材料力学教案-组合变形
09.材料力学-组合变形

2 1 , 2 0, 3 2 2 2 2 2
然后,选用强度理论建立强度条件。因手柄用钢材制成,应 选用第三或第四强度理论。若采用第三强度理论,可得其强度 条件为
2
2
r 3 4
2
2
≤
作出AB杆的弯矩图和AC段的轴力图,如图(c)所示。从图中 可以看出, C 点截面左侧,其弯矩值为最大,而轴力与其它截 面相同,故为危险截面。 开始试算时,可以先不考虑轴力Fx的影响,只根据弯曲强度
条件选取工字钢。这时截面系数为
W≥
M 120 10 m 120cm 100 106
350
M
FN
(a)
(b)
t .max
(c)
c.max
21
解:首先,根据截面尺寸计算横 截面面积,确定截面形心位置,求 出截面对形心主惯性轴y的主惯性矩
y1
z0
y
z1
50
Iy。计算结果为
150 50 150
A 15103 mm2 ,z1 75 mm, I y 531010 mm
30
若采用第四强度理论,可将上述三个主应力代入公式,其 强度条件成
r 4 2 3 2 ≤
若将式
M W
MT WP
2 M 2 MT
代入上两式,并注意到对圆截面杆有 WP = 2W ,则以上两式 改写成
r3
r4
W
2 M 2 0.75M T
≤ ≤
A1 Wz1
200
300
200 P
350000 350 50 6 0.2 0.3 0.2 0.32 11.7 MPa
材料力学-组合变形
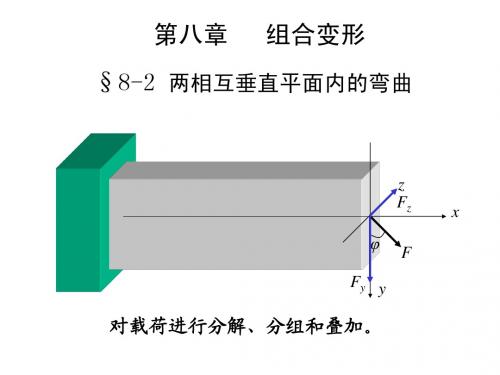
组合变形
§8-2 两相互垂直平面内的弯曲
z Fz φ Fy y F
x
对载荷进行分解、分组和叠加。 对载荷进行分解、分组和叠加。
一、应力与变形的计算
1. 应力计算
z x Fy y z Fz x 中性轴 σamax σlmax
y
z Fz φ x l My z Mz Fy y F
x
M y = Fz (l x) = F sin φ (l x) M z = Fy (l x) = F cos φ (l x) M y = M sin φ = F (l x) sin φ M z = M cos φ = F (l x) cos φ
x
M z = Fy (l x)
M y = Fz (l x)
FN M y z A M z y A σ= + + A Iz Iy
Fx = bh
-
Fz (l x) × 30
b h / 12
3
+
Fy (l x) × 20
bh 3 / 12
2. 3. 4. 5.
中性轴离开坐标原点, 中性轴离开坐标原点,且与形心主轴斜交 截面上到中性轴距离最大的点, 截面上到中性轴距离最大的点,正应力值最大 多边形截面的最大的正应力均发生在角点, 多边形截面的最大的正应力均发生在角点, 曲线周边截面通过推中性轴平行线, 曲线周边截面通过推中性轴平行线,至截面周边的 方法来确定最大正应力的位置。 方法来确定最大正应力的位置。
压缩+ 压缩+平面弯曲
3)求应力 求应力
FN = 3kN M max = 8kN m
σ t ,max
FN M max ± = σ c,max A W
材料力学-组合变形

7
4、刚度计算
y
f y max
f max
Fy L3 3EI z
,
Fz L3 f z max 3EI y
Fy L3
Fsz z
z
F
y
Fsy
y
3 F L f y2 f z2 ( )2 ( z )2 3EI z 3EI y
48.44o
2 2 2 2 f max wz ) max wy max 11.99 10.63 16.02(m m
f max
3.3 103 16.02(m m) w 16.5(m m) 200
10
例 图示悬臂梁,承受载荷F1与F2作用,已知F1=800N,F2=1.6kN,l= 1m,许用应力[σ ]=160MPa。试分别按下列要求确定截面尺寸: (1) 截面为矩形,h=2b;(2) 截面为圆形。
z (1)中性轴不过截面形心,与外力无关,与偏心距及截面形状、尺寸有 ez 关; (2)中性轴的截距与偏心距符号相反,表明外力作用点与中性轴分别在 截面形心的相对两侧; (3)外力作用点越是向形心靠拢,中性轴离形心越远,甚至移到截面外 面。当中性轴移到与截面相切或截面以外时,截面上则只存在压应力或拉 22 应力;
a y1 h 2
i ey
2 y
2 z
④D
b 6 b 6
z
2
①
A
a z1
az
2 iy
ay
ez
b
3
1
h 6
y
b 23 12 hb i A 12 bh
2 z
Iy
4h
重庆大学材料力学教案组合变形

重庆大学材料力学教案组合变形一、教学目标1. 理解组合变形的基本概念和特点;2. 掌握组合变形的受力分析和应力计算方法;3. 能够应用组合变形的理论知识解决实际工程问题。
二、教学内容1. 组合变形的基本概念和特点;2. 组合变形的受力分析方法;3. 组合变形的应力计算方法;4. 组合变形的变形和失效分析;5. 组合变形的应用实例。
三、教学方法1. 采用讲授法,讲解组合变形的基本概念、特点和受力分析方法;2. 采用案例分析法,分析组合变形的应力计算方法和应用实例;3. 采用问题讨论法,引导学生思考和解决实际工程问题。
四、教学准备1. 教案和教学大纲;2. 教材和相关参考书籍;3. 教学PPT和多媒体课件;4. 案例分析和问题讨论的相关资料。
五、教学过程1. 导入:简要介绍组合变形的基本概念和特点,激发学生的兴趣;2. 讲解:详细讲解组合变形的受力分析方法,结合实例进行分析;3. 计算:引导学生掌握组合变形的应力计算方法,进行相关计算练习;4. 分析:分析组合变形的变形和失效原因,引导学生思考实际工程问题;5. 应用:介绍组合变形的应用实例,让学生了解其在工程中的重要性;6. 总结:对本节课的内容进行总结,强调重点和难点;7. 作业:布置相关作业,巩固学生对组合变形的理解和应用能力。
六、教学评估1. 课堂问答:通过提问方式检查学生对组合变形概念的理解和掌握情况;2. 作业批改:评估学生对组合变形应力计算和应用实例的分析和计算能力;4. 期末考试:设计相关的试题,全面评估学生对组合变形的理解和应用水平。
七、教学拓展1. 引导学生关注组合变形在工程实际中的应用,了解最新的研究动态和发展趋势;2. 鼓励学生参加相关的学术活动和实践活动,提高学生的综合能力和创新意识。
八、教学反思1. 总结本节课的教学效果,反思教学方法和策略的优缺点;2. 根据学生的反馈和作业情况,调整教学内容和难度,提高教学效果;3. 不断学习和探索新的教学方法,提高自身的教学水平和能力。
直梁的弯曲及组合变形与压杆稳定——教案

直梁的弯曲及组合变形与压杆稳定——教案一、教学目标:1. 让学生了解直梁弯曲的基本概念,掌握梁弯曲的弹性理论。
2. 使学生理解组合变形及压杆稳定的基本原理,能够分析实际工程中的相关问题。
3. 培养学生的动手实践能力,通过实例分析提高学生解决工程问题的能力。
二、教学内容:1. 直梁弯曲的基本概念:直梁、弯曲、剪力、弯矩等。
2. 梁弯曲的弹性理论:弯曲应力、弯曲变形、弯曲强度计算等。
3. 组合变形:拉伸、压缩、弯曲、剪切等组合变形的分析方法。
4. 压杆稳定的基本原理:压杆稳定条件、压杆失稳现象、压杆稳定计算等。
5. 实例分析:分析实际工程中的直梁弯曲、组合变形与压杆稳定问题。
三、教学方法:1. 采用讲授与讨论相结合的方式,让学生掌握直梁弯曲及组合变形与压杆稳定的基本理论。
2. 通过案例分析,使学生能够将理论知识应用于实际工程问题。
3. 利用动画、图片等辅助教学手段,帮助学生形象地理解抽象的概念。
4. 安排课堂讨论,鼓励学生提问、发表观点,提高学生的参与度。
四、教学安排:1. 课时:本章共计12课时。
2. 教学方式:讲授、案例分析、课堂讨论。
3. 教学进程:第1-4课时:直梁弯曲的基本概念及弹性理论。
第5-8课时:组合变形及压杆稳定的基本原理。
第9-12课时:实例分析及练习。
五、教学评价:1. 课堂表现:观察学生在课堂上的参与程度、提问回答等情况,给予相应的表现评价。
2. 课后作业:布置相关练习题,检验学生对知识的掌握程度。
3. 课程报告:要求学生选择一个实际工程案例进行分析,报告应包括问题分析、计算过程和结论。
通过课程报告评价学生的实践能力。
4. 期末考试:设置有关直梁弯曲、组合变形与压杆稳定的题目,考察学生的综合运用能力。
六、教学资源:1. 教材:《材料力学》、《结构力学》等相关教材。
2. 辅助材料:PPT课件、动画、图片、案例资料等。
3. 实验设备:力学实验仪、弯曲实验装置、压杆实验装置等。
4. 网络资源:相关学术期刊、在线课程、论坛等。
14-1组合变形-材料力学

Fz F sin
五、自由端的变形
z
A
y
y
FL3 cos
3EI z
z
B y
x
B z
FL3 sin
3EI y
B
z
y
查表7-1(3)
在 Fz B点的位移 z :
例题14.1 图所示屋架结构。已知屋面坡度为1:2, 两屋架之间的距离为4m,木檩条梁的间距为1.5m, 屋面重(包括檩条)为1.4kN/m2。若木檩条梁采
"
Iy
Iy
'
M z y M y z
Iz
Iy
cos sin
M ( y z)
Iz
Iy
四、斜弯曲时的强度条件
1、中性轴的位置
M (
Iz
yo
sin
Iy
zo )
0
tan yo Iz tan
zo
和扭矩图如图c、d
危险截面在杆的根部(固定端)
(3)应力分析
B
M W
T
T Wp
在杆的根部取一单元体分析
y 0, x B , xy T
计算主应力
1
3
B
2
( B
2
)2
2 T
2 0
(4)强度分析
选择第三、第四强度理论
r3
入偏心拉伸的强度条
4
32
件校核
32.4106 32.4MPa 35MPa
满足强度条件,最后选用立柱直 d = 12.5cm
材料力学(单辉祖)第十章组合变形

弯压组合
可见,危险截面为C截面 其轴力和弯矩分别为
FNC 3 kN M c M max 4 2 8kN m
A
FAy
10kN m a x
g g f
C m
FBy
B
危险点 截面C上的最低点f 和最高点g
FN M c s A W
f
18
弯压组合
A I
4
10kN
解 首先计算折杆的支座反力 由平衡方程可得 FAx A
FAx 0, FAy 5kN, FBy 5kN
FAy
m
10kN
C 1.2m B 1.6m FBy
a x 1.6m
m
由于折杆左右对称,所以只需分析一半即可。 折杆AC部分任一截面上的内力
FN FAy sin 3 kN FS FAy cos 4 kN M xFAy cos
杆件变形分析步骤 首先, 在杆件原始尺寸上分别计算由横向力和 轴向力引起变形、应力 然后, 利用叠加原理,合成在横向力和轴向力 共同作用下杆件变形、应变和应力等物理量 若杆件抗弯刚度EI较大,轴力引起杆件的弯曲 变形较小,可以忽略
10
弯拉组合
细长杆件强度问题, 受力如图,抗弯刚度 EI,截面抗弯模量W , 横截面面积A。
n
e n
P
z b h y
30
偏心拉伸(压缩)
解: 1. 力系简化 力P对竖直杆作用等效于作 用在杆轴线上一对轴力P和 一对作用在竖直平面内力 偶mz=Pe
FN P 2000 N, M z mz Pe 120 N m
mz P
n
e n
P
mz P
可见,竖直杆发生弯拉组合变形
材料力学第十章 组合变形

r 3 2 4 2
r3
2 M y M z2 T 2
W
M 2 T 2 W
r 4 3
2
2
2 M y M z2 0.75T 2
r4
W
M 2 0.75T 2 W
例3 图示空心圆杆,
内径d=24mm,外
径D=30mm, P1=600N, []=100MPa,试用 第三强度理论校核 A
Lmax D1
⑤变形计算
ymax D 2
f f
2 y 2 z
fz
f
tg
fy fz
f fy
当j = 时,即为平面弯曲。
例1结构如图,P过形心且与z轴成j角,求此梁的最大应力与挠度。 解:危险点分析如图 中性轴 h Pz
x
Py
P z j z
D2 P 变形计算 Py y
P
P
10203 [ 1020252 ] 12 7.27105 mm4
M 5P 3 500Nm 10
P N M
20 20
y yC z
应力分析如图
100
N M z max max A I yc
P
100 103 500 55 103 6 800 10 7.27107
P Mz y Myz x A Iz Iy
三、中性轴方程
P M z y0 M y z0 x 0 A Iz Iy
对于偏心拉压问题 P Py y Pz z P yP y0 z P z0 P 0 P 0 (1 2 2 )0 y 2 2 A Aiz Aiy A iz iy y
1
材料力学 第7章 组合变形

1
z x
1
式中M——危险截面的弯矩 T——危险截面的扭矩
2
y
2
例 3 某齿轮传动轴上装有两个直圆柱齿轮,C轮的输入功
率NkC=15kW,不考虑功率损耗,轴的转速n=850r/min, 直径d=50mm,材料的[]=50MPa,两轮节圆直径分别为 D1=300mm, D2=120mm,压力角=20,试校核轴的强度。
FAx
800
.
D
.
A
.
. .
C
.
B 1500
2500
c max
FN M max A Wz
A FAy y
FC
FCx
FCy C
F B
F x
40 10 12 10 4 26.1 10 141 10 6
3 3
FN 40kN
12kNm M
100.5 MPa [ ]
第七章
作业
7-2 7-4 7-5 7-8 7-13 7-17 7-21
第七章
7.1 7.2
组合变形杆的强度
组合变形的概念 弯曲与拉伸(压缩)的组合
7.3
偏心压缩与截面核心
7.4 扭转与弯曲的组合 7.5 复合梁的强度计算
7.6
开口薄壁梁的切应力
组合变形杆的强度
7.1
组合变形概念
F
截面核心—— 在轴向压力作用下,使杆的横截面上只产 生压应力的载荷作用区域
偏心压缩与截面核心
五、截面核心
2.确定方法
压力作用区域。 当压力作用在此区域内时,横截面上无拉应力。 ay 截面核心 az
材料力学——8组合变形

F m
B
T 15kN m
M max 20kN m
W
15kN· m
D 3
32
(1 )
4
+
r3
20kN· m
-
M2 T2 157.26MPa [ ] W
例题8 传动轴如图所示。在A处作用一个外力偶矩
m=1kN· m,皮带轮直径 D=300mm,皮带轮紧边拉力为 F1,松边拉力为F2。且F1=2F2,L=200mm,轴的许用 应力[]=160MPa。试用第三强度理论设计轴的直径
例3 直径为d=0.1m的圆杆受力如图,T=7kNm,P=50kN, []=100MPa,试按第三强度理论校核此杆的强度。 解:拉扭组合,危险点应力状态如图 T P A T P
P 450 10 3 6.37 MPa A 0.12
T 167000 35 .7MPa 3 Wn 0.1
P
P
1
1
a a
a a
未开槽前 立柱为轴向压缩
N P P P 1 2 A A (2a) 4a2
开槽后 立柱危险截面为偏心压缩;
P
1
P
1
a a
a a
P
1
Pa/2
1
N M P Pa 2 2P 2 2 A W 2 a a 1 2a 2 a a 6 2 P a2 开槽后立柱的最大压应力 8 2 P 4a 未开槽前立柱的最大压应力
2、相当应力计算 第三强度理论,计算相当力
2 0
r 3 1 3 2 4 2
第四强度理论,计算相当应力
r 4 2 3 2
3、强度校核
《材料力学》第八章组合变形

(2)内力分析,确定危险截面—整个轴;
M=600(kN·cm) FN=15(kN)
(3)应力计算,确定危险点—a、b点;
P产生拉伸正应力: t
FN AFNd 2源自4FNd 24
M拉产弯生组弯合曲:的正应力:wmax
M Wy
M
d3
32
32M
d3
P M= a Pe
补例8.1 已知: P=2kN,L求=:1mσm,Iazx=628×104mm4,Iy=64×1040mm2740 2844
解:1.分解P力。 Py Pcos φ Pz Psin φ 2.画弯矩图,确定危险截面--固定端截面。 3.画应力分布图,确定危险点—A、 B点
σ” σ’
A
x
y
Pyl
M
z
践中,在计算中,往往忽略轴力的影响。
4.大家考虑扭转、斜弯曲与拉(压)的组合怎么处理?
例8.5 图8.14a是某滚齿机传动轴AB的示意图。轴的直径为35 mm,材料为45钢, [σ]=85 MPa。轴是由P=2.2kW的电动机通过
带轮C带动的,转速为n=966r/min。带轮的直径为D=132 mm,
Mz Py l - x Pcosφ l - x Mcosφ My Pz l - x Psinφ l - x Msinφ
式中的总弯矩为:M Pl- x
3.计算两个平面弯曲的正应力。在x截面上任取一点A(z 、y),
与弯矩Mz、My对应的正应力分别为σ’和σ”,故
- Mz y , - M yz
第八章 组合变形
基本要求: 掌握弯曲与拉伸(或压缩)的组合、扭转与弯曲的组合 的强度计算。
重点: 弯曲与拉伸(或压缩)的组合,扭转与弯曲的组合。
材料力学课件(组合变形)

(2)矩形截面 解:截面形心为点O 主惯性轴y、z 当中性轴切于边AB时
z A中性轴
b
12 o
y
C
B
h
截距
a y1
h 2
,a
z1
核心边界点1
yF1
iz2 a y1
h 6
,z
F1
i
2 y
az1
0
(iy
b 12
,iz
h) 12
类似地,可定点2
y F2
八、组合变形 (Combined deformation)
杆件有两种或两种以上基本变形的应力分量相当 两种基本变形组合的类型:
拉(压)+扭;拉(压)+弯;扭+弯;平面弯+平面弯
分析方法(线弹性、小变形假设下): 按基本变形分解外力与内力 计算各基本变形的应力与 变形分量 根据叠加原理综合各基本变形的结果 确定组合变形的危险截面与危险点的应力状态
(1
zF z
i
2 y
yF iz2
y
)
在截面上线性分布
中性轴
1
zF z
i
2 y
z0
yF y iz2
y0
0
——不过形心C的直线
截矩
ay
iz2 yF
,az
iy2 zF
距离中性轴最远点:D1——tmax, D2——cmax
横截面外周边具有棱角时,最大正应力在角点上
最大正应力点处于单向应力状态,强度条件 max [ ] 截面形心的位移 w wy2 wz2 x2
练习: P288习题8-16
M I
材料力学 第十章组合变形(1,2,3)

1.2m
解:求支反力,由平衡方程
FB B
FA
' FA
F ' A 0,
FA FB 5kN
A
1.6m 1.6m
m g f A
10kN C
m FAy
作折杆的受力图,折杆及 受力对称,只需分析一半 即杆AC 将FA分解, 得杆的轴力 FN、弯矩M (x)
B
FAx
FN FAx 3kN
3 10 8 10 t 81.1 2 3 c d / 4 d / 32 81.9
3 3
M W
[例10-2]圆截面杆的偏心压缩时不产生拉 力的载荷作用范围
P
y
P
y
Pa
a
z
z
CL11TU12
P
y
Pa
y
P
y
Pa
z
z
z
P
y y
Pa
y
P
z
Pa
z P
y y
z
Pa
y
P
CL11TU10
解: X A 3kN, A 4kN Y
任意横截面x上的内力:
FN X A 3kN FS YA 4kN M ( x) YA x 4 x
1 1截面上危险截面, 其上:FN 3kN,M 8kN m
FN A
M W
t FN M c A W
CL11TU5
y0 Iz tg tg z0 Iz
为中性轴与z轴夹角
3.强度计算:
1)危险截面:当x=0时 M Z , M y 同时取最大,固定端处为危险面 2)危险点:危险面上 D1 , D2点 3)最大应力
组合变形—拉伸(压缩)与弯曲的组合变形(材料力学)

一、受力特点 既有轴向拉(压)力,还有横向力
二、变形特点 杆件将发生拉伸 (压缩 )与弯 曲组合变形
q W8.2 拉伸(压缩Fra bibliotek与弯曲的组合变形
三、应力分析
x
q F
l x
= FN
A
tmax = M y
Iz
cmax
t max
c max
= M y + FN
2m
FCy
C
B
1m F
A
C
B FN图
18
12
A
C
B M图
c1
t2 c2
Iz
A
8.2 拉伸(压缩)与弯曲的组合变形
四、强度条件
由于危险点处的应力状态仍为单向应力状态,故其强度条件为:
max [ ]
当材料的许用拉应力和许用压应力不相等时,应分别建立杆件 的抗拉和抗压强度条件。
tmax [ t ] cmax [ c ]
8.2 拉伸(压缩)与弯曲的组合变形
四、例题
1.5m
A
C
B
FAx A
FAy
2m
1m F
FC
FCy
C
B
FCx
2m
1m F
8.2 拉伸(压缩)与弯曲的组合变形
(2)画内力图
(3)C 截面是危险截面
C
FN A
MC Wz
18 103 12 106 2613 .1 141 103
91.9MPa
(4)横梁AB是安全的。
FAx A
FAy
FCx
如图所示起重机的最大吊重F=12kN,横梁AB工字钢为16号,许用
材料力学:12 组合变形

Iy
Iz
A
偏心拉(压)计算的中性轴截距表达式
ay1
iz2 yF
az1
iy2 zF
作一系列与截面周边相切的直线 作为中性轴…
z 1
O
y 1
ay1
az1
其截距为ay1、az1,对应的偏心力 作用点的坐标(yF1,zF1)
az1
yF1
iz2 a y1
zF1
iy2 az1
z 1
5
3
2O 4 2
y 15
4 3 ay1
Mr4
M
2 yB
M
2 zB
0.75T
2
3642 10002 0.7510002 1372N m
பைடு நூலகம்
r4
Mr4 W
1372N m W
[ ]
W πd 3 32
解得
d 3 321372103 51.9m
π 100
Δ组合变形小结
1、组合变形解题步骤 ①外力分析:横力向弯心简化并沿形心主惯性轴分解
Mr3
M
2 z
M
2 y
T
2
Mr4
M
2 z
M
2 y
0.75T
2
§2、斜弯曲——两相互垂直平面内的弯曲
斜弯曲的弯曲正应力与位移计算
F2 a
m
z C
z
O
x
m y F1 y
x
m z
O MZ
MY m
y
F2 单独作用,梁在竖直平面内发生平面弯曲,z轴为 中性轴;
F1 单独作用,梁在水平平面内发生平面弯曲,y轴为中 性轴。
上述两个互相垂直的平面弯曲之组合即为斜弯曲。
材料力学-第八章组合变形

M z y M y sin
Iz
Iz
x
M y z M z cos
Iy
Iy
x
y
z
y
z
M
y sin
z
cos
对于圆形截面
因为过形心的任意轴均为截面的对称轴,所以当横 截面上同时作用两个弯矩时,可以将弯矩用矢量表示, 然后求二者的矢量和。于是,斜弯曲圆截面上的应力计 算公式为:
A
C
B
D
2 kN 5 kN
300 500
2 kN (a)
500
解:
1.5 kN Am
7 kN
C
1.5 kN m
B
D
(1)分析载荷 如图b所示
5 kN
12 kN (b)
T 1.5 kN m
(2)作内力图 x
如图c、d、e、f 所示
(c)
MC MD
1.5 kN Am
7 kN
C
1.5 kN m
B
FN A
F (2a)2
1 4
F a2
(2)开槽后的正应力
My
FN F
My
Fa 2
FN
2
max
FN A
My Wy
F 2a2
Fa / 2 2a2 a2 /
6
2
F a2
2a
2a
z
a
所以:
2
1
8
y
§8.3 斜弯曲
F1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(Combined Deformation)
=
+
=
+
+
(Combined Deformation)
§8-2 拉伸(或压缩)与弯曲的组合
(Combined axial loading and bending)
一、受力特点 (Character of external force)
使之每个力(或力偶)对应一种基本变形
2.内力分析(Analysis of internal force ) 求每个外力分量对应的内力方程和内力图,确定危险截面.分
别计算在每一种基本变形下构件的应力和变形
3.应力分析(Stress analysis)
画出危险截面的应力分布图,利用叠加原理 将基本变形下的
1.2m F 1.2m
FRAy FRAx A
F
Fy
FNAB
30°
B
D Fx
cmax
0.866F A
0.6F Wz
94.37MPa [ ]
(Combined Deformation)
例题2 小型压力机的铸铁框架如图所示.已知材料的许用拉应力
[t] =30MPa ,许用压应力 [c] =160MPa.试按立柱的强度确定压
F2
A
最大弯曲正应力
max
Mmax W
F1l 4W
杆危险截面 下边缘各点处上的拉应力为
t max
max
F2 A
F1l 4W
(Combined Deformation) 五、强度条件(Strength condition)
由于危险点处的应力状态仍为单向应力状态,故其强度条件 为:
max [ ]
(Combined Deformation)
§8-1 组合变形和叠加原理(Combined deformation and superposition method)
一、组合变形的概念(Concepts of combined deformation)
构件在荷载作用下发生两种或两种以上的基本变形,则构件 的变形称为组合变形.
当材料的许用拉应力和许用压应力不相等时,应分别建立 杆件的抗拉和抗压强度条件.
tmax [ t ]
cmax [ c ]
(Combined Deformation)
例题1 悬臂吊车如图所示,横梁用20a工字钢制成. 其抗弯刚度Wz = 237cm3,横截面面积 A=35.5cm2,总荷载F= 34kN,横梁材料的许
(Combined Deformation)
例题3 正方形截面立柱的中间处开一个槽,使截面面积为原来截
面面积的一半.求开槽后立柱的的最大压应力是原来不开槽的几
倍.
F
F
aa
aa
(Combined Deformation)
解: 未开槽前立柱为轴向压缩
1
FN A
F A
F (2a)2
F 4a 2
开槽后1-1是危险截面
y
(Combined Deformation)
2.以横截面具有两对称轴的等直杆承受偏心拉力 F 为例
(1)将外力向截面形心简化,使每个力(或力偶)只产生一种 基本变形形式
轴向拉力 F 力偶矩 M = F e,
将 M向y轴和z轴分解
F
z
M y Fe sin
Mz
Fe cos
FzF FyF
O1
A(yF,zF)
AA
FN
z
Mz (y,z)
My
C
y
由 My 产生的正应力
M y z F zF z
Iy
Iy
由 Mz 产生的正应力
Mz y F yF y
Iz
Iz
(Combined Deformation)
由于 C 点在第一象限内,根据杆件的变形可知,
, , 均为拉应力
由叠加原理,得 C点处的正应力为
§8-3 偏心拉(压)• 截面核心 (Eccentric loads &the kern of a section)
一、偏心拉(压) (Eccentric loads)
1.定义(Definition) 当外力作用线与杆的轴线平行但不重合时,
将引起轴向拉伸(压缩)和平面弯曲两种基本变形.
F
O1
z A(yF,zF)
(Combined Deformation)
第八章 组合变形 (Combined deformation)
§8-1 组合变形和叠加原理 (Combined deformation and superposition method)
§8-2 拉伸(压缩)与弯曲的组合 (Combined axial and flexural loads) §8-3 偏心拉(压)•截面核心(Eccentric loads &the kern(or core)of a section) §8-4 扭转与弯曲的组合 (Combined torque and flexural loads)
用应力为[]=125MPa.校核横梁AB的强度.
解:(1) 分析AB的受力情况
C
M A 0 FNAB sin30 2.4 1.2F 0
FNAB F
Fx 0 FRAx 0.866F
A
30°
B
D
1.2m F 1.2m
Fy 0 FRAy 0.5F
FRAy
AB杆为平面弯曲与轴向压缩组合变形
(Combined Deformation)
z
a
b
c
F2
A
F1
x
P
y B
(Combined Deformation)
四、处理组合变形的基本方法 (Basic method for solving combined deformation)
1.外力分析(Analysis of external force) 将外力简化并沿主惯性轴分解,将组合变形分解为基本变形,
轴力 FN= F F
弯矩
M y FzF
M
z
FyF
My O1 Mz
y
n
n
FN Mz
z
My
y
(Combined Deformation)
三、任意横截面 n-n 上C 点的应力分析
(Stress analysis at point C on cross section n-n)
由 F产生的正应力
FN F
三、内力分析(Analysis of internal force)
横截面上内力(internal force on cross section)
1.拉(压) :轴力 FN (axial force)
FSMz
O
z x
FN
y
弯矩 Mz (bending moment)
2.弯曲 剪力Fs(shear force)
FN Mz y
A Iz
( z,y)
Mz
z
O
x
FN
y
(Combined Deformation)
3.危险截面的确定(Determine the danger cross section)
作内力图
F1
轴力(axial force)
F2
F2
பைடு நூலகம்
FN F2
弯矩(bending moment)
Fy
FNAB
中间截面为危险截面.最大压应力 FRAx A
30°
B
发生在该截面的上边缘
F D Fx
(Combined Deformation)
(2) 压缩正应力
C
FRAx 0.866F
A
A
(3) 最大弯曲正应力
max
1.2FR Ay Wz
0.6F Wz
(4)危险点的应力
A
30°
B
D
因为引起的切应力较小,故一般不考虑.
(Combined Deformation)
四、应力分析(Analysis of stress)
横截面上任意一点 ( z, y) 处的正应 力计算公式为
1.拉伸正应力
FN
A
(Axial normal stress)
2.弯曲正应力
Mz y
(Bending normal stress) Iz
()
cmax
M y z1 Iy
425 12.5F 5310
MPa
()
n
n
FN My
(Combined Deformation)
F 350
F
n
拉
z0 y z1
n
z 150
50 150
50 F
压
n
n
FN My
(3)叠加 在截面内侧有最大拉应力
t max
tmax
F 15
425 7.5F 5310
作用在杆件上的外力既有轴向拉( 压 )力,还有横向力
二、变形特点(Character of deformation)
杆件将发生拉伸 (压缩 )与弯曲组合变形
示例1 F1 产生弯曲变形
F2
F1
F2
示例2
F2 产生拉伸变形 Fy 产生弯曲变形 Fx 产生拉伸变形
Fy
F
Fx
(Combined Deformation)
危险截面为偏心压缩
F F Fa/2
1
1
将力 F 向1-1形心简化
2
FN A
M W
F 2a a
Fa / 2 1 2a a2
