一道高考填空题的解法探究
高考数学填空题答题套路和技巧

高考数学填空题答题套路和技巧考试答题,对分数影响最为关键的就是答案的正确性。
下面是为大家整理的高考数学填空题答题套路和技巧相关内容,以供参考,一起来看看!高考数学填空题答题套路和技巧1、直接法这是解填空题的基本方法,它是直接从题设条件出发、利用定义、定理、性质、公式等知识,通过变形、推理、运算等过程,直接得到结果。
2、特殊化法当填空题的结论唯一或题设条件中提供的信息暗示答案是一个定值时,可以把题中变化的不定量用特殊值代替,即可以得到正确结果。
3、数形结合法对于一些含有几何背景的填空题,若能数中思形,以形助数,则往往可以简捷地解决问题,得出正确的结果。
4、等价转化法通过“化复杂为简单、化陌生为熟悉”,将问题等价地转化成便于解决的问题,从而得出正确的结果。
5、图像法借助图形的直观形,通过数形结合,迅速作出判断的方法称为图像法。
文氏图、三角函数线、函数的图像及方程的曲线等,都是常用的图形。
6、构造法在解题时有时需要根据题目的具体情况,来设计新的模式解题,这种设计工作,通常称之为构造模式解法,简称构造法。
高考数学答题规范1、答题工具答选择题时,必须用合格的2B铅笔填涂,如需要对答案进行修改,应使用绘图橡皮轻擦干净,注意不要擦破答题卡。
禁止使用涂改液、修正带或透明胶带改错。
必须用0.5毫米黑色墨水签字笔作答,作图题可先用铅笔绘出,确认后,再用0.5毫米黑色墨水签字笔描清楚。
2、答题规则与程序①先填空题,再做解答题;②先填涂再解答;③先易后难。
3、答题位置按题号在指定的答题区域内作答,如需对答案进行修改,可将需修改的内容划去,然后紧挨在其上方或其下方写出新的答案,修改部分在书写时与正文一样,不能超出该题答题区域的黑色矩形边框,否则修改的答案无效。
4、解题过程及书写格式要求关于填空题,常见的错误或不规范的答卷方式有:字迹不工整、不清晰、字符书写不规范或不正确、分式写法不规范、通项和函数表达式书写不规范、函数解析式书写正确但不注明定义域、要求结果写成集合的不用集合表示、集合的对象属性描述不准确。
从一道高考的填空题谈思维

思路 3 能 否直接 用公式 ( ) 1 呢?若用 的话 则必 须 求高 , 如何求 高便成 了此 问题 的关键. 已知有 什 么? 目 标是什么?强烈的 目标意识 告诉 我们构造等量关 系( 方
程思想 ) 表示出高.
已知 有 A B=2 又 知 道 , 另两边 的大 小关 系 , 目标 是
・ 教学论坛 ・
十。 7 (l 第 期・ 中 ) 7 擞・ 2o 6 高 版 o年
1 5
数 学 问题 解 决教 学 策 略探 析
505 广 东实验 中学 10 5
问题解决 是 当今 数 学教育 中越 来越 受人 瞩 目的课 题 .目前 , 世界上几乎所有 的国家 都把 提高学生 的问题 解决 能 力作为数 学教 学的 主要 目的之一. 因而 , 习 怎 学 样解决 问题就成 为学 习数学 的根本原 因. 要培 养学生 的 问题解决 能 力 , 不 是单 靠某 些 技 能 的传 递 就 能形 成 并 的, 也不 是仅仅靠 多做几 个 习题 就 能形成 的 , 而需 要教 师努力地 去改进 教学 方法 , 有效 地创 设学 习空 间, 让学 生有可 能 在 自主 的探 索 活动 中 经历 “ 顿悟 ” 获 取 “ , 智 慧” 从 而寻找 到问题解决的策略. ,
C
我们需求 的 目标是三角形 的面积 , 如何选取适 当的 面积公式 准确地表示 出三角形 的面积 , 构建 函数模 型是 问题 的核 心 , 于是在脑海里搜 索三角形 的面积公式 :
1 1
表示出 A B上 的高 h 能 否将 , 它们联系起来呢?只要我们 有最基 本 的方程 意识 , 即设 A
的 “ 近发 展 区 ” 最 .
= 十 一 = √一1 2l 4 3 ,
课改区高考填空题解题策略探究

点评: 掌握基 本 的概 念 、 算 性质 , 运 记住 一 些常 用
的结论 , 练运 用基 本 的解 题 技 能 即 能 快速 解答 , 熟 反
思解题 思 维的 流程 , 有什 么启 发? 会
3 特 殊 值 法 .
根 据题 设 条 件 , 取恰 当 的特 殊 值 、 殊 图形 或 选 特 特 殊情 况进行 处 理 , 而 得 出正 确 的结 论 . 字母 不 从 含
分 析 : 决 这 类 问题 的 关 键 就 是 找 到 定 价 增 加 后 该 解
供 游客 居住 , 当每 个 房 间 的定 价 为 每 天 2 O元 时 , O 房
间可 以住满 . 当每个房 间每天 的定 价 每 增加 1 0元 时 , 就 会有 一个 房 问空 闲. 有 游 客 人 住 的 房 间 , 馆 需 对 宾 对 每个 房 间每 天 支 出 2 0元 的各 种 费 用. 每 个 房 间 设
析 , 辅 之 以 简 单 计 算 得 出结 论 的 方 法 . 既 是 方 法 , 并 它
ቤተ መጻሕፍቲ ባይዱ
更是 重 要的数 学思 想) 【 4 ( ( 7 山东 ) 例 】 2) , O 与直 线 + 一2 —0和 曲 线 。 + 一 1z一1 + 5 —0都相 切 的半 径 最小 的 2 2 4 圆的标 准方程 是 . 分析: 曲线化 为 ( 一6 。 ( ) + 一6 1 , 圆心 )一 8 其
常见 的补形 方法 是将 四面体 补成 正方 体或 者 长方体 . 【 5 ( O 8 山东 ) 三棱 锥 的 三 个 侧 面 两 两 例 】 20, 若
宾馆每 天的入住量 , 类试 题都 可以转化 为二 次函数 的 此 最值 问题 , 再利用二次函数 的 图象和性质加 以解 决.
探究高考英语语法填空解题技巧

探究高考英语语法填空解题技巧发表时间:2017-11-10T11:57:24.897Z 来源:《教育学文摘》2017年11月总第245期作者:张家琼[导读] 有效的复习策略能提高应试能力,达到事半功倍的效果。
四川省简阳市养马中学641402摘要:语法填空是近年来高考英语科新推出的一种题型。
这种题型能全面检测学生在英语词汇、语法甚至是句法上的运用能力,能更科学地反映学生的英语综合水平。
有效的复习策略能提高应试能力,达到事半功倍的效果。
关键词:考纲语法填空思路技巧首先、研读考纲,把握方向。
2017年高考英语考试大纲、考试说明明确提出:要完善新题型,突出考查综合语言运用能力。
对语法填空题的题干说明部分进行了完善,语法填空题所填内容只分为两种情况:第一种是没有提示词,主要填写一些语法功能性的词语,这种情况就只能填写一个词;第二种是给提示词的情况,是根据所给的提示词写出正确的形式。
语法填空题的备考建议是要加强学生的知识储备能力,尤其是基础知识的储备,包括考纲所列出的3500词的记忆与复习,灵活掌握单词的拼写、词性、搭配及词义的拓展,要特别注意常考动词的特殊过去式和过去分词的变化情况。
语法知识方面尤其要掌握动词的时态、语态,非谓语动词的正确使用,名词的单复数,连词的选用以及形容词和副词的转换、比较级的正确使用等。
当然,介词、代词、冠词的基本用法也是考生必须掌握的知识点。
因此,我对语法填空题解题技巧做了一些探究和尝试,愿与大家分享。
其次,探究语法填空解题技巧。
1.解题思路。
(1)通读全文,把握大意。
在解题前,快速浏览短文,把握全文大意,这一步非常重要。
(2)结合语境,试填空格。
读懂短文之后,要结合短文所提供的特定的语言环境,从句子结构的完整性去分析思考空格所缺单词的词性,再根据句子的结构和意义以及句子之间的逻辑关系来确定具体要填的单词和所给词的正确形式。
(3)重读全文,解决难题。
在解题过程中要先易后难,在大部分空格填好后,再经过仔细推敲,难题也就不再难了。
高考数学-填空题的解法技巧

(1)已知点
P(x,y)的坐标
x,y
满足x-2y+1≥0, |x|-y-1≤0,
则 x2+y2-6x+9 的取值范围是
________________________________________________________________________.
(2)(2016·枣庄模拟)已知函数
填空题的解法技巧
题型概述 填空题是一种只要求写出结论,不要求解答过程的客观性试题,有小巧灵活、覆盖面广、跨 度大等特点,突出考查准确、严谨、灵活运用知识的能力. 由于填空题不像选择题那样有备选提示,不像解答题那样有步骤得分,所填结果必须准确、 规范,因此得分率较低,解答填空题的第一要求是“准”,然后才是“快”、“巧”,要合 理灵活地运用恰当的方法,不可“小题大做”. 方法一 直接法 直接法就是直接从题设出发,利用有关性质或结论,通过巧妙地变形,直接得到结果的方法.要 善于透过现象抓本质,有意识地采取灵活、简捷的方法解决问题.直接法是求解填空题的基 本方法.
解题规律和解题技巧的灵活应用,将计算过程简化从而得到结果,这是快速准确地求解填空
题的关键.
跟踪演练 1 (1)已知 F 为双曲线 C:x92-1y62 =1 的左焦点,P,Q 为 C 上的点.若 PQ 的长等
于虚轴长的 2 倍,点 A(5,0)在线段 PQ 上,则△PQF 的周长为________.
解析 (1)令 α=0°, 则原式=cos20°+cos2120°+cos2240°=32. (2)要满足各个截面使分得的两个三棱锥体积相等,则需满足与截面对应的交点 E,F,G 分 别为中点即可.故可以将三条棱长分别取为 OA=6,OB=4,OC=2, 如图,则可计算 S1=3 5,
高考数学填空题解法

二、 定义
法
有些问题直接
去解很难奏效,
而利用定义去
解可以大大地x 2 化繁为简,速25
y2 9
1
达目的
例3.到椭圆 右焦点的距离 与到定直线x
解:据抛物 线定义,结 合图1知:
轨迹是以(5, 0)为顶点, P=2且开口 方向向左的抛 物线,故其方 程为:
y2 4(x5)
三、特殊化
解:直接计算 f(n+1)-f(n) ,可得2(n+1) 个
例2.现时盛行的足球彩票,其规则如 下:全部13场足球比赛,每场比赛有 3种结果:胜、平、负,13长比赛全 部猜的为特等奖,仅猜中12场为一等 奖,其它不设奖,则某人获得特等奖 的概率为 ————
解:此人猜中某一场的概率为,且猜中每 场比赛结果的事件为相互独立事件,故某 人全部猜中即获得特等奖的概率为 1
题型特点四
形态短小精悍、 跨度大、知识 覆盖面广、考 查目标集中, 形式灵活,答 案简短、明确、 具体,评分客 观、公正、准 确
考试对学生
的要求
突出训练学生 严谨、灵活运 用知识的能力 和基本运算能 力(较容易)
突出训练学生 准确、全面的 运用知识的综 合能力和数据 处理能力(较 难)
解答填空题时, 由于不反映过 程,只要求结 果,故对正确 性的要求比解 答题更高、更 严格,《考试 说明》中对解 答填空题提出 的基本要求是 “正确、合理、
的解集为A,
4xx2 (a1)x
且
A {x|0x2},
那么实数a的取值范围
是 解:据不等式的几何。意义,作函数 y 4xx2
和函数 y(a的1)图x 象(如图),
从图上容易得实数a的取值范围是 a2, 。
一道高考数学填空题的解法探究

,
+
t n [ a t
这是一道关于 “ 三角函数” 的填充题 ,主要考 查三角函数 的基础知识 和三角恒等 一 阻 变换等基本思想方法 ,考查 的知识点为解三角形 、正弦定理 、余弦定理的灵活运用.
本题 构思巧妙 ,内涵丰富 、结构和谐 ,解法 多样 ,是一道全方位考查 三角变换 与
1 持 “ 法” . 坚 通 ,定 能 “ 到 最 后 ” . 笑 B —宝 C { 所谓 “ 通法 ”就是采用平时处理这类问题的一般方法 : , 切化弦+ 正弦定理+ 弦定理. 余
蹶 由 6C 手6Z- ,n2 c 以 + = +=o, +:一be 2= 2 ac 得 s ×+c故 + 争 , a 一 b 所 e
下 图所示 的直角坐
标 系 , 设 A , , B
(,)则 cs = , 。 0, oC x
U
y 、
2 . 在斜 AA C中 , A, C所 对的边分别为 Ⅱ b B 角 B, ,,
一j 2  ̄b-
a2 c 2
-
一
c
0c
iA c。 n
1 .
o(+ ) 则角 A 的值 为— s _ A) t C aD si s i
s
sC = i n
s iZ nC
_ =C 箍 s 2 =
e b+ c2
-
盟
t nC a
一
’
a2
—
—
—
=
—
—
M
专 =icA= 丽Cs s o n
=222 丽ca= b_ +
2 2e- 2 ( +2b a )
2 巧妙 “ 值” . 赋 ,定 能 “ 得 最 美 ” . 笑
对一道高考填空题的探究

结合厂 ( ) 的图象可得, ( ) 的最大值为1 6 .
还可以如下求厂 ( ) 的最大值 :
另解 : ) = ( 1 - - x ) ( 2 + + 1 5 ) 一( 卅1 ) ( 一 1 ) ( + 3 ) ・ ( + 5 )
= 一
因为厂 ( ) = ( 1 - x ) ( 2 + 似+ 6 ) ,
2 0 1 3年 1 1 月
解 法 探 究
学 谋
对 一道 高 考填 空题 的探 究
⑩ 安 徽 省 枞 阳 县 会 宫 中 学 王 怀 明
题
( 2 0 1 3 年课标 I 理1 6 ) 若 函数厂 ( ) = ( 1 ) ( 。 +
解法4 : 因为厂 ( ) 的图 象关于直线 = _ 2 对称 , 所以厂 ( _ 4 )
因为: 厂 ( ) = 一 4 x 3 - 3 a g . c 2 + ( 2 — 2 b ) x + a ,
mY ( 一 2 ) = 0 得2 8 + 4 b = 1 l a .
②
解法1 : 易 知点 ( 1 , 0 ) , ( 一 1 , 0 ) 在厂 ( ) 的图像上 , 因为
所1 A ) f ( 一 4 ) = [ 1 一 ( - 4 ) ] [ ( 一 4 - x ) 2 + 0 ( 一 4 ) + l 6 ]
= 一
( + 4 + 3 ) ( + 4 一 5 ) .
I x + ( 1 6 一 a ) x + ( 9 5 + 6 — 1 2 a ) X 2 + ( 2 4 8 — 4 7 a + 8 b ) +
当 = 一 2 + 、 / 时, . 厂 ( ) 的极 大值为 1 6 _
解得a = 8 , b = 1 5 .
一道浙江数学高考题引发的探究与教学启示

图1
&+y = m
+ 8kx + 4 - 4m二0,由韦达定理得xx + x2 =
FT乔g 滤 - 2%2,于是有I x2
丁,又由看=2岗得衍 1 + 4k
8丨 I 二
8
W
ቤተ መጻሕፍቲ ባይዱ
1+4厂4山+缶
8 2
=2,当且仅当I k\ =*时等号成
处取得最大值4,即点B的横坐标的绝对值取得最大 值2.
点评:解法2主要由两点坐标间的关系代 入椭圆方程,通过“消元”思想把点B横坐标的平方 珂转化为关于参数m的一个二次函数,运用二次函 数性质快速求解出m以及丨靭丨的最大值,让人耳目
一新,瞬间觉得“山重水复疑无路,柳暗花明又一 村”.该解法有效地避免了分类讨论,巧妙地简化了 繁琐的代数运算,解法虽很优美,但难点是如何巧妙 “消元”、构造二次函数,基础一般的同学恐怕难以 想到这个思路.
3.换元法的视角(三角换元,快速突破) 解法3:由题意设点B坐标为(2 Jocose,
y/msinO),于是由4P 二 2 PB 可得4( - 40^cos&,3 2 v^sin^),把力"两点坐标代入椭圆方程得
1.韦达定理模型的视角(韦达定理,凸显通法) 解法1:如图1分类讨论:①当直线的斜率不
2020年第2期
中学数学研究
・17・
存在时,由题知4(0, -伍)上(0,丽),于是得TH =9 ,xB = 0.
②当直线AB的斜率存 在时,设AP方程为y =蠢+
方程组
1y = kx + 1, x*12 2 =(i 〃)/
解问题,使学生掌握一些合理设计算法形成简便运 算的方法,体会数学思想,培养核心素养.本教学片 段针对学生的运算困惑和解题思路给予了合理的指 导和点拨.
高考完形填空答题技巧

高考完形填空答题技巧高考完形填空答题技巧完形填空在高考试卷中是拉开考生得分的一道关键题型,因此掌握完形填空的解题技巧对考生而言尤为重要。
下面是店铺收集整理的高考完形填空答题技巧,希望对你有所帮助!1:通过主旨大意解题在完形填空题中,理解主旨大意十分重要,正确把握主旨大意有助于考生对文章细节的正确理解,特别是长难句的分析和突破可以帮助考生提高解题的正确率。
完形填空题的第一句往往不设空,这句话一般是文章的主题句,考生在解题时一定不要忽略首句的内容。
【典例】As a general rule, all forms of activity lead to boredom when they are performed on a routine(常规) basis. As a matter of fact, we can see this __41__ at work in people of all 42(ages).41.A. principle B. Habit C. way D. power【分析】A根据首句信息可知,这里是指”当各种活动变成常规的时候都会让人厌倦”这个准则。
principle”原则,准则”;habit”习惯”;way”方式”;power”权力”。
由首句的信息再结合选项可知,A选项正确。
2:通过文化背景解题完形填空的语篇信息常渗透着各类相关的文化背景知识。
有些选项的设置与文化背景相关,这就要求考生有较宽的知识面,同时要具备一定的文化意识,特别是要有对英语国家文化的敏感性和鉴别力,只有这样才能既快速又准确地解题。
3:通过复现词解题这类题多为同义词、近义词和反义词的复现或同义词、近义词和反义词的异形的复现。
这类试题主要是考查考生的整体篇章意识和对上下文的推断能力。
【典例】In particular, there was (and perhaps still is) a beliefin fairies. Not all of these __1__ are the friendly, people-loving characters that appear in Disney films, and in some folk tales they are __2__ and cause much human suffering.1.A. babies B. Beliefs C. fairies D. supermen2.A. powerful B. Cruel C. frightened D. extraordinary【分析】 1.C根据空前的”a belief in fairies”可知,此处选C。
高考英语(上海卷)选词填空解题策略探究

20·实践智慧·高考英语(上海卷)选词填空解题策略探究邵华【上海市陆行中学,上海 200120】随着高考改革在上海不断深化,英语卷的试题类型也做出了相应变化,取消了原有的语法词汇单选题,取而代之的是将对语法词汇的考核都以语篇填空的形式出现。
这在很大程度上提高了对学生阅读能力的要求。
针对这一题型的解题策略主要集中在如何提高词汇量、如何在语境中理解具体词语的功能、词义的内涵和外延以及使用者的意图和态度,同时因为这一题型仍然脱不开语篇的框架,所以解题策略的另一方面就是要关注阅读能力的提高。
一、拓展词汇量词汇又称语汇,是一种语言中所有词和词组的总和。
词是语言的基础,也是最小的语言单位。
学习词汇不仅涉及到记忆单词的音、形、义,更重要的是在语篇中,通过各种语言活动,理解与各种主题相关的信息或观点。
拓展词汇量可以注意学习构词法、归类联想记忆以及在语境中培养词块意识。
(一)学习构词法,有效快速地扩充随着人类社会的不断发展,语言也会相应地发展。
很多旧词因为失去了原有存在的语境而逐渐消亡,取而代之的则是新兴词汇的诞生。
而新词的产生,也基本遵循语法的规则,或以词根为基础添加前后缀,或转化旧词的词性又或者将几个词合并成为新词。
这种“以新代旧”不断完善和发展的过程体现出一种规律——构词法(word-formation)。
《上海市高中英语学科教学基本要求》中对构词法的学习内容分成四类:派生法、转化法、合成法和首字母缩略法。
选词填空题型中给出的待选单词大多从派生、转化和合成三个方面着手,这样设置题目,看似词汇都是出自《高考英语词汇手册(上海卷)》,但是几乎每个都发生了一定的变化,所以学习构词法是应对这一题型最基本也是最有效的方法。
当然同时这种知识的学习也是突破记忆单词难关的有效手段。
1.派生派生法中最常见的是前缀后缀法,也是在中学阶段构词法学习的重点。
通常是由一个有意义的词根加词缀构成。
前缀改变词义,而后缀改变词性。
一道高考数学填空题的分析及其启示

由此 可知 , ( x ∈ 0 ,n∈Z,.任意 ∈(, f2 ) 【 , " . 0+ 。 ,函数, 。 ) )的值域为 [,o ,故②正确. 0+o )
3 启 示 .
填空题不 同于选择题 ,选择题 的答案就在 四个选
我们 也可 以找到 一般化 方法 ,取 f(m 】则 i 2, , 2
两 项是对 的 ,本 题也 只有 两项正 确 ,结果 把对 的 改
错 ,其 实此类 问题什 么情况都可能 出现 ;四是填② 的 时候 ,后 面还带 了一笔 ,分不清是②还是⑧ ,给评卷 带来疑 问和困难 ;五是没有思路 ,思维僵化 ,随便填
答案 .
【, ) 02 , 此时 2 x∈( ,】 f 4)2 (x E【,) 此时 4 ∈ 2 4; (x=f2 ) 0 4 , x
( = )
_ )= “ . 厂 2 ’ 解析式求 出来 了,下面 的问题就容易 了. 本题 的函数实 际上是一 个分 段 函数 ( 图) 如 ,即
过程 中 ,要注意研究性 学习和研究性 复习 ,提高我们 的研究 能力 ,比如 一题 多解 的研究 ,一 理 多用 的研
究 ,或者 多题 一解 的研究 ,对 问题 进行 一些 变式 拓
三是受平 时思维定势影 响 ,以为平 时类似 的问题 只有
m∈ Z,有 .2)O 厂m . ( = 事 实 上 ,我 们 也 可 以找 到 一 般 化 的方 法 :
I2 (・ )2 ( : 2 厂2= , 厂 2 2 =f2 …= l )0 故①正确. ( ) (
对 ② , 1 】 , ( = - 01; f2)2() ∈(, 时 fx 2 xE[, 而 ( =fx ∈ 2 ) ) x
一道高考立体几何填空题的解答辨析
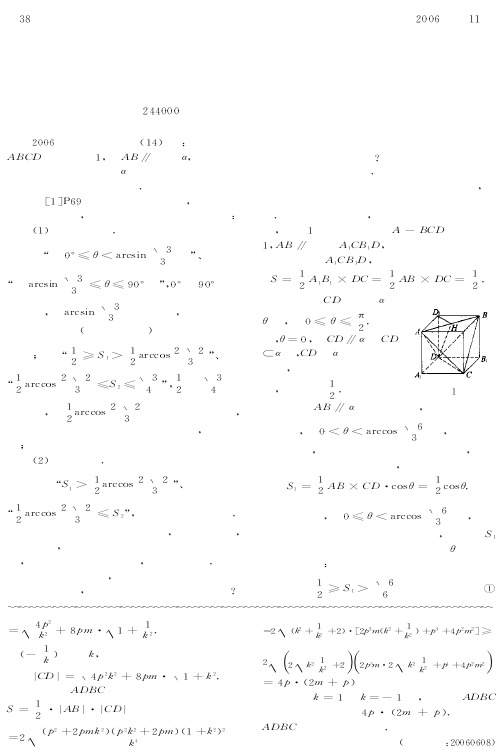
射影 图 形的 面 积从 大 到小 或 从小 到 大 的 变化
过程 又 如 何 展 示 出 来I在 复 习 课 上 教 师 是 应 该要 向学 生讲 清楚的 0
我 们 用 运 动 变 化 的 观 点 来 帮 助 思 考 -只 需考 虑 正四 面 体的 顶 点的 射 影连 成 图 形 的面
积0先 求 它的 最 大值 -借助 正 方体 的 模 型 来观
图形 &当 -. /01123466 时 &平 面 !"89 %&
射影 图形 的面积 等于 (!"8的面 积 4:67
由上 &当 /01123465 ; -; /01123466 时&射 影图 形是 等腰 三角 形&其 面积 <=变化 的 趋势 是在 下面 的 范 围中 随 -的增 大 而由 小 变
W+,WK @"R!S! T URV O @&T S!0 于是 四边 形 ),*+的 面积 为
FK
& !
OW)*WOW+,W
@ K!
%R! T!RVS!’%R!S!T !RV’%&TS!’! S"
@ K!
%S!T
& S!
T!’O1!RAV%S!T
S&!’TR"T"R!V!2E来自@X@ YX @ Y !
中学数学
6N
当 平 面 !"# $ %时&相 当 于图 ’中 的 (!#" 绕 # 点 逆 时 针 旋 转 )#’#*+* 为
!"的中 点,&即 -. /01123465 时&射 影图 形 由四 边形 变为 等腰 三角 形&其面 积 为 4557正 四面 体 继 续作 旋 转 运 动 &此 时 正 四 面 体 的 射 影图 形实 际上 是正 ( !"8在 平面 %上 的射 影
高考数学填空题解题方法

高考数学填空题解题方法填空题是一种传统的题型,也是高考试卷中罕见题型.查字典数学网为大家引荐了高考数学填空题解题方法,请大家细心阅读,希望你喜欢。
一、直接法这是解填空题的基本方法,它是直接从题设条件动身、应用定义、定理、性质、公式等知识,经过变形、推理、运算等进程,直接失掉结果。
它是解填空题的最基本、最常用的方法。
运用直接法解填空题,要擅长经过现象看实质,熟练运用解方程和解不等式的方法,自觉地、无看法地采取灵敏、简捷的解法。
二、特殊化法当填空题的结论独一或题设条件中提供的信息暗示答案是一个定值时,而条件中含有某些不确定的量,可以将题中变化的不定量选取一些契合条件的恰当特殊值(或特殊函数,或特殊角,图形特殊位置,特殊点,特殊方程,特殊模型等)停止处置,从而得出探求的结论。
这样可大大地简化推理、论证的进程。
三、数形结合法"数缺形时少直观,形缺数时难入微。
"数学中少量数的效果前面都隐含着形的信息,图形的特征上也表达着数的关系。
我们要将笼统、复杂的数量关系,经过形的笼统、直观提醒出来,以到达"形帮数"的目的;同时我们又要运用数的规律、数值的计算,来寻觅处置形的方法,来到达"数促形"的目的。
关于一些含有几何背景的填空题,假定能数中思形,以形助数,那么往往可以简捷地处置效果,得出正确的结果。
四、等价转化法经过"化复杂为复杂、化生疏为熟习",将效果等价地转化成便于处置的效果,从而得出正确的结果。
数学里常用的几种经典解题方法引见:1、配方法所谓配方,就是把一个解析式应用恒等变形的方法,把其中的某些项配成一个或几个多项式正整数次幂的和方式。
经过配方处置数学效果的方法叫配方法。
其中,用的最多的是配成完全平方式。
配方法是数学中一种重要的恒等变形的方法,它的运用十分十分普遍,在因式分解、化简根式、解方程、证明等式和不等式、求函数的极值和解析式等方面都经常用到它。
高考英语完形填空解题方法探究

单击添加副标题
Methods & Skills
202X C l o z e Te s t
阅读下面的片段,根据上下文,在A、B、 C、D中选择最佳答案。
I’m not sure about it. Now, we have been (1) of music in its common meaning--- the kind of music we hear in the concert hall. (2) if we look some parts of music more closely, we discover them in our everyday life too---in the rhythm of the sea, the singing of a bird in the woods and (3).
1. A. because B. since
2. A. almost
B. always
C. if C. possibly
D. unless D. never
高考数学填空题的解法技巧

高考数学填空题的解法技巧题型概述填补空白是一个客观的测试,只需要写一个结论,不需要解决过程。
它具有体积小、灵活、覆盖面广、跨度大的特点。
它强调了准确、严谨和灵活运用知识的能力由于填空题不像选择题那样有备选提示,不像解答题那样有步骤得分,所填结果必须准确、规范,因此得分率较低.解答填空题的第一要求是“准”,然后才是“快”、“巧”,要合理灵活地运用恰当的方法,不可“小题大做”.方法一直接法直接法是直接从问题设计入手,利用相关的性质或结论,通过巧妙的变形直接获得结果,要善于通过现象抓住本质,有意识地采用灵活、简单的方法来解决问题,直接法是解决毛坯填充问题的基本方法。
log21-x?+1,x<1,?例1(1)已知函数f(x)=?-2如果f(a)=3,那么a=____x,x≥1,?sin2a(2)(2021北京)在△abc中,a=4,b=5,c=6,则=________.Sinc分析(1)∵ 当≥ 1,f(a)≤ 1.不合适∴f(a)=log2(1-a)+1=3∴a=3。
(2)根据余弦定理:b2+c2-a225+36-1637cosa===,∴sina=,2bc442×5×6a2+b2-c216+25-36137cosc===,∴sinc=,2ab882×肆×伍仟叁佰柒拾贰××44sin2a∴==1.sinc378答案(1)-3(2)1思维升华利用直接法求解填空题要根据题目的要求灵活处理,多角度思考问题,注意一些解题规律和解题技巧的灵活应用,将计算过程简化,从而得到结果,这是快速准确地求解填空题的关键.x2y2跟踪演练1(1)已知f为双曲线c:-=1的左焦点,p,q为c上的点.若pq的长等于916是假想轴长度的两倍,点a(5,0)位于段PQ上,然后是△ PQF是____(2)(2021安徽)已知数列{an}是递增的等比数列,a1+a4=9,a2a3=8,则数列{an}的前n项和等于________.答案(1)44(2)2n-1(1)从问题的意义可以得出PQ=16。
对一道高考填空题的研究性学习案例

得a4=0 于是就认为当k=1 时, (k =0 1 . 4 fa ) .
我说, 虽然得到的是正确答案, 但恐怕没有 根据.
3 .纠 正
fa4 0 fa5 (1)= , (1)≈ 0 2006, (,) . 0016 fa6 ≈ 0
0 40 13 , . 0 0 3 3 故该命题 为假命题. 0
追问3 { ( )是一个单调数列吗? ,血 )
是的.利用复合函数的单调性 即可判断: 当
这时一旁有学生在说: 函数 fx = s + () i n
tn a 是一个奇函数, 个条件肯定要用的. 这
或许是 得到了这位同学 的启发,不一会儿, 另一位学生给 出了他的正确解答:
d≠0 若fa)t (2 +… +fa7 =0 则 . (1-fa) - (2) , 当 =— — 时, (k =0 fa ) .
2 误解 .
刚读完题 目, 一位学生就立即报 出了正确答
追问1 { ( ) ,n )是一个数列吗? 是的. 对于任意一个正整数礼∈【 21( 1 7 根 , , 据数列是一类特殊 的函数) 有唯一确定的 a 与 n 之对应, 又对于每一个 a , n 有唯一确定的 fa ) (. n 与之对应, .n )是一个关于n 故{ (竹) 厂 , 的函数, 又由 于定义域的特殊性, { ( )是一个数列. 故 ,n ) . 追问2 判断命题“厂 } . ( ) 是一个等差数 【0 .
性、奇偶性、等差数 列、数列的 函数本性以及
复合 函数等多个 知识点, 因而容 易造成 思维 障
碍. 所以我想通过追问以使学生能对{ ( ] .0)的 厂 l
把 握 更 深入 .
已知函数 , ()= s X+tn i n a .项数为 2 7
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一道高考填空题的解法探究-中学数学论文
一道高考填空题的解法探究
贾周德
(赣榆中等专业学校,江苏连云港222100)
摘要:本文探究了一道高考填空题的多种解法,开扩了学生的解题思路,培养了学生的创新思维.教学实践证明,在数学教学中开展一题多解训练,有利于学生掌握数学基础知识和基本方法,提高解题能力。
关键词:基本不等式;判别式;三角换元;几何;导数
中图分类号:G633文献标识码:A文章编号:1005-6351(2013)-11-0020-01 在数学教学中,笔者引导学生对下面一道高考填空题的解法作了一番探究,得到了多种不同的解法,现总结如下,供解题参考。
题目:设x,y,z为正实数,满足x-2y+3z=0,则y2xz的最小值是。
(2008年江苏高考数学卷第11题)
一、基本不等式法
解法1:由x-2y+3z=0,得y=x+3z2.将此式代入y2xz中,整理得y2xz=x4z+9z4x+32.由题设知,x4z,9z4x均为正实数,由基本不等式,得x4z+9z4x+32≥2x4z.9z4x+32=3,即y2xz≥3(当x=y=3z时,取“=”),所以y2xz的最小值是3.
点评:上述解法1是用基本不等式ab≤a+b2(a≥0, b≥0)求解的。
本题也可以这样解,将已知等式化为y=x+3z2,由基本不等式,得y≥3xz0,即y2xz≥3,从而得解。
利用基本不等式求最值时,要注意满足“一正数、二定值、三相等”的条件。
二、判别式法
解法2:设y2xz=t (t0),则y2=txz.由已知等式,得y=x+3z2.将此式代入y2=txz 中,整理得(xz)2+(6-4t)xz+9=0.因为这个关于xz的二次方程有正实数根,所以判别式Δ=(6-4t)2-36≥0,解得t≥3或t≤0(舍去),即y2xz≥3(当x=y=3z 时,取“=”).所以y2xz的最小值是3.
点评:上述解法2是将y2xz用新变量t表示,结合已知等式,用代入法消去y,整理得关于xz的二次方程,从而利用“判别式法”得解.利用判别式法求函数的最值时,要注意检验其结论的正确性,防止出现“误判”或“漏判”的情形. 三、三角换元法
解法3:将x-2y+3z=0化为x2y+3z2y=1.令x2y=cos2θ,3z2y=sin2θ,θ∈(0,π2).两式相乘并整理,得y2xz=3sin22θ.因为2θ∈(0,π),所以1sin22θ≥1,于是y2xz≥3.当θ=π4时, 1sin22θ取最小值1,从而y2xz取最小值3,此时x=y=3z.所以y2xz的最小值是3.
点评:上述解法3是将已知等式化为x2y+3z2y=1,利用三角换元法把问题转化为求三角函数的最值问题而得解的。
这里得出x2y+3z2y=1后,也可以利用基本不等式求解。
四、几何法
解法4:作线段AP=x,延长AP至点B,使PB=3z,则AB=x+3z=2y(x,y,z为正实数).
以线段AB为直径作圆O (如图),作半径OC,使OC⊥AB,则OC=y.过点P作PE⊥AB,交圆O于点E,则3xz=PE2≤OC2,即3xz≤y2,所以y2xz≥3.显然,当点P 与圆心O重合时,此不等式取“=”,此时x=y=3z.所以y2xz的最小值是3.
点评:上述解法4是通过作圆,在圆中创造条件,利用几何平均值ab的几何意义,得3xz=PE2,再根据“半弦不大于半径”而得解。
五、导数法
解法5:设y2xz=t (t0),由上述解法1知,t=x4z+9z4x+32.令xz=u(u0),则t=u4+94u+32(u0).将此函数记为t=g(u),u∈(0,+∞).求导数g′(u),由g′(u)=14-94u2=0,解得u1=3,u2=-3(舍). 当u∈(0,3)时, g′(u)0;当u∈(3,+∞)时,g′(u)0.所以函数t=g(u)在u=3处取得极小值3(唯一),也是最小值.所以y2xz的最小值是3.
点评:上述解法5是通过换元,将问题转化为求一元函数的最值问题,从而利用“导数法”得解。
应用导数法求函数的最值时,要注意检验,正确判断函数的最值。
通过此题多种解法的探究,开扩了学生的解题思路,培养了学生的创新思维,收到了良好的教学效果。
教学实践证明,在数学教学中开展一题多解训练,有利于学生掌握数学基础知识和基本方法,有利于培养学生的解题能力和探索精神。
参考文献:
[1]单墫.普通高中课程标准实验教科书数学5(必修)[M].江苏教育出版社,2005.
[2]徐小伍.利用平均值不等式解题的误区[J].中学数学教学,2000,(2). [3]单墫. 普通高中课程标准实验教科书数学(选修1-1)[M].江苏教育出版
社,2005.。
