除法器的实现
电路中的除法器设计

电路中的除法器设计在电路设计中,除法器是一种十分重要的组件。
它可以将输入的数字进行除法运算,将商和余数输出。
除法器在计算机和数字信号处理器等电子设备中被广泛使用,因此其设计和优化具有重要意义。
一、除法器的基本原理除法运算是一种复杂的运算,要实现除法器的设计,首先需要了解其基本原理。
除法器的基本原理是通过移位和减法实现的。
在将被除数和除数输入除法器后,除法器将被除数和除数进行比较,并开始迭代过程。
在每一次迭代中,被除数的位数向左移动,直到其高位与除数相等或超过除数。
然后,除法器进行减法操作,将除数减去被除数,结果作为商的一位。
此后,商持续左移,被减数保持不变,重复上述过程,直到所有的商位都得出。
二、除法器的设计策略在除法器的设计中,有几种常见的策略可以考虑。
1. 组合逻辑除法器:这种类型的除法器使用组合逻辑电路实现,通过减法器、比较器和移位器等组件的组合来实现除法运算。
组合逻辑除法器的优点是速度较快,但缺点是占用较多的电路资源。
2. 串行逻辑除法器:与组合逻辑除法器相反,串行逻辑除法器使用顺序逻辑电路实现。
它通过一个时钟信号,逐位地进行计算,因此典型的串行逻辑除法器速度较慢。
但串行逻辑除法器更节省电路资源,因此在一些资源有限的场景中得到了广泛应用。
3. 重复系列除法器:这种除法器通过多个并行的子除法器实现,并行计算多个位的商。
重复系列除法器具有较高的性能,但需要更多的电路资源和功耗。
三、除法器的优化方法为了提高除法器的性能和效率,可以采用一些优化方法。
1. 位级并行思路:通过将除法器分解为多位的子除法器,并行计算多个子除法器,可以大幅提高除法器的速度。
这种方法在重复系列除法器中得到了广泛应用。
2. 乘法相关技巧:利用乘法器计算除法运算,可以加速除法器的运算速度。
通过将除数进行逆运算,转化为乘法操作,可以利用乘法器的高速性能,提升除法器的效率。
3. 进制转换思想:将数字进行二进制到十进制的转换,然后进行简单的除法运算,可以减少运算的复杂程度,提高除法器的运算速度。
基于VHDL的8位除法器的实现

基于VHDL的8位除法器的实现The Design of 8 Division With VHDL摘要:介绍了利用VHDL实现八位除法,采用层次化设计,给出了实现除法的子模块程序。
使用Altera公司的MAX+PLUSII10.2开发软件进行功能仿真并给出仿真波形。
关键词:二进制除法 VHDL MAX+PLUS2Abstract:The design of division(8/8) by hierarchy technique is proposed. Schematic documents and submodule program with VHDL language are also given. At the end of the article, using MAX+PLUS2, the flow char is given and the simulation result is attached.Keywords: division VHDL MAX+PLUS2引言除法是数值计算和数据分析中最常用的运算之一,许多高级运算如平方根、指数、三角函数等都与其有关。
在FPGA中,有加、减、乘、除的算法指令,但除法中除数必须是2的幂,因此无法实现除数为任意数的除法。
本文用VHDL编写了除法运算,可实现任意八位数的除法。
除法器的设计本文所采用的除法原理是:对于八位无符号被除数A,先对A转换成高八位是0低八位是A的数C,在时钟脉冲的每个上升沿C向左移动一位,最后一位补零,同时判断C的高八位是否大于除数B,如是则C的高八位减去B,同时进行移位操作,将C的第二位置1。
否则,继续移位操作。
经过八个周期后,所得到的C的高八位为余数,第八位为商。
从图(1)可清楚地看出此除法器的工作原理。
此除法器主要包括比较器、减法器、移位器、控制器等模块。
1、比较模块设计中所用的八位比较器是由两个四位比较器级联而成的。
verilog除法器 srt算法

verilog除法器srt算法Verilog实现SRT除法器算法在数字电路设计中,除法是一种常见的数值运算。
在Verilog中,可以使用SRT (Sweeney-Robertson-Tocher)算法来实现除法器。
SRT算法是一种用于计算除法的算法,它可以实现高精度和高效率的除法运算。
本文将详细介绍如何使用Verilog实现SRT除法器算法,以及该算法的原理和实现步骤。
SRT除法器算法的原理SRT除法器算法是一种通过连续的减法和移位操作来计算除法的算法。
它采用了一种逐位比较的策略,可以在不考虑余数的情况下,实现整数除法的计算。
SRT 算法的核心思想是将被除数和除数进行比较,并根据比较结果来进行减法和移位操作,以得到商数。
SRT算法的步骤如下:1. 将被除数和除数进行比较,得到初始估计商数。
2. 进行减法运算,得到余数。
3. 对余数进行移位操作,得到新的估计商数。
4. 重复步骤2和3,直到得到最终的商数。
SRT算法的优点是可以实现高精度和高效率的除法运算,适用于多种除法场景。
Verilog实现SRT除法器算法的步骤接下来,我们将详细介绍如何使用Verilog实现SRT除法器算法。
第一步:定义模块和端口首先,我们需要在Verilog中定义SRT除法器的模块和端口。
模块包括被除数、除数和商数等参数,端口包括输入端口和输出端口。
定义模块和端口的代码如下:verilogmodule srt_divider (input [N-1:0] dividend, 被除数(N位)input [N-1:0] divisor, 除数(N位)output reg [2*N-1:0] quotient, 商数(2N位)output reg [N-1:0] remainder 余数(N位));在上面的代码中,我们定义了一个包括被除数、除数、商数和余数的SRT除法器模块,并设置了相应的输入端口和输出端口。
第二步:实现SRT算法的核心逻辑接下来,我们需要在Verilog中实现SRT算法的核心逻辑。
模拟除法器电路原理

模拟除法器电路原理一、引言除法运算是数字电路中常用的一种运算方式,而除法器电路则是实现除法运算的重要组成部分。
本文将介绍模拟除法器电路的原理和工作过程。
二、模拟除法器电路的基本原理模拟除法器电路是一种能够对两个输入数进行除法运算的电路,它能够将除数和被除数作为输入,输出商和余数。
模拟除法器电路的设计和实现需要考虑除法运算的特性和数电电路的基本原理。
三、模拟除法器电路的设计要点1. 除法器电路的输入包括除数和被除数,输出包括商和余数。
除数和被除数的位数决定了除法器电路的复杂度和精度。
2. 除法器电路通常采用串行除法算法或并行除法算法来实现除法运算。
串行除法算法需要多个时钟周期完成一次运算,而并行除法算法能够在一个时钟周期内完成运算。
3. 除法器电路中需要包含除法运算所需的基本运算单元,如加法器、减法器、比较器等。
这些基本运算单元能够完成除法算法中的各个步骤。
4. 除法器电路中需要考虑特殊情况的处理,如除数为0、被除数为0等,这些情况需要特殊的处理逻辑来确保电路的正确运行。
四、模拟除法器电路的工作过程1. 输入除数和被除数,将它们送入除法器电路。
2. 电路根据选择的算法和电路设计,进行除法运算。
3. 电路输出商和余数,可以通过显示屏、LED灯等方式显示。
五、模拟除法器电路的应用模拟除法器电路广泛应用于各种需要进行除法运算的场合,如数值计算、信号处理、通信系统等。
除法器电路能够高效地对输入数据进行除法运算,为各种应用提供了便利。
六、模拟除法器电路的优缺点1. 优点:模拟除法器电路能够高效地进行除法运算,能够满足各种应用的需求。
2. 缺点:模拟除法器电路的设计和实现比较复杂,需要考虑各种特殊情况的处理,电路的规模较大。
七、总结模拟除法器电路是一种能够对两个输入数进行除法运算的电路,它能够将除数和被除数作为输入,输出商和余数。
模拟除法器电路的设计和实现需要考虑除法运算的特性和数电电路的基本原理。
模拟除法器电路在各种应用中起到了重要的作用,能够高效地进行除法运算。
基于VHDL的8位除法器的实现

基于VHDL的8位除法器的实现The Design of 8 Division With VHDL摘要:介绍了利用VHDL实现八位除法,采用层次化设计,给出了实现除法的子模块程序。
使用Altera公司的MAX+PLUSII10.2开发软件进行功能仿真并给出仿真波形。
关键词:二进制除法 VHDL MAX+PLUS2Abstract:The design of division(8/8) by hierarchy technique is proposed. Schematic documents and submodule program with VHDL language are also given. At the end of the article, using MAX+PLUS2, the flow char is given and the simulation result is attached.Keywords: division VHDL MAX+PLUS2引言除法是数值计算和数据分析中最常用的运算之一,许多高级运算如平方根、指数、三角函数等都与其有关。
在FPGA中,有加、减、乘、除的算法指令,但除法中除数必须是2的幂,因此无法实现除数为任意数的除法。
本文用VHDL编写了除法运算,可实现任意八位数的除法。
除法器的设计本文所采用的除法原理是:对于八位无符号被除数A,先对A转换成高八位是0低八位是A的数C,在时钟脉冲的每个上升沿C向左移动一位,最后一位补零,同时判断C的高八位是否大于除数B,如是则C的高八位减去B,同时进行移位操作,将C的第二位置1。
否则,继续移位操作。
经过八个周期后,所得到的C的高八位为余数,第八位为商。
从图(1)可清楚地看出此除法器的工作原理。
此除法器主要包括比较器、减法器、移位器、控制器等模块。
1、比较模块设计中所用的八位比较器是由两个四位比较器级联而成的。
加法器除法器FPGA实现总结文档

加法器除法器FPGA实现总结文档FPGA实现加法器和除法器总结文档引言FPGA(Field-Programmable Gate Array)是一种可编程逻辑芯片,可以根据需要进行配置和重新编程,具有灵活性和可重复性。
在数字电路设计中,加法器和除法器是非常常见且基础的功能模块。
本文将总结FPGA实现加法器和除法器的过程和结果,并对实现的优势和不足进行分析。
一、加法器的实现在FPGA中实现加法器有多种方法,最基本也是最常见的是使用全加器构建一个完整的加法器。
全加器是一个三输入一输出的电路,可以实现两个二进制位的加法。
通过级联多个全加器,就可以构造出任意位数的加法器。
1.实现步骤:(1)定义加法器的输入和输出位数:假设我们要实现一个4位加法器,那么就需要4个输入(A[3:0]、B[3:0])和一个4位输出(SUM[3:0])。
(2)使用VHDL或Verilog等硬件描述语言来描述全加器和加法器的逻辑。
(3)使用逻辑综合工具将硬件描述语言代码综合为逻辑电路连接。
(5)验证加法器的功能和正确性。
2.实现优势:FPGA实现加法器的优势主要体现在以下几个方面:(1)灵活性:FPGA可以根据需要重新编程,可以方便地修改加法器的位数和功能。
(2)速度:FPGA中的逻辑电路是并行计算的,可以实现高速的加法运算。
(3)资源利用:FPGA可以利用其内部的查找表(lookup table)实现逻辑运算,节省了硬件资源的使用。
3.实现不足:FPGA实现加法器也存在一些不足之处:(1)成本高:FPGA价格相对较高,成本较高,适合于需要较高性能和灵活性的应用场景。
(2)资源有限:FPGA的资源有限,实现复杂的逻辑电路可能会导致资源不足的问题。
二、除法器的实现除法器是一个更为复杂的数字电路,用于实现两个二进制数的除法运算。
在FPGA中实现除法器需要使用一种称为"非冗余算法"的方法,通过迭代运算来实现除法的功能。
verilog 乘法 除法

verilog 乘法除法Verilog是一种硬件描述语言,广泛应用于数字电路设计和验证。
本文将介绍Verilog中的乘法和除法原理及其在实际应用中的实现。
一、Verilog乘法器原理与实现1.原理Verilog乘法器的原理是基于位级运算。
输入的两个二进制数按位进行与运算,得到乘积的位级表示。
然后通过移位和加法运算,将位级乘积转换为最终的整数乘积。
2.实现Verilog乘法器的实现主要分为三个部分:全加器、位级乘法器和移位器。
全加器用于处理乘数和被乘数的各位与运算结果;位级乘法器用于计算乘数和被乘数的各位与运算;移位器用于调整位级乘积的位数。
3.实例以下是一个简单的Verilog乘法器实例:```module multiplier(input [7:0] a, b [7:0], output [15:0] result);wire [15:0] partial_product;wire [15:0] temp_result;// 位级乘法器wire [15:0] product [7:0];genvar i;generatefor (i = 0; i < 8; i = i + 1) beginassign product[i] = a * b[i];endendgenerate// 移位器assign partial_product = {product[7], product[6:0]};// 全加器assign temp_result = partial_product + result;assign result = temp_result;endmodule```二、Verilog除法器原理与实现1.原理Verilog除法器的原理是采用迭代算法,将除法问题转化为加法和减法问题。
除数和被除数按位进行与运算,得到余数的位级表示。
然后通过循环移位和加法运算,将余级表示转换为最终的整数商和余数。
加减交替阵列除法器的设计与仿真实现

加减交替阵列除法器的设计与仿真实现一、引言随着数字电路的发展,除法器在计算机和通信系统中的应用越来越广泛。
加减交替阵列除法器是一种高效的除法器,具有运算速度快、面积小等优点。
本文将详细介绍加减交替阵列除法器的设计与仿真实现。
二、加减交替阵列除法器原理加减交替阵列除法器是一种基于移位和加减运算的快速除法器。
其主要原理如下:1. 将被除数左移n位,得到一个n+1位的数(其中最高位为0)。
2. 对于每个n+1位的数,采用加减交替的方式进行运算。
3. 在第n步时,判断商是否已经求出。
4. 如果商未求出,则返回第1步。
三、加减交替阵列除法器设计1. 系统框图加减交替阵列除法器由以下模块组成:被除数寄存器、商寄存器、余数寄存器、控制单元、计算单元和状态机。
系统框图如下所示:2. 系统模块设计(1)被除数寄存器被除数寄存器用于存储待处理的被除数。
它由一个n位的寄存器和一个移位器组成,可以将被除数左移n位。
(2)商寄存器商寄存器用于存储计算得到的商。
它由一个n位的寄存器和一个移位器组成,可以将商左移1位。
(3)余数寄存器余数寄存器用于存储计算得到的余数。
它由一个n+1位的寄存器和一个移位器组成,可以将余数左移1位。
(4)控制单元控制单元用于控制整个系统的运行。
它根据状态机的输出信号来控制各个模块之间的数据传输和运算。
(5)计算单元计算单元是加减交替阵列除法器最核心的部分,用于进行加减运算。
它由若干个加法器和减法器组成,每个加法器或减法器都能够进行一次加或减运算。
(6)状态机状态机用于控制控制单元的工作状态,并输出相应的信号。
它有以下三种状态:a. 初始化状态:在这个状态下,被除数、商、余数等变量都被初始化。
b. 运行状态:在这个状态下,加减交替阵列除法器按照原理进行运算。
c. 结束状态:在这个状态下,商已经求出,整个系统停止工作。
四、加减交替阵列除法器仿真实现1. 系统仿真为了验证加减交替阵列除法器的正确性,需要对其进行仿真。
阵列除法器设计与实现

课程设计报告课程设计名称:计算机组成原理课程设计课程设计题目:阵列除法器设计与实现院(系):计算机学院专业:班级:学号:姓名:指导教师:完成日期:2016年1月12日目录第1章总体设计方案 01。
1设计原理 01.2设计思路 (2)1.3设计环境 (2)第2章详细设计方案 (4)2.1功能模块的设计与实现 (4)2。
1。
1细胞模块的设计与实现 (4)2.1.2除法器模块的设计与实现 (6)2.2仿真调试 (8)参考文献 (10)附录(电路原理图).11第1章总体设计方案1.1 设计原理在原码除法中,原码除法符号位是单独处理的,商符由两数符号位进行异或运算求得,商值由两数绝对值相除求得.原码除法中由于对余数的处理不同,又可分为恢复余数法和不恢复余数法(加减交替法)。
在机器操作中通常采用加减交替法,因为加减交替法机器除法时间短,操作规则。
加减交替法的运算规则如下:(1)当余数为正时,上商1,余数左移一位后减去除数得下一位余数.(2)当余数为负时,上商0,余数左移一位后加上除数得下一位余数.阵列除法器是一种并行运算部件,采用大规模集成电路制造,与早期的串行除法器相比,阵列除法器不仅所需的控制线路少,而且能提供令人满意的高速运算速度。
阵列除法器有多种形式,如不恢复余数阵列除法器、补码阵列除法器等等。
本实验设计的是加减交替阵列除法器。
本实验利用的细胞单元是一个可控加法/减法CAS单元,利用它组成的流水阵列来实现四位小数的除法.CAS单元有四个输入端、四个输出端。
其中有一个控制输入端P,当P=0时,CAS作加法运算;当P=1时,CAS作减法运算。
逻辑结构图如图1。
1所示。
图1。
1 可控加法/减法(CAS)单元逻辑结构图CAS单元的输入与输出的关系可用如下逻辑方程来表示:Si=Ai⊕(Bi⊕P)⊕CiCi+1=(Ai+Ci)(Bi⊕P)+AiCi当P=0时,CAS单元就是一个全加器,如下:Si=Ai⊕B⊕iCiCi+1=AiBi+BiCi+AiCi当P=1时,则得求差公式:Si=Ai⊕B⊕iCiCi+1=AiBi+BiCi+AiCi其中有Bi=Bi⊕1在减法中,输入称为借位输入,而称为借位输出。
除法器的工作原理

除法器的工作原理
除法器是一种电子电路或计算机硬件模块,用于实现数值的除法运算。
其基本工作原理是通过不断迭代的过程,将被除数逐步减去除数,并记录需要的迭代次数来获得商及余数。
具体来说,除法器通常利用移位及减法等算法来实现除法运算。
以下是一种常见的除法器工作原理示例:
1. 首先,将被除数输入除法器,并与除数进行比较。
如果被除数小于除数,则商为0,余数为被除数本身。
2. 如果被除数大于除数,则进入迭代过程。
首先,将除数左移一位(相当于除以2),然后减去被除数的值。
如果减法结果
大于等于0,则将商的对应位置标记为1,表示商在该位上有值;否则,商的对应位置为0,并将减法结果作为新的被除数。
3. 迭代过程会一直进行,直到除数左移至最高位或者被除数为0为止。
最终,商的各个位对应的值就是最终的商,而最后的
被除数值就是余数。
除法器可以采用不同的设计方法和算法,以满足不同的需求和性能要求。
其中,一些高性能除法器还会使用查表法、预计算和流水线等技术来加速除法运算。
总之,除法器通过迭代的方式,不断将被除数减去除数,并记录迭代次数,来实现数值的除法运算。
它是计算机中重要的基
本模块之一,可以广泛应用于数字信号处理、图像处理、网络通信等各个领域中。
高性能CPU中除法器的设计与实现

同济大学硕士学位论文高性能CPU中除法器的设计与实现姓名:石松华申请学位级别:硕士专业:电子科学与技术指导教师:林正浩20050301摘要摘要在CPtJ的发展过程中,由于对运算精度的要求不断提高,浮点运算单元成为构成CPU的不呵缺少的部件之一。
除法相对于加法、减法和乘法来说,是属于较少用到的运算,但因为运算较复杂,使得其延迟时间比其他运算长,其性能优劣将直接影响CPU的整体处理能力,因此,设计高性能的浮点除法单元成为提高CPU性能的关键。
本文首先介绍了浮点数的标准和运算规则,在此基础上分析了浮点除法的基本原理,然后介绍了目前流行的基于减法和基于乘法的经典浮点除算法,在比较几种算法优劣的基础上选择了基4SRT算法作为本设计的算法。
接下来应用基4SRT算法设计了浮点除法器的体系结构,对此结构中的关键部件进行了分析与选择。
在此基础上通过VerilogHDL编码和综合优化给出了该除法器的基于.1Sum工艺库的门级网表。
本文的主要工作集中在浮点除法器的算法选择、体系结构设计和综合优化。
难点是算法选择,各种算法各有优缺点,需综合考虑,进行取舍。
重点是体系结构设计。
创新点是综合优化,在不改变源代码的前提下,应用不同的优化策略较之标准编译过程可以有效地提高设计的性能。
关键词:浮点除法SRTVerilog综合优化AbstracfABSTRACTTherequirementofcomputationalprecisionisrisinginthedevelopmentofCPU,sothefloating—pointunitespeciallythefloating—pointdividerunitbecomesoneofthenecessarybasicpartofCPU.Divisionistheleastusedoperationascomparetoaddition,subtractionandmultiplication.Butdivisionoperationismorecomplex,itstime—delayislongerthanotheroperation,theperformanceoffloating—pointdividerunithasadirecteffectonCPU,Soahi曲performancefloating—pointdividerunitiscriticaltothedesignofCPU.Inthisarticle,standardandcomputingruleareintroducedfirst.Onthisbase,theoryoffloating—pointdivisionisanalyzed.Thensomepopularfloating-pointdivisionarithmeticisintroduced.Basedonthecomparisonofdifferentarithmetic,Radix.4SRTarithmeticischosentorealizethisdesign.Thenarchitectureoffloating—pointdivisionbasedonradix-4arithmeticisdesigned.OnthisbasebyVerilogHDLcodingandsynthesisoptimization,netlistbasedon.18urntechnologylibraryisprovided.Finallylow—powerdesignisdiscussed.Themainworkofthisarticlefocusesonchoosingoffloating-pointdivisionarithmetic,architecturedesignandsynthesisoptimization.Thedifficultyischoosingoffloating-pointdivisionarithmetic,eacharithmetichasitsOWnadvantageandisdisadvantage,choosingisdependedonwholeconsideration.Thekeypointarchitecturedesign.Theinnovationalpartissynthesisoptimization.Applicationofdifferentoptimizationstrategycaneffectivelyenhancetheperformanceofdesignascomparetostandardcompileprocess.KeyWords:floating-pointdivisionSRTVerilogSynthesisOptimization】I学位论文版权使用授权书本人完全了解同济大学关于收集、保存、使用学位论文的规定,同意如下各项内容:按照学校要求提交学位论文的印刷本和电子版本;学校有权保存学位论文的印刷本和电子版,并采用影印、缩印、扫描、数字化或其它手段保存论文;学校有权提供目录检索以及提供本学位论文全文或者部分的阅览服务;学校有权按有关规定向国家有关部门或者机构送交论文的复印件和电子版;在不以赢利为目的的前提下,学校可以适当复制论文的部分或全部内容用于学术活动。
高效除法器verilog实现

整理文本西北工业大学《 FPGA 技术实验》实验报告二(高效除法器 )学院:软件与微电子学院学号:姓名:专业:微电子学实验时间:2011.10.12实验地点:毅字楼 335指导教师:王少熙西北工业大学2010年 10 月一、实验目的及要求实验目的 : 1.进一步了解熟悉verilog 语句语法掌握条件语句在简单建模中的应用,学会建模仿真综合 .2.熟练运用 modelsim进行调试模拟仿真 .3.初步学会运用综合工具进行综合,熟悉 synplify.实验要求 :用verilog实现一个被除数为8 位,除数为 4 位的高效除法器 .二、实验设备(环境)及要求ModelSim SE 6.2b及 Synplify Pro 9.6.2三、实验内容与步骤1.实验总体设计思路由于只有加法器 ,除法在计算机中是通过部分余数左移加除数补码或 0 实现 ,我们由此可以得到启示 ,也按照如此的思路进行 .整体思路是先将八位 (本来余数是四位的但是我们这里的余数不仅仅充当余数 ,还当中间变量把被除数从最高位一位一位的移到余数里 )余数清零 ,然后把被除数的最高位拼接到余数后面 ,此时余数与除数比较 , 若余数大于除数 ,则把他们俩的差作为新的余数 ,且把对应的商值为记 1; 若余数小于除数 ,则把对应位的商值记 0;进行下一步之前把被除数的第二高位继续拼接到余数后面 ,如此进行 ,循环八次即可 .最后结果是得到商和余数的形式 .其算法流图如下所示 :Start余数 rem=0;商 quo=0; i=7rem={rem[6:0],did[i]}是否rem>disquo[i]=1;i=i-1;quo[i]=0;rem=rem-dis;rem=rem;i=i-1;i<0否是得到 quo,rem.是 4 位,除数 (dis)是 2 位,商(quo)是 4 位 ,余数 (rem)是 4 位,设 did=0110,dis=10,我们来看看是怎么执行的.首先余数和商都清零 ,即 rem=0,quo=0;把被除数的最高位0 拼接到 rem的最低位 ,此时 rem=0000B,由于 rem 小于除数 dis=10,则商 quo[3]=0;下面进行第二次计算,把 did[2]拼接到 rem 最低位 ,此时 rem=0001,dis=10>rem,故 quo[2]=0;继续计算 , 把 did[1]拼接到 rem 最低位 ,此时 rem=0011,dis=10<rem,故quo[1]=1,rem=rem-quo=0011-10=0001;进行最后一轮运算 , 把 did[0]拼接到 rem 最低位 ,此时 rem=0010,dis=10=rem,因此 quo[0]=1,rem=rem-dis=0010-10=0000,至此我们已计算完毕商quo=0011,余数 rem=0000;计算简单快速 .2.测试平台设计模块设计`timescale 1ns/1nsmodule divider_8_4(did,// Divident被除数dis,// Divisor除数quo,// Quotient商rem,// Remainder 余数error//错误,如果除数为0.则error置1);parameter M=7;//被除数,余数,商的位数parameter N=3;//除数的位数input [M:0] did;input [N:0] dis;output [M:0] quo;output [M:0] rem;output error;reg [M:0] quo;reg [M:0] rem;reg error;integer i;//整数,用于计数always @(did or dis)//被除数,除数beginquo=0;rem=0;//开始余数和商清零if(dis==0)error=1;//若除数为0则显示错误else if(did<dis)//为了提高效率,在被除数小于除数时begin//商0,余数为除数rem=dis;quo=0;error=0;endelsebeginerror=0;for (i=8;i>0;i=i-1) //循环8次beginrem={rem[M-1:0],did[i-1]}; //把did[i-1]连接到rem后quo=quo<<1;//商左移一位if(rem>=dis)//若拼接后rem>=除数disbeginquo=quo+1; //商值自加1rem=rem-dis; //新余数变为旧余数减除数endendendend//结束endmoduleTesebench如下 :`timescale 1ns/1nsmodule divider_bench;reg [7:0] did;reg [3:0] dis;wire [7:0] quo;wire [7:0] rem;integer i;//整数,用于控制被除数变化integer j;//整数,用于控制除数变化divider_8_4 d1(did,dis,quo,rem,error); //实例化initialbeginfor(i=0;i<=255;i=i+1)//被除数从0到255begindid=i;for(j=0;j<=15;j=j+1)//除数从0到15变化#1 dis=j;endendinitialbegin$monitor($time,"divident=% divisor=%d quotient=%dremainder=%d",did,dis,quo,rem) ;endinitialbegin#1000 $finish;// 1000ns 时停止仿真endendmodule四、实验结果与数据处理1.Modelsim 仿真结果,波形图,代码覆盖率图等为了严谨 ,把所有的数值都测了一遍 (did 从 0 到 255,dis 从 0 到 15),从modeldim 仿真结果看到程序的正确性 ,鉴于数据较多这里只选择几组数据给予展示 :上图中从上到下一次代表被除数,除数 ,错误 ,商和余数 ,当被除数是 4.除数分别是 9,10,11,12,13,14,15时商为 0,余数分别 9,10,11,12,13,14,15.当被除数为 147,除数分别为 1,2,3,4,5,6,7时 ,商分别为 147,73,49,36,29,24,21,余数分别为 0,1,0,3,2,3,0结.果正确 .由上图可见代码覆盖率已达100%,非常好 .2.综合结果,布局布线结果,关键路径,资源利用率等。
VHDL实现32位除法器(可选有无符号运算)

除法器模块说明1.前言在本项目中,需要用到非2的整数次幂的除法操作,所以不能通过移位操作来完成,而且不允许使用既有的IP核,这样,就需要在VHDL环境下自建一个除法功能模块,以在环路计算中实现除法操作。
2.任务分析此除法模块必须能够被重复调用,实现环路计算时对此模块时分复用,以达到节约逻辑资源的目的。
另外,经过对环路数据的计算,需要除法操作的数据可以控制在二进制下32位宽度以内,所以,本次除法器的设计是以32位有符号数的运算为目的的。
3.设计原理除法器的设计主要有两种方法,一是基于乘法操作,另一是基于减法操作。
基于乘法操作的算法是把除法看做乘法的逆运算,实现时需要顺次进行,因此运算速度较慢且需要耗费大量的逻辑资源,在FPGA中实现是不推荐此种方法,在此也不做讨论和采用;与此相比,在FPGA环境下,基于减法的操作不仅速度快,而且节省资源,而且通过除数与被除数的符号位判断,还能够实现有符号数运算,本次除法器的设计即采用基于减法的操作。
除法的数学运算公式为:A = B * Q + R (1)其中,A为被除数,B为除数,Q为商数,R为余数。
实现原理与步骤阐述如下:要方便的利用FPGA的特性进行求商运算,需先阐明一个运算关系。
二进制下数值的左右移位等同于此数与2的n次幂的乘法,左移n位后低位补零结果等于原数值与2的n次幂的乘积,右移n位后高位补零结果等于原数值除以2的n 次幂的结果。
例如,十进制数14,二进制表示为1110原数左移2位并补零后为 111000,即56,56=14*2*2。
原数右移1位并补零后为 0111,即7,7=14/2。
利用这个移位的性质,结合FPGA方便的移位操作,可以实现快速的除法运算。
一个被除数A,仍以1110(14)为例,可以表示为3210+++,1*21*21*20*2可以由最高位或者最低位开始,任意截取连续的几位数据去做运算,相当于原数据进行了移位后进行的运算,运算结果只需要再进行逆向的移位操作即可得到正确的结果。
模拟除法器电路原理

模拟除法器电路原理一、引言除法运算是数学中基础的运算之一,而在电子电路中,除法运算同样非常重要。
为了实现除法运算,人们设计出了除法器电路,使用模拟电路来模拟实现除法运算。
本文将介绍模拟除法器电路的原理和工作方式。
二、模拟除法器电路的基本原理模拟除法器电路的基本原理是通过模拟电压值来模拟除法运算。
在模拟除法器电路中,输入的被除数通过电路经过一系列的运算,最终得到输出的商。
下面将介绍模拟除法器电路的基本原理和工作过程。
1. 输入端模拟除法器电路的输入端包括被除数和除数两个输入。
被除数是需要被除的数,而除数是用来除的数。
这两个输入通过输入端进入除法器电路。
2. 运算电路模拟除法器电路的核心是运算电路,它通过一系列的运算来实现除法运算。
运算电路包括比较器、积分器和运算放大器等组成部分。
(1) 比较器比较器用于比较被除数和除数的大小关系,并输出比较结果。
如果被除数大于等于除数,则比较器输出高电平;如果被除数小于除数,则比较器输出低电平。
(2) 积分器积分器用于对比较器输出的高电平进行积分,得到积分值。
积分器的输出电压与时间的积分成正比。
(3) 运算放大器运算放大器用于放大积分器输出的电压,使其达到适当的电压范围。
运算放大器通常采用差动放大电路,具有高增益和低失真的特点。
3. 输出端模拟除法器电路的输出端为商,即除法运算的结果。
输出端通过输出电压来表示商的大小。
输出电压的大小与被除数和除数的比例成正比。
三、模拟除法器电路的工作方式模拟除法器电路的工作方式如下:1. 输入被除数和除数的值,并通过输入端进入除法器电路。
2. 比较器对被除数和除数进行比较,输出比较结果。
3. 根据比较器输出的结果,积分器开始对高电平进行积分,并输出积分值。
4. 运算放大器对积分器输出的电压进行放大,使其达到适当的电压范围。
5. 输出端通过输出电压来表示商的大小,即除法运算的结果。
四、总结模拟除法器电路通过模拟电压值来实现除法运算,其原理和工作方式可以总结为:输入被除数和除数的值,经过比较器、积分器和运算放大器等运算电路的处理,最终得到输出端的商。
除法器的工作原理

除法器的工作原理
除法器是一种数字电路,用于执行除法操作。
它的工作原理可以分为以下几个步骤:
1. 导入除数和被除数:除法器接收输入信号,将除数和被除数导入电路中。
2. 对齐操作:除法器需要将除数和被除数进行对齐,使它们的小数点位置相同。
这可能需要移位操作。
3. 比较操作:除法器需要将除数与被除数进行比较,以确定商的各个位。
4. 商的计算:通过重复减法和比较操作,除法器逐位地计算商的各个位。
5. 商的校正:在商的计算过程中,商可能会偏离实际结果。
因此,除法器可能需要进行商的校正,以确保得到正确的商结果。
6. 结果输出:除法器将商和余数输出到指定的输出端口。
这些步骤的具体实现方式可能会因使用的具体除法算法而有所不同。
一些常见的除法算法包括原码除法、补码除法以及余数-商模型除法等。
除法器的设计和实现是数字电路设计中的重
要部分,涉及到逻辑门、多路复用器、触发器等基本电路元件的使用。
计算机组成原理--除法器原理

计算机组成原理--除法器原理
除法器是计算机中的一种基本逻辑功能模块,用于实现除法运算。
除法器的实现原理与方法有很多种,以下是其中一种常见的实现原理:
1. 物理实现
除法器通常由大量的逻辑门电路组成,可以采用不同的实现方式,如串行除法器、并行除法器、移位除法器、余数-商除法器等。
其中,
移位除法器和余数-商除法器是最常用的两种。
2. 操作流程
以余数-商除法器为例,其操作流程如下:
(1)将除数和被除数输入除法器。
(2)将除法器初始化,即将商和余数的初始值设置为0。
(3)按照一定的算法,在每个时钟周期内进行一次除法运算。
(4)在计算过程中,如果余数小于除数,则商的相应位清零,
否则商的相应位为1,并将余数减去除数。
(5)在除法执行完毕后,商即为结果的整数部分,余数即为结
果的小数部分。
3. 特点
除法器的特点包括:
(1)实现较为复杂,需要大量的逻辑门电路,占用较多的芯片
面积和功耗。
(2)除法运算的速度相比加减乘运算较慢,需要多个时钟周期
才能计算完毕。
(3)除法器较为容易出错,需要考虑除法中各种特殊情况的处
理方法,如被除数为0、除数为0、商或余数超出范围等。
(4)除法器通常作为CPU中的一个模块存在,与其他逻辑电路
协同工作,在计算机系统中发挥重要作用。
计算机组成原理--除法器原理及c代码

计算机组成原理--除法器原理及c代码除法器是计算机中的一个重要组成部分,用于实现除法运算。
除法器可以由硬件电路或软件实现。
硬件电路实现速度快,但成本高,而软件实现则速度慢但成本低。
下面是一些关于除法器原理及C代码的介绍:除法器原理:除法器的原理就是将被除数不断减去除数,直到被除数小于除数为止,被减的次数即为商。
这个过程可以用一个简单的while循环来实现。
除法器的步骤如下:1.读入被除数和除数。
2.判断除数是否为0,若为0,则除法操作失败。
3.对被除数除以除数,在每一次迭代中将被除数减去除数。
4.计算商的值,即被减的次数。
C代码实现:下面是一个简单的C代码实现,实现了除法器的基本功能:```。
#include <stdio.h>。
int main()。
int dividend, divisor, quotient = 0;。
printf("Enter dividend: ");。
scanf("%d", ÷nd);。
printf("Enter divisor: ");。
scanf("%d", &divisor);。
if(divisor == 0) 。
printf("Division by zero error!\n");。
return 0;。
}。
while(dividend >= divisor) 。
dividend = dividend - divisor;。
quotient++;。
}。
printf("Quotient: %d\n", quotient);。
return 0;。
}。
```。
在这个代码段中,我们首先读入了被除数和除数。
然后,我们检查除数是否为0,如果是,则输出错误提示,并退出程序。
接着,我们使用一个while循环来迭代计算商的值。
加减交替阵列除法器的设计与仿真实现实验报告

加减交替阵列除法器的设计与仿真实现实验报告一、引言加减交替阵列除法器是一种常用的数字逻辑电路,用于计算两个数的除法运算。
它能够将一个除数和被除数作为输入,输出商和余数。
本实验报告将详细介绍加减交替阵列除法器的设计原理、电路结构以及仿真实现结果。
二、设计原理1. 加减交替阵列除法器的基本原理是通过将除法运算转化为连续的减法和加法运算来实现。
具体步骤如下:- 将除数和被除数输入除法器。
- 如果被除数大于等于除数,则进行减法运算,将结果存储为商,并将被除数减去除数。
- 如果被除数小于除数,则进行加法运算,将结果存储为商,并将被除数加上除数。
- 重复上述过程,直到被除数小于除数为止。
2. 加减交替阵列除法器的电路结构主要由以下几个部分组成:- 除法单元:负责执行减法和加法运算。
- 商和余数寄存器:用于存储每一步的商和余数。
- 控制模块:用于控制除法运算的步骤和判断条件。
三、电路结构加减交替阵列除法器的电路结构如下所示:1. 除法单元:由一个减法器和一个加法器组成,用于执行减法和加法运算。
2. 商和余数寄存器:包括商寄存器和余数寄存器。
商寄存器用于存储每一步的商,余数寄存器用于存储每一步的余数。
3. 控制模块:根据被除数和除数的大小关系,确定执行减法还是加法运算,并控制除法运算的步骤和判断条件。
四、仿真实现我们使用Verilog语言进行仿真实现。
首先,我们定义了除法单元、商和余数寄存器以及控制模块的输入输出端口,并根据设计原理实现了相应的功能。
然后,通过编写测试程序,对设计的加减交替阵列除法器进行了仿真测试。
仿真结果显示,加减交替阵列除法器能够正确执行除法运算,并输出正确的商和余数。
在不同的测试案例中,除法器的运算速度和准确性都得到了验证。
五、实验总结本实验通过对加减交替阵列除法器的设计与仿真实现,深入理解了其工作原理和电路结构。
加减交替阵列除法器在计算中起到了重要的作用,能够高效地完成除法运算。
通过本次实验,我们对数字逻辑电路的设计和仿真有了更深入的了解,并提高了我们的实践能力。
计算机组成原理--除法器原理及c代码

计算机组成原理--除法器原理及c代码除法器是计算机中的一种重要的算术逻辑单元,用于实现除法运算。
除法器的设计是计算机组成原理中的重要内容之一,本文将从除法器的原理和相关的C代码实现两个方面进行介绍。
一、除法器原理除法器的原理主要包括除法算法和硬件实现两个方面。
1.除法算法在计算机中,除法可以采用多种算法实现,其中最常用的算法是连续除法和恢复余数法。
连续除法是将除数逐位地与被除数相减,判断余数的大小来进行下一步的操作。
具体操作如下:1)将被除数置于一边,余数和商置于另一边;2)被除数减去除数,得到当前位上的余数;3)余数进行左移,并加上下一位的被除数;4)重复上述操作直到计算完所有位。
恢复余数法是将除法过程中的余数加上除数,然后与被除数进行比较,得到商和下一位的余数。
具体操作如下:1)将被除数放在寄存器的高位,余数和商放在低位;2)将寄存器与除数进行比较,若寄存器大于等于除数,说明商的该位为1,余数等于当前寄存器减去除数;3)将寄存器进行左移,并加上下一位的被除数;4)重复上述操作直到计算完所有位。
2.硬件实现硬件实现除法器可以采用著名的Restoring、Non-Restoring和SRT 等算法。
其中Restoring算法是最常用的硬件实现方式。
Restoring算法中,通过比较、左移、减法等操作进行计算。
具体操作如下:1)将除数和被除数放入寄存器的高位和低位,商和余数置零;2)将寄存器与除数进行比较,若寄存器大于等于除数,说明商的该位为1,余数等于当前寄存器减去除数;3)将寄存器逻辑左移一位;4)循环执行2-3步,直到计算完所有位。
二、C代码实现以下是C语言中使用Restoring算法实现的除法器代码:```c#include <stdio.h>unsigned int divide(unsigned int dividend, unsigned int divisor)unsigned int quotient = 0;unsigned int remainder = 0;//32位无符号整数除法for (int i = 31; i >= 0; i--)remainder = (remainder << 1) , ((dividend >> i) & 1); // 将被除数逻辑左移一位,并加上下一位的被除数if (remainder >= divisor) // 判断余数是否大于等于除数remainder -= divisor; // 余数减去除数quotient ,= (1u << i); // 商的该位为1}}return quotient;int mainunsigned int dividend = 53;unsigned int divisor = 5;unsigned int result = divide(dividend, divisor);printf("%u / %u = %u\n", dividend, divisor, result);return 0;```以上的代码实现了一个32位无符号整数的除法操作,通过Restoring算法将除法运算转化为逐位比较、逻辑左移和减法等操作,最终得到商。
除法器的实现
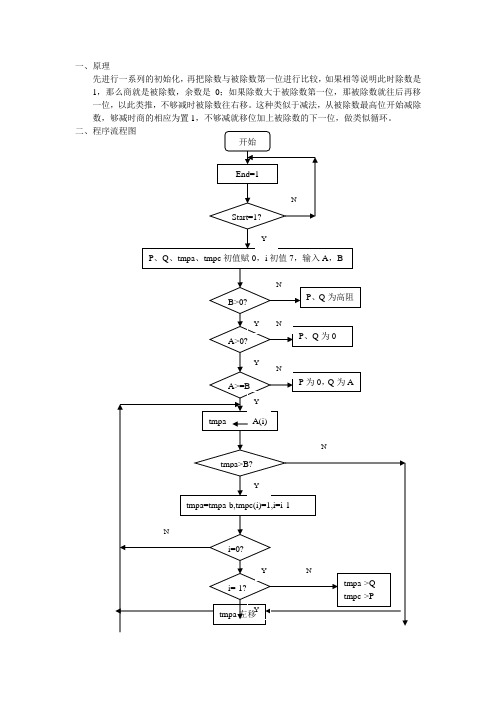
一、原理先进行一系列的初始化,再把除数与被除数第一位进行比较,如果相等说明此时除数是1,那么商就是被除数,余数是0;如果除数大于被除数第一位,那被除数就往后再移一位,以此类推,不够减时被除数往右移。
这种类似于减法,从被除数最高位开始减除数,够减时商的相应为置1,不够减就移位加上被除数的下一位,做类似循环。
二、程序流程图开始End=1Start=1?P、Q、tmpa、tmpc初值赋0,i初值7,输入A,BB>0?P、Q为高阻A>0?P、Q为0A>=BP为0,Q为Atmpa A(i)tmpa>B?tmpa=tmpa-b,tmpc(i)=1,i=i-1i=0?i=-1? tmpa左移tmpa->Qtmpc->P NY Y YYY Y NNNNNNY三、程序代码LIBRARY IEEE;USE IEEE.std_logic_1164.ALL;USE IEEE.std_logic_ARITH.ALL;USE IEEE.std_logic_unsigned.ALL;ENTITY cjd ISPORT(A,B:IN std_logic_vector(3 DOWNTO 0);--A是被除数,B是除数P,Q:OUT std_logic_vector(3 DOWNTO 0));--P是商,Q余数END cjd;ARCHITECTURE one OF cjd ISBEGINPROCESS(a,b)V ARIABLE tmpa, tmpc:std_logic_vector(3 DOWNTO 0);-- tmpa被除数中间量,tmpc 除数中间量BEGINtmpa:="0000";tmpc:="0000";if B>0 thenif A>0 thenif A>B thenfor i in 3 downto 0 looptmpa(0):=a(i);if tmpa<B thentmpc(i):='0';elsetmpc(i):='1';tmpa:=tmpa-B;end if;if i>0 thenfor j in 3 downto 1 looptmpa(j):=tmpa(j-1);end loop;tmpa(0):='0';end if;end loop;P<=tmpc;Q<=tmpa;elsif A<B thenP<="0000";Q<=A;elseP<="0001";Q<="0000";end if;elseP<="0000";Q<="0000";end if;elseP<="ZZZZ";Q<="ZZZZ";end if;END PROCESS;END one;三、波形仿真1、功能仿真A,B都是去符号数,所以先排除A=0或者B=0的情况。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、 原理
先进行一系列的初始化,再把除数与被除数第一位进行比较, 如果相等说明此时除数是
1,那么商就是被除数,余数是 0;如果除数大于被除数第一位,那被除数就往后再移 一位,以
此类推,不够减时被除数往右移。
这种类似于减法, 从被除数最高位开始减除
数,够减时商的相应为置 1,不够减就移位加上被除数的下一位,做类似循环。
二、
程序流程图 开始
End=1
P 、Q 、tmpa 、tmpc 初值赋0, i 初值7,输入A , B
N
N
Y
N
P 、Q 为 0
>—
Y
N
P 为0, Q 为A
Y
tmpa=tmpa-b,tmpc(i)=1,i=i-1
Start=1?
Y
B>0?
A>0? * P 、Q 为高阻
Y
A(i)
tmpa
N
i=-1?
tmpa 左移
tmpa->Q
tmpc->P
三、程序代码
LIBRARY IEEE;
USE lEEE.std」o gic_1164.ALL;
USE IEEE.std_logic_ARITH.ALL;
USE IEEE.std_logic_ un sig ned.ALL;
ENTITY cjd IS
PORT(A,B:IN std」ogic_vector(3 DOWNTO 0);--A 是被除数,B 是除数
P, Q:OUT std」ogic_vector(3 DOWNTO 0));--P 是商,Q 余数
END cjd;
ARCHITECTURE one OF cjd IS
BEGIN
PROCESS(a,b)
VARIABLE tmpa, tmpc:std_logic_vector(3 DOWNTO 0);-- tmpa 被除数中间量, 除数中间量
tmpc BEGIN
tmpa:="OOOO"; tmpc:="OOOO";
if B>0 then
if A>0 the n
if A>B the n
for i in 3 dow nto 0 loop
tmpa(0):=a(i);
if tmpa<B the n
tmpc(i):='0';
else
tmpc(i):='1'; tmpa:=tmpa-B; end if;
if i>0 the n
for j in 3 dow nto 1 loop
tmpa(j):=tmpa(j-1);
end loop;
tmpa(0):='0';
end if;
end loop;
P<=tmpc;
Q<=tmpa;
elsif A<B the n
P<="0000";
Q<=A;
else
P<="0001";
Q<="0000";
end if;
else
P<="0000";
Q<="0000";
end if;
else
P<="ZZZZ";
Q<="ZZZZ";
end if;
END PROCESS;
END one;
三、波形仿真
1、功能仿真
A, B都是去符号数,所以先排除A=0或者B=0的情况。
当A=0时,波形验证如下图:
S iLMul at ion ■avef or>s:
Simulation mode: Functional
Mas tex Time E 吉x*: 16- 25 ns jjjJ Paint |~7. 78 ns~ I nt erval x ["―S. 47 ns St&Ft :
Name Value
16.2
E3 HU
E3
E IS A
ALO]
AE1]
AT^l
A [3] Ei
E
BLO]
ELI]
BT^l
B[3] Ei F
P[0]
PE1]
PT21
P[3]
Ei Q
Q[0]
QtJ]
QT2]
Q[3]
1001r mi DC0111< 0011>
j
厂L
L
0000
Jf
当B=0时,波形验证如下图:
当A<B时,红色线是具体例子;当B=1时,绿色线是例子。
波形验证如下图: SimLilatioii nodei Functional
当A>B 时,波形验证如下: 2、时序仿真 Master Tine Ear: 93.0 ns H
J Pointer : 289.26 ns Interval : 196.26 ns Start:
End: n 3 H -
I —I
I —I T J T J T J T J T J T J T
J T J 1J 1J 0 1 2 3 0
1 2 3 0 1 2 3 r L r L r L r L r L r L r L r L r L r L r L
r L A A A A A E
E
E E
E F F F F F 0
Q B
Vs. Tut 2S7. 79 ns 288. 73 ns 2B9. 79 ns
290
-弹
291. 丁9 ns
292. 79 甲
93. £
B 1
1100
c 1101
E
r
E
E E
B 1
,111/
0011
xoiii yr
0100
X
0000
I ioo& XiiTn
E E
r
E
—r
-L
r E r B 0
0011
□SiYoDGoojr -
oooo -
Moooi)L 0011 \一
-QODL
X
E 1
nr
T~
B r
m
r
~L
B
1
J
1
J
T
J
T J o
1 2 3 r L r L r L r L Q Q Q Q E
血14?烦讹 mil 狮腕躺。
饰0&S 近虱近而丽5而柑而湎烦妙粗询厂丽厂呦施顽i
1
II 1
II ~1 1
I
n r n i i r _r~u ------ 1
n _ i n - r
r
un _____ i _。
