高考专题突破三(1)
2022版高考英语一轮复习语法专项突破专题三不可忽视的小词_代词冠词和介词短语第三讲介词短语学案含解

第三讲介词(短语)Ⅰ.单句语法填空1.(2020·高考某某卷)Some time after 10,000 BC, people made the first real attempt to control the world they lived ,through agriculture.解析:考查介词。
分析句子结构可知,they lived 是定语从句,修饰先行词the world;省略了关系代词,说明关系代词在从句中作宾语。
根据语法常识知,live常和介词in搭配,意为“居住在……〞。
省略了的关系代词作in的宾语。
答案:in2.(2020·高考全国卷Ⅲ)The artist was finally humbled (谦卑) by the greatest artist earth, Mother Nature.解析:考查介词。
此处on earth相当于in the world,意思是“在世上,在人间〞。
答案:on3.(2020·新高考全国卷Ⅰ)Museums must pete people's spare time and money with other amusements.Most museums also wele school groups and arrange special activities for children.解析:考查介词。
pete for...with...为了……而与……竞争,为固定搭配。
答案:forⅡ.单句改错1.(2020·高考全国卷Ⅱ)I'm glad to know that you've e China to learn kung fu in a school in my hometown.解析:考查介词。
句意:知道你来到中国在我家乡的一所学校学习功夫我很高兴。
e为不与物动词,后面加宾语时,需加介词。
高考二轮复习专题突破:3-1 ATP和酶

蔗糖是二糖,在蔗糖酶作用下水解为葡 萄糖和果糖;麦芽糖是二糖,在麦芽糖 酶作用下水解为2分子葡萄糖。因此由图 可知,六边形即丙,代表葡萄糖;五边形即丁,代表果糖,A错误。 图中显示蔗糖在蔗糖酶作用下发生水解,而麦芽糖在蔗糖酶作用下无 法水解,体现了酶的专一性,未体现高效性,B错误。 酶与底物结合时,结构会有所改变,形成酶-底物复合物,C正确。 酶活性可用在单位时间内产物生成量或底物消耗量表示,D错误。
123456
题组三 酶的影响因素及相关实验分析 5.除了温度和pH对酶活性有影响外,一些抑制剂也会降低酶的催化效果。 图甲为酶作用机理及两种抑制剂影响酶活性的机理示意图,图乙为相同 酶溶液在无抑制剂、添加不同抑制剂的条件下,酶促反应速率随底物浓 度变化的曲线。下列说法不正确的是
123456
A.图甲中非竞争性抑制剂降低酶活性的机理 与高温、低温对酶活性抑制的机理不同
123456
6.酶分子具有相应底物的活性中心,用于结合并催化底物反应。在37 ℃、 适宜pH等条件下,用NaCl和CuSO4溶液,研究Cu2+、Cl-对唾液淀粉酶 催化淀粉水解速率的影响,得到实验结果如图所示。已知Na+和 SO24-几 乎不影响该反应,下列相关分析正确的是 A.实验中的无关变量是无机盐溶液的种类
水解产生的腺苷没有放射性(2021·海南,14)( √ )
判断正误
(5)某些蛋白质在蛋白激酶和蛋白磷酸酶的作用下,可在特定氨基酸位 点发生磷酸化和去磷酸化,参与细胞信号传递,如图所示,因此作为
能量“货币”的ATP能参与细胞信号传递(2021·湖南,5)( √ )
判断正误
(6)将A、B两种物质混合,T1时加入酶C,如图为最适温度下A、B浓 度的变化曲线。则T2后B增加缓慢是酶活性降低导致的(2017·天津,3)
专题突破卷03 语法填空之新闻报道(学生版) 2025年高考英语一轮复习考点通关卷(新高考通用)

专题突破卷03语法填空之新闻报道2024年高考模拟真题(2024·湖北·二模)阅读下面短文,在空白处填入1个适当的单词或括号内单词的正确形式。
Tianshui in Northwest China’s Gansu Province is sweeping social media with one of its unique dishes.This city is stepping into the spotlight now that its local street dish malatang has become increasingly1 (influence)on social media.According to the China News Agency,one restaurant owner in Tianshui2(note),“we have been serving at least400customers a day,as people from other provinces drive to the city to get3taste of the local cuisine.”“There has been a long queue outside my restaurant even on weekdays,”said the shop owner. The growing4(popular)of this kind of street food can also be reflected in its main ingredient,the Gangu chili pepper,or lamb’s horn pepper,grown in Gangu county,a place well-known5the “Hometown of Chili Peppers”in China.The sales of products such as the broth for Tianshui malatang and Gangu chili peppers have been surging recently.In some places,the sales of Gangu chili peppers6(increase)tenfold in the past two weeks. Young customers born in the1990s have become the leading force for its consumption,7(account)for 40percent of chili pepper product sales.At the same time,related hashtags such as“going for malatang in Gansu by high-speed train”have been trending on China’s Sina Weibo,8on the short video platform Douyin, the topic Tianshui has been viewed more than12billion times.The successful tourism experience9(earn)by the cities of Zibo and Harbin has paved the way for Tianshui,10the culinary dish is becoming a main force for the city to stand out.(2024·广东广州·三模)阅读下面短文,在空处填入1个适当的单词或括号内单词的正确形式。
2021届高考语文复习知识专题突破专题三 古代诗歌阅读 含解析

2021届高考语文复习知识专题突破专题三古代诗歌阅读含解析----ada23ed2-6ea1-11ec-80d9-7cb59b590d7d2021届高考语文复习知识专题突破专题三古代诗歌阅读含解析话题三古诗词阅读绝招七读懂诗歌,分析特征――形象题鉴赏古诗意象,就是要把握古诗意象的特征,品味其内涵,进而了解作者的思想感情,总结其象征意义或社会意义。
问题类型分类人物形象1选材特点:欣赏诗歌风景形象1选材特点:实物形象1选材特点:主要针对具有特定内涵的事物。
诗歌中的人物形象是分析诗歌场景形象中人物的肖像、动态形象、意境和技巧。
通过对事物形象特征的分析,得出事物的形象、表情、性格、情感、面貌和功能。
命题特点:概括要点、情境等内容,把握特点,探索符号与本体的联系。
2.命题特点:系统分析、把握诗歌的思想情感。
2.命题特征:概括事物形象的个体特征。
它可以分为两类:塑造人物形象和抒情主人公形象。
2.命题特征:主要测试场景、特征和情感。
在欣赏景物形态特征的同时,简要分析了物象的内涵,挖掘了物象的内在特征,找到了书面物与口头意志的“契合点”。
检查并总结人物的特征和形象,以及联系和欣赏诗人的人物的命运。
形象无论是欣赏人物、景物的意象,都要首先把握诗歌的内容、命题的共性,解读诗歌的意义和情感基调,注意诗歌中所描述的意象意义,尤其是常见意象的意义,注意作者描述意象的方法,并把握作者在形象中所体现的特殊情感。
该考试网站是国家新课程标准中的一个圆形考试网站,2022、国家新课程标准量表I考查了该测试站点,以问题类型为主要观察问题。
《国家新课程标准解题特长教学法》中考察的形象主要集中在人物和景物上,从未涉及对事物形象的考察。
因此,我们在这里主要解释人物和风景的形象。
类型一鉴赏人物形象常见设问1.这首诗(词)塑造了一人物形象个怎样的诗(词)人(抒情主准确审题1.题干中有“形象”字样,包答题要点1.概括形象:性格+身份。
2.分析形象:人公)形象?试加以分析。
高考语文 最后四十天专题突破训练 3语言知识和语言表达正确使用标点符号

第一模块:语言知识和语言表达专题三正确使用标点符号(测试时间:45分钟)四川省江油市明镜中学校:刘海燕姓名:成绩:1.下列句中划横线的标点符号,使用正确的一项是A.人中国每人平均每年总要吃四、五百斤粮食,还要有种子、饲料和工业用粮。
B.这件事为什么还要等一、二年?就是希望在这段时间里同各方面进行磋商。
C.其余四分之一的人口在发达国家,包括俄罗斯,东欧(东欧不能算很发达),西欧,北美,,大洋洲的澳大利亚、新西兰,共近20亿亿人口。
D.他常用“烧香找错庙门”、“蚊子叮泥菩萨,看错了对象”等四川俗语,幽默诙谐地批评那些不重视侦察和调查,指挥莽撞,办事马虎的同志。
2下列各句中,标点符号有错误的一句是A.虽然是满月,天上却有一层淡淡的云,所以不能朗照;但我以为这恰是到了好处——酣眠固不可少,小睡也别有风味的。
B.最出色的要数“林教头风雪山神庙”,写那纷纷扬扬的漫天大雪,只一句:“那雪正下得紧。
”C.但我们没有人根据了“礼尚往来”的仪节,说道:拿来!D.她不是“苟活到现在的”我的学生,是为了中国而死的中国的青年。
3.下列标点符号没有错误的一项是A.人什么叫有中国特色的?什么叫的初级阶段?我们过去对这个问题的认识不是完全清醒的。
B.据克鲁普斯卡娅说,列宁“从不凭记忆‘大致不差地’来叙述事实,他叙述事实是极确切的。
”C.“没有调查研究就没有发言权”,这句话虽然曾经被人讥为“狭隘经验论”的,我却至今不悔。
D.李卜克内西回忆说:“马克思在语言和风格问题上十分考究,有时到了咬文嚼字的程度”,“他对于语言的简洁和正确是一丝不苟的”,“马克思是个严格的修辞家;他常常花很多时间力求找到需要的字句。
”(《回忆马克思恩格斯》第104、108页)4.选出标点正确的一句A.山海关,这号称天下“第一关”的山海关! B.山海关,这号称:“天下第一关”的山海关!C.山海关,这号称“天下第一关”的山海关!D.山海关!这号称“天下第一关”的山海关!5.指出下列句中破折号的用法A.表示意思的递进 B.表示意思的转折 C.表示解释、说明 D.表示说话中断或声音延长①在1942年,我们曾经把解决人民内部矛盾的这种民主的方法,具体化为一个公式,叫做“团结——批评——团结”。
2022届高三化学二轮总复习 专题突破 专题三 离子反应 氧化还原反应(76张)

不守恒,正确的离子方程式为3NO2 + H2 O === 2H+ + 2NO−
3 +NO,B项错误;
________________________________________________;
+H2O
(8)将H2S气体通入CuSO4溶液中:
H2S+Cu2+===2H++CuS↓
________________________________________________;
(9)将少量SO2气体通入Na2CO3溶液中:
(11)Al和NaOH溶液的反应:
+ − + = − +3H2↑
__________________________________________________;
(12)AlCl3和过量氨水的反应:
+ + · = ↓ ++
3
2H2O
C.硫酸铝溶液中滴加少量氢氧化钾溶液:Al3+ + 4OH − == AlO2− +
2H2O
D.氯化铜溶液中通入硫化氢:Cu2++S2-===CuS↓
答案:A
3.[2020·江苏卷]下列指定反应的离子方程式正确的是(
)
A.Cl2通入水中制氯水:Cl2+H2O⇌2H++Cl-+ClO-
B.NO2通入水中制硝酸:22 + 2 === 2 + + 3− +
与CO2−
、SO
,Ag
4
4
3
3
②因发生氧化还原反应不能大量共存:具有氧化性的离子与具有还
2020版高考语文(江苏)新增分大一轮复习第三章文言文阅读专题三核心突破一理解实词含义讲义含解析
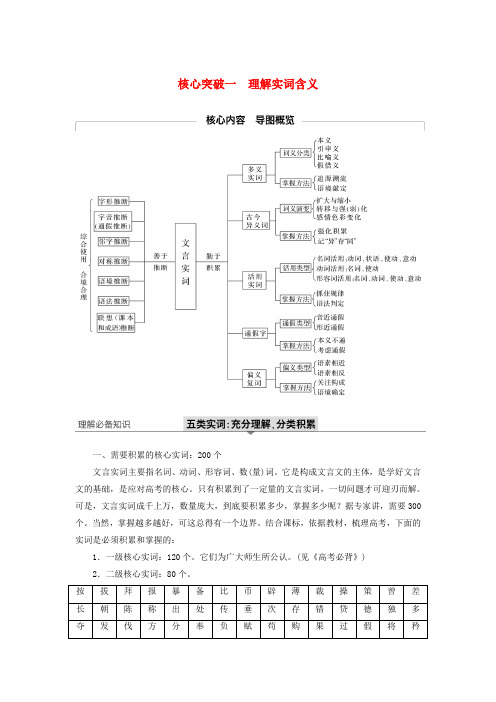
核心突破一理解实词含义一、需要积累的核心实词:200个文言实词主要指名词、动词、形容词、数(量)词。
它是构成文言文的主体,是学好文言文的基础,是应对高考的核心。
只有积累到了一定量的文言实词,一切问题才可迎刃而解。
可是,文言实词成千上万,数量庞大,到底要积累多少,掌握多少呢?据专家讲,需要300个。
当然,掌握越多越好,可这总得有一个边界。
结合课标,依据教材,梳理高考,下面的实词是必须积累和掌握的:1.一级核心实词:120个。
它们为广大师生所公认。
(见《高考必背》)2.二级核心实词:80个。
上面的实词是从教材出现频率,尤其是从近十年各地高考频率梳理、总结出来的,具有一定的权威性。
二、需要理解、积累的知识点:五类实词(一)多义实词:追源溯流,语境敲定多义实词是实词的主体,数量庞大,掌握它们众多的义项耗时费力。
除了要通过教材、试题和大量阅读积累外,还要注意两点:1.追源溯流,寻找义项联系一词多义在文言文中相当普遍,是学习的重点与难点。
如果能弄清其词义演变的规律和特点,那么,无论是记忆还是临场推断,效果都会大大增强。
(1)词义演变规律词的本义,就是词的本来意义,即词产生时的最初的根本的意义。
如“道”的本义是“路途、道路”,“本”的本义是“树木的根”。
词的引申义,就是词由本义派生出的与本义相关的其他意义。
如“道”的本义是“路途、道路”,“方向、方法、道理”为其引申义;“本”的本义是“树木的根”,“根本、本来、原本、基本”就是它的引申义。
又如“孟尝君至关,关法鸡鸣而出客”中,“关”本指“门闩”,由于作用相似引申为“关卡”。
词的比喻义,就是词建立在比喻基础上所产生的意义。
如“爪牙”的本义是“鸟兽的爪子和牙齿”,比喻义是“得力的帮手或武士”,现在属贬义词;“草菅人命”中的“草菅”,本义是“野草”,比喻义是“不值得珍惜的事物”。
词的假借义,就是因假借而产生的含义。
古文中常常出现通假现象。
“通假”就是“通用、借代”,即用读音相同或相近的字代替本字。
高中数学高考2022届高考数学一轮复习(新高考版) 第6章 高考专题突破三 高考中的数列问题

(1)求a4的值;
解 因为 4Sn+2+5Sn=8Sn+1+Sn-1,a1=1,a2=32,a3=54,
当n=2时,4S4+5S2=8S3+S1,
即 4×1+32+54+a4+5×1+32=8×1+32+45+1,
解得 a4=78.
(2)证明:an+1-12an为等比数列.
证明 由4Sn+2+5Sn=8Sn+1+Sn-1(n≥2), 得4Sn+2-4Sn+1+Sn-Sn-1=4Sn+1-4Sn(n≥2), 即4an+2+an=4an+1(n≥2). 当 n=1 时,有 4a3+a1=4×54+1=6=4a2,∴4an+2+an=4an+1, ∴aan+n+2-1-2112aan+n 1=44aan+n+2-1-22aan+n 1=4an4+a1-n+a1-n-22aan n+1=222aann++11--aann=12, ∴数列an+1-12an是以 a2-12a1=1 为首项,12为公比的等比数列.
4.错位相减法 如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构 成的,那么这个数列的前n项和即可用此法来求,如等比数列的前n项和 公式就是用此法推导的.
题型突破 核心探究
TIXINGTUPO HEXINTANJIU
题型一 数列与数学文化
自主演练
1.(多选)(2020·山东曲阜一中月考)在《增删算法统宗》中有这样一则故事:
2.我国古代数学名著《算法统宗》中说:“九百九十六斤棉,赠分八子
做盘缠.次第每人多十七,要将第八数来言.务要分明依次第,孝和休惹
外人传.”意为:“996斤棉花,分别赠送给8个子女做旅费,从第1个孩
Байду номын сангаас
子开始,以后每人依次多17斤,直到第8个孩子为止.分配时一定要按照
新高考生物专题训练1—细胞:第3讲 细胞的生命历程(学生版含答案详解)

新高考生物专题突破训练(三)细胞的生命历程一、单项选择题:本题共12小题,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列关于细胞增殖、分化、衰老和凋亡的叙述,错误的是()A.一般情况下,细胞分化程度越高,细胞的分裂能力越低B.细胞分化使细胞形态结构和功能改变,但遗传信息不变C.细胞衰老会导致酪氨酸酶缺失从而导致老年人头发变白D.被新型冠状病毒侵染的细胞与相应的效应T细胞接触后会凋亡2.肝脏是人体可以自我再生的内部器官。
下列叙述错误的是()A.肝脏是人体内重要器官之一,其大小主要决定于肝细胞数量的多少B.肝癌手术部分切除肝脏后,会通过有丝分裂再生出与机体大小相适应的肝脏C.肝脏再生过程中存在细胞的形态、结构和遗传物质发生稳定性差异的过程D.肝癌细胞表面的糖蛋白等物质减少,使得肝癌细胞容易在体内分散和转移3.为研究某一时相细胞的代谢、增殖、基因表达或凋亡,常需采取一些方法使细胞处于细胞周期的同一时相,下列说法正确的是()A.阻断DNA的合成,多数细胞将停滞于前期B.阻断DNA的合成,多数细胞将停滞于间期C.抑制纺锤体的形成,多数细胞将停滞于间期D.抑制纺锤体的形成,多数细胞将停滞于末期4.“”如图表示某生物的纺锤体,纺锤体由动粒微管、极微管和星体微管组成,细胞分裂后期需要马达蛋白的作用。
下列相关叙述错误的是()A.此图一定不是高等植物的分裂图B.如图所示的时期可能为细胞分裂中期C.微管的化学本质是纤维素D.马达蛋白的运动需要消耗能量5.真核细胞中的细胞周期蛋白A可促进DNA的复制。
细胞中某种特异性siRNA(一种双链RNA)可以导致细胞周期蛋白A的mRNA降解。
下列分析错误的是() A.细胞周期蛋白A可能需进入细胞核发挥作用B.此种siRNA会使细胞周期缩短C.细胞周期蛋白A的合成会受此种siRNA影响D.这种特异性siRNA内一定含有氢键6.真核细胞的细胞周期分为间期和分裂期,受多种物质的调控,分裂间期又分为G1、S、G2三个阶段。
2020年高考化学提升突破专题三 化学与中华民族优秀传统文化(含答案)

专题03化学与中华民族优秀传统文化——立德树人形成核心价值观教育部考试中心提出高考所有学科必须渗透“一点四面”的考查,即以立德树人为核心(一点),强化社会主义核心价值观、中华优秀传统文化、依法治国和创新精神(四面)的考查。
中考、高考升学考试都应增加中华优秀传统文化内容的比重。
通过加强对中国优秀传统文化的考查,引导学生提高人文素养,传承民族精神,树立民族自信心和自豪感。
高考化学试题中对于中华优秀传统文化的考查,不是简简单单地考查死记硬背的知识,而是遵循继承、弘扬、创新的发展路径,注重传统文化在现实中的创造性和创新性发展。
试题起点和立意较高,题干内容多数以古代化学史、古文献中的优秀传统文化为背景,考查学生的文学功底和文本解读能力。
但落点适中,侧重考查教材中的基本知识、基本方法和基本应用。
1.【2019新课标Ⅱ】“春蚕到死丝方尽,蜡炬成灰泪始干”是唐代诗人李商隐的著名诗句,下列关于该诗句中所涉及物质的说法错误的是A.蚕丝的主要成分是蛋白质B.蚕丝属于天然高分子材料C.“蜡炬成灰”过程中发生了氧化反应D.古代的蜡是高级脂肪酸酯,属于高分子聚合物【答案】D【解析】A.蚕丝的主要成分是蛋白质,A项正确;B.蚕丝的主要成分是蛋白质,蛋白质是天然高分子化合物,B项正确;C.“蜡炬成灰”指的是蜡烛在空气中与氧气反应,属于氧化反应,C项正确;D.高级脂肪酸酯不属于高分子聚合物,D项错误;答案选D。
【素养解读】“春蚕到死丝方尽,蜡炬成灰泪始干”十分熟悉的诗句,我们要从中挖掘出解题关键“春蚕”和“蜡炬”,进而进一步分析物质性质和发生的反应。
这些古诗句写者无意,我们学者要有心,根据诗句中现象分析其蕴含的化学知识。
2.【2017新课标1卷】《本草衍义》中对精制砒霜过程有如下叙述:“取砒之法,将生砒就置火上,以器覆之,令砒烟上飞着覆器,遂凝结累然下垂如乳,尖长者为胜,平短者次之。
”文中涉及的操作方法是A.蒸馏B.升华C.干馏D.萃取【答案】B【解析】“将生砒就置火上,以器覆之,令砒烟上飞着覆器,遂凝结”,属于固体直接转化为气体,类似于碘的升华,因此涉及的操作方法是升华,答案选B。
高考历史二轮复习第一板块中国古代史专题突破练三中国古代的经济与社会生活含解析

专题突破练三中国古代的经济与社会生活一、选择题1.(2021·辽宁沈阳一模)有研究表明:“定居聚落获取食物的开发领地半径约5千米,而采集渔猎等流动经济型聚落的领地半径则为10千米。
”这有利于印证( )A.采集渔猎是一种先进生产方式B.农业产生对人类居住环境的影响C.人类的生产活动范围越来越大D.交通运输的不断进步与发展2.(2021·山东淄博一模)战国时期,各国货币出现交变现象。
行铜贝的楚国在晚期亦铸行布币,行刀币的齐、燕亦铸行圜钱。
这说明战国时期( )A.由分裂走向统一的趋势B.统一市场逐渐形成C.区域间商贸联系的加强D.货币使用状况混乱3.(2021·山西太原一模)西汉政府在丝织业发达地区设置官营丝织作坊,如齐郡有“三服官”主管制作“天子之服”,所属“作工各数千人,一岁费数巨万”。
长安有东、西织室,汉元帝时,每年花费五千万钱以上。
这反映出汉朝( )A.丝织业的生产技术高超B.官营生产超过私营作坊C.官营丝织业生产规模大D.丝织业为政府垄断专卖4.(2021·广东梅州一模)汉朝的国有土地称为“公田”,除了使用士兵、服役农民耕种之外,遇到灾荒时还“假”(出租借贷)给百姓耕种并征收一定数量的假税,称为“假民公田”。
从东汉永平九年(公元66年)到元兴元年(公元105年),政府假民公田近20次。
这一措施( )A.有利于维护政权的稳定B.改变了土地所有制C.打击了地主豪强的势力D.扩大了自耕农群体5.(2021·北京西城期末)魏晋南北朝时期,社会经济在曲折中发展,南方的开发初见成效。
促进南方开发的有利因素是( )A.大部分时期处于分裂状态,社会动荡B.北魏孝文帝将都城从平城迁至洛阳C.北民南迁带来先进生产工具和技术D.汉族与内迁民族从冲突到和平交往6.(2021·山东济宁一模)据《文献通考》载,孝文帝颁行均田令:“令有盈者无受不还,不足者受种如法,盈者得卖其盈,不足者得买所不足,不得卖其分,亦不得买过所足。
高考英语一轮总复习 语法专题突破 专题三 谓语动词

6.(2021·浙江卷)The little home was painted
(paint) white.It was
sweet and fresh.Mary loved it.
7.(2021·全国甲卷)We hired (hire) our bikes from the rental place at the
【用法点拨】 1.过去将来时的构成 主动语态:would+动词原形 被动语态:would be+过去分词 2.过去将来时的主要用法 过去将来时表示在过去预计将来的某一时间要发生的动作或存在的状态。
I thought that Jack was going to write a letter to his father.
专题三 谓语动词
语法专题
突
破
英语
内容索引
增素能 精准突破 测效果 课堂评价
增素能 精准突破
一、一般现在时及其被动语态
【真题语境】
1.(2023·全国乙卷)The remarkable development of this city,which is
consciously designed to protect the past while stepping into the modern world,
仅表示在过去某一时间点,一个动作正在进 行,有什么样的结果不得而知
时间上
凡有明确的过去时间的情况均用过去时,不能用完成时,如含有 ago,last year,just now,the other day
结果上
强调的是动作发生在 “过去”,和现在毫无关 系
强调的是对“现在”的影响和结果,动作到现 在刚完成或还在继续
2020年高考历史热点单元突破专题三:古代中国的思想文化(带答案解析)

专题03 古代中国的思想文化【重难点梳理】一、春秋战国时期的百家争鸣1.百家争鸣局面形成的原因(百家争鸣,启于春秋,兴盛于战国,它是特定的历史时代的产物)①春秋战国时期,生产力的发展是百家争鸣出现的根本原因,为学术繁荣提供了物质条件;②社会变革和各国纷争的局面促成了思想自由的社会环境;③私学兴起,教育相对普及,培养了大批人才④各诸侯国为了富国强兵,竞相礼贤下士,重用人才2.诸子百家的代表人物及思想主张●儒家:孔子哲学思想——思想核心是“仁”、“礼”(仁者爱人,克己复礼)政治思想——①主张为政以德(含民本思想)②提出“正名”主张教育思想——“有教无类”、“因材施教”评价:①当时未受重视,后经改造形成完整的儒家思想体系,成为中国传统文化的主流;②在世界文化史上有重要影响。
被推崇为“圣人”孟子政治思想——“仁政”(核心)、“民贵君轻”哲学思想——“性善说”道德思想——先义后利,舍生取义人格精神——要求人们要有“富贵不能淫、贫贱不能移、威武不能屈”的人格精神评价:①《孟子》一书被当作经典,后列为“四书”之一②建立一套系统的政治学说“仁政”,成为儒家学派的重要奠基人。
③继承并发展了孔子学说,被尊为“亚圣”,对传统文化产生很大影响。
荀子哲学思想——①“天行有常”“制天命而用之”(唯物主义)②“性恶论”(但教育可使人由恶变善)政治主张——以礼教为主,礼法并施评价:①基本继承了儒家思想,但不为正统儒家重视。
②作为战国百家思想的集大成者,对中国哲学影响深远。
●道家:老子哲学思想——①“道”是天地万物的本源,否定“天命论”②辩证法思想(矛盾对立面及转化)政治主张——“无为而治”、“小国寡民”评价:①中国第一个探讨宇宙本源的哲学家②思想体系博大精深,对中国文化,产生了深远影响。
庄子哲学思想——“齐物”(任何事物在本质上都是相同的);“逍遥”(对事物变化要采取旁观、超然的态度)天与人“不相胜”,人必须顺从自然●法家:韩非思想主张——①主张法、术、势结合,建立君主专制中央集权②认为历史是发展的,主张变法革新。
江苏2020版高考语文第四章古诗词鉴赏专题三核心突破一鉴赏古诗形象讲义(含解析)

核心突破一鉴赏古诗形象(说明:在诗歌中,形象与意象是可以合二为一的,但从理论上看,二者还是有区别的。
意象是隶属诗歌形象的,诗歌形象所指范围广,既可是具体的,也可是抽象的情感或理趣;而意象只能是客观的、具体的。
诗歌形象可以是人,也可以是物、情、理等,而意象通常只是自然景象、物象。
)题点一人物形象——因形悟神人物形象大致有两类:一是主观形象(作者塑造的抒情主人公,即作者自己);二是客观形象(作者描写或刻画的人物)。
每首诗都有抒情主人公形象,但不一定都有客观的人物形象。
诗中客观的人物形象只是抒情主人公抒情达意的途径之一。
如苏轼的《念奴娇·赤壁怀古》,词中的周瑜,风流倜傥,指挥若定,是词中的人物形象,而那中年失意、壮志未酬又略显旷达的苏轼,就是主观形象。
结合课本知识填空。
《琵琶行》一诗中的客观人物形象是琵琶女,其形象特征是年老色衰、沦落江湖。
主观人物形象是作者(白居易),其形象特征是怀才不遇、沦落江湖、忧愁痛苦。
古诗中八类人物形象及其特征①正直之士:不慕权贵、豪放洒脱、傲岸不羁。
②爱国之士:心忧天下、忧国忧民。
③隐士:寄情山水、归隐田园。
④失意之士:怀才不遇、壮志难酬。
⑤报国之士:矢志报国、慷慨愤世。
⑥游子:友人送别、思念故乡。
⑦疆场将士:献身边疆、反对征伐。
⑧痴情儿女:缠绵悱恻、爱恨情长。
1.(2017·全国Ⅱ)阅读下面这首宋诗,然后回答问题。
送子由使契丹苏轼云海相望寄此身,那因远适更沾巾。
不辞驿骑凌风雪,要使天骄识凤麟。
沙漠回看清禁月①,湖山应梦武林春②。
单于若问君家世,莫道中朝第一人③。
注①清禁:皇宫。
苏辙时任翰林学士,常出入宫禁。
②武林:杭州的别称。
苏轼时知杭州。
③唐代李揆被皇帝誉为“门地、人物、文学皆当世第一”。
后来入吐蕃会盟,酋长问他:“闻唐有第一人李揆,公是否?”李揆怕被扣留,骗他说:“彼李揆,安肯来邪?”本诗首联表现了诗人什么样的性格?请加以分析。
答:________________________________________________________________________答案表现了诗人旷达的性格。
2020高考数学核心突破《专题三 三角函数、解三角形与平面向量》(含往年真题分析)

专题三三角函数、解三角形与平面向量第1讲三角函数的图象与性质题型一三角函数的图象1.(1)要得到函数f (x )=cos ⎝⎛⎭⎫2x +π3的图象,只需将函数g (x )=sin ⎝⎛⎭⎫2x +π3的图象( C ) A .向左平移π2个单位长度B .向右平移π2个单位长度C .向左平移π4个单位长度D .向右平移π4个单位长度(2) (2017·山西朔州模拟)函数f (x )=A sin(ωx +φ)⎝⎛⎭⎫A >0,ω>0,|φ|<π2的部分图象如图所示,则函数f (x )在区间⎣⎡⎦⎤0,π2上的最小值为__-1__.突破点拨(1)先利用诱导公式将两函数化为同名三角函数,再利用平移法则求解. (2)先求函数f (x )的解析式,再利用解析式求最值. 解析 (1)因为f (x )=cos ⎝⎛⎭⎫2x +π2-π6 =sin ⎝⎛⎭⎫π6-2x =sin ⎝⎛⎭⎫2x +5π6=sin ⎣⎡⎦⎤2⎝⎛⎭⎫x +π4+π3, 所以要得到函数f (x )=cos ⎝⎛⎭⎫2x +π3的图象,只需将函数g (x )=sin ⎝⎛⎭⎫2x +π3的图象向左平移π4个单位长度.故选C. (2)由函数f (x )=A sin(ωx +φ)⎝⎛⎭⎫A >0,ω>0,|φ|<π2的部分图象,可得A =2,14·2πω=5π6-7π12,解得ω=2.再根据图象经过点⎝⎛⎭⎫7π12,0, 可得2·7π12+φ=π+2k π,k ∈Z .因为|φ|<π2,所以φ=-π6,故函数f (x )=2sin ⎝⎛⎭⎫2x -π6. 因为x ∈⎣⎡⎦⎤0,π2,所以2x -π6∈⎣⎡⎦⎤-π6,5π6, 故函数f (x )的最小值为2×⎝⎛⎭⎫-12=-1. 2. 某同学用“五点法”画函数f (x )=A sin(ωx +φ)⎝⎛⎭⎫ω>0,|φ|<π2在某一个周期内的图象时,列表并填入了部分数据,如下表:(1)(2)将y =f (x )图象上所有点向左平行移动θ(θ>0)个单位长度,得到y =g (x )的图象.若y=g (x )图象的一个对称中心为⎝⎛⎭⎫5π12,0,求θ的最小值.突破点拨(1)由表中数据先写出A ,ω,φ的值,再由ωx +φ=0,π,2π,求出其余值. (2)写出函数y =g (x )的解析式,由y =sin x 图象的对称中心为(k π,0),k ∈Z ,利用整体思想建立关于θ的方程,根据k ∈Z 及θ>0,求出θ的最小值.解析 (1)根据表中已知数据,解得A =5,ω=2,φ=-π6.数据补全如下表.且函数表达式为f (x )=5sin ⎝⎛⎭⎫2x -π6. (2)由(1)知f (x )=5sin ⎝⎛⎭⎫2x -π6, 得g (x )=5sin ⎝⎛⎭⎫2x +2θ-π6. 因为y =sin x 的对称中心为(k π,0),k ∈Z . 令2x +2θ-π6=k π,解得x =k π2+π12-θ,k ∈Z .由于函数y =g (x )的图象关于点⎝⎛⎭⎫5π12,0中心对称, 令k π2+π12-θ=5π12,解得θ=k π2-π3,k ∈Z . 由θ>0可知,当k =1时,θ取得最小值π6.(1)三角函数图象平移问题需注意三点:一是函数名称是否一致;二是弄清由谁平移得到谁;三是左右的平移是自变量本身的变化.(2)对于由三角函数的图象确定函数解析式的问题,一般由函数的最值可确定A ,由函数的周期可确定ω,由对称轴或对称中心和φ的范围确定φ.题型二 三角函数的性质1. 已知函数f (x )=sin ⎝⎛⎭⎫π2-x sin x -3cos 2x . (1)求f (x )的最小正周期和最大值; (2)讨论f (x )在⎣⎡⎦⎤π6,2π3上的单调性. 突破点拨(1)先将已知解析式化简,然后求解.(2)根据y =A sin(ωx +φ)+k (A >0,ω>0)与y =sin x 的关系求解. 解析 (1)f (x )=sin ⎝⎛⎭⎫π2-x sin x -3cos 2x =cos x sin x -32(1+cos 2x ) =12sin 2x -32cos 2x -32=sin ⎝⎛⎭⎫2x -π3-32. 因此f (x )的最小正周期为π,最大值为2-32.(2)当x ∈⎣⎡⎦⎤π6,2π3时,0≤2x -π3≤π,从而当0≤2x -π3≤π2,即π6≤x ≤5π12时,f (x )单调递增; 当π2<2x -π3≤π,即5π12<x ≤2π3时,f (x )单调递减.综上可知,f (x )在⎣⎡⎦⎤π6,5π12上单调递增;在⎝⎛⎦⎤5π12,2π3上单调递减. 2. 设函数f (x )=sin ωx +sin ⎝⎛⎭⎫ωx -π2,x ∈R . (1)若ω=12,求f (x )的最大值及相应x 的集合;(2)若x =π8是f (x )的一个零点,且0<ω<10,求ω的值和f (x )的最小正周期.突破点拨(1)先用公式化简,再利用三角函数的性质求解. (2)将x =π8代入,求ω,则周期可求.解析 由已知得f (x )=sin ωx -cos ωx =2sin ⎝⎛⎭⎫ωx -π4. (1)若ω=12,则f (x )=2sin ⎝⎛⎭⎫12x -π4. 又x ∈R ,则2sin ⎝⎛⎭⎫12x -π4≤2,所以f (x )max =2,此时12x -π4=2k π+π2,k ∈Z ,即f (x )取最大值时,x 的取值集合为⎩⎨⎧⎭⎬⎫x ⎪⎪x =4k π+3π2,k ∈Z .(2)∵x =π8是函数f (x )的一个零点,∴2sin ⎝⎛⎭⎫π8ω-π4=0,∴π8ω-π4=k π,k ∈Z . 又0<ω<10,∴ω=2,∴f (x )=2sin ⎝⎛⎭⎫2x -π4,其最小正周期为π.求解函数y =A sin(ωx +φ)的性质的三种意识(1)转化意识:利用三角恒等变换将所求函数转化为f (x )=A sin(ωx +φ)的形式. (2)整体意识:类比y =sin x 的性质,只需将y =A sin(ωx +φ)中的“ωx +φ”看成y =sin x 中的“x ”,采用整体代入的方法求解.(3)讨论意识:当A 为参数时,求最值应分情况讨论.三角函数的综合应用【预测】 已知函数f (x )=sin ⎝⎛⎭⎫2ωx -π6-4sin 2ωx +2(ω>0),其图象与x 轴相邻两个交点的距离为π2.(1)求函数f (x )的解析式;(2)若将f (x )的图象向左平移m (m >0)个单位长度,得到的函数g (x )的图象恰好经过点⎝⎛⎭⎫-π3,0,求当m 取得最小值时,g (x )在⎣⎡⎦⎤-π6,7π12上的单调递增区间. 思维导航(1)解题导引:①先化简函数f (x )的解析式,再利用图象与x 轴相邻两个交点的距离是半个周期求解析式;②先求函数g (x )的解析式,再求在⎣⎡⎦⎤-π6,7π12上的单调递增区间. (2)方法指导:三角函数的综合应用主要是将三角函数的图象和性质与三角变换相结合,通过变换将函数化为y =A sin(ωx +φ)的形式再研究其性质,解题时注意观察角、名、结构等特征,注意整体思想的应用.规范解答(1)函数f (x )=sin ⎝⎛⎭⎫2ωx -π6-4sin 2ωx +2 =32sin 2ωx -12cos 2ωx -4×1-cos 2ωx 2+2 =32sin 2ωx +32cos 2ωx =3sin ⎝⎛⎭⎫2ωx +π3(ω>0). 根据函数f (x )的图象与x 轴相邻两个交点的距离为π2,可得函数f (x )的最小正周期为2×π2=2π2ω,得ω=1. 故函数f (x )=3sin ⎝⎛⎭⎫2x +π3. (2)将f (x )的图象向左平移m (m >0)个单位长度得到函数 g (x )=3sin ⎣⎡⎦⎤2(x +m )+π3=3sin ⎝⎛⎭⎫2x +2m +π3的图象.根据g (x )的图象恰好经过点⎝⎛⎭⎫-π3,0, 可得3sin ⎝⎛⎭⎫-2π3+2m +π3=0, 即sin ⎝⎛⎭⎫2m -π3=0, 所以2m -π3=k π(k ∈Z ),m =k π2+π6(k ∈Z ).因为m >0,所以当k =0时,m 取得最小值,且最小值为π6.此时,g (x )=3sin ⎝⎛⎭⎫2x +2π3. 令2k π-π2≤2x +2π3≤2k π+π2,k ∈Z ,得k π-7π12≤x ≤k π-π12,k ∈Z ,故函数g (x )的单调递增区间为⎣⎡⎦⎤k π-7π12,k π-π12,k ∈Z . 结合x ∈⎣⎡⎦⎤-π6,7π12,可得g (x )在⎣⎡⎦⎤-π6,7π12上的单调递增区间为⎣⎡⎦⎤-π6,-π12和⎣⎡⎦⎤5π12,7π12. 【变式考法】 已知向量a =(m ,cos 2x ),b =(sin 2x ,n ),函数f (x )=a·b ,且y =f (x )的图象过点⎝⎛⎭⎫π12,3和点⎝⎛⎭⎫2π3,-2. (1)求m ,n 的值;(2)将y =f (x )的图象向左平移φ (0<φ<π)个单位后得到函数y =g (x )的图象,若y =g (x )图象上各最高点到点(0,3)的距离的最小值为1,求y =g (x )的单调递增区间.解析 (1)由题意,知 f (x )=a·b =m sin 2x +n cos 2x .因为y =f (x )的图象经过点⎝⎛⎭⎫π12,3和⎝⎛⎭⎫2π3,-2, 所以⎩⎨⎧3=m sin π6+n cos π6,-2=m sin 4π3+n cos 4π3,即⎩⎨⎧3=12m +32n ,-2=-32m -12n ,解得m =3,n =1.(2)由(1)知f (x )=3sin 2x +cos 2x =2sin ⎝⎛⎭⎫2x +π6. 由题意知g (x )=f (x +φ)=2sin ⎝⎛⎭⎫2x +2φ+π6. 设y =g (x )的图象上符合题意的最高点为(x 0,2),由题意知x 20+1=1,所以x 0=0,即y =g (x )的图象上到点(0,3)的距离为1的最高点为(0,2). 将其代入y =g (x )并整理得sin ⎝⎛⎭⎫2φ+π6=1, 因为0<φ<π,所以φ=π6.因此g (x )=2sin ⎝⎛⎭⎫2x +π2=2cos 2x . 由2k π-π≤2x ≤2k π,k ∈Z ,得k π-π2≤x ≤k π,k ∈Z ,所以函数y =g (x )的单调递增区间为⎣⎡⎦⎤k π-π2,k π,k ∈Z .1.(教材回归)下列函数中,最小正周期为π且图象关于原点对称的函数是( A ) A .y =cos ⎝⎛⎭⎫2x +π2 B .y =sin ⎝⎛⎭⎫2x +π2 C .y =sin 2x +cos 2xD .y =sin x +cos x解析 y =cos ⎝⎛⎭⎫2x +π2=-sin 2x ,符合题意,故选A. 2.(2017·广西南宁质检)将函数y =cos ⎝⎛⎭⎫2x +π3的图象向左平移π6个单位长度后,得到f (x )的图象,则( B )A .f (x )=-sin 2xB .f (x )的图象关于直线x =-π3对称C .f ⎝⎛⎭⎫7π3=12D .f (x )的图象关于点⎝⎛⎭⎫π12,0对称 解析 将函数y =cos ⎝⎛⎭⎫2x +π3的图象向左平移π6个单位长度,得到的图象对应的解析式为f (x )=cos ⎣⎡⎦⎤2⎝⎛⎭⎫x +π6+π3=cos ⎝⎛⎭⎫2x +2π3.函数f (x )的图象的对称轴满足2x +2π3=k π(k ∈Z ),即对称轴方程为x =k π2-π3(k ∈Z ),所以f (x )的图象关于直线x =-π3对称;令2x +2π3=k π+π2,得x =k π2-π12(k ∈Z ),即f (x )的图象关于点⎝⎛⎭⎫-π12,0对称;f ⎝⎛⎭⎫7π3=-12.故选B. 3.(2017·湖北襄阳模拟)同时具有性质“①最小正周期是4π;②直线x =π3是图象的一条对称轴;③在区间⎝⎛⎭⎫2π3,5π6上是减函数”的一个函数是( D )A .y =sin ⎝⎛⎭⎫2x -π6B .y =cos ⎝⎛⎭⎫2x -π6 C .y =cos ⎝⎛⎭⎫x 2+π3D .y =sin ⎝⎛⎭⎫x 2+π3解析 对于A 项,B 项,∵T =2π2=π,故A 项,B 项不正确.对于C 项,若直线x =π3为其图象的一条对称轴,则π3×12+π3=k π,k ∈Z ,得π2=k π,k ∈Z ,k 不存在,不满足题意,故C 项不正确.对于D 项,因为T =2π12=4π,且由x 2+π3=k π+π2,k ∈Z ,解得图象的对称轴方程为x =2k π+π3,k ∈Z ;当k =0时,x =π3为图象的一条对称轴.由2k π+π2≤x 2+π3≤2k π+3π2,k ∈Z ,解得单调递减区间为⎣⎡⎦⎤4k π+π3,4k π+7π3,k ∈Z ,所以函数在区间⎝⎛⎭⎫2π3,5π6上是减函数,故D 项正确.故选D.4.(2017·山西晋中考前测试)已知函数f (x )=A sin(ωx +φ)⎝⎛⎭⎫A >0,ω>0,|φ|<π2的部分图象如图所示,将函数y =f (x )的图象向左平移4π3个单位长度,得到函数y =g (x )的图象,则函数y =g (x )在区间⎣⎡⎦⎤π2,5π2上的最大值为( C )A .3B .332C.322D .22解析 由图象可知函数y =f (x )的周期为2⎝⎛⎭⎫7π3-π3=4π, ∴ω=12.又点⎝⎛⎭⎫π3,0,⎝⎛⎭⎫0,-32在函数y =f (x )的图象上, ∴⎩⎨⎧A sin ⎝⎛⎭⎫π6+φ=0,A sin φ=-32,且|φ|<π2.∴φ=-π6,A =3,则f (x )=3sin ⎝⎛⎭⎫12x -π6, ∴g (x )=3sin ⎣⎡⎦⎤12⎝⎛⎭⎫x +4π3-π6=3cos 12x . 由x ∈⎣⎡⎦⎤π2,5π2,可得12x ∈⎣⎡⎦⎤π4,5π4,则3cos 12x ∈⎣⎡⎦⎤-3,322,即g (x )的最大值为322.5.(书中淘金)某城市一年中12个月的平均气温与月份的关系可近似地用三角函数y =a +A cos ⎣⎡⎦⎤π6(x -6)(x =1,2,3,…,12)来表示,已知6月份的月平均气温最高,为28 ℃,12月份的平均气温最低,为18 ℃,则10月份的平均气温为__20.5__℃.解析 依题意知,a =28+182=23,A =28-182=5,所以y =23+5cos ⎣⎡⎦⎤π6(x -6),当x =10时,y =23+5cos ⎝⎛⎭⎫π6×4=20.5. 答案 20.56.(高考改编)把函数y =sin 2x 的图象沿x 轴向左平移π6个单位,纵坐标伸长到原来的2倍(横坐标不变)后得到函数y =f (x )的图象,对于函数y =f (x )有以下四个判断:①该函数的解析式为y =2sin ⎝⎛⎭⎫2x +π6;②该函数图象关于点⎝⎛⎭⎫π3,0对称;③该函数在⎣⎡⎦⎤0,π6上是增函数;④若函数y =f (x )+a 在⎣⎡⎦⎤0,π2上的最小值为3,则a =2 3. 其中,正确判断的序号是__②④__.解析 将函数y =sin 2x 的图象向左平移π6个单位得到y =sin 2⎝⎛⎭⎫x +π6=sin ⎝⎛⎭⎫2x +π3的图象,然后纵坐标伸长到原来的2倍得到y =2sin ⎝⎛⎭⎫2x +π3的图象,所以①不正确.f ⎝⎛⎭⎫π3=2sin ⎝⎛⎭⎫2×π3+π3=2sin π=0,所以函数图象关于点⎝⎛⎭⎫π3,0对称,所以②正确.由-π2+2k π≤2x +π3≤π2+2k π,k ∈Z ,得-5π12+k π≤x ≤π12+k π,k ∈Z ,∴函数的单调增区间为⎣⎡⎦⎤-5π12+k π,π12+k π,k ∈Z ,而⎣⎡⎦⎤0,π6⃘⎣⎡⎦⎤-512π+k π,π12+k π(k ∈Z ),所以③不正确.y =f (x )+a =2sin ⎝⎛⎭⎫2x +π3+a ,当0≤x ≤π2时,π3≤2x +π3≤4π3,所以当2x +π3=4π3,即x =π2时,函数取得最小值,y min =2sin 4π3+a =-3+a ,令-3+a =3,得a =23,所以④正确.所以正确的判断为②④.7.(考点聚焦)设函数f (x )=32-3sin 2ωx -sin ωx ·cos ωx (ω>0),且y =f (x )的图象的一个对称中心到最近的对称轴的距离为π4.(1)求ω的值;(2)求f (x )在区间⎣⎡⎦⎤π,3π2上的最大值和最小值. 解析 (1)f (x )=32-3sin 2ωx -sin ωx cos ωx =32-3·1-cos 2ωx 2-12sin 2ωx =32cos 2ωx -12sin 2ωx =-sin ⎝⎛⎭⎫2ωx -π3=sin ⎝⎛⎭⎫2ωx +2π3. 因为图象的一个对称中心到最近的对称轴的距离为π4,又ω>0,所以2π2ω=4×π4.因此ω=1.(2)由(1)知f (x )=-sin ⎝⎛⎭⎫2x -π3. 当π≤x ≤3π2时,5π3≤2x -π3≤8π3,所以-32≤sin ⎝⎛⎭⎫2x -π3≤1. 因此-1≤f (x )≤32.故f (x )在区间⎣⎡⎦⎤π,3π2上的最大值和最小值分别为32,-1. 8.(2018·山东青岛调考)已知函数f (x )=2sin x sin ⎝⎛⎭⎫x +π6. (1)求函数f (x )的最小正周期和单调递增区间; (2)当x ∈⎣⎡⎦⎤0,π2时,求函数f (x )的值域. 解析 (1)f (x )=2sin x ⎝⎛⎭⎫32sin x +12cos x=3×1-cos 2x 2+12sin 2x=sin ⎝⎛⎭⎫2x -π3+32. 函数f (x )的最小正周期为T =π. 由-π2+2k π≤2x -π3≤π2+2k π,k ∈Z ,解得-π12+k π≤x ≤5π12+k π,k ∈Z ,所以函数f (x )的单调递增区间是⎣⎡⎦⎤-π12+k π,5π12+k π,k ∈Z . (2)当x ∈⎣⎡⎦⎤0,π2时,2x -π3∈⎣⎡⎦⎤-π3,2π3, sin ⎝⎛⎭⎫2x -π3∈⎣⎡⎦⎤-32,1, 可得函数f (x )的值域为⎣⎡⎦⎤0,1+32. 9.(母题营养)已知函数f (x )=sin x cos x +12cos 2x .(1)若tan θ=2,求f (θ)的值;(2)若函数y =g (x )的图象是由函数y =f (x )的图象上所有的点向右平移π4个单位长度而得到,且g (x )在区间(0,m )内是单调函数,求实数m 的最大值.解析 (1)因为tan θ=2,所以sin θ=2cos θ. 代入sin 2θ+cos 2θ=1,得cos 2θ=15.所以f (θ)=sin θcos θ+12cos 2θ=2cos 2θ+12(2cos 2θ-1)=3cos 2θ-12=110.(2)由已知得f (x )=12sin 2x +12cos 2x =22sin ⎝⎛⎭⎫2x +π4. 依题意,得g (x )=22sin ⎣⎡⎦⎤2⎝⎛⎭⎫x -π4+π4, 即g (x )=22sin ⎝⎛⎭⎫2x -π4. 因为x ∈(0,m ),所以2x -π4∈⎝⎛⎭⎫-π4,2m -π4. 又因为g (x )在区间(0,m )内是单调函数,所以-π4<2m -π4≤π2,即0<m ≤3π8,故实数m的最大值为3π8.10.(母题营养)设函数f (x )=sin 2ωx +23sin ωx ·cos ωx -cos 2ωx +λ(x ∈R )的图象关于直线x =π对称,其中ω,λ为常数,且ω∈⎝⎛⎭⎫12,1.(1)求函数f (x )的最小正周期;(2)若y =f (x )的图象经过点⎝⎛⎭⎫π4,0,求函数f (x )在x ∈⎣⎡⎦⎤0,π2上的值域. 解析 (1)因为f (x )=sin 2ωx +23sin ωx ·cos ωx -cos 2ωx +λ=-cos 2ωx +3sin 2ωx +λ=2sin ⎝⎛⎭⎫2ωx -π6+λ,由直线x =π是y =f (x )图象的一条对称轴,可得sin ⎝⎛⎭⎫2ωπ-π6=±1,所以2ωπ-π6=k π+π2(k ∈Z ),即ω=k 2+13(k ∈Z ).又ω∈⎝⎛⎭⎫12,1,k ∈Z ,所以k =1,从而ω=56. 所以f (x )的最小正周期是6π5.(2)由y =f (x )的图象过点⎝⎛⎭⎫π4,0,得f ⎝⎛⎭⎫π4=0, 即λ=-2sin ⎝⎛⎭⎫56×π2-π6=-2sin π4=-2, 即λ=- 2.故f (x )=2sin ⎝⎛⎭⎫53x -π6-2, ∵x ∈⎣⎡⎦⎤0,π2,∴53x -π6∈⎣⎡⎦⎤-π6,2π3, ∴函数f (x )的值域为[-1-2,2-2].1.函数f (x )=cos(w x +φ)的部分图象如图所示,则f (x )的单调递减区间为( D )A.⎝⎛⎭⎫k π-14,k π+34,k ∈Z B.⎝⎛⎭⎫2k π-14,2k π+34,k ∈Z C.⎝⎛⎭⎫k -14,k +34,k ∈Z D.⎝⎛⎭⎫2k -14,2k +34,k ∈Z 解析 由题图可知T 2=54-14=1,所以T =2.结合题图可知,在⎣⎡⎦⎤-34,54(f (x )的一个周期)内,函数f (x )的单调递减区间为⎝⎛⎭⎫-14,34.由f (x )是以2为周期的周期函数可知,f (x )的单调递减区间为⎝⎛⎭⎫2k -14,2k +34,k ∈Z ,故选D. 2.下列函数中,最小正周期为π且图象关于原点对称的函数是( A ) A .y =cos ⎝⎛⎭⎫2x +π2 B .y =sin ⎝⎛⎭⎫2x +π2 C .y =sin 2x +cos 2xD .y =sin x +cos x解析 y =cos ⎝⎛⎭⎫2x +π2=-sin 2x 是奇函数,图象关于原点对称,且最小正周期为π,A 项正确.y =sin ⎝⎛⎭⎫2x +π2=cos 2x ,是偶函数,B 项错误.y =sin 2x +cos 2x =2sin ⎝⎛⎭⎫2x +π4,非奇非偶,C 项错误.y =sin x +cos x =2sin ⎝⎛⎭⎫x +π4,非奇非偶,D 项错误.故选A. 3.为了得到函数y =sin(2x +1)的图象,只需把函数y =sin 2x 的图象上所有的点( A ) A .向左平行移动12个单位长度B .向右平行移动12个单位长度C .向左平行移动1个单位长度D .向右平行移动1个单位长度 解析 ∵y =sin(2x +1)=sin 2⎝⎛⎭⎫x +12, ∴只需把y =sin 2x 图象上所有的点向左平移12个单位长度即得到y =sin(2x +1)的图象.故选A.4.将函数y =sin(2x +φ)的图象沿x 轴向左平移π8个单位后,得到一个偶函数的图象,则φ的一个可能取值为( C )A.3π4 B .π2C.π4D .-π4解析 y =sin(2x +φ)――→左移π8sin ⎣⎡⎦⎤2⎝⎛⎭⎫x +π8+φ=sin ⎝⎛⎭⎫2x +π4+φ是偶函数,即π4+φ=k π+π2(k ∈Z )⇒φ=k π+π4(k ∈Z ),当k =0时,φ=π4,故选C.5.如图,某港口一天6时到18时的水深变化曲线近似满足函数y =3sin ⎝⎛⎭⎫π6x +φ+k ,据此函数可知,这段时间水深的最大值为( C )A .5 mB .6 mC .8 mD .10 m解析 由题意可知,当sin ⎝⎛⎭⎫π6x +φ=-1时,函数取得最小值2,即3×(-1)+k =2,∴k =5.因此,函数的最大值是8,故水深的最大值为8 m.6.将函数y =3cos x +sin x (x ∈R )的图象向左平移m (m >0)个单位长度后,所得到的图象关于y 轴对称,则m 的最小值是( B )A.π12 B .π6C.π3D .5π6解析 y =3cos x +sin x =2sin ⎝⎛⎭⎫x +π3,向左平移m 个单位长度后得到y =2sin ⎝⎛⎭⎫x +π3+m ,由它关于y 轴对称可得sin ⎝⎛⎭⎫π3+m =±1,∴π3+m =k π+π2,k ∈Z ,∴m =k π+π6,k ∈Z ,又m >0,∴m 的最小值为π6.7.已知函数f (x )=A sin(w x +φ)(A ,w ,φ均为正的常数)的最小正周期为π,当x =2π3时,函数f (x )取得最小值,则下列结论正确的是( A )A .f (2)<f (-2)<f (0)B .f (0)<f (2)<f (-2)C .f (-2)<f (0)<f (2)D .f (2)<f (0)<f (-2)解析 ∵ω>0,∴T =2πω=π,∴ω=2.又A >0,∴f ⎝⎛⎭⎫2π3=-A , 即sin ⎝⎛⎭⎫4π3+φ=-1,得φ+4π3=2k π+32π(k ∈Z ), 即φ=2k π+π6(k ∈Z ).又∵φ>0,∴可取f (x )=A sin ⎝⎛⎭⎫2x +π6, ∴f (2)=A sin ⎝⎛⎭⎫4+π6, f (-2)=A sin ⎝⎛⎭⎫-4+π6,f (0)=A sin π6. ∵π<4+π6<3π2,∴f (2)<0.∵-7π6<-4+π6<-π,且y =sin x 在⎝⎛⎭⎫-7π6,-π上为减函数, ∴sin ⎝⎛⎭⎫-4+π6<sin ⎝⎛⎭⎫-7π6=sin π6,且sin ⎝⎛⎭⎫-4+π6>sin(-π)=0,从而有0<f (-2)<f (0).故有f (2)<f (-2)<f (0).故选A.8.将函数f (x )=sin 2x 的图象向右平移φ⎝⎛⎭⎫0<φ<π2个单位后得到函数g (x )的图象.若对满足|f (x 1)-g (x 2)|=2的x 1,x 2,有|x 1-x 2|min =π3,则φ=( D )A.5π12B .π3C.π4D .π6解析 g (x )=sin[2(x -φ)] =sin(2x -2φ). ∵|f (x )|≤1,|g (x )|≤1, ∴|f (x )-g (x )|≤2,当且仅当f (x 1)=1,g (x 2)=-1或f (x 1)=-1,g (x 2)=1时,满足|f (x 1)-g (x 2)|=2. 不妨设A (x 1,-1)是函数f (x )图象的一个最低点,B (x 2,1)是函数g (x )图象的一个最高点, 于是x 1=k 1π+3π4(k 1∈Z ),x 2=k 2π+π4+φ(k 2 ∈Z ).∴|x 1-x 2|≥⎪⎪⎪⎪3π4-⎝⎛⎭⎫π4+φ=⎪⎪⎪⎪π2-φ. ∵φ ∈⎝⎛⎭⎫0,π2,|x 1-x 2|min =π3, ∴π2-φ=π3,即φ=π6,故选D. 9.已知函数f (x )=2sin x +φ2cos x +φ2⎝⎛⎭⎫|φ|<π2,且对于任意的x ∈R ,f (x )≤f ⎝⎛⎭⎫π6,则( C ) A .f (x )=f (x +π) B .f (x )=f ⎝⎛⎭⎫x +π2 C .f (x )=f ⎝⎛⎭⎫π3-xD .f (x )=f ⎝⎛⎭⎫π6-x解析 f (x )=sin(x +φ).由题意,可知f (x )≤f ⎝⎛⎭⎫π6对于任意的x ∈R 恒成立,即sin(x +φ)≤sin ⎝⎛⎭⎫π6+φ.又因为|φ|<π2,所以π6+φ=π2,所以φ=π3,所以f (x )=sin ⎝⎛⎭⎫x +π3.f ⎝⎛⎭⎫π3-x =sin ⎝⎛⎭⎫π3-x +π3=sin ⎣⎡⎦⎤-⎝⎛⎭⎫π3+x +π=sin ⎝⎛⎭⎫x +π3=f (x ).故选C. 10.已知函数f (x )=3sin w x +cos w x (w >0)的图象与x 轴的交点的横坐标可构成一个公差为π2的等差数列,把函数f (x )的图象沿x 轴向左平移π6个单位,得到函数g (x )的图象.下列说法正确的是( D )A .g (x )在⎣⎡⎦⎤π4,π2上是增函数B .g (x )的图象关于直线x =-π4对称C .函数g (x )是奇函数D .当x ∈⎣⎡⎦⎤π6,2π3时,函数g (x )的值域是[-2,1]解析 f (x )=3sin ωx +cos ωx =2sin ⎝⎛⎭⎫ωx +π6,由题意知T 2=π2,∴T =π,∴ω=2πT=2,∴f (x )=2sin ⎝⎛⎭⎫2x +π6.把函数f (x )的图象沿x 轴向左平移π6个单位,得到g (x )=2sin ⎣⎡⎦⎤2⎝⎛⎭⎫x +π6+π6=2sin ⎝⎛⎭⎫2x +π2=2cos 2x 的图象,易知g (x )是偶函数且在⎣⎡⎦⎤π4,π2上是减函数,其图象不关于直线x =-π4对称,所以A 项,B 项,C 项错误.当x ∈⎣⎡⎦⎤π6,2π3时,2x ∈⎣⎡⎦⎤π3,4π3,则g (x )min =2cos π=-2,g (x )max =2cos π3=1,即函数g (x )的值域为[-2,1],故选D.11.函数f (x )=2x -4sin x ,x ∈⎣⎡⎦⎤-π2,π2的图象大致是( D )解析 因为函数f (x )是奇函数,所以排除A ,B 项,f ′(x )=2-4cos x ,令f ′(x )=2-4cos x =0,得x =±π3,故选D.12.函数f (x )=A sin w x (A >0,w >0)的部分图象如图所示,则f (1)+f (2)+f (3)+…+f (2 018)的值为( A )A .2+2B .32C .62D .-2解析 由题图可知,A =2,T =8,2πω=8,ω=π4,∴f (x )=2sin π4x ,∴f (1)=2,f (2)=2,f (3)=2,f (4)=0,f (5)=-2,f (6)=-2,f (7)=-2,f (8)=0,而2 018=8×252+2,∴f (1)+f (2)+…+f (2 018)=f (1)+f (2)=2+ 2.故选A.第2讲 三角变换与解三角形题型一三角恒等变换1.(1)(2018·河南郑州模拟)若tan α=13,tan(α+β)=12,则tan β=( A )A.17 B .16C .57D .56(2) (2017·河北唐山中学模拟)已知α是三角形的内角,sin ⎝⎛⎭⎫α+π3=45,则cos ⎝⎛⎭⎫5π12-α=( D )A.210B .-210C .-7210D .7210突破点拨(1)注意到β=(α+β)-α,再结合已知条件求tan β的值. (2)注意到cos ⎝⎛⎭⎫5π12-α=-cos ⎣⎡⎦⎤⎝⎛⎭⎫α+π3+π4,再实施运算. 解析 (1)tan β=tan[(α+β)-α] =tan (α+β)-tan α1+tan (α+β)·tan α=12-131+12×13=17.故选A.(2)∵α是三角形的内角,sin ⎝⎛⎭⎫α+π3=45<32, ∴α+π3是钝角,∴cos ⎝⎛⎭⎫α+π3=-35,cos ⎝⎛⎭⎫5π12-α=-cos ⎣⎡⎦⎤π-⎝⎛⎭⎫5π12-α=-cos ⎝⎛⎭⎫712π+α=-cos ⎣⎡⎦⎤⎝⎛⎭⎫α+π3+π4=-cos ⎝⎛⎭⎫α+π3·cos π4+sin ⎝⎛⎭⎫α+π3sin π4=7210.故选D. 2. 已知cos ⎝⎛⎭⎫π6+α·cos ⎝⎛⎭⎫π3-α=-14,α∈⎝⎛⎭⎫π3,π2. (1)求sin 2α的值; (2)求tan α-1tan α的值. 突破点拨(1)利用诱导公式转化为二倍角公式,再利用同角三角函数基本关系式求解. (2)切化弦,转化为二倍角公式,再利用(1)的结论求解. 解析 (1)cos ⎝⎛⎭⎫π6+α·cos ⎝⎛⎭⎫π3-α =cos ⎝⎛⎭⎫π6+α·sin ⎝⎛⎭⎫π6+α=12sin ⎝⎛⎭⎫2α+π3=-14, 即sin ⎝⎛⎭⎫2α+π3=-12. ∵α∈⎝⎛⎭⎫π3,π2,∴2α+π3∈⎝⎛⎭⎫π,4π3, ∴cos ⎝⎛⎭⎫2α+π3=-32, ∴sin 2α=sin ⎣⎡⎦⎤⎝⎛⎭⎫2α+π3-π3=sin ⎝⎛⎭⎫2α+π3cos π3-cos ⎝⎛⎭⎫2α+π3sin π3=12. (2)∵α∈⎝⎛⎭⎫π3,π2,∴2α∈⎝⎛⎭⎫2π3,π, 又由(1)知sin 2α=12,∴cos 2α=-32.∴tan α-1tan α=sin αcos α-cos αsin α=sin 2α-cos 2αsin α cos α=-2cos 2αsin 2α=-2×-3212=2 3.利用三角恒等变换公式解题的常用技巧(1)项的分拆与角的配凑:如sin 2α+2cos 2α=(sin 2α+cos 2α)+cos 2α,α=(α-β)+β等. (2)降幂与升幂:通过二倍角公式得到. (3)弦、切互化:一般是切化弦. 题型二 解三角形1. 已知a ,b ,c 分别为△ABC 内角A ,B ,C 的对边,sin 2B =2sin A sin C . (1)若a =b ,求cos B ;(2)设B =90°,且a =2,求△ABC 的面积. 突破点拨(1)根据正弦定理把已知条件转化为边的关系,然后利用余弦定理求解.(2)利用勾股定理得到边的一个方程,结合已知条件解方程组求得边长,然后求面积.解析 (1)由题设及正弦定理可得b 2=2ac . 又a =b ,可得b =2c ,a =2c . 由余弦定理可得cos B =a 2+c 2-b 22ac =14.(2)由(1)知b 2=2ac . 因为B =90°,由勾股定理得a 2+c 2=b 2,故a 2+c 2=2ac ,进而可得c =a = 2. 所以△ABC 的面积为12×2×2=1.【变式考法】 (1)在本例条件下,求角B 的范围. (2)在本例条件下,若B =60°,b =2,求a 的值. 解析 (1)因为b 2=2ac ,所以cos B =a 2+c 2-b 22ac ≥2ac -2ac2ac =0,又因为0<B <π,所以0<B ≤π2.(2)因为b 2=2ac ,b =2,所以ac =1, 又因为b 2=a 2+c 2-2ac cos B ,所以a 2+c 2=3, 所以a +c =5, 所以a =5+12或5-12. 2. △ABC 中,D 是BC 上的点,AD 平分∠BAC ,△ABD 面积是△ADC 面积的2倍. (1)求sin ∠B sin ∠C; (2)若AD =1,DC =22,求BD 和AC 的长. 突破点拨(1)利用面积关系得边的关系,再利用正弦定理求解. (2)先利用面积比求BD ,再利用余弦定理求解. 解析 (1)S △ABD =12AB ·AD sin ∠BAD ,S △ADC =12AC ·AD sin ∠CAD .因为S △ABD =2S △ADC ,∠BAD =∠CAD ,所以AB =2AC . 由正弦定理可得sin ∠B sin ∠C =AC AB =12.(2)因为S △ABD ∶S △ADC =BD ∶DC ,所以BD = 2. 在△ABD 和△ADC 中,由余弦定理知 AB 2=AD 2+BD 2-2AD ·BD cos ∠ADB , AC 2=AD 2+DC 2-2AD ·DC cos ∠ADC . 故AB 2+2AC 2=3AD 2+BD 2+2DC 2=6. 由(1)知AB =2AC ,所以AC =1.利用正、余弦定理解三角形的技巧解三角形问题一般要利用正、余弦定理和三角形内角和定理,正弦定理可以将角转化为边,也可以将边转化成角,当涉及边的平方关系时,一般利用余弦定理,要根据题目特点和正、余弦定理的结构形式,灵活选用.有关解三角形的综合问题(1)求∠ACP ;(2)若△APB 的面积是332,求sin ∠BAP .思维导航(1)由已知条件选择余弦定理求得AP .(2)由三角形的面积和(1)结论解得PB ,再由余弦定理及正弦定理求得AB 和sin ∠BAP . 规范解答(1)在△APC 中,因为∠P AC =60°,PC =2,AP +AC =4, 由余弦定理得PC 2=AP 2+AC 2-2AP ·AC ·cos ∠P AC ,所以22=AP 2+(4-AP )2-2AP ·(4-AP )·cos 60°,整理得AP 2-4AP +4=0,解得AP =2,所以AC =2.所以△APC 是等边三角形,所以∠ACP =60°.(2)因为∠APB 是△APC 的外角,所以∠APB =120°.因为△APB 的面积是332,所以12AP ·PB ·sin ∠APB =332,所以PB =3.在△APB 中,AB 2=AP 2+PB 2-2AP ·PB ·cos ∠APB =22+32-2×2×3×cos 120°=19,所以AB =19.在△APB 中,由正弦定理得AB sin ∠APB =PBsin ∠BAP,所以sin ∠BAP =3sin 120°19=35738.【变式考法】 (2017·广州模拟)如图,在△ABC 中,∠ABC =30°,AB =3,AC =1,AC <BC ,P 为BC 右上方一点,满足∠BPC =90°.(1)若BP =2,求AP 的长; (2)求△BPC 周长的最大值.解析 由题意知1=AC 2=AB 2+BC 2-2AB ·BC ·cos ∠ABC =3+BC 2-3BC ,解得BC =2(BC =1舍去,则∠CAB =90°.又∠BPC =90°,且BP =2,所以∠PBC =45°,从而∠ABP =75°.连接AP ,由余弦定理得AP =3+2-2×3×2×6-24=6+22. (2)由(1)可知BC =2或BC =1,又因为求△BPC 周长的最大值,所以BC =2,设BP =m ,PC =n ,则m 2+n 2=4.由于BC 长为定值,因此求△BPC 周长的最大值只需求BP +PC =m +n 的最大值即可. 又4=m 2+n 2≥(m +n )22,则m +n ≤22, 当且仅当m =n =2时取等号,此时△BPC 的周长取得最大值,为2+2 2.1.(教材回归)sin 20°cos 10°-cos 160°sin 10°=( D ) A .-32B .32C .-12D .12解析 原式=sin 20°cos 10°+cos 20°sin 10°=sin(20°+10°)=sin 30°=12,故选D.2.(2017·“江南十校”模拟)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .若C=2B ,则sin Bsin A=( D )A.c 2a 2+b 2-c 2 B .b 2a 2+b 2-c 2C.a 2a 2+b 2-c2 D .c 2a 2+c 2-b2解析 由已知,得sin C =sin 2B =2sin B cos B , 所以sin C sin B =2cos B .由正弦定理及余弦定理,得c b =2×a 2+c 2-b 22ac ,则b a =c 2a 2+c 2-b2. 再由正弦定理,得sin B sin A =c 2a 2+c 2-b 2,故选D.3.已知tan α=-2,tan(α+β)=17,则tan β的值为__3__.解析 tan β=tan[(α+β)-α]=tan (α+β)-tan α1+tan (α+β)tan α=17-(-2)1+17×(-2)=3.4.(2017·河南郑州调考)已知△ABC 中,角C 为直角,D 是边BC 上一点,M 是AD 上一点,且CD =1,∠DBM =∠DMB =∠CAB ,则MA =__2__.解析 如图,设∠DMB =θ,则∠ADC =2θ,∠DAC =π2-2θ,∠AMB =π-θ,∠ABM =π2-2θ,在Rt △ABC 中,cos θ=cos ∠CAB =ACAB ;在△CDA 中,由正弦定理得CD sin ⎝⎛⎭⎫π2-2θ=ACsin 2θ; 在△AMB 中,由正弦定理得MA sin ⎝⎛⎭⎫π2-2θ=ABsin (π-θ), ∴CD MA =AC ·sin θAB ·sin 2θ=AC ·sin θ2AB ·sin θcos θ=12,从而MA =2. 5.在△ABC 中,a =4,b =5,c =6,则sin 2Asin C=__1__.解析 在△ABC 中,由余弦定理的推论可得cos A =b 2+c 2-a 22bc =52+62-422×5×6=34,由正弦定理可知sin 2A sin C =2sin A cos A sin C =2a ·cos Ac =2×4×346=1.6.(书中淘金)如图,一辆汽车在一条水平的公路上向正西行驶,到A 处时测得公路北侧一山顶D 在西偏北30°的方向上,行驶600 m 后到达B 处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD解析 依题意有AB =600,∠CAB =30°,∠CBA =180°-75°=105°,∠DBC =30°,DC ⊥CB . ∴∠ACB =45°,在△ABC 中,由AB sin ∠ACB =CB sin ∠CAB ,得600sin 45°=CBsin 30°, 有CB =3002,在Rt △BCD 中,CD =CB ·tan 30°=1006, 则此山的高度CD =100 6 m.7.(考点聚焦)已知函数f (x )=2sin ωx +m cos ωx (ω>0,m >0)的最小值为-2,且图象上相邻两个最高点的距离为π.(1)求ω和m 的值;(2)若f ⎝⎛⎭⎫θ2=65,θ∈⎝⎛⎭⎫π4,3π4,求f ⎝⎛⎭⎫θ+π8的值. 解析 (1)易知f (x )=2+m 2sin(ωx +φ)(φ为辅助角), ∴f (x )min =-2+m 2=-2,∴m = 2.由题意知函数f (x )的最小正周期为π,∴2πω=π,∴ω=2.(2)由(1)得f (x )=2sin 2x +2cos 2x =2sin ⎝⎛⎭⎫2x +π4, ∴f ⎝⎛⎭⎫θ2=2sin ⎝⎛⎭⎫θ+π4=65, ∴sin ⎝⎛⎭⎫θ+π4=35, ∵θ∈⎝⎛⎭⎫π4,3π4,∴θ+π4∈⎝⎛⎭⎫π2,π,∴cos ⎝⎛⎭⎫θ+π4=-1-sin 2⎝⎛⎭⎫θ+π4=-45, ∴f ⎝⎛⎭⎫θ+π8=2sin ⎣⎡⎦⎤2⎝⎛⎭⎫θ+π8+π4=2sin ⎝⎛⎭⎫2θ+π2 =2sin ⎣⎡⎦⎤2⎝⎛⎭⎫θ+π4=4sin ⎝⎛⎭⎫θ+π4cos ⎝⎛⎭⎫θ+π4 =4×35×⎝⎛⎭⎫-45=-4825. 8.(教材回归)在△ABC 中,已知AB =2,AC =3,A =60°. (1)求BC 的长; (2)求sin 2C 的值.解析 (1)由余弦定理知,BC 2=AB 2+AC 2-2AB ·AC ·cos A =4+9-2×2×3×12=7,所以BC =7.(2)由正弦定理知sin C =AB BC ·sin A =2sin 60°7=217.因为AB <BC ,所以C <A ,所以C 为锐角, 则cos C =1-sin 2C =1-37=277. 因此sin 2C =2sin C ·cos C =2×217×277=437. 9.(2017·河北唐山二模)已知△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,a 2+b 2=λab . (1)若λ=6,B =5π6,求sin A ;(2)若λ=4,AB 边上的高为3c6,求C . 解析 (1)已知B =5π6,a 2+b 2=6ab ,结合正弦定理得4sin 2A -26sin A +1=0,解得sin A =6±24. 因为0<A <π6,所以sin A <12,所以sin A =6-24.(2)由题意可知S △ABC =12ab sin C =312c 2,得12ab sin C =312(a 2+b 2-2ab cos C )=312(4ab -2ab cos C ). 从而有3sin C +cos C =2,即sin ⎝⎛⎭⎫C +π6=1. 又π6<C +π6<7π6,所以C =π3.10.(2017·山东淄博模拟)已知a ,b ,c 分别为△ABC 的内角A ,B ,C 的对边,且a cos C +3a sin C -b -c =0.(1)求A ;(2)若a =2,求△ABC 面积的最大值.解析 (1)由a cos C +3a sin C -b -c =0及正弦定理, 得sin A cos C +3sin A sin C -sin B -sin C =0. 因为B =π-A -C ,所以3sin A sin C -cos A sin C -sin C =0. 易知sin C ≠0,所以3sin A -cos A =1, 所以sin ⎝⎛⎭⎫A -π6=12.又0<A <π,所以A =π3. (2)方法一 由(1)得B +C =2π3⇒C =2π3-B ⎝⎛⎭⎫0<B <2π3,因为a sin A =2sin π3=43, 所以由正弦定理得b =43sin B ,c =43sin C . 所以S △ABC =12bc sin A =12×43sin B ×43sin C ·sin π3=433sin B ·sin C =433·sin B ·sin ⎝⎛⎭⎫2π3-B =433⎝⎛⎭⎫32sin B cos B +12sin 2B =sin 2B -33cos 2B +33=233sin ⎝⎛⎭⎫2B -π6+33.易知-π6<2B -π6<7π6, 故当2B -π6=π2,即B =π3时,S △ABC 取得最大值,最大值为233+33= 3.方法二 由(1)知A =π3,又a =2,由余弦定理得22=b 2+c 2-2bc cos π3,即b 2+c 2-bc =4⇒bc +4=b 2+c 2≥2bc ⇒bc ≤4,当且仅当b =c=2时,等号成立.所以S △ABC =12bc sin A =12×32bc ≤34×4=3,即当b =c =2时,S △ABC 取得最大值,最大值为 3.1.已知函数f (x )=2cos 2x -sin ⎝⎛⎭⎫2x -7π6. (1)求函数f (x )的最大值,并写出f (x )取最大值时x 的取值集合;(2)已知△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若f (A )=32,b +c =2,求实数a的取值范围.解析 (1)f (x )=(1+cos 2x )-⎝⎛⎭⎫sin 2x cos 7π6-cos 2x sin 7π6 =1+32sin 2x +12cos 2x =1+sin ⎝⎛⎭⎫2x +π6, ∴函数f (x )的最大值为2,当且仅当sin ⎝⎛⎭⎫2x +π6=1, 即2x +π6=2k π+π2,k ∈Z ,即x =k π+π6,k ∈Z 时取到.∴函数f (x )取最大值时x 的取值集合为x ⎪⎪⎭⎬⎫x =k π+π6,k ∈Z . (2)由题意,f (A )=sin ⎝⎛⎭⎫2A +π6+1=32, 化简得sin ⎝⎛⎭⎫2A +π6=12. ∵A ∈(0,π),∴2A +π6∈⎝⎛⎭⎫π6,13π6, ∴2A +π6=5π6,∴A =π3.在△ABC 中,a 2=b 2+c 2-2bc cos π3=(b +c )2-3bc .由b +c =2,知bc ≤⎝⎛⎭⎫b +c 22= 1,即a 2≥1,当b =c =1时取等号. 又由b +c >a ,得a <2, ∴a 的取值范围是[1,2).2.已知a ,b ,c 分别是△ABC 的内角A ,B ,C 所对的边,且c =2,C =π3.(1)若△ABC 的面积等于3,求a ,b ; (2)若sin C +sin(B -A )=2sin 2A ,求A 的值. 解析 (1)∵c =2,C =π3,∴由余弦定理得4=a 2+b 2-2ab cos π3=a 2+b 2-ab .∵△ABC 的面积等于3, ∴12ab sin C =3,∴ab =4, 联立⎩⎪⎨⎪⎧ a 2+b 2-ab =4,ab =4,解得⎩⎪⎨⎪⎧a =2,b =2.(2)∵sin C +sin(B -A )=2sin 2A , ∴sin(B +A )+sin(B -A )=4sin A cos A , ∴sin B cos A =2sin A cos A . ①当cos A =0时,A =π2;②当cos A ≠0时,sin B =2sin A ,由正弦定理得b =2a ,联立⎩⎪⎨⎪⎧a 2+b 2-ab =4,b =2a ,解得⎩⎨⎧a =233,b =433,∴b 2=a 2+c 2,∵C =π3,∴A =π6.综上所述,A =π2或A =π6.3.(2017·浙江重点中学联考)已知△ABC 的三个内角A ,B ,C 的对边分别为a ,b ,c . (1)若C =2B ,求证:cos A =3cos B -4cos 3B ;(2)若b sin B -c sin C =a ,且△ABC 的面积S =b 2+c 2-a 24,求角B .解析 (1)证明:∵C =2B ,∴A =π-3B , ∴cos A =cos(π-3B )=-cos(B +2B ) =-cos B cos 2B +sin B sin 2B =-cos B (2cos 2B -1)+2sin 2B cos B=cos B -2cos 3B +2cos B (1-cos 2B )=3cos B -4cos 3B , ∴cos A =3cos B -4cos 3B .(2)在△ABC 中,∵S =b 2+c 2-a 24,∴S =b 2+c 2-a 24=12bc sin A .由余弦定理知b 2+c 2-a 24=12bc cos A ,∴12bc cos A =12bc sin A ,∴tan A =1, 而A ∈(0,π),∴A =π4.∵b sin B -c sin C =a ,由正弦定理,得 sin 2B -sin 2C =sin A =22, ∴cos 2C -cos 2B = 2.∵2C =2π-2A -2B =3π2-2B ,∴-sin 2B -cos 2B =2,∴sin ⎝⎛⎭⎫2B +π4=-1. ∵B ∈(0,π),∴2B +π4=3π2,∴B =5π8.4.(2017·武汉武昌五月调研)已和函数f (x )=sin(ωx +φ)⎝⎛⎭⎫ω>0,0<φ<π2的图象经过点⎝⎛⎭⎫0,12,且相邻两条对称轴的距离为π2.(1)求函数f (x )的解析式及其在[0,π]上的单调递增区间;(2)在△ABC 中,a ,b ,c 分别是内角A ,B ,C 的对边,若f ⎝⎛⎭⎫A 2-cos A =12,bc =1,b +c =3,求a 的值.解析 (1)将⎝⎛⎭⎫0,12代入f (x )的解析式,得sin φ=12. 又因为0<φ<π2,所以φ=π6.又因为最小正周期T =π2×2=π,所以ω=2.所以函数f (x )的解析式为f (x )=sin ⎝⎛⎭⎫2x +π6. 因为x ∈[0,π], 所以π6≤2x +π6≤13π6,所以2x +π6∈⎣⎡⎦⎤π6,π2或2x +π6∈⎣⎡⎦⎤3π2,13π6时,f (x )递增,即x ∈⎣⎡⎦⎤0,π6或x ∈⎣⎡⎦⎤2π3,π时,f (x )递增.所以函数f (x )在[0,π]上的单调递增区间是⎣⎡⎦⎤0,π6,⎣⎡⎦⎤2π3,π. (2)由(1)知f ⎝⎛⎭⎫A 2=sin ⎝⎛⎭⎫A +π6,代入已知等式得 sin ⎝⎛⎭⎫A +π6-cos A =32sin A +12cos A -cos A =32sin A -12cos A =sin ⎝⎛⎭⎫A -π6=12, 所以A -π6=π6或5π6,即A =π3或A =π(舍去).又因为bc =1,b +c =3,由余弦定理,得a 2=b 2+c 2-2bc ·cos A =b 2+c 2-bc =(b +c )2-3bc =6,所以a = 6. 5.(2018·山东青岛模拟)在△ABC 中,边a ,b ,c 的对角分别为A ,B ,C ,且b =4,A =π3,面积S =2 3. (1)求a 的值;(2)设f (x )=2(cos C sin x -cos A cos x ),将f (x )图象上所有点的横坐标变为原来的12(纵坐标不变)得到g (x )的图象,求g (x )的单调增区间.解析 (1)在△ABC 中,∵S =12bc sin A ,∴23=12×4×c ×32,∴c =2.∴a =b 2+c 2-2bc cos A =16+4-2×4×2×12=2 3.(2)∵a sin A =b sin B ,即2332=4sin B,∴sin B =1, 又0<B <π,∴B =π2,∴C =π6,∴f (x )=2(cos C sin x -cos A cos x )=2sin ⎝⎛⎭⎫x -π6, 将f (x )图象上所有点的横坐标变为原来的12(纵坐标不变),得到的图象对应的函数解析式为g (x )=2sin ⎝⎛⎭⎫2x -π6, 令2k π-π2≤2x -π6≤2k π+π2(k ∈Z ),解得k π-π6≤x ≤k π+π3(k ∈Z ),故g (x )的单调增区间为⎣⎡⎦⎤k π-π6,k π+π3(k ∈Z ). 6.(2018·辽宁协作体一模)设△ABC 是锐角三角形,三个内角A ,B ,C 所对的边分别为a ,b ,c ,且(sin A -sin B )(sin A +sin B )=sin ⎝⎛⎭⎫π3+B sin ⎝⎛⎭⎫π3-B . (1)求角A 的值;(2)若AB →·AC →=12,a =27,求b ,c (其中b <c ).解析 (1)∵(sin A -sin B )(sin A +sin B )=sin ⎝⎛⎭⎫π3+B ·sin ⎝⎛⎭⎫π3-B ,∴sin 2A -sin 2B =⎝⎛⎭⎫32cos B +12sin B⎝⎛⎭⎫32cos B -12sin B , 即sin 2A =34cos 2B -14sin 2B +sin 2B=34(cos 2B +sin 2B )=34, ∵角A 为锐角△ABC 的内角,∴sin A >0, ∴sin A =32,∴A =π3. (2)AB →·AC →=bc cos A =12,∴bc =24,又a 2=b 2+c 2-2bc cos A =(b +c )2-3bc =(27)2, ∴b +c =10,又∵b <c ,∴b =4,c =6.第3讲 平面向量题型一 向量的概念及线性运算高考中常从以下角度命题:1. (1)平面内给定三个向量a=(3,2),b=(-1,2),c=(4,1).若(a+k c)∥(2b-a),则k=-1613.(2)如图,E为平行四边形ABCD的边DC的中点,F为△ABD的重心,且AB→=a,AD→=b,则FE→=23b+16a.突破点拨(1)利用向量的坐标运算和向量共线定理求解.(2)利用向量加、减法的几何意义和重心公式求解.解析(1)因为(a+k c)∥(2b-a),又a+k c=(3+4k,2+k),2b-a=(-5,2),所以2×(3+4k)-(-5)×(2+k)=0,所以k=-1613.(2)由F为△ABD的重心,得AF→=23×12AC→=13(a+b).又AE→=AD→+DE→=b+12a,所以FE→=AE→-AF→=23b+16a.2.(1)在△ABC中,点M,N满足AM→=2MC→,BN→=NC→.若MN→=xAB→+yAC→,则x=12,y=-16.(2)已知向量a=(2,1),b=(1,-2),若m a+n b=(9,-8)(m,n∈R),则m-n的值为__-3__.突破点拨(1)画出图形,利用向量加减法则求解.(2)利用向量的坐标运算求解.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考专题突破三 高考中的数列问题【考点自测】1.(2017·苏北四市模拟)在公比为q 且各项均为正数的等比数列{a n }中,S n 为{a n }的前n 项和.若a 1=1q 2,且S 5=S 2+2,则q 的值为________.答案5-12解析 由题意得a n =q n -3(q >0),因为S n 为{a n }的前n 项和且S 5=S 2+2,所以S 5-S 2-2=0,即a 3+a 4+a 5-2=0,整理得q 2+q -1=0,解得q =5-12⎝ ⎛⎭⎪⎫q =-5-12舍. 2.已知等差数列{a n }的前n 项和为S n ,a 5=5,S 5=15,则数列⎩⎨⎧⎭⎬⎫1a n a n +1的前100项和为________.答案100101解析 设等差数列{a n }的首项为a 1,公差为d .∵a 5=5,S 5=15,∴⎩⎨⎧a 1+4d =5,5a 1+5×(5-1)2d =15,∴⎩⎪⎨⎪⎧a 1=1,d =1, ∴a n =a 1+(n -1)d =n . ∴1a n a n +1=1n (n +1)=1n -1n +1, ∴数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1a n a n +1的前100项和为⎝⎛⎭⎫1-12+⎝⎛⎭⎫12-13+…+⎝⎛⎭⎫1100-1101=1-1101=100101. 3.若a ,b 是函数f (x )=x 2-px +q (p >0,q >0)的两个不同的零点,且a ,b ,-2这三个数适当排序后可成等差数列,也可适当排序后成等比数列,则p +q 的值为________. 答案 9解析 由题意知,a +b =p ,ab =q ,∵p >0,q >0,∴a >0,b >0.在a ,b ,-2这三个数的6种排序中,成等差数列的情况有a ,b ,-2;b ,a ,-2;-2,a ,b ;-2,b ,a ;成等比数列的情况有a ,-2,b ;b ,-2,a .∴⎩⎪⎨⎪⎧ ab =4,2b =a -2或⎩⎪⎨⎪⎧ ab =4,2a =b -2,解得⎩⎪⎨⎪⎧ a =4,b =1或⎩⎪⎨⎪⎧a =1,b =4.∴p =5,q =4,∴p +q =9.4.已知数列{a n }是等比数列,数列{b n }是等差数列,若a 1·a 6·a 11=33,b 1+b 6+b 11=7π,则tanb 3+b 91-a 4·a 8的值是________.答案 - 3解析 {a n }是等比数列,{b n }是等差数列,且a 1·a 6·a 11=33,b 1+b 6+b 11=7π, ∴a 36=(3)3,3b 6=7π,∴a 6=3,b 6=7π3, ∴tanb 3+b 91-a 4·a 8=tan2b 61-a 26=tan 2×7π31-(3)2 =tan ⎝⎛⎭⎫-7π3=tan ⎝⎛⎭⎫-2π-π3 =-tan π3=- 3.5.(2013·江苏)在正项等比数列{a n }中,a 5=12,a 6+a 7=3.则满足a 1+a 2+…+a n >a 1a 2…a n 的最大正整数n 的值为________. 答案 12解析 设{a n }的公比为q (q >0),则由已知可得⎩⎨⎧a 1q 4=12,12(q +q 2)=3,解得⎩⎪⎨⎪⎧a 1=132,q =2.于是a 1+a 2+…+a n =132(1-2n )1-2=132(2n -1),a 1a 2…a n =(1)(1)2211()232n n n n nn a q--=. 由a 1+a 2+…+a n >a 1a 2…a n ,可得132(2n -1)> (1)21()232n n n -,整理得211522212.-n nn-+>由2n >2115222n n-+,可得n >12n 2-112n +5,即n 2-13n +10<0,解得13-1292<n <13+1292,取n =12,可以验证当n =12时满足a 1+a 2+…+a n >a 1a 2…a n ,n ≥13时不满足a 1+a 2+…+a n >a 1a 2…a n , 故n 的最大值为12.题型一 数列的通项与求和例1 已知等差数列{a n }的公差为2,前n 项和为S n ,且S 1,S 2,S 4成等比数列. (1)求数列{a n }的通项公式; (2)令b n =(-1)n-14na n a n +1(n ∈N *),求数列{b n }的前n 项和T n . 解 (1)因为S 1=a 1,S 2=2a 1+2×12×2=2a 1+2,S 4=4a 1+4×32×2=4a 1+12,由题意得(2a 1+2)2=a 1(4a 1+12), 解得a 1=1,所以a n =2n -1(n ∈N *). (2)b n =(-1)n -14na n a n +1=(-1)n -14n(2n -1)(2n +1)=(-1)n -1⎝ ⎛⎭⎪⎫12n -1+12n +1. 当n 为偶数时,T n =⎝⎛⎭⎫1+13-⎝⎛⎭⎫13+15+…+⎝ ⎛⎭⎪⎫12n -3+12n -1-⎝ ⎛⎭⎪⎫12n -1+12n +1=1-12n +1=2n 2n +1.当n 为奇数时,T n =⎝⎛⎭⎫1+13-⎝⎛⎭⎫13+15+…-⎝ ⎛⎭⎪⎫12n -3+12n -1+⎝ ⎛⎭⎪⎫12n -1+12n +1=1+12n +1=2n +22n +1.所以T n=⎩⎪⎨⎪⎧2n +22n +1,n 为奇数,2n2n +1,n 为偶数.⎝ ⎛⎭⎪⎫或T n =2n +1+(-1)n -12n +1思维升华 (1)一般求数列的通项往往要构造数列,此时从要证的结论出发,这是很重要的解题信息.(2)根据数列的特点选择合适的求和方法,常用的求和方法有错位相减法、分组转化法、裂项相消法等.跟踪训练1 已知数列{a n }的前n 项和为S n ,且a 1=12,a n +1=n +12n a n(n ∈N *).(1)证明:数列⎩⎨⎧⎭⎬⎫a n n 是等比数列;(2)求数列{a n }的通项公式与前n 项和S n . (1)证明 ∵a 1=12,a n +1=n +12n a n ,当n ∈N *时,a nn≠0,又a 11=12,a n +1n +1∶a n n =12(n ∈N *)为常数, ∴⎩⎨⎧⎭⎬⎫a n n 是以12为首项,12为公比的等比数列.(2)解 由⎩⎨⎧⎭⎬⎫a n n 是以12为首项,12为公比的等比数列,得a n n =12·⎝⎛⎭⎫12n -1,∴a n =n ·⎝⎛⎭⎫12n . ∴S n =1·12+2·⎝⎛⎭⎫122+3·⎝⎛⎭⎫123+…+n ·⎝⎛⎭⎫12n , 12S n =1·⎝⎛⎭⎫122+2·⎝⎛⎭⎫123+…+(n -1)⎝⎛⎭⎫12n +n ·⎝⎛⎭⎫12n +1, ∴两式相减得12S n =12+⎝⎛⎭⎫122+⎝⎛⎭⎫123+…+⎝⎛⎭⎫12n -n ·⎝⎛⎭⎫12n +1=12-⎝⎛⎭⎫12n +11-12-n ·⎝⎛⎭⎫12n +1, ∴S n =2-⎝⎛⎭⎫12n -1-n ·⎝⎛⎭⎫12n =2-(n +2)·⎝⎛⎭⎫12n .综上,a n =n ·⎝⎛⎭⎫12n ,S n =2-(n +2)·⎝⎛⎭⎫12n . 题型二 等差数列、等比数列的综合问题例2 (2013·江苏)设{a n }是首项为a ,公差为d 的等差数列(d ≠0),S n 是其前n 项的和.记b n =nS nn 2+c,n ∈N *,其中c 为实数. (1)若c =0,且b 1,b 2,b 4成等比数列,证明:S nk =n 2S k (k ,n ∈N *); (2)若{b n }是等差数列,证明:c =0. 证明 由题设知,S n =na +n (n -1)2d .(1)由c =0,得b n =S nn =a +n -12d .又因为b 1,b 2,b 4成等比数列,所以b 22=b 1b 4,即⎝⎛⎭⎫a +d 22=a ⎝⎛⎭⎫a +32d , 化简得d 2-2ad =0.因为d ≠0,所以d =2a . 因此,对于所有的m ∈N *, 有S m =ma +m (m -1)2·2a =m 2a .从而对于所有的k ,n ∈N *,有S nk =(nk )2a =n 2k 2a =n 2S k . (2)设数列{b n }的公差是d 1,则b n =b 1+(n -1)d 1,即nS nn 2+c =b 1+(n -1)d 1,n ∈N *,代入S n 的表达式,整理得,对于所有的n ∈N *,有⎝⎛⎭⎫d 1-12d n 3+⎝⎛⎭⎫b 1-d 1-a +12d n 2+cd 1n =c (d 1-b 1).令A =d 1-12d ,B =b 1-d 1-a +12d ,D =c (d 1-b 1),则对于所有的n ∈N *,有An 3+Bn 2+cd 1n =D .(*) 在(*)式中分别取n =1,2,3,4,得A +B +cd 1=8A +4B +2cd 1=27A +9B +3cd 1=64A +16B +4cd 1,从而有⎩⎪⎨⎪⎧7A +3B +cd 1=0, ①19A +5B +cd 1=0, ②21A +5B +cd 1=0, ③由②③得A =0,cd 1=-5B ,代入方程①,得B =0, 从而cd 1=0.即d 1-12d =0,b 1-d 1-a +12d =0,cd 1=0.若d 1=0,则由d 1-12d =0,得d =0,与题设矛盾,所以d 1≠0.又因为cd 1=0,所以c =0.思维升华 关于等差(比)数列的基本运算,其实质就是解方程或方程组,需要认真计算,灵活处理已知条件.容易出现的问题主要有两个方面:一是计算出现失误,特别是利用因式分解求解方程的根时,不注意对根的符号进行判断;二是不能灵活运用等差(比)数列的基本性质转化已知条件,导致列出的方程组较为复杂,增大运算量.跟踪训练2 已知首项为32的等比数列{a n }不是递减数列,其前n 项和为S n (n ∈N *),且S 3+a 3,S 5+a 5,S 4+a 4成等差数列. (1)求数列{a n }的通项公式;(2)设T n =S n -1S n (n ∈N *),求数列{T n }的最大项的值与最小项的值.解 (1)设等比数列{a n }的公比为q , 因为S 3+a 3,S 5+a 5,S 4+a 4成等差数列, 所以S 5+a 5-S 3-a 3=S 4+a 4-S 5-a 5,即4a 5=a 3, 于是q 2=a 5a 3=14.又{a n }不是递减数列且a 1=32,所以q =-12.故等比数列{a n }的通项公式为a n =32×⎝⎛⎭⎫-12n -1 =(-1)n -1·32n (n ∈N *).(2)由(1)得S n =1-⎝⎛⎭⎫-12n =⎩⎨⎧1+12n ,n 为奇数,1-12n ,n 为偶数.当n 为奇数时,S n 随n 的增大而减小, 所以1<S n ≤S 1=32,故0<S n -1S n ≤S 1-1S 1=32-23=56.当n 为偶数时,S n 随n 的增大而增大, 所以34=S 2≤S n <1,故0>S n -1S n ≥S 2-1S 2=34-43=-712.综上,对于n ∈N *,总有-712≤S n -1S n ≤56. 所以数列{T n }的最大项的值为56,最小项的值为-712.题型三 数列与其他知识的交汇 命题点1 数列与函数的交汇例3 设等差数列{a n }的公差为d ,点(a n ,b n )在函数f (x )=2x 的图象上(n ∈N *). (1)若a 1=-2,点(a 8,4b 7)在函数f (x )的图象上,求数列{a n }的前n 项和S n ;(2)若a 1=1,函数f (x )的图象在点(a 2,b 2)处的切线在x 轴上的截距为2-1ln 2,求数列⎩⎨⎧⎭⎬⎫a nb n 的前n 项和T n .解 (1)由已知,得b 7=72a,b 8=82a=4b 7, 有82a=4×72a=722a +,解得d =a 8-a 7=2,所以S n =na 1+n (n -1)2d =-2n +n (n -1)=n 2-3n .(2)f ′(x )=2x ln 2,f ′(a 2)=22aln 2,故函数f (x )=2x 在(a 2,b 2)处的切线方程为y -22a=22aln 2(x -a 2), 它在x 轴上的截距为a 2-1ln 2.由题意,得a 2-1ln 2=2-1ln 2,解得a 2=2, 所以d =a 2-a 1=1. 从而a n =n ,b n =2n ,a n b n =n2n .所以T n =12+222+323+…+n -12n -1+n 2n ,2T n =11+22+322+…+n2n -1.两式相减,得2T n -T n =1+12+122+…+12n -1-n 2n=2-12n -1-n2n=2n +1-n -22n.所以T n =2n +1-n -22n.命题点2 数列与不等式的交汇例4 设同时满足条件:①b n +b n +22≥b n +1;②b n ≤M (n ∈N *,M 是常数)的无穷数列{b n }叫做P数列.已知数列{a n }的前n 项和S n 满足S n =aa -1(a n-1)(a 为常数,且a ≠0,a ≠1). (1)求数列{a n }的通项公式;(2)设b n =2S n a n +1,若数列{b n }为等比数列,求a 的值,并证明数列⎩⎨⎧⎭⎬⎫1b n 为P 数列.解 (1)因为S 1=aa -1(a 1-1)=a 1,所以a 1=a .当n ≥2时,a n =S n -S n -1=aa -1(a n -a n -1), 整理得a na n -1=a ,即数列{a n }是以a 为首项,a 为公比的等比数列,所以a n =a ·a n -1=a n .(2)由(1)知,b n =2×a a -1(a n -1)a n +1=(3a -1)a n -2a(a -1)a n .(*)由数列{b n }是等比数列,可得b 22=b 1·b 3, 故⎝ ⎛⎭⎪⎫3a +2a 2=3·3a 2+2a +2a 2, 解得a =13,再将a =13代入(*)式得b n =3n .由于1b n +1b n +22=13n +13n +22>213n ·13n +22=13n +1=1b n +1,满足条件①; 又由于1b n =13n ≤13,故存在M ≥13满足条件②.故数列⎩⎨⎧⎭⎬⎫1b n 为P 数列.命题点3 数列应用题例5 某企业为了进行技术改造,设计了两种方案,甲方案:一次性贷款10万元,第一年便可获利1万元,以后每年比前一年增加30%的利润;乙方案:每年贷款1万元,第一年可获利1万元,以后每年比前一年增加5千元.两种方案的使用期都是10年,到期一次性归还本息.若银行两种形式的贷款都按年息5%的复利计算,试比较两种方案中哪种获利更多?(参考数据:取1.0510≈1.629,1.310≈13.786,1.510≈57.665)解 甲方案中,每年所获利润组成等比数列,首项为1,公比为(1+30%),所以10年所获得的总利润为S 10=1+(1+30%)+(1+30%)2+…+(1+30%)9 =1.310-10.3≈42.62(万元),贷款到期时,需要偿还银行的本息是 10(1+5%)10≈16.29(万元),故使用甲方案所获纯利润为42.62-16.29=26.33(万元). 乙方案中,每年的利润组成等差数列,首项为1,公差为0.5, 所以10年所获得的总利润为T 10=1+(1+0.5)+(1+2×0.5)+…+(1+9×0.5)=10×1+10×92×0.5=32.5(万元),从第一年起,每年的贷款在到期时所产生的本息组成等比数列,首项为1×(1+5%)10万元,公比为11+5%,故贷款到期时,需要偿还银行的本息是 1×[(1+5%)10+(1+5%)9+…+(1+5%)] =1.05×1.0510-10.05≈13.21(万元),故使用乙方案所获纯利润为32.5-13.21=19.29(万元). 综上可知,甲方案获利更多.思维升华 数列与其他知识交汇问题的常见类型及解题策略 (1)数列与函数的交汇问题①已知函数条件,解决数列问题,此类问题一般利用函数的性质研究数列问题;②已知数列条件,解决函数问题,解决此类问题一般要充分利用数列的范围、公式、求和方法对式子化简变形.另外,解题时要注意数列与函数的内在联系,灵活运用函数的思想方法求解,在问题的求解过程中往往会遇到递推数列,因此掌握递推数列的常见解法有助于该类问题的解决.(2)数列与不等式的交汇问题①函数方法:即构造函数,通过函数的单调性、极值等得出关于正实数的不等式,通过对关于正实数的不等式特殊赋值得出数列中的不等式;②放缩方法:数列中不等式可以通过对中间过程或者最后的结果放缩得到; ③比较方法:作差或者作商比较. (3)数列应用题①根据题意,确定数列模型; ②准确求解模型;③问题作答,不要忽视问题的实际意义.跟踪训练3 某企业在第1年年初购买一台价值为120万元的设备M ,M 的价值在使用过程中逐年减少,从第2年到第6年,每年年初M 的价值比上一年年初减少10万元;从第7年开始,每年年初M 的价值为上一年年初的75%. (1)求第n 年年初M 的价值a n 的表达式;(2)设A n =a 1+a 2+…+a nn ,若A n 大于80万元,则M 继续使用;否则,必须在第n 年年初对M 更新.证明:必须在第9年年初对M 更新.(1)解 当n ≤6时,数列{a n }是首项为120,公差为-10的等差数列,a n =120-10(n -1)=130-10n ;当n ≥6时,数列{a n }是以a 6为首项,公比为34的等比数列,又a 6=70,所以a n =70×⎝⎛⎭⎫34n -6.因此,第n 年年初M 的价值a n 的表达式为a n =⎩⎪⎨⎪⎧130-10n ,n ≤6,n ∈N *,70×⎝⎛⎭⎫34n -6,n ≥7,n ∈N *.(2)证明 设S n 表示数列{a n }的前n 项和,由等差及等比数列的求和公式,得 当1≤n ≤6时,S n =120n -5n (n -1), A n =120-5(n -1)=125-5n ; 当n ≥7时,由于S 6=570, 故S n =S 6+(a 7+a 8+…+a n ) =570+70×34×4×⎣⎡⎦⎤1-⎝⎛⎭⎫34n -6 =780-210×⎝⎛⎭⎫34n -6, A n =780-210×⎝⎛⎭⎫34n -6n,因为{a n }是递减数列,所以{A n }也是递减数列. 又A 8=780-210×⎝⎛⎭⎫3428=824764>80,A 9=780-210×⎝⎛⎭⎫3439=767996<80,所以必须在第9年年初对M 更新.1.设数列{a n }的前n 项和为S n ,n ∈N *.已知a 1=1,a 2=32,a 3=54,且当n ≥2时,4S n +2+5S n=8S n +1+S n -1. (1)求a 4的值;(2)证明:⎩⎨⎧⎭⎬⎫a n +1-12a n 为等比数列;(3)求数列{a n }的通项公式.(1)解 当n =2时,4S 4+5S 2=8S 3+S 1, 即4⎝⎛⎭⎫1+32+54+a 4+5⎝⎛⎭⎫1+32 =8⎝⎛⎭⎫1+32+54+1, 解得a 4=78.(2)证明 因为4S n +2+5S n =8S n +1+S n -1(n ≥2), 所以4S n +2-4S n +1+S n -S n -1=4S n +1-4S n (n ≥2), 即4a n +2+a n =4a n +1 (n ≥2),当n =1时,4a 3+a 1=4×54+1=6=4a 2,所以n =1也满足此式, 所以4a n +2+a n =4a n +1 (n ∈N *), 因为a n +2-12a n +1a n +1-12a n =4a n +2-2a n +14a n +1-2a n=4a n +1-a n -2a n +14a n +1-2a n =2a n +1-a n 2(2a n +1-a n )=12,所以数列⎩⎨⎧⎭⎬⎫a n +1-12a n 是以a 2-12a 1=1为首项,12为公比的等比数列.(3)解 由(2)知,数列⎩⎨⎧⎭⎬⎫a n +1-12a n 是以a 2-12a 1=1为首项,12为公比的等比数列,所以a n +1-12a n =⎝⎛⎭⎫12n -1. 即a n +1⎝⎛⎭⎫12n +1-a n ⎝⎛⎭⎫12n =4, 所以数列⎩⎨⎧⎭⎬⎫a n ⎝⎛⎭⎫12n 是以a 112=2为首项,4为公差的等差数列,所以a n ⎝⎛⎭⎫12n =2+(n -1)×4=4n -2,即a n =(4n -2)×⎝⎛⎭⎫12n=(2n -1)×⎝⎛⎭⎫12n -1, 所以数列{a n }的通项公式是a n =(2n -1)×⎝⎛⎭⎫12n -1.2.已知递增的等比数列{a n }满足:a 2+a 3+a 4=28,且a 3+2是a 2和a 4的等差中项. (1)求数列{a n }的通项公式;(2)若b n =a n log 12a n ,S n =b 1+b 2+…+b n ,求使S n +n ·2n +1>62成立的正整数n 的最小值.解 (1)由题意,得⎩⎪⎨⎪⎧a 1q +a 1q 2+a 1q 3=28,a 1q +a 1q 3=2(a 1q 2+2),解得⎩⎪⎨⎪⎧a 1=2,q =2或⎩⎪⎨⎪⎧a 1=32,q =12,∵{a n }是递增数列,∴a 1=2,q =2,∴数列{a n }的通项公式为a n =2·2n -1=2n (n ∈N *). (2)∵b n =a n log 12a n =2n ·log 122n =-n ·2n ,∴S n =b 1+b 2+…+b n =-(1×2+2×22+…+n ·2n ),① 则2S n =-(1×22+2×23+…+n ·2n +1),②②-①,得S n =(2+22+…+2n )-n ·2n +1=2n +1-2-n ·2n +1, 则S n +n ·2n +1=2n +1-2,解2n +1-2>62,得n >5, ∴n 的最小值为6.3.(2014·江苏)设数列{a n }的前n 项和为S n .若对任意的正整数n ,总存在正整数m ,使得S n =a m ,则称{a n }是“H 数列”.(1)若数列{a n }的前n 项和S n =2n (n ∈N *),证明:{a n }是“H 数列”.(2)设{a n }是等差数列,其首项a 1=1,公差d <0.若{a n }是“H 数列”,求d 的值.(3)证明:对任意的等差数列{a n },总存在两个“H 数列”{b n }和{c n },使得a n =b n +c n (n ∈N *)成立.(1)证明 由已知,当n ≥1时, a n +1=S n +1-S n =2n +1-2n =2n .于是对任意的正整数n ,总存在正整数m =n +1, 使得S n =2n =a m . 所以{a n }是“H 数列”.(2)解 由已知,得S 2=2a 1+d =2+d . 因为{a n }是“H 数列”,所以存在正整数m ,使得S 2=a m , 即2+d =1+(m -1)d ,于是(m -2)d =1. 因为d <0,所以m -2<0,故m =1.从而d =-1.当d =-1时,a n =2-n ,S n =n (3-n )2是小于2的整数,n ∈N *.于是对任意的正整数n ,总存在正整数m =2-S n =2-n (3-n )2,使得S n =2-m =a m , 因为{a n }是“H 数列”. 所以d 的值为-1.(3)证明 设等差数列{a n }的公差为d ,则a n =a 1+(n -1)d =na 1+(n -1)(d -a 1)(n ∈N *). 令b n =na 1,c n =(n -1)(d -a 1),则a n =b n +c n (n ∈N *). 下证{b n }是“H 数列”.设{b n }的前n 项和为T n ,则T n =n (n +1)2a 1(n ∈N *).于是对任意的正整数n ,总存在正整数m =n (n +1)2,使得T n =b m ,所以{b n }是“H 数列”. 同理可证{c n }也是“H 数列”.所以,对任意的等差数列{a n },总存在两个“H 数列”{b n }和{c n },使得a n =b n +c n (n ∈N *)成立.4.(2017·江苏南师附中质检)已知数列{a n }和{b n }满足a 1a 2a 3…a n =n b(n ∈N *).若{a n }为等比数列,且a 1=2,b 3=6+b 2. (1)求{a n }和{b n }的通项公式;(2)设c n =1a n -1b n (n ∈N *),记数列{c n }的前n 项和为S n .(i)求S n ;(ii)求正整数k ,使得对任意n ∈N *均有S k ≥S n .解 (1)∵a 1a 2a 3…a n =n b(n ∈N *), ①当n ≥2,n ∈N *时,a 1a 2a 3…a n -1=1n b -,②由①②知a n =1n n b b --,令n =3,则有a 3=32b b -.∵b 3=6+b 2,∴a 3=8.∵{a n }为等比数列,且a 1=2,设{a n } 的公比为q , ∴则q 2=a 3a 1=4,由题意知a n >0,∴q >0,∴q =2. ∴a n =2n (n ∈N *).又由a 1a 2a 3…a n =n b(n ∈N *),得21×22×23…×2n =n b ,即(1)22n n +=n b,∴b n =n (n +1)(n ∈N *). (2)(i)∵c n =1a n -1b n =12n -1n (n +1)=12n -⎝ ⎛⎭⎪⎫1n -1n +1,∴S n =c 1+c 2+c 3+…+c n=12-⎝⎛⎭⎫11-12+122-⎝⎛⎭⎫12-13+…+12n -⎝ ⎛⎭⎪⎫1n -1n +1 =12+122+…+12n -⎝ ⎛⎭⎪⎫1-1n +1 =1-12n -1+1n +1=1n +1-12n .(ii)∵c 1=0,c 2>0,c 3>0,c 4>0, 当n ≥5时,c n =1n (n +1)⎣⎢⎡⎦⎥⎤n (n +1)2n -1,而n (n +1)2n -(n +1)(n +2)2n +1=(n +1)(n -2)2n +1>0,得n (n +1)2n ≤5×(5+1)25<1,∴当n ≥5时,c n <0.综上,对任意的n ∈N *恒有S 4≥S n ,故k =4.5.(2016·江苏)记U ={1,2,…,100}.对数列{a n }(n ∈N *)和U 的子集T ,若T =∅,定义S T =0;若T ={t 1,t 2,…,t k },定义S T =12.++…+k t t t a a a 例如:T ={1,3,66}时,S T =a 1+a 3+a 66.现设{a n }(n ∈N *)是公比为3的等比数列,且当T ={2,4}时,S T =30. (1)求数列{a n }的通项公式;(2)对任意正整数k (1≤k ≤100),若T ⊆{1,2,…,k },求证:S T <a k +1; (3)设C ⊆U ,D ⊆U ,S C ≥S D ,求证:S C +S C ∩D ≥2S D . (1)解 当T ={2,4}时,S T =a 2+a 4=a 2+9a 2=30, ∴a 2=3,a 1=a 23=1,故a n =a 1q n -1=3n -1.(2)证明 对任意正整数k (1≤k ≤100). 由于T ⊆{1,2,…,k },则S T ≤a 1+a 2+a 3+…+a k =1+3+32+…+3k -1=3k -12<3k =a k +1.(3)证明 设A =∁C (C ∩D ),B =∁D (C ∩D ),则A ∩B =∅,S C =S A +S C ∩D ,S D =S B +S C ∩D ,S C +S C ∩D -2S D =S A -2S B , ∴S C +S C ∩D ≥2S D 等价于S A ≥2S B . 由条件S C ≥S D 可得S A ≥S B .①若B =∅,则S B =0,所以S A ≥2S B 成立; ②若B ≠∅,由S A ≥S B 可知A ≠∅,设A 中的最大元素为I ,B 中的最大元素为m , 若m ≥I +1,则由(2)得S A <S I +1≤a m ≤S B ,矛盾. 又∵A ∩B =∅,∴I ≠m ,∴I ≥m +1,∴S B ≤a 1+a 2+…+a m =1+3+32+…+3m -1<a m +12≤a I 2≤S A2,即S A >2S B 成立. 综上所述,S A ≥2S B . 故S C +S C ∩D ≥2S D 成立.6.(2018届江苏常州三校联考)已知数列{a n },{b n },其中,a 1=12,数列{a n }满足(n +1)a n =(n-1)a n -1 (n ≥2,n ∈N *),数列{b n }满足b 1=2,b n +1=2b n . (1)求数列{a n },{b n }的通项公式;(2)是否存在自然数m ,使得对于任意n ∈N *,n ≥2,有1+1b 1+1b 2+…+1b n <m -84恒成立?若存在,求出m 的最小值;(3)若数列{c n }满足c n =⎩⎪⎨⎪⎧1na n ,n 为奇数,b n ,n 为偶数,求数列{c n }的前n 项和T n .解 (1)由(n +1)a n =(n -1)a n -1, 即a n a n -1=n -1n +1(n ≥2). 又a 1=12,所以a n =a n a n -1·a n -1a n -2·a n -2a n -3·…·a 3a 2·a 2a 1·a 1=n -1n +1·n -2n ·n -3n -1·…·24·13·12=1n (n +1).当n =1时,上式成立,故a n =1n (n +1).因为b 1=2,b n +1=2b n ,所以{b n }是首项为2,公比为2的等比数列, 故b n =2n .(2)由(1)知,b n =2n ,则1+1b 1+1b 2+…+1b n =1+12+122+…+12n =2-12n . 假设存在自然数m ,使得对于任意n ∈N *,n ≥2,有1+1b 1+1b 2+…+1b n <m -84恒成立,即2-12n <m -84恒成立,由m -84≥2,解得m ≥16. 所以存在自然数m ,使得对于任意n ∈N *,n ≥2,有1+1b 1+1b 2+…+1b n <m -84恒成立,此时,m 的最小值为16. (3)当n 为奇数时,T n =⎝⎛⎭⎫1a 1+13a3+…+1na n+(b 2+b 4+…+b n -1) =[2+4+…+(n +1)]+(22+24+…+2n -1)=2+n +12·n +12+4⎝⎛⎭⎫1-412n -1-4=n 2+4n +34+43(2n -1-1);当n 为偶数时,T n =⎣⎢⎡⎦⎥⎤1a 1+13a 3+…+1(n -1)a n -1+(b 2+b 4+…+b n )=(2+4+…+n )+(22+24+…+2n )=2+n 2·n 2+4⎝⎛⎭⎫1-42n1-4=n 2+2n 4+43(2n -1). 所以T n=⎩⎪⎨⎪⎧n 2+4n +34+43(2n -1-1),n 为奇数,n 2+2n 4+43(2n-1),n 为偶数.。
