第六章静电场-资料

合集下载

第六章静电场(1)

F12
q1、q2同号（排斥力）
q1
er12
F21
er 21 q2
F12
q1、q2异号（吸引力）
第六章静电场
讨论
库仑定律：
F
1
4π 0
q1q2 r3
r
（1）点电荷是带电体的理想模型。
（2）库仑定律是实验定律，它仅适用于静止的点电荷之间。
3. 静电力叠加原理
设有n个点电荷组成的点电荷系，点电荷 q 受到
其他点电荷qi作用的总静电力为 :
qi
F
i
Fi
1
4π 0
i
qqi ri 3
ri
q
ri
第六章静电场
二、电场强度 1、电场（electric field）
(1)对电场的认识过程
1）“超距作用”的观点：电荷
2）“场”的观点：电荷
电场
电荷电荷
即：电荷周围存在着的一种特殊物质——电场。
电荷 (2)场与实物的关系
1）对场中的其他带电体有作用力 2）当带电体在电场中移动时，电场力对带电体作功，这表明电场具有能量 3）使引入其中的导体或电介质分别产生静电感应现象和极化现象
第六章静电场
2、电场强度（electric field strength）
(1)试验电荷q0：
1）点电荷 2）电荷量足够小 3）正电荷
各个点电荷单独存在时在该点产生的电场强度的矢量和。
这一结论称为场强的叠加原理。
E1
《大学物理》第六章教学课件（1）
西南大学：杨亚玲
第六章静电场
第六章静电场【本章内容】
1 第一节电场强度库仑定律、电场强度、高斯定理

高中物理：第6章静电场

第6章静电场第1讲电场力的性质板块一主干梳理·对点激活知识点1 电荷守恒点电荷Ⅰ库仑定律Ⅱ1．元电荷、点电荷（1）元电荷：e＝1.6×10-19 C，最小的电荷量，所有带电体的电荷量都是元电荷的整数倍，其中质子、正电子的电荷量与元电荷相同。

电子的电荷量q＝－1.6×10－19 C。

（2）点电荷：忽略带电体的大小和形状的理想化模型。

（3）比荷：带电粒子的电荷量与其质量之比。

2．电荷守恒定律（1）内容：电荷既不能创生，也不能消失，只能从一个物体转移到另一个物体，或者从物体的一部分转移到另一部分，在转移的过程中电荷的总量保持不变。

（2）起电方法：摩擦起电、感应起电、接触起电。

（3）带电实质：物体带电的实质是得失电子。

（4）电荷的分配原则：两个形状、大小相同的导体，接触后再分开，二者带相同电荷；若两导体原来带异种电荷，则电荷先中和，余下的电荷再平分。

3．库仑定律（1）内容：真空中两个静止点电荷之间的相互作用力，与它们的电荷量的乘积成正比，与它们的距离的二次方成反比，作用力的方向在它们的连线上。

（2）表达式：F ＝k q 1q 2r 2，式中k ＝9.0×109 N ·m 2/C 2，叫静电力常量。

（3）适用条件：真空中的点电荷。

①在空气中，两个点电荷的作用力近似等于真空中的情况，可以直接应用公式。

②当两个带电体的间距远大于本身的大小时，可以把带电体看成点电荷。

③两个点电荷间的距离r →0时，不能再视为点电荷，也不遵循库仑定律，它们之间的库仑力不能认为趋于无穷大。

（4）库仑力的方向由相互作用的两个带电体决定，且同种电荷相互排斥，为斥力；异种电荷相互吸引，为引力。

知识点2 静电场 Ⅰ 电场强度、点电荷的场强 Ⅱ1．电场（1）定义：存在于电荷周围，能传递电荷间相互作用的一种特殊物质。

（2）基本性质：对放入其中的电荷有力的作用。

2．电场强度（1）定义：放入电场中某点的电荷所受到的静电力F 跟它的电荷量q 的比值。

第六章静电场详解

R2 1 )0 2
1
1
R2 0
x2
2 x2
2020/10/1
第六章静电场
16
6.1静电场的概念--电场强度
17-4 一个细玻璃棒被弯成半径为R的半圆形，沿其上半部分均匀分布有电荷+Q，沿其下半部分均匀分布有电荷－Q，如图所示。试求圆心O处的电场强度。
解：把所有电荷都当作正电荷处理.
y
在q处取微小电荷dq = dl = 2Qd / ， dq
4π
qx
0(x2
R2 )3
2
2020/10/1
第六章静电场
12
6.1静电场的概念--电场强度
E
4π
0
qx (x2
R2
)3
2
讨论
（1） x R
q
E 4π 0x2
（点电荷电场强度）
（2） x 0, E0 0
（3） dE 0, x 2 R
dx
2
y dq dl
qR
o
z
r
x
P x E
2R E
2
xRdR 2 0 (x2 R2 )3 2
y dq 2π RdR
R (x2 R2 )1/2
zR0
o
x
P
dE
x
dR q π R02
2020/10/1
第六章静电场
14
6.1静电场的概念--电场强度
dEx
2 0
xRdR (x2 R2)3
2
E dEx
x
2 0
R0 RdR 0 (x2 R2 )3/2
y
zR0
R o
dR
P
dE

第六章真空中的静电场总结

第六章真空中的静电场§6-1 电荷库仑定律5.电荷的量子化效应：到目前为止的所以实验表明，一切带电体包括微观粒子所带的电量 q ，都是某一基本电荷量的整数倍，这个基本电荷就是 e = 1.60210-19 库仑一个带电体带的电量 q = ne n = 1,2,3,... 只能取不连续的值，这称为电荷的量子化。

宏观带电体的带电量 q e ，准连续二、库仑定律与叠加原理库仑定律是两个点电荷相互作用的定律。

2.库仑定律实验给出：k = 8.988010 9 N·m2/C212120022014q q q q F k r r r r πε==▲ 库仑定律适用的条件：• 真空中点电荷间的相互作用• 电荷对观测者静止41πε=k 0 —真空介电常量2212o m /N C 1085.841⋅⨯==-k πε3.静电力的叠加原理作用于某电荷上的总静电力等于其他点电荷单独存在时作用于该电荷的静电力的矢量和。

离散状态:∑==N i iF F 12004i ii i r r q q Fπε=连续分布02004r rdq q F d πε=⎰=Fd F结论：库仑力比万有引力大得多，所以在原子中，作用在电子上的力，主要是电场力，万有引力完全可以忽略不计。

§6-2 静电场电场强度一、电场电荷间的相互作用是通过场来传递的 2. 静电场的对外表现：静电场：相对于观察者静止的电荷所产生的电场称为静电场。

静电场最重要的表现有两方面：（1）力的表现: 对电荷（带电体）施加作用力；（2）功的表现: 电场力对电荷（带电体）作功。

★研究方法：电场能量—引入电势 UE电场力—引入场强二、电场强度1.试验电荷 q 0 及条件{点电荷(尺寸小)q 0 足够小，对待测电场影响小4.场强叠加原理设有若干个静止的点电荷q1、q2、…… qN ，它们单独存在时的场强分别为NE E E ,2,1，则它们同时存在时的场强为三、电场强度的计算 1.点电荷的电场强度0002144πq q F qE r r q q rε==⋅=特点: (1)是球对称的; (2)是与 r 平方成反比的非均匀场。

第六章静电场62(新课标复习资料)

金版教程
高三物理
选修 3-1
选修3-1
第六章静电场
金版教程
高三物理
第六章静电场
选修3-1
第六章静电场
金版教程
高三物理
第2单元电场的能的性质
选修3-1
第六章静电场
金版教程
基础知识梳理考技案例导析易错易混分析
选修3-1
基础知识梳理
第六章静电场
高三物理
混分
该点电势比零电势高(低)．
析
选修3-1
第六章静电场
金版教程
高三物理
基础
(4)相对性：电势具有相相对性，同一点的电势因选取
知识
零电势点的不同而不同．
梳
理
2．等势面
随堂针对训
练
考
(1)定义：电场中电势相等的各点组成的面．
技
案例
(2)四个特点
导析
①等势面一定与电场场线线垂直，即跟场强的方向垂垂直直．
金版教程
高三物理
基础
选项
诊断
结论
知识梳理
试探电荷＋q 若由 a 点释放，将受到
随堂
针
C 变化的电场力的作用，所以试探电荷 ×
对训
练
考
不会沿弯曲的电场线运动
技
案
例导析
将试探电荷由 a 点移到 b 点过程中，
D
√
限
电场力做正功，电荷的电势能减小
时规
范
易
错易
[答案] BD
特训
混
分
析
特训
易混
零场强不不一一定定为为零零势能一一定定为为零零

静电场(全课件)

PA R T. 0 1
静电场(全课件)
单击此处添加文本具体内容
CONTENTS
目录
静电场的简介
电场的基本概念
静电场的计算方法
静电场的实际应用
静电场的未来发展
PA R T. 0 2
静电场的简介
单击此处添加文本具体内容
静电场的定义
静电场是保守场，即电场力做功与路径无关，只与初末位置的电势差有关。静电场是由静止电荷产生的电场，其电场线从正电荷出发，终止于负电荷或无穷远处。
定义
电场强度是描述电场中电场力性质的物理量，用矢量表示，单位为牛/库或伏/米。
计算公式
在点电荷产生的电场中，电场强度的大小等于点电荷的电量与距离的平方的比值，方向由点电荷指向其周围的电场线。
电场强度的叠加原理
在空间中某一点的电场强度等于各个点电荷在该点产生的电场强度的矢量和。
电势
电势是描述电场中电势能性质的物理量，用标量表示，单位为伏特。
电场的基本概念
单击此处添加文本具体内容
电场线
电场线是用来描述电场分布的假想线，其密度表示电场强度的大小。描述电场分布电场线的方向电场线的切线电场线的方向与电场强度矢量方向一致，从正电荷或无穷远指向负电荷或无穷远。电场线的切线方向表示电场强度的方向，切线的长度表示电场强度的大小。
电场强度
离子交换离子交换是一种常用的水处理技术，通过电场的作用，使带电离子在电场中发生定向迁移，从而实现离子的交换和去除。
电场在生物医学中的应用
医学成像
01
医学成像技术如X光、CT等利用电场的作用，使不同物质在电
场中的吸收和散射程度不同，从而实现医学成像。
电刺激细胞

教材第六章静电场资料

第三部分电磁学前面研究了机械运动和热运动，现在开始研究电磁运动。

大量实验事实证明，物件间相互作用不是超距发生的，而是由场传递的。

电磁力就是由电磁场传递的。

正是场与实物间的相互作用，才导致了实物间的相互作用。

电磁学研究物质间电磁相互作用，研究电磁场的产生、变化和运动的规律。

（1）什么是电磁学电磁学是研究电磁运动及其规律的科学，它的主要内容有：（2）电磁学的主要内容电荷、电流产生电场和磁场的规律；电场和磁场的相互作用；电磁场对电流、电荷的作用；电磁场中物质的各种性质。

（3）学习电磁学的意义电磁运动是物质的一种基本运动形式，电磁相互作用是自然界已知的四种相互作用之一。

在日常生活和生产活动中，在对物质结构的深入认识过程中，都要涉及电磁运动。

因此理解和掌握电磁运动的基本规律，在理论和实践中都有重要的意义。

学好电磁学是学习电工学、无线电电子学、自动控制、计算机技术等学科的基础，在现代物理学中的地位也是非常重要的。

（4）研究方法：电磁学：归纳法——从几个基本实验规律出发，经过建立模型，定义概念，数学外推与大胆假设，把理论预言与实验相对照，进行归纳总结，得出基本规律。

电磁学两条线：主线——实验规律副线——建立方Maxwell程组第六章静电场§6-1电荷电荷守恒定律库仑定律静电场1．摩擦起电、电荷（１）电荷人们对电荷的认识是从摩擦起电（electrification by friction ）现象和雷电开始的。

公元3世纪晋朝张华的《博物志》中记载“今人梳头、解著衣，有随梳解结，有光者，亦有咤声。

”人们发现不同材料的两种物质互相摩擦后会吸引纸屑等轻小物体，人们把能够吸引轻小物体的属性称为带电，该物体称为带电体，带电体所带的称为电荷。

（2）电荷的分类及作用将两个用丝绸摩擦过的玻璃棒或毛皮摩擦过的硬橡胶棒互相靠近会发现他们互相排斥、而丝绸摩擦过的玻璃棒和毛皮摩擦过的硬橡胶棒之间互相吸引，这说明丝绸摩擦过的玻璃棒和毛皮摩擦过的硬橡胶棒它们所带的是两种不同性质的电荷，实验发现，自然界的电荷只有两种或与丝绸摩擦过的玻璃棒上的电荷相同或者与毛皮摩擦过的硬橡胶棒上的电荷相同，前者称为正电荷（positive charge ）、后者称为负电荷（negative charge ），电荷的正负是人为规定的，原则上是任意的，首先是由美国的富兰克林命名的一直沿用至今。

第六章静电场6-1(新课标复习资料)

FF 公式：E＝，单位：N/C，或 V/m E＝ q N/C q
随堂针对训练
考技案例导析
易错易混分析
是描述电场的力的性质的物理量．力的性质
限时规范特训
选修3-1
第六章静电场
金版教程
基础知识梳理
高三物理
矢量三性
电场强度 E 是表示电场力的性质的一个物理量，规定正电荷所受电场力方向为该点场强的方向．正电荷所受电场力
易错易混分析
限时规范特训
矢量性存在时在该点所产生的场强的矢量和.
选修3-1
第六章静电场
金版教程
基础知识梳理
高三物理
电场线
1．几种典型电场的电场线(见下图)
随堂针对训练
考技案例导析
易错易混分析
限时规范特训
选修3-1
第六章静电场
限时规范特训随堂针对训练
考技案例导析
易错易混分析
选修3-1
第六章静电场
金版教程
基础知识梳理
高三物理
5kq2 A. l＋ 2k0l2 5kq2 C. l－ 4k0l2
kq2 B. l－ 2 k0l 5kq2 D. l－ 2k0l2
随堂针对训练
易错易混分析
感应起电 ②感应起电
接触起电 ③接触起电
选修3-1
第六章静电场
金版教程
基础知识梳理
高三物理
(2)三种起电方式虽然不同，但本质相同，都是电荷的
转移转移.

大学物理学第6章-静电场

6.1 库仑定律静电力叠加原理
6.1.1 电荷
1.电荷两种电荷正电荷和负电荷电性力同号相斥、异号相吸
电荷量物体带电的多少 (q, Q)
2.电荷量子化
q ne n 1,2,3,
• e为电子电量
• 宏观带电体的带电量qe，准连续
夸克模型理论预言,夸克带有或1 e 的2电e量,以四味
4πε0r
4
(1-
l 2r
)2
(1
l )2 2r
r l
EA
2p
4π 0 r 3
考虑方向：
EA
2p
4π 0r3
（2）电偶极子中垂线上B点的场强
如图选取坐标系
q E E- 4πε0r2
E 2E cos
l
2
4πε0
q (r 2
l2 22
)
(r
2
2
l2 22
)
1 2
l2
忽略，B点场强与P反方向
4
EB
均匀带电直线的场强
例求真空中长为L、均匀带电，线电荷密度为的直线的场强。场点与直线的垂直距离为d、场点与直线两端连线和直线的夹角
分别为1和2。
解：取直角坐标oxy如图
dEy dEy
dq dx
dE
1
4π 0
dx
r2
dEx
dE cos
dx 4π0r 2
cos
dEx
P
π 2
1
dr
2
LOx dx
dE
Rd 4π 0 R 2
y
dl
由对称性
dEx 0
E
dEy
2
2
d 4π 0 R

大学物理第六章静电场详解(全)

向运动，并将涂料微粒吸附在工件表面的一种喷涂方法。
优点
02
涂料利用率高，可达80%~90%；涂装效率高，适合大批量生
产；涂层质量好，附着力强。
缺点
03
对工件的形状和大小有一定限制；对涂料的电阻率有一定要求
；设备投资较大。
26
静电除尘技术原理及优缺点
原理
含尘气体经过高压静电场时被电分离，尘粒与负离子结合带上负电后，趋向阳极表面放电而沉积。
放电过程
使充电后的电容器失去电荷的过程叫做放电。此过程中，电容器将储存的电场能转化为其他形式的能。同时，随着电容器两极板上电荷量的减少，电容器两极板间的电势差也逐渐减小。
2024/1/28
25
静电喷涂技术原理及优缺点
2024/1/28
原理
01
利用高压静电电场使带负电的涂料微粒沿着电场相反的方向定
2024/1/28
格林函数的求解与应用
利用格林函数的性质，结合边界条件，求解格林函数的具体形式；再将格林函数应用于原问题的求解，得到静电场的分布。
23
06
静电场应用举例
2024/1/28
24
电容器充放电过程分析
充电过程
将电容器两极板分别与电源的正负极相连，使电容器带电的过程叫做充电。此过程中，电源内部的非静电力做功，将其他形式的能转化为电场能，储存于电容器中。同时，随着电容器两极板上电荷量的积累，电容器两极板间的电势差也逐渐增大。
电势和电场强度的计算
利用点电荷和镜像电荷的电势叠加原理，计算空间任意一点的电势；再通过电势梯度计算电场强度。
2024/1/28
21
分离变量法求解二维边值问题
2024/1/28

物理-静电场知识点汇总

2.电场强度的计算：
（1）定义-矢量叠加
点电荷
E
1
4 0
q r2
er
连续带电体
E
dE
1
4 0
dq r2
er
方法
场源电荷分布
球面、球壳无限长棒、圆柱无线大平面
（2）高斯定理：
1
E dS
S
0
q int
3.电势的计算：
（1）定义法已知场强分布方法
（2）叠加法已知电荷分布
Vp
稳恒磁场中，磁感应强度沿任意闭合路径 L 的线积分(也称的环B流)，等于该路径 L 包围的所有电流强度的代数和的
倍 μ0
说明
积分路径方向
(1)电流正I 负的规定：与I 成L右螺旋时，为I正；反之为负.
(2) 环路上各点的B为空间所有电流的贡献
Edr
p
dq
V dV =
Q
Q 40r
➢ 电势差的计算： U AB =VA VB
B
Edl
A
WAB =
B A
q0
E
d
l
=q0
B
E dl
A
q0U AB
例1 求均匀带电球壳的电场与电势分布，已知半径R，带电量q。
解：由高斯定理求出场强分布
0
E
q
4 0 r 2
er
rR rR
++
+ +O
O
40r 2
er
r R2
r
电势差 A,B
一.毕奥－萨伐尔定律
✓ 实验定律，反映电流元在空间激发磁场的规律
dB
I

选修3-1 第六章静电场

第六章静电场第一部分电场的力的性质,物质的电结构、点电荷、电荷守恒Ⅰ(考纲要求)1.物质的电结构(1)原子是由带的原子核和带的电子构成，原子核的正电荷数与电子的负电荷数相等．(2)金属中离原子核最远的电子往往会脱离原子核的束缚而在金属中自由活动，这种电子叫做．2．点电荷、元电荷(1)元电荷：e＝，所有带电体的电荷量都是元电荷的，其中质子、正电子的电荷量与元电荷相同．电子的电荷量q＝．(2)点电荷：①本身的线度比相互之间的距离的带电体．②点电荷是理想化模型．3．电荷守恒定律(1)内容：电荷既不能创生，也不能消失，只能从物体的一部分到另一部分，或者从一个物体到另一个物体，在的过程中电荷的总量保持不变．(2)起电方法：摩擦起电、、接触起电．(3)带电实质：物体带电的实质是．,库仑定律Ⅱ(考纲要求)1.内容：中两个静止点电荷之间的相互作用力与它们的成正比，与它们的成反比．作用力的方向在．2．表达式：F＝，式中k＝ N·m2/C2，叫静电力常量．3．适用条件：中的．,静电场Ⅰ、电场强度、点电荷的电场强度Ⅱ(考纲要求)1．静电场(1)定义：存在于电荷周围，能传递电荷间的一种特殊物质．(2)基本性质：对放入其中的电荷有．2．电场强度(1)定义：放入电场中某点的电荷受到的电场力F与它的电荷量的．(2)定义式：E＝．单位：N/C或V/m(3)点电荷形成电场中某点的电场强度真空中点电荷形成的电场：E＝．(4)方向：规定在电场中某点所受的方向为该点的电场强度方向．(5)电场强度的叠加：电场中某点的电场强度为各个点电荷单独在该点产生的电场强度的 .电场线Ⅰ(考纲要求)1.定义为了形象地描述电场中各点电场强度的强弱及方向，在电场中画出一些曲线，曲线上每一点的都跟该点的电场强度方向一致，曲线的表示电场的强弱.2.电场线的特点3.几种典型电场的电场线(如图所示).一、基础自测1.M和N是两个不带电的物体，它们互相摩擦后M带正电1.6×10－10 C，下列判断正确的有().A.在摩擦前M和N的内部没有任何电荷B.摩擦的过程中电子从M转移到NC.N在摩擦后一定带负电1.6×10－10 CD.M在摩擦过程中失去1.6×10－10个电子2.关于点电荷，以下说法正确的是().A.足够小的电荷，就是点电荷B.一个电子，不论在何种情况下均可视为点电荷C.在实际中点电荷并不存在D.一个带电体能否看成点电荷，不是看它尺寸的大小，而是看它的形状和尺寸对相互作用力的影响能否忽略不计3.(2012·广东模拟)当在电场中某点放入电荷量为q的正试探电荷时，测得该点的电场强度为E，若在同一点放入电荷量为q′＝2q的负试探电荷时，测得该点的电场强度().A.大小为2E，方向与E相同B.大小为2E，方向与E相反C.大小为E，方向与E相同D.大小为E，方向与E相反4.在真空中有甲、乙两个点电荷，其相互作用力为F.要使它们之间的相互作用力为2F，下列方法可行的是().A.使甲、乙电荷量都变为原来的2倍B.使甲、乙电荷量都变为原来的1 2C.使甲、乙之间距离变为原来的2倍D.使甲、乙之间距离变为原来的1 2 .5.某电场的电场线的分布如图所示．一个带电粒子只在电场力作用下由M点沿图中虚线所示的路径运动通过N 点．则下列判断正确的是().A.粒子带负电B.粒子在M点的加速度大C.粒子在N点的速度大D.电场力对粒子做正功二、高考体验（一）库仑定律的应用(中频考查)1．(2010·海南卷，4)如图所示，M、N和P是以MN为直径的半圆弧上的三点，O点为半圆弧的圆心，∠MOP ＝60°.电荷量相等、符号相反的两个点电荷分别置于M、N两点，这时O点电场强度的大小为E1；若将N点处的点电荷移到P点，则O点的电场强度大小变为E2.E1与E2之比为()．A．1∶2 B．2∶1C．2∶ 3 D．4∶ 32．(2011·海南卷)三个相同的金属小球1、2、3分别置于绝缘支架上，各球之间的距离远大于小球的直径．球1的带电荷量为q，球2的带电荷量为nq，球3不带电且离球1和球2很远，此时球1、2之间作用力的大小为F.现使球3先与球2接触，再与球1接触，然后将球3移至远处，此时球1、2之间作用力的大小仍为F，方向不变．由此可知()．A．n＝3 B．n＝4 C．n＝5 D．n＝6（二）对电场强度的理解及叠加(中频考查)3．(2009·上海)两带电荷量分别为q和－q的点电荷放在x轴上，相距为L，能正确反映两电荷连线上电场强度大小E与x关系的是图()．4．(2011·重庆卷，19)如图所示，电荷量为＋q 和－q 的点电荷分别位于正方体的顶点，正方体范围内电场强度为零的点有( )．A ．体中心、各面中心和各边中点B ．体中心和各边中点C ．各面中心和各边中点D ．体中心和各面中心(三）对电场线的理解及应用(高频考查) 5．(2010·上海高考)三个点电荷电场的电场线分布如图所示，图中a 、b 两点处的电场强度大小分别为E a 、E b ，电势分别为φa 、φb ，则( )．A ．E a >E b ，φa >φbB ．E a <E b ，φa <φbC ．E a >E b ，φa <φbD ．E a <E b ，φa >φb 6．(2010·课标全国)静电除尘器是目前普遍采用的一种高效除尘器．某除尘器模型的收尘板是很长的条形金属板，下图中直线ab 为该收尘板的横截面．工作时收尘板带正电，其左侧的电场线分布如图所示；粉尘带负电，在电场力作用下向收尘板运动，最后落在收尘板上．若用粗黑曲线表示原来静止于P 点的带电粉尘颗粒的运动轨迹，下列4幅图中可能正确的是(忽略重力和空气阻力)( )．7．(2011·上海单科，1)电场线分布如图所示，电场中a 、b 两点的电场强度大小分别为E a 和E b ，电势分别为φa 和φb ，则( )．A ．E a >E b ，φa >φbB ．E a >E b ，φa <φbC ．E a <E b ，φa >φbD ．E a <E b ，φa <φb第二部分电场的电的性质,电势能、电势 Ⅰ(考纲要求)1.电势能(1)电场力做功①特点：电场力做功与无关，只与有关． ②计算方法a ．W ＝，只适用于匀强电场，其中d 为沿的距离．b ．W AB ＝qU AB ，适用于． (2)电势能①定义：电荷在电场中具有的势能，数值上等于将电荷从该点移到位置时电场力所做的功． ②电场力做功与电势能变化的关系：电场力做的功等于，即W AB ＝E p A －E p B ＝－ΔE p . 2．电势(1)定义：电荷在电场中某一点的电势能与它的电荷量的比值，叫做这一点的电势，用φ表示．在数值上等于单位正电荷由该点移到零电势时，电势是标量，只有大小，没有方向，但有正负．(2)公式：φ＝E p q(与试探电荷无关) (3)单位：伏特(V)(4)电势与电场线的关系：沿电场线方向电势降低．(电场线指向电势降低最快的方向)(5)零电势位置的规定：电场中某一点的电势的数值与零电势的选择有关，即电势的数值决定于零电势的选择．(大地或无穷远默认为零)3．等势面(1)定义：电场中电势相同的各点构成的面叫做等势面．(2)等势面的特点①等势面一定和电场线垂直．②等势面上各点电势相等，在等势面上移动电荷时电场力不做功．③电场线总是由电势高的等势面指向电势低的等势面．④电场线越密的地方，等差等势面越密．,电势差Ⅱ(考纲要求)1.定义：电荷在电场中，由一点A移到另一点B时，与移动电荷的的比值．2．定义式：U AB＝．3．电势差与电势的关系：U AB＝，U AB＝－U BA.4．影响因素：电势差U AB由电场本身的性质决定，与移动的电荷q及电场力做的功W AB，与零电势点的选取．,匀强电场中电势差与电场强度的关系Ⅰ(考纲要求)1．电势差与电场强度的关系式：U AB＝Ed，其中d为电场中两点间的距离．(如右上图所示)2．电场强度的方向和大小：电场中，电场强度方向是指最快的方向．在匀强电场中，电场强度在数值上等于沿方向每单位距离上降低的电势．特别提醒：(1)U＝Ed只适于匀强电场的定量计算．(2)在非匀强电场中也可用U＝Ed定性判断电势差的大小.静电现象的解释Ⅰ(考纲要求)1.静电感应、静电平衡：把金属导体放在外电场中，导体内的自由电子受电场力作用而，使导体的两面出现等量的电荷，这种现象叫静电感应；当导体内自由电子的定向移动时，导体处于静电平衡状态.2.静电屏蔽金属壳或金属网罩所包围的区域，不受电场的影响，这种现象叫做静电屏蔽.一、基础测试1.下列关于电荷在电场中电势能的说法正确的是().A.电荷在电场强度大的地方，电势能一定大B.电荷在电场强度为零的地方，电势能一定为零C.电荷只在电场力的作用下从某点移动到另一点，电荷的电势能一定减少D.电荷只在电场力的作用下从某点移动到另一点，电荷的电势能可能增加，也可能减少2.下列说法正确的是().A.A、B两点的电势差等于将正电荷从A点移到B点时电场力所做的功B.电势差是一个标量，但是有正值或负值之分C.由于电场力做功跟移动电荷的路径无关，所以电势差也跟移动电荷的路径无关，只跟这两点的位置有关D.A、B两点的电势差是恒定的，不随零电势面的不同而改变，所以U AB＝U BA3.(2012·重庆模拟)如下图左所示，正点电荷Q产生的电场中，已知A、B间的电势差为U，现将电荷量为q的正点电荷从B移到A，则().A.外力克服电场力做功QU，电势能增加qUB.外力克服电场力做功qU，电势能增加QUC.外力克服电场力做功qU，电势能增加qUD.外力克服电场力做功QU，电势能减少QU4.(2012·湖北宜昌高三检测)如上图右所示是一个匀强电场的等势面，每两个相邻等势面相距2 cm，由此可以确定电场强度的方向和数值是().A.竖直向下，E＝100 V/mB.水平向左，E＝100 V/mC.水平向左，E＝200 V/mD.水平向右，E＝200 V/m5.(2012·江苏盐城、泰州联考)如图所示，虚线a、b、c代表电场中的三个等势面，相邻等势面之间的电势差相等，即U ab＝U bc，实线为一带正电的质点仅在电场力作用下通过该区域时的运动轨迹，P、Q是这条轨迹上的两点．据此可知().A.三个等势面中，c的电势最高B.带电质点通过P点时的电势能较Q点大.带电质点通过P点时的动能较Q点大D.带电质点通过P点时的加速度较Q点大二、高考体验（一）电场的能的性质(高频考查)1．(2009·上海)位于A、B处的两个带有不等量负电的点电荷在平面内电势分布如图所示，图中实线表示等势线，则()．A．a点和b点的电场强度相同B．正电荷从c点移到d点，电场力做正功C．负电荷从a点移到c点，电场力做正功D．正电荷从e点沿图中虚线移到f点电势能先减小后增大2．(2010·天津理综，5)在静电场中，将一正电荷从a点移到b点，电场力做了负功，则()．A．b点的电场强度一定比a点大B．电场线方向一定从b指向aC．b点的电势一定比a点高D．该电荷的动能一定减小3．(2010·山东理综，20)某电场的电场线分布如图，以下说法正确的是()．A．c点电场强度大于b点电场强度B．a点电势高于b点电势C．若将一试探电荷＋q由a点释放，它将沿电场线运动到b点D．若在d点再固定一点电荷－Q，将一试探电荷＋q由a移至b的过程中，电势能减小4．(2011·江苏卷，8)一粒子从A点射入电场，从B点射出，电场的等势面和粒子的运动轨迹如图所示，图中左侧前三个等势面彼此平行，不计粒子的重力．下列说法正确的有()．A．粒子带负电荷B．粒子的加速度先不变，后变小C．粒子的速度不断增大D．粒子的电势能先减小，后增大（二）电势、电势差、与电场强度的关系(中频考查)5．(2010·江苏单科，5)空间有一沿x轴对称分布的电场，其电场强度E随x变化的图象如图示．下列说法中正确的是()．A．O点的电势最低B．x2点的电势最高C．x1和－x1两点的电势相等D．x1和x3两点的电势相等6．(2010·安徽理综)如图所示，在xOy平面内有一个以O为圆心、半径R＝0.1 m的圆，P为圆周上的一点，O、P两点连线与x轴正方向的夹角为θ.若空间存在沿y轴负方向的匀强电场，电场强度大小E＝100 V/m，则O、P两点的电势差可表示为()．A．U OP＝－10sin θ(V)B．U OP＝10sin θ(V)C．U OP＝－10cos θ(V)D．U OP＝10cos θ(V)7．(2011·海南卷，1)关于静电场，下列说法正确的是()．A．电势等于零的物体一定不带电B．电场强度为零的点，电势一定为零C．同一电场线上的各点，电势一定相等D．负电荷沿电场线方向移动时，电势能一定增加第三部分电容器带电粒子在电场中的运动,常见电容器电容器的电压、电荷量和电容的关系 Ⅰ(考纲要求)1．常见电容器(1)组成：由两个彼此又相互的导体组成． (2)带电荷量：一个极板所带电荷量的． (3)电容器的充、放电充电：使电容器带电的过程，充电后电容器两板带上等量的，电容器中储存．放电：使充电后的电容器失去电荷的过程，放电过程中转化为其他形式的能． 2．电容(1)定义：电容器所带的与电容器两极板间的电势差U 的比值．(2)定义式：C ＝．(3)物理意义：表示电容器本领大小的物理量． (4)单位：法拉(F)1 F ＝ μF ＝1012pF 3．平行板电容器(1)影响因素：平行板电容器的电容与成正比，与介质的介电常数成正比，与两板间的距离成反比． (2)决定式：C ＝，k 为静电力常量．,带电粒子在匀强电场中的运动 Ⅱ(考纲要求)1.带电粒子在电场中的加速带电粒子沿与电场线平行的方向进入电场，带电粒子将做运动．有两种分析法： (1)用动力学观点分析：a ＝qE m ，E ＝U d，v 2－v 20＝2ad . (2)用功能观点分析：粒子只受电场力作用，电场力做的功等于物体动能的变化．qU ＝12mv 2－12mv 202．带电粒子在匀强电场中的偏转(1)研究条件：带电粒子垂直于电场方向进入匀强电场． (2)处理方法：类似于平抛运动，应用运动的的方法．①沿初速度方向做运动，运动时间t ＝l v 0②沿电场力方向，做运动⎩⎪⎨⎪⎧加速度：a ＝F m ＝qE m ＝Uq md离开电场时的偏移量：y ＝12at 2＝Uql 22mdv2离开电场时的偏转角：tan θ＝v yv 0＝Uql mdv20示波管 Ⅰ(考纲要求)1.构造：(1) ，(2) ，(3)2.工作原理(如右上图所示)(1)如果在偏转电极XX ′和YY ′之间都没有加电压，则电子枪射出的电子沿直线运动，打在荧光屏，在那里产生一个亮斑.(2)YY′上加的是待显示的，XX ′上是机器自身产生的锯齿形电压，叫做扫描电压，若所加扫描电压和信号电压的周期相同，就可以在荧光屏上得到待测信号在一个周期内变化的稳定图象. 一图二结论（如右下图）结论：(1)粒子以一定速度v 0垂直射入偏转电场．粒子从偏转电场中射出时，就像是从极板间的l/2处沿直线射出的.(2)经过相同电场加速，又经过相同电场偏转的带电粒子，其运动轨迹重合，与粒子的带电荷量和质量无关. 一、基础自测1.下列关于电容的说法正确的是( ). A.电容器简称电容B.电容器A 的电容比B 的大，说明A 的带电荷量比B 多C.电容在数值上等于使两极板间的电势差为1 V 时电容器需要带的电荷量D.由公式C ＝QU知，电容器的电容与电容器两极板间的电势差成反比，与电容器所带的电荷量成正比2.(2012·徐州高三检测)如图所示，用静电计可以测量已充电的平行板电容器两极板之间的电势差U ，现使B 板带正电，则下列判断正确的是( ). A.增大两极板之间的距离，静电计指针张角变大 B.将A 板稍微上移，静电计指针张角将变大C.若将玻璃板插入两板之间，则静电计指针张角变大D.若将A 板拿走，则静电计指针张角变为零3.一个带电小球，用细绳悬挂在水平方向的匀强电场中，当小球静止后把悬绳烧断，小球将做( ). A.自由落体运动 B.匀变速曲线运动方向 C.沿悬绳的延长线方向做匀加速直线运动 D.变加速直线运动4.电子以初速度v 0沿垂直电场强度方向射入两平行金属板间的匀强电场中，现增大两极板间的电压，但仍使电子能够穿过平行金属板，则电子穿过平行金属板所需要的时间( ). A.随电压的增大而减小 B.随电压的增大而增大 C.加大两板间距离，时间将减小 D.与电压及两板间距离均无关5.(2011·长春调研)如图所示，静止的电子在加速电压为U 1的电场作用下从O 经P 板的小孔射出，又垂直进入平行金属板间的电场，在偏转电压为U 2的电场作用下偏转一段距离．现使U 1加倍，要想使电子的运动轨迹不发生变化，应该( ).A.使U 2加倍B.使U 2变为原来的4倍C.使U 2变为原来的2倍D.使U 2变为原来的12倍二、高考体验（一）平行电容器的动态分析问题(高频考查)1．(2009·海南)一平行板电容器两极板间距离为d 、极板面积为S ，电容为ε0Sd ，其中ε0是常量．对此电容器充电后断开电源．当增加两板间距时，电容器极板间( )．A ．电场强度不变，电势差变大B ．电场强度不变，电势差不变C ．电场强度减小，电势差不变D ．电场强度减小，电势差减小 2．(2010·北京理综)用控制变量法，可以研究影响平行板电容器电容的因素(如图所示)．设两极板正对面积为S ，极板间的距离为d ，静电计指针偏角为θ.实验中，极板所带电荷量不变，若( )．A ．保持S 不变，增大d ，则θ变大B ．保持S 不变，增大d ，则θ变小C ．保持d 不变，减小S ，则θ变小D ．保持d 不变，减小S ，则θ不变3．(2011·天津卷，5)板间距为d 的平行板电容器所带电荷量为Q 时，两极板间电势差为U 1，板间电场强度为E 1.现将电容器所带电荷量变为2Q ，板间距变为12d ，其他条件不变，这时两极板间电势差为U 2，板间电场强度为E 2，下列说法正确的是( )．A ．U 2＝U 1，E 2＝E 1B ．U 2＝2U 1，E 2＝4E 1C ．U 2＝U 1，E 2＝2E 1D ．U 2＝2U 1，E 2＝2E 1 （二）带电粒子在电场中的运动(高频考查) 4．(2011·安徽卷，20)如图(a)所示，两平行正对的金属板A 、B 间加有如图(b)所示的交变电压，一重力可忽略不计的带正电粒子被固定在两板的正中间P 处．若在t 0时刻释放该粒子，粒子会时而向A 板运动，时而向B 板运动，并最终打在A 板上．则t0可能属于的时间段是( )．A ．0<t 0<T 4 B.T 2<t 0<3T4C.3T 4<t 0<T D ．T <t 0<9T85．(2011·安徽卷，18)图(a)所示为示波管的原理图．如果在电极YY ′之间所加的电压按图(b)所示的规律变化，在电极XX ′之间所加的电压按图(c)所示的规律变化，则在荧光屏上会看到的图形是( )．6．(2011·福建卷，20)反射式速调管是常用的微波器件之一，它利用电子团在电场中的振荡来产生微波，其振荡原理与下述过程类似．如图所示，在虚线MN 两侧分别存在着方向相反的两个匀强电场，一带电微粒从A 点由静止开始，在电场力作用下沿直线在A 、B 两点间往返运动．已知电场强度的大小分别是E 1＝2.0×103 N/C和E 2＝4.0×103 N/C ，方向如图所示，带电微粒质量m ＝1.0×10－20 kg ，带电荷量q ＝－1.0×10－9C ，A 点距虚线MN 的距离d 1＝1.0 cm ，不计带电微粒的重力，忽略相对论效应．求： (1)B 点距虚线MN 的距离d 2；(2)带电微粒从A 点运动到B 点所经历的时间t .。

第6章静电场中的导体与介质

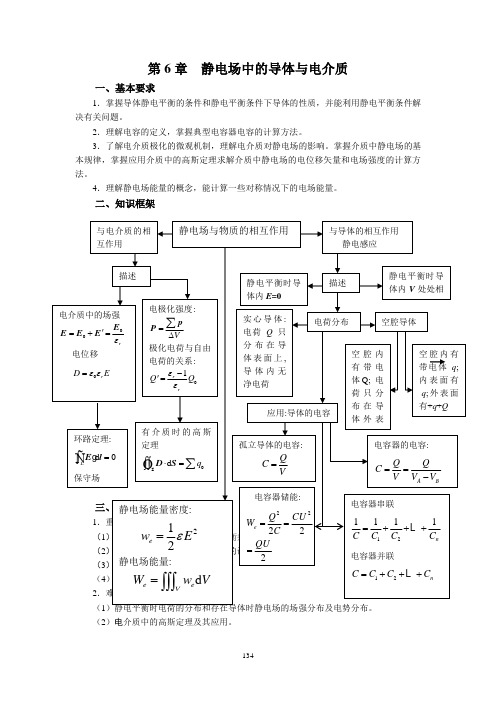
第6章静电场中的导体与电介质一、基本要求1．掌握导体静电平衡的条件和静电平衡条件下导体的性质，并能利用静电平衡条件解决有关问题。

2．理解电容的定义，掌握典型电容器电容的计算方法。

3．了解电介质极化的微观机制，理解电介质对静电场的影响。

掌握介质中静电场的基本规律，掌握应用介质中的高斯定理求解介质中静电场的电位移矢量和电场强度的计算方法。

4．理解静电场能量的概念，能计算一些对称情况下的电场能量。

二、知识框架三、知识要点 1．重点（2）电介质中的高斯定理及其应用。

1C ++n C ++d 0L =⎰E l 保守场Sd q ⋅=∑⎰⎰D S 静电场能量密度:1四、基本概念及规律1．导体的静电平衡条件及其性质（1）导体的静电平衡条件导体内部电场强度处处为零，即 0=内E （2）导体处于静电平衡时的性质 ① 导体是等势体，导体表面是等势面。

② 导体表面的场强处处与导体表面垂直，导体表面附近的场强大小与该处导体表面的面密度σ成正比，即0 E e nσε=表面 ③ 电荷只分布在导体外表面。

（3）静电屏蔽在静电平衡条件下，空腔导体内部电场不受外部电场的影响，接地空腔导体内部与外部电场互不影响，这种现象称为静电屏蔽。

2．电容C（1）孤立导体的电容 Vq C =电容的物理意义：使导体每升高单位电势所需的电量。

（2）电容器的电容 BA V V qC -=（3）电容器两极板间充满电介质后的电容 0C C r ε= 其中C 0是两极板间为真空时的电容，r ε是电介质的相对介电常数。

（4）几种常见电容器的电容① 平行板电容器 dSC r εε0=② 同心球形电容器 AB BA rR R R R C -=επε04 （R B ＞R A ）③ 同轴圆柱形电容器 AB rR R lC ln 20επε= （R B ＞R A ）（5）电容器的串并联① 电容器串联后的总电容3211111C C C C ++=+…+nC 1② 电容器并联后的总电容 C = C 1+ C 2 + C 3+ … + C n 3．电介质中的静电场（1）电极化强度电介质中任一点的电极化强度等于单位体积中所有分子的电偶极矩的矢量和，即 iV∆∑P P =① 对于各向同性的电介质 00(1)r e εεχε-=P =E E 其中1-=r e εχ称为电介质的极化率。

第六章静电场6-3(新课标复习资料)

随堂针对训练
考技案例导析
易错易混分析
限时规范特训
选修3-1
第六章静电场
金版教程
基础知识梳理
高三物理
(2)用功能观点分析：粒子动能的变化量等于电场力对它所做的功(电场可以是匀强或非匀强电场)．若粒子的初
随堂针对训练
考技案例导析
1 2 速度为零，则：qU＝ mv ⇒v＝ 2
2qU ；若粒子的初速度 m 2qU 2 v0＋ . m
限时规范特训
1 2 1 2 不为零，则：qU＝ mv － mv0⇒v＝ 2 2
易错易混分析
选修3-1
第六章静电场
金版教程
基础知识梳理
高三物理
例 2 飞行时间质谱仪可对气体分子进行分析．如图所示，在真空状态下，脉冲阀 P 喷出微量气体，经激光照射产生电荷量为 q、质量为 m 的正离子，自 a 板小孔进入
高三物理
(2)第二类动态变化
随堂针对训练
考技案例导析
易错易混分析
限时规范特训
选修3-1
第六章静电场
金版教程
基础知识梳理
高三物理
关键一点：
考技案例导析
在分析平行板电容器的电容及其他参
随堂针对训练
量的动态变化时，有两个技巧：(1)确定不变量，(2)选择合适的公式分析．
随堂针对训练
考技案例导析
易错易混分析
限时规范特训
选修3-1
第六章静电场
金版教程

第6章静电场.ppt

er 0i
例：设电荷的分布如右图所示，图中 q1=1.5×10-3C， q2= –0.5×10-3C，q3= 0.2×10-3C，AC = r1=1.2m， BC=r2=0.5m，试求作用在电荷q3上的合力。
解: q1和q3之间的力是斥力
q2 B
F1

q1q3
4 0 r12
q1
1.875103 N
F

n Fi
i 1

n
q0 Fi
q0
q0
q i1 0
qi n
E Ei i 1
即： n 个点电荷产生的电场中某点的电场强度等于各点电荷单独存在时在该点产生的电场强度的矢量和。
它是电力叠加原理的直接结果，是求解电场的一个重要基础。
四、点电荷的场强公式
由库仑定律由场强定义
，证明了微小粒子带电量的变化不连续性。
+
3.电荷数：微观粒子所带的基元电荷的个数。
Q Ne
现代物理预言夸克

1 3
e

2 3
e
3. 电荷守恒
1. 表述：在一个和外界没有电荷交换的系统内，正负电荷的代数和在任何物理过程中保持不变。电荷守恒定律是物理学中普遍的基本定律。
2. 正、负电子的湮灭和产生：电子对的“产生”和“湮灭”并不破坏电荷守恒 [光子] → [电子] + [正电子] 产生电荷： (+e) + (-e) 0 [电子] + [正电子] → [光子] 湮灭电荷： 0 (+e) + (-e)
检验电荷
电量充分地小线度足够地小
实验发现: 在电场中任取A点处
Q