高中文科数学高考模拟试卷
高三高考文科模拟试卷数学

一、选择题(本大题共10小题,每小题5分,共50分)1. 已知函数f(x) = ax^2 + bx + c,其中a ≠ 0,且f(1) = 2,f(2) = 8,f(3) = 18。
则a、b、c的值分别为:A. 1, 3, 0B. 2, 2, 0C. 3, 1, 0D. 1, 1, 22. 下列函数中,有最小值的是:A. y = x^2B. y = x^3C. y = -x^2D. y = x^43. 若复数z满足|z - 1| = |z + 1|,则复数z的取值范围是:A. 实轴上B. 第一象限C. 第二象限D. 第四象限4. 已知数列{an}的前n项和为Sn,且a1 = 1,an = an-1 + 2n。
则数列{an}的通项公式是:A. an = n^2 - n + 1B. an = n^2C. an = n(n + 1)D. an = n^2 + 15. 若等差数列{an}的前n项和为Sn,且a1 = 1,公差d = 2。
则S10的值为:B. 90C. 100D. 1106. 已知等比数列{bn}的前n项和为Tn,且b1 = 1,公比q = 2。
则T5的值为:A. 31B. 32C. 33D. 347. 在直角坐标系中,点P(2, 3)关于直线y = x的对称点为:A. (3, 2)B. (2, 3)C. (3, 3)D. (2, 2)8. 函数y = log2(x - 1)的图像大致为:A. 上升的曲线B. 下降的曲线C. 平坦的直线D. 抛物线9. 已知直线l的方程为x - y + 1 = 0,点A(2, 3)到直线l的距离为:A. 1B. 2C. 310. 若直线y = kx + b与圆x^2 + y^2 = 4相切,则k和b的关系为:A. k^2 + b^2 = 4B. k^2 + b^2 = 16C. k^2 - b^2 = 4D. k^2 - b^2 = 16二、填空题(本大题共10小题,每小题5分,共50分)11. 若复数z满足|z - 1| = |z + 1|,则z的实部为______。
高三数学文科模拟试题

高三数学文科模拟试题一、选择题(本题共8小题,每小题5分,共40分。
每小题只有一个选项符合题意)1. 下列函数中,哪一个是奇函数?A. y = x^2B. y = x^3C. y = x^2 + 1D. y = x + 12. 已知圆的方程为(x-1)^2 + (y-2)^2 = 9,该圆的圆心坐标是?A. (1, 2)B. (-1, 2)C. (1, -2)D. (-1, -2)3. 函数f(x) = 2x + 3在区间[1, 3]上的最大值是?A. 5B. 7C. 8D. 114. 若直线l的斜率为2,且过点(1, 3),则直线l的方程为?A. y = 2x + 1B. y = 2x - 1C. y = -2x + 5D. y = -2x - 15. 已知向量a = (3, -1),向量b = (2, 4),则向量a与向量b的数量积为?A. 10B. -2C. 8D. -106. 函数y = sin(x) + cos(x)的值域是?A. [-1, 1]B. [0, 2]C. [-√2, √2]D. [1, √2]7. 已知等差数列{an}的首项a1 = 2,公差d = 3,则该数列的前5项和S5为?A. 25B. 40C. 55D. 708. 双曲线x^2/a^2 - y^2/b^2 = 1的渐近线方程为?A. y = ±(b/a)xB. y = ±(a/b)xC. y = ±xD. y = ±√2x二、填空题(本题共4小题,每小题5分,共20分)9. 已知抛物线y^2 = 4x的焦点坐标为______。
10. 函数f(x) = x^2 - 4x + 3的对称轴为直线x = ______。
11. 已知三角形ABC的三边长分别为a, b, c,且a^2 + b^2 = c^2,若a = 3, b = 4,则c = ______。
12. 已知正弦函数y = sin(2x)的周期为π,则该函数的最小正周期为______。
高考数学(文科)模拟试卷及答案3套

又∵ AD / /BC ,∴ BC BD .
又∵ D1D BD D , BD 平面 D1BD , D1D 平面 D1BD ,
∴ BC 平面 D1BD ,( 4 分)
而 BC 平面 D1BC ,
∴平面 D1BC 平面 D1BD ;(6 分)
(2)∵ D1D 平面 ABCD ,
∴ D1BD 即为直线 D1B 与底面 ABCD 所成的角,即
D1 BD
,( 7 分)
6
而 BD 2 3 ,∴ DD 1 2 . ( 8 分)
V V 又 C MNQ
Q CMN
1 4 VQ BDC ,∴ VC MNQ
111 23 2 1
432
3
( 12 分)
6
20. 解:( 1)依题意可设圆 C 方程为 x2 y 2 b2 ,
Q 圆 C 与直线 x y
2 0 相切, b
椭圆 C 的短半轴长为半径的圆与直线 x y 2 0 相切.
(1)求椭圆 C 的方程; (2)如图,过定点 P( 2,0)的直线 l 交椭圆 C 于 A,B 两点, 连接 AF 并延长交 C于 M,求证:∠ PFM=∠ PFB.
文科试卷 4
21、(本小题满分 12 分)
已知函数
.
(Ⅰ)求函数
极值;
a2019
.
15、已知 a 0,b 0,ab 8, 则当 a 的值为
时 log 2 a log2 2b 取得最大值 .
16、一个倒置圆锥形容器, 底面直径与母线长相等, 容器内存有部分水,
向容器内放入一个半径为 1 的铁球, 铁球恰好完全没入水中 (水面与铁
球相切)则容器内水的体积为 _____ .
则这三天中至少有两天有强浓雾的概率近似为(
高考数学(文科)模拟试卷及答案3套

高考数学(文科)模拟试卷及答案3套模拟试卷一第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的. 1.已知复数ii z 1-=,则=||z ( ) .A 2 .B22.C 1 .D 2 2.已知集合}02|{2<-=x x x A ,集合}2,121,0,1{,-=B ,则集合B A I 的子集个数为( ).A 1 .B 2 .C 4 .D 83.已知向量,满足2||||||=-==,则=+||( ).A 72 .B 2 .C 52 .D 324.已知函数x x x f sin 12cos2)(2⎪⎭⎫⎝⎛-=,则函数)(x f 的最小正周期和最大值分别为( ) .A π和1 .B π和21.C π2和1 .D π2和215.中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其意思为:有一个人要走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地,请问第二天走了( ) .A 24里 .B 48里 .C 96里 .D 192里 6.已知函数x x x f +=ln )(,则函数)(x f 在1=x 处的切线方程为( ).A 012=--y x .B 012=++y x .C 02=-y x .D 012=+-y x7.设函数⎩⎨⎧≤+>=-0,120,log )(3x x x x f x,若2)(=a f ,则实数a 的值为( ).A 9 .B 0或9 .C 0 .D 1-或98.已知双曲线1324:22=-y x C 的左右焦点分别为21,F F ,点P 是双曲线C 右支上一点,若||||221PF F F =,︒=∠3021F PF ,则||1PF 的长为( ).A 324+ .B )63(2+ .C 832+ .D 632+9.若数列}12{+n a 是等差数列,其公差1=d ,且53=a ,则10a =( ).A 18 .B217 .C 219 .D 12 10.已知三棱柱111C B A ABC -,棱⊥1AA 面ABC ,ABC ∆是边长为2的等边三角形,且41=AA ,点M 是棱1AA 的中点,则异面直线CM 与AB 所成角的余弦值为( ).A 41 .B 21 .C 42 .D 4311.已知圆1:22=+y x O ,过直线02:=-+y x l 上第一象限内的一动点M 作圆O 的两条切线,切点分别为B A ,,过B A ,两点的直线与坐标轴分别交于Q P ,两点,则OPQ ∆面积的最小值为( ).A 1 .B 21 .C 41 .D 8112.已知函数x x ax x f ln 2)(2++=存在极值,若这些极值的和大于7-,则实数a 的取值范围为( ).A )4,52(-- .B ),4()4,(+∞--∞Y .C )52,4()4,52(Y -- .D )4,(--∞第Ⅱ卷(非选择题 共90分)本试卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须作答.第22题~第23题为选考题,考生根据要求作答.二、填空题:本大题共4小题,每小题5分,共20分.将答案填在机读卡上相应的位置.13.已知0>x ,则xx x 42+-的最小值是 ;14.某班随机抽查了B A ,两组各10名学生的数学成绩,分数制成如图的茎叶图,试比较B A ,两组学生的平均分A x B x ;(用“>”或“<”或“=”连接)15.已知抛物线x y C 4:2=的焦点为F ,倾斜角为3π的直线l 过点F ,且与抛物线C 交于B A ,两点,则AOB ∆的面积为________;16.水平放置一个底面半径为20cm ,高为100cm 的圆柱形水桶(不计水桶厚度),内装高度为50cm 的水,现将一个高为10cm 圆锥形铁器放入水桶中并完全没入水中(圆锥的底面半径小于20cm),圆柱形水桶的水面高度上升了2.5cm,则圆锥形铁器的侧面积为________2cm .三、解答题:本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤. 17. (本小题满分12分)在ABC ∆中,设边c b a ,,所对的角分别为C B A ,,,cb aC A +-=2cos cos . (Ⅰ)求角A 的大小;(Ⅱ)若,2=b ABC ∆的面积为32,求a 的值. 18.(本小题满分12分)在三棱锥BCD A -中,G 是ACD ∆的重心,⊥AB 平面BCD ,且F 在棱AB 上,满足FB AF 2=,22,2====CD BD BC AB ,(1)求证://GF 平面BCD ;(2)求三棱锥BCD G -的体积.19.(本小题满分12分)2020年哈尔滨市第六中学为了响应市政府倡议的“百万青少年上冰雪”活动的号召.开展了丰富的冰上体育兴趣课,为了了解学生对冰球的兴趣,随机从该校高三年级抽取了100名学生进行调查,其中男生和女生中对冰球运动有兴趣的人数比是3: 2,男生有15人对冰球没有兴趣,占男生人数的31. (1)从被调查的对冰球有兴趣的学生中抽取男生3人,女生2人,再从中抽取2人,求抽到的都是女生的概率. ?有兴趣 没兴趣 合计 男 女 合计附表:20()P K k ≥0.150 0.100 0.050 0.025 0.0100k2.072 2.7063.841 5.024 6.635))()()(()(22d b c a d c b a bc ad n K ++++-=,其中d c b a n +++=20.(本小题满分12分)已知函数)0(,2)2(ln )(2>++-+=a x a x a x x f (1) 讨论函数)(x f 的单调性;(2)若函数x x a x f x g ln )()()(--=在⎥⎦⎤⎢⎣⎡e e ,1上有两个零点,求a 的取值范围.21.(本小题满分12分)在平面直角坐标系中,已知动点M 与到定点)(0,1F 距离到定直线2=x 的距离比为22. (Ⅰ)求动点M 轨迹C 的方程;(Ⅱ)过点F 的直线l 交轨迹C 于B A ,两点,若轨迹C 上存在点P ,使OB OA OP 23+=,求直线l 的方程.请考生在22、23两题中任选一题作答,如果多做,则按所做的的第一题记分. 22.(本小题满分10分) 选修4-4:坐标系与参数方程 已知曲线1C 的参数方程为⎩⎨⎧=+=θθsin cos 1y x (θ为参数),以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线2C 的极坐标方程为θρsin 32=.(Ⅰ)写出曲线1C 的极坐标方程,并求出曲线1C 与2C 公共弦所在直线的极坐标方程; (Ⅱ)若射线)(20πϕϕθ<<=与曲线1C 交于A O ,两点,与曲线2C 交于B O ,两点,且2||=AB ,求ϕ的值.23.(本小题满分10分) 选修4—5:不等式选讲 设|1|||)(ax a x x f ++-=(0>a ) (Ⅰ)证明:2)(≥x f ;(Ⅱ)若3)2(>f ,求a 的取值范围.答案一、选择题ACDBC ABDBC BA二、填空题 13.3 14.< 15.334 16.2)(3200cm π 三、解答题17.(本小题满分12分) 解:(1)由正弦定理可得:CB AC A sin sin 2sin cos cos +-=0cos sin cos sin sin cos 2=++C A A C B A0sin cos sin 2=+B A B ————————3分0sin ),,0(>∴∈B B πΘ————————4分,21cos -=∴A ————————5分32π=A ————————6分 (2)将32π=A ,322==S b ,,代入A bc S sin 21=可得4=c ————————9分由余弦定理可得72=a ————————————12分 18. (本小题满分12分)(1)证明:连接FG ,连接AG 并延长交CD 于点E ,连接BE ,G Θ是ACD ∆的重心,2=∴,又Θ2=,BE GF //∴————————2分又⊄FG Θ平面BCD ,————————————3分 且⊂BE 平面BCD ————————————4分//GF ∴平面BCD ————————————6分由(1)可知//GF 平面BCD ,所以BCD F BCD G V V --=————————————8分 且⊥AB 平面BCD ,FB ∴为三棱锥BCD F -的高,32231||=⨯=FB ————————————9分 则22221=⨯⨯=∆BCDS ————————————10分 9423231=⨯⨯==--BCD F BCD G V V ————————————12分19.(本小题满分12分)解:(1)设“抽到的都是女生 ”为事件D ——————————1分不妨设3个男生分别是:321,,n n n ,两个女生分别为:21,A A从中任选两人有:()21,n n ,()31,n n ,()11,A n ,()21,A n ,()32,n n ,()12,A n ,()22,A n ,()13,A n ,()23,A n ,()21,A A共10种,——————————3分 其中都是女生:()21,A A 共1种,则101)(=D P ——————————4分 (2)男生总数:45315=⨯人,男生中有兴趣的301545=-人——————————5分女生中有兴趣的20230=⨯——————————6分22100(30352015)1009.091 2.7065050455511K ⨯-⨯==≈>⨯⨯⨯——————————11分有%90的把握认为“性别与对冰球是否有兴趣有关”——————————12分20. (本小题满分12分) (1)xx a x a x a x x f )1)(2()2(2)('--=+-+=——————————1分 当20<<a 时,)(x f 的单调增区间为),1(),2,0(+∞a ;减区间为)1,2(a——————————2分当2=a 时,)(x f 的单调增区间为),0(+∞,无减区间;——————————3分当2>a 时,)(x f 的单调增区间为),2(),1,0(+∞a ;减区间为)2,1(a ——————————4分 (2)2)2(ln )(2++-+=x a x x x x g ,02)2(ln 2=++-+x a x x x 将变量与参数分开得:xx x a 2ln 2++=+——————————5分令xx x x h 2ln )(++= xx x x x x x x x h )1)(2(2211)('222-+=-+=-+=,——————————6分可得)(x h 的单调减区间是)1,1(e,单调减区间是),1(e ,即1=x 是极小值点(需列表)—————8分ee e h e e e h h 21)(,112)1(,3)1(++=+-==——————————9分)1()(eh e h <Θ——————————10分e e a 2123++≤+<∴即ee a 211+-≤<∴——————————12分21. (本小题满分12分)解(Ⅰ)设)(y x M ,因为,M 到定点)(0,1F 的距离与到定直线2=x 的距离之比为22,所以有|2|||x MF -=——————————————2分代入得1222=+y x ————————————4分 (Ⅱ)由题意直线l 斜率存在,设),(),,(),1(:2211y x B y x A x k y l -=(2)联立方程得,⎪⎩⎪⎨⎧-==+)1(1222x k y y x ,0124)12(2222=-+-+k x k x k ,∴0>∆恒成立∴⎪⎪⎩⎪⎪⎨⎧+-=+=+122212422212221k k x x k k x x ,---------5分OB OA OP 23+=,所以,23,232121y y y x x x p p +=+=代入椭圆有223223221221=+++)()(y y x x ,又222121=+y x ,222222=+y x ————————6分得22349212122222121=+++++)()()(y y x x y x y x02232121=++y y x x ,——————————————————9分 得02)(212232212212=++-++k x x k x x k )( 代入得612=k ——————————————11分直线方程l :)1(66-±=x y —————————12分 22.(本小题满分10分)解:(Ⅰ)曲线1C 的极坐标方程为θρcos 2=—————————2分θρsin 32=,θρcos 2=,得33tan =θ————————3分 所在直线的极坐标方程)(R ∈=ρπθ6,(或6πθ=和67πθ=)——————5分 (Ⅱ)把)(20πϕϕθ<<=,代入θρsin 32=,θρcos 2=, 得ϕcos 2||=OA ;ϕsin 32||=OB ——------6分 又2||=AB ,则2|cos 2sin 32|=-ϕϕ,),(,)(36621|6sin |πππϕπϕ-∈-=-——————9分 所以3πϕ=------10分23.(本小题满分10分)(Ⅰ)证明:2|1||1||1|||)(≥+=---≥++-=a a a x a x a x a x x f ;——————5分 (Ⅱ)aa a a f 11|2|3|12||2|)2(-<-⇔<++-=————————7分23102151211+<<+⇒<-<-a a a a ————————10分模拟试卷二一、选择题:共12 小题,每小题 5 分,共 60 分.1、若全集R U =,集合),4()1,(+∞--∞=Y A ,{}2||≤=x x B ,则如图阴影部分所表示的集合为 A.{}42<≤-x x B.{}42≥≤x x x 或 C.{}12-≤≤-x x D.{}21≤≤-x x 2、已知)1)(1(ai i -+0>(i 为虚数单位),则实数a 等于( ) A.1- B.0 C.1D.23、已知函数()xx x f )31(3-=,则()x f ( )A .是奇函数,且在 R 上是增函数B .是偶函数,且在 R 上是增函数C .是奇函数,且在 R 上是减函数D .是偶函数,且在 R 上是减函数 4、,是单位向量,“2)(2<+”是“,的夹角为钝角”的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件5、已知圆C 的圆心在坐标轴上,且经过点()0,6及椭圆141622=+y x 的两个顶点,则该圆的标准方程为( )A. ()16222=+-y x B. 72)6(22=-+y x C.91003822=+⎪⎭⎫ ⎝⎛-y x D. 91003822=+⎪⎭⎫ ⎝⎛+y x 6、古代数学著作《九章算术》有如下的问题:“今有女子善织,日自倍,五日织五尺,问日织几何?”意思是:“一女子善于织布,每天织的布都是前一天的2倍,己知她5天共织布5尺,问这女子每天分别织布多少?”根据上述己知条件,若要使织布的总尺数不少于30尺,则至少需要( ) A .6天 B .7天 C .8天 D .9天 7、过点()1,1P 的直线,将圆形区域(){}4,22≤+y x y x 分两部分,使.这两部分的面积之差最大,则该直线的方程为( )A.02=-+y xB.1=yC. 0=-y xD.043=-+y x 8、若1cos()86απ-=,则cos(2)4α3π+=( ) A .1819 B .1718 C .1718- D .1819-9、已知21,F F 是双曲线12222=-by a x 的左右焦点,P 是右支上的动点, M F 2垂直于21PF F ∠ 的平分线,垂足为M ,则点M 的轨迹是( )A 、抛物线弧B 、双曲线弧C 、椭圆弧D 、圆弧 10、已知A 、B 、C 是球O 的球面上三点,三棱锥ABC O -的高为22,且3π=∠ABC , 2=AB ,4=BC , 则球O 的表面积为( )A.π24B.π32C.π48D.π19211、抛物线()02:21>=p py x C 的焦点与双曲线136:222=-y x C 的右焦点的连线在第一象限内与1C 交于点M .若1C 在点M 处的切线平行于2C 的一条渐近线,则=P ( ) A.163 B. 82 C. 223 D. 334 12.函数()1,0252sin 2,0,6x x f x x x ππ⎧≤⎪⎪=⎨⎛⎫⎪+<< ⎪⎪⎝⎭⎩,,若方程()f x a =恰有三个不同的解,记为123,,x x x ,则123x x x ++的取值范围是( )A .10102,33ππ⎛⎫-⎪⎝⎭ B .552,33ππ⎛⎫-⎪⎝⎭ C .10101,33ππ⎛⎫-⎪⎝⎭ D .551,33ππ⎛⎫-⎪⎝⎭二.填空题:本大题共 4 小题,每小题 5 分,共 20 分.13、已知实数,x y 满足65125=+y x的最小值等于 .14、已知椭圆131222=+y x 的左右焦点为21,F F ,点P 在椭圆上,若线段1PF 的中点在y 轴上,则1PF 是2PF 的 倍。
高三数学试卷模拟题文科版

一、选择题(本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1. 已知函数f(x) = x^2 - 2ax + 1,若f(x)的图像关于x=a对称,则a的值为()A. 0B. 1C. -1D. 22. 下列各式中,绝对值最小的是()A. |2x-3|B. |3x-2|C. |x-2|D. |x+2|3. 若复数z满足|z+2i|=|z-1|,则z的实部为()A. 1B. -1C. 2D. -24. 已知数列{an}的通项公式为an = 3n - 2,则数列{an}的前n项和S_n为()A. n(n+1)B. n(n-1)C. 3n(n+1)D. 3n(n-1)5. 已知向量a = (2, 3),向量b = (-1, 2),则向量a·b的值为()A. -1B. 1C. 0D. 56. 若等差数列{an}的首项为2,公差为3,则第10项a_10为()A. 25B. 28C. 31D. 347. 已知函数f(x) = log2(x+1),若f(2x-1) = 3,则x的值为()A. 3B. 4C. 5D. 68. 在△ABC中,若∠A = 60°,∠B = 45°,则∠C的度数为()A. 75°B. 90°C. 105°D. 120°9. 已知等比数列{bn}的首项为b_1,公比为q,若b_3 = 8,b_6 = 32,则b_1的值为()A. 1B. 2C. 4D. 810. 若函数f(x) = x^3 - 3x + 2在x=1处取得极值,则该极值为()A. 0B. -1C. 1D. 2二、填空题(本大题共5小题,每小题5分,共25分。
)11. 若复数z满足|z+1|=|z-1|,则z在复平面上的几何意义是______。
12. 数列{an}的前n项和S_n = n^2 + n,则数列{an}的通项公式an = ______。
高三数学试卷文科模拟

一、选择题(本大题共10小题,每小题5分,共50分)1. 若复数z满足|z-1|=2,则复数z在复平面内的轨迹是()A. 以(1,0)为圆心,2为半径的圆B. 以(1,0)为圆心,1为半径的圆C. 以(1,0)为圆心,2为半径的圆的内部D. 以(1,0)为圆心,2为半径的圆的外部2. 已知函数f(x) = ax^2 + bx + c,其中a≠0,若f(2) = 3,f'(2) = -1,则f(0) = ()A. 3B. -1C. 0D. 23. 下列函数中,定义域为实数集R的是()A. y = 1/xB. y = √(x^2 - 1)C. y = log2(x + 1)D. y = sin(x)4. 已知数列{an}满足an = 2an-1 - 1,且a1 = 1,则数列{an}的通项公式是()A. an = 2^n - 1B. an = 2^nC. an = 2^n + 1D. an = 2^n - 25. 若等差数列{an}的前n项和为Sn,且S5 = 20,S9 = 60,则a1 = ()A. 2B. 4C. 6D. 86. 已知向量a = (2, -3),向量b = (-1, 2),则向量a与向量b的夹角余弦值是()A. 1/5B. -1/5C. 2/5D. -2/57. 若函数f(x) = x^3 - 3x在区间[0, 2]上单调递增,则实数a的取值范围是()A. a ≤ 0B. a ≥ 0C. a < 0D. a > 08. 已知圆C的方程为x^2 + y^2 - 2x - 4y + 5 = 0,则圆C的半径是()A. 1B. 2C. √5D. 59. 若直线y = kx + 1与圆x^2 + y^2 = 1相切,则实数k的取值范围是()A. k < 0B. k ≥ 0C. k > 0D. k ≤ 010. 若函数f(x) = x^3 - 3x^2 + 4x + 1在x = 1处取得极值,则f'(1) = ()A. 0B. 1C. -1D. 2二、填空题(本大题共5小题,每小题5分,共25分)11. 若复数z满足|z-1| = 2,则z的实部是______。
完整)全国卷高考文科数学模拟题

完整)全国卷高考文科数学模拟题本试卷共23小题,满分150分,考试用时120分钟。
一、选择题:本大题共12小题,每小题5分,满分60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若A = {(x。
y)|x+y=0.x。
y∈R}。
B = {(x。
y)|x-y-2=0.x。
y∈R},则集合AB=({(1.-1)}。
{(x。
-1)|x∈R}),故选D。
2.函数f(x) = -x+√(x+1)的定义域为[-1.∞),f'(x) = -1+1/(2√(x+1)),f'(x) < 0,故f(x)在[-1.∞)内是减函数,故选A。
3.若x < 0,则f(x) = x(x+1),f(x) = 0的解为x = 0.-1;若x ≥ 0,则f(x) = x(x-1),f(x) = 0的解为x = 0.1.故函数f(x)的零点个数为4,故选D。
4.根据已知条件列方程组:a1+a3=a2+a8,a2+a8=15-a5.解得a1+a3=15-a5,a5=2a1+2a3-15.又因为a1+a5=a2+a8,代入得a3=a2+a5-a1=3a1+3a3-15,化简得a3=3a1.又因为a1+a3+a5=3a1+a1+3a1=7a1=-8,故a1=-8/7,a3=-24/7,a5=-2/7.故a5=2,故选C。
5.f(-x) = (-x)^4-a(-x)+4 = x^4+ax+4 = f(x),故f(x)为偶函数,故选B。
6.向量a·b = 1·4+x·4 = 4(x+1),|a|=√2,|b|=4,故|a||b|=8,故8=|a||b|=|a·b|=4(x+1),故x=1,故选A。
7.根据已知条件列出方程组:a1+a15=2a8+2,a15-a1=14d,解得a1=-4,d=1,故a5=a1+4d=0,故选B。
8.命题①中,若l//α,则由平面几何基本定理可知l//β,故命题①为真;命题②中,___⊥α,则由平面几何基本定理可知___⊥β,故命题②为真;命题③中,若l//α,则由平面几何基本定理可知m//α,故命题③为假;命题④中,由平面几何基本定理可知l⊥m,m⊥β,故命题④为真。
高考文科数学试卷模拟卷

一、选择题(本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1. 已知函数f(x) = x^2 - 2x + 1,其图像的对称轴是:A. x = 1B. x = 0C. y = 1D. y = 02. 在△ABC中,a=3,b=4,c=5,则△ABC是:A. 直角三角形B. 等腰三角形C. 等边三角形D. 不等边三角形3. 若等差数列{an}的首项a1=2,公差d=3,则第10项an=?A. 27B. 30C. 33D. 364. 下列命题中,正确的是:A. 函数y = log2(x - 1)的定义域为x > 1B. 函数y = 2^x的值域为(0, +∞)C. 函数y = |x|的对称轴为y轴D. 函数y = x^3的增减性为单调递增5. 若复数z满足|z - 1| = |z + 1|,则复数z位于:A. x轴B. y轴C. 第一象限D. 第二象限6. 已知向量a = (2, -1),向量b = (-3, 4),则向量a与向量b的夹角θ满足:A. θ = 0°B. θ = 90°C. θ = 180°D. θ = 270°7. 在下列函数中,奇函数是:A. f(x) = x^2B. f(x) = |x|C. f(x) = x^3D. f(x) = 1/x8. 若等比数列{an}的首项a1=1,公比q=2,则第n项an=?A. 2^nB. 2^(n-1)C. 2^(n+1)D. 2^(n-2)9. 下列不等式中,正确的是:A. |x| > 2B. x^2 > 4C. |x| < 2D. x^2 < 410. 已知函数f(x) = ax^2 + bx + c,若a < 0,b = 0,c > 0,则函数f(x)的图像是:A. 抛物线开口向下B. 抛物线开口向上C. 直线D. 双曲线二、填空题(本大题共5小题,每小题5分,共25分。
高考数学(文科)模拟试卷及答案3套

高考数学(文科)模拟试卷及答案3套(一)第Ⅰ卷 选择题(60分)一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知集合,,}02{B }3,2,1,0,1{A ≤-=-=x x |x 2则A B =I A .}2,1{ B.}2,0,1{- C .}2,1,0{ D.}3,2,1,0{3.已知πlog ,c 9.0,b π9.0π1.0===a ,则c b a ,,的大小关系是A.c a b >>B.b c a >>C.a c b >>D.c b a >>4.为考察A ,B 两种药物预防某疾病的效果,进行动物实验,分别得到如下等高条形图:药物A 实验结果患病未患病服用药没服用药0.10.20.30.40.50.60.70.80.91药物B 实验结果患病未患病服用药没服用药0.10.20.30.40.50.60.70.80.91根据图中信息,在下列各项中,说法最佳的一项是 A .药物A 的预防效果优于药物B 的预防效果 B .药物B 的预防效果优于药物A 的预防效果 C .药物A 、B 对该疾病均有显著的预防效果 D .药物A 、B 对该疾病均没有预防效果5.定义在R 上的奇函数)(x f 满足)3()(x f x f +=-,2)2020(=f ,则)1(f 的值是 A .-1 B .-2 C .1 D . 26.设n m ,是两条不同的直线,βα,是两个不同的平面,,平面直线平面且直线βn αm ⊂⊂,下列命题为真命题的是A.“n m ⊥”是“αn ⊥”的充分条件B.“n m //”是“βm //”的既不充分又不必要条件C.“βα//”是“n m //”的充要条件D.“n m ⊥”是“βα⊥”的必要条件7.已知等差数列}{n a 的前n 项和为n S ,11=a ,若151m m 1m =++-+a a a ,且27S =m ,则m 的值是A .7B .8C . 9D . 10 8.函数)0(3cos y <-=b x b a 的最大值为23,最小值为21-,则]π)4[(sin x b a y -=的周期是A.31 B.32 C.3π D.3π2 9.在ABC ∆中,已知向量AB 与AC 满足AB AC()BC |AB||AC|+⊥u u u r u u u ru u u r u u ur u u u r 且21=•|AC ||AB |,则是ABC ΔA.三边均不相同的三角形 B .直角三角形 C .等腰非等边三角形 D .等边三角形10.在△ABC 中,若115031tan ===︒BC C A ,,,则△ABC 的面积S 是A.833- B.433- C.833+ D.433+ 11. 正方体1111D C B A ABCD -中,11Q D C 点是线段的中点,点P 满足1113A P A A =u u u r u u u r ,则异面直线PQ AB 与所成角的余弦值为A.210 B.210 C.210- D.3712.众所周知的“太极图”,其形状如对称的阴阳两鱼互抱在一起,因而也被称为“阴阳鱼太极图”.如图是放在平面直角坐标系中的“太极图”,整个图形是一个圆形,其中黑色阴影区域在y 轴右侧部分的边界为一个半圆.给出以下命题: ①在太极图中随机取一点,此点取自黑色阴影部分的概率是12; ②当43a =-时,直线(2)y a x =-与黑色阴影部分有公共点; ③黑色阴影部分中一点()y x ,,则y x +的最大值为2.其中所有正确结论的序号是( ) A .① B .② C .①③ D .①②第Ⅱ卷 非选择题(90分)二、填空题:本大题共4小题,每小题5分,共20分.13. 若向量a ,b 满足:(a -b )⋅(2a +b )=-4,且|a |=2,|b |=4,则a 与b 的夹角是__________.14.按照程序框图(如图所示)执行,第4个输出的数是__________.15.已知双曲线1222=-y ax (a >0)的左、右焦点分别为F 1,F 2,离心率为2,开始输出A结束是否1A =1S =5?S ≤2A A =+1S S =+第12题图P 为双曲线右支上一点,且满足4||||2221=-PF PF ,则△PF 1F 2的周长为 .16.已知直线l 与曲线x x f sin )(=切于点)sin (A α α,,且直线l 与曲线x x f sin )(=交于点)sin (B β β,,若π=β-α,则的值为α tan ________.三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)为庆祝新中国成立70周年,某市工会组织部分事业单位职工举行“迎国庆,广播操比赛”活动.现有200名职工参与了此项活动,将这200人按照年龄(单位:岁)分组:第一组[15,25),第二组[25,35),第三组[35,45),第四组[45,55),第五组[55,65],得到的频率分布直方图如图所示.记事件A 为“从这200人中随机抽取一人,其年龄不低于35岁”,已知P (A )=0.75. (1)求b a,的值;(2)在第二组、第四组中用分层抽样的方法抽取6人,再从这6人中随机抽取2人作为活动的负责人,求这2人恰好都在第四组中的概率.18.(本小题满分12分)已知等差数列}{n a 的首项为6,公差为d ,且4312,2,a a a +成等比数列.(1)求}{n a 的通项公式;(2)若0<d ,求||a ...||a ||a ||a n ++++321的值.19.(本小题满分12分)如图,多面体ABCDEF 中,12===AD DE AB ,,平面CDE ⊥平面ABCD ,四边形ABCD 为矩形,BC ∥EF ,点G 在线段CE 上,且AB GC EG 3222==. (1) 求证:DE ⊥平面ABCD ;(2) 若BC EF 2=,求多面体ABCDEF 被平面BDG 分成的大、小两部分的体积比.20.(本小题满分12分)已知函数()()()()21112ln 02f x ax a x a x a =+-+->. (1)若2x =是函数的极值点,求a 的值及函数()f x 的极值; (2)讨论函数的单调性.21.(本小题满分12分)已知抛物线C 的顶点为坐标原点O ,焦点F 在y 轴的正半轴上,过点F 的直线l 与抛物线相交于A ,B 两点,且满足.43-=⋅OB OA (Ⅰ)求抛物线C 的方程;(Ⅱ)若P 是抛物线C 上的动点,点N M ,在x 轴上,圆1122=-+)(y x 内切于PMN ∆,求PMN ∆面积的最小值.选考题:共10分.请考生在第22、23题中任选一题作答. 22.[选修4-4:坐标系与参数方程](10分).在平面直角坐标系xoy 中,曲线C 的参数方程为为参数),,(θθθ⎩⎨⎧+=+=sin 24y cos 23x 以原点为极点,x 轴的非负半轴为极轴建立极坐标系.(1)求曲线C 的极坐标方程;(2)在平面直角坐标系xOy 中,A (﹣2,0),B (0,﹣2),M 是曲线C 上任意一点,求△ABM 面积的最小值.23.[选修4-5:不等式选讲](10分).设函数.|2|||5)(+---=x a x x f (1)当1=a 时,求不等式0)(≥x f 的解集; (2)若1)(≤x f ,求a 的取值范围.答案一、选择题: CBDAB BCBDA DD 二、填空题:13.120° 14.7 15. 3310 16.2π三、解答题:17.解:(1)由题意知P(A)=10×(a +0.030+0.010)=0.75,解得a =0.035,又10×(b +0.010)=0.25,所以b =0.015. ……4分(2)在第二组、第四组中用分层抽样的方法抽取6人,则第二组中应抽取2人,分别记为21a a ,,第四组中应抽取4人,分别记为4321b b b b ,,,. ……5分从这6人中抽取2人的所有可能情况有)(11b ,a , )(21b ,a ,)(31b ,a ,)(41b ,a ,)(12b ,a ,)(22b ,a ,)(32b ,a ,)(42b ,a ,)(21a ,a ,)(21b ,b ,)(31b ,b ,)(41b ,b ,)(32b ,b ,)(42b ,b ,)(43b ,b ,共15种. ……8分其中从这6人中抽取的2个人恰好都在第四组中的情况有)(21b ,b ,)(31b ,b ,)(41b ,b ,)(32b ,b ,)(42b ,b ,)(43b ,b ,共6种. ……9分所以所求概率为52156=. ……10分18. 解:(1) d.a d a d a 36266431+=+=∴=,,,公差为Θ Θ又43122a a a ,,+成等差数列,.21)2(22341=-=+=⋅∴d d a a a 或,解得 .42271n n +==-==n a d n a -d 时,;当时,当故.427}{+==n a n -a a n n n 或的通项公式为·······5分 (2)∵d <0,∴d =-1,此时.n 7n -=a.2132.......07n n -a a a |a ||a ||a |a n 2n 21n 21n +=+++=+++≥≤,时,当·······7分 )....(.......07n 98721n 21n a a a a a a |a ||a ||a |a n +++-+++=+++<>,时,当 .422n 132n 2)n 71)(7n (26072+-=-+---+=)(·······11分 故⎪⎩⎪⎨⎧>+-≤+=+++.422137213 (7)n n 2n n n 2n -|a ||a ||a |22n 21,, ·······12分 19. 解:(1)因为四边形ABCD 为矩形,所以CD=AB.因为AB=DE=2,所以CD=DE=2.因为点G 在线段CE 上,且EG=2GC=322AB ,所以EC=2AB=2CD=22所以.CD DE ,EC CD DE 222⊥=+即又平面CDE ⊥平面ABCD ,平面CDE ⋂平面ABCD=CD,DE ⊂平面CDE , 所以DE ⊥平面ABCD.·······5分(2)方法1:由(1)知,//,,BC AD DC DA DE DC AD ABCD DE 两两垂直,又,所以,且平面⊥⊥ 所以易知.CDE BC 平面⊥设,,222,1=====BC EF DE AB BC,,34323231====∆∆∆∆CDE EDG CDE CDG S S S S .9431,9231=⨯==⨯=∆-∆-BC S V BE BC S V EDG GDE B CDG CDE B ,则连接所以因为,平面所以易知所以ADEF AB EF AD AD BC EF BC ⊥,//,//,// 2313)(2=⨯==+⋅=∆-∆AB S V EF AD DE S ADEF ADEF B ADEF ,所以922=+--ADEF B DEG B V V 所以 故多面体ABCDEF 被平面BDG 分成的大、小两部分的体积比为11:1 方法2:设三棱锥G-BCD 的体积为1,连接EB,AE. 因为EG=2GC,所以CG=31EC,所以3V 3V BCD G BCD E ==--.易知.3V V ABD E BCD E ==--又EF=2BC,BC ∥EF ,所以.V V 2S S 2AEF B ABD B EFA ABD --∆∆==,故 又6,3===---AEF B ABD E ABE B V V V 所以, 故.111336=-++=++---BDG E ABD E AFE B V V V故多面体ABCDEF 被平面BDG 分成的大、小两部分的体积比为11:1.·······12分20.解:(1∴()()()10f x ax a x=++'->,···········1分14a =,···········2分当01x <<和2x >时,()0f x '>,()f x 是增函数, 当12x <<时,()0f x '<,()f x 是减函数,···········4分 所以函数()f x 在1x =和2x =处分别取得极大值和极小值.故函数()f x 的极大值为()1351848f =-=-, 极小值为()13112ln2ln212222f =-+=-.···········6分(2)由题意得()()121a f x ax a x-=+-+'()()2112ax a x a x +-+-=()()1210a a x x a x x-⎛⎫-- ⎪⎝⎭=>,···········7分01x <<时,()0f x '<,()f x 单调递减; 当1x >时,()0f x '>,()f x 单调递增.···········8分②当1201a a -<<,即1132a <<时, 则当120ax a-<<和1x >时,()0f x '>,()f x 单调递增;当121a x a -<<时,()0f x '<,()f x 单调递减.···········9分 ③当121a a ->,即103a <<时,则当01x <<和12ax a->时,()0f x '>,()f x 单调递增;当121ax a -<<时,()0f x '<,()f x 单调递减.···········10分④当121a a -=,即13a =时,()0f x '≥,所以()f x 在定义域()0,+∞上单调递增.···········11分 综上:①当103a <<时,()f x 在区间121,a a -⎛⎫⎪⎝⎭上单调递减,在区间()0,1和12,a a -⎛⎫+∞ ⎪⎝⎭上单调递增; ②当13a =时,()f x 在定义域()0,+∞上单调递增; ③当1132a <<时,()f x 在区间12,1a a -⎛⎫ ⎪⎝⎭上单调递减,在区间120,a a -⎛⎫⎪⎝⎭和()1,+∞上单调递增;()f x 在区间()0,1上单调递减,在区间()1,+∞上单调递增.······12分21.解:(1)由题意,设抛物线C 的方程为)0(22>=p py x ,则焦点F 的坐标为),(20p . 设直线l 的方程为,,,,,)()(22211y x B y x A pkx y +=·······1分 联立方程得,得消去044,0222222222>+=∆=--⎪⎩⎪⎨⎧+==p k p p pkx x y p kx y py x 所以.4222122121p y y p x x pk x x =-==+,,·······3分因为.1432121=-=+=⋅p y y x x OB OA ,所以故抛物线的方程为y x 22=.·······5分(2)设)0()0()0)((0000,,,,,n N m M y x y x P ≠易知点M ,N 的横坐标与P 的横坐标均不相同.不妨设m>n.易得直线PM 的方程为)(00m x mx y y --=化简得0)(000=---my y m x x y ,又圆心(0,1)到直线PM 的距离为1,所以,1)(||202000=-++-m x y my m x 所以2020*******)(2)()(y m m x my m x y m x +-+-=+-不难发现,,故上式可化为02)2(200200=-+->y m x m y y 同理可得,02)2(0020=-+-y n x n y所以m ,n 可以看作是02)2(0020=-+-y t x t y 的两个实数根,则,,2220000--=--=+y y mn y x n m 所以.)2(8444)()(200202022--+=-+=-y y y x mn n m n m 因为)(00y x P ,是抛物线C 上的点,所以0202y x =则,2022)2(4)(-=-y y n m 又20>y ,所以,2200-=y y n m -从而 84)24)(2(2424222)(2100000200000=+--≥+-+-=-=⋅-=-=∆y y y y y y y y y y n m S PMN当且仅当4)2(20=-y 时取得等号,此时22,400±==x y故△PMN 面积的最小值为8.·······12分 22.解:(1)∵曲线C 的参数方程为,(θ为参数),∴曲线C 的直角坐标方程为(x ﹣3)2+(y ﹣4)2=4, 将,代入得曲线C 的极坐标方程为:ρ2﹣6ρcos θ﹣8ρsin θ+21=0.(2)设点M (3+2cos θ,4+2sin θ)到直线AB :x +y +2=0的距离为d ,2|9)4sin(2|2|9cos 2sin 2|+π+θ=+θ+θ=d 则,当sin ()=﹣1时,d 有最小值, 所以△ABM 面积的最小值S ==9﹣2.23解:(1)当1=a 时,⎪⎩⎪⎨⎧>+-≤≤--<+=142122262)x x x x x f(x ,,,可得0)(≥x f 的解集为}23-{≤≤a |x .(2)1)(≤x f 等价于.4|2||≥++-x |a x而|a |x |a x 2|2||+≥++-,当且仅当0)2)((≤+-x a x 时等号成立.故1)(≤x f 等价于42≥+|a |.由42≥+|a |可得26≥-≤a a 或.所以a 的取值范围是(-∞,-6]∪[2,+∞)文科数学模拟试卷二一、选择题:本题共12小题,每小题5分,共60分。
高三模拟数学文科试卷

一、选择题(本大题共12小题,每小题5分,共60分)1. 若函数f(x)=(2x-1)ln(2x+1)在(-1,+∞)上单调递增,则实数a的取值范围是()A. a≤0B. a>0C. a≥0D. a<02. 已知向量a=(1,2),b=(2,1),则向量a与向量b的夹角θ的余弦值为()A. 0B. 1/2C. 1D. -1/23. 若等差数列{an}的前n项和为Sn,且a1=3,S5=55,则公差d为()A. 4B. 5C. 6D. 74. 若函数f(x)=x^3-3x+1在区间(0,2)上单调递增,则实数a的取值范围是()A. a≥0B. a>0C. a≤0D. a<05. 已知函数y=(x-1)^2+2,则函数的图像()A. 向上开口B. 向下开口C. 水平开口D. 垂直开口6. 若等比数列{an}的首项a1=2,公比q=3,则第5项an为()A. 162B. 48C. 18D. 67. 已知函数y=ln(x+1)的图像上一点P(a,b),若该点处的切线斜率为1,则a的值为()A. 0B. 1C. -1D. 28. 若函数f(x)=ax^2+bx+c在区间(-∞,1)上单调递减,在区间(1,+∞)上单调递增,则a、b、c的关系为()A. a>0,b>0,c>0B. a>0,b<0,c>0C. a<0,b>0,c>0D. a<0,b<0,c>09. 已知等差数列{an}的前n项和为Sn,且a1=1,S10=55,则第10项an为()A. 5B. 6C. 7D. 810. 若函数y=x^2+ax+1的图像与x轴有两个不同的交点,则a的取值范围是()A. a>0B. a<0C. a≥0D. a≤011. 已知函数f(x)=x^3-3x^2+4x-1在区间(0,1)上单调递增,则实数a的取值范围是()A. a≤0B. a>0C. a≥0D. a<012. 若函数y=2^x在区间(0,1)上单调递增,则实数a的取值范围是()A. a>0B. a<0C. a≥0D. a≤0二、填空题(本大题共6小题,每小题5分,共30分)13. 已知等差数列{an}的前n项和为Sn,且a1=2,S10=100,则公差d为______。
高三数学模拟高考试卷文科

一、选择题(本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1. 函数f(x) = ax^2 + bx + c(a≠0)的图像是抛物线,若抛物线的对称轴为x = -2,且顶点坐标为(-2, 3),则下列结论正确的是()A. a > 0,b < 0B. a < 0,b > 0C. a > 0,b > 0D. a < 0,b < 02. 已知等差数列{an}的前n项和为Sn,若S10 = 100,S20 = 300,则数列的公差d为()A. 1B. 2C. 3D. 43. 在△ABC中,角A、B、C的对边分别为a、b、c,若cosA = 1/2,sinB = 3/5,则sinC的值为()A. 4/5B. 3/5C. 2/5D. 1/54. 已知复数z = 1 + i,则|z - 3i|^2的值为()A. 8B. 10C. 12D. 145. 下列函数中,在区间(0,+∞)上单调递增的是()A. y = x^2B. y = 2^xC. y = log2xD. y = e^x6. 已知函数f(x) = x^3 - 3x + 2,若f(x) = 0的两根之积为4,则f(x) = 0的两根之和为()A. 0B. 2C. 3D. 47. 下列各式中,正确的是()A. sin30° = 1/2,cos60° = √3/2B. sin45° = √2/2,cos45° = √2/2C. tan30° = √3/3,cot60° = √3/3D. sec60° = 2,csc30° = 28. 在平面直角坐标系中,点P(2, 3)关于直线y = x的对称点为()A. (3, 2)B. (2, 3)C. (3, 3)D. (2, 2)9. 已知等比数列{an}的前n项和为Sn,若a1 = 2,q = 3,则S6的值为()A. 1098B. 1215C. 1512D. 181510. 下列各式中,正确的是()A. sin(α + β) = sinαcosβ + cosαsinβB. cos(α + β) = cosαcosβ - sinαsinβC. tan(α + β) = (tanα + tanβ) / (1 - tanαtanβ)D. cot(α + β) = (cotα + cotβ) / (1 - cotαcotβ)二、填空题(本大题共5小题,每小题5分,共25分。
模拟高考文科数学试卷

一、选择题(本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1. 已知函数f(x) = x^2 - 4x + 3,则f(2)的值为()A. 1B. 3C. 5D. 72. 下列不等式中正确的是()A. x > 2B. x < 2C. x ≤ 2D. x ≥ 23. 若等差数列{an}的前n项和为Sn,且S5 = 15,S10 = 45,则数列的公差d为()A. 1B. 2C. 3D. 44. 在△ABC中,角A、B、C的对边分别为a、b、c,若a = 5,b = 7,c = 8,则sinA的值为()A. 4/5B. 3/5C. 2/5D. 1/55. 已知函数f(x) = ax^2 + bx + c,若f(1) = 2,f(2) = 5,则f(3)的值为()A. 7B. 8C. 9D. 106. 下列复数中,实部为0的是()A. 2 + 3iB. 4 - 2iC. 1 + 2iD. -3 - 4i7. 若log2(x - 1) = 3,则x的值为()A. 2B. 3C. 4D. 58. 已知等比数列{an}的首项a1 = 3,公比q = 2,则数列的第5项an为()A. 48B. 24C. 12D. 69. 在平面直角坐标系中,点P(2, -3)关于y轴的对称点为()A. (2, 3)B. (-2, 3)C. (-2, -3)D. (2, -3)10. 下列函数中,y = x^3 - 3x在x = 0处取得极小值的是()A. y = x^2B. y = x^3C. y = -x^3D. y = -x^2二、填空题(本大题共5小题,每小题10分,共50分。
)11. 已知等差数列{an}的首项a1 = 3,公差d = 2,则数列的第10项an为______。
12. 若log2(x + 3) - log2(x - 1) = 1,则x的值为______。
高三数学文科模拟试卷

一、选择题(本大题共10小题,每小题5分,共50分)1. 下列函数中,定义域为实数集R的是:A. \( f(x) = \sqrt{x^2 - 1} \)B. \( f(x) = \frac{1}{x} \)C. \( f(x) = \log_2(x - 1) \)D. \( f(x) = x^3 - x \)2. 已知函数 \( f(x) = ax^2 + bx + c \)(\( a \neq 0 \))的图象开口向上,且与x轴有两个不同的交点,则下列说法正确的是:A. \( a > 0 \) 且 \( b^2 - 4ac < 0 \)B. \( a > 0 \) 且 \( b^2 - 4ac > 0 \)C. \( a < 0 \) 且 \( b^2 - 4ac < 0 \)D. \( a < 0 \) 且 \( b^2 - 4ac > 0 \)3. 下列命题中,正确的是:A. 若 \( a^2 + b^2 = 1 \),则 \( a \) 和 \( b \) 不可能同时为正或同时为负B. 若 \( a^2 + b^2 = 0 \),则 \( a \) 和 \( b \) 必须同时为0C. 若 \( a^2 + b^2 = 0 \),则 \( a \) 和 \( b \) 必须同时为0D. 若 \( a^2 + b^2 = 1 \),则 \( a \) 和 \( b \) 必须同时为04. 已知函数 \( f(x) = 2^x \),则 \( f(x) \) 的单调递增区间是:A. \( (-\infty, 0) \)B. \( (0, +\infty) \)C. \( (-\infty, +\infty) \)D. \( \emptyset \)5. 已知 \( \sin x + \cos x = \sqrt{2} \),则 \( \sin 2x \) 的值为:B. -1C. 0D. 26. 下列函数中,周期为 \( \pi \) 的是:A. \( f(x) = \sin x \)B. \( f(x) = \cos 2x \)C. \( f(x) = \tan x \)D. \( f(x) = \sec x \)7. 已知 \( \triangle ABC \) 中,\( a = 3 \),\( b = 4 \),\( c = 5 \),则 \( \cos A \) 的值为:A. \( \frac{3}{5} \)B. \( \frac{4}{5} \)C. \( \frac{5}{3} \)D. \( \frac{5}{4} \)8. 下列方程中,无解的是:A. \( 2x + 3 = 0 \)B. \( x^2 - 4 = 0 \)C. \( x^2 + 1 = 0 \)D. \( x^2 - 1 = 0 \)9. 已知 \( \log_2 x + \log_2 (x - 1) = 3 \),则 \( x \) 的值为:A. 8B. 4C. 210. 下列命题中,正确的是:A. 若 \( a > b \),则 \( a^2 > b^2 \)B. 若 \( a > b \),则 \( a^2 < b^2 \)C. 若 \( a > b \),则 \( a^2 > b^2 \) 或 \( a^2 < b^2 \)D. 若 \( a > b \),则 \( a^2 > b^2 \) 或 \( a^2 = b^2 \)二、填空题(本大题共5小题,每小题5分,共25分)11. 函数 \( f(x) = -2x^2 + 3x + 1 \) 的对称轴方程是 ________。
高三数学模考文科试卷答案

一、选择题(每题5分,共50分)1. 【答案】C解析:根据函数的定义,当x=0时,f(x)=0,因此C选项正确。
2. 【答案】A解析:由等差数列的性质可知,第n项an=a1+(n-1)d,其中d为公差。
代入题目中的数据,得a5=a1+4d=10,a10=a1+9d=30,解得a1=2,d=4,因此a1+a5=2+10=12,A选项正确。
3. 【答案】D解析:根据复数的性质,实部相同,虚部相反的两个复数互为共轭复数。
因此,-1-2i的共轭复数为-1+2i,D选项正确。
4. 【答案】B解析:由三角函数的性质可知,sin(π/2-x)=cosx,因此B选项正确。
5. 【答案】C解析:根据向量的数量积公式,a·b=|a||b|cosθ,其中θ为a和b的夹角。
由题意可知,|a|=|b|=2,且a和b的夹角θ=π/3,代入公式得a·b=2×2×cos(π/3)=2,C选项正确。
二、填空题(每题5分,共25分)6. 【答案】x=1解析:由一元二次方程的定义可知,x=1是方程x^2-3x+2=0的解。
7. 【答案】a=-2,b=1解析:根据韦达定理,一元二次方程ax^2+bx+c=0的根满足x1+x2=-b/a,x1x2=c/a。
代入题目中的数据,得x1+x2=-b/a=-1/2,x1x2=c/a=-1/2,解得a=-2,b=1。
8. 【答案】π解析:由三角函数的性质可知,sin(π/2)=1,因此π/2的对应角是π。
9. 【答案】3解析:由等比数列的性质可知,an=a1q^(n-1),其中q为公比。
代入题目中的数据,得a5=a1q^4=80,a1q^2=20,解得q=√(80/20)=2,因此a1=20/q=10,所以a1+a5=10+80=90。
10. 【答案】1/2解析:由复数的性质可知,|z|=√(a^2+b^2),其中z=a+bi。
代入题目中的数据,得|z|=√(1^2+1^2)=√2,因此z的模为√2。
高考文科模拟卷数学试卷

一、选择题(本大题共10小题,每小题5分,共50分)1. 若函数f(x) = x^3 - 3x + 1在区间[1, 2]上存在极值,则f(x)在区间[1, 2]上的极值点个数是:A. 0个B. 1个C. 2个D. 3个2. 已知等差数列{an}的前n项和为Sn,若a1 = 3,S3 = 21,则数列的公差d为:A. 2B. 3C. 4D. 53. 若复数z满足|z - 1| = |z + 1|,则复数z的实部是:A. 0B. 1C. -1D. 24. 下列函数中,定义域为全体实数的是:A. y = √(x^2 - 1)B. y = log2(x - 1)C. y = x^2 + 1D. y = 1/x5. 已知向量a = (2, -3),向量b = (1, 2),则向量a与向量b的夹角θ的余弦值是:A. 1/5B. 2/5C. 3/5D. 4/56. 若不等式x^2 - 4x + 3 < 0的解集是A,则不等式x^2 - 4x + 3 > 0的解集是:A. A的补集B. AC. R(实数集)D. 空集7. 已知函数y = sin(2x + π/6)的图象向右平移π个单位后,得到的函数的解析式是:A. y = sin(2x + π/6)B. y = sin(2x - 5π/6)C. y = sin(2x + 5π/6)D. y = sin(2x - π/6)8. 在三角形ABC中,∠A = 30°,∠B = 45°,则sinC的值为:A. √3/2B. 1/2C. √2/2D. 1/√29. 若直线y = kx + 1与圆x^2 + y^2 = 1相切,则k的取值范围是:A. (-∞, -1] ∪ [1,+∞)B. (-1, 1)C. (-1, 0) ∪ (0, 1)D. (-∞, 0) ∪ (0, +∞)10. 若数列{an}的前n项和为Sn,且an = 3^n - 2^n,则S5的值为:A. 441B. 462C. 482D. 502二、填空题(本大题共5小题,每小题5分,共25分)11. 函数f(x) = x^2 - 4x + 3的零点是______。
高考数学(文科)模拟试卷及答案3套
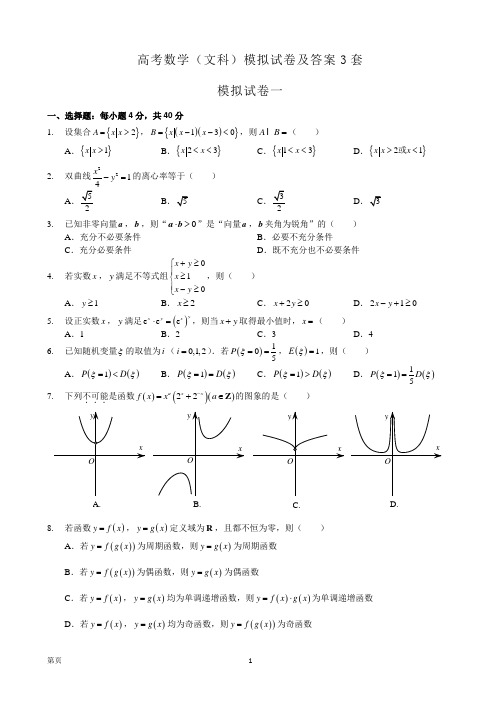
高考数学(文科)模拟试卷及答案3套模拟试卷一一、选择题:每小题4分,共40分1. 设集合{}2A x x =>,()(){}130B x x x =--<,则A B =I ( )A .{}1x x >B .{}23x x <<C .{}13x x <<D .{}21x x x ><或2. 双曲线2214x y -=的离心率等于( )A .52B .5C .32D .33. 已知非零向量a ,b ,则“0⋅>a b ”是“向量a ,b 夹角为锐角”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件4. 若实数x ,y 满足不等式组010x y x x y +≥⎧⎪≥⎨⎪-≥⎩,则( )A .1y ≥B .2x ≥C .20x y +≥D .210x y -+≥5. 设正实数x ,y 满足()e e e yx y x ⋅=,则当x y +取得最小值时,x =( ) A .1 B .2 C .3 D .46. 已知随机变量ξ的取值为i (0,1,2i =).若()105P ξ==,()1E ξ=,则( )A .()()1P D ξξ=<B .()()1P D ξξ==C .()()1PD ξξ=>D .()()115P D ξξ==7. 下列不可能...是函数()()()22a x x f x x a -=+∈Z 的图象的是( ) D.C.B.A.xxxyyyyxOOOO8. 若函数()y f x =,()y g x =定义域为R ,且都不恒为零,则( ) A .若()()y f g x =为周期函数,则()y g x =为周期函数 B .若()()y f g x =为偶函数,则()y g x =为偶函数C .若()y f x =,()y g x =均为单调递增函数,则()()y f x g x =⋅为单调递增函数D .若()y f x =,()y g x =均为奇函数,则()()y f g x =为奇函数9. 已知椭圆22221x y a b+=(0a b >>)的左右焦点分别为1F ,2F ,抛物线22y px =(0p >)的焦点为2F .设两曲线的一个交点为P ,若221216PF F F p ⋅=u u u u r u u u u r ,则椭圆的离心率为( )A .12B .22C .34D .3210. 已知非常数数列{}n a 满足12n nn a a a αβαβ+++=+(*n ∈N ,α,β为非零常数).若0αβ+≠,则( )A .存在α,β,对任意1a ,2a ,都有数列{}n a 为等比数列B .存在α,β,对任意1a ,2a ,都有数列{}n a 为等差数列C .存在1a ,2a ,对任意α,β,都有数列{}n a 为等差数列D .存在1a ,2a ,对任意α,β,都有数列{}n a 为等比数列二、填空题:单空题每题4分,多空题每题6分,共36分11. 设复数z 满足()1i 2i z +⋅=(i 为虚数单位),则z = ,z = .12. 已知二项式()60a x a x ⎛⎫+> ⎪⎝⎭的展开式中含2x 的项的系数为15,则a = ,展开式中各项系数和等于 .13. 在ABC △中,BAC ∠的平分线与BC 边交于点D ,sin 2sin C B =,则BDCD= ;若1AD AC ==,则BC = .14. 已知函数()()()210cos 0x x f x x x π⎧-≤⎪=⎨>⎪⎩,则()2019f f =⎡⎤⎣⎦ ;若关于x 的方程()0f x a +=在(),0-∞内有唯一实根,则实数a 的取值范围是 .15. 杭州亚运会启动志愿者招募工作,甲、乙等5人报名参加了A ,B ,C 三个项目的志愿者工作,因工作需要,每个项目仅需1名志愿者.若甲不能参加A ,B 项目,乙不能参加B ,C 项目,那么共有 种不同的选拔志愿者的方案.(用数字作答)16. 已知函数()39f x x x =-,()()23g x x a a =+∈R .若方程()()f x g x =有三个不同的实数解1x ,2x ,3x ,且它们可以构成等差数列,则a = .17. 在平面凸四边形ABCD 中,2AB =,点M ,N 分别是边AD ,BC 的中点,且32MN =,若()32MN AD BC ⋅-=u u u u r u u u r u u u r ,则AB CD ⋅=u u u r u u u r .三、解答题:5小题,共74分18. (本题满分14分)已知函数()22sin cos 3f x x x π⎛⎫=-+ ⎪⎝⎭(x ∈R ).(1)求()f x 的最小正周期;(2)求()f x 在区间,34ππ⎡⎤-⎢⎥⎣⎦上的值域.19. (本题满分15分)已知函数()212f x x k x =+--.(1)当1k =时,求函数()f x 的单调递增区间. (2)若2k ≤-,试判断方程()1f x =-的根的个数.20. (本题满分15分)如图,在ABC △中,23BAC π=∠,3AD DB =u u u r u u u r ,P 为CD 上一点,且满足12AP mAC AB =+u u u r u u u r u u u r,若ABC △的面积为23.(1)求m 的值;(2)求AP u u u r的最小值.PBDAC21. (本题满分15分)设公差不为0的等差数列{}n a 的前n 项和为n S ,等比数列{}n b 的前n 项和为n T ,若2a 是1a 与4a 的等比中项,612a =,11221a b a b ==. (1)求n a ,n S 与n T ;(2)若n n n c S T =⋅,求证:12(2)2n n n c c c ++++<L .22. (本题满分15分)设函数()e x f x ax =+,a ∈R .(1)若()f x 有两个零点,求a 的取值范围;(2)若对任意[)0,x ∈+∞均有()2223f x x a +≥+,求a 的取值范围.模拟试卷二一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知集合⎭⎬⎫⎩⎨⎧=ππcos 2sin,A ,⎭⎬⎫⎩⎨⎧-+-+-=x x ,x x B sin sin 2cos cos ,则A B I 为( ▲ ) A . {0,1}- B .{1,1}-C .{1}-D .{0}2.若复数()()14i t i +-的模为52,则实数t 的值为( ▲ )A . 1B . 2C . 2±D .3±3.某几何体的三视图如下图所示,它的体积为( ▲ )A . π192B .π240C . π384D .π5764.设等比数列{a n }的前n 项和为S n ,若S 5=2 S 10,则5151052S S S S +=-( ▲ )A . 52B . 92-C . 72D . 112-5.已知A 、B 是抛物线x y 42=上异于原点O 的两点,则“OA ·OB =0”是“直线AB 恒过定点(0,4)”的( ▲ )A .充分非必要条件B .充要条件C .必要非充分条件D .非充分非必要条件6.数列921,,,a a a ⋅⋅⋅中,恰好有6个7,3个4,则不相同的数列共有( ▲ )个 A .67C B .49C C .39C D .36C7.已知双曲线]2,2[)0,0(12222∈>>=-e b a by a x 的离心率,则一条渐近线与实轴所构成的角的取值范围是( ▲ )A .⎥⎦⎤⎢⎣⎡4,6ππB .⎥⎦⎤⎢⎣⎡3,6ππC .⎥⎦⎤⎢⎣⎡3,4ππD . ⎥⎦⎤⎢⎣⎡2,3ππ 8.已知函数()()242log ,041234(4)x x f x x x x ⎧<≤⎪=⎨⎪-+>⎩,若方程()(=∈f x t t )R 有四个不同的实数 根1x ,2x ,3x ,4x ,则1x 2x 3x 4x 的取值范围为( ▲ )A .(30,34)B .(30,36)C .(32,34)D .(32,36)9.已知,x y 都是正实数,则44x yx y x y+++的最大值为( ▲ )A .32B .43C . 52D . 5410.已知在矩形ABCD 中,2AB =,4AD =,E ,F 分别在边AD ,BC 上,且1AE =,3BF =,如图所示, 沿EF 将四边形AEFB 翻折成A EFB '',则在翻折过程中,二面角B CD E '--的大小为θ,则tan θ的最大值为( ▲ )A .325 33B.5 32C.4 33D.4非选择题部分二、填空题(本大题7小题,多空题每题6分,单空题每题4分,共36分.) 11.已知函数()ln 2020f x x x =+,则()1f '= ▲ ,0(12)(1)lim x f x f x∆→-∆-∆的值等于▲ .12.已知点P(x,y)满足条件y x z k k y x x y x 3),(02,,0+=⎪⎩⎪⎨⎧≤++≤≥若为常数的最大值为12, 则k = ▲ .13.如果x +x 2+x 3+……+x 9+x 10=a 0+a 1(1+x )+a 2(1+x )2+……+a 9(1+x )9+a 10(1+x )10,则a 9=______ _,10a = ▲ .14.已知A 袋内有大小相同的1个红球和3个白球,B 袋内有大小相同的2个红球和4个白球.现从A 、B 两个袋内各任取2个球,设取出的4个球中红球的个数为ξ,则(1)P ξ== ▲ ,ξ的数学期望为 ▲ .15.抛物线x y 22=顶点为O ,焦点为F ,M 是抛物线上的动点,则MFMO 取最大值时M 点的横坐标为▲ .16.已知ABC ∆中,BC 中点为M ,()BC AC AB ⊥+,AB AC AB AC BC ⋅=--2222,CA CN 31=,3=AB ,则 B ∠= ▲ ,=MN ▲ .17.已知函数()222sin 2,2cos 2a a f a a a θθθ++=++()0,,≠∈a R a θ,则函数(),f a θ的值域是 ▲ .三、解答题(本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.) 18.(本题满分14分) 在ABC ∆中,,,A B C 所对边分别为,,a b c .已知3,b =2()4cos 23sin 23,f x x x =+- (Ⅰ)求()f x 单调递减区间和最大值M ;(Ⅱ)若(),f B M =求ABC ∆面积的最大值. 19.(本小题满分15分)如图,ABEF 是等腰梯形, EF AB //,BF AF ⊥,矩形ABCD 和ABEF 所在的平面互相垂直.已知2=AB ,1=EF .(Ⅰ)求证:平面⊥DAF 平面CBF ;(Ⅱ)求直线AB 与平面CBF 所成角的正弦值. 20、(本小题满分15分) 已知数列{}n a 的前n 项和n S 满足:()121--=n n a S . (Ⅰ)求{}n a 的通项公式;(Ⅱ)设11111n n n c a a +=++-,数列{}n c 的前n 项和为T n . 求证:123n T n >-.21、(本小题满分15分)已知圆S :020422=-++y x x ,T 是抛物线x y 82=的焦点,点P 是圆S 上的动点,Q 为PT 的中点,过Q 作Q G ⊥PT 交PS 于G(1)求点G 的轨迹C 的方程;(2)过抛物线x y 82—=的焦点E 的直线l 交G 的轨迹C 于点M 、N ,且满足364sin =∠⋅MON ON OM ,(O 为坐标原点),求直线l 的方程.22.(本小题满分15分)对于定义在I 上的函数()y f x =,若存在0x I ∈,对任意的x I ∈,都有()()0f x f x m ≥=或者()()0f x f x M ≤=,则称0()f x 为函数()f x 在区间I 上的“最小值m ”或“最大值M ”.(Ⅰ)求函数2()ln(2)f x x x =-+在]1,0[上的最小值;(Ⅱ)若把“最大值M ”减去“最小值m ”的差称为函数()f x 在I 上的“和谐度G ”, 试求函数()23F x x x a a =-+>(0)在[1,2]上的“和谐度G ”;(Ⅲ)类比函数()f x 的“和谐度G ”的概念, 请求出(,)(1)(1)11x yx y x y y xϕ=--++++在{}(,),[0,1]I x y x y =∈上的“和谐度G ”.参考答案:CDBDB CCCBC11.【答案】2021,-4042.12.【答案】9-13.【答案】-9,1 14.【答案】 7(1)15P ξ==,76E ξ= ξ可能的取值为0123,,,.1(0)5P ξ==,7(1)15P ξ==, 13224611(3)30C P C C ξ===·.从而3(2)1(0)(1)(3)10P P P P ξξξξ==-=-=-==.ξ的分布列为ξ 0 1 23Pmnp qξ的数学期望17317012351510306E ξ=⨯+⨯+⨯+⨯=.15.【答案】1.【解析】设抛物线方程为x y 22=,则顶点及焦点坐标为()00,O ,⎪⎭⎫ ⎝⎛021,F ,若设点M 坐标为 (),M x y ,则2⎪⎭⎫⎝⎛MF MO ==+⎪⎭⎫ ⎝⎛-+222221y x y x =+⎪⎭⎫ ⎝⎛-+x x x x 22122241222+++x x x x令41222+++=x x x x t 得,()()04212=+-+-t x t x t ,由0≥∆得34≤t ,由4123422+++=x x x x 得1=x 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中文科数学高考模拟试卷一、选择题:本大题共12小题,每小题5分,满分60分.1.如果复数)()2(Raiai∈+的实部与虚部是互为相反数,则a的值等于A.2B.1C.2-D.1-2.已知两条不同直线1l和2l及平面α,则直线21//ll的一个充分条件是A.α//1l且α//2l B.α⊥1l且α⊥2lC.α//1l且α⊄2l D.α//1l且α⊂2l3.在等差数列}{na中,69327aaa-=+,nS表示数列}{na的前n项和,则=11SA.18B.99C.198D.2974.右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是A.π32B.π16C.π12D.π85.已知点)43cos,43(sinππP落在角θ的终边上,且)2,0[πθ∈,则θ的值为A.4πB.43πC.45πD.47π6.按如下程序框图,若输出结果为170,则判断框内应补充的条件为A.5i>B.7i≥C.9i>D.9i≥7.若平面向量)2,1(-=与的夹角是︒180,且||=A.)6,3(-B.)6,3(-C.)3,6(-8.若函数)(log)(bxxfa+=的大致图像如右图,其中则函数baxg x+=)(的大致图像是A B C D9.设平面区域D是由双曲线1422=-xy的两条渐近线和椭圆1222=+yx的右准线所围成的三角形(含边界与内部).若点Dyx∈),(,则目标函数yxz+=的最大值为A.1B.2C.3D.610.设()11xf xx+=-,又记()()()()()11,,1,2,,k kf x f x f x f f x k+===则()2009=f xA.1x-B.x C.11xx-+D.11xx+-俯视图11. 等差数列{}n a 中,8776,S S S S ><,真命题有__________(写出所有满足条件的序号)①前七项递增,后面的项递减②69S S <③1a 是最大项④7S 是n S 的最大项 A .②④B .①②④C .②③④D .①②③④12. 已知()f x 是定义在R 上的且以2为周期的偶函数,当01x ≤≤时,2()f x x =,如果直线y x a =+与曲线()y f x =恰有两个交点,则实数a 的值为A .0B .2()k k Z ∈C .122()4k k k Z -∈或 D .122()4k k k Z +∈或 二、填空题:本大题共4小题,每小题4分,满分16分。
13.某大型超市销售的乳类商品有四种:纯奶、酸奶、婴幼儿奶粉、成人奶粉,且纯奶、酸奶、婴幼儿奶粉、成人奶粉分别有30种、10种、35种、25种不同的品牌.现采用分层抽样的方法从中抽取一个容量为n 的样本进行三聚氰胺安全检测,若抽取的婴幼儿奶粉的品牌数是7,则=n 。
14.若关于x 的不等式2||20ax x a -+<的解集为∅,则实数a 的取值范围为。
15.在ABC Rt ∆中,若a BC b AC C ===∠,,900,则ABC ∆外接圆半径222b a r +=。
运用类比方法,若三棱锥的三条侧棱两两互相垂直且长度分别为c b a ,,,则其外接球的半径R =。
16. 在OAB 中,O 为坐标原点,(1,cos ),(sin ,1),0,2A B πθθθ⎡⎤-∈⎢⎥⎣⎦。
⑴若,OA OB OA OB θ+=-=则 ,⑵OAB ∆的面积最大值为 。
三、解答题:本大题6小题,满分74分。
17.(本小题满分12分)已知函数2()2cos cos()sin cos 6f x x x x x x π=-+.(Ⅰ)求()f x 的最小正周期;(Ⅱ)设]2,3[ππ-∈x ,求()f x 的值域.18.(本小题满分10分)先后随机投掷2枚正方体骰子,其中x 表示第1枚骰子出现的点数,y 表示第2枚骰子出现的点数.(Ⅰ)求点),(y x P 在直线1-=x y 上的概率; (Ⅱ)求点),(y x P 满足x y 42<的概率.19.(本小题满分13分)如图,AB 为圆O 的直径,点E 、F 在圆O 上,EF AB //,矩形ABCD 所在的平面 和圆O 所在的平面互相垂直,且2=AB ,1==EF AD . (Ⅰ)求证:⊥AF 平面CBF ;(Ⅱ)设FC 的中点为M ,求证://OM 平面DAF ;(Ⅲ)设平面CBF 将几何体EFABCD 分成的两个锥体的体积分别为ABCD F V -,CBE F V -,求ABCD F V -CBE F V -:.20.(本题满分12分)已知函数d cx bx ax x f +++=23)(,)(R x ∈在任意一点))(,(00x f x 处的切线的斜率为)1)(2(00+-=x x k 。
(1)求c b a ,,的值;(2)求函数)(x f 的单调区间;(3)若)(x f y =在23≤≤-x 上的最小值为25,求)(x f y =在R 上的极大值。
21.(本题满分13分)如图,两条过原点O 的直线21,l l 分别与x 轴、y 轴成︒30的角,已知线段PQ 的长度为2,且点),(11y x P 在直线1l 上运动,点),(22y x Q 在直线2l 上运动. (Ⅰ)求动点),(21x x M 的轨迹C 的方程;(Ⅱ)设过定点)2,0(T 的直线l 与(Ⅰ)中的轨迹C 交于不同的两点A 、B ,且AOB ∠为锐角,求直线l 的斜率k 的取值范围.22.(本小题满分14分)设数列{}n a 的前n 项和为n S ,11=a ,且对任意正整数n ,点()n n S a ,1+在直线022=-+y x 上. (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)是否存在实数λ,使得数列⎭⎬⎫⎩⎨⎧+⋅+n n n S 2λλ为等差数列?若存在,求出λ的 值;若不存在,则说明理由.(Ⅲ)求证:21)1)(1(26111<++≤∑=+-n k k k k a a .高中文科数学高考模拟试卷答案及评分标准一、ABBCD DABCD CC二、13.20. 14.)4+∞.15.2222c b a ++. 16.8,23π. 三、解答题:本大题满分74分.17.解:(Ⅰ)∵2()cos sin )sin cos f x x x x x x x =++22sin )2sin cos x x x x =-+x x 2sin 2cos 3+=)32sin(2π+=x .)(x f ∴的最小正周期为π.(Ⅱ)∵]2,3[ππ-∈x ,34323πππ≤+≤-∴x , ………… 9分 又)32sin(2)(π+=x x f ,]2,3[)(-∈∴x f ,()f x 的值域为]2,3[-.18.解:(Ⅰ)每颗骰子出现的点数都有6种情况,所以基本事件总数为3666=⨯个. 2分记“点),(y x P 在直线1-=x y 上”为事件A ,A 有5个基本事件:)}5,6(),4,5(),3,4(),2,3(),1,2{(=A , .365)(=∴A P …… 5分 (Ⅱ)记“点),(y x P 满足x y 42<”为事件B ,则事件B 有17个基本事件: 当1=x 时,;1=y 当2=x 时,2,1=y ; …………… 6分当3=x 时,3,2,1=y ;当4=x 时,;3,2,1=y ……………… 8分 当5=x 时,4,3,2,1=y ;当6=x 时,4,3,2,1=y ..3617)(=∴B P ………… 10分19.(Ⅰ)证明: 平面⊥ABCD 平面ABEF ,AB CB ⊥,平面 ABCD 平面ABEF =AB ,⊥∴CB 平面ABEF , ⊂AF 平面ABEF ,CB AF ⊥∴ ,又AB 为圆O 的直径,BF AF ⊥∴, ⊥∴AF 平面CBF 。
…………………… 5分(Ⅱ)设DF 的中点为N ,则MN //CD 21,又AO //CD 21,则MN //AO ,MNAO 为平行四边形,//OM ∴AN ,又⊂AN 平面DAF ,⊄OM 平面DAF ,//OM ∴平面DAF 。
(Ⅲ)过点F 作AB FG ⊥于G , 平面⊥ABCD 平面ABEF ,⊥∴FG 平面ABCD ,FG FG S V ABCD ABCD F 3231=⋅=∴-, ⊥CB 平面ABEF ,CB S V V BFE BFE C CBE F ⋅==∴∆--31FG CB FG EF 612131=⋅⋅⋅=,ABCD F V -∴1:4:=-CBE F V .20.(本小题满分12分)解:(1)c bx ax x f ++='23)(2(1分)而)(x f 在))(,(00x f x 处的切线斜率)1)(2(23)(000200+-=++='=x x c bx ax x f k∴2,12,13-=-==c b a ∴31=a ,21-=b ,2-=c (3分)(2)∵d x x x x f +--=22131)(23由0)1)(2(2)(2≥+-=--='x x x x x f 知)(x f 在]1,(--∞和),2[+∞上是增函数 由0)1)(2()(≤+-='x x x f 知)(x f 在]2,1[-上为减函数(7分) (3)由)1)(2()(+-='x x x f 及23≤≤-x 可列表)(x f 在]2,3[-由d f +-=-215)3(,d f +-=310)2(知)2()3(f f <-(9分)于是25215)3(=+-=-d f 则10=d (11分)∴667)1()(=-=f x f 极大值 即所求函数)(x f 在R 上的极大值为667(12分)21.解:(Ⅰ)由已知得直线21l l ⊥,1l :x y 33=, 2l :x y 3-=, ……… 2分),(11y x P 在直线1l 上运动,),(22y x Q 直线2l 上运动,1133x y =∴,223x y -=, …………………… 3分 由2=PQ 得4)()(22222121=+++y x y x ,即44342221=+x x ,⇒132221=+x x , …………………… 4分∴动点),(21x x M 的轨迹C 的方程为1322=+y x . …………………… 5分(Ⅱ)直线l 方程为2+=kx y ,将其代入1322=+y x , 化简得0912)31(22=+++kx x k , ……… 7分 设),(11y x A 、),(22y x B0)31(36)12(22>+⨯-=∆∴k k ,12>⇒k ,且221221319,3112kx x k kx x x +=+-=+, …………………… 9分 AOB ∠ 为锐角,0>⋅∴, …………………… 9分 即02121>+y y x x ,⇒0)2)(2(2121>+++kx kx x x , 04)(2)1(21212>++++∴x x k x x k .将221221319,3112k x x k kx x x +=+-=+代入上式, 化简得03131322>+-k k ,3132<⇒k .…………………… 11分 由12>k 且3132<k ,得339,1()1,339( --∈k .……………………13分 22.(本小题满分14分)设数列{}n a 的前n 项和为n S ,11=a ,且对任意正整数n ,点()n n S a ,1+在直线022=-+y x 上.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)是否存在实数λ,使得数列⎭⎬⎫⎩⎨⎧+⋅+nn n S 2λλ为等差数列?若存在,求出λ的值;若不存在,则说明理由.(Ⅲ)求证: 21)1)(1(26111<++≤∑=+-n k k k k a a .K^S*5U.C#O%M解:(Ⅰ)由题意可得: .0221=-++n n S a ①2≥n 时,.0221=-+-n n S a ②…………………… 1分①─②得()22102211≥=⇒=+-++n a a a a a n n n n n , 2122,12121=⇒=+=a a a a (3)分∴{}n a 是首项为1,公比为21的等比数列,.211-⎪⎭⎫⎝⎛=∴n n a ……………… 4分(Ⅱ)解法一:.2122112111--=--=n nn S ……………… 5分 若⎭⎬⎫⎩⎨⎧+n n S 2λ为等差数列,则3322123,22,2λλλλλλ++++++S S S 成等差数列,……………… 6分2,82547231492328252349312λλλλλλ+++=⎪⎭⎫⎝⎛+⇒+++=⎪⎭⎫ ⎝⎛+S S S 得.2=λ……………… 8分又2=λ时,22222+=++n n S n n ,显然{}22+n 成等差数列,故存在实数2=λ,使得数列⎭⎬⎫⎩⎨⎧++n n n S 2λλ成等差数列. ……………… 9分解法二:.2122112111--=--=n nn S ……………… 5分 ().2122221221n n n n n n n n S -++=++-=++∴-λλλλλλ…………… 7分欲使⎭⎬⎫⎩⎨⎧+⋅+n n n S 2λλ成等差数列,只须02=-λ即2=λ便可.……………8分故存在实数2=λ,使得数列⎭⎬⎫⎩⎨⎧++n n n S 2λλ成等差数列.……………… 9分(Ⅲ)=+++)1)(1(11k k a a(21)121)(121(11k k k =++--+1211k )12111+-k …… 10分 ∑∑==+--+=++∴nk k n k kt k k a a 1111211()1)(1(2)12111+-k ………… 11分++-+=)1111211( ++-+)12111211(2-++1211(t )12111+-k++-=1111211+k 21122-+=k k ………… 12分 又函数=+=122x x y 1211+x 在),1[∞+∈x 上为增函数,K^S*5U.C#O%M112212211<+≤+∴k k , ………… 13分 211211222132-<-+≤-∴k k ,21)1)(1(26111<++≤∑=+-n k k k k a a . ……… 14分 向你推荐高考状元复习法: 朱坤(北京大学光华管理学院学生,高考文科状元):数学是我最讨厌,也是最头疼的科目之一。
