重庆八中高2023级数学高一上国庆作业题一(终版)+参考答案
重庆市第八中学2023-2024学年高一上学期九月检测(一)数学试题含答案

重庆八中高2026级高一(上)数学检测试题(一)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设命题p :x ∀∈R ,20x +>,则p ¬为()A.x ∃∈R ,20x +>B.x ∃∈R ,20x +≤C.x ∃∈R ,20x +<D.x ∀∈R ,20x +≤2.已知集合{}1,2,3,4,5U =,{}1,3A =,{}1,2,4B =,则U B A = ()A.{}1,3,5 B.{}1,3 C.{}1,2,4 D.{}1,2,4,53.已知集合{A =,{}1,B m =,且A B A = ,则m 等于()A.0B.1C.0或3D.1或3或04.下列说法中正确的个数为()①0.333Q ∈;②0∈∅;③{}0∅⊆;④{}{}0∅⊆;⑤{}0∅=;⑥{}{}11,2,3∈;⑦{}{}22x x m m ≥=≥;⑧{}{}2211x y x y y x =+==+A.2B.3C.4D.55.已知p 是r 的充分条件,q 是r 的充分不必要条件,s 是r 的必要条件,p 是s 的必要条件,现有下列命题:①r 是p 的必要不充分条件;②r 是s 的充分不必要条件;③q 是p 的充分不必要条件;④s 是q 的充要条件.正确的命题序号是()A.①B.②C.③D.④6.若{}{}2,0,1,,0a a b −=,则20232023a b +的值是()A.1− B.0C.1D.27.已知全集U =R ,集合{}18,P x x x Z =−<≤∈,{}05M x x x =∈≤>R 或之间关系的Venn 图如图所示,则阴影部分所示的集合中的元素共有()A.8个B.6个C.5个D.4个8.对于集合M ,N ,定义{},M N x x M x N −=∈∉,()()M N M N N M ⊕−⊂−,设9,4A x x x =≥−∈R ,{}0,B x x x =<∈R ,则A B ⊕=()A.9,04 −B.9,04−C.[)9,0,4−∞−+∞D.()9,0,4−∞−+∞二、选择题:本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.下列说法正确的是()A.a Q ∈是a ∈R 的充分不必要条件B.x y =是x y =的必要不充分条件C.21x >是1x >的充分不必要条件 D.0a b +<是0a <,0b <的必要不充分条件10.下列命题正确的是()A.x ∃∈R ,x x> B.x ∀∈R ,2350x x −−>C.{}x y y ∀∈是无理数,4x 是有理数D.,a b ∃∈R ,()2210a b −++≤11.下列命题为真命题的是( ). A.若0a b >>,则11a b a b+>+ B.若0m n >>,则11m mn n +<+C.如果0c a b >>>,那么a c a −D.1a b ≥>−,则11a ba b ≥++12.若非空实数集M 满足任意,x y M ∈,都有x y M +∈,x y M −∈,则称M 为“优集”.已知A ,B 是优集,则下列命题中正确的是()A.A B 是优集B.A B 是优集C.若A B 是优集,则A B ⊆或B A ⊆D.若A B 是优集,则A B 是优集三、填空题:本大题共4小题,每小题5分,共20分.13.已知实数x ,y 满足12x −≤<,01y <≤,则2x y −的取值范围是______.14.已知(){},12A x y xy ==,(){},,,B x y x y y x =∈<N ,则A B = ______.15.命题“x ∃∈R ,()()22210a x a x +++−≥”为假命题,则实数a 的取值范围为______.16.若集合{}1,2,3,4,5,6,7M ,且M 中至少含有两个奇数,则满足条件的集合M 的个数是______.四、解答题:本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.17.设集合{},03U A x x ==≤≤R ,{}12B x m x m =−≤≤.(1)3m =,求()U A B ; (2)若B A ,求m 的取值范围.18.新冠肺炎疫情防控期间,学校为做好预防消毒工作,开学初购进A ,B 两种消毒液,购买A 种消毒液花费了2500元,购买B 种消毒液花费了2000元,且购买A 种消毒液数量是购买B 种消毒液数量的2倍,已知购买一桶B 种消毒液比购买一桶A 种消毒液多花30元. (1)求购买一桶A 种、一桶B 种消毒液各需多少元?(2)为了践行“把人民群众生命安全和身体健康摆在第一位”的要求,加强学校防控工作,保障师生健康安全,学校准备再次购买一批防控物资.其中A ,B 两种消毒液准备购买共50桶.如果学校此次购买A 、B 两种消毒液的总费用不超过3250元,那么学校此次最多可购买多少桶B 种消毒液?19.现有A ,B ,C ,D 四个长方体容器,A ,B 的底面积均为2x ,高分别为x ,y ;C ,D 的底面积均为2y ,高分别为x ,y (其中x y ≠).现规定一种两人的游戏规则:每人从四种容器中取两个盛水,盛水多者为胜.问先取者在未能确定x 与y 大小的情况下有没有必胜的方案?若有的话,有几种? 20.设{}1,3A =−,{}230Bx xax b =−+=,已知B ≠∅,且“x B ∈”是“x A ∈”的充分条件,求34a b +的值.21.已知a ,b 是实数,求证:44221a b b −−=成立的充要条件是221a b −=. 22.已知n 为正整数,集合(){}{}122,,,,1,1,1,2,,2ni A x x x x i n αα==⋅⋅⋅∈−=⋅⋅⋅∣具有性质P :“对于集合A中的任意元素()122,,,n x x x α=⋅⋅⋅,1220n x x x ++⋅⋅⋅+=,且120i x x x ++⋅⋅⋅+ ,其中1,2,,21i n =⋅⋅⋅−”.(1)当3n =时,写出满足条件的集合A ;(2)当9n =时,求129x x x ++⋅⋅⋅+的所有可能的取值.重庆八中高2026级高一(上)数学检测试题(一)参考答案1 2 3 4 5 6 7 8 9 10 11 12 B ACBCBCCABDADBCD ACD13.[)3,2−14.()()(){}12,1,6,2,4,315.62a −<≤−16.871.命题是全称命题,则命题的否定是特称命题即p ¬:x ∃∈R ,20x +≤,故选B2.由{}3,5U B = ,而{}1,3A =,所以{}1,3,5U B A = .故选:A3.由题意,集合{A =,{}1,B m =,因为A B A = ,可得B A ⊆,则满足3m =或m =1m ≠,解得3m =或0m =.故选:C. 4.①③⑦正确,故选:B.5.因为p 是r 的的充分条件,所以p r ⇒.因为q 是r 的充分不必要条件,所以q r ⇒,r q . 因为s 是r 的必要条件,所以r s ⇒.因为p 是s 的必要条件,所以s p ⇒. 因为r s ⇒,s q ⇒,所以r p ⇒,r 是p 的充分条件,命题①错误;因为s p ⇒,p r ⇒,所以s r ⇒,又r s ⇒,所以r 是s 的充要条件,命题②错误;因为q r ⇒,r s ⇒,s p ⇒,所以q p ⇒,p q ,故q 是p 的充分不必要条件,命题③正确; 因为r q ,r s ⇔,所以s q ,又q s ⇒,所以s 是p 的必要不充分条件,命题④错误,故选:C.6.因为{}{}2,0,1,,0a a b −=,所以①21a a b ==−或②21a b a = =− ,由①得01a b = =− 或11a b = =− ,其中01a b = =− 与元素互异性矛盾,舍去,11a b = =− 符合题意,由②得11b a = =− ,符合题意,两种情况代入202320230a b +=,答案相同.故选:B7.因为{}05M x x x =∈≤>R 或,所以{}05U M x x =<≤ .题图中阴影部分表示的集合为()UP M ,因为{}{}18,0,1,2,3,4,5,6,7,8P x x x Z =−<≤∈=,所以(){}1,2,3,4,5UP M = ,所以该集合中共有5个元素.8.集合9,4A x x x =≥−∈R ,{}0,B x x x =<∈R ,则R9,4A x x x =<−∈R , {}R 0,B x x x =≥∈R ,由定义可得:{}{}[)R 0,0,A B x x A x B A B x x x −=∈∉==≥∈=+∞R 且 ,{}R 99,,44B A x x B x A B A x x x−=∈∉==<−∈=−∞−R 且 ,所以()()[)9,0,4A B A B B A⊕=−−=−∞−+∞,选项ABD 错误,选项C 正确.故选:C.9.对于A ,a Q ∈是a R ∈的充分不必要条件,正确;对于B ,x y =等价于x y =±是x y =的必要不充分条件,正确; 对于C ,21x >等价于1x >或1x <−是1x >的必要不充分条件,错误; 对于D ,0a b +<是0a <,0b <的必要不充分条件,正确;故选:ABD 10.对于A :当0x <时,0x x x =−>>,故A 正确;对于B :当1x =时,23570x x −−=−<,故B 错误; 对于C :当x π=时,4x 是无理数,故C 错误;对于D :2a =,1b =−时,()()22210a b −++=,A 正确;故选:AD. 11.对于A ,令2a =,12b =,则11a b a b+=+,A 错误; 对于B ,()1011m m n m n n n n +−−=<++,11m mn n+<+,B 正确. 对于C ,000a b a b c a c b >>⇒−<−<⇒<−<−,同乘以()()1c a c b −−,得110c b c a<<−−,又0a b >>,∴a bc a c b>−−,C 正确. 对于D ,1a b >− ,则110a b +≥+>,()()11a b a ab b ab b a +=+≥+=+,则11a ba b≥++,D 正确.故选BCD.12.对于A 中,任取x A B ∈ ,y A B ∈ ,因为集合A ,B 是优集,则x y A +∈,x y B +∈,则x y A B +∈ ,x y A −∈,x y B −∈,则x y A B −∈ ,所以A 正确;对于B 中,取{}2,Ax x k k Z ==∈,{}3,Bx x m m Z ==∈,则{}23,A B x x k x k k Z ===∈或 ,令3x =,2y =,则5x y A B +=∉ ,所以B 不正确;对于C 中,任取x A ∈,y B ∈,可得,x y A B ∈ ,因为A B 是优集,则x y A B +∈ ,x y A B −∈ ,若x y B +∈,则()x x y y B =+−∈,此时A B ⊆;若x y A +∈,则()y x y x A =+−∈,此时B A ⊆,所以C 正确;对于D 中,A B 是优集,可得A B ⊆,则A B A = 为优集;或B A ⊆,则A B B = 为优集,所以A B 是优集,所以D 正确.故选:ACD.13.因为01y <≤,所以220y −≤−<,因为12x −≤<,所以322x y −≤−<,所以2x y −的取值范围是[)3,2−14.由12,xy x y y x=∈ <N 解得121x y == 或62x y = = 或43x y = = ,所以,()()(){}12,1,6,2,4,3A B = . 15.命题“x ∃∈R ,()()22210a x a x +++−≥”的否定为:“x ∀∈R ,()()22210a x a x +++−<”,因为原命题为假命题,所以其否定为真,所以当20a +=即2a =−时,10−<恒成立,满足题意;当20a +≠即2a ≠−时,只需()()220Δ2420a a a +< =+++< ,解得:62a −<<− .综上所述,实数a 的取值范围是62a −<≤−.16.考虑反面的两种情况:若M 中不含有奇数,则集合M 的个数等价于集合{}2,4,6的子集的个数,即328=.若M 中只含有一个奇数,则有4种可能,集合M 的个数等价于集合{}2,4,6的子集的个数的4倍,即32432×=.不考虑奇数条件时集合M 共721127−=,故共有12783287−−=个. 17.解:(1)由题意知当3m =时,{}26B x x =≤≤,故{}26U B x x x =<>或 , 而{}03A x x =≤≤,故()[)0,2UA B =(2)当B =∅时,12m m −>,∴1m <−,符合题意;当B ≠∅时,需满足012312m m m m≤−≤ −≤,且01m ≤−,23m ≤中等号不能同时取得,解得312m ≤≤, 综上所述,m 的取值范围为1m <−或312m ≤≤. 18.解:(1)设购买一桶A 种消毒液x 元,购买一桶B 种消毒液y 元,则有25002000230xy y x =×−=, 解得5080x y ==所以,购买一桶A 种消毒液需50元,购买一桶B 种消毒液需80元. (2)设购买A 种消毒液m 桶,购买B 种消毒液n 桶, 则有5050803250m n m n +=+≤ ,(),N m n ∈得()5050803250n n −+≤,解得25n ≤,所以最多可以购买25桶B 种消毒液19.解:①当x y >时,则3223x x y xy y >>>,即A B C D >>>;在此种条件下取A ,B 能够稳操胜券 ②当x y <时,则3223y y x yx x >>>,即D C B A >>>;在此种条件下取D ,C 能够稳操胜券.③又()()()()332232322()0x y xy x y x x y y xy x y x y +−+=−+−=−+>.∴在不知道x ,y 的大小的情况下,取A ,D 能够稳操胜券,其他的都没有必胜的把握. 故可能有1种,就是取A ,D . 20.详解:因为B A ⊆,B ≠∅,所以①当{}1B =−时,则222Δ4301(1)303a a b b a b =− −×⇒ =−++=, 所以()1143432433a b +=×−+×=−, ②当{}3B =时,则226Δ43033330a a b b a b =−× ⇒ =−+=, 所以34364330a b +=×+×=③当{}1,3B =−时,则2Δ4302131133a b a a b b −×>=−+=⇒=− −×=, 所以()3432412a b +=×+×−=,综述:①当{}1B =−即213a b =−=时,14343a b +=−, ②当{}3B =即63a b == 时,3430a b +=,③当{}1,3B =−即21a b ==−时,342a b +=. 21.解:先证明充分性:若221a b −=,则()()44222222222222221a b b a b ab b a b b a b −−=−+−=+−=−=成立.所以“221a b −=”是“44221a b b −−=”成立的充分条件; 再证明必要性:若44221a b b −−=,则442210a b b −−−=, 即()442210a b b −++=, ∴()24210a b −+=,∴()()2222110a b a b ++−−=, ∵2210a b ++≠, ∴2210a b −−=, 即221a b −=成立.所以“221a b −=”是“44221a b b −−=”成立的必要条件. 综上:44221a b b −−=成立的充要条件是221a b −=.22.解:(1)3n =时,由题设,在126,,,x x x ⋅⋅⋅中,有3个1+,3个1−集合A 中的元素为()11,1,1,1,1,1α=−−−,()21,1,1,1,1,1α=−−−,()31,1,1,1,1,1α=−−−,()41,1,1,1,1,1α−−−,()51,1,1,1,1,1α=−−−∴()()()()(){}1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1A=−−−−−−−−−−−−−−−(2)9n =时,首先证明11x =,且181x =−,在120i x x x ++⋅⋅⋅+ 中,令1i =,得10x ,从而有11x =, 在120i x x x ++⋅⋅⋅+ 中,令17i =,得12170x x x ++⋅⋅⋅+ .又12180x x x ++⋅⋅⋅+=,故)1812170x x x x =−++⋅⋅⋅+ ,从而有181x =−,考虑()1,,1,1,,1α=⋅⋅⋅−⋅⋅⋅−,即1291x x x ==⋅⋅⋅==,1011181x x x ==⋅⋅⋅==−此时1299x x x ++⋅⋅⋅+=为最大值,现交换9x 与10x ,使得91x =−,101x =,此时1297x x x ++⋅⋅⋅+=,现将91x =−逐项前移,直至21x =−,在前移过程中,显然1297x x x ++⋅⋅⋅+=不变,这一过程称为1次“移位”,依此类推,每次“移位”,129x x x ++⋅⋅⋅+的值依次递减2,经过有限次移位,129,,,x x x ⋅⋅⋅一定可以调整为1,1−交替出现.注意到9n =为奇数,所以1291x x x ++⋅⋅⋅+=为最小值, 所以129x x x ++⋅⋅⋅+的所有可能取值,1,3,5,7,9.。
重庆八中2020-2021学年高一上学期国庆假期数学作业(二) PDF版含答案

(2)若 A B = ,求实数 a 的取值范围.
第6页 共8页
21.(12 分) 已知函数 f (x) = x + 4 . x
(1)用函数单调性的定义证明 f (x) 在区间[2, +) 上为增函数; (2)解不等式: f (x2 − 2x + 4) f (7) .
第7页 共8页
22.(12 分) 已知二次函数 f (x) = x2 − 2ax + 5 ,其中 a 1 . (1)若函数 f (x) 的定义域和值域均为[1, a] ,求实数 a 的值;
1.已知全集U = R ,集合 A, B 满足 A B ,则下列选项正确的有( )
A. A B = B
B. A B = B
C. ( U A) B =
D. A ( U B) =
2.已知集合 A, B 均为全集U =1, 2,3, 4 的子集,且 U ( A B) = 4, B = 1, 2 ,则
A U B 等于( )
(2) 若 函 数 f (x) 在 区 间 (−, 2] 上 单 调 递 减 , 且 对 任 意 的 x1, x2 [1, a +1] , 总 有
f (x1) − f (x2 ) 3 成立,求实数 a 的取值范围.
第8页 共8页
重庆八中高 2023 级国庆假期数学作业(二)答案
一、选择题
1
2
3
4
a =3 3a 4
,解得 a = 3;
当 a<0 时, B = {x 3a x a} ,应满足:
3a = 2
a
4
,解得 a .
当 a = 0 时, B = , A B = ,舍去;
a = 3 时, A B = {x 3 x 4} .
重庆市第八中学校2023-2024学年高一上学期期中数学试题

题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若 P = {(1, 2),(1,3)} ,则集合 P 中元素的个数是( )
A.1
B.2
C.3
2.命题“ "x Î R , x2 - 2x +12 £ 0”的否定为( )
五、证明题 19.已知 VABC 的三边长为 a, b, c ,其中 a = 2 .求证: VABC 为等边三角形的充要条件
是 b2 + c2 - 2(b + c) = bc - 4 .
六、解答题 20.如图,现将正方形区域 ABCD 规划为居民休闲广场,八边形 HGTQPMKL 位于正
方形 ABCD 的正中心,计划将正方形 WUZV 设计为湖景,造价为每平方米 20 百元;在 四个相同的矩形 EFUW , IJVW ,VZON,UZRS 上修鹅卵石小道,造价为每平方米 2 百元;
22.若在函数 f ( x) 的定义域内存在区间[a,b] ,使得 f ( x) 在[a,b] 上单调,且函数值的
取值范围是[ma, mb] ( m 是常数),则称函数 f ( x) 具有性质 M .
(1)当
m
=
1 2
时,函数
f
(
x)
=
x 否具有性质 M ?若具有,求出 a , b ;若不具有,说明
理由;
(2)若定义在 (0, 2) 上的函数
f
(x) =
x+
4 x
-5
具有性质 M
m ,求 的取值范围.
试卷第51 页,共33 页
重庆市2023-2024学年高一上学期10月月考数学试题解析

重庆2023—2024学年度(上)高2026级国庆学情检测数学试题数学试题(答案在最后)注意事项:1.本试卷分第Ⅰ卷和第Ⅱ卷两部分,满分150分,考试时间120分钟.2.答卷前,请考生将自己的姓名、准考证号填涂在答题卡上.3.作答时,请将答案写在答题卡指定的区域,超出答题区域或写在试题卷、草稿纸上无效.4.做选考题时,按要求作答,并用2B 铅笔在答题卡上把所选题目的题号涂黑.第Ⅰ卷(选择题)一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知命题:p x R ∀∈,2210x +>,命题p 的否定是()A.x ∀∈R ,2210x +≤B.x ∃∈R ,2210x +>C.x ∃∈R ,2210x +<D.x ∃∈R ,2210x +≤【答案】D 【解析】【分析】利用含有一个量词的命题的否定的定义求解即可.【详解】命题:p x R ∀∈,2210x +>的否定是:x ∃∈R ,2210x +≤故选:D2.函数()11f x x =+-的定义域为()A.[)2,-+∞B.()1,+∞C.[)()2,11,-⋃+∞ D.()()2,11,-⋃+∞【答案】C 【解析】【分析】根据函数的定义域列不等式组求解即可.【详解】由题意,得2010x x +≥⎧⎨-≠⎩,解得2x ≥-且1x ≠,即函数()f x 的定义域为[)()2,11,-⋃+∞.故选:C .3.游泳池原有一定量的水.打开进水阀进水,过了一段时间关闭进水阀.再过一段时间打开排水阀排水,直到水排完.已知进水时的流量、排水时的流量各保持不变.用h 表示游泳池的水深,t 表示时间.下列各函数图象中能反映所述情况的是()A. B.C. D.【答案】D 【解析】【分析】函数图像不过原点,排除AC ;函数值有一段时间不变,排除B ,得到答案.【详解】游泳池原有一定量的水,故函数图像不过原点,排除AC ;再过一段时间打开排水阀排水,故函数值有一段时间不变,排除B .故选:D4.已知函数243,0()3,0x x x f x x x ⎧++≤=⎨->⎩,则((5))f f =()A.1B.0C.1- D.2-【答案】C 【解析】【分析】根据分段函数解析式求解即可.【详解】解:由题知()5352f =-=-,所以()((5))24831f f f =-=-+=-.故选:C5.若a b c >>,且0a b c ++=,则下列不等式中一定成立的是()A.ab ac > B.ac bc> C.a b c b> D.222a b c >>【答案】A 【解析】【分析】题目已知a b c >>,且0a b c ++=,于是可以推出得到最大数0a >和最小数0c <,而b 为正、负、零均有可能,所以每个选项代入不同的b ,逐一验证.【详解】解:a b c >> 且0a b c ++=.当0a ≤时,0c b a << ,则0a b c ++<,与已知条件0a b c ++=矛盾,所以必有0a >,同理可得0c <.A 项,()0ab ac a b c -=->,即ab ac >,故A 项正确;B 项,()0ac bc c a b -=-<,即ac bc <,故B 项错误;C 项,0b =时,a b c b =,故C 项错误;D 项,当1a =,0b =,1c =-时,222a c b =>,故D 项错误.故选A【点睛】本题主要考查给定条件判断不等式的性质,注意考虑,,a b c 的正负.6.中国南宋大数学家秦九韶提出了“三斜求积术”,即已知三角形三边长求三角形面积的公式:设三角形的三条边长分别为a 、b 、c ,则三角形的面积S 可由公式S =求得,其中p 为三角形周长的一半,这个公式也被称为海伦-秦九韶公式,现有一个三角形的边长满足3a =,5b c +=,则此三角形面积的最大值为()A.32B.3C.D.【答案】B 【解析】【分析】由公式列出面积的表达式,代入已知3a =,然后由基本不等式求得最大值.【详解】由题意()13542p =+=S =()83b c ==≤-+=,当且仅当44-=-b c ,即b c =时等号成立﹐∴此三角形面积的最大值为3.故选:B .【点睛】易错点睛:利用基本不等式求最值时,要注意其必须满足的三个条件:(1)“一正二定三相等”“一正”就是各项必须为正数;(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方7.如果对于任意实数x ,[x ]表示不超过x 的最大整数,例如[π]=3,[0.6]=0,[-1.6]=-2,那么“[x ]=[y ]”是“|x -y |<1”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分又不必要条件【答案】A 【解析】【分析】根据高斯函数的定义以及充分必要条件的定义推导即可.【详解】如果[][],Z x y n n ==∈,则有[)1212,,,0,1x n d y n d d d =+=+∈,x y ∴-=121d d -<,所以[][]=x y 是1x y -<的充分条件;反之,如果1x y -<,比如 3.9, 4.1x y ==,则有0.21x y -=<,根据定义,[][][][]3,4,x y x y==≠,即不是必要条件,故[][]=x y 是1x y -<的充分不必要条件;故选:A .8.若两个正实数x ,y 满足142x y +=,且不等式24y x m m +<-有解,则实数m 的取值范围是()A.()1,2- B.()(),21,-∞-+∞ C.()2,1- D.()(),12,-∞-+∞ 【答案】D 【解析】【分析】利用基本不等式求得4yx +的最小值,根据不等式存在性问题,解一元二次不等式求得m 的取值范围.【详解】若不等式24y x m m +<-有解,即2min 4y m m x ⎛⎫->+ ⎪⎝⎭即可,因为两个正实数x ,y 满足142x y +=,即1212x y+=,则1221124428⎛⎫⎛⎫+=++=++≥+= ⎪ ⎪⎝⎭⎝⎭y y x y x x x y y x ,当且仅当28x yy x=,即1,4x y ==时,等号成立,即min24y x ⎛⎫+= ⎪⎝⎭,可得22m m ->,即220m m -->,解得m>2或1m <-,所以实数m 的取值范围是()(),12,-∞-+∞ .故选:D.二、多项选择题:本题共4小题,每题5分,共20分.在每个小题给出的选项中,有多项是符合题目要求的,全部选对得5分,部分选对得3分,错选不得分.9.下列各组函数表示的是不同函数的是()A.()f x =()g x x =B.()f x x =与()g x =C.()1f x x =+与()0g x x x =+D.()f x =与()g x =【答案】ACD 【解析】【分析】利用相同函数的定义求解.【详解】A.()f x ={}|0x x ≤,且()f x ==-,()g x x =的定义域为{}|0x x ≤,解析式不同,所以不是同一函数,故错误;B.()f x x =的定义域为R,()g x x ==定义域为R ,且解析式相同,所以是同一函数,故正确;C.()1f x x =+的定义域为R ,()0g x x x =+的定义域为{}|0x x ≠,所以不是同一函数,故错误;D.,由010x x ≥⎧⎨+≥⎩得0x ≥,所以()f x =的定义域为{}|0x x ≥,由20x x +≥,得0x ≥或1x ≤-,所以函数()g x =的定义域为{|0x x ≥或}1x ≤-,所以不是同一函数,故错误;故选:ACD10.下列不等式,其中正确的是()A.3322(,R)a b a b ab a b +≥+∈B.()232x x x R +>∈C.222()11f x x x =+≥- D.222(1)a b a b +≥--【答案】BD 【解析】【分析】结合不等式的性质及基本不等式分别检验各选项即可判断.【详解】解:332222222()()()()()()a b a b ab a a b b b a a b a b a b a b +--=-+-=--=-+ ,2()0a b - ,a b +的符号不定,所以33+a b 与22a b ab +的大小不定,A 错误;2223(1)220x x x -+=-+> ,故232x x +>,B 正确;222222()1111f x x x x x =+=-++--,当210x -<时,()0f x <,故C 错误.2222222(1)(1)0a b a b a b +-++=-++ ,故222(1)a b a b +-- ,D 正确;故选:BD .【点睛】利用基本不等式求最值时,要注意其必须满足的三个条件:(1)“一正二定三相等”“一正”就是各项必须为正数;(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方11.若正实数a ,b 满足2a b +=,则下列说法正确的是()A.ab 有最大值1B.有最大值2C.11a b+有最小值2 D.22a b +有最大值2【答案】ABC【解析】【分析】根据基本不等式,即可判断选项.【详解】对于A 项,因为212a b ab +⎛⎫≤= ⎪⎝⎭,当且仅当1a b ==时取等号,则ab 的最大值为1,故A 正确;对于B 项,()()224a b a b a b a b =+++++=+=,当且仅当1a b ==时取等号,+的最大值为2,故B 正确;对于C 项,因为()1111111222222b a a b a b a b a b ⎛⎛⎫⎛⎫+=++=++≥+= ⎪ ⎪ ⎝⎭⎝⎭⎝,当且仅当1a b ==时取等号,所以11a b+的最小值为2,故C 正确;对于D 项,因为()2222424212a b a b ab ab +=+-=-≥-⨯=,当且仅当1a b ==时取等号,所以22a b +的最小值为2,故D 错误.故选:ABC12.已知有限集{}()12,,,2,n A a a a n n =⋅⋅⋅≥∈N ,如果A 中元素()1,2,3,,i a i n =⋅⋅⋅满足1212n n a a a a a a ++⋅⋅⋅+=⨯⨯⋅⋅⋅⨯,就称A 为“完美集”下列结论中正确的有()A.集合{11---不是“完美集”B.若1a 、2a 是两个不同的正数,且{}12,a a 是“完美集”,则1a 、2a 至少有一个大于2C.2n =的“完美集”个数无限D.若*i a ∈N ,则“完美集”A 有且只有一个,且3n =【答案】BCD 【解析】【分析】根据题设中的“完美集”的定义,结合集合的运算,以及一元二次方程的性质,可判定A 错误,B 和C 正确;设A 中123n a a a a <<<⋅⋅⋅<,得到121n a a a n -⋅⋅⋅<,分2n =和3n =,两种情况分类讨论,可判定D 正确.【详解】对于A 中,((112-+-+=-,(112--+=-,集合{11--+是“完美集”,所以A 错误;对于B 中,若1a 、2a 是两个不同的正数,且{}12,a a 是“完美集”,设12120a a a a t +=⋅=>,根据根和系数的关系1a 和2a 相当于20x tx t -+=的两根,由240t t ∆=->,解得4t >或0t <(舍去),所以124a a ⋅>,所以1a 、2a 至少有一个大于2,所以B 正确;对于C 中,由B 知,一元二次方程20x tx t -+=,当t 取不同的值时,12,a a 的值是不同的,所以二元“完美集”有无穷多个,所以所以C 正确;对于D 中,不妨设A 中123n a a a a <<<⋅⋅⋅<,由1212n n n a a a a a a na ⋅⋅⋅=++⋅⋅⋅+<,得121n a a a n -⋅⋅⋅<,当2n =时,即有12a <,所以11a =,于是221a a +=,2a 无解,即不存在满足条件的“完美集”;当3n =时,123a a <,故只能11a =,22a =,求得33a =,于是“完美集”A 只有一个,为{}1,2,3.当4n ≥时,由()1211231n a a a n -⋅⋅⋅≥⨯⨯⨯⋅⋅⋅⨯-,即有()1231n n >⨯⨯⨯⋅⋅⋅⨯-,事实上,()()()()221231123222n n n n n n n n ⨯⨯⨯⋅⋅⋅⨯-≥--=-+=--+>,矛盾,所以当4n ≥时不存在完美集A ,所以D 正确.故选:BCD.第Ⅱ卷(非选择题)三、填空题:本题共4小题,每小题5分,共20分.13.函数()y f x =的图象如图所示,那么其中只有唯一的x 值与之对应的y 值的范围是______.【答案】[)(]1,24,5U【解析】【分析】根据图中数据即可求解.【详解】解:由题中图形可得,只有唯一的x 值与之对应的y 值的范围是:[)(]1,24,5U 故答案为:[)(]1,24,5U .14.已知集合{}2210,A xax x x =++=∈R ∣的子集只有两个,则实数a 的值为______.【答案】0或1【解析】【分析】分类讨论确定集合A 中元素或元素个数后得出其子集个数,从而得结论.【详解】0a =时,1{}2A =-,子集只有两个,满足题意,0a ≠时,若440∆=-<a 即1a >,则A =∅,子集只有1个,不满足题意;若0∆>,即1a <,则集合A 有两个元素,子集有4个,不满足题意,1a =时,Δ0=,{1}A =-,子集只有两个,满足题意,所以0a =或1.故答案为:0或1,15.函数2,02()28,2x x x f x x x ⎧+<<=⎨-+≥⎩,若()(2)f a f a =+,则()2f a =__________.【答案】4【解析】【分析】根据函数2,02()28,2x x x f x x x ⎧+<<=⎨-+≥⎩各段的定义域,分02a <<,2a ≥两种情况,由()(2)f a f a =+求解.【详解】当02a <<时,则22a +>,因为()(2)f a f a =+,所以()2228a a a +=-++,即2340a a +-=,解得1a =或4a =-(舍去),所以()22284f a =-⨯+=.当2a ≥时,则22a +>,因为()(2)f a f a =+,所以()28228a a -+=-++无解.综上:()24f a =故答案为:4【点睛】本题主要考查分段函数求值问题,还考查了分类讨论思想和运算求解的能力,属于中档题.16.已知a >b >0,且a +b =1,则411()a b b a b a b b++---的最小值为______.【答案】12【解析】【分析】两次利用基本不等式求最值即可.【详解】∵a >b >0,且a +b =1,∴2424812(22)22a b b b a b a b b a b b -++≥=+=--⋅-+⎛⎫⎪⎝⎭,当且仅当4a b b b a b -=-且2a b b -=,即334a b ==时,等号同时取到,故答案为:12四、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.17.已知集合:{}{}2237,560A x x B x x x =-≤=--<:(1)求集合A 、B ;(2)求A B ⋃和()R A B ⋂ð.【答案】(1){}25A x x =-≤≤,{}16B x x =-<<(2){}26A B x x ⋃=-≤<,(){}56R A B x x ⋂=<<ð【解析】【分析】(1)解绝对值不等式求得集合A ,解一元二次不等式求得集合B ;(2)利用并集的定义可得A B ⋃,由补集的定义可得R A ð,再根据交集的定义即可求得()R A B ⋂ð.【小问1详解】∵237x -≤,∴7237x -≤-≤,解得25x -≤≤,∴{}25A x x =-≤≤,∵2560x x --<,∴()()610x x -+<,解得16x -<<,∴{}16B x x =-<<【小问2详解】∵{}25A x x =-≤≤,{}16B x x =-<<,∴{}26A B x x ⋃=-≤<,{2R A x x =<-ð或}5x >,∴(){}56R A B x x ⋂=<<ð18.已知定义在R 上的函数满足:()()2223f x f x x x +-=-+.(1)求函数()f x 的表达式;(2)若不等式()21f x ax ≥-在[]1,3上恒成立,求实数a 的取值范围.【答案】(1)()21213f x x x =++(2)13a ≤+【解析】【分析】(1)利用方程组法求函数解析式即可;(2)要使()21f x ax ≥-在[]1,3上恒成立,分离参数结合基本不等式求解即可.【小问1详解】将()()2223f x f x x x +-=-+的x 替换为x -得()()2223f x f x x x -+=++,联立()()()()22223223f x f x x x f x f x x x ⎧+-=-+⎪⎨-+=++⎪⎩解得()21213f x x x =++【小问2详解】不等式()21f x ax ≥-为2121213x x ax ++≥-,化简得116x a x≤++,要使其在[]1,3上恒成立,则min 116x a x ⎛⎫≤++⎪⎝⎭,111163x x ++≥+=+,当且仅当x =取等,所以13a ≤+.19.党的二十大报告提出,积极稳妥推进碳达峰碳中和,立足我国能源资源禀赋,坚持先立后破,有计划分步骤实施碳达峰行动,深入推进能源革命,加强煤炭清洁高效利用,加快规划建设新型能源体系,积极参与应对气候变化全球治理.在碳达峰、碳中和背景下,光伏发电作为我国能源转型的中坚力量发展迅速.在可再生能源发展政策的支持下,今年前8个月,我国光伏新增装机达到4447万千瓦,同比增长2241万千瓦.某公司生产光伏发电机的全年固定成本为1000万元,每生产x (单位:百台)发电机组需增加投入y(单位:万元),其中2240,040180001652250,40100x x x y x x x ⎧+≤<⎪=⎨+-≤≤⎪⎩,该光伏发电机年产量最大为10000台.每台发电机的售价为16000元,全年内生产的发电机当年能全部售完.(1)将利润P (单位:万元)表示为年产量x (单位:百台)的函数;(2)当年产量为何值时,公司所获利润最大?最大利润为多少万元?(总收入=总成本+利润).【答案】(1)221201000,0401800051250,40100x x x P x x x ⎧-+-≤<⎪=⎨--+≤≤⎪⎩;(2)当年产量为3000台时,公司所获利润最大,最大利润为800万元.【解析】【分析】(1)根据利润、成本、收入之间的关系分类讨论即可;(2)根据二次函数的性质,结合基本不等式进行求解即可.【小问1详解】当040x ≤<时,()22160240100021201000P x x x x x =-+-=-+-;当40100x ≤≤时,18000180001601652250100051250P x x x x x=--+-=--+,即221201000,0401800051250,40100x x x P x x x ⎧-+-≤<⎪=⎨--+≤≤⎪⎩;【小问2详解】当040x ≤<时,22212010002(30)800P x x x =-+-=--+,所以当30x =时,max 800P =,当40100x ≤≤时,36001250512505650P x x ⎛⎫=-+≤-⨯ ⎪⎝⎭,当且仅当3600x x=时取等号,即60x =时取等号,∵800650>,∴当年产量为3000台时,公司所获利润最大,最大利润为800万元.20.已知关于x 的不等式2(2)20ax a x -++≤.(1)若a<0,求不等式的解集;(2)若0a >,不等式的解集中恰有3个整数,求实数a 的取值范围.【答案】(1)[)2,1,a ⎛⎤-∞+∞ ⎥⎝⎦(2)12,23⎛⎤ ⎥⎝⎦【解析】【分析】(1)根据一元二次不等式的解法求解即可;(2)先根据一元二次不等式的解法解含参不等式,再结合不等式的解集中恰有3个整数,即可得解.【小问1详解】当a<0时,令2(2)20ax a x -++=,解得1221,x x a ==,此时21a>,则由2(2)20ax a x -++≤,得2(1)0x x a ⎛⎫--≥ ⎪⎝⎭,故不等式解集为[)2,1,a ⎛⎤-∞+∞ ⎥⎝⎦;【小问2详解】当0a >时,令2(2)20ax a x -++=,解得1221,x x a ==,若21a <,即02a <<时,不等式解集为21,a ⎡⎤⎢⎥⎣⎦,此时要使解集中恰有3个整数,这3个整数只能是1,2,3,所以02234a a <<⎧⎪⎨≤<⎪⎩,解得1223a <≤;若21a=,即2a =时,不等式解集为{}1,此时不符合题意;若若21a >,即2a >时,不等式解集为2,1a ⎡⎤⎢⎥⎣⎦,而201a <<,此时不等式解集2,1a ⎡⎤⎢⎥⎣⎦只有一个整数解1,故不符合题意,综上所述,实数a 的取值范围为12,23⎛⎤⎥⎝⎦.21.已知集合{}{}222|320,|(2)210A x x x B x x a x a a =-+==-++-+=.(1)当{}1A B ⋂=时,求实数a 的值;(2)若R R A B ⋃=ð时,求实数a 的取值范围.【答案】(1)0a =(2)(]{}8,01,7⎛⎫-∞+∞ ⎪⎝⎭【解析】【分析】(1)由1B ∈解方程求出a 的值,再检验即可;(2)由R R A B ⋃=ð得出B A ⊆,结合子集的定义得出B 可能为∅,{}1,{}2,{}1,2,分别讨论这四种情况,得出实数a 的取值范围.【小问1详解】{}{}2|3201,2A x x x =-+==,∵{}1A B ⋂=,∴1B ∈,即221(2)210a a a -++-+=,解得0a =或1a =.当0a =时,{}{}2|2101B x x x =-+==,符合题意;当1a =时,{}{}2|3201,2B x x x =-+==,{}1,2A B = ,不合题意,综上,0a =.【小问2详解】∵R R A B ⋃=ð,∴B A ⊆,即B 可能为∅,{}1,{}2,{}1,2.当B =∅时,22(2)4()021a a a ∆-+=+-<,即2780a a ->,解得a<0或87a >,当集合B 中只有一个元素时,22(2)4()021a a a ∆-+=+-=,解得0a =或87a =,当0a =时,{}{}2|2101B x x x =-+==,符合题意;当87a =时,117B ⎧⎫=⎨⎬⎩⎭,不符合题意;当{}1,2B =时,由根与系数的关系可知22122112a a a +=+⎧⎨-+=⨯⎩,又22(2)4()021a a a ∆-+=+->,解得1a =,∴所求实数a 的取值范围是(]{}8,01,7⎛⎫-∞+∞ ⎪⎝⎭.22.对于函数32(1)(1)(0)y mx ax b x b a =++-+-≠,若存在0x ∈R ,使得320000(1)(1)mx ax b x b x ++-+-=成立,则称0x 为函数32(1)(1)(0)y mx ax b x b a =++-+-≠的“囧点”.(1)当m =2,a =-3,b =2时,求函数32(1)(1)(0)y mx ax b x b a =++-+-≠的“囧点”;(2)当m =0时,对任意实数b ,函数32(1)(1)(0)y mx ax b x b a =++-+-≠恒有“囧点”,求a 的取值范围.【答案】(1)“囧点”1=1x ,212x =-(2)10a -≤<【解析】【分析】(1)利用“囧点”定义布列方程,即可得到结果;(2)函数32(1)(1)(0)y mx ax b x b a =++-+-≠恒有“囧点”,等价于函数2(1)(1)(0)y ax b x b a =+++-≠恒有“囧点”,结合判别式即可得到结果.【小问1详解】当m =2,a =-3,b =2时,32231y x x x =-++,由题意知:∴32231x x x x -++=,∴()()22110x x +-=,解得1=1x ,212x =-,所以当m =2,a =-3,b =2时,函数32(1)(1)(0)y mx ax b x b a =++-+-≠的“囧点”1=1x ,212x =-.【小问2详解】由题知:2(1)(1)(0)ax b x b x a +-+-=≠,所以2(2)(1)0ax b x b +-+-=,由于函数2(1)(1)(0)y ax b x b a =+++-≠恒有“囧点”,所以2(2)4(1)0b a b ∆=---≥,即24(1)4(1)0b a b a -+++≥,又因为b 是任意实数,所以()110a a ∆=+≤,。
高一数学国庆假期作业参考答案

高一数学国庆假期作业参考答案【选择题答案】1.C2.D3.C4.A5.D6.D7.D8.A9.A 10.D 注:其中第7题涉及函数奇偶性,可不做【填空题答案】11. {1,2,3} 12. (1)x x + 13. {|01}x x x <>或14. [2,7]- 15. 1,1x x -+(答案不唯一)注:其中第12、15题涉及函数奇偶性,可不做【解答题答案】16.(1)(){6,5,4,3,2,1,0}A B C A ==±±±±±±(2)(){6,5,4,3,2,1,0}A A C B C =------17.(1)根据211()211x f x x x -==+--,可判断函数在(1,)+∞上为减函数, 用单调性定义证明(此处略);(2)法一:直接解不等式2111x x ->-可得01x x <>或 法二:利用函数211()211x f x x x -==+--的图象,可直观得到01x x <>或 18. 集合2{|40,}{4,0}A x x x x R =+=∈=-根据A B B B A =⇔⊆ 可知,集合B 须分B =∅与B ≠∅两种情况考虑:①当B =∅时,即方程222(1)10x a x a +++-=无实根,因此0∆<,即 224(1)4(1)0a a +--<,所以1a <-;②当B ≠∅时,要使B A ⊆,则{4}{0}{4,0}B B B =-==-或或当0∆=即1a =-时{0}B =,符合;({4}B =-不可能)当{4,0}B =-时,根据2402(1)401a a -+=-+-⨯=-且,解得1a =;综上可知,11a a ≤-=或。
19.(1)函数1()f x x x =+的定义域为(,0)(0,)-∞+∞ ,且1()()()f x x f x x -=-+=-,故函数1()f x x x=+为奇函数; (2)21()[()1](1)1(0)F x x f x x x x x x x=-=+-=-+≠所以函数()y F x =的值域为333(,)[,1)(1,)[,)444+∞+∞=+∞【附加题答案】: (1)()()()2f x f x g x +-=是偶函数,()()()2f x f x h x --=是奇函数; (2)()()()()()()()22f x f x f x f x f xg xh x +---=+=+ (3)结论:任意一个定义域关于原点对称的函数()f x ,都可以表示为一个偶函数与一个奇函数的和,其中偶函数为()()()2f x f x g x +-=,奇函数为()()()2f x f x h x --=。
重庆八中高2023级数学高一上国庆作业题一(终版答案)

3, ⩽13, ⩽1
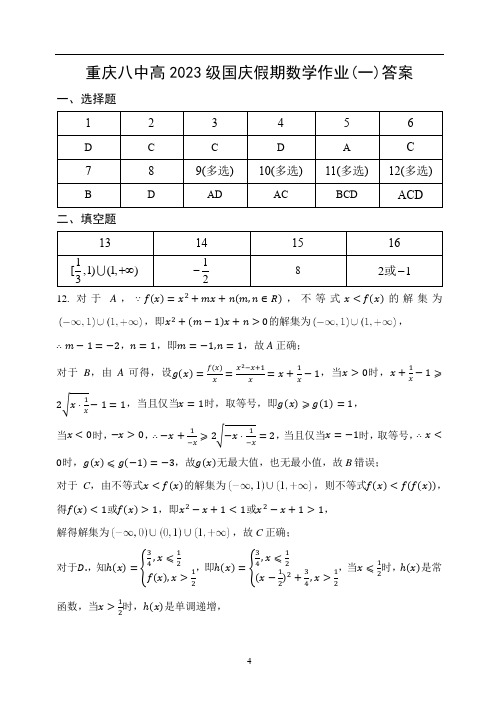
对于.,知ℎ()={42,即ℎ()={42
,当 ⩽1时,ℎ()是常
(), >1
2
函数,当 >1时,ℎ()是单调递增,
2
( −1
2
+3, >12
42
⩽1
2
>1
311
若ℎ()< ℎ(2+2),则{或
2 + 2 >1
2
∴ > (2− )得 > 2,即 = {| > 2};
(Ⅱ)不等式( − 3)( − − 2) < 0,
①当3 > 2 + ,即 > 1时,解集 = (2 + , 3),
若 ∈ 是 ∈ 的必要不充分条件,则 ⫋ ,
∴ 2 + ≥ 2此时 ∈ (1, +∞).
存在 > 3,使得() > 1成立,即存在 > 3,使得 >
成立.
令()=,∈(3,+∞),则>().
2−6
2−6
+62
()
,即2+ (−1)+ >0的解集 ,
∴ − 1 = −2, = 1,即 = −1, = 1,故A正确;
对于B,由A可得,设()=()=−+11,当>0时,+1− 1⩾
= + − 1
2√ ·1
− 1 = 1
,当且仅当 = 1时,取等号,即() ⩾ (1) = 1,
围是,故D正确.
,解得− < ⩽或 >
242
,∴ 的取值范
重庆八中高2023级数学高一上国庆作业题一 含答案

重庆八中高2023级高一(上)国庆假期数学作业(一)满分:150分 测试时间:120分钟姓名:__________ 班级:__________ 学号:__________ 一、 选择题(共12题,1~8题为单选题,每题5分,9~12题为多选题,全部选对得5分,部分选对得3分,错选或不选得0分,共60分)1.已知集合{}2|1M x x ==,{}|2N x ax ==,若N M ⊆,则实数a 的取值集合为( ) A .{}2 B .{}2,2- C .{}2,0-D .{}2,2,0-2.已知集合{}2,0A =,{}|,,B z z x y x A y A ==+∈∈ ,则集合B 的非空子集的个数为( ) A .3 B .4 C .7D .83.一元二次方程()24005ax x a ++=≠有一个正根和一个负根的一个充分不必要条件是( ) A .0a < B .0a > C .2a <-D .1a >4.已知关于x 的不等式22430(0)x ax a a -+<<的解集为12(,)x x ,则1212ax x x x ++的最大值是( ) AB. CD.5.设集合{}2|60A x x x =->-,{}0|()(2)B x x k x k =---<,若A B ≠∅,则实数k 的取值范围是( ) A .{}21|k k k <->或 B .{}|21k k -<< C .{}43|k k k <->或D .{}|43k k -<<6.下列各式:①212a a +>;②12xx +≥2≤;④22111x x +≥+. 其中正确..的个数是( ) A .0 B .1 C .2D .37.已知函数()1(1)3(1)f x x x x x +≤⎧=⎨-+>⎩,则52f f ⎡⎤⎛⎫= ⎪⎢⎥⎝⎭⎣⎦( ) A .12 B .32 C .52D .728.设0c <,()f x 是区间[],a b 上的减函数,下列命题中正确..的是( ) A .()f x c +在[],a b 上有最小值()f a c + B .()f x 在[],a b 上有最小值()f a C .()f x c -在[],a b 上有最小值()f a c - D .()cf x 在[],a b 上有最小值()cf a9.【多选题】若01,1a b c <<>>,则下列结论中正确..的有( ) A .111a b c>++ B .c a cb a b->-C >D .21b a ->-10.【多选题】设[]x 表示不大于实数x 的最小整数(例如:[2.5]2=,[2.2]3-=-),则满足关于x 的不等式2[][]120x x +-≤的解可以为( )A B .C .π-D .5-11.【多选题】下列说法中正确..的有( ) A .命题“32,1x x x ∀∈>+R ”的否定是“32,1x x x ∃∈<+R ”B .若不等式210ax bx ++>的解集为{}|13x x -<<,则不等式23650ax bx ++<的解集为(,1)(5,)-∞-+∞C .22,421x ax x x ∀∈+≥-R 恒成立,则实数a 的取值范围是[6,)+∞ D .已知211:3,:()10(0)2p x q x a x a a≤≤-++≤>,若p 是q 的充分不必要条件,则实数a 的取值范围是1(0,][3,)3+∞12.【多选题】已知函数2()(,)f x x mx n m n =++∈R ,不等式()x f x <的解集为(,1)(1,)-∞+∞,则( )A .1,1m n =-=B .设()()f x g x x=,则()g x 的最小值为(1)1g = C .不等式()(())f x f f x <的解集为(,0)(0,1)(1,)-∞+∞。
重庆八中高2023级数学高一上国庆作业题一(终版答案)

,故 C 正确;
3
4
1
3
, ⩽ 2
4
1
, ⩽ 2
1
对于.,知ℎ() = {
1,即ℎ() = {
1
3
1,当 ⩽ 2时,ℎ()是常
(), >
( − )2 + , >
2
2
1
函数,当 > 2时,ℎ()是单调递增,
1
4
2
1
⩽2
1
3
1
1
若 ℎ() < ℎ(2 + 2),则{
则 = × × =
= 15( +
,
400
+ 40) ≥ 1200,
60
7
≤ ≤ 80
当且仅当 = 20时取等号,所以当 DQ 的长为 20 时,S 最小,且为 1200.
(2) ∵ ≥ 1600,结合(1)中 S 的表达式列出不等式,化简得
∴ 3 2 − 200 + 1200 ≥ 0,
3
③当3 < 2 + ,即 < 1时解集 = (3, 2 + ),
若 ∈ 是 ∈ 的必要不充分条件,则 ⫋ 成立,
2
∴ 3 ≥ 2此时 ∈ [3 , 1).
(1)当 = 4时, = {| − 2 < < 2},
则⋂ = {|1 ≤ < 2}, ⋃ = {| − 2 < ≤ 3},
(2) = {| < 1, 或 > 3},因为 ⊆ ,所以√ ≤ 1,解得0 < < 1。
18.解:(1)因为不等式 2 − 4 + 3 < 0的解集为{|1 < < },
八中高2024级高一上半期试题及答案

重庆八中2021—2022学年度(上)半期考试高一年级数学试题一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求.1.已知集合{}0,1,2,3A =,{}2,3,4,5B =,记集合P A B = ,B A Q =,则A .1P∈B .4P∉C .5Q∈D .3Q∉2.命题“对x R ∀∈,都有1sin -≤x ”的否定为A .对x R ∀∈,都有sin 1x >-B .对x R ∀∈,都有sin 1x C .0x R ∃∈,使得0sin 1x >-D .0x R ∃∈,使得0sin 1x - 3.下列函数中,既是奇函数又是增函数的为A .||y x x =B .3y x =-C .23y x =+D .1y x=-4.函数111y x =-+的值域是A .(,1)-∞-B .(1,)-+∞C .),1()1,(+∞---∞ D .(,)-∞+∞5.函数2()(1)32x f x m x =-+-+在区间(]5,∞-上单调递增,则实数m 的取值范围是A .(,6]-∞B .[6,)+∞C .[4,)-+∞D .(,4]-∞-6.已知0>a ,0>b ,2=+b a ,则)2)(2(bb a a ++的最小值为A .8B .434-C .9D .434+7.如图所示,A ,B 是非空集合,定义集合#A B 为阴影部分表示的集合.若x ,y R ∈,{|1A x y ==,{|2,0}B y y x x ==>,则#A B 为A .{|03}x x <<B .{|13}x x <C .{|013}x x x 或D .{|03}x x x =>或8.已知0a >,k R ∈,设函数2,,(),x x x s f x kx x s ⎧-⎪=⎨+->⎪⎩,若对任意的实数(2,2)s ∈-,都有()f x 在区间(,)-∞+∞上至少存在两个零点,则A .4a ,且1k B .4a ,且01k < C .04a <<,且1k D .04a <<,且01k < 二、选择题:本题共4小题,每小题5分,共20分.每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.已知集合{|||,}M y y x x x R ==-∈,12{|},0N y y x x ≠==,则下列选项错误的有A .M N=B .N M⊆C .R M N=ðD .R N MÜð10.下列各组函数中,表示同一函数的是A .2()f t t =,2()g s s=B .()1f x x =+,21()1x g x x -=-C .()||f x x =,(0)()(0)t t g t t t ⎧=⎨-<⎩ D .()f x x =,2()g x =11.已知1m n >>,下列不等式中正确的是A .2m mn>B .2n mn-<-C .12n n+≤D .1111m n <--12.已知集合0{|01}A x x =<<.给定一个函数()y f x =,定义集合{|()n A y y f x ==,1}n x A -∈.若1n n A A -=∅ 对任意的*n N ∈成立,则称该函数()y f x =具有性质“p ”.则下列函数中具有性质“p ”的是A .1y x =+B .1y x=C .2y x =D .1y x x=+三、填空题:本题共4小题,每小题5分,共20分.13.若幂函数()y f x =的图象过点1(4,)2,则()2f 的值为.14.若||1x a -<成立的充分不必要条件是23x <<,则实数a 的取值范围是.15.已知()f x 为奇函数,当0x <时,2()31f x x x =+-;当0x >时,()f x 的解析式为()f x =.16.设x R ∈,对于使22x x M - 恒成立的所有常数M 中,我们把M 的最大值1-叫做22x x -的下确界,若0a >,0b >,且11121a a b+=++,则2a b +的下确界为.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(10分)已知幂函数ax a a x f )22()(2--=(R a ∈)在),0(+∞上单调递增.(1)求函数)(x f 的解析式;(2)解不等式)3()5(2x x f x f -<+18.(12分)已知集合{}042)23(22≤+++-=a a x a x x A ,{}106≤≤=x x B (1)当6=a 时,求B A ,)(B C A R (2)从①R A C B R =)( ;②“B x ∈”是“A x ∈”的必要不充分条件;③φ=)(B C A R 这三个条件中任选一个,补充在下面横线上,并进行解答.问题:若,求实数a 的取值范围.19.(12分)如图,边长为1的正三角形纸片ABC ,M 、N 分别为边AB 、AC 上的点,MN ∥BC ,将纸片沿着MN 折叠,使得点A 落至点1A ,1MA 交BC 于点P ,1NA 交BC 于点Q ,记x AM =,四边形MNQP 的面积为y .(1)建立变量y 与x 之间的函数关系式)(x f y =,并写出函数)(x f y =的定义域;(2)求四边形MNQP 的面积y 的最大值以及此时的x 的值.20.(12分)已知关于x 的不等式052>+-n x mx 的解集为),3()2,(+∞-∞∈ x .(1)求实数n m ,的值;(2)当0>+y x ,1->z ,且满足11=+++z ny x m 时,有5222+-≥++t t z y x 恒成立,求实数t 的取值范围.21.(12分)北京时间2021年10月16日0时23分,搭载神舟十三号载人飞船的长征二号F 遥十三运载火箭,在酒泉卫星发射中心精准发射,约582秒后,飞船与火箭成功分离,进入预定轨道,发射取得圆满成功,这是我国载人航天工程立项实施以来的第21次飞行任务,也是空间站阶段的第2次载人飞行任务。
重庆八中高2023级数学高一上国庆作业题二(终版答案)

x +1 2 x +1 −2 0 −x +5 0 x −5 0,
x−2
x−2
x−2
x−2
所以
(
x
− 5)( x
−
2)
0,
解得
x
2
或
x
5
A
=
x
x
2或
x
5 ,
x − 2 0,
B = x −x2 + x + 6 0 , B = x x −2 或 x 3 ,
A B = x x −2 或 x 5
f (x)max = max f (1), f (a +1).
又 f (1) − f (a +1) = 6 − 2a − (6 − a2 ) = a(a − 2) 0, 所以 f (x)max = f (1) = 6 − 2a. 因为对任意的 x1, x2 [1, a +1] ,总有 f (x1) − f (x2 ) 3 , 所以 f (x)max − f (x)min 3 ,即 6 − 2a − (−a2 + 5) 3 ,解得1− 3 a 1+ 3 , 又因为 a 2 ,所以 2 a 1+ 3 ,即实数 a 的取值范围为[2,1+ 3].
重庆八中高 2023 级国庆假期数学作业(二)答案
一、选择题
1
2
3
4
5
6
D
A
D
D
C
C
7
8
9(多选) 10(多选) 11(多选) 12(多选)
C
A
BD
AD
ABD
ABC
二、填空题
13
14
15
重庆八中高2023级数学高一上国庆作业题一(终版)

重庆八中高2023级高一(上)国庆假期数学作业(一)满分:150分 测试时间:120分钟姓名:__________ 班级:__________ 学号:__________ 一、 选择题(共12题,1~8题为单选题,每题5分,9~12题为多选题,全部选对得5分,部分选对得3分,错选或不选得0分,共60分)1.已知集合{}2|1M x x ==,{}|2N x ax ==,若N M ⊆,则实数a 的取值集合为( ) A .{}2 B .{}2,2− C .{}2,0−D .{}2,2,0−2.已知集合{}2,0A =,{}|,,B z z x y x A y A ==+∈∈ ,则集合B 的非空子集的个数为( ) A .3 B .4 C .7D .83.一元二次方程()24005ax x a ++=≠有一个正根和一个负根的一个充分不必要条件是( ) A .0a < B .0a > C .2a <−D .1a >4.已知关于x 的不等式22430(0)x ax a a −+<<的解集为12(,)x x ,则1212ax x x x ++的最大值是( ) A.3 B.3−C.3D.3−5.设集合{}2|60A x x x =−>−,{}0|()(2)B x x k x k =−−−<,若A B ≠∅,则实数k 的取值范围是( ) A .{}21|k k k <−>或 B .{}|21k k −<< C .{}43|k k k <−>或D .{}|43k k −<<6.下列各式:①212a a +>;②12xx +≥2≤;④22111x x +≥+. 其中正确..的个数是( ) A .0 B .1 C .2D .37.已知函数()1(1)3(1)f x x x x x +≤⎧=⎨−+>⎩,则52f f ⎡⎤⎛⎫= ⎪⎢⎥⎝⎭⎣⎦( ) A .12 B .32 C .52D .728.设0c <,()f x 是区间[],a b 上的减函数,下列命题中正确..的是( ) A .()f x c +在[],a b 上有最小值()f a c + B .()f x 在[],a b 上有最小值()f a C .()f x c −在[],a b 上有最小值()f a c − D .()cf x 在[],a b 上有最小值()cf a9.【多选题】若01,1a b c <<>>,则下列结论中正确..的有( ) A .111a b c>++ B .c a cb a b−>−C >D .21b a −>−10.【多选题】设[]x 表示不大于实数x 的最小整数(例如:[2.5]2=,[2.2]3−=−),则满足关于x 的不等式2[][]120x x +−≤的解可以为( ) AB.C .π−D .5−11.【多选题】下列说法中正确..的有( ) A .命题“32,1x x x ∀∈>+R ”的否定是“32,1x x x ∃∈<+R ”B .若不等式210ax bx ++>的解集为{}|13x x −<<,则不等式23650ax bx ++<的解集为(,1)(5,)−∞−+∞C .22,421x ax x x ∀∈+≥−R 恒成立,则实数a 的取值范围是[6,)+∞D .已知211:3,:()10(0)2p x q x a x a a≤≤−++≤>,若p 是q 的充分不必要条件,则实数a 的取值范围是1(0,][3,)3+∞12.【多选题】已知函数2()(,)f x x mx n m n =++∈R ,不等式()x f x <的解集为(,1)(1,)−∞+∞,则( )A .1,1m n =−=B .设()()f x g x x=,则()g x 的最小值为(1)1g = C .不等式()(())f x f f x <的解集为(,0)(0,1)(1,)−∞+∞D .已知31,42()1(),2x h x f x x ⎧≤⎪⎪=⎨⎪>⎪⎩,若()(22)h x h x <+,则x 的取值范围是3(,)4−+∞二、填空题(共4题,每题5分,共20分)13.函数11y x=−的定义域是________________.14.已知函数11x f x x −⎛⎫=⎪+⎝⎭,则(3)f 的值为________________. 15.某游泳馆出售冬季学生游泳卡,每张240元,使用规定:不记名,每卡每次只限1人,每天只限1次.某班有48名学生,老师打算组织同学们集体去游泳,除需购买若干张游泳卡外,每次还要包一辆汽车,无论乘坐多少名同学,每次的车费均为40元.若使每个同学游8次,则购买________________张游泳卡最合算.16.若不等式2322x ax a −−≤+≤−有唯一解,则实数a 的值为________________.三、解答题(共6题,共70分)17.(10分) 设全集为{}{}22,430,0(0)A x x x B x x a a =−+≤=−<>R . (1)当4a =时,求,A B A B ;(2)若B A ⊆R,求实数a 的取值范围.18.(12分) 已知关于x 的不等式2430ax x −+<的解集为{}1x x b <<. (1)求,a b 的值; (2)解关于x 的不等式12bx ax −≤+.19.(12分) 已知函数()23f x x =−. (1)解不等式2()f x x <;(2)设函数()()g x x f x =−的最大值为m ,设正实数,a b 满足2a b m +=,求141a b++的最小值.20.(12分) 学校里两条相互垂直的道路,AM AN 旁有一矩形花园ABCD ,现欲将其扩建成一个更大的三角形花园APQ ,要求点,B P 在AM 上,点,D Q 在AN 上,且PQ 过点C ,其中100,30,20AM AN AB AD ====,如图,记三角形花园APQ的面积为S .(1)设(0)DQ x x =>,建立三角形花园APQ 的面积S 关于x 的表达式及S 的最小值; (2)要使三角形花园APQ 的面积不小于1600,请问DQ 的长应该在什么范围内?21.(12分) 已知命题2000:[1,1],0p x x x m ∃∈−−−≥是假命题. (1)求实数m 的取值集合B ;(2)设不等式(3)(2)0x a x a −−−<的解集为A .若x B ∈是x A ∈的必要不充分条件,求实数a 的取值范围.22.(12分) 已知函数22()(0)6kxf x k x k=>+.(1)若()f x m >的解集为{}32x x x <−>−或,求不等式2530mx kx ++>的解集; (2)若存在3x >,使得()1f x >成立,求k 的取值范围.。
重庆市第八中学校2023-2024学年高一数学第一学期期末考试试题含解析

y
sin
2
x
8
sin
2x
4
故选 A 2、D 【解析】根据平均数和方差的计算性质即可计算.
【详解】设甲、乙两班学生成绩分别为 xi , yi ,甲班平均成绩为 x ,乙班平均成绩为 y ,因为甲、乙两班的平均成绩相
等,所以甲、乙两班合在一起后平均成绩依然为 x ,
1 30
因为
30 i1
f
x
2
cos
x
sin
x
6
1 2
0
这两个条件中任选一个,补充在下而问题中,并解
答.
已知______,函数 f x 的图象相邻两条对称轴之间的距离为 .
2
(1)若
f
x 在0, 上的值域为
1 2
,1
,求
a
的取值范围;
(2)求函数 f x 在0, 2 上的单调递增区间.
21.化简下列各式:
重庆市第八中学校 2023-2024 学年高一数学第一学期期末考试试题
注意事项: 1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。 2.答题时请按要求用笔。 3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。 4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。 5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
3 30 1,
0 sin 1, 10
log
0.3
sin
10
3 .
故选:A
6、C
【解析】根据直线的点斜式方程可得直线过定点 A(3, 0) ,曲线 y 1 (x 1)2 表示以 (1, 0) 为圆心,1 为半径的半圆,作
重庆市2023-2024学年高一上学期10月月考数学试题含解析

2023年重庆高2026届高一上期10月月考数学(答案在最后)注意事项:1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上.2.答选择题时,必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其他答案标号.3.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上.4.所有题目必须在答题卡上作答,在试题卷上答题无效.一、单选题(本大题共8个小题,每题只有一个选项正确,每小题5分,共40分)1.命题“0,320x x ∀>->”的否定是()A.000,320x x ∃>-≤B.000,320x x ∃≤-≤C.0,320x x ∀≤->D.0,320x x ∀>-≤【答案】A 【解析】【分析】由特称命题的否定:任意改存在并否定原结论,即可确定答案.【详解】由全称命题的否定为特称命题,则原命题的否定为000,320x x ∃>-≤.故选:A2.已知集合{}()2|20,{|30}A x x x B x x x =--≤=->,则A B ⋃=()A.[]0,2 B.(]0,2 C.[)1,3- D.[]1,3-【答案】C 【解析】【分析】解一元二次不等式求解集,再由集合的并运算求集合.【详解】由题设{}|12,{|03}A x x B x x =-≤≤=<<,则{|13}[1,3)A B x x =-≤<=- .故选:C3.若102x <<的最大值是()A.14B.24C.12D.22【答案】B 【解析】【分析】利用基本不等式求积的最大值.21224x x +-=≤=,当且仅当12124x x x =-⇒=时等号成立.4.故选:B4.如图,已知全集U =R ,集合{}{}2Z |90,|20A x x B x x =∈-≤=-≥,则图中阴影部分表示的集合中的元素个数为()A.7B.6C.5D.4【答案】C 【解析】【分析】解一元二次、一元一次不等式求集合,再由阴影部分的集合为()U A B ð,应用交补运算求集合,即可得答案.【详解】由题设{}{}Z |33{3,2,1,0,1,2,3},|2A x x B x x =∈-≤≤=---=≥,由图知:阴影部分为()U A B ð,而{}|2U B x x =<ð,则(){3,2,1,0,1}U A B =--- ð,所以阴影部分共有5个元素.故选:C5.设实数,a b 满足111b a>>,则下列不等式一定成立的是()A.a b <B.2ab b <C.11a ab b +<+ D.1a b ab +<+【答案】D 【解析】【分析】先由题设不等式可得01b a <<<,故可判断A 的正误,利用作差法可判断BCD 的正误,故可得正确的选项.【详解】因为111b a>>,故01b a <<<,故A 错误.又0a b ->,故()20ab b b a b -=->,故2ab b >,故B 错误.又110b +>>,()()()()1110111a b b a a a a b b b b b b b +-++--==>+++,故11a ab b +>+,故C 错误.又()11(1)(1)(1)ab a b a b b a b +--=---=--,由01b a <<<可得10,10a b -<-<,故()()110a b -->,故10ab a b +-->即1ab a b +>+,故D 正确.故选:D.6.已知:p “()2()3x m x m ->-”是:q “2340x x --≤”成立的必要不充分条件,则实数m 的取值范围为()A.][(),44,-∞-⋃+∞ B.()(),44,∞∞--⋃+C.()4,4- D.[]4,4-【答案】B 【解析】【分析】解一元二次不等式求,q p 为真对应x 的范围,根据必要不充分条件求参数范围.【详解】由()2:()3()[(3)]0p x m x m x m x m x m ->-⇒--+>⇒<或3x m >+,由2:340(4)(1)014q x x x x x --≤⇒-+≤⇒-≤≤,又p 是q 成立的必要不充分条件,则q p ⇒且p ¿q ,所以4m >或314m m +<-⇒<-,故m 的取值范围为()(),44,∞∞--⋃+.故选:B7.已知集合{}2|10,R ,{|0}A x x ax x B x x =-+=∈=>,若A B ⋂=∅,则实数a 的取值范围为()A.2a <B.22a -<<C.2a >- D.2a ≥【答案】A 【解析】【分析】由题设2()10f x x ax =-+=在(0,)+∞上无解,结合二次函数性质求参数范围即可.【详解】对于2()1f x x ax =-+开口向上且对称轴为2ax =,(0)10=>f ,由A B ⋂=∅,即()0f x =在(0,)+∞上无解,若0a >时,只需24022a a ∆=-<⇒-<<,即02a <<;若0a ≤时,此时对称轴02a≤且(0)10=>f ,故满足题设;综上,2a <.故选:A8.已知关于x 的不等式组()224502525x x x x x k ⎧-++<⎪⎨+<-+⎪⎩的解集中有且仅有一个整数,则实数k 的取值范围为()A.()()6,23,4-⋃ B.[)(]6,23,4-⋃C.][()5,34,5-⋃ D.][5,34,5⎡⎤-⋃⎣⎦【答案】B 【解析】【分析】解一元二次不等式且两不等式解集的交集中有且仅有一个整数,讨论参数k 求其范围.【详解】对于245(5)(1)01x x x x x --=-+>⇒<-或5x >,而22(25)5(25)()0x k x k x x k +++=++<解集与{|1x x <-或5}x >的交集中有且仅有一个整数,当52k <时,解集为5{|}2x x k -<<-,此时2662k k -<-≤⇒-≤<满足要求;当52k =时,解集为∅,此时不可能满足题设;当52k >时,解集为5{|}2x k x -<<-,此时4334k k -≤-<-⇒<≤满足要求;综上,实数k 的取值范围为[)(]6,23,4-⋃.故选:B二、多选题(本大题共4个小题,每小题5分,共20分.在每小题给出的选项中,有多项是符合题目要求的.全部选对的得5分,部分选对的得2分,有选错的得0分)9.已知命题:p “2R,20x x ax a ∀∈-+>恒成立”为真命题,下列选项中可以作为p 的充分不必要条件的有()A.103a <<B.01a <<C.01a <≤D.1132a <<【答案】AD 【解析】【分析】由已知命题为真,根据一元二次不等式恒成立有2440a a ∆=-<求参数范围,再由充分、必要性定义判断p 的充分不必要条件.【详解】由“2R,20x x ax a ∀∈-+>恒成立”为真命题,故244001a a a ∆=-<⇒<<,所以103a <<、1132a <<是p 的充分不必要条件,01a <<是p 的充要条件,01a <≤是p 的必要不充分条件.故选:AD10.若1,x A A x ∀∈∈,则称集合A 为幸福集合.对集合11,0,,1,2,32M ⎧⎫=-⎨⎬⎩⎭的所有非空子集,下列叙述正确的是()A.幸福集合个数为8B.幸福集合个数为7C.不含1的幸福集合个数为4D.元素个数为3的幸福集合有2个【答案】BD 【解析】【分析】根据题意写出所有的幸福集合,逐项分析即可得解.【详解】具有“幸福关系”的元素组有:11;,2;12-三组,含一组的有{1},{}1-,1{,2}2共3个,含二组的有{1,1}-,1{1,,2}2,1{1,,2}2-共3个,含三组的有1{1,1,,2}2-共1个.所以M 的非空子集中幸福集合的个数为7个,故A 错B 对;其中不含1的幸福集合个数为3个,故C 错误;其中元素个数为3的幸福集合有2个,故D 正确.故选:BD11.已知集合{}{}()22|60,|00A x x x B x ax bx c a =-->=++≤≠,若A B =R ,{|35}A B x x =<≤ ,则()A.0a >B.关于x 的不等式20cx bx a ++>解集为1|2x x ⎧<-⎨⎩或15x ⎫>⎬⎭C.0a b c ++>D.101bc a >-【答案】AD 【解析】【分析】解一元二次不等式求集合A ,再由交并集的结果可得{|25}B x x =-≤≤,即2,5-是20ax bx c ++=的两个根且a<0,再结合各项判断正误.【详解】由题设{|2A x x =<-或3}x >,又A B =R ,{|35}A B x x =<≤ ,所以{|25}B x x =-≤≤,故2,5-是20ax bx c ++=的两个根且0a >,A 对;则331010bb a ac c a a⎧-=⎪=-⎧⎪⇒⎨⎨=-⎩⎪=-⎪⎩,则120a b c a ++=-<,C 错;222(1031)010310(51)(21)0cx bx a a x x x x x x ++=-+->⇒+-<⇒-+<,所以,解集为11{|}25x x -<<,B 错;22111013010130(066bc a a a a -+=-+=-+>,即101bc a >-,D 对.故选:AD12.已知正实数,x y 满足21xy x y --=,则()A.xy的最小值为22+B.x y +1C.2x y +32+D.22x y +2+【答案】BC 【解析】【分析】利用基本不等式构造一元二次不等式判断A ,根据xy 和x y +得关系判断B ,利用多变量变单变量法判断C ,构造关于xy 的二次函数关系判断D.【详解】因为,x y 为正实数,选项A :因为21xy x y --=,则21x y xy +=-≥2210-≥,12+≥,22xy ≥,当且仅当12x y +==时等号成立,故A 错误;选项B :因为21x y xy +=-,所以()()min min 211x y xy +=-=,当且仅当12x y +==时取得最小值,故B 正确;选项C :由21xy x y --=得()211x y y -=+,当12y =时显然不符合题意,所以12y ≠,则1021y x y +=>-,得12y >或1y <-(舍去),则()1131332242121242222y x y y y y y ++=+=++-+≥+=+--当且仅当()3142422y y =--即24y +=时等号成立,故C 正确;选项D :()()22222212x y x y xy xy xy +=+-=--,令xy t =,由A 可知22t ≥,则()222223523521222224224x y t t t ⎛⎫+⎛⎫+=--=--≥⨯-=+ ⎪ ⎪ ⎪⎝⎭⎝⎭当且仅当22t +=时等号成立,故D 错误;故选:BC三、填空题(本大题共4个小题,每小题5分,共20分)13.若命题“()0,x ∃∈+∞,使得2a x x>+成立”是假命题,则实数a 的取值范围是__________.【答案】a ≤【解析】【分析】由原命题的否定为真命题可求参数的取值范围.【详解】因为命题“()0,x ∃∈+∞,使得2a x x>+成立”是假命题,故其否定为真命题,即()0,x ∀∈+∞,2a x x≤+为真命题,而2x x+≥x =时等号成立,故a ≤故答案为:a ≤14.设全集{}21,3,9U m m =+-,集合{}{}1,,3U A m A ==ð,则实数m =__________.【答案】3-【解析】【分析】根据已知可得29m m m +-=,解方程求参数,结合集合中元素的互异性确定参数值.【详解】由{}21,3,9U m m =+-且{}{}1,,3U A m A ==ð,则22993m m m m m +-=⇒=⇒=±,当3m =,则293m m m +-==,不满足集合元素的互异性;当3m =-,此时{}1,3,3U =-,{}1,3=-A 满足题设;综上,3m =-.故答案为:3-15.某校高一年级组织趣味运动会,其中“毛毛虫”和“两人三足”两个比赛项目深受学生喜爱,报名踊跃.已知某班学生参加“毛毛虫”的人数是该班全体人数的四分之一;参加“两人三足”的人数比参加“毛毛虫”的人数多2人;两个项目都参加的人数比两个项目都不参加的学生人数少26人;则该班参加“两人三足”比赛的人数是__________.【答案】16【解析】【分析】设该班总人数为4n ,两个项目都参加的人数为x ,根据题设并利用容斥原理列方程求n ,即可得答案.【详解】设该班总人数为4n ,则参加“毛毛虫”的人数为n ,参加“两人三足”的人数为2n +,若两个项目都参加的人数为x ,则两个项目都不参加的学生人数为26x +,所以226414n n x x n n ++-++=⇒=,故该班参加“两人三足”比赛的人数是16.故答案为:1616.对任意的正实数,,a b c ,且满足2b c +=,则234181ab a bc a +++的最小值为__________.【答案】6-##6-+【解析】【分析】根据题意将原式整理成()223181a b b c bc a ⎡⎤++⎣⎦++,利用基本不等式可得2341818611ab a a bc a a ++≥+++,再利用基本不等式可求得当1a =-,24,33b c ==时234181ab a bc a +++的最小值为6-.【详解】由正实数,,a b c ,且2b c +=可得()()()2222223344234181818181111a b b c a b a b c bc ab a bc a bc a bc a bc a ⎡⎤++++++⎣⎦+=+=+=+++++4181818226111b c a a a c b a a a ⎛⎫⎛⎫=+++≥+=+ ⎪ ⎪ ⎪+++⎝⎭⎝⎭;当且仅当4b cc b=时,即24,33b c ==时,等号成立;又181866666611a a a a +=++-≥=-++,当且仅当()18611a a+=+,即1a=-时,等号成立;所以当1a =,24,33b c ==时,等号成立,此时234181ab a bc a+++的最小值为6.故答案为:6-四、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)17.已知3{}(0),|,A xa xb b a B y y x A x ⎧⎫=<<>>==∈⎨⎬⎩⎭∣(1)若1,32a b ==,求A B ⋂与()A B ⋃R ð;(2)是否存在,a b ,满足4a b +=,且使得A B A B = ,存在则求出,a b 的值,不存在则说明理由.【答案】(1){}|13A B x x ⋂=<<,()1{|2A B x x ⋃=≤R ð或6}x ≥.(2)存在1,3a b ==,使得A B A B = ,理由见解析.【解析】【分析】(1)根据交集、并集和补集的定义可求A B ⋂与()A B ⋃R ð;(2)就01a <<、12a ≤<分类讨论后可求,a b 的值.【小问1详解】当1,32a b ==时,1{|3}2A x x =<<,故{}16|B x x =<<,故{}|13A B x x =<< ,1|62A B x x ⎧⎫=<<⎨⎬⎩⎭,故()1{|2A B x x ⋃=≤R ð或6}x ≥.【小问2详解】因为0b a >>,故40a a ->>,故02a <<.由题设有33|4B x x a a ⎧⎫=<<⎨⎬-⎩⎭,若01a <<,则344a a ->-且()()()21334340a a a a a a a a---+--==>,故34a a >-且34a a>-,故3|44A B x x a a ⎧⎫=<<-⎨⎬-⎩⎭ ,3|A B x a x a ⎧⎫=<<⎨⎬⎩⎭,由A B A B = 可得343401a a a a a ⎧=⎪-⎪⎪-=⎨⎪<<⎪⎪⎩,无解.若12a ≤<,则()()()13340a a a a a ----=≤,故34a a ≤-且34a a ≤-,故3|A B x a x a ⎧⎫=<<⎨⎬⎩⎭ ,3|44A B x x a a ⎧⎫=<<-⎨⎬-⎩⎭ ,由A B A B = 可得343412aa a a a ⎧=⎪-⎪⎪-=⎨⎪≤<⎪⎪⎩,故1a =.综上,存在1,3a b ==,使得A B A B = .18.关于x 的不等式()()2220R x a x a a -++≤∈的解集为A ,(1)求A ;(2){}2|5217B x x a =≤+≤-,若A 是B 的真子集,求a 的取值范围.【答案】(1)答案见解析;(2)4a >.【解析】【分析】(1)讨论参数a 求不等式解集即可;(2)由题设可得a ≥或a ≤-A B 并讨论参数确定范围即可.【小问1详解】由()222()(2)0x a x a x a x -++=--≤,当2a <时,解集{|2}A x a x =≤≤;当2a =时,解集{2}A =;当2a >时,解集{|2}A x x a =≤≤;【小问2详解】由2|242a B x x ⎧⎫=≤≤-≠∅⎨⎬⎩⎭,则2422a a -≥⇒≥a ≤-,又AB ,当a ≤-{|2}A x a x =≤≤,显然不满足;当a ≥{|2}A x x a =≤≤,则()()224282402a a a a a a ->⇒--=+->⇒2a <-或4a >,此时4a >;综上,a 的取值范围为4a >.19.已知函数()221,R f x x x x =-+∈,命题[]():0,2,p x f x a ∃∈<;命题q :已知190,0,1,x y a x y x y>>+=≤+恒成立.(1)若p 为真命题,求a 的取值范围;(2)若p ,q 这两个命题中存在假命题,求a 的取值范围.【答案】(1)0a >;(2)(,0](16,)-∞+∞ .【解析】【分析】(1)由题意[]0,2x ∈上()min a f x >,由二次函数性质求函数最小值,即可得参数范围;(2)由q 为真命题时min ()a x y ≤+,应用基本不等式“1”的代换求目标式最小值,即得参数范围,讨论p ,q 存在假命题的情况求对应参数范围.【小问1详解】由p 为真命题,则[]0,2x ∈上()min (1)0a f x f >==,故0a >.【小问2详解】若q 为真命题,则min ()a x y ≤+,而199()()101016y x x y x y x y x y +=++=++≥+=,当且仅当94,12y x x y x y=⇒==时等号成立,故16a ≤,而p 为真时0a >,由于p ,q 这两个命题中存在假命题,且p 为假0a ≤,q 为假16a >,当p 真q 假时,a 的取值范围16a >;当q 真p 假时,a 的取值范围0a ≤;当q 、p 假时,a 的取值范围∅;综上,a 的范围为(,0](16,)-∞+∞ .20.某中学为了迎接建校100周年校庆,决定在学校校史馆利用一侧原有墙体,建造一间墙高为3米,底面积为24平方米,且背面靠墙的长方体形状的荣誉室.由于荣誉室的后背靠墙,无需建造费用.甲乙两支队伍参与竞标,甲工程队给出的报价为:荣誉室前面新建墙体的报价为每平方米400元,左右两面新建墙体报价为每平方米300元,屋顶和地面以及其他报价共计12600元,设荣举室的左右两面墙的长度均为x 米()16x ≤≤,乙工程队给出的整体报价为()18002a x x +元(0)a >,综合考虑各种条件,学校决定选择报价较低的队伍施工,如果报价相同,则选择乙队伍.(1)若10a =,问学校该怎样选择;(2)在竞争压力下,甲工程队主动降价5400元,若乙工程队想要确保自己被选中,求实数a 的最大值.【答案】(1)选择乙工程队进行建造.(2)9【解析】【分析】(1)设甲工程队的总造价为1y 元,得到1161800()12600y x x =++,结合基本不等式求得()1min 27000y =,设乙工程队的总造价为2y 元,得到[]2218000(1),1,6xy x ⨯+∈=,结合函数的单调性,求得()2min 24000y =,比较即可得到答案;(2)根据题意,得到甲工程队的最低报价为21600,要使得乙工程队确保自己被选中,则满足()2min 21600y ≤,列出不等式,即可求解.【小问1详解】解:设甲工程队的总造价为1y 元,因为荣举室的左右两面墙的长度均为x 米,且长方体底面积为24平方米,可得底面长方形的另一边长为24x米,则甲工程队的总造价为:[]12416233003400126001800()12600,1,6y x x x x x =⨯⨯+⨯⨯++=++∈,又由168x x +≥=,当且仅当4x =时,等号成立,所以()1min 180081260027000y =⨯+=(元),当10a =时,设乙工程队的总造价为2y 元,则()[]21800102218000(11,6y x x x x⨯+=⨯∈=+,因为函数21y x=+在[]1,6x ∈上为单调递减函数,所以()2min 24000y =(元),由2700024000>,所以学校选择乙工程队进行建造.【小问2详解】解:若甲工程队主动降价5400元,则甲工程队的最低报价为270000540021600-=(元),若乙工程队确保自己被选中,则满足()2min 21600y ≤,又由乙工程队的造价为()[]2180022180601(1,)a x y a x xx =∈+=+,由(1)知,当6x =时,()2min 21800(124006y a a =⋅+=,由022400016a ≤,解得9a ≤,因为0a >,所以09a <≤,所以实数a 的最大值为9.21.已知()()20f x ax bx c a =++≠,非空集合(){}()(){}120,0A x f x A x f f x ====∣∣(1)证明:12A A ⊆的充要条件是0c =;(2)若12A A =,求b 的取值范围.【答案】(1)证明见解析;(2)04b ≤<【解析】【分析】(1)首先证明充分性:当0c =时可求得集合{}210A xax bx =+=∣,对参数b 是否为零进行分类讨论,可得集合2A 中至少含有1A 中的所有元素;再证明必要性:若12A A ⊆可得方程()0f x =的所有实数根都是方程()()0f f x =的实根,即()00f c ==,得出证明;(2)根据(1)的结论可知0c =,然后对于参数b 是否为零进行分类讨论,易知当0b =时符合题意,当0b ≠时,对于方程220a x abx b ++=的根的个数结合判别式进行讨论,并利用集合间的包含关系求得b 的取值范围是04b ≤<.【小问1详解】充分性:若0c =,则(){}{}2100A x f x x ax bx ===+=∣∣;当0b ≠时,可得10,b A a ⎧⎫=-⎨⎬⎩⎭若()()0f f x =,可得()0f x =或()bf x a =-;当()0f x =时,120,b x x a ==-;即可得()20,b b A x f x a a ⎧⎫⎧⎫==-⋃-⎨⎬⎨⎬⎩⎭⎩⎭∣所以可得集合2A 中至少含有0,b a-两个元素,可知12A A ⊆,当0b =时,可得{}10A =;此时当()()0f f x =时()0f x =,即可得{}20A =;此时12A A =,满足12A A ⊆;综上可知充分性成立;必要性:因为1A 为非空集合,所以可知当12A A ⊆时,可知方程()0f x =的所有实数根都是方程()()0ff x =的实根,即可得()()()00f f x f ==,即()0000f a b c =⨯+⨯+=,可得0c =,所以必要性成立;综上可得,12A A ⊆的充要条件是0c =;【小问2详解】若12A A =时,满足12A A ⊆;由(1)中的结论可得0c =,此时(){}{}2100A x f x x ax bx ===+=∣∣;当0b =时,可得{}10A =,此时()(){}(){}2100A xf f x x f x A =====∣∣,符合题意;当0b ≠时,可得10,b A a ⎧⎫=-⎨⎬⎩⎭,此时()20,b b A x f x a a ⎧⎫⎧⎫==-⋃-⎨⎬⎨⎬⎩⎭⎩⎭∣;为使12A A =可知,集合(){}2200,b b x f x x a x abx b a a ⎧⎫⎧⎫=-=++=⊆-⎨⎬⎨⎬⎩⎭⎩⎭∣∣;对于方程220a x abx b ++=,令()()222244ab a b a b b ∆=-=-①当Δ0<时,即04b <<时,()0,b b xf x a a ⎧⎫⎧⎫=-=∅⊆-⎨⎬⎨⎬⎩⎭⎩⎭∣,符合题意;②当Δ0=时,即4b =时,此时()2b b x f x a a ⎧⎫⎧⎫=-=-⎨⎬⎨⎬⎩⎭⎩⎭∣,但02b a -≠且2b b a a -≠-,不合题意;③当0∆>时,即0b <或4b >时,()44,2222b b b x f x a a a a a ⎧⎪⎧⎫=-=-+--⎨⎬⎨⎬⎩⎭⎪⎪⎩⎭∣,为使12A A =,需满足422b b a a a -+=-或422b b a a a --=-,即42b a =,解得0b =;这与大前提0b ≠矛盾,不合题意;综合①②③可得04b <<符合题意;综上可知,满足题意的b 的取值范围为04b ≤<【点睛】关键点点睛:本题在求解参数b 的取值范围时,要结合(1)的结论将0c =代入计算,并根据12A A =将集合{}220xa x abxb ++=∣转化成集合0,b a ⎧⎫-⎨⎬⎩⎭的子集,再对参数b 进行分类讨论后再利用判别式进行讨论计算可得结果.22.已知集合{}*123,,N n A a a a a =⋯⋯⊆,其中N n ∈且1233,n n a a a a ≥<<<⋯⋯<,若对任意的(),x y A x y ∈≠,都有xy x y k-≥,则称集合A 具有性质k M .(1)集合{}1,2,A a =具有性质3M ,求a 的最小值;(2)已知A 具有性质15M ,求证:111115n n a a --≥;(3)已知A 具有性质15M ,求集合A 中元素个数的最大值,并说明理由.【答案】(1)6;(2)证明见解析;(3)7,理由见解析.【解析】【分析】(1)由性质3M 定义列不等式组求参数范围,结合*N a ⊆即可得最小值;(2)根据定义11||,(1,2,3,...,1)15i i i i a a a a i n ++-≥=-,进而有111115i i a a +-≥,应用累加法即可证结论;(3)首先应用放缩有11115n a ->求得16n <,同理可得()15i n i -<恒成立,假设8n ≥得出矛盾,再讨论7n ≤并应用基本不等式证恒成立,即可确定元素个数最大值.【小问1详解】由性质3M 定义知:313622623a a a a a a a ⎧-≥⎧⎪≥⎪⎪⇒⇒≥⎨⎨⎪⎪≥-≥⎩⎪⎩,且*N a ⊆,所以a 的最小值为6.【小问2详解】由题设11||,(1,2,3,...,1)15i i i i a a a a i n ++-≥=-,且1n a a <⋯⋯<,所以111111,(1,2,3,...,1)1515i i i i i i a a a a i n a a +++-≥⇒-≥=-,所以122311********* (15)n n n n a a a a a a a a ---+-++-=-≥,得证.【小问3详解】由(2)知:1111115116151n n a n a -⎧>-⎪⇒<⇒<⎨⎪≥⎩,同(2)证明得1115i n n i a a --≥且1,2,3,...,1i n =-,故115i n i a ->,又i a i ≥,所以1()1515n i i n i i ->⇒-<在1,2,3,...,1i n =-上恒成立,当8n ≥,取3i =,则3(3)15n -≥,故8n <,当7n ≤,则22()()1544i n i n i n i n +--≤=<⇒<,即7n ≤.综上,集合A 中元素个数的最大值为7.【点睛】关键点点睛:第二问,根据定义得111115i i a a +-≥为关键;第三问,应用放缩法确定16n <,同理得到()15i n i -<恒成立为关键.。
重庆八中 2022——2023 学年度(上)半期考试高一年级数学参考答案

重庆八中2022——2023学年度(上)半期考试高一年级参考答案13.13π+ 14. 8- 15.2()f x x =(答案不唯一)16.[4-,]8-8.解:因为正实数x ,y 满足11y x y x ->-,整理得1()(1)0y x xy-+>,即0y x >>.选项A :11y y x x +<+满足糖水不等式,故选项A 正确;选项B :11xy <整理得11y x ,构造函数1()f x x=,易知()f x 在(0,)+∞单调递增,11y x <,故选项B 正确;选项C :构造函数221()|1|1x x x f x x x x x x ⎧≥⎪=-=⎨<<⎪⎩- -+ 0,可知函数()f x 在(0,)+∞不具有单调性,故选项C 错误;选项D :由0y x >>,可得110y x +>+>,所以2110y x +>+>,故选项D 正确;12.解:函数()(1)21111f x ax a a x a x x =++=-++--,根据题意有1(1)2f x a ax x+-=+,则函数(1)2y f x a =+-为奇函数,函数()f x 图像关于(1,2)a 成中心对称,所以选项A 正确.选项B :当0a >时,()(1)211f x a x a x =-++-可由函数1y ax x=+向右平移1个单位,向上平移2a 个单位得到.又易知函数1y axx=+在)+∞上单调递增,所以()f x 在1,)++∞上单调递增,∴选项B 错误;选项C :21()111ax a f x ax a x x -+=++=--,()0f x =有解,即210ax a -+=有解,所以4(1)00a a a ∆=--+≥⎧⎨≠⎩,即(,0)[1,)a ∈-∞∞+,选项C 正确;选项D :当12a =时,()f x 关于(1,1)中心对称,又函数()g x 关于(1,1)中心对称,112220222022()()()220224044x y x y x y ∴++++++=⨯=,故选项D 正确;故选:ACD . 16.解:()f x ,()g x 的隔离直线为4y x b =-+,则2234x x x b -≥-+对一切实数x 成立,即220x x b +-对一切实数x 成立,故△180b =+,解得18b ≤-△;又14x b x -+对一切0x <恒成立,即14(0)b x x x+<恒成立,当0x <时,1142(4x x x+--=-,当且仅当14x x -=-,即12x =-时取等号,4b ∴-△;由△△,得148b --,∴实数b 的取值范围是[4-,1]8-.17.解:(1){}2{|50}1,65A x x x +=-==,当1a =时,{1}B =,则{}()5Z A B =;………5分 (2)无论选择△△△中的哪一个,均有B A ⊆, 当B =∅时,0a =,此时满足B A ⊆,当B ≠∅时,即0a ≠时,1{}B a=,此时若满足B A ⊆,则11a =或15a =,解得1a =或15, 综上10,,15C ⎧⎫=⎨⎬⎩⎭..……………………………………………………………………………… 10分18.解:(1)由函数21()(57)m f x m m x -=-+是幂函数,则2571m m -+=,解得2m =或3m =;当2m =时,()f x x =,不合题意;当3m =时,2()f x x =,满足题意.故2()f x x =.………………………………………………………………………………………5分 (2)由(1)可得,()()()2211f x x g x f x x ==++, ()()()()2222222222211111a b a b a b g a g b a b a b ++∴+=+==++++,化简有221a b =,故1ab =. ()()2222f a f b a b ab ∴+=+≥=,当且仅当1a b ==时,()()min 2f a f b +=⎡⎤⎣⎦..…………………………………………………12分19.解:(1)()max{()M x f x =,243,[4,)(,1]()}1,(1,4)x x x g x x x ⎧-+∈+∞-∞=⎨-∈⎩,()M x 图象如下图所示:………………………………6分(2)由(1)中图象可知:函数()M x 在[0x ∈,1]上单调递减,在(1x ∈,4]上单调递增,在(4x ∈,)+∞上单调递增,当01a <时,2()()43223min M a a x g a a ==-+=-,12a ∴=或3a =(舍),当1a >时,()()1min M x f =2023a==-,3a ∴=故实数a 的取值集合为:1{,3}2.………………………………………………………………12分20.解:(1)由表中的数据可知,当时间变化时,日销售量有增有减并不单调, 所以选择模型△:()|20|Q x a x b =-+,从表中任取两组值,不妨令(10)10110(20)120Q a b Q b =+=⎧⎨==⎩,解得1120a b =-⎧⎨=⎩,即()|20|120Q x x =--+,显然表中其它各组值均满足这个函数,故函数的解析式()|20|120(130Q x x x =--+,x ∈N )*.……………………………………5分 (2)由(1)知,**100,120,()|20|120140,2030,x x x Q x x x x x ⎧+∈=--+=⎨-+<∈⎩N N , *100101,120,*()()()140139,2030,x x x x T x P x Q x x x x x ⎧++∈⎪⎪=⋅=⎨⎪-++<∈⎪⎩N N , 当120x ,*x ∈N ,100()101T x x x=++在[1,10]上单调递减,在[10,20]上单调递增,当10x =时,()T x 取得最小值(10)121T =(元),当2030x <,*x ∈N ,140()139T x x x=-++在(20,30]上单调递减,当30x =时,()T x 取得最小值2341(30)11312133T =+=<(元),则当130x ,*x ∈N ,341()(30)3min T x T ==(元),故商品的日销售收入的最小值为3413元.………………………………………………………12分21.解:(1)结合题意易知函数()f x 为奇函数且在()4,4-上单调递增,下面证明之,取0x y ==得到(0)2027(0)f f =,所以(0)0f =,故()16()()16x y f f x f y xy +⎡⎤=+⎢⎥+⎣⎦, 一方面,取y x =-,则(0)()()0f f x f x =+-=,即()()f x f x =--,所以函数()f x 为奇函数,……………………………………………………3分另一方面,对任意的12,x x ∈()4,4-,不妨设12x x <, 则()2121211216()()()()16x x f x f x f x f x f x x -⎡⎤-=+-=⎢⎥-⎣⎦, 因为210x x ->,12160x x ->,故()211216016x x x x ->-,又()()()2112121216444401616x x x x x x x x -+--=<--,故()2112160416x x x x -<<-, 所以有()2121211216()()()()016x x f x f x f x f x f x x -⎡⎤-=+-=>⎢⎥-⎣⎦, 故:21()()f x f x >,所以函数()f x 在()4,4-上单调递增;……………………………………7分(2)由(1)易知,()f x 在()4,4-上单调递增,因为3(1)()0x f x f x-++≤,即33(1)()(x x f x f f x x --+≤-=-), 因为函数()f x 在()4,4-上单调递增,故:31414344x x x x x x -⎧+≤-⎪⎪-<+<⎨⎪-⎪-<<⎩,解得(]35,3,15x ⎛⎤∈-- ⎥⎝⎦,故不等式的解集为(]35,3,15⎛⎤-- ⎥⎝⎦.……………………………………………………………12分22.解:(1)()f x=()2()222f x gx ∴=+=+;)2()202f x x ∴=+≤≤,易知2()f x 在()0,1x ∈递增,在()1,2x ∈递减,故[]2()24f x ∈,,()0f x >,所以()f x ⎤∈⎦.……………………………………………3分(2)令()f x t ⎤=∈⎦,则()2()2a h x t t t a ϕ-==++, △当0a <时,()t ϕ的对称轴10t a=<,故()t ϕ在t ⎤∈⎦递增,故()()22m a a ϕ==-; 当0a >时,分三种情况讨论:(i )当102a ⎛⎤∈ ⎥⎝⎦,时,()t ϕ在t ⎤∈⎦递增,故()()22m a a ϕ==-; (ii )当122a ⎛∈⎝⎭,时,()t ϕ在t ∈递增,在1,2t a ⎛⎫∈ ⎪⎝⎭递减,故()112m a a a a ϕ⎛⎫==+⎪⎝⎭;(iii )当a ⎫∈+∞⎪⎣⎭时,()t ϕ在t ⎤∈⎦递减,故()m a ϕ==综上:()m a=12,0211,2222a a a a a a a ⎧-≤≠⎪⎪⎪+<<⎨⎪≥且;……………………………………………………………8分△当2a⎫∈+∞⎪⎢⎣⎭时,(10a∈,此时需分三种情况讨论: (i )当1a ∈⎣,即a∈⎣时,()1m a m a ⎛⎫== ⎪⎝⎭ (ii )当112a ⎡∈⎢⎣⎭,即a ⎤∈⎦时,()112a m a m a a ⎛⎫=+ ⎪⎝⎭,解得a =; (iii )当110,2a ⎛⎫∈ ⎪⎝⎭,即()2a ∈+∞,时,()12m a m a a ⎛⎫===- ⎪⎝⎭,解得2a =; 当122a⎛∈ ⎝⎭时,即)1a ∈时,()112m a a m a a ⎛⎫=+== ⎪⎝⎭a =(舍); 当10,2a ⎛⎤∈ ⎥⎝⎦时,即()12,a ∈+∞时,()12m a a m a ⎛⎫=-= ⎪⎝⎭2a =(舍);当(),0a ∈-∞时,即()1,0a ∈-∞时,()1122m a a m a a ⎛⎫=-==- ⎪⎝⎭,解得1a =-;综上:{}12a ∈-⎢⎣.………………………………………………………………………12分。
重庆八中 2023——2024 学年度(上)期末考试高一年级数学模拟试卷

重庆八中2023——2024学年度(上)期末考试高一年级数学模拟试题一.单选题:题号12345678答案DDCDBCAA3.解:设扇形的圆心角的弧度数为α,由扇形的面积公式:212S R α=,因为扇形的半径长为2R =,面积为4S =,所以扇形的圆心角的弧度数是2.故选.C 4.解:根据题意可得02815n C =⋅,则当10A I =时,101528n n t ⋅=⋅,所以,20233log 2log 23228(28(28(56h 2332n t -=⋅=⋅=⋅=,即当放电电流10A I =,放电时间为56h .故选:D .5.解:函数()()26f x ln x x =---,0x <时函数是连续函数,(2)2460f ln -=+-< ,()1260f e e -=+->,故有(2)()0f f e --< ,根据函数零点的判定定理可得,函数()()26f x ln x x =---的零点所在的区间为(,2)e --,故选:B .6.解:由于函数2tan()63y x ππ=-+在一个周期内单调递减,令()2632k x k k Z ππππππ-+<+<+∈,解得6561()k x k k Z -<<+∈,故函数2tan()63y x ππ=-+的单调递减区间为(65k -,61)()k k Z +∈.故选:C .7.解:根据题意,()f x 对任意的x R ∈都有51()(22f x f x +=-,则有(3)()f x f x +=,即函数()f x 是周期为3的周期函数,则(2020)(16733)f f f =+⨯=(1),(2019)(0)f f =,又由函数()f x 是定义在R 上的奇函数,则(0)0f =,又由当3(,0)2x ∈-时,2()log (1)f x x =--,则2(1)log (11)1f -=-+=-,则f (1)(1)1f =--=,故(2020)(2019)10f f f -=-=(1)(0)1f -=;故选:A .8.解: 函数(1)y f x =+是偶函数,(1)y f x ∴=+的图象关于y 轴对称,(1)y f x =+ 向右平移1个单位得到()y f x =,()y f x ∴=的图象关于直线1x =对称,若对任意a 、[1,)()b a b ∈+∞≠总有()()()()af b bf a af a bf b +<+成立,即()()()()0a b f a f b -->,()f x ∴在[1,)+∞上单调递增,()f x ∴在(,1)-∞上单调递减,因此由()(2)4f x f <,可得2141x -<-,即213x -<,所以3213x -<-<,解得12x -<<,即不等式()(2)4f x f <的解集为(1,2)-,故选A .二.多选题题号9101112答案BCDABDABDCD9.解:cos()cos θθ-=,A 不符合题意;cos()cos πθθ+=-,B 符合题意;sin(cos 2πθθ-=-,C 符合题意;3sin()cos 2πθθ-=-,D 符合题意.故选:BCD .10.解:对于A ,1113a a b a b a a b a b a b ++=+=+++= ,当且仅当12a b ==时取等号,故A 项正确;对于B ,2323()4545a b a b a b a b ab ab ab b a++++++===+,所以454545()()99a b a b b a b a b a+=++=+++ ,当且仅当2a =,即5a =-,4b =-时取等号,故B 项正确;对于C ,211222125(1)(21)(22)(21)(2228a b a b a b +++++=++⨯= ,当且仅当2221a b +=+,即14a =,34b =时取等号,故C 项错误;对于D ,因为0a >,0b >,1a b +=,所以01a <<,22244(1)(2)a b a a a +=+-=-,又因为01a <<,所以22(2)(02)4a -<-=,即244a b +<,故D 项正确.故选:ABD .11.解: 将()sin 2f x x =的图象向右平移(0)ϕϕ>个单位长度,得到函数()sin(22)g x x ϕ=-的图象,故当4πϕ=时,()sin(22)sin(2)cos 22g x x x x πϕ=-=-=-,为偶函数,故A 正确;当12x π=时,求得(sin(2)16123f x πππ+=⨯+=,为最大值,可得12x π=是函数(6f x π+的一条对称轴,故B 正确;()sin(222)sin(2cos 2422g x x x x πππϕϕϕ+-=+--=-=- ,当[4x π∈,23π,2[2x π∈,43π,故()4g x πϕ+-没有单调性,故C 错误;若函数()1sin(22)1y g x x ϕ=+=-+的一个对称中心为(3π,1),则223k πϕπ⨯-=,k Z ∈,即23k πϕπ=-+,令1k =-,可得56πϕ=,故D 正确,故选:ABD .12.解: 函数()cos([])2f x x π=,其中[]x 表示不超过x 的最大整数,由10x -< ,[]1x =-,()1f x =;由01x < ,[]0x =,()1f x =;由12x < ,[]1x =,()0f x =;由23x < ,[]2x =,()1f x =-,由34x < ,[]3x =,()0f x =;⋯,11()(0)122f f -+==,11(22f f +=(1)0=,1111((2222f f -+≠+,函数1(2y f x =+不是偶函数,所以A 不正确;则()f x 的值域为{1-,0,1},故B 不正确;由上面的分析可得()f x 为周期函数,且最小正周期4T =,故C 正确;()f x 与7log |1|y x =-的图象恰有一个公共点,故D 正确.故选:CD .三.填空题13.1(,1)2-;14.8-;15.9[,)4+∞;16.015.解:对x R ∀∈,()3f x 恒成立,即为13x x ae e + ,由0xe >,可得231x xa e e - 恒成立,设2231139()()24x x x g x e e e =-=--+,当132x e =即23x ln =时,()g x 取得最大值94,可得94a ,即有a 的取值范围为9[4,)+∞.16..解: (0,2cos()24ππααα∈=-,2sin 2sin )2ααα∴=+,两边平方可得:21sin 2(1sin 2)2αα=+,即22sin 2sin 210αα--=,2(0,)απ∈ ,sin 20α>,∴解得sin 21α=,可得cos 20α=.四.解答题17.解:(1)211log 313(0.008)2254(3)0.2232(52)lg lg lg lg π+--++++=-++⨯++356210ππ=-+++=+.(2)3sin()cos()tan()cos()cos (sin )tan (sin )222cos sin(2)tan()sin()sin (tan )sin πππααπαααααααπααπαπααα--++-⋅-⋅⋅-==-------⋅-⋅19.18.解:(1)2()12sin cos 2sin f x x x x ωωω=+-sin 2cos2x x ωω=+4x πω=+;所以()f x 的最小正周期为2|2|T ππω==,1ω=;(2)所以()sin()1424f πππ=+=;(3)由02x π- ,得32444x πππ-+ ,所以2sin(2)[1,]42x π+∈-;当242x ππ+=-,即38x π=-时,()f x取得最小值为.19.解:(1)由已知可得2sin cos αα=-,则1tan 2α=-,所以2222sin cos cos 2tan 11sin cos cos 215tan sin cos tan ααααααααααα++-+===++;(2)由2tan 6tan 1ββ-=,可得22tan 1tan 213tan βββ==--,则11tan tan 223tan(2)1111tan tan 2123αβαβαβ--++===---⨯,因为(0,2πβ∈,所以2(0,)βπ∈,又13tan 233β=->-,则52(,)6πβπ∈,因为(0,)απ∈,1tan 23α=->-,则5(,)6παπ∈,则52(,2)3παβπ+∈,所以724παβ+=.20.解:(1) 不搞促销活动,该产品的年销售量只能是2万件,即0m =时,2x =,2401∴=-+k ,解得2=k ,则2401x m =->+,816161.5(816)36(0)1x y x x m m m x m +∴=⨯-+-=--+ ;(2)16163637(1)11y m m m m =--=--+++3737829-=-= ,当且仅当1611m m =++,即3m =时,等号成立,故该厂家2020年的促销费用投入3万元时,厂家的利润最大.21.解:(1)由题意可知,T π=,所以22Tπω==,所以()2cos(2)f x x ϕ=+;因为()f x 的图象过点5(6π,2),所以52cos(2)26πϕ⨯+=,解得523k πϕπ=-,k Z ∈;因为0ϕπ<<,所以3πϕ=,所以()2cos(23f x x π=+;(2)由(1)可得()2cos(2cos(2)136g x x x ππ=++-+2cos(2))133x x ππ=++++4sin(2)136x ππ=+++4cos 21x =+;设()t g x =,因为1cos 21x - ,所以3()5g x - ;又因为不等式2()(32)()230g x m g x m -+-- 恒成立,即2()(32)230h t t m t m =-+-- 在[3-,5]上恒成立,则(3)0(5)0h h -⎧⎨⎩ ,即93(32)230255(32)230m m m m ++--⎧⎨-+--⎩ ,解得112m - ,所以m 的取值范围是1[2-,1].22.解:(1)由题知,当0x >,21()()log x g x f x x+==,设0x <.则0x ->,所以2211()log log x x g x x x-+--==-,因为()g x 是奇函数,所以2()log 1x g x x =-,又因为(0)0g =所以221log ,0()0,0log ,01x x x g x x x x x +⎧>⎪⎪==⎨⎪⎪<-⎩;(2)令2221()log ()log ()0h x a x x=++=,整理得210ax x +-=,因为()h x 有且只有一个零点,所以方程210ax x +-=有且只有一根或两相等根,当0a =时,1x =,符合题意,当0a ≠时,只需△140a =+=,所以14a =-,此时2x =,符合题意,综上,14a =-或0a =.(3)在(0,)+∞上任取1x ,2x ,且12x x <,则1211a a x x +>+,221211log ()log ()a a x x +>+,所以12()()f x f x >,所以()f x 在(0,)+∞上单调递减,所以函数()f x 在[t ,1]t +上的最大值与最小值分别为()f t ,(1)f t +,所以2222211(1)1()(1)log ()log ()log 11(1)at a t f t f t a a t t at a t +++-+=+-+=+++ ,即2(1)10at a t ++- ,对任意1[,1]2t ∈成立,因为0a >,所以函数2(1)1y at a t =++-的图象开口向上,对称轴102a t a+=-<,所以函数2(1)1y at a t =++-在(0,)+∞上单调递增,所以当12t =时,y 有最小值3142a -,所以31042a - ,解得23a ,所以a 的取值范围为2[,)3+∞.。
重庆八中高2023级数学高一上国庆作业题一(终版答案)
重庆八中高2023级国庆假期数学作业(一)答案一、选择题二、填空题3212.对于A ,∵f(x)=x 2+mx +n(m,n ∈R),不等式x <f(x)的解集为,即x 2+(m −1)x +n >0的解集为,∴m −1=−2,n =1,即m =−1,n =1,故A 正确; 对于B ,由A 可得,设g(x)=f(x)x=x 2−x+1x=x +1x −1,当x >0时,x +1x −1⩾2√x ·1x −1=1,当且仅当x =1时,取等号,即g(x)⩾g(1)=1, 当x <0时,−x >0,∴−x +1−x⩾2√−x ·1−x =2,当且仅当x =−1时,取等号,∴x <0时,g(x)⩽g(−1)=−3,故g(x)无最大值,也无最小值,故B 错误; 对于C ,由不等式x <f(x)的解集为,则不等式f(x)<f(f(x)),得f(x)<1或f(x)>1,即x 2−x +1<1或x 2−x +1>1, 解得解集为,故C 正确;对于D.,知ℎ(x)={34,x ⩽12f(x),x >12,即ℎ(x)={34,x ⩽12(x −12)2+34,x >12,当x ⩽12时,ℎ(x)是常函数,当x >12时,ℎ(x)是单调递增,若 ℎ(x)<ℎ(2x +2),则{x ⩽122x +2>12或x >12,解得−34<x ⩽12或x >12,∴x 的取值范围是,故D 正确.故选ACD .16.若不等式-3≤x 2-2ax +a≤-2有唯一解,则方程x 2-2ax +a =-2有两个相等的实根,解得a=21-或三、解答题17.解:由已知条件可得:A ={x |1≤x ≤3},B ={x |−√a <x <√a}, (1)当a =4时,B ={x |−2<x <2},则A⋂B ={x |1≤x <2},A⋃B ={x |−2<x ≤3},(2)C R A ={x |x <1,或x >3},因为B ⊆C R A ,所以√a ≤1,解得0<a <1。
2024-2025学年重庆八中高一(上)期中数学试卷(含答案)

2024-2025学年重庆八中高一(上)期中数学试卷一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.命题“∀x∈R,x2−x+1>0”的否定是( )A. ∃x∈R,x2−x+1>0B. ∃x∈R,x2−x+1≤0C. ∀x∈R,x2−x+1>0D. ∀x∈R,x2−x+1≤02.已知全集U=R,集合A={0,1,2,3,4,5},B={x∈R|x≥3},则A∩∁U B=( )A. {4,5}B. {3,4,5}C. {0,1,2}D. {0,1,2,3}3.下列各组函数表示同一函数的是( )A. f(x)=1,g(x)=xB. f(x)=x,g(x)=x2xC. f(x)=x,g(x)=3x3D. f(x)=x2,g(x)=(x)24.已知函数f(x)=ax2+bx+c,若a>b>c,且a+b+c=0,则函数f(x)的图象可能是( )A. B. C. D.5.设x∈R,用[x]表示不超过x的最大整数,如[1.2]=1,[2]=2,[−1.2]=−2,则“x>y”是“[x]>[y]”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件6.对任意两个实数a,b,定义min{a,b}={a,a≤bb,a>b,若f(x)=2−x2,g(x)=x2−2,则下列关于函数m(x)=min{f(x),g(x)}的说法错误的是( )A. 函数m(x)是偶函数B. 方程m(x)=−2有两个根C. 不等式m(x)>−x的解集为(1,2)D. 函数m(x)的值域为(−∞,0])<f(−2),则实数x的取值7.已知函数f(x)是定义在[−4,a−1]上的偶函数,在[−4,0]上单调递增.若f(x+a5范围是( )A. (−∞,−3)∪(1,+∞)B. (−3,1)C. [−5,−3)∪(1,3]D. [−3,1)∪(3,5]8.对于函数f(x),若存在x0∈R,f(x0)=x0,则称x0为f(x)的不动点.若函数f(x)=mx2+(n−1)x+n−8对∀n∈R恒有两个相异的不动点,则实数m的取值范围是( )A. (−∞,0]∪[6,+∞)B. (−∞,0)∪(6,+∞)C. (0,6]D. (0,6)二、多选题:本题共3小题,共18分。
2022-2023学年重庆市第八中学校高一上学期期中数学试题(解析版)

2022-2023学年重庆市第八中学校高一上学期期中数学试题一、单选题1.命题200,2x R x ∃∈>的否定是( ) A .2,2x R x ∃∈≤ B .2,2x R x ∃∈< C .2,2x R x ∀∈< D .2,2x R x ∀∈≤【答案】D【分析】根据特称命题的否定变换形式即可得出选项.【详解】命题200,2x R x ∃∈>的否定为:2,2x R x ∀∈≤.故选:D2.函数()13f x x=-的定义域为( ) A .[)1,-+∞ B .[)()1,33,-⋃+∞ C .()()1,33,-+∞D .[)3,+∞【答案】B【分析】利用根式与分式有意义,结合交集的定义即可求解.【详解】要使()f x 有意义,则1030x x +≥⎧⎨-≠⎩,解得1x ≥-且3x ≠.所以函数()13f x x=-的定义域为[)()1,33,-⋃+∞. 故选:B.3.已知a R ∈,则2a >是22a a >的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【答案】A【分析】首先解不等式22a a >,再根据不等式的解集即可得到答案. 【详解】因为220(2)02a a a a a ->⇒->⇒>或a<0. 所以2a >是22a a >的充分不必要条件. 故选:A【点睛】本题主要考查充分不必要条件,同时考查了二次不等式,属于简单题.4.函数()f x 满足()112f x x-=,则()2f =( ) A .2 B .2-C .12D .12-【答案】B【分析】令122x -=,求出x ,再代入计算可得. 【详解】解:因为()112f x x-=,令122x -=,解得12x =-,所以()12212f ==--. 故选:B 5.函数()232xf x x =-的图象大致为( ) A . B .C .D .【答案】D【分析】根据函数的定义域可排除B ,再利用特殊值的函数值的符号即可排除AC. 【详解】解:220x -≠,则2x ≠± 所以函数的定义域为{}2x x ≠,故排除B ; 当2x ()0f x >,故排除A ;()110f =-<,故排除C.故选:D.6.新冠肺炎疫情防控中,核酸检测是新冠肺炎确诊的有效快捷手段.某医院在成为新冠肺炎核酸检测定点医院并开展检测工作的第n 天,每个检测对象从接受检测到检测报告生成平均耗时()t n (单位:小时)大致服从的关系为()0n N t n n N <=≥(00,t N 为常数).已知第16天检测过程平均耗时为10小时,第65天和第68天检测过程平均耗时均为5小时,那么可得到第49天检测过程平均耗时约为( ) A .9小时 B .7小时C .6小时D .5小时【答案】C【分析】按照题目所给的条件,算出0t 和0N ,再代入计算即可.【详解】解:因为第65天和第68天检测过程平均耗时均为5小时,所以016N <,10=,即040t =5=,解得064N =, 所以()645,64n t n n <=≥⎩,所以()404967t ==≈(小时). 故选:C7.已知函数()29,1,1x ax x f x ax x ⎧---≤⎪=⎨>⎪⎩在R 上单调递增,则实数a 的取值范围为( ) A .[)5,0- B .(],2-∞-C .[]5,2--D .(),0∞-【答案】C【分析】根据分段函数每段递增,以及左边一段的最高点不高于右边一段的最低点,列不等式组求解即可.【详解】函数()29,1,1x ax x f x ax x ⎧---≤⎪=⎨>⎪⎩在R 上单调递增 12019aa a a ⎧-≥⎪⎪∴<⎨⎪---≤⎪⎩,解得52a -≤≤- 故选:C.8.若正实数,x y 满足11y x y x->-,则下列结论错误的是( ) A .11x x y y +<+ B11yx<C .11x x y y -<-D .121x y +<+【答案】C【分析】根据条件化简得到y x >,计算得到A 正确,根据函数()1f x x x =-的单调性得到B 正确,取特殊值判断C 错误,平方得到D 正确,得到答案. 【详解】11y x y x ->-,即()110y x xy ⎛⎫-+> ⎪⎝⎭,(),0,x y ∈+∞,故y x >. 要11x x y y +<+,即xy x xy y +<+,即x y <,A 正确; 易知函数()1f x x x=-在()0,∞+上单调递增,故()()f x f y <,11x y x y-<-,即11x y y x+<+,B 正确;取1,12x y ==,代入11x x y y -<-计算得到104<,不成立,C 错误;121x y +<+,平方得到121x y +<+,即2x y <,成立,D 正确.故选:C.二、多选题9.图中矩形表示集合,,U A B 是U 的两个子集,则阴影部分可以表示为( )A .()()U U AB ⋂ B .()U A B ⋂C .()BA BD .()()UUA B ⋂【答案】BC【分析】根据阴影部分不在集合A 中,在集合B 中可得答案, 【详解】根据图形可得阴影部分不在集合A 中,在集合B 中, 即阴影部分可以表示为()()U BA B A B ⋂⋂,,故选:BC10.若0,0a b >>,且3a b +=,则下列结论正确的是( )A .2292a b +≥B 32≥C D .3183a b +≥【答案】AC【分析】利用基本不等式即可判断ABC ,根据()311313a b a b a b ⎛⎫+=++ ⎪⎝⎭结合基本不等式即可判断D.【详解】解:因为()()22222292ab a b a b a b +=++≥=+,当且仅当32a b ==时,取等号, 所以2292a b +≥,故A 正确;对于B 322a b +=,当且仅当32a b ==时,取等号,故B 错误;对于C ,因为()2222a b +≥++,当且仅当32a b ==时,取等号,C 正确;对于D ,()3113113144333b a a b a b a b a b ⎛⎛⎫⎛⎫+=++=++≥+= ⎪ ⎪ ⎝⎭⎝⎭⎝当且仅当3b aa b=,即)312a ==时取等号,故D 错误.故选:AC.11.已知函数()f x 是定义在R 上的偶函数,且在[)0,∞+上单调递增,若()10f =,则下列说法正确的是( )A .x ∀∈R ,M ∃∈R ,使()f x M ≥B .若()()13f x f -<,则(),4x ∈-∞C .若()0xf x <,则()(),10,1x ∈-∞-⋃D .()f x 的解析式可以为()223f x x x =+-【答案】ACD【分析】取()0M f ≤可判断A 选项;利用函数()f x 的单调性与奇偶性解不等式()()13f x f -<,可判断B 选项;分0x <、0x >解不等式()0xf x <,可判断C 选项;验证()223f x x x =+-满足题干中的条件,可判断D 选项.【详解】对于A 选项,因为函数()f x 是定义在R 上的偶函数,且在[)0,∞+上单调递增,若()10f =, 故函数()f x 在(],0-∞上单调递减,故()()min 0f x f =,故x ∀∈R ,M ∃∈R ,当()0M f ≤时,()f x M ≥恒成立,A 对; 对于B 选项,若()()13f x f -<,且函数()f x 在[)0,∞+上单调递增,所以,()()13f x f -<,可得13x -<,即313x -<-<,解得24-<<x ,B 错; 对于C 选项,由题意可知()()110f f -==.当0x <时,由()0xf x <,可得()()01f x f >=-,所以,1x <-; 当0x >时,由()0xf x <,可得()()01f x f <=,所以,01x <<. 若()0xf x <,则()(),10,1x ∈-∞-⋃,C 对;对于D 选项,若()223f x x x =+-,则该函数的定义域为R ,()()()222323f x x x x x f x -=-+--=+-=,即函数()223f x x x =+-为偶函数,当0x ≥时,()223f x x x =+-,则函数()f x 在[)0,∞+上单调递增,且()10f =,故()f x 的解析式可以为()223f x x x =+-,D 对.故选:ACD.12.我们知道,函数()y f x =的图象关于坐标原点成中心对称图形的充要条件是函数()y f x =为奇函数.有同学发现可以将其推广为:函数()y f x =的图象关于点(),P a b 成中心对称图形的充要条件是函数()y f x a b =+-为奇函数.现已知函数()11f x ax a x =++-,则下列说法正确的是( ) A .函数()12y f x a =+-为奇函数 B .当0a >时,()f x 在()1,+∞上单调递增 C .若方程()0f x =有实根,则()[),01,a ∞∞∈-⋃+ D .设定义域为R 的函数()g x 关于()1,1中心对称,若12a =,且()f x 与()g x 的图象共有2022个交点,记为()(),1,2,,2022i i i A x y i =,则()()()112220222022x y x y x y ++++++的值为4044【答案】ACD【分析】对于A.根据题意改写函数得到新解析式即可判断;对于B.可用特殊值法判断错误,也可根据增函数定义进行判断;对于C.令()0f x =写出a 的解析式即可判断a 的取值范围;对于D 根据题意可知()f x 和()g x 关于()1,1中心对称,所以交点关于()1,1中心对称,即对称的横或纵坐标之和为2,由此得出答案. 【详解】对于A.()()11121211f x a a x a a ax x x+-=+++-=++-由解析式可知1y ax x=+是奇函数,故A 正确;对于B.特殊值法33152322212f a a a ⎛⎫=++=+ ⎪⎝⎭-,()1223121f a a a =++=+- 即3(2)122a f f ⎛⎫-=- ⎪⎝⎭,若02a <<,则()f x 在()1,+∞上不是单调递增,故B 错误.对于C.令()101f x ax a x =++=-,分离参数后211a x=-,()(]21,0)(0,1x ∞-∈-⋃ 故()[)21,01,1x ∞∞∈-⋃+-,C 正确; 对于D.由A 可知,当12a =时,()f x 关于()1,1中心对称,且()g x 关于()1,1中心对称,所以这2022个交点关于()1,1对称,故()()122022122022202220224044x x x y y y +++++++=+=,D 正确.故选:ACD 【点睛】思路点睛:①奇函数+奇函数=奇函数,偶函数+偶函数=偶函数,奇函数⨯奇函数=偶函数, 偶函数⨯偶函数=偶函数,奇函数⨯偶函数=奇函数;②关于对称中心对称的两个点,两个点横坐标之和等于两倍对称中心的横坐标,两个点纵坐标之和等于两倍对称中心的纵坐标.三、填空题13.计算:021632727(2)8⎛⎫⎡⎤---= ⎪⎣⎦⎝⎭__________. 【答案】13π+##π13+【分析】根据指数幂的运算性质计算即可.【详解】解:021632727(2)8⎛⎫⎡⎤--- ⎪⎣⎦⎝⎭()21363231π32⨯⨯=-+-+91π3813π=-+-+=+.故答案为:13π+.14.已知函数()f x 为奇函数,当0x ≥时,()32f x x m =-,则()()1f f -=__________.【答案】8-【分析】先利用()00f =求出m ,利用奇函数的定义,求出()1f -,再求()()1f f -. 【详解】函数()f x 为奇函数()020f m ∴=-=,2m =∴当0x ≥时,()3f x x =∴()()(31121f f -=-=-=-,()()()()(312228f f f f -=-=-=-=-故答案为:8-.15.写出一个同时具有下列性质①②的函数()f x :__________.①函数()f x 对其定义域内的任意两个不等实数12,x x 都满足不等式()()121222f x f x x x f ++⎛⎫< ⎪⎝⎭;②函数()f x 为偶函数.【答案】()2f x x =(答案不唯一)【分析】本题属于开放性问题,只需写出符合题意的函数解析式即可,不妨令()2f x x =,利用奇偶性的定义判断②,利用重要不等式判断①.【详解】解:令()2f x x =,则()()()22f x x x f x -=-==,即()2f x x =为偶函数,满足条件②,设12,R x x ∀∈且12x x ≠,则()211f x x =,()222f x x =,222121212122224x x x x x x x x f ++++⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭, 所以()()222211221222224f x f x x x x x +++==,因为2212122x x x x +>,所以222212121222244x x x x x x +++>, 即()()121222f x f x x x f ++⎛⎫> ⎪⎝⎭,故满足①; 故答案为:()2f x x =(答案不唯一)16.若存在常数k 和b ,使得函数()F x 和()G x 分别对其定义域上的任意实数x 都满足:()F x kx b +和()G x kx b +恒成立,则称此直线y kx b =+为()F x 和()G x 的“隔离直线”,已知函数()()()2123,(0)f x x x x g x x x=-∈=<R ,若函数()f x 和()g x 之间存在隔离直线4y x b =-+,则实数b 的取值范围是__________.【答案】14,8⎡⎤--⎢⎥⎣⎦【分析】根据题意得到2234x x x b -≥-+,计算180b =+≤得到一个范围,再根据双勾函数的单调性得到函数()14K x x x=+的最大值,综合得到答案. 【详解】2234x x x b -≥-+,即220x x b +-≥恒成立,故180b =+≤,解得18b ≤-;14x b x ≤-+,即14x b x +≤,函数()14K x x x =+在1,2⎛⎫-∞- ⎪⎝⎭上单调递增,在1,02⎡⎫-⎪⎢⎣⎭上单调递减,故()max 142K x K ⎛⎫=-=- ⎪⎝⎭,故b 4≥-.综上所述:14,8b ⎡⎤∈--⎢⎥⎣⎦.故答案为:14,8⎡⎤--⎢⎥⎣⎦四、解答题17.已知{}2650A x x x =-+=,{}10B x ax =-=.(1)若1a =,求()Z A B ⋂; (2)从①()AB =RR ;②A B B =;③()B A ⋂=∅R 这三个条件中任选一个,补充在下面横线上,并进行解答.问题:若__________,求实数a 的所有取值构成的集合C . 注:如果选择多个条件分别解答,按第一个解答计分. 【答案】(1)(){}Z5AB =(2)条件选择见解析,10,,15C ⎧⎫=⎨⎬⎩⎭【分析】(1)当1a =时,求出集合B 、A ,利用补集和交集的定义可求得集合()Z A B ⋂; (2)选①,分0a =、0a ≠两种情况讨论,在0a =时,直接验证即可;在0a ≠时,求得1B a ⎧⎫=⎨⎬⎩⎭,根据()AB =RR 可得出关于a 的等式,综合可得出集合C ;选②,分析可知B A ⊆,分0a =、0a ≠两种情况讨论,在0a =时,直接验证即可;在0a ≠时,求得1B a ⎧⎫=⎨⎬⎩⎭,根据B A ⊆可得出关于a 的等式,综合可得出集合C ;选③,分0a =、0a ≠两种情况讨论,在0a =时,直接验证即可;在0a ≠时,求得1B a ⎧⎫=⎨⎬⎩⎭,根据()B A ⋂=∅R ,可得出关于a 的等式,综合可得出集合C .【详解】(1)解:当1a =时,{}{}101B x x =-==,又因为{}{}26501,5A x x x =-+==,故(){}Z5AB =.(2)解:若选①,当0a =时,B =∅,则B =RR ,满足()AB =RR ,当0a ≠时,1B a ⎧⎫=⎨⎬⎩⎭,若()AB =RR ,则11a =或5,解得1a =或15. 综上所述,10,,15C ⎧⎫=⎨⎬⎩⎭;若选②,A B B =,则B A ⊆.当0a =时,B =∅,满足B A ⊆;当0a ≠时,1B a ⎧⎫=⎨⎬⎩⎭,因为B A ⊆,则11a =或5,解得1a =或15.综上所述,10,,15C ⎧⎫=⎨⎬⎩⎭;若选③,当0a =时,B =∅,满足()B A ⋂=∅R ;当0a ≠时,则1B a ⎧⎫=⎨⎬⎩⎭,因为()B A ⋂=∅R ,则11a =或5,解得1a =或15.综上所述,10,,15C ⎧⎫=⎨⎬⎩⎭.18.已知幂函数()()2157m f x m m x -=-+,且()()=f x f x -.(1)求函数()f x 的解析式; (2)若()()(),,1f xg x a b f x =+均为正数且()()1g a g b +=,求()()f a f b +的最小值.【答案】(1)()2f x x =(2)2【分析】(1)根据幂函数得到2571m m -+=,解方程再验证函数的奇偶性得到答案.(2)代入数据计算得到2211111a b +=++,再利用均值不等式计算得到答案. 【详解】(1)幂函数()()2157m f x m m x -=-+,则2571m m -+=,解得2m =或3m =,当2m =时,()f x x =是奇函数,舍去;当3m =时,()2f x x =是偶函数,满足.故()2f x x =.(2)()()()22211111f x x g x f x x x ===-+++,()()221111111g a g b a b +=-+-=++, 即2211111a b +=++, ()()2222112f a f b a b a b +=+=+++-()()22222222222211111122211111111b a b a a b b a b a b a +=+++⎛⎫+⎡⎤+++⨯-=⎣⎦++≥⋅= ⎪+++++⎝⎭, 当22221111b a a b ++=++,即1a b ==时等号成立,故()()f a f b +的最小值为2. 19.已知函数()()21,43,f x x g x x x x =-=-+∀∈R ,用()M x 表示()(),f x g x 中的较大者,记为()()(){}max ,M x f x g x =.(1)写出函数()M x 的解析式,并画出它的图象;(2)当[]0,x a ∈时,若函数()M x 的最小值为322a-,求实数a 的取值集合.【答案】(1)()[]()()21,1,443,,14,x x M x x x x ∞∞⎧-∈⎪=⎨-+∈-⋃+⎪⎩,图象见解析(2)1,32⎧⎫⎨⎬⎩⎭【分析】(1)分别求出()()f x g x ≥,()()f x g x <的解集,即可得出函数()M x 的解析式,再根据一次函数和二次函数的图象作图即可;(2)分01a <<和1a ≥两种情况讨论,求出函数的最小值,从而可得出答案. 【详解】(1)解:当2143x x x -≥-+,即14x ≤≤时,()1M x x =-,当当2143x x x -<-+,即>4x 或1x <时,()243M x x x =-+,所以()[]()()21,1,443,,14,x x M x x x x ∞∞⎧-∈⎪=⎨-+∈-⋃+⎪⎩, 函数图象如图所示:(2)解:由(1)可得,函数()M x 在(),1-∞上递减,在()1,+∞上递增, 当01a <<时,函数()M x 在[]0,a 上递减,所以()()2min 34322a M x M a a a ==-+=-,解得12a =或3(舍去),当1a ≥时,函数()M x 在[]0,a 上的最小值为()31022aM ==-,解得3a =, 综上实数a 的取值集合为1,32⎧⎫⎨⎬⎩⎭.20.北京2022年冬奥会和冬残奥会,向世界传递了挑战自我、积极向上的体育精神,引导了健康、文明、快乐的生活方式.冬奥会吉祥物“冰墩墩”和冬残奥会吉祥物“雪容融”一亮相,好评不断,这是一次中国文化与奥林匹克精神的完美结合,是一次现代设计理念的传承与突破.为了进一步宣传2022年北京冬奥会和冬残奥会,某赞助商开发了一款纪念产品,通过对这款产品的销售情况调查发现:该产品在过去的一个月内(以30天计)的日销售价格()P x (单位:元)与时间x (单位:天)的函数关系近似满足()11P x =+,该商品的日销售量()Q x (单位:个)与时间x 部分数据如下表所示:x (天)5 10 15 20 25 30(1)给出以下三种函数模型:①()Q x ax b =+,②()20Q x a x b =-+,③()Q x c =, 请你根据上表中的数据,从中选择你认为最合适的一种函数模型来描述该商品的日销售量()Q x 与时间x 的关系,并求出该函数的解析式;(2)求该商品的日销售总收入()(*130,T x x x N ≤≤∈)(单位:元)的最小值.(注:日销售总收入=日销售价格⨯日销售量)【答案】(1)模型②,()()*20120130,Q x x N x x =--≤≤∈+(2)3413【分析】(1)根据数据的对称性选择模型②,再代入数据计算参数得到答案.(2)计算()T x 的解析式,根据函数的单调性和均值不等式,分段计算函数的最小值,再比较得到答案.【详解】(1)根据表格数据,()Q x 的函数值关于120对称,故选择()20Q x a x b =-+合适.()552015105Q a b a b =-+=+=,()10102010110Q a b a b =-+=+=,解得1,120a b =-=,故()20120Q x x =--+,验证均满足.故()()*20120130,N Q x x x x =--+≤≤∈(2)()()()()**100101,120,N 1120120140139,2030,N x x x xT x P x Qx x x x x x x ⎧++≤≤∈⎪⎪⎛⎫=⋅=+⋅--+=⎨ ⎪⎝⎭⎪-++<≤∈⎪⎩当*120,N x x ≤≤∈时,()100101101121T x x x =++≥=,当100x x =,即10x =时等号成立;当*2030,N x x <≤∈时,()140139T x x x-++=在(]20,30上单调递减,故最小值为()1403413013930330T -++==. 综上所述:当30x =时,()T x 有最小值为3413元. 21.设函数()f x 的定义域为()4,4-,且满足:()()()()20250f x y f x f y f +=++,且当04x <<时,()0f x >.(1)根据函数奇偶性和单调性的定义证明函数()f x 在定义域上的奇偶性和单调性; (2)求关于x 不等式()310x f x f x -⎛⎫++≤ ⎪⎝⎭的解集.【答案】(1)证明见解析 (2)(]35,3,15⎛⎤-- ⎥⎝⎦【分析】(1)令0x y ==,即可求出()0f ,从而得到()()()f x y f x f y +=+,再令y x =-,即可说明函数的奇偶性,再利用定义法证明函数的单调性;(2)根据奇偶性与单调性将函数不等式转化为自变量的不等式,解得即可,需注意函数的定义域. 【详解】(1)解:因为()()()()20250f x y f x f y f +=++, 令0x y ==,可得()()()()00020250f f f f =++,解得()00f =, 所以()()()f x y f x f y +=+,令y x =-,则()()()0f f x f x =+-,即()()f x f x -=-,所以()f x 为奇函数, 设()124,4,x x ∈-∀且12x x <,则212111211121()()()()()()()()f x f x f x x x f x f x x f x f x f x x -=-+-=-+-=-, 因为12x x <,所以210x x ->,故21()0f x x ->, 所以()f x 在()4,4-上单调递增;(2)解:因为()f x 为()4,4-上单调递增的奇函数,所以不等式()310x f x f x -⎛⎫++≤ ⎪⎝⎭等价于()31x f x f x -⎛⎫+≤ ⎪⎝⎭, 等价于31344414x x x x x x -⎧+≤⎪⎪-⎪-<<⎨⎪-<+<⎪⎪⎩,解得53x -<≤-或315x <≤, 即不等式的解集为(]35,3,15⎛⎤--⎥⎝⎦.22.已知函数()()f x g x ==(1)证明:()()222f x g x =+,并求函数()f x 的值域;(2)已知a 为非零实数,记函数()()()x x h f g x a =-的最大值为()m a . ①求()m a ;②求满足()1m a m a ⎛⎫= ⎪⎝⎭的所有实数a .【答案】(1)证明见解析,函数()f x的值域为2⎤⎦(2)①()()12,,00,211,22a a m a a a a a ∞∞⎧⎛⎤⎪-+∈-⋃ ⎥⎪⎝⎦⎪⎛⎪=+∈ ⎨ ⎝⎭⎪⎫∈+⎪⎪⎣⎭⎩;②1a =-a ≤≤【分析】(1)分别求出两函数的定义域,计算即可得证,求出函数()g x 的值域,从而可得出答案; (2)①由(1)得()()212f xg x =-,令(),t f x t ⎤=∈⎦,分a<0,102a <≤,a ≥和12a <<四种情况讨论,结合二次函数的最值即可得出答案;(2)求出1m a ⎛⎫ ⎪⎝⎭,再分a<0,102a <≤,12a <<a ≤≤2a <<和2a ≥六种情况讨论,从而可得出答案.【详解】(1)解:由函数()f x得020x x ≥⎧⎨-≥⎩,解得02x ≤≤,所以函数()f x 的定义域为[]0,2,由函数()g x =,得()20x x -≥,解得02x ≤≤,所以函数()g x 的定义域为[]0,2,所以()()2222f x x x g x =+-+=+,()g x =因为[]0,1x ∈,所以()[]2110,1x --+∈,所以()[]0,1g x ∈,所以()[]22,4f x ∈,又()0f x ≥,所以函数()fx 的值域为2⎤⎦;(2)解:①由(1)得()()212f xg x =-,则()()()()()22a h f f a x x x x x a f g =-+-+=, 令(),t f x t ⎤=∈⎦,则()2,2a h t t t a t ⎤=-++∈⎦, 对称轴为1t a =, 当a<0时,则10a<, 所以()()max 22h t h a ==-+, 当12a ≥,即102a <≤时,()()max 22h t h a ==-+,当10a <≤a ≥()max h t h ==12a <,即12a <<()max 112h t h a a a ⎛⎫==+ ⎪⎝⎭,综上所述()()12,,00,211,22a a m a a a a a ∞∞⎧⎛⎤⎪-+∈-⋃ ⎥⎪⎝⎦⎪⎛⎪=+∈ ⎨ ⎝⎭⎪⎫∈+⎪⎪⎣⎭⎩; ②因为()()12,,00,211,22a a m a a a a a ∞∞⎧⎛⎤⎪-+∈-⋃ ⎥⎪⎝⎦⎪⎛⎪=+∈ ⎨ ⎝⎭⎪⎫∈+⎪⎪⎣⎭⎩, 所以()[))(12,,02,11,22a a am a a a a ∞∞⎧-+∈-⋃+⎪⎪⎪⎛⎫=+∈⎨ ⎪⎝⎭∈⎩,当a<0时,122a a -+=-+,解得1a =-(1a =舍去),当102a <≤时,2a -+=2a =,当12a <<时,12a a +=a =,a ≤≤时,()1m a m a ⎛⎫== ⎪⎝⎭2a <12a a +,解得a =,当2a ≥12a =-+,解得a =,综上1a =-a ≤≤. 【点睛】本题考查了求含根号函数的值域问题及二次函数的最值问题,考查了分类讨论思想及数据分析能力,解决第二问的关键在于找到讨论的临界点,可以借助数轴的手段来进行讨论.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x1
+
x2
+
a x1 x2
的最大值是(
)
A. 6 3
B. − 2 3 3
C. 4 3 3
D. − 4 3 3
第1页 共8页
{ } 5.设集合 A = x | x2 − x − 6 > 0 ,B = {x | (x − k)(x − k − 2) < 0} ,若 A I B ≠ ∅ ,
则实数 k 的取值范围是( )
12.【多选题】已知函数 f (x) = x2 + mx + n(m, n ∈ R) ,不等式 x < f (x) 的解集为
(−∞,1) U (1, +∞) ,则( )
A. m = −1, n = 1 B.设 g(x) = f (x) ,则 g(x) 的最小值为 g(1) = 1
x C.不等式 f (x) < f ( f (x)) 的解集为 (−∞, 0) U (0,1) U (1, +∞)
A.{k | k < −2或k > 1}
B.{k | −2 < k < 1}
C.{k | k < −4或k > 3}
D.{k | −4 < k < 3}
6.下列各式:① a2
+1 > 2a ;②
x+ 1 x
≥ 2 ;③ m + n mn
≤ 2 ;④ x2
+
x
1 2+
1
≥
1
.
其中正.确.的个数是( ) A.0
B.1
C.2
D.3
7.已知函数
f
(x)
=
x +1 −x + 3
(x (x
≤ 1) > 1)
,则
f
f
5 2
=(
)
ห้องสมุดไป่ตู้
A. 1 2
B. 3 2
C. 5 2
D. 7 2
8.设 c < 0 , f ( x) 是区间[a,b] 上的减函数,下列命题中正.确.的是( )
A. f ( x) + c 在[a,b] 上有最小值 f (a) + c
重庆八中高 2023 级高一(上)国庆假期数学作业(一)
满分:150 分 测试时间:120 分钟 姓名:__________ 班级:__________ 学号:__________ 一、选择题(共 12 题,1~8 题为单选题,每题 5 分,9~12 题为多选题,全 部选对得 5 分,部分选对得 3 分,错选或不选得 0 分,共 60 分)
D.已知
h(x)
=
f
3,x 4 ( x),
≤1 2
x>1 2
,若
h(
x)
<
h(2x
+
2)
,则
x
的取值范围是
(−
3 4
,
+∞ )
第3页 共8页
二、填空题(共 4 题,每题 5 分,共 20 分)
13.函数 y = 3x −1 + 1 的定义域是________________. 1− x
14.已知函数
B. c − a > c b−a b
C. ab > c
D. b − 2a > −1
第2页 共8页
10.【多选题】设[x] 表示不大于实数 x 的最小整数(例如:[2.5] = 2 ,[−2.2] = −3),
则满足关于 x 的不等式[x]2 + [x] −12 ≤ 0 的解可以为( )
A. 3 + 5 C. −π
的解集为 (−∞, −1) U (5, +∞)
C. ∀x ∈ R, ax2 + 4x ≥ 2x2 −1 恒成立,则实数 a 的取值范围是[6, +∞)
D.已知 p : 1 ≤ x ≤ 3, q : x2 − (a + 1 )x +1 ≤ 0(a > 0) ,若 p 是 q 的充分不必要条件,
2
a
则实数 a 的取值范围是 (0, 1] U[3, +∞) 3
{ } 1.已知集合 M = x | x2 = 1 , N = {x | ax = 2} ,若 N ⊆ M ,则实数 a 的取值集合
为( )
A.{2}
B.{−2, 2}
C. {−2, 0}
D.{−2, 2,0}
2.已知集合 A = {2, 0} , B = {z | z = x + y, x ∈ A, y ∈ A} ,则集合 B 的非空子集的
元.若使每个同学游 8 次,则购买________________张游泳卡最合算.
16.若不等式 −3 ≤ x2 − 2ax + a ≤ −2 有唯一解,则实数 a 的值为________________. 三、解答题(共 6 题,共 70 分)
{ } { } 17.(10 分) 设全集为 R, A = x x2 − 4x + 3 ≤ 0 , B = x x2 − a < 0 (a > 0) .
B. f ( x) 在[a,b] 上有最小值 f (a)
C. f ( x) − c 在[a,b] 上有最小值 f (a) − c
D. cf ( x) 在[a,b] 上有最小值 cf (a)
9.【多选题】若 0 < a < 1, b > c > 1 ,则下列结论中正.确.的有( )
A. 1 > 1 a +1 b+c
个数为( )
A.3
B.4
C.7
D.8
3.一元二次方程 ax2 + 5x + 4 = 0(a ≠ 0) 有一个正根和一个负根的一个充分不必要
条件是( )
A. a < 0
B. a > 0
C. a < −2
D. a > 1
4 . 已 知 关 于 x 的 不 等 式 x2 − 4ax + 3a2 < 0(a < 0) 的 解 集 为 (x1, x2 ) , 则
f
1− 1+
x x
=
x
,则
f
(3)
的值为________________.
15.某游泳馆出售冬季学生游泳卡,每张 240 元,使用规定:不记名,每卡每次只限
1 人,每天只限 1 次.某班有 48 名学生,老师打算组织同学们集体去游泳,除需购买
若干张游泳卡外,每次还要包一辆汽车,无论乘坐多少名同学,每次的车费均为 40
(1)当 a = 4 时,求 A I B, A U B ;
(2)若 B ⊆ ðR A ,求实数 a 的取值范围.
第4页 共8页
{ } 18.(12 分) 已知关于 x 的不等式 ax2 − 4x + 3 < 0 的解集为 x 1 < x < b .
(1)求 a, b 的值; (2)解关于 x 的不等式 bx − a ≤ 1.
B. 2 5 D. −5
11.【多选题】下列说法中正.确.的有( )
A.命题“ ∀x ∈ R, x3 > x2 +1”的否定是“ ∃x ∈ R, x3 < x2 +1”
B.若不等式 ax2 + bx +1 > 0 的解集为{x | −1 < x < 3} ,则不等式 3ax2 + 6bx + 5 < 0
