数列求和方法总结(课堂PPT)
合集下载
数列求和的几种方法PPT课件

第2页/共11页
练习:(2003s)设f x 1 ,利用课本中
2x 2 推导等差数列前n项和的公式的方法,可求得
f 5 f 4 f 0 f 5 f 6
的值为 3 2 。
第3页/共11页
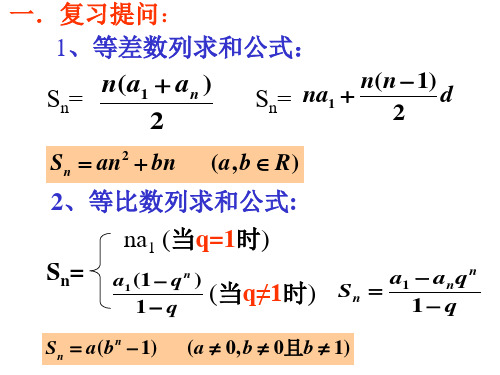
2、错位相减法
例2:求: 1 2
2 22
3 23
n 2n
1 an n 2n
问题:什么时候用错位相减的方法求数列和?
通过拆项,能将数列转化成两个或若干个等差或等比数 列的和或差的形式来求和。
第6页/共11页
4、拆项抵消
例4:求: 1 1
2
1 2
3
1
nn
1
1 11
an nn 1 n n 1
问题:什么时候用拆项抵消的方法求数列和?
将数列的每一项(实际就是通项)拆分成两项, 在求和时除前、后若干项外,中间各项能够相互抵消。
n
1 2
5 4
9 8
......
4n 2n
3.
5 求:S
n
1
3 2
5 4
7 8
......
(1)n1
2n 1 2n1
.
第10页/共11页
感谢观看!
第11页/共11页
1 2
1
1 3
1 ...... 2 2 3
1 n 1
. n
第9页/共11页
练习:
(1)求数列 :1 1,2 1,3 1 3 9 27
,, n
1 3n
的
和S
.
n
(2)求数列 :1 ,11,111,,111(n个1) 的和Sn.
(3)求:S
n
1 1
3
1
练习:(2003s)设f x 1 ,利用课本中
2x 2 推导等差数列前n项和的公式的方法,可求得
f 5 f 4 f 0 f 5 f 6
的值为 3 2 。
第3页/共11页
2、错位相减法
例2:求: 1 2
2 22
3 23
n 2n
1 an n 2n
问题:什么时候用错位相减的方法求数列和?
通过拆项,能将数列转化成两个或若干个等差或等比数 列的和或差的形式来求和。
第6页/共11页
4、拆项抵消
例4:求: 1 1
2
1 2
3
1
nn
1
1 11
an nn 1 n n 1
问题:什么时候用拆项抵消的方法求数列和?
将数列的每一项(实际就是通项)拆分成两项, 在求和时除前、后若干项外,中间各项能够相互抵消。
n
1 2
5 4
9 8
......
4n 2n
3.
5 求:S
n
1
3 2
5 4
7 8
......
(1)n1
2n 1 2n1
.
第10页/共11页
感谢观看!
第11页/共11页
1 2
1
1 3
1 ...... 2 2 3
1 n 1
. n
第9页/共11页
练习:
(1)求数列 :1 1,2 1,3 1 3 9 27
,, n
1 3n
的
和S
.
n
(2)求数列 :1 ,11,111,,111(n个1) 的和Sn.
(3)求:S
n
1 1
3
1
数列的求和方法(ppt)

分组求和法:有一等比或者其他常见数列(即可用倒序相加,错位相减或 裂项相消求和的数列),然后分别求和,之后再进行合并即可算出原数列的前n项 和。
错位相减法:形如An=BnCn,其中{Bn}为等差数列,首项为b1,公差为d;{Cn}为等 比数列,首项为c1,公比为q。对数列{An}进行求和,首先列出Sn,记为①式;再把① 式中所有项同乘等比数列{Cn}的公比q,即得qSn,记为②式;然后①②两式错开一位 做差,从而得到{An}的前n项和。这种数列求和方式叫作错位相减。
数列的求和方法(ppt)
演讲人
目录
01
数列概念
02
等差数列思维导图
数列求和的七种方法:倒序相加法、分组求和法、错位相减法、裂项相消法、乘 公比错项相减(等差×等比)、公式法、迭加法。
倒序相加法:如果一个数列{an},与首末两端等“距离”的两项和相等或者等于 同一个常数,则求该数列的前n项和即可用倒序相加法。例如等差数列的求和公 式,就可以用该方法进行证明。
等差数列思维导图
一般地来说如果一个数列从第2项起,每一项与它的前一项的差等于同一个常 数,这个数列就叫做等差数列,这个常数叫做等差数列的公差,公差通常用字 母d表示,前n项和用Sn表示。
谢谢
裂项相消法:裂项相消法把数列的通项拆成两项之差,在求和时中间的一些项可以相互 抵消,从而求得其和。
乘公比错项相减(等差×等比):这种方法是在推导等比数列的前 n 项和公式时所用的 方法,这种方法主要用于求数列(anxbn)的前n项和,其中(an),(bn)分别是 等差数列和等比数列。
公式法:对等差数列、等比数列,求前n项和Sn可直接用等差、等 比数列的前n项和公式进行求解。运用公式求解的注意事项:首先 要注意公式的应用范围,确定公式适用于这个数列之后,再计算。
错位相减法:形如An=BnCn,其中{Bn}为等差数列,首项为b1,公差为d;{Cn}为等 比数列,首项为c1,公比为q。对数列{An}进行求和,首先列出Sn,记为①式;再把① 式中所有项同乘等比数列{Cn}的公比q,即得qSn,记为②式;然后①②两式错开一位 做差,从而得到{An}的前n项和。这种数列求和方式叫作错位相减。
数列的求和方法(ppt)
演讲人
目录
01
数列概念
02
等差数列思维导图
数列求和的七种方法:倒序相加法、分组求和法、错位相减法、裂项相消法、乘 公比错项相减(等差×等比)、公式法、迭加法。
倒序相加法:如果一个数列{an},与首末两端等“距离”的两项和相等或者等于 同一个常数,则求该数列的前n项和即可用倒序相加法。例如等差数列的求和公 式,就可以用该方法进行证明。
等差数列思维导图
一般地来说如果一个数列从第2项起,每一项与它的前一项的差等于同一个常 数,这个数列就叫做等差数列,这个常数叫做等差数列的公差,公差通常用字 母d表示,前n项和用Sn表示。
谢谢
裂项相消法:裂项相消法把数列的通项拆成两项之差,在求和时中间的一些项可以相互 抵消,从而求得其和。
乘公比错项相减(等差×等比):这种方法是在推导等比数列的前 n 项和公式时所用的 方法,这种方法主要用于求数列(anxbn)的前n项和,其中(an),(bn)分别是 等差数列和等比数列。
公式法:对等差数列、等比数列,求前n项和Sn可直接用等差、等 比数列的前n项和公式进行求解。运用公式求解的注意事项:首先 要注意公式的应用范围,确定公式适用于这个数列之后,再计算。
数列求和方法专题课ppt课件

数列求和方法专题
(第一课时)
1
知识梳理
1.公式法
数 2.分组求和法
列
求 3.裂项相消法
和
方 法
4.错位相减法
5.倒序相加法
6.奇偶并项法 7.绝对值法 8.周期法
……
2
1.公式法:
直接用求和公式,求数列的前n项和。
①等差数列的前n项和公式:Sn
n(a1 2
an )
na1
n(n 1) 2
d
②等比数列的前n项和公式
an1 an
a=1 a 1
注意:在求等比数列前n项和时, 当q不确定时要对q分q=1和q≠1两 种情况讨论求解。
4
2.分组求和法:
若数列{an} 的通项可转化为an bn cn
s s 的形式,且数列 {bn}、{cn}可求出前n项和
、
b
c
则
5
例2:求下面数列的前n项和。
11 1
1
2 ,4 ,6 , 4 8 16
Sn
na1 (q a1(1
1) qn )
1 q
a1 anq 1 q
(q
1)
③ 12 22 32 n2 1 n(n 1)(2n 1)
6
④ 13 23 33
n3
n(n 1) 2 2
3
例1 求和:1+(1/ a)+(1/a2)+……+(1/an)
n 1,
解: S
an+1 1
(4)
1 n+
n+1=
n+1-
n;
(5)
1 n+
n+k=1k(
n+k-
n).
(6) nn+11n+2=12[nn1+1-n+11n+2];
(第一课时)
1
知识梳理
1.公式法
数 2.分组求和法
列
求 3.裂项相消法
和
方 法
4.错位相减法
5.倒序相加法
6.奇偶并项法 7.绝对值法 8.周期法
……
2
1.公式法:
直接用求和公式,求数列的前n项和。
①等差数列的前n项和公式:Sn
n(a1 2
an )
na1
n(n 1) 2
d
②等比数列的前n项和公式
an1 an
a=1 a 1
注意:在求等比数列前n项和时, 当q不确定时要对q分q=1和q≠1两 种情况讨论求解。
4
2.分组求和法:
若数列{an} 的通项可转化为an bn cn
s s 的形式,且数列 {bn}、{cn}可求出前n项和
、
b
c
则
5
例2:求下面数列的前n项和。
11 1
1
2 ,4 ,6 , 4 8 16
Sn
na1 (q a1(1
1) qn )
1 q
a1 anq 1 q
(q
1)
③ 12 22 32 n2 1 n(n 1)(2n 1)
6
④ 13 23 33
n3
n(n 1) 2 2
3
例1 求和:1+(1/ a)+(1/a2)+……+(1/an)
n 1,
解: S
an+1 1
(4)
1 n+
n+1=
n+1-
n;
(5)
1 n+
n+k=1k(
n+k-
n).
(6) nn+11n+2=12[nn1+1-n+11n+2];
数列求和的基本方法和技巧ppt课件

1
ppt精选版
数列求和基本方法:
公式法 分组求和法 错位相减法 裂项相消法 并项求合法
2
ppt精选版
一.公式法:即 直 接 用 求 和 公 式 , 求 数 列 的 前 n 和 S n
①等差数列的前n项和公式:
Sn
n(a1 2
an )
na1
n(n 1) 2
d
②等比数列的前n项和公式 ③ 1 23 n 1 n (n 1)
:Sn
na1(q a1(1
1) qn )
1 q
a1 anq 1 q
(q
1)
2
④ 12 22 32
n2
1n(n1)(2n1) 6
⑤ 13 23 33
n3
n (n 1) 2 2
ppt精选版
3
例1:求和:
1 . 4 6 8 … … + ( 2 n + 2 )
2.1111 1
37
ppt精选版
2.(2013·唐山统考)在等比数列{an}中,a2a3=32,a5=32. (1)求数列{an}的通项公式;
(2)设数列{an}的前 n 项和为 Sn,求 S1+2S2+…+nSn.
解:(1)设等比数列{an}的公比为 q,依题意得
a1q·a1q2=32, a1q4=32,
解得 a1=2,q=2,
20
ppt精选版
常见的裂项公式有:
1. 1 1 1 n(n1) n n1
2. 1 1(1 1 ) n(nk) k n nk
3. 1 1( 1 1) (2n1)2 (n1) 22n12n1
4. 1 1 ( a b) a b ab
5 . 1 1 [ 1 1 ] n (n 1 )n ( 2 ) 2n (n 1 ) (n 1 )n ( 2 )
ppt精选版
数列求和基本方法:
公式法 分组求和法 错位相减法 裂项相消法 并项求合法
2
ppt精选版
一.公式法:即 直 接 用 求 和 公 式 , 求 数 列 的 前 n 和 S n
①等差数列的前n项和公式:
Sn
n(a1 2
an )
na1
n(n 1) 2
d
②等比数列的前n项和公式 ③ 1 23 n 1 n (n 1)
:Sn
na1(q a1(1
1) qn )
1 q
a1 anq 1 q
(q
1)
2
④ 12 22 32
n2
1n(n1)(2n1) 6
⑤ 13 23 33
n3
n (n 1) 2 2
ppt精选版
3
例1:求和:
1 . 4 6 8 … … + ( 2 n + 2 )
2.1111 1
37
ppt精选版
2.(2013·唐山统考)在等比数列{an}中,a2a3=32,a5=32. (1)求数列{an}的通项公式;
(2)设数列{an}的前 n 项和为 Sn,求 S1+2S2+…+nSn.
解:(1)设等比数列{an}的公比为 q,依题意得
a1q·a1q2=32, a1q4=32,
解得 a1=2,q=2,
20
ppt精选版
常见的裂项公式有:
1. 1 1 1 n(n1) n n1
2. 1 1(1 1 ) n(nk) k n nk
3. 1 1( 1 1) (2n1)2 (n1) 22n12n1
4. 1 1 ( a b) a b ab
5 . 1 1 [ 1 1 ] n (n 1 )n ( 2 ) 2n (n 1 ) (n 1 )n ( 2 )
数列求和各种方法总结归纳课件PPT

[冲关锦囊]
用错位相减法求和时,应注意 (1)要善于识别题目类型,特别是等比数列公比为负数
的情形; (2)在写出“Sn”与“qSn”的表达式时应特别注意将两式“
错项对齐”以便下一步准确写出“Sn-qSn”的表达式.
[精析考题] [例3] (2011·全国新课标卷)等比数列{an}的各项均为正数,且2a1+ 3a2=1,a32=9a2a6. (1)求数列{an}的通项公式; (2)设bn=log3a1+log3a2+…+log3an,求数列{b1n}的前n项和.
(1)an=kn+b,利用等差数列前n项和公式直接求解;
所以,当n>1时,①-②得 用错位相减法求和时,应注意
①转化的思想,即将一般数列设法转化为等差或等比数列,这一思想方法往往通过通项分解或错位相减来完成.
①转化的思想,即将一般数列设法转化为等差或等比数列,这一思想方法往往通过通项分解或错位相减来完成.
数列求和各种方法总结归纳
二、非等差、等比数列求和的常用方法 1.倒序相加法
如果一个数列{an},首末两端等“距离”的两项的和相等 或等于同一常数,那么求这个数列的前n项和即可用倒 序相加法,如等差数列的前n项和即是用此法推导的.
2.分组求和法 若一个数列的通项公式是由若干个等差数列或等比数列 或可求和的数列组成,则求和时可用分组转化法,分别 求和而后相加减.
∴bn+1+1=2bn+2=2(bn+1).
∴((11b))要a1n=善=0于k,n识b+1别b+,题1利=目用1类≠等0型.差n1,数-特列别n前是+n1等项比1和数公列=式公直-比接为求n负解2+数n;1.
所以数列{b1n}的前n项和为-n2+n1.
[巧练模拟]—————(课堂突破保分题,分分必保!)
数列求和方法总结PPT课件

有一类数列,既不是等差数列,也不是等比 数列,若将这类数列适当拆开,可分为几个等差、 等比或常见的数列,然后分别求和,再将其合并 即可.
-
6
例2:求数列的前n项和:1 1, 1 4, 1 7, , 1 3n 2,…
a a2
a n1
-
7
练习 : 求数列1 1 2
,3 1 4
,5
1 8
-
1
本节概要 数列求和的常用方法
-
2
等差数列前 n 项和公式:
Sn
n(a1 2
an )
na1
n(n 1) 2
d
.
等比数列前 n
项和公式:
Sn
na1(q a1(1
1) qn)
1 q
a1 anq 1 q
(q
1)
.
自然数方幂和公式:1 2 3 n 1 n(n 1) 2
12 22 32 n2 1 n(n 1)(2n 1) 6
2n 2n
…………………………………①
1 2
Sn
2 22
4 23
6 24
2n 2 n1
………………………………②
(设制错位)
①-②得(1
1 2
)S
n
2 2
2 22
2 23
2 24
2 2n
2n 2 n 1
2 1 2n 2n1 2n1
∴
Sn
4
n2 2 n 1
-
17
这是推导等差数列的前n项和公式时所用的 方法,就是将一个数列倒过来排列,再把它与原 数列相加。
-
18
例
5.设
f
(x)
4 x , 则f 4x 2
数列求和的常用方法完整版课件
解 设等比数列{an}的公比为q(q>1),
则由 a2+a4=90,a3=27,得aa11qq+ 2=a21q7,3=90,
解得aq1==33,
a1=243, 或q=13
(舍去),
故an=3×3n-1=3n. 因为 bn+1=bnb+n 1(n∈N*), 所以bn1+1=b1n+1,
又 b1=1,所以b1n是首项为 1,公差为 1 的等差数列. 于是,b1n=1+(n-1)×1=n,故 bn=1n.
√A.1 011
B.1 008
C.1 009
D.1 010
解析 由an+2Sn-1=n得an+1+2Sn=n+1, 两式相减得an+1-an+2an=1⇒an+1+an=1⇒S2 021=a1+(a2+a3)+… +(a2 018+a2 019)+(a2 020+a2 021)=1 010×1+1=1 011.
②
②-①得2an+1=2(n2+2n+2)an+1-(n+1)2an+2-(n+1)2an,
所以2(n+1)2an+1=(n+1)2an+2+(n+1)2an,
化简得2an+1=an+2+an,
所以{an}是等差数列.
由2S1=(1+1)2a1-a2可得a2=4,
所以公差d=a2-a1=4-2=2,
故an=2+2(n-1)=2n.
由 b1=a1,nbn+1=anbn 以及 an=2n 可知,b1=2,bbn+n 1=2,所以数列{bn} 是以 2 为首项,2 为公比的等比数列, 故bn=2×2n-1=2n.
(2)若数列{cn}满足cn=an+bn(n∈N*),求数列{cn}的前n项和Tn.
=2n+1-2+n-2 1-n
=2n+1-n2-52. ∴Tn=22nn++11-+2n2n--252,,nn为为奇偶数数,.
第讲数列的求和精选课件

若一个数列是由等比数列或是等差数列组成,以 考查公式为主,可先分别求和,再将各部分合并,这就是我们说 的分组求和.
【互动探究】 1.(2019 年陕西)已知{an}是公差不为零的等差数列,a1=1,
且 a1,a3,a9 成等比数列. (1)求数列{an}的通项公式; (2)求数列{2 a n}的前 n 项和 Sn.
4.数列 112,214,318,…,n+21n,…的前 n 项和 Sn=______ __12_n_(n_+__1_)_+__1_-__21_n___.
5.数列{an}的通项公式 an=
1 n+
n+1,若前
n
项的和为
10,
则项数 n=___1_2_0___.
考点1 利用公式或分组法求和
例1:(2011 年重庆)设{an}是公比为正数的等比数列,a1=2, a3=a2+4.
数列求和常用的方法
1.公式法 (1)等差数列{an}的前
n
项和公式:Sn=nnaa1+ 12+nann2-,1d.
(2)等比数列{an}的前n项和Sn:①当q=1时,Sn=__n_a_1_;
a11-qn
a1-anq
②当 q≠1 时,Sn=____1_-__q___=____1_-__q__.
2.分组求和法 把一个数列分成几个可以直接求和的数列. 3.错位相减法 适用于一个等差数列和等比数列对应项相乘构成的数列求 和. 4.裂项相消法 有时把一个数列的通项公式分成两项差的形式,相加过程消 去中间项,只剩有限项再求和.
解析:(1)P1(-1,0),an=n-2,bn=2n-2. (2)f(n)=n2- n-2, 2,n为 n为奇偶数数,. 假设存在符合条件. ①若 k 为偶数,则 k+5 为奇数. 有 f(k+5)=k+3,f(k)=2k-2. 如果 f(k+5)=2f(k)-2,则 k+3=4k-6⇒k=3 与 k 为偶数矛 盾.故不符(舍去). ②若 k 为奇数,则 k+5 为偶数, 有 f(k+5)=2k+8,f(k)=k-2. ∴2k+8=2(k-2)-2 这样的 k 也不存在. 综上所述:不存在符合条件的 k.
【互动探究】 1.(2019 年陕西)已知{an}是公差不为零的等差数列,a1=1,
且 a1,a3,a9 成等比数列. (1)求数列{an}的通项公式; (2)求数列{2 a n}的前 n 项和 Sn.
4.数列 112,214,318,…,n+21n,…的前 n 项和 Sn=______ __12_n_(n_+__1_)_+__1_-__21_n___.
5.数列{an}的通项公式 an=
1 n+
n+1,若前
n
项的和为
10,
则项数 n=___1_2_0___.
考点1 利用公式或分组法求和
例1:(2011 年重庆)设{an}是公比为正数的等比数列,a1=2, a3=a2+4.
数列求和常用的方法
1.公式法 (1)等差数列{an}的前
n
项和公式:Sn=nnaa1+ 12+nann2-,1d.
(2)等比数列{an}的前n项和Sn:①当q=1时,Sn=__n_a_1_;
a11-qn
a1-anq
②当 q≠1 时,Sn=____1_-__q___=____1_-__q__.
2.分组求和法 把一个数列分成几个可以直接求和的数列. 3.错位相减法 适用于一个等差数列和等比数列对应项相乘构成的数列求 和. 4.裂项相消法 有时把一个数列的通项公式分成两项差的形式,相加过程消 去中间项,只剩有限项再求和.
解析:(1)P1(-1,0),an=n-2,bn=2n-2. (2)f(n)=n2- n-2, 2,n为 n为奇偶数数,. 假设存在符合条件. ①若 k 为偶数,则 k+5 为奇数. 有 f(k+5)=k+3,f(k)=2k-2. 如果 f(k+5)=2f(k)-2,则 k+3=4k-6⇒k=3 与 k 为偶数矛 盾.故不符(舍去). ②若 k 为奇数,则 k+5 为偶数, 有 f(k+5)=2k+8,f(k)=k-2. ∴2k+8=2(k-2)-2 这样的 k 也不存在. 综上所述:不存在符合条件的 k.
数列求和的常用方法总结归纳PPT

等比数列)的数列,可采用错位相减的方法进行求和.
例6:(1)已知数列{an}的首项a1 2,an 3an1 (2 n 2),
bn log3(an 1),cn anbn n. ①证明:{an 1}是等比数列; ②求数列{cn }的前n项和S n .
Sn
3 4
(1 2
n
1 )3n1 4
(2)已知{an}是递增的等差数列,a2,a4是方程x2 5x 6 0的根.
(2)求和Sn
1
(1
1) 2
(1
1 2
1) 4
(1
1 2
1 4
1 2n1 ).
Sn
1 2n1
2n 2
三、并项求和法: 若数列的通项公式中含有形如(1)n,或通项公式
需分奇偶讨论的数列,可采用并项的方法进行求和.
例3:(1)设Sn是数列{an}的前n项和,已知 a1 1,S n 2 2an1. ①求数列{an}的通项公式;
4x 4x
2
, 令bn
g
(
an ), 2021
求数列{bn
}的前2020项和T2020
.
T2020 1010
五 、 裂 项 相 消 法 : 若通项项公式为分式,可 待定系数法 对定系数法
对分式进行裂项 .
例5:(1)设数列{an}满足a1 3a2 (2n 1)an 2n.
2
①求数列{an}的通项公式;
D.10200
四 、 倒 序 相 加 法 :若数列首末两端等“距离”的两项和相等(通项公式常与
函数有关),可采用倒序相加的方法进行求和.
例4:(1)已知函数 y f (x)满足f (x) f (1 x) 1,若数列{an}满足
例6:(1)已知数列{an}的首项a1 2,an 3an1 (2 n 2),
bn log3(an 1),cn anbn n. ①证明:{an 1}是等比数列; ②求数列{cn }的前n项和S n .
Sn
3 4
(1 2
n
1 )3n1 4
(2)已知{an}是递增的等差数列,a2,a4是方程x2 5x 6 0的根.
(2)求和Sn
1
(1
1) 2
(1
1 2
1) 4
(1
1 2
1 4
1 2n1 ).
Sn
1 2n1
2n 2
三、并项求和法: 若数列的通项公式中含有形如(1)n,或通项公式
需分奇偶讨论的数列,可采用并项的方法进行求和.
例3:(1)设Sn是数列{an}的前n项和,已知 a1 1,S n 2 2an1. ①求数列{an}的通项公式;
4x 4x
2
, 令bn
g
(
an ), 2021
求数列{bn
}的前2020项和T2020
.
T2020 1010
五 、 裂 项 相 消 法 : 若通项项公式为分式,可 待定系数法 对定系数法
对分式进行裂项 .
例5:(1)设数列{an}满足a1 3a2 (2n 1)an 2n.
2
①求数列{an}的通项公式;
D.10200
四 、 倒 序 相 加 法 :若数列首末两端等“距离”的两项和相等(通项公式常与
函数有关),可采用倒序相加的方法进行求和.
例4:(1)已知函数 y f (x)满足f (x) f (1 x) 1,若数列{an}满足
数列求和ppt课件

1
20
(2)设bn=
,数列{bn}的前n项和为Sn,若Sm= ,求m的值.
·+1
41
1
1
1
1
1
【解析】(2)由(1)知,bn=
=
= ·(
),
·+1 (2−1)(2+1) 2 2−1 2+1
1
1
1 1
1
1
1
1
所以Sn= [(1- )+( - )+…+(
)]= (1)=
.
2
3
3
D.
2
【解析】选C.S2 023=a1+(a2+a3+a4)+(a5+a6+a7)+…+(a2 021+a2 022+a2 023)=
1+cos
2π
5π
2 018π
2 021π
2π
5π
+cos +…+cos
+cos
=1+337×(cos +cos )=1.
3
3
3
3
3
3
)
2 , 当为奇数时,
和.形如an=(-1)nf(n)类型,可采用两项合并求解.
考点二裂项相消法求和
模型一
1
b n=
({an}为等差数列)型
+1
1
[例1](1)数列{an}中,an=
,则数列{an}的前2
(+1)
024项和S2 024=
1
1 1
【解析】由题意得,an=
= - ,
20
(2)设bn=
,数列{bn}的前n项和为Sn,若Sm= ,求m的值.
·+1
41
1
1
1
1
1
【解析】(2)由(1)知,bn=
=
= ·(
),
·+1 (2−1)(2+1) 2 2−1 2+1
1
1
1 1
1
1
1
1
所以Sn= [(1- )+( - )+…+(
)]= (1)=
.
2
3
3
D.
2
【解析】选C.S2 023=a1+(a2+a3+a4)+(a5+a6+a7)+…+(a2 021+a2 022+a2 023)=
1+cos
2π
5π
2 018π
2 021π
2π
5π
+cos +…+cos
+cos
=1+337×(cos +cos )=1.
3
3
3
3
3
3
)
2 , 当为奇数时,
和.形如an=(-1)nf(n)类型,可采用两项合并求解.
考点二裂项相消法求和
模型一
1
b n=
({an}为等差数列)型
+1
1
[例1](1)数列{an}中,an=
,则数列{an}的前2
(+1)
024项和S2 024=
1
1 1
【解析】由题意得,an=
= - ,
第四节 数列求和 课件(共48张PPT)

-
1 n+3
)=
1 2
56-n+1 2-n+1 3. 答案:1256-n+1 2-n+1 3
考点1 分组转化法求和 [例1] (2020·焦作模拟)已知{an}为等差数列,且 a2=3,{an}前4项的和为16,数列{bn}满足b1=4,b4= 88,且数列{bn-an}为等比数列. (1)求数列{an}和{bn-an}的通项公式; (2
an=n(n1+k)型
[例2] (2020·中山七校联考)已知数列{an}为公差 不为0的等差数列,满足a1=5,且a2,a9,a30成等比数列.
(1)求{an}的通项公式; (2)若数列{bn}满足bn+1-bn=an(n∈N*),且b1=
3,求数列b1n的前n项和Tn.
1.裂项时常用的三种变形.
(1)n(n1+1)=n1-n+1 1.
(2)n(n1+2)=12n1-n+1 2.
(3)(2n-1)1(2n+1)=122n1-1-2n1+1.
(4)
1 n+
n+1=
n+1-
n.
2.应用裂项相消法时,应注意消项的规律具有对称 性,即前面剩第几项则后面剩倒数第几项.
3.在应用错位相减法求和时,若等比数列的公比为 参数,应分公比等于1和不等于1两种情况求解.
) B. 2 020-1
C. 2 021-1 D. 2 021+1
解析:由f(4)=2,可得4α=2,解得α=12,
则f(x)= x.
所以an=
1 f(n+1)+f(n)
=
1 n+1+
= n
n+1 -
n,
所以S2 020=a1+a2+a3+…+a2 020=( 2 - 1 )+ ( 3- 2)+( 4- 3)+…+( 2 021- 2 020)=
数列求和的几种方法课件ppt
2、设法消去中间项:
(2)乘公比,错位相减(对“A·G”型);
(3)裂通项,交替相消
1、转化成等差、等比数列求和
(公式法、分组求和法、错位相减法、 裂(并)项法求和)
练习: 指出下列求和的方法:
合并项求和
特殊的数列,在求数列的和时,可将一些项放在一起先求和,然后再求Sn.
[例] 在各项均为正数的等比数列中,若
的值.
求和: (1)Sn=1+(3+4)+(5+6+7)+…+(2n-1+2n+ …+3n-2); (2)Sn=12-22+32-42+…+(-1)n-1·n2.
(1)一般应从通项入手,若无通项,先求通项,然后通过对通项变形,转化为适用特点的形式,从而求和.
数列求和的方法
(2)解决非等差、等比和,两种思路: ①转化的思想,即化为等差或等比数列. ②裂项相消法、错位相减法、倒序相加法等求和.
数列求和的常用方法:
(1) 拆项(对A±G型 如果拆项不明显,写出通项,如例2 )
na1+ d
n(n+1)(2n+1)
n2(n+1)2
倒序相加
令
例题1. 求和
(1)
[解Байду номын сангаас原式=
n(n+3)/2
(x≠1)
(x=1)
分析:原式=(1+2+3+…+n)+
我们把这种类型的数列称为“A+G”型。而求此类数列的和,一般是把数列的每一项分成两项,再分别利用等差和等比数列的求和公式求解。此方法称为分组求和法。
(2)乘公比,错位相减(对“A·G”型);
(3)裂通项,交替相消
1、转化成等差、等比数列求和
(公式法、分组求和法、错位相减法、 裂(并)项法求和)
练习: 指出下列求和的方法:
合并项求和
特殊的数列,在求数列的和时,可将一些项放在一起先求和,然后再求Sn.
[例] 在各项均为正数的等比数列中,若
的值.
求和: (1)Sn=1+(3+4)+(5+6+7)+…+(2n-1+2n+ …+3n-2); (2)Sn=12-22+32-42+…+(-1)n-1·n2.
(1)一般应从通项入手,若无通项,先求通项,然后通过对通项变形,转化为适用特点的形式,从而求和.
数列求和的方法
(2)解决非等差、等比和,两种思路: ①转化的思想,即化为等差或等比数列. ②裂项相消法、错位相减法、倒序相加法等求和.
数列求和的常用方法:
(1) 拆项(对A±G型 如果拆项不明显,写出通项,如例2 )
na1+ d
n(n+1)(2n+1)
n2(n+1)2
倒序相加
令
例题1. 求和
(1)
[解Байду номын сангаас原式=
n(n+3)/2
(x≠1)
(x=1)
分析:原式=(1+2+3+…+n)+
我们把这种类型的数列称为“A+G”型。而求此类数列的和,一般是把数列的每一项分成两项,再分别利用等差和等比数列的求和公式求解。此方法称为分组求和法。
数列求和ppt课件

法,分别求和后相加减.
把数列的通项拆成两项之差,在求和时中间的
一些项可以相互抵消,从而求得前n项和.
如果一个数列的各项是由一个等差数列和一个等
比数列的对应项之积构成的,那么求这个数列的前n项
和即可用错位相减法求解.
如果一个数列{an}与首末两端等“距离”的
(4)倒序相加法:
两项的和相等或等于同一个常数,那么求这个数
an,n 为奇数,
2.若数列{cn}的通项公式为 cn=
其中数列{an},{bn}
bn,n 为偶数,
是等比数列或等差数列,可采用分组求和法求{cn}的前 n 项和.
聚焦必备知识
11
突破核心命题
限时规范训练
1.(2023·全国乙卷)记Sn为等差数列{an}的前n项和,已知a2=11,S10
=40.
(1)求{an}的通项公式;
列的前n项和即可用倒序相加法求解.
(3)错位相减法:
聚焦必备知识
4
常用结论
1.一些常见的数列的前 n 项和
n(n+1)
(1)1+2+3+…+n=
;
2
(2)2+4+6+…+2n=n(n+1);
(3)1+3+5+…+2n-1=n2.
突破核心命题
限时规范训练
聚焦必备知识
5
突破核心命题
限时规范训练
裂项相消法:适用的通项公式如下
( + ) +
聚焦必备知识
16
突破核心命题
考 点 二 裂项相消法求和
1
(1)数列{an}的前 n 项和为 Sn.若 an=
,则 Sn=____
n(n+1)
训练2
已知Sn是数列{an}的前n项和,Sn=n2.
把数列的通项拆成两项之差,在求和时中间的
一些项可以相互抵消,从而求得前n项和.
如果一个数列的各项是由一个等差数列和一个等
比数列的对应项之积构成的,那么求这个数列的前n项
和即可用错位相减法求解.
如果一个数列{an}与首末两端等“距离”的
(4)倒序相加法:
两项的和相等或等于同一个常数,那么求这个数
an,n 为奇数,
2.若数列{cn}的通项公式为 cn=
其中数列{an},{bn}
bn,n 为偶数,
是等比数列或等差数列,可采用分组求和法求{cn}的前 n 项和.
聚焦必备知识
11
突破核心命题
限时规范训练
1.(2023·全国乙卷)记Sn为等差数列{an}的前n项和,已知a2=11,S10
=40.
(1)求{an}的通项公式;
列的前n项和即可用倒序相加法求解.
(3)错位相减法:
聚焦必备知识
4
常用结论
1.一些常见的数列的前 n 项和
n(n+1)
(1)1+2+3+…+n=
;
2
(2)2+4+6+…+2n=n(n+1);
(3)1+3+5+…+2n-1=n2.
突破核心命题
限时规范训练
聚焦必备知识
5
突破核心命题
限时规范训练
裂项相消法:适用的通项公式如下
( + ) +
聚焦必备知识
16
突破核心命题
考 点 二 裂项相消法求和
1
(1)数列{an}的前 n 项和为 Sn.若 an=
,则 Sn=____
n(n+1)
训练2
已知Sn是数列{an}的前n项和,Sn=n2.
第七章 第四节 数列求和 课件(共42张PPT)

1.一些常见数列的前 n 项和公式 (1)1+2+3+4+…+n=n(n+ 2 1) ; (2)1+3+5+7+…+2n-1=n2; (3)2+4+6+8+…+2n=n2+n.
2.三种常见的拆项公式
1 (1)n(n+1)
=1n
-n+1 1
;
1 (2)(2n-1)(2n+1)
=12
2n1-1-2n1+1
答案: (1)× (2)√ (3)√
2.(必修 5P47T4 改编)数列{an}的前 n 项和为 Sn,若 an=n(n1+1) ,
则 S5 等于( )
A.1
B.56
C.16
D.310
B [∵an=n(n1+1) =1n -n+1 1 ,∴S5=a1+a2+…+a5=1-12 +12 -13 +…+15 -16 =56 .]
所以 an=-2n1+1 (n 为正奇数), 若 n 为奇数,则 an-1=-2an+21n =(-2)-2n1+1 +21n , 所以 an=21n (n 为正偶数), 所以 a3=-214 =-116 , 因为 an=-2n1+1 (n 为正奇数),所以-a1=--212 =212 ,
因为 an=21n (n 为正偶数),所以 a2=212 , 所以-a1+a2=2×212 , 因为-a3=--214 =214 ,a4=214 , 所以-a3+a4=2×214 , …… -a99+a100=2×21100 .
(2)因为 an=2n,所以 bn=(n+1)log2an=(n+1)log22n=n(n+1), 所以,2n2b+n2 2n =n(n2+1) =21n-n+1 1 , 所以 Tn=21-12+12-13+…+1n-n+1 1 =21-n+1 1 =n2+n1 .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数列求和方法总结
主讲人:陈鑫城 1
本节概要 数列求和的常用方法 公式法 分组求和法 裂项相消法 错位相减法 倒序相加法
2
一、公式法
等差数列前 n 项和公式:
Sn
n(a1 2
an )
na1
n(n 1) 2
d
.
等比数列前 n
项和公式:
Sn
na1(q a1(1
1) qn)
1 q
a1 anq 1 q
①-②得( 1 1 2 )S n 2 2 2 2 2 2 2 3 2 2 4 2 2 n 2 2 n n 1221n1
2n
2n1
∴
Sn
4n2 2n1
16
17
五、倒序相加法
这是推导等差数列的前n项和公式时所用的 方法,就是将一个数列倒过来排列,再把它与原 数列相加。
18
例
5.设
f
(x)
a a2
an 1
7
练:习 求数 11 2列 ,31 4,51 8,,2n121n,
的n 前 项.和
8
三、裂项相消法
“裂项相消法”,此法常用于形如{1/f(n)g(n)} 的数列求和,其中f(n),g(n)是关于n(n∈N)的 一次函数。把数列中的每一项都拆成两项或几项 的差,从而产生一些可以相消的项,最后剩下有 限的几项
9
例 3 : Sn求 1 1221 3 n(1 n 1 )
10
练习:
11
12
13
四、错位相减法
这种方法是在推导等比数列的前n项和公式时 所用的方法,这种方法主要用于求数列{an· bn} 的前n项和,其中{ an }、{ bn }分别是等差数列和 等比数列.
14
例4:求和 :S n 1 3 x 5 x 2 7 x 3 ( 2 n 1 ) x n 1
为数列{ Sn n
} 的前n项Fra bibliotek和,求Tn .
4
练习:求 1 + a + a 2 + a 3 + …… + a n (a为非零实数)的值
5
二、分组求和法
有一类数列,既不是等差数列,也不是等比 数列,若将这类数列适当拆开,可分为几个等差、 等比或常见的数列,然后分别求和,再将其合并 即可.
6
例2:求数列的前n项和:11 ,14,17,, 13n2,…
4x 4x 2
, 则f
1 11
f 2 11
f
3 11
f
10 11
(
)
A.4
B. 5
C. 6
D. 10
19
课后作业
已知数列{an}是递增的等比数列, a1 a4 9, a2a3 8 ,则数列{an}的前 n 项和等于
.
数列 {an } 满足
a1
1,且 an1
an
(q
1)
.
自然数方幂和公式:1 2 3 n 1 n(n 1) 2
12 22 32 n2 1 n(n 1)(2n 1) 6
13 23 33 n3 [1 n(n 1)]2 2
3
例
1.设{an}为等差数列, Sn 为数列{an}的前
n
项和,已知
S7
7,
S15
75
, Tn
15
练习:求数列 22,242,263,,22nn ,前n项的和
解:由题可知,{ 2 n 2n
}的通项是等差数列{2n}的通项与等比数列{
1 2n
}的通项之积
设 Sn2 22422632 2n n …………………………………①
1 2Sn2 2 22 4 32 6 42 2 n n 1 ………………………………② (设制错位)
n
1( n N*
),则数列{ 1 }的前 an
10
项和为
【2015 高考山东,理 18】设数列an 的前 n 项和为 Sn .已知 2Sn 3n 3 . (I)求an 的通项公式; (II)若数列bn 满足 anbn log3 an ,求bn 的前 n 项和Tn .
20
谢谢
21
主讲人:陈鑫城 1
本节概要 数列求和的常用方法 公式法 分组求和法 裂项相消法 错位相减法 倒序相加法
2
一、公式法
等差数列前 n 项和公式:
Sn
n(a1 2
an )
na1
n(n 1) 2
d
.
等比数列前 n
项和公式:
Sn
na1(q a1(1
1) qn)
1 q
a1 anq 1 q
①-②得( 1 1 2 )S n 2 2 2 2 2 2 2 3 2 2 4 2 2 n 2 2 n n 1221n1
2n
2n1
∴
Sn
4n2 2n1
16
17
五、倒序相加法
这是推导等差数列的前n项和公式时所用的 方法,就是将一个数列倒过来排列,再把它与原 数列相加。
18
例
5.设
f
(x)
a a2
an 1
7
练:习 求数 11 2列 ,31 4,51 8,,2n121n,
的n 前 项.和
8
三、裂项相消法
“裂项相消法”,此法常用于形如{1/f(n)g(n)} 的数列求和,其中f(n),g(n)是关于n(n∈N)的 一次函数。把数列中的每一项都拆成两项或几项 的差,从而产生一些可以相消的项,最后剩下有 限的几项
9
例 3 : Sn求 1 1221 3 n(1 n 1 )
10
练习:
11
12
13
四、错位相减法
这种方法是在推导等比数列的前n项和公式时 所用的方法,这种方法主要用于求数列{an· bn} 的前n项和,其中{ an }、{ bn }分别是等差数列和 等比数列.
14
例4:求和 :S n 1 3 x 5 x 2 7 x 3 ( 2 n 1 ) x n 1
为数列{ Sn n
} 的前n项Fra bibliotek和,求Tn .
4
练习:求 1 + a + a 2 + a 3 + …… + a n (a为非零实数)的值
5
二、分组求和法
有一类数列,既不是等差数列,也不是等比 数列,若将这类数列适当拆开,可分为几个等差、 等比或常见的数列,然后分别求和,再将其合并 即可.
6
例2:求数列的前n项和:11 ,14,17,, 13n2,…
4x 4x 2
, 则f
1 11
f 2 11
f
3 11
f
10 11
(
)
A.4
B. 5
C. 6
D. 10
19
课后作业
已知数列{an}是递增的等比数列, a1 a4 9, a2a3 8 ,则数列{an}的前 n 项和等于
.
数列 {an } 满足
a1
1,且 an1
an
(q
1)
.
自然数方幂和公式:1 2 3 n 1 n(n 1) 2
12 22 32 n2 1 n(n 1)(2n 1) 6
13 23 33 n3 [1 n(n 1)]2 2
3
例
1.设{an}为等差数列, Sn 为数列{an}的前
n
项和,已知
S7
7,
S15
75
, Tn
15
练习:求数列 22,242,263,,22nn ,前n项的和
解:由题可知,{ 2 n 2n
}的通项是等差数列{2n}的通项与等比数列{
1 2n
}的通项之积
设 Sn2 22422632 2n n …………………………………①
1 2Sn2 2 22 4 32 6 42 2 n n 1 ………………………………② (设制错位)
n
1( n N*
),则数列{ 1 }的前 an
10
项和为
【2015 高考山东,理 18】设数列an 的前 n 项和为 Sn .已知 2Sn 3n 3 . (I)求an 的通项公式; (II)若数列bn 满足 anbn log3 an ,求bn 的前 n 项和Tn .
20
谢谢
21
