电路——邱关源PPT课件
电路课件(邱关源五版)

04
三相电路
三相电源
三相电源的组成
三相电源由三个频率相同、幅值相等、相位差互为120度的交流 电源组成。
星形连接与三角形连接
三相电源可以接成星形或三角形,两种连接方式下的电压和电流特 性不同。
三相电源的功率
三相电源的总功率等于各相功率之和,且总功率恒定。
产生原因
非正弦周期电压和电流的产生通常是由于电路中存在非线性元件,如电阻、电容、电感等 ,这些元件的伏安特性不是线性的,因此会导致电压或电流随时间变化呈现出非正弦周期 的特性。
特点
非正弦周期电压和电流具有随机性和复杂性,其波形通常由多个不同频率的正弦波叠加而 成,因此难以用简单的数学模型描述。
非正弦周期电路的谐波分析法
一阶电路的时域分析
一阶电路
由一个动态元件和电阻组成的简单电路。
一阶电路的响应特性
电压和电流随时间按指数规律变化,具有延 时、振荡和稳态等不同阶段。
时域分析方法
采用一阶常微分方程描述电路,通过求解微 分方程得到电压和电流的时域响应。
一阶电路的分析步骤
建立微分方程、求解微分方程、分析响应特 性。
二阶电路的时域分析
频率响应
频率响应分析电路在不同频率下 的性能表现,包括幅频特性和相
频特性。
一阶电路分析
一阶电路是指包含一个动态元件 的电路,其分析方法主要是三要
素法。
功率计算
有功功率
有功功率是指电路中实际消耗的功率,用于衡量 能量转换的效果。
无功功率
无功功率是指电路中交换的功率,用于衡量储能 元件的能量交换。
视在功率
电路课件(邱关源五版 )
电路第五版邱关源ppt课件.ppt

。例如电阻、电感、电容。..
返回 上页 下页
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
2.集总参数电路
由集总元件/构成的电路
集总元件
假定发生的电磁过程都集中在元
件内部进行。
集总条件 d
注意集总参数电路中u、i 可以是时间的函数,
电压参考方向的三种表示方式: (1) 用箭头表示:
u
(2)用正、负极性表示:
+u
(3)用双下标表示:
A
uAB
B
返回 上页 下页
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
3.关联参考方向
元件或支路的u,i 采用相同的参考方向称为关联 参考方向。反之,称为非关联参考方向。
问题 在复杂电路或交变电路中,两点间电压的
实际方向往往不易判别,给实际电路问题 的分析、计算带来困难。
电压(降)的参考方向
参考方向
+
u
–
假设高电位指向低电 位的方向。
参考方向
+
u
–
+ 实际方向 – – 实际方向 +
u >0
u <0
返回 上页 下页
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
电路第五版邱关源罗先觉课件.ppt
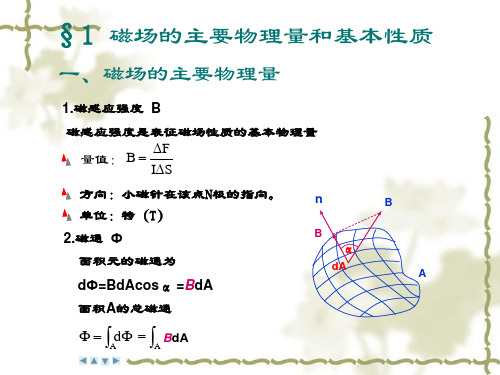
该磁通势取正,反之取负。
3.磁路欧姆定律
μ
A
Φ
l
因为 H B
磁位差
B A
Um
Hl
B
l
l A
Rm
式中
Rm
l A
欧姆定律
Um Rm
H
(3)
磁导率 μ 用来衡量物质的磁性能,μ大物质的导磁性能强, μ小物质的导磁性能弱。 单位: 亨/米 (H/m)
真空的磁导率
0 4 10 7 H / m
非铁磁物质的磁导率 0 铁磁物质的磁导率 》0
相对磁导率:物质的磁导率与真空磁导率的比。
r
0
或
r0
非铁磁物质 r 1
铁磁物质μr很大,如硅钢片 r 6000 ~ 8000
磁场强度 H 为分析磁场和电流的依存关系引入的物理量
H B
方向:小磁针N极所指的方向 单位:安/米(A/m)
二、磁场的基本性质
1. 磁通的连续性 磁场中任一闭合面的总磁通恒等于零。
AB dA 0
2. 安培环路定律 磁场强度矢量H沿任何路径的线积分等于穿过此路径所围成 的面的电流代数和。电流的正负要根据它的方向和所选路径的 方向之间是否符合右手螺旋法则而定。
l H dl I
安培环路定律的应用
l H dl I1 I2
I1 H
dl
I2
§2 铁磁物质的磁化曲线
一、铁磁物质的磁化 铁磁物质在外磁场的作用下,产生于外磁场方向一致而且很强的 附加磁场,这种现象叫铁磁物质的磁化。
H
二、磁化曲线
1.起始磁化曲线
Bμ
a3 B H
a2
μH
a1 B μ0H
0
H
邱关源电路三相电路PPT课件

三 相 负 载
W1
A
B
C
*
*
*
*
W2
三 相 负 载
W2
A
B
C
*
*
*
*
W1
三 相 负 载
W1
A
B
C
*
*
*
*
W2
若W1的读数为P1 , W2的读数为P2 ,则三相总功率为:
P=P1+P2
证明:
=P1+P2
三 相 负 载
W1
A
B
C
*
*
*
*
W2
在对称三相电路中: 式中φ为负载的阻抗角。 1 :uAC 与iA的相位差, 2 :uBC 与iB的相位差。 P=UACIAcos 1 + UBCIBcos 2
三相总功率: P=3Pp=3UpIpcos
1. 平均功率
A’
B’
C’
Z
Z
Z
A’
B’
C’
Z
Z
Z
*
1
注
2
为相电压与相电流的相位差角(阻抗角),不要误以为是线电压与线电流的相位差。
3
cos为每相的功率因数,在对称三相制中三相功率因数: cos A= cos B = cos C = cos 。
4
,三角形连接负载(复)阻抗
,负载的三相功率
,求三相电源供出的功率P。
例1:
三角形连接负载相电流
线电流:
负载端三角形变换为星形,
则电源相电压:
线电压:
所以电源三相功率:
Z’
Z’
Z’
或:
解:
邱关源-电路第五版课件-第11章.pptx

返回 上页 下页
I1( j)
I2 ( j)
U1( j)
线性 网络
U2 ( j)
激励是电压源
H
(
j
)
I2 ( j) U1( j)
转移 导纳
H
(
j
)
U 2 U1
( (
j) j)
转移 电压比
激励是电流源
H
(
j
)
U2 ( j) I1( j)
H
( j)
I2 ( j) I1( j)
转移 阻抗
转移 电流比
第6页/共56页
第4页/共56页
返回 上页 下页
激H (励j是) 电UI流((jj源),) 响应是策电动压点阻抗U ( j) I( j)
线性 网络
激励是电压源,响应是电流
H
(
j)
I( j) U ( j)
策动点导纳
转移函数(传递函数) I1( j)
I2 ( j)
U1( j)
线性 网络
U2 ( j)
第5页/共56页
uC
Im
0C
sin(0t
90o )
L C
I
m
c
os0t
wC
1 2
CuC2
1 2
LIm2
cos2 0t
电场能量
wL
1 2
Li2
1 2
LIm2
sin 2 0t
表明
磁场能量
①电感和电容能量按正弦规律变化,最大值相等
WLm=WCm。L、C的电场能量和磁场能量作周期
振荡性的交换,而不与电源进行能量交换。
第19页/共56页
C C及Q。
完整版电路邱关源第五版05第五章课件

uo =[(R1 + R2)/R2 ] ui
=(1+ R1/R2) ui
②当R2=,R1=0时, uo=ui,为电压跟随器 ③输入、输出关系与运放本身参数无关。
返回 上页 下页
③电压跟随器
电 路
A
+ u_i
_
+ +
+电
uo_
路 B
特点 ① 输入阻抗无穷大(虚断);
② 输出阻抗为零; ③ uo= ui。 应用:在电路中起隔离前后两级电路的作用。
②合理地运用这两条规则,并与结点电压法相结合。
返回 上页 下页
2. 典型电路
①加法器
u-= u+=0 i-=0
ui1
R1
ui2 R2
ui3 R3
Rf
i-
_ uu+ +
+
+ u_o
ui1/R1+ ui2 /R2+ ui3 /R3 =-uo /Rf
uo= -(Rf /R1 ui1 +Rf /R2 ui2+Rf /R3 ui3)
uo
un2
G1 Gf
Gf
( AGo
Gf
)
Gf (AGo Gf ) (G1 Gi Gf )
( Gf
Go
GL) ui
返回 上页 下页
uo
un2
G1 Gf
Gf
( AGo
Gf
)
Gf (AGo Gf ) (G1 Gi Gf )
( Gf
Go
GL) ui
因A一般很大,上式分母中Gf(AGo-Gf)一项的值比
• 本章完!
|ud| < 则 uo=Aud
第10章电路邱关源课件PPT

电路第十章含有耦合电感的电路电路§1010--1 1 互互感1121i 111'22'L 2N 2L 1N 1i 222212ΨΨΨ+±=12111ΨΨΨ±=电路22122111i L Mi ΨMi i L Ψ+±=±=1111i L Ψ=2222i L Ψ=21212i M Ψ=12121i M Ψ=**ML 1L 2+−i 1i 2u 1u 2+−11'22'dt di Mdt di L dt d u 21111±=Ψ=dtdi L dt di M dt d u 22122+±=Ψ=ML 1L 2+−i 1i 2u 1u 2+−122122111i L Mi ΨMi i L Ψ+±=±=2111I M j I L j U &&&ωω+=2212I L j I M j U &&&ωω+=Mj Z M ω=121≤=L L Mk 22211112ΨΨΨΨ=k电路§1010--2 2 含有耦合电感电路的计算含有耦合电感电路的计算I L j R U &&)(111ω+=[]I M L L j R R U &&)22121(−+++=ω1R R 1L −+1u −+uM••i 1R R ML −21−+1u −+ui I L j R U &&)(222ω+=[]I M I M j L j R &&)(−=−+11ωω[]I M I M j L j R &&)(−=−+22ωω电路[])22121(M L L j R R U I−+++=ω&&))222111((M M L j R Z L j R Z −−+=+=ωω)22121(M L L j R R Z −+++=ω))222111((M M L j R Z L j R Z ++=++=ωω)22121(M L L j R R Z ++++=ω电路cos10002**12M1R 2+−iu s4522000°∠Z cos 22121×L L ∠2电路1R R 1L −+1u −+uM••i SS 826.05.125.782121=×===L L ML L M k ωωωΩ−∠=−=−+=o46.904.35.03)(111j M L j R Z ωΩ∠=+=−+=o4237.65.45)(222j M L j R Z ωΩ∠=+=+=o57.2694.84821j Z Z Z o &050∠=U57.2659.557.2694.8050−∠=∠∠==oo &&Z U I1212121Z I X jI R I S =+=AV 63.14025.1564237.659.52222⋅+=∠×==j Z I S oAV 12525057.2659.550*⋅+=∠×==j I U S o &&21S S S +=A V .....⋅−=−∠×=631575934690435952j o1R R 2L j ω1L j ω−+U&••I&1I &I &Mj ω2111I j I L j R U M &&&ωω++=)(1R R 2L j ω1L j ω−+U&••I&1I &I &Mj ω22212111)()(I L j R I j U I j I L j R U M M &&&&&&ωωωω++−=−+=2221I L j R I j U M &&&)(ωω++=2112I I I I I I &&&&&&−=−=[]I j I M L j R M &&m ωω±+=111)(1R R ML −1−+U&I&1I &I &ML −21R R ML +1−+U&I&1I &I &ML +222212111)()(I L j R I j U I j I L j R U M M &&&&&&ωωωω++±=±+=[]222I M L j R I j U M &m &&)(ωω++±=)()(1111I I j I L j R U M &&&&−±+=ωω电路410CL =ωH 05.0662410510411===−×××C L ωA87.36025.0240320010)(2111o o &&−∠=+∠=−+−+=j M L M L j R U I AB ωV13.53387.36025.0120)(12o o &&∠=−∠×=−=j I M L j U ED ωW2.0025.03202211=×==I R P电路+−U S500 V o13ΩIR 25Ω1j ωL 2I 1**j ωM+−U S500 V o13ΩIR 25Ω1j (+)ωL M 2I 1()22电路()+−U S500 V o13ΩIR 25Ω1j (+)ωL M 2I 1电路§1010--3 3 空心变压器空心变压器()21111I j I L j R U M &&&ωω++=11Z22Z MZ 2221112221111)(Y M Z U Y Z Z U I M ω+=−=&&&1R 1L j ω••−+1U &1′••2R 2L j ωR ω••2′2221)(0I jX R L j R I j L L M &&++++=ωω1222⋅−=I Z Z I M &1⋅I电路11222111112221112)(Y M jX R L j R U MY j Y Z Z U Y Z I L L M M ωωω++++−=−−=&&&−+1U &222)(Y M ω1I 12221112221111)(Y M Z U Y Z Z U I M ω+=−=&&&Z 2I −+111U MY j &ω1222⋅−=I Z Z I M &电路1R 1L j ω••−+1U &1′••2R 2L j ωR ω••2′Ω==50111j L j Z ωΩ+=++=123222j jX R L j Z L L ωΩ−=+=37.3184.7123400)(222j j Y M ωo &021001∠=U o &&2.675.337.3184.7502/100)(2221111−∠=−+=+=j j Y M Z U I ωo o &&84.12666.51232.675.3202212∠=+−∠×=−=j j Z I M j I ω)84.12610cos(266.5)2.6710cos(25.321oo +=−=t i t i电路cos3142115**+−u sa i 112L 1L 2R LM电路+−a b422Ω−Ωj189U 1I 1电路§1010--3 3 理想变压器理想变压器1N ••1−+1u ••2N ••−+u 21i n −••1−+1••11u n 2211N u N u =12211=+i N i N 122211=+i u i u 1N N电路11N ••1−+1u ••2N ••−+u 21in ••1−+1••11u n −22211nu u N N u −=−=212112ii i n N N ==电路11N ••1−+1u ••2N ••Z ••1−+1u 11I U Z in &&=1N ••1−+1u ••2N ••Z Ln in Z n I U n I U Z 221211=−==&&&&L n Z n I U n 2212=−=&&电路1−+s u ••Z −+2u −+1u 110:Ω+=+×==300300)33(1022j j Z n Z L in inZ −+sU &1I 13003001000220011j Z R U I in s ++∠=+=&&09.3644.0−∠=211I nI &&−=12I n I &&=A9.364.4−∠=电路21210I nI I &&&==1−+s u ••−+2u −+1u 1n sU U &&=1000221∠==s c U nU &&22I U Z in &&=Ω===1)1(12111R n I n U n &&9.364.433102202−∠=++∠=+=j Z Z U I L in oc &&in−+oc u 2i电路1••iI &−+1U &22••2I &−+2U &−+1u 1:2R 1I &ii I U R &&1=221212)11(1I U R R U R &&&−=++−11U U n &&=)(22112R U U I n I n I i &&&&&−−=−=121U U n &&=i I n R n nR nR U &&=−++)211(2121Ω==381ii I U R &&电路Ω−5j V 4=sU &Ω−=)5(222j n Z in Ω+−=5120141222n j j Y 05120122=+−n j j 22=n 2211Z n Z in =100=Ω=42Z 100421=n 51=n W 04.01004422m ax=×=×=ssUR U P电路)1(21==R R 21122111I L j I M j U I M j I L j U &&&&&&ωωωω+=+=21,1)2(L L M k ==1R 1L j ω••−+1U &1′••2R 2L j ωR ω••2′−+2U&2121u u L L =121212L L L L L L 221212221111I L j I L L j U I L L j I L j U &&&&&&ωωωω+=+=n=电路nL L L =∞→211211i ni −=212111I L L L j U I &&&−=ω2121I L L I &&−=n L L =21)3(221111I L L j I L j U &&&ωω+=电路M j Z L j R Z L j R Z M ωωω=+=+=222111221211I Z I Z U I Z I Z U M M &&&&&&+±=±=U Z Z Z Z Z I MM &m &22121−=U Z Z Z Z Z I MM &m &22112−=U Z Z Z Z Z Z I I I M M &m &&&2212121−+=+=22212111)()(I L j R I j U I j I L j R U M M &&&&&&ωωωω++±=±+=电路。
电路-邱关源教材课件-第3章

03
线性电阻电路的分析方法
支路电流法
01
02
03
04
总结词
通过设定未知的支路电流,建 立独立方程求解电路的方法。
详细描述
支路电流法是以支路电流为未 知量,根据基尔霍夫定律建立 独立方程,通过求解线性方程 组得到各支路电流的方法。该 方法适用于具有多个支路的电 路系统。
适用范围
适用于求解具有多个支路的复 杂电路系统。
注意事项
在设定未知量时,应尽量减少 未知量的个数,以简化计算过 程。
节点电压法
总结词
详细描述
适用范围
注意事项
通过设定未知的节点电压,建 立独立方程求解电路的方法。
节点电压法是以节点电压为未 知量,根据基尔霍夫定律建立 独立方程,通过求解线性方程 组得到各节点电压的方法。该 方法适用于具有多个节点的电 路系统。
电路-邱关源教材课件-第3章
目
CONTENCT
录
• 线性电阻电路 • 基尔霍夫定律 • 线性电阻电路的分析方法 • 线性电容电路 • 线性电感电路 • 一阶动态电路
01
线性电阻电路
电阻元件
定义
电阻元件是一种将电能转换为热能的元件,其特性 可以用阻值来描述。
种类
电阻元件有多种类型,包括固定电阻器、可变电阻 器和敏感电阻器等。
时间常数
决定RL电路暂态过程持续时间的参 数,计算公式为$tau = L/R$。
一阶动态电路的分析方法
初始状态
分析电路的初始状态,即电路接通电源前各元件 的电压和电流值。
时域分析
利用电路的微分方程进行求解,得到各元件的电 压和电流值随时间的变化情况。
《电路》第五版邱关源罗先觉课件

网络函数随频率变化的特性,包括幅频特性和相频特性。
频率特性的分析方法
通过求解电路在正弦稳态下的响应,得到网络性
RC电路的基本构成
由电阻和电容元件组成的电路。
RC电路的频率特性
随着频率的变化,RC电路的阻抗、 相位等都会发生变化,表现出不 同的频率响应特性。
视在功率为电压与电流的复数模的乘积,有功功率 为平均功率,无功功率为电路中储能元件与电源之 间交换的功率
功率因数的提高
通过改善电路元件参数或采用补偿装置来提 高功率因数,减少无功功率的传输,提高电 力系统的效率
06 频率特性及多频正弦稳态 电路分析
网络函数与频率特性
网络函数的定义
表示线性时不变电路在单一频率正弦激励下,响应的相量 与激励相量比值,即电压传递函数或电流传递函数。
电功率与电能
电功率
单位时间内电场力所做的功称为 电功率。
电能
一段时间内电场力所做的功称为电 能。
功率守恒
在一个闭合电路中,电源发出的功 率等于各负载吸收的功率之和。
电阻元件及欧姆定律
电阻元件
表示消耗电能的元件,用R表示。
欧姆定律
在一段不含电源的导体中,导体 中的电流I与导体两端的电压U成 正比,与导体的电阻R成反比。
串联谐振电路的应用
在通信、电子测量等领域广泛应用,如选频 电路、振荡电路等。
RLC并联谐振电路
RLC并联电路的基本构成
由电阻、电感和电容元件并联组成的 电路。
并联谐振的概念
当电路中的感抗等于容抗时,电路发 生谐振,此时电路的阻抗最大,电压 最高。
并联谐振电路的频率特性
在谐振频率附近,电路的幅频特性出 现深谷,相频特性发生突变。
电路 邱关源第五版通用课件

时域分析法
时域分析法是一种基于微分方 程或差分方程的方法,直接在 时间域内对非正弦周期电压和 电流进行分析,可以更直观地 了解电路的工作过程。
复数分析法
复数分析法是一种基于复数运 算的方法,通过将实数域中的 非正弦周期电压和电流转换为 复数域进行分析,可以简化计 算过程。
非正弦周期电流电路的功率
非正弦周期功率的概念
总结词
网孔电流法是一种求解电路中电压和电流的方法,通过设置网孔电流并利用基尔 霍夫定律建立方程式求解。
详细描述
网孔电流法的基本思想是将电路中的网孔电流作为未知数,根据基尔霍夫电压定 律建立网孔电压方程,然后求解网孔电流。通过网孔电流法,我们可以得到电路 中各支路的电流和电压。
叠加定理
总结词
叠加定理是一种求解线性电路中电压和电流的方法,它基于 线性电路的性质,即多个激励源共同作用时,各激励源分别 产生的响应可以叠加起来得到总响应。
在正弦稳态电路中,有功功率是指电 路中消耗的功率,其计算公式为 $P=UIcostheta$,其中$U$和$I$分 别为电压和电流的有效值,$theta$ 为电压与电流之间的相位差。无功功 率是指电路中交换的功率,其计算公 式为$Q=UIsintheta$。有功功率和 无功功率都是标量,但无功功率带有 符号。
非正弦周期功率是指非正弦周期电压和电流在一定时间内 所做的功或所消耗的能量,其计算需要考虑电压和电流的 有效值和相位差等因素。
非正弦周期功率的计算方法
非正弦周期功率可以通过计算电压和电流的有效值之积, 再乘以时间得到。也可以通过傅里叶级数展开的方法,分 别计算各次谐波的功率再求和得到。
非正弦周期功率的测量方法
电场力对电荷所做的功,通常用符号U表示。电压的 大小等于电场力把单位正电荷从一点移动到另一点 所做的功。
电路课件(邱关源版)

返 回 上 页 下 页
1.对称三相电源的产生
同步发电机结构:
A Y º I º N S X Z
定子
w
B
A
+
–
B
+
–
C
+
–
转子
X
Y
Z
C
铁心(作为导磁路经) 匝数相同 定子: 三相绕组 空间排列互差120
转子 : 直流励磁的电磁铁
返 回 上 页 下 页
三相同步发电机
A Y C º I º N S X
Z
w
B
通常由三相同步发电机 产 生 , 三 相 绕 组 在 空 间 互 差 120° , 当 转 子 以 均 匀角速度 w 转动时,在三相 绕组中产生感应电压,从而 形成对称三相电源。
返 回
上 页
下 页
③Y形联接的对称三相负载,根据相、线电压、电 3U 30 , I I 流的关系得: U AB AN A A'
2. Y–联接
+
IA
A’
A’ Z/3
设 U A U0
0
UA
UB U 120 o UC U120 o Z | Z | φ
A
UB U 120 o UC U120 o U AB U A U0o UBC UB U 120 o U CA UC U120 o
线电压等于对应的相电压
注意 ①以上关于线电压和相电压的关系也适用
电路第五版 邱关源 课件

叠加定理
总结词
叠加定理是线性电路分析的基本定理之一,它表明在多个独立源共同作用的线性 电路中,任何一个元件的响应等于各个独立源单独作用于该元件所产生的响应的 代数和。
详细描述
叠加定理是线性电路分析的重要工具,它可以用来求解多个独立源共同作用下的 电路问题。通过应用叠加定理,可以将多个独立源分别单独作用于电路,然后将 其对电路的影响(即电压或电流)叠加起来,得到最终的响应。
电路第五版 邱关源 课件
目录
• 电路的基本概念 • 电路分析方法 • 正弦稳态电路分析 • 三相电路 • 非正弦周期电流电路 • 一阶动态电路分析
01
电路的基本概念
Chapter
电流、电压和电阻
电流
电荷在导体中流动的现象称为电流。电流的大小用单位时间内通过导体横截面的电荷量来 表示,通常用字母I表示。
由三个幅值相等、频率相同、相 位互差120度的正弦电压源组成 。
三相负载
分为对称和不对称两类。对称负 载有星形和三角形连接方式,不 对称负载则可能存在单相或多相 的连接方式。
三相电路的分析方法
相电压和线电压
在三相四线制中,相电压 是各相与中性点之间的电 压,线电压是任意两相之 间的电压。
相电流和线电流
}}{1.732}$。
视在功率
表示电路的总功率,计算公式为 $S = sqrt{P^2 + Q^2}$。
05
非正弦周期电流电路
Chapter
非正弦周期电流电路的分析方法
傅里叶级数展开法
将非正弦周期电流或电压表示为傅里叶级数的形式,然后对每一 个展开项分别进行计算。
平均值法
将非正弦周期函数表示为直流和交流成分的平均值,适用于分析线 性非正弦周期电路。
《电路》邱关源第五版第一章课件

欧姆定律的应用非常广泛, 它可以帮助我们计算电流、
电压和电阻等电路参数。
通过欧姆定律,我们可以计算出 电流 $I = frac{V}{R}$ 或 $V = IR$,以及电阻 $R = frac{V}{I}$。 这些公式可以帮助我们解决电路 中的各种问题,例如计算功率、
分析电路的动态响应等。
基尔霍夫定律
描述了电路中电流和电压 的约束关系,包括电流定 律和电压定律。
功率守恒定律
描述了电路中功率的约束 关系,即任意电路中输入 功率等于输出功率。
03
电路的基本定律
欧姆定律
总结词
详细描述
总结词
详细描述
欧姆定律是电路分析中最基 本的定律之一,它描述了电 路中电压、电流和电阻之间
的关系。
欧姆定律是指在一个线性电阻元 件中,电压与电流成正比,即 $V = IR$,其中 $V$ 是电压,$I$ 是 电流,$R$ 是电阻。这个定律适 用于金属导体和电解液等线性元
动态变化
暂态过程中,电路中的电压和电流会随时间动态变化。
持续时间短
暂态过程的时间常数很小,通常在微秒或毫秒级别。
能量转换
暂态过程中,电路中的储能元件会进行能量的转换和传递 。
一阶电路的暂态过程
01
一阶电路的数学模 型
一阶电路由一个电容或一个电感 组成,其数学模型可以用微分方 程表示。
02
一阶电路的暂态过 程分析
电压
电场力做功的量度,表示为V 。
电功率
表示电场力做功快慢的物理量 ,表示为P。
电能量
表示电荷在电场中做功本领大 小的物理量,表示为W。
02
电路的状态和元件的约束关系
电流和电压
第2章电路邱关源课件PPT

等效电阻
Req = ∑ Rk
k =1
n
各电阻上的电压为
Rk uk = Rk i = u, k = 1, 2,L, n Req
各电阻上的分压值与其电阻值成正比
电阻的并联
i 1 i1 + u
i2
G1
−
G2
Gn
i 1 + u
−
Geq
1′
1′
根据KCL 根据KCL写作 KCL写作
i = i1 + i2 + L + in
n个电流源并联, 个电流源并联,可等效为一个电流源
iS 1 iS 2 iSn
n
iS = iS 1 + iS 2 + L + iSn = ∑ iSk
k =1
iS
电 路
+ us −
+ us −
+ us −
iS
iS
iS
iS
只有电压相等极性一致的电压源才允许并联, 只有电压相等极性一致的电压源才允许并联, 等效电路为 其中任一电压源。 其中任一电压源。 只有电流相等且方向一致的电流源才允许串联, 只有电流相等且方向一致的电流源才允许串联, 等效电路 为其中任一电流源. 为其中任一电流源. 电阻电路的等效变换
ia
+
1 ib G2
ic + G1 U1
−
2
is1 + U2
−
G4
3
+
Us
−
G3
U3
is 2
−
1 ib G2
+
2
is1 + U2
− +
1
电路第五版课件邱关源罗先觉第十一章-2.ppt

1026
1611 -1034 577 UR2=0.346
返回 上页 下页
UR=UR/|Z| (mA) UR0=10 UR1=0.304 UR2=0.346
UR(f )
U R1 3.04% U R 2 3.46%
UR0
UR0
∴收到北京台820kHz的节目。
1mA
LR
5 0.5mH
U U S 50V 2
C 0.002μ F
P UI0 0.05W
返回 上页 下页
11.6 滤波器简介
滤波器 工程上根据输出端口对信号频率范围的要求,设计 专门的网络,置于输入—输出端口之间,使输出端口 所需要的频率分量能够顺利通过,而抑制或削弱不需 要的频率分量,这种具有选频功能的中间网络,工程 上称为滤波器。
在谐振点响应出现峰值,当 偏离0时,输出
下降。即串联谐振电路对不同频率信号有不同的 响应,对谐振信号最突出(响应最大),而对远离谐 振频率的信号具有抑制能力。这种对不同输入信 号的选择能力称为“选择性”。
②谐振电路的选择性与Q成正比 Q越大,谐振曲线越陡。电路对非谐振频率的信
号具有强的抑制能力,所以选择性好。因此Q是反映 谐振电路性质的一个重要指标。
谐 振 时 电 路 中 电 磁 场 的总 储 能 2π 谐 振 时 一 周 期 内 电 路 消耗 的 能 量
Q是反映谐振回路中电磁振荡程度的量,Q越大,
总能量就越大,维持振荡所消耗的能量愈小,振荡程
度越剧烈。则振荡电路的“品质”愈好。一般在要求
发生谐振的回路中希望尽可能提高Q值。
返回 上页 下页
例
o 640 820 1200 f (kHz)
电路邱关源第五版课件第三章ppt.ppt
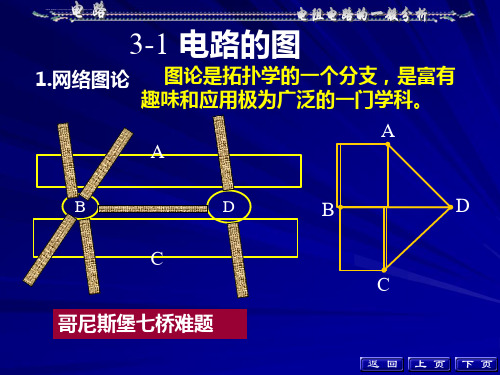
这一步可 以省去
2
回路1 u2u3u10 回路2 u4u5u30
回路3 u1u5u6uS0
应用欧姆定律消去支路电压得
R2 i2
i3
R4 i4
1
1
R3 2
3
R1 i1
i5 R5
34
i6
R 2i2R 3i3R 1 i10 R 4i4R 5i5R 3 i30 R 1 i1R 5 i5R 6 i6u S
R6 + uS –
bnl1 结点、支路和
基本回路关系
返回 上页 下页
从使用情况来看,闭胸式的使用比较 广泛。 敞开式 盾构之 中有挤 压式盾 构、全 部敞开 式盾构 ,但在 近些年 的城市 地下工 程施工 中已很 少使用 ,在此 不再说 明。
例1-1 图示为电路的图,画出三种可能的树及其对
应的基本回路。
1解 45
86 3 72
结论 • KVL的独立方程数=基本回路数= b-( n-1)。
• n个结点、b条支路的电路, 独立的KCL和KVL方 程数为
(n 1 )b(n 1 )b
返回 上页 下页
从使用情况来看,闭胸式的使用比较 广泛。 敞开式 盾构之 中有挤 压式盾 构、全 部敞开 式盾构 ,但在 近些年 的城市 地下工 程施工 中已很 少使用 ,在此 不再说 明。
5
86 7
4 86
3
4
8 2
3
注意
网孔数为基本回路数。
返回 上页 下页
从使用情况来看,闭胸式的使用比较 广泛。 敞开式 盾构之 中有挤 压式盾 构、全 部敞开 式盾构 ,但在 近些年 的城市 地下工 程施工 中已很 少使用 ,在此 不再说 明。
3-2 KCL和KVL的独立方程数
第6章电路邱关源课件PPT

线性电容
C +q + u -q -
du i =C dt
1 t uc (t ) = ∫ ic (ξ )d ξ C -∞
任意时刻
1 t uc (t ) = uc (t0 ) + ∫t ic (ξ )dξ C 0
1 0+ uc (0 + ) = uc (0 − ) + ∫0 ic dt C −
电 路
t0 = 0- t = 0+
3 −3
一 阶 电 路
电 路 例3 图示电路, 图示电路,t<0时,开关S 开关S闭合, 闭合,电路已达稳态。 电路已达稳态。在t=0时 刻,打开开关S 打开开关S,求初始值iL(0+)、uC(0+)、 i(0+)、 iC(0+)、 du C uL(0+)、 diL 、 和稳态值iL(∞)、uC(∞) 。 dt 0+ dt 0+ 解 : t<0 时 , 电容相当于开 i 路,电感相当于短路
换路前i 换路前i1(0-)+i2(0-)≠0,换路后i 换路后i1(0+)+i2(0+) =0(KCL), =0(KCL),i1、i2 发生跃变, 发生跃变 ,但总磁链不变 一 阶 电 路
§6-2 一阶电路的零输入响应
电 路
零输入响应: 没有外施激励( 没有外施激励(输入为零), 输入为零),由电路中动态元件 ),由电路中动态元件 的初始储能引起的响应。 的初始储能引起的响应。 S (t = 0 )
一 阶 电 路
线性电感
i + L u (t) -
dψ di(t ) u (t ) = =L dt dt
电 路
换路 0-到 0+的瞬间
《电路原理》邱关源ppt课件

单位正电荷q 从电路中一点移至另一点时 电场力做功(W)的大小
U
def
dW
dq
为什么要设电流参考方
向?
简单电a 路
+
+
I
U
E
Uab
-
b-
I1 R1
R2 I2
复杂+ 电路
U6
I3
-
IS
I4
R3
R4
电流的实际方向 可知
各电I5流+ 的US 实- 际方向 未知
(b) 若iS为变化的电源,则某一时刻的伏安关系也是 这样 电流为零的电流源,伏安曲线与 u 轴重合, 相当于开路元件
(4). 理想电流源的短路与开路
i
(a) 短路:R=0, i= iS ,u=0 ,电流
+
源被短路。
iS
u
R (b) 开路:R,i= iS ,u 。若强
_
迫断开电流源回路,电路模型为病
i为有限值时,u=0。
当R=,视其为开路。
u为有限值时,i=0。 * 理想导线的电阻值为零。
5.其他电阻元件
负电阻: (negative resistance),在u、i 取关联参考方向时,负电阻的电压、
电流关系位于Ⅱ、Ⅳ象限,即R<0,G<0 。负电阻将输出电功率(电功率
小于零),对外提供电能。所以负电阻是一种有源元件(active element)。
例 i
+
AU B
-
电压电流参考方向如图中所标, 问:对A、两部分电路电压电流参考方向 关联否?
答: A 电压、电流参考方向非关联;
B 电压、电流参考方向关联。
电路(邱关源第五版)课件第十章

总结词
电源的等效变换是指将复杂的电源网络 通过一定的方法简化为单一电源或电阻 的形式,以便于分析和计算。
VS
详细描述
电源的等效变换是电路分析中常用的方法 之一。通过电源的等效变换,我们可以将 复杂的电源网络简化为单一电源或电阻的 形式,从而简化电路分析和计算。等效变 换的方法包括电压源的串联等效和电流源 的并联等效等。
基尔霍夫定律
总结词
基尔霍夫定律是电路分析的基本定律,包括基尔霍夫电流定 律和基尔霍夫电压定律。
详细描述
基尔霍夫电流定律指出,在电路中,流入节点的电流之和等 于流出节点的电流之和;基尔霍夫电压定律指出,在电路中 ,绕行一周的电压降之和等于零。这两个定律是电路分析的 基础,适用于任何集总参数电路。
欧姆定律
详细描述
当非线性电阻并联在电路中时,其总电阻的倒数 等于各电阻倒数之和。在并联电路中,各支路电 压相等,电流则可能会因非线性电阻的特性而发 生变化。
非线性电阻电路的分析方法
总结词:解析法 总结词:图解法
详细描述:解析法是通过数学解析的方式来求解 非线性电阻电路的方法。这种方法需要建立电路 的数学模型,然后通过求解方程来得到电路的解 。
详细描述:图解法是通过绘制电路图的方式来直 观地分析非线性电阻电路的方法。这种方法需要 绘制出电路的伏安特性曲线,然后通过分析曲线 的交点和性质来得到电路的解。
THANKS FOR WATCHING
感谢您的观看
替代定理
总结词
替代定理是电路分析中的一个基本定理,它表明在具 有唯一解的线性电路中,如果将某个未知支路的电流 或电压用另一个已知的电流或电压替代,则电路的状 态不变。
详细描述
替代定理指出,在具有唯一解的线性电路中,如果将 某个未知支路的电流或电压用另一个已知的电流或电 压替代,整个电路的状态不会发生变化。这个定理在 电路分析中非常有用,因为它允许我们用已知的电流 或电压来替代未知的电流或电压,从而简化电路的分 析过程。
电路 邱光源 第一章课件

u1
-
i2
u2
X
控制支路
受控支路
说明:
1. 控制支路: 反映控制量 u1 , i1
电流i1 ( 短路)
电压u1 ( 开路 )
电流源 i2 (
i2 )
2. 受控支路: 反映被控量 u2 , i2
电 压源 (
三. 理想受控源分类
+ ) u2 i2
1. 电流控制电流源 (CCCS )
控制关系 i2 i1
发出
P5V uS i 5 (2) 10 W 发出
满足:P(发)=P(吸)
X
+
_
计算图示电路各元件的功率
i
2A
例. 图示电路中 , U CD ?
1A
A
AD间开路 , 则电压 U AB ? UBC ?
2A
3 +
C
3
3V
U AD ?
D
B
1
I
1 V
3A
解:
由广义节点知: I=0
u 10 V
p 10W
pI S 30W
u 10 V
p 10W ( 吸收 )
Is :
pI S 10W
pI S 10W (发出 )
X
⑤ 电流源不能开路
Is
Is
可以短路
X
例
解
i iS 2A u 5V P2 A iS u 2 5 10 W
+
5V u
330kV
10kV 10kV 400V
电工理论学科是电力工业主要依靠的技术学科
X
电路应用举例
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
2
3
4
D
24K
KD
R30
HEAD
C20 2n2(M)
KC
C
R29 12K
C39 103(M)
C33 22uF
R28 220
REC
KA
330K
D3
C40
1N4148
1uF
R23
1N4148 D2
R22 4.7K
C23
C24 47uF
B
1uF
C22
203
C2
1uF
R8 1.2K
BAT
6V
DC
POWSKT D1
DVC
C18 220uF
R6 CHANG
1K
BATTT3 8050 D
R7 24(0.5W)
C
C30 470uF
9
16 1
15 2
14 3
13 4
12 5
11 6
10 7
U4 TA7738
L4 47uH
C11 4.7uF
R37 2.2k
SPKSKT
C29 100uF
R42 68
C32 470uF
11
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
You Know, The More Powerful You Will Be
Thank You
在别人的演说中思考,在自己的故事里成长
1 2 3 4 5 6 7 8 9 10 11 12
R3
1UF
R1
22K DAO C8
8
U1D 4066
1K
Title
8520new-M
A
C7
220u
C6
4D.7V
100uF
202
Size A4
Number 2001.4.1
Revision
Date: File:
10-Feb-2003
H:\新建文件夹\j ob\8520ne w-.DDB
R27
6.8K
2
U1A 4066
R32 47K
R17 10K
C42 1uF
13
1 MIC
MICSKT
MIC
VCC
SPK
R15 470
DVCC
C19 104 C14
47uF
DC
R4 10K
C4
R12 10K
1UF
R13
T8
10K
8050
C12 1UF
C17
D5
104
4.7V
RESET
T2 9014
D11 4148
Thinking In Other People‘S Speeches,Growing Up In Your Own Story
讲师:XXXXXX XX年XX月XX日
•
1831年,法拉第
(英国,1791~1867)
• 发现了电磁感应现象,
指出圆形软铁两边绕
上AB两个线圈,在A
线圈与电池接通断开
的瞬间,B线圈中感应
出电流,后来根据这
个原理制成了变压器;
磁铁和导线的闭合回
路有相对运动时,回
路中产生感生电流,
由此发明了发电机。
•
1864年,麦克斯韦
(英国,1831~1879)
电路的基本概念、 电路的基本理论、 电路的基本分析方法 • 课程难度中等
电路理论circuit theory
• 基尔霍夫定律 Kirchhoff ’s Law-----KVL 、KCL
• 叠加定理superposition theorem • 替代定理substitution theorem • 戴维南定理Thevenin ‘s theorem • 诺顿定理Norton ‘s theorem
电路分析基础
BASIC CIRCUIT THEORY
要想了解一门学科, 最好的办法是先读读它的历史。
•
1773年,库仑
(法国,1736~1806)
• 发现库仑定律,它 描述了电荷间的作 用力和磁极间的作 用力,它是静电学 的理论基础。
• 1802年,安培
(法国,1775~1836)。
• 发现了电磁效应, 指出通电的线圈与 磁铁相似,进而发 现两根截流导线相 互作用。它描述的 是电流的磁效应, 是磁路设计的基础, 研究的是稳恒磁场。
ADIN S3
1N4001
A
C9
220uF
C16
1000uF
1
R33
18kK
R21 27K R18 18K
C21 153
C37 103
C34 561
C26 4.7uF
R19 330K
KB
C41
104
DVCC
R36
3.3K
R31 3.3K
C31 220uF
C28
C13 47uF
C15 104
100uF
• 发表论文《电磁场的 动力Байду номын сангаас理论》,提出 了联系着电荷,电流 电场,磁场的基本微
分方程,电磁场的波 动方程,预见了电磁 波的存在,并把光学
和磁学统一起来。他 在1873年出版了二卷 本《电磁理论》,成
为经典物理学的重要 支柱之一。
• 1892年,洛伦兹 (荷兰,1853~1928)
• 发表电子论,指出一切 物质的分子都含有电子, 从而建立了经典电子学。 随之而来的是电子技术 的飞速发展,特别是在 信息技术上的广泛应用。
Sheet of Drawn By :
2
3
4
电器件种类繁多,功能各异。
开关
电容器
发光二极管 灯泡
电池
接线柱
保险丝
运放
电位器
电阻器
指示灯座
晶体管
线圈
电路课程介绍
• 电气工程师的“看家本领”、“面包和黄油” • 重要的专业技术基础课 • 前续课程:高等数学、线性代数、物理
后续课程:模拟电子、数字电子、数字信号处理、 自动控制原理、自动化仪表、电气检测技术等 • 本课程重点(三句):
R46 51K
U1C 4066
MIC R34 10K C3 104
4
3
R26 10K
D9
5
5.1V
9
6 C5
VCC R43 1K
R45 10K
R35 22k
R39 10K
MOT
T6 9014
T5 9014
VDD GND RESET DVC HIFI DGND NC CHK ADIN MOT DAOUT MIC
学习方法
• 上课认真听讲 • 勤于动脑、动手(举一反三、触类旁通),
多做习题。 • 善于归纳总结。读书由厚到薄,再由薄到
厚。
• 遵循从简到繁、从易到难的原则 • 体系上先静态(直流电路分析)
后稳态(正弦和非正弦周期电路) 再暂态(过渡过程分析)
浏览目录,纵览全书
参考书: <电路基础>(英文版)James W.Nilsson著 《电路分析基础》(第三版)李翰逊 《电路分析》胡翔骏 《电路原理》周守昌
R40 47
DVCC
R5 10K H/L
8
R41
12
4.7
C36
1
8
RP1 1k
C27
104
2
7
47uF
U1B
U6
C35
561
R24
R20
10
4066 C43
680
430
VR1
1uf
50KVR
3
2402
6
VR3
4
5
10K
B CON1
C25 1uF
C38 222(M)
T1 8050
R2 1K
T4 9V0D14D
