关于驻波能量的基本认识
6-驻波

驻波
波动
驻波系统的驻波原理: 驻波系统的驻波原理: 简正模式的频率称为系统的的固有频率 简正模式的频率称为系统的的固有频率,一个 固有频率, 驻波系统有多个固有频率, 驻波系统有多个固有频率,这与弹簧振子只有 一个固有频率不同. 一个固有频率不同. 当外界驱动源以驻波系统的某个固有频率振 动时,会激起强驻波,这种现象也称为共振 共振. 动时,会激起强驻波,这种现象也称为共振. 系统究竟按哪种模式振动取决于初始条件, 系统究竟按哪种模式振动取决于初始条件,一 般驻波系统的振动频率是各种简正模式的叠 加.
y = 2 A cos2π cos2π ν t
x
λ
y
λ 2
例 x=±
λ 3λ
4 λ
4
,
为波节
o
x
x
λ2
x
4
x
λ
4
<x<
, cos2 π > 0
λ
3λ x < x < , cos2 π < 0 4 4 λ
λ
y = 2 A cos 2 π
y = 2 Acos2 π
λ
cos 2π ν t
cos(2 πν t + π)
驻波
波动
B
o
y反
驻波方程: 驻波方程:
y = y入 + y反
2π t 2π ( 3 λ x ) 4 = A cos T λ 2π t 2π x 3π = A cos( + ) T λ 2
2πt 2πx π 2πt 2πx 3π = A cos( + ) + A cos( + ) T λ 2 T λ 2 2π x 2π t π λ = 2 A cos( ) cos( + ) n = 0, x1 = λ T 2 4
驻波解析

原点描写合成驻波。由于绳很长,可不考虑反射。 绳上的波速设为u 。
解 设左端的振动为y1 =Acos t,则右端的振动 为 y2=Acos ( t + )。
设右行波的波动表达式(以绳的中心为坐标原点)
y1Acos(t[ux)1]
设左行波的波动表达式(以绳的中心为坐标原点)
dE k2dV A 22co 2(2 s πx)si2 nt dE p2dV A 22si2n 2 πxco 2st
(1) cos t = ±1 各质点的位移达到最大,dEk为零,
势能dEp不为零。波节处势能最大;在波腹处势 能最小。势能集中在波节附近。
波腹处势能始终为0
(2) cos t = 0 各质点都回到平衡位置,此时所有
反射波在B点的振动方程
tl y反 BAco2 s([T)]
反射波的表达式
y 反 A co 2 (T s t [ l) 2 (l x )]
y反
Acos2( t T
212x)
Acos2(t x)
T
(2)驻波的表达式为
yy入y反
Acos2(t x)Acos2(t x)
T
T
2Asin2xsin2t
x k
2
点O 到点B 之间的波节
x 0 ,,,3 ,2 ,5 , 3 ,7 ,4 ,9 ,5
22 2 2 2
波腹的坐标
sin 2π x 1 2π x(2k1)π x (2k 1)
2
4
x ,3 ,5 ,7 ,9 ,1 ,1,3 1 ,5 1,7 19
4444444 4 4 4
例题* 两人各执长为l 的绳的一端,以相同的角 频率和振幅在绳上激起振动,右端的 ]A co (t sx [l)]
机械波的驻波问题

机械波的驻波问题引言:机械波是一种在介质中传播的能量和信息的形式。
驻波是机械波在传播过程中出现的一种特殊现象,它是由于波的传播过程中发生的干涉造成的。
驻波在许多领域中有着广泛的应用,如声波、横波、纵波等。
本文将从驻波的定义、特征和应用等方面进行探讨。
一、驻波的定义和特征1.1 定义驻波是指波的前进和反射波之间的干涉效应形成的一种特殊波动形式。
当两个具有相同频率、方向、幅度但传播方向相反的波沿同一介质传播时,则它们之间会发生干涉,形成驻波。
1.2 特征1)驻波的节点和腹部:在驻波中,波峰和波谷位置保持不变,形成一系列不动的节点和腹部。
节点是波动方向振动幅度的最小值,而腹部则是振动幅度的最大值。
2)驻波的波长和频率:在驻波中,波动方向中的振动模式是由两波相互叠加形成的。
波长是两个传播波的波长之比。
3)驻波的单一模式:驻波只能形成某种特定的波动模式,而不会形成多种波动模式。
4)驻波的能量传递:在驻波中,能量在波峰和波谷之间来回传递,而不会在波动方向上传播。
二、驻波的数学描述和实验现象2.1 数学描述驻波的数学描述是通过波函数来进行的。
设波函数为y(x,t),驻波的数学描述可以表示为y(x,t) = A*sin(kx)*cos(ωt),其中A为振幅,k为波数,ω为角频率。
2.2 实验现象通过实验可以观察到驻波的形成和特征。
一种常见的实验是通过绳子来观察驻波现象。
将一根绳子固定在一端,然后在另一端通过振动源产生波动,当波动传播到固定端时,会发生反射并与传入的波动叠加形成驻波。
在绳子上可以观察到波节和波腹的形成,波节为绳子不振动的位置,波腹为绳子振动幅度最大的位置。
三、驻波的应用驻波在许多领域中有着广泛的应用。
3.1 声波的驻波在乐器中,驻波是产生声音的基本原理之一。
当乐器振动时,空气中的声波在乐器内传播并与传入的声波叠加形成驻波,产生特定的音调。
不同的乐器具有特定的驻波形式,因此可以通过驻波来区分不同乐器的声音。
公开课——驻波
本征频率;基频;谐频
2. 一端固定一端自由的弦振动的简正模式
l (n 1) n n 1,2,
22
l 1
4
l 32
4
l 53
4
第五节 驻
波
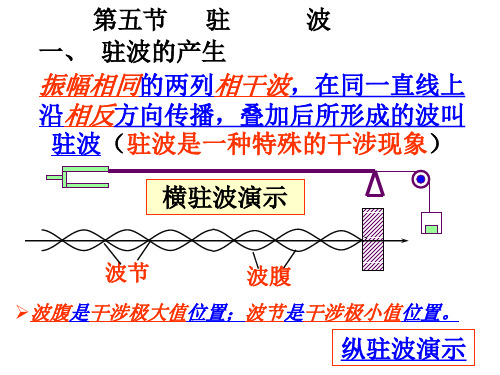
一、 驻波的产生
振幅相同的两列相干波,在同一直线上
沿相反方向传播,叠加后所形成的波叫
驻波(驻波是一种特殊的干涉现象)
横驻波演示
波节
波腹
➢波腹是干涉极大值位置;波节是干涉极小值位置。
纵驻波演示
二、 驻 波方 程
负向: 正向:
y1
A cos(t
2
x
1)
y2
A cos(t
2
x
2)
y
y1
y
结论: 相邻两个波腹之间的距离为半个波长。
2 2 x=2 x 2
(2)波节位置(为干涉极小值位置)
2
2
x
2
1
(2k+1)
,
k 0,1. 2,
✓求出的X即为波节处.
相邻两个波节之间的距离也为半个波长.
2
y
o
2
x
应用:可用测量波腹或波节间的距离, 来确定波长
3. 位 相
y 2A cos( 2 x ) cos( t )
2 x (2K 1) ,
2
(k 0,1,2,)
✓求出的 x 即为波节的位置。
❖方法二(求出X处质点两分振动的位相差)
y1
A cos(t
2
x 1)
,
y2
A cos(tBiblioteka 2 x2)
2
2
x 2
1
(1)波腹位置(为干涉极大值位置)
大学物理 驻波(一)2024

大学物理驻波(一)引言概述:驻波是在介质中传播的波在与逆向传播的波相遇时形成的一种特殊波动现象。
它在大学物理中有着重要的应用和理论意义。
本文将从驻波的基本概念和特点入手,详细介绍了驻波的形成条件,驻波的数学描述以及驻波的实验观察等。
正文:1. 驻波的基本概念和特点- 驻波是由两个相同频率、振幅相等而方向相反的波在空间中相遇而形成的。
- 驻波的震动节点是固定不动的,而虚节点一直在不断地交替出现。
- 驻波是由于波的干涉而形成的,不会传输能量或物质。
2. 驻波的形成条件- 驻波形成的必要条件是波的传播速度相同,波长相等且频率相同。
- 在一维情况下,驻波形成的充分条件是两波的幅值、频率、相位相同。
3. 驻波的数学描述- 驻波可以用数学方程来描述,常用的方程为y(x,t) = Acos(kx)cos(ωt + φ),其中A为振幅,k为波数,ω为角频率,φ为初相位。
- 驻波方程中的k和ω与波长λ和周期T之间有着确定的关系:k = 2π/λ,ω = 2π/T。
4. 驻波的实验观察- 驻波可以通过在一定条件下的波的传播介质中观察到,如绳上的驻波、声管中的驻波等。
- 在实验观察中,可以通过调节波的频率、振幅、传播介质的长度等参数来观察驻波的形成与特性。
5. 驻波的应用- 驻波在声学、光学、电磁学以及其他物理学领域中有着广泛的应用,如乐器共鸣现象、干涉仪的工作原理等。
- 驻波还可以用于测量波的参数,如测量波速、波长等。
总结:驻波是在介质中传播的波在与逆向传播的波相遇时形成的一种特殊波动现象。
它具有震动节点固定、虚节点不断交替出现的特点,是由波的干涉形成的。
驻波的形成需要满足波的传播速度相等、波长相等且频率相同的条件。
驻波可以通过实验观察到,并可用数学方程进行描述,有着广泛的应用价值。
驻波的工作原理

驻波的工作原理首先,让我们了解什么是驻波。
驻波是指在两个波沿传播方向相对立的波叠加形成的波现象。
当一条波沿某一介质中传播时,如果遇到另一条相同频率和振幅的波从相对方向传播而来,两条波会相互叠加形成驻波。
驻波的工作原理可以通过以下几个步骤来解释:1. 信号源产生波:首先,一个信号源会产生一条波。
这个信号源可以是电磁波源、声波源或其他波源。
2. 波在传输介质中传播:波从信号源出发,在传输介质中传播。
传输介质可以是空气、水、电缆等。
3. 波遇到障碍物或反射点:在传输过程中,波会遇到障碍物或者反射点。
这些障碍物或者反射点会使波反射或折射。
4. 反射波与源波叠加形成驻波:当反射波遇到源波时,如果它们满足相位差为整数倍关系,那么它们就会相互叠加形成驻波。
驻波的反映波和源波振幅可以相互增强或相互抵消。
5. 驻波节点和驻波腹:在驻波中,存在一些位置振幅为零的点,称为节点。
同时,存在振幅最大的位置,称为腹。
驻波的节点和腹是由波的叠加效应形成的。
6. 驻波在传输介质中保持不变:一旦驻波形成,它会在传输介质中保持不变。
这是因为驻波是由源波和反射波的叠加效应形成的,当两者相遇并满足一定条件时,波的能量不会再继续传播。
驻波的工作原理可以用数学公式来描述。
对于一维驻波,其数学表达式可以表示为:A(x, t) = A_0 * sin(kx) * cos(ωt)其中,A(x, t)是波的振幅,x是位置坐标,t是时间,A_0是振幅的最大值,k是波数,ω是角频率。
这个表达式说明了驻波的位置和时间的关系。
驻波在实际应用中有许多重要的应用。
例如,在乐器中,弦乐器上的驻波使得我们可以产生不同的音调。
此外,在安全检测中,通过发送或接收信号源产生的波与反射波的驻波可用于探测目标物体的位置和性质。
此外,通过使用驻波技术还可以制造微波炉、无线电天线和光纤通信系统等设备。
综上所述,驻波是由源波和反射波的叠加效应形成的。
通过满足一定条件,波的振幅在某些位置形成节点和腹,从而形成驻波现象。
电磁驻波中的能量与能流分布探讨

电磁驻波是电磁学中一个重要的研究课题。
它不仅可以提供精确的电磁场数据,而且可以用来探索电磁场中的能量和能量流分布。
首先,讨论电磁驻波中的能量分布。
电磁驻波中的能量主要来自电场和磁场,即电磁能量。
电场和磁场的能量密度分布可以用电磁能量密度的概念来解释。
它表明,电磁驻波中的能量密度分布是电磁功率的功率密度的函数。
电磁功率的功率密度可以用电功率和磁功率的功率密度的概念来解释。
其次,讨论电磁驻波中的能量流分布。
电磁驻波中的能量流是由电场和磁场的能量流决定的,它是一种电磁能流密度的概念。
电磁能流密度可以用电功率和磁功率的功率密度的概念来解释,电磁功率的功率密度是电磁能量的功率密度的函数。
因此,电磁驻波中的能量流分布与电磁能量的分布相关。
综上所述,电磁驻波中的能量主要来自电场和磁场,而电磁驻波中的能量流分布与电磁能量的分布相关。
电磁能量的功率密度可用电功率和磁功率的功率密度的概念来解释,而电磁能流密度可以用电磁功率的功率密度来解释。
因此,电磁驻波中的能量和能量流分布是电磁功率的功率密度的函数,可以反映电磁场的状态。
驻波的原理

驻波的原理驻波是指在传播介质中产生的一种特殊的波动情况,其特点是波动形式呈现出相互干涉的现象。
驻波的形成是由于波的传播过程中发生反射现象,在介质中由传播方向相对相反的两个波相遇产生干涉。
驻波的形成原理可以通过以下几个步骤来解释:1. 波的传播:当一波传播到介质中时,它会遇到终端或者障碍物。
在遇到障碍物时,波会发生反射,并以相反的方向传播。
2. 反射:当波达到障碍物时,一部分能量被反射回传了原来的方向,而另一部分能量继续传播。
反射波与入射波在介质中相互干涉,形成驻波。
3. 干涉:当入射波与反射波相遇时,它们会相互干涉。
干涉是指波的相位和振幅的叠加效应。
如果入射波与反射波的振幅相等,相位相反,它们将相互抵消,形成驻波。
在某些点上,波的振幅为零,这些点称为节点;而在其他点上,振幅达到最大值,这些点称为腹部。
4. 波长和频率:驻波的形成需要一定的波长和频率条件。
波长需要满足几何限制,以使得反射波与入射波之间的干涉产生稳定的驻波。
频率则取决于波的源和介质的性质。
总结起来,驻波的形成是通过反射波与入射波在介质中相互干涉产生的,它要求在一定波长和频率下波的振幅和相位满足特定条件。
驻波在电磁波、声波等不同媒介中都有普遍存在,具有重要的理论和应用价值。
继续驻波的原理,我们可以从数学角度来理解。
驻波的形成是由于在传播介质中存在对称的波和反射波之间的相互干涉。
考虑一维情况下的驻波,我们可以将介质分为两个相同的部分,每个部分的波动由自由传播波和反射波构成。
假设传播介质中的波形为 $y(x, t) = A \sin(kx - \omega t)$,其中 $A$ 表示振幅,$k$ 表示波数,$x$ 表示位置,$\omega$ 表示角频率,$t$ 表示时间。
当波达到反射边界时,一部分波会以相反的方向反射回来,并产生反射波。
反射波的形式为 $y(x, t) = A \sin(-kx - \omega t) = -A \sin(kx + \omega t)$。
对于驻波能量的定量研究

对于驻波能量的定量研究驻波是一种特殊的波动现象,它由两个同频率但反向传播的波叠加而成。
驻波形成的条件是波的传播方向与波的反射方向一致,而反射方向的振幅与传播方向相反。
驻波在物理学中有着广泛的应用,比如在声学中,驻波能够形成声学共振,而在电磁学中,驻波可以形成共振腔。
对于驻波能量的定量研究,我们可以从驻波的能量分布和传播特性入手进行分析。
首先,我们需要研究驻波的能量分布。
在一维驻波中,驻波的能量密度与振幅的平方成正比。
对于一根被两端固定的弦,根据能量守恒定律,驻波的能量在弦的各个位置分布应该是均匀的。
但是,在一维驻波中,振幅和能量的分布并不均匀,而是呈现“波腹”和“波节”的分布规律。
波腹处能量密度最大,而波节处能量密度为零。
我们可以通过测量波腹和波节处的振幅来定量研究驻波的能量分布。
其次,我们可以通过传播特性来研究驻波的能量。
对于一维驻波,驻波的频率与波长有着特定的关系。
在一个封闭的管道中,当管道的长度等于波长的整数倍时,会产生共振现象,能量传递效果更为明显。
我们可以通过改变波长或改变驻波的条件来调节驻波的能量传输效果。
在三维空间中,驻波的能量分布和传播特性与一维驻波有所不同。
对于三维驻波,波场分布更为复杂,而且驻波的能量分布往往不再是均匀的,而是呈现出球面波的特点。
我们可以使用模拟方法或实验方法来研究三维驻波的能量分布和传播特性。
总的来说,驻波能量的定量研究需要结合能量分布和传播特性来进行分析。
通过测量振幅、频率和波长等参数,可以定量研究驻波能量在空间中的分布和传播特性。
驻波能量的定量研究对于理解波动现象以及在声学、电磁学等领域的应用具有重要意义。
驻波的能量特点

驻波的能量特点
驻波(Standing wave)是在一定空间范围内来回反射形成的波动模式。
它具有以下能量特点:
1. 能量局限:驻波的能量被局限在空间的特定区域内。
在驻波中,波峰和波谷形成固定的位置,能量在这些位置上来回传递,而在波节处能量几乎为零。
这导致能量在空间上被限制在驻波模式所占据的区域内。
2. 能量稳定:由于反射和干涉的作用,驻波中的能量处于稳定状态。
波峰和波谷之间的能量交换导致能量在区域内持续循环,而不会传播到其他区域。
这使得驻波的能量保持相对稳定,不会随时间推移而减弱或增强。
3. 最大与最小能量点:在一个驻波模式中,存在能量最大和能量最小的位置。
能量最大的位置位于波峰,而能量最小的位置位于波节。
这种分布使得驻波具有不同位置上能量密度的变化,形成特定的振动模式。
4. 振幅变化:驻波中的能量随着位置的变化而发生振幅的周期性变化。
在波峰处,振幅达到最大值;而在波节处,振幅几乎为零。
这种振幅变化形成了驻波模式的特征。
需要注意的是,驻波的能量特点与波长、频率等参数密切相关。
具体的能量分布和特性取决于驻波的模式和系统的几何形状。
驻波在许多领域中都有重要的应用,包括声学、光学和电磁学等。
1/ 1。
对于驻波能量的定量研究

玉林师范学院本科生毕业论文对于驻波能量的定量研究The Quantitative Study Of Standing Save Energy院系物理科学与工程技术学院专业物理学学生班级姓名学号指导教师单位物理科学与工程技术学院指导教师姓名指导教师职称对于驻波能量的定量研究物理学2008级1班指导教师摘要驻波是由两列振幅、频率相同,但传播方向相反的简谐波叠加而成的。
关于驻波的能量问题,在多数普通物理力教材中只作了简单介绍。
不过笔者认为,驻波是力学的重要组成部分,因此对这个问题的讨论,应该有一个定量的解析式分析,才能使之更富有普遍性和说服力。
本文通过“驻波是由两列振幅、频率相同,但传播方向相反的简谐波叠加而成”和“驻波方程”两个角度,首先阐明了弹性介质驻波形成的原理及其特点,导出了弹性介质中驻波质元的动能和势能的表达式,进一步导出了驻波能量的表达式,然后定量分析弹性介质中驻波的波节、波腹与波节(波腹)、波腹(波节)之间的能量分布及波节(波腹)、波腹(波节)之间能量的相互转换问题。
最后文章指出在驻波中没有引起能量的重新分布,但发生了能量的转换.并且在波节和波腹处,都没有能量的传递和通过,能量只能在相邻波节和波腹之间转换、流动。
关键词:驻波,波节,波腹,能量,转换和流动The quantitative study of Standing wave energyPhysics 2008-1 Zhou Shi- kunSupervisor Guan Xiao-rongAbstractStanding wave is by two columns of amplitude, frequency and same, but spread in the opposite direction of Jane harmonic a stack. In the energy of the wave problem about, in the most ordinary physical force only in the teaching material are introduced. But I think, as the in-depth discussions on this problem, should have a quantitative analytical analysis, can make it more rich universality and persuasive.This article through the standing wave by two columns amplitude frequency is same, but spread in the opposite direction of Jane harmonic superposition of standing wave equation into and two Angle, first expounded the elastic medium standing wave form the principle and features of the elastic medium are standing wave of mass yuan kinetic energy and potential formula, further derived and the expression of the standing wave energy, and quantitative analysis of the elastic medium standing wave wave quarter wave abdomen and wave festival (wave abdomen) wave abdomen (nodes) of energy between the distribution and wave festival (wave abdomen) wave abdomen (nodes) of energy conversion between each other last the article points out that in the standing wave did not cause the redistribution of energy, but happened the transfer of energy. And in the nodes and wave in the abdomen, all have no energy transfer and through, energy can only in adjacent nodes and wave abdomen convert between flow.Key words:standing wave;node;lop;energy;Conversion and flow目录1前言 (1)2驻波 (1)2.1驻波的形成 (1)2.2驻波方程 (2)2.3驻波振动的特点 (3)3驻波的能量 (5)3.1简谐波介质中质元的动能、势能、机械能 (5)3.2驻波介质中质元的动能、势能、机械能 (7)3.3简谐波的能流密度 (10)3.4驻波的能流密度 (10)3.5驻波在相邻波节(波腹)、波腹(波节)之间的能量 (12)3.6波在相邻波节(波腹)、波腹(波节)之间的动能 (13)3.7波在相邻波节(波腹)、波腹(波节)之间的势能 (14)4结论 (15)致谢 (16)参考文献 (16)玉林师范学院本科毕业生论文1前言对于驻波,大家都有所认识,它是一种常见的物理现象。
驻波能量分析

驻波能量分析摘要:驻波是由振幅、频率、和传播速度都相同的两列相干波,在同一直线沿相反方向传播时叠加而成的一种特殊形式的干涉现象。
但是它不同于行波,它不定向传播能量,只是在波腹和波节间转移。
本文以定量的方式来讨论驻波能量问题。
关键词:驻波能量定量解释不定向传播一、驻波的方程现在假设两个振幅、频率、和传播速度都相同、初相为零的两列简谐波,其波动方程分别为:y1=Α cos2π (νt− X/λ); (1)y2=Α cos2π (νt+ X/λ); (2)式中Α为波的振幅,ν为频率,λ为波长。
则其形成的驻波的波函数为:y=2Acos2πx/λcos2πνt; (3)上式表明驻波上各点做振幅为|2Acos2πx/λ|、频率为ν的简谐运动。
由驻波的波函数易得其波节位置为:x=±(2k+1)λ/4, k=0,1,2,⋯波腹位置为:x=±kλ/2, k=0,1,2,⋯二、驻波的动能、势能、总能量、能量密度下面我们以下图所示的棒为例,假设其为弹性均匀介质。
考察距棒x处一段长为dx的体积元。
该棒的密度为ρ,截面积为S,则该体积元体积为dV=Sdx,质量为dm=ρSdx。
当波传到了该体积元时,若它的左端发生了位移y,右端位移为y+dy,这表明它不仅发生了运动,而且还发生了被拉伸dy的形变,所以它应同时具有振动动能和弹性势能。
d W k=1/2(dm)υ; (4)由式(3),该体积元的振动速度为:υ=∂y/∂t=−2πν·2 Acos2π x/λ cos2πνt=−4πν Acos2π x/λ cos2πνt(5)所以sin22πνt; (6)d W k=1/2ρdV 16π2ν2A2cos22πxλ同时,体积元因形变而具有的弹性势能d W p=k(dy)2/2, 此处k为棒的劲度系数,而k与弹性模量E的关系为k=SE/dx。
于是弹性势能为:d W p=k(dy)2/2= SE/dx·(dy)2/2= SE·dx(dy/dx)2/2;又因为υ=E/ρ.所以上式为:d W p =1/2ρυ2(dy/dx)2;而此时dy/dx =∂y/∂x =−2π/λ·2A sin 2π x/λ cos 2πνt;所以d W p =1/2 ρdV 16π2ν2A 2sin 22πxλ cos 22πνt ; (7) 所以体积元的总能量为dW=d W k + d W p =8 ρdV π2ν2A 2(cos 22πxλsin 22πνt +sin 22πxλcos 22πνt); (8)其能量密度为: W =dWdV =8ρπ2ν2A 2(cos 22πxλ sin 22πνt +sin 22πxλcos 22πνt); (9)三、驻波能量在波节波腹间的变化①相邻波节、波腹之间的能量为W= dW= 8ρ π2ν2A 2(cos 22πx λ sin 22πνt +sin 22πx λcos 22πνt)dV =S8ρ π2ν2A 2(cos 22πx λ sin 22πνt +sin 22πx λcos 22πνt)dx (2k+1)λ/42k λ/4=8S ρ π2ν2A 2[sin 22πνt ·(12x +λ8πsin 4π x/λ)|2k λ/4(2k+1)λ/4+ cos 22πνt ·(12x −λ8πsin 4π x/λ)|2k λ/4(2k+1)λ/4]=8S ρ π2ν2A 2·12·λ4(cos 22πνt +sin 22πνt)=8S ρ π2ν2A 2·12·λ4= S ρ π2ν2A 2λ (10) ②任意不相邻的波节与波腹之间的能量W= dW= 8ρ π2ν2A 2(cos 22πx λ sin 22πνt +sin 22πx λ cos 22πνt)dV =S8ρ π2ν2A 2(cos 22πx λ sin 22πνt +sin 22πx λcos 22πνt)dx 2k+1 λ4+N λ22k λ/4=(2N+1) S ρ π2ν2A 2λ 其中N 为波节、波腹间隔的个数N= 0,±1,±2,±3,⋯ (11)③对应位置之间的能量W= dW= 8ρ π2ν2A 2(cos 22πx λ sin 22πνt +sin 22πx λ cos 22πνt)dV =S8ρ π2ν2A 2(cos 22πx λ sin 22πνt +sin 22πx λcos 22πνt)dx 2k+1 λ4+N λ2+∆x 2k λ/4+∆x=(2N +1) S ρ π2ν2A 2λ 其中N 为波节、波腹间隔的个数N= 0,±1,±2,±3,⋯ (12)由上述三点可以得出这样一个结论:驻波的能量在任一波节及波腹间都保持不变,且在相对应的位置之间的能量之和也保持不变。
驻波的概念

驻波的概念驻波啊,就像是一场超级奇特的音乐派对,只不过这个派对上的客人都很“固执”。
你想象一下,有一群波的小伙伴,他们不是像普通波那样自由自在地跑来跑去传播,而是原地踏步,就好像一群士兵被下了定身咒一样。
这驻波就像是在一根绳子上玩跷跷板的小精灵。
当你在绳子一端制造了一个波动,这个波动跑啊跑,跑到另一端又被弹回来,然后就和后面来的波撞在一起。
这一撞可不得了,就像两个莽撞的小孩,撞得晕头转向之后就开始在那里叠加起来,形成了驻波这种奇妙的东西。
如果把普通的波比作是在草原上奔驰的骏马,那驻波就是马厩里原地打转的马。
它被困在一个小天地里,来回折腾,高高低低地起伏,就像一个被困在蹦床上的小怪兽,只能在那个小范围里上蹿下跳。
驻波的节点就更有趣了,那简直是波的“墓地”。
波到了那里就像是被黑洞吸进去一样,消失得无影无踪,没有一点波动的痕迹,就好像是一个超级安静的魔法禁区,周围的波都得绕道走。
而腹点呢,那可是驻波的“狂欢中心”。
这里的波动幅度超级大,像是一群精力过剩的小矮人在举行跳高比赛,一个比一个跳得高。
如果把驻波想象成一个海洋,那腹点就是浪尖,节点就是平静得像镜子一样的海面。
驻波在乐器里也是个神奇的存在。
就拿琴弦来说吧,当你拨动琴弦,驻波就像一群在琴弦上跳集体舞的小跳蚤。
它们按照特定的规则排列,让琴弦发出美妙的声音。
如果没有驻波,那琴弦就像一个哑巴,啥声音都发不出来。
从能量的角度看,驻波就像是一个吝啬鬼。
普通的波会把能量到处传播,像个散财童子。
可驻波呢,它把能量都紧紧地锁在自己的地盘里,不肯多分给别人一点,就在那几个节点和腹点之间来回捣鼓自己的能量。
有时候,驻波又像一个爱搞怪的魔术师。
在一些光学现象里,它能让光线出现一些奇特的图案,就像把光变成了一个个漂亮的小花朵或者神秘的几何图形,让人看了惊叹不已。
驻波这个东西,虽然看起来有点怪,但是它无处不在。
就像一个调皮的小幽灵,在物理世界的各个角落时不时地冒出来,给我们展示它那独特的魅力。
驻波

2p x cos = 0 l ? x ? (2k
②波腹:振幅最大的点 (两振动同相位,相互加强)
2p x cos = 1 l
2p x \ = l
(k
kp
l ? x ?k 2 两相邻波腹间的距离:
0,1, 2,......)
l D x = xk+ 1 - xk = 2 相邻的波节和波腹间的距离: l 4
∴能量始终在相邻的波节和波腹之间传递
————驻波不传播能量
二 . 两端固定的弦中的驻波 若弦中激起横向振动,经两端反射后,会形 成两列反向行进的波,叠加后形成驻波。 ∵弦的两端固定 ∴弦长 l = n l 驻波的波长 频率
2
∴两端为波节
2l (n = 1, 2, 3......) ln = n u nu nn = = u是波速 ln 2l
∴合振动的位移: 2p x x = x1 + x2 = 2A cos cos w t l
振幅因子
2p x x2 = A cos w t + ( ) l
( 不具 备传播 相位中无 x 的特征)
y
2A 0 0 0 0 x x x
t=0
t = T/ 8 t = T/4
t = 3T/8 t = T/2
振动范围 波腹
————驻波不传播波形
(3)相位特点: ①相邻波节之间质点的振动相位相同 波节: x k
xk + 1
xk < x < xk + 1 :
2p x k p = kp + l 2 2p x k + 1 3p = kp + l 2 p 2p x 3p kp + < < kp + 2 l 2
驻波波节处动能和势能

驻波波节处动能和势能1.引言1.1 概述概述驻波是物理学中一种重要的现象,它是由于传播方向相反的两个波在同一介质中叠加而形成的。
在驻波中,存在一些特殊的位置称为波节,这些位置上的振动幅度为零。
本文将重点讨论驻波波节处的动能和势能。
在物理学中,动能是指物体由于运动而具有的能量。
而势能是指物体由于位置或状态而具有的能量。
在驻波波节处,由于振动幅度为零,物体在该位置上的运动速度为零,因此其动能也为零。
与此同时,波节处的位置通常对应着波的能量最低的位置,因此在该位置上物体具有最低的势能。
驻波波节处的动能和势能之间存在着密切的关系。
当物体在波节处静止不动时,它具有最低的动能和势能。
随着物体离开波节,其动能和势能都会增加。
当物体到达波的振幅最大值处时,它具有最大的动能和势能。
因此,波节处的动能和势能是相互关联的,它们之间的变化是相反且对称的。
了解驻波波节处的动能和势能对于理解波动现象以及相关领域的研究具有重要意义。
例如,在乐器的设计和声音调整中,了解波节处的动能和势能可以帮助我们调整乐器的共振频率和音量。
此外,在无线电通信和光学通信中,了解驻波波节处的动能和势能可以帮助我们优化信号传输和接收的效果。
本文将进一步探讨驻波波节处动能和势能的定义、特点以及影响因素。
通过对相关领域的意义和应用的展望,我们可以更好地理解和应用驻波波节处的动能和势能。
文章结构部分的内容可以按照以下方式编写:1.2 文章结构本文共分为引言、正文和结论三个部分。
引言部分主要介绍了本文的概述、结构以及目的。
我们将会首先对驻波波节处动能和势能进行全面的定义和解释,并讨论它们的特点和影响因素。
接着,我们将在正文部分分别深入探讨驻波波节处动能和势能的内涵和相关理论。
最后,通过总结驻波波节处动能和势能之间的关系,我们将得出结论并展望其在相关领域中的意义和应用。
正文部分将分为两个小节,分别讨论驻波波节处动能和驻波波节处势能。
2.1 驻波波节处动能在这一小节中,我们将详细定义和解释驻波波节处动能的概念,包括它的物理意义和数学表达式。
驻波的能量分析

驻波的能量分析宋德山1,张秀珍21 驻波的能量密度设两列相干简谐波中的一列沿x轴正方向传播,另一列沿x轴负方向传播.选取共同的坐标原点和计时起点,使他们的波方程表示为y1=A cos k t-2πλx,(1)y2=A cos k t+2πλx,(2)y=y1+y2=A co s k t-2πλx+A cos k t+2πλx=2A cos2πλx co s k t.(3)形成驻波的相干波可以是纵波或横波.现就固体中的横波讨论驻波能量,但结论对纵波也适用.由(3)式可求出介质体元的速度和相对形变u=yt=-2A k cos2πλx sin k t.(4)j=yx=-2A2πλx sin2πλcos k t.(5)由此得介质体元的动能和剪切形变的势能d E k=12d d vu2=2d A2k2d v co s22πλx sin2k t,(6)d E p=12N j2d v=2d A2k2d v sin22πλx co s2k t.(7)介质体元的总能量为d E=d E k+d E p=2d A2k2d v co s22πλx sin2k t+sin22πλx cos2k t,介质内的能量密度为W=d E d v=2d A2k2cos22πλx sin2k t+sin22πλx co s2k t.(8)2 驻波中能量的定向传播由(3)式可知,驻波的波动曲线始终关于通过波腹(或波节)并与y轴平行的直线对称,这一对称性决定了波腹(或波节)附近体元的能量传播规律是:能量要么从两侧同时向波腹(或波节)处传播,要么从波腹(或波节)处同时向两侧传播,但能量不会从波腹(或波节)的一侧向另一侧传播,即在驻波振动过程中,不存在能量的定向传播.3 驻波中能量在波腹和波节间的转移下面讨论x=0(波腹)到x=λ/4(波节)之间的各体元从t=0到t=T/2这段时间内的能量变化.当t=0时,由(6)、(7)式可知,各体元的动能d E k =0,而各体元的势能则达到最大值d E p=2d A2k2d v sin22πλx,波腹处的势能为零,从波腹到波节势能逐渐增大,能量以势能的形式主要集中在波节附近.由(8)式可知,此时波腹处的能量密度为零,从波腹到波节能量密度逐渐增大,在波节处达到最大值.当t=T/4时,由(6)、(7)式可知,各体元的势能d E p=0,而各体元的动能则达到最大值d E k= 2d A2k2d v cos22πλx,从波节到波腹动能逐渐增大,能量以动能的形式主要集中在波腹附近.由(8)式可知,此时波节处的能量密度为零,从波节到波腹能量密度逐渐增大,波腹处的能量密度最大.当0<t<T/4时,由(6)、(7)式可知,除波腹处和波节处外,其他各体元既有动能,又有势能.随着各体元的振动,从波节到波腹的各个体元的势能逐渐减小,动能则逐渐增大.由(8)式可知,此过程中波腹处的能量密度逐渐增大,波节处的能量密度则逐渐减小,即在前T/4时间内能量逐渐由波节附近向波腹附近转移.在后T/4时间内,能量的变化与上述情况相反,即能量逐渐由波腹附近向波节附近转移.能量在波腹与波节间的转移是依靠弹性力做功来实现的.在前T/4时间内,各体元从各自的最大位移处向平衡位置运动,沿x轴(设正方向向右)正方向,右边的体元依靠弹性力对左边的体元做正功,能量由右边的体元向左边的体元转移.在后T/4时间内,各体元从各自的平衡位置向最大位移处运动,沿x轴正方向,左边的体元依靠弹性力对右边的体元做正功,能量由左边的体元向右边的体元转移.综上所述,在驻波振动过程中,不存在能量的定向传播,但能量可以在波腹与波节间转移.作者单位: 1.驻马店师专物理系;2.驻马店市橡林一中第17卷 第5期2002年10月天中学刊Jour nal o f T ianzhongV o l.17 N o.5O ct.2002DOI:10.14058/ k i.tzxk.2002.05.044。
公开课——驻波

2π 2 A cos( x + Φ) λ
2.波腹和波节的位置 2.波腹和波节的位置
方法一(若已知驻波方程) 方法一(若已知驻波方程)
2π y = 2A cos( x + Φ) ⋅ cos(ω t + Ψ) λ
2π cos( x + Φ) = 1 λ
(1)波腹: 令 波腹:
2π x + Φ = kπ , λ
ωt+Ψ
ωt+Ψ+π
2π [ 当 cos( x + Φ) > 0 时] λ
2π [ 当 cos( x + Φ) < 0 时] λ
A(X) o x
结论: 结论:相邻两个波节之间的 y
各点是同位相的;一个波节 o 各点是同位相的; 两侧的点是反相的。 两侧的点是反相的。
思考题:右下图, 思考题:右下图,某时刻若 已知A点的位相为 点的位相为π 则求该 已知 点的位相为π/4,则求该 时刻B点和 点的位相。 点和C点的位相 时刻 点和 点的位相。
∆ϕ = 2πx + ϕ + π ⇒ ϕ = 2π 3 3 = 10 π + ϕ + π 取 ϕ = 2π 3 3 =π
− 10 π
y反 = 0.01cos[4t+π x+2π ] (SI) 3
例. 图中画出一向右传播的简谐波在t时刻 的波形图, 为波密介质的反射面, 的波形图,BC为波密介质的反射面,波由P 点反射,则反射波在t时刻的波形图为 [ B ]
y1 = A cos(ω t + + y 2 = A cos(ω t-
2π
则另一列波的波动方程必可设为
λ
x+
驻波的能量与能流

x
,
乙 由能 流 密度 连续 性方 程
刁
甲
了二
分
W t
刁
J
l
X
W I
J
J
( 8) 故 可 以 肯定 存在 能流
,
( 式) 可 知 由7
,
才
一
附( x
,
) l ,
等
`
, 0
我们 不 必 解 出式 ( ) 8
的微分 方程 度 L
,
可 由形成 驻 波 的 相 向传 播 的 行 波 的 能 流 密度 I
第
期
李锦英等
y 一x
驻波的能量与能流 图 象 和 卜 x 图象
I
:
下 图描绘 出 的是驻 波 不 同时刻 的 图中
曲线为
y 一x
曲线 为
一x
扬州 工 学院学报
年
几 点结论
能 流在 波腹与波节 间 回 荡 由图 可 见 每隔
_ _
, ,
在 腹 点 与节 点 ,
,
一
。
,
,
在 (0
,
哥
)日 寸间 内 I 指 向腹 点 ; 在 (
y
Z
一 `
“
二
,
`
手 奇
、
+
) 波 长 和 周期
。
口 而成 的 迭力
式中
,
A
、
、
“
T
分另 “ 为“ 波的 振幅
。
显然
二
一 、
叠
处 为驻
波波 腹
,
在二
一
2 、+ (
驻波精品文档

实验结果分析:通 过波形图分析驻波 的特点和影响因素
实验步骤
准备实验器材: 包括弦线、振 动测量仪器、 信号发生器等
安装弦线:将 弦线固定在两 个端点上,确
保弦线绷紧
信号发生器连 接:将信号发 生器连接到弦 线上,以产生
振动信号
振动测量:使 用振动测量仪 器测量弦线的 振动幅度和频
率
数据记录与分 析:记录实验 数据,并进行 分析,以得出
弦的振动与琴弓 的摩擦产生音乐
不同弦乐器利用 不同长度的弦产 生不同音调
电磁波的传播
无线通信:利用驻波实现信号传输 雷达系统:通过驻波进行目标探测和定位 卫星通信:利用驻波实现地球与卫星之间的信号传输 电磁波的传播方式:驻波是其中的一种重要形式,具有特定的传播特性
地震波传播
地震波传播原理
地震波传播的衰减规律
驻波
汇报人:XX
目录
01 02 03 04 05
驻驻驻驻驻 波波波波波 的的的的的 形特应实未 成点用验来
研发 究展
01
驻波的形成
波的干涉现象
波的干涉定义:两列或两 列以上的波在空间相遇时 发生叠加,形成新的波动 现象。
形成条件:频率相同、振 动方向相同、相位差恒定。
干涉现象:在波的干涉区 域内,某些点的振动加强 ,某些点的振动减弱,形 成稳定的强弱分布。
输和存储方式。
在特定频率下产生共振
驻波的特点之一是在 特定频率下产生共振。
驻波的能量在空间中 分布均匀,不会向外
传播。
驻波的振幅和相位在空 间中保持不变,只在特
定频率下产生共振。
驻波的频率与产生它 的振源的频率相同。
03
驻波的应用
ห้องสมุดไป่ตู้
关于驻波能量的基本认识

关于驻波能量的基本认识姓名:李昕学号:D3******* 专业:生物工程一、什么是机械波机械振动在介质中的传播称为机械波(mechanical产wave)。
机械波与电磁波既有相似之处又有不同之处,机械波由机械振动产生,电磁波由电磁振荡生;机械波的传播需要特定的介质,垂直,则这种波称为横波;如果振动波的方向与波的方向平行,则称为纵波。
)在不同介质中的传播速度也不同,在真空中根本不能传播,而电磁波(例如光波)可以在真空中传播;机械波可以是横波和纵波,(如果振动方向与波的传播方向但电磁波只能是横波;机械波与电磁波的许多物理性质,如:折射、反射等是一致的,描述它们的物理量也是相同的。
常见的机械波有:水波、声波、地震波。
机械波传播的基本条件:有波源和传播机械振动的介质。
这是产生机械波的两个基本条件。
波的传播实质即波动实质上是波的振动状态在介质中的传播。
而且传播过程有两个特点:1、介质中各质点都在做与波源同方向同频率的振动。
2、沿着波的传播方向,介质中各质点的振动相位是逐一落后的二、机械波的能量因为在机械波传播的过程中,各质元即由静止开始振动,同时也发生了形变。
所以机械波传播的过程中一定有动能与弹性势能的转化。
振动动能+形变势能=波的能量在平衡点,其振动速度最大,故动能最大。
同时该处的形变最大因此该处质点的动能和势能为最大,其总能量也就最大。
而位于波峰的A点和位于波谷的C点其动能和形变最小为零所位于平衡位置的以其能量最小。
所以介于平衡位置和波峰之间的点和介于平衡位置和波谷之间的点其能量介于最大和零之间。
离平衡位置越近的质点,它的能量就越大,即能量在波的传播方向上也呈现周期性的分布,随着波形的向前传播,这种能量分布的状态也以波的传播速度向前传递。
三、驻波的能量驻波是频率和振幅均相同、振动方向一致、传播方向相反的两列波叠加后形成的波。
波在介质中传播时其波形不断向前推进,故称行波;上述两列波叠加后波形并不向前推进,故称驻波。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关于驻波能量的基本认识
姓名:李昕学号:D3******* 专业:生物工程
一、什么是机械波
机械振动在介质中的传播称为机械波(mechanical产wave)。
机械波与电磁波既有相似之处又有不同之处,机械波由
机械振动产生,电磁波由电磁振荡生;机械波的传播需要特定
的介质,垂直,则这种波称为横波;如果振动波的方向与波的
方向平行,则称为纵波。
)在不同介质中的传播速度也不同,在
真空中根本不能传播,而电磁波(例如光波)可以在真空中传
播;机械波可以是横波和纵波,(如果振动方向与波的传播方向
但电磁波只能是横波;机械波与电磁波的许多物理性质,如:
折射、反射等是一致的,描述它们的物理量也是相同的。
常见
的机械波有:水波、声波、地震波。
机械波传播的基本条件:有波源和传播机械振动的介质。
这是产生机械波的两个基本条件。
波的传播实质即波动实
质上是波的振动状态在介质中的传播。
而且传播过程有两
个特点:
1、介质中各质点都在做与波源同方向同频率的振动。
2、沿着波的传播方向,介质中各质点的振动相位是逐一
落后的
二、机械波的能量
因为在机械波传播的过程中,各质元即由静止开始振动,同时也
发生了形变。
所以机械波传播的过程中一定有动能与弹性势能的转化。
振动动能+形变势能=波的能量
在平衡点,其振动速度最大,故动能最大。
同时该处的形变最大因此该处质点的动能和势能为最大,其总能量也就最大。
而位于波峰的A点和位于波谷的C点其动能和形变最小为零所位于平衡位置的以其能量最小。
所以介于平衡位置和波峰之间的点和介于平衡位置和波谷之间的点其能量介于最大和零之间。
离平衡位置越近的质点,它的能量就越大,即能量在波的传播方向上也呈现周期性的分布,随着波形的向前传播,这种能量分布的状态也以波的传播速度向前传递。
三、驻波的能量
驻波是频率和振幅均相同、振动方向一致、传播方向相反的两列波叠加后形成的波。
波在介质中传播时其波形不断向前推进,故称行波;上述两列波叠加后波形并不向前推进,故称驻波。
例如,如图所示,一弦线的一端与音叉一臂相连,另一端经支点O并跨过滑轮后与一重物相连。
音叉振动后在弦线上产生一自左向右传播的行波,
传到支点 O 后发生反射,弦线中产生一自右向左传播的反射波,当
弦长接近1/2波长的整数倍时。
两列波叠加后弦线上各点的位移为(设音叉振动规律为u=Acosωt) u(x,t)=2Asin(x)sin(ωt )=A(x)sin(ωt),弦线上每个固定的点均作简谐运动,但不同点的振幅不同,由x值决定。
振幅为零的点称为波节,振幅最大处称
为波腹。
波节两侧的振动相位相反。
相邻两波节或波腹间的距离都是
半个波长。
在行波中能量随波的传播而不断向前传递,其平均能流密度不为零;但驻波的平均能流密度等于零,能量只能在波节与波腹间来回运行。
测量两相邻波节间的距离就可测定波长。
各种乐器,包括弦乐器、管乐器和打击乐器,都是由于产生驻波而发声。
为得到最强的驻波,弦或管内空气柱的长度L必须等于半波长的整数倍,即,k为整数,λ为波长。
因而弦或管中能存在的驻波波长为,相应的振动频率为,υ为波速。
k=1时,,称为基频,除基频外,还可存在频率为kn1的倍频。
简谐波在弹性介质中传播时,波所经过的质元都在各自平衡位置附近振动,具有动能,同时弹性介质产生了形变,又具
有弹性势能。
现在以横波为例,研究体元的动能、势能以及总
的机械能。
在有简谐横波传播的介质内,取一微小体元,根据简谐波方程2.2.1可求其振动速度。
形成驻波的简谐波可以是纵波
或横波,现就横波为例定量讨论驻波的能量,但是结论对纵波
也适用。
同样驻波在弹性介质中传播时,波所经过的质元都在
各自平衡位置附近振动,具有动能,同时弹性介质产生了形变,
又具有弹性势能。
因此驻波的能量为弹性介质中质元的动能和
势能之和。
设驻波在密度为 的弹性介质中传播,在介质中取
一体元V ,则该质元的质量为m ,则该质元的质量
为Vm 同理,在有驻波传播的介质内,
按照求“平面简谐波的动能、势能、总机械能”的方法,可求其驻波振动速度。
①在驻波传播中,波节处的各质元始终不动,动能为零,只有弹性势能,弹性势能随时间作周期变化;波腹处的各质元没有形变,弹性势能为零,只有动能,动能随时间作周期性变化。
其它位置上的质元既有动能,又有弹性势能。
②在驻波传播中,能量只在相邻波节(波腹)、波腹(波节)之间流动,每一段{波节(波腹)和波腹(波节)之间}都可看作一个独立单元,没有能量通过波节和波腹,任一单元内各部分同时达到最大位移,又同时回到平衡位置。
并且各段上的总能量守恒,与时间无关。
在驻波传播中,相邻波节(波腹)、波腹(波节)之间的动能与势能不断地相互转换,当所有质元都振动到平衡位置时,相邻波节和波腹之间的能量会全部转化为动能。
当所有质元都振动到最大位移时,相邻波节和波腹之间的能量会全部转化为势能。
由于驻波在传播过程中能量只在局部区域内流动,没有沿某一固定方向传播,所以得出驻波能量的主要特征是:能量只在波节波腹间来回振荡,并且不向外传播,不存在沿单一方向的能流。
