戴维南定理和诺顿定理在电路中的分析应用
戴维南定理、诺顿定理和最大功率传输的验证及分析

戴维南定理、诺顿定理和最大功率传输的验证及分析一.戴维南定理1.实验目的:1)掌握戴维南定理相关知识2)掌握利用Mulstim软件分析验证相关的原理3)加深对等效变换的理解。
2.实验原理:戴维南定理:含独立电源的线性电阻单口网络N,就端口特性而言,可以等效为一个电压源和电阻串联的单口网络。
Uoc称为开路电压,R0称为戴维南等效电阻。
当单口网络视为电源时,称此电阻为输出电阻R0;当单口网络视为负载时,则称为输入电阻Ri。
电压源Uoc和电阻R0的串联单口网络,称为戴维南等效电路。
3.实验步骤:1)画出电路2)算出理论值3)利用Mulstim软件分析验证4)得出结论理论值:R1电流I1=U/I=6A U=IR=12V二.诺顿定理1.实验目的:1)掌握诺顿定理相关知识2)掌握利用Mulstim软件分析验证相关的原理3)加深对等效变换的理解。
2.实验原理:诺顿定理:含独立源的线性电阻单口网络N,就端口特性而言,可以等效为一个电流源和电阻的并联。
电流源的电流等于单口网络从外部短路时的端口电流isc;电阻R0是单口网络内全部独立源为零值时所得网络N0的等效电阻。
4.实验步骤:1)画出电路2)算出理论值3)利用Mulstim软件分析验证4)得出结论理论值:U=1A×2×2/(2+2)=1V I=1V/2/2×(2+2)=1A三.最大功率传输1.实验目的:1)掌握最大功率传输相关知识2)掌握利用Mulstim软件分析验证相关的原理3)加深对等效变换的理解。
2.实验原理:最大功率传输定理是关于使含源线性阻抗单口网络向可变电阻负载传输最大功率的条件。
定理满足时,称为最大功率匹配,此时负载电阻(分量)RL获得的最大功率为:Pmax=Uoc^2/4R0。
直流电路含源线性电阻单口网络(Ro>0)向可变电阻负载RL传输最大功率的条件是:负载电阻RL与单口网络的输出电阻Ro相等。
满足RL=Ro条件时,称为最大功率匹配,此时负载电阻RL获得的最大功率为:Pmax=Uoc^2/4R0。
戴维南定理和诺顿定理实验报告

竭诚为您提供优质文档/双击可除戴维南定理和诺顿定理实验报告篇一:电路实验报告戴维南定理和诺顿定理的验证戴维南定理和诺顿定理的验证一、实验目的1.验证戴维南定理和诺顿定理的正确性,加深对该定理的理解。
2.掌握测量有源二端网络等效参数的一般方法。
二、原理说明任何一个线性含源网络,如果仅研究其中一条支路的电压和电流,则可将电路的其余部分看作是一个有源二端网络(或称为含源一端口网络)。
戴维南定理指出:任何一个线性有源网络,总可以用一个电压源与一个电阻的串联来等效代替,此电压源的电动势us等于这个有源二端网络的开路电压uoc,其等效内阻R0等于该网络中所有独立源均置零(理想电压源视为短接,理想电流源视为开路)时的等效电阻。
诺顿定理指出:任何一个线性有源网络,总可以用一个电流源与一个电阻的并联组合来等效代替,此电流源的电流Is等于这个有源二端网络的短路电流Isc,其等效内阻R0定义同戴维南定理。
四、实验内容被测有源二端网络如图3-4(c)(d),需要自行连接电路。
(c)Tx型设备实验电路图(d)等效图图3-4实验电路图和等效图1.用开路电压、短路电流法测定戴维南等效电路的uoc、R0和诺顿等效电路的Isc、R0。
按图3-4(a)或3-4(c)接入稳压电源us=12V和恒流源Is=10mA,不接入RL。
测出uoc 和Isc,并计算出R0(测uoc时,不接入mA表),填入右表中。
2.负载实验按图3-4(a)或3-4(c)连线,接入RL。
根据下表中负载RL3.验证戴维南定理:从电阻箱上取得按步骤“1”所得的等效电阻R0之值,然后令其与直流稳压电源(调到步骤“1”时所测得的开路电压uoc之值)相串联,如图3-4(b)或3-4(d)所示,仿照步骤“2”测4.验证诺顿定理:从电阻箱上取得按步骤“1”所得的等效电阻R0之值,然后令其与直流恒流源(调到步骤“1”时所测得的短路电流Isc之值)相并联,如图3-5所示,仿照步骤“2”测其外特性,对诺顿定图3-5Tx型设备电流源电路图及等效图五、实验注意事项1.测量时应注意电流表量程的更换。
戴维南定理、诺顿定理

戴维南定理、诺顿定理戴维南定理和诺顿定理是电路分析中常用的两个重要定理。
它们分别用于简化复杂电路的计算和分析,为工程师提供了便利。
本文将依次介绍戴维南定理和诺顿定理的原理和应用。
一、戴维南定理戴维南定理是一种将电路中的电源和负载分离计算的方法。
它通过将电源和负载分别替换为等效电源和等效电阻,简化了电路的计算过程。
根据戴维南定理,我们可以将电源替换为一个等效电压源,其电压等于原电源的电压,内阻等于原电源的内阻。
同样地,我们可以将负载替换为一个等效电阻,其阻值等于原负载的阻值。
通过这样的替换,原本复杂的电路被简化为一个等效电压源和一个等效电阻的串联电路。
这样的简化使得电路的计算更加便捷,尤其适用于大规模复杂电路的分析。
二、诺顿定理诺顿定理是一种将电路中的电源和负载分离计算的方法。
它通过将电源和负载分别替换为等效电流源和等效电阻,简化了电路的计算过程。
根据诺顿定理,我们可以将电源替换为一个等效电流源,其电流等于原电源的电流,内阻等于原电源的内阻。
同样地,我们可以将负载替换为一个等效电阻,其阻值等于原负载的阻值。
通过这样的替换,原本复杂的电路被简化为一个等效电流源和一个等效电阻的并联电路。
这样的简化使得电路的计算更加便捷,尤其适用于大规模复杂电路的分析。
三、戴维南定理和诺顿定理的应用戴维南定理和诺顿定理在电路分析中有着广泛的应用。
它们可以用于计算电路中的电流、电压、功率等参数,帮助工程师进行电路设计和故障排查。
通过戴维南定理,我们可以将复杂的电路转化为等效电路,从而简化计算。
例如,在求解电路中某个分支的电流时,我们可以将其他分支看作一个等效电阻,这样就可以利用欧姆定律直接计算电流。
而诺顿定理则更适用于电流的计算。
通过将电路中的电源和负载分离,我们可以更方便地计算负载电流。
例如,在计算电路中某个负载的电流时,我们可以将电源看作一个等效电流源,利用欧姆定律计算电流。
戴维南定理和诺顿定理为电路分析提供了重要的工具和方法。
实验五 戴维南定理和诺顿定理

实验五戴维南定理和诺顿定理一、实验目的1.验证戴维南定理和诺顿定理的正确性,加深对两个定理的理解。
2.掌握含源二端网络等效参数的一般测量方法。
3.验证最大功率传递定理。
二、原理说明戴维南定理与诺顿定理在电路分析中是一对“对偶”定理,用于复杂电路的化简,特别是当“外电路”是一个变化的负载的情况。
在电子技术中,常需在负载上获得电源传递的最大功率。
选择合适的负载,可以获得最大的功率输出。
1.戴维南定理任何一个线性有源网络,总可以用一个含有内阻的等效电压源来代替,此电压源的电动势Es等于该网络的开路电压Uoc,其等效内阻Ro等于该网络中所有独立源均置零(理想电压源视为短接,理想电流源视为开路)时的等效电阻。
2.诺顿定理任何一个线性含源单口网络,总可以用一个含有内阻的等效电流源来代替,此电流源的电流Is等于该网络的短路电流Isc,其等效内阻Ro等于该网络中所有独立源均置零时的等效电阻。
Uoc、Isc和Ro称为有源二端网络的等效参数。
3.最大功率传递定理在线性含源单口网络中,当把负载RL以外的电路用等效电路(Es+Ro或Is∥Ro)取代时,若使R L=Ro,则可变负载R L上恰巧可以获得最大功率:P MAX=I sc2.R L/4=Uoc2/4RL (1)4.有源二端网络等效参数的测量方法⑴开路电压Uoc的测量方法①直接测量法直接测量法是在含源二端网络输出端开路时,用电压表直接测其输出端的开路电压Uoc,如图5-1(a)所示。
它适用于等效内阻Ro较小,且电压表的内阻Rv>>Ro的情况下。
②零示法在测量具有高内阻(Ro>>Rv)含源二端网络的开路电压时,用电压表进行直接测量会造成较大的误差,为了消除电压表内阻的影响,往往采用零示测量法,如图5-1(b)所示。
零示法测量原理是用一低内阻的稳压电源与被测有源二端网络进行比较,当稳压电源的输出电压Es与有源二端网络的开路电压Uoc相等时,电压表的读数将为“0”,然后将电路断开,测量此时稳压电源的输出电压,即为被测有源二端网络的开路电压。
戴维南和诺顿定理的验证实验报告

戴维南和诺顿定理的验证实验报告实验目的:验证戴维南和诺顿定理。
实验原理:戴维南和诺顿定理是电路理论中的基本定理之一。
它表示任何包含电压源和电流源的线性电路可以用其电压源和电流源的代数和来等效为一个独立电压源和电流源的并联电路。
实验装置:- 直流电源- 滑动变阻器- 电阻器- 电压表- 电流表- 连接线实验步骤:1. 将实验装置按照电路图连接好,确保电路没有接错。
2. 设置直流电压源的电压值为一定值,例如5V。
3. 测量并记录电路中各个元件的电压和电流数值。
4. 更改电路中的滑动变阻器的阻值,测量并记录电路中各个元件的电压和电流数值。
5. 使用戴维南和诺顿定理,将实验得到的电压和电流数据进行计算,验证定理的成立。
实验结果:表格1:电路1的各个元件的电压和电流数据元件电压(V)电流(A)电压源 5.0 0.5电流源0.0 1.0电阻器R1 2.5 0.5电阻器R2 2.5 0.5总电阻(R1+R2) 5.0 1.0表格2:电路2的各个元件的电压和电流数据元件电压(V)电流(A)电压源 5.0 0.5电流源0.0 1.0电阻器R1 2.0 0.4电阻器R2 3.0 0.6总电阻(R1+R2) 5.0 1.0根据戴维南和诺顿定理,两个电路的电压源和电流源的代数和应该相等。
计算结果:对于电路1:电压源的代数和= 5.0V + 0.0V = 5.0V,电流源的代数和= 0.5A + 1.0A = 1.5A。
对于电路2:电压源的代数和= 5.0V + 0.0V = 5.0V,电流源的代数和= 0.5A + 1.0A = 1.5A。
实验结论:通过实验结果和计算可以看出,戴维南和诺顿定理在实际电路中成立,验证了定理的准确性。
戴维南定理和诺顿定理的验证实验报告 -回复

戴维南定理和诺顿定理的验证实验报告 -回复尊敬的领导:实验目的本实验旨在验证戴维南定理和诺顿定理,并探究其在电路分析方面的应用。
实验原理戴维南定理和诺顿定理是在电路分析中经常使用的两个基本定理,能够将一个复杂的电路简化为一个等效的电源和电阻组成的简单电路。
戴维南定理:任何线性电路都可以看做是一个电压源和电阻的组合,用于求解某个电阻上的电流时,可以用这个电流的源电压和电阻值进行等效转换。
即:$I=\frac{V_S}{R_S+R_L}$$V_S$为等效电源电压,$R_S$为等效电源内阻,$R_L$为负载电阻。
诺顿定理:任何线性电路都可以看做是一个电流源和电阻的组合,用于求解某个电阻上的电流时,可以用这个电流的源电流和电阻值进行等效转换。
即:$I=\frac{I_S \cdot R_N}{R_N+R_L}$$I_S$为等效电流源电流,$R_N$为等效电流源内阻,$R_L$为负载电阻。
实验设计本实验设计了两组电路,分别用于验证戴维南定理和诺顿定理。
具体电路图如下:戴维南定理验证电路图:诺顿定理验证电路图:实验步骤1. 按照实验设计,搭建电路图。
2. 测量各元件的电阻值,并分别记录在表中。
3. 连接电流计和电压计,并记录电流和电压值。
4. 根据戴维南定理和诺顿定理公式,计算出等效电源电压、等效电源内阻、等效电流源电流和等效电流源内阻等值。
5. 测量负载电阻值,并根据公式计算出电路中的电流值。
6. 将负载电阻值替换为理论计算的电流值,再次测量电路中的电流值,并进行对比分析。
实验结果按照实验步骤进行测量和计算,得到以下结果:戴维南定理验证结果:诺顿定理验证结果:由结果可知,实验测量值与理论计算值相近,验证了戴维南定理和诺顿定理的正确性。
实验分析本实验从实际电路出发,验证了戴维南定理和诺顿定理的准确性,并说明了两个定理在电路分析上的实际应用。
实验结果也提示我们,实际电路中各元件的阻值存在一定的误差,因此在实际应用中需要谨慎处理。
实验三戴维南定理和诺顿定理的验证

实验三戴维南定理和诺顿定理的验证一、实验目的1、理解戴维南定理和诺顿定理的内涵与应用。
2、初步掌握使用直流电桥、电流表、电压表等测量仪器的能力。
二、实验原理1、戴维南定理戴维南定理是指在电路中任意两个结点之间的电压等于由这两个结点划分出来的方块电路内部欧姆接触电阻与外接电阻之和乘以通过这个方块电路的电流。
戴维南定理的实际应用与布朗—博利定理类似,也是希望通过这个定理来简化电路分析和设计过程中繁琐的计算。
学习戴维南定理主要是为了在电路分析和设计中寻找我们需要的信息。
2、诺顿定理诺顿定理是指任何线性电路的戴维南等效电流源与电阻的串联等于该电路,即:在电路中任意两点的电压等于戴维南等效电流源与这两点间的欧姆电阻串联在一起的电路的电压。
诺顿定理与戴维南定理是等价的,因此学习它们两个定理的任一一个都可以很好地理解和应用它们两个。
三、实验器材和器件示波器万用表直流电源初始化电阻电箱直流电桥四、实验步骤(1)连接和调节实验电路:按照实验电路图连接电路。
(2)找寻电路中的方块电路:将电路按照结点手法分成方块,再将方块内的欧姆电阻与外接电阻相加,求出它们的和R。
(3)测量电路电流:在电路中加入电流表I01、I02,分别测量出I01、I02,作为通过方块电路的电流Ip。
(5)计算电路方块的电压:将U01 - U02的值除以Ip,求出方块电路的电压Up。
(6)实验验证:实验中得到的Up和实际测量值的误差小于5%,表明戴维南定理的应用正确。
(2)求出诺顿等效电流源的电流:通过电路中的电阻电箱,依次取出100Ω、1kΩ、10kΩ、100kΩ等不同阻值的电阻,将它们依次串联在电路中,通过万用表测量电阻电箱电阻值并各自记下,然后将测量出的电流值与电阻值计算出来,可以得到诺顿等效电流源的电流。
(3)在电路中加入一电阻:通过电路中的电阻电箱,在电路中加入一电阻表现为RL。
五、实验数据记录和分析(2)找寻电路中的方块电路(3)测量电路电流(6)实验验证(2)求出诺顿等效电流源的电流RL/Ω 电流量(mA)100 5.0001k 0.82410k 0.100100k 0.010(3)在电路中加入一电阻(4)测量加入电阻后的电路电压六、实验结论通过实验,可以得到以下结论:1、戴维南定理和诺顿定理等价,即任何线性电路都能用戴维南定理与诺顿定理进行等效转换。
戴维南定理和诺顿定理的应用场景

戴维南定理和诺顿定理的应用场景1. 引言嘿,朋友们,今天我们来聊聊两个电路分析的超级英雄——戴维南定理和诺顿定理。
没错,它们可不是出现在漫威电影里的角色,但绝对能在电路的世界里大显身手。
说到电路,很多人可能觉得这东西像外星语言一样晦涩难懂,但其实只要掌握了这两位英雄的技能,分析电路就像吃西瓜一样简单。
接下来,咱们就来看看它们的应用场景,保准让你对这两个定理爱不释手。
1.1 戴维南定理的魅力首先,咱们得说说戴维南定理。
这个定理的核心思想是把复杂的电路“简化”,用一个等效的电压源和串联电阻来替代。
听起来有点拗口?别担心,想象一下你把一堆麻烦的事情都简化成了一个简单的任务。
比如说,你的朋友约你去看电影,结果他带了十个朋友,最后你变成了一个大杂烩。
但如果你只需约一个人,那岂不是简单多了?这就是戴维南定理的神奇之处。
你可以把复杂的电路看成一大堆麻烦的事情,而戴维南就像那个靠谱的朋友,帮你把它们整理得清清爽爽。
那么,戴维南定理常用在哪些场景呢?想象一下你在设计一个电路,电流和电压波动得像过山车。
你可能需要快速分析一下不同组件的影响,哎呀,电阻、源电压,这些玩意儿全都搅合在一起。
这时候,戴维南定理就像你的导航仪,帮你一眼看出这电路的“本质”,让你轻松解决问题。
1.2 诺顿定理的实用性接下来,咱们再来聊聊诺顿定理。
这个家伙跟戴维南有点像,但它更注重的是电流源和并联电阻的组合。
你可以把它想象成一个时尚搭配的高手,总能把各种元素巧妙组合在一起。
诺顿定理的精髓在于,无论你面对的是怎样的电路,最终都能将其简化为一个电流源和并联电阻。
想象一下,你正在参加一个聚会,各种小圈子让你感觉像在迷宫里转悠。
可是,如果你知道哪个圈子最热闹,哪个人最有趣,那你就能迅速融入进去。
诺顿定理就是帮你找到这些“热点”,让你在复杂的电路中游刃有余。
2. 应用场景2.1 实际电路分析现在咱们来看看这两个定理在实际电路分析中的应用。
比如说,你正在修理一个老旧的收音机,里面的电路像是一个年代久远的秘密花园。
戴维南定理和诺顿定理

01
பைடு நூலகம்
戴维南定理
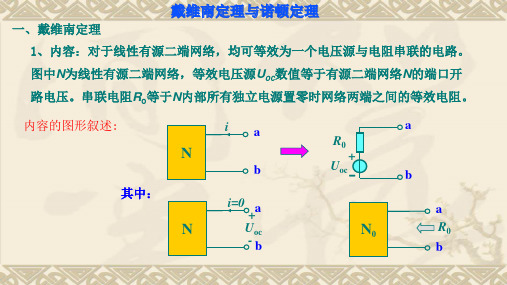
任何有源线性二端网络,总可以用一个电压源和一个电阻串联来表示。
电压源的电压等于网络的开路电压,电阻等于网络内部所有独立源为零
时的等效电阻。
02
诺顿定理
任何有源线性二端网络,总可以用一个电流源和一个电阻并联来表示。
电流源的电流等于网络的短路电流,电阻等于网络内部所有独立源为零
时的等效电阻。
交叉学科研究
随着电子工程与其他学科的交叉融合,戴维南定理和诺顿定理可以与其他学科的理论和方法相结合,开 展交叉学科的研究和应用。
THANKS
戴维南定理与诺顿定理在电路分析中的应用选择
选择应用戴维南定理或诺顿定理取决于具体电路的特性和需求。如果需要计算一端口网络的开路电压 或短路电流,则应用戴维南定理;如果需要计算一端口网络的等效电阻或等效电流,则应用诺顿定理 。
在实际应用中,可以根据一端口网络的性质和电路分析的目的选择合适的定理。例如,对于一个无源 一端口网络,如果需要计算其等效电阻,则可以选择应用诺顿定理;对于一个有源一端口网络,如果 需要计算其开路电压或短路电流,则可以选择应用戴维南定理。
诺顿定理
任何一个有源线性二端网络,对其外部电路来说,都可以用一个等效的理想电流 源和电阻并联的电源模型来代替。其中,理想电流源的电流等于有源线性二端网 络的短路电流,电阻等于该网络的开路电压与电流源电流的比值。
戴维南定理和诺顿定理的重要性
简化电路分析
通过应用戴维南定理和诺顿定理,可以将复杂的有源电路简化为简单的电源模型,从而简化电路 分析过程。
电子设备设计
在电子设备设计中,可以利用戴维南定理来计算电路的性能 参数,如电压放大倍数、输入电阻等。
诺顿等效电路

uS R1 isc i2 i3 iS2 iS1 iS2 R1 R2 R3
Ro
( R1 R2 ) R3 R1 R2 R3
诺顿定理
• 三、含源线性电阻单口网络的等效电路 • 从戴维南——诺顿定理的学习中可以知道,含 源线性电阻单口网络可以等效为一个电压源和电阻 的串联或一个电流源和电阻的并联[(b)和(c)]。
戴维南定理
• 例4-7 求图所示单口网络的戴维南等效电路。
戴维南定理
• 解:先求开路电压Uoc • 在单口网络的端口上标明开路电压Uoc的 参考方向,注意到i=0,可求得
i=0
u oc 1V (2) 2A 3V
戴维南定理
• • 求等效电阻Ro
将单口网络内1V电压源用短路代替,2A电流 源用开路代替,得到图(b)电路,由此求得
12 u oc 12 V (24 V) 4V 12 24
诺顿定理
• 为求isc,将单口短路,并设isc的参考方向 由a指向b,如图4-2-20(b)所示。
isc i1 i2
12 V (24 12)V 0.5A 12 24
诺顿定理
• 为求Ro,将单口内的电压源用短路代替, 得到图4-22(c)电路,用电阻并联公式求得
戴维南定理
图 4-10
uoc称为开路电压。Ro称为戴维南等效电阻。
戴维南定理
电压源 uoc和电阻Ro的串联单口网络,称 为戴维南等效电路。
戴维南定理
当单口网络的端口电压和电流采用关联参 考方向时,其端口电压、电流关系方程可表示 为
u Ro i uoc
戴维南定理
戴维南定理的应用
戴维南定理的主要用途是简化电路,便于计算。特别适 用于计算电路中某一支路的电流、电压、功率等,或者求某 一支路的元件参数之类的特殊计算。 (1) 开路电压Uo c 的计算 戴维南等效电路中电压源电压等于将外电路断开时的开路 电压Uo c,电压源方向与所求开路电压方向有关。计算Uoc的方 法视电路形式选择前面学过的任意方法进行计算。 (2)等效电阻RO的计算 等效电阻就是将单口网络内部独立电源全部置零 ( 电压 源短路,电流源开路)后,所得无源单口网络的输入电阻。
戴维南定理和诺顿定理 实验

一、基本原理:A.戴维南定理和诺顿定理:戴维南定理:含独立源的线性电阻单口网络N,就其端口来看,可等效为一个电压源串联电阻的支路。
其中电压源的电压等于网络N的开路电压uoc,串联的电阻等于网络N中所有独立源置零时所得网络N0的等效电阻R0。
诺顿定理:含独立源的线性电阻单口网络N,就其端口来看,可等效为一个电流源与电阻并联的组合。
其中电流源的电流等于网络N的短路电流isc,并联的电阻等于网络N中所有独立源置零时所得网络N0的等效电阻R0。
测量实际二端网络(EEL-53)的开路电压(用电压表)和短路电流(电流表),得到二端网络的内阻,改变负载的电阻,记下不同电阻的电压和电流。
通过一个等效电路,电流源和电阻并联(诺顿定理),和另一个等效电路,电压源和电阻串联(戴维南定理)在不同负载电阻的电流和电压与其比对,若作出的数据图表拟合性好,证明验证戴维南定理和诺顿定理成功,否则失败。
B.有源二端网络等效参数的测量方法:开路电压、短路电流法在有源二端网络输出端开路时,用电压表直接测其暑促段的开路电压U,然后再将其输出端短路,测其短路电流I,则其内阻是:R=U/IC.置换定理一个有唯一解的电阻电路N,若已知其中一个单口网络NK的端口电压,用一个电压值为a的电压源置换该单口网络NK,若置换后的电路也有唯一解,则置换前后电路其余部分的电流和电压值保持不变。
测量电路只接12V电压源,只接6V电压源,两个同时接上时,EEL-52各个支路和元件的电流和电压,由数据记录的叠加,验证叠加定理二、简要实验步骤:A.任务一:1.按实验书原理图接好电路。
2.S1上拔,S2右拔,记录电压。
3.S1下拔,S2左拔,记录电流。
4.计算内阻R 。
任务二:1.在原电路加负载。
2.记录下各阻值下的电流和电压。
任务三:1.按实验书电流源和电阻并联。
2.记录下各阻值下的电流和电压。
3.按实验书电压源和电阻串联。
4记录下各阻值下的电流和电压。
5.作图比较拟合程度。
戴维南定理和诺顿定理
(3)求得诺顿等效电路后,将4Ω电阻接上,得图(c),由此可得: I 9.6 1.67 2.78A 4 1.67
含受控源电路戴维南定理的应用
例3. 求U0 。 6
– 6I + a
+
I
9V 3
–
解: (1) 求开路电压Uoc
+ 3 U0
– b
R0
+ Uoc
–
6
– 6I + a
+
I
9V 3
–
+
Uoc=6I+3I
Uoc
I=9/9=1A
–
b
a +
3 U0 -
b
Uoc=9V
(2) 求等效电阻R0 方法1:外加电源法
内部独立 源置零
6 3
– 6I + I
I0 a
+
U0 –
b
U0=6I+3I=9I I=I06/(6+3)=(2/3)I0
R0 = U0 /I0=6
N0
a
b a R0 b
2、适用范围 只求解复杂电路中的某一条支路电流或电压时。
3、应用举例 【例1】用戴维南定理求图 (a)电路中的电流I。
解:(1)求开路电压Uoc,如图(b)电路所示。
(a)
(b)
U oc
U
' oc
U
" oc
R1
R3
R3
U
s
[R2
(R1
//
R3 )]I s
12 12 (4 6 12 ) 0.5 8 4 12V
戴维南定理和诺顿定理在电路中的分析应用

期中考试(论文)(2014届)题目戴维南定理和诺顿定理在电路分析中应用学院物理与电子工程学院专业电子信息工程班级14电子信息工程(1)班学号1430220014学生姓名毛征姜指导教师孙运旺副教授完成日期2015年4月戴维南定理和诺顿定理在电路分析中应用The Application of Thevenin's Theorem and Norton's Theorem in circuit analysis学生姓名:毛征姜Student: Mao Zheng Jiang指导老师:孙运旺副教授Adviser: Vice Professor Sun Yunwang台州学院物理与电子工程学院School of Physics & Electronics EngineeringTaizhou UniversityTaizhou, Zhejiang, China2015年4月May2015摘要介绍了戴维南定理和诺顿定理在电路中的分析应用关键词戴维南定理;诺顿定理。
目录1.引言 (4)2.戴维南定理 (4)2.1戴维南定理介绍 (4)2.2戴维南等效电路的计算 (5)2.3注意事项 (6)3.诺顿定理 (7)3.1诺顿定理介绍 (7)3.2诺顿等效电路的计算 (7)3.3注意事项 (8)4.戴维南定理和诺顿定理 (9)4.1戴维南定理和诺顿定理在含受控源电路中的应用 (9)4.2戴维南等效电路和诺顿等效电路的相互转换 (11)5.结论 (12)参考文献 (13)引言戴维南定理和诺顿定理在电路分析中是非常重要的。
希望通过这次论文能让我加深对戴维南定理和诺顿定理的了解和对毕业论文设计的模式有一些了解。
2戴维南定理2.1戴维南定理介绍戴维南定理(Thevenin's theorem)又称等效电压源定律,是由法国科学家L·C·戴维南于1883年提出的一个电学定理。
由于早在1853年,亥姆霍兹也提出过本定理,所以又称亥姆霍兹-戴维南定理。
戴维南定理、诺顿定理

戴维南定理、诺顿定理戴维南定理和诺顿定理是电路理论中的两个重要定理,它们在电路分析和设计中有着广泛的应用。
本文将分别介绍这两个定理的概念和应用,并探讨它们在电路领域中的重要性。
一、戴维南定理戴维南定理,也称为戴维南-诺顿定理,是电路理论中的基本定理之一。
它是由英国科学家戴维南和诺顿在19世纪末提出的,用于简化复杂电路的分析。
该定理表明,任何一个线性电路都可以用一个电压源和一个串联的电阻模型等效代替。
戴维南定理的核心思想是将电路分为两部分:被测电路和测量电路。
被测电路是指需要分析的电路,而测量电路是指用于测量电路参数的电路。
根据戴维南定理,可以将被测电路的复杂结构简化为一个等效的电压源和串联电阻。
通过戴维南定理,我们可以方便地计算电路中的电流和电压。
例如,在分析直流电路时,可以通过测量电压源的电压和串联电阻的电流,来确定整个电路的特性。
这样,我们可以将复杂的电路问题转化为简单的电路问题,从而更容易解决。
二、诺顿定理诺顿定理,也称为诺顿-戴维南定理,是电路理论中的另一个重要定理。
它与戴维南定理相似,也是用于简化电路分析的工具。
诺顿定理表明,任何一个线性电路都可以用一个电流源和一个并联的电导模型等效代替。
诺顿定理的思想与戴维南定理相似,同样将电路分为被测电路和测量电路。
不同的是,诺顿定理通过一个电流源和并联电导来简化被测电路。
这样,我们可以通过测量电流源的电流和并联电导的电压,来确定整个电路的特性。
诺顿定理的应用同样广泛。
在分析交流电路时,诺顿定理可以帮助我们简化电路结构,从而更方便地计算电流和功率。
通过将复杂的电路分解为简单的电路,我们可以更加精确地预测电路的性能,并进行相应的设计和调整。
三、戴维南定理与诺顿定理的关系戴维南定理和诺顿定理虽然在表述上有所不同,但实质上是等效的。
它们都可以将复杂的电路简化为一个等效的电源和电阻或电流源和电导。
两者的转换关系可以通过一些简单的数学运算实现。
具体而言,戴维南定理可以通过将电流源的电流与串联电阻的阻值相除,得到等效的电压源和串联电阻。
戴维南定理和诺顿定理

主要内容:戴维南定理和诺顿定理
重点难点:戴维南定理
4-3戴维南定理和诺顿定理
一、定理
对于任一含源线性二端网络,就其两个端钮而言,都可以用一条最简单支路对外部等效。
1.以一条实际电压源支路对外部等效,其中电压源的电压值等于该含源线性二端网络端钮处开路时的开路电压 ,其串联电阻值等于该含源线性二端网络中所有独立源令为零时,由端钮处看进去的等效电阻 ,此即戴维南定理。
将上述网络中的独立源分成两组,即线性含源二端网络中的所有独立源为一组,电流源I为一组。
当线性含源二端网络中的独立源共同作用时,电流源I断开,如图(c),此时求得的电压分量 ,即为a、b支路断开时的开路电压UOC,得 。
当电流源I单独作用时,原线性含源二端网络中的所有独立源令为零值,如图(d),此时从a、b两点向左看即为等效电阻 ,则 (注意参考方向)。
则
可见,分析过程中使用了求等效电阻的一般方法、电流源的分裂方法及叠加定理三个知识点。
最大功率传输
主要内容:最大功率传输
重点难点:最大功率传输
4-3最大功率传输
一、利用戴维南定理分析含受控源的电路
原则:1.被等效电路内部与负载内部不应有任何联系(控制量为端口U或I除外)
2.求 要用一般方法
例1:电路如图4-17(a)所示,用戴维南定理求电压U。
(a)(b)
图4-19
我们知道: 而
利用数学中求极值的方法:
令 ,得
即:当负载电阻RL与戴维南等效电阻Req相等时,负载电阻可从含源线性二端网络获得最大功率。此时最大功率为:
而戴维南等效电路中电源Uoc的效率
可见此时等效电源Uoc的效率只达50%,而Uoc所产生的功率有一半白白地损耗在等效电阻Req上,这在电力系统中是决不允许的,故电力系统中通常取RL>>Req。负载电阻吸收的功率和电源Uoc的效率随负载电阻变化的曲线如图4-20所示。
实验八 戴维南定理和诺顿定理

实验八戴维南定理和诺顿定理一、实验目的1.验证戴维南定理和诺顿定理的正确性,加深对两个定理的理解。
2.掌握含源二端网络等效参数的一般测量方法。
3.验证最大功率传递定理。
二、原理说明戴维南定理与诺顿定理在电路分析中是一对“对偶”定理,用于复杂电路的化简,特别是当“外电路”是一个变化的负载的情况。
在电子技术中,常需在负载上获得电源传递的最大功率。
选择合适的负载,可以获得最大的功率输出。
1.戴维南定理任何一个线性有源网络,总可以用一个含有内阻的等效电压源来代替,此电压源的电动势Es等于该网络的开路电压Uoc,其等效内阻Ro等于该网络中所有独立源均置零(理想电压源视为短接,理想电流源视为开路)时的等效电阻。
2.诺顿定理任何一个线性含源单口网络,总可以用一个含有内阻的等效电流源来代替,此电流源的电流Is等于该网络的短路电流Isc,其等效内阻Ro等于该网络中所有独立源均置零时的等效电阻。
Uoc、Isc和Ro称为有源二端网络的等效参数。
3.最大功率传递定理在线性含源单口网络中,当把负载RL以外的电路用等效电路(Es+Ro或Is∥Ro)取代时,若使R L=Ro,则可变负载R L上恰巧可以获得最大功率:P MAX=I sc2.R L/4=Uoc2/4RL (1)4.有源二端网络等效参数的测量方法⑴开路电压Uoc的测量方法①直接测量法直接测量法是在含源二端网络输出端开路时,用电压表直接测其输出端的开路电压Uoc,如图8-1(a)所示。
它适用于等效内阻Ro较小,且电压表的内阻Rv>>Ro的情况下。
②零示法在测量具有高内阻(Ro>>Rv)含源二端网络的开路电压时,用电压表进行直接测量会造成较大的误差,为了消除电压表内阻的影响,往往采用零示测量法,如图8-1(b)所示。
零示法测量原理是用一低内阻的稳压电源与被测有源二端网络进行比较,当稳压电源的输出电压Es与有源二端网络的开路电压Uoc相等时,电压表的读数将为“0”,然后将电路断开,测量此时稳压电源的输出电压,即为被测有源二端网络的开路电压。
4.3.戴维南定理和诺顿定理

–– 66II++ Io
II
+ ++ 3UU0UC 0
– ––
Uoc=9V
②求等效电阻Req 方法1:加压求流
独立源置零
U=6I+3I=9I
U =9 (2/3)I0=6Io
I=Io6/(6+3)=(2/3)Io Req = U /Io=6
方法2:开路电压、短路电流 6
6I –+
(Uoc=9V) 6 I1 +3I=9 6I+3I=0
i
Req
u i
b
b
③开路电压,短路电流法。 Req
Req
uoc isc
+ Uoc
-
2 3 方法更有一般性。
i
a +
u
-b
注意
① 外电路可以是任意的线性或非线性电路,外电路 发生改变时,含源一端口网络的等效电路不变(伏 -安特性等效)。
② 当一端口内部含有受控源时,控制电路与受控
源必须包含在被化简的同一部分电路中。 a
Uoc 50 25 5
60 30
2A
50V
PL
5I
2 L
5
4
20W
–
+
例4 已知开关S
1 A =2A
线性 + S
1 2
2
+ 1A
+1A
3 +
含源 4V 网络-
A5
V -
5 U -
U -
2 V =4V 求开关S打向3,电压U等于多少。
解 iSc 2A Uoc 4V
等效电源定理及应用

电压源的电压等于有源二端网络的开路电压uoc;串联电阻等于有源二端网络全部独立源置零后的等效电阻Ri.
关于无源二端网络的等效电阻的三种计算方法:
I 等效电源定理包括戴维南定理和诺顿定理.
例3、求如图所示电路中3.
18 2A
6 3 (b)中电压源电阻串联电路为戴维南等效电路,电压源电压等于有源二端网络的开路电压,如图(c)所示;
解:(1)求开路电压UOC: 断开所求支路6Ω电阻后得一含源二端网络,如图(b)
所示。由电路图可求二端网络的开路电压为 UOC=2×2=4v
(2)求等效电阻Ri:
将含源泉二端网络中的所有独立源置零,如图(c)所示。 则二端网络的等效电阻为:
Ri=2Ω (3)求支路电流I。
用戴维南等效电路代替含源二端网络,如图(d)所
串联电阻等于有源二端网络除源后得到的无源二端网络的等效电阻,如图(d)所示。
电路如图所示,US1=8V,US2=4V,R1=R2=4Ω,R3=2Ω。
2Ω电阻的电压:用出戴维南等效电路,接上3.
( d ) 图 ( a ) 的 等 效 电 路 下图为戴维南定理示意图:(a)中所示NS为含有独立源、线性电阻或受控源的有源二端网络。
例3、求如图所示电路中3.2Ω电阻两端的电压Uo
解(1)求开路电压UOC 如图(b)所示,则
I1I261401A UOC10I14I2101416V
(2)求等效电阻Ri
电路如图(c)所示: 独立电压源短路后,
外加电源电压U,设 端口电流为I 则有
I
1
6
4
4
I
0.4I
U 10I1 6I1 16I1 6.4I
图(a)的等效电路,如图(d)所示,由图可求得I为: 例1、用戴维南定理求如图所示电路中的电流I
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
戴维南定理和诺顿定理在电路中的分析应用期中考试(论文)( 2014届)题目戴维南定理和诺顿定理在电路分析中应用学院物理与电子工程学院专业电子信息工程班级14电子信息工程(1)班学号1430220014学生姓名毛征姜指导教师孙运旺副教授2 / 15完成日期2015年4月戴维南定理和诺顿定理在电路分析中应用The Application of Thevenin's Theorem and Norton's Theorem in circuit analysis学生姓名:毛征姜Student: Mao Zheng Jiang指导老师:孙运旺副教授Adviser: Vice Professor Sun Yunwang台州学院物理与电子工程学院School of Physics & Electronics EngineeringTaizhou UniversityTaizhou, Zhejiang, China2015年4月May2015摘要介绍了戴维南定理和诺顿定理在电路中的分析应用关键词戴维南定理;诺顿定理。
目录1.引言 (4)2.戴维南定理 (4)2.1戴维南定理介绍 (4)2.2戴维南等效电路的计算 (5)2.3注意事项 (6)3.诺顿定理 (7)3.1诺顿定理介绍 (7)3.2诺顿等效电路的计算 (7)3.3注意事项 (8)4.戴维南定理和诺顿定理 (9)4.1戴维南定理和诺顿定理在含受控源电路中的应用 (9)4.2戴维南等效电路和诺顿等效电路的相互转换 (11)5.结论 (12)参考文献 (13)引言戴维南定理和诺顿定理在电路分析中是非常重要的。
希望通过这次论文能让我加深对戴维南定理和诺顿定理的了解和对毕业论文设计的模式有一些了解。
2戴维南定理2.1戴维南定理介绍戴维南定理(Thevenin's theorem)又称等效电压源定律,是由法国科学家L·C·戴维南于1883年提出的一个电学定理。
由于早在1853年,亥姆霍兹也提出过本定理,所以又称亥姆霍兹-戴维南定理。
其内容是:一个含有独立电压源、独立电流源及电阻的线性网络的两端,就其外部型态而言,在电性上可以用一个独立电压源V和一个松弛二端网络的串联电阻组合来等效。
在单频交流系统中,此定理不仅适用于电阻,也适用于广义的阻抗。
此定理陈述出一个具有电压源及电阻的电路可以被转换成戴维南等效电路,这是用于电路分析的简化技巧。
戴维南等效电路对于电源供应器及电池(里面包含一个代表内阻抗的电阻及一个代表电动势的电压源)来说是一个很好的等效模型,此电路包含了一个理想的电压源串联一个理想的电阻。
2.2戴维南等效电路计算在计算戴维南等效电路时,必须联立两个由电阻及电压两个变数所组成的方程,这两个方程可经由下列步骤来获得,但也可以使用端口在其他条件下的状态得出:1. 在AB两端开路(在没有任何外电流输出,亦即当AB点之间的阻抗无限大)的状况下计算输出电压V AB,此输出电压就是V Th。
2. 在AB两端短路(亦即负载电阻为零)的状况下计算输出电流I AB,此时R Th等于V Th除以I AB。
•此等效电路是由一个独立电压源V Th与一个电阻R Th串联所组成。
其中的第2项也可以考虑成:a. 首先将原始电路系统中的电压源以短路取代,电流源以开路取代。
b. 此时,用一个电阻计从AB两端测得系统的总电阻R,即等效电阻R Th。
2.3注意事项(1)戴维南定理只对外电路等效,对内电路不等效。
也就是说,不可应用该定理求出等效电源电动势和内阻之后,又返回来求原电路(即有源二端网络内部电路)的电流和功率。
(2)应用戴维南定理进行分析和计算时,如果待求支路后的有源二端网络仍为复杂电路,可再次运用戴维南定理,直至成为简单电路。
(3)戴维南定理只适用于线性的有源二端网络。
如果有源二端网络中含有非线性元件时,则不能应用戴维南定理求解。
(4)戴维南定理和诺顿定理的适当选取将会大大化简电路3 诺顿定理3.1诺顿定理的介绍诺顿定理(Norton's theorem)指的是一个由电压源及电阻所组成的具有两个端点的电路系统,都可以在电路上等效于由一个理想电流源I与一个电阻R并联的电路。
对于单频的交流系统,此定理不只适用于电阻,亦可适用于广义的阻抗。
诺顿等效电路是用来描述线性电源与阻抗在某个频率下的等效电路,此等效电路是由一个理想电流源与一个理想阻抗并联所组成的。
诺顿定理是戴维宁定理的一个延伸,于1926年由两人分别提出,他们分别是西门子公司研究员汉斯·梅耶尔(1895年-1980年)及贝尔实验室工程师爱德华·劳笠·诺顿(1898-1983)。
实际上梅耶尔是两人中唯一有在这课题上发表过论文的人,但诺顿只在贝尔实验室内部用的一份技术报告上提及过他的发现。
3.2诺顿等效电路的计算任何只包含电压源、电流源及电阻的黑箱系统,都可以转换成诺顿等效电路要计算出等效电路,需:1. 在AB两端短路(亦即负载电阻为零)的状况下计算输出电流I AB。
此为I NO。
2. 在AB两端开路(在没有任何往外电流输出,亦即当AB点之间的阻抗无限大)的状况下计算输出电压V AB,此时R No等于V AB除以I NO。
•此等效电路是由一个独立电流I NO与一个电阻R NO并联所组成。
其中的第2项也可以考虑成:•2a.将原始电路系统中的独立电压源以短路取代,而且将独立电流源以开路取代。
•2b.若电路系统中没有非独立电源的话,则R No为移走所有独立电源后的电阻*。
3.3注意事项•(1)诺顿定理只对外电路等效,对内电路不等效。
也就是说,不可应用该定理求出等效电源电动势和内阻之后,又返回来求原电路(即有源二端网络内部电路)的电流和功率。
•(2)应用诺顿定理进行分析和计算时,如果待求支路后的有源二•11诺顿定理端网络仍为复杂电路,可再次运用诺顿定理,直至成为简单电路。
•(3)诺顿定理只适用于线性的有源二端网络。
如果有源二端网络中含有非线性元件时,则不能应用诺顿定理求解。
4戴维南和诺顿定理4.1 戴维南定理和诺顿定理在含受控源电路中的应用例如图4-1 所示含源一端口的戴维南等效电路和诺顿等效电路。
一端口内部有电流控制电流源,i c=0.75i1。
解先求开路电压u oc。
在图4-1(a)中,当端口1—1'开路时,有i2=i1+i c=1.75i1对网孔1列KVL方程,得5*1000*i1+20*1000i2=40代入i2=1.75i1,可以求得i1=1mA。
而开路电压u oc=20*1000*i2=35V当1-1'短路时,可求的短路电流isc【见图4-1(b)】。
此时i1=40/5000A=8mAi sc=i1+i c=1.75i1=14mA故得R eq=u oc/i sc=2.5kΩ对应的戴维南等效电路和诺顿等效电路分别如图4-1(c)和图4-1(d)所示。
图4-1注意:当含源一端口内部含受控源时,在它的内部独立电源置零后,输入电阻有可能为零或无限大。
如果R eq=0而开路电压u oc为有限值,此时含源一端口存在戴维南等效电路且仅为一个无伴电压源(即u oc),而无电阻与之串联,但因G eq与i sc均趋向无限大,故不存在诺顿等效电路。
如果求的R eq为无限大(或G eq=0)而短路电流i sc为有限值,此时含源一端口存在诺顿等效电路且仅为一个无伴电流源(即i sc),而无电阻与之并联,但因R eq与u oc均趋于无限大,故不存在戴维南等效电路。
通常情况下,两种等效电路都是存在的。
4.2 戴维南等效电路和诺顿等效电路的相互转换图4-2(1)诺顿等效电路转换为戴维南等效电路如图4-2所示,左边为诺顿等效电路,右边为戴维南等效电路,诺顿等效电路与戴维南等效电路之间的关系,可由下列方程来描述:其中、、及分别代表戴维南等效电阻、诺顿等效电阻、戴维南等效独立电压源以及诺顿独立电流源。
(2)戴维南等效电路转换为诺顿等效电路如图4-2所示,左边是诺顿等效电路,右边是戴维宁等效电路,可用下列方程将诺顿等效电路转换成戴维宁等效电路:其中、、及分别代表戴维宁等效电阻、诺顿等效电阻、戴维宁等效独立电压源以及诺顿独立电流源结论本次期中考试论文我选择了戴维南定理和诺顿定理在电路分析中应用这个课题。
通过查阅资料,我确定了自己本次论文的思路:分别介绍戴维南定理和诺顿定理在电路中的作用。
通过这次论文,我学到了很多,从中受益匪浅:首先,在这次论文中,我对戴维南定理和诺顿定理及其作用有了一个更加深刻的了解。
其次,在写论文的整个过程中,我也遇到了一些问题,特别是在刚开始查阅资料的时候,很茫然,那时候还没有确定好思路,不知道该从哪里下手。
现在,论文已圆满完成。
在这个过程中,我不仅学会了查阅资料的技巧,还学会了坚持。
不论是在生活,学习还是工作中,我们都会遇到许许多多的困难,面对困难,我们要保持积极乐观的心态,尽自己最大的努力去寻找解决问题的办法,只有这样,才能一步一步走向成功。
参考文献1.维基百科:戴维南定理、诺顿定理;2.百度百科:戴维南定理、诺顿定理;3.电路第五版4-3 戴维宁定理和诺顿定理;。
