§10-5 两个自由度体系的自由振动(柔度法)
合集下载
吸振器
2
D1 P k 22 2 m2 k12 P2 1 D2 P2 k11 2
k 21 k11 m1
2
m k
1
21P 1
D
k 21
0
如果荷载频率θ与任一个自振频率 ω1、 ω2重合，则D0=0, 当D1、D2 不全为零时，则出现共振现象
5
例：质量集中在楼层上m1、m2 ，层间侧移刚度为k1、k2 解：荷载幅值：P1=P，P2=0，求刚度系数： k11=k1+k2 , k21=－k2 , k22=k2 , k12=－k2
两个主振型相互正交，因与质量有关，称为第一正交关系。 3
由功的互等定理：
2 2 (m112Y11 )Y12 (m212Y21 )Y22 (m12 Y12 )Y11 (m22 Y22 )Y21
m1Y11Y12 m2Y21Y22 0(15.51)
上式分别乘以ω12、ω22，则得：
如图示对称结构在对称荷载作用下。
k11 k22 , k12 k21
与ω2相应的振型是
Psinθt m l/3 l/3
Psinθt m l/3
Y12 k12 2 2 =－1 k 22 2 m k11 2 m k12 k 21 2 2 m Y22 k11
当θ=ω2 ，D0=0 ，也有： 对称体系在对称荷载作用下时， 只有当荷载频率与对称主振型的自 2 D1 P k 22 2 m2 k12 P2 振频率相等时才发生共振；当荷载 P k 22 2 m k12 P 0 1 频率与反对称主振型的自振频率相 2 D2 P2 k11 2 m1 k 21P 等时不会发生共振。同理可知：对 P k11 2 m k 21P 0 1 称体系在反对称荷载作用下时，只 有当荷载频率与反对称主振型的自 D1 D2 不会趋于无穷大，不发生共振， Y1 , Y2 振频率相等时才发生共振。 D0 D0 共振区只有一个。
D1 P k 22 2 m2 k12 P2 1 D2 P2 k11 2
k 21 k11 m1
2
m k
1
21P 1
D
k 21
0
如果荷载频率θ与任一个自振频率 ω1、 ω2重合，则D0=0, 当D1、D2 不全为零时，则出现共振现象
5
例：质量集中在楼层上m1、m2 ，层间侧移刚度为k1、k2 解：荷载幅值：P1=P，P2=0，求刚度系数： k11=k1+k2 , k21=－k2 , k22=k2 , k12=－k2
两个主振型相互正交，因与质量有关，称为第一正交关系。 3
由功的互等定理：
2 2 (m112Y11 )Y12 (m212Y21 )Y22 (m12 Y12 )Y11 (m22 Y22 )Y21
m1Y11Y12 m2Y21Y22 0(15.51)
上式分别乘以ω12、ω22，则得：
如图示对称结构在对称荷载作用下。
k11 k22 , k12 k21
与ω2相应的振型是
Psinθt m l/3 l/3
Psinθt m l/3
Y12 k12 2 2 =－1 k 22 2 m k11 2 m k12 k 21 2 2 m Y22 k11
当θ=ω2 ，D0=0 ，也有： 对称体系在对称荷载作用下时， 只有当荷载频率与对称主振型的自 2 D1 P k 22 2 m2 k12 P2 振频率相等时才发生共振；当荷载 P k 22 2 m k12 P 0 1 频率与反对称主振型的自振频率相 2 D2 P2 k11 2 m1 k 21P 等时不会发生共振。同理可知：对 P k11 2 m k 21P 0 1 称体系在反对称荷载作用下时，只 有当荷载频率与反对称主振型的自 D1 D2 不会趋于无穷大，不发生共振， Y1 , Y2 振频率相等时才发生共振。 D0 D0 共振区只有一个。
两个自由度体系的自由振动
根据达朗伯原理，列平衡方程
y1 r1 0 m1 y2 r2 0 m2
(a)
r2 与结构的位移 y1 、 y2 之间 图10-30c中，结构所受的力 r1 、 满足刚度方程。
r1 k11 y1 k12 y2 r2 k 21 y1 k 22 y2
Y1 和 Y不全为零的解答，则： 2 k12 k11 2 m1 0 D 2 k22 m2 k21
(4-3a)
式(4-3a)称为频率方程或特征方程，可求频率。
将式（4-3a）展开：
Hale Waihona Puke (k11 m1 )(k22 m2 ) k12k21 0
2 2
2 2
（4-3b)
（4-2）
Y11 k12 Y21 k11 12 m1
（4-5a）
这个比值确定的振动形式：第一圆频率1相对应 的振型，称为第一振型或基本振型。 同样，由
第二振 型中质 点1的振 幅
2
得：
Y12 k12 2 Y22 k11 2 m1
第二振型中质 点2的振幅
（4-5b）
求出的两个振型分别如图10-31b、c
在一般情况下，两个自由振动体系的自由振动可 看作是两个频率及其主振型的组合振动，即，
方程（41）的全 解
y1 (t ) AY 1 11 sin(1t 1 ) A2Y 12 sin(2t 2 ) y2 (t ) AY 1 21 sin(1t 1 ) A2Y22 sin(2t 2 )
1
2
2 (11m1 22m2 ) (1122m1m2 1221m1m2 ) 0
(11m1 22 m2 ) (11m1 22 m2 ) 2 4(11 22 12 21 )m1m2 1 2 2
多自由度自由振动.
2
1、刚度法：（建立力的平衡方程）
两个自由度的体系
y2(t)
质点动平衡方程:
m2 .y.2 r2
y2(t) r2
m1 y..1 r1 0, m2 y..2 r2 0
r1=k11y1+k12y2 r2=k21y1+k22y2
y1(t) m1.y.1 r1 y1(t) r1
即: m1 y..1 k11 y1 k12 y2 0 m2 y..2 k21 y1 k22 y2 0
(m111 )Y1 m212Y2 0 m1 21Y1 (m2 22 )Y2 0 D m111 m212 0
m1 21 m2 22
振型方程：其中：λ=1/ω2
Y1 ，Y2不能全为零。
频率方程
不能有振型方程求出Y1 ，Y2的解，只能求出它们的比值。
Y1 12m2 Y2 11m1
Y12 12m2
1.125m/ EI
1
Y22 11m1 2 2.5m/ EI 1.125m/ EI 1
2 1
1 1
Yij为正时 表示质量mi的
运动方向与计 算柔度系数时 置于其上的单 位力方向相同， 为负时，表示 与单位力方向 相反。
m1Y11Y12
m2Y21Y22
m 2
(2) (1)
32
..
mi yi ri 0
(i 1,2,..., n)
ri ki1 y1 ki2 y2 ... kin yn
(i 1,2,..., n)
m.mmm.1.12n.y....yy....12n.m..2..k.kk.1.21n.11y.yy.111....m.k.kkn.1.22n.22y.y.y2yy...y..2...2.1.n2................kkk.k.1.2nk.k111.1.n2n.ynn..ynykkk..nn1n2.222...0..00............
1、刚度法：（建立力的平衡方程）
两个自由度的体系
y2(t)
质点动平衡方程:
m2 .y.2 r2
y2(t) r2
m1 y..1 r1 0, m2 y..2 r2 0
r1=k11y1+k12y2 r2=k21y1+k22y2
y1(t) m1.y.1 r1 y1(t) r1
即: m1 y..1 k11 y1 k12 y2 0 m2 y..2 k21 y1 k22 y2 0
(m111 )Y1 m212Y2 0 m1 21Y1 (m2 22 )Y2 0 D m111 m212 0
m1 21 m2 22
振型方程：其中：λ=1/ω2
Y1 ，Y2不能全为零。
频率方程
不能有振型方程求出Y1 ，Y2的解，只能求出它们的比值。
Y1 12m2 Y2 11m1
Y12 12m2
1.125m/ EI
1
Y22 11m1 2 2.5m/ EI 1.125m/ EI 1
2 1
1 1
Yij为正时 表示质量mi的
运动方向与计 算柔度系数时 置于其上的单 位力方向相同， 为负时，表示 与单位力方向 相反。
m1Y11Y12
m2Y21Y22
m 2
(2) (1)
32
..
mi yi ri 0
(i 1,2,..., n)
ri ki1 y1 ki2 y2 ... kin yn
(i 1,2,..., n)
m.mmm.1.12n.y....yy....12n.m..2..k.kk.1.21n.11y.yy.111....m.k.kkn.1.22n.22y.y.y2yy...y..2...2.1.n2................kkk.k.1.2nk.k111.1.n2n.ynn..ynykkk..nn1n2.222...0..00............
《理论力学 动力学》 第十一讲 两个自由度系统的自由振动
两个自由度系统的振动理论曾凡林哈尔滨工业大学理论力学教研组本讲主要内容1、两个自由度系统的自由振动2、两个自由度系统的受迫振动1、两个自由度系统的自由振动（1）模型的简化同一物体的振动可以简化为不同的振动模型。
C研究上下平移振动研究前后颠簸振动两个自由度系统的自由振动模型112122222122()00mxk k x k x m x k x k x ++-=üý-+=þ&&&&2212121m k d m k c m k k b ==+=，，令方程变为：11221200xbx cx x dx dx +-=-+=&&&&，根据微分方程理论，可设上列方程组的解为：)sin()sin(21q w q w +=+=t B x t A x ，其中：A 、B 是振幅；ω为角频率，θ是初始相位角。
将上式代入微分方程组，得到：)sin()sin()sin(0)sin()sin()sin(22=+++++-=+-+++-q w q w q w w q w q w q w w t dB t dA t B t cB t bA t A 整理后得到：0)(0)(22=++-=--B d dA cB A b w w ，系统振动时，方程组具有非零解, 则方程组的系数行列式必须等于零，即：22=----ww d dc b —频率行列式①固有频率1、两个自由度系统的自由振动)()(24=-++-c b d d b w w 行列式展开后得到：—系统的本征方程，又称为频率方程21,22b d w +=m 2b d +=m i ω2的两个根都是实数，而且都是正数。
ii ω2的第一个根较小，称为第一固有频率。
iii ω2的第二个根较大，称为第二固有频率。
结论：两个自由度系统具有两个固有频率，这两个固有频率只与系统的质量和刚度等参数有关，而与振动的初始条件无关。
第六节 两个自由度体系的自由振动
4l 3 = , 243EI
δ 12 = δ 21
7l 3 = 486 EI
(2)求自振频率 求自振频率 将柔度系数及m 代入式(11-48)求得 将柔度系数及 1=m2=m代入式 代入式 求得
15ml 3 λ1 = (δ 11 + δ 12 )m = , 486 EI
于是得到两个自振频率
ml 3 λ2 = (δ 11 − δ 12 )m = 486 EI
y1 (t ) = −m1 ɺɺ1 (t )δ 11 − m2 ɺɺ2 (t )δ 12 y y y 2 (t ) = −m1 ɺɺ1 (t )δ 21 − m2 ɺɺ2 (t )δ 22 y y
或
δ 11m1 ɺɺ1 (t ) + δ 12 m2 ɺɺ2 (t ) + y1 (t ) = 0 y y δ 21m1 ɺɺ1 (t ) + δ 22 m2 ɺɺ2 (t ) + y 2 (t ) = 0 y y
大值)和 小值)如下 由此可解出 λ 的两个正实根 λ 1 (大值 和λ 2 (小值 如下： 大值 小值 如下：
λ1, 2 = [(δ 11 m1 + δ 22 m2 ) ± (δ 11 m1 − δ 22 m2 ) 2 + 4m1 m2δ 12 2 ]
1 2
λ1, 2 = [(δ 11 m1 + δ 22 m 2 ) ± (δ 11 m1 − δ 22 m2 ) 2 + 4m1 m2δ 12 2 ]
试求图a所示等截面简支梁的自振频率和主振型 所示等截面简支梁的自振频率和主振型。 例11-9 试求图 所示等截面简支梁的自振频率和主振型。
解：(1)求柔度系数 求柔度系数 体系有两个自由度。 如图b、 所示 所示。 体系有两个自由度。作 M 1、M图，如图 、c所示。由图乘法求得柔度系数 2
25 两个自由度体系的自由振动计算(柔度法)
(m111 − ) m1 21
m212 = 0 (m222 − )
2
−
(m111
+
m222
)
+
m1m2
(1122
−
2 12
)
=
0
1
=
m111
+ m222
2
+
(m111
+
m222 )2
−ቤተ መጻሕፍቲ ባይዱ
4m1m2 (1122
−
2 12
)
2
2
=
m111
+ m222
2
−
(m111
+
m2 22
)2
−
4m1m2
(11 22
25 、两个自由度体系的自由振动（柔度法）
25.1、运动方程的建立 图1a所示为两个自由度体系(梁的质量略去不计)，质点m1 和m2的位移分别为y1(t)和y2(t)，它们都是从静平衡位置量 取并以向下为正。可以认为在自由振动过程中的任一瞬
时，质点m1、m2的位移y1(t)和y2(t)是由惯性力 −m1 y1(t)
2 ) A1 (m2 22
+ m212 A2 −1 2 ) A2
= =
0
0
上式是A1 和A2的齐次线性代数方程组。其中零解对应于无振动的情况，不是所 要求的解答。为使上述方程组具有非零解，则其系数行列式必须等于零，即
频率方程
D=
(m111
−
1 2
)
m1 21
m212
=0
(m2 22
−
1 2
)
= 1 2
式中，A1 、A2分别是质点m1 、m2 的位移幅值，ω为体系的自振频率。
多自由度自由振动
2
486 EI
20
3m
例：求图示体系对称振动情况下的频率。 m/2 1 m EI
m m EI 3m m
1
0.25 2 1 0.875
M1
0.5 1
3m
EI 3m
M2
4.5 1.6875 1.125 1 11 0 22 4.5 12 21 M1 , M1 相乘:11 EI EI EI EI 4. m ) ( 4.5 m )2 4(1 3 )m m m 1 ( 11m( 5 22 .6875) 11m1 1.22 2 ) 2 4 (4.51.687521.1252 )2 2 11 22 12 1 1 0相乘 6875 1 1122 MEI 2:1 1.6875( 2 M ,22 22 2 0 2 2 M 10 M2 EI 0 1 M 2 ,.M10相乘或M1 ，M 2 相乘.596 EI , 1 0.943 EI 2 8125 / EI m 0 3 1 2 1 m m 1 2 2 1. /1.125 125m EI 12 21 EI
k21=－k2 ,
k22=k2 ,
k12=－k2
12
3 5 k k 0.38197 2 m m k 2 3 5 k 2 2.61803 2 m m
21
22
2
1 0.61803 2 1.61803
k k
m m
9
求振型： Y11 ω1→第一主振型：
Y21
k 1 k12 2 2k 0.38197 1.618 k k11 1 m1
§10-5 多自由度体系的自由振动
工程中的结构有些可简化为单自由度体系分析 单层工业厂房 水塔 有些不能作为单自由度体系分析，需简化为多自由度体系 进行分析 多层房屋、高层建筑 不等高厂房排架和块式基础
486 EI
20
3m
例：求图示体系对称振动情况下的频率。 m/2 1 m EI
m m EI 3m m
1
0.25 2 1 0.875
M1
0.5 1
3m
EI 3m
M2
4.5 1.6875 1.125 1 11 0 22 4.5 12 21 M1 , M1 相乘:11 EI EI EI EI 4. m ) ( 4.5 m )2 4(1 3 )m m m 1 ( 11m( 5 22 .6875) 11m1 1.22 2 ) 2 4 (4.51.687521.1252 )2 2 11 22 12 1 1 0相乘 6875 1 1122 MEI 2:1 1.6875( 2 M ,22 22 2 0 2 2 M 10 M2 EI 0 1 M 2 ,.M10相乘或M1 ，M 2 相乘.596 EI , 1 0.943 EI 2 8125 / EI m 0 3 1 2 1 m m 1 2 2 1. /1.125 125m EI 12 21 EI
k21=－k2 ,
k22=k2 ,
k12=－k2
12
3 5 k k 0.38197 2 m m k 2 3 5 k 2 2.61803 2 m m
21
22
2
1 0.61803 2 1.61803
k k
m m
9
求振型： Y11 ω1→第一主振型：
Y21
k 1 k12 2 2k 0.38197 1.618 k k11 1 m1
§10-5 多自由度体系的自由振动
工程中的结构有些可简化为单自由度体系分析 单层工业厂房 水塔 有些不能作为单自由度体系分析，需简化为多自由度体系 进行分析 多层房屋、高层建筑 不等高厂房排架和块式基础
10-5两个自由度体系的自由振动
Ymn
m
代表质点的振幅
n
代表振动的频率
y1 (t ) = AY 1 11 sin(ω1t + α1 ) + A2Y 12 sin(ω2 t + α 2 ) ⎫ ⎬ y2 (t ) = AY sin( ω t + α ) + A Y 1 21 1 1 2 22 sin(ω2 t + α 2 ) ⎭
A1 A2 α1 α 2 由初始条件来确定。
大
Y11 = 1
Y12 = 1
ω1 = 0.618
ω2 = 1.618
第一主振型
第二主振型
2
2013-6-25
1. 刚度法
1. 刚度法
讨论：
m2
m1 = nm2
k2
k1 = nk2
2 2 2 2
mn
yn (t )
− mn yn mn rn
n
拓展：
n个自由度体系
[(n + 1)k 2 − ω nm2 ](k 2 − ω m2 ) − k = 0
k12 =0 k12 − ω 2 m2
k1 = k2 = k
2
2 ω2 = 2.618
第一 主振型 第二 主振型
Y11 k12 k 1 =− = = Y21 k11 − ω12 m1 2k − 0.382k 1.618
(k11 − ω 2m1 )( k 22 − ω 2 m2 ) − k12 k21 = 0
频率 方程
主振型
作业
习题 P483：10-18、19
k11 − ω m1 k21
2
k12 =0 k12 − ω 2 m2
Y11 k12 =− Y21 k11 − ω12 m1
两个自由度体系的自由振动.
2
1 1,2 m1 22 m 2 11
Y1 12 m2 1 Y2 11m1 2
22 m2
1
21m1
2
1
1
1
1
Y1 12 m2 (1) 1 Y2 11m1 2
(1)
1
2
2
Y1 12 m2 (2) 1 Y2 11m1 2
2 (1) (2) 2 2
(1)
(2) (2)
m21 Y2 Y2
Y Y
0 称第一正交关系 0 第一主振型惯性力在第二 0 主振型上所做的虚功为零
2 (1) 2
（2）刚度法
•微分方程建立
思路：取质量m1和m2为 隔离体，建立动力平衡方 程。0 m2 y
1 t 11 m2 2 t 12 y1 t m1 y y y2 t m1 y1 t 21 m2 y2 t 22
ij 是体系的柔度系数
设 y1 t Y1sin t y1 t Y1 常数 y t Y 2 y2 t Y2sin t 2 惯性力 惯性力幅值 1 t m1Y1 2sin t m1 2Y1 m1 y 2 2 t m2Y2 sin t m 2 2Y2 m2 y
15.4 两个自由度体系的自由振动
两种方法：刚度法和柔度法。 刚度法通过建立动力平衡方程求解 ，柔度法通过建立位移协调方程求解。
（1）柔度法
•微分方程建立
y2
y1
2 m y 1 m y
21
22
11
P 1 1 12
思路： P2 1 各质量的位 移等于体系 在当时惯性 力作用下所 产生的静力 位移。
1 1,2 m1 22 m 2 11
Y1 12 m2 1 Y2 11m1 2
22 m2
1
21m1
2
1
1
1
1
Y1 12 m2 (1) 1 Y2 11m1 2
(1)
1
2
2
Y1 12 m2 (2) 1 Y2 11m1 2
2 (1) (2) 2 2
(1)
(2) (2)
m21 Y2 Y2
Y Y
0 称第一正交关系 0 第一主振型惯性力在第二 0 主振型上所做的虚功为零
2 (1) 2
（2）刚度法
•微分方程建立
思路：取质量m1和m2为 隔离体，建立动力平衡方 程。0 m2 y
1 t 11 m2 2 t 12 y1 t m1 y y y2 t m1 y1 t 21 m2 y2 t 22
ij 是体系的柔度系数
设 y1 t Y1sin t y1 t Y1 常数 y t Y 2 y2 t Y2sin t 2 惯性力 惯性力幅值 1 t m1Y1 2sin t m1 2Y1 m1 y 2 2 t m2Y2 sin t m 2 2Y2 m2 y
15.4 两个自由度体系的自由振动
两种方法：刚度法和柔度法。 刚度法通过建立动力平衡方程求解 ，柔度法通过建立位移协调方程求解。
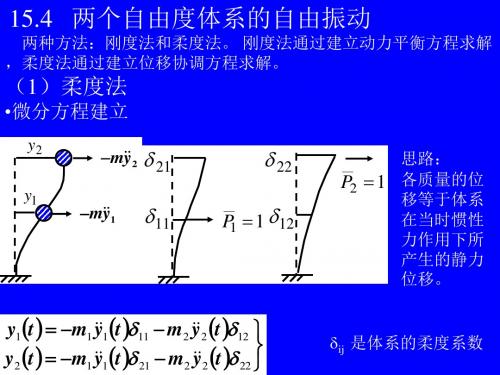
（1）柔度法
•微分方程建立
y2
y1
2 m y 1 m y
21
22
11
P 1 1 12
思路： P2 1 各质量的位 移等于体系 在当时惯性 力作用下所 产生的静力 位移。
两个自由度体系的自由振动
两个自由度体系的自由振动
• 引言 • 两个自由度体系的模型建立 • 两个自由度体系的自由振动分析
• 两个自由度体系的振动控制 • 实验验证与结果分析 • 结论与展望
01
引言
背景介绍
ቤተ መጻሕፍቲ ባይዱ
自由振动是物理学中一个重要的概念，它描述了系统在没有外部作用力的情况下 ，通过自身内部能量进行的振动。两个自由度体系是指具有两个独立方向的振动 体系，例如弹簧振荡器、单摆等。
02
通过理论分析和数值模拟，我 们发现某些参数条件下，两个 自由度体系可以发生共振或反 共振现象。
03
系统的能量在振动过程中会在 两个自由度之间转移，表现出 能量的分散和集中现象。
研究不足与展望
1
当前的研究主要集中在理论分析和数值模拟上， 缺乏实验验证，因此需要进一步开展实验研究。
2
对于两个自由度体系自由振动的动力学行为，仍 有许多未知领域需要探索，例如更高维度的自由 度体系、不同阻尼机制等。
3
需要进一步研究两个自由度体系在受到外部激励 或约束条件下的振动行为，以及与其他动力学现 象的相互作用。
THANKS
感谢观看
分析振动响应的特性，如频率、振幅、相位等，以 了解系统的自由振动行为。
03
两个自由度体系的自由振动分析
振动特性分析
固有频率
描述体系对振动的敏感程度，与体系的质量和刚度有关。
阻尼比
描述体系能量耗散的快慢，与阻尼系数和固有频率有关。
模态振型
描述体系在不同方向的振动形态，是振动特性的重要参数。
振动频率计算
自由振动在工程、自然界和日常生活中广泛存在，如乐器振动、地震波传播、桥 梁振动等。
研究意义
自由振动研究有助于深入理解物理现象的本质，探究系统内部能量转换和 传递机制。
• 引言 • 两个自由度体系的模型建立 • 两个自由度体系的自由振动分析
• 两个自由度体系的振动控制 • 实验验证与结果分析 • 结论与展望
01
引言
背景介绍
ቤተ መጻሕፍቲ ባይዱ
自由振动是物理学中一个重要的概念，它描述了系统在没有外部作用力的情况下 ，通过自身内部能量进行的振动。两个自由度体系是指具有两个独立方向的振动 体系，例如弹簧振荡器、单摆等。
02
通过理论分析和数值模拟，我 们发现某些参数条件下，两个 自由度体系可以发生共振或反 共振现象。
03
系统的能量在振动过程中会在 两个自由度之间转移，表现出 能量的分散和集中现象。
研究不足与展望
1
当前的研究主要集中在理论分析和数值模拟上， 缺乏实验验证，因此需要进一步开展实验研究。
2
对于两个自由度体系自由振动的动力学行为，仍 有许多未知领域需要探索，例如更高维度的自由 度体系、不同阻尼机制等。
3
需要进一步研究两个自由度体系在受到外部激励 或约束条件下的振动行为，以及与其他动力学现 象的相互作用。
THANKS
感谢观看
分析振动响应的特性，如频率、振幅、相位等，以 了解系统的自由振动行为。
03
两个自由度体系的自由振动分析
振动特性分析
固有频率
描述体系对振动的敏感程度，与体系的质量和刚度有关。
阻尼比
描述体系能量耗散的快慢，与阻尼系数和固有频率有关。
模态振型
描述体系在不同方向的振动形态，是振动特性的重要参数。
振动频率计算
自由振动在工程、自然界和日常生活中广泛存在，如乐器振动、地震波传播、桥 梁振动等。
研究意义
自由振动研究有助于深入理解物理现象的本质，探究系统内部能量转换和 传递机制。
两个自由度体系自由振动例题.ppt
4A 3 A 1 2 0 6 A 8 A 0 1 2
3. 频率方程
D
2
4. 求主振型 将λ=λ1代入振型方程， 得
4
6
3 0 8
12 14 0
10 . 6904 , 1 . 3096 1 2
1
6EI 1 EI 0 . 7499 ml3 1 ml3
4A 3 A 1 2 0 A 6 A 8 1 2 0
A 21 1 4 2 .230 A 3 11
6EI 1 EI 2 2 . 140 ml3 2 ml3
1 A 2 . 230
1 1 21 2 2 22
a/2 a 1
3 3 a a , 11 22 6 EI EI
a3 12 21 4EI
m
a
1
m
a a
2
2. 振型方程
) A m A 0 1 12 2 2 2 1 21m 22m2 2 )A2 0 1A 1 ( (11m 1 1
3 a3 1 a 解：1. 运动方程 m A mA 0 2 2 1 6EI 4 EI 3 3 y ( t ) m y ( t ) m y ( t ) a a 1 1 1 1 11 2 2 12 mA m A 0 1 2 EI 4EI 2
3
0
2 14 15 0
12 . 8310 , 1 . 1690 1 2
1 2
12EI 1 EI 0 . 9671 ma3 1 ma3 12EI 1 EI 3 . 2039 ma3 2 ma3
第5讲 两自由度系统的振动
(4)
，式中常数u1和u2起振幅的作用。 请
将方程(4)代入方程(3)，得
m1u1 f(t)+ (k11u1 + k12u2 ) f (t ) = 0 m2u2 f (t)+ (k21u1 + k22u2 ) f (t ) = 0
2015/3/24 机械系统动力学-多自由度系统的振动
现在关心的问题是，在初值条件下，如何求解 这个方程。这里，有两个问题需要确定： 1、坐标x1和x2是否有相同的随时间的变化规律 2、x1和x2是否是简谐函数
2015/3/24
机械系统动力学-多自由度系统的振动
14
有趣的“同步化” 现象
最早观察到同步化现象的科学家是
课 件荷兰的物理学家克里斯蒂安 · 惠更斯 仅 供(Christian Huygens 1629-1695)。根据 学 习伽利略(Galileo Galilei 1564-1642)发现 复 习 的钟摆的等时性原理，他于1656年把单 之 用 ，摆引入了机械钟，研制成第一个摆钟。 请
勿标，它们能够完全描述了系统在任何时刻的运动：x1和 它 用x2不仅表示出质量m1和m2的运动，而且也描述了
弹簧
。 曹k 、k 和k 的运动。因此，该系统是一个两自由度系统。 1 2 3
2015/3/24 机械系统动力学-多自由度系统的振动 8
两自由度系统的自由振动（微分方程）
f1 f2
课 件 仅 供 x1 x2 学 k2 (x2 − x1 ) 习 k1 x1 m1 m2 k3 x2 复 习 f1 f2 之 用 设运动x1和x2是微幅的，振动系统是线性的。由牛 ，顿定律建立运动微分方程 ：
引言
2015/3/24
机械系统动力学-多自由度系统的振动
§10-5 两个自由度体系的自由振动(柔度法)
11
a
3
2
a
1
M1
a a
1
a
EI
, 12 21
EI ma
3
a
3
4EI
, 22
a
3
6EI
1 0 .9 6 7
2 3 .2 0 3
EI ma
3
（2）振型
(1)
M
2
0.5a
0.277 1
第一振型
1 0 .2 7 7
(2)
1
2
3. 主振型 （1）第一振型
（对应于ω1 的Y1/Y2相对值）
幅 值 方 程
1 m 1 1 1 2 m 1 21
m 2 1 2 m 2 2 2
Y1 0 Y 1 2 2
将ω1 代入幅值方程任一式，可得：
Y1
(i)
1
简记为 (i)
2( i ) 其中 可由（5）式中 ( i ) （n－1)个独立方程解出。 n
▲多自由度体系自由振动的特点小结
1.n自由度体系有n个自振频率： 1 、 2 、 n
（由基频依次到高频）
2.每个ωi 对应有相应的主振型，有n个主振型；
2 (i ) i
（5）
K 2 M
0
(i )
∴ 方程组只有（n-1）个独立方程，只能求出Y 的相对值。
求法： 令质量m1的振幅
Y1 ( i ) 1 (i) (i) Y 2 标准化 2 Y (i ) ( i ) n n
a
3
2
a
1
M1
a a
1
a
EI
, 12 21
EI ma
3
a
3
4EI
, 22
a
3
6EI
1 0 .9 6 7
2 3 .2 0 3
EI ma
3
（2）振型
(1)
M
2
0.5a
0.277 1
第一振型
1 0 .2 7 7
(2)
1
2
3. 主振型 （1）第一振型
（对应于ω1 的Y1/Y2相对值）
幅 值 方 程
1 m 1 1 1 2 m 1 21
m 2 1 2 m 2 2 2
Y1 0 Y 1 2 2
将ω1 代入幅值方程任一式，可得：
Y1
(i)
1
简记为 (i)
2( i ) 其中 可由（5）式中 ( i ) （n－1)个独立方程解出。 n
▲多自由度体系自由振动的特点小结
1.n自由度体系有n个自振频率： 1 、 2 、 n
（由基频依次到高频）
2.每个ωi 对应有相应的主振型，有n个主振型；
2 (i ) i
（5）
K 2 M
0
(i )
∴ 方程组只有（n-1）个独立方程，只能求出Y 的相对值。
求法： 令质量m1的振幅
Y1 ( i ) 1 (i) (i) Y 2 标准化 2 Y (i ) ( i ) n n
§10-5 两个自由度体系的自由振动(刚度法)解析
0 y1 k11 m2 y2 k21
2
y (t ) 0
m1 矩阵式： 0
k12 y1 0 k22 y2 0
两自由度体系 自振微分方程
（对角质量矩阵）
（刚度矩阵）
振动方程：
m1 y1(t ) k11 y1(t ) k12 y2 (t ) 0 m2 y2 (t ) k21 y1(t ) k22 y2 (t ) 0
2.频率方程和频率 y1 (t ) Y1 sin(t ) ① 假设位移
（振动方程的解，简谐）
y2 (t ) Y2 sin(t )
y1 (t ) Y1 =常数 y2 (t ) Y2
a）在振动过程中，两个质点具有相同的频率和相同的相位角；
b）在振动过程中，两个质点的位移之比为常数。
1 第一振型 1
(1)
y1 (t ) A2Y12 sin( 2 t 2 ) 1 (2) 第二振型 y2 (t ) A2Y22 sin( 2 t 2 ) 2
（2）通解
—— 两个特解的线性组合
（两自由度体系自由振动是两种频率及其主振型的组合振动）
② 幅值方程
（位移代入振动方程， 消去sin( )项，得）
(k11 2 m1 )Y1 k12Y2 0 2 k21Y1 (k22 m2 )Y2 0
当然 Y1=Y2=0 为零解（无意义解）； 而非零解的条件是：系数行列式＝0 。
③ 频率方程（特征方程） (k11 2m1 )
▲两个自由度体系自由振动的特点小结
1 、2 1.有两个自振频率：
(1 (基频） 2 )
2
y (t ) 0
m1 矩阵式： 0
k12 y1 0 k22 y2 0
两自由度体系 自振微分方程
（对角质量矩阵）
（刚度矩阵）
振动方程：
m1 y1(t ) k11 y1(t ) k12 y2 (t ) 0 m2 y2 (t ) k21 y1(t ) k22 y2 (t ) 0
2.频率方程和频率 y1 (t ) Y1 sin(t ) ① 假设位移
（振动方程的解，简谐）
y2 (t ) Y2 sin(t )
y1 (t ) Y1 =常数 y2 (t ) Y2
a）在振动过程中，两个质点具有相同的频率和相同的相位角；
b）在振动过程中，两个质点的位移之比为常数。
1 第一振型 1
(1)
y1 (t ) A2Y12 sin( 2 t 2 ) 1 (2) 第二振型 y2 (t ) A2Y22 sin( 2 t 2 ) 2
（2）通解
—— 两个特解的线性组合
（两自由度体系自由振动是两种频率及其主振型的组合振动）
② 幅值方程
（位移代入振动方程， 消去sin( )项，得）
(k11 2 m1 )Y1 k12Y2 0 2 k21Y1 (k22 m2 )Y2 0
当然 Y1=Y2=0 为零解（无意义解）； 而非零解的条件是：系数行列式＝0 。
③ 频率方程（特征方程） (k11 2m1 )
▲两个自由度体系自由振动的特点小结
1 、2 1.有两个自振频率：
(1 (基频） 2 )
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Y1 0 1 Y m2 22 2 2 m212
将ω1 代入幅值方程任一式，可得：
Y11 12 m2 1 Y21 11m1 2
标准化 (1)
1
1 1 1 2 m111 1 1 m212
K M 0
2
M
1
2
I 0
—— 展开为ω2的n次方程，可解得n个自频ω1 …ωn 。 基频为ω1，由低到高依次排列。
5.主振型（n个） —— 对应于ωi 的振型为Y( i )
将ωi 代入幅值方程：
K M Y 0
（2）第二振型
（对应于ω2 的Y1/Y2相对值） 将ω2 代入幅值方程任一式，可得：
Y12 12 m2 1 Y22 11m1 2
标准化 (2)
2
1 1 1 m111 2 2 2 m212
§10-5 两个自由度体系的自由振动(续)
二、柔度法
1.建立振动方程（建立位移方程）
y2(t)
—— y1(t)、y2(t) 是两个惯性力共同作用下的静力位移
m2 2 y m1 1 y
m2 m1
y1(t ) m11(t )11 m2 2 (t )12 y y
y2 (t ) m11(t ) 21 m2 2 (t )22 y y
（n×n）
回弹力
2.假设特解 （位移）
y Y sin(t )
（n×1）
3.幅值方程（位移代入振动方程， 消去sin(
)项，得）
K M Y 0
2
1 M 2 I Y 0
4.频率方程
(1)
M1
M2
0.5a
0.277 1
第一振型
(2)
1 3.61
3.61 1
第二振型
▲一般多自由度体系的自由振动
刚度法 柔度法
1.振动方程
惯性力
y M K y 0
（n×n）
（对角阵）
y y － M
（n×1） （n×n） ×n） （n 惯性力
y2 (t ) Y2 sin(t )
y2 (t )
Y2
a）在振动过程中，两个质点具有相同的频率和相同的相位角；
b）在振动过程中，两个质点的位移之比为常数。
② 幅值方程
（位移代入振动方程， 消去sin( )项，得）
1 m111 2 m 1 21
Y1 0 1 Y2 m2 22 2 m212
3.对应第i 振型的初始条件下，体系将以频率ωi 按照第i 振型 作简谐振动； 4.一般初始条件下的自由振动是各个振型的叠加；
5.两个不同振型之间存在着正交关系（振型分解法要用到）
[例1] 试求图示梁的自振频率和主振型，梁的EI已知。 m 1 m 解：（1）计算频率
2
a
1
a a
1
a
a3 a3 a3 11 , 12 21 , 22 EI 4 EI 6 EI
EI EI 1 0.967 2 3.203 3 ma ma3
（2）振型
1 0.277
第10章 结构的动力计算
§10-1 动力计算的特点和动力自由度 §10-2 单自由度体系的自由振动 ▲ 结构的刚、柔度系数复习 §10-3 单自由度体系的强迫振动 §10-4 阻尼对振动的影响 §10-5 两个自由度体系的自由振动 §10-7 两个自由度体系在简谐荷载下的 强迫振动 §10-11 近似法求自振频率
简记为
(i )
2( i ) 其中 可由（5）式中 ( i ) （n－1)个独立方程解出。 n
▲多自由度体系自由振动的特点小结
1.n自由度体系有n个自振频率： 1 、2 、 n
（由基频依次到高频）
2.每个ωi 对应有相应的主振型，有n个主振型；
11、12、 21、 22—ຫໍສະໝຸດ 柔度系数y1(t)
（1）
12 m1 0 1 y y 矩阵式： 1 － 11 0 m y2 21 22 2 y2 2.频率方程和频率 y1 (t ) Y1 sin(t ) y1 (t ) Y1 ① 假设位移 =常数 （2） （振动方程的解，简谐）
（3）
当然 Y1=Y2=0 为零解；而非零解的条件是：系数行列式＝0 。
③ 频率方程（特征方程）
D m111 1
2
m212 m2 22 1
0
（4）
m1 21
2
展开为关于（1/ω2）的二次方程，可解出
ω1、ω2 。 令
1
2 (11m1 22m2 ) (11 22m1m2 12 21m1m2 ) 0
2 (i ) i
（5）
K 2 M 0
(i )
∴ 方程组只有（n-1）个独立方程，只能求出Y
的相对值。
求法： 令质量m1的振幅 Y1(i ) 1
Y1( i ) (i ) Y2 Yn( i )
标准化
1 ( i ) 2 n( i )
2
2
1 1 (11m1 22m2 ) (11m1 22m2 )2 4(11 22 12 21 )m1m2 2
1
1
1
2
1
2
3. 主振型 （1）第一振型
（对应于ω1 的Y1/Y2相对值）
幅 值 方 程
1 m111 2 m 1 21