高考数学刷题首秧专题突破练5立体几何的综合问题文含解析
2023年高考数学立体几何真题练习(含答案解析)

2023年高考数学立体几何真题练习(含答案解析)1.(2022·北京·高考真题)已知正三棱锥−P ABC 的六条棱长均为6,S 是ABC 及其内部的点构成的集合.设集合{}5T Q S PQ =∈≤,则T 表示的区域的面积为( ) A .34πB .πC .2πD .3π【答案】B 【解析】设顶点P 在底面上的投影为O ,连接BO ,则O 为三角形ABC 的中心,且263BO =⨯=PO 因为5PQ =,故1OQ =,故S 的轨迹为以O 为圆心,1为半径的圆,而三角形ABC 内切圆的圆心为O ,半径为2364136=>⨯, 故S 的轨迹圆在三角形ABC 内部,故其面积为π 故选:B2.(2022·浙江·高考真题)如图,已知正三棱柱1111,ABC A B C AC AA −=,E ,F 分别是棱11,BC AC 上的点.记EF 与1AA 所成的角为α,EF 与平面ABC 所成的角为β,二面角F BC A −−的平面角为γ,则( )A .αβγ≤≤B .βαγ≤≤C .βγα≤≤D .αγβ≤≤【答案】A【解析】如图所示,过点F 作FP AC ⊥于P ,过P 作PM BC ⊥于M ,连接PE ,则EFP α=∠,FEP β=∠,FMP γ=∠, tan 1PE PE FP AB α==≤,tan 1FP AB PE PE β==≥,tan tan FP FPPM PEγβ=≥=, 所以αβγ≤≤, 故选:A .3.(多选题)(2022·全国·高考真题)如图,四边形ABCD 为正方形,ED ⊥平面ABCD ,,2FB ED AB ED FB ==∥,记三棱锥E ACD −,F ABC −,F ACE −的体积分别为123,,V V V ,则( )A .322V V =B .31V V =C .312V V V =+D .3123V V =【答案】CD 【解析】设22AB ED FB a ===,因为ED ⊥平面ABCD ,FB ED ,则()2311114223323ACDV ED Sa a a =⋅⋅=⋅⋅⋅=, ()232111223323ABCV FB Sa a a =⋅⋅=⋅⋅⋅=,连接BD 交AC 于点M ,连接,EM FM ,易得BD AC ⊥,又ED ⊥平面ABCD ,AC ⊂平面ABCD ,则ED AC ⊥,又ED BD D =,,ED BD ⊂平面BDEF ,则AC ⊥平面BDEF ,又12BM DM BD ===,过F 作FG DE ⊥于G ,易得四边形BDGF 为矩形,则,FG BD EG a ===,则,EM FM ==,3EF a =,222EM FM EF +=,则EM FM ⊥,212EFMSEM FM =⋅,AC =, 则33123A EFM C EFM EFMV V V AC S a −−=+=⋅=,则3123V V =,323V V =,312V V V =+,故A 、B 错误;C 、D 正确. 故选:CD.4.(多选题)(2022·全国·高考真题)已知正方体1111ABCD A B C D −,则( ) A .直线1BC 与1DA 所成的角为90︒ B .直线1BC 与1CA 所成的角为90︒ C .直线1BC 与平面11BB D D 所成的角为45︒ D .直线1BC 与平面ABCD 所成的角为45︒【答案】ABD【解析】如图,连接1B C 、1BC ,因为11//DA B C ,所以直线1BC 与1B C 所成的角即为直线1BC与1DA 所成的角,因为四边形11BB C C 为正方形,则1B C ⊥1BC ,故直线1BC 与1DA 所成的角为90︒,A 正确;连接1AC ,因为11A B ⊥平面11BB C C ,1BC ⊂平面11BB C C ,则111A B BC ⊥, 因为1B C ⊥1BC ,1111A B B C B =,所以1BC ⊥平面11A B C ,又1AC ⊂平面11A B C ,所以11BC CA ⊥,故B 正确; 连接11AC ,设1111ACB D O =,连接BO ,因为1BB ⊥平面1111D C B A ,1C O ⊂平面1111D C B A ,则11C O B B ⊥, 因为111C O B D ⊥,1111B D B B B ⋂=,所以1C O ⊥平面11BB D D , 所以1C BO ∠为直线1BC 与平面11BB D D 所成的角,设正方体棱长为1,则1C O =1BC =1111sin 2C O C BO BC ∠==, 所以,直线1BC 与平面11BB D D 所成的角为30,故C 错误;因为1C C ⊥平面ABCD ,所以1C BC ∠为直线1BC 与平面ABCD 所成的角,易得145C BC ∠=,故D 正确. 故选:ABD5.(多选题)(2021·全国·高考真题)在正三棱柱111ABC A B C -中,11AB AA ==,点P 满足1BP BC BB λμ=+,其中[]0,1λ∈,[]0,1μ∈,则( )A .当1λ=时,1AB P △的周长为定值B .当1μ=时,三棱锥1P A BC −的体积为定值C .当12λ=时,有且仅有一个点P ,使得1A P BP ⊥ D .当12μ=时,有且仅有一个点P ,使得1A B ⊥平面1AB P 【答案】BD 【解析】易知,点P 在矩形11BCC B 内部(含边界).对于A ,当1λ=时,11=BP BC BB BC CC μμ=++,即此时P ∈线段1CC ,1AB P △周长不是定值,故A 错误;对于B ,当1μ=时,1111=BP BC BB BB B C λλ=++,故此时P 点轨迹为线段11B C ,而11//B C BC ,11//B C 平面1A BC ,则有P 到平面1A BC 的距离为定值,所以其体积为定值,故B 正确.对于C ,当12λ=时,112BP BC BB μ=+,取BC ,11B C 中点分别为Q ,H ,则BP BQ QH μ=+,所以P 点轨迹为线段QH ,不妨建系解决,建立空间直角坐标系如图,1A ⎫⎪⎪⎝⎭,()0,0P μ,,10,,02B ⎛⎫⎪⎝⎭,则112A P μ⎛⎫=−− ⎪ ⎪⎝⎭,10,,2BP μ⎛⎫=− ⎪⎝⎭,()110A P BP μμ⋅=−=,所以0μ=或1μ=.故,H Q 均满足,故C 错误; 对于D ,当12μ=时,112BP BC BB λ=+,取1BB ,1CC 中点为,M N .BP BM MN λ=+,所以P 点轨迹为线段MN .设010,,2P y ⎛⎫ ⎪⎝⎭,因为0,0A ⎫⎪⎪⎝⎭,所以01,2AP y ⎛⎫=− ⎪ ⎪⎝⎭,11,122A B ⎛⎫=−− ⎪ ⎪⎝⎭,所以00311104222y y +−=⇒=−,此时P 与N 重合,故D 正确. 故选:BD .6.(2020·海南·高考真题)已知直四棱柱ABCD –A 1B 1C 1D 1的棱长均为2,∠BAD =60°.以1DBCC 1B 1的交线长为________.【答案】2. 【解析】如图:取11B C 的中点为E ,1BB 的中点为F ,1CC 的中点为G ,因为BAD ∠=60°,直四棱柱1111ABCD A B C D −的棱长均为2,所以△111D B C 为等边三角形,所以1D E =111D E B C ⊥,又四棱柱1111ABCD A B C D −为直四棱柱,所以1BB ⊥平面1111D C B A ,所以111BB B C ⊥, 因为1111BB B C B =,所以1D E ⊥侧面11B C CB ,设P 为侧面11B C CB 与球面的交线上的点,则1D E EP ⊥,1D E =||EP =所以侧面11B C CB 与球面的交线上的点到E因为||||EF EG ==11B C CB 与球面的交线是扇形EFG 的弧FG , 因为114B EFC EG π∠=∠=,所以2FEG π∠=,所以根据弧长公式可得22FG π==..。
高三数学一轮专题突破训练《立体几何》(理)及答案
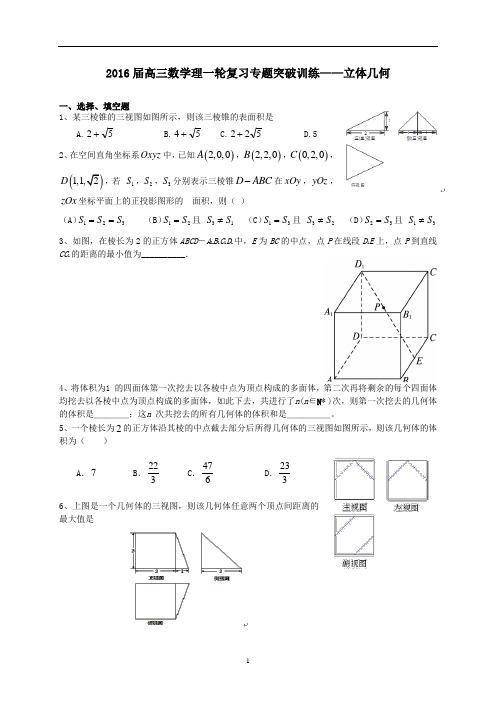
2016届高三数学理一轮复习专题突破训练——立体几何一、选择、填空题1、某三棱锥的三视图如图所示,则该三棱锥的表面积是A.52+B.54+C.522+D.52、在空间直角坐标系Oxyz 中,已知()2,0,0A ,()2,2,0B ,()0,2,0C ,(D ,若 1S ,2S ,3S 分别表示三棱锥D ABC -在xOy ,yOz ,zOx 坐标平面上的正投影图形的 面积,则( )(A )123S S S == (B )12S S =且 31S S ≠ (C )13S S =且 32S S ≠ (D )23S S =且 13S S ≠ 3、如图,在棱长为2的正方体ABCD -A 1B 1C 1D 1中,E 为BC 的中点,点P 在线段D 1E 上,点P 到直线CC 1的距离的最小值为__________.4、将体积为1 的四面体第一次挖去以各棱中点为顶点构成的多面体,第二次再将剩余的每个四面体均挖去以各棱中点为顶点构成的多面体,如此下去,共进行了n (n ∈N * )次,则第一次挖去的几何体的体积是____;这n 次共挖去的所有几何体的体积和是_____。
5、一个棱长为2的正方体沿其棱的中点截去部分后所得几何体的三视图如图所示,则该几何体的体积为( )A .7B .223 C .476D .2336、上图是一个几何体的三视图,则该几何体任意两个顶点间距离的最大值是(A) 4 (B) 5(C) (D) 7、若空间中有(5)n n ≥个点,满足任意四个点都不共面,且任意两点的连线都与其它任意三点确定的平面垂直,则这样的n 值( ) (A )不存在(B )有无数个(C )等于5(D )最大值为88、在如图所示的空间直角坐标系O xyz -中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为( )A .①和② B.③和① C.③和④ D.④和② 9、一个几何体的三视图如图所示,则该几何体的体积的是 ( )10、已知直线m 和平面α,β,则下列四个命题中正确的是A. 若αβ⊥,m β⊂,则m α⊥B. 若//αβ,//m α,则//m βC. 若//αβ,m α⊥,则m β⊥D. 若//m α,//m β,则//αβN MD 1C 1A 1D CBA11、某三棱锥的三视图如图所示,则该三棱锥的全面积是 A .4+.8 C .4+ D.12、已知直线l ⊥平面α,直线m ⊂平面β,有下列四个命题:①若αβ∥,则l m ⊥;②若αβ⊥,则l m ∥;③若l m ∥,则αβ⊥;④若l m ⊥,则αβ∥.以上命题中,正确命题的序号是(A )①② (B )①③ (C )②④ (D )③④13、如图,网格纸的各小格都是正方形,粗线画出的是一个三棱锥的侧视图和俯视图,则该三棱锥的正视图可能是14、如图,网格纸上小正方形的边长为1,粗实线画出的 是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )D. 315、在正方体1111ABCD A B C D -中,已知M ,N 分别是11A B ,1BB 的中点,过点M ,N ,1C 的截面截正方体所得的几何体,如图所示,那么该几何体的侧视图是二、解答题1、如图,在四棱锥A EFCB -中,EF A ∆为等边三角形,平面⊥∆EF A 平面EFCB ,EF∥BC,BC=4,2EF a =,60EBC FCB ∠=∠=︒,O 为EF 的中点.(Ⅰ) 求证:AO BE ⊥;(Ⅱ) 求二面角F AE B --的余弦值; (Ⅲ) 若BE ⊥平面AOC ,求a 的值.2、如图,正方形AMDE 的边长为2,C B ,分别为MD AM ,的中点,在五棱锥ABCDE P - 中,F 为棱PE 的中点,平面ABF 与棱PC PD ,分别交于点H G ,. (1)求证:FG AB //;(2)若⊥PA 底面ABCDE ,且PE AF ⊥,求直线BC 与平面ABF 所成角的大小,并 求线段PH 的长.3、如图,在三棱柱ABC -A 1B 1C 1中,AA 1C 1C 是边长为4的正方形.平面ABC ⊥平面AA 1C 1C ,AB =3,BC =5,(1)求证:AA 1⊥平面ABC ;(2)求二面角A 1-BC 1-B 1的余弦值;(3)证明:在线段BC 1上存在点D ,使得AD ⊥A 1B ,并求1BDBC 的值.4、如图,正方形 ADEF 与梯形 ABCD 所在平面互相垂直,已知 AB ∥CD ,AD ⊥CD , AB = AD =12CD .(1)求证: BF ∥平面CDE ;(2)求平面BDF 与平面CDE 所成锐二面角的余弦值;(3)线段EC 上是否存在点M ,使得平面BDM ⊥平面BDF ?若存在,求出EMEC的值;若不存在, 说明理由.-的侧面BEFC是边长为1的正方形,侧面BEFC⊥侧面ADEB,5、如图,三棱柱ABC DEFAB=,604∠= ,G是DE的中点.DEB(Ⅰ)求证:CE∥平面AGF;(Ⅱ)求证:GB⊥平面BEFC;--为45 ,若存在,求BP的长;若不存(Ⅲ)在线段BC上是否存在一点P,使二面角P GE B在,说明理由.AC⊥,且6、在如图所示的多面体中,EA⊥平面ABC,DB⊥平面ABC,BCBCAC,M是AB的中点.=AEBD22===(Ⅰ)求证:CM⊥EM;(Ⅱ)求平面EMC与平面BCD所成的锐二面角的余弦值;(Ⅲ)在棱DC上是否存在一点N,使得直线MN与平面EMC所成的角为60︒.若存在,指出点N的位置;若不存在,请说明理由.7、在如图所示的几何体中,四边形ABCD 为正方形,PA ⊥平面ABCD ,PA //BE ,AB =PA =4,BE =2. (Ⅰ)求证:CE //平面PAD ;(Ⅱ)求PD 与平面PCE 所成角的正弦值;(Ⅲ)在棱AB 上是否存在一点F ,使得平面DEF ⊥平面PCE ?如果存在,求AFAB的值; 如果不存在,说明理由.8、如图所示,在四棱锥P ABCD -中, //AB CD ,AB AD ⊥,22AB AD AP CD ====,M 是棱PB 上一点.(Ⅰ)若2BM MP =,求证://PD 平面MAC ; (Ⅱ)若平面PAB ⊥平面A B C D ,平面PAD ⊥平面A B C D ,求证:PA ⊥平面ABCD ;(Ⅲ)在(Ⅱ)的条件下,若二面角B AC M --的余弦值为23,求PM PB的值.A CDEFB9、如图,多面体ABCDEF 中,平面ADEF ⊥平面ABCD ,正方形ADEF 的边长为2,直角梯形ABCD 中,AB ∥CD ,AD ⊥DC ,AB =2,CD =4.(Ⅰ)求证:BC ⊥平面BDE ;(Ⅱ)试在平面CDE 上确定点P ,使点P 到 直线DC 、DE 的距离相等,且AP 与平面BEF 所成的角等于30°.10、如图,在五面体 ABCDEF 中,四边形 ABCD 是边长为 4 的正方形,EF ∥AD ,平面 ADEF ⊥ 平面 ABCD ,且BC = 2EF , AE = AF ,点G 是EF 的中点。
2021届高考数学专题突破直线、平面垂直的判定和性质(解析版)

2021届高考数学立体几何突破性讲练 05直线、平面垂直的判定和性质一、考点传真:1.以立体几何的定义、公理和定理为出发点,认识和理解空间中线面垂直的有关性质与判定定理;2.能运用公理、定理和已获得的结论证明一些空间图形的垂直关系的简单命题. 二、知识点梳理:1.直线与平面垂直 (1)直线和平面垂直的定义:直线l 与平面α内的任意一条直线都垂直,就说直线l 与平面α互相垂直.(2)直线与平面垂直的判定定理及性质定理:一条直线与一个平面内的两条相交直线都,则该直线与垂直于同一个平面的 ⎣⎢⎡⎦⎥⎤❶如果一条直线与平面内再多(即无数条)的直线垂直,但这些直线不相交就不能说明这条直线与此平面垂直. 2.平面与平面垂直的判定定理与性质定理一个平面过另一个平,则这两两个平面垂直,则一个平面内垂直于交线的直线与另一个平面[❷要求一平面只需过另一平面的垂线.]二、常用结论汇总直线与平面垂直的五个结论(1)若一条直线垂直于一个平面,则这条直线垂直于这个平面内的任意直线. (2)若两条平行线中的一条垂直于一个平面,则另一条也垂直于这个平面. (3)垂直于同一条直线的两个平面平行.(4)一条直线垂直于两平行平面中的一个,则这一条直线与另一个平面也垂直. (5)两个相交平面同时垂直于第三个平面,它们的交线也垂直于第三个平面. 三、例题:例1. (2019全国II 文17)如图,长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形,点E 在棱AA 1上,BE ⊥EC 1.(1)证明:BE ⊥平面EB 1C 1;(2)若AE =A 1E ,AB =3,求四棱锥11E BB C C -的体积. 【解析】(1)由已知得B 1C 1⊥平面ABB 1A 1,BE ⊂平面ABB 1A 1, 故11B C BE ⊥.又1BE EC ⊥,所以BE ⊥平面11EB C .(2)由(1)知∠BEB 1=90°.由题设知Rt △ABE ≌Rt △A 1B 1E ,所以1145AEB A EB ︒∠=∠=,故AE =AB =3,126AA AE ==.作1EF BB ⊥,垂足为F ,则EF ⊥平面11BB C C ,且3EF AB ==. 所以,四棱锥11E BB C C -的体积1363183V =⨯⨯⨯=.例2. (2019全国III 文19)图1是由矩形ADEB 、Rt △ABC 和菱形BFGC 组成的一个平面图形,其中AB =1,BE =BF =2,∠FBC =60°.将其沿AB ,BC 折起使得BE 与BF 重合,连结DG ,如图2.(1)证明图2中的A ,C ,G ,D 四点共面,且平面ABC ⊥平面BCGE ; (2)求图2中的四边形ACGD 的面积.【解析】(1)由已知得AD BE ,CG BE ,所以AD CG ,故AD ,CG 确定一个平面,从而A ,C ,G ,D 四点共面.由已知得AB ⊥BE ,AB ⊥BC ,故AB ⊥平面BCGE . 又因为AB ⊂平面ABC ,所以平面ABC ⊥平面BCGE . (2)取CG 的中点M ,联结EM ,DM .因为AB DE ∥,AB ⊥平面BCGE ,所以DE ⊥平面BCGE ,故DE ⊥CG . 由已知,四边形BCGE 是菱形,且60EBC ∠=︒得EM ⊥CG ,故CG ⊥平面DEM . 因此DM ⊥CG .在Rt △DEM 中,1DE =,EM =,故2DM =.所以四边形ACGD 的面积为4.-中,PA⊥平面ABCD,底部ABCD为例3. (2019北京文18)如图,在四棱锥P ABCD菱形,E为CD的中点.(Ⅰ)求证:BD⊥平面PAC;(Ⅱ)若∠ABC=60°,求证:平面PAB⊥平面PAE;(Ⅲ)棱PB上是否存在点F,使得CF∥平面PAE?说明理由.【解析】(Ⅰ)因为PA⊥平面ABCD,且BD⊂平面ABCD,⊥.所以PA BD⊥.又因为底面ABCD为菱形,所以BD AC=,又PA⊂平面PAC,AC⊂平面PAC,PA AC A所以BD⊥平面PAC.(Ⅱ)因为PA⊥平面ABCD,AE⊂平面ABCD,所以PA⊥AE.因为底面ABCD 为菱形,∠ABC =60°,且E 为CD 的中点, 所以AE ⊥CD .又//AB CD ,所以AB ⊥AE .又PA ⊂平面PAB ,AB ⊂平面PAB ,PAAB A =,所以AE ⊥平面PAB .又AE ⊂平面PAE ,所以平面PAB ⊥平面PAE .(Ⅲ)棱PB 上存在点F ,且F 为PB 的中点,使得CF ∥平面PAE . 取F 为PB 的中点,取G 为PA 的中点,连结CF ,FG ,EG . 因为G ,F 分别为PA ,PB 的中点,则FG ∥AB ,且FG =12AB . 因为底面ABCD 为菱形,且E 为CD 的中点, 所以CE ∥AB ,且CE =12AB . 所以FG ∥CE ,且FG =CE . 所以四边形CEGF 为平行四边形, 所以CF ∥EG .因为CF ⊄平面PAE ,EG ⊂平面PAE , 所以CF ∥平面PAE .例4. (2019天津文17)如图,在四棱锥中,底面为平行四边形,为等边三角形,平面平面,,,,(Ⅰ)设分别为的中点,求证:平面; (Ⅱ)求证:平面;(Ⅲ)求直线与平面所成角的正弦值. 【解析】 (Ⅰ)连接,易知,.又由,故,又因为平面,平面,所以平面.(Ⅱ)取棱的中点,连接.依题意,得,又因为平面平面,P ABCD -ABCDPCD PAC ⊥PCD PA CD ⊥2CD =3AD =G H ,PB AC ,GH ∥PAD PA ⊥PCD AD PAC BD ACBD H =BH DH =BG PG =GH PD ∥GH ⊄PAD PD ⊂PAD GH ∥PAD PC N DN DN PC ⊥PAC ⊥PCD平面平面,所以平面,又平面,故.又已知,,所以平面.(Ⅲ)连接,由(Ⅱ)中平面,可知为直线与平面所成的角,因为PCD △为等边三角形,且为的中点,所以又, 故在Rt AND △中,. 所以,直线与平面所成角的正弦值为. 例5. (2018全国卷Ⅱ)如图,在三棱锥-P ABC 中,==AB BC4====PA PB PC AC ,O 为AC 的中点.(1)证明:PO ⊥平面ABC ;(2)若点M 在棱BC 上,且2=MC MB ,求点C 到平面POM 的距离.【解析】(1)因为4===AP CP AC ,O 为AC 的中点,所以OP ⊥AC ,且=OP 连结OB .因为2==AB BC AC ,所以∆ABC 为等腰直角三角形, 且OB ⊥AC ,122==OB AC . 由222OP OB PB +=知,OP ⊥OB .由OP ⊥OB ,OP ⊥AC 知PO ⊥平面ABC .PACPCD PC =DN ⊥PAC PA ⊂PAC DN PA ⊥PA CD ⊥CD DN D =PA ⊥PCD AN DN ⊥PAC DAN ∠AD PAC 2CD =N PC DN =DN AN ⊥sin 3DN DAN AD ∠==AD PAC 3O MPCBA(2)作CH⊥OM,垂足为H.又由(1)可得OP⊥CH,所以CH⊥平面POM.故CH的长为点C到平面POM的距离.由题设可知122==OC AC,23==CM BC,45∠=ACB.所以=OM,sin5⋅⋅∠==OC MC ACBCHOM.例6. (2018全国卷Ⅲ)如图,矩形ABCD所在平面与半圆弧CD所在平面垂直,M是CD 上异于C,D的点.(1)证明:平面AMD⊥平面BMC;(2)在线段AM上是否存在点P,使得MC∥平面PBD?说明理由.【解析】(1)由题设知,平面CMD⊥平面ABCD,交线为CD.因为BC⊥CD,BC平面ABCD,所以BC⊥平面CMD,故BC⊥DM.因为M为CD上异于C,D的点,且DC为直径,所以DM⊥CM.又BC CM=C,所以DM⊥平面BMC.而DM平面AMD,故平面AMD⊥平面BMC.(2)当P为AM的中点时,MC∥平面PBD.HOMPCBAA BCDM⊂⊂证明如下:连结AC交BD于O.因为ABCD为矩形,所以O为AC中点.连结OP,因为P为AM中点,所以MC∥OP.MC⊄平面PBD,OP⊂平面PBD,所以MC∥平面PBD.四、巩固练习:1.若l,m是两条不同的直线,m垂直于平面α,则“l⊥m”是“l∥α”的() A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】B【解析】∵m⊥α,若l∥α,则必有l⊥m,即l∥α⇒l⊥m.但l⊥m⇒/ l∥α,∵l⊥m时,l可能在α内.故“l⊥m”是“l∥α”的必要不充分条件.2.设a,b是两条不同的直线,α,β是两个不同的平面,则能得出a⊥b的是() A.a⊥α,b∥β,α⊥βB.a⊥α,b⊥β,α∥βC.a⊂α,b⊥β,α∥βD.a⊂α,b∥β,α⊥β【答案】C【解析】对于C项,由α∥β,a⊂α可得a∥β,又b⊥β,得a⊥b,故选C.3.设m,n表示两条不同的直线,α,β表示两个不同的平面,下列命题为真命题的是() A.若m⊥α,α⊥β,则m∥βB.若m∥α,m⊥β,则α⊥βC.若m⊥n,m⊥α,则n∥αD.若m∥α,n∥β,α⊥β,则m⊥n【答案】B【解析】对于A,m可以在β内,故A错;对于C,n可以在α内,故C错误;对于D,m与n可以平行,故D错.4.已知P A垂直于以AB为直径的圆所在的平面,C为圆上异于A,B两点的任一点,则下列关系不正确的是()A.P A⊥BC B.BC⊥平面P ACC.AC⊥PB D.PC⊥BC【答案】C【解析】由P A⊥平面ACB⇒P A⊥BC,故A不符合题意;由BC⊥P A,BC⊥AC,P A∩AC =A,可得BC⊥平面P AC,所以BC⊥PC,故B、D不符合题意;AC⊥PB显然不成立,故C符合题意.5.已知P为△ABC所在平面外一点,且P A,PB,PC两两垂直,有下列结论:①P A⊥BC;②PB⊥AC;③PC⊥AB;④AB⊥BC.其中正确的是()A.①②③B.①②④C.②③④D.①②③④【答案】A【解析】如图,因为P A⊥PB,P A⊥PC,PB∩PC=P,且PB⊂平面PBC,PC⊂平面PBC,所以P A⊥平面PBC.又BC⊂平面PBC,所以P A⊥BC,同理可得PB⊥AC,PC⊥AB,故①②③正确.6.如图,在四面体ABCD中,已知AB⊥AC,BD⊥AC,那么点D在平面ABC内的射影H必在()A.直线AB上B.直线BC上C.直线AC上D.△ABC内部【答案】A【解析】因为AB⊥AC,BD⊥AC,AB∩BD=B,所以AC⊥平央ABD,又AC⊂平面ABC,所以平面ABC⊥平面ABD,所以点D在平面ABC内的射影H必在直线AB上.7.如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,且BC1⊥AC,过C1作C1H⊥底面ABC,垂足为H,则点H在()A.直线AC上B.直线AB上C.直线BC上D.△ABC内部【答案】 B【解析】连接AC1,如图.∵∠BAC =90°,∴AC ⊥AB , ∵BC 1⊥AC ,BC 1∩AB =B , ∴AC ⊥平面ABC 1.又AC 在平面ABC 内,∴根据面面垂直的判定定理,知平面ABC ⊥平面ABC 1,则根据面面垂直的性质定理知,在平面ABC 1内一点C 1向平面ABC 作垂线,垂足必落在交线AB 上.故选B.8.在正方体ABCD -A 1B 1C 1D 1中,点M 、N 分别是直线CD 、AB 上的动点,点P 是△A 1C 1D 内的动点(不包括边界),记直线D 1P 与MN 所成角为θ,若θ的最小值为π3,则点P 的轨迹是( )A .圆的一部分B .椭圆的一部分C .抛物线的一部分D .双曲线的一部分【答案】B【解析】 把MN 平移到平面A 1B 1C 1D 1中,直线D 1P 与MN 所成角为θ,直线D 1P 与MN 所成角的最小值是直线D 1P 与平面A 1B 1C 1D 1所成角,即原问题转化为:直线D 1P 与平面A 1B 1C 1D 1所成角为π3,点P 在平面A 1B 1C 1D 1的投影为圆的一部分,因为点P 是△A 1C 1D 内的动点(不包括边界),所以点P 的轨迹是椭圆的一部分.故选B.9.如图,在正四面体P -ABC 中,D ,E ,F 分别是AB ,BC ,CA 的中点,则下面四个结论不成立的是( )A .BC ∥平面PDFB .DF ⊥平面P AEC .平面PDF ⊥平面P AED .平面PDE ⊥平面ABC【答案】D【解析】因为BC ∥DF ,DF ⊂平面PDF ,BC ⊄平面PDF ,所以BC ∥平面PDF ,故选项A 正确.在正四面体中,AE ⊥BC ,PE ⊥BC ,AE ∩PE =E ,所以BC ⊥平面P AE ,又DF ∥BC ,则DF ⊥平面P AE ,从而平面PDF ⊥平面P AE .因此选项B 、C 均正确.10.如图,在正方形ABCD 中,E ,F 分别是BC ,CD 的中点,G 是EF 的中点,现在沿AE ,AF 及EF 把这个正方形折成一个空间图形,使B ,C ,D 三点重合,重合后的点记为H ,那么在这个空间图形中必有( )A.AG ⊥平面EFHB.AH ⊥平面EFHC.HF ⊥平面AEFD.HG ⊥平面AEF 【答案】 B【解析】 根据折叠前、后AH ⊥HE ,AH ⊥HF 不变,又HE ∩HF =H ,∴AH ⊥平面EFH ,B 正确.∵过A 只有一条直线与平面EFH 垂直,∴A 不正确.∵AG ⊥EF ,EF ⊥GH ,AG ∩GH =G ,∴EF ⊥平面HAG ,又EF ⊂平面AEF ,∴平面HAG ⊥平面AEF ,过H 作直线垂直于平面AEF ,一定在平面HAG 内,∴C 不正确.由条件证不出HG ⊥平面AEF ,∴D 不正确.11.如图,在下列四个正方体1111ABCD A B C D 中,E ,F ,G 均为所在棱的中点,过E ,F ,G 作正方体的截面,则在各个正方体中,直线1BD 与平面EFG 不垂直的是( )【答案】D【解析】对于选项D 中图形,由于E ,F ,为AB ,11A B 的中点,所以1//EF BB ,故11B BD ∠为异面直线所成的角且11TAN B BD ∠=11B BD ∠不为直角,故1BD 与平面EFG 不可能垂直,故选D.12.如图,在矩形ABCD 中,AB =3,BC =1,将△ACD 沿AC 折起,使得D 折起后的位置为D 1,且D 1在平面ABC 上的射影恰好落在AB 上,在四面体D 1ABC 的四个面中,有n 对平面相互垂直,则n 等于( )A.2B.3C.4D.5【答案】 B【解析】 设D 1在平面ABC 上的射影为E ,连接D 1E ,则D 1E ⊥平面ABC .∵D 1E ⊂平面ABD 1,∴平面ABD 1⊥平面ABC .∵D 1E ⊥平面ABC ,BC ⊂平面ABC ,∴D 1E ⊥BC ,又AB ⊥BC ,D 1E ∩AB =E ,∴BC ⊥平面ABD 1.又BC ⊂平面BCD 1,∴平面BCD 1⊥平面ABD 1.∵BC ⊥平面ABD 1,AD 1⊂平面ABD 1,∴BC ⊥AD 1,又CD 1⊥AD 1,BC ∩CD 1=C ,∴AD 1⊥平面BCD 1,又AD 1⊂平面ACD 1,∴平面ACD 1⊥平面BCD 1.∴共有3对平面相互垂直.故选B.13.已知PD 垂直于正方形ABCD 所在的平面,连接PB ,PC ,P A ,AC ,BD ,则一定互相垂直的平面有________对.【答案】7【解析】由于PD ⊥平面ABCD ,故平面P AD ⊥平面ABCD ,平面PDB ⊥平面ABCD ,平面PDC ⊥平面ABCD ,平面PDA ⊥平面PDC ,平面P AC ⊥平面PDB ,平面P AB ⊥平面P AD, 平面PBC ⊥平面PDC ,共7对.14.如图,在长方体ABCD -A 1B 1C 1D 1中,AB =BC =2,AA 1=1,则AC 1与平面A 1B 1C 1D 1所成角的正弦值为________.【答案】 13【解析】 连接A 1C 1,则∠AC 1A 1为AC 1与平面A 1B 1C 1D 1所成的角.因为AB =BC =2,所以A 1C 1=AC =22,又AA 1=1,所以AC 1=3, 所以sin ∠AC 1A 1=AA 1AC 1=13. 15.在直三棱柱ABC -A 1B 1C 1中,平面α与棱AB ,AC ,A 1C 1,A 1B 1分别交于点E ,F ,G ,H ,且直线AA 1∥平面α.有下列三个命题:①四边形EFGH 是平行四边形;②平面α∥平面BCC 1B 1;③平面α⊥平面BCFE .其中正确命题的序号是________.【答案】①③【解析】如图所示,因为AA 1∥平面α,平面α∩平面AA 1B 1B =EH ,所以AA 1∥EH .同理AA 1∥GF ,所以EH ∥GF ,又ABC -A 1B 1C 1是直三棱柱,易知EH =GF =AA 1,所以四边形EFGH 是平行四边形,故①正确;若平面α∥平面BB 1C 1C ,由平面α∩平面A 1B 1C 1=GH ,平面BCC 1B 1∩平面A 1B 1C 1=B 1C 1,知GH ∥B 1C 1,而GH ∥B 1C 1不一定成立,故②错误;由AA 1⊥平面BCFE ,结合AA 1∥EH 知EH ⊥平面BCFE ,又EH ⊂平面α,所以平面α⊥平面BCFE ,故③正确.16.如图,在直三棱柱ABC -A 1B 1C 1中,侧棱长为2,AC =BC =1,∠ACB =90°,D 是A 1B 1的中点,F 是BB 1上的动点,AB 1,DF 交于点E ,要使AB 1⊥平面C 1DF ,则线段B 1F 的长为________.【答案】 12【解析】 设B 1F =x ,因为AB 1⊥平面C 1DF ,DF ⊂平面C 1DF ,所以AB 1⊥DF ,由已知可得A 1B 1=2,设Rt △AA 1B 1斜边AB 1上的高为h ,则DE =12h . 又12×2×2=12×h 22+(2)2,所以h =233,DE =33.在Rt △DB 1E 中,B 1E =⎝⎛⎭⎫222-⎝⎛⎭⎫332=66.由面积相等得12×66×x 2+⎝⎛⎭⎫222=12×22x ,得x =12.17.如图,在四棱锥P -ABCD 中,PD ⊥平面ABCD ,底面ABCD 为正方形,BC =PD =2,E 为PC 的中点,CB =3CG .(1)求证:PC ⊥BC ;(2)AD 边上是否存在一点M ,使得P A ∥平面MEG ?若存在,求出AM 的长;若不存在,请说明理由.【解析】(1)证明:因为PD ⊥平面ABCD ,BC ⊂平面ABCD ,所以PD ⊥BC .因为四边形ABCD 是正方形,所以BC ⊥CD .又PD ∩CD =D ,PD ⊂平面PCD ,CD ⊂平面PCD ,所以BC ⊥平面PCD .因为PC ⊂平面PCD ,所以PC ⊥BC .(2)连接AC ,BD 交于点O ,连接EO ,GO ,延长GO 交AD 于点M ,连接EM ,则P A ∥平面MEG .证明如下:因为E 为PC 的中点,O 是AC 的中点,所以EO ∥P A .因为EO ⊂平面MEG ,P A ⊄平面MEG ,所以P A ∥平面MEG . 因为△OCG ≌△OAM ,所以AM =CG =23, 所以AM 的长为23. 18.如图,四棱锥P -ABCD 的底面ABCD 是圆内接四边形(记此圆为W ),且P A ⊥平面ABCD .(1)当BD 是圆W 的直径时,P A =BD =2,AD =CD =3,求四棱锥P -ABCD 的体积.(2)在(1)的条件下,判断在棱P A 上是否存在一点Q ,使得B Q ∥平面PCD ?若存在,求出A Q 的长;若不存在,请说明理由.【解析】(1)因为BD 是圆W 的直径,所以BA ⊥AD ,因为BD =2,AD =3,所以AB =1.同理BC =1,所以S 四边形ABCD =AB ·AD = 3.因为P A ⊥平面ABCD ,P A =2,所以四棱锥P -ABCD 的体积V =13S 四边形ABCD ·P A =233. (2)存在,A Q =23.理由如下. 延长AB ,DC 交于点E ,连接PE ,则平面P AB 与平面PCD 的交线是PE .假设在棱P A 上存在一点Q ,使得B Q ∥平面PCD ,则B Q ∥PE ,所以A Q P A =AB AE. 经计算可得BE =2,所以AE =AB +BE =3,所以A Q =23. 故存在这样的点Q ,使B Q ∥平面PCD ,且A Q =23.19.如图1,在矩形ABCD 中,AB =4,AD =2,E 是CD 的中点,将△ADE 沿AE 折起,得到如图2所示的四棱锥D 1-ABCE ,其中平面D 1AE ⊥平面ABCE .(1)证明:BE ⊥平面D 1AE ;(2)设F 为CD 1的中点,在线段AB 上是否存在一点M ,使得MF ∥平面D 1AE ,若存在,求出AM AB的值;若不存在,请说明理由. 【解析】(1)证明:∵四边形ABCD 为矩形且AD =DE =EC =BC =2,∴∠AEB =90°,即BE ⊥AE ,又平面D 1AE ⊥平面ABCE ,平面D 1AE ∩平面ABCE =AE ,∴BE ⊥平面D 1AE .(2)当AM AB =14时,MF ∥平面D 1AE ,理由如下: 取D 1E 的中点L ,连接FL ,AL ,∴FL ∥EC ,又EC ∥AB ,∴FL ∥AB ,且FL =14AB , ∴M ,F ,L ,A 四点共面,又MF ∥平面AD 1E ,∴MF ∥AL .∴四边形AMFL 为平行四边形, ∴AM =FL =14AB ,AM AB =14. 20.如图所示的五面体ABEDFC 中,四边形ACFD 是等腰梯形,AD ∥FC ,∠DAC =60°,BC ⊥平面ACFD ,CA =CB =CF =1,AD =2CF ,点G 为AC 的中点.(1)在AD 上是否存在一点H ,使GH ∥平面BCD ?若存在,指出点H 的位置并给出证明;若不存在,说明理由;(2)求三棱锥G -ECD 的体积.【解析】(1)存在点H 使GH ∥平面BCD ,此时H 为AD 的中点.证明如下.取点H 为AD 的中点,连接GH ,因为点G 为AC 的中点,所以在△ACD 中,由三角形中位线定理可知GH ∥CD ,又GH ⊄平面BCD ,CD ⊂平面BCD ,所以GH ∥平面BCD .(2)因为AD ∥CF ,AD ⊂平面ADEB ,CF ⊄平面ADEB ,所以CF ∥平面ADEB ,因为CF ⊂平面CFEB ,平面CFEB ∩平面ADEB =BE ,所以CF ∥BE ,又CF ⊂平面ACFD ,BE ⊄平面ACFD ,所以BE ∥平面ACFD ,所以V G -ECD =V E -GCD =V B -GCD .因为四边形ACFD 是等腰梯形,∠DAC =60°,AD =2CF =2AC ,所以∠ACD =90°, 又CA =CB =CF =1,所以CD =3,CG =12, 又BC ⊥平面ACFD , 所以V B -GCD =13×12CG ×CD ×BC =13×12×12×3×1=312. 所以三棱锥G -ECD 的体积为312.。
专题10 立体几何-五年(2017-2021)高考数学真题分项详解(新高考地区专用)(解析版)

连 ,在正方体 中,
M是 的中点,所以 为 中点,
又N是 的中点,所以 ,
平面 平面 ,
所以 平面 .
因为 不垂直 ,所以 不垂直
则 不垂直平面 ,所以选项B,D不正确;
在正方体 中, ,
平面 ,所以 ,
,所以 平面 ,
平面 ,所以 ,
且直线 是异面直线,
所以选项C错误,选项A正确.
故选:A.
本题考查了旋转体的理解和应用,解题的关键是掌握圆锥底面周长即为侧面展开图半圆的弧长,圆锥的母线长即为侧面展开图半圆的半径,考查了逻辑推理能力与运算能力,属于基础题.
【2021·江苏高考】在正三棱柱 中, ,点P满足 ,其中 , ,则
A.当 时, 的周长为定值
B.当 时,三棱锥 的体积为定值
C.当 时,有且仅有一个点P,使得
而 面BCD, 面BCD, ,
面BCD, 面BCD,
, 是直角三角形,且 ,
设DF与面DBC所成角为 ,则 即为CH与面DBC的夹角,
且 ,
在 中, ,
,
.
【知识点】线面垂直的判定、直线与平面所成的角、面面垂直的性质、线面垂直的性质
【解析】本题主要考查空间直线互相垂直的判定和性质,以及直线与平面所成角的几何计算问题,考查了空间想象能力和思维能力,平面与空间互相转化是能力,几何计算能力,以及逻辑推理能力,本题属综合性较强的题.
D.当 时,有且仅有一个点P,使得 平面
【答案】BD
【知识点】圆柱、圆锥、圆台的侧面积、表面积和体积
【解析】解:对于A,当 时, ,即 ,所以 ,
故点P在线段 上,此时 的周长为 ,
当点P为 的中点时, 的周长为 ,
当点P在点 处时, 的周长为 ,
2023届高考数学专项练习立体几何解答题最全归纳总结含答案

2023届高考数学专项练习立体几何解答题最全归纳总结【题型归纳目录】题型一:非常规空间几何体为载体题型二:立体几何存在性问题题型三:立体几何折叠问题题型四:立体几何作图问题题型五:立体几何建系繁琐问题题型六:两角相等(构造全等)的立体几何问题题型七:利用传统方法找几何关系建系题型八:空间中的点不好求题型九:创新定义【典例例题】题型一:非常规空间几何体为载体例1.如图,P为圆锥的顶点,O为圆锥底面的圆心,圆锥的底面直径AB=4,母线PH=22,M是PB的中点,四边形OBCH为正方形.(1)设平面POH∩平面PBC=l,证明:l∥BC;(2)设D为OH的中点,N是线段CD上的一个点,当MN与平面PAB所成角最大时,求MN的长.例2.如图所示,圆锥的底面半径为4,侧面积为162π,线段AB为圆锥底面⊙O的直径,C在线段AB上,且BC=3CA,点D是以BC为直径的圆上一动点;(1)当CD=CO时,证明:平面PAD⊥平面POD(2)当三棱锥P-BCD的体积最大时,求二面角B-PD-A的余弦值.例3.如图,圆锥PO 的母线长为6,△ABC 是⊙O 的内接三角形,平面PAC ⊥平面PBC .BC =23,∠ABC =60°.(1)证明:PA ⊥PC ;(2)设点Q 满足OQ =λOP ,其中λ∈0,1 ,且二面角O -QB -C 的大小为60°,求λ的值.例4.如图,D 为圆锥的顶点,O 为圆锥底面的圆心,AB 为底面直径,C 为底面圆周上一点,DA =AC =BC =2,四边形DOAE 为矩形,点F 在BC 上,且DF ⎳平面EAC .(1)请判断点F 的位置并说明理由;(2)平面DFO 将多面体DBCAE 分成两部分,求体积较大部分几何体的体积.例5.如图,在直角△POA 中,PO ⊥OA ,PO =2OA ,将△POA 绕边PO 旋转到△POB 的位置,使∠AOB =90°,得到圆锥的一部分,点C 为AB的中点.(1)求证:PC ⊥AB ;(2)设直线PC 与平面PAB 所成的角为φ,求sin φ..例6.如图,四边形ABCD 为圆柱O 1O 2的轴截面,EF 是该圆柱的一条母线,EF =2EA ,G 是AD 的中点.(1)证明:AF ⊥平面EBG ;(2)若BE =3EA ,求二面角E -BG -A 的正弦值.例7.例7.如图,几何体是圆柱的一部分,它是由矩形ABCD (及其内部)以AB 边所在直线为旋转轴旋转120°得到的,G 是DF的中点.(1)设P 是CE 上的一点,且AP ⊥BE ,求证BP ⊥BE ;(2)当AB =3,AD =2时,求二面角E -AG -C 的大小.例8.如图,四边形ABCD 是一个半圆柱的轴截面,E ,F 分别是弧DC ,AB 上的一点,EF ∥AD ,点H 为线段AD 的中点,且AB =AD =4,∠FAB =30°,点G 为线段CE 上一动点.(1)试确定点G 的位置,使DG ⎳平面CFH ,并给予证明;(2)求二面角C -HF -E 的大小.例9.坐落于武汉市江汉区的汉口东正教堂是中国南方唯一的拜占庭式建筑,象征着中西文化的有机融合.拜占庭建筑创造了将穹顶支承于独立方柱上的结构方法和与之相呼应的集中式建筑形制,其主体部分由一圆柱与其上方一半球所构成,如图所示.其中O 是下底面圆心,A ,B ,C 是⊙O 上三点,A 1,B 1,C 1是上底面对应的三点.且A ,O ,C 共线,AC ⊥OB ,C 1E =EC ,B 1F =13FB ,AE 与OF 所成角的余弦值为36565.(1)若E 到平面A 1BC 的距离为233,求⊙O 的半径.(2)在(1)的条件下,已知P 为半球面上的动点,且AP =210,求P 点轨迹在球面上围成的面积.例10.如图,ABCD 为圆柱OO 的轴截面,EF 是圆柱上异于AD ,BC 的母线.(1)证明:BE ⊥平面DEF ;(2)若AB =BC =6,当三棱锥B -DEF 的体积最大时,求二面角B -DF -E 的正弦值.例11.如图,O1,O分别是圆台上、下底的圆心,AB为圆O的直径,以OB为直径在底面内作圆E,C为圆O的直径AB所对弧的中点,连接BC交圆E于点D,AA1,BB1,CC1为圆台的母线,AB=2A1B1=8.(1)证明;C1D⎳平面OBB1O1;(2)若二面角C1-BC-O为π3,求O1D与平面AC1D所成角的正弦值.例12.某市在滨海文化中心有滨海科技馆,其建筑有鲜明的后工业风格,如图所示,截取其中一部分抽象出长方体和圆台组合,如图所示,长方体ABCD-A1B1C1D1中,AB=4,AD=AA1=2,圆台下底圆心O为AB的中点,直径为2,圆与直线AB交于E,F,圆台上底的圆心O1在A1B1上,直径为1.(1)求A1C与平面A1ED所成角的正弦值;(2)圆台上底圆周上是否存在一点P使得FP⊥AC1,若存在,求点P到直线A1B1的距离,若不存在则说明理由.题型二:立体几何存在性问题例13.如图,三棱锥P-ABC中,PA⊥平面ABC,PA=1,AB=1,AC=2,∠BAC=60°.(1)求三棱锥A-PBC的体积;(2)在线段PC上是否存在一点M,使得BM⊥AC?若存在,求MCPM的值,若不存在,请说明理由.例14.已知四棱锥P-ABCD中,底面ABCD是矩形,且AD=2AB,△PAD是正三角形,CD⊥平面PAD,E、F、G、O分别是PC、PD、BC、AD的中点.(1)求平面EFG与平面ABCD所成的锐二面角的大小;(2)线段PA上是否存在点M,使得直线GM与平面EFG所成角的大小为π6,若存在,求出PMPA的值;若不存在,说明理由.例15.已知三棱柱ABC-A1B1C1中,∠ACB=90°,A1B⊥AC1,AC=AA1=4,BC=2.(1)求证:平面A1ACC1⊥平面ABC;(2)若∠A1AC=60°,在线段AC上是否存在一点P,使二面角B-A1P-C的平面角的余弦值为34若存在,确定点P的位置;若不存在,说明理由.例16.如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD⎳BC,AD⊥CD,且AD=CD,BC=2CD,PA=2AD.(1)证明:AB⊥PC;(2)在线段PD上是否存在一点M,使得二面角M-AC-D的余弦值为1717,若存在,求BM与PC所成角的余弦值;若不存在,请说明理由.例17.如图,△ABC是边长为6的正三角形,点E,F,N分别在边AB,AC,BC上,且AE=AF=BN=4,M 为BC边的中点,AM交EF于点O,沿EF将三角形AEF折到DEF的位置,使DM=15.(1)证明:平面DEF⊥平面BEFC;(2)试探究在线段DM上是否存在点P,使二面角P-EN-B的大小为60°?若存在,求出DPPM的值;若不存在,请说明理由.例18.图1是直角梯形ABCD ,AB ⎳CD ,∠D =90∘,AB =2,DC =3,AD =3,CE =2ED ,以BE 为折痕将△BCE 折起,使点C 到达C 1的位置,且AC 1=6,如图2.(1)求证:平面BC 1E ⊥平面ABED ;(2)在棱DC 1上是否存在点P ,使得C 1到平面PBE 的距离为62?若存在,求出二面角P -BE -A 的大小;若不存在,说明理由.例19.如图所示,在四棱柱ABCD -A 1B 1C 1D 1中,侧棱A 1A ⊥底面ABCD ,AB ⊥AC ,AB =1,AC =AA 1=2,AD =CD =5,E 为棱AA 1上的点,且AE =12.(1)求证:BE ⊥平面ACB 1;(2)求二面角D 1-AC -B 1的余弦值;(3)在棱A 1B 1上是否存在点F ,使得直线DF ∥平面ACB 1?若存在,求A 1F 的长;若不存在,请说明理由.例20.如图,在五面体ABCDE中,已知AC⊥BD,AC⊥BC,ED⎳AC,且AC=BC=2ED=2,DC=DB =3.(1)求证:平面ABE⊥与平面ABC;(2)线段BC上是否存在一点F,使得平面AEF与平面ABE夹角余弦值的绝对值等于54343,若存在,求BFBC的值;若不存在,说明理由.题型三:立体几何折叠问题例21.如图1,在边上为4的菱形ABCD中,∠DAB=60°,点M,N分别是边BC,CD的中点,AC∩BD=O1,AC∩MN=G.沿MN将△CMN翻折到△PMN的位置,连接PA,PB,PD,得到如图2所示的五棱锥P -ABMND.(1)在翻折过程中是否总有平面PBD⊥平面PAG?证明你的结论;(2)当四棱锥P-MNDB体积最大时,求直线PB和平面MNDB所成角的正弦值;(3)在(2)的条件下,在线段PA上是否存在一点Q,使得二面角Q-MN-P余弦值的绝对值为1010若存在,试确定点Q的位置;若不存在,请说明理由.例22.如图,在等腰直角三角形PAD中,∠A=90°,AD=8,AB=3,B、C分别是PA、PD上的点,且AD⎳BC,M、N分别为BP、CD的中点,现将△BCP沿BC折起,得到四棱锥P-ABCD,连接MN.(1)证明:MN⎳平面PAD;(2)在翻折的过程中,当PA=4时,求二面角B-PC-D的余弦值.例23.如图1,在平面四边形PDCB中,PD∥BC,BA⊥PD,PA=AB=BC=2,AD=1.将△PAB沿BA 翻折到△SAB的位置,使得平面SAB⊥平面ABCD,如图2所示.(1)设平面SDC与平面SAB的交线为l,求证:BC⊥l;(2)点Q在线段SC上(点Q不与端点重合),平面QBD与平面BCD夹角的余弦值为66,求线段BQ的长.例24.如图,在平面五边形PABCD 中,△PAD 为正三角形,AD ∥BC ,∠DAB =90°且AD =AB =2BC =2.将△PAD 沿AD 翻折成如图所示的四棱锥P -ABCD ,使得PC =7.F ,Q 分别为AB ,CE 的中点.(1)求证:FQ ∥平面PAD ;(2)若DE PE=12,求平面EFC 与平面PAD 夹角的余弦值.例25.如图,在平行四边形ABCD 中,AB =3,AD =2,∠A =60°,E ,F 分别为线段AB ,CD 上的点,且BE =2AE ,DF =FC ,现将△ADE 沿DE 翻折至△A 1DE 的位置,连接A 1B ,A 1C .(1)若点G 为线段A 1B 上一点,且A 1G =3GB ,求证:FG ⎳平面A 1DE ;(2)当三棱锥C -A 1DE 的体积达到最大时,求二面角B -A 1C -D 的正弦值.例26.如图1,四边形ABCD是边长为2的正方形,四边形ABEF是等腰梯形,AB=BE=12EF,现将正方形ABCD沿AB翻折,使CD与C D 重合,得到如图2所示的几何体,其中D E=4.(1)证明:AF⊥平面AD E;(2)求二面角D -AE-C 的余弦值.例27.如图,在梯形ABCD中,AD∥BC,AB=BC=2,AD=4,现将△ABC所在平面沿对角线AC翻折,使点B翻折至点E,且成直二面角E-AC-D.(1)证明:平面EDC⊥平面EAC;(2)若直线DE与平面EAC所成角的余弦值为12,求二面角D-EA-C的余弦值.例28.如图1,在△ABC 中,∠ACB =90°,DE 是△ABC 的中位线,沿DE 将△ADE 进行翻折,使得△ACE 是等边三角形(如图2),记AB 的中点为F .(1)证明:DF ⊥平面ABC .(2)若AE =2,二面角D -AC -E 为π6,求直线AB 与平面ACD 所成角的正弦值.题型四:立体几何作图问题例29.已知四棱锥P -ABCD 中,底面ABCD 为正方形,O 为其中心,点E 为侧棱PD 的中点.(1)作出过O 、P 两点且与AE 平行的四棱锥截面(在答题卡上作出该截面与四棱锥表面的交线,并写出简要作图过程);记该截面与棱CD 的交点为M ,求出比值DM MC (直接写出答案);(2)若四棱锥的侧棱与底面边长均相等,求AE 与平面PBC 所成角的正弦值.例30..如图,已知底面为平行四边形的四棱锥P-ABCD中,平面MNGH与直线PB和直线AC平行,点E为PD的中点,点F在CD上,且DF:FC=1:2.(1)求证:四边形MNGH是平行四边形;(2)求作过EF作四棱锥P-ABCD的截面,使PB与截面平行(写出作图过程,不要求证明).截面的定义:用一个平面去截一个几何体,平面与几何体的表面的交线围成的平面图形.例31.如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为棱B1C1的中点,F,G分别是棱CC1,BC上的动点(不与顶点重合).(1)作出平面A1DG与平面CBB1C1的交线(要求写出作图过程),并证明:若平面A1DG⎳平面D1EF,则EF⎳A1D;(2)若G为棱BC的中点,是否存在F,使平面D1EF⊥平面DGF,若存在,求出CF的所有可能值;若不存在,请说明理由.例32.如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为棱B1C1的中点,F,G分别是棱CC1,BC上的动点(不与顶点重合).(1)作出平面A1DG与平面CBB1C1的交线(要求写出作图过程),并证明:若平面A1DG⎳平面D1EF,则EF⎳A1D;(2)若F,G均为其所在棱的中点,求点G到平面D1EF的距离.例33.如图多面体ABCDEF中,面FAB⊥面ABCD,△FAB为等边三角形,四边形ABCD为正方形,EF⎳BC,且EF=32BC=3,H,G分别为CE,CD的中点.(1)求二面角C-FH-G的余弦值;(2)作平面FHG与平面ABCD的交线,记该交线与直线AB交点为P,写出APAB的值(不需要说明理由,保留作图痕迹).例34.如图,已知多面体EABCDF的底面ABCD是边长为2的正方形,EA⊥底面ABCD,FD⎳EA,且FD =12EA=1.(1)求多面体EABCDF的体积;(2)记线段BC的中点为K,在平面ABCD内过点K作一条直线与平面ECF平行,要求保留作图痕迹,但不要求证明.例35.四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠DAB=2π3.AC∩BD=O,且PO⊥平面ABCD,PO=3,点F,G分别是线段PB.PD上的中点,E在PA上.且PA=3PE.(Ⅰ)求证:BD⎳平面EFG;(Ⅱ)求直线AB与平面EFG的成角的正弦值;(Ⅲ)请画出平面EFG与四棱锥的表面的交线,并写出作图的步骤.题型五:立体几何建系繁琐问题例36.如图,已知三棱柱ABC-A1B1C1的底面是正三角形,侧面BB1C1C是矩形,M,N分别为BC,B1C1的中点,P为AM上一点.过B1C1和P的平面交AB于E,交AC于F.(1)证明:AA1⎳MN,且平面A1AMN⊥平面EB1C1F;(2)设O为△A1B1C1的中心.若AO⎳平面EB1C1F,且AO=AB,求直线B1E与平面A1AMN所成角的正弦值.例37.如图,在锥体P-ABCD中,ABCD是边长为1的菱形,且∠DAB=60°,PA=PD=2,PB=2,E,F 分别是BC,PC的中点(1)证明:AD⊥平面DEF(2)求二面角P-AD-B的余弦值.例38.如图,AEC 是半径为a 的半圆,AC 为直径,点E 为AC的中点,点B 和点C 为线段AD 的三等分点,平面AEC 外一点F 满足FB =FD =5a ,EF =6a .(1)证明:EB ⊥FD ;(2)已知点Q ,R 为线段FE ,FB 上的点,FQ =23FE ,FR =23FB ,求平面BED 与平面RQD 所成二面角的正弦值.例39.《九章算术》是中国古代的一部数学专著,是《算经十书》中最重要的一部,成于公元一世纪左右.它是一本综合性的历史著作,是当时世界上最简练有效的应用数学,它的出现标志着中国古代数学形成了完整的体系.《九章算术》中将由四个直角三角形组成的四面体称为“鳖臑”,已知在三棱锥P -ABC 中,PA ⊥平面ABC .(1)从三棱锥P -ABC 中选择合适的两条棱填空: BC ⊥ ,则三棱锥P -ABC 为“鳖臑”;(2)如图,已知AD ⊥PB ,垂足为D ,AE ⊥PC ,垂足为E ,∠ABC =90°.(ⅰ)证明:平面ADE ⊥平面PAC ;(ⅱ)设平面ADE 与平面ABC 的交线为l ,若PA =23,AC =2,求二面角E -l -C 的大小.例40.已知四面体ABCD,AD=CD,∠ADB=∠CDB=120°,且平面ABD⊥平面BCD.(Ⅰ)求证:BD⊥AC;(Ⅱ)求直线CA与平面ABD所成角的大小.例41.已知四面体ABCD,∠ADB=∠CDB=120°,且平面ABD⊥平面BCD.(Ⅰ)若AD=CD,求证:BD⊥AC;(Ⅱ)求二面角B-CD-A的正切值.题型六:两角相等(构造全等)的立体几何问题例42.如图,在三棱锥A-BCD中,ΔABC是等边三角形,∠BAD=∠BCD=90°,点P是AC的中点,连接BP,DP(1)证明:平面ACD⊥平面BDP;(2)若BD=6,cos∠BPD=-33,求三棱锥A-BCD的体积.例43.如图,在三棱锥A-BCD中,ΔABC是等边三角形,∠BAD=∠BCD=90°,点P是AC的中点,连接BP,DP.(1)证明:平面ACD⊥平面BDP;(2)若BD=6,且二面角A-BD-C为120°,求直线AD与平面BCD所成角的正弦值.例44.如图,四棱锥F-ABCD中,底面ABCD为边长是2的正方形,E,G分别是CD、AF的中点,AF=4,∠FAE=∠BAE,且二面角F-AE-B的大小为90°.(1)求证:AE⊥BG;(2)求二面角B-AF-E的余弦值.例45.如图,四棱锥E-ABCD中,四边形ABCD是边长为2的菱形,∠DAE=∠BAE=45°,∠DAB=60°.(Ⅰ)证明:平面ADE⊥平面ABE;(Ⅱ)当直线DE与平面ABE所成的角为30°时,求平面DCE与平面ABE所成锐二面角的余弦值.例46.如图,在四面体ABCD中,已知∠ABD=∠CBD=60°,AB=BC=2,(1)求证:AC⊥BD;(2)若平面ABD⊥平面CBD,且BD=52,求二面角C-AD-B的余弦值.题型七:利用传统方法找几何关系建系例47.如图:长为3的线段PQ与边长为2的正方形ABCD垂直相交于其中心O(PO>OQ).(1)若二面角P-AB-Q的正切值为-3,试确定O在线段PQ的位置;(2)在(1)的前提下,以P,A,B,C,D,Q为顶点的几何体PABCDQ是否存在内切球?若存在,试确定其内切球心的具体位置;若不存在,请说明理由.例48.在四棱锥P-ABCD中,E为棱AD的中点,PE⊥平面ABCD,AD⎳BC,∠ADC=90°,ED=BC= 2,EB=3,F为棱PC的中点.(Ⅰ)求证:PA⎳平面BEF;(Ⅱ)若二面角F-BE-C为60°,求直线PB与平面ABCD所成角的正切值.例49.三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=2,侧面BCC1B1为矩形,∠A1AB=2π3,二面角A-BC-A1的正切值为12.(Ⅰ)求侧棱AA1的长;(Ⅱ)侧棱CC1上是否存在点D,使得直线AD与平面A1BC所成角的正切值为63,若存在,判断点的位置并证明;若不存在,说明理由.例50.如图,在四棱锥P-ABCD中,底面四边形ABCD内接于圆O,AC是圆O的一条直径,PA⊥平面ABCD,PA=AC=2,E是PC的中点,∠DAC=∠AOB(1)求证:BE⎳平面PAD;(2)若二面角P-CD-A的正切值为2,求直线PB与平面PCD所成角的正弦值.例51.如图所示,PA⊥平面ABCD,ΔCAB为等边三角形,PA=AB,AC⊥CD,M为AC中点.(Ⅰ)证明:BM⎳平面PCD;(Ⅱ)若PD与平面PAC所成角的正切值为62,求二面角C-PD-M的正切值.题型八:空间中的点不好求例52.如图,直线AQ⊥平面α,直线AQ⊥平行四边形ABCD,四棱锥P-ABCD的顶点P在平面α上,AB =7,AD=3,AD⊥DB,AC∩BD=O,OP⎳AQ,AQ=2,M,N分别是AQ与CD的中点.(1)求证:MN⎳平面QBC;(2)求二面角M-CB-Q的余弦值.例53.如图,四棱锥S-ABCD中,AB⎳CD,BC⊥CD,侧面SAB为等边三角形.AB=BC=2,CD=SD=1.(1)证明:SD⊥平面SAB(2)求AB与平面SBC所成角的正弦值.例54.如图,四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=2,DC=SD=2,点M在侧棱SC上,∠ABM=60°.(Ⅰ)证明:M是侧棱SC的中点;(Ⅱ)求二面角S-AM-B的余弦值.例55.如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD为直角梯形,其中AB⎳CD,∠CDA=90°,CD=2AB=2,AD=3,PA=5,PD=22,点E在棱AD上且AE=1,点F为棱PD的中点.在棱AD上且AE=1,点F位棱PD的中点.(1)证明:平面BEF⊥平面PEC;(2)求二面角A-BF-C的余弦值的大小.例56.如图,在四棱锥A-BCFE中,四边形EFCB为梯形,EF⎳BC,且EF=34BC,ΔABC是边长为2的正三角形,顶点F在AC上的射影为点G,且FG=3,CF=212,BF=52.(1)证明:平面F GB⊥平面ABC;(2)求二面角E-AB-F的余弦值.例57.三棱柱ABC-A1B1C1的底面ABC是等边三角形,BC的中点为O,A1O⊥底面ABC,AA1与底面ABC所成的角为π3,点D在棱AA1上,且AD=32,AB=2.(1)求证:OD⊥平面BB1C1C;(2)求二面角B-B1C-A1的平面角的余弦值.例58.如图,将矩形ABCD沿AE折成二面角D1-AE-B,其中E为CD的中点,已知AB+2,BC=1.BD1 =CD1,F1为D1B的中点.(1)求证:CF⎳平面AD1E;(2)求AF与平面BD1E所成角的正弦值.题型九:创新定义例59.蜂房是自然界最神奇的“建筑”之一,如图1所示.蜂房结构是由正六棱柱截去三个相等的三棱锥H-ABC,J-CDE,K-EFA,再分别以AC,CE,EA为轴将△ACH,△CEJ,△EAK分别向上翻转180°,使H,J,K三点重合为点S所围成的曲顶多面体(下底面开口),如图2所示.蜂房曲顶空间的弯曲度可用曲率来刻画,定义其度量值等于蜂房顶端三个菱形的各个顶点的曲率之和,而每一顶点的曲率规定等于2π减去蜂房多面体在该点的各个面角之和(多面体的面角是多面体的面的内角,用弧度制表示).例如:正四面体在每个顶点有3个面角,每个面角是π3,所以正四面体在各顶点的曲率为2π-3×π3=π.(1)求蜂房曲顶空间的弯曲度;(2)若正六棱柱底面边长为1,侧棱长为2,设BH=x(i)用x表示蜂房(图2右侧多面体)的表面积S(x);(ii)当蜂房表面积最小时,求其顶点S的曲率的余弦值.例60.类比于二维平面中的余弦定理,有三维空间中的三面角余弦定理;如图1,由射线PA,PB,PC构成的三面角P-ABC,∠APC=α,∠BPC=β,∠APB=γ,二面角A-PC-B的大小为θ,则cosγ=cosαcosβ+sinαsinβcosθ.时,证明以上三面角余弦定理;(1)当α、β∈0,π2(2)如图2,四棱柱ABCD-A1B1C1D1中,平面AA1C1C⊥平面ABCD,∠A1AC=60°,∠BAC=45°,①求∠A1AB的余弦值;②在直线CC1上是否存在点P,使BP⎳平面DA1C1?若存在,求出点P的位置;若不存在,说明理由.例61.(1)如图,对于任一给定的四面体A1A2A3A4,找出依次排列的四个相互平行的平面α1,α2,α3,α4,使得A i ∈αi i=1,2,3,4,且其中每相邻两个平面间的距离都相等;(2)给定依次排列的四个相互平行的平面α1,α2,α3,α4,其中每相邻两个平面间的距离为1,若一个正四面体A1A2A3A4的四个顶点满足:A i∈αi i=1,2,3,4,求该正四面体A1A2A3A4的体积.例62.已知a =(x 1,y 1,z 1),b =(x 2,y 2,z 2),c =(x 3,y 3,z 3),定义一种运算:(a ×b )⋅c =x 1y 2z 3+x 2y 3z 1+x 3y 1z 2-x 1y 3z 2-x 2y 1z 3-x 3y 2z 1,已知四棱锥P -ABCD 中,底面ABCD 是一个平行四边形,AB =(2,-1,4),AD =(4,2,0),AP =(-1,2,1)(1)试计算(AB ×AD )⋅AP 的绝对值的值,并求证PA ⊥面ABCD ;(2)求四棱锥P -ABCD 的体积,说明(AB ×AD )⋅AP 的绝对值的值与四棱锥P -ABCD 体积的关系,并由此猜想向量这一运算(AB ×AD )⋅AP 的绝对值的几何意义.立体几何解答题最全归纳总结【题型归纳目录】题型一:非常规空间几何体为载体题型二:立体几何存在性问题题型三:立体几何折叠问题题型四:立体几何作图问题题型五:立体几何建系繁琐问题题型六:两角相等(构造全等)的立体几何问题题型七:利用传统方法找几何关系建系题型八:空间中的点不好求题型九:创新定义【典例例题】题型一:非常规空间几何体为载体例1.如图,P 为圆锥的顶点,O 为圆锥底面的圆心,圆锥的底面直径AB =4,母线PH =22,M 是PB 的中点,四边形OBCH 为正方形.(1)设平面POH ∩平面PBC =l ,证明:l ∥BC ;(2)设D 为OH 的中点,N 是线段CD 上的一个点,当MN 与平面PAB所成角最大时,求MN 的长.【解析】(1)因为四边形OBCH 为正方形,∴BC ∥OH ,∵BC ⊄平面POH ,OH ⊂平面POH ,∴BC ∥平面POH .∵BC ⊂平面PBC ,平面POH ∩平面PBC =l ,∴l ∥BC .(2)∵圆锥的母线长为22,AB =4,∴OB =2,OP =2,以O 为原点,OP 所在的直线为z 轴,建立如图所示的空间直角坐标系,则P 0,0,2 ,B 0,2,0 ,D 1,0,0 C 2,2,0 ,M 0,1,1 ,设DN =λDC =λ,2λ,0 0≤λ≤1 ,ON =OD +DN =1+λ,2λ,0 ,MN =ON -OM =1+λ,2λ-1,-1 ,OD =1,0,0 为平面PAB 的一个法向量,设MN 与平面PAB 所成的角为θ,则sin θ=1+λ,2λ-1,-1 ⋅1,0,0 1+λ 2+2λ-1 2+1 =1+λ5λ2-2λ+3,令1+λ=t ∈1,2 ,则sin θ=t 5t 2-12t +10=15-12t +101t 2=1101t -35 2+75所以当1t =35时,即λ=23时,sin θ最大,亦θ最大,此时MN =53,13,-1 ,所以MN =MN =53 2+13 2+-1 2=353.例2.如图所示,圆锥的底面半径为4,侧面积为162π,线段AB 为圆锥底面⊙O 的直径,C 在线段AB 上,且BC =3CA ,点D 是以BC 为直径的圆上一动点;(1)当CD =CO 时,证明:平面PAD ⊥平面POD(2)当三棱锥P -BCD 的体积最大时,求二面角B -PD -A 的余弦值.【解析】(1)∵PO 垂直于圆锥的底面,∴PO ⊥AD ,当CD =CO 时,CD =OC =AC ,∴AD ⊥OD ,又OD ∩PO =O ,∴AD ⊥平面POD ,又AD ⊂平面PAD ,∴平面PAD ⊥平面POD ;(2)由题可知OA =OB =4,4π⋅PB =162π,∴PB =42,∴PO =4,当三棱锥P -BCD 的体积最大时,△DBC 的面积最大,此时D 为BC的中点,如图,建立空间直角坐标系O -xyz ,则A (0,-4,0),B (0,4,0),P (0,0,4),D 3,1,0 ,∴BP =0,-4,4 ,PD =3,1,-4 ,AP =(0,4,4),设平面PAD 的法向量为n 1 =(a ,b ,c ),则n 1 ⋅AP =0n 1 ⋅PD =0 ,即4b +4c =03a +b -4c =0,令a =5,则b =-3,c =3,∴n 1 =(5,-3,3),设平面PBD 的法向量n 2 =x ,y ,z ,则n 2 ⋅BP =0n 2 ⋅PD =0 ,即-4y +4z =03x +y -4z =0,令x =1,则y =1,z =1,∴n 2 =1,1,1 ,则cos n 1 ,n 2 =n 1 ⋅n 2 n 1 n 2 =5-3+33×52+-3 2+32=5129129,∴二面角B -PD -A 的余弦值为-5129129.例3.如图,圆锥PO 的母线长为6,△ABC 是⊙O 的内接三角形,平面PAC ⊥平面PBC .BC =23,∠ABC =60°.(1)证明:PA ⊥PC ;(2)设点Q 满足OQ =λOP ,其中λ∈0,1 ,且二面角O -QB -C 的大小为60°,求λ的值.【解析】(1)∵PA =PB =PC =6,BC =23,PB 2+PC 2=BC 2,∴PB ⊥PC∵平面PAC ⊥平面PBC 且平面PAC ∩平面PBC =PC ,PB ⊂平面PBC ,PB ⊥PC ,∴PB ⊥平面PAC ,又PA ⊂平面PAC ,∴PB ⊥PA ,∴AB =PA 2+PB 2=23,∴∠ABC =60°,∴△ABC 是正三角形,AC =23,∵PA 2+PC 2=AC 2∴PA ⊥PC ;(2)在平面ABC 内作OM ⊥OB 交BC 于M ,以O 为坐标原点,OM ,OB ,OP 所在直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系O -xyz 如图所示:易知OB =OC =2,OP =PB 2-OB 2=2,所以B 2,0,0 ,P 0,0,2 ,C -1,3,0 ,Q 0,0,2λ ,QB =2,0,-2λ ,BC =-3,3,0 ,设平面OBC 的法向量n 1 =x ,y ,z ,依题意n 1 ⋅QB =0n 1 ⋅CB =0 ,即2x -2λz =0-3x +3y =0 ,不妨令y =3λ,得n 1 =λ,3λ,2 ,易知平面OQB 的法向量n 2 =0,1,0 ,由λ∈0,1 可知cos n 1 ,n 2 =n 1 ⋅n 2 n 1 ⋅n 2=cos60°,即3λλ2+(3λ)2+2 2=12,解得λ=12例4.如图,D 为圆锥的顶点,O 为圆锥底面的圆心,AB 为底面直径,C 为底面圆周上一点,DA =AC =BC =2,四边形DOAE 为矩形,点F 在BC 上,且DF ⎳平面EAC .(1)请判断点F 的位置并说明理由;(2)平面DFO 将多面体DBCAE 分成两部分,求体积较大部分几何体的体积.【解析】(1)点F 是BC 的中点,取BC 的中点F ,连接OF ,DF ,因为O 为AB 的中点,所以OF ⎳AC ,又AC ⊂平面AEC ,OF ⊄平面AEC ,所以OF ⎳平面AEC ,由四边形DOAE 为矩形,所以DO ⎳AE ,又AE ⊂平面AEC ,OD ⊄平面AEC ,所以OD ⎳平面AEC ,因为DO ∩OF =O ,DO ,OF ⊂平面DOF ,所以平面DOF ⎳平面AEC ,因为DF ⊂平面DOF ,所以DF ⎳平面AEC ,(2)由(1)知点F 是BC 的中点,因为DA =AC =BC =2,所以AB =AC 2+BC 2=22,所以OA =OC =OB =2,且OC ⊥AB ,所以OD =AD 2-OA 2=2,所以三棱锥D -BOF 的体积V D -BOF =13S △BOF ⋅DO =13×12×2×22×2=26;又三棱锥D -BOC 的体积V D -BOC =13S △BOC ⋅DO =13×12×2×2×2=23,所以四棱锥C -DOAE 的体积V C -DOAE =13S DOAE ×2=13×2 2×2=223,所以几何体DBCAE 的体积V DBCAE =V D -BCO +V C -DOAE =2,所以体积较大部分几何体的体积为V DBCAE -V D -BOF =2-26=526;例5.如图,在直角△POA 中,PO ⊥OA ,PO =2OA ,将△POA 绕边PO 旋转到△POB 的位置,使∠AOB =90°,得到圆锥的一部分,点C 为AB 的中点.(1)求证:PC ⊥AB ;(2)设直线PC 与平面PAB 所成的角为φ,求sin φ.【解析】(1)证明:由题意知:PO ⊥OA ,PO ⊥OB ,OA ∩OC =0∴PO ⊥平面AOB ,又∵AB ⊂平面AOB ,所以PO ⊥AB .又点C 为AB 的中点,所以OC ⊥AB ,PO ∩OC =0,所以AB ⊥平面POC ,又∵PC ⊂平面POC ,所以PC ⊥AB .(2)以O 为原点,OA ,OB ,OP 的方向分别作为x ,y ,z 轴的正方向建立如图所示的空间直角坐标系,设OA =2,则A 2,0,0 ,B 0,2,0 ,P 0,0,4 ,C 2,2,0 ,所以AB =-2,2,0 ,AP =-2,0,4 ,PC =2,2,-4 .设平面PAB 的法向量为n =a ,b ,c ,则n ⋅AB =-2a +2b =0,n ⋅AP =-2a +4c =0, 取c =1,则a =b =2可得平面PAB 的一个法向量为n =2,2,1 ,所以sin φ=cos n ,PC =n ⋅PC n PC =42-465=210-5 15.例6.如图,四边形ABCD 为圆柱O 1O 2的轴截面,EF 是该圆柱的一条母线,EF =2EA ,G 是AD 的中点.(1)证明:AF ⊥平面EBG ;(2)若BE =3EA ,求二面角E -BG -A 的正弦值.【解析】(1)由已知EF ⊥平面ABE ,BE ⊂平面ABE ,所以EF ⊥BE ,因为AB 是圆O 1的直径,所以AE ⊥BE ,因为AE ∩FE =E ,所以BE ⊥平面AFE ,AF ⊂平面AFE ,故BE ⊥AF ,因为EF =2EA =2AG ,所以EA =2AG ,易知:Rt △AEG ∼Rt △EFA ,所以∠GEA +∠EAF =90°,从而AF ⊥EG ,又BE ∩EG =E ,所以AF ⊥平面EBG .(2)以E 为坐标原点,EA 为x 轴正方向,EA 为单位向量,建立如图所示的空间直角坐标系E -xyz ,则AB =2,BE =3,EF =2,从而A 1,0,0 ,B 0,3,0 ,D 1,0,2 ,F 0,0,2 ,AB =-1,3,0 ,AD =0,0,2 ,设n =x ,y ,z 位平面BGA 的法向量,则{n ⋅AB =0n ⋅AD =0⇒{-x +3y =02z =0⇒{x =3y =1z =0,所以n =3,1,0 ,由(1)知:平面BEG 的法向量为AF =-1,0,2 ,因为cos n ,AF =n ⋅AF n ⋅AF=-12,所以二面角E -BG -A 的正弦值为32.例7.例7.如图,几何体是圆柱的一部分,它是由矩形ABCD (及其内部)以AB 边所在直线为旋转轴旋转120°得到的,G 是DF的中点.(1)设P 是CE 上的一点,且AP ⊥BE ,求证BP ⊥BE ;(2)当AB =3,AD =2时,求二面角E -AG -C 的大小.【解析】(1)因为AP ⊥BE ,AB ⊥BE ,AB ,AP ⊂平面ABP ,AB ∩AP =A ,所以BE ⊥平面ABP ,又BP ⊂平面ABP ,所以BP ⊥BE .(2)以B 为坐标原点,分别以BE ,BP ,BA 所在的直线为x ,y ,z 轴,建立如图所示的空间直角坐标系.由题意得A (0,0,3),E (2,0,0),G (1,3,3),C (-1,3,0),故AE =(2,0,-3),AG =(1,3,0),CG =(2,0,3).设m =x 1,y 1,z 1 是平面AEG 的一个法向量,由m ·AE =0m ·AG =0 可得2x 1-3z 1=0,x 1+3y 1=0.取z 1=2,可得平面AEG 的一个法向量m =(3,-3,2).设n =x 2,y 2,z 2 是平面ACG 的一个法向量,由n ·AG =0n ·CG =0,可得x 2+3y 2=0,2x 2+3z 2=0. 取z 2=-2,可得平面ACG 的一个法向量n =(3,-3,-2).所以cos ‹m ,n ›=m ⋅n |m |⋅|n |=12, 因为<m ,n >∈[0,π],故所求的角为60°.例8.如图,四边形ABCD 是一个半圆柱的轴截面,E ,F 分别是弧DC ,AB 上的一点,EF ∥AD ,点H 为线段AD 的中点,且AB =AD =4,∠FAB =30°,点G 为线段CE 上一动点.(1)试确定点G 的位置,使DG ⎳平面CFH ,并给予证明;(2)求二面角C -HF -E 的大小.【解析】(1)当点G 为CE 的中点时,DG ∥平面CFH .证明:取CF 得中点M ,连接HM ,MG .∵G ,M 分别为CE 与CF 的中点,∴GM ∥EF ,且GM =12EF =12AD ,又H 为AD 的中点,且AD ∥EF ,AD =EF ,∴GM ∥DH ,GM =DH .四边形GMHD 是平行四边形,∴HM ∥DG又HM ⊂平面CFH ,DG ⊄平面CFH∴DG ∥平面CFH(2)由题意知,AB 是半圆柱底面圆的一条直径,∴AF ⊥BF .∴AF =AB cos30°=23,BF =AB sin30°=2.由EF ∥AD ,AD ⊥底面ABF ,得EF ⊥底面ABF .∴EF ⊥AF ,EF ⊥BF .以点F 为原点建立如图所示的空间直角坐标系,则F (0,0,0),B (0,2,0),C (0,2,4),H (23,0,2)FH =(23,0,2),FC =(0,2,4)设平面CFH 的一个法向量为n =(x ,y ,z )所以n ⋅FH =23x +2z =0n ⋅FC =2y +4z =0则令z =1则y =-2,x =-33即n =-33,-2,1由BF ⊥AF ,BF ⊥FE ,AF ∩FE =F .得BF ⊥平面EFH ∴平面EFH 的一个法向量为FB =(0,2,0)设二面角C -HF -E 所成的角为θ∈0,π2则cos θ=∣cos ‹n ,FB ›=|n ⋅FB ||n ||FB |=0×-33 +(-2)×2+1×02×13+4+1=32 ∴二面角C -HF -E 所成的角为π6.例9.坐落于武汉市江汉区的汉口东正教堂是中国南方唯一的拜占庭式建筑,象征着中西文化的有机融合.拜占庭建筑创造了将穹顶支承于独立方柱上的结构方法和与之相呼应的集中式建筑形制,其主体部分由一圆柱与其上方一半球所构成,如图所示.其中O 是下底面圆心,A ,B ,C 是⊙O 上三点,A 1,B 1,C 1是上底面对应的三点.且A ,O ,C 共线,AC ⊥OB ,C 1E =EC ,B 1F =13FB ,AE 与OF 所成角的余弦值为36565.(1)若E 到平面A 1BC 的距离为233,求⊙O 的半径.(2)在(1)的条件下,已知P 为半球面上的动点,且AP =210,求P 点轨迹在球面上围成的面积.【解析】(1)如图,取BB 1,CE 上的点N ,M .连接OM ,OF ,FM .过N 作NH ⊥A 1B 于H ,则OM ∥AE ,由题意知cos ∠FOM =36565,设⊙O 的半径为r ,AA 1=h ,由勾股定理知OF =r 2+916h 2,OM =r 2+116h 2,FM =2r 2+14h 2,由余弦定理知cos ∠FOM =OF 2+OM 2-FM 22×OF ×OM.代入解得h =2r ,因为EN ∥BC ,EN ⊄面A 1BC ,所以EN ∥面A 1BC ,故N 到面A 1BC 的距离是233,因为BC ⊥AB ,BC ⊥AA 1,AA 1∩AB =A ,所以BC ⊥面A 1AB ,BC ⊥NH ,因为NH ⊥BC ,NH ⊥A 1B ,A 1B ∩BC =B ,所以NH ⊥面A 1BC ,NH =233,而sin ∠A 1BB 1=NH BN =A 1B 1A 1B ,即233×h 2=2r 2r 2+h 2,解得r =2,h =4,即⊙O 的半径为2.(2)设上底面圆心为O 1,则O 1P =2,O 1O 2与O 1P 的夹角为θ,所以|AP |=|AO 1 +O 1P |=20+4+85cos θ=210,解得cos θ=255,过P 作PO 2⊥AO 1于O 2,则O 2P =O 1P ⋅sin θ=255,所以点P 的轨迹是以O 2为圆心,以255为半径的圆,因此可作出几何体被面AOA 1所截得到的截面,如图所示.设弧A 1C 1旋转一周所得到的曲面面积为S 1,弧PP 得到的为S 2,则S 2S 1=1-cos θS 1=12×4πr2 ,因此S 2=2πr 2(1-cos θ)=8π1-255 .因此P 点轨迹在球面上围成的面积为8π1-255.例10.如图,ABCD 为圆柱OO 的轴截面,EF 是圆柱上异于AD ,BC 的母线.(1)证明:BE ⊥平面DEF ;(2)若AB =BC =6,当三棱锥B -DEF 的体积最大时,求二面角B -DF -E 的正弦值.【解析】(1)证明:如图,连接AE ,由题意知AB 为⊙O 的直径,所以AE ⊥BE .因为AD ,EF 是圆柱的母线,所以AD ∥EF 且AD =EF ,所以四边形AEFD 是平行四边形.所以AE ⎳DF ,所以BE ⊥DF .因为EF 是圆柱的母线,所以EF ⊥平面ABE ,又因为BE ⊂平面ABE ,所以EF ⊥BE .又因为DF ∩EF =F ,DF 、EF ⊂平面DEF ,所以BE ⊥平面DEF .(2)由(1)知BE 是三棱锥B -DEF 底面DEF 上的高,由(1)知EF ⊥AE ,AE ∥DF ,所以EF ⊥DF ,即底面三角形DEF 是直角三角形.设DF =AE =x ,BE =y ,则在Rt △ABE 中有:x 2+y 2=6,所以V B -DEF =13S △DEF ⋅BE =13⋅12x ⋅6⋅y =66xy ≤66⋅x 2+y 22=62,当且仅当x =y =3时等号成立,即点E ,F 分别是AB ,CD的中点时,三棱锥B -DEF 的体积最大,。
高三数学一轮复习专题突破训练立体几何 Word版含答案

江苏省年高考一轮复习专题突破训练立体几何一、填空题、(常州市届高三上期末)已知四棱锥-的底面是边长为,锐角为°的菱形,侧棱⊥底面,=,若点是的中点,则三棱锥-的体积为、(年江苏高考)现有橡皮泥制作的底面半径为,高为的圆锥和底面半径为,高为的圆柱各一个,若将它们制作成总体积和高均保持不变,但底面半径相同的新圆锥和圆柱各一个,则新的底面半径为。
、(年江苏高考)设甲、乙两个圆柱的底面积分别为,体积分别为,若它们的侧面积相等,,则▲ .、(南京市届高三三模)已知α,β是两个不同的平面,,是两条不同直线,⊥α,⊂β.给出下列命题:①α∥β⇒⊥;②α⊥β⇒∥;③∥α⇒⊥β;④⊥β⇒∥α.其中正确的命题是. (填.写所有正确命题的........序号..).、(南通、扬州、泰州三市届高三二模)在体积为的四面体中,平面,,,,则长度的所有值为▲.、(南通市届高三一模)已知正方体的棱长为,点是棱的中点,则三棱锥的体积为、(苏锡常镇四市届高三一模)如图,正方体的棱长为,是棱的中点,则四棱锥的体积为.、(苏锡常镇四市市届高三二模)设棱长为的正方体的体积和表面积分别为,,底面半径和高均为的圆锥的体积和侧面积分别为,,若,则的值为▲.、(镇江市届高三一模)设,表示两条直线,α,β表示两个平面,现给出下列命题:①若⊂α,∥α,则∥;②若⊂,∥,则∥;③若∥α,α⊥β,则⊥β;④若∥α,⊥β,则α⊥β.其中正确的命题是.(写山所有正确命题的序号)、(南通市海安县届高三上期末)正四棱锥的底面边长为,侧面与底面所成二面角的大小为°,则该四棱锥的侧面积为、(苏州市届高三上期末)将半径为的圆分割成面积之比为的三个扇形作为三个圆锥的侧面,设这三个圆锥的底面半径依次为,则=▲、(泰州市届高三第一次模拟)如图,长方体中,为的中点,三棱锥的体积为,四棱锥的体积为,则的值为▲ .二、解答题、(年江苏高考)如图,在直三棱柱中,,分别为,的中点,点在侧棱上,且,.求证:()直线∥平面;()平面⊥平面.。
高考数学压轴题突破训练——立体几何(含详解)

高考数学压轴题突破训练——立体几何1. 1. 如图,平面如图,平面VAD VAD⊥平面⊥平面ABCD ABCD,△,△,△VAD VAD 是等边三角形,是等边三角形,ABCD ABCD 是矩形,是矩形,AB AB AB∶∶AD AD==2∶1,F 是AB 的中点.的中点.(1)求VC 与平面ABCD 所成的角;所成的角; (2)求二面角V-FC-B 的度数;的度数;(3)当V 到平面ABCD 的距离是3时,求B 到平面VFC 的距离.的距离.2.2.如图正方体如图正方体ABCD-1111D C B A 中,中,E E 、F 、G 分别是B B 1、AB AB、、BC 的中点.的中点.(1)证明:F D 1⊥EG EG;; (2)证明:F D 1⊥平面AEG AEG;; (3)求AE <cos ,>B D 1.3. 3. 在直角梯形在直角梯形P 1DCB 中,中,P P 1D//CB D//CB,,CD//P 1D 且P 1D D = = 6,BC = = 33,DC =6,A 是P 1D 的中点,沿AB 把平面P 1AB 折起到平面PAB 的位置,使二面角P -CD CD--B 成45°角,设E 、F 分别是线段AB AB、、PD 的中点.的中点. ((1)求证:)求证:AF//AF//AF//平面平面PEC PEC;; ((2)求平面PEC 和平面PAD 所1. 1. 如图,平面如图,平面VAD VAD⊥平面⊥平面ABCD ABCD,△,△,△VAD VAD 是等边三角形,ABCD 是矩形,是矩形,AB AB AB∶∶AD AD==2∶1,F 是AB 的中点.的中点.D B C F E A P (1)求VC 与平面ABCD 所成的角;所成的角; (2)求二面角V-FC-B 的度数;的度数;(3)当V 到平面ABCD 的距离是3时,求B 到平面VFC 的距离.的距离.2.2.如图正方体如图正方体ABCD-1111D C B A 中,中,E E 、F 、G 分别是B B 1、AB AB、、BC 的中点.的中点.(1)证明:F D 1⊥EG EG;; (2)证明:F D 1⊥平面AEG AEG;; (3)求AE <cos ,>B D 1.3. 3. 在直角梯形在直角梯形P 1DCB 中,中,P P 1D//CB D//CB,,CD//P 1D 且P 1D D = = 6,BC = = 33,DC =6,A 是P 1D 的中点,沿AB 把平面P 1AB 折起到平面PAB 的位置,使二面角P -CD CD--B 成45°角,设E 、F 分别是线段AB AB、、PD 的中点.的中点. ((1)求证:)求证:AF//AF//AF//平面平面PEC PEC;; ((2)求平面PEC 和平面PAD 所成的二面角的大小;所成的二面角的大小; ((3)求点D 到平面PEC 的距离.的距离. 成的二面角的大小;成的二面角的大小; ((3)求点D 到平面PEC 的距离.的距离.BC DA P 1 DBCF E A P4. 4. 如图四棱锥如图四棱锥ABCD P -中,中,^PA 底面ABCD ,4=PA 正方形的边长为2 (1)求点A 到平面PCD 的距离;的距离;(2)求直线PA 与平面PCD 所成角的大小;所成角的大小; (3)求以PCD 与PAC 为半平面的二面角的正切值。
高考数学最新真题专题解析—立体几何综合(新高考卷)

高考数学最新真题专题解析—立体几何综合(新高考卷)【母题来源】2022年新高考I卷【母题题文】已知正方体ABCD−A1B1C1D1,则()A. 直线BC1与DA1所成的角为90∘B. 直线BC1与CA1所成的角为90∘C. 直线BC1与平面BB1D1D所成的角为45∘D. 直线BC1与平面ABCD所成的角为45∘【答案】ABD【分析】本题主要考查直线与直线所成角及直线与平面所成角,属于中档题.【解答】解:如图,因为BC1⊥B1C,B1C//DA1,所以BC1⊥DA1,故A正确;对于选项B:因为直线BC1⊥平面CDA1B1,且CA1⊂平面CDA1B1,所以直线BC1⊥CA1,故B正确;对于选项C:连接A1C1与B1D1交于点O1,则∠O1BC1即为直线BC1与平面BB1D1D所成的角,sin∠O1BC1=O1C1BC1=12,所以∠O1BC1=30∘,故C错误;对于选项D:直线BC1与平面ABCD所成的角即为∠C1BC=45∘,所以D 正确.【母题来源】2022年新高考I卷【母题题文】如图,直三棱柱ABC−A1B1C1的体积为4,△A1BC的面积为2√2.(1)求A到平面A1BC的距离;(2)设D为A1C的中点,AA1=AB,平面A1BC⊥平面ABB1A1,求二面角A−BD−C的正弦值.【答案】解:(1)设A到平面A1BC的距离为d,因为直三棱柱ABC−A1B1C1的体积为4,即可得S△ABC·AA1=4,故V A1−ABC =13S△ABC·AA1=43,又V A1−ABC =V A−A1BC=13S△A1BC·d=13×2√2×d=43,解得d =√2,所以A 到平面A 1BC 的距离为√2;(2)连接AB 1,因为直三棱柱ABC −A 1B 1C 1中,AA 1=AB , 故AA 1B 1B 为正方形,即AB 1⊥A 1B ,又平面A 1BC ⊥平面ABB 1A 1,平面A 1BC ∩平面ABB 1A 1=A 1B ,AB 1⊂平面ABB 1A 1, 故AB 1⊥平面A 1BC ,所以AB 1⊥BC ,又因为AA 1⊥BC ,AB 1,AA 1⊂平面ABB 1A 1,且AB 1∩AB 1=A , 故BC ⊥平面ABB 1A 1,则BC ⊥AB , 所以BB 1,AB,BC 三条直线两两垂直, 故如图可以以B 为原点建立空间直角坐标系,设AA 1=AB =a ,BC =b ,则A 1B =√2a ,由条件可得{12a ×b ×a =412×√2a ×b =2√2,解得{a =2b =2, 则B(0,0,0),C(2,0,0),A(0,2,0),A 1(0,2,2),A 1C 的中点D(1,1,1), 所以BA ⃗⃗⃗⃗⃗ =(0,2,0),BD ⃗⃗⃗⃗⃗⃗ =(1,1,1),BC ⃗⃗⃗⃗⃗ =(2,0,0) 设平面ABD 的一个法向量为n 1⃗⃗⃗⃗ =(x,y,z),{n1⃗⃗⃗⃗ ⋅BA⃗⃗⃗⃗⃗ =0n1⃗⃗⃗⃗ ⋅BD⃗⃗⃗⃗⃗⃗ =0⇒{2y=0x+y+z=0,取n1⃗⃗⃗⃗ =(1,0,−1),同理可求得平面BCD的一个法向量为n2⃗⃗⃗⃗ =(0,1,−1)所以|cos<n1⃗⃗⃗⃗ ,n2⃗⃗⃗⃗ >|=|n1⃗⃗⃗⃗⃗ ·n2⃗⃗⃗⃗⃗ ||n1⃗⃗⃗⃗⃗ |·|n2⃗⃗⃗⃗⃗ |=12,所以二面角A−BD−C的正弦值为√32.【母题来源】2022年新高考II卷【母题题文】如图,四边形ABCD为正方形,ED⊥平面ABCD,FB//ED,AB=ED=2FB,记三棱锥E−ABC,E−ACF,F−ABC的体积分别为V1,V2,V3,则()A. V3=2V2B. V3=2V1C. V3=V1+V2D. 2V3=3V1【答案】CD【解析】【分析】本题主要考查三棱锥的体积,属于基础题.【解答】解:设AB=ED=2FB=2,则V1=13×2×2=43,V2=13×2×1=23.连结BD交AC于M,连结EM、FM,则FM=√3,EM=√6,EF=3,故S△EMF=1 2⋅√3⋅√6=3√22,V3=13S△EMF×AC=2,V3=V1+V2,2V3=3V1.【母题来源】2022年新高考II卷【母题题文】如图,PO是三棱锥P−ABC的高,PA=PB,AB⊥AC,E是PB的中点.(1)证明:OE//平面PAC;(2)若∠ABO=∠CBO=30∘,PO=3,PA=5,求二面角C−AE−B正弦值.【答案】解:(1)法一:连接OA、OB,因为PO是三棱锥P−ABC的高,所以PO⊥平面ABC,所以PO⊥OA,PO⊥OB,所以∠POA=∠POB=90∘,又PA=PB,PO=PO,所以△POA≌△POB,所以OA=OB,作AB中点D,连接OD、DE,则有OD⊥AB,又AB⊥AC,所以OD//AC,又因为OD⊄平面PAC,AC⊂平面PAC,所以OD//平面PAC,又D、E分别为AB、PB的中点,所以,在△BPA中,DE//PA又因为平面PAC,PA⊂平面PAC,所以DE//平面PAC,又OD、DE⊂平面ODE,OD∩DE=D,所以平面ODE//平面PAC,又OE⊂平面ODE,所以OE//平面PAC;法二:(1)连接OA、OB,因为PO是三棱锥P−ABC的高,所以PO⊥平面ABC,所以PO⊥OA,PO⊥OB,所以∠POA=∠POB=90∘,又PA=PB,PO=PO,所以△POA≌△POB,所以OA=OB,又AB⊥AC,在Rt△ABF,O为BF中点,延长BO,交AC于F,连接PF,所以在△PBF中,O、E分别为BF、PB的中点,所以EO//PF,因为EO⊄平面PAC,PF⊂平面PAC,所以EO//平面PAC;(2)法一:过点D作DF//OP,以DB为x轴,DO为y轴,DF为z轴.建立如图所示的空间直角坐标系.因为PO=3,PA=5,由(1)OA=OB=4,又∠ABO=∠CBO=30∘,所以OD=2,DB=2√3,),所以P(0,2,3),B(2√3,0,0),A(−2√3,0,0),E(√3,1,32设AC=a,则C(−2√3,a,0),平面AEB的法向量设为n1⃗⃗⃗⃗ =(x1,y1,z1),直线AB的方向向量可设为a⃗=(1,0,0),直线DP⊂平面AEB,直线DP的方向向量为b⃗ =(0,2,3){a ⃗ ⋅n 1⃗⃗⃗⃗ =0b ⃗ ⋅n 1⃗⃗⃗⃗ =0,所以{x 1=02y 1+3z 1=0,所以x 1=0,设y 1=3,则z 1=−2,所以n 1⃗⃗⃗⃗ =(0,3,−2);平面AEC 的法向量设为n 2⃗⃗⃗⃗ =(x 2,y 2,z 2),AC ⃗⃗⃗⃗⃗ =(0,a,0),AE ⃗⃗⃗⃗⃗ =(3√3,1,32) {AC ⃗⃗⃗⃗⃗ ⋅n 2⃗⃗⃗⃗ =0AE ⃗⃗⃗⃗⃗ ⋅n 2⃗⃗⃗⃗ =0,所以{ay 2=03√3x 2+y 2+32z 2=0,所以y 2=0,设x 2=√3,则z 2=−6,所以n ⃗ =(√3,0,−6);所以cos <n 1⃗⃗⃗⃗ ,n 2⃗⃗⃗⃗ >=n 1⃗⃗⃗⃗⃗ ·n 2⃗⃗⃗⃗⃗ |n 1⃗⃗⃗⃗⃗ |⋅|n 2⃗⃗⃗⃗⃗ |=√13×√39=13√3=4√313, 二面角C −AE −B 的平面角为θ,则sinθ=√1−cos 2θ=1113, 所以二面角C −AE −B 的正弦值为1113法二:(2)过点A 作AF//OP ,以AB 为x 轴,AC 为y 轴,AF 为z 轴 建立所示的空间直角坐标系.因为PO =3,PA =5,由(1)OA =OB =4,又∠ABO =∠CBO =30°,所以,AB =4√3,所以P(2√3,2,3),B(4√3,0,0), A(0,0,0),E(3√3,1,32),设AC =a ,则C(0,a,0),平面AEB 的法向量设为n 1⃗⃗⃗⃗ =(x 1,y 1,z 1),AB ⃗⃗⃗⃗⃗ =(4√3,0,0),AE ⃗⃗⃗⃗⃗ =(3√3,1,32) {AB ⃗⃗⃗⃗⃗ ⋅n 1⃗⃗⃗⃗ =0AE ⃗⃗⃗⃗⃗ ⋅n 2⃗⃗⃗⃗ =0,所以{4√3x 1=03√3x 1+y 1+32z 1=0,所以x 1=0设z 1=−2,则y 1=3, 所以n 1⃗⃗⃗⃗ =(0,3,−2);平面AEC 的法向量设为n 2⃗⃗⃗⃗ =(x,y,z),AC ⃗⃗⃗⃗⃗ =(0,a,0),AE ⃗⃗⃗⃗⃗ =(3√3,1,32) {AC ⃗⃗⃗⃗⃗ ⋅n 2⃗⃗⃗⃗ =0AE ⃗⃗⃗⃗⃗ ⋅n 2⃗⃗⃗⃗ =0,所以{ay 2=03√3x 2+y 2+32z 2=0,所以y 2=0,设x 2=√3,则z 2=−6,所以n 2⃗⃗⃗⃗ =(√3,0,−6);所以cos <n 1⃗⃗⃗⃗ ,n 2⃗⃗⃗⃗ >=n 1⃗⃗⃗⃗⃗ ·n 2⃗⃗⃗⃗⃗ |n 1⃗⃗⃗⃗⃗ |⋅|n 2⃗⃗⃗⃗⃗ |=√13×√39=√1213√3=4√313二面角C −AE −B 的平面角为θ,则sinθ=√1−cos 2θ=1113, 所以二面角C −AE −B 的正弦值为1113. 【命题意图】考察棱柱、棱锥棱台、圆柱、圆锥、圆台及其简单组合体的结构特征,能画出简单空间图形并能识别立体图形的模型,考察几何体中的点线面关系,考察线线、线面、面面之间的平行和垂直关系,考察异面直线所成的角,直线和平面所成的角,二面角的平面角等的求解,考察数形结合思想,空间想象力及逻辑推导能力。
压轴题05 立体几何压轴题(解析版)--2023年高考数学压轴题专项训练(全国通用-理)

压轴题05立体几何压轴题题型/考向一:点、线、面间的位置关系和空间几何体的体积、表面积题型/考向二:外接球、内切球等相关问题题型/考向三:平行关系、垂直关系、二面角等相关问题一、空间几何体的体积、表面积热点一空间几何体的侧面积、表面积柱体、锥体、台体和球的表面积公式:(1)若圆柱的底面半径为r,母线长为l,则S侧=2πrl,S表=2πr(r+l).(2)若圆锥的底面半径为r,母线长为l,则S侧=πrl,S表=πr(r+l).(3)若圆台的上、下底面半径分别为r′,r,则S侧=π(r+r′)l,S表=π(r2+r′2+r′l +rl).(4)若球的半径为R,则它的表面积S=4πR2.热点二空间几何体的体积柱体、锥体、台体和球的体积公式:(1)V柱体=Sh(S为底面面积,h为高);Sh(S为底面面积,h为高);(2)V锥体=13(S上+S下+S上S下)h(S上、S下分别为上、下底面面积,h为高);(3)V台体=13(4)V球=4πR3.3二、外接球、内切球问题类型一外接球问题考向1墙角模型墙角模型是三棱锥有一条侧棱垂直于底面且底面是直角三角形模型,用构造法(构造长方体)解决,外接球的直径等于长方体的体对角线长.长方体同一顶点的三条棱长分别为a,b,c,外接球半径为R.则(2R)2=a2+b2+c2,即2R=a2+b2+c2.常见的有以下三种类型:考向2对棱相等模型对棱相等模型是三棱锥的三组对棱长分别相等模型,用构造法(构造长方体)解决,外接球的直径等于长方体的体对角线长,如图所示,(2R )2=a 2+b 2+c 2(长方体的长、宽高分别为a ,b ,c ),即R 2=18(x 2+y 2+z 2),如图.考向3汉堡模型汉堡模型是直三棱柱、圆柱的外接球模型,模型如下,由对称性可知,球心O 的位置是△ABC 的外心O 1与△A 1B 1C 1的外心O 2的连线的中点,算出小圆O 1的半径AO 1=r ,OO 1=h 2,所以R 2=r 2+h 24.考向4垂面模型垂面模型是有一条侧棱垂直底面的棱锥模型,可补为直棱柱内接于球;如图所示,由对称性可知球心O 的位置是△CBD 的外心O 1与△AB 2D 2的外心O 2连线的中点,算出小圆O1的半径CO1=r,OO1=h2,则R=r2+h24.类型二内切球问题内切球问题的解法(以三棱锥为例)第一步:先求出四个表面的面积和整个锥体的体积;第二步:设内切球的半径为r,建立等式V P-ABC=V O-ABC+V O-P AB+V O-P AC+V O-PBC⇒V P-ABC=13S△ABC·r+13S△P AB·r+13S△P AC·r+13S PBC·r=13(S△ABC+S△P AB+S△P AC+S△PBC)r;第三步:解出r=3V P-ABCS△ABC+S△P AB+S△P AC+S△PBC.类型三球的截面问题解决球的截面问题抓住以下几个方面:(1)球心到截面圆的距离;(2)截面圆的半径;(3)直角三角形(球心到截面圆的距离、截面圆的半径、球的半径构成的直角三角形).三、平行关系和垂直关系的证明、二面角等热点一空间线、面位置关系的判定判断空间线、面位置关系的常用方法(1)根据空间线面平行、垂直的判定定理和性质定理逐项判断,解决问题.(2)利用直线的方向向量、平面的法向量判断.(3)必要时可以借助空间几何模型,如从长方体、四面体等模型中观察线、面的位置关系,并结合有关定理进行判断.热点二几何法证明平行、垂直1.直线、平面平行的判定及其性质(1)线面平行的判定定理:a⊄α,b⊂α,a∥b⇒a∥α.(2)线面平行的性质定理:a∥α,a⊂β,α∩β=b⇒a∥b.(3)面面平行的判定定理:a⊂β,b⊂β,a∩b=P,a∥α,b∥α⇒α∥β.(4)面面平行的性质定理:α∥β,α∩γ=a,β∩γ=b⇒a∥b.2.直线、平面垂直的判定及其性质(1)线面垂直的判定定理:m⊂α,n⊂α,m∩n=P,l⊥m,l⊥n⇒l⊥α.(2)线面垂直的性质定理:a⊥α,b⊥α⇒a∥b.(3)面面垂直的判定定理:a⊂β,a⊥α⇒α⊥β.(4)面面垂直的性质定理:α⊥β,α∩β=l,a⊂α,a⊥l⇒a⊥β.热点三空间向量法证明平行、垂直1.用向量证明空间中的平行关系(1)设直线l 1和l 2的方向向量分别为v 1和v 2,则l 1∥l 2(或l 1与l 2重合)⇔v 1∥v 2.(2)设直线l 的方向向量为v ,在平面α内的两个不共线向量v 1和v 2,则l ∥α或l ⊂α⇔存在两个实数x ,y ,使v =x v 1+y v 2.(3)设直线l 的方向向量为v ,平面α的法向量为u ,则l ∥α或l ⊂α⇔v ⊥u .(4)设平面α和β的法向量分别为u 1,u 2,则α∥β⇔u 1∥u 2.2.用向量证明空间中的垂直关系(1)设直线l 1和l 2的方向向量分别为v 1和v 2,则l 1⊥l 2⇔v 1⊥v 2⇔v 1·v 2=0.(2)设直线l 的方向向量为v ,平面α的法向量为u ,则l ⊥α⇔v ∥u .(3)设平面α和β的法向量分别为u 1和u 2,则α⊥β⇔u 1⊥u 2⇔u 1·u 2=0.四、空间角、距离问题热点一异面直线所成的角求异面直线所成角的方法方法一:综合法.步骤为:①利用定义构造角,可固定一条直线,平移另一条直线,或将两条直线同时平移到某个特殊的位置;②证明找到(或作出)的角即为所求角;③通过解三角形来求角.方法二:空间向量法.步骤为:①求出直线a ,b 的方向向量,分别记为m ,n ;②计算cos 〈m ,n 〉=m ·n|m ||n |;③利用cos θ=|cos 〈m ,n 〉|,以及θ,π2,求出角θ.热点二直线与平面所成的角求直线与平面所成角的方法方法一:几何法.步骤为:①找出直线l 在平面α上的射影;②证明所找的角就是所求的角;③把这个角置于一个三角形中,通过解三角形来求角.方法二:空间向量法.步骤为:①求出平面α的法向量n 与直线AB 的方向向量AB →;②计算cos 〈AB →,n 〉=AB →·n |AB →||n |;③利用sin θ=|cos 〈AB →,n 〉|,以及θ∈0,π2,求出角θ.热点三平面与平面的夹角求平面与平面的夹角方法方法一:几何法.步骤为:①找出二面角的平面角(以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角就是二面角的平面角);②证明所找的角就是要求的角;③把这个平面角置于一个三角形中,通过解三角形来求角.求二面角的平面角的口诀:点在棱上,边在面内,垂直于棱,大小确定.方法二:空间向量法.步骤为:①求两个平面α,β的法向量m ,n ;②计算cos 〈m ,n 〉=m ·n|m |·|n |;③设两个平面的夹角为θ,则cos θ=|cos 〈m ,n 〉|.热点四距离问题1.空间中点、线、面距离的相互转化关系2.空间距离的求解方法有:(1)作垂线段;(2)等体积法;(3)等价转化;(4)空间向量法.一、单选题1.在正方体1111ABCD A B C D -中,直线m 、n 分别在平面ABCD 和11ABB A 内,且m n ⊥,则下列命题中正确的是()A .若m 垂直于AB ,则n 垂直于AB B .若m 垂直于AB ,则n 不垂直于ABC .若m 不垂直于AB ,则n 垂直于ABD .若m 不垂直于AB ,则n 不垂直于AB【答案】C【详解】AB 选项,若m 垂直于AB ,由面ABCD ⊥面11ABB A ,面ABCD ⋂面11ABB A AB =,可得m 垂直于面11ABB A ,即面11ABB A 内的所有直线均与m 垂直,而n 可能垂直于AB ,也可能不垂直于AB ,故A 错误,B 错误;CD 选项,若m 不垂直于AB ,则,BC m 为面ABCD 内的两条相交直线,由题可知BC n ⊥,m n ⊥,则n 垂直面ABCD ,又AB ⊂面ABCD ,所以n 垂直于AB ,故C 正确,D 错误.故选:C2.在中国古代数学经典著作《九章算术》中,称图中的多面体ABCDEF 为“刍甍”.书中描述了刍甍的体积计算方法:求积术曰,倍下袤,上袤从之,以广乘之,又以高乘之,六而一,即()216V AB EF AD h =+⨯⨯,其中h 是刍甍的高,即点F 到平面ABCD 的距离.若底面ABCD 是边长为4的正方形,2EF =,且//EF AB ,ADE V 和BCF △是等腰三角形,90AED BFC ∠=∠= ,则该刍甍的体积为()A .3B .3C .D .403【答案】B【详解】如图所示,设点F 在底面的射影为G ,,H M 分别为,BC AD 的中点,连接,,EM FH MH ,则FG 即为刍甍的高,-P ABC 面积恰为该容器的表面积)展开后是如图所示的边长为10的正方形123APP P (其中点B 为23P P 中点,点C为12PP 中点),则该玩具的体积为()A .6253B .1253C .125D .2503【答案】B【详解】该玩具为三棱锥-P ABC ,即三棱锥A PBC -,则PA ⊥底面PBC ,且10PA =,PBC 面积为252,所以12512510323P ABC V -=⨯⨯=.故选:B.4.攒尖是中国古代建筑中屋顶的一种结构形式,宋代称为撮尖,清代称攒尖.通常有圆形攒尖、三角攒尖、四角攒尖、八角攒尖,也有单檐和重檐之分,多见于亭阁式建筑、园林建筑.如图所示的建筑屋顶是圆形攒尖,可近似看作一个圆锥,已知其轴截面(过圆锥旋转轴的截面)是底边长为6m ,腰长为5m 的等腰三角形,则该屋顶的体积约为()A .38πmB .39πmC .310πmD .312πm 【答案】D【详解】如图所示为该圆锥轴截面,由题知该圆锥的底面半径为15.已知为两条不同的直线,,为两个不同的平面,则下列命题中正确的是()A .若//,//a b b α,则//a αB .若//,,//a b a b αβ⊥,则αβ⊥C .若//,//,//a b αβαβ,则//a bD .若//,//,a b αβαβ⊥,则a b⊥【答案】B【详解】对于A ,若//,//a b b α,则//a α或a α⊂,故A 错误;对于B ,若//,//a b b β,则a β⊂或//a β,若a β⊂,因为a α⊥,则αβ⊥,若//a β,如图所示,则在平面β一定存在一条直线//m a ,因为a α⊥,所以m α⊥,又m β⊂,所以αβ⊥,综上若//,,//a b a b αβ⊥,则αβ⊥,故B 正确;对于C ,若//,//,//a b αβαβ,则直线,a b 相交或平行或异面,故C 错误;对于D ,若//,//,a b αβαβ⊥,则直线,a b 相交或平行或异面,故D 错误.故选:B.6.在直三棱柱111ABC A B C -中,ABC 为等腰直角三角形,若三棱柱111ABC A B C -的体积为32,则该三棱柱外接球表面积的最小值为()A .12πB .24πC .48πD .96π7.已知三棱锥-P ABC 中,底面ABC 是边长为的正三角形,点P 在底面上的射影为底面的中心,且三棱锥-P ABC 外接球的表面积为18π,球心在三棱锥-P ABC 内,则二面角P AB C --的平面角的余弦值为()A .12B .13C 22D 即PDC ∠为二面角P AB C --的平面角,由23AB =,得22OC OD ==,显然三棱锥线段PO 上,由三棱锥-P ABC 的外接球的表面积为8.已知三棱锥-P ABC 的四个顶点都在球O的球面上,4PB PC AB AC ====,2PA BC ==,则球O 的表面积为()A .316π15B .79π15C .158π5D .79π5而,,AB AC A AB AC =⊂ 平面ABC ,因此在等腰ABC 中,4,2AB AC BC ===,则215sin 1cos ABC ABC ∠=-∠=,二、多选题9.已知直线a ,b ,c 两两异面,且a c ⊥,b c ⊥,下列说法正确的是()A .存在平面α,β,使a α⊂,b β⊂,且c α⊥,c β⊥B .存在平面α,β,使a α⊂,b β⊂,且c α∥,c β∥C .存在平面γ,使a γ∥,b γ∥,且c γ⊥D .存在唯一的平面γ,使c γ⊂,且a ,b 与γ所成角相等【答案】ABC【详解】对于A,平移直线b 到与直线a 相交,设平移后的直线为b ',因为b c ⊥,所以b c '⊥,设直线,a b '确定的平面为α,则a c ⊥,b c '⊥,直线b '和a 相交,所以c α⊥,同理可得:c β⊥,故A 对;对于B,平移直线c 到与直线a 相交,设平移后的直线为c ',设直线,a c '确定的平面为α,因为c //c ',且α⊄c ,所以c α∥,同理可得:c β∥,故B 对;对于C,同时平移直线b 和直线a ,令平移后的直线相交,设平移后的直线为,a b '''',因为a c ⊥,b c ⊥,所以a c ''⊥,b c ''⊥,设直线,a b ''''确定的平面为γ,则a γ∥,b γ∥,且c γ⊥,故C 对;对于D ,由对称性可知,存在两个平面γ,使c γ⊂,且a ,b 与γ所成角相等,故D 错误;故选:ABC.10.已知正方体1111ABCD A B C D -的外接球表面积为12π,,,M N P 分别在线段1BB ,1CC ,1DD 上,且,,,A M N P 四点共面,则().A .AP MN=B .若四边形AMNP 为菱形,则其面积的最大值为C .四边形AMNP 在平面11AAD D 与平面11CC D D 内的正投影面积之和的最大值为6D .四边形AMNP 在平面11AA D D 与平面11CC D D 内的正投影面积之积的最大值为4设正方体1111ABCD A B C D -依题意,234π()12π2a ⋅=,解得因为平面11BCC B ∥平面ADD则M 在平面11AA D D 上的投影落在设为H ,则四边形AGHP 为四边形AMNP 由于,AM PN GM HN ==,则(当1x y ==时取“=”),故C 错误,D 正确,故选:ABD三、解答题11.如图,四棱锥S ABCD -的底面为菱形,60BAD ∠=︒,2AB =,4SD =,SD ⊥平面ABCD ,点E 在棱SB 上.(1)证明:AC DE ⊥;(2)若三棱锥E ABC -,求点E 到平面SAC 的距离.【详解】(1)证明:如图,连接BD ,因为四边形ABCD 为菱形,所以AC BD ⊥,因为SD ⊥平面ABCD ,AC ⊂平面ABCD ,所以SD AC ⊥,又因为SD BD D = ,所以AC ⊥平面SBD ,又因为DE ⊂平面SBD ,所以AC DE ⊥.(2)解:设点E 到平面ABC 则三棱锥E ABC -的体积V (11sin 18032AB BC =⨯⨯⨯⨯︒-12.如图,在三棱锥A BCD -中,平面ABD ⊥平面BCD ,,AB AD O =为BD 的中点.(1)证明:OA CD ⊥;(2)已知OCD 是边长为1的等边三角形,已知点E 在棱AD 的中点,且二面角E BC D --的大小为45 ,求三棱锥A BCD -的体积.【详解】(1)证明:AB AD = ,O 为BD 的中点,AO BD ∴⊥,又平面ABD ⊥平面BCD ,平面ABD ⋂平面BCD BD =,AO ⊂平面BCD ,所以AO ⊥平面BCD ,又CD ⊂平面BCD ,AO CD ∴⊥.(2)取OD 的中点F ,因为OCD 为等边三角形,所以CF OD ⊥,过O 作//OM CF ,与BC 交于M ,则OM OD ⊥,由(1)可知OA ⊥平面BCD ,设OA a =,因为OA ⊥平面BCD ,所以设平面BCE 的一个法向量为n =3300x y n BC ⎧+=⎪⎧⋅= ○热○点○题○型二外接球、内切球等相关问题一、单选题1.已知ABC 是边长为3的等边三角形,其顶点都在球O 的球面上,若球O 的体积为323π,则球心O 到平面ABC 的距离为()A B .32C .1D 因为ABC 是边长为3的等边三角形,且所以13O B =,又因为球O 的体积为32π2.已知三棱锥-P ABC 的底面ABC 是边长为1的正三角形,侧棱,,PA PB PC 两两垂直,若此三棱锥的四个顶点都在同一个球面上,则该球的表面积是()A .3πB .πC .3π4D .3π23.一个圆锥的底面圆和顶点都恰好在一个球面上,且这个球的半径为5,则这个圆锥的体积的最大值时,圆锥的底面半径为()A .103B .2C .3D 【答案】C【详解】解:如图,设圆锥的底面半径为r ,球半径5R =,球心为O .过圆锥的顶点P 作底面的垂线2125OO r =-.所以圆锥的高h PO =4.已知圆锥的侧面积为2π,母线与底面所成角的余弦值为2,则该圆锥的内切球的体积为()A .4π3B .43π9C.27D5.如图,几何体Ω为一个圆柱和圆锥的组合体,圆锥的底面和圆柱的一个底面重合,圆锥的顶点为A ,圆柱的上、下底面的圆心分别为B 、C ,若该几何体Ω存在外接球(即圆锥的顶点与底面圆周在球面上,且圆柱的底面圆周也在球面上).已知24BC AB ==,则该组合体的体积等于()A .56πB .70π3C .48πD .64π【答案】A【详解】设该组合体外接球的球心为O ,半径为R ,易知球心在BC 中点,则224R AO ==+=.6.已知矩形ABCD的顶点都在球心为的体积为43,则球O的表面积为()A.76πB.112πC D.3故球的表面积为:2476πR π=,故选:A .7.水平桌面上放置了4个半径为2的小球,4个小球的球心构成正方形,且相邻的两个小球相切.若用一个半球形的容器罩住四个小球,则半球形容器内壁的半径的最小值为()A .4B .2C .2D .6此时,如上图示,O 为半球的球心,体的体对角线,且该小球与半球球面上的切点与8.已知三棱锥-PABC的四个顶点均在球的球面上,,PB AC== PC AB=Q为球O的球面上一动点,则点Q到平面PAB 的最大距离为()A2211BC2211D2223BD BE AB∴+==,BD2226BD BE BF∴++=,∴球在PAB中,cosABABP∠=二、填空题9.在三棱锥-P ABC 中,PA ⊥平面ABC ,14AB AC PA AB AC ⊥=+=,,,当三棱锥的体积最大时,三棱锥-P ABC 外接球的体积为______.则三棱锥-P ABC 外接球的直径为2R PA =因此,三棱锥-P ABC 外接球的体积为34π3R10.如图,在直三棱柱111中,1.设为1的中点,三棱锥D ABC -的体积为94,平面1A BC ⊥平面11ABB A ,则三棱柱111ABC A B C -外接球的表面积为______.【答案】27π【详解】取1A B 的中点E ,连接AE ,如图.因为1AA AB =,所以1AE A B ⊥.又面1A BC ⊥面11ABB A ,面1A BC ⋂面111ABB A A B =,且AE ⊂面11ABB A ,所以⊥AE 面1A BC ,BC ⊂面1A BC ,所以AE BC ⊥.在直三棱柱111ABC A B C -中,1BB ⊥面ABC ,BC ⊂面ABC ,所以1BB BC ⊥.又AE ,1BB ⊂面11ABB A ,且AE ,1BB 相交,所以BC ⊥面11ABB A ,AB ⊂面11ABB A ,所以BC AB ⊥.11.如图,直三棱柱111的六个顶点都在半径为1的半球面上,,侧面11BCC B 是半球底面圆的内接正方形,则直三棱柱111ABC A B C -的体积为___________.12.如图所示的由4个直角三角形组成的各边长均相等的六边形是某棱锥的侧面展开图,若该六边形的面积为12+,则该棱锥的内切球半径为___.由题意,侧面展开图的面积由,PD AD PD DC ⊥⊥,○热○点○题○型三平面关系、垂直关系、二面角等相关问题1.已知多面体ABCDEF 中,四边形CDEF 是边长为4的正方形,四边形ABCD 是直角梯形,90ADC DAB ∠=∠=︒,36BE AB ==,4=AD .(1)求证:平面ADF ⊥平面BCE ;(2)求直线AF 与平面BCF 所成角的正弦值.【详解】(1)因为四边形CDEF 是边长为4的正方形,所以CE ⊥DF ,ED ⊥DC ,因为四边形ABCD 是直角梯形,90ADC DAB ∠=∠=︒,所以AD ⊥CD ,AB ⊥AD ,故直线AF与平面BCF所成角的正弦值为-PA 2.如图,在四棱锥P ABCD平面PAD⊥平面ABCD.Array(1)证明:平面CDM⊥平面PAB;(2)若AD BC ∥,2AD BC =,2AB =,直线PB 与平面MCD ,求三棱锥P MCD -的体积.【详解】(1)取AD 中点为N ,连接PN ,因为PAD 为等边三角形,所以PN AD ^,且平面PAD ⊥平面ABCD ,平面PAD ⋂平面ABCD AD =,PN ⊂面PAD ,所以PN ^平面ABCD ,又AB ⊂平面ABCD ,所以PN AB ⊥,又因为PD AB ⊥,PN PD P = ,,PN PD ⊂平面PAD ,所以AB ⊥平面PAD ,又因为DM ⊂平面PAD ,所以AB DM ⊥,因为M 为AP 中点,所以DM PA ⊥,且PA AB A = ,,PA PB ⊂平面PAD ,所以DM ⊥平面PAB ,且DM ⊂平面CDM ,所以平面CDM ⊥平面PAB .(2)由(1)可知,PN AB ⊥且PD AB ⊥,PN PD P = ,所以AB ⊥平面PAD ,△为边长为6的等边三角形,E为BD的中点,F为AE的三等分点,且2AF FE ABD=.(1)求证://FM 面ABC ;(2)若二面角A BD C --的平面角的大小为23π,求直线EM 与面ABD 所成角的正弦值.【详解】(1)在BE 上取一点N ,使得12BN NE =,连接FN ,NM ,∵6BD =,∴116BN BD ==,2NE =,3ED =,∵12AF FE =,∴12BN AF NE FE ==,则FN AB ∥,又FN ⊄面ABC ,AB ⊂面ABC ,∴FN ∥面ABC ,∵15BN CM ND MD ==,∴NM BC ∥.∵NM ⊄面ABC ,BC ⊂面ABC ,∴NM ∥面ABC ,∵FN NM N = ,,FN NM ⊂面FNM ,∴面FNM ∥面ABC ,又FM ⊂面FNM ,4.已知底面是正方形,平面,,,点E 、F 分别为线段PB 、CQ 的中点.(1)求证://EF平面PADQ ;(2)求平面PCQ 与平面CDQ 夹角的余弦值;(3)线段PC 上是否存在点M ,使得直线AM 与平面PCQ 所成角的正弦值是7,若存在求出PM MC的值,若不存在,说明理由.【详解】(1)证明:法一:分别取AB 、CD 的中点G 、H ,连接EG 、GH 、FH ,由题意可知点E 、F 分别为线段PB 、CQ 的中点.所以//EG PA ,//FH QD ,因为//PA DQ ,所以//EG FH ,所以点E 、G 、H 、F 四点共面,因为G 、H 分别为AB 、CD 的中点,所以//GH AD ,因为AD ⊂平面ADQP ,GH ⊄平面ADQP ,所以//GH 平面ADQP ,又因为//FH QD ,QD ⊂平面ADQP ,FH ⊄平面ADQP ,所以//FH 平面ADQP ,法二:因为ABCD 为正方形,且以点A 为坐标原点,以AB 、空间直角坐标系,则()0,0,3P 、()3,3,0C 、()0,3,1Q 所以()0,3,1EF =- ,易知平面PADQ 所以0a EF ⋅= ,所以E F a ⊥ ,EF ⊄ADQP EF所在平面和圆所在的平面互相垂直,已知2,1AB EF ==.(1)求证:平面DAF ⊥平面CBF ;(2)当AD 的长为何值时,二面角C EF B --的大小为60︒?设()0AD t t =>,则(1,0,C -∴(1,0,0)EF = ,33,22CF ⎛= ⎝6.如图,在三棱柱111中,四边形11是边长为4的菱形,AB BC =,点D 为棱AC 上的动点(不与A 、C 重合),平面1B BD 与棱11AC 交于点E .(1)求证1BB DE //;(2)若平面ABC ⊥平面11AAC C ,160A AC ∠= ,判断是否存在点D 使得平面11A ABB 与平面1B BDE 所成的锐二面角为π3,并说明理由.【详解】(1)11//BB CC ,且1BB ⊂/平面11ACC A ,1CC ⊂平面11ACC A ,∴1//BB 平面11ACC A ,又∵1BB ⊂平面1B BD ,且平面1B BD 平面11ACC A DE =,∴1BB DE //;(2)连接1AC ,取AC 中点O ,连接1AO ,BO ,在菱形11ACC A 中,160A AC ∠=︒,∴1A AC △是等边三角形,又∵O 为AC 中点,∴1A O ⊥∵平面ABC ⊥平面11ACC A ,平面ABC ⋂平面11ACC A AC =∴1A O ⊥平面ABC ,OB ⊂平面。
专题8.8 立体几何综合问题(精练)-2021年新高考数学一轮复习学与练(解析版)

专题8.8 立体几何综合问题一、选择题1.(2020·浙江高三月考)“直线l与平面α内无数条直线垂直”是“直线l与平面α垂直”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不必要也不充分条件【答案】B【解析】设命题p:直线l与平面α内无数条直线垂直,命题q:直线l与平面α垂直,⇒,所以p是q的必要不充分条件.则p q,但q p故选:B、是空间两个不同的平面,则“平面α上存在不共线的三点到2.(2020·上海市建平中学月考)已知αβαβ”的()平面β的距离相等”是“//A.充分非必要条件B.必要非充分条件C.充要条件D.非充分非必要条件【答案】B【解析】、是空间两个不同的平面,若平面α内存在不共线的三点到平面β的距离相等,已知αβαβ或相交,可得//αβ,则平面α上存在不共线的三点到平面β的距离相等;反之,若//αβ”的必要不充分条件.所以“平面α上存在不共线的三点到平面β的距离相等”是“//故选:B.3.(2020·浙江高三月考)设m,n是空间两条不同直线,α,β是空间两个不同平面,则下列选项中不正确的是()A.当n⊥α时,“n⊥β”是“α∥β”成立的充要条件⊥”的充分不必要条件B.当时,“m⊥β”是“αβC.当时,“n//α”是“”必要不充分条件D .当时,“”是“”的充分不必要条件【答案】C 【解析】A,B,D 正确;C 错误.,////m n m n m n αα⊂⇒或与异面;,////;m n m n n ααα⊂⇒⊂或所以当m α⊂时,//n α是//m n 的既不充分又不必要条件.故选C3.(2020·河北新华·石家庄二中高三月考(理))如图,正方体1111ABCD A BC D -中,P 为底面ABCD 上的动点,1PE A C ⊥于E ,且,PA PE =则点P 的轨迹是( )A .线段B .圆C .椭圆的一部分D .抛物线的一部分【答案】A【解析】 连结1AP ,可证11A AP A EP ≌,即11A A A E =,即点E 是体对角线1AC 上的定点,直线AE 也是定直线.PA PE =,∴动点P 必定在线段AE 的中垂面α上,则中垂面α与底面ABCD 的交线就是动点P 的轨迹,所以动点P 的轨迹是线段.故选:A5.(2020·河南月考(理))3D 打印属于快速成形技术的一种,它是一种以数字模型文件为基础,运用粉末状金属或塑料等可粘合材料,通过逐层堆叠累积的方式来构造物体的技术(即“积层造型法”).过去常在模具制造、工业设计等领域被用于制造模型,现正用于一些产品的直接制造,特别是一些高价值应用(比如髋关节、牙齿或一些飞机零部件等).已知利用3D 打印技术制作如图所示的模型.该模型为在圆锥底内挖去一个正方体后的剩余部分(正方体四个顶点在圆锥母线上,四个顶点在圆锥底面上),圆锥底面直径为31 g/cm,不考虑打印损耗,制作该模型所需原料的质量约为()(取π 3.14=,精确到0.1)A.609.4g B.447.3g C.398.3g D.357.3g【答案】C【解析】如图,是几何体的轴截面,因为圆锥底面直径为,所以半径为OB=.因为母线与底面所成角的正切值为tan B,所以圆锥的高为10cmPO=.设正方体的棱长为a,DE=1010a-=,解得5a=.所以该模型的体积为(()2331500ππ105125cm33V=⨯⨯-=-.所以制作该模型所需原料的质量为()500π500π1251125398.3g33⎛⎫-⨯=-≈⎪⎝⎭.故选:C.6.(2020·上海浦东新·华师大二附中月考)运用祖暅原理计算球的体积时,夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意一个平面所截,若截面面积都相等,则这两个几何体的体积相等.构造一个底面半径和高都与球的半径相等的圆柱,与半球(如图①)放置在同一平面上,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥后得到一新几何体(如图②),用任何一个平行于底面的平面去截它们时,可证得所截得的两个截面面积相等,由此可证明新几何体与半球体积相等.现将椭圆221916x y +=绕y 轴旋转一周后得一橄榄状的几何体(如图③),类比上述方法,运用祖暅原理可求得其体积等于( )A .64πB .48πC .16πD .32π【答案】B【解析】 构造一个底面半径为3,高为4的圆柱,在圆柱中挖去一个以圆柱下底面圆心为顶点的圆锥,则当截面与顶点距离为(04)h h 时,小圆锥的底面半径为r ,则43h r =, 34r h ∴=, 故截面面积为26991h ππ-,把y h =代入椭圆221916x y +=可得x =, ∴橄榄球形几何体的截面面积为221699h x πππ=-, 由祖暅原理可得橄榄球形几何体的体积()1229494483V V V πππ⎛⎫=-=⨯-⨯⨯= ⎪⎝⎭圆柱圆锥. 故选:B .7.(2018·浙江高考真题)已知四棱锥S ABCD -的底面是正方形,侧棱长均相等,E 是线段AB 上的点(不含端点),设SE 与BC 所成的角为1θ,SE 与平面ABCD 所成的角为2θ,二面角S AB C --的平面角为3θ,则( )A .123θθθ≤≤B .321θθθ≤≤C .132θθθ≤≤D .231θθθ≤≤【答案】D【解析】 设O 为正方形ABCD 的中心,M 为AB 中点,过E 作BC 的平行线EF ,交CD 于F ,过O 作ON 垂直EF 于N ,连接SO 、SN 、OM ,则SO 垂直于底面ABCD ,OM 垂直于AB ,因此123,,,SEN SEO SMO θθθ∠=∠=∠= 从而123tan ,tan ,tan ,SN SN SO SO EN OM EO OMθθθ==== 因为SN SO EO OM ≥≥,,所以132tan tan tan ,θθθ≥≥即132θθθ≥≥,选D.8.(2019·山西高二期中(理))如图,在Rt ABC ∆中,D ,E 分别为AB ,AC 边上的中点,且4AB =,2BC =.现将ABC ∆沿DE 折起,使得A 到达1A 的位置,且二面角1A DE B --为60︒,则1AC =( )A .B .3CD .【答案】A【解析】 ,D E 分别为,AB AC 中点 //DE BC ∴ DE BD ∴⊥,1DE A D ⊥又1,BD A D ⊂平面1A BD ,1BD A D D = DE ∴⊥平面1A BD二面角1A DE B --的平面角为1A DB ∠ 160A DB ∴∠=12A D BD == 12A B ∴=//BC DE BC ∴⊥平面1A BD ,又1A B ⊂平面1A BD 1BC A B ∴⊥1AC ∴===故选:A9.(2020·浙江诸暨·)正方体1111ABCD A BC D -中,在111A B D ∆内部(不含边界)存在点P ,满足点P 到平面11ACC A 的距离等于点P 到棱1BB 的距离.分别记二面角P AD B --为α,P AC B --为β,P BC A --为γ,则下列说法正确的是( )A .αβγ>>B .αγβ<<C .αβγ<<D .以上说法均不正确【答案】C【解析】如图所示,作PQ ⊥面ABCD 于Q ,作QE AD ⊥于E ,QF BC ⊥于F ,QG AC ⊥于G ,连PE ,PF ,PG , 则PEQ α=∠,PGQ β=∠,PFQ γ=∠. 因此tan PQ QE α=,tan PQ QG β=,tan PQ QFγ=, 作111PE A D ⊥于1E ,111PF B C ⊥于1F ,111PG AC ⊥于1G ,1PG 即点P 到平面11ACC A 的距离,1PB 即点P 到棱1BB 的距离,因此11PB PG =,因为111QF PF PB PG QG =<==,因此tan tan βγ<,因为11QG PG PE QE =<=,因此tan tan αβ<综上有:tan tan tan αβγ<<,即αβγ<<,故选:C10.(2020·安徽合肥·高三三模(理))在长方体1111ABCD A B C D -中,6AB AD ==,12AA =,M 为棱BC 的中点,动点P 满足APD CPM ∠=∠,则点P 的轨迹与长方体的面11DCC D 的交线长等于()A .23πB .πC .43πD【答案】A【解析】如下图所示:当P 在面11DCC D 内时,AD ⊥面11DCC D ,CM ⊥面11DCC D ;又APD MPC ∠=∠, 在Rt PDA △与Rt PCM 中,∵6AD =,则3MC =, ∴tan tan AD MC APD MPC PD PC ∠==∠=,则63PD PC =, 即2PD PC =.在平面11DCC D 中,以DC 所在直线为x 轴,以DC 的垂直平分线为y 轴建立平面直角坐标系, 则()3,0D -,()3,0C ,设(),P x y , 由2PD PC ==整理得:221090x x y -++=,即()22516x y -+=.∴点P 的轨迹是以()5,0F 为圆心,半径为4的圆.设圆F 与面11DCC D 的交点为E 、M ,作EK 垂直x 轴于点K ,则21sin 42EK EFK EF ∠===; ∴6EFK π∠=;故点P 的轨迹与长方体的面11DCC D 的交线为劣弧ME ,所以劣弧ME 的长为2463ππ⨯=. 故选:A .二、多选题 11.(2020·广东宝安·高三开学考试)如图,正方体1111ABCD A BC D -的棱长为1,线段11B D 上有两个动点E 、F ,且12EF =,则下列结论中正确的是( )A .AC BE ⊥B .//EF 平面ABCDC .AEF 的面积与BEF 的面积相等D .三棱锥A BEF -的体积为定值【答案】ABD【解析】可证AC ⊥平面11D DBB ,从而AC BE ⊥,故A 正确;由11//B D 平面ABCD ,可知//EF 平面ABCD ,B 也正确;连结BD 交AC 于O ,则AO 为三棱锥A BEF -的高,1111224BEF S =⨯⨯=△,三棱锥A BEF -的体积为1134224⨯⨯=为定值,D 正确;很显然,点A 和点B 到的EF 距离是不相等的,C 错误. 故选:ABD 12.(2020·江苏赣榆一中高一月考)已知在矩形ABCD 中,4AB =,3BC =,将矩形ABCD 沿对角线AC 折成大小为θ的二面角B AC D --,若折成的四面体ABCD 内接于球O ,则下列说法正确的是( ) A .四面体ABCD 的体积的最大值是245 B .球的体积随θ的变化而变化C .球心O 为原矩形的两条对角线的交点D .球O 的表面积为定值25π 【答案】ACD【解析】如图,(1)当面ACD ⊥面ABC 时,四面体ABCD 的体积最大,此时,如图,过点D 作AC 的垂线,交AC 于点E ,则DE 即为四面体ABCD 的高,由等面积法得:AC DE AD DC ⨯=⨯,∴ 125DE = , ∴四面体ABCD 的最大值为11112243433255ABC V S h =⋅=⨯⨯⨯⨯=, 故A 选项正确; (2)在四面体ABCD 内,AC 的中点O 到点,,,A B C D 的距离相等,∴点O 为外接球的球心,此时球的半径522AC R ==,球的体积242533V R ππ== ,为定值,球的表面积2425S R ππ== ,为定制,故B 选项错误,,C D 正确,故选,,A C D 13.(2020·湖北江岸·期末)向体积为1的正方体密闭容器内注入体积为x (01x <<)的液体,旋转容器,下列说法正确的是( )A .当12x =时,容器被液面分割而成的两个几何体完全相同 B .不管注入多少液体,液面都可以成正三角形形状CD 【答案】AC【解析】对于A ,当12x =时,题目等价于过正方体中心的平面截正方体为两部分, 根据对称性知两部分完全相同,所以A 正确; 对于B ,取12x =,此时液面过正方体中心,截面不可能为三角形,所以B 错误; 对于C ,当液面与正方体的体对角线垂直时,液面为如图所示正六边形时面积最大,其中正六边形的顶点均为对应棱的中点,所以液面面积的最大值为162S ==,C 正确; 对于D ,当液面过1DB 时,截面为1B NDG ,将1111D C B A 绕11C D 旋转2π,如图所示;则111DN B N DN B N DB ''+=+≥= 当D 、N 、1B '三点共线时等号成立,所以液面周长最小值为D 错误. 故选:AC.14.(2020·广东深圳·高二月考)(多选题)如图,在直三棱柱111ABC A B C -中,1223AA AC AB ===,AB AC ⊥,点D ,E 分别是线段BC ,1BC 上的动点(不含端点),且1EC DC B C BC=.则下列说法正确的是( )A .//ED 平面1ACCB .该三棱柱的外接球的表面积为68πC .异面直线1BC 与1AA 所成角的正切值为32 D .二面角A EC D --的余弦值为413【答案】AD【解析】在直三棱柱111ABC A B C -中,四边形11BCC B 是矩形, 因为1EC DC B C BC=,所以11////ED BB AA ,ED 不在平面1ACC 内,1AA ⊂平面1ACC , 所以//ED 平面1ACC ,A 项正确; 因为1223AA AC AB ===,所以3AB =, 因为AB AC ⊥,所以BC ==1BC 易知1BC 是三棱柱外接球的直径,所以三棱柱外接球的表面积为22417πππ=⨯=⎝⎭,所以B 项错误; 因为11//AA BB ,所以异面直线1BC 与1AA 所成角为1BB C ∠.在1Rt B BC 中,12BB =,BC =,所以11tan BC BB C BB ∠==C 项错误; 二面角A EC D --即二面角1A B C B --,以A 为坐标原点,以AB ,AC ,1AA 的方向分别为x ,y ,z 轴的正方向,建立空间直角坐标系,如图则1(0,0,0),(3,0,0),(0,2,0),(3,0,2)A B C B ,1(3,0,2)AB ∴=,(3,2,0)BC =-,1(3,2,2)BC =--, 设平面1ABC 的法向量(,,)n x y z =,则1100n AB n B C ⎧⋅=⎪∴⎨⋅=⎪⎩,即3203220x z x y z +=⎧⎨-+-=⎩,令2x =可得(2,0,3)n =-, 设平面1BB C 的一个法向量为(,,)m x y z =,则100m BC m B C ⎧⋅=⎪⎨⋅=⎪⎩,即3203220x y x y z -+=⎧⎨-+-=⎩,令2x =可得(2,3,0)m = 故二面角A EC D --413=,所以D 项正确. 故选:AD.三、填空题15.(2020·浙江高三月考)在2000多年前,古希腊数学家阿波罗尼斯采用平面切割圆锥的方法来研究圆锥曲线:用垂直于锥轴的平面去截圆锥,得到的是圆;把平面渐渐倾斜,得到椭圆;当平面倾斜到“和且仅和”圆锥的一条母线平行时,得到抛物线;当平面再倾斜一些就可以得到双曲线.已知一个圆锥的高和底面半径都为2,则用与底面呈45的平面截这个圆锥,得到的曲线是___________.【答案】抛物线【解析】因为圆锥的高和底面半径都为2,因此有, ︒tan 145OS SAO SAO AO︒∠==⇒∠=所以母线SA 与底面所成的角为45,因为用与底面呈45的平面截这个圆锥,所以该平面一定会与圆锥的某条母线(如SA )平行,由题中所给的结论可知:用与底面呈45的平面截这个圆锥,得到的曲线是抛物线.故答案为:抛物线16.(2020·江西其他(文))《九章算术》是我国古代著名数学经典,其中对勾股定理的论述,比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小;以锯锯之,深一寸,锯道长一尺,问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深1寸,锯道长1尺,问这块圆柱形木料的直径是多少?长为0.5丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示(阴影部分为镶嵌在墙体内的部分).己知弦尺,弓形高寸,估算该木材镶嵌墙内部分的体积约为______立方寸.(注:一丈=10尺=100寸,,答案四舍五入,只取整数...........)【答案】317 【解析】如图,设圆半径为寸(下面长度单位都是寸),连接,已知,, 在中,,即,解得, ︒︒︒1AB =1CD =53.14,sin 22.513π≈≈r ,OA OD 152AD AB ==1OD OC CD r =-=-Rt ADO 222AD OD OA 2225(1)r r +-=13r =由得,所以, 图中阴影部分面积为扇形(平方寸), 镶嵌在墙体中木材是以阴影部分为底面,以锯刀长为高的柱体,所以其体积为(立方寸)故答案为:317.17.(2020·河北新华·石家庄二中高二月考)如图,在四棱锥中,四边形为菱形,且是等边三角形,点是侧面内的一个动点,且满足,则点所形成的轨迹长度是_______.【解析】根据题意,连接AC ,BD ,记其交点为O ,取PC 上一点为M ,连接MB ,MD ,作图如下:5sin 13AD AOD AO ∠==22.5AOD ∠=︒45AOB ∠=︒S S =214131012 6.332522AOB S πππ-=⨯⨯-⨯⨯≈△6.332550317V Sh =≈⨯≈P ABCD -ABCD 2,60,AB DAB PAD =∠=∆PB Q =PBC DQ AC ⊥Q若满足题意,又,故平面DBQ ,则点Q 只要在平面DBQ 与平面PBC 的交线上即可.假设如图所示:平面DBM 与平面DBQ 是同一个平面,则Q 点的轨迹就是线段BM.根据假设,此时直线平面DBM ,则.故三角形MOC 为直角三角形.因为三角形PAD 是等边三角形,三角形BAD 也是等边三角形,故AD ,又因为BC //AD ,故BC PB ,故三角形PBC 为直角三角形,故故在三角形PAC 中,由余弦定理可得:故在直角三角形MOC 中, 在直角三角形PBC 中, 在三角形BCM 中: 故可得:. DQ AC ⊥AC BD ⊥AC ⊥AC ⊥AC MO ⊥PB ⊥⊥2210PC PB BC +2,23,10PA AC PC ===33021023cos PCA ∠==⨯210OC MC cos PCA ==∠BC cos PCB PC ∠=1010=2222829BM BC CM BC CM cos PCB =+-⨯⨯⨯∠=27BM =故答案为. 18.(2021·福建其他)《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑.在如图所示的鳖臑中,平面,,,,为中点,为内的动点(含边界),且.①当在上时,______;②点的轨迹的长度为______.【答案】【解析】 (1)当在上时,因为平面,故,又,故平面.故.又,为中点,故所以为中点.故. (2)取中点则由(1)有平面,故,又,设平面则有平面.故点的轨迹为.又此时,,故. 所以3P ABC -PA ⊥ABC 90ACB ∠=︒4CA =2PA =D AB E PAC ∆PC DE ⊥E AC AE =E E AC PA ⊥ABC PA DE ⊥PC DE ⊥DE ⊥PAC DE AC ⊥90ACB ∠=︒D AB //DE BC E AC 122AE AC ==AC F DF ⊥PAC PC DF ⊥PC DE ⊥DEF PC G ⋂=PC ⊥DGF E FG 2CF =1tan 2PA PCA AC ∠==sin PCA ∠==sin 5FG CF PCA =⋅∠==故答案为:19.(2020·全国高三专题练习(文))现代足球运动是世上开展得最广泛、影响最大的运动项目,有人称它为“世界第一运动”.早在2000多年前的春秋战国时代,就有了一种球类游戏“蹴鞠”,后来经过阿拉伯人传到欧洲,发展成现代足球.1863年10月26日,英国人在伦敦成立了世界上第一个足球运动组织——英国足球协会,并统一了足球规则.人们称这一天是现代足球的诞生日.如图所示,足球表面是由若干黑色正五边形和白色正六边形皮围成的,我们把这些正五边形和正六边形都称为足球的面,任何相邻两个面的公共边叫做足球的棱.已知足球表面中的正六边形的面为20个,则该足球表面中的正五边形的面为______个,该足球表面的棱为______条.【答案】12 90【解析】足球每块黑色皮子的5条边分别与5块白色皮子的边缝在一起;每块白色皮子的6条边中,有3条边与黑色皮子的边缝在一起,另3条边则与其他白色皮子的边缝在一起.所以设这个足球有x 块正五边形,一共有5x 条边,其中白皮三条边和黑皮相连,又足球表面中的正六边形的面为20个,根据题意可得方程:,解得,该足球表面中的正五边形的面为12个;因为任何相邻两个面的公共边叫做足球的棱,所以每条棱由两条边组成,该足球表面的棱为:条.故答案为:12;90.20.如图在三棱锥S ABC -中,SA SB SC ==,且2ASB BSC CSA π∠=∠=∠=,M N 、分别是AB 和SC 的中点.则异面直线SM 与BN 所成的角的余弦值为______,直线SM 与面SAC 所成角大小为5203x =⨯12x =()125+206290⨯⨯÷=_________.4π 【解析】 因为2ASB BSC CSA π∠=∠=∠=,所以以S 为坐标原点,SA,SB,SC 为x,y,z 轴建立空间直角坐标系.设2SA SB SC ===,则(1,1,0),(0,2,0),(0,0,1),(2,0,0),(0,0,2).M B N A C因为2(1,1,0),(0,2,1),cos ,2SM BNSM BN -==-==,所以异面直线SM 与BN 所成的角的余弦值为5,面SAC 一个法向量为(0,2,0),SB =则由2cos ,22SM SB ==得π,4SM SB =,即直线SM 与面SAC 所成角大小为π4. 21.(2020·包头市第九中学高一期末)设三棱锥的底面和侧面都是全等的正三角形,是棱的中点.记直线与直线所成角为,直线与平面所成角为,二面角的平面角为,则,,中最大的是_________,最小的是________.【答案】【解析】S ABC -P SA PB AC αPB ABC βP AC B --γαβγαβ作交于,由于,, 所以为正三棱锥,由对称性知,取中点,连接,作平面,交平面于,连接, 作平面,交平面于,连接,作,交于,连接,所以, 由于,所以,由于平面,所以,由于,平面,所以,, 因为,在上,平面于,平面于, 所以.所以.所以, 由于都是锐角,所以, 由于在上,由对称性,而,则,由于也是锐角,所以,由,,所以 综上所述,三个角中的最小角是,最大角是.故答案为:①;②.四、解答题//PD CA SC D AB BC CA ==SA SB SC ==S ABC -BD PB =PD E BE EH ⊥ABC ABC H BH PF ⊥ABC ABC F BF PG AC ⊥AC G GF BE PD ⊥//PD AC BPD α=∠PF ⊥ABC PBF β=∠PG AC ⊥PF ⊥ABC PGF γ=∠sin BE EH BP BP BP BPα==>=//PD CA E PD EH ⊥ABC H PF ⊥ABC F EH PF =sin PF EH BP BPβ==sin sin αβ>,αβαβ>P SA PB CP =CP PG >sin sin PF PF PF PG CP BP γβ=>==γγβ>PB BG<sin BE EH PF BP BP BP α==>==sin PF PGγ>=αγβααβ22.(2019·北京西城·高三三模)如图,在正四棱柱1111ABCD A BC D -中,1AB =,13AA =,过顶点A ,1C 的平面与棱1BB ,1DD 分别交于M ,N 两点(不在棱的端点处).(1)求证:四边形1AMC N 是平行四边形;(2)求证:AM 与AN 不垂直;(3)若平面1AMC N 与棱BC 所在直线交于点P ,当四边形1AMC N 为菱形时,求PC 长.【答案】(1)证明见解析;(2)证明见解析;(3)=2PC .【解析】(1)依题意1AM C N ,,,都在平面1AC 上, 因此AM ⊆平面1AC ,1NC ⊆平面1AC ,又AM ⊆平面11ABB A ,1NC ⊆平面11DCC D ,平面11ABB A 与平面11DCC D 平行,即两个平面没有交点,则AM 与1NC 不相交,又AM 与1NC 共面,所以//AM 1NC ,同理可证//AN 1MC ,所以四边形1AMC N 是平行四边形;(2)因为M ,N 两点不在棱的端点处,所以11MN BD AC <=,又四边形1AMC N 是平行四边形,1MN AC ≠,则1AMC N 不可能是矩形,所以AM 与AN 不垂直;(3)如图,延长1C M 交CB 的延长线于点P ,若四边形1AMC N 为菱形,则1AM MC =,易证11Rt ABM Rt C B M ≅,所以1BM B M =,即M 为1BB 的中点, 因此112BM CC =,且1//BM CC ,所以BM 是1PCC 的中位线, 则B 是PC 的中点,所以22PC BC ==.23.(2019·全国高三专题练习)如图,正△ABC 的边长为4,CD 为AB 边上的高,E ,F 分别是AC 和BC 边的中点,现将△ABC 沿CD 翻折成直二面角A -DC -B .(1)试判断直线AB 与平面DEF 的位置关系,并说明理由;(2)在线段BC 上是否存在一点P ,使AP DE ⊥?如果存在,求出BP BC 的值;如果不存在,请说明理由. 【答案】(1)//AB 平面DEF ,理由见解析;(2)13. 【解析】(1)AB∥平面DEF ,理由如下:在△ABC 中,由E ,F 分别是AC ,BC 的中点,得EF∥AB.又因为AB ⊄平面DEF ,EF ⊂平面DEF ,所以AB∥平面DEF.(2)以点D 为坐标原点,直线DB ,DC ,DA 分别为x 轴,y 轴,z 轴,建立空间直角坐标系(如图所示),则A(0,0,2),B(2,0,0),C(0,0),E(01),故DE =(01).假设存在点P(x ,y ,0)满足条件,则AP =(x ,y ,-2),AP ·DE 20-=,所以y =.又BP =(x 2-,y ,0),PC =(-x ,y ,0),BP ∥PC ,所以(x 2-)(y )=xy -y +=把y =代入上式得4x 3=,所以BP =1BC 3, 所以在线段BC 上存在点P 使AP⊥DE,此时BP 1BC 3=. 24.(2019·上海市金山中学高二月考)几何特征与圆柱类似,底面为椭圆面的几何体叫做“椭圆柱”,如图所示的“椭圆柱”中,A B ''、AB 和O '、O 分别是上下底面两椭圆的长轴和中心,1F 、2F 是下底面椭圆的焦点,其中长轴的长度为2,两中心O '、O M 、N 分别是上、下底面椭圆的短轴端点,且位于平面AA B B ''的两侧.(1)求证:OM ∥平面A B N '';(2)求点M 到平面A B N ''的距离;(3)若点Q 是下底面椭圆上的动点,Q '是点Q 在上底面的投影,且1Q F '、2Q F '与下底面所成的角分别为α、β,试求出tan()αβ+的取值范围.【答案】(1)证明见解析;(2(3)tan()[5αβ+∈-. 【解析】(1)连接,,O M O N ON '',M N 分别为上下椭圆的短轴端点 //O M ON '∴∴四边形O MPN '为平行四边形 //OM O N '∴O N '⊂平面A B N '',OM ⊄平面A B N '' //OM ∴平面A B N ''(2)连接OO '由“椭圆柱”定义可知OO '⊥平面12F NFON ⊂平面12F NF OO ON '∴⊥ O N '∴==由对称性可知:A N B N ''= O N A B '''∴⊥1122A B N S A B O N ''∆'''∴=⋅=⨯=又12A B M S A B O M ''∆'''=⨯⋅=,OO '1133N A B M A B M V S OO ''''-∆'∴=⋅==设点M 到平面A B N ''的距离为d ,则13M A B N N A B M A B N V V S d ''''''--∆==⋅==解得:7d =,即点M 到平面A B N ''的距离为7(3)连接12,QF QF由题意知:QQ '⊥平面12F F Q,QQ '=1Q FQ '∴∠即为1Q F'与下底面所成角;2Q F Q '∠即为2Q F '与下底面所成角 即1Q FQ α'∠=,2Q F Q β'∠= 设1QF m =,由椭圆定义知:2QF m =1tan QQ QF α'∴==,2tan QQ QF β'== ()tan tan tan 1tan tan 1αβαβαβ+∴+===-21m ⎡⎤∈⎣⎦[]265,4m∴-+-∈-- ()tan 5αβ⎡∴+∈-⎢⎣⎦25.(2016·天津高考真题(理))如图,正方形ABCD 的中心为O ,四边形OBEF 为矩形,平面OBEF⊥平面ABCD ,点G 为AB 的中点,AB=BE=2.(Ⅰ)求证:EG∥平面ADF ;(Ⅱ)求二面角O −EF −C 的正弦值;(Ⅲ)设H 为线段AF 上的点,且AH=23HF ,求直线BH 和平面CEF 所成角的正弦值. 【答案】(Ⅰ)详见解析;(Ⅱ)√33;(Ⅲ)√721.【解析】依题意,OF ⊥平面ABCD ,如图,以O 为点,分别以AD ⃗⃗⃗⃗⃗ ,BA⃗⃗⃗⃗⃗ ,OF ⃗⃗⃗⃗⃗ 的方向为x 轴、y 轴、z 轴的正方向建立空间直角坐标系,依题意可得O(0,0,0),A(−1,1,0),B(−1,−1,0),C(1,−1,0),D(1,1,0),E(−1,−1,2),F(0,0,2),G(−1,0,0).(Ⅰ)证明:依题意,AD ⃗⃗⃗⃗⃗ =(2,0,0),AF⃗⃗⃗⃗⃗ =(1,−1,2). 设n 1=(x,y,z)为平面ADF 的法向量,则{n 1⋅AD ⃗⃗⃗⃗⃗ =0n 1⋅AF⃗⃗⃗⃗⃗ =0 ,即{2x =0x −y +2z =0 . 不妨设z =1,可得n 1=(0,2,1),又EG ⃗⃗⃗⃗⃗ =(0,1,−2),可得EG⃗⃗⃗⃗⃗ ⋅n 1=0, 又因为直线EG ⊄平面ADF ,所以EG//平面ADF .(Ⅱ)解:易证,OA⃗⃗⃗⃗⃗ =(−1,1,0)为平面OEF 的一个法向量. 依题意,EF⃗⃗⃗⃗⃗ =(1,1,0),CF ⃗⃗⃗⃗⃗ =(−1,1,2).设n 2=(x,y,z)为平面CEF 的法向量,则{n 2⋅EF ⃗⃗⃗⃗⃗ =0n 2⋅CF⃗⃗⃗⃗⃗ =0 ,即{x +y =0−x +y +2z =0 . 不妨设x =1,可得n 2=(1,−1,1).因此有cos <OA ⃗⃗⃗⃗⃗ ,n 2>=OA⃗⃗⃗⃗⃗⃗ ⋅n 2|OA ⃗⃗⃗⃗⃗⃗ |⋅|n 2|=−√63,于是sin <OA ⃗⃗⃗⃗⃗ ,n 2>=√33, 所以,二面角O −EF −C 的正弦值为√33.(Ⅲ)解:由AH =23HF ,得AH =25AF .因为,所以AH ⃗⃗⃗⃗⃗⃗ =25AF ⃗⃗⃗⃗⃗ =(25,−25,45),进而有H(−35,35,45),从而BH⃗⃗⃗⃗⃗⃗=(25,85,45),因此cos <BH ⃗⃗⃗⃗⃗⃗ ,n 2>=BH⃗⃗⃗⃗⃗⃗ ⋅n 2|BH ⃗⃗⃗⃗⃗⃗ |⋅|n 2|=−√721. 所以,直线BH 和平面CEF 所成角的正弦值为√721.26.(2018·天津高考真题(理))如图,且AD =2BC ,,且EG =AD ,且CD =2FG ,,DA =DC =DG =2.(I )若M 为CF 的中点,N 为EG 的中点,求证:;(II )求二面角的正弦值;(III )若点P 在线段DG 上,且直线BP 与平面ADGE 所成的角为60°,求线段DP 的长.【答案】(Ⅰ)证明见解析;(Ⅱ);(Ⅲ). 【解析】依题意,可以建立以D 为原点, 分别以,,的方向为x 轴,y 轴,z 轴的正方向的空间直角坐标系(如图),可得D (0,0,0),A (2,0,0),B (1,2,0),C (0,2,0),//AD BC AD CD ⊥//EG AD //CD FG DG ABCD ⊥平面MN CDE 平面E BC F --103DA DC DGE (2,0,2),F (0,1,2),G (0,0,2),M (0,,1),N (1,0,2).(Ⅰ)依题意=(0,2,0),=(2,0,2).设n 0=(x ,y ,z )为平面CDE 的法向量,则 即不妨令z =–1,可得n 0=(1,0,–1).又=(1,,1),可得,又因为直线MN 平面CDE ,所以MN ∥平面CDE .(Ⅱ)依题意,可得=(–1,0,0),,=(0,–1,2).设n =(x ,y ,z )为平面BCE 的法向量,则 即 不妨令z =1,可得n =(0,1,1).设m =(x ,y ,z )为平面BCF 的法向量,则 即不妨令z =1,可得m =(0,2,1).因此有cos <m ,n>=,于是sin <m ,n.所以,二面角E –BC–F . 32DC DE 0000DC DE ⎧⋅=⎪⎨⋅=⎪⎩,,n n 20220y x z ,,=⎧⎨+=⎩MN 32-00MN n ⋅=⊄BC ()122BE =-,,CF 00n BC n BE ,,⎧⋅=⎨⋅=⎩0220x x y z -=⎧⎨-+=⎩,,00m BC m CF ⎧⋅=⎨⋅=⎩,,020x y z -=⎧⎨-+=⎩,,10⋅=m nm n(Ⅲ)设线段DP 的长为h (h ∈[0,2]),则点P 的坐标为(0,0,h ),可得. 易知,=(0,2,0)为平面ADGE 的一个法向量,故=sinh0,2].所以线段27.(2020届浙江省宁波市余姚中学高考模拟)如图,ABC 为正三角形,且2BC CD ==,CD BC ⊥,将ABC 沿BC 翻折.(1)若点A 的射影在BD 上,求AD 的长;(2)若点A 的射影在BCD 中,且直线AB 与平面ACD ,求AD 的长. 【答案】(1)2 (2【解析】(1)过A 作AE BD ⊥交BD 于E ,则AE ⊥平面BCD .取BC 中点O ,连接AO ,OE ,∵AE ⊥平面BCD ,BC ⊂平面BCD ,∴AE BC ⊥,又ABC 是正三角形,∴BC AO ⊥,又AE AO A =,AE ,AO ⊂平面AOE ,∴BC ⊥平面AOE ,∴BC OE ⊥.又BC CD ⊥,O 为BC 的中点,∴E 为BD 的中点.()12BP h =--,,DC BP DCcos BP DC BP DC h ⋅⋅==DP∵2BC CD ==,∴112OE CD ==,AO =BD =∴DE =AE =∴2AD =;(2)取BC 中点为,O 过点A 作平面BCD 的垂线,垂足为E ,连接AO ,因为,AB AC OE BC =∴⊥.以O 为原点,以BC 为x 轴,以OE 为y 轴,以平面BCD 的过O 的垂线为z 轴建立空间直角坐标系,如图所示:设二面角D BC A --为θ,因为AE ⊥平面BCD ,与(1)同理可证BC ⊥平面AOE ,OE BC ⊥,AOE θ∴∠=,AO则)A θθ,(1,0,0)B -,(1,0,0)C ,(1,2,0)D .∴(1,)BA θθ=,(0,2,0)CD =,(1)CA θθ=-,设平面ACD 的法向量为(,,)n x yz =,则200n CD y n CA x y z θθ⎧⋅==⎪⎨⋅=-⋅+⋅=⎪⎩, 令1z =,得(3sin ,0,1)n θ=.∴cos ,n BA <>==解得sin 6θ=. ∴1(0,,22A ,又(1,2,0)D ,∴AD ==。
高考数学立体几何复习指要含模拟考全国考试题分析和强化练习及答案

高考数学立体几何复习指要含模拟考全国考试题分析和强化练习及答案立体几何高考复习指要立体几何高考试题选择、填空题主要考查立几中的计算型问题和多重判断问题, 而解答题着重考查立几中的逻辑推理问题, 解答题一般为一证一算型或先证后算型问题.在一些同时选用A、B版本教材的省市,立体几何解答题还兼顾传统几何法或向量法两种方法,因此所选的载体往往比较规则.从近几年的各地考题来看, 以多面体为载体的线面位置关系的论证、角与距离的探求仍是常考常新的重点.我们在复习备考中既要抓住这些重点知识和方法的复习,又要留意对重点知识考查的不同命题角度,同时不要忽视可以命制一些小、巧、活试题的知识点的演练.在立体几何的总复习中,首先应从解决“平行与垂直”的有关问题着手,通过较为基本的问题,熟悉公理、定理的内容和功能,通过对问题的分析与概括,掌握立体几何中解决问题的规律——充分利用线线平行(垂2直)、线面平行(垂直)、面面平行(垂直)相互转化的思想,提高逻辑思维能力和空间想象能力.空间的角和距离是空间图形中最重要的数量关系.空间的角主要研究射影以及与射影有关的定理、空间两直线所成的角、直线和平面所成的角、以及二面角和二面角的平面角等.解这类问题的基本思路是把空间问题转化为平面问题去解决.空间的距离问题,主要是求空间两点之间、点到直线、点到平面、两条异面直线之间(限于给出公垂线段的)、平面和它的平行直线、以及两个平行平面之间的距离.求距离的一般方法和步骤是:一作——作出表示距离的线段;二证——证明它就是所要求的距离;三算——计算其值.例1 对于直线m、n和平面a,下面命题中的真命题是(A)如果,,m a n a m⊂⊄、n是异面直线,那么//n a(B)如果,,⊂⊄、n是异面直线,那么n与m a n a ma相交(C)如果,//,⊂、n共面,那么//m nm a n a m(D)如果//,//,m a n a m、n.3解析:本题考查空间直线与平面位置关系的判定,涉及到异面直线,直线与平面的三种位置关系,两条直线平行的判定等内容,体现出文字语言、符号语言转化为图形语言的能力,判断几何命题真假的方法与能力,体现出思维能力与空间想像能力的综合,属于中等题.在解决这类问题时,读题画图是关键,往往采用举例排除的方法进行判断.首先要读懂题,将文字语言、符号语言转化为图形语言进行研究.在选项(A)(B)中,n a 包含两种情况,//n a或n与a只有一个交点,这两种情况都可以使m、n为异面线,因此(A)和(B)都不正确.选项(C)恰是由线面平行推出线线平行定理的语言符号表述,是正确的.于是选项(D)肯定不正确,就不用再判断了.在立几重点知识中,直线与平面垂直在距离与角度的计算中占有尤4其重要的地位,二面角知识也成为重中之重.请看下例:例 2 如图,已知四棱锥 P—ABCD,PB⊥AD侧面PAD为边长等于2的正三角形,底面ABCD为菱形,侧面PAD与底面ABCD所成的二面角为120°.(I)求点P到平面ABCD的距离;(II)求面APB与面CPB所成二面角的大小.本题反映的是目前全国各地高考中常见的的命题形式:先证后算或一证一算.考查的内容是立体几何的主干知识:平行与垂直、距离与角度. 直线与平面垂直在(I)中固然要用,在(II)中作二面角的平面角也是必不可少的.面二面角的知识既成为本题中的条件,也成为(II)中待求的结果.解析:(I)求点到平面的距离思路有三:一是直接作点到平面的垂线段,一般需要找到或构造互相垂直的两平面,利用两平面垂直的性质定理在一个平面内作垂直于交线的56直线,也可通过特殊三棱锥顶点在底面内的射影是底面的外心或内心、垂心等性质作图,然后进行计算;二是借助三棱锥利用等积法求高;三是通过建立空间坐标系,求已知点P 与平面上任意一点A 所连的向量在平面的一个法向量上的投影长||||a l =.本小题作PO ⊥平面ABCD ,垂足为点O.连结OB 、OA 、OD 、OB 与AD 交于点E ,连结PE.可证∠PEB 为面PAD 与面ABCD 所成二面角的平面角,可求出点P 到平面ABCD 的距离PO 为23. (II )二面角的求解方法是丰富多彩的.设法找到或作出一个半平面的垂线段,利用三垂线定理作出二面角的平面角是最重要的方法.也可根据二面角的平面角的定义直接作图,或作二面角的棱的垂面找出交线,然后进行计算.而不需直接作出二面角的平面角,通过建立空间坐标系或面积射影法求二面角也是切实可行的方法.本小题取PB 的中点G ,PC 的中点F ,则∠AGF 是所求二面角的7平面角,所求二面角的大小为π-arctan 23.也可建立直角坐标系,设PB 的中点为G ,可证θ的夹角BC GA PB BC PB GA ,.⊥⋅⊥等于所求二面角的平面角,于是,772||||cos -=⋅=BC GA BCGA θ所以所求二面角的大小为772arccos -π .立体几何的重点知识在高考中可能以开放性试题的面目出现,突出考查创新能力.开放性试题虽然没有固定的解题模式可套,解法灵活多样,但在解立体几何开放性试题中,我们可以通过执果索因、猜想证明、设未知数解方程等方法进行探究.例3 如图,在棱长为1的正方体1111ABCD A B C D -中,P 是侧棱1CC 上的一点,CP m =. (Ⅰ)、试确定m ,使直线AP 与平面11BDD B 所成角的正切值为32;(Ⅱ)、在线段11A C上是否存在一个定点Q,使得对任意的m,D1Q在平面1APD上的射影垂直于AP,并证明你的结论.解析:(Ⅰ)把通常的给定点的位置计算夹角,变为给出直线AP与平面11BDD B所成角求点P的位置,应属执果索因,题中给出了未知数m(否则应设出),渗透了方程的思想.本小题用几何法或向量法易得m=31.(II)可以先推测点Q应当是A I C I 的中点O1,通过证明D1O1⊥平面ACC1A1,D1O1⊥AP.根据三垂线定理知,D1O1在平面APD1的射影与AP垂直.也可在空间坐标系中,设在A1C1上存在这样的点Q,此点的横坐标为x,依题意,对任意的m要使D1Q在平面APD1上的射影垂直于AP,等价于D1Q⊥AP11 0(1)0.2AP D Q x x x⇔⋅=⇔-+-=⇔=即Q为A1C1的中点时,满足题设要求.在立体几何的复习中,一类被称为“隐棱”8二面角的知识应引起我们的高度重视.在二面角的计算中,若用传统几何方法往往需要通过垂线法和垂面法过棱上一点,分别在两个半平面内作出垂直于棱的射线,从而得到二面角的平面角,然后进行计算.若所要求的二面角的棱处于”隐蔽”状态怎么办?对于这种“隐棱”的二面角,一是通过两个半平面内两线平行,利用线面平行的性质定理找棱;二是通过两个半平面内两线相交,通过这两线的交点找棱,找到棱后就问题就转化为常规问题了.这种题型若应用空间向量的方法,可以通过建立空间坐标系,将几何元素之间的关系数量化,进而通过计算解决求角、证明的问题,空间向量更显现出解题的优势.例 4 如图,在底面是直角梯形的四棱锥S—ABCD中,∠ABC=90°,SA⊥面ABCD,1.SA=AB=BC=1,AD=2910 (Ⅰ)求四棱锥S —ABCD 的体积;(Ⅱ)求面SCD 与面SBA 所成的二面角的正切值.解析:(Ⅰ)可求得V S —ABCD =31·SA ·S ABCD =41. (Ⅱ)延长CD 、BA 交于点E ,连结SE ,SE 即平面CSD 与平面BSA 的交线.又DA ⊥平面SAB ,过A 点作SE 的垂线交于F .由三垂线定理可证得∠DFA 为二面角的平面角.∴tan DFA =22 FA DA即所求二面角的正切值. 可以思考:本题若将ABCD 改为矩形,如何在(II )中找出二面角的棱进而作出二面角的平面角求解?本题(II )还可通过建立空间坐标系,求出两个平面的法向量,利用向量夹角的公式求出二面角的大小.利用等积法将点到平面的距离等问题转化成求三棱锥的高是常用的解题方法.但利用等积法求线面角对很多同学来说就不是很习惯了.例5 已知棱长为a 的正方体1111D C B A ABCD -,E 为BC 的中点.(1)求证:平面⊥D C B 11平面ED B 1;(2)求直线DC 和平面ED B 1所成的角的正弦值.解析:(1)设D B 1的中点为O ,连EO ,设D C 1的中点为F ,连OF 、CF ,易证⊥OE 平面D C B 11,从而得出平面⊥D C B 11平面ED B 1. (2)设C 到平面ED B 1的距离为d ,则有ED B C CED B V V 11--=,解得6ad =.设点C 在面ED B 1上的射影为H ,则∠CDH 是直线DC 和平面ED B 1所成的角,其正弦值为66.立体几何中的一些问题虽不成为知识的主干,但体现了高考注重“考查能力,在知识交汇点命制试题”的思想,应引起足够的注意.如图形的翻折与展开问题、与球面上两点间的距离相关的问题、立体几何中的轨迹问题都在成为高考命题新的热点.例6 已知球O 的半径为1,A 、B 、C三点都在球面上,且每两点之间的球面距离均为2π,则球心O 到平面ABC 的距离为 (A) 31 (B)33 (C) 32 (D)36 解析:由球面上两点间的距离的定义知,在四面体中,2π=∠=∠=∠BOC AOC AOB , 又OA =OB =OC =1,可用等积法求出O 到平面ABC 的距离为33.选(B ).例7如图,在正方体ABCD-A 1B 1C 1D 1中,P 是侧面BB 1C 1C 内一动点,若P 到直线BC与直线C 1D 1的距离相等,则动点P 的轨迹所在的曲线是(A)直线 (B)圆 (C)双曲线(D)抛物线解析:由于1111B BCC C D 平面⊥,连1PC ,有111D C PC ⊥,则P 到点C 1与P 到直线BC 的距离相等,由平面解析几何知识知点P 的轨迹是抛物线.选(D ).例8 如图,在正三棱柱ABC=A 1B 1C 1中,AB=3,AA 1=4,M 为AA 1的中点,P 是BC 上一点,且由P 沿棱柱侧面经过棱CC 1到M 的最短路线长为29,设这条最短路线与CC 1的交点为N ,求:(I )该三棱柱的侧面展开图的对角线长;(II )PC 和NC 的长;(III )平面NMP 与平面ABC 所成二面角(锐角)的大小(用反三角函数表示).解析:(I )正三棱柱ABC -A 1B 1C 1的侧面展开图是一个长为9,宽为4的矩形,其对角线长为974922=+.(II )将侧面BB 1C 1C 绕棱CC 1旋转120°使其与侧面AA 1C 1C 在同一平面上,点P 运动到点P 1的位置,连接MP 1,则MP 1就是由点P 沿棱柱侧面经过棱CC 1到点M的最短路线. PC =2.,NC=54. (III )连接PP 1,则PP 1就是平面NMP与平面ABC 的交线,作NH ⊥PP 1于H ,由三垂线定理证得∠NHC 就是平面NMP 与平面ABC 所成二面角的平面角(锐角),其大小为arctan 54. 随着新课程的实验和新教材的使用,立体几何正从复习耗时较多而考试得分偏低的题型变为得分较高的题型. 只要依据课本,熟化知识, 掌握基本方法,构建空间思维网络,突出重点, 我们在解答立体几何题时定会成竹在胸.巩固练习:1.对于平面α和共面的直线m 、,n 下列命题中真命题是(A )若,,m m n α⊥⊥则n α∥ (B )若m αα∥,n ∥,则m ∥n(C )若,m n αα⊂∥,则m ∥n (D )若m 、n 与α所成的角相等,则m ∥n2.表面积为23 的正八面体的各个顶点都在同一个球面上,则此球的体积为 A .23π B .13π C .23π D .22π3.已知球O 的半径是1,,,A B C 三点都在球面上,,A B 两点和,A C 两点的球面距离都是4π,,B C 两点的球面距离是3π,则二面角B OA C --的大小是(A )4π(B )3π (C )2π (D )23π 4.如图,O 是半径为l 的球心,点A 、B 、C 在球面上,OA 、OB 、OC 两两垂直,E 、F 分别是大圆弧AB 与AC 的中点,则点E 、F 在该球面上的球面距离是(A)4π (B)3π (C)2π (D)42π5.矩形ABCD 中,AB=4,BC=3,沿AC将矩形ABCD 折成一个直二面角B -AC -D ,则四面体ABCD 的外接球的体积为(A )π12125 (B )π9125 (C )π6125 (D )π3125 6.正方体ABCD -A 1B 1C 1D 1的棱长为1,O 是底面A 1B 1C 1D 1的中心,则O 到平面ABC 1D 1的距离为(A )21 (B )42 (C )22 (D )237.把正方形ABCD 沿对角线AC 折起,当以A 、B 、C 、D 四点为顶点的正棱锥体积最大时,直线BD 和平面ABC 所成的角的大小为(A )90O (B )60O(C ) 45O (D ) 30O8.若三棱锥A-BCD 的侧面ABC 内一动点P 到底面BCD 的距离与到棱AB 的距离相等,则动点P 的轨迹与ABC ∆组成图形可能是P(A ) (B )(C )(D )9.设P 是60的二面角l αβ--内一点,PA⊥平面α,PB ⊥平面β ,A 、B 为垂足,4,2,PA PB ==则AB 的长为(A )3 (B )25 (C )27 (D )4210.如图,在直三棱C ABBC A A B C P A B CP A B C P柱ABC -A 1B 1C 1中,底面为直角三角形,∠ACB =90︒,AC =6,BC =CC 12,P 是BC 1上一动点,则CP +PA 1的最小值是___________11.在正三棱柱111C B A ABC -中,1=AB .若二面角1C AB C --的大小为60,则点C 到平面1ABC 的距离为_____________.12.在三棱锥0ABC -中,三条棱,,OA OB OC 两两互相垂直,且,OA OB OC M ==是AB 边的中点,则OM 与平面ABC 所成角的大小是________________(用反三角函数表示)13.四棱锥S -ABCD 的底面是边长为1的正方形,SD ⊥底面ABCD ,SB =3.(I )求证:BC ⊥SC ;(II )求面ASD 与面BSC 所成二面角的大小;(III )设棱SA 的中点为M ,求异面直线DM 与SB 所成角的大小.14.如图所示的多面体是由底面ABCD为菱形的直平行六面体被平面AEFG 所截而得的,其中∠BAD =60O ,AB=4,BE =2,CF =3. (I )求证:EG ⊥AC ;(II )求截面AEFG 与底面ABCD 所成锐二面角的大小;(III )求点C 到截面AEFG 的距离.15.如图,在三棱锥P -ABC 中,AB ⊥BC ,AB =BC =kPA ,点O 、D分别是AC 、PC 的中点,OP ⊥底面ABC .(Ⅰ)求证:OD ∥平面PAB ;(Ⅱ)当k =21时,求直线PA 与平面PBC 所成角的大小;(Ⅲ) 当k 取何值时,O 在平面PBC 内的射影恰好为△PBC 的重心?16.如图,在四棱锥P —ABCD 中,底面ABCD 为矩形,侧棱PAA BC D O P⊥底面ABCD ,AB=3,BC=1,PA=2,E 为PD 的中点.(Ⅰ)求直线AC 与PB 所成角的余弦值;(Ⅱ)在侧面PAB 内找一点N ,使NE ⊥面PAC ,并求出N 点到AB 和AP 的距离.答案:1.C 2.A 3.C 4.B 5.C6.B7.C8.D9.C 10.5211.34 12.2arctan 13.(II )45O ;(III )90O14.(II )21arctan ; (III)556 15.(II )arcsin 21030;(III )k=116.(I )1473;(II )1,63。
2024年高考数学立体几何大题突破(解析版)

立体几何立体几何是高考数学的必考内容,在大题中一般分两问,第一问考查空间直线与平面的位置关系证明;第二问考查空间角、空间距离等的求解。
考题难度中等,常结合空间向量知识进行考查。
2024年高考有很大可能延续往年的出题方式。
题型一:空间异面直线夹角的求解1(2023·上海长宁·统考一模)如图,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,O为BD的中点.(1)求证:AO⊥CD;(2)若BD⊥DC,BD=DC,AO=BO,求异面直线BC与AD所成的角的大小.【思路分析】(1)利用面面垂直的性质、线面垂直的性质推理即得.(2)分别取AB,AC的中点M,N,利用几何法求出异面直线BC与AD所成的角.【规范解答】(1)在三棱锥A-BCD中,由AB=AD,O为BD的中点,得AO⊥BD,而平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AO⊂平面ABD,因此AO⊥平面BCD,又CD⊂平面BCD,所以AO⊥CD.(2)分别取AB,AC的中点M,N,连接OM,ON,MN,于是MN⎳BC,OM⎳AD,则∠OMN是异面直线BC与AD所成的角或其补角,由(1)知,AO ⊥BD ,又AO =BO ,AB =AD ,则∠ADB =∠ABD =π4,于是∠BAD =π2,令AB =AD =2,则DC =BD =22,又BD ⊥DC ,则有BC =BD 2+DC 2=4,OC =DC 2+OD 2=10,又AO ⊥平面BCD ,OC ⊂平面BCD ,则AO ⊥OC ,AO =2,AC =AO 2+OC 2=23,由M ,N 分别为AB ,AC 的中点,得MN =12BC =2,OM =12AD =1,ON =12AC =3,显然MN 2=4=OM 2+ON 2,即有∠MON =π2,cos ∠OMN =OM MN =12,则∠OMN =π3,所以异面直线BC 与AD 所成的角的大小π3.1、求异面直线所成角一般步骤:(1)平移:选择适当的点,线段的中点或端点,平移异面直线中的一条或两条成为相交直线.(2)证明:证明所作的角是异面直线所成的角.(3)寻找:在立体图形中,寻找或作出含有此角的三角形,并解之.(4)取舍:因为异面直线所成角θ的取值范围是0,π2,所以所作的角为钝角时,应取它的补角作为异面直线所成的角.2、可通过多种方法平移产生,主要有三种方法:(1)直接平移法(可利用图中已有的平行线);(2)中位线平移法;(3)补形平移法(在已知图形中,补作一个相同的几何体,以便找到平行线).3、异面直线所成角:若n 1 ,n 2分别为直线l 1,l 2的方向向量,θ为直线l 1,l 2的夹角,则cos θ=cos <n 1 ,n 2 > =n 1 ⋅n 2n 1 n 2.1(2023·江西萍乡·高三统考期中)如图,在正四棱台ABCD -A 1B 1C 1D 1中,E ,F 分别是BB 1,CD 的中点.(1)证明:EF ⎳平面AB1C 1D ;(2)若AB =2A 1B 1,且正四棱台的侧面积为9,其内切球半径为22,O 为ABCD 的中心,求异面直线OB 1与CC 1所成角的余弦值.【答案】(1)证明见解析;(2)45【分析】(1)根据中位线定理,结合线面平行判定定理以及面面平行判定定理,利用面面平行的性质,可得答案;(2)根据题意,结合正四棱台的几何性质,求得各棱长,利用线线角的定义,可得答案.【解析】(1)取CC 1中点G ,连接GE ,GF ,如下图:在梯形BB 1C 1C 中,E ,G 分别为BB 1,CC 1的中点,则EG ⎳B 1C 1,同理可得FG ⎳C 1D ,因为EG ⊄平面AB 1C 1D ,B 1C 1⊂平面AB 1C 1D ,所以EG ⎳平面AB 1C 1D ,同理可得GF ⎳平面AB 1C 1D ,因为EG ∩FG =G ,EG ,FG ⊆平面EFG ,所以平面EFG ⎳平面AB 1C 1D ,又因为EF ⊆平面EFG ,所以EF ⎳平面AB 1C 1D ;(2)连接AC ,BD ,则AC ∩BD =O ,连接A 1O ,A 1C 1,B 1O ,在平面BB 1C 1C 中,作B 1N ⊥BC 交BC 于N ,在平面BB 1D 1D 中,作B 1M ⊥BD 交BD 于M ,连接MN ,如下图:因为AB =2A 1B 1,则OC =A 1C 1,且OC ⎳A 1C 1,所以A 1C 1CO 为平行四边形,则A 1O ⎳CC 1,且A 1O =CC 1,所以∠A 1OB 1为异面直线OB 1与CC 1所成角或其补角,同理可得:B 1D 1DO 为平行四边形,则B 1O =D 1D ,在正四棱台ABCD -A 1B 1C 1D 1中,易知对角面BB 1D 1D ⊥底面ABCD ,因为平面ABCD ∩平面BB 1D 1D =BD ,且B 1M ⊥BD ,B 1M ⊂平面BB 1D 1D ,所以B 1M ⊥平面ABCD ,由内切球的半径为22,则B 1M =2,在等腰梯形BB 1C 1C 中,BC =2B 1C 1且B 1N ⊥BC ,易知BN =14BC ,同理可得BM =14BD ,在△BCD 中,BN BC=BM BD =14,则MN =14CD ,设正方形ABCD 的边长为4x x >0 ,则正方形A 1B 1C 1D 1的边长为2x ,MN =x ,由正四棱台的侧面积为9,则等腰梯形BB 1C 1C 的面积S =94,因为B 1M ⊥平面ABCD ,MN ⊂平面ABCD ,所以B 1M ⊥MN ,在Rt △B 1MN ,B 1N =B 1M 2+MN 2=2+x 2,可得S =12⋅B 1N ⋅B 1C 1+BC ,则94=12×2+x 2×4x +2x ,解得x =12,所以BC =2,B 1C 1=1,BN =14BC =12,B 1N =32,则A 1B 1=1,在Rt △BB 1N 中,BB 1=B 1N 2+BN 2=102,则CC 1=DD 1=102,所以在△A 1OB 1中,则cos ∠A 1OB 1=A 1O 2+B 1O 2-A 1B 212⋅A 1O ⋅B 1O=1022+102 2-12×102×102=45,所以异面直线OB 1与CC 1所成角的余弦值为45.2(2023·辽宁丹东·统考二模)如图,平行六面体ABCD -A 1B 1C 1D 1的所有棱长都相等,平面CDD 1C 1⊥平面ABCD ,AD ⊥DC ,二面角D 1-AD -C 的大小为120°,E 为棱C 1D 1的中点.(1)证明:CD ⊥AE ;(2)点F 在棱CC 1上,AE ⎳平面BDF ,求直线AE 与DF 所成角的余弦值.【答案】(1)证明见解析;(2)37【分析】(1)根据面面垂直可得线面垂直进而得线线垂直,由二面角定义可得∠D 1DC =120°,进而根据中点得线线垂直即可求;(2)由线面平行的性质可得线线平行,由线线角的几何法可利用三角形的边角关系求解,或者建立空间直角坐标系,利用向量的夹角即可求解.【解析】(1)因为平面CDD 1C 1⊥平面ABCD ,且两平面交线为DC ,AD ⊥DC ,AD ⊂平面ABCD , 所以AD ⊥平面CDD 1C 1,所以AD ⊥D 1D ,AD ⊥DC ,∠D 1DC 是二面角D 1-AD -C 的平面角,故∠D 1DC =120°.连接DE ,E 为棱C 1D 1的中点,则DE ⊥C 1D 1,C 1D 1⎳CD ,从而DE ⊥CD .又AD ⊥CD ,DE ∩AD =D ,DE ,AD ⊂平面AED ,所以CD ⊥平面AED ,ED ⊂平面AED ,因此CD ⊥AE .(2)解法1:设AB =2,则DE =D 1D 2-12D 1C 1 2=3,所以CE =AE =AD 2+DE 2=7.连AC 交BD 于点O ,连接CE 交DF 于点G ,连OG .因为AE ⎳平面BDF ,AE ⊂平面AEC ,平面AEC ∩平面BDF =OG ,所以AE ∥OG ,因为O 为AC 中点,所以G 为CE 中点,故OG =12AE =72.且直线OG 与DF 所成角等于直线AE 与DF 所成角.在Rt △EDC 中,DG =12CE =72,因为OD =2,所以cos ∠OGD =722+72 2-(2)22×72×72=37.因此直线AE 与DF 所成角的余弦值为37.解法2;设AB =2,则DE =D 1D 2-12D 1C 1 2=3,所以CE =AE =AD 2+DE 2=7.取DC 中点为G ,连接EG 交DF 于点H ,则EG =DD 1=2.连接AG 交BD 于点I ,连HI ,因为AE ⎳平面BDF ,AE ⊂平面AGE ,平面AGE ∩平面BDF =IH ,所以AE ∥IH .HI 与DH 所成角等于直线AE 与DF 所成角.正方形ABCD 中,GI =13AG ,DI =13DB =223,所以GH =13EG ,故HI =13AE =73.在△DHG 中,GH =13EG =23,GD =1,∠EGD =60°,由余弦定理DH =1+49-1×23=73.在△DHI 中,cos ∠DHI =732+73 2-223 22×73×73=37.因此直线AE 与DF 所成角的余弦值为37.解法3:由(1)知DE ⊥平面ABCD ,以D 为坐标原点,DA为x 轴正方向,DA为2个单位长,建立如图所示的空间直角坐标系D -xyz .由(1)知DE =3,得A 2,0,0 ,B 2,2,0 ,C 0,2,0 ,E (0,0,3),C 1(0,1,3).则CC 1=(0,-1,3),DC =(0,2,0),AE =(-2,0,3),DB =(2,2,0).由CF =tCC 1 0≤t ≤1 ,得DF =DC +CF =(0,2-t ,3t ).因为AE ⎳平面BDF ,所以存在唯一的λ,μ∈R ,使得AE =λDB +μDF=λ2,2,0 +μ(0,2-t ,3t )=2λ,2λ+2μ-tμ,3μt ,故2λ=-2,2λ+2μ-tμ=0,3μt =3,解得t =23,从而DF =0,43,233 .所以直线AE 与DF 所成角的余弦值为cos AE ,DF =AE ⋅DF|AE ||DF |=37.题型二:空间直线与平面夹角的求解2(2024·安徽合肥·统考一模)如图,三棱柱ABC -A 1B 1C 1中,四边形ACC 1A 1,BCC 1B 1均为正方形,D ,E 分别是棱AB ,A 1B 1的中点,N 为C 1E 上一点.(1)证明:BN ⎳平面A 1DC ;(2)若AB =AC ,C 1E =3C 1N,求直线DN 与平面A 1DC 所成角的正弦值.【思路分析】(1)连接BE ,BC 1,DE ,则有平面BEC 1⎳平面A 1DC ,可得BN ⎳平面A 1DC ;(2)建立空间直角坐标系,利用空间向量进行计算即可.【规范解答】(1)连接BE ,BC 1,DE .因为AB ⎳A 1B 1,且AB =A 1B 1,又D ,E 分别是棱AB ,A 1B 1的中点,所以BD ⎳A 1E ,且BD =A 1E ,所以四边形BDA 1E 为平行四边形,所以A 1D ⎳EB ,又A 1D ⊂平面A 1DC ,EB ⊄平面A 1DC ,所以EB ⎳平面A 1DC ,因为DE ⎳BB 1⎳CC 1,且DE =BB 1=CC 1,所以四边形DCC 1E 为平行四边形,所以C 1E ⎳CD ,又CD ⊂平面A 1DC ,C 1E ⊄平面A 1DC ,所以C 1E ⎳平面A 1DC ,因为C 1E ∩EB =E ,C 1E ,EB ⊂平面BEC 1,所以平面BEC 1⎳平面A 1DC ,因为BN ⊂平面BEC 1,所以BN ⎳平面A 1DC .(2)四边形ACC 1A 1,BCC 1B 1均为正方形,所以CC 1⊥AC ,CC 1⊥BC ,所以CC 1⊥平面ABC .因为DE ⎳CC 1,所以DE ⊥平面ABC ,从而DE ⊥DB ,DE ⊥DC .又AB =AC ,所以△ABC 为等边三角形.因为D 是棱AB 的中点,所以CD ⊥DB ,即DB ,DC ,DE 两两垂直.以D 为原点,DB ,DC ,DE 所在直线为x ,y ,z 轴,建立如图所示的空间直角坐标系D -xyz .设AB =23,则D 0,0,0 ,E 0,0,23 ,C 0,3,0 ,C 10,3,23 ,A 1-3,0,23 ,所以DC =0,3,0 ,DA 1=-3,0,23 .设n=x ,y ,z 为平面A 1DC 的法向量,则n ⋅DC=0n ⋅DA 1 =0,即3y =0-3x +23z =0 ,可取n=2,0,1 .因为C 1E =3C 1N ,所以N 0,2,23 ,DN =0,2,23 .设直线DN 与平面A 1DC 所成角为θ,则sin θ=|cos ‹n ,DN ›|=|n ⋅DN ||n |⋅|DN |=235×4=1510,即直线DN 与平面A 1DC 所成角正弦值为1510.1、垂线法求线面角(也称直接法):(1)先确定斜线与平面,找到线面的交点B 为斜足;找线在面外的一点A ,过点A 向平面α做垂线,确定垂足O ;(2)连结斜足与垂足为斜线AB 在面α上的投影;投影BO 与斜线AB 之间的夹角为线面角;(3)把投影BO 与斜线AB 归到一个三角形中进行求解(可能利用余弦定理或者直角三角形)。
高考数学难点突破训练 立体几何(含答案)

高考数学难点突破训练立体几何(含答案)高考数学难点突破训练-立体几何(含答案)高考数学难点的突破训练——立体几何acd30,?acb?45?,1.将两块三角板按图甲方式拼好,其中?b??d?90?,交流电?2.现在沿AC折叠三角形板ACD,使D在平面ABC上的投影正好在AB上,如图B所示(1)求证:ad?平面bdc;w.w.w.k.s.5.u.c.o.m(2)求二面角d?ac?b的大小;(3)找出AC和BD之间的角度2.如图,在正三棱柱abc?a1b1c1中,各棱长都等于a,d、 E分别是AC1和BB1的中点,(1)求证:de是异面直线ac1与bb1的公垂线段,并求其长度;(2)找到二面角e?ac1?C)房间的大小;(3)求从点C1到平面AEC的距离3.如图,在棱长为a的正方体abcd?a1b1c1d1中,e、f分别为棱ab和bc的中点,ef 交bd于h.(1)二面角?1.ef?B的正切值;(2)试在棱b1b上找一点m,使d1m?平面efb1,并证一明你的结论;(3)求出从点D1到平面efb1的距离4.如图,斜三棱柱abc―a1b1c1的底面是直角三角形,ac⊥cb,∠abc=45°,侧面A1abb1是边长为a且垂直于底部ABC的钻石,∠ a1ab=60°,e和F分别为Ab1和BC 的中点(1)求证ef//平面a1acc1;(2)找到EF和a1abb1侧之间的角度;(3)求出a-bce三角金字塔的体积5.已知直三棱柱abc―a1b1c1中,△abc为等腰直角三角形,∠bac=90°,且ab=aa1,d、e、f分别为b1a、c1c、bc的中点。
(i)验证:de‖plane ABC;(二)验证:B1F⊥ 飞机AEF;(iii)求二面角b1―ae―f的大小(用反三角函数表示)。
二6.在直角梯形abcd中,∠a=∠d=90°,ab<cd,sd⊥平面abcd,ab=ad=a,SD=2A,在线段SA上取一个点E(不包括终点),使EC=AC,横截面CDE和Sb在点F 处相交。
专题05 立体几何专项高考真题总汇(带答案与解析)

专题05立体几何(选择题、填空题)1.【2021·浙江高考真题】某几何体的三视图如图所示,则该几何体的体积是()A .32B .3C.2D.【答案】A【分析】根据三视图可得如图所示的几何体,根据棱柱的体积公式可求其体积.【解析】几何体为如图所示的四棱柱1111ABCD A B C D -,其高为1,底面为等腰梯形ABCD ,,下底为12=,故1111131222ABCD A B C D V -=⨯+⨯⨯=,故选:A.2.【2021·北京高考真题】某四面体的三视图如图所示,该四面体的表面积为()A .332+B .4C .33D .2【答案】A【分析】根据三视图可得如图所示的几何体(三棱锥),根据三视图中的数据可计算该几何体的表面积.【解析】根据三视图可得如图所示的几何体-正三棱锥O ABC -,其侧面为等腰直角三角形,底面等边三角形,由三视图可得该正三棱锥的侧棱长为1,故其表面积为213333112242+⨯⨯⨯+⨯=,故选:A.3.【2021·浙江高考真题】如图已知正方体1111ABCD A B C D -,M ,N 分别是1A D ,1D B 的中点,则()A .直线1A D 与直线1DB 垂直,直线//MN 平面ABCD B .直线1A D 与直线1D B 平行,直线MN ⊥平面11BDD BC .直线1AD 与直线1D B 相交,直线//MN 平面ABCD D .直线1A D 与直线1D B 异面,直线MN ⊥平面11BDD B 【答案】A【分析】由正方体间的垂直、平行关系,可证1//,MN AB A D ⊥平面1ABD ,即可得出结论.【解析】连1AD ,在正方体1111ABCD A B C D -中,M 是1A D 的中点,所以M 为1AD 中点,又N 是1D B 的中点,所以//MN AB ,MN ⊄平面,ABCD AB ⊂平面ABCD ,所以//MN 平面ABCD .因为AB 不垂直BD ,所以MN 不垂直BD 则MN 不垂直平面11BDD B ,所以选项B,D 不正确;在正方体1111ABCD A B C D -中,11AD A D ⊥,AB ⊥平面11AA D D ,所以1AB A D ⊥,1AD AB A ⋂=,所以1A D ⊥平面1ABD ,1D B ⊂平面1ABD ,所以11A D D B ⊥,且直线11,A D D B 是异面直线,所以选项B 错误,选项A 正确.故选:A.【点睛】关键点点睛:熟练掌握正方体中的垂直、平行关系是解题的关键,如两条棱平行或垂直,同一个面对角线互相垂直,正方体的对角线与面的对角线是相交但不垂直或异面垂直关系.4.【2021·全国高考真题(理)】已如A ,B ,C 是半径为1的球O 的球面上的三个点,且,1AC BC AC BC ⊥==,则三棱锥O ABC -的体积为()A .212B .312C .24D .34【答案】A【分析】由题可得ABC 为等腰直角三角形,得出ABC 外接圆的半径,则可求得O 到平面ABC 的距离,进而求得体积.【解析】,1AC BC AC BC ⊥== ,ABC ∴ 为等腰直角三角形,AB ∴=,则ABC 外接圆的半径为22,又球的半径为1,设O 到平面ABC 的距离为d ,则2d ==,所以1112211332212O ABC ABC V S d -=⋅=⨯⨯⨯⨯=.故选:A.【点睛】关键点睛:本题考查球内几何体问题,解题的关键是正确利用截面圆半径、球半径、球心到截面距离的勾股关系求解.5.【2021·全国高考真题(理)】在正方体1111ABCD A B C D -中,P 为11B D 的中点,则直线PB 与1AD 所成的角为()A .π2B .π3C .π4D .π6【答案】D【分析】平移直线1AD 至1BC ,将直线PB 与1AD 所成的角转化为PB 与1BC 所成的角,解三角形即可.【解析】如图,连接11,,BC PC PB ,因为1AD ∥1BC ,所以1PBC ∠或其补角为直线PB 与1AD 所成的角,因为1BB ⊥平面1111D C B A ,所以11BB PC ⊥,又111PC B D ⊥,1111BB B D B ⋂=,所以1PC ⊥平面1P B B ,所以1PC PB ⊥,设正方体棱长为2,则111112BC PC D B ===1111sin 2PC PBC BC ∠==,所以16PBC π∠=.故选:D6.【2021·全国高考真题】已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的母线长为()A .2B.C .4D.【答案】B【分析】设圆锥的母线长为l ,根据圆锥底面圆的周长等于扇形的弧长可求得l 的值,即为所求.【解析】设圆锥的母线长为l,由于圆锥底面圆的周长等于扇形的弧长,则2l ππ=解得l =.故选:B.7.【2021·北京高考真题】定义:24小时内降水在平地上积水厚度(mm )来判断降雨程度.其中小雨(10mm <),中雨(10mm 25mm -),大雨(25mm 50mm -),暴雨(50mm 100mm -),小明用一个圆锥形容器接了24小时的雨水,如图,则这天降雨属于哪个等级()A .小雨B .中雨C .大雨D .暴雨【答案】B【分析】计算出圆锥体积,除以圆面的面积即可得降雨量,即可得解.【解析】由题意,一个半径为()200100mm 2=的圆面内的降雨充满一个底面半径为()20015050mm 2300⨯=,高为()150mm 的圆锥,所以积水厚度()22150150312.5mm 100d ππ⨯⨯==⨯,属于中雨.故选:B.8.【2021·全国高考真题】在正三棱柱111ABC A B C -中,11AB AA ==,点P 满足1BP BC BB λμ=+,其中[]0,1λ∈,[]0,1μ∈,则()A .当1λ=时,1AB P △的周长为定值B .当1μ=时,三棱锥1P A BC -的体积为定值C .当12λ=时,有且仅有一个点P ,使得1A P BP ⊥D .当12μ=时,有且仅有一个点P ,使得1A B ⊥平面1AB P 【答案】BD【分析】对于A ,由于等价向量关系,联系到一个三角形内,进而确定点的坐标;对于B ,将P 点的运动轨迹考虑到一个三角形内,确定路线,进而考虑体积是否为定值;对于C ,考虑借助向量的平移将P 点轨迹确定,进而考虑建立合适的直角坐标系来求解P 点的个数;对于D ,考虑借助向量的平移将P 点轨迹确定,进而考虑建立合适的直角坐标系来求解P 点的个数.【解析】易知,点P 在矩形11BCC B 内部(含边界).对于A ,当1λ=时,11=BP BC BB BC CC μμ=++,即此时P ∈线段1CC ,1AB P △周长不是定值,故A 错误;对于B ,当1μ=时,1111=BP BC BB BB B C λλ=++,故此时P 点轨迹为线段11B C ,而11//B C BC ,11//B C 平面1A BC ,则有P 到平面1A BC 的距离为定值,所以其体积为定值,故B 正确.对于C ,当12λ=时,112BP BC BB μ=+,取BC ,11B C 中点分别为Q ,H ,则BP BQ QH μ=+,所以P 点轨迹为线段QH ,不妨建系解决,建立空间直角坐标系如图,13,0,12A ⎛⎫ ⎪ ⎪⎝⎭,()0,0P μ,,10,,02B ⎛⎫⎪⎝⎭,则13,0,12A P μ⎛⎫=-- ⎪ ⎪⎝⎭,10,,2BP μ⎛⎫=- ⎪⎝⎭ ,()110A P BP μμ⋅=-=,所以0μ=或1μ=.故,H Q 均满足,故C 错误;对于D ,当12μ=时,112BP BC BB λ=+ ,取1BB ,1CC 中点为,M N .BP BM MN λ=+ ,所以P 点轨迹为线段MN .设010,,2P y ⎛⎫ ⎪⎝⎭,因为0,02A ⎛⎫ ⎪ ⎪⎝⎭,所以01,22AP y ⎛⎫= ⎪ ⎪⎝⎭,11,,122A B ⎛⎫=-- ⎪ ⎪⎝⎭,所以00311104222y y +-=⇒=-,此时P 与N 重合,故D 正确.故选:BD .【点睛】本题主要考查向量的等价替换,关键之处在于所求点的坐标放在三角形内.9.【2021·全国高考真题(理)】以图①为正视图,在图②③④⑤中选两个分别作为侧视图和俯视图,组成某三棱锥的三视图,则所选侧视图和俯视图的编号依次为_________(写出符合要求的一组答案即可).【答案】③④(答案不唯一)【分析】由题意结合所给的图形确定一组三视图的组合即可.【解析】选择侧视图为③,俯视图为④,如图所示,长方体1111ABCD A B C D -中,12,1AB BC BB ===,,E F 分别为棱11,BC BC 的中点,则正视图①,侧视图③,俯视图④对应的几何体为三棱锥E ADF -.故答案为:③④.【点睛】三视图问题解决的关键之处是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系.10.【2020年高考全国Ⅰ卷理数】埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥.以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为A .514-B .512-C .514D .512+【答案】C【解析】如图,设,CD a PE b ==,则22224a PO PE OEb =-=-由题意得212PO ab =,即22142a b ab-=,化简得24()210b b a a -⋅-=,解得14b a +=(负值舍去).故选C .【点晴】本题主要考查正四棱锥的概念及其有关计算,考查学生的数学计算能力,是一道容易题.11.【2020年高考全国Ⅱ卷理数】如图是一个多面体的三视图,这个多面体某条棱的一个端点在正视图中对应的点为M ,在俯视图中对应的点为N ,则该端点在侧视图中对应的点为A .EB .FC .GD .H【答案】A【解析】根据三视图,画出多面体立体图形,14D D 上的点在正视图中都对应点M ,直线34B C 上的点在俯视图中对应的点为N,∴在正视图中对应M ,在俯视图中对应N 的点是4D ,线段34D D ,上的所有点在侧试图中都对应E ,∴点4D 在侧视图中对应的点为E .故选A.【点睛】本题主要考查了根据三视图判断点的位置,解题关键是掌握三视图的基础知识和根据三视图能还原立体图形的方法,考查了分析能力和空间想象,属于基础题.12.【2020年高考全国II 卷理数】已知△ABC 是面积为934O 的球面上.若球O 的表面积为16π,则O 到平面ABC 的距离为A 3B .32C .1D .32【答案】C【解析】设球O 的半径为R ,则2416R π=π,解得:2R =.设ABC △外接圆半径为r ,边长为a ,ABC △是面积为934的等边三角形,21393224a ∴⨯=,解得:3a =,22229933434a r a ∴=-=⨯-,∴球心O 到平面ABC 的距离22431d R r =-=-=.故选:C .【点睛】本题考查球的相关问题的求解,涉及到球的表面积公式和三角形面积公式的应用;解题关键是明确球的性质,即球心和三角形外接圆圆心的连线必垂直于三角形所在平面.13.【2020年高考全国Ⅲ卷理数】如图为某几何体的三视图,则该几何体的表面积是A .2B .4+42C .3D .4+23【答案】C 【解析】根据三视图特征,在正方体中截取出符合题意的立体图形根据立体图形可得:12222ABC ADC CDB S S S ===⨯⨯=△△△根据勾股定理可得:22AB AD DB ===∴ADB △是边长为的等边三角形根据三角形面积公式可得:2113sin 60222ADB S AB AD =⋅⋅︒=⋅=△∴该几何体的表面积是:632=⨯++.故选:C .【点睛】本题主要考查了根据三视图求立体图形的表面积问题,解题关键是掌握根据三视图画出立体图形,考查了分析能力和空间想象能力,属于基础题.14.【2020年高考全国Ⅰ卷理数】已知,,A B C 为球O 的球面上的三个点,⊙1O 为ABC △的外接圆,若⊙1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为A .64πB .48πC .36πD .32π【答案】A【解析】设圆1O 半径为r ,球的半径为R ,依题意,得24,2r r π=π=∴, ABC 为等边三角形,由正弦定理可得2sin 60AB r =︒=,1OO AB ∴==,根据球的截面性质1OO ⊥平面ABC ,11,4OO O A R OA ∴⊥====,∴球O 的表面积2464S R ππ==.故选:A.【点睛】本题考查球的表面积,应用球的截面性质是解题的关键,考查计算求解能力,属于基础题.15.【2020年高考天津】若棱长为为A .12πB .24πC .36πD .144π【答案】C【解析】这个球是正方体的外接球,其半径等于正方体的体对角线的一半,即3R ==,所以,这个球的表面积为2244336S R πππ==⨯=.故选:C .【点睛】本题考查正方体的外接球的表面积的求法,求出外接球的半径是本题的解题关键,属于基础题.求多面体的外接球的面积和体积问题,常用方法有:(1)三条棱两两互相垂直时,可恢复为长方体,利用长方体的体对角线为外接球的直径,求出球的半径;(2)直棱柱的外接球可利用棱柱的上下底面平行,借助球的对称性,球心为上下底面外接圆的圆心连线的中点,再根据勾股定理求球的半径;(3)如果设计几何体有两个面相交,可过两个面的外心分别作两个面的垂线,垂线的交点为几何体的球心.16.【2020年高考北京】某三棱柱的底面为正三角形,其三视图如图所示,该三棱柱的表面积为A .6+B .6+C .12+D .12+【答案】D 【解析】由题意可得,三棱柱的上下底面为边长为2的等边三角形,侧面为三个边长为2的正方形,则其表面积为:()1322222sin 60122S ⎛⎫=⨯⨯+⨯⨯⨯⨯︒=+⎪⎝⎭故选:D .【点睛】(1)以三视图为载体考查几何体的表面积,关键是能够对给出的三视图进行恰当的分析,从三视图中发现几何体中各元素间的位置关系及数量关系.(2)多面体的表面积是各个面的面积之和;组合体的表面积应注意重合部分的处理.(3)圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将这个曲面展为平面图形计算,而表面积是侧面积与底面圆的面积之和.17.【2020年高考浙江】某几何体的三视图(单位:cm )如图所示,则该几何体的体积(单位:cm 3)是A .73B .143C .3D .6【答案】A 【解析】由三视图可知,该几何体是上半部分是三棱锥,下半部分是三棱柱,且三棱锥的一个侧面垂直于底面,且棱锥的高为1,棱柱的底面为等腰直角三角形,棱柱的高为2,所以几何体的体积为11117211212232233⎛⎫⎛⎫⨯⨯⨯⨯+⨯⨯⨯=+=⎪ ⎪⎝⎭⎝⎭.故选:A【点睛】本小题主要考查根据三视图计算几何体的体积,属于基础题.18.【2020年高考浙江】已知空间中不过同一点的三条直线l ,m ,n .“l ,m ,n 共面”是“l ,m ,n 两两相交”的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件【答案】B【解析】依题意,,m n l 是空间不过同一点的三条直线,当,,m n l 在同一平面时,可能////m n l ,故不能得出,,m n l 两两相交.当,,m n l 两两相交时,设,,m n A m l B n l C ⋂=⋂=⋂=,根据公理2可知,m n 确定一个平面α,而,B m C n αα∈⊂∈⊂,根据公理1可知,直线BC 即l α⊂,所以,,m n l 在同一平面.综上所述,“,,m n l 在同一平面”是“,,m n l 两两相交”的必要不充分条件.故选:B【点睛】本小题主要考查充分、必要条件的判断,考查公理1和公理2的运用,属于中档题.19.【2020年新高考全国Ⅰ卷】日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O ),地球上一点A 的纬度是指OA 与地球赤道所在平面所成角,点A 处的水平面是指过点A 且与OA 垂直的平面.在点A 处放置一个日晷,若晷面与赤道所在平面平行,点A 处的纬度为北纬40°,则晷针与点A 处的水平面所成角为A .20°B .40°C .50°D .90°【答案】B 【解析】画出截面图如下图所示,其中CD 是赤道所在平面的截线;l 是点A 处的水平面的截线,依题意可知OA l ⊥;AB 是晷针所在直线.m 是晷面的截线,依题意依题意,晷面和赤道平面平行,晷针与晷面垂直,根据平面平行的性质定理可得可知//m CD 、根据线面垂直的定义可得AB m ⊥..由于40,//AOC m CD ∠=︒,所以40OAG AOC ∠=∠=︒,由于90OAG GAE BAE GAE ∠+∠=∠+∠=︒,所以40BAE OAG ∠=∠=︒,也即晷针与点A 处的水平面所成角为40BAE ∠=︒.故选:B.【点睛】本小题主要考查中国古代数学文化,考查球体有关计算,涉及平面平行,线面垂直的性质,属于中档题.20.【2019年高考全国Ⅰ卷理数】已知三棱锥P −ABC 的四个顶点在球O 的球面上,PA =PB =PC ,△ABC 是边长为2的正三角形,E ,F 分别是PA ,AB 的中点,∠CEF =90°,则球O 的体积为A .B .C .D 【答案】D【解析】解法一:,PA PB PC ABC == △为边长为2的等边三角形,P ABC ∴-为正三棱锥,PB AC ∴⊥,又E ,F 分别为PA ,AB 的中点,EF PB ∴∥,EF AC ∴⊥,又EF CE ⊥,,CE AC C EF =∴⊥ 平面PAC ,∴PB ⊥平面PAC ,APB PA PB PC ∴∠=90︒,∴===,P ABC ∴-为正方体的一部分,2R ==364466,π2338R V R =∴=π=⨯=,故选D .解法二:设2PA PB PC x ===,,E F 分别为,PA AB 的中点,EF PB ∴∥,且12EF PB x ==,ABC △为边长为2的等边三角形,CF ∴=又90CEF ∠=︒,12CE AE PA x ∴===,AEC △中,由余弦定理可得()2243cos 22x x EAC x +--∠=⨯⨯,作PD AC ⊥于D ,PA PC = ,D \为AC 的中点,1cos 2AD EAC PA x ∠==,2243142x x x x+-+∴=,221221222x x x ∴+=∴==,,,PA PB PC ∴===,又===2AB BC AC ,,,PA PB PC ∴两两垂直,2R ∴==,62R ∴=,34466338V R ∴=π=π⨯=,故选D.【名师点睛】本题主要考查学生的空间想象能力,补体法解决外接球问题.可通过线面垂直定理,得到三棱两两互相垂直关系,快速得到侧棱长,进而补体成正方体解决.21.【2019年高考全国Ⅱ卷理数】设α,β为两个平面,则α∥β的充要条件是A .α内有无数条直线与β平行B .α内有两条相交直线与β平行C .α,β平行于同一条直线D .α,β垂直于同一平面【答案】B【解析】由面面平行的判定定理知:α内两条相交直线都与β平行是αβ∥的充分条件,由面面平行性质定理知,若αβ∥,则α内任意一条直线都与β平行,所以α内两条相交直线都与β平行是αβ∥的必要条件,故选B .【名师点睛】本题考查了空间两个平面的判定与性质及充要条件,渗透直观想象、逻辑推理素养,利用面面平行的判定定理与性质定理即可作出判断.面面平行的判定问题要紧扣面面平行判定定理,最容易犯的错误为定理记不住,凭主观臆断,如:“若,,a b a b αβ⊂⊂∥,则αβ∥”此类的错误.22.【2019年高考全国Ⅲ卷理数】如图,点N 为正方形ABCD 的中心,△ECD 为正三角形,平面ECD ⊥平面ABCD ,M 是线段ED 的中点,则A .BM =EN ,且直线BM ,EN 是相交直线B .BM ≠EN ,且直线BM ,EN 是相交直线C .BM =EN ,且直线BM ,EN 是异面直线D .BM ≠EN ,且直线BM ,EN 是异面直线【答案】B【解析】如图所示,作EO CD ⊥于O ,连接ON ,BD ,易得直线BM ,EN 是三角形EBD 的中线,是相交直线.过M 作MF OD ⊥于F ,连接BF ,平面CDE ⊥平面ABCD ,,EO CD EO ⊥⊂平面CDE ,EO ∴⊥平面ABCD ,MF ⊥平面ABCD ,MFB ∴△与EON △均为直角三角形.设正方形边长为2,易知12EO ON EN ===,,5,,22MF BF BM ==∴=BM EN ∴≠,故选B .【名师点睛】本题考查空间想象能力和计算能力,解答本题的关键是构造直角三角形.解答本题时,先利用垂直关系,再结合勾股定理进而解决问题.23.【2019年高考浙江卷】祖暅是我国南北朝时代的伟大科学家,他提出的“幂势既同,则积不容异”称为祖暅原理,利用该原理可以得到柱体的体积公式V柱体=Sh,其中S是柱体的底面积,h是柱体的高.若某柱体的三视图如图所示(单位:cm),则该柱体的体积(单位:cm3)是A.158B.162C.182D.324【答案】B【解析】由三视图得该棱柱的高为6,底面可以看作是由两个直角梯形组合而成的,其中一个上底为4,下底为6,高为3,另一个的上底为2,下底为6,高为3,则该棱柱的体积为2646336162 22++⎛⎫⨯+⨯⨯=⎪⎝⎭.故选B.【名师点睛】本题首先根据三视图,还原得到几何体——棱柱,根据题目给定的数据,计算几何体的体积,常规题目.难度不大,注重了基础知识、视图用图能力、基本计算能力的考查.易错点有二,一是不能正确还原几何体;二是计算体积有误.为避免出错,应注重多观察、细心算.24.【2019年高考浙江卷】设三棱锥V–ABC的底面是正三角形,侧棱长均相等,P是棱VA 上的点(不含端点).记直线PB与直线AC所成的角为α,直线PB与平面ABC所成的角为β,二面角P–AC–B的平面角为γ,则A.β<γ,α<γB.β<α,β<γC.β<α,γ<αD.α<β,γ<β【答案】B【解析】如图,G 为AC 中点,连接VG ,V 在底面ABC 的投影为O ,则P 在底面的投影D 在线段AO 上,过D 作DE 垂直于AC 于E ,连接PE ,BD ,易得PE VG ∥,过P 作PF AC ∥交VG 于F ,连接BF ,过D 作DH AC ∥,交BG 于H ,则,,BPF PBD PED αβγ=∠=∠=∠,结合△PFB ,△BDH ,△PDB 均为直角三角形,可得cos cos PF EG DH BD PB PB PB PB αβ===<=,即αβ>;在Rt △PED 中,tan tan PD PD ED BD γβ=>=,即γβ>,综上所述,答案为B.【名师点睛】本题以三棱锥为载体,综合考查异面直线所成的角、直线与平面所成的角、二面角的概念,以及各种角的计算.解答的基本方法是通过明确各种角,应用三角函数知识求解,而后比较大小.而充分利用图形特征,则可事倍功半.常规解法下易出现的错误有,不能正确作图得出各种角,未能想到利用“特殊位置法”,寻求简便解法.25.【2020年高考全国Ⅱ卷理数】设有下列四个命题:p 1:两两相交且不过同一点的三条直线必在同一平面内.p 2:过空间中任意三点有且仅有一个平面.p 3:若空间两条直线不相交,则这两条直线平行.p 4:若直线l ⊂平面α,直线m ⊥平面α,则m ⊥l .则下述命题中所有真命题的序号是__________.①14p p ∧②12p p ∧③23p p ⌝∨④34p p ⌝∨⌝【答案】①③④【解析】对于命题1p ,可设1l 与2l 相交,这两条直线确定的平面为α;若3l 与1l 相交,则交点A 在平面α内,同理,3l 与2l 的交点B 也在平面α内,所以,AB α⊂,即3l α⊂,命题1p 为真命题;对于命题2p ,若三点共线,则过这三个点的平面有无数个,命题2p 为假命题;对于命题3p ,空间中两条直线相交、平行或异面,命题3p 为假命题;对于命题4p ,若直线m ⊥平面α,则m 垂直于平面α内所有直线,直线l ⊂平面α,∴直线m ⊥直线l ,命题4p 为真命题.综上可知,,为真命题,,为假命题,14p p ∧为真命题,12p p ∧为假命题,23p p ⌝∨为真命题,34p p ⌝∨⌝为真命题.故答案为:①③④.【点睛】本题考查复合命题的真假,同时也考查了空间中线面关系有关命题真假的判断,考查推理能力,属于中等题.26.【2020年高考全国Ⅲ卷理数】已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为_________.【答案】23【解析】易知半径最大球为圆锥的内切球,球与圆锥内切时的轴截面如图所示,其中2,3BC AB AC ===,且点M 为BC 边上的中点,设内切圆的圆心为O ,由于223122AM =-=,故1222222S =⨯⨯=△ABC 设内切圆半径为r ,则:ABC AOB BOC AOC S S S S =++△△△△111222AB r BC r AC r =⨯⨯+⨯⨯+⨯⨯()1332222r =⨯++⨯=解得:22r =,其体积:34233V r =π=π.故答案为:23π.【点睛】与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.27.【2020年高考浙江】已知圆锥的侧面积(单位:cm 2)为2π,且它的侧面展开图是一个半圆,则这个圆锥的底面半径(单位:cm )是_______.【答案】1【解析】设圆锥底面半径为r ,母线长为l ,则21222r l r l ππππ⨯⨯=⎧⎪⎨⨯⨯=⨯⨯⨯⎪⎩,解得1,2r l ==.故答案为:1【点睛】本小题主要考查圆锥侧面展开图有关计算,属于基础题.28.【2020年高考江苏】如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2cm ,高为2cm ,内孔半轻为0.5cm ,则此六角螺帽毛坯的体积是▲cm.【答案】2π【解析】正六棱柱体积为2624⨯⨯⨯,圆柱体积为21()222ππ⋅=,所求几何体体积为2π.故答案为:2π-【点睛】本题考查正六棱柱体积、圆柱体积,考查基本分析求解能力,属基础题.29.【2020年新高考全国Ⅰ卷】已知直四棱柱ABCD –A 1B 1C 1D 1的棱长均为2,∠BAD =60°.以1D 为球心,为半径的球面与侧面BCC 1B 1的交线长为________.【答案】22π.【解析】如图:取11B C 的中点为E ,1BB 的中点为F ,1CC 的中点为G ,因为BAD ∠=60°,直四棱柱1111ABCD A B C D -的棱长均为2,所以△111D B C 为等边三角形,所以1D E =111D E B C ⊥,又四棱柱1111ABCD A B C D -为直四棱柱,所以1BB ⊥平面1111D C B A ,所以111BB B C ⊥,因为1111BB B C B = ,所以1D E ⊥侧面11B C CB ,设P 为侧面11B C CB 与球面的交线上的点,则1D E EP ⊥,,1D E =,所以||EP ===,所以侧面11B C CB 与球面的交线上的点到E ,因为||||EF EG ==11B C CB 与球面的交线是扇形EFG 的弧 FG ,因为114B EF C EG π∠=∠=,所以2FEG π∠=,所以根据弧长公式可得 22FGπ==.故答案为:22π.【点睛】本题考查了直棱柱的结构特征,考查了直线与平面垂直的判定,考查了立体几何中的轨迹问题,考查了扇形中的弧长公式,属于中档题.30.【2019年高考全国Ⅲ卷理数】学生到工厂劳动实践,利用3D 打印技术制作模型.如图,该模型为长方体1111ABCD A B C D -挖去四棱锥O —EFGH 后所得的几何体,其中O 为长方体的中心,E ,F ,G ,H 分别为所在棱的中点,16cm 4cm AB =BC =, AA =,3D 打印所用原料密度为0.9g/cm 3,不考虑打印损耗,制作该模型所需原料的质量为___________g.【答案】118.8【解析】由题意得,214642312cm 2EFGH S =⨯-⨯⨯⨯=四边形,∵四棱锥O −EFGH 的高为3cm ,∴3112312cm 3O EFGH V -=⨯⨯=.又长方体1111ABCD A B C D -的体积为32466144cm V =⨯⨯=,所以该模型体积为3214412132cm O EFGH V V V -=-=-=,其质量为0.9132118.8g ⨯=.【名师点睛】本题考查几何体的体积问题,理解题中信息联系几何体的体积和质量关系,从而利用公式求解.根据题意可知模型的体积为长方体体积与四棱锥体积之差进而求得模型的体积,再求出模型的质量即可.31.【2019年高考北京卷理数】某几何体是由一个正方体去掉一个四棱柱所得,其三视图如图所示.如果网格纸上小正方形的边长为1,那么该几何体的体积为__________.【答案】40【解析】如图所示,在棱长为4的正方体中,三视图对应的几何体为正方体去掉棱柱1111MPD A NQC B -之后余下的几何体,则几何体的体积()3142424402V =-⨯+⨯⨯=.【名师点睛】本题首先根据三视图,还原得到几何体,再根据题目给定的数据,计算几何体的体积.属于中等题.(1)求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系,利用相应体积公式求解;(2)若所给几何体的体积不能直接利用公式得出,则常用等积法、分割法、补形法等方法进行求解.32.【2019年高考北京卷理数】已知l ,m 是平面α外的两条不同直线.给出下列三个论断:①l ⊥m ;②m ∥α;③l ⊥α.以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:__________.【答案】如果l ⊥α,m ∥α,则l ⊥m .【解析】将所给论断,分别作为条件、结论,得到如下三个命题:(1)如果l ⊥α,m ∥α,则l ⊥m ,正确;(2)如果l ⊥α,l ⊥m ,则m ∥α,不正确,有可能m 在平面α内;(3)如果l ⊥m ,m ∥α,则l ⊥α,不正确,有可能l 与α斜交、l ∥α.故答案为:如果l ⊥α,m ∥α,则l ⊥m.【名师点睛】本题主要考查空间线面的位置关系、命题、逻辑推理能力及空间想象能力.将所给论断,分别作为条件、结论加以分析即可.33.【2019年高考天津卷理数】2的正方形,5若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为_____________.【答案】π4【解析】由题意,的正方形,借助勾股定理,2=.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,一个底面的圆心为四棱锥底面的中心,故圆柱的高为1,圆柱的底面半径为12,故圆柱的体积为21ππ124⎛⎫⨯⨯= ⎪⎝⎭.【名师点睛】根据棱锥的结构特点,确定所求的圆柱的高和底面半径.注意本题中圆柱的底面半径是棱锥底面对角线长度的一半、不是底边棱长的一半.34.【2019年高考江苏卷】如图,长方体1111ABCD A B C D -的体积是120,E 为1CC 的中点,则三棱锥E −BCD 的体积是▲.【答案】10【解析】因为长方体1111ABCD A B C D -的体积为120,所以1120AB BC CC ⋅⋅=,因为E 为1CC 的中点,所以112CE CC =,由长方体的性质知1CC ⊥底面ABCD ,所以CE 是三棱锥E BCD -的底面BCD 上的高,所以三棱锥E BCD -的体积1132V AB BC CE =⨯⋅⋅=111111201032212AB BC CC =⨯⋅⋅=⨯=.【名师点睛】本题蕴含“整体和局部”的对立统一规律.在几何体面积或体积的计算问题中,往往需要注意理清整体和局部的关系,灵活利用“割”与“补”的方法解题.由题意结合几何体的特征和所给几何体的性质可得三棱锥的体积.35.【2019年高考全国Ⅱ卷理数】中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有________个面,其棱长为_________.(本题第一空2分,第二空3分.)【答案】261【解析】由图可知第一层(包括上底面)与第三层(包括下底面)各有9个面,计18个面,第二层共有8个面,所以该半正多面体共有18826+=个面.如图,设该半正多面体的棱长为x ,则AB BE x ==,延长CB 与FE 的延长线交于点G ,延长BC 交正方体的棱于H ,由半正多面体对称性可知,BGE △为等腰直角三角形,22,21)122BG GE CH x GH x x x ∴===∴=⨯+=+=,1x ∴=1.。
高三数学文一轮复习专题突破训练立体几何 Word版含解析

山东省届高三数学文一轮复习专题突破训练
立体几何
一、选择、填空题
、(年山东高考)一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为
()()()()
、(年山东高考)已知等腰直角三角形的直角边的长为,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )
()()()()
、(年山东高考)一个六棱锥的体积为,其底面是边长为的正六边形,侧棱长都相等,则该六棱锥的侧面积为。
、(临沂市届高三月期中质量检测)某几何体的三视图如图,则此几何体的体积为
、(齐鲁名校协作体届高三上学期第二次调研联考)某几何体的三视图如图所示,则该几何体的表面积为
、(泰安市届高三二模)如图,四棱锥—的底面为正方形,上底面,则下列结论中不正确的是
.
.平面
.平面⊥平面
.平面
、(东营市、潍坊市届高三高三三模)如图,网格纸上小正方形的边长为,粗线画出的是某几何体的三视图,则该几何体的外接球的表面积为.
、(济宁市届高三三模)某几何体的三视图如图所示,则该几何体的体积为.。
2020高考数学刷题专题突破练5立体几何的综合问题文含解析2019050644

专题突破练(5) 立体几何的综合问题一、选择题1.已知直线a ⊂平面α,直线b ⊂平面β,则“a ∥b ”是“α∥β”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分又不必要条件 答案 D解析 “a ∥b ”不能得出“α∥β”,反之由“α∥β”也得不出“a ∥b ”.故选D . 2.如图,三棱柱ABC -A 1B 1C 1中,AA 1⊥平面ABC ,A 1A =AB =2,BC =1,AC =5,若规定正视方向垂直平面ACC 1A 1,则此三棱柱的侧视图的面积为( )A .455B .2 5C .4D .2 答案 A解析 在△ABC 中,AC 2=AB 2+BC 2=5,∴AB ⊥BC .作BD ⊥AC 于D ,则BD 为侧视图的宽,且BD =2×15=255,∴侧视图的面积为S =2×255=455.故选A .3.平行六面体ABCD -A 1B 1C 1D 1中,既与AB 共面也与CC 1共面的棱的条数为( ) A .3 B .4 C .5 D .6 答案 C解析 如图,既与AB 共面也与CC 1共面的棱有CD ,BC ,BB 1,AA 1,C 1D 1,共5条.故选C .4.在四边形ABCD 中,AB =AD =CD =1,BD =2,BD ⊥CD .将四边形ABCD 沿对角线BD 折成四面体A ′-BCD ,使平面A ′BD ⊥平面BCD ,则下列结论正确的是( )A .A ′C ⊥BDB .∠BA ′C =90°C .CA ′与平面A ′BD 所成的角为30° D .四面体A ′-BCD 的体积为13答案 B解析 ∵AB =AD =1,BD =2,∴AB ⊥AD .∴A ′B ⊥A ′D .∵平面A ′BD ⊥平面BCD ,CD ⊥BD ,∴CD ⊥平面A ′BD ,∴CD ⊥A ′B ,∴A ′B ⊥平面A ′CD ,∴A ′B ⊥A ′C ,即∠BA ′C=90°.故选B .5.(2018·河南豫东、豫北十校测试)鲁班锁是中国传统的智力玩具,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙,原为木质结构,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称.从外表上看,六根等长的正四棱柱体分成三组,经90度榫卯起来,若正四棱柱体的高为4,底面正方形的边长为1,则该鲁班锁的表面积为 ( )A .48B .60C .72D .84 答案 B解析 复杂的图形表面积可以用三视图投影的方法计算求得;如图所示:投影面积为4×2+1×2=10,共有6个投影面积,所以该几何体的表面积为10×6=60.故选B .6.如图所示,已知在多面体ABC-DEFG中,AB,AC,AD两两垂直,平面ABC∥平面DEFG,平面BEF∥平面ADGC,AB=AD=DG=2,AC=EF=1,则该多面体的体积为( )A.2 B.4 C.6 D.8答案 B解析如图所示,将多面体补成棱长为2的正方体,那么显然所求的多面体的体积即为该正方体体积的一半,于是所求几何体的体积为V=12×23=4.故选B.7.(2018·湖北黄冈中学二模)一个几何体的三视图如图所示,其中正视图是边长为2的等边三角形,俯视图是半圆(如图).现有一只蚂蚁从点A出发沿该几何体的侧面环绕一周回到A点,则蚂蚁所经过路程的最小值为( )A.π B.6+ 2C.6- 2 D.π+2答案 B解析由三视图可知,该几何体是半圆锥,其展开图如图所示,则依题意,点A,M的最短距离,即为线段AM.∵PA=PB=2,半圆锥的底面半圆的弧长为π,∴展开图中的∠BPM=πPB =π2,∵∠APB =π3,∴∠APM =5π6,∴在△APM 中,根据余弦定理有,MA 2=22+22-2×2×2cos 5π6=8+43=(6+2)2,∴MA =6+2,即蚂蚁所经过路程的最小值为6+2,故选B .8.已知圆锥的底面半径为R ,高为3R ,在它的所有内接圆柱中,表面积的最大值是( ) A .22πR 2 B .94πR 2C .83πR 2D .52πR 2 答案 B解析 如图所示,为组合体的轴截面,记BO 1的长度为x ,由相似三角形的比例关系,得PO 13R =x R,则PO 1=3x ,圆柱的高为3R -3x ,所以圆柱的表面积为S =2πx 2+2πx ·(3R -3x )=-4πx 2+6πRx ,则当x =34R 时,S 取最大值,S max =94πR 2.故选B .9.如图,在正方体ABCD -A 1B 1C 1D 1中,点E 为正方形ABCD 的两条对角线的交点,点F 是棱AB 的中点,则异面直线AC 1与EF 所成角的正切值为( )A .- 2B .-22C .22D . 2 答案 D解析 在正方体ABCD -A 1B 1C 1D 1中,依题意知,EF ∥AD ,所以异面直线AC 1与EF 所成角为∠C 1AD .连接C 1D ,因为AD ⊥平面C 1CDD 1,所以AD ⊥DC 1,设正方体的棱长为1,则tan ∠C 1AD =C 1D AD =21=2,所以异面直线AC 1与EF 所成角的正切值为2.故选D .10.(2018·河北唐山第一次摸底)在长方体ABCD -A 1B 1C 1D 1中,AB =BC =2AA 1,则异面直线A 1B 与B 1C 所成角的余弦值为( )A .105 B .15 C .55 D .155答案 B解析 在长方体ABCD -A 1B 1C 1D 1中,连接A 1D ,可得A 1D ∥B 1C ,所以异面直线A 1B 与B 1C 所成的角即为直线A 1B 与直线A 1D 所成的角,即∠DA 1B 为异面直线A 1B 与B 1C 所成的角,在长方体ABCD -A 1B 1C 1D 1中,设AB =BC =2AA 1=2,则A 1B =A 1D =5,BD =22,在△A 1BD 中,由余弦定理得cos ∠DA 1B =A 1B 2+A 1D 2-BD 22A 1B ·A 1D =5+5-82×5×5=15.故选B .11.在正方体ABCD -A 1B 1C 1D 1中,P 为正方形A 1B 1C 1D 1四边上的动点,O 为底面正方形ABCD 的中心,M ,N 分别为AB ,BC 边的中点,点Q 为平面ABCD 内一点,线段D 1Q 与OP 互相平分,则满足MQ →=λMN →的实数λ的值有( )A .0个B .1个C .2个D .3个 答案 C解析 本题可以转化为在MN 上找点Q 使OQ 綊PD 1,可知只有Q 点与M ,N 重合时满足条件.故选C .12.(2019·四川第一次诊断)如图,在Rt △ABC 中,∠ACB =90°,AC =1,BC =x (x >0),D 是斜边AB 的中点,将△BCD 沿直线CD 翻折,若在翻折过程中存在某个位置,使得CB ⊥AD ,则x 的取值范围是( )A .22,2 B .[3,23] C .(0,2) D .(0,3] 答案 D解析 由题意得,AD =CD =BD =x 2+12,BC =x ,取BC 中点E ,翻折前,在图1中,连接DE ,CD ,则DE =12AC =12,翻折后,在图2中,此时CB ⊥AD .∵BC ⊥DE ,BC ⊥AD ,∴BC ⊥平面ADE ,∴BC ⊥AE ,又E 为BC 中点,∴AB =AC =1,∴AE =1-14x 2,AD =x 2+12,在△ADE 中:①x 2+12+12>1-14x 2,②x 2+12<12+1-14x 2,③x >0;由①②③可得0<x <3.如图3,翻折后,当△B 1CD 与△ACD 在一个平面上,AD 与B 1C 交于M ,且AD ⊥B 1C ,AD =B 1D =CD =BD ,∠CBD =∠BCD =∠B 1CD ,又∠CBD +∠BCD +∠B 1CD =90°,∴∠CBD =∠BCD =∠B 1CD =30°,∴∠A =60°,BC =AC tan60°,此时x =1×3=3,综上,x 的取值范围为(0,3].故选D .二、填空题13.如图,已知球O 的面上有四点A ,B ,C ,D ,DA ⊥平面ABC ,AB ⊥BC ,DA =AB =BC =2,则球O 的体积等于________.答案 6π解析 如图,以DA ,AB ,BC 为棱长构造正方体,设正方体的外接球O 的半径为R ,则正方体的体对角线长即为球O 的直径,所以|CD |=(2)2+(2)2+(2)2=2R ,所以R =62,故球O 的体积V =4πR33=6π.14.(2018·湖南湘潭四模)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有仓,广三丈,袤四丈五尺,容粟一万斛,问高几何?”其意思为:“今有一个长方体(记为ABCD -A 1B 1C 1D 1)的粮仓,宽3丈(即AD =3丈),长4丈5尺,可装粟一万斛,问该粮仓的高是多少?”已知1斛粟的体积为2.7立方尺,一丈为10尺,则下列判断正确的是________.(填写所有正确结论的编号)①该粮仓的高是2丈;②异面直线AD 与BC 1所成角的正弦值为31313;③长方体ABCD -A 1B 1C 1D 1的外接球的表面积为133π4平方丈.答案 ①③解析 由题意,因为10000×2.7=30×45×AA 1,解得AA 1=20尺=2丈,故①正确;异面直线AD 与BC 1所成角为∠CBC 1,则sin ∠CBC 1=21313,故②错误;此长方体的长、宽、高分别为4.5丈、3丈、2丈,故其外接球的表面积为4π 4.52+32+2222=133π4平方丈,所以③正确.15.如图,用一个边长为2的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个巢,将半径为1的球体放入其中,则球心与巢底面的距离为__________.答案3+12解析 由题意知,折起后原正方形顶点间最远的距离为1,如图中的DC ;折起后原正方形顶点到底面的距离为12,如图中的BC .由图知球心与巢底面的距离OF =1-122+12=3+12. 16.(2018·珠海摸底)用一张16×10的长方形纸片,在四个角剪去四个边长为x 的正方形(如图),然后沿虚线折起,得到一个无盖的长方体纸盒,则这个纸盒的最大容积是________.答案 144解析 沿虚线折出纸盒后,该纸盒的长为16-2x ,宽为10-2x ,高为x ,则0<x <5,其容积为V =x (16-2x )·(10-2x )=4x 3-52x 2+160x ,所以V ′=12x 2-104x +160=4(x -2)(3x -20),令V ′=0,得x =2或x =203>5(舍去),当x ∈(0,2)时,V ′>0,即在(0,2)上,V (x )是增函数;当x ∈(2,5),V ′<0,即在(2,5)上,V (x )是减函数,所以当x =2时,V (x )有最大值为144.三、解答题17.(2018·广东华南师大附中测试二)如图,AB 为圆O 的直径,点E ,F 在圆O 上,AB ∥EF ,矩形ABCD 所在平面和圆O 所在的平面互相垂直,已知AB =2,EF =1.(1)求证:平面DAF ⊥平面CBF ;(2)设几何体F -ABCD ,F -BCE 的体积分别为V 1,V 2,求V 1∶V 2的值. 解 (1)证明:如图,在矩形ABCD 中,CB ⊥AB ,∵平面ABCD ⊥平面ABEF ,平面ABCD ∩平面ABEF =AB , ∴CB ⊥平面ABEF , ∵AF ⊂平面ABEF , ∴AF ⊥CB ,又∵AB 为圆O 的直径, ∴AF ⊥BF ,∵CB ∩BF =B ,CB ,BF ⊂平面CBF , ∴AF ⊥平面CBF ,∵AF ⊂平面DAF ,∴平面DAF ⊥平面CBF .(2)几何体F -ABCD 是四棱锥,F -BCE 是三棱锥,过点F 作FH ⊥AB ,交AB 于H . ∵平面ABCD ⊥平面ABEF ,∴FH ⊥平面ABCD . 则V 1=13AB ·BC ·FH ,V 2=13×12EF ·FH ·BC ,∴V 1V 2=2AB EF =2×21=4.18.(2018·厦门开学考试)如图,直三棱柱ABC -A ′B ′C ′中,AC =BC =5,AA ′=AB =6,D ,E 分别为AB 和BB ′上的点,且AD DB =BEEB ′.(1)当D 为AB 中点时,求证:A ′B ⊥CE ;(2)当D 在AB 上运动时,求三棱锥A ′-CDE 体积的最小值. 解 (1)证明:∵三棱柱ABC -A ′B ′C ′为直三棱柱,AA ′=AB , ∴平行四边形ABB ′A ′为正方形, ∵D 为AB 的中点,故E 为B ′B 的中点, ∴DE ⊥A ′B .∵AC =BC ,D 为AB 的中点,∴CD ⊥AB . ∵三棱柱ABC -A ′B ′C ′为直三棱柱, ∴CD ⊥平面ABB ′A ′,又A ′B ⊂平面ABB ′A ′,∴CD ⊥A ′B . 又CD ∩DE =D ,∴A ′B ⊥平面CDE , ∵CE ⊂平面CDE ,∴A ′B ⊥CE . (2)设BE =x ,则AD =x ,DB =6-x ,B ′E =6-x .由已知可得点C 到平面A ′DE 的距离等于△ABC 的边AB 上的高h =AC 2-AB22=4,∴V 三棱锥A ′-CDE =V 三棱锥C -A ′DE=13(S 正方形ABB ′A ′-S △AA ′D -S △DBE -S △A ′B ′E )·h =1336-3x -12(6-x )x -3(6-x )·h =23(x 2-6x +36) =23[(x -3)2+27], ∴当x =3,即D 为AB 的中点时,三棱锥A ′-CDE 的体积有最小值18.19.(2018·厦门质检一)如图,平面ACEF ⊥平面ABCD ,四边形ABCD 是菱形,∠ABC =60°,AF ∥CE ,AF ⊥AC ,AB =AF =2,CE =1.(1)求四棱锥B -ACEF 的体积;(2)在BF 上有一点P ,使得AP ∥DE ,求BP PF的值.解 (1)∵四边形ABCD 是菱形,∴BD ⊥AC , 又平面ACEF ⊥平面ABCD .平面ACEF ∩平面ABCD =AC ,BD ⊂平面ABCD , ∴BD ⊥平面ACEF . 在△ABC 中,∠ABC =60°,AB =AC =2,设BD ∩AC =O ,则可得AC =2,BO =3, 在梯形ACEF 中,AF ∥CE ,AF ⊥AC ,AC =AF =2,CE =1,∴梯形ACEF 的面积S =12×(1+2)×2=3, ∴四棱锥B -ACEF 的体积为V =13·S ·BO =13×3×3=3.(2)在平面ABF 内作BM ∥AF ,且BM =1,连接AM 交BF 于P ,则点P 满足AP ∥DE ,证明如下:∵AF ∥CE ,CE =1,∴BM ∥CE ,且BM =CE ,∴四边形BMEC 是平行四边形,∴BC ∥ME ,BC =ME ,又在菱形ABCD 中,BC ∥AD ,BC =AD ,∴ME ∥AD ,ME =AD ,∴四边形ADEM 是平行四边形,∴AM ∥DE ,即AP ∥DE ,∵BM ∥AF ,∴△BPM ∽△FPA ,又BM =1,∴BP FP =BM FA =12.20.(2018·河南考前适应测试)如图所示,在四棱锥P -ABCD 中,底面ABCD 为直角梯形,AB ∥CD ,∠BAD =90°,DC =DA =2AB =25,点E 为AD 的中点,BD ∩CE =H ,PH ⊥平面ABCD ,且PH =4.(1)求证:PC ⊥BD ;(2)线段PC 上是否存在一点F ,使三棱锥P -BFD 的体积为52?若存在,请找出点F 的位置;若不存在,请说明理由.解 (1)证明:∵AB ∥CD ,∠BAD =90°,∴∠EDC =∠BAD =90°.∵DC =DA =2AB ,E 为AD 的中点,∴AB =ED .∴△BAD≌△EDC.∴∠DBA=∠DEH.∵∠DBA+∠ADB=90°,∴∠DEH+∠ADB=90°.∴BD⊥EC.又∵PH⊥平面ABCD,BD⊂平面ABCD,∴BD⊥PH.又∵PH∩EC=H,且PH,EC⊂平面PEC,∴BD⊥平面PEC.又∵PC⊂平面PEC,∴PC⊥BD.(2)假设线段PC上存在一点F满足题意,由(1)可知,△DHE∽△DAB,∴DHDA=EHBA=DEDB,∵BD=EC=(25)2+(5)2=5,AB=DE=5,∴EH=1,HC=4,DH=2,HB=3.∵PH,EC,BD两两垂直,且PH=HC=4,∴∠HPC=45°.∵BD⊥平面PEC,∴V三棱锥P-BFD=V三棱锥B-PHF+V三棱锥D-PHF=13S△PHF·BD=13×12×PH·PF·sin45°×5=523PF=52,∴PF=3.∵PC=42>3,∴线段PC上存在满足条件的点F,点F的位置满足PF=3.。
2023高考精品系列之数学(文)专题立体几何解答题(解析版)

2023高考精品系列之数学(文)专题立体几何解答题(解析版)专题11立体几何解答题考纲解读三年高考分析1、对于线面关系中的存在性问题,首先假设存在,垂直关系的证明和平行关系的证明是考查的重然后在该假设条件下,利用线面关系的相关定理、点,解题时常用到平行判定定理、垂直判定定理、性质进行推理论证,寻找假设满足的条件,若满垂直性质定理、平行性质定理,考查学生的数学足则肯定假设,若得出矛盾的结论则否定假设.逻辑推理能力、数学运算能力、直观想象能力,对于探索性问题用向量法比较容易入手.一般先假设存在,设出空间点的坐标,转化为代数方程是否有解的问题,若有解且满足题意则存在,若有解但不满足题意或无解则不存在.2、空间几何体体积问题的常见类型及解题策略(1)若所给定的几何体是可直接用公式求解的柱体、锥体或台体,则可直接利用公式进行求解.(2)若所给定的几何体的体积不能直接利用公式得出,则常用转换法、分割法、补形法等方法进行求解.题型以选择填空题和解答题为主,中等难度.1、直线、平面平行的判定及其性质是高考中的重点考查内容,涉及线线平行、线面平行、面面平行的判定及其应用等内容.题型主要以解答题的形式出现,解题要求有较强的推理论证能力,广泛应用转化与化归的思想.2、直线、平面垂直的判定及其性质是高考中的重点考查内容,涉及线线垂直、线面垂直、面面垂直的判定及其应用等内容.题型主要以解答题的形式出现,解题要求有较强的推理论证能力,(3)若以三视图的形式给出几何体,则应先根据三视广泛应用转化与化归的思想.图得到几何体的直观图,然后根据条件求解.3、空间几何体与球接、切问题的求解方法(1)求解球与棱柱、棱锥的接、切问题时,一般过球心及接、切点作截面,把空间问题转化为平面图形与圆的接、切问题,再利用平面几何知识寻找几何中元素间的关系求解.(2)若球面上四点P,A,B,C构成的三条线段PA,PB,PC两两互相垂直,且PA=a,PB=b,PC=c,一般把有关元素“补形”成为一个球内接长方体,利用4R2=a2+b2+c2求解.1.【2023年天津文科17】如图,在四棱锥P﹣ABCD中,底面ABCD为平行四边形,△PCD为等边三角形,平面PAC⊥平面PCD,PA⊥CD,CD=2,AD=3.(Ⅰ)设G,H分别为PB,AC的中点,求证:GH∥平面PAD;(Ⅱ)求证:PA⊥平面PCD;(Ⅲ)求直线AD与平面PAC所成角的正弦值.【解答】证明:(Ⅰ)连结BD,由题意得AC∩BD=H,BH=DH,又由BG=PG,得GH∥PD,∵G H?平面PAD,PD?平面PAD,∴GH∥平面PAD.(Ⅱ)取棱PC中点N,连结DN,依题意得DN⊥PC又∵平面PAC⊥平面PCD,平面PAC∩平面PCD=PC,∴DN⊥平面PAC又PA?平面PAC,∴DN⊥PA,又PA⊥CD,CD∩DN=D,∴PA⊥平面PCD.解:(Ⅲ)连结AN,由(Ⅱ)中DN⊥平面PAC,知∠DAN是直线AD与平面PAC所成角∵△PCD是等边三角形,CD=2,且N为PC中点,∴DN,又DN⊥AN.在Rt△AND中,sin∠DAN∴直线AD与平面PAC所成角的正弦值为.【解答】解:(1)证明:由已知可得AD∥BE,CG∥BE,即有AD∥CG,则AD,CG确定一个平面,从而A,C,G,D四点共面;由四边形ABED为矩形,可得AB⊥BE,由△ABC为直角三角形,可得AB⊥BC,又BC∩BE=E,可得AB⊥平面BCGEAB?平面ABC,可得平面ABC⊥平面BCGE;(2)连接BG,AG由AB⊥平面BCGE,可得AB⊥BG在△BCG中,BC=CG=2,∠BCG=120°,可得BG=2BCsin60°=2可得AG在△ACG中,AC可得cos∠ACG,CG=2,AG,即有s in∠ACG则平行四边形ACGD的面积为24.3.【2023年新课标2文科17】如图,长方体ABCD﹣A1B1C1D1的底面ABCD是正方形,点E在棱AA1上BE⊥EC1.(1)证明:BE⊥平面EB1C1;(2)若AE=A1E,AB=3,求四棱锥E﹣BB1C1C的体积.【解答】解:(1)证明:由长方体ABCD﹣A1B1C1D1,可知B1C1⊥平面ABB1A1,BE?平面ABB1A1∴B1C1⊥BE∵BE⊥EC1,B1C1∩EC1=C1,∴BE⊥平面EB1C1;(2)由(1)知∠BEB1=90°,由题设可知RtRt∴∠AEB=∠A1EB1=45°,∴AE=AB=3,AA1=2AE=6∵在长方体ABCD﹣A1B1C1D1中,AA1∥平面BB1C1C,E∈AA1,AB⊥平面BB1C1C,∴E到平面BB1C1C的距离d=AB=3,∴四棱锥E﹣BB1C1C 的体积V3×6×3=18.4.【2023年新课标1文科19】如图,直四棱柱ABCD﹣A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.(1)证明:MN∥平面C1DE;(2)求点C到平面C1DE的距离.【解答】解法一:。
高三数学一轮复习立体几何知识点突破训练含答案解析

第八章⎪⎪⎪立 体 几 何 第一节空间几何体的三视图、直观图、表面积与体积突破点(一) 空间几何体的三视图和直观图基础联通 抓主干知识的“源”与“流” 1.空间几何体的结构特征 (1)多面体的结构特征 多面体 结构特征棱柱 有两个面平行,其余各面都是四边形且每相邻两个面的交线都平行且相等棱锥 有一个面是多边形,而其余各面都是有一个公共顶点的三角形 棱台棱锥被平行于底面的平面所截,截面和底面之间的部分叫做棱台(2)旋转体的形成 几何体 旋转图形 旋转轴圆柱 矩形 矩形任一边所在的直线 圆锥 直角三角形 一条直角边所在的直线圆台 直角梯形或等腰梯形直角腰所在的直线或等腰梯形上下底中点的连线球半圆或圆直径所在的直线2.空间几何体的三视图 (1)三视图的名称几何体的三视图包括:正视图、侧视图、俯视图. (2)三视图的画法①在画三视图时,能看见的轮廓线和棱用实线表示,重叠的线只画一条,不能看见的轮廓线和棱用虚线表示.②三视图的正视图、侧视图、俯视图分别是从几何体的正前方、正左方、正上方观察几何体的正投影图.3.空间几何体的直观图空间几何体的直观图常用斜二测画法来画,其规则是:(1)原图形中x 轴、y 轴、z 轴两两垂直,直观图中,x ′轴,y ′轴的夹角为45°或135°,本节主要包括3个知识点:1.空间几何体的三视图和直观图;2.空间几何体的表面积与体积;3.与球有关的切、接应用问题.z′轴与x′轴和y′轴所在平面垂直.(2)原图形中平行于坐标轴的线段,直观图中仍分别平行于坐标轴;平行于x轴和z轴的线段在直观图中保持原长度不变;平行于y轴的线段在直观图中长度为原来的一半.考点贯通抓高考命题的“形”与“神”空间几何体的结构特征[例1](1)用任意一个平面截一个几何体,各个截面都是圆面,则这个几何体一定是()A.圆柱B.圆锥C.球体D.圆柱、圆锥、球体的组合体(2)下列说法正确的是()A.有两个平面互相平行,其余各面都是平行四边形的多面体是棱柱B.四棱锥的四个侧面都可以是直角三角形C.有两个平面互相平行,其余各面都是梯形的多面体是棱台D.棱台的各侧棱延长后不一定交于一点[解析](1)截面是任意的且都是圆面,则该几何体为球体.(2)A错,如图(1);B正确,如图(2),其中底面ABCD是矩形,PD⊥平面ABCD,可证明∠PAB,∠PCB,∠PDA,∠PDC都是直角,这样四个侧面都是直角三角形;C错,如图(3);D错,由棱台的定义知,其侧棱的延长线必相交于同一点.[答案](1)C(2)B[方法技巧]解决与空间几何体结构特征有关问题的三个技巧(1)把握几何体的结构特征,要多观察实物,提高空间想象能力;(2)紧扣结构特征是判断的关键,熟悉空间几何体的结构特征,依据条件构建几何模型,如例1(2)中的A,C两项易判断失误;(3)通过反例对结构特征进行辨析.空间几何体的三视图1.画三视图的规则长对正、高平齐、宽相等,即俯视图与正视图一样长;正视图与侧视图一样高;侧视图与俯视图一样宽.2.三视图的排列顺序先画正视图,俯视图放在正视图的下方,侧视图放在正视图的右方.[例2](1)(2017·贵州七校联考)如图所示,四面体ABCD的四个顶点是长方体的四个顶点(长方体是虚拟图形,起辅助作用),则四面体ABCD的三视图是(用①②③④⑤⑥代表图形,按正视图,侧视图,俯视图的顺序排列)()A.①②⑥B.①②③C.④⑤⑥D.③④⑤(2)(2016·天津高考)将一个长方体沿相邻三个面的对角线截去一个棱锥,得到的几何体的正视图与俯视图如图所示,则该几何体的侧(左)视图为()[解析](1)正视图应该是边长为3和4的矩形,其对角线左下到右上是实线,左上到右下是虚线,因此正视图是①;侧视图应该是边长为5和4的矩形,其对角线左上到右下是实线,左下到右上是虚线,因此侧视图是②;俯视图应该是边长为3和5的矩形,其对角线左上到右下是实线,左下到右上是虚线,因此俯视图是③.(2)先根据正视图和俯视图还原出几何体,再作其侧(左)视图.由几何体的正视图和俯视图可知该几何体为图①,故其侧(左)视图为图②.[答案](1)B(2)B[方法技巧]三视图问题的常见类型及解题策略(1)由几何体的直观图求三视图注意正视图、侧视图和俯视图的观察方向;注意能看到的部分用实线表示,不能看到的部分用虚线表示.(2)由几何体的部分视图画出剩余的视图解决此类问题,可先根据已知的一部分视图,还原、推测直观图的可能形式,然后再找其剩下部分视图的可能形式.当然作为选择题,也可将选项逐项代入检验.(3)由几何体的三视图还原几何体的形状要熟悉柱、锥、台、球的三视图,明确三视图的形成原理,结合空间想象将三视图还原为实物图.空间几何体的直观图直观图与原图形面积的关系按照斜二测画法得到的平面图形的直观图与原图形面积的关系:(1)S直观图=24S原图形.(2)S原图形=22S直观图.[例3]用斜二测画法画一个水平放置的平面图形的直观图为如图所示的一个正方形,则原来的图形是()[解析]由直观图可知,在直观图中多边形为正方形,对角线长为2,所以原图形为平行四边形,位于y轴上的对角线长为2 2.[答案] A能力练通抓应用体验的“得”与“失”1.[考点一]如果四棱锥的四条侧棱都相等,就称它为“等腰四棱锥”,四条侧棱称为它的腰,以下四个命题中,假命题是()A.等腰四棱锥的腰与底面所成的角都相等B.等腰四棱锥的侧面与底面所成的二面角都相等或互补C.等腰四棱锥的底面四边形必存在外接圆D.等腰四棱锥的各顶点必在同一球面上解析:选B因为“等腰四棱锥”的四条侧棱都相等,所以它的顶点在底面的射影到底面的四个顶点的距离相等,故A,C是真命题;且在它的高上必能找到一点到各个顶点的距离相等,故D是真命题;B是假命题,如底面是一个等腰梯形时结论就不成立.2.[考点二]一几何体的直观图如图,下列给出的四个俯视图中正确的是()解析:选B由直观图可知,该几何体由一个长方体和一个截角三棱柱组成.从上往下看,外层轮廓线是一个矩形,矩形内部是一条水平线段连接两个三角形.3.[考点二]已知三棱锥的俯视图与侧视图如图所示,俯视图是边长为2的正三角形,侧视图是有一条直角边为2的直角三角形,则该三棱锥的正视图可能为()解析:选C当正视图为等腰三角形时,则高应为2,且应为虚线,排除A,D;当正视图是直角三角形时,由条件得一个直观图如图所示,中间的线是看不见的线PA形成的投影,应为虚线,故答案为C.4.[考点三]用斜二测画法画出的某平面图形的直观图如图,边AB平行于y轴,BC,AD平行于x轴.已知四边形ABCD的面积为2 2 cm2,则原平面图形的面积为()A.4 cm2B.4 2 cm2C.8 cm2D.8 2 cm2解析:选C依题意可知∠BAD=45°,则原平面图形为直角梯形,上下底面的长与BC ,AD 相等,高为梯形ABCD 的高的22倍,所以原平面图形的面积为8 cm 2.5.[考点二](2017·南昌模拟)如图,在正四棱柱ABCD -A 1B 1C 1D 1中,点P 是平面A 1B 1C 1D 1内一点,则三棱锥P -BCD 的正视图与侧视图的面积之比为( )A .1∶1B .2∶1C .2∶3D .3∶2解析:选A 根据题意,三棱锥P -BCD 的正视图是三角形,且底边为正四棱柱的底面边长、高为正四棱柱的高;侧视图是三角形,且底边为正四棱柱的底面边长、高为正四棱柱的高.故三棱锥P -BCD 的正视图与侧视图的面积之比为1∶1.突破点(二) 空间几何体的表面积与体积基础联通 抓主干知识的“源”与“流” 1.圆柱、圆锥、圆台的侧面展开图及侧面积公式圆柱圆锥圆台侧面展开图侧面积公式S 圆柱侧=2πrlS 圆锥侧=πrlS 圆台侧=π(r +r ′)l圆柱、圆锥、圆台侧面积间的关系:S 圆柱侧=2πrl ――→r ′=rS 圆台侧=π(r +r ′)l ――→r ′=0S 圆锥侧=πrl . 2.空间几何体的表面积与体积公式名称 几何体表面积 体积柱体 (棱柱和圆柱)S 表面积=S 侧+2S 底V =Sh 锥体 (棱锥和圆锥)S 表面积=S 侧+S 底V =13Sh台体 (棱台和圆台)S 表面积=S 侧+S 上+S 下V =13(S 上+S 下+S 上S 下)h球S =4πR 2V =43πR 3考点贯通 抓高考命题的“形”与“神”空间几何体的表面积[例1] (1)(2017·安徽江南十校联考)某几何体的三视图如图所示,其中侧视图的下半部分曲线为半圆弧,则该几何体的表面积为( )A .4π+16+4 3B .5π+16+4 3C .4π+16+2 3D .5π+16+2 3(2)一个四面体的三视图如图所示,则该四面体的表面积是( )A .1+ 3B .2+ 3C .1+2 2D .2 2[解析] (1)由三视图可知该几何体是一个正三棱柱和一个半圆柱的组合体,三棱柱的两个侧面面积之和为2×4×2=16,两个底面面积之和为2×12×2×3=23;半圆柱的侧面积为π×4=4π,两个底面面积之和为2×12×π×12=π,所以几何体的表面积为5π+16+23,故选D.(2)根据三视图还原几何体如图所示,其中侧面ABD ⊥底面BCD ,另两个侧面ABC ,ACD 为等边三角形,则有S 表面积=2×12×2×1+2×34×(2)2=2+3.[答案] (1)D (2)B[方法技巧]求空间几何体表面积的常见类型及思路(1)求多面体的表面积,只需将它们沿着棱“剪开”展成平面图形,利用求平面图形面积的方法求多面体的表面积.(2)求旋转体的表面积,可以从旋转体的形成过程及其几何特征入手,将其展开后求表面积,但要搞清它们的底面半径、母线长与对应侧面展开图中的边长关系.(3)求不规则几何体的表面积时,通常将所给几何体分割成基本的柱体、锥体、台体,先求出这些基本的柱体、锥体、台体的表面积,再通过求和或作差,求出所给几何体的表面积.空间几何体的体积柱体、锥体、台体体积间的关系[例2] (1)(2016·北京高考)某三棱锥的三视图如图所示,则该三棱锥的体积为( )A.16B.13C.12D .1 (2)某几何体的三视图如图所示,则该几何体的体积为( )A.13+2π B.13π6 C.7π3D.5π2[解析] (1)通过三视图可还原几何体为如图所示的三棱锥P -ABC ,通过侧视图得高h =1,通过俯视图得底面积S =12×1×1=12,所以体积V =13Sh =13×12×1=16. (2)由三视图可知,该几何体是一个圆柱和半个圆锥组合而成的几何体,其体积为π×12×2+12×13π×12×1=13π6.[答案] (1)A (2)B [方法技巧]求空间几何体体积的常见类型及思路(1)若所给定的几何体是柱体、锥体或台体等规则几何体,则可直接利用公式进行求解.其中,等积转换法多用来求三棱锥的体积.(2)若所给定的几何体是不规则几何体,则将不规则的几何体通过分割或补形转化为规则几何体,再利用公式求解.(3)若以三视图的形式给出几何体,则应先根据三视图得到几何体的直观图,然后根据条件求解.能力练通 抓应用体验的“得”与“失”1.[考点二](2016·山东高考)一个由半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为( )A.13+23πB.13+23πC.13+26π D .1+26π 解析:选C 由三视图知,四棱锥是底面边长为1,高为1的正四棱锥,结合三视图可得半球半径为22,从而该几何体的体积为13×12×1+12×4π3×⎝⎛⎭⎫223=13+26π.故选C.2.[考点二]已知一个几何体的三视图如图所示,则该几何体的体积为( )A.5π3 cm 3 B .2π cm 3 C.7π3cm 3 D .3π cm 3解析:选C 该几何体为一个圆柱挖去半个球得到的几何体,其体积V =π×12×3-12×4π×133=7π3(cm 3).3.[考点一]某几何体的三视图如图所示,则它的表面积为( )A .125+20B .242+20C .44D .12 5解析:选A 由三视图得,这是一个正四棱台,且上、下底面的边长分别为2,4,则侧面梯形的高h = 22+⎝⎛⎭⎫4-222=5,所以该正四棱台的表面积S =(2+4)×52×4+22+42=125+20.4.[考点一]某几何体的三视图如图所示,则该几何体的表面积等于( )A .8+2 2B .11+2 2C .14+2 2D .15解析:选B 由三视图知,该几何体是一个直四棱柱,上、下底面为直角梯形,如图所示.直角梯形斜腰长为12+12=2,所以底面周长为4+2,侧面积为2×(4+2)=8+22,两底面的面积和为2×12×1×(1+2)=3,所以该几何体的表面积为8+22+3=11+2 2.5.[考点二]中国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器——商鞅铜方升,其三视图如图所示(单位:寸):若π取3,其体积为12.6(立方寸),则图中的x 的值为________.解析:由三视图知,商鞅铜方升由一圆柱和一长方体组合而成,由题意得:(5.4-x )×3×1+π·⎝⎛⎭⎫122x =12.6,解得x =1.6.答案:1.6突破点(三) 与球有关的切、接应用问题1.球的表面积和体积是每年高考的热点,且多与三视图、多面体等综合命题,常以选择题、填空题的形式出现.解决此类问题时,一是要善于把空间问题平面化,把平面问题转化到直角三角形中处理;二是要将变化的模型转化到固定的长方体或正方体中.2.与球有关的组合体问题主要有两种,一种是内切问题,一种是外接问题.解题时要认真分析图形,明确切点和接点的位置,确定有关“元素”间的数量关系,并作出合适的截面图.考点贯通 抓高考命题的“形”与“神”多面体的内切球问题[例1] 若一个正四面体的表面积为S 1,其内切球的表面积为S 2,则S 1S 2=________.[解析] 设正四面体棱长为a , 则正四面体表面积为S 1=4×34·a 2=3a 2,其内切球半径为正四面体高的14, 即r =14×63a =612a ,因此内切球表面积为S 2=4πr 2=πa 26, 则S 1S 2=3a 2π6a 2=63π. [答案] 63π[方法技巧]处理与球有关内切问题的策略解答此类问题时首先要找准切点,通过作截面来解决.如果内切的是多面体,则作截面时主要抓住多面体过球心的对角面来作.多面体的外接球问题处理与球有关外接问题的策略把一个多面体的几个顶点放在球面上即为球的外接问题.解决这类问题的关键是抓住外接的特点,即球心到多面体的顶点的距离等于球的半径.[例2] (1)(2017·抚顺模拟)已知直三棱柱ABC -A 1B 1C 1的6个顶点都在球O 的球面上,若AB =3,AC =4,AB ⊥AC ,AA 1=12,则球O 的半径为( )A.3172 B .210 C.132D .310(2)正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为( )A.81π4 B .16π C .9πD.27π4(3)一个正方体削去一个角所得到的几何体的三视图如图所示(图中三个四边形都是边长为2的正方形),则该几何体外接球的体积为________.[解析] (1)如图所示,由球心作平面ABC 的垂线,则垂足为BC 的中点M .又AM =12BC =52,OM =12AA 1=6,所以球O 的半径R =OA =⎝⎛⎭⎫522+62=132.(2)如图所示,设球半径为R ,底面中心为O ′且球心为O , ∵正四棱锥P -ABCD 中AB =2, ∴AO ′= 2. ∵PO ′=4,∴在Rt △AOO ′中,AO 2=AO ′2+OO ′2, ∴R 2=(2)2+(4-R )2, 解得R =94,∴该球的表面积为4πR 2=4π×⎝⎛⎭⎫942=81π4.(3)依题意可知,新的几何体的外接球也就是原正方体的外接球,球的直径就是正方体的体对角线,∴2R =23(R 为球的半径),∴R =3, ∴球的体积V =43πR 3=43π.[答案] (1)C (2)A (3)43π [方法技巧]与球有关外接问题的解题规律(1)直棱柱外接球的球心到直棱柱底面的距离恰为棱柱高的12.(2)正方体外接球的直径为正方体的体对角线的长.此结论也适合长方体,或由同一顶点出发的两两互相垂直的三条棱构成的三棱柱或三棱锥.(3)求多面体外接球半径的关键是找到由球的半径构成的三角形,解三角形即可.能力练通 抓应用体验的“得”与“失”1.[考点一]一块石材表示的几何体的三视图如图所示,将该石材切削、打磨、加工成球,则能得到的最大球的半径等于( )A .1B .2C .3D .4解析:选B 该几何体为直三棱柱,底面是边长分别为6,8,10的直角三角形,侧棱长为12,故能得到的最大球的半径等于底面直角三角形内切圆的半径,其半径为r =2Sa +b +c =2×12×6×86+8+10=2,故选B.2.[考点二]如图是某几何体的三视图,则该几何体的外接球的表面积为( )A .200πB .150πC .100πD .50π解析:选D 由三视图知,该几何体可以由一个长方体截去4个角后得到,此长方体的长、宽、高分别为5,4,3,所以外接球半径R 满足2R =42+32+52=52,所以外接球的表面积为S =4πR 2=4π×⎝⎛⎭⎫5222=50π,故选D. 3.[考点二](2016·太原模拟)如图,平面四边形ABCD 中,AB =AD =CD =1,BD =2,BD ⊥CD ,将其沿对角线BD 折成四面体A ′-BCD ,使平面A ′BD ⊥平面BCD ,若四面体A ′-BCD 的顶点在同一个球面上,则该球的表面积为( )A .3π B.32π C .4π D.34π 解析:选A 由图示可得BD =A ′C =2,BC =3,△DBC 与△A ′BC 都是以BC 为斜边的直角三角形,由此可得BC 中点到四个点A ′,B ,C ,D 的距离相等,即该三棱锥的外接球的直径为3,所以该外接球的表面积S =4π×⎝⎛⎭⎫322=3π. 4.[考点二]设一个球的表面积为S 1,它的内接正方体的表面积为S 2,则S 1S 2的值等于( )A.2πB.6πC.π6D.π2解析:选D 设球的半径为R ,其内接正方体的棱长为a ,则易知R 2=34a 2,即a =233R ,则S 1S 2=4πR 26×⎝⎛⎭⎫233R 2=π2.[全国卷5年真题集中演练——明规律] 1.(2016·全国甲卷)如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )A .20πB .24πC .28πD .32π解析:选C 由三视图知该几何体是圆锥与圆柱的组合体,设圆柱底面圆半径为r ,周长为c ,圆锥母线长为l ,圆柱高为h .由图得r =2,c =2πr =4π,h =4,由勾股定理得,l =22+(23)2=4,S 表=πr 2+ch +12cl =4π+16π+8π=28π.2.(2016·全国丙卷)在封闭的直三棱柱ABC -A 1B 1C 1内有一个体积为V 的球.若AB ⊥BC ,AB =6,BC =8,AA 1=3,则V 的最大值是( )A .4πB.9π2C .6πD.32π3解析:选B 设球的半径为R ,∵△ABC 的内切圆半径为6+8-102=2,∴R ≤2.又2R ≤3,∴R ≤32,∴V max =43×π×⎝⎛⎭⎫323=9π2.故选B. 3.(2015·新课标全国卷Ⅱ)一个正方体被一个平面截去一部分后,剩余部分的三视图如下图,则截去部分体积与剩余部分体积的比值为()A.18 B.17C.16D.15解析:选D 由已知三视图知该几何体是由一个正方体截去了一个“大角”后剩余的部分,如图所示,截去部分是一个三棱锥.设正方体的棱长为1,则三棱锥的体积为V 1=13×12×1×1×1=16,剩余部分的体积V 2=13-16=56.所以V 1V 2=1656=15,故选D. 4.(2015·新课标全国卷Ⅱ)已知A ,B 是球O 的球面上两点,∠AOB =90°,C 为该球面上的动点.若三棱锥O -ABC 体积的最大值为36,则球O 的表面积为( )A .36πB .64πC .144πD .256π解析:选C 如图,设球的半径为R ,∵∠AOB =90°,∴S △AOB =12R 2.∵V O -ABC =V C -AOB ,而△AOB 面积为定值,∴当点C 到平面AOB 的距离最大时,V O -ABC 最大,∴当C 为与球的大圆面AOB 垂直的直径的端点时,体积V O -ABC 最大,为13×12R 2×R =36,∴R =6,∴球O 的表面积为4πR 2=4π×62=144π.故选C.5.(2015·新课标全国卷Ⅰ)圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r =( )A .1B .2C .4D .8解析:选B 如图,该几何体是一个半球与一个半圆柱的组合体,球的半径为r ,圆柱的底面半径为r ,高为2r ,则表面积S =12×4πr 2+πr 2+4r 2+πr ·2r =(5π+4)r 2.又S =16+20π,∴(5π+4)r 2=16+20π,∴r 2=4,r =2,故选B.6.(2015·新课标全国卷Ⅰ)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( )A .14斛B .22斛C .36斛D .66斛解析:选B 设米堆的底面半径为r 尺,则π2r =8,所以r =16π,所以米堆的体积为V=14×13π·r 2·5=π12×⎝⎛⎭⎫16π2×5≈3209(立方尺).故堆放的米约有3209÷1.62≈22(斛).故选B. 7.(2014·新课标全国卷Ⅱ)如图,网格纸上正方形小格的边长为1(表示1 cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3 cm ,高为6 cm 的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )A.1727B.59C.1027D.13解析:选C 原毛坯的体积V =(π×32)×6=54π(cm 3),由三视图可知该零件为两个圆柱的组合体,其体积V ′=V 1+V 2=(π×22)×4+(π×32)×2=34π(cm 3),故所求比值为1-V ′V =1027.8.(2013·新课标全国卷Ⅰ)某几何体的三视图如图所示,则该几何体的体积为( )A .16+8πB .8+8πC .16+16πD .8+16π解析:选A根据三视图可以判断该几何体由上、下两部分组成,其中上面部分为长方体,下面部分为半个圆柱,所以组合体的体积为2×2×4+12×22×π×4=16+8π,故选A.9.(2012·新课标全国卷)已知三棱锥S-ABC的所有顶点都在球O的球面上,△ABC是边长为1的正三角形,SC为球O的直径,且SC=2,则此棱锥的体积为()A.26 B.36 C.23 D.22解析:选A由于三棱锥S-ABC与三棱锥O-ABC底面都是△ABC,O是SC的中点,因此三棱锥S-ABC的高是三棱锥O-ABC高的2倍,所以三棱锥S-ABC的体积也是三棱锥O-ABC体积的2倍.在三棱锥O-ABC中,其棱长都是1,如图所示,S△ABC=34×AB2=34,高OD=12-⎝⎛⎭⎫332=63,所以V S-ABC=2V O-ABC=2×13×34×63=26.[课时达标检测] 重点保分课时——一练小题夯双基,二练题点过高考[练基础小题——强化运算能力]1.下列结论正确的是()A.各个面都是三角形的几何体是三棱锥B.以三角形的一条边所在直线为旋转轴,其余两边绕旋转轴旋转形成的曲面所围成的几何体叫圆锥C.棱锥的侧棱长与底面多边形的边长都相等,则该棱锥可能是六棱锥D.圆锥的顶点与底面圆周上的任意一点的连线都是母线解析:选D A错误,如图①是由两个相同的三棱锥叠放在一起构成的几何体,它的各个面都是三角形,但它不是三棱锥;B错误,如图②,若△ABC不是直角三角形,或△ABC是直角三角形但旋转轴不是直角边,所得的几何体都不是圆锥;C错误,若该棱锥是六棱锥,由题设知,它是正六棱锥.易证正六棱锥的侧棱长必大于底面边长,这与题设矛盾.2.如图是一个空间几何体的三视图,其中正视图、侧视图都是由边长为4和6的矩形以及直径等于4的圆组成,俯视图是直径等于4的圆,该几何体的体积是( )A.41π3B.62π3C.83π3D.104π3解析:选D 由题意得,此几何体为球与圆柱的组合体,其体积V =43π×23+π×22×6=104π3. 3.某空间几何体的三视图如图所示,则该几何体的表面积为( )A .12+4 2B .18+8 2C .28D .20+8 2解析:选D 由三视图可知该几何体是底面为等腰直角三角形的直三棱柱,如图.则该几何体的表面积为S =2×12×2×2+4×2×2+22×4=20+82,故选D.4.《九章算数》中,将底面是直角三角形的直三棱柱称为“堑堵”,已知某“堑堵”的三视图如图所示,俯视图中虚线平分矩形的面积,则该“堑堵”的侧面积为( )A .2B .4+2 2C .4+4 2D .6+4 2解析:选C 由题可知,该几何体的底面为等腰直角三角形,等腰直角三角形的斜边长为2,腰长为2,棱柱的高为2.所以其侧面积S =2×2+22×2=4+42,故选C.5.已知一个正方体的所有顶点在一个球面上,若球的体积为9π2,则正方体的棱长为________.解析:设正方体棱长为a ,球半径为R ,则43πR 3=9π2,∴R =32,∴3a =3,∴a = 3.答案: 3[练常考题点——检验高考能力]一、选择题1.已知圆锥的表面积为a ,且它的侧面展开图是一个半圆,则这个圆锥的底面直径是( )A.a2 B.3πa3πC.23πa 3πD.23a 3π解析:选C 设圆锥的底面半径为r ,母线长为l ,由题意知2πr =πl ,∴l =2r ,则圆锥的表面积S 表=πr 2+12π(2r )2=a ,∴r 2=a 3π,∴2r =23πa 3π.2.在梯形ABCD 中,∠ABC =π2,AD ∥BC ,BC =2AD =2AB =2.将梯形ABCD 绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )A.2π3B.4π3C.5π3D .2π解析:选C 过点C 作CE 垂直AD 所在直线于点E ,梯形ABCD 绕AD 所在直线旋转一周而形成的旋转体是由以线段AB 的长为底面圆半径,线段BC 为母线的圆柱挖去以线段CE 的长为底面圆半径,ED 为高的圆锥,如图所示,该几何体的体积为V =V 圆柱-V 圆锥=π·AB 2·BC -13·π·CE 2·DE =π×12×2-13π×12×1=5π3,故选C. 3.一个几何体的三视图如图所示,则该几何体的体积为( )A.163B.203C.152D.132解析:选D 该几何体可视为正方体截去两个三棱锥所得,如图所示,所以其体积为23-13×12×2×2×2-13×12×1×1×1=132.故选D.4.已知正四面体的棱长为2,则其外接球的表面积为( ) A .8π B .12π C.32π D .3π 解析:选D 如图所示,过顶点A 作AO ⊥底面BCD ,垂足为O ,则O 为正三角形BCD 的中心,连接DO 并延长交BC 于E ,又正四面体的棱长为2,所以DE =62,OD =23DE =63,所以在直角三角形AOD 中,AO =AD 2-OD 2=233.设正四面体外接球的球心为P ,半径为R ,连接PD ,则在直角三角形POD 中,PD 2=PO 2+OD 2,即R 2=⎝⎛⎭⎫233-R 2+⎝⎛⎭⎫632,解得R =32,所以外接球的表面积S =4πR 2=3π. 5.(2017·郑州质检)如图所示是一个几何体的三视图,则这个几何体外接球的表面积为( )A .8πB .16πC .32πD .64π解析:选C 还原三视图可知该几何体为一个四棱锥,将该四棱锥补成一个长、宽、高分别为22,22,4的长方体,则该长方体外接球的半径r =(22)2+(22)2+422=22,则所求外接球的表面积为4πr 2=32π.6.已知四棱锥P -ABCD 的三视图如图所示,则四棱锥P -ABCD 的四个侧面中面积的最大值是( )A .6B .8C .2 5D .3解析:选A 四棱锥如图所示,作PN ⊥平面ABCD ,交DC 于点N ,PC =PD =3,DN =2,则PN =32-22=5,AB =4,BC =2,BC ⊥CD ,故BC ⊥平面PDC ,即BC ⊥PC ,同理AD ⊥PD .设M 为AB 的中点,连接PM ,MN ,则PM =3,S △PDC =12×4×5=25,S △PBC =S△PAD=12×2×3=3,S △PAB =12×4×3=6,所以四棱锥P -ABCD 的四个侧面中面积的最大值是6.二、填空题7.在棱长为3的正方体ABCD -A 1B 1C 1D 1中,P 在线段BD 1上,且BP PD 1=12,M 为线段B 1C 1上的动点,则三棱锥M -PBC 的体积为________.解析:∵BP PD 1=12,∴点P 到平面BC 1的距离是D 1到平面BC 1距离的13,即三棱锥P -MBC 的高h =D 1C 13=1.M 为线段B 1C 1上的点, ∴S △MBC =12×3×3=92,∴V M -PBC =V P -MBC =13×92×1=32. 答案:328.一个几何体的三视图如图所示(单位:m),则该几何体的体积为________m 3.解析:由三视图可得该几何体是组合体,上面是底面圆的半径为2 m 、高为2 m 的圆。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A.4 5 5
B.2
5
C.4 D.2
答案 A
解析 在△ABC 中,AC2=AB2+BC2=5,∴AB⊥BC.作 BD⊥AC 于 D,则 BD 为侧视图的宽,
且 BD=2 × 1=2 5,∴侧视图的面积为 S=2×2 5=4 5.故选 A.
55
5
5
3.平行六面体 ABCD-A1B1C1D1 中,既与 AB 共面也与 CC1 共面的棱的条数为( )
所成的角即为直线 A1B 与直线 A1D 所成的角,即∠DA1B 为异面直线 A1B 与 B1C 所成的角,在
长方体 ABCD-A1B1C1D1 中,设 AB=BC=2AA1=2,则 A1B=A1D= 5,BD=2 2,在△A1BD 中,
由余弦定理得 cos∠DA1B=A1B22+A1AB1·DA21-D BD2=2
A.3 B.4 C.5 D.6
答案 C
1
解析 如图,既与 AB 共面也与 CC1 共面的棱有 CD,BC,BB1,AA1,C1D1,共 5 条.故选 C.
4.在四边形 ABCD 中,AB=AD=CD=1,BD= 2,BD⊥CD.将四边形 ABCD 沿对角线 BD 折成四面体 A′-BCD,使平面 A′BD⊥平面 BCD,则下列结论正确的是( )
专题突破练(5) 立体几何的综合问题
一、选择题 1.已知直线 a⊂平面 α,直线 b⊂平面 β,则“a∥b”是“α∥β”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分又不必要条件 答案 D 解析 “a∥b”不能得出“α∥β”,反之由“α∥β”也得不出“a∥b”.故选 D. 2.如图,三棱柱 ABC-A1B1C1 中,AA1⊥平面 ABC,A1A=AB=2,BC=1,AC= 5,若规 定正视方向垂直平面 ACC1A1,则此三棱柱的侧视图的面积为( )
2
A.48 B.60 C.72 D.84 答案 B
解析 复杂的图形表面积可以用三视图投影的方法计算求得;如图所示: 投影面积为 4×2+1×2=10,共有 6 个投影面积,所以该几何体的表面积为 10×6=60.故 选 B. 6.如图所示,已知在多面体 ABC-DEFG 中,AB,AC,AD 两两垂直,平面 ABC∥平面 DEFG,平面 BEF∥平面 ADGC,AB=AD=DG=2,AC=EF=1,则该多面体的体积为( )
A.2 B.4 C.6 D.8 答案 B
解析 如图所示,将多面体补成棱长为 2 的正方体,那么显然所求的多面体的体积即为
3
该正方体体积的一半,于是所求几何体的体积为 V=1×23=4.故选 B. 2
7.(2018·湖北黄冈中学二模)一个几何体的三视图如图所示,其中正视图是边长为 2 的 等边三角形,俯视图是半圆(如图).现有一只蚂蚁从点 A 出发沿该几何体的侧面环绕一周回 到 A 点,则蚂蚁所经过路程的最小值为( )
2,所以异面直线 AC1 与 EF 所成角的正切值为
2.故选 D.
10.(2018·河北唐山第一次摸底)在长方体 ABCD-A1B1C1D1 中,AB=BC=2AA1,则异面 直线 A1B 与 B1C 所成角的余弦值为( )
5
A. 10 B.1 C. 5 D. 15
5
5
5
5
答案 B
解析 在长方体 ABCD-A1B1C1D1 中,连接 A1D,可得 A1D∥B1C,所以异面直线 A1B 与 B1C
A.A′C⊥BD B.∠BA′C=90° C.CA′与平面 A′BD 所成的角为 30° D.四面体 A′-BCD 的体积为1
3 答案 B 解析 ∵AB=AD=1,BD= 2,∴AB⊥AD.∴A′B⊥A′D.∵平面 A′BD⊥平面 BCD,CD⊥ BD,∴CD⊥平面 A′BD,∴CD⊥A′B,∴A′B⊥平面 A′CD,∴A′B⊥A′C,即∠BA′C= 90°.故选 B. 5.(2018·河南豫东、豫北十校测试)鲁班锁是中国传统的智力玩具,起源于古代汉族建 筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙, 原为木质结构,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称.从外表上 看,六根等长的正四棱柱体分成三组,经 90 度榫卯起来,若正四棱柱体的高为 4,底面正 方形的边长为 1,则该鲁班锁的表面积为 ( )
A.π B. 6+ 2 C. 6- 2 D.π+2 答案 B
解析 由三视图可知,该几何体是半圆锥,其展开图如图所示,则依题意,点 A,M 的
最短距离,即为线段 AM.∵PA=PB=2,半圆锥的底面半圆的弧长为 π,∴展开图中的∠BPM=
π=π,∵∠APB=π,∴∠APM=5π,∴在△APM 中,根据余弦定理有,MA2=22+22-
5+5-8 × 5×
=1.故选 B. 55
11.在正方体 ABCD-A1B1C1D1 中,P 为正方形 A1B1C1D1 四边上的动点,O 为底面正方形 ABCD 的中心,M,N 分别为 AB,BC 边的中点,点 Q 为平面 ABCD 内一点,线段 D1Q 与 OP 互相平分, 则满足M→Q=λ M→N的实数 λ 的值有( )
得PO1=x,则 3R R
PO1=3x,圆柱的高为
3R-3x,所以圆柱的表面积为
S=2πx2+2πx·(3R-3x)=
-4πx2+6πRx,则当
x=3R 4
时,S
取最大值,Smax=94πR2.故选
B.
9.如图,在正方体 ABCD-A1B1C1D1 中,点 E 为正方形 ABCD 的两条对角线的交点,点 F 是棱 AB 的中点,则异面直线 AC1 与 EF 所成角的正切值为( )
A.-
2
B.- 2 2
C. 2 2
D.
2
答案 D
解析 在正方体 ABCD-A1B1C1D1 中,依题意知,EF∥AD,所以异面直线 AC1 与 EF 所成角
为∠C1AD.连接 C1D,因为 AD⊥平面 C1CDD1,所以 AD⊥DC1,设正方体的棱长为 1,则 tan∠C1AD
=C1D= 2= AD 1
PB 2
3
6
2×2×2cos5π=8+4 6
3=(
6+
2)2,∴MA=
6+
2,即蚂蚁所经过路程的最小值为
6+
2,故选 B.
8.已知圆锥的底面半径为 R,高为 3R,在它的所有内接圆柱中,表面积的最大值是( )
A.22πR2 B.9πR2 4
4
C.8πR2 D.5πR2
32答案 BFra bibliotek解析 如图所示,为组合体的轴截面,记 BO1 的长度为 x,由相似三角形的比例关系,
