最新北师大版八年级数学上册第一、二单元检测题及答案

合集下载

北师大版八年级上册数学第一章、第二章单元测试卷 2套(Word版,含答案)

北师大版八年级上册数学第一章勾股定理单元测试卷（满分120分；时间：120分钟）一、选择题（本题共计10 小题，每题3 分，共计30分，）1. 以下列各组数据为边长作三角形，其中能组成直角三角形的是（）A.7、24、25B.36、12、13C.4、6、8D.3、5、32. 已知一个Rt△的两边长分别为3和4，则第三边长的平方是()A.25B.14C.7D.7或253. 如图所示，一个梯子AB长2.5米，顶端A靠墙AC上，这时梯子下端B与墙角C距离为1.5米，梯子滑动后停在DE的位置上，测得BD长为0.5米，则梯子顶端A下落了()米．A.1B.0.5C.0.6D.0.84. 用四个边长均为a、b、c的直角三角板，拼成如图中所示的图形，则下列结论中正确的是（）A.c2=a2+b2B.c2=a2+2ab+b2C.c2=a2−2ab+b2D.c2=(a+b)2．5. 如图，以Rt△ABC的三边分别向外作正方形，则以AC为边的正方形的面积S2等于（）A.6B.26C.4D.246. 下列各组数据不是勾股数的是()A.2，3，4B.3，4，5C.5，12，13D.6，8，107. 如图，透明的圆柱形玻璃容器（容器厚度忽略不计）的高为16cm，在容器内壁离容器底部4cm的点B处有一滴蜂蜜，此时一只蚂蚁正好在容器外壁，位于离容器上沿4cm的点A处，若蚂蚁吃到蜂蜜需爬行的最短路径为20cm，则该圆柱底面周长为()A.12cmB.14cmC.20cmD.24cm8. 如图，在一块平地上，停在一辆大客车前9m处有一棵大树．在一次强风中，这棵树从离地面6m处正对大客车方向折断倒下，若倒下部分的长是10m，则大树倒下时会碰到客车吗？（）A.不会B.可能会C.一定会D.无法确定9. 有长度分别为5，7，9，12，13，15，16，20，24，25的木棒，用它来摆成直角三角形，可以重复使用，问可摆成不同的直角三角形的个数为（）A.2个B.3个C.4个D.5个10. 如图所示，是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案，已知大正方形面积为49，小正方形面积为4，若用x，y表示直角三角形的两直角边(x>y)，下列四个说法：①x2+y2=49，②x−y=2，③2xy+4=49，④x+y=9．其中说法正确的是（）A.①②B.①②③C.①②④D.①②③④二、填空题（本题共计8 小题，每题3 分，共计24分，）11. 在△ABC中，若a2=b2−c2，则△ABC是________三角形，________是直角；若a2<b2−c2，则∠B是________．12. 一个圆锥体形状的水晶饰品，母线长是10cm，底面圆的直径是5cm，点A为圆锥底面圆周上一点，从A点开始绕圆锥侧面缠绕一圈彩带回到A点，则彩带最少用________厘米．（接口处重合部分忽略不计）13. 如图，把长、宽、对角线的长分别是a、b、c的矩形沿对角线剪开，与一个直角边长为c的等腰直角三角形拼接成右边的图形，用面积割补法能够得到的一个等式是________．14. 如图，一个上方无盖的长方体盒子紧贴地面，一只蚂蚁由盒外A处出发，沿着盒子面爬行到盒内的点B处，已知，AB=9，BC=9，BF=6，这只蚂蚁爬行的最短距离是________．15. 如图，起重机吊运物体，∠ABC=90∘．若BC=5m，AC=13m，则AB=________m．16. 如图，圆柱形玻璃杯高为12cm、底面周长为18cm，在杯内离杯底4cm的点C处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿4cm与蜂蜜相对的点A处，则蚂蚁到达蜂蜜的最短距离为________cm．17. 如图．是用4个全等的直角三角形和一个小正方形镶嵌而成的正方形图案，已知大正方形的面积是49，小正方形的面积为1，若用a、b表示直角三角形的两条直角边(a> b)，则(a+b)2＝________．18. 如图，长方体的长、宽、高分别是3cm、1cm、6cm，如果一只小虫从点A开始爬行，经过2个侧面爬行到另一个侧棱的中点B处，则所爬行的最短的长度为________．三、解答题（本题共计7 小题，共计66分，）19. 如图，一只蚂蚁沿边长是3的正方体表面从顶点A爬到顶点B，求它走过的最短路程，并画出示意图．20. 如图，已知在△ABC中，CD⊥AB于点D，AC=20，BC=15，DB=9.(1)求CD，AB的长；(2)求证：△ABC是直角三角形．21. 已知，如图，在四边形ABCD中，∠ABC=90∘，CD⊥AD，AD2+CD2=2AB2，求证：AB=BC．22. 如图，两个直角三角形的直角边a，b在同一直线上，斜边为c，请利用三角形和梯形面积公式验证勾股定理．23. 如图，有一个底面半径为6cm，高为24cm的圆柱，在圆柱下底面的点A有一只蚂蚁，它想吃到上底面上与点A相对的点B处的食物后再返回到A点处休息，请问它需爬行的最短路程约是多少？(π取整数3)24. 消防队员进行消防演练，在模拟现场，有一建筑物发生了火灾，消防车到达后，发现离建筑物的水平距离最近为12m，如图，即AD=BC=12m，此时建筑物中距地面12.8m高的P处有一被困人员需要救援，已知消防云梯车的车身高AB是3.8m，问此消防车的云梯至少应伸长多少米？25. 如图所示，A、B两块试验田相距200米，C为水源地，AC=160m，BC=120m，为了方便灌溉，现有两种方案修筑水渠．甲方案：从水源地C直接修筑两条水渠分别到A、B；乙方案；过点C作AB的垂线，垂足为H，先从水源地C修筑一条水渠到AB所在直线上的H处，再从H分别向A、B进行修筑．（1）请判断△ABC的形状（要求写出推理过程）；（2）两种方案中，哪一种方案所修的水渠较短？请通过计算说明．参考答案一、选择题（本题共计10 小题，每题 3 分，共计30分）1.【答案】A【解答】解：A、72+242=252，能构成直角三角形；B、122+132≠362，不能构成直角三角形；C、42+62≠82，不能构成直角三角形；D、32+32≠52，不能构成直角三角形；故选A．2.【答案】D【解答】解：分两种情况：①3，4都为直角边，由勾股定理得，第三边长是√42+32=5，∴ 第三边长的平方为25.②3为直角边，4为斜边，由勾股定理得，第三边长是√42−32=√7，∴ 第三边长的平方是7.故选D．3.【答案】B【解答】解：在Rt△ABC中，AB=2.5米，BC=1.5米，故AC=√AB2−BC2=√2.52−1.52=2米，在Rt△ECD中，AB=DE=2.5米，CD=(1.5+0.5)米，故EC=√DE2−CD2=√2.52−22=1.5米，故AE=AC−CE=2−1.5=0.5米．故选B.4.【答案】A【解答】解：由题意得到四个完全一样的直角三角板围成的四边形为正方形，其边长为c，里边的小四边形也为正方形，边长为b−a，则有c2=1ab×4+(b−a)2，整理得：c2=a2+b2．故选A．5.【答案】C【解答】∴ △ABC是直角三角形，∴ AC2+BC2＝AB2，即S1+S2＝S3，∴ S2＝S3−S1＝5−1＝4．6.【答案】A【解答】解：A，22+32≠42，不能构成直角三角形，所以不是勾股数，故符合题意；B，32+42=52，能构成直角三角形，所以是勾股数，故不符合题意；C，52+122=132，能构成直角三角形，所以是勾股数，故不符合题意；D，62+82=102，能构成直角三角形，所以是勾股数，故不符合题意.故选A.7.【答案】D【解答】解：将圆柱侧面展开，如图，过ED作A的对称点A′，连接A′B，则A′B即为最短距离，则AD=A′D=4cm.由题意得EF=16cm，BF=CG=4cm，A′B=20cm∴ A′C=16−4+4=16(cm)，∴ BC=√A′B2−A′C2=√202−162=12(cm)，∴ 底面周长=2BC=24(cm).故选D.8.【答案】A【解答】如图所示，AB＝10米，AC＝6米，根据勾股定理得，BC=√AB2−AC2=√102−62=8米<9米．9.【答案】D【解答】解：∴ 52+122=132，72+242=252，92+122=152，122+162=202，152+202= 252，∴ 可摆成不同的直角三角形5个．故选D．10.【答案】B【解答】解：①大正方形的面积是49，则其边长是7，显然，利用勾股定理可得x2+y2=49，故选项①正确；②小正方形的面积是4，则其边长是2，根据图可发现y+2=x，即x−y=2，故选项②正确；③根据图形可得四个三角形的面积+小正方形的面积=大正方形的面积，即4×12xy+4= 49，化简得2xy+4=49，故选项③正确；④{x2+y2=492xy+4=49，则x+y=√94，故此选项不正确．故选B．二、填空题（本题共计8 小题，每题 3 分，共计24分）11.【答案】直角,∠B,钝角【解答】解：∴ a2=b2−c2，∴ a2+c2=b2，∴ 这个三角形是直角三角形，b是最长边，∴ b边所对的∠B为直角．故答案为：直角；∠B；在△ABC中，∴ a2<b2−c2，∴ a 2+c 2<b 2，由余弦定理可得：cos B =a 2+c 2−b 22ac<0，∴ ∠B 为钝角，故答案为：钝角． 12. 【答案】10√2【解答】解：由两点间直线距离最短可知，圆锥侧面展开图AA′最短，由题意可得出：OA =OA′=10cm ， AA ′̂=nπ×10180=5π，解得：n =90∘， ∴ ∠AOA′=90∘，∴ AA′=√OA 2+OA ′2=10√2(cm)，故答案为：10√2．13. 【答案】a 2+b 2=c 2【解答】解：此图可以这样理解，有三个Rt △其面积分别为 12ab ，12ab 和 12c 2．还有一个直角梯形，其面积为 12(a +b)(a +b)．由图形可知：12(a +b)(a +b)=12ab +12ab +12c 2，整理得(a +b)2=2ab +c 2，a 2+b 2+2ab =2ab +c 2， ∴ a 2+b 2=c 2．故答案为：a 2+b 2=c 2．14.【答案】15【解答】解：如图所示，AB′=√92+(6+6)2=15．故答案为：15．15.【答案】12【解答】解：由题意可得：AB=√AC2−BC2=12(m)．故答案为：12．16.【答案】15【解答】解：沿过A的圆柱的高剪开，得出矩形EFGH，过C作CQ⊥EF于Q，作A关于EH的对称点A′，连结A′C交EH于P，连结AP，则AP+PC就是蚂蚁到达蜂蜜的最短距离，∴ AE=A′E，A′P=AP，∴ AP+PC=A′P+PC=A′C.×18cm=9cm，A′Q=12cm−4cm+4cm=12cm，∴ CQ=12在Rt△A′QC中，由勾股定理得：A′C=√122+92=15(cm)，故答案为：15.17.【答案】97【解答】利用勾股定理得a2+b2＝49；利用小正方形的边长得到a−b＝1，则(a−b)2＝1，可得：2ab＝48，所以(a+b)2＝49+48＝97，18.【答案】5cm【解答】解：分为三种情况：①如图将正面与右面展开在同一平面，连接AB，由勾股定理得：AB=√(3+1)2+32=5(cm)；②如图将下底面与后面展开在同一平面，连接AB，由勾股定理得：AB=√(3+1)2+32=5(cm)；③如图将下底面与右面展开在同一平面，连接AB，由勾股定理得：AB=√(3+3)2+12=√37cm>5cm，即从A处爬到B处的最短路程是5cm．故答案为5cm．三、解答题（本题共计7 小题，每题10 分，共计70分）19.【答案】解：如图所示：将正方体展开，连接A、B，根据两点之间线段最短，AB=√32+62=3√5．【解答】解：如图所示：将正方体展开，连接A、B，根据两点之间线段最短，AB=√32+62=3√5．20.【答案】(1)解：∴ 在Rt△BCD中，BC=15，BD=9，∴ CD=√BC2−BD2=√152−92=12．在Rt△ADC中，AC=20，CD=12，∴ AD=√AC2−CD2=√202−122=16．∴ AB=AD+DB=16+9=25．(2)证明：∴ AB=25，AC=20，BC=15，∴ AB2=252=625，AC2+BC2=202+152=625，∴ AB2=AC2+BC2，∴ △ABC是直角三角形．【解答】(1)解：∴ 在Rt△BCD中，BC=15，BD=9，∴ CD=√BC2−BD2=√152−92=12．在Rt△ADC中，AC=20，CD=12，∴ AD=√AC2−CD2=√202−122=16．∴ AB=AD+DB=16+9=25．(2)证明：∴ AB=25，AC=20，BC=15，∴ AB2=252=625，AC2+BC2=202+152=625，∴ AB2=AC2+BC2，∴ △ABC是直角三角形．21.【答案】证明：∴ ∠ABC=90∘，∴ AB2+BC2=AC2，∴ CD⊥AD，∴ ∠ADC=90∘，∴ AD2+CD2=AC2，∴ AD2+CD2=2AB2，∴ AC2=2AB2，∴ AB2+BC2=2AB2，∴ AB2=BC2，∴ AB=BC．【解答】证明：∴ ∠ABC=90∘，∴ AB2+BC2=AC2，∴ CD⊥AD，∴ ∠ADC=90∘，∴ AD2+CD2=AC2，∴ AD2+CD2=2AB2，∴ AC2=2AB2，∴ AB2+BC2=2AB2，∴ AB2=BC2，∴ AB=BC．22.【答案】解：由图可得，12×(a+b)(a+b)=12ab+12c2+12ab，整理得，a 2+2ab+b22=2ab+c22，∴ a2+2ab+b2=2ab+c2，∴ a2+b2=c2．【解答】解：由图可得，12×(a+b)(a+b)=12ab+12c2+12ab，整理得，a 2+2ab+b22=2ab+c22，∴ a2+2ab+b2=2ab+c2，∴ a2+b2=c2．23.【答案】解：将圆柱体展开，连接A、B，根据两点之间线段最短，根据题意可得：BC=24cm，AC是圆周的一半，∴ AC=12×2×π×6=18cm，∴ AB=√AC2+BC2=30cm，∴ 它需爬行的最短路程约是60cm．【解答】解：将圆柱体展开，连接A、B，根据两点之间线段最短，根据题意可得：BC=24cm，AC是圆周的一半，∴ AC=12×2×π×6=18cm，∴ AB=√AC2+BC2=30cm，∴ 它需爬行的最短路程约是60cm．24.【答案】解：由题意可知：AB=CD=3.8m，AD=12m，PC=12.8m，∠ADP=90∘，∴ PD=PC−CD=9m，在Rt△ADP中，AP=√AD2+PD2=15m.答：此消防车的云梯至少应伸长15米.【解答】解：由题意可知：AB=CD=3.8m，AD=12m，PC=12.8m，∠ADP=90∘，∴ PD=PC−CD=9m，在Rt△ADP中，AP=√AD2+PD2=15m.答：此消防车的云梯至少应伸长15米.25.【答案】解：(1)△ABC是直角三角形；理由如下：∴ AC2+BC2=1602+1202=40000，AB2=2002=40000，∴ AC2+BC2=AB2，∴ △ABC是直角三角形，∠ACB=90∘；（2）甲方案所修的水渠较短；理由如下：∴ △ABC是直角三角形，∴ △ABC的面积=12AB⋅CH=12AC⋅BC，∴ CH=AC⋅BCAB =160×120200=96(m)，∴ CH⊥AB，∴ ∠AHC=90∘，∴ AH=√AC2−CH2=√1602−962=128(m)，∴ BH=AB−AH=72m，∴ AC+BC=160m+120m=280m，CH+AH+BH=96m+200m=296m，∴ AC+BC<CH+AH+BH，∴ 甲方案所修的水渠较短．【解答】解：(1)△ABC是直角三角形；理由如下：∴ AC2+BC2=1602+1202=40000，AB2=2002=40000，∴ AC2+BC2=AB2，∴ △ABC是直角三角形，∠ACB=90∘；（2）甲方案所修的水渠较短；理由如下：∴ △ABC是直角三角形，∴ △ABC的面积=12AB⋅CH=12AC⋅BC，∴ CH =AC⋅BC AB=160×120200=96(m)，∴ CH ⊥AB ， ∴ ∠AHC =90∘，∴ AH =√AC 2−CH 2=√1602−962=128(m)， ∴ BH =AB −AH =72m ，∴ AC +BC =160m +120m =280m ，CH +AH +BH =96m +200m =296m ， ∴ AC +BC <CH +AH +BH ， ∴ 甲方案所修的水渠较短．北师大版八年级上册数学第二章实数单元测试卷一、选择题(每小题3分,共30分) 1.下列四个选项中,属于无理数的是 ( ) A .3.1415926 B .3.21C .√93D .-√1162.下列二次根式中,是最简二次根式的是 ( ) A .√8B .√10C .√16D .√273.下列说法不正确的是 ( ) A .125的平方根是±15B .(-4)3的立方根是-4C .√4的算术平方根是2D .-√273=-34.下列计算正确的是 ( ) A .√52=±5 B .√2÷√3=√63 C .2√3×2√3=4√3 D .√2+√3=√55.估计√153的大小在 ( ) A .2与3之间 B .3与4之间C .4与5之间D .5与6之间6.设a=(-√3)2,b=√(-3)2,则a ,b 的大小关系是 ( ) A .a=bB .a>bC .a<bD .a+b=07.下列各实数比较大小,其中正确的是 ( ) A .√7<2.5B .√16<2.2C .1π>√5D .√3-13<13 8.已知a ,b 互为倒数,c ,d 互为相反数,则-√ab 3+√c +d +1的平方根为 ( ) A .1B .-1C .0D .±19.若x+y=3+2√2,x-y=3-2√2,则√x 2-y 2的值为 ( ) A .4√2B .1C .6D .3-2√210.已知a ,b ,c 在数轴上的对应点的位置如图所示,则化简√a 2-|a+c|+√(c -b )2的结果是 ( )A .2c-bB .-bC .bD .-2a-b二、填空题(每小题4分,共24分) 11.计算:|√3-2|= .12.已知a=√3,则a 的倒数是 .13.已知√2.021≈1.422,√20.21≈4.496,则√2021≈ .14.√643的平方根是 .15.有边长为5厘米的正方形和长为18厘米,宽为8厘米的长方形,现要制作一个面积为这两个图形面积之和的正方形,则此正方形的边长应为厘米.16.已知y=√(x -4)2-x+5,当x 分别取1,2,3,…,2021时,所对应y 值的总和是 . 三、解答题(共46分)17.(4分)计算:(1)√24×4√12÷√48;(2)3√20-√45+10√15.18.(4分)计算:(1)(3-√7)(3+√7)+√2(2-√2);(2)2√13×√9-√12+√78-13.19.(6分)(1)已知x=√3+1,y=√3-1,求x2+2xy+y2的值;(2)已知x=√2-1,求x2+3x-1的值.20.(6分)站在海拔为h米的地方看到的水平距离为d米,它们之间的关系可近似地表示为.d=8√ℎ5(1)当h=1000时,求d的值;(2)某登山者从海拔n米处登上海拔2n米处的山顶(n>0),那么他看到的水平距离是原来的多少倍?21.(8分)阅读下面的文字,解答问题.例如:因为√4<√7<√9,即2<√7<3,所以√7的整数部分为2,小数部分为√7-2.请解答:(1)√17的整数部分是,小数部分是;(2)已知:5-√17的小数部分是m,6+√17的小数部分是n,且(x+1)2=m+n,请求出满足条件的x 的值.22.(8分)图①是由8个同样大小的正方体组成的魔方,体积为64.(1)求出这个魔方的棱长;(2)图中阴影部分是一个正方形ABCD,求出阴影部分的面积及边长;(3)把正方形ABCD放到数轴上,如图②,使得点A与表示-1的点重合,那么点D在数轴上表示的数为.23.(10分)先观察下列各式,再回答问题:√1+112+122=112;√1+122+132=116;√1+132+142=1112.(1)根据上面三个等式提供的信息,请猜想√1+142+152的结果,不用验证;(2)按照上面各等式反映的规律,试写出用含n(n为正整数)的式子表示的等式,不用验证.答案1.C2.B3.C4.B5.A6.A7.D8.C 9.B10.A [解析] 根据数轴可以得到a<b<0<c ,且|a|>|c|,则a+c<0,c-b>0,则原式=-a+(a+c )+(c-b )=-a+a+c+c-b=2c-b.11.2-√3 12.√33 13.44.9614.±2 15.13 16.203317.解:(1)原式=2√6×4×√22÷4√3=8√3÷4√3=2.(2)原式=6√5-3√5+2√5=5√5.18.解:(1)原式=9-7+2√2-2=2√2.(2)原式=2×√33×3-2√3-12=-12.19.解:(1)当x=√3+1,y=√3-1时,原式=(x+y )2=(√3+1+√3-1)2=(2√3)2=12.(2)当x=√2-1时,原式=(√2-1)2+3(√2-1)-1=2+1-2√2+3√2-3-1=√2-1.20.解:(1)当h=1000时,d=8√10005=80√2.(2)因为8√2n 5÷8√n 5=√2,所以他看到的水平距离是原来的√2倍.21.[解析] (1)因为√16<√17<√25,所以4<√17<5,所以√17的整数部分是4,小数部分是√17-4.解:(1)4√17-4(2)因为5-√17的小数部分是m,6+√17的小数部分是n,所以m=5-√17,n=6+√17-10=√17-4,所以m+n=1,所以(x+1)2=1,所以x+1=1或x+1=-1,则x=0或x=-2.22.解:(1)√643=4.因此,这个魔方的棱长为4.(2)因为魔方的棱长为4,所以每个小正方体的棱长为2.所以阴影部分的面积为12×2×2×4=8,边长为√8=2 √2.因此,阴影部分的面积是8,边长是2√2.(3)-1-2√223.解:(1)观察可得√1+142+152=1120.(2)√1+1n2+1(n+1)2=1+1n(n+1)(n为正整数).。

北师大版数学八年级上册全册全套单元试题及答案

北师大版数学八年级上册全册单元试卷第一章勾股定理一、选择题1．以下列各组数据为三角形三边，能构成直角三角形的是（）（A ）4cm ，8cm ，7cm （B ） 2cm ，2cm ，2cm （C ） 2cm ，2cm ，4cm （D ）13cm ，12 cm ，5 cm2．一个三角形的三边长分别为15cm ，20cm ，25cm ，则这个三角形最长边上的高为（）（A ）12cm （B ）10cm （C ）12.5cm （D ）10.5cm3．Rt ∆ABC 的两边长分别为3和4，若一个正方形的边长是∆ABC 的第三边，则这个正方形的面积是（）（A ）25 （B ）7 （C ）12 （D ）25或74．有长度为9cm ，12cm ，15cm ，36cm ，39cm 的五根木棒，可搭成（首尾连接）直角三角形的个数为（）（A ）1个（B ）2个（C ）3个（D ）4个5．将直角三角形的三边长扩大相同的倍数后，得到的三角形是（）（A ）直角三角形（B ）锐角三角形（C ）钝角三角形（D ）以上结论都不对 6．在△ABC 中，AB =12cm ， AC =9cm ，BC =15cm ，下列关系成立的是（）（A ）B C A ∠+∠>∠ （B ）B C A ∠+∠=∠ （C ）B C A ∠+∠<∠ （D ）以上都不对7．小刚准备测量河水的深度,他把一根竹竿插到离岸边1.5m 远的水底，竹竿高出水面0.5m ，把竹竿的顶端拉向岸边，竿顶和岸边的水平刚好相齐，河水的深度为（）（A ）2m （B ）2.5cm （C ）2.25m （D ）3m 8．若一个三角形三边满足ab c b a 2)(22=-+，则这个三角形是（）（A ）直角三角形（B ）等腰直角三角形（C ）等腰三角形（D ）以上结论都不对 9．一架250cm 的梯子斜靠在墙上，这时梯足与墙的终端距离为70cm ，如果梯子顶端沿墙下滑40cm ，那么梯足将向外滑动（）（A ）150cm（B ）90cm（C ）80cm（D ）40cm10．三角形三边长分别为12+n 、n n 222+、1222++n n （n 为自然数），则此三角形是（）（A ）直角三角形（B ）等腰直角三角形（C ）等腰三角形（D ）以上结论都不对二、填空题11．写四组勾股数组.______，______，______，______.12．若一个直角三角形的三边为三个连续的偶数，则它的周长为____________。

北师大版八年级数学上册单元测试题全套及答案

最新北师大版八年级数学上册单元测试题全套及答案第一章勾股定理综合测评时间：满分：120分一、精心选一选（每小题4分，共32分）1. 在△ABC中，∠B=90°，若BC=3，AC=5，则AB等于（）A.3B.4C.5D.62.下列几组数中，能组成直角三角形的是（）A.13，14，15B.3，4，6C.5，12，13D.0.8，1.2，1.53.如图1，正方形ABCD的面积为100 cm2，△ABP为直角三角形，∠P=90°，且PB=6 cm，则AP的长为（）A.10 cmB.6 cmC.8 cmD.无法确定4.两只小鼹鼠在地下打洞，一只朝前方挖，每分钟挖8 cm，另一只朝左挖，每分钟挖6 cm，10分钟后，两只小鼹鼠相距（）A.50 cmB.80 cmC.100 c mD.140 cm5.已知a，b，c为△ABC的三边，且满足()()22222a b a b c-+-＝0，则它的形状为（）A.直角三角形B.等腰三角形C.等腰直角三角形D.等腰三角形或直角三角形6.图2中的小方格都是边长为1的正方形，试判断△ABC的形状为（）A．钝角三角形 B. 锐角三角形 C. 直角三角形 D.以上都有可能7.如图3,一圆柱高8 cm，底面半径为2 cm，一只蚂蚁从点A爬到点B处吃食，要爬行的最短路程（π取3）是（）A.20 cmB.10 cmC.14 cmD.无法确定8.已知Rt△ABC中，∠C=90°，若BC＋AC＝14 cm，AB＝10 cm，则该三角形的面积是（）A.24 cm2B.36 cm2C.48 cm2D.60 cm2二、耐心填一填（每小题4分，共32分）9.写出两组勾股数： .10.在△ABC中，∠C＝90°，若BC∶AC＝3∶4，AB＝10，则BC＝_____，AC＝_____.11.如图4，等腰三角形ABC的底边长为16，底边上的高AD长为6，则腰AB的长度为_____.PC BD A12.如图5，∠OA B ＝∠OBC ＝∠OCD ＝90°，AB ＝BC ＝CD ＝1，OA ＝2，则2OD ＝____.13.一个三角形的三边长之比为5∶12∶13，它的周长为60，则它的面积是______.14.图6是一个三级台阶，它的每一级长、宽、高分别是2米，0.3米，0.2米，A ，B 是这个台阶上两个相对的端点，A 点有一只蚂蚁，想到B 点去吃可口的食物，则蚂蚁沿台阶面爬行到B 点的最短路程是_____米.15.一天，小明买了一张底面是边长为260 cm 的正方形，厚30 cm 的床垫回家，到了家门口，才发现屋门只有242 cm 高，100 cm 宽．你认为小明能把床垫拿进屋吗？．（填“能”或“不能”）16.图7是一束太阳光线从仓库窗户射入的平面示意图，小强同学测得BN ＝35米，NC ＝34米，BC ＝1米，AC ＝4.5米，MC ＝6米，则太阳光线MA 的长度为_____米.三、细心做一做（共56分）17.（10分）如图8，甲渔船以8海里/时的速度离开港口O 向东北方向航行，乙渔船以6海里/时的速度离开港口O 向西北方向航行，它们同时出发.一个半小时后，甲、乙两渔船相距多少海里？18.（10分）如图9，已知在△ABC 中，AB=13，AD=12，AC=15，CD=9，求△ABC 的面积．19.（12分）如图10，在一棵树的10米高处有两只猴子，一只猴子爬下树后走到离树20米处的池塘A 处．另一只爬到树顶D 后直接跃到A 处，距离以直线计算，若两只猴子所经过的距离相等，试求该树的高度.20.（12分）如图11，一块草坪的形状为四边形ABCD ，其中∠B=90°，AB=8 m ，BC=6 m ，CD=24 m ，AD=26 m ．求这块草坪的面积．21. （12分）对任意符合条件的直角三角形保持其锐角顶点A 不动，改变BC 的位置，使B →E ，C →D ，且∠BAE ＝90°，∠CAD ＝90°（如图12）．【分析】所给数据如图中所示，且四边形ACFD 是一个正方形，它的面积和四边形ABFE 的面积相等.【解答】结合上面的分析过程验证勾股定理.第一章勾股定理综合测评一、1.B 2.C 3.C 4.C 5.D 6.C 7.B 8.A二、9. 答案不唯一，如3,4,5；60,80,100 10.6 8 11.10 12.7 13.120 14.2.5 15.能16.7.5三、17.解：由题意得38122OA =⨯=（海里），3692OB =⨯=（海里），90AOB ∠=︒，所以△AOB 是直角三角形.由勾股定理，得222OA OB AB +=，即2AB =92+122=225，所以AB ＝15（海里）.答略.18.解：因为AD=12，AC=15，CD=9，所以AD 2+CD 2=144+81=225= AC 2，所以△ADC 为直角三角形，且∠ADC=90°.在Rt △ABD 中，AB=13，AD=12，由勾股定理得BD ２=ＡＢ２－ＡＤ２＝２５，所以ＢＤ=5，所以BC ＝BD+DC=5+9=14．所以S △ABC =21·BC ·AD=21×14×12=84． 19.解：由题意知AD+DB=BC+CA ，且CA=20米，BC=10米，设BD=x ，则AD=30-x ．在Rt △ACD 中，CD 2+CA 2=AD 2，即（30-x ）2=（10+x ）2+202，解得x=5，故树高CD=10+x=15（米）.20.解：如图，连接AC ，因为∠B=90°，所以在Rt △ABC 中，由勾股定理得AC 2=AB 2+BC 2=82+62=100，所以AC=10.又因为CD=24，AD=26，所以在△ACD 中，AC 2+CD 2=AD 2，所以△ACD 是直角三角形．所以S 四边形ABCD =S △ACD -S △ABC =21AC•CD -21AB•BC=21×10×24-21×8×6=120-24=96（m 2）．故该草坪的面积为96 m 2．21.解：由分析可得S 正方形ACFD ＝S 四边形ABFE =S △BAE ＋S △BFE ．即b 2＝12c 2+12（b +a ）（b -a ）．整理，得2b 2=c 2+（b +a ）（b -a ）.所以a 2+b 2=c 2．第二章实数检测题【本检测题满分：100分，时间：90分钟】一、选择题（每小题3分，共30分）1．下列无理数中，在－2与1之间的是（）A ．－B ．－C ．D ．2．（2014·南京中考）8的平方根是（）A ．4B ．±4C ． 2D ．3. 若a ,b 为实数，且满足|a －2|+2b -=0，则b －a 的值为（）A ．2B ．0C ．－2D ．以上都不对 4. 下列说法错误的是（）A ．5是25的算术平方根B ．1是1的一个平方根C ．(－4)2的平方根是－4D ．0的平方根与算术平方根都是0 5. 要使式子有意义，则x 的取值范围是（）A ．x ＞0B ．x ≥－2C ．x ≥2D ．x ≤2 6. 若a ，b 均为正整数，且a ＞7，b ＞32，则a ＋b 的最小值是（） A.3 B.4 C.5 D.6 7. 在实数，，，－3.14，中，无理数有（）A.1个B.2个C.3个D.4个8. 已知3a ＝－1，b ＝1，212c ⎛⎫- ⎪⎝⎭＝0，则abc 的值为（）A.0 B ．－1 C.－12 D.129.若(m -1)2+2n +＝0，则m ＋n 的值是（） A ．－1 B ．0 C ．1 D ．210. 有一个数值转换器，原理如图所示：当输入的x =64时，输出的y 等于（）A ．2B ．8C ．32D ．22 二、填空题（每小题3分，共24分）11. 已知：若 3.65≈1.910，36.5≈6.042，则365000≈ ，±0.000365≈ . 12. 绝对值小于π的整数有 .13. 0.003 6的平方根是，81的算术平方根是 . 14. 已知|a －5|＋3b +＝0，那么a －b ＝ .15. 已知a ，b 为两个连续的整数，且a ＞28＞b ，则a ＋b ＝ . 16．计算：（2+1）（2-1）＝________.17.使式子1+x 有意义的x 的取值范围是________. 18.）计算：﹣＝_________.三、解答题（共46分）19.（6分）已知，求的值.20.（6分）若5+7的小数部分是a ，5－7的小数部分是b ，求ab +5b 的值. 21.（6分）先阅读下面的解题过程，然后再解答：形如n m 2±的化简，只要我们找到两个数a ，b ，使m b a =+，n ab =，即m b a =+22)()(，n b a =⋅，那么便有：b a b a n m ±=±=±2)(2)(b a >.例如：化简：347+. 解：首先把347+化为1227+，这里7=m ，12=n ，因为，，即7)3()4(22=+，1234=⨯，所以347+1227+32)34(2+=+.根据上述方法化简：42213-.22.（6分）比较大小，并说明理由：（1）与6；（2）与．23.（6分）大家知道是无理数，而无理数是无限不循环小数，因此的小数部分我们不能全部写出来，于是小平用－1来表示的小数部分，你同意小平的表示方法吗？事实上小平的表示方法是有道理的，因为的整数部分是1，用这个数减去其整数部分，差就是小数部分.请解答：已知：5＋的小数部分是，5－的整数部分是b ，求＋b 的值.24.（8分）计算：（1）862⨯-82734⨯+；（2）)62)(31(-+-2)132(-. 25.（8分）阅读下面计算过程：12)12)(12()12(1121-=-+-⨯=+；();23)23)(23(231231-=-+-⨯=+()25)25)(25(251251-=-+-⨯=+.试求：（1）671+的值；（2）nn ++11（n 为正整数）的值.（3122334989999100++++++++的值.第二章实数检测题参考答案一、选择题1.B 解析：即－32；,即－2－1即1223，所以选B.2.D 解析：8的平方根是±点拨：注意一个正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根．3.C 解析：∵ |a －2|0，∴ a ＝2，b ＝0,∴b －a ＝0－2=－2．故选C ．4.C 解析：A.，所以A 项正确；B.＝±1，所以1是1的一个平方根说法正确；C.4，所以C 项错误；D.00，所以D 项正确. 故选C ．5.D 解析：∵ 二次根式的被开方数为非负数，∴ 2－x ≥0，解得x ≤2.6.C 解析：∵a ，b 均为正整数，且a b a 的最小值是3，b 的最小值是2，则a ＋b 的最小值是5．故选C ．7.A2，所以在实数23-，0， 3.1423-，0，－3.14是无理数.8.C ＝－11，212c ⎛⎫- ⎪⎝⎭＝0，∴a ＝－1，b ＝1，c ＝12，∴abc ＝－12．故选C ．9.A 解析：根据偶次方、算术平方根的非负性，由(m -1)20,得m －1＝0，n ＋2＝0，解得m ＝1，n ＝－2，∴m ＋n ＝1＋(－2)=－1.10.D 解析：由图得64的算术平方根是8，8的算术平方根是故选D ．二、填空题11.604.2 ±0.019 1 604.2≈±0.019 1. 12.±3，±2，±1,0 解析：π≈3.14，大于－π的负整数有：－3，－2，－1，小于π的正整数有：3，2，1，0的绝对值也小于π.13.±0.06 3 解析：0.06±，9的算术平方根是3 3.14.8 解析：由|a －5|＝0，得a ＝5，b ＝－3，所以a －b ＝5－(－3) ＝8.15.11 解析：∵a＞28＞b，a，b为两个连续的整数，又25＜28＜36，∴a＝6，b＝5，∴a＋b＝11.16.1 解析：根据平方差公式进行计算，（2＋1）（2－1）＝()22－12＝2－1＝1.17.x≥0 解析：根据二次根式的被开方数必须是非负数，要使1+x有意义，必须满足x≥0.18.332解析：12－343333=23.222--==三、解答题19.解：因为，，即，所以.故，从而，所以，所以.20.解：∵ 2＜7＜3，∴ 7＜5+7＜8，∴a=7－2.又可得2＜5－7＜3，∴b=3－7.将a＝7－2，b=3－7代入ab＋5b中，得ab＋5b＝（7－2）（3－7）＋5（3－7）＝37－7－6＋27＋15－57＝2.21.解：根据题意，可知，因为，所以.22.分析：（1）可把6转化成带根号的形式，再比较它们的被开方数，即可比较大小；（2）可采用近似求值的方法来比较大小．解：（1）∵3635＜3635 6.（2）∵51≈－2.236+1＝－1.2362≈－0.707，1.236＞0.707，51223. 解：∵ 4＜5＜9，∴ 2＜＜3，∴ 7＜5＋＜8，∴ ＝－2.又∵ －2＞－＞－3，∴ 5－2＞5－＞5－3，∴ 2＜5－＜3，∴ b ＝2，∴ ＋b ＝－2＋2＝.24. 解：(1)原式＝62333223-+⨯ （2）原式＝()266321343-+--- ＝623663-+ ＝432213--. ＝136233-.1(76)25.17 6.76(76)(76)⨯-==-++-解：（）（2）1(1)11(1)(1)n n n n n n n n n n ⨯+-==+-+++++-.（3）122334989999100+++⋅⋅⋅+++++++＝－11001＋10＝9.第三章位置与坐标检测题（本检测题满分：100分，时间：90分钟）一、选择题（每小题3分，共30分）1.（2016•湖北荆门中考）在平面直角坐标系中，若点A （a ，﹣b ）在第一象限内，则点B （a ，b ）所在的象限是（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 2.在如图所示的直角坐标系中，点M ，N 的坐标分别为（） A . M （－1，2），N （2，1） B .M （2，－1），N （2，1） C.M （－1，2），N （1，2） D .M （2，－1），N （1，2）第2题图第3题图3.如图，长方形BCDE 的各边分别平行于x 轴或y 轴，物体甲和物体乙分别由点A （2，0）同时出发，沿长方形BCDE 的边作环绕运动，物体甲按逆时针方向以1个单位长度/秒匀速运动，物体乙按顺时针方向以2个单位长度/秒匀速运动，则两个物体运动后的第2012 次相遇点的坐标是（）A .（2，0）B .（－1，1）C .（－2，1）D .（－1，－1） 4.已知点P 的坐标为，且点P 到两坐标轴的距离相等，则点P 的坐标是（）A .（3，3）B .（3，－3）C .（6，－6）D .（3，3）或（6，－6）5.（2016•福州中考）平面直角坐标系中，已知平行四边形ABCD 的三个顶点坐标分别是A （m ，n ），B （2，﹣1），C （﹣m ，﹣n ），则点D 的坐标是（） A.（﹣2，1）B.（﹣2，﹣1）C.（﹣1，﹣2）D.（﹣1，2）6.在直角坐标系中，一个图案上各个点的横坐标和纵坐标分别加正数，那么所得的图案与原图案相比（）A .形状不变，大小扩大到原来的倍B .图案向右平移了个单位长度C .图案向上平移了个单位长度D .图案向右平移了个单位长度，并且向上平移了个单位长度7.（2016·武汉中考）已知点A (a ，1)与点A ′(5，b )关于坐标原点对称，则实数a 、b 的值是（） A ．a ＝5，b ＝1 B ．a ＝－5，b ＝1 C ．a ＝5，b ＝－1 D ．a ＝－5，b ＝－18.如图，若将直角坐标系中“鱼”的每个“顶点”的横坐标保持不变，纵坐标分别变为原来的21，则点A 的对应点的坐标是（） A .（－4，3） B .（4，3）C .（－2，6）D .（－2，3）9．如果点),(n m A 在第二象限,那么点,(m B │n │）在（）A .第一象限B .第二象限C .第三象限D .第四象限 10.（湖南株洲中考）在平面直角坐标系中，孔明做走棋游戏，其走法是：棋子从原点出发，第1步向右走1个单位，第2步向右走2个单位，第3步向上走1个单位，第4步向右走1个单位……依次类推，第n 步的走法是：当n 能被3整除时，则向上走1个单位；当n 被3除，余数是1时，则向右走1个单位，当n 被3除，余数为2时，则向右走2个单位，当走完第100步时，棋子所处位置的坐标是（） A .（66，34） B .（67，33） C .（100，33） D .（99，34）二、填空题（每小题3分，共24分）第8题图11.在平面直角坐标系中，点A （2，2m +1）一定在第象限． 12点和点关于轴对称，而点与点C （2,3）关于轴对称，那么，，点和点的位置关系是 .13.一只蚂蚁由点（0，0）先向上爬4个单位长度，再向右爬3个单位长度，再向下爬2个单位长度后，它所在位置的坐标是 . 14.（2015·南京中考）在平面直角坐标系中，点A 的坐标是（2,3）,作点A 关于x 轴的对称点，得到点A ′，再作点A ′关于y 轴的对称点，得到点A ″,则点A ″的坐标是（____,____）. 15.（2016·杭州中考）在平面直角坐标系中，已知A (2，3),B （0,1）， C （3,1），若线段AC 与BD 互相平分，则点D 关于坐标原点的对称点的坐标为 .16.如图，正方形ABCD 的边长为4，点A 的坐标为（－1，1），AB平行于x 轴，则点C 的坐标为 _.17.已知点(1)M a -，和(2)N b ，不重合. （1）当点M N ，关于对称时,21a b ==，；（2）当点M N ，关于原点对称时,a = ,b = .18.（2015·山东青岛中考）如图，将平面直角坐标系中“鱼”的每个“顶点”的纵坐标保持不变，横坐标分别变为原来的31，那么点A 的对应点A '的坐标是＿＿＿＿＿＿＿．第18题图三、解答题（共46分）19.（6分）如图所示，三角形ABC 三个顶点A ，B ，C 的坐标分别为A （1，2），B （4，3），C （3，1）.把三角形A 1B 1C 1向右平移4个单位长度，再向下平移3个单位长度，恰好得到三角形ABC ，试写出三角形A 1B 1C 1三个顶点的坐标.第19题图第20题图20.（6分）如图,在平面网格中每个小正方形的边长为1个单位长度，（1）线段CD 是线段AB 经过怎样的平移后得到的？（2）线段AC 是线段BD 经过怎样的平移后得到的？ 21.（6分）在直角坐标系中，用线段顺次连接点A （，0），B （0，3），C （3，3），D （4，0）．第16题图（1）这是一个什么图形；（2）求出它的面积；（3）求出它的周长．22.（6分）如图，点用表示，点用表示．若用→→→→表示由到的一种走法，并规定从到只能向上或向右走（一步可走多格），用上述表示法写出另两种走法，并判断这几种走法的路程是否相等．23.（6分）（湖南湘潭中考）在边长为1的小正方形网格中，△AOB的顶点均在格点上，（1）B点关于y轴的对称点的坐标为；（2）将△AOB向左平移3个单位长度得到△A1O1B1，请画出△A1O1B1；（3）在（2）的条件下，点A1的坐标为．24.（8分）如图所示.（1）写出三角形③的顶点坐标.（2）通过平移由三角形③能得到三角形④吗？（3）根据对称性由三角形③可得三角形①，②，它们的顶点坐标各是什么？25.（8分）有一张图纸被损坏，但上面有如图所示的两个标志点A（－3，1），B（－3，－3）可见，而主要建筑C（3，2）破损，请通过建立直角坐标系找到图中C点的位置．第三章位置与坐标检测题参考答案一、选择题1.D解析：根据各象限内点的坐标特征解答即可．∵点A（a，﹣b）在第一象限内，∴a＞0，﹣b＞0，∴b＜0，第22题图第23题图第24题图第25题图∴ 点B （a ，b ）所在的象限是第四象限．故选D ．2.A 解析：本题利用了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解题的关键，四个象限的符号特点分别是：第一象限（＋，＋）；第二象限（－，＋）；第三象限（－，－）；第四象限（＋，－）．3.D 解析：长方形的边长为4和2，因为物体乙的速度是物体甲的速度的2倍，时间相同，物体甲与物体乙的路程比为1︰2，由题意知： ①第一次相遇物体甲与物体乙行的路程和为12×1，物体甲行的路程为12×31=4，物体乙行的路程为12×32＝8，在BC 边相遇； ②第二次相遇物体甲与物体乙行的路程和为12×2，物体甲行的路程为12×2×31＝8，物体乙行的路程为12×2×32＝16，在DE 边相遇； ③第三次相遇物体甲与物体乙行的路程和为12×3，物体甲行的路程为12×3×31＝12，物体乙行的路程为12×3×32＝24，在A 点相遇，此时甲、乙回到出发点，则每相遇三次，两物体回到出发点.因为2 012÷3=670……2，故两个物体运动后的第2012次相遇点与第二次相遇点为同一点，即物体甲行的路程为 12×2×31=8，物体乙行的路程为12×2×32＝16，在DE 边相遇，此时相遇点的坐标为：（－1，－1），故选D ．4.D 解析：因为点P 到两坐标轴的距离相等，所以，所以a =－1或a =－4.当a =－1时，点P 的坐标为（3,3）；当a =－4时，点P 的坐标为（6，－6）. 5.A 解析：∵ A （m ，n ），C （﹣m ，﹣n ），∴ 点A 和点C 关于原点对称. ∵ 四边形ABCD 是平行四边形，∴ 点D 和B 关于原点对称. ∵ B （2，﹣1），∴ 点D 的坐标是（﹣2，1）．故选A ．6.D7.D 解析：因为点A (a ，1)与点A ′(5，b )关于坐标原点对称，而点（a ，b ）关于坐标原点的对称点的坐标是（-a ，-b ），所以a ＝－5，b ＝－1.故选D. 8.A 解析：点A 变化前的坐标为（－4，6），将横坐标保持不变，纵坐标变为原来的21，则点A 的对应点的坐标是（－4，3）,故选A ．9.A 解析:因为点A 在第二象限,所以,0,0><n m 所以,0>-m ︱n ︱＞0,因此点B 在第一象限. 10.C 解析：在1至100这100个数中：（1）能被3整除的为33个，故向上走了33个单位；（2）被3除，余数为1的数有34个，故向右走了34个单位；（3）被3除，余数为2的数有33个，故向右走了66个单位，故总共向右走了34＋66＝100（个）单位，向上走了33个单位.所以走完第100步时所处位置的横坐标为100，纵坐标为33.故选C .二、填空题11.一解析：因为2m ≥0，1＞0，所以纵坐标2m +1＞0.因为点A 的横坐标2＞0，所以点A 一定在第一象限． 12.关于原点对称解析：因为点A （a ,b ）和点关于轴对称，所以点的坐标为（a ,-b ）;因为点与点C （2,3）关于轴对称，所以点的坐标为（－2,3），所以a ＝－2,b ＝－3，点和点关于原点对称.13.（3，2）解析：一只蚂蚁由点（0，0）先向上爬4个单位长度，坐标变为（0，4），再向右爬3个单位长度，坐标变为（3，4），再向下爬2个单位长度，坐标变为（3，2），所以它所在位置的坐标为（3，2）. 14.3 解析：点A 关于x 轴的对称点A ′的坐标是（2，3），点A ′关于y 轴的对称点A ″的坐标是（2,3）.15.（-5，-3）解析：如图所示，∵ A （2，3），B （0，1），C （3，1），线段AC 与BD 互相平分，∴ D 点坐标为：（5，3），∴ 点D 关于坐标原点的对称点的坐标为（-5，-3）．第15题答图16.（3,5）解析：因为正方形ABCD 的边长为4，点A 的坐标为（－1，1），所以点C 的横坐标为4－1＝3，点C 的纵坐标为4＋1＝5，所以点C 的坐标为（3，5）．17.（1）x 轴（2）－2 1 解析:两点关于x 轴对称时,横坐标相等,纵坐标互为相反数;两点关于原点对称时,横、纵坐标都互为相反数. 18.（2，3）解析：点A 的坐标是（6，3），它的纵坐标保持不变，把横坐标变为原来的31，得到它的对应点A ＇的坐标是16,33⎛⎫⨯ ⎪⎝⎭，即A ＇（2，3）.三、解答题19.解：设△A 1B 1C 1的三个顶点的坐标分别为A 1（,将它的三个顶点分别向右平移4个单位长度，再向下平移3个单位长度，则此时三个顶点的坐标分别为（,由题意可得=2，2x ＋4＝4,2y －3＝3,3x ＋4＝3,3y －3＝1,所以A 1（－3,5），B 1（0,6），.20. 解：（1）将线段AB 向右平移3个单位长度（向下平移4个单位长度），再向下平移4个单位长度（向右平移3个单位长度），得线段CD .（2）将线段BD 向左平移3个单位长度（向下平移1个单位长度），再向下平移1个单位长度（向左平移3个单位长度），得到线段AC ． 21. 解：（1）因为点B （0，3）和点C （3，3）的纵坐标相同，点A 2,04,0D （－）和点（）的纵坐标也相同，所以BC ∥AD . 因为AD BC ，所以四边形是梯形．作出图形如图所示. （2）因为，，高，故梯形的面积是21227．（3）在Rt △中，根据勾股定理,得，同理可得，因而梯形的周长是．22.解：走法一：；走法二：.答案不唯一．路程相等.23.分析：（1）根据关于y 轴对称的点的横坐标互为相反数，纵坐标相等解答；（2）根据网格结构找出点A ，O ，B 向左平移后的对应点A 1，O 1，B 1的位置，然后顺次连接即可；（3）根据平面直角坐标系写出坐标即可．解：（1）B 点关于y 轴的对称点的坐标为（－3，2）；（2）△A 1O 1B 1如图所示；（3）点A 1的坐标为（－2，3）．第21题答图第23题答图24.分析：（1）根据坐标的确定方法，读出各点的横、纵坐标，即可得出各个顶点的坐标；（2）根据平移过程中点的坐标的变化规律：横坐标右移加，左移减；纵坐标上移加，下移减，可得三角形④不能由三角形③通过平移得到；（3）根据对称性，即可得到三角形①，②顶点的坐标．解：（1）（－1，－1），（－4，－4），（－3，－5）. （2）不能．（3）三角形②的顶点坐标分别为（－1，1），（－4，4），（－3，5）（三角形②与三角形③关于轴对称）；三角形①的顶点坐标分别为（1，1），（4，4），（3，5）（由三角形③与三角形①关于原点对称可得三角形①的顶点坐标）． 25.分析：先根据点A （－3，1），B （－3，－3）的坐标，确定出x 轴和y 轴，再根据C 点的坐标（3，2），即可确定C 点的位置．解：点C 的位置如图所示.第四章一次函数检测题（本检测题满分：100分，时间：90分钟）一、选择题（每小题3分，共30分）1.（2015•上海中考）下列y 关于x 的函数中，是正比例函数的为（）A .2y x = B .2y x =C .2x y =D .12x y +=2.（2016•南宁中考）已知正比例函数y =3x 的图象经过点（1，m ），则m 的值为（）A ．B ．3 C.﹣D.﹣33.（2016•陕西中考）设点A （a ，b ）是正比例函数y =﹣x 图象上的任意一点，则下列等式一定成立的是（）A ．2a +3b =0B ．2a ﹣3b =0C ．3a ﹣2b =0D ．3a +2b =04.（2016·湖南邵阳中考）一次函数y =﹣x +2的图象不经过的象限是（） A.第一象限 B.第二象限 C.第三象限 D.第四象限5.已知一次函数y ＝kx ＋b 中y 随x 的增大而减小，且kb ＜0，则在直角坐标系内它的大致图象是（）6.已知直线y ＝kx －4（k ＜0）与两坐标轴所围成的三角形面积等于4，则直线的表达式为（）A ．y ＝－x －4B ．y ＝－2x －4C ．y ＝－3x ＋4D ．y ＝－3x －47.小敏从A 地出发向B 地行走，同时小聪从B 地出发向A 地行走，如图所示，相交于点P 的两条线段l 1、l 2分别表示小敏、小聪离B 地的距离y km 与已用时间x h 之间的关系，则小敏、小聪行走的速度分别是（）A ．3 km/h 和4 km/hB ．3 km/h 和3 km/hC ．4 km/h 和4 km/hD ．4 km/h 和3 km/h8.若甲、乙两弹簧的长度y cm 与所挂物体质量x kg 之间的函数表达式分别为y =k 1x +b 1和y =k 2x +b 2，如图所示，所挂物体质量均为2 kg 时，甲弹簧长为y 1，乙弹簧长为y 2，则y 1与y 2的大小关系为（） A.y 1＞ y 2 B.y 1＝y 2 C.y 1＜y 2 D.不能确定 9.如图所示，已知直线l ：y =3x ，过点A （0，1）作y 轴的垂线交直线l 于点B ，过点B 作直线l 的垂线交y 轴于点A 1；过点A 1作y 轴的垂线交直线于点B 1，过点B 1作直线l 的垂线交y 轴于点A 2；…；按此作法继续下去，则点A 4的坐标为（） A ．（0，64） B ．（0，128） C ．（0，256） D ．（0，512）第7题图第9题图第10题图第8题图y x O yx O y x O y x O C10.如图所示，在平面直角坐标系中，直线y ＝23x －23与矩形ABCO 的边OC 、BC 分别交于点E 、F ，已知OA =3，OC =4，则△CEF 的面积是（）A ．6B ．3C ．12D ．43二、填空题（每小题3分，共24分）11. 已知函数y =（m －1）2m x ＋1是一次函数，则m = .12.（ 2015·天津中考）若一次函数y =2x +b （b 为常数）的图象经过点（1，5），则b 的值为 .13.已知A 地在B 地正南方3 km 处，甲、乙两人同时分别从A 、B 两地向正北方向匀速直行，他们与A 地的距离s （km ）与所行的时间t （h ）之间的函数图象如图所示，当行走3 h 后，他们之间的距离为 km. 14.（2015·海南中考）点（-1，1y ）、（2，2y ）是直线y =2x +1上的两点，则1y ________2y .（填“＞”或“＝”或“＜”） 15.如图所示，一次函数y =kx ＋b （k ＜0）的图象经过点A ．当y ＜3时，x 的取值范围是 .16.函数y =－3x ＋2的图象上存在点P ,使得点P •到x •轴的距离等于3，则点P •的坐标为 . 17.（浙江金华中考）小明从家跑步到学校，接着马上步行回家. 如图是小明离家的路程y （米）与时间t （分）的函数图象，则小明回家的速度是每分钟步行米．第17题图18.据有关资料统计，两个城市之间每天的电话通话次数T •与这两个城市的人口数m 、n （单位：万人）以及两个城市间的距离d （单位：km ）有T =2kmnd 的关系（k 为常数）．•现测得A 、B 、C 三个城市的人口数及它们之间的距离如图所示，且已知A 、B 两个城市间每天的电话通话次数为t ，那么B ，C 两个城市间每天的电话通话次数为_______（用t 表示）．三、解答题（共46分） 19.（6分）已知一次函数的图象经过点A （2，0）与B （0，4）．（1）求一次函数的表达式，并在直角坐标系内画出这个函数的图象；（2）如果（1）中所求的函数的值在－4≤≤4的范围内，求相应的的值在什么范围内．第15题图stO 4 2BA CD第18题图20.（6分）已知一次函数，（1）为何值时，它的图象经过原点？（2）为何值时，它的图象经过点（0，）?21.（6分）已知与成正比例，且时.（1）求与之间的函数关系式；（2）当时，求的值.22.（6分）如图，过A点的一次函数的图象与正比例函数y=2x的图象相交于点B，求这个一次函数的表达式.第22题图23.（6分）小李从西安通过某快递公司给在南昌的外婆寄一盒樱桃，快递时，他了解到这个公司除收取每次6元的包装费外，樱桃不超过1kg收费22元，超过1kg，则超出部分按每千克10元加收费用．设该公司从西安到南昌快寄樱桃的费用为y（元），所寄樱桃为x（kg）．（1）求y与x之间的函数表达式；（2）已知小李给外婆快寄了2.5kg樱桃，请你求出这次快寄的费用是多少元？24.（8分）已知某服装厂现有A种布料70米，B种布料52米，•现计划用这两种布料生产M、N两种型号的时装共80套．已知做一套M型号的时装需用A种布料1.1米，B种布料0.4米，可获利50元；做一套N型号的时装需用A种布料0.6米，B种布料0.9米，可获利45元．设生产M型号的时装套数为，用这批布料生产两种型号的时装所获得的总利润为y元．（1）求y（元）与（套）之间的函数表达式，并求出自变量的取值范围.（2）当生产M型号的时装多少套时，能使该厂所获利润最大？最大利润是多少？25.（8分）（2015·天津中考）1号探测气球从海拔5 m处出发，以1 m/min的速度上升.与此同时，2号探测气球从海拔15 m处出发，以0.5 m/min的速度上升.两个气球都匀速上升了50 min.设气球上升时间为x min（0≤x≤50）.（1上升时间/min 10 30 (x)1号探测气球所在位置的海拔/m 15 …2号探测气球所在位置的海拔/m 30 …（2能，请说明理由.（3）当30≤x≤50时，两个气球所在的位置的海拔最多相差多少米？第四章一次函数检测题参考答案一、选择题1.C 解析：2y x =中x 的指数是2，2y x =中2x 不是整式，2=x y 是正比例函数，111222x y x +==+是一次函数.2.C 解析：∵ 正比例函数y =3x 的图象经过点（1，m ），∴ 把点（1，m ）代入正比例函数y =3x ，可得m =3，故选B. 3.D 解析：把点A （a ，b ）代入正比例函数y =﹣x ，可得﹣3a =2b ，所以3a +2b =0，故选D.4.C 解析：∵ 一次函数y =﹣x +2中k =﹣1＜0，b =2＞0， ∴ 该函数图象经过第一、二、四象限．故选C ．5.A 解析：∵ 一次函数y ＝kx ＋b 中y 随着x 的增大而减小，∴ k ＜0.又∵ kb ＜0，∴ b ＞0，∴ 此一次函数图象经过第一、二、四象限，故选A ．6.B 解析：直线y =kx －4（k ＜0）与两坐标轴的交点坐标为（0，－4），40k ⎛⎫⎪⎝⎭，， ∵ 直线y =kx －4（k ＜0）与两坐标轴所围成的三角形面积等于4，∴ 4×4k ⎛⎫- ⎪⎝⎭×12=4，解得k =－2，则直线的表达式为y =－2x －4．故选B ．7.D 解析：∵ 通过图象可知的函数表达式为=3，的函数表达式为=－4+11.2 , ∴ 小敏行走的速度为11.2÷2.8=4（km/h ），小聪行走的速度为4.8÷1.6=3（km/h ）.故选D. 8.A 解析：∵ 点（0，4）和点（1，12）在上， ∴ 得到方程组解得∴ y 1＝8x ＋4（x ＞0）．∵ 点（0，8）和点（1，12）在上， ∴ 得到方程组解得∴ y 2＝4x ＋8（x ＞0）．当时，，，∴ ．故选A ．9.C 解析：∵ 点A 的坐标是（0，1），∴ OA =1.∵ 点B 在直线y =3x 上， ∴ OB =2，∴ OA 1=4，∴ OA 2=16，得出OA 3=64，∴ OA 4=256， ∴ A 4的坐标是（0，256）．故选C ．10.B 解析：当y =0时，23x －23=0，解得=1，∴ 点E 的坐标是（1，0），即OE =1.∵ OC =4，∴ EC =OC －OE =4－1=3，点F 的横坐标是4，∴ y =23×4－23=2，即CF =2.∴ △CEF 的面积=·CE ·CF =×3×2=3．故选B ．二、填空题11.－1 解析：若两个变量和y 间的关系式可以表示成y =k +b （k ，b 为常数，k ≠0）的形式，则称y 是的一次函数（为自变量，y 为因变量）．因而有m 2=1，解得m =±1.又m －1≠0，∴ m =－1． 12. 3 解析：一次函数y =2x +b 的图象经过点（1,5），所以5=2+b ，解得b =3. 13.23解析：由题意可知甲走的是路线，乙走的是路线，因为直线过点（0，0），（2，4），所以．因为直线过点（2，4），（0，3），所以.当时，．14.＜解析：∵ 一次函数y =2x +1中k =2＞0，∴ y 随x 的增大而增大，∵ -1＜2，由21x x <，得1y ＜2y .15.x ＞2 解析：由函数图象可知，此函数y 随x 的增大而减小，当y =3时，x =2，故当y ＜3时，x ＞2．故答案为x ＞2. 16.13⎛⎫- ⎪⎝⎭，3或53⎛⎫ ⎪⎝⎭，-3 解析：∵ 点P 到轴的距离等于3，∴ 点P 的纵坐标为3或－3. 当时，；当时，，∴ 点P 的坐标为或．17.80 解析：由图象知，小明回家走了15－5＝10（分钟），路程是800米，故小明回家的速度是每分钟步行80010＝80（米）.18.2t 解析：根据题意，有t =25080160⨯k ，∴ k =325t ．因此，B 、C 两个城市间每天的电话通话次数为T BC =k ×280100325.5642320t t⨯=⨯=三、解答题19. 解：（1）由题意，得20,2,4,4,a b a b b +==-⎧⎧⎨⎨==⎩⎩解得 ∴ 这个一次函数的表达式为，函数图象如图所示．（2）∵ ，－4≤≤4，第19题答图∴－4≤≤4，∴0≤≤4．20.分析：（1）把点的坐标代入一次函数表达式，并结合一次函数的定义求解即可；（2）把点的坐标代入一次函数表达式即可．解：（1）∵图象经过原点，∴点（0，0）在函数图象上，代入函数表达式，得，解得．又∵是一次函数，∴3－k≠0，∴k≠3．故符合．∴当k为9时，它的图象经过原点.（2）∵图象经过点（0，），∴（0，－2）满足函数表达式，代入，得－2＝－2k＋18，解得．由（1）知k≠3，故符合.∴当k为10时，它的图象经过点（0，－2）.21.解：（1）因为与成正比例，所以可设将代入，得所以与之间的函数关系式为（2）将代入，得=1.22.解：∵B点在正比例函数y=2x的图象上，横坐标为1，∴y=2×1=2，∴B（1，2）.设这个一次函数表达式为y=kx+b，∵这个一次函数的图象过点A（0，3），与正比例函数y=2x的图象相交于点B（1，2），∴可得出方程组32bk b=⎧⎨+=⎩，，解得31bk=⎧⎨=-⎩，，则这个一次函数的表达式为y=－x+3.23.分析：（1）根据快递的费用=包装费+运费，当0＜x≤1和x＞1时，可以求出y与x之间的函数表达式；（2）由（1）的表达式可以得出x=2.5＞1，代入表达式就可以求解．解：（1）由题意，得当0＜x≤1时，y=22+6=28；当x＞1时，y=28+10（x－1）=10x＋18，∴y=()()01 1018.1xx x⎧<≤⎨+>⎩28，（2）当x=2.5时，y=10×2.5+18=43．∴小李这次快寄的费用是43元．24.解：（1）．∵两种型号的时装共用A种布料[1.1+0.•6（80－）]米≤70米，共用B种布料[0.4+0.9（80－）]米≤52米，解得40≤≤44.而为整数，∴=40，41，42，43，44，∴y与的函数表达式是y=5+3 600（=40，41，42，43，44）.（2）∵y随的增大而增大，∴当=44时，y最大=3 820，即生产M型号的时装44套时，该厂所获利润最大，最大利润是3 820元．25.解：（1）35，x+5;20,0.5x+15。

北师大版八年级上册数学第一二章测试题及参考答案

八年级数学上册第一、二章测试题一．填空题：（每小题2分，共20分）1．已知直角三角形的三边长为6、8、x ，x 为斜边，则以x 为边的正方形的面积为____ _； 2．如右图：图形A 的面积是；3．2)3(-=________，327- =_________， 0)5(-的立方根是；4．210-的算术平方根是，16的平方根是；5．计算(508)2-÷的结果是． 6．比较下列实数的大小（在填上 > 、< 或＝） ①3-2-； ②215- 21； ③112 53。

7．若a 、b 互为相反数，c 、d 互为倒数，则______3=++cd b a ；8．在2,3.0,10,1010010001.0,125,722,0,1223π---•- 中，负无理数集合：｛｝；9．有两棵树，一棵高6米，另一棵高2米，两树相距5米，一只小鸟从一棵树的树梢飞到另一棵树的树梢，至少飞了米； 10．一只蚂蚁从长、宽都是3，高是8的长方体纸箱的A 点沿纸箱爬到B 点，那么它所行的最短路线的长是_____________；二．选择题：（每小题3分，共24分） 11、数轴上点P 表示的数可能是（）A 、B 、C 、D 、12．五根小木棒，其长度分别为7，15，20，24，25，现将他们摆成两个直角三角形，其中正确的是（）715242520715202425157252024257202415(A)(B)(C)(D)13．已知一直角三角形的木版，三边的平方和为1800cm 2，则斜边长为（）（A ） 80cm （B ） 30cm （C ） 90cm （D ） 120cmAB第10题图144225A14．下列语句中正确的是（）（A ）9-的平方根是3-（B ）9的平方根是3（C ）9的算术平方根是3±（D ）9的算术平方根是3 15．下列运算中，错误的是（） ①1251144251=，②4)4(2±=-，③22222-=-=-，④2095141251161=+=+ （A ） 1个（B ） 2个（C ） 3个（D ） 4个16．若9,422==b a ，且0<ab ，则b a -的值为（）（A ） 2- （B ） 5± （C ） 5 （D ） 5-17、如下图，正方形网格中，每个小正方形的边长为1，则网格上的三角形ABC 中，边长为无理数的边数为（）A ．0B ．1C ．2D ．318、如图，有一块直角三角形纸片，两直角边AC=6cm,BC=8cm,现将直角边AC 沿直线AD 折叠，使它落在斜边AB 上，且与AE 重合，则CD 等于（）A. 2cmB. 3cm B.C. 4cmD. 5cm三．计算题：（每小题3分，共20分） 19． 24612⨯ )32)(32(-+()2132-7002871+- |322|21121--⎪⎭⎫⎝⎛--19、（6分）求下列图形中阴影部分的面积.（2）1414220、（6分）请在同一个数轴上用尺规作出 2 和 5 的对应的点。

(完整版)北师大版八年级上册数学第一章《勾股定理》单元测试卷(含答案),推荐文档

7 7第一章《勾股定理》单元测试卷班别：姓名：一、选择题（本题共10 小题，每小题3 分，满分30 分）1.一直角三角形的斜边长比一直角边长大2，另一直角边长为6，则斜边长为（）A．4 B．8 C．10 D．122.已知a=3，b=4，若a，b，c 能组成直角三角形，则c=（）A.5B.C.5 或D.5 或63.如图中字母A 所代表的正方形的面积为（）A．4 B．8 C．16 D．644.将直角三角形的三条边长同时扩大同一倍数，得到的三角形是（）A．钝角三角形B．锐角三角形C．直角三角形D．等腰三角形5．直角三角形的一直角边长是7cm，另一直角边与斜边长的和是49cm，则斜边的长（）A．18cm B．20cm C．24cm D．25cm6．适合下列条件的△ABC 中，直角三角形的个数为（）①a= ，b=，c= ②a=6，∠A=45°；③∠A=32°，∠B=58°；④a=7，b=24，c=25 ⑤a=2，b=2，c=4A．2 个B．3 个C．4 个D．5 个7．在△ABC 中，若a=n2﹣1，b=2n，c=n2+1，则△ABC 是（）A．锐角三角形B．钝角三角形C．等腰三角形D．直角三角形3 8. 直角三角形斜边的平方等于两条直角边乘积的2 倍，这个三角形有一个锐角是（） A ．15°B ．30°C ．45°D ．60°9. 已知，如图长方形 ABCD 中，AB=3cm ，AD=9cm ，将此长方形折叠，使点B 与点 D 重合，折痕为 EF ，则△ABE 的面积为（） A ．3cm 2B ．4cm 2C ．6cm 2 D.12cm 210. 已知，如图，一轮船以 16 海里/时的速度从港口 A 出发向东北方向航行，另一轮船以 12 海里/时的速度同时从港口 A 出发向东南方向航行，离开港口 2 小时后，则两船相距（） A ．25 海里B ．30 海里C ．35 海里D ． 40 海里二、填空题（本题共 8 小题，每小题 3 分，满分 24 分）11. 一个三角形三边长度之比为 1∶2∶ ，则这个三角形的最大角为度．12. 如图，等腰△ABC 的底边 BC 为 16，底边上的高 AD 为 6，则腰长 AB 的长为． 13．如图，某人欲横渡一条河，由于水流的影响，实际上岸地点 C 偏离欲到达点 B200m ，结果他在水中实际游了 520m ，求该河流的宽度为m ．14.小华和小红都从同一点O 出发，小华向北走了9 米到A 点，小红向东走到B 点时,当两人相距为15 米，则小红向东走了米．15.一个三角形三边满足(a +b)2 -c2 = 2ab ,则这个三角形是三角形．16.木工做一个长方形桌面，量得桌面的长为60cm，宽为32cm，对角线为68cm，这个桌面（填”合格”或”不合格”）．17.直角三角形一直角边为12cm，斜边长为13cm，则它的面积为cm2．18.如图，一个三级台阶，它的每一级的长宽和高分别为20、3、2，A 和B 是这个台阶两个相对的端点，A 点有一只蚂蚁，想到B 点去吃可口的食物，则蚂蚁沿着台阶面爬到B 点最短路程是．三、解答题（共46 分）19.在RtΔABC 中，∠A CB=90°，AB=5，AC=3，CD⊥AB 于D，求CD 的长．CA BD21．（7 分）如图，在△ABC 中，AD⊥BC 于D，AB=3，BD=2，DC=1，求AC 的值．22．（8 分）如图，一个牧童在小河的南4km 的A 处牧马，而他正位于他的小屋B 的西8km 北7km 处，他想把他的马牵到小河边去饮水，然后回家.他要完成这件事情所走的最短路程是多少？小河北牧童A东B 小屋23．如图，A 城气象台测得台风中心在A 城正西方向320km 的B 处，以每小时40km 的速度向北偏东60°的BF 方向移动，距离台风中心200km 的范围内是受台风影响的区域．（1）A 城是否受到这次台风的影响？为什么？（2）若 A 城受到这次台风影响，那么 A 城遭受这次台风影响有多长时间？《勾股定理》单元测试卷答案一、选择题（共10 小题，每小题3 分，满分30 分）1．C．2．C．3．D．4．C．5．D．6．A．7．D．8．C．9．C．10．D．二、填空题（共8 小题，每小题3 分，满分24 分）11．900 ．12．10 ．13．480 m．14．12 米．15．直角．16．合格．17．30 cm2．18．25 ．三、解答题（共46 分）19．略20．解：∵∠ACB=90°，AB=5，AC=3，∴BC2 = AB2 -AC2=42，∴BC=4，∵CD⊥AB，1 1 12∴AB·CD= AC·BC，∴5CD=12，∴CD=．2 2 5．21.解：∵AD⊥BC 于D，∴∠ADB=∠ADC=90°∵AB=3，BD=2∴AD2=AB2﹣BD2=5∵DC=1，∴AC2=AD2+DC2=5+1=6．∴AC=22.解：设矩形的长是a，宽是b，根据题意，得：，（2）+（1）×2，得（a+b）2=196，即a+b=14，所以矩形的周长是14×2=28m．23.如图，作出A 点关于MN 的对称点A′，则A′A=8 km,连接A′B 交MN 于点P，则A′B 就是最短路线.在Rt△A′DB 中，A′D=15 km,BD=8 km由勾股定理得A′B2= A′D 2+BD2=289∴A′D =17kmA′M P NAD B24.解：（1）由A 点向BF 作垂线，垂足为C，在Rt△ABC 中，∠ABC=30°，AB=320km，则AC=160km，因为160＜200，所以A 城要受台风影响；（2）设BF 上点D，DA=200 千米，则还有一点G，“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。

北师大版八年级数学(上)第一二三章测试试卷完整版.doc

北师大版八年级数学(上)第一二三章测试试卷一选择题（每小题3分，共36分）1下列四组数据中，不能．．作为直角三角形的三边长是（）（A ）3，4，6 （B ）7，24，25 （C ）6，8，10 （D ）9，12，152、已知三角形的三边长为6，8，10，则这个三角形最长边上的高是（） A 、10 B 、 8 C 、2.4 D 4.8 3. 下列计算结果正确的是（）A. 332=）（－B. 636±=C. 523=+D.35323=+4．在平面直角坐标系中，点A （1，－3）在（）（A ）第一象限（B ）第二象限（C ）第三象限（D ）第四象限5、在-2)5(-、2π、4.0、71、0 、311 中无理数个数为（）A 、1个B 、2个C 、3个D 、4个6、三角形的三边长c b a ,,满足()bc a b c 222+=+,则这个三角形是( )A 、等边三角形B 、钝角三角形C 、直角三角形D 、锐角三角形7、下列计算正确的是（）A 、235=-B 、()ππ-=-332C 、5315=D 、1535=⨯ 8、分析下列说法：①实数与数轴上的点一一对应；②2a -没有平方根；③任何实数的立方根有且只有一个；④平方根与立方根相同的数是0和1。

其中正确的有（）A 、1个B 、2个C 、3个D 、4个9. 如图，在直角坐标系中，△AOB 是等边三角形，若B 点的坐标是（2，0），则A 点的坐标是（）A. （2，1） B.（1，2）4cm2cm5cmPQC.（3，1 ）D.（1， 3 ）10、已知点P （1，－2），点Q(－1，2)，点 R (－1，－2)，点H(1,2)，下面选项中关于y 轴对称的是（）.A. P 和Q B. P 和H C. Q 和R D. P 和R11、估算243+的值（） A 、在5和6之间B 、在6和7之间C 、在7和8之间D 、在8和9之间12．实数a 、b 在数轴上对应点的位置如图，则2a b a --的结果是( )A 、2a-bB 、b-2aC 、bD 、-b二、填空题（每小题3分，共18分）13、16的算术平方根是 , 14．比较大小：23-______32-． 15已知点A （2，y ）与点B （x ，－3）关于x 轴对称，则xy ＝__________ 16、已知实数a 、b 满足()0622=++-b a ，那么（b a -）的立方根是 ,17．如右图，长方体的底面边长分别为2 cm 和4 cm ，高为5 cm ．若一只蚂蚁从P 点开始经过4个侧面爬行一圈到达Q 点，则蚂蚁爬行的最短路径长为cm ．18、如下图，一块直角三角形的纸片，两直角边6c m A C =，8c m B C =．现将直角边AC 沿直线AD 折叠，使它落在斜边AB 上，且与AE 重合，则C D 等于三、计算题（每题2分，共16分）19、（1）2)221(- 2)32(- 24612⨯（2）、（2 +3）2 （3）、baDBEADCBA （4）（5）3181083315275－－+（6）483122+四、解答题：20、（7分）如图所示的一块草坪，已知AD =12m ，CD =9m ，∠ADC =90°，AB =39 m ，BC =36 m ，求这块草坪的面积．21（6分）、已知x-1的平方根是±3，2x+y+7的立方根是2，求 7-x-y 的平方根。

北师大版数学八年级上册全册单元测试题(附答案_可打印)

北师大版八年级数学上册单元测试卷（含答案）第一章勾股定理测试题一、选择题1、下列各组数中不能作为直角三角形的三边长的是 ( ) A. 1.5, 2, 3; B. 7, 24, 25; C. 6 ,8, 10; D. 9, 12, 15.2、适合下列条件的△ABC 中, 是直角三角形的个数为 ( ) ①;51,41,31===c b a ②,6=a ∠A=450; ③∠A=320, ∠B=580; ④ ;25,24,7===c b a ⑤.4,2,2===c b aA. 2个;B. 3个;C. 4个;D. 5个.3、已知直角三角形两直角边的长为A 和B ，则该直角三角形的斜边的长度为（） A 、A ＋B B 、2AB C 、B -A D 、22B A +4、直角三角形的两直角边分别为5厘米、12厘米，则斜边上的高是（） A 、6厘米 B 、8厘米 C 、1380厘米 D 、1360厘米5、若等腰三角形腰长为10cm ，底边长为16 cm,那么它的面积为 ( )A. 48 cm 2B. 36 cm 2C. 24 cm 2D.12 cm 26、如图，一棵大树在一次强台风中于离地面5米处折断倒下，倒下部分与地面成30°夹角，这棵大树在折断前的高度为（） A ．10米 B ．15米 C ．25米 D ．30米7、若一个直角三角形的一条直角边长是7cm ，另一条直角边比斜边短1cm ，则斜边长为（） A.18 cm B.20 cm C.24 cm D.25 cm8、一部电视机屏幕的长为58厘米,宽为46厘米,则这部电视机大小规格（实际测量误差忽略不计）（）A.34英寸（87厘米）B. 29英寸（74厘米）C. 25英寸（64厘米）D.21英寸（54厘米）9、一块木板如图所示，已知AB ＝4，BC ＝3，DC ＝12，AD ＝13，∠B ＝90°，木板的面积为( )A ．60B ．30C ．24D ．1210、小明想知道学校旗杆的高，他发现旗杆上的绳子垂到地面还多1m ，当它把绳子的下端拉开5m 后，发现下端刚好接触地面，则旗杆的高为（） A ．8cm B ．10cm C ．12cm D ．14cm30°6 A DBC第9题北南 A 东第12题图11、已知Rt △ABC 中，∠C ＝90°，若14=+b a cm ，10=c cm ，则Rt △ABC 的面积为（）．A.24cm 2B.36cm 2C.48cm 2D.60cm 212、已知，如图，一轮船以16海里/时的速度从港口A 出发向东北方向航行，另一轮船以12海里/时的速度同时从港口A 出发向东南方向航行，离开港口2小时后，则两船相距（） A 、25海里 B 、30海里 C 、35海里 D 、40海里二、填空题13、在△ABC 中，∠C ＝90°，若 a ＝5，b ＝12，则 c ＝． 14、在△ABC 中，∠C ＝90°，若c ＝10，a ∶ b ＝3∶4，则S Rt △AB ＝．15、如图，从电线杆离地面3米处向地面拉一条长为5米的拉线，这条拉线在地面的固定点距离电线杆底部有米。

北师大版八年级数学数学上册单元测试题全套

北师大版八年级数学数学上册单元测试题全套(含答案)(总44页) --本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--北师大版八年级数学上册单元测试题全套（含答案）第一章检测卷(120分，90分钟)题号一二三总分得分一、选择题(每题3分，共301．下列各组数中，能够作为直角三角形的三边长的一组是( )A．1，2，3 B．2，3，4 C．4，5，6 D．3，4，52．在Rt△ABC中，∠C＝90°，若角A，B，C所对的三边分别为a，b，c，且a＝7，b＝24，则c的长为( )A．26 B．18 C．25 D．21(第3题)3．如图中有一个正方形，此正方形的面积是( )A．16 B．8 C．4 D．24．适合下列条件的△ABC中，直角三角形的个数为( )①a＝6，b＝8，c＝10；②a∶b∶c＝1∶2∶2；③∠A＝32°，∠B＝58°；④a＝8，b＝15，c＝17.A．1个 B．2个 C．3个 D．4个5．若△ABC的三边长分别为a，b，c，且满足(a－b)(a2＋b2－c2)＝0，则△ABC是( )A．直角三角形 B．等腰三角形C．等腰直角三角形 D．等腰三角形或直角三角形(第6题)6．如图是医院、公园和超市的平面示意图，超市在医院的南偏东25°的方向，且到医院的距离为300 m，公园到医院的距离为400 m．若公园到超市的距离为500 m，则公园在医院的( )A．北偏东75°的方向上 B．北偏东65°的方向上C．北偏东55°的方向上 D．无法确定7．如图，将长方形纸片ABCD折叠，使边DC落在对角线AC上，折痕为CE，且D点落在对角线上的D′处．若AB＝3，AD＝4，则ED的长为( )B．3 C．1(第7题) (第8题) (第9题) (第10题)8．如图，在△ABC中，AD是BC边上的中线，AC＝17，BC＝16，AD＝15，则△ABC的面积为( )A．128 B．136 C．120 D．2409．如图，长方形ABCD的对角线AC＝10，BC＝8，则图中五个小长方形的周长和为( )A．14 B．16 C．20 D．2810．如图，长方体的高为9 m，底面是边长为6 m的正方形，一只蚂蚁从顶点A开始，爬向顶点B，那么它爬行的最短路程为( )A．10 m B．12 m C．15 m D．20 m二、填空题(每题3分，共24分)11．在Rt△ABC中，a，b为直角边，c为斜边，若a2＋b2＝16，则c＝________．12．如图，在△ABC中，AB＝5 cm，BC＝6 cm，BC边上的中线AD＝4 cm，则∠ADB＝________．(第12题) (第13题) (第17题) (第18题)13．如图，一架长为4 m的梯子，一端放在离墙脚m处，另一端靠墙，则梯子顶端离墙脚________．14．木工师傅要做一个长方形桌面，做好后量得长为80 cm，宽为60 cm，对角线长为100 cm，则这个桌面________．(填“合格”或“不合格”)15．若直角三角形的两边长为a，b，且满足(a－3)2＋|b－4|＝0，则该直角三角形的斜边长为________．16．在△ABC中，AB＝13 cm，AC＝20 cm，BC边上的高为12 cm，则△ABC的面积为________．17．如图，以Rt△ABC的三边为斜边分别向外作等腰直角三角形．若斜边AB＝3，则图中阴影部分的面积为________．18．《中华人民共和国道路交通安全法实施条例》规定：小汽车在没有道路中心线的城市街道上的行驶速度不得超过30 km/h.如图，一辆小汽车在一条没有道路中心线的城市街道上直道行驶时，某一时刻刚好行驶到路对面车速检测仪观测点A正前方30 m的C处，过了4 s后，行驶到B处的小汽车与车速检测仪间的距离变为50 m．请你判断：这辆小汽车________．(填“超速”或“未超速”)三、解答题(19～21题每题8分，22～24题每题10分，25题12分，共66分)19．如图，正方形网格中有△ABC，若小方格的边长为1，请你根据所学的知识解答下列问题：(1)求△ABC的面积；(2)判断△ABC是什么形状，并说明理由．(第19题)20．如图，在△ADC中，AD＝15，AC＝12，DC＝9，点B是CD延长线上一点，连接AB.若AB＝20，求△ABD的面积．(第20题)21．已知一个直角三角形的周长是12 cm，两条直角边长的和为7 cm，则此三角形的面积是多少？22．如图，将断落的电线拉直，使其一端在电线杆顶端A处，另一端落在地面C处，这时测得BC＝6 m，再把电线沿电线杆拉直，且电线上的D点刚好与B点重合，并量出电线剩余部分(即CD)的长为2 m，你能由此算出电线杆AB的高吗？(第22题)23．如图，在△ABC中，AB∶BC∶CA＝3∶4∶5，且周长为36 cm，点P从点A开始沿AB边向B点以1 cm/s 的速度移动，点Q从点B开始沿BC边向点C以2 cm/s的速度移动，如果同时出发，问过3 s时，△BP Q的面积为多少？(第23题)24．如图，圆柱形玻璃容器高19 cm，底面周长为60 cm，在外侧距下底cm的点A处有一只蜘蛛，在蜘蛛正对面的圆柱形容器的外侧，距上底cm处的点B处有一只苍蝇，蜘蛛急于捕捉苍蝇充饥，请你帮蜘蛛计算它沿容器侧面爬行的最短距离．(第24题)25．图甲是任意一个直角三角形ABC ，它的两条直角边长分别为a ，b ，斜边长为c.如图乙、丙那样分别取四个与直角三角形ABC 全等的三角形，放在边长为a ＋b 的正方形内．(1)由图乙、图丙，可知①是以________为边长的正方形，②是以________为边长的正方形，③的四条边长都是________，且每个角都是直角，所以③是以________为边长的正方形．(2)图乙中①的面积为________，②的面积为________，图丙中③的面积为________． (3)图乙中①②面积之和为________．(4)图乙中①②的面积之和与图丙中③的面积有什么关系为什么由此你能得到关于直角三角形三边长的关系吗(第25题)答案一、 7．A二、 ° m 14.合格或5 cm 2或66 cm 218.超速三、19.解：(1)用正方形的面积减去三个三角形的面积即可求出△ABC 的面积．S △ABC ＝4×4－12×1×2－12×4×3－12×2×4＝5，所以△ABC 的面积为5.(2)△ABC 是直角三角形．理由如下：因为AB 2＝12＋22＝5，AC 2＝22＋42＝20，BC 2＝32＋42＝25，所以AC 2＋AB 2＝BC 2.所以△ABC 是直角三角形．20．解：在△ADC 中，因为AD ＝15，AC ＝12，DC ＝9，所以AC 2＋D C 2＝122＋92＝152＝AD 2.所以△ADC 是直角三角形，且∠C＝90°.在Rt △ABC 中，AC 2＋BC 2＝AB 2，所以BC ＝16.所以BD ＝BC －DC ＝16－9＝7.所以S △ABD ＝12×7×12＝42.21．解：设两条直角边长分别为a cm ，b cm ，斜边长为c cm .由题意可知a ＋b ＋c ＝12①，a ＋b ＝7②，a 2＋b 2＝c 2③，所以c ＝12－(a ＋b)＝5，(a ＋b)2＝a 2＋b 2＋2ab ＝49，2ab ＝49－25＝24.所以ab ＝12.所以S ＝12ab ＝12×12＝6(cm 2)．22．解：设AB ＝x m ，则AC ＝AD ＋CD ＝AB ＋CD ＝(x ＋2)m .在Rt △ABC 中，有(x ＋2)2＝x 2＋62，解得x ＝8.即电线杆AB 的高为8 m .23．解：设AB 为3x cm ，则BC 为4x cm ，AC 为5x cm . 因为△ABC 的周长为36 cm ，所以AB ＋BC ＋AC ＝36 cm ，即3x ＋4x ＋5x ＝36.解得x ＝3. 所以AB ＝9 cm ，BC ＝12 cm ， AC ＝15 cm .因为AB 2＋BC 2＝AC 2，所以△ABC 是直角三角形，且∠B＝90°.过3 s 时，BP ＝9－3×1＝6(cm )，BQ ＝2×3＝6(cm )，所以S △BPQ ＝12BP·BQ＝12×6×6＝18(cm 2)．故过3 s 时，△BPQ 的面积为18 cm 2.24．解：如图，将圆柱侧面展开成长方形MNQP ，过点B 作BC⊥MN 于点C ，连接AB ，则线段AB 的长度即为所求的最短距离．在Rt △ACB 中，AC ＝MN －AN －CM ＝16 cm ，BC 的长等于上底面的半圆周的长，即BC ＝30 cm .由勾股定理，得AB 2＝AC 2＋BC 2＝162＋302＝1 156＝342，所以AB ＝34 cm .故蜘蛛沿容器侧面爬行的最短距离为34 cm .(第24题)25．解：(1)a ；b ；c ；c (2)a 2；b 2；c 2(3)a 2＋b 2(4)图乙中①②的面积之和与图丙中③的面积相等．由大正方形的边长为a ＋b ，得大正方形的面积为(a ＋b)2，图乙中把大正方形分成了四部分，分别是边长为a 的正方形，边长为b 的正方形，还有两个长为a ，宽为b 的长方形．根据面积相等得(a ＋b)2＝a 2＋b 2＋2ab.由图丙可得(a ＋b)2＝c 2＋4×12ab.所以a 2＋b 2＝c 2.能得到关于直角三角形三边长的关系：两直角边的平方和等于斜边的平方．第二章检测卷(120分，90分钟)一、选择题(每题3分，共30分) 1．9的平方根是( ) A ．±3 B．±13C ．3D ．－32．下列4个数：9，227，π，(3)0，其中无理数是( )C ．πD ．(3)03．下列说法错误的是( )A ．1的平方根是1B ．－1的立方根是－1 是2的一个平方根 D ．－3是(－3)2的一个平方根 4．下列各式计算正确的是( ) ＋3＝ 5 B ．43－33＝1 C ．23×23＝4 3 ÷3＝3 5．已知a ＋2＋|b －1|＝0，那么(a ＋b)2 017的值为( )A ．－1B ．1C ．32 017D ．－32 0176．若平行四边形的一边长为2，面积为45，则此边上的高介于( ) A ．3与4之间 B ．4与5之间 C ．5与6之间 D ．6与7之间7．实数a ，b 在数轴上对应点的位置如图所示，且|a|＞|b|，则化简a 2－|a ＋b|的结果为( )(第7题)A ．2a ＋bB ．－2a ＋bC ．bD ．2a －b8．已知a ，b 为Rt △ABC 的两直角边的长，且斜边长为6，则a 2＋b 2－3的值是( ) A ．3 B ．6 C ．33 D ．369．已知a ＝3＋2，b ＝3－2，则a 2＋b 2的值为( ) A ．4 3 B ．14 D ．14＋4310．若6－13的整数部分为x ，小数部分为y ，则(2x ＋13)y 的值是( ) A ．5－313 B ．3 C ．313 D ．－3 二、填空题(每题3分，共24分)的相反数是________；绝对值等于2的数是________．12．若式子x ＋1在实数范围内有意义，则x 的取值范围是________． 13．估算比较大小：(1)－10________－；(2)3130________5. 14．计算：8＋(－1)2 018－|－2|＝________．15．已知x ，y 都是实数，且y ＝x －3＋3－x ＋4，则y x＝________. 16．若2x ＋7＝3，(4x ＋3y)3＝－8，则3x ＋y ＝________．17．一个长方形的长和宽分别是6 2 cm 与2cm ，则这个长方形的面积等于________，周长等于________． 18．任何实数a ，可用[a]表示不超过a 的最大整数，如[4]＝4，[3]＝1.现对72进行如下操作：72――→第一次[72]＝8――→第二次[8]＝2――→第三次[2]＝1，这样对72只需进行3次操作后变为1，类似地，对81只需进行________次操作后变为1；只需进行3次操作后变为1的所有正整数中，最大的是________．三、解答题(20题12分，23，24题每题8分，25，26题每题10分，其余每题6分，共66分) 19．求下列各式中x 的值．(1)4x 2＝25； (2)(x －3＝.20．计算下列各题：(1)8＋32－2； (2)3216－3－3－38×400；(3)(6－215)×3－612； (4)(548－627＋12)÷ 3.21.已知a ，b ，c 在数轴上对应点的位置如图所示，化简：||a －||a ＋b ＋（c －a ）2＋||b －c .(第21题)22．已知x ＝1－2，y ＝1＋2，求x 2＋y 2－xy －2x ＋2y 的值．23．一个正方体的表面积是2 400 cm 2. (1)求这个正方体的体积；(2)若该正方体的表面积变为原来的一半，则体积变为原来的多少？24．如图，在四边形ABCD中，AB＝AD，∠BAD＝90°，若AB＝22，CD＝43，BC＝8，求四边形ABCD的面积．(第24题)25．“保护环境，节约资源”一直是现代社会所提倡的．墨墨参加了学校组织的“节约资源，废物利用”比赛，他想将一个废旧易拉罐的侧面制作成一个正方体(有底有盖)的储存盒，经过测量得知废旧易拉罐的高是20 cm，底面直径是10 cm，废旧易拉罐的侧面刚好用完，正方体储存盒的接头部分忽略不计．求墨墨所做的正方体储存盒的棱长．(π取3)26．阅读材料：小王在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如3＋22＝(1＋2)2.善于思考的小王进行了以下探索：设a＋b2＝(m＋n2)2(其中a，b，m，n均为整数)，则有a＋b2＝m2＋2n2＋2mn 2.所以a＝m2＋2n2，b＝2mn.这样小王就找到了一种把类似a＋b2的式子化为平方式的方法．请你仿照小王的方法探索并解决下列问题：(1)当a ，b ，m ，n 均为正整数时，若a ＋b 3＝(m ＋n 3)2，用含m ，n 的式子分别表示a ，b ，得a ＝________，b ＝________；(2)利用所探索的结论，找一组正整数a ，b ，m ，n 填空：________＋________3＝(________＋________3)2；(3)若a ＋43＝(m ＋n 3)2，且a ，m ，n 均为正整数，求a 的值．答案一、 6．B二、11.－6；± 2 ≥－1 13．(1)> (2)> ＋115．64 16.－1 cm 2；14 2 cm 18．3；255三、19.解：(1)因为4x 2＝25，所以x 2＝254.所以x ＝±52.(2)因为(x －3＝，所以x －＝.所以x ＝1.20．解：(1)原式＝22＋42－2＝5 2.(2)原式＝6－⎝ ⎛⎭⎪⎫－32×20＝36.(3)原式＝18－245－32＝32－65－32＝－6 5. (4)原式＝(203－183＋23)÷3＝43÷3＝4.21．解：由数轴可知b ＜a ＜0＜c ，所以a ＋b ＜0，c －a ＞0，b －c ＜0.所以原式＝－a －[－(a ＋b)]＋(c －a)＋[－(b －c)]＝－a ＋a ＋b ＋c －a －b ＋c ＝－a ＋2c.22．解：因为x ＝1－2，y ＝1＋2，所以x －y ＝(1－2)－(1＋2)＝－22，xy ＝(1－2)(1＋2)＝－1.所以x 2＋y 2－xy －2x ＋2y ＝(x －y)2－2(x －y)＋xy ＝(－22)2－2×(－22)＋(－1)＝7＋4 2.23．解：(1)设这个正方体的棱长为a cm ，由题意得6a 2＝2 400. 可得a ＝20，则体积为203＝8 000(cm 3)．(2)若该正方体的表面积变为原来的一半，则有6a 2＝1 200. 所以a ＝10 2.所以体积为(102)3＝2 0002(cm 3)．所以2 00028 000＝24.即体积变为原来的24.24．解：因为AB ＝AD ，∠BAD＝90°，AB ＝22，所以BD ＝AB 2＋AD 2＝4.因为BD 2＋CD 2＝42＋(43)2＝64，BC 2＝64，所以BD 2＋CD 2＝BC 2.所以△BCD 为直角三角形，且∠BDC＝90°.所以S 四边形ABCD＝S △ABD ＋S △BCD ＝12×22×22＋12×43×4＝4＋8 3.25．解：设正方体储存盒的棱长为x cm ，由题意得6x 2＝20×π×10，解得x ＝10.所以墨墨所做的正方体储存盒的棱长为10 cm . 26．解：(1)m 2＋3n 2；2mn (2)21；12；3；2(答案不唯一)(3)由题意，得a ＝m 2＋3n 2，b ＝2mn ，所以4＝2mn ，且m ，n 为正整数．所以m ＝2，n ＝1或m ＝1，n ＝2.所以a ＝22＋3×12＝7或a ＝12＋3×22＝13.第三章检测卷(120分，90分钟)一、选择题(每题3分，共30分) 1．点P(4，3)所在的象限是( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限 2．根据下列表述，能确定位置的是( )A ．红星电影院2排B ．北京市四环路C ．北偏东30° D．东经118°，北纬40° 3．如果座位表上“5列2行”记作(5，2)，那么(4，3)表示( ) A ．3列5行 B ．5列3行 C ．4列3行D ．3列4行 4．如图，在直角坐标系中，卡片盖住的数可能是( ) A ．(2，3) B ．(－2，1) C ．(－2，－ D ．(3，－2)(第4题) (第7题) (第9题) 5．点P(－2，3)关于x 轴对称的点的坐标是( ) A ．(－3，2) B ．(2，－3) C ．(－2，－3) D ．(2，3)6．已知点A(－1，－4)，B(－1，3)，则( )A．点A，B关于x轴对称 B．点A，B关于y轴对称C．直线AB平行于y轴 D．直线AB垂直于y轴7．如图，若在象棋盘上建立直角坐标系，使“将”位于点(0，－1)，“象”位于(2，－1)，则“炮”位于点( )A．(－3，2) B．(－4，3) C．(－3，0) D．(1，－1)8．点C在x轴上方，y轴左侧，距离x轴2个单位长度，距离y轴3个单位长度，则点C的坐标为( ) A．(2，3) B．(－2，－3) C．(－3，2) D．(3，－2)9．如图，动点P从(0，3)出发，沿图中所示方向运动，每当碰到长方形的边时反弹，反弹时反射角等于入射角，当点P第2 015次碰到长方形的边时，点P的坐标为( )A．(1，4) B．(5，0) C．(6，4) D．(8，3)10．在平面直角坐标系中，孔明做走棋的游戏，其走法是：棋子从原点出发，第1步向右走1个单位长度，第2步向右走2个单位长度，第3步向上走1个单位长度，第4步向右走1个单位长度，……以此类推，第n步的走法是：当n能被3整除时，向上走1个单位长度；当n被3除，余数为1时，向右走1个单位长度；当n被3除，余数为2时，向右走2个单位长度，当走完第100步时，棋子所处位置的坐标是( ) A．(66，34) B．(67，33) C．(100，33) D．(99，34)二、填空题(每题3分，共24分)11．写出平面直角坐标系中一个第三象限内点的坐标：________．12．在直角坐标系中，第四象限内一点P到x轴的距离为2，到y轴的距离为5，那么点P的坐标是________．13．如图是益阳市行政区域图，图中益阳市区所在地用坐标表示为(1，0)，安化县城所在地用坐标表示为(－3，－1)，那么南县县城所在地用坐标表示为________．(第13题) (第15题) (第17题)14．第二象限内的点P(x，y)满足|x|＝9，y2＝4，则点P的坐标是__________．15．如图，等腰三角形AOC的底边OC在x轴的正半轴上，点O是坐标原点，点A在第一象限，若AO＝5，OC ＝6，则顶点A的坐标为________．16．如果将点(－b，－a)称为点(a，b)的“反称点”，那么点(a，b)也是点(－b，－a)的“反称点”，此时，点(a，b)和点(－b，－a)互为“反称点”．容易发现，互为“反称点”的两点有时是重合的，例如(0，0)的“反称点”还是(0，0)．请写出一个这样的点：________.17．如图，点A，B的坐标分别为(2，4)，(6，0)，点P是x轴上一点，且△ABP的面积为6，则点P的坐标为________．18．在平面直角坐标系中，点A的坐标为(1，1)，点B的坐标为(11，1)，点C到直线AB的距离为4，△ABC是直角三角形且∠C不是直角，则满足条件的点C有________个．三、解答题(19题6分，20题8分，21，23题每题9分，22题10分，其余每题12分，共66分)19．(1)在坐标平面内画出点P(2，3)；(2)分别作出点P关于x轴、y轴的对称点P1，P2，并写出P1，P2的坐标．20．已知点A(1＋2a，4a－5)，且点A到两坐标轴的距离相等，求点A的坐标．21．春天到了，七(1)班组织同学到人民公园春游，张明、李华对着景区示意图(如图)描述牡丹园的位置(图中小正方形的边长为100 m)．(第21题)张明：“牡丹园的坐标是(300，300)．”李华：“牡丹园在中心广场东北方向约420 m处．”实际上，他们所说的位置都是正确的．根据所学的知识解答下列问题：(1)请指出张明同学是如何在景区示意图上建立平面直角坐标系的，并在图中画出所建立的平面直角坐标系．(2)李华同学是用什么来描述牡丹园的位置的？请用张明同学所用的方法，描述出公园内其他地方的位置．22．如图，在平面直角坐标系中，O，A，B，C的坐标分别为(0，0)，(－1，2)，(－3，3)和(－2，1)．(1)将图中的各个点的纵坐标不变，横坐标都乘－1，与原图案相比，所得图案有什么变化？画出图形并说明一下变化．(2)将图中的各个点的横坐标不变，纵坐标都乘－1，与原图案相比，所得图案有什么变化？画出图形并说明一下变化．(第22题)23．如图，A，B，C为一个平行四边形的三个顶点，且A，B，C三点的坐标分别为(3，3)，(6，4)，(4，6)．(1)请直接写出这个平行四边形第四个顶点的坐标；(2)求这个平行四边形的面积．(第23题)24．在平面直角坐标系xOy中，我们把横、纵坐标都是整数的点叫做整点．如图，已知点A(0，4)，点B是x轴正半轴上的整点，记△AOB内部(不包括边界)的整点个数为m.(1)当m＝3时，求点B的横坐标的所有可能值；(2)当点B的横坐标为4n(n为正整数)时，用含n的代数式表示m.(第24题)25．先阅读一段文字，再回答问题：已知在平面内两点的坐标为P1(x1，y1)，P2(x2，y2)，则该两点间的距离公式为P1P2＝（x2－x1）2＋（y2－y1）2.同时，当两点在同一坐标轴上或所在直线平行于x轴或垂直于x轴时，两点间的距离公式可化简成|x2－x1|或|y2－y1|.(1)若已知两点A(3，5)，B(－2，－1)，试求A，B两点间的距离．(2)已知点A，B在平行于y轴的直线上，点A的纵坐标为5，点B的纵坐标为－1，试求A，B两点间的距离．(3)已知一个三角形各顶点的坐标分别为A(0，6)，B(－3，2)，C(3，2)，你能判断此三角形的形状吗？试说明理由．答案一、 6．C二、11.(－1，－1)(答案不唯一) 12．(5，－2) 13.(2，4) 14．(－9，2) 15.(3，4) 16．(－2，2)(答案不唯一)17．(3，0)或(9，0) 点拨：设点P 的坐标为(x ，0)，根据题意得12×4×|6－x|＝6，解得x ＝3或9，所以点P 的坐标为(3，0)或(9，0)．18．4三、19.解：(1)点P(2，3)如图所示．(2)点P 1，P 2如图所示，P 1(2，－3)，P 2(－2，3)．(第19题)20．解：根据题意，分两种情况讨论： ①1＋2a ＝4a －5，解得a ＝3，所以1＋2a ＝4a －5＝7. 所以点A 的坐标为(7，7)． ②1＋2a ＋4a －5＝0，解得a ＝23，所以1＋2a ＝73，4a －5＝－73.所以点A 的坐标为⎝ ⎛⎭⎪⎫73，－73.故点A 的坐标为(7，7)或⎝ ⎛⎭⎪⎫73，－73.21．解：(1)张明同学是以中心广场为原点、正东方向为x 轴正方向、正北方向为y 轴正方向建立平面直角坐标系的，图略．(2)李华同学是用方向和距离描述牡丹园的位置的．用张明同学所用的方法，描述如下：中心广场(0，0)，音乐台(0，400)，望春亭(－200，－100)，游乐园(200，－400)，南门(100，－600)．22．解：(1)将各个点的纵坐标不变，横坐标都乘－1，得到新的坐标分别为(0，0)，(1，2)，(3，3)，(2，1)．在坐标系中描出各点，再连接各点，如图所示．所得图案与原图案关于y轴对称．[第22(1)题](2)将各个点的横坐标不变，纵坐标都乘－1，得到新的坐标分别为(0，0)，(－1，－2)，(－3，－3)，(－2，－1)．在坐标系中描出各点，再连接各点，如图所示．所得图案与原图案关于x轴对称．[第22(2)题]23．解：(1)(7，7)或(1，5)或(5，1)．(2)这个平行四边形的面积为8.24．解：(1)如图①，当点B的横坐标为3或4时，m＝3，即当m＝3时，点B的横坐标的所有可能值是3和4.(第24题)(2)如图②，当点B的横坐标为4n＝4时，n＝1，m＝3；当点B的横坐标为4n＝8时，n＝2，m＝9；当点B的横坐标为4n＝12时，n＝3，m＝15……当点B的横坐标为4n(n为正整数)时，m＝6n－3.25．解：(1)AB＝（－2－3）2＋（－1－5）2＝61. (2)AB ＝|－1－5|＝6. (3)能．理由：因为AB ＝（－3－0）2＋（2－6）2＝5， BC ＝[3－（－3）]2＋（2－2）2＝6， AC ＝（3－0）2＋（2－6）2＝5，所以△ABC 为等腰三角形．第四章检测卷(120分，90分钟)得分一、选择题(每题3分，共30分)1．下列图象中，表示y 是x 的函数的个数有( )(第1题)A ．1个B ．2个C ．3个D ．4个 2．直线y ＝x ＋3与y 轴的交点坐标是( ) A ．(0，3) B ．(0，1) C ．(1，0) D ．(3，0)3．如图，直线O A 是某正比例函数的图象，下列各点在该函数图象上的是( ) A ．(－4，16) B ．(3，6) C ．(－1，－1) D ．(4，6)(第3题) (第4题) (第6题)4．如图，与直线AB 对应的函数表达式是( )A ．y ＝32x ＋3B ．y ＝－32x ＋3C ．y ＝－23x ＋3D ．y ＝23x ＋35．关于一次函数y ＝12x －3的图象，下列说法正确的是( )A ．图象经过第一、二、三象限B ．图象经过第一、三、四象限C ．图象经过第一、二、四象限D ．图象经过第二、三、四象限6．一次函数y 1＝kx ＋b 与y 2＝x ＋a 的图象如图所示，则下列结论中：①k<0；②a>0；③b>0；④当x ＝3时，y 1＝y 2.正确的有( )A ．0个B ．1个C ．2个D ．3个7．弹簧挂上物体后会伸长，测得一弹簧的长度y(cm )与所挂物体质量x(kg )间有如下关系(其中x≤12)．下列说法不正确的是( )A.x与y都是变量，且x是自变量B．弹簧不挂物体时的长度为10 cmC．物体质量每增加1 kg，弹簧长度y增加 cmD．所挂物体质量为7 kg，弹簧长度为 cm8．若直线y＝－3x＋m与两坐标轴所围成的三角形的面积是6，则m的值为( )A．6 B．－6 C．±6 D．±39．A，B两地相距20 km，甲、乙两人都从A地去B地，如图，l1和l2分别表示甲、乙两人所走路程s(km)与时间t(h)之间的关系，下列说法：①乙晚出发1 h；②乙出发3 h后追上甲；③甲的速度是4 km/h；④乙先到达B地．其中正确的个数是( )A．1 B．2 C．3 D．4(第9题) (第10题)10．一天，小亮看到家中的塑料桶中有一个竖直放置的玻璃杯，桶和玻璃杯的形状都是圆柱形，桶口的半径是杯口半径的2倍，其从正面看得到的图形如图所示．小亮决定做个实验：把塑料桶和玻璃杯看成一个容器，对准杯口匀速注水，注水过程中玻璃杯始终竖直放置，则下列能反映容器最高水位h与注水时间t之间关系的大致图象是( )二、填空题(每题3分，共24分)11．下列函数：①y＝πx；②y＝2x－1；③y＝1x＋8；④y＝kx＋3；⑤y＝x2－(x－2)2.其中一定属于一次函数的是________．12．直线y＝－3x＋5不经过的象限为________．13．若一次函数y＝2x＋b(b为常数)的图象经过点(1，5)，则b＝________.14．在平面直角坐标系中，已知一次函数y＝2x＋1的图象经过P1(x1，y1)，P2(x2，y2)两点，若x1<x2，则y1________y2.(填“>”“<”或“＝”)15．如图，一次函数的图象经过点E，且与正比例函数y＝－x的图象交于点F，则该一次函数的表达式为____________．(第15题) (第17题) (第18题) 16．已知点(3，5)在直线y ＝ax ＋b(a ，b 为常数，且a≠0)上，则ab －5＝________．17．如图，l 1反映了某公司的销售收入与销售量的关系，l 2反映了该公司产品的销售成本与销售量的关系，当销售量x________时，该公司盈利(收入大于成本)．18．将正方形A 1B 1C 1O 和正方形A 2B 2C 2C 1按如图所示方式放置，点A 1，A 2在直线y ＝x ＋1上，点C 1，C 2在x 轴上．已知点A 1的坐标是(0，1)，则点B 2的坐标为________．三、解答题(19题6分，20，21题每题9分，22题10分，23题8分，其余每题12分，共66分) 19．已知y ＋2与x －1成正比例，且当x ＝3时，y ＝4. (1)求y 与x 之间的函数关系式； (2)当y ＝1时，求x 的值．20．作出函数y ＝3x ＋1的图象，根据图象回答： (1)当x 取什么值时，函数值y 大于零？(2)直接写出方程3x ＋1＝0的解．21．已知直线y 1＝－23x ＋3与x 轴交于点A ，与y 轴交于点B ，直线y 2＝2x ＋b 经过点B ，且与x 轴交于点C ，求△ABC 的面积．22．请你根据如图所示的图象所提供的信息，解答下面问题：(1)分别写出直线l 1，l 2对应的函数中变量y 的值随x 的变化而变化的情况；(2)求出直线l 1对应的函数表达式．(第22题)23．一次函数y ＝ax －a ＋1(a 为常数，且a≠0)．(1)若点⎝ ⎛⎭⎪⎫－12，3在一次函数y ＝ax －a ＋1的图象上，求a 的值； (2)当－1≤x≤2时，函数有最大值2，请求出a 的值．24．某校实行学案式教学，需印制若干份数学学案．印刷厂有甲、乙两种收费方式，除按印刷份数收取印刷费外，甲种方式还需收取制版费而乙种不需要．两种收费方式的费用y(元)与印刷份数x(份)之间的函数关系如图所示．(1)填空：甲种收费方式的函数关系式是__________，乙种收费方式的函数关系式是__________； (2)该校某年级每次需印制100～450(含100和450)份学案，选择哪种收费方式较合算？(第24题)25．甲、乙两车分别从A ，B 两地同时出发相向而行，并以各自的速度匀速行驶，甲车途经C 地休息了1 h ，然后按原速度继续前进到达B 地；乙车从B 地直接到达A 地，如图是甲、乙两车和B 地的距离y(km )与甲车出发时间x(h )的函数图象．(1)直接写出a，m，n的值；(2)求出甲车与B地的距离y(km)与甲车出发时间x(h)的函数表达式(写出自变量x的取值范围)；(3)当两车相距120 km时，乙车行驶了多长时间？(第25题)答案一、5．B 点拨：一次函数y＝12x－3.其中k＝12＞0，b＝－3＜0.其图象如图所示．(第5题)6．D二、11.①②⑤ 12.第三象限 14．< ＝x ＋216．－13 点拨：将(3，5)代入y ＝ax ＋b ，得3a ＋b ＝5.所以b －5＝－3a ，因为a≠0，所以b≠5.所以a b －5＝a －3a ＝－13. 17．>4 18．(3，2)三、19.解：(1)由y ＋2与x －1成正比例可设y ＋2＝k(x －1)，将x ＝3，y ＝4代入上式得4＋2＝k(3－1)，解得k ＝3，所以y ＋2＝3(x －1)，即y ＝3x －5.(2)当y ＝1时，得1＝3x －5，解得x ＝2，即当y ＝1时，x ＝2. 20．解：列表：图象如图所示．(1)当x>－13时，y>0.(第20题)(2)x ＝－13.21．解：令x ＝0，则y 1＝3；令y 1＝0，则0＝－23x ＋3，即x ＝92.所以点A 的坐标为⎝ ⎛⎭⎪⎫92，0，点B 的坐标为(0，3)．又因为点B 在直线y 2＝2x ＋b 上，所以b ＝3，即y 2＝2x ＋3.令y 2＝0，则0＝2x ＋3，所以x ＝－32.所以点C 的坐标为⎝ ⎛⎭⎪⎫－32，0.(第21题)如图，AC ＝⎪⎪⎪⎪⎪⎪－32＋92＝6，OB ＝3，∴S △ABC ＝12AC·OB＝12×6×3＝9.22．解：(1)直线l 1对应的函数中，y 的值随x 的增大而增大；直线l 2对应的函数中，y 的值随x 的增大而减小．(2)设直线l 1对应的函数表达式为y ＝a 1x ＋b 1，由题意得a 1＋b 1＝1，b 1＝－1，可得a 1＝2，所以直线l 1对应的函数表达式为y ＝2x －1.23．解：(1)把⎝ ⎛⎭⎪⎫－12，3代入y ＝ax －a ＋1，得－12a －a ＋1＝3，解得a ＝－43.(2)当a>0时，y 随x 的增大而增大，则当x ＝2时，y 有最大值2，把x ＝2，y ＝2代入函数关系式得2＝2a －a ＋1，解得a ＝1；当a<0时，y 随x 的增大而减小，则当x ＝－1时，y 有最大值2，把x ＝－1，y ＝2代入函数关系式得2＝－a －a ＋1，解得a ＝－12.所以a ＝－12或a ＝1.24．解：(1)y ＝＋6；y ＝(2)当甲、乙两种收费方式费用相同时，有 0．12x ＝＋6， x ＝300.因此可得其函数图象交点横坐标为300. 如图，由函数图象可得(第24题)当100≤x＜300时选择乙种收费方式较合算；当x ＝300时，选择甲、乙两种收费方式费用一样；当300<x≤450时，选择甲种收费方式较合算． 25．解：(1)a ＝90，m ＝，n ＝.(2)①休息前，0≤x＜，设甲车与B 地的距离y(km )与甲车出发时间x(h )的函数表达式为y ＝kx ＋b(k≠0)．因为函数图象经过点(0，300)，故b ＝300.把点，120)的坐标代入y ＝kx ＋300中得k ＝－120. 所以y ＝－120x ＋300； ②休息时，≤x＜，y ＝120；③休息后，≤x≤，设甲车与B 地的距离y(km )与甲车出发时间x(h )的函数表达式为y ＝px ＋n(p≠0)．把点，120)，，0)的坐标分别代入y ＝px ＋n 中得p ＝－120，n ＝420. 所以y ＝－120x ＋420.综上可知，y 与x 的函数表达式为 y ＝⎩⎪⎨⎪⎧－120x ＋300（0≤x<），120（≤x<），－120x ＋420（≤x≤）.(3)设两车相距120 km 时，乙车行驶了t h ，甲车的速度为(300－120)÷＝120(km/h)，乙车的速度为120÷2＝60(km/h)．①若两车相遇前相距120 km ，则120t ＋60t ＝300－120，解得t ＝1；②若两车相遇后相距120 km ，则120(t －1)＋60t ＝300＋120，解得t ＝3.所以当两车相距120 km 时，乙车行驶了1 h 或3 h.第五章检测卷(120分，90分钟)一、选择题(每题3分，共30分)1．二元一次方程x －2y ＝3有无数多个解，下列四组值中不是该方程的解的是( )2．下列方程组中，是二元一次方程组的是( )3．用代入法解方程组⎩⎪⎨⎪⎧2y －3x ＝1，x ＝y －1，下面的变形正确的是( )A ．2y －3y ＋3＝1B ．2y －3y －3＝1C ．2y －3y ＋1＝1D ．2y －3y －1＝14．已知⎩⎪⎨⎪⎧x ＝4，y ＝－1是方程12x －ky ＝3的一个解，那么k 的值是( )A ．1B ．2C ．－2D ．－15．若|3－a|＋2＋b ＝0，则a ＋b 的值是( ) A ．2 B ．1 C ．0 D ．－16．在函数y ＝kx ＋b 中，当x ＝3时，y ＝－4；当x ＝4时，y ＝－3，则k ，b 的值分别为( ) A ．1，－7 B ．7，－1 C ．－1，7 D ．－7，17．已知⎩⎪⎨⎪⎧x ＝2，y ＝1是方程组⎩⎪⎨⎪⎧ax ＋by ＝5，bx ＋ay ＝1的解，则a －b 的值是( )A ．－1B ．2C ．3D ．48．小亮用作图象的方法解二元一次方程组时，在同一直角坐标系内作出了相应的两个一次函数的图象l 1，l 2，如图所示，他解的这个方程组是( )(第8题) (第10题)9．已知方程组⎩⎪⎨⎪⎧2x ＋y ＝3，4x －z ＝－1，6x ＋y ＋z ＝8，则z 的值为( )B ．1C ．2D ．310．用如图①中的长方形和正方形纸板作侧面和底面，做成如图②的竖式和横式的两种无盖纸盒．现在仓库里有m 张长方形纸板和n 张正方形纸板，如果做两种纸盒若干个，恰好使库存的纸板用完，则m ＋n 的值可能是( )A ．2 013B ．2 014C ．2 015D ．2 016 二、填空题(每题3分，共24分)11．把方程5x －2y ＋12＝0写成用含x 的代数式表示y 的形式为________． 12．已知(n －1)x |n|－2ym －2 014＝0是关于x ，y 的二元一次方程，则n m＝________.13．方程组⎩⎪⎨⎪⎧x ＋y ＝12，y ＝2的解为________．14．在△ABC 中，∠A－∠B＝20°，∠A＋∠B＝140°，则∠A＝________，∠C＝________.15．已知⎩⎪⎨⎪⎧x ＝2，y ＝1是二元一次方程组⎩⎪⎨⎪⎧mx ＋ny ＝7，nx －my ＝1的解，则m ＋3n 的立方根为________．16．对于实数x ，y ，定义新运算x*y ＝ax ＋by ＋1，其中a ，b 为常数，等式右边为通常的加法和乘法运算，若3*5＝14，4*7＝19，则5*9＝________.17．如图，两根铁棒直立于桶底水平的木桶中，在桶中加入水后，一根露出水面的长度是它的13，另一根露出水面的长度是它的15，两根铁棒长度之和为220 cm ，此时木桶中水的深度是________．(第17题) (第18题)18．在一次越野跑中，当小明跑了1 600 m 时，小刚跑了1 400 m ，小明、小刚在此后所跑的路程y(m )与时间t(s )之间的函数关系如图所示，则这次越野跑的全程为________．三、解答题(19，25题每题12分，20～23题每题8分，24题10分，共66分) 19．解下列方程组：(1)⎩⎪⎨⎪⎧x －2y ＝3，3x ＋y ＝2； (2)⎩⎪⎨⎪⎧x 3－y 2＝6，x －y 2＝9；(3)⎩⎪⎨⎪⎧3（x ＋y ）－4（x －y ）＝6，x ＋y 2－x －y 6＝1； (4)⎩⎪⎨⎪⎧x －y ＋z ＝0，4x ＋2y ＋z ＝0，25x ＋5y ＋z ＝60.20．已知关于x ，y 的方程组⎩⎪⎨⎪⎧mx ＋ny ＝7，2mx －3ny ＝4的解为⎩⎪⎨⎪⎧x ＝1，y ＝2，求m ，n 的值．21．某村粮食专业队去年计划生产水稻和小麦共150 t ，实际完成了170 t ．其中水稻超产15%，小麦超产10%.问：该专业队去年实际生产水稻、小麦各多少吨？22．已知一个三位数，十位上的数字比个位上的数字大1，百位上的数字是十位上的数字的2倍，如果把百位上的数字与个位上的数字对调，那么得到的新的三位数比原来的三位数小297.求原来的三位数．23．如图，过点A(0，2)，B(3，0)的直线AB与直线CD：y＝56x－1交于点D，C为直线CD与y轴的交点．求：(1)直线AB对应的函数表达式；(2)S△ADC.(第23题)24．某地区为了鼓励市民节约用水，计划实行生活用水按阶梯式水价计费，每月用水量不超过10 t时，每吨按基础价收费；每月用水量超过10 t时，超过的部分每吨按调节价收费．例如，第一个月用水16 t，需交水费元，第二个月用水20 t，需交水费23元．(1)求每吨水的基础价和调节价；(2)设每月用水量为n t，应交水费为m元，写出m与n之间的函数表达式；(3)若某月用水12 t，则应交水费多少元？。

北师大版八年级数学上册单元测试题全套含答案

北师大版八年级数学上册单元测试题全套含答案（含期中期末试题，共12套）第一章检测题(时间：120分钟满分：120分)一、选择题(每小题3分，共30分)1．如图，在边长为1个单位长度的小正方形组成的网格中，点A ，B 都是格点，则以AB 为边的正方形的面积为( A )A ．10B ．9C ．100D ．25,第3题图)2．在△ABC 中，AB ＝15，BC ＝12，AC ＝9，则△ABC 的面积为( C ) A ．180 B ．90 C ．54 D ．1083．如图，AB ⊥CD 于点B ，△ABD 和△BCE 都是等腰三角形，如果CD ＝17，BE ＝5，那么AC 的长为( D )A ．12B ．7C ．5D ．134．(荆门中考)如图，在△ABC 中，AB ＝AC ，AD 是∠BAC 的角平分线，已知AB ＝5，AD ＝3，则BC 的长为( C )A ．5B ．6C ．8D ．105．在Rt △ABC 中，∠C ＝90°，AC ＝9，BC ＝12，则点C 到AB 的距离为( A ) A .365 B .1225 C .94 D .3346．若一个三角形的三边长为a ，b ，c 且满足(a ＋b ＋c)(a 2－b 2－c 2)＝0，则这个三角形是( B ) A ．等腰三角形 B ．直角三角形 C ．锐角三角形 D ．钝角三角形7．一架2.5米长的梯子，斜立在一竖直的墙上，这时梯子的底端离墙0.7米，如果梯子的顶端沿墙下滑0.4米，那么梯子底端在水平方向上滑动( B )A ．0.9米B ．0.8米C ．0.5米D ．0.4米8．如图，圆柱高8 cm ，底面圆的半径为6πcm ，一只蚂蚁从点A 爬到点B 处吃蜂蜜，则要爬行的最短路程是( B )A ．20 cmB ．10 cmC ．14 cmD ．无法确定,第8题图) ,第10题图)9．在△ABC 中，AB ＝13，AC ＝15，高AD ＝12，则BC 的长为( B ) A ．14 B ．14或4 C ．8 D ．4或810．如图，将长方形纸片ABCD 折叠，使边DC 落在对角线AC 上，折痕为CE ，且D 点落在对角线D′处，若AB ＝3，AD ＝4，则ED 的长为( A )A .32B ．3C ．1D .43二、填空题(每小题3分，共18分)11．请写出两组你所熟悉的勾股数：__3，4，5__或__6，8，10__等．12．如图，两个正方形的面积分别为9和16，则直角三角形的斜边长为__5__.,第12题图) ,第13题图)13．如图，由四个全等的直角三角形拼成的“赵爽弦图”，在Rt △ABF 中，∠AFB ＝90°，AF ＝3，AB ＝5，则四边形EFGH 的面积是__1__.14．如图有一个棱长为9 cm 的正方体，一只蜜蜂要沿正方体的表面从顶点A 爬到C 点(C 点在一条棱上，距离顶点B 3 cm 处)，则需爬行的最短路程是__15__cm .,第14题图) ,第15题图)15．(漳州中考)如图，在△ABC 中，AB ＝AC ＝5，BC ＝8.点D 是底边BC 上的一个动点，若线段AD 的长为整数，则满足条件的点D 共有__5__个．16．定义：如图，点M ，N 将线段AB 分割成线段AM ，MN ，NB ，且以AM ，MN ，NB 为边可组成一个直角三角形，点M ，N 是线段AB 的勾股分割点．若M ，N 是线段AB 的勾股分割点，且AM ＝3，BN ＝5，则MN 2的值为__16或34__.三、解答题(本大题9小题，共72分)17．(6分)如图，正方形网格中有△ABC ，若小方格边长为1，请你根据所学的知识解答下列问题： (1)求△ABC 的面积；(2)判断△ABC 是什么形状，并说明理由．解：(1)用正方形的面积减去三个小三角形的面积即可求出△ABC 的面积．S △ABC ＝4×4－1×2×12－4×3×12－2×4×12＝16－1－6－4＝5，所以△ABC 的面积为5(2)△ABC 是直角三角形．理由如下：因为AB 2＝12＋22＝5，AC 2＝22＋42＝20，BC 2＝32＋42＝25，所以AC2＋AB2＝BC2，所以△ABC是直角三角形18．(6分)如图，AF⊥DE于F，且DF＝15 cm，EF＝6 cm，AE＝10 cm.求正方形ABCD的面积．解：在Rt△AEF中，AF2＝AE2－EF2＝64，在Rt△AFD中，AD2＝AF2＋DF2＝289，所以正方形ABCD的面积是289 cm219．(7分)有一只喜鹊在一棵高(AB)3米的小树的树梢上觅食，它的巢筑在距离该树24米(BC)，高(EC)为14米的一棵大树上，且巢D离大树顶部E为1米，这时，它听到巢中幼鸟求助的叫声，立刻赶过去，如果它的飞行速度为每秒5米，那么它几秒能赶回巢中？解：由题意知AB＝3，BC＝24，CD＝13，作AG⊥CD于点G，则在Rt△ADG中，AG＝24，DG＝10，∴AD＝102＋242＝26(米)，t＝265＝5.2(秒)．答：它5.2秒能赶回巢中20．(7分)(达州期末)如图，甲轮船以16海里/小时的速度离开港口O向东南方向航行，乙轮船同时同地向西南方向航行，已知他们离开港口一个半小时后分别到达B，A两点，且知AB＝30海里，问乙轮船每小时航行多少海里？解：甲轮船向东南方向航行，乙轮船向西南方向航行，所以AO⊥BO，因为甲轮船以16海里/小时的速度航行了一个半小时，所以OB＝16×1.5＝24(海里)，又AB＝30海里，所以在Rt△AOB中，AO＝AB2－OB2＝302－242＝18，所以乙轮船每小时航行18÷1.5＝12(海里)21．(8分)如图，在等腰直角三角形ABC中，∠ABC＝90°，D为AC边上的中点，过D点作DE ⊥DF，交AB于点E，交BC于点F，若AE＝4，FC＝3，求EF的长．解：连接BD，证△BDE≌△CDF，得BE＝FC，所以AB＝7，BF＝4，在Rt△BEF中，EF2＝BE2＋BF2＝25，即EF＝522．(8分)如图，∠AOB＝90°，OA＝45 cm，OB＝15 cm，一智能机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O，智能机器人立即从点B出发，沿直线匀速前进拦截小球，恰好在点C处截住了小球．如果小球滚动的速度与智能机器人行走的速度相等，那么智能机器人行走的路程BC是多少？解：小球滚动的速度与智能机器人行走的速度相同，时间相同，即BC＝CA，设AC＝x，则OC＝45－x，在Rt△BOC中，OB2＋OC2＝BC2，即152＋(45－x)2＝x2，解得x＝25.所以机器人行走的路程BC是25 cm23．(8分)如图，已知∠MBN＝60°，在BM，BN上分别截取BA＝BC，P是∠MBN内的一点，连接PA，PB，PC，以BP为边作∠PBQ＝60°，且BQ＝BP，连接CQ.(1)观察并猜想AP与CQ之间的大小关系，并证明你的结论；(2)若PA∶PB∶PC＝3∶4∶5，连接PQ，求证：∠PQC＝90°.解：(1)AP＝CQ.因为∠ABP＋∠PBC＝60°，∠QBC＋∠PBC＝60°，所以∠ABP＝∠QBC，又因为AB＝BC，BP＝BQ，所以△ABP≌△CBQ，AP＝CQ(2)设PA＝3a，PB＝4a，PC＝5a，连接PQ，在△PBQ中，因为PB＝BQ＝4a，且∠PBQ＝60°，所以△PBQ为等边三角形，所以PQ＝4a，在△PQC中，因为PQ2＋QC2＝16a2＋9a2＝25a2＝PC2，所以△PQC 为直角三角形，即∠PQC ＝90°24．(10分)如图，在长方形ABCD 中，AB ＝8，BC ＝6，P 为AD 上一点，将△ABP 沿BP 翻折至△EBP ，PE 与CD 相交于点O ，且OE ＝OD.(1)试证明DG ＝EP ； (2)求AP 的长．解：(1)因为四边形ABCD 是长方形，所以∠D ＝∠A ＝∠C ＝90°，AD ＝BC ＝6，CD ＝AB ＝8.由折叠的性质可知EP ＝AP ，BE ＝AB ＝8，∠E ＝∠A ＝90°，所以∠E ＝∠D.在△ODP 和△OEG 中，⎩⎨⎧∠D ＝∠E ，OD ＝OE ，∠DOP ＝∠EOG ，所以△ODP ≌△OEG ，所以OP ＝OG ，PD ＝GE ，所以DO ＋OG ＝PO ＋OE ，所以DG ＝EP(2)设AP ＝EP ＝DG ＝x ，则GE ＝PD ＝AD －AP ＝6－x ，所以CG ＝DC －DG ＝8－x ，BG ＝BE －GE ＝8－(6－x)＝2＋x.在Rt △CGB 中，由勾股定理得BC 2＋CG 2＝BG 2，即62＋(8－x)2＝(x ＋2)2，解得x ＝4.8，所以AP ＝4.825. (12分)如图，在△ABC 中，AC ＝BC ，∠ACB ＝90°，点D ，E 是线段AB 上两点．∠DCE ＝45°.(1)当CE ⊥AB 时，点D 与点A 重合，求证：DE 2＝AD 2＋BE 2； (2)当点D 不与点A 重合时，求证：DE 2＝AD 2＋BE 2；(3)当点D 在BA 的延长线上时，(2)中的结论是否成立？画出图形，说明理由．解：(1)因为CE ⊥AB ，所以AE ＝BE ，因为点D 与点A 重合，所以AD ＝0，所以DE 2＝AD 2＋BE 2 (2)如图①，过点A 作AF ⊥AB ，使AF ＝BE ，连接DF ，CF ，因为在△ABC 中，AC ＝BC ，∠ACB ＝90°，所以∠CAB ＝∠B ＝45°，所以∠FAC ＝45°，所以△CAF ≌△CBE(SAS )，所以CF ＝CE ，∠ACF ＝∠BCE ，因为∠ACB ＝90°，∠DCE ＝45°，所以∠ACD ＋∠BCE ＝∠ACB －∠DCE ＝90°－45°＝45°，因为∠ACF ＝∠BCE ，所以∠ACD ＋∠ACF ＝45°，即∠DCF ＝45°，所以∠DCF ＝∠DCE ，又因为CD ＝CD ，所以△CDF ≌△CDE(SAS )，所以DF ＝DE ，因为AD 2＋AF 2＝DF 2，所以AD 2＋BE 2＝DE 2(3)结论仍然成立．理由：如图②，过点A 作AF ⊥AB ，使AF ＝BE ，连接DF ，CF ，因为在△ABC 中，AC ＝BC ，∠ACB ＝90°，所以∠CAB ＝∠B ＝45°，所以∠FAC ＝45°，所以△CAF ≌△CBE(SAS )，所以CF ＝CE ，∠ACF ＝∠BCE ，因为∠BCE ＋∠ACE ＝90°，所以∠ACF ＋∠ACE ＝90°，即∠FCE＝90°，因为∠DCE ＝45°，所以∠DCF ＝45°，所以∠DCF ＝∠DCE ，又因为CD ＝CD ，所以△CDF ≌△CDE(SAS )，所以DF ＝DE ，因为AD 2＋AF 2＝DF 2，所以AD 2＋BE 2＝DE 2第二章检测题(时间：120分钟满分：120分)一、选择题(每小题3分，共30分)1．下列四个实数中，不是无理数的是( B )A . 2B .38C ．1.01001000100001……D .π22．121的平方根是( C )A ．11B ．－11C ．±11D ．±113．(铁岭中考)二次根式x －4有意义，则实数x 的取值范围是( D ) A ．x>4 B ．x<4 C ．x ＝4 D ．x ≥4 4．(达州期中)下面计算正确的是( B ) A ．3＋3＝3 3 B .27÷3＝3C .2·3＝ 5D .4＝±25．实数a ，b 在数轴上的位置如图所示，且|a|>|b|，则化简a 2－|a ＋b|的结果为( C )A ．2a ＋bB ．－2a ＋bC ．bD ．2a －b6．已知k ，m ，n 为三个整数，若135＝k 15，450＝15m ，180＝6n ，则下列关于k ，m ，n 的大小关系正确的是( D )A ．k<m ＝nB ．m ＝n<kC ．m<n<kD ．m<k<n7．下列说法：①5是25的算术平方根；②56是2536的一个平方根；③(－4)2的平方根是－4；④立方根和算术平方根都等于自身的数是0和1.其中正确的个数有( C )A ．1个B ．2个C ．3个D ．4个8．如图，下列各数中，数轴上点A 表示的可能是( C )A ．4的算术平方根B ．4的立方根C ．8的算术平方根D ．8的立方根 9．下列各式中，正确的是( C ) A .22＋32＝2＋3B ．32＋53＝(3＋5)2＋3C .152－122＝15＋12·15－12D .412＝21210．(泸州中考)已知三角形的三边长分别为a ，b ，c ，求其面积问题，中外数学家曾经进行过深入研究，古希腊的几何学家海伦(Heron ，约公元50年)给出求其面积的海伦公式S ＝p （p －a ）（p －b ）（p －c ），其中p ＝a ＋b ＋c2；我国南宋时期数学家秦九韶(约1202－1261)曾提出利用三角形的三边求其面积的秦九韶公式S ＝12a 2b 2－（a 2＋b 2－c 22）2，若一个三角形的三边长分别为2，3，4，则其面积是( B )A .3158B .3154C .3152D .152二、填空题(每小题3分，共18分) 11．(南京中考)计算：（－3）2＝__3__.12．(陕西中考)在实数－5，－3，0，π，6中，最大的一个数是__π__. 13．(荆门中考)已知实数m ，n 满足|n －2|＋m ＋1＝0，则m ＋2n 的值为__3__. 14．(鄂州中考)若y ＝x －12＋12－x －6，则xy ＝__－3__. 15.15－x 是有理数，则x 的最大整数值是__15__.16．若两个代数式M 与N ，满足M ·N ＝－1，则称这两个代数式为“互为友好因式”，则3＋5的“互为友好因式”是2三、解答题(本大题9小题，共72分) 17．(8分)计算：(1)(达州中考)20170－|1－2|＋(13)－1＋2×22；解：5(2)1＋(－12)－1－（3－2）2÷(13－3)0.解：－3＋318．(8分)先化简，再求值：(1)(a －2b)(a ＋2b)＋ab 3÷(－ab)，其中a ＝2，b ＝3；解：原式＝a 2－5b 2＝－13(2)(2x ＋3)(2x －3)－4x(x －1)＋(x －2)2，其中x ＝－ 3. 解：原式＝x 2－5＝－219．(9分)计算：(1)32＋50＋1345－18；解：62＋5 (2)22÷52×1234；解：35 (3)(6－412＋38)÷2 2. 解：123＋220．(6分)若31－2x 与33y －2互为相反数，求1＋2x y的值．解：由题意得(1－2x)＋(3y －2)＝0，整理得1＋2x ＝3y ，所以1＋2x y ＝3yy＝321．(8分)甲同学用如下图所示的方法作出了C 点，表示数13，在△OAB 中，∠OAB ＝90°，OA ＝2，AB ＝3，且点O ，A ，C 在同一数轴上，OB ＝OC.(1)请说明甲同学这样做的理由；(2)仿照甲同学的做法，在如下所给数轴上描出表示－29的点F.解：(1)在Rt △OAB 中，由勾股定理得OB 2＝OA 2＋AB 2，所以OC ＝OB ＝OA 2＋AB 2＝22＋32＝13，即点C表示数13(2)画图略．在△ODE中，∠EDO＝90°，OD＝5，DE＝2，则OF＝OE＝29，即F点为－2922．(8分)如果正方形网格中的每一个小正方形的边长都是1，则每个小格的顶点叫做格点．(1)如图①，以格点为顶点的△ABC中，请判断AB，BC，AC三边的长度是有理数还是无理数？(2)在图②中，以格点为顶点画一个三角形，使三角形的三边长分别为3，5，2 2.解：(1)AB＝4，AC＝32＋32＝32，BC＝12＋32＝10，所以AB的长度是有理数，AC和BC的长度是无理数(2)图略23．(6分)已知实数x，y满足x＋y＝－7，xy＝12，求y xy＋xyx的值．解：因为x＋y＝－7，xy＝12，所以x<0，y<0，所以y xy＋xyx＝－xy－xy＝－2xy＝－212＝－4324．(8分)小丽想用一块面积为400 cm2的正方形纸片沿着边的方向剪出一块面积为300 cm2的长方形，并使长方形纸片的长宽之比为3∶2，请问小丽能否剪出符合要求的长方形纸片，请说明理由．解：小丽不能剪出符合要求的长方形纸片．理由为：设长方形纸片的长为3x cm，宽为2x cm，由题意则有：3x·2x＝300，6x2＝300，x2＝50，所以x＝50，所以长方形纸片的长为3x＝350，又因为50>49＝7，所以3x＝350>21(cm)，而原正方形纸片的边长为20 cm，故小丽不能剪出符合要求的长方形纸片25．(11分)阅读下列材料，然后解答下列问题：在进行代数式化简时，我们有时会碰上如53，23＋1这样的式子，其实我们还可以将其进一步化简：(一)53＝5×33×3＝533；(二)23＋1＝2×（3－1）（3＋1）（3－1）＝2（3－1）（3）2－1＝3－1；(三)23＋1＝3－13＋1＝（3）2－123＋1＝（3＋1）（3－1）3＋1＝3－1.以上这种化简的方法叫分母有理化．(1)请用不同的方法化简25＋3：①参照(二)式化简25＋3＝；②参照(三)式化简25＋3＝(2)化简：13＋1＋15＋3＋17＋5＋…＋199＋97.解：(1)①2×（5－3）（5＋3）（5－3）＝2（5－3）（5）2－（3）2＝5－3②5－35＋3＝（5）2－（3）25＋3＝（5＋3）（5－3）5＋3＝5－3(2)原式＝3－12＋5－32＋7－52＋…＋99－972＝99－12＝311－12第三章检测题(时间：120分钟满分：120分)一、选择题(每小题3分，共30分)1．(聊城中考)在平面直角坐标系中，点M(－3，4)在( B )A．第一象限B．第二象限C．第三象限D．第四象限2．八(2)班有45人参加学校运动会的入场式，队伍共9排5列，如果用(2，4)表示第2排从左到右第4列站着的同学，那么站在队伍最中间的点表示为( D )A．(15，4) B．(2，3) C．(3，0) D．(5，3)3．若点A(m，n)在第三象限，则点B(－m，n)在( D )A．第一象限B．第二象限C．第三象限D．第四象限4．如果M(m＋3，2m＋4)在y轴上，那么点M的坐标是( B )A．(－2，0) B．(0，－2) C．(1，0) D．(0，1)5．如果P 点的坐标为(a ，b)，它关于y 轴的对称点为P 1，P 1关于x 轴的对称点为P 2，已知P 2的坐标为(－2，3)，则点P 的坐标为( B )A ．(－2，－3)B ．(2，－3)C ．(－2，3)D ．(2，3)6．(资阳期末)如图，小明从点O 出发，先向西走40米，再向南走30米到达点E ，如果点E 的位置用(－40，－30)表示，那么(10，20)表示的位置是( B )A ．点AB ．点BC ．点CD ．点D,第6题图) ,第7题图)7．如图，在平面直角坐标系中，以O 为圆心，适当长为半径画弧，交x 轴于点M ，交y 轴于点N ，再分别以点M ，N 为圆心，大于12MN 的长为半径画弧，两弧在第二象限交于点P.若点P 的坐标为(2a ，b ＋1)，则a 与b 的数量关系为( B )A ．a ＝bB ．2a ＋b ＝－1C ．2a －b ＝1D ．2a ＋b ＝18．在平面直角坐标系中，A ，B ，C 三点的坐标分别为(0，0)，(0，－5)，(－2，－2)，以这三点为平行四边形的三个顶点，则第四个顶点不可能在( A )A ．第一象限B ．第二象限C ．第三象限D ．第四象限9. 已知A(a ，0)和B 点(0，10)两点，且AB 与坐标轴围成的三角形的面积等于20，则a 的值为( D ) A ．2 B ．4C ．0或4D ．4或－410．如图，点A 的坐标是(2，2)，若点P 在x 轴上，且△APO 是等腰三角形，则点P 的坐标不可能是( B )A ．(4，0)B ．(1，0)C ．(－22，0)D ．(2，0) 二、填空题(每小题3分，共18分)11．点P(1，2)关于x 轴的对称点P 1的坐标是__(1，－2)__，点P(1，2)关于y 轴的对称点P 2的坐标是__(－1，2)__．12．如图，如果所在的位置坐标为(－1，－2)，所在的位置坐标为(2，－2)，则所在的位置坐标为__(－3，3)__．,第12题图) ,第14题图)13．已知点A(4，3)，AB ∥y 轴，且AB ＝3，则B 点的坐标为__(4，0)或(4，6)__．14．如图，正方形A 1A 2A 3A 4，A 5A 6A 7A 8，A 9A 10A 11A 12，…(每个正方形从第三象限的顶点开始，按顺时针方向，依次记为A 1，A 2，A 3，A 4；A 5，A 6，A 7，A 8；A 9，A 10，A 11，A 12；…)的中心均在坐标原点O ，各边均与x 轴或y 轴平行，若它们的边长依次是2，4，6…，则顶点A 20的坐标为__(5，－5)__．15．(湘潭中考)阅读材料：设a →＝(x 1，y 1)，b →＝(x 2，y 2)，如果a →※b →，则x 1·y 2＝x 2·y 1.根据该材料填空：已知a →＝(2，3)，b →＝(4，m)，且a →※b →，则m ＝__6__.16．如图，将正方形OABC 放在平面直角坐标系中，O 是原点，A 的坐标为(1，3)，则点B 的坐标为3)__．三、解答题(本大题9小题，共72分)17．(6分)有一张图纸被损坏，但上面有如图所示的两个标志点A(－3，1)，B(－3，－3)可见，而主要建筑C(3，2)破损，请通过建立直角坐标系找到图中建筑C 的位置．解：如图：18．(6分)图中标明了小强家附近的一些地方．(1)写出公园、游艺场和学校的坐标；(2)早晨，小强从家里出发，沿(－3，－1)，(－1，－2)，(0，－1)，(2，－2)，(1，0)，(1，3)，(－1，2)路线转了一下，又回到家里，写出他路上经过的地方．解：(1)公园(3，－1)，游艺场(3，2)，学校(1，3)(2)邮局——移动通讯——幼儿园——消防队——火车站——学校——糖果店19．(6分)一位老人制作的仿真郑和宝船尺寸如图，已知在某一直角坐标系中，点A坐标为(9，0)．(1)请你直接在图中画出该坐标系；(2)写出其余5点的坐标．解：(1)画图略(2)B(5，2)，C(－5，2)，D(－9，0)，E(－5，－2)，F(5，－2)20．(6分)如图，分别说明：△ABC从(1)→(2)，再从(2)→(3)…一直到(5)，它的横、纵坐标依次是如何变化的？解：(1)→(2)纵坐标不变，横坐标都加1(2)→(3)横坐标不变，纵坐标都加1(3)→(4)横、纵坐标都乘以－1(4)→(5)横坐标不变，纵坐标都乘以－121．(9分)已知点A(a－3，a2－4)，求分别满足下列条件的a及点A的坐标：(1)当点A在x轴上；(2)当点A在y轴上；(3)已知点B(2，5)，且AB∥x轴．解：(1)因为点A(a－3，a2－4)在x轴上，所以a2－4＝0，所以a＝±2.点A的坐标为(－1，0)或(－5，0)(2)因为点A在y轴上，所以a－3＝0，所以a＝3，点A的坐标为(0，5)(3)因为AB∥x轴，所以a2－4＝5，所以a＝±3.当a＝±3时，a－3≠2，故a＝±3，点A的坐标为(0，5)或(－6，5)22．(10分)如图所示，在平面直角坐标系中有A，B，C三点．(1)写出A，B，C三点坐标；(2)画出△ABC关于x轴对称图形△A1B1C1，并写出A1，B1，C1的坐标；(3)在图中描出D(2，4)，E(3，1)，F(1，3)，观察△DEF与△ABC有什么关系？(4)如果三角形ABC中任意一点M的坐标为(x，y)，那么它关于y轴对称的点N的坐标是什么？解：(1)A(－2，4)，B(－3，1)，C(－1，3)(2)图略，A1(－2，－4)，B1(－3，－1)，C1(－1，－3)(3)△DEF与△ABC关于y轴对称(4)N(－x，y)23．(8分)如图所示，OABC是一张放在平面直角坐标系中的长方形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA＝10，OC＝8.在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处，求D，E两点的坐标．解：由题意可知，折痕AD是四边形OAED的对称轴，在Rt△ABE中，AE＝AO＝10，AB＝8，BE＝AE2－AB2＝102－82＝6，所以CE＝4，所以E(4，8)．在Rt△DCE中，DC2＋CE2＝DE2，又因为DE＝OD，所以(8－OD)2＋42＝OD2，解得OD＝5，所以D(0，5)24．(9分)如图，在平面直角坐标系中有三点A(－2，1)，B(3，1)，C(2，3)．(1)在平面直角坐标系内描出点A，B，C的位置，并将点A，B，C，A用线段依次连接起来；(2)求出以A，B，C三点为顶点的三角形的面积；(3)在y轴上是否存在点P，使以A，B，P三点为顶点的三角形的面积为10？若存在，请直接写出点P的坐标；若不存在，请说明理由．解：(1)图略(2)依题意，得AB∥x轴，且AB＝3－(－2)＝5，所以S△ABC＝12×5×2＝5(3)存在．因为AB＝5，S△ABP＝10，所以P点到AB的距离为4.又因为点P在y轴上，所以点P的坐标为(0，5)或(0，－3)25．(12分)如图，在平面直角坐标系中，直线l是第一、三象限的角平分线．实验与探究：(1)由图观察可知点A(0，2)与点A1(2，0)关于直线l对称，请你在图中标明点B(3，5)，C(3，－5)，D(－3，－5)，E(－5，0)关于直线l的对称点B1，C1，D1，E1的位置，并写出它们的坐标；归纳与发现：(2)结合图形并观察以上五组点的坐标，你会发现：坐标平面内任意一点P(a，b)关于直线l的对称点P1的坐标为__(b，a)__；拓展与应用：(3)若点M(4，2＋5y)与点N(－3，3x＋1)关于第一、三象限的角平分线对称，求点(x，y)的坐标．解：(1)B1(5，3)，C1(－5，3)，D1(－5，－3)，E1(0，－5)(3)根据任意一点P(a，b)关于直线y＝x的对称点P1的坐标为(b，a)可知，2＋5y＝－3，3x＋1＝4，解得x＝1，y＝－1，所以点(x，y)的坐标为(1，－1)第四章检测题(时间：120分钟满分：120分)一、选择题(每小题3分，共30分)1．下列图象中，表示y是x的函数的个数有( B )A．1个B．2个C．3个D．4个2．(宜宾期末)一名老师带领x名学生到动物园参观，已知成人票每张30元，学生票每张10元．设门票的总费用为y元，则y与x的函数关系为( A )A．y＝10x＋30 B．y＝40xC．y＝10＋30x D．y＝20x3．(白银中考)在平面直角坐标系中，一次函数y＝kx＋b的图象如图所示，观察图象可得( A ) A．k>0，b>0 B．k>0，b<0C．k<0，b>0 D．k<0，b<0,第3题图),第9题图),第10题图) 4．下列四个点中，不在同一个正比例函数上的点是( D )A．(－4，－8) B．(1，2)C．(－3，－6) D．(2，－4)5．P1(x1，y1)，P2(x2，y2)是一次函数y＝－2x＋5图象上的两点，且x1＜x2，则y1与y2的大小关系是( C )A．y1＜y2B．y1＝y2C．y1＞y2D．y1＞y2＞06．对于函数y＝－12x＋3，下列说法错误的是( C )A．图象经过点(2，2)B．y随着x的增大而减小C．图象与y轴的交点是(6，0)D．图象与坐标轴围成的三角形面积是97．已知一次函数y＝32x＋m和y＝－12x＋n的图象都经过点A(－2，0)，且与y轴分别交于B，C两点，那么△ABC的面积是( C )A．2 B．3C．4 D．68．已知一次函数y＝kx＋b的图象与y＝x平行，且过点(1，2)，那么它必过点( A )A．(－1，0) B．(2，－1)C．(2，1) D．(0，－1)9．如图，把Rt△ABC放在直角坐标系内，其中∠CAB＝90°，BC＝5，点A，B的坐标分别为(1，0)，(4，0)，将△ABC沿x轴向右平移，当点C落在直线y＝2x－6上时，线段BC扫过的面积为( C )A．4 B．8C．16 D．8210．(成都期末)甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500 m，先到终点的人原地休息．已知甲先出发2 s．在跑步过程中，甲、乙两人的距离(m)与乙出发的时间t(s)之间的关系如图所示，给出以下结论：①a＝8；②b＝92；③c＝123.其中正确的是( A )A．①②③B．①②C．①③D．②③二、填空题(每小题3分，共18分)11．将直线y＝2x向上平移1个单位长度后得到的直线是__y＝2x＋1__.12．(盐城中考)函数y＝x－2x－4自变量x的取值范围是__x≥2且x≠4__.13．一次函数y＝(m＋2)x＋1，若y随x的增大而增大，则m的取值范围是__m＞－2__.14．已知某一次函数的图象经过点A(0，2)，B(1，3)，C(a ，1)三点，则a 的值是__－1__.15．某农场租用播种机播种小麦，在甲播种机播种2天后，又调来乙播种机参与播种，直至完成800亩的播种任务．播种亩数与天数之间的函数关系如图，那么乙播种机参与播种的天数是__4__.16．一次函数y ＝kx ＋b ，当0≤x ≤4时，－7≤y ≤－3，则k ＝__1或－1__. 三、解答题(本大题9小题，共72分)17．(7分)已知一次函数y ＝kx ＋b 的图象经过M(0，2)，N(1，3)两点． (1)求k ，b 的值；(2)若一次函数y ＝kx ＋b 的图象与x 轴的交点为A(a ，0)，求a 的值．解：(1)由题意得b ＝2，把⎩⎪⎨⎪⎧x ＝1，y ＝3代入y ＝kx ＋2中得k ＝1(2)由(1)得y ＝x ＋2，当y ＝0时，x ＝－2，即a ＝－218．(6分)一次函数y ＝－4x ＋b 与x 轴交于点A ，与y 轴交于点B ，△OAB 的面积是2，求一次函数的表达式．解：令y ＝0得－4x ＋b ＝0，x ＝b 4，所以S △AOB ＝12×|b4|×|b|＝2，所以b ＝±4，所以一次函数的表达式为y ＝－4x ＋4或y ＝－4x －419．(8分)联通公司手机话费收费有A 套餐(月租费15元，通话费每分钟0.1元)和B 套餐(月租费0元，通话费每分钟0.15元)两种．设A 套餐每月话费为y 1(元)，B 套餐为y 2(元)，月通话时间为x 分钟．(1)分别表示出y 1与x ，y 2与x 的函数关系式； (2)月通话时间多长时，A ，B 两种套餐收费一样？(3)什么情况下A 套餐更省钱？解：(1)y 1＝0.1x ＋15，y 2＝0.15x(2)由y 1＝y 2得0.1x ＋15＝0.15x ，解得x ＝300 (3)当通话时间多于300分钟时，A 套餐省钱20．(7分)设函数y ＝x ＋n 的图象与y 轴交于点A ，函数y ＝－3x －m 的图象与y 轴交于点B ，两个函数的图象交于点C(－3，1)，D 为AB 的中点．(1)求m ，n 的值；(2)求直线DC 的一次函数表达式．解：(1)m ＝8，n ＝4(2)由(1)得A(0，4)，B(0，－8)．因为D 是AB 的中点，所以D(0，－2)，设直线CD 的表达式为y＝kx ＋b ，则⎩⎨⎧b ＝－2，－3k ＋b ＝1，解得⎩⎨⎧k ＝－1，b ＝－2，即y ＝－x －221．(7分)某生物小组观察一植物生长，得到植物的高度(单位：厘米)与观察时间(单位：天)的关系，并画出如下的图象(AC 是线段，直线CD 平行于x 轴．)(1)该植物从观察时起，多少天以后停止长高？(2)求直线AC 的表达式，并求该植物最高长多少厘米？解：(1)50天后(2)设直线AC 的表达式为y ＝kx ＋6，将(30，12)代入，得12＝30k ＋6，解得k ＝15，表达式为y ＝15x ＋6，最高长16厘米22．(8分)1号探测气球从海拔5 m 处出发，以1 m /min 的速度上升．与此同时，2号探测气球从海拔15 m 处出发，以0.5 m /min 的速度上升，两个气球都匀速上升了50 min .设气球上升时间为 x min (0≤x ≤50)(1)根据题意，填写下表：果不能，请说明理由；(3)当30≤x ≤50时，两个气球所在位置的海拔最多相差多少米？解：(2)能．由x ＋5＝0.5x ＋15得x ＝20，所以x ＋5＝25，即气球上升20 min 时位于海拔25 m 处 (3)当30≤x ≤50时，1号气球始终在2号气球上方，设两气球的海拔差为y ，则y ＝(x ＋5)－(0.5x ＋15)＝0.5x －10，由函数的性质知y 随x 的增大而增大，所以当x ＝50时，y 的值最大，为15米23．(9分)如图，直线y ＝kx ＋6与x 轴、y 轴分别相交于点E ，F ，点E 的坐标为(－8，0)，点A 的坐标为(－6，0)，点P(x ，y)是第二象限内的直线上的一个动点．(1)求k 的值；(2)在点P 的运动过程中，写出△OPA 的面积S 与x 的函数表达式，并写出自变量x 的取值范围；(3)探究：当P 运动到什么位置(求P 的坐标)时，△OPA 的面积为278解：(1)k ＝34(2)由(1)得y ＝34x ＋6，所以S ＝12×6×(34x ＋6)，所以S ＝94x ＋18(－8<x<0)(3)由S ＝94x ＋18＝278得x ＝－132，y ＝34×(－132)＋6＝98，所以P(－132，98)，即P 运动到点(－132，98)时，△OPA 的面积为27824．(9分)(长春中考)甲、乙两车间同时开始加工一批服装．从开始加工到加工完这批服装甲车间工作了9小时，乙车间在中途停工一段时间维修设备，然后按停工前的工作效率继续加工，直到与甲车间同时完成这批服装的加工任务为止．设甲、乙两车间各自加工服装的数量为y(件)，甲车间加工的时间为x(时)，y 与x 之间的函数图象如图所示．(1)甲车间每小时加工服装件数为__80__件；这批服装的总件数为__1140__件； (2)求乙车间维修设备后，乙车间加工服装数量y 与x 之间的函数关系式； (3)求甲、乙两车间共同加工完1000件服装时甲车间所用的时间．解：(2)乙车间每小时加工服装件数为120÷2＝60(件)，乙车间修好设备的时间为9－(420－120)÷60＝4(时)，所以乙车间维修设备后，乙车间加工服装数量y 与x 之间的函数关系式为y ＝120＋60(x －4)＝60x －120(4≤x ≤9)(3)甲车间加工服装数量y 与x 之间的函数关系式为y ＝80x ，当80x ＋60x －120＝1000时，x ＝8.答：甲、乙两车间共同加工完1000件服装时甲车间所用的时间为8小时25．(11分)双11购物节期间，某电器商城推出了两种促销方式，且每次购买电器时只能使用其中一种方式：第一种是打折优惠，凡是在该商城购买家用电器的客户均可享受八折优惠；第二种方式是：赠送优惠券，凡在商城三天内购买家用电器的金额满400元且少于600元的，赠优惠券100元；不少于600元的，所赠优惠券是购买电器金额的14，另再送50元现金．(1)以上两种促销方式中第二种方式，可用如下形式表达：设购买电器的金额为x(x ≥400)元，优惠券金额为y 元，则：①当x ＝500时，y ＝__100__；②当x ≥600时，y ＝__14x__；(2)如果小张想一次性购买原价为x(400≤x ＜600)元的电器，可以使用优惠券，在上面的两种促销方式中，试通过计算帮他确定一种比较合算的方式？(3)如果小张在促销期间内在此商城先后两次购买电器时都得到了优惠券(两次购买均未使用优惠券)，第一次购买金额在600元以内，第二次购买金额超过600元，所得优惠券金额累计达800元，设他购买电器的金额为W 元，W 至少应为多少？(W ＝支付金额－所送现金金额)解：(2)设y 1＝0.8x ，y 2＝x －100，因为由0.8x ＝x －100得x ＝500，此时y 1＝y 2；当400≤x ＜500时y 1＞y 2；当500＜x ＜600时y 1＜y 2，所以当x ＝500时，两种方式一样合算；当400≤x ＜500时，选第二种方式合算；当500＜x ＜600时，选第一种方式合算(3)设第一次购买花了m 元，第二次花了n 元，当400≤m ＜600，n ≥600时，100＋14n ＝800，得n＝2800，W ＝m ＋n －50＝m ＋2750，因为400≤m ＜600，所以3150≤W ＜3350，即W 至少为3150元第五章检测题(时间：120分钟满分：120分)一、选择题(每小题3分，共30分)1．下列方程组中，是二元一次方程组的是( D ) A .⎩⎪⎨⎪⎧x ＋13＝1y ＝x 2 B .⎩⎪⎨⎪⎧3x －y ＝52y －z ＝6C .⎩⎪⎨⎪⎧x 5＋y 2＝1xy ＝1D .⎩⎪⎨⎪⎧x 2＝3y －2x ＝42．由方程组⎩⎪⎨⎪⎧2x ＋m ＝1，y －3＝m可得出x 与y 的关系是( A )A ．2x ＋y ＝4B ．2x －y ＝4C ．2x ＋y ＝－4D ．2x －y ＝－43．已知3a 2x －1b 2y 与－3a －3y b 3x ＋6是同类项，则x ＋y 的值为( D ) A .113 B .3113 C .1513 D ．－1134．如图，以两条直线l 1，l 2的交点坐标为解的方程组是( C )A .⎩⎪⎨⎪⎧3x －4y ＝63x －2y ＝0 B .⎩⎪⎨⎪⎧3x －4y ＝63x ＋2y ＝0 C .⎩⎪⎨⎪⎧3x －4y ＝－63x －2y ＝0 D .⎩⎪⎨⎪⎧－3x ＋4y ＝63x ＋2y ＝05．(眉山中考)已知关于x ，y 的二元一次方程组⎩⎪⎨⎪⎧2ax ＋by ＝3，ax －by ＝1的解为⎩⎨⎧x ＝1，y ＝－1，则a －2b 的值是( B )A ．－2B ．2C ．3D ．－36．(随州中考)小明到商店购买“五四青年节”活动奖品，购买20只铅笔和10本笔记本共需110元，但购买30支铅笔和5本笔记本只需85元，设每支铅笔x 元，每本笔记本y 元，则可列方程组( B )A .⎩⎪⎨⎪⎧20x ＋30y ＝11010x ＋5y ＝85B .⎩⎪⎨⎪⎧20x ＋10y ＝11030x ＋5y ＝85C .⎩⎪⎨⎪⎧20x ＋5y ＝11030x ＋10y ＝85D .⎩⎪⎨⎪⎧5x ＋20y ＝11010x ＋30y ＝85 7．一个两位数，个位上的数字与十位上的数字之和为7，如果这个两位数加上45，则恰好成为个位数字与十位数字对调后组成的新两位数，则原来的两位数是( B )A ．61B ．16C ．52D ．258．已知等腰三角形的两边长为x ，y 满足方程组⎩⎪⎨⎪⎧2x －y ＝3，3x ＋2y ＝8.则此等腰三角形的周长为( A )A ．5B ．4C ．3D ．5或49．由方程组⎩⎨⎧2x ＋y ＝7，2y ＋z ＝8，2z ＋x ＝9，可得到x ＋y ＋z 的值为( A )A ．8B ．9C ．10D ．11.710．有一根长40 cm 的金属棒，欲将其截成x 根7 cm 长的小段和y 根的9 cm 长的小段，剩余部分作废料处理．若使废料最少，则正整数x ，y 应分别为( B )A ．x ＝1，y ＝3B ．x ＝3，y ＝2C ．x ＝4，y ＝1D ．x ＝2，y ＝3 二、填空题(每小题3分，共18分)11．写出一个解为⎩⎪⎨⎪⎧x ＝1，y ＝2的二元一次方程组是__⎩⎪⎨⎪⎧x ＋y ＝3x －y ＝－1__.12．(包头中考)若关于x ，y 的二元一次方程组⎩⎪⎨⎪⎧x ＋y ＝3，2x －ay ＝5的解是⎩⎨⎧x ＝b ，y ＝1，则a b的值为__1__.13．如果直线y ＝2x ＋3与直线y ＝3x －2b 的交点在x 轴上，那么b 的值为__－94__.14．八年级(1)班为了奖励学习进步的学生，购买了单价为3元的笔记本与单价为5元的钢笔两种奖品，共花35元，则有__2__种购买方案．15．(乐山中考)二元一次方程组x ＋y 2＝2x －y3＝x ＋2的解是__⎩⎪⎨⎪⎧x ＝－5y ＝－1__.16．在同一直角坐标系内分别作出一次函数y ＝12x ＋1和y ＝2x －2的图象，则下面的说法：①函数⎪⎧2y －x ＝2，⎪⎧x ＝2，1＝2x －2的图象交点的坐标为(－2，2)；④两直线与y 轴所围成的三角形的面积为 3.其中正确的有__②④__.(填序号)三、解答题(本大题9小题，共72分) 17．(12分)解下列方程组：(1)⎩⎪⎨⎪⎧y ＋x ＝1，5x ＋2y ＝8； (2)⎩⎪⎨⎪⎧x 2＋y 3＝132，4x －3y ＝18；解：⎩⎪⎨⎪⎧x ＝2y ＝－1 解：⎩⎪⎨⎪⎧x ＝9y ＝6(3)⎩⎪⎨⎪⎧x －2y ＝－1，x －y ＝2－2y ； (4)⎩⎪⎨⎪⎧x ＋y ＝－1，2x －y ＋3z ＝1，x －2y －z ＝6.解：⎩⎪⎨⎪⎧x ＝1y ＝1 解：⎩⎪⎨⎪⎧x ＝1y ＝－2z ＝－118．(6分)直线a 与直线y ＝2x ＋1的交点的横坐标是2，与直线y ＝－x ＋2的交点的纵坐标是1，求直线a 对应的表达式．解：将x ＝2代入y ＝2x ＋1得y ＝5，将y ＝1代入y ＝－x ＋2得x ＝1，设直线a 的表达式为y ＝kx＋b ，即⎩⎨⎧5＝2k ＋b ，1＝k ＋b ，解得⎩⎨⎧k ＝4，b ＝－3，所以直线a 的表达式为y ＝4x －319．(6分)已知关于x ，y 的方程组⎩⎪⎨⎪⎧ax ＋2by ＝4，x ＋y ＝1与⎩⎪⎨⎪⎧x －y ＝3，bx ＋（a －1）y ＝3的解相同，求a ，b 的值．解：解方程组⎩⎪⎨⎪⎧x ＋y ＝1，x －y ＝3得⎩⎨⎧x ＝2，y ＝－1，将⎩⎪⎨⎪⎧x ＝2，y ＝－1代入方程组⎩⎪⎨⎪⎧ax ＋2by ＝4，bx ＋（a －1）y ＝3得⎩⎪⎨⎪⎧a －b ＝2，2b －a ＝2解得⎩⎪⎨⎪⎧a ＝6b ＝420．(6分)如图，8块相同的长方形地砖拼成了一个长方形图形(地砖间的缝隙忽略不计)，求每块地砖的长和宽．解：设每块地砖的长为x 厘米，宽为y 厘米，由题意得⎩⎨⎧x ＋y ＝60，3y ＋x ＝2x ，解得⎩⎪⎨⎪⎧x ＝45，y ＝15.答：每块地砖的长和宽分别为45厘米，15厘米21．(7分)如图，在东北大秧歌的踩高跷表演中，已知演员身高是高跷长度的2倍，高跷与腿重合部分的长度为28 cm ，演员踩在高跷上时，头顶距离地面的高度为224 cm .设演员的身高为x cm ，高跷的长度为y cm ，求x ，y 的值．解：依题意得⎩⎨⎧x ＝2y ，x ＋y －28＝224，解得⎩⎪⎨⎪⎧x ＝168y ＝8422．(7分)学校组织学生乘汽车去自然保护区野营，前13路段为平路，其余路段为坡路，已知汽车在平路上行驶的速度为60 km /h ，在坡路上行驶的速度为30 km /h .汽车从学校到自然保护区一共行驶了6.5 h ，求汽车在平路和坡路上各行驶多少时间？解：设汽车在平路上行驶x h ，在坡路上行驶y h ，则依题意得⎩⎨⎧x ＋y ＝6.5，60x ×2＝30y ，解得⎩⎪⎨⎪⎧x ＝1.3y ＝5.2。

全新北师大版八年级数学上册各单元测试卷(全册共61页附答案)

全新北师大版八年级数学上册各单元测试卷（全册共61页附答案）目录第一章达标测试卷一、选择题(每题3分，共30分)1．把一个直角三角形的两直角边长同时扩大到原来的3倍，则斜边长扩大到原来的( ) A．2倍B．3倍C．4倍D．5倍2．下列各组线段能构成直角三角形的一组是( )A．30，40，50 B．7，12，13 C．5，9，12 D．3，4，63．已知一个直角三角形的两直角边长分别为5和12，则第三边长的平方是( ) A．169 B．119 C．13 D．1444．如图，阴影部分是一个长方形，则长方形的面积是( )A．3 cm2B．4 cm2C．5 cm2D．6 cm2(第4题) (第7题) (第10题)5．满足下列条件的△ABC，不是直角三角形的为( )A．∠A＝∠B－∠C B．∠A∶∠B∶∠C＝1∶1∶2C．b2＝a2－c2D．a∶b∶c＝2∶3∶46．已知一轮船以18 n mile/h的速度从港口A出发向西南方向航行，另一轮船以24 n mile/h 的速度同时从港口A出发向东南方向航行，离开港口1.5 h后，两轮船相距( ) A．30 n mile B．35 n mile C．40 n mile D．45 n mile7．如图，在△ABC中，AB＝AC＝13，BC＝10，点D为BC的中点，DE⊥AB，垂足为点E，则DE等于( )A.1013B.1513C.6013D.75138．若△ABC的三边长a，b，c满足(a－b)(a2＋b2－c2)＝0，则△ABC是( ) A．等腰三角形B．直角三角形C．等边三角形D．等腰三角形或直角三角形9．已知直角三角形的斜边长为5 cm，周长为12 cm，则这个三角形的面积是( ) A．12 cm2B．6 cm2C．8 cm2D．10 cm210．如图，分别以直角三角形的三条边为边向外作正方形，然后分别以三个正方形的中心为圆心，正方形边长的一半为半径作圆，记三个圆的面积分别为S1，S2，S3，则S1，S2，S3之间的关系是( )A．S1＋S2＞S3B．S1＋S2＝S3C．S1＋S2＜S3D．无法确定二、填空题(每题3分，共24分)11．如图，在等腰三角形ABC中，AB＝AC，AD是底边上的高，若AB＝5 cm，BC＝6 cm，则AD＝__________．(第11题) (第12题) (第13题)12．如图，某人欲横渡一条河，由于水流的影响，实际上岸地点C偏离欲到达点B 300 m，结果他在水中实际游了500 m，则该河流的宽度为________．13．如图，在Rt△ABC中，∠B＝90°，AB＝3 cm，AC＝5 cm，将△ABC折叠，使点C与点A 重合，得折痕DE，则△ABE的周长等于________．14．已知a，b，c是△ABC的三边长，且满足关系式(a2－c2－b2)2＋||c－b＝0，则△ABC的形状为_________________________________________．15．如图是一个长方体，则AB＝________，阴影部分的面积为________．(第15题) (第16题)16．如图是“赵爽弦图”，△ABH，△BCG，△CDF和△DAE是四个全等的直角三角形，四边形ABCD和EFGH都是正方形．如果AB＝10，且AH∶AE＝3∶4.那么AH等于________．17．红方侦察员小马的正前方400 m处有一条东西走向的公路，突然发现一辆蓝方汽车在公路上行驶，他拿出红外线测距仪测得汽车与他相距400 m，10 s后又测得汽车与他相距500 m，则蓝方汽车的速度是________m/s.18．在一根长90 cm的灯管上缠满了彩色丝带，已知可近似地将灯管看成圆柱体，且底面周长为4 cm，彩色丝带均匀地缠绕了30圈(如图为灯管的部分示意图)，则彩色丝带的总长度为__________．(第18题)三、解答题(19～22题每题9分，其余每题10分，共66分)19．某消防部队进行消防演练．在模拟现场，有一建筑物发生了火灾，消防车到达后，发现离建筑物的水平距离最近为12 m，如图，即AD＝BC＝12 m，此时建筑物中距地面12.8 m高的P处有一被困人员需要救援．已知消防云梯车的车身高AB是3.8 m，问此消防车的云梯至少应伸长多少米？20．如图，在4³4的正方形网格中，每个小正方形的边长都是1.线段AB，AE分别是图中两个1³3的长方形的对角线，请你说明：AB⊥AE.21．如图，四边形ABCD是边长为a的正方形，点E在CD上，DE＝b，AE＝c，延长CB至点F，使BF＝b，连接AF，试利用此图说明勾股定理．22．如图，一根12 m的电线杆AB用铁丝AC，AD固定，现已知用去的铁丝AC＝15 m，AD＝13 m，又测得地面上B，C两点之间的距离是9 m，B，D两点之间的距离是5 m，则电线杆和地面是否垂直，为什么？23．如图，∠AOB＝90°，OA＝9 cm，OB＝3 cm，一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O，机器人立即从点B出发，沿BC方向匀速前进拦截小球，恰好在点C处截住了小球，如果小球滚动的速度与机器人行走的速度相等，那么机器人行走的路程BC是多少？24．如图，在长方形ABCD中，DC＝5 cm，在DC上存在一点E，沿直线AE把△AED折叠，使点D恰好落在BC边上，设落点为F，若△ABF的面积为30 cm2，求△ADE的面积．25．有一个如图所示的长方体透明玻璃水缸，其长AD＝8 cm，高AB＝6 cm，水深为AE＝4 cm，在水面线EF上紧贴内壁G处有一粒食物，且EG＝6 cm，一只小虫想从水缸外的A处沿水缸壁爬进水缸内的G处吃掉食物．(1)小虫应该沿怎样的路线爬才能使爬的路线最短呢？请你画出它爬行的最短路线，并用箭头标注．(2)求小虫爬行的最短路线长(不计缸壁厚度)．答案一、1.B 2.A 3.A 4.C 5.D 6.D 7．C 8.D 9.B 10.B二、11.4 cm 12.400 m 13.7 cm 14．等腰直角三角形 15．13；30 16.6 17.3018．150 cm 点拨：因为灯管可近似看成圆柱，而圆柱的侧面展开图是一个长方形，所以假设把灯管的侧面展开后，得到一个由30个完全相同的小长方形组成的大长方形，且每个小长方形的长等于灯管的底面周长，小长方形的高等于灯管长度的130，则丝带的长度等于小长方形对角线长的30倍．三、19.解：因为CD ＝AB ＝3.8 m ，所以PD ＝PC －CD ＝9 m. 在Rt △ADP 中，AP 2＝AD 2＋PD 2，得AP ＝15 m.所以此消防车的云梯至少应伸长15 m.20．解：如图，连接BE .(第20题)因为AE 2＝12＋32＝10，AB 2＝12＋32＝10，BE 2＝22＋42＝20，所以AE 2＋AB 2＝BE 2.所以△ABE 是直角三角形，且∠BAE ＝90°，即AB ⊥AE .21．解：在△ADE 和△ABF 中，⎩⎪⎨⎪⎧AD ＝AB ＝a ，∠D ＝∠ABF ，DE ＝BF ＝b ，所以△ADE ≌△ABF .所以AE ＝AF ＝c ，∠DAE ＝∠BAF ，S △ADE ＝S △ABF .所以∠EAF ＝∠EAB ＋∠BAF ＝∠EAB ＋∠DAE ＝∠DAB ＝90°，S 正方形ABCD ＝S 四边形AECF .连接EF ，易知S 四边形AECF ＝S △AEF ＋S △ECF ＝12[c 2＋(a －b )(a ＋b )]＝12(a 2＋c 2－b 2)，S 正方形ABCD＝a 2，所以12(a 2＋c 2－b 2)＝a 2.所以a 2＋b 2＝c 2. 22．解：垂直．理由如下：因为AB ＝12 m ，AC ＝15 m ，BC ＝9 m ，所以AC 2＝BC 2＋AB 2. 所以∠CBA ＝90°. 又因为AD ＝13 m ，AB ＝12 m ，BD ＝5 m ，所以AD 2＝BD 2＋AB 2. 所以∠ABD ＝90°，因此电线杆和地面垂直．点拨：要判定电线杆和地面垂直，只需说明AB ⊥BD 且AB ⊥BC 即可，利用勾股定理的逆定理即可判定△ABD 和△ABC 为直角三角形，从而得出电线杆和地面垂直． 23．解：根据题意，BC ＝AC ＝OA －OC ＝9－OC .因为∠AOB ＝90°，所以在Rt △BOC 中，根据勾股定理，得OB 2＋OC 2＝BC 2，所以32＋OC 2＝(9－OC )2，解得OC ＝4 cm. 所以BC ＝5 cm.24．解：由折叠可知AD ＝AF ，DE ＝EF .由S △ABF ＝12BF ²AB ＝30 cm 2，AB ＝DC ＝5 cm ，得BF ＝12 cm.在Rt △ABF 中，由勾股定理，得AF ＝13 cm ，所以BC ＝AD ＝AF ＝13 cm. 设DE ＝x cm ，则EC ＝(5－x )cm ，EF ＝x cm ，FC ＝13－12＝1(cm)．在Rt △ECF 中，由勾股定理，得EC 2＋FC 2＝EF 2，即(5－x )2＋12＝x 2，解得x ＝135.所以S △ADE ＝12AD ²DE ＝12³13³135＝16.9 (cm 2)．25．解：(1)如图，作点A 关于BC 的对称点A ′，连接A ′G 与BC 交于点Q ，则AQ ＋QG 为最短路线．(第25题)(2)因为AE ＝4 cm ，AA ′＝12 cm ，所以A ′E ＝8 cm.在Rt △A ′EG 中，EG ＝6 cm ，A ′E ＝8 cm ，A ′G 2＝A ′E 2＋EG 2＝102，所以A ′G ＝10 cm ，所以AQ ＋QG ＝A ′Q ＋QG ＝A ′G ＝10 cm. 所以最短路线长为10 cm.第二章达标测试卷一、选择题(每题3分，共30分) 1．8的平方根是( )A ．4B ．±4C ．2 2D ．±2 2的立方根是( )A ．－1B ．0C ．1D ．±13．有下列各数：0.456，3π2，(－π)0，3.14，0.801 08，0.101 001 000 1…(相邻两个1之间0的个数逐次加1)，4，12.其中是无理数的有( ) A ．1个B ．2个C ．3个D ．4个4．有下列各式：①2；②13；③8x >0).其中，最简二次根式有( )A ．1个B ．2个C ．3个D ．4个5．下列语句不正确的是( )A ．数轴上的点表示的数，如果不是有理数，那么一定是无理数B ．大小介于两个有理数之间的无理数有无数个C ．－1的立方是－1，立方根也是－1D ．两个实数，较大者的平方也较大 6．下列计算正确的是( )A.12＝2 3B.32＝32＝＝x7．设n 为正整数，且n <65<n ＋1，则n 的值为( )A ．5B ．6C ．7D ．88．如图，在数轴上表示－5和19的两点之间表示整数的点有( )A ．7个B ．8个C ．9个D ．6个(第8题)(第10题)9(y ＋3)2＝0，则x －y 的值为( )A ．－1B ．1C ．－7D ．710．按如图所示的程序计算，若开始输入的n 值为2，则最后输出的结果是( )A ．14B ．16C ．8＋52D ．14＋2二、填空题(每题3分，共24分)11 ________ 5 (填“＞”或“＜”)．12．利用计算器计算12³3－5时，正确的按键顺序是________________，显示器上显示的数是________．13．如图，数轴上表示数3的是点________．。

北师大八年级数学上册单元测试题全套及答案

最新北师大版八年级数学上册单元测试题全套及答案第一章勾股定理综合测评时间：满分：120分、精心选一选（每小题4分，共32 分）1. 在厶 ABC 中，/ B=90° ，若 BC=3 AC=5,贝U AB 等于（）A.3B.4C.5D.62. 下列几组数中，能组成直角三角形的是（）4.两只小鼹鼠在地下打洞，一只朝前方挖，每分钟挖8 cm,另一只朝左挖，每分钟挖 6 cm,10分钟后，两只小鼹鼠相距（）6.图2中的小方格都是边长为 1的正方形，试判断厶 ABC 的形状为（）、耐心填一填（每小题4分，共32 分）9. 写出两组勾股数： ________________ . _______________10. 在厶ABC 中，ZC = 90° , 若 BC ： AC = 3 ：4 , AB= 10,则 BC= ___ , AC = _____ .班级: ________ 姓名： _______ 得分： _______1 1 1A.—,B.3 ,4, 6C.5 ,12, 13D.0.8 , 1.2 , 1.53 4 ，53.如图 1, 正方形 ABCD 的面积为 100 cm 2, △ ABP 为直角三角形， / P=90 ° ,且PB=6 cm ,则AP 的长为 ( )A.10 cmB.6 cmC.8 cmD.无法确定A.50 cmB.80 cmC.100 cm D.140 cm5.已知a , b , cABC 的三边，且满足 a 2 b 2 a 2 b 2 c 2 = 0，则它的形状为（ A.直角三角形C.等腰直角三角形B.等腰三角形D. 等腰三角形或直角三角形A .钝角三角形 B. 锐角三角形 C.直角三角形 D.以上都有可能［来源：学科网7. 如图3, 一圆柱高8 cm,底面半径为2 cm, —只蚂蚁从点 A 爬到点B 处吃食，要爬行的最短路程（取3 )是()A. 20 cmB.10 cmC.14 cmD.无法确定8.已知 Rt △ ABC 中，/ C=90°, 若 BC + AC = 14 cm , AB= 10 cm ,则该三角形的面积是（ 2A.24 cm2B.36 cmC.48 cm2D.60 cm11. 如图4，等腰三角形ABC的底边长为16,底边上的高AD长为6,则腰AB的长度为___________13. 一个三角形的三边长之比为 5 ： 12 ： 13，它的周长为60,则它的面积是 _______ . 14. 图6是一个三级台阶，它的每一级长、宽、高分别是2米，0.3米，0.2米，A ，B 是这个台阶上两个相对的端点，A 点有一只蚂蚁，想到B 点去吃可口的食物，则蚂蚁沿台阶面爬行到B 点的最短路程是米.屋门只有242 cm 高，100 cm 宽.你认为小明能把床垫拿进屋吗？________________________________________________________________________ .（填"能”或"不能”）16.图7是一束太阳光线从仓库窗户射入的平面示意图，小强同学测得米，AC = 4.5米，MC= 6米，则太阳光线 MA 的长度为 _______ 米.17. （10分）如图8，甲渔船以8海里/时的速度离开港口 O 向东北方向航行，乙渔船以5 4 BN ^ —米，NC=—米，BC = 133三、细心做一做（共56分）12.如图 5，/ OAB =Z OBC=Z OCD= 90°, AB= BC = CD= 1, OA= 2，贝U OD 2 = _____15. 一天，小明买了一张底面是边长为 260 cm 的正方形，厚30 cm 的床垫回家，至U 了家门口，才发现6海里/时的10,在一棵树的10米高处有两只猴子，一只猴子爬下树后走到离树 20米处的池塘D 后直接跃到A 处，距离以直线计算，若两只猴子所经过的距离相等，试求该树的19. （12分）如图 A 处.另一只爬到树顶速度离开港口 O 向西北方向航行，它们同时出发 .一个半小时后，甲、乙两渔船相距多少海里?9，已知在厶 ABC 中，AB=13, AD=12 AC=15, CD=9 求厶 ABC 的面积.18. （10分）如图高度.20. （12分）如图11, 一块草坪的形状为四边形 ABCDr 其中/ B=90 , AB=8 m BC=6 m CD=24 mAD=26 m.求这块草坪的面积.来源:Z#xx#]21. （12分）对任意符合条件的直角三角形保持其锐角顶点 A 不动，改变BC 的位置，使 E , D ，且/ BAE = 90°,/ CAD = 90° （如图 12）.【分析】所给数据如图中所示，且四边形 ACFD 是一个正方形，它的面积和四边形ABFE 的面积相等.第一章勾股定理综合测评一、 1.B 2.C 3.C 4.C 5.D 6.C 7.B 8.A二、 9.答案不唯一，如 3,4,5 ; 60,80,100 10.6 8 11.10 12.7 13.120 14.2.5 15.台匕冃匕16.7.533三、 17.解：由题意得 OA — 812 （海里），OB — 69 （海里）， AOB 90，所以△ AOB22是直角三角形.由勾股定理，得 OA 2 OB 2 AB 2，即AB 2 =92+122=225,所以AB= 15 （海里）.答略.18. 解：因为 AD=12 AC=15 CD=9所以AD+cD=144+8仁225= AC 2，所以△ ADC 为直角三角形，且/ ADC=90 .在 Rt △ ABD 中，AB=13, AD=12 由勾股定理得 BD 2 =AB 2 - AD 2 = 25，所以ED =5,所以 BC = BD+DC=5+9=1411所以 S AABC =• BC• AD=— X 14X 12=84 .2 219. 解：由题意知 AD+DB=BC+CA 且 CA=20米，BC=10米，设 BD=x 贝U AD=30-x .【解答】结合上面的分析过程验证勾股定理［来源：学科网］在Rt △ ACD中，CD+CA^AE2，即(30-x ) 2= ( 10+x) 2+202，解得x=5，故树高CD=10+x=15 (米).20. 解：如图，连接AC,因为/ B=90，所以在Rt△ ABC中，由勾股定理得AC2=AB2+BC2=82+62=100, 所以AC=10.又因为CD=24, AD=26所以在△ ACD中, AC+CD^A E J，所以△ ACD是直角三角形.1 1 1 1” *所以S 四边形ABC=S^ACD-S△ AB(= — AC?CD ——AB?BC —X 10X 24 -——X 8X6 =120-24=96 (m)."22 2 2 2/故该草坪的面积为96 m. '-一/21解：由分析可得S 正方形ACFD= S 四边形ABFE=S^ BAE+ S^ BFE・1 1即b2= c2+ (b+a) (b-a).2 2整理，得2b2= c2+ (b+ a) (b-a) .*源学一科网心所以a2+ b2= c2.第二章实数检测题【本检测题满分：100分，时间：90分钟】、选择题（每小题3分，共30分）1 .下列无理数中，在一2与1之间的是（)A. —LB.—:;C.D .2. （2014 •南京中考）8的平方根是（)A . 4B . ±4C .2 .刁D . ±皿3.若a,b为实数，且满足|a—2|+ . b2 =0, 则b —a的值为（)A . 2B . 0C.—2 D . 以上都不对4.卜列说法错误的是（）A. 5是25的算术平方根B.1是1的一个平方根C . （—4）2的平方根是一4D.0的平方根与算术平方根都是5.要使式子- x有意义，则x的取值范围是（）A . x> 0 B. x>- 2 C. x> 2 D. x< 26.若a, b均为正整数，且a> .7 , b> 3 2，则a + b的最小值是( )A. 3B.4C.57.在实数-，。

(完整版)北师大版八年级数学上册第一二单元检测题及答案

北师版八年级数学上册第一、二单元综合检测题（满分为120 分, 时间100 分钟）班级姓名分数一. 选择题（请将下列各题中的答案填在下面的表格中, 每小题3 分, 共30 分）1.49 的算术平方根是( )A. 7B. －7C.D. ±772．下列各组数中，不是“勾股数”的是()A．7，24，25 B. 1 ，2，3 C. 6，8，10 D. 9 ，12，15 3．下列各式中, 属于最简二次根式的是（）13A. B. 20 C. 22 D. 1214．在下列各数 3 、0 、-0.2 、 4 、8 、0.3737737773 （相邻两个 3 之间的7 的个数逐次加1）中，无理数的个数是()A. 4B. 3C. 2D. 15．如图1, 三个正方形围成一个直角三角形，64、400 分别为所在正方形的面积，则图中字母M 所代表的正方形面积是（）A .336 B.164096 C.464 D .155904图16. 将直角三角的三条边同时扩大 4 倍后，得到的三角形为（）A. 直角三角形B. 锐角三角形C. 钝角三角形 D . 不能确定7. 如果一个数的立方根是它本身，那么这个数是()A. 1 、0B. - 1C. 0D. 1、- 1 、08. 下列说法中正．确．的是(A. 带根号的数都是无理数)B. 无限小数都是无理数C. 无理数都是无限小数D. 无理数就是开方开不尽的数9．一个直角三角形两直角边长分别为 3 和4, 下列说法正确的是( )A. 斜边长为25B. 三角形的周长为25125C. 斜边长上的高为D. 三角形的面积为2010．下列说法中正．确．的有 ( )381 的平方根是 8 2( 2) 22 都是 2 ，③①8 的立方根，② 3，④A. 1 个B. 2个C. 3个 D. 4个二. 填空题（每小题 3 分, 共 24 分）2211. 一个三角形三边满足 (a+b) －c ＝ 2ab, 则这个三角形是三角形 .12. 已知 5＋ 11 的小数部分为 a ，5－ 11 的小数部分为 b ，则 a ＋b= 。

北师大版八年级数学上册第一章单元检测试题及答案

北师大版八年级数学上册第一章单元检测试题及答案一.单选题(每题3分,共30分)1．我国古代数学名著《九章算术》中记载:"今有竹高一丈.末折抵地,去本三尺．问折者高几何?翻译:现有竹子高一丈,折断的末端撑着地,离地面竹根三尺远,问折断处离地面有多高?(1丈=10尺)设折断处离地的高度为x 尺,则下列方程正确的是( )A ．()222310x x +=-B ．()222310x x -=-C ．()222310x x +-=D ．()222103x x +-=2．如图,在高为3米,斜坡长为5米的楼梯台阶上铺地毯,则地毯的长度至少要()A ．4米B ．5米C ．6米D ．7米3．下列各数是勾股数的是( )A ．B ．2.3.4C ．3.4.5D ．4.5.64．如图所示,在ABC 中,90ACB ∠=︒,分别以AB .BC .AC 为边向外作正方形,若三个正方形的面积分别为225.400.S ,则S 的值为( )A ．25B ．175C ．600D ．6255．如图1,一棵大树在一次强烈的地震中于离地面5米处折断倒下,树顶落在离树根12米处,图2是这棵大树折断的示意图,则这棵大树在折断之前的高是( )A ．20米B ．18米C ．16米D ．15米6．直角三角形中,有两边的长分别为6和8,那么第三边的长为(　)A ．10B ．14C ．或10D ．7．如图,圆柱形容器的高17cm ,底面周长是24cm ,在外侧底面S 处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口处1cm 点F 处有一苍蝇,急于捕获苍蝇充饥的蜘蛛所走的最短路线长度是( )A ．20cmB ．CD ．24cm8．如图,在直线m 上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别是3,6,9,正放置的四个正方形的面积依次是1S ,2S ,3S ,4S ,则14S S +＝( )A ．6B ．6.5C ．7D ．89．如图,在四边形ABDE 中,AB DE ∥,AB BD ⊥,点C 是边BD 上一点,BC DE a ==,CD AB b ==,AC CE c ==．下列结论:①ABC CDE ≌△△；②A C C E ⊥；③四边形ABDE 的面积是222121b ab a ++；④()2221112222a b c ab +-=⨯；⑤222+=a b c ．其中正确的结论个数是( )A ．2B ．3C ．4D ．510．三角形的三边长为a ,b ,c ,且满足22()2a b c ab +=+,则这个三角形是( )A ．等边三角形B ．钝角三角形C ．直角三角形D ．锐角三角形．二.填空题(每题3分,共30分)11．若直角三角形两直角边平方和为36,则它的斜边长为______．12．如图,有两棵树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少要飞______m ．13．在Rt ABC △中,90C ∠=︒,6AC =,8BC =,D ,E 分别是斜边AB 和直角边CB 上的点,把ABC 沿着直线DE 折叠,顶点B 的对应点是点B ',如果点B '和顶点A 重合,则CE 的长为___________．14．如图,有一张直角三角形的纸片,90,5,3ACB AB AC ∠=︒==．现将三角形折叠,使得边AC 与AB 重合,折痕为AE ．则CE 长为_____________．15．在等腰直角ABC 中,90B Ð=°,2BC =,则AC =______．16．如图,在44⨯的正方形网格中,每个小正方形的边长均为1,点A ,B ,C 都在格点上,BD AC ⊥于D ,则BD 的长为______．17．如图,一个梯子斜靠在一竖直的墙AO 上,测得4m AO =,若梯子的顶端沿墙下滑1m ,这时梯子的底端也向右滑1m ,则梯子AB 的长度为________.18．用四个全等的直角三角形镶嵌而成的正方形如图所示,已知大正方形的面积为49,小正方形的面积为4,若x ,y 表示直角三角形的两直角边长(x ＞y ),给出下列四个结论正确的是 _____．(填序号即可)①x ﹣y ＝2；②2249x y +=；③2xy ＝45；④x +y ＝9．19．如图,在ABC 中,90ACB ∠=︒,10cm AB =,6cm BC =,若动点P 从点A 出发,以1cm/s 的速度沿折线A C B A ---运动．设运动时间为t (0t >)s ．当点P 运动到恰好到点A 和点B 的距离相等的位置时,t 的值为______．20．如图,在Rt ABC △中,90C ∠=︒,分别以AB .AC .BC 为直径向外作半圆,它们的面积分别记作1S .2S .3S ,其中125S π=,216S π=,3S = __________(用含π的代数式表示)三.解答题(共60分)21．我国古代数学家赵爽的"勾股圆方图"是由四个全等的直角三角形(如图1)与中间的一个小正方形拼成一个大正方形(如图2)．(1)利用图2正方形面积的等量关系得出直角三角形勾股的定理,该定理的结论用字母表示: ；(2)用图1这样的两个直角三角形构造图3的图形,满足AE BC a ==,DE AC b ==,AD AB c ==,90AED ACB ==︒∠∠,求证(1)中的定理结论；(3)如图,由四个全等的直角三角形拼成的图形,设CE m =,HG n =,求正方形BDFA 的面积．(用m ,n 表示)22．我们知道,有一个内角是直角的三角形是直角三角形,其中直角所在的两条边叫直角边,直角所对的边叫斜边((如图①所示)．数学家还发现:在一个直角三角形中,两条直角边长的平方和等于斜边长的平方,即如果一个直角三角形的内条直角边长度分别是a 和b ,斜边长度是c ,那么222+=a b c ．(1)直接填空:如图①,若34a b ==，,则c =__________；(2)观察图②,其中两个相同的直角三角形边AE .EB 在一条直线上,请利用几何图形的之间的面积关系,试说明222+=a b c ．(3)如图③所示,折叠长方形ABCD 的一边AD ,使点D 落在BC 边的点F 处,已知810AB BC ==，,利用上面的结论求EF 的长?23．如图,甲乙两船同时从A 港出发,甲船沿北偏东35°的方向,航速是12海里/时,2小时后,两船同时到达了目的地．若C .B 两岛的距离为30海里,问乙船的航速是多少?24．如图1,AB BC ⊥于点B ,射线CM BC ⊥于点C ,P 是线段BC (不与点B ,C 重合)上的动点,过点P 作DP AP ⊥交射线CM 于点D ．(1)若AP DP =,求证:ABP PCD ≅ ；(2)如图2,若,3,9AP PC AB BC ===,求ABP 的面积；(3)如图3,连结AD ,若DP 平分ADC ∠,试猜测PB 和PC 的数量关系,并说明理由．25．如图,Rt ABC △中,90ACB ∠=︒,AC BC =,AD CD ⊥,BE CD ⊥,垂足分别为点D ,E ．(1)求证:ACD CBE ≌；(2)若1AD =,2DE =,求AC 的长．26．如图,在四边形ABCD 中,AC ,BD 是对角线,将点B 绕点C 逆时针旋转60︒得到点E ,连接AE ,BE ,CE ．(1)求CBE ∠的度数；(2)若ACD 是等边三角形,且30ABC ∠=︒,3AB =,5BD =,求BE 的长．27．如图,某城市接到台风警报,在该市正南方向260km 的B 处有一台风中心,沿BC 方向以15/km h 的速度移动,已知城市A 到BC 的距离100AD km =．(1)台风中心经过多长时间从B 移动到D 点?(2)已知在距台风中心30km 的圆形区域内都会受到不同程度的影响,若在点D 的工作人员早上6:00接到台风警报,台风开始影响到台风结束影响要做预防工作,则他们要在什么时间段内做预防工作?28．已知ABC 中,=90B ∠︒,6cm BC =,8cm AB =,P .Q 是ABC 边上的两个动点,其中点P 从点A 开始沿A B →方向运动且速度为每秒2cm,点Q 从点B 开始沿B C A →→方向运动,在BC 边上的运动速度是每秒3cm ,在AC 边上的运动速度是每秒5cm ,它们同时出发,当其中一个点到达终点时,另一个点也随之停止,设运动时间为t 秒,(1)线段AC =________；(2)当1t =秒时,求BPQ V 的面积；(3)当点AP CP =时,CQ =________；(4)若PQ 将ABC 周长分为5:7两部分,直接写出t 的值．参考答案:1．A2．D3．C4．D5．B6．C7．A8．A9．C10．C11．612．1013．7414．3215．16．9517．5m ##5米18．①②③19．254或19##19或25420．9π21．(1)解:∵大正方形的面积2c =,大正方形的面积()2142a b b a =⨯⨯⨯+-,∴()22142c a b b a =⨯⨯⨯+-,∴222c a b =+,故答案为:222c a b =+；(2)证明:如图:连接BD ,∵Rt Rt ABC DAE ≌△△,∴ADE BAC ∠=∠,∴90DAE ADE DAE BAC ∠+∠=︒=∠+∠,∴90DAB ∠=︒,∵()21122ABCD S c a b a =+-四边形, ()11222ABCD ab b b a S ⨯+=-四边形,∴()()2211122212ab b b a c a b a ++-=-⨯,∴222c a b =+；(3)解:由题意可得:CE CD DE =+,GH AG AH =-,∴m a b =+,n b a =-,∴2m n a -=,2m n b +=,∴22222222BD BC CD a b m n ==++=+,∴正方形BDFA 的面积为222m n +．22(1)解:∵222+=a b c ,∴5c =,故答案为:5；(2)根据题意得:21111()()2222a b a b ab ab c +⨯+=++,则22211(2)22a ab b abc ++=+,∴222111222a ab b abc ++=+,∴222111222a b c +=,∴222+=a b c ；(3)∵折叠长方形ABCD 的一边AD ,使点D 落在BC 边的点F 处,∴DE EF =,10AD AF ==,∴6BF ===,∴4CF =,设DE EF x ==,则8CE x =-,在Rt EFC △中,222EF FC EC =+,即2224(8)x x =+-,解得5x =,∴5EF =．23．根据题意得:1222430AB BC =⨯==，,90BAC ∠=︒,∴222AC AB BC +=．∴222223024324AC BC AB =-=-=∴18AC =．∴乙船的航速是:1829÷=(海里/时)．24(1)证明:∵AB BC CM BC⊥⊥，∴90B C ∠=∠=∵DP AP⊥∴90APD ∠=∴90A APB DPC APB ∠∠∠∠+=+=o∴A DPC∠=∠∵AP DP=∴ABP PCD ≌；(2)解:设BP =x∴9AP PC x==-∵AB BC ⊥,∴222AB BP AP +=∴()22239x x +=-解得4x =∴ABP 的面积14362=⨯⨯=；(3)证明:BP CP =,理由如下:延长DC ,AP 交于点E,∵DP 平分ADC ∠,∴ADP EDP ∠=∠,∵DP AP ⊥,∴90DPA DPE ∠∠==o ,∵DP DP =,∴ΔΔDPA DPE ≅,∴AP PE =,∵90B PCE APB EPC ∠∠∠∠===o ，,∴ΔΔABP ECP ≅,∴BP CP =．25．(1)证明:90AD CD BE CD ACB ⊥⊥∠=︒ ，，,909090ADC CEB ACD BCE ACD CAD ∴∠=∠=︒∠+∠=︒∠+∠=︒，，,BCE CAD ∴∠=∠,在ACD 和CBE △中,90ADC CEB CAD BCECA BC ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,()AAS ACD CBE ∴ ≌；(2)解:()AAS ACD CBE ≌,1CE AD ∴==,123CD CE DE ∴=+=+=,AC ∴==26．(1)解:∵将点B 绕点C 逆时针旋转60︒得到点E,∴CB CE =,60BCE ∠=︒,∴BCE 是等边三角形,∴60CBE ∠=︒,∴CBE ∠的度数为60°；(2)∵ACD 是等边三角形,∴AC DC =,60ACD ∠=︒.∵60ACD BCE ∠=∠=︒,∴ACD ACB BCE ACB ∠+∠=∠+∠,∴ACE BCD ∠=∠.∵BC CE =,AC DC =,∴ACE △≌DCB △(SAS ),∴5AE BD ==.∵60CBE ∠=︒,30ABC ∠=︒,∴90ABE CBE ABC ∠=∠+∠=︒.在Rt ABE △中,3AB =,∴4BE ===,∴BE 的长为4．27．解:(1)在Rt △ABD 中,根据勾股定理,得BD =km ,所以,台风中心经过240÷15=16小时从B 移动到D 点,答:台风中心经过16小时时间从B 移动到D 点；(2)如图,∵距台风中心30km 的圆形区域内都会受到不同程度的影响,∴BE =BD -DE =240-30=210km ,BC =BD +CD =240+30=270km ,∵台风速度为15km /h ,∴210÷15=14时,270÷15=18,∵早上6:00接到台风警报,∴6+14=20时,6+18=24时,∴他们要在20时到24时时间段内做预防工作．28．(1)解:∵=90B ∠︒,∴10AC ==,故答案为:10；(2)解:∵22,33AP t BQ t ====,∴826BP AB AP =-=-=,∴211639cm 22BPQ S BP BQ =⋅=⨯⨯= ；(3)解:设AP CP x ==,则8BP x =-,在Rt BCP △中,由勾股定理得,222CP BP BC -=,∴()22286x x --=,∴254x =,∴25252248t =÷=>,∴点Q 在AC 上,∴25455288CQ ⎛⎫=⨯-= ⎪⎝⎭,故答案为:458；(4)解: ()568101057++⨯=+,241014-=,当02t <<时,10BP BQ +=时,82310t t -+=,解得∶2t =(舍去),当14BP BQ +=时,82314t t -+=,解得∶6t =(舍去),当24t ≤<时,当10AP AQ +=时,()2105210t t +--=,解得:103t =,当14AP AQ +=时,()2105214t t +--=,解得:2t =,综上所述:2t =或103．。

北师大版八年级数学上册各章测试题带答案(全册)

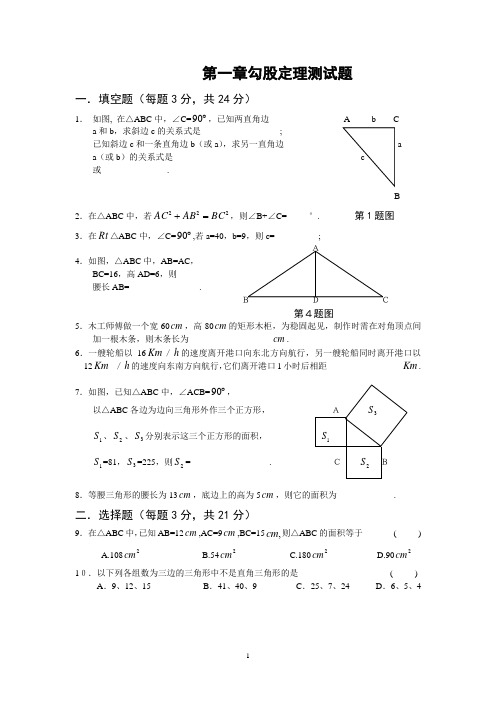
第一章勾股定理测试题一．填空题（每题3分，共24分）1．如图, 在△ABC 中，∠C=︒90，已知两直角边 A b Ca 和b ，求斜边c 的关系式是__________________;已知斜边c 和一条直角边b （或a ），求另一直角边 a a （或b ）的关系式是________________ 或_______________. B 2．在△ABC 中，若222BC AB AC =+，则∠B+∠C=_____°. 第1题图 3．在Rt △ABC 中，∠C=︒90,若a=40，b=9，则c=__________; Ａ 4．如图，△ABC 中，AB=AC ，BC=16，高AD=6，则腰长AB=________________.ＢＤＣ第４题图5．木工师傅做一个宽60cm ，高80cm 的矩形木柜，为稳固起见，制作时需在对角顶点间加一根木条，则木条长为___________________cm . 6．一艘轮船以16Km ／h 的速度离开港口向东北方向航行，另一艘轮船同时离开港口以12Km ／h 的速度向东南方向航行，它们离开港口1小时后相距_________________Km .7．如图，已知△ABC 中，∠ACB=︒90，以△ABC 各边为边向三角形外作三个正方形，Ａ 3S1S 、2S 、3S 分别表示这三个正方形的面积， 1S1S =81，3S =225，则2S =__________________. Ｃ 2S Ｂ8．等腰三角形的腰长为13cm ，底边上的高为5cm ，则它的面积为_____________.二．选择题（每题3分，共21分）9．在△ABC 中，已知AB=12cm ,AC=9cm ,BC=15,cm 则△ABC 的面积等于 ( )A.1082cm B.542cm C.1802cm D.902cm1０．以下列各组数为三边的三角形中不是直角三角形的是 ( ) A ．9、12、15 B ．41、40、9 C ．25、7、24 D ．6、5、411．如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A 爬到点B 处吃食, 要爬行的最短路程(π取3)是( )A.20cm;B.10cm;C.14cm;D.无法确定.12．一个三角形三边之比为3∶4∶5,则这个三角形三边上的高之比为 ( )A.3：4：5B.5：4：3C.20：15：12D.10：8：2 13．一个三角形的三边长为a 、b 、c,且满足等式ab c b a 2)(22=-+,则此三角形是 ( ) A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形 14. 如图，为求出湖两岸的A 、B 两点之间的距离,一个观测者在点C 设桩,使△ABC 恰好为直角三角形,且∠B=︒90,测得AC=160米,BC=128米,则A 、B 两点间的距离为 ( )B A ．96米 B ．100米C ．86米D ．90米C A 15．一直角三角形的斜边长比直角边长大2，另一直角边长为6，则斜边长为（）（A ）4 （B ）8 （C ）10 （D ）12三．解答题16．已知：如图，⊿ABC 中，∠ACB =︒90，AB = 5cm ，BC = 3 cm ，CD ⊥AB 于D ，求CD 的长及三角形的面积.（16分）17．在图中所示的长方形零件示意图中，根据所给的部分尺寸，求两孔中心Ａ和Ｂ的距离（单位：mm ）（10分）B C A D18．小强到某海岛上去探宝，登陆后先往东走10千米，又往北走2千米，遇到障碍后又往西走3千米，再折向北走到4千米处往东拐，仅走1千米便找到宝藏，问登陆点到宝藏埋藏点的直线距离是多少千米？（10分）19．八（2）班数学课外活动小组的同学测量学校旗杆的高度时，发现升旗的绳子垂到地面要多1米，当他们把绳子的下端拉开5米后，发现下端刚好接触地面。

北师大版八年级数学上册第一二章测试题

最新北师大版八年级数学上册第一----二测真题〔含答案〕一、选择题1. 4 的平方根是〔〕A . 2B . 16 C. ±2 D .±16 【答案】C 2.设a =19－1，a 在两个相邻整数之间，则这两个整数是〔〕A ．1和2B ．2和3C ．3和4D ．4和5 【答案】C3.实数a 在数轴上的位置如下图，则22(4)(11)a a -+- 化简后为A ． 7B ．－7C ． 2a －15D ．无法确定【答案】A4. 〔202XXX ，1，3分〕4的算术平方根是〔〕A . 2B . －2C . ±2D . 16【答案】A5. 〔202XXX ，5，3分〕假设0)3(12=++-+y y x ，则y x -的值为〔〕[来A ．1B ．－1C ．7D ．－7【答案】C6. 〔202XXX ，1，3分〕(-2)2的算术平方根是〔〕〔A 〕2 〔B 〕 ±2 〔C 〕-2 〔D 〕2【答案】A7. 〔202XXX ，7 ，3分〕以下运算正确的选项是〔〕A.25=±5B.43-27=1C.18÷2=9D.24·32=6 【答案】D8. 〔202XXX ，1，3分〕在实数0、3-、2、2-中，最小的是〔〕A ．2-B ．3-C ．0D ．2 【答案】A9. 〔202XXX ，5,4分〕如果2(21)12a a -=-，则〔〕A ．a ＜12 B. a ≤12 C. a ＞12 D. a ≥12【答案】B10．〔202XXX ，1，3〕以下各式中，正确的选项是〔〕A ．2(3)3-=- B ．233=- C 2(3)3±± D 233±【答案】B11. 〔202XX 省，7，3分〕已知21+=m ，21-=n ，则代数式mn n m 322-+的值为〔〕A .9B .±3C .3D . 5【答案】C12. 〔202XX 台北，4〕计算75147-＋27之值为何？ A ．53 B ．33 C ．311 D ． 911【答案】A13. 〔202XX 全区，17〕17．计算631254129⨯÷之值为何？ A ．123 B ．63 C ．33 D ．433 【答案】Ｂ14. 〔202XXX ，1，3分〕8的立方根是〔〕A ．2B ．-2C ．3D ．4【答案】A15. 〔202XXX ，4，3分〕以下各式计算正确的选项是A ．235+=B ．2222+=C ．33222-=D ．1210652-=- 【答案】C16. 〔202XXX ，1，3分〕下面计算正确的选项是〔〕A.3333+=B.2733÷=C.235=D.2(2)2-=-【答案】B17. 〔202XXX ，7，3分〕如图，△ABC 中，∠C =90°，AC =3，∠B =30°，点P 是BC 边上的动点，则AP 长不可能是〔第7题图〕〔A 〕3.5 〔B 〕4.2 〔C 〕5.8 〔D 〕7【答案】D18. 〔202X X ，9，3分〕如图3，在△ABC 中，∠C=90°，BC=6,D,E 分别在AB,AC 上，将△ABC 沿DE 折叠，使点A 落在点A ′处，假设A ′为CE 的中点，则折痕DE 的长为〔〕A ．21B ．2C ．3D ．4【答案】B19. 〔202XXX ，7,4分〕如图是油路管道的一局部，延伸外围的支路恰好构成一个直角三角形，两直角边分别为6m 和8m.按照输油中心O 到三条支路的距离相等来连接管道，则O 到三条支路的管道总长〔计算时视管道为线，中心O 为点〕是〔〕A2m B.3mC.6mD.9m【答案】C20. 〔202XXX ，2，3分〕以下运算正确的选项是〔〕A ．(1)1x x --+=+B ．954-=C ．3223-=-D ．222()a b a b -=-【答案】C21. 〔202XX 襄阳，6，3分〕以下说法正确的选项是A.0)2(π是无理数B.33是有理数C.4是无理数D.38-是有理数【答案】D22. 〔202XXX ，6，3分〕如图，矩形OABC 的边OA 长为2 ，边AB 长为1，O A 在数轴上，以原点O 为圆心，对角线OB 的长为半径画弧，交正半轴于一点，则这个点表示的实数是〔第6题图〕〔A 〕2.5 〔B 〕2 2 〔C 〕 3 〔D 〕 5【答案】D23．(202XXX ，1，2分9A ．3B ．－3C ．±3D ． 3【答案】A 24. 〔202XXX ，3，3327A. ±3 B .3 C . ±3 D . 3 【答案】D.25. 〔202XXX ，4，3分〕计算221－631＋8的结果是〔〕 A ．32－23 B ．5－2C ．5－3D ．22 【答案】A二填空题26 〔202XXX ，16，5分〕我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图〞，后人称其为“赵爽弦图〞〔如图1〕．图2由弦图变化得到，它是用八个全等的直角三角形拼接而成，记图中正方形ABCD ，正方形EFGH ，正方形MNKT 的面积分别为S 1,S 2，O〔第7题图〕S 3．假设S 1，S 2，S 3＝10，则S 2的值是．【答案】103 27. 〔202XX 凉山州，15，4分〕把命题“如果直角三角形的两直角边长分别为a 、b ，斜边长为c ，那么222a b c +=〞的逆命题改写成“如果……，那么……〞的形式：。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

北师版八年级数学上册第一、二单元综合检测题
（满分为120分,时间100分钟）班级姓名分数一. 选择题（请将下列各题中的答案填在下面的表格中,每小题3分,共30分） 1.49的算术平方根是( )
A. 7
B.－7
C. 7
D. ±7 2．下列各组数中，不是“勾股数”的是 ( )
A ．7，24，25 B. 1，2，3 C. 6，8，10 D. 9，12，15 3．下列各式中, 属于最简二次根式的是（）
A.
3
1
B. 20
C. 22
D. 121 4．在下列各数 3、0、-0.2 、4、8、0.3737737773…（相邻两个3之间的7的个数逐次加1）中，无理数的个数是( )
A. 4
B. 3
C. 2
D. 1
5．如图1, 三个正方形围成一个直角三角形，64、400分别为所在正方形的面积，则图中字母M 所代表的正方形面积是（）
A .336 B.164096 C.464 D .155904
图1
6. 将直角三角的三条边同时扩大4 倍后，得到的三角形为（） A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D . 不能确定
7. 如果一个数的立方根是它本身，那么这个数是 ( )
A. 1、0
B. - 1
C. 0
D. 1 、 - 1、 0 8. 下列说法中正确．．
的是 ( ) A.带根号的数都是无理数 B. 无限小数都是无理数 C. 无理数都是无限小数 D. 无理数就是开方开不尽的数 9．一个直角三角形两直角边长分别为3和4,下列说法正确的是( ) A.斜边长为25 B.三角形的周长为25 C.斜边长上的高为
5
12
D.三角形的面积为20
10．下列说法中正确．．
的有( ) ① 2±都是8的立方根，②2)2(2-=-，③ 81的平方根是3，④
283
=-- A. 1个 B. 2个 C. 3个 D. 4个二. 填空题（每小题3分, 共24分）
11.一个三角形三边满足(a+b)2－c 2＝2ab, 则这个三角形是三角形. 12.已知5＋11的小数部分为a ，5－11的小数部分为b ，则a ＋b= ________。

13. 比较大小：
2
1
5- 21 .(填 “＞”或 “＜”号)
14.在Rt △ABC 中，斜边BC=2，则AB 2+AC 2+BC 2=________。

15. 已知一个正数的平方根是13+a 和11+a ，则这个正数的立方根是________。

16. 16. 31-的相反数是_________，︱31-︱= _________；
=-2)31( 。

17. 已知直角三角形两边的长为3和4，则此三角形第三边长为。

18。

若a 、b 互为相反数，c 、d 互为倒数，则______3=++cd b a 。

三. 计算题 (每小题5分，共30分)
19．计算：（1）32583- （2）2
)52(+
（3） ()3
2
22
143-⎪⎭
⎫
⎝⎛-⨯+ （4）
322
1
3
32⨯+-
（5）)32)(32(-+ （6） 3
12
27-+5
D
C
B
A
A
C
B
四.解答题（共36分）
.20.已知a 、b 、c 为三角形三边长，且满足()2
342100a b c -+-+-，试判断
三角形的形状。

（5分）
21.已知x 、y 都是实数，且334y x x --，求x y 的平方根（5分）
22. 如图，一块草坪的规划图形状为四边形ABCD ，其中∠B=90º，AB=3㎝，BC=4㎝，CD=12㎝，AD=13㎝，求这块草坪的面积。

（6分）
23.一架长25米的云梯，斜靠在一面墙上，梯子底端离墙7米，(1)求梯子顶端到地面的距离。

（2）如果梯子的顶端下滑4米，那么云梯的底端在水平方向将滑多少米？(6分)
D
O
24.如图，长方体盒子（无盖）的长、宽、高分别是12cm ,8cm,30cm,在AB 中点C 处有一滴食物，一只小虫从P 处爬到C 处去吃，则最短路程是多少？（6分）
A
B
C
D
.12
8
30
25. （一）. 阅读下面内容：
12)
12)(12()
12(1121-=-+-⨯=+； (
)
;23)23)(23(2
31231-=-+-⨯
=
+
()
25)
25)(25(2
512
51-=-+-⨯=
+.
仿例子完成以下各题（8分）（二）. 计算：（1）6
71+；（2）
3
134-；
（3
）
⋅⋅⋅+
八年级数学答案一．选择题：1A2B3C4B5A6A7D8C9C10A
二．填空题:11.直角三角形12. 1 。

13、＞14. 8 15、4 16、三个空均为
13- 17、5或7 18、1
三．计算题：19（1）214-（2）7+102(3)-7(4)-2.52+6(5)-1(6)6 20题、直角三角形21.X=3 Y=4平方根为8、-8 22题.36 23、（1）24米（2） 8米 24、25cm 25.(1)7-6(2)313+(3)9。

最新北师大版八年级数学上册第一、二单元检测题及答案

北师大版八年级上册数学第一章、第二章单元测试卷 2套(Word版,含答案)

北师大版数学八年级上册全册全套单元试题及答案

北师大版八年级数学上册单元测试题全套及答案

北师大版八年级上册数学第一二章测试题及参考答案

(完整版)北师大版八年级上册数学第一章《勾股定理》单元测试卷(含答案),推荐文档