同济大学朱慈勉 结构力学12章
同济大学朱慈勉版结构力学课后答案(下)
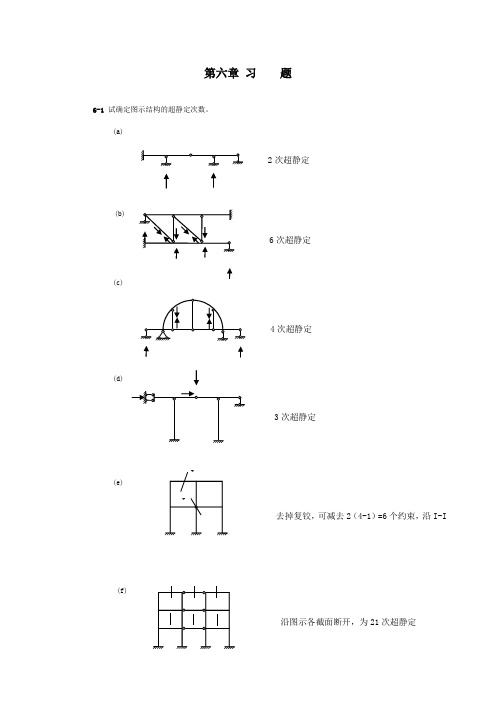
第六章习题6-1 试确定图示结构的超静定次数。
(a)(b)(c)(d)(f)2次超静定6次超静定4次超静定3次超静定去掉复铰,可减去2(4-1)=6个约束,沿I-I 沿图示各截面断开,为21次超静定(g) 所有结点均为全铰结点(h)6-2 试回答:结构的超静定次数与力法基本结构的选择是否有关力法方程有何物理意义 6-3 试用力法计算图示超静定梁,并绘出M 、F Q 图。
(a) 解:上图=l1M p M01111=∆+p X δ其中:EIl l l l l l l EI l l l l EI 8114232332623232333211311=⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯+⨯⨯⨯+⎪⎭⎫ ⎝⎛⨯⨯⨯⨯=δ2l 3l 3II刚片I 与大地组成静定结构,刚片II 只需通过一根链杆和一个铰与I 连接即可,故为4题目有错误,为可变体系。
+lF 2 X=1EIl F l lF l lF EI l pp p p817332322263231-=⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯=∆0817*******=-EIl F X EI l p p F X 211=p M X M M +=11l F p 61l F p 61 p Q X Q Q +=11p F 21p 2(b) 解:基本结构为:l1Ml l2l 2l2lEI =常数l 2M 图Q 图F PXXl 2Ml F p 21p Ml F p 31⎪⎩⎪⎨⎧=∆++=∆++0022221211212111p p X X X X δδδδ p M X M X M M ++=2211p Q X Q X Q Q ++=22116-4 试用力法计算图示结构,并绘其内力图。
(a)解:基本结构为:3m6m6m20kN/m1 MpM1111=∆+pXδpMXMM+=11(b)解:基本结构为:计算1M,由对称性知,可考虑半结构。
1M4a2a4a4a6810810X2计算pM:荷载分为对称和反对称。
结构力学课后习题答案(朱慈勉)

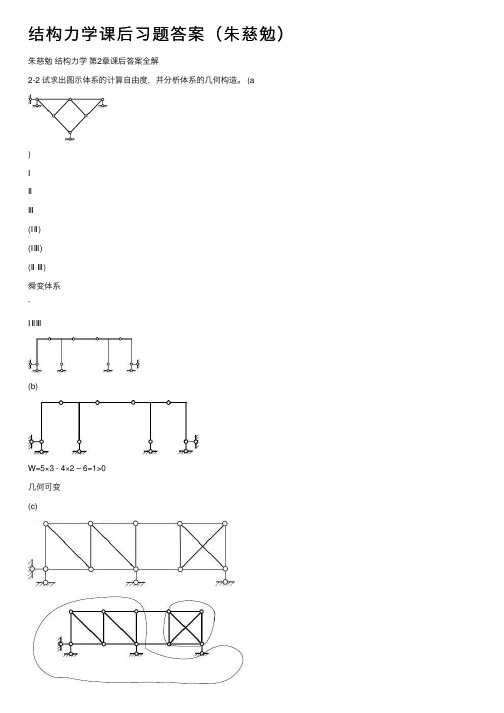
朱慈勉 结构力学 第2章课后答案全解2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a)(ⅠⅡ)(ⅠⅢ)舜变体系ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0几何可变(c)有一个多余约束的几何不变体系(d)W=3×3 - 2×2 – 4=1>0可变体系2-3 试分析图示体系的几何构造。
(a)(ⅡⅢ)Ⅲ几何不变2-4 试分析图示体系的几何构造。
(a)几何不变(b)W=4×3 -3×2 -5=1>0几何可变体系(ⅠⅢ)(ⅡⅢ)几何不变(d)Ⅲ(ⅠⅢ)有一个多余约束的几何不变体(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系(f)(ⅠⅢ)(ⅡⅢ)无多余约束内部几何不变(h)二元体W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)Ⅲ(ⅡⅢ)(ⅠⅢ)同济大学朱慈勉 结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)2P F a 2P F a4P F Q34P F 2P F(b)aa aaa2m6m2m4m2m2020Q10/326/310(c)18060(d)3m2m2m3m3m4m3m2m 2m2mA2m2m2m2m7.5514482.524MQ3-3 试作图示刚架的内力图。
(a)242018616MQ18(b)4kN ·m3m3m6m1k N /m2kN A CBD6m10kN3m3m 40kN ·mABC D30303011010QM 210(c)45MQ(d)3m3m6m6m2m 2m444444/32MQN(e)4481``(f)4m4m2m3m4m222220M3-4 试找出下列各弯矩图形的错误之处,并加以改正。
(a)F P(b)(c)(d)(e)(f)F3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件,确定E 、F两铰的位lx l lx置。
同济大学朱慈勉 结构力学12章

四、确定极限荷载三个定理
1、上限定理(亦称“机动定理”、或“极小定理”)
对于比例加载作用下的给定结构,按任意可能的破坏
机构,由平衡条件求得的荷载将大于或等于极限荷载。
或:“可破坏荷载的最小值是极限荷载的上限”。 p
或:“极限荷载是可破坏荷载的最小值” 2、下限定理(亦称“静力定理”、或“极大定理”) pu
依上限定理:
pu
1.33
Mu a
例题3 求图示结构的极限荷载。
pp
q 2pa
1.2 p
A
EF B
C
D
a a a 2a
p
p Mu
q 2pa
2
Mu 3
机构1
p
Mu
p
q 2pa
aa
1.2 p
1.2 p
Mu
MG
MH
经验算各截面弯矩值满足屈服条件,
pu
2.27
Mu a
解:试算法
试 取 机 构 (1)
qu1
qu2
Mu
Mu
Mu
Mu
2、不同结构,只要材料、截面积、截面形状相同,塑性弯矩一定相同。
Mu Wu s
3、材料、截面积、截面形状相同的不同结构,qu不一定相同。
qu1
qu2
Mu1
Mu1 Mu2 qu1 qu2
Mu2
Mu2
四、如何确定单跨梁的极限荷载
1、机理
q
qu1
ql 2
12
计
三、基本假设 1、材料为“理想弹塑性材料” 。 2、拉压时,应力、应变关系相同。 3、满足平截面假定。即无论弹、塑性阶段,保持平截面不变。
结构力学课后习题答案(朱慈勉)

取虚线所示的两个隔离体有:
M B 0,
2 2
FN
2
a
FN 1
a
Fx 0, FN1
2 2
FN
2
4 3
a
2a
联立方程解得:FN1
a 3
,
FN 2
2a 3
杆3的内力可以通过D节点求得
a
a
a
a
FN 3 P
(c)
先去除结构中的零力杆
2
再求出支座反力
1
在A, B点用节点法可求得
43
FN1
13 2
1.5qa
FP
)
FP
FP
FP
FP
、
3-12 试求图示桁架各指定杆件的内力。 (b)
3m
3 ×3m
D
1
1
B
3
2KN
4m
7.5KN
4m
2kN
E
2 3kN
1
A F3
10.5KN
4m
然后再依次隔离A, B, D点不难求得 F2 7.5KN (), FBD 3KN , F1 4KN ()
先求出支座反力,如图所示。零杆亦示于图中。 取1-1截面以上部分分析
$
2-3 试分析图示体系的几何构造。 (a)
(ⅠⅢ) (ⅠⅡ)
Ⅰ
Ⅱ
Ⅲ
几何不变
(Ⅱ Ⅲ)
,
(b)
(ⅠⅡ) Ⅰ
(ⅡⅢ) Ⅱ
(ⅠⅢ)
Ⅲ
几何不变
<
2-4 试分析图示体系的几何构造。
(a)
(ⅠⅢ)
·
(b)
Ⅰ
Ⅱ
(ⅠⅡ)
Ⅲ
最新完整的结构力学答案-同济大学朱慈勉
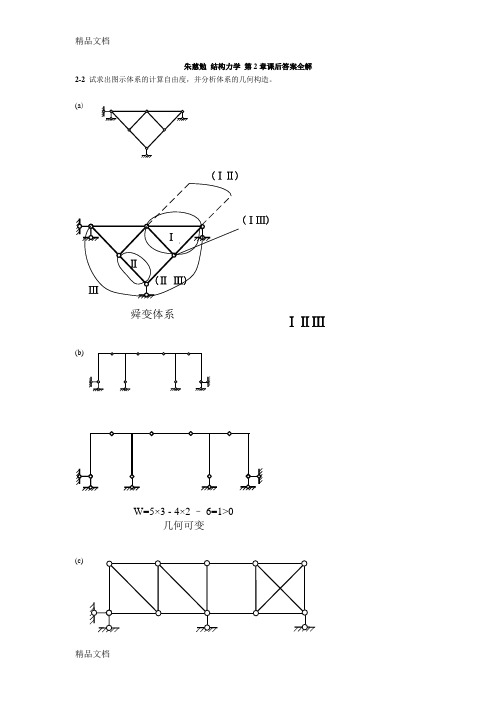
对B点求矩
20 9 (4.5 3) RF 6 RF 45() M E 0.5 20 92 45 9 405, RE 135() MCF 45 3 135, MCD 0.5 20 9 90 M BA 0.5 20 9 90
精品文档
精品文档
(b)
1
M
5.75
精品文档
精品文档
5FP
5FP
5FP
5 4
FP
5 4
FP
5FP
2FP
5 4
FP
2FP k
由节点法知:
对A节点 对E节点
FNAD =- 5FP
FNEC
5 4
FP
FNAE 2FP
FNEF
5 4
FP
1
由节点法知:
k
对A节点
FNAD =-
5 2
FNAE 1
yc
F N FNPl EA
1 EA
2
qa 2
q
G
H
qa2 IJ
B
C
a
a
3qa 2 2
qa 2
a
3qa 2 2
qa 2 2
a
对H点求矩:
qa 2
qa 2 2
HC
a
HC
1.5qa()
对F点求矩:
qa 1.5a H A a 0 H A 1.5qa() H D 0, MGF qa2, MGH 1.5qa2
qa 2
qa 2 2
xB
1 EI
M ( )M ( )ds
1
2
qR2(1 cos )R sin Rd
1
qR 4 ()
EI 0
2EI
结构力学朱慈勉版课后答案【重要】

朱慈勉 结构力学 第2章课后答案全解(b)解:基本结构为:1M2Mp M M()EIEI 1086623323326611=⨯⨯+⨯⨯+⨯⨯=δ EI=常数6m6m6mEDACB20kN/m X1 X120kN/mX2 X2363361 11 118090 15030150()03323326612=⨯⨯-⨯⨯=EI δ ()EIEI 1086623323326622=⨯⨯+⨯⨯+⨯⨯=δEI EI p 27003231806212362081632323180621121=⎪⎪⎭⎫ ⎝⎛⨯⨯⨯⨯+⨯⎪⎭⎫ ⎝⎛⨯⨯⨯⨯+⨯⨯⨯⨯=∆EI EI p 5403231806212362081632323180621122=⎪⎪⎭⎫ ⎝⎛⨯⨯⨯⨯-⨯⎪⎭⎫ ⎝⎛⨯⨯⨯⨯+⨯⨯⨯⨯=∆ ⎩⎨⎧-=-=⇒⎪⎪⎩⎪⎪⎨⎧=+=+5250540108027001082111X X EI X EIEIX EI m KN M CA ⋅=⨯-⨯-=9035253180 m KN M CB ⋅=⨯+⨯-=12035253180 ()m KN M CD ⋅-=-⨯=3056(c)解:基本结构为: ⊕6m 3m5III 10kN ·m10kN ·mEA =∞C ABD 5I12m10kN ·m10kN ·mX110kN ·m 119 339 10kN ·m10kN ·m 10 101N 1M p M()EI I E EI 5558293299233256633263111=⨯⎥⎦⎤⎢⎣⎡⨯⨯+⨯⨯+⨯⨯⨯+⎪⎭⎫ ⎝⎛⨯⨯⨯=δ ()EI I E p 1442103109109231025661-=⨯⎥⎦⎤⎢⎣⎡⨯+⨯+⨯⨯+⨯⨯⨯-=∆ 01111=∆+p X δ29.11=⇒Xm KN M AC ⋅=-⨯=61.11029.19m KN M DA ⋅-=-⨯=13.61029.13 m KN M DC ⋅=⨯=87.329.13M题6-6图6-7 试用力法计算图示组合结构,求出链杆轴力并绘出M 图。
同济大学朱慈勉结构力学课后习题答案

更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
同济大学-朱慈勉版-结构力学-课后答案(上)

2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a)(ⅠⅡ)(ⅠⅢ)舜变体系ⅠⅡⅢ(b)【W=5×3 - 4×2 – 6=1>0几何可变(c)】有一个多余约束的几何不变体系(d)|2-3 试分析图示体系的几何构造。
(a)/W=3×3 - 2×2 – 4=1>0可变体系(ⅡⅢ) (b);Ⅲ几何不变2-4 试分析图示体系的几何构造。
(a)几何不变-(b)~(ⅠⅢ)(ⅡⅢ)几何不变~W=4×3 -3×2 -5=1>0几何可变体系(d)Ⅲ(ⅠⅢ)有一个多余约束的几何不变体@(e)(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系…(f)?(ⅠⅢ)(ⅡⅢ)无多余约束内部几何不变(g):(h)|二元体W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)%(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)!Ⅲ(ⅡⅢ)(ⅠⅢ)`3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)%aa *a a2P F a 2P F a4P F Q34P F 2P F(b)"2020Q10/326/310(c){2m6m`4m2m3m2m2m3m3m4m18060(d)]7.5514482.524MQ3-3 试作图示刚架的内力图。
(a)3m2m2m2m2m2m 2m2m4kNm%6m1k N /m2kNCB{242018616MQ18(b),30303011010QM 2106m10kN>3m3m40kNmAB CD:45MQ(d)…444444/32MQN3m3m6m)2m2m(e))4481``(f)#222220M…4m2m3m4m/3-4试找出下列各弯矩图形的错误之处,并加以改正。
(a)F P(b)(c)—(d)(e)(f)F3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件,确定E 、F 两铰的位置。
(完整版)!完整的结构力学答案-同济大学朱慈勉!

朱慈勉 结构力学 第2章课后答案全解2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a )ⅠⅡⅢ(ⅠⅡ)(ⅠⅢ)(Ⅱ Ⅲ)舜变体系`ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0几何可变(c)有一个多余约束的几何不变体系(d)2-3 试分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(Ⅱ Ⅲ)几何不变W=3×3 - 2×2 – 4=1>0可变体系ⅠⅡⅢ(ⅠⅡ)(ⅠⅢ)(ⅡⅢ)几何不变2-4 试分析图示体系的几何构造。
(a)(ⅠⅢ)(ⅠⅡ)(ⅡⅢ)ⅠⅡⅢ几何不变(b)W=4×3 -3×2 -5=1>0几何可变体系ⅢⅠⅡ(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)几何不变(d)(ⅠⅡ)ⅢⅠⅡ(ⅡⅢ)(ⅠⅢ)二元杆有一个多余约束的几何不变体ⅠⅡⅢ(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系(f)ⅠⅡⅢ(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)无多余约束内部几何不变ⅠⅡⅢ(ⅠⅢ)(ⅠⅡ)(ⅡⅢ)二元体(h)ⅠⅡⅢ(ⅠⅢ)(ⅠⅡ)(ⅡⅢ)二元体多余约束W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)(ⅠⅢ)几何不变同济大学朱慈勉 结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)4P F a2P F a 2P F a M4P F Q34P F 2P F(b)ABCaa aaaF P a DEFF P2m6m2m4m2mABCD10kN2kN/m42020M Q10/326/3410(c)21018018040M1560704040Q(d)3m2m2mA B CEF15kN 3m3m4m20kN/mD 3m2m2m2mA2m 2m2mABCD E FG H 6kN ·m4kN ·m 4kN2m7.5514482.524MQ3-3 试作图示刚架的内力图。
同济大学朱慈勉版结构力学课后(上)
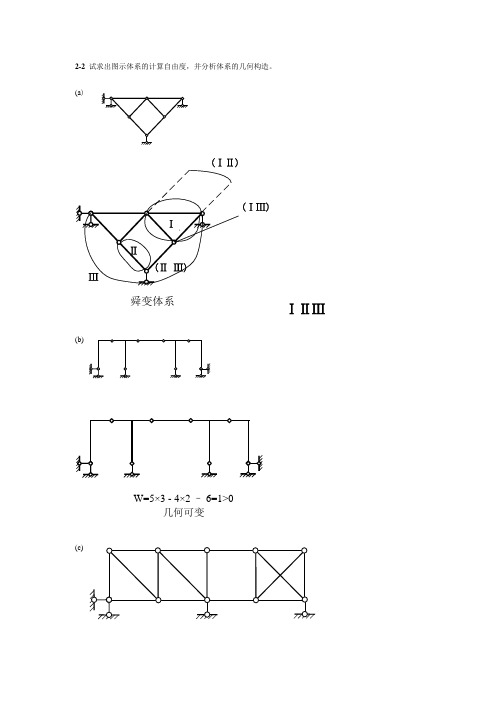
2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a )(ⅠⅡ)(ⅠⅢ)舜变体系ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0几何可变(c)有一个多余约束的几何不变体系(d)W=3×3 - 2×2 – 4=1>0可变体系2-3 试分析图示体系的几何构造。
(a)(ⅡⅢ)Ⅲ几何不变2-4 试分析图示体系的几何构造。
(a)几何不变(b)W=4×3 -3×2 -5=1>0几何可变体系(ⅠⅢ)(ⅡⅢ)几何不变(d)Ⅲ(ⅠⅢ)有一个多余约束的几何不变体(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系(f)(ⅠⅢ)(ⅡⅢ)无多余约束内部几何不变(h)二元体W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)Ⅲ(ⅡⅢ)(ⅠⅢ)3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)2P F a 2P F a4P F Q34P F 2P F(b)2020Q10/326/310aa aaa2m6m2m4m2m(c)18060(d)7.5514482.524M Q 3m2m2m3m 3m 4m3m2m 2m 2mA2m 2m 2m 2m3-3 试作图示刚架的内力图。
(a)242018616MQ18(b)30303011010QM 2104kN ·m3m3m6m1k N /m2kN A CBD6m10kN3m3m 40kN ·mABC D(c)45MQ(d)444444/32MQN(e)3m3m6m6m2m 2m4m4m4481``(f)222220M3-4 试找出下列各弯矩图形的错误之处,并加以改正。
2m3m4mF P (b)(c)(d)(e)(f)F3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件,确定E 、F 两铰的位置。
结构力学答案-同济大学朱慈勉

朱慈勉结构力学第2章课后答案全解2-2试求出图示体系的计算自由度,并分析体系的几何构造。
(a)(ⅠⅡ)(ⅠⅢ)Ⅰ`Ⅱ(ⅡⅢ)Ⅲ舜变体系ⅠⅡⅢ(b)W=5×3-4×2–6=1>0几何可变(c)有一个多余约束的几何不变体系(d)W=3×3-2×2–4=1>0可变体系2-3试分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅢ几何不变(ⅠⅡ)Ⅱ(ⅡⅢ)(ⅡⅢ)(ⅠⅡ)ⅠⅡ(ⅠⅢ)Ⅲ几何不变2-4试分析图示体系的几何构造。
(a)ⅠⅡ(ⅡⅢ)(ⅠⅡ)(ⅠⅢ)Ⅲ几何不变(b)W=4×3-3×2-5=1>0几何可变体系(ⅠⅢ)(ⅡⅢ)Ⅰ(ⅠⅡ)ⅡⅢ几何不变(d)二元杆ⅡⅠ(ⅠⅡ)Ⅲ(ⅡⅢ)(ⅠⅢ)有一个多余约束的几何不变体ⅢⅠⅡ(ⅡⅢ)(ⅠⅢ)(ⅠⅡ)舜变体系(f)Ⅲ(ⅠⅢ)(ⅡⅢ)ⅠⅡ(ⅠⅡ)无多余约束内部几何不变(ⅠⅢ)(ⅠⅡ)二元体(ⅡⅢ)ⅠⅡⅢ(h)(ⅡⅢ)(ⅠⅢ)Ⅱ多余约束Ⅰ(ⅠⅡ)ⅢW=3×8-9×2–7=-1,有1个多余约束二元体2-5试从两种不同的角度分析图示体系的几何构造。
(a)ⅡⅠ(ⅠⅡ)Ⅲ(ⅠⅢ)舜变体系(ⅡⅢ)(b)(ⅡⅢ)几何不变ⅡⅠ(ⅠⅡ)Ⅲ(ⅠⅢ)同济大学朱慈勉结构力学第3章习题答案3-2试作图示多跨静定梁的弯矩图和剪力图。
(a)FP F P aA B CD E Fa a a a aMF aP2F aP2F aP4QFP4FP23FP4(b)2kN/m10kNA B C D2m6m2m4m2mM结构力学答案-同济大学朱慈勉2020Q (c)410/310426/315kN20kN/mA B C D E F2m2m3m3m3m4m180M4018070210Q4015(d)606kN·m4kN·m404kNA B C D E F G H3m2m2m2m2m2m2m2m1/ 结构力学答案-同济大学朱慈勉M7.5148Q 5442.523-3 试作图示刚架的内力图。
结构力学完整.1同济大学_朱慈勉PPT课件
41
3、截面内力 截开一根梁式杆件的截面上有三个内力(分量),
即:轴力FN 、剪力FQ和弯矩Μ 。 1、内力的定义
FN:截面上平行于截面外法线方向的正应力的代数 和,一般以受拉为正。
FQ:截面上垂直于截面法 线方向的切应力的代数和, 以使隔离体产生顺时针转 动为正。
Μ:截面上正应力对截面
中性轴的力矩代数和,对
刚片中任一两点间的距离保持不变,既由刚片中 任意两点间的一条直线的位置可确定刚片中任一点 的位置。所以可由刚片中的一条直线代表刚片。
精选PPT课件
9
二、研究体系几何组成的任务和目的:
1、研究结构的基本组成规则,用及判定体系是否 可作为结构以及选取结构的合理形式。
2、根据结构的几何组成,选择相应的计算方法和 计算途径。
§1-2 结构计算简图
1、结构计算简图的概念 2、结构计算简图的简化原则是:
1)计算简图要能反映实际结构的主要受力和变 形特点,即要使计算结果安全可靠;
2)便于计算,即计算简图的简化程度要与计算 手段以及对结果的要求相一致。
精选PPT课件
2
精选PPT课件
3
3、结构计算简图的几个要点:
空间杆件结构的平面简化 杆件构件的简化:以杆件的轴线代替杆件;
桁架:由若干直杆在两端用铰结点连接构成。桁 架杆件主要承受轴向变形,是拉压构件。
组合结构:由梁式构件和拉压构件构成。 拱:一般由曲杆构成。在竖向荷载作用下有水 平支座反力。
2、按计算方法分类: 静定结构, 超静定结构。
精选PPT课件
6
§1-4 荷载分类
1、按作用时间分类: 恒载:永久作用在结构上。如结构自重、永久
平面内最简体系的自由度数:
结构力学课后习题答案(朱慈勉)
结构⼒学课后习题答案(朱慈勉)朱慈勉结构⼒学第2章课后答案全解2-2 试求出图⽰体系的计算⾃由度,并分析体系的⼏何构造。
(a)ⅠⅡⅢ(ⅠⅡ)(ⅠⅢ)(ⅡⅢ)舜变体系`ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0⼏何可变(c)有⼀个多余约束的⼏何不变体系(d)2-3 试分析图⽰体系的⼏何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)⼏何不变W=3×3 - 2×2 – 4=1>0可变体系ⅠⅡⅢ(ⅠⅡ)(ⅠⅢ)(ⅡⅢ)⼏何不变2-4 试分析图⽰体系的⼏何构造。
(a)(ⅠⅢ)(ⅠⅡ)(ⅡⅢ)ⅠⅡ(b)W=4×3 -3×2 -5=1>0⼏何可变体系ⅢⅠⅡ(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)⼏何不变(d)(ⅠⅡ)ⅢⅠⅡ(ⅡⅢ)(ⅠⅢ)⼆元杆有⼀个多余约束的⼏何不变体Ⅲ(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系(f)ⅠⅡⅢ(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)⽆多余约束内部⼏何不变ⅠⅡⅢ(ⅠⅢ)(ⅠⅡ)(ⅡⅢ)⼆元体(ⅠⅡ)(ⅡⅢ)⼆元体多余约束W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的⾓度分析图⽰体系的⼏何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)(ⅠⅢ)⼏何不变同济⼤学朱慈勉结构⼒学第3章习题答案3-2 试作图⽰多跨静定梁的弯矩图和剪⼒图。
(a)4P F aP F Q34P F 2 P F (b)ABCaa aaaF P a D EFF P2m6m2m4m2mABCD10kN 2kN/m 42020M Q(c)210 180 18040M1560704040Q (d)3m2m2mA B CEF15kN 3m 3m4m20kN/m D 3m2m2m2m2m 2m 2mAB6kN ·m4kN ·m 4kN2m7.5514482.524MQ3-3 试作图⽰刚架的内⼒图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一系列 可破坏 荷载的 最小值
…… ……
pu
极限荷载 一系列 可接受 荷载的 最大值
“ 既是可破坏荷载,又是可接受荷载,则此荷载是极限荷载”。 或:“极限荷载是唯一的”
12.4 超静定梁的极限荷载
一、确定极限荷载的三种方法 • 1、机动法 • 2、静力法 • 3、试算法 二、机动法
1、依据:机动法是以上限定理为依据的。 2、步骤:先假设出所有的破坏机构,而后利用虚位移原理计算 出各机构相应的极限荷载。依据上限定理,这些可破坏荷载中 的最小者即为极限荷载。 三、试算法 1、依据:试算法是以单值定理为依据的。 2、步骤:先试算出相应于某一破坏机构的可破坏荷载,而后验 算该荷载是否满足屈服条件,若满足,该荷载即为极限荷载。
三、破坏机构 由于足够多的塑性铰的出现,使原结构成为机构(几何可变体系), 失去继续承载的能力,该几何可变体系称为“机构”。 1、不同结构在荷载作用下,成为机构,所需塑性铰的数目不同。
q u1
qu 2
Mu Mu
M u Wu s
Mu
Mu
2、不同结构,只要材料、截面积、截面形状相同,塑性弯矩一定相同。
M u qu 2 l 2 Mu 2 8
(4)极限状态
2、确定单跨梁极限荷载的机动法
q
l
qu
A
x
Mu x
l 2
2
B
dx C
Mu
Mu
临 界 状 态 时 , 由 虚 功程 方: 2 x qu dx M u M u M u 2
1 2 l qu 4 M u 4 16M u qu l2
例题2 试用试算法求图示结构的极限荷载。 p 解 法2 : 1.1 p
A D B E
C
试取机构( 2) p2 a M u M u 2 Mu a 绘 出 与机 构 ( 2) 相应的 M图 , p2 3
2a
a
1.1 p
a
a
p
2
Mu
验 算 屈服 条 件 :
Mu
M DA
Mu
q
1.1 p
Mu
p
x
q
机构(4)
结论:机构(1)、(2)不会出现,各跨可单独考虑。
q
弯矩( M)、剪力( Q)与荷载集度 (q) 关系:
0
A
ql 2
q
B
N
q( x )
M
M+dM N+dN Q
x
dx
l
ql 2
q
dx
Q+dQ
x
q( x ) q
q
y0
ql qx 2
ql 2
x
dQ q( x ) dx
E
Ms s 1 2 bh 6
y s y0
y
1 2 M s bh s 6
h 2 h 2
y s
h 2 h 2
2.弹塑性阶段
y
s
y0
s h s Ey0 2 y0
s 2 y0 h
y0 y0
2 2 2 2 y0 bh2 s 3 2 y0 h h 3 2 y0 M s b( y0 )( y0 ) s b ( 2 ) Ms ( 2 ) 2 2 3 6 2 h 2 h M 1 [3 ( s ) 2 ] Ms 2
三、基本假设
1、材料为“理想弹塑性材料” 。 2、拉压时,应力、应变关系相同。
3、满足平截面假定。即无论弹、塑性阶段,保持平截面不变。
y
卸载时有残余变形
§12-2 纯弯曲梁的极限弯矩和塑性铰
1. 弹性阶段
b b 2 2
M
M
y / E 2 s s s h/2 Eh
z
同时满足机构条件、平衡条件和屈服条件的荷载。它既是可破坏荷 载,又是可接受荷载。
四、确定极限荷载三个定理 1、上限定理(亦称“机动定理”、或“极小定理”) 对于比例加载作用下的给定结构,按任意可能的破坏 机构,由平衡条件求得的荷载将大于或等于极限荷载。 或:“可破坏荷载的最小值是极限荷载的上限”。 或:“极限荷载是可破坏荷载的最小值” 2、下限定理(亦称“静力定理”、或“极大定理”) 或:“可接受荷载的最大值是极限荷载的下限”。 或:“极限荷载是可接受荷载的最大值” 3、单值定理(亦称“唯一定理”)
p
A
C
M u1 M u2
D
M u2
B A C
p
D
B
p
机构(一)A C M u2 D
M u2 M u1
M u2
B 情况(1)
M u1
C A B
p
D B
p
C D
机构(二)A
M u2
情况(2)
M u2
p
M u1
M u1
B C A
p
D
机构(三)A
C
M u2
D
B
M u2
不可能出现,为什么? 情况(3)
试确定图示单跨梁的极限荷载
3、材料、截面积、截面形状相同的不同结构,qu不一定相同。
q u1
qu 2
Mu1
M u1 M u 2 qu1 qu 2
Mu2 Mu2
四、如何确定单跨梁的极限荷载 1、机理 q
ql 2 12 ql 2 12
ql 2 24
q u1
Mu
q u1 l Mu 12
q u1 l 2 M u 24 2
p1
Mu Mu
p2
B
Mu
p1
p2
B
p1
p2
B
Mu
机构(一)
Mu
机构(一)M 图情况
Mu
p1
p2
B
Mu
p1
p2
B
机构(二)
Mu
Mu
机构(二)M 图情况
Mu
p1
机构(三)
p2
B
M u2
不可能出现,为什么?
12.3 确定极限荷载的几个定理
一、几点假设 1、比例加载
a ) p1 1 p, p2 2 p, , pn n p b) q1 1q, q2 2q , , qn nq
2、小变形假设(几何线形),变形后仍用变形前的几何尺寸。 3、略去弹性变形(弹塑性材料,刚塑性变形。)
qu 2
Mu
Mu 4、不计剪力、轴力对极限荷载的影响
5、正负极限弯矩值相等
Mu Mu
Mu
二、结构极限状态时应满足的三个条件 1、机构条件
当荷载达到极限值时,结构上必须有足够多的塑性铰,而使结构变 成机构。
p
2
p2 3
Mu a
Mu
Mu
Mu 依 上 限 定 理 : pu 2.27 a
机构(2)
例题1 试用机动法求图示结构的极限荷载。 (1)分析弯矩与曲率的关系 : p 1.1 p
A D B E
C
1
y
M EI
(a )当M为 正 值 时 , 曲 率 为 负 ; 值
2a
dM Q( x ) dx
ql 2
M 0
Q( x )
Q
x
ql 2 8 ql 1 M ( x) x q x 2 2 2
d 2M q( x ) 2 dx
M
例题2 试用试算法求图示结构的极限荷载。 p 解 法1 : 1.1 p
A D B E
C
试取机构( 1) 1.1p1 2a M u 3 M u 2 Mu a 绘出与 机构( 1) 相应的 M图, p1 2.27
p
解: 机构( 1) p1 2a p1 a M u M u 3 p1 1.33 Mu a
p
q 2p
a
1.2 p
A
E
F
B
C
D
a
p
机构1
2
a
a
p Mu
3
2a
q 2p a
a
a
1.2 p
机构( 2) p2 a p2 2a M u 2 M u 3 p1 1.67
s 弹性极限弯矩 塑性极限弯矩 (屈服弯矩)
Mu s
3. 塑性流动阶段
b
3. 塑性流动阶段
h h 1 2 M u s b bh s 2 2 4 1 M s bh2 s 6
Mu 1 截面形状系数 Ms 塑性铰(plastic hinge)的概念
压
拉
h 2 h 2
2a
a
1.1 p
Mu
a
a
p
验算屈 服条件:
M EC 1 1 p1 2a M u 4 2 M 1 1 ( 2.27 u ) 2a M u 4 a 2 0.635M u M u
2
Mu
3
机构(1)
1.1 p
Mu
p
Mu
M图
M EC
经验算各截面弯矩值足 满屈服条件, M pu 2.27 u a
a
1.1 p
Mu 机构(3)
a
p
a
Mu
(b)当M为 负 值 时 , 曲 率 为 正 。 值
x
M
M
y
(2)分析弯矩与荷载集度 (q)关系:
d 2M q dx2 (a )当q为 正 值 (向 下 ) 时 , 曲 率 为 负 ; 值 (b)当q为 负 值 (向 上 ) 时 , 曲 率 为 正 。 值
