定积分不等式
探讨定积分不等式的证明方法

探讨定积分不等式的证明方法定积分是微积分中重要的概念之一,它在数学和其他学科中有着广泛的应用。
定积分不等式是对定积分的一种推广和扩展,它可以用来证明数学中的很多重要不等式。
定积分不等式的证明方法有很多种。
下面将介绍其中的几种常见证明方法。
1.利用积分的定义定积分的定义是通过极限来定义的,可以用积分和极限的性质来证明定积分不等式。
一般的证明步骤如下:(1)通过积分的定义,将定积分转化为极限的形式。
(3)利用极限的性质,对被积函数和不等式进行变换和处理,最终得到待证不等式。
2.利用积分的性质和中值定理(1)利用中值定理,将定积分表示为导数的形式。
(3)利用中值定理和被积函数的性质,对待证不等式进行变换和处理,最终得到待证不等式。
3.利用积分的性质和数学归纳法数学归纳法是数学中常用的证明方法之一,可以用来证明定积分不等式。
具体的证明方法如下:(1)利用积分的性质,将待证不等式转化为一系列具有相似性质的子不等式。
(2)对待证不等式的子不等式进行归纳证明,即先证明基本情况,然后假设第n个不等式成立,再通过已知的前n个不等式得到第n+1个不等式。
(3)通过数学归纳法的证明,得到待证不等式。
这种证明方法的优点是简单直接,能够通过归纳证明得到待证不等式,但需要对数学归纳法的性质和待证不等式的子不等式非常熟悉。
除了以上的方法,还可以利用几何意义、特殊函数的性质、不等式的基本性质等进行证明。
不同的证明方法适用于不同的场合和问题,需要根据具体情况选择合适的方法。
综上所述,定积分不等式的证明方法有很多种,可以利用积分的定义、性质和中值定理,数学归纳法等进行证明。
不同的证明方法有不同的优点和适用范围,需要根据具体情况选择合适的方法。
对于定积分不等式的证明方法的深入理解和熟练应用,对于深化对定积分的理解和掌握具有重要意义。
利用定积分证明不等式

热点追踪Җ㊀广东㊀李文东㊀㊀不等式的证明是高考的重要内容,证明的方法多㊁难度大,特别是一些数列和型的不等式.这类不等式常见于高中数学竞赛题和高考压轴题中,由于证明难度较大,往往令人望而生畏.其中有些不等式若利用定积分的几何意义证明,则可达到以简驭繁㊁以形助数的解题效果.1㊀利用定积分证明数列和型不等式数列和型不等式的一般模式为ðni =1a i <g (n )(或ðni =1a i >g (n )),g (n )可以为常数.不失一般性,设数列a n =f (n )>0,此类问题可以考虑如下的定积分证明模式.(1)若f (x )单调递减.因为f (i )<ʏii -1f (x )d x ,从而ðni =1a i =ðn i =1f (i )<ðni =1ʏii-1f (x )d x =ʏn0f (x )d x .㊀㊀又因为ʏi i -1f (x )d x <f (i -1),从而ʏn +11f (x )d x =ðn +1i =2ʏi i-1f (x )d x <ðn +1i =2f (i -1)=ðni =1a i.㊀㊀(2)若f (x )单调递增.因为f (i )>ʏi i -1f (x )d x ,从而ðni =1a i=ðni =1f (i )>ðni =1ʏii-1f (x )d x =ʏn0f (x )d x .㊀㊀又因为ʏii -1f (x )d x >f (i -1),从而ʏn +11f (x )d x =ðn +1i =2ʏii-1f (x )d x >ðn +1i =2f (i -1)=ðni =1a i .例1㊀(2013年广东卷理19,节选)证明:1+122+132+ +1n2<74(n ɪN ∗).分析㊀本题证法大多采用裂项放缩来证明,为了得到更一般的结论,我们这里采用定积分来证明.证明㊀因为函数y =1xα(α>0且αʂ1)在(0,+ɕ)上单调递减,故ʏii -11x αd x >1iα(i ȡ3),从而当αʂ1时,ðni =11i α<1+12α+ðni =3ʏii -11x αd x =1+12α+ʏn21x αd x =1+12α-1(α-1)x α-1n 2=1+12α+1(α-1)2α-1-1(α-1)nα-1.㊀㊀利用这个不等式可以得到一些常见的不等式.若α=12,则ðn i =11i<1-32+2n =2n -1+(2-32)<2n -1.㊀㊀当α>1时,ðni =11iα<1+12α+1(α-1)2α-1=1+α+1α-1 12α.特别地,若α=2,则ðni =11i 2<1+2+12-1 122=74;若α=3,则ðni =11i3<1+3+13-1 123=54;若α=32,则ðni =11ii<1+32+132-1 1232=1+524<3;若α=1,则1n<ʏnn -11x d x =l n x nn -1=l n n -l n (n -1),从而可以得到12+13+ +1n +1<ʏn +111xd x =l n (n +1),1n +1+1n +2+ +12n<ʏ2nn1xd x =l n2.㊀㊀另一方面,1n -1>ʏnn -11xd x =l n x n n -1=l n n -l n (n -1),则1+12+13+ +1n -1>ʏn11x d x =l n n .㊀㊀当α=1时,借助定积分的几何意义上述不等式42热点追踪还可以进一步加强.图1是函数y =1x的部分图象,显然S 曲边梯形A B C F <S 梯形A B C F ,于是ʏn +1n1x d x <12(1n +1n +1),得l n (1+1n )<12(1n +1n +1),令n =1,2, ,n ,并采用累加法可得1+12+13+ +1n>l n (n +1)+n2(n+1)(n ȡ1).图1例2㊀证明:l n 42n +1<ðni =1i4i 2-1(n ɪN ∗).分析㊀由于i 4i 2-1=14(12i -1+12i +1),l n 42n +1=14l n (2n +1),故证明l n (2n +1)<ðni =1(12i -1+12i +1).构造函数f (x )=12x +1,显然f (x )单调递减,考虑到ðni =1(12i -1+12i +1)的结构,对函数f (x )采用类似图1中的梯形面积放缩.证明㊀由分析得ʏii -112x +1d x <12(12i -1+12i +1),故12l n (2n +1)=ʏn012x +1d x =ðni =1ʏii -112x +1d x <12ðni =1(12i -1+12i +1),不等式两边除以12即为所证.例3㊀证明13+15+17+ +12n +1<12l n (n +1)(n ɪN ∗).分析㊀若考虑函数y =12x +1,则有12i +1<ʏii -112x +1d x ,则ðni =112i +1<ðni =1ʏii -112x +1d x =ʏn012x +1d x =12l n (2x +1)n0=12l n (2n +1),达不到所证的精度,必须改变定积分放缩的精度.证明㊀结合不等式的右边,考虑函数f (x )=1x.如图2所示,在区间[i ,i +1]上,取区间的中点i +12,并以1i +12为高作矩形A E F B ,则S 矩形A E F B <ʏi +1i 1x d x .于是有22i +1=1i +12<ʏi +1i1xd x ,则ðni =122i +1<ðni =1ʏi +1i1xd x =ʏn +111xd x =l n (n +1),即ðn i =112i +1<12ln (n +1).图2例4㊀设n 是正整数,r 为正有理数.(1)求函数f (x )=(1+x )r +1-(r +1)x -1(x >-1)的最小值;(2)证明:n r +1-(n -1)r +1r +1<n r<(n +1)r +1-nr +1r +1;(3)设x ɪR ,记[x ]为不小于x 的最小整数,例如[2]=2,[π]=4,[-32]=-1.令S =381+382+383+ +3125,求[S ]的值.(参考数据:8043ʈ344 7,8143ʈ350 5,12543ʈ625 0,12643ʈ631 7.)分析㊀出题者的本意是利用第(1)问中的伯努利不等式来证明后两问,但这里我们利用积分来证明.证明㊀(1)f m i n (x )=0(求解过程略).(2)因为r 为正有理数,函数y =x r 在(0,+ɕ)上单调递增,故ʏnn -1x r d x <nr,而52热点追踪ʏnn -1x rd x =x r +1r +1n n -1=n r +1-(n -1)r +1r +1,故n r +1-(n -1)r +1r +1<n r.同理可得n r<ʏn +1n x rd x =x r +1r +1n +1n =(n +1)r +1-n r +1r +1,从而n r +1-(n -1)r +1r +1<n r<(n +1)r +1-n r +1r +1.(3)由于i 13<ʏi +1i x 13d x <(i +1)13,故S =ð125i =81i13<ð125i =81ʏi +1ix 13dx =ʏ12681x 13dx =34x 4312681=34(12643-8143),34(12543-8043)=34x 4312580=ʏ12580x 13d x =ð124i =80ʏi +1ix 13d x <ð124i =80(i +1)13=S .34(12543-8043)<S <34(12643-8043).代入数据,可得34(12543-8043)ʈ210.2,34(12643-8143)ʈ210.9.由[S ]的定义,得[S ]=211.2㊀利用积分证明函数不等式我们知道ʏx 2x 1fᶄ(x )d x =f (x 2)-f (x 1),因此,对于与f (x 2)-f (x 1)有关的问题,可以从定积分的角度去思考.若f (x )的导数f ᶄ(x )在区间(a ,b )上单㊀图3调递减且f ᶄ(x )为凹函数,如图3所示.设A C 的中点为B ,过点B 作B G ʅx 轴与f (x )交于点G ,过点G 作f (x )的切线与直线AH 和C D 分别交于点F 和I .设A (x 1,0),C (x 2,0),则f (x 2)-f (x 1)=ʏx 2x 1fᶄ(x )d x =S 曲边梯形A C J H ,S 矩形A C D E =f ᶄ(x 2+x 12)(x 2-x 1).因为S 曲边三角形E G H >S әE F G =S әD I G >S 曲边三角形J D G ,S 曲边梯形A C J H -S 矩形A C D E =S 曲边三角形E G H -S 曲边三角形J D G >0,于是有f (x 2)-f (x 1)x 2-x 1>f ᶄ(x 2+x 12).借助上述几何意义,一般地我们有如下结论.(1)若函数f (x )的导数f ᶄ(x )在区间(a ,b )上为凹函数,则对于任意的a <x 1<x 2<b ,有f (x 2)-f (x 1)x 2-x 1>f ᶄ(x 2+x 12);(2)若函数f (x )的导数f ᶄ(x )在区间(a ,b )上为凸函数,则对于任意的a <x 1<x 2<b ,有f (x 2)-f (x 1)x 2-x 1<f ᶄ(x 2+x12).例5㊀(1)函数f (x )=l n x ,因为f ᶄ(x )=1x在(0,+ɕ)上为凹函数,则对任意0<x 1<x 2,有l n x 2-l n x 1x 2-x 1>1x 2+x 12,即x 2-x 1l n x 2-l n x 1<x 1+x 22,此为对数均值不等式.(2)函数f (x )=x l n x ,因为f ᶄ(x )=1+l n x 在(0,+ɕ)上为凸函数,则对任意0<x 1<x 2,有x 2l n x 2-x 1l n x 1x 2-x 1<1+l n x 2+x 12.许多考题都是以此为背景命题,比如,如下高三模拟考试的压轴题.例6㊀已知函数f (x )=l n x -a x 22+(a -1)x -32a(a >0),在函数f (x )的图象上是否存在不同两点A (x 1,y 1),B (x 2,y 2),线段A B 中点的横坐标为x 0,直线A B 的斜率为k ,使得k >f ᶄ(x 0).简证㊀由于f ᶄ(x )=1x-a x +a -1(a >0)在(0,+ɕ)上为凹函数,可见结论成立!例7㊀设函数f (x )=xex ,若x 1ʂx 2,且f (x 1)=f (x 2),证明:x 1+x 2>2.分析㊀本题的本质是极值点偏移问题,常见证法是利用对称性构造函数,这里采用定积分来证明.证明㊀不妨设x 1<x 2,由f ᶄ(x )=1-x ex ,可知f (x )在(-ɕ,1]上单调递增,在[1,+ɕ)上单调递减,且f (0)=0.当x >0时,f (x )>0,可知0<x 1<1<x 2.设x 1e x 1=x 2e x 2=t ,则x 1+x 2=t (e x 1+e x 2),x 2-x 1=t (e x 2-e x 1),考虑函数y =e x ,则根据定积分的梯形面积放缩有e x 2-e x 1=ʏx 2x 1e xd x <(e x 1+e x2)(x 2-x 1)2,则x 2-x 1t <12 x 2+x 1t(x 2-x 1),故x 1+x 2>2.(作者单位:广东省中山市中山纪念中学)62。
定积分的计算和积分不等式 数学

定积分的计算和积分不等式摘要:本文首先介绍了定积分的几种计算方法:牛顿—莱布尼兹公式,分部积分法,换元积分法,积分值的估计。
其次再介绍了积分不等式的几种证明:用微分学的方法证明积分不等式,利用被积函数的不等式证明积分不等式,在不等式两端取变限积分证明新的不等式,利用积分性质证明不等式,利用积分中值定理证明不等式。
关键字:定积分;牛顿—莱布尼兹公式;分部积分法;换元积分法The Definite Integral Compute and Integral InequalityAbstract: In this paper, firstly, mainly introduced a few kinds computational method of definite integral: Newton-Leibniz, definite integration by parts, integration by substitution, definite integral by estimate value. Secondly, this paper also introduced a few kinds of integral invariant: using the method of differential calculus to prove integral invariant; making use of integrand invariant to prove integral invariant; using transfinite integrate to prove integral invariant; using integral characteristic to prove integral invariant; making use of integral mean value theorem to prove integral invariant.Key word:Definite integral; Newton-Leibniz; definite integration by parts; integration by substitution.引言数学分析是数学专业中一门重要的基础课,定积分的计算和积分不等式无疑是数学分析中一个重要的方面。
定积分不等式及其最佳常数的两种证明方法

定积分不等式及其最佳常数的两种证明方法定积分不等式是指对于$f(x)$在$[a,b]$上连续,$g(x)$在$[a,b]$上单调递增和非负,有以下不等式成立:$$\int_a^bf(x)g(x)dx\le\frac{b-a}{2}\left(\int_a^bf^2(x)dx+\frac{1}{g^2(a)}\int_a^bg^2(x)dx\ right)$$其中等号成立当且仅当$f(x)=k\cdot g(x)$,其中$k$是一个常数。
这个不等式也被称为“加权平均值-平方根平均值不等式”,可以用两种不同的证明方法:一种是基于几何意义的证明,另一种是基于分部积分的证明。
方法一:首先考虑一个几何上的问题:对于函数$f(x)$,我们可以将其图像在区间$[a,b]$上折叠,形成一个平行四边形,可以证明该平行四边形的面积等于$\int_a^bf(x)dx$。
现在我们假设将平行四边形“割”成两半,所得的两个“三角形”的底分别为$\frac{b-a}{2}$和$\frac{b-a}{2}g(a)$。
则根据三角形面积公式,这两个“三角形”的面积分别为$\frac{1}{2}\int_a^bf^2(x)dx$和$\frac{1}{2g^2(a)}\int_a^bg^2(x)dx$。
由于$g(x)$是单调递增且非负的,所以可以想象这两个“三角形”肯定包含在一条斜率为$k$(其中$k$为常数)的直线下方。
因此,我们可以将这个直线逆时针旋转一定角度,得到一个新的平行四边形,其底仍为$\frac{b-a}{2}$和$\frac{b-a}{2}g(a)$,高为$\frac{1}{2}(k+\frac{1}{g(a)})$(即平行四边形的两个高之和的一半)。
根据面积公式,这个新的平行四边形的面积为$\frac{b-a}{2}(k+\frac{1}{g(a)})\cdot\int_a^bf(x)g(x)dx$。
由于这个新平行四边形的面积应不小于原平行四边形的面积,因此我们可以得到不等式:$$\int_a^bf(x)g(x)dx\le\frac{b-a}{2}\left(\int_a^bf^2(x)dx+\frac{1}{g^2(a)}\int_a^bg^2(x)dx\ right)$$并且等号成立当且仅当$f(x)=k\cdot g(x)$。
定积分中的柯西不等式

定积分中的柯西不等式在数学的世界里,有一个非常酷的家伙叫做柯西不等式。
这家伙就像是我们生活中的一位老朋友,可能不常见,但一出现,总能让我们感受到它的魅力。
你看,定积分本身就像一场美妙的旅程,像是在寻找隐藏的宝藏。
而柯西不等式就像是给我们指路的明灯,让我们在这条路上走得更顺畅,找到那些意想不到的惊喜。
什么是柯西不等式呢?它简单得让人惊叹,像是老天爷给我们留的一个小秘密。
我们知道,在任何一个数列中,如果我们把两个数的平方相乘再求和,通常会得到一个比我们想象中还要大的结果。
这就是柯西不等式的精髓所在。
这家伙让我们意识到,合在一起的东西,往往能产生出意想不到的力量。
就像是你和朋友一起合作做个项目,结果总比你一个人要强大许多。
现在,咱们来聊聊这位不等式的具体应用。
想象一下,我们在做积分时,想要评估某个函数的表现。
这里,柯西不等式就像是一位数学界的老顽童,总能给你带来灵感。
通过将两个函数的积分进行结合,我们能轻松地估计出它们的关系。
就像在厨房里,拿出几个材料,按照自己的想法调配出一道美味的菜肴,意外的美味总能让人惊喜连连。
使用柯西不等式的时候,我们可以大胆地组合不同的函数,就好比拼图游戏,努力把每一块拼得恰到好处。
比如说,假设我们有两个函数,f(x)和g(x),通过柯西不等式,我们能知道它们的积分的平方和总是大于等于它们的乘积的积分的平方。
听上去是不是有点复杂?但别担心,慢慢来,像是在研究一个新的游戏规则,最后你会发现,掌握这个不等式后,数学的世界瞬间变得更加有趣。
这个不等式对我们有什么启示呢?它提醒我们,在生活中,我们和他人之间的关系也是如此。
无论是工作还是学习,团队的力量总是超过个体的总和。
想想看,几个人一起加班,气氛轻松了,效率也提高了,真是一举两得。
柯西不等式正是这种理念的数学体现,让我们懂得团结的重要性。
咱们还得说说如何使用这个不等式来解决实际问题。
举个例子,假设你想要估算某个不规则图形的面积,直接计算可能会让你头疼不已。
考研数学一:定积分及其等式与不等式问题
1
b
f ( x )dx 2
a
若
a b
f ( x )dx 0 ,则取
ξ = a 或 b 即可
若
a
f ( x )dx 0 ,则 F (a )F (b) 0 ,根据零值定理,
存在ξ(a , b) 使
F ( ) f (t )dt
a
1
b
f ( x )dx 0 2
ξ[ a , b] 使成立
x
1b f ( x )dx f ( x )dx 2a a
1
解 设 F ( x)
a
f (t )dt
b
f ( x )dx ,则 F(x) 在 a , b上连续 , 2
a
b
且
F (a )
b
1
f ( x )dx 2
a
, F (b)
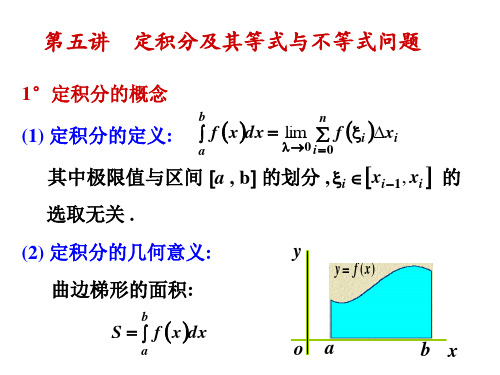
第五讲 定积分及其等式与不等式问题
1°定积分的概念
b
(1) 定积分的定义:
f x dx lim f i xi
0 i 0
n
a
其中极限值与区间 a , b 的划分 , i xi 1 , xi 的
选取无关 .
(2) 定积分的几何意义:
曲边梯形的面积:
a
b
x
a
f ( t )dt f ( t )dt
x
F '' ( x ) 2 f ( x ) 0
F(x) 是 a , b 上的凸函数
x
例9 设
F ( x ) tf ( x t )dt
0
2
2
, 其中 f (x(0) 0 , f' (0 ) 1 , F x ~ cx ,
定积分不等式word文档良心出品

第三章一元积分学第三节定积分值的估计及不等式定积分值的估计及不等式证明是一个较难的问题,方法多样,用到的知识(微分学的知识,积分学的知识等)也很多。
总的说来:(1)主要用积分学的知识,除了定积分的性质、积分中值定理、计算方法外,以下几个简单的不等式也是有用的:b b(i)若f(x) <g(x)(x 引a,b]),则J f (x)dx < J g(x)dx .a ab b(ii) I f f(x)dx| 兰f l f (x) |dx.ad b(iii )若f(X)>0(X 引a,b]), a<c<d<b,则f f (x)dx < f f (x)dx.9 £(iv)(柯西不等式)[f f (x)g(x)dxr < a f 2(x)dx a g2(x)dx(2)主要用微分学的知识,包括前面己讲过的利用微分学知识证明不等式的一切方法.(3)利用二重积分、级数等.值得注意的是:题目的解法往往有多种,同一题目其解答过程中往往要用到各种知识和方法.、■莎 2例1.判断积分[sin x dx的符号分析:这个积分值是求不出来的.如果被积函数在积分区间上有确切的符号,那么积分值的符号很容易判断.如果被积函数在积分区间上有正、有负,那么应根据被积函数的正、负情况将积分区间分成部分区间,然后利用积分学等方面的知识比较在这些部分区间上的积分值(实际上是比较积分值的绝对值).本题中被积函数si nx2在积分区间上有正、有负,先作,一2*烦2 1 ^sin t换兀:t =x ,把积分变为(sinx dx=5t -^dt后,问题更清晰,因而想到/莎 2 1 2;rs int 1 F兀sin t ,^si ntsinxdx=?0 ;r dt=2d寅dx+J兀至此积分的符号凭直觉已经能判断了. 但严格说明还需做一些工作,上式右端两个积分的积分区间不一样,为了方便比较,应将两个积分放在同一积分区间上进行比较. 有了这些分析和思路后,解答就容易了.解:令t =x2,则0 sin/dx^L 于dt—2(0 于dx+J兀于dt)2兀sin t 兀一sin u 兀sin t对上式右端后一积分换元,u*得d r 右du—0右dt从而广sinx2dx—丄(f字dx-f严dt) 0 2 0JT看V u +兀1兀1 1=-f (k -- )sintdt >02 J t+J注:本题的解答过程不复杂,但其过程中有两个技巧很有用(1)将积分区间分成部分区间 (尤其是等分区间,特别是二等分) (2)如要比较两个在不同积分区间上的积分的大小,可通过换元变成相同积分区间上的积分,然后比较.迟. 3例 2 .设a A 0,证明:(xa sinx dx『a ■sinx dx > 亍分析::从形式上看很象柯西不等式,但两个积分的积分区间不一样,前面的积分可用教材上介绍的一个等式0,f(sinx)dx = jr 02 f(sinx)dx变为[0,亍]上的积分,再用柯西不等式便可得结论。
定积分与不等式证明

21 0 1年 8月
赤 峰 学 院 学 报 (科 学 教 育 版 )
J u a o hf gU i r t si c o r l f i n n es y(c n e&e u a o ) n C e v i e d ctn i
Vn13 No8 . . Aug 201 . 1
不 等 式 的 证 明 在 数学 分析 中起 着 重 要 作 用 . 有 足 积 分 笛
的不等式较 为常见 , 根据含积分 不等式的特点 , 般可 以考 一 虑 以下几种求证方法 :
应分积法:xd x 』 L 用部分有』x}l, ̄ x 2l d n = n一x x l n x 4  ̄
1 充分运用积分运算方法 . 2 换元积分法 , 分部积分法不仅能求解积分 , 在积 分不等
证 引入参数 1 考察 f ) )x, 1 , . + 【 )由题设 上式在[b ( uf x ( a] ,上
对任何实数 U 都不能恒为“”不然 , 0, 若假设有实数 u使得 ,
rx uf)O (+ x(= ) x
ufx (d+ufxx (d+』[x2 >  ̄x x2 f)xx f)d 0 ) (e ) (1x
=
1 灵活 运 用 性 质 与 运 算 方 法 证 明
[n {l2- + 手x n 1 孚 一 nn -2
11 应用积分性质 .
一
<
些不等式的证明一般不必计算 出定 积分 ,因此对 于
再
等n孚 1 l + n 一
n -I
含抽象函数 的定 积分不等式证 明, 可灵 活应用积分性质.
一
式 的证 明中也起了重要的作 用.
例 2 证明不等式 1( 1 n n -
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
a sin
x dx
3
0
0
4
分析:: 从形式上看很象柯西不等式,但两个积分的积分区间不一样,前面的积分可用教材上介
绍的一个等式
xf (sin x)dx
2
f (sin x)dx 变为[0,
] 上的积分,再用柯西不等式便可得结
0
0
2
论。
解:
xasin x dx
2 a sin x dx
证:令 F(x)
x
ax
tf (t)dt
x
f (t)dt ,则 F (a) 0, 且
a
2a
F (x) x a f (x) 1
x
1
f (t)dt
x
[ f (x) f (t)]dt 0
2
2a
2a
从而 F(x) F(a) 0, x [a,b]
取 x b ,便得 F (b) 0 ,结论得证.
a
a
b
b
(ii)| f (x)dx | | f (x) | dx .
a
a
d
b
(iii)若 f (x) 0 (x [a,b]), a c d b ,则 f (x)dx f (x)dx .
c
a
(iv)(柯西不等式)[ b f (x)g(x)dx]2 b f 2 (x)dx b g 2 (x)dx
a
2
被积函数中因子 x a b 关于积分区间中点具有某种对称性,而 f (x) 又单调,因此可想到前 2
面介绍的利用对称性计算积分的有关公式去处理.思路三:基于思路二的考虑,将积分区间二
等分,然后用积分中值定理或其它方法去证.思路四:由于 b (x a b ) f ( a b ) 0 故
a
a
a
(2)主要用微分学的知识,包括前面己讲过的利用微分学知识证明不等式的一切方法.
(3)利用二重积分、级数等.值得注意的是:题目的解法往往有多种,同一题目其解答过程
中往往要用到各种知识和方法.
例1.判断积分 2 sin x 2dx 的符号 0
分析:这个积分值是求不出来的.如果被积函数在积分区间上有确切的符号,那么积分值的 符号很容易判断.如果被积函数在积分区间上有正、有负,那么应根据被积函数的正、负情 况将积分区间分成部分区间,然后利用积分学等方面的知识比较在这些部分区间上的积分值
( f (2 )
f (1 ))
0
注:第一种方法我们称之为变易常数法,即把某个常数(在积分中一般是积分上限或下限)换 成变量,从而化为一个函数不等式,再利用微分学的知识及其它知识去证明,这是一种常用的技 巧。本题若把条件“连续且单调增加”改为“单调且有界”,结论仍成立。但变易常数法不能用(为 什么?)。
2 sin t dt)
0
20 t
20 t
t
对上式右端后一积分换元 t u 得
2 sin t dt
sin u du
sin t
dt
t
0 u
0 t
从而 2 sin x2dx 1 ( sin t dx sin t dt)
0
20 t
0 t
Page - 1 - of 11
a
2
2
b (x a b) f (x)dx 0
b
(x
a
b)(
f
(x)
f
(a
b))dx
0
a
2
a
2
2
就一目了然.思路五:变形为
(b a)
b
xf (x)dx
b2
a2
b
f (x)dx
b
b
1dx xf (x)dx
b
b
xdx f (x)dx
a
2a
a
a
a
a
那么看过例 6 后就知道怎么做了.
2
两边在[a,b] 上积分并注意到 b (x a b )dx 0 得
a
2
b
ab 1
f (x)dx (b a) f ( )
b f ( )(x a b)2 dx ,从而得
a
2
2a
2
|
b f (x)dx (b a) f ( a b) | 1 |
b f ( )(x a b)2 dx | M
a
2a
2a
不做(2)的证明过程中的第二步放大,便可证出上面结论:
b f 2 (x)dx
b
{(x a)
x[ f (t)]2 dt}dx
b
(
x
[
f
(t)]2
dt)d
(x
a)2
,再分部即可.
a
a
a
aa
2
例4.设 f (x) 在[a,b] 上有二阶连续导数, M max | f (x) | ,证明: x[ a ,b ]
b
bb
bb
而左边亦可化为二重积分:(b a) g(x) f (x)dx f (x)g(x)dxdy f ( y)g( y)dxdy
例 6.设 f (x), g(x) 在[a,b] 上连续且单调增加,求证:
b
b
b
(b a)a g(x) f (x)dx a f (x)dxa g(x)dx
分析:右端出现了两个积分,若将两个积分的积分变量换成不同符号则可化为二重积分:
b
b
b
b
bb
bb
a f (x)dxa g(x)dx a f ( y)dya g(x)dx a a f ( y)g(x)dxdy a a f (x)g( y)dxdy
2
2 22 2 2
62
(1)—(2)得
F (b)
F (a)
F ( a
2
b )(b
a)
(b
a)3 48
(F (1 )
F (2
))
(2)
所以
|
b a
f (x)dx
f ( a b)(b a) | (b a)3
2
48
|
f (1 )
f (2 ) |
M (b a)3 24
例5.设 f (x) 在[a,b] 上连续且单调增加,求证:
a
2
0
2
2
2
2
2
2
ba 2
x[
f
(a
b
x)
f
(a
b)
x]dx
0)
0
2
2
或: b (x a b) f (x)dx
a
2
ab 2
(x
a
b)
f
(x)dx
a
2
b ab
2
(x
a
2
b)
f
(x)dx
f (1 )
ab
2 (x
a
a b)dx 2
f (2 )
b
ab (x
2
a b)dx 2
(b a)2 2
0
0
xasin xdx
2 a sin x dx
sห้องสมุดไป่ตู้n x
2 (a 2 )dx
sin x
2 (a 2 )2 dx (
2 1dx)2
3
0
0
0
0
0
4
例3.设 f (x) 在[a,b] 上有一阶连续导数,且 f (a) 0 ,证明:
(1)| b f (x)dx | (b a)2 max | f (x) |
b xf (x)dx a b
b
f (x)dx
a
2a
分析:本题有多种证明方法,思路一:这里有两个参数 a, b ,把 b 改成变量 x ,欲证
x
tf
(t)dt
a
x
x
f (t)dt
a
2a
左右两边均是函数,可利用导数这一工具去证明.思路二:变形为 b (x a b ) f (x)dx 0
| b f (x)dx (b a) f ( a b) | M (b a)3
a
2 24
方法一:利用上一节中的例 10 中的(2),或练习题 21 可证出结论。
方法二:由泰勒公式有
f (x) f ( a b) f ( a b)(x a b) 1 f ( )(x a b)2
2
2
22
f (x) f (x) f (a) f ( )(x a)
从而 | f (x) || f ( )(x a) | M (x a), x [a,b]
所以
|
b
f (x)dx |
b
| f (x) | dx
b M (x a)dx (b a)2 M
a
a
a
2
Page - 2 - of 11
第三章 一元积分学 第三节 定积分值的估计及不等式 定积分值的估计及不等式证明是一个较难的问题,方法多样,用到的知识(微分学的知识, 积分学的知识等)也很多。总的说来: (1)主要用积分学的知识,除了定积分的性质、积分中值定理、计算方法外,以下几个简单 的不等式也是有用的:
b
b
(i)若 f (x) g(x) (x [a,b]) ,则 f (x)dx g(x)dx .
Page - 4 - of 11
或:
b
(x
a
b)
f
(x)dx
1
b[(x a b) f (x) (a b x a b) f (a b x)]dx
a
2
2a
2
2
1
b
(x
a
b)(
f
(x)
f
(a
b
