影院座位设计
数学建模综合题影院座位设计问题概要

数学模型张峰华材料学院材料成型及控制工程04班20123631 刘泽材料学院材料成型及控制工程04班20123627 杨海鹏材料学院冶金工程03班20123203一、问题重述影院座位的满意程度主要取决于视角α和仰角β,视角是观众眼睛到屏幕上下边缘的视线的夹角,越大越好;仰角是观众眼睛到屏幕上边缘视线与水平线的夹角,太大使人的头部过分上仰,引起不适,一般要求仰角β不超过030;记影院的屏幕高为h,上边缘距离地面高为H,影院的地板线通常与水平线有一个倾角θ,第一排和最后一排与屏幕水平距离分别为,d D,观众的平均座高为c(指眼睛到地面的距离),已知参数h=1.8. H=5, 4.5,19==,c=1.1(单位m)。
d D求解以下问题:θ时,求最佳座位的所在位置。
(1) 地板线的倾角010=(2) 地板线的倾角θ一般超过020,求使所有观众的平均满意程度最大时的地板线倾角。
二、问题的分析电影院座位的设计应满足什么要求,是一个非常现实的问题。
根据题意观众对座位的满意程度主要取决于观看时的视角α和仰角β,α越大越好,而β越小越好,最佳位置就是要在这两者之间找到一个契合点,使观众对两者的综合满意程度达到最大。
本文通过对水平视角α和仰角β取权重,建立适当的坐标系,从而建立一个线形型满意度函数。
针对问题一,已知地板线倾角,求最佳座位所在,即将问题转化求综合满意度函数的最大值,建立离散加权的函数模型并利用Matlab数学软件运算求解;针对问题二,将所有观众视为离散的点,要使所有观众的平均满意程度达到最大,即将问题转化求满意度函数平均值的最大值。
对此利用问题一所建立的满意度函数,将自变量转化为地板线倾角;在问题二的基础上对地板线形状进行优化设计,使观众的平均满意程度可以进一步提高。
本文在满意度呈线性的基础上来建立模型的,为使模型简化,更好地说明问题,文中将作以下假设。
三、模型假设1.忽略因视力或其他方面因素影响观众的满意度;2.观众对座位的仰角的满意程度呈线性;3.观众对座位的水平视角的满意程度呈线性;4.最后排座位的最高点不超过屏幕的上边缘;5.相邻两排座位间的间距相等,取为0.8m;6.对于同一排座位,观众的满意程度相同;7.所有观众的座位等高为平均座高;8.影院的的地板成阶梯状。
电影空间陈设方案

电影空间陈设方案1. 引言电影作为一种流行的娱乐形式,吸引了大量观众。
在影院中,观众不仅可以享受电影本身,还可以享受舒适的环境。
一个好的电影空间陈设方案可以提升观众的观影体验,增加观众的满意度和忠诚度。
本文将提供一个电影空间陈设方案的详细设计,包括座位布局、灯光设计、音效设计等方面。
2. 座位布局座位布局是电影空间陈设中最重要的部分之一,它直接影响观众的舒适度和观影效果。
以下是一个适用于中等规模电影空间的座位布局方案:•座位之间的距离应足够宽敞,以便观众有足够的腿部空间和活动空间。
•座位应该合理安排,以便观众可以清楚地看到屏幕,并且不被其他观众的头部遮挡。
•座位的角度应该使观众的视线在垂直于屏幕的方向上能够接近水平。
3. 灯光设计灯光设计在电影空间陈设中起到了关键的作用。
以下是一个适用于电影空间的灯光设计方案:•主要灯光应集中在屏幕上,以确保观众可以清楚地看到电影。
•在电影播放期间,其他灯光应该保持较暗的灯光状况,以减少观众在观影过程中对外界干扰的感受。
•当观众需要离开座位时,应有足够的照明以确保观众的安全。
4. 音效设计音效在电影观影中起到了非常重要的作用。
以下是一个适用于电影空间的音效设计方案:•声音应该清晰、真实,使观众感觉自己置身于电影的场景中。
•音箱应该布置在合适的位置,以确保观众可以听到均衡的音效。
•音响系统应该具备良好的调节功能,以适应不同类型的电影和音效要求。
5. 装饰设计装饰设计是电影空间陈设中不可忽视的一部分。
以下是一个适用于电影空间的装饰设计方案:•墙面可以选择黑色或深色系的颜色,以减少光线的反射,增强视觉效果。
•座位可以选择舒适的布质材料,配备可调节座椅和扶手,以提供更好的观影体验。
•在空间的其他区域,可以增加一些电影相关的装饰品,如电影海报、明星照片等,以增加观众的兴趣和身临其境的感觉。
6. 其他注意事项除了以上的设计方案,还有一些其他的注意事项需要考虑:•座位数量应该根据影院的容量和可用空间进行合理的安排。
影院座位设计的数学模型
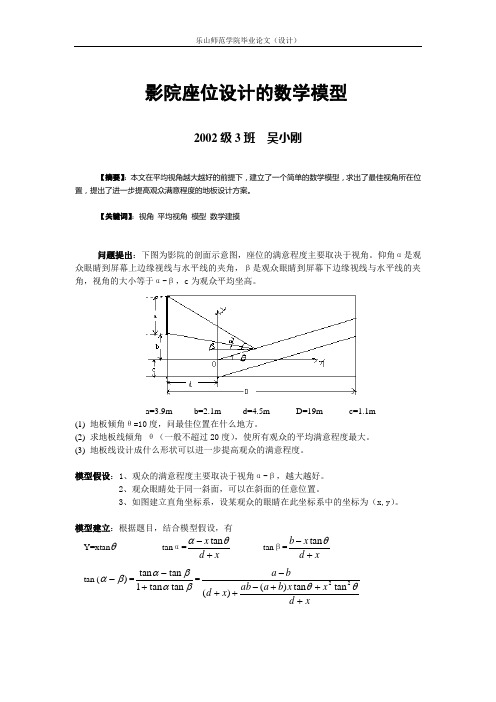
影院座位设计的数学模型2002级3班 吴小刚【摘要】:本文在平均视角越大越好的前提下,建立了一个简单的数学模型,求出了最佳视角所在位置,提出了进一步提高观众满意程度的地板设计方案。
【关键词】:视角 平均视角 模型 数学建摸问题提出:下图为影院的剖面示意图,座位的满意程度主要取决于视角。
仰角α是观众眼睛到屏幕上边缘视线与水平线的夹角,β是观众眼睛到屏幕下边缘视线与水平线的夹角,视角的大小等于α-β,c 为观众平均坐高。
a=3.9m b=2.1m d=4.5m D=19m c=1.1m(1) 地板倾角θ=10度,问最佳位置在什么地方。
(2) 求地板线倾角 θ(一般不超过20度),使所有观众的平均满意程度最大。
(3) 地板线设计成什么形状可以进一步提高观众的满意程度。
模型假设:1、观众的满意程度主要取决于视角α-β,越大越好。
2、观众眼睛处于同一斜面,可以在斜面的任意位置。
3、如图建立直角坐标系,设某观众的眼睛在此坐标系中的坐标为(x,y )。
模型建立:根据题目,结合模型假设,有Y=xtan θ tan α=tan x d x αθ-+ tan β=tan b x d x θ-+ tan ()βα-=βαβαtan tan 1tan tan +-=xd x x b a ab x d b a +++-++-θθ22tan tan )()(模型求解:(1)令f(x)=(d+x)+xd x x b a ab +++-θθ22tan tan )( )tan(20βαπβα-∴<-< 为增函数要使tan(βα-)最大,即视角βα-最大,只需f(x)最小,为此,我们对f(x)求导f ′(x)=1+2222)()tan tan )(())(tan )(tan 2(x d x x b a ab x d b a x +++--++-θθθθ =1+22222)(tan )(tan )(tan x d ab d b a d d x +-+--+θθθ 令f ′(x)=0x=1tan tan )(tan 222+++=θθθab d b a d (0≤x ≤14.5) 0≤x<1tan tan )(tan 222+++=θθθab d b a d f’(x)>0 1tan tan )(tan 222+++=θθθab d b a d <x ≤14.5 f’(x)<0 因此,tan(βα-)在x=1tan tan )(tan 222+++=θθθab d b a d 处取得最大值。
电影院看电影坐什么位置比较好

电影院看电影坐什么位置比较好电影院看电影坐什么位置比较好根据具体的观影环境和个人喜好,以下是几个座位选择的实践建议:利用前排座位。
通常来说,前排座位能够更好地捕捉到屏幕上的细节,对于视力不好的观众来说尤其适合。
同时,前排座位的视觉角度和音效体验也相对出色。
当然,如果你希望更轻松地观看电影,避免视角过于陡峭而导致视觉疲劳,可以选择稍微靠后的座位。
了解电影院布局。
在选择座位之前,可以先了解电影院的整体布局,包括屏幕的尺寸、音箱的位置等。
这可以帮助你更好地选择一个适合自己的座位。
与邻座交流。
如果你选择了连在一起的座位,可以事先了解邻座的观影喜好,以便在观影过程中更好地交流和分享。
例如,如果邻座是电影发烧友,可以一起探讨电影情节和拍摄技巧;如果邻座是小孩,可以避免选择过于刺激的影片,以避免影响其他观众。
注意安全。
在选择座位时,需要注意安全因素。
如果座位太靠近出口或者紧急通道,可能会在发生意外时受到影响。
因此,在选择座位时应该尽量避免这些区域。
电影院看电影选择座位的重要性在电影院观看电影时,座位的选择直接影响到观影效果。
首先,座位的设计需要考虑人体工学,以确保观众在观影过程中保持舒适状态,避免长时间久坐引起的身体不适。
其次,座位的选择需要兼顾视野和音效。
一个好的座位应该能够让观众完整地看到屏幕,并享受到出色的音效体验。
最后,座位的选择还直接影响到观影过程中的互动体验,比如与邻座交流、分享零食等。
电影院看电影座位选择的基本原则在选择座位时,可以遵循以下几个基本原则:面向电影院大门的右侧通常被认为是最佳座位。
这个位置可以避免屏幕反射造成的视觉干扰,同时可以欣赏到最佳的屏幕图像和音效。
如果可以,可以选择背后有墙的座位。
这种座位通常比较舒服,因为背后有一个支撑点,同时可以减少来自其他观众的干扰。
如果想要与朋友一起观影,可以选择连在一起的座位。
这种座位方便聊天和分享零食,同时可以更好地掌控自己的观影体验。
电影院看电影座位选择总结选择一个合适的座位对于观看电影至关重要。
小型电影院设计规范改

小型电影院设计规范改随着人们对文化娱乐需求的提升,电影院已经成为人们常去的休闲场所之一、为了满足人们对于电影观影体验的需求,小型电影院的设计规范也应不断进行改进。
本文将从空间布局、影院设备、舒适度和安全性等方面提出几项改进规范。
一、空间布局1.座位数量和距离:小型电影院的座位数量应根据场地面积和观影需求进行合理配置,座位与屏幕之间的距离应符合观影距离的要求。
一般来说,座位数不宜超过150个,距离屏幕的最佳观影距离为1.5倍屏幕宽度。
2.紧凑空间设计:小型电影院的空间相对较小,因此应注重紧凑的空间设计,避免浪费空间。
可采用弯曲座椅或圆形座椅等设计,提高观众的观影体验。
3.通道设计:为了方便观众进出电影院,通道的设计应宽敞且合理,以避免拥挤和堵塞。
二、影院设备1.声音设备:小型电影院的声音设备应具备良好的音质和高保真度,并且能够提供适当的音量。
建议采用环绕声系统,以提升观众的听觉体验。
2.屏幕设备:屏幕的质量对于观影效果有着重要的影响。
应选择适合小型电影院的高清晰度屏幕,并确保投影质量清晰、亮度适中。
3.观众席设备:观众席座椅的设计应符合人体工程学原理,提供舒适的观影体验。
座椅的角度、高度和宽度等参数应根据人体工程学数据进行合理调整,同时考虑到通道的宽度和配置。
三、舒适度1.空调设备:小型电影院的空调设备应具备较大的制冷和制热能力,以便适应不同季节的需求。
同时,应考虑到座位与通道的通风情况,保持影院内的舒适温度。
2.灯光设计:观影时,灯光应能提供适宜的亮度,既能照亮观众席,又不影响屏幕的观看效果。
在开场前和结束后的时间段,可以通过控制灯光亮度和颜色来提升观众的观影体验。
3.降噪设备:小型电影院周围可能存在各种噪音干扰,如交通噪音、外部设备噪音等。
为了提供良好的观影环境,建议采用降噪设备,降低外界噪音的影响。
四、安全性1.疏散通道:小型电影院应设置合理的疏散通道,确保观众在紧急情况下能够迅速安全地离开电影院。
影院座位间距标准

影院座位间距标准
影院座位间距标准因国家和地区的建筑规范和标准不同而有所差异。
但一般来说,以下是一些常见的规范:
1.中国大陆:根据《公共建筑设计标准》规定,影院座位排距宽度不小于1.2米,排距长度不小于1米,排数不宜超过10排,每排座位数不宜超过18座。
2.香港:排距宽度不小于1.08米,每排不宜超过14座,每个座位与楼梯之间的距离不小于1米。
3.日本:排距宽度不小于1.1米,每排座位数不宜超过14座,每个座位与楼梯之间的距离不小于0.7米。
4.美国:排距宽度不小于2.5英尺(约0.76米),每排不宜超过20座,每个座位与楼梯之间的距离不小于1英尺(约0.3米)。
需要提醒的是,以上规范只是参考标准,不同影院的具体间距可能会有所不同。
影院设计规范

影院设计规范影院设计规范是指在建筑设计过程中,针对影院的特殊需求和特点制定的一系列规范和标准。
下面是一份关于影院设计规范的草稿,仅供参考。
1. 影院布局:影院应按照观众的视野和舒适度进行布局。
大多数影院采用倾斜式座椅布局,使每个座位都有较好的视野和观看体验。
此外,还应设立轮椅、残疾人专用座椅,并设置便利设施。
2. 屏幕大小:影院屏幕大小应根据影院内部空间尺寸和座位数量进行合理设置。
较大的屏幕能够提供更好的观看效果,但也需要考虑到观众距离屏幕的距离,以确保观影舒适度。
根据常见标准,屏幕高度应占据影院高度的1/3至1/2之间。
3. 音响系统:影院音响系统是影院设计中的重要组成部分。
音响系统应具备高保真度、高分辨率和均衡的声音分配,以提供观众沉浸式的视听体验。
同时,应确保音响系统能够在大音量和小音量情况下都有良好的表现。
4. 灯光设计:灯光设计对影院氛围的营造和观影体验起着重要作用。
应根据不同场景和需要,设计合适的灯光效果。
例如,在电影开始前和结束后,可以使用柔和的灯光;而在电影播放期间,应保持暗淡的照明,以增强观众对电影的投入感。
5. 空调系统:影院内应安装高效的空调系统,以确保观众在观影过程中的舒适度。
空调温度和湿度应能够适应观众的需求,并考虑到影院内人员密集导致的热量和湿气增加。
6. 座位布局:影院座位布局应合理,以提供观众最佳的观影体验。
座椅的高度、宽度和靠背角度都应符合人体工程学标准,以保证观众的舒适度。
同时,要提供足够的脚部空间,以便观众在观影过程中调整姿势。
7. 紧急出口和安全设施:影院需要设置多个紧急出口,以便观众在紧急情况下迅速疏散。
此外,还应配备自动喷水灭火系统、疏散指示标志等安全设施,以确保观众的安全。
8. 听力辅助设备:应为听力有障碍的观众提供听力辅助设备,如无线听力辅助系统和耳麦等。
同时,应设立听力辅助设备位置,并提供指引和服务。
9. 售票和排队区域:影院的售票和排队区域应设计合理,以提供良好的观众服务。
影院座位设计范文

影院座位设计范文现代影院座位设计,是为了能够给观众带来更加舒适的观影体验。
座位设计不仅要考虑观众的舒适性,还需要考虑到观众的视线和声音等因素。
首先,座位的舒适性是最基本的要求。
座位设计应该考虑到人的体型和姿势,使观众在长时间的观影过程中感到舒适。
座位的宽度和深度应适中,以使观众能够有足够的空间坐下和伸展双腿。
座位的背部设计应符合人体工学原理,使观众的背部得到一定的支撑,以减轻身体的压力和疲劳感。
其次,座位的视线设计也非常重要。
观众在观影时,希望能够有一个清晰且不受遮挡的视线。
为此,座位的高度和角度应设计得合理,以保证观众能够看到屏幕上的内容。
座位和座位之间的距离也要考虑到观众之间的视野干扰问题,应尽量避免相互之间的遮挡。
此外,影院座位的声音设计也不容忽视。
影院一般都会配备环绕声音系统,为观众带来身临其境的音效体验。
座位的设计应该考虑到声音传递的问题,以保证观众能够充分地感受到影片的音效效果。
座位和座位之间的间距和高度应该经过精确的计算,以使声音能够均匀地传播到观众每个位置。
随着科技的进步和观影需求的不断提升,现代影院座位设计也在不断创新。
一些高端影院开始采用豪华电动座椅,观众可以通过调整座位的角度和高度,来获得更加舒适的观影体验。
还有一些影院开始引入智能化座位,观众可以通过手机App来预定座位、调整座椅位置和享受个性化的服务。
这些创新不仅提高了观众的观影体验,也使影院座位成为了一种豪华和时尚的象征。
总的来说,现代影院座位设计是一个综合性的工程,需要考虑到观众的舒适性、视线和声音等因素。
随着科技的发展,影院座位设计也在不断创新,为观众提供更加舒适和个性化的观影体验。
影院座位作为观众与电影之间的连接点,对于观影体验的影响不可小觑,因此,对于影院座位的设计,应该给予足够的重视和关注。
影院座位设计的优化模型

参 考 文 献: [ 1 】周人 忠 . 电影 院建 筑设 计 [ . 京 : 国建 筑 工 业 出 M】 北 中
5 { t ( ̄ . ( )<a 3) no
t =( L —d t ( )+C ) nO a
如图 1
,
( +h > 时为正 ) £
收稿 日期 :0 00 1 2 1.3 9
—
霎 漱
川 拱… … ~ ; 姬
38 6 因此 , 可得 目标 函数 :
( : )
四川理 工 学 院学报 ( 自然科 学版 )
=
21 0 0年 6月
2 .4 9 , 时 =6 9 即最佳 位 置在 中央 一 列 67 2 。 此 . m,
约束 条 件 : 影 院 中每排 据屏 幕 的距 离 可 表示 为 :
=
看电影 的效果都会略有下降 , 出现这一结果的原因主要
是 因 为 在 前 面 3排 时 , 然 视 角 比较 大 , 仰 角也 比较 虽 但 大 并且 还 超过 了 3 。 而 在后 面 几排 , 然 仰 角 较 小 , 0, 虽 但 视 角也 很 小 , 因此效 果也 不 是 很 好 。所 以这 一 结 果对 整
体 效果 来 说是 非 常 合 理 的。 此 模 型 还 可 以 用 于 大 型 场
d+0 8 n一1 n ∈ Z .( )( 且 ≤ n≤ m)
其 中: 表示观众眼睛到水平 面的距离 , 表示影 院中座 n
位 的排 数 。
对 于 这个 多 目标 问 题 , “ 目标优 化 法 ” 用 主 对模 型进
行求解 。进一步分析 , 人们看 电影 时 , 角大时能达 到 视
更 好 的观 看 效 果 , 通 过 调 整 颈 部 的 扭 转 角 度 , 而 只要 角
影院影厅设计技术参数要求

影院影厅设计技术参数要求影院影厅设计技术参数要求是指影院在设计和建设过程中,对影厅设备、音效、画面等方面的要求。
这些参数要求的目的是为了创造一个能够提供优质观影体验的环境,使观众能够享受到高品质的音画效果。
下面是一些常见的影院影厅设计技术参数要求。
1.影院座位布局:影院的座位布局应该合理,座位之间的间距要适中,以保证观众的观影舒适度,同时要满足消防安全的要求。
2.屏幕尺寸和位置:屏幕是影院影厅的核心装备,其尺寸和位置对影院的观影效果至关重要。
一般来说,屏幕尺寸与观众距离之比应保持在1:6到1:8之间,以保证观众可以充分享受到大屏幕的视觉冲击力。
3.投影仪和放映设备:好的投影仪和放映设备是保证影院画面清晰度和色彩还原度的关键。
投影仪的分辨率应不低于2K,为了满足未来4K和8K等高清画质的发展,最好选择支持4K或以上分辨率的投影仪。
4.音效系统:影院的音效系统应该具备高保真度和立体声效果,以提供更加逼真的声音享受。
一般来说,影院应配备杜比全景声系统或者类似的音效系统,以提供环绕立体声效果。
5.灯光设计:影院的灯光设计需要考虑观影过程中的环境舒适度和效果呈现。
一般来说,在观影过程中,灯光应该保持较暗的状态,以减少观众的视觉干扰,同时保持一定的照明度,以方便观众进出影厅。
6.空调和通风系统:影院影厅通常会因为人员密集和长时间封闭而产生较高的温度和湿度,因此需要配备良好的空调和通风系统,以确保观众在观影过程中的舒适度。
7.声学设计:影院的声学设计非常重要,它关系到声音在影厅内的传播和反射,直接影响观众听觉体验的质量。
影院应该采用吸音材料和隔音设计,以减少外界噪音的干扰,并提升声音的清晰度和环绕感。
8.观众入口和出口:影院的观众入口和出口设计要合理,确保观众能够方便进出影厅,并满足消防安全的要求。
以上是影院影厅设计技术参数要求的一些主要内容。
这些参数要求在影院的设计和建设中都应该得到充分考虑和满足,以创造一个能够提供高品质观影体验的环境。
影院装修设计方案

影院装修设计方案1. 背景介绍电影院作为一种娱乐休闲场所,其装修设计直接影响着观众的舒适感和审美体验。
一套合理且创新的装修设计方案不仅能够提升观影效果,还能增加影院的吸引力和竞争力。
本文将针对影院装修设计提出一套方案,旨在营造舒适的观影环境和独特的视觉感受。
2. 空间布局影院的空间布局是影响观影体验的重要因素之一。
为了营造更佳的观影效果,我们建议采取以下布局方案:•座位布置:采用倾斜式座椅布置,使每个座位都有良好的视野,并提供足够的腿部空间。
座位之间的间距要合理,以确保观众的舒适度和隐私性。
•走道设计:合理规划走道的位置和宽度,确保观众进出影院和观影过程中的便利性。
•大荧幕位置:将大荧幕放置在影院的正中央,这样观众无论坐在哪个位置都可以有良好的视觉体验。
3. 灯光设计灯光设计可以为影院增添独特的氛围和观影体验。
以下是一些建议的灯光设计方案:•入口灯光:通过设计独特的入口灯光,营造观众进入影院的仪式感,使用柔和的照明,让观众感到舒适和欢迎。
•观影区灯光:在影院的观影区域使用柔和的照明,避免过亮或过暗的灯光,以提供舒适的观影环境。
可以考虑设置可调节灯光,使观影过程中的光线适应不同电影场景的需要。
•阶梯灯光:在阶梯或走道上设置合适的灯光,既可以提供照明功能,又可以增加空间层次感和视觉效果。
注意避免灯光过亮,以免影响观影体验。
4. 声音设计影院的声音设计直接关系到观众对电影剧情的理解和感受。
以下是一些建议的声音设计方案:•声音系统:采用先进的音响系统,确保声音的清晰度和立体感,并使观众能够沉浸在影片的音效中。
•音量控制:设置合适的音量控制系统,使观影时的音量适应电影的剧情需求,避免音量过高或过低对观影体验的影响。
•隔音设计:对影院进行隔音处理,减少室内外噪音对观影体验的干扰,提供良好的声音环境。
5. 装饰设计装饰设计是影院装修的重要组成部分,能够给观众带来独特的视觉感受和观影体验。
以下是一些建议的装饰设计方案:•色彩搭配:选用适合的色彩搭配方案,营造出舒适和谐的氛围。
小型影院设计方案

小型影院设计方案小型影院设计方案建议:1. 座席布局- 影院座位数量应根据场地的大小和容纳人数来确定,一般可考虑每排5-8个座位,每排座位之间应有足够的间距。
- 座椅设计应舒适,选择柔软的座椅材料,并考虑到使用者的身体和腿部支持,提供合适的靠背和靠头。
- 座位之间应设置足够的过道,方便观众进出。
- 对于VIP座位区域,可以考虑使用更豪华舒适的座椅,并额外提供更宽敞的腿部空间。
2. 屏幕和音响系统- 选用高品质的屏幕和投影设备,确保观众可以享受到清晰、逼真的影像效果。
- 音响系统应考虑到空间大小和声场效果,选择合适的声音分布和音箱布局,以提供立体感和沉浸感的音响体验。
- 为了确保音响效果的最佳表现,可以在影院内部进行声学调整和吸音处理,减少音频回声和杂音。
3. 灯光和环境氛围- 影院设计应注重舒适和温馨的环境氛围,利用柔和的灯光和适当的装饰元素,营造出放松和享受电影的氛围。
- 可以使用LED灯带或灯光控制系统,根据不同影片的场景和情节,调整灯光的颜色和亮度,增加观影的感官体验。
4. 声光控制系统- 建议使用智能化的声光控制系统,可根据观影需求调整音频和灯光效果。
- 室内温度和湿度控制也非常重要,为观众提供适宜的观影环境。
5. 进场和票务系统- 影院应配备快速、高效的进场和票务系统,便于观众购票、选座和入场。
- 可考虑使用电子票务系统和自助售票机,提高观影的便利性和效率。
6. 后勤和维护设施- 影院应设置食品饮料区,提供各种小吃和饮品,为观众提供更好的观影体验。
- 应配备洗手间和婴儿换洗室等基本设施,提供便利的生活条件。
- 影院设施需要定期检查和维护,确保设备的正常运转和观影环境的良好状态。
7. 环保和安全措施- 影院设计应符合环保要求,选择节能设备和材料,减少能源消耗和环境污染。
- 应配备适当的消防系统和紧急疏散通道,确保观众的安全。
通过以上设计方案,希望能够为小型影院的建设提供参考和指导,营造出一流的观影体验,吸引更多观众前来观影。
imax影院坐第几排好

IMAX影院坐第几排好IMAX影院作为一种高端的电影观赏技术,给观众带来了超凡的视听体验。
但是,在IMAX影院中,选择一个好的座位位置对于观影体验至关重要。
很多人不知道在IMAX影院中坐哪一排比较好,下面我将根据自己的经验和一些专业知识,给大家提供一些建议。
1. 排数和观影体验的关系IMAX影院座位通常分为多个排数,一般从前往后递增,排数越靠前,离屏幕越近。
对于IMAX影院而言,坐在较前排可以给观众带来更加震撼的视觉效果。
离屏幕越近,屏幕所呈现的画面尺寸越大,效果也就越好。
但是,这样也可能会带来一些问题。
比如,坐在太靠前的位置容易导致观影时颈椎不适或者眼睛疲劳。
作为观众,我们的目标是找到一个既能让我们享受到IMAX影院的震撼效果,又能保护我们的身体健康的位置。
下面我将给大家介绍一些建议。
2. 中间位置是首选在IMAX影院中,中间位置是观影体验最好的选择。
这个位置可以保证观众能够获得最佳的观影角度和视野,感受到最强烈的沉浸感。
一般而言,排数越中间,观影效果越佳。
当然,如果是IMAX影院的后排,也可以选择靠中间位置,因为屏幕较大,观影效果也比较好。
但是,如果是前排的话,还是建议选择靠近中间的位置。
3. 避免靠近屏幕的位置尽管坐在前排可以获得更大的屏幕尺寸,但是靠近屏幕的位置并不是最好的选择。
靠近屏幕会导致观影时眼睛需要转动更大的角度,容易导致视觉疲劳。
同时,这个位置的观影角度也相对较大,可能会对观影体验产生一些负面影响。
因此,建议大家在选择座位时尽量避免靠近屏幕的位置,以免影响观影效果和身体健康。
4. 尝试斜坐位置IMAX影院的座位通常是沿着电影放映的屏幕弧线排列的。
这样设计的目的是为了使观众能够获得更好的观影效果。
因此,如果你坐在了屏幕两侧的座位上,可能会感觉到屏幕的失真或者画面有些扭曲的感觉。
为了避免这种情况,建议大家尝试一下斜坐的位置,这样可以获得更好的观影效果。
5. 考虑安全距离在挑选IMAX影院的座位时,除了以上给出的观影角度和视野因素外,还应该考虑安全距离。
影院座位设计优化模型

下图为影院的剖面示意图,座位的满意程度主要取决于视角α和仰角β。
视角α是观众眼睛到屏幕上、下边缘视线的夹角,α越大越好;仰角β是观众眼睛到屏幕上边缘视线与水平线的夹角,β如果太大会使人的头部过分上仰,引起不舒适感,一般要求β不超过30︒。
(1) 地板线倾角θ=10︒,问最佳座位在什么地方。
(2) 求地板线倾角θ(一般不超过20︒),使所有观众的平均满意程度最大。
(3) 地板线设计成什么形状可以进一步提高观众的满意程度。
吕华军陈霞曹智芳摘要:本文针对影院座位设计问题,利用三角形正切,建立了视角α与仰角β关于地板线倾角θ的数学模型。
并通过Matlab、Lingo、VB等软件,利用求极值的方法解答了问题一,得当倾角θ为10︒时,最佳座位在(6.228,1.4)处。
对于问题二,我们通过泛函分析等方法,将座位分成n排,得出排与排之间的距离是14.5/n,对每排观众的视角α和仰角β进行求和,得出视角α和仰角β的平均值,从而取得平均满意度,再通过求极值的方法算出当θ为15.14︒时,观众的平均满意度最大。
此外,在β角不超过30︒的前提下我们还对地板线的设计进行改进(将第一排座位抬高),通过方程组(7)的解答,可得到最佳的地板线设计,进一步提高观众的满意度。
我们还对模型进行了误差分析,若n越大,模型的精确度就越高。
关键词:座位设计仰角视角平均满意度一、问题的重述下图为影院的剖面示意图,座位的满意程度主要取决于视角α和仰角β。
视角α是观众眼睛到屏幕上、下边缘视线的夹角,α越大越好;仰角β是观众眼睛到屏幕上边缘视线与水平线的夹角,β如果太大会使人的头部过分上仰,引起不舒适感,一般要求β不超过30︒。
(1) 地板线倾角θ=10︒,问最佳座位在什么地方。
(2) 求地板线倾角θ(一般不超过20︒),使所有观众的平均满意程度最大。
(3) 地板线设计成什么形状可以进一步提高观众的满意程度。
二、模型假设1、假设观众的座高是一致的;2、影院排与排之间的距离相等;3、观众的平均满意度只取决于视角α和仰角β,其他因素忽略不计;4、假设屏幕的长度与座位的排长相等;5、把观众的眼睛看作一个点。
影院设计方案

影院设计方案话说前阵子我去看了一场电影,那体验真是一言难尽。
座位不舒服,音响效果也差强人意,整个影厅的设计感觉就是凑合事儿。
这让我深深意识到,一个好的影院设计是多么重要!咱们先来聊聊影厅的布局。
座位的安排可不能马虎,得根据人体工程学来,保证观众无论坐在哪个位置,都能有舒适的观影角度,不会被前面的人挡住视线。
比如说,每一排座位的高度差要恰到好处,不能让后排的观众只能看到前排人的后脑勺。
我就记得有一次看电影,因为座位安排不合理,我全程歪着脖子,那叫一个难受!然后是屏幕。
屏幕的大小和位置得精心设计,要让整个影厅的观众都能感受到最佳的视觉效果。
大屏幕固然震撼,但要是比例不协调,画面变形,那可就糟糕了。
还有屏幕的亮度和对比度也得调好,不能太亮刺眼,也不能太暗看不清。
音响系统也不能忽视。
环绕音响要分布均匀,让观众感觉声音是从四面八方传来的,就像真的置身于电影场景之中。
记得有一回看一部动作片,音响效果不好,打斗场面的声音都糊成一团,完全没有那种紧张刺激的感觉。
再来说说灯光。
开场前和散场时的灯光要明亮但不刺眼,方便观众找到座位和离场。
而在观影过程中,过道的灯光要足够微弱,不能影响观众的观影体验。
还有装修风格。
影院可以根据不同的影片类型打造不同的主题风格,比如科幻片可以是充满未来感的,爱情片可以是温馨浪漫的。
这样能让观众在走进影厅的那一刻,就仿佛走进了电影的世界。
通风系统也很关键。
影厅里人多,空气不流通可不行。
得保证有良好的新风系统,让观众在观影过程中能呼吸到新鲜的空气,不然闷得慌,哪还有心思好好看电影。
另外,影厅的出入口要设计得合理,不能造成拥堵。
厕所的位置也要方便,不能让观众为了上个厕所跑大老远。
总之,一个好的影院设计要考虑到方方面面的细节,从观众的舒适度到观影的效果,每一个环节都不能马虎。
只有这样,才能让观众真正享受到一场精彩的电影之旅,而不是被各种糟糕的设计影响心情。
希望未来的影院都能用心做好设计,让我们能开开心心地看电影!。
大班科学《电影院里的座位》教案

一、教学目标1. 让幼儿了解电影院的座位分布和排列规律。
2. 培养幼儿的观察力、空间感知能力和逻辑思维能力。
3. 引导幼儿学会合作、交流和分享,提高团队意识。
二、教学重点与难点重点:认识电影院的座位分布和排列规律。
难点:能够独立观察并描述电影院的座位分布特点。
三、教学准备1. 教具:电影院座位图、座位模型、指示牌等。
2. 学具:每人一份座位图、铅笔、彩笔等。
3. 环境:安静、舒适的学习氛围。
四、教学过程1. 导入:教师出示电影院座位图,引发幼儿兴趣,引导幼儿观察座位图。
2. 新课导入:介绍电影院的座位分布和排列规律。
3. 操作活动:a. 教师分发座位图和学具,引导幼儿独立观察座位图,找出座位排列的规律。
b. 幼儿相互交流自己的发现,教师巡回指导。
c. 教师组织幼儿进行小组讨论,总结座位排列的规律。
4. 实践活动:a. 教师出示座位模型,引导幼儿根据座位排列规律,尝试摆放指示牌。
b. 幼儿动手操作,教师巡回指导。
c. 幼儿展示自己的成果,教师评价、总结。
5. 巩固练习:a. 教师出示不同类型的电影院座位图,引导幼儿独立观察并描述座位排列的规律。
b. 幼儿相互交流自己的答案,教师巡回指导。
c. 教师组织幼儿进行小组讨论,总结座位排列的规律。
6. 总结与反思:教师引导幼儿总结本节课所学内容,让幼儿分享自己的收获。
五、教学评价1. 观察幼儿在实践活动中的表现,评价幼儿对电影院座位排列规律的掌握程度。
2. 关注幼儿在小组讨论中的参与程度,评价幼儿的合作和交流能力。
3. 收集幼儿的作业作品,评价幼儿在课堂学习中的动手操作能力。
六、教学延伸活动1. 家园共育:教师与家长沟通,让家长了解幼儿园的教学内容,鼓励家长在家中与孩子一起观察家庭影院或客厅的座位分布,并尝试绘制座位图。
2. 区域活动:在角色区设置电影院场景,让幼儿扮演电影院工作人员,引导幼儿运用所学知识为顾客指路、安排座位。
七、教学反思1. 教师在课后对自己的教学过程进行反思,分析教学目标的达成情况,思考如何改进教学方法,提高教学效果。
数学建模综合题影院座位设计问题概要

数学模型张峰华材料学院材料成型及控制工程04班20123631 刘泽材料学院材料成型及控制工程04班20123627 杨海鹏材料学院冶金工程03班20123203一、问题重述影院座位的满意程度主要取决于视角α和仰角β,视角是观众眼睛到屏幕上下边缘的视线的夹角,越大越好;仰角是观众眼睛到屏幕上边缘视线与水平线的夹角,太大使人的头部过分上仰,引起不适,一般要求仰角β不超过030;记影院的屏幕高为h ,上边缘距离地面高为H ,影院的地板线通常与水平线有一个倾角θ,第一排和最后一排与屏幕水平距离分别为,d D ,观众的平均座高为c (指眼睛到地面的距离),已知参数h =1.8. H =5, 4.5,19d D ==,c =1.1(单位m)。
求解以下问题:(1) 地板线的倾角010=θ时,求最佳座位的所在位置。
(2) 地板线的倾角θ一般超过020,求使所有观众的平均满意程度最大时的地板线倾角。
二、问题的分析电影院座位的设计应满足什么要求,是一个非常现实的问题。
根据题意观众对座位的满意程度主要取决于观看时的视角α和仰角β,α越大越好,而β越小越好,最佳位置就是要在这两者之间找到一个契合点,使观众对两者的综合满意程度达到最大。
本文通过对水平视角α和仰角β取权重,建立适当的坐标系,从而建立一个线形型满意度函数。
针对问题一,已知地板线倾角,求最佳座位所在,即将问题转化求综合满意度函数的最大值,建立离散加权的函数模型并利用Matlab 数学软件运算求解;针对问题二,将所有观众视为离散的点,要使所有观众的平均满意程度达到最大,即将问题转化求满意度函数平均值的最大值。
对此利用问题一所建立的满意度函数,将自变量转化为地板线倾角;在问题二的基础上对地板线形状进行优化设计,使观众的平均满意程度可以进一步提高。
本文在满意度呈线性的基础上来建立模型的,为使模型简化,更好地说明问题,文中将作以下假设。
三、模型假设1.忽略因视力或其他方面因素影响观众的满意度;2.观众对座位的仰角的满意程度呈线性;3.观众对座位的水平视角的满意程度呈线性;4.最后排座位的最高点不超过屏幕的上边缘;5.相邻两排座位间的间距相等,取为0.8m ;6.对于同一排座位,观众的满意程度相同;7.所有观众的座位等高为平均座高;8.影院的的地板成阶梯状。
电影院选座那个位置最好

电影院选座那个位置最好
去电影院看电影时坐什么位置最好?这里面也有不少讲究,为了更好地获得视觉和听觉享受,去影院看电影一定要选好位置。
电影院选座那个位置最好?就让的根据计算,观众水平方向上的视角(也就是屏幕两侧的视线方向夹角)至少要为36°。
其次,要避免颈部疲劳。
到荧幕顶端的视线与水平面呈的角度必须要小于35°。
最后,要避免回声干扰。
一般来说,一个影厅有6组音响。
三组在银幕的后面,分别为左路、中路、右路;一组低音喇叭在银幕下方,还有两个环境声分别在影厅两侧。
“声像不同步,声音传输需要一定时间,如果影厅太大,这个现象就会体现得比较明显,糟糕的效果如同是在看模糊的枪版电影。
”由于中间的座位受回声影响最弱,听觉效果会比较好。
小厅(如10-15排)5 6排最佳
中厅(如16-20排)7 8排最佳
大厅(如21-25排)9 10排位置最佳
其原理是荧幕宽度的2-3倍,太靠前感觉荧幕会变形,且视角比较疲劳;太靠后光线有些暗,音响效果也会减弱。
同时,中间两侧10个左右的位置均效果不错。
但有些设计较好的影院,坐哪都差不多,比如座位下有独立音响的,双放映机甚至多放映机播放的,这时候凭爱好选择即可。
以上就是为您提供了关于电影院选座那个位置最好的解答,真心希望对您有所帮助!您要了解更多关于电影院最佳位置,电影院座椅该如何正确保养及影院安全知识等相关内容请您多多关注吧!。
影院设计规范范文

影院设计规范范文影院作为一个集观影、娱乐、休闲为一体的综合性场所,在设计上既要满足观影者的需求,又要考虑到工程的实施、运营和管理方面的要求。
因此,影院设计规范是非常重要的,下面将从空间布局、座位设计、音响设备和灯光设计等方面详细介绍。
一、空间布局1.观众安全:设计应保证观众的安全,包括应设置足够数量的安全出口和疏散通道,确保在紧急情况下观众能够迅速有效地离开影院。
2.舒适度:观众在影院中观影的时间一般较长,因此座椅和走道的设计应考虑到观众的舒适度,如座椅宽敞舒适、视线良好、走道宽阔等。
3.视觉效果:影院设计应注重观影效果,包括选择合适的屏幕尺寸和高度、安排观众席的观看角度、减少光线干扰等。
4.影音隔离:应对音响设备和放映机进行隔离,以减少噪音对观众的干扰。
二、座椅设计1.座位间距:座位之间应保留足够的间距,以确保观众能够自如地出入座椅,并避免头部和膝盖间的碰撞。
2.坐姿舒适度:座椅设计应考虑到观众的舒适度,包括座位的宽度、角度、颈椎和腰椎的支撑等。
3.观看角度:座位的高低应适当调整,以保证观众能够有良好的视觉效果,避免因身高差异而影响观影体验。
4.优先座位:应设立优先座位,以方便老年人、残障人士等特殊观众就坐。
三、音响设备1.声场设计:影院的音响系统应能提供清晰逼真的声音效果,包括平衡的音量、立体的声场和清晰的对话声。
2.设备布置:音响设备应根据影院的实际情况进行合理布置,以保证音响效果的最佳体验。
3.声音控制:应设置合适的声音限制,确保影院内的声音不超过观众可以接受的范围。
4.音响维护:应定期对音响设备进行维护和保养,以确保设备的正常运行和持久使用。
四、灯光设计1.舞台照明:灯光设计应满足影片放映和表演的需求,包括背景灯、特效灯、聚光灯等。
2.观众照明:观众席的照明应舒适柔和,既能满足观众的需求,又不影响观看屏幕的效果。
3.紧急疏散照明:应设置紧急疏散照明装置,以确保在紧急情况下观众能够迅速有效地离开影院。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
影院座位设计
摘要
本文研究了电影院座位设计问题,由于座位的满意程度主要取决于视角α和仰角β,我们建立了满意程度的数学模型,并进行最优求解。
问题一,首先利用了加权平均数建立满意度随座位与屏幕距离的变化而变化的模型,并利用matlab软件对该函数进行分析,结果当座位在最后一排时,观众的满意度最大。
问题二,在问题一的模型的基础上,将θ角也定为变量,建立满意程度随座位与屏幕距离和θ角的变化而变化的模型,再对变量x求相应区间的定积分,从而可以得到平均满意度随θ角变化的模型,再用matlab软件分析模型,求得当θ=20︒时,平均满意度最大。
关键词:加权平均数满意度函数定积分
一、问题重述
影院座位的满意程度主要取决于视角α和仰角β。
视角α是观众眼睛到屏幕上、下边缘视线的夹角,α越大越好;仰角β是观众眼睛到屏幕上边缘视线与水平线的夹角,β太大是人的头部过分上仰,引起不舒适感,一般要求β不超过30︒.
记影院屏幕高h,上边缘距地面高H,地板线倾角θ,第一排和最后一排座位与屏幕水平距离分别为d和D,观众平均坐高为c(指眼睛到地面的距离)。
已知参数h=1.8m,H=5m,D=19m,c=1.1m。
1)地板线倾角θ=10︒,问最佳作为在什么地方?
2)求地板线倾角θ(一般不超过20︒),使所有观众平均满意
度最大。
二、问题的分析
根据观众对座位的满意程度主要取决于观看时的视角α和仰角β,α越大越好,β越小越好,最佳位置β就是在这两者之间找一个平衡点,使观众的综合满意度最大。
既然β>30︒不可避免,那么在建立模型时,必须将α与β同时考虑。
于是本文通过对α与β分别设立权重,建立适当的坐标系,从而形成一个线性的满意度函数。
对于问题一,已知地板线倾角,求最佳座位所在,即将问题转化为求综合满意度函数的最大值,用matlab软件做出综合满意度图像,在进行求解。
对于第二问,将所有的座位想像为一个个连续的点,此时,综合满意度为关于x与θ的二元函数,先对x求所在区间的积分,从而求
出其在所有位置上的平均满意度,再利用matlab做出平均满意度关于θ的函数的图形,从而可进行直观求解。
三、模型假设
1.忽略因视力或其他方面因素影响观众的满意度;
2.观众对座位的仰角的正切值的满意程度呈线性;
3.观众对座位的水平视角的正切值呈线性;
4.所有的观众的座位等高,且为平均坐高。
四、符号说明
α视角
β仰角
θ地板线与水平线的倾角
D 最后一排离屏幕的水平距离
d 第一排离屏幕的水平距离
h 屏幕的高度
H 屏幕上边缘离地面的高度
Pα主观给定α的权重
Pβ主观给定β的权重
五、模型的建立
1、问题一
以第一排观众的眼睛为原点,建立直角坐标系如图1所示:
图1
其中,AB为屏幕,MS为地板线,OE为所有的观众的眼睛所在的直线。
则由图可设视觉线OE上任意一点P的坐标为(x,xtan ),屏幕上下点的坐标分别为A(-d,H-c),B(-d,H-h-c),PA的斜率记为k PA,PB的斜率记为k PB。
则直线PA与PB的斜率分别为
k PA=xtanθ−H+c
x+d
k PB=xtanθ−H+ℎ+c
x+d
则
tanα=k PB−k PA 1+k PA k PB
=
ℎ(x+d)
(x+d)2+(xtanθ−H+c)(xtanθ−H+ℎ+c) tanβ=−k PA=
H−c−xtanθ
x+d
而
A
tan(30°−β)=tan30°−tanβ1+tan30°tanβ
由我们假设的模型可知,满意度S的表达式为:
S=Pαtanα+Pβtan(30°−β)
这里主观设定Pα=Pβ=0.5,再对S关于x的函数分析可得到其在其定义域上的最大值,即所求。
2、问题二
如上文建立坐标系,将θ角设为变量,可得此时满意度
S1=Pαtanα+Pβtan(30°−β)
再对S1求其x∈[0,D-d]上的定积分得到总的观众满意度,再除以D-d 得到平均满意度S2,即:
S2=∫S1dx D−d
D−d
则得到的S2是关于θ的函数,再对该函数进行分析,得到最大值及满足条件的θ。
六、模型求解
1、问题一
运用matlab软件对上面的S函数作图(见附录二),如图2所示:
图2
由上图知,当x=D-d=14.5时,观众的满意度最大,即对于我们所建立的模型,最后一排的满意度最大。
2、问题二
运用matlab软件求出上述S2函数,在对S2作图(见附录三),如图3所示:
图3
由图可知,观众的平均满意度S2随θ增大而增大,故当θ=20︒时,观众的平均满意度最大。
七、附录
附录一参考资料
1、郑阿奇曹弋《MATLAB实用教程》(第三版)
2、王正林刘明《精通MATLAB》(升级版)
3、吴礼斌闫云侠《经济数学与建模》
附录二问题一的matlab语言
x=0:0.05:14.5;
y1=(1.8*(x+4.5))./((x+4.5).^2-(x*tan(pi/18)-5+1.1).*(x*tan(pi/18)-5+1 .8+1.1));
y2=(5-1.1-x*tan(pi/18))./(x+4.5);
y3=(tan(pi/6)-(5-1.1-x*tan(pi/18))./(x+4.5))./(1+tan(pi/6)*(5-1.1-x*t an(pi/18))./(x+4.5));
y=0.5*y1+0.5*y3;
plot(x,y)
附录三问题二的matlab语言
x=linspace(0,14.5,300);
t=linspace(0,pi/9,300);
y1=(1.8*(x+4.5))./((x+4.5).^2-(x.*tan(t)-5+1.1).*(x.*tan(t)-5+1.8+1.1 ));
y2=(5-1.1-x.*tan(t))./(x+4.5);
y3=(tan(pi/6)-y2)./(1-tan(pi/6)*y2);
y=0.5*y1+0.5*y3;
Y=sym(y);
ya=int(Y,'x');
ya=int(Y,'x','0','14.5');
ya=double(ya);
yb=ya./14.5;
plot(t,yb)。
