傅里叶(Fourier)级数的指数形式与傅里叶变换
傅里叶级数与傅里叶变换

傅里叶级数与傅里叶变换傅里叶级数和傅里叶变换是现代数学以及工程学领域中非常重要的概念。
它们广泛应用于信号处理、图像处理、通信系统、电子电路等方面。
本文将介绍傅里叶级数和傅里叶变换的基本概念、原理和应用。
一、傅里叶级数傅里叶级数是一种用正弦函数和余弦函数的线性组合来表示周期函数的方法。
对于任意周期为T的函数f(t),其傅里叶级数表示为:f(t) = a0 + Σ(an*cos(nωt) + bn*sin(nωt))其中,a0为零频率分量的系数,an和bn为一系列傅里叶系数,n为正整数,ω=2π/T为基本频率。
傅里叶级数展开式中的每一项都代表了函数f(t)中具有不同频率的分量。
通过计算适当的系数an和bn,我们可以将任意周期函数表示为一系列正弦和余弦函数的线性组合。
这使得我们能够分析、合成和处理不同频率的信号。
二、傅里叶变换傅里叶变换是将一个时域函数转换为频域函数的过程。
对于非周期函数f(t),它的傅里叶变换表示为:F(ω) = ∫[f(t)e^(-jωt)]dt其中,F(ω)为频域函数,ω为连续频率参数,e为自然对数的底,j为虚数单位。
傅里叶变换将时域函数转换为频域函数,可以帮助我们理解和分析信号在不同频率上的能量分布。
频域函数F(ω)表示了原始信号中不同频率的幅度和相位信息。
通过傅里叶变换,我们可以在频域对信号进行滤波、调制、解调等操作,从而实现对信号的处理和传输。
三、傅里叶级数与傅里叶变换的关系傅里叶级数和傅里叶变换在数学上是相互关联的。
傅里叶级数是对周期函数进行频谱分析的方法,而傅里叶变换则适用于各种非周期信号的频谱分析。
当周期T趋于无穷大时,傅里叶级数就变成了傅里叶变换的极限形式。
傅里叶变换可以看作是傅里叶级数的一个推广,将其应用于非周期信号的频谱分析。
四、傅里叶级数与傅里叶变换的应用傅里叶级数和傅里叶变换在信号处理和通信领域有着广泛的应用。
以下是一些典型的应用场景:1. 信号滤波:通过傅里叶变换,我们可以在频域对信号进行滤波操作,以去除不需要的频率成分或者保留感兴趣的频率成分。
第一节傅立叶级数与傅里叶积分

理意义(从频谱的角度来描述函数的特征),
因而在许多领域被广泛地应用.离散和快速
Fourier变换在计算机时代更是特别重要.
Fourier 变换是在周期函数的 Fourier
6. 离散频谱与频谱图 a n jbn a0 a n jbn , , c n 分析 由 c0 , cn 2 2 2
An 1 2 2 a n bn , 得 c0 A0 , | cn | | c n | 2 2
arg cn arg c n θn , ( n 0) .
1 j t j t (D) f (t ) [ f ( t ) e d t ] e dω 2π 1 在 f (t ) 的间断处,公式的左端应为 [ f ( t 0) f ( t 0)] . 2
级数的基础上发展起来的。在微积分课程
中已经学习了Fourier 级数的有关 内容,
因此本节将先简单地回顾一下 Fourier
级数展开。
§8.1 Fourier 级数与Fourier 积分
一、周期函数的 Fourier 级数 二、非周期函数的 Fourier级数即
Fourier积分
一、周期函数的 Fourier 级数
n 1
A0 a n cos n 0 t bn sin n 0 t
n 1
A0 An cos(n 0 t n ) .
n 1
3. Fourier 级数的三角形式 定理 ( Dirichlet 定理)设 fT (t )是以 T 为周期的实值函数,且在 区间 [T /2 , T /2] 上满足如下条件(称为 Dirichlet 条件): (1) 连续或只有有限个第一类续点处有
傅里叶级数和傅里叶变换

傅里叶级数和傅里叶变换傅里叶级数和傅里叶变换是数学中常见且重要的概念,它们在信号处理、图像处理、电路分析以及物理学等领域中起着重要的作用。
本文将介绍傅里叶级数和傅里叶变换的基本原理、应用以及它们之间的关系。
一、傅里叶级数傅里叶级数是将一个周期性函数表示为正弦函数和余弦函数的无限级数。
在数学上,一个周期为T的函数f(t)可以表示为傅里叶级数的形式:f(t) = a0/2 + ∑(an*cos(nω0t) + bn*sin(nω0t))其中,a0表示直流分量,an和bn分别表示函数f(t)在一个周期内的cosine分量和sine分量,n为正整数,ω0为角频率,ω0 = 2π/T。
傅里叶级数的基本原理是,任何一个函数都可以用一系列基本的正弦和余弦函数来表示。
通过计算函数f(t)在一个周期内的各种正弦和余弦分量的系数,我们可以将函数f(t)展开成傅里叶级数的形式。
傅里叶级数在信号处理中有广泛的应用,例如音频信号的分析与合成、图像压缩等。
通过对信号进行傅里叶级数分解,我们可以得到信号的频率成分,从而对信号进行频域分析和处理。
二、傅里叶变换傅里叶变换是将一个非周期性函数或一个有限区间内的函数表示为连续频谱的方法。
傅里叶变换可以将一个时域上的函数转换为频域上的函数,从而能够更方便地观察信号在不同频率上的分量。
函数f(t)的傅里叶变换定义为:F(ω) = ∫f(t) * exp(-jωt) dt其中,F(ω)表示函数f(t)的频域表示,ω为频率。
傅里叶变换将函数f(t)从时域转换到频域,提供了频域上对信号进行分析和处理的方法。
傅里叶变换在信号处理中有广泛的应用,例如频率滤波、信号去噪、图像处理等。
通过对信号进行傅里叶变换,我们可以将信号表示为一系列复指数函数的线性组合,从而得到信号的频谱信息。
三、傅里叶级数与傅里叶变换的关系傅里叶级数和傅里叶变换之间存在着密切的关系。
事实上,傅里叶级数可以看作是傅里叶变换的一种特殊形式,即周期为T的函数的傅里叶级数可以看作是傅里叶变换在频率上的离散表示。
傅里叶级数与傅里叶变换关系与应用

论文题目傅里叶级数与傅里叶变换的关系与应用目录摘要: 0关键词 0Abstract 01绪论 (1)2傅里叶级数的概念 (1)2.1周期函数 (2)2.2傅里叶级数的定义 (2)3 傅里叶变换的概念及性质 (10)3.1傅里叶变换的概念 (10)3.2傅立叶变换的性质 (11)4傅里叶变换与傅里叶级数之间的区别与联系 (12)5傅里叶级数和傅里叶变换的应用 (12)5.1傅里叶级数的应用 (12)5.2傅里叶变换的应用 (13)参考文献 (15)傅里叶级数与傅里叶变换的关系与应用摘要:傅里叶级数是对周期性现象做数学上的分析,而傅里叶变换则可以看作傅里叶级数的极限形式,它也可以看作是对周期现象进行数学上的分析。
除此之外,傅里叶变换还是处理信号领域的一种很重要的算法。
傅里叶变换是一种分析信号的方法,它可分析信号的成分,也可用这些成分合成信号。
很多波形可以作为信号的成分,例如余弦波,方波,锯齿波等等,傅里叶变换作为信号的成分。
在电子类学科,物理学科,信号处理学科等众多领域都有着广泛的应用。
傅里叶级数针对的是周期性函数,傅里叶变换针对的是非周期性函数,它们在本质上都是一种把信号表示成复正选信号的叠加,存在相似的特性。
关键词:傅里叶级数;傅里叶变换;周期性Fourier series And Fourier TransformsAbstract: Fourier series is made mathematical analysis to cyclical phenomenon, and Fourier transform can be seen as the limit form of Fourier series, it also can be regarded as a mathematical analysis of cycle phenomenon. In addition, the Fourier transform is a kind of very important in the field of signal processing algorithms.Fourier transform is a method of signal analysis, it can analyze signal component, also can use these ingredients synthetic signal. Many waveform can be used as a signal of ingredients, such as cosine wave, square wave, sawtooth wave, etc., the Fourier transform as a signal of composition. In electronics disciplines, physics, signal processing disciplines etc many fields have a wide range of applications.Fourier series is for periodic function, Fourier transform for is a periodic function, they are in essence a kind of papers said the signal into a complex signal superposition, similar features.Key words: Fourier series; Fourier Transform; Periodic1绪论傅里叶级数是法国数学家J.-B.-J.傅里叶在研究偏微分方程的边值问题时提出来的,从而极大的推动了偏微分方程理论的发展,在数学物理以及工程中都具有重要的应用。
复变函数第1节 傅氏积分,傅氏变换

解. 由Fourier变换的定义
F (w) F [ f (t)] f (t) e-iw td t -
1 e-iw t d t e-iwt 1 2sinw
-1
-iw -1
w
再求F(w)的Fourier逆变换即得 f(t)的积分表达式,
f (t) F -1[F (w)] 1 F (w) eiwtd w
1
1/2
t
二、单位脉冲函数及其傅氏变换
在物理学和工程技术中,除了连续分布量之外, 还有集中作用在一点的量. 例如,点电荷、点热源、 质点、单位脉冲等. 下面分析在原点处的单位脉冲.
设矩形电流脉冲:
(t
)
1
/
0
0t
其它
- (t)dt 1
(t)
1/
O
t
lim
0
(
t
)
0
t 0 t 0
引进狄拉克(Dirac)的函数,
i
-
f
( ) sin w(t
-
)d
dw
1
2p
-
-
f
(
)
cos w (t
-
)
d
d
w
(1.5)
由
f (t) 1
2p
-
-
f
(
)
cos w (t
-
)
d
d
w
(1.5)
可得
f (t) 1
p
0
-
f ( ) cosw(t
-
)
d
d
w
(1.6)
傅氏积分公式的三角形式
-
)
d
d
傅里叶级数与傅里叶变换

最常见的三角级数是傅立叶级数。
傅立叶级数
直线
y kx b
y x
抛物线 y ax2 bx c
y x
傅立叶级数展开(T=2l)
y
f (x)
a0 2
n x
(an cos
二维Hartley变换
F f (x)eix d x
一维傅立叶变换
FF
,
F f
x, y
f (x, y)ei2 x yd x d y
二维傅立叶变换
傅立叶变换存在问题:核函数中出现了复数,这就意 味着即使在空域中的实序列经过傅立叶变换之后也会 变成复数,如果实序列用复序列来处理,问题本身将 被复杂化。
恩格斯把傅里叶的数学成就与他所推崇的哲学家黑格尔的辩证法 相提并论。他写道:傅里叶是一首数学的诗,黑格尔是一首辩证 法的诗。
傅立叶级数
常见的表示函数的工具:幂级数和三角级数。
幂级数简单、方便,但条件苛刻,要求函数在相应的区 间内不仅必须无限次可微,还有其它一些要求(例如收 敛性等),因而从理论上说其使用范围比较有限。
周期函数展开成傅立叶级数的核心思想是:f(x)可以分解 为不同频率的谐波之和。
傅立叶级数 例2:周期为τ =1的方波函数
傅立叶级数
若设f(x)是定义在(-∞,+∞)区间上的非周期函数,它 是否可以表示为不同频率谐波的迭加?
设f(x),及其一阶导数f΄(x)在任意一个有限区间上
分段连续,且
f xd存x 在。
由于
1 1 1 , n
l l
n
lim l
傅里叶级数与傅里叶变换

傅里叶级数与傅里叶变换傅里叶级数和傅里叶变换是数学中重要的概念,广泛应用于信号处理、图像处理、通信系统等领域。
它们为我们理解和分析周期信号以及非周期信号提供了有效的数学工具。
本文将分别介绍傅里叶级数和傅里叶变换的基本概念、性质和应用。
一、傅里叶级数傅里叶级数是指将一个周期函数表示成一系列正弦和余弦函数的和。
它的基本思想是利用正弦和余弦函数的基本频率,将一个周期函数分解成多个不同频率的谐波分量,从而得到函数的频谱内容。
在数学上,傅里叶级数表示为:\[f(t) = \sum_{n=-\infty}^{\infty}c_ne^{i \omega_n t}\]其中,$c_n$代表系数,$e^{i \omega_n t}$是正弦和余弦函数的复数形式,$\omega_n$是频率。
将周期函数用傅里叶级数表示的好处是,可以通过调整系数来控制频谱内容,进而实现信号的滤波、合成等操作。
傅里叶级数的性质包括线性性、对称性、频谱零点等。
线性性意味着可以将不同的周期函数的傅里叶级数叠加在一起,得到它们的叠加函数的傅里叶级数。
对称性则表示实函数的傅里叶级数中系数满足一定的对称关系。
频谱零点表示在某些特殊条件下,函数的傅里叶级数中某些频率的系数为零。
傅里叶级数的应用广泛,例如在音频信号处理中,利用它可以进行音乐合成、乐音分析和音频压缩等操作。
此外,在图像处理领域,傅里叶级数被广泛应用于图像滤波、增强、噪声消除等方面。
二、傅里叶变换傅里叶变换是傅里叶级数的推广,用于处理非周期信号。
它将时域的信号转换为频域的信号,从而可以对信号进行频谱分析和处理。
傅里叶变换的定义为:\[F(\omega) = \int_{-\infty}^{\infty}f(t)e^{-i \omega t}dt\]其中,$F(\omega)$表示信号的频域表示,$f(t)$为时域信号,$\omega$为连续的角频率。
傅里叶变换可以将时域的信号分解成不同频率的复指数函数,并用复数表示频谱信息。
傅里叶级数和傅里叶变换

第九章 傅里叶级数和傅里叶变换在自然界中广泛地存在各种各样的周期性运动(即相隔一定时间间隔往复循返的过程)。
例如,日月星球的运动,海洋潮汐的运动,电磁波与声波的运动,工厂里机器部件的往复运动,时钟摆的摆动以及人体心脏的跳动等等,都是周期性运动。
为了描述周期性的运动过程,数学上是借助某类函数来描述的。
当然这类函数也要体现出周期性。
这类函数称为周期函数。
在前面几章中,为了研究函数的性质,常常采用分析表示法,将这些函数在某区域展开成幂级数的形式,如泰勒级数或罗朗级数。
但是,这种幂级数形式的展开式是体现不出周期性来的,那么,对于周期性函数应采取怎样的分析表示法呢?这就是本章要讨论的内容。
9.1 周期函数和傅里叶级数9.1.1 周期函数 凡满足以下关系式:)()(x f T x f =+ (T 为常数) (9.1.1) 的函数,都称为周期函数。
周期的定义(1) 满足式(9.1.1)的T 值中的最小正数,即为该函数的周期; (2) 一个常数以任何正数为周期。
9.1.2 基本三角函数系按某一规律确定的函数序列称为函数系。
如下形式的函数系:1,x l πcos,x l πsin,x l π2cos ,x l π2sin ,…,x l k πcos ,x lk πsin ,… (9.1.2)称为基本三角函数系。
所有这些函数具有各自的周期,例如x l k πcos 和x lk πsin 的周期为kl2,但它们的共有周期为l 2(即所有周期的最小公倍数)。
通常这个周期命名为函数系的周期。
所以式(9.1.2)的三角函数系的周期为l 2。
如果我们将基本三角函数系中的函数,任意取n 个组合,则我们可以得到一个较复杂的函数。
例如图9.1(a )是两个函数的组合x lx l x f ππ2sin 21sin )(-=;图9.1(b )是三个函数的组合x lx l x l x f πππ3sin 312sin 21sin )(+-=。
傅里叶变换
傅里叶分析不仅仅是一个数学工具,更是一种可以彻底颠覆一个人以前世界观的思维模式。
一、什么叫频域从我们出生,我们看到的世界都以时间贯穿,股票的走势、人的身高、汽车的轨迹都会随着时间发生改变。
这种以时间作为参照来观察动态世界的方法我们称其为时域分析。
而我们也想当然的认为,世间万物都在随着时间不停的改变,并且永远不会静止下来。
但如果我告诉你,用另一种方法来观察世界的话,你会发现世界是永恒不变的,你会不会觉得我疯了?我没有疯,这个静止的世界就叫做频域。
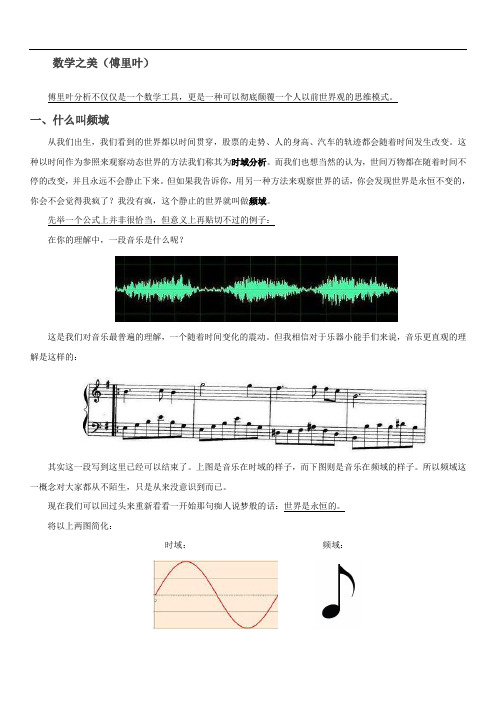
先举一个公式上并非很恰当,但意义上再贴切不过的例子:在你的理解中,一段音乐是什么呢?这是我们对音乐最普遍的理解,一个随着时间变化的震动。
但我相信对于乐器小能手们来说,音乐更直观的理解是这样的:其实这一段写到这里已经可以结束了。
上图是音乐在时域的样子,而下图则是音乐在频域的样子。
所以频域这一概念对大家都从不陌生,只是从来没意识到而已。
现在我们可以回过头来重新看看一开始那句痴人说梦般的话:世界是永恒的。
将以上两图简化:时域:频域:在时域,我们观察到钢琴的琴弦一会上一会下的摆动,就如同一支股票的走势;而在频域,只有那一个永恒的音符。
你眼中看似落叶纷飞变化无常的世界,实际只是躺在上帝怀中一份早已谱好的乐章。
傅里叶同学告诉我们,任何周期函数,都可以看作是不同振幅,不同相位正弦波的叠加。
在第一个例子里我们可以理解为,利用对不同琴键不同力度,不同时间点的敲击,可以组合出任何一首乐曲。
贯穿时域与频域的方法之一,就是传中说的傅里叶分析。
傅里叶分析可分为傅里叶级数(Fourier Serie)和傅里叶变换(Fourier Transformation),我们从简单的开始谈起。
二、傅里叶级数(Fourier Series)举个栗子并且有图有真相才好理解。
如果我说我能用前面说的正弦曲线波叠加出一个带90 度角的矩形波来,你会相信吗?你不会,就像当年的我一样。
但是看看下图:第一幅图是一个郁闷的正弦波cos(x)第二幅图是2 个卖萌的正弦波的叠加cos(x)+a.cos(3x)第三幅图是4 个发春的正弦波的叠加第四幅图是10 个便秘的正弦波的叠加随着正弦波数量逐渐的增长,他们最终会叠加成一个标准的矩形,大家从中体会到了什么道理?(只要努力,弯的都能掰直!)随着叠加的递增,所有正弦波中上升的部分逐渐让原本缓慢增加的曲线不断变陡,而所有正弦波中下降的部分又抵消了上升到最高处时继续上升的部分使其变为水平线。
第4(5)章 傅里叶级数和变换

t0
2 2
f (t ) cos( n1t )dt
2 T1
2
E cos( n1t )dt
4 T1
0
E cos( n1t )dt
2
4E 1 sin n1t T1 n1
变
0
不 变
2E n an sin n T1
n sin 2E n T1 n n T1 T1 2 E n Sa ( ) T1 T1
§4.1 引言 信号与系统的时域分析→变换域分析(频域分析)
第四章 连续系统的频域分析P116
任一周期信号都可以用三角函数的线性组合来表示
1822年,法国数学家傅里叶提出;
Poisson、Gauss等将其应用到电学中;
20世纪后,谐振电路、滤波器、正弦振荡器等为傅立 叶分析的应用开辟了广阔的前景 周期信号——傅里叶级数 非周期信号——傅里叶变换
T 2 T 2 T 2 T 2
(3) 半波重迭信号 fT(t)=f(t±T/2)
f (t )
-T/2
T/2
t
半波重叠周期信号只含有正弦与余弦 的偶次谐波分量,而无奇次谐波分量。
(4) 半波镜像信号 fT(t)=f(t±T/2)
f (t )
T/2 0 T
t
半波镜像周期信号只含有正弦与余弦的奇 次谐波分量,而无直流分量与偶次谐波分量。
④ t =±π,±2π,…±nπ;Sa(t)=0
正弦分量的幅度: bn
2 T1
t 0 T1
2 2
t0
f (t ) sin( n1t )dt
2 T1
已知傅里叶级数求傅里叶变换

已知傅里叶级数求傅里叶变换傅里叶级数和傅里叶变换是信号处理和数学中非常重要的概念,它们在科学、工程、物理学和数学各个领域都有着广泛的应用。
傅里叶级数用于描述周期性信号的频域特性,而傅里叶变换则适用于非周期性信号,将信号从时域转换到频域。
通过对这两个概念的深入了解,我们可以更好地理解信号的频谱特性和信号处理的方法。
接下来,让我们来深入探讨已知傅里叶级数如何求傅里叶变换。
一、傅里叶级数的基本概念在深入研究傅里叶变换之前,我们需要首先了解傅里叶级数的基本概念。
傅里叶级数可以表示任意周期信号为一系列正弦和余弦函数之和的形式,它的数学表达式为:\[ f(t) = \frac{a_0}{2} + \sum\limits_{n=1}^{\infty} (a_n\cos{(\frac{2\pi nt}{T})} + b_n \sin{(\frac{2\pi nt}{T})}) \]其中,\[ f(t) \] 代表信号的时域表示,\[ T \] 代表信号的周期,\[ a_0, a_n, b_n \] 为傅里叶系数。
二、傅里叶级数到傅里叶变换当我们已知一个信号的傅里叶级数,想要求出其傅里叶变换时,我们可以通过一定的方法将傅里叶级数转换为傅里叶变换。
这里需要引入复数形式的傅里叶级数,即欧拉公式:\[ e^{ix} = \cos{x} + i\sin{x} \]通过欧拉公式,我们可以将之前的正弦和余弦函数转化为指数形式的复数函数。
这为我们求解傅里叶变换提供了便利。
傅里叶变换的数学定义是:\[ F(\omega) = \int_{-\infty}^{\infty} f(t)e^{-i\omega t} dt \]其中,\[ f(t) \] 为时域信号,\[ F(\omega) \] 为频域信号,表示信号在频域上的频谱特性。
三、从傅里叶级数推导傅里叶变换对于已知傅里叶级数的情况,我们可以通过一些步骤将其转换为傅里叶变换。
根据欧拉公式将傅里叶级数中的正弦和余弦函数转化为指数形式的复数函数。
6.1 傅里叶积分定理

]
上连续或只有有限个第一类间断点;
2)
在
[
T 2
,
T 2
]
上只有有限个极值点,
则函数 f T(x)在
[
T 2
,
T2上] 可以展开成傅里叶级数.
在 fT (t) 的连续点处,
其中
,且
傅里叶级数的三角形式
an
2 T
T
2 T
fT (t) cos nt d t
(n 0,1, 2,)
2
bn
2 T
T
(t
)d
d
因 f ( )sin(t )d是的奇函数,
f (t) 1
2
f
( )cos(t
)
d
d
又由于 f ( )cos(t )d是 的偶函数,
从 f (t) 1
2
f
(
)
cos(t
)d
d
可得 f (t) 1
0
f
(
) cos (t
)d
d
利用三角函数公式
2 2
fT
(t)cos
nt
i sin
nt dt
1
T
T2 T 2
fT
(t )e int dt
dn
1 T
T T
2 2
fT
(t)cos
nt
i sin
nt dt
1
T
T2 T 2
fT
(t)eintdt cn
上述两个系数可以合并为一个
cn
1 T
T2 T 2
fT
(t )e int dt
n 0,1, 2,
推导过程如下
信号分析与处理-傅里叶变换

第三章傅里叶变换本章提要:◆傅里叶级数(Fourier Series)◆非周期信号的傅里叶变换◆傅里叶变换的性质◆周期信号的傅里叶变换◆采样信号和采样定理J.B.J. 傅里叶(Fourier)◆1768年生于法国◆1807年提出“任何周期信号都可用正弦函数级数表示”,但其数学证明不很完善。
◆拉普拉斯赞成,但拉格朗日反对发表◆1822年首次发表在《热的分析理论》◆1829年狄里赫利第一个给出收敛条件周期信号都可表示为谐波关系的正弦信号的加权和非周期信号都可用正弦信号的加权积分表示傅里叶分析方法的应用:(1)泊松(Possion)、高斯(Gauss)等将其应用于电学中;(2)在电力系统中,三角函数、指数函数及傅里叶分析等数学工具得到广泛的应用。
(3)20世纪以后,在通信与控制系统的理论研究与实际应用中开辟了广阔的前景。
(4)力学、光学、量子物理和各种线性系统分析等得到广泛而普遍的应用。
§ 3.1 周期信号的傅立叶级数◆三角函数形式的傅里叶级数◆复指数形式的傅里叶级数◆几种典型周期信号的频谱◆吉伯斯现象一、三角函数形式的傅里叶级数∞Tianjin University Tianjin University二、复指数形式的傅里叶级数周期信号的复数频谱图三、几种典型周期信号的频谱+-1T t tjn ωTianjin UniversityTianjin University∞n A τωτ思考题:KHz T f T 100101011 26=⨯===-,πω2. 奇函数:f (t )= -f (-t)1tω只含正弦项n F =3.奇谐函数T四、吉伯斯现象)(t f有限项的N越大,误差越小例如: N=11§ 3.2 非周期信号的傅立叶变换∞从物理意义来讨论傅立叶变换(FT)Tianjin University Tianjin UniversityTianjin UniversityTianjin University )0>arctg -=)(t f时域中信号变化愈尖锐,其频域所包含的高频分量就愈丰富;反之,信号在时域中变化愈缓慢,其频域所包含的低频分量就愈多。
数学物理方法第五章傅里叶变换

l
l
l
l kx nx
sin cos dx0
l
l
l
l
1 2 dx 2 l
l
l
sin
2 k x dx
l
l
l
cos
2 k x dx
l
l
2、可以由函数的正交性求出傅立叶级数中的系数;
a f 1 l
0 2l l
xdx
a f 1l n l l
xconsxdx
l
(n1,2,3, )
b f 1l n l l
( a k cos
kπx l
b k sin
kπx )
l
k 1
2
2l l
说明 1、三角函数族是两两正交的
l kx
cos d x 0
l
l
(k 0),
l kx
sin d x 0
l
l
l kx nx
cos cos d x 0 (k n)
l
l
l
l kx nx
sin sin dx0 (kn),
f (x)
a
x
l
延拓到(- l,l)后再周期延拓,如图做偶延拓:
f (x)
a
l 0 l
x
所以
1l
x
a
a0
l
a(1
0
l
)dx 2
ak2 l0 la(1x l)co k lx sd x 2(2 4 n a 0 1 )2(k (k 2n )2n1 )
如图做奇延拓: f (x)
a
l
0l
x
2l x kx 2a
An 2cn
A n 称为f ( x)的振幅频谱(简称为频谱).它描述了各次谐波 的振幅随频率变化的分布情况。它清楚地表明了一个非正旋 周期函数包含了哪些频率分量及各分量所占的比重(如振幅 的大小)。因此频谱图在工程技术中应用比较广泛.所谓频谱 图,通常是指频率和振幅的关系图。
(完整版)傅立叶级数的指数形式(图)

傅立叶级数的指数形式(图)上一回说到,利用傅立叶级数(Fourier Series,简称FS)这个数学法宝,可以将一般的周期信号分解为直流成分、基波和无穷多个高次谐波成分的叠加,从而方便地确定其频谱。
但上述的傅立叶级数表达式只是傅立叶级数的三角形式,在实用中还有傅立叶级数的指数形式,本文介绍。
一、傅立叶级数的三角形式对于一个周期为T的周期函数f T(t),在一定条件下可以在连续点t处展开为傅立叶级数的三角形式,即:(1)其中ω1=2π/T为周期函数的圆频率,也就是信号的基频;傅立叶系数分别为(2)(3)(4)在信号分析理论中a0叫做直流分量,a n叫做余弦分量系数,b n叫做正弦分量系数。
二、傅立叶级数的指数形式根据欧拉公式有(5)其中j为虚数单位,即(6)不难从傅立叶级数的三角形式导出傅立叶级数的指数形式:(7)其中傅立叶系数一般为复数(8)三、傅立叶级数的指数形式与三角形式的关系根据欧拉公式由式(7)有(9)不难看出傅立叶级数的指数形式与三角形式可以描述同一个周期信号,只是数学形式不同而已。
其中两种形式的傅立叶系数关系如下:(10)或(11)可以看出傅立叶级数的指数形式中的傅立叶系数不再是实数,而是复数。
四、周期信号的频谱分析从傅立叶级数的指数形式也可以进行频谱分析。
由式(9)得(12)可知,周期函数f T(t)包含的直流分量为(13)基波分量的振幅为(14)基波初相位为各高次谐波分量的振幅为(16)各高次谐波分量的初相位为(17)这样,周期信号f T(t)的振幅频谱函数可表示为(18)五、为什么需要傅立叶级数的指数形式?实际上,如果考虑信号的双边频谱,用傅立叶级数的指数形式更方便。
在双边频域(∞,-∞)内,周期信号的频谱函数就是傅立叶系数,即(19)傅立叶系数一般为复数,可写成(20)其模就是双边的振幅频谱其幅角φn就是双边频率各次谐波成分的初相位,其中n为整数。
再看看傅立叶级数的指数形式可写成(22)其数学含义就是说,一般周期信号可以分解为无穷多个离散频率分量的叠加,各分量的频率是基频的整数倍,振幅是傅立叶系数C n的复模,初相位是傅立叶系数C n的幅角。
傅里叶变换(周期和非周期信号)

f (t) Fne jn0t n
n1
e e jn0t jn0t
e e jn0t jn0t
a0 (an
n1
2
bn
2j
)
a0
n1
( an
- jbn 2
e
jn0t
an
2
jbn
e
jn0t
)
*
F0 Fne jn0t F en jn0t
n1
n1
*
F0 a0 是实数,Fn与 F n 是一对共轭复数
n1
c0 a0
cn an2 bn2
a0
1 T
T
2 -T
f (t) dt
2
an
2 T
T
2 T
2
f (t) cosn0t dt
bn
2 T
T
2 T
2
f (t)sin n0t dt
周期信号的傅里叶变换——傅里叶级数
1、 三角函数式傅里叶级数
若周期函数 f (t) 满足狄里赫利( Dirichlet)条件:
或
f (t) c0 cn cos(n0t n ) n1
谐波形式
ω0是基谐波角频率,简称基波频率。
例1 已知周期信号f(t)如下, 画出其频谱图。
f (t) 1
2
c
os0t
c
os(20t
5
4
)
2
s in 0t
1 2
sin
30t
解 : 将f(t)整理为标准形式
f
(t)
1 2 cos(0t
4
f (t) a0 (an cos0t bn sin0t)
n1
a0
傅里叶变换(周期和非周期信号)

例1的频谱图
周期信号的傅里叶变换——傅里叶级数
2、指数形式的傅里叶级数
式中,
f (t) Fne jn0t n
1
Fn T
T
2 T
f (t )e jn0tdt
2
证明
- n
傅里叶复系数
周期信号的傅里叶变换——傅里叶级数
2、指数形式的傅里叶级数
式中,
f (t) Fne jn0t n
1
Fn T
A
T1
2 A sin n1
n1 n
2
cos n1t
A
T1
2A sin
1
2
cos1t
A
sin
1
cos 21t
2A sin
3
31
2
cos 31t
......
2. 指数形式的傅里叶级数
周期矩形脉冲
f (t) Fne jn1t n
Fn
1 T1 A T1
T1
2 T1
f (t )e jn1tdt
2. T不变,τ减小,则频谱的幅度也将减小,谱线密度 保持不变,但包络过零点的间隔将增大。
A
F0 T
Back
非周期信号的傅立里叶变换
两个重要公式:
f ( t ) F( ) : F( ) f ( t )e jtdt
F( ) f (t ):
F -1F( ) f ( t ) 1 F( )e jtd
1、 三角函数式傅里叶级数
若周期函数 f (t) 满足狄里赫利( Dirichlet)条件:
(1)在任意周期内存在有限个第一类间断点; (2)在任意周期内存在有限个的极值点; (3)在任意周期上是绝对可积的,即
傅里叶(Fourier)级数的指数形式与傅里叶变换

傅里叶(Fourier )级数的指数形式与傅里叶变换专题摘要:根据欧拉(Euler )公式,将傅里叶级数三角表示转化为指数表示,进而得到傅里叶积分定理,在此基础上给出傅里叶变换的定义和数学表达式。
在通信与信息系统、交通信息与控制工程、信号与信息处理等学科中,都需要对各种信号与系统进行分析。
通过对描述实际对象数学模型的数学分析、求解,对所得结果给以物理解释、赋予其物理意义,是解决实际问题的关键。
这种数学分析方法主要针对确定性信号的时域和频域分析,线性时不变系统的描述以及信号通过线性时不变系统的时域分析与变换域分析。
所有这些分析方法都离不开傅里叶变换、拉普拉斯变换和离散时间系统的z 变换。
而傅里叶变换的理论基础是傅里叶积分定理。
傅里叶积分定理的数学表达式就是傅里叶级数的指数形式。
不但傅里叶变换依赖于傅里叶级数,就是纯数学分支的调和分析也来源于函数的傅里叶级数。
因此,傅里叶级数无论在理论研究还是在实际应用中都占有非常重要的地位。
我们承认满足狄里克莱(Dirichlet )条件下傅里叶级数的收敛性结果,不去讨论和深究傅里叶展式的唯一性问题。
傅里叶级数的指数形式一个以T 为周期的函数)(t f ,在]2,2[TT 上满足狄里克莱条件:1o)(t f 连续或只有有限个第一类间断点;2o只有有限个极值点。
那么)(t f 在]2,2[TT -上就可以展成傅里叶级数。
在连续点处 ∑∞=++=1)sin cos (2)(n n n t n b t n a a t f ωω, (1)其中 Tπω2=, ),2,1,0(,cos )(222Λ==⎰-n dt t n t f T a TT n ω, (2)),3,2,1(,sin )(222Λ==⎰-n dt t n t f T b TT n ω, (3)根据欧拉(Euler )公式:θθθsin cos j e j +=,(1)式化为∑∞=--⎥⎦⎤⎢⎣⎡-+++=10222)(n t jn t jn n t jn t jn n j e e b e e a a t f ωωωω∑∞=-⎥⎦⎤⎢⎣⎡++-+=10222n t jn n n t jn n n e jb a e jb a a ωω, (4) 若令dt t f T c TT ⎰-=220)(1Λ,3,2,1,)(1]sin )[cos (1sin )(1cos )(1222222222==-=-=-=⎰⎰⎰⎰-----n dt e t f T dt t n j t n t f T dtt n t f T j dt t n t f T jb a c TT t jn TT TT T T n n n ωωωωωΛ,3,2,1,)(122==⎰--n dt e t f T c TT t jn nω 综合n n c c c -,,0,可合并成一个式子Λ,2,1,0,)(122±±==⎰--n dt e t f T c TT t jn n ω, (5)若令Λ,2,1,0,±±==n n n ωω,则(1)式可写为∑∑+∞-∞=∞=--=++=n tj nn tj n tj n n n n e c ec ec c t f ωωω10)()(, (6)这就是傅里叶(Fourier)级数的指数形式。
3.2 周期信号的傅里叶级数分析

1
∞
f (t) = a0 + ∑(an cos nω1t + bn sin nω1t), n为正整数
n=1
∞
1 直流分量: a 0 = T1
∫
t 0 + T1
t0
f ( t ) dt
2 t0 +T1 余弦分量的幅度:n = ∫ a f (t ) cos(nω1t )dt T1 t0
2 正弦分量的幅度: bn = T1
sin(ω1t )
4 T1 a1 = ∫ 2 f (t) cos(ω1t)dt T 0 1
4 T1 b = ∫ 2 f (t) sin( ω1t)dt 1 T 0 1
cos(2ω1t )
sin(2ω1t )
∞
令:Fn = Fn e
∞
jϕn
1 − jϕn 1 = (an − jbn ) F−n = F−n e = (an + jbn ) 2 2
jnwt 1
f (t) = F0 + ∑Fne
n=1
+ ∑F−ne
n=1
∞
− jnwt 1
= ∑Fne
n=0
∞
jnwt 1
+ ∑Fne jnw1t
n=−∞
−1
周期函数: f (t) =
7
周期信号的复数频谱 F0
complex frequency spectrum
F = Fn n − F = c0 0
1 = cn 2
8
周期信号的功率特性
1 t0 +T1 2 周期信号f (t )的平均功率 : P = f (t ) = ∫ f (t )dt T1 t0
2
傅里叶变换 拉普拉斯变换

傅里叶变换拉普拉斯变换傅里叶变换傅里叶变换(Fourier Transform)是一种将时域信号转换为频域信号的数学工具。
它是以法国数学家约瑟夫·傅里叶的名字命名的,用于分析周期性信号和非周期性信号。
1. 傅里叶级数傅里叶级数是傅里叶变换的前身,它是一种将周期函数表示为正弦和余弦函数的无限级数的方法。
根据欧拉公式,正弦和余弦函数可以表示为复指数形式:$$\sin(x)=\frac{e^{ix}-e^{-ix}}{2i}$$$$\cos(x)=\frac{e^{ix}+e^{-ix}}{2}$$假设一个连续周期函数$f(t)$可以表示为以下级数:$$f(t)=a_0+\sum_{n=1}^{\infty}(a_n\cos(n\omegat)+b_n\sin(n\omega t))$$其中$\omega$是角频率,$a_0,a_n,b_n$是系数。
这个级数就称为$f(t)$的傅里叶级数。
通过求解系数$a_0,a_n,b_n$,可以得到$f(t)$在周期内任意时刻$t$的值。
2. 傅里叶变换对于非周期信号,我们无法使用傅里叶级数进行分析。
此时,我们需要使用傅里叶变换。
傅里叶变换将一个时域信号$f(t)$转换为一个频域函数$F(\omega)$,它表示了$f(t)$中各个频率成分的强度和相位。
傅里叶变换的定义如下:$$F(\omega)=\int_{-\infty}^{\infty}f(t)e^{-i\omega t}dt$$其中$\omega$是角频率,$e^{-i\omega t}$是复指数形式的正弦函数。
$F(\omega)$表示了$f(t)$在频率为$\omega$时的贡献。
3. 傅里叶逆变换傅里叶变换可以将一个时域信号转换为一个频域函数,那么我们是否可以将一个频域函数转换回时域信号呢?答案是肯定的,这就需要用到傅里叶逆变换。
傅里叶逆变换的定义如下:$$f(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}F(\omega)e^{i\omegat}d\omega$$其中$F(\omega)$是$f(t)$的傅里叶变换。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题摘要:根据欧拉(Euler)公式,将傅里叶级数三角表示转化为指数表示,进而得到傅 里叶积分定理,在此基础上给出傅里叶变换的定义和数学表达式。
在通信与信息系统、交通信息与控制工程、信号与信息处理等学科中,都需要对各种 信号与系统进行分析。通过对描述实际对象数学模型的数学分析、求解,对所得结果给以物 理解释、赋予其物理意义,是解决实际问题的关键。这种数学分析方法主要针对确定性信号 的时域和频域分析,线性时不变系统的描述以及信号通过线性时不变系统的时域分析与变换 域分析。所有这些分析方法都离不开傅里叶变换、拉普拉斯变换和离散时间系统的 z 变换。 而傅里叶变换的理论基础是傅里叶积分定理。傅里叶积分定理的数学表达式就是傅里叶级数 的指数形式。
f (t) 。于是有
f (t)
lim 1 T T
n
T
2 T
2
fT
(
)e
j n
d
e
j n t
。
可以证明(详细过程可参阅文[46]),当T 时,有
f
(t)
1 2
f
( )e j d e jt d
,
(8)
公式(8)称为傅里叶积分公式。从而得到一个非周期函数可用傅里叶积分公式表示的傅里
F ( ) 叫做 f (t) 的象函数,(10)式叫做 F ( ) 的傅里叶逆变换,记为
f (t) = F -1[F ( )].
f (t) 叫做 F ( ) 的原象函数。
叶积分定理。
傅里叶变换
根据傅里叶积分定理,设
F ( ) f (t)e jt dt ,
(9)
则
f (t) 1
F
(
)e
j
t
d
,
2
(10)
从上两式可以看出, f (t) 和 F ( ) 通过指定的积分运算可以相互表达。(9)式叫做 f (t) 的
傅里叶变换,记为
F () F[ f (t)] .
有限个第一类间断点;2o 只有有限个极值点。那么 f (t) 在[ T , T ] 上就可以展成傅里叶级 22
数。在连续点处
f
(t)
a0 2
(an
n1
cos nt
bn
sin nt) ,
其中
2 ,
T
an
2 T
T
2 T
f (t) cos ntdt,
2
(n 0,1,2,) ,
(1) (2)
bn
不但傅里叶变换依赖于傅里叶级数,就是纯数学分支的调和分析也来源于函数的傅里 叶级数。因此,傅里叶级数无论在理论研究还是在实际应用中都占有非常重要的地位。我们 承认满足狄里克莱(Dirichlet)条件下傅里叶级数的收敛性结果,不去讨论和深究傅里叶展 式的唯一性问题。 傅里叶级数的指数形式
一个以 T 为周期的函数 f (t) ,在[ T , T ] 上满足狄里克莱条件:1o f (t) 连续或只有 22
e jn t
an
jbn 2
e
jn
t
,
c0
1 T
T
2 T
f (t)dt
2
(4)
cn
an
jbn 2
1 T
T
2 T
2
f
(t) cos ntdt
1 j T
T
2 T
f (t) sin ntdt
2
1
T
T
2 T
f (t)[cos nt
j sin nt]dt
2
1
T
T2Leabharlann Tf (t)e jnt dt,
n1
n
(5) (6)
这就是傅里叶(Fourier)级数的指数形式。或写成
f (t)
1 T
n
T
2 T
2
f
(
)e
j n
d
e
j n t
。
傅里叶积分定理
(7)
因为任何一个非周期函数 f (t) 都可以看成是由某个周期函数 fT (t) 当 T 时转化
而来的,即 lim T
fT (t)
2 T
T
2 T
f (t) sin ntdt,
2
(n 1,2,3,) ,
(3)
根据欧拉(Euler)公式: e j cos j sin ,(1)式化为
若令
f (t)
a0 2
an
n1
e jn t
e jn t 2
bn
e jn t
e jn t
2j
a0 2
an n1
jbn 2
2
n 1,2,3,
cn
1 T
T
2 T
f (t)e jnt dt,
2
n 1,2,3,
综合 c0 , cn , cn ,可合并成一个式子
cn
1 T
T
2 T
f (t)e jnt dt,
2
n 0, 1, 2, ,
若令n n, n 0, 1, 2, ,则(1)式可写为
f (t) c0 (cne jnt cne jnt ) cne jnt ,
