从二次函数图象-抛物线获得信息
二次函数的图像和性质PPT课件

你们喜欢篮球吗?:投篮时,篮球运动的路 线是什么曲线?怎样计算篮球达到最高点 时的高度?
今天让我们来研究一下二次函数的图像 和性质吧
开县德阳中学
教师
二次函数:
一般地,形如 y=ax2+bx+c(a、b、c为常数,a≠0)的函 数,叫做二次函数.其中,x是自变量,a,b,c分别是函数表
达式的二次项系数、一次项系数和常数项.
(1) 求此抛物线的函数解析式 (2)写出这个二次函数图象的对称轴,顶点坐标及开口方向
;
(3解)(判1断)点把((-1,-2-,4)-8是)否代在入此抛y=物a线x2上,得; -8=a(-2)2,解出a= -2,所求函数解析式为y= -2x2.
(2)对称轴:y轴,顶点坐标:(0,0),开口向下.
(3)因为 4 2(1)2 ,所以点B(-1 ,-4) 不在此抛物线上。
开县德阳中学
教师
1. 二次函数的图像都是什么图形? 2. 抛物线y=ax2的图像性质: (1) 抛物线y=ax2的对称轴是y轴,顶点是原点.
(2)当a>0时,抛物线的开口向上,顶点是 抛物线的最低点;
当a<0时,抛物线的开口向下,顶点是 抛物线的最高点;
(3)抛物线的增减性
(4)|a|越大,抛物线的开口越小;
8
y=x2
7
6
5
坐标平面中描点(x,y),
4
再用平滑曲线顺次连
3 2
接各点,就得到y=x2的
1 -5 -4 -3 -2 -1 o 1
2
3
4
5
x
图像.
开县德阳中学
教师
请画函数y=-x2的图像 解:(1) 列表 x … -3 -2 -1 0 1 2 3 …
二次函数图像与性质完整归纳

二次函数图像与性质完整归纳二次函数的图像与性质二次函数是高中数学中的重要内容之一,掌握其图像与性质是必不可少的。
二次函数的基本形式是y=ax^2,其中a表示开口方向和抛物线开口大小,x^2表示自变量的平方。
根据a的正负,抛物线的开口方向和顶点的坐标可以得到不同的性质。
当a>0时,抛物线开口向上,顶点坐标为(0,0),对称轴为y轴;当a<0时,抛物线开口向下,顶点坐标为(0,0),对称轴为y轴。
在y=ax^2的基础上,加上常数项c可以得到y=ax^2+c的形式,其中c表示抛物线在y轴上的截距。
根据a和c的正负,抛物线的开口方向、顶点坐标和对称轴可以得到不同的性质。
当a>0,c>0时,抛物线开口向上,顶点坐标为(0,c),对称轴为y轴;当a>0,c0时,抛物线开口向下,顶点坐标为(0,c),对称轴为y轴;当a<0,c<0时,抛物线开口向下,顶点坐标为(0,c),对称轴为y轴。
除了基本形式和加上常数项的形式,二次函数还有一种顶点式的形式y=a(x-h)^2+k,其中(h,k)表示顶点坐标。
根据a的正负,抛物线的开口方向和顶点坐标可以得到不同的性质。
当a>0时,抛物线开口向上,顶点坐标为(h,k),对称轴为直线x=h;当a<0时,抛物线开口向下,顶点坐标为(h,k),对称轴为直线x=h。
在顶点式的基础上,加上常数项k可以得到y=a(x-h)^2+k的形式。
根据a和k的正负,抛物线的开口方向、顶点坐标和对称轴可以得到不同的性质。
当a>0,k>0时,抛物线开口向上,顶点坐标为(h,k),对称轴为直线x=h;当a>0,k0时,抛物线开口向下,顶点坐标为(h,k),对称轴为直线x=h;当a<0,k<0时,抛物线开口向下,顶点坐标为(h,k),对称轴为直线x=h。
二次函数图象的平移二次函数的图像可以通过平移来得到新的图像。
平移的步骤是先确定顶点坐标,然后根据顶点坐标的变化来确定平移方向和距离。
二次函数及其图象和性质

二次函数及其图象和性质(二)一、内容提要(一)二次函数的解析式:1.一般式:y=ax2+bx+c;其中a≠0, a, b, c 为常数2.顶点式:y=a(x-h)2+k;其中a≠0, a, h, k 为常数,(h,k)为顶点坐标。
3.交点式:y=a(x-x1)(x-x2);其中a≠0, a, x1,x2为常数,x1,x2是抛物线与横轴两交点的横坐标。
注:这种形式可以作为了解内容,重点是前两种。
(二)二次函数的图象:抛物线(三)性质:1.对称轴,顶点坐标:2.开口方向:a>0, 抛物线开口向上,并向上无限延伸。
a<0, 抛物线开口向下,并向下无限延伸。
3.增减性:(Ⅰ)a>0时,当x时,y随x增大而减少当x>时,y随x增大而增大(Ⅱ)a<0时,当x时,y随x增大而增大当x>时,y随x增大而减小4.最值:(Ⅰ)a>0时,当x=时,(Ⅱ)a<0时,当x= 时,5.抛物线与y轴交点坐标:(0,C)特别地当C=0时,抛物线过原点,反之也成立。
6.抛物线与x轴的位置关系:(Ⅰ)Δ=b2-4ac<0,抛物线与x轴无交点。
(Ⅱ)Δ=b2-4ac=0,抛物线与x轴只有一个交点,交点坐标为(,0)(Ⅲ)Δ=b2-4ac>0,抛物线与x轴有两个交点,交点坐标为(,0)二、典型例题:例1.已知+3x+6是二次函数,求m的值,并判断此抛物线开口方向,写出顶点坐标及对称轴。
解:由题意得解得 m=-1∴y=-3x2+3x+6=,开口向下,顶点坐标(),对称轴x=。
说明:在y=a(x-h)2+k中,(h,k)是抛物线的顶点坐标,所以一般求抛物线的顶点坐标时,常常利用配方法把解析式转化为上述表达形式,直接写出顶点坐标,对称轴方程,也可以用顶点坐标公式()求得,解题时可根据系数的情况选择适当的方法。
例2.已知抛物线y=ax2+bx+c 如图所示,直线x=-1是其对称轴,(1)确定a,b,c, Δ=b2-4a c的符号,(2)求证:a-b+c>0, (3)当x取何值时,y>0, 当x取何值时y<0。
九年级数学二次函数的图象与性质湘教版知识精讲

九年级数学二次函数的图象与性质湘教版【本讲教育信息】一. 教学内容:二次函数的图象与性质教学要求:(一)知识与技能要求1. 知道二次函数的图象是抛物线,并且知道抛物线的顶点2. 通过“列表、描点、连线”三步作二次函数y=ax2,y=a(x+d)2,y=a(x+d)2+k,y=ax2+bx+c的图象3. 能说出上述抛物线的对称轴、顶点坐标、开口方向4. 能根据二次函数的图象说明函数值随自变量取值的变化而升或降的性质5. 知道抛物线的顶点坐标与抛物线的最大值(最小值)之间的关系,并能依据抛物线的开口方向确定抛物线的最值(二)过程与方法要求1. 经历探索二次函数y=ax2,y=a(x+d)2,y=a(x+d)2+k,y=ax2+bx+c的图象的作法和性质的过程2. 体会数形结合的思想(三)情感态度与价值观要求1. 积极投入到探索活动中,勇于发表个人意见。
2. 数学活动中充满着探索性,通过认识、观察、归纳、类比可以获得数学猜想二. 重点、难点重点:1. 二次函数y=ax2(a≠0)的性质2. 二次函数y=ax2+bx+c的平移规律3. 求二次函数的最大值或最小值难点:二次函数的性质的应用三. 主要内容:(一)y=ax2(a≠0)的图象及性质1. 二次函数y=ax2的图象是一条抛物线当a>0时,抛物线开口向上,且向上无限伸展a<0时,抛物线开口向下,并且向下无限伸展2. 二次函数y=ax2的性质对称轴是y轴,顶点在原点处a>0,开口向上;a<0,开口向下(二)二次函数y=ax2+bx+c的图象1. 二次函数y=ax2+k的图象可由抛物线y=ax2向上(下)平移得到当k>0时,抛物线y=ax2向上平移|k|个单位,得y=ax2+kk<0时,抛物线y =ax 2向下平移|k|个单位,得y =ax 2+k2. 二次函数y =a (x +d )2的图象由抛物线y =ax 2向左(右)平移 当d>0,抛物线y =ax 2向左平移|d|个单位,得y =a (x +d )2d<0,抛物线y =ax 2向右平移|d|个单位,得y =a (x +d )23. 一般地,抛物线y =a (x +d )2+k 与y =ax 2的形状相同,只是位置不同。
二次函数的三种表示方式(解析版)

二次函数的三种表示方式高中必备知识点1:一般式形如下面的二次函数的形式称为一般式:y =ax 2+bx +c (a ≠0);典型考题【典型例题】已知抛物线y =ax 2+bx +c 的对称轴为x =﹣1,且过点(﹣3,0),(0,﹣3). (1)求抛物线的表达式.(2)已知点(m ,k )和点(n ,k )在此抛物线上,其中m ≠n ,请判断关于t 的方程t 2+mt +n =0是否有实数根,并说明理由.【答案】(1)y =x 2+2x ﹣3;(2)方程有两个不相等的实数根. 【解析】(1)抛物线y =ax 2+bx +c 的对称轴为x =﹣1,且过点(﹣3,0),(0,3) 9a ﹣3b +c =0930312a b c c b a⎧⎪-+=⎪=-⎨⎪⎪-=-⎩ 解得a =1,b =2,c =﹣3 ∴抛物线y =x 2+2x ﹣3;(2)∵点(m ,k ),(n ,k )在此抛物线上, ∴(m ,k ),(n ,k )是关于直线x =﹣1的对称点, ∴+2m n=﹣1 即m =﹣n ﹣2 b 2﹣4ac =m 2﹣4n =(﹣n ﹣2)2﹣4n =n 2+4>0∴此方程有两个不相等的实数根.【变式训练】抛物线的图象如下,求这条抛物线的解析式。
(结果化成一般式)【答案】【解析】由图象可知抛物线的顶点坐标为(1,4),设此二次函数的解析式为y=a(x-1)2+4把点(3,0)代入解析式,得:4a+4,即a=-1所以此函数的解析式为y=-(x-1)2+4故答案是y=-x2+2x+3.【能力提升】如图,在平面直角坐标系中,抛物线先向右平移2个单位,再向下平移2个单位,得到抛物线. (1)求抛物线的解析式(化为一般式);(2)直接写出抛物线的对称轴与两段抛物线弧围成的阴影部分的面积.【答案】(1) ;(2)4.【解析】 (1)抛物线的顶点坐标为,把点先向右平移2个单位,再向下平移2个单位后得到的点的坐标为,抛物线的解析式为;(2)顶点坐标为,且抛物线的对称轴与两段抛物线弧围成的阴影部分的面积,抛物线的对称轴与两段抛物线弧围成的阴影部分的面积.高中必备知识点2:顶点式形如下面的二次函数的形式称为顶点式:y =a (x -h )2+k (a ≠0),其中顶点坐标是(h ,k ).典型考题【典型例题】已知二次函数21322y x x =-++. ⑴用配方法将此二次函数化为顶点式; ⑵求出它的顶点坐标和对称轴方程.【答案】(1)()21122y x =--+;(2)(1,2),直线1x = 【解析】 (1)21322y x x =-++()21232y x x =--- ()2121132y x x =--+--()212142y x x ⎡⎤=--+-⎣⎦ ()21142y x ⎡⎤=---⎣⎦()21122y x =--+(2)∵()21122y x =--+∴顶点坐标为(1,2),对称轴方程为直线1x =.【变式训练】已知二次函数的图象的顶点是(﹣1,2),且经过(1,﹣6),求这个二次函数的解析式. 【答案】二次函数的解析式为y=﹣2(x+1)2+2. 【解析】∵二次函数的图象的顶点是(﹣1,2),∴设抛物线顶点式解析式y=a (x+1)2+2,将(1,﹣6)代入得,a (1+1)2+2=﹣6, 解得a=﹣2,所以,这个二次函数的解析式为y=﹣2(x+1)2+2.【能力提升】二次函数的图象经过点(03)A -,,(23)B -,,(10)C -,. (1)求此二次函数的关系式; (2)求此二次函数图象的顶点坐标;(3)填空:把二次函数的图象沿坐标轴方向最少..平移 个单位,使得该图象的顶点在原点.【答案】(1)322--=x x y ;(2)(1,-4);(3)5【解析】(1)设c bx ax y ++=2,把点(03)A -,,(23)B -,,(10)C -,代入得 ⎪⎩⎪⎨⎧=---=++-=03343b a c b a c ,解得⎪⎩⎪⎨⎧-=-==321c b a∴322--=x x y ;(2)∵4)1(3222--=--=x x x y∴函数的顶点坐标为(1,-4); (3)∵|1-0|+|-4-0|=5∴二次函数的图象沿坐标轴方向最少平移5个单位,使得该图象的顶点在原点.高中必备知识点3:交点式形如下面的二次函数的形式称为交点式:y =a (x -x 1) (x -x 2) (a ≠0),其中x 1,x 2是二次函数图象与x 轴交点的横坐标.典型考题【典型例题】已知在平面直角坐标系中,二次函数 y =x 2+2x +2k ﹣2 的图象与 x 轴有两个交点. (1)求 k 的取值范围;(2)当 k 取正整数时,请你写出二次函数 y =x 2+2x +2k ﹣2 的表达式,并求出此二次函数图象与 x 轴的两个交点坐标.【答案】(1)k <;(2)(﹣2,0)和(0,0).【解析】(1)∵图象与x轴有两个交点,∴方程有两个不相等的实数根,∴解得(2)∵k 为正整数,∴k=1.∴令y=0,得解得∴交点为(﹣2,0)和(0,0).【变式训练】已知二次函数的图象经过点(3,-8),对称轴是直线x=-2,此时抛物线与x轴的两交点间距离为6.(1)求抛物线与x轴两交点坐标;(2)求抛物线的解析式.【答案】(1)(-5,0),(1,0);(2)y=-x2-2x+.【解析】(1) ∵因为抛物线对称轴为直线x=-2,且图象与x轴的两个交点的距离为6,∴点A、B到直线x=-2的距离为3,∴A为(-5,0),B为(1,0);(2)设y=a(x+5)(x-1).∵点(3,-8)在抛物线上,∴-8=a(3+5)(3-1),a=-,∴y=-x2-2x+.【能力提升】已知二次函数y=x2﹣4x+3.(1)求该二次函数与x轴的交点坐标和顶点;(2)在所给坐标系中画出该二次函数的大致图象,并写出当y<0时,x的取值范围.【答案】(1)二次函数与x轴的交点坐标为(1,0)(3,0),抛物线的顶点坐标为(2,﹣1);(2)图见详解;当y<0时,1<x<3.【解析】(1)当y=0时,x2﹣4x+3=0,解得x1=1,x2=3,所以该二次函数与x轴的交点坐标为(1,0)(3,0);因为y=x2﹣4x+3=x2﹣4x+4﹣1=(x﹣2)2﹣1,所以抛物线的顶点坐标为(2,﹣1);(2)函数图象如图:由图象可知,当y<0时,1<x<3.专题验收测试题1.将抛物线y=﹣2(x+1)2﹣2向左平移2个单位,向下平移3个单位后的新抛物线解析式为()A.y=﹣2(x﹣1)2+1 B.y=﹣2(x+3)2﹣5C.y=﹣2(x﹣1)2﹣5 D.y=﹣2(x+3)2+1【答案】B【解析】解:将抛物线y=﹣2(x+1)2﹣2向左平移2个单位,向下平移3个单位后的新抛物线解析式为:y=﹣2(x+3)2﹣5.故选:B.2.二次函数y=﹣2(x﹣1)2+3的图象的顶点坐标是()A.(1,3)B.(﹣1,3)C.(1,﹣3)D.(﹣1,﹣3)【答案】A【解析】解:二次函数y=﹣2(x﹣1)2+3的图象的顶点坐标为(1,3).故选:A.3.若二次函数y=(k+1)x2﹣2x+k的最高点在x轴上,则k的值为()A.1 B.2 C.﹣1 D.﹣2【答案】D【解析】∵二次函数y=(k+1)x2﹣2x+k的最高点在x轴上,∴△=b2﹣4ac=0,即8﹣4k(k+1)=0,解得:k1=1,k2=﹣2,当k=1时,k+1>0,此时图象有最低点,不合题意舍去,则k的值为:﹣2.故选:D.4.已知二次函数为常数,且),()A.若,则的增大而增大;B.若,则的增大而减小;C.若,则的增大而增大;D.若,则的增大而减小;【答案】C【解析】解:∵y=ax2+(a+2)x-1对称轴直线为,x=-=-.由a<0得,->0.∴->-1.又∵a<0∴抛物线开口向下.故当x<-时,y随x增大而增大.又∵x<-1时,则一定有x<-.∴若a<0,则x<-1,y随x的增大而增大.故选:C.5.二次函数y=3(x﹣1)2+2,下列说法正确的是()A.图象的开口向下B.图象的顶点坐标是(1,2)C.当x>1时,y随x的增大而减小D.图象与y轴的交点坐标为(0,2)【答案】B【解析】解:A、因为a=3>0,所以开口向上,错误;B、顶点坐标是(1,2),正确;C、当x>1时,y随x增大而增大,错误;D、图象与y轴的交点坐标为(0,5),错误;故选:B.6.将抛物线y=x2﹣x+1先向左平移2个单位长度,再向上平移3个单位长度,则所得抛物线的表达式为()A.y=x2+3x+6 B.y=x2+3x C.y=x2﹣5x+10 D.y=x2﹣5x+4【答案】A【解析】,当向左平移2个单位长度,再向上平移3个单位长度,得.故选A.7.把抛物线y=ax2+bx+c图象先向左平移2个单位长度,再向下平移3个单位长度,所得的图象的解析式是y=x2+5x+6,则a﹣b+c的值为()A.2 B.3 C.5 D.12【答案】B【解析】y=x2+5x+6=(x+)2﹣.则其顶点坐标是(﹣,﹣),将其右左平移2个单位长度,再向上平移3个单位长度后得到(﹣).故原抛物线的解析式是:y=(x+)2+=x2+x+3.所以a=b=1,c=3.所以a﹣b+c=1﹣1+3=3.故选B.8.已知二次函数y=﹣(x﹣k+2)(x+k)+m,其中k,m为常数.下列说法正确的是()A.若k≠1,m≠0,则二次函数y的最大值小于0B.若k<1,m>0,则二次函数y的最大值大于0C.若k=1,m≠0,则二次函数y的最大值小于0D.若k>1,m<0,则二次函数y的最大值大于0【答案】B【解析】∵y=﹣(x﹣k+2)(x+k)+m=﹣(x+1)2+(k﹣1)2+m,∴当x=﹣1时,函数最大值为y=(k﹣1)2+m,则当k<1,m>0时,则二次函数y的最大值大于0.故选:B.9.关于抛物线,下列说法错误..的是().A.开口向上B.与轴只有一个交点C.对称轴是直线D.当时,的增大而增大【答案】B【解析】解:A、,抛物线开口向上,所以A选项的说法正确;B、当时,即,此方程没有实数解,所以抛物线与x轴没有交点,所以B选项的说法错误;C、抛物线的对称轴为直线,所以C选项的说法正确;D、抛物线开口向上,抛物线的对称轴为直线,则当时,y随x的增大而增大,所以D选项的说法正确.故选:B.10.将抛物线y=﹣3x2+1向左平移2个单位长度,再向下平移3个单位长度,所得到的抛物线为()A.y=﹣3(x﹣2)2+4 B.y=﹣3(x﹣2)2﹣2C.y=﹣3(x+2)2+4 D.y=﹣3(x+2)2﹣2【答案】D【解析】将抛物线y=﹣3x2+1向左平移2个单位长度所得直线解析式为:y=﹣3(x+2)2+1;再向下平移3个单位为:y=﹣3(x+2)2+1﹣3,即y=﹣3(x+2)2﹣2.故选D.11.已知抛物线经过点,则该抛物线的解析式为__________.【答案】【解析】解:将A、O两点坐标代入解析式得:,解得:,∴该抛物线的解析式为:y=.12.二次函数y=(a-1)x2-x+a2-1 的图象经过原点,则a的值为______.【答案】-1【解析】解:∵二次函数y=(a-1)x2-x+a2-1 的图象经过原点,∴a2-1=0,∴a=±1,∵a-1≠0,∴a≠1,∴a的值为-1.故答案为:-1.13.将二次函数y=x2的图象先向上平移1个单位,然后向右平移2个单位,得到新的二次函数的顶点式为______.【答案】y=(x-2)2+1【解析】解:将抛物线y=x2的图象先向上平移1个单位,然后向右平移2个单位后,得到的抛物线的表达式为y=(x-2)2+1,故答案为:y=(x-2)2+1.14.将抛物线y=2x2平移,使顶点移动到点P(﹣3,1)的位置,那么平移后所得新抛物线的表达式是_____.【答案】y=2(x+3)2+1【解析】抛物线y=2x2平移,使顶点移到点P(﹣3,1)的位置,所得新抛物线的表达式为y=2(x+3)2+1.故答案为:y=2(x+3)2+115.在平面直角坐标系xOy 中,函数y = x2的图象经过点M (x1 , y1 ) ,N (x2 , y2 ) 两点,若- 4< x1<-2,0< x2<2 ,则y1 ____ y2 . (用“ <”,“=”或“>”号连接)【答案】>【解析】解:抛物线y=x2的对称轴为y轴,而M(x1,y1)到y轴的距离比N(x2,y2)点到y轴的距离要远,所以y1>y2.故答案为:>.16.小颖从如图所示的二次函数的图象中,观察得出了下列信息:;;;;.你认为其中正确信息的个数有______.【答案】【解析】解:抛物线的对称轴位于y轴左侧,则a、b同号,即,抛物线与y轴交于正半轴,则,所以,故错误;如图所示,当时,,所以,故正确;对称轴,,则如图所示,当时,,,,故正确;如图所示,当时,,故错误;综上所述,正确的结论是:.故答案是:.17.已知二次函数y=﹣x2+bx﹣c的图象与x轴的交点坐标为(m﹣2,0)和(2m+1,0).(1)若x<0时,y随x的增大而增大,求m的取值范围;(2)若y =1时,自变量x 有唯一的值,求二次函数的解析式. 【答案】(1)31=m (2)y =﹣x 2﹣4x ﹣3和y =﹣x 2﹣16x ﹣63. 【解析】解:(1)由题意可知,二次函数图象的对称轴为x =2213122m m m -++-=,∵a =﹣1<0,∴二次函数的图象开口向下, ∵x <0时,y 随x 的增大而增大,∴312m -≥0, 解得m ≥13,(2)由题意可知,二次函数的解析式为y =﹣(x ﹣312m -)2+1, ∵二次函数的图象经过点(m ﹣2,0), ∴0=﹣(m ﹣2﹣312m -)2+1, 解得m =﹣1和m =﹣5,∴二次函数的解析式为y =﹣x 2﹣4x ﹣3和y =﹣x 2﹣16x ﹣63. 18.设二次函数y 1=ax 2+bx +a ﹣5(a ,b 为常数,a ≠0),且2a +b =3. (1)若该二次函数的图象过点(﹣1,4),求该二次函数的表达式;(2)y 1的图象始终经过一个定点,若一次函数y 2=kx +b (k 为常数,k ≠0)的图象也经过这个定点,探究实数k ,a 满足的关系式;(3)已知点P (x 0,m )和Q (1,n )都在函数y 1的图象上,若x 0<1,且m >n ,求x 0的取值范围(用含a 的代数式表示).【答案】(1)y =3x 2﹣3x ﹣2;(2)k =2a ﹣5;(3)x 0<.【解析】解:(1)∵函数y 1=ax 2+bx +a ﹣5的图象经过点(﹣1,4),且2a +b =3 ∴,∴,∴函数y 1的表达式为y =3x 2﹣3x ﹣2; (2)∵2a +b =3∴二次函数y1=ax2+bx+a﹣5=ax2+(3﹣2a)x+a﹣5,整理得,y1=[ax2+(3﹣2a)x+a﹣3]﹣2=(ax﹣a+3)(x﹣1)﹣2∴当x=1时,y1=﹣2,∴y1恒过点(1,﹣2)∴代入y2=kx+b得∴﹣2=k+3﹣2a得k=2a﹣5∴实数k,a满足的关系式:k=2a﹣5(3)∵y1=ax2+(3﹣2a)x+a﹣5∴对称轴为x=﹣,∵x0<1,且m>n∴当a>0时,对称轴x=﹣,解得,当a<0时,对称轴x=﹣,解得(不符合题意,故x0不存在)故x0的取值范围为:19.已知二次函数y=x2+bx+c的图象经过点A和点B(1)求该二次函数的解析式;(2)写出该抛物线的对称轴及顶点坐标.【答案】(1) y=x2﹣4x﹣6;(2)对称轴为x=2;顶点坐标是(2,﹣10).【解析】(1)根据题意,得,解得,∴所求的二次函数的解析式为y=x2﹣4x﹣6.(2)又∵y=x2﹣4x﹣6=(x﹣2)2﹣10,∴函数图象的对称轴为x=2;顶点坐标是(2,﹣10).20.如图,对称轴为直线x=-1的抛物线y=x2+bx+c与x轴相交于A、B两点,其中A点的坐标为(-3,0),C为抛物线与y轴的交点.(1)求抛物线的解析式;(2)若点P在抛物线上,且S△POC=2S△BOC,求点P的坐标.【答案】(1)y=x2+2x﹣3;(2)点P的坐标为(2,5)或(﹣2,﹣3)【解析】(1)∵抛物线的对称轴为x=﹣1,A点的坐标为(﹣3,0),∴点B的坐标为(1,0).将点A和点B的坐标代入抛物线的解析式得:解得:b=2,c=﹣3,∴抛物线的解析式为y=x2+2x﹣3.(2)∵将x=0代y=x2+2x﹣3入,得y=﹣3,∴点C的坐标为(0,﹣3).∴OC=3.∵点B的坐标为(1,0),∴OB=1.设点P的坐标为(a,a2+2a﹣3),则点P到OC的距离为|a|.∵S△POC=2S△BOC,∴12OC•|a|=12OC•OB,即12×3×|a|=2×12×3×1,解得a=±2.当a=2时,点P的坐标为(2,5);当a=﹣2时,点P的坐标为(﹣2,﹣3).∴点P的坐标为(2,5)或(﹣2,﹣3).21.已知抛物线y=ax2﹣3ax﹣4a(a≠0).(1)直接写出该抛物线的对称轴.(2)试说明无论a为何值,该抛物线一定经过两个定点,并求出这两个定点的坐标.【答案】(1);(2)抛物线一定经过点.【解析】解:(1)该抛物线的对称轴为x=-;(2)可化为,当,即时,,抛物线一定经过点.22.如图,已知点A(-1,0),B(3,0),C(0,)在抛物线y=ax2+bx+c 上.(1)求抛物线解析式;(2)在第一象限的抛物线上求一点P,使△PBC的面积为.【答案】(1);(2)点P的坐标为(1,2)或(2,).【解析】(1)设抛物线的解析式为y=a(x+1)(x-3),将C(0,)代入,得-3a=,解得∴抛物线的解析式为(2)过点P作PD⊥x轴于D.设点,∴S四边形ACOB=S梯形PDOC+S△PBD =(=∴S△PBC=S四边形PCOB- S△BOC=整理得,解得x=1或x=2.∴点P的坐标为(1,2)或(2,)。
二次函数y=ax2的图象和性质ppt课件

例4 如图, 四个二次函数的图象分别对应 ① y=ax2 ;② y=bx2;
③ y=cx2;④ y=dx2,且①与③,②与④分别关于x 轴对称.
(1)比较a,b,c,d 的大小; (2)说明a 与c,b 与d 的数量关系.
解:(1)由抛物线的开口方向,知 a > 0,b > 0,c < 0,d < 0,
由抛物线的开口大小,知 |a| > |b|,|c| > |d|, 因此a > b,c < d. ∴ a > b > d > c. (2)∵①与③,②与④分别关于x 轴对称,
∴①与③,②与④的开口大小相同,方向相反. ∴ a+c=0,b+d=0.
课堂练习
1、下列函数中,y总随x增大而减小的是( B )
归纳总结
位置开 开口向上,在x轴上方 开口向下,在x轴下方
口方向
a的绝对值越大,开口越小
对称性 顶点最值
关于y轴对称,对称轴方程是直线x=0 顶点坐标是原点(0,0)
当x=0时,y最小值=0 当x=0时,y最大值=0
增减性
在对称轴左侧递减 在对称轴左侧递增 在对称轴右侧递增 在对称轴右侧递减
1、如右图,观察函数y=( k-1)x2的图象, 则k的取值范围是 k>1 .
复习引入
1.二次函数的一般形式是怎样的? y=ax²+bx+c(a,b,c是常数,a≠ 0)
2.下列函数中,哪些是二次函数?
①
②
③
④
⑤
3.一次函数的图象是一条 直线.
4.通常怎样画一个函数的图象? 列表、描点、连线
那么,二次函数的图象会是什么样的图形呢?这节课我们 来学习最简单的二次函数y=ax2的图像
不同点: a的值越大,开口越小.
二次函数图象信息题的四种常见类型

抛物线开口向上的图像
1
特点
图像开口朝上,a>0。
2
性质在抛物ຫໍສະໝຸດ 的中心处,函数取得最小值,也称为“顶点”,坐标为(f(g),-h(f(g)))。
3
例题
如果抛物线y=ax^2+bx+c的顶点是(-1,4),则方程的形式是什么?
抛物线开口向下的图像
特点
图像开口朝下,a<0。
性质
函数的最大值位于抛物线的中心 处,其坐标为(f(g),-h(f(g)))。
二次函数图象信息题的四 种常见类型
在学习二次函数时,掌握常见的四种图像类型对于学生们是非常重要的。这 个幻灯片将介绍这些类型,以及如何轻松应对与它们相关的信息问题。
什么是二次函数?
1 定义
二次函数是形如y=ax^2+bx+c的函数,其中a,b,c为常数,a不等于零。图像为开口朝 上或朝下的轮廓类似于一个U形。
例题
如果抛物线y=ax^2+bx+c的最大 值点是(2,5),则a的值是多少?
两个实根的图像
特点
图像与x轴有两个交点(实 根),a>0。
性质
当x趋近于正无穷或负无穷时, 二次函数趋近于无穷大。此 外,抛物线的轴线是根的平 均值。
例题
给定二次函数y=-2(x-4)(x-3), 求它的零点是多少?
无实根的图像
1
特点
图像可以用a(x-h)^2+k的形式表示,其中a<0。
2
性质
在抛物线的中心处,函数达到最大值。图像完全位于或高于x轴上方。
3
例题
二次方程y=x^2+4x+13有实根吗?如果不是,图像是什么样子的?
初三数学. 二次函数的图象判断和几何变换

二次函数的图象判断和几何变换模块一:二次函数的图象判断1.二次函数图象与系数的关系 (1)a 决定抛物线的开口方向当0a >时,抛物线开口向上;当0a <时,抛物线开口向下.反之亦然. (2)b 和a 共同决定抛物线对称轴的位置:“左同右异”当0b =时,抛物线的对称轴为y 轴;当a 、b 同号时,对称轴在y 轴的左侧;当a 、b 异号时,对称轴在y 轴的右侧.(3)c 的大小决定抛物线与y 轴交点的位置当0c =时,抛物线与y 轴的交点为原点;当0c >时,交点在y 轴的正半轴;当0c <时,交点在y 轴的负半轴.2.二次函数的图象信息(1)根据抛物线的开口方向判断a 的正负性. (2)根据抛物线的对称轴判断b 的正负性. (3)根据抛物线与y 轴的交点,判断c 的正负性. (4)根据抛物线与x 轴有无交点,判断24b ac -的正负性. (5)根据抛物线的对称轴可得2ba-与1±的大小关系,可得2a b ±的正负性. (6)根据抛物线所经过的已知坐标的点,可得到关于a ,b ,c 的等式.(7)根据抛物线的顶点,判断244ac b a -的大小.模块二:二次函数的几何变换 1.二次函数图象的平移平移规律:在原有函数的基础上“左加右减”,“上加下减”.2.二次函数图象的对称一般有五种情况,可以用一般式或顶点式表达. (1)关于x 轴对称关于x 轴对称后,得到的解析式是.2()y a x h k =-+关于x 轴对称后,得到的解析式是2()y a x h k =---. (2)关于轴对称关于y 轴对称后,得到的解析式是.2()y a x h k =-+关于y 轴对称后,得到的解析式是2()y a x h k =++. (3)关于原点对称关于原点对称后,得到的解析式是.2y ax bx c =++2y ax bx c =---y 2y ax bx c =++2y ax bx c =-+2y ax bx c =++2y ax bx c =-+-2()y a x h k =-+关于原点对称后,得到的解析式是2()y a x h k =-+-. (4)关于点(,)m n 对称2()y a x h k =-+关于点(,)m n 对称后,得到的解析式是2(2)2y a x h m n k =-+-+- 3.二次函数图象的翻折函数的图象可以由函数通过关于x 轴的翻折变换得到.具体规则为函数图象在x 轴上方的部分不变,在x 轴下方的部分翻折到x 轴上方.|()|y f x =()y f x =()y f x =模块一 二次函数的图象判断题组一:(1)二次函数2y ax bx c =++的图象如图1-1,则一次函数()y a b x ac =++的图象不经过( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限(2)二次函数2y ax bx c =++的图象如图1-2,则下列六个代数式:ab 、ac 、a b c ++、a b c -+、2a b +、2a b -、24b ac -中,其值为正的式子的个数是( ) A .5个 B .4个 C .3个 D .2个(3)二次函数2y ax bx c =++的图象如图1-3,则22a b c a b c a b a b ++--+++--_______0.(填“>”、“<”或“=”).图1-1 图1-2 图1-3题组二:(1)如图2-1,二次函数2y ax bx c =++的图象经过点(1,2)-,下列结论:①420a b c -+<;②20a b -<;③2b <-;④22()a c b +<,其中正确的结论有________.(填序号)(2)如图2-2,已知二次函数2y ax bx c =++的图象经过点(1,2),下列结论:①20a b +<;②0abc <;③1a c +<-;④284b a ac +<,其中正确结论的有________.(填序号)(3)(成外半期)二次函数2(0)y ax bx c a =++≠的图象如图2-3所示,有下列5个结论:①0abc <;②b a c <+;③420a b c ++>;④240b ac ->;⑤()a b m am b +>+,(1m ≠的实数),其中正确的结论的有________.(填序号)图2-1 图2-2 图2-3题组三:(1)已知二次函数2(0)y ax bx c a =++≠的图像如图3-1所示,它与x 轴两个交点分别为(1,0)-,30(,).对于下列命题:①20b a -=;②0abc <;③102a b c --+<;④80a c +>.其中正确的有________.(填序号)(2)如图3-2,抛物线2(0)y ax bx c a =++≠的对称轴是1x =-,且过点1,02⎛⎫ ⎪⎝⎭,有下列结论:①0abc >;②240a b c -+=;③251040a b c -+=;④320b c +>.其中正确的结论有________.(填序号) (3)如图3-3,已知二次函数2(0)y ax bx c a =++≠的图象与x 轴交于点(10A -,),对称轴为直线1x =,与y 轴的交点B 在(0,2)和(0,3)之间(包括这两点),下列结论:①当3x >时,0y <;②30a b +<;③213a -≤≤-;④248acb a ->;其中正确的结论是_________.(填序号)图3-1 图3-2 图3-3题组四:(1)已知二次函数y ax bx c 2=+++2的图象如图4-1所示,顶点为(,)-10,下列结论:①abc <0;②b ac 2-4=0;③a >2;④a b c 4-2+>0.其中正确结论的个数是____________.(填序号) (2)二次函数2y ax bx c =++的图象如图4-2所示,给出下列结论:①20a b +>;②若11m n -<<<,则bm n a+<-;③3||||2||a cb +<;④b ac >>,其中正确的结论有____________.(填序号)图4-1 图4-2yAO xx =1模块二 二次函数的几何变换题组一:(1)二次函数2241y x x =-++的图象如何移动就得到22y x =-的图象( ). A .向左移动1个单位,向上移动3个单位 B .向右移动1个单位,向上移动3个单位 C .向左移动1个单位,向下移动3个单位D .向右移动1个单位,向下移动3个单位(2)一抛物线向右平移3个单位,再向下平移2个单位后得抛物线224y x x =-+,则平移前抛物线的解析式为________________.(3)如果将抛物线228y x =-+向右平移a 个单位后,恰好过点(3,6),那么a 的值为__________. 题组二:(1)如图6-1所示,已知抛物线0C 的解析式为22y x x =-,则抛物线0C 的顶点坐标____________;将抛物线0C 每次向右平移2个单位,平移n 次,依次得到抛物线1C 、2C 、3C 、…、n C (n 为正整数),则抛物线n C 的解析式为___________. (2)如图6-2,把抛物线212y x =平移得到抛物线m ,抛物线m 经过点(6,0)A -和原点(0,0)O ,它的顶点为P ,它的对称轴与抛物线212y x =交于点Q ,则图中阴影部分的面积为___________.图6-1 图6-2题组三:已知二次函数221y x x =--,求:(1)与此二次函数关于x 轴对称的二次函数解析式为_____________________; (2)与此二次函数关于y 轴对称的二次函数解析式为_____________________; (3)与此二次函数关于原点对称的二次函数解析式为_____________________. 题组四:已知二次函数2441y ax ax a =++-的图象是1C . (1)求1C 关于点(1,0)R 中心对称的图象2C 的解析式;(2)设曲线1C 、2C 与y 轴的交点分别为A ,B ,当||18AB =时,求a 的值.xyO…C nC 1C 0题组五:作出2|5|y x x =+的函数图象. 题组七:已知关于x 的一元二次方程22410x x k ++-=有实数根,k 为正整数. (1)求k 的值;(2)当此方程有两个非零的整数根时,将关于x 的二次函数2241y x x k =++-的图象向下平移8个单位,求平移后的图象的解析式;(3)在(2)的条件下,将平移后的二次函数的图象在x 轴下方的部分沿x 轴翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当直线1()2y x b b k =+<与此图象有两个公共点时,b 的取值范围.复习巩固模块一 二次函数的图象判断(1)二次函数2y ax bx c =++的图象如图1-1,则一次函数by ax c =-的图象不经过第________象限.(2)如图1-2,二次函数2y ax bx c =++的图象经过点(1,2)-和(1,0),给出五个结论:①0abc <;②20a b +>;③1a c +=;④1a >;⑤9640a b c ++>.其中结论正确的是________.(3)二次函数2y ax bx c =++的图象如图1-3,小丹观察得出了下面五条信息:①0c <;②0abc >;③0a b c -+>;④230a b -=;⑤40c b ->,其中结论正确的是________.图1-1 图1-2 图1-3(1)已知二次函数2y ax bx c =++的图象如图2-1所示,有下列结论:①240b ac ->;②0abc >;③20a b +>;④930a b c ++<;⑤80a c +>.其中结论正确的是________.(填序号即可)(2)如图2-2,抛物线2y ax bx c =++的图象交x 轴于1(,0)A x 、(2,0)B ,交y 轴正半轴于C ,且OA OC =.下列结论:①0a b c ->;②1ac b =-;③12a =-;④22bc +=,其中结论正确的是________.图2-1 图2-2Oyx模块二 二次函数的几何变换(1)(树德实验半期)把抛物线2y x =-向左平移1个单位,然后向上平移3个单位,则平移后的抛物线的解析式为________.(2)将函数2y x x =+的图象向右平移(0)a a >个单位,得到函数232y x x =-+的图象,则a 的值为________.(3)如图,在平面直角坐标xOy 中,抛物线1C 的顶点为(1,4)A --,且过点(3,0)B -: ①将抛物线1C 向右平移2个单位得抛物线2C ,则抛物线2C 的解析式_____________; ②写出阴影部分的面积S =_____________.(1)在平面直角坐标系中,先将抛物线22y x x =+-关于x 轴作轴对称变换,再将所得的抛物线关于y 轴作轴对称变换,则经两次变换后所得的新抛物线的解析式为________.(2)已知二次函数234y x x =--的图象,将其函数图象在x 轴下方的部分沿x 轴翻折,图象的其余部分保持不变,得到一个新的图象,结合图象写出当直线(1)y x n n =+<与这个新图象有两个公共点时,n 的取值范围为__________.y xOyxO AB。
例析利用二次函数的图象求一元二次方程的根

例析利用二次函数的图象求一元二次方程的根二次函数是一个常见的二次方程方程的图象,通过利用二次函数的图象可以求解一元二次方程的根。
一元二次方程的一般形式为:ax^2 + bx + c = 0,其中a、b、c为常数,且a≠0。
首先,我们来分析二次函数的图象。
二次函数的标准形式为y =ax^2 + bx + c,其中a≠0,对应的图象是一个抛物线。
如果a>0,那么抛物线开口向上,最低点在y轴上方,如果a<0,那么抛物线开口向下,最低点在y轴下方。
我们可以通过观察二次函数的图象,抛物线与x轴相交的点就是一元二次方程的根。
根据图象的特点,我们可以得出下面的结论:1.如果二次函数图象与x轴有两个交点,那么一元二次方程有两个不同的实数根;2.如果二次函数图象与x轴有且只有一个交点,那么一元二次方程有一个实数根;3.如果二次函数图象与x轴没有交点,那么一元二次方程没有实数根。
接下来,我们以一个具体的例子来说明如何利用二次函数的图象求解一元二次方程的根。
例1:求解方程x^2-3x+2=0的根。
首先,我们将方程的系数与一元二次方程的一般形式对应起来,可以看出a=1,b=-3,c=2我们可以通过求解方程的判别式来判断该方程有几个实数根。
判别式的计算公式为D=b^2 - 4ac,其中D为判别式的值。
根据判别式的值可以得出以下结论:1.如果D>0,方程有两个不同的实数根;2.如果D=0,方程有一个实数根;3.如果D<0,方程没有实数根。
我们将系数代入计算判别式:D=(-3)^2-4*1*2=9-8=1根据判别式的结果,我们可以得知方程有两个不同的实数根。
接下来,我们可以画出二次函数的图象来求解方程的根。
首先,我们可以画出抛物线的大致形状。
由于判别式大于0,所以抛物线开口向上。
现在,我们需要找到抛物线与x轴的交点。
我们可以看出,抛物线与x轴的交点对应方程的根。
根据题意,我们需要求解方程的两个根,所以我们需要找到抛物线与x轴的两个交点。
《二次函数y=ax^2的图象与性质》知识点解读

《二次函数y=ax²的图象与性质》知识点解读知识点1 二次函数y=ax²的图象及有关概念二次函数的图象函数y=ax2(a≠0)的图象是一条关于y轴对称的曲线,这条曲线叫做抛物线。
实际上,二次函数的图象都是抛物线,y轴是抛物线y=ax2(a≠0)的对称轴,对称轴与抛物线的交点是抛物线的顶点。
用描点法画二次函数y=ax2(a≠0)的图象(1)按步骤列表、描点、连线。
(2)用描点法画二次函数y=ax2(a≠0)的图象时,应在O(0,0)点左右两侧(或在对称轴左右两侧)对称的选取自变量x的值,在计算y的值,这样的对应值选择月密集,描出的图象越精准。
通常情况下,画图一般选取9个点,草图通常取5或7个点,但必须画出抛物线的顶点,然后对称的取其他各点。
实际问题应在自变量取值范围内选取适当的几个点,一般选7个点,再进行描点。
连线时要注意图象的平滑,特别是顶点处更要注意,不能画得太平或者太尖,要顺势用平滑曲线连接。
知识点2 二次函数y=ax²的性质(1)二次函数y=ax2(a≠0)的图象是一条抛物线。
我们把二次函数y=ax2(a≠0)的图象叫做抛物线y=ax2。
(2)抛物线y=ax2(a≠0)的对称轴是y轴(即直线x=0),顶点是原点。
(3)当a>0时,抛物线y=ax2的开口向上,顶点是它的最低点,抛物线在x轴上方(顶点在x轴上),并且向上无限延伸;当a<0时,抛物线y=ax2的开口向下,顶点是它的最高点,抛物线在x 轴下方(顶点在x轴上),并且向下无限延伸。
(4)当a>0时,在y 轴左侧,y随x的增大而减小,在y 在右侧,y随x 的增大而减大,函数y的值,当x=0时最小,最小值是0;当a<0时,在y 在左侧,y随x的增大而增大,在y 在右侧,y随x 的增大而减小,函数y的值,当x=0时最大,最大值是0。
(5)当a 的绝对值越大,图象越靠近y 轴,抛物线开口越窄;当a 的绝对值越小,图象越远离y 轴,抛物线开口越宽。
二次函数图表总结

【最新】二次函数图表总结二次函数图表总结y=a_图象2a>0ay=a_+k图象2a>0a0开口对称性顶点k0ky=a(_-h)2图象a>0a0开口对称性顶点增减性h0hy=a(_-h)+k2a>0a0,k>0h>0,k0,kh0顶点是最低点左右平移y=a_2+k上下平移y=a(_h)2+k上下平移y=a(_h)2左右平移y=a_2一般地,抛物线y=a(_-h)+k与y=a_2的形状相同,位置不同.2y=a_2向上(k>0)【或向下(k0)【或左(h0)【或左(h0)【或下(k0)【或左(h0)【或下(k扩展阅读:二次函数单元总结二次函数单元总结【知识归纳和总结】一.知识网络二次函数的定义ya_2b_c(a0)ya_2(a0)二次函数的图像ya(_m)2k(a0)ya_2b_c(a0)二次函数二次函数的性质开口方向.对称轴.顶点坐标.增减性,二次函数与一元二次方程的关系二次函数的应用最大面积.利润等二.知识要点分布1.二次函数的定义:形如ya_2b_c(a.b.c为常数,a0〕的函数叫二次函数.任何一个二次函数的表达式都可以化为ya_2b_c的形式,这就是二次函数的一般形式.2.二次函数表达式的几种形式:〔1〕y=a_2;〔2〕y=a_2+k;〔3〕y=a(_+h)2;〔4〕〔5〕y=a_2+b_+c(a0).y=a(_+h)2+k;3.二次函数表达式的形式及对称轴.顶点坐标.〔1〕一般式:ya_b_c(a.b.c为常数,a0〕,其对称轴为直线_=-2b,顶点2ab4ac-b2坐标为-,.2a4a〔2〕顶点式:y=a(_+h)+k(a.h.k为常数,a0〕,其对称轴为直线_=-h,顶点坐标为-h,k.〔3〕交点式:y=a_-_1_-_2,其中a0,_1._2是抛物线与_轴两个交点的横坐标,即一元二次方程a_-_1_-_2=0的两个根.4.二次函数图像之间的平移关系1向上〔k>0〕或向下〔k0〕或向下〔k0〕或向下〔k0a对称轴顶点坐标直线_=-b2a 直线_=-b2ab4ac-b2-,2a4a当_-小;当_-大;b4ac-b2-,2a4a当_-大;性质增减性b 时,y随_的增大而减2ab时,y随_的增大而增2ab时,y随_的增大而增2ab时,y 随_的增大而减2a当_-小;最值当_=-b时,y有最小值,2a当_=-b时,y有最大值,2a4ac-b2y最小值=4a〞,〞p〞:{“h〞:19.298,〞w〞:9.111,〞_〞:407.786,〞y〞:455.644,〞z〞:象而具体了.7.抛物线的平移与解析式的变化.抛物线上最重要的点是它的顶点,最重要的线是它的对称轴,抛物线的平移首先表现为对称轴和顶点的平移.在抛物线y=a_-h+k中,令_-h=0易得对称轴为直线_=h,抛物线向右〔左〕平移那么对称轴也向右〔左〕平移,h的值将随之增大〔减小〕,反之也成立;抛物线上〔下〕平移,对称轴不会改变,即顶点的横坐标h的值不变,但顶点的纵坐标k的值将随之增大〔减小〕,反之也成立.抛物线的平移不会改变抛物线的形状,即a不变.在抛物线y=a_2+b_+c中研究平移是很不方便的,要先将y=a_2+b_+c的形式转化成2y=a(_-h)2+k再研究.抛物线平移的题型一般有以下几种:〔1〕抛物线的解析式,求平移后抛物线的解析式.例1将抛物线y=-3(_-1)2-3先向左平移2个单位,再向上平移5个单位,所得抛物线的解析式为.〔2〕平移后抛物线是解析式,求原抛物线的解析式.例2将抛物线y=a(_-h)2+k先向左平移5个单位,再向下平移4个单位后所得抛物线为y=-12_+2-3,那么原抛物线的解析式为.222〔3〕平移前后抛物线的解析式,求平移的方式.例3将抛物线y=-2_-2-5经过怎样的平移,可得抛物线y=-2_+4+3?8.图像共存问题的解法解决此类问题的关键是分析两函数的解析式有什么共同的特点,从这些特点入手,在利用抛物线的顶点位置和开口方向.双曲线所在象限.直线所在象限加以判断,决定取舍.例函数y=a_与函数y=a_+a在同一直角坐标系中的图像大致为〔〕A.B.C.D.29.抛物线的对称性的妙用.二次函数的图像是一条抛物线,其具有轴对称性.假设设抛物线上两个对称点的坐_+_标为_1,y1._2,y2,那么一定有y1=y2,且该抛物线的对称轴为直线_=12,利用它2可以简便.快捷地解决相关问题.例:二次函数y=a_2+b_+c的局部对应值如下表:_y……-37-200-81-93-557……二次函数y=a_2+b_+c的图形的对称轴为直线_=;_=2对应的函数值y=.【典型例题分析】题型一利用图像求二次函数y=a_2+b_+c的增减性例1二次函数y=-12_+_+4.2〔1〕试确定抛物线的开口方向.顶点坐标和对称轴;〔2〕_为何值时,y有最大〔小〕值?〔3〕求出抛物线与两坐标轴的交点;1〔4〕画出函数图形的草图,并说明该图像是y=-_2经过怎样的平移得到的; 2〔5〕根据图像答复,当_取何值时,y>0?y=0?y题型三二次函数与几何知识的综合应用例3如下图,某场地为一直角三角形,∠C=90°,AC=6m,BC=12m,现在要对四边形ABPQ进行装修,装修费为50元/m,且四边形ABPQ的边AQ为PC的一半,问怎样设计四边形ABPQ才能使装修费最少?2B例4如下图,二次函数y=-_2+a_+b的图形与_轴交于PCQA1A-,0.B2,0两点,且与y轴交于点C,求该抛物线的解析2式,并判断△ABC 的形状.题型四二次函数与其他函数的综合应用例5二次函数y=a_+b_+c的图像如下图,反比例函数y=在同一坐标系中的大致图像可能是〔〕2a与正比例函数y=b+c__A.B.C.D.题型五二次函数在生活.生产中的应用例6王亮同学善于改良学习方法,他发现对解题过程进行回忆反思,效果会更好.某一天他利用30分钟时间进行自主学习.假设他用于解题的时间_〔单位:分钟〕与学习收益量y的关系如图甲所示,用于回忆反思的时间_〔单位:分钟〕与学习收益量y的关系如图乙所示〔其中OA是抛物线的一局部,A为抛物线的顶点〕,且用于回忆反思的时间不超过用于解题的时间.〔1〕求王亮解题的学习收益量y与用于解题的时间_的函数解析式,并写出自变量_的取值范围;〔2〕求王亮回忆反思的学习收益量y与用于回忆反思的时间_之间的函数解析式;〔3〕王亮如何分配解题和回忆反思的时间,才能使这30分钟的学习收益总量最大?〔学习收益总量=解题的学习收益量+回忆反思的学习收益量〕y4O2_甲例7甲车在弯路做刹车试验,收集到的数据如下表所示:速度_/〔kmh〕10510152025…刹车距离y/m034215416354…〔1〕请用上表中的各对数据〔_,y〕作为点的坐标,在如图所示的坐标系中画出刹车距离y〔m〕与速度_〔kmh〕的函数图像,并求函数的解析式;〔2〕在一个限速为40kmh的弯路上,甲.乙两车相向而行,同时刹车,但还是相撞了,事后测得甲.乙两车刹车距离分别为12m和10.5m,又知乙车刹车距离y〔m〕与速度_〔km/h〕满足函数y析相撞原因.11_,请你就两车速度方面分4题型六二次函数与图形变换相结合例8如下图,在矩形ABCD中,BC=acm,AB=bcm,ab,且a.b是方程8-4_2_+3+=1的两个根.P是BC上一动点,动点Q在PC或_(_+5)_+5其延长线上,BP=PQ,以PQ为一边的正方形为PQRS.点P从B点开始沿射线BC方向运动.设BP=_cm,正方形PQRS与矩形ABCD重叠局部的面积为ycm. 〔1〕求a.b的值;〔2〕分别求出0_2和2_4时,y与_之间的函数关系式.2SADRBPCQ。
二次函数的图像和性质
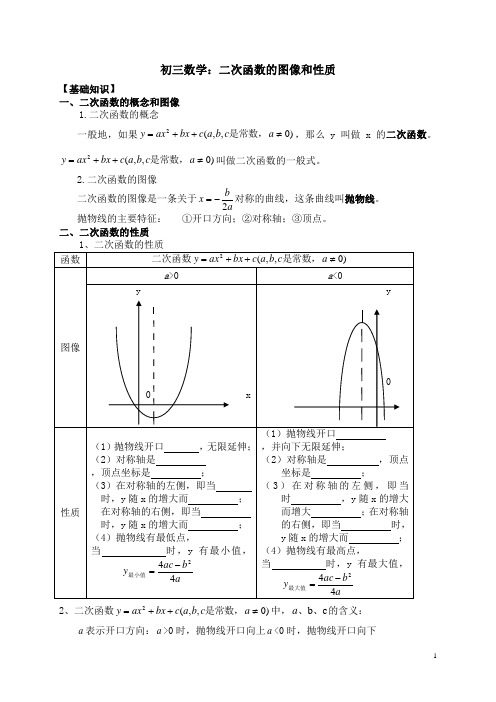
初三数学:二次函数的图像和性质【基础知识】一、二次函数的概念和图像 1.二次函数的概念一般地,如果)0,,(2≠++=a c b a c bx ax y 是常数,,那么y 叫做x 的二次函数。
)0,,(2≠++=a c b a c bx ax y 是常数,叫做二次函数的一般式。
2.二次函数的图像二次函数的图像是一条关于abx 2-=对称的曲线,这条曲线叫抛物线。
抛物线的主要特征: ①开口方向;②对称轴;③顶点。
二、二次函数的性质2、二次函数)0,,(2≠++=a c b a c bx ax y 是常数,中,c b 、、a 的含义:a 表示开口方向:a >0时,抛物线开口向上a <0时,抛物线开口向下yO1c+-1 b 与对称轴的位置有关(左同右异):对称轴为x=ab2- c 看抛物线与y 轴的交点坐标: 三、二次函数图象的平移2. 平移规律“左加右减,上加下减”. 【典型例题】如图,矩形ABCD 的两边长AB =18cm ,AD =4cm ,点P 、Q 分别从A 、B 同时出发,P 在边AB 上沿AB 方向以每秒2cm 的速度匀速运动,Q 在边BC 上沿BC 方向以每秒1cm 的速度匀速运动.设运动时间为x 秒,△PBQ 的面积为y (cm 2). (1)求y 关于x 的函数关系式,并写出x 的取值范围; (2)求△PBQ 的面积的最大值.对应练习:1. 二次函数2y ax bx c =++的图象如图所示,则反比例函数ay x=与一次函数y bx c =+在同一坐标系中的大致图象是( ).2. 如图,已知二次函数c bx x y ++=2的图象经过点(-1,0), (1,-2),当y 随x 的增大而增大时,x 的取值范围是 . 3. 已知二次函数c bx ax y ++=2的图像如图,其对称轴1-=x ,给出 下列结果①ac b 42>②0>abc ③02=+b a ④0>++c b a ⑤0<+-c b a , 则正确的结论是( )A ①②③④B ②④⑤C ②③④D ①④⑤ 【课堂检测】 22.(2013哈尔滨)把抛物线y=(x+1)2向下平移2个单位,再向右平移1个单位,所得到的抛物线是( ).(A)y=(x+2)2+2 (B)y=(x+2)2-2 (C)y=x 2+2 (D)y=x 2-24.(2011重庆)已知抛物线()20y ax bx c a =++≠在平面直角坐标系中的位置如图所示,则下列结论中,正确的是( ) A 、a >0 B 、b <0 C 、c <0 D 、a +b +c >05.(2011浙江)已知二次函数的图象(0≤x ≤3)如图所示,关于该函数在所给自变量取值范围内,下列说法正确的是( )A 、有最小值0,有最大值3B 、有最小值﹣1,有最大值0C 、有最小值﹣1,有最大值3D 、有最小值﹣1,无最大值 6.(2013•广安)已知二次函数y=ax 2+bx+c 的图象如图所示,对称轴是直线x=1.下列结论:①abc >O ,②2a+b=O ,③b 2﹣4ac <O ,④4a+2b+c >O7.(2012重庆)已知二次函数)0(2≠++=a c bx ax y 的图象如图所示对称轴为21-=x 。
二次函数图象和性质知识点总结

二次函数的图象和性质知识点总结一、知识点回顾1. 二次函数解析式的几种形式:①一般式:(a、b、c为常数,a≠0)②顶点式:(a、h、k为常数,a≠0),其中(h,k)为顶点坐标。
③交点式:,其中是抛物线与x轴交点的横坐标,即一元二次方程的两个根,且a≠0,(也叫两根式)。
2. 二次函数的图象①二次函数的图象是对称轴平行于(包括重合)y轴的抛物线,几个不同的二次函数,如果a相同,那么抛物线的开口方向,开口大小(即形状)完全相同,只是位置不同。
②任意抛物线可以由抛物线经过适当的平移得到,移动规律可简记为:[左加右减,上加下减],具体平移方法如下表所示。
③在画的图象时,可以先配方成的形式,然后将的图象上(下)左(右)平移得到所求图象,即平移法;也可用描点法:也是将配成的形式,这样可以确定开口方向,对称轴及顶点坐标。
然后取图象与y轴的交点(0,c),及此点关于对称轴对称的点(2h,c);如果图象与x轴有两个交点,就直接取这两个点(x1,0),(x2,0)就行了;如果图象与x轴只有一个交点或无交点,那应该在对称轴两侧取对称点,(这两点不是与y轴交点及其对称点),一般画图象找5个点。
(1)抛物线开口向(1)抛物线开口向(1)抛物线(1)抛物线4. 求抛物线的顶点、对称轴和最值的方法①配方法:将解析式化为的形式,顶点坐标为(h,k),对称轴为直线,若a>0,y有最小值,当x=h时,;若a<0,y有最大值,当x=h时,。
②公式法:直接利用顶点坐标公式(),求其顶点;对称轴是直线,若若,y有最大值,当5. 抛物线与x轴交点情况:对于抛物线①当时,抛物线与x轴有两个交点,反之也成立。
②当时,抛物线与x轴有一个交点,反之也成立,此交点即为顶点。
③当时,抛物线与x轴无交点,反之也成立。
二、考点归纳考点一求二次函数的解析式例1.已知二次函数f(x)满足f(2)=-1,f(-1)=-1,且f(x)的最大值是8,试求f(x)。
(完整版)非常好的讲义二次函数图像与性质

二次函数图像及性质一、二次函数的定义一般地,形如2y ax bx c =++(a b c ,,为常数,0a ≠)的函数称为x 的二次函数,其中x 为自变量,y 为因变量,a 、b 、c 分别为二次函数的二次项、一次项和常数项系数.注意:和一元二次方程类似,二次项系数0a ≠,而b 、c 可以为零.二次函数的自变量的取值范围是全体实数.二、二次函数的图象 1.二次函数图象与系数的关系 (1)a 决定抛物线的开口方向 当0a >时,抛物线开口向上;当0a <时,抛物线开口向下.反之亦然.a 决定抛物线的开口大小:a 越大,抛物线开口越小;a 越小,抛物线开口越大. 温馨提示:几条抛物线的解析式中,若a 相等,则其形状相同,即若a 相等,则开口及形状相同,若a 互为相反数,则形状相同、开口相反. (2)b 和a 共同决定抛物线对称轴的位置(抛物线的对称轴:2b x a=-) 当0b =时,抛物线的对称轴为y 轴; 当a 、b 同号时,对称轴在y 轴的左侧; 当a 、b 异号时,对称轴在y 轴的右侧.(3)c 的大小决定抛物线与y 轴交点的位置(抛物线与y 轴的交点坐标为()0c ,) 当0c =时,抛物线与y 轴的交点为原点; 当0c >时,交点在y 轴的正半轴;当0c <时,交点在y 轴的负半轴.2.二次函数图象的画法 五点绘图法:利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.一般我们选取的五点为:顶点、与y 轴的交点()0c ,、以及()0c ,关于对称轴对称的点()2h c ,、与x 轴的交点()10x ,,()20x ,(若与x 轴没有交点,则取两组关于对称轴对称的点).画草图时应抓住以下几点:开口方向,对称轴,顶点,与x 轴的交点,与y 轴的交点. 3。
第1讲二次函数的图象和性质复习课件(共39张PPT)

大师导航 归类探究 自主招生交流平台 思维训练
第二种是在瑞典本国流行的说法.在诺贝尔立遗嘱期 间,瑞典最有名望的数学家就是米塔格·勒弗列尔,诺贝尔 很明白,如果设立数学奖,这项奖金在当时必然会授予这位 数学家,而诺贝尔很不喜欢他.所以诺贝尔不设立数学奖.
全效优等生
大师导航 归类探究 自主招生交流平台 思维训练
全效优等生
大师导航 归类探究 自主招生交流平台 思维训练
从函数图象中获取信息 a的作用:决定开口的方向和大小. (1)a>0开口向上,a<0开口向下; (2)a越大,抛物线的开口越小. b的作用:决定顶点的位置. 左(对称轴在y轴左边) 同(a,b同号) 右(对称轴在y轴右边) 异(a,b异号) c的作用:决定抛物线与y轴交点的位置. 上(抛物线与y轴的交点在y轴正半轴)
全效优等生
大师导航 归类探究 自主招生交流平台 思维训练
【解析】 ①∵图象与x轴的交点A,B的横坐标分别为-1,3, ∴AB=4, ∴对称轴 x=-2ba=1, 即2a+b=0, 故①错误; ②根据图示可知,当x=1时,y<0,即a+b+c<0, 故②错误; ③∵点A的坐标为(-1,0), ∴a-b+c=0,且b=-2a, ∴a+2a+c=0,即c=-3a, 故③正确;
大师导航 归类探究 自主招生交流平台 思维训练
第一章 二次函数
第1讲 二次函数的图象和性质
全效优等生
全效优等生
大师导航 归类探究 自主招生交流平台 思维训练
诺贝尔为什么没有设数学奖 诺贝尔奖在全世界有很高的地位,许多科学家梦想着能 获得诺贝尔奖.数学被誉为“科学女皇的骑士”却得不到每年由 瑞典科学院颁发的诺贝尔奖,过去没有,将来也不会有.因为 瑞典著名化学家诺贝尔留下的遗嘱中没有提出设立数学奖.对 此,外界流传着两种说法. 第一种是在法国和美国流行的说法.与诺贝尔同时期的 瑞典著名数学家米塔格·勒弗列尔曾是俄国彼得堡科学院的外 籍院士,后来又是前苏联科学院的外籍院士.米塔格·勒弗列 尔曾侵犯过诺贝尔的夫人,诺贝尔对他非常厌恶.为了对他所 从事的数学研究进行报复,所以诺贝尔不设立数学奖.
二次函数系数与图像的关系(共32张PPT)

⑤、a-b+c>0,⑥、4a+2b+c<0,⑦、4a-2b+c<0.
小结:二次函数y=ax2+bx+c(a≠0)的系数a,b,c,△与
抛物线的关系
数
形
a a决定开口方向:a>0时开口向上,
a<0时开口向下
a、b同时决定对称轴位置:a、b同号时对称轴在y轴左侧
b
a、b异号时对称轴在y轴右侧
b=0时对称轴是y轴
由抛物线捕捉对称信息的方式有:
抛物线y=ax2+bx+c如图所示,试确定a、b、c的符号:
⑤、a-b+c>0,⑥、4a+2b+c<0,⑦、4a-2b+c<0.
3个
对称轴是y轴: b=0
三、随堂演练
1.根据图象判断a、b、c的符号
y
a _>___0
y
b__<__0
0
c__<___0
0
x
a _<___0
抛物线的关系
数
形
a决定开口方向:a>0时开口向上,
a
a<0时开口向下
a、b同时决定对称轴位置:a、b同号时对称轴在y轴左侧
b
a、b异号时对称轴在y轴右侧
b=0时对称轴是y轴
c决定抛物线与y轴的交点:c>0时抛物线交于y轴的正半轴
c
c=0时抛物线过原点
c<0时抛物线交于y轴的负半轴
△决定抛物线与x轴的交点:△>0时抛物线与x轴有两个交点
y
2、当x=-1时, y=a-b+c
3、当x=2时,
y=4a+2b+c
4、当x=-2时, y=4a-2b+c
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
从二次函数图象------抛物线中获取信息2015.01.05
一.选择题(共19小题)
1.如图为二次函数y=ax2+bx+c的图象,在下列说法中:
①abc>0;②方程ax2+bx+c=0的根为x1=﹣1,x2=3;③a+b+c>0;④当x>1时,y随着x的增大而增大.
正确的说法个数是()
2.小明从二次函数y=ax+bx+c的图象(如图)中观察得到了下面四条信息:①c<0;②abc<0;③a﹣b+c>0;
④2a+3b=0;你认为正确的信息是()
3.(2005•武汉)抛物线y=ax2+bx+c的图象如图,则下列结论:①abc>0;②a+b+c=2;③a>;④b<1.其中正确的结论是()
4.抛物线y=ax+bx+c的图象如图,则下列结论:①abc>0;②a+b+c=2;③a﹣b+c<0;④b﹣4ac<0.其中正确的结论是()
5.(2002•哈尔滨)已知二次函数y=ax+bx+c的图象如图,下列结论:①abc>0;②b=2a;③a+b+c<0;④a﹣b+c>0.其中正确的个数是()
6.已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论正确的有()个.
①abc<0,②2a+b=0,③a﹣b+c>0,④4a+2b+c>0,⑤b>﹣2c.
7.二次函数y=ax2+bx+c的图象如图,则下列各式中成立的个数是()
(1)abc<0;(2)a+b+c<0;(3)a+c>b;(4)a<﹣.
8.如图,已知二次函数y=ax2+bx+c的图象,下列结论:
①a+b+c<0;②a﹣b+c>0;③abc<0;④b=2a;⑤△<0.正确的个数是()
中正确的有()
10.如图是二次函数y=ax2+bx+c(a≠0)的图象,请你根据图中的信息判断下列四个结论:
①abc<0;②a+b+c<0;③9a+3b+c<0;④b=2a.其中正确的结论有()
11.如图是二次函数y=ax2+bx+c的图象,下列结论中:①abc>0;②b=2a;③a+b+c<0;④a﹣b+c>0;⑤4a+2b+c <0.正确的个数是()
12.如图,二次函数y=ax2+bx+c(a≠0)的图象与X轴的交点的横坐标为﹣1和3,给出下列说法:(1)abc<0;(2)方程ax2+bx+c=0的根为x1=﹣1,x2=3;(3)4a+2b+c>0;(4)8a+c<0;其中正确的结论的个数是()
13.如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(﹣1,2)和(1,0)且与y轴交于负半轴.结论:①abc<0;②2a+b>0;③a+c=1;(4)a>1.其中正确的结论的序号是()
14.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列四个结论:
①b2﹣4ac<0;②方程ax2+bx+c=0的根是x1=﹣3,x2=1;③abc>0;④a+b+c=0.
其中正确的个数有()
15.(2010•崇左)二次函数y=ax2+bx+c的图象如图所示,给出下列说法:①abc<0;②方程ax2+bx+c=0的根为x1=﹣1、x2=3;③当x>1时,y随x值的增大而减小;④当y>0时,﹣1<x<3.其中正确的说法是()
16.小明从二次函数y=ax2+bx+c的图象(如图)中观察得出了下面五条信息:
①c<0;②abc>0;③a﹣b+c>0;④2a﹣3b=0;⑤c﹣4b>0.你认为其中正确的信息是()
17.如图为抛物线y=ax2+bx+c的图象,A、B、C为抛物线与坐标轴的交点,且OA=OC=1,AB>AO,下列几个结论:
(1)abc<0;(2)b>2a;(3)a﹣b=﹣1;(4)4a﹣2b+1<0.
其中正确的个数是()
18.已知二次函数y=ax2+bx+c(a≠0)的图象如图,在下列代数式中(1)a+b+c>0;(2)﹣4a<b<﹣2a(3)abc >0;(4)5a﹣b+2c<0;其中正确的个数为()
19.(2011•雅安)已知二次函数y=ax2+bx+c的图象如图,其对称轴x=﹣1,给出下列结果①b2>4ac;②abc>0;
③2a+b=0;④a+b+c>0;⑤a﹣b+c<0,则正确的结论是()
二.填空题(共11小题)
20.如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,
给出下列命题:
①abc<0;②b>2a;③a+b+c=0 ④ax2+bx+c=0的两根分别为﹣3和1;⑤8a+c>0.
其中正确的命题是.
21.如图,已知二次函数y=ax2+bx+c(a≠0)的图象,则下列结论正确序号是(只填序号).
①abc>0;②c=﹣3a;③b2+ac>0.
22.如图,直线x=1是二次函数y=ax2+bx+c的图象的对称轴,则①a+b+c>0,②b<a+c,③abc<0,④2a=b中正确的是.(请把正确的序号填上)
23.已知抛物线y=ax2+bx+c的图象如图,则下列结论:①abc>0;②a+b+c=2;③a>;④b<1.其中正确的结论是.
24.已知y=ax2+bx+c的图象如图,则:a0,b0,c0,a﹣b+c0,b2﹣4ac0.
25.如图为二次函数y=ax2+bx+c的图象,则a0,b0,c0,b2﹣4ac0.
26.如图,由二次函数y=ax2+bx+c的图象确定下列各式的符号:b0,b2﹣4ac0,
a﹣b+c0.
27.已知抛物线y=ax2+bx+c(a≠0)如图.则abc0,a﹣b+c0,b2﹣4ac0.
28.已知二次函数y=ax2+bx+c的部分图象如图所示,则下列结论:①关于x的一元二次方程ax2+bx+c=0的解为﹣1,3;②abc>0;③2a+b=0;④4a+2b+c>0;⑤5a+2c>b中正确的有.(填写正确的序号)
29.二次函数y=ax2+bx+c的图象如图所示,以下结论:
①a+b+c=0;②4a+b=0;③abc<0;④4ac﹣b2<0;⑤当x≠2时,总有4a+2b>ax2+bx
其中正确的有(填写正确结论的序号).
30.抛物线y=ax2+bx+c中,b=4a,它的图象如图,有以下结论:
①c>0;②a+b+c>0;③a﹣b+c>0 ④b2﹣4ac<0;⑤abc<0;⑥4a>c;其中正确的为(填序号).。
