【中考必备】最新中考数学试题分类解析专题54 图形的旋转变换

合集下载

【中考数学专题】三大变换之旋转（旋转的性质）

【中考数学专题】三大变换之旋转（旋转的性质）
旋转是三大几何变换中考察最多、难度最大的，平移、对称从图像观察角度来说直接显然，对应的结论也很容易用到．而旋转变换得到的图形相对复杂些，有时候解题的突破口隐藏得更深，导致无从下手．本篇将从基本的性质开始，到一些常见的模型，最后说说关于构造旋转能给我们带来什么，全方位了解旋转在中考题中的考察．01基本性质
如下图，将△ABC绕点A旋转一定角度得到△ADE．
性质一：对应边相等
结论：AB=AD，AC=AE．
补充：当然还可以得到BC=DE，但这并没有什么用，因为BC与DE并没有特殊位置关系．
性质二：对应角相等
结论：∠B=∠D，∠C=∠E，∠BAC=∠DAE．
补充：如果不是特殊角，此性质并没有什么用，但由性质二可以推性质三．
性质三：旋转角都相等
结论：∠BAD=∠CAE=∠BFD．
补充：∠BAD=∠CAE易证，
∠BAD=∠BFD可用“8字”模型证明：
∵∠BAD+∠B=∠BFD+∠D，且∠B=∠D，
∴∠BAD=∠BFD．
且第三组夹角往往用得最多．
02真题速览
2019眉山中考-三角形的旋转
2019内江中考-旋转得等边
2019阜新中考-特殊角的旋转
2019包头中考-旋转角都相等
2018镇江中考-隐藏的特殊角
2019山西中考-解三角形2017吉林中考-矩形的旋转2019梧州中考-菱形的旋转2018陇南中考-正方形的旋转2019贺州中考-旋转的思考2019营口中考-动态的旋转来源：有一点数学，作者刘岳。

中考数学几何图形的变换历年真题解析

中考数学几何图形的变换历年真题解析几何图形的变换是中考数学中的重要内容，涉及平移、旋转、翻转等多种变换方式。

通过对历年真题的解析，我们可以更好地理解和掌握这些变换的方法和应用。

下面将对数学中考几何图形的变换部分进行详细解析。

一、平移变换平移变换是指将一个图形在平面上沿着一定方向移动一定的距离，保持图形形状和大小不变。

在中考中，常常要求计算平移后的图形坐标或者确定平移向量的特征等。

例题1：已知点A(3,4)，将点A沿向量(2,-3)平移，记平移后的点为B。

求点B的坐标。

解析：根据平移的定义和向量的性质，我们知道平移后点的坐标等于原来点的坐标加上平移向量的坐标。

所以，点B的坐标为(3+2, 4-3)，即B(5,1)。

例题2：如图，平行四边形ABCD经过平移变换得到新的平行四边形A'B'C'D'，其中AB=3cm，CB=4cm，平移向量为v，求平移向量v的坐标。

解析：首先，我们可以利用平行四边形的性质推导出平移向量v的坐标与平行四边形的对应边的向量相等。

由于AB在变换前和变换后分别与A'B'、B'C'平行，所以v的坐标等于AB的坐标，即v=(3, 0)。

二、旋转变换旋转变换是指将一个图形绕着一定的旋转中心按一定的角度旋转。

在中考中，常常要求计算旋转后的图形坐标或者确定旋转角度的特征等。

例题3：如图，A、B、C三点在平面内，点A经过逆时针旋转90°得到点B，点B经过逆时针旋转90°得到点C，求点C的坐标。

解析：根据旋转的性质，我们可以得出旋转90°后，点的坐标分别等于原来点的y坐标、-x坐标。

所以，点C的坐标为(-2, 3)。

例题4：如图，正方形ABCD绕顶点A顺时针旋转90°得到新图形，求旋转后点C的坐标。

解析：根据旋转的性质，我们可以将旋转90°看作将原点逆时针旋转90°。

因此，旋转后点C的坐标为(-1, 1)。

2022年中考数学真题分类汇编：图形的旋转(含答案)

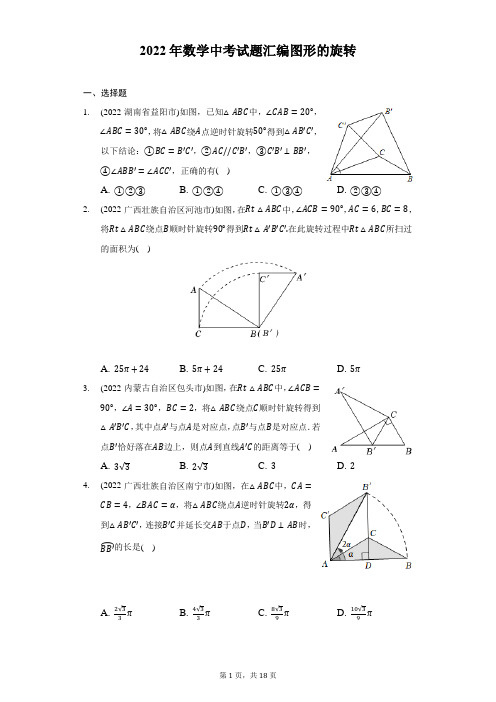
2022年数学中考试题汇编图形的旋转一、选择题1.(2022·湖南省益阳市)如图，已知△ABC中，∠CAB=20°，∠ABC=30°，将△ABC绕A点逆时针旋转50°得到△AB′C′，以下结论：①BC=B′C′，②AC//C′B′，③C′B′⊥BB′，④∠ABB′=∠ACC′，正确的有( )A. ①②③B. ①②④C. ①③④D. ②③④2.(2022·广西壮族自治区河池市)如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，将Rt△ABC绕点B顺时针旋转90°得到Rt△A′B′C′.在此旋转过程中Rt△ABC所扫过的面积为( )A. 25π+24B. 5π+24C. 25πD. 5π3.(2022·内蒙古自治区包头市)如图，在Rt△ABC中，∠ACB=90°，∠A=30°，BC=2，将△ABC绕点C顺时针旋转得到△A′B′C，其中点A′与点A是对应点，点B′与点B是对应点．若点B′恰好落在AB边上，则点A到直线A′C的距离等于( )A. 3√3B. 2√3C. 3D. 24.(2022·广西壮族自治区南宁市)如图，在△ABC中，CA=CB=4，∠BAC=α，将△ABC绕点A逆时针旋转2α，得到△AB′C′，连接B′C并延长交AB于点D，当B′D⊥AB时，BB′⏜的长是( )A. 2√33π B. 4√33π C. 8√39π D. 10√39π5.(2022·内蒙古自治区赤峰市)如图，AB是⊙O的直径，将弦AC绕点A顺时针旋转30°得到AD，此时点C的对应点D落在AB上，延长CD，交⊙O于点E，若CE=4，则图中阴影部分的面积为( )A. 2πB. 2√2C. 2π−4D. 2π−2√26.(2022·天津市)如图，在△ABC中，AB=AC，若M是BC边上任意一点，将△ABM绕点A逆时针旋转得到△ACN，点M的对应点为点N，连接MN，则下列结论一定正确的是( )A. AB=ANB. AB//NCC. ∠AMN=∠ACND. MN⊥AC7.(2022·贵州省遵义市)在平面直角坐标系中，点A(a,1)与点B(−2,b)关于原点成中心对称，则a+b的值为( )A. −3B. −1C. 1D. 38.(2022·湖南省娄底市)如图，等边△ABC内切的图形来自我国古代的太极图，等边三角形内切圆中的黑色部分和白色部分关于等边△ABC的内心成中心对称，则圆中的黑色部分的面积与△ABC的面积之比是( )A. √3π18B. √318C. √3π9D. √399.(2022·湖南省)下列图形中，既是轴对称图形又是中心对称图形的是( )A. B.C. D.10.(2022·湖南省娄底市)下列与2022年冬奥会相关的图案中，是中心对称图形的是( )A. B.C. D.11.(2022·湖南省)下列图形中，既是轴对称图形又是中心对称图形的是( )A. B.C. D.12.(2022·湖南省)下列图形中，既是轴对称图形又是中心对称图形的是( )A. B.C. D.13.(2022·湖南省)下列图形中，既是轴对称图形又是中心对称图形的是( )A. B.C. D.14.(2022·湖南省)下列图形中，既是轴对称图形又是中心对称图形的是( )A. B.C. D.15.(2022·湖南省)下列图形中，既是轴对称图形又是中心对称图形的是( )A. B.C. D.16.(2022·上海市)有一个正n边形旋转90°后与自身重合，则n为( )A. 6B. 9C. 12D. 15二、填空题17.(2022·青海省西宁市)如图，在△ABC中，∠C=90°，∠B=30°，AB=6，将△ABC绕点A逆时针方向旋转15°得到△AB′C′，B′C′交AB于点E，则B′E=______．18.(2022·湖北省随州市)如图1，在矩形ABCD中，AB=8，AD=6，E，F分别为AB，AD的中点，连接EF.如图2，将△AEF绕点A逆时针旋转角θ(0°<θ<90°)，使EF⊥AD，连接BE并延长交DF于点H.则∠BHD的度数为，DH的长为．19.(2022·吉林省)第二十四届北京冬奥会入场式引导牌上的图案融入了中国结和雪花两种元素．如图，这个图案绕着它的中心旋转角α(0°<α<360°)后能够与它本身重合，则角α可以为______度．(写出一个即可)20.(2022·辽宁省盘锦市)如图，在△ABC中，AB=AC，∠ABC=30°，点D为BC的中点，将△ABC绕点D逆时针旋转得到△A′B′C′，当点A的对应点A′落在边AB上时，点C′在BA的延长线上，连接BB′，若AA′=1，则△BB′D的面积是______．21.(2022·湖南省永州市)如图，图中网格由边长为1的小正方形组成，点A为网格线的交点．若线段OA绕原点O顺时针旋转90°后，端点A的坐标变为______．三、解答题22.(2022·广西壮族自治区河池市)如图、在平面直角坐标系中，△ABC的三个顶点的坐标分别为A(4,1)，B(2,3)，C(1,2)．(1)画出与△ABC关于y轴对称的△A1B1C1；(2)以原点O为位似中心，在第三象限内画一个△A2B2C2，使它与△ABC的相似比为2：1，并写出点B2的坐标．23.(2022·吉林省)图①，图②均是4×4的正方形网格，每个小正方形的顶点称为格点．其中点A，B，C均在格点上，请在给定的网格中按要求画四边形．(1)在图①中，找一格点D，使以点A，B，C，D为顶点的四边形是轴对称图形；(2)在图②中，找一格点E，使以点A，B，C，E为顶点的四边形是中心对称图形．24.(2022·江苏省常州市)如图，点A在射线OX上，OA=a.如果OA绕点O按逆时针方向旋转n°(0<n≤360)到OA’，那么点A’的位置可以用(a,n°)表示．(1)按上述表示方法，若a=3，n=37，则点A’的位置可以表示为______；(2)在(1)的条件下，已知点B的位置用(3,74°)表示，连接A’A、A’B.求证：A’A=A’B．25.(2022·湖北省武汉市)如图是由小正方形组成的9×6网格，每个小正方形的顶点叫做格点．△ABC的三个顶点都是格点．仅用无刻度的直尺在给定网格中完成画图，画图过程用虚线表示．(1)在图(1)中，D，E分别是边AB，AC与网格线的交点．先将点B绕点E旋转180°得到点F，画出点F，再在AC上画点G，使DG//BC；(2)在图(2)中，P是边AB上一点，∠BAC=α.先将AB绕点A逆时针旋转2α，得到线段AH，画出线段AH，再画点Q，使P，Q两点关于直线AC对称．26.(2022·四川省广安市)数学活动课上，张老师组织同学们设计多姿多彩的几何图形，如图都是由边长为1的小等边三角形构成的网格，每个网格图中有3个小等边三角形已涂上阴影，请同学们在余下的空白小等边三角形中选取一个涂上阴影，使得4个阴影小等边三角形组成一个轴对称图形或中心对称图形，请画出4种不同的设计图形．(规定：凡通过旋转能重合的图形视为同一种图形)，1.【答案】B【解析】解：①∵△ABC绕A点逆时针旋转50°得到△AB′C′，∴BC=B′C′.故①正确；②∵△ABC绕A点逆时针旋转50°，∴∠BAB′=50°．∵∠CAB=20°，∴∠B′AC=∠BAB′−∠CAB=30°．∵∠AB′C′=∠ABC=30°，∴∠AB′C′=∠B′AC．∴AC//C′B′.故②正确；③在△BAB′中，AB=AB′，∠BAB′=50°，∴∠AB′B=∠ABB′=12(180°−50°)=65°．∴∠BB′C′=∠AB′B+∠AB′C′=65°+30°=95°．∴CB′与BB′不垂直．故③不正确；④在△ACC′中，AC=AC′，∠CAC′=50°，∴∠ACC′=12(180°−50°)=65°．∴∠ABB′=∠ACC′.故④正确．∴①②④这三个结论正确．故选：B．2.【答案】A【解析】解：∵∠ACB=90°，AC=6，BC=8，∴AB=10，∴Rt△ABC所扫过的面积=90⋅π×102360+12×6×8=25π+24，故选：A．3.【答案】C【解析】解：连接AA′，如图，∵∠ACB =90°，∠BAC =30°，BC =2， ∴AC =√3BC =2√3，∠B =60°， ∵将△ABC 绕点C 顺时针旋转得到△A′B′C ， ∴CA =CA′，CB =CB′，∠ACA′=∠BCB′， ∵CB =CB′，∠B =60°，∴△CBB′为等边三角形，∴∠BCB′=60°，∴∠ACA′=60°，∴△CAA′为等边三角形，过点A 作AD ⊥A′C 于点D ，∴CD =12AC =√3，∴AD =√3CD =√3×√3=3， ∴点A 到直线A′C 的距离为3，故选：C ． 4.【答案】B【解析】解：根据题意可得， AC′//B′D ，∵B′D ⊥AB ，∴∠C′AD =∠C′AB′+∠B′AB =90°， ∵∠C′AD =α，∴α+2α=90°，∴α=30°，∵AC =4，∴AD =AC ⋅cos30°=4×√32=2√3， ∴AB =2AD =4√3，∴BB′⏜的长度l =nπr 180=60×π×4√3180=4√33．【解析】解：连接OE，OC，BC，由旋转知AC=AD，∠CAD=30°，∴∠BOC=60°，∠ACE=(180°−30°)÷2=75°，∴∠BCE=90°−∠ACE=15°，∴∠BOE=2∠BCE=30°，∴∠EOC=90°，即△EOC为等腰直角三角形，∵CE=4，∴OE=OC=2√2，∴S阴影=S扇形OEC−S△OEC=90π×(2√2)2360−12×2√2×2√2=2π−4，故选：C．6.【答案】C【解析】解：A、∵AB=AC，∴AB>AM，由旋转的性质可知，AN=AM，∴AB>AN，故本选项结论错误，不符合题意；B、当△ABC为等边三角形时，AB//NC，除此之外，AB与NC不平行，故本选项结论错误，不符合题意；C、由旋转的性质可知，∠BAC=∠MAN，∠ABC=∠ACN，∵AM=AN，AB=AC，∴∠ABC=∠AMN，∴∠AMN=∠ACN，本选项结论正确，符合题意；D、只有当点M为BC的中点时，∠BAM=∠CAM=∠CAN，才有MN⊥AC，故本选项结论错误，不符合题意；【解析】解：∵点A(a,1)与点B(−2,b)关于原点成中心对称，∴a =2，b =−1，∴a +b =1，故选：C ．8.【答案】A【解析】解：作AD ⊥BC 于点D ，作BE ⊥AC 于点E ，AD 和BE 交于点O ，如图所示，设AB =2a ，则BD =a ，∵∠ADB =90°，∴AD =√AB 2−BD 2=√3a ， ∴OD =13AD =√33a ， ∴圆中的黑色部分的面积与△ABC 的面积之比是：π×(√33a)2×122a⋅√3a2=√3π18，故选：A ． 9.【答案】C【解析】解：A.是轴对称图形，不是中心对称图形，故本选项错误；B .不是轴对称图形，是中心对称图形，故本选项错误；C .既是轴对称图形，又是中心对称图形，故本选项正确；D .是轴对称图形，不是中心对称图形，故本选项错误．故选C ．10.【答案】D【解析】解：A.不是中心对称图形，故此选项不合题意；B .不是中心对称图形，故此选项不合题意；C .不是中心对称图形，故此选项不合题意；D .是中心对称图形，故此选项符合题意；故选：D ．11.【答案】D【解析】解：A.是中心对称图形，不是轴对称图形，故此选项不合题意；B .不是中心对称图形，也不是轴对称图形，故此选项不合题意；C.不是中心对称图形，是轴对称图形，故此选项不合题意；D.既是中心对称图形，也是轴对称图形，故此选项符合题意；故选：D．12.【答案】D【解析】解：A.不是中心对称图形，是轴对称图形，故此选项不合题意；B.是中心对称图形，不是轴对称图形，故此选项不合题意；C.不是中心对称图形，是轴对称图形，故此选项不合题意；D.既是中心对称图形，也是轴对称图形，故此选项符合题意；故选：D．13.【答案】C【解析】解：A.是轴对称图形，不是中心对称图形，故此选项不合题意；B.是轴对称图形，不是中心对称图形，故此选项不合题意；C.既是轴对称图形又是中心对称图形，故此选项符合题意；D.是轴对称图形，不是中心对称图形，故此选项不合题意；故选：C．14.【答案】C【解析】解：A.既不是中心对称图形，也不是轴对称图形，故此选项不合题意；B.既不是中心对称图形，也不是轴对称图形，故此选项不合题意；C.既是中心对称图形，也是轴对称图形，故此选项符合题意；D.不是中心对称图形，是轴对称图形，故此选项不合题意；故选：C．15.【答案】C【解析】解：A.不是中心对称图形，是轴对称图形，故此选项不合题意；B.是中心对称图形，不是轴对称图形，故此选项不合题意；C.既是中心对称图形，也是轴对称图形，故此选项符合题意；D.不是中心对称图形，是轴对称图形，故此选项不合题意；故选：C．16.【答案】C【解析】解：A.正6边形旋转90°后不能与自身重合，不合题意；B.正9边形旋转90°后不能与自身重合，不合题意；C.正12边形旋转90°后能与自身重合，符合题意；D.正15边形旋转90°后不能与自身重合，不合题意；故选：C．17.【答案】3√3−3【解析】解：在△ABC中，∵∠C=90°，∠B=30°，AB=6，∴AC=3，BC=3√3，∠CAB=60°，∵将△ABC绕点A逆时针方向旋转15°得到△AB′C′，∴△ABC≌△AB′C′，∠C′AE=45°，∴AC=AC′=C′E=3，BC=B′C′=3√3，∴B′E=B′C′−C′E=3√3−3．先在含30°锐角的直角三角形中计算出两条直角边，再根据旋转性质得到对应边相等、对应角相等得到AC=AC′=C′E=3，BC=B′C′=3√3，即可解答．18.【解析】解：如图，设EF交AD于点J，AD交BH于点O，过点E作EK⊥AB于点K．∵∠EAF=∠BAD=90°，∴∠DAF=∠BAE，∵AFAD =AEAB=12，∴AFAE =ADAB，∴△DAF∽△BAE，∴∠ADF=∠ABE，∵∠DOH=∠AOB，∴∠DHO=∠BAO=90°，∴∠BHD=90°，∵AF=3，AE=4，∠EAF=90°，∴EF=√32+42=5，∵EF⊥AD，∴12⋅AE⋅AF=12⋅EF⋅AJ，∴AJ =125，∴EJ =√AE 2−AJ 2=√42−(125)2=165， ∵EJ//AB ，∴OJ OA =EJ AB ，∴OJOJ+125=1658， ∴OJ =85， ∴OA =AJ +OJ =125+85=4， ∴OB =√AB 2+AO 2=√42+82=4√5，OD =AD −AO =6−4=2，∵cos∠ODH =cos∠ABO ，∴DH OD =AB BO ， ∴DH 2=4√5， ∴DH =4√55．故答案为：90°，4√55． 19.【答案】72(答案不唯一)．【解析】解：360°÷5=72°，则这个图案绕着它的中心旋转72°后能够与它本身重合，故答案为：72(答案不唯一)． 20.【答案】3√34【解析】解：如下图所示，设A′B′与BD 交于点O ，连接A′D 和AD ，∵点D 为BC 的中点，AB =AC ，∠ABC =30°，∴AD ⊥BC ，A′D ⊥B′C′，A′D 是∠B′A′C′的角平分线，AD 是∠BAC ，∴∠B′A′C′=120°，∠BAC=120°，∴∠BAD=∠B′A′D=60°，∵A′D=AD，∴△A′AD是等边三角形，∴A′A=AD=A′D=1，∵∠BA′B′=180°−∠B′A′C′=60°，∴∠BA′B′=∠A′AD，∴A′B′//AD，∴A′O⊥BC，∴A′O=12A′D=12，∴OD=√1−14=√32，∵A′B′=2A′D=2，∵∠A′BD=∠A′DO=30°，∴BO=OD，∴OB′=2−12=32，BD=2OD=√3，∴S△BB′D=12×BD×B′O=12×√3×32=3√34．先证明△A′AD是等边三角形，再证明A′O⊥BC，再利用直角三角形30°角对应的边是斜边的一半分别求出A′B′和A′O，再利用勾股定理求出OD，从而求得△BB′D的面积．21.【答案】(2,−2)【解析】解：线段OA绕原点O顺时针旋转90°如图所示，则A′(2,−2)，则旋转后A点坐标变为：(2,−2)，故答案为：(2,−2)．22.【答案】解：(1)如图，△A1B1C1为所作；(2)如图，△A2B2C2为所作，点B2的坐标为(−4,−6)；【解析】(1)根据关于y轴对称的点的坐标得到A1、B1、C1的坐标，然后描点即可；(2)把A、B、C的坐标都乘以−2得到A2、B2、C2的坐标，然后描点即可．本题考查了位似变换：在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或−k.也考查了轴对称变换．23.【答案】解：(1)作点B关于直线AC的对称点D，连接ABCD，四边形ABCD为筝形，符合题意．(2)将点A向右平移1个单位，再向上平移1个单位可得点D，连接ABCD，AD//BC且AD= BC，∴四边形ABCD为矩形，符合题意．24.【答案】(1)解：由题意，得A′(a,n°)，∵a=3，n=37，∴A′(3,37°)，故答案为：(3,37°)；(2)证明：如图：∵A′(3,74°)，B(3,74°)，∴∠AOA′=37°，∠AOB=74°，OA=OB=3，∴∠A′OB=∠AOB−∠AOA′=74°−37°=37°，∵OA′=OA′，∴△AOA′≌△BOA′(SAS)，∴A′A=A′B．25.【答案】解：(1)如图(1)中，点F，点G即为所求；(2)如图(2)中，线段AH，点Q即为所求．26.【答案】解：图形如图所示：【解析】利用轴对称图形，中心对称图形的性质，画出图形即可．本题考查利用作图设计图案，等边三角形的判定和性质，轴对称图形，中心对称图形等知识，解题的关键是理解题意，灵活运用所学知识解决问题．。

中考数学综合题专题复习【旋转】专题解析含答案

一、旋转真题与模拟题分类汇编（难题易错题）1．小明在矩形纸片上画正三角形，他的做法是：①对折矩形纸片ABCD(AB>BC)，使AB与DC重合，得到折痕EF，把纸片展平；②沿折痕BG折叠纸片，使点C落在EF上的点P 处，再折出PB、PC，最后用笔画出△PBC(图1)．（1）求证：图1中的PBC是正三角形：（2）如图2，小明在矩形纸片HIJK上又画了一个正三角形IMN，其中IJ=6cm，且HM=JN．①求证：IH=IJ②请求出NJ的长；（3）小明发现：在矩形纸片中，若一边长为6cm，当另一边的长度a变化时，在矩形纸片上总能画出最大的正三角形，但位置会有所不同．请根据小明的发现，画出不同情形的示意图(作图工具不限，能说明问题即可)，并直接写出对应的a的取值范围．【答案】（1）证明见解析；（2）①证明见解析；②1233）3＜a＜3，a＞3【解析】分析：（1）由折叠的性质和垂直平分线的性质得出PB=PC，PB=CB，得出PB=PC=CB即可；（2）①利用“HL”证Rt△IHM≌Rt△IJN即可得；②IJ上取一点Q，使QI=QN，由Rt△IHM≌Rt△IJN知∠HIM=∠JIN=15°，继而可得∠NQJ=30°，设NJ=x，则IQ=QN=2x、3，根据IJ=IQ+QJ求出x即可得；（3）由等边三角形的性质、直角三角形的性质、勾股定理进行计算，画出图形即可．（1）证明：∵①对折矩形纸片ABCD(AB>BC)，使AB与DC重合，得到折痕EF∴PB=PC∵沿折痕BG折叠纸片，使点C落在EF上的点P处∴PB=BC∴PB=PC=BC∴△PBC是正三角形：（2）证明：①如图∵矩形AHIJ∴∠H=∠J=90°∵△MNJ 是等边三角形∴MI=NI在Rt △MHI 和Rt △JNI 中MI NI MH NJ =⎧⎨=⎩∴Rt △MHI ≌Rt △JNI （HL ）∴HI=IJ②在线段IJ 上取点Q ，使IQ=NQ∵Rt △IHM ≌Rt △IJN ，∴∠HIM=∠JIN ，∵∠HIJ=90°、∠MIN=60°，∴∠HIM=∠JIN=15°，由QI=QN 知∠JIN=∠QNI=15°，∴∠NQJ=30°，设NJ=x ，则IQ=QN=2x ，QJ=22=3QN NJ -x ，∵IJ=6cm ，∴2x+3x=6，∴x=12-63，即NJ=12-63（cm ）．（3）分三种情况：①如图：设等边三角形的边长为b ，则0＜b≤6，则tan60°=3=2ab，∴a=32b，∴0＜b≤632=33；②如图当DF与DC重合时，DF=DE=6，∴a=sin60°×DE=632=33，当DE与DA重合时，a=643sin603==︒，∴33＜a＜43；③如图∵△DEF是等边三角形∴∠FDC=30°∴DF=643cos303==︒∴a＞3点睛：本题是四边形的综合题目，考查了折叠的性质、等边三角形的判定与性质、旋转的性质、直角三角形的性质、正方形的性质、全等三角形的判定与性质等知识；本题综合性强，难度较大．2．在平面直角坐标系中，O为原点，点A（0，4），点B（﹣2，0），把△ABO绕点A逆时针旋转，得△AB′O′，点B、O旋转后的对应点为B′、O′．（1）如图①，若旋转角为60°时，求BB′的长；（2）如图②，若AB′∥x轴，求点O′的坐标；（3）如图③，若旋转角为240°时，边OB上的一点P旋转后的对应点为P′，当O′P+AP′取得最小值时，求点P′的坐标（直接写出结果即可）【答案】（1）252）点O′的坐标为（855，55+4）；（3）点P′的坐标为（﹣83 5，365．【解析】分析：（1）由点A、B的坐标可得出AB的长度，连接BB′，由旋转可知：AB=AB′，∠BAB′=60°，进而可得出△ABB′为等边三角形，根据等边三角形的性质可求出BB′的长；（2）过点O′作O′D⊥x轴，垂足为D，交AB′于点E，则△AO′E∽△ABO，根据旋转的性质结合相似三角形的性质可求出AE、O′E的长，进而可得出点O′的坐标；（3）作点A关于x轴对称的点A′，连接A′O′交x轴于点P，此时O′P+AP′取最小值，过点O′作O′F⊥y轴，垂足为点F，过点P′作PM⊥O′F，垂足为点M，根据旋转的性质结合解直角三角形可求出点O′的坐标，由A、A′关于x轴对称可得出点A′的坐标，利用待定系数法即可求出直线A′O′的解析式，由一次函数图象上点的坐标特征可得出点P的坐标，进而可得出OP的长度，再在Rt△O′P′M中，通过解直角三角形可求出O′M、P′M的长，进而可得出此时点P′的坐标．详解：（1）∵点A（0，4），点B（﹣2，0），∴OA=4，OB=2，∴AB22OA OB5．在图①中，连接BB′．由旋转可知：AB=AB′，∠BAB′=60°，∴△ABB′为等边三角形，∴BB′=AB5（2）在图②中，过点O′作O′D⊥x轴，垂足为D，交AB′于点E．∵AB′∥x轴，O′E⊥x轴，∴∠O′EA=90°=∠AOB．由旋转可知：∠B′AO′=∠BAO，AO′=AO=4，∴△AO′E∽△ABO，AEAO='O EBO='AOAB，即4AE ='2O E =25，∴AE =855，O ′E =455，∴O ′D =455+4，∴点O ′的坐标为（8545，+4）．（3）作点A 关于x 轴对称的点A ′，连接A ′O ′交x 轴于点P ，此时O ′P +AP ′取最小值，过点O ′作O ′F ⊥y 轴，垂足为点F ，过点P ′作PM ⊥O ′F ，垂足为点M ，如图3所示．由旋转可知：AO ′=AO =4，∠O ′AF =240°﹣180°=60°，∴AF =12AO ′=2，O ′F =3AO ′=23，∴点O ′（﹣23，6）．∵点A （0，4），∴点A ′（0，﹣4）．设直线A ′O ′的解析式为y =kx +b ，将A ′（0，﹣4）、O ′（﹣23，6）代入y =kx +b ，得： 4236b k b =-⎧⎪⎨-+=⎪⎩，解得：5334k b ⎧=-⎪⎨⎪=-⎩，∴直线A ′O ′的解析式为y =﹣53x ﹣4．当y =0时，有﹣53x ﹣4=0，解得：x =﹣43，∴点P （﹣43，0），∴OP =O ′P ′=435．在Rt △O ′P ′M 中，∠MO ′P ′=60°，∠O ′MP ′=90°，∴O ′M =12O ′P ′=23，P ′M =3O ′P ′=65，∴点P ′的坐标为（﹣23+23，6+65），即（﹣83365，）．点睛：本题考查了函数图象及旋转变换、待定系数法求一次函数解析式、等边三角形的判定与性质、一次函数图象上点的坐标特征以及解直角三角形，解题的关键是：（1）利用等边三角形的性质找出BB ′的长；（2）通过解直角三角形求出AE 、O ′E 的长；（3）利用两点之间线段最短找出当O ′P +AP ′取得最小值时点P 的位置．3．在Rt △ACB 和△AEF 中，∠ACB ＝∠AEF ＝90°，若点P 是BF 的中点，连接PC ，PE.特殊发现：如图1，若点E 、F 分别落在边AB ，AC 上，则结论：PC ＝PE 成立（不要求证明）．问题探究：把图1中的△AEF 绕点A 顺时针旋转．(1)如图2，若点E 落在边CA 的延长线上，则上述结论是否成立？若成立，请给予证明；若不成立，请说明理由；(2)如图3，若点F 落在边AB 上，则上述结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由；(3)记AC BC＝k ，当k 为何值时，△CPE 总是等边三角形？（请直接写出后的值，不必说）【答案】()1 PC PE =成立 ()2 ，PC PE =成立 ()3当k 3CPE 总是等边三角形【解析】【分析】（1）过点P 作PM ⊥CE 于点M ，由EF ⊥AE ，BC ⊥AC ，得到EF ∥MP ∥CB ，从而有EM FP MC PB=，再根据点P 是BF 的中点，可得EM=MC ，据此得到PC=PE ．（2）过点F 作FD ⊥AC 于点D ，过点P 作PM ⊥AC 于点M ，连接PD ，先证△DAF ≌△EAF ，即可得出AD=AE ；再证△DAP ≌△EAP ，即可得出PD=PE ；最后根据FD ⊥AC ，BC ⊥AC ，PM ⊥AC ，可得FD ∥BC ∥PM ，再根据点P 是BF 的中点，推得PC=PD ，再根据PD=PE ，即可得到结论．（3）因为△CPE 总是等边三角形，可得∠CEP=60°，∠CAB=60°；由∠ACB=90°，求出∠CBA=30°；最后根据AC k BC =，AC BC =tan30°，求出当△CPE 总是等边三角形时，k 的值是多少即可．【详解】解：（1）PC=PE 成立，理由如下：如图2，过点P 作PM ⊥CE 于点M ，∵EF ⊥AE ，BC ⊥AC ，∴EF ∥MP ∥CB ，∴EM FP MC PB=，∵点P 是BF 的中点，∴EM=MC ，又∵PM ⊥CE ，∴PC=PE ；（2）PC=PE 成立，理由如下：如图3，过点F 作FD ⊥AC 于点D ，过点P 作PM ⊥AC 于点M ，连接PD ，∵∠DAF=∠EAF ，∠FDA=∠FEA=90°，在△DAF 和△EAF 中，∵∠DAF=∠EAF ，∠FDA=∠FEA ，AF=AF ，∴△DAF ≌△EAF （AAS ），∴AD=AE ，在△DAP 和△EAP 中，∵AD=AE ，∠DAP=∠EAP ，AP=AP ，∴△DAP ≌△EAP （SAS ），∴PD=PE ，∵FD ⊥AC ，BC ⊥AC ，PM ⊥AC ，∴FD ∥BC ∥PM ， ∴DM FP MC PB=， ∵点P 是BF 的中点，∴DM=MC ，又∵PM ⊥AC ，∴PC=PD ，又∵PD=PE ，∴PC=PE ；（3）如图4，∵△CPE 总是等边三角形，∴∠CEP=60°，∴∠CAB=60°，∵∠ACB=90°，∴∠CBA=90°﹣∠ACB=90°﹣60°=30°，∵AC k BC =，AC BC=tan30°，∴k=tan30°=3，3∴当k为3时，△CPE总是等边三角形．【点睛】考点：1．几何变换综合题；2．探究型；3．压轴题；4．三角形综合题；5．全等三角形的判定与性质；6．平行线分线段成比例．4．在正方形ABCD中，连接BD．（1）如图1，AE⊥BD于E．直接写出∠BAE的度数．（2）如图1，在（1）的条件下，将△AEB以A旋转中心，沿逆时针方向旋转30°后得到△AB′E′，AB′与BD交于M，AE′的延长线与BD交于N．①依题意补全图1；②用等式表示线段BM、DN和MN之间的数量关系，并证明．（3）如图2，E、F是边BC、CD上的点，△CEF周长是正方形ABCD周长的一半，AE、AF 分别与BD交于M、N，写出判断线段BM、DN、MN之间数量关系的思路．（不必写出完整推理过程）【答案】（1）45°；（2）①补图见解析；②BM、DN和MN之间的数量关系是BM2+MD2=MN2，证明见解析；（3）答案见解析.【解析】（1）利用等腰直角三角形的性质即可；（2）依题意画出如图1所示的图形，根据性质和正方形的性质，判断线段的关系，再利用勾股定理得到FB2+BM2=FM2，再判断出FM=MN即可；（3）利用△CEF周长是正方形ABCD周长的一半，判断出EF=EG，再利用（2）证明即可．解：（1）∵BD是正方形ABCD的对角线，∴∠ABD=∠ADB=45°，∵AE⊥BD，∴∠ABE=∠BAE=45°，（2）①依题意补全图形，如图1所示，②BM、DN和MN之间的数量关系是BM2+MD2=MN2，将△AND绕点D顺时针旋转90°，得到△AFB，∴∠ADB=∠FBA，∠BAF=∠DAN，DN=BF，AF=AN，∵在正方形ABCD中，AE⊥BD，∴∠ADB=∠ABD=45°，∴∠FBM=∠FBA+∠ABD=∠ADB+∠ABD=90°，在Rt△BFM中，根据勾股定理得，FB2+BM2=FM2，∵旋转△ANE得到AB1E1，∴∠E1AB1=45°，∴∠BAB1+∠DAN=90°﹣45°=45°，∵∠BAF=DAN，∴∠BAB1+∠BAF=45°，∴∠FAM=45°，∴∠FAM=∠E1AB1，∵AM=AM，AF=AN，∴△AFM≌△ANM，∴FM=MN，∵FB2+BM2=FM2，∴DN2+BM2=MN2，（3）如图2，将△ADF绕点A顺时针旋转90°得到△ABG，∴DF=GB，∵正方形ABCD的周长为4AB，△CEF周长为EF+EC+CF，∵△CEF周长是正方形ABCD周长的一半，∴4AB=2（EF+EC+CF），∴2AB=EF+EC+CF∵EC=AB﹣BE，CF=AB﹣DF，∴2AB=EF+AB﹣BE+AB﹣DF，∴EF=DF+BE，∵DF=GB，∴EF=GB+BE=GE，由旋转得到AD=AG=AB，∵AM=AM，∴△AEG≌△AEF，∠EAG=∠EAF=45°，和（2）的②一样，得到DN2+BM2=MN2．“点睛”此题是四边形综合题，主要考查了正方形的性质、旋转的性质，三角形的全等，判断出（△AFN≌△ANM，得到FM=MM），是解题的关键.5．如图，△ABC是等边三角形，AB=6cm，D为边AB中点．动点P、Q在边AB上同时从点D出发，点P沿D→A以1cm/s的速度向终点A运动．点Q沿D→B→D以2cm/s的速度运动，回到点D停止．以PQ为边在AB上方作等边三角形PQN．将△PQN绕QN的中点旋转180°得到△MNQ．设四边形PQMN与△ABC重叠部分图形的面积为S（cm2），点P运动的时间为t（s）（0＜t＜3）．（1）当点N落在边BC上时，求t的值．（2）当点N到点A、B的距离相等时，求t的值．（3）当点Q沿D→B运动时，求S与t之间的函数表达式．（4）设四边形PQMN的边MN、MQ与边BC的交点分别是E、F，直接写出四边形PEMF 与四边形PQMN的面积比为2：3时t的值．【答案】（1）（2）2（3）S=S菱形PQMN=2S△PNQ=t2；（4）t=1或【解析】试题分析：（1）由题意知：当点N落在边BC上时，点Q与点B重合，此时DQ=3；（2）当点N到点A、B的距离相等时，点N在边AB的中线上，此时PD=DQ；（3）当0≤t≤时，四边形PQMN与△ABC重叠部分图形为四边形PQMN；当≤t≤时，四边形PQMN与△ABC重叠部分图形为五边形PQFEN．（4）MN、MQ与边BC的有交点时，此时＜t＜，列出四边形PEMF与四边形PQMN的面积表达式后，即可求出t的值．试题解析：（1）∵△PQN与△ABC都是等边三角形，∴当点N落在边BC上时，点Q与点B重合．∴DQ=3∴2t=3．∴t=；（2）∵当点N到点A、B的距离相等时，点N在边AB的中线上，∴PD=DQ，当0＜t＜时，此时，PD=t，DQ=2t∴t=2t∴t=0（不合题意，舍去），当≤t＜3时，此时，PD=t，DQ=6﹣2t∴t=6﹣2t，解得t=2；综上所述，当点N到点A、B的距离相等时，t=2；（3）由题意知：此时，PD=t，DQ=2t当点M在BC边上时，∴MN=BQ∵PQ=MN=3t，BQ=3﹣2t∴3t=3﹣2t∴解得t=如图①，当0≤t≤时，S△PNQ=PQ2=t2；∴S=S菱形PQMN=2S△PNQ=t2，如图②，当≤t≤时，设MN、MQ与边BC的交点分别是E、F，∵MN=PQ=3t，NE=BQ=3﹣2t，∴ME=MN﹣NE=PQ﹣BQ=5t﹣3，∵△EMF是等边三角形，∴S△EMF=ME2=（5t﹣3）2．；（4）MN、MQ与边BC的交点分别是E、F，此时＜t＜，t=1或．考点：几何变换综合题6．正方形ABCD 中，点E 、F 分别是边AD 、AB 的中点，连接EF ．（1）如图1，若点G 是边BC 的中点，连接FG ，则EF 与FG 关系为：；（2）如图2，若点P 为BC 延长线上一动点，连接FP ，将线段FP 以点F 为旋转中心，逆时针旋转90°，得到线段FQ ，连接EQ ，请猜想BF 、EQ 、BP 三者之间的数量关系，并证明你的结论．（3）若点P 为CB 延长线上一动点，按照（2）中的作法，在图3中补全图形，并直接写出BF 、EQ 、BP 三者之间的数量关系：．【答案】（1）证明见解析（2）BF+EQ=BP （3）BF+BP=EQ【解析】试题分析：（1）EF 与FG 关系为垂直且相等（EF=FG 且EF ⊥FG ）．证明如下： ∵点E 、F 、G 分别是正方形边AD 、AB 、BC 的中点，∴△AEF 和△BGD 是两个全等的等腰直角三角形．∴EF=FG ，∠AFE=∠BFG=45°．∴∠EFG=90°，即EF ⊥FG ．（2）取BC 的中点G ，连接FG ，则由SAS 易证△FQE ≌△FPG ，从而EQ=GP ，因此)EF 2BP EQ =-．（3）同（2）可证△FQE ≌△FPG （SAS ），得EQ=GP ，因此，))EF GF 2BG 2GP BP 2EQ BP ===-=-．7．在平面直角坐标系中，四边形AOBC 是矩形，点(0,0)O ，点(5,0)A ，点(0,3)B .以点A 为中心，顺时针旋转矩形AOBC ，得到矩形ADEF ，点O ，B ，C 的对应点分别为D ，E ，F .（Ⅰ）如图①，当点D 落在BC 边上时，求点D 的坐标；（Ⅱ）如图②，当点D 落在线段BE 上时，AD 与BC 交于点H .①求证ADB AOB △△≌；②求点H 的坐标.（Ⅲ）记K 为矩形AOBC 对角线的交点，S 为KDE △的面积，求S 的取值范围（直接写出结果即可）.【答案】（Ⅰ）点D 的坐标为(1,3).（Ⅱ）①证明见解析；②点H 的坐标为17(,3)5.（Ⅲ3033430334S -+≤≤. 【解析】分析：（Ⅰ）根据旋转的性质得AD=AO=5,设CD=x ，在直角三角形ACD 中运用勾股定理可CD 的值，从而可确定D 点坐标；（Ⅱ）①根据直角三角形全等的判定方法进行判定即可；②由①知BAD BAO ∠=∠，再根据矩形的性质得CBA OAB ∠=∠.从而BAD CBA ∠=∠，故BH=AH ，在Rt △ACH 中，运用勾股定理可求得AH 的值，进而求得答案；（Ⅲ）303343033444S -+≤≤. 详解：（Ⅰ）∵点()5,0A ，点()0,3B ，∴5OA =，3OB =.∵四边形AOBC 是矩形，∴3AC OB ==，5BC OA ==，90OBC C ∠=∠=︒.∵矩形ADEF 是由矩形AOBC 旋转得到的，∴5AD AO ==.在Rt ADC 中，有222AD AC DC =+， ∴22DC AD AC -22534-=.∴1BD BC DC =-=.∴点D 的坐标为()1,3.（Ⅱ）①由四边形ADEF 是矩形，得90ADE ∠=︒.又点D 在线段BE 上，得90ADB ∠=︒.由（Ⅰ）知，AD AO =，又AB AB =，90AOB ∠=︒，∴Rt ADB Rt AOB ≌.②由ADB AOB ≌，得BAD BAO ∠=∠.又在矩形AOBC 中，//OA BC ，∴CBA OAB ∠=∠.∴BAD CBA ∠=∠.∴BH AH =.设BH t =，则AH t =，5HC BC BH t =-=-.在Rt AHC 中，有222AH AC HC =+，∴()22235t t =+-.解得175t =.∴175BH =. ∴点H 的坐标为17,35⎛⎫ ⎪⎝⎭.（Ⅲ）303343033444S -+≤≤. 点睛：本大题主要考查了等腰三角形的判定和性质，勾股定理以及旋转变换的性质等知识，灵活运用勾股定理求解是解决本题的关键.8．如图，已知Rt △ABC 中，∠ACB =90°，AC =BC ，D 是线段AB 上的一点（不与A 、B 重合）．过点B 作BE ⊥CD ，垂足为E ．将线段CE 绕点C 顺时针旋转90︒，得到线段CF ，连结EF ．设∠BCE 度数为α.（1）①补全图形；②试用含α的代数式表示∠CDA ．（2）若32EF AB = ，求α的大小．（3）直接写出线段AB 、BE 、CF 之间的数量关系．【答案】（1）①答案见解析；②45α︒+；（2）30α=︒；（3）22222AB CF BE =+．【解析】试题分析：（1）①按要求作图即可；②由∠ACB=90°，AC=BC ，得∠ABC=45°,故可得出结论；（2）易证FCE ∆∽ ACB ∆，得32CF AC =；连结FA ，得△AFC 是直角三角形，求出∠ACF=30°，从而得出结论；（3）222A 22B CF BE =+.试题解析：（1）①补全图形．②∵∠ACB=90°，AC=BC ，∴∠ABC=45°∵∠BCE=α ∴∠CDA=45α︒+（2）在FCE ∆和ACB ∆中，45CFE CAB ∠=∠=︒ ，90FCE ACB ∠=∠=︒ ∴ FCE ∆∽ ACB ∆∴CF EF AC AB = 3EF AB =∴ 3CF AC =连结FA ．90,90FCA ACE ECB ACE ∠=︒-∠∠=︒-∠∴ FCA ECB ∠=∠=α在Rt CFA ∆中，90CFA ∠=︒，3cos FCA ∠= ∴ 30FCA ∠=︒即30α=︒. （3）22222AB CF BE =+。

初中数学中考冲刺必备(旋转几个类型题)

初中数学中考冲刺必备(旋转几个类型题)
几何图形变换包括平移、旋转和翻折三种基本变换。

这些变换是根据确定的法则对给定的图形进行位置变化，然后在新的图形中分析有关图形之间的关系。

在这些变换中，旋转是其中一种基本变换。

旋转是指根据确定的旋转中心和旋转角度，将图形绕旋转中心旋转一定角度，得到新的图形。

在初中数学中考中，常见的旋转图形有三种类型：正三角形、正方形和等腰直角三角形。

对于正三角形类型的旋转题目，一般要求根据旋转角度和旋转中心，求出图形中某些线段的长度或角度。

例如，在正三角形ABC中，如果将ΔABP绕A点逆时针旋转60°，使得
AB与AC重合，那么需要求∠APB的度数。

对于正方形类型的旋转题目，一般要求根据旋转角度和旋转中心，求出正方形的面积或其他相关的线段长度或角度。

例如，在正方形ABCD中，如果将ΔABP绕B点顺时针旋转90°，使得BA与BC重合，那么需要求正方形ABCD的面积。

对于等腰直角三角形类型的旋转题目，一般要求根据旋转角度和旋转中心，求出图形中某些线段的长度或角度。

例如，在等腰直角三角形ABC中，如果将ΔAPC绕C点逆时针旋转90°，使得AC与BC重合，那么需要求∠___的度数。

通过以上三种类型的旋转题目的练，可以帮助学生更好地理解几何图形变换，提高他们的几何图形变换能力。

九年级数学图形的旋转专题讲解+六大题型解析+专题训练,收藏学习

九年级数学图形的旋转专题讲解+六大题型解析+专题训练，收藏学习九年级数学图形的旋转专题讲解+六大题型解析+专题训练，收藏学习 -九年级数学图形的旋转专题讲解+六大题型解析+专题训练，收藏学习图形的旋转这一章节是初中几何内容中非常重要的一个章节，对于图形的运动的形式和规律以及旋转的性质都是我们在对几何的初步认识当中的一个过程，掌握其重要的性质之后，对于几何综合题型当中辅助线的运用起到了非常重要的作用。

并且图形的旋转加上已经学习过的平移和轴对称。

对几何图形的变化有充分地了解，建立几何空间思维的正确认识,对于几何空间能力的提升起到了非常重要的促进作用。

首先，在学习图形的旋转这一章节我们主要围绕以下两个重要的内容来展开:第一，掌握图形的旋转和中心对称的概念；第二，掌握旋转的本质。

这也是我们学习过程中的重点和难点内容。

因为在旋转前后的两个图形中，对应点与旋转中心之间的距离总是相同的，所以对应点必然分别在以旋转中心为圆心，以对应点到旋转中心的距离为半径的一组同心圆上，对应点与旋转中心连线所成的角等于且等于旋转角。

唐老师提醒大家，旋转过程中保持静止的点就是旋转的中心，不变的量就是对应的元素。

其次，旋转的三个要素：旋转中心、旋转的角度和旋转方向.第三，旋转的性质：（1）图形中的每一点都绕着旋转中心旋转了同样大小的连线所成的角度；—整体角度（2）对应点到旋转中心的距离相等；（3）对应线段相等，对应角相等；——局部角度（4）图形的形状和大小都没有发生变化，即旋转不改变图形的形状和大小.—变换结果.第四，简单图形的旋转作图：（1）确定旋转中心；（2）确定图形中的关键点；（3）将关键点沿指定的方向旋转指定的角度；(4)连接这些点，得到原始图形的旋转图形。

(以上四个步骤是我们在制作简单旋转图的过程中应该遵循的步骤。

按照以上步骤画图，可以提高大家的学习效率，保证其在画图过程中的正确率。

)第五，旋转对称图形：平面图形绕某点旋转一定角度(小于圆角)后，可以与自身重叠。

图形的旋转(共30题)(学生版)--2023年中考数学真题分项汇编

图形的旋转(30题)一、单选题1(2023·江苏无锡·统考中考真题)如图，△ABC 中，∠BAC =55°，将△ABC 逆时针旋转α(0°<α<55°),得到△ADE ，DE 交AC 于F ．当α=40°时，点D 恰好落在BC 上，此时∠AFE 等于()A.80°B.85°C.90°D.95°2(2023·天津·统考中考真题)如图，把△ABC 以点A 为中心逆时针旋转得到△ADE ，点B ，C 的对应点分别是点D ，E ，且点E 在BC 的延长线上，连接BD ，则下列结论一定正确的是()A.∠CAE =∠BEDB.AB =AEC.∠ACE =∠ADED.CE =BD3(2023·四川宜宾·统考中考真题)如图，△ABC 和△ADE 是以点A 为直角顶点的等腰直角三角形，把△ADE 以A 为中心顺时针旋转，点M 为射线BD 、CE 的交点．若AB =3，AD =1．以下结论：①BD =CE ；②BD ⊥CE ；③当点E 在BA 的延长线上时，MC =3-32；④在旋转过程中，当线段MB 最短时，△MBC 的面积为12．其中正确结论有()A.1个B.2个C.3个D.4个4(2023·山东聊城·统考中考真题)如图，已知等腰直角△ABC ，∠ACB =90°，AB =2，点C 是矩形ECGF 与△ABC 的公共顶点，且CE =1，CG =3；点D 是CB 延长线上一点，且CD =2．连接BG ，DF ，在矩形ECGF绕点C按顺时针方向旋转一周的过程中，当线段BG达到最长和最短时，线段DF对应的长度分别为m和n，则mn的值为()A.2B.3C.10D.13二、填空题5(2023·江苏连云港·统考中考真题)以正五边形ABCDE的顶点C为旋转中心，按顺时针方向旋转，使得新五边形A B CD E 的顶点D 落在直线BC上，则正五边ABCDE旋转的度数至少为°．6(2023·湖南张家界·统考中考真题)如图，AO为∠BAC的平分线，且∠BAC=50°，将四边形ABOC 绕点A逆时针方向旋转后，得到四边形AB O C ，且∠OAC =100°，则四边形ABOC旋转的角度是．7(2023·湖南常德·统考中考真题)如图1，在Rt△ABC中，∠ABC=90°，AB=8，BC=6，D是AB上一点，且AD=2，过点D作DE∥BC交AC于E，将△ADE绕A点顺时针旋转到图2的位置．则图2中BDCE的值为．8(2023·江苏无锡·统考中考真题)已知曲线C1、C2分别是函数y=-2x(x<0),y=kx(k>0,x>0)的图像，边长为6的正△ABC的顶点A在y轴正半轴上，顶点B、C在x轴上(B在C的左侧)，现将△ABC绕原点O顺时针旋转，当点B在曲线C1上时，点A恰好在曲线C2上，则k的值为．9(2023·辽宁·统考中考真题)如图，线段AB=8，点C是线段AB上的动点，将线段BC绕点B顺时针旋转120°得到线段BD，连接CD，在AB的上方作RtΔDCE，使∠DCE=90°,∠E=30°，点F为DE的中点，连接AF，当AF最小时，ΔBCD的面积为．10(2023·江西·统考中考真题)如图，在▱ABCD中，∠B=60°，BC=2AB，将AB绕点A逆时针旋转角α(0°<α<360°)得到AP，连接PC，PD．当△PCD为直角三角形时，旋转角α的度数为．11(2023·上海·统考中考真题)如图，在△ABC中，∠C=35°，将△ABC绕着点A旋转α(0°<α< 180°)，旋转后的点B落在BC上，点B的对应点为D，连接AD，AD是∠BAC的角平分线，则α=．12(2023·湖南郴州·统考中考真题)如图，在Rt△ABC中，∠BAC=90°，AB=3cm，∠B=60°．将△ABC绕点A逆时针旋转，得到△AB C ，若点B的对应点B 恰好落在线段BC上，则点C的运动路径长是cm(结果用含π的式子表示)．13(2023·内蒙古·统考中考真题)如图，在Rt△ABC中，∠ACB=90°,AC=3,BC=1，将△ABC绕点A逆时针方向旋转90°，得到△AB C ．连接BB ，交AC于点D，则ADDC的值为．14(2023·黑龙江绥化·统考中考真题)已知等腰△ABC，∠A=120°，AB=2．现将△ABC以点B为旋转中心旋转45°，得到△A BC ，延长C A 交直线BC于点D．则A D的长度为．15(2023·浙江嘉兴·统考中考真题)一副三角板ABC和DEF中，∠C=∠D=90°，∠B=30°，∠E= 45°，BC=EF=12．将它们叠合在一起，边BC与EF重合，CD与AB相交于点G(如图1)，此时线段CG 的长是，现将△DEF绕点C(F)按顺时针方向旋转(如图2)，边EF与AB相交于点H，连结DH，在旋转0°到60°的过程中，线段DH扫过的面积是．三、解答题16(2023·北京·统考中考真题)在△ABC中、∠B=∠C=α0°<α<45°，AM⊥BC于点M，D是线段MC上的动点(不与点M，C重合)，将线段DM绕点D顺时针旋转2α得到线段DE．(1)如图1，当点E在线段AC上时，求证：D是MC的中点；(2)如图2，若在线段BM上存在点F(不与点B，M重合)满足DF=DC，连接AE，EF，直接写出∠AEF的大小，并证明．17(2023·四川自贡·统考中考真题)如图1，一大一小两个等腰直角三角形叠放在一起，M，N分别是斜边DE，AB的中点，DE=2,AB=4．(1)将△CDE绕顶点C旋转一周，请直接写出点M，N距离的最大值和最小值；(2)将△CDE绕顶点C逆时针旋转120°(如图2)，求MN的长．18(2023·四川达州·统考中考真题)如图，网格中每个小正方形的边长均为1，△ABC 的顶点均在小正方形的格点上．(1)将△ABC 向下平移3个单位长度得到△A 1B 1C 1，画出△A 1B 1C 1；(2)将△ABC 绕点C 顺时针旋转90度得到△A 2B 2C 2，画出△A 2B 2C 2；(3)在(2)的运动过程中请计算出△ABC 扫过的面积．19(2023·辽宁·统考中考真题)在Rt ΔABC 中，∠ACB =90°，CA =CB ，点O 为AB 的中点，点D 在直线AB 上(不与点A ,B 重合)，连接CD ，线段CD 绕点C 逆时针旋转90°，得到线段CE ，过点B 作直线l ⊥BC ，过点E 作EF ⊥l ，垂足为点F ，直线EF 交直线OC 于点G ．(1)如图，当点D 与点O 重合时，请直接写出线段AD 与线段EF 的数量关系；(2)如图，当点D 在线段AB 上时，求证：CG +BD =2BC ；(3)连接DE ，△CDE 的面积记为S 1，△ABC 的面积记为S 2，当EF :BC =1:3时，请直接写出S 1S 2的值．20(2023·四川乐山·统考中考真题)在学习完《图形的旋转》后，刘老师带领学生开展了一次数学探究活动【问题情境】刘老师先引导学生回顾了华东师大版教材七年级下册第121页“探索”部分内容：如图，将一个三角形纸板△ABC绕点A逆时针旋转θ到达△AB C 的位置，那么可以得到：AB=AB ，AC =AC ，BC=B C ；∠BAC=∠B AC ，∠ABC=∠AB C ，∠ACB=∠AC B ()刘老师进一步谈到：图形的旋转蕴含于自然界的运动变化规律中，即“变”中蕴含着“不变”，这是我们解决图形旋转的关键；故数学就是一门哲学．【问题解决】(1)上述问题情境中“( )”处应填理由：；(2)如图，小王将一个半径为4cm，圆心角为60°的扇形纸板ABC绕点O逆时针旋转90°到达扇形纸板A BC 的位置．①请在图中作出点O；②如果BB =6cm，则在旋转过程中，点B经过的路径长为；【问题拓展】小李突发奇想，将与(2)中完全相同的两个扇形纸板重叠，一个固定在墙上，使得一边位于水平位置，另一个在弧的中点处固定，然后放开纸板，使其摆动到竖直位置时静止，此时，两个纸板重叠部分的面积是多少呢？如图所示，请你帮助小李解决这个问题．21(2023·浙江绍兴·统考中考真题)在平行四边形ABCD中(顶点A,B,C,D按逆时针方向排列)，AB =12,AD=10,∠B为锐角，且sin B=45．(1)如图1，求AB边上的高CH的长．(2)P是边AB上的一动点，点C,D同时绕点P按逆时针方向旋转90°得点C ,D ．①如图2，当点C 落在射线CA上时，求BP的长．②当△AC D 是直角三角形时，求BP的长．22(2023·四川南充·统考中考真题)如图，正方形ABCD中，点M在边BC上，点E是AM的中点，连接ED，EC．(1)求证：ED=EC；(2)将BE绕点E逆时针旋转，使点B的对应点B 落在AC上，连接MB′．当点M在边BC上运动时(点M 不与B，C重合)，判断△CMB′的形状，并说明理由．(3)在(2)的条件下，已知AB=1，当∠DEB′=45°时，求BM的长．在综合实践活动课上，李老师让同桌两位同学用相同的两块含30°的三角板开展数学探究活动，两块三角板分别记作△ADB和△A D C,∠ADB=∠A D C=90°,∠B=∠C=30°，设AB=2．【操作探究】如图1，先将△ADB和△A D C的边AD、A D 重合，再将△A D C绕着点A按顺时针方向旋转，旋转角为α0°≤α≤360°，旋转过程中△ADB保持不动，连接BC．(1)当α=60°时，BC=；当BC=22时，α=°；(2)当α=90°时，画出图形，并求两块三角板重叠部分图形的面积；(3)如图2，取BC的中点F，将△A D C绕着点A旋转一周，点F的运动路径长为．如图1，在正方形ABCD中，对角线AC、BD相交于点O．在线段AO上任取一点P(端点除外)，连接PD、PB．①求证：PD=PB；②将线段DP绕点P逆时针旋转，使点D落在BA的延长线上的点Q处．当点P在线段AO上的位置发生变化时，∠DPQ的大小是否发生变化？请说明理由；③探究AQ与OP的数量关系，并说明理由．(2)[迁移探究]如图2，将正方形ABCD换成菱形ABCD，且∠ABC=60°，其他条件不变．试探究AQ与CP的数量关系，并说明理由．25(2023·湖北随州·统考中考真题)1643年，法国数学家费马曾提出一个著名的几何问题：给定不在同一条直线上的三个点A，B，C，求平面上到这三个点的距离之和最小的点的位置，意大利数学家和物理学家托里拆利给出了分析和证明，该点也被称为“费马点”或“托里拆利点”，该问题也被称为“将军巡营”问题．(1)下面是该问题的一种常见的解决方法，请补充以下推理过程：(其中①处从“直角”和“等边”中选择填空，②处从“两点之间线段最短”和“三角形两边之和大于第三边”中选择填空，③处填写角度数，④处填写该三角形的某个顶点)当△ABC的三个内角均小于120°时，如图1，将△APC绕，点C顺时针旋转60°得到△A P C，连接PP ，由PC=P C，∠PCP =60°，可知△PCP 为三角形，故PP =PC，又P A =PA，故PA+PB+PC =PA +PB+PP ≥A B，由可知，当B，P，P ，A在同一条直线上时，PA+PB+PC取最小值，如图2，最小值为A B，此时的P点为该三角形的“费马点”，且有∠APC=∠BPC=∠APB=；已知当△ABC有一个内角大于或等于120°时，“费马点”为该三角形的某个顶点．如图3，若∠BAC≥120°，则该三角形的“费马点”为点．(2)如图4，在△ABC中，三个内角均小于120°，且AC=3，BC=4，∠ACB=30°，已知点P为△ABC的“费马点”，求PA+PB+PC的值；(3)如图5，设村庄A，B，C的连线构成一个三角形，且已知AC=4km，BC=23km，∠ACB=60°．现欲建一中转站P沿直线向A，B，C三个村庄铺设电缆，已知由中转站P到村庄A，B，C的铺设成本分别为a 元/km，a元/km，2a元/km，选取合适的P的位置，可以使总的铺设成本最低为元．(结果用含a的式子表示)26(2023·四川·统考中考真题)如图1，已知线段AB，AC，线段AC绕点A在直线AB上方旋转，连接BC，以BC为边在BC上方作Rt△BDC，且∠DBC=30°．(1)若∠BDC=90°，以AB为边在AB上方作Rt△BAE，且∠AEB=90°，∠EBA=30°，连接DE，用等式表示线段AC与DE的数量关系是；(2)如图2，在(1)的条件下，若DE⊥AB，AB=4，AC=2，求BC的长；(3)如图3，若∠BCD=90°，AB=4，AC=2，当AD的值最大时，求此时tan∠CBA的值．27(2023·湖北黄冈·统考中考真题)【问题呈现】△CAB和△CDE都是直角三角形，∠ACB=∠DCE=90°,CB=mCA,CE=mCD，连接AD，BE，探究AD，BE的位置关系．(1)如图1，当m=1时，直接写出AD，BE的位置关系：；(2)如图2，当m≠1时，(1)中的结论是否成立？若成立，给出证明；若不成立，说明理由．【拓展应用】(3)当m=3,AB=47,DE=4时，将△CDE绕点C旋转，使A,D,E三点恰好在同一直线上，求BE的长．28(2023·内蒙古赤峰·统考中考真题)数学兴趣小组探究了以下几何图形．如图①，把一个含有45°角的三角尺放在正方形ABCD 中，使45°角的顶点始终与正方形的顶点C 重合，绕点C 旋转三角尺时，45°角的两边CM ，CN 始终与正方形的边AD ，AB 所在直线分别相交于点M ，N ，连接MN ，可得△CMN ．【探究一】如图②，把△CDM 绕点C 逆时针旋转90°得到△CBH ，同时得到点H 在直线AB 上．求证：∠CNM =∠CNH ；【探究二】在图②中，连接BD ，分别交CM ，CN 于点E ，F ．求证：△CEF ∽△CNM ；【探究三】把三角尺旋转到如图③所示位置，直线BD 与三角尺45°角两边CM ，CN 分别交于点E ，F ．连接AC 交BD 于点O ，求EFNM的值．29(2023·湖南·统考中考真题)问题情境：小红同学在学习了正方形的知识后，进一步进行以下探究活动：在正方形ABCD的边BC上任意取一点G，以BG为边长向外作正方形BEFG，将正方形BEFG绕点B顺时针旋转．特例感知：(1)当BG在BC上时，连接DF，AC相交于点P，小红发现点P恰为DF的中点，如图①．针对小红发现的结论，请给出证明；(2)小红继续连接EG，并延长与DF相交，发现交点恰好也是DF中点P，如图②，根据小红发现的结论，请判断△APE的形状，并说明理由；规律探究：(3)如图③，将正方形BEFG绕点B顺时针旋转α，连接DF，点P是DF中点，连接AP，EP，AE，△APE 的形状是否发生改变？请说明理由．30(2023·贵州·统考中考真题)如图①，小红在学习了三角形相关知识后，对等腰直角三角形进行了探究，在等腰直角三角形ABC中，CA=CB,∠C=90°，过点B作射线BD⊥AB，垂足为B，点P在CB上．(1)【动手操作】如图②，若点P在线段CB上，画出射线PA，并将射线PA绕点P逆时针旋转90°与BD交于点E，根据题意在图中画出图形，图中∠PBE的度数为度；(2)【问题探究】根据(1)所画图形，探究线段PA与PE的数量关系，并说明理由；(3)【拓展延伸】如图③，若点P在射线CB上移动，将射线PA绕点P逆时针旋转90°与BD交于点E，探究线段BA,BP, BE之间的数量关系，并说明理由．。

图形的旋转、翻折与平移-三年中考数学真题分项汇编(解析版)

图形的旋转、翻折与平移一、单选题1．（2022·浙江湖州）如图，将△ABC沿BC方向平移1cm得到对应的△A′B′C′．若B′C=2cm，则BC′的长是（）A．2cm B．3cm C．4cm D．5cm【答案】C【分析】据平移的性质可得BB′=CC′=1，列式计算即可得解．【详解】解：∵∵ABC沿BC方向平移1cm得到△A′B′C′，∵BB′=CC′=1cm，∵B′C=2cm，∵BC′= BB′+ B′C+CC′=1+2+1=4（cm）．故选：C．【点睛】本题考查了平移的性质，熟记性质得到相等的线段是解题的关键．2．（2022·浙江嘉兴）“方胜”是中国古代妇女的一种发饰，其图案由两个全等正方形相叠组成，寓意是同心''''，形成一个“方吉祥．如图，将边长为2cm的正方形ABCD沿对角线BD方向平移1cm得到正方形A B C D胜”图案，则点D，B′之间的距离为（）A．1cm B．2cm C．2－1)cm D．21)cm【答案】D【分析】先求出BD，再根据平移性质求得BB'=1cm，然后由BD BB-′求解即可．【详解】解：由题意，BD=22cm，由平移性质得BB'=1cm，∵点D，B′之间的距离为DB'=BD BB-′=（221-）cm，【点睛】本题考查平移性质、正方形的性质，熟练掌握平移性质是解答的关键．3．（2021·浙江丽水）四盏灯笼的位置如图．已知A，B，C，D的坐标分别是(−1，b)，(1，b)，(2，b)，(3.5，b)，平移y轴右侧的一盏灯笼，使得y轴两侧的灯笼对称，则平移的方法可以是（）A．将B向左平移4.5个单位B．将C向左平移4个单位C．将D向左平移5.5个单位D．将C向左平移3.5个单位【答案】C【分析】直接利用利用关于y轴对称点的性质得出答案．【详解】解：∵点A (−1，b) 关于y轴对称点为B (1，b)，C (2，b)关于y轴对称点为(-2，b)，需要将点D (3.5，b) 向左平移3.5+2=5.5个单位，故选：C．【点睛】本题主要考查了关于y轴对称点的性质，正确记忆横纵坐标的关系是解题关键．4．（2021·浙江绍兴）数学兴趣小组同学从“中国结”的图案（图1）中发现，用相同的菱形放置，可得到更多的菱形．如图2，用2个相同的菱形放置，得到3个菱形．下面说法正确的是（）A．用3个相同的菱形放置，最多能得到6个菱形B．用4个相同的菱形放置，最多能得到16个菱形C．用5个相同的菱形放置，最多能得到27个菱形D．用6个相同的菱形放置，最多能得到41个菱形【分析】根据平移和大菱形的位置得出菱形的个数进行判定即可【详解】如图所示，用2个相同的菱形放置，最多能得到3个菱形；用3个相同的菱形放置，最多能得到8个菱形，用4个相同的菱形放置，最多能得到16个菱形，用5个相同的菱形放置，最多能得到29个菱形，用6个相同的菱形放置，最多能得到47个菱形．故选：B．【点睛】本题考查了生活中的平移现象，菱形的判定，正确的识别图形是解题的关键．5．（2020·浙江台州）如图，把∵ABC 先向右平移3个单位，再向上平移2个单位得到∵DEF ，则顶点C （0，-1）对应点的坐标为（）A ．（0，0）B ．（1，2）C ．（1，3）D ．（3，1）【答案】D 【分析】先找到顶点C 的对应点为F ，再根据直角坐标系的特点即可得到坐标．【详解】∵顶点C 的对应点为F ，由图可得F 的坐标为（3，1），故选D ．【点睛】此题主要考查坐标与图形，解题的关键是熟知直角坐标系的特点．6．（2022·浙江台州）如图是战机在空中展示的轴对称队形．以飞机B ，C 所在直线为x 轴、队形的对称轴为y 轴，建立平面直角坐标系．若飞机E 的坐标为(40，a )，则飞机D 的坐标为（）A ．(40,)a -B ．(40,)a -C ．(40,)a --D ．(,40)a -【答案】B 【分析】直接利用关于y 轴对称，纵坐标相同，横坐标互为相反数，进而得出答案．【详解】解：根据题意，点E 与点D 关于y 轴对称，∵飞机E 的坐标为(40，a )，∵飞机D 的坐标为(-40，a )，【点睛】此题主要考查了关于y 轴对称点的性质，正确记忆横纵坐标的符号关系是解题关键．7．（2020·浙江台州）把一张宽为1cm 的长方形纸片ABCD 折叠成如图所示的阴影图案，顶点A ，D 互相重合，中间空白部分是以E 为直角顶点，腰长为2cm 的等腰直角三角形，则纸片的长AD （单位：cm ）为（）A ．732+B ．742+C ．832+D ．842+【答案】D 【分析】如图，过点M 作MH∵A'R 于H ，过点N 作NJ∵A'W 于J ．想办法求出AR ，RM ，MN ，NW ，WD 即可解决问题．【详解】解：如图，过点M 作MH∵A'R 于H ，过点N 作NJ∵A'W 于J ．由题意∵EMN 是等腰直角三角形，EM=EN=2，MN=22∵四边形EMHK 是矩形，∵EK= A'K=MH=1，KH=EM=2，∵∵RMH 是等腰直角三角形，∵RH=MH=1，RM=2，同法可证NW=2，题意AR=R A'= A'W=WD=4，∵AD=AR+RM+MN+NW+DW=4+2+22+2+4=842+.故答案为：D.【点睛】本题考查翻折变换，等腰直角三角形的判定和性质，矩形的性质等知识，解题的关键是学会添加常用辅助线，构造特殊三角形或特殊四边形解决问题．8．（2022·浙江衢州）下列图形是中心对称图形的是（）A ．B ．C ．D ．【分析】根据中心对称图形的定义（在平面内，把一个图形绕某点旋转180 ，如果旋转后的图形与另一个图形重合，那么这两个图形互为中心对称图形）逐项判断即可得．【详解】解：A、不是中心对称图形，此项不符合题意；B、是中心对称图形，此项符合题意；C、不是中心对称图形，此项不符合题意；D、不是中心对称图形，此项不符合题意；故选：B．【点睛】本题考查了中心对称图形，熟记中心对称图形的定义是解题关键．9．（2020·浙江绍兴）如图，点O为矩形ABCD的对称中心，点E从点A出发沿AB向点B运动，移动到点B停止，延长EO交CD于点F，则四边形AECF形状的变化依次为（）A．平行四边形→正方形→平行四边形→矩形B．平行四边形→菱形→平行四边形→矩形C．平行四边形→正方形→菱形→矩形D．平行四边形→菱形→正方形→矩形【答案】B【分析】根据对称中心的定义，根据矩形的性质，可得四边形AECF形状的变化情况．【详解】解：观察图形可知，四边形AECF形状的变化依次为平行四边形→菱形→平行四边形→矩形．故选：B．【点睛】考查了中心对称，矩形的性质，平行四边形的判定与性质，菱形的性质，根据EF与AC的位置关系即可求解．二、填空题10．（2022·浙江台州）如图，△ABC的边BC长为4cm．将△ABC平移2cm得到△A′B′C′，且BB′∵BC，则阴影部分的面积为______2cm．【答案】8【分析】根据平移的性质即可求解．【详解】解：由平移的性质S △A ′B ′C ′=S △ABC ，BC =B ′C ′，BC ∵B ′C ′，∵四边形B ′C ′CB 为平行四边形，∵BB ′∵BC ，∵四边形B ′C ′CB 为矩形，∵阴影部分的面积=S △A ′B ′C ′+S 矩形B ′C ′CB -S △ABC=S 矩形B ′C ′CB=4×2=8(cm 2)．故答案为：8．【点睛】本题考查了矩形的判定和平移的性质：∵平移不改变图形的形状和大小；∵经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．11．（2022·浙江金华）如图，在Rt ABC 中，90,30,2cm ACB A BC ∠=︒∠=︒=．把ABC 沿AB 方向平移1cm ，得到A B C '''，连结CC '，则四边形AB C C ''的周长为_____cm ．【答案】823+【分析】通过勾股定理，平移的特性，特殊角的三角函数，分别计算出四边形的四条边长，再计算出周长即可．【详解】解：∵90,30,2cm ACB A BC ∠=︒∠=︒=，∵AB =2BC =4，∵AC =2216423AB BC -=-=，∵把ABC 沿AB 方向平移1cm ，得到A B C '''，∵1CC '=，=4+1=5AB '， =2B C BC ''=，∵四边形的周长为：23152823+++=+，故答案为：823+．【点睛】本题考查勾股定理，平移的特性，特殊角的三角函数，能够熟练掌握勾股定理是解决本题的关键． 12．（2022·浙江嘉兴）如图，在扇形AOB 中，点C ，D 在AB 上，将CD 沿弦CD 折叠后恰好与OA ，OB 相切于点E ，F ．已知120AOB ∠=︒，6OA =，则EF 的度数为_______；折痕CD 的长为_______．【答案】 60°##60度 46【分析】根据对称性作O 关于CD 的对称点M ，则点D 、E 、F 、B 都在以M 为圆心，半径为6的圆上，再结合切线的性质和垂径定理求解即可．【详解】作O 关于CD 的对称点M ，则ON =MN连接MD 、ME 、MF 、MO ，MO 交CD 于N∵将CD 沿弦CD 折叠∵点D 、E 、F 、B 都在以M 为圆心，半径为6的圆上∵将CD 沿弦CD 折叠后恰好与OA ，OB 相切于点E ，F ．∵ME ∵OA ，MF ∵OB∵90MEO MFO ∠=∠=︒∵120AOB ∠=︒∵四边形MEOF 中36060EMF AOB MEO MFO ∠=︒-∠-∠-∠=︒即EF 的度数为60°；∵90MEO MFO ∠=∠=︒，ME MF =∵MEO MFO ≅（HL ）∵1302EMO FMO FME ∠=∠=∠=︒ ∵643cos cos30ME OM EMO ===∠︒∵23MN =∵MO ∵DC∵222216(23)262DN DM MN CD =-=-== ∵46CD =故答案为：60°；46【点睛】本题考查了折叠的性质、切线的性质、垂径定理、勾股定理；熟练掌握折叠的性质作出辅助线是解题的关键．13．（2020·浙江金华）图1是一个闭合时的夹子，图2是该夹子的主视示意图，夹子两边为AC ，BD （点A与点B 重合），点O 是夹子转轴位置，O E ∵AC 于点E ，OF ∵BD 于点F ，OE=OF=1cm ，AC =BD =6cm ， CE =DF ， CE :AE =2:3.按图示方式用手指按夹子，夹子两边绕点O 转动．(1)当E ，F 两点的距离最大值时，以点A ，B ，C ，D 为顶点的四边形的周长是_____ cm ．(2)当夹子的开口最大（点C 与点D 重合）时，A ，B 两点的距离为_____cm ．【答案】1660 13【分析】（1）当E、O、F三点共线时，E、F两点间的距离最大，此时四边形ABCD是矩形，可得AB=CD=EF=2cm，根据矩形的性质求出周长即可．（2）当夹子的开口最大（点C与D重合）时，连接OC并延长交AB于点H，可得CH AB⊥，AH=BH，利用已知先求出125CE cm=，在Rt△OEF中利用勾股定理求出CO的长，由sinOE AHECOCO AAC∠==，求出AH，从而求出AB=2AH的长．【详解】（1）当E、O、F三点共线时，E、F两点间的距离最大，此时四边形ABCD是矩形，∵AB=CD=EF=2cm，∵以点A，B，C，D为顶点的四边形的周长为2+6+2+6=16cm．（2）当夹子的开口最大（点C与D重合）时，连接OC并延长交AB于点H，∵CH AB⊥，AH=BH，∵AC=BD=6cm，CE∵AE=2∵3，∵125CE cm=，在Rt△OEF中，2213 5CO OE CE=+=，∵sinOE AHECOCO AAC∠==，3013AH=，∴AB=2AH=60 13．故答案为16，60 13．【点睛】本题主要考查了勾股定理与旋转的结合，做题时准确理解题意利用已知的直角三角形进行求解是解题的关键．三、解答题14．（2022·浙江温州）如图，在26⨯的方格纸中，已知格点P，请按要求画格点图形（顶点均在格点上）．(1)在图1中画一个锐角三角形，使P为其中一边的中点，再画出该三角形向右平移2个单位后的图形．(2)在图2中画一个以P为一个顶点的钝角三角形，使三边长都不相等，再画出该三角形绕点P旋转180︒后的图形．【答案】(1)见解析(2)见解析【分析】（1）根据题意画出合适的图形即可，注意本题答案不唯一，主要作出的图形符合题意即可；（2）根据题意画出合适的图形即可，注意本题答案不唯一，主要作出的图形符合题意即可．（1）画法不唯一，如图1或图2等．（2）画法不唯一，如图3或图4等．【点睛】本题考查作图—旋转变换、作图—平移变换，解答本题的关键是明确题意，画出相应的图形，注意不要忘记画出平移后或旋转后的图形．15．（2022·浙江丽水）如图，在66的方格纸中，点A，B，C均在格点上，试按要求画出相应格点图形．(1)如图1，作一条线段，使它是AB向右平移一格后的图形；(2)如图2，作一个轴对称图形，使AB和AC是它的两条边；(3)如图3，作一个与ABC相似的三角形，相似比不等于1．【答案】(1)画图见解析(2)画图见解析(3)画图见解析【分析】（1）分别确定A，B平移后的对应点C，D，从而可得答案；（2）确定线段AB，AC关于直线BC对称的线段即可；（3）分别计算ABC的三边长度，再利用相似三角形的对应边成比例确定DEF的三边长度，再画出DEF 即可．（1）解：如图，线段CD即为所求作的线段，（2）如图，四边形ABDC是所求作的轴对称图形，（3）如图，如图，DEF 即为所求作的三角形，由勾股定理可得：221310,2,AB AC而2,BC = 同理：2226210,22,DFDE 而4,EF1,2AB AC BC DF DE EF.ABC DFE ∽【点睛】本题考查的是平移的作图，轴对称的作图，相似三角形的作图，掌握平移轴对称的性质，相似三角形的判定方法是解本题的关键．16．（2021·浙江温州）如图44⨯与66⨯的方格都是由边长为1的小正方形组成．图1是绘成的七巧板图案，它由7个图形组成，请按以下要求选择其中一个并在图2、图3中画出相应的格点图形（顶点均在格点上）．（1）选一个四边形画在图2中，使点P 为它的一个顶点，并画出将它向右平移3个单位后所得的图形．（253中．【答案】（1）见解析；（2）见解析【分析】（1）七巧板中有两个四边形，分别是正方形和平行四边形，根据题意可画出4种图形任意选一种即可，（2）七巧板中有五个等腰直角三角形，有直角边长2的两个，直角边长22的两个，直角边长2 的一个，根据题意利用数形结合的思想解决问题即可．【详解】解：（1）画法不唯一，当选四边形为正方形时可以是如图1或图2；当四边形式平行四边形时可以是图3或图4．（2）画法不唯一，当直角边长为2时，扩大5即直角边长为10利用勾股定理画出直角边长为10直角三角形可以是如图5或图6当直角边长为22时，扩大5即直角边长为210利用勾股定理画出直角边长为210直角三角形可以是如图7或图8等．【点睛】本题考查基本作图，平移，二次根式的乘法，以及勾股定理的应用，解题的关键是学会利用数形结合的思想解决问题，属于中考常考题型．17．（2022·浙江宁波）图1，图2都是由边长为1的小等边三角形构成的网格，每个小等边三角形的顶点称为格点，线段AB的端点均在格点上，分别按要求画出图形．(1)在图1中画出等腰三角形ABC，且点C在格点上．（画出一个即可）(2)在图2中画出以AB为边的菱形ABDE，且点D，E均在格点上．【答案】(1)见解析(2)见解析【分析】利用轴对称图形、中心对称图形的特点画出符合条件的图形即可；（1）答案不唯一．（2）【点睛】本题考查了轴对称图形、中心对称图形的特点，熟练掌握特殊三角形与四边形的性质才能准确画出符合条件的图形．18．（2020·浙江宁波）图1，图2都是由边长为1的小等边三角形构成的网格，每个网格图中有3个小等边三角形已涂上阴影．请在余下的空白小等边三角形中，分别按下列要求选取一个涂上阴影：（1）使得4个阴影小等边三角形组成一个轴对称图形．（2）使得4个阴影小等边三角形组成一个中心对称图形．（请将两个小题依次作答在图1，图2中，均只需画出符合条件的一种情形）【答案】（1）见解析；（2）见解析【分析】（1）根据轴对称图形的定义画出图形构成一个大的等边三角形即可（答案不唯一）．（2）根据中心对称图形的定义画出图形构成一个平行四边形即可（答案不唯一）．【详解】解：（1）轴对称图形如图1所示．（2）中心对称图形如图2所示．【点睛】本题考查利用中心对称设计图案，利用轴对称设计图案，解题的关键是理解题意，灵活运用所学知识解决问题．19．（2020·浙江金华）如图，在∵ABC 中，AB =42∵B =45°，∵C =60°．（1）求BC 边上的高线长．（2）点E 为线段AB 的中点，点F 在边AC 上，连结EF ，沿EF 将∵AEF 折叠得到∵PEF ． ∵如图2，当点P 落在BC 上时，求∵AEP 的度数． ∵如图3，连结AP ，当PF ∵AC 时，求AP 的长．【答案】（1）4;（2）∵90°；∵26【分析】（1）如图1中，过点A 作AD∵BC 于D ．解直角三角形求出AD 即可．（2）∵证明BE=EP ，可得∵EPB=∵B=45°解决问题． ∵如图3中，由（1）可知：AC=83sin 603AD =︒，证明∵AEF∵∵ACB ，推出AF AE AB AC =，由此求出AF 即可解决问题．【详解】解：（1）如图1，过点A 作AD ∵BC 于点D ，在Rt∵ABD 中，sin 45AD AB =⋅︒=2422⨯=4.（2）∵如图2，∵∵AEF ∵∵PEF ， ∵AE ＝EP . 又∵AE ＝BE ， ∵BE ＝EP ， ∵∵EPB ＝∵B ＝45°， ∵∵AEP ＝90°.∵如图3，由（1）可知：在Rt∵ADC 中，83sin 603AD AC ==︒. ∵PF ∵AC ， ∵∵PF A ＝90°. ∵∵AEF ∵∵PEF ，∵∵AFE ＝∵PFE ＝45°，则∵AFE ＝∵B . 又∵∵EAF ＝∵CAB ， ∵∵EAF ∵∵CAB ，∵AF AB＝AE AC ，即42AF ＝22833， ∵AF ＝23,在Rt∵AFP 中，AF ＝PF ，则AP ＝2AF ＝26.【点睛】本题属于三角形综合题，考查了解直角三角形的应用，翻折变换，全等三角形的性质，相似三角形的判定和性质等知识，解题的关键是正确寻找相似三角形解决问题，属于中考常考题型．20．（2021·浙江嘉兴）小王在学习浙教版九上课本第72页例2后，进一步开展探究活动：将一个矩形ABCD 绕点A 顺时针旋转()090αα︒<≤︒，得到矩形'''AB C D[探究1]如图1，当90α=︒时，点'C 恰好在DB 延长线上．若1AB =，求BC 的长．[探究2]如图2，连结'AC ，过点'D 作'//'D M AC 交BD 于点M ．线段'D M 与DM 相等吗？请说明理由．[探究3]在探究2的条件下，射线DB 分别交'AD ，'AC 于点P ，N （如图3），MN ，PN 存在一定的数量关系，并加以证明．【答案】[探究1]152BC +=；[探究2]'D M DM =，证明见解析；[探究3]2MN PN DN =⋅，证明见解析【分析】[探究1] 设BC x =，根据旋转和矩形的性质得出''//D C DA ，从而得出''D C B ADB ∆∆∽，得出比例式'''D C D BAD AB=，列出方程解方程即可； [探究2] 先利用SAS 得出''AC D DBA ∆∆≌，得出'DAC ADB ∠=∠，'ADB AD M ∠=∠，再结合已知条件得出''MDD MD D ∠=∠，即可得出'D M DM =；[探究3] 连结AM ，先利用SSS 得出ADM ADM ∆∆≌，从而证得MN AN =，再利用两角对应相等得出NPA NAD ∆∆∽，得出PN ANAN DN=即可得出结论．【详解】[探究1]如图1，设BC x =．∵矩形ABCD 绕点A 顺时针旋转90︒得到矩形'''AB C D ， ∵点A ，B ，'D 在同一直线上．∵'AD AD BC x ===，'1DC AB AB ===， ∵''1D B AD AB x =-=-． ∵'90BAD D ∠=∠=︒， ∵//D C DA ''．又∵点'C 在DB 延长线上， ∵''D C B ADB ∆∆∽， ∵'''D C D BAD AB =，∵111x x -=．解得1152x +=，2152x -=（不合题意，舍去）∵152BC +=． [探究2] 'D M DM =．证明：如图2，连结'DD ．∵'//'D M AC ， ∵'''AD M D AC ∠=∠．∵'AD AD =，''90AD C DAB ∠=∠=︒，''D C AB =，∵()''AC D DBA SAS ∆∆≌．∵'D AC ADB '∠=∠，'ADB AD M ∠=∠，∵AD AD =，''ADD AD D ∠=∠，∵''MDD MD D ∠=∠，∵'D M DM =．[探究3]关系式为2MN PN DN =⋅．证明：如图3，连结AM ．∵'D M DM =，'AD AD =，AM AM =，∵()ADM AD M SSS '∆∆≌．∵'MAD MAD ∠=∠，∵AMN MAD NDA ∠=∠+∠，'NAM MAD NAP ∠=∠+∠，∵AMN NAM ∠=∠，∵MN AN =．在NAP ∆与NDA ∆中，ANP DNA ∠=∠，NAP NDA ∠=∠，∵NPA NAD ∆∆∽，∵PN AN AN DN=， ∵2AN PN DN =⋅．∵2MN PN DN =⋅．【点睛】本题考查了矩形的性质，旋转的性质，全等三角形的判定和性质，相似三角形的判定和性质，解一元二次方程等，解题的关键是灵活运用这些知识解决问题．21．（2020·浙江绍兴）如图1，矩形DEFG中，DG＝2，DE＝3，Rt∵ABC中，∵ACB＝90°，CA＝CB＝2，FG，BC的延长线相交于点O，且FG∵BC，OG＝2，OC＝4．将∵ABC绕点O逆时针旋转α（0°≤α＜180°）得到∵A′B′C′．（1）当α＝30°时，求点C′到直线OF的距离．（2）在图1中，取A′B′的中点P，连结C′P，如图2．∵当C′P与矩形DEFG的一条边平行时，求点C′到直线DE的距离．∵当线段A′P与矩形DEFG的边有且只有一个交点时，求该交点到直线DG的距离的取值范围．【答案】（1）点C′到直线OF的距离为23；（2）∵点C′到直线DE的距离为22±2；∵2≤d＜4417或d＝3．【分析】（1）过点C′作C′H∵OF于H．根据直角三角形的边角关系，解直角三角形求出CH即可．（2）∵分两种情形：当C′P∵OF时，过点C′作C′M∵OF于M；当C′P∵DG时，过点C′作C′N∵FG于N．通过解直角三角形，分别求出C′M，C′N即可．∵设d为所求的距离．第一种情形：当点A′落在DE上时，连接OA′，延长ED交OC于M．当点P落在DE上时，连接OP，过点P作PQ∵C′B′于Q．结合图象可得结论．第二种情形：当A′P与FG相交，不与EF相交时，当点A′在FG上时，A′G＝25﹣2，即d＝25﹣2；当点P落在EF上时，设OF交A′B′于Q，过点P作PT∵B′C′于T，过点P作PR∵OQ交OB′于R，连接OP．求出QG可得结论．第三种情形：当A′P经过点F时，此时显然d＝3．综上所述即可得结论．【详解】解：（1）如图，过点C′作C′H∵OF于H．∵∵A′B′C′是由∵ABC绕点O逆时针旋转得到，∵C′O=CO=4，在Rt∵HC′中，∵∵HC′O＝α＝30°，∵C′H＝C′O•cos30°＝23，∵点C′到直线OF的距离为23．（2）∵如图，当C′P∵OF时，过点C′作C′M∵OF于M．∵∵A′B′C′为等腰直角三角形，P为A′B′的中点，∵∵A′C′P=45°，∵∵A′C′O=90°，∵∵OC′P=135°.∵C′P∵OF，∵∵O＝180°﹣∵OC′P＝45°，∵∵OC′M是等腰直角三角形，∵C′M ＝C′O•cos45°=4×22=22， ∵点C′到直线DE 的距离为222-．如图，当C′P∵DG 时，过点C′作C′N∵FG 于N ．同法可证∵OC′N 是等腰直角三角形，∵C′N ＝22，∵GD=2，∵点C′到直线DE 的距离为222+．∵设d 为所求的距离．第一种情形：如图，当点A′落在DE 上时，连接OA′，延长ED 交OC 于M ．∵OC=4，AC=2，∵ACO=90°，2216425OA CO AC =+∴+==∵OM ＝2，∵OMA′＝90°，∵A′M ＝22A O OM '-＝()22252-＝4，∵DM=2，∵A′D＝A′M-DM=4-2=2，即d＝2，如图，当点P落在DE上时，连接OP，过点P作PQ∵C′B′于Q．∵P为A′B′的中点，∵A′C′B′=90°，∵PQ∵A′C′，∵'12 B P C Q PQB A BC A C'''''''===∵B′C′=2∵PQ＝1，C'Q=1，∵Q点为B′C′的中点，也是旋转前BC的中点，∵OQ=OC'+C'Q=5∵OP＝2251+＝26，∵PM＝2226422OP OM-=-=，∵PD＝222PM DM-=-，∵d＝22﹣2，∵2≤d≤22﹣2．第二种情形：当A′P与FG相交，不与EF相交时，当点A′在FG上时，A′G＝25﹣2，即d＝25﹣2，如图，当点P落在EF上时，设OF交A′B′于Q，过点P作PT∵B′C′于T，过点P作PR∵OQ交OB′于R，连接OP．由上可知OP＝26，OF＝5，∵FP＝22OP OF-＝2625-＝1，∵OF＝OT，PF＝PT，∵F＝∵PTO＝90°，∵Rt∵OPF∵Rt∵OPT（HL），∵∵FOP＝∵TOP，∵PR∵OQ，∵∵OPR＝∵POF，∵∵OPR＝∵POR，∵OR＝PR，∵PT2+TR2＝PR2，22215PR PR∴+（﹣）＝∵PR＝2.6，RT＝2.4，∵∵B′PR∵∵B′QO，∵B ROB''＝PRQO，∵3.46＝2.6OQ，∵OQ＝78 17，∵QG＝OQ﹣OG＝4417，即d＝4417∵25﹣2≤d＜44 17，第三种情形：当A′P经过点F时，如图，此时FG=3，即d＝3．综上所述，2≤d＜4417或d＝3．【点睛】（1）本题考查了通过解直角三角形求线段长，解决本题的关键是构建直角三角形，熟练掌握直角三角形中边角关系.（2）∵本题综合性较强，考查了平行线的性质，解直角三角形，解决本题的关键是正确理解题意，能够根据题目条件进行分类讨论，然后通过解直角三角形求出相应的线段长即可.∵本题综合性较强，考查了辅助线的作法，平行线的性质以及解直角三角形，解决本题的关键是正确理解题意，能够根据情况对题目进行分类讨论，通过不同情形，能够作出辅助线，在解决本题的过程中要求熟练掌握直角三角形中的边角关系. 22．（2020·浙江嘉兴）在一次数学研究性学习中，小兵将两个全等的直角三角形纸片ABC和DEF拼在一起，使点A与点F重合，点C与点D重合（如图1），其中∵ACB＝∵DFE＝90°，BC＝EF＝3cm，AC＝DF＝4cm，并进行如下研究活动．活动一：将图1中的纸片DEF沿AC方向平移，连结AE，BD（如图2），当点F与点C重合时停止平移．【思考】图2中的四边形ABDE是平行四边形吗？请说明理由．【发现】当纸片DEF平移到某一位置时，小兵发现四边形ABDE为矩形（如图3）．求AF的长．活动二：在图3中，取AD的中点O，再将纸片DEF绕点O顺时针方向旋转α度（0≤α≤90），连结OB，OE （如图4）．【探究】当EF平分∵AEO时，探究OF与BD的数量关系，并说明理由．【答案】【思考】是，理由见解析；【发现】94；【探究】BD ＝2OF ，理由见解析；【分析】【思考】由全等三角形的性质得出AB ＝DE ，∵BAC ＝∵EDF ，则AB ∵DE ，可得出结论；【发现】连接BE 交AD 于点O ，设AF ＝x （cm ），则OA ＝OE ＝12（x +4），得出OF ＝OA ﹣AF ＝2﹣12x ，由勾股定理可得()2221123424x x ⎛⎫-+=+ ⎪⎝⎭，解方程求出x ，则AF 可求出；【探究】如图2，延长OF 交AE 于点H ，证明∵EFO ∵∵EFH （ASA ），得出EO ＝EH ，FO ＝FH ，则∵EHO ＝∵EOH ＝∵OBD ＝∵ODB ，可证得∵EOH ∵∵OBD （AAS ），得出BD ＝OH ，则结论得证．【详解】解：【思考】四边形ABDE 是平行四边形．证明：如图，∵∵ABC ∵∵DEF ，∵AB ＝DE ，∵BAC ＝∵EDF ，∵AB ∵DE ，∵四边形ABDE 是平行四边形；【发现】如图1，连接BE 交AD 于点O ，∵四边形ABDE 为矩形，∵OA ＝OD ＝OB ＝OE ，设AF ＝x （cm ），则OA ＝OE ＝12（x +4），∵OF ＝OA ﹣AF ＝2﹣12x ，在Rt∵OFE 中，∵OF 2+EF 2＝OE 2，∵()2221123424x x ⎛⎫-+=+ ⎪⎝⎭，解得：x ＝94， ∵AF ＝94cm ．【探究】BD ＝2OF ，证明：如图2，延长OF 交AE 于点H ，∵四边形ABDE 为矩形，∵∵OAB ＝∵OBA ＝∵ODE ＝∵OED ，OA ＝OB ＝OE ＝OD ，∵∵OBD ＝∵ODB ，∵OAE ＝∵OEA ，∵∵ABD +∵BDE +∵DEA +∵EAB ＝360°，∵∵ABD +∵BAE ＝180°，∵AE ∵BD ，∵∵OHE ＝∵ODB ，∵EF 平分∵OEH ，∵∵OEF ＝∵HEF ，∵∵EFO ＝∵EFH ＝90°，EF ＝EF ，∵∵EFO ∵∵EFH （ASA ），∵EO ＝EH ，FO ＝FH ，∵∵EHO ＝∵EOH ＝∵OBD ＝∵ODB ，∵∵EOH ∵∵OBD （AAS ），∵BD ＝OH ＝2OF ．【点睛】本题考查了图形的综合变换，涉及了三角形全等的判定与性质、平行四边形的判定与性质等，准确识图，熟练掌握和灵活运用相关知识是解题的关键．。

中考专题图形的变换-旋转

图形的变换-旋转知识点梳理一、旋转的理解1. 将图形绕一个定点旋转一定的角度，这样的图形运动称为图形的旋转，如图所示；2. 旋转前后的两个图形全等，即旋转只改变图形的位置，不改变图形的大小与形；状如△AOB ≌△A 1OB 1；3. 图形的旋转，本质上是图形上的点在同心圆上作同步运动；4. 以每组对应点和旋转中心为顶点的三角形相似，且都是等腰三角形，如等腰△AOA 1∽等腰△BOB'1；5. 当旋转角为特殊角时，如60°、90°等，会出现特殊等腰三角形，如等边三角形、等腰直角三角形；6. 当旋转角不大于90°时，对应线段所在直线的夹角等于旋转角，如AB 与A 1B 1所在直线的夹角等于∠AOA 1；7. 当旋转角不大于90时，两组对应点连线所在直线（如AA 1与BB 1)的夹角等于∠AOB 。

旋转运用<1>：共顶点模型的旋转全等1. 如图1-1，△ABC 绕点A 旋转到△AB 1C 1，则有△ABB 1≌△ACC 1（SAS ）；2. 如图1-2，若△ABC 与△AED 式等边三角形，则△ABE ≌△ACD （SAS ）；3. 如图1-3，若△ABC 与△AED 式等腰直角三角形，则△ABD ≌△ACE （SAS ）；旋转运用<2>：角含半角旋转模型1. 如图2-1，在正方形 ABCD 中，若∠EBF=45°，将△BAE 绕点B 旋转至△BCG ，则有①EF=AE+CF ；②BE 平分∠AEF ；③BF 平分教EFC .2. 如图2-2，在四边形ABCD 中，若BA=BC ，∠ABC+∠D=180°，且∠EBF=12∠ABC，则有①EF=AE+CF ；②BE 平分∠AEF ；③BF 平分教EFC .图2-1 图2-23. 如图2-3，等腰Rt △ABC 中，若∠DAE=45°可将△ABD 绕点A 旋转至△ACF ，则有DE 2=BD 2+CE 2；4. 如图2-4，等腰Rt △ABC 中，若∠DAE=45°可将△ABD 绕点A 旋转至△ACF ，则DE 2=BD 2+CE 2；5. 如图2-5，等腰Rt △ABC 中，若∠DAE=135°可将△ABD 绕点A 旋转至△ACF ，则DE 2=BD 2+CE 2；图2-3 图2-4 图2-5旋转运用<3>：对角互补模型1. 如图3-1，已知四边形ABCD 中，∠BDC=∠BAC=90°，且DB=DC ，则有AB+AC=2AD ；2. 如图3-2，已知四边形ABCD 中，∠BDC=∠BAC=90°，且DB=DC ，则有AB-AC=2AD ；图3-1 图3-23. 如图3-3，已知等边△ABC ，且∠BPC=120°，则有PA=PB+PC ；4. 如图3-4，已知等边△ABC ，且∠BPC=30°，则有PA 2=PB 2+PC 2；图3-3 图3-45. 如图3-5，已知等腰△ABC ，且∠BAC=120°，且∠BPC=60°，则有PB+PC=3PA；6. 如图3-6，已知等腰△ABC ，且∠BAC=120°，且∠BPC=120°，则有PC-PB=3PA ；图3-5 图3-6【练习】1. 如图，P 为等边三角形ABC 内的一点，且P 到三个顶点A ，B ，C 的距离分别为3，4，5，则△ABC 的面积为（）A.B ．C ．D ．2. 如图，等边三角形ABC 内有一点P ，分別连结AP 、BP 、CP ，若AP ＝6，BP ＝8，CP ＝10．则S △ABP +S △BPC ＝．3. 如图，△ABC、△BDE 都是等腰直角三角形，BA ＝BC ，BD ＝BE ，AC ＝4，DE ＝2．将△BDE 绕点B 逆时针方向旋转后得△BD ′E ′，当点E ′恰好落在线段AD ′上时，则CE ′＝．4．如图，正方形ABCD 和Rt △AEF ，AB ＝5，AE ＝AF ＝4，连接BF ，DE ．若△AEF 绕点A 旋转，当∠ABF 最大时，S △ADE ＝．5.如图，在△ABC 中，AB ＝AC ＝2，∠BAC ＝120°，点D 、E 都在边BC 上，∠DAE ＝60°．若BD ＝2CE ，则DE 的长为．6.如图，如四边形ABCD 中，AD=CD ，∠ABC=75°，∠ADC=60°，AB=2，BC=2，求四边形ABCD 的面积.7.（1）如图1，已知∠ACB ＝∠DCE ＝90°,AC ＝BC ＝6，CD ＝CE ，AE ＝3,∠CAE ＝45°,求AD 长．（2）如图2，已知∠ACB ＝∠DCE ＝90°，∠ABC ＝∠CED ＝∠CAE ＝30°，AC ＝3，AE ＝8，求AD 长．8.（1）如图1，已知等腰Rt △ABC ，∠BAC=90°，且∠ADB=45°，BD=4，CD=41，求AD的长.（2）如图2，已知等腰Rt △ABC ，∠BAC=90°，且∠ADB=75°，BD=6，AD=52，求CD 的长. （3）如图3，在四边形ABCD 中，BC=CD ，∠BCD=90°，若AB=4，AD=3，求对角线AC 的最大值.图1 图2 图39. （1）如图1，AC ，BD 是四边形ABCD 的对角线，若∠ACB ＝∠ACD ＝∠ABD ＝∠ADB ＝60°，则线段BC ，CD ，AC 三者之间有何等量关系？（2）如图2，如果把“∠ACB ＝∠ACD ＝∠ABD ＝∠ADB ＝60°”改为“∠ACB ＝∠ACD ＝∠ABD ＝ ∠ADB ＝45°”，其它条件不变，那么线段BC ，CD ，AC 三者之间有何等量关系？（3）如图3，如果把“∠ACB ＝∠ACD ＝∠ABD ＝∠ADB ＝60°”改为“∠ACB ＝∠ACD ＝∠ABD ＝∠ADB ＝α”，其它条件不变，那么线段BC ，CD ，AC 三者之间有何等量关系？图1 图2 图310. 【操作发现】如图①，在边长为1个单位长度的小正方形组成的网格中，△ABC 三个顶点均在格点上．（1）请按要求画图：将△ABC 绕点A 按顺时针方向旋转90°，点B 的对应点为B′，点C 的对应点为C′，连接BB′；（2）在（1）所画图形中，∠AB′B=．【问题解决】如图②，在等边三角形ABC 中，AC=7，点P 在△ABC 内，且∠APC=90°，∠BPC=120°，求△APC 的面积．小明同学通过观察、分析、思考，对上述问题形成了如下想法：想法一：将△APC 绕点A 按顺时针方向旋转60°，得到△AP′B ，连接PP′，寻找PA ，PB ，PC 三条线段之间的数量关系；想法二：将△APB 绕点A 按逆时针方向旋转60°，得到△AP′C′，连接PP′，寻找PA ，PB ，PC 三条线段之间的数量关系． …请参考小明同学的想法，完成该问题的解答过程．（一种方法即可）【灵活运用】如图③，在四边形ABCD 中，AE ⊥BC ，垂足为E ，∠BAE=∠ADC ，BE=CE=2，CD=5，AD=kAB （k 为常数），求BD 的长（用含k 的式子表示）．问题背景：如图①设P是等边△ABC内一点，PA＝6，PB＝8，PC＝10，求∠APB的度数．小君研究这个问题的思路是：将△ACP绕点A逆时针旋转60°得到△ABP'，易证：△APP'是等边三角形，△PBP'是直角三角形，所以∠APB＝∠APP'+∠BPP'＝150°．简单应用：（1）如图2，在等腰直角△ABC中，∠ACB＝90°．P为△ABC内一点，且PA＝5，PB＝3，PC＝2，则∠BPC＝_________°（2）如图3，在等边△ABC中，P为△ABC内一点，且PA＝5，PB＝12，∠APB＝150°，则PC＝__________．拓展廷伸：①如图4，∠ABC＝∠ADC＝90°，AB＝BC．求证：BD＝AD+DC．②若图4中的等腰直角△ABC与Rt△ADC在同侧如图5，若AD＝2，DC＝4，请直接写出BD的长．（宜兴市二模）【问题提出】如图1，四边形ABCD 中，AD CD =，120ABC ∠=︒，60ADC ∠=︒，2AB =，1BC =，求四边形ABCD 的面积．【尝试解决】旋转是一种重要的图形变换，当图形中有一组邻边相等时，往往可以通过旋转解决问题．（1）如图2，连接BD ，由于AD CD =，所以可将DCB ∆绕点D 顺时针方向旋转60︒，得到DAB ∆'，则BDB ∆'的形状是____________．（2）在（1）的基础上，求四边形ABCD 的面积．【类比应用】如图3，四边形ABCD 中，AD CD =，75ABC ∠=︒，60ADC ∠=︒，2AB =，2BC =，求四边形ABCD 的面积．（2019•亭湖区二模）【阅读材料】小明遇到这样一个问题：如图1，点P 在等边三角形ABC 内，且150APC ∠=︒，3PA =，4PC =，求PB 的长．小明发现，以AP 为边作等边三角形APD ，连接BD ，得到ABD ∆；由等边三角形的性质，可证ACP ABD ∆≅∆，得PC BD =；由已知150APC ∠=︒，可知PDB ∠的大小，进而可求得PB 的长．（1）请回答：在图1中，PDB ∠=________︒，PB =____．【问题解决】（2）参考小明思考问题的方法，解决下面问题：如图2，ABC ∆中，90ACB ∠=︒，AC BC =，点P 在ABC ∆内，且1PA =，17PB=，22PC =，求AB 的长．【灵活运用】（3）如图3，在Rt ABC ∆中，90ACB ∠=︒，BAC α∠=，且4tan 3α=，点P 在ABC ∆外，且3PB =，1PC =，直接写出PA 长的最大值．。

2020年全国中考数学试题分类(13)——图形的旋转(含答案)

2020年全国中考数学试题分类（13）——图形的旋转一．旋转的性质（共20小题）1．（2020•陕西）如图，在5×5的网格中，每个小正方形的边长均为1，点A 、B 、O 都在格点上．若将△OAB 绕点O 逆时针旋转90°，得到△OA ′B ′，A 、B 的对应点分别为A ′、B ′，则A 、B ′之间的距离为（）A ．2√5B ．5C ．√13D ．√102．（2020•德阳）如图，Rt △ABC 中，∠A ＝30°，∠ABC ＝90°．将Rt △ABC 绕点B 逆时针方向旋转得到△A 'BC '．此时恰好点C 在A 'C '上，A 'B 交AC 于点E ，则△ABE 与△ABC 的面积之比为（）A ．13B ．12C ．23D ．34 3．（2020•大连）如图，△ABC 中，∠ACB ＝90°，∠ABC ＝40°．将△ABC 绕点B 逆时针旋转得到△A ′BC ′，使点C 的对应点C ′恰好落在边AB 上，则∠CAA ′的度数是（）A ．50°B ．70°C ．110°D ．120°4．（2020•绵阳）如图，在四边形ABCD 中，AD ∥BC ，∠ABC ＝90°，AB ＝7，AD ＝4，将△ABC 绕点C 顺时针方向旋转后得△A ′B ′C ，当A ′B ′恰好经过点D 时，△B ′CD 为等腰三角形，则AA ′＝（）A ．25√185B ．2√3C ．√13D ．√145．（2020•孝感）如图，点E 在正方形ABCD 的边CD 上，将△ADE 绕点A 顺时针旋转90°到△ABF 的位置，连接EF ，过点A 作EF 的垂线，垂足为点H ，与BC 交于点G ．若BG ＝3，CG ＝2，则CE 的长为（）A ．54B ．154C ．4D ．92 6．（2020•河北）如图，将△ABC 绕边AC 的中点O 顺时针旋转180°．嘉淇发现，旋转后的△CDA 与△ABC 构成平行四边形，并推理如下：小明为保证嘉淇的推理更严谨，想在方框中“∵CB ＝AD ，”和“∴四边形…”之间作补充，下列正确的是（）A ．嘉淇推理严谨，不必补充B ．应补充：且AB ＝CDC ．应补充：且AB ∥CDD ．应补充：且OA ＝OC7．（2020•天津）如图，在△ABC 中，∠ACB ＝90°，将△ABC 绕点C 顺时针旋转得到△DEC ，使点B 的对应点E 恰好落在边AC 上，点A 的对应点为D ，延长DE 交AB 于点F ，则下列结论一定正确的是（）A ．AC ＝DEB ．BC ＝EF C ．∠AEF ＝∠D D ．AB ⊥DF8．（2020•齐齐哈尔）有两个直角三角形纸板，一个含45°角，另一个含30°角，如图①所示叠放，先将含30°角的纸板固定不动，再将含45°角的纸板绕顶点A 顺时针旋转，使BC ∥DE ，如图②所示，则旋转角∠BAD 的度数为（）A ．15°B ．30°C ．45°D ．60°9．（2020•苏州）如图，在△ABC 中，∠BAC ＝108°，将△ABC 绕点A 按逆时针方向旋转得到△AB 'C '．若点B '恰好落在BC 边上，且AB '＝CB '，则∠C '的度数为（）A ．18°B ．20°C ．24°D ．28°10．（2020•聊城）如图，在Rt △ABC 中，AB ＝2，∠C ＝30°，将Rt △ABC 绕点A 旋转得到Rt △AB ′C ′，使点B 的对应点B ′落在AC 上，在B ′C ′上取点D ，使B ′D ＝2，那么点D 到BC 的距离等于（）A ．2（√33+1） B ．√33+1 C ．√3−1 D ．√3+111．（2020•绍兴）如图，等腰直角三角形ABC 中，∠ABC ＝90°，BA ＝BC ，将BC 绕点B 顺时针旋转θ（0°＜θ＜90°），得到BP ，连结CP ，过点A 作AH ⊥CP 交CP 的延长线于点H ，连结AP ，则∠P AH 的度数（）A ．随着θ的增大而增大B ．随着θ的增大而减小C ．不变D ．随着θ的增大，先增大后减小12．（2020•海南）如图，在Rt △ABC 中，∠C ＝90°，∠ABC ＝30°，AC ＝1cm ，将Rt △ABC 绕点A 逆时针旋转得到Rt △AB 'C '，使点C '落在AB 边上，连接BB '，则BB '的长度是（）A ．1cmB ．2cmC ．√3cmD ．2√3cm13．（2020•菏泽）如图，将△ABC 绕点A 顺时针旋转角α，得到△ADE ，若点E 恰好在CB 的延长线上，则∠BED 等于（）A ．α2B ．23αC ．αD ．180°﹣α14．（2020•阜新）如图，在△ABC 中，∠ABC ＝90°，AB ＝BC ＝2．将△ABC 绕点B 逆时针旋转60°，得到△A 1BC 1，则AC 边的中点D 与其对应点D 1的距离是．15．（2020•眉山）如图，在Rt △ABC 中，∠BAC ＝90°，AB ＝2．将△ABC 绕点A 按顺时针方向旋转至△AB 1C 1的位置，点B 1恰好落在边BC 的中点处，则CC 1的长为．16．（2020•天水）如图，在边长为6的正方形ABCD 内作∠EAF ＝45°，AE 交BC 于点E ，AF 交CD 于点F ，连接EF ，将△ADF 绕点A 顺时针旋转90°得到△ABG ．若DF ＝3，则BE 的长为．17．（2020•滨州）如图，点P 是正方形ABCD 内一点，且点P 到点A 、B 、C 的距离分别为2√3、√2、4，则正方形ABCD 的面积为．18．（2020•金华）图1是一个闭合时的夹子，图2是该夹子的主视示意图，夹子两边为AC，BD（点A与点B重合），点O是夹子转轴位置，OE⊥AC于点E，OF⊥BD于点F，OE＝OF＝1cm，AC＝BD＝6cm，CE＝DF，CE：AE＝2：3．按图示方式用手指按夹子，夹子两边绕点O转动．（1）当E，F两点的距离最大时，以点A，B，C，D为顶点的四边形的周长是cm．（2）当夹子的开口最大（即点C与点D重合）时，A，B两点的距离为cm．19．（2020•广州）如图，正方形ABCD中，△ABC绕点A逆时针旋转到△AB'C'，AB'，AC'分别交对角线BD 于点E，F，若AE＝4，则EF•ED的值为．20．（2020•玉林）如图，四边形ABCD中，对角线AC与BD交于点O，且OA＝OB＝OC＝OD=√22AB．（1）求证：四边形ABCD是正方形；（2）若H是边AB上一点（H与A，B不重合），连接DH，将线段DH绕点H顺时针旋转90°，得到线段HE，过点E分别作BC及AB延长线的垂线，垂足分别为F，G．设四边形BGEF的面积为s1，以HB，BC为邻边的矩形的面积为s2，且s1＝s2．当AB＝2时，求AH的长．二．旋转对称图形（共1小题）21．（2020•镇江）点O是正五边形ABCDE的中心，分别以各边为直径向正五边形的外部作半圆，组成了一幅美丽的图案（如图）．这个图案绕点O至少旋转°后能与原来的图案互相重合．三．中心对称（共3小题）22．（2020•绍兴）如图，点O为矩形ABCD的对称中心，点E从点A出发沿AB向点B运动，移动到点B 停止，延长EO交CD于点F，则四边形AECF形状的变化依次为（）A．平行四边形→正方形→平行四边形→矩形B．平行四边形→菱形→平行四边形→矩形C．平行四边形→正方形→菱形→矩形D．平行四边形→菱形→正方形→矩形23．（2020•泰安）如图，将正方形网格放置在平面直角坐标系中，其中，每个小正方形的边长均为1，点A，B，C的坐标分别为A（0，3），B（﹣1，1），C（3，1）．△A'B'C′是△ABC关于x轴的对称图形，将△A'B'C'绕点B'逆时针旋转180°，点A'的对应点为M，则点M的坐标为．24．（2020•台州）用四块大正方形地砖和一块小正方形地砖拼成如图所示的实线图案，每块大正方形地砖面积为a，小正方形地砖面积为b，依次连接四块大正方形地砖的中心得到正方形ABCD．则正方形ABCD 的面积为．（用含a，b的代数式表示）四．中心对称图形（共3小题）25．（2020•黄石）下列图形中，既是中心对称又是轴对称图形的是（）A．B．C．D．26．（2020•天水）下列图形中，是中心对称图形但不是轴对称图形的是（）A．B．C．D．27．（2020•呼伦贝尔）下列图形中，既是轴对称图形，又是中心对称图形的是（）A．B．C．D．五．关于原点对称的点的坐标（共1小题）28．（2020•淮安）在平面直角坐标系中，点（3，2）关于原点对称的点的坐标是（）A．（2，3）B．（﹣3，2）C．（﹣3，﹣2）D．（﹣2，﹣3）六．坐标与图形变化-旋转（共6小题）29．（2020•青岛）如图，将△ABC先向上平移1个单位，再绕点P按逆时针方向旋转90°，得到△A′B′C′，则点A的对应点A′的坐标是（）A．（0，4）B．（2，﹣2）C．（3，﹣2）D．（﹣1，4）30．（2020•枣庄）如图，平面直角坐标系中，点B在第一象限，点A在x轴的正半轴上，∠AOB＝∠B＝30°，OA＝2．将△AOB绕点O逆时针旋转90°，点B的对应点B'的坐标是（）A．（−√3，3）B．（﹣3，√3）C．（−√3，2+√3）D．（﹣1，2+√3）31．（2020•黄石）在平面直角坐标系中，点G的坐标是（﹣2，1），连接OG，将线段OG绕原点O旋转180°，得到对应线段OG'，则点G'的坐标为（）A．（2，﹣1）B．（2，1）C．（1，﹣2）D．（﹣2，﹣1）32．（2020•恩施州）如图，在平面直角坐标系中，△ABC的顶点坐标分别为：A（﹣2，0），B（1，2），C （1，﹣2）．已知N（﹣1，0），作点N关于点A的对称点N1，点N1关于点B的对称点N2，点N2关于点C 的对称点N3，点N3关于点A的对称点N4，点N4关于点B的对称点N5，…，依此类推，则点N2020的坐标为．33．（2020•烟台）如图，已知点A （2，0），B （0，4），C （2，4），D （6，6），连接AB ，CD ，将线段AB绕着某一点旋转一定角度，使其与线段CD 重合（点A 与点C 重合，点B 与点D 重合），则这个旋转中心的坐标为．34．（2020•衡阳）如图，在平面直角坐标系中，点P 1的坐标为（√22，√22），将线段OP 1绕点O 按顺时针方向旋转45°，再将其长度伸长为OP 1的2倍，得到线段OP 2；又将线段OP 2绕点O 按顺时针方向旋转45°，长度伸长为OP 2的2倍，得到线段OP 3；如此下去，得到线段OP 4，OP 5，…，OP n （n 为正整数），则点P 2020的坐标是．七．作图-旋转变换（共6小题）35．（2020•广西）如图，在平面直角坐标系中，△ABC 的三个顶点分别是A （1，1），B （4，1），C （5，3）．（1）将△ABC 向左平移6个单位长度得到△A 1B 1C 1，请画出△A 1B 1C 1，并写出点A 1，C 1的坐标．（2）请画出△ABC 关于原点O 成中心对称的△A 2B 2C 2．36．（2020•巴中）如图所示，△ABC在边长为1cm的小正方形组成的网格中．（1）将△ABC沿y轴正方向向上平移5个单位长度后，得到△A1B1C1，请作出△A1B1C1，并求出A1B1的长度；（2）再将△A1B1C1绕坐标原点O顺时针旋转180°，得到△A2B2C2，请作出△A2B2C2，并直接写出点B2的坐标；（3）在（1）（2）的条件下，求线段AB在变换过程中扫过图形的面积和．37．（2020•贵港）如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别为A（1，4），B（4，1），C（4，3）．（1）画出将△ABC向左平移5个单位得到的△A1B1C1；（2）画出将△ABC绕原点O顺时针旋转90°得到的△A2B2C2．38．（2020•阜新）如图，△ABC在平面直角坐标系中，顶点的坐标分别为A（4，4），B（1，1），C（4，1）．（1）画出与△ABC关于y轴对称的△A1B1C1；（2）将△ABC绕点O1顺时针旋转90°得到△A2B2C2，弧AA2是点A所经过的路径，则旋转中心O1的坐标为；（3）求图中阴影部分的面积（结果保留π）．39．（2020•桂林）如图，在平面直角坐标系中，△ABC的三个顶点分别是A（1，3），B（4，4），C（2，1）．（1）把△ABC向左平移4个单位后得到对应的△A1B1C1，请画出平移后的△A1B1C1；（2）把△ABC绕原点O旋转180°后得到对应的△A2B2C2，请画出旋转后的△A2B2C2；（3）观察图形可知，△A1B1C1与△A2B2C2关于点（，）中心对称．40．（2020•常州）如图1，点B在线段CE上，Rt△ABC≌Rt△CEF，∠ABC＝∠CEF＝90°，∠BAC＝30°，BC＝1．（1）点F到直线CA的距离是；（2）固定△ABC，将△CEF绕点C按顺时针方向旋转30°，使得CF与CA重合，并停止旋转．①请你在图1中用直尺和圆规画出线段EF经旋转运动所形成的平面图形（用阴影表示，保留画图痕迹，不要求写画法）．该图形的面积为；②如图2，在旋转过程中，线段CF与AB交于点O，当OE＝OB时，求OF的长．八．利用旋转设计图案（共1小题）41．（2020•枣庄）如图的四个三角形中，不能由△ABC 经过旋转或平移得到的是（）A ．B ．C ．D ．九．几何变换综合题（共9小题） 42．（2020•锦州）已知△AOB 和△MON 都是等腰直角三角形（√22OA ＜OM ＝ON ），∠AOB ＝∠MON ＝90°．（1）如图1：连AM ，BN ，求证：△AOM ≌△BON ；（2）若将△MON 绕点O 顺时针旋转，①如图2，当点N 恰好在AB 边上时，求证：BN 2+AN 2＝2ON 2；②当点A ，M ，N 在同一条直线上时，若OB ＝4，ON ＝3，请直接写出线段BN 的长．43．（2020•葫芦岛）在等腰△ADC 和等腰△BEC 中，∠ADC ＝∠BEC ＝90°，BC ＜CD ，将△BEC 绕点C 逆时针旋转，连接AB ，点O 为线段AB 的中点，连接DO ，EO ．（1）如图1，当点B 旋转到CD 边上时，请直接写出线段DO 与EO 的位置关系和数量关系；（2）如图2，当点B 旋转到AC 边上时，（1）中的结论是否成立？若成立，请写出证明过程，若不成立，请说明理由；（3）若BC ＝4，CD ＝2√6，在△BEC 绕点C 逆时针旋转的过程中，当∠ACB ＝60°时，请直接写出线段OD 的长．44．（2020•沈阳）在△ABC 中，AB ＝AC ，∠BAC ＝α，点P 为线段CA 延长线上一动点，连接PB ，将线段PB 绕点P 逆时针旋转，旋转角为α，得到线段PD ，连接DB ，DC ．（1）如图1，当α＝60°时，①求证：P A ＝DC ；②求∠DCP的度数；（2）如图2，当α＝120°时，请直接写出P A和DC的数量关系．（3）当α＝120°时，若AB＝6，BP=√31，请直接写出点D到CP的距离为．45．（2020•长春）如图①，在△ABC中，∠ABC＝90°，AB＝4，BC＝3．点P从点A出发，沿折线AB﹣BC以每秒5个单位长度的速度向点C运动，同时点D从点C出发，沿CA以每秒2个单位长度的速度向点A运动，点P到达点C时，点P、D同时停止运动．当点P不与点A、C重合时，作点P关于直线AC的对称点Q，连结PQ交AC于点E，连结DP、DQ．设点P的运动时间为t秒．（1）当点P与点B重合时，求t的值．（2）用含t的代数式表示线段CE的长．（3）当△PDQ为锐角三角形时，求t的取值范围．（4）如图②，取PD的中点M，连结QM．当直线QM与△ABC的一条直角边平行时，直接写出t的值．46．（2020•鄂尔多斯）（1）【操作发现】如图1，在边长为1个单位长度的小正方形组成的网格中，△ABC的三个顶点均在格点上．①请按要求画图：将△ABC绕点A顺时针方向旋转90°，点B的对应点为点B′，点C的对应点为点C′．连接BB′；②在①中所画图形中，∠AB′B＝°．（2）【问题解决】如图2，在Rt△ABC中，BC＝1，∠C＝90°，延长CA到D，使CD＝1，将斜边AB绕点A顺时针旋转90°到AE，连接DE，求∠ADE的度数．（3）【拓展延伸】如图3，在四边形ABCD中，AE⊥BC，垂足为E，∠BAE＝∠ADC，BE＝CE＝1，CD＝3，AD＝kAB（k 为常数），求BD的长（用含k的式子表示）．47．（2020•十堰）如图1，已知△ABC≌△EBD，∠ACB＝∠EDB＝90°，点D在AB上，连接CD并延长交AE于点F．（1）猜想：线段AF与EF的数量关系为；（2）探究：若将图1的△EBD绕点B顺时针方向旋转，当∠CBE小于180°时，得到图2，连接CD并延长交AE 于点F ，则（1）中的结论是否还成立？若成立，请证明；若不成立，请说明理由；（3）拓展：图1中，过点E 作EG ⊥CB ，垂足为点G ．当∠ABC 的大小发生变化，其它条件不变时，若∠EBG ＝∠BAE ，BC ＝6，直接写出AB 的长．48．（2020•包头）如图，在Rt △ABC 中，∠ACB ＝90°，AC ＝4，BC ＝2，Rt △ABC 绕点C 按顺时针方向旋转得到Rt △A ′B ′C ，A ′C 与AB 交于点D ．（1）如图1，当A ′B ′∥AC 时，过点B 作BE ⊥A ′C ，垂足为E ，连接AE ．①求证：AD ＝BD ；②求α△αααα△ααα的值；（2）如图2，当A ′C ⊥AB 时，过点D 作DM ∥A ′B ′，交B ′C 于点N ，交AC 的延长线于点M ，求αααα的值．49．（2020•东营）如图1，在等腰三角形ABC 中，∠A ＝120°，AB ＝AC ，点D 、E 分别在边AB 、AC 上，AD ＝AE ，连接BE ，点M 、N 、P 分别为DE 、BE 、BC 的中点．（1）观察猜想．图1中，线段NM 、NP 的数量关系是，∠MNP 的大小为．（2）探究证明把△ADE 绕点A 顺时针方向旋转到如图2所示的位置，连接MP 、BD 、CE ，判断△MNP 的形状，并说明理由；（3）拓展延伸把△ADE 绕点A 在平面内自由旋转，若AD ＝1，AB ＝3，请求出△MNP 面积的最大值．50．（2020•威海）发现规律（1）如图①，△ABC 与△ADE 都是等边三角形，直线BD ，CE 交于点F ．直线BD ，AC 交于点H ．求∠BFC 的度数．（2）已知：△ABC与△ADE的位置如图②所示，直线BD，CE交于点F．直线BD，AC交于点H．若∠ABC＝∠ADE＝α，∠ACB＝∠AED＝β，求∠BFC的度数．应用结论（3）如图③，在平面直角坐标系中，点O的坐标为（0，0），点M的坐标为（3，0），N为y轴上一动点，连接MN．将线段MN绕点M逆时针旋转60°得到线段MK，连接NK，OK．求线段OK长度的最小值．2020年全国中考数学试题分类（13）——图形的旋转参考答案与试题解析一．旋转的性质（共20小题）1．【解答】解：如图，由旋转的性质作出△A 'OB '，连接AB '，∵每个小正方形的边长均为1，∴AB '=√22+32=√13，故选：C ．2．【解答】解：∵∠A ＝30°，∠ABC ＝90°，∴∠ACB ＝60°，∵将Rt △ABC 绕点B 逆时针方向旋转得到△A 'BC '，∴BC ＝BC '，∠ACB ＝∠A 'C 'B ＝60°，∴△BCC '是等边三角形，∴∠CBC '＝60°，∴∠ABA '＝60°，∴∠BEA ＝90°，设CE ＝a ，则BE =√3a ，AE ＝3a ，∴αααα=13， ∴αααα=34， ∴△ABE 与△ABC 的面积之比为34．故选：D ．3．【解答】解：∵∠ACB ＝90°，∠ABC ＝40°，∴∠CAB ＝90°﹣∠ABC ＝90°﹣40°＝50°，∵将△ABC 绕点B 逆时针旋转得到△A ′BC ′，使点C 的对应点C ′恰好落在边AB 上，∴∠A ′BA ＝∠ABC ＝40°，A ′B ＝AB ，∴∠BAA ′＝∠BA ′A =12（180°﹣40°）＝70°，∴∠CAA '＝∠CAB +∠BAA ′＝50°+70°＝120°．故选：D ．4．【解答】解：过D 作DE ⊥BC 于E ，则BE ＝AD ＝4，DE ＝7，设B ′C ＝BC ＝x ，则DC =√2x ，∴DC 2＝DE 2+EC 2，即2x 2＝49+（x ﹣4）2，解得：x ＝5（负值舍去），∴BC ＝5，AC =√74，在AB 上取一点F ，使得BF ＝BC ＝5，连接DF ，则△DFC ∽△CB ′B ，且相似比为√2：1，∴AF ＝7﹣5＝2，∵AD ＝4，∴DF ＝2√5，∴BB ′=√2=√10， ∵将△ABC 绕点C 顺时针方向旋转后得△A ′B ′C ，∴∠DB ′C ＝∠ABC ＝90°，B ′C ＝BC ，A ′C ＝AC ，∠A ′CA ＝∠B ′CB ，∴△A ′CA ∽△B ′CB ，∴α′αα′α=αααα，∴AA ′=√745×√10=25√185，故选：A ．5．【解答】解：如图所示，连接EG ，由旋转可得，△ADE ≌△ABF ，∴AE ＝AF ，DE ＝BF ，又∵AG ⊥EF ，∴H 为EF 的中点，∴AG 垂直平分EF ，∴EG ＝FG ，设CE ＝x ，则DE ＝5﹣x ＝BF ，FG ＝8﹣x ，∴EG ＝8﹣x ，∵∠C ＝90°，∴Rt △CEG 中，CE 2+CG 2＝EG 2，即x 2+22＝（8﹣x ）2，解得x =154， ∴CE 的长为154，故选：B ．6．【解答】解：∵CB ＝AD ，AB ＝CD ，∴四边形ABCD 是平行四边形，故应补充“AB ＝CD ”，故选：B ．7．【解答】解：由旋转可得，△ABC ≌△DEC ，∴AC ＝DC ，故A 选项错误，BC ＝EC ，故B 选项错误，∠AEF ＝∠DEC ＝∠B ，故C 选项错误，∠A ＝∠D ，又∵∠ACB ＝90°，∴∠A +∠B ＝90°，∴∠D +∠B ＝90°，∴∠BFD ＝90°，即DF ⊥AB ，故D 选项正确，故选：D ．8．【解答】解：如图，设AD与BC交于点F，∵BC∥DE，∴∠CF A＝∠D＝90°，∵∠CF A＝∠B+∠BAD＝60°+∠BAD，∴∠BAD＝30°故选：B．9．【解答】解：∵AB'＝CB'，∴∠C＝∠CAB'，∴∠AB'B＝∠C+∠CAB'＝2∠C，∵将△ABC绕点A按逆时针方向旋转得到△AB'C'，∴∠C＝∠C'，AB＝AB'，∴∠B＝∠AB'B＝2∠C，∵∠B+∠C+∠CAB＝180°，∴3∠C＝180°﹣108°，∴∠C＝24°，∴∠C'＝∠C＝24°，故选：C．10．【解答】解：方法一：∵在Rt△ABC中，AB＝2，∠C＝30°，∴BC＝2√3，AC＝4，∵将Rt△ABC绕点A旋转得到Rt△AB′C′，使点B的对应点B′落在AC上，∴AB′＝AB＝2，B′C′＝BC＝2√3，∴B′C＝2，延长C′B′交BC于F，∴∠CB′F＝∠AB′C′＝90°，∵∠C＝30°，∴∠CFB′＝60°，B′F=√33B′C=2√33，∵B′D＝2，∴DF＝2+2√3 3，过D作DE⊥BC于E，∴DE=√32DF=√32×（2+2√33）=√3+1，方法二：过B′作B′F⊥BC于F，B′H⊥DE于H，则B′F＝HE，B′H＝EF，在Rt△ABC中，AB＝2，∠C＝30°，∴BC＝2√3，AC＝4，∵将Rt△ABC绕点A旋转得到Rt△AB′C′，使点B的对应点B′落在AC上，∴AB′＝AB＝2，B′C′＝BC＝2√3，∴B′C＝2，∴B′F=12AB＝1，∴HE＝1，∵∠B′HD＝∠HEC＝90°，∴∠HB′C＝∠C＝30°，∴∠DB′H＝60°，∴∠B′DH＝30°，∴B′H＝1，DH=√3，∴DE=√3+1，故选：D．11．【解答】解：∵将BC绕点B顺时针旋转θ（0°＜θ＜90°），得到BP，∴BC＝BP＝BA，∴∠BCP＝∠BPC，∠BP A＝∠BAP，∵∠CBP+∠BCP+∠BPC＝180°，∠ABP+∠BAP+∠BP A＝180°，∠ABP+∠CBP＝90°，∴∠BPC+∠BP A＝135°＝∠CP A，∵∠CP A＝∠AHC+∠P AH＝135°，∴∠P AH＝135°﹣90°＝45°，∴∠P AH的度数是定值，故选：C．12．【解答】解：∵在Rt△ABC中，∠C＝90°，∠ABC＝30°，AC＝1cm，∴AC=12AB，则AB＝2AC＝2cm．又由旋转的性质知，AC′＝AC=12AB，B′C′⊥AB，∴B′C′是△ABB′的中垂线，∴AB′＝BB′．根据旋转的性质知AB ＝AB ′＝BB ′＝2cm ．故选：B ．13．【解答】解：∵∠ABC ＝∠ADE ，∠ABC +∠ABE ＝180°，∴∠ABE +∠ADE ＝180°，∴∠BAD +∠BED ＝180°，∵∠BAD ＝α，∴∠BED ＝180°﹣α．故选：D ．14．【解答】解：连接BD 、BD 1，如图，∵∠ABC ＝90°，AB ＝BC ＝2，∴AC =√22+22=2√2，∵D 点为AC 的中点，∴BD =12AC =√2，∵△ABC 绕点B 逆时针旋转60°，得到△A 1BC 1，∴BD 1＝BD ，∠DBD 1＝60°，∴△BDD 1为等边三角形，∴DD 1＝BD =√2．故答案为√2．15．【解答】解：∵在Rt △ABC 中，∠BAC ＝90°，将该三角形绕点A 按顺时针方向旋转到△AB 1C 1的位置，点B 1恰好落在边BC 的中点处，∴AB 1=12BC ，BB 1＝B 1C ，AB ＝AB 1，∴BB 1＝AB ＝AB 1，∴△ABB 1是等边三角形，∴∠BAB 1＝∠B ＝60°，∴∠CAC 1＝60°，∵将△ABC 绕点A 按顺时针方向旋转至△AB 1C 1的位置，∴CA ＝C 1A ，∴△AC 1C 是等边三角形，∴CC 1＝CA ，∵AB ＝2，∴CA ＝2√3，∴CC 1＝2√3．故答案为：2√3．16．【解答】解：法一：由题意可得，△ADF ≌△ABG ，∴DF ＝BG ，∠DAF ＝∠BAG ，∵∠DAB ＝90°，∠EAF ＝45°，∴∠DAF +∠EAB ＝45°，∴∠BAG +∠EAB ＝45°，∴∠EAF ＝∠EAG ，在△EAG 和△EAF 中，{αα=αααααα=αααααα=αα，∴△EAG ≌△EAF （SAS ），∴GE ＝FE ，设BE ＝x ，则GE ＝BG +BE ＝3+x ，CE ＝6﹣x ，∴EF ＝3+x ，∵CD ＝6，DF ＝3，∴CF ＝3，∵∠C ＝90°，∴（6﹣x ）2+32＝（3+x ）2，解得，x ＝2，即BE ＝2，法二：设BE ＝x ，连接GF ，如下图所示，∵四边形ABCD 为正方形，∴∠ABE ＝∠GCF ＝90°，∵△ADF 绕点A 顺时针旋转90°得到△ABG ，∴∠CAF ＝90°，GA ＝F A ，∴△GAF 为等腰直角三角形，∵∠EAF ＝45°，∴AE 垂直平分GF ，∴∠AEB +∠CGF ＝90°，∵在Rt △AEB 中，∠AEB +∠BAE ＝90°，∴∠BAE ＝∠CGF ，∴△BAE ∽△CGF ，∴αααα=αααα， ∵CF ＝CD ﹣DF ＝6﹣3＝3，GC ＝BC +BG ＝BC +DF ＝6+3＝9， ∴α3=69，∴x ＝2，即BE ＝2，故答案为：2．17．【解答】解：如图，将△ABP 绕点B 顺时针旋转90°得到△CBM ，连接PM ，过点B 作BH ⊥PM 于H ．∵BP ＝BM =√2，∠PBM ＝90°，∴PM =√2PB ＝2，∵PC ＝4，P A ＝CM ＝2√3，∴PC 2＝CM 2+PM 2，∴∠PMC ＝90°，∵∠BPM ＝∠BMP ＝45°，∴∠CMB ＝∠APB ＝135°，∴∠APB +∠BPM ＝180°，∴A ，P ，M 共线，∵BH ⊥PM ，∴PH ＝HM ，∴BH ＝PH ＝HM ＝1，∴AH ＝2√3+1，∴AB 2＝AH 2+BH 2＝（2√3+1）2+12＝14+4√3，∴正方形ABCD 的面积为14+4√3．解法二：连接AC ，利用勾股定理求出AC 即可．故答案为14+4√3．18．【解答】解：（1）当E ，F 两点的距离最大时，E ，O ，F 共线，此时四边形ABCD 是矩形， ∵OE ＝OF ＝1cm ，∴EF ＝2cm ，∴AB ＝CD ＝2cm ，∴此时四边形ABCD 的周长为2+2+6+6＝16（cm ），故答案为16．（2）如图3中，连接EF 交OC 于H ．由题意CE ＝CF =25×6=125（cm ）， ∵OE ＝OF ＝1cm ，∴CO 垂直平分线段EF ，∵OC =√αα2+αα2=√(125)2+12=135（cm ）， ∵12•OE •EC =12•CO •EH ， ∴EH =1×125135=1213（cm ），∴EF ＝2EH =2413（cm ）∵EF ∥AB ，∴αααα=αααα=25， ∴AB =52×2413=6013（cm ）．故答案为6013． 19．【解答】解：∵四边形ABCD 是正方形，∴∠BAC ＝∠ADB ＝45°，∵把△ABC 绕点A 逆时针旋转到△AB 'C '，∴∠EAF ＝∠BAC ＝45°，∵∠AEF ＝∠DEA ，∴△AEF ∽△DEA ，∴αααα=αααα，∴EF •ED ＝AE 2，∵AE ＝4，∴EF •ED 的值为16，故答案为：16．20．【解答】（1）证明：∵OA ＝OB ＝OC ＝OD ，∴四边形ABCD 是平行四边形，∴AC ＝BD ，∴平行四边形ABCD 是矩形，∵OA ＝OB ＝OC ＝OD =√22AB ，∴OA 2+OB 2＝AB 2，∴∠AOB ＝90°，即AC ⊥BD ，∴四边形ABCD 是正方形；（2）解：∵EF ⊥BC ，EG ⊥AG ，∴∠G ＝∠EFB ＝∠FBG ＝90°，∴四边形BGEF 是矩形，∵将线段DH 绕点H 顺时针旋转90°，得到线段HE ，∴∠DHE ＝90°，DH ＝HE ，∴∠ADH +∠AHD ＝∠AHD +∠EHG ＝90°，∴∠ADH ＝∠EHG ，∵∠DAH ＝∠G ＝90°，∴△ADH ≌△GHE （AAS ），∴AD ＝HG ，AH ＝EG ，∵AB ＝AD ，∴AB ＝HG ，∴AH ＝BG ，∴BG ＝EG ，∴矩形BGEF 是正方形，设AH ＝x ，则BG ＝EG ＝x ，∵s 1＝s 2．∴x 2＝2（2﹣x ），解得：x =√5−1（负值舍去），∴AH =√5−1．二．旋转对称图形（共1小题）21．【解答】解：连接OA ，OE ，则这个图形至少旋转∠AOE 才能与原图象重合，∠AOE =360°5=72°．故答案为：72．三．中心对称（共3小题）22．【解答】解：观察图形可知，四边形AECF形状的变化依次为平行四边形→菱形→平行四边形→矩形．故选：B．23．【解答】解：将△A'B'C'绕点B'逆时针旋转180°，如图所示：所以点M的坐标为（﹣2，1），故答案为：（﹣2，1）．24．【解答】解：如图，连接DK，DN，∵∠KDN＝∠MDT＝90°，∴∠KDM＝∠NDT，∵DK＝DN，∠DKM＝∠DNT＝45°，∴△DKM≌△DNT（ASA），∴S△DKM＝S△DNT，∴S四边形DMNT＝S△DKN=14a，∴正方形ABCD的面积＝4×14a+b＝a+b．故答案为（a+b）．四．中心对称图形（共3小题）25．【解答】解：A、既不是中心对称图形，又不是轴对称图形，故本选项不符合题意；B、是中心对称图形，但不是轴对称图形，故本选项不符合题意；C、不是中心对称图形，是轴对称图形，故本选项不符合题意；D、既是中心对称图形，又是轴对称图形，故本选项符合题意；故选：D．26．【解答】解：A、是轴对称图形，不是中心对称图形，故本选项不合题意；B、既是轴对称图形，又是中心对称图形，故本选项不合题意；C、是中心对称图形但不是轴对称图形，故本选项符合题意；D、是轴对称图形，不是中心对称图形，故本选项不合题意．故选：C．27．【解答】解：A、不是轴对称图形，是中心对称图形，故此选项错误；B、是轴对称图形，不是中心对称图形，故此选项错误；C、既是轴对称图形，也是中心对称图形，故此选项正确；D、是轴对称图形，不是中心对称图形，故此选项错误；故选：C．五．关于原点对称的点的坐标（共1小题）28．【解答】解：点（3，2）关于原点对称的点的坐标是：（﹣3，﹣2）．故选：C．六．坐标与图形变化-旋转（共6小题）29．【解答】解：如图，△A′B′C′即为所求，则点A的对应点A′的坐标是（﹣1，4）．故选：D．30．【解答】解：如图，过点B′作B′H⊥y轴于H．在Rt△A′B′H中，∵A′B′＝2，∠B′A′H＝60°，∴A′H＝A′B′cos60°＝1，B′H＝A′B′sin60°=√3，∴OH＝2+1＝3，∴B′（−√3，3），故选：A．31．【解答】解：由题意G与G′关于原点对称，∵G（﹣2，1），∴G′（2，﹣1），故选：A．32．【解答】解：由题意得，作出如下图形：N 点坐标为（﹣1，0），N 点关于A 点对称的N 1点的坐标为（﹣3，0），N 1点关于B 点对称的N 2点的坐标为（5，4），N 2点关于C 点对称的N 3点的坐标为（﹣3，﹣8），N 3点关于A 点对称的N 4点的坐标为（﹣1，8），N 4点关于B 点对称的N 5点的坐标为（3，﹣4），N 5点关于C 点对称的N 6点的坐标为（﹣1，0），此时刚好回到最开始的点N 处，∴其每6个点循环一次，∴2020÷6＝336……4，即循环了336次后余下4，故N 2020的坐标与N 4点的坐标相同，其坐标为（﹣1，8）．故答案为：（﹣1，8）．33．【解答】解：平面直角坐标系如图所示，旋转中心是P 点，P （4，2）．故答案为（4，2）．34．【解答】解：∵点P 1的坐标为（√22，√22），将线段OP 1绕点O 按逆时针方向旋转45°，再将其长度伸长为OP 1的2倍，得到线段OP 2；∴OP 1＝1，OP 2＝2，∴OP 3＝4，如此下去，得到线段OP 4＝23，OP 5＝24…，∴OP n ＝2n ﹣1，由题意可得出线段每旋转8次旋转一周，∵2020÷8＝252…4，∴点P2020的坐标与点P4的坐标在同一直线上，正好在y轴的负半轴上，∴点P2020的坐标是（0，﹣22019）．故答案为：（0，﹣22019）．七．作图-旋转变换（共6小题）35．【解答】解：（1）如图，△A1B1C1即为所求，∴A1（﹣5，1）C1（﹣1，3）；（2）如图，△A2B2C2即为所求．36．【解答】解：（1）如图所示，△A1B1C1即为所求，α1α1=3√2αα；（2）如图，△A2B2C2即为所求，B2（4，﹣4）；（3）在（1）（2）的条件下，线段AB在变换过程中扫过图形的面积和为：5×3+12π×（4√2）2−12π×（√2）2＝（15+15π）cm2．37．【解答】解：（1）如图所示，△A1B1C1即为所求．（2）如图所示，△A2B2C2即为所求．38．【解答】解：（1）如图，△A1B1C1为所作；（2）旋转中心O1的坐标为（2，0），故答案为（2，0）；（3）设旋转半径为r，则r2＝22+42＝20，∴阴影部分的图形面积为：α阴影=14⋅αα2−12×2×4−12×2×2+12×1×1=5π−112．39．【解答】解：（1）如图所示，△A1B1C1即为所求；（2）如图所示，△A2B2C2即为所求；（3）由图可得，△A1B1C1与△A2B2C2关于点（﹣2，0）中心对称．故答案为：﹣2，0．40．【解答】解：（1）如图1中，作FD⊥AC于D，∵Rt △ABC ≌Rt △CEF ，∠ABC ＝∠CEF ＝90°，∠BAC ＝30°，BC ＝1．∴∠ACB ＝60°，∠FCE ＝∠BAC ＝30°，AC ＝CF ，∴∠ACF ＝30°，∴∠BAC ＝∠FCD ，在△ABC 和△CDF 中，{∠ααα=∠ααααααα=αααααα=αα，∴△ABC ≌△CDF （AAS ），∴FD ＝BC ＝1，法二：∵∠ECF ＝∠FCD ＝30°，FD ⊥CD ，FE ⊥CE ，∴DF ＝EF ，∵EF ＝BC ＝1，∴DF ＝1．故答案为1；（2）线段EF 经旋转运动所形成的平面图形如图所示，此时点E 落在CF 上的点H 处．S 阴＝S △EFC +S 扇形ACF ﹣S 扇形CEH ﹣S △AHC ＝S 扇形ACF ﹣S 扇形ECH =30⋅α⋅22360−30⋅α⋅(√3)2360=α12．故答案为α12．（3）如图2中，过点E 作EH ⊥CF 于H ．设OB ＝OE ＝x ．在Rt △ECF 中，∵EF ＝1，∠ECF ＝30°，EH ⊥CF ，∴EC =√3EF =√3，EH =√32，CH =√3EH =32，在Rt △BOC 中，OC =√αα2+αα2=√1+α2， ∴OH ＝CH ﹣OC =32−√1+α2，在Rt △EOH 中，则有x 2＝（√32）2+（32−√1+α2）2，解得x =√73或−√73（不合题意舍弃），∴OC =1+(√73)2=43， ∵CF ＝2EF ＝2，∴OF ＝CF ﹣OC ＝2−43=23．八．利用旋转设计图案（共1小题）41．【解答】解：由题意，选项A ，C ，D 可以通过平移，旋转得到，选项B 可以通过翻折得到．故选：B ．九．几何变换综合题（共9小题）42．【解答】（1）证明：如图1中，∵∠AOB ＝∠MON ＝90°，∴∠AOM ＝∠BON ，∵AO ＝BO ，OM ＝ON ，∴△AOM ≌△BON （SAS ）．（2）①证明：如图2中，连接AM ．同法可证△AOM≌△BON，∴AM＝BN，∠OAM＝∠B＝45°，∵∠OAB＝∠B＝45°，∴∠MAN＝∠OAM+∠OAB＝90°，∴MN2＝AN2+AM2，∵△MON是等腰直角三角形，∴MN2＝2ON2，∴NB2+AN2＝2ON2．②如图3﹣1中，设OA交BN于J，过点O作OH⊥MN于H．∵△AOM≌△BON，∴AM＝BN，∠OAM＝∠OBN，∵∠AJN＝∠BJO，∴∠ANJ＝∠JOB＝90°，∵OM＝ON＝3，∠MON＝90°，OH⊥MN，∴MN＝3√2，MH＝HN═OH=3√2 2，∴AH=√αα2−αα2=42−(3√22)2=√462，∴BN＝AM＝MH+AH=√46+3√22．如图3﹣2中，同法可证AM＝BN=√46−3√22．43．【解答】解：（1）DO⊥EO，DO＝EO；理由：当点B旋转到CD边上时，点E必在边AC上，∴∠AEB＝∠CEB＝90°，在Rt△ABE中，点O是AB的中点，∴OE＝OA=12AB，∴∠BOE＝2∠BAE，在Rt△ABD中，点O是AB的中点，∴OD＝OA=12AB，∴∠DOE＝2∠BAD，∴OD＝OE，∵等腰△ADC，且∠ADC＝90°，∴∠DAC＝45°，∴∠DOE＝∠BOE+∠DOE＝2∠BAE+2∠BAD＝2（∠BAE+∠DAE）＝2∠DAC＝90°，∴OD⊥OE；（2）仍然成立，理由：如图2，延长EO到点M，使得OM＝OE，连接AM，DM，DE，∵O是AB的中点，∴OA＝OB，∵∠AOM＝∠BOE，∴△AOM≌△BOE（SAS），∴∠MAO＝∠EBO，MA＝EB，∵△ACD和△CBE是等腰三角形，∠ADC＝∠CEB＝90°，∴∠CAD＝∠ACD＝∠EBC＝∠BCE＝45°，∵∠OBE＝180°﹣∠EBC＝135°，∴∠MAO＝135°，∴∠MAD＝∠MAO﹣∠DAC＝90°，∵∠DCE＝∠DCA+∠BCE＝90°，∴∠MAD＝∠DCE，∵MA＝EB，EB＝EC，∴MA＝EC，∵AD＝DC，∴△MAD≌△ECD，∴MD＝ED，∠ADM＝∠CDE，∵∠CDE+∠ADE＝90°，∴∠ADM+∠ADE＝90°，∴∠MDE＝90°，∵MO＝EO，MD＝DE，∴αα=12αα，OD⊥ME，∵αα=12αα，∴OD＝OE，OD⊥OE；（3）①当点B在AC左侧时，如图3，延长EO到点M，使得OM＝OE，连接AM，DM，DE，同（2）的方法得，△OBE≌△OAM（SAS），∴∠OBE＝∠OAM，OM＝OE，BE＝AM，∵BE＝CE，∴AM＝CE，在四边形ABECD中，∠ADC+∠DCE+∠BEC+∠OBE+∠BAD＝540°，∵∠ADC＝∠BEC＝90°，∴∠DCE＝540°﹣90°﹣90°﹣∠OBE﹣∠BAD＝360°﹣∠OBE＝360°﹣∠OAM﹣∠BAD，∵∠DAM+∠OAM+∠BAD＝360°，∴∠DAM＝360°﹣∠OAM﹣∠BAD，∴∠DAM＝∠DCE，∵AD＝CD，∴△DAM≌△DCE（SAS），∴DM＝DE，∠ADM＝∠CDE，∴∠EDM＝∠ADM+∠ADE＝∠CDE+∠ADE＝∠ADC＝90°，∵OM＝OE，∴OD＝OE=12ME，∠DOE＝90°，在Rt△BCE中，CE=√22BC＝2√2，过点E作EH⊥DC交DC的延长线于H，在Rt△CHE中，∠ECH＝180°﹣∠ACD﹣∠ACB﹣∠BCE＝180°﹣45°﹣60°﹣45°＝30°，∴EH=12CE=√2，根据勾股定理得，CH=√3EH=√6，∴DH＝CD+CH＝3√6，在Rt△DHE中，根据勾股定理得，DE=√αα2+αα2=2√14，∴OD=√22DE＝2√7，②当点B在AC右侧时，如图4，同①的方法得，OD＝OE，∠DOE＝90°，连接DE，过点E作EH⊥CD于H，在Rt△EHC中，∠ECH＝30°∴EH=12CE=√2，根据勾股定理得，CH=√6，∴DH＝CD﹣CH=√6，在Rt△DHE中，根据勾股定理得，DE＝2√2，∴OD=√22DE＝2，即：线段OD的长为2或2√7．44．【解答】（1）①证明：如图1中，∵将线段PB绕点P逆时针旋转，旋转角为α，得到线段PD，∴PB＝PD，∵AB＝AC，PB＝PD，∠BAC＝∠BPD＝60°，∴△ABC，△PBD是等边三角形，∴∠ABC＝∠PBD＝60°，∴∠PBA＝∠DBC，∵BP＝BD，BA＝BC，∴△PBA≌△DBC（SAS），∴P A＝DC．②解：如图1中，设BD交PC于点O．∵△PBA≌△DBC，∴∠BP A＝∠BDC，∵∠BOP＝∠COD，∴∠OBP＝∠OCD＝60°，即∠DCP＝60°．（2）解：结论：CD=√3P A．理由：如图2中，∵AB ＝AC ，PB ＝PD ，∠BAC ＝∠BPD ＝120°，∴BC ＝2•AB •cos30°=√3BA ，BD ═2BP •cos30°=√3BP ，∴αααα=αααα=√3，∵∠ABC ＝∠PBD ＝30°，∴∠ABP ＝∠CBD ，∴△CBD ∽△ABP ，∴αααα=αααα=√3，∴CD =√3P A ．（3）过点D 作DM ⊥PC 于M ，过点B 作BN ⊥CP 交CP 的延长线于N ．如图3﹣1中，当△PBA 是钝角三角形时，在Rt △ABN 中，∵∠N ＝90°，AB ＝6，∠BAN ＝60°，∴AN ＝AB •cos60°＝3，BN ＝AB •sin60°＝3√3，∵PN =√αα2−αα2=√31−27=2，∴P A ＝3﹣2＝1，由（2）可知，CD =√3P A =√3，∵∠BP A ＝∠BDC ，∴∠DCA ＝∠PBD ＝30°，∵DM ⊥PC ，∴DM =12CD =√32如图3﹣2中，当△ABP 是锐角三角形时，同法可得P A ＝2+3＝5，CD ＝5√3，DM =12CD =5√32，综上所述，满足条件的DM 的值为√32或5√32．故答案为√32或5√32．45．【解答】解：（1）当点P 与B 重合时，5t ＝4，解得t =45．（2）在Rt △ABC 中，∵∠B ＝90°，AB ＝4，BC ＝3，∴AC =√αα2+αα2=√42+32=5，∴sin A =35，cos A =45，如图①中，当点P 在线段AB 上时，在Rt △APE 中，AE ＝AP •cos A ＝4t ，∴EC ＝5﹣4t ．如图③中，当点P 在线段BC 上时，在Rt △PEC 中，PC ＝7﹣5t ，cos C =35， ∴EC ＝PC •cos C =35（7﹣5t ）=215−3t ．（3）当△PDQ 是等腰直角三角形时，则PE ＝DE ，如图④中，当点P 在线段AB 上时，在Rt △APE 中，PE ＝P A •sin A ＝3t ，∵DE ＝AC ﹣AE ﹣CD ＝5﹣4t ﹣2t ＝5﹣6t ，∵PE ＝DE ，∴3t ＝5﹣6t ，∴t =59．如图⑤中，当点P 在线段BC 上时，在Rt △PCE 中，PE ＝PC •sin C =45（7﹣5t ）=285−4t ，∵DE ＝CD ﹣CE ＝2t −35（7﹣5t ）＝5t −215，∴285−4t ＝5t −215，解得t =4945．∵△PDQ 是锐角三角形，∴观察图象可知满足条件的t 的值为0＜t ＜59或4945＜t ＜75．（4）如图⑥中，当点P 在线段AB 上，QM ∥AB 时，过点Q 作QG ⊥AB 于G ，延长QM 交BC 于N ，过点D 作DH ⊥BC 于H ．∵PB ∥MN ∥DH ，PM ＝DM ，∴BN ＝NH ，在Rt △PQG 中，PQ ＝2PE ＝6t ，∴QG =45PQ =245t ，在Rt △DCH 中，HC =35DC =65t ，∵BC ＝BH +CH =245t +245t +65t ＝3，解得t =518．如图⑦中，当点P 在线段BC 上，QM ∥BC 时，过点D 作DH ⊥BC 于H ，过点P 作PK ⊥QM 于K ．∵QM ∥BC ，DM ＝PM ，∴DH ＝2PK ，在Rt △PQK 中，PQ ＝2PE =85（7﹣5t ），∴PK =35PQ =2425（7﹣5t ），在Rt △DCH 中，DH =45DC =85t ，∵DH ＝2PK ，∴85t ＝2×2425（7﹣5t ），解得t =65，综上所述，满足条件的t 的值为518或65．46．【解答】解：（1）①如图1中，△AB ′C ′即为所求．②由作图可知，△ABB ′是等腰直角三角形，∴∠AB ′B ＝45°，故答案为45．（2）如图2中，过点E 作EH ⊥CD 交CD 的延长线于H ．∵∠C ＝∠BAE ＝∠H ＝90°，∴∠B+∠CAB＝90°，∠CAB+∠EAH＝90°，∴∠B＝∠EAH，∵AB＝AE，∴△ABC≌△EAH（AAS），∴BC＝AH，EH＝AC，∵BC＝CD，∴CD＝AH，∴DH＝AC＝EH，∴∠EDH＝45°，∴∠ADE＝135°．（3）如图3中，连接AC，∵AE⊥BC，BE＝EC，∴AB＝AC，将△ABD绕点A逆时针旋转得到△ACG，连接DG．则BD＝CG，∵∠BAD＝∠CAG，∴∠BAC＝∠DAG，∵AB＝AC，AD＝AG，∴∠ABC＝∠ACB＝∠ADG＝∠AGD，∴△ABC∽△ADG，∵AD＝kAB，∴DG＝kBC＝2k，∵∠BAE+∠ABC＝90°，∠BAE＝∠ADC，∴∠ADG+∠ADC＝90°，∴∠GDC＝90°，∴CG=√αα2+αα2=√4α2+9．∴BD＝CG=√4α2+9．47．【解答】解：（1）延长DF到K点，并使FK＝DC，连接KE，如图1所示，∵△ABC≌△EBD，∴DE＝AC，BD＝BC，∴∠CDB＝∠DCB，且∠CDB＝∠ADF，∴∠ADF＝∠DCB，∵∠ACB＝90°，∴∠ACD+∠DCB＝90°，∵∠EDB＝90°，∴∠ADF+∠FDE＝90°，∴∠ACD＝∠FDE，∵FK+DF＝DC+DF，∴DK＝CF，在△ACF 和△EDK 中，{αα=αααααα=αααααα=αα，∴△ACF ≌△EDK （SAS ），∴KE ＝AF ，∠K ＝∠AFC ，又∠AFC ＝∠KFE ，∴∠K ＝∠KFE∴KE ＝EF∴AF ＝EF ，故AF 与EF 的数量关系为：AF ＝EF ．故答案为：AF ＝EF ；（2）仍然成立，理由如下：延长DF 到K 点，并使FK ＝DC ，连接KE ，如图2所示，设BD 延长线DM 交AE 于M 点，∵△ABC ≌△EBD ，∴DE ＝AC ，BD ＝BC ，∴∠CDB ＝∠DCB ，且∠CDB ＝∠MDF ，∴∠MDF ＝∠DCB ，∵∠ACB ＝90°，∴∠ACD +∠DCB ＝90°，∵∠EDB ＝90°，∴∠MDF +∠FDE ＝90°，∴∠ACD ＝∠FDE ，∵FK +DF ＝DC +DF ，∴DK ＝CF ，在△ACF 和△EDK 中，{αα=αααααα=αααααα=αα，∴△ACF ≌△EDK （SAS ），∴KE ＝AF ，∠K ＝∠AFC ，又∠AFC ＝∠KFE ，∴∠K ＝∠KFE ，∴KE ＝EF ，∴AF ＝EF ，故AF 与EF 的数量关系为：AF ＝EF ．（3）当点G 在点B 右侧时，如图3所示，过点E 作EG ⊥BC 交CB 的延长线于G ， ∵BA ＝BE ，∴∠BAE ＝∠BEA ，∵∠BAE ＝∠EBG ，∴∠BEA ＝∠EBG ，∴AE ∥CG ，∴∠AEG +∠G ＝180°，∴∠AEG ＝90°，∴∠ACG ＝∠G ＝∠AEG ＝90°，∴四边形AEGC 为矩形，∴AC ＝EG ，且AB ＝BE ，∴Rt △ACB ≌Rt △EGB （HL ），∴BG ＝BC ＝6，∠ABC ＝∠EBG ，又∵ED ＝AC ＝EG ，且EB ＝EB ，∴Rt △EDB ≌Rt △EGB （HL ），∴DB＝GB＝6，∠EBG＝∠ABE，∴∠ABC＝∠ABE＝∠EBG＝60°，∴∠BAC＝30°，在Rt△ABC中，由30°所对的直角边等于斜边的一半可知：AB＝2BC＝12．当点G在点B左侧时，如图4所示，由旋转知，∠ABC＝∠ABE，AB＝BE，∴∠BAE＝∠BEA，∵∠BAE＝∠EBG＝2∠ABC＝2∠ABE，∴∠BAE＝∠AEB＝2∠ABE，∵∠AEB+∠BAE+∠ABE＝180°，∴2∠ABE+2∠ABE+∠ABE＝180°，∴∠BAE＝36°，∴∠ABC＝36°，在Rt△ABC中，cos36°=αααα，∴AB=ααααα36°=6ααα36°，即满足条件的AB＝12或6ααα36°．48．【解答】解：（1）①∵A ′B ′∥AC ，∴∠B ′A ′C ＝∠A ′CA ，∵∠B ′A ′C ＝∠BAC ，∴∠A ′CA ＝∠BAC ，∴AD ＝CD ，∵∠ACB ＝90°，∴∠BCD ＝90°﹣∠ACD ，∵∠ABC ＝90°﹣∠BAC ，∴∠CBD ＝∠BCD ，∴BD ＝CD ，∴AD ＝BD ；②∵∠ACB ＝90°，BC ＝2，AC ＝4，∴AB =√22+42=2√5，∵BE ⊥CD ，∴∠BEC ＝∠ACB ＝90°，∵∠BCE ＝∠ABC ，∴△BEC ∽△ACB ，∴αααα=αααα，即αα2=2√5， ∴CE =25√5，∵∠ACB ＝90°，AD ＝BD ， ∴CD =12AB =√5， ∴CE =25CD ，∴S △ACE =23S △ADE ，∵AD ＝BD ，∴S △ABE ＝2S △ADE ，∴α△αααα△ααα=13；（2）∵CD ⊥AB ，∴∠ADC ＝90°＝∠A ′CB ′，∴AB ∥CN ，∴△MCN ∽△MAD ，∴αααα=αααα，∵α△ααα=12αα⋅αα=12αα⋅αα，∴αα=αα⋅αααα=4×22√5=45√5，∴AD =√αα2−αα2=85√5，∵DM ∥A ′B ′，。

中考数学复习----《图形的旋转变换》知识点总结与专项练习题

中考数学复习----《图形的旋转变换》知识点总结与专项练习题知识点总结1.旋转的定义：在平面内，把一个图形绕着某一个点O旋转一个角度的图形变换叫做旋转．点O 叫做旋转中心，转动的角叫做旋转角，如果图形上的点P经过旋转变为点P′，那么这两个点叫做对应点。

2.旋转的要素：①旋转中心；②旋转方向；③旋转角。

3.旋转的性质：①旋转前后的两个图形全等。

即有对应边相等，对应角相等。

②对应点到旋转中心的连线距离相等。

③对应点与旋转中心的连线构成的夹角等于旋转角。

4.旋转对称图形：若一个图形旋转一定角度（小于360°）之后与原图形重合，则这个图形叫做旋转对称图形。

如正多边形或圆。

5.中心对称：①定义：把一个图形绕着某个点旋转180°，如果它能够与另一个图形重合，那么就说这两个图形关于这个点对称或中心对称，这个点叫做对称中心，这两个图形中的对应点叫做关于中心的对称点。

②性质：I：关于中心对称的两个图形能够完全重合；II：关于中心对称的两个图形，对应点的连线都经过对称中心，并且被对称中心平分。

6. 坐标的旋转变换：①若点()y x P ，顺时针或逆时针旋转90°，则横纵坐标的绝对值互换，符号看象限。

②若点()y x P ，顺时针或逆时针旋转180°，即关于原点成中心对称，则横纵坐标变为原来的相反数。

即()y x P −−，7. 旋转作图：基本步骤：①确定旋转方向与旋转角；②把图形的关键点按照旋转方向与旋转角进行旋转，得到关键点的对应点；③将对应点按照原图形连接。

练习题1、（2022•德州）下列图形是中心对称图形的是（）A ．B ．C ．D ．【分析】根据中心对称图形的概念判断．把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形．【解答】解：选项A 、C 、D 都不能找到这样的一个点，使图形绕某一点旋转180°后与原来的图形重合，所以不是中心对称图形．选项B 能找到这样的一个点，使图形绕某一点旋转180°后与原来的图形重合，所以是中心对称图形．故选：B ．2、（2022•黄石）下面四幅图是我国一些博物馆的标志，其中既是轴对称图形又是中心对称图形的是（）A．温州博物馆B．西藏博物馆C．广东博物馆D．湖北博物馆【分析】根据中心对称图形与轴对称图形的概念进行判断即可．【解答】解：A．既是中心对称图形，又是轴对称图形，故此选项符合题意；B．不是中心对称图形，是轴对称图形，故此选项不合题意；C．不是中心对称图形，也不是轴对称图形，故此选项不合题意；D．不是中心对称图形，是轴对称图形，故此选项不合题意；故选：A．3、（2022•河池）如图，在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，将Rt△ABC绕点B 顺时针旋转90°得到Rt△A'B'C'．在此旋转过程中Rt△ABC所扫过的面积为（）A．25π+24 B．5π+24 C．25πD．5π【分析】根据勾股定理得到AB，然后根据扇形和三角形的面积公式即可得到结论．【解答】解：∵∠ACB＝90°，AC＝6，BC＝8，∴AB＝10，∴Rt△ABC所扫过的面积＝+×6×8＝25π+24，故选：A ．4、（2022•呼和浩特）如图．△ABC 中，∠ACB ＝90°，将△ABC 绕点C 顺时针旋转得到△EDC ，使点B 的对应点D 恰好落在AB 边上，AC 、ED 交于点F ．若∠BCD ＝α，则∠EFC 的度数是（用含α的代数式表示）（）A ．90°+21αB ．90°﹣21αC ．180°﹣23αD ．23α 【分析】由旋转的性质可知，BC ＝CD ，∠B ＝∠EDC ，∠A ＝∠E ，∠ACE ＝∠BCD ，因为∠BCD ＝α，所以∠B ＝∠BDC ＝＝90°﹣，∠ACE ＝α，由三角形内角和可得，∠A ＝90°﹣∠B ＝．所以∠E ＝．再由三角形内角和定理可知，∠EFC ＝180°﹣∠ECF ﹣∠E ＝180°﹣α．【解答】解：由旋转的性质可知，BC ＝CD ，∠B ＝∠EDC ，∠A ＝∠E ，∠ACE ＝∠BCD ， ∵∠BCD ＝α，∴∠B ＝∠BDC ＝＝90°﹣，∠ACE ＝α，∵∠ACB ＝90°，∴∠A ＝90°﹣∠B ＝． ∴∠E ＝． ∴∠EFC ＝180°﹣∠ECF ﹣∠E ＝180°﹣α．故选：C ．5、（2022•包头）如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，BC＝2，将△ABC绕点C 顺时针旋转得到△A'B'C，其中点A'与点A是对应点，点B'与点B是对应点．若点B'恰好落在AB边上，则点A到直线A'C的距离等于（）A．33B．23C．3 D．2【分析】由直角三角形的性质求出AC＝2，∠B＝60°，由旋转的性质得出CA＝CA′，CB＝CB′，∠ACA′＝∠BCB′，证出△CBB′和△CAA′为等边三角形，过点A作AD⊥A'C于点D，由等边三角形的性质及直角三角形的性质可得出答案．【解答】解：连接AA′，如图，∵∠ACB＝90°，∠BAC＝30°，BC＝2，∴AC＝BC＝2，∠B＝60°，∵将△ABC绕点C顺时针旋转得到△A'B'C，∴CA＝CA′，CB＝CB′，∠ACA′＝∠BCB′，∵CB＝CB′，∠B＝60°，∴△CBB′为等边三角形，∴∠BCB′＝60°，∴∠ACA′＝60°，∴△CAA′为等边三角形，过点A作AD⊥A'C于点D，∴CD＝AC＝，∴AD＝CD＝＝3，∴点A到直线A'C的距离为3，故选：C．6、（2022•常德）如图，在Rt△ABC中，∠ABC＝90°，∠ACB＝30°，将△ABC绕点C顺时针旋转60°得到△DEC，点A，B的对应点分别是D，E，点F是边AC的中点，连接BF，BE，FD．则下列结论错误的是（）A．BE＝BC B．BF∥DE，BF＝DEC．∠DFC＝90°D．DG＝3GF【分析】根据等边三角形的判定定理得到△BCE为等边三角形，根据等边三角形的性质得到BE＝BC，判断A选项；证明△ABC≌△CFD，根据全等三角形的性质判断B、C选项；解直角三角形，用CF分别表示出GF、DF，判断D选项．【解答】解：A、由旋转的性质可知，CB＝CE，∠BCE＝60°，∴△BCE为等边三角形，∴BE＝BC，本选项结论正确，不符合题意；B、在Rt△ABC中，∠ABC＝90°，∠ACB＝30°，点F是边AC的中点，∴AB＝AC＝CF＝BF，由旋转的性质可知，CA＝CD，∠ACD＝60°，∴∠A＝∠ACD，在△ABC和△CFD中，，∴△ABC≌△CFD（SAS），∴DF＝BC＝BE，∵DE＝AB＝BF，∴四边形EBFD为平行四边形，∴BF∥DE，BF＝DE，本选项结论正确，不符合题意；C、∵△ABC≌△CFD，∴∠DFC＝∠ABC＝90°，本选项结论正确，不符合题意；D、在Rt△GFC中，∠GCF＝30°，∴GF＝CF，同理可得，DF＝CF，∴DF＝3GF，故本选项结论错误，符合题意；故选：D．7、（2022•天津）如图，在△ABC中，AB＝AC，若M是BC边上任意一点，将△ABM绕点A逆时针旋转得到△ACN，点M的对应点为点N，连接MN，则下列结论一定正确的是（）A．AB＝AN B．AB∥NC C．∠AMN＝∠ACN D．MN⊥AC【分析】根据旋转变换的性质、等边三角形的性质、平行线的性质判断即可．【解答】解：A、∵AB＝AC，∴AB＞AM，由旋转的性质可知，AN＝AM，∴AB＞AN，故本选项结论错误，不符合题意；B、当△ABC为等边三角形时，AB∥NC，除此之外，AB与NC不平行，故本选项结论错误，不符合题意；C、由旋转的性质可知，∠BAC＝∠MAN，∠ABC＝∠ACN，∵AM＝AN，AB＝AC，∴∠ABC＝∠AMN，∴∠AMN＝∠ACN，本选项结论正确，符合题意；D、只有当点M为BC的中点时，∠BAM＝∠CAM＝∠CAN，才有MN⊥AC，故本选项结论错误，不符合题意；故选：C．8、（2022•南充）如图，将直角三角板ABC绕顶点A顺时针旋转到△AB′C′，点B′恰好落在CA的延长线上，∠B＝30°，∠C＝90°，则∠BAC′为（）A ．90°B ．60°C ．45°D ．30°【分析】利用旋转不变性，三角形内角和定理和平角的意义解答即可．【解答】解：∵∠B ＝30°，∠C ＝90°，∴∠CAB ＝180°﹣∠B ﹣∠C ＝60°，∵将直角三角板ABC 绕顶点A 顺时针旋转到△AB ′C ′，∴∠C ′AB ′＝∠CAB ＝60°．∵点B ′恰好落在CA 的延长线上，∴∠BAC ′＝180°﹣∠CAB ﹣∠C ′AB ′＝60°．故选：B ．9、（2022•内蒙古）如图，边长为1的正方形ABCD 绕点A 逆时针旋转30°到正方形AB ′C ′D ′，图中阴影部分的面积为（）A ．21B ．33C ．1﹣33D ．1﹣43 【分析】设B ′C ′与CD 的交点为E ，连接AE ，利用“HL ”证明Rt △AB ′E 和Rt △ADE 全等，根据全等三角形对应角相等∠DAE ＝∠B ′AE ，再根据旋转角求出∠DAB ′＝60°，然后求出∠DAE ＝30°，再解直角三角形求出DE ，然后根据阴影部分的面积＝正方形ABCD 的面积﹣四边形ADEB ′的面积，列式计算即可得解．【解答】解：如图，设B′C′与CD的交点为E，连接AE，在Rt△AB′E和Rt△ADE中，，∴Rt△AB′E≌Rt△ADE（HL），∴∠DAE＝∠B′AE，∵旋转角为30°，∴∠DAB′＝60°，∴∠DAE＝×60°＝30°，∴DE＝1×＝，∴阴影部分的面积＝1×1﹣2×（×1×）＝1﹣．故选：C．10、（2022•朝阳）如图，在矩形ABCD中，AD＝23，DC＝43，将线段DC绕点D 按逆时针方向旋转，当点C的对应点E恰好落在边AB上时，图中阴影部分的面积是．【分析】由旋转的性质可得DE＝DC＝4，由锐角三角函数可求∠ADE＝60°，由勾股定理可求AE的长，分别求出扇形EDC和四边形DCBE的面积，即可求解．【解答】解：∵将线段DC绕点D按逆时针方向旋转，∴DE＝DC＝4，∵cos∠ADE＝＝＝，∴∠ADE＝60°，∴∠EDC＝30°，∴S扇形EDC＝＝4π，∵AE＝＝＝6，∴BE＝AB﹣AE＝4﹣6，∵四边形ABCD是矩形，∴EB∥CD，∠B＝∠DCB＝90°，∵EB≠CB，∴四边形DCBE是直角梯形，∴S四边形DCBE＝＝24﹣6，∴阴影部分的面积＝24﹣6﹣4π，故答案为：24﹣6﹣4π．11、（2022•西宁）如图，在△ABC中，∠C＝90°，∠B＝30°，AB＝6，将△ABC绕点A逆时针方向旋转15°得到△AB′C′，B′C′交AB于点E，则B′E＝．【分析】先在含30°锐角的直角三角形中计算出两条直角边，再根据旋转性质得到对应边相等、对应角相等得到AC＝AC'＝C'E＝3，BC＝B'C'＝3，即可解答．【解答】解：在△ABC中，∵∠C＝90°，∠B＝30°，AB＝6，∴AC＝3，BC＝3，∠CAB＝60°，∵将△ABC绕点A逆时针方向旋转15°得到△AB′C′，∴△ABC≌△AB′C′，∠C'AE＝45°，∴AC＝AC'＝C'E＝3，BC＝B'C'＝3，∴B'E＝B'C'﹣C'E＝3﹣3．12、（2022•上海）有一个正n边形旋转90°后与自身重合，则n为（）A．6 B．9 C．12 D．15【分析】如果某一个图形围绕某一点旋转一定的角度（小于360°）后能与原图形重合，那么这个图形就叫做旋转对称图形．直接利用旋转对称图形的性质，结合正多边形中心角相等进而得出答案．【解答】解：A．正六边形旋转90°后不能与自身重合，不合题意；B．正九边形旋转90°后不能与自身重合，不合题意；C．正十二边形旋转90°后能与自身重合，符合题意；D．正十五边形旋转90°后不能与自身重合，不合题意；故选：C．13、（2022•遵义）在平面直角坐标系中，点A（a，1）与点B（﹣2，b）关于原点成中心对称，则a+b的值为（）A．﹣3 B．﹣1 C．1 D．3【分析】由中心对称的性质可求a，b的值，即可求解．【解答】解：∵点A（a，1）与点B（﹣2，b）关于原点成中心对称，∴a＝2，b＝﹣1，∴a+b＝1，故选：C．14、（2022•雅安）在平面直角坐标系中，点（a+2，2）关于原点的对称点为（4，﹣b），则ab的值为（）A．﹣4 B．4 C．12 D．﹣12【分析】首先根据关于原点对称的点的坐标特点可得a+2＝﹣4，﹣b＝﹣2，分别求出a、b的值，再代入即可得到答案．【解答】解：∵在平面直角坐标系中，点（a+2，2）关于原点的对称点为（4，﹣b），则∴得a+2＝﹣4，﹣b＝﹣2，解得a＝﹣6，b＝2，∴ab＝﹣12．故选：D．15、（2022•湘西州）在平面直角坐标系中，已知点P（﹣3，5）与点Q（3，m﹣2）关于原点对称，则m＝．【分析】平面直角坐标系中任意一点P（x，y），关于原点的对称点是（﹣x，﹣y），即求关于原点的对称点时，横、纵坐标都变成原数的相反数．【解答】解：根据两个点关于原点对称，则横、纵坐标都是原数的相反数，得m﹣2＝﹣5，∴m＝﹣3．故答案为：﹣3．16、（2022•怀化）已知点A（﹣2，b）与点B（a，3）关于原点对称，则a﹣b＝．【分析】根据关于原点对称的点的坐标，可得答案．【解答】解：∵点A（﹣2，b）与点B（a，3）关于原点对称，∴a＝2，b＝﹣3，∴a﹣b＝2+3＝5，故答案为：5．17、（2022•枣庄）如图，将△ABC先向右平移1个单位，再绕点P按顺时针方向旋转90°，得到△A′B′C′，则点B的对应点B′的坐标是（）A．（4，0）B．（2，﹣2）C．（4，﹣1）D．（2，﹣3）【分析】作出旋转后的图形即可得出结论．【解答】解：作出旋转后的图形如下：∴B'点的坐标为（4，﹣1），故选：C．18、（2022•青岛）如图，将△ABC先向右平移3个单位，再绕原点O旋转180°，得到△A'B'C'，则点A的对应点A'的坐标是（）A．（2，0）B．（﹣2，﹣3）C．（﹣1，﹣3）D．（﹣3，﹣1）【分析】利用平移的性质得出对应点位置，再利用关于原点对称点的性质直接得出答案．【解答】解：由图中可知，点A（﹣2，3），将△ABC先向右平移3个单位，得坐标为：（1，3），再绕原点O旋转180°，得到△A'B'C'，则点A的对应点A'的坐标是（﹣1，﹣3）．故选：C．19、（2022•聊城）如图，在直角坐标系中，线段A1B1是将△ABC绕着点P（3，2）逆时针旋转一定角度后得到的△A1B1C1的一部分，则点C的对应点C1的坐标是（）A ．（﹣2，3）B ．（﹣3，2）C ．（﹣2，4）D ．（﹣3，3）【分析】根据旋转的性质解答即可．【解答】解：连接AP ，A 1P ．∵线段A 1B 1是将△ABC 绕着点P （3，2）逆时针旋转一定角度后得到的△A 1B 1C 1的一部分，∴A 的对应点为A 1，∴∠APA 1＝90°，∴旋转角为90°，∴点C 绕点P 逆时针旋转90°得到的C 1点的坐标为（﹣2，3），故选：A ．20、（2022•杭州）如图，在平面直角坐标系中，已知点P （0，2），点A （4，2）．以点P 为旋转中心，把点A 按逆时针方向旋转60°，得点B ．在M 1（﹣33，0），M 2（﹣3，﹣1），M 3（1，4），M 4（2，211）四个点中，直线PB 经过的点是（）A．M1B．M2C．M3D．M4【分析】根据含30°角的直角三角形的性质可得B（2，2+2），利用待定系数法可得直线PB的解析式，依次将M1，M2，M3，M4四个点的一个坐标代入y＝x+2中可解答．【解答】解：∵点A（4，2），点P（0，2），∴PA⊥y轴，PA＝4，由旋转得：∠APB＝60°，AP＝PB＝4，如图，过点B作BC⊥y轴于C，∴∠BPC＝30°，∴BC＝2，PC＝2，∴B（2，2+2），设直线PB的解析式为：y＝kx+b，则，∴，∴直线PB的解析式为：y＝x+2，当y＝0时，x+2＝0，x＝﹣，∴点M1（﹣，0）不在直线PB上，当x＝﹣时，y＝﹣3+2＝﹣1，∴M2（﹣，﹣1）在直线PB上，当x＝1时，y＝+2，∴M3（1，4）不在直线PB上，当x＝2时，y＝2+2，∴M4（2，）不在直线PB上．故选：B．21、（2022•贺州）如图，在平面直角坐标系中，△OAB为等腰三角形，OA＝AB＝5，点B到x轴的距离为4，若将△OAB绕点O逆时针旋转90°，得到△OA′B′，则点B′的坐标为．【分析】过点B作BN⊥x轴，过点B′作B′M⊥y轴，先求出ON＝8，再证明△AOB≌△A′OB′（AAS），推出OM＝ON＝8，B′M＝BN＝4，从而求出点B′的坐标．【解答】解：过点B作BN⊥x轴，过点B′作B′M⊥y轴，∴∠B′MO＝∠BNO＝90°，∵OA＝AB＝5，点B到x轴的距离为4，∴AN＝3，∴ON＝8，∵将△OAB绕点O逆时针旋转90°，得到△OA′B′，∴∠BOB′＝90°，OB＝OB′，∴∠BOA′+∠B′OA′＝∠BOA+∠BOA′，∴∠BOA＝∠B′OA′，∴△NOB≌△MOB′（AAS），∴OM＝ON＝8，B′M＝BN＝4，∴B′（﹣4，8），故答案为：（﹣4，8）．。

2023年中考数学讲练必考重点04 几何变换之旋转问题(含答案)

[选择题]必考重点04 几何变换之旋转问题几何变换中的旋转问题,江苏省各地考查频率较高且考查难度较高,综合性较强,通常有线段的旋转、三角形及四边形的旋转问题,在解决此类问题时,要牢牢把握旋转的性质,即旋转前后的图形全等,对应角相等,对应边相等,结合几何图形本身的性质,找到旋转过程中变化的量和不变的量,运用三角形全等或相似的有关知识,求解有关角、线段及面积问题。

0,2,点B是x轴正半轴上的一点,将线段AB绕点A按逆时[2022·江苏苏州·中考母题]如图,点A的坐标为()m,则m的值为（）针方向旋转60°得到线段AC．若点C的坐标为(),3A B C D．3[考点分析]本题考查直角坐标系中的旋转变换,解题的关键是熟练应用勾股定理,用含m的代数式表示相关线段的长度．[思路分析]过C作CD⊥x轴于D ,CE⊥y轴于E ,根据将线段AB绕点A按逆时针方向旋转60°得到线段AC ,可得△ABC是等边三角形,又A（0 ,2）,C（m ,3）,即得AC BC AB=,可得=,即可解得m=．BD,OB=,m<,将ABC以点A为中心逆时针旋转得到ADE,点[2022·江苏扬州·中考母题]如图,在ABC∆中,AB ACD 在BC 边上 ,DE 交AC 于点F ．下列结论：①AFE DFC △△ ;②DA 平分BDE ∠ ;③CDF BAD ∠=∠ ,其中所有正确结论的序号是（）A ．①②B ．②③C ．①③D ．①②③[考点分析]本题考查了性质的性质 ,等边对等角 ,相似三角形的性质判定与性质 ,全等三角形的性质 ,掌握以上知识是解题的关键．[思路分析]根据旋转的性质可得对应角相等 ,对应边相等 ,进而逐项分析判断即可求解．[2020·江苏宿迁·中考母题]如图 ,在平面直角坐标系中 ,Q 是直线y=﹣12x+2上的一个动点 ,将Q 绕点P(1 ,0)顺时针旋转90° ,得到点Q ' ,连接OQ ' ,则OQ '的最小值为( )A B C D [考点分析]本题考查了一次函数图象上点的坐标特征 ,一次函数的性质 ,三角形全等的判定和性质 ,坐标与图形的变换-旋转 ,二次函数的性质 ,勾股定理 ,表示出点的坐标是解题的关键．[思路分析]利用等腰直角三角形构造全等三角形 ,求出旋转后Q′的坐标 ,然后根据勾股定理并利用二次函数的性质即可解决问题．1．（2022·江苏·九年级专题练习）如图将△ABC 绕点C 逆时针旋转得到△A ’B ’C ,点B 恰好落在A ’B ’上 ,若∠A =25° ,∠BCA ’=45° ,则∠A ’CA = （）A．30°B．35°C．40°D．45°2．（2022·江苏泰州·九年级专题练习）在正方形ABCD中,AB＝8 ,若点E在对角线AC上运动,将线段DE 绕点D逆时针旋转90°得到线段DF ,连接EF、CF．点P在CD上,且CP＝3PD．给出以下几个结论①222=+,②EF, ③线段PF的最小值是,④△CFE的面积最大是16．其中正确的是EF AE CE（）A．①②④B．②③④C．①②③D．①③④3．（2022·江苏苏州·一模）如图,直角三角形ACB中,两条直角边AC=8 ,BC=6 ,将△ACB绕着AC中点M旋转一定角度,得到△DFE ,点F正好落在AB边上,DE和AB交于点G ,则AG的长为（）A．1.4 B．1.8 C．1.2 D．1.64．（2022·江苏徐州·二模）如图,△ABC中,∠ABC＝45° ,BC＝8 ,tan∠ACB＝3 ,AD⊥BC于D ,若将△ADC 绕点D逆时针方向旋转得到△FDE ,当点E恰好落在AC上,连接AF．则AF的长为（）A B C ．D ．45．（2022·江苏盐城·一模）如图 ,在AOB 中 ,2AO = ,3BO AB ==.将AOB 绕点O 逆时针方向旋转90° ,得到A OB ''△ ,连接AA '.则线段AA '的长为（）A ．2B ．3C ．D ．6．（2022·江苏·宜兴外国语学校一模）如图 ,在矩形ABCD 中 ,AB ＝3 ,BC ＝4 ,P 是对角线AC 上的动点 ,连接DP ,将直线DP 绕点P 顺时针旋转使∠DPE ＝∠DAC ,且过D 作DE ⊥PE ,连接CE ,则CE 最小值为（）A ．65B ．3625C ．3225D ．857．（2022·江苏扬州·模拟）如图 ,将矩形ABCD 绕点B 按顺时针方向旋转一定角度得到矩形A B C D ''''．此时点A 的对应点A '恰好落在对角线AC 的中点处．若AB ＝3 ,则点B 与点D 之间的距离为（）A．3 B．6 C．D．8．（2022·江苏·九年级专题练习）如图所示,已知ABC是等边三角形,点D是BC边上一个动点(点D不与,B C重合) ,将ADC绕点A顺时针旋转一定角度后得到AFB△,过点F作BC的平行线交AC于点E,连接②为等边三角形;③四边形BCEF为平行四边形;DF,下列四个结论中：①旋转角为60︒;ADF④．其中正确的结论有（）=BF AEA．1B．2C．3D．49．（2022·江苏南京·模拟）如图,在Rt ABC中,∠ACB=90° ,BC=2 ,∠BAC=30° ,将ABC绕顶点C逆时针旋转得到△A'B'C' , M是BC的中点,P是A'B'的中点, 连接PM ,则线段PM的最大值是（）A．4 B．2 C．3 D．10．（2022·江苏苏州·二模）如图,将ABC绕点A顺时针旋转角α,得到ADE,若点E恰好在CB的延长线上,则BED∠等于（）A ．2αB ．23αC ．αD ．180α︒-11．（2022·江苏·阳山中学一模）如图 ,在△ABC 中 ,∠BAC ＝45° ,AC ＝8 ,动点E 从点A 出发沿射线AB 运动 ,连接CE ,将CE 绕点C 顺时针旋转45°得到CF ,连接AF ,则△AFC 的面积变化情况是（）．A ．先变大再变小B ．先变小再变大C ．逐渐变大D ．不变12．（2022·江苏·南通市启秀中学九年级阶段练习）如图 ,点E 是正方形ABCD 的边DC 上一点 ,把ADE ∆绕点A 顺时针旋转90︒到ABF ∆的位置．若四边形AECF 的面积为20 ,DE=2 ,则AE 的长为（）A ．4B ．C ．6D ．13．（2022·江苏·九年级专题练习）如图1 ,在Rt ABC 中 ,AC BC = ,90C ∠=︒ ,点D 为AB 边的中点 ,90EDF ∠=︒ ,将EDF ∠绕点D 旋转 ,它的两边分别交AC 、CB 所在直线于点E 、F ,有以下4个结论：①CE BF = ;②180DEC DFC ∠+∠=︒ ;③222EF DE = ;④如图2 ,当点E 、F 落在AC 、CB 的延长线上时 ,12DEF CEF ABC S S S -=△△△ ,在旋转的过程中上述结论一定成立的是（）A ．①②B ．②③C ．①②③D ．①③④14．（2022·江苏扬州·三模）如图 ,已知正方形ABCD 的边长为4 ,点E 是AB 边上一动点 ,连接ED ,将ED 绕点E 顺时针旋转90°到EF ,连接DF ,CF ,则DF ＋CF 的最小值是（）A ．B ．C ．D ．15．（2022·江苏南京·一模）在平面直角坐标系中 ,点A 的坐标是()2,3- ,将点A 绕点C 顺时针旋转90°得到点B ．若点B 的坐标是()5,1- ,则点C 的坐标是（）A ．()0.5, 2.5--B ．()0.25,2--C ．()0, 1.75-D ．()0, 2.75-16．（2022·江苏南京·模拟）如图 ,在Rt ABC 中 ,AB =AC =10 ,∠BAC =90°,等腰直角三角形ADE 绕点A 旋转 ,∠DAE =90°,AD =AE =4 ,连接DC ,点M 、P 、N 分别为DE 、DC 、BC 的中点 ,连接MP 、PN 、MN ．①PMN为等腰直角三角形 ;②MN ≤;③△PMV 面积的最大值是494;④PMN 周长的最小值为6+ ）A．4个B．3个C．2个D．1个17．（2022·江苏无锡·一模）如图,已知直线AB与y轴交于点(0,A,与x轴的负半轴交于点B ,且∠ABO ＝60° ,在x轴正半轴上有一点C ,点C坐标为()1,0,将线段AC绕点A逆时针旋转120° ,得线段AD ,连接BD．则BD的长度为（）A．B．4C D．15 218．（2022·江苏·无锡市积余实验学校一模）如图1 ,在Rt△ABC中,90A∠=︒,AB AC=,点D ,E分别在边AB ,AC上,AD AE=,连接DC ,点M、P、N分别为DE、DC、BC的中点．将△ADE绕点A在平面内自由旋转（如图2）,若4=AD,10AB=,则△PMN面积的最大值是（）A．494B．18 C．492D．25219．（2022·江苏·无锡市天一实验学校一模）如图,扇形OAB中,90AOB∠=︒,将扇形OAB绕点B逆时针旋转,得到扇形BDC,若点O刚好落在弧AB上的点D处,则ADAC的值为（）A B C D 20．（2022·江苏·苏州市平江中学校二模）如图 ,在BAC 中 ,90BAC ∠=︒ ,2AB AC = ,将BAC 绕点A 顺时针旋转至DAE △ ,点D 刚好落在BC 直线上 ,则BDE 的面积为（）A ．24BD B ．22BC C ．4BC BD ⋅ D ．22AB 21．（2022·江苏·淮安市浦东实验中学九年级开学考试）如图 ,直线1y x =+与x 轴、y 轴分别相交于点A 、B ,过点B 作BC AB ⊥ ,使2BC BA =．将 ABC ∆绕点O 顺时针旋转 ,每次旋转90︒．则第2022次旋转结束时 ,点C 的对应点C '落在反比例函数k y x=的图象上 ,则k 的值为( )A ．4-B ．4C ．6-D ．622．（2022·江苏无锡·九年级期末）如图 ,在Rt △ABC 中 ,90BAC ∠=︒ ,6AB AC == ,点D 、E 分别是AB 、AC 的中点．将△ADE 绕点A 顺时针旋转60°,射线BD 与射线CE 交于点P ,在这个旋转过程中有下列结论：①△AEC ≌△ADB ;②CP 存在最大值为3+;③BP 存在最小值为3 ;④点P 运动的路径长为．其中 ,正确的（）A ．①②③B ．①②④C ．①③④D ．②③④23．（2022·江苏无锡·模拟）如图 ,在正方形ABCD 中 ,6AB = ,点H 为BC 中点 ,点E 绕着点C 旋转 ,且4CE = ,在DC 的右侧作正方形DEFG ,则线段FH 的最小值是（）A．9-B ．8- C ．9-D ．10-24．（2022·江苏·常州市金坛区水北中学二模）如图 ,在矩形ABCD 中 ,5AB = ,BC =,点P 在线段BC 上运动（含B 、C 两点） ,连接AP ,以点A 为中心 ,将线段AP 逆时针旋转60°到AQ ,连接DQ ,则线段DQ 的最小值为（）A ．52B ．CD ．325．（2022·江苏南京·模拟）如图 ,在ABC ∆中 ,5,AB AC BC === ,D 为边AC 上一动点（C 点除外） ,把线段BD 绕着点D 沿着顺时针的方向旋转90°至DE ,连接CE ,则CDE ∆面积的最大值为（）A ．16B ．8C ．32D ．10[选择题]必考重点04 几何变换之旋转问题几何变换中的旋转问题,江苏省各地考查频率较高且考查难度较高,综合性较强,通常有线段的旋转、三角形及四边形的旋转问题,在解决此类问题时,要牢牢把握旋转的性质,即旋转前后的图形全等,对应角相等,对应边相等,结合几何图形本身的性质,找到旋转过程中变化的量和不变的量,运用三角形全等或相似的有关知识,求解有关角、线段及面积问题。

中考数学考点15 旋转变换(解析版)

旋转变换通常结合全等三角形探索角的数量关系，线段与线段之间的位置关系与数量关系，经常作为作为中等偏难一点的题型出现．旋转的性质有：①旋转角是对应点与旋转中心所连线段的夹角是旋转角；②旋转前后的图形全等；③对应点到旋转中心的距离相等．如图，△ABC绕点O逆时针方向旋转∠AOA′到△A′B′C′的位置，则①旋转角是∠AOA′＝∠BOB′＝∠COC′；②△ABC≌△A′B′C′；③OA＝OA′，OB＝OB′，OC＝OC′．1.注意旋转的三要素：旋转中心，旋转方向，旋转角；2.抓住旋转只是改变图形的位置，不改变图形的形状和大小，即旋转前后的图形全等；3.能够用旋转解题的图形的基本特征是有公共端点且相等的两条线段，这个公共端点往往会是旋转中心．例1.如图，将Rt△ABC（其中∠B＝35°，∠C＝90°）绕点A按顺时针方向旋转到△AB1C1的位置，使得点C，A，B1在同一条直线上，那么旋转角等于( )A. 55°B. 70°C. 125°D. 155°【答案】C例2.如图，点P为定角∠AOB的平分线上的一个定点，且∠MPN与∠AOB互补，若∠MPN在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：（1）PM＝PN恒成立；（2）OM＋ON 的值不变；（3）四边形PMON的面积不变；（4）MN的长不变，其中正确的个数为（）A. 4B. 3C. 2D. 1【答案】B学科@网【精细解读】因为角平分线上的点到角的两边的距离相等，所以存在着隐性的有公共端点的相等线段的特征，故可考虑过点P作∠AOB的两边的垂线，再结合旋转的性质求解．如图作PE⊥OA于E，PF⊥OB于F．例3.如图1，在△ABC中，∠ACB＝90°，点P为△ABC内一点.（1）连接PB，PC，将△BCP沿射线CA方向平移，得到△DAE，点B，C，P的对应点分别为点D、A、E，连接CE.①依题意，请在图2中补全图形；②如果BP⊥CE，BP＝3，AB＝6，求CE的长．（2）如图3，以点A为旋转中心，将△ABP顺时针旋转60°得到△AMN，连接P A、PB、PC，当AC＝3，AB＝6时，根据此图求P A＋PB＋PC的最小值．【答案】（1）33（2）37∵△BCP沿射线CA方向平移，得到△DAE，∴BC∥AD且BC＝AD，∵∠ACB＝90°，∴四边形BCAD是矩形，∴CD＝AB＝6，∵BP＝3，∴DE＝BP＝3，∵BP⊥CE，BP∥DE，∴DE⊥CE，∴在Rt△DCE中，22CE=CD DE=369=27=33--；（2）证明：如图所示，1.把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′，边BC与D′C′交于点O，则四边形ABOD′的周长是 ( )A. 6B. 6C. 3D. 3＋3【答案】A【解析】试题解析：连接BC′，∵旋转角∠BAB′＝45°，∠BAD′＝45°，∴B在对角线AC′上，∵B′C′＝AB′＝3，在Rt△AB′C′中，AC′＝，∴BC′＝3－3，在等腰Rt△OBC′中，OB＝BC′＝3－3，在直角三角形OBC′中，OC′＝（3－3）＝6－3，∴OD′＝3－OC′＝3－3，∴四边形ABOD′的周长是：2AD′＋OB＋OD′＝6＋3－3＋3－3＝6．故选A．2.两个全等的三角尺重叠放在△ACB的位置，将其中一个三角尺绕着点C按逆时针方向旋转至△DCE的位置，使点A恰好落在边DE上，AB与CE相交于点F．已知∠ACB＝∠DCE＝90°，∠B＝30°，AB＝8cm，则CF ＝_________cm．【答案】33.如图，菱形ABCD中，边长为2，∠B＝60°，将△ACD绕点C旋转，当AC（即A′C）与AB交于一点E，CD（即CD′）同时与AD交于一点F时，点E，F和点A构成△AEF．试探究△AEF的周长是否存在最小值，如果不存在，请说明理由；如果存在，请计算出△AEF周长的最小值.【答案】2＋3（每道试题10分，总计100分）1.如图，在□ABCD中，AE⊥BC于点E，以点B为中心，取旋转角等于∠ABC，把△BAE顺时针旋转，得到△BA′E′，连接DA′，若∠ADC＝60°，∠ADA′＝50°，则∠DA′E′的大小为（）A. 130°B. 150°C. 160°D. 170°【答案】C【解析】根据平行四边形对角相等、邻角互补，得∠ABC＝60°，∠DCB＝120°，再由∠A′DC＝10°，可运用三角形外角求出∠DA′B＝130°，再根据旋转的性质得到∠BA′E′＝∠BAE＝30°，从而得到答案．解：∵四边形ABCD是平行四边形，∠ADC＝60°，∴∠ABC＝60°，∠DCB＝120°，∵∠ADA′＝50°，∴∠A′DC＝10°，∴∠DA′B＝130°，∵AE⊥BC于点E，∴∠BAE＝30°，∵△BAE顺时针旋转，得到△BA′E′，∴∠BA′E′＝∠BAE＝30°，∴∠DA′E′＝∠DA′B＋∠BA′E′＝160°．故选C．2.如图，中，，，将绕点顺时针旋转得到，当点、、三点共线时，旋转角为，连接，交于点．下面结论：①为等腰三角形；②；③；④中，正确的是（）A. ①③④B. ①②④C. ②③④D. ①②③④【答案】B3.三角板ABC中，∠ACB＝90°，∠B＝30°，AC＝23，三角板绕直角顶点C逆时针旋转，当点A的对应点A′落在AB边的起始位置上时即停止转动，则B点转过的路径长为（）A. 32πB.433πC. 2πD. 3π【答案】C4.如图，将△ABC绕点B逆时针旋转60°得到△A′C′B，且BC＝2，那么CC′的长是___________.【答案】2；【解析】试题解析：∵△ABC绕点B逆时针旋转60°得到△A′C′B，∴BC＝BC′＝2，∠CBC′＝60°，∴△BCC′为等边三角形，∴CC′＝BC＝BC′＝2.学科@网5.如图，在△ABC中，∠ACB＝90°，∠ABC＝60°，AB＝12cm，将△ABC以点B为中心顺时针旋转，使点C 旋转到AB边延长线上的点D处，则AC边扫过的图形（阴影部分）的面积是_____cm2．（结果保留π）．【答案】36π6.在Rt△ABC中，∠C＝90°，AC＝1，BC＝，点O为Rt△ABC内一点，连接AO、BO、CO，且∠AOC＝∠COB＝∠BOA＝120°，则OA＋OB＋OC＝__________．【答案】7【解析】试题解析：∵∠ACB＝90°，AC＝1，BC＝，∴tan∠ABC＝，∴∠ABC＝30°，∵△AOB绕点B顺时针方向旋转60°，∴∠A′BC＝∠ABC＋60°＝30°＋60°＝90°，∴A′B⊥CB，∵∠ACB＝90°，AC＝1，∠ABC＝30°，∴AB＝2AC＝2，∵△AOB绕点B顺时针方向旋转60°，得到△A′O′B，∴A′B＝AB＝2，BO＝BO′，A′O′＝AO，∴△BOO′是等边三角形，∴BO＝OO′，∠BOO′＝∠BO′O＝60°，∵∠AOC＝∠COB＝∠BOA＝120°，∴∠COB＋∠BOO′＝∠BO′A′＋∠BO′O＝120°＋60°＝180°，∴C、O、A′、O′四点共线，在Rt△A′BC中，A′C＝，∴OA＋OB＋OC＝A′O′＋OO′＋OC＝A′C＝．7.如图，⊙P的半径为5，A、B是圆上任意两点，且AB＝6，以AB为边作正方形ABCD（点D、P在直线AB两侧）．若AB边绕点P旋转一周，则CD边扫过的面积为____．【答案】9π8.如图，四边形ABCD是正方形，△ADF按顺时针方向旋转一定角度后得到△ABE，若AF＝4，AB＝7.（1）旋转中心为______；旋转角度为______；（2）DE的长度为______；（3）指出BE与DF的位置关系如何？并说明理由.【答案】（1）A，90°；（2）3；（3）BE⊥DF，理由见解析.9.如图（1），已知△ABC中，∠BAC＝90°，AB＝AC，AE是过A的一条直线，且B、C在A、E的异侧，BD ⊥AE于D，CE⊥AE于E（1）试说明：BD＝DE＋CE．（2）若直线AE绕A点旋转到图（2）位置时（BD＜CE），其余条件不变，问BD与DE、CE的关系如何？请直接写出结果；（3）若直线AE 绕A 点旋转到图（3）位置时（BD ＞CE ），其余条件不变，问BD 与DE 、CE 的关系如何？请直接写出结果，不需说明理由．【答案】（1）证明见解析；（2）DE ＝BD ＋CE ；（3）DE ＝BD ＋CE ．10.（1）探究：如图，四边形ABCD 中，已知AB AD =， 90BAD ∠=︒，点E F 、分别在边BC CD 、上， 45EAF ∠=︒；①如图1，若B ADC ∠∠、都是直角，把ABE V 绕点A 逆时针旋转90︒至ADG V ，使AB 与AD 重合，则能证得EF BE DF =+，请写出推理过程；②如图2，若B D ∠∠、不是直角，则当B D ∠∠、满足数量关系时，仍有EF BE DF =+；（2）拓展：如图3，在ABC V 中， 90BAC ∠=︒， 22AB AC ==，点D E 、均在边BC 上，且45DAE ∠=︒，若1BD =，求DE 的长．【答案】（1）①证明见解析； ②当∠B ＋∠ADC ＝180°时，EF ＝BE ＋DF ；(2) DE ＝53. 【解析】试题分析: （1）①根据旋转的性质得出AE ＝AG ，∠BAE ＝∠DAG ，BE ＝DG ，求出∠EAF ＝∠GAF ＝45°，根据SAS 推出△EAF ≌△GAF ，根据全等三角形的性质得出EF ＝GF ，即可求出答案；②根据旋转的性质得出AE ＝AG ，∠B ＝∠ADG ，∠BAE ＝∠DAG ，求出C 、D 、G 在一条直线上，根据SAS 推出△EAF ≌△GAF ，根据全等三角形的性质得出EF ＝GF ，即可求出答案；（2）根据等腰直角三角形性质好勾股定理求出∠ABC ＝∠C ＝45°，BC ＝4，根据旋转的性质得出AF ＝AE ，∠FBA ＝∠C ＝45°，∠BAF ＝∠CAE ，求出∠F AD ＝∠DAE ＝45°，证△F AD ≌△EAD ，根据全等得出DF ＝DE ，设DE ＝x ，则DF ＝x ，BF ＝CE ＝3−x ，根据勾股定理得出方程，求出x 即可．②当∠B ＋∠ADC ＝180°时，EF ＝BE ＋DF ；把△ACE 旋转到ABF 的位置，连接DF ，则∠F AB ＝∠CAE .∵∠BAC ＝90°，∠DAE ＝45°，∴∠BAD ＋∠CAE ＝45°，又∵∠F AB ＝∠CAE ，∴∠F AD ＝∠DAE ＝45°，则在△ADF 和△ADE 中， AD AD FAD DAE AF AE =⎧⎪∠=∠⎨⎪=⎩，∴△ADF ≌△ADE ，∴DF ＝DE ，∠C ＝∠ABF ＝45°，∴∠BDF ＝90°，∴△BDF 是直角三角形，∴222BD BF DF +=，∴222BD CE DE +=．∵∠BAC ＝90°，AB ＝AC ＝22，∴BC ＝4，∵BD ＝1，∴DC ＝3，EC ＝3－DE ，∴()2213DE DE +-=，解得DE ＝53．学科@网。

初三数学旋转试题及答案

初三数学旋转试题及答案在解答初三数学旋转试题时，我们首先需要理解旋转的概念和性质，然后应用这些知识来解决具体的几何问题。

以下是一些典型的旋转试题及其答案。

1. 题目：在平面直角坐标系中，点A的坐标为(3,4)，若将点A绕原点O逆时针旋转90°，求旋转后点A的新坐标。

答案：首先，我们需要知道逆时针旋转90°后，点的坐标变换规则是(x, y)变为(-y, x)。

因此，点A(3,4)旋转后的新坐标为(-4, 3)。

2. 题目：已知三角形ABC，其中∠A=30°，∠B=60°，∠C=90°，边AB的长度为6，边BC的长度为4，求将三角形ABC绕点C逆时针旋转90°后，点A的新位置。

答案：由于三角形ABC是一个直角三角形，且∠C=90°，旋转后点A 将位于点B的正上方，且与点B的距离等于AB的长度。

因此，点A的新位置可以通过计算得到，即点A的新坐标为(4, 6)。

3. 题目：在平面直角坐标系中，点P的坐标为(2, -1)，若将点P绕点Q(1, 2)顺时针旋转45°，求旋转后点P的新坐标。

答案：首先，我们需要计算点P相对于点Q的向量，即(2-1, -1-2)=(1, -3)。

然后，将这个向量顺时针旋转45°，可以通过旋转矩阵来实现。

旋转矩阵为：\[\begin{bmatrix}\cos(-45°) & -\sin(-45°) \\\sin(-45°) & \cos(-45°)\end{bmatrix}=\begin{bmatrix}\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \\-\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}\end{bmatrix}\]将向量(1, -3)与旋转矩阵相乘，得到新的向量为(\(\frac{\sqrt{2}}{2} - \frac{3\sqrt{2}}{2}\), \(-\frac{\sqrt{2}}{2} - \frac{3\sqrt{2}}{2}\))。

全国181套中考数学试题分类汇编54图形的旋转变换

54：图形的旋转变换一、选择题1.（浙江湖州3分）如图，△AOB 是正三角形，OC ⊥OB ，OC ＝OB ，将△AOB绕点O 按逆时针方向旋转，使得OA 与OC 重合，得到△OCD，则旋转角度是A ．150ºB ．120ºC ．90ºD ．60º【答案】A 。

【考点】旋转的性质，等边三角形的性质，等腰直角三角形的性质。

【分析】由题意，∠AOC 就是旋转角，根据等边三角形每个角都是60°的性质和OC ⊥OB ，即可求得旋转角∠AOC=∠AOB+∠BOC=60°＋90°=150°。

故选A 。

2.（浙江宁波3分）如图，Rt△ABC 中，∠ACB=90°，AC=BC=Rt△绕边AB 所在直线旋转一周，则所得几何体的表面积为(A)4π (B) (C)8π (D) 【答案】D 。

【考点】圆锥的计算，勾股定理，【分析】所得几何体的表面积为2个底面半径为2，母线长为∵Rt△ABC 中，∠ACB=90°，AC=BC=4=。

∴所得圆锥底面半径为2，∴几何体的表面积=2³π³2³。

故选D 。

3.（黑龙江哈尔滨3分）如罔，在Rt△ABC 中，∠BAC=900，∠B=600，△A 11C B 可以由△ABC 绕点 A 顺时针旋转900得到(点B 1与点B 是对应点，点C 1与点C 是对应点)，连接CC’，则∠CC’B’的度数是。

(A) 450 (B) 300 (C) 250 (D) 150 【答案】D 。

【考点】旋转的性质，等腰直角三角形的性质，三角形内角和定理。

【分析】由∠BAC=900，∠B=600可知，∠ACB=300。

由旋转的性质可知，AC=AC ′，又∠CAC′=90°，可知△CAC′为等腰直角三角形，∴∠CC′A=45°。

也由旋转的性质可知，∠A C′ B′=∠ACB=300。

2024年中考数学高频考点专题复习——旋转综合题(含解析)

2024年中考数学高频考点专题复习——旋转综合题1．如图，△ABC 和△DEF 关于某点对称（1）在图中画出对称中心O ；（2）连结AF 、CD ，判断四边形ACDF 的形状，并说明理由．2．在平面直角坐标系中的位置如图所示，其中每个小正方形的边长为1个单位．（1）画出关于原点O 的中心对称图形；（2）在（1）的条件下，请分别写出点A 、B 、C 的对应点、、的坐标．ABC ABC 111A B C 1A 1B 1C3．如图1，图2，△ABC 是等边三角形，D 、E 分别是AB 、BC 边上的两个动点（与点A 、B 、C 不重合），始终保持BD=CE.（1）当点D 、E 运动到如图1所示的位置时,求证：CD=AE.（2）把图1中的△ACE 绕着A 点顺时针旋转60°到△ABF 的位置（如图2），分别连结DF 、EF.①找出图中所有的等边三角形(△ABC 除外)，并对其中一个给予证明；②试判断四边形CDFE 的形状,并说明理由.4．如图，矩形中，，将矩形绕点C 顺时针旋转得到矩形 .设旋转角为，此时点恰好落在边上，连接 .（1）当恰好是中点时，此时；（2）若，求旋转角及的长.5．将线段AB 绕点A 逆时针旋转60°得到线段AC ，继续旋转α（0°＜α＜120°）得到线段AD ，连接CD 、BD ．（1）如图，若α=80°，则∠BDC 的度数为；（2）请探究∠BDC 的大小是否与角α的大小有关，并说明理由．ABCD 4BC =ABCD A B C D ''''αB 'AD B B 'B 'AD α=75AB B ︒∠='αAB6．在平面直角坐标系中，小方格都是边长为1的正方形，△ABC ≌△DEF ，其中点A 、B 、C 、都在格点上，请你解答下列问题：（1）如图（a ）在方格纸中，选择标有序号①②③④中的一个小正方形涂黑，与图中阴影部分构成中心对称图形，涂黑的小正方形的序号为．（2）画出△ABC 关于y 轴对称的△A 1B 1C 1；画出△ABC 绕点P （1，﹣1）顺时针旋转90°后的△A 2B 2C 2；（3）△A 1B 1C 1与△A 2B 2C 2成中心对称吗？若成中心对称请你求出对称中心的坐标；若不成，则说明理由．7．图1是某小型汽车的侧面示意图，其中矩形表示该车的后备箱，在打开后备箱的过程中，箱盖可以绕点A 逆时针方向旋转，当旋转角为时，箱盖落在的位置（将后备箱放大后如图2所示）．已知厘米，厘米，厘米．在图2中求：（1）点到的距离（结果保留根号）；（2）E 、两点的距离（结果保留根号）．ABCD ADE 60︒ADE AD E ''90AD =30DE =40EC =D 'BC E '8．如图，是等腰直角三角形，是直角三角形，，点为边中点将绕点顺时针旋转，旋转角记为，点为边的中点．（1）如图，求初始状态时的大小；（2）如图，在旋转过程中，若点构成平行四边形，请直接写出此时的值；（3）在旋转过程中，若点和点重合，请在图中画出并连接，判断此时是否有 ?如果成立，请证明；如果不成立，请说明理由．ABC 90,ABC BDE ∠=︒ 30E ∠=︒D BC BDE D (0360)αα<<︒F BE AEC ∠,,,B D F B 'a F B ,B DE ' AE AE ED ⊥9．如图，在菱形中，，将边绕点逆时针旋转至，记旋转角为．过点作于点，过点作直线于点，连接．（1）（探索发现）填空：当时， = ．的值是（2）（验证猜想）当时，（1）中的结论是否仍然成立?若成立，请仅就图2的情形进行证明；若不成立，请说明理由；（3）（拓展应用）在（2）的条件下，若，当是等腰直角三角形时，请直接写出线段的长．ABCD 120BAD ∠= AB A 'AB αD DF BC ⊥F B BE ⊥'B D E EF 60α= 'EBB ∠ 'EF DB 0360α<< AB =BDE ∆EF10．如图(1),在△ABC中,AB=BC,P为AB边上一点,连接CP,以PA、PC为邻边作APCD，AC与PD 相交于点E，已知∠ABC=∠AEP= (0°< <90°).（1）求证: ∠EAP=∠EPA;（2）APCD是否为矩形?请说明理由;（3）如图(2),F为BC中点,连接FP,将∠AEP绕点E顺时针旋转适当的角度,得到∠MEN(点M、N分别是∠MEN的两边与BA、FP延长线的交点).猜想线段EM与EN之间的数量关系，并证明你的结论.αα11．定义：有一组邻边相等，且它们的夹角为60°的四边形叫做半等边四边形．（1）已知在半等边四边形ABCD 中，AB=AD ，∠BAD=60°，∠BCD=120°．①如图1，若∠B=∠D ，求证：BC=CD ；②如图2，连结AC ，探索线段AC 、BC 、CD 之间的数量关系，并说明理由；（2）如图3，已知∠MAC=30°，AC=10+10，点D 是射线AM 上的一个动点，记∠DCA=a ，点B 在直线AC 的下方，若四边形ABCD 是半等边四边形，且CB=CD ．问：当点D 在15°≤a≤45°的变化过程中运动时，点B 也随之运动，请直接写出点B 所经过的路径长．12．已知，把45°的直三角板的直角顶点E 放在边长为6的正方形ABCD 的一边BC 上，直三角板的一条直角边经过点D ，以DE 为一边作矩形DEFG ，且GF 过点A ，得到图1.（1）求矩形DEFG 的面积；（2）若把正方形ABCD 沿着对角线AC 剪掉一半得到等腰直角三角形ABC ，把45°的直三角板的一个45°角的顶点与等腰直角三角形ABC 的直角顶点B 重合，直三角板夹这个45°角的两边分别交CA 和CA 的延长线于点H 、P ，得到图2.猜想：CH 、PA 、HP 之间的数量关系，并说明理由；（3）若把边长为6的正方形ABCD 沿着对角线AC 剪掉一半得到等腰直角三角形ABC ，点M 是Rt △ABC 内一个动点，连接MA 、MB 、MC ，设MA+MB+MC ＝y ，直接写出的最小值.2y13．（1）观察猜想：如图①，在Rt △ABC 和Rt △BDE 中，∠ABC ＝∠EBD ＝90°，AB ＝BC ，BE ＝BD ，连接AE ，点F 是AE 的中点，连接CD 、BF ，当点D 、B 、C 三点共线时，线段CD 与线段BF 的数量关系是，位置关系是 .（2）探究证明：在（1）的条件下，将Rt △BDE 绕点B 顺时针旋转至图②位置时，（1）中的结论是否仍然成立？如果成立，请你就图②的情形进行证明；如果不成立，请说明理由；（3）拓展延伸：如图③，在Rt △ABC 和Rt △BDE 中，∠ABC ＝∠EBD ＝90°，BC ＝2AB ＝8，BD ＝2BE ＝4，连接AE ，点F 是AE 的中点，连结CD 、BF ，将△BDE 绕点B 在平面内自由旋转，请直接写出BF 的取值范围，14．请认真阅读下面的数学小探究系列，完成所提出的问题：（1）探究1，如图1，在等腰直角三角形ABC 中，，，将边AB 绕点B 顺时针旋转90°得到线段BD ，连接CD ，过点D 作BC 边上的高DE ，则DE 与BC 的数量关系是，的面积为；（2）探究2，如图2，在一般的中，，（，），将边AB 绕点B 顺时针旋转90°得到线段BD ，连接CD ，请用含m ，n 的式子表示的面积，并说明理由.（3）探究3：如图3，在等腰三角形ABC 中，，（，，），将边AB 绕点B 顺时针旋转90°得到线段BD ，连接CD ，试探究用含a ，b ，c 的式子表示的面积，要有探究过程.90ACB ∠=︒5BC =BCD Rt ABC 90ACB ∠=︒22()()BC m n m n =+--0m >0n >BCD AB AC =BC a b c =++0a >0b >0c >BCD15．如图1，在△ABC中，∠A＝120°，AB＝AC，点D，E分别在边AB，AC上，AD＝AE，连接BE，点M，N，P分别为DE，BE，BC的中点，连接NM，NP.（1）图1中，线段NM，NP的数量关系是，∠MNP的度数为；（2）把△ADE绕点A顺时针旋转到如图2所示的位置，连接MP.求证：△MNP是等边三角形；（3）把△ADE绕点A在平面内旋转，若AD＝2，AB＝5，请直接写出△MNP面积的最大值.16．（1）问题发现：如图①，正方形ABCD的边长为4，对角线AC、BD相交于点O，E是AB上点（点E不与A、B重合），将射线OE绕点O逆时针旋转90°，所得射线与BC交于点F，则四边形OEBF的面积为 .（2）问题探究：如图②，线段BQ＝10，C为BQ上点，在BQ上方作四边形ABCD，使∠ABC＝∠ADC＝90°，且AD ＝CD，连接DQ，求DQ的最小值；（3）问题解决：“绿水青山就是金山银山”，某市在生态治理活动中新建了一处南山植物园，图③为南山植物园花卉展示区的部分平面示意图，在四边形ABCD中，∠ABC＝∠ADC＝90°，AD＝CD，AC＝600米.其中AB、BD、BC为观赏小路，设计人员考虑到为分散人流和便观赏，提出三条小路的长度和要取得最大，试求AB+BD+BC的最大值.17．如图14-1，在平面直角坐标系xOy 中，直线l 2：y=与x 轴交于点B ，与直线l 1交于点c ，c点到x 轴的距离CD 为2 ，直线1交x 轴于点A(-3，0) ．（1）求直线l 1的函数表达式；（2）如图14-2，y 轴上的两个动点E 、F(E 点在F 点上方)满足线段EF 的长为，连接CE 、AF ，当线段CE+EF+AF 有最小值时，求出此时点F 的坐标，以及CE+EF+AF 的最小值；（3）如图14-3，将△ACB 绕点B 逆时针方向旋转60°，得到△BGH ，使点A 与点H 重合，点C 与点G 重合(C 、G 两点恰好关于x 轴对称)，将ABGH 沿直线BC 平移，记平移中的△BGH 为△B'G'H'，在平移过程中，设直线B'H'与x 轴交于点M ，是否存在这样的点M ，使得△B'MG'为等腰三角形？若存在，请直接写出此时点M 的坐标；若不存在，说明理由．18．如图（1）问题发现：如图1，已知点C 为线段上一点，分别以线段为直角边作两个等腰直角三角形，，连接，线段之间的数量关系为；位置关系为 .（2）拓展研究：如图2，把绕点C 逆时针旋转，线段交于点F ，则之间的关系是否仍然成立，说明理由；x AB ,AC BC 90,,ACD CA CD CB CE ︒∠===,AE BD ,AE BD Rt ACD ∆,AF BD ,AE BD（3）解决问题：如图3，已知，连接，把线段AB 绕点A 旋转，若，请直接写出线段的取值范围.19．如图1，在中， , ，点分别是的中点，连接 .（1）探索发现：图1中，的值为；的值为；（2）拓展探究若将绕点逆时针方向旋转一周，在旋转过程中的大小有无变化，请仅就图2的情形给出证明；（3）问题解决当旋转至三点在同一直线时，直接写出线段的长.,,90AC CD BC CE ACD BCE ︒==∠=∠=,,AB AE AD 7,5AB AC ==AE ABC 2AB AC ==120BAC ∠=︒,D E ,AC BC DE AB BC AD BE CDE C AD BECDE ,,A D E BE20．有两个形状、大小完全相同的直角三角板ABC 和CDE ，其中∠ACB ＝∠DCE ＝90°．将两个直角三角板ABC 和CDE 如图①放置，点A ，C ，E 在直线MN 上．（1）三角板CDE 位置不动，将三角板ABC 绕点C 顺时针旋转一周，①在旋转过程中，若∠BCD ＝35°，则∠ACE ＝ ▲ °；②在旋转过程中，∠BCD 与∠ACE 有怎样的数量关系？请依据图②说明理由．（2）在图①基础上，三角板ABC 和CDE 同时绕点C 顺时针旋转，若三角板ABC 的边AC 从CM 处开始绕点C 顺时针旋转，转速为12°/秒，同时三角板CDE 的边CE 从CN 处开始绕点C 顺时针旋转，转速为2°/秒，当AC 旋转一周再落到CM 上时，两三角板都停止转动．如果设旋转时间为t 秒，则在旋转过程中，当∠ACE ＝2∠BCD 时，t 为多少秒？21．我们做如下的规定：如果一个三角形在运动变化时保持形状和大小不变，则把这样的三角形称为三角形板.把两块边长为4的等边三角形板和叠放在一起，使三角形板的顶点与三角形板的AC 边中点重合，把三角形板固定不动，让三角形板绕点旋转，设射线与射线相交于点M ，射线与线段相交于点N.ABC DEF DEF D ABC O ABC DEF O DE AB DF BC（1）如图1，当射线经过点，即点N 与点重合时，易证△ADM ∽△CND.此时，AM·CN= .（2）将三角形板由图1所示的位置绕点沿逆时针方向旋转，设旋转角为 .其中，问AM·CN 的值是否改变？说明你的理由.（3）在（2）的条件下，设AM= x ，两块三角形板重叠面积为，求与的函数关系式.（图2，图3供解题用）22．已知抛物线（，，是常数，）的顶点为，与轴相交于，两点（点在点的左侧），与轴相交于点．（1）若点，求点和点的坐标；（2）将点绕点逆时针方向旋转，点的对应点为，若，两点关于点中心对称，求点的坐标和抛物线解析式：（3）在（1）的条件下，点为直线下方抛物线上的一个动点，过点作轴，与相交于点，过点作轴，与轴相交于点，求的最大值及此时点的坐标．DF B B DEF O α090α<< y y x 2y ax bx c =++a b c 0a ≠()14M -，x A B A B y C ()03C -，A B A B 90︒A 1A A 1A M 1A P BC P PD x BC D P PE y x E PD PE +P答案解析部分1．【答案】（1）解：对称中心O 如图所示；（2）解：∵A 与F ，C 与D 是对应点，∴AO=DO ，CO ＝FO ，∴四边形ACDF 是平行四边形．2．【答案】（1）解：如图所示：（2）解：由图可知：，，．3．【答案】（1）证明：∵△ABC 是正三角形，∴BC=CA ，∠B=∠ECA=60°.又∵BD=CE ，∴△BCD ≌△CAE.∴CD=AE.（2）解：① 图中有2个正三角形，分别是△BDF ，△AFE.由题设，有△ACE ≌△ABF ，∴CE=BF ，∠ECA=∠ABF=60°又∵BD=CE ，∴BD=CE=BF ，∴△BDF 是正三角形，∵AF=AE ，∠FAE=60°，∴△AFE 是正三角形.1(12)A -，1(33)B -，1(40)C ，② 四边形CDFE 是平行四边形.∵∠FDB=∠ABC =60°∴FD ∥EC.又∵FD=FB=EC ，∴四边形CDFE 是平行四边形.4．【答案】（1）60°（2）解：∵四边形是矩形，∴ ，∴ .由旋转的性质得，∴ ，∴ ，即旋转角为30°.作于点E.则 .5．【答案】（1）30°（2）解：无关．理由如下：由旋转变换可知：∠BAC=60°，∠CAD=α， = ， AB=AC=AD ，∴ ，，ABCD //AD BC 75CBB AB B ︒'∠=∠='CB CB ='75CB B CBB ︒∠'=∠='180757530BCB ︒︒︒︒∠--='=αB E BC '⊥122AB B E CB '='==()1180602ADB α∠=︒-+︒⎡⎤⎣⎦1202α︒-()11802ADC α∠=︒-()11202ADB α︒∠=-∴∠BDC=∠ADC-∠ADB= - =30° ，∴∠BDC 的大小与ɑ的度数无关．6．【答案】（1）②（2）解：如图（3）解：如图所示：△A 1B 1C 1与△A 2B 2C 2成中心对称图形，对称中心的坐标为：（1，0）．7．【答案】（1）解：过点作，垂足为点H ，交于点F ．由题意得（厘米），．∵四边形是矩形，∴ ，．在中，又∵ ，，∴ ．∴ （厘米）答：点到的距离是（厘米）．（2）解：连结、、．()11802α︒-()11202α︒-D 'D H BC '⊥AD 90AD AD =='60DAD ∠='︒ABCD AD BC 90AFD BHD ∠'=∠='︒Rt AD F ∆'sin 90sin 60D F AD DAD ︒=⋅∠=⋅='''40CE =30DE =70FH=70)D H D F FH ='++'=D 'BC ()70+AE AE 'EE '由题意得，．∴ 是等边三角形．∴ ．∵四边形是矩形，∴ ．在中，，，∴（厘米）答：E 、两点的距离是厘米．8．【答案】（1）解：∵∠BED ＝30°，△BDE 是直角三角形，∴∠EBD ＝90°－∠BED ＝60°．又∵D 是BC 的中点，∴DE 是BC 的垂直平分线．∵BE ＝CE ，∠BEC ＝60°，∴△BCE 是等边三角形．∴BC ＝BE ．∵△ABC 是等腰三角形，∠ABC ＝90°，∴AB ＝BC ．∴BE ＝AB ．∵AB ⊥BC ，DE ⊥BC ，∴AB ∥DE ，∴∠ABE ＝∠BED ＝30°．∴∠BAE ＝∠BEA ＝ (180°－∠ABE)＝75°．∴∠AEC ＝∠BAE ＋∠BEC ＝135°．（2）解：∵四边形BDFB ＇是平行四边形，∠FB ＇D ＝60°∴B ＇F ∥BD ，∴∠B D B ＇＝∠FB ＇D ＝60°AE AE ='60EAE ∠='︒AEE ∆'EE AE '=ABCD 90ADE ∠=︒Rt ADE ∆90AD =30DE =AE ===E '12即＝60°．（3）解：△B ＇DE 如图所示，AE ⊥DE 不成立，理由如下：DE 与AB 相交于点G ，假设AE ⊥DE ，则△AEG ∽△DBG ，设BG ＝a ，∠BDG ＝30°，∴DG ＝2a ，BD ＝ a ，AB ＝2 BD ＝ a ．∴AG ＝AB －BG ＝（－1）a ，B ＇D ＝BD ＝a ．∴DE ＝＝3a．∴GE ＝DE －DG＝3a －2a ＝a ．∴ ，．∴ 与假设矛盾．∴AE ⊥DE 不成立．9．【答案】（1）30（2）解：当时，（1）中的结论仍然成立．证明：如图1，连接．a tan 30B D＇AG DG ==1GE a GB a ==AG GE DG GB≠0360α<< BD，，．，．．．，即．，，．．，（3）解：线段的长为或．连接，交于点．，，，，∵DE=BE ，∠DEB=90°，∴∠EDB=∠EBD=45°，．，∠B′EB=90°，，．，．．'AB AD AB == 1'(180)9022AB B αα∴∠=︒-=︒-1'[180(120)]3022AB D αα∠=︒-︒-=︒+'180''180(90)(306022EB B AB D AB B αα∴∠=︒-∠-∠=︒-︒--︒+=︒'30EBB ∴∠=︒11(180)3022CBD ABC BAD∠=∠=︒-∠=︒ 'EBB CBD ∴∠=∠'''EBB FBB CBD FBB ∴∠+∠=∠+∠'DBB EBF ∠=∠cos BF DBF BD ∠== cos ''BE EBB BB ∠=='BF BE BD BB ∴='DBB FBE ∆∆∽''EF BE DB BB ∴==EF 3+3-AC BD O AC DB ⊥ 1602BAO BAD ∠=∠=︒sin OB AB BAO ∴=⋅∠=2BD OB ∴==sin DE BE BD DBE ∴==⋅∠=='AB AD AB == 1'(180)9022AB B αα∴∠=︒-=︒-1'[180(120)]3022AB D αα∠=︒-︒-=︒+'180''180(90)(306022EB B AB D AB B αα∴∠=︒-∠-∠=︒-︒--︒+=︒'30EBB ∴∠=︒'tan '2EB BE EBB ∴=⋅∠==分两种情况：如图，，∵∠B′BE=∠DBF=30°，∴cos ∠B′BE=cos ∠DBF=，又∵∠B′BE+∠EBD=∠EBD+∠DBF ，∴∠B′BD=∠EBF ，∴△B′BD ∽△EBF ，∴ ，．如图，．①''2B D DE BE =+=+EB FB B B DB ='=EB FB EF B B DB B D '='2)3EF D '∴==+=②''2B D DE B E =-=∵∠B′BE=∠DBF=30°，∴cos ∠B′BE=cos ∠DBF=，又∵∠B′BE-∠FBB′=∠DBF-∠FBB′，∴∠B′BD=∠EBF ，∴△B′BD ∽△EBF ，∴ ，．综上所述，线段的长为或．10．【答案】（1）证明：(1)在△ABC 和△AEP 中,∠ABC=∠AEP,∠BAC=∠EAP, ∠ACB=∠APE,在△ABC 中,AB=BC. ∠ACB=∠BAC,∠EPA=∠EAP,（2）解： APCD 是矩形.四边形APCD 是平行四边形,AC=2EA,PD=2EP.由(1)知, ∠EPA=∠EAP.EA=EP ，进而AC=PDAPCD 是矩形.（3）解：EM=ENEA=EP, ∠EPA=90° - ∠EAM=180°-∠EAP =180°-∠EPA= 180°-(90°-)=90°+ 由(2)知, ∠CPB=90°,F 是BC 的中点, FP=FB,∠FPB=∠ABC= ，∠EPN=∠EPA+∠APN=∠EPA+∠FPB=90° -+ =90°+ ∠EAM=∠EPN∠AEP 绕点E 顺时针旋转适当的角度，得到∠MEN ，EB FB B B DB ='=EB FB EF B B DB B D '='2)3EF B D ∴===-'EF 33 ∴∴∴ ∴∴∴ ∴12α∴12α12α∴∴α∴12αα12α∴∠AEP-∠AEN =∠MEN-∠AEN,即∠MEA=∠NEP.△EAM ≌△EPN,EM=EN.11．【答案】（1）解：①证明：连结AC ，∵∠A+∠B+∠C+∠D=360°，且∠A=60°，∠C=120°，∴∠B+∠D=180°，且∠B=∠D ，∴∠B=∠D=90°，∵AB=AD ，AC=AC ，∴△ABC ≌△ADC （HL ），∴BC=DC ；②解：延长CB ，使得CD=BE ，∵∠BAD=60°，∠BCD=120°，∴∠ABC+∠D=180°，且∠ABC+∠ABE=180°，∴∠D=∠ABE ，又∵AB=AD∴△ABE ≌△ADC ，∴AE=AC，∴∴∴∠BAE=∠DAC ，∴∠EAC=∠BAE+∠BAC=∠DAC+∠BAC=∠BAD=60°，∴△ACE 是等边三角形，∴AC=CE=CB+BE=CB+CD（2）解：如图，设∠ACD=15°，∠DCD‘=30°，作CM ⊥AD ，D‘H ⊥AC ，由旋转图形的特点可知，CB=CD ，CB‘=CD’，∠BCB'=DCD‘=30°，∴△∠BCB'≌△DCD‘，BB'=DD’，设D'H=x ，由勾股定理得：， HC=x，则，解得x=10，即D'H=10，得，AD’=20，在Rt △AMC 中，∵，∠DAC=30°，∴，AM=（，-5，，∴DD’为D 点的运动路程，则BB‘的运动路程也为10 .12．【答案】（1）解：∵四边形ABCD 是正方形，∴∠ADC ＝∠DCE ＝90°，∵四边形DEFG 是矩形，∴∠AGD ＝∠GDE ＝90°，∴∠DCE ＝∠AGD ＝90°，∠ADC ＝∠GDE ＝90°，∴∠ADC ﹣∠ADE ＝∠GDE ﹣∠ADE ，∴∠EDC ＝∠ADG ，∵∠EDC ＝∠ADG ，∠DCE ＝∠AGD ＝90°，∴△ECD ∽△AGD ，∴ ，∴DG•DE ＝DC•DA ＝6×6＝36，∴矩形DEFG 的面积＝DG•DE ＝36；（2）解：，证明：把△BAP 绕着点B 顺时针旋转90°得到△BCK ，连接KH ，由旋转得△BAP ≌△BCK ，∴BK ＝BP ，∠PBA ＝∠KBC ，∠BCK ＝∠BAP ＝，∴∠HCK ＝＝，∴由勾股定理得，，∵∠PBE ＝45°，∴∠PBA+∠ABE ＝45°，∵∠PBA ＝∠KBC ，∴∠KBC+∠ABE ＝45°，∵∠ABC ＝90°，∴∠HBK ＝45°，∵∠PBE ＝45°，∴∠HBK ＝∠PBE ＝45°，∵BK ＝BP ，∠HBK ＝∠PBE ，BH ＝BH ，∴△BHP ≌△BHK （SAS ），CD DE DG DA=222CH PA HP +＝18045135︒-︒=︒BCK BCA ∠-∠1354590︒-︒=︒222CH PA KH +＝∴HK ＝HP ，∵ ，∴ ；（3）解：把△BMC 绕着点B 顺时针旋转60°得到△BKN ，连接MK ，BN ，NC ，由旋转得，△BMC ≌△BKN ，∴MC ＝KN ，BM ＝BK ，∵BM ＝BK ，∠MBK ＝60°，∴△BKM 是等边三角形，∴MK ＝BM ，∴MA+MB+MC ＝AM+MK+KN ，当A ，M ，K ，N 四点共线时，AN 就是所求的MA+MB+MC 的最小值，过N 作NQ ⊥AB 交AB 的延长线于Q ，∵ ，∠BQN ＝90°，∴QN ＝BN•sin30°＝6× ＝3，BQ ＝BN•cos30°＝，∴AQ ＝AB+BQ ＝，在Rt △AQN 中，由勾股定理得，，∴ 的最小值为 .13．【答案】（1）CD=2BF ；BF ⊥CD（2）解：BF ⊥CD ，CD=2BF 成立，证明：∵△ABC 与△DBE 都是等腰直角三角形，∴AB=BC ，DB=EB ，∠ABC=∠DBE=90°，222CH PA KH +＝222CH PA HP +＝180906030NBQ ∠︒-︒-︒=︒＝126=6+(222226372AN AQ QN +=++=+＝2y 72+如图②，将△ABE 绕点B 顺时针旋转90°得到△CBG ，点E 、F 的对应点分别是G 、H ，连BH ，则△ABE ≌△CBG ，BE=BG ，AE=CG ，BF=BH ，∠FBH=∠EBG=90°，AF=CH ，EF=GH ， ∴BF ⊥BH ，∵AF=EF ，∴CH=GH ，∵∠DBE=90°，∴∠DBE+∠EBG=180°，∴D 、B 、G 三点共线，∴BH ∥CD ，，∴BF ⊥CD ，，即CD=2BF ，∴BF ⊥CD ，CD=2BF 成立；（3）14．【答案】（1）DE=BC ；12.5（2）解：过点D 作BC 边上的高DE ，如图，∵∠ABC+∠A=90°，∠ABC+∠DBE=90°，∴∠A=∠DBE ，又∵∠ACB=∠E=90°，AB=BD ，∴ ，∴，12BH CD =12BF CD =13BF ≤≤ACB BED ≌BC DE =又 .∴ 的面积为：.（3）解：作于G ，过点D 作BC 边上的高DE ，如图，由（2）同理，可证，∴ ，又，∵AB=AC ，，∴ .∴ 的面积为： .15．【答案】（1）NM=NP ；60°（2）证明：由旋转得：∠BAD=∠CAE ，又∵AB=AC ，AD=AE ，∴△ABD ≌△ACE （SAS ），∴BD=CE ，∠ABD=∠ACE ，∵点M ，N ，P 分别为DE ，BE ，BC 的中点，∴MN= BD ，PN= CE ，MN ∥BD ，PN ∥CE ，∴MN=PN ，∠ENM=∠EBD ，∠BPN=∠BCE ，∴∠ENP=∠NBP+∠NPB=∠NBP+∠ECB ，∵∠EBD=∠ABD+∠ABE=∠ACE+∠ABE ，∴∠MNP=∠MNE+∠ENP=∠ACE+∠ABE+∠EBC+∠EBC+∠ECB=180°-∠BAC=60°，∴△MNP 是等边三角形；（322()()4mn BC m n m n =+--=BCD 221448m n 2mn mn ⨯⨯=AGB BED ≌BG DE =BC a b c =++BC a b c =++11()22BG BC a b c ==++BCD 2111()()()224a b c a b c a b c ⨯++⨯++=++121216．【答案】（1）4（2）解：如图②中，连接BD ，取AC 的中点O ，连接OB ，OD.∵∠ABD ＝∠ADC ＝90°，AO ＝OC ，∴OA ＝OC ＝OB ＝OD ，∴A ，B ，C ，D 四点共圆，∴∠DBC ＝∠DAC ，∵DA ＝DC ，∠ADC ＝90°，∴∠DAC ＝∠DCA ＝45°，∴∠DBQ ＝45°，根据垂线段最短可知，当QD ⊥BD 时，QD 的值最短，DQ 的最小值＝BQ ＝5 .（3）解：如图③中，将△BDC 绕点D 顺时针旋转90°得到△EDA ， ∵∠ABC+∠ADC ＝180°，∴∠BCD+∠BAD ＝∠EAD+BAD ＝180°，∴B ，A ，E 三点共线，∵DE ＝DB ，∠EDB ＝90°，∴BE ＝ BD ，∴AB+BC ＝AB+AE ＝BE ＝BD，∴BC+BC+BD ＝（ +1）BD ，∴当BD 最大时，AB+BC+BD 的值最大，∵A ，B ，C ，D 四点共圆，∴当BD 为直径时，BD 的值最大，∵∠ADC ＝90°，∴AC 是直径，∴BD ＝AC 时，AB+BC+BD 的值最大，最大值＝600（ +1）.17．【答案】（1）解：∵点C 的纵坐标为2 ，点c 在直线l 2：y= ∴点C(-1，2 )设l 1的表达式为y= kx+ b将A(-3，0)、C(-1，2)代入，解得故直线l 1的表达式为：y=x+3 （2）解：作点a关于y 轴的对称点A(3，0)，将点a4向上平移个单位长度得E (3，)连接E'C 交y 轴于点E ，在E下方取EF= ，则点F是所求点，将点C 、E' 的坐标代入一次函数表达式，同理可得： CE' 的函数表达式为：y= 故点E(0，)，点F(0，)CE+EF+4F 的最小值=FE+CE'= +．（3）M(5+8，0)或(5-8，0)或(-3，0)或(-19，0) x +03k bk b=-+⎧⎪⎨=-+⎪⎩k b ⎧=⎪⎨=⎪⎩x +18．【答案】（1）AE=BD ；AE ⊥BD（2）解：仍然成立.由题意得，∵△ACD 和△BCE 是等腰直角三角形即，∴∴ .∴∴ .（3）解：连接BD.由（2）可知，AE=BD ，在△ABD 中，且，所以即在AB 绕点A 旋转过程中，当A ，B ，D 三点在一条直线上时，或者,AE BD AE BD =⊥90ACD DCE ECB DCE DCE ︒∴∠+∠=∠+∠=+∠,,ACE DCB AC CD EC CB ∠=∠==ACE DCB∆≅∆,12AE DB =∠=∠180(4512)90EFB ︒︒︒∠=--∠+∠=AE BD⊥77AE -≤≤7AD AB ===77BD <<+77AE -<<+7AE =7AE =∴ ≤AE≤ 19．【答案】（1（2）解：无变化,理由: 由(1)知,CD=1, ,∴,∴ ,由(1)知,∠ACB=∠DCE=30°,∴∠ACD=∠BCE,∴△ACD ∽△BCE,∴,（3）解：线段BE 的长为或，理由如下：当点D 在线段AE 上时,如图2,过点C 作CF ⊥AE 于F,∠CDF=180°﹣∠CDE=60°,∴∠DCF=30°,∴ ,∴,7-7+CE BE ==CD CE =AC BC =CD AC CE BC ==AD AC BE BC ==1122DF CD ==CF ==在Rt △AFC 中,AC=2,根据勾股定理得, ,∴AD=AF+DF=,由(2)知, ,∴当点D在线段AE 的延长线上时,如图3,过点C 作CG ⊥AD 交AD 的延长线于G,∵∠CDG=60°,∴∠DCG=30°,∴ ,∴ ,在Rt △ACG 中,根据勾股定理得,,∴ ,由(2)知,,∴即:线段BE 的长为或.AF ==AD BE =BE ==1122DG CD ==CG ==AG =AD AG DG =-=AD BE =BE ==20．【答案】（1）①145；②∠BCD+∠ACE ＝180°，理由如下：∵∠ACE ＝∠ACB+∠BCE ，∴∠BCD+∠ACE ＝∠BCD+∠ACB+∠BCE ＝∠ACB+∠DCE ＝90°+90°＝180°；（2）解：三角板ABC 和CDE 重合之前，∠ACE ＝180°-10°t ，∠BCD ＝10°t ，依题意有180°-10°t ＝2×10°t ，解得t ＝6；三角板ABC 和CDE 重合之后，∠ACE ＝10°t-180°，∠BCD ＝360°-10°t ，依题意有10°t-180°＝2×（360°-10°t ），解得t ＝30．故当t ＝6或30秒时，有∠ACE ＝2∠BCD ．故答案为：6或30．21．【答案】（1）4（2）解：AM•CN 的值不会改变.连接BD ，在△ADM 与△CND 中，∵∠A=∠C=60°，∠DNC=∠DBN+∠BDN=30°+α，∠ADM=30°+α，∴∠ADM=∠CND ，∴△ADM ∽△CND∴ ，∴AM•CN=AD•CD=2×2=4，∴AM•CN 的值不会改变；（3）解：情形1，当0°＜α＜60°时，1＜AM ＜4，即1＜x ＜4，此时两三角形板重叠部分为四边形AD AM CN CD如图2，过D 作DQ ⊥AB 于Q ，DG ⊥BC 于G ，∴DQ=DG= ，由（2）知，AM•CN=4，得CN=，于是y=（1＜x ＜4）；情形2，当60°≤α＜90°时，AM≥4时，即x≥4，此时两三角形板重叠部分为△DPN ，如图3，过点D 作DH ∥BC 交AM 于H ，易证△MBP ∽△MHD ，∴ ，又∵MB=x-4，MH=x-2，DH=2,∴BP=，∴PN=4－，于是y= ，综上所述，1＜x ＜4时，y=；x≥4时，y= 22．【答案】（1）解：设抛物线解析式为，将点代入得，4x 21122AB AM DQ CN DG x -⋅-⋅=BP MB DH MH=282x x --4282x x x ---114284222x PN DG x x -⎛⎫⋅=--= ⎪-⎝⎭x ()214y a x =--()03C -，解得：∴抛物线解析式为当时，解得：，∵点在点的左侧，∴，；（2）解：∵，抛物线，与轴相交于，两点∴，对称轴为直线，设，则，∴∵点绕点逆时针方向旋转得到，则点一定在第四象限，如图所示，则，，∵，两点关于点中心对称，∴解得：，则∴，1a =()214y x =--0y =()2140x --=1213x x =-=，A B ()10A -，()30B ，()14M -，2y ax bx c =++x A B 0a >1x =()0A m ，()20B m -，222AB m m m=--=-A B 90︒A 'A '22BA BA m ='=-()222A m m '--，A 1A M 228m -=-3m =-()58A '-，()30A -，()50B ，将点代入得，解得：∴抛物线解析式为；（3）解：如图所示，设交于点，由（1）可得，，设直线的解析式为，将点代入得，解得所以直线的解析式为，∵抛物线解析式为，设，则，∴，∵轴，轴，由∵则是等腰直角三角形，∴()30A -，()214y a x =--1640a -=14a =()21144y x =--PE BC F ()30B ，()03C -，BC 3y kx =-()30B ，330k -=1k =BC 3y x =-()221423y x x x =--=--()223P t t t --，()0E t ，()3F t t -，223233FP t t t t t =--++=-+223PE t t =-++PD x PE y OC OB=OCB 45FDP OBC ∠=∠=︒∴也是等腰直角三角形，∴∴∴当时，取得最大值此时，即．PDF PD PF=PD PE+22323t t t t =-+-++2253t t =-++252525232168t t ⎛⎫=--+++ ⎪⎝⎭2549248t ⎛⎫=--+ ⎪⎝⎭54t =PD PE +498225632314416t t ⎛⎫--=--=- ⎪⎝⎭563416P ⎛⎫- ⎪⎝⎭。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2012年全国中考数学试题分类解析汇编(159套63专题）专题54：图形的旋转变换一、选择题1. （2012天津市3分）将下列图形绕其对角线的交点逆时针旋转900，所得图形一定与原图形重合的是【】（A ）平行四边形（B ）矩形（C ）菱形（D ）正方形【答案】D 。

【考点】旋转对称图形【分析】根据旋转对称图形的性质，可得出四边形需要满足的条件：此四边形的对角线互相垂直、平分且相等，则这个四边形是正方形。

故选D 。

2. （2012广东佛山3分）如图，把一个斜边长为2且含有300角的直角三角板ABC 绕直角顶点C 顺时针旋转900到△A 1B 1C ，则在旋转过程中这个三角板扫过的图形的面积是【】A ．πBC ．34π D ．1112π 【答案】D 。

【考点】旋转的性质，勾股定理，等边三角形的性质，扇形面积。

【分析】因为旋转过程中这个三角板扫过的图形的面积分为三部分扇形ACA 1、 BCD 和△ACD 计算即可：在△ABC 中，∠ACB =90°，∠BAC =30°，AB =2，∴BC =12AB =1，∠B =90°－∠BAC =60°。

∴AC∴ABC 1S BC AC 2∆=⨯⨯=设点B 扫过的路线与AB 的交点为D ，连接CD ， ∵BC =DC ，∴△BCD 是等边三角形。

∴BD =CD =1。

∴点D 是AB 的中点。

∴ACD ABC 11S S 22∆∆===S 。

∴1ACD ACA BCD ABC S S S ∆∆=++扇形扇形的面扫过积故选D 。

3. （2012广东汕头4分）如图，将△ABC 绕着点C 顺时针旋转50°后得到△A ′B ′C ′．若∠A =40°．∠B ′=110°，则∠BCA ′的度数是【】A ．110°B ．80°C ．40°D ．30°【答案】B 。

【考点】旋转的性质，三角形内角和定理。

【分析】根据旋转的性质可得：∠A ′=∠A ，∠A ′CB ′=∠ACB ，∵∠A =40°，∴∠A ′=40°。

∵∠B ′=110°，∴∠A ′CB ′=180°﹣110°﹣40°=30°。

∴∠ACB =30°。

∵将△ABC 绕着点C 顺时针旋转50°后得到△A ′B ′C ′，∴∠ACA ′=50°， ∴∠BCA ′=30°+50°=80°，故选B 。

4. （2012江苏苏州3分）如图，将△AOB 绕点O 按逆时针方向旋转45°后得到△A ＇OB ＇，若 ∠AOB =15°，则∠AOB ＇的度数是【】BA ＇AB ＇OA .25°B .30°C .35°D . 40°【答案】B 。

【考点】旋转的性质。

【分析】根据旋转的性质，旋转前后图形全等以及对应边的夹角等于旋转角，从而得出答案：∵将△AOB 绕点O 按逆时针方向旋转45°后得到△A ′OB ′， ∴∠A ′OA =45°，∠AOB =∠A ′OB ′=15°，∴∠AOB ′=∠A ′OA －∠A ′OB =45°－15°=30°。

故选B 。

5. （2012福建龙岩4分）如图，矩形ABCD 中，AB =1，BC =2，把矩形ABCD 绕AB 所在直线旋转一周所得圆柱的侧面积为【】A ．10πB ．4πC ．2πD ．2【答案】B 。

【考点】矩形的性质，旋转的性质。

【分析】把矩形ABCD 绕AB 所在直线旋转一周所得圆柱是以BC =2为底面半径，AB =1为高。

所以，它的侧面积为221=4ππ⋅⋅。

故选B 。

6. （2012湖北十堰3分）如图，O 是正△ABC 内一点，OA =3，OB =4，OC =5，将线段BO 以点B 为旋转中心逆时针旋转60°得到线段BO ′，下列结论：①△BO ′A 可以由△BOC 绕点B 逆时针旋转60°得到；②点O与O ′的距离为4；③∠AOB =150°；④AOBO S 四形边AOCAOBS S+=是【】A ．①②③⑤B ．①②③④C ．①②③④⑤D ．①②③【答案】A 。

【考点】旋转的性质，全等三角形的判定和性质，等边三角形的判定和性质，勾股定理的逆定理。

【分析】∵正△ABC ，∴AB =CB ，∠ABC =600。

∵线段BO 以点B 为旋转中心逆时针旋转60°得到线段BO ′，∴BO =BO ′，∠O ′AO =600。

∴∠O ′BA =600－∠ABO =∠OBA 。

∴△BO ′A ≌△BOC 。

∴△BO ′A 可以由△BOC 绕点B 逆时针旋转60°得到。

故结论①正确。

连接OO ′，∵BO =BO ′，∠O ′AO =600，∴△OBO ′是等边三角形。

∴OO ′=OB =4。

故结论②正确。

∵在△AOO ′中，三边长为O ′A =OC =5，OO ′=OB =4，OA =3，是一组勾股数，∴△AOO ′是直角三角形。

∴∠AOB =∠AOO ′＋∠O ′OB =900＋600=150°。

故结论③正确。

AOO OBO AOBO 11S S S 34+422∆'∆''=+=⋅⋅⋅⋅四形边。

故结论④错误。

如图所示，将△AOB 绕点A 逆时针旋转60°，使得AB 与AC 重合，点O 旋转至O ″点．易知△AOO ″是边长为3的等边三角形，△COO ″是边长为3、4、5的直角三角形。

则AOC AOB AOCO COO AOO 11S S S S S 34+322∆∆"∆"∆"+==+=⋅⋅⋅。

故结论⑤正确。

综上所述，正确的结论为：①②③⑤。

故选A 。

7. （2012湖南岳阳3分）如图，两个边长相等的正方形ABCD 和EFGH ，正方形EFGH 的顶点E 固定在正方形ABCD 的对称中心位置，正方形EFGH 绕点E 顺时针方向旋转，设它们重叠部分的面积为S ，旋转的角度为θ，S 与θ的函数关系的大致图象是【】A ．B ．C ．D ．【答案】B 。

【考点】旋转问题的函数图象，正方形的性质，旋转的性质，全等三角形的判定和性质。

【分析】如图，过点E 作EM ⊥BC 于点M ，EN ⊥AB 于点N ，∵点E 是正方形的对称中心，∴EN =EM ，EMBN 是正方形。

由旋转的性质可得∠NEK =∠MEL ，在Rt △ENK 和Rt △EML 中，∠NEK =∠MEL ，EN =EM ，∠ENK =∠EML ， ∴△ENK ≌△ENL （ASA ）。

∴阴影部分的面积始终等于正方形面积的14，即它们重叠部分的面积S 不因旋转的角度θ的改变而改变。

故选B 。

8. （2012四川绵阳3分）如图，P 是等腰直角△ABC 外一点，把BP 绕点B 顺时针旋转90°到BP ′，已知∠AP ′B =135°，P ′A ：P ′C =1：3，则P ′A ：PB =【】。

A．1B．1：2 C 2 D．1【答案】B。

【考点】旋转的性质，等腰直角三角形的判定和性质，全等三角形的判定和性质，勾股定理。

【分析】如图，连接AP，∵BP绕点B顺时针旋转90°到BP′，∴BP=BP′，∠ABP+∠ABP′=90°。

又∵△ABC是等腰直角三角形，∴AB=BC，∠CBP′+∠ABP′=90°，∴∠ABP=∠CBP′。

在△ABP和△CBP′中，∵BP=BP′，∠ABP=∠CBP′，AB=BC，∴△ABP≌△CBP′（SAS）。

∴AP=P′C。

∵P′A：P′C=1：3，∴AP=3P′A。

连接PP′，则△PBP′是等腰直角三角形。

∴∠BP′P=45°，PP′= 2 PB。

∵∠AP′B=135°，∴∠AP′P=135°-45°=90°，∴△APP′是直角三角形。

设P′A=x，则AP=3x，在Rt△APP′中，PP'==。

在Rt△APP′中，PP'=。

，解得PB=2x。

∴P′A：PB=x：2x=1：2。

故选B。

9. （2012四川泸州2分）将如图所示的直角梯形绕直线l旋转一周，得到的立体图形是【】【答案】D。

【考点】点、线、面的关系，旋转的性质。

【分析】将如图所示的直角梯形绕直线l旋转一周得到圆台。

故选D。

10. （2012四川泸州2分）如图，边长为a的正方形ABCD绕点A逆时针旋转30°得到正方形A′B′C′D′，图中阴影部分的面积为【】A 、21a 2B 2C 、2a ⎛ ⎝⎭D 、2a ⎛⎝⎭【答案】D 。

【考点】正方形的性质，旋转的性质，全等三角形的判定和性质，三角形内角和定理，锐角三角函数定义，特殊角的三角函数值。

【分析】设B ′C ′与CD 交于点E ，连接AE .在△AB ′E 与△ADE 中，∠AB ′E =∠ADE =90°，AE =AE , AB ′=AD , ∴△AB ′E ≌△ADE （HL ）。

∴∠B ′AE =∠DAE 。

∵∠BAB ′=30°，∠BAD =90°，∴∠B ′AE =∠DAE =30°。

∴DE =AD •tan ∠DAE a 。

∴2ADE AB ED 1S 2S 2a a a 233∆'==⋅⋅⋅=四边形。

∴2ABCD AB ED S S 1 a '=-=-正方形四边形阴影部分的面积（。

故选D 。

11. （2012贵州黔东南4分）点P 是正方形ABCD 边AB 上一点（不与A 、B 重合），连接PD 并将线段PD 绕点P 顺时针旋转90°，得线段PE ，连接BE ，则∠CBE 等于【】A ．75°B ．60°C ．45°D ．30°【答案】C 。

【考点】正方形的性质，旋转的性质，全等三角形的判定和性质，等腰直角三角形的判定和性质。

【分析】过点E 作EF ⊥AF ，交AB 的延长线于点F ，则∠F =90°，∵四边形ABCD 为正方形，∴AD =AB ，∠A =∠ABC =90°。

∴∠ADP +∠APD =90°。

由旋转可得：PD =PE ，∠DPE =90°，∴∠APD +∠EPF =90°。

∴∠ADP =∠EPF 。

在△APD 和△FEP 中，∵∠ADP =∠EPF ，∠A =∠F ，PD =PE ， ∴△APD ≌△FEP （AAS ）。

【中考必备】最新中考数学试题分类解析 专题54 图形的旋转变换

【中考数学专题】三大变换之旋转（旋转的性质）

中考数学几何图形的变换历年真题解析

2022年中考数学真题分类汇编：图形的旋转(含答案)

中考数学综合题专题复习【旋转】专题解析含答案

初中数学中考冲刺必备(旋转几个类型题)

九年级数学图形的旋转专题讲解+六大题型解析+专题训练,收藏学习

图形的旋转(共30题)(学生版)--2023年中考数学真题分项汇编

图形的旋转、翻折与平移-三年中考数学真题分项汇编(解析版)

中考专题 图形的变换-旋转

2020年全国中考数学试题分类(13)——图形的旋转(含答案)

中考数学复习----《图形的旋转变换》知识点总结与专项练习题

2023年中考数学讲练必考重点04 几何变换之旋转问题(含答案)

中考数学 考点15 旋转变换(解析版)

初三数学旋转试题及答案

全国181套中考数学试题分类汇编54图形的旋转变换

2024年中考数学高频考点专题复习——旋转综合题(含解析)

【中考必备】最新中考数学试题分类解析专题54 图形的旋转变换

中考专题图形的变换-旋转

中考数学考点15 旋转变换(解析版)