洛伦兹变换
相对论知识:洛伦兹变换——相对论中的坐标系变换

相对论知识:洛伦兹变换——相对论中的坐标系变换洛伦兹变换是相对论中的坐标系变换,是指在不同惯性参考系之间进行相互转换的数学方法。
相对论是爱因斯坦在1905年提出的,它考察的是运动物体的物理现象,因此必须将观察者的运动状态考虑在内。
在相对论中,时间和空间不具有绝对性,而是相对于观察者的运动状态而言的。
洛伦兹变换就是这种相对性的体现。
首先,我们要理解什么是惯性参考系。
惯性参考系是指一个不受力作用的、作匀速直线运动的参考系。
在相对论中,任何两个相对运动的惯性参考系之间都可以进行转换,而这种转换就是洛伦兹变换。
换句话说,洛伦兹变换是一种坐标系变换,可以将同一事件在两个不同的惯性参考系中的描述进行转换。
洛伦兹变换有两种形式:时间变换和坐标变换。
时间变换主要是指时间的变化,在不同的惯性参考系中,同一个事件发生的时间也是不同的。
当一个事件在一个惯性参考系中发生时,其时间为t1,在另一个惯性参考系中的时间为t2。
这两个时间之间的关系可以用下面的公式表示:t2 = γ(t1 - vx/c²)其中,γ是洛伦兹因子,v是相对速度,c是光速。
这个公式表示在相对于第一个参考系以速度V运动的第二个参考系中,时间的变化规律。
γ的大小取决于相对速度的大小,当速度很小时,γ趋近于1,相当于牛顿力学中常用的时间变换公式;而当速度趋近于光速时,γ趋近于无穷大,表示时间的变化越来越慢。
坐标变换主要是指空间坐标的变化。
在不同的惯性参考系中,同一物体的位置是不同的。
当一个物体在一个惯性参考系中的位置为(x1, y1, z1)时,在另一个惯性参考系中的位置为(x2, y2, z2)。
这两个位置之间的关系可以用下面的公式表示:x2 = γ(x1 - vt1)y2 = y1z2 = z1其中,γ、v、t1的含义和上面相同。
这个公式表示在相对于第一个参考系以速度V运动的第二个参考系中,坐标的变化规律。
与时间变换类似,当速度很小时,坐标变换公式也可以简化为牛顿力学中常用的变换公式。
大学物理下相对论-洛伦兹变换

100%
长度收缩
在相对论中,当物体以接近光速 运动时,其长度相对于静止观察 者会缩短,这种现象被称为长度 收缩。
80%
相对论的多普勒效应
当光源或观察者以接近光速运动 时,光波的频率或波长会发生改 变,这种现象被称为相对论的多 普勒效应。
相对论的速度合成法则
相对论的速度合成法则
当两个物体以接近光速相对运动时,它们的相对速度不能简单地通过矢量相加得到,而是需要使用洛伦兹变换进 行计算。
速度合成法则的应用
在高速运动和强引力场中,相对论的速度合成法则对于精确描述物体的运动状态非常重要。
相对论的质量-能量关系(E=mc^2)
质量-能量等效原理
在相对论中,物体的质量与能量是等效的,即存在一个固定的转换关系 E=mc^2。
质能方程的应用
质能方程在核能、粒子物理和宇宙学等领域有广泛的应用,如核反应释放能量、黑洞的形成和演化等 。
洛伦兹变换公式描述了不同参 考系之间的长度和时间的关系 ,是相对论中的基本公式之一 。
通过洛伦兹变换公式,可以推 导出相对论中的其他重要结论 ,如时间膨胀和长度收缩。
04
洛伦兹变换的应用
时间和空间的测量
80%
时间膨胀
在相对论中,当物体以接近光速 运动时,其内部的时间相对于静 止观察者会变慢,这种现象被称 为时间膨胀。
洛伦兹变换的性质
线性性质
洛伦兹变换是线性变换,即变换前后线性组合的结 果与单个变换的结果相同。
逆变换
如果知道从一个参考系到另一个参考系的洛伦兹变 换,则可以推导出从另一个参考系回到原参考系的 逆变换。
相对性
对于任意两个惯性参考系之间的变换,其逆变换与 原变换是等价的。
03
洛伦兹变换

11 – 2
洛伦兹变换
第十一章 狭义相对论
相对论速度正变换式
说明
当 S 系观察者测得光 信号速度为c时,S测得
ux v u x v 1 2 ux c 2 uy v u y 1 2 v c 1 2 ux c 2 uz v u 1 2 z v c 1 2 ux c
S S
11 – 2
洛伦兹变换
第十一章 狭义相对论
例1 在惯性系 S 中,有两个事件同时发生在 x 轴 上相距 1000m 的两点,而在另一惯性系 S(沿 x 轴方 向相对于 S 系运动)中测得这两个系事件发生的地点 相距 2000m。求在 系中测得这两个事件的时间间隔 . 解: 已知 t 0 x 1000 m 正 变 换
v
( x, y, z, t ) y y ' P ( x' , y ' , z ' , t ' ) S S
z
o
z'
o'
x' x
v c
1 1
2Hale Waihona Puke 11 – 2洛伦兹变换
第十一章 狭义相对论
正 变 换
x' ( x vt ) y' y z' z v t ' (t 2 x) c
二
洛伦兹变换
第十一章 狭义相对论
洛伦兹速度变换
洛伦兹坐标正变换式
x x vt y y z z v t t 2 c
dx dx vdt dy dy dz dz
v dt dt 2 dx x c dx v ux v d x d t u x dt 1 v dx 1 v u 2 x 2 c c dt
洛伦兹变换

洛伦兹变换编辑由于爱因斯坦提出的假说否定了伽利略变换,因此需要寻找一个满足相对论基本原理的变换式。
洛伦兹导出了这个变换式,一般称它为洛伦兹变换式。
中文名洛伦兹变换外文名Lorentz transformation别称洛伦兹变换式提出者亨德里克·洛伦兹提出时间1904年应用学科数学适用领域范围狭义相对论目录1简介2理论3释义4推导▪公设一▪公设二▪过程▪另一种方式5区别6四维矢量改写1简介编辑洛伦兹变换(Lorentz transformation)是观测者在不同惯性参照系之间对物理量进行测量时所进行的转换关系,在数学上表现为一套方程组。
洛伦兹变换因其创立者——荷兰物理学家亨德里克·洛伦兹而得名。
洛伦兹变换最初用来调和19世纪建立起来的经典电动力学同牛顿力学之间的矛盾,后来成为狭义相对论中的基本方程组。
2理论编辑洛伦兹变换(Lorentz transformation)是狭义相对论中关于不同惯性系之间物理事件时空坐标变换的基本关系式。
设两个惯性系为S系和S′系,它们相应的笛卡尔坐标系彼此平行,S′系相对于S系沿x 方向运动,速度为v,且当t=t′=0时,S′系与S系的坐标原点重合,则事件在这两个惯性系的时空坐标之间的洛伦兹变换为式中,;c为真空中的光速。
其逆变换形式为不同惯性系中的物理定律必须在洛伦兹变换下保持形式不变。
19世纪后期建立了麦克斯韦方程组,标志着经典电动力学取得了巨大成功。
然而麦克斯韦方程组在经典力学的伽利略变换下并不是协变的。
由麦克斯韦方程组可以得到电磁波的波动方程,由波动方程解出真空中的光速是一个常数。
按照经典力学的时空观,这个结论应当只在某个特定的惯性参照系中成立,这个参照系就是以太。
其它参照系中测量到的光速是以太中光速与观察者所在参照系相对以太参照系的速度的矢量叠加。
然而1887年的迈克耳孙-莫雷实验测量不到地球相对于以太参照系的运动速度。
1904年,洛伦兹提出了洛伦兹变换用于解释迈克耳孙-莫雷实验的结果。
14.4 洛伦兹变换

∆x′ =
∆x −u∆t 1−u2 / c2
=
100 − 0.8×3×108 ×10 1− 0.82
= −4.0×109 m
因此, 因此, S' 系中测得选手跑过的路程为
| ∆x′ |= 4.0×109 m
(2) S' 系中选手从起点到终点的时间间隔为 ∆t'
u 0.8×100 ∆t − 2 ∆x 10 − c 3×108 =16.7 s ∆t′ = = 2 2 1−u / c 1− 0.82
14.4 洛伦兹变换
一、洛伦兹变换
在两参考系中的时间间隔、 在两参考系中的时间间隔、空间间隔的变换关系 时间间隔 洛仑兹速度变换
二、由洛仑兹变换看相对论时空观
• 同时性的相对性 • 时间延迟 • 长度收缩
一、洛伦兹变换 y'
u S' 时刻, 在t = t′=0 时刻, S , S′ 原点重合 O' z' 线 性 变 换 关 系 x' z
∆t' = 0,
∆x' ≠ 0
同时异地事件 不是同时事件
∆t' + u∆x' c2≠ 0 ∆t = 1− β2
原时 ∆t' = τ0 ≠ 0
S′
∆x' = 0,
∆t =
同地异时事件
S
∆t' + u∆x' c2 1− β
2
∴ τ = ∆t =
τ0 1− β2
∴ τ 0 <τ 原时最短
(3) 长度收缩 a b u
∆t =10 s
∆x =100 m
l0 = 100 m
∆t' ∆x' l
写出洛伦兹变换及其逆变换的形式。

洛伦兹变换及其逆变换是狭义相对论中的重要概念,它描述了当两个惯性系之间相对运动时,时间和空间的变化规律。
本文将从以下几个方面展开讨论:一、洛伦兹变换的推导1.1 介绍洛伦兹变换的背景狭义相对论是爱因斯坦在19世纪初提出的一种理论,它颠覆了牛顿力学的观念,重新定义了时间和空间的概念。
在狭义相对论中,运动状态并不是绝对的,而是相对于观察者的。
当两个惯性系相对运动时,时间和空间的观测数值会发生变化,而这种变化规律由洛伦兹变换来描述。
1.2 推导洛伦兹变换的数学表达式根据狭义相对论的基本原理和洛伦兹对称性,可以推导出洛伦兹变换的数学表达式。
假设有两个惯性系S和S',它们之间以速度v相对运动。
假设在S系中有事件的时空坐标为(x, y, z, t),在S'系中的时空坐标为(x', y', z', t'),那么洛伦兹变换的数学表达式可以表示为:\[x'=\frac{x-vt}{\sqrt{1-\frac{v^2}{c^2}}}, y'=y, z'=z, t'=\frac{t-\frac{v}{c^2}x}{\sqrt{1-\frac{v^2}{c^2}}}.\]其中c为光速。
1.3 推导出洛伦兹变换的矩阵形式将洛伦兹变换的以上数学表达式整理成矩阵形式,并引入矩阵运算的概念,可以得到洛伦兹变换的矩阵形式如下:\[ \begin{bmatrix} x' \\ y' \\ z' \\ t' \end{bmatrix}= \begin{bmatrix} \frac{1}{\sqrt{1-\frac{v^2}{c^2}}} 0 0 -\frac{v}{c^2}\frac{1}{\sqrt{1-\frac{v^2}{c^2}}} \\ 0 1 0 0 \\ 0 0 1 0 \\ -\frac{v}{c^2}\frac{1}{\sqrt{1-\frac{v^2}{c^2}}} 0 0\frac{1}{\sqrt{1-\frac{v^2}{c^2}}} \end{bmatrix}\begin{bmatrix} x \\ y \\ z \\ t \end{bmatrix}.\]二、洛伦兹变换的逆变换形式2.1 介绍洛伦兹变换的逆变换洛伦兹变换的逆变换即是将事件的时空坐标从S'系变换到S系的坐标变换规律。
洛伦兹变换的三个公式

洛伦兹变换是狭义相对论中描述时间和空间之间的关系的数学工具,可以用来描述相对论速度变换以及时间和空间的相对性。
洛伦兹变换有三个主要的公式,分别是:
时间间隔的洛伦兹变换公式:Δt' = γ(Δt - vΔx/c^2) 其中,Δt' 是观测者在运动的参考系中测得的时间间隔,Δt 是静止参考系中的时间间隔,v 是两个参考系之间的相对速度,Δx 是两个参考系之间的相对位置,c 是光速,γ是洛伦兹因子,其值为γ= 1/√(1 - v^2/c^2)。
空间坐标的洛伦兹变换公式: x' = γ(x - vt) 其中,x' 是观测者在运动的参考系中测得的空间坐标,x 是静止参考系中的空间坐标,v 是两个参考系之间的相对速度,t 是时间。
时间坐标的洛伦兹变换公式: t' = γ(t - vx/c^2) 其中,t' 是观测者在运动的参考系中测得的时间坐标,t 是静止参考系中的时间坐标,v 是两个参考系之间的相对速度,c 是光速,γ是洛伦兹因子,其值为γ = 1/√(1 - v^2/c^2)。
这些公式描述了时间和空间之间的变换关系,在相对论中起到了重要的作用。
它们表达了相对论效应,如时间膨胀和长度收缩,以及相对速度的影响。
通过使用洛伦兹变换,我们可以更准确地描述和理解高速运动物体的运动和相互作用。
大学物理精品课件3.1 洛伦兹变换

伽利略变换式
牛顿的绝对时空观
第三章 相对论
伽利略速度变换公式
u' x u x v
s
y
vt
y
s'
y'
y'
u' y u y
u'z uz
加速度变换公式
v
x'
P ( x, y , z )
*
( x', y', z ' )
o
a' x ax
a' y a y
a a' F ma ' F ma
25
伽利略变换式
牛顿的绝对时空观
第三章 相对论
速度变换
考虑一质点 P 在空间 的运动,从 S 和 S′ 系来看,速度分别是:
y
S
y'
S'
V
P
O
v v'
x ( x' )
O'
z
z'
dx dy dz v x dt , v y dt , vz dt dx dy dz v'x dt , v'y dt , v'z dt
4
伽利略变换式
牛顿的绝对时空观
第三章 相对论
y
(1)同时的绝对性
V
y'
event 1
event 2
o
S系, t1 t 2
o'
x
x'
两个事件同时发生
据伽利略变换,S/系
同时的绝对性
t1 t 2
在其他惯性系中,两个事件也一定同时发生。
8.2洛伦兹变换

推导时间 t ' 与 t 之间的变换关系:
x
( x ut)
t
1 u
x
x
把 x ( x ut) 代入,得
t
1 u
x源自(xut)
u
1
2
1 x
ut
把 1 2 (1 u2 c2 ) 代入,得:
t
t
u c2
x
1 u2 c2
【例】一宇宙飞船相对地面以 0.8c 的 速度飞行,飞船上的观察者测得飞船的长 度为100m。一光脉冲从船尾传到船头, 求地面上的观察者测量,光脉冲 “从船尾 发出” 和 “到达船头” 这两个事件的空间间 隔是多少?
解 只涉及时空变换的问题称为运动学 问题,一般按以下步骤求解:
只需推导:
( x, t) ~ ( x, t) 之间的变换关系
伽利略变换 x x ut
注意:( x ut) 是同一参考系 S 中长度的合成,
只能整体地随 u 变化,所以新变换可表示为:
x ( x ut)
x ( x ut)
, 待定参量
根据爱因斯坦相对性原理:
(3)洛伦兹变换,求两事件在S系中的空间间隔。
已知:x2 x1 100m, t2 t1 ( x2 x1 ) c
x2
x1
( x2
x1 ) u(t2 1 u2 c2
t1 )
100 0.8 100
m 300 m
1 0.82
编者:陈信义
新变换可简单地写成:
x ( x ut) x ( x ut)
洛伦兹变换

设t = t' = 0时, O与O' 重合
S Px, y, z,t
yS
y' S' u
ut P
S Px, y, z, t
o
o' x'
x'
两个参考系中相应的
x
x
坐标值之间的关系:
x x ut (x ut) 1u2 c2
z y y
z'
z z
t'
t u x c2
(t u x)
x ( x ut)
则
t
(
t
u c2
x)
x ( x ut)
逆变换
t
(
t
u c2
x)
u c 1 1 2
二、由洛伦兹变换看长度的收缩(length contraction)
标尺相对 S系静止
y y'
在 S系中测量
l0 x'2 x'1 l'
s
s'
u
x'1
l0
x'2 x'
O'
说明上海站的乙火车先开,
时序颠倒!!
O z
ቤተ መጻሕፍቲ ባይዱ
x
狭义相对论的时空观: 两个事件在不同的惯性系看来,它们的空间关
系是相对的,时间关系也是相对的,时间和空间的 量度与参考系的选择有关。也就是说时间、空间和 运动三者之间紧密联系,是不可分割的一个整体。
光速 C 是建立不同惯性系间时空变换的纽带。
试求宇航员参考系中测得的甲乙两列火车发车的时间 间隔,哪一列先开?
解:取地面为 S 系,和飞船一起运动的参考系为 S 系,
大学物理第4章第4节-洛伦兹变换

一. 洛仑兹坐标变换 洛仑兹变换描述相对论的时空关系.
y
S
S
y
u
( x, y , z ; t ) P ( x, y , z , t )
ut
o
z
o
x
x, x
z
x
1. 坐标变换
y
S
S
y
u
( x, y , z ; t ) P ( x, y , z , t )
ut
o
z
o
x
x, x
z
x
在 S 系中观测, 由运动尺度收缩效应,
(在 S 系中, x 静止, x 运动)
x ut x 1 2 (1)
x
x ut 1 2
y
S
S
y
u
( x, y , z ; t ) P ( x, y , z , t )
即同地事件的同时性的绝对的, 异地事 件的同时性是相对的.
2. 关于事件的时序问题 因果事件: 表示结果的事件 B 发生在 表示原因的事件 A 之后.
t1 t2 t 2 t1 1
2
(u c 2 )( x2 x1 ) 1 2
t 2 t1 u x2 x1 1 2 2 1 c t 2 t1
(2) 在垂直方向上的速度发生变化是由 于时间间隔存在相对论效应; (3) 当 v 沿 x 轴方向或 v 沿 x 轴方向时
vu v , v v x z 0 y 0, 2 1 (uv c ) v u vx , v y 0, v z 0 2 1 (uv c )
x ( x ut), y y, z z , t [t (u c 2 ) x]
洛伦兹变换的速度公式

洛伦兹变换的速度公式洛伦兹变换是描述相对论情况下空间时间坐标之间的关系的数学方法。
在狭义相对论中,当观察者的参考系以速度v相对于光速运动时,由于光速不变原理,时间和空间会发生相对论效应的变换。
速度变换公式推导假设存在两个参考系,分别为S系和S’系,S’系以速度v相对于S系运动。
考虑一个运动速度为u相对于S系的物体,我们要求其在S’系中的速度u’。
根据洛伦兹变换,时间的变换公式为:$$ \\Delta t' = \\gamma (\\Delta t - \\frac{v}{c^2} \\Delta x) $$空间的变换公式为:$$ \\Delta x' = \\gamma (\\Delta x - v \\Delta t) $$其中,$\\gamma = \\frac{1}{\\sqrt{1 - \\frac{v^2}{c^2}}}$。
考虑速度是空间坐标对时间的导数,即$u = \\frac{dx}{dt}$,$u' =\\frac{dx'}{dt'}$,代入变换公式,得到速度变换的公式为:$$ u' = \\frac{dx'}{dt'} = \\frac{\\gamma(dx - vdt)}{\\gamma(dt -\\frac{v}{c^2}dx)} $$将dx=udt代入,整理得到:$$ u' = \\frac{U - v}{1 - \\frac{vU}{c^2}} $$其中,U为速度u的分量,即U = u/c。
结论洛伦兹变换的速度变换公式表达了相对论情况下,观察者在不同参考系中测得的物体速度之间的关系。
这个公式揭示了在相对论情况下速度的变换会受到光速不变原理的影响,导致速度的合成与经典物理中不同。
通过相对论性的速度变换公式,我们可以更好地理解相对论情况下的运动问题。
洛伦兹变换

u << c
x' x ut t' t
绝对时空观是低速情况下,相对论时空观的近似
(2) 光速是各种物体运动的一个极限速度
uc
1 u 2 / c2
虚数
任何物体的运动都不会超过光速
(3) 两事件在S、S’系中的时间间隔、空间间隔的变换关系
S
事件1 事件2 空间间隔 时间间隔
S
x'1 , t'1 x'2 , t'2 x' x'2 x'1 t' t'2 t'1
( x', y', z', t' )
事件 (x,y,z ,t) x
y' y z' z
t' b1 x b2 t x' a1 x a2 t
其中,a1 a2 b1 b2 待定系数 原点O' : S 系中 x = ut ; S' 系中 x' =0
0 a1 ut a2t
a2 a1 u
S
?
地球表面 S 大气
验证: l 9000 1 u 2 / c 2 569 m
一. 洛伦兹变换
y' y
u
S 在t = t’=0 时刻, ' S
(x,y,z ,t) ( x', y', z', t' ) P
S , S' 原点重合
O' z' 线 性 变 换 关 系 z S系 x' O x
y' y z' z
t' b1 x b2 t x' a1 ( x ut )
§11-2洛伦兹变换

1
一、狭义相对论的基本假设
1.相对性原理
在所有惯性系中物理规律(力、热、光、 电、…)都是一样的.
力学的相对性原理的推广. 2.光速不变原理 在所有惯性系测量真空中的光速都是c. 光速不满足伽俐略速度变换式,抛弃了绝对 时空观。
令
x2-x1 u' 信号速度 t2-t1
即事件1发生后,发出一信号,经(t2 - t1)时间传 播(x2 - x1)距离到达2处,触发事件2发生.
16
因果关系的绝对性
因为u < c, u ´ c , 由
t1 (t 2 t1 )[1 t2
c
u' ]
有 t 2 - t 1 和 t2 - t1 同号,S中和S中时序相同。 结论:有因果关系的事件,时序不会颠倒,因果 关系不变.
15
因果关系的绝对性
若两事件有因果关系,时序是不会颠倒的。
S中:若t2 - t1 > 0,即事件1---因(先), 2---果(后)
t1 [( t 2 t1 ) t2
c ( x2 x1 ) (t2 t1 )[1 ] c (t2 t1 )
( x2 x1 )]
14
举例
从飞船上看
若飞船的速度u = 0.6c可得t 2 - t 1 =0, 甲乙同时出生不分哥弟 若u = 0.8c可得t 2 - t 1 <0,甲后乙先 甲---弟 乙---哥 时序颠倒了 由相对论变换,会不会得到如此情况: 问题1 子弹先打到靶上而后出枪口? 问题2 儿子先出生而爸爸后出生?
13. 2 洛伦兹变换
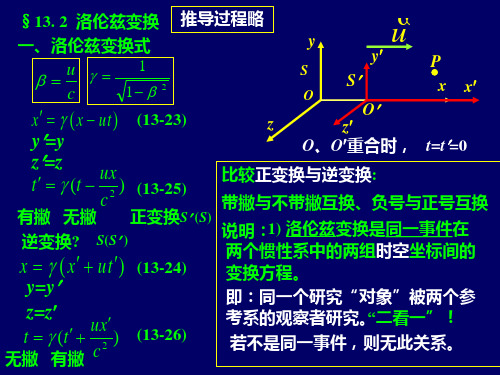
推导过程略 y
S
2
y
u
P x x
O
S
O
x ( x ut ) (13-23) y=y z=z ux t (t 2 ) (13-25)
c
z
z O、O重合时, t=t=0
z1 z1
z 2 z2
“2”“1” ?
例1.在S 惯性系中观测到相距x=9108m的两地点相隔t=5s 发 生两事件,而在相对S系沿x方向匀速运动的S系中发现此两事件 恰好发生在同一地点。试求在S系中此两事件的时间间隔。
x = 9108m t =5 解: S:
S: x=0,
2
4) 物体运动速度的极限为 c 。 u<c ux u t (t 2 0 =1 5) 当u<<c时, c c x=xut y =y z =z t =t 洛伦兹变换 伽利略变换 经典力学是相对论力学的极限情况,仅在u<<c时成立。 uc时,用相对论; u<<c时,可以用经典理论。
带撇与不带撇互换、负号与正号互换
即:同一个研究“对象”被两个参 考系的观察者研究。 “二看一”! 若不是同一事件,则无此关系。
1 说明: 1) 洛伦兹变换是同一事件在两个惯性 u c 1 系中的两组时空坐标间的变换方程。
“二看一”! x ( x ut ) 2) 各惯性系的时间、空间度量基准必须一致。 y=y 各惯性系中的观察者、钟、尺必须相 对各自惯性系保持静止。 3) 时间、空间和物质运动密不可分!
A
x
A
B A
S:x=0 t=t=? 1 v x ( t ) t = t 2 c 1 2
洛伦兹变换推导过程详细

洛伦兹变换推导过程详细洛伦兹变换是狭义相对论中的一个重要概念,用于描述不同参考系之间的时空坐标转换关系。
它的推导过程可以从狭义相对论的两个基本假设出发,逐步推导出洛伦兹变换的形式。
在狭义相对论中,有两个基本假设:光速不变原理和惯性参考系原理。
光速不变原理指出,光在真空中的传播速度在任何惯性参考系中都是恒定的,即与观察者的运动状态无关。
惯性参考系原理则认为,任何惯性参考系中的物理规律都应该是相同的。
基于这两个假设,可以推导出洛伦兹变换的形式。
假设有两个参考系S和S',它们之间的相对速度为v。
设S系中某一事件的时空坐标为(x, y, z, t),在S'系中的时空坐标为(x', y', z', t')。
根据相对性原理,两个参考系之间的坐标变换应该是线性的。
为了推导洛伦兹变换,我们需要考虑两个基本情况:在S系中的事件在S'系中的时间和空间坐标,以及在S'系中的事件在S系中的时间和空间坐标。
根据相对性原理和光速不变原理,可以得到以下两个关系式:1. 在S系中的事件在S'系中的时间坐标:t' = γ(t - vx/c^2)2. 在S系中的事件在S'系中的空间坐标:x' = γ(x - vt)其中,γ是洛伦兹因子,定义为γ = 1 / sqrt(1 - v^2/c^2),c是光速。
类似地,可以推导出在S'系中的事件在S系中的时间和空间坐标的变换关系:1. 在S'系中的事件在S系中的时间坐标:t = γ(t' + vx'/c^2)2. 在S'系中的事件在S系中的空间坐标:x = γ(x' + vt')这样,就得到了洛伦兹变换的完整形式。
洛伦兹变换的推导过程并不复杂,但需要严密的逻辑推理和数学推导。
通过这个变换,我们可以描述不同参考系之间的时空关系,揭示了狭义相对论中的一些奇特现象,如时间膨胀和长度收缩等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
′ ′ t 2 − t1 1− β 2
1 − β 2 ∆t
即运动时大于固有时,或说运动的时钟变慢了. 运动时大于固有时,或说运动的时钟变慢了 运动的时钟变慢
上页
下页
返回
结束
第十二章 相对论简介
§12.2.4 尺缩钟慢的实验检验
[例题 有文献报道在高为 例题1] 有文献报道在高为1981m的山顶上测得 个µ 的山顶上测得563个 例题 的山顶上测得 子进入大气层,在海平面测得 个 示意如图 示意如图12.5. 已知 µ 子进入大气层 在海平面测得408个.示意如图 在海平面测得 子下降速率为0.995c,c表示真空中光速 试解释上述测 , 表示真空中光速 表示真空中光速.试解释上述测 子下降速率为 得结果. 得结果 [解] µ子速率已达 解 子速率已达0.995c,非常接近 非常接近 光速,应用相对论 但为了与经典观 光速 应用相对论.但为了与经典观 应用相对论 点比较,先按经典的时空观求解 按 点比较 先按经典的时空观求解,按 先按经典的时空观求解 非相对论时空观,时间是绝对的 非相对论时空观,时间是绝对的, 因而 µ子运动时和静止的半衰期相 同,即亦为τ0 . µ子降落时间为 t =1981/0. 995c 即亦为
′ l 0 = x′ − x1 2
y S x
y′ S′
r u
x′ 2
z
z′
′ x1
x′
上观察, 同时测出棒各端点坐标 在S上观察,必须同时测出棒各端点坐标, 上观察 必须同时测出棒各端点坐标,
l = x2 − x1 ′ ′ l0 = x2 − x1 = γ ( x 2 − x1 )
上页 下页
l
返回 结束
上页 下页 返回 结束
第十二章 相对论简介 2.运动的杆缩短 运动的杆缩短 静长度(固有长度 静长度 固有长度)——相对观察者静止时的长度 l0. 固有长度 相对观察者静止时的长度 运动时, 当棒相对观察者以 u 运动时,观测长度 l=? 方向, 设棒与S′ 系固定 u为x方向 棒相对于 ′ 的长度为 棒与 系固定, 为 方向 棒相对于S
上页 下页 返回 结束
第十二章 相对论简介
n = n 0e −αt
α = ln 2 / τ 0
≈ 27
n = 563 × e
−(ln 2 / 2×10 −6 )×1981 / 0.995 c
即仅有27个 子到达海平面,与实验结果不合 与实验结果不合. 即仅有 个µ 子到达海平面 与实验结果不合 现在运用相对论研究.首先以地球为参考系 现在运用相对论研究 首先以地球为参考系, µ 子运动 首先以地球为参考系 时间仍为 t =1981/0.995c.但因动钟变慢 运动的µ 介子 但因动钟变慢,运动的 但因动钟变慢 运动的µ 的半衰期应为
上页
下页
返回பைடு நூலகம்
结束
第十二章 相对论简介 讨论: 讨论: 上同时不同地点的两事件) ①若 ∆t = 0 ∆ x ≠ 0(S上同时不同地点的两事件) 上同时不同地点的两事件
u u ∆t ′ = −γ 2 ∆x = −γ 2 ( x 2 − x1 ) ≠ 0 c c
②
不同时
∆ x = 0 ∆t = 0 ∆ t ′= 0
d 1 × 10 − 1 t= = s = 4 .5 × 10 −10 s v 2 .24 × 10 8
K0粒子的固有寿命应为
t0 = t 1 − β 2 = 4.5 × 10 −10 ≈ 3.0 × 10 −10 s 5.02 × 1016 1− s 16 8.99 × 10
t 0 < t 表明固有时间间隔最短 表明固有时间间隔最短.
x 2 + y 2 + z 2 − c 2t 2 = 0
系而言,其波面(波前) 对于S′ 系而言,其波面(波前)到达 ( x ′, y ′, z ′ ) 处所需时间, 处所需时间,根据光速不变原理得
x′2 + y′2 + z′2 t′ = c
x ′ 2 + y′ 2 + z ′ 2 − c 2 t ′ 2 = 0
r u
y′ S′ z′ x′
O′
t = t ′ = 0、x′ = x = 0, 发光
上页 下页 返回 结束
第十二章 相对论简介 对于S系而言,其波面 波前 到达(x, , 处所需 波前)到达 对于 系而言,其波面(波前 到达 ,y,z)处所需 系而言 时间为: 时间为:
x2 + y2 + z2 t= c
c = 2.99792458 × 10 8 m ⋅ s −1
上页 下页 返回 结束
第十二章 相对论简介
§12.2.2 洛伦兹变换
洛伦兹变换——新的时空变换关系 该变换满足: 新的时空变换关系,该变换满足 洛伦兹变换 新的时空变换关系 该变换满足: (1)光速不变原理和狭义相对性原理 )光速不变原理和狭义相对性原理; (2)当物体运动速率远小于真空中的光速时,新 )当物体运动速率远小于真空中的光速时, 的变换关系能使伽利略变换重新成立. 的变换关系能使伽利略变换重新成立 r y S y Su y′ S′ O′ O z′ z x′ x z O x
−(ln 2 / 2.2×10−6 )×1981 1−0.9952 / 0.995c
再从与µ子一起运动的参考系研究 此参考系中 再从与µ子一起运动的参考系研究.此参考系中µ子静
n = n0 × e
≈ 415
与前面结果相同. 与前面结果相同
上页
下页
返回
结束
第十二章 相对论简介 [例题 例题2] 如图表示气泡室中一些 例题 基本粒子的轨迹. 其中描写一π 基本粒子的轨迹 其中描写一π 介 子与质子相碰产生其他粒子, 子与质子相碰产生其他粒子,图 中 K+ 即碰撞处。 即碰撞处。我们仅考虑它们 之中的K 粒子.它经 它经d=1×10-1m 的 之中的 0粒子 它经 × 距离便衰变为两个具有相反电荷 介子.若 的 π介子 若 K0的速度为 v=2.24×108m/s,试求其固有寿命 × 试求其固有寿命. 试求其固有寿命
上页
下页
返回
结束
第十二章 相对论简介 根据相对性原理知 ,新的时空关系必须是线 性的,这样才能保证在 系的匀速直线运动 系的匀速直线运动, 性的,这样才能保证在S系的匀速直线运动,在S′ ′ 系也是匀速直线运动,可推导得 系也是匀速直线运动,
x′ = γ ( x − ut ) y′ = y z′ = z u t′ = γ (t − 2 x) c
第十二章 相对论简介
l = l0 1 − β 2
对给定的杆,在相对于它静止的坐标系中,长度最大. 对给定的杆 在相对于它静止的坐标系中,长度最大 在相对于它静止的坐标系中 注意:长度的缩短是相对的 注意:长度的缩短是相对的. 3.运动的时钟变慢 运动的时钟变慢 设在S′ 系中同一地点 ′=ξ处发生二个事件的时间间隔为 设在 ′ 系中同一地点x′ ξ
K K+
e
+
e−
π +0
π− − π
π+
µ+
e+
π
上页
下页
返回
结束
第十二章 相对论简介 [解] 粒子的速率已达 解 粒子的速率已达2.24×108m/s ,达光速 达光速70%以上 以上, × 达光速 以上 应当用相对论计算.题中 和 显然是实验室中测得 应当用相对论计算 题中d和v显然是实验室中测得 题中 的.从实验室测得的粒子运动的时间间隔为 从实验室测得的粒子运动的时间间隔为
′ ′ ∆ t ′ = t 2 − t1
上看, 在S上看,二事件发生于 1和t2,相隔 上看 二事件发生于t
u u ′ ′ ∆ t = t 2 − t1 = γ ( t 2 + 2 ξ ) − γ ( t1 + 2 ξ ) c c
上页 下页 返回 结束
第十二章 相对论简介
′ ′ = γ ( t 2 − t1 ) =
上页 下页 返回 结束
(3) 若 |u|<<c, γ →1, β→ 0
上页
下页
返回
结束
第十二章 相对论简介
§12.2.3 洛伦兹变换蕴含的时空观
1.同时的相对性 同时的相对性
S中 : 两件事( x1 , t1 ), ( x2 , t 2 ) ∆t = t 2 − t1 ∆x = x2 − x1
′ ′ S ′中 : ∆ t ' = t 2 − t 1 u u = γ ( t 2 − 2 x 2 ) − γ ( t1 − 2 x1 ) c c u ∆ t′ = γ (∆ t − 2 ∆ x ) c
τ =τ0 / 1− β 2
n = n0 × e
−(ln 2× 1− β 2 / τ 0 ) t
−(ln2× 1− 0.995 2 / 2.2×10−6 )×1981/ 0.995c ( )
上页 下页 返回
= 563×e
≈ 415
结束
第十二章 相对论简介 此结果与实验基本符合. 此结果与实验基本符合 但因“ 止,故其半衰期仍为τ 0 ;但因“动尺缩短”,山的高度 故其半衰期仍为 但因 动尺缩短” 山的高度 成为 1981 1 − 0 .995 2 m 故得
第十二章 相对论简介
§12.2 洛伦兹变换
§12.2.1 狭义相对论的基本假设 §12.2.2 洛伦兹变换 §12.2.3 洛伦兹变换蕴含的时空观 §12.2.4 尺缩钟慢的实验检验
上页
下页
返回
结束
第十二章 相对论简介
§12.2 洛伦兹变换
§12.2.1 狭义相对论的基本假设
1. 相对性原理 物理定律在所有惯性系中都是同形的, 惯性系中都是同形的 物理定律在所有惯性系中都是同形的,因此各 个惯性系中都是等价的,不存在特殊的绝对惯性系 个惯性系中都是等价的,不存在特殊的绝对惯性系. 或:物理定律在所有惯性系中具有数学形式不 变性,即协变性 变性,即协变性. 2. 光速不变原理 所有的惯性系中,光在真空 真空中的传播速率具有 所有的惯性系中,光在真空中的传播速率具有 相同的值c 相同的值 .
