第三章线性系统的时域分析法第三四五讲
合集下载
第3章线性系统的时域分析法自动控制原理课件

不同而有一簇, 见教材P.87图3-10. h() 1, 下面由
h(t) 1
1
1 2
e nt sin( n
12t )
根据动态性能指标的定义, 推导各项动态性能指标的计
算公式.
(1) 延迟时间 td : 由定义, 令 h(td ) 0.5 , 代入上式
ntd
1
ln
2sin(
1 2 tn d cos1 ) 1 2
(4) 脉冲信号(脉冲函数) 先看下面图型:
r (t )
具有左图形状的信号被称为矩型脉动信号,
R
0
其数学表达式为:
0 t 0
t
r(t)
R
0
0t t
由图可见, 脉动信号 的面积为R. 当脉动
信号的宽度 0
时, 其高度为 , 但
面积乃为R. 把宽度 0时的矩型脉动信号定义为脉
冲信号, 而其面积R称为脉冲信号的脉冲强度.
尼, 0 1叫欠阻尼, 下面主要讨论欠阻尼时的动态
性能,欠阻尼时系统的两个极点为:
s1,2 n j数, d n 1 2 叫阻尼
振荡角频率,两个极点在s平面上的分布如下图所示, 图中
j
n
d n 1 2
cos , sin 1 2 ,
3-1 系统时间响应的性能指标
一﹑典型输入信号
工程上经常碰到的典型输入信号有以下几种:
(1) 阶跃信号(阶跃函数) 其数学表达式和图形为:
0 t 0 r(t) R t 0
r(t) R
0
t
上式中R为常数, 当t=0时, r(0)不定, 且r(0 ) R, r(0) 0
当R=1时, 称为单位阶跃信号, 记为1(t).
第三章 线性系统的时域分析法(第三四五讲)
若变号系统不稳定!
变号的次数为特征根在s右半平面的个数!
劳斯表出现零行
设系统特征方程为:
s4+5s3+7s2+5s+6=0 劳 斯 表
s4 1 s3 5 1 s2 6 1 s1 0 2 s0 1 7 6 1 5 6 1 这是零行
① 有大小相等符号相反的 特征根时会出现零行 ② 由零行的上一行构成 辅助方程:
或 %
100%
tg
e
100%
欠阻尼二阶系统动态性能计算
tr d
tr 特征根的虚部
弧度
tp d
tp 特征根的虚部
cos
5%
3.5 ts n
% e
1 2
100%
tg
3.5 ts 特征根的实部
n=[0.05 10]; d=[0.0025 0.5125 2.52 4.01 3]; sys=tf(n,d); step(sys)
第三章 系统的时域性能指标
3.1 系统的时域性能指标 3.2 一阶系统的时域分析 3.3 二阶系统的时域分析
3.4 高阶系统的时域分析
3.5 线性系统的稳定性分析 3.6 线性系统的稳态误差计算
1
t T 2 2
0<ξ<1 s1, 2 n jjn 1 2 ξ=0 0<ξ<1
0
h( t ) 1 ξ=0 e n t 1
2
j 0 0 j
sin(,d jn 欠阻尼t ) s1 2
0 零阻尼 h(t ) 1 cos n t
欠阻尼二阶系统动态性能分析
它们的阶跃响应曲线如图所示,试在同一平面画出3个系统闭环 极点的相对位置,并说明理由。
变号的次数为特征根在s右半平面的个数!
劳斯表出现零行
设系统特征方程为:
s4+5s3+7s2+5s+6=0 劳 斯 表
s4 1 s3 5 1 s2 6 1 s1 0 2 s0 1 7 6 1 5 6 1 这是零行
① 有大小相等符号相反的 特征根时会出现零行 ② 由零行的上一行构成 辅助方程:
或 %
100%
tg
e
100%
欠阻尼二阶系统动态性能计算
tr d
tr 特征根的虚部
弧度
tp d
tp 特征根的虚部
cos
5%
3.5 ts n
% e
1 2
100%
tg
3.5 ts 特征根的实部
n=[0.05 10]; d=[0.0025 0.5125 2.52 4.01 3]; sys=tf(n,d); step(sys)
第三章 系统的时域性能指标
3.1 系统的时域性能指标 3.2 一阶系统的时域分析 3.3 二阶系统的时域分析
3.4 高阶系统的时域分析
3.5 线性系统的稳定性分析 3.6 线性系统的稳态误差计算
1
t T 2 2
0<ξ<1 s1, 2 n jjn 1 2 ξ=0 0<ξ<1
0
h( t ) 1 ξ=0 e n t 1
2
j 0 0 j
sin(,d jn 欠阻尼t ) s1 2
0 零阻尼 h(t ) 1 cos n t
欠阻尼二阶系统动态性能分析
它们的阶跃响应曲线如图所示,试在同一平面画出3个系统闭环 极点的相对位置,并说明理由。
线性系统的时域分析法

三、动态性Leabharlann 和稳态性能动态性能:通常在阶跃函数作用下,测定或计算系统的动
态性能。一般认为阶跃输入对系统来说是最严峻的工作状态。
描述稳定的系统在阶跃函数作用下,动态过程随时间的
变化状况的指标称为动态性能指标。通常包括:
延迟时间 td :指响应曲线第一次到达稳态值一半所需的时间。
上升时间 tr :指响应第一次 h(t) % 误差带
洛比特法则
lim lim
(s pi )N (s)
(s pi )N (s) N (s) N ( pi )
s pi
D(s)
s pi
D(s)
D( pi )
f (t) L1
F (s)
L1
n i1
Ai s pi
n i 1
Aie pi t
② 具有多重极点的有理函数的反变换
F (s)
误差平方积分(ISE,Integral of Square Error)
ISE e2 (t)dt 0
( e(t)是输入输出之间存在的误差)
时间乘误差平方积分(ITSE,Integral of Timed Square Error)
ITSE te2 (t)dt 0
误差绝对值积分(IAE,Integral of Absoluted Error)
(s a
j)F (s) sa j
N (s) D(s)
sa j
k1
e j
思考:为何 k1,k2 必为共轭复数?
f
(t)
L1 F (s)
L1
s
A1 p1
k1 sa
j
k2 sa
j
A1e p1t
k1e(a j)t
《自动控制原理》第三章-3-5-稳态误差计算

伺服电动机
R(s)
E(s)
1
C(s)
-
s(s 1)
K 1, 1
r(t) 1(t),k p , ess 0
r(t) t, kv 1, ess 1
r(t)
1 2
t2, ka
0, ess
位置随动系统
能源与动力学院 第三章 线性系统的时域分析法
14
4.扰动作用下稳态误差
R(s)
-
E(s)
R(s) E(s) 20
s4
N (s)
+
2
C(s)
s(s 2)
能源与动力学院 第三章 线性系统的时域分析法
28
3-20
R
-
K1
U
K2 S(T1S 1)
C
G(s)
K1K 2
B
s(T1s 1)(T2s 1)
1 T2S 1
(s)
C(s) R(s)
T1T2 s 3
K1K2 (T2s 1) (T1 T2 )s2 s
1
能源与动力学院 第三章 线性系统的时域分析法
7
3.输入作用下稳态误差计算
(1)阶跃作用下的稳态误差
r(t) R 1(t), R(s) R s
ess
Lim sR(s) s0 1 G(s)H (s)
Lim s1R(s)
s0
K Lim s
s0
1
R LimG(s)H (s)
Lim s R
s0
K Lim s
27
参考答案: Kp= ,kv=5,ka=0,essr=0.4,essn=-0.2
四、控制系统如图, r(t) 1 2t, n(t) 1(t), 试计算
《自动控制理论》第三章 线性系统的时域分析PPT课件

电子笔
12
五、正弦函数(Sinusoidal function)
定义为:
自
r(t)= A Sinωt
动
控
制 式中,A为振幅;
理 论
ω为角频率。
用频率不同的正弦函数作为输入信号,可求得系统此时
的稳态响应,在频率法中广泛使用。
首页 上页 下页 末页 结束
2020/7/17
电子笔
13
3.3 控制系统的时域性能指标
电子笔
15
二. 动态过程和稳态过程
➢ 1.瞬时响应和稳态响应 Transient Response & Steady_state Response
自 动
➢ 在典型输入信号作用下,任何一个控制系统的时
控
间响应。
制
理 论
➢
瞬态响应 指系统从初始状态到最终状态的
响应过程。由于实际控制系统具有惯性、摩擦、
论
道的,可以用解析的方法或者曲线表示。
首页 上页 下页 末页 结束
2020/7/17
电子笔
6
➢ 在分析和设计控制系统时,对各种控制系统性能得有评判、
比较的依据。这个依据也许可以通过对这些系统加上各种输
入信号,比较它们对特定的输入信号的响应来建立。
自 动
➢ 许多设计准则就建立在这些信号的基础上,或者建立在系统
➢ 分析控制系统的第一步是建立模型,数学模型一旦建立,第
二步 分析控制性能,分析有多种方法,主要有时域分析法,
频域分析法,根轨迹法等。每种方法,各有千秋。均有他们
自 的适用范围和对象。本章讨论时域法。
动
控 制
➢ 实际上,控制系统的输入信号常常是不知的,而是随机的。
线性系时域分析法-精品文档78页

ts w4n
5% 2%
wn
% h(tp)h( )10 % 0 e1 2 10 % 0
h( )
ess 0
南 京 理 工 大 学 自 动 化 系 NJUST AUTOMATION
南 京 理 工 大 学 自 动 化 系 NJUST AUTOMATION
,t 0
n e n ts i d t n ) (d e n tc o d t ) s 0 (
12
tg 1 2
tg(dt )
dtp0,,2,
,根据峰值时间定义,应取
dtp
tpd 1 2 2 dd 1 2 T d
2、过阻尼情况( 1)
南 京 理 工 大 学 自 动 化 系 NJUST AUTOMATION
二、二阶系统单位阶跃响应 3、临界阻尼情况( 1)
南 京 理 工 大 学 自 动 化 系 NJUST AUTOMATION
二、二阶系统单位阶跃响应 4、欠阻尼情况( 0 1)
在控制工程中,除了那些不容许产生振荡响应的系统 外,通常都希望控制系统具有适度的阻尼、快速的响应速 度和较短的调节时间。
12
e
nt sind(tr
)0
dtr
tr d
一定,即 一定,n tr ,响应速度越快
南 京 理 工 大 学 自 动 化 系 NJUST AUTOMATION
t p (峰值时间)
h (t) 1 1 12e n tsin d t ( )
Uc
r(t)
R(s)
C (s)
TC(t)C(t)r(t)
传递函数为:(s)C(s) 1
5% 2%
wn
% h(tp)h( )10 % 0 e1 2 10 % 0
h( )
ess 0
南 京 理 工 大 学 自 动 化 系 NJUST AUTOMATION
南 京 理 工 大 学 自 动 化 系 NJUST AUTOMATION
,t 0
n e n ts i d t n ) (d e n tc o d t ) s 0 (
12
tg 1 2
tg(dt )
dtp0,,2,
,根据峰值时间定义,应取
dtp
tpd 1 2 2 dd 1 2 T d
2、过阻尼情况( 1)
南 京 理 工 大 学 自 动 化 系 NJUST AUTOMATION
二、二阶系统单位阶跃响应 3、临界阻尼情况( 1)
南 京 理 工 大 学 自 动 化 系 NJUST AUTOMATION
二、二阶系统单位阶跃响应 4、欠阻尼情况( 0 1)
在控制工程中,除了那些不容许产生振荡响应的系统 外,通常都希望控制系统具有适度的阻尼、快速的响应速 度和较短的调节时间。
12
e
nt sind(tr
)0
dtr
tr d
一定,即 一定,n tr ,响应速度越快
南 京 理 工 大 学 自 动 化 系 NJUST AUTOMATION
t p (峰值时间)
h (t) 1 1 12e n tsin d t ( )
Uc
r(t)
R(s)
C (s)
TC(t)C(t)r(t)
传递函数为:(s)C(s) 1
第三章3 线性系统的时域分析方法(3.4)

自动控制原理
总结: 闭环零点的作用为减少峰值时间,使系统响应速度加 快,并且闭环零点越接近虚轴,这种作用越显著。 闭环非主导极点的作用为增大峰值时间,使系统响应 速度变缓。 若闭环零、极点彼此接近,则他们对系统响应速度的 影响相互削弱。 高阶系统的主导极点常常是共轭复数极点,因此高 阶系统可以常用主导极点构成的二阶系统来近似。相应 的性能指标可按二阶系统的各项指标来估计。在设计高 阶系统时,常利用主导极点的概念来选择系统参数,使 系统具有预期的一对共轭复数主导极点,这样,就可以 近似的用二阶系统的性能指标来设计系统。
q r
Bk ( s + ξ k ω nk ) + C k ω nk 1 − ξ k s 2 + 2ξ k ω nk s + ω 2 nk
2
式中
Α 0 、 Α i 、Β k和 C k
都是进行部分分式展开时所确定的常数。 对上式进行拉氏反变换,求得系统在零初始条件下的单位阶 跃响应为
C (t ) = Α 0 + ∑ Α i e pi t + ∑ Βk e −ξ kω nk t cos(ω nk 1 − ξ 2 k × t ) i =1 k =1 (3-27) r (t ≥ 0 ) + ∑ Ck e −ξ ω t sin(ω nk 1 − ξ k 2 × t )
3.4
高阶系统的时域响应
若描述系统的微分方程高于二阶,则该系统为高阶 系统。在控制工程中,大多数控制系统都是高阶系统。从 理论上讲,高阶系统也可以直接由传递函数求出它的时域 响应,然后按上述二阶系统的分析方法来确定系统的瞬态 性能指标。但是,高阶系统的分布计算比较困难,同时, 在工程设计的许多问题中,过分讲究精确往往是不必要 的,甚至是无意义的。因此,工程上通常把高阶系统适当 地简化成低阶系统进行分析。下面简单地介绍高阶系统时 域响应的确定方法及研究高阶系统性能的思路和途径。
总结: 闭环零点的作用为减少峰值时间,使系统响应速度加 快,并且闭环零点越接近虚轴,这种作用越显著。 闭环非主导极点的作用为增大峰值时间,使系统响应 速度变缓。 若闭环零、极点彼此接近,则他们对系统响应速度的 影响相互削弱。 高阶系统的主导极点常常是共轭复数极点,因此高 阶系统可以常用主导极点构成的二阶系统来近似。相应 的性能指标可按二阶系统的各项指标来估计。在设计高 阶系统时,常利用主导极点的概念来选择系统参数,使 系统具有预期的一对共轭复数主导极点,这样,就可以 近似的用二阶系统的性能指标来设计系统。
q r
Bk ( s + ξ k ω nk ) + C k ω nk 1 − ξ k s 2 + 2ξ k ω nk s + ω 2 nk
2
式中
Α 0 、 Α i 、Β k和 C k
都是进行部分分式展开时所确定的常数。 对上式进行拉氏反变换,求得系统在零初始条件下的单位阶 跃响应为
C (t ) = Α 0 + ∑ Α i e pi t + ∑ Βk e −ξ kω nk t cos(ω nk 1 − ξ 2 k × t ) i =1 k =1 (3-27) r (t ≥ 0 ) + ∑ Ck e −ξ ω t sin(ω nk 1 − ξ k 2 × t )
3.4
高阶系统的时域响应
若描述系统的微分方程高于二阶,则该系统为高阶 系统。在控制工程中,大多数控制系统都是高阶系统。从 理论上讲,高阶系统也可以直接由传递函数求出它的时域 响应,然后按上述二阶系统的分析方法来确定系统的瞬态 性能指标。但是,高阶系统的分布计算比较困难,同时, 在工程设计的许多问题中,过分讲究精确往往是不必要 的,甚至是无意义的。因此,工程上通常把高阶系统适当 地简化成低阶系统进行分析。下面简单地介绍高阶系统时 域响应的确定方法及研究高阶系统性能的思路和途径。
第三章-线性系统的时域分析法(简)

注意:此时系统不为稳定系统,而是临界稳定系统
劳斯表出现全零行:
系统在s平面有对称分布的根:
①大小相等符号相反的实根
j
0
②共轭虚根
j
③对称于实轴的两对共轭复根
j
0
0
• 特殊情况3:多行元素全为零
Routh表出现多个全零行,系统在s平面有重共轭虚根, 则系统不稳定。
参看:《现代控制系统》第八版 Richard C.Dorf Robert H.Bishop著
名称
时域表达式 复数域表达式
单位阶跃信号 1(t) , t 0
1 s
单位斜坡信号 t , t 0
1 s2
单位加速度信号 1 t 2 , t 0
2
1 s3
单位脉冲信号 (t) , t 0
1
正弦信号
A
As
Asint Acost s2 2 s2 2
二、 动态过程与稳态过程 P78
➢ 动态过程(过渡过程、瞬态过程): 在典型输入信号作用下,系统输出量从初始状
s5
1
5
6 解决方法:
s4
1
由全0行的上一行元素构
5
6 成辅助方程F(s)=0,并
s3 0 4 0 10 0 对其求导后,用所得系数
s2 5/2
6
代替全0行的元素。
s1 2/ 5
例如:F(s) s4 5s2 6 0
s0
6
求导得: F(s) 4s3 10s1 0
s1,2 j 2 s3,4 j 3 s5 1
第三章 线性系统的时域分析法
本章主要内容: 3.I 系统时间响应的性能指标 3.2 一阶系统的时域分析 3.3 二阶系统的时域分析 3.4 高阶系统的时域分析 3.5 线性系统的稳定性分析 3.6 线性系统的稳态误差计算
劳斯表出现全零行:
系统在s平面有对称分布的根:
①大小相等符号相反的实根
j
0
②共轭虚根
j
③对称于实轴的两对共轭复根
j
0
0
• 特殊情况3:多行元素全为零
Routh表出现多个全零行,系统在s平面有重共轭虚根, 则系统不稳定。
参看:《现代控制系统》第八版 Richard C.Dorf Robert H.Bishop著
名称
时域表达式 复数域表达式
单位阶跃信号 1(t) , t 0
1 s
单位斜坡信号 t , t 0
1 s2
单位加速度信号 1 t 2 , t 0
2
1 s3
单位脉冲信号 (t) , t 0
1
正弦信号
A
As
Asint Acost s2 2 s2 2
二、 动态过程与稳态过程 P78
➢ 动态过程(过渡过程、瞬态过程): 在典型输入信号作用下,系统输出量从初始状
s5
1
5
6 解决方法:
s4
1
由全0行的上一行元素构
5
6 成辅助方程F(s)=0,并
s3 0 4 0 10 0 对其求导后,用所得系数
s2 5/2
6
代替全0行的元素。
s1 2/ 5
例如:F(s) s4 5s2 6 0
s0
6
求导得: F(s) 4s3 10s1 0
s1,2 j 2 s3,4 j 3 s5 1
第三章 线性系统的时域分析法
本章主要内容: 3.I 系统时间响应的性能指标 3.2 一阶系统的时域分析 3.3 二阶系统的时域分析 3.4 高阶系统的时域分析 3.5 线性系统的稳定性分析 3.6 线性系统的稳态误差计算
第3章 线性系统的时域分析法

n n 1 2
n n 1 2
2 (1 1 entp ) n 2
ts
3
n
( 5%)
(2)临界阻尼单位斜坡响应
c(t)
t
2
n
2
n
1
1 2
n
tቤተ መጻሕፍቲ ባይዱ
e
nt
(t 0)
css
(t
)
t
2
n
ctt
(t)
2
n
1
1 2
nt ent
e(t)
t
c(t)
2
n
2
n
1
1 2
n
t
e
nt
ts
4.1
2% (0 0.9)
5%
1
n
1
n
4
ln
3 ln
1 1 2
1 1 2
n
2% 5%
二阶系统单位阶跃响应的性能指标归纳如下:
1 0.6 0.2 2
td
n
或
tr d
n 1 2
1 0.7 td n
tp
d
n
1 2
% e / 1 2 100%
实际上,上述各项性能 指标之间的存在矛盾, 例如上升时间(响应速 度)和超调量(阻尼程 度或相对稳定性)
sin( n
1 2tr ) 1
1 2
sin(n 1 2 tr ) 0
tr
d
n
1 2
(3)峰值时间 t p 的计算
dh(t ) dt ttp
n e nt p sin d t p 0 1 2
sin d t p 0
d t p 0, , 2 ,
第三章 线性系统的时域分析

1
R(s) L (t) 1 0
t
考查系统在脉冲扰动下的恢复情况
各函数间关系:
t 积分1t 积分 t 1t 积分 1 t 2 1t
求导 求导
求导 2
(5)正弦函数
f(t)
rt Asint
R(s) LAsint A 0
t
s2 2
考查随动系统在波浪环境中的控制和跟随能力
二. 阶跃响应的时域性能指标
轴上,使得系统的响应表现为 s2
过阻尼的。
s1 0
s1,2 n n 2 1
(2) ξ=1时,特征根为一对等值的负实根,位于s 平面的负实轴上, 使得系统的响应表现为临界阻尼的。
(3) 0 < ξ < 1 时,特征根为一对具有负实部的共轭复根,位于s平面
c阶 (t)
即单位斜坡响应的导数是单位阶跃响应。
3.2.3
单位脉冲响应 [R(s)=1]
C(s) 1 Ts 1
h(t) 1/T
它恰是系统的闭环传函,这
时输出称为脉冲(冲激)响应
函数,以g(t)标志。
g (t
)
C脉冲
(t)
1 T
e
t T
0.368/T
0.135/T
0.05/T
0 T 2T 3T
t
于0。有差跟踪。
斜坡响应(续)
2.初始速度:dc(t
dt
)
|t0
1
e
t T
|t0 11 0
t
3
e ss
lim[r(t) c(t)] lim(T
t
t
Te
T )T
表明一阶系统在过渡过程结束后,其稳态输出与单 位斜坡输入之间,在位置上仍有误差。
机械控制工程资料第三章线性系统的时域分析法

稳态过程:系统在典型信号作用下,时间t趋于无穷〔较大〕 时,系统的输出状态。研究系统的稳态特性,以确定输出信号 对输入信号跟踪〔伺服、复现〕能力。稳态过程又称稳态响应, 提供稳态误差信息,用稳态性能〔稳态误差〕描述。
6
3 动态性能与稳态性能
R(S) E(S) G(S) C(S) B(S) H(S)
23
c(t)L 1[C (S) ]1T T 1 21 1eT 1 1tT T 1 21 1eT 1 2t
r (t )
c(t) 0
t
24
(2) 临界阻尼 1
c (t )
r (t ) 1
r(t)1(t) , R(s)1
c(t)
S
C (s)(S n2n)2S 1S 1(S nn)2S 1n 0
(s)C R((ss))S22n2nn2
n2
K Tm
n
K Tm
n-自然频率(或无阻尼振荡频率)
2
n
1 Tm
1 2 Tm K
-阻尼比(相对阻尼系数)
二阶系统的闭环特征方程为
S22nSn20
特征方程的两个根(闭环极点) S1,2nn 21
特征根的性质取决于 的大小,下面分四种情况讨论。
21
对上式取拉氏反变换,得
t
c(t) 1e T
t 0
c(t)
1
0.632
t
c(t) 1e T
1 T
63.2% 86.5% 95% 98.2% 99.3%
0
T
2T 3T 4T 5T
图3-3 指数响应曲线
注解:
传递函数的极点产生系
统响应的瞬态分量。这一
个结论不仅适用于一阶线
性定常系统,而且也适用
6
3 动态性能与稳态性能
R(S) E(S) G(S) C(S) B(S) H(S)
23
c(t)L 1[C (S) ]1T T 1 21 1eT 1 1tT T 1 21 1eT 1 2t
r (t )
c(t) 0
t
24
(2) 临界阻尼 1
c (t )
r (t ) 1
r(t)1(t) , R(s)1
c(t)
S
C (s)(S n2n)2S 1S 1(S nn)2S 1n 0
(s)C R((ss))S22n2nn2
n2
K Tm
n
K Tm
n-自然频率(或无阻尼振荡频率)
2
n
1 Tm
1 2 Tm K
-阻尼比(相对阻尼系数)
二阶系统的闭环特征方程为
S22nSn20
特征方程的两个根(闭环极点) S1,2nn 21
特征根的性质取决于 的大小,下面分四种情况讨论。
21
对上式取拉氏反变换,得
t
c(t) 1e T
t 0
c(t)
1
0.632
t
c(t) 1e T
1 T
63.2% 86.5% 95% 98.2% 99.3%
0
T
2T 3T 4T 5T
图3-3 指数响应曲线
注解:
传递函数的极点产生系
统响应的瞬态分量。这一
个结论不仅适用于一阶线
性定常系统,而且也适用
自控原理课件-第三章线性系统的时域分析法

0.1hs
ts
t
tdtr
稳态误差ess ±2%或±5%
ts
t
上升时间tr:振荡——第一次上升到终值所需时间;
非振荡——从终值10%上升到终值90%所需的时间。
延迟时间td: 第一次达到其终值一半所需的时间。
峰值时间tp:超过其终值到达第一个峰值所需的最短时间。
调节时间ts: 到达并保持在终值±2%(± 5%)内所需的最短时
实际中,常用tr, tp ,ts和Mp (σ%)
tr,tp——评价系统的响应速度;
Mp (σ%)——评价系统的阻尼程度;值越小、响应快、性能好
ts——评价速度和阻尼程度的综合指标。
18
2.稳态性能:又称静态性能
稳态误差是稳态性能的一种性能指标。 通常在阶跃函数、斜坡函数、加速度函作用下, 进行测定或计算。(单位阶跃输入下的稳态误差也 称为余差) (将在后面专节讨论。§3-3)
等加速度信号;脉冲信号;正弦信号。
4
1、阶跃函数
表达式:r(t)
A 0
t0 t0
A为常数,A=1的阶跃函数称为单位阶跃函数。
r(t - t0 ):称为延迟t0时刻阶跃函数 拉氏变换: R(s) L[1(t)] 1
s
5
2、斜坡函数(速度函数)
表达式:
r(t
)
At 0
t0 t0
A为常数,A=1的斜坡函数称为单位斜坡函数。
t r(t)
t r(t)
t r(t)
t
10
二、动态过程和稳态过程
对于线性定常系统,输入为:r(t,) 输出为:c(t) 用微分方程描述如下:
dn
d n-1
d
dt n c(t ) a1 dt n-1 c(t ) an-1 dt c(t ) anc(t )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
= 设开环传递函数G(s)H(s)
i1
s n (Tjs 1)
注意:s → 0时,G0H0一定→1 j1
G0H0
k 此时的 为开环增益 其实k limsG(s)H(s) s0 sν表示开环有ν个极点在坐标原点
ν= 0 称为0型系统
ν= 1 称为Ⅰ型系统 提个醒! 1 k
ν= 2 称为Ⅱ型系统
2ν
G 2 (s)
s(s
7(s 3) 4)(s2 2s
2)
Ⅰ型
k=21/8 ess= 8/21
r3(t)=t2
8(0.5s 1)
G 3 (s) s2 (0.1s 1)
× Ⅱ型 k=8 ess=1/8
例题4
求图示系统的essn。
n(t)=1(t)
r=0
2
5
(0.1s+1)(0.5s+1)
s
解:
R(s)
32 C(s) 左: Gr(s) = s/4
s(s+4)
右: Gr(s) = 2
0.5
注意,不可变为单位反馈后再加Gr(s)!
若是输入端定义:ess=0.5 左:Gr=s/8 右:Gr=2
例题6
已知图示系统的调节时间ts= 0.3秒,
试求r(t)=3t 时输出端定义的误差终值ess。
R(s)
1.
G(s)
19 1.786s2 4.1s
1
2.
1
G c (s)
kc s
0 < k c < 0.12
上海交通大学 硕士研究生入学考试试题
• 考虑一个单位负反馈三阶系统,其开环传递 函数的分子为常数,要求:
• 在单位斜坡作用下的稳态误差为1.2 • 三阶系统的一对闭环主导极点为试求同时满
足上述条件的系统开环传递函数
j0
0
0
j
hξ(=t) 01
e n t 1 2
s欠isn阻1(,2尼dt j)n
h(t) 1 零c阻o尼s0nt
欠阻尼二阶系统动态性能分析
j
n
β
n
0
cosβ=ξ
(s)
s2
n2 2 ns
n2
0 < ξ<1时:
s1,2 n jn 1 2
h(t) 1
1
1
2
e nt
sin(
dt
)
欠阻尼二阶系统动态性能计算
5 G(s) s(0.5s2 3.5s 6)
tr d
弧度
tr 特征根的c虚o部s
tp d
tp 特征根的虚部
ts
3.5 n
5%
3.5 ts 特征根的实部
% e 12 100%
e 或 %
tg
100%
例:①已知 0.3 ,求 % ②已知系统的结构如图所示,要求超调量
% 16.3% ,峰值时间tp 1s , 求 K
传递函数:
(s)
A1s (s a)2
B1 b2
零极点分布图:
运动模态2
K(t)=Ae-atsin(bt+α)
j
b
-a 0
0
传递函数:
(s)
A1s B1 s2 b2
零极点分布图:
运动模态3
K(t)=Asin(bt+α)
j
b
0
0
传递函数:
(s)
A1s (s a)2
B1 b2
零极点分布图:
2 按扰动的稳态全补过偿程 设系统这稳就定是,按N(扰s)=动1/的s ,全则补偿
全 essn=
-limsC(各s) 种=-干l扰im信1号 k1G
s→0
s→0
k1
n
(s)
∴Gn(s)= -1/k1
误差计算
系统如图,其中扰动信号n(t)=1(t),问仅仅改变k 的值,能否使系统在扰动信号作用下的误差终值 为-0.099?
ν= 3 称为Ⅲ型系统
例题3
已知单位反馈系统开
环传递函数为G(s),输
入为r(t),试求稳态误
差ess。
r1(t)=1(t)
10
G1(s) (0.1s 1)(0.5s 1)
解:
系统2不稳定,∴ ess→∞ 系统3的A=2, ∴ ess=1/4
√ 0型 k=10 ess=1/11
× r2(t)=t
n2
s2 2 ns n2
s2 2ns n2 s 1/ T1 s 1/T2
1 T1 / T2
2 T1 / T2
1T 4T2 ts 3T1
1ts 4.75T1
无零点的过阻尼二阶系统阶跃响应无振荡无超调
六、二阶系统性能的改善----校正
控制系统常用的两种校正方式:比例微分校正和测速反馈校正 原二阶系统
N(s)
R(s)
E(s) k
10 (0.1s 1)(0.2s 1)(0.5s 1)
C(s)
例题2 求二阶无差度的ko和τ k0
R(s)
k(s 1)
C(s)
(T1s 1)(T2s 1)
T1>0,T2>0,k>0
0<k0<1时系统稳定
k0
1 k
,
T1
T2
系统型别与开环增益
m
k (is 1)
1 C(s) 0.01s
(s) 1 / kh 0.01s / kh 1
kh
ts=3T=0.03/kh=0.3
E(s) R(s)
1
30
H(s) 1 G(s)H(s) s(s 10)
∴kh=0.1
ess= 3
R(s) 1 s3
Gr (s)
E(s) 2
s
50 s1
Gr
(s)
s2
s 1 50
高阶系统的时域分析
一、高阶系统的单位阶跃响应
n=[0.05 10]; d=[0.0025 0.5125
2.52 4.01 3]; sys=tf(n,d); step(sys)
第三章 系统的时域性能指标
3.1 系统的时域性能指标 3.2 一阶系统的时域分析 3.3 二阶系统的时域分析 3.4 高阶系统的时域分析 3.5 线性系统的稳定性分析 3.6 线性系统的稳态误差计算
试确定Gr (s)使系统稳态误差为0。
清华考研试题(15分)
设无零点的单位反馈二阶系统h(t)曲线如图所示,
1、试求出该系统的开环传递函数及参数; 2、确定串联校正装置的传递函数,使系统
对阶跃输入的稳态误差为零。
1.25 0.95
0
ess 0.05
% 0.3 0.95
tp 1s
=0.344,n 3.346
GH
k
(s 1)(s 2)(s 4)
特征方程为:s3 5s2 2s k 8 0
这样简单吧!
第三章 系统的时域性能指标
3.1 系统的时域性能指标 3.2 一阶系统的时域分析 3.3 二阶系统的时域分析 3.4 高阶系统的时域分析 3.5 线性系统的稳定性分析 3.6 线性系统的稳态误差计算
s4 4s2 a 0 可见s1,2 j 5
s4 2 s3 0
s2 s1
8 0
2a
令s设4ja代4入2辅5得a助:方0程得可:s4见,5 s3
2
1
s0
(2 5)(2 1) 0
令原式 (s4 4s2 5)(s b) (s2 5)(s2 1)(s b) 0
让所有极点在s=-2之左: s3
1.138s 2.994 s2 1.737s 2.994
0.5 % 16.3%
引入测速反馈校正
第三章 系统的时域性能指标
3.1 系统的时域性能指标 3.2 一阶系统的时域分析 3.3 二阶系统的时域分析 3.4 高阶系统的时域分析 3.5 线性系统的稳定性分析 3.6 线性系统的稳态误差计算
运动模态4
K(t)=Aeatsin(bt+α)
j
0
b
0a
运动模态小结
j
j
j
j
j
0
0
0
0
0
已知系统特征方程试确定正实部根的个数。
s4 s3 23s2 32s 120 0
已知特征方程 s5 2s4 4s3 8s2 as 2a 0
有一对纯虚根,试求出所有根。
辅助方程
s5 1 4 a
s2
s1
s0
1
-6
12 -8
s3 8s2 22s k 0
8
-32 32
用s 2代替原来的s,得新的特征方程:
22 -44
k
(s 2)3 8(s 2)2 22(s 2) k 0
1
2
2 k-20
让所有极点在s=-1之左: 用s 1代替原来的s,得新GH:
GH
k
s(s 3)(s 5)
引入比例微分校正
引入测速反馈校正
引入比例微分校正
引入了一个比例微分校 正的二阶系统,其输出量同 时受偏差信号和偏差信号微 分的双重控制。
比例微分校正
0.173 57.6%
G(s) 5 s(1.67s 1)
G(s) 5(0.38s 1) s(1.67s 1)
(s)
G(s) 1 G(s)
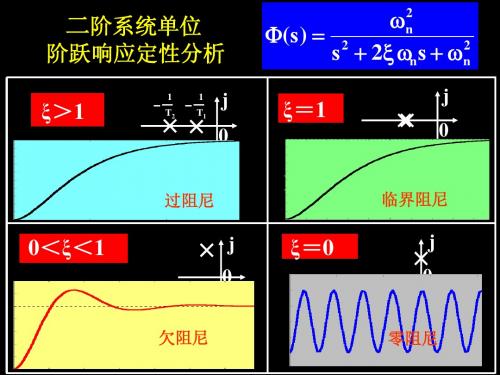
二阶系统单位
阶跃响应定性分析
(s)
s2
n2 2 ns
n2
ξ>ξ>11
1 1j
s1,2
T2
T1
n
n
2ξ= 11
0
jj 00
hξ(=t)1 1
e
t T1
T2
T1
1s1过阻TTes12尼2Tt21n
