流水线加法器
十大基本功之流水线设计

第一,什么是流水线流水线设计就是将组合逻辑系统地分割,并在各个部分(分级)之间插入寄存器,并暂存中间数据的方法。
目的是将一个大操作分解成若干的小操作,每一步小操作的时间较小,所以能提高频率,各小操作能并行执行,所以能提高数据吞吐率(提高处理速度)。
第二,什么时候用流水线设计使用流水线一般是时序比较紧张,对电路工作频率较高的时候。
典型情况如下:1)功能模块之间的流水线,用乒乓buffer来交互数据。
代价是增加了memory的数量,但是和获得的巨大性能提升相比,可以忽略不计。
2)I/O瓶颈,比如某个运算需要输入8个数据,而memroy只能同时提供2个数据,如果通过适当划分运算步骤,使用流水线反而会减少面积。
3)片内sram的读操作,因为sram的读操作本身就是两极流水线,除非下一步操作依赖读结果,否则使用流水线是自然而然的事情。
4)组合逻辑太长,比如(a+b)*c,那么在加法和乘法之间插入寄存器是比较稳妥的做法。
第三,使用流水线的优缺点:1)优点:流水线缩短了在一个时钟周期内给的那个信号必须通过的通路长度,增加了数据吞吐量,从而可以提高时钟频率,但也导致了数据的延时。
举例如下:例如:一个2级组合逻辑,假定每级延迟相同为Tpd,1.无流水线的总延迟就是2Tpd,可以在一个时钟周期完成,但是时钟周期受限制在2Tpd;2.流水线:每一级加入寄存器(延迟为Tco)后,单级的延迟为Tpd+Tco,每级消耗一个时钟周期,流水线需要2个时钟周期来获得第一个计算结果,称为首次延迟,它要2*(Tpd+Tco),但是执行重复操作时,只要一个时钟周期来获得最后的计算结果,称为吞吐延迟(Tpd+Tco)。
可见只要Tco小于Tpd,流水线就可以提高速度。
特别需要说明的是,流水线并不减小单次操作的时间,减小的是整个数据的操作时间,请大家认真体会。
2)缺点:功耗增加,面积增加,硬件复杂度增加,特别对于复杂逻辑如cpu的流水线而言而言,流水越深,发生需要hold 流水线或reset 流水线的情况时,时间损失越大。
我们将tl和tk的比值定义为k级线性流水线的加速比

2.6.4 浮点运算器实例
1.CPU之外的浮点运算器 之外的浮点运算器 80×87是美国 是美国Intel公司为处理浮点数等数据的算术运算和多种 × 是美国 公司为处理浮点数等数据的算术运算和多种 函数计算而设计生产的专用算术运算处理器。 函数计算而设计生产的专用算术运算处理器。由于它们的算 术运算是配合80× 进行的, 术运算是配合 ×86CPU进行的,所以又称为协处理器 进行的 (1)以异步方式与 以异步方式与80386并行工作,80×87相当于 并行工作, × 相当于 相当于386的一个 的一个I/O 以异步方式与 并行工作 的一个 部件,本身有它自己的指令,但不能单独使用, 部件,本身有它自己的指令,但不能单独使用,它只能作为 386主CPU的协处理器才能运算。因为真正的读写主存的工 的协处理器才能运算。 主 的协处理器才能运算 作不是80× 完成 而是由386执行的。如果 完成, 执行的。 作不是 ×87完成,而是由 执行的 如果386从主存读 从主存读 取的指令是80× 浮点运算指令 浮点运算指令, 取的指令是 ×87浮点运算指令,则它们以输出的方式把该 指令送到80× , × 接受后进行译码并执行浮点运算 接受后进行译码并执行浮点运算。 指令送到 ×87,80×87接受后进行译码并执行浮点运算。 80×87进行运算期间,386可取下一条其他指令予以执行, 进行运算期间, 可取下一条其他指令予以执行, × 进行运算期间 可取下一条其他指令予以执行 因而实现了并行工作。如果在80× 执行浮点运算指令过程 因而实现了并行工作。如果在 ×87执行浮点运算指令过程 又取来了一条80× 指令 指令, 以给出“ 中386又取来了一条 ×87指令,则80×87以给出“忙”的 又取来了一条 × 以给出 标志信号加以拒绝, 暂停向80× 发送命令 发送命令。 标志信号加以拒绝,使386暂停向 ×87发送命令。只有待 暂停向 80×87完成浮点运算而取消“忙”的标志信号以后,386才 完成浮点运算而取消“ 的标志信号以后, × 完成浮点运算而取消 才 可以进行一次发送操作。 可以进行一次发送操作。
基于流水线加法器的数字相关器设计

基于流水线加法器的数字相关器设计作者:雷青锋,郏文海来源:《现代电子技术》2010年第16期摘要: 数字相关器在数字扩频通信系统中应用广泛,受数字信号处理器件速度限制,无法应用于高速宽带通信系统,在此提出了一种基于流水线加法器的数字相关处理算法。
该算法最大限度地减少了加法器进位操作,解决了基于全加器型数字相关器存在的进位延迟过大的问题,实现了时分多址体制下的同步段数字相关,提高了同步段相关的可靠性。
关键词:扩频通信; 数字相关; FPGA; 流水线加法器; 相关器中图分类号:TN911-34文献标识码:A文章编号:1004-373X(2010)16-0151-03Design of Digital Correlator Based on Pipeline AdderLEI Qing-feng,JIA Wen-hai(No. 20th Institute, CETC, Xi’an 710068, China)Abstract:Digital correlator is widely applied in digital spread-spectrum communication system, but it cannot be used in high speed wide-band communication system due to the limitation of low-speed DSP device. In this paper, a full-adder based digital correlation processing algorithm is proposed, which largely decreased the carry operation in the full-adder, solved the problem of carry time-delay existing in the full-adder based digital correlator, achieved the synchronization processing in time-division-multiple-access based system and improved the reliability of the synchronization correlation.Keywords:spread-spectrum communication;digital correlation;FPGA;pipelineadder;correlation device0 引言数字相关器是扩频通信体制下数字中频接收机核心部件之一,在数字扩频通信系统中应用广泛,但由于受数字信号处理器件速度限制,无法应用于高速宽带通信系统。
流水线技术在高速数字电路设计中的应用

摘要:流水线技术是设计高速数字电路的一种最佳选择之一,对其实现原理作了较形象的阐述。
针对加法器在DSP中的重要作用,对流水线加法器中流水线技术的应用作了较深入的说明。
同时,对流水线技术中引入寄存器事项也作了较全面的阐述。
1 前言数字信号处理技术(DSP)在许多领域都得到广泛的应用,在数字电路设计时,设计者都希望设计出具有理想速度的电路系统。
目前,并行技术、流水线技术等都是很好的备选方案。
对于组合逻辑电路占主要成分的电路中,流水线技术是首先考虑的技术。
现在,现场可编程门阵列FPGA的集成度已达到很高的程度,且设计灵活,可在实验室里进行,并具有丰富的寄存器,适合设计人员使用流水线技术来进行设计以提高数字电路的整体运行速度。
2 流水线技术的作用原理流水线技术就是把在一个时钟周期内执行的操作分成几步较小的操作,并在多个较高速的时钟内完成。
如图1、2所示,对图1中的两个寄存器间的数据通路,在图2中将其分成了3级,并在其间插入了两个寄存器,这就是流水线技术的使用。
图1常规的数据通路图2采用流水线技术数据通路对图1中的数据通路,设tpd≈x,则该电路(不考虑寄存器的影响)从输入到输出的最高时钟频率就为1/x。
而在图z中,假设在理想情况下所分成的3级,每级的tpd≈x/3,则该电路从输入到输出的最高频率可提高到原来的3倍,采用流水线技术有效地提高了系统的时钟频率,因而在多个时钟周期连续工作情况下,就提高了整个系统的数据处理量。
当然,这不包括电路中所加入的寄存器时延,因此每级的实际延迟应比x/ 3稍大。
但在多个时钟周期连续工作情况下,可忽略不计,所以流水线技术能提高系统的数据流量。
3 流水线技术的设计应用加法运算是最基本的数字信号处理(DSP)运算,减法、乘法、除法或FFT运算都可分解为加法运算。
因此进行加法运算的加法器就成为实现DSP的最基本器件,因而研究如何提高其运行速度很有必要。
流水线技术在提高系统整体运行速率方面绩效显著,因而采用流水线技术的流水线加法器就成为继串联加法器、并行加法器之后在选择加法器时的首选。
基于流水线的复数阵列加法器的设计与实现

图 1 加法器阵列功能框 图
2 设计实现
模块 里 的所有 加 法 运 算均 采 用 C r — ok A— ar lo — y ha 法器 ; 法则 转 换 为 加 法进 行 运 算 , 过 对 ed加 减 通 减数 求补 把模块 里 的所有 减 法均转 换为 加法 进行运
算 模块采用四级流水线结构 , 从收到数据第五个周 期 开始 输 出数据 。
输 入数 实 部 R , bR ,d 虚部 I, , , aR , cR , aI I I b c d的 数 据 宽度均 为 1 ; 次 向加法 器阵列 只送 一个 操 9位 每
要的部件… 。所有基本算术运算 ( 减 、 、 最 加、 乘 除) 终都 可 归结 为加 法 运 算 J 。本 文 就 是 根 据 实 际 要
线。功能验证 、 电路综合及 布局布线的结果表 明设计正确 , 实现 了复数加法运 算 , 时序性能好 , 耗用 资源少。
关键 词
加法器
超前进位
复数 阵列 流水 线 文献标识码 A
中图法分 类号
T 322 ; P 3 . 1
算 术逻辑 单元 ( L 不 仅 能 完成 算 术 运 算 , A U) 也 能完 成逻 辑运 算 , 是微 处 理 器 芯 片 中的 一个 十分 重
维普资讯
科
学
技
术
与
工
程
7卷
2 1 4位 C A 加法器 . L
A, B为输 入 的两 个 4位 加 数 , I 为 低 位 的进 CN
位。 .
进位 传播 : P= A l B; 进位 产生 :G = A & B; 第 0位 的进位 : cr 0 = CN; ar y[ ] I 第 1位 的进位 : Cl 1 : CN}P 0 a y[ ] T I [ ]+G[ ] 0 ; 第 2位 的进位 :
流水线乘法累加器的混合输入设计

1乘法 累 加器 的 基本 原 理 在二 进制 乘法 中,乘法 的 基本算 法 常可用 所谓 的一 位乘 法和 两位 乘法 进 行 。进 行这 种乘 法运 算时 ,通 常分别 用 乘数 的一位 或 二位 与被 乘数 相乘, 再 把 部 分积 加起 来 。移 位相 加 是最 基 本 的乘 法器 设 计 思路, 实现起 来 较 为简 单 。 它的设 计 思想 就是 根据 乘数 的 每一 位 是否 为 1 行计 算, 若 为 1则将 进 被 乘数 移位 相加 。 这 种方 法硬件 资源耗 用较 少 。 以 8位移 位相 加乘 法器 为 例 , 其 实现 过 程 如下 。 先对 乘 数的最 低位 进行 判 断是否 为 l 如 果 为 l 则把 被乘 数相 加, 然 。 , 后 被乘 数 向高位 移 1 , 乘数 向低 位移 1 : 如 果为 0 则 被乘 数不 相加 而 位 位 , 仍 然 向高位 移 1 , 乘数 向低 位移 1 。 如 此循 环判 断 8次, 结束运 算 。 位 位 纯组 合逻 辑 电路 构成 的乘 法器 虽 然工 作速 度 比较 快 , 但过 于占用 硬件 资 源 , 于实现 多 为乘 法器 : 难 因此 本课 题将 介绍 由 8位加 法 器 构成 的来 设 计流 水 线乘法 累加 器 的混合 输入 , 这种 设计 能够 比较 方便 实现 两个8 二进 制数 的 位 乘 法运算 。 2设 计 思路 用 V D 文 本输 入设 计方 法, 计一 个 8 流水 线乘 法累 加器 的混 合输 入, HL 设 位 进行系统 仿真 。 算 术流 水线 主要 是 指运 算操 作步 骤 的并行 。如流水 乘 法器 , 例如 :T R SA~ 10 4 0 为 级流水 运 算器, I A C为 8 T—S 级流 水运 算器 , R Y 1 l 级 流水 运算 器 CA 为 4 等: 设 l 先 6位初 始和 为零 , 1 键 和键 2分 别输 入 乘数 的低 4位 、高 4位 : 3 键 和键 4输入 被 乘数 的 低 4位 、 高 4位 。由波形 可 见, 1 c c o k的第 一 上升 沿 个 由锁 存器输 入 的乘数 和被 乘数 为 0 所 以在 第二 个上 升沿 后得 到结 果 为 S O× , 02 + 3× 1= 4 , 53 5 而第 三个 上升 沿后 得 到结 果为 S 2 3× 1+ 3× 1=9 , 第 52 56 0 而 四个上 升沿 后得 到结 果为 S 2 : 3× 1+ 6× 2 :8 , 此 等等 。如此 往 复, 51 1 6 1如 直 至 8个时 钟脉 冲 后, 流水 线 乘 法累 加 器 过程 终 止 。 2 设计 文件 2 1顶 层原 理 图 如图 l 所示 , l 由 6位加 法器 (D E 1 B 、8 锁存 器 (A C 8 1 和 调入 ADR6) 位 L T H )
一种三级流水线加法器设计

中 。第 三 级 流 水 线完 成相 似 的操 作 , 直到输 出运
算结 果 ( 见图1 )。 3 . 电 路 仿 真 与 综 合
—
u
I
心
利 用 上 述 架 构 ,利 用 V e r i o g — R D L 对 电 路 进 行 描 述 。在 M o d e l S i m I 具 下对 系 统 进 行 仿 真 , 得 到 的 三级 流 水 线 加 法 器 的 仿 真 结 果 如 图 2 , 从 图 中可 以 看 出 , 三 级 流 水 线 加 法 器 功 能 正 确。在C a n d e n c e 工作环境 下,基于C S M C O . 5 m
襻设计卟 微电子学与计算机, 2 0 0 6 , 2 3 ( 4 ] : 4 8 — 4 9 . f 3 ] 郭天 天, 张志勇, 卢焕章. 快速浮 点加法器 的F P G A实卿 Ⅱ ] 计 算机 工程, 2 0 0 5 , 3 1 ( 1 6 ) : 2 0 2 - 2 0 4 .
屯-  ̄t t t 界 一1 4 3
1 . 引 言
伟 澜
加 法运 算 是 一种 最 基本 的 运算 形 式 ,乘 法 、 除法 甚 至 开 方 等 运 算 都 可 以 分 化 为 基 本 的 加 法
运 算 ,提 高 加 法 器 的 运 行 速 度 可 以 有 效 地 提 高
运 算 单 元 的速 度 , 目前 ,超 前 进 位 加 法 器 可 以 有 效 地 提 高 加 法 器 的 运 算 速 度 , 但 是 对 于 很 高 位 数 的 加 法 运 算 , 超 前 进 位 加 法 器 对 运 算 速 度 的提 高有 限 1 。 对 于 高 佩 的加 法 器 采 用 流 水 线 ] 结 构 是 一 种 很 好 的 选 择 , 论 文 以 一 种 采 用 三 级 流 水线实现 的I 2 位 加 法 器 为 例 ,阐 述 了 流 水 线 加 法 器 的设 计 思想 ,并 最终 对 加 法 器进 行 硬件 综 合 和布 局 布线 。
FPGA八位加法器

FPGA 实验报告(信息科学与工程学院)实验名称:流水线设计技巧设计加法器专业:通信071学生姓名:喻明富学号:07437126 2010 ~2010学年第一学期第一次试验实验日期:10月30号指导教师:刘威成绩:审阅教师:信息科学与工程学院电子与信息技术实验中心教务处一、实验目的1、理解流水线设计技巧的原理;2、通过比较普通加法器和流水线加法器的性能验证后者的优越性。
二、实验要求1、用《EDA技术》课程所学方法设计一个8位加法器;2、用流水线技巧设计一个2级流水线的8位加法器;3、比较普通加法器和流水线加法器的性能。
三、实验原理1、设计一个普通加法器,用8个一位加法器级联,组成行波进位式加法器;图1-1 行波进位式加法器为了方便进行时间分析,需要在输入和输出端分别加上寄存器。
输入端(图1-2)图1-2 输入端所加的寄存器输出端(图1-3)图1-3 输出端所加的寄存器处理后可进行delay time分析、setup/hold time分析和频率分析。
2、流水线设计方法流水线设计就是将一个时延比较大的复杂的组合逻辑系统地分割,在各个部分(分级)之间插入寄存器以暂存中间数据的方法。
目的是将一个大操作分解成若干的小操作,每一步小操作的耗时较小,各小操作能并行执行,所以数据可以像流水线一样轮流进入每一步小操作进行处理,这样整体地来看系统,数据可以更快地进入和流出系统,所以能提高数据吞吐率(提高处理速度)。
这样的流水线的速率取决于每一步小操作所耗费的时间。
由于采用同步寄存器分割组合逻辑,只要每个组合逻辑的时延小于寄存器的时钟周期,那么系统的频率取决于系统的时钟频率。
流水线处理是高速设计中的一个常用设计手段。
如果某个设计的处理流程分为若干步骤,而且整个数据处理是“单流向”的,即没有反馈或者迭代运算,前一个步骤的输出是下一个步骤的输入,则可以考虑采用流水线设计方法来提高系统的工作频率。
例如,利用FPGA设计8位加法器时,考虑到:1>FPGA每个逻辑单元规模小,一般为4输入LUT,如果加法器位数大于4bit,则会受到LUT容量限制。
32位双重快速跳跃进位链六级流水线加法器Verilog的实现

32位双重快速跳跃进位链六级流水线加法器Verilog的实现DLUT-SOFTWARE-0819Mr Xie2011/6/28`timescale 1ns / 1ps //定义时间单位为1ns,时间精度为1ps////////////////////////////////////////////////////////////////////////////////// //模块名: fullAdder32//端口说明: clk: 输入的时钟A:输入的32加数B:输入的32位被加数Cin:输入的最低位进位Cout:输出的最高位进位Sum:两个数相加的和//目标器件: Veritex4系列的XC4VSX35//工具版本: Xilinx-ISE10.1、ISE Simulator(VHDL/Verilog)、Synplify Pro9.6.2 //依懒关系: 不依懒于其它模块//创建日期: 08:43:38 06/21/2011//创建人:////////////////////////////////////////////////////////////////////////////////// module fullAdder32(clk,A,B,Cin,Cout,Sum);input clk; //声明clk为1位的线网型输入变量input [31:0] A; //声明A为32位的线网型输入变量input [31:0] B; //声明B为32位的线网型输入变量,input Cin; //声明Cin为1位的线网型输入变量output Cout; //声明Cout为1位的线网型输出变量output [31:0] Sum; //声明Sum为32位的线网型输出变量reg [31:0] Sum; //对Sum进行重新声明为寄存器型reg Cout; //对Cout进行重新声明为寄存器型reg [30:0] C; //每一位相加时产生的进位reg [30:0]tmpC1, tmpC2, tmpC3; //临时变量,对进位作一个暂存reg [31:0]d; //小组的本地进位reg [31:0]tmpd1, tmpd2, tmpd3;//临时变量,对本地进位作一个暂存reg [31:0]t; //小组的传递进位reg [31:0]tmpt1, tmpt2, tmpt3;//临时变量,对传递进位作一个暂存reg [8:1]D; //大组的本地进位reg [8:1]tmpD1; //临时变量,对大组的本地进位作一个暂存reg [8:1]T; //大组的传递进位reg [8:1]tmpT1; //临时变量,对大组的传递进位作一个暂存reg [31:0]tmpA1, tmpA2, tmpA3, tmpA4, tmpA5;//对输入变量A作暂存reg [31:0]tmpB1, tmpB2, tmpB3, tmpB4, tmpB5; //对输入变量B作暂存reg tmpCin1, tmpCin2, tmpCin3, tmpCin4, tmpCin5;//对输入变量Cin作暂存reg tmpCout1, tmpCout2;//对输出变量Cout作一个暂存//////////////////第一个时钟周期//////////////////////////////////计算小组的本地进位d和传递进位t//对输入的加数A,被加数B,低位进位Cin作一级暂存always @(posedge clk) begind <= A&B;t <= A|B;tmpA1 <= A;tmpB1 <= B;tmpCin1 <= Cin;end//////////////////第二个时钟周期/////////////////////////////////对输入的加数A,被加数B,低位进位Cin作二级暂存//对小组的本地进位d,传递进位t作一级暂存//计算进位C[0],C[1],C[2]//计算大组的本地进位D、传递进位Talways @(posedge clk) begintmpd1 <= d;tmpt1 <= t;tmpA2 <= tmpA1;tmpB2 <= tmpB1;tmpCin2 <= tmpCin1;C[0] <= d[0] | t[0]&tmpCin1;C[1] <= d[1] | t[1]&d[0] | t[1]&t[0]&tmpCin1;C[2] <= d[2] | t[2]&d[1] | t[2]&t[1]&d[0] | t[2]&t[1]&t[0]&tmpCin1;D[1] <= d[3] | &{t[3],d[2]} | &{t[3:2],d[1]} | &{t[3:1],d[0]};T[1] <= &t[3:0]; //t[3]&t[2]&t[1]&t[0];D[2] <= d[7] | &{t[7],d[6]} | &{t[7:6],d[5]}| &{t[7:5],d[4]};T[2] <= &t[7:4]; //t[3]&t[2]&t[1]&t[0];D[3] <= d[11] | &{t[11],d[10]} | &{t[11:10],d[9]}| &{t[11:9],d[8]};T[3] <= &t[11:8]; //t[11]&t[10]&t[9]&t[8];D[4] <= d[15] | &{t[15],d[14]} | &{t[15:14],d[13]}| &{t[15:13],d[12]};T[4] <= &t[15:12]; //t[15]&t[14]&t[13]&t[12];D[5] <= d[19] | &{t[19],d[18]} | &{t[19:18],d[17]}| &{t[19:17],d[16]};T[5] <= &t[19:16]; //t[19]&t[18]&t[17]&t[16];D[6] <= d[23] | &{t[23],d[22]} | &{t[23:22],d[21]}| &{t[23:21],d[20]};T[6] <= &t[23:20]; //t[23]&t[22]&t[21]&t[20];D[7] <= d[27] | &{t[27],d[26]} | &{t[27:26],d[25]}| &{t[27:25],d[24]};T[7] <= &t[27:24]; //t[27]&t[26]&t[25]&t[24];D[8] <= d[31] | &{t[31],d[30]} | &{t[31:30],d[29]}| &{t[31:29],d[28]};T[8] <= &t[31:28]; //t[31]&t[30]&t[29]&t[28];end////////////////////////t第三个时钟周期///////////////////////////对输入的加数A,被加数B,低位进位Cin作三级暂存//对小组的本地进位d,传递进位t作二级暂存//对大组的本地进位D,传递进位T作一级暂存//对进位部分进位C作二级暂存//计算进位C[3],C[7],C[11],C[15]always @ (posedge clk) begintmpd2 <= tmpd1;tmpt2 <= tmpt1;tmpA3 <= tmpA2;tmpB3 <= tmpB2;tmpCin3 <= tmpCin2;tmpD1 <= D;tmpT1 <= T;tmpC1[2:0] <= C[2:0];tmpC1[3] <= D[1] | T[1]&tmpCin2;tmpC1[7] <= D[2] | T[2]&tmpCin2;tmpC1[11] <= D[3] | T[3]&tmpCin2;tmpC1[15] <= D[4] | T[4]&tmpCin2;end////////////////////////t第四个时钟周期///////////////////////// //对输入的加数A,被加数B,低位进位Cin作四级级暂存//对小组的本地进位d,传递进位t作三级暂存//对进位部分进位C作二级暂存//计算进位C[6:4],C[10:8],C[14:12],C[19:16],C[23],C[27]//计算最高进位Coutalways @ (posedge clk) begintmpd3 <= tmpd2;tmpt3 <= tmpt2;tmpA4 <= tmpA3;tmpB4 <= tmpB3;tmpCin4 <= tmpCin3;tmpC2[0] <= tmpC1[0];tmpC2[1] <= tmpC1[1];tmpC2[2] <= tmpC1[2];tmpC2[3] <= tmpC1[3];tmpC2[7] <= tmpC1[7];tmpC2[11] <= tmpC1[11];tmpC2[15] <= tmpC1[15];tmpC2[4] <= tmpd2[4] | tmpt2[4]&tmpC1[3];tmpC2[5] <= tmpd2[5] | tmpt2[5]&tmpd2[4] | tmpt2[5]&tmpt2[4]&tmpC1[3];tmpC2[6] <= tmpd2[6] | tmpt2[6]&tmpd2[5] |tmpt2[6]&tmpt2[5]&tmpt2[4]&tmpC1[3];tmpC2[8] <= tmpd2[8] | tmpt2[8]&tmpC1[7];tmpC2[9] <= tmpd2[9] | tmpt2[9]&tmpd2[8] | tmpt2[9]&tmpt2[8]&tmpC1[7];tmpC2[10]<=tmpd2[10] | tmpt2[10]&tmpd2[9]| tmpt2[10]&tmpt2[9]&tmpt2[8]&tmpC1[7];tmpC2[12] <= tmpd2[12] | tmpt2[12]&tmpC1[11];tmpC2[13] <= tmpd2[13] | tmpt2[13]&tmpd2[12]| tmpt2[13]&tmpt2[12]&tmpC1[11];tmpC2[14] <= tmpd2[14] | tmpt2[14]&tmpd2[13]|tmpt2[14]&tmpt2[13]&tmpt2[12]&tmpC1[11];tmpC2[16] <= tmpd2[16] | tmpt2[16]&tmpC1[15];tmpC2[17] <= tmpd2[17] | tmpt2[17]&tmpd2[16]| tmpt2[17]&tmpt2[16]&tmpC1[15];tmpC2[18]<=tmpd2[18] | tmpt2[18]&tmpd2[17]| tmpt2[18]&tmpt2[17]&tmpt2[16]&tmpC1[15];tmpC2[19] <= tmpD1[5] | tmpT1[5]&tmpC1[15];tmpC2[23] <= tmpD1[6] | tmpT1[6]&tmpC1[15];tmpC2[27] <= tmpD1[7] | tmpT1[7]&tmpC1[15];tmpCout1 <= tmpD1[8] | tmpT1[8]&tmpC1[15];end////////////////////////t第五个时钟周期///////////////////////////对输入的加数A,被加数B,低位进位Cin作五级级暂存//对进位部分进位C作三级暂存//对最高进位Cout作一级暂存//计算进位C[22:20],C[26:24],C[30:28]always @ (posedge clk) begintmpA5 <= tmpA4;tmpB5 <= tmpB4;tmpCin5 <= tmpCin4;tmpC3[19:0] <= tmpC2[19:0];tmpC3[23] <= tmpC2[23];tmpC3[27] <= tmpC2[27];tmpCout2 <= tmpCout1;tmpC3[20] <= tmpd3[20] | tmpt3[20]&tmpC2[19];tmpC3[21] <= tmpd3[21] | tmpt3[21]&tmpd3[20]| tmpt3[21]&tmpt3[20]&tmpC2[19];tmpC3[22] <= tmpd3[22] | tmpt3[22]&tmpd3[21]| tmpt3[22]&tmpt3[21]&tmpd3[20]| tmpt3[22]&tmpt3[21]&tmpt3[20]&tmpC2[19];tmpC3[24] <= tmpd3[24] | tmpt3[24]&tmpC2[23];tmpC3[25] <= tmpd3[25] | tmpt3[25]&tmpd3[24]| tmpt3[21]&tmpt3[20]&tmpC2[23];tmpC3[26] <= tmpd3[26] | tmpt3[26]&tmpd3[25]| tmpt3[26]&tmpt3[25]&tmpd3[23]| tmpt3[26]&tmpt3[25]&tmpt3[24]&tmpC2[23];tmpC3[28] <= tmpd3[28] | tmpt3[28]&tmpC2[27];tmpC3[29] <= tmpd3[29] | tmpt3[29]&tmpd3[28]| tmpt3[29]&tmpt3[28]&tmpC2[27];tmpC3[30] <= tmpd3[30] | tmpt3[30]&tmpd3[29]| tmpt3[30]&tmpt3[29]&tmpd3[28]| tmpt3[30]&tmpt3[29]&tmpt3[28]&tmpC2[27]; end////////////////////////第六个时钟周期///////////////////////////所有的进位已经产生//计算A、B两个数的和Sum//输出最高进位always @ (posedge clk) beginSum <= tmpA5^tmpB5^{tmpC3[30:0],tmpCin5};Cout <= tmpCout2;endendmodule// module fullAdder32(clk,A,B,Cin,Cout,Sum);测试代码如下:`timescale 1ns / 1ps //定义时间单为及时间精度//////////////////////////////////////////////////////////////////////////////////模块名: test.v//输入输出端口:无//目标器件: Veritex4系列的XC4VSX35//工具版本: Xilinx-ISE10.1、ISE Simulator(VHDL/Verilog)、Synplify Pro9.6.2 //创建日期: 08:44:52 06/23/2011//创建人://////////////////////////////////////////////////////////////////////////////// module test;// 输入信号reg clk;reg [31:0] A;reg [31:0] B;reg Cin;//输出信号wire Cout;wire [31:0] Sum;// 实例化要测试的模块fullAdder32 uut (.clk(clk),.A(A),.B(B),.Cin(Cin),.Cout(Cout),.Sum(Sum));initial begin// 初始化输入信号clk = 1;A = 32'd1112111;B = 32'd2221222;Cin = 0;//下面为仿真激励信号foreverfork#20 A <= A + 1; //加数每隔一个时钟周期加1#20 B <= B + 1; //被加数每隔一个时钟周期加1joinendalways#10 clk <= ~clk; //时钟周期为20nsendmodule1.加法器的仿真仿真时序波形如下所示:2.加法器的综合Technology Hierarchical View如下图所示:。
流水线分类

线性流水线与非线性流水线按照流水线的各个流水段之间是否有反馈信号,可以把流水线分为线性流水线和非线性流水线两类。
线性流水线(Linear Pipelining)是将流水线的各段逐个串接起来。
输入数据从流水线的一端进入,从另一端输出。
数据在流水线中的各个流水段流过时,每一个流水段都流过一次,而且仅仅流过一次。
一条线性流水线通常只完成一种固定的功能。
在现代计算机系统中,线性流水线已经被非常广泛地应用于指令执行过程、各种算术运算操作、存储器访问操作等。
在上一节中介绍的流水线中,如图5.13所示的指令流水线,图5.14所示的浮点加法器流水线等都属于线性流水线。
非线性流水线(Nonlinear Pipelining)在流水线的各个流水段之间除了有串行的连接之外,还可以有前馈和反馈连接。
图5.17是一种简单的非线性流水线。
流水线的流水段S2的输出可能直接传送给流水段S3,也可能反馈到本流水段的输入。
图5.17 一种简单的非线性流水线在图5.17中,虽然总共只有三个流水段,但是,输入任务经过流水线到达输出,往往不只是经过三个时钟周期;其中,流水段S2可能要被多次调用,这也是非线性流水线与线性流水线的一个主要区别。
因此,在非线性流水线中,只用图5.17这样一种连接图并不能表示出一个任务在流水线中实际流动的过程。
表示非线性流水线的工作情况除了需要流水线的连接图之外,通常还需要一张“预约表”,用两者共同来表示流水线的工作情况。
在预约表中可以很清楚地表示出反馈回路的使用次数。
例如,图5.18表示图5.17中反馈回路仅使用一次的预约表,图中用“×”表示这一个流水段在相应的这一段时间内有效,即任务经过了这一个流水段。
图5.18 非线性流水线的预约表一条非线性流水线可以对应有很多张预约表,同样,一张预约表实际上仅表示了一条非线性流水线的一种工作方式。
线性流水线实际上也有预约表,只不过它的预约表是确定的。
首先,预约表的水平方向与垂直方向的格数一定是相等,即组成一个正方形。
VHDL流水线加法器

可编程实验报告实验报告要求:1、任务的简单描述2、画出电路图3、写出源代码4、仿真结果5、分析和讨论1、3-8译码器源代码:LIBRARY ieee;USE ieee.std_logic_1164.all;USE ieee.std_logic_arith.all;USE ieee.std_logic_signed.all;ENTITY dc38 ISPORT(sel : in std_logic_vector(2 downto 0);y : out std_logic_vector(7 downto 0)); END dc38;ARCHITECTURE behavior OF dc38 ISBEGINy <= "11111110" WHEN sel = "000" else"11111101" WHEN sel = "001" else"11111011" WHEN sel = "010" else"11110111" WHEN sel = "011" else"11101111" WHEN sel = "100" else"11011111" WHEN sel = "101" else"10111111" WHEN sel = "110" else"01111111" WHEN sel = "111" else"ZZZZZZZZ";END behavior;仿真结果:一位全加器A B CI S CO0 0 0 0 00 0 1 1 00 1 0 1 00 1 1 0 11 0 0 1 01 0 1 0 11 1 0 0 11 1 1 1 1四级流水加法器library ieee;use ieee.std_logic_1164.all;use ieee.std_logic_unsigned.all;use ieee.std_logic_arith.all;entity adder isport(clk,rst : in std_logic;a,b : in std_logic_vector(3 downto 0);sum : out std_logic_vector(3 downto 0);c : out std_logic);end entity adder;architecture depict of adder issignal reg1: std_logic_vector(7 downto 0);signal reg2: std_logic_vector(6 downto 0);signal reg3: std_logic_vector(5 downto 0);beginbit0:process(clk,rst)beginif(rst='1') thenreg1<="00000000";elsif(rising_edge(clk)) thenreg1(0)<= a(0) xor b(0);reg1(1)<= a(0) and b(0);reg1(2)<= a(1);reg1(3)<= b(1);reg1(4)<= a(2);reg1(5)<= b(2);reg1(6)<= a(3);reg1(7)<= b(3);end if;end process bit0;bit1:process(clk,rst)beginif(rst='1') thenreg2<="0000000";elsif(rising_edge(clk)) thenreg2(0)<= reg1(0);reg2(1)<= reg1(1) xor reg1(2) xor reg1(3);reg2(2)<= (reg1(1) and reg1(2))or(reg1(1)and reg1(3))or(reg1(2)and reg1(3));reg2(6 downto 3)<=reg1(7 downto 4);end if;end process bit1;bit2:process(clk,rst)beginif(rst='1') thenreg3<="000000";elsif(rising_edge(clk)) thenreg3(1 downto 0)<=reg2(1 downto 0);reg3(2)<=reg2(2)xor reg2(3)xor reg2(4);reg3(3)<=(reg2(2)and reg2(3))or(reg2(2)and reg2(4))or(reg2(3)and reg2(4));reg3(5 downto 4)<=reg2( 6 downto 5);end if;end process bit2;bit3:process(clk,rst)beginif(rst='1') thensum<="0000";c<='0';elsif(rising_edge(clk)) thensum(2 downto 0)<=reg3(2 downto 0);sum(3)<=reg3(3)xor reg3(4)xor reg3(5);c<=(reg3(3)and reg3(4))or(reg3(3)and reg3(5))or(reg3(4)and reg3(5));end if;end process bit3;end depict;library ieee;use ieee.std_logic_1164.all; use ieee.std_logic_unsigned.all; use ieee.std_logic_arith.all;entity noadd isport(clk,rst : in std_logic;a,b : in std_logic_vector(3 downto 0);sum : out std_logic_vector(3 downto 0);c : out std_logic);end entity noadd;architecture depict of noadd issignal reg : std_logic_vector(4 downto 0);signal rega: std_logic_vector(4 downto 0);signal regb: std_logic_vector(4 downto 0);beginprocess(clk)beginif(rising_edge(clk))thenrega<='0'& a;regb<='0'& b;end if;end process;process(clk)beginif(rst='1')thenreg<="00000";elsif(rising_edge(clk))thenreg<=rega+regb;end if;end process;sum<=reg(3 downto 0);c<=reg(4);end depict;4位十进制数计数器library ieee;use ieee.std_logic_1164.all; use ieee.std_logic_unsigned.all; use ieee.std_logic_arith.all; entity dec_disp is port(clk_cnt : in std_logic;sel1 : out std_logic_vector(3 downto 0);sel2 : out std_logic_vector(3 downto 0);sel3 : out std_logic_vector(3 downto 0);sel4 : out std_logic_vector(3 downto 0));end dec_disp;architecture behav of dec_disp issignal data1 : std_logic_vector(3 downto 0); signal data2 : std_logic_vector(3 downto 0); signal data3 : std_logic_vector(3 downto 0); signal data4 : std_logic_vector(3 downto 0);begincount:process(clk_cnt)beginif(rising_edge(clk_cnt))thenif(data1="1001")thendata1<="0000";elseif(data2="1001")thendata2<="0000";data1<=data1+1;elseif(data3="1001")thendata3<="0000";data2<=data2+1;elseif(data4="1001")thendata4<="0000";data3<=data3+1;elsedata4<=data4+1;end if;end if;end if;end if;end if;end process count;sel1<=data1;sel2<=data2;sel3<=data3;sel4<=data4;end behav;正弦波发生器sin.mif文件depth=256;width=8;address_radix=dec; data_radix=dec; contentbegin0: 131;1: 134;2: 137;3: 141;4: 144;5: 147;6: 150;7: 153;8: 156;9: 159;10: 162;11: 165;12: 168; 13: 171;14: 174;15: 177;16: 180;17: 183;18: 186;19: 188;20: 191;21: 194;22: 196;23: 199;24: 202;25: 204;26: 207;27: 209;28: 212;29: 214;30: 216;31!219;32:221;33:223;34:225;35:227;36:229;37:231;38:233;39:234;40:236;41:238;42:239;43:241;44:242;45:244;46:245;47:246;48:247;49:249;50:250;51:250;52:251;53:252; 54:253; 55:254; 56:254; 57:255; 58:255; 59:255; 60:255; 61:255; 62:255; 63:255; 64:255; 65:255; 66:255; 67:255; 68:255; 69:255; 70:254; 71:254; 72:253; 73:252; 74:251; 75:250; 76:250; 77:249; 78:247; 79:246; 80:245; 81:244; 82:242; 83:241; 84:239; 85:238; 86:236; 87:234; 88:233; 89:231; 90:229; 91:227; 92:225; 93:223; 94:221; 95:219; 96:216;97:214;98:212;99:209;100:207;101:204;102:202;103:199;104:196;105:194;106:191;107:188;108:186;109:183;110:180;111:177;112:174;113:171;114:168;115:165;116:162;117:159;118:156;119:153;120:150;121:147;122:144;123:141;124:137;125:134;126:131;127:128;128:125;129:122;130:119;131:115;132:112;133:109;134:106;135:103;136:10;137:97;138:94;139:91;140:88;141:85;142:82;143:79;144:76;145:73;146:70;147:68;148:65;149:62;150:60;151:57;152:54;153:52;154:49;155:47;156:44;157:42;158:40;159:37;160:35;161:33;162:31;163:29;164:27;165:25;166:23;167:22;168:20;169:18;170:17;171:15;172:14;173:12;174:11;175:10;176:9;177:7;178:6;179:6;180:5;181:4;182:3;183:2;184:2;185:1; 186:1; 187:1; 188:0; 189:0; 190:0; 191:0; 192:0; 193:0; 194:0; 195:1; 196:1; 197:1; 198:2; 199:2; 200:3; 201:4; 202:5; 203:6; 204:6; 205:7; 206:9; 207:10; 208:11; 209:12; 210:14; 211:15; 212:17; 213:18; 214:20; 215:22; 216:23; 217:25; 218:27; 219:29; 220:31; 221:33; 222:35; 223:37; 224:40; 225:42; 226:44; 227:47; 228:49; 229:52; 230:54; 231:57; 232:60; 233:62; 234:65; 235:68; 236:70 ; 237:73; 238:76; 239:79; 240:82; 241:85; 242:88; 243:91; 244:94; 245:97; 246:100; 247:103; 248:106; 249:109; 250:112; 251:115; 252:119; 253:122; 254:125; 255:128; end;。
一种深度流水线的浮点加法器

关键 词 : 浮点加法器;P A 流水线; FG ; 吞吐量
中图分 类号 : N 3 . T 4 12
文献 标识码 : A
文章 编 号 :o 59 9 ( o 7 O -9 o l o -4 O 2 o ) 3o 儿-4
b t d xo rt na dma t s p r t n, d io ds b rcinwees p r t p r sp e n e Fo i— o hi e p ai ni ao ai n e o n s e o a dt na u t t r e aae a a t i n a o d wa rs td e rsn
.
gepeio 3 i ) p rt n we s tr ’ Srt Ifmi h ,ahee ru h u ts n r ta 5 l r s n(2bt o ai , e Al aS t i I a l c i ci d t o g p t ae oe h n3 6 ci s e o u d e a x y p v h r r
S HAO Ji , U n ln YU n c e g e Wa —e g. Ha —h n
(olg f If r t nS i c n eh oo y, n igUnvri f rn ui C l e n omai c n e d T cn lg Na jn ies yo Aeoa t s& As 0 “i5 e o o e a t c tm t , r c " 1 0 6 C ∞ ) g2 0 1
M Hzb ih-tg epy pp l i . yeg t a ed e l iei u s ng Ke o d :la ig p i ta d r PGA ;p p l i g h o g p t y w r s fo tn - on d e ;F iei n ;t r u h u n
经典:计算机组成原理-第2章-运算方法和运算器

第二章:运算方法和运算器
2.1 数据与文字的表示方法 2.2 定点加法、减法运算 2.3 定点乘法运算 2.4 定点除法运算 2.5 定点运算器的组成 2.6 浮点运算方法和浮点运算器
其中尾数域所表示的值是1.M。因为规格化的浮点数的尾数域最
左位(最高有效位)总是1。故这一位经常不予存储,而认为隐藏
在小数点的左边。
64位的浮点数中符号位1位,阶码域11位,尾数域52位,指数偏
移值是1023。因此规格化的64位浮点数x的真值为:
x=(-1)s ×(1.M) × 2E-1023 e=E-1023
[X]反=1.x1x2...xn 对于0,有[+0]反=[-0]反之分:
[+0]反=0.00...0
[-0]反=1.11...1
我们比较反码与补码的公式
[X]反=2-2-n+X
[X]补=2+X
可得到 [X]补=[X]反+2-n
8
若要一个负数变补码,其方法是符号位置1,其余各位0变1,1变 0,然后在最末位(2-n)上加1。
10100.10011=1.010010011*24 e=4 于是得到:S=0,E=4+127=131=10000011, M=010010011 最后得到32位浮点数的二进制存储格式为: 0100 0001 1010 0100 1100 0000 0000 0000=(41A4C000)164
基于FPGA的流水线珠算加法器设计

中图法分类号
T P 3 3 2 . 2 1 ;
文献标志码
B
加法运算是数 字信号处理 中最基本也是 最常
用 的一 种操作 , 加 法器 的性 能 对整 个 处 理 过程 的速 度和效 率 起 着 重 要 的影 响。 目前 常 用 的 提 高 加 法
器运算 速度 的途径 有 3种 。
设计 提 供 了更 高 的 计 算 性 能 , 并 具 有 深 入 研 究 的
理, 采用珠算算法设计 了一个流水结构 的并行高速硬件加法器; 并在 X i l i n x V i  ̄ e x — I I的 F P G A上实现 了设 计方 案。在 F P G A上
集成 8个处理单元完成并行计算 , 处理单元运用流水线结构 , 提 高运 算频率 ; 并 采用数据调 度模块解 决流水 线上“ 数 据相关”
发模块解决 “ 数据相关 ” 问题。实验结果表 明 , 本
2 0 1 3年 6月 1 8日收到 国家 自然科学基金 ( 6 0 3 7 2 0 5 8 , 6 0 7 7 2 1 0 1 ) 资助 第一作 者简介 : 王 悦, 硕士研究 生。研究方向 : 嵌入 式系统研究 与
变了原算盘档上算珠 的权值 , 采用上档 1 个权值 为 8的算珠 和下档 7个权 值 为 1的算 珠组 成 J 。由于 算盘结构 的变化 , 原有珠 算 口诀 已不适 用 于本设
本 文跳 出 现 代 数 学 对 可 解 析 性 的 一 味 追 求 ,
运算的精髓 , 算盘操作是根据适 当的珠算 口诀在当
前 档 向上或 向下拨 动若 干算 珠 , 当所 有档 的操 作都 执 行完后 , 算 盘盘 面上 即显 示运 算结果 。 1 . 2 珠 算 口诀设计
关于加法器
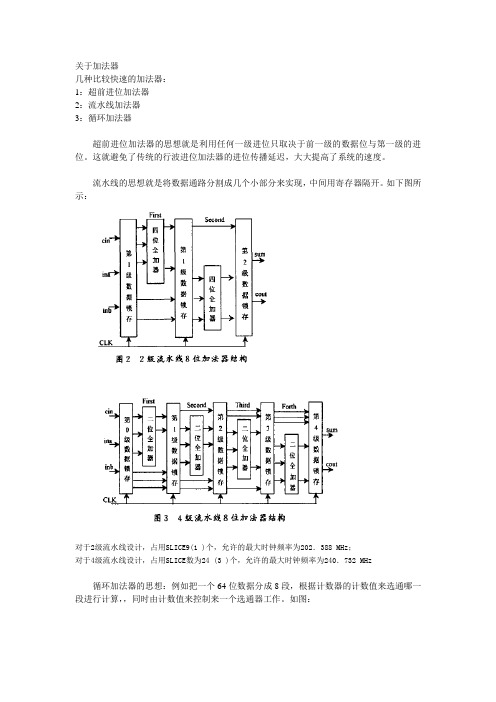
关于加法器几种比较快速的加法器:1:超前进位加法器2:流水线加法器3:循环加法器超前进位加法器的思想就是利用任何一级进位只取决于前一级的数据位与第一级的进位。
这就避免了传统的行波进位加法器的进位传播延迟,大大提高了系统的速度。
流水线的思想就是将数据通路分割成几个小部分来实现,中间用寄存器隔开。
如下图所示:对于2级流水线设计,占用SLICE9(1 )个,允许的最大时钟频率为202.388 MHz;对于4级流水线设计,占用SLICE数为24 (3 )个,允许的最大时钟频率为240.732 MHz循环加法器的思想:例如把一个64位数据分成8段,根据计数器的计数值来选通哪一段进行计算,,同时由计数值来控制来一个选通器工作。
如图:比较传统的方法是使用行波进位加法器,所谓行波就是进位像波浪一样一级一级往前推,这种方法的最大缺点是系统的速度取决于所加数的字长,字长越长速度越慢,既要传递的进位越多。
但是,针对具体的情况,这种方法的加法器也能比较快,能够满足大多数场合的需要。
例如,对于Virtex—E型FPGA,每一个Virtex—E的CLB包含2个SLICE,每个SLICE由2个LC构成,在每个SLICE中都有专用进位逻辑,从而为高速算术功能提供快速的算术进位能力。
算术逻辑中包括1个异或门,使每个LC单元可以实现一个1位全加器。
与传统的全加器相比,他在结构上有一些适当的调整,这样一方面缩短了进位传递的时间(约为组合逻辑输出的1O ),另一方面又可以在低级进位到达时,更快速地输出该位的和运算结果。
此外,在FPGA内部同一列的两个SLICE间,还专门为进位传递保留了一条最短连线。
正是基于这样的一种结构,Virtex—E器件可以实现快速的行波进位加法器。
基本电路实验

数字逻辑课程设计实验报告四位ALU1. 需求分析设计四位ALU 需要具有8种不同的操作,分别为:A 加B 、A 加B 加1、A 加1、A 减B 、A 减B 减1、A 减1、传送A 、传送B 。
操作数作为无符号数进行运算。
设计模块的输入信号为:四位操作数A0,A1,A2,A3,四位操作数B0,B1,B2,B3;操作码控制S0,S1,S2;模块输出信号为:四位结果F0,F1,F2,F3,进借位Cn 。
输入信号由拨动开关控制,输出信号送到指示灯。
电路必须用基本门电路搭建。
2. 设计原理操作数A 和B 依据操作码的不同实现不同的运算。
操作码的分配SO,S1,S2为:A 加B(000)、A 加B 加1(001)、A 加1(010)、A 减B(011)、A 减B 减1(100)、A 减1(101)、传送A(110)、传送B(111)。
所有的加减功能都可以通过全加器来实现,如果进行A 减B 就用A 加B 加1,其他的减法运算就类似算,就是要注意此时的进位标志Cn 要取反,因为116++=+-=-B A B A B A ,此时若A 大于等于B ,进位位必为1,如A 小于B ,进位位必为0,刚好与我们要的结果相反。
需要处理的情况有三种:A 减B (1++B A ),A 减B 减1(B A +),A 减1(15+A )。
当有运算需要加一时,我是通过在低位的全加器进位输入上加上1,使得在A 加B 加1(1++B A )、A 加1(1+A )、A 减B(1++B A )三种情况下有一个进位1从最低位输入,其他的情况下,此处的输入为0。
3. 设计总体框图及流程通过对输入信号(S0,S1,S2)的分析,控制输入A ,B 在各种情况下的输出,最终利用加法器完成必要的功能。
在设计过程中:首先是完成了A 处理逻辑(functiona )和B 处理逻辑(functionb)设计。
它们的输入是控制信号(SO,S1,S2)和A 或B 得每位。
8位4级流水线加法器verilog程序

8位4级流水线加法器verilog程序module adder8pip(cout,sum,cin,ina,inb,clk);input cin,clk;input[7:0] ina,inb;output cout;output[7:0] sum;reg cout,tempcin;reg[7:0] sum,tempa,tempb;reg firstco,secondco,thirdco; //前三级加法的进位输出reg[1:0] firstsum,thirdina,thirdinb;reg[3:0] secondsum,secondina,secondinb;reg[5:0] thirdsum,firstina,firstinb;always@ (posedge clk)begintempcin=cin;tempa=ina;tempb=inb;//输入数据缓存endalways@ (posedge clk)begin{firstco,firstsum}=tempa[1:0]+tempb[1:0]+tempcin;//第一级低2位相加firstina=tempa[7:2];firstinb=tempb[7:2];//未参加计算的数据缓存endalways@ (posedge clk)begin{secondco,secondsum}={firstina[1:0]+firstinb[1:0]+firstco,firstsum};//第二级2位相加,并与前一级结果合并secondina=firstina[5:2];secondinb=firstinb[5:2];//未参加计算的数据缓存endalways@ (posedge clk)begin{thirdco,thirdsum}={secondina[1:0]+secondinb[1:0]+secondco,secondsum};//第三级2位相加,并与前一级结果合并thirdina=secondina[3:2];thirdinb=secondinb[3:2];//未参加计算的数据缓存endalways@ (posedge clk)begin{cout,sum}={thirdina[1:0]+thirdinb[1:0]+thirdco,thirdsum};//第四级最高2位相加,并与前一级结果合并endendmodule综合之后发现如下警告:FF/Latch (without init value) has a constant value of 0 in block . This FF/Latch will be trimmed during the optimization process. 再看RTL电路图:果然cout被接地了。
一种基于FPGA的32位快速加法器设计

由此可 以看到先行进位加法器 的结 构由两部分组 成 ,进 位计算模块和本位和计算模块。由式 (7),容易求 出 8位先 行进位加法器的公式 ,得到内部 的设计结构如 图 1所示 。
1 4级流 水 线 结 构 的 32位 加 法 器
图 1 8位 先 行 进位 加 法 器 内部 设 计 结构
并 对 这 个 流 水线 结 构 进 行 了分 析改 进 ,设 计 了一 个 两 级 流水 线 结 构 的 32位加 法 器 。
关 键 词 :流水 线 ;an法 器 ;先 行 进位
中图 分 类号 :TP23
文 献 标 识 码 :A
文 章 编 号 :1006—0707(2011)07—0078—04
刘 昌锦 (1958一 ),男 ,教授 ,硕士生导师 ,主要从事通信与信息系统研究 。
岳伟 甲 ,等 :一 种基 于 FPGA 的 32位 快速 加 法器设计
79
器 平 均 每 个 系 统 时 钟 完 成 一 次 32位 加 运 算 ,但 是 系 统 的 延 时较 大 为 4个 系 统 时 钟 。不 能 满 足 对 于 转 换 速 度 要 求 较 高 的场合 。因此采用一种新的方式 ,综合 流水线技术 和先行进
第 32卷 第 7期 【自动化 技术 】
四 川 兵 工 学 报
2011年 7月
一 种 基 于 FPGA 的 32位 快 速 加 法 器 设 计
岳 伟 甲 ,刘 昌锦
(炮 兵 学 院 ,合 肥 230031)
摘要 :针对采用流水线结构设计的 32位 加法器系统延迟 时间长 的问题 ,设计 了一个 4级流水线结构 的 32位加法器 ,
2 对流水线结构 的改进
g +∑ (gl-m-l I I PJ) +c0 B
浮点运算流水线

浮点运算流水线计算机的流水处理过程同工厂中的流水装配线类似。
为了实现流水,首先必须把输入的任务分割为一系列的子任务,使各子任务能在流水线的各个阶段并发地执行。
将任务连续不断地输入流水线,从而实现了子任务的并行。
因此流水处理大幅度地改善了计算机的系统性能,是在计算机上实现时间并行性的一种非常经济的方法。
在流水线中,原则上要求各个阶段的处理时间都相同。
若某一阶段的处理时间较长,势必造成其他阶段的空转等待。
因此对子任务的划分,是决定流水线性能的一个关键因素,它取决于操作部分的效率、所期望的处理速度,以及成本价格等等。
假定作业T 被分成 k 个子任务,可表达为T={T1,T2,···,T k}各个子任务之间有一定的优先关系:若i<j,则必须在 T i完成以后,T j才能开始工作。
具有这种线性优先关系的流水线称为线性流水线。
线性流水线处理的硬件基本结构如图所示。
图中,处理一个子任务的过程为过程段(S i)。
线性流水线由一系列串联的过程段组成,各个过程之间设有高速的缓冲寄存器(L),以暂时保存上一过程子任务处理的结果。
在一个统一的时钟(C)控制下,数据从一个过程段流向相邻的过程段。
设过程段 S i所需的时间为τi,缓冲寄存器的延时为τl,线性流水线的时钟周期定义为(2.44)故流水线处理的频率为 f=1/τ。
在流水线处理中,当任务饱满时,任务源源不断的输入流水线,不论有多少级过程段,每隔一个时钟周期都能输出一个任务。
从理论上说,一个具有k 级过程段的流水线处理n 个任务需要的时钟周期数为(2.45)其中k个时钟周期用于处理第一个任务。
k个周期后,流水线被装满,剩余的n-1个任务只需n-1个周期就完成了。
如果用非流水线的硬件来处理这n个任务,时间上只能串行进行,则所需时钟周期数为T L=n·k(2.46)我们将T L和T k的比值定义为k级线性流水线的加速比:(2.47)当 n>>k 时, C k->k 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
module add_line (a,b,clk,out);
parameter width=16,
width1=8, //lsb
width2=8; //msb
// r3 r1 input [width-1:0] a; //a<=00010111_00000001
input [width-1:0] b; //b<=11111111_00000000
output [width:0] out; // r4 r2
input clk;
reg [width1-1:0] r1,r2,r5;
reg [width2-1:0] r3,r4,r6;
reg c1,c2;
reg [width:0] sum;
always @(posedge clk) //---first
begin
r1[width1-1:0]=a[width1-1:0]; //
r2[width1-1:0]=b[width1-1:0]; //
r3[width2-1:0]=a[width-1:width1];
r4[width2-1:0]=b[width-1:width1];
end
always @(posedge clk) //---- second
begin
{c1,r5}=r1+r2;
{c2,r6}=r3+r4+c1;
sum={c2,r5,r6};
end
assign out=sum;
endmodule
图Ⅰ
图Ⅱ
上图Ⅱ是没有assign out=sum;时的rtl级仿真结果;
错误1:Warning (10034): Output port "out[1]" at add_line.v(9) has no driver
原因:out没有驱动,out根本就没有用;
错误2:
永远有多远(1057978105) 10:43:30
这样不好有时序又有组合
永远有多远(1057978105) 10:46:04
最好把它都放在时序里面width改成width0
★(1003704680) 10:47:54
那个地方是时序,哪个地方是组合
永远有多远(1057978105) 10:48:17
always 时序assign组合
module add_line (a,b,clk,out);
parameter width=16,
width1=8, //lsb
width2=8; //msb
// r3 r1
input [width-1:0] a; //a<=00010111_00000001
input [width-1:0] b; //b<=11111111_00000000
output [width:0] out; // r4 r2
input clk;
reg [width1-1:0] r1,r2,r5;
reg [width2-1:0] r3,r4,r6;
reg c1,c2;
reg [width:0] out;
always @(posedge clk) //---first
begin
r1[width1-1:0]<=a[width1-1:0]; //
r2[width1-1:0]<=b[width1-1:0]; //
r3[width2-1:0]<=a[width-1:width1];
r4[width2-1:0]<=b[width-1:width1];
end
always @(posedge clk) //---- second
begin
{c1,r5}<=r1+r2;
{c2,r6}<=r3+r4+c1;
out<={c2,r5,r6};
end
endmodule
图Ⅲ
上图用阻塞赋值的rtl;
图Ⅳ
上图是用非阻塞赋值的rtl;
下图是用非阻塞赋值运算结果:有两个地方进位错误!第一个进位推迟一个时钟;
图Ⅴ
下图是用阻塞赋值结果:
图Ⅵ
错误原因:非阻塞赋值语句中,数值的转移须等到下一个时钟周期;
与组合逻辑的比较:
module add(a,b,sum);
input [15:0] a,b;
output [16:0] sum;
assign sum=a+b;
Endmodule
图Ⅶ
所谓流水线设计实际上就是把规模较大、层次较多的组合逻辑电路分为几个级,在每
一级插入寄存器组暂存中间数据。
K 级的流水线就是从组合逻辑的输入到输出恰好有K 个寄存器组(分为K 级,每一级都有一个寄存器组)上一级的输出是下一级的输入而又无反馈的电路。
图5.6 表示了如何将把组合逻辑设计转换为相同组合逻辑功能的流水线设计。
这个组合逻辑包括两级。
第一级的延迟是T1 和T3 两个延迟中的最大值;第二级的延迟等于T2 的延迟。
为了通过这个组合逻辑得到稳定的计算结果输出,需要等待的传播延迟为
[max(T1,T3)+T2]个时间单位。
在从输入到输出的每一级插入寄存器后,流水线设计的第一级寄存器所具有的总的延迟为T1 与T3 时延中的最大值加上寄存器的Tco(触发时间)。
同样,第二级寄存器延迟为T2 的时延加上Tco。
采用流水线设计为取得稳定的输出总体计
算周期为:
max(max(T1,T3)+Tco,(T2+Tco))
流水线设计需要两个时钟周期来获取第一个计算结果,而只需要一个时钟周期来获取随后的计算结果。
开始时用来获取第一个计算结果的两个时钟周期被称为采用流水线设计的首次延迟(latency)。
对于CPLD 来说,器件的延迟如T1、T2 和T3 相对于触发器的Tco 要长得多,并且寄存器的建立时间Tsu 也要比器件的延迟快得多。
只有在上述关于硬件时延的假设为真的情况下,流水线设计才能获得比同功能的组合逻辑设计更高的性能。
采用流水线设计的优势在于它能提高吞吐量(throughput)。
假设T1、T2 和T3 具有同样的传递延迟Tpd。
对于组合逻辑设计而言,总的延迟为2*Tpd。
对于流水线设计来说,计算周期为(Tpd+Tco)。
前面提及的首次延迟(latency)的概念实际上就是将(从输入到输出)最长的路径进行初始化所需要的时间总量;吞吐延迟则是执行一次重复性操作所需要的时间总量。
在组合逻辑设计中,首次延迟和吞吐延迟同为2*Tpd。
与之相比,在流水线设计中,首次延迟是2*(Tpd+Tco),而吞吐延迟是Tpd+Tco。
如果CPLD 硬件能提供快速的
Tco,则流水线设计相对于同样功能的组合逻辑设计能提供更大的吞吐量。
典型的富含寄存器资源的CPLD 器件(如Lattice 的ispLSI 8840)的Tpd 为8.5ns,Tco 为6ns。
流水线设计在性能上的提高是以消耗较多的寄存器资源为代价的。
对于非常简单的用于数据传输的组合逻辑设计,例如上述例子,将它们转换成流水线设计可能只需增加很少的寄存器单元。
随着组合逻辑变得复杂,为了保证中间的计算结果都在同一时钟周期内得到,必须在各级之间加入更多的寄存器。
如果需要在CPLD 中实现复杂的流水线设计,以获取更优良的性能,具有丰富寄存器资源的CPLD 结构并且具有可预测的延迟这两大特点的FPGA 是一个很有吸引力的选择。
