解三角形专项训练(经典题型)
完整版)高考解三角形大题(30道)

完整版)高考解三角形大题(30道)1.在三角形ABC中,已知内角A,B,C的对边分别为a,b,c,且有以下等式:frac{\cos A - 2\cos C}{2c-a} = \frac{\cos B b}{\sin C}$$求该等式右侧的值,以及:2)若$\cos B=\frac{1}{4}$,$b=2$,求三角形ABC的面积S。
2.在三角形ABC中,角A,B,C的对边分别为a,b,c,已知$\sin C+\cos C=1$,求:1)$\sin C$的值;2)若$a+b=4a-8$,求边c的值。
3.在三角形ABC中,角A,B,C的对边分别为a,b,c。
1)若$\sin(A+\frac{2}{3}\pi)=2\cos A$,求角A的值;2)若$\cos A=\frac{3}{c}$,求$\sin C$的值。
4.在三角形ABC中,D为边BC上的一点,且$BD=\frac{3}{3}$,$\sin B=\frac{5}{3}$,$\cos\angleADC=\frac{\sqrt{3}}{5}$,求AD。
5.在三角形ABC中,角A,B,C的对边分别为a,b,c,已知$a=1$,$b=2$,$\cos C=-\frac{1}{4}$,求:1)三角形ABC的周长;2)$\cos(A-C)$的值。
6.在三角形ABC中,角A,B,C的对边分别为a,b,c,已知$\sin A+\sin C=\frac{1}{2}\sin B$,且$ac=\frac{1}{2}b$。
1)求a,c的值;2)若角B为锐角,求p的取值范围,其中$p=\frac{1}{5}$,$b=1$。
7.在三角形ABC中,角A,B,C的对边分别为a,b,c,且$2a\sin A=(2b+c)\sin B+(2c+b)\sin C$。
1)求角A的值;2)求$\sin B+\sin C$的最大值。
8.在三角形ABC中,角A,B,C的对边分别为a,b,c,已知$\cos 2C=-\frac{1}{4}$。
解三角形练习题及答案

解三角形练习题及答案一、解三角形练习题1. 已知三角形ABC,AB=5cm,AC=8cm,BC=7cm,求角A的大小。
2. 已知三角形DEF,DE=6cm,EF=9cm,DF=12cm,求角D的大小。
3. 已知三角形GHI,GH=5cm,HI=5cm,GI=7cm,求角G的大小。
4. 已知三角形JKL,JK=8cm,KL=10cm,JL=12cm,求角K的大小。
5. 已知三角形MNO,MN=4cm,NO=6cm,MO=8cm,求角M的大小。
二、解三角形练习题答案1. 解题过程:根据已知条件,我们可以使用余弦定理来求解角A的大小。
余弦定理公式为:cos(A) = (b^2 + c^2 - a^2) / (2b*c)其中,a、b、c分别表示三角形对应边的长度。
代入已知条件可得: cos(A) = (7^2 + 8^2 - 5^2) / (2*7*8)= (49 + 64 - 25) / 112= 88 / 112≈ 0.786通过查表或计算器的反余弦函数,可以得到角A的近似值为38°。
2. 解题过程:同样利用余弦定理,我们可以求解角D的大小。
代入已知条件可得:cos(D) = (9^2 + 12^2 - 6^2) / (2*9*12)= (81 + 144 - 36) / 216= 189 / 216≈ 0.875通过反余弦函数,可以得到角D的近似值为 30°。
3. 解题过程:同理,利用余弦定理求解角G的大小。
代入已知条件可得:cos(G) = (5^2 + 7^2 - 5^2) / (2*5*7)= (25 + 49 - 25) / 70= 49 / 70≈ 0.7通过反余弦函数,可以得到角G的近似值为 45°。
4. 解题过程:利用余弦定理求解角K的大小。
代入已知条件可得:cos(K) = (10^2 + 12^2 - 8^2) / (2*10*12)= (100 + 144 - 64) / 240= 180 / 240= 3 / 4= 0.75通过反余弦函数,可以得到角K的近似值为 41.4°。
数学-2023年解三角形高频题型精选

解三角形高频题型精选1.(2023·全国·高一专题练习)△ABC 的内角A 、B 、C 的对边分别为a 、b 、c ,则下列说法不正确的是( )A .若A >B ,则sin A >sin BB .若A =30∘,b =4,a =3,则△ABC 有两解C .若△ABC 为钝角三角形,则a 2+b 2>c 2D .若三角形ABC 为斜三角形,则tan A +tan B +tan C =tan A tan B tan C2.(2019春·安徽芜湖·高一芜湖一中校考期中)在△ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,a =2,b =3,B =π3,那么A =( )A .3π4B .π4C .3π4或π4D .π33.(2020秋·陕西西安·高二西安建筑科技大学附属中学校联考期中)在△ABC 中,若∠A =60°,b =1,S △ABC =3,则a +b +c sin A +sin B +sin C的值为( )A .2633B .2393C .393D .13334.(2021春·河北·高三统考学业考试)在△ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c .若a =1,c =17,sin A =1717,则cos B =( )A .178B .14C .34D .17175.(2023·江西赣州·统考一模)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若a ,b ,c 成等差数列,C =2A +B ,则b a =( )A .75B .32C .53D .746.(2020秋·广东清远·高二校考期中)已知a ,b ,c 为△ABC 的三个内角A ,B ,C 所对的边,若3b cos C =c (1-3cos B ),则sin C ∶sin A =( )A .3∶1B .3∶2C .1∶3D .4∶37.(2023·河南郑州·统考一模)记△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知角C =π4,b sin π4+A -a sin π4+B =c ,则角B =( )A .π8B .π6C .5π8D .π38.(2023·河北·高三学业考试)在△ABC 中,a ,b ,c 分别为内角A ,B ,C 的对边,若a 2-b 2=3bc ,sin C =23sin B ,则A 等于( )A .5π6B .2π3C .π3D .π69.(2023春·江西赣州·高三统考阶段练习)在锐角△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .已知a =1,且b cos A -cos B =1,则3sin B +2sin 2A 的取值范围是( )A .0,3+1B .2,3+1C .1,3D .2,3 10.(2022秋·江西吉安·高二江西省吉水县第二中学校考开学考试)在△ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c ,且c =2a cos B ,则△ABC 的形状为( )A .等腰三角形B .直角三角形C .等腰直角三角形D .等腰三角形或直角三角形11.(2023秋·浙江宁波·高三期末)在△ABC 中,内角A ,B ,C 的对应边分别为a ,b ,c ,已知b sin (B +C )=a sinA +C 2,且△ABC 的面积为23,则△ABC 周长的最小值为( )A .22B .23C .62D .6+2312.(2023·陕西榆林·统考一模)△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,若a sin A +b +λa sin B =c sin C ,则λ的取值范围为( )A .-2,2B .0,2C .-2,2D .0,213.(2022·北京·统考模拟预测)已知△ABC 的三个内角A 、B 、C 所对的边分别为a 、b 、c ,且3a cos B =b sin A ,则B =( )A .π6B .π4C .π3D .π214.(2023秋·陕西西安·高二统考期末)在△ABC 中,内角A ,B ,C 所对的边为a ,b ,c ,若a =4,b =43,A =30°,则B =( )A .30°B .30°或150°C .60°D .60°或120°15.(2023·全国·高三专题练习)“奔驰定理”是平面向量中一个非常优美的结论,因为这个定理对应的图形与“奔驰”轿车(Mercedesbenz )的log o 很相似,故形象地称其为“奔驰定理”.奔驰定理:已知O 是△ABC 内的一点,△BOC ,△AOC ,△AOB 的面积分别为S A ,S B ,S C ,则有S A ⋅OA +S B ⋅OB +S C ⋅OC =0 .设O 是锐角△ABC 内的一点,∠BAC ,∠ABC ,∠ACB 分别是△ABC 的三个内角,以下命题不正确的有( )A .若OA +OB +OC =0 ,则O 为△ABC 的重心B .若OA +2OB +3OC =0 ,则S A :S B :S C =1:2:3C .若OA =OB =2,∠AOB =5π6,2OA +3OB +4OC =0 ,则S △ABC =92D .若O 为△ABC 的垂心,则tan ∠BAC ⋅OA +tan ∠ABC ⋅OB +tan ∠ACB ⋅OC =016.(2023·全国·高一专题练习)不解三角形,判断下列三角形解的个数.(1)a =5,b =4,A =120°;(2)a =9,b =10,A =60°;(3)b =72,c =50,C =135°.17.(山西省部分学校2023届高三下学期质量检测试题)已知a ,b ,c 分别为△ABC 三个内角A ,B ,C 的对边,c 1+cos B =3b sin C .(1)求角B 的大小;(2)若b =2,a +c =4,求△ABC 的面积.18.(河北省石家庄市2023届高三质量检测(一)数学试题)△ABC 的内角A ,B ,C 的对边长分别为a ,b ,c ,设a +bc -b =sin C +sin B sin A (1)求C ;(2)若3+1 a +2b =6c ,求sin A .19.(2023·湖南·模拟预测)在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,若b sin A =a cos B -π6 .(1)求角B 的大小;(2)若b =13.且a +c =5,求△ABC 的面积.20.(2023·福建福州·统考二模)记ΔABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知b 2-a 2=2c 2.(1)求tan B tan A的值:(2)求C 的最大值.21.(2023·云南昆明·高三昆明一中校考阶段练习)已知△ABC 的内角A ,B ,C 所对边分别为a ,b ,c ,且sin A =3a 2+c 2-b 2 2bc .(1)求B 的大小;(2)若△ABC 为钝角三角形,且b =3,求△ABC 的周长的取值范围.22.(2023·湖北·统考模拟预测)记△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知2b cos C =2a +c .(1)求B ;(2)设b =9,若点M 是边AC 上一点,2AM =MC ,且∠MAB =∠MB A ,求△BMC 的面积.23.(2023春·四川资阳·高三四川省乐至中学校考开学考试)在△ABC 中,内角A 、B 、C 满足sin 2A =sin 2B +sin 2C -2sin B sin C .(1)求A ;(2)若AB 边上的高等于13AB ,求cos C .24.(2023春·浙江温州·高三统考开学考试)记△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知b cos C +3b sin C a +c=1.(1)求B ;(2)若a +c =43,△ABC 内切圆的面积为π,求△ABC 的面积.25.(2023·全国·高三专题练习)已知△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,b =3,a <c ,且sin π3-Acos π6+A =14.(1)求A 的大小;(2)若a sin A +c sin C =43sin B ,求△ABC 的面积.26.(2023·山东临沂·统考一模)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,已知a cos B +b cos A =2c cos C .(1)求C ;(2)若c =1,求△ABC 面积的取值范围.27.(2023春·湖南长沙·高三雅礼中学校考阶段练习)已知△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且2sin C -sin B =tan A cos B .(1)求A ;(2)若a =2,求2c -b 的取值范围.28.(2023·河南·高三信阳高中校联考阶段练习)已知△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,若2a sin C =ctan A .(1)求角A 的大小;(2)若a =2,D 为BC 的中点,求线段AD 长度的最大值.29.(2023春·湖北武汉·高三华中师大一附中校考阶段练习)在锐角△ABC 中,角A ,B ,C 所对的边分别是a ,b ,c ,满足c 2=b b +a .(1)求证:C =2B ;(2)求1tan B -1tan C+3sin C 的取值范围.30.(2021春·四川成都·高一四川省成都市盐道街中学校考阶段练习)在△ABC 中,三个内角A ,B ,C 的对边分别为a ,b ,c ,b =2sin B ,tan A +tan C =2sin B cos A.(1)求角C 和边c 的大小.(2)求△ABC 周长的范围.31.(2023秋·浙江绍兴·高三期末)记锐角△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,△ABC 外接圆的半径为R ,已知a cos B -b cos A =R .(1)若B =π4,求A 的值;(2)求R -c b 的取值范围.32.(2023春·湖北·高三统考阶段练习)已知a ,b ,c 分别为锐角△ABC 三个内角A ,B ,C 的对边,且m =a ,2b -c ,n =cos A ,cos C ,且m ⎳n.(1)求角A 的大小;(2)求b c的取值范围.33.(2023春·河北石家庄·高三石家庄二中校考阶段练习)已知△ABC 内角A ,B ,C 所对的边分别为a ,b ,c ,面积为23,且3b 2+c 2-a 2 =2ac sin B ,求:(1)求角A 的大小;(2)求BC 边中线AD 长的最小值.34.(2020春·陕西西安·高二交大附中分校校考阶段练习)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且满足ctan C =3a cos B +b cos A .(1)求角C 的大小.(2)若c =43,求△ABC 面积的最大值.35.(2022秋·云南昆明·高二昆明市第三中学校考阶段练习)在△ABC中,角A,B,C 的对边分别为a,b,c,且2c-a=2b cos A.(1)求角B的大小;(2)若b=2,求△ABC周长l的取值范围.36.(2023·全国·校联考一模)在△ABC中,角A,B,C所对的边分别为a,b,c,c2+ ac=b2.(1)证明:B=2C;(2)求a+bc的取值范围.37.(2019春·安徽芜湖·高一芜湖一中校考期中)设△ABC的内角A,B,C的对边分别为a,b,c,a=b tan A,且B为钝角.(1)证明:B-A=π2;(2)求sin A+sin C的取值范围.38.(2023·全国·高三专题练习)已知函数f(x)=cos2(ωx)+3sin(ωx)cos(ωx)-12,其中ω>0,且函数f(x)的两个相邻零点间的距离为π2,(1)求ω的值及函数f(x)的对称轴方程;(2)在△ABC中,a,b,c分别是角A,B,C的对边,若f(A)=-1,a=3,求△ABC 周长的取值范围.39.(2023秋·陕西汉中·高二统考期末)在①a sin C-sin Asin C+sin B=c-b;②sin2A+sin2C-sin2B=sin A sin C;③2a-cb=cos Ccos B.这三个条件中任选一个,补充在下面的问题中并作答.在△ABC中,内角A,B,C所对的边分别是a,b,c,__________.(1)求B;(2)若b=4,求△ABC的周长的取值范围.40.(2023·辽宁沈阳·统考一模)在△ABC中,角A、B、C的对边分别为a、b、c.已知sin A+3cos A=0.(1)求角A的大小;(2)给出以下三个条件:①a=43,b=4;②b2-a2+c2+10b=0;③S△ABC= 153.若这三个条件中仅有两个正确,请选出正确的条件并回答下面问题:(i)求sin B的值;(ii)∠BAC的角平分线交BC于点D,求AD的长.参考答案:1.C【分析】根据正弦定理、余弦定理、三角恒等变换的知识对选项进行分析,从而确定正确答案.【详解】对于A 选项,若A >B ,则a >b ,由正弦定理可得2R sin A >2R sin B ,所以,sin A >sin B ,故A 选项正确;对于B 选项,b sin A =4sin30∘=2,则b sin A <a <b ,如图:所以△ABC 有两解,B 选项正确;对于C 选项,若△ABC 为钝角三角形且C 为钝角,则cos C =a 2+b 2-c 22ab<0,可得a 2+b 2<c 2,C 选项错误;对于D ,因为tan (B +C )=tan B +tan C 1-tan B tan C,所以tan B +tan C =tan (B +C )(1-tan B tan C )因为tan B +C =tan π-A =-tan A ,所以tan B +tan C =tan (B +C )(1-tan B tan C )=tan A tan B tan C -tan A ,所以tan A +tan B +tan C =tan A tan B tan C ,所以D 正确.故选:C2.B【分析】利用正弦定理可求出sin A ,再结合大边对大角即可得解.【详解】因为a =2,b =3,B =π3,由正弦定理a sin A=b sin B ,可得sin A =a sin B b =2sin π33=22,又因为a <b ,所以A <B ,故0<A <π3,所以A =π4.故选:B .3.B 【分析】根据三角形面积公式可得c =4,再由余弦定理计算可得a =13,根据正弦定理可知a +b +c sin A +sin B +sin C =a sin A,代入计算即可得出结果.【详解】根据三角形面积公式可得S △ABC =12bc sin A =12×32c =3,即c =4;由余弦定理可知a 2=b 2+c 2-2bc cos A =1+16-2×1×4×12=13,可得a =13;由正弦定理可得a +b +c sin A +sin B +sin C =a sin A =1332=2393.答案第1页,共2页4.D【分析】利用正弦定理求得sin C ,再利用诱导公式求解即可.【详解】由正弦定理可得a sin A=csin C ,即11717=17sin C ,解得sin C =1,因为△ABC 中C ∈0,π ,所以C =π2,所以B =π2-A ,cos B =cos π2-A=sin A =1717,故选:D 5.C【分析】根据题意和等差数列等差中项的应用可得C =2π3、2b =a +c ,利用余弦定理化简计算即可求解.【详解】由C =2A +B ,A +B +C =π,得C =2π3,由a ,b ,c 成等差数列,得2b =a +c ,由余弦定理,得cos C =a 2+b 2-c 22ab,即-12=a 2+b 2-(2b -a )22ab ,整理,得5ab -3b 2=0,由b ≠0得5a -3b =0,由a ≠0得ba =53.故选:C .6.A【分析】利用正弦定理及三角恒等变换即可求解.【详解】由正弦定理得3sin B cos C =sin C (1-3cos B ),即3sin B cos C +3sin C cos B =sin C ,3sin B +C =sin C ,∵A +B +C =π,∴3sin π-A =sin C ,即3sin A =sin C ,sin Csin A=3,故选:A .7.C【分析】先由正弦定理把边转化为角,再展开化简求得B 与A 的关系,进一步计算得出结果.【详解】已知角C =π4,b sin π4+A -a sin π4+B =c ,由正弦定理可得sin B sin π4+A -sin A sin π4+B =sin C ,整理得22sin B cos A -sin A cos B =22,即sin B -A =1,因为A ,B ∈0,3π4 ,所以B -A ∈-3π4,3π4 ,所以B -A =π2.又B +A =3π4,所以B =5π8.8.D【分析】根据正弦定理把sin C=23sin B化为c=23b,再结合余弦定理求角即可【详解】∵sin C=23sin B,∴c=23b,结合a2-b2=3bc即可求得a=7b.由余弦定理可得cos A=b2+c2-a22bc=b2+12b2-7b22×b×23b=32.又∵A∈0,π,∴A=π6.故选:D 9.B【分析】由正弦定理边化角可得B=2A,由△ABC为锐角三角形可得π6<A<π4,运用降次公式及辅助角公式将问题转化为求三角函数y=2sin2A-π6+1在π6,π4上的值域.【详解】∵b cos A-cos B=1,即:b cos A=cos B+1,a=1,∴b cos A=(cos B+1)a,∴由正弦定理得:sin B cos A=(cos B+1)sin A,即:sin B cos A=sin A cos B+sin A,∴sin(B-A)=sin A,∴B-A=A或B-A+A=π,解得:B=2A或B=π(舍),又∵△ABC为锐角三角形,则C=π-A-B=π-3A,∴0<A<π20<B<π20<C<π2⇒0<A<π20<2A<π20<π-3A<π2,解得:π6<A<π4,∴3sin B+2sin2A=3sin2A+1-cos2A=2sin2A-π6+1,又∵π6<A<π4,∴π6<2A-π6<π3,∴12<sin2A-π6<32,∴2<2sin2A-π6+1<3+1,即3sin B+2sin2A的取值范围(2,3+1).故选:B.10.A【分析】已知条件用正弦定理边化角,由sin C=sin A+B展开后化简得tan A=tan B,可得出等腰三角形的结论.【详解】c=2a cos B,由正弦定理,得sin C=sin A+B=2sin A cos B,即sin A cos B+cos A sin B=2sin A cos B,∴sin A cos B=cos A sin B,可得tan A=tan B,又0<A<π,0<B<π,∴A=B,则△ABC的形状为等腰三角形.故选:A.11.C【分析】首先利用正弦定理及诱导公式,二倍角公式对原式化简得sin B2=12,即求出B的大小,再利用三角形面积公式得ac=8,从而求出a+c的最小值,最后得到C△ABC=(a+c) +(a+c)2-24,利用函数单调性即可求出其最小值.【详解】因为b sin A=a sin π-B 2,根据正弦定理及诱导公式得sin B⋅sin A=sin A⋅cos B 2,∵A∈0,π,∴sin A≠0,∴sin B=cos B 2,即2sin B2cosB2=cosB2,∵B∈0,π,则B2∈0,π2,则cos B2≠0解得sin B2=12,所以B2=π6⇒B=π3,所以S=12ac sin B=3ac4=23,所以ac=8,a+c≥2ac=42,当且仅当a=c=22时等号成立,根据余弦定理得b=a2+c2-2ac cos B,即b=a2+c2-ac,设△ABC的周长为C,所以C△ABC=a+c+(a+c)2-3ac=(a+c)+(a+c)2-24,设a+c=t,t≥42,则f t =t+t2-24,根据复合函数单调性及增函数加增函数为增函数的结论得:f t 在42,+∞上为单调增函数,故f t min=f42=62,故C△ABCmin=62,当且仅当a=b=c=22时取等.故选:C.12.A【分析】根据正弦、余弦定理可得λ=-2cos C,结合C∈0,π即可求解.【详解】因为a sin A+b+λasin B=c sin C,由正弦定理得c2=a2+b2+λab.又c2= a2+b2-2ab cos C,所以λ=-2cos C.因为C∈0,π,所以cos C∈-1,1,故λ∈-2,2.故选:A.13.C【分析】由正弦定理化简得出tan B的值,结合角B的取值范围可求得角B的值.【详解】因为3a cos B=b sin A,由正弦定理可得3sin A cos B=sin B sin A,∵A、B∈0,π,则sin A>0,所以,3cos B=sin B>0,所以,tan B =3,故B =π3.故选:C .14.D【分析】根据a =4,b =43,A =30°,利用正弦定理求解.【详解】解:在△ABC 中,a =4,b =43,A =30°,由正弦定理得a sin A=bsin B ,所以sin B =b ⋅sin A a =43⋅sin30∘4=32,所以B =60°或120°,故选:D 15.C【分析】对于A ,假设D 为AB 的中点,连接OD ,由已知得O 在中线CD 上,同理可得O 在其它中线上,即可判断;对于选项B ,利用奔驰定理可直接得出B 正确;对于C ,根据奔驰定理可得S A :S B :S C =2:3:4,再利用三角形面积公式可求得S C =1,即可计算出S △ABC =94,可得C 错误;选项D ,由垂心的性质、向量数量积的运算律OB ∙AC =OB ∙OC -OB ∙OA=0,得到OA :OB :OC=cos ∠BAC :cos ∠ABC :cos ∠BCA ,结合三角形面积公式及角的互补关系得结论.【详解】对于A :如下图所示,假设D 为AB 的中点,连接OD ,则OA +OB =2OD =CO,故C ,O ,D 共线,即O 在中线CD 上,同理可得O 在另外两边BC ,AC 的中线上,故O 为△ABC 的重心,即A 正确;对于B :由奔驰定理O 是△ABC 内的一点,△BOC ,△AOC ,△AOB 的面积分别为S A ,S B ,S C ,则有S A ⋅OA +S B ⋅OB +S C ⋅OC=0可知,若OA +2OB +3OC =0,可得S A :S B :S C =1:2:3,即B 正确;对于C :由|OA |=|OB|=2,∠AOB =5π6可知,S C =12×2×2×sin 5π6=1,又2OA +3OB +4OC =0 ,所以S A :S B :S C =2:3:4由S C =1可得,S A =12,S B =34;所以S △ABC =S A +S B +S C =12+34+1=94,即C 错误;对于D :由四边形内角和可知,∠BOC +∠BAC =π,则OB ∙OC=OB OCcos ∠BOC =-OB OC cos ∠BAC ,同理,OB ∙OA =OB OA cos ∠BOA =-OB OAcos ∠BCA ,因为O 为△ABC 的垂心,则OB ∙AC =OB ∙(OC -OA )=OB ∙OC -OB ∙OA=0,所以OC cos ∠BAC =OA cos ∠BCA ,同理得OC cos ∠ABC =OB cos ∠BCA ,OA cos ∠ABC =OB cos ∠BAC ,则OA :OB :OC=cos ∠BAC :cos ∠ABC :cos ∠BCA ,令OA =m cos ∠BAC ,OB =m cos ∠ABC ,OC=m cos ∠BCA ,由S A =12OB OCsin ∠BOC ,则S A =12OB OC sin ∠BAC =m 22cos ∠ABC cos ∠BCA sin ∠BAC ,同理:S B =12OAOC sin ∠ABC =m 22cos ∠BAC cos ∠BCA sin ∠ABC ,S C =12OA OB sin ∠BCA =m 22cos ∠BAC cos ∠ABC sin ∠BCA ,综上,S A :S B :S C =sin ∠BAC cos ∠BAC :sin ∠ABC cos ∠ABC :sin ∠BCAcos ∠BCA=tan ∠BAC :tan ∠ABC :tan ∠BCA ,根据奔驰定理得tan ∠BAC ⋅OA +tan ∠ABC ⋅OB +tan ∠ACB ⋅OC =0,即D 正确.故选:C【点睛】关键点点睛:利用向量数量积定义、运算律和垂心性质得到向量模的比例,结合三角形面积公式和奔驰定理判断结论即可.16.(1)一解(2)两解(3)无解【分析】使用正弦定理、正弦函数的性质及三角形内角和、大边对大角等知识进行判断即可.【详解】(1)由正弦定理a sin A=bsin B ,∴sin B =b a sin A =45×32<32,∵A =120°,∴B =180°-A +C =60°-C <60°,∴B 只有一解,三角形解的个数为一解.(2)由正弦定理a sin A=bsin B ,∴sin B =b a sin A =109×32=539,∴32<sin B <1,∵A =60°,a <b ,∴60°<B <120°,∴B 有两解,三角形解的个数为两解.(3)∵b >c ,∴B >C =135°,∴B +C >270°,∴B 无解,三角形无解.17.(1)B =π3(2)3【分析】(1)利用正弦定理化边为角,再结合辅助角公式即可得解;(2)利用余弦定理求得ac ,再根据三角形的面积公式即可得解.【详解】(1)因为c 1+cos B =3b sin C ,所以sin C 1+cos B =3sin B sin C ,因为C ∈0,π ,所以sin C ≠0,所以1+cos B =3sin B ,得2sin B -π6 =1,即sin B -π6 =12,因为B ∈0,π ,所以B -π6∈-π6,5π6,所以B -π6=π6,所以B =π3;(2)由余弦定理得b 2=a 2+c 2-2ac cos B =a +c 2-3ac =16-3ac ,即22=16-3ac ,解得ac =4,所以S △ABC =12ac sin B =12×4×32=3.18.(1)2π3(2)sin A =6-24【分析】(1)利用正弦定理边角互化结合余弦定理求解即可;(2)利用正弦定理边角互化结合三角恒等变换求解即可.【详解】(1)根据题意,由正弦定理可得a +bc -b=c +b a ,即c 2=a 2+b 2+ab ,所以根据余弦定理cos C =a 2+b 2-c 22ab=-12及△ABC 中C ∈0,π 可得C =2π3.(2)根据题意,由正弦定理可得3+1 sin A +2sin B =6sin C ,所以3+1 sin A +2sin A +2π3 =3+1 sin A +2-12sin A +32cos A =3sin A +cos A =322,解得sin A +cos A =62①,因为sin 2A +cos 2A =1②,①②联立可解得sin A =6+24或6-24,又因为C =2π3,则A <π3,sin 2A <34,6+242=2+34>34(舍去),所以sin A=6-2 4.19.(1)B=π3(2)S△ABC=3【分析】(1)由正弦定理和两角差的余弦公式,化简已知等式,求得tan B,可求角B的大小;(2)由已知条件利用余弦定理求得ac,根据三角形面积公式求△ABC的面积.【详解】(1)在△ABC中,由正弦定理asin A=bsin B,可得b sin A=a sin B,又由b sin A=a cos B-π6,得a sin B=a cos B-π6即sin B=cos B-π6,由sin B=cos B-π6=32cos B+12sin B,有32cos B=12sin B可得tan B=3,又因为B∈(0,π),所以B=π3.(2)b=13.且a+c=5,B=π3,由余弦定理:b2=a2+c2-2ac cos B=a+c2-2ac-2ac cos B,有13=25-2ac-ac,解得ac=4,∴S△ABC=12ac sin B=12×4×32=3.20.(1)tan Btan A=-3(2)π6【分析】(1)通过余弦定理、正弦定理将条件中的边转化为角即可求出结果;(2)由余弦定理表示出cos C,借助条件消去边c,利用基本不等式求出cos C的范围,进而求出C的最大值.【详解】(1)由余弦定理可得b2=c2+a2-2ac cos B,代入b2-a2=2c2,得到c2+a2-2ac cos B-a2=2c2,化简得c2+2ac cos B=0,即c+2a cos B=0.由正弦定理可得sin C+2sin A cos B=0,即sin A+B+2sin A cos B=0,展开得sin A cos B+cos A sin B+2sin A cos B= 0,即3sin A cos B=-cos A sin B,所以tan Btan A=-3.(2)由b2-a2=2c2得c2=b2-a2 2,故cos C=a2+b2-c22ab=a2+b2-b2-a222ab=3a2+b24ab=3a4b+b4a≥2316=32,当且仅当b2=3a2,即b=3a时等号成立.因为C ∈0,π ,所以C ≤π6,所以C 的最大值为π6.21.(1)π3(2)23,3+3【分析】(1)根据正余弦定理,将条件变形,求角B 的大小;(2)根据正弦定理,将周长表示为三角函数,根据函数的定义域,求周长的取值范围.【详解】(1)根据余弦定理可知,a 2+c 2-b 22ac=cos B ,所以sin A =3⋅2ac cos B 2bc ,即sin A =3a cos Bb⇔sin A =3sin A cos Bsin B,则tan B =3,B ∈0,π ,所以B =π3;(2)设∠A ∈π2,2π3,根据正弦定理可知a sin A =c sin C =b sin B =3sinπ3=2,所以a =2sin A ,c =2sin C =2sin 2π3-A ,所以周长a +b +c =2sin A +2sin 2π3-A +3=2sin A +232cos A +12sin A+3=3sin A +3cos A +3=23sin A +π6 +3,因为A ∈π2,2π3 ,A +π6∈2π3,5π6 ,所以sin A +π6 ∈12,32 ,所以23<23sin A +π6 +3<3+3,所以△ABC 的周长为23,3+3 .22.(1)B =2π3(2)932【详解】(1)依题意,由2b cos C =2a +c 及正弦定理得2sin B cos C =2sin A +sin C ,即2sin B cos C =2sin B +C +sin C =2sin B cos C +2cos B sin C +sin C ,所以2cos B sin C =-sin C .因为C ∈0,π ,所以sin C ≠0,所以cos B =-12,又B ∈0,π ,所以B =2π3.(2)如图所示:因为2AM =MC,所以AM =3,MC =6.又∠MAB =∠MB A ,所以BM =AM =3.在△ABC 中,由余弦定理得b 2=a 2+c 2-2ac cos B ,即a 2+c 2+ac =81.①又2AM =MC ,所以BM=23BA +13BC,两边平方得BM 2=49BA 2+19BC 2+49BA ⋅BC,即9=49c 2+19a 2+49ac cos B ,所以a 2+4c 2-2ac =81.②②-①得3c 2=3ac ,所以a =c ,代入①得a =c =33,在△BMC 中,BM 2+BC 2=32+33 2=36=MC 2,所以△BMC 是以∠MB C 为直角的三角形,所以△BMC 的面积为12×3×33=932.23.(1)A =π4(2)-1010【分析】(1)利用正弦定理及余弦定理可求得cos A 的值,结合角A 的取值范围可求得角A 的值;(2)由三角形的面积公式可得出c 2=3ab sin C ,利用正弦定理以及两角和的正弦公式可得出sin C =-3cos C ,由同角三角函数的平方关系以及sin C >0可求得cos C 的值.【详解】(1)解:因为sin 2A =sin 2B +sin 2C -2sin B sin C ,令△ABC 的三内角A ,B ,C 所对的边分别为a ,b ,c ,所以由正弦定理可得a 2=b 2+c 2-2bc ,所以由余弦定理可得cos A =b 2+c 2-a 22bc =2bc 2bc=22,因为A ∈0,π ,所以A =π4.(2)由三角形的面积公式可得S △ABC =12ab sin C =12×13c 2,则c 2=3ab sin C ,由正弦定理可得sin 2C =3sin A sin B sin C ,因为C ∈0,π ,则sin C >0,所以,sin C =3sin A sin B ,即sin C =322sin B ,即sin C =322sin C +π4 =32sin C +32cos C ,整理可得sin C =-3cos C ,所以,sin C =-3cos Csin 2C +cos 2C =0sin C >0,解得cos C =-1010.24.(1)π3(2)33【分析】(1)利用正弦定理边化角结合三角恒等变换求解;(2)利用等面积法可得12ac sin B =12(a +b +c )r ,从而得32ac =43+b ,再根据余弦定理,联立方程组求出b =23,从而可求三角形的面积.【详解】(1)因为b cos C +3b sin Ca +c=1,所以b cos C +3b sin C -a -c =0,所以sin B cos C +3sin B sin C -sin A -sin C =0因为A +B +C =π,所以sin B cos C +3sin B sin C -sin (B +C )-sin C =0.所以3sin B sin C -cos B sin C -sin C =0,又因为C ∈0,π ,sin C >0,所以3sin B -cos B =1,所以sin B -π6 =12,因为B ∈0,π ,所以B -π6∈-π6,5π6 ,所以B -π6=π6,所以B =π3.(2)因为△ABC 内切圆的面积为π,所以内切圆半径r =1.由于S △ABC =12ac sin B =12(a +b +c )r ,所以32ac =43+b ,①由余弦定理b 2=a 2+c 2-2ac cos B 得,b 2=a +c 2-3ac ,即b 2=48-3ac ,②联立①②可得b 2=48-38+233b,即b 2+23b -24=0,解得b =23或b =-43(舍去),所以S △ABC =12(a +b +c )×r =33.25.(1)A =π6(2)334【分析】(1)已知等式利用诱导公式和倍角公式化简,可求A 的大小;(2)条件中的等式,利用正弦定理角化边,再用余弦定理求得c 边,用面积公式计算面积.【详解】(1)sin π3-Acos π6+A =cos π2-π3-A cos π6+A =cos 2π6+A =cos π3+2A +12=14,∴cos π3+2A =-12,因为0<A <π,得π3<π3+2A <7π3,所以π3+2A =2π3或π3+2A =4π3,解得A =π6或A =π2,因为a <c ,得A <π2,∴A =π6.(2)由(1)知,A =π6,a sin A +c sin C =43sin B ,由正弦定理,得a 2+c 2=43b =12,由余弦定理,得a 2=b 2+c 2-2bc ⋅cos A ,即12-c 2=3+c 2-23c ⋅32,整理,得2c 2-3c -9=0,由c >0得c =3,所以S △ABC =12bc sin A =12×3×3×12=334.26.(1)C =π3;(2)0,34.【分析】(1)利用正弦定理边化角,再利用和角的正弦化简作答.(2)由(1)的结论,利用余弦定理结合均值不等式求出三角形面积范围作答.【详解】(1)在△ABC 中,由已知及正弦定理得:sin A cos B +sin B cos A =2sin C cos C ,即有sin A +B =2sin C cos C ,即sin C =2sin C cos C ,而0<C <π,sin C >0,则cos C =12,所以C =π3.(2)在△ABC 中,由余弦定理c 2=a 2+b 2-2ab cos C 得:1=a 2+b 2-ab ,因此1≥2ab -ab ,即0<ab ≤1,当且仅当a =b 时取等号,又S △ABC =12ab sin C =12×32ab =34ab ∈0,34 ,所以△ABC 面积的取值范围是0,34.27.(1)A =π3(2)-2,4 【分析】(1)利用同角三角函数的商数关系及两角和的正弦公式的逆用,结合三角形的内角和定理及三角函数的特殊值对应特殊角注意角的范围即可;(2)利用同角三角函数的商数关系及正弦定理的边化角,根据(1)的结论得出角B 的范围及余弦函数的性质即可求解.【详解】(1)由题意知,2sin C -sin B =sin A cos A×cos B ,所以2cos A sin C -cos A sin B =sin A cos B ,则2cos A sin C =sin A cos B +cos A sin B =sin A +B =sin C ,又C ∈0,π ,所以sin C ≠0,所以cos A =12,又A ∈0,π ,所以A =π3.(2)由(1)得2sin C -sin B =sin A cos A ×cos B ,由正弦定理得2c -b =a cos B cos A ,又a =2,A =π3,所以2c -b =4cos B .因为B ∈0,2π3,所以cos B ∈-12,1 ,所以4cos B ∈-2,4 ,故2c -b ∈-2,4 ,即2c -b 的取值范围为-2,4 .28.(1)A =π4(2)2+1【分析】(1)利用正弦定理求得正确答案.(2)利用圆的几何性质求得AD 的最大值.【详解】(1)依题意,2a sin C =ctan A ,由正弦定理得2sin A sin C =sin C ⋅sin A cos A,由于A ,C 是三角形的内角,所以sin A >0,sin C >0,所以cos A =22,则A 为锐角,所以A =π4.(2)设三角形ABC 外接圆的半径为r ,圆心为O ,则2r =2sin π4=22,r =2,由于A =π4,所以A 在三角形ABC 外接圆上运动,且只在优弧BC (不包括端点)上运动,如图所示,则∠BOC =π2,OD =2 2-12=1,当A ,O ,D 三点共线时,AD 最大,所以AD 长度的最大值是2+1.29.(1)证明见解析(2)1336,4【分析】(1)利用正余弦定理化简得sin A =sin B 2cos c +1 ,再利用两角和差的正弦公式及三角形的性质得sin C -B =sin B ,得证;(2)弦切互化转化为正弦复合函数,先求角C 的范围,然后换元,利用函数单调性求范围.【详解】(1)由c 2=b 2+ab 及余弦定理c 2=a 2+b 2-2ab cos C得a =b 2cos C +1 ,由正弦定理得:sin A =sin B 2cos C +1 ,又A +B +C =π,∴sin A =sin B +C =sin B cos C +cos B ⋅sin C =2sin B cos C +sin B ,∴cos B sin C -sin B cos C =sin B ,∴sin C -B =sin B ,∵A ,B ,C 都是锐角,∴C -B =B ,即C =2B .(2)令y =1tan B -1tan C +3sin C =cos B sin B -cos C sin C+3sin C =sin C cos B -cos C ⋅sin B sin B ⋅sin C +3sin C =sin C -B sin B ⋅sin C +3sin C ,由(1)C =2B 得y =1sin C +3sin C ,在锐角三角形ABC 中,0<A <π20<B <π20<C <π2 ,即0<π-B +C <π20<B =C 2<π20<C <π2,解得π3<C <π2,∴sin C ∈32,1,令t =sin C ∈32,1 ,∴y =f t =1t +3t ,t ∈32,1,又函数y =f t =1t +3t 在32,1上单调递增,∴y =f t ∈1336,4 ,故1tan B -1tan C+3sin C 的取值范围是1336,4 .30.(1)c =62,C =π3(2)6,362【分析】(1)由三角恒等变换化简等式tan A +tan C =2sin B cos A ,结合角的范围可得C ,再由正弦定理及b =2sin B 求得c ;(2)结合正弦定理有a +b +c =2sin A +sin B +62,结合角的关系及三角恒等变换化简求范围即可.【详解】(1)2sin B cos A=tan A +tan C =sin A cos A +sin C cos C =sin A cos C +cos A sin C cos A cos C =sin A +C cos A cos C =sin π-B cos A cos C =sin B cos A cos C ,∵A 、B 、C ∈0,π ,sin B cos A≠0,∴cos C =12,∴C =π3.由b =2sin B 及正弦定理得2=b sin B =c sin C ⇒c =2sin C =62;(2)由正弦定理得a sin A =b sin B =2⇒a =2sin A ,∴a +b =2sin A +sin B =2sin 2π3-B +sin B=232cos B +32sin B =612cos B +32sin B =6sin B +π6.∵B ∈0,2π3 ,∴B +π6∈π6,5π6 ,∴a +b =6sin B +π6∈62,6 .∴△ABC 周长a +b +c ∈6,362.31.(1)A =5π12(2)(-1,0)【分析】(1)已知等式由正弦定理边化角解得A -B =π6,又B =π4,可求A 的值;(2)锐角△ABC 且A -B =π6,可求角B 的范围,利用正弦定理边化角得R -c b =2sin B -π3 ,可求取值范围.【详解】(1)根据正弦定理a sin A=b sin B =c sin C =2R ,有a =2R sin A ,b =2R sin B ,c =2R sin C ,由a cos B -b cos A =R ,有2R sin A cos B -2R sin B cos A =R ,得sin (A -B )=12,因为A ,B ∈0,π2 ,所以A -B ∈-π2,π2 ,所以A -B =π6,由B =π4,解得A =5π12.(2)因为A =π6+B ,所以C =π-(A +B )=5π6-2B ,因为0<A <π20<B <π20<C <π2 ,即0<π6+B <π20<B <π20<5π6-2B <π2 ,所以B ∈π6,π3 ,则R -c b=R -2R sin C 2R sin B =1-2sin C 2sin B =1-2sin 5π6-2B 2sin B =1-cos2B -3sin2B 2sin B=2sin 2B -23sin B cos B 2sin B =sin B -3cos B =2sin B -π3 ,B ∈π6,π3 ,有B -π3∈-π6,0 ,所以2sin B -π3 ∈(-1,0),所以R -c b 的取值范围为(-1,0).32.(1)A =π3(2)12,2 【分析】(1)根据向量平行和正弦定理得cos A =12,则得到A 的大小;(2)首先根据锐角三角形求出C 的范围,再利用正弦定理进行边换角得b c =32tan C +12,根据tan C 的范围即可得到答案.【详解】(1)由m ⎳n得a cos C =2b -c cos A ,∴a cos C +c cos A =2b cos A ,根据正弦定理得sin A cos C +sin C cos A =2sin B cos A ,所以sin A +C =2sin B cos A ,又A +C =π-B ,所以sin B =2sin B cos A .又sin B ≠0,∴cos A =12,又A ∈0,π ,∴A =π3;(2)由(1)得A =π3,B +C =2π3,∵B ,C 为锐角,所以0<C <π20<2π3-C <π2,∴C ∈π6,π2 ,根据正弦定理得b c =sin B sin C =sin 2π3-C sin C =32cos C +12sin C sin C =32tan C +12,其中tan C ∈33,+∞ ,∴32tan C ∈0,32 ,即32tan C+12∈12,2 ,综上可知,b c 的取值范围是12,2 .33.(1)π3(2)6【分析】(1)先使用余弦定理,再用正弦定理进行角变边即求得结果;(2)由平面向量可知AD =12AB +AC ,两边平方,用三角形的边及角表示并结合基本不等式得出结果.【详解】(1)∵3b 2+c 2-a 2 =2ac sin B ,由余弦定理可得23bc cos A =2ac sin B ,即3b cos A =a sin B ,由正弦定理可得3sin B cos A =sin A sin B ,∵B ∈0,π ,∴sin B ≠0.∴3cos A =sin A ,即tan A =3,又A ∈0,π ,所以A =π3.(2)由(1)知,A =π3,△ABC 的面积为23,所以12bc sin π3=23,解得bc =8.由平面向量可知AD =12AB +AC ,所以AD 2=14(AB +AC )2=14AB 2+AC 2+2AB ⋅AC=14b 2+c 2+2bc cos π3 =14b 2+c 2+bc ≥142bc +bc =34bc =6,当且仅当b =c =22时取等号,故BC 边中线AD 的最小值为6.34.(1)π3(2)123【分析】(1)根据正弦定理边角互化,结合两角和的正弦的公式求解即可;(2)利用余弦定理和基本不等式得到ab ≤48,再利用三角形的面积公式求解即可.【详解】(1)根据题意,由正弦定理,可得sin C tan C =3sin A cos B +sin B cos A =3sin A +B ,又因为△ABC 中A +B =π-C ,且C ∈0,π ,所以sin C tan C =3sin C ,即tan C =3,所以C =π3.(2)由余弦定理,可得c 2=a 2+b 2-2ab cos C ,即48=a 2+b 2-ab所以48+ab =a 2+b 2≥2ab ,当且仅当a =b 时等号成立,所以ab ≤48,所以S △ABC =12ab sin C ≤12×48×32=123,所以△ABC 面积的最大值为123.35.(1)π3(2)4,6 【分析】(1)根据正弦定理边化角结合三角形内角和与诱导公式得出2sin A cos B =sin A ,根据三角形内角范围可知sin A ≠0,即可得出cos B =12,再根据角围得出答案;(2)根据已知结合余弦定理即可得出a 、c 关系,再根据基本不等式得出a +c 范围,即可得出答案.【详解】(1)由正弦定理,得2sin C -sin A =2sin B cos A ,因为A +B +C =π,所以sin C =sin A +B ,所以2sin (A +B )-sin A =2sin B cos A ,即2sin A cos B +2cos A sin B -sin A =2sin B cos A ,所以2sin A cos B =sin A ,因为0<A <π,所以sin A ≠0,所以cos B =12,又0<B <π,所以B =π3;(2)由(1)可得B =π3,若b =2,则由余弦定理,得4=a 2+c 2-ac =a +c 2-3ac ,所以3ac =a +c 2-4≤3×a +c 2 2,即14a +c 2≤4,所以a +c ≤4,当且仅当a =c 时等号成立,又a +c >b =2,所以2<a +c ≤4,即4<a +b +c ≤6,所以△ABC 周长的取值范围为4,6 .36.(1)证明见解析.(2)(1,5).【分析】(1)运用余弦定理得2c ⋅cos B =a -c ,再运用正弦定理边化角化简计算即可.(2)运用三角形内角范围求得角C 的范围,进而求得cos C 范围,运用边化角将问题转化为求关于cos C 的二次函数在区间上的值域.【详解】(1)∵c 2+ac =b 2,∴c 2-b 2=-ac ,∴由余弦定理得:cos B =a 2+c 2-b 22ac =a 2-ac 2ac =a -c 2c,即:2c ⋅cos B =a -c ,由正弦定理得:2sin C ⋅cos B =sin A -sin C ,∴2sin C ⋅cos B =sin (B +C )-sin C =sin B cos C +sin C cos B -sin C ,整理得:sin B cos C -sin C cos B -sin C =0,即:sin (B -C )=sin C ,又∵B 、C ∈(0,π),∴B -C =C ,即:B =2C .(2)∵B =2C ,∴A =π-3C ,又∵sin2C =2sin C ⋅cos C ,sin3C =sin (C +2C )=sin C ⋅cos2C +cos C ⋅sin2C =sin C ⋅cos2C +2sin C ⋅cos 2C ,sin C ≠0,∴由正弦定理得:a +b c =sin A +sin B sin C =sin (π-3C )+sin2C sin C =sin3C +sin2C sin C=sin C⋅cos2C+2sin C⋅cos2C+2sin C⋅cos Csin C=cos2C+2cos2C+2cos C =2cos2C-1+2cos2C+2cos C=4cos2C+2cos C-1,又∵0<A<π0<B<π0<C<π⇒0<π-3C<π0<2C<π0<C<π⇒0<C<π3,∴12<cos C<1,令t=cos C,则a+bc=4t2+2t-1,12<t<1,∵y=4t2+2t-1对称轴为t=-1 4,∴y=4t2+2t-1在12,1上单调递增,当t=12时,y=4×14+2×12-1=1;当t=1时,y=4+2-1=5,∴1<a+bc<5,即:a+bc的范围为(1,5).37.(1)证明见解析(2)2 2,98【分析】(1)利用同角的商数关系与正弦定理的边角变换化简得到sin B=cos A,再由条件和诱导公式求得B=π2+A,由此得证;(2)先由(1)求出A的范围,再由诱导公式和二倍角的余弦公式变形化简得到sin A+sin C =-2sin2A+sin A+1,从而利用换元法和二次函数的性质即可求出式子的范围.【详解】(1)因为a=b tan A,所以ab=tan A=sin Acos A,由正弦定理可得sin Acos A=ab=sin Asin B,又0<A<π,所以sin A>0,故sin B=cos A,则sin B=sinπ2+A ,又B为钝角,则0<A<π2,因此B∈π2,π,π2+A∈π2,π,所以B=π2+A,即B-A=π2;(2)由(1)知,C=π-(A+B)=π-2A+π2=π2-2A>0,所以A<π4,又0<A<π2,所以0<A<π4,则0<sin A<22,所以sin A+sin C=sin A+sinπ2-2A=sin A+cos2A=-2sin2A+sin A+1=-2sin A-142+98,令t=sin A,则0<t<22,sin A+sin C=-2t-142+98,对于y=-2t-1 42+98=-2t2+t+1,其开口向下,对称轴为t=14,所以y=-2t-1 42+98在0,14上单调递增,在14,22上单调递减,故当t=14时,y=-2t-142+98取得最大值为98,又当t=0时,y=1,当t=22时,y=22,所以y=-2t-1 42+98的值域为22,98,故22<-2sin A-142+98≤98,即22<sin A+sin C≤98,所以sin A+sin C的取值范围是22,98 .38.(1)ω=1,对称轴方程为:x=kπ2+π6k∈Z;(2)(23,2+3].【分析】(1)根据降幂公式、辅助角公式,结合正弦型函数的零点性质、周期公式、对称轴方程进行求解即可;(2)根据正弦定理、辅助角公式、正弦型函数的单调性进行求解即可.【详解】(1)f(x)=cos2(ωx)+3sin(ωx)cos(ωx)-12=1+cos(2ωx)2+3sin(2ωx)2-1 2,f x =sin2ωx+π6,因为函数f(x)的两个相邻零点间的距离为π2,所以函数f(x)的最小正周期为2×π2=π,因为ω>0,所以2π2ω=π⇒ω=1,即f x =sin2x+π6,令2x+π6=kπ+π2k∈Z⇒x=kπ2+π6k∈Z,所以对称轴为x=kπ2+π6k∈Z;(2)由f(A)=-1⇒sin2A+π6=-1,因为A∈(0,π),所以2A+π6∈π6,13π6⇒2A+π6=3π2⇒A=2π3,因为a=3,所以由正弦定理可知:asin A=bsin B=csin C=332=2⇒b=2sin B,c=2sin C,所以三角形的周长为3+2sin B+2sin C=3+2sin B+2sinπ3-B ,=3+2sin B +232cos B -12sin B=3cos B +sin B +3=2sin B +π3 +3,因为B ∈0,π3 ,所以B +π3∈π3,2π3 ,因此sin B +π3∈32,1 ⇒2sin B +π3 +3∈(23,2+3],所以△ABC 周长的取值范围为(23,2+3].39.(1)π3(2)8,12 【分析】(1)选①或②:由正弦定理得到a 2+c 2-b 2=ac ,再由余弦定理得到cos B =12,结合B ∈0,π ,求出B =π3;选③:由正弦定理化简得到2sin A cos B -sin C cos B =sin B cos C ,进而得到2sin A cos B =sin A ,cos B =12,求出B =π3;(2)由余弦定理结合基本不等式可得出a +c ≤8,从而可求得△ABC 的周长的取值范围.【详解】(1)选①,∵a sin C -sin A sin C +sin B=c -b ,∴sin A sin C -sin A sin C +sin B=sin C -sin B ∴sin A sin C -sin 2A =sin 2C -sin 2B∴sin A sin C =sin 2A +sin 2C -sin 2B∴ac =a 2+c 2-b 2,又∵a 2+c 2-b 2=2ac cos B∴cos B =12,又∵0<B <π,∴B =π3.选②,∵sin 2A +sin 2C -sin 2B =sin A sin C ∴a 2+c 2-b 2=ac ,又∵a 2+c 2-b 2=2ac cos B∴cos B =12,又∵0<B <π,∴B =π3.选③,∵2a -c b=cos C cos B ,∴2sin A -sin C sin B =cos C cos B ∴2sin A cos B -sin C cos B =sin B cos C∴2sin A cos B =sin C cos B +sin B cos C =sin (B +C )=sin A∵sin A ≠0,∴cos B =12,又∵0<B <π,∴B =π3.(2)由余弦定理得:b 2=a 2+c 2-2ac cos B ,∴16=a 2+c 2-ac =(a +c )2-3ac ≥a +c 2-3a +c 24=a +c 24,当且仅当a =c =4时,取等号.∴a +c 2≤64,∴a +c ≤8,又∵a +c >4,∴4<a +c ≤8,∴8<a +c +b ≤12。
解三角形图形类问题(十大题型)(原卷版)

重难点突破02解三角形图形类问题目录01方法技巧与总结 (2)02题型归纳与总结 (2)题型一:妙用两次正弦定理(两式相除消元法) (2)题型二:两角使用余弦定理建立等量关系 (4)题型三:张角定理与等面积法 (5)题型四:角平分线问题 (6)题型五:中线问题 (7)题型六:高问题 (9)题型七:重心性质及其应用 (10)题型八:外心及外接圆问题 (11)题型九:两边夹问题 (13)题型十:内心及内切圆问题 (14)03过关测试 (15)解决三角形图形类问题的方法:方法一:两次应用余弦定理是一种典型的方法,充分利用了三角形的性质和正余弦定理的性质解题;方法二:等面积法是一种常用的方法,很多数学问题利用等面积法使得问题转化为更为简单的问题,相似是三角形中的常用思路;方法三:正弦定理和余弦定理相结合是解三角形问题的常用思路;方法四:构造辅助线作出相似三角形,结合余弦定理和相似三角形是一种确定边长比例关系的不错选择;方法五:平面向量是解决几何问题的一种重要方法,充分利用平面向量基本定理和向量的运算法则可以将其与余弦定理充分结合到一起;方法六:建立平面直角坐标系是解析几何的思路,利用此方法数形结合充分挖掘几何性质使得问题更加直观化.题型一:妙用两次正弦定理(两式相除消元法)【典例1-1】(2024·河南·三模)已知P 是ABC 内一点,π3π,,,44PB PC BAC BPC ABP ∠∠∠θ====.(1)若π,224BC θ=,求AC ;(2)若π3θ=,求tan BAP ∠.【典例1-2】ABC 的内角,,A B C 的对边分别为,,,a b c AD 为BAC ∠平分线,::32:3c AD b =(1)求A ∠;(2)AD 上有点,90M BMC ∠= ,求tan ABM ∠.【变式1-1】如图,在平面四边形ABCD 中,90ACB ADC ∠=∠=︒,AC =30BAC ∠=︒.(1)若CD =BD ;(2)若30CBD ∠=︒,求tan BDC ∠.【变式1-2】(2024·广东广州·二模)记ABC 的内角A 、B 、C 的对边分别为a 、b 、c ,已知cos cos b A a B b c -=-.(1)求A ;(2)若点D 在BC 边上,且2CD BD =,cos 3B =,求tan BAD ∠.【变式1-3】在ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,且2cos (cos cos )A c B b C a +=.(1)求角A ;(2)若O 是ABC 内一点,120AOB ∠=︒,150AOC ∠=︒,1b =,3c =,求tan ABO ∠.题型二:两角使用余弦定理建立等量关系【典例2-1】如图,四边形ABCD 中,1cos 3BAD ∠=,3AC AB AD ==.(1)求sin ABD ∠;(2)若90BCD ∠=︒,求tan CBD ∠.【典例2-2】如图,在梯形ABCD 中,AB CD ∥,AD ==(1)求证:sin C A =;(2)若2C A =,2AB CD =,求梯形ABCD 的面积.【变式2-1】(2024·全国·模拟预测)在锐角ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,2232cos 235cos22C C π⎛⎫=-- ⎪⎝⎭.(1)求角C ;(2)若点D 在AB 上,2BD AD =,BD CD =,求AC BC的值.【变式2-2】平面四边形ABCD 中,1AB =,2AD =,πABC ADC ∠+∠=,π3BCD ∠=.(1)求BD ;(2)求四边形ABCD 周长的取值范围;(3)若E 为边BD 上一点,且满足CE BE =,2BCE CDE S S =△△,求BCD △的面积.题型三:张角定理与等面积法【典例3-1】(2024·吉林·模拟预测)ABC 的内角,,A B C 的对边分别是,,a b c ,且sin sin sin A B a c C a b --=+,(1)求角B 的大小;(2)若3b =,D 为AC 边上一点,2BD =,且BD 为B ∠的平分线,求ABC 的面积.【典例3-2】(2024·黑龙江哈尔滨·二模)记ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知4b =,2cos sin cos tan b B A A c C=+.(1)求角B 的大小;(2)已知直线BD 为ABC ∠的平分线,且与AC 交于点D ,若3BD =,求ABC 的周长.【变式3-1】(2024·吉林通化·梅河口市第五中学校考模拟预测)已知锐角ABC 的内角,,A B C 的对边分别为,,a b c ,且sin sin sin sin a B C b c A C-=+-.(1)求B ;(2)若bB 的平分线交AC 于点D ,1BD =,求ABC 的面积.【变式3-2】(2024·江西抚州·江西省临川第二中学校考二模)如图,在ABC 中,4AB =,1cos 3B =,点D 在线段BC 上.(1)若3π4ADC ∠=,求AD 的长;(2)若2BD DC =,ACD sin sin BAD CAD ∠∠的值.题型四:角平分线问题【典例4-1】(2024·全国·模拟预测)已知在△ABC 中,内角,,A B C 的对边分别为,,a b c ,且6,60a A =∠=︒.(1)若AD 为BC 边上的高线,求AD 的最大值;(2)已知AM 为BC 上的中线,BAC ∠的平分线AN 交BC 于点N ,且sin tan 2cos A B A=-,求△AMN 的面积.【典例4-2】如图所示,在ABC 中,3AB AC =,AD 平分BAC ∠,且AD kAC =.(1)若2DC =,求BC 的长度;(2)求k 的取值范围;(3)若1ABC S =△,求k 为何值时,BC 最短.【变式4-1】在ABC 中,角A ,B ,C 所对的边分别是a ,b ,c ,已知2π3A =,22cos c b ac C -=.(1)求tan C ;(2)作角A 的平分线,交边BC 于点D ,若AD =AC 的长度;(3)在(2)的条件下,求ABC 的面积.【变式4-2】已知ABC 的内角,,A B C 的对边分别为,,a b c ,其面积为S ,且()()sin sin sin 6a b c a A B C S+-++=(1)求角A 的大小;(2)若3,a BA AC A ∠=⋅=-的平分线交边BC 于点T ,求AT 的长.题型五:中线问题【典例5-1】如图,在ABC 中,已知2AB =,AC =,45BAC ∠=︒,BC 边上的中点为M ,点N 是边AC 上的动点(不含端点),AM ,BN 相交于点P .(1)求BAM ∠的正弦值;(2)当点N 为AC 中点时,求MPN ∠的余弦值.(3)当NA NB ⋅ 取得最小值时,设BP BN λ= ,求λ的值.【典例5-2】(2024·辽宁沈阳·东北育才双语学校校考一模)如图,设ABC 中角A ,B ,C 所对的边分别为a ,b ,c ,AD 为BC 边上的中线,已知1c =且12sin cos sin sin sin 4c A B a A b B b C =-+,cos BAD ∠=(1)求b 边的长度;(2)求ABC 的面积;(3)设点E ,F 分别为边AB ,AC 上的动点(含端点),线段EF 交AD 于G ,且AEF △的面积为ABC 面积的16,求AG EF 的取值范围.【变式5-1】阿波罗尼奥斯(Apollonius )是古希腊著名的数学家,他提出的阿波罗尼奥斯定理是一个关于三角形边长与中线长度关系的定理,内容为:三角形两边平方的和,等于所夹中线及第三边之半的平方和的两倍,即如果AD 是ABC 中BC 边上的中线,则222222BC AB AC AD ⎡⎤⎛⎫+=+⎢⎥ ⎪⎝⎭⎢⎥⎣⎦.(1)若在ABC 中,5AB =,3AC =,π3BAC ∠=,求此三角形BC 边上的中线长;(2)请证明题干中的定理;(3)如图ABC 中,若AB AC >,D 为BC 中点,3BD DC ==,()sin 3sin 3sin a A b B b A C +=-,2ABC S =△,求cos DAC ∠的值.【变式5-2】在ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,30B ︒=.(1)已知b =cos cos 2b A a B +=(i )求C ;(ii )若a b <,D 为AB 边上的中点,求CD 的长.(2)若ABC 为锐角三角形,求证:3a c <【变式5-3】(2024·江苏南通·模拟预测)在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,已知2a =,2c BA BC =⋅- ,其中S 为ABC 的面积.(1)求角A 的大小;(2)设D 是边BC 的中点,若AB AD ⊥,求AD 的长.题型六:高问题【典例6-1】(2024·河北秦皇岛·三模)在ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,π3C =且7a b +=,ABC (1)求ABC 的面积;(2)求ABC 边AB 上的高h .【典例6-2】(2024·四川·模拟预测)在ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且()sin cos B b A B b ++=.(1)求角C 的大小;(2)若8a =,ABC 的面积为AB 边上的高.【变式6-1】在ABC 中,角,,A B C 所对的边分别为,,a b c ,已知7,8a c ==.(1)若4sin 7C =,求角A 的大小;(2)若5b =,求AC 边上的高.【变式6-2】(2024·山东枣庄·一模)在ABC 中,角,,A B C 的对边分别为,,a b c ,且sin tan 22a C A c =.(1)求C ;(2)若8,5,ab CH ==是边AB 上的高,且CH mCA nCB =+ ,求m n .题型七:重心性质及其应用【典例7-1】(2024·四川内江·一模)ABC 的内角A 、B 、C 所对的边分别为a 、b 、c ,6a =,sin sin 2B C b a B +=.(1)求角A 的大小;(2)M 为ABC 的重心,AM 的延长线交BC 于点D ,且AM =ABC 的面积.【典例7-2】(2024·江西景德镇·一模)如图,已知△ABD 的重心为C ,△ABC 三内角A 、B 、C 的对边分别为a ,b ,c .且2cos 22A b c c+=(1)求∠ACB 的大小;(2)若π6CAB ∠=,求sin CDA ∠的大小.【变式7-1】(2024·高三·福建福州·期中)已知ABC 内角A ,B ,C 的对边分别为a ,b ,c ,点G 是ABC的重心,且0AG BG ⋅= .(1)若π6GAB ∠=,①直接写出AG CG=______;②设CAG α∠=,求tan α的值(2)求cos ACB ∠的取值范围.【变式7-2】(2024·浙江温州·模拟预测)ABC 的角,,A B C 对应边是a ,b ,c ,三角形的重心是O .已知3,4,5OA OB OC ===.(1)求a 的长.(2)求ABC 的面积.题型八:外心及外接圆问题【典例8-1】(2024·广东深圳·二模)已知在ABC 中,角,,A B C 的对边分别为,,,6,2,1a b c a b c ===.(1)求角A 的余弦值;(2)设点O 为ABC 的外心(外接圆的圆心),求,AO AB AO AC ⋅⋅ 的值.【典例8-2】已知ABC 的内角,,A B C 所对的边分别为,,,3,22cos a b c a c b a B =-=.(1)求A ;(2)M 为ABC 外心,AM 的延长线交BC 于点D ,且MD =ABC 的面积.【变式8-1】ABC 的内角,,A B C 的对边分别为,,,,20,a b c c b AB AC ABC >⋅= 的面积为(1)求A ∠;(2)设O 点为ABC 外心,且满足496OB OC ⋅=- ,求a .【变式8-2】(2024·河南·模拟预测)已知ABC 的外心为O ,点,M N 分别在线段,AB AC 上,且O 恰为MN 的中点.(1)若1BC OA ==,求ABC 面积的最大值;(2)证明:AM MB AN NC ⋅=⋅.【变式8-3】(2024·安徽黄山·三模)记ABC 的内角,,A B C 的对边分别为,,a b c ,已知c =(1cos )sin b C B +=.(1)求角C 的大小和边b 的取值范围;(2)如图,若O 是ABC 的外心,求OC AB CA CB ⋅+⋅ 的最大值.题型九:两边夹问题【典例9-1】在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,若2cos sin 0sin cos A A B B +-=+,则a b c +的值是()A .2B 3C 2D .1【典例9-2】在ABC ∆中,a 、b 、c 分别是A ∠、B ∠、C ∠所对边的边长.若2cos sin 0cos sin A A B B +-=+,则a b c+的值是().A .1B 2C 3D .2【变式9-1】在ABC ∆中,已知边,,a b c 所对的角分别为,,A B C ,若2223sin 2sin sin si 2si n sin n C A B C B A ++=,则tan A =_________________【变式9-2】(2024·江苏苏州·吴江中学模拟预测)在ABC ∆中,已知边,,a b c 所对的角分别为,,A B C ,若22252cos 3cos 2sin sin sin sin --=+B C A B C A ,则tan A =_____.【变式9-3】在ABC ∆中,已知边a 、b 、c 所对的角分别为A 、B 、C ,若5a =,2223sin 2sin sin si 2si n sin n C A B C B A ++=,则ABC ∆的面积S =______.【变式9-4】在ABC 中,若(cos sin )(cos sin )2A A B B ++=,则角C =__.题型十:内心及内切圆问题【典例10-1】(2024·全国·模拟预测)设ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,且满足2cos 2a B b c +=,5a =.(1)求ABC 的周长的取值范围;(2)若ABC 的内切圆半径r =ABC 的面积S .【典例10-2】(2024·湖南永州·一模)在ABC 中,设,,A B C 所对的边分别为,,a b c ,且满足cos cos c A a C a b -=+.(1)求角C ;(2)若5,c ABC = 的内切圆半径4r =,求ABC 的面积.【变式10-1】(2024·全国·模拟预测)已知ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,sin cos c A C -=.(1)求角A 的大小;(2)若7a =,ABC 外接圆的半径为R ,内切圆半径为r ,求R r的最小值.【变式10-2】(2024·全国·模拟预测)在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且22sin 2sin 2sin sin 4A B A B ⋅⋅=.(1)求C ;(2)若2c =,求ABC 内切圆半径取值范围.【变式10-3】(2024·广西南宁·一模)在ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知2a =,且sin sin sin A B b c C b a+-=-.(1)求ABC 的外接圆半径R ;(2)求ABC 内切圆半径r 的取值范围.【变式10-4】(2024·吉林·二模)已知ABC 的三个内角,,A B C 的对边分别为,,,a b c ABC 的外接圆半径为222sin sin sin sin sin B C B C A +-=.(1)求a ;(2)求ABC 的内切圆半径r 的取值范围1.如图所示,在ABC 中,设,,a b c 分别为内角,,A B C 的对边,已知3b c a +=,()4b c a =-.(1)求角C ;(2)若7c =,过B 作AC 的垂线并延长到点D ,使,,,A B C D 四点共圆,AC 与BD 交于点E ,求四边形ABCD 的面积.2.如图,在梯形ABCD 中,//AB CD ,60D ∠= .(1)若3AC =,求ACD 周长的最大值;(2)若2CD AB =,45BCD ∠= ,求tan DAC ∠的值.3.(2024·全国·模拟预测)在ABC 中,已知sin()sin sin BAC B B C ∠-∠=+.(1)求BAC ∠.(2)若2AC AB =,BAC ∠的平分线交BC 于点D ,求cos ADB ∠.4.(2024·四川成都·模拟预测)在ABC 中,角,,A B C 所对的边分别为,,a b c 3sin sin 2B C b a B +=,边BC 上有一动点D .(1)当D 为边BC 中点时,若3,2AD b ==,求c 的长度;(2)当AD 为BAC ∠的平分线时,若4a =,求AD 的最大值.5.(2024·安徽合肥·模拟预测)已知函数()π2π1sin sin 332f x x x ⎛⎫⎛⎫=+⋅+- ⎪ ⎪⎝⎭⎝⎭,角A 为△ABC 的内角,且()0f A =.(1)求角A 的大小;(2)如图,若角A 为锐角,3AB =,且△ABC 的面积S E 、F 为边AB 上的三等分点,点D 为边AC 的中点,连接DF 和EC 交于点M ,求线段AM 的长.6.(2024·全国·模拟预测)在ABC 中,角,,A B C ,的对边分别为,,a b c ,ABC 的面积为S ,()2sin 213sin A B S b B ⎡⎤+=+⎢⎥⎣⎦.(1)求角A .(2)若ABC 的面积为a =,D 为边BC 的中点,求AD 的长.7.(2024·四川成都·三模)在ABC 中,15,6,cos 8BC AC B ===.(1)求AB 的长;(2)求AC 边上的高.8.(2024·江苏南通·三模)在ABC 中,角,,A B C 的对边分别为(),,,2cos cos a b c b c A a C -=.(1)求A ;(2)若ABCBC 边上的高为1,求ABC 的周长.9.(2024·高三·河南·开学考试)在ABC 中,内角,,A B C 所对的边分别为,,a b c ,且满足()()()10sin sin sin sin 2sin 2sin 3a b c A B C a B c A b c C ++++=+++.(1)求cos C ;(2)若AB 边上的高为2,c =,a b .10.(2024·高三·山东济南·开学考试)在ABC 中,内角A ,B ,C 的对边分别为a ,b ,c .已知()cos 2cos b A a B =-.(1)求c a;(2)若2π3B =,且AC ABC 的周长.11.在ABC 中,设a ,b ,c 分别表示角A ,B ,C 对边.设BC 边上的高为h ,且2a h =.(1)把b cc b +表示为sin cos x A y A +(x ,R y ∈)的形式,并判断b c c b+能否等于(2)已知B ,C 均不是直角,设G 是ABC 的重心,BG CG ⊥,c b >,求tan B 的值.12.(2024·江苏苏州·二模)记ABC 的内角,,A B C 的对边分别为,,a b c ,已知sin sin sin sin a b C B c A B+-=-.(1)求角A ;(2)若6a =,点M 为ABC 的重心,且AM =ABC 的面积.13.(2024·河南开封·模拟预测)记ABC 的内角,,A B C 的对边分别为,,a b c,已知sin cos cos ,B a C c A b G -==为ABC 的重心.(1)若2a =,求c 的长;(2)若AG =ABC 的面积.14.(2024·辽宁抚顺·一模)记ABC 的内角,,A B C 的对边分别为,,a b c ,已知()()()sin sin sin sin a b A B c C B +-=-.(1)求角A ;(2)若6a =,点M 为ABC的重心,且AM =ABC 的面积.15.在ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且a ,b ,c 是公差为2的等差数列.(1)若2sin 3sin C A =,求ABC 的面积.(2)是否存在正整数b ,使得ABC 的外心在ABC 的外部?若存在,求b 的取值集合;若不存在,请说明理由.16.(2024·湖北·模拟预测)已知ABC 的外心为O ,,M N 为线段,AB AC 上的两点,且O 恰为MN 中点.(1)证明:||||||||AM MB AN NC ⋅=⋅(2)若||AO ||1OM =,求AMN ABCS S V V 的最大值.17.在ABC 中,角,,A B C 所对的边分别为,,a b c ,满足3cos 5c a B b =+.(1)求cos A 的值;(2)当BC 与BC 边上的中线长均为2时,求ABC 的周长;(3)当ABC 内切圆半径为1时,求ABC 面积的最小值.18.已知ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,且()cos b c a C C +=+.(1)求A ;(2)若2a =,求ABC 内切圆周长的最大值.19.(2024·浙江杭州·模拟预测)已知ABC 的周长为20,角A ,B ,C 所对的边分别为a ,b ,c (1)若π4C =,7c =,求ABC 的面积;(2)若ABC 7a =,求tan A 的值.20.(2024·高三·江苏扬州·开学考试)已知ABC 的内角,,A B C 的对边分别为,,a b c ,23A π=,10b =,6c =,ABC 的内切圆I 的面积为S .(1)求S 的值;(2)若点D 在AC 上,且,,B I D 三点共线,求BD BC ⋅ 的值.21.(2024·贵州·模拟预测)在ABC 中,AB =2AC =,π6C ∠=,N 为AB 的中点,A ∠的角平分线AM 交CN 于点O .(1)求CN 的长;(2)求AOC 的面积.22.(2024·广东梅州·二模)在ABC 中,角A ,B ,C 所对应的边分别为a ,b ,ccos sin B b A -=,2c =,(1)求A 的大小:(2)点D 在BC 上,(Ⅰ)当AD AB ⊥,且1AD =时,求AC 的长;(Ⅱ)当2BD DC =,且1AD =时,求ABC 的面积ABC S .23.(2024·甘肃陇南·一模)在ABC 中,内角A ,B ,C 的对边分别为,,a b c .已知cos cos 3c A a C +=.(1)求b ;(2)D 为边AC 上一点,π26AD DC,DBC ,AB BD =∠=⊥,求BD 的长度和ADB ∠的大小.24.(2024·全国·模拟预测)如图,四边形ABCD 为梯形,//AB CD ,2AB CD ==tan2A =,1cos 3ADB ∠=.的值;(1)求cos BDC(2)求BC的长.。
专题解三角形大题(含答案)

专题解三角形大题(含答案)靠自己打拼出来的天下,才是最美的;靠自己获得的一切,才是最珍贵的。
今天,你,做数学题了吗?1.在△ABC中,已知bcosA+a=c,求B的大小和△ABC的面积。
根据正弦定理和余弦定理,可以得到sinBcosA+sinA=sinC和cosB=(c-a2-b2)/2ab。
代入已知条件,解得B=π/3,S△ABC=absinB=√3/4.2.在△ABC中,已知(b-a)sinB+asinA=csinC,且c=2,求角C的度数和△ABC面积的最大值。
同样利用正弦定理和余弦定理,可以得到a2+b2-c2=ab和cosB=(c-a2-b2)/2ab。
解得C=π/3,S△ABC=absinC=√3.3.在△ABC中,已知a+b+c=2,求sinC和如果△ABC是钝角三角形,求其面积。
根据余弦定理,可以得到cosC=(a2+b2-c2)/2ab。
代入已知条件,解得sinC=√3/2,若△ABC是钝角三角形,面积为0.4.在△ABC中,已知2cosC(acosB+bcosA)=c,求角C和如果c=2,求△ABC面积的最大值。
根据余弦定理,可以得到cosC=(a2+b2-c2)/2ab。
代入已知条件,解得C=π/3,S△ABC=absinC=√3.当c=2时,代入面积公式,解得S△ABC=√3.5.在四边形ABCD中,已知∠D=2∠B,且AD=2,CD=6,cosB=1/3,求△ACD的面积和AB的长。
根据余弦定理,可以得到AC2=40-24cosB=32,再根据海龙公式和正弦定理,可以解得S△ACD=8√3和AB=2√7.6.在△ABC中,已知bsin(A+C)=asinC,且a=2c,求sinB和△ABC的周长。
代入正弦定理和已知条件,解得sinB=1/2,周长为3c。
1.由$a^2+b^2-c^2=ab$,得到$ab+4=a^2+b^2$。
由不等式$a^2+b^2\geq 2ab$,得到$ab+4\geq 2ab$,因此$ab\leq 4$。
解三角形专题高考题练习【附答案】

解三角形专题(高考题)练习【附答案】1、在ABC ∆中,已知内角3A π=,边23BC =.设内角B x =,面积为y .(1)求函数()y f x =的解析式和定义域;(2)求y 的最大值. 2、已知ABC ∆中,1||=AC ,0120=∠ABC ,θ=∠BAC , 记→→∙=BC AB f )(θ,(1)求)(θf 关于θ的表达式; (2)(2)求)(θf 的值域;3、在△ABC 中,角A 、B 、C 所对的边分别是a ,b ,c ,且.21222ac b c a =-+ (1)求B CA 2cos 2sin 2++的值;(2)若b =2,求△ABC 面积的最大值. 4、在ABC ∆中,已知内角A 、B 、C 所对的边分别为a 、b 、c ,向量()2sin ,3m B =-,2cos 2,2cos 12B n B ⎛⎫=- ⎪⎝⎭,且//m n 。
(I )求锐角B 的大小;(II )如果2b =,求ABC ∆的面积ABC S ∆的最大值。
5、在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且.cos cos 3cos B c B a C b -= (I )求cos B 的值;(II )若2=⋅BC BA ,且22=b ,求c a 和b 的值. 6、在ABC ∆中,5cos 5A =,10cos 10B =. (Ⅰ)求角C ;(Ⅱ)设2AB =,求ABC ∆的面积.7、在△ABC 中,A 、B 、C 所对边的长分别为a 、b 、c ,已知向量(1,2sin )m A =,(sin ,1cos ),//,3.n A A m n b c a =++=满足(I )求A 的大小;(II )求)sin(6π+B 的值.8、△ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,且有sin2C+3cos (A+B )=0,.当13,4==c a ,求△ABC 的面积。
AB C1209、在△ABC 中,角A 、B 、C 所对边分别为a ,b ,c ,已知11tan ,tan 23A B ==,且最长边的边长为l.求:(I )角C 的大小;(II )△ABC 最短边的长.10、在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c.已知a+b=5,c=7,且.272cos 2sin 42=-+C B A (1)求角C 的大小;(2)求△ABC 的面积. 11、已知△ABC 中,AB=4,AC=2,23ABC S ∆=. (1)求△ABC 外接圆面积.(2)求cos(2B+3π)的值. 12、在ABC ∆中,角A B C 、、的对边分别为a b c 、、,(2,)b c a =-m ,(cos ,cos )A C =-n ,且⊥m n 。
中考数学关于解直角三角形的18道经典题
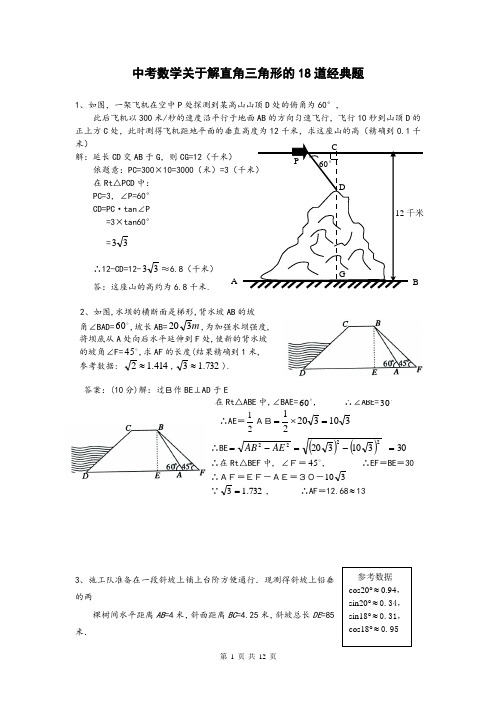
中考数学关于解直角三角形的18道经典题1、如图,一架飞机在空中P 处探测到某高山山顶D 处的俯角为60°,此后飞机以300米/秒的速度沿平行于地面AB 的方向匀速飞行,飞行10秒到山顶D 的正上方C 处,此时测得飞机距地平面的垂直高度为12千米,求这座山的高(精确到0.1千米) 解:延长CD 交AB 于G ,则CG=12(千米)依题意:PC=300×10=3000(米)=3(千米) 在Rt △PCD 中: PC=3,∠P=60° CD=PC ·tan ∠P =3×tan60°=33∴12-CD=12-33≈6.8(千米) 答:这座山的高约为6.8千米.2、如图,水坝的横断面是梯形,背水坡AB 的坡 角∠BAD=60,坡长AB=m 320,为加强水坝强度, 将坝底从A 处向后水平延伸到F 处,使新的背水坡 的坡角∠F= 45,求AF 的长度(结果精确到1米,参考数据: 414.12≈,732.13≈).答案:(10分)解:过B作BE ⊥AD 于E在Rt △ABE 中,∠BAE= 60, ∴∠ABE= 30 ∴AE =21AB31032021=⨯=∴BE ()()303103202222=-=-=AE AB∴在Rt △BEF 中, ∠F= 45, ∴EF =BE =30 ∴AF=EF-AE=30-310∵732.13=, ∴AF =12.68≈133、施工队准备在一段斜坡上铺上台阶方便通行.现测得斜坡上铅垂的两棵树间水平距离AB =4米,斜面距离BC =4.25米,斜坡总长DE =85米.参考数据cos20°≈0.94, sin20°≈0.34, sin18°≈0.31, cos18°≈0.95AB12千米P C D G60°(1)求坡角∠D 的度数(结果精确到1°);(2)若这段斜坡用厚度为17cm 的长方体台阶来铺,需要铺几级台阶?解:(1) cos ∠D =cos ∠ABC =BC AB =25.44≈0.94, …………………………………3分 ∴∠D ≈20°. ………………………………………………………………………1分 (2)EF =DE sin ∠D =85sin20°≈85×0.34=28.9(米) , ……………………………3分 共需台阶28.9×100÷17=170级. ………………………………………………1分4、在玉溪州大河旁边的路灯杆顶上有一个物体,它的抽象几何图形如图, 若 60ABC 10,AC 4,AB =∠==, 求B 、C 两点间的距离.解:过A 点作AD ⊥BC 于点D , …………1分在Rt △ABD 中,∵∠ABC=60°,∴∠BAD=30°. …………2分 ∵AB=4,∴BD=2, ∴AD=23. …………4分 在Rt △ADC 中,AC=10,∴CD=22AD AC -=12100-=222 . …………5分 ∴BC=2+222 . …………6分 答:B 、C 两点间的距离为2+222. …………7分5、在东西方向的海岸线l 上有一长为1km 的码头MN(如图),在码头西端M 的正西19.5 km 处有一观察站A .某时刻测得一艘匀速直线航行的轮船位于 A 的北偏西30°,且与A 相距40km 的B 处;经过1小时20分钟,又测得该轮船位于A 的北偏东NM 东北BCAlCBA17cm(第19题) A BCF60°,且与A相距83的C处.(1)求该轮船航行的速度(保留精确结果);(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.答案解:(1)由题意,得∠BAC=90°,………………(1分)∴2240(83)167BC=+=.…………(2分)∴轮船航行的速度为41671273÷=时.……(3分)(2)能.……(4分)作BD⊥l于D,CE⊥l于E,设直线BC交l于F,则BD=AB·cos∠BAD=20,CE=AC·sin∠CAE=43,AE=AC·cos∠CAE=12.∵BD⊥l,CE⊥l,∴∠BDF=∠CEF=90°.又∠BFD=∠CFE,∴△BDF∽△CEF,……(6分)∴,DF BDEF CE=∴3220343EFEF+=,∴EF=8.……(7分)∴AF=AE+EF=20.∵AM<AF<AN,∴轮船不改变航向继续航行,正好能行至码头MN靠岸.6、如图是某货站传送货物的平面示意图. 为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°. 已知原传送带AB长为4米.(1)求新传送带AC的长度;(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物MNQP 是否需要挪走,并说明理由.(说明:⑴⑵的计算结果精确到0.1米,参考数据:2≈1.41,3≈1.73,5≈2.24,6≈2.45)答案(1)如图,作AD⊥BC于点D……………………………………1分Rt△ABD中,AD=AB sin45°=42222=⨯……2分在Rt△ACD中,∵∠ACD=30°FEDlAC北东M NABE FQ P ∴AC =2AD =24≈6.5………………………3分即新传送带AC 的长度约为6.5米. ………………………………………4分 (2)结论:货物MNQP 应挪走. ……………………………………5分 解:在Rt △ABD 中,BD =AB cos45°=42222=⨯……………………6分 在Rt △ACD 中,CD =AC cos30°=622324=⨯∴CB =CD —BD =)26(22262-=-≈2.1∵PC =PB —CB ≈4—2.1=1.9<2 ………………………………7分 ∴货物MNQP 应挪走. …………………………………………………………8分7、如图,大海中有A 和B 两个岛屿,为测量它们之间的距离,在海岸线PQ 上点E 处测得∠AEP =74°,∠BEQ =30°;在点F 处测得∠AFP =60°,∠BF Q =60°,EF =1km .(1)判断ABAE 的数量关系,并说明理由;(2)求两个岛屿A 和B 之间的距离(结果精确到0.1km ).(参考数据:3≈1.73,sin74°≈,cos74°≈0.28,tan74°≈3.49,sin76°≈0.97,cos76°≈0.24)答案 (1)相等30,6030BEQ BFQ EBF EF BF ∠=∠=∴∠=∴=....................................2分 又6060AF P BFA ∠∠=∴∠=在AEF 与△ABF 中,,EF BF AFE AFB AF AFAFE AFB AE AB=∠=∠=∴≅∴=...........................................................................5分 (2)法一:作AH PQ ⊥,垂足为H 设 AE=x 则AH=xsin74°HE= xcos74° HF=xcos74°+1 ...............................................................................................7分tan60Rt AHF AH HF=中,所以xsin74°=(xcos74°+1)tan60°即0.96x=(0.28x+1)×1.73所以 3.6x≈即AB 3.6km≈法二:设AF与BE的交点为G,在Rt△EGF中,因为EF=1, 所以 EG=3在Rt△AEG中376,cos760.24 3.6 AEG AE EG∠==÷=÷≈答: 两个岛屿A与B之间的距离约为3.6km8、在一个阳光明媚、清风徐来的周末,小明和小强一起到郊外放风筝﹒他们把风筝放飞后,将两个风筝的引线一端都固定在地面上的C处(如图).现已知风筝A的引线(线段AC)长20m,风筝B的引线(线段BC)长24m,在C处测得风筝A的仰角为60°,风筝B的仰角为45°.(1)试通过计算,比较风筝A与风筝B谁离地面更高?(2)求风筝A与风筝B的水平距离.(精确到0.01 m;参考数据:sin45°≈0.707,cos45°≈0.707,tan45°=1,sin60°≈0.866,cos60°=0.5,tan60°≈1.732)解:(1)分别过A,B作地面的垂线,垂足分别为D,E.在Rt△ADC中,∵AC﹦20,∠ACD﹦60°,AB45°60°C E D∴AD ﹦20×sin 60°﹦103≈17.32m在Rt △BEC 中,∵BC ﹦24,∠BEC ﹦45°,∴BE ﹦24×sin 45°﹦122≈16.97 m∵17.32>16.97∴风筝A 比风筝B 离地面更高. ……………………………………………3分 (2)在Rt △ADC 中,∵AC ﹦20,∠ACD ﹦60°, ∴DC ﹦20×cos 60°﹦10 m在Rt △BEC 中,∵BC ﹦24,∠BEC ﹦45°,∴EC ﹦BC ≈16.97 m∴EC -DC ≈16.97-10﹦6.97m即风筝A 与风筝B 的水平距离约为6.97m .…………………………………3分9、为了缓解长沙市区内一些主要路段交通拥挤的现状,交警队在一些主要路口设立了交通路况显示牌(如图).已知立杆AB 高度是3m ,从侧面D 点测得显示牌顶端C 点和底端B 点的仰角分别是60°和45°.求路况显示牌BC 的高度.解:∵在Rt △ADB 中,∠BDA =45°,AB =3 ∴DA =3 …………2分 在Rt △ADC 中,∠CDA =60°∴tan60°=CAAD∴CA =33 …………4分 ∴BC=CA -BA =(33-3)米答:路况显示牌BC 的高度是(33-3)米 ………………………6分10、永乐桥摩天轮是天津市的标志性景观之一.某校数学兴趣小组要测量摩天轮的高度.如图,他们在C 处测得摩天轮的最高点A 的仰角为45︒,再往摩天轮的方向前进50 m 至D 处,测得最高点A 的仰角为60︒. 求该兴趣小组测得的摩天轮的高度AB (3 1.732≈,第19题图A45°60°结果保留整数).解:根据题意,可知45ACB ∠=︒,60ADB ∠=︒,50DC =.在Rt △ABC 中,由45BAC BCA ∠=∠=︒,得BC AB =. 在Rt △ABD 中,由tan ABADB BD∠=, 得3tan tan 60AB AB BD AB ADB ===∠︒. ..............................6分 又 ∵ BC BD DC -=,∴ 350AB AB -=,即(33)150AB -=. ∴ 11833AB =≈-.答:该兴趣小组测得的摩天轮的高度约为118 m. .....................8分11、小明想知道湖中两个小亭A 、B 之间的距离,他在与小亭A 、B 位于同一水平面且东西走向的湖边小道l 上某一观测点M 处,测得亭A 在点M 的北偏东30°, 亭B 在点M 的北偏东60°,当小明由点M 沿小道l 向东走60米时,到达点N 处,此时测得亭A 恰好位于点N 的正北方向,继续向东走30米时到达点Q 处,此时亭B 恰好位于点Q 的正北方向,根据以上测量数据,请你帮助小明计算湖中两个小亭A 、B 之间的距离.25.连结AN 、BQ∵点A 在点N 的正北方向,点B 在点Q 的正北方向 ∴l AN ⊥ l BQ ⊥--------------------------1分 在Rt △AMN 中:tan ∠AMN=MNAN∴AN=360-----------------------------------------3分 在Rt △BMQ 中:tan ∠BMQ=MQBQ∴BQ=330----------------------------------------5分 过B 作BE ⊥AN 于点E 则:BE=NQ=30∴AE= AN -BQ -----------------------------------8分 在Rt △ABE 中,由勾股定理得:222BE AE AB +=22230)330(+=AB∴AB=60(米)12、我们知道当人的视线与物体表面互相垂直时的视觉效果最佳.如图是小明站在距离墙壁1.60米处观察装饰画时的示意图,此时小明的眼睛与装饰画底部A 处于同一水平线上,视线恰好落在装饰画中心位置E 处,且与AD 垂直.已知装饰画的高度AD 为0.66米, 求:⑴ 装饰画与墙壁的夹角∠CAD 的度数(精确到1°);⑵ 装饰画顶部到墙壁的距离DC (精确到0.01米).解:⑴ ∵AD =0.66,∴AE =21CD =0.33. 在Rt △ABE 中,………………1分 ∵sin ∠ABE =AB AE =6.133.0, ∴∠ABE ≈12°. ………………4分∵∠CAD +∠DAB =90°,∠ABE +∠DAB =90°, ∴∠CAD =∠ABE =12°.∴镜框与墙壁的夹角∠CAD 的度数约为12°. ………………5分 ⑵ 解法一:在Rt △∠ABE 中, ∵sin ∠CAD =ADCD, ∴CD =AD ·sin ∠CAD =0.66×sin12°≈0.14. ………………7分ACD EBABCD第19题图解法二: ∵∠CAD =∠ABE , ∠ACD =∠AEB =90°,∴△ACD ∽△BEA. ………………6分 ∴AB ADAE CD =. ∴6.166.033.0=CD . ∴CD ≈0.14. ………………7分∴镜框顶部到墙壁的距离CD 约是0.14米.………………8分13、如图,某天然气公司的主输气管道从A 市的东偏北30°方向直线延伸,测绘员在A 处测得要安装天然气的M 小区在A 市东偏北60°方向,测绘员沿主输气管道步行2000米到达C 处,测得小区M 位于C 的北偏西60°方向,请你在主输气管道上寻找支管道连接点N ,使到该小区铺设的管道最短,并求AN 的长.第23题图解:过M 作MN ⊥AC ,此时MN 最小,AN =1500米1、(2010山东济南)图所示,△ABC 中,∠C =90°,∠B =30°,AD 是△ABC 的角平分线,若AC 3求线段AD 的长.解:∵△ABC 中,∠C =90º,∠B =30º,∴∠BAC =60º,∵AD 是△ABC 的角平分线,∴∠CAD =30º, ··················· 1分 ∴在Rt △ADC 中,cos30ACAD =︒············· 2分=3×3··········· 3分=2 . ·············· 4分14、热气球的探测器显示,从热气球A 处看一栋高楼顶部的仰角为45°,看这栋高楼底部的俯角为60°,A 处与高楼的水平距离为60m ,这栋高楼有多高?(结果精确到0.1m ,参考数据:2 1.414,3 1.732≈≈)答案: 解:过点A 作BC 的垂线,垂足为D 点 ……………1分由题意知:∠CAD = 45°, ∠BAD =60°, AD = 60m在Rt △ACD 中,∠CAD = 45°, AD ⊥BC∴ CD = AD = 60 ……………………3分 在Rt △ABD 中,∵BDtan BAD AD∠=……………………4分 ∴ BD = AD ·tan ∠BAD= 603 ……………………5分∴BC = CD+BD= 60+603 ……………………6分≈ 163.9 (m) …………………7分答:这栋高楼约有163.9m . …………………8分 (本题其它解法参照此标准给分)15、如图,直角ABC ∆中,90C ∠=︒,25AB =,5sin B =,点P 为边BC 上一动点,PD ∥AB ,PD 交AC 于点D ,连结AP . (1)求AC 、BC 的长;(2)设PC 的长为x ,ADP ∆的面积为y .当x 为何值时,y 最大,并PD CBA求出最大值.22.(1)在Rt ABC ∆中,5sin B =,25AB =, 得5AC AB =,∴2AC =,根据勾股定理得:4BC =. …… 3分(2)∵PD ∥AB ,∴ABC ∆∽DPC ∆,∴12DC AC PC BC == 设PC x =,则12DC x =,122AD x =- ∴2211111(2)(2)122244ADP S AD PC x x x x x ∆=⋅=-⋅=-+=--+ ∴当2x =时,y 的最大值是1. ……… 8分16、小明家所在居民楼的对面有一座大厦AB ,AB =80米.为测量这座居民楼与大厦之间的距离,小明从自己家的窗户C 处测得大厦顶部A 的仰角为37°,大厦底部B 的俯角为48°.求小明家所在居民楼与大厦的距离CD 的长度.(结果保留整数) (参考数据:o o o o 33711sin37tan37sin 48tan48541010≈≈≈≈,,,)答案:解:设CD = x .在Rt △ACD 中,tan37AD CD︒=, 则34AD x=, ∴34AD x =. 在Rt △BCD 中,tan48° = BD CD, 则1110BD x=, ∴1110BD x =. ∵AD +BD = AB , B37° 48° D CA 第19题图∴31180 410x x+=.解得:x≈43.17、在市政府广场进行了热气球飞行表演,如图,有一热气球到达离地面高度为36米的A处时,仪器显示正前方一高楼顶部B的仰角是37°,底部C的俯角是60°.为了安全飞越高楼,气球应至少再上升多少米?(结果精确到0.1米)(参考数据:,75.037tan,80.037cos,60.037sin≈︒≈︒≈︒73.13≈)解:过A作AD⊥CB,垂足为点D.………………………1分在Rt△ADC中,∵CD=36,∠CAD=60°.∴AD=31233660tan==︒CD≈20.76.……5分在Rt△ADB中,∵AD≈20.76,∠BAD=37°.∴BD=37tan⨯AD≈20.76×0.75=15.57≈15.6(米).………8分答:气球应至少再上升15.6米.…………………………9分18、图1为已建设封顶的16层楼房和其塔吊图,图2为其示意图,吊臂AB与地面EH平行,测得A点到楼顶D点的距离为5m,每层楼高3.5m,AE、BF、CH都垂直于地面,EF=16m,求塔吊的高CH的长.【答案】解:根据题意得:DE=3.5×16=56,AB=EF=16∵∠ACB=∠CBG-∠CAB=15°,∴∠ACB =∠ CAB∴CB=AB=16.∴CG=BCsin30°=8CH=CG+HG=CG+DE+AD=8+56+5=69.∴塔吊的高CH的长为69m.BACD。
解三角形大题第一问专练13个类型练到位原卷版

专题3解三角形大题第一问专练·13个类型练到位目录高考真题回顾与梳理 (3)2023.新高考一卷T17(1):出现了3个角时 拆角 (3)2022.新高考二卷T18(2):式子变形后出现了三边的平方 余弦 (3)2019.全国Ⅲ卷高考真题:出现两角之和 变为第三个角 (4)题型一正弦定理+和差公式 (5)类型1 出现了3个角(拆角,正向使用和差公式) (5)类型2 反向使用和差公式 (6)类型3 拆角后再用辅助角公式合并求角 (6)题型二用余弦定理 (8)类型1 出现了边的平方 (8)类型2 出现角的余弦(正弦走不通) (9)题型三多解问题分析 (11)题型四通过诱导公式统一函数名 (12)类型1 半角降幂扩角 (13)类型2余弦二倍角转变为1元二次方程 (13)题型六切化弦 (14)题型七判断三角形的形状或验证角度之间的关系 (15)题型七遇到两角之和化为第三个角 (17)一、基本定理公式(1)正余弦定理:在△ABC 中,角A ,B ,C 所对的边分别是a ,b ,c ,R 为△ABC 外接圆半径,则111sin sin sin 222S ABC ab C bc A ac B ∆=== 1()42abc S ABC a b c r R ∆==++⋅(r 是三角形内切圆的半径,并可由此计算R ,r . ) (3)二倍角公式sin 22sin cos A A A =,2222cos 22cos 112sin cos sin A A A A A =−=−=−二、相关应用 (1)正弦定理的应用①边化角,角化边::sin :sin :sin a b c A B C ⇔=②大边对大角 大角对大边sin sin cos cos a b A B A B A B >⇔>⇔>⇔<③合分比:b 2sin sin sin sin sin sin sin sin sin sin sin B sin a bc a b b c a c a cR A B C A B B C A C A C+++++=======+++++(2)ABC △内角和定理(结合诱导公式):A B C π++= ①sin sin()sin cos cos sin CA B A B A B =+=+cos cos c a B b A ⇔=+ 同理有:cos cos a b C c B +,cos cos b c A a C +.②cos cos()cos cos sinAsinB CA B A B −=+=−; ③斜三角形中,tan tan tan tan()1tan tan A BCA B A B+−=+=−⋅tan tan tanC tan tan tanC A B A B ⇔++=⋅⋅④sin()cos 22A B C +=;cos()sin 22A B C+= ⑤在ABC ∆中,内角A B C ,,成等差数列2,33BA C ππ⇔=+=.(3)2倍角公式的扩角降幂21cos cos 22C C +=.,21cos sin 22C C −= 忘记了可以用二倍角公式推导:记2Ct =, 则22cos cos 22cos 112sin C t t t ==−=−故221cos 2cos22cos 1cos 2t t t t +=−⇒=,221cos 2cos 212sin sin 2tt t t −=−⇒=高考真题回顾与梳理2023·新高考一卷T17(1):出现了3个角时 拆角已知在ABC 中,()3,2sin sin A B C A C B +=−=,求sin A .2022·新高考二卷T18(2):式子变形后出现了三边的平方 余弦2019·全国Ⅲ卷高考真题:出现两角之和 变为第三个角题型一 正弦定理+和差公式类型1 出现了3个角(拆角,正向使用和差公式)1.在ABC cos cos CA =,求A 的值2.△ABC 的内角A,B,C 的对边分别为a,b,c ,且2sin 6b c A π+,求C.重点题型·归类精类型2 反向使用和差公式中,角A,B,C的对边分别为a,b,c,已知4.(2023·重庆二模)在ABC类型3 拆角后再用辅助角公式合并求角7.(2023届·深圳市一模)记△ABC的内角A,B,C的对边分别为a,b,c,已知2sin 6b c a C π+=+ ,求A .8.在 ABC sin sin cos sin B CC C A++=,求A .题型二 用余弦定理 类型1 出现了边的平方11.已知ABC 内角,,A B C 所对的边长分别为2222,,cos 2cos a b c B b ab C a c +=++,求B .12.在ABC ∆中,角A ,B ,C 的对边分别为a ,b ,c ,已知c =2sin cos sin sin sin a C B a A b B C =−+,求b2023届·湖南四大名校团队模拟冲刺卷(一)2023·广东省六校高三第四次联考14.已知ABC 的角A ,B ,C 的对边分别为a ,b ,c ,且类型2 出现角的余弦(正弦走不通)17.(2023·广州二模)记ABC 的内角A 、B 、C 的对边分别为a 、b 、c ,已知cos cos b A a B b c −=−,求A .18.(2023·深圳二模)已知,,a b c 分别为ABC 三个内角,,A B C 的对边,且()sin 2sin A B C −=,证明:22.ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知sin =sin b c B b A C −−,求角A .题型三 多解问题分析23.(易漏解)△ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,且有()sin 20C A B ++=, 求角C .24.(2023上·肇庆·二模)在ABC 中,角,,A B C 的对边分别为,,a b c .已知()cos cos cos 0b c A a B a C +−−=,求角A .题型四 通过诱导公式统一函数名25.在ABC 中,内角,,A B C 所对的边分别为,,a b c .已知πsin cos 6a B b A=−,求A 的值26.(2023下·华中师大一附中5月压轴卷(一)·模拟预测)已知ABC 中,角A ,B ,C 所对边分别为a ,b ,c ,若满足(sin 2cos cos )sin sin 0a A B C b A C −+=,求角A 的大小.cos cos b C c B =,求A 的值.题型五 降幂,半角,二倍角 类型1 半角降幂扩角28.(2023·重庆八中二模)记ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,已知223cos cos 222C A a c b +=.证明:sin sin 2sin A C B +=29.在ABC ∆中,内角A ,B ,C 所对的边分别a ,b ,c ,且223(coscos )()222C Aa c a cb ac ++−=,求角B 的大小;类型2 余弦二倍角转变为1元二次方程30.在△ABC 中,角A ,B ,C 对应的边分别是a ,b ,c ,已知cos2A -3cos (B +C )=1,求角A 的大小.题型六 切化弦长沙市长郡中学、长沙一中、雅礼中学、湖南师大附中2023届5月“一起考” 31.在ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,sin sin tan cos cos B CA B C+=+,求A ∠.32.(2023·青岛·三模)记ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知()2sin2tan c B a c C =−,求33.在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且满足πsin 3tan πsin 6C B C+=−,求A .题型七判断三角形的形状或验证角度之间的关系重庆市巴蜀中学校2023届高三下学期适应性月考(十)三角形38.记ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知2cos a c b A +=,证明:2B A =.39.在锐角ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且2cos c b A b −=,求证:2A B =.2023届·武汉市华中师范大学第一附属中学5月压轴卷(二)40.ABC 的内角,,A B C 的对边分别为,,a b c 且()()sin cos cos sin A B CB AC −=−,判断ABC 的形状;题型七 遇到两角之和化为第三个角41.(2023sinsin 2A Bc A +=,求角C 的大小.Cc=,求B2。
高中数学解三角形精选题目(附答案)

高中数学解三角形精选题目(附答案)一、解三角解三角形的常见类型及方法(1)已知三边:先由余弦定理求出两个角,再由A+B+C=π,求第三个角.(2)已知两边及其中一边的对角:先用正弦定理求出另一边的对角,再由A +B+C=π,求第三个角,最后利用正弦定理或余弦定理求第三边.(3)已知两边及夹角:先用余弦定理求出第三边,然后再利用正弦定理或余弦定理求另两角.(4)已知两角及一边:先利用内角和求出第三个角,再利用正弦定理求另两边.1.设锐角△ABC的内角A,B,C的对边分别为a,b,c,且有a=2b sin A.(1)求B的大小;(2)若a=33,c=5,求b.1.解:(1)由a=2b sin A,根据正弦定理得sin A=2sin B sin A,所以sin B=1 2,由于△ABC是锐角三角形,所以B=π6.(2)根据余弦定理,得b2=a2+c2-2ac cos B=27+25-45=7,所以b=7.注:利用正、余弦定理来研究三角形问题时,一般要综合应用三角形的性质及三角函数关系式,正弦定理可以用来将边的比和对应角正弦值的比互化,而余弦定理多用来将余弦值转化为边的关系.2.在△ABC中,内角A,B,C的对边分别是a,b,c,若a2-b2=3bc,sin C=23sin B,则A=()A.30°B.60°C.120°D.150°解析:选A 由正弦定理可知c =23b ,则cos A =b 2+c 2-a 22bc =-3bc +c 22bc =-3bc +23bc 2bc =32,所以A =30°,故选A.3.在△ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c .若c 2=(a -b )2+6,C =π3,则△ABC 的面积是( )A .3B.932C.332 D .33解析:选C ∵c 2=(a -b )2+6,∴c 2=a 2+b 2-2ab +6.①∵C =π3,∴c 2=a 2+b 2-2ab cos π3=a 2+b 2-ab .②由①②得-ab +6=0,即ab =6. ∴S △ABC =12ab sin C =12×6×32=332.4.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .已知A =π6,a =1,b =3,则B =________.解析:依题意得,由正弦定理知:1sin π6=3sin B ,sin B =32,又0<B <π,b >a ,可得B =π3或2π3.答案:π3或2π35.△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c .(1)若a ,b ,c 成等差数列,证明:sin A +sin C =2sin(A +C );(2)若a ,b ,c 成等比数列,求cos B 的最小值.解:(1)证明:∵a ,b ,c 成等差数列,∴a +c =2b .由正弦定理得sin A +sin C =2sin B .∵sin B =sin[π-(A +C )]=sin(A +C ),∴sin A +sin C =2sin(A +C ).(2)∵a ,b ,c 成等比数列,∴b 2=ac .由余弦定理得cos B =a 2+c 2-b 22ac =a 2+c 2-ac 2ac≥2ac -ac 2ac =12, 当且仅当a =c 时等号成立.∴cos B 的最小值为12.二、三角形的形状判定三角形中的常用结论(1)A +B =π-C ,A +B 2=π2-C 2. (2)在三角形中大边对大角,反之亦然.(3)任意两边之和大于第三边,任意两边之差小于第三边.6.在△ABC 中,a ,b ,c 分别表示三个内角A ,B ,C 的对边,如果(a 2+b 2)sin(A -B )=(a 2-b 2)·sin(A +B ),试判断该三角形的形状.[解] ∵(a 2+b 2)sin(A -B )=(a 2-b 2)·sin(A +B ),∴a 2[sin(A -B )-sin(A +B )]=b 2[-sin(A +B )-sin(A -B )],∴2a 2cos A sin B =2b 2sin A cos B .法一:(化边为角)由正弦定理得2sin 2A cos A sin B =2sin 2B sin A cos B , 即sin 2A ·sin A sin B =sin 2B ·sin A sin B .∵0<A <π,0<B <π,∴sin 2A =sin 2B ,∴2A =2B 或2A =π-2B ,即A =B 或A +B =π2.∴△ABC 是等腰三角形或直角三角形.法二:(化角为边)2a 2cos A sin B =2b 2cos B sin A ,由正弦、余弦定理得a 2b ·b 2+c 2-a 22bc =b 2a ·a 2+c 2-b 22ac ,∴a 2(b 2+c 2-a 2)=b 2(a 2+c 2-b 2),即(a 2-b 2)(c 2-a 2-b 2)=0.∴a =b 或c 2=a 2+b 2,∴△ABC 为等腰三角形或直角三角形.注:根据所给条件判断三角形的形状的途径(1)化边为角.(2)化角为边,转化的手段主要有:①通过正弦定理实现边角转化;②通过余弦定理实现边角转化;③通过三角变换找出角之间的关系;④通过对三角函数值符号的判断以及正、余弦函数的有界性来确定三角形的形状.7.在△ABC 中,内角A ,B ,C 所对的边长分别是a ,b ,c .若c -a cos B =(2a -b )cos A ,则△ABC 的形状为( )A .等腰三角形B .直角三角形C .等腰直角三角形D .等腰或直角三角形解析:选D ∵c -a cos B =(2a -b )cos A ,C =π-(A +B ),∴由正弦定理得sin C -sin A cos B =2sin A cos A -sin B cos A ,∴sin A cos B +cos A sin B -sin A cos B =2sin A cos A -sin B cos A ,∴cos A (sin B -sin A )=0,∴cos A =0或sin B =sin A ,∴A =π2或B =A 或B =π-A (舍去).故△ABC 为直角三角形或等腰三角形.8.在△ABC 中,已知3b =23a sin B ,且A ,B ,C 成等差数列,则△ABC 的形状为( )A .直角三角形B .等腰三角形C .等边三角形D .等腰直角三角形解析:选C ∵A ,B ,C 成等差数列,∴A +C =2B ,即3B =π,解得B =π3.∵3b =23a sin B ,∴根据正弦定理得3sin B =23sin A sin B .∵sin B ≠0,∴3=23sin A ,即sin A =32,即A =π3或2π3,当A =2π3时,A +B =π不满足条件.∴A =π3,C =π3.故A =B =C ,即△ABC 的形状为等边三角形.9.在△ABC 中,a ,b ,c 分别为内角A ,B ,C 的对边,且2a sin A =(2b +c )sin B +(2c +b )sin C .(1)求A 的大小;(2)若sin B +sin C =1,试判断△ABC 的形状.解:(1)由已知,根据正弦定理得2a 2=(2b +c )b +(2c +b )c ,即a 2=b 2+c 2+bc .由余弦定理,a 2=b 2+c 2-2bc cos A ,∴bc =-2bc cos A ,cos A =-12. 又0<A <π,∴A =2π3.(2)由(1)知sin 2A =sin 2B +sin 2C +sin B sin C ,∴sin 2A =(sin B +sin C )2-sin B sin C .又sin B +sin C =1,且sin A =32,∴sin B sin C =14,因此sin B =sin C =12.又B ,C ∈⎝ ⎛⎭⎪⎫0,π2,故B =C . 所以△ABC 是等腰的钝角三角形.三、实际应用(1)仰角与俯角是相对水平线而言的,而方位角是相对于正北方向而言的.(2)利用方位角或方向角和目标与观测点的距离即可唯一确定一点的位置.10.如图,渔船甲位于岛屿A 的南偏西60°方向的B 处,且与岛屿A 相距12海里,渔船乙以10海里/小时的速度从岛屿A 出发沿正北方向航行,若渔船甲同时从B 处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上.(1)求渔船甲的速度;(2)求sin α的值.[解] (1)依题意,∠BAC =120°,AB =12海里,AC =10×2=20(海里),∠BCA =α.在△ABC 中,由余弦定理,得BC 2=AB 2+AC 2-2AB ×AC ×cos ∠BAC =122+202-2×12×20×cos 120°=784.解得BC =28海里.∴渔船甲的速度为BC 2=14(海里/小时).(2)在△ABC 中,AB =12海里,∠BAC =120°,BC =28海里,∠BCA =α,由正弦定理,得AB sin α=BC sin 120°.即sin α=AB sin 120°BC=12×3228=3314.故sin α的值为33 14.注:应用解三角形知识解决实际问题的步骤(1)读题.分析题意,准确理解题意,分清已知与所求,尤其要理解题中的有关名词、术语,如坡度、仰角、俯角、方位角等;(2)图解.根据题意画出示意图,并将已知条件在图形中标出;(3)建模.将所求解的问题归结到一个或几个三角形中,通过合理运用正弦定理、余弦定理等有关知识正确求解;(4)验证.检验解出的结果是否具有实际意义,对结果进行取舍,得出正确答案.11.要测量底部不能到达的电视塔AB的高度,如图,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD=40 m,则电视塔的高度为()A.10 2 m B.20 mC.20 3 m D.40 m解析:选D设电视塔的高度为x m,则BC=x,BD=3x.在△BCD中,根据余弦定理得3x2=x2+402-2×40x×cos 120°,即x2-20x-800=0,解得x =40或x=-20(舍去).故电视塔的高度为40 m.12.北京国庆阅兵式上举行升旗仪式,如图,在坡度为15°的观礼台上,某一列座位与旗杆在同一个垂直于地面的平面上,在该列的第一排和最后一排测得旗杆顶端的仰角分别为60°和30°,且第一排和最后一排的距离为10 6 m,则旗杆的高度为________m.解析:设旗杆高为h m,最后一排为点A,第一排为点B,旗杆顶端为点C,则BC=hsin 60°=233h.在△ABC中,AB=106,∠CAB=45°,∠ABC=105°,所以∠ACB=30°,由正弦定理,得106sin 30°=233hsin 45°,故h=30(m).答案:3013.某高速公路旁边B处有一栋楼房,某人在距地面100米的32楼阳台A处,用望远镜观测路上的车辆,上午11时测得一客车位于楼房北偏东15°方向上,且俯角为30°的C处,10秒后测得该客车位于楼房北偏西75°方向上,且俯角为45°的D处.(假设客车匀速行驶)(1)如果此高速路段限速80千米/小时,试问该客车是否超速?(2)又经过一段时间后,客车到达楼房的正西方向E处,问此时客车距离楼房多远?解:(1)在Rt△ABC中,∠BAC=60°,AB=100米,则BC=1003米.在Rt△ABD中,∠BAD=45°,AB=100米,则BD=100米.在△BCD中,∠DBC=75°+15°=90°,则DC=BD2+BC2=200米,所以客车的速度v=CD10=20米/秒=72千米/小时,所以该客车没有超速.(2)在Rt△BCD中,∠BCD=30°,又因为∠DBE=15°,所以∠CBE=105°,所以∠CEB=45°.在△BCE中,由正弦定理可知EBsin 30°=BCsin 45°,所以EB=BC sin 30°sin 45°=506米,即此时客车距楼房506米.巩固练习:1.在△ABC中,若a=7,b=3,c=8,则其面积等于()A.12 B.21 2C.28D.63解析:选D由余弦定理得cos A=b2+c2-a22bc=32+82-722×3×8=12,所以sin A=32,则S△ABC=12bc sin A=12×3×8×32=6 3.2.在△ABC中,内角A,B,C所对的边分别为a,b,c.若3a=2b,则2sin2B-sin2Asin2A的值为()A.19 B.13C.1 D.7 2解析:选D由正弦定理可得2sin2B-sin2Asin2A=2b2-a2a2=2·⎝ ⎛⎭⎪⎫32a2-a2a2=72.3.在△ABC中,已知AB=2,BC=5,△ABC的面积为4,若∠ABC=θ,则cos θ等于()A.35B.-35C.±35D.±45解析:选C∵S△ABC =12AB·BC sin∠ABC=12×2×5×sin θ=4.∴sin θ=45.又θ∈(0,π),∴cos θ=±1-sin2θ=±3 5.4.某人从出发点A向正东走x m后到B,向左转150°再向前走3 m到C,测得△ABC的面积为334m2,则此人这时离开出发点的距离为()A.3 m B. 2 mC.2 3 m D. 3 m解析:选D在△ABC中,S=12AB×BC sin B,∴334=12×x×3×sin 30°,∴x= 3.由余弦定理,得AC=AB2+BC2-2AB×BC×cos B=3+9-9=3(m).5.在△ABC中,A=60°,AB=2,且△ABC的面积S△ABC=32,则边BC的边长为()A.3B.3C.7D.7解析:选A∵S△ABC =12AB·AC sin A=32,∴AC=1,由余弦定理可得BC2=AB2+AC2-2AB·AC cos A=4+1-2×2×1×cos 60°=3,即BC= 3.6.设△ABC的内角A,B,C所对的边分别为a,b,c,若b cos C+c cos B =a sin A,则△ABC的形状为()A.锐角三角形B.直角三角形C.钝角三角形D.不确定解析:选B∵b cos C+c cos B=b·b2+a2-c22ab+c·c2+a2-b22ac=b2+a2-c2+c2+a2-b22a=2a22a=a=a sin A,∴sin A=1.∵A∈(0,π),∴A=π2,即△ABC是直角三角形.7.在△ABC中,B=60°,b2=ac,则△ABC的形状为____________.解析:由余弦定理得b2=a2+c2-2ac cos B,即ac=a2+c2-ac,∴(a-c)2=0,∴a=c.又∵B=60°,∴△ABC为等边三角形.答案:等边三角形8.在△ABC中,a=b+2,b=c+2,又知最大角的正弦等于32,则三边长为________.解析:由题意知a边最大,sin A=32,∴A=120°,∴a2=b2+c2-2bc cos A.∴a2=(a-2)2+(a-4)2+(a-2)(a-4).∴a2-9a+14=0,解得a=2(舍去)或a=7.∴b=a-2=5,c=b-2=3.答案:a=7,b=5,c=39.已知三角形ABC的三边为a,b,c和面积S=a2-(b-c)2,则cos A=________.解析:由已知得S=a2-(b-c)2=a2-b2-c2+2bc=-2bc cos A+2bc.又S=12bc sin A,∴12bc sin A=2bc-2bc cos A.∴4-4cos A=sin A,平方得17cos2A-32cos A+15=0.∴(17cos A-15)(cos A-1)=0.∴cos A=1(舍去)或cos A=15 17.答案:15 1710.在△ABC中,内角A,B,C的对边分别为a,b,c.已知cos A=23,sin B=5cos C.(1)求tan C的值;(2)若a=2,求△ABC的面积.解:(1)因为0<A<π,cos A=2 3,所以sin A=1-cos2A=5 3,又5cos C=sin B=sin(A+C)=sin A cos C+cos A sin C=53cos C+23sin C,所以253cos C=23sin C,tan C= 5.(2)由tan C=5得sin C=56,cos C=16,于是sin B =5cos C =56. 由a =2及正弦定理a sin A =c sin C 得c =3,所以△ABC 的面积S △ABC =12ac sinB =12×2×3×56=52. 11.如图,在△ABC 中,∠B =π3,AB =8,点D 在BC 边上,且CD =2,cos ∠ADC =17.(1)求sin ∠BAD ;(2)求BD ,AC 的长.解:(1)在△ADC 中,因为cos ∠ADC =17,所以sin ∠ADC =437.所以sin ∠BAD =sin(∠ADC -∠B )=sin ∠ADC cos B -cos ∠ADC sin B=437×12-17×32=3314.(2)在△ABD 中,由正弦定理得BD =AB ·sin ∠BAD sin ∠ADB =8×3314437=3. 在△ABC 中,由余弦定理得AC 2=AB 2+BC 2-2AB ·BC ·cos B=82+52-2×8×5×12=49. 所以AC =7.12.已知△ABC 的内角A ,B ,C 所对的边分别是a ,b ,c ,设向量m =(a ,b ),n =(sin B ,sin A ),p =(b -2,a -2).(1)若m ∥n ,求证:△ABC 为等腰三角形;(2)若m ⊥p ,c =2,C =π3,求△ABC 的面积.解:(1)证明:∵m∥n,∴a sin A=b sin B,∴a·a=b·b,即a2=b2,a=b,∴△ABC为等腰三角形.(2)由m⊥p,得m·p=0,∴a(b-2)+b(a-2)=0,∴a+b=ab.由余弦定理c2=a2+b2-2ab cos C,得4=a2+b2-ab=(a+b)2-3ab,即(ab)2-3ab-4=0,解得ab=4(ab=-1舍去),∴S△ABC =12ab sin C=12×4×sinπ3= 3.。
解三角形经典练习题集锦

解三角形经典练习题集锦解三角形一、选择题1.在△ABC中,若C=90°,a=6,B=30°,则c-b等于()A.1B.-1C.2/3D.-2/32.若A为△ABC的内角,则下列函数中一定取正值的是()A.sinAB.cosAC.XXXD.1/tanA3.在△ABC中,角A,B均为锐角,且cosA>sinB,则△ABC的形状是()A.直角三角形B.锐角三角形C.钝角三角形D.等腰三角形4.等腰三角形一腰上的高是3,这条高与底边的夹角为60°,则底边长为()A.2B.3/2C.3D.2/35.在△ABC中,若b=2asinB,则A等于()A.30°或60°B.45°或60°C.120°或60°D.30°或150°6.边长为5,7,8的三角形的最大角与最小角的和是()A.90°B.120°C.135°D.150°二、填空题1.在Rt△ABC中,C=90°,则sinAsinB的最大值是1/2.2.在△ABC中,若a^2=b^2+bc+c^2,则A=120°。
3.在△ABC中,若b=2,B=30°,C=135°,则a=2√3.4.在△ABC中,若5.在△ABC中,AB=6-2,C=30°,则AC+BC的最大值是2√7.三、解答题1.在△ABC中,若acosA+bcosB=ccosC,则△ABC为等腰三角形。
2.在△ABC中,证明:a/b-cosBcosA/a-c=b/a-c。
3.在锐角△ABC中,证明:XXX>XXX。
4.在△ABC中,设a+c=2b,A-C=π/3,则sinB=1/2.5.在△ABC中,若(a+b+c)(b+c-a)=3bc,则A的度数为()A.90B.60C.135D.150解析:根据余弦定理,有$b^2+c^2-2bc\cos A=a^2$,代入$(a+b+c)(b+c-a)=3bc$中,整理得$\cos A=-\frac{1}{2}$,即$A=120^\circ$,选项B正确。
专题1.3 解直角三角形的中考常考题专项训练(50道)(举一反三)(北师大版)(原卷版)

专题1.3 解直角三角形的中考常考题专项训练(50道)【北师大版】考卷信息:本套训练卷共50题,其中选择题15题,填空题15题,解答题20题. 题型针对性较高,覆盖面广,选题有深度,涵盖了解直角三角形的中考常考题的综合问题的所有类型!一、选择题(共15题)1.(2022·湖北武汉·中考真题)由4个形状相同,大小相等的菱形组成如图所示的网格,菱形的顶点称为格点,点A,B,C都在格点上,∠O=60°,则tan∠ABC=()A.13B.12C.3D.22.(2022·江苏连云港·中考真题)如图,△ABC中,BD⊥AB,BD、AC相交于点D,AD=47AC,AB=2,∠ABC=150°,则△DBC的面积是()A B C D3.(2022·浙江宁波·中考真题)如图,在△ABC中,∠B=45°,∠C=60°,AD⊥BC于点D,BDE,F分别为AB,BC的中点,则EF的长为()A B C.1D4.(2022·黑龙江·中考真题)如图,在正方形ABCD中,对角线AC与BD相交于点O,点E在BC的延长线上,连接DE,点F是DE的中点,连接OF交CD于点G,连接CF,若CE=4,OF=6.则下列结论:①GF=2;②OD=;③tan∠CDE=12;④∠ODF=∠OCF=90°;⑤点D到CF()A.①②③④B.①③④⑤C.①②③⑤D.①②④⑤5.(2022·四川宜宾·中考真题)如图,在△ABC中,点O是角平分线AD、BE的交点,若AB=AC=10,BC=12,则tan∠OBD的值是()A.12B.2C.3D.46.(2022·湖北荆州·中考真题)如图,在平面直角坐标系中,点A,B分别在x轴负半轴和y轴正半轴上,点C在OB上,OC:BC=1:2,连接AC,过点O作OP∥AB交AC的延长线于P.若P(1,1),则tan∠OAP的值是()A B C .13D .37.(2022·四川乐山·中考真题)如图,在Rt △ABC 中,∠C =90°,BC =D 是AC 上一点,连接BD .若tan ∠A =12,tan ∠ABD =13,则CD 的长为( )A .B .3CD .28.(2022·广西贵港·中考真题)如图,在4×4网格正方形中,每个小正方形的边长为1,顶点为格点,若△ABC 的顶点均是格点,则cos ∠BAC 的值是( )A B C D .459.(2022·黑龙江牡丹江·中考真题)如图,在△ABC 中,sinB=13, tanC=2,AB=3,则AC 的长为( )AB C D .210.(2022·四川绵阳·中考真题)公元三世纪,我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形的面积是125,小正方形面积是25,则(sin θ−cos θ)2=( )A .15B .5C .5D .9511.(2022·贵州遵义·中考真题)构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图.在Rt △ACB 中,∠C =90°,∠ABC =30°,延长CB 使BD =AB ,连接AD ,得∠D =15°,所以tan15°=ACCD=1=tan22.5°的值为( )A+1B 1C D .1212.(2022·浙江绍兴·中考真题)如图,Rt △ABC 中,∠BAC =90°,cos B =14,点D 是边BC 的中点,以AD 为底边在其右侧作等腰三角形ADE ,使∠ADE =∠B ,连结CE ,则CEAD 的值为( )A .32B C D .213.(2022·山东淄博·中考真题)如图,在Rt △ABC 中,∠ACB =90°,CE 是斜边AB 上的中线,过点E 作EF ⊥AB 交AC 于点F .若BC =4,△AEF 的面积为5,则sin ∠CEF 的值为( )A .35B .5C .45D .514.(2022·四川巴中·中考真题)如图,点A 、B 、C 在边长为1的正方形网格格点上,下列结论错误的是( )A .sinB =13B .sin C =C .tan B =12D .sin 2B +sin 2C =115.(2022·浙江丽水·中考真题)如图,已知菱形ABCD 的边长为4,E 是BC 的中点,AF 平分∠EAD 交CD 于点F , FG∥AD 交AE 于点G ,若cos B =14,则FG 的长是( )A .3B .83C D .52二、填空题(共15题)16.(2022·内蒙古·中考真题)如图,在矩形ABCD 中,BD 是对角线,AE ⊥BD ,垂足为E ,连接CE .若∠ADB =30°,则如tan ∠DEC 的值为_____.17.(2022·广东深圳·中考真题)如图,已知四边形ABCD ,AC 与BD 相交于点O ,∠ABC =∠DAC =90°,tan ∠ACB =12,BOOD =43,则S △ABDS △CBD=___.18.(2022·广东·中考真题)如图,在▱ABCD 中,AD =5,AB =12,sin A =45.过点D 作DE ⊥AB ,垂足为E ,则sin ∠BCE =______.19.(2022·广西贵港·中考真题)如图,在矩形ABCD 中,BD 是对角线,AE ⊥BD ,垂足为E ,连接CE ,若tan ∠ADB =12,则tan ∠DEC 的值是________.20.(2022·山东滨州·中考真题)如图,在△ABC 中,∠ACB =90°,∠BAC =30°,AB =2.若点P 是△ABC 内一点,则PA +PB +PC 的最小值为____________.21.(2022·山东德州·中考真题)如图.在4×4的正方形方格图形中,小正方形的顶点称为格点.ΔABC 的顶点都在格点上,则∠BAC的正弦值是__________.22.(2022·江苏镇江·中考真题)如图,△ABC中,∠BAC>90°,BC=5,将△ABC绕点C按顺时针方向旋转90°,点B对应点B′落在BA的延长线上.若sin∠B′AC=9,则AC=_____.1023.(2022·上海·中考真题)如图,在△ABC中,AB=AC,BC=8,tanC=3,如果将△ABC沿直线l翻折后,2点B落在边AC的中点处,直线l与边BC交于点D,那么BD的长为________.24.(2022·江苏盐城·中考真题)如图,在△ABC中,BC=∠C=45°,AB=,则AC的长为________.25.(2022·四川·中考真题)如图,由10个完全相同的正三角形构成的网格图中,∠α、∠β如图所示,则cos(α+β)=______.26.(2022·江苏淮安·中考真题)如图,在矩形ABCD中,AB=3,BC=2,H是AB的中点,将ΔCBH沿CH 折叠,点B落在矩形内点P处,连接AP,则tan∠HAP=__.27.(2022·山东济南·中考真题)如图,在矩形ABCD中,AB=4,BCE为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF=1,则CE=_____.228.(2022·山东潍坊·中考真题)如图,矩形ABCD中,点G,E分别在边BC,DC上,连接AG,EG,AE,将△ABG 和△ECG分别沿AG,EG折叠,使点B,C恰好落在AE上的同一点,记为点F.若CE=3,CG=4,则sin∠DAE= _______.29.(2022·江苏常州·中考真题)如图,点C在线段AB上,且AC=2BC,分别以AC、BC为边在线段AB的同侧作正方形ACDE、BCFG,连接EC、EG,则tan∠CEG=_________.30.(2022·江苏常州·中考真题)如图,在△ABC中,AC=3,BC=4,点D、E分别在CA、CB上,点F在△ABC 内.若四边形CDFE是边长为1的正方形,则sin∠FBA=________.三、解答题(共20题)31.(2022·黑龙江哈尔滨·中考真题)如图,方格纸中每个小正方形的边长均为1,线段的两个端点均在小正方形的顶点上.(1)在图中画出以为底、面积为12的等腰,且点在小正方形的顶点上;(2)在图中画出平行四边形,且点和点均在小正方形的顶点上,,连接,请直接写出线段的长.32.(2022·贵州毕节·中考真题)如图,在▱ABCD中过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.(1)求证:△ABF∽△BEC;,求AF的长.(2)若AD=5,AB=8,sinD=4533.(2022·江苏扬州·中考真题)如图,将△ABC沿着射线BC方向平移至△A′B′C′,使点A′落在∠ACB的外角平分线CD上,连接A A′.(1)判断四边形AC C′A′的形状,并说明理由;(2)在△ABC中,∠B=90°,AB=24,cos∠BAC=12,求C B′的长.1334.(2022·山东潍坊·中考真题)如图,点M是正方形ABCD边CD上一点,连接AM,作DE⊥AM于点E,BF⊥AM于点F,连接BE.(1)求证:AE=BF;(2)已知AF=2,四边形ABED的面积为24,求∠EBF的正弦值.35.(2022·上海·中考真题)如图,已知△ABC中,AB=BC=5,tan∠ABC=3.4(1)求边AC的长;(2)设边BC的垂直平分线与边AB的交点为D,求AD的值.DB36.(2022·广西贺州·中考真题)如图,在△ABC中,∠ACB=90°,O、D分别是边AC、AB的中点,过点C 作CE∥AB交DO的延长线于点E,连接AE.(1)求证:四边形AECD是菱形;(2)若四边形AECD的面积为24,tan∠BAC=3,求BC的长.437.(2022·黑龙江绥化·中考真题)如图,在矩形ABCD中,AD=5,CD=4,点E是BC边上的点,BE=3,连接AE,DF⊥AE交于点F.(1)求证:△ABE≌△DFA;(2)连接CF,求sin∠DCF的值;(3)连接AC交DF于点G,求AG的值.GC38.(2022·湖南常德·中考真题)如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB=1,AD=1.3(1)求BC的长;(2)求tan∠DAE的值.39.(2022·浙江绍兴·中考真题)在△ABC中,∠CAB=90°,AD⊥BC于点D,点E为AB的中点,EC与AD 交于点G,点F在BC上.(1)如图1,AC∶AB=1∶2,EF⊥CB,求证∶EF=CD.(2)如图2,AC∶AB=1EF⊥CE,求EF∶EG的值.40.(2022·广西梧州·中考真题)如图,在RtΔABC中,∠C=90°,D为BC上一点,AB=5,B D=1,tan B=3.4(1)求AD的长;(2)求sinα的值.41.(2022·湖北宜昌·中考真题)如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F 落在AD上.(1)求证:△ABF∽△DFE;(2)若,求tan∠EBC的值.42.(2022·福建厦门·中考真题)已知ABCD,对角线AC与BD相交于点O,点P在边AD上,过点P分别作PE⊥AC、PF⊥BD,垂足分别为E、F,PE=PF.(1)如图,若PE EO=1,求∠EPF的度数;(2)若点P是AD的中点,点F是DO的中点,BF =BC+4,求BC的长.43.(2022·山东滨州·中考真题)如图,菱形ABCD的边长为10,∠ABC=60°,对角线AC,BD相交于点O,点E在对角线BD上,连接AE,作∠AEF=120°且边EF与直线DC相交于点F.(1)求菱形ABCD的面积;(2)求证AE=EF.44.(2022·广东广州·中考真题)如图,在菱形ABCD中,∠BAD = 120°,AB = 6,连接BD.(1)求BD的长;(2)点E为线段BD上一动点(不与点B,D重合),点F在边AD上,且BE,①当CE丄AB时,求四边形ABEF的面积;②当四边形ABEF的面积取得最小值时,CE的值是否也最小?如果是,求CE的最小值;如果不是,请说明理由.45.(2022·湖南邵阳·中考真题)如图,在Rt△ABC中,点P为斜边BC上一动点,将△ABP沿直线AP折叠,使得点B的对应点为B′,连接A B′,C B′,B B′,P B′.(1)如图①,若P B′⊥AC,证明:P B′=A B′.(2)如图②,若AB=AC,BP=3PC,求cos∠B′AC的值.(3)如图③,若∠ACB=30°,是否存在点P,使得AB=C B′.若存在,求此时PC的值;若不存在,请说明BC理由.46.(2022·山东济南·中考真题)在等腰△ABC中,AC=BC,△ADE是直角三角形,∠DAE=90°,∠ADE=1∠ACB,连接BD,BE,点F是BD的中点,连接CF.2(1)当∠CAB=45°时.①如图1,当顶点D在边AC上时,请直接写出∠EAB与∠CBA的数量关系是 .线段BE与线段CF 的数量关系是 ;②如图2,当顶点D在边AB上时,(1)中线段BE与线段CF的数量关系是否仍然成立?若成立,请给予证明,若不成立,请说明理由;学生经过讨论,探究出以下解决问题的思路,仅供大家参考:思路一:作等腰△ABC底边上的高CM,并取BE的中点N,再利用三角形全等或相似有关知识来解决问题;思路二:取DE的中点G,连接AG,CG,并把△CAG绕点C逆时针旋转90°,再利用旋转性质、三角形全等或相似有关知识来解快问题.(2)当∠CAB=30°时,如图3,当顶点D在边AC上时,写出线段BE与线段CF的数量关系,并说明理由.47.(2022·四川南充·中考真题)如图,点E在正方形ABCD边AD上,点F是线段AB上的动点(不与点A.重合).DF交AC于点G,GH⊥AD于点H,AB=1,DE=13(1)求tan ∠ACE .(2)设AF =x ,GH =y ,试探究y 与x 的函数关系式(写出x 的取值范围).(3)当∠ADF =∠ACE 时,判断EG 与AC 的位置关系并说明理由.48.(2022·山东烟台·中考真题)(1)【问题呈现】如图1,△ABC 和△ADE 都是等边三角形,连接BD ,CE .求证:BD =CE .(2)【类比探究】如图2,△ABC 和△ADE 都是等腰直角三角形,∠ABC =∠ADE =90°.连接BD ,CE .请直接写出BD CE 的值.(3)【拓展提升】如图3,△ABC 和△ADE 都是直角三角形,∠ABC =∠ADE =90°,且AB BC =AD DE =34.连接BD ,CE .①求BD CE 的值;②延长CE 交BD 于点F ,交AB 于点G .求sin ∠BFC 的值.49.(2022·贵州安顺·中考真题)如图1,在矩形ABCD 中,AB =10,AD =8,E 是AD 边上的一点,连接CE ,将矩形ABCD 沿CE 折叠,顶点D 恰好落在AB 边上的点F 处,延长CE 交BA 的延长线于点G .(1)求线段AE 的长;(2)求证四边形DGFC为菱形;(3)如图2,M,N分别是线段CG,DG上的动点(与端点不重合),且∠DMN=∠DCM,设DN=x,是否存在这样的点N,使△DMN是直角三角形?若存在,请求出x的值;若不存在,请说明理由.50.(2022·黑龙江齐齐哈尔·中考真题)综合与实践数学是以数量关系和空间形式为主要研究对象的科学.数学实践活动有利于我们在图形运动变化的过程中去发现其中的位置关系和数量关系,让我们在学习与探索中发现数学的美,体会数学实践活动带给我们的乐趣.如图①,在矩形ABCD中,点E、F、G分别为边BC、AB、AD的中点,连接EF、DF,H为DF的中点,连接GH.将△BEF绕点B旋转,线段DF、GH和CE的位置和长度也随之变化.当△BEF绕点B顺时针旋转90°时,请解决下列问题:(1)图②中,AB=BC,此时点E落在AB的延长线上,点F落在线段BC上,连接AF,猜想GH与CE之间的数量关系,并证明你的猜想;(2)图③中,AB=2,BC=3,则GH=;CE(3)当AB=m , BC=n时.GH=.CE(4)在(2)的条件下,连接图③中矩形的对角线AC,并沿对角线AC剪开,得△ABC(如图④).点M、N 分别在AC、BC上,连接MN,将△CMN沿MN翻折,使点C的对应点P落在AB的延长线上,若PM平分∠APN,则CM长为.。
经典解三角形练习题(含答案)

解三角形练习题一、选择题1、在△ABC 中,a =3,b =7,c =2,那么B 等于()A . 30°B .45°C .60°D .120° 2、在△ABC 中,a =10,B=60°,C=45°,则c 等于 ( )A .310+B .()1310-C .13+D .3103、在△ABC 中,a =32,b =22,B =45°,则A 等于()A .30°B .60°C .60°或120°D . 30°或150° 4、在△ABC 中,a =12,b =13,C =60°,此三角形的解的情况是( )A .无解B .一解C . 二解D .不能确定 5、在△ABC 中,已知bc c b a ++=222,则角A 为()A .3π B .6πC .32πD . 3π或32π 6、在△ABC 中,若B b A a cos cos =,则△ABC 的形状是( )A .等腰三角形B .直角三角形C .等腰直角三角形D .等腰或直角三角形 7、已知锐角三角形的边长分别为1,3,a ,则a 的范围是()A .()10,8B .()10,8C .()10,8D .()8,108、在△ABC 中,已知C B A sin cos sin 2=,那么△ABC 一定是 ( )A .直角三角形B .等腰三角形C .等腰直角三角形D .正三角形9、在△ABC 中,已知===B b x a ,2, 60°,如果△ABC 两组解,则x 的取值范围是()A .2>xB .2<xC .3342<<x D . 3342≤<x 10、在△ABC 中,周长为7.5cm ,且sinA :sinB :sinC =4:5:6,下列结论:①6:5:4::=c b a ②6:5:2::=c b a ③cm c cm b cm a 3,5.2,2=== ④6:5:4::=C B A 其中成立的个数是 ( ) A .0个 B .1个 C .2个 D .3个 11、在△ABC 中,3=AB ,1=AC ,∠A =30°,则△ABC 面积为 ( )A .23B .43C .23或3 D .43 或23 12、已知△ABC 的面积为23,且3,2==c b ,则∠A 等于 ( )A .30°B .30°或150°C .60°D .60°或120°13、已知△ABC 的三边长6,5,3===c b a ,则△ABC 的面积为 ( )A . 14B .142C .15D .15214、某市在“旧城改造”中计划内一块如图所示的三角形空地上种植草皮以美化环境,已知这种草皮每平方米a 元,则购买这种草皮至少要( )A . 450a 元B .225 a 元C . 150a 元D . 300a 元15、甲船在岛B 的正南方A 处,AB =10千米,甲船以每小时4千米的速度向正北航行,同时乙船自B 出发以每小时6千米的速度向北偏东60°的方向驶去,当甲,乙两船相距最近时,它们所航行的时间是( )A .7150分钟 B .715分钟 C .21.5分钟 D .2.15分钟16、飞机沿水平方向飞行,在A 处测得正前下方地面目标C 得俯角为30°,向前飞行10000米,到达B 处,此时测得目标C 的俯角为75°,这时飞机与地面目标的距离为( ) A . 5000米B .50002 米C .4000米D .24000 米17、在△ABC 中,10sin =a °,50sin =b °,∠C =70°,那么△ABC 的面积为( )A .641B .321 C .161 D .81 18、若△ABC 的周长等于20,面积是310,A =60°,则BC 边的长是( ) A . 5 B .6 C .7 D .819、已知锐角三角形的边长分别为2、3、x ,则x 的取值范围是( ) A .51<<x B .135<<x C .50<<x D .513<<x20、在△ABC 中,若cCb B a A sin cos cos ==,则△ABC 是( ) A .有一内角为30°的直角三角形 B .等腰直角三角形C .有一内角为30°的等腰三角形D .等边三角形 二、填空题21、在△ABC 中,若∠A:∠B:∠C=1:2:3,则=c b a :: 22、在△ABC 中,===B c a ,2,33150°,则b =23、在△ABC 中,A =60°,B =45°,12=+b a ,则a = ;b = 24、已知△ABC 中,===A b a ,209,181121°,则此三角形解的情况是25、已知三角形两边长分别为1和3,第三边上的中线长为1,则三角形的外接圆半径为 26、在△ABC 中,()()()6:5:4::=+++b a a c c b ,则△ABC 的最大内角的度数是20米30米150°三、解答题27、在△ABC 中,已知210=AB ,A =45°,在BC 边的长分别为20,3320,5的情况下,求相应角C 。
(完整版)解三角形经典练习题集锦(附答案)

(完整版)解三角形经典练习题集锦(附答案)解三角形一、选择题1.在△ABC中,若0030,6,90BaC,则bc 等于() A.1 B.1 C.32 D.32 2.若A为△ABC的内角,则下列函数中一定取正值的是()A.Asin B.Acos C.Atan D.Atan1 3.在△ABC中,角,AB均为锐角,且,sincosBA则△ABC的形状是()A.直角三角形 B.锐角三角形 C.钝角三角形 D.等腰三角形 4.等腰三角形一腰上的高是3,这条高与底边的夹角为060,则底边长为() A.2 B.23 C.3 D.32 5.在△ABC中,若Babsin2,则A等于() A.006030或 B.006045或 C.0060120或 D.0015030或6.边长为5,7,8的三角形的最大角与最小角的和是()A.090 B.0120 C.0135 D.0150 二、填空题 1.在Rt△ABC中,090C,则BAsinsin的最大值是_______________。
2.在△ABC中,若Acbcba 则,222_________。
3.在△ABC中,若aCBb则,135,30,200_________。
4.在△ABC中,若sinA∶sinB∶sinC7∶8∶13,则C_____________。
5.在△ABC中,,26AB030C,则ACBC的最大值是________。
三、解答题1.在△ABC中,若,coscoscosCcBbAa则△ABC的形状是什么?2.在△ABC中,求证:)coscos(aAbBcabba 3.在锐角△ABC中,求证:CBACBAcoscoscossinsinsin。
4.在△ABC中,设,3,2CAbca求Bsin的值。
解三角形一、选择题1.在△ABC中,::1:2:3ABC,则::abc等于() A.1:2:3 B.3:2:1 C.1:3:2 D.2:3:1 2.在△ABC 中,若角B为钝角,则sinsinBA的值()A.大于零B.小于零C.等于零D.不能确定3.在△ABC中,若BA2,则a等于()A.Absin2 B.Abcos2 C.Bbsin2 D.Bbcos2 4.在△ABC中,若2lgsinlgcoslgsinlgCBA,则△ABC的形状是()A.直角三角形B.等边三角形C.不能确定D.等腰三角形5.在△ABC中,若,3))((bcacbcba则A ( ) A.090 B.060 C.0135 D.0150 6.在△ABC中,若1413cos,8,7Cba,则最大角的余弦是() A.51 B.61 C.71 D.81 7.在△ABC中,若tan2ABabab,则△ABC的形状是()A.直角三角形B.等腰三角形 C.等腰直角三角形 D.等腰三角形或直角三角形二、填空题1.若在△ABC中,060,1,3,ABCAbS则CBAcbasinsinsin=_______。
专题4-5 解三角形大题归类-(解析版)

专题4-4 解三角形大题归类目录一、热点题型归纳【题型一】巧用“拆”面积法解决角平分线题型 ................................................................................... 1 【题型二】角平分线的扩展结论 .............................................................................................................. 4 【题型三】中线的处理方法 ...................................................................................................................... 6 【题型四】三角形高的类型 .................................................................................................................... 10 【题型五】三角形内心 ............................................................................................................................ 11 【题型六】外接圆 .................................................................................................................................... 14 【题型七】双三角形 ................................................................................................................................ 16 【题型八】四边形 .................................................................................................................................... 18 【题型九】四边形图形最值 .................................................................................................................... 20 二、真题再现 ............................................................................................................................................ 22 三、模拟检测 .. (29)【题型一】巧用“拆”面积法解决角平分线题型【典例分析】(2022·湖北·高三开学考试)在ABC 中,2AB AC =,点D 在BC 边上,AD 平分BAC ∠.(1)若cos ACB ∠=,求cos BAC ∠;(2)若AD AC =,且ABC BC 的长.【答案】【分析】(1)在ABC 中,利用正弦定理可得sin ABC ∠=,从而可得cos ABC ∠=,再由()cos cos CAB ABC ACB ∠∠∠=-+,展开即可求解;(2)利用三角形的面积公式可得111sin sin sin 2222AC AD AB AD AB AC θθθ⋅⋅+⋅⋅=⋅⋅,从而解得3cos 4θ=,根据三角形的面积求出24b =,再由余弦定理即可求解.(1)由cos ACB ∠=,得sin ACB ∠=,在ABC 中,由正弦定理可得sin AB ACABC =∠,又2AB AC =,所以sin ABC ∠=AB AC >,故cos ABC ∠=所以()()cos cos cos CAB ABC ACB ABC ACB ∠π∠∠∠∠=--=-+,即cos sin sin cos cos CAB ABC ACB ABC ACB ∠∠∠∠∠=-,所以cos CAB ∠==(2)由已知,设22AB AC t ==,所以AD AC t ==,另设CAD θ∠=.由ABC ACD ABD S S S =+△△△,可得1112sin2sin 2sin 222t t t t t t θθθ⋅⋅⋅=⋅⋅+⋅⋅⋅,所以12sin cos sin sin 2θθθθ⋅=+,因为sin 0θ≠,所以3cos 4θ=,所以21cos22cos 18θθ=-=,又02,sin2θπθ<<==,又212sin22ABC S t t θ==⋅⋅⋅=,所以24t =,所以222299422cos241822BC t t t t t θ=+-⋅⋅⋅==⨯=,所以BC =【提分秘籍】基本规律角平分线“拆”面积法:ABC ACD ABDS S S =+△△△1.(2022·湖北·高三开学考试)已知ABC 的角,,A B C 的对边分别为 ,,a b c ,且sin (cos cos )sin sin sin A c B b C c B c C b B +-=+, (1)求角A ;(2)若AD 平分BAC ∠交线段BC 于点D ,且2,2AD BD CD ==,求ABC 的周长.【答案】(1)23A π=(2)9+【分析】(1)先利用余弦定理化简cos cos c B b C +,然后代入已知式子中利用正弦定理统一成边的形式,再利用余弦定理可求出角A ,(2)由ABCBADCAD SSS=+结合AD 平分BAC ∠,23A π=可得22bc b c =+,作AE BC ⊥于E ,则由ABD ACDS S 结合已知条件可得2cb=,解方程组可求得,b c ,再利用余弦定理可求出a ,从而可求出三角形的周长.(1)由余弦定理得222222cos cos 22a c b a b c c B b C c b a ac ab+-+-+=⨯+⨯= 所以sin (cos cos )sin sin sin A c B b C c B c C b B +-=+可化为sin sin sin sin a A c B c C b B -=+ 再由正弦定理,得222a cb c b -=+,得222c b a bc +-=-,所以2221cos 22b c a A bc +-==-.因为(0,)A π∈, 所以23A π= (2)因为AD 平分BAC ∠,所以3BAD CAD π∠=∠=.由1211sin sin sin 232323ABCBADCADSSSb c c AD b AD πππ=+⇒⋅=⋅+⋅, 得22bc b c =+.作AE BC ⊥于E ,则11sin 232211sin 232ABD ACD c AD BD AES c BD S b DCb AD CD AE ππ⋅⋅==⇒==⋅⋅. 由222bc b cc b =+⎧⎨=⎩,解得6,3,c b =⎧⎨=⎩由余弦定理,得2222cos 63a b c bc A ,所以37a故ABC 的周长为937+2.(2022·江苏·盐城中学高三开学考试)在①()()()sin sin sin sin A C a b c B C -=-+,①()2222cos 2a b c a c B a+--=,①()sin cos 6a B C B b π⎛⎫+=- ⎪⎝⎭这三个条件中选一个,补充在下面问题中,并解答.已知ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且__________. (1)求B(2)若b =ABC ∠的平分线交AC 于点D ,且BD =,求ABC 的面积. 【答案】(1)=3B π【分析】(1)若选条件①,先用正弦定理将角转化为边的关系,再利用余弦定理即可;若选条件①,先用余弦定理将边转化为角的关系,再利用正弦定理即可;若选条件①,先用三角形的内角之和为π,再利用正弦定理即可;(2)利用角平分线的性质得到ABC ABD BCD S S S =+△△△,结合余弦定理和三角形的面积公式即可 (1)选择条件①:根据正弦定理,可得:()()()a c a b c b c -=-+可得:222a c b ac +-=根据余弦定理,可得:2221cos 22a cb B ac +-==()0,,=3B B ππ∈∴ 选择条件①:根据余弦定理,可得:2cos (2)cos =cos 2ab Ca c Bb C a-=根据正弦定理,可得:(2sin sin )cos sin cos A C B B C -=整理可得:2sin cos sin()sin A B B C A =+= 。
解三角形经典题型

在 ABC 中,已知角 A, B,C 的对边分别为 a,b,c,且 a b, sin A 3 cos A 2sin B 。
(1)求角 C 的大小;(2)求 a b 的最大值。 c
解析:(1)由 sin A
3
cos
A
2 sin
B
得
2 sin
A
3
(1)求 A;
(2)若 2a b 2c ,求 sinC.
解三角形
题型一:边长、周长、面积等取值范围转化为角度求解 题型二:边化角 题型三:角化边 题型四:化切为弦 题型五:实际应用
才哥数学
才哥数学
题型一:边长、周长、面积等取值范围转化为角度求解
1.(19 全国 3 理、文 18).(12 分)
△ABC 的内角 A,B,C 的对边分别为 a,b,c,已知 a sin A C b sin A . 2
3
36
所以
1 2
sin
A
3
3
.
2
由此有 3 2
3
sin
A
3
3 2
3,
所以, cos A sin C 的取值范围为
3 2
,3 2
.
才哥数学
4. 在 ABC 中,已知 b, B ,求 ma nc 【或 ABC 周长】的取值范围
(1)求 B; (2)若△ABC 为锐角三角形,且 c=1,求△ABC 面积的取值范围.
解:(1)由题设及正弦定理得 sin Asin A C sin B sin A . 2
解三角形经典题型

专题一:解三角形一:边长、周长、面积等取值范围转化为角度求解 例.(19全国3理、文18).(12分)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知sinsin 2A Ca b A +=. (1)求B ;(2)若△ABC 为锐角三角形,且c =1,求△ABC 面积的取值范围.变式:.锐角ABC ∆,若c b C c A b B a 则,1,sin 2)cos cos (3==+的取值范围3.△ABC 的外接圆半径为R ,C =60°,则a +bR的取值范围是4.在ABC ∆中,已知角,,A B C 的对边分别为a ,b ,c ,且,sin 2sin a b A A B ≥+=。
(1)求角C 的大小;(2)求a bc+的最大值。
三.形如:在ABC ∆中,已知B ∠,求C n A m cos sin +的取值范围例:(07全国卷1理)设锐角三角形ABC 的内角A B C ,,的对边分别为a b c ,,,2sin a b A =. (Ⅰ)求B 的大小;(Ⅱ)求cos sin A C +的取值范围.四.形如:在ABC ∆中,已知B b ∠,,求nc ma +【或ABC ∆周长】的取值范围例:在ABC ∆中,60,B AC ==2AB BC +的最大值。
变式:在ABC ∆中,已知角,,A B C 的对边分别为a ,b ,c ,且,sin 2sin a b A A B ≥=。
(1)求角C 的大小;(2)求a bc+的最大值。
五.形如:在ABC ∆中,已知B b ∠,,求22nc ma +的取值范围 例:在ABC ∆中,已知3,3π=∠=B b ,求22c a +的取值范围例:在ABC ∆中,已知D 为BC 上一点,且BC AD BC AD =⊥,求bc +的取值范围在ABC ∆中,已知D 为BC 上一点,且BC AD BC AD 63,=⊥求bcc b +的取值范围七:边化角 消元思想例题:已知ABC ∆三内角A 、B 、C 的对边分别为a 、b 、c ,且cos 0a C A b c --=,(1)求角A 的值;(2)求函数()cos 24sin sin f x x A x =+在区间23[,]74ππ的值域。
解三角形经典练习题集锦

解三角形一、选择题1.在厶ABC 中,若C 900,a 6, B 300,则c b等于(解三角形2. _______________________________________________ 在厶ABC 中,若a2 b2 bc c2,则A ________________________ 。
3. _____________________________________________________ 在厶ABC 中,若b 2, B 30°, C 135°,则a _____________________ 。
4. 在厶ABC 中,若si nA : sin B : si nC 7 : 8 : 13,贝UC ___________ 。
°5. 在厶ABC中,AB .、6 2, C 30°,则AC BC的最大值是。
三、解答题一、选择题1. 在厶ABC 中,A: B: C 1:2:3,则a:b:c 等于()A. 1: 2:3 B . 3:2:1 C . 1: .3:2 D . 2^ 3 :12. 在厶ABC中,若角B为钝角,则si nB si nA的值()A.大于零B.小于零C.等于零D .不能确定3. 在厶ABC中,若A 2B,则a等于()A . 2b si nAB . 2b cos AC . 2bsi nBD . 2b cosB4. 在厶ABC 中,若Ig si nA Ig cos B Ig sin C Ig 2,则△ ABC的形状是()A.直角三角形 B .等边三角形 C .不能确定 D .等腰三角形A B a b7.在厶ABC中,若tan ,则△ ABC的形状是()2 a b形或直角三角形、填空题A. 1B. 1C. 2.3D. 2.32. 若A ABC的内角,则下列函数中一定取正值的是()1A. sin AB. cosA C . tanA D .- tan A3. 在厶ABC中,角A, B均为锐角,且cos A sinB,则厶ABC的形状是()A.直角三角形 B .锐角三角形 C •钝角三角形 D .等腰三角形4. 等腰三角形一腰上的高是3,这条高与底边的夹角为600,则底在锐角△ ABC中,求证sin A sin B sinC cosA cosB cosC。
解三角形专项题目型及高考题目

正余弦定理的专项题型题型1:利用正余弦定理判断三角形形状两种途径:(1)利用正、余弦定理把已知条件转化为边边关系,通过因式分解、配方等得出边的相应关系,从而判断三角形的形状;(2)利用正、余弦定理把已知条件转化为内角的三角函数间的关系,通过三角函数恒等变形,得出内角的关系,从而判断出三角形的形状,此时要注意应用A +B +C =π这个结论. 例1.在中,a,b,c 分别表示三个内角A,B,C的对边,如果2222()sin()()sin()a b A B a b A B +-=-+ ,判断三角形的形状.例2.在△ABC 中,已知22tan tan a B b A =,试判断此三角形的形状。
【同类型强化】1.在∆ABC 中,若B b A a cos cos =,试判断∆ABC 的形状【同类型强化】2.(2010上海文数)若ABC ∆的三个内角满足sin :sin :sin 5:11:13A B C =,则ABC∆( )A .一定是锐角三角形.B .一定是直角三角形.C .一定是钝角三角形.D .可能是锐角三角形,也可能是钝角三角形【同类型强化】3.△ABC 中,2sinAcosB=sinC ,则此三角形的形状是 ( ) (A)等腰△ (B) 等腰或者直角△ (C)等腰直角△ (D)直角△题型2:利用正余弦定理求三角形的面积三角形一般由三个条件确定,比如已知三边a ,b ,c ,或两边a ,b 及夹角C ,可以将a ,b ,c 或a ,b ,C 作为解三角形的基本要素,根据已知条件,通过正弦定理、余弦定理、面积公式等利用解方程组等手段进行求解,必要时可考虑作辅助线,将所给条件置于同一三角形中.例3.在ABC ∆中,角A,B,C 所对的边分别为a,b,c 且满足(1)求△ABC 的面积;(2)若c =1,求a 的值.例4.(2010·辽宁营口检测)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且满足3sin A -cos A =0,cos B =45,b =2 3.(1)求sin C 的值;(2)求△ABC 的面积.例5.(2009·安徽)在△ABC 中,sin(C -A )=1,sin B = 13. (1)求sin A 的值;(2)设AC = 6,求△ABC 的面积.【同类型强化】1. 在ABC △中,已知角A 、B 、C 所对的边分别是a 、b 、c ,边72c =,且tan tan 3tan tan 3A B A B +=⋅-,又ABC △的面积为332,求a b +的值.【同类型强化】2. 在锐角三角形中,边a 、b 是方程22320x x -+=的两根,角A 、B 满足()2sin 30A B +-=,求角C 的度数,边c 的长度及ABC △的面积.【同类型强化】3.(2009湖北卷文)(本小题满分12分) 在锐角△ABC 中,a 、b 、c 分别为角A 、B 、C 所对的边,且A c a sin 23=(Ⅰ)确定角C 的大小(Ⅱ)若c =7,且△ABC 的面积为233,求a+b 的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解三角形专项训练
知识梳理
1.正弦定理:
2sin sin sin a b c
R A B C
===或变形:::sin :sin :sin a b c A B C =. 2.余弦定理: 222222
2222cos 2cos 2cos a b c bc A b a c ac B c b a ba C
⎧=+-⎪=+-⎨⎪=+-⎩ 或 222222222
cos 2cos 2cos 2b c a A bc a c b B ac b a c C ab ⎧+-=⎪⎪
+-⎪=⎨⎪⎪+-=
⎪⎩
.
3.(1)两类正弦定理解三角形的问题:已知两角和任意一边,求其他的两边及一角;已知两边和其中一边的对角,求其他边角.
(2)两类余弦定理解三角形的问题:已知三边求三角;已知两边及其夹角,求第三边和其他两角.
4.面积公式:()r c b a R abc B ac A bc C ab S ABC ⋅++==
===∆2
1
4sin 21sin 21sin 21,.)(r R r 、,并可由此计算是三角形内切圆的半径
5.判定三角形形状时,可利用正余弦定理实现边角转化,统一成边的形式或角的形式. 6.解题中利用ABC ∆中A B C π++=,以及由此推得的一些基本关系式进行三角变换的运算,如:sin()sin ,A B C +=cos()cos ,A B C +=-tan()tan ,A B C +=-
sin cos ,cos sin ,tan cot 222222
A B C A B C A B C
+++===.、 走进高考
1.(2018全国新课标Ⅰ理)下图来自古希腊数学家希波克拉底所研究的几
何图形.此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC 的斜边BC ,直角边AB ,AC .ABC △的三边所围成的区域记为Ⅰ,黑色部分记为Ⅱ,其余部分记为Ⅲ.在整个图形中随机取一点,此点取自Ⅰ,Ⅱ,Ⅲ的概率分别记为p 1,p 2,p 3,则( )
A .p 1=p 2
B .p 1=p 3
C .p 2=p 3
D .p 1=p 2+p 3
2.(2018全国新课标Ⅱ文、理)在ABC △中,5cos
25
C =,1BC =,5AC =,则AB =( )
A .42
B .30
C .29
D .25
3.(2018全国新课标Ⅲ文、理)ABC △的内角A ,B ,C 的对边分别为a ,b ,
c .若ABC △的面积为
222
4a b c +-,则C =( ) A .π2
B .π3
C .π
4 D .π6
4.(2018北京文)若ABC △的面积为
()2
2234
a c
b +-,且C ∠为钝角,则B ∠=_________;
c
a
的取值范围是_________. 5.(2018江苏)在ABC △中,角,,A B C 所对的边分别为,,a b c ,
120ABC ∠=︒,ABC ∠的平分线交AC 于点D ,且1BD =,则4a c +的最小值为 .
6.(2018浙江)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .若a =7,
b =2,A =60°,则sin B =___________,
c =___________.
7.(2018全国新课标Ⅰ文)△ABC 的内角A B C ,,的对边分别为a b c ,
,,已知sin sin 4sin sin b C c B a B C +=,2228b c a +-=,则△ABC 的面积为________. 8.(2018北京理)在△ABC 中,a =7,b =8,cos B =–17
.
(Ⅰ)求∠A ;
(Ⅱ)求AC 边上的高.
9.(2018天津理)在ABC △中,内角A ,B ,C 所对的边分别为a ,b ,c.已知
sin cos()6
b A a B π
=-.(I )求角B 的大小; (II )设a =2,c =3,求b 和sin(2)
A B -的值.
10.(2018全国新课标Ⅰ理)在平面四边形ABCD 中,90ADC ∠=,45A ∠=,2AB =,5BD =.
(1)求cos ADB ∠; (2)若22DC =,求BC . 小题狂练
1、在△ABC 中,a =3,b =7,c =2,那么B 等于( )
A . 30°
B .45°
C .60°
D .120° 2、在△ABC 中,a =10,B=60°,C=45°,则c 等于 ( )
A .310+
B .()
1310- C .13+ D .310
3、在△ABC 中,a =32,b =22,B =45°,则A 等于( )
A .30°
B .60°
C .60°或120°
D . 30°或150° 4、在△ABC 中,a =12,b =13,C =60°,此三角形的解的情况是( )
A .无解
B .一解
C . 二解
D .不能确定 5、在△ABC 中,已知bc c b a ++=222,则角A 为( )
A . 3π
B .6π
C .32π
D . 3
π
或32π
6、在△ABC 中,若B b A a cos cos =,则△ABC 的形状是( )
A .等腰三角形
B .直角三角形
C .等腰直角三角形
D .等腰或直角三角形 7、已知锐角三角形的边长分别为1,3,a ,则a 的范围是( )
A .()10,8
B .()10,8
C . ()10,8
D .()
8,10 8、在△ABC 中,已知C B A sin cos sin 2=,那么△ABC 一定是 ( )
A .直角三角形
B .等腰三角形
C .等腰直角三角形
D .正三角形
9、在△ABC 中,已知===B b x a ,2, 60°,如果△ABC 两组解,则x 的取值范围是( )
A .2>x
B .2<x
C .3342<<x
D . 33
42≤<x 10、在△ABC 中,周长为7.5cm ,且sinA :sinB :sinC =4:5:6,下列结论:
①6:5:4::=c b a ②6:5:2::=c b a
③cm c cm b cm a 3,5.2,2=== ④6:5:4::=C B A
其中成立的个数是 ( ) A .0个 B .1个 C .2个 D .3个
11、在△ABC 中,3=AB ,1=AC ,∠A =30°,则△ABC 面积为 ( ) A .
2
3 B .4
3 C .
2
3
或3 D .
43 或2
3 12、已知△ABC 的面积为
2
3
,且3,2==c b ,则∠A 等于 ( ) A .30° B .30°或150° C .60° D .60°或120° 13、已知△ABC 的三边长6,5,3===c b a ,则△ABC 的面积为 ( )
A . 14
B .142
C .15
D .152 14、某市在“旧城改造”中计划内一块如图所示的三角形空地上种植草皮以美
化环境,已知这种草皮每平方米a 元,则购买这种草皮至少要( )
A . 450a 元
B .225 a 元
C . 150a 元
D . 300a 元 15、甲船在岛B 的正南方A 处,AB =10千米,甲船以每小时4千米的速度向正北航行,同时乙船自B 出发以每小时6千米的速度向北偏东60°的方向驶去,当甲,乙两船相距最近时,它们所航行的时间是( )
A . 7150分钟
B .7
15
分钟 C .21.5分钟 D .2.15分钟
16、飞机沿水平方向飞行,在A 处测得正前下方地面目标C 得俯角为30°,向前飞行10000米,到达B 处,此时测得目标C 的俯角为75°,这时飞机与地面目标的距离为( ) A . 5000米 B .50002 米 C .4000米 D .24000 米
17、在△ABC 中,10sin =a °,50sin =b °,∠C =70°,那么△ABC 的面积为( )
A . 641
B .321
C .16
1
D .81
18、若△ABC 的周长等于20,面积是310,A =60°,则BC 边的长是( )
A . 5
B .6
C .7
D .8
19、已知锐角三角形的边长分别为2、3、x ,则x 的取值范围是( ) A .51<<x B .135<<x C .50<<x D .513<<x
20、在△ABC 中,若c
C
b B a A sin cos cos ==,则△ABC 是( ) A .有一内角为30°的直角三角形 B .等腰直角三角形 C .有一内角为30°的等腰三角形 D .等边三角形
20米
30米
150°。
