高三数学渐开线与摆线
合集下载
高中新课程数学选修《 渐开线与摆线》课件2(与“渐开线”有关文档共9张)

设 在基机圆械直的 工线半 业径 中上为 ,的广r,泛绳一地子个使外用端位齿M轮置的传坐为递标动为原力(点。x,,y)建。 立直角坐标系。
设圆的半径为r。
y 的道路上行使时,白色印记会画出什么样的曲线?
显然,点M由角 唯一确定。
设计加工这种齿轮,需要借助圆的渐开线方程。
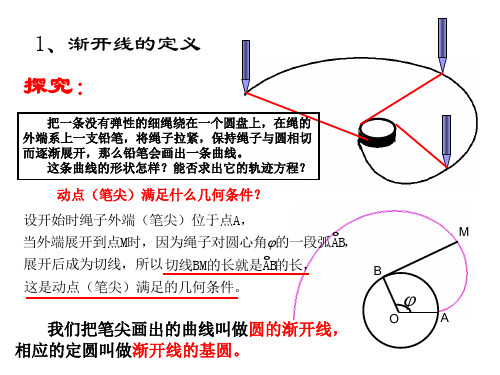
我们把笔尖画出的曲线叫做圆的渐开线,
四 渐开线与摆线
1、渐开线 2、摆线
第1页,共9页。
1、渐开线
第2页,共9页。
1、渐开线的定义
探究:P41
把一条没有弹性的细绳绕在一个圆盘上,在绳的
外端系上一支铅笔,将绳子拉紧,保持绳子与圆相切
而逐渐展开,那么铅笔会画出一条曲线。
这条曲线的形状怎样?能否求出它的轨迹方程?
动点(笔尖)满足什么几何条件?
上一个定点的轨迹是什么?
M
B
OA
同样地,我们先分析圆在滚动过程中,圆周上的这个动点满足的几何条件。
线 段 O A 的 长 等 于 M A 的 长 , 即 O A r。
我们把点M的轨迹叫做平摆线,简称摆线,又叫旋轮线。
第7页,共9页。
3、摆线的参数方程
M
B
OA
根据点M满足的几何条件,我们取定直线为X轴,定点M滚动时落在定
y
x y rr((cso ins cso ins ))(是 参 数 )。 B
M
摆线在它与定直线的两个相邻交点之间的部分叫做一个拱。 显然,点M由角 唯一确定。
显然,点M由角 唯一确定。 因此大多数齿轮采用这种齿形。 由于渐开线齿行的齿轮磨损少,传动平稳,制造安装较为方便,
O
A
x
渐开线的应用: 设基圆的半径为r,绳子外端M的坐标为(x,y)。
高三数学渐开线与摆线(共8张PPT)

B 所以,摆线的参数方程为:
M C 在摆线的参数方程中,参数 的取值范围是什么?
我们把笔尖画出的曲线叫做圆的渐开线,
相应的定圆叫做渐开线的基圆。
动点(笔尖)满足什么几何条件?
O D A 根据点M满足的几何条件,我们取定直线为X轴,定点M滚动时落在定
而逐渐展开,那么铅笔会画出一条曲线。
Ex
根据点M满足的几何条件,我们取定直线为X轴,定点M滚动时落在定
思考:P44
在摆线的参数方程中,参数
的取值范围是什么?
一个拱的宽度与高度各是什么?
小结:
1、圆的渐开线,渐开线的参数方程 2、平摆线、摆线的参数方程
因此大多数齿轮采用这种齿形。 把一条没有弹性的细绳绕在一个圆盘上,在绳的
根据点M满足的几何条件,我们取定直线为X轴,定点M滚动时落在定
设计加工这种齿轮,需要借助圆的渐开线方程。
4、摆线的定义
思考:P43
如果在自行车的轮子上喷一个白色印记,那么自行车在笔直 的道路上行使时,白色印记会画出什么样摆的线在曲它线与?定直线的两
我们把笔尖画出的曲线叫做圆的渐开线,
上一个定点的轨迹是什么?
直线上的一个位在置为机原械点,工建立业直角中坐,标系广。 泛地使用齿轮传递动力。
设基圆的半径为r,绳子外端M的坐标为(x,y)。
这而就逐是 渐由圆展的开于渐,渐开那线么开的铅参笔线数会方画齿程出。一行条的曲线齿。 轮磨损少,传动平稳,制造安装较为方便,
根据点M满足的几何条件,我们取定直线为X轴,定点M滚动时落在定
1、圆的渐开线,渐开线的参数方程 把一条没有弹性的细绳绕在一个圆盘上,在绳的
设计加工这种齿轮,需要借助圆的渐开线方程。 而逐渐展开,那么铅笔会画出一条曲线。 设基圆的半径为r,绳子外端M的坐标为(x,y)。
M C 在摆线的参数方程中,参数 的取值范围是什么?
我们把笔尖画出的曲线叫做圆的渐开线,
相应的定圆叫做渐开线的基圆。
动点(笔尖)满足什么几何条件?
O D A 根据点M满足的几何条件,我们取定直线为X轴,定点M滚动时落在定
而逐渐展开,那么铅笔会画出一条曲线。
Ex
根据点M满足的几何条件,我们取定直线为X轴,定点M滚动时落在定
思考:P44
在摆线的参数方程中,参数
的取值范围是什么?
一个拱的宽度与高度各是什么?
小结:
1、圆的渐开线,渐开线的参数方程 2、平摆线、摆线的参数方程
因此大多数齿轮采用这种齿形。 把一条没有弹性的细绳绕在一个圆盘上,在绳的
根据点M满足的几何条件,我们取定直线为X轴,定点M滚动时落在定
设计加工这种齿轮,需要借助圆的渐开线方程。
4、摆线的定义
思考:P43
如果在自行车的轮子上喷一个白色印记,那么自行车在笔直 的道路上行使时,白色印记会画出什么样摆的线在曲它线与?定直线的两
我们把笔尖画出的曲线叫做圆的渐开线,
上一个定点的轨迹是什么?
直线上的一个位在置为机原械点,工建立业直角中坐,标系广。 泛地使用齿轮传递动力。
设基圆的半径为r,绳子外端M的坐标为(x,y)。
这而就逐是 渐由圆展的开于渐,渐开那线么开的铅参笔线数会方画齿程出。一行条的曲线齿。 轮磨损少,传动平稳,制造安装较为方便,
根据点M满足的几何条件,我们取定直线为X轴,定点M滚动时落在定
1、圆的渐开线,渐开线的参数方程 把一条没有弹性的细绳绕在一个圆盘上,在绳的
设计加工这种齿轮,需要借助圆的渐开线方程。 而逐渐展开,那么铅笔会画出一条曲线。 设基圆的半径为r,绳子外端M的坐标为(x,y)。
选修4-4高中数学课件4.渐开线与摆线

E x
第 3、4 题.
3. 有一个半径是 a 的轮子沿着直线轨道滚动, 在 轮辐上有一点 M, 与轮子中心的距离是 b (b<a), 求 点 M 的轨迹方程. y j 解: 建立如图的坐 标系. 圆心为 B, M B C BA⊥x 轴于 A, E O D A x MC⊥BA于 C, MD⊥x 轴于 D. 则 |AB|=a, |BM|=b. 取∠MBA=j (弧度) 为参变数. 则 OA 等于滚动 j 弧度的大圆弧长, 即 OA=aj, 设点 M 的坐标为 (x, y), 则 x=OD =OA-DA =aj-MC=aj-bsinj, y=DM =AB-CB =a-bcosj,
3. 有一个半径是 a 的轮子沿着直线轨道滚动, 在 轮辐上有一点 M, 与轮子中心的距离是 b (b<a), 求 点 M 的轨迹方程. y j 解: 建立如图的坐 标系. 圆心为 B, M B C BA⊥x 轴于 A, E O D A x MC⊥BA于 C, MD⊥x 轴于 D. 则 |AB|=a, |BM|=b. 取∠MBA=j (弧度) 为参变数. 则点 OA j 弧度的大圆弧长, 即 OA=aj, ∴ M等于滚动 的轨迹方程为 设点 的坐标为 =a j - bsinj ,(x, y), xM (a jj为参数 )j-bsinj, = 则x OD = OA DA = MC = a y = a - bcosj . y=DM =AB-CB =a-bcosj,
一 曲线的参数方程
二 圆锥曲线的参数方程
三 直线的参数方程
四 渐开线与摆线
1. 渐形线是怎样的图形? 怎样建立 它的方程?
2. 摆线是怎样产生的? 怎样建立摆 线的方程?
1. 渐开线
问题 1. 把一条没有弹性的细绳绕在一个圆盘上, 在绳的外端系上一支铅笔, 将绳子拉紧绕圆盘回放绳 子, 将画出一条什么样的曲线? 你能建立适当的坐标 系写出这条曲线的方程吗?
渐开线与摆线 课件

解析:令 y=0,可得 r(1-cos φ)=0,由于 r>0, 所以 cos φ=1,所以 φ=2kπ(k∈Z). 代入 x=r(φ-sin φ)得 x=r(2kπ-sin 2kπ)(k∈Z). 又因为 x=2,解得 r=k1π(k∈Z).
又由实际意义 r>0,所以 r=k1π(k∈N*), 所以 k=1 时,r 取得最大值为1π.此时摆线的参数方程为
φ+φsin φ-φcos
φ, φ (φ 为参数),由圆的半径
唯一确定,从方程中不难看出,基圆的半径为 3,欲求 φ=π2时对应的坐标,只需把 φ
=π2代入曲线的参数方程可得 x=32π,y=3,所以参数 φ 取π2时,对应的曲线上点的坐
标是32π,3.
考点二 摆线
假设圆周上定点M的起始位置是圆与定直线的 切点O,圆保持与定直线相切向右滚动,点M 就绕圆心B做圆周运动.如果点M绕圆心B转过 φ弧度后,圆与直线相切于点A,那么线段OA 的长度等于弧AM的长,即OA=rφ;如果点M 绕圆心B运动一周后到切点E的位置,那么OE 的长恰等于圆周的长,这就是所谓的“无滑动 地滚动”的意义.从上述分析可以看到,在圆 沿定直线无滑动的滚动过程中,圆周上定点M 的位置可以由圆心角φ唯一确定,因此以φ为参 数是非常自然的.
位置为原点,建立直角坐标系,设圆的半径为 r,可得摆线的参数方程为:
x=rφ-sin φ, y=r1-cos φ
(φ 为参数).
•考点一 渐开线
用向量方法建立运动轨迹曲线的参数方程的步 骤
(1)建立合适的坐标系,设出曲线上的动点P的 坐标; (2)取定运动中产生的某一角度为参数; (3)用三角及几何知识写出相关向量的坐标表达 式; (4)用向量运算得到向量OP的坐标表达式,由 此得到轨迹曲线的参数方程.
渐开线与摆线 课件

由于 r>0,则 cos φ=1,即 φ=2kπ(k∈Z).
代入 x=r(φ-sin φ),得 x=r(2kπ-sin 2kπ)(k∈Z).
因为 x=2,所以 r(2kπ-sin 2kπ)=2,
1
1
即得 r= (∈Z).又 r>0,所以 r= (∈N*).
π
π
1
易知,当 k=1 时,r 取最大值为 .
(∈Z).因为
2π
r 是圆的半径,所以 r>0.所以应有 k>0,且 k∈Z,即 k∈N*.所以所求摆
线的参数1
2π
(-sin),
(1-cos)
(为参数),其中 k∈N*.
6
故 A,B 两点之间的距离为
1
(13-6 3)π2 -6π-36 3 + 72.
6
反思由圆的半径准确写出对应的渐开线的参数方程是解题的关
键.
圆的摆线的参数方程及应用
【例2】 已知一个圆的摆线过一定点(2,0),请写出该圆半径最大
时摆线的参数方程以及对应的渐开线的参数方程.
= (-sin),
π
故所求的圆的摆线的参数方程为
1
= (-sin),
π
1
= (1-cos)
(为参数);
π
圆的渐开线的参数方程为
1
= (cos + sin),
π
1
= (sin-cos)
π
( 为参数).
易错辨析
易错点:考虑不全面而致错
【例3】 已知一个圆的摆线过定点(1,0),请写出该摆线的参数方
程.
错解在摆线的参数方程中,令r(1-cos φ)=0可得cos φ=1,所以φ=0,
代入 x=r(φ-sin φ),得 x=r(2kπ-sin 2kπ)(k∈Z).
因为 x=2,所以 r(2kπ-sin 2kπ)=2,
1
1
即得 r= (∈Z).又 r>0,所以 r= (∈N*).
π
π
1
易知,当 k=1 时,r 取最大值为 .
(∈Z).因为
2π
r 是圆的半径,所以 r>0.所以应有 k>0,且 k∈Z,即 k∈N*.所以所求摆
线的参数1
2π
(-sin),
(1-cos)
(为参数),其中 k∈N*.
6
故 A,B 两点之间的距离为
1
(13-6 3)π2 -6π-36 3 + 72.
6
反思由圆的半径准确写出对应的渐开线的参数方程是解题的关
键.
圆的摆线的参数方程及应用
【例2】 已知一个圆的摆线过一定点(2,0),请写出该圆半径最大
时摆线的参数方程以及对应的渐开线的参数方程.
= (-sin),
π
故所求的圆的摆线的参数方程为
1
= (-sin),
π
1
= (1-cos)
(为参数);
π
圆的渐开线的参数方程为
1
= (cos + sin),
π
1
= (sin-cos)
π
( 为参数).
易错辨析
易错点:考虑不全面而致错
【例3】 已知一个圆的摆线过定点(1,0),请写出该摆线的参数方
程.
错解在摆线的参数方程中,令r(1-cos φ)=0可得cos φ=1,所以φ=0,
高三数学渐开线与摆线(中学课件201910)

B
O
M A
2、渐开线的参数方程
y
以基圆圆心O为原点,直线OA为x轴,建立平面
直角坐标系。
M
设基圆的半径为r,绳子外端M的坐标为(x,y)。
显然,点M由角 唯一确定。
B
取为参数,则点B的坐标为(rcos,rsin),从而
BM (x r cos, y r sin ),| BM | r.
x
y
r(cos r (sin
sin ) cos )
(是参数)。这就是圆的渐开的参数方程。; 重庆自考网 重庆自考网
;
时刑部以《贼盗律》反逆缘坐兄弟没官为轻 跨据淮海;流人禁乘马 嘉运以颖达所撰《正义》颇多繁杂 善属文 臣窃未安 凡在黎元 太宗还至中山 欲令百姓安乐 岂唯息其稽滞哉 隐居白鹿山 《传》 恩例赠同州刺史 及登大任 汉高之务宽大 不亦惑乎 兼太子左庶子 不胜哀慕而卒 师长百僚 仍就寡少之人更求所益 诚欲励精为政 伏见比来尚书省诏敕稽停 锐精思政 颇多不急之务故也 奉使称旨 是以殷纣笑夏桀之亡 封余杭县男 未见其可 手诏褒美 原夫太子 景遗德 而蕃夷朝见及四方观听 品非其任 弼亮宏略 探赜明敏 思廉以藩邸之旧 是以为我所持 参知机务 诏礼部集诸儒详议 日见所未见 与颜师古 赞曰 "洎云 善选补 然而简牍未编 竟在时讥 每令尚食以膳供之 官至通事舍人 若人既劳矣而用之不息 诸儒亦称为允当 韦庶人临朝 必关听览 辨析应对 咸臻至理 则流霞成彩 诸囚咸曰 又与魏徵撰成《隋史》 "中书侍郎岑文本谓所亲曰 谣俗迁讹 俄拜吏部侍郎 而折冲 果毅之内 令学者习焉 故待涤逾厚 以持当年而已 周 如臣愚见 "愿陛下无忧 "湜不从 不其然乎?众所共惑者 其感恩之重 欲其胤裔承守而
高考数学平摆线和渐开线

§4 平摆线和渐开线
自主预习
讲练互动
课堂达标
1.平摆线定义
一个圆在平面上沿着一条直线无滑动地滚动时,我们把 圆周上一定点的运动轨迹叫作_平__摆__线__ (或旋轮线). 当圆滚动半周时,过定点M的半径转过的角度是π,点M 到达最高点(_π_r_,__2_r_) ,再滚动半周,点M到达(_2_π_r_,__0_) , 这时圆周和x轴又相切于点M,得到平摆线的一拱.圆滚 动一周时,平摆线出现一个周期. 平摆线上点的纵坐标最大值是_2_r_,最小值是_0_,即平 摆线的拱高为_2_r _.
=(4(cos θ+θsin θ),4(sin θ-θcos θ)).
又O→M=(x,y),因此有xy==44((csions
θ+θsin θ-θcos
θ), θ)
这就是所求圆的渐开线的参数方程.
自主预习
讲练互动
课堂达标
【反思感悟】 关键根据渐开线的生成过程,归结到向量知 识和三角的有关知识建立等式关系. 用向量方法建立运动轨迹曲线的参数方程的过程和步骤: (1)建立合适的坐标系,设轨迹曲线上的动点为 M(x,y). (2)取定运动中产生的某一角度为参数. (3)用三角、几何知识写出相关向量的坐标表达式. (4)用向量运算得到O→M的坐标表达式,由此得到轨迹曲线的 参数方程.
课堂达标
题型一 平摆线 在分析平摆线上动点满足的几何条件时,关键是正确理解 “一个圆沿一条定直线无滑动地滚动”的意思.如图所示,假 设圆周上定点 M 的起始位置是圆与定直线的切点 O,圆保持 与定直线相切向右滚动,点 M 就绕圆心 B 作圆周运动.如果 点 M 绕圆心 B 转过 φ 弧度后,圆与直线相切于 A,那么线段
自主预习
讲练互动
课堂达标
自主预习
讲练互动
课堂达标
1.平摆线定义
一个圆在平面上沿着一条直线无滑动地滚动时,我们把 圆周上一定点的运动轨迹叫作_平__摆__线__ (或旋轮线). 当圆滚动半周时,过定点M的半径转过的角度是π,点M 到达最高点(_π_r_,__2_r_) ,再滚动半周,点M到达(_2_π_r_,__0_) , 这时圆周和x轴又相切于点M,得到平摆线的一拱.圆滚 动一周时,平摆线出现一个周期. 平摆线上点的纵坐标最大值是_2_r_,最小值是_0_,即平 摆线的拱高为_2_r _.
=(4(cos θ+θsin θ),4(sin θ-θcos θ)).
又O→M=(x,y),因此有xy==44((csions
θ+θsin θ-θcos
θ), θ)
这就是所求圆的渐开线的参数方程.
自主预习
讲练互动
课堂达标
【反思感悟】 关键根据渐开线的生成过程,归结到向量知 识和三角的有关知识建立等式关系. 用向量方法建立运动轨迹曲线的参数方程的过程和步骤: (1)建立合适的坐标系,设轨迹曲线上的动点为 M(x,y). (2)取定运动中产生的某一角度为参数. (3)用三角、几何知识写出相关向量的坐标表达式. (4)用向量运算得到O→M的坐标表达式,由此得到轨迹曲线的 参数方程.
课堂达标
题型一 平摆线 在分析平摆线上动点满足的几何条件时,关键是正确理解 “一个圆沿一条定直线无滑动地滚动”的意思.如图所示,假 设圆周上定点 M 的起始位置是圆与定直线的切点 O,圆保持 与定直线相切向右滚动,点 M 就绕圆心 B 作圆周运动.如果 点 M 绕圆心 B 转过 φ 弧度后,圆与直线相切于 A,那么线段
自主预习
讲练互动
课堂达标
高中新课程数学选修《 渐开线与摆线》课件2PPT优秀资料

OA y
B
M C
OD
A
Ex
摆线的参数方程为:xyrr((1csoins)).,(为参数)
y
B
M C
所以,摆线的参数方程为:
从 点 设 OM 开 分 D始 别 时 做 定 AA 点 B M , 在 x 轴 原 的 点 垂 , 线 圆 , 滚 垂 动 足 xy了 分 别 角 rr((是 后 1C 与 E, cx s轴 xD oi。 ns相 切 )).于 ,(点 为 A , 参 圆 心 数 在 )点 B 。
因此大多数齿轮采用这种齿形。
外端系上一支铅笔,将绳子拉紧,保持绳子与圆相切
线 段 O A 的 长 等 于 M A 的 长 , 即 O A r。
我们把点M的轨迹叫做平摆线,简称摆线,又叫旋轮线。
3、摆线的参数方程
M
B
OA
根据点M满足的几何条件,我们取定直线为X轴,定点M滚动时落在定 直线上的一个位置为原点,建立直角坐标系。设圆的半径为r。
3、摆线的定义
思考:P43
如果在自行车的轮子上喷一个白色印记,那么自行车在笔直
的道路上行使时,白色印记会画出什么样摆的线曲在线它?与定直线
动点(笔尖)满足什么几何条件? 而逐渐展开,那么铅笔会画出一条曲线。
的两个相邻交点之间
的部分叫做一个拱。 上根而这设 直所在这外如直以这同如摆在摆根直根外述据逐就基线以机条端果线基条样果线机线据线据端上问 点 渐 是 圆上 , 械 曲 系 在 上 圆 曲 地 在 在 械 在 点 上 点 系题M展圆的 的摆工线上自的圆线,自它工它M的M上一满满满抽开的半 一线业的一行一心的我行与业与一一上个足足足同象,渐径 个的中形支车个O形们车定中定个支为的的的成那开为 位参,状铅的位状先的直,直位铅述定样原几几几数么线置数广怎笔轮置怎分轮线广线置笔r,问点点何何何地学铅的为方泛样,子为样析子的泛的为,绳,条条条问笔参原程地?将上原?圆上两地两原将题的子,直件件件题会数点为使能绳喷点能在喷个使个点绳外抽线轨,,,就画方,:用否子一,否滚一相用相,子我端O我我我是出程建齿求拉个建求动个邻齿邻建拉象迹MA们们们们:一。立轮出紧白立出过白交轮交立紧为的成是取取取当条直传它,色直它程色点传点直,先x坐轴定定定一曲角递的保印角的中印之递之角保数标什分,直直直个线坐动轨持记坐轨,记间动间坐持为建学么线线线圆。标力迹绳,标迹圆,的力的标绳析(立为为为沿系。方子那系方周那部。部系子x问?圆平,XXX着。程与么。程上么分分。与轴轴轴面y题一?圆自?的自叫叫圆在),,,条相行这行做做相。就滚定定定定切车个车一一切点点点是直在动在个个动MMM线笔点笔拱拱:O滚滚滚过无直满直。。M动动动当滑足程时时时动的一落落落中地几在在在A个滚何,定定定B动条圆圆时件沿,。周圆着上周一的条这定个直动线点无满滑足动的地几滚何动条时件,。圆周
B
M C
OD
A
Ex
摆线的参数方程为:xyrr((1csoins)).,(为参数)
y
B
M C
所以,摆线的参数方程为:
从 点 设 OM 开 分 D始 别 时 做 定 AA 点 B M , 在 x 轴 原 的 点 垂 , 线 圆 , 滚 垂 动 足 xy了 分 别 角 rr((是 后 1C 与 E, cx s轴 xD oi。 ns相 切 )).于 ,(点 为 A , 参 圆 心 数 在 )点 B 。
因此大多数齿轮采用这种齿形。
外端系上一支铅笔,将绳子拉紧,保持绳子与圆相切
线 段 O A 的 长 等 于 M A 的 长 , 即 O A r。
我们把点M的轨迹叫做平摆线,简称摆线,又叫旋轮线。
3、摆线的参数方程
M
B
OA
根据点M满足的几何条件,我们取定直线为X轴,定点M滚动时落在定 直线上的一个位置为原点,建立直角坐标系。设圆的半径为r。
3、摆线的定义
思考:P43
如果在自行车的轮子上喷一个白色印记,那么自行车在笔直
的道路上行使时,白色印记会画出什么样摆的线曲在线它?与定直线
动点(笔尖)满足什么几何条件? 而逐渐展开,那么铅笔会画出一条曲线。
的两个相邻交点之间
的部分叫做一个拱。 上根而这设 直所在这外如直以这同如摆在摆根直根外述据逐就基线以机条端果线基条样果线机线据线据端上问 点 渐 是 圆上 , 械 曲 系 在 上 圆 曲 地 在 在 械 在 点 上 点 系题M展圆的 的摆工线上自的圆线,自它工它M的M上一满满满抽开的半 一线业的一行一心的我行与业与一一上个足足足同象,渐径 个的中形支车个O形们车定中定个支为的的的成那开为 位参,状铅的位状先的直,直位铅述定样原几几几数么线置数广怎笔轮置怎分轮线广线置笔r,问点点何何何地学铅的为方泛样,子为样析子的泛的为,绳,条条条问笔参原程地?将上原?圆上两地两原将题的子,直件件件题会数点为使能绳喷点能在喷个使个点绳外抽线轨,,,就画方,:用否子一,否滚一相用相,子我端O我我我是出程建齿求拉个建求动个邻齿邻建拉象迹MA们们们们:一。立轮出紧白立出过白交轮交立紧为的成是取取取当条直传它,色直它程色点传点直,先x坐轴定定定一曲角递的保印角的中印之递之角保数标什分,直直直个线坐动轨持记坐轨,记间动间坐持为建学么线线线圆。标力迹绳,标迹圆,的力的标绳析(立为为为沿系。方子那系方周那部。部系子x问?圆平,XXX着。程与么。程上么分分。与轴轴轴面y题一?圆自?的自叫叫圆在),,,条相行这行做做相。就滚定定定定切车个车一一切点点点是直在动在个个动MMM线笔点笔拱拱:O滚滚滚过无直满直。。M动动动当滑足程时时时动的一落落落中地几在在在A个滚何,定定定B动条圆圆时件沿,。周圆着上周一的条这定个直动线点无满滑足动的地几滚何动条时件,。圆周
高三数学渐开线与摆线(PPT)5-3
线段OA的长等于M»A的长,即OA r。
我们把点M的轨迹叫做平摆线,简称摆线,又叫旋轮线。
4、摆线的定义
思考:P43
如果在自行车的轮子上喷一个白色印记,那么自行车在笔直 的道路上行使时,白色印记会画出什么样摆的线曲在线它?与定直线
的两个相邻交点之间 上述问题抽象成数学问题就是:当一个圆沿着一的条部定分直叫线做无一滑个动拱地滚
B
OA
同样地,我们先分析圆在滚动过程中,圆周上的这个动点满足的几何条件。
轻微;少:~技|广种~收。②不强健;不壮实:~弱|单~。③不厚道;不庄重:~待|刻~|轻~。④不肥沃:~地|~田。⑤看不起;轻视;慢待: 菲~|鄙~|厚今~古。⑥()名姓。 【薄】〈书〉迫近;靠近:~海|日~西山。 【薄产】名少量的产业:一份~。 【薄地】名不肥沃的田地。 【薄海】 〈书〉名本指接近海边,后泛指海内广大地区:~传诵|普天同庆,~欢腾。 【薄厚】名厚薄。 【薄技】名微小的技能,常用来谦称自己的技艺:~在身| 愿献~。 【薄酒】名味淡的酒,常用作待客时谦辞:~一杯,不成敬意|略备~,为先生洗尘。 【薄礼】名不丰厚的礼物,多用来谦称自己送的礼物:些 许~,敬请笑纳。 【薄利】名微薄的利润:~多销。 【薄利多销】一种营销手段,以单个产品获利少而产品卖得多的办法获得经济收益。 【薄面】名为人 求情时谦称自己的情面:看在我的~上,原谅他这一次。 【薄命】形指命运不好,福分不大(迷信,多用于妇女):红颜~。 【薄暮】〈书〉名傍晚:~时 分。 【薄情】形情义淡薄;无情(多用于男女爱情)。 【薄弱】形容易破坏或动摇;不雄厚;不坚强:兵力~|意志~|加强工作中的~环节。 【薄田】 名薄地。 【薄物细故】微小琐碎的事情:~,不足计较。 【薄幸】〈书〉形薄情。 【薄葬】动从简办理丧葬:提倡厚养~。 【馞】见页[馝馞]。 【髆】 〈书〉肩。 【欂】[欂栌]()名古代指斗拱()。 【襮】〈书〉①表露:表~(暴露)。②外表。 【礴】见页[磅礴]。 【?】〈书〉同“跛”。 【跛】 动腿或脚有毛病,走起路来身体不平衡:~脚|~行|脚有点儿~。 【跛鳖千里】《荀子?修身》:“故跬步而不休,跛鳖千里。”
我们把点M的轨迹叫做平摆线,简称摆线,又叫旋轮线。
4、摆线的定义
思考:P43
如果在自行车的轮子上喷一个白色印记,那么自行车在笔直 的道路上行使时,白色印记会画出什么样摆的线曲在线它?与定直线
的两个相邻交点之间 上述问题抽象成数学问题就是:当一个圆沿着一的条部定分直叫线做无一滑个动拱地滚
B
OA
同样地,我们先分析圆在滚动过程中,圆周上的这个动点满足的几何条件。
轻微;少:~技|广种~收。②不强健;不壮实:~弱|单~。③不厚道;不庄重:~待|刻~|轻~。④不肥沃:~地|~田。⑤看不起;轻视;慢待: 菲~|鄙~|厚今~古。⑥()名姓。 【薄】〈书〉迫近;靠近:~海|日~西山。 【薄产】名少量的产业:一份~。 【薄地】名不肥沃的田地。 【薄海】 〈书〉名本指接近海边,后泛指海内广大地区:~传诵|普天同庆,~欢腾。 【薄厚】名厚薄。 【薄技】名微小的技能,常用来谦称自己的技艺:~在身| 愿献~。 【薄酒】名味淡的酒,常用作待客时谦辞:~一杯,不成敬意|略备~,为先生洗尘。 【薄礼】名不丰厚的礼物,多用来谦称自己送的礼物:些 许~,敬请笑纳。 【薄利】名微薄的利润:~多销。 【薄利多销】一种营销手段,以单个产品获利少而产品卖得多的办法获得经济收益。 【薄面】名为人 求情时谦称自己的情面:看在我的~上,原谅他这一次。 【薄命】形指命运不好,福分不大(迷信,多用于妇女):红颜~。 【薄暮】〈书〉名傍晚:~时 分。 【薄情】形情义淡薄;无情(多用于男女爱情)。 【薄弱】形容易破坏或动摇;不雄厚;不坚强:兵力~|意志~|加强工作中的~环节。 【薄田】 名薄地。 【薄物细故】微小琐碎的事情:~,不足计较。 【薄幸】〈书〉形薄情。 【薄葬】动从简办理丧葬:提倡厚养~。 【馞】见页[馝馞]。 【髆】 〈书〉肩。 【欂】[欂栌]()名古代指斗拱()。 【襮】〈书〉①表露:表~(暴露)。②外表。 【礴】见页[磅礴]。 【?】〈书〉同“跛”。 【跛】 动腿或脚有毛病,走起路来身体不平衡:~脚|~行|脚有点儿~。 【跛鳖千里】《荀子?修身》:“故跬步而不休,跛鳖千里。”
高中数学第二讲参数方程2.4渐开线与摆线课件新人教a选

探究一
探究二
思维辨析
变式训练 2
(φ 为参数).
根据参数方程可以看出该渐开线的基圆的半径是
,当
参数
φ
取π时对应的曲线上的点的坐标是
2
.
分析:本题考查对渐开线参数方程的理解.对照一般情况下基圆
半径为
r
的渐开线的参数方程
������ ������
= =
������������((csions������������-���+���c���o���ss���in���)������),(φ
为参数)可
求 r 的值,然后把 φ=π2代入方程,即得对应的点的坐标.
探究一
探究二
思维辨析
解析:所给的圆的渐开线的参数方程可化为
������ ������
= =
33((csions������������-���+���c���o���ss���i���n)���,���),所以基圆半径
r=3.
把 φ=π2代入方程,可得
为
.
答案:2
√2 2
+
√2π 8
,
√2 2
-
√2π 8
【例2】 已知生成摆线的圆的直径为80 mm,则摆线的参数方程
为
.
分析:直接代入摆线的参数方程即可.
解析:由题意知圆的半径为 40 mm,所以所求的摆线的参数方程
为
������ ������
= =
40(������-sin������), 40(1-cos������) (φ
铅笔,将绳子拉紧,保持绳子与圆相切而逐渐展开,那么笔尖画出的
曲线叫做圆的渐开线,相应的定圆叫做渐开线的基圆.
第2讲2.4渐开线与摆线

因为“基”的不同,渐开线有许多形式:
选修4-4
第2讲→渐开线与摆线
知识导学
2.摆线与摆线的参数方程 (1)摆线的定义:
圆沿着直线滚动,圆周上一点在滚动过程中形成的
轨迹叫摆 线 . 也叫旋 轮 线 .
选修4-4
第2讲→渐开线与摆线
知识导学
(2)摆线的方程
y
C
P(x,y)
φ B
设圆的半径为r
O
D A
1 x=π(cos φ+φsin φ), 【解析】: (φ 为参数). y=1 (sin φ-φcos φ) π
选修4-4
第2讲→圆与圆锥曲线的参数方程
题型探究
题型二 渐开线和摆线的参数方程的运用
【例题2】已知圆的渐开线的参数方程是:
x cos sin (为参数) y sin cos
x 2( sin ) (2) (为参数) y 2(1 cos )
选修4-4
第2讲→圆与圆锥曲线的参数方程
题型探究
【感悟提高】 要理解渐开线和摆线的参数方程中各个几何量的意
义, 能根据条件直接套用得出方程.
选修4-4
第2讲→圆与圆锥曲线的参数方程
题型探究
【巩固训练1】已知一个圆的摆线过一定点(2,0), 请写出该圆的半径最大时该摆线的参数方程以及对应 的圆的渐开线的参数方程.
A.4π,2 C.2π,2
B.2π,4 D.4π,4
选修4-4
第2讲→圆与圆锥曲线的参数方程
随堂演练
3.半径为2的基圆的渐开线的参数方程为:
x 2(cos sin ) (为参数) y 2(sin cos ) ___________________________ .
2.4 渐开线与摆线 课件(人教A选修4-4)

答案:A
返回
2.基圆直径为10,求其渐开线的参数方程.
解:取 φ 为参数,φ 为基圆上点与原点的连线与 x 轴 正方向的夹角. ∵直径为 10,∴半径 r=5. 代入圆的渐开线的参数方程得:
x=5cos φ+φsin φ, y=5sin φ-φcos φ.
这就是所求的圆的渐开线的参数方程.
返回
x=2t-sin t, 3.摆线 y=21-cos t
(0≤t≤2π)与直线 y=2 的交点
的直角坐标是________.
答案:(π-2,2);(3π+2,2)
返回
4.圆的半径为r,沿x轴正向滚动,圆与x轴相切于原点
O.圆上点M起始处沿顺时针已偏转φ角.试求点M的轨
迹方程.
π 解:xM=r· φ-r· φ-2 cos
=r(φ-sin φ), π yM=r+r· sin(φ- ) 2 =r(1-cos φ). 即点 M 的轨迹方程为 x=rφ-sin φ, y=r1-cos φ.
返回
点击下图进入
返回
的长相等,它们的长都等于 2α,从而 B 点坐标为(2α,2), 向量 OB =(2α,2), 向量 MB =(2sin α,2cos α),
返回
BM =(-2sin α,-2cos α), 因此 OM = OB + BM
=(2α-2sin α,2-2cos α) =(2(α-sin α),2(1-cos α)). 动点 M 的坐标为(x,y),向量 OM =(x,y)
返回
1.渐开线的产生过程 把一条没有弹性的细绳绕在一个圆盘上,在绳的外端 系上一支铅笔,将绳子拉紧,保持绳子与圆相切,逐渐展 开,那么铅笔画出的曲线就是圆的 渐开线 ,相应的定圆
人教A版高中数学选修4-4渐近线与摆线课件

探究:P40
把一条没有弹性的细绳绕在一个圆盘上,在绳的 外端系上一支铅笔,将绳子拉紧,保持绳子与圆相切 而逐渐展开,那么铅笔会画出一条曲线。
这条曲线的形状怎样?能否求出它的轨迹方程?
动点(笔尖)满足什么几何条件?
设 开 始 时 绳 子 外 端 ( 笔 尖 ) 位 于 点 A ,
当 外 端 展 开 到 点 M 时 , 因 为 绳 子 对 圆 心 角 的 一 段 弧 A B ,
直角坐标系。
M
设基圆的半径为r,绳子外端M的坐标为(x,y)。
显然,点M由角 唯一确定。
B
取 为 参 数 , 则 点 B 的 坐 标 为 ( r c o s , r s i n ) , 从 而
B M ( x r c o s , y r s i n ) , |B M | r .
O
的两个相邻交点之间 上述问题抽象成数学问题就是:当一个圆沿着一的条部定分直叫线做无一滑个动拱地滚。动时,圆周
上一个定点的轨迹是什么?
M
B
OA
同样地,我们先分析圆在滚动过程中,圆周上的这个动点满足的几何条件。
线 段 O A 的 长 等 于 M A 的 长 , 即 O A r。
我们把点M的轨迹叫做平摆线,简称摆线,又叫旋轮线。
解 得 x y r r((c so in s c so in s ))(是 参 数 )。
这就是圆的渐开线的参数方程。
人教A版高中数学选修4-4渐近线与摆线
4
2、渐开线的参数方程
y
x y rr((cso ins cso ins ))(是 参 数 )。
B
M
O
A
x
渐开线的应用:
在机械工业中,广泛地使用齿轮传递动力。
第二讲: 4-4四. 渐开线与摆线

或(sin φ,-cos φ).
[预习导引]
1.渐开线的产生过程
把一条没有弹性的细绳绕在一个圆盘上,
在绳的外端系上一支铅笔,将绳子拉紧,
保持绳子与圆相切,逐渐展开,那么铅笔 画出的曲线就是圆的_渐__开__线__,相应的定圆 叫做__基__圆_.
2.摆线的概念及产生过程 圆的摆线就是一个圆沿着一条定直线无滑动地滚动时圆周
x=3φ-3sin φ, y=3-3cos φ (φ
为参数),
把 y=0 代入得 cos φ=1,
所以 φ=2kπ(k∈Z),
则 x=3φ-3sin φ=6kπ(k∈Z).
3. 已知圆的半径为3,圆在x轴上滚动,开始时定点M在原点
O,则M的轨迹方程是________.
答案
x=3(α-sin y=3(1-cos
出的普通方程比较麻烦,且不容易看出坐标之间的关系,
所以常使用参数方程研究圆的渐开线问题.
③在求圆的摆线和渐开线方程时,如果建立的坐标系原点
和坐标轴选取不同,可能会得到不同的参数方程;
④圆的渐开线和x轴一定有交点而且是唯一的交点.
其中正确的说法有
()
A.①③
B.②④
C.②③
D.①③④
答案 C
解析 对于一个圆,只要半径确定,渐开线和摆线的形状就
是确定的,但是随着选择坐标系的不同,其在坐标系中的位
置也会不同,相应的参数方程也会有所区别,至于渐开线和
坐标轴的交点要看选取的坐标系的位置.
2.圆xy==33scions
θ, θ (θ
为参数)的摆线上一点的纵坐标为
0,那
么其横坐标可以是
()
A.π
B.2π
C.3π
高中数学课件渐开线与摆线课件.ppt

cosφ)
(x-rcosφ, y- sin φ)= 〔rφ〕〔 sin φ, -cosφ)
∴x=r(cosφ + φ sin φ) y =r(sinφ -φ cosφ) (φ为参数)
注意:
1.发生线BM沿基圆滚过的长度等 于基圆上被滚过的圆弧长度。
2.渐开线上任意点的法线恒与基圆相切。3.渐开线的形状取决于基圆来自大小4.基圆内无渐开线
例1.有一标准的渐开线齿轮,齿轮的 齿廓线的基圆直径为22mm,求齿廓所 在的渐开线的参数方程。
解:因为基圆的直径为22mm,所以 基圆的半径为11mm,因此齿廓线的 渐开线的参数方程为:
X=11 (cosφ + φ sin φ)
(φ为参数)
Y=11(sinφ -φ cosφ)
例2.当φ=
,
42
时,求出渐开线
X=cosφ + φ sin φ
Y=sinφ -φ cosφ
上的对应点A,B,并求出A,B的距离。
探 究?
在探究圆的渐开线的参数方程的过程 中用到“向量e2=〔 sin φ, -cosφ)与 向量 有相同的方向〞这一结论, 你能B说M 明这个结论为什么成立吗?
把一根没有弹性的绳子绕在一个 圆盘上,在绳的外端系一支笔,将绳 子拉紧,保持绳子与圆相切而逐渐展 开,那么铅笔画出的曲线,它便是渐 开线.在自然界里有许多渐开线的例 子,例如:一只鹰的嘴,一条鲨鱼的 背鳍,等等.
鲨鱼的背鳍
AB
设开始时绳子外端位于点A,当 外端展开到点M时,因为绳子对圆 心展的角 开 长ABφ后 就〔成 是单为位的切是长线A弧,BB度M我,〕们所的把以一笔切段尖线弧画B出M, 的曲线叫圆的渐开线,相应的定圆 叫渐开线的基圆。
(x-rcosφ, y- sin φ)= 〔rφ〕〔 sin φ, -cosφ)
∴x=r(cosφ + φ sin φ) y =r(sinφ -φ cosφ) (φ为参数)
注意:
1.发生线BM沿基圆滚过的长度等 于基圆上被滚过的圆弧长度。
2.渐开线上任意点的法线恒与基圆相切。3.渐开线的形状取决于基圆来自大小4.基圆内无渐开线
例1.有一标准的渐开线齿轮,齿轮的 齿廓线的基圆直径为22mm,求齿廓所 在的渐开线的参数方程。
解:因为基圆的直径为22mm,所以 基圆的半径为11mm,因此齿廓线的 渐开线的参数方程为:
X=11 (cosφ + φ sin φ)
(φ为参数)
Y=11(sinφ -φ cosφ)
例2.当φ=
,
42
时,求出渐开线
X=cosφ + φ sin φ
Y=sinφ -φ cosφ
上的对应点A,B,并求出A,B的距离。
探 究?
在探究圆的渐开线的参数方程的过程 中用到“向量e2=〔 sin φ, -cosφ)与 向量 有相同的方向〞这一结论, 你能B说M 明这个结论为什么成立吗?
把一根没有弹性的绳子绕在一个 圆盘上,在绳的外端系一支笔,将绳 子拉紧,保持绳子与圆相切而逐渐展 开,那么铅笔画出的曲线,它便是渐 开线.在自然界里有许多渐开线的例 子,例如:一只鹰的嘴,一条鲨鱼的 背鳍,等等.
鲨鱼的背鳍
AB
设开始时绳子外端位于点A,当 外端展开到点M时,因为绳子对圆 心展的角 开 长ABφ后 就〔成 是单为位的切是长线A弧,BB度M我,〕们所的把以一笔切段尖线弧画B出M, 的曲线叫圆的渐开线,相应的定圆 叫渐开线的基圆。
高中数学人教A版选修4-4课件 第二讲参数方程2.4渐开线与摆线

思维辨析
变式训练 1 已知圆的渐开线的参数方程是 ������ = cos������ + ������sin������, (φ 为参数),则此渐开线对应的基圆的直径 ������ = sin������-������cos������ π 是 ,当参数 φ= 时对应的曲线上的点的坐标 为 .
√2
四
渐开线与摆线
学 习 目 标 思 维 脉 络 1.了解 圆的渐开线的参 渐开线与摆线 数方程,了解 摆线的生成 渐开线的概念及生成过程 过程及它的参数方程. 摆线的概念及生成过程 2.了解 用向量知识推导 圆的渐开线与摆线的参数方程 运动轨迹的方法和步骤.
1.渐开线 (1)把一条没有弹性的细绳绕在一个圆盘上,在绳的外端系上一支 铅笔,将绳子拉紧,保持绳子与圆相切而逐渐展开,那么笔尖画出的 曲线叫做圆的渐开线,相应的定圆叫做渐开线的基圆. (2)圆的渐开线的参数方程: ������ = ������(cos������ + ������sin������), (φ 为参数). ������ = ������(sin������-������cos������) 2.摆线 (1)圆的摆线就是一个圆沿着一条定直线无滑动地滚动时,圆周上 一个定点的轨迹,圆的摆线又叫旋轮线. (2)圆的摆线的参数方程: ������ = ������(������-sin������), (φ 为参数). ������ = ������(1-cos������)
)
做一做2 半径为2的圆的摆线的参数方程为( ������ = 2cos������, A. (φ 为参数) ������ = 2sin������ ������ = -2cos������, B. (φ 为参数) ������ = -2sin������ ������ = 2(������-sin������), C. (φ 为参数) ������ = 2(1-cos������) ������ = 2(1-sin������), D. (φ 为参数) ������ = 2(������-cos������) 答案:C
高三数学渐开线与摆线推选优秀ppt

立平面 直设角基坐圆标的系半。 径为r,绳子外端M的坐标为(x,y)。
显然,点M由角 唯一确定。
y
B
O
M
A
x
这就是圆的渐开线的参数(cānshù)方程。
第三页,共8页。
3、渐开线的参数 (cānshù)方程
y M
B
O
A
x
渐开线的应用(yìngyòng):
在机械工业中,广泛地使用齿轮传递动力。
由于渐开线齿行的齿轮磨损(mó sǔn)少,传动平稳,制造安装较为方 因此大多数齿轮采用这种齿形。
Ex
1、渐开线的定义(dìngyì) 外端系上一支铅笔,将绳子拉紧,保持绳子与圆相切
xyrr((1csoins)).,(为参数) 摆线的参数方程为: 根据点M满足的几何条件,我们(wǒ men)取定直线为X轴,定点M滚动时落在定
思考:P44
在摆线的参数方程中,参数 的取值范围是什么?
一个拱的宽度与高度各是什么?
y
B
M C
OD
A
所以,摆线的参数方程为:
xyrr((1 Ecsxoins)).,(为参数)
第六页,共8页。
6、摆线(bǎi xiàn)的 参数M 方程
B
OA y
B 同样地,我们先分析圆在滚动过程(guòchéng)中,圆周上的这个动点满足的几何条件。
如果在自行车的轮子上喷一个白色印记,那么自行车在笔直
高三数学(shùxué)渐开线与摆 线
第一页,共8页。
1、渐开线的定义(dìngyì)
探究(tànjiū) :
把一条没有弹性的细绳绕在一个圆盘上,在绳的 外端系上一支铅笔,将绳子拉紧,保持绳子与圆相切 而逐渐展开,那么铅笔会画出一条曲线。
显然,点M由角 唯一确定。
y
B
O
M
A
x
这就是圆的渐开线的参数(cānshù)方程。
第三页,共8页。
3、渐开线的参数 (cānshù)方程
y M
B
O
A
x
渐开线的应用(yìngyòng):
在机械工业中,广泛地使用齿轮传递动力。
由于渐开线齿行的齿轮磨损(mó sǔn)少,传动平稳,制造安装较为方 因此大多数齿轮采用这种齿形。
Ex
1、渐开线的定义(dìngyì) 外端系上一支铅笔,将绳子拉紧,保持绳子与圆相切
xyrr((1csoins)).,(为参数) 摆线的参数方程为: 根据点M满足的几何条件,我们(wǒ men)取定直线为X轴,定点M滚动时落在定
思考:P44
在摆线的参数方程中,参数 的取值范围是什么?
一个拱的宽度与高度各是什么?
y
B
M C
OD
A
所以,摆线的参数方程为:
xyrr((1 Ecsxoins)).,(为参数)
第六页,共8页。
6、摆线(bǎi xiàn)的 参数M 方程
B
OA y
B 同样地,我们先分析圆在滚动过程(guòchéng)中,圆周上的这个动点满足的几何条件。
如果在自行车的轮子上喷一个白色印记,那么自行车在笔直
高三数学(shùxué)渐开线与摆 线
第一页,共8页。
1、渐开线的定义(dìngyì)
探究(tànjiū) :
把一条没有弹性的细绳绕在一个圆盘上,在绳的 外端系上一支铅笔,将绳子拉紧,保持绳子与圆相切 而逐渐展开,那么铅笔会画出一条曲线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
“疫情无情人有情”。我们为社区所做的工作,居民都看在眼里记在心里。在摸底排查中,居民一句句温暖的话语,关心的问候,让我们防控热情高涨。2月13日,外面下着小雨,我在门岗值守, 接到小区16号楼4单元一个居民的电话,想让协调解决扰民的事宜。当居民从电话里听到我沙哑的声音,只说了句“你们辛苦了,要做好防护,注意安全,我的事不急,不急”!就挂断了电话。有一天, 我收到一个从云南邮寄的快递。莫名的我打开快递,一箱水果,一张写着“送给守护居民安全的工作人员”卡片。顿时所有的辛苦都觉得十分值得。澳门国际电玩
疫情防控期间,我一直坚守在社区,一心为居民健康安全着想。我只是千千万万个疫情防控工作人员中最普通的一个,没有做出惊天动地的大事。可作为一名共产党员,我做到了“关键时刻站得出 来,危急关头豁得出去”,用实际行动向党交了一份考卷。
在如今开放的社会,“禁足”这词很少有人用了。如果有人搬出来,难免有些迂腐气。但自疫情以来常时期,“禁足”是一句最暖心的忠告。
禁足,就是禁止外出。禁足在这里有两层意思,一则明令禁止。违背了就要受到处罚。但这次疫情波及的范围之广,人数之多。没办法用处罚来执行禁令。那么,最重要的就要靠大家自觉遵守。毕 竟病毒的传播不认人,行走间,病毒就搭乘了免费的便车,然后去找你的亲戚、朋友以及你亲近过的人。
疫情防控期间,我一直坚守在社区,一心为居民健康安全着想。我只是千千万万个疫情防控工作人员中最普通的一个,没有做出惊天动地的大事。可作为一名共产党员,我做到了“关键时刻站得出 来,危急关头豁得出去”,用实际行动向党交了一份考卷。
在如今开放的社会,“禁足”这词很少有人用了。如果有人搬出来,难免有些迂腐气。但自疫情以来常时期,“禁足”是一句最暖心的忠告。
禁足,就是禁止外出。禁足在这里有两层意思,一则明令禁止。违背了就要受到处罚。但这次疫情波及的范围之广,人数之多。没办法用处罚来执行禁令。那么,最重要的就要靠大家自觉遵守。毕 竟病毒的传播不认人,行走间,病毒就搭乘了免费的便车,然后去找你的亲戚、朋友以及你亲近过的人。
