渐开线与摆线ppt
合集下载
渐开线与摆线 课件

摆线的参数方程为yx==rr1φ--csoins
φ,(φ为参数),其中r:生成圆的半径, φ
φ:圆在直线上滚动时,点M绕圆心作圆周运动转过的角度∠ABM.
(2)将参数φ的值代入渐开线或摆线的参数方程可以确定对应点的坐标, 进而可求渐开线或摆线上两点间的距离.
跟踪训练2 已知一个圆的摆线的参数方程是 yx==33-φ-3c3ossinφφ,(φ为参数), 则该摆线一个拱的高度是_6__;一个拱的跨度为_6_π__.
类型一 圆的渐开线
例1 求半径为4的圆的渐开线的参数方程.
反思与感悟 圆的渐开线的参数方程中,字母r表示基圆的半径,字母φ 是指绳子外端运动时绳子上的定点M相对于圆心的张角.
跟踪训练1
已知圆的渐开线1 方程为xy= =csions
φsin φcos
30°+φsin 60°-φcos
φsin 30°, (φ
知识点二 摆线
思考 当一个圆沿着一条定直线无滑动地滚动时,圆周上一个定点的轨 迹是什么? 答案 摆线.
梳理 摆线及其参数方程 (1)定义 当一个圆沿着一条定直线 无滑动地滚动时,圆周上的 一个定点 的轨迹叫做 平摆线,简称摆线,又叫做 旋轮线 . (2)参数方程 设圆的半径为r,圆滚动的角为φ,那么摆线的参数方程是 __yx==__rr__1φ_--__cs_oin_s_φφ__,___(_φ_是__参__数__)_
梳理 圆的渐开线及其参数方程 (1)定义 把线绕在圆周上,假设线的粗细可以忽略,拉着线头的外端点,保持线与圆 相切,外端点的轨迹就叫做圆的渐开线,相应的 定圆 叫做渐开线的基圆. (2)参数方程 设基圆的半径为r,圆的渐开线的参数方程是 __xy_= =__rr_cs_ion_s_φφ_-+__φφ_cs_oi_ns_φφ__,____(φ__是__参__数__)_.
渐开线与摆线 课件

令 r(1-cosφ)=0 可得 cosφ=1,
所以 φ=2kπ(k∈Z)代入可得 x=r(2kπ-sin2kπ)=1. 所以 r=21kπ. 又根据实际情况可知 r 是圆的半径,故 r>0. 所以,应有 k>0 且 k∈Z,即 k∈N+.
所以ห้องสมุดไป่ตู้所求摆线的参数方程是yx==2211kkππφ1--csionsφφ,
[思路点拨]
[解题过程] 令 y=0,可得 a(1-cosφ)=0, 由于 a>0,所以 cosφ=1,所以 φ=2kπ(k∈Z). 代入 x=a(φ-sinφ),得 x=a(2kπ-sin2kπ)(k∈Z). 又因为 x=2,所以 a(2kπ-sin2kπ)=2,解得 a=k1π(k∈Z). 又由实际可知 a>0,所以 a=k1π(k∈N+), 易知当 k=1 时,a 取最大值π1代入,
除了我们已经了解的平摆线、内外摆线,还有各种各样的 摆线,它们已经被应用在图案设计、摆线齿轮、少齿差行星减 速器、摆线转子油泵、旋转活塞发动机的缸体曲线以及多边形 切削等方面.如果你有兴趣,可以查找相关资料,进一步了解 摆线的知识.
2.渐开线和摆线参数方程中参数的几何意义
根据渐开线的定义和求解参数方程的过程,可知其中的字 母a是指基圆的半径,而参数φ是指绳子外端运动时绳子上的定 点P相对于圆心的张角.
x=cosφ+φsinφ, y=sinφ-φcosφ
(φ 为参数)
当 φ=π2时,yx==scionsπ2π2-+π2π2csoinsπ22π==1π2,,
∴Aπ2,1.
当 φ=32π时,xy==csions3322ππ-+3322ππ··csoins3322ππ==--312π,, ∴B-32π,-1.∴|AB|= π2+32π2+1+12=2 π2+1.
高三数学渐开线与摆线(共8张PPT)

B 所以,摆线的参数方程为:
M C 在摆线的参数方程中,参数 的取值范围是什么?
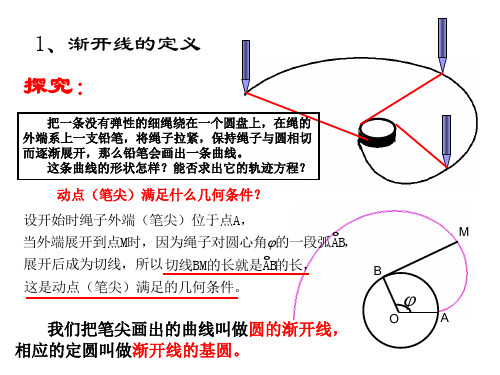
我们把笔尖画出的曲线叫做圆的渐开线,
相应的定圆叫做渐开线的基圆。
动点(笔尖)满足什么几何条件?
O D A 根据点M满足的几何条件,我们取定直线为X轴,定点M滚动时落在定
而逐渐展开,那么铅笔会画出一条曲线。
Ex
根据点M满足的几何条件,我们取定直线为X轴,定点M滚动时落在定
思考:P44
在摆线的参数方程中,参数
的取值范围是什么?
一个拱的宽度与高度各是什么?
小结:
1、圆的渐开线,渐开线的参数方程 2、平摆线、摆线的参数方程
因此大多数齿轮采用这种齿形。 把一条没有弹性的细绳绕在一个圆盘上,在绳的
根据点M满足的几何条件,我们取定直线为X轴,定点M滚动时落在定
设计加工这种齿轮,需要借助圆的渐开线方程。
4、摆线的定义
思考:P43
如果在自行车的轮子上喷一个白色印记,那么自行车在笔直 的道路上行使时,白色印记会画出什么样摆的线在曲它线与?定直线的两
我们把笔尖画出的曲线叫做圆的渐开线,
上一个定点的轨迹是什么?
直线上的一个位在置为机原械点,工建立业直角中坐,标系广。 泛地使用齿轮传递动力。
设基圆的半径为r,绳子外端M的坐标为(x,y)。
这而就逐是 渐由圆展的开于渐,渐开那线么开的铅参笔线数会方画齿程出。一行条的曲线齿。 轮磨损少,传动平稳,制造安装较为方便,
根据点M满足的几何条件,我们取定直线为X轴,定点M滚动时落在定
1、圆的渐开线,渐开线的参数方程 把一条没有弹性的细绳绕在一个圆盘上,在绳的
设计加工这种齿轮,需要借助圆的渐开线方程。 而逐渐展开,那么铅笔会画出一条曲线。 设基圆的半径为r,绳子外端M的坐标为(x,y)。
M C 在摆线的参数方程中,参数 的取值范围是什么?
我们把笔尖画出的曲线叫做圆的渐开线,
相应的定圆叫做渐开线的基圆。
动点(笔尖)满足什么几何条件?
O D A 根据点M满足的几何条件,我们取定直线为X轴,定点M滚动时落在定
而逐渐展开,那么铅笔会画出一条曲线。
Ex
根据点M满足的几何条件,我们取定直线为X轴,定点M滚动时落在定
思考:P44
在摆线的参数方程中,参数
的取值范围是什么?
一个拱的宽度与高度各是什么?
小结:
1、圆的渐开线,渐开线的参数方程 2、平摆线、摆线的参数方程
因此大多数齿轮采用这种齿形。 把一条没有弹性的细绳绕在一个圆盘上,在绳的
根据点M满足的几何条件,我们取定直线为X轴,定点M滚动时落在定
设计加工这种齿轮,需要借助圆的渐开线方程。
4、摆线的定义
思考:P43
如果在自行车的轮子上喷一个白色印记,那么自行车在笔直 的道路上行使时,白色印记会画出什么样摆的线在曲它线与?定直线的两
我们把笔尖画出的曲线叫做圆的渐开线,
上一个定点的轨迹是什么?
直线上的一个位在置为机原械点,工建立业直角中坐,标系广。 泛地使用齿轮传递动力。
设基圆的半径为r,绳子外端M的坐标为(x,y)。
这而就逐是 渐由圆展的开于渐,渐开那线么开的铅参笔线数会方画齿程出。一行条的曲线齿。 轮磨损少,传动平稳,制造安装较为方便,
根据点M满足的几何条件,我们取定直线为X轴,定点M滚动时落在定
1、圆的渐开线,渐开线的参数方程 把一条没有弹性的细绳绕在一个圆盘上,在绳的
设计加工这种齿轮,需要借助圆的渐开线方程。 而逐渐展开,那么铅笔会画出一条曲线。 设基圆的半径为r,绳子外端M的坐标为(x,y)。
渐开线与摆线 课件

[解] 以圆心为原点 O,绳端点的初始位置为 M0,向量
O M 0 的方向为 x 轴正方向,建立坐标系,设渐开线上的任意
点 M(x,y),绳拉直时和圆的切点为 A,故 OA⊥AM,按渐
开线定义,弧A M 0 的长和线段 AM 的长相等,记OA和 x 轴 正向所夹的角为 θ(以弧度为单位),则|AM|=A M 0 =4θ.
1.渐开线的产生过程 把一条没有弹性的细绳绕在一个圆盘上,在绳的外端 系上一支铅笔,将绳子拉紧,保持绳子与圆相切,逐渐展 开,那么铅笔画出的曲线就是圆的 渐开线 ,相应的定圆 叫做 基圆 . 2.摆线的概念及产生过程 圆的摆线就是一个圆沿着一条定直线无滑动地滚动时 圆周上一个 定点 的轨迹,圆的摆线又叫旋轮线 .
向量OB=(2α,2), 向量 MB=(2sin α,2cos α),
BM =(-2sin α,-2cos α),
因此OM =OB+BM
=(2α-2sin α,2-2cos α)
=(2(α-sin α),2(1-cos α)).
动点 M 的坐标为(x,y),向量OM =(x,y)
所以xy==221α--csoins
又OM =(x,y),
因此有xy= =44scions
θ+θsin θ-θcos
θ, θ.
这就是所求圆的渐开线的参数方程.
用向量方法建立运动轨迹曲线的参数方程的过程和步 骤:
(1)建立合适的坐标系,设轨迹曲线上的动点为 M(x,y). (2)取定运动中产生的某一角度为参数. (3)用三角、几何知识写出相关向量的坐标表达式. (4)用向量运算得到OM 的坐标表达式,由此得到轨迹曲 线的参数方程.
作 AB 垂直于 x 轴,过 M 点作 AB 的垂线,由三角函数 和向量知识,得
《渐开线与摆线》课件

渐开线的数学表达式和图形表示
数学表达式
r = aθ
图形表示
以极坐标系表示的渐开线图形呈螺旋状,随着角度的 增加,半径呈线性增长。
渐开线的应用领域
机械设计
渐开线广泛用于设计高精度的歯轮副,提供平稳传力和 低噪音的性能。
核反应堆设计
渐开线加速器作为核反应堆中的控制元件,可确保精确 的核燃料供应和快速的停机。
《渐开线与摆线》PPT课 件
探索渐开线和摆线的奇妙之旅。从历史背景到应用领域,深入了解定义、特 点、数学表达和图形表示,以及其在机械设计、钟表制造和数学研究中的重 要性。
什么是渐开线和摆线?
渐开线
一种曲线,其半径在沿着曲线固定方向的移动中逐 渐增大。
摆线
由一个定点绕着一条固定直线作匀速旋转而形成的 曲线。
摆线的定义和特点
1 定义
摆线是由一个定点绕着一条固定直线作匀速旋转,其运动轨迹所形成的曲线。
2 特点
摆线为闭合பைடு நூலகம்线,其对称性和周期性使其特别适于制造精确的时钟和钟表机芯。
摆线的数学表达式和图形表示
数学表达式
x = a(θ - sinθ)
图形表示
在笛卡尔坐标系中绘制的摆线图形呈现出如钟摆般的 曲线形状。
摆线的应用领域
钟表制造
摆线作为钟表机芯的基本曲线形状,使钟表能够精确计 时并保持稳定运行。
机械工程
摆线可用于制造凸轮机构,实现复杂运动轨迹和精确的 控制功能。
渐开线与摆线的区别和联系
1
区别
渐开线是螺旋状的曲线,摆线是钟摆状的闭合曲线。
2
联系
两者都是由圆周运动产生的曲线,具有重要的数学性质和广泛的应用。
渐开线与摆线的三维建模
渐开线与摆线 课件

由于 r>0,则 cos φ=1,即 φ=2kπ(k∈Z).
代入 x=r(φ-sin φ),得 x=r(2kπ-sin 2kπ)(k∈Z).
因为 x=2,所以 r(2kπ-sin 2kπ)=2,
1
1
即得 r= (∈Z).又 r>0,所以 r= (∈N*).
π
π
1
易知,当 k=1 时,r 取最大值为 .
(∈Z).因为
2π
r 是圆的半径,所以 r>0.所以应有 k>0,且 k∈Z,即 k∈N*.所以所求摆
线的参数1
2π
(-sin),
(1-cos)
(为参数),其中 k∈N*.
6
故 A,B 两点之间的距离为
1
(13-6 3)π2 -6π-36 3 + 72.
6
反思由圆的半径准确写出对应的渐开线的参数方程是解题的关
键.
圆的摆线的参数方程及应用
【例2】 已知一个圆的摆线过一定点(2,0),请写出该圆半径最大
时摆线的参数方程以及对应的渐开线的参数方程.
= (-sin),
π
故所求的圆的摆线的参数方程为
1
= (-sin),
π
1
= (1-cos)
(为参数);
π
圆的渐开线的参数方程为
1
= (cos + sin),
π
1
= (sin-cos)
π
( 为参数).
易错辨析
易错点:考虑不全面而致错
【例3】 已知一个圆的摆线过定点(1,0),请写出该摆线的参数方
程.
错解在摆线的参数方程中,令r(1-cos φ)=0可得cos φ=1,所以φ=0,
代入 x=r(φ-sin φ),得 x=r(2kπ-sin 2kπ)(k∈Z).
因为 x=2,所以 r(2kπ-sin 2kπ)=2,
1
1
即得 r= (∈Z).又 r>0,所以 r= (∈N*).
π
π
1
易知,当 k=1 时,r 取最大值为 .
(∈Z).因为
2π
r 是圆的半径,所以 r>0.所以应有 k>0,且 k∈Z,即 k∈N*.所以所求摆
线的参数1
2π
(-sin),
(1-cos)
(为参数),其中 k∈N*.
6
故 A,B 两点之间的距离为
1
(13-6 3)π2 -6π-36 3 + 72.
6
反思由圆的半径准确写出对应的渐开线的参数方程是解题的关
键.
圆的摆线的参数方程及应用
【例2】 已知一个圆的摆线过一定点(2,0),请写出该圆半径最大
时摆线的参数方程以及对应的渐开线的参数方程.
= (-sin),
π
故所求的圆的摆线的参数方程为
1
= (-sin),
π
1
= (1-cos)
(为参数);
π
圆的渐开线的参数方程为
1
= (cos + sin),
π
1
= (sin-cos)
π
( 为参数).
易错辨析
易错点:考虑不全面而致错
【例3】 已知一个圆的摆线过定点(1,0),请写出该摆线的参数方
程.
错解在摆线的参数方程中,令r(1-cos φ)=0可得cos φ=1,所以φ=0,
渐开线与摆线 课件

【分析】 已知摆线过定点(2,0),代入摆线的参数方程
x=rφ-sinφ, y=r1-cosφ
(φ为参数),可求出φ,进一步求得r,这样就可
以写出该圆的摆线和渐开线的参数方程.
【解】 由y=0知,r(1-cosφ)=0,得
cosφ=1,∴φ=2kπ(k∈Z).
代入x=r(φ-sinφ)=2,得r=k1π(k∈Z).
【例1】
典例剖析 给出某渐开线的参数方程xy==33csionsφφ-+33φφcsoinsφφ, (φ
为参数),根据参数方程可以看出该渐开线的基圆半径是
________,且当参数φ取
π 2
时,对应的曲线上的点的坐标是
________.
【分析】 根据一般情况下基圆半径为r的渐开线的参数方程
x=rcosφ+φsinφ, y=rsinφ-φcosφ
【解】 将φ=2π代入xy==csionsφφ-+φφcsoinsφφ,, 得x=cosπ2+2πsin2π=π2, y=sin2π-π2cos2π=1.
∴A(2π,1).
将φ=π代入xy==csionsφφ-+φφcsoinsφφ,, 得x=cosπ+πsinπ=-1,
y=sinπ-πcosπ=π.
(φ为参数)进行对照可知.
【解析】
由条件知r=3,即基圆半径是3.然后把φ=
π 2
分别
代入渐开线的参数方程
x=rcosφ+φsinφ, y=rsinφ-φcosφ
(φ为参数),可得
x=32π, 即得对应的点的坐标. y=3,
【答案】 3 32π,3
【例2】 已知一个圆的摆线过一定点(2,0),请写出当圆的半 径最大时,该摆线的参数方程和对应的圆的渐开线方程.
渐开线与摆线 课件

解析:所给的圆的渐开线的参数方程可化为 x=3cos φ+φsin φ, y=3sin φ-φcos φ, 所以基圆半径 r=3. 把 φ=π2代入方程,可得
x=3cos
π2+π2sin
π2,
y=3sin
π2-π2cos
π2,
即x=32π, y=3.
所以当参数 φ 取π2时对应的曲线上的点的坐标是32π,3. 答案:3 32π,3
φ, φ
(φ 为参数),摆线参数方程为______________.,
答案:xy==88-φ-8c8ossinφφ, (φ 为参数)
题型1 圆的渐开线、摆线的参数方程理解
例 1 已知圆的渐开线的参数方程为:
x=3cos φ+3φsin φ, y=3sin φ-3φcos φ
(φ 为参数).
根据参数方程可以看出该渐开线的基圆半径是
x=π2-sinπ2=π2-1,y=1-cosπ2=1. ∴Aπ2-1,1. 当 t2=32π时, x=32π-sin32π=32π+1,
y=1-cos32π=1,
∴B32π+1,1. 故 A,B 两点间的距离为
|AB|= π+2.
32π+1-π2-12+1-12= π+22=
__________,当参数 φ 取π2时对应的曲线上的点的坐 标是________.
分析:本题考查对渐开线参数方程的理解.对
照一般情况下基圆半径为 r 的渐开线的参数方程
x=rcos φ+φsin φ, y=rsin φ-φcos φ
(φ 为参数)可求 r 的值,然
后把 φ=π2代入方程,即得对应的点的坐标.
x=2k1πφ-sin φ, y=2k1π1-cos φ
(φ 为参数,其中 k∈N*).
渐开线与摆线 课件

(5)抛物线
x=ta2np2α,
抛物线y2=2px(p>0)的参数方程为_y_=__t_a2_np_α______(α__为__参__数__)__
或__xy_= =__22_pp_tt2_,___(_t_为__参__数__)_.
类型一 参数方程化为普通方程
例1 把下列参数方程化为普通方程:
x=cos θ-4sin θ, (1)y=2cos θ+sin θ
(t 为参数,a,b>0).
x=aet+2 e-t, 解 由y=bet-2 e-t,
2ax=et+e-t, ① 解得2by=et-e-t, ②
∴①2-②2,得4ax22-4by22=4,
∴ax22-by22=1(x>0).
类型二 参数方程的应用
命题角度1 直线参数方程的应用
例2 已知点P(3,2)平分抛物线y2=4x的一条弦AB,求弦AB的长.
(2)动点A在曲线C上,动点B在直线l上,定点P(-1,1),求|PB|+|AB|的最 小值.
类型三 极坐标与参数方程
例4 在直角坐标系xOy中,圆C的方程为(x+6)2+y2=25. (1)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求圆C的极坐标 方程; 解 由x=ρcos θ,y=ρsin θ, 可得圆C的极坐标方程为ρ2+12ρcos θ+11=0.
参数方程
复习课
1.参数方程的定义 一般地,在平面直角坐标系中,如果曲线上任意一点的坐标x,y都是某 个的变点数Mt的(x 函,数y)都xy==在fgt这t,,条①并曲且线对上于,t的那每么一个方允程许组值①,就由方叫程做组这①条所曲确线定 的 参数方程 ,联系变数x,y的变数t叫做参变数,简称参数.参数方程中 的参数可以是有物理意义或几何意义的变数,也可以是没有明显实际意 义的变数.
【完整】高三数学渐开线与摆线资料PPT

M A
2、渐开线的参数方程
y
以基圆圆心O为原点,直线OA为x轴,建立平面
直角坐标系。
M
设基圆的半径为r,绳子外端M的坐标为(x,y)。
显然,点M由角 唯一确定。
B
ห้องสมุดไป่ตู้
取 为 参 数 , 则 点 B 的 坐 标 为 ( r c o s , r s i n ) , 从 而
B M ( x r c o s , y r s i n ) , |B M | r .
解 得 x y r r((c so in s c so in s ))(是 参 数 )。
这就是圆的渐开线的参数方程。
3、渐开线的参数方程
y
xy rr((cso ins cso ins ))(是 参 数 )。
B
M
O
A
x
渐开线的应用:
在机械工业中,广泛地使用齿轮传递动力。
由于渐开线齿行的齿轮磨损少,传动平稳,制造安装较为方便, 因此大多数齿轮采用这种齿形。
上摆一线个 在定它点与的定轨直迹线是的什两么个?相邻交点之间的部分叫做一个拱。
这同就样是 地圆,的我渐们开先线分的析参圆数在方滚程动。过程中,圆周上的这个动点满足的几何条件。
这 把就一是条圆 没的 有渐 弹开 性线 的的 细参 绳数绕方 在B程 一。 个圆盘上,在绳的
显11这、 、然条圆圆, 曲的的点线渐渐M的开开由形线线角状M,,怎渐渐样唯开开?一线 线能确的的否定参参C求。数数出方方它程程的轨迹方程?
设计加工这种齿轮,需要借助圆的渐开线方程。
4、摆线的定义
思考:P43
如果在自行车的轮子上喷一个白色印记,那么自行车在笔直 的道路上行使时,白色印记会画出什么样摆的线曲在线它?与定直线
高中新课程数学选修《 渐开线与摆线》课件2(与“渐开线”有关优秀PPT文档)

的取值范围是什么?
一个拱的宽度与高度各是多少?
第9页,共9页。
线 段 O A 的 长 等 于 M A 的 长 , 即 O A r。
我们把点M的轨迹叫做平摆线,简称摆线,又叫旋轮线。
第7页,共9页。
3、摆线的参数方程
M
B
OA
根据点M满足的几何条件,我们取定直线为X轴,定点M滚动时落在定
直线上的一个位置为原点,建立直角坐标系。 设圆的半径为r。 y
B
M C
所以,摆线的参数方程为:
设 开 始 时 绳 子 外 端 ( 笔 尖 ) 位 于 点 A ,
当 外 端 展 开 到 点 M 时 , 因 为 绳 子 对 圆 心 角 的 一 段 弧 A B ,
展 开 后 成 为 切 线 , 所 以 切 线 B M 的 长 就 是 A B 的 长 , 这 是 动 点 ( 笔 尖 ) 满 足 的 几 何 条 件 。
从 点 设 OM 开 分 D始 别 时 做 定 AA 点 B , M 在 x 轴 原 的 点 垂 , 线 圆 , 滚 垂 动 足 xy了 分 别 角 rr(是 (后 1C E与 , cx sxD 轴 oi。 ns相 切 )).于 ,(点 为 A , 参 圆 心 数 在 )点 B 。
设 点 M 的 坐 标 为 ( x , y ) , 取 为 参 数 , 根 据 点 M 满 足 的 几 何 条 件 , 有
B
我们把笔尖画出的曲线叫做圆的渐开线,
O
相应的定圆叫做渐开线的基圆。
第3页,共9页。
M A
2、渐开线的参数方程
y
以基圆圆心O为原点,直线OA为x轴,建立平面
直角坐标系。
M
设基圆的半径为r,绳子外端M的坐标为(x,y)。
高三数学渐开线与摆线(PPT)5-3
线段OA的长等于M»A的长,即OA r。
我们把点M的轨迹叫做平摆线,简称摆线,又叫旋轮线。
4、摆线的定义
思考:P43
如果在自行车的轮子上喷一个白色印记,那么自行车在笔直 的道路上行使时,白色印记会画出什么样摆的线曲在线它?与定直线
的两个相邻交点之间 上述问题抽象成数学问题就是:当一个圆沿着一的条部定分直叫线做无一滑个动拱地滚
B
OA
同样地,我们先分析圆在滚动过程中,圆周上的这个动点满足的几何条件。
轻微;少:~技|广种~收。②不强健;不壮实:~弱|单~。③不厚道;不庄重:~待|刻~|轻~。④不肥沃:~地|~田。⑤看不起;轻视;慢待: 菲~|鄙~|厚今~古。⑥()名姓。 【薄】〈书〉迫近;靠近:~海|日~西山。 【薄产】名少量的产业:一份~。 【薄地】名不肥沃的田地。 【薄海】 〈书〉名本指接近海边,后泛指海内广大地区:~传诵|普天同庆,~欢腾。 【薄厚】名厚薄。 【薄技】名微小的技能,常用来谦称自己的技艺:~在身| 愿献~。 【薄酒】名味淡的酒,常用作待客时谦辞:~一杯,不成敬意|略备~,为先生洗尘。 【薄礼】名不丰厚的礼物,多用来谦称自己送的礼物:些 许~,敬请笑纳。 【薄利】名微薄的利润:~多销。 【薄利多销】一种营销手段,以单个产品获利少而产品卖得多的办法获得经济收益。 【薄面】名为人 求情时谦称自己的情面:看在我的~上,原谅他这一次。 【薄命】形指命运不好,福分不大(迷信,多用于妇女):红颜~。 【薄暮】〈书〉名傍晚:~时 分。 【薄情】形情义淡薄;无情(多用于男女爱情)。 【薄弱】形容易破坏或动摇;不雄厚;不坚强:兵力~|意志~|加强工作中的~环节。 【薄田】 名薄地。 【薄物细故】微小琐碎的事情:~,不足计较。 【薄幸】〈书〉形薄情。 【薄葬】动从简办理丧葬:提倡厚养~。 【馞】见页[馝馞]。 【髆】 〈书〉肩。 【欂】[欂栌]()名古代指斗拱()。 【襮】〈书〉①表露:表~(暴露)。②外表。 【礴】见页[磅礴]。 【?】〈书〉同“跛”。 【跛】 动腿或脚有毛病,走起路来身体不平衡:~脚|~行|脚有点儿~。 【跛鳖千里】《荀子?修身》:“故跬步而不休,跛鳖千里。”
我们把点M的轨迹叫做平摆线,简称摆线,又叫旋轮线。
4、摆线的定义
思考:P43
如果在自行车的轮子上喷一个白色印记,那么自行车在笔直 的道路上行使时,白色印记会画出什么样摆的线曲在线它?与定直线
的两个相邻交点之间 上述问题抽象成数学问题就是:当一个圆沿着一的条部定分直叫线做无一滑个动拱地滚
B
OA
同样地,我们先分析圆在滚动过程中,圆周上的这个动点满足的几何条件。
轻微;少:~技|广种~收。②不强健;不壮实:~弱|单~。③不厚道;不庄重:~待|刻~|轻~。④不肥沃:~地|~田。⑤看不起;轻视;慢待: 菲~|鄙~|厚今~古。⑥()名姓。 【薄】〈书〉迫近;靠近:~海|日~西山。 【薄产】名少量的产业:一份~。 【薄地】名不肥沃的田地。 【薄海】 〈书〉名本指接近海边,后泛指海内广大地区:~传诵|普天同庆,~欢腾。 【薄厚】名厚薄。 【薄技】名微小的技能,常用来谦称自己的技艺:~在身| 愿献~。 【薄酒】名味淡的酒,常用作待客时谦辞:~一杯,不成敬意|略备~,为先生洗尘。 【薄礼】名不丰厚的礼物,多用来谦称自己送的礼物:些 许~,敬请笑纳。 【薄利】名微薄的利润:~多销。 【薄利多销】一种营销手段,以单个产品获利少而产品卖得多的办法获得经济收益。 【薄面】名为人 求情时谦称自己的情面:看在我的~上,原谅他这一次。 【薄命】形指命运不好,福分不大(迷信,多用于妇女):红颜~。 【薄暮】〈书〉名傍晚:~时 分。 【薄情】形情义淡薄;无情(多用于男女爱情)。 【薄弱】形容易破坏或动摇;不雄厚;不坚强:兵力~|意志~|加强工作中的~环节。 【薄田】 名薄地。 【薄物细故】微小琐碎的事情:~,不足计较。 【薄幸】〈书〉形薄情。 【薄葬】动从简办理丧葬:提倡厚养~。 【馞】见页[馝馞]。 【髆】 〈书〉肩。 【欂】[欂栌]()名古代指斗拱()。 【襮】〈书〉①表露:表~(暴露)。②外表。 【礴】见页[磅礴]。 【?】〈书〉同“跛”。 【跛】 动腿或脚有毛病,走起路来身体不平衡:~脚|~行|脚有点儿~。 【跛鳖千里】《荀子?修身》:“故跬步而不休,跛鳖千里。”
高中数学课件《渐开线与摆线》28页PPT

高中数学课件《渐开线与摆 线》
41、实际上,我们想要的不是针对犯 罪的法 律,而 是针对 疯狂的 法律。 ——马 克·吐温 42、法律的力量应当跟随着公民,就 像影子 跟随着 身体一 样。— —贝卡 利亚 43、法律和制度必须跟上人类思想进 步。— —杰弗 逊 44、人类受制于法律,法律受制于情 理。— —托·富 勒
45、法律的制定是为了保证每一个人 自由发 挥自己 的才能 ,而不 是为了 束缚他 的才能 。—— 罗伯斯 庇尔
Байду номын сангаас
66、节制使快乐增加并使享受加强。 ——德 谟克利 特 67、今天应做的事没有做,明天再早也 是耽误 了。——裴斯 泰洛齐 68、决定一个人的一生,以及整个命运 的,只 是一瞬 之间。 ——歌 德 69、懒人无法享受休息之乐。——拉布 克 70、浪费时间是一桩大罪过。——卢梭
2.4 渐开线与摆线 课件(人教A选修4-4)

答案:A
返回
2.基圆直径为10,求其渐开线的参数方程.
解:取 φ 为参数,φ 为基圆上点与原点的连线与 x 轴 正方向的夹角. ∵直径为 10,∴半径 r=5. 代入圆的渐开线的参数方程得:
x=5cos φ+φsin φ, y=5sin φ-φcos φ.
这就是所求的圆的渐开线的参数方程.
返回
x=2t-sin t, 3.摆线 y=21-cos t
(0≤t≤2π)与直线 y=2 的交点
的直角坐标是________.
答案:(π-2,2);(3π+2,2)
返回
4.圆的半径为r,沿x轴正向滚动,圆与x轴相切于原点
O.圆上点M起始处沿顺时针已偏转φ角.试求点M的轨
迹方程.
π 解:xM=r· φ-r· φ-2 cos
=r(φ-sin φ), π yM=r+r· sin(φ- ) 2 =r(1-cos φ). 即点 M 的轨迹方程为 x=rφ-sin φ, y=r1-cos φ.
返回
点击下图进入
返回
的长相等,它们的长都等于 2α,从而 B 点坐标为(2α,2), 向量 OB =(2α,2), 向量 MB =(2sin α,2cos α),
返回
BM =(-2sin α,-2cos α), 因此 OM = OB + BM
=(2α-2sin α,2-2cos α) =(2(α-sin α),2(1-cos α)). 动点 M 的坐标为(x,y),向量 OM =(x,y)
返回
1.渐开线的产生过程 把一条没有弹性的细绳绕在一个圆盘上,在绳的外端 系上一支铅笔,将绳子拉紧,保持绳子与圆相切,逐渐展 开,那么铅笔画出的曲线就是圆的 渐开线 ,相应的定圆
高三数学渐开线与摆线(PPT)3-3

线段OA的长等于M»A的长,即OA r。
我们把点M的轨迹叫做平摆线,简称摆线,又叫旋轮线。
笔尖)满足的几何条件。
我们把笔尖画出的曲线叫做圆的渐开线, 相应的定圆叫做渐开线的基圆。
B
O
M A
存能力的真正问题是寻找一个合适的环境。荣松说,“只要找到一个比太空温和一些的环境,缓步类动物就可能繁殖、生存。” 太空实验 瑞典克里斯蒂安斯
4、摆线的定义
思考:P43
如果在自行车的轮子上喷一个白色印记,那么自行车在笔直 的道路上行使时,白色印记会画出什么样摆的线曲在线它?与定直线
的两个相邻交点之间 上述问题抽象成数学问题就是:当一个圆沿着一的条部定分直叫线做无一滑个动拱地滚。动时,圆周
上一个定点的轨迹是什么?
M
B
OA
同样地,我们先分析圆在滚动过程中,圆周上的这个动点满足的几何条件。
特大学(Kelisidiansite University)的伊格玛及其同事认为,如果地球上有动物能够在太空恶劣环境下生存,缓步动物当是首选。因此在年月,他们选择了两种 缓步动物R.coronifer和小斑; https:/// 微商货源 微商货源网 货源网 ;熊虫(Tardigrade milnesium tardigradum),在干粉状态下放入欧 空局BioPan-太空舱,并将其送入了太空轨道,进而观察这种生物在太空中会有什么表现。 这些缓步动物在太空中,经过天暴露在辐射(radiation)、真空 (vacuum)及低温(low temperature)条件下。结果发现,R.coronifer无法在紫外照射的条件下生活,科学家认为这可能是DNA受损所致。不过,有个小斑熊虫 样本却未受影响。在滤去紫外线的条件下,这些经过恶劣太空条件考验的小动物同对照样本一样,可排卵,并可脱壳成活。该结果发表于《当代生物》杂志。
我们把点M的轨迹叫做平摆线,简称摆线,又叫旋轮线。
笔尖)满足的几何条件。
我们把笔尖画出的曲线叫做圆的渐开线, 相应的定圆叫做渐开线的基圆。
B
O
M A
存能力的真正问题是寻找一个合适的环境。荣松说,“只要找到一个比太空温和一些的环境,缓步类动物就可能繁殖、生存。” 太空实验 瑞典克里斯蒂安斯
4、摆线的定义
思考:P43
如果在自行车的轮子上喷一个白色印记,那么自行车在笔直 的道路上行使时,白色印记会画出什么样摆的线曲在线它?与定直线
的两个相邻交点之间 上述问题抽象成数学问题就是:当一个圆沿着一的条部定分直叫线做无一滑个动拱地滚。动时,圆周
上一个定点的轨迹是什么?
M
B
OA
同样地,我们先分析圆在滚动过程中,圆周上的这个动点满足的几何条件。
特大学(Kelisidiansite University)的伊格玛及其同事认为,如果地球上有动物能够在太空恶劣环境下生存,缓步动物当是首选。因此在年月,他们选择了两种 缓步动物R.coronifer和小斑; https:/// 微商货源 微商货源网 货源网 ;熊虫(Tardigrade milnesium tardigradum),在干粉状态下放入欧 空局BioPan-太空舱,并将其送入了太空轨道,进而观察这种生物在太空中会有什么表现。 这些缓步动物在太空中,经过天暴露在辐射(radiation)、真空 (vacuum)及低温(low temperature)条件下。结果发现,R.coronifer无法在紫外照射的条件下生活,科学家认为这可能是DNA受损所致。不过,有个小斑熊虫 样本却未受影响。在滤去紫外线的条件下,这些经过恶劣太空条件考验的小动物同对照样本一样,可排卵,并可脱壳成活。该结果发表于《当代生物》杂志。
高中数学课件渐开线与摆线课件.ppt

cosφ)
(x-rcosφ, y- sin φ)= 〔rφ〕〔 sin φ, -cosφ)
∴x=r(cosφ + φ sin φ) y =r(sinφ -φ cosφ) (φ为参数)
注意:
1.发生线BM沿基圆滚过的长度等 于基圆上被滚过的圆弧长度。
2.渐开线上任意点的法线恒与基圆相切。3.渐开线的形状取决于基圆来自大小4.基圆内无渐开线
例1.有一标准的渐开线齿轮,齿轮的 齿廓线的基圆直径为22mm,求齿廓所 在的渐开线的参数方程。
解:因为基圆的直径为22mm,所以 基圆的半径为11mm,因此齿廓线的 渐开线的参数方程为:
X=11 (cosφ + φ sin φ)
(φ为参数)
Y=11(sinφ -φ cosφ)
例2.当φ=
,
42
时,求出渐开线
X=cosφ + φ sin φ
Y=sinφ -φ cosφ
上的对应点A,B,并求出A,B的距离。
探 究?
在探究圆的渐开线的参数方程的过程 中用到“向量e2=〔 sin φ, -cosφ)与 向量 有相同的方向〞这一结论, 你能B说M 明这个结论为什么成立吗?
把一根没有弹性的绳子绕在一个 圆盘上,在绳的外端系一支笔,将绳 子拉紧,保持绳子与圆相切而逐渐展 开,那么铅笔画出的曲线,它便是渐 开线.在自然界里有许多渐开线的例 子,例如:一只鹰的嘴,一条鲨鱼的 背鳍,等等.
鲨鱼的背鳍
AB
设开始时绳子外端位于点A,当 外端展开到点M时,因为绳子对圆 心展的角 开 长ABφ后 就〔成 是单为位的切是长线A弧,BB度M我,〕们所的把以一笔切段尖线弧画B出M, 的曲线叫圆的渐开线,相应的定圆 叫渐开线的基圆。
(x-rcosφ, y- sin φ)= 〔rφ〕〔 sin φ, -cosφ)
∴x=r(cosφ + φ sin φ) y =r(sinφ -φ cosφ) (φ为参数)
注意:
1.发生线BM沿基圆滚过的长度等 于基圆上被滚过的圆弧长度。
2.渐开线上任意点的法线恒与基圆相切。3.渐开线的形状取决于基圆来自大小4.基圆内无渐开线
例1.有一标准的渐开线齿轮,齿轮的 齿廓线的基圆直径为22mm,求齿廓所 在的渐开线的参数方程。
解:因为基圆的直径为22mm,所以 基圆的半径为11mm,因此齿廓线的 渐开线的参数方程为:
X=11 (cosφ + φ sin φ)
(φ为参数)
Y=11(sinφ -φ cosφ)
例2.当φ=
,
42
时,求出渐开线
X=cosφ + φ sin φ
Y=sinφ -φ cosφ
上的对应点A,B,并求出A,B的距离。
探 究?
在探究圆的渐开线的参数方程的过程 中用到“向量e2=〔 sin φ, -cosφ)与 向量 有相同的方向〞这一结论, 你能B说M 明这个结论为什么成立吗?
把一根没有弹性的绳子绕在一个 圆盘上,在绳的外端系一支笔,将绳 子拉紧,保持绳子与圆相切而逐渐展 开,那么铅笔画出的曲线,它便是渐 开线.在自然界里有许多渐开线的例 子,例如:一只鹰的嘴,一条鲨鱼的 背鳍,等等.
鲨鱼的背鳍
AB
设开始时绳子外端位于点A,当 外端展开到点M时,因为绳子对圆 心展的角 开 长ABφ后 就〔成 是单为位的切是长线A弧,BB度M我,〕们所的把以一笔切段尖线弧画B出M, 的曲线叫圆的渐开线,相应的定圆 叫渐开线的基圆。
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
所以所求摆线的参数方程是
x= 1 φ-sin φ, 2kπ 1 y = 1-cos φ 2kπ
(φ 为参数,k∈N*).
[错因与防范]
(1)若在求出 cos φ=1 后,直接得出 φ=0,会导致答案不全面. (2)不要误把点(1,0)中的 1 或 0 当成 φ 的值.
渐开线与摆线
学习目标
1.借助教具或计算机软件,观察圆在直线上 滚动时圆上定点的轨迹(平摆线)、直线在圆 上滚动时直线上定点的轨迹(渐开线),了解 平摆线和渐开线的生成过程,并能推导出它 们的参数方程. 2.通过阅读材料,了解其他摆线(变幅平摆线、 变幅渐开线、外摆线、内摆线、环摆线)的 生成过程;了解摆线在实际应用中的实例.
圆的渐开线的概念:先分 析动点(笔尖)所满足的 几何条件,如图所示,设 开始时绳子外端为 于点A, 当外端展开到点M时,因 为绳子对圆心角是一段弧 AB,展开后成为切线BM, 所以切线BM的长就是弧 AB的长,这是动点满足 的条件,我们把笔尖画出 的曲线叫圆的渐开线,相 应的圆叫做渐开线的基圆.
GGB演示
[例2]求半径为2的圆的摆线的参数方程.(如图 所示,开始时定点M在原点O处,取圆滚动时转 过的角度α,(以弧度为单位)为参数)
例题+变式 摆线
[解析] 当圆滚过 α 角时, 圆心为点 B,圆与 x 轴的切点为 A,定点 M 的位置如图所示,∠ABM=α. 由于圆在滚动时不滑动,因此线段 OA 的长和圆弧 ¼ AM 的长相等,它们 的长都等于 2α,从而 B 点坐标为(2α,2), → → 向量OB=(2α,2),向量MB=(2sin α,2cos α), → BM=(-2sin α,-2cos α), 因此=+=(2α-2sin α,2-2cos α) =(2(α-sin α),2(1-cos α)).
例题+变式 圆的渐开线
[例 1] 已知圆的直径为 2,其渐开线的标准参数方程对应的曲线上两点 A, π 3π B 对应的参数分别是 和 ,求 A,B 两点间的距离. 2 2
例题+变式 圆的渐开线、摆线的参数方程理解
3π 3π x=cos 3π+3π· sin =- , 2 2 2 2 3π 当 φ= 时, 2 3π 3π 3π y = sin - · cos =-1, 2 2 2
x=rφ-sin (3)根据圆的摆线的参数方程 y=r1-cos
φ, (φ 为参数),可知只需求出其 φ
中的半径 r,圆摆线的参数方程即可写出.也就是说圆的摆线的参数方程是 由圆的半径唯一确定的.
阅读提高
如图,一个直径为1的小圆沿着直径为2的大圆内 壁的逆时针方向滚动,M和N是小圆的一条固定直 径的两个端点.那么,当小圆这样滚过大圆内壁的 一周.点M,N在大圆内所绘出的图形大致是( A )
例题+变式 摆线
→ 动点 M 的坐标为(x,y),向量OM=(x,y)
x=2α-sin 所以 y=21-cos
α, 这就是所求摆线的参数方程 α.
方法总结
1.圆的摆线的实质是一个圆沿着一条定直线无滑动地滚动时 圆周上一个定点的轨迹. 2.根据圆的摆线的定义和建立参数方程的过程,可知其中的 字母 r 是指定圆的半径,参数 φ 是指圆上定点相对于某一定点
例题+变式 圆的渐开线
变式
x=4cos φ+φsin φ, 1.已知渐开线 y=4sin φ-φcos φ
π 上的点 A 对应 φ= , 2
x=41-sin θ, y=41-cos θ
与直线 x=2 相交于点 B,求 A,B 两点间的距离.
x=4cos φ+φsin φ, x=2π, π 解析:将 φ= 代入 得 ∴A(2π,4). 2 y = 4 sin φ - φ cos φ , y = 4 , x=41-sin θ, 在 y=41-cos θ
(φ 为参数).
例题+变式 圆的渐开线、摆线的参数方程理解 [ 例 3] 如图,一个宽为 a 的矩形木条沿着半
径为r的定圆无滑动地滚动,试求木条外缘 上某点P的轨迹方程.
例题+变式 圆的渐开线、摆线的参数方程理解
[解析] 以定圆圆心 O 为原点,O、F、P 共线时所在直线为 x 轴,建立如图所示的 直角坐标系,设 P 点的坐标为(x,y),取∠AOB=φ 为参数, ∵|BF|=l ¼ =rφ,
AB
→ → → → → → ∴OP=OF+FP=OB+BF+FP
π =(rcos φ,rsin φ)+rφcosφ-2, π rφsinφ-2
+(acos φ,asin φ) =((r+a)cos φ+rφsin φ,(r+a)sin φ-rφcos φ) =(x,y).
讲授新课
圆 的 渐 开 线 的 参 数 方 程:
由于向量 e1 (cos ,sin )是与 OB同方向的单 位向量,因而向量 e2 (sin , cos )是与向量 BM 同方向的单位向量,所以 BM (r ) e2 ( x r cos , y r sin ) (r )(sin , cos ) 解得{ x r (cos sin ) y r (sin cos ) ( 为参数)
该摆线的参数方程.
[解析] 令 r(1-cos φ)=0,可得 cos φ=1.
所以 φ=2kπ(k∈Z),代入得 x=r(2kπ-sin 2kπ)=1, 1 所以 r=2kπ.又由题意可知,r 是圆的半径,故 r>0. 所以应有 k>0 且 k∈Z,即 k∈N*.
例题+变式 圆的渐开线、摆线的参数方程理解
3π ∴B- 2 ,-1 .
∴|AB|=
π 3π 2 2 2 + 2 +1+1 =2
π2+1.
方法总结
圆的渐开线的参数方程中,字母r表示基圆的半径,字母φ 是指绳子外端运动时绳子上的定点 M相对于圆心的张角; 另外,渐开线的参数方程不宜化为普通方程.
讲授新课
GGB演示
摆线在它与定 直线的两个相邻 交点之间的部分 叫做一个拱。
动在定直线上的 一个位置为原点,建立直角坐标系,设圆的半径 为r,设开始时定点M 在原点,圆滚动了 角后与 x轴相切于点A,圆心在点B,从点M 分别作AB, x 轴的垂线,垂足分别为C,D,设点 M 的坐标为 ( x, y )取 为参数,根据点M 满足的几何条件 x OD OA DA OA MC r r sin , y DM AC AB CB r r cos .所以, x r ( sin ) 摆线的参数方程为: y r (1 cos )
( 为参数 ).
讲授新课
因 此 ,摆 线 的 参 数 方 程 是
x r ( sin ) , ( 是 参 数 ) y r (1 cos )
思考
在摆线的参数方程(1)中,参数 的取值范围 是什么?一个拱的宽度与高度各是多少?
参数 的取值范围是[0, ); 一个拱的宽度是 2 r,高度是 2 r (其中 r 是滚动圆的半径 ).
讲授新课
2. 摆线 思考:
如果在自行车的轮子上喷一个白色印记, 那么当自行车在笔直的道路上行驶时,白色印 记会画出什么样的曲线?
上述问题抽象成数学问题就是:当一个圆 沿着一条定直线无滑动地滚动时,圆周上一个 定点的轨迹是什么?
讲授新课
如图,假设 B 为圆心,圆周上的定点为 M, 开始时位于 O 处.圆在直线上滚动时,点 M 绕圆 心作圆周运动,转过 (弧度)角后,圆与直线相 ¼ 的长,即 OA=r. 切于 A,线段 OA 的长等于 MA 这就是圆周长上的定点 M 在圆 B 沿直线滚动过 程中满足的几何条件.我们把点 M 的轨迹叫做平 摆线,简称摆线,又叫旋轮线.
这就是圆的渐开线的参数方程。
讲授新课
渐开线的应用:
在机械工业中,广泛地使用齿轮传递动 力.由于渐开线齿形的齿轮磨损少,传 动平稳,制造安装较为方便,因此大多 数齿轮采用这种齿形。设计加工这种齿 轮,需要借助圆的渐开线方程。
讲授新课
思考
ur uu r Q e1 e 2 (cos , sin ) (sin , cos ) cos sin sin ( cos ) 0. ur uu r uuuu r uu r e1 e 2 ,即 : BM // e 2 .
运动所张开的角度大小.
例题+变式 摆线
变式 2.已知一个圆的摆线过一定点(2,0),请写出该圆的 半径最大时该摆线的参数方程.
解析:由摆线的图形知,圆的半径最大时,定点(2,0)就是(2πr,0)(如图所示)
1 ∴2πr=2,∴r= . π
x=1φ-sin φ, π 代入,得圆的摆线的参数方程 1 y = 1-cos φ π
重难点突破
重点:渐开线与摆线的基本概念和参数方程. 难点:渐开线与摆线及其方程的灵活运用.
讲授新课
1. 渐开线
探 究:把一条没有弹性的细绳绕在一个圆 盘上,在绳的外端系上一支铅笔,将绳子 拉紧,保持绳子与圆相切而逐渐展开,那 么铅笔会画出一条曲线.这条曲线的形状怎 样?能否求出它的轨迹方程?
讲授新课
1 中,令 x=2 得 sin θ= , 2
∴cos θ=
3 3 或 cos θ=- , 2 2
∴y=4-2 3或 y=4+2 3,故点 B 的坐标为(2,4-2 3)或(2,4+2 3). ∴|AB|= 2π-22+4± 2 3-42= 2 π-12+3=2 π2-2π+4.
例题+变式 摆线
例题+变式 圆的渐开线、摆线的参数方程理解
所以所求的点 P 轨迹的参数方程为
x=r+acos φ+rφsin φ, y=r+asin φ-rφcos φ
x= 1 φ-sin φ, 2kπ 1 y = 1-cos φ 2kπ
(φ 为参数,k∈N*).
[错因与防范]
(1)若在求出 cos φ=1 后,直接得出 φ=0,会导致答案不全面. (2)不要误把点(1,0)中的 1 或 0 当成 φ 的值.
渐开线与摆线
学习目标
1.借助教具或计算机软件,观察圆在直线上 滚动时圆上定点的轨迹(平摆线)、直线在圆 上滚动时直线上定点的轨迹(渐开线),了解 平摆线和渐开线的生成过程,并能推导出它 们的参数方程. 2.通过阅读材料,了解其他摆线(变幅平摆线、 变幅渐开线、外摆线、内摆线、环摆线)的 生成过程;了解摆线在实际应用中的实例.
圆的渐开线的概念:先分 析动点(笔尖)所满足的 几何条件,如图所示,设 开始时绳子外端为 于点A, 当外端展开到点M时,因 为绳子对圆心角是一段弧 AB,展开后成为切线BM, 所以切线BM的长就是弧 AB的长,这是动点满足 的条件,我们把笔尖画出 的曲线叫圆的渐开线,相 应的圆叫做渐开线的基圆.
GGB演示
[例2]求半径为2的圆的摆线的参数方程.(如图 所示,开始时定点M在原点O处,取圆滚动时转 过的角度α,(以弧度为单位)为参数)
例题+变式 摆线
[解析] 当圆滚过 α 角时, 圆心为点 B,圆与 x 轴的切点为 A,定点 M 的位置如图所示,∠ABM=α. 由于圆在滚动时不滑动,因此线段 OA 的长和圆弧 ¼ AM 的长相等,它们 的长都等于 2α,从而 B 点坐标为(2α,2), → → 向量OB=(2α,2),向量MB=(2sin α,2cos α), → BM=(-2sin α,-2cos α), 因此=+=(2α-2sin α,2-2cos α) =(2(α-sin α),2(1-cos α)).
例题+变式 圆的渐开线
[例 1] 已知圆的直径为 2,其渐开线的标准参数方程对应的曲线上两点 A, π 3π B 对应的参数分别是 和 ,求 A,B 两点间的距离. 2 2
例题+变式 圆的渐开线、摆线的参数方程理解
3π 3π x=cos 3π+3π· sin =- , 2 2 2 2 3π 当 φ= 时, 2 3π 3π 3π y = sin - · cos =-1, 2 2 2
x=rφ-sin (3)根据圆的摆线的参数方程 y=r1-cos
φ, (φ 为参数),可知只需求出其 φ
中的半径 r,圆摆线的参数方程即可写出.也就是说圆的摆线的参数方程是 由圆的半径唯一确定的.
阅读提高
如图,一个直径为1的小圆沿着直径为2的大圆内 壁的逆时针方向滚动,M和N是小圆的一条固定直 径的两个端点.那么,当小圆这样滚过大圆内壁的 一周.点M,N在大圆内所绘出的图形大致是( A )
例题+变式 摆线
→ 动点 M 的坐标为(x,y),向量OM=(x,y)
x=2α-sin 所以 y=21-cos
α, 这就是所求摆线的参数方程 α.
方法总结
1.圆的摆线的实质是一个圆沿着一条定直线无滑动地滚动时 圆周上一个定点的轨迹. 2.根据圆的摆线的定义和建立参数方程的过程,可知其中的 字母 r 是指定圆的半径,参数 φ 是指圆上定点相对于某一定点
例题+变式 圆的渐开线
变式
x=4cos φ+φsin φ, 1.已知渐开线 y=4sin φ-φcos φ
π 上的点 A 对应 φ= , 2
x=41-sin θ, y=41-cos θ
与直线 x=2 相交于点 B,求 A,B 两点间的距离.
x=4cos φ+φsin φ, x=2π, π 解析:将 φ= 代入 得 ∴A(2π,4). 2 y = 4 sin φ - φ cos φ , y = 4 , x=41-sin θ, 在 y=41-cos θ
(φ 为参数).
例题+变式 圆的渐开线、摆线的参数方程理解 [ 例 3] 如图,一个宽为 a 的矩形木条沿着半
径为r的定圆无滑动地滚动,试求木条外缘 上某点P的轨迹方程.
例题+变式 圆的渐开线、摆线的参数方程理解
[解析] 以定圆圆心 O 为原点,O、F、P 共线时所在直线为 x 轴,建立如图所示的 直角坐标系,设 P 点的坐标为(x,y),取∠AOB=φ 为参数, ∵|BF|=l ¼ =rφ,
AB
→ → → → → → ∴OP=OF+FP=OB+BF+FP
π =(rcos φ,rsin φ)+rφcosφ-2, π rφsinφ-2
+(acos φ,asin φ) =((r+a)cos φ+rφsin φ,(r+a)sin φ-rφcos φ) =(x,y).
讲授新课
圆 的 渐 开 线 的 参 数 方 程:
由于向量 e1 (cos ,sin )是与 OB同方向的单 位向量,因而向量 e2 (sin , cos )是与向量 BM 同方向的单位向量,所以 BM (r ) e2 ( x r cos , y r sin ) (r )(sin , cos ) 解得{ x r (cos sin ) y r (sin cos ) ( 为参数)
该摆线的参数方程.
[解析] 令 r(1-cos φ)=0,可得 cos φ=1.
所以 φ=2kπ(k∈Z),代入得 x=r(2kπ-sin 2kπ)=1, 1 所以 r=2kπ.又由题意可知,r 是圆的半径,故 r>0. 所以应有 k>0 且 k∈Z,即 k∈N*.
例题+变式 圆的渐开线、摆线的参数方程理解
3π ∴B- 2 ,-1 .
∴|AB|=
π 3π 2 2 2 + 2 +1+1 =2
π2+1.
方法总结
圆的渐开线的参数方程中,字母r表示基圆的半径,字母φ 是指绳子外端运动时绳子上的定点 M相对于圆心的张角; 另外,渐开线的参数方程不宜化为普通方程.
讲授新课
GGB演示
摆线在它与定 直线的两个相邻 交点之间的部分 叫做一个拱。
动在定直线上的 一个位置为原点,建立直角坐标系,设圆的半径 为r,设开始时定点M 在原点,圆滚动了 角后与 x轴相切于点A,圆心在点B,从点M 分别作AB, x 轴的垂线,垂足分别为C,D,设点 M 的坐标为 ( x, y )取 为参数,根据点M 满足的几何条件 x OD OA DA OA MC r r sin , y DM AC AB CB r r cos .所以, x r ( sin ) 摆线的参数方程为: y r (1 cos )
( 为参数 ).
讲授新课
因 此 ,摆 线 的 参 数 方 程 是
x r ( sin ) , ( 是 参 数 ) y r (1 cos )
思考
在摆线的参数方程(1)中,参数 的取值范围 是什么?一个拱的宽度与高度各是多少?
参数 的取值范围是[0, ); 一个拱的宽度是 2 r,高度是 2 r (其中 r 是滚动圆的半径 ).
讲授新课
2. 摆线 思考:
如果在自行车的轮子上喷一个白色印记, 那么当自行车在笔直的道路上行驶时,白色印 记会画出什么样的曲线?
上述问题抽象成数学问题就是:当一个圆 沿着一条定直线无滑动地滚动时,圆周上一个 定点的轨迹是什么?
讲授新课
如图,假设 B 为圆心,圆周上的定点为 M, 开始时位于 O 处.圆在直线上滚动时,点 M 绕圆 心作圆周运动,转过 (弧度)角后,圆与直线相 ¼ 的长,即 OA=r. 切于 A,线段 OA 的长等于 MA 这就是圆周长上的定点 M 在圆 B 沿直线滚动过 程中满足的几何条件.我们把点 M 的轨迹叫做平 摆线,简称摆线,又叫旋轮线.
这就是圆的渐开线的参数方程。
讲授新课
渐开线的应用:
在机械工业中,广泛地使用齿轮传递动 力.由于渐开线齿形的齿轮磨损少,传 动平稳,制造安装较为方便,因此大多 数齿轮采用这种齿形。设计加工这种齿 轮,需要借助圆的渐开线方程。
讲授新课
思考
ur uu r Q e1 e 2 (cos , sin ) (sin , cos ) cos sin sin ( cos ) 0. ur uu r uuuu r uu r e1 e 2 ,即 : BM // e 2 .
运动所张开的角度大小.
例题+变式 摆线
变式 2.已知一个圆的摆线过一定点(2,0),请写出该圆的 半径最大时该摆线的参数方程.
解析:由摆线的图形知,圆的半径最大时,定点(2,0)就是(2πr,0)(如图所示)
1 ∴2πr=2,∴r= . π
x=1φ-sin φ, π 代入,得圆的摆线的参数方程 1 y = 1-cos φ π
重难点突破
重点:渐开线与摆线的基本概念和参数方程. 难点:渐开线与摆线及其方程的灵活运用.
讲授新课
1. 渐开线
探 究:把一条没有弹性的细绳绕在一个圆 盘上,在绳的外端系上一支铅笔,将绳子 拉紧,保持绳子与圆相切而逐渐展开,那 么铅笔会画出一条曲线.这条曲线的形状怎 样?能否求出它的轨迹方程?
讲授新课
1 中,令 x=2 得 sin θ= , 2
∴cos θ=
3 3 或 cos θ=- , 2 2
∴y=4-2 3或 y=4+2 3,故点 B 的坐标为(2,4-2 3)或(2,4+2 3). ∴|AB|= 2π-22+4± 2 3-42= 2 π-12+3=2 π2-2π+4.
例题+变式 摆线
例题+变式 圆的渐开线、摆线的参数方程理解
所以所求的点 P 轨迹的参数方程为
x=r+acos φ+rφsin φ, y=r+asin φ-rφcos φ
