圆周角定理ppt
合集下载
圆周角定理 课件

AD=BD=5
3 2 cm.
在 Rt△AOD 中,OD=
OA2-AD2
=
5 2
cm,所以
∠OAD=30°,
所以∠AOD=60°.
所
以
∠AOB
=
2∠AOD
=
120
°
,
所
以
∠ACB
=
1 2
∠AOB=60°.因为∠AOB=120°,所以劣弧A︵EB的度数为
︵ 120°,优弧ACB的度数为 240°.
所以∠AEB=12×240°=120°. 所以此弦所对的圆周角为 60°或 120°.
所以 OG∥CF.所以∠AOB=∠FCB,(2 分) 所以∠DAO=90°-∠AOB, ∠FBC=90°-∠FCB,(4 分) 所以∠DAO=∠FBC.(6 分)
(2)连接 AB,AC, 因为 BC 为直径, 所以∠BAC=π2, 又因为 AD⊥BC, 所以∠BAD=∠BCA,(8 分)
︵︵ 又因为AB=AF, 所以∠ABF=∠BCA,(9 分) 所以∠ABF=∠BAD, 所以 AE=BE.(10 分)
类型 2 利用定理及推论进行证明(规范解答)
[典例 2] 如图所示,BC 是半圆 O 的直径,AD⊥BC, ︵︵
垂足为 D,AB=AF,BF 与 AD、AO 分别交于点 E、G. (1)证明:∠DAO=∠FBC; (2)证明:AE=BE.
︵︵ [规范解答] (1)连接 FC,OF,因为AB=AF,OB =OF, 所以点 G 是 BF 的中点, OG⊥BF. 因为 BC 是⊙O 的直径, 所以 CF⊥BF.(1 分)
反过来,弧的度数相等,它们所对圆心角的度数也相 等.2.由于圆心角的度数与它所对弧的度数相等,所以圆周 角的度数等于它所对弧的度数的一半.
2第4课时圆周角PPT课件(人教版)

• 课后作业:“学生用书”的“课后作业”部 分.
第4课时 圆周角
学习目标
• 1. 学习圆周角、圆内接多边形的概念,圆 周角定理及推论.
• 2. 掌握圆周角与圆心角、直径的关系,能 用分类讨论的思想证明圆周角定理.
• 3. 会用圆周角定理及推论进行证明和计算.
一、概念 顶点在圆上,并且两边都和圆相交的角
顶点在圆上,并且两边都和圆相交的角.
D
【针对训练】
(1)(3)(4)
120
25
C 60°
探究点二 圆周角定理及其推论的 应用
针对训练】
1.两个概念:圆周角,圆内接四边形. 2.圆周角定理及其推论. 3.圆内接四边形的性质. 4.分类讨论的数学思想方法.
C C
C
C 40
课后作业
• 上交作业: 教科书第89页习题24.1第4,5,6题 .
A
试找出图中的圆周角 C
O·
E
BB
探究点一 圆周角定理及其推论的推导 1.圆周角定理的推导
D A
C
O·
E
B
2.
思考:
半圆(或直径)所对的圆周角是多少度?90°的圆周角 所对的弦是什么?
在半径不等的圆中,如果两个圆周角相等,它们所对的 弧相等吗?
在同圆或等圆中,如果两个圆周角相等,它们所对的弧 一定相等吗?为什么?圆内接四边形的两组对角分别有 怎样的关系?
第4课时 圆周角
学习目标
• 1. 学习圆周角、圆内接多边形的概念,圆 周角定理及推论.
• 2. 掌握圆周角与圆心角、直径的关系,能 用分类讨论的思想证明圆周角定理.
• 3. 会用圆周角定理及推论进行证明和计算.
一、概念 顶点在圆上,并且两边都和圆相交的角
顶点在圆上,并且两边都和圆相交的角.
D
【针对训练】
(1)(3)(4)
120
25
C 60°
探究点二 圆周角定理及其推论的 应用
针对训练】
1.两个概念:圆周角,圆内接四边形. 2.圆周角定理及其推论. 3.圆内接四边形的性质. 4.分类讨论的数学思想方法.
C C
C
C 40
课后作业
• 上交作业: 教科书第89页习题24.1第4,5,6题 .
A
试找出图中的圆周角 C
O·
E
BB
探究点一 圆周角定理及其推论的推导 1.圆周角定理的推导
D A
C
O·
E
B
2.
思考:
半圆(或直径)所对的圆周角是多少度?90°的圆周角 所对的弦是什么?
在半径不等的圆中,如果两个圆周角相等,它们所对的 弧相等吗?
在同圆或等圆中,如果两个圆周角相等,它们所对的弧 一定相等吗?为什么?圆内接四边形的两组对角分别有 怎样的关系?
圆周角定理的推论课件

图 3-4-6
圆周角定理的推论
10
[ 解 析 ] 首 先 利 用 等 腰 三 角 形 的 性 质 得 出 ∠DBC = ∠DCB,进而利用圆内接四边形的性质得出∠EAD=∠DCB, 再利用圆周角定理得出∠DAE 与∠DAC 相等.
解:∠DAE 与∠DAC 相等. 理由:∵DB=DC,∴∠DBC=∠DCB.
6
[解析] 连接 AD,由 AB 是⊙O 的直径得到∠ADB=90°,再 根据直角三角形两锐角互余计算出∠A 的度数,然后根据圆周角 定理即可得到∠C 的度数.
解:连接 AD,如图.
∵AB 是⊙O 的直径,∴∠ADB=90°.
∵∠ABD=55°,
∴∠A=90°-55°=35°,
∴∠BCD=∠A=35°.
∵∠DAE 是四边形 ABCD 的一个外角,
∴∠DAE+∠DAB=∠DCB+∠DAB=180°,
∴∠DAE=DCB,
∴∠DBC=∠DAE.
又∵∠DAC=∠DBC,∴∠DAE=∠DAC.
圆周角定理的推论
11
[归纳总结]圆内接四边形性质的推广: 圆内接四边形的对角互补,外角等于与它相邻的内角的对角.因此常利用圆 内接四边形的性质,结合圆周角定理及其推论来探求角的相等关系或互补关 系.在进行有关计算或证明时,常添加辅助线构造圆周角或圆内接四边形.
圆周角定理的推论
17
圆周角定理的推论
7
观察与思考
如图,在⊙O中,∠ABD =110°,求∠C的大小.
A B
四边形ABCD的四个点都在 ⊙O上,像这样的四边形叫做 圆内接四边形,这个圆叫做 C 四边形的外接圆。
D
思考:1、∠ABD与∠C有怎样的关系? 2、由此我们可以得到怎样的结论?
圆周角-PPT课件

E
20°
30°
∴∠ABF=∠D=20°,∠FBC=∠E=30°.
∴∠x=∠ABF+∠FBC=50°.
A F
C
下列说法是否正确,为什么?
拓展巩固
“在同圆或等圆中,同弦或等弦所对的圆周角相等”.
一条弦所对应的圆周角有两类.
D
如图所示,连接BO、EO. 显然,∠C与∠D所对应的圆心角和为 ,
O.
所以36根0°据圆周角定理可知∠C+∠D = . 180°
通过积极引导,帮助学生有意识地积累活动经验,获得成功的 体验.
知识回顾
O
1.圆心角的定义?
顶点在圆心的角叫圆心角.
A
B
2.图中∠ACB 的顶点和边有哪些特点?
C
考考你:你能仿照圆心角的定义,给下
图中象∠ACB 这样的角下个定义吗?
O
A
B
探索新知
顶点在圆上,并且两边都和圆相交 的角叫圆周角.(两个条件必须同时具备,缺一不可)
24.1 圆的有关性质
24.1.4 圆周角
教学目标
【知识目标】 理解圆周角的概念。探索圆周角与同弧所对的圆心角之间的关
系,并会用圆周角定理及推论进行有关计算和证明. 【能力目标】
经历探索圆周角定理的过程,初步体会分类讨论的数学思想, 渗透解决不确定的探索型问题的思想和方法,提高学生的发散思维能 力. 【情感目标】
意两点,连接AB,AC,BD,CD.∠A与∠D相等吗? 请说明理由.
D
同弧所对的圆周角相等.
问题2 如图,若
,那么 ∠A与∠B相等吗?
想一想: 反过来,若∠A=∠B,那么
成立吗?
AB E
O
C
圆周角定理 课件

(2)因为△ABE∽△ADC, 所以AABE=AADC,即 AB·AC=AD·AE. 又 S=12AB·AC·sin ∠BAC,且 S=12AD·AE, 所以 AB·AC·sin ∠BAC=AD·AE. 则 sin ∠BAC=1. 又∠BAC 为三角形内角, 所以∠BAC=90°.
2.已知 AD 是△ABC 的高,AE 是△ABC 的外接圆的直径. 求证:∠BAE=∠DAC. 证明:连接 BE,因为 AE 为直径, 所以∠ABE=90°. 因为 AD 是△ABC 的高,所以∠ADC=90°. 所以∠ADC=∠ABE. 因为∠E=∠C,所以∠BAE=90°-∠E, ∠DAC=90°-∠C. 所以∠BAE=∠DAC.
5.如图,△ABC 的角平分线 AD 的延长线交 它的外接圆于点 E. (1)证明:△ABE∽△ADC; (2)若△ABC 的面积 S=12AD·AE, 求∠BAC 的大小. 解:(1)证明:由已知条件可得∠BAE=∠CAD. 因为∠AEB 与∠ACB 是同弧上的圆周角, 所以∠AEB=∠ACD. 故△ABE∽△ADC.
利用圆周角进行计算
[例 2] 如图,已知 BC 为半⊙O 的直径, AD⊥BC,垂足为 D,BF 交 AD 于 E,且 AE =BE.
(1)求证: AB= AF ; (2)如果 sin ∠FBC=35,AB=4 5,求 AD 的长. [思路点拨] BC 为半⊙O 的直径,连接 AC,构造 Rt△ABC.
4.如图,△ABC ຫໍສະໝຸດ 接于⊙O,OD⊥BC 于 D,∠A=50°,则
∠OCD 的度数是
()
A.40° C.50°
B.25° D.60°
解析:连接 OB.因为∠A=50°,所以弦 BC 所 对的圆心角∠BOC=100°,∠COD=12∠BOC =50°,∠OCD=90°-∠COD=40°. 答案:A
《圆周角》课件精品 (公开课)2022年数学PPT全

第二十四章 圆
24.1 圆的有关性质
24.1.4 圆周角
导入新课
讲授新课
当堂练习
课堂小结
学习目标
1.理解圆周角的概念,会叙述并证明圆周角定理. 2.理解圆周角与圆心角的关系并能运用圆周角定理解 决简单的几何问题.(重点、难点) 3.理解掌握圆周角定理的推论及其证明过程和运用. (难点)
导入新课
复习引入
(5)√
A B
(6)√
二 圆周角定理及其推论
测量与猜测
如图,连接BO,CO,得圆心角∠BOC.试猜想∠BAC与 ∠BOC存在怎样的数量关系.
BAC1BOC 2
推导与论证
圆心O在∠BAC 的一边上
圆心O 在∠BAC
的 内部
圆心O在∠BAC 的外部
n圆心O在∠BAC的一边上(特殊情形)
OA=OC ∠A= ∠C ∠BOC= ∠ A+ ∠C
证明猜想
∵ 弧BCD和弧BAD所对的圆心角的和是周角, ∴∠A+∠C=180°, 同理∠B+∠D=180°,
归纳总结
推论:圆的内接四边形的对角互补.
想一想
图中∠A与∠DCE的大小有何关系?
∵ 弧BCD和弧BAD所对的圆心角的和是周角,
∴∠A+∠C=180°,
D
同理∠B+∠D=180°, A
延长BC到点E,有
2∠BOC. 求证:∠ACB=2∠BAC.
证明: ACB1AOB,
2
1
BAC BOC,
O
2
∠AOB=2∠BOC,
A
C B
∴∠ACB=2∠BAC
9.船在航行过程中,船长通过测定角数来确定是否遇到
暗礁,如图,A、B表示灯塔,暗礁分布在经过A、B两
24.1 圆的有关性质
24.1.4 圆周角
导入新课
讲授新课
当堂练习
课堂小结
学习目标
1.理解圆周角的概念,会叙述并证明圆周角定理. 2.理解圆周角与圆心角的关系并能运用圆周角定理解 决简单的几何问题.(重点、难点) 3.理解掌握圆周角定理的推论及其证明过程和运用. (难点)
导入新课
复习引入
(5)√
A B
(6)√
二 圆周角定理及其推论
测量与猜测
如图,连接BO,CO,得圆心角∠BOC.试猜想∠BAC与 ∠BOC存在怎样的数量关系.
BAC1BOC 2
推导与论证
圆心O在∠BAC 的一边上
圆心O 在∠BAC
的 内部
圆心O在∠BAC 的外部
n圆心O在∠BAC的一边上(特殊情形)
OA=OC ∠A= ∠C ∠BOC= ∠ A+ ∠C
证明猜想
∵ 弧BCD和弧BAD所对的圆心角的和是周角, ∴∠A+∠C=180°, 同理∠B+∠D=180°,
归纳总结
推论:圆的内接四边形的对角互补.
想一想
图中∠A与∠DCE的大小有何关系?
∵ 弧BCD和弧BAD所对的圆心角的和是周角,
∴∠A+∠C=180°,
D
同理∠B+∠D=180°, A
延长BC到点E,有
2∠BOC. 求证:∠ACB=2∠BAC.
证明: ACB1AOB,
2
1
BAC BOC,
O
2
∠AOB=2∠BOC,
A
C B
∴∠ACB=2∠BAC
9.船在航行过程中,船长通过测定角数来确定是否遇到
暗礁,如图,A、B表示灯塔,暗礁分布在经过A、B两
圆周角优秀课件

1.圆周角定义:顶点在圆上,并且两边都和圆相 交的角叫圆周角.
2.半圆或直径所对的圆周角等于90° 90°的圆周角所对的弦是直径
3.在同圆(或等圆)中,同弧或等弧所对的圆周角相 等,同弧或等弧所对的圆周角等于圆心角的一半;相 等的圆周角所对的弧相等。
在同圆或等圆中,如果两个圆周角相等, 它们所对弧一定相等吗?为什么?
2
∠BAD+∠CAD= 1∠ BOD+ 1∠COD
2
2
即∠BAC= 1 ∠BOC 2
3.第三种情况:
A
证明:作射线AO交⊙O于D。
由第1种情况得 ∠CAD= 1 ∠ COD
2
O C
DB
∠BAD=
1 2
∠ BOD
∠CAD-∠BAD= ห้องสมุดไป่ตู้ ∠ COD- 1 ∠BOD
2
2
即∠BAC= 1 ∠BOC 2
归纳总结
A
E B
C D
E
●O
C
A⌒C所对的圆周角∠ AEC ∠ ABC
∠ ADC的大小有什么关系?
B
规律:都相等,都等于圆心角∠AOC的一半
D
结论:同弧或等弧所对的圆周角相等。
练习:
1、如图,在⊙O中,ABC=50°,
则∠AOC等于( D)
A、50°;
B、80°;
C、90°;
D、100°
A
BO C
2、如图,△ABC是等边三角形,动点P
圆周角定理
C
在同圆或等圆中,同弧(或等弧)所对 的圆周角相等;同弧(或等弧)所对的 圆周角等于圆心角的一半.
D A
O·
B E
推论
C2
C1
C3
直径(或半圆)所对的圆周角是 直角, 90°的圆周角所对的弦是 A
2.半圆或直径所对的圆周角等于90° 90°的圆周角所对的弦是直径
3.在同圆(或等圆)中,同弧或等弧所对的圆周角相 等,同弧或等弧所对的圆周角等于圆心角的一半;相 等的圆周角所对的弧相等。
在同圆或等圆中,如果两个圆周角相等, 它们所对弧一定相等吗?为什么?
2
∠BAD+∠CAD= 1∠ BOD+ 1∠COD
2
2
即∠BAC= 1 ∠BOC 2
3.第三种情况:
A
证明:作射线AO交⊙O于D。
由第1种情况得 ∠CAD= 1 ∠ COD
2
O C
DB
∠BAD=
1 2
∠ BOD
∠CAD-∠BAD= ห้องสมุดไป่ตู้ ∠ COD- 1 ∠BOD
2
2
即∠BAC= 1 ∠BOC 2
归纳总结
A
E B
C D
E
●O
C
A⌒C所对的圆周角∠ AEC ∠ ABC
∠ ADC的大小有什么关系?
B
规律:都相等,都等于圆心角∠AOC的一半
D
结论:同弧或等弧所对的圆周角相等。
练习:
1、如图,在⊙O中,ABC=50°,
则∠AOC等于( D)
A、50°;
B、80°;
C、90°;
D、100°
A
BO C
2、如图,△ABC是等边三角形,动点P
圆周角定理
C
在同圆或等圆中,同弧(或等弧)所对 的圆周角相等;同弧(或等弧)所对的 圆周角等于圆心角的一半.
D A
O·
B E
推论
C2
C1
C3
直径(或半圆)所对的圆周角是 直角, 90°的圆周角所对的弦是 A
圆周角定理ppt课件
∴∠A=∠C .
o
又 ∠AOB=∠A+∠C,
B A
∴∠AOB=2∠C. 即
类比转化 考虑两种一般情况:
2.圆心O在圆周角的内部: C
.O
3.圆心O在圆周角的外部:
.C
O
A
B
D
c o
D AB
B A
圆周角定理
一条弧所对的圆周角等于它 所对的圆心角的一半.
符号表示:
∵ A⌒B 所对的圆周角为∠ACB
A⌒B 所对的圆心角为∠AOB
圆周角和圆心O的位置关系:
①圆心在圆周角 ②圆心在圆周 的一条边上; 角的内部;
C
O·
A
B
C
O·
A
B
③圆心在圆 周角的外部.
C
O·
B A
证 明 1.圆心在圆周角的一条边上:
(
已知:在⊙O中,AB 所对的圆周角是 ∠C,圆心
角是 ∠AOB. 求证: ∠C = 1 ∠AOB. 2
c
证明: ∵OA=OC ,
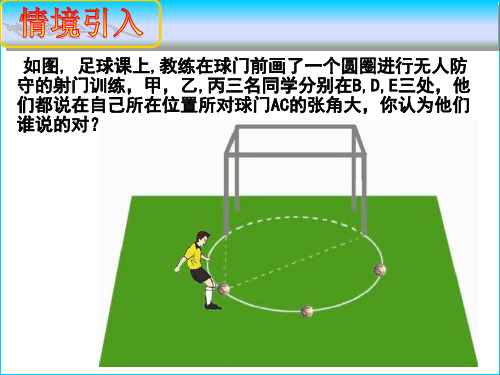
如图, 足球课上,教练在球门前画了一个圆圈进行无人防 守的射门训练,甲,乙,丙三名同学分别在B,D,E三处,他 们都说在自己所在位置所对球门AC的张角大,你认为他们 谁说的对?
回顾圆心角的定义,给下图中像∠ACB这样的角下定义.
1.顶点在圆心的角叫 圆心角 ;
2.顶点在圆上,并且两边都和 圆相交的角叫做 圆周角 .
辨一辨 下列各图中,哪些是圆周角?
探 究 同弧(弧AB)所对的圆周角∠ACB与圆心角∠AOB的关系
1.画一画,量一量
C
在⊙O上任取一条弧,作
出这条弧所对的圆周角和
圆心角, 测量它们的度数,
圆周角定理PPT课件

关系?
n 为了解决这个问题,我们先探究同弧所对的圆周角和 圆心角之间有的关系.
你会画同弧所对的圆周角和圆心角吗?
精选2021最新课件
5
探究同一条弧所对的圆周角和圆心角的关系
1、分别量一量图23.1.10中弧AB所对的两 个圆周角的度数比较一下. 再变动点C在 圆周上的位置,看看圆周角的 度数有没有变化. 你发 现其中有什么规律吗?
C
O.
A
B
顶点在圆上
两边都与圆相交
这样的角叫圆周角。
精选2021最新课件
3
问题探讨:
判断下列图形中所画的∠P是否为圆周角?并说明理
由。
P
P
P
P 不是
顶点不 在圆上。
是
顶点在圆上, 两边和圆相 交。
不是
两边不和 圆相交。
精选2021最新课件
不是 有一边和圆 不相交。
4
类比圆心角 探知 圆周角
• 在同圆或等圆中,同弧或等弧所对的圆心角相等. • 在同圆或等圆中,同弧或等弧所对的圆周角有什么
B
n老师提示:能否转化为1的情况? n过点B作直径BD.由1可得:
AD C
n∠ABD
=
∠1 AOD,∠CBD
2
=
∠1 COD,
2
●O
∴ ∠ABC = ∠1 AOC.
2
B
同弧所对的圆周角等于它所对
你能写出这个命题吗?
的圆心角的一半.
精选2021最新课件
11
圆周角和圆心角的关系 A
C
• 如果圆心不在圆周角的一边上,结果 会怎样?
四边形ABCD的对角线把4个内角分成8个角,
这些角中哪些是相等的角?
n 为了解决这个问题,我们先探究同弧所对的圆周角和 圆心角之间有的关系.
你会画同弧所对的圆周角和圆心角吗?
精选2021最新课件
5
探究同一条弧所对的圆周角和圆心角的关系
1、分别量一量图23.1.10中弧AB所对的两 个圆周角的度数比较一下. 再变动点C在 圆周上的位置,看看圆周角的 度数有没有变化. 你发 现其中有什么规律吗?
C
O.
A
B
顶点在圆上
两边都与圆相交
这样的角叫圆周角。
精选2021最新课件
3
问题探讨:
判断下列图形中所画的∠P是否为圆周角?并说明理
由。
P
P
P
P 不是
顶点不 在圆上。
是
顶点在圆上, 两边和圆相 交。
不是
两边不和 圆相交。
精选2021最新课件
不是 有一边和圆 不相交。
4
类比圆心角 探知 圆周角
• 在同圆或等圆中,同弧或等弧所对的圆心角相等. • 在同圆或等圆中,同弧或等弧所对的圆周角有什么
B
n老师提示:能否转化为1的情况? n过点B作直径BD.由1可得:
AD C
n∠ABD
=
∠1 AOD,∠CBD
2
=
∠1 COD,
2
●O
∴ ∠ABC = ∠1 AOC.
2
B
同弧所对的圆周角等于它所对
你能写出这个命题吗?
的圆心角的一半.
精选2021最新课件
11
圆周角和圆心角的关系 A
C
• 如果圆心不在圆周角的一边上,结果 会怎样?
四边形ABCD的对角线把4个内角分成8个角,
这些角中哪些是相等的角?
圆周角定理 课件

2 点评:只要是在圆中考查角的关系,那么就要考虑弧的 中介作用.
已知AD是△ABC的高,AE是△ABC的外接 圆的直径,求证:∠BAE=∠DAC.
分析:题目中出现圆的直径,想到直径所对的圆周角 是直角.因此,连结BE,得到∠ABE=90°,同时,在 △ABE与△ADC中,又有同弧所对的圆周角∠C与∠E相等, 从而结论得以证明.
圆周角定理
1.圆周角定理:圆上一条弧所对的圆周角等于它所对的圆 心角的________.
应当注意的是,圆周角与圆心角一定是对着__________,它 们才有上面定理中所说的数量关系.
2.圆心角定理:圆心角的度数________它所对弧的度数.
3.圆周角定理的推论:
推论1:同弧或等弧所对的圆周角________;同圆或等圆中, 相等的圆周角所对的弧________.
所以 AD=BD= 5 3 (cm).在 Rt△AOD 中,OD= OA2 AD2 2
= 5 (cm),所以∠OAD=30,所以∠AOD=60.所以∠AOB= 2
2∠AOD=120,所以∠ACB= 1 ∠AOB=60.因为∠AOB=120, 2
所以 AEB 的度数为 120, ACB 的度数为 240.所以∠AEB= 1 240=120.所以此弦所对的圆周角为 60或 120. 2
推论2:半圆(或直径)所对的圆周角是________;90°的圆 周角所对的弦是________.
1.一半 同一条弧 2.等于
3.相等 也相等 直角 直径
在半径为5 cm的圆内有长为5 3 cm的弦AB,求 此弦所对的圆周角.
OD 经过圆心,
点评:弦所对的圆周角有两个,易丢掉120°而导致错
误.另外,求圆周角时应用到解三角形的知识.
已知AD是△ABC的高,AE是△ABC的外接 圆的直径,求证:∠BAE=∠DAC.
分析:题目中出现圆的直径,想到直径所对的圆周角 是直角.因此,连结BE,得到∠ABE=90°,同时,在 △ABE与△ADC中,又有同弧所对的圆周角∠C与∠E相等, 从而结论得以证明.
圆周角定理
1.圆周角定理:圆上一条弧所对的圆周角等于它所对的圆 心角的________.
应当注意的是,圆周角与圆心角一定是对着__________,它 们才有上面定理中所说的数量关系.
2.圆心角定理:圆心角的度数________它所对弧的度数.
3.圆周角定理的推论:
推论1:同弧或等弧所对的圆周角________;同圆或等圆中, 相等的圆周角所对的弧________.
所以 AD=BD= 5 3 (cm).在 Rt△AOD 中,OD= OA2 AD2 2
= 5 (cm),所以∠OAD=30,所以∠AOD=60.所以∠AOB= 2
2∠AOD=120,所以∠ACB= 1 ∠AOB=60.因为∠AOB=120, 2
所以 AEB 的度数为 120, ACB 的度数为 240.所以∠AEB= 1 240=120.所以此弦所对的圆周角为 60或 120. 2
推论2:半圆(或直径)所对的圆周角是________;90°的圆 周角所对的弦是________.
1.一半 同一条弧 2.等于
3.相等 也相等 直角 直径
在半径为5 cm的圆内有长为5 3 cm的弦AB,求 此弦所对的圆周角.
OD 经过圆心,
点评:弦所对的圆周角有两个,易丢掉120°而导致错
误.另外,求圆周角时应用到解三角形的知识.
沪科版九年级下册数学24.3:圆周角定理及其推论-课件-(共20张PPT)

B O·
B
C
AO·ຫໍສະໝຸດ A CO·C A(1) √
A
顶点(不2)在圆上 B
B 边AC(没3有)和圆相交
CC
O·
A O·
·O
A B
B
C
顶点不在圆上
(5)√
√ (6)
圆周角定理
合作探究 问题1 如图,点A、B、C、D都是☉O 上的点,请问图中哪些是 圆周角?哪些是圆心角?分别指出对应哪条弧?是同一条弧吗?
圆心角:∠BOC
x 60 °
B
x
D 20
°
E
30 °
A FC
拓展提升:如图,在△ABC中,AB=AC, 以AB为直径的圆交BC于D,交AC于E, (1)BD与CD的大小有什么关系?为什么? (2)求证:BD DE .
B
A
E DC
课堂小结
定义
1.顶点在圆上; 2.两边都与圆相交的角
二者必须同时具备
圆
周
定理
角
同弧所对的圆周角等于它 所对的圆心角的一半.
明理由.
D
同弧所对的圆周角相等
问题2 如图,若 CD EF,∠A与∠B相等吗? A B
E O
反过来,若∠A=∠B, 那么 等弧所对的圆周角相等
C
F
D
CD EF 成立吗?
圆周角定理推论
推论1 在同圆或等圆中,同弧或等弧所对的圆周角相等,
相等的圆周角所对的弧也相等. A B
D
E
O
C
F
D
C1
推论2:半圆或直径所对的圆周角是直角;
2
2
A
O
DAC1DOC
2
C
《圆周角》PPT课件

O
1.(2008东莞调研文、理)如图所示,圆O上一点C在直径AB上的射影为D,CD=4,BD=8,则圆O的半径等于 .ABOD
C
分析:由射影定理得
2.如图, ⊙O的直径 AB 为10cm,弦AC为6cm,∠ACB 的平分线交⊙O于 D, 求BC、AD、BD的长.
我能行
3.如图,BC为⊙O的直径,AD⊥BC,垂足为D, ,BF和AD相交于E,求证:AE=BE。
比一比,看谁最快!
2、如上题图,若∠3=∠7,则____=____.
圆周角定理的推论3:
半圆(或直径)所对的圆周角是 , 90°的圆周角所对的弦是 。
直角
直径
如图,∠AC1B=∠AC2B=∠AC3B=
例1 如图,AD是△ABC的高,AE是△ABC的外接圆直径。求证:
A
B
C
D
E
顶点在圆上,并且两边都与圆相交的角叫做圆周角。
顶点在圆心的角叫做圆心角。
什么叫做圆周角?圆心角呢?
下列各图中的∠CDE哪些是圆周角?
E
⑴
⑵
⑶
⑷
√
×
√
×
看一看,谁理解?
如图,观察圆周角∠ACB与圆心角∠AOB,它们的大小有什么关系?
一条弧所对的圆周角等于它所对的圆心角的一半.
圆周角定理:
1、如图,∠A是⊙O的圆周角,∠BOC=80°,则∠A= ,2、如图,∠E=46°则∠DOC=_____,∠OCD=______.
∴AE=BE
3.3 圆周角定理
- .
本节学习目标:1、理解圆周角定理、圆心角定理以及两个 推论;2、会利用圆周角定理、圆心角定理以及 两个推论进行计算、证明。
右图中 所对的圆周角是 , 所对的圆心角是 .
1.(2008东莞调研文、理)如图所示,圆O上一点C在直径AB上的射影为D,CD=4,BD=8,则圆O的半径等于 .ABOD
C
分析:由射影定理得
2.如图, ⊙O的直径 AB 为10cm,弦AC为6cm,∠ACB 的平分线交⊙O于 D, 求BC、AD、BD的长.
我能行
3.如图,BC为⊙O的直径,AD⊥BC,垂足为D, ,BF和AD相交于E,求证:AE=BE。
比一比,看谁最快!
2、如上题图,若∠3=∠7,则____=____.
圆周角定理的推论3:
半圆(或直径)所对的圆周角是 , 90°的圆周角所对的弦是 。
直角
直径
如图,∠AC1B=∠AC2B=∠AC3B=
例1 如图,AD是△ABC的高,AE是△ABC的外接圆直径。求证:
A
B
C
D
E
顶点在圆上,并且两边都与圆相交的角叫做圆周角。
顶点在圆心的角叫做圆心角。
什么叫做圆周角?圆心角呢?
下列各图中的∠CDE哪些是圆周角?
E
⑴
⑵
⑶
⑷
√
×
√
×
看一看,谁理解?
如图,观察圆周角∠ACB与圆心角∠AOB,它们的大小有什么关系?
一条弧所对的圆周角等于它所对的圆心角的一半.
圆周角定理:
1、如图,∠A是⊙O的圆周角,∠BOC=80°,则∠A= ,2、如图,∠E=46°则∠DOC=_____,∠OCD=______.
∴AE=BE
3.3 圆周角定理
- .
本节学习目标:1、理解圆周角定理、圆心角定理以及两个 推论;2、会利用圆周角定理、圆心角定理以及 两个推论进行计算、证明。
右图中 所对的圆周角是 , 所对的圆心角是 .
圆周角定理 课件

∴ACDD=BEDD,即63=E5D,
∴ED=2.5 cm. 【名师点评】 和圆周角有关的线段、角的计算,不仅可以 通过计算弧、圆心角、圆周角的度数来求相关的角、线段, 有时,还可以通过比例线段,相似比来计算.
又 OB=OC,∴∠OCB=∠OBC=30°, ∴∠BOD=60°,∴∠CAB=∠BOD. (2)在 Rt△ABC 中,∠ABC=30°,得 AC=12AB, 又 OB=12AB,∴AC=OB. 由 BD 切⊙O 于点 B,得∠OBD=90°. 在△ABC 和△ODB 中,
∠CAB=∠BOD ∠ACB=∠OBD , AC=OB
的弦是直__径__.
考点突破
考点一 与圆周角定理相关的证明 例1 (高考课标全国卷)如图,D,E 分别为△ABC 边 AB ,AC 的中点,直线 DE 交△ABC 的外接圆于 F ,G 两点.若 CF ∥ AB ,
证明:(1) CD=BC;
(2)△BCD∽△GBD. 【证明】 (1)因为 D,E 分别为 AB,AC 的中点,所以 DE ∥BC.又已知 CF∥AB,故四边形 BCFD 是平行四边形,所以 CF=BD=AD.而 CF∥AD,连接 AF,所以四边形 ADCF 是 平行四边形,故 CD=AF.
圆周角定理
1.圆周角定理 圆上一条弧所对的圆周角等于它所对的圆心角的_一__半__. 应当注意的是,圆周角与圆心角一定是对着_同__一__条__弧____,它
们才有上面定理中所说的数量关系.
2.圆心角定理 圆心角的度数_等__于___它所对弧的度数. 3.圆周角定理的推论 推论 1:同弧或等弧所对的圆周角相__等__;同圆或等圆中,相等 的圆周角所对的弧也相__等__. 推论 2:半圆(或直径)所对的圆周角是直__角__;90°的圆周角所对
∴ED=2.5 cm. 【名师点评】 和圆周角有关的线段、角的计算,不仅可以 通过计算弧、圆心角、圆周角的度数来求相关的角、线段, 有时,还可以通过比例线段,相似比来计算.
又 OB=OC,∴∠OCB=∠OBC=30°, ∴∠BOD=60°,∴∠CAB=∠BOD. (2)在 Rt△ABC 中,∠ABC=30°,得 AC=12AB, 又 OB=12AB,∴AC=OB. 由 BD 切⊙O 于点 B,得∠OBD=90°. 在△ABC 和△ODB 中,
∠CAB=∠BOD ∠ACB=∠OBD , AC=OB
的弦是直__径__.
考点突破
考点一 与圆周角定理相关的证明 例1 (高考课标全国卷)如图,D,E 分别为△ABC 边 AB ,AC 的中点,直线 DE 交△ABC 的外接圆于 F ,G 两点.若 CF ∥ AB ,
证明:(1) CD=BC;
(2)△BCD∽△GBD. 【证明】 (1)因为 D,E 分别为 AB,AC 的中点,所以 DE ∥BC.又已知 CF∥AB,故四边形 BCFD 是平行四边形,所以 CF=BD=AD.而 CF∥AD,连接 AF,所以四边形 ADCF 是 平行四边形,故 CD=AF.
圆周角定理
1.圆周角定理 圆上一条弧所对的圆周角等于它所对的圆心角的_一__半__. 应当注意的是,圆周角与圆心角一定是对着_同__一__条__弧____,它
们才有上面定理中所说的数量关系.
2.圆心角定理 圆心角的度数_等__于___它所对弧的度数. 3.圆周角定理的推论 推论 1:同弧或等弧所对的圆周角相__等__;同圆或等圆中,相等 的圆周角所对的弧也相__等__. 推论 2:半圆(或直径)所对的圆周角是直__角__;90°的圆周角所对
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
.
课 时 作 业
菜
单
新课标 ·数学 选修4-1
课 前 自 主 导 学
在半径为 5 cm 的圆内有长为 5 3 cm 的弦, 求 此弦所对的圆周角.
当 堂 双 基 达 标
课 堂 互 动 探 究
【思路探究】 过圆心作弦的垂线构造直角三角形.先 求弦所对的圆心角度数,再分两种情况求弦所对的圆周角的 度数.
当 堂 双 基 达 标
课 堂 互 动 探 究
所在圆上的特殊性,寻求相关的圆周角作为桥梁; (2)当圆中出现直径时,要注意寻找直径所对的圆周角, 然后在直角三角形中处理相关问题.
课 前 自 主 导 学
【提示】 不一定相等.一般有两种情况:相等或互补, 弦所对的优弧与所对劣弧上的点所成的圆周角互补,所对同 一条弧上的圆周角都相等,直径所对的圆周角既相等又互
当 堂 双 基 达 标
课 堂 互 动 探 究
补. 2. 在推论 1 中, 把“同弧或等弧”改为“同弦或等弦”
的话,结论还成立吗? 【提示】 不成立.因为一条弦所对的圆周角有两种可
课 时 作 业
菜
单
新课标 ·数学 选修4-1
课 前 自 主 导 学
AB AD (2) 因为△ ABE ∽△ ADC ,所以 = ,即 AB· AC = AE AC AD· AE. 1 1 又 S=2AB· ACsin∠BAC 且 S= 2AD· AE, 故 AB· ACsin∠BAC=AD· AE, 则 sin∠BAC=1,又∠BAC 为三角形内角,所以∠BAC =90° .
当 堂 双 基 达 标
课 堂 互 动 探 究
课 时 作 业
菜
单
新课标 ·数学 选修4-1
课 前 自 主 导 学
1. 解答本题(2)时关键是利用 AB· AC=AD· AE 以及面积 S 1 = AB· ACsin∠BAC 确定 sin∠BAC 的值. 2 2.利用圆中角的关系证明时应注意的问题 (1)分析已知和所求,找好所在的三角形,并根据三角形
课 时 作 业
菜
单
新课标 ·数学 选修4-1
课 前 自 主 导 学
1.圆周角定理及其推论 (1)圆周角定理:圆上一条弧所对的 圆周角 对的 圆心角 的一半. (2) 推 论 1 : 等于它所
当 堂 双 基 达 标
同弧或等弧
所对的圆周角相等;
课 时 作 业
课 堂 互 动 探 究
同圆或等圆
中,相等的圆周角所对的 弧 也相等.
新课标 ·数学 选修4-1课 前 自 主 ຫໍສະໝຸດ 学当 堂 双 基 达 标
课 堂 互 动 探 究
课 时 作 业
菜
单
新课标 ·数学 选修4-1
一
课 前 自 主 导 学
圆周角定理
当 堂 双 基 达 标
课 堂 互 动 探 究
课 标 1.了解圆心角定理. 解 2.理解圆周角定理及其两个推论,并能解决有关问题. 读
课 前 自 主 导 学
(2)利用(1)的结论及面积相等求 sin∠BAC 的大小,从而 求∠BAC 的大小.
【自主解答】 (1)由已知条件,可得∠BAE=∠CAD.
当 堂 双 基 达 标
课 堂 互 动 探 究
因为∠AEB 与∠ACB 是同弧上的圆周角,所以∠AEB= ∠ACD. 故△ABE∽△ADC.
课 时 作 业
菜
单
新课标 ·数学 选修4-1
【自主解答】 如图所示,过点 O 作 OD⊥AB 于点 D.
课 前 自 主 导 学
∵OD⊥AB,OD 经过圆心 O, 5 3 ∴AD=BD= 2 cm.
当 堂 双 基 达 标
课 堂 互 动 探 究
课 时 作 业
菜
单
新课标 ·数学 选修4-1
在 Rt△AOD 中, 5 OD= OA -AD = cm, 2
【解】
课 前 自 主 导 学
∵
,
当 堂 双 基 达 标
∴∠ADB=∠CDE. 又∵ ,
∴∠BAD=∠ECD.
课 堂 互 动 探 究
∴△ABD∽△CED. AD BD 6 5 ∴CD=ED.即3=ED. ∴ED=2.5 cm.
课 时 作 业
菜
单
新课标 ·数学 选修4-1
如图 2-1-2,△ABC 的角平分线 AD 的延长
菜 单
当 堂 双 基 达 标
课 堂 互 动 探 究
的度数为 120° ,优弧
课 时 作 业
新课标 ·数学 选修4-1
课 前 自 主 导 学
1 . 解答本题时应注意弦所对的圆周角有两个,它们互 为补角. 2 .和圆周角定理有关的线段、角的计算,不仅可以通
当 堂 双 基 达 标
课 堂 互 动 探 究
过计算弧、圆心角、圆周角的度数来求相关的角、线段,有 时,还可以通过比例线段,相似比来计算.
2 2
课 前 自 主 导 学
∴∠OAD=30° ,∴∠AOD=60° . ∴∠AOB=2∠AOD=120° . 1 ∴∠ACB=2∠AOB=60° . ∵∠AOB=120° ,∴劣弧 . 的度数为 240° 1 ∴∠AEB=2×240° =120° , ∴此弦所对的圆周角为 60° 或 120° .
课 时 作 业
菜
单
新课标 ·数学 选修4-1
已知如图 2-1-1,△ABC 内接于⊙O,
课 前 自 主 导 学
,点
当 堂 双 基 达 标
D是
上任意一点,AD=6 cm,BD=5 cm, CD= 3 cm,
求 DE 的长.
课 堂 互 动 探 究
课 时 作 业
图 2-1-1
菜 单
新课标 ·数学 选修4-1
(3)推论 2:半圆 (或 直径 )所对的圆周角是直角;90° 的圆周角所对的弦是 直径 .
菜
单
新课标 ·数学 选修4-1
课 前 自 主 导 学
2.圆心角定理 圆心角的 度数 等于它所对弧的度数 .
当 堂 双 基 达 标
课 堂 互 动 探 究
课 时 作 业
菜
单
新课标 ·数学 选修4-1
1.圆的一条弦所对的圆周角都相等吗?
课 前 自 主 导 学
线交它的外接圆于点 E.
当 堂 双 基 达 标
课 堂 互 动 探 究
图 2-1-2 (1)证明:△ABE∽△ADC;
1 (2)若△ABC 的面积 S= AD· AE,求∠BAC 的大小. 2
菜 单
课 时 作 业
新课标 ·数学 选修4-1
【思路探究】 (1)通过证明角相等来证明三角形相似.
课 时 作 业
能,在一般情况下是不相等的.
菜 单
新课标 ·数学 选修4-1
3.“相等的圆周角所对的弧相等”,正确吗?
课 前 自 主 导 学
【提示】 不正确.“相等的圆周角所对的弧相等”是 在“同圆或等圆中”这一大前提下成立的,如图.
当 堂 双 基 达 标
课 堂 互 动 探 究
若 AB∥DG,则∠BAC=∠EDF,但
