三角函数与解三角形
三角函数与解三角形-新高考数学新情景、新文化问题(新高考地区专用)(解析版)

三角函数与解三角形一、单选题1.(2021·云南昆明市·高三(文))东寺塔与西寺塔为“昆明八景”之一,两塔一西一东,遥遥相对,已有1100多年历史.东寺塔基座为正方形,塔身有13级,塔顶四角立有四只铜皮做成的鸟,俗称金鸡,所以也有“金鸡塔”之称.如图,在A 点测得:塔在北偏东30°的点D 处,塔顶C 的仰角为30°,且B 点在北偏东60°.AB 相距80(单位:m ),在B 点测得塔在北偏西60°,则塔的高度CD 约为( )mA .69B .40C .35D .23【答案】B 【分析】根据题意构造四面体C -ABD ,再运用线面位置关系及三角形相关知识求解出相应的线段长即可. 【详解】如图,根据题意,图中CD ⊥平面ABD ,30CAD ∠=︒,30,60,80BAD ABD AB ∠=︒∠=︒=ABD 中,30,60BAD ABD ∠=︒∠=︒, 90ADB ∴∠=︒cos 80?cos30AD AB BAD ∴=∠=︒=又CD ⊥平面ABD ,ACD ∴是直角三角形Rt ACD中,30,90,CAD ADC AD ∠=︒∠=︒=·tan 3040CD AD ∴=︒==,选项B 正确,选项ACD 错误 故选:B.2.(2021·山东枣庄八中高一期中)《数书九章》是中国南宋时期杰出数学家秦九韶的著作,全书十八卷共八十一个问题,分为九类,每类九个问题,《数书九章》中记录了秦九昭的许多创造性成就,其中在卷五“三斜求积"中提出了已知三角形三边a ,b ,c 求面积的公式,这与古希腊的海伦公式完全等价,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上,以小斜幂乘大斜幂减上,余四约之,为实,一为从隅,开平方得积.”若把以上这段文字写成公式,即S =现在有周长为10+ABC满足sin :sin :sin 2:A B C =,则用以上给出的公式求得ABC 的面积为( ) A.B.C.D .12【答案】A 【分析】利用正弦定理结合三角形的周长可求得ABC 的三边边长,利用题中公式可求得ABC 的面积. 【详解】由题意结合正弦定理可得:::sin :sin :sin 2:a b c A B C ==ABC周长为10+10a b c ++=+4a ∴=,6b =,c =所以S == 故选:A.3.(2021·安徽淮北一中高一月考)“赵爽弦图”是由四个全等的直角三角形与一个小正方形拼成的一个大正方形(如图),若大、小正方形的面积分别为25和1,直角三角形中较大的锐角为θ,则cos2θ等于( )A .725B .725-C .925D .925-【答案】B 【分析】根据题意可得出1sin cos 5θθ-=,平方可得24sin 225θ=,即可求出.【详解】因为大正方形的面积为25,小正方形的面积为1,所以大正方形的边长为5,小正方形的边长为1, 所以5sin 5cos 1θθ-=,即1sin cos 5θθ-=,两边平方得11sin 225θ-=,即24sin 225θ=. 因为θ是直角三角形中较大的锐角,所以42ππθ<<,所以22πθπ<<,所以7cos 225θ==-. 故选:B.4.(2021·蚌埠铁路中学高三开学考试(文))勒洛三角形是一种特殊三角形,指分别以正三角形的三个顶点为圆心,以其边长为半径作圆弧,由这三段圆弧组成的曲边三角形.勒洛三角形的特点是:在任何方向上都有相同的宽度,即能在距离等于其圆弧半径(等于正三角形的边长)的两条平行线间自由转动,并且始终保持与两直线都接触.机械加工业上利用这个性质,把钻头的横截面做成勒洛三角形的形状,就能在零件上钻出正方形的孔来.如在勒洛三角形ABC 内随机选取一点,则该点位于正三角形ABC 内的概率为( )AB C D 【答案】A 【分析】由题意可得曲边三角形的面积为一个扇形加两个拱形的面积,或者3个扇形面积减去2个三角形的面积,然后由几何概型的概率公式求出概率. 【详解】解:由题意可得正三角形的边长为半径的三段圆弧组成的曲边三角形的面积S 曲=S 扇形CAB +2S 拱=123π⋅⋅22+2(S 扇形﹣S △ABC )=23π⋅3﹣2⋅22=2π﹣三角形ABC 的面积S △ABC 22所以由几何概型的概率公式可得:所求概率=ABCS S ∆曲 故选:A .5.(2021·江苏高一期中)公元前6世纪,古希腊的毕达哥拉斯学派研究过正五边形和正十边形的作图方法,发现了“黄金分割”.“黄金分割”是工艺美术、建筑、摄影等许多艺术门类中审美的要素之一,它表现了恰到好处的和谐,0.618≈,这一比值也可以表示为2sin18m =︒,若228m n +=,=( ) A.2 B .4 C .D .【答案】C 【分析】由题知28cos 18n =,再根据二倍角公式化简整理即可得答案. 【详解】解:因为2sin18m =︒,228m n +=, 所以2228288sin 188cos 18n m =-=-=,2sin1822cos1822sin 3622cos54cos54⨯===故选:C6.(2021·贵州贵阳·高三开学考试(文))水车(如图1),又称孔明车,是我国最古老的农业灌溉工具,主要利用水流的动力灌溉农作物,是先人们在征服世界的过程中创造出来的高超劳动技艺,是珍贵的历史文化遗产,相传为汉灵帝时毕岚造出雏形,经三国时孔明改造完善后在蜀国推广使用,隋唐时广泛用于农业灌溉,有1700余年历史.下图2是一个水车的示意图,它的直径为3m ,其中心(即圆心)O 距水面0.75m .如果水车每4min 逆时针转3圈,在水车轮边缘上取一点P ,我们知道在水车匀速转动时,P 点距水面的高度h(单位:m )是一个变量,它是时间t (单位:s )的函数.为了方便,不妨从P 点位于水车与水面交点Q 时开始记时()0t =,则我们可以建立函数关系式()()sin h t A t k ωϕ=++(其中0A >,0>ω,2πϕ<)来反映h 随t 变化的周期规律.下面关于函数()h t 的描述,正确的是( )A .最小正周期为80πB .一个单调递减区间为[]30,70C .()y h t =的最小正周期为40D .图像的一条对称轴方程为403t =- 【答案】D 【分析】首先求得()33sin 24064h t t ππ⎛⎫=-+ ⎪⎝⎭,[)0,t ∈+∞,然后结合选项由三角函数的图象和性质判断即可.【详解】依题意可知,水车转动的角速度32(rad /s)46040ππω⨯==⨯, 3324A k +=+,3324A k -+=-+,解得32A =,34k =,由()330sin sin 024h A k ϕϕ=+=+=得1sin 2ϕ=-,又2πϕ<,则6πϕ=-,所以()33sin 24064h t t ππ⎛⎫=-+ ⎪⎝⎭,[)0,t ∈+∞.对于选项A :函数()h t 的最小正周期为2=8040ππ,故A 错误;对于选项B :当[]30,70t ∈时,719,4061212t ππππ⎡⎤-∈⎢⎥⎣⎦,因为3719,21212πππ⎡⎤∈⎢⎥⎣⎦, 所以函数()h t 在[]30,70上不具有单调性,故B 错误; 对于选项C :()()353340sin 02642h h π=+=≠,所以C 错误;对于选项D :40333sin 32244h π⎛⎫⎛⎫-=-+=- ⎪ ⎪⎝⎭⎝⎭(最小值),所以D 正确.故选:D.7.(2021·江苏南京市·高一期中)托勒密(C .Ptolemy ,约90-168),古希腊人,是天文学家、地理学家、地图学家、数学家,所著《天文集》第一卷中载有弦表.在弦表基础上,后人制作了正弦和余弦表(部分如下图所示),该表便于查出0°~90°间许多角的正弦值和余弦值,避免了冗长的计算.例如,依据该表,角2°12′的正弦值为0.0384,角30°0′的正弦值为0.5000,则角34°36′的正弦值为( )A .0.0017B .0.0454C .0.5678D .0.5736【答案】C 【分析】先看左边列找34︒,再往右找对第一行的36'即可. 【详解】由题意查表可得3436︒'的正弦值为0.5678. 故选:C .8.(2021·江苏镇江·高一期中)今年是伟大、光荣、正确的中国共产党成立100周年.“红星闪闪放光彩”,正五角星是一个非常优美的几何图形,庄严美丽的国旗和国徽上的大五角星是中国共产党的象征,如图为一个正五角星图形,由一个正五边形的五条对角线连结而成,已知C ,D 为AB 的两个黄金分割点,即AC BD AB AB =.则cos DEC ∠=( )ABCD【答案】A 【分析】根据图形和已知条件表示出,,CE DE CD ,然后用余弦定理求解即可 【详解】由正五角星的对称性知:BC CE DE AD ===, 不妨设BC CE DE AD x ====,则CD AC AD =-, 又AC BC AC AD AB +=+=,AB AC ==则AC AD AC +=,所以AD =,AC AD AD ==,CD AC AD x x =-=-=22222224cos 122x DE CE CDDEC DE CEx +-∠===⨯ 故选:A二、多选题9.(2021·河北唐山·高三开学考试)声音是由物体振动产生的波,每一个音都是由纯音合成的.已知纯音的数学模型是函数sin y A t ω=.我们平常听到的乐音是许多音的结合,称为复合音.若一个复合音的数学模型是函数()1sin sin 22f x x x =+,则( )A .()f x 的最大值为32B .2π为()f x 的最小正周期C .π2x =为()y f x =曲线的对称轴 D .()π,0为曲线()y f x =的对称中心【答案】BD 【分析】分析函数sin y x =与1sin 22y x =不能同时取得最大值可判断A ;由sin y x =的最小正周期是2π,1sin 22y x=的最小正周期是2ππ2=可判断B ;计算ππ22f x f x ⎛⎫⎛⎫+=- ⎪ ⎪⎝⎭⎝⎭是否成立可判断C ;计算()()2π0f x f x +-=是否成立可判断D ;进而可得正确选项. 【详解】对于A :若()f x 的最大值为32,则sin y x =与1sin 22y x =同时取得最大值,当sin y x =取得最大值1时,cos 0x =,可得1sin 2sin cos 02y x x x ===取不到12,若1sin 22y x =取得最大值12时,sin 21x =,此时()ππZ 4x k k =+∈,而πsin sin π4y x k ⎛⎫==+= ⎪⎝⎭1,所以sin y x =与1sin 22y x =不可能同时取得最大值,故选项A 不正确;对于B :因为sin y x =的最小正周期是2π,1sin 22y x =的最小正周期是2ππ2=, 且()()()()112πsin 2πsin 22πsin sin 222f x x x x x f x +=+++=+=,()()()()11πsin πsin 2πsin sin 222f x x x x x f x +=+++=-+≠所以2π为()f x 的最小正周期,故选项B 正确;对于C :ππ1π1sin sin 2cos sin 222222f x x x x x ⎛⎫⎛⎫⎛⎫+=+++=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,ππ1π1sin sin 2cos sin 222222f x x x x x ⎛⎫⎛⎫⎛⎫-=-+-=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,所以ππ22f x f x ⎛⎫⎛⎫+=- ⎪ ⎪⎝⎭⎝⎭不恒成立,即ππ22f x f x ⎛⎫⎛⎫+≠- ⎪ ⎪⎝⎭⎝⎭,所以π2x =不是曲线()y f x =的对称轴,故选项C 不正确;对于D :()()()112πsin 2πsin 22πsin sin 222f x x x x x -=-+-=--,所以()()2π0f x f x +-=对于任意的x 恒成立,所以()π,0为曲线()y f x =的对称中心,故选项D 正确; 故选:BD.10.(2021·江苏)由倍角公式2cos 22cos 1x x =-,可知cos2x 可以表示为cos x 的二次多项式.一般地,存在一个n (n *∈N )次多项式()12012n n n n n P t a t a ta t a --=+++⋅⋅⋅+(012,,,n a a a a ⋅⋅⋅∈R ),使得()cos cos n nx P x =,这些多项式()n P t 称为切比雪夫(P .L .Tschebyscheff )多项式.运用探究切比雪夫多项式的方法可得( )A .()3343P t t t =-+ B .()424881P t t t =-+C .sin18︒=D .cos18︒=【答案】BC 【分析】通过求cos3,cos 4,cos5x x x ,来判断出正确选项. 【详解】()cos3cos 2cos2cos sin 2sin =+=-x x x x x x x()222cos 1cos 2sin cos x x x x =-- ()()222cos 1cos 21cos cos x x x x =--- 34cos 3cos x x =-,所以()3343P t t t =-,A 错误.()()222222cos 4cos 22cos 2sin 22cos 14sin cos x x x x x x x =⋅=-=--()42224cos 4cos 141cos cos x x x x =-+--428cos 8cos 1x x =-+,所以()424881P t t t =-+,B 正确.()cos5cos 4cos4cos sin 4sin x x x x x x x =+=- ()428cos 8cos 1cos 2sin 2cos2sin x x x x x x =-+- ()53228cos 8cos cos 4sin 2cos 1cos x x x x x x =-+--()()53228cos 8cos cos 41cos 2cos 1cos x x x x x x =-+--- 5316cos 20cos 5cos x x x =-+.所以()53cos90cos 51816cos 1820cos 185cos180︒=⨯︒=︒-︒+︒=,由于cos180︒≠,所以4216cos 1820cos 1850︒-︒+=,由于cos18cos30︒>︒,所以223cos 18cos 304︒>︒=,所以由4216cos 1820cos 1850︒-︒+=解得2cos 18︒=,所以sin18︒=,C正确. 2=≠⎝⎭,所以D 错误. 故选:BC 【点睛】三角函数化简求值问题,关键是根据题意,利用三角恒等变换的公式进行化简.11.(2021·全国)海水受日月的引力,在一定的时候发生涨落的现象叫潮汐.早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近船坞;卸货后,在落潮时返回海洋.一艘货船的吃水深度(船底到水面的距离)为4m.安全条例规定至少要有2.25m 的安全间隙(船底到海底的距离),下表给出了某港口在某季节每天几个时刻的水深.若选用一个三角函数()f x 来近似描述这个港口的水深与时间的函数关系,则下列说法中正确的有( ) A .() 2.5cos 56x x f π⎛⎫=+⎪⎝⎭B .() 2.5sin 56f x x π⎛⎫=+⎪⎝⎭C .该货船在2:00至4:00期间可以进港D .该货船在13:00至17:00期间可以进港 【答案】BCD 【分析】依据题中所给表格,写出()f x 的表达式而判断选项A ,B ;再根据船进港的条件列出不等式,求解即可判断选项C ,D. 【详解】依据表格中数据知,可设函数为()sin f x A x k ω=+,由已知数据求得 2.5A =,5k =,周期12T =,所以26T ππω==﹐ 所以有() 2.5sin 56f x x π⎛⎫=+⎪⎝⎭,选项A 错误;选项B 正确; 由于船进港水深至少要6.25,所以 2. 5sin 5 6.256x π⎛⎫+ ⎪⎝⎭≥,得1sin 62x π⎛⎫⎪⎝⎭≥, 又024046x x ππ≤≤⇒≤≤,则有5666x πππ≤≤或1317666x πππ≤≤,从而有1 5 x ≤≤或1317x ≤≤,选项C ,D 都正确. 故选:BCD 【点睛】解三角不等式sin()(||1)x m m ωϕ+≥<关键在于:找准不等式中的函数值m 所对角; 长为一个周期的区间内相位x ωϕ+所在范围.12.(2020·全国高三月考)斐波那契螺线又叫黄金螺线,广泛应用于绘画、建筑等,这种螺线可以按下列方法画出:如图,在黄金矩形ABCD AB BC ⎛= ⎝⎭中作正方形ABFE ,以F 为圆心,AB 长为半径作弧BE ;然后在黄金矩形CDEF 中作正方形DEHG ,以H 为圆心,DE 长为半径作弧EG ;;如此继续下去,这些弧就连接成了斐波那契螺线.记弧BE ,EG ,GI 的长度分别为l ,m ,n ,则下列结论正确的是( )A .l m n =+B .2m l n =⋅C .2m l n =+D .111m l n=+ 【答案】AB 【分析】设1AB =,则2BC =,再由14圆弧分别求得l ,m ,n ,然后再逐项判断.【详解】不妨设1AB =,则2BC =,所以121)4l π=⨯⨯=.因为3ED =所以12(34m π=⨯⨯=.同理可得124)4n π=⨯⨯=所以l m n =+,2m l n =⋅,2m l n ≠+,111m l n≠+,所以A ,B 正确,C ,D 错误. 故选:AB三、填空题13.(2021·安徽高三开学考试(理))正割(secant )及余割(cosecant )这两个符号是荷兰数学家基拉德在《三角学》中首先使用,后经欧拉采用得以通行.在三角中,定义正割1sec cos αα=,余割1csc sin αα=.已知0t >,且22sec csc 16x t x +≥对任意的实数,2k x x k Z π⎛⎫≠∈ ⎪⎝⎭均成立,则t 的最小值为__________. 【答案】9 【分析】根据正余割的定义,得到和为1,结合基本不等式1的代入即可求解 【详解】 由题得:22111sec csc x x+=, 所以()22222211sec csc sec csc 16sec csc x t x x t x x x ⎛⎫+=++≥ ⎪⎝⎭即:2222csc sec 11sec csc t x xt x x t ≥+++++116t ++5-3,所以9t ≥故答案为:914.(2021·江苏仪征中学高一月考)赵爽是我国古代数学家,大约在公元222年,赵爽在为《周髀算经》,作序时,介绍了“勾股圆方图”,亦称为“赵爽弦图”.可类似地构造如图所示的图形,由三个全等的三角形与中间的一个小等边三角形拼成一个大的等边三角形,设2DF FA =,若AB =ABD △的面积为____________.【答案】【分析】设BD x =,可得出3AD x =,23ADB π∠=,利用余弦定理求出x 的值,再利用三角形的面积公式可求得ABD △的面积. 【详解】设BD x =,则3AD x =,因为DEF 为等边三角形,则3ADE π∠=,故23ADB π∠=, 在ABD △中,由余弦定理得()222252323cos3AB x x x x π==+-⨯⨯⨯,解得2x =,故6AD =,2BD =,因此,ABD △的面积为1226sin23ABD S π=⨯⨯⨯=△故答案为:15.(2021·安徽阜阳·高一期末)筒车是一种水利灌溉工具(如图1所示),筒车上的每一个盛水筒都做逆时针匀速圆周运动,筒车转轮的中心为O ,筒车的半径为r ,筒车转动的周期为24s ,如图2所示,盛水桶M在0P 处距水面的距离为0h .4s 后盛水桶M 在1P 处距水面的距离为1h ,若10h h -=,则直线0OP 与水面的夹角为______.【答案】π12【分析】根据题意构建平面几何模型,在借助三角函数求解答案. 【详解】如图,过O 作直线l 与水面平行,过0P 作0P A l ⊥于A ,过1P 作1PB l ⊥于B . 设0AOP α∠=,1BOP β∠=,则,4π2π243βα-=⨯=,π3βα∴=+由图知,0sin P A r α=,1sin PB r β=,0101sin sin P A h h PB r r r βα--=-==,所以πsin sin 3αα⎛⎫+-= ⎪⎝⎭πsin 3α⎛⎫-= ⎪⎝⎭,则ππ34α-=-,即π12α=.故答案为:π12. 16.(2021·广东深圳·高三)著名的费马问题是法国数学家皮埃尔德费马(1601-1665)于1643年提出的平面几何极值问题:“已知一个三角形,求作一点,使其与此三角形的三个顶点的距离之和最小.”费马问题中的所求点称为费马点,已知对于每个给定的三角形,都存在唯一的费马点,当ABC 的三个内角均小于120︒时,则使得120APB BPC CPA ∠=∠=∠=︒的点P 即为费马点.已知点P 为ABC 的费马点,且AC BC ⊥,若||||||PA PB PC λ+=,则实数λ的最小值为_________.【答案】2 【分析】根据题意120APB BPC CPA ∠=∠=∠=︒,不妨设PCB α∠=,故,,326CBP ACP CAP πππααα∠=-∠=-∠=-,进而得,63ππα⎛⎫∈ ⎪⎝⎭,所以在BCP 和ACP △中,由正弦定理得sin sin 3BP PC απα=⎛⎫- ⎪⎝⎭,sin 2sin 6PA PC παπα⎛⎫- ⎪⎝⎭=⎛⎫- ⎪⎝⎭,故sin sin 2sin sin 36πααλππαα⎛⎫- ⎪⎝⎭=+⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭,在结合三角恒等变换化简整理求函数最值即可.【详解】根据题意, 点P 为ABC 的费马点,ABC 的三个内角均小于120︒, 所以120APB BPC CPA ∠=∠=∠=︒,设PCB α∠=,所以在BCP 和ACP △中,,,3236CBP ACP CAP ACP ππππααα∠=-∠=-∠=-∠=-,且均为锐角,所以,63ππα⎛⎫∈ ⎪⎝⎭所以由正弦定理得:sin sin 3BPPC παα=⎛⎫- ⎪⎝⎭,sin sin 26PA PCππαα=⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭,所以sin sin 3BP PC απα=⎛⎫- ⎪⎝⎭,sin 2sin 6PA PC παπα⎛⎫- ⎪⎝⎭=⎛⎫- ⎪⎝⎭, 因为||||||PA PB PC λ+=所以sin cos sin sin cos sin 2sin sin 36πααααααλππαα⎛⎛⎫- - ⎪⎝⎭=+==⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭11==,因为,63ππα⎛⎫∈ ⎪⎝⎭,所以22,33ππα⎛⎫∈ ⎪⎝⎭,所以(2sin 20,2α,)12,⎡∈+∞⎣故实数λ的最小值为2.故答案为:2【点睛】本题考查数学文化背景下的解三角形,三角恒等变换解决三角函数取值范围问题,考查运算求解能力,数学建模能力,化归转化思想,是难题.本题解题的关键在于根据题目背景,通过设PCB α∠=,进而建立解三角形的模型,再根据正弦定理及三角恒等变换化简求最值即可.四、解答题17.(2021·海安市南莫中学高一期中)下图所示的毕达格拉斯树画是由图(i )利用几何画板或者动态几何画板Geogebra 做出来的图片,其中四边形ABCD ,AEFG ,PQBE 都是正方形.如果改变图(i )中EAB ∠的大小会得到更多不同的“树形”.(1)在图(i )中,21AB ,AE ==,且AE AB ⊥,求AQ ;(2)在图(ii )中,21AB ,AE ==,设(0)EAB θθπ∠=<<,求AQ 的最大值.【答案】(1(2)9. 【分析】(1)由已知条件结合诱导公式求得cos ABQ ∠,在ABQ △中,利用余弦定理,即可求解;(2)由已知条件结合余弦定理,求得BE ,再利用正弦定理、余弦定理及三角函数的性质,即可求解. 【详解】(1)当AE AB ⊥时,BE BQ ==则()cos cos2ABQ ABE π∠=+∠sin AE ABE BE =-∠=-=在ABQ △中,由余弦定理可得2222cos 45413AQ AB BQ AB BQ ABQ =+-⋅∠=++=,所以AQ =(2)在ABE △中,由余弦定理知,2222cos 54cos BE AB AE AB AE θθ⋅=-⋅=+-,所以BE BQ ==在ABE △中,由正弦定理知sin sin AE BEABE θ=∠,可得sin ABE ∠=在ABQ △中,由余弦定理可得2222cos()2AQ AB BQ AB BQ ABE π=+-⋅⋅+∠454cos 4θ=+-+4(sin cos )994πθθθ⎛⎫=-+=-+ ⎪⎝⎭,所以当3(0,)4πθπ=∈时,AQ 的取最大值9.答:(1)AQ =(2)AQ 的最大值为9.18.(2021·昆明·云南师大附中高一期中)仰望星空,时有流星划过天际,令我们感叹生命的短暂,又深深震撼我们凡俗的心灵.流星是什么?从古至今,人们作过无数种猜测.古希腊亚里士多德说,那是地球上的蒸发物,近代有人进一步认为,那是地球上磷火升空后的燃烧现象.10世纪波斯著名数学家、天文学家阿尔·库希设计出一种方案,通过两个观测者异地同时观察同一颗流星,来测定其发射点的高度.如图,假设地球是一个标准的球体,O 为地球的球心,AB 为地平线,有两个观测者在地球上的A ,B 两地同时观测到一颗流星S ,观测的仰角分别为SAD α∠=,SBD β∠=,其中,90DAO DBO ∠=∠=︒,为了方便计算,我们考虑一种理想状态,假设两个观测者在地球上的A ,B 两点测得30α=︒,15β=︒,地球半径为R 公里,两个观测者的距离3RAB π=. 1.73 1.5≈)(1)求流星S 发射点近似高度ES ;(2)在古希腊,科学不发达,人们看到流星以为这是地球水分蒸发后凝结的固体,已知对流层高度大约在18公里左右,若地球半径6370R ≈公里,请你据此判断该流星S 是地球蒸发物还是“天外来客”?并说明理由.【答案】(1)0.5ES R =公里;(2)该流星不是地球蒸发物,而是“天外来客”,理由见解析. 【分析】(1)由已知条件在ASB △中利用正弦定理求出1)AS R =,在SAC 中再利用余弦定理求出OS ,从而可得ES OS R =-;(2)由(1)求出的值可得流星S 发射点近似高度为3185公里,远远大于对流层最高近似高度18公里,从而可得结论 【详解】 (1)因为3AB R π=,则60AOB ∠=︒,所以AOB 为等边角形,所以AB R =.又因为90DAO DBO ∠=∠=︒,所以30∠=∠=︒DAB DBA ,所以30∠=∠=︒DAB DBA ,所以60SAB ∠=︒,45SBA ∠=︒,75ASB ∠=︒.在ASB △中,由正弦定理:sin 75sin 45AB AS =︒︒,得()sin 4530sin 45R AS ︒=︒+︒, 解得1)AS R =,在SAC 中,由余弦定理:2222222212cos 1)1)(42OS SA OA SA OA SAO R R R R ⎛⎫=+-⋅∠=+-⨯-= ⎪⎝⎭.所以 1.5OS R =≈≈,所以0.5ES OS R R =-=公里.(2)0.53185ES R ≈≈公里,所以流星S 发射点近似高度为3185公里,远远大于对流层最高近似高度18公里,所以该流星不是地球蒸发物,而是“天外来客”.(言之有理即可).19.(2021·奉新县第一中学高一月考)重庆是我国著名的“火炉”城市之一,如图,重庆某避暑山庄O 为吸引游客,准备在门前两条小路OA 和OB 之间修建一处弓形花园,使之有着类似“冰淇淋”般的凉爽感,已知π6AOB ∠=,弓形花园的弦长AB =M ,π6MAB MBA ∠=∠=,设OBA θ∠=.(1)将OA 、OB 用含有θ的关系式表示出来;(2)该山庄准备在M 点处修建喷泉,为获取更好的观景视野,如何设计OA 、OB 的长度,才使得喷泉M 与山庄O 的距离的值最大?【答案】(1)OA θ=,6OB πθ⎛⎫=+ ⎪⎝⎭;(2)当OA OB =OM 取最大值4+ 【分析】(1)本题可通过正弦定理得出OA θ=、6OB πθ⎛⎫=+ ⎪⎝⎭;(2)本题首先可根据题意得出2AM BM ==,然后通过余弦定理得出2222cos 6OM OB BM OB BM πθ⎛⎫=+-⋅⋅⋅+ ⎪⎝⎭,通过转化得出222283OM πθ⎛⎫=-++ ⎪⎝⎭,最后通过50,6πθ⎛⎫∈ ⎪⎝⎭以及正弦函数的性质即可求出最值.【详解】(1)因为sin sin sin OA OB AB OAB AOBθ==∠∠,π6AOB ∠=,AB =所以56OAB πθ∠=-,OA θ=,566OB ππθθ⎛⎫⎛⎫=-=+⎪ ⎪⎝⎭⎝⎭.(2)因为AB =π6MAB MBA ∠=∠=,所以2AM BM ==, 在OMB △中,由余弦定理易知2222cos 6OM OB BM OB BM πθ⎛⎫=+-⋅⋅⋅+ ⎪⎝⎭,即2248sin 4cos 666OM πππθθθ⎛⎫⎛⎫⎛⎫=++-++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭248sin 2428224cos 22286333ππππθθθθ⎛⎫⎛⎫⎛⎫⎛⎫=+-+-+=-+-++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭122sin 2282283233πππθθθ⎤⎛⎫⎛⎫⎛⎫=-++++=-++⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎦,因为50,6πθ⎛⎫∈ ⎪⎝⎭,所以2272,333πππθ⎛⎫+∈ ⎪⎝⎭,2sin 23πθ⎡⎛⎫+∈-⎢⎪⎝⎭⎣⎭, 当2sin 213πθ⎛⎫+=- ⎪⎝⎭,即512πθ=时, 2OM 取最大值28+OM 取最大值4+此时51264OA πππ⎛⎫==+= ⎪⎝⎭ 512643OB ππππ⎛⎫⎛⎫=+=+= ⎪ ⎪⎝⎭⎝⎭故当OA OB =时,OM 取最大值4+ 【点睛】关键点点睛:本题考查解三角形的实际应用,考查正弦定理与余弦定理的应用,考查三角恒等变换,考查根据正弦函数的性质求最值,考查化归与转化思想,体现了综合性,是难题.20.(2021·江苏省镇江中学)古希腊数学家普洛克拉斯曾说:“哪里有数学,哪里就有美,哪里就有发现……”,对称美是数学美的一个重要组成部分,比如圆,正多边形……,请解决以下问题:(1)魏晋时期,我国古代数学家刘徽在《九章算术注》中提出了割圆术:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”,割圆术可以视为将一个圆内接正n 边形等分成n 个等腰三角形(如图所示),当n 变得很大时,等腰三角形的面积之和近似等于圆的面积,运用割圆术的思想,求sin3︒的近似值(结果保留π).(2)正n 边形的边长为a ,内切圆的半径为r ,外接圆的半径为R ,求证:2tan2a R r nπ+=.【答案】(1)60π;(2)详见解析.【分析】(1)将一个单位圆分成120个扇形,每个扇形的圆心角为3︒,再根据120个等腰三角形的面积之和近似等于圆的面积求解;(2)设O 为内切圆的圆心,OA ,OB 分别为外接圆和内切圆的半径R ,r ,易知 1,2AB a nπθ==,然后在Rt OAB 中,利用三角函数的定义求得R ,r ,利用三角恒等变换证明.【详解】(1)将一个单位圆分成120个扇形,每个扇形的圆心角为3︒, 因为这120个等腰三角形的面积之和近似等于圆的面积, 所以11211sin 32π⨯⨯⨯⨯≈ sin 360π≈;(2)设O 为内切圆的圆心,OA ,OB 分别为外接圆和内切圆的半径R ,r ,则,OA R OB r ==, 如图所示:所以1,2AB a nπθ==, 在Rt OAB 中,sin AB OAθ=,即12sin an Rπ=,所以2sin a R n π=, cos OB OA θ=,即cos r n Rπ=,所以coscos 2sin a n r R n nπππ==, 所以1cos cos2sin 2sin 2sina a a n n R r n n nπππππ⎛⎫+ ⎪⎝⎭+=+=, 22cos 24sincos2tan222a a nnnnππππ==.21.(2021·上海徐汇·高一期末)主动降噪耳机工作的原理是:先通过微型麦克风采集周国的噪声,然后降噪芯片生成与噪声振幅相同、相位相反的声波来抵消噪声(如图所示).已知某噪声的声波曲线f(x)=Asin (2π3x +φ)(A >0,0≤φ<π),其中的振幅为2,且经过点(1,-2)(1)求该噪声声波曲线的解析式f(x)以及降噪芯片生成的降噪声波曲线的解析式g(x); (2)证明:g(x)+g(x +1)+g(x +2)为定值. 【答案】(1)f(x)=2sin (2π3x +5π6), g(x)=−2sin (2π3x +5π6);(2)证明见解析.【分析】(1)首先根据振幅为2求出A ,将点(1,-2)代入解析式即可解得; (2)由(1),结合诱导公式和两角和差的余弦公式化简即可证明.【详解】(1)∵振幅为2,A >0,∴A =2,f(x)=2sin (2π3x +φ),将点(1,-2)代入得:−2=2sin (2π3+φ)⇒sin (2π3+φ)=−1,∵0≤φ<π,∴2π3+φ∈[2π3,5π3),∴2π3+φ=3π2⇒φ=5π6,∴f(x)=2sin (2π3x +5π6),易知g(x)与f(x)关于x 轴对称,所以g(x)=−2sin (2π3x +5π6).(2)由(1)g(x)=−2sin (2π3x +5π6)=−2sin (2π3x +π3+π2)=−2cos (2π3x +π3)g(x)+g(x +1)+g(x +2)=−2cos (2π3x +π3)−2cos (2π3x +π)−2cos (2π3x +2π3+π)=−2cos (2π3x +π3)+2cos2π3x +2cos (2π3x +2π3)=−2(cos2π3x ⋅12−sin2π3x ⋅√32)+2cos2π3x +2[cos2π3x ⋅(−12)−sin2π3x ⋅√32]=0.即定值为0.22.(2021·合肥市第六中学高一期末)合肥逍遥津公园是三国古战场,也是合肥最重要的文化和城市地标,是休闲游乐场,更是几代合肥人美好记忆的承载地.2020年8月启动改造升级工作,欲对该公园内一个平面凸四边形ABCD 的区域进行改造,如图所示,其中4DC a =米,2DA a =米,ABC 为正三角形.改造后BCD △将作为人们旅游观光、休闲娱乐的区域,ABD △将作为对三国历史文化的介绍区域.(1)当3ADC π∠=时,求旅游观光、休闲娱乐的区域BCD △的面积;(2)求旅游观光、休闲娱乐的区域BCD △的面积的最大值.【答案】(1)()22m ;(2)(()224m a +.【分析】(1)由余弦定理求得AC ,再由正弦定理求得ACD ∠,求出BC BC ⊥,易得面积;(2)不妨设ADC θ∠=,ACD α∠=,用余弦定理表示出2AC ,用正弦定理表示出sin α,再用余弦定理表示出cos α,然后表示出BCD △的面积,利用两角和的正弦公式展开代入2sin ,cos ,AC αα,再利用两角差的正弦公式化简,然后利用正弦函数性质得最大值. 【详解】解析:(1)2222cos3AC AD DC AD DC π=+-⋅⋅,∴AC =,又sin sin3ACADACD π=∠,∴1sin 2ACD ∠=,易知ACD ∠是锐角,所以6π∠=ACD ,∴2BCD π∠=,()2214m 2BCD S a =⨯⨯=△,(2)不妨设ADC θ∠=,ACD α∠=,于是由余弦定理得()222016cos AC a θ=-①,22sin sin sin sin AC a a ACθαθα=⇒=②, 22222124168cos cos 8AC a a AC a aAC a a aAC+=+-⋅⇒=③, ∴14sin 23BCDS a AC πα⎛⎫=⨯⨯⋅+ ⎪⎝⎭△2(sin cos cos sin )33a AC ππαα=⋅+2222sin 128a AC a AC AC AC θ⎡⎤+=⋅⎢⎥⎣⎦((2222sin 4sin 43a a a πθθθ⎛⎛⎫=-+=-++ ⎪ ⎝⎝≤⎭,当且仅当5 326πππθθ-=⇒=时取等号,∴BCD S △最大值为(()224m a +.【点睛】本题考查解三角形的应用,解题关键是选用一个角为参数,然后把其他量表示为参数的三角函数,这里注意正弦定理和余弦定理的应用,然后利用三角函数恒等变换公式化简变形,最后利用正弦函数性质求得最值.。
三角函数与解三角形

课程标题三角函数与解三角形求三角函数得定义域实质就就就是解三角不等式(组)、一般可用三角函数得图象或三角函数线确定三角不等式得解、列三角不等式,既要考虑分式得分母不能为零;偶次方根被开方数大于等于零;对数得真数大于零及底数大于零且不等于1,又要考虑三角函数本身得定义域;求三角函数得值域得常用方法:1、化为求得值域;,引入辅助角,化为求解方法同类型。
2、化为关于(或)得二次函数式;,设,化为二次函数在上得最值求之;周期问题一般将函数式化为(其中为三角函数,)、)②y=tanx图象得对称中心(,0)(二)主要方法:1、函数得单调增区间可由解出,单调减区间可由解出; 周期2、函数得单调减区间可由解出,单调增区间呢。
(自己导出)周期3、函数得单调增区间可由解出。
(无增区间,重点掌握) 周期课堂练习:1.已知函数得定义域为,值域为,求常数得值 (化为求得值域)、2、函数得单调递减区间就就是3、函数得单调增区间为2、函数,、(Ⅰ)求函数得最小正周期;(Ⅱ)求函数在区间上得最小值与最大值、(化为求得值域)、3、函数得一个单调增区间就就是ﻩﻩﻩﻩ4、若函数,则就就是最小正周期为得奇函数最小正周期为得奇函数最小正周期为得偶函数最小正周期为得偶函数5、函数得最大值6、当函数得最大值为时,求得值、7、函数得最大值就就是8、已知函数,、(1)求得最大值与最小值;(2)f(x)得最小正周期。
(3)若不等式在上恒成立,求实数得取值范围、解三角形正弦定理:,余弦定理:推论:正余弦定理得边角互换功能① ,,②,,③==④(4)面积公式:S=ab*sinC=bc*sinA=ca*sinB课堂练习:1、在中,角得对边分别为,已知,则( )A、1 ﻩB.2 C、ﻩﻩﻩD、2、在△ABC中,AB=3,BC=,AC=4,则边AC上得高为( )A、B、 C、D、3、在ΔABC中,已知a=,b=,B=45°,求角A,角C得大小及边c得长度。
三角函数与解三角形题型归纳及习题含详解

题型 53 终边相同的角的集合的表示与区别 思路提示
(1) 终边相同的角的集合的表示与识别可用列举归纳法和双向等差数列的方 法解决.
(2) 注意正角、第一象限角和锐角的联系与区别,正角可以是任一象限角,也 可以是坐标轴角;锐角是正角,也是第一象限角,第一象限角不包含坐标
4. 熟练运用同角三角函数函数关系式和诱导公式进行三角函数式的化简、求值
和简单恒等式的证明.
命题趋势探究
1.一般以选择题或填空题的形式进行考查.
2.角的概念考查多结合函数的基础知识.
3.利用同角三角函数关系式和诱导公式进行三角函数式的化简、求值是重要考点. 知识点精讲 一、基本概念
正角---逆时针旋转而成的角; (1)任意角 负角---顺时针旋转而成的角;
二、任意角的三角函数 1.定义 已 知 角 终 边 上 的 任 一 点 P(x, y) ( 非 原 点 O ), 则 P 到 原 点 O 的 距 离
r OP x2 y2 0 . sin y , cos x , tan y .
r
r
x
此定义是解直三角形内锐角三角函数的推广.类比,对 y ,邻 x ,斜 r , 如图 4-2 所示.
的终边逆时针旋转整数圈,终边位置不变.
注:弧度或 rad 可省略 (5)两制互化:一周角= 3600 2 r 2 (弧度),即 1800 .
r
1(弧度)
180
0
57.30
57018
故在进行两制互化时,只需记忆 1800 ,10 两个换算单位即可:如: 180
5 5 1800 1500 ; 360 36 .
C. 0, ,是第一、二象限角
2022年高考数学真题:三角函数与解三角形(解析版)

第3讲三角函数与解三角形一、单选题1.(2022·全国·高考真题(理))双曲线C 的两个焦点为12,F F ,以C 的实轴为直径的圆记为D ,过1F 作D 的切线与C 的两支交于M ,N 两点,且123cos 5F NF ,则C 的离心率为()AB .32C .132D .172【答案】C 【解析】【分析】依题意不妨设双曲线焦点在x 轴,设过1F 作圆D 的切线切点为G ,可判断N 在双曲线的右支,设12F NF ,21F F N ,即可求出sin ,sin ,cos ,在21F F N 中由12sin sin F F N 求出12sin F F N ,再由正弦定理求出1NF ,2NF ,最后根据双曲线的定义得到23b a ,即可得解;【详解】解:依题意不妨设双曲线焦点在x 轴,设过1F 作圆D 的切线切点为G ,所以1OG NF ,因为123cos 05F NF,所以N 在双曲线的右支,所以OG a ,1OF c ,1GF b ,设12F NF ,21F F N ,由123cos 5F NF,即3cos 5 ,则4sin 5=,sin a c ,cos b c ,在21F F N 中,12sin sin sin F F N 4334sin cos cos sin 555b a a bc c c,由正弦定理得211225sin sin sin 2NF NF c c F F N ,所以112553434sin 2252c c a b a b NF F F N c,2555sin 222c c a a NF c 又12345422222a b a b aNF NF a,所以23b a ,即32b a ,所以双曲线的离心率132c e a故选:C2.(2022·全国·高考真题)若sin()cos()sin 4,则()A . tan 1B . tan 1C . tan 1D . tan 1【答案】C 【解析】【分析】由两角和差的正余弦公式化简,结合同角三角函数的商数关系即可得解.【详解】由已知得:sin cos cos sin cos cos sin sin 2cos sin sin ,即:sin cos cos sin cos cos sin sin 0 ,即: sin cos 0 ,所以 tan 1 ,故选:C3.(2022·全国·高考真题)记函数()sin (0)4f x x b的最小正周期为T .若23T ,且()y f x 的图象关于点3,22中心对称,则2f()A .1B .32C .52D .3【答案】A【解析】【分析】由三角函数的图象与性质可求得参数,进而可得函数解析式,代入即可得解.【详解】由函数的最小正周期T 满足23T ,得223,解得23 ,又因为函数图象关于点3,22对称,所以3,24k k Z ,且2b ,所以12,63k k Z ,所以52 ,5()sin 224f x x ,所以5sin 21244f .故选:A4.(2022·全国·高考真题(理))设函数π()sin 3f x x在区间(0,π)恰有三个极值点、两个零点,则 的取值范围是()A .513,36B .519,36C .138,63D .1319,66【答案】C 【解析】【分析】由x 的取值范围得到3x的取值范围,再结合正弦函数的性质得到不等式组,解得即可.【详解】解:依题意可得0 ,因为 0,x ,所以,333x,要使函数在区间 0, 恰有三个极值点、两个零点,又sin y x ,,33x的图象如下所示:则5323 ,解得13863 ,即138,63.故选:C .5.(2022·全国·高考真题(理))沈括的《梦溪笔谈》是中国古代科技史上的杰作,其中收录了计算圆弧长度的“会圆术”,如图, AB 是以O 为圆心,OA 为半径的圆弧,C 是的AB 中点,D 在 AB 上,CD AB .“会圆术”给出 AB 的弧长的近似值s 的计算公式:2CD s AB OA.当2,60OA AOB 时,s ()A .112B .112C D .92【答案】B 【解析】【分析】连接OC ,分别求出,,AB OC CD ,再根据题中公式即可得出答案.【详解】解:如图,连接OC ,因为C 是AB 的中点,所以OC AB ,又CD AB ,所以,,O C D 三点共线,即2OD OA OB ,又60AOB ,所以2AB OA OB ,则OC 2CD所以22211222CD s AB OA.故选:B.6.(2022·全国·高考真题(理))函数 33cos x xy x 在区间ππ,22的图象大致为()A .B .C .D .【答案】A 【解析】【分析】由函数的奇偶性结合指数函数、三角函数的性质逐项排除即可得解.【详解】令33cos ,,22x xf x x x,则 33cos 33cos x x x xf x x x f x ,所以 f x 为奇函数,排除BD ;又当0,2x时,330,cos 0x x x ,所以 0f x ,排除C.故选:A.7.(2022·全国·高考真题(文))将函数π()sin (0)3f x x的图像向左平移π2个单位长度后得到曲线C ,若C 关于y 轴对称,则 的最小值是()A .16B .14C .13D .12【答案】C 【解析】【分析】先由平移求出曲线C 的解析式,再结合对称性得,232k kZ ,即可求出 的最小值.【详解】由题意知:曲线C 为sin sin()2323y x x,又C 关于y 轴对称,则,232k kZ ,解得12,3k kZ ,又0 ,故当0k 时, 的最小值为13.故选:C.二、填空题8.(2022·全国·高考真题(理))记函数 cos (0,0π)f x x 的最小正周期为T ,若3()2f T ,9x 为()f x 的零点,则 的最小值为____________.【答案】3【解析】【分析】首先表示出T ,根据f T ,再根据π9x 为函数的零点,即可求出 的取值,从而得解;【详解】解:因为 cos f x x ,(0 ,0π )所以最小正周期2πT,因为 2π3cos cos 2πcos 2f T,又0π ,所以π6 ,即 πcos 6f x x,又π9x为 f x 的零点,所以ππππ,Z 962k k ,解得39,Z k k ,因为0 ,所以当0k 时min 3 ;故答案为:39.(2022·全国·高考真题(理))已知ABC 中,点D 在边BC 上,120,2,2ADB AD CD BD .当ACAB取得最小值时,BD ________.1## 【解析】【分析】设220CD BD m ,利用余弦定理表示出22AC AB 后,结合基本不等式即可得解.【详解】设220CD BD m ,则在ABD △中,22222cos 42AB BD AD BD AD ADB m m ,在ACD △中,22222cos 444AC CD AD CD AD ADC m m ,所以 2222224421214441243424211m m m AC m m AB m m m mm m44 当且仅当311mm 即1m 时,等号成立,所以当ACAB取最小值时,1m .1.三、解答题10.(2022·全国·高考真题)记ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,分别以a ,b ,c 为边长的三个正三角形的面积依次为123,,S S S ,已知1233123S S S B .(1)求ABC 的面积;(2)若2sin sin 3A C ,求b .【答案】(2)12【解析】【分析】(1)先表示出123,,S S S ,再由123S S S 2222a c b ,结合余弦定理及平方关系求得ac ,再由面积公式求解即可;(2)由正弦定理得22sin sin sin b acB A C,即可求解.(1)由题意得22221231,,2S a a S b S c ,则2221234442S S S a b c,即2222a c b ,由余弦定理得222cos 2a c b B ac ,整理得cos 1ac B ,则cos 0B ,又1sin 3B ,则cos B ,1cos ac B 1sin 2ABC S ac B (2)由正弦定理得:sin sin sin b a cB AC ,则223294sin sin sin sin sin 423b ac ac B A C A C,则3sin 2b B ,31sin 22b B .11.(2022·全国·高考真题)记ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知cos sin 21sin 1cos2A BA B.(1)若23C,求B ;(2)求222a b c的最小值.【答案】(1)π6;(2)5.【解析】【分析】(1)根据二倍角公式以及两角差的余弦公式可将cos sin 21sin 1cos2A BA B化成cos sin A B B ,再结合π02B,即可求出;(2)由(1)知,π2C B ,π22A B ,再利用正弦定理以及二倍角公式将222a b c 化成2224cos 5cos B B,然后利用基本不等式即可解出.(1)因为2cos sin 22sin cos sin 1sin 1cos 22cos cos A B B B BA B B B,即1sin cos cos sin sin cos cos 2B A B A B A B C,而π02B ,所以π6B ;(2)由(1)知,sin cos 0B C ,所以πππ,022C B ,而πsin cos sin 2B C C,所以π2C B,即有π22A B .所以222222222sin sin cos 21cos sin cos a b A B B B c C B2222222cos 11cos 24cos 555cos cos B BB BB.当且仅当2cos 2B 时取等号,所以222a b c的最小值为5.12.(2022·全国·高考真题(文))记ABC 的内角A ,B ,C 的对边分别为a ,b ,c ﹐已知 sin sin sin sin C A B B C A .(1)若2A B ,求C ;(2)证明:2222a b c 【答案】(1)5π8;(2)证明见解析.【解析】【分析】(1)根据题意可得, sin sin C C A ,再结合三角形内角和定理即可解出;(2)由题意利用两角差的正弦公式展开得sin sin cos cos sin sin sin cos cos sin C A B A B B C A C A ,再根据正弦定理,余弦定理化简即可证出.(1)由2A B , sin sin sin sin C A B B C A 可得, sin sin sin sin C B B C A ,而π02B,所以 sin 0,1B ,即有 sin sin 0C C A ,而0π,0πC C A ,显然C C A ,所以,πC C A ,而2A B ,πA B C ,所以5π8C .(2)由 sin sin sin sin C A B B C A 可得,sin sin cos cos sin sin sin cos cos sin C A B A B B C A C A ,再由正弦定理可得,cos cos cos cos ac B bc A bc A ab C ,然后根据余弦定理可知,22222222222211112222a c b b c a b c a a b c ,化简得:2222a b c ,故原等式成立.27.(2022·全国·高考真题(理))记ABC 的内角,,A B C 的对边分别为,,a b c ,已知sin sin()sin sin()C A B B C A .(1)证明:2222a b c ;(2)若255,cos 31a A ,求ABC 的周长.【答案】(1)见解析(2)14【解析】【分析】(1)利用两角差的正弦公式化简,再根据正弦定理和余弦定理化角为边,从而即可得证;(2)根据(1)的结论结合余弦定理求出bc ,从而可求得b c ,即可得解.(1)证明:因为 sin sin sin sin C A B B C A ,所以sin sin cos sin sin cos sin sin cos sin sin cos C A B C B A B C A B A C ,所以2222222222222a c b b c a a b c ac bc ab ac bc ab,即22222222222a c b a b c b c a ,所以2222a b c ;(2)解:因为255,cos 31a A ,由(1)得2250bc ,由余弦定理可得2222cos a b c bc A ,则50502531bc ,所以312bc,故 2222503181b c b c bc ,所以9b c ,所以ABC 的周长为14a b c .。
三角函数及解三角形知识点总结

1. 任意角的三角函数的定义: 设〉是任意一个角,p (x,y )是〉的终边上的任意一点(异于原点),它与原点的距离是「“x 2r 2.o ,位置无关。
2. 三角函数在各象限的符号:(一全二正弦,三切四余弦)+L i+ ——L+ _ - + ------ ■——+ -■sin : cos : tan :3. 同角三角函数的基本关系式:4.三角函数的诱导公式 k 二.一诱导公式(把角写成2…形式,利用口诀:奇变偶不变,符(2)商数关系:tan-E屮一、cos 。
(用于切化弦) (1)平方关系: 2 2 2sin 工 cos ■■ -1,1 tan : 1cos 2:※平方关系一般为隐含条件,直接运用。
注意“ 1”的代换si …y,cos 」那么r三角函数值只与角的大小有关,而与终边上点5. 特殊角的三角函数值度 0s30cA45“A60“90 120cA135“150s 180c 270° 360弧31JIJI2n3兀 5兀 JI3兀 2兀度64323462si n 。
01 竝迈1旦1 01222222cosa亦11念力12_112 2222号看象限)sin (2k .亠 x ) = sin x cos (2k ■亠 x ) = cosx [)tan (2k ,亠 x )二 tanxsin ( -x ) - - sin x cos (-x ) =cosx H )tan(-x ) - - tanxm )|sin (,亠 x ) = -sin x cos (m ) = - cosx tan (二 x ) IV ) Sin (兀 _x ) =sin x cos (兀—x ) = —cosx tan (兀一sin (— -〉)= cos ..zsin (㊁:)=cos :V )-?) = sin :6. 三角函数的图像及性质7.函数厂Asi n( X J图象的画法:n 5m —兀-2兀①“五点法” __设X-x…•,令X = 0, 2,,2,求出相应的X 值,计算得出五点的坐标,描点后得出图象;②图象变换法:这是作函数简图常用方法。
第5章 三角函数与解三角形公式

三角函数与解三角形公式总结【预备知识点】一、任意角与弧度制(一)任意角1.任意角的概念:规定一条射线绕其端点任意方向旋转所形成的角。
2.任意角的分类:(1)正角:规定一条射线绕其端点逆时针方向旋转所形成的角。
(2)负角:规定一条射线绕其端点顺时针方向旋转所形成的角。
(3)零角:规定一条射线绕其端点无任意方向旋转所形成的角,始边与终边重合的角。
口诀:正逆负顺零重合3.相等角、相反角与角的运算(1)相等角:旋转方向相同且旋转量相等。
(2)相反角:旋转方向相反且旋转量相等。
(3)角的运算:线性加减运算与数乘运算。
4.常见误区:(1)锐角是第一象限角,但是第一象限角不一定是锐角,因为有周期。
例如420°。
(2)钝角是第二象限角,但是第二象限角不一定是钝角,因为有周期。
例如495°。
(3)直角不是任意象限角,属于y轴的特殊角。
(4)平角、周角属于轴线角,它不属于任何一个象限角。
(二)弧度制1.弧长公式及其意义(1)弧长公式:l=nπr180⟺lr=n∗π180=|α|⟺l=|α|r(2)弧长公式的意义:(i)圆心角α所对的弧长与半径r的比值,只与α大小有关。
(ii)弧长长度等于半径长的圆弧所对的圆心角叫做1弧度的角,用rad表示,读作弧度。
其中rad可省略。
(3)一般地,正角的弧度数是正数,零角的弧度数是0,负角的弧度数是一个负数。
2.角度制与弧度制的互换依据:180°=π rad{1°=π180rad≈0.01745 rad 1 rad=(180π)°≈57.30°=57°18′(三)常见的角度制与弧度制互换表示二、三角函数常用特殊值【大重点,熟练背诵】【必考知识点】一、三角函数概念(1)定义式【熟记理解】(2)同角三角函数的基本关系【大重点题型:化弦为切经常用到,结合诱导公式与恒等变换】(i)平方关系【重点记第一个】sin2x+cos2x=11+cot2x=csc2x1+tan2x=sec2x(ii)商数关系【重点记第一个】tanx=sinx cosxcotx=cosx sinx(iii)倒数关系tanx∗cotx=1sinx∗cscx=1cosx∗secx=1(3)三角函数在各象限的符号【大重点并背诵】二、诱导公式【大重点,以下表格全背】诱导公式的基本思路【以第1组~第4组为例】:(1)首先,任意负角的三角函数转化成任意正角的三角函数【用公式3或1】(2)其次,任意正角的三角函数转化成0∼2π的三角函数【用公式1】(3)最后,0∼2π的三角函数转化成锐角三角函数【用公式2或4】三、三角恒等变换【大重点,所有公式都要背】1.两角和与差的正弦、余弦、正切Cα−β:cos(α−β)=cosα∗cosβ+sinα∗sinβCα+β:cos(α+β)=cosα∗cosβ−sinα∗sinβSα−β:sin(α−β)=sinα∗cosβ−cosα∗sinβSα+β:sin(α+β)=sinα∗cosβ+cosα∗sinβTα−β:tan(α−β)=tanα−tanβ1+tanα∗tanβTα+β:tan(α+β)=tanα+tanβ1−tanα∗tanβ扩展:三角和公式Cα+β+γ:cos(α+β+γ)=cosα∗cosβ∗cosγ−cosα∗sinβ∗sinγ−sinα∗cosβ∗sinγ−sinα∗sinβ∗cosγSα+β+γ:sin(α+β+γ)=sinα∗cosβ∗cosγ+cosα∗sinβ∗cosγ+cosα∗cosβ∗sinγ−sinα∗sinβ∗sinγTα+β+γ:tan(α+β+γ)=tanα+tanβ+tanγ−tanα∗tanβ∗tanγ1−tanα∗tanβ−tanα∗tanγ−tanβ∗tanγ2.二倍角的正弦、余弦、正切C2α: cos2α=cos2α−sin2α=1−2sin2α=2cos2α−1; cos2α=1+cos2α2,sin2α=1−cos2α2S2α: sin2α=2sinα∗cosαT2α: tan2α=2tanα1−tan2α扩展1:半角公式Cα2: cosα2=±√1+cosα2Sα2: sinα2=±√1−cosα2Tα2: tanα2=sinα1+cosα=1−cosαsinα=±√1−cosα1+cosα注意:正负由α2所在的象限决定!其中Cα: cosα=cos2α2−sin2α2=1−2sin2α2=2cos2α2−1=1−tan2α21+tan2α2Sα: sinα=2sin α2∗cosα2=2∗tanα21+tan2α2Tα:tanα=2∗tanα2 1−tan2α2扩展2:三倍角公式S3α: sin3α=3sinα−4sin3α=4sinα∗sin(π3−α)∗sin(π3+α)C3α: cos3α=4cos3α−3cosα=4cosα∗cos(π3−α)∗cos(π3+α)T3α: tan3α=3tanα−tan3α1−3tan3α=tanα∗tan(π3−α)∗tan(π3+α)扩展3:四倍角公式S4α: sin4α=−4∗[cosα∗sinα∗(2sin2α−1)]C4α: cos4α=1−8∗cos2α∗sin2αT4α: tan4α=4tanα−4tan3α1−6tan2α+tan4α扩展4:五倍角公式S5α: sin5α=16sin5α−20sin3α+5sinαC5α: cos5α=16cos5α−20cos3α+5cosαT5α: tan5α=5−10tan2α+tan4α1−10tan2α+5tan4α3.和差化积公式sin α+sin β=2sin α+β2∗cosα−β2sin α−sin β=2cos α+β2∗sinα−β2cos α+cos β=2cos α+β2∗cosα−β2cos α−cos β=−2sin α+β2∗sinα−β2tan α+tan β=sin(α+β) cosα∗cosβtan α−tan β=sin(α−β) cosα∗cosβcot α+cot β=sin(α+β) sinα∗sinβcot α−cot β=−sin(α−β) sinα∗sinβtan α+cot β=cos(α−β) cosα∗sinβtan α−cot β=−cos(α+β) cosα∗sinβsin2α−sin2β=sin(α+β)∗sin(α−β)cos2α−cos2β=−sin(α+β)∗sin(α−β)sin2α−cos2β=−cos(α+β)∗cos(α−β)cos2α−sin2β=cos(α+β)∗cos(α−β)记忆口诀:同名和差三角积,(sin α±sin β或cos α±cos β:等式左边只有同是正弦或同是余弦才可以相加减。
高考《三角函数与解三角形》(解析版)

专题四 三角函数与解三角形第十二讲 解三角形答案部分 2019年1.解:(1)由已知得222sin sin sin sin sin B C A B C +-=,故由正弦定理得222b c a bc +-=.由余弦定理得2221cos 22b c a A bc +-==. 因为0180A ︒︒<<,所以60A ︒=.(2)由(1)知120B C ︒=-,()sin 1202sin A C C ︒+-=,1sin 2sin 2C C C ++=,可得()cos 602C ︒+=-.由于0120C ︒︒<<,所以()sin 60C ︒+=,故 ()sin sin 6060C C ︒︒=+-()()sin 60cos60cos 60sin 60C C ︒︒︒︒=+-+=. 2.解析:由余弦定理有2222cos b a c ac B =+-, 因为6b =,2a c =,π3B =,所以222π36(2)4cos 3c c c =+-,所以212c =,21sin sin 2ABC S ac B c B ===△3.解析(1)由题设及正弦定理得sin sinsin sin 2A CA B A +=. 因为sin 0A ≠,所以sinsin 2A CB +=.由180A B C ︒++=,可得sincos 22A C B +=,故cos 2sin cos 222B B B=. 因为cos02B ≠,故1sin 22B =,因此60B =︒. (2)由题设及(1)知△ABC的面积4ABC S a =△. 由正弦定理得()sin 120sin 1sin sin 2C c A a C C ︒-===.由于ABC △为锐角三角形,故090A ︒<<︒,090C ︒<<︒,由(1)知120A C +=︒,所以3090C ︒<<︒,故122a <<ABC S <<△. 因此,ABC △面积的取值范围是,82⎛⎫⎪ ⎪⎝⎭.4.解析 设()2AD AB A AO C λλ==+u u u u r u u u u u r u u u rr ,1()(1)3AO AE EO AE EC AE AC AE AE AC AB ACμμμμμμ-=+=+=+-=-+=+u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r ,所以1232λμλμ-⎧=⎪⎪⎨⎪=⎪⎩,解得1214λμ⎧=⎪⎪⎨⎪=⎪⎩,所以11()24AO AD AB AC ==+u u u r u u u r u u u r u u u r ,13EC AC AE AB AC =-=-+u u u r u u u r u u u r u u ur u u u r ,221131266()()()43233AO EC AB AC AB AC AB AB AC AC ⋅=⨯+⨯-+=-+⋅+=u u u r u u u r u u u r u u u r u u u r u u u r u u ur u u u r u u u r u u u r221322AB AB AC AC -+⋅+u u ur u u u r u u u r u u u r , 因为221322AB AC AB AB AC AC ⋅=-+⋅+u u u r u u u r u u u r u u u r u u u r u u u r ,所以221322AB AC =u u ur u u u r ,所以223AB AC=u u u r u u u r,所以AB AC =. 5.解析 (1)由余弦定理222cos 2a c b B ac +-=,得2222(3)323c c c c +-=⨯⨯,即213c =.所以3c =. (2)因为sin cos 2A Ba b =, 由正弦定理sin sin a b A B =,得cos sin 2B Bb b=,所以cos 2sin B B =. 从而22cos (2sin )B B =,即()22cos 41cos B B =-,故24cos 5B =.因为sin 0B >,所以cos 2sin 0B B =>,从而25cos B =. 因此π25sin cos 2B B ⎛⎫+== ⎪⎝⎭. 6.解析:在直角三角形ABC 中,4AB =,3BC =,5AC =,4sin 5C =, 在BCD △中,sin sin BD BC C BDC=∠,可得122BD =;135CBD C ∠=-o ,224372sin sin(135)(cos sin )225510CBD C C C ⎛⎫∠=-=+=⨯+=⎪⎝⎭o , 所以()72cos cos 90sin ABD CBD CBD ∠=-∠=∠=o.7.解析:(I )由余弦定理2222cos b a c ac B =+-,得22213232b c c ⎛⎫=+-⨯⨯⨯-⎪⎝⎭. 因为2b c =+,所以()222123232c c c ⎛⎫+=+-⨯⨯⨯- ⎪⎝⎭.解得5c =, 所以7b =.(II )由1cos 2B =-得sin B =.由正弦定理得sin sin c C B b ==在ABC △中,B ∠是钝角,所以C ∠为锐角.所以11cos 14C ==. 所以()sin sin cos cos sin B C B C B C -=-=. 8.解析(Ⅰ)在ABC △中,由正弦定理sin sin b cB C=,得sin sin b C c B =,又由3sin 4sin c B a C =,得3sin 4sin b C a C =,即34b a =.又因为2b c a +=,得到43b a =,23c a =.由余弦定理可得222222416199cos 22423a a a a cb B a a +-+-===-⋅⋅.(Ⅱ)由(Ⅰ)可得sin 4B ==,从而sin 22sin cos 8B B B ==-,227cos 2cos sin 8B B B =-=-,故πππ71sin 2sin 2cos cos 2sin 66682B B B ⎛⎫+=+=-⨯= ⎪⎝⎭.2010-2018年1.A 【解析】因为213cos 2cos121255=-=⨯-=-C C ,所以由余弦定理, 得22232cos 251251()325=+-⋅=+-⨯⨯⨯-=AB AC BC AC BC C ,所以=AB A .2.C 【解析】根据题意及三角形的面积公式知2221sin 24a b c ab C +-=,所以222sin cos 2a b c C C ab +-==,所以在ABC ∆中,4C π=.故选C . 3.A 【解析】由sin (12cos )2sin cos cos sin B C A C A C +=+,得sin 2sin cos sin cos sin B B C A C B +=+,即2sin cos sin cos B C A C =,所以2sin sin B A =,即2b a =,选A . 4.A 【解析】由余弦定理得213931AC AC AC =++⇒=,选A.5.C 【解析】设△ABC 中角A ,B ,C 的对边分别是a ,b ,c ,由题意可得1sin 34a c π==,则a =.在△ABC 中,由余弦定理可得222222295322b ac c c c c =+-=+-=,则b =.由余弦定理,可得22222259cos 2c c c b c a A bc +-+-===C . 6.B 【解析】11sin 22AB BC B ⋅⋅=,∴sin 2B =,所以45B =o 或135B =o. 当45B =o时,1AC ==,此时1,AB AC BC ===90A =o 与“钝角三角形”矛盾;当135B =o时,AC ==.7.A 【解析】因为A B C π++=,由1sin 2sin()sin()2A ABC C A B +-+=--+得1sin 2sin 2sin 22A B C ++=, 即1sin[()()]sin[()()]sin 22A B A B A B A B C ++-++--+=, 整理得1sin sin sin 8A B C =, 又111sin sin sin 222S ab C bc A ac B ===,因此322222211sin sin sin 864S a b c A B C a b c ==,由12S ≤≤ 得222311264a b c ≤≤,即8abc ≤≤C 、D 不一定成立.又0b c a +>>,因此()8bc b c bc a +>⋅≥,即()8bc b c +>,选项A 一定成立.又0a b c +>>,因此()8ab a b +>,显然不能得出()ab a b +>B 不一定成立.综上所述,选A .8.C 【解析】由22()6c a b =-+可得22226a b c ab +-=-①,由余弦定理及3C π=可得222a b c ab +-=②.所以由①②得6ab =,所以1sin 23ABC S ab π∆==9.C 【解析】∵tan15tan(6045)2=-=o o o∴60tan 6060tan151)BC =-=o o.10.D 【解析】225cos 10A -=,1cos 5A =,由余弦定理解得5b =. 11.A 【解析】边换角后约去sin B ,得1sin()2A C +=,所以1sin 2B =,但B 非最大角,所以6B π=.12.C 【解析】由余弦定理可得AC =sin 10A =. 13.B 【解析】∵cos cos sin bC c B a A +=,∴由正弦定理得2sin cos sin cos sin B C C B A +=,∴2sin()sin B C A +=,∴2sin sin A A =,∴sin 1A =,∴△ABC 是直角三角形.14.B 【解析】由正弦定理得:sin sin sin 60sin 45BC AC ACAC A B ︒︒=⇔=⇔=15.D 【解析】由正弦定理,得22sin sin sin cos A B B A A +=,即22sin (sin cos )B A A A ⋅+=,sin B A =,∴sin sin b B a A== 16.D 【解析】设AB c =,则AD c =,BD =,BC =ΔABD 中,由余弦定理得2222413cos 23c c c A c +-==,则sin 3A =,在ΔABC 中,由正弦定理得sin sin 3c BC C A ==,解得sin C =.17.A 【解析】因为120C ∠=o,c =,所以2222cos c a b ab C =+-,222122()2a ab ab =+--所以22,0,aba b ab a b a b a b-=-=>>+ 因为0,0a b >>,所以0aba b a b-=>+,所以a b >.故选A .18.9【解析】因为120ABC ∠=︒,ABC ∠的平分线交AC 于点D ,所以60ABD CBD ∠=∠=o,由三角形的面积公式可得111sin120sin 60sin 60222ac a c =+o o o , 化简得ac a c =+,又0a >,0c >,所以111a c+=,则1144(4)()559c a a c a c a c a c +=++=+++=≥, 当且仅当2c a =时取等号,故4a c +的最小值为9. 19.7;3【解析】因为a =2b =,60A =o,所以由正弦定理得2sin sin 7b AB a⨯===.由余弦定理2222cos a b c bc A =+-可得2230c c --=,所以3c =.202222224241cos 22424AB BC AC ABC AB BC +-+-∠===⨯⨯⨯⨯,由22sin cos 1ABC ABC ∠+∠=所以sin4ABC∠===,1sin2BDCS BD BC DBC∆=⨯⨯∠11sin()sin22BD BC ABC BD BC ABCπ=⨯⨯-∠=⨯⨯∠1222=⨯⨯=.C因为BD BC=,所以D BCD∠=∠,所以2ABC D BCD D∠=∠+∠=∠,cos cos24ABCBDC∠∠====.21.2【解析】单位圆内接正六边形是由6个边长为1的正三角形组成,所以61611sin602S=⨯⨯⨯⨯=o.22.2113【解析】∵4cos5A=,5cos13C=,所以3sin5A=,12sin13C=,所以()63sin sin sin cos cos sin65B AC A C A C=+=+=,由正弦定理得:sin sinb aB A=解得2113b=.23.1 【解析】由1sin2B=得6Bπ=或56π,因为6Cπ=,所以56Bπ≠,所以6Bπ=,于是23Aπ=.有正弦定理,得21sin32bπ=,所以1b=.24.7【解析】由已知得ABC ∆的面积为1sin 20sin 2AB AC A A ⋅==所以sin A =,(0,)2A π∈,所以3A π=. 由余弦定理得2222cos BC AB AC AB AC A =+-⋅=49,7BC =. 25.【解析】如图作PBC ∆,使75∠=∠=oB C ,2BC =,作出直线AD 分别交线段PB 、PC 于A 、D 两点(不与端点重合),且使75∠=oBAD ,则四边形ABCD 就是符合题意的四边形,过C 作AD 的平行线交PB 于点Q ,在PBC ∆中,可求得BP =QBC ∆中,可求得BQ =,所以AB 的取值范围为.26.1【解析】∵2223cos 24b c a A bc +-==, 而sin 22sin cos 243cos 21sin sin 64A A A a A C C c ⨯==⨯=⨯⨯=. 27.8 【解析】 因为0A π<<,所以sin A ==又1sin 28ABC S bc A ∆===24bc ∴=, 解方程组224b c bc -=⎧⎨=⎩,得6b =,4c =,由余弦定理得2222212cos 64264644a b c bc A ⎛⎫=+-=+-⨯⨯⨯-= ⎪⎝⎭,所以8a =.28.ο30=∠BAC ,ο105=∠ABC ,在ABC ∆中,由ο180=∠+∠+∠ACB BAC ABC ,所以ο45=∠ACB ,因为600=AB ,由正弦定理可得οο30sin 45sin 600BC=, 即2300=BC m ,在BCD Rt ∆中,因为ο30=∠CBD ,2300=BC , 所以230030tan CDBC CD ==ο,所以6100=CD m .29.150【解析】在三角形ABC 中,AC =,在三角形MAC 中,sin 60sin 45MA AC=o o,解得MA =在三角形MNA sin 60==o ,故150MN =. 30.2【解析】由b B c C b 2cos cos =+得:sin cos sin cos 2sin B C C B B +=,即sin()2sin B C B +=,sin 2sin A B =,∴2a b =,故2ab=. 31.π32【解析】3sin 5sin A B =, π32212cos 2,53222=⇒-=-+=⇒=+=⇒C ab c b a C a c b b a ,所以π32.32sin sin()cos 2BAC BAD BAD π∠=∠+=∠=∴根据余弦定理可得222cos 2AB AD BD BAD AB AD+-∠=•,2223BD ∴==33.①②③【解析】①222221cos 2223a b c ab ab ab c C C ab ab π+-->⇒=>=⇒< ②2222224()()12cos 2823a b c a b a b a b c C C ab ab π+-+-++>⇒=>≥⇒< ③当2C π≥时,22232233c a b c a c b c a b ≥+⇒≥+>+与333a b c +=矛盾④取2,1a b c ===满足()2a b c ab +<得:2C π<⑤取2,1a b c ===满足22222()2a b c a b +<得:3C π<.34.4【解析】根据余弦定理可得2214(7)22(7)()4b b b =+--⨯⨯-⨯-,解得b =4. 35. 在ABC ∆中,根据sin sin sin AB AC BCC B A==,得sin sin 2sin sin ACAB C C C B=⋅==,同理2sin BC A =, 因此22sin 4sin AB BC C A +=+22sin 4sin()3C C π=+-4sin )C C C ϕ=+=+.36【解析】根据sin sin AB ACC B=得5sin sin 7AB C B AC ===11cos 14C ==, 所以sin sin[()]sin cos cos sin A B C B C B C π=-+=+111142-= 37.4【解析】(方法一)考虑已知条件和所求结论对于角A 、B 和边a 、b 具有轮换性.当A =B 或a =b 时满足题意,此时有:1cos 3C =,21cos 1tan 21cos 2C C C -==+,tan22C =,1tan tan tan 2A B C===,tan tan tan tan C CA B+= 4. (方法二)226cos 6cos b aC ab C a b a b+=⇒=+, 2222222236,22a b c c ab a b a b ab +-⋅=++=tan tan sin cos sin sin cos sin sin()tan tan cos sin sin cos sin sin C C C B A B A C A B A B C A B C A B +++=⋅=⋅21sin cos sin sin C C A B =⋅.由正弦定理,得:上式22222214113cos ()662c c c c C ab a b =⋅===+⋅.38.6π【解析】由sin cos 2B B +=得12sin cos 2B B +=,即sin 21B =, 因02B π<<,所以2,24B B ππ==.又因为2,2,a b ==由正弦定理得22sin sin 4A π=,解得1sin 2A =,而,a b <则04A B π<<=,故6a π=. 39.【解析】(1)在ABC ∆中,∵1cos 7B =-,∴(,)2B ππ∈,∴243sin 1cos B B =-=. 由正弦定理得sin sin a b A B=⇒7sin 43A =,∴3sin A =. ∵(,)2B ππ∈,∴(0,)2A π∈,∴π3A ∠=.(2)在ABC ∆中,∵sin sin()sin cos cos sin C A B A B A B =+=+=31143()2727⨯-+⨯=3314. 如图所示,在ABC ∆中,∵sin hC BC=,∴sin h BC C =⋅=33337⨯=, ∴AC 边上的高为33.40.【解析】(1)在ABD △中,由正弦定理得sin sin BD ABA ADB=∠∠. 由题设知,52sin 45sin ADB=︒∠,所以2sin ADB ∠=.由题设知,90ADB ∠<︒,所以cos 5ADB ∠==.(2)由题设及(1)知,cos sin 5BDC ADB ∠=∠=. 在BCD △中,由余弦定理得2222cos BC BD DC BD DC BDC =+-⋅⋅⋅∠258255=+-⨯⨯25=. 所以5BC =.41.【解析】(1)在ABC △中,由正弦定理sin sin a bA B=,可得sin sin b A a B =, 又由πsin cos()6b A a B =-,得πsin cos()6a B a B =-,即πsin cos()6B B =-,可得tan B =又因为(0π)B ∈,,可得3B π=.(2)在ABC △中,由余弦定理及2a =,3c =,3B π=,有2222cos 7b a c ac B =+-=,故b =.由πsin cos()6b A a B =-,可得sin A =a c <,故cos A =.因此sin 22sin cos A A A ==21cos 22cos 17A A =-=.所以,sin(2)sin 2cos cos 2sin A B A B A B -=-=11727214-⨯= 42.【解析】(1)由题设得21sin 23sin a ac B A =,即1sin 23sin ac B A=由正弦定理得1sin sin sin 23sin AC B A =. 故2sin sin 3B C =.(2)由题设及(1)得121cos()cos cos sin sin 632B C B C B C +=-=-=-所以2π3B C +=,故π3A =. 由题设得21sin 23sin a bc A A=,即8bc =.由余弦定理得229b c bc +-=,即2()39b c bc +-=,得b c +=.故ABC △的周长为343.【解析】(1)由已知得tan A =,所以23A π=. 在ABC ∆中,由余弦定理得222844cos 3c c π=+-,即2+224=0c c -.解得6c =-(舍去),4c = (2)有题设可得2CAD π∠=,所以6BAD BAC CAD π∠=∠-∠=.故ABD ∆面积与ACD ∆面积的比值为1sin26112AB AD AC AD π⋅⋅=⋅. 又ABC ∆的面积为142sin 2BAC ⨯⨯∠=ABD ∆44.【解析】由题设及A B C π++=得2sin 8sin 2B B =,故sin 4(1cos )B B =-. 上式两边平方,整理得217cos 32cos 150B B -+=, 解得cos 1B =(舍去),15cos 17B =. (2)由15cos 17B =得8sin 17B =,故14sin 217ABC S ac B ac ∆==. 又2ABCS ∆=,则172ac =.由余弦定理及6a c +=得22222cos ()2(1cos )b a c ac B a c ac B =+-=+-+1715362(1)4217=-⨯⨯+=. 所以2b =.45.【解析】(Ⅰ)在ABC △中,因为a b >,故由3sin 5B =,可得4cos 5B =. 由已知及余弦定理,有2222cos 13b a c ac B =+-=,所以b =.由正弦定理sin sin a bA B=,得sin sin a B A b ==.所以,bsin A的值为13. (Ⅱ)由(Ⅰ)及a c <,得cos 13A =,所以12sin 22sin cos 13A A A ==, 25cos 212sin 13A A =-=-.故πππsin(2)sin 2cos cos 2sin 44426A A A +=+=. 46.【解析】(Ⅰ)在△ABC 中,因为60A ∠=︒,37c a =,所以由正弦定理得sin 3sin 7c A C a ==. (Ⅱ)因为37c a a =<,所以60C A ∠<∠=o,由7a =,所以3737c =⨯=.由余弦定理2222cos a b c bc A =+-得222173232b b =+-⨯⨯, 解得8b =或5b =-(舍).所以△ABC的面积11sin 8322S bc A ==⨯⨯=47.【解析】(Ⅰ)由tan tan 2(tan tan )cos cos A BA B B A +=+得sin sin sin 2cos cos cos cos cos cos C A BA B A B A B⨯=+,所以C B C sin sin sin +=2,由正弦定理,得c b a 2=+.(Ⅱ)由abc ab b a ab c b a C 22222222--+=-+=)(cos22233311112222()2c c a b ab =--=-=+….所以C cos 的最小值为12.48.【解析】(I )证明:由正弦定理sin sin sin a b cA B C==可知 原式可以化解为cos cos sin 1sin sin sin A B CA B C+==∵A 和B 为三角形内角 , ∴sin sin 0A B ≠则,两边同时乘以sin sin A B ,可得sin cos sin cos sin sin B A A B A B += 由和角公式可知,()()sin cos sin cos sin sin sin B A A B A B C C π+=+=-= 原式得证。
三角函数和解三角形知识点汇总
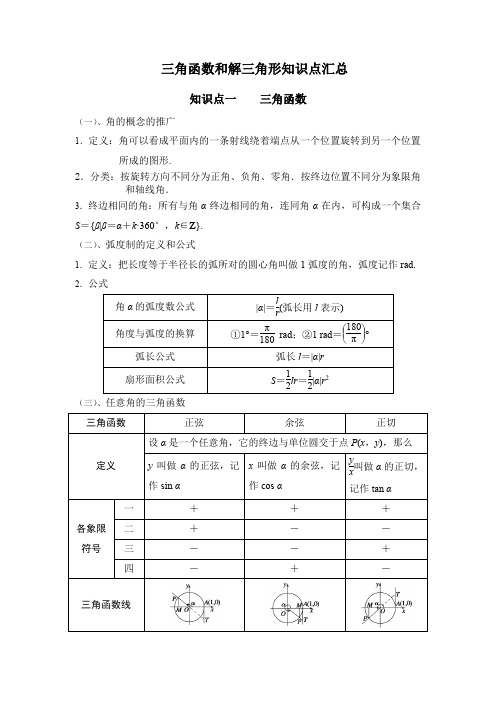
三角函数和解三角形知识点汇总知识点一三角函数(一)、角的概念的推广1.定义:角可以看成平面内的一条射线绕着端点从一个位置旋转到另一个位置所成的图形.2.分类:按旋转方向不同分为正角、负角、零角.按终边位置不同分为象限角和轴线角.3.终边相同的角:所有与角α终边相同的角,连同角α在内,可构成一个集合S={β|β=α+k·360°,k∈Z}.(二)、弧度制的定义和公式1.定义:把长度等于半径长的弧所对的圆心角叫做1弧度的角,弧度记作rad. 2.公式(三)、任意角的三角函数(四)、同角三角函数的基本关系 1.平方关系:sin 2α+cos 2α=1. 2.商数关系:sin αcos α=tan α.(五)、三角函数的诱导公式知识点二 三角函数的图像与性质(一)、用五点法作正弦函数和余弦函数的简图1.正弦函数y =sin x ,x ∈[0,2π]的图象中,五个关键点是:(0,0),⎝ ⎛⎭⎪⎫π2,1,(π,0),⎝ ⎛⎭⎪⎫3π2,-1,(2π,0).2.余弦函数y =cos x ,x ∈[0,2π]的图象中,五个关键点是:(0,1),⎝ ⎛⎭⎪⎫π2,0,(π,-1),⎝ ⎛⎭⎪⎫3π2,0,(2π,1).(二)、正弦、余弦、正切函数的图象与性质(下表中k ∈Z )知识点三函数y=A sin(ωx+φ)的图像及应用(一)、“五点法”作函数y=A sin(ωx+φ)(A>0,ω>0)的简图“五点法”作图的五点是在一个周期内的最高点、最低点及与x轴相交的三个点,作图时的一般步骤为:1.定点:如下表所示.2.作图:在坐标系中描出这五个关键点,用平滑的曲线顺次连接得到y=A sin(ωx+φ)在一个周期内的图象.3.扩展:将所得图象,按周期向两侧扩展可得y=A sin(ωx+φ)在R上的图象.(二)、函数y=A sin(ωx+φ)中各量的物理意义当函数y=A sin(ωx+φ)(A>0,ω>0),x∈[0,+∞) 表示一个振动量时,几个相关的概念如下表:(三)、函数y =sin x 的图象经变换得到y =A sin(ωx +φ)的图象的两种途径知识点四 三角恒等变换(一)、两角和与差的正弦、余弦和正切公式sin(α±β)=sin αcos β±cos αsin β. cos(α∓β)=cos αcos β±sin αsin β. tan(α±β)=tan α±tan β1∓tan αtan β.(二)、二倍角的正弦、余弦、正切公式sin 2α=2sin αcos α.cos 2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α. tan 2α=2tan α1-tan 2α.(三)、有关公式的逆用、变形等 1.tan α±tan β=tan(α±β)(1∓tan αtan β). 2.cos 2α=1+cos 2α2, sin 2α=1-cos 2α2. 3.1+sin 2α=(sin α+cos α)2, 1-sin 2α=(sin α-cos α)2,sin α±cos α=2sin ⎝ ⎛⎭⎪⎫α±π4.(四)、函数f (α)=a sin α+b cos α(a ,b 为常数),可以化为f (α)=a 2+b 2sin(α+φ)⎝ ⎛⎭⎪⎫其中tan φ=b a 或f (α)=a 2+b 2cos(α-φ)⎝ ⎛⎭⎪⎫其中tan φ=a b .知识点五 解三角形(一)、正、余弦定理在△ABC 中,若角A ,B ,C 所对的边分别是a ,b ,c ,R 为△ABC 外接圆半径,则(二)、S△ABC=12ab sin C=12bc sin A=12ac sin B=abc4R=12(a+b+c)·r(r是三角形内切圆的半径),并可由此计算R,r.(三)、实际问题中的常用角1.仰角和俯角:在同一铅垂平面内的水平视线和目标视线的夹角,目标视线在水平视线上方叫仰角,目标视线在水平视线下方叫俯角(如图1).2.方位角:从某点的指北方向线起按顺时针转到目标方向线之间的水平夹角叫作方位角.如B点的方位角为α(如图2).3.方向角:正北或正南方向线与目标方向线所成的锐角,如南偏东30°,北偏西45°等.4.坡度:坡面与水平面所成的二面角的正切值.。
第九章 三角函数与解三角形

第九章 三角函数、三角恒等变换与解三角§9.1三角函数的概念、同角三角函数的关系和诱导公式【高考考点】(1)理解任意角的概念、弧度的意义能正确地进行弧度与角度的换算.(2)掌握任意角的正弦、余弦、正切的定义;掌握同角三角函数的基本关系式;掌握正弦、余弦的诱导公式.【知识点梳理】1、与角α终边相同的角的集合为{}360,k k ββα=⋅+∈Z2、角度制与弧度制的互化(1)1弧度角:长度等于半径长的弧所对的圆心角叫做1弧度的角; (2)弧度制与角度制的换算公式:2360π=,1180π=,180157.3π⎛⎫=≈ ⎪⎝⎭(3)弧长及扇形面积公式: 22121,...R lR S R l αα==⋅=扇形其中扇形的圆心角为()αα为弧度制,半径为r ,弧长为l 。
(4)特殊角的角度与弧度(请完成表格)(5)特殊角的三角函数值:3、任意角的三角函数设α是一个任意角,它的终边上一点p (x,y ), r=22y x + (1)正弦sin α=r y 余弦cos α=r x 正切:tan α=xy1弧度LR(2)各函数在不同象限的符号:正弦 余弦 正切4.同角三角函数的基本关系:(1)平方关系:sin 2α+ cos 2α=1 (2)商数关系:ααcos sin =tan α (在利用已知角的某一三角函数值求另外三角函数值时,还可用解直角三角形得出结论,但一定要注意函数值的取值符号。
) 5.诱导公式: 记忆口诀:把a k ±2π的三角函数化为a 的三角函数 概括为:奇变偶不变,符号看象限。
()()1sin 2sin k παα+=,()cos 2cos k παα+=, ()()tan 2tan k k παα+=∈Z . ()()2sin sin παα+=-,()cos cos παα+=-,()t a n t a nπαα+=. ()()3sin sin αα-=-, ()c o s c o s αα-=, ()t a n t a n αα-=-. ()()4sin sin παα-=, ()cos cos παα-=-, ()t a n t a n παα-=-. ()5sin cos 2παα⎛⎫-=⎪⎝⎭cos sin 2παα⎛⎫-= ⎪⎝⎭; ()6sin cos 2παα⎛⎫+=⎪⎝⎭,cos sin 2παα⎛⎫+=- ⎪⎝⎭.【课前预习】1. _____240sin =o _____390cos =o=π34tan_________ 2.一扇形圆心角为,120o半径为1,则圆心角所对的弧长为:_______3.已知角α的终边经过点P (2,-3),则:sin sin α=_______,cos α=________tan α=________【典型例题】【例1】cos300︒=( )yx xy O — + — +y O — + + —+ + — _ xA. B.-12 C.12 D.【解析】()1cos300cos 36060cos 602︒=︒-︒=︒=【例2】若4sin ,tan 05θθ=->,则cos θ= .【解析】由已知,θ在第三象限,∴3cos 5θ===-.【例3】求函数y =|tan |tan cos |cos ||sin |sin x xx x x x ++的值域. 【解析】对x 进行分类讨论得出函数值。
三角函数与解三角形

高中三角函数公式大全三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) =tanAtanB -1tanB tanA + tan(A-B) =tanAtanB1tanBtanA +-倍角公式 tan2A =Atan 12tanA2-Sin2A=2SinA•CosACos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A 半角公式 sin(2A )=2cos 1A - cos(2A )=2cos 1A + tan(2A )=A A cos 1cos 1+- tan(2A )=A A sin cos 1-=AAcos 1sin +和差化积 诱导公式sin(-a) = -sina cos(-a) = cosa sin(2π-a) = cosa cos(2π-a) = sina sin(2π+a) = cosa cos(2π+a) = -sina sin(π-a) = sina cos(π-a) = -cosa sin(π+a) = -sina cos(π+a) = -cosa tgA=tanA =a acos sin万能公式sina=2)2(tan 12tan2a a + cosa=22)2(tan 1)2(tan 1a a +- tana=2)2(tan 12tan2aa- 其它公式a•sina+b•cosa=)b (a 22+×sin(a+c) [其中tanc=ab]a•sin(a)-b•cos(a) =)b (a 22+×cos(a-c) [其中tan(c)=ba]1+sin(a) =(sin 2a +cos 2a )2 1-sin(a) = (sin 2a -cos 2a)2其他非重点三角函数 csc(a) =asin 1 sec(a) =a cos 1公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin (2kπ+α)= sinα cos (2kπ+α)= cosα tan (2kπ+α)= tanα 公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin (π+α)= -sinα cos (π+α)= -cosα tan (π+α)= tanα公式三:任意角α与 -α的三角函数值之间的关系:sin (-α)= -sinα cos (-α)= cosα tan (-α)= -tanα cot (-α)= -cotα 公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin (π-α)= sinα cos (π-α)= -cosα tan (π-α)= -tanα 公式五:利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:sin (2π-α)= -sinα cos (2π-α)= cosα tan (2π-α)= -tanα cot (2π-α)= -cotα 公式六:2π±α及23π±α与α的三角函数值之间的关系:sin (2π+α)= cosα cos (2π+α)= -sinα sin (2π-α)= cosα cos (2π-α)= sinαsin (23π+α)= -cosα cos (23π+α)= sinα tan (23π+α)= -cotαsin (23π-α)= -cosα cos (23π-α)= -sinα tan (23π-α)= cotα求未知角的三角函数值例1:已知3sin35πα⎛⎫+=⎪⎝⎭,,26ππα⎛⎫∈-⎪⎝⎭,求:(1)sinα(2)sin2α例2:已知113cos,cos()714ααβ=-=,且02πβα<<<.(1)求tan2α;(2)求β.例3:已知344ππβα<<<<,335cos,sin45413ππαβ⎛⎫⎛⎫-=+=⎪ ⎪⎝⎭⎝⎭,求()sinαβ+的值.例4:设12cos,sin,,,0,292322βαππαβαπβ⎛⎫⎛⎫⎛⎫⎛⎫-=--=∈∈⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,求()cosαβ+例5:已知sin sin sin 0,cos cos cos 0αβγαβγ++=++=,则()cos αβ-=( ) A. 1 B. 1- C. 12 D. 12-例6:已知()124sin ,sin 135ααβ=+=,且,αβ均为锐角,求cos 2β例7:已知πβπα<<<<20,53sin =α,54)cos(-=+βα,则=βsin _______例8:已知cos sin 6παα⎛⎫-+= ⎪⎝⎭7sin 6πα⎛⎫+ ⎪⎝⎭的值是______________例9:已知11,0,tan ,tan 237παππβαβ<<-<<=-=-,求2αβ+例10:已知在ABC 中,3sin 4cos 6,4sin 3cos 1A B B A +=+=,则角C 的大小为( )A. 30B. 150C. 30或150D. 90三角函数的值域与最值二、典型例题例1:已知向量()()()cos ,sin 3cos ,cos 3sin ,sin ,a x x x b x x x f x a b =+=--=⋅ (1)求函数()f x 的单调递增区间 (2)当,64x ππ⎡⎤∈-⎢⎥⎣⎦时,求()f x 的取值范围例2:已知函数()cos 22sin sin 344f x x x x πππ⎛⎫⎛⎫⎛⎫=-+-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ (1)求函数()f x 的最小正周期和图像的对称轴方程(2)求函数()f x 在区间,122ππ⎡⎤-⎢⎥⎣⎦的值域例3:函数27cos sin cos24y x x x =--+的最大值为___________例4:设函数()sin cos2f x x x =+,若,62x ππ⎡⎤∈-⎢⎥⎣⎦,则函数()f x 的最小值是______例5:函数()3sin 2sin xf x x-=+的值域为___________例6:函数()2sin cos xf x x-=的值域为____________例7:设函数()sin 2,,66f x x x a ππ⎛⎫⎡⎤=+∈- ⎪⎢⎥⎝⎭⎣⎦的值域是1,12⎡⎤-⎢⎥⎣⎦,则实数a 的取值范围是_____________例8:已知函数()2cos sin cos 2a f x a x b x x =--的最大值为12,且3f π⎛⎫= ⎪⎝⎭3f π⎛⎫-= ⎪⎝⎭ ( )A. 12B. 4-C. 12-或4D. 12-或4例9:当02x π<<时,函数()21cos28sin sin 2x xf x x ++=的最小值为__________例10:求函数()sin cos sin cos 1f x x x x x =+-+的值域三角函数及函数()sin y A x ωϕ=+性质典型例题:例1:函数()2cos2f x x x + ( ) A. 在,36ππ⎛⎫-- ⎪⎝⎭上单调递减 B. 在,63ππ⎛⎫⎪⎝⎭上单调递增 C. 在,06π⎛⎫- ⎪⎝⎭上单调递减 D. 在0,6π⎛⎫⎪⎝⎭上单调递增例2:函数22cos 14y x π⎛⎫=+- ⎪⎝⎭的一个单调递减区间为( ) A. 3,22ππ⎛⎫⎪⎝⎭B. 3,44ππ⎛⎫⎪⎝⎭C. ,22ππ⎛⎫- ⎪⎝⎭D. ,44ππ⎛⎫- ⎪⎝⎭例3:sin 23y x π⎛⎫=-⎪⎝⎭的递减区间为( ) A. 52,2,1212k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦ B. 5114,4,33k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦C. 511,,1212k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦ D. 5,,1212k k k Z ππππ⎡⎤---∈⎢⎥⎣⎦例4:已知函数sin cos 1212y x x ππ⎛⎫⎛⎫=-- ⎪ ⎪⎝⎭⎝⎭,则下列关于函数性质判断正确的是( ) A. 最小正周期为π,一个对称中心是,012π⎛⎫⎪⎝⎭B. 最小正周期为π,一个对称中心是,06π⎛⎫⎪⎝⎭ C. 最小正周期为2π,一个对称中心是,012π⎛⎫⎪⎝⎭D. 最小正周期为2π,一个对称中心是,06π⎛⎫⎪⎝⎭例5:函数()ln sin 26f x x π⎛⎫⎛⎫=-⎪ ⎪⎝⎭⎝⎭的单调递增区间为( ) A. (),123k k k Z ππππ⎛⎫++∈⎪⎝⎭ B.(),63k k k Z ππππ⎛⎫-++∈ ⎪⎝⎭C. ()7,312k k k Z ππππ⎛⎫++∈ ⎪⎝⎭D.()5,36k k k Z ππππ⎛⎫++∈⎪⎝⎭例6:设函数()sin 23f x x π⎛⎫=+⎪⎝⎭,则下列关于函数()f x 的说法中正确的是( ) A. ()f x 是偶函数 B. ()f x 的最小正周期是π C. ()f x 图像关于点,06π⎛⎫-⎪⎝⎭对称 D. ()f x 在区间7,312ππ⎡⎤⎢⎥⎣⎦上是增函数 例7:函数2sin 46y x π⎛⎫=+ ⎪⎝⎭的图像的两条相邻对称轴间的距离为( ) A.8π B. 4π C. 2πD. π 例8:已知函数()sin 2cos2f x x a x =+的图像关于直线8x π=-对称,则a 的值为_______例9:已知()()2sin 0f x x ωω=>在,34ππ⎡⎤-⎢⎥⎣⎦单调递增,求ω的取值范围例10:已知函数()sin 0y x ωω=>在区间0,2π⎡⎤⎢⎥⎣⎦上为增函数,且图像关于点()3,0π对称,则ω的取值集合为______________图像变换在三角函数中的应用典型例题:例1:要得到函数sin 23y x π⎛⎫=- ⎪⎝⎭的图像,只需要将函数sin 2y x =的图像( ) A. 向左平移3π个单位 B. 向右平移3π个单位 C. 向右平移6π个单位 D. 向左平移6π个单位例2:把函数sin y x =的图像上所有的点横坐标都缩小到原来的一半,纵坐标保持不变,再把图像向右平移34π个单位,这是对应于这个图像的解析式是( ) A. cos 2y x = B. cos 2y x =- C. 13sin 24y x π⎛⎫=-⎪⎝⎭ D. 13sin 28y x π⎛⎫=-⎪⎝⎭例3:为了得到函数sin 26y x π⎛⎫=- ⎪⎝⎭的图像,可以将函数cos 2y x =的图像( ) A. 向左平移3π个单位 B. 向右平移3π个单位 C. 向右平移6π个单位 D. 向左平移6π个单位例4:要得到sin y x =的图像只需将sin 23x y π⎛⎫=+ ⎪⎝⎭的图像( ) A. 先向左平移23π个单位,再将图像上各点的横坐标缩短至原来的12 B. 先向右平移23π个单位,再将图像上各点的横坐标缩短至原来的12C. 先将图像上各点的横坐标缩短至原来的12,再将图像向左平移3π个单位D. 先将图像上各点的横坐标扩大为至原来的2倍,再将图像向右平移3π个单位例5:为了得到函数x x y 3cos 3sin +=的图像,可以将函数x y 3sin 2=的图像( )A.向右平移4π个单位 B.向左平移4π个单位C.向右平移12π个单位D.向左平移12π个单位例6:将函数()sin 2y x ϕ=+的图像沿x 轴向左平移8π个单位后,得到一个偶函数的图像,则ϕ的一个可能取值为( ) A .4π- B .0 C .4π D .43π例7:若将函数()sin y x ωϕ=+0,2πωϕ⎛⎫><⎪⎝⎭的图像向右平移6π个单位可得到一个奇函数的图像,向左平移3π个单位可得到一个偶函数的图像,则,ωϕ可取的一组值是( ) A. 2,3πωϕ== B. 2,6πωϕ==-C. 1,6πωϕ==D. 1,26πωϕ==例8:若把函数sin y x ω=图像向左平移3π个单位,则与函数cos y x ω=的图像重合,则ω的值可能是( ) A. 13 B. 12 C. 23 D. 32例9.将函数()()sin 222f x x ππθθ⎛⎫=+-<< ⎪⎝⎭的图象向右平移()0ϕϕ>个单位长度后得到函数()g x 的图象,若()(),f x g x 的图象都经过点30,2P ⎛⎫⎪ ⎪⎝⎭,则ϕ的值可以是( )A.53πB.56πC.2πD.6π例10:函数()sin()f x A x ωϕ=+(其中)2,0πϕ<>A )的图象如图所示,为了得到()sin g x x ω=的图象,则只要将)(x f 的图象( )A .向右平移6π个单位长度 B .向右平移12π个单位长度C .向左平移6π个单位长度 D .向左平移12π个单位长度函数()sin y A x ωϕ=+解析式的求解典型例题:例1:化简:()22sin cos 42f x x x π⎛⎫=-- ⎪⎝⎭例2:化简:()22cos 23sin cos 1f x x x x =+-例3:()sin 2cos 263f x x x ππ⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭例4:如图,函数()()sin 0,02y A x A ωϕϕπ=+><<的图像经过点7,0,,066ππ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭,且该函数的最大值为2,最小值为2-,则该函数的解析式为( ) A. 32sin 24x y π⎛⎫=+⎪⎝⎭ B. 2sin 24x y π⎛⎫=+ ⎪⎝⎭C. 32sin 26y x π⎛⎫=+ ⎪⎝⎭D. 2sin 26x y π⎛⎫=+ ⎪⎝⎭例5:如图所示为函数()()sin 0,02f x A x πωϕωϕ⎛⎫=+>≤≤ ⎪⎝⎭的部分图像,其中,A B 两点之间的距离为5,那么()1f -=_________例6:已知函数()()()sin 0,0,0f x A x A ωϕωϕπ=+>><<,其导函数()'f x 的部分图像如图所示,则函数()f x 的解析式是( )A. ()12sin 24f x x π⎛⎫=+⎪⎝⎭ B. ()14sin 24f x x π⎛⎫=+ ⎪⎝⎭C. ()2sin 4f x x π⎛⎫=+ ⎪⎝⎭D. ()134sin 24f x x π⎛⎫=+⎪⎝⎭例7:已知函数()()cos f x A x ωϕ=+的图像如图所示,223f π⎛⎫=- ⎪⎝⎭,则()0f =( ) A. 23- B. 12- C. 23 D. 12例8:已知函数()()sin ,(0,0,0)2f x A x x R A πωϕωϕ=+∈>><<的图像与x 轴的交点中,相邻两个交点之间的距离为2π,且图像上一个最低点为2,23M π⎛⎫-⎪⎝⎭,则()f x 的解析式为____________例9:已知函数()sin 0,02y A x m A πωϕϕ⎛⎫=++><< ⎪⎝⎭的最大值为4,最小值为0,两条对称轴之间最短距离为2π,直线6x π=是其图像的一条对称轴,则函数解析式为________例10:已知,,,,A B C D E 是函数()sin 0,02y x πωϕωϕ⎛⎫=+><<⎪⎝⎭一个周期内图像上的五个点,如图所示,,06A π⎛⎫- ⎪⎝⎭,B 为y 轴上的点,C 为图像上的最低点,E 为该函数图象的一个解三角形中的要素三角形的中线定理与角平分线定理(1)三角形中线定理:如图,设AD 为ABC 的一条中线,则()22222AB AC AD BD +=+ (知三求一)证明:在ABD 中2222cos AB AD BD AD BD ADB =+-⋅ ① 2222cos AC AD DC AD DC ADC =+-⋅ ②D 为BC 中点 BD CD ∴=ADB ADC π∠+∠= cos cos ADB ADC ∴=-∴ ①+②可得:()22222AB AC AD BD +=+(2)角平分线定理:如图,设AD 为ABC 中BAC ∠的角平分线,则AB BDAC CD= 证明:过D 作DE ∥AC 交AB 于EBD BEDC AE∴= EDA DAC ∠=∠ EAAD 为BAC ∠的角平分线EAD DAC ∴∠=∠ EDA EAD ∴∠=∠EAD ∴为等腰三角形 EA ED ∴=BD BE BEDC AE ED ∴==而由BED BAC 可得:BE ABED AC=AB BDAC CD ∴=二、典型例题:例1:(1)ABC 的内角,,A B C 所对的边分别为,,a b c,若60c b B ===,则C =_____(2))ABC 的内角,,A B C 所对的边分别为,,a b c,若30c b C ===,则B =_____例2:在ABC 中,2,60BC B ==,若ABCAC 边长为_________例3:(2012课标全国)已知,,a b c 分别为ABC 三个内角,,A B C的对边,且有cos sin 0a C C b c +--= (1)求A(2)若2a =,且ABC,b c例4:如图,在ABC 中,D 是边AC 上的点,且,2,2AB AD AB BC BD ===,则sin C 的值为___________例5:已知ABC 中,,,a b c 分别是角,,A B C 所对边的边长,若ABC 的面积为S ,且()222S a b c =+-,则tan C等于___________例6:在ABC ∆ 中,内角,,A B C 所对的边分别为,,a b c ,已知ABC ∆的面积为,12,cos ,4b c A -==- 则a 的值为 .例7:设ABC 的内角,,A B C 所对边的长分别为,,a b c,若sin cos 0b A B -=,且2b ac =,则a cb+的值为( ) A.2B.C. 2D. 4例8:设ABC 的内角,,A B C 所对边的长分别为,,a b c ,且22,6b a bc A π=+=,则C =( )A. 6πB. 4πC. 34πD. 4π或34π例9:已知ABC 的三边长为三个连续的自然数,且最大内角是最小内角的2倍,则最小内角的余弦值是( ) A. 34 B. 56 C. 710 D. 23例10:在ABC 中,D 为边BC 上一点,1,120,22BD CD ADB AD =∠==,若ADC的面积为3BAC ∠=_________解三角形中的不等问题二、例题精析:B例1:△ABC 各角的对应边分别为c b a ,,,满足1b c a c a b+≥++,则角A 的范围是 A .(0,]3πB .(0,]6πC .[,)3ππD .[,)6ππ例2:在ABC 中,角,,A B C 所对的边分别为,,a b csin cC = (1)求A 的大小(2)若6a =,求b c +的取值范围例3:在锐角ABC 中,角,,A B C 所对的边分别为,,a b c ,且2cos 2b C a c =- (1)求角B (2)求sin sin A C 的取值范围例4:在ABC 中,角,,A B C 所对的边分别为,,a b c ,已知()sin sin sin A C p B p R +=∈,且214ac b =(1)当5,14p b ==时,求,a c 的值 (2)若角B 为锐角,求p 的取值范围例5:若ABC ∆的内角满足sin 2sin A B C =,则cos C 的最小值是例6:在锐角ABC ∆中2,A B ∠=∠B ∠、C ∠的对边长分别是b 、c ,则+bb c的取值范围是( ) A .11(,)43 B .11(,)32 C . 12(,)23 D .23(,)34例7:已知ABC 的角,,A B C 所对的边分别是,,a b c ,且22223a b c ab +=+,若ABC 的外接圆半径为2,则ABC 面积的最大值为__________例9:已知△ABC 中,角A,B,C 所对的边分别为,,a b c ,且BC 边上的高为a ,则b cc b+的取值范围为______.例10:(2014,重庆)已知ABC 的内角,,A B C 满足()1sin2sin()sin 2A ABC C A B +-+=--+,面积S 满足12S ≤≤,记,,a b c 分别是,,A B C 所对的边,则下列不等式一定成立的是( )A. ()8bc b c +>B. ()ab a b +>612abc ≤≤ D. 1224abc ≤≤。
三角函数与解三角形

三角函数与解三角形在数学中,三角函数是研究角度和三角形之间关系的重要工具。
通过三角函数的使用,我们可以解决很多与角度和三角形相关的问题。
本文将介绍三角函数的基本概念以及如何应用三角函数解决三角形的各类问题。
一、三角函数的基本概念1. 正弦函数(sine function)正弦函数常用符号为sin,对于任意角θ,其正弦值sinθ等于对边与斜边的比值:sinθ = 对边/斜边。
2. 余弦函数(cosine function)余弦函数常用符号为cos,对于任意角θ,其余弦值cosθ等于邻边与斜边的比值:cosθ = 邻边/斜边。
3. 正切函数(tangent function)正切函数常用符号为tan,对于任意角θ,其正切值tanθ等于对边与邻边的比值:tanθ = 对边/邻边。
4. 余切函数(cotangent function)余切函数常用符号为cot,对于任意角θ,其余切值cotθ等于邻边与对边的比值:cotθ = 邻边/对边。
5. 正割函数(secant function)正割函数常用符号为sec,对于任意角θ,其正割值secθ等于斜边与邻边的比值:secθ = 斜边/邻边。
6. 余割函数(cosecant function)余割函数常用符号为csc,对于任意角θ,其余割值cscθ等于斜边与对边的比值:cscθ = 斜边/对边。
二、解三角形的常用方法1. 已知边长求角度假设我们已知一个三角形的两条边长a和b,以及它们之间的夹角θ。
我们可以利用正弦、余弦或正切函数求解这个角度。
- 已知边长a和b,以及夹角θ,可以使用正弦函数来求解:sinθ = a/b,从而可以解得角度θ。
- 已知边长a和b,以及夹角θ,可以使用余弦函数来求解:cosθ = a/b,从而可以解得角度θ。
- 已知边长a和b,以及夹角θ,可以使用正切函数来求解:tanθ = a/b,从而可以解得角度θ。
2. 已知角度求边长假设我们已知一个三角形的一条边长a,以及与这条边相连的两个角度θ和φ。
三角函数与解三角形题型总结

三角函数与解三角形热点一 解三角形高考对解三角形的考查,以正弦定理、余弦定理的综合应用为主.其命题规律可以从以下两方面看:(1)从内容上看,主要考查正弦定理、余弦定理以及三角函数公式,一般是以三角形或其他平面图形为背景,结合三角形的边角关系考查学生利用三角函数公式处理问题的能力;(2)从命题角度看,主要是在三角恒等变换的基础上融合正弦定理、余弦定理,在知识的交汇处命题.【例1】在△ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,且2cos A cos C (tan A tan C -1)=1.(1)求B 的大小;(2)若a +c =332,b =3,求△ABC 的面积.【解析】(1)由2cos A cos C (tan A tan C -1)=1,得2(sin A sin C -cos A cos C )=1,即cos(A +C )=-12,∴cos B =-cos(A +C )=12,又0<B <π,∴B =π3.(2)由余弦定理得cos B =a 2+c 2-b 22ac =12,∴(a +c )2-2ac -b 22ac =12,又a +c =332,b =3,∴274-2ac -3=ac ,即ac =54,∴S △ABC =12ac sin B =12×54×32=5316.【变式1】若本题第(2)问条件变为“若b =3,S △ABC =332”,试求a +c 的值.【解析】由已知S △ABC =12ac sin B =332,∴12ac ×32=332,则ac =6.由余弦定理,得b 2=a 2+c 2-2ac cos B =(a +c )2-3ac ,所以(a +c )2=b 2+3ac =21,所以a +c =21.【变式2】在本例条件下,若b =3,求△ABC 面积的最大值.【解析】由余弦定理,得b 2=a 2+c 2-2ac cos B =a 2+c 2-ac ,则3=a 2+c 2-ac ≥2ac -ac ,所以ac ≤3(当且仅当a =c =3时取等号).所以S △ABC =12ac sin B ≤12×3×sin π3=334.故△ABC 面积的最大值为334.【类题通法】利用正弦定理、余弦定理解三角形的步骤第一步:找条件:寻找三角形中已知的边和角,确定转化方向.第二步:定工具:根据已知条件和转化方向,选择使用的定理和公式,实施边角之间的转化.第三步:求结果:根据前两步分析,代入求值得出结果.第四步:再反思:转化过程中要注意转化的方向,审视结果的合理性.【对点训练】△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知sin(A +C )=8sin 2B2.(1)求cos B ;(2)若a +c =6,△ABC 的面积为2,求b .【解析】(1)由题设及A +B +C =π得sin B =8sin 2 B 2,即sin B =4(1-cos B),故17cos 2B -32cos B +15=0,解得cos B =1517或cos B =1(舍去). (2)由cos B =1517,得sin B =817,故S △ABC =12ac sin B =417ac .又S △ABC =2,则ac =172.由余弦定理及a +c =6得b 2=a 2+c 2-2ac cos B =(a +c )2-2ac (1+cos B)=36-2×172×⎝ ⎛⎭⎪⎫1+1517=4. 所以b =2.热点二 三角函数的图象和性质注意对基本三角函数y =sin x ,y =cos x 的图象与性质的理解与记忆,有关三角函数的五点作图、图象的平移、由图象求解析式、周期、单调区间、最值和奇偶性等问题的求解,通常先将给出的函数转化为y =A sin(ωx +φ)的形式,然后利用整体代换的方法求解.【例2】已知函数f (x )=(sin x +cos x )2+cos 2x -1.(1)求函数f (x )的最小正周期;(2)求函数f (x )在区间⎣⎢⎡⎦⎥⎤-π4,π4上的最大值和最小值. 【解析】(1)∵f (x )=(sin x +cos x )2+cos 2x -1=2sin x cos x +cos 2x =sin 2x +cos 2x =2sin ⎝ ⎛⎭⎪⎫2x +π4, ∴函数f (x )的最小正周期T =2π2=π.(2)由(1)可知,f (x )=2sin ⎝ ⎛⎭⎪⎫2x +π4. ∵x ∈⎣⎢⎡⎦⎥⎤-π4,π4, ∴2x +π4∈⎣⎢⎡⎦⎥⎤-π4,3π4, ∴sin ⎝ ⎛⎭⎪⎫2x +π4∈⎣⎢⎡⎦⎥⎤-22,1. 故函数f (x )在区间⎣⎢⎡⎦⎥⎤-π4,π4上的最大值和最小值分别为2,-1. 【类题通法】解决三角函数图象与性质综合问题的步骤(1)将f (x )化为a sin x +b cos x 的形式;(2)构造f (x )=a 2+b 2a a 2+b 2·sin x +b a 2+b 2·cos x ; (3)和角公式逆用,得f (x )=a 2+b 2sin(x +φ)(其中φ为辅助角);(4)利用f (x )=a 2+b 2sin(x +φ)研究三角函数的性质;(5)反思回顾,查看关键点、易错点和答题规范.【对点训练】已知函数f (x )=12sin 2x -32cos 2x .(1)求f (x )的最小正周期和最大值;(2)讨论f (x )在⎣⎢⎡⎦⎥⎤π6,2π3上的单调性. 【解析】(1)f (x )=12sin 2x -32cos 2x =sin ⎝ ⎛⎭⎪⎫2x -π3. 因此f (x )的最小正周期为π,最大值为1.(2)当x ∈⎣⎢⎡⎦⎥⎤π6,2π3时,0≤2x -π3≤π,从而当0≤2x -π3≤π2,即π6≤x ≤5π12时,f (x )单调递增. 当π2≤2x -π3≤π,即5π12≤x ≤2π3时,f (x )单调递减.综上可知,f (x )在⎣⎢⎡⎦⎥⎤π6,5π12上单调递增,在⎣⎢⎡⎦⎥⎤5π12,2π3上单调递减. 热点三 三角函数与平面向量结合三角函数、解三角形与平面向量的结合主要体现在以下两个方面:(1)以三角函数式作为向量的坐标,由两个向量共线、垂直、求模或求数量积获得三角函数解析式;(2)根据平面向量加法、减法的几何意义构造三角形,然后利用正、余弦定理解决问题.【例3】已知向量m =(2sin ωx ,cos 2ωx -sin 2ωx ),n =(3cos ωx ,1),其中ω>0,x ∈R .若函数f (x )=m ·n 的最小正周期为π.(1)求ω的值;(2)在△ABC 中,若f (B )=-2,BC =3,sin B =3sin A ,求BA→·BC →的值. 【解析】(1)f (x )=m ·n =23sin ωx cos ωx +cos 2ωx -sin 2ωx =3sin 2ωx +cos 2ωx =2sin ⎝⎛⎭⎪⎫2ωx +π6. ∵f (x )的最小正周期为π,∴T =2π2|ω|=π. ∵ω>0,∴ω=1.(2)设△ABC 中角A ,B ,C 所对的边分别是a ,b ,c .∵f (B )=-2,∴2sin ⎝⎛⎭⎪⎫2B +π6=-2, 即sin ⎝⎛⎭⎪⎫2B +π6=-1,解得B =2π3(B ∈(0,π)). ∵BC =3,∴a =3,∵sin B =3sin A ,∴b =3a ,∴b =3. 由正弦定理,有3sin A =3sin 2π3, 解得sin A =12.∵0<A <π3,∴A =π6.∴C =π6,∴c =a = 3.∴BA →·BC →=ca cos B =3×3×cos 2π3=-32.【类题通法】1.破解平面向量与“三角”相交汇题的常用方法是“化简转化法”,即先活用诱导公式、同角三角函数的基本关系式、倍角公式、辅助角公式等对三角函数进行巧“化简”;然后把以向量共线、向量垂直形式出现的条件转化为“对应坐标乘积之间的关系”;再活用正、余弦定理,对三角形的边、角进行互化.2.这种问题求解的关键是利用向量的知识将条件“脱去向量外衣”,转化为三角函数的相关知识进行求解.【对点训练】在△ABC 中,内角A ,B ,C 的对边分别是a ,b ,c ,向量m =⎝ ⎛⎭⎪⎫a 2,c 2,n =(cos C ,cos A ),且n ·m =b cos B .(1)求角B 的值;(2)若cos A -C 2=3sin A ,且|m |=5,求△ABC 的面积.【解析】(1)由m ·n =b cos B ,得a 2cos C +c 2cos A =b cos B ,sin A cos C +sin C cos A =2sin B cos B ,即sin(A +C )=2sin B cos B ,sin B =2sin B cos B ,∵0<B<π,sin B≠0,∴cos B=12,∴B=π3.(2)C=π-A-B=2π3-A,cos A-C2=3sin A⇒cos⎝⎛⎭⎪⎫A-π3=3sin A⇒cos A=3sin A⇒tan A=33.∵0<A<23π⇒A=π6,∴C=π-π6-π3=π2.在Rt△ABC中,∵a=c sin π6=12c,又|m|=5,即a2+c2=20,∴a=2,c=4,b=16-4=23,△ABC的面积S=12×2×23=2 3.。
2023届高考数学《三角函数与解三角形》典型例题讲解

2023届高考数学《三角函数与解三角形》典型例题讲解【典型例题】例1.(2022·全国·高三校联考阶段练习)已知函数2()cos cos )sin f x x x x x =+−.(1)求函数f (x )的单调递增区间和最小正周期;(2)若当ππ,122x ⎡⎤∈⎢⎥⎣⎦时,关于x 的不等式. (),f x m ≥求实数m 的取值范围. 请选择①恒成立,②有解,两条件中的一个,补全问题(2),并求解.注意:如果选择①和②两个条件解答,以解答过程中书写在前面的情况计分.【解析】(1)222()cos cos )sin cos cos sin f x x x x x x x x x =+−=+−π2cos22sin(2)6x x x +=+. 所以函数()f x 的最小正周期πT =. 由πππ2π22π,Z 262k x k k −+++∈剟,解得ππππ,Z 36k x k k −++∈剟. 所以函数()f x 的单调增区间为ππ[π,π],Z 36k k k −++∈,(2)若选择①由题意可知,不等式()f x m …恒成立,即min ()m f x …. 因为ππ,122x ⎡⎤∈⎢⎥⎣⎦,所以ππ7π2366x +剟. 故当π7π266x +=,即π2x =时,()f x 取得最小值,且最小值为1π2f ⎛⎫=− ⎪⎝⎭. 所以1m −…,实数m 的取值范围为(],1−∞−.若选择②由题意可知,不等式()f x m …有解,即max ()m f x …. 因为ππ,122x ⎡⎤∈⎢⎥⎣⎦,所以ππ7π2366x +剟.故当ππ262x +=,即π6x =时,()f x 取得最大值,且最大值为π26f ⎛⎫= ⎪⎝⎭. 所以2m …,实数m 的取值范围(],2−∞.例2.(2022春·重庆渝中·高三重庆巴蜀中学校考阶段练习)已知,,a b c 分别为ABC 内角,,A B C 的对边,若ABC 同时满足下列四个条件中的三个:①a 2b =;③sin sin sin ++=−B C a c A b c ;④21cos sin sin 24−⎛⎫−= ⎪⎝⎭B C B C . (1)满足有解三角形的序号组合有哪些?(2)请在(1)所有组合中任选一组,求对应ABC 的面积.【解析】(1)对于③,()22212π,0,223b c a c a c b B B a b c ac π+++−=⇒=−∈∴=−; 对于④,()()1cos 11sin sin cos 2sin sin 242B C B C B C B C +−−=⇒−−=−, 即()1cos 2B C +=−,且π,0,,πA B C A B C ++=<<,则π3A =,故③,④不能同时存在,则满足有解三角形的序号组合为①②③,①②④.(2)选①②③:2π2,3a b B ===时, 由余弦定理:22221cos22a c b B ac +−=⇒−=整理得:210c −=且0c >,则c =,ABC ∴的面积为31sin 28ABC S ac B ==.选①②④:π2,3a b A ===时, 由余弦定理:2222143cos 224b c a c A bc c+−+−=⇒=, 整理得:2210c c −+=,则1c =,ABC ∴的面积1sin 2ABC S bc A ==. 例3.(2022春·浙江·高二期中)在①(sin sin )()(sin sin )c A C a b A B −=−+,②2cos 2b A a c +=,222sin B a c b =+−三个条件中任选一个,补充在下面问题中,并解答.(1)求角B 的大小; (2)如图所示,当sin sin A C +取得最大值时,若在ABC 所在平面内取一点D (D 与B 在AC 两侧),使得线段2,1DC DA ==,求BCD △面积的最大值.【解析】(1)若选①(sin sin )()(sin sin )c A C a b A B −=−+,由正弦定理得,()()()c a c a b a b −=−+,整理得222a c b ac +−=, 所以2221cos 222a cb ac B ac ac +−===,又0πB <<,所以π3B =; 若选②2cos 2b A a c +=, 由余弦定理得222222b c a b a c bc+−+=,化简得222a c b ac +−= 所以2221cos 222a cb ac B ac ac +−===,又0πB <<,所以π3B =;222sin B a c b =+−,sin 2cos B ac B =, 化简得tan B 0πB <<,所以π3B =;(2)由(1)得2π3A C +=,故2π03A <<,所以2π3πsin sin sin sin sin 326A C A A A A A ⎛⎫⎛⎫+=+−==+ ⎪ ⎪⎝⎭⎝⎭ 由ππ5π666A <+<,所以当ππ62A +=即π3A =时,sin sin A C + 令,ACD ADC θα∠=∠=,AB AC BC a ===, 在ACD 中由正弦定理可得,1sin sin a αθ=,所以sin sin a αθ=, 由余弦定理可得22221221cos 54cos a αα=+−⨯⨯⨯=−,所以()2222222cos 1sin sin a a a a θθθ=−=−()22254cos sin cos 4cos 42cos ααααα=−−=−+=−, 因为1,2DA DC ==,可得π02θ<<,所以cos 2cos a θα=−,1π12sin cos sin 232BCD S a a θθθ⎛⎫=⨯⨯⨯+=+ ⎪⎝⎭)1π2cos sin sin 23ααα⎛⎫=−+=− ⎪⎝⎭ 当且仅当ππ=32α−即5π=6α时,等号成立, 所以BCD △.本课结束。
三角函数及解直角三角形

三角函数及解直角三角形1、知识点梳理知识点一:锐角三角函数定义:在Rt△ABC中,∠C=900, ∠A、∠B、∠C的对边分别为a、b、c,则∠A的正弦可表示为:sinA= ,∠A的余弦可表示为cosA= ∠A的正切:tanA= ,它们统称为∠A的锐角三角函数注意:1、sinA、∠cosA、tanA表示的是一个整体,是两条线段的比,没有单位,这些比值只与有关,与直角三角形的无关2、取值范围<sinA< ,cosA< ,tanA>知识点二:特殊角的三角函数值:ΑSinαcosαtanα300450600注意:1、三个特殊角的三角函数值都是根据定义应用直角三角形性质算出来的,要在理解的基础上结合表格进行记忆2、正弦和正切值随着角度的增大而余弦值随着角度的增大而知识点三:解直角三角形:1、定义:由直角三角形中除直角外的个已知元素,求出另外个未知元素的过程叫解直角三角形2、解直角三角形的依据:Rt∠ABC中,∠C=900 三边分别为a、b、c⑴三边关系:⑵两锐角关系⑶边角之间的关系:sinA cosA tanAsinB cosB tanB注意:解直角三角形中已知的两个元素应至少有一个是当没有直角三角形时应注意构造直角三角形,再利用相应的边角关系解决】3、解直角三角形应用中的有关概念⑴仰角和俯角:如图:在图上标上仰角和俯角⑵坡度坡角:如图:斜坡AB的垂直度h和水平宽度l的比叫做坡度,用i表示,即i=坡面与水平面得夹角为用字母α表示,则i=tanα=hl。
⑶方位角:是指南北方向线与目标方向所成的小于900的水平角如图:OA表示OB表示OC表示OD表示(也可称东南方向)铅直水平线3、 利用解直角三角形知识解决实际问题的一般步骤:⑴把实际问题抓化为数学问题(画出平面图形,转化为解直角三角形的问题)⑵根据条件特点,选取合适的锐角三角函数去解直角三角形⑶解出数学问题答案,从而得到实际问题的答案注意:在解直角三角形实际应用中,先构造符合题意的三角形,解题的关键是弄清在哪个直角三角形中用多少度角的哪种锐角三角函数解决2、近几年真题再现:1.(天津)tan60°的值等于( )A .1BCD .22.(温州)如图,在△ABC 中,∠C=90°,AB=5,BC=3,则sinA 的值是( )A .3B . 4C .3D . 4A .B .C .D .A .B .C .D .A .12B .C .米D .7 (潍坊)一渔船在海岛A 南偏东20°方向的B 处遇险,测得海岛A 与B 的距离为20海里,渔船将险情报告给位于A 处的救援船后,沿北偏西80°方向向海岛C 靠近,同时,从A 处出发的救援船沿南偏西10°方向匀速航行,20分钟后,救援船在海岛C 处恰好追上渔船,那么救援船航行的速度为( )A ./小B .30海里/小时C ./小时D ./小时8(东营)某校研究性学习小组测量学校旗杆AB 的高度,如图在教学楼一楼C 处测得旗杆顶部的仰角为60°,在教学楼三楼D 处测得旗杆顶部的仰角为30°,旗杆底部与教学楼一楼在同一水平线上,已知每层楼的高度为3米,则旗杆AB 的高度为 米.精确到0.1)11 (莱芜)如图,有一艘渔船在捕鱼作业时出现故障,急需抢修,调度中心通知附近两个小岛A 、B 上的观测点进行观测,从A 岛测得渔船在南偏东37°方向C 处,B 岛在南偏东66°方向,从B 岛测得渔船在正西方向,已知两个小岛间的距离是72海里,A 岛上维修船的速度为每小时20海里,B 岛上维修船的速度为每小时28.8海里,为及时赶到维修,问调度中心应该派遣哪个岛上的维修船?(参考数据:cos37°≈0.8,sin37°≈0.6,sin66°≈0.9,cos66°≈0.4)3、考点训练考点一:锐角三角函数的概念例1 (贵阳)如图,P 是∠α的边OA 上一点,点P 的坐标为(12,5),则tan α等于( )A . 513B .1213C .512D .125对应训练1.如图,将∠AOB 放置在5×5的正方形网格中,则tan ∠AOB 的值是( )A .23B .32C .13D .13考点二:特殊角的三角函数值对应训练2.计算6tan45°-2cos60°的结果是()A.B.4 C.D.5考点三:化斜三角形为直角三角形3.如图,四边形ABCD的对角线AC,BD相交于点O,且BD平分AC.若BD=8,AC=6,∠BOC=120°,则四边形ABCD的面积为.(结果保留根号)考点四:解直角三角形的应用例4 (2015•舟山)某学校的校门是伸缩门(如图1),伸缩门中的每一行菱形有20个,每个菱形边长为30厘米.校门关闭时,每个菱形的锐角度数为60°(如图2);校门打开时,每个菱形的锐角度数从60°缩小为10°(如图3).问:校门打开了多少米?(结果精确到1米,参考数据:sin5°≈0.0872,cos5°≈0.9962,sin10°≈0.1736,cos10°≈0.9848).思路分析:先求出校门关闭时,20个菱形的宽即大门的宽;再求出校门打开时,20个菱形的宽即伸缩门的宽;然后将它们相减即可.点评:本题考查了菱形的性质,解直角三角形的应用,难度适中.解题的关键是把实际问题转化为数学问题,只要把实际问题抽象到解直角三角形中,一切将迎刃而解.对应训练4.如图,益阳市梓山湖中有一孤立小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PD,小张在小道上测得如下数据:AB=80.0米,∠PAB=38.5°,∠PBA=26.5.请帮助小张求出小桥PD的长并确定小桥在小道上的位置.(以A,B为参照点,结果精确到0.1米)(参考数据:sin38.5°=0.62,cos38.5°=0.78,tan38.5°=0.80,sin26.5°=0.45,cos26.5°=0.89,tan26.5°=0.50)。
解三角形与三角函数最全知识总结

三角形与三角比1.(包括角α在平面几何里,我们把周角分成360等份,每一份叫做1度的角,这种用“度”作为单位来度量角的单位制叫做角度制;我们也可以用圆弧的长与圆半径的比值来表示这个圆弧或圆弧所对的圆心角的大小;把弧长等于半径的弧所对的圆心角叫做1弧度的角,用符号rad 表示,读作弧度;用“弧度”作为单位来度量角的单位制叫做弧度制;如果一个半径为r 的圆的圆心角α所对的弧长为l ,那么比值l r 就是角α的弧度数的绝对值,即lrα=,这里α的正负由它的终边的旋转方向决定;零角的弧度数为零;弧度制与角度制的换算关系:1弧度180π︒=;1180π︒=弧度;在弧度制下,角的集合与实数集R 之间建立起一一对应的关系;例如,与角α终边相同的角可以表示为{|2,k ββπα=+}k ∈Z ,与角α终边共线的角可以表示为{|,}k k ββπα=+∈Z ;弧长公式:||l r α=;扇形面积公式:211||22S r lr α==扇形;附表:由α的象限判断2α、3α、2α、3α的象限:2.(r >sin α在平面直角坐标系中,称以原点O 为圆心,以1为半径的圆为单位圆,把点(,)P x y 看作角α的终边与单位圆的交点,如图,过点P 作x 轴的垂线,垂足为M ,过点(1,0)A 作单位圆的切线,这条切线必然平行于y 轴,设它与角α的终边或其反向延长线相交于点T ;于是,cos x OM α==,sin y PM α==,tan yAT xα==;所以点P 坐标总可以表示成(cos ,sin )αα;我们把PM 、OM 、AT 这三条线段分别叫做角α的正弦线、余弦线、正切线,这些线段通称为三角函数线;由三角函数线得出的常用三角不等式:①2πsin tan x x x << 3.①切割化弦,“切”通过商数关系化为“弦”,“割”通过倒数关系化为“弦”;②弦化切,一般和“齐次式”有关,通过分式上下同时除以cos 或2cos 得到“切”;③1的代换,通过平方关系,将1代换成所需的三角比;(2)诱导公式:奇变偶不变,符号看象限;第一组:sin(2)sin k παα+=;cos(2)cos k παα+=;tan(2)tan k παα+=;第二组:sin()sin αα-=-;cos()cos αα-=;tan()tan αα-=-;第三组:sin()sin παα+=-;cos()cos παα+=-;tan()tan παα+=;第四组:sin()sin παα-=;cos()cos παα-=-;tan()tan παα-=-;第五组:sin()cos 2παα-=;cos()sin 2παα-=;tan()cot 2παα-=;第六组:sin()cos 2παα+=;cos()sin 2παα+=-;tan()cot 2παα+=-;4.三角恒等变换(1)和与差公式cos(α-sin(α+tan(α+由cos ϕ)3πα±;cos 2α=sin2α=①2α=2α=;21sin 2(sin cos )ααα±=±;1tan tan()1tan 4απαα±=± ;tan tan tan()(1tan tan )αβαβαβ±=± ;⑥常见角的变换:()ααββ=+-;22αα=⋅;()()244πππαα=++-;2()()ααβαβ=++-;2()()βαβαβ=+--;()()222αββααβ+=---;(()222αββααβ-=+-+;5.解三角形(1)三角形面积公式(其中R 是三角形外接圆半径,r 是内切圆半径,2a b cp ++=)111sin sin sin 222ABC S bc A ac B C ∆===;22sin sin sin 4ABC abc S R A B C R ∆==;ABC S pr ∆==;222b ac =+222c a b =+②sin 2A =③,,A B C ④,,A B C ①sin(A +②sin2A B +三角函数1.sin y x =,合是{|2x x =sin y x =的最小正周期;sin()y A x ωϕ=+的周期是2||T πω=;(3)奇偶性:sin y x =是奇函数;(4)单调性:sin y x =在闭区间[2,2]()22k k k ππππ-+∈Z 上都是增函数;在闭区间3[2,2]()22k k k ππππ++∈Z 上都是减函数;(5)对称性:正弦函数sin y x =既是轴对称图形,又是中心对称图形,对称轴是2x k ππ=+()k ∈Z ,对称中心(,0)k π()k ∈Z ;2.余弦函数图像对任意一个实数x 都有唯一确定的值cos x 与它对应,按照这个对应法则所建立的函数,表示为cos y x =,它叫做余弦函数,它的定义域是实数集R ;(1)值域和最值:余弦函数cos ,y x x =∈R 的值域是[1,1]-,max 1y =,此时x 的集合是{|2,}x x k k π=∈Z ,min 1y =-,此时x 的集合是{|2,}x x k k ππ=+∈Z ;cos(y A x ω=+(4)]()k π+∈Z 上是减函数;);对称中心(,0)2k ππ+(k 3.表示为tan y =(1)值域和最值:由tan y x =的定义可以得到它的值域是实数集R ,无最值;(2)周期性:由tan()tan x x π+=可知正切函数是周期函数,π是它的最小正周期;(3)奇偶性:由tan()tan x x -=-(,)2x k k ππ≠+∈Z 可知正切函数是奇函数;(4)单调性:正切函数tan y x =在区间(,)22k k ππππ-+()k ∈Z 内都是增函数;(5)对称性:正切函数tan y x =是中心对称图形,对称中心是(,0)2k π()k ∈Z ;4.函数sin()y A x ωϕ=+的图像与性质函数sin()y A x ωϕ=+(0,0)A ω>>中的常数,,A ωϕ对其图像有如下影响:正数A 决定了函数sin()y A x ωϕ=+的值域为[,]A A -,A 叫做该正弦曲线的振幅;如图,sin y x =与2sin y x =的图像对比,横坐标不变,纵坐标变成原来的2倍;正数ω12T ωπ==叫做该ϕϕ叫做初相;如图,sin y =sin y x =纵坐标变成原来的上加下减5.反三角函数函数sin ,[,]22y x x ππ=∈-的反函数叫做反正弦函数,记作arcsin ,[1,1]y x x =∈-;函数cos ,[0,]y x x π=∈的反函数叫做反余弦函数,记作arccos ,[1,1]y x x =∈-;函数tan ,(,)22y x x ππ=∈-的反函数叫做反正切函数,记作arctan ,(,)y x x =∈-∞+∞;arcsin y x =arccos y x =arctan y x=(1)值域:arcsin [,]22y x ππ=∈-;arccos [0,]y x π=∈;arctan (,)22y x ππ=∈-;(2)奇偶性:arcsin y x =与arctan y x =为奇函数;arccos y x =为非奇非偶函数;(0,2πsin(arcsin )x =cos(arccos )x =tan(arctan )x =arcsin x +6.(1)sin x a =(2)cos x a =(3)tan x a =的解集为{|arctan ,}x x k a k π=+∈Z .。
三角函数与解三角形

高考三角函数与解三角形必记知识点⎧⎪⎨⎪⎩正角:按逆时针方向旋转形成的角1、任意角负角:按顺时针方向旋转形成的角零角:不作任何旋转形成的角2、角α的顶点与原点重合,角的始边与x 轴的非负半轴重合,终边落在第几象限,则称α为第几象限角.第一象限角的集合为{}36036090,k k k αα⋅<<⋅+∈Z第二象限角的集合为{}36090360180,k k k α⋅+<⋅+∈Z第三象限角的集合为{}360180360270,k k k αα⋅+<<⋅+∈Z第四象限角的集合为{}360270360360,k k k αα⋅+<<⋅+∈Z3、与角α终边相同的角的集合为{}360,k k ββα=⋅+∈Z4、弧度制与角度制的换算公式:0180=π 5、同角三角函数的基本关系:()221sin cos 1αα+=()2222sin 1cos ,cos 1sin αααα=-=-;()sin 2tan cos ααα=sin sin tan cos ,cos tan αααααα⎛⎫== ⎪⎝⎭.6、函数的诱导公式:口诀:把∂看作锐角,奇变偶不变,符号看象限。
7、①的图象上所有点向左(右)平移ϕ个单位长度,得到函数()sin y x ϕ=+的图象;再将函数()sin y x ϕ=+的图象上所有点的横坐标伸长(缩短)到原来的1ω倍(纵坐标不变),得到函数()sin y x ωϕ=+的图象;再将函数()sin y x ωϕ=+的图象上所有点的纵坐标伸长(缩短)到原来的A 倍(横坐标不变),得到函数()sin y x ωϕ=A +的图象.②数sin y x =的图象上所有点的横坐标伸长(缩短)到原来的1ω倍(纵坐标不变),得到函数sin y x ω=的图象;再将函数sin y x ω=的图象上所有点向左(右)平移ϕω个单位长度,得到函数()sin y x ωϕ=+的图象;再将函数()sin y x ωϕ=+的图象上所有点的纵坐标伸长(缩短)到原来的A 倍(横坐标不变),得到函数()sin y x ωϕ=A +的图象.8、函数()()sin 0,0y x ωϕω=A +A >>的性质:①振幅:A;②周期:2πωT=;③频率:12fωπ==T;④相位:xωϕ+;⑤初相:ϕ函数()siny xωϕ=A++B,当1x x=时,取得最小值为miny;当2x x=时,取得最大值为maxy,则()max min12y yA=-,()max min12y yB=+,()21122x x x xT=-<.8、正弦函数、余弦函数和正切函数的图象与性质:siny x=cosy x=tany x=图象定义域R R,2x x k kππ⎧⎫≠+∈Z⎨⎬⎩⎭值域[]1,1-[]1,1-R 最值当22x kππ=+()k∈Z时,max1y=;当22x kππ=-()k∈Z时,min1y=-.当()2x k kπ=∈Z时,max1y=;当2x kππ=+()k∈Z时,min1y=-.既无最大值也无最小值周期性2π2ππ奇偶性奇函数偶函数奇函数单调性在2,222k kππππ⎡⎤-+⎢⎥⎣⎦()k∈Z上是增函数;在32,222k kππππ⎡⎤++⎢⎥⎣⎦()k∈Z上是减函数.在[]()2,2k k kπππ-∈Z上是增函数;在[]2,2k kπππ+()k∈Z上是减函数.在,22k kππππ⎛⎫-+⎪⎝⎭()k∈Z上是增函数.对称性对称中心()(),0k kπ∈Z对称轴()2x k kππ=+∈Z对称中心(),02k kππ⎛⎫+∈Z⎪⎝⎭对称轴()x k kπ=∈Z对称中心(),02kkπ⎛⎫∈Z⎪⎝⎭无对称轴函数性质9、两角和与差的正弦、余弦和正切公式: ⑴()cos cos cos sin sin αβαβαβ-=+;⑵()cos cos cos sin sin αβαβαβ+=-;⑶()sinsin cos cos sin αβαβαβ-=-;⑷()sin sin cos cos sin αβαβαβ+=+;⑸()tan tan tan1tan tan αβαβαβ--=+ ⇒ (()()tan tan tan 1tan tan αβαβαβ-=-+);⑹()tan tan tan1tan tan αβαβαβ++=- ⇒ (()()tan tan tan 1tan tan αβαβαβ+=+-).10、二倍角的正弦、余弦和正切公式: ⑴sin 22sin cos ααα=⑵2222cos2cos sin 2cos 112sin ααααα=-=-=-⑶22tan tan 21tan ααα=-.11、合一变形⇒把两个三角函数的和或差化为“一个三角函数,一个角,一次方”的B x A y ++=)sin(ϕϖ形式。
专题2 三角函数与解三角形

一、三角函数的图象与性质 1.如何用“五点法”作正弦函数和余弦函数的简图?
(1)正弦函数 y=sin x,x∈[0,2π]的图象中,五个关键点分别是
(0,0),
π 2
,1
,(π,0),
3π 2
,-1
,(2π,0).
(2)余弦函数 y=cos x,x∈[0,2π]的图象中,五个关键点分别是
一、选择题和填空题的命题特点 (一)三角函数的图象与性质是高考考查的重点和热点,考查主要从以下两个方面进行:(1)三角 函数的图象,主要涉及图象变换以及由图象确定解析式;(2)利用三角函数的性质求解三角函数中 的参数、最值、值域、单调区间等问题.
1.(2019 年全国Ⅱ卷,文 T8 改编)若 x1=π3,x2=43π是函数 f(x)=sin ωx(ω>0)两个相邻的极值点,则
ω=( ).
A.2 B.3 C.1 D.1
2
2
解析▶
由题意知,f(x)=sin
ωx 的周期 T=2π=2
4π 3
-
π 3
=2π,解得ω=1.故选 C.
答案▶ C 2.(2018 年全国Ⅰ卷,文 T8 改编)已知函数 f(x)=2cos22x+5,则( ). A.f(x)的最小正周期为π,最大值为 7 B.f(x)的最小正周期为 2π,最小值为 5 C.f(x)的最小正周期为 2π,最大值为 7
tan(α±β)= tan ±tan .
1∓ tan tan
(2)二倍角的正弦、余弦、正切公式: sin 2α= 2sin αcos α . cos 2α= cos2α-sin2α=2cos2α-1=1-2sin2α .
tan 2α=
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角函数与解三角形
.(·天津模拟)在△中,内角,,的对边分别是,,,若+=-. ()求的值;
()若-=,且=,求.
解:()由已知,+-=-,
在△中,≠,因而-=,
则-+=,
因而=.
()由已知=,结合(),
得=.
法一:利用正弦定理和余弦定理得
=×得=(-).
又-=,∴=,在△中,≠,∴=.
法二:∵=+-,
∴=-,
在△中,≠,∴=+,
又=,由正弦定理,则=,
解得=.
.(·甘肃模拟)如图,在△中,边上的中线长为,且∠=,∠=-. ()求∠的值;
()求边的长.
解:()∵∠=,∴∠=.
∵∠=-,∴∠=,
∴∠=(∠-∠)
=×-×=.
()在△中,由=,得=,
解得=,故=,
在△中,=+-··∠
=+-×××=.
故=.
.(·山东高考)在△中,角,,的对边分别为,,.已知( + )=)+). ()证明:+=;
()求的最小值.
解:()证明:由题意知
)+( )))=)+),
化简得( +)=+,
即(+)=+ .
因为++=π,
所以+=,
由正弦定理得+=.
()由()知=,
所以==
=·-≥,
当且仅当=时,等号成立,
故的最小值为.
.(·天津高考)已知函数()=·-.
()求()的定义域与最小正周期;
()讨论()在区间上的单调性.
解:()()的定义域为.
()=-
=-
=+(()) ))-
=+-
=+(-)-
=-=.
所以()的最小正周期==π.
()令=-,则函数=的单调递增区间是,∈.
由-+π≤-≤+π,
得-+π≤≤+π,∈.
设=,
=,
易知∩=.
所以当∈时,()在区间上单调递增,在区间上单调递减.
.(·龙岩质检)某同学用“五点法”画函数()=(ω+φ)在某一个周期内的图象时,列表并填入的数据如下表:。
