(优选)第三章分布函数的计算ppt讲解
合集下载
概率论课件之分布函数

(1) F( x ) 为单调不降函数, 即若 x1 ≤ x2 , 则有F( x1 ) ≤ F( x2 ) .
(2) 0≤F( x ) ≤1,且
lim F (x ) 1 , lim F (x ) 0
x
x
(3) F( x ) 是右连续函数,即
xl im x0F(x)F(x0) 分布函数的性质可用来确定某一函数是否为随 机变量的分布函数,或求解分布函数.
X
O
x
x
(2) 利用分布函数可以更方便求研究随 机变量在某一区间内取值的概率.
如P{X(a,b]} P { X ( ,b ] } P { X ( ,a ] }
P {X b } P {X a }
F(b)F(a)
当3 ≤ x 时,
X -1 O 1 2 3 x x
F(x) = P{X≤x } = P{ Ω } = 1 .
故随机变量X 的分布函数
(
x)
6 1 2
,
1
x < 1; 1 x < 1;
1 x < 2; x2
从而随机变量X的分布率为
X 1 1 2
111
P
632
例 计算并画出参数 p 的两点分布的分布函数。 解:两点分布的分布律是:
P ( X = 0 ) = q, P ( X = 1 ) = p ; q = 1 – p 由于 X 只可能取 0、1 两个值,因此
F(x) =
0, x<0, q ,0 ≤ x < 1 , 1, x≥1 。
2.3 分布函数
1. 分布函数的定义 2. 分布函数的性质 3. 例题讲解
1.分布函数的定义
定义:设X是一个随机变量, x 是任意实 数,称函数
分布函数与概率密度函数的求法ppt文件

04
分布函数与概率密度函数的求解方法
离散型随机变量的求解方法
定义法
根据随机变量的定义,利用公式计算离散型随机变量的概率,从而得到其分布函 数和概率密度函数。
表格法
将随机变量取值的所有可能结果列成一个表格,计算每个可能结果的概率,从而 得到其分布函数和概率密度函数。
连续型随机变量的求解方法
公式法
连续型随机变量的关系
• 连续型随机变量的分布函数是一个连续函数,它描述了随机变量取某个范围内的概率。例如,正态分布的 分布函数可以表示为
• f(x) = 1/√(2πσ^2) * exp(-(x-μ)^2/(2σ^2)), x∈R • 其中,μ是均值,σ是标准差。 • 连续型随机变量的概率密度函数是一个连续函数,它描述了随机变量取某个范围内的概率密度。例如,正
分布函数与概率密度函数的 求法
xx年xx月xx日
contents
目录
• 分布函数的定义与性质 • 概率密度函数的定义与性质 • 分布函数与概率密度函数的关系 • 分布函数与概率密度函数的求解方法 • 分布函数与概率密度函数的应用
01
分布函数的定义与性质
分布函数的定义
离散型随机变量的分布函数
对于离散型随机变量X,其分布函数F(x)定义为事件{X≤x}的概率,即F(x)=P(X≤x)。
分布函数与概率密度函数在统计分析中的应用
参数估计
假设检验
方差分析
相关分析
回归分析
利用样本数据估计未知 参数,包括点估计和区 间估计。
利用样本数据对未知参 数进行假设检验,包括 参数检验和非参数检验 。
分析多个因素对观测值 的影响,判断各因素对 观测值的影响是否显著 。
研究两个或多个变量之 间的相关关系,包括线 性相关和非线性相关。
三章5节函数的分布ppt课件
。
目 录 前一页 后一页 第2退6页 出
第三章 随机变量及其分布 §5 多维随机变量函数分布
更一般地,我们有如下 结论:
如果随机变量
X
,
1
X
,
2
,
Xn
相互独立,
X i
~
N
,
i
2 i
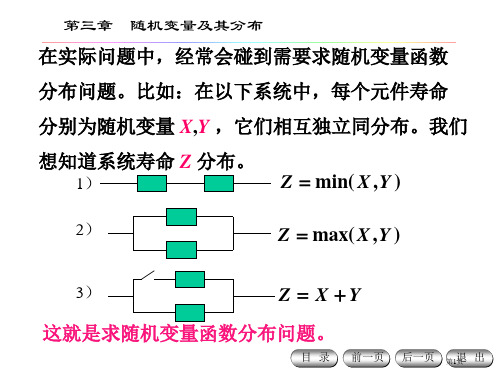
第三章 随机变量及其分布
在实际问题中,经常会碰到需要求随机变量函数
分布问题。比如:在以下系统中,每个元件寿命
分别为随机变量 X,Y ,它们相互独立同分布。我们
想知道系统寿命 Z 分布。
1)
Z min( X ,Y )
2)
Z max(X ,Y )
3)
Z X Y
这就是求随机变量函数分布问题。
目 录 前一页 后一页 第1退页 出
例 1(续)
f x, y
1
x2 y2
e2
2
x,y
所以,Z X 2 Y 2 的分布函数为
FZ z PZ z P X 2 Y 2 z
若 z 0 ,则 FZ z 0
若 z 0 ,则 FZ z P X 2 Y 2 z
f x, ydxdy
x2 y2 z
FZ
z
0
e
2 rdr 0
z0 z0
所以,Z X 2 Y 2 的密度函数为
f Z
z
ze
z2 2
0
z0 z0
目 录 前一页 后一页 第6退页 出
第三章 随机变量及其分布
§5 多维随机变量函数分布
例 2 设随机变量 X 与Y 相互独立,X ~ U 0, 1,
Y ~ 参数为1的指数分布,令 Z X 2Y,
第三章 随机变量及其分布 §5 多维随机变量函数分布
《概率论》课程PPT : 随机变量的分布函数

4
(1, 5)
0 其它
求 X 的分布函数
y
解 当x1时
x
F (x) f (x)dx
0 1 2345 x x
当1 < x 5 时F (x)
x
f (x)dx
1
f (x)dx
x
f (x)dx
1
0 x 1 dx 1 (x 1)
14
(2)X 的密度函数
(1) P(0.3 X 0.7) F(0.7) F(0.3) 0.72 0.32 0.4
(2)密度函数为
f
(x)
F(x)
2x 0
0 x 1 otherwise
例:已知密度函数求分布函数
已知连续型随机变量X的概率密度为
1
f
(
x)
随机变量的分布函数
Distribution Function 分布函数的定义
设X为一随机变量,则对任意实数x,(X<x) 是一个随机事件,称
F(x) P(X x)
为随机变量X的分布函数
F(x)是一个
普通的函数!
定义域为 (-∞,+∞); 值域为 [0,1]。
分布函数表示事件的概率
引进分布函数F(x)后,事件的概率都可以用 F(x)的函数值来表示。
解
X的概率密度
3 e3x x 0 f (x)
0 x 0
P(x1 X x2)
x2 f (x)dx
x1
P(X 1)
f (x)dx
3e3xdx e3
1
1
分布函数PPT课件

(4) 设X为连续型随机变量 , 则
10
x
F( x) P{ X x} f (t)d t
20 若 f ( x) 在点 x 处连续, 有 F( x) f ( x)
30 P{a X b} P{a X b} P{a X b}
b
P{a X b} a f ( x)dx F (b) F (a),
f
(
x)
(1
1 x)2
,
x 0,
0,
x 0.
P{ X 3} P{ X 3} F (3) 3 / 4,
P{2 X 5} P{2 X 5} F (5) F (2) 5 / 6,
P{ X 1} 1 P{ X 1} 1 F (1) 1 1 / 2 1 / 2.
(2) 0 F ( x) 1, x (, )并且
F () lim F ( x) 0, F () lim F ( x) 1;
x
x
(3)
lim
x x0
F
(
x)
F
(
x0
),
( x0 ).
即任一分布函数处处右连续.
重要公式
(1) P{a X b} F (b) F (a),
(2) P{X a} 1 F (a). (3)设 X 是离散型随机变量,其分布律为
2.4 分布函数
1. 分布函数的定义 2. 分布函数的性质 3. 例题讲解 4. 小结
1.分布函数的定义
定义 设 X 是一个随机变量, x是任意实数,函数
F(x) P{X x} x
称为X的分布函数. 说明 (1) F ( x) P{ X x} 即 P{ X (, x]}
(2) 利用 分布函数可以更方便求研究随机变 量在某一区间内取值的概率. 如 P{ X (a, b]} P{ X (, b]} P{ X (, a]}
第三章 分布函数的计算-PPT精选文档

(三)下侧概率、上侧概率和分位点 下侧概率的定义:
F ( x ) P ( X x ) ( x ) dx p
x
上侧概率的定义:
1 F ( x ) P ( X x ) ( x ) dx p
x
利用分布函数我们可以计算随机变量X落在某一范围的概率, 或者说我们掌握了该随机变量的规律了。例如随机变量X小于分位 点的概率即下侧概率,大于分位点的概率即上侧概率。而随机变量 落入x1和x2之间的概率可用以下公式计算。
(2)抛物线求积公式 Cotes系数为1/6,4/6,1/6
1
1 / 2 x dx (0 . 5 40 . 75 1 ) 0 . 4309 0 。 5 6
(3)取7个点
Cotes系数为41/840,9/35,9/280,34/105,9/280, 9/35,/41/840
1
0 .5
第三章 分布函数的计算
1、密度函数和分布函数 2、分布函数的一般计算方法 3、标准正态分布的计算方法 4、统计工具箱的各种分布计算 5、统计推断原理 6、非参数统计分析 7、习题
分布函数的计算在整个信息统计分析应用中起着基础性的作用, 当我们建立了某个统计模型后,会产生很多的统计量,用它们对某 个假设进行检验。这时必须知道这些统计量的分布,某一点的概率、 某概率的分位点。在学习概率论时我们已经知道用查表的方法进行 计算。本章介绍分布函数的计算方法,以及如何用MATLAB的统计 工具箱计算各种分布的概率与分位点的计算。
例3.1.5:分别作出连续型和离散型随机变量的inv和cdf (1)设男性大学生的身高X的平均值为1.7米,标准差为0.1米。 作密度函数和分布函数。利用MATLAB中的正态分布norminv和 normcdf命令进行计算 X=linspace(1.4,2.1,100); P = normcdf(X,1.7,0.1); p = norminv(X,1.7,0.1); subplot(1,2,1),plot(X,p),title('身高密度函数') subplot(1,2,2),plot(X,P),title('身高分布函数')
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x!
这里 为参数,表示随机变量的平均值和方差。
设平均值为5,算出0到10的分布律
X=0:10;
Y = poissinv(X,5); % 计算泊松分布每点的概率
stem(X,Y)
% 作分布律图形
(二)分布函数cdf
分布函数是对密度函数进行积分,其表达式为:
连续型
x
F( x) P( X x) p( x)dx
计算结果为:P=0.6827
X = norminv(0.95,1.70,0.1) % 计算下侧概率的分位点
计算结果为:X=1.8645,即有95%的人身高在1.86以下。
正态分布的密度函数 p 表达式为:
p( x)
1
x 2
e 2 2
2
其中参数:
:为平均值。是随机变量中心趋势的描述。
:为标准差。是随机变量离散程度的描述。
• 分布律(inv) 对于离散型随机变量,分布律相当于连续型随机变量的密度函数。 例3.1.4:作泊松分布随机变量的分布律图形。
p( x | ) x e
(优选)第三章分布函数的计 算ppt讲解
分布函数的计算在整个信息统计分析应用中起着基础性的作用, 当我们建立了某个统计模型后,会产生很多的统计量,用它们对某 个假设进行检验。这时必须知道这些统计量的分布,某一点的概率、 某概率的分位点。在学习概率论时我们已经知道用查表的方法进行 计算。本章介绍分布函数的计算方法,以及如何用MATLAB的统计 工具箱计算各种分布的概率与分位点的计算。
(1)设男性大学生的身高X的平均值为1.7米,标准差为0.1米。 作密度函数和分布函数。利用MATLAB中的正态分布norminv和 normcdf命令进行计算
X=linspace(1.4,2.1,100); P = normcdf(X,1.7,0.1); p = norminv(X,1.7,0.1); subplot(1,2,1),plot(X,p),title('身高密度函数') subplot(1,2,2),plot(X,P),title('身高分布函数')
设某汽车站7点到7点05分等车的人数为一变量X,显然X可取 值0,1,2,3,…。则X是一个离散型的随机变量。事实上这种随 机变量称为服从泊松分布规律的随机变量。
投一硬币,正面为1,反面为0。记该随机变量为X,则其结果 空间为{0,1}。也是一个离散随机变量。
(一)密度函数和分布律
随机变量X在没有发生时我们不知到,也不能预测其结果,看 似随机变量没有规律。但是我们进行大量抽样或实验时,却可以看 见明显的规律。
n
离散型
F ( x) P( X x) pi ( xi )
i0
分布函数函数具有以下性质:
1)对任意x有
0 F(x) 1
2)单调不降,
x1 x2 F( x1 ) F( x2 )
利用分布函数我们可以计算随机变量X落在某一范围的概率, 或者说我们掌握了该随机变量的规律了。
例3.1.5:分别作出连续型和离散型随机变量的inv和cdf
1、密度函数和分布函数
密度函数和分布函数是反映随机变量的总体规律的函数,当 一个变量X在没有抽样之前不知会有什么结果,但结果的范围是 知道的,这样的变量称为随机变量。随机变量可以分为: (1)连续型随机变量 (2)离散型随机变量 (1)连续型随机变量 随机变量的结果空间是实数,例如服从(0,1)上的均匀分布随 机数、人体身高随机数等。 例3.1.1 续型随机变量的例子:
(三)下侧概率、上侧概率和分位点 下侧概率的定义:
x
F( x) P( X x) p( x)dx
上侧概率的定义:
1 F( x) P( X x) x p( x)dx
利用分布函数我们可以计算随机变量X落在某一范围的概率, 或者说我们掌握了该随机变量的规律了。例如随机变量X小于分位 点的概率即下侧概率,大于分位点的概率即上侧概率。而随机变量 落入x1和x2之间的概率可用以下公式计算。
从例3.1.3可以看出,大学生身高的一些特点。
1)首先身高在平均值附近的人数特别多。
2)从直方图中我们可以看出身高的趋势具有对称性。
3)离平均值越远数量越少。
这是典型的正态分布的特点。可以想象当我们抽样量增大应该 有一个理论函数这个理论函数为连续型随机变量的密度函数,上图中的红线所显 示的就是密度函数的图形。在MATLAB这密度函数用inv来表示。
P( x1 X x2 ) F( x2 ) F( x1)
例3.1.6:男性大学生身高X的平均值为1.7米,标准差为0.1米。 1)计算身高小于1.8米大于1.6米发生的概率,即随机变量X落入 区间(1.6, 1.8)的概率。 2)求下侧概率为0.95的分位点。 解:本题利用分布函数进行计算
P(1.6<X<1.8)=F(1.8)-F(1.6) % 例 3.1.6 计算身高小于1.8米大于1.6米发生的概率 P = normcdf(1.8,1.7,0.1)- normcdf(1.6,1.7,0.1)
例3.1.3: 对男性大学生随机抽检,共抽400名大学生测量其身高。 将身高区间(1.50, 2.1)分划分成若干段,计算每段学生身高的 数量,并作直方图。
% 第三章,例3.1.3 R = normrnd(1.7,0.1,400,1); % 产生正态分布的随机数 histfit(R,12) % 作直方图并建立拟合曲线
大学生男性身高X、随机抽一个大学生量其身高得随机变量 的一个实现,例如x=1.75米。则X是一个连续型的随机变量。这 种随机变量服从正态分布。正态分布是统计分析中极其重要的分 布。
(2)离散型随机变量 当一个随机变量X的结果空间有有限个元素或可列个元素时,
称该随机变量为离散型随机变量。
例3.1.2 离散型随机变量的例
(2)设X服从均值为5的泊松分布,作分布律和分布函数图形。
X=0:10; Y = poissinv(X,5); Y1= poisscdf(X,5) subplot(1,2,1),stem(X,Y),title('泊松分布律') subplot(1,2,2),stairs(X,Y1),title('泊松分布函数')
这里 为参数,表示随机变量的平均值和方差。
设平均值为5,算出0到10的分布律
X=0:10;
Y = poissinv(X,5); % 计算泊松分布每点的概率
stem(X,Y)
% 作分布律图形
(二)分布函数cdf
分布函数是对密度函数进行积分,其表达式为:
连续型
x
F( x) P( X x) p( x)dx
计算结果为:P=0.6827
X = norminv(0.95,1.70,0.1) % 计算下侧概率的分位点
计算结果为:X=1.8645,即有95%的人身高在1.86以下。
正态分布的密度函数 p 表达式为:
p( x)
1
x 2
e 2 2
2
其中参数:
:为平均值。是随机变量中心趋势的描述。
:为标准差。是随机变量离散程度的描述。
• 分布律(inv) 对于离散型随机变量,分布律相当于连续型随机变量的密度函数。 例3.1.4:作泊松分布随机变量的分布律图形。
p( x | ) x e
(优选)第三章分布函数的计 算ppt讲解
分布函数的计算在整个信息统计分析应用中起着基础性的作用, 当我们建立了某个统计模型后,会产生很多的统计量,用它们对某 个假设进行检验。这时必须知道这些统计量的分布,某一点的概率、 某概率的分位点。在学习概率论时我们已经知道用查表的方法进行 计算。本章介绍分布函数的计算方法,以及如何用MATLAB的统计 工具箱计算各种分布的概率与分位点的计算。
(1)设男性大学生的身高X的平均值为1.7米,标准差为0.1米。 作密度函数和分布函数。利用MATLAB中的正态分布norminv和 normcdf命令进行计算
X=linspace(1.4,2.1,100); P = normcdf(X,1.7,0.1); p = norminv(X,1.7,0.1); subplot(1,2,1),plot(X,p),title('身高密度函数') subplot(1,2,2),plot(X,P),title('身高分布函数')
设某汽车站7点到7点05分等车的人数为一变量X,显然X可取 值0,1,2,3,…。则X是一个离散型的随机变量。事实上这种随 机变量称为服从泊松分布规律的随机变量。
投一硬币,正面为1,反面为0。记该随机变量为X,则其结果 空间为{0,1}。也是一个离散随机变量。
(一)密度函数和分布律
随机变量X在没有发生时我们不知到,也不能预测其结果,看 似随机变量没有规律。但是我们进行大量抽样或实验时,却可以看 见明显的规律。
n
离散型
F ( x) P( X x) pi ( xi )
i0
分布函数函数具有以下性质:
1)对任意x有
0 F(x) 1
2)单调不降,
x1 x2 F( x1 ) F( x2 )
利用分布函数我们可以计算随机变量X落在某一范围的概率, 或者说我们掌握了该随机变量的规律了。
例3.1.5:分别作出连续型和离散型随机变量的inv和cdf
1、密度函数和分布函数
密度函数和分布函数是反映随机变量的总体规律的函数,当 一个变量X在没有抽样之前不知会有什么结果,但结果的范围是 知道的,这样的变量称为随机变量。随机变量可以分为: (1)连续型随机变量 (2)离散型随机变量 (1)连续型随机变量 随机变量的结果空间是实数,例如服从(0,1)上的均匀分布随 机数、人体身高随机数等。 例3.1.1 续型随机变量的例子:
(三)下侧概率、上侧概率和分位点 下侧概率的定义:
x
F( x) P( X x) p( x)dx
上侧概率的定义:
1 F( x) P( X x) x p( x)dx
利用分布函数我们可以计算随机变量X落在某一范围的概率, 或者说我们掌握了该随机变量的规律了。例如随机变量X小于分位 点的概率即下侧概率,大于分位点的概率即上侧概率。而随机变量 落入x1和x2之间的概率可用以下公式计算。
从例3.1.3可以看出,大学生身高的一些特点。
1)首先身高在平均值附近的人数特别多。
2)从直方图中我们可以看出身高的趋势具有对称性。
3)离平均值越远数量越少。
这是典型的正态分布的特点。可以想象当我们抽样量增大应该 有一个理论函数这个理论函数为连续型随机变量的密度函数,上图中的红线所显 示的就是密度函数的图形。在MATLAB这密度函数用inv来表示。
P( x1 X x2 ) F( x2 ) F( x1)
例3.1.6:男性大学生身高X的平均值为1.7米,标准差为0.1米。 1)计算身高小于1.8米大于1.6米发生的概率,即随机变量X落入 区间(1.6, 1.8)的概率。 2)求下侧概率为0.95的分位点。 解:本题利用分布函数进行计算
P(1.6<X<1.8)=F(1.8)-F(1.6) % 例 3.1.6 计算身高小于1.8米大于1.6米发生的概率 P = normcdf(1.8,1.7,0.1)- normcdf(1.6,1.7,0.1)
例3.1.3: 对男性大学生随机抽检,共抽400名大学生测量其身高。 将身高区间(1.50, 2.1)分划分成若干段,计算每段学生身高的 数量,并作直方图。
% 第三章,例3.1.3 R = normrnd(1.7,0.1,400,1); % 产生正态分布的随机数 histfit(R,12) % 作直方图并建立拟合曲线
大学生男性身高X、随机抽一个大学生量其身高得随机变量 的一个实现,例如x=1.75米。则X是一个连续型的随机变量。这 种随机变量服从正态分布。正态分布是统计分析中极其重要的分 布。
(2)离散型随机变量 当一个随机变量X的结果空间有有限个元素或可列个元素时,
称该随机变量为离散型随机变量。
例3.1.2 离散型随机变量的例
(2)设X服从均值为5的泊松分布,作分布律和分布函数图形。
X=0:10; Y = poissinv(X,5); Y1= poisscdf(X,5) subplot(1,2,1),stem(X,Y),title('泊松分布律') subplot(1,2,2),stairs(X,Y1),title('泊松分布函数')
