ch.1-18 自由能和吉布斯函数
吉布斯自由能公式

吉布斯自由能公式在物理化学中,吉布斯自由能公式是一个非常重要的概念。
它描述了一个系统在恒温恒容条件下的平衡状态和非平衡状态之间的转化能力。
吉布斯自由能公式由19世纪的物理化学家吉布斯提出,成为了理解和预测自然界中化学反应和相变的关键工具。
1. 吉布斯自由能的定义吉布斯自由能(Gibbs Free Energy)用符号G表示,它定义为一个系统在恒温恒容条件下可用于做非体积功的最大能量。
当系统处于平衡状态时,吉布斯自由能呈极小值。
吉布斯自由能的公式为:G = H - TS其中,H为焓(enthalpy),T为温度,S为熵(entropy)。
这个公式描述了系统的能量变化和熵变化之间的关系。
2. 吉布斯自由能的物理意义吉布斯自由能可以帮助我们理解化学反应和相变的发生条件。
在恒温恒容条件下,一个系统的吉布斯自由能的变化ΔG可以通过以下公式计算:ΔG = ΔH - TΔS当ΔG小于0时,系统会朝着更稳定的状态转化,化学反应会发生。
当ΔG大于0时,系统不会发生化学反应。
当ΔG等于0时,系统处于平衡状态。
3. 吉布斯自由能在化学反应中的应用吉布斯自由能可以帮助我们预测化学反应的方向和条件。
根据ΔG的大小,我们可以确定一个反应是放热还是吸热,是自发的还是非自发的。
通过调控温度和压力,可以改变系统的吉布斯自由能,从而控制化学反应的进行。
吉布斯自由能公式在化学工程、生物化学等领域都有着广泛的应用。
它不仅可以解释许多自然界现象,还可以指导实际工程和制备过程的设计和优化。
结论吉布斯自由能公式是物理化学中的一个重要概念,通过它我们可以深入理解系统平衡状态和非平衡状态之间的能量变化和熵变化关系。
吉布斯自由能的理论为化学反应和相变的预测提供了重要工具,有着广泛的应用前景。
通过对吉布斯自由能的深入研究,我们可以更好地理解和控制自然界中的化学过程。
自由能

右式上面的横线代表对所有非平衡态过程的平均。Jarzynski恒等式 假设初始态为平衡态,终态则不必是。 物理文献中常称其为自由能,并以F表示。也有文献使用A表示
Thank
You!!!
,其中是化学势。一个重要的推论是。也就是说每 个粒子的平均吉布斯自由能等于化学势
吉布斯自由能 在标准状况下,存在一个一般规律:
物理意义
“任何一个封闭系统都尽量使自由能最小”
因此,根据这个自然界的基本趋势,如果对于一个潜在反应,距离 势 这个最小值进行定量测量,当热力学的计算显示吉布斯自由能ΔG的 变化是负值的时候。本质上,这表明了那样一个反应更容易发生并 且将释放能量。释放的能量等于这个化学反应所能够做的最大的功。 相反,如果ΔG为正值,能量必须通过做功的方式进入反应系统使得 此反应能够进行。 吉布斯自由能的物理含义是在等温等压过程中,除体积变化所做的 功以外,从系统所能获得的最大功。换句话说,在等温等压过程中, 除体积变化所做的功以外,系统对外界所做的功只能等于或者小于 吉布斯自由能的减小。数学表示是: 不足
吉布斯自由能 吉布斯自由能(Gibbs free energy),或称吉布斯函数 (Gibbs function)、自由焓(Free Enthalpy)是热力学中描 述等温、等压过程的一个重要参量,常用G表示,它的定义是:
,其中U是系统的内能,T是温度,S是熵,p是压强,V是体积, H是焓。 吉布斯自由能的微分形式是:
Ndg+gdN=SdT+Vdp+μdN
,现在假想保证原来物体属性的情况下,切掉体系的一小部分 dN。这时dT,dp,dg,这些强度量的变化为零。所以必然有
μ=g=G/N
亥姆霍兹自由能
定义
ቤተ መጻሕፍቲ ባይዱ
自由能和吉布斯函数

1.吉布斯函数的定义
G = U − TS + pV
2.吉布斯函数判据
dU ≤ TdS + dW → dG = dU − TdS + Vdp + pdV ≤ −SdT+Vdp + pdV + dW 等温等压:dT = 0,dp = 0,dW = 0 dG ≤ 0
吉布斯函数判据:在等温等压条件下,系 统发生的不可逆过程,总是朝吉布斯函数 减少的方向进行。当吉布斯函数达到最小 值时,系统达到平衡态。
一、 熵判据
热力学第二定律:dU ≤ TdS + dw 孤立系统: dU=0 , dW=0 熵判据:孤立系统内部任何自发过程总是 朝熵增加的方向进行,当熵达到最大值时,系 统达到平衡态。
二、自由能及自由能判据
1.自由能的定义 F = U − TS 2.自由能判据
等温过程系统吸热: Q ≤ T ( S B − S A ) 根据热力学第一定律 U B − U A = W + Q 则 - W ≤ (U A − U B ) − T ( S A − S B ) 即 - W ≤ FA − FB
最大功原理:在等温过程中,系统对外所 作的功不大于其自由能的减少。
等温等容: dT = 0, dV = 0, dW = 0 FB − FA ≤ 0
自由能判据:在等温等容过程中,系统的自由 能永不增加,系统中发生的不可逆过程总是朝 自由能减少的方向进行。当自由能达到最小值 时,系统达到平衡态。
3.吉布斯函数及吉布斯函数判据
吉布斯自由能的定义

吉布斯自由能的定义自由能是热力学中一个重要的概念,它描述了系统在恒温恒压条件下的可用能量。
吉布斯自由能(Gibbs free energy)是由美国化学家吉布斯提出的,用来描述一个系统在恒温恒压条件下的稳定性和可逆性。
吉布斯自由能的定义可以帮助我们理解化学反应的方向和速率,以及系统是否能够达到平衡状态。
吉布斯自由能的定义包括以下几个要点:首先,吉布斯自由能是一个状态函数,它只与系统的初始状态和最终状态有关,而与系统变化的路径无关。
其次,吉布斯自由能可以用以下公式表示:ΔG = ΔH - TΔS,其中ΔG表示系统的吉布斯自由能的变化,ΔH表示系统的焓变,ΔS表示系统的熵变,T表示系统的温度。
当ΔG小于0时,系统是稳定的,反应是自发的;当ΔG等于0时,系统处于平衡状态;当ΔG大于0时,系统是不稳定的,反应是不自发的。
吉布斯自由能的定义对于化学反应的研究具有重要意义。
在化学反应中,如果一个反应的ΔG小于0,那么这个反应是自发的,反应物会转化为生成物,释放出能量;如果一个反应的ΔG大于0,那么这个反应是不自发的,需要外界输入能量才能进行;如果一个反应的ΔG等于0,那么这个反应处于平衡状态,反应物和生成物的浓度保持不变。
吉布斯自由能的定义也可以应用于生物学领域。
生物体是开放系统,需要不断输入能量来维持生命活动。
通过吉布斯自由能的计算,可以了解生物体内各种代谢反应的稳定性和动力学特性,从而更好地理解生物体内的能量转化过程。
吉布斯自由能的定义是热力学中一个重要的概念,它描述了系统的稳定性和可逆性,对于化学反应和生物代谢过程的研究具有重要意义。
通过对吉布斯自由能的理解,我们可以更深入地了解能量转化的规律,为科学研究和工程应用提供重要参考。
希望本文能够帮助读者更好地理解吉布斯自由能的定义及其在热力学中的应用。
吉布斯函数

吉布斯函数,即吉布斯自由能(G)。
ΔG=ΔH-TΔS
式中H为焓;T为热力学温度;S为熵。
在恒温恒压和理想状态下,一个化学反应能够做的最大有用功等于反应后吉布斯自由能的减少;而反应自发性的正确标志也正是它产生有用功的能力。
因此,从某一反应的吉布斯自由能变量ΔG可以判断反应能否自发进行;ΔG<0时,反应在恒温恒压下可以产生有用功,因而反应是自发的;ΔG>0 时,反应是非自发的;ΔG=0 时,反应体系处于平衡状态。
从公式ΔG=ΔH-TΔS 看,化学反应的推动力(ΔG)依赖于两个量:①形成或断开化学键所产生的能量变化(ΔH);②体系无序性变化与温度的乘积。
这个公式后来被称为吉布斯方程。
它是化学中最有用的方程之一。
自吉布斯方程为化学界普遍接受后,人们终于从本质上辨明了化学反应的推动力。
过去一切有关的含糊不清的概念得到了澄清。
ch.2-1 内能、焓、自由能和吉布斯函数的全微分

(循环关系)
(链式关系)
(复合函数求导法)
2z 2z = xy yx
(全微分条件法)
① 基本方程记忆规则
a.函数的相邻两量为自变量,对应两量为系数。 b.箭头离开系数,取负;箭头指向系数,取正。 例如,与U相邻的两自变量分别为S和V,对应的系数为T和 p,前者箭头指向系数,后者箭头离开系数,故可写出
dU=TdS-pdV
用同样的方法,可方便的写出其他三个基本方程。
② 八个偏导数的记忆方法
由(2.1.2)式dH=TdS+Vdp ,有
H H T , V S p p S
(2.1.6)
由(2.1.3)式dF=-SdT-pdV ,有
F S , T V F p V T (2.1.7)
从四个基本方程出发,利用系数比较法,可很方便地写 出八个偏导数。例如,由dU=TdS-pdV出发,设U=U(S,V), 写出U的全微分,然后比较系数,即可得到
③ 麦氏关系的记忆方法
沿顺时针方向,例如,从S出法,S对V求导T不变,等 于p对T求导V不变。箭头都指向不变量或都离开不变量取 正,一个指向不变量,而一个离开不变量则取负,得
S V T p p T
热力学关系的记忆方法
四个基本方程,八个偏导,四个麦 氏关系。 首先,画两正交箭头,从上到下为 S→T,从左到右为P→V。 为了便于记住箭头的方向,可默读 一个英文句子: The Sun is pouring down his rays upon the Trees, and the brook is flowing from the Peak to the Valley. 然后,按顺时针方向加上E(=U)、F、 G和H。
内能晗自由能和吉布斯函数全微分记忆顺口溜

内能晗自由能和吉布斯函数全微分记忆顺口溜内能的全微分顺口溜:内能全微分,记清记明现在。
熵变热交与工过程表达我用它。
温度压强体积不说变化量就以du。
吉布斯函数全微分顺口溜:吉布斯全微分,内容真全面。
化学势等熵增温度压强凭借它。
迈尔关系慢慢用变化量就以dG。
在热力学中,内能和吉布斯函数是两个重要的物理量。
它们的全微分描述了系统的变化过程中的能量变化和物理性质的变化。
以下是对这两个全微分的顺口溜解释。
首先是内能,内能全微分的表达方式是dU。
内能是系统中分子的平均能量,它受到熵变、热交和功的影响。
在内能的全微分中,我们需要记住以下要点:- 系统的熵变(entropy change)和热交(heat exchange)与内能有关。
- 进行的过程可以通过表达式表示,我们用它(we use it)来描述。
-温度、压强和体积的变化通常会对内能产生影响,但在这个表达中我们不明确指出。
- 整个过程的变化量可以用du来表示,du是内能的全微分符号。
接下来是吉布斯函数,吉布斯函数全微分的表达方式是dG。
吉布斯函数是系统的自由能,在化学过程中具有重要的意义。
-吉布斯函数的全微分对系统的变化进行了全面描述。
-化学势的变化和熵的增加与吉布斯函数存在关系。
-温度、压强也与吉布斯函数有关,它们是这个表达式的关键因素。
-迈尔关系是一个重要的概念,使用它可以推导出吉布斯函数与其他物理性质之间的关系。
-整个过程的变化量可以用dG来表示,dG是吉布斯函数的全微分符号。
通过这样的顺口溜,我们可以更加容易地记住内能和吉布斯函数的全微分表达方式,并更好地理解它们在热力学中的作用和意义。
第二章 热力学函数及关系

d (U 0HM ) TdS pdV 0MdH 定义包括了磁介质在磁场中势能的内能:U * U 0HM ,则
dU * TdS pdV 0MdH
24
定义磁介质系统的吉布斯函数:G U * TS pV ,那么
dG SdT Vdp 0MdH
因为G是一个态函数,存在全微分,即在数学上
21
它常决定物体的性质,可看成是一个热力学系统, 状态参量:温度T、表面张力σ、表面积ξ。 物态方程:f (T,σ,ξ)=C, 外界对系统所做的功为
A d
dF SdT d
S F , T
F
T
注意:表面积扩大系外界对系统做功的结果,因此对于非气体 系统的广义位型变化前加一个负号。
22
下面这个图是解释表面张力的一个理想试验。一个光滑的金属 框,有一边是可以自由滑动的。把这个框在水里浸一下,框里 就形成一层水膜。水膜有上下两个表面。表面上的水分子有使 表面减小的倾向,所以必须施加一定的力F才能对抗这个力从 而保持住水膜面积。很显然,这个力F的大小与那个边的长度l 成正比。而这个比例是水的一种基本性质,与力F 和边l无关。 在界面科学里,这个比例被定义为表面张力,它的单位是力除 以长度,牛顿/米。
dG
G T
p,H
dT
G p
T
,H
dp
G H
T
,
p
dH
比较以上两个等式的右边对应项,可得
0M
G H
, T , p
V
G p
T ,H
对两者求混合偏导,有
0M
p
T
,
H
V H
T , p
此式将压缩效应(左边)与磁致伸缩效应(右边)
第三章 热力学第二定律
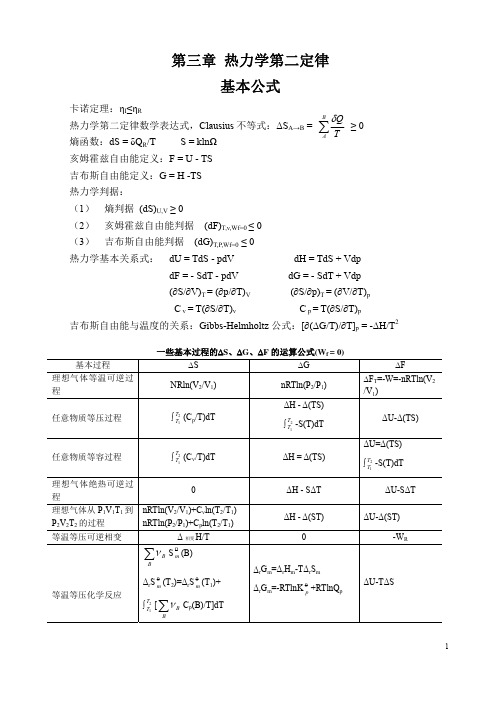
第三章热力学第二定律基本公式卡诺定理:ηI≤ηR热力学第二定律数学表达式,Clausius不等式:ΔS A→B = ∑BATQδ≥ 0熵函数:dS = δQ R/T S = klnΩ亥姆霍兹自由能定义:F = U - TS吉布斯自由能定义:G = H -TS热力学判据:(1) 熵判据 (dS)U,V≥ 0(2) 亥姆霍兹自由能判据(dF)T,v,Wf=0 ≤ 0(3) 吉布斯自由能判据(dG)T,P,Wf=0≤ 0热力学基本关系式:dU = TdS - pdV dH = TdS + VdpdF = - SdT - pdV dG = - SdT + Vdp(∂S/∂V)T = (∂p/∂T)V(∂S/∂p)T = (∂V/∂T)pC v = T(∂S/∂T)v C p = T(∂S/∂T)p吉布斯自由能与温度的关系:Gibbs-Helmholtz公式:[∂(ΔG/T)/∂T]p = -ΔH/T2一些基本过程的ΔS、ΔG、ΔF的运算公式(W例题例1 一个理想卡诺热机在温差为100K的两个热源之间工作,若热机效率为25%,计算T1、T2和功,已知每一循环中T1热源吸热1000J,假定所作的功W以摩擦热的形式完全消失在T2热源上,求该热机每一循环后熵变和环境的熵变。
解:卡诺热机效率η = (T2 - T1)/T225% =100K/T2, T2=400K, T1 = 300K热机效率定义:η = W/Q2η = W/(Q1+ W), 25% =W/(1000J + W), W =333.3JQ2 = W/η = 333.3J/25% = 1333JΔS体 =0(热机循环一周回到原态)由题意知,热机对环境所作的功完全以摩擦热的形式释放在T2热源上。
故T2热源得到了W的热量。
放出了Q2的热量。
ΔS环 =Q环,1/T1 + Q环,2/T2 = Q1/T1 + (Q2+W)/T2=1000J/300K + (-1333+333.3)J/400K =0.83J.K -1例2 有一绝热体系,中间隔板为导热壁,右边容积为左边容积的2倍,已知气体的C V,m = 28.03 J.mol-1,试求:1mol O2 273K 2mol N2 298K(a)不抽掉隔板达平衡后的ΔS ;(b) 抽去隔板达平衡后的ΔS。
自由能

意义:
① 当G < 0时, Wmax< 0,表明自由能被用来
对环境作最大有用功,是自发过程。
② 当G > 0时, Wmax> 0, 表明过程非自发,要使过程进行,必须由 环境对体系做功。 问题:G是否为状态函数? ③ 自由能是状态函数
4
二、吉布斯-赫姆霍兹方程
(Gibbs–HelmnoltzEquation): G = H TS G(T) = H TS 应用条件?
7
五、热力学函数的变化
1. G (T) = H TS,
2. G = Wmax 。 G > 0, Wmax > 0,非自发过程 G < 0 ,Wm < 0,是自发过程 G是过程自发性的判据; G > 0:非自发过程, G < 0:自发过程
8
rHm > 0,rSm < 0 G > 0 rHm > 0,rSm > 0 G = H TS 低温时 G > 0 高温时 G 有可能< 0 rHm < 0, rSm < 0 低温时 G< 0 高温时 G > 0
解: CaCO3(s) CaO(s) + CO2(g) fHm /kJ· mol-1 -1206.9 -635.1 -393.5 Sm /J· mol-1K-1 92.9 39.7 213.6 fGm /kJ· mol-1 -1128.8 -604.2 -394.4 298K时: rGm = -394.4 - 604.2 + 1128.8 = 130.2 kJ· mol-1 298K时非自发 rHm = 178.3 kJ· mol-1, rSm = 164.4 J· mol-1K-1 该反应在高温下自发,反应的温度为: rGm = rHm - T rSm 0 T rHm /rSm = 178.3 103/164.4 = 1111 K
吉布斯自由能详细资料大全

吉布斯自由能详细资料大全吉布斯自由能(Gibbs free energy)在化学热力学中为判断过程进行的方向而引入的热力学函式。
又称自由焓、吉布斯自由能或自由能。
自由能指的是在某一个热力学过程中,系统减少的内能中可以转化为对外做功的部分。
自由能(free energy)在物理化学中,按照亥姆霍兹的定容自由能F与吉布斯的定压自由能G的定义。
吉布斯自由能是自由能的一种。
基本介绍•中文名:吉布斯自由能•外文名:Gibbs free energy•拼音:jibusi ziyouneng•别称:吉布斯函式•相关领域:热力学•表示字母:G简介,提出,定义,特点,等温公式,物理意义,自由能,平衡常数,原理,简介吉布斯自由能又叫吉布斯函式,(英Gibbs free energy,Gibbs energy or Gibbs function; also known as free enthalpy)是热力学中一个重要的参量,常用G表示,它的定义是: G = U − TS + pV = H − TS,其中U是系统的内能,T是温度(绝对温度,K),S是熵,p 是压强,V是体积,H是焓。
吉布斯自由能的微分形式是:dG = −SdT + Vdp + μdN,其中μ是化学势,也就是说每个粒子的平均吉布斯自由能等于化学势。
提出1876年美国著名数学物理学家,数学化学家吉布斯在康乃狄克科学院学报上发表了奠定化学热力学基础的经典之作《论非均相物体的平衡》的第一部分。
1878年他完成了第二部分。
这一长达三百余页的论文被认为是化学史上最重要的论文之一,其中提出了吉布斯自由能,化学势等概念,阐明了化学平衡、相平衡、表面吸附等现象的本质。
ΔG=ΔH-TΔS (Kj/mol)G叫做吉布斯自由能。
因为H、T、S均为状态函式,所以G为状态函式。
吉布斯自由能相关书籍封面(1)特点ΔG叫做吉布斯自由能变吉布斯自由能的变化可作为恒温、恒压过程自发与平衡的判据。
第二章 自由能、化学势和溶液 公式

第二章 自由能、化学势和溶液 公式1.第一和第二定律的联合公式为2.吉布斯自由能定义式G = U + PV – TS = H – TS △G = △H -T △S(G----体系的状态函数, ( J ) , 绝对值无法测量 ) 3.在定温定压下,有如下关系: ΔG=W’最大4.吉布斯自由能判据< 不可逆过程, 自发过程 = 可逆过程, 平衡态 > 反方向为自发过程5.判断过程方向及平衡条件的总结6定压下.对任意相变或化学变化 7.定温物理变化∆G 的计算(W’=0的封闭体系). 理想气体定温过程. 纯液体或纯固体的定温过程0≥'+--W dV P dU dS T e eδ0,,≤'W P T dG 0,,≤∆'W P T G S TGP ∆-=∂∆∂)(⎰⎰===∆212112ln P P P P T P P nRT dP PnRT dP V G ⎰-==∆21)(12P P l l T P P V dP V G ⎰-==∆21)(12P P s s T P P V dP V G. 定温定压可逆相变 dG = -SdT + VdP dT =0 dP =0 ∆G T , P, W' = 0。
定温定压不可逆相变必须设计可逆过程 来求算, 由于△G 定温条件下的计算公式简单, 因此设计定温变压可逆途径 求解. 而计算不可逆相变的 ∆H 和 ∆S 时 , 是设计定压变温可逆途径进行求解.8.化学反应∆G 的计算 化学反应△ r Gm θ的计算 。
由物质的△fGm θ求算△rG θm = ∑νB △fG θm ,B 。
由反应的△rH θm 和 △rS θm 求算 △rG θm = △rH θm - T △rS θm 。
估计该反应能自发进行的最高温度< 0 不可逆过程, 自发过程 △rG θm = △rH θm - T △rS θm = 0 可逆过程, 平衡态> 0 反方向为自发过程 9.在指定压力下温度对反应自发性的影响 10.偏摩尔量的定义式: 条件:定温定压(Z 代表任一广度性质 )对于纯物质的均相系统,偏摩尔量即为该物质的摩尔量11.偏摩尔量的集合公式12.化学势定义式13.化学势(偏摩尔吉布斯自由能)集合公式在一定的温度, 压力和浓度的条件下,多组分体系处于一定的状态, 体系的吉布斯自由能可用下式计算纯组分:K S H T mrm r 3144241012.1333=-⨯-=∆∆=θθ)B (,,,≠⎪⎪⎭⎫ ⎝⎛∂∂=j n P T B mB j nz Z m P T m B V nVV =∂∂=,,)(∑=Bm B B Z n Z ,jn P T ii n G,,(∂∂=μ∑=B BB n G μmG nG ==μ14.化学势与温度的关系15.化学势与压力的关系16.化学势判据在定温、定压、W ´=0 的封闭体系中< 自发过程≤ 0 = 可逆过程或平衡态> 反方向为自发过程17.化学势判据与相平衡设在定温、定压、W ´=0 的条件下, 有dni mol 的 i 物质从 α相转移到 β 相,dG T, P, W ´=0 = (μi β -μi α)dni(1)若 μi β < μi α 则 dG < 0 ; 物质从α→β相的转移 是自发过程; (2)若 μi β > μi α 则 dG > 0 ; 物质从β→α相的转移是自发过程; (3)若 μi β = μi α 则 dG = 0 ; 体系处于相平衡状态. 18.化学势判据与化学平衡对定温、定压、W ´= 0 ,且 ξ = 1mol 的化学反应 a A + b B → g G + h H< 0 , 反应正方向自发= 0 , 反应达到平衡 > 0 , 逆反应方向自发( 定T , 定P , W ´ = 0 的封闭体系 , 化学反应方向与限度的判据. 由化学势高的物质自发生成化学势低的物质) 19.气体的化学势与标准态mB n P B S T ,,)(-=∂∂∑μmB n T B V P,,)(=∂∂∑μ∑=B B dn dG μBA H G BB m b a h g rG μμμμμν--+==∆∑20.拉乌尔定律 (PA,PA*分别表示定温时稀溶液中的溶剂的饱和蒸气压与该温度时的纯溶剂的饱和蒸气压,xA 是溶液中溶剂的摩尔分数).溶液的蒸气压下降∆p =p*-p = p* - p*xA =p*(1-xA)= p*xB .溶液沸点升高∆tb = tb -tb* = Kb. bB (Kb ——沸点上升常数,与溶剂有关。
自由能

自由能free energy其他名称:亥姆霍兹函数(Helmholtz function)定义1:热力系工质的一种状态参数,等于内能减去绝对温度与熵之积。
应用学科:电力(一级学科);通论(二级学科)定义2:在恒温、恒压条件下,体系中可用于做功的能量。
符号为“G”。
应用学科:细胞生物学(一级学科);细胞生理(二级学科)以上内容由全国科学技术名词审定委员会审定公布求助编辑百科名片自由能free energy :在热力学当中,自由能指的是在某一个热力学过程中,系统减少的内能中可以转化为对外作功的部分,它衡量的是:在一个特定的热力学过程中,系统可对外输出的“有用能量”。
可分为亥姆霍兹自由能和吉布斯自由能目录生物反应中的自由能自由能的分类自由能做功化学反应中的自由能生物反应中的自由能呼吸链中电子对传递时自由能的变化自由能free energy 在物理化学中,按照亥姆霍兹的定容自由能F与吉布斯的定压自由能G的定义,G=A+PV (p为压力,V为体积)。
在生物的反应中,因为△(PV)可以忽略不计,所以两者是相同的。
只有这样,A的变化△A=△U-T△S 才成为主要讨论的问题(U、T、S分别是该系统的内能、绝对温度、熵)。
△A给出了生物反应中释放出来可用于做功的能量上限。
其变化量(一般用△G*表示)在生物学上使用时必须注意下列事项:(1)水的活度,可随意设为1.0进行计算:(2)因[H+]=1M并不符合实际情况,一般认为[H+]=10-7M(pH7),为了区别其符号写成△G0′;(3)例如反应,因各种成分并非标准浓度(1M),把实际浓度代入下式后其值△G′就有问题了;(4)在共轭反应中,要注意各种成分反应的变化量之和;(5)把△G0改为用平衡常数[1](Keq)表示,往往是很有用的。
例如在25℃下△G0=-RT1nKeq=-1363log10Keq自由能的分类亥姆霍兹自由能设体系从温度为T环的热源吸取热量δQ,根据第二定律的基本公亥姆霍兹dS - δQ/T环≥0;代入第一定律的公式δQ=dU十δW,得δW≤-(dU-T环ds)若体系的最初与最后温度和环境的温度相等,即T1=T2=T环,则δW≤- d (U-Ts) (.2.27)令F===U-TS (中间横线上为def) (2.28) ,F称为亥姆霍兹自由能(Helmholz free energy),亦称亥姆霍兹函数,又称为功函(work function),它显然是体系的状态函数。
吉布斯自由能

吉布斯自由能[编辑]维基百科,自由的百科全书(重定向自生成吉布斯自由能)跳转至:导航、搜索本条目需要补充更多来源。
(2014年10月31日)请协助添加多方面可靠来源以改善这篇条目,无法查证的内容可能会被提出异议而移除。
吉布斯自由能(英语:Gibbs free energy),或称吉布斯函数(Gibbs function)、自由焓(Free Enthalpy)是热力学中描述等温、等压过程的一个重要参量,常用表示,它的定义是:,其中是系统的内能,是温度,是熵,是压强,是体积,是焓。
吉布斯自由能的微分形式是:,其中是化学势。
一个重要的推论是。
也就是说每个粒子的平均吉布斯自由能等于化学势。
目录[隐藏]∙ 1 物理意义∙ 2 生成吉布斯自由能o 2.1 部分物质的生成自由能[1]∙ 3 范特霍夫等温公式∙ 4 吉布斯自由能与熵和焓o 4.1 推导o 4.2 相变∙ 5 吉布斯自由能与平衡常数∙ 6 吉布斯自由能与电化学∙7 参阅∙8 参考文献物理意义[编辑]在标准状况下,存在一个一般规律:“任何一个封闭系统都尽量使自由能最小”因此,根据这个自然界的基本趋势,如果对于一个潜在反应,距离这个最小值进行定量测量,当热力学的计算显示吉布斯自由能ΔG的变化是负值的时候。
本质上,这表明了那样一个反应更容易发生并且将释放能量。
释放的能量等于这个化学反应所能够做的最大的功。
相反,如果ΔG为正值,能量必须通过做功的方式进入反应系统使得此反应能够进行。
吉布斯自由能的物理含义是在等温等压过程中,除体积变化所做的功以外,从系统所能获得的最大功。
换句话说,在等温等压过程中,除体积变化所做的功以外,系统对外界所做的功只能等于或者小于吉布斯自由能的减小。
数学表示是:如果没有体积变化所做的功,即,上式化为:也就是说,在等温等压过程前后,吉布斯自由能不可能增加。
如果发生的是不可逆过程,反应总是朝着吉布斯自由能减少的方向进行。
特别地,吉布斯自由能是一个广延量,单位摩尔物质的吉布斯自由能就是化学势,也就是说。
化学反应的自由能变化

化学反应的自由能变化自由能是描述化学反应在常温下能否自发进行的重要指标之一。
通过计算反应体系的自由能变化,可以判断反应的可逆性及其驱动力。
本文将介绍自由能的概念、计算自由能变化的方法以及自由能变化对化学反应的影响。
一、自由能的概念自由能是热力学中的重要概念,表示了化学反应在常温下能否自发进行。
它由吉布斯自由能(Gibbs free energy)或哈耳自由能(Helmholtz free energy)来描述。
1. 吉布斯自由能(Gibbs free energy):吉布斯自由能是指在恒定温度和压力下,化学体系发生变化时可以做可逆功的最大能量。
它的数学表达式为:$$G=H-TS$$其中,G代表吉布斯自由能,H代表焓,T代表温度,S代表熵。
2. 哈耳自由能(Helmholtz free energy):哈耳自由能是指在恒定温度和体积下,化学体系发生变化时可以做可逆功的最大能量。
它的数学表达式为:$$A=U-TS$$其中,A代表哈耳自由能,U代表内能,T代表温度,S代表熵。
二、计算自由能变化的方法化学反应的自由能变化可以通过化学平衡常数(K)和标准自由能变化(ΔG°)之间的关系进行计算。
具体计算方法如下:1. 标准自由能变化(ΔG°):标准自由能变化指的是在标准状态下,反应物转化为生成物时的吉布斯自由能变化值。
计算公式如下:$$\Delta G^{\circ}=\sum \nu_{i} \Delta G_{i}^{\circ}$$其中,ΔG°代表标准自由能变化,νi代表生成物(产物)的系数,ΔGi°代表生成物(产物)的标准摩尔自由能变化。
2. 化学平衡常数(K)与自由能变化之间的关系:对于一般化学反应:$$aA+bB\rightarrow cC+dD$$其化学平衡常数(K)与反应的标准自由能变化(ΔG°)满足以下关系:$$\Delta G^{\circ}=-RT \ln K$$其中,R为理想气体常数,T为温度,K为化学反应的平衡常数。
吉布斯自由能

热力学第二定律:论述在一定条件下变化过程进行的 方向与限度,及相平衡与化学平衡的有关问题。
热力学第三定律:研究低温下物质的运动状态及标准 熵的数值。
“在0 K时,任何完整晶体(只有一种排列方式)的 熵等于零。”
热力学方法
i
( Qi Ti
)R
0
或
Q
( T )R 0
R---可逆 δQR ----表示无限小可逆过程的热效 应
T----热源的温度,在可逆过程中也 是体系的温度
——克劳修斯原理
用一闭合曲线代表任意可逆循环。
在曲线上任意取A,B两点,把循环分成AB和 BA两个可逆过程。
根据任意可逆循环热温商的公式:
对于隔离体系 环境与体系间既无热的交换,又无功的交换,
dSiso 0
或ΔSiso ≥ 0
“>” 号为自发过程 “=” 号为可逆过程或平衡态
即 隔离体系内的一切实际过程都是向着熵增大的方 向进行/隔离体系的熵永远不减少。
∵环境不作用于隔离体系 ∴隔离体系中所发生的任何不可逆过程必然是自发过程
有时把与体系密切相关的环境也包括在一起, 当作一个隔离体系,即:
Q
( T )R 0
可分成两项的加和
B Q
( AT
)R1
A Q
( BT
)R2
0
移项得:
B A
(
Q T
)R1
ቤተ መጻሕፍቲ ባይዱ
B A
(
Q T
)R2
说明任意可逆过程的热温商 的值决定于始终状态,而与可 逆途径无关,这个热温商具有 状态函数的性质。
热力学与统计物理第二章知识总结

§内能、焓、自由能和吉布斯函数的全微分热力学函数中的物态方程、内能和熵是基本热力学函数,不仅因为它们对应热力学状态描述第零定律、第一定律和第二定律,而且其它热力学函数也可以由这三个基本热力学函数导出。
焓:自由能:吉布斯函数:下面我们由热力学的基本方程(1)即内能的全微分表达式推导焓、自由能和吉布斯函数的全微分焓、自由能和吉布斯函数的全微分o焓的全微分由焓的定义式,求微分,得,将(1)式代入上式得(2)o自由能的全微分由得(3)o吉布斯函数的全微分(4)从方程(1)(2)(3)(4)我们容易写出内能、焓、自由能和吉布斯函数的全微分dU,dH,dF,和dG独立变量分别是S,V;S,P;T,V和T,P所以函数U(S,V),H(S,P),F(T,V),G(T,P)就是我们在§将要讲到的特性函数。
下面从这几个函数和它们的全微分方程来推出麦氏关系。
二、热力学(Maxwell)关系(麦克斯韦或麦氏)(1)U(S,V)利用全微分性质(5)用(1)式相比得(6)再利用求偏导数的次序可以交换的性质,即(6)式得(7)(2)H(S,P)同(2)式相比有由得(8)(3)F(T,V)同(3)式相比(9)(4)G(T,P)同(4)式相比有(10)(7),(8),(9),(10)式给出了热力学量的偏导数之间的关系,称为麦克斯韦()关系,简称麦氏关系。
它是热力学参量偏导数之间的关系,利用麦氏关系,可以从以知的热力学量推导出系统的全部热力学量,可以将不能直接测量的物理量表示出来。
例如,只要知道物态方程,就可以利用(9),(10)式求出熵的变化,即可求出熵函数。
§麦氏关系的简单应用证明1. 求选T,V为独立变量,则内能U(T,V)的全微分为(1)熵函数S(T,V)的全微分为( 2)又有热力学基本方程(3)由(2)代入(3)式得(4)(4)相比可得(5)(6)由定容热容量的定义得(7)2. 求选T 、P为独立参量,焓的全微分为(8)焓的全微分方程为(9)以T、P为自变量时熵S(T、P)的全微分表达式为(10)将(10)代入(9)得(11) (8)式和(11)式相比较得(12)(13)(14)3求由(7) (14)式得(15)把熵S看作T,V的函数,再把V看成T,P的函数,即对上式求全微分得∴代入(15)式得由麦氏关系得(16)即得证4、P,V,T三个变量之间存在偏导数关系而可证(17)§气体的节流过程和绝热膨胀过程气体的节流过程(节流膨胀)和绝热膨胀是获得低温的两种常用方法,我们利用热力学函数来分析这两种过程的性质一,气体的节流(焦耳---汤姆逊效应)1、定义:如图所示有一由绝热材料制成的管子,中间用一多孔塞(节流阀)隔开,塞子一边维持较高的压强P,另一边维持较低的压强P,在压力的作用下,气体由高压的一边经过多孔塞流向低压的一边。
化学反应的吉布斯自由能

化学反应的吉布斯自由能
一、啥是化学反应的吉布斯自由能
嘿,同学们!今天咱们来聊聊化学反应中的一个超级重要的概念——吉布斯自由能。
简单来说,吉布斯自由能就像是化学反应的“指南针”,它能告诉我们这个反应能不能自发进行。
比如说,有些反应不用外界帮忙,自己就能发生,像铁生锈啦,这就是自发反应。
而有些反应,必须得给它加点外力,比如通电啥的,才能进行,这就是非自发反应。
而吉布斯自由能就是判断一个反应是自发还是非自发的关键指标。
二、吉布斯自由能咋计算
那吉布斯自由能到底咋算呢?这可得用到一些公式啦。
一般来说,吉布斯自由能等于反应的焓变减去温度乘以熵变。
焓变呢,就是反应前后热量的变化。
熵变呢,就是混乱程度的变化。
温度嘛,就是咱们平常说的那个温度啦。
听起来有点复杂,是不?但其实只要把相关的数据带进公式里,就能算出吉布斯自由能的大小啦。
三、吉布斯自由能有啥用
算出来吉布斯自由能可太有用啦!如果吉布斯自由能是负数,那这个反应就能自发进行;要是正数,就得外界给点力才能进行;要是等于零,那反应就处于平衡状态。
在实际生活中,比如化工生产里,咱们可以通过计算吉布斯自由能来判断一个反应能不能大规模进行,能不能赚钱。
在研究化学反应的原理和方向上,吉布斯自由能也是超级重要的哦!
好啦,同学们,今天关于化学反应的吉布斯自由能就讲到这里啦,希望大家都能搞明白这个有趣又重要的概念!。
吉布斯自由能计算

在讨论单组份系统两相平衡时的温度与压力关系时, 则通过式( 3) 和等温等压下平衡时 ∃G = 0 的条
件,
得到
Clapeyron
方程:
dp dT
=
∃#∀H m T ∃#∀Vm
.
3 吉布斯自由能与化学平衡
对有化学反应的系统, 由式( 2) 讨论:
∀ ∀ dG = - SdT + Vdp +
B dnB = - S dT + V dp +
5 Li X, Grace J R, Watldnson A P, et a1. Equilibrium modeling of gasification: a free energy minimization approach and its application to a circulating fluidized bedcoal gasifier J . Fuel, 2001, 80( 2) : 195- 207.
对复相反应体系, 如果凝聚相均处于纯态, 不形成固溶体或溶液, 则 B ∃
&B (
& B
是纯凝聚相在
标准
压
力下的化学势) .
将研究体系中参入反应物质同一状态下的 B 表达式代入式( 6) 中, 得到化学反应的等温方程式 3 :
% ∃rGm =
∃rG
& m
+
RT ln
aVb B
( 9)
B
反应达到平衡时, ∃rGm =
BvB d%
B
B
在等温等压下, ∃rGm =
∀ G
%
T,
p
=
VB B
B
自发 0 平衡
自由能和吉布斯函数的全微分

自由能和吉布斯函数的全微分在第一章我们根据热力学的基本规律引出了三个基本的热力学函数,物态方程。
内能和熵,并导出了热力学的基本方程dU=TdS-pdV (2.1.1)不论连接两个平衡态的过程可逆与否,式(2.1.1)都是成立的。
因此,可以把式(2.1.1)理解为U 作为S.V 的函数的全微分表达式。
根据式( 1.6.5),焓的定义是H=U+pV 。
求微分,并将式(2.1.1)代入,即得dH=TdS-Vdp (2.1.2)式(2.1.2)是H 作为S ,p 的函数的全微分表达式。
根据式(1.18.3),自由能的定义F=U-TS 。
求微分,并将式式(2.1.1) 代入,即得dF= -SdT-pdV (2.1.3)根据式(1.18.7),吉布斯函数的定义是G=U-TS+Pv求微分,并将代入,即得dG=-SdT+VdP (2.1.4)式(2.1.4)是G 作为T ,p 函数的全微分的表达式。
函数U (S ,V ),H (S ,p ),F (T ,V )和G (T ,p )是在§2.5中将要讲到的特性函数的几个例子。
U 作为S ,V 的函数U=U (S ,V ),其全微分为 dU =(S U ∂∂)v dS+(S VU )∂∂dV 与式(2.1.1)比较,得 (S U ∂∂)v = T , (S VU )∂∂= p (2.1.5) 考虑到求偏导数的次序可以交换,即 V S U ∂∂∂2=SV U ∂∂∂2(VT ∂∂)S = --- (S p ∂∂)V (2.1.6) 类似地,由焓的全微分表达式(2.1.2)可得 (S H ∂∂)p = T ,(p H ∂∂)S = V (2.1.7) (pT ∂∂)S =(S V ∂∂)p (2.1.8) 由自由能的全微分表达式(2.1.3)可得 (T F ∂∂)V = -S , (V F ∂∂)T= -p (2.1.9) (V S ∂∂)T =(T p ∂∂)V (2.1.10) 由吉布斯函数的全微分表达式(2.1.4)可得(T G ∂∂)p = -S ,(pG ∂∂)t =V (2.1.5). (2.1.7). (2.1.9).和 (2.1.11).四式将S ,T ,P ,V 这四个量用热力学函数U ,H ,F ,G 的偏导表达出来。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014年9月17日星期三
第一章 热力学的基本定律
2014年9月17日星期三
第一章 热力学的基本定律
(2)若把不可逆过程包括在内,式(1.12.15)应写为
dG≤-SdT+Vdp-dW1 (1.12.17) 对于等温等压,且不存在非体积功情况下的系统,即 dT=0, dp=0,dW1=0的系统,过程进行的方向由 dG≤0 (1.12.18) 决定。它表明当吉布斯函数达到最小值时,系统达到平衡 态。即等温等压没有非体积功的系统中进行的过程吉布斯 函数绝不会增加,平衡态对应于吉布斯函数最小的状态。
2014年9月17日星期三
第一章 热力学的基本定律
2.自由能 F 定义: F=U-TS。 (1.18.8) 求F的全微分,并将(1.18.3)式代入,得 dF=-SdT-pdV (1.18.9) 上式是F作为T、V的函数的全微分表达式。自由能的性质 如下:
(1)若系统经历一等温的可逆过程, dT=0,由(1.18.9)式 知 dF = pdV.这表明在不可逆的等温过程中,系统所作的 体积功等于系统自由能的减少。自由能一词正是由此得来 的。内能分为两部分,一部分是束缚能TS,它不能被转变 为功;另一部分即自由能F,它可以被转变为功,因而是 “自由”的。
§1.18 自由能和吉布斯函数
上一章,我们导出了热力学基本方程 dU ≤ TdS+đW。 (1.18.2) 为讨论方便起见,将đW分为两部分: đW=-pdV+dW1, 其中,dW1是除体积膨胀时压强作的功以外,其它广义力 所作的功,简称为非膨胀功。对于可逆过程,如果只考虑 体积功,则上式可简化为 dU = TdS-pdV 。 (1.18.3) 上式是内能U作为S、V 的函数的全微分表达式,是今后经常 要用到的一个公式。
2014年9月17日星期三
第一章 热力学的基本定律
Q (3)如果考虑到非膨胀功 ,则由 S B S A T
代入 S S U B U A W B A
T
由F的定义,有
FB FA W
说明系统自由能的减少是在等温过程中从系统所能获 得的最大功(此结论也称为最大功定理)。
2014年9月17日星期三
2014年9月17日星期三 第一章 热力学的基本定律
(2)如果把不可逆过程包括在内,且只考虑体积功,则 式(1.18.9)应为 dF≤ -SdT-pdV。 (1.18.10)
若系统进行的是等温和等容过程,即dT=0, dV=0, 则过程进行的方向由下式决定 dF等容过程中,系统的自由能绝不增 加。当该系统达到平衡态时,自由能最小。
第一章 热力学的基本定律
下面讨论焓的性质: 如果系统经历一等压过程,dp=0,由(1.18.4)式得 (dH)p=(TdS)p=(dQ)p (1.18.5) 上式说明,等压过程中系统吸收的热量等于焓的增量。如 果把不可逆过程也考虑在内,则(1.18.4)式应为 dH ≤ TdS+Vdp (1.18.6) 若过程是绝热等压过程,即dS=0, dp=0, 则过程进行的方 向由 dH≤0 (1.18.7) 决定。即,对于绝热的等压过程,系统的焓绝不增加。当 焓达到最小值时,系统达到平衡态。
在上面的讨论中,我们给出了焓、自由能和吉布斯函 数的定义、物理意义以及在给定系统中过程进行方向的判 断方法。
2014年9月17日星期三 第一章 热力学的基本定律
另外,我们还应注意:焓、自由能和吉布斯函数都是广 延量,具有可加性,这从它的定义式以及广延量和强度量的 特性可以看出。公式(1.12.2)、(1.12.4)、(1.12.9)和(1.12.13)也 叫做热力学基本微分方程。后面将会看到,这四个基本微分 方程就是我们解决系统所有热力学问题的依据。
2014年9月17日星期三
第一章 热力学的基本定律
现在,我们在不同的外界条件下再引入几个新的态函 数,或称热力学函数。
1.焓H 定义: H=U+pV。 (1.18.4) 写出H的全微分,并将(1.18.3)代入,得 dH=TdS+Vdp (1.18.5) 上式是H作为S、p的函数的全微分表达式。
2014年9月17日星期三
第一章 热力学的基本定律
3.吉布斯函数G 定义: G=U-TS+pV。 (1.12.12) 求全微分,并将(1.12.2)式代入,得 dG=-SdT+Vdp (1.12.13) 上式是G作为T、p的函数的全微分表达式。
2014年9月17日星期三
第一章 热力学的基本定律
吉斯函数的性质如下: (1) 如果将系统对外界所作的功分为体积和非体积功两部分, 并考虑所进行的是可逆过程,则由式(1.12.1),有 dU=TdS-pdV+dW1 (1.12.14) 代入G的全微分中,得 dG=-SdT+Vdp-dW1 (1.12.15) 对于等温等压过程,dT=0, dp=0, 上式变为 -dG=dW1 (1.12.16) 上式说明,系统对外所作的非体积功等于系统吉布斯 函数的减少。这意味着系统中的能量有一部分能以非体积 功的形式被自由释放出来,因此,吉布斯函数也称为吉布 斯自由能。
