席位分配问题(含Jefforson的除子法)
席位分配问题数学建模

席位分配问题是一个常见的实际问题,涉及到资源的分配和管理。
为了解决这个问题,我们可以使用数学建模的方法,通过建立数学模型来分析和优化席位的分配方案。
一、问题描述假设有一个大型会议,需要分配给不同的参与者席位。
每个参与者可能有不同的资格和需求,我们需要根据一定的规则来分配席位。
具体问题包括:1. 参与者数量和席位数量2. 参与者的资格和需求3. 席位分配的规则和标准二、数学建模为了解决席位分配问题,我们可以使用以下数学模型:1. 参与者集合P:表示所有的参与者。
2. 席位集合S:表示所有的席位。
3. 资格矩阵A:表示每个参与者的资格情况,每一行表示一个参与者,每一列表示一个资格类型(例如,专业、身份等)。
4. 需求矩阵D:表示每个参与者对席位的需求情况,每一行表示一个参与者,每一列表示一个席位类型(例如,地点、时间等)。
5. 分配规则R:表示席位的分配规则和标准,如按照资格优先、按照需求优先、按照公平分配等。
根据以上描述,我们可以建立如下的数学模型:目标函数:最小化席位浪费(即席位数与参与者需求之差)约束条件:1. 资格约束:每个参与者的资格必须满足分配规则的要求。
2. 需求约束:每个参与者所需席位类型必须得到满足。
3. 数量约束:总的席位数必须不超过总席位数量。
4. 可行性约束:分配的席位必须是有效的,即不存在冲突和重复的情况。
三、求解方法根据上述数学模型,我们可以使用以下方法进行求解:1. 枚举法:逐个尝试所有可能的席位分配方案,找到满足约束条件的方案。
这种方法需要大量的计算时间和空间,但在某些情况下可能找到最优解。
2. 优化算法:使用优化算法如遗传算法、粒子群算法等,通过不断迭代找到最优解。
这种方法需要一定的编程知识和技能,但通常能够快速找到满意的解。
3. 启发式算法:使用启发式算法如模拟退火、蚁群算法等,通过不断尝试找到满意解。
这种方法相对简单易行,但可能无法找到最优解。
4. 数学软件求解:使用专门的数学软件如Matlab、Python等,通过编程求解上述数学模型。
数学论文席位的公平分配问题

数学建模论文席位的公平分配问题姓名:学号:18 15 20公平的委员分配问题摘要:1.我们首先是用惯例分配法来解决这委员分配问题的,由于方法来解决存在很大的缺陷,因此,通过组内的讨论,我们想出了Q值法来解决此问题,发现这样能作到相对公平。
我们这一组开始就考虑到了该怎样分配能作到相对公平,就这个问题,我们开始了研讨。
我们采用惯例分配法分析发现:各楼所得到的委员数A 、B 、C楼分别为:3、3、4人,而Q值法其结果为:A、B、C楼分别为:2、3、5人。
2.“取其精华,去其糟粕”我们发现Q值法能很好的解决委员分配问题,Q 值法:我们用Qi=(Pi*Pi)/[n(n+1)],其中i=A、B、C,Pi为第i楼的人数,n 为分配到的委员数,我们采用将剩下的一位委员名额分给Q值最大的一方。
通过计算得到Qa=9204.16、Qb=9240.75、Qc=9331.2比较得到:Qa>Qb>Qc,所以我们决定把剩下的一名委员分给C楼。
3.我们用惯例分配法发现有一名委员不好分配,不知道分给谁更公平些。
建议:我们的思维不能太单一了,在考虑问题方面要做到全面些,这样才会少走弯路。
(无论在哪方面都一样。
)关键字:委员分配、比例法、Q值法1.1问题的重述分配问题是日常生活中经常遇到的问题,它涉及到如何将有限的人力或其他资源以“完整的部分”分配到下属部门或各项不同任务中.分配问题涉及的内容十分广泛,例如:学校共有1000学生,235人住在A楼,333人住B楼,432人住C楼,学校要组织一个10人委员会,试用惯例分配法和Q值方法分配各楼的委员数并比较结果。
1.2问题的分析数学中通常人们用比例的方法来分配各个楼要派出几个人来组建委员会,当比例中有小数时人们有按照惯例使得各组中小数最大的组拥有更多的人数。
然而人们是怎样分配的呢?又因为没栋楼所占比例不是整数,可以会出现不公平的现象。
为了让席位分配更加公平我们不应该采用比例法,要引用不比例法更好的Q值法对其进行求解。
《离散模型——公平的席位分配》示范公开课教学PPT课件【高中数学人教版】

pi ni pi ni i=1 103 11 114 11 i=2 63 7 64 6 i=3 34 3 34 4 和 200 21 212 21
pi ni
pi
ni
103 10 114(+10.6%) 11
63 6 63
6
34 4 38(+11.8%) 3
200 20 215
20
“公平”分配方法 衡量公平分配的数量指标
模 已知: m方人数分别为 p1, p2,… pm, 记总人数 型 为 P= p1+p2+…+pm, 待分配的总席位为N.
记 qi=Npi /P, 称为第i方的份额(i =1,2, …m)
要 已知份额向量q=(q1, …, qm)>0, 找一个非负 求 整数分配向量n=(n1, …, nm), 使n与q最接近.
• 对于非负整数n定义一个非负单调增函数d(n) • 当总席位为s时第i方分配的席位记作fi(p, s), fi(p, 0)=0 • 让s每次1席地递增至N,按照以下准则分配:
记ni=fi(p, s),若
pk
/ d(nk )
Max
i 1, 2,, m
pi
/ d (ni )
则令fk(p, s+1)= nk+1, fi(p, s+1) = ni (i≠k)
公平的席位分配
8/10/2021
1
公平的席位分配
每十年,美国联邦政府进行一次全国人口普查(census)。 各州在联邦众议院的代表名额也据此重新确定。
2000年人口普查后,犹他州(Utah)向联邦政府提出 控诉,说分配给卡罗莱纳州的名额应该是他们的。
事实上,过去200年来,美国国会在名额分配上打过多 起法律官司,曾有过长期争论并用过四种分配方案。
数学建模论文-席位公平分配问题

数学建模论文-席位公平分配问题数学建模论文(席位公平分配问题)席位公平分配问题摘要本文讨论了席位公平分配问题以使席位分配方案达到最公平状态。
我主要根据了各系人数因素对席位获得的影响,首先定义了公平的定义及相对不公平的定义,采用了比例模型、汉丁顿模型和Q值模型制定了一个比较合理的分配方案。
首先,我根据相关资料的查阅,定义了公平的定义和不公平的定义以及不公平程度的定义和相对不公平数的定义以便来检验模型的公平性程度。
其次,我建立了一个比例模型,采用了比例相等的方法,列出一个关于所获席位与总席位数和各系人数与各系总人数的等式,进而求得所获席位数。
同时我建立了一D+Q值模型,通过汉丁顿模型和Q值模型的结合,最终得出一个比较合理的分配方案。
最后,我用相对不公平数来检验两个模型的公平性程度。
关键词:数学建模公平定义 Q值模型 d'Hondt(汉丁顿)模型1目录一、问题重述与分析: ................................... 3 1.1问题重述: ........................................ 3 1.2问题分析: ........................................ 3 二、模型假设 .......................................... 4 三、符号说明 .......................................... 4 四、模型建立: ........................................ 5 4.1公平的定义: ...................................... 5 4.2不公平程度的表示: ................................ 5 4.3相对不公平数的定义: .............................. 5 4.4模型一的建立:(比例分配模型) ...................... 6 4.5模型二的建立:(d'hondt模型和Q值模型) (6)五、模型求解 .......................................... 8 5.1模型一求解: ...................................... 8 5.2模型二的求解: .................................... 8 六、模型分析与检验 ..................................... 9 七、模型的评价: ...................................... 11 7.1、优点: ......................................... 11 7.2、缺点: ......................................... 11 7.3、改进方向: ..................................... 11 八、模型优化 ......................................... 11 九、参考文献 (12)2一、问题重述与分析:1.1问题重述:三个系学生共200名(甲系100,乙系60,丙系40),代表会议共20席,按比例分配,三个系分别为10,6,4席。
公平席位分配问题

200
学生人数比例 103/200 63/200 34/200
按比例分配席位 10.3
6.3
3.4
20
按惯例席位分配 10
6
4
20
惯例席位分配方法为:比例分配出现小数时,先按整数 分配席位,余下席位按小数的大小依次分配之
为改变总席位为偶数出现表决平局现象,决定增加一 席,总席位变为21个学生代表席位,还按惯例分配席位, 有
1032 1011
96.4
Q2
632 67
94.5
应该将席位分给甲
Q3
342 3 4
96.3
第21席的分配由Q值决定为
1032
632
Q1 1112 80.4 Q2 6 7 94.5
应该将席位分给丙
342 Q3 3 4 96.3
最后的席位分配 为:
Qi
pi2 ni (ni 1)
于是增加的席位分配由Qi的最小值决定,它可 以推广到一般情况,即n个组
模型求解
先按应分配的整数部分分配,余下的部分按Q值分配。
本问题的整数名额共分配了19席,具体 为
甲
10.815 n1=10
乙
6.615 n2=6
丙
3.570 n3=3
第20席的分配由Q值决定
Q1
1、 p1 p2 说明此一席给 A,对A还不公平,应给 A n1 1 n2
2、 p1 p2 说明此一席给A,对B不公平, n1 1 n2
不公平值为rB (n1
1, n2 )
(n1 1) p2 p1n2
1
3、p1 p2 说明此一席给B,还对A不公平, n1 n2 1
数学建模论文 - 席位公平分配问题1

数学建模论文(席位公平分配问题)席位公平分配问题摘要本文讨论了席位公平分配问题以使席位分配方案达到最公平状态。
我主要根据了各系人数因素对席位获得的影响,首先定义了公平的定义及相对不公平的定义,采用了比例模型、汉丁顿模型和Q值模型制定了一个比较合理的分配方案。
首先,我根据相关资料的查阅,定义了公平的定义和不公平的定义以及不公平程度的定义和相对不公平数的定义以便来检验模型的公平性程度。
其次,我建立了一个比例模型,采用了比例相等的方法,列出一个关于所获席位与总席位数和各系人数与各系总人数的等式,进而求得所获席位数。
同时我建立了一D+Q值模型,通过汉丁顿模型和Q 值模型的结合,最终得出一个比较合理的分配方案。
最后,我用相对不公平数来检验两个模型的公平性程度。
关键词:数学建模公平定义 Q值模型 d'Hondt(汉丁顿)模型目录一、问题重述与分析: (3)1.1问题重述: (3)1.2问题分析: (3)二、模型假设 (4)三、符号说明 (4)四、模型建立: (5)4.1公平的定义: (5)4.2不公平程度的表示: (5)4.3相对不公平数的定义: (5)4.4模型一的建立:(比例分配模型) (6)4.5模型二的建立:(d'hondt模型和Q值模型) (6)五、模型求解 (8)5.1模型一求解: (8)5.2模型二的求解: (8)六、模型分析与检验 (9)七、模型的评价: (11)7.1、优点: (11)7.2、缺点: (11)7.3、改进方向: (11)八、模型优化 (11)九、参考文献 (12)一、问题重述与分析:1.1问题重述:三个系学生共200名(甲系100,乙系60,丙系40),代表会议共20席,按比例分配,三个系分别为10,6,4席。
现因学生转系,三系人数为103, 63, 34, 问20席如何分配。
若增加为21席,又如何分配。
因此存在席位公平分配问题,以下针对各系自身人数对所获席位数目的影响建立相关模型,解得最优的席位公平分配方案。
席位分配问题

席位分配问题一、问题背景席位分配是日常生活中经常遇到的问题,对于企业、公司、学校、政府等部门都能解决实际的问题。
席位可是是代表大会、股东会议、公司企业员工大会等的具体座位。
二、问题提出学校共1000名学生,235人住在A宿舍,333人住在B宿舍,432人住在C宿舍.学生们要组织一个10人的委员会,试用下列办法分配各宿舍的委员数:(1). 按比例分配取整数的名额后,剩下的名额按惯例分给小数部分较大者;(2). 用?2.1中的Q值方法分配,要求编一个通用程序解决此类分配问题;(3).d’Ho ndt方法:将A、B、C各宿舍的人数用正整数n=1,2,3,……相除,其商数如下表:1 2 3 4 5A 235 117.5 78.3 58.75 …B 333 166.5 111 83.25 …C 432 216 144 108 86.4将所得商数从大到小取前10个(10为席位数),在数字下标以横线,表中A、B、C行有横线的数分别为2,3,5,这就是3个宿舍分配的席位.请解释此方法的原理,并编程求解。
(4)如果委员会从10个人增至15人,用以上3种方法再分配名额,将3种方法两次分配的结果列表比较.三、模型的建立与求解(1)通常分配结果的公布与否以每个代表席位所代表的人数相等或相近来衡量,目前沿用的惯例分配方法为按比例分配方法,即: 席位分配数总人数比例总席位数=,按比例分配取整数的名额后,剩下的名额按惯例分给小数部分较大者,所以分配情况如表一所示。
表一宿舍学生人数学生人数比例按比例分配的席位按惯例分配的席位A 235 0.235 2.35 3B 333 0.333 3.33 3C 432 0.432 4.32 4总和 1000 10 10 学生们要组织的10人的委员会,分配各宿舍的委员数分别为:A宿舍3人,B宿舍3人,C宿舍4人。
ipn(2)Q值法:有m方分配席位的情况,设第方人数为,已占有个席位,im,1,2,,.ii2pi当总席位增加1席时,计算应将这一席分给值最大的一方,Q,1,2,,Qim,,i(1)nn,ii这种席位分配方法称为值法。
关于代表席位公平分配问题

2 0
2 O
Z 1
2 1
们反而 比原来减 少 了一席 ) 这 一事 实 说 明, , 这种 “ 小数 即 , 总有若 干个 b 不 是 整数 . 尾数优先”的惯例 并非永 远合 理.文 [3因此提 出相对 1 任 何 一个 可行 的代表 席 位分 配方 案 不公平度的概念并建立 了 Q值方法 的数学 模型. 用这个 ( , 2 , m 1 … )
现在考 虑代表 席位 分 配 问题 的一 般情 形. 设某 社
团共有 m个 单位 , 数分 别 为 , … , 社 团总人 人 p , p,
例 1 人数 分别 为 1 3 3 3 0 ,6 和 4的 A, C三个 B, 单 位 的一个 2 0人 的代 表 会 议 , 一 届 按 照 人 数 比例 上
摘 要 针对代表 席位公平分 配问题及 Q值方 法模 型提出F值方法 和G值方法 的方差 最小模型 , 可获得与 Q
值 方 法 同样 结 果 , 比 Q值 方 法 较 为 简便 , 但 因为 无 须 用 小 数 尾 数 优 先 的 惯 例 先 作 出少 1席 的分 配 . 例说 明 在 某 些 实 情 况 下 Q值 方 法 可 能 给 出 不 正 确 的结 果 ; 者 不 能 作 出决 定 . 理 论 上 进 一 步 证 明 只要 所 涉 及 的 两 个 单 位 人 数 不 或 从
记 b 的小数 尾 数
C 3 4
1 7
34 .
4
350 . 7
3
r 一 b一l , j且 b
一k ,
总 合 0 1 0 20 0
若 k 0 则 每个 b都 是 整数 , 是绝 对公 平 的理 想情 一 , 这 增加一席的分配结果显然对单位 C不公平 ( 因为他 况 , 它一 般 很 难 出现 .实 际 上 ,k总 是 某 个 正 整 数 ,
【数学建模】公平席位的分配问题

【数学建模】公平席位的分配问题基础案列某展会,AB双⽅根据⼈数分配席位:衡量公平的数量指标: p1/n1=p2/n2。
此时对AB均公平。
p1/n1>p2/n2。
此时对A不公平,因为对A放来说,每个席位相对应的⼈数⽐率更⼤。
绝对不公平度定义: p1/n1-p2/n2 = 对A的绝对不公平度问题:/*情况1*/p1=150, n1=10, p1 /n1=15 p2=100, n2=10, p2 /n2=10/*情况2*/ p1=1050, n1=10, p1 /n1=105 p2=1000, n2=10, p2 /n2=100两者对A的不公平度相同,但是很明显后者对A的不公平成都已经⼤⼤降低。
相对不公平度定义:说明:由定义知对某⽅的不公平值越⼩,某⽅在席位分配中越有利,因此可以⽤使不公平值尽量⼩的分配⽅案来减少分配中的不公平使⽤不公平值的⼤⼩确定分配⽅案: 设A, B已分别有n1 , n2 席,若增加1席,问应分给A, 还是B 不妨设分配开始时 p1 /n1> p2 /n2 ,即对A不公平。
分情况讨论: 1. 2.,说明此以⼀席给A后,对B不公平,则计算对B的不公平度。
rB(n1+1,n2). 3.,说明此⼀席给B后,对A不公平,不公平值为,rA(n1,n2+1). 4.p1/n1<p2/n2+1,这种情况不可能出现。
上⾯的分配⽅法在第1和第3种情况可以确定新席位的分配,但在第2种情况时不好确定新席位的分配。
⽤不公平值的公式来决定席位的分配,对于新的席位分配,若有则应该增加给A⼀席,否则则应该增加给B⼀席。
提炼模型: ————>引⼊公式: 于是知道增加的席位分配可以由Qk的最⼤值决定,且它可以推⼴到多个组的⼀般情况。
⽤Qk的最⼤值决定席位分配的⽅法称为Q值法。
席位分配

1引言席位分配是一个非常有趣而重要的问题,它在政治学管理和对策论等领域具有广泛的应用价值。
处理的方法最早的有尾数最大法;然后是Q值法;1974年引入了席位分配问题的公理体系研究方法,并于1982年证明了同时满足五个所用的比例分配方法存在较大缺陷分配为11,7,3名额。
其结果是,单位增加一个先进名额后,丙部门反而减少了一个名额。
公理的席位分配方法是不存在的。
后又有一些新的算法,如:新值法,最大熵法,0-1规划法,法,值法最小极差法和最大概率法等。
但有时我们遇到大会上遇到少数情况,某个部门的人数较少,按上述方法分不到席位。
本文讨论的是“少数原则”下解决席位分配问题,在解决“少数原则”情况下较方便。
正文问题:2.1问题:在一次民族代表会中,有一个民族的人口在该国占有极少比例,但大会必须考虑政策给一个席位的分配资格。
如果我们遇到同样的问题该如何处理呢?下面我们给出少数分配的原则,并讨论在该特殊问题下的分配问题。
少数原则:在席位分配中,各部门都有分配资格,当席位数n大于单位(部门)数i时至少分配一个席位。
2.2问题的一般表述一个单位由m个部门组成,其中第i个部门的人数为ai (1)i m≤≤,学校总人数为a。
如果该单位需要召开一个由n个代表参加的代表大会,且每个部门尽可能分配一个名额,组织者必须把n个席位尽可能公平的分配到个部门中去。
记每个部门最后应分配到的席位数为ni ,试问ni是多少?模型假设要解决这样的问题首先必须舍弃原有的公平分配体系,让更多的部门拥有席位分配的资格,建立相对公平的指标。
建立数量指标首先我们必须讨论总席位数n和总部门数i之间的关系1)当n〈i时,由于不可能保证每个部门都可一分到席位,这时我们尽可能的让更多的部门分到席位,可以由D’Hondt法(备注2)中的ai/1来做比较,由值的大小来决定分配与否(由值的大小由大到小按顺序来排,依次给予一个席位直到分配完)2)当n=i时,由少数原则,每个部门必须分到,刚好每个部门分配一个3)当n〉i时,每个部门至少可以分到一个名额。
六、公平的席位分配
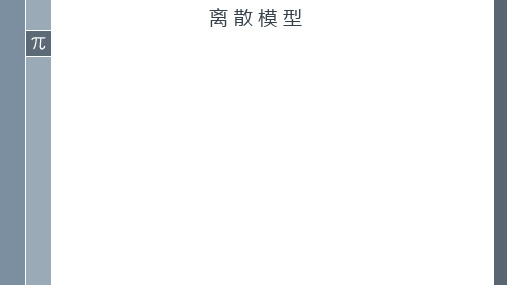
公平度 rA , rB 讨论当总席位增加1席时,应该分配给A还是B.
设 p1 / n1 p2 / n2 ,大于号成立时对A不公平。若增加的1席分配 给A, n1 就变为 n1 1 ;分配给B就有 n2 1 ,原不等式可能出现以 下3种情况。
p1 p2 1. n 1 n ,说明即使A增加1席仍然对A不公平,这一席显然应 1 2
是整数,所以通常 p1 / n1 p2 / n2 ,分配不公平,并且是对比值
较大的一方不公平。
不妨设 p1 / n1 p2 / n2,不公平程度可以用数值 p1 / n1 p2 / n2
衡量,但是这种衡量指标无法区分不公平程度明显不同的情况,
因此需要改进。 为了改进上述的绝对标准,自然想到用相对标准。定义 p1 / n1 p2 / n2 rA (n1 , n2 ) p2 / n2 为A的相对不公平度。若 p2 / n2 p1 / n1 ,定义 p2 / n2 p1 / n1 rB (n1 , n2 ) p1 / n1 为B的相对不公平度。
a1+a2+„+as=h, 怎么才能让第i州取得a i(i=1, 2, 3,„, s)个议员名额, 并且“尽可能地”满足美国宪法所规定的“按人口比例分配” 的原则?这就是“席位分配问题”。
例1.
某学校有3个系共200名学生,其中甲系100名,乙系60名,丙 系40名。若学生代表会议设20个席位,公平又简单的席位分配 办法是按学生人数的比例分配,显然甲乙丙三系应分别占10,6, 4个席位。
甲 乙 丙 总和
103 63 34 200
51.5 31.5 17.0 100
虽然从Q值法与最大剩余法对着具体问题不同的分配结果看,难以 对二者进行评判,可是Q值法不仅有明确的不公平度指标,而且由 于是每增加1席地计算Q值,所以不会出现席位悖论(也可以证明 不会出现人口悖论)。实际上,这个方法是20世纪20年代由哈弗 大数学家E.V.Huntington提出和推荐的一系列席位分配方法中的一 个。
最新席位分配PPT课件
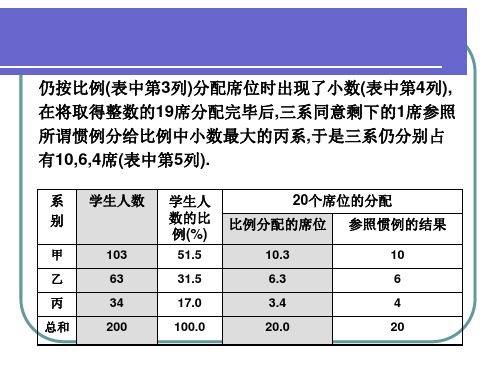
设第i方人数为pi,i=1,2…,m,总人数
m
P pi
,待
i 1
分配的席位为N, qi=N*(pi/P)为按比例的席位数,ni为理想
化的席位数。
n i 是N和pi的函数,记
ni ni(N ,p1, ,pm ),
q qi,qi 分别为 i 向左取整和向右取整。
原则一 按比例分配原则
q i n i q i , i 1 , 2 , , m , 即 n i 必 q i , q i 取 二者之一
同上.Q3最大,于是这一席应分给丙系. 这样,21个席位的分配结果是三系分别占有11,6,4席,丙 系保住了险些丧失的1席.你觉得这种分配方法公平吗?
席位分配表
前 系 学 学生 19 别 生 人数 席
人 的比 的 数 例(%) 分
配
甲 103 51.5 10
乙 63 31.5 6
丙 34 17.0 3
例:p1=11,n1=2,每5.5个人拥有一个席位。 p2=100, n2=20 ,每5个人拥有一个席位。 p1/n1>p2/n2
对A方不公平。试给A方加1席,因为 p1/(n1+1)<p2/n2 即11/3<5
所以,对B方不公平。相对不公平度为 rB =p2*(n1+1)/p1*n2 – 1=0.36=36/100
n11,0 n26,n33
然后再用Q值方法分配第20席和第21席. 第20席:计算
Q 1 1 1 1 0 2 0 1 9 3 .4 6 ,Q 2 6 6 2 7 3 9 .5 4 ,Q 3 3 3 2 4 4 9 .3 6 .
Q1最大
于是这一席应分给甲系.
第21席:计算 Q11110123280.4,Q2Q3
罗浩 2010562009

一:五种除数法.现在有5方人,共分配100个席位.记第i 方人数为p i,且记p =(p 1,p2,p3,p4,p5),P =∑=51i ip.席位的分配是寻求n =(n 1,n 2,n 3,n 4,n 5),其中n i 是第i 方分得的席位,满足∑=51i i n =N ,且均为非负整数.首先计算第i 方的精确的席位份额,记为q i ,显然q i =NPpi,i=1,2,3,4,5.若q i 为整数,令n i =q i 即可完成分配,否则,记[]q i为q i的整数部分,先将[]q i 分给第i 方,然后将尚未分配的r=[]∑=51i iq 个席位在作分配.五种除数法都是据公式)(n p ii d 来作为不公平指标来分配剩余的r 个席位,每增加一个席位就分配给)(n pii d 值大的,增加第二个席位时,分配到席位的)(n p iid 值改变,而其它方)(n piid 值不变,据此分配增加的第二个席位,再增加席位方法一样.最后通过利用五种除数法得出各组分配的席位数,如下表:p iq iGD MF EP HM SD1 5117 51.7 52 51 51 51 51 2 4400 44 45 44 44 44 443 162 1.62 1 2 2 2 24 161 1.61 1 2 2 2 25 160 1.60 1 2 2 2 2总和 10000 100 100 100 100 100 100二:最大剩余法(GR)解:设第i方人数为pi,已占有n i个席位(其中n i为第i方人数与总人数的比再乘上总席位数,然后通过取整函数取整所得),(i=1,2,3,4,5)题意得:p1=5117,n1=51;p2=4400,n2=44;p3=162,n3=1;p4=161,n4=1;p5=60,n5=1.现在5方人已经分得100个席位中的98个,还有2个未分配。
据Q值法公式Qi =)1(2+nnpiii.第99席:Q1=525151172⨯=9873.2,Q2=454444002⨯= 9777.8,Q3=21162⨯=13122,Q4=211612⨯=12960.5,Q5=211602⨯=12800.因为Q3最大, 所以将第99席分给第3方.第100席: 第3方增加一席之后Q3=321622⨯=4374,Q1,Q2,Q4,Q5同上,这时Q4最大,所以将第100席分给第4方.最后席位的分配如下表:即最后的席位分配为:第1方51个席位,第2方44个席位,第3方2个席位,第4方2个席位,第5方1个席位.三:份额法(QM)份额法即满足定义:第i方分配第s+1个席位合格是指n i〈qi=(s+1)Ppi(即不违反份额上线)的前提下,当s 每增加一个席位时,据公式E i =1+np ii来分配新增加的一个席位,而且将新增加的一个席位分给E i 值大的那个.设第i 方人数为p i ,已占有n i 个席位(其中n i 为第i 方人数与总人数的比再乘上总席位数,然后通过取整函数取整所得),(i=1,2,3,4,5) 题意得:p 1=5117,n 1=51;p 2=4400,n 2=44;p 3=162,n 3=1;p 4=161,n 4=1;p5=60,n 5=1.第99席:因为n 1=51〉99⨯100005117=(s+1)P p 1,n 2=44〉99⨯100004400=(s+1)Pp2,也就是说第99席如果分给第1方或第2方,此时的分配都是不合格的.现在只考虑第3,4,5方.因为E 3=81,E 4=80.5,E 5=80,此时E 3最大,且n 3=1〈10000162⨯100=1.6,即分配给第3方是合格的.所以将第99席分给第3方.第100席:因为n 1=51〈100⨯100005117=51.17,且此时E 1=98.4,E 2=97.8, E 3=54,E4=80.5,E 5=80,即E 1最大,所以将第100个席位分给第1方.所以最后的分配如下表:。
公平的席位分配

公平的席位分配问题提出:某学校有3个系⼀共200名学⽣,其中甲系100名,⼄系60名,丙系40名。
如果学校代表会议设置20个席位,怎样公平地分配席位?思考:按照传统的思维⽅式,按照每个系的⽐例进⾏席位的分配。
在该问题中,甲⼄丙三个系的⼈数⽐例为100:60:40=5:3:2。
因此按照这个⽐例进⾏席位的分配可以公平简单的实现席位分配。
但是上⾯的例⼦有些特殊,因为每个系的⼈数⽐例正好是整数,并且能够恰好分配所有的席位。
现在将问题进⼀步⼀般化。
假设甲系学⽣103⼈,⼄系学⽣63⼈,丙系学⽣34⼈。
此时甲⼄丙学⽣⼈数所占⽐例分⽐为51.5%、31.%、17.0%。
仍然分配20个席位,此时甲⼄丙按⽐例分配的席位个数分别为:10.3、6.3、3.4三个系进过协商同意将最后⼀个席位分配给⽐例中⼩数部分最⼤的丙系。
此时甲⼄丙席位分别为10、6、4现在问题进⼀步复杂。
由于决策过程可能出现10:10的现象,会议决定将增加⼀个席位。
依旧按照上述的将最后⼀个席位分配给⼩数⽐例最⼤的那个系。
见下⾯表格不过现在通过表格可以看出:总席位的增加,反⽽导致丙系由4个席位减少⾄3个席位,这样的分配⽅法(将最后⼀个席位分配给⼩数⽐例最⼤的那个系)对丙系不公平。
因此问题出现在分配席位的⽅法上⾯。
该分配席位的⽅法称为最⼤剩余法或者最⼤分数法最⼤分数法明显的缺陷:⼈⼝悖论,某⽅⼈⼝增加反⽽导致该⽅席位数⽬减少。
例如上述三系学⽣变为114,64,34.按照最⼤剩余法,21个席位的分配结果应该是:11、6、4,⼄系学⽣⼈数增加席位反⽽⽐原来少1席,丙系学⽣数量不变席位反⽽多了1席。
为了寻找新的公平的席位分配⽅法,先讨论衡量公平的数量指标不公平度指标为了简单,只考虑A,B两⽅分配席位的情况。
设两⽅⼈数分别为p1,p2,占有席位分别为n1,n2.则⽐例p1/n1,p2/n2为两⽅每个席位所代表的⼈数。
显然只有当p1/n1=p2/n2时,分配才公平。
席位分配问题

席位分配问题三个系学生共200名(甲系100,乙系60,丙系40),代表会议共20席,按比例分配,三个系分别为10,6,4席。
现在学生转系,三系人数为130,63,34,问20席位如何分配。
系别学生人数比例 20席位分配(%) 比例结果甲 103 51.5 10.3 , 乙 63 31.5 6.3 , 丙 34 17.0 3.4 , 总和 200 1000 20用四舍五入,,Hamilton方法如何解决四舍五入的缺陷/1, 先让各系取的比例的整数部分。
2(,按照小数的大小顺序将余额逐个分配。
结果为10 6 4如果席位增加到21怎么分配,此时各系比例为:10.815 6.615 3.570 结果为:11 7 3 增加席位时丙反而见减少一个席位。
舍去惯列,建立衡量公平的指标。
人数席位A P1 N1B P2 N2当p1/n1=p2/n2时,分配公平当p1/n1>p2/n2时,对A不公平,”绝对不公平度” 当p1/n1-p2/n2 对A的这样做就可以完全解决问题吗?-“绝对不公平度”也有缺陷如:p1=150,n1=10,p1/n1=15 p1=10050,n1=10,p1/n1=1005P2=100,n2=10,p2/p2=10 p2=10000,n2=10,p2/n2=1000P1/n1-p2/n2=5 p1/n1-p2/n2=5二者的绝对不公平度相同,但后者对A的不公平程度已大大降低了~~~将绝对度量改为相对度量,若p1/n1》p2/n2则定义:(p1/n1-p2/n2)/(p2/n2)=Ra(n1,n2)——对A 相对不公平度类似的定义Rb(n1,n2) 公平的分配的方案应使Ra,Rb尽量的小根据此原理,再增加一席后,应该给A还是B,将一次性的席位分配转化为懂太多饿席位分配,即:设AB已分配了n1,n2席,再增加一席应该给谁, 新的分配方案:设,分配开始时p1/n1>p2/n2,即对A不公平.1),若p1/(n1n+1)>p2/n2, 这席位该给A2),若p1/(n1+1)<p2/n2,席位给A不一定公平重新计算Rb(n+1,n2)再计算Ra(n1,n2+1) //Rb(n+1,n2)<Ra(n1,n2+1)——给ARb(n1+1,n2)>Ra(n1,n2+1)——给B推广到n个代表方时22pp21当Rb(n1+1,n2)<Ra(n1,n2+1)——推出——席位给A ,nnnn(1)(1),,221122pp21定义:该席位给Q值较大的一方。
公平席位分配问题 数学建模

公平席位分配问题数学建模数学建模,公平席位问题所在系别:地球科学与资源系专业班级:10级土管6班姓名:刘强1一、摘要本文就是席位分配公平与否的问题。
需要联系生活想象。
它就是在达到所有系最公平的条件下寻求最好的方法,通过对各个合理的计算和研究,总结找出最佳方案。
首先用比例分配法求出本题的答案,然而考虑到实际的多重因素下,在假设一组数据进行检验,然后便发现了问题,即:很多时候根本没有公平的分配方法,我需要另寻其他方法。
找到了以下关于分配的方法:Hamilton (哈密顿)方法、d’Hondt 接着我(汉丁顿)方法、Q值方法、d’Hondt(汉丁顿)方法+Q值法。
将对这些方法进行逐一分析与检验,使得得出一套最佳的合理方案。
即:使得各系席位分配最公平。
关键词:公平分配、最佳方案、最公平二、问题的重述某校有200名学生,甲系100名,乙系60名,丙系40名,若学生代表会议设20个席位,问三系各有多少个席位,三、问题的提出与分析分配问题是日常生活中经常遇到的问题,它涉及到如何将有限的人力或其他资源以“完整的部分”分配到下属部门或各项不同任务中。
它涉及的内容十分广泛。
此题一个自然的问题是如何分配席位名额才是公平的呢,反映公平分配的数量指标可用每席位代表的人数来衡量。
即:mi / xi当各系每席位代表的人数相等时,则就是最公平的分配方法。
此题公平的席位分配办法是按学生人数的比例分配,显然甲、乙、丙三系分别占有10、6、4个席位。
但是比例分配在实际生活中的应用并不广泛,原因是当所得结果并非整数时,就难以解决了。
此时就需要另寻其他方法了。
Hamilton (哈密顿)方法、d’Hondt(汉丁顿)方法、Q值方法均是求如何分配所总结的方法。
那么什么方法使得能够更大的获得公平呢,四、符号的约定• N 表示总席位数• s 表示系数• ni(i=1.2.3……s) 表示第i个系• mi(i=1.2.3……s) 表示各系中的人数• xi(i=1.2.3……s) 表示各系所获得的席位数?、采用比例分配法xi=(mi/N)*总席数20个席位的分配结果如下表人数系别ni 所占比例分配方案席位数xi mi甲 100 100/200 (50/100)*20=10 102乙 60 60/200 (30/100)*20=6 6丙 40 40/200 (20/100)*20=4 4• 但是我发现实际生活中结果是整数的情况少之又少,• 所以对此我们假设下面这种情况作为参考。
关于席位分配问题的进一步讨论

pi2 , i 1,2,...., s . 大的那个州, Qi ni (ni 1)
(1)先证明存在性.考虑 f ( x1 , x2 ,..., xs )
( x q ) .x R , i 1,2,..., s 显
2 i 1 i i i
s
然 f 是一个连续函数,当 ( x1 , x2 ,..., xs ) (q1 , q2 ,..., qs ) 时,fmin=0 而对于 f (n1 , n2 ,..., ns ) ,有 n1 n2 ... ns N .
* * n1 n2 n1 n 2 .
1,2,..., s且j i, s.t.n* 1,2,..., s, s.t.ni* ni . 则 j 事实上,若 i j nj,
* 因为 n N n N nl ni .从而与 ni n i 矛盾.
[qi ] 表示向 qi 方向取整, [qi ] 表示向 qi 方向取整. 这样,
[qi ] ni [qi ] , i 1,2,..., s .
关于 qi 的取值情况有且仅有两种.也就是说 f (n1 , n2 ,..., ns ) 至多存在 2 s 个正实值,并剔除那些 n1 n2 ... ns N 的情况,在剩余的这有限多 个点中,必存在最小值点,记为 f (n1, n 2, ..., n s ) .于是,我们知道,
* * n1 n1 1, n 2 n2 1 ,则:
差值 f f (n1 , n 2 , ..., n s ) f (n , n ,..., n )
* 1 * 2 * s
2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Hamilton 法解释
Hamilton 法的数学模型 q = (q1,…,qs)T: 份额向量. n = (n1,…,ns)T: 分配向量. 1Tq=Σqi =N 1Tn=Σni =N 它们均位于s维空间的s-1维单形 (s维空间的 超平面)中 .
Hamilton 法解释
对于 s = 3 的情形(则2维单行就是正三角形): 经 变形,有 10. n, q 是正三角形上的点,该点到三个边的 距离为它们的坐标。 20. 将三角形各边N等分,分别以平行各边的 直线连接相应的等分点。连线在三角形内的交点 将是三角形上有整数坐标的格点,这些点构成席 位分配向量的集合{n}。 30. 连线将三角形分为若干小三角形。份额向 量q为三角形上任意一点。该点到它所在的小三角 形三个边的距离分别为三个坐标的小数部分。
一、问题与背景
2. 背景
•1787年美国颁布宪法, 规定“众议院议员的名额…将 根据各州的人口比例分配”, 并于1788年生效. •1791年 Hamilton 提出了议员席位分配的方法, 并于 1792年通过. •1792年 Thomas Jefforson 提出了议员席位分配的除 子法。 •1851年开始用Hamilton法分配议员的席位。
例:某学院有3个专业,学生会名额为20个,甲系: 100人,乙希:60人,丙系:40人。要想把学生会的 名额公平的分配给各个系应该怎样分配为好? 若人数变为103、64、43人呢?
二. Hamilton 法及有关悖论
Hamilton 法:
(1.)先让各州取得份额qi的整数部分[qi]; (2.)让ri=qi-[qi],按照从小到大的顺序排列,将余下 的名额逐个分配给各相应的州,即小数部分最大的 州优先获得余下的第一个名额,次大的取得余下名 额中的第二个,以此类推,直到名额分配完毕.
Hamilton 法解释
40. 按照最大小数部分增加一个席位的Hamilton法相当于在 q 所在的小三角形中选择最靠近 q 点的顶点(格点 n)为席 位分配方案。 50. Hamilton 分配域:作小三角形内心,则可以构成以 n 为 重心,以上述若干内心为顶点的正六边形。 如果 q 落入某个小六边形内,则选择该六边形的中心 n 为席位的分配方案。
有关悖论 (1). Alabama 悖论: 人口不变, 总席位增加 导致某州席位减少. 例1. P = 200, s = 3, N = 2021 州 pi pi/p qi ni qi ni A 103 0.515 10.3 10 10.815 11 B 63 0.315 6.3 6 6.615 7 C 34 0.170 3.4 4 3.570 3
(2.) 人口悖论: 人口增长, 分额增加的州 可能失掉席位. (3.) 新州悖论: 原州人数不变, 增加新州 (人数增), 席位按比例增, 将导致原州席位减 少.
三. Jefforson的除子法
考虑 Σqi = N 且 Σ[qi] < N 的情形: 选择适当的除子 λ, 计算 qi* = qi/λ, 使得Σ[qi*] =N. 则取 ni = [qi*] . 此方法的名额分配域,以s=3为例,均是以 三角形顶点的楔形的交集
席位分配问题
组员:陆遥 金辉 罗胤达
一、问题与背景
1. 问题:美国众议院如何根据各州人口的比例分配众 议院议员的名额? •s-- 州数, pi-- 第 i 州人口数, p =Σ pi--总人口数 •N--议员数, ni--第 i 州议员数, N=Σni. •根据按人口比例分配的原则给出公平的议员席位分配 的方案{n1, …, ns}. •qi=(pi/p)N: 第 i 州应占有的议员的份额. •求{ni},与{qi}最接近。
按照常理,对于某个非整数份额qi,它所取 的名额数ai应满足[qi]<a<[qi]+1.这就是“公 平分摊原则”但是除子法依旧可能出现不 满足此原则的情况。
人口悖论的几何模型
首先考察人口增长率p’i/pi.若第i州的人口增 长率大于第j州的人口增长率,有p’i/pi>p’j/pj, 即p’i/p’j>pi/pj.在名额分配图上,p’i/p’j为常数, 表示为从正三角形某个顶点出发的一条射 线,两州人口增长率有差异表示为这条射线 离开正三角形的一边而靠拢另一边的偏转. 当这条射线同名额分配域的边界相交而非 重合时,在交点附近可能产生人口悖论.
四、席位分配问题的公理化模型
1. 公理化建模: 事先根据具体的实际问题给 出一系列的约束, 称之为“公理”. 它是所研究问题的基本要求,或所希望 达到的基本目标。 并据此寻求适当的数学结构来满足这些 基本的要求。
如果存在唯一确定的数学结构, 将它表达 出来。 如果不可能有一个数学系统与公理体系相 容,则需要找出虽然违背公理 要寻出其中最优者。
遗憾的是………..
1980年 Balinsky 和 Young 研究的结果表明: 不存在既能避免所有席位分配的悖论同 时又满足份额法则的席位分配的方法. 这就是有名的: 席位分配的不可能定理.
O(∩_∩)O 谢谢!
2. 席位公平分配的公理模型 公理I. (份额单调性) 一个州人口的增加不会导致它 失去席位. 公理II.(无偏性) 在整个时间上平均, 每个州应得到 它自己应分摊的份额. 公理III.(席位单调性) 总席位增加不会导致某个州名 额减少. 公理IV. (公平分摊性) 任何州的席位数都不会偏离其 比例的份额数. 公理V. (接近份额性) 没有从一个州到另一个州的名 额转让会使得这两个州都接近它们应得的份额.
