广东省数学建模讲座
数学建模讲座--预测模型

年份
1963 1964 1965 1966 1967 1968 1969 1970 1971 1972 1973
时序 ( t) 12 13 14 15 16 17 18 19 20 21 22
总额 ( yt ) 604.5 638.2 670.3 732.8 770.5 737.3 801.5 858.0 929.2 1023.3 1106.7
k
(一) 直线趋势外推法
适用条件:时间序列数据(观察值)呈直线 上升或下降的情形。 该预测变量的长期趋势可以用关于时间 的直线描述,通过该直线趋势的向外延伸 (外推),估计其预测值。 两种处理方式:拟合直线方程与加权拟合直线 方程
例 3.1 某家用电器厂 1993~2003 年利润额数据资料如表 3.1 所示。试预测 2004、2005年该企业的利润。
二 、趋势外推法经常选用的数学模型
根据预测变量变动趋势是否为线性,又分为线性趋势外推法 和曲线趋势外推法。
ˆt b0 b (一)线性模型y 1t (二)曲线模型 1.多项式曲线模型 2.简单指数曲线模型 3.修正指数曲线模型 4.生长曲线模型 (龚珀资曲线模型)
2
ˆt b0 b1t b2t bk t y 多项式模型一般形式:
预测模型简介
数学模型按功能大致分三种: 评价、优化、预测 最近几年,在大学生数学建模竞赛常常出 现预测模型或是与预测有关的题目:
1.疾病的传播; 2.雨量的预报; 3.人口的预测。
统计预测的概念和作用
(一)统计预测的概念
概念: 预测就是根据过去和现在估计未来,预测未来。 统计预测属于预测方法研究范畴,即如何利用科学的统计 方法对事物的未来发展进行定量推测.
数学建模知识讲座教案模板精选

数学建模知识讲座教案模板精选一、教学内容本节课选自高中数学教材《数学建模》第五章第一节“数学建模的基本概念和方法”,内容包括数学建模的定义、分类、步骤以及常用的数学建模方法。
二、教学目标1. 了解数学建模的定义、分类和基本步骤,掌握常用的数学建模方法。
2. 能够运用所学知识解决实际问题,提高数学应用能力。
3. 培养学生的团队合作意识和创新精神。
三、教学难点与重点重点:数学建模的定义、分类、步骤和常用方法。
难点:如何运用所学知识解决实际问题。
四、教具与学具准备1. 教具:多媒体课件、黑板、粉笔。
2. 学具:教材、练习本、计算器。
五、教学过程1. 导入新课通过展示一个实际问题的案例,引导学生思考如何运用数学知识解决实际问题,从而引出数学建模的概念。
2. 基本概念(1)数学建模的定义:用数学语言和方法对现实世界中的问题进行抽象、简化和描述的过程。
(2)数学建模的分类:定性建模、定量建模、混合建模。
(3)数学建模的基本步骤:问题提出、分析研究、建立模型、求解模型、验证模型、应用模型。
3. 常用数学建模方法(1)差分法:将连续问题离散化,用差分方程描述。
(2)有限元法:将连续问题离散化,用有限元方法求解。
(3)回归分析法:根据已知数据,建立变量之间的回归方程。
(4)优化方法:求解最优化问题。
4. 实践情景引入给出一个实际问题的案例,让学生分组讨论,尝试运用所学知识建立数学模型。
5. 例题讲解讲解一个具体的数学建模例题,引导学生分析问题、建立模型、求解模型。
6. 随堂练习让学生独立完成一个数学建模练习题,巩固所学知识。
六、板书设计1. 定义、分类、步骤2. 常用数学建模方法3. 实践情景引入4. 例题讲解5. 随堂练习七、作业设计1. 作业题目:(1)运用差分法解决一个实际问题。
(2)运用回归分析法建立两个变量之间的回归方程。
2. 答案:(1)根据问题特点,建立差分方程。
(2)根据已知数据,求解回归方程。
八、课后反思及拓展延伸1. 反思:本节课通过实际案例引入数学建模的概念,让学生了解数学建模的基本步骤和常用方法,提高学生的数学应用能力。
建模培训讲座第一讲(回归模型以及SAS)

i 1
i 1
从而得到回归方程 yˆ aˆ bˆx
按照上述准则,我们可求出前面例子中灌溉 面积y对最大积雪深度x的回归方程是:
yˆ 142 364x
可以看出, 最大积雪深度每增加一个单位, 灌溉面积平均增加364个单位.
可以证明,我们用最小二乘法求出的估计
分别aˆ是, bˆ a, b 的无偏估计, 它们都是 y1,y2, …,yn
为一元线性回归模型.
由(1)式, 我们不难算得y的数学期望:
E(y)=a+bx
该式表示当x已知时,可以精确地算出E(y).
由于ε是不可控制的随机因素,通常就用E(y)作为y的估计,
记作 . 这样我们得到
yˆ
yˆ aˆ bˆx
(2)
称此方程为y关于x的回归方程 .
y=a+bx+ε, ε ~N(0, )2 (1)
对任意两个变量的一组观察 (xi, yi), i=1, 2, …, n
都可以用最小二乘法形式上求得 y 对 x的回归方程, 如果y 与x 没有 线性相关关系, 这种形式的回归方程就没有意义 .
因此需要考察 y 与 x 间是否确有线性相关关系, 这就是回归效果的 检验问题.
我们注意到 yˆ aˆ bˆx 只反映了x对y的
在回归分析中, 当变量只有两个时, 称为一元回归分析; 当变量 在两个以上时, 称为多元回归分析. 变量间成线性关系, 称线性回归, 变量间不具有线性关系, 称非线性回归.
一元回归
线性
非线性
多元回归
在这一讲里, 我们主要讨论的是一元线性回归. 它是处理两个变 量之间关系的最简单的模型. 它虽然比较简单, 但我们从中可以了解 到回归分析的基本思想、方法和应用.
《数学建模讲座》课件

讲者:李教授,XX大学数学系副教授。
感谢您的聆听!
数学建模的基本步骤
1
研究问题
了解和分析实际问题,明确目标和需求。
2
建立模型
根据实际问题,选择适当的数学模型,并进行建模。
3
求解模型
利用数学工具和方法求解建立的数学模型。
4
模型分析
对求解的结果进行分析和评价,寻找优劣及改进方案。
数学建模中的数学工具及其应用
优化方法
优化方法可以帮助 我们寻找问题的最 优解或最佳决策。
统计学方法
统计学方法可以帮 助我们分析和理解 数据,揭示其中的 规律和趋势。
线性代数
线性代数在数学建 模中有广泛的应用, 如矩阵运算、线性 方程组的求解等。
概率论与数 理统计
概率论与数理统计 可以帮助我们分析 和预测随机现象, 并进行决策和风险 评估。
结论
数学建模的重要性
数学建模是将数学与实践相结合的要途径,对推动科学和社会的发展具有重要意义。
《数学建模讲座》PPT课件
# 数学建模讲座PPT课件 ## 概述 本讲座将介绍以下内容: 1. 什么是数学建模 2. 数学建模的意义 3. 数学建模的基本步骤 4. 数学建模中的数学工具及其应用
什么是数学建模
1 定义
数学建模是指利用数学语言和工具对真实世界中的问题进行化简、抽象和数学描述的过 程。
将知识转化为实践的能力
通过数学建模,我们可以将抽象的数学理论应用于实际问题的求解与分析。
建立对世界的更深理解
数学建模可以帮助我们深入分析问题,寻找最佳解决方案,从而提高对世界的理解。
Q&A
1 时间
讲座时间:2021年6月15日,上午10点至11点。
广东省大学生数学建模竞赛初评结果

2015年广东省大学生数学建模竞赛获奖名单(初稿)根据《广东省教育厅关于做好2015年广东省本科高校大学生相关学科竞赛工作的通知》(粤教高函〔2015〕37号)安排,省教育厅委托中山大学组织开展2015年广东省大学生数学建模竞赛。
竞赛于9月11日至9月14日分本科和高职高专两个组别进行,全省共有86所高校1581支代表队伍共计4740位选手报名参赛。
初步评审已于日前结束,共评出本科组一等奖114项,二等奖195项,三等奖317项;高职高专组一等奖24项,二等奖44项,三等奖68项。
现将2015年广东省大学生数学建模竞赛获奖名单(初稿)公布如下,异议期为一个月,即2015年10月9日-2015 年11月 9日。
说明:1.获奖名单公布之日起的一个月内,任何个人和单位可以提出异议,由广东省组委会负责受理。
2.受理异议的重点是违反竞赛章程的行为,包括竞赛期间教师参与、队员与他人讨论,不公正的评阅等。
对于要求将答卷复评以提高获奖等级的申诉,原则上不予受理。
3.异议须以书面形式提出。
个人提出的异议,须写明本人的真实姓名、工作单位、通信地址(包括联系电话或电子邮件地址等),并有本人的亲笔签名;单位提出的异议,须写明联系人的姓名、通信地址(包括联系电话或电子邮件地址等),并加盖公章。
广东省组委会对提出异议的个人或单位给予保密。
4.与受理异议有关的学校管理部门,有责任协助组委会对异议进行调查,并提出处理意见。
组委会应在异议期结束后两个月内向申诉人答复处理结果。
5.广东省组委会对异议期结束后一年内发现的违规行为继续承担按章处理义务。
本科组一等奖本科组二等奖本科组三等奖高职高专组一等奖高职高专组二等奖高职高专组三等奖广东省数学建模竞赛组织委员会2015年10月9日。
数学建模竞赛专题讲座辅导安排-南昌大学-理学院

南昌大学第十四届数学建模竞赛专题讲座及辅导安排
1、第一次4月29日(星期六)下午14:00——18:00
讲座地点:前湖校区教学主楼135
主讲:尹洪位,陈涛
讲座内容:数学建模认知与数学软件
2、第二次5月6日(星期六)下午14:00——18:00
讲座地点:前湖校区教学主楼135
主讲:阮小军
讲座内容:数学建模初探
3、第三次5月7日(星期日)下午14:00——18:00
讲座地点:前湖校区教学主楼135
主讲:肖水明
讲座内容:概率模型应用
4、第四次5月13日(星期六)下午14:00——18:00
讲座地点:前湖校区教学主楼135
主讲:蔡用
讲座内容:数学建模方法与案例一
5、第五次5月14日(星期日)下午14:00——18:00
讲座地点:前湖校区教学主楼135
主讲:余国松
讲座内容:数学建模方法与案例之二
6、第六次5月21日(星期日)下午14:00——18:00
讲座地点:前湖校区教学主楼135
主讲:刘斌斌
讲座内容:金融时间序列模型
上机安排:2017年南昌大学第十四届数学建模竞赛将于5月23日下午3:00 ~5月31日下午3:00举行, 竞赛期间理学院数学系数学实验室(前湖校区理生楼B708机房)将进行全面开放,为参赛队员提供计算机用机和上网免费服务,具体开放时间将在QQ群内发布。
5月08日-----5月16日现场报名(理生楼B711)
5月31日13:30—17:00交卷(理生楼B711)。
数学建模论文讲座心得体会

一、引言数学建模是近年来备受关注的研究领域,它将数学理论应用于实际问题,为解决实际问题提供了一种有效的方法。
近日,我有幸参加了一场关于数学建模论文写作的讲座,通过此次讲座,我对数学建模论文的写作有了更深入的了解,以下是我对讲座的心得体会。
二、讲座内容回顾1. 数学建模论文的基本结构讲座首先介绍了数学建模论文的基本结构,包括引言、问题背景、模型建立、模型求解、结果分析与讨论、结论等部分。
这些部分构成了一个完整的数学建模论文,有助于读者全面了解论文的研究内容。
2. 数学建模论文的写作技巧讲座重点讲解了数学建模论文的写作技巧,包括以下几个方面:(1)引言部分:应简要介绍研究背景、研究目的、研究意义,以及论文的主要贡献。
(2)问题背景部分:应详细阐述研究问题的来源、研究问题的重要性,以及研究问题的现状。
(3)模型建立部分:应介绍模型的选择、模型的假设、模型的参数等。
(4)模型求解部分:应介绍求解模型的方法、求解过程、求解结果。
(5)结果分析与讨论部分:应分析求解结果的意义、求解结果的局限性,以及与现有研究的比较。
(6)结论部分:应总结论文的主要发现、论文的创新点,以及论文的不足之处。
3. 数学建模论文的写作规范讲座还介绍了数学建模论文的写作规范,包括以下几个方面:(1)格式规范:遵循学术期刊的格式要求,包括字体、字号、行距等。
(2)参考文献规范:按照学术规范引用参考文献,确保论文的学术性。
(3)图表规范:图表应清晰、简洁、规范,便于读者理解。
三、心得体会1. 数学建模论文写作的重要性通过讲座,我深刻认识到数学建模论文写作的重要性。
数学建模论文不仅是对数学理论的应用,更是对实际问题的解决。
一篇优秀的数学建模论文,有助于推动数学理论的发展,为实际问题的解决提供有力支持。
2. 数学建模论文写作的技巧讲座中提到的数学建模论文写作技巧,为我今后的写作提供了宝贵的经验。
在今后的写作过程中,我将遵循这些技巧,提高论文的质量。
数学建模广东省公布成绩
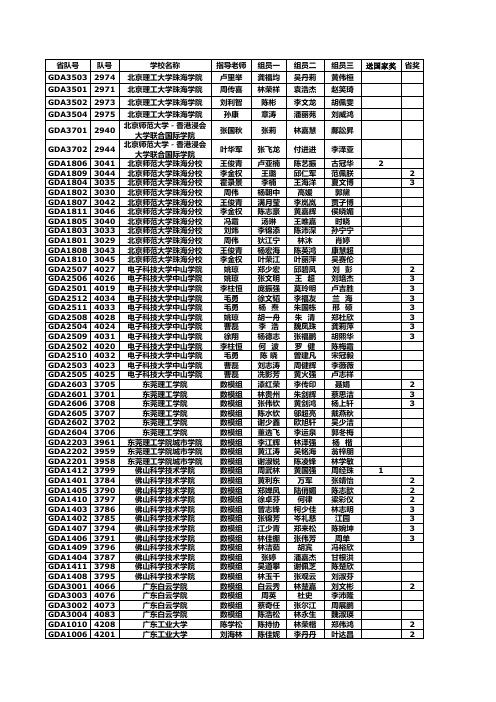
4121 4122 4127 4125 4130 4129 3101 3000 3008 3006 2999 3001 4277 4283 4278 4285 4282 4284 4189 4194 4191 4195 4187 4193 4188 4184 4186 4303 4289 4302 4299 4286 4301 4297 4304 4294 4307 4293 4296 4309 4306 4295 4311 4287 4292 4310 4305 4096 4108 4099 4098 4097 4092 4100 4109 4103 4105 3780 3782 3779
4199 4202 4196 4215 4198 4200 4212 4205 4214 4211 4197 4207 4170 4171 4169 3121 3111 3103 3119 3105 3110 3114 3118 3108 3106 3107 3109 3104 4229 4228 4227 4231 3991 3984 3994 3983 4001 4217 4223 3234 3230 3232 3241 3231 3240 3236 3245 3242 3233 3243 3237 3886 3885 3882 3880 3908 3915 3913 3907 3909
组员三 黄伟桓 赵笑琦 胡佩雯 刘威鸿 鄺訟昇 李泽亚 古冠华 范佩朕 夏文博 郭黛 贾子博 侯晓媚 时晓 孙宁宁 肖婷 康慧超 吴赛伦 刘 彭 刘培杰 卢吉胜 兰 海 邢 硕 郑杜欣 龚莉萍 胡熙华 陈梅霜 宋冠毅 李薇薇 卢志祥 聂娟 蔡思洁 杨上轩 戴燕秋 吴少洁 郭冬梅 杨 楷 翁梓朋 林学敏 周经珠 张靖怡 陈志歆 梁彩仪 林志明 江园 陈婉坤 周单 冯裕欣 甘根洪 陈楚欣 刘淑芬 刘文彬 李沛隆 周展鹏 魏淑瑛 郑伟鸿 叶达昌
2010年数学建模广东省公布成绩

送国家奖 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2
GDC2006 3921 GDC3105 4180 GDC3807 3059 GDC3812 3064 GDC3104 4179 GDC5704 3220 GDC7004 3253 GDC2001 3916 GDC2005 3920 GDC3806 3058 GDC3809 3061 GDC3810 3062 GDC3904 3128 GDC5101 4112 GDC7005 3254 GDC2004 3919 GDC2002 3917 GDC3823 3081 GDC3915 3145 GDC3903 3127 GDC5302 4133 GDC3828 3090 GDC3815 3070 GDC7003 3251 GDC3107 4182 GDC3804 3053 GDC7002 3250 GDC3801 3050 GDC3901 3122 GDC3813 3066 GDC4103 3766 GDC4104 3767 GDC3826 3086 GDC7001 3249 GDC3808 3060 GDC3805 3057 GDC1503 3725 GDC3905 3135 GDC4806 4013 GDC5902 2932 GDC3002 4087 GDC3907 3137 GDC5001 4060 GDC5304 4137 GDC6202 4240 GDC3102 4173
胡煜 数模组 数模组 数模组 关占荣 陈锐彬 黎捷 冯冰 梁炼 数模组 王明福 齐松茹 段振华 数模组 白静 数模组 数模组 陈锐彬 钟剑龙 罗福生 数模组 数模组 袁福坤 数模组 雷田礼 数模组 数模组 数模组 邢婷文 罗建华 田红梅 数模组 傅秀莲 罗福生 谭旭平 邓小红 数模组 黄静 李宗涛 数模组 数模组 数模组 数模组 数模组 姚新钦 数模组 赵坤
数学教研活动讲座记录(3篇)

第1篇一、讲座背景为了提高数学教师的教学水平,加强教师之间的交流与合作,我校于2021年10月20日举办了数学教研活动讲座。
本次讲座邀请了知名数学教育专家李教授主讲,主题为“数学核心素养与课堂教学策略”。
以下是本次讲座的详细记录。
二、讲座内容1. 数学核心素养的内涵李教授首先介绍了数学核心素养的内涵。
她指出,数学核心素养是指学生在数学学习过程中形成的具有持久价值的思维品质、情感态度和价值观。
数学核心素养包括以下几个方面:(1)数学抽象:培养学生从具体事物中抽象出数学概念、规律和模型的能力。
(2)逻辑推理:培养学生运用数学语言进行推理、论证的能力。
(3)数学建模:培养学生运用数学知识解决实际问题的能力。
(4)直观想象:培养学生运用图形、图像等直观方式理解和解决问题的能力。
(5)数学运算:培养学生准确、高效地进行数学运算的能力。
2. 课堂教学策略李教授结合实际案例,详细阐述了如何将数学核心素养融入课堂教学。
以下是一些具体策略:(1)创设情境,激发兴趣在教学中,教师应关注学生的生活实际,创设具有趣味性和启发性的情境,激发学生的学习兴趣。
例如,在教授“平面图形”时,可以让学生观察生活中的平面图形,如窗户、桌子等,引导学生思考这些图形的特点。
(2)注重探究,培养能力教师应鼓励学生积极参与课堂活动,通过探究、讨论、合作等方式,培养学生的数学思维能力和创新能力。
例如,在教授“函数”时,可以让学生自主探究函数的性质,发现函数的规律。
(3)强化运算,提高效率在教学中,教师应注重培养学生的数学运算能力,提高学生的运算效率。
可以通过以下方法实现:①引导学生掌握运算规律,提高运算速度。
②鼓励学生进行口算、心算等练习,提高运算准确率。
③运用现代教育技术,如计算器、计算机等,辅助学生进行运算。
(4)关注差异,因材施教教师应关注学生的个体差异,根据学生的实际情况进行分层教学。
对于基础较弱的学生,教师应加强基础知识的教学,帮助他们逐步提高;对于基础较好的学生,教师应适当提高教学难度,激发他们的学习兴趣。
数学建模讲座ppt课件

2.多项式的常用函数
roots(p) %返回多项式的根向量 注1:多项式p是一个行向量,而poly(p)是一个
例1 求x,使 Ax b 其中:
1 0 1 1
A
2
1
0
b
2
3 2 5 1
解1 用逆阵法 >> A=[1,0,1 2,1,0 -3,2,-5]; >> b=[1,2,-1]'; >> x=inv(A)*b
解2 用左/2
1/3
1/3
1/4
c=
335/113
>> format compact
>> A,c
A=
1
1/2
1/2
1/3
1/3
1/4
c=
335/113
%要空行
1/3 1/4 1/5
%不要空行
1/3 1/4 1/5
二、矩阵运算与数组运算
1、矩阵运算
>> A(:,1:3) ans = 123 678 11 12 13 >> A([1,2],[1,3,5]) ans = 135 6 8 10
例2 将向量中满足不超过0.5的元素提取出来 先编写一个M-文件 rand('seed',0); x=rand(1,10); L=x<=0.5; x x=x(L) 用tiquyuansu.m为名存盘,然后回到MATLAB环
数学建模大会策划书3篇

数学建模大会策划书3篇篇一数学建模大会策划书一、活动主题“创新改变世界,数学建模演绎精彩”二、活动目的本次数学建模大会旨在为广大数学爱好者提供一个学习交流的平台,提高学生的数学建模能力和创新能力,培养学生的团队合作精神和综合素质。
三、活动时间和地点时间:[具体时间]地点:[具体地点]四、活动对象全校学生五、活动内容1. 数学建模讲座:邀请数学建模专家进行数学建模的讲座,介绍数学建模的基本方法和技巧,以及数学建模在实际问题中的应用。
2. 数学建模培训:组织数学建模培训,通过实际案例分析和编程实践,帮助学生掌握数学建模的方法和步骤。
3. 数学建模竞赛:举办数学建模竞赛,要求学生在规定时间内完成一个实际问题的建模和求解,并提交论文。
4. 数学建模展览:展示学生的数学建模作品,包括论文、模型和实物等,同时邀请获奖学生进行现场讲解和演示。
5. 颁奖仪式:举行颁奖仪式,对获奖学生进行表彰和奖励。
六、活动组织1. 活动筹备组:负责活动的策划、组织和协调工作。
2. 专家顾问组:邀请数学建模专家担任顾问,为活动提供指导和支持。
3. 培训教师组:组织数学建模培训教师,负责培训的教学工作。
4. 竞赛评审组:邀请数学教师和专家担任竞赛评审,负责竞赛论文的评审工作。
5. 宣传报道组:负责活动的宣传报道工作,包括制作海报、宣传单、拍摄照片和视频等。
6. 后勤保障组:负责活动的后勤保障工作,包括场地布置、设备调试、物资采购等。
七、活动宣传1. 海报宣传:在学校宣传栏张贴活动海报,宣传活动的时间、地点和内容。
2. 网络宣传:在学校网站、公众号、微博等平台发布活动通知和宣传信息,吸引更多的学生参与。
3. 班级宣传:通过学生会、班级干部等渠道,向学生宣传活动的信息,鼓励学生积极参与。
八、活动预算1. 讲座费用:[X]元2. 培训费用:[X]元3. 竞赛奖品费用:[X]元4. 宣传费用:[X]元5. 其他费用:[X]元九、活动注意事项1. 活动期间要注意安全,确保学生的人身安全和财产安全。
数学建模讲座

讲座内容
数学建模 讲座内容
1、数学建模的含义与意义 2、数学建模能力的培养与提升 3、数学建模竞赛的相关介绍
4、 数学建模论文的设计与排版艺术
10/16/2020
2
数学建模的含义和意义
1 什么是数学建模
问题:树上有十只鸟,开枪打死一只, 还剩几只?
9只? 还是 0只?
分析:这是一道数学应用题(应该是小学生 的)。但他一样是数学建模问题,不过答案 就不重要了,重要的是过程。
2 数学建模的意义
1)体现了数学的应用价值 2)有利于学生理论联系实际能力的培养 3)有利于培养学生的科研素养 4)有利于增加同学参加课外学术活动的 经验并在评优时更有竞争力。
3 江西师大的数学建模
肯定:从我校学生参加数学建模竞赛的成绩来看,是相当值得 肯定的,每年的高教杯和国际赛都会有很多优秀的参赛队获得 很好的奖项。
杨玉花 夏成 周志刚 吴姗 付晓 高海龙 管莉莉 张丽 魏莎 袁海霞 吕琦 蒋漓 张一帆
袁定欢 宗志英 廖智霖 康悦 刘庆龙 刘涛 杜晨 阳春燕 李鹏飞 鄢婷芳 黄过伟 汪茵芸 王晴
指导 教师
教练组
获奖 等级
国2
教练组 1
教练组 2
教练组 2
教练组 2
教练组 3
教练组 3
教练组 国 1
教练组 国 2
10
2. 如何培养和提升建模能力
1)培养对数学建模的兴趣 2)学会自学学会研究 3)增强数学理论知识 4)平时多领悟建模过程 5)多参加比赛,在实践中体会平时学到的理论 知识从而得到领悟和进步 6)研读优秀论文
数学建模竞赛的相关介绍
1. Mcm/Icm国际数学建模竞赛
政府
发展学生数学建模素养的实际问题背景优化——以“整式的加减——去括号”教学为例

至简教学
2023 年 5 月下半月
1
2
+12× -
6
3
(
)
=2+ -8
3 体现不同设计意图的教学引入设计比对
=12×
3.
1 从实际问题出发的教学引入
(
2) 12×
半个多 世 纪,于 2006 年 7 月 1 日 建 成 通 车 .
它从西宁
=12×
至拉萨全长 1956km,是世界上海拔 最 高、线 路 最 长、
想.
然后进行例 1 和例 2 教学,再将引言问题后 置 到 巩
表 3 多版本教材的教学引入方式比对
教学引入方式
版本及问题类型
设计目的
从实际问题
背景引入
如人教版“冻土问题”、北 师 大 版 和 鲁 教 版 “计
算火柴棒问题”、青岛版“购书问题”等 .
通过实 际 问 题 的 求 解 得 出 含 有 括 号 的 代 数
5h,如果列车通过冻
土地 段 需 要 u h,那 么 这 段 铁 路 的 全 长 可 以 怎 么 样 表
)
=-6;
3.
1.
1 创设情境,导入课题
教师:(出 示 图 片:青 藏 铁 路 )青 藏 铁 路 这 个 离 天
最近的铁路,被人们形象地称为“天路”.
它的建设 历 经
(
)
(
1)
2h 后两船相距多远?
材和课标的 理 解,针 对 不 同 教 学 意 图,分 别 从 实 际 问
的运算法则和运算律来 学 习 整 式 的 运 算,有 了 一 定 的
基础之一,是学生认知 数 量 关 系、探 索 数 学 规 律、建 立
学中教师应把握数 与 式 的 整 体 性 .
数学建模优秀讲座-模糊综合评价基础与入门

0.3,
0.3,
0.1
0.3, 0.4, 0.2, 0.1
为了更好地理解和解释评价的结果,我们一般会
把评价结果进行归一化:
B' b1' , b2' ,..., bm'
1
m
b1,b2 ,..., bm
bi
i 1
B’表示最终的评价结果,bi' 表示为评价对象属于第i个评语 的百分比。
将上述所得的式子进行归一化处理:
0.5 , 0.3 , 0.3 , 0.2 0.38,0.25,0.25,0.12
1.3 1.3 1.3 1.3
它表示持权重A的顾客对这种服装的评价为: “很喜欢”的程度是38%,“较喜欢”的程度是25%, “不太喜欢”的程度是25%,“不喜欢”的程度是12%。 所以,我们根据最大隶属度原则,得出结论顾客对某件 衣服应该是“很喜欢”。
0.06,
0.3,
0.4,
0.15,
0.09,
0
0.056,
0.251,
0.345,
0.227,
0.105,
0.016
0, 0.23, 0.37, 0.26, 0.12, 0.02
将结果归一化处理:
0.056 , 0.251 , 0.345 , 0.227 , 0.105 , 0.016 0.056,0.251,0.345,0.227 ,0.105,0.016
隶属度:表示在模糊集合中每一个元素u属于模糊集合 A 的隶
属程度,记作 uA (u)。U可在[0,1]区间连续取值
例:年龄20岁,30岁,40岁与“年轻”的模糊界限之间的隶
属度
可以分别是1,0.6,0.3;
数学建模知识讲座教案模板精选

数学建模知识讲座教案模板精选一、教学内容本讲座依据《数学建模》教材第四章“数学模型的建立与求解”,具体内容包括:线性规划模型、非线性规划模型、整数规划模型及其应用案例分析。
二、教学目标1. 理解数学建模的基本概念,掌握数学建模的基本方法。
2. 学会运用线性规划、非线性规划和整数规划等方法解决实际问题。
3. 培养学生的团队合作意识和创新思维能力。
三、教学难点与重点教学难点:非线性规划模型的建立与求解。
教学重点:线性规划、非线性规划和整数规划模型的建立及其在实际问题中的应用。
四、教具与学具准备1. 教具:多媒体教学设备、黑板、粉笔。
2. 学具:教材、《数学建模》学习指导书、计算器、草稿纸。
五、教学过程1. 实践情景引入(10分钟)利用多媒体展示实际生活中的数学建模案例,引导学生思考数学建模在实际问题中的应用。
2. 理论讲解(40分钟)(1)线性规划模型:讲解线性规划的基本概念、数学模型及其求解方法。
(2)非线性规划模型:讲解非线性规划的基本概念、数学模型及其求解方法。
(3)整数规划模型:讲解整数规划的基本概念、数学模型及其求解方法。
3. 例题讲解(40分钟)选择典型例题,分别讲解线性规划、非线性规划和整数规划模型的建立与求解过程。
4. 随堂练习(20分钟)学生独立完成练习题,教师巡回指导,解答学生疑问。
5. 小组讨论(20分钟)学生分组讨论,共同解决实际问题,培养团队合作意识。
六、板书设计1. 黑板左侧:列出线性规划、非线性规划和整数规划的基本概念、数学模型。
2. 黑板右侧:展示例题的解题步骤及关键公式。
七、作业设计1. 作业题目:(1)求下列线性规划问题的最优解:maximize z = 2x + 3ysubject to x + y ≤ 42x + y ≤ 5x, y ≥ 0(2)求解下列非线性规划问题:maximize z = x^2 + y^2subject to x + y = 1x, y ≥ 0(3)将实际问题转化为整数规划模型,并求解。
高中生数学思维的培养路径——以“指数函数与对数函数交点个数问题”的教学为例

2024年第6期教育教学SCIENCE FANS 对于高中生数学思维的培养,一线教师一直在探索各种有效的途径。
本文以“指数函数与对数函数交点个数问题”的教学为例,详细探讨如何培养高中生的数学思维,以期有效提升学生的数学 成绩。
1 培养高中生数学思维的重要性高中数学作为一门重要学科,对于高中生的学习和发展具有重要的作用。
在高中数学教学中培养学生的数学思维,可以促进学生逻辑思维能力、创新能力以及问题解决能力的提高,而这些能力对于学生未来的学习和职业发展都非常重要。
高中阶段正是培养学生数学思维的关键阶段,教师应将培养学生的数学思维作为教学重点。
2 “指数函数与对数函数交点个数问题”的背景和意义第一,指数函数与对数函数交点个数问题是高中数学中的一个经典问题,其中蕴含着深刻的数学思维。
指数函数和对数函数是数学中的重要函数,它们被广泛应用于科学、工程等各个领域[1]。
第二,指数函数与对数函数交点个数问题的研究旨在探索这两类函数的交点个数的规律和特征,以帮助学生深入理解指数函数和对数函数的性质和变化趋势,拓宽学生的数学视野,培养学生的探究精神和数学思维能力[2]。
第三,通过解决指数函数与对数函数交点个数问题,学生可以锻炼抽象思维能力,培养观察、分析、推理和解决实际问题的能力。
同时,对指数函数与对数函数交点个数问题进行研究,也可以为后续的高等数学学习奠定坚实的基础[3]。
总之,研究指数函数与对数函数交点个数问题不仅具有重要的理论意义,而且对于高中生数学思维的培养具有重要的实践意义,可以让学生在解决实际问题的过程中感受到数学的奇妙,从而培养学生的数学学习兴趣和创新意识,促进学生全面发展。
因此,高中数学教师应指导学生积极探索指数函数与对数函数交点个数问题,以提升学生的数学思维能力和解决问题的能力[4]。
3 探讨“指数函数与对数函数交点个数问题”的解决方法指数函数与对数函数交点个数问题是一个典型的数学分析问题,解决这一问题的关键在于熟练掌握函数图象、基本性质和求解方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例如:金融衍生产品如何定 价?如何估计风险?金融危 机与经济危机如何预测?在 衍生证卷的定价理论中,著 名经济学家、诺贝尔奖获得 者Black-Scholes建立的定价 理论成为华尔街的操盘法律。
(K)房地产业;
例如:房地产价格评估问题; 房地产行业的泡沫问题等;
(L)租赁和商务服务业;
例如:2005年高教社杯全国 大学生数学建模竞赛题目 B题
· 单因子方差分析方法建模 · 一元回归分析方法建模。
(2)连续系统方法建模 ·差分方程方法建模—黑箱模型
· 差分方程简介 · 差分方程方法建模 · 差分方程组方法建模 (特征:数据等时间间隔变化)
· 微分方程方法建模—白箱模型 ·微分方程简介 ·一阶线性常微分方程建模 · 二阶线性常微分方程建模 · 线性常微分方程组建模 · 常微分方程定性理论应用
视频1
管如此,现代生命科学在20世纪 的下半视频2叶还是取得了丰盛的成果。 正如美国科学院院长、分子生物 学家阿尔伯特(B.Albert)所说, “在一个基因克隆占主要地位的
时代,当今许多优秀的科学家在 不具备任何定量研究的能力下仍 然取得了巨大的成绩”。但是, 随着后基因组时代的到来,生物
视频1
06历史视频学2 0601考古学 0602中国史 0603世界史
同时,案例分析(涉及的问题) 遍布所有行业和日常生活
(1)行业的国家标准 (GB/T4754-2002)规定国 民经济行业分20个门类, 我们对各门类中存在的问 题作简单分析。
(A)农、林、牧、渔业;
例如:中药种植业发展中的三个 关键问题—中药材资源的可持续 发展、中药材基地建设、中药材 规范化种植及GAP认证;
·排队论方法建模 ·存储论方法建模 ·对策论方法建模 ·决策论方法建模
(4)对不确定性问题的随机建模 · 随机系统建模
· 随机过程的概念及分类 · 两个重要过程及应用 · 马氏链模型 · 连续时间马氏过程模型
·时间序列分析方法建模 · 时间序列分析简介 · 时间序列分析方法建模 · 蒙特卡罗方法简介 · 随机决策
高兴趣、宽知识、阔视野、强能力 的数学建模培训模式
广东省数学建模讲座
谭忠
厦门大学
1
标题解读
一、高兴趣:提高学习数学、应用数学的兴趣 二、宽知识:拓宽大学生的数学知识面 三、阔视野:开阔大学生的学科和行业视野
了解数学在其中的应用,拓宽就业渠道 四、强能力:强化大学生应用数学解决实际问题
的能力—创新能力,提高大学生的持久竞争力
(1)教务处、数学科学学院 第一时间在网上宣传;
(2)认真编写广告在各校区 进行宣传,学生踊跃报名。
三、扩大大学生知 识面,首先是数学 知识面
首先从大学数学课程开设看大学 数学的知识结构
第一学年: 数论
高代
数分(一元)
解析几何
运筹学
常微分方程
第二学年: 离散数学
概率论
实变函数
数分(多元)
第三学年: 抽象代数 数理统计 偏微分方程
例如:节能问题;污水治理问
(E)建筑业;
例如:建筑的抗震问题等;
例如:建筑设计中的问题:伊拉克裔 天才女设计师哈迪德,最初选择学习 数学而不是建筑学,在那里她学会了 分析和缜密的思考,还获得很多关于 几何学的抽象知识。在上世纪70年 代初到伦敦后, 她才开始学习建筑。
(F)批发和零售业;
例如:烟草制品批发与零售的精 准投放问题;超市进货问题等;
0711系统科学
0712科学技术史0713生态学
0714视统频1 计学
08工学视频2
0801力学
0802机械工程
0803光学工程
0804仪器科学与技术
0805材料科学与工程 0806冶金工程 0807动力工程及工程热物理 0808电视频1气工程 0809电子科学与技术 0810信视频2息与通信工程 0811控制科学与工程 0812计算机科学与技术 0813建筑学
0833城乡规划学 0834风景园林学 0835软件工程 0836生视频1物工程 0837安全科学与工程 0838公视频2安技术
09农学
0901作物学 0902园艺学
0903农业资源与环境
0904视植频1 物保护学 0905畜牧学 0906兽医学
0907视林频2 学
0908水产学
0909草学
10医学
(5)多元统计分析方法建模 · 方差分析方法建模 · 多元回归分析方法建模 · 相关性分析法建模 · 主成分分析法建模 · 因子分析法建模
· 统计推断方法建模 · 统计模拟方法建模 ·模拟方法建模 · 随机行为的模拟 · 随机服务模型
(6)模糊系统方法建模 · 模糊数学方法建模
· 模糊数学简介 · 模糊聚类分析方法建模 · 模糊模式识别方法建模 · 模糊综合评判方法建模
0710生物学
数学在生命科学中的最新应用: 分子生物学的诞生使传统的生物 学研究视频1转变为现代实验科学。但 是,在视频2生命科学领域的实验科学 与其它实验科学如实验物理学相 比,更多地是注重经验,而非抽 象的理论或概念。此外,这些
们大多关注定性的研究,以发现 新基因或新蛋白质为主要目标, 对于定量的研究,如分子动力学 过程等没有给予足够的重视。尽
学研究者的定量研究能力和知识 已不再视频2是可有可无的了,而是大 势所趋。
英国生物学家保罗.纳斯(Paul Nurse)因细胞周期方面的卓越研 究成为了2001年度生理学医学诺 奖的得主。他曾在一篇回顾20世
视频1
纪细胞周期研究的综述文章中写 道:“视频我2 们需要进入一个更为抽 象的陌生世界,一个不同于我们 日常所想象的细胞活动的、能根 据数学有效地进行分析的世界。”
·利用导数思想建模(变化率) ·初等连续优化模型(求极值) · 初等代数与几何方法建模 · 矩阵与代数方程组建模 (由投入产出问题到填充问题) · 初等几何方法建模
·初等数据处理方法建模 · 数据拟合方法建模 · 插值方法建模
·初等概率方法建模 · 概率分布、期望与方差 · 概率分布方法建模
·初等统计方法建模 · 数据的收集与整理 · 经验模型的建立 · 模型的参数估计 · 模型的误差分析 · 模型检验
最后数学软件的使用!
• 中间过程:组队
四、开阔视野、提高能力的重 要阶段
第二阶段:案例分析
8月21日-9月11日
案例分析遍布所有学科、科学 与工程技术领域
训练布置:
每个队必须两天完成一 个综合案例分析,并必须在 当天晚上12点之前通过邮件 发给我们点评。
许多学生都是凌晨一两 点提交论文,个别凌晨5点。
(G)交通运输、仓储和邮政业;
例如:物流公司的最佳运输路径 问题;最佳装载问题;最佳仓储 问题等
(H)住宿和餐饮业;
例如:酒店的评级问题;
(I)信息传输、计算机服务和软 件业;
例如:计算机是数学家发明的; 高新技术的本质是数学;数据处 理和存储服务问题;件等IT公司
(J)金融业;
例如:金融、保险、证券行 业定价问题;银行系统(理 财、财务分析师)保险公司 (精算)、证券分析师;风 险和损失评估问题;汇率问 题等
·灰色系统分析方法建模 · 灰色系统基本理论 · 灰色系统关联度分析 · 灰色系统预测模型 · 灰色系统预测案例分析
·层次分析方法建模 · 层次分析一般方法 · 层次分析方法建模
· 综合评价方法建模—在管理界 十分流行
还有更抽象的数学如微分几何、 黎曼几何在更复杂的问题中需要 应用。比如:Mong-Ampere方程的 建立,源头问题是一个最优化问 题。
才成为科学”
03法学 0301法学 0302政治学 0303社会学 0304民族学 0305视马频1 克思主义理论 0306公安学 04教育视频2 学 0401教育学 0402心理学(教育学、理学学位) 0403体育学
05文学 0501中国语言文学 0502外国语言文学 0503新视频1闻传播学
2
一、提高兴趣的几种方式
物理
化学化工 计算机 生物
几
各学科 案例
科学
生态
种
内容新颖有趣—源头问题且案例具有时代感
方
式 各行业 案例
航空航 天行业
材料工程 行业
金融证券
银行保 险行业
模式别具一格—研究性、协同学习相结合模式
以学 生为 主体
三人 一组3
协同 研讨
论文 陈述
教师 点评
1、这些年,为案例的何时代感总有“怪 风”来袭?
例如:造林和更新问题;例如: 渔业养殖与捕捞问题;例如:农 业生产最佳灌溉系统问题。
(B)采矿业;
例如:烟煤和无烟煤开采洗选 合理配置问题;
例如:对煤矿瓦斯气(煤层气) 的开采问题,瓦斯爆炸的运动 方程与预防。
(C)制造业;
例如:加工过程中的最佳方案 问题等
(D)电力、燃气及水的生产 和供应业;
(M)科学研究、技术服务和 地质勘查业;
例如:自然灾害和自然现象的 分析与预测 (1)石油开采模型 (2)新材料的合成 晶体生长、聚合物材料的特性
(N)水利、环境和公共设施 管理业;
例如:2005年高教社杯全国 大学生数学建模竞赛题目 A题: 长江水质的评价和预测
(O)居民服务和其他服务业;
例如:菜市场选址问题;菜 篮子工程的优化问题;
·偏微分方程建模—白箱模型 · 偏微分方程建模特征 · 偏微分方程模型经典解法
·变分法建模—白箱模型 · 变分法简介 · 变分法思想建模
(3)离散优化方法建模 · 线性规划模型 · 整数规划模型 · 非线性规划模型 · 动态规划建模
·图论模型 · 经典问题
·组合数学模型 · 组合计数 · 组合设计 · 组合矩阵
(1)数学建模与自然科 学各学科
07理学视频1 0701数学 0702物理学
