电磁场与电磁波(第四版)课后答案_第三章习题
谢处方《电磁场与电磁波》(第4版)课后习题-第3章 静态电磁场及其边值问题的解【圣才出品】

第3章 静态电磁场及其边值问题的解(一)思考题3.1 电位是如何定义的?中的负号的意义是什么?答:由静电场基本方程▽×E=0和矢量恒等式可知,电场强度E 可表示为标量函数φ的梯度,即式中的标量函数φ称为静电场的电位函数,简称电位;式中负号表示场强方向与该点电位梯度的方向相反。
3.2“如果空间某一点的电位为零,则该点的电场强度也为零”,这种说法正确吗?为什么?答:不正确。
因为电场强度大小是该点电位的变化率。
3.3“如果空间某一点的电场强度为零,则该点的电位为零”,这种说法正确吗?为什么?答:不正确。
此时该点电位可能是任一个不为零的常数。
3.4 求解电位函数的泊松方程或拉普拉斯方程时,边界条件有何意义?答:边界条件起到给方程定解的作用。
3.5 电容是如何定义的?写出计算电容的基本步骤。
答:两导体系统的电容为任一导体上的总电荷与两导体之间的电位差之比,即其基本计算步骤:①根据导体的几何形状,选取合适坐标系;②假定两导体上分别带电荷+q和-q;③根据假定电荷求出E;④由求得电位差;⑤求出比值3.6 多导体系统的部分电容是如何定义的?试以考虑地面影响时的平行双导线为例,说明部分电容与等效电容的含义。
答:多导体系统的部分电容是指多导体系统中一个导体在其余导体的影响下,与另一个导体构成的电容。
计及大地影响的平行双线传输线,如图3-1-1所示,它有三个部分电容C11、C12和C22,导线1、2间的等效电容为;导线1和大地间的等效电容为;导线2和大地间的等效电容为图3-1-13.7 计算静电场能量的公式和之间有何联系?在什么条件下二者是一致的?答:表示连续分布电荷系统的静电能量计算公式,虽然只有ρ≠0的区域才对积分有贡献,但不能认为静电场能量只存在于有电荷区域,它只适用静电场。
表示静电场能量存在于整个电场区域,所有E≠0区域对积分都有贡献,既适用于静电场,也用于时变电磁场,当电荷分布在有限区域内,闭合面S无限扩大时,有限区内的电荷可近似为点电荷时,二者是一致的。
《电磁场与电磁波》(第四版)课后习题解答(全)

第一章习题解答【习题1.1解】222222222222222222222222222222222222cos cos cos cos cos cos 1xx x y z yx y z z x y z x y z x y z x y z x y z x y z x y z 矢径r 与轴正向的夹角为,则同理,矢径r 与y 轴正向的夹角为,则矢径r 与z 轴正向的夹角为,则可得从而得证a a b b g g a b g =++=++=++++=++++++++++==++ 【习题1.2解】924331329(243)54(9)(243)236335x y z x y z x y z x y z x y z x y z x y z x y z A B e e e e e e e e e A B e e e e e e e e e A B e e e e e e A B +=--+-+=-+=----+=---∙=--∙-+=+-=⨯()()-()(9)(243)19124331514x y z x y z x y z x y ze e e e e e e e e e e e =--⨯-+=---=--+【习题1.3解】已知,38,x y z x y z A e be ce B e e e =++=-++ (1)要使A B ⊥,则须散度 0A B =所以从 1380A B b c =-++=可得:381b c +=即只要满足3b+8c=1就可以使向量错误!未找到引用源。
和向量错误!未找到引用源。
垂直。
(2)要使A B ,则须旋度 0A B ⨯= 所以从1(83)(8)(3)0138xy zx y z e e e A B b c b c e c e b e ⨯==--+++=-可得 b=-3,c=-8 【习题1.4解】已知129x y z A e e e =++,x y B ae be =+,因为B A ⊥,所以应有0A B ∙= 即()()1291290xy z x y ee e ae be a b ++∙+=+= ⑴又因为 1B =; 所以221=; ⑵由⑴,⑵ 解得 34,55a b =±=【习题1.5解】由矢量积运算规则123233112()()()x y zx y z x x y y z ze e e A Ca a a a z a y e a x a z e a y a x e xyzB e B e B e B =?=-+-+-=++取一线元:x y z dl e dx e dy e dz =++则有xy z xyz e e e dlB B B dx dy dzB ?=则矢量线所满足的微分方程为 x y zd x d y d z B B B == 或写成233112()dx dy dzk a z a y a x a z a y a x==---=常数 求解上面三个微分方程:可以直接求解方程,也可以采用下列方法k xa a y a a z a d z a a x a a y a d y a a z a a x a d =-=-=-323132132231211)()()( (1)k x a y a z zdzz a x a y ydy y a z a x xdx =-=-=-)()()(211332 (2)由(1)(2)式可得)()(31211y a a x a a k x a d -=)()(21322z a a x a a k y a d -= (3))()(32313x a a y a a k z a d -= )(32xy a xz a k xdx -=)(13yz a xy a k ydy -= (4))(21xz a yz a k zdz -=对(3)(4)分别求和0)()()(321=++z a d y a d x a d 0)(321=++z a y a x a d0=++zdz ydy xdx 0)(222=++z y x d所以矢量线方程为1321k z a y a x a =++ 2222k z y x =++【习题1.6解】已知矢量场222()()(2)x y z A axz x e by xy e z z cxz xyz e =++++-+- 若 A 是一个无源场 ,则应有 div A =0即: div A =0y x zA A A A x y z∂∂∂∇⋅=++=∂∂∂ 因为 2x A axz x =+ 2y A by xy =+ 22z A z z cxz xyz =-+- 所以有div A =az+2x+b+2xy+1-2z+cx-2xy =x(2+c)+z(a-2)+b+1=0 得 a=2, b= -1, c= - 2 【习题1.7解】设矢径 r的方向与柱面垂直,并且矢径 r到柱面的距离相等(r =a ) 所以,2sssr ds rds a ds a ah πΦ===⎰⎰⎰=22a h π=【习题1.8解】已知23x y φ=,223y z A x yze xy e =+而 A A A A rot⨯∇+⨯∇=⨯∇=φφφφ)()(2222(6)3203xy zx y ze e e A xy x y e y e xyze x y z x yz xy ∂∂∂∇⨯==--+∂∂∂ 2223[(6)32]x y z A x y xy x y e y e xyze φ∴∇⨯=--+又y x z y x e x e xy ze y e x e 236+=∂∂+∂∂+∂∂=∇φφφφ 232233222630918603xy z x y z e e e A xyx x y e x y e x y ze x yz xy φ∇⨯==-+所以222()3[(6)32]x y z rot A A A x y xy x y e y e xyze φφφ=∇⨯+∇⨯=--+ +z y x e z y x e y x e y x 2332236189+-=]49)9[(3222z y x e xz e y e x x y x+--【习题1.9解】已知 222(2)(2)(22)x y zA y x z e x y z e x z y z e =++-+-+ 所以()()1144(22)0xyzyy x x z z x y z x yzx y z A A A A A A rot A A x y z y z z x x y A A A xz xz y y e e ee e e e e e ∂∂⎛⎫⎛⎫∂∂∂∂∂∂∂⎛⎫=∇⨯==-+-+- ⎪ ⎪ ⎪∂∂∂∂∂∂∂∂∂⎝⎭⎝⎭⎝⎭-++-+-=由于场A 的旋度处处等于0,所以矢量场A 为无旋场。
电磁场与电磁波第四版第三章部分答案

电磁场与电磁波第三章无限大导体平板分别置于k = 0和x - d处,板间充满电荷,其体电荷密度为p =-:极板间的电位分别为0和如图所示,求两d级板之间的电位和电场强度。
解:由泊松定理得d2* _ 1dx2电o d3解得二:6«od|在久=0处* * = 0,故B = 0在X二d处,"二%故U。
二-页j亠Ad证明:同轴线单位长度的静电储能$二巴。
式中山为单位长度上的电臼2C|6 c od +荷量,C为单位长度上的电容。
解:由高斯定理可知:故内外导体间的电压为qj Qi h------- d P = ---- ------ ln-则电容为有一半径为a,带电量q的导体球,其球心位于介电常数分别为5和F.汕勺两种介质的分界面上,该分界面为无限大平面。
试求:(1)导体球的电容;(2)总的静电常量解:根据边界条件则Eit = E2t,故有□二E?二日,由于I ■ I _■_ _,所以一- I |_ 1 1;l)iSi I P2S2 = q即 2 n r2 f ]E 十2^r2- Qn qE =-------- ---------------2 n r2( e 1 + e 2)导体球的电位为“(日)二J’Edr二N77:+ 二心电容为「二為=2肌(£ 1亠5)』⑵总的静能量为1I | I在一块厚度为d的导电板上,由两个半径分别为卜汇4的圆弧和夹角为u 的两半径割出的一块扇形体,如图所示。
试求:(1)沿厚度方向的电阻;(2)两圆弧面之间的电阻;(3)沿方向的两电极间的电阻。
设导电板的电导率为。
&解:(1)设沿厚度方向的两电极的电压为f U1则El 二7aUiJ1二晌二〒11 = JiSi =晋-7(ra2一n2)故得到沿厚度方向的电阻为无限长直线电流I 垂直于磁导率分别为「1和叫的两种磁介质的分界 鸟 1辺 应rd (3)设沿 . 一―一 J 厂頁 i'2 u dU 3------- d r… a r ri 1 0 dU 3 r 2 ------ 1 n — a nu 3 a Rj =—= h o din — ri 2dIl a O (r 22 - \'\(2)设内外两圆弧面电极之间的电流为1 [2 I 2 J2肓a rd12比 12 匚2E^dr = -------In 一F LCL rd V] 故两圆弧面之间的电阻为<1K^rd® o 沿d 方向的电阻为1_ (u - jio)l7 _ U 憑_ H _ 五u 叶 心—T ;'=0以z 轴为中心, 为半径做一个圆形回路C,由安培环路定理得其厚度可忽略不计。
电磁场与电磁波课后习题答案第3章(杨儒贵编着)

第三章 静电场3-1 已知在直角坐标系中四个点电荷分布如习题图3-1所示,试求电位为零的平面。
解 已知点电荷q 的电位为rq 4πεϕ=,令)0,1,0(1q q -=,)0,1,3(2q q +=,)0,0,1(3q q -=,)0,0,0(4q q +=,那么,图中4个点电荷共同产生的电位应为∑=414ii r q πεϕ令0=ϕ,得 0 4 4 4 44321=+-+-r qr q r q r q πεπεπεπε 由4个点电荷的分布位置可见,对于x =1.5cm 的平面上任一点,4321 ,r r r r ==,因此合成电位为零。
同理,对于x =0.5cm 的平面上任一点,3241 ,r r r r ==,因此合成电位也为零。
所以,x =1.5cm 及x =0.5cm 两个平面的电位为零。
3-2 试证当点电荷q 位于无限大的导体平面附近时,导体表面上总感应电荷等于)(q -。
证明 建立圆柱坐标,令导体表面位于xy 平面,点电荷距离导体表面的高度为h ,如图3-2所示。
那么,根据镜像法,上半空间的电场强度为32023101 4 4r q r q πεπεr r E -=X 习题图3-1(r , z )习题图3-2电通密度为)(43223110r r q r r E D -==πε 式中 232231])([h z r r -+=; 232232])([h z r r ++=那么,⎥⎥⎥⎦⎤⎪⎪⎪⎭⎫ ⎝⎛+++-++-+⎢⎢⎢⎣⎡⎪⎪⎪⎭⎫ ⎝⎛++--+=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧++++--+-+=z z zh z r hz h z r h z h z r r h z r r q h z r h z r h z r h z r q e e e e e e D r r r 232223222322232223222322])([])([ ])([])([4 ])([)(])([)(4ππ 已知导体表面上电荷的面密度n s D =ρ,所以导体表面的感应电荷为2322232223220)(2][][4h r qh h r h h r h q D z zs +-=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧++-+-===ππρ 则总的感应电荷为q h r r r qh r r S q s ss -=+-===⎰⎰⎰∞∞2322)(d d 2d 'πρρ3-3 根据镜像法,说明为什么只有当劈形导体的夹角为π的整数分之一时,镜像法才是有效的?当点电荷位于两块无限大平行导体板之间时,是否也可采用镜像法求解。
电磁场与电磁波(第四版)课后答案__谢处方

电磁场 与电磁波(第四版) 课后答案第一章 习 题 解答1.1 给定三个矢量A 、B 和C 如下: 23x y z =+-A e e e4y z =-+B e e 52x z =-C e e求:(1)A a ;(2)-A B ;(3)A B ;(4)AB θ;(5)A 在B 上的 分量;(6)⨯A C ;(7)()⨯A B C 和()⨯A B C ;(8)()⨯⨯A B C 和()⨯⨯A B C 。
解 (1)23A x y z +-===+-e e e A a e e e A (2)-=A B (23)(4)x y z y z +---+=e e e ee 64x y z +-=e e e (3)=A B (23)x y z +-e e e (4)y z -+=e e -11 (4)由c o sAB θ=11238=A B A B ,得1c o s AB θ-=(135.5= (5)A 在B 上的分 量 B A =A c o s AB θ==A B B (6)⨯=A C 123502xyz-=-e e e 41310x y z ---e e e (7)由于⨯=B C 041502xyz-=-e e e 8520x y z ++e e e⨯=A B 123041xyz-=-e e e 1014x y z ---e e e所以 ()⨯=A B C (23)x y z +-e e e (8520)4x y z ++=-e e e ()⨯=A B C (1014)x y z ---e e e (52)42x z -=-e e (8)()⨯⨯=A B C 1014502xyz---=-e e e 2405x y z -+e e e()⨯⨯=A B C 1238520x y z -=e e e 554411x y z --e e e1.2 三角形的三个顶点 为1(0,1,2)P -、2(4,1,3)P -和3(6,2,5)P 。
《电磁场与电磁波》第4版(谢处方 编)课后习题答案 高等教育出版社三章习题解答

三章习题解答3.1 真空中半径为a 的一个球面,球的两极点处分别设置点电荷q 和q -,试计算球赤道平面上电通密度的通量Φ(如题3.1图所示)。
解 由点电荷q 和q -共同产生的电通密度为33[]4q R R π+-+-=-=R R D 22322232()(){}4[()][()]r z r z r z a r z a q r z a r z a π+-++-+-++e e e e 则球赤道平面上电通密度的通量d d zz SSS Φ====⎰⎰D S D e22322232()[]2d 4()()aq a ar r r a r a ππ--=++⎰22121)0.293()aqaq q r a ==-+ 3.2 1911年卢瑟福在实验中使用的是半径为a r 的球体原子模型,其球体内均匀分布有总电荷量为Ze -的电子云,在球心有一正电荷Ze (Z 是原子序数,e 是质子电荷量),通过实验得到球体内的电通量密度表达式为02314ra Ze r r r π⎛⎫=- ⎪⎝⎭D e ,试证明之。
解 位于球心的正电荷Ze 球体内产生的电通量密度为 124rZer π=D e 原子内电子云的电荷体密度为 333434a a Ze Zer r ρππ=-=- 电子云在原子内产生的电通量密度则为 32234344r r a r Ze r r r ρπππ==-D e e 故原子内总的电通量密度为 122314r a Ze r r r π⎛⎫=+=- ⎪⎝⎭D D D e3.3 电荷均匀分布于两圆柱面间的区域中,体密度为30C m ρ, 两圆柱面半径分别为a 和b ,轴线相距为c )(a b c -<,如题3.3图()a 所示。
求空间各部分的电场。
解 由于两圆柱面间的电荷不是轴对称分布,不能直接用高斯定律求解。
但可把半径为a 的小圆柱面内看作同时具有体密度分别为0ρ±的两种电荷分布,这样在半径为b 的整个圆柱体内具有体密度为0ρ的均匀电荷分布,而在半径为a 的整个圆柱体内则具有体密度为0ρ-的均匀电荷分布,如题3.3图()b 所示。
电磁场与电磁波(第4版)第3章部分习题参考解答
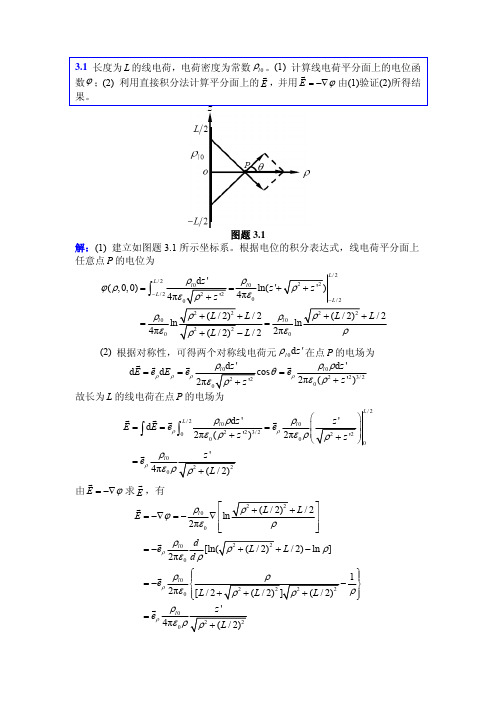
ρ ≥ a 时, E = −∇ϕ = −eρ
G
G ∂ ∂ρ
3.4 已知 y > 0 的空间中没有电荷,试判断下列函数中哪些是可能的电位解? (1) e− y cosh x ;(2) e− y cos x ;(3) e− 2 sin x cos x ;(4) sin x sin y sin z 。 解:在电荷体密度 ρ = 0 的空间,电位函数应满足拉普拉斯方程 ∇ 2ϕ = 0 。
∂2 − y ∂2 − y ∂2 − y (e cosh x) + 2 (e cosh x) + 2 (e cosh x) = 2e− y cosh x ≠ 0 (1) ∂x 2 ∂y ∂z −y 所以函数 e cosh x 不是 y > 0 空间中的电位解; ∂2 − y ∂2 − y ∂2 − y (e cos x) + 2 (e cos x) + 2 (e cos x) = −e− y cos x + e− y cos x = 0 (2) ∂x 2 ∂y ∂z −y 所以函数 e cos x 是 y > 0 空间中可能的电位解; ∂ − 2 ∂ ∂ (e sin x cos x) + 2 (e− 2 sin x cos x) + 2 (e − 2 sin x cos x) (3) 2 ∂x ∂y ∂z
G ρ = −eρ l 0 2πε 0 G = eρ
ρl 0 4πε 0 ρ
⎧ ρ 1⎫ ⎪ ⎪ − ⎬ ⎨ 2 2 2 2 ρ⎪ ⎪[ L / 2 + ρ + ( L / 2) ] ρ + ( L / 2) ⎩ ⎭ z'
ρ 2 + ( L / 2) 2
3.2 点电荷 q1 = q 位于 P 1 ( − a, 0, 0) ,另一点电荷 q2 = −2q 位于 P 2 ( a, 0, 0) ,求空间的 零电位面。 解:两个点电荷 + q 和 −2q 在空间产生的电位 ⎤ q 1 ⎡ 2q ϕ ( x, y , z ) = − ⎢ ⎥ 2 2 2 2 2 2 4 πε 0 ⎢ ( ) ( ) ⎥ x a y z x a y z + + + − + + ⎣ ⎦ 1 2 − =0 令 ϕ ( x, y, z ) = 0 ,则有 2 2 2 2 ( x + a) + y + z ( x − a) + y 2 + z 2
《电磁场与电磁波》第4版(谢处方 编)课后习题答案 高等教育出版社三章习题解答

三章习题解答3.1 真空中半径为a 的一个球面,球的两极点处分别设置点电荷q 和q -,试计算球赤道平面上电通密度的通量Φ(如题3.1图所示)。
解 由点电荷q 和q -共同产生的电通密度为33[]4q R R π+-+-=-=R R D 22322232()(){}4[()][()]r z r z r z a r z a q r z a r z a π+-++-+-++e e e e 则球赤道平面上电通密度的通量d d zz SSS Φ====⎰⎰D S D e223222320()[]2d 4()()aq a ar r r a r a ππ--=++⎰ 22121)0.293()aqaq q r a =-=-+ 3.2 1911年卢瑟福在实验中使用的是半径为a r 的球体原子模型,其球体内均匀分布有总电荷量为Ze -的电子云,在球心有一正电荷Ze (Z 是原子序数,e 是质子电荷量),通过实验得到球体内的电通量密度表达式为02314ra Ze r r r π⎛⎫=- ⎪⎝⎭D e ,试证明之。
解 位于球心的正电荷Ze 球体内产生的电通量密度为 124rZer π=D e 原子内电子云的电荷体密度为333434a a Ze Zer r ρππ=-=- 电子云在原子内产生的电通量密度则为 32234344r ra r Ze rr r ρπππ==-D e e 故原子内总的电通量密度为 122314ra Ze r r r π⎛⎫=+=- ⎪⎝⎭D D D e 3.3 电荷均匀分布于两圆柱面间的区域中,体密度为30C m ρ, 两圆柱面半径分别为a 和b ,轴线相距为c )(a b c -<,如题3.3图()a 所示。
求空间各部分的电场。
解 由于两圆柱面间的电荷不是轴对称分布,不能直接用高斯定律求解。
但可把半径为a 的小圆柱面内看作同时具有体密度分别为0ρ±的两种电荷分布,这样在半径为b 的整个圆柱体内具有体密度为0ρ的均匀电荷分布,而在半径为a 的整个圆柱体内则具有体密度为0ρ-的均匀电荷分布,如题 3.3图()b 所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2e y chx 0
y 函数 e chx 不是 y 0 空间中电位的解。
(2)
2 y 2 y 2 y y y ( e cos x ) ( e cos x ) ( e cos x ) e cos x e cos x 0 2 2 2 x y z
sin x cos x 0
sin x cos x 不是 y 0 空间中电位的解。
(4)
2 2 2 2 (sin x sin y sin z) 2 (sin x sin y sin z) 2 2 (sin x sin y sin z) 2 x y x z
sin x sin y sin z sin x sin y sin z sin x sin y sin z 0
0
0 x 3 Ax B 解得 6 0d 在x=0处 0 ,B=0
在x=d处 U 0 ,故
0d 3 U0 Ad 6 0 d U 0 0d A d 6 0
3 x 因此 0 6 0d
U 0 0 d x d 6 0
第三章 习题
3.3 有一半径为 a 的圆柱体,已知柱内外的电位函数分别为 0 ra
a2 A(r ) cos r
ra
(1)求圆柱内、外的电场强度; (2)这个圆柱是什么材料制成的?表面有电荷分布吗?试求之。 解: (1)电场
在
ra
e E (er ez ) r r z
2
1
强度 H1 H2
(1)利用安培环路定律,当 a 时, 有 I I 2 B0 0 2 2 B0 0 2 a a 2 a
在 a b 的区域内,有
H1 H2 I
即
B1 B2 I 1 2
函数 e y cos x 是 y 0 空间中电位的解。
(3)
2 (e 2 x
2 2y sin x cos x) 2 (e y 2 2y sin x cos x) 2 (e z 2y
sin x cos x)
2y
e
函数 e
2y
2y
(cos2 x sin2 x) 2e
B e
故
12 I 1 2
a b
同轴线中单位长度存储的磁场能量为
1 b B02 1 b B2 1 b B2 Wm 2 d d d a a a 2 0 2 1 2 2 1 a 1 0 I 1 1 1 b 1 1 2 I 2 d d 2 0 a 2 0 2 a 2 1 2 0 1 2 0 I 2 12 I 2 b ln 16 2 1 2 a
1 bU 2 h (l h) 0 2 d
液体所受的沿高度方向的电场力为
bU 2 W bU 2 F (h l 0 h 0 ) ( 0 ) h h d 2d
这个力应与水平面以上的液体重量相平衡,即
( 为体积)所以有
解:在 y 0 的空间中无电荷分布,电位函数因满足拉普拉斯方程, 题中几个函数中凡满足拉普拉斯方程的函数,便为 y 0 空间电位的解
(1)
2 2 2 2 y 2 y 2 y 2 2 2 (e chx) 2 (e chx) 2 (e chx) 2 x y z x y z
M 1
0
B2 H e
0 I
20
则磁化电流体密度
1 d J m M ez M d ez
0 I
20
1 d 1 0 d
由 B2 H e I 看出 0 处有奇异性,所以在磁介质中 2 0 处存在磁化线电流 I m 以z轴为中心、 为半径做一个圆形
B1
和
B2
解:由安培环路定律,有
H H I 2
z
I
O
1 0
利用边界条件
即
H1t H2t
2
H1t H2t H
B H
( z 0)
( z 0)
及本构关系
有
0 I B1 0 H 2
B2 H
I 2
(2)介质的磁化强度
0 x 2 U 0 0 d E ex ex x 2 0 d d 6 0
3.9 有一半径
a ,带电量 q 的导体球,其球心位于两种介质的
分界面上,此两种介质的介电常数分别为 1 和 2 ,分界面可视 为无限大平面,求(1)球的电容;(2)总静电能。 解: (1)由于电场分布仍沿径向方向,所以在两种介质的 分界面上,根据边界条件有
0 Er
r a
2 A 0 cos
3. 已知 y 0 的空间中没有电荷,下列几个函数中哪个可能 是电位函数解?
(1) exp y cosh x (3) exp( 2 y)sin x cos x (2)
exp( y) cos x
(4) sin x sin y sin z
处
a2 a2 E er A cos (1 2 ) e A(1 2 sin ) r r 即 a2 A a2 A E er ( A 2 ) cos e ( A 2 sin ) (r a) r r
在 ra 处
E 0
(2)这个圆柱体是由导体制成的,表面有电荷存在, 其电荷密度为
函数 sin x sin y sin z 不是 y 0 空间中电位的解。
3.7无限大导体平板分别置于x=0 和 x=d处,板间充满电荷,其体
0 x 电荷密度为 d ,极板电位分别为0和U0,求两极板间的电位
和电场强度。 解:两导体间的电位满足泊松方程 2
d 2 1 0 x 因此有 2 dx 0 d
2 2
1 2 (2)由 Wm LI ,得到单位长度的自感为 2
2Wm 0 12 b L 2 ln I 8 1 2 a
3.23一电荷量为 q 质量为 m 的小带电体,放置在无限长导体 平面下方,与平面距离 h 。求 q 的值以使带电体上受到的 3 静电力恰好与重力相平衡(设 m 2 10 kg, h 0.02m)。
其中 为液体的质量密度 证:设电容极板面积为 S bl
b 为宽,
1
( l 为极板高),液面升高为 。电容器的电容为两个电容并联, h
即 C
bh 0b(l h) d d
电容器的储能为
2 1 U bh 0b(l h) 2 W CU 2 2 d d
E1t E2t E
En 0
所以此题仍可用高斯定理
S
D dS q
求解,即
D1S1 D2 S2 q
4 r 2 4 r 2 1E 2E q 2 2
所以
E
q 2 r 2 (1 2 )
孤立导体球的电位为 a E dr
a
a
q q dr 2 2 r (1 2 ) 2 a(1 2 )
F mg g
bU 2 ( 0 ) hbdg 2d
液面升高为
U 2 ( 0 ) 1 U 2 h ( 0 )( ) 2 2d g 2 g d
3.15 无限长直线电流 I 垂直于磁导率分别为 1 和 2 的两种 磁介质的交界面,试求(1)两种媒质中的磁感应 (2)磁化电流分布
回路C,由安培环路定律有
I Im
1
0
c
B dl
I 0
因此得到
I m 1 I 0
在磁介质表面上,磁化电流面密度为
J ms M ez |z0 e
0 I
20
3.19同轴线内导体是半径为a的圆柱,外导体是半径为b的薄圆柱 面,其厚度可忽略不计。内外导体间填充有磁导率不同的介质。 设同轴线中通过的电流为I,试求 (1)同轴线中单位长度所储存的磁场能量; (2)单位长度的自感 解:同轴线的内外导体之间的磁场沿φ方 向,在两种介质分界面上,磁场只有法向 分量,根据边界条件可知,两种介质的 磁感应强度 B1 B2 B e B 但磁场
3.29如图所示,请求出槽内的电位分布。y , 有限】
y
U0
a
x
题7图
故球的电容为
C
q
a
2 a(1 2 )
2 1 q (2)总的静电能量为 W a q 2 4 a(1 2 )
3.10 两平行的金属板,板间距离为 d ,竖直地插在介电常数为 的液体中,板间电压为 U。证明液体面升高为
U 2 h ( 0 )( ) 2 g d
解:小带电体可视为一点电荷 q ,它所受静电力,来自导体
' 平板的感应电荷,也就是镜像电荷 q(平面上方 h 处, q ' q )对它的作用力。
q2 fe 4 0 (2h)2
吸力,向上。
令 fe 与重力mg大小相等,有
q2 mg 2 4 0 (2h)
解得
q 5.9 108 C
