自适应复化求积法
复化梯形积分的自适应算法

复化梯形积分的自适应算法复合梯形积分是一种数值积分方法,用于计算积分形式为∫a^b f(x)dx的近似值。
它是复合模拟辛普森法的一种变体,它使用了梯形规则来估计函数的积分。
自适应算法是指积分算法自动地调整区间的长度和位置,以满足某些精度要求。
这使得自适应算法能够更有效地计算复杂函数的积分。
下面是一个简单的复合梯形积分自适应算法的步骤:1. 设置初始区间[a, b]和精度要求eps。
2. 计算区间[a, b]上的积分值I,使用复合梯形法。
3. 将区间[a, b]划分为两个子区间[a, c]和[c, b],其中c=(a+b)/2。
4. 计算子区间[a, c]和[c, b]上的积分值I1和I2,使用复合梯形法。
5. 计算I的近似误差E=|I-(I1+I2)|。
6. 如果E>eps,则递归调用算法,计算子区间[a, c]和[c, b]的积分值。
否则,返回I作为积分的近似值。
这个算法可以递归地将区间划分为更小的子区间,直到达到精度要求为止。
它的时间复杂度是O(n),其中的n是递归的次数,取决于函数的复杂度和所需的精度。
复合梯形积分自适应算法有一些优点,包括:•它可以自动地调整区间长度和位置,以满足精度要求。
•它可以有效计算复杂函数的积分。
•它的时间复杂度比较低,在大多数情况下都能满足实际需求。
但是,复合梯形积分自适应算法也有一些缺点,包括:•它需要较多的计算,因为必须多次计算函数的值。
•它可能在边界处产生较大的误差。
•它对初始区间的选择有一定的要求,如果选择的初始区间不合适,可能会导致较大的误差。
总的来说,复合梯形积分自适应算法是一种有效的数值积分方法,它可以有效计算复杂函数的积分。
但是,在实际应用中,还应该根据函数的特点和精度要求选择合适的积分算法。
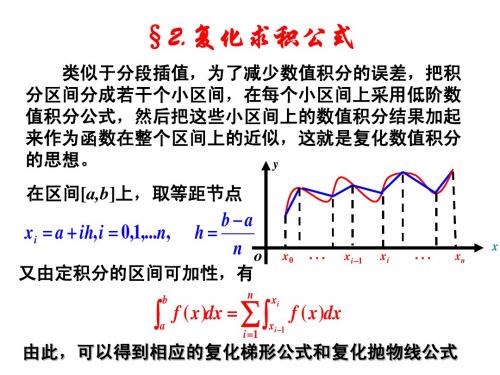
复化求积公式

h[ 2
f ( x0 )
n1
2
k 1
f ( xk )
f ( xn )]
复化梯形公式
Tn
h 2
[
f
(
x0
)
n1
2
k 1
f ( xk )
f ( xn )]
复化梯形公式
计算方法
2.复化辛浦生公式
计算方法
在每个小区间[xk1, xk ]上应用辛浦生公式得:
xk
xk 1
则
f
b
( x)dx h[ f 6
计算方法
在 每 个 小 区 间[ xk1, xk ]上 应 用 梯 形 公 式 得 :
xk xk 1
f ( x)dx
h 2
[
f
(
xk1
)
f ( xk )]
则
b
n
f (x)dx =
xk f (x)dx
a
k 1 xk1
n k 1
h[ f 2
(xk1)
f
(xk )]
计算方法
x0 x1 x2 x3
2
三、区间逐次分半求积法
计算方法
复化求积公式可有效提高计算精度,但对给定 的误差限,如何确定节点的个数,即[a,b]应多少等 份?由截断误差可以估计步长的取值情况,但需要 给出各阶导数的最大值,这往往是比较困难的,且 估计值往往偏大.
接下来,我们将考虑步长的更为实用的选取方 法.
计算方法
若用Tn及T2n分别表示将[a, b]n等分及2n等分的复化 梯形公式,则
f(x) 1 0.997 0.9896 0.976 0.95 0.936 0.908 0.877 0.841 3978 158 7267 8851 1556 8516 1925 4709
数值分析(18)复化求积法

1 2
h2
b
4
a
,
直到 T2n Tn 为止,将T2n作为积分的近似值。
数值分析
数值分析
下面推导由n到2n的复化梯形公式
给出误差限,将[a,b]n等分,步长hn
b
a n
,
用复化梯形公式:
在[xk , xk1 ]上,T1k
hn 2
(
f
( xk )
f ( xk1 ))
在[a, b]上,
T (hn ) Tn
理查逊外推算法流程 1,0
1,1 2,0
1,2 2,1 3,0
M
M
MO
1,n 2,n1 3,n2 L n1,0
数值分析
数值分析
二、龙贝格(Romberg)方法
龙贝格(Romberg)算法是将理查逊(Richardson)外推法应 用于数值积分,由低精度求积公式推出高精度求积公式的算法。
h
ba 2k
数值分析
数值分析
变步长复化梯形公式的递推公式: (由n到2n)
T2n
1 2 Tn
Hn 2
其中Tn
hn 2
(
f (a)
n1
f (b)) hn
k 1
f ( xk )
n1
H n
hn
k0
f
(
x
k
1
)
2
实际计算中的递推公式为
ba
T1
[ f (a) f (b)] 2
1
b a n1
ba
T2n 2 Tn
复 化 梯 形 公 式 的 截 断 误差 有 展 开 式
b a
f ( x)dx Tn
C2h2
chap4第2节 复化求积公式
Rn [ f ]
h (b a )
2
f ( ), (a , b)
12
如果记 M 2 max f ( x )
a xb
则有 Rn [ f ]
b
a
f ( x )dx Tn
( b a )h 12
2
M2
(b a ) 12n
2
3
M2
上式说明复化梯形公式是收敛的。
这时由
xk x k 1
得到
h h f f ( x )dx f ( xk 1 ) 4 f ( x 1 ) f ( xk ) k 2880 6 2 n
5
(4)
( k )
b
a
f ( x )dx
i 1
xk
f ( x )dx
x k 1
5 n h h (4) f ( k ) f ( x k 1 ) 4 f ( x 1 ) f ( x k ) 2880 k 1 k k 1 6 2
1
1 4 4 4 2 2 2 1 4 6 1 1 9 9
3.1230
4 )3
而梯形公式的结果为
1 x
0
1
4
2
dx
1 0 2
(
4
1 0 11
例 4.4 用复化梯形公式计算积分 I 0 e dx ,应将区间 [0,1]多少等分,才可以使其截断误差不超过 1 10 4
x
1
2
解:复化梯形公式的误差为
Rn [ f ] f ( x )dx Tn
a b
(b a ) 12n
复化求积公式的算法及其应用

摘要在数值计算中,低阶牛顿柯特斯求积方法存在很多缺陷,从余项公式可以看出其要求提高求积公式的代数精度,必须增加结点个数,会导致插值多项式出现龙格现象,且数值稳定性不能保证.基于以上原因,我们往往采用复化求积方法,此方法不仅可以克服以上缺点而且便于在计算机上实现,值得研究和学习.在本课程设计中,我们首先从复化求积公式的思想引入,然后详细介绍复化梯形求积公式、复化辛普森求积公式和复化柯特斯求积公式的推导过程和相关性质,再对三种求积公式进行比较和总结,其次画出三种求积公式的流程图,最后通过求解例题写出三种求积算法的程序设计.关键词复化求积算法;流程图;程序设计目录引言 0第一章复化求积算法 (2)§1.1复化求积公式 (2)§1.1复化求积公式的思想 (3)§1.2复化求积公式的构造 (3)§1.2复化梯形求积公式 (3)§1.2.1复化梯形求积公式的推导过程 (3)§1.2.2复化梯形求积公式的性质 (3)§1.3复化辛普森求积公式 (4)§1.3.1复化辛普森求积公式的推导过程 (4)§1.3.2复化辛普森求积公式的性质 (4)§1.4复化柯特斯求积公式 (5)§1.4.1复化柯特斯求积公式的推导过程 (5)§1.4.2复化柯特斯求积公式的性质 (5)§1.5三种复化求积公式的比较及总结 (6)第二章复化求积公式算法的流程图及其应用 (9)§2.1 流程图 (9)§2.2 应用 (12)参考文献 (15)附录A (16)附录B (17)附录C (18)引言积分计算在分析数学领域里是个古老的问题,在数值分析中已被广泛应用.但在计算机上却不能像在分析数学中那样,用原函数[满足)()('x f x F =的函数)(x F 就是函数)(x f 的原函数]计算积分.这是因为在实际问题中,函数关系往往是用列表数据或曲线给出的.即使知道了函数的表达式,求其一个原函数并非一个简单问题.许多函数难以用初等函数表示(如2,/sin x e x x -等).在计算机上,通常利用函数的若干个离散值,以代数运算近似计算积分值,这类近似计算法称为数值积分法.设给定区间],[b a 上的函数)(x f .需要建立计算积分dx x f f I ba ⎰=)()(的近似方法.数值积分的基本思想是试图用一个简单又易于积分的函数逼近)(x f ,以计算积分)(f I .显然插值多项式是一个很好的选择,因为插值多项式可由)(x f 的若干值构造出来,其积分很容易计算.为此,需将],[b a 分为n 等分n i x x i i ,,2,1],,[1 =+,其中b x x x x a n =<<<<=+1321 .分割步长h ,因此,1,3,2,/)1(1+=-+=n i h i x x i 对应的函数值)()(,),(),()(121b f x f x f x f a f n ==+ .显然)(f I 可以表示为所有小区间上各函数的积分的和,即)()(1f I f I ni i ∑==其中 dx x f I i ix x i ⎰+=1)(通常把为每个)(f I i 建立的计算公式简称为求积公式,而把)(f I 建立的求积公式称为复化求积公式.由于在实际计算时,不宜使用高阶的牛顿——柯特斯公式,但若积分区间较大,单独用一个低阶的牛顿——柯特斯公式来计算积分的近似值,显然精度不好,为了提高数值求积的精确度,可利用积分对区间的可加性来解决这个问题,这就是通常采用的复合求积法.而且使用这种方法之后,求积公式的收敛性和稳定性也得到了改善.第一章 复化求积算法牛顿—柯特斯公式的求积余项表明,求积节点n 越大,对应的求积公式精度越高,但由于牛顿—柯特斯公式在8>n 时数值不稳定,因此不能用增加求积节点数的方法来提高计算精度.实用中常将求积区间],[b a 分成若干个小区间,然后在每个小区间上采用数值稳定的牛顿—柯特斯公式求小区间上的定积分,最后把所有小区间上的计算结果相加来作为原定积分的近似值.采用这种方法构造的求积公式就称为复合求积公式.复合求积公式具有计算简单且可以任意逼近所求定积分值的特点,这是牛顿—柯特斯公式一般做不到的.常用的复合求积公式有复合梯形求积公式和复合辛普森求积公式以及复合柯特斯求积公式.以下我们将从三种复化求积算法的构造、余项、稳定性、收敛性等几方面进行讨论,并写出相应的流程图以及应用中所涉及到的算法的程序设计.§1.1复化求积公式§1.1.1 复化求积公式的思想n 很大时,牛顿——柯特斯求积公式出现了不稳定、不收敛现象,往往使用低阶牛顿——柯特斯求积公式,误差比较大,故将],[b a 若干等分,在每个子区间上反复使用低阶牛顿——柯特斯公式,进行累加.而构造出来的新的求积公式,称之为复化求积公式.在构造求积公式的过程中,我们将求积区间],[b a 进行等距细分:n i nab ia x i ,,1,0, =-+=,在每个小区间],[1i i x x -上用相同的“基本”求积公式(如梯形公式;中矩形公式;左(右)矩形公式或辛普森公式)计算出dx x f i i x x ⎰-1)(的近似值i S .§1.1.2 复化求积公式的的构造将定积分⎰ba dx x f )(的区间],[b a 划分为n 等分,各节点为kh a x k +=,n k ,,1,0 =,nab h -=,在子区间)1,,1,0](,[1-=+n k x x k k 上使用牛顿——柯特公式,将],[1+k k x x 分割为l 等份,步长为l h,节点为1,,2,,+=+++k k k k k x llhx l h x l h x x记121,,,,++++=k ll k lk lk k x xxxx为在],[1+k k x x 上作)(x f 的l 阶牛顿——柯特斯求积公式.∑∑⎰=++=+=-=≈+li li k l i li k li l i k k k i x x xf C h xf C x x I dx x f k)(0)(1)()()()()(1由积分区间的可加性,可得nli k n k li l i n k k l n k k k baI xf C h I dxx f dx x f ==≈=+-==-=-=+∑∑∑∑⎰⎰)()()(100)(1)(11§1.2 复化梯形求积公式§1.2.1 复化梯形求积公式的的推导过程将积分区间],[b a 划分等分,步长nab h -=,求积节点kh a x k +=,n k ,,1,0 =在每个小区间)1,,1,0](,[1-=+n k x x k k 上应用梯形公式)]()([2)(11++≈⎰+k k x x x f x f hdx x f k k然后将它们累加求和,作为所求积分I 的近似值.])()(2)([2)]())()()((2)([2)]()([2)()(11121011011∑∑∑⎰⎰---+-=-=++=+++++=+≈==+n i k n n k k n k n k x x bab f x f a f hx f x f x f x f x f hx f x f hdx x f dx x f I k k记n T )]()(2)([211b f x f a f hn i k ++=∑-=式为复化梯形求积公式,下标n 表示将区间n 等分,若把区间n 2等分,在每个小区间上仍用梯形求积公式,则可得到n n T T ,2和n H 间的关系为:)(212n n n H T T +=其中∑=--+=nk n nab k a f h H 1]2)12([ §1.2.2复化梯形求积公式的性质性质1.1复化梯形求积公式余项当)(x f 在],[b a 上有连续的二阶导数,则复化梯形公式的余项:)(12)()(''2ηf h a b T dx x f R n ba T --=-=⎰ ],[b a ∈η 性质1.2稳定性若],[,)(''b a x M x f ∈≤,则有估计式M na b R nT 2312)(-≤ 复化梯形求积公式的系数均大于零,且满足a b nh n hA ni i -==+-+=∑=]1)1(21[2因此,复化梯形求积公式的计算过程是数值稳定的.性质1.3收敛性可证复化梯形求积公式是收敛的. 性质1.4代数精度定义1.1 若积分⎰b adx x f )(的数值积分公式⎰badx x f )()(0k nk k x f A ∑=≈对于任意一个次数不高于m 次的多项式都精确成立,且存在一个1+m 次多项式使之不精确成立,则称该数值积分公式的代数精度为m .可证复化梯形求积公式的代数精度为2.§1.3 复化辛普森求积公式§1.3.1 复化辛普森求积公式的的推导过程将积分区间],[b a 划分等分,记子区间],[1+k k x x 的中点为h x x k k 2121+=+在每个小区间上应用辛普森公式,则有))()(2)(4)((6)444(6)]()(4)([6)()(101121211223112101211011b f x f x f a f hf f f f f f f f f hx f x f x f hdxx f dx x f I n k n k k k n n n k k k n k n k x x bak k+++=+++++++++=++≈==∑∑∑∑⎰⎰-=-=+--++-=-=+其中h x xk k 2121+=+记 )]()(2)(4)([6111021b f x f x f a f hS n k k n k k n +++=∑∑-=-=+式为复化辛普森求积公式§1.3.2复化辛普森求积公式的性质性质1.5复化辛普森求积公式余项当)(x f 在],[b a 上有连续的四阶导数,复化辛普森公式的求积余项为:)(2880)()2(180)4(4)4(4ηηf h a b f h a b R S --=--= ],[b a ∈η 性质1.6稳定性同复化梯形求积公式,复化辛普森求积公式的系数均大于零,且满足总和为a b - 因此,复化辛普森求积公式的计算过程是数值稳定的.性质1.7收敛性可证复化辛普森求积公式是收敛的. 性质1.8代数精度可证复化辛普森求积公式的代数精度为4.§1.4 复化柯特斯求积公式§1.4.1 复化柯特斯求积公式的的推导过程将积分区间],[b a 划分等分,若把每个子区间],[1+k k x x 四等份,内点依次记为432141,,+++k k k xxx,同理可得复化柯特斯求积公式)](7)(14)(32)(12)(32)(7[9010101143211041b f x f x f x f x f a f hC n k n k n k k k k n k k n +++++=∑∑∑∑-=-=-=++-=+(1-1)其中h x xh x x h x x k k k k k k 43;21;41432141+=+=+=+++ 记(1-1)为复化柯特斯求积公式§1.4.2复化柯特斯求积公式的性质性质1.9复化柯特斯求积公式余项当)(x f 在],[b a 上有连续的四阶导数,复化柯特斯公式的求积余项为:)()4(945)(2)6(6ηf h a b R c --= ],[b a ∈η性质1.10稳定性同复化梯形求积公式,复化柯特斯求积公式的系数均大于零,且满足总和为a b - 因此,复化柯特斯求积公式的计算过程是数值稳定的.性质1.11收敛性可证复化柯特斯求积公式是收敛的. 性质1.12代数精度可证复化柯特斯求积公式的代数精度为6.§1.5 三种复化求积公式的比较及总结为了更形象的表述三种复化求积公式之间的关系,我们通过一个例子来进行比较例1.1使用各种复化求积公式计算定积分dx xxI ⎰=10sin 为简单起见,依次使用8阶复化梯形公式、4阶复化辛普森公式和2阶复化柯特斯公式,可得各节点的值如下表表1-1节点值94569086.0)]1()(2)0([161718=++=∑=f x f f T k k 94608331.0)]1()(2)(4)0([2413031214=+++=∑∑==+f x f x f f S k k k k 94608307.0)]1(7)(14)](32)(12)(32[)0(7[180111104342412=+++++=∑∑==+++f x f x f x f x f f C k k k k k k 比较三个公式的结果:精度最低 94569086.08=T 精度次高 94608331.04=S 精度最高 94608307.02=C原积分的精确值为6719460830703.0sin 10==⎰dx xxI . 我们知道,三种求积公式的余项分别如表1-2表1-2 复化梯形、辛普森、柯特斯求积公式的余项定义1.2对于复化求积公式n I 若存在0>p 及0≠c ,使其余项n I I -满足c h I I pnh =-→0lim则称复化求积公式n I 是p 阶收敛的 P 阶收敛性的意义:对于一个数值求积公式来说,收敛阶越高,近似值n I 收敛到真值dx x f ba ⎰)(的速度就越快.由于三种求积公式的余项分别是h 的2,4,6阶无穷小量 所以n n n C S T ,,趋于定积分I 的速度依次更快.从这三种求积公式的构造过程中可以看出,它们都属于机械求积公式,但不属于插值行和牛顿柯特斯公式.都具有稳定性和收敛性,且收敛速度一个比一个快,一个比一准确.在使用函数值个数相等的情况下,248,,C S T 的精度逐渐升高.第二章复化求积公式算法的流程图及其应用§2.1 流程图1.复化梯形求积公式图2.1 复化梯形求积公式算法的流程图Step1给出被积函数)(x f 、区间],[b a 端点b a ,和等分数n ; Step2求出,kh x k =nab h -=; Step3计算∑-=1)(),(),(n k k x f b f a f ;Step4得)]()()([211b f x f a f h T n k k n ++=∑-=2. 复化辛普森求积公式图2.2 复化辛普森求积公式算法的流程图Step1 给出被积函数)(x f 、区间],[b a 端点b a ,和等分数n ; Step2求出,kh x k =nab h -=; Step3计算∑∑-=+-=1211)(,)(),(),(n k k n k k xf x f b f a f ;Step4得)]()(2)(4)([6111021b f x f x f a f hS n k k n k k n +++=∑∑-=-=+3. 复化柯特斯求积公式图2.3 复化柯特斯求积公式算法的流程图Step1给出被积函数)(x f 、区间],[b a 端点b a ,和等分数n ; Step2求出,kh x k =nab h -=; Step3计算∑∑∑∑-=-=+-=+-=+11143121141)(,)(,)(,)(),(),(n k k n k k n k k n k k x f xf xf xf b f a f ;Step4得)](7)(14)(32)(12)(32)(7[9010101143211041b f x f x f x f x f a f hC n k n k n k k k k n k k n +++++=∑∑∑∑-=-=-=++-=+§2.2 应用例2.1.分别用复化梯形,复化辛普森,复化柯特斯公式计算函数32)(x x x f -=在区间]1,0[上的弧长S .(要求写出源程序和运行结果) *注 在],[b a 上的弧长dx x f S ba⎰+=2'))((11.用复化梯形公式计算S 的过程:(1).写出变量说明表2-1 复化梯形求积公式程序设计的变量说明Step1 输入n ,nab h -=,被积函数0),(1=s x f ; Step2 for 1=k to 1-n ;{计算11)(s kh a f s →++}))(2)((21b f s a f hs ++=; Step3 输出近似值s .(3) 写出源程序和运行结果(见附录A) 2.用复化辛普森公式计算S 的过程: (1).写出变量说明表2-2 复化辛普森求积公式程序设计的变量说明Step1:输入n ,nab h -=,被积函数0),(1=s x f 0,2=s ; Step2:for 1=i to 1-n ,2+=i i ;{计算11)2/*(s h i a f s →++} Step3:for 2=j to 1-n ,2+=j j ; {计算22)2/*(s h j a f s →++}))(24)((621b f s s a f hs +++=; Step4:输出近似值s .(3).写出源程序和运行结果(见附录B) 3.用复化柯特斯公式计算S 的过程: (1).写出变量说明表2-3 复化柯特斯求积公式程序设计的变量说明Step1输入n ,nab h -=,被积函数0),(1=s x f 0,2=s 0,3=s ; Step2 for 1=i to 1-n ,2+=i i ;{计算11)4/*(s h i a f s →++} Step3:for 2=j to 1-n ,4+=j j ; {计算22)4/*(s h j a f s →++} Step4: for 4=k to 2-n ,2+=k k ; {计算33)4/*(s h k a f s →++}))(141232)((90321b f s s s a f hs ++++=; Step5:输出近似值s .(3).写出源程序和运行结果(见附录C)根据运行结果可知,由三种复化求积公式求得的S 的值分别为064837.1、061199.1、061189.1,精度逐渐升高.参考文献[1] 薛毅,耿美英.数值分析[M]. 北京:北京工业大学出版社.2003年. [2] 刘长安.数值分析教程[M].西安:西北工业大学出版社.2005年.[3] 朝伦巴根,贾德彬.数值计算方法[M].北京:中国水利水电出版社.2007年.[4] 韩旭里,万中.数值分析与实验[M].北京: 科学出版社.2006年.[5] 林成森.数值分析[M].北京: 科学出版社.2007年.[6] 封建湖,车刚明,聂玉峰.数值分析原理. 北京: 科学出版社.2001年.附录A1.复化梯形求积公式的程序设计:(1).源程序:#include<stdio.h>#include<math.h>double f(double x){double z;z=sqrt(1+pow((2*x-3*pow(x,2)),2));return z;}main(){ int n,k;float h;float a;float b;double s=0.0;double s1=0.0;double t;printf("Please input the deng fen ;");scanf("%d",&n);printf("Please input qujian a ;");scanf("%f",&a);printf("Please input qujian b ;");scanf("%f",&b);h=(b-a)/n;for (k=1;k<n;k++){ t=a+k*h;s1=s1+f(t);}s=(h/2)*(f(a)+2*s1+f(b));printf("%f\n",s);}(2).运行结果:图1 复化梯形求积公式计算弧长结果附录B2.复化辛普森求积公式的程序设计:(1).源程序:#include<stdio.h>#include<math.h>double f(double x){double z;z=sqrt(1+pow((2*x-3*pow(x,2)),2));return z;}main(){ int n,i,j;float h;float a;float b;double s=0.0;double s1=0.0,s2=0.0;double t,l;printf("Please input the deng fen ;");scanf("%d",&n);printf("Please input qujian a ;");scanf("%f",&a);printf("Please input qujian b ;");scanf("%f",&b);h=(b-a)/n;for(i=1;i<8;i=i+2){t=a+i*h/2;s1=s1+4*f(t);}for(j=2;j<8;j=j+2){l=a+j*h/2;s2=s2+2*f(l);}s=(h/6)*(f(a)+s1+s2+f(b));printf("%f\n",s);}(2).运行结果:图2 复化辛普森求积公式计算弧长结果附录C3.复化柯特斯求积公式的程序设计:(1).源程序:#include<stdio.h>#include<math.h>double f(double x){double z;z=sqrt(1+pow((2*x-3*pow(x,2)),2));return z;}main(){int n,i,j,k;float h;float a;float b;double s=0.0;double s1=0.0,s2=0.0,s3=0.0;double t,l,m;printf("Please input the deng fen ;"); scanf("%d",&n);printf("Please input qujian a ;");scanf("%f",&a);printf("Please input qujian b ;");scanf("%f",&b);h=(b-a)/n;for(i=1;i<8;i=i+2){t=a+i*h/4;s1=s1+32*f(t);}for(j=2;j<7;j=j+4){l=a+j*h/4;s2=s2+12*f(l);}for(k=4;k<6;k=k+2){m=a+k*h/4;s3=s3+14*f(m);}s=(h/90)*(7*f(a)+s1+s2+s3+7*f(b)); printf("%f\n",s);}(2).运行结果:图3 复化柯特斯求积公式计算弧长结果。
自适应求积分

自适应求积分
1. 基本原理
自适应求积分的基本步骤如下:
(1) 将整个积分区间划分为若干个小区间;
(2) 在每个小区间上应用某种数值积分公式(如复化trapezoid规则、Simpson规则等)计算部分积分值;
(3) 估计每个小区间上的积分误差;
(4) 对误差较大的区间继续细分,重复步骤(2)和(3),直到所有区间的误差之和满足给定的精度要求。
2. 误差估计
误差估计是自适应求积分的关键步骤。
常用的误差估计方法有: (1) 重复嵌套规则:使用不同阶数的积分公式,根据结果的差值估计误差;
(2) Romberg积分:通过Richardson外推估计误差上限;
(3) 双重积分:利用高斯求积公式的嵌套性质,估计误差上限。
3. 自适应策略
不同的自适应策略对应不同的区间划分方式。
常见的策略包括: (1) 均匀划分:将区间等分为若干个小区间;
(2) 分治策略:将区间一分为二,分别处理两个子区间;
(3) 最大误差优先:优先细分误差最大的区间。
4. 应用实例
自适应求积分在工程计算、数值模拟等领域有着广泛应用,例如:
(1) 计算流体力学中的升力系数;
(2) 求解偏微分方程的边界积分项;
(3) 计算路径规划中的能量消耗等。
通过自适应求积分技术,可以在保证精度的前提下,提高计算效率,从而解决许多复杂的工程和科学计算问题。
自适应辛普森求积方法

自适应辛普森求积方法自适应辛普森求积方法是一种用于数值积分的数值计算方法。
它是对辛普森求积方法的改进和优化。
在数学中,积分是求解一个函数在某个区间内的面积或曲线下的总长度。
然而,很多函数的积分无法通过解析方法求得,因此需要使用数值方法进行近似计算。
辛普森求积方法是一种常见的数值积分方法之一。
辛普森求积方法基于一个假设:在每个小区间内,被积函数的形状近似为一个二次函数。
它将整个积分区间分割成若干个小区间,然后在每个小区间内使用一个二次函数来近似被积函数。
通过对这些二次函数的积分,可以得到整个区间内的近似积分值。
具体的计算公式如下:[int_{a}^{b} f(x) ,dx approx frac{b-a}{6} left( f(a) +4fleft(frac{a+b}{2}ight) + f(b)ight)]辛普森求积方法的优点是计算简单,精度较高。
然而,当被积函数在某些小区间上变化非常剧烈时,辛普森求积方法的精确度可能会降低。
为了解决这个问题,可以使用自适应辛普森求积方法。
自适应辛普森求积方法的基本思想是,在计算整个积分区间的近似积分值时,根据被积函数的变化情况,对不同的小区间使用不同的步长。
对于变化剧烈的区间,使用较小的步长,以提高精确度;对于变化平缓的区间,使用较大的步长,以提高计算效率。
具体的步骤如下:1. 将整个积分区间[a, b]等分成n个小区间,其中n为一个大于1的整数。
2. 在每个小区间上使用辛普森求积方法计算近似积分值。
3. 将得到的近似积分值相加,得到整个区间的近似积分值。
4. 检查每个小区间的近似积分值与整个区间的近似积分值之差,如果差值超过预设的精度要求,则将该小区间再次等分,并重复步骤2和3,直到满足精度要求为止。
通过自适应辛普森求积方法,可以在保持较高精度的同时,尽可能地减少计算量。
然而,需要注意的是,自适应辛普森求积方法的计算复杂度较高,对于复杂的被积函数和较大的积分区间,可能需要较长的计算时间。
复化求积公式

复化求积公式复化求积公式是计算定积分的一种常用方法。
它的基本思想是将区间分成多个小区间,用每个小区间上的函数近似代替原函数,然后将这些小区间的近似结果相加得到总的近似结果。
这个方法的优点是能够适用于各种函数类型,而且在计算机上也可以很方便地实现。
具体来说,我们可以将区间[a, b]均匀地分成n个小区间,每个小区间的长度都为Δx = (b-a)/n。
然后我们在每个小区间上选择一个点xi(可以是小区间的左端点、右端点、中点等)作为代表,然后计算这些小区间上的函数值f(xi)。
这样我们就得到了n个高度为f(xi)的矩形,它们的面积就是Δx * f(xi)。
将这n个矩形的面积相加,就得到了近似的定积分的结果。
单个小区间的近似结果可以表示为Δx * f(xi)。
为了得到更精确的结果,我们可以进一步增加小区间的数量,即取n趋向于无穷大的极限。
这样,我们就可以得到复化求积公式的一般形式:∫[a, b] f(x) dx ≈ Δx/2 * [f(x0) + 2f(x1) + 2f(x2) + ... + 2f(x(n-1)) + f(xn)]其中,Δx = (b-a)/n,x0 = a,xn = b,xi 是每个小区间上的代表点。
复化求积公式的精确度与小区间的数量n有关,通常情况下,n越大,近似结果越精确。
但是同时也需要注意,小区间的数量过大会导致计算量过大,需要更多的时间和计算资源。
复化求积公式在实际应用中有很重要的作用,特别是在数值计算和科学工程领域。
通过这个方法,我们可以近似地计算各种复杂的函数的定积分,例如概率密度函数、信号处理中的卷积运算等。
同时,复化求积公式也为数值积分提供了一种计算机实现的思路,可以通过编程语言实现自动计算定积分的功能。
总之,复化求积公式是计算定积分的一种重要方法,通过将区间分成多个小区间,用每个小区间上的函数近似代替原函数,并将这些小区间结果相加,从而获得近似结果。
它在实际应用中具有广泛的适用性和指导意义,为求解各种复杂问题提供了一种有效的数值计算方法。
数值分析考试复习总结汇总

第一章1 误差相对误差和绝对误差得概念 例题:当用数值计算方法求解一个实际的物理运动过程时, 一般要经历哪几个阶段? 在哪些阶段将有哪些误差产生? 答: 实际问题-数学模型-数值方法-计算结果 在这个过程中存在一下几种误差:建立数学模型过程中产生:模型误差 参数误差选用数值方法产生:截断误差 计算过程产生:舍入误差 传播误差6.设937.0=a 关于精确数x 有3位有效数字,估计a 的相对误差. 对于x x f -=1)(,估计)(a f 对于)(x f 的误差和相对误差.解 a 的相对误差:由于 31021|)(|-⋅≤-≤a x x E . x ax x E r -=)(, 221018110921)(--⋅=⨯≤x E r . (1Th ))(a f 对于)(x f 的误差和相对误差.|11||)(|a x f E ---==()25.021011321⨯⋅≤-+---ax x a =310-33104110|)(|--⨯=-≤a f E r . □2有效数字基本原则:1 两个很接近的数字不做减法:2: 不用很小得数做分母(不用很大的数做分子)例题:4.改变下列表达式使计算结果比较精确:(1) ;1||,11211<<+--+x xxx 对(2) ;1,11>>--+x xx xx 对(3)1||,0,cos 1<<≠-x x xx对.解 (1) )21()1(22x x x ++. (2) )11(2x x x x x-++.(3) xxx x x x x cos 1sin )cos 1(sin cos 12+≈+=-. □ 第二章拉格朗日插值公式(即公式(1))∑==ni i i n x l y x p 0)()(插值基函数(因子)可简洁表示为)()()()()()(0i n i n nij j j i j i x x x x x x x x x l ωω'-=--=∏≠= 其中: ()∏∏≠==-='-=nij j j i i nnj jn x x x xx x 00)(,)()(ωω. 例1 n=1时,线性插值公式 )()()()()(010110101x x x x y x x x x y x P --⨯+--⨯=, 例2 n=2时,抛物插值公式))(())(())(())(())(())(()(1202102210120120102102x x x x x x x x y x x x x x x x x y x x x x x x x x y x P ----⨯+----⨯+----⨯= 牛顿(Newton )插值公式由差商的引入,知(1) 过点10,x x 的一次插值多项式为)()()(0101x x c x f x p -+=其中],[)()(1001011x x f x x x f x f c =--=⇒ )](,[)()(01001x x x x f x f x p -+=(2) 过点210,,x x x 的二次插值多项式为))(()()(10212x x x x c x p x p --+=其中],,[)()()()(21002010112122x x x f x x x x x f x f x x x f x f c =------=⇒ ))(](,,[)()(1021012x x x x x x x f x p x p --+=))(](,,[)](,[)(102100100x x x x x x x f x x x x f x f --+-+=重点是分段插值: 例题:1. 利用Lagrange 插值公式求下列各离散函数的插值多项式(结果要简化):(1)(2)解(2):方法一. 由 Lagrange 插值公式)()()()()(332211003x l f x l f x l f x l f x L ⋅+⋅+⋅+⋅= 可得: )21()(23-=x x x L 方法二. 令)()21()(3B Ax x x x L +-=由 23)1(3-=-L , 21)1(3=L , 定A ,B (称之为待定系数法) □15.设2)(x x f =,求)(x f 在区间]1,0[上的分段线性插值函数)(x f h ,并估计误差,取等距节点,且10/1=h .解 2)(x x f =, ih x i = , 10,,1,0 =i , 101=h设 1+≤≤i i x x x ,则: ii ii i i i i h x x x x x f x x x x x f x f --+--⋅=++++1111)()()(h ihx h i h h i x h i -++-+-⋅=22))1(()1()( 100)1(10)12(+-+=i i x i 误差估计: ))1(()(!2|)()(|max)1(h i x ih x f x f x f hi x ix h +--''≤-+≤≤. □第三章最佳一致逼近:(了解) 最佳平方逼近 主要分两种情形:1. 连续意义下在空间],[2b a L 中讨论2. 离散意义下在n 维欧氏空间n R 中讨论,只要求提供f 的样本值1. 最佳逼近多项式的法方程组设],[2b a L 的1+n 维子空间 n P =span },,,1{2n x x x , 其中 n x x x ,,,12 是],[2b a L 的线性无关多项式系.对],[2b a L f ∈∀,设其最佳逼近多项式*φ可表示为: ∑==ni i i x a 0**φ由 n P f ∈∀=-φφφ ,0),(*⇒ ∑===-ni j i i n j x x a f 0*)1(0,0),(即 ∑===nj ij j i n i x f a x x 0*)1(0),,(),((*2) 其中⎰⎰⎰⋅==⋅=+b ab abai iji jijidx x x f x f dx x dx x x x x)(),( ,),(称(*2)式为最佳逼近多项式的法方程组(或正规方程组). 由n i i x 0}{=的线性无关性,可证明G 正定,即 上述法方程组的解存在且唯一 .11、 求x x f πcos )(= ,]1,0[∈x 的一次和二次最佳平方逼近多项式. 解: 设 x a a x P 10*1)(+= , 2210*2)(x b x b b x P ++= 分别为)(x f 的一次、二次最佳平方逼近多项式。
自适应求积分

自适应求积分
自适应求积分的基本思想是将积分区间划分为多个子区间,对每个子区间进行积分,然后将所有子区间的积分值相加得到最终的积分结果。
在这个过程中,算法会根据被积函数在每个子区间内的变化情况动态调整子区间的大小,从而确保在变化剧烈的区域使用更小的步长,在变化平缓的区域使用更大的步长。
自适应求积分算法通常包括以下几个步骤:
1. 初始化积分区间和误差容限。
2. 对整个积分区间进行初步估计,得到一个初始的积分值和误差估计值。
3. 如果误差估计值小于误差容限,则返回积分值作为最终结果。
4. 否则,将积分区间一分为二,对两个子区间分别进行积分和误差估计。
5. 对于每个子区间,重复步骤3和4,直到所有子区间的误差估计值之和小于误差容限。
6. 将所有子区间的积分值相加,得到最终的积分结果。
自适应求积分算法的优点在于能够自动调整步长,从而在保证精度的同时提高计算效率。
它特别适用于被积函数在某些区域变化剧烈,而在其他区域变化平缓的情况。
该算法广泛应用于数值计算、物理建模、工程分析等领域。
复化求积公式的算法及其应用

复化求积公式的算法及其应用复化求积公式是数值计算方法中重要的一种技术,用于近似计算函数的积分值。
该方法通过将积分区间等分为多个小区间,并在每个小区间上使用求积公式来估计函数在该区间上的积分值。
本文将介绍复化求积公式的算法及其应用。
一、复化求积公式算法1.复化梯形求积公式复化梯形求积公式是复化求积公式中最简单的一种,其基本思想是将积分区间等分为若干个小区间,然后在每个小区间上使用梯形求积公式计算积分值,最后将所有小区间的积分值相加得到最终的积分值。
算法步骤:1)将积分区间[a,b]等分为n个小区间,每个小区间的长度为h=(b-a)/n。
2) 在每个小区间上使用梯形求积公式计算积分值,即Ii=h/2*(f(xi)+f(xi+1)),其中xi=a+i*h,i=0,1,2,...,n-13)将所有小区间的积分值相加得到最终的积分值,即I≈I0+I1+I2+...+In-12. 复化Simpson求积公式复化Simpson求积公式是一种更为精确的复化求积公式,它通过在每个小区间上使用Simpson求积公式来计算积分值,从而提高了计算精度。
算法步骤:1)将积分区间[a,b]等分为n个小区间,每个小区间的长度为h=(b-a)/n。
2) 在每个小区间上使用Simpson求积公式计算积分值,即Ii=h/6*(f(xi)+4f(xi+h/2)+f(xi+h)),其中xi=a+i*h,i=0,1,2,...,n-13)将所有小区间的积分值相加得到最终的积分值,即I≈I0+I1+I2+...+In-1二、复化求积公式应用1.数学分析中的数值积分计算,用于计算函数的定积分值。
2.物理学中的积分计算,用于计算物理量的平均值或总量。
3.统计学中的积分计算,用于计算概率密度函数的面积值。
4.工程学中的积分计算,用于计算工程问题中的各种积分量。
5.金融学中的积分计算,用于计算金融衍生品的价格或价值。
总结:复化求积公式是一种重要的数值计算方法,在数学、物理、统计、工程、金融等领域中有广泛的应用。
4-3复化求积公式

1 n1 min f ( x ) f ( k ) max f ( x ) a xb a xb n k 0
故存在 [a , b] 使
1 n1 f ( ) f ( k ) n k 0
所以复化梯形公式的积分余项为
h3 RTn I Tn nf ( ) 12 ba 2 h f ( ) 12 3 b a [a , b] f ( ) 2 12n
由此解得
n 6616.67
2
所以
n 79
即至少要把区间[1,2]分为79等份。
对本例题的进一步思考:h是否越小越好?
前面介绍的复化求积公式对提高精度是行之 有效的,但使用前必须给出合适的步长h。
h太小则计算量增加
误差有积累,更需计算稳定
h太大则精度不满足
(收敛性)
计算方案:事先估计法 变步长(事后估计) 自适应步长法
2.系数Ak >0,满足 Ak b a ,故方法是稳定的.
k 0
n
三、例题
x
0
f(x)
1 0.9973978
ቤተ መጻሕፍቲ ባይዱ
sin x 举例 对于函数 f ( x ) x , 1/8
试利用下表计算积分
I
1 sin
1/4
3/8 1/2 5/8 3/4 7/8
0.9896158
0.9767267 0.9588510 0.9361556 0.9088516 0.8771925
3*. 复化柯特斯公式 如果将每个小区间[xk,xk+1]四等分,内分点 依次记为 xk 1 , xk 1 , xk 3 ,
4 2 4
则相应地可得复化柯特斯公式。
数值计算方法 复化求积公式 - 复化求积公式

nn
(t
0 j0
j )dt
jk
柯
特点: 插值型的、节点等距
特 斯
存在问题: 节点较多时,高次插值的不稳定导致高阶N-
公
K
式
解决办法公:式的复不化稳求定积。
复化求积法:区间分成若干子区间,在每个子区间上用低 阶求积公式。
N=1时的牛-柯公式
1
梯 形 公 式 T b a f a f b
牛 顿 -
xk1 xk
f
( x )dx
h[ 2
f
(xk )
f
(
xk
1
)]
h3 12
f ''(k )
k [ xk , xk1]
求和可得
I
b
n1
f (x)dx
xk1 f ( x )dx
a
k0 xk
h 2
n1
[
k0
f
(
xk
)
f ( xk1)]
Rn ( f )
2
记
Tn
h 2
n1 k0
[
f
(
xk
)
f ( xk1)]
b
lim
n
T
n
a
f ( x)dx,
复 化
事实上
h n1
Tn
2
[
k0
f
(
xk
)
Hale Waihona Puke f ( xk1 )]梯 形 公
1 b a n1
ba n
2 n
f (xk )
k0
n
f ( xk ).
k 1
式 的 收
lim
复化求积公式

第 二 节 复化求积公式
一、复化求积公式 复化求积公式的基本思想: 将区间[a , b] 分为若干个小子区间,在每个 小子区间上使用低阶的Newton-Cotes公式。然后
把它们加起来,作为整个区间上的求积公式。
数值分析
数值分析
1、复化梯形公式
将区间 a , b n等分, ba h , xk a kh, ( k 0,1, , n), n 在每个小区间 xk , xk 1 ,(k 0,1, , n 1) 上用梯形公式:
数值分析
数值分析
数值试验
复化Simpson公式Matlab程序
function rs= simpson(s,a,b,n) h = (b-a)/n; r= feval(s,a)+feval(s,b); for j = 1:2:n-1 x=a+j*h ; r= r+ 4*feval(s,x); end for j = 2:2:n-2 x=a+j*h ; r= r+ 2*feval(s,x); end 将此程序存于work目录中 rs = r*h/3;
n 1
复化Simpson公式的截断误差为
(b a ) 4 (4) 4 R( Sn ) h f ( ) O(h ) a, b 2880
数值分析
数值分析
数值分析
数值分析
Example 1
Approximate the integral
1 0.9 0.8 f(x)=sin(x)/x 0.7 0.6 0.5 0.4 0.3 0.2
s in x dx x 0
Using the Composite Trapezoidal rule and Composite Simpson’s rule
复化求积公式

复化求积公式复化求积复化求积是数值计算中一种常用的数值积分方法,用于近似计算函数的定积分。
1. 方法介绍复化求积的基本思想是将要求解的定积分区间划分为若干个小区间,并对每个小区间采用数值积分方法进行近似计算,最后将各小区间的积分结果相加得到整个定积分的近似值。
2. 公式列表以下是复化求积的常用公式:矩形公式矩形公式是最简单的复化求积公式,将每个小区间近似为一个矩形,并取矩形的高度为该小区间上函数值的平均值。
矩形公式的表达式如下:∫[a, b] f(x) dx ≈ (b - a) * (f(a) + f(b)) / 2其中,a和b为积分区间的上下限。
梯形公式梯形公式是复化求积中常用的公式,将每个小区间近似为一个梯形,并取梯形的高度为该小区间上函数值的平均值。
梯形公式的表达式如下:∫[a, b] f(x) dx ≈ (b - a) * (f(a) + f(b)) / 2其中,a和b为积分区间的上下限。
辛普森公式辛普森公式是复化求积中精度更高的公式,将每个小区间近似为一个二次曲线,并取二次曲线的高度为该小区间上函数值的平均值。
辛普森公式的表达式如下:∫[a, b] f(x) dx ≈ (b - a) * (f(a) + 4 * f((a + b) / 2) + f(b)) / 6其中,a和b为积分区间的上下限。
3. 示例说明以求解函数f(x) = x^2在区间[0, 1]上的定积分为例,通过复化求积方法进行近似计算。
矩形公式计算将区间[0, 1]划分为n个小区间,每个小区间的宽度为h = (1 - 0) / n。
利用矩形公式计算每个小区间的积分值,然后将所得结果相加。
∫[0, 1] x^2 dx ≈ (1 - 0) * (f(0) + f(1)) / 2= (1 - 0) * (0^2 + 1^2) / 2= 1/2梯形公式计算同样将区间[0, 1]划分为n个小区间,每个小区间的宽度为h = (1 - 0) / n。
自适应辛普森法积分算法推导

自适应辛普森法积分算法推导自适应辛普森法积分算法推导1. 引言在数学和工程领域中,积分算法是一项重要的计算工具,用于求解曲线下的面积、求解定积分等问题。
辛普森法是一种常用的数值积分方法,而自适应辛普森法则是在辛普森法的基础上进行改进的一种算法。
本文将对自适应辛普森法积分算法进行推导和解析,帮助读者深入理解该算法的原理和应用。
2. 自适应辛普森法积分算法概述自适应辛普森法是一种数值积分方法,通过对被积函数进行区间划分,利用辛普森公式进行数值积分。
在每个小区间上计算辛普森公式的近似值,然后根据精度要求和误差估计值来决定是否对当前区间进行进一步的划分,从而实现自适应性。
该算法的优点是能够适应被积函数的不规则性,同时具有较高的数值积分精度。
3. 自适应辛普森法推导下面,我们将对自适应辛普森法进行推导。
假设被积函数为f(x),要计算区间[a, b]上的定积分∫f(x)dx。
我们将区间[a, b]等分为n个小区间,每个小区间长度为h=(b-a)/n。
利用辛普森公式对每个小区间进行数值积分:∫f(x)dx ≈ (h/6) * (f(a) + 4*f((a+b)/2) + f(b))将所有小区间上的积分值相加,得到整个区间[a, b]上的近似积分值。
我们计算近似解的误差估计值,如果误差估计值大于预设的精度要求,就对误差较大的小区间进行进一步划分,重复以上步骤,直到满足精度要求为止。
4. 自适应辛普森法的应用与优点自适应辛普森法在实际应用中具有广泛的应用价值。
该算法能够适应被积函数的不规则性,对于具有较大波动的函数能够给出较为精确的数值积分结果。
由于该算法具有自适应性,能够根据不同函数的特点进行区间划分和积分计算,因此适用于多种类型的函数积分计算。
5. 个人观点与总结自适应辛普森法作为一种数值积分方法,不仅具有较高的数值积分精度,同时也具有较强的适应性和灵活性。
在工程实践中,我曾经使用自适应辛普森法对复杂函数进行积分计算,取得了较为满意的结果。
3.1复化数值求积法

2
f (b)
记
Tn
下面考虑余项,先从每个小区间上考虑余项,
因为每个小区间上是N-C公式中当n=1时的梯形公式。
定理7 若f ( x) C 2[a, b] , 则复化梯形公式的余项为
b
a f ( x)dx Tn
(b a)h2 12
f ( ),
a b,
b
及渐近估计式 a f ( x)dx Tn 1 ( f (a) f (b)), h 0。
(1)
f ( xi ) f (i ) f ( i )( xi i ) O(( xi i )2 )
(2)
(2) (1),得 f ( xi ) f ( xi1) hf (i ) O(h2 ),i 1,2,,n
即
hf (i ) [ f ( xi ) f ( xi1)] O(h2 ),i 1,2,,n
b
对[a,b] 上的任何连续函数 f (x),都有
lim
n
Tn
a
f ( x)dx
但对代数多项式
f (x)
x2, b a
f ( x)dx Tn
0, n 1,2,
定义4将区间 [a, b]n等分,h b ,a 用某一基本求积公式
n
In
生成的复化求积公式,若对充分光滑的被积函数 f (,x)有
)]
b f (x)dx h[ f (a)
a
6
n1
n
f (b) 2 f (xi ) 4
i 1
i 1
f
(
x
i
1
)]
S
n
2
12 Sn 3 Tn 3 Hn
由
2T2n
Tn
H
,得
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[ ]变为两个更小的子区间[ ],从而[ ]上的积分值为
于是
其中h=(b-a)/n
实验硬件及软件平台:
Matlab 2010a
实验步骤:
1.根据算法事先写出相应程序。
2.启动PC机,在Matlab中输入代码。
3.编译调试。
4.调试通过,计算出正确结果。
实验内容(包括实验具体内容、算法分析、源代码等等):
zishitixing.m
clear
clc
a=input('区间左端点:');
b=input('区间右端点:');
z=input('精度:');
h=b-a;
s2=h*(a+b)/2;
s1=0;
k=1;
s=0;
while abs(s1-s2)>=z
s1=s2;
s=0;
for i=1:1:k
s=s+f(a+(i-1/2)*h);
同时在实验过程中了解到在运用复化求积公式进行计算时,步长h取得太大时难以保证,步长太小时则会增加计算工作量,这时就必须要求进行反复利用求积公式进行计算,直到所求得的积分值满足精度要求为止。
指导教师意见:
签名: 年 月 日
实 验 报 告
实验课程名称数值计算方法
实验项目名称自适应复化梯形求积法
年 级2012级
专 业应用数学
学生姓名
学 号
理 学 院
实验时间:2014 年 4月 24日
学生所在学院:理学院 专业:应用数学 班级:应数121
姓 名
学 号
实验组
实验时间
2014.4.24指导教师Βιβλιοθήκη 成 绩实验项目名称
自适应复化梯形求积法
实验目的及要求:
复合梯形公式是提高精度的行之有效的方法,但是在使用求积公式之前,必须先给出步长。步长取得太大精度难以保证,步长太小则导致计算量的增加,而事先给出一个合适的步长往往是困难的,因此提出了在求积过程中根据精度要求自动确定积分步长的梯形公式的逐次分半加速法。
实验(或算法)原理
记 为n等分[a,b]后用复化梯形公式算得的积分值,于是
end
s2=s1/2+h*s/2;
k=2*k;
h=h/2;
end
disp('满足精度的值为:');
s2
f.m
function y=f(x)
y=exp(-x^2);
end
用上述程序计算 。
可见,用程序计算的结果和真实结果相同。
实验结果与讨论:
通过本实验的学习,初步掌握了使用自适应复化求积法。更进一步加深了对自适应复化求积法的基本原理和技巧的理解,初步学会使用自适应复化求积法解决一些简单的问题。
