高等数学讲义2
(高等数学)第二章 连续函数

周 世 国 讲 义第二章 连续函数第一节 连续函数一.连续函数的概念引:许多物理量都是随时间而连续变化的。
例如:自由落体的高度或冷却中固体的温度等。
通常我们说物理量()t f 随时间t 的变化而连续变化,其确切含义啥?那就是说,物理量()t f 在变化过程中不会突然发生跳跃,只要时间t 的改变量非常小,相应地量()t f 的改变也应该非常小.用极限的语言来说: ()()00l i m t t f t f t →=.推广上述的说法,就得到一般函数在一点处连续的概念.1.定义1.设函数()x f 在0x 的邻域()0U x 内有定义,如果()()00lim x x f x f x →=,则称()x f 在0x 点处连续,并称0x 点为函数()x f 的连续点. 注意:(1)由定义1可见,函数在0x 点处连续,则0x 点必属于()x f 的定义域,这()0lim x x f x A →=定义的前提有本质的区别;(2)如果()x f 在0x 点处连续,则函数()x f 在0x 点首先必有极限,而且极限值就 是函数()x f 在0x 点处的定义值,因此()x f 在连续点处的极限很好求; (3)如果()x f 在0x 点处连续,则()()lim x x x x f x f lim x →→=.2.连续的第一个等价定义:设函数()x f 在0x 的邻域()0U x 内有定义,如果对0,0>∃>∀δε,使当0x x ε-<时,就有()()0f x f x ε-<成立,称()x f 在0x 点处连续,并称0x 点为函数()x f 的连续点. 注意:定义中,不再象函数极限定义中那样,要求00x x <-(为何?) 函数在一点处连续还有第二种等价定义,为此要先介绍一个新概念----增量.3.定义2.若自变量从初始值0x 变化到终值x ,相应地函数值由()0f x 变化到()x f ,则称0x x -为自变量的增量,并计为0x x x ∆=-;而称()()0f x f x -为函数的增量,计为()()0y f x f x ∆=-.注意:显然()()0y f x f x ∆=-又可表示为:()()00y f x x f x ∆=+∆-由此可见()()0y f x f x ∆=-是0x x x ∆=-的函数.4.连续的第二种等价定义:设函数()x f 在0x 的邻域()0U x 内有定义,如果lim 0x y ∆→∆=,则称()x f 在0x 点处连续,并称0x 点为函数()x f 的连续点.二.左、右连续1.定义3.如果()()00lim x x f x f x -→=,则称()x f 在0x 点处左连续,并称0x 点为函数()x f 的左连续点;2.定义4.如果()()00lim x x f x f x +→=,则称()x f 在0x 点处右连续,并称0x 点为函数()x f 的右连续点.定理1.()x f 在x 0点处连续⇔()x f 在x 0点处既左连续又,右连续. 注意:连续函数的几何意义是:函数()x f y =的曲线在0x 点处没有断.三.函数在区间上连续定义5.若函数()x f 在开区间()b a ,内每一点0x 处都连续,则称函数()x f 在开区间()b a ,内连续;若函数()x f 在开区间()b a ,内每一点0x 处都连续,而且在点a 处右连续,在点b 处左连续则称函数()x f 在闭区间[]b a ,上连续.注意:在在闭区间[]b a ,上连续的函数的图形特征是曲线位于[]b a ,上方的一段是连续不间断的.例1.证明常值函数()c x f ≡在()+∞∞-,连续.证明:任取0x ()+∞∞-∈,,下证()x f 在0x 点处连续,即要证()()00lim x x f x f x →=,也就是要证: c c x x =→0lim .事实上,对,0>∀ε要使()()0||||0f x f x c c ε-=-=<,可取δ为任意正实数,则当0||x x ε-<时,就有 ()()0||f x f x ε-<成立。
考研高数讲义新高等数学上册辅导讲义——第二章上课资料

第二章导数与微分第一节导数概念一、导数的定义 定义:若极限()()lim lim 0000x x f x x f x y x x∆→∆→+∆-∆=∆∆存在,则称函数()y f x =在点0x 处可导,此极限值称为函数()y f x =在点0x 处的导数。
记为: ()0f x '、0x x y ='、0x x dy dx =、()0x x df x dx = (或极限()()lim 000x x f x f x x x →--存在也可)()()lim lim 0000x x f x x f x y x x∆→∆→+∆-∆=∆∆单侧导数:左导数:()()lim 000x f x x f x x-∆→+∆-=∆()()lim 000x x f x f x x x -→--存在,则称左导数存在,记为:()0f x -'。
右导数:()()lim 000x f x x f x x+∆→+∆-=∆()()lim 000x x f x f x x x +→--存在,则称右导数存在,记为:()0f x +'。
【例1】(89一)已知()32f '=,则【例2】(87二)设()f x 在x a =处可导,则(A )()f a '. (B )()2f a '.(C )0. (D )()2f a '.【例3】(89二)设()()()()12f x x x x x n =+++,则()0f '= .(C)可导,但导数不连续. (D)可导,但导数连续.处的(A)左、右导数都存在. (B)左导数存在,但右导数不存在.(C)左导数不存在,但右导数存在.(D)左、右导数都不存在.【例7】(96二)设函数()f x在区间(,)-δδ内有定是()f x的(A)间断点. (B)连续而不可导的点. (C)可导的点,且()00f'=.(D)可导的点,且()00f'≠.【例8】(90三)设函数()f x 对任意的x 均满足等式()()1f x af x +=,且有()0f b '=,其中a 、b 为非零常数,则(A )()f x 在1x =处不可导.(B )()f x 在1x =处可导,且()1f a '=.(C )()f x 在1x =处可导,且()1f b '=.(D )()f x 在1x =处可导,()1f ab '=.二、导数的几何意义和物理意义导数的几何意义: 切线的斜率为:()()tan lim 00x x f x f x k x x →-==-α, ()()00f x f x x x --导数的物理意义:某变量对时间t 的变化率,常见的有速度和加速度。
《高等数学》课件第2章

2.2 函数的求导法则
2.2.1 导数的四则运算法则
引例2-3(物体的运动速度) 已知某物体作直线运动,路 程s(单位m)与时间t(单位s)的函数关系为s=t2-tlnt+5,t∈[1, 5]. 求物体在t=2 s时的速度.
分析: 问题即为求导数 ds . 因为s的表达式较复杂,
dt t=2
所以直接用定义求解很繁琐,是否有便捷的方法呢?可以看 到,s是由t2、t、lnt、5这四个基本初等函数通过加、 减、 乘 法运算组成的,而这四个基本初等函数的导数都有现成的公 式可用,因此若能找到导数的四则运算法则,则问题迎刃 而解.
解 因为y′=3x2,由导数的几何意义可知,曲线y=x3 在 点(1,1)处的切线斜率为
K=y′|x=1=3
y-1=3(x-1)
y=3x-2
y 1 1 (x 1) 3
即
y 1x 4
33
2.1.4 可导与连续的关系
设函数y=f(x)在点x处可导,即 lim y f (x) 存在,由极
x0 x
限的运算法则得
如图2-1所示,设曲线y=f(x)上有定点M0(x0,y0)和动点 M(x+Δx,y+Δy),作割线M0M. 当动点M沿着曲线趋向于定 点M0时,割线M0M的极限位置M0T就定义为曲线在点M0处的 切线,过M0且与切线垂直的直线叫做曲线在点M0处的法线.
图2-1
割线M0M
tan y
x
其中φ为割线M0M的倾斜角. 当Δx→0时,点M将沿着 曲线无限趋于点M0,上式的极限存在,即
ds [2t ln t 1] 4 ln 2 1 2.3069 dt t=2
即物体在t=2 s时的速度约为2.3069 m/s.
高等数学随堂讲义二重积分概念

二重积分的性质
即若把曲线 K 按 x x0 , x1 , , xn ,分成 n 个小段
则每一小段都能被以
xi 为宽, i 为高的小矩形所
覆盖. 由于这 n 个小矩形面积的总和
n
i xi
i1
b
a
n i1
xi
,
因此由定理21.1 的推论即得曲线 K 的面积为零.
推论 1
参量方程 x (t ), y (t ) ( t ) 所表示的
I P 为 P 的外面积.
定义1
若平面图形 P 满足
I P = I P , 则称 P 为可求面积
的图形, 并把共同值 IP I P I P 作为 P 的面积.
§1二重积分概念
平面图形的面积
二重积分的定义及其存在性
二重积分的性质
定理20.1
平面有界图形 P 可求面积的充要条件是:
对任给的 0 , 总存在直线网 T,
所以也有 SK (T ) . 由上述推论, P 的边界K 的面积
为零.
§1二重积分概念
平面图形的面积
二重积分的定义及其存在性
二重积分的性质
定理21.3
若曲线 K 为定义在 [a , b] 上的连续函数
的图象, 则曲线 K 的面积为零.
f (x)
证 由于 f ( x) 在闭区间 [a , b]上连续, 所以它在
的网眼 (小闭矩形)
i 可分为三类:
(i) i 上的点都是 P 的内点;
(ii) i 上的点都是 P 的外点, 即
i
(iii) i 上含有 P 的边界点.
这时直线网 T
P ;
§1二重积分概念
平面图形的面积
二重积分的定义及其存在性
高等数学讲义第二章

⾼等数学讲义第⼆章24 第⼆章⼀元函数微分学§2.1 导数与微分(甲)内容要点⼀、导数与微分概念 1、导数的定义设函数)(x f y =在点0x 的某领域内有定义,⾃变量x 在0x 处有增量x ?,相应地函数增量)()(00x f x x f y -?+=?。
如果极限x x f x x f x yx x ?-?+=??→?→?)()(lim lim0000存在,则称此极限值为函数)(x f 在0x 处的导数(也称微商),记作0()f x ',或0x x y =',x x dxdy=,)(x x dxx df =等,并称函数)(x f y =在点0x 处可导。
如果上⾯的极限不存在,则称函数)(x f y =在点0x 处不可导。
导数定义的另⼀等价形式,令x x x ?+=0,0x x x -=?,则0000()()()l i mx x f x f x f x x x →-'=- 我们也引进单侧导数概念。
右导数:0000000()()()()()lim lim x x x f x f x f x x f x f x x x x +++→?→-+?-'==-? 左导数:0000000()()()()()lim lim x x x f x f x f x x f x f x x x x---→?→-+?-'==-? 则有)(x f 在点0x 处可导)(x f ?在点0x 处左、右导数皆存在且相等。
程:000()()()y f x f x x x '-=-25法线⽅程:00001()()(()0)()y f x x x f x f x '-=--≠' 设物体作直线运动时路程S 与时间t 的函数关系为)(t f S =,如果0()f t '存在,则0()f t '表⽰物体在时刻0t 时的瞬时速度。
3.函数的可导性与连续性之间的关系如果函数)(x f y =在点0x 处可导,则)(x f 在点0x 处⼀定连续,反之不然,即函数)(x f y =在点0x 处连续,却不⼀定在点0x 处可导。
高等数学讲义第二章:导数与微分2-第四节初等函数的求导问题双曲函数与反双曲函数的导数

(3)(u)vu vu v,
(4)
( u ) v
uvuv
(v0).
v2
设 yf(u )而 , u(x)则复y合 f[(函 x)的 ] 数
导数为
ddxydduyddux或 y (x ) f( u )(x ).
利用上述公式及法那么,初等函数求导问题可完 全 解注决意.:初等函数的导数仍为初等函数.
二、双曲函数与反双曲函数的导数
(sh)xchx (ch)xshx
(th)x( shx ) ch2xsh2x, 即 (thx) 1
chx
ch2x
ch2x
ar s ln x h ( 1 x x 2 )
(ars)h(xx1x2) x1x2
1 (1 x ) 1 .
x1x2
1x2 1 x2
同理
(arc)hx 1 ; x21
(arth)x 1 . 1x2
(loagx)
1 x ln a
(lnx)
1 x
(arcsxi)n 1 1 x2
(actraxn ) 1 1 x2
(arccxo)s 1 1 x2
(accrox)t 1 1 x2
2.函数的和、差、积、商的求导法那么
设u u( x), v v( x)可导,那么 (1)(uv)uv, (2)(cu)cu (其c中 是常 ). 数
结论 任何初等函数的导数都可以按常数和根本 初等函数的求导公式和上述求导法那么求出.
等都是初等函数。
2 yxarcxsi4 n2 x
(C ) 0 (sinx) co xs
( x ) x1
(coxs) six n
(taxn)se2cx
(coxt) cs2x c
(sexc) se x tc a xn (csxc) cx s cc x ot
《高等数学》课件 第2章

再设函数 x(t),y(t)都可导,且 '(t) 0 .由
复合函数及反函数的求导法那么与反函数的求导公式,
有
ddyxddyt ddxt ddyt d1x
(t) (t)
dt
dy
即
dy dx
dt dx
dt
34
第四节 高阶导数
定义2.4.1
函数 y= f(x) 的导数 y'= f' (x) 仍是 x 的函数,我们称
证
设函数 f ( x) 在点 x 0 处可导,即
lim y f (x) x0 x
存在,那么 lim y li x m 0 x y x li x m 0 x y li x m 0 x f(x 0 )0 0 .
所以函数在该点处连续.
注意: 函数在点 x 处连续未必可导.
即 ddx2y2 (t)(t) 3(t)(t)(t).
第五节 函数的微分及其应用
一、微分的概念
1.引例
一块正方形金属薄片受温度变化的影响,其边长由
x0变到x0 + Δx问此薄片面积改变了多少?
设薄片边长为 x , 面积为 A , 那么A=x2,当 x 在x0取得
增量Δx时,面积的增量为
A(x0x)2x02 2x0x(x)2
令xx0 x
f(x ) f(x 0 ) f(x 0 )(x x 0 )
f(x ) f(x 0 ) f(x 0 )(x x 0 )
(1) n1x 11x
常
n
用
(2) sinxx
的
近 似
(3) tanxx
公 式
(4) ex 1x
(5) ln(1x)x
v f (t) f (t0) t t0
高等数学上2_课件2.ppt

达标后的函数值:
f (x) A
2.2.2 x趋于有限值x0时函数的极限
●至此,我们用 N ”、“ X ”、“ ” 的语言定 义了七种极限, 下面将列表类比对照.
极限形式: 接近程度指标:
lim f (x) A
x
实现时刻:
X
实现时刻后的自变量: x X
达标后的函数值:
f (x) A
定义 2.2
*在定义 2.2 中, 将“ f (x) 在 b, 上有定义”换作 “ f (x) 在 , a上有定义;将“ x X ”换作“ x X ”
lim
x
f
(x)
A或
f
(x)
A(x
)
.
2.2.1 x趋于无穷大时函数的极限
定义 2.3 设 f (x) 在 , a b, (a ≤b) 上有定义,A
推 论 若 在 x0 的 某 去 心 邻 域 内 f (x) ≥ 0 ( 或
f
(
x)
≤
0
)且
lim
xx0
f
(x)
A ,则 A≥0 ( A≤0 ).
2.2.3 函数极限的性质
● 在 2.2.1,2.2.2 中我们共列举了六种类型的极限:
(1)
lim
x
f
(x) ;
(2)
lim
x
f
(x) ;
(3)
lim
2.2.1 x趋于无穷大时函数的极限
自变量 x 趋向于无穷大有下面三种方式: x ,表示 x 沿 x 轴无限向右推进,趋于正无穷大; x ,表示 x 沿 x 轴无限向左推进,趋于负无穷大; x ,表示 x 沿 x 轴无限向任何一方推进,即 x 趋于 .
《高等数学第二章》课件

高阶导数及其应用
高阶导数的 定义
解释高阶导数的概 念和计算方法,以 及与一阶导数的关 系。
阶乘
讨论阶乘的定义和 性质,以及在高阶 导数中的应用。
幂指函数的 导数
给出幂指函数的导 数计算公式和性质。
洛必达法则 及其应用
介绍洛必达法则的 原理和应用方法, 解决极限的问题。
极限的定义
清晰地定义函数的极限,包括左极限和右极限。
极限的性质
介绍极限的性质,如极限的唯一性和四则运算法则。
连续性
连续函数的概念
解释连续函数的定义和性质,以及在实际问 题中的应用。
连续函数的性质
讨论连续函数的重要性质,如介值定理和最 值定理。
导数
导数的定义
给出导数的几何和 代数定义,以及导 数的计算法则。
导数的性质
介绍导数的性质, 如导数的唯一性和 四则运算法则。
导数的计算
探讨不同类型函数 的导数计算方法, 如幂函数、三角函 数和复合函数的求 导法则。
几何意义和 物理意义
解释导数在几何和 物理中的意义和应 用。
微分学基本公式
函数的四则运算及其微分
给出函数的加减乘除法则,并给出微分的法 则。
复合函数的微分
《高等数学第二章》PPT 课件
欢迎大家来到《高等数学第二章》课件。本课将介绍函数的基本概念、常用 函数、极限、连续性、导数、微分学基本公式、高阶导数及其应用,以及函 数的图形与曲率。让我们一起探索数学的魅力吧!
导言
概述
介绍《高等数学第二章》的重要性和内容 概览。
常用符号说明
解释常见的数学符号的意义和用法。
常用函数
幂函数、指数函 数、对数函数
高等数学随堂讲义含参量反常积分

(A) sup xJ
A f ( x, y)dy
0 ( A ).
注2 由定义, ( x)
f ( x, y)dy在 I 上不一致收敛
c
的充要条件是
使得
0 0, M c, A M及 x0 J ,
A
f ( x0 ,
y)dy
0
.
§2 含参量反常积分 一致收敛性 一致收敛性的判别
性质
含参量无界函数的反常积分
含参量无界函数的反常积分
魏尔斯特拉斯 M 判别法
设有函数 g(y), 使得
f ( x, y) g( y) , (x,y) I [c, ) .
若 g( y)dy 收敛, 则 f ( x, y)dy 在 I 上一致收敛.
c
c
证
由于
c
g(
y)dy
收敛,
N
c,A1 ,
A2
N,
因此
A2 g( y)dy . A1
是 x 的连续函数. 在上面不等式中令 x b , 得到当
A A M 时,
A
A f (b, y)dy .
而 是任给的, 因此 f ( x, y)dy 在 x b 处收敛, c
这与假设矛盾. 所以积分 f ( x, y)dy 在 [a, b) 上 c
不一致收敛.
§2 含参量反常积分 一致收敛性 一致收敛性的判别
1 1 x2
,
及反常积分
0
1
dx x2
收敛,
故由魏尔斯特拉斯M判
别法, 含参量反常积分(10)在 (, ) 上一致收敛.
§2 含参量反常积分 一致收敛性 一致收敛性的判别
性质
含参量无界函数的反常积分
例4 证明含参量反常积分
《高等数学讲义》(上、下册)--目录 樊映川等编

第一篇解析几何《高等数学讲义》 (上、下册) -- 目录第五章极坐标樊映川等编12.平面束的方程第一章行列式及线性方程组1.二阶行列式和二元线性方程组2.三阶行列式3.三阶行列式的主要性质4.行列式的按行按列展开5.三元线性方程组6.齐次线性方程组7.高阶行列式概念第二章平面上的直角坐标曲线及其方程1.轴和轴上的线段2.直线上点的坐标数轴3.平面数的点的笛卡儿直角坐标4.坐标变换问题5.两点间的距离6.线段的定比分点7.平面上曲线方程的概念8.两曲线的交点第三章直线与二元一次方程1.过定点有定斜率的直线方程2.直线的斜截式方程3.直线的两点式方程4.直线的截距式方程5.直线的一般方程6.两直线的交角7.直线平息及两直线垂直的条件8.点到直线的距离9.直线束第四章圆锥曲线与二元一次方程1.圆的一般方程2.椭圆及其标准方程3.椭圆形状的讨论4.双曲线及其标准方程5.双曲线形状的讨论6.抛物线及其标准方程7.抛物线形状的讨论8.椭圆及双曲线的准线9.利用轴的平移简化二次方程10.利用轴的旋转简化二次方程11.一般二元二次方程的简化1.极坐标的概念2.极坐标与直角的关系3.曲线的极坐标方程4.圆锥曲线的极坐标方才第六章参数方程1.参数方程的概念2.曲线的参数方程3.参数方程的作图法第七章控件直角坐标与矢量代数1.间点的直角坐标2.基本问题3.矢量的概念矢径4.矢量的加减法5.矢量与数量的乘法6.矢量在轴上的投影投影定理7.矢量的分解与矢量的坐标8.矢量的模矢量的方向余弦与方向数9.两矢量的数量积10.两矢量的夹角11.两矢量的矢量积12.矢量的混合积第八章曲面方程与曲线方程1.曲面方程的概念2.球面方程3.母线平行于坐标的柱面方程二次柱面4.控件曲线作为两曲面的交线5.空间曲线的参数方程6.空间曲线在坐标面上的投影第九章空间的平面于曲线1.过一点并已知一法线矢量的平面方程2.平面的一般方程的研究3.平面的截距式方程4.点到平面的距离5.两平面的夹角6.直线作为两平面的交线7.直线的方程8.两直线的夹角9.直线与平面的夹角10.直线与平面的交点11.杂例第十章二次曲面1.旋转曲面2.椭秋面3.单叶双曲面4.双叶双曲面5.椭圆抛物面6.双曲抛物面7.二次锥面第二篇第一章函数及其图形1.实数与数轴2.区间3.实数的绝对值邻域4.常量与变量5.函数概念6.函数的表示法7.函数的几种特性8.反函数概念9.基本初等函数的图形10.复合函数初等函数第二章数列的极限及函数的极限1.数列及其简单性质2.数列的极限3.函数的极限4.无穷大无穷小5.关于无穷小的定理6.极限的四则运算7.极限存在的准则两个重要极限8.双曲函数9.无穷小的比较第三章函数的连续性1.函数连续性的定义2.函数的间断点3.闭区间上连续函数的基本性质4.连续函数的和积及商的连续性5.反函数与复合函数的连续性6.初等函数的连续性第四章导数及微分1.几个物力学上的概念2.导数概念3.导数的几何意义4.求导数的例题导数的基本公式表5.函数的和积商的导数6.反函数的导数7.复合函数的导数8.高阶导数9.参数方程所确定的函数的导数10.微分概念11.微分的求法微分形式不变性12.微分应用与近似计算及误差的估计第五章中值定理1.中值定理2.罗必塔法则3.泰勒公式第六章导数的应用1.函数的单调增减性的判定法2.函数的极值及其求法3.最大值及最小值的求法4.曲线的凹性及其判定法5.曲线的拐点及其求法6.曲线的渐进线7.函数图形的描绘方法8.弧微分曲率9.曲率半径曲率中心10.方程的近似解第七章不定积分1.原函数与不定积分的概念2.不定积分的性质3.基本积分表4.换元积分法5.分步积分法6.有理函数的分解7.有理函数的积分8.三角函数的有理式的积分9.简单无理函数的积分10.二项微分式的积分11.关于积分问题的一些补充说明第八章定积分1.曲边梯形的面积变力所作的功2.定积分的概念3.定积分的简单性质中值定理4.牛顿-莱布尼兹公式5.用换元法计算定积分6.用分部积分法计算定积分7.定积分的近似公式8.广义积分第九章定积分的应用1.平面图形的面积2.体积3.曲线的弧长4.定积分在物力力学上的应用第十章级数I. 常数项级数1.无穷级数概念2.无穷级数的基本性质收敛的必要条件3. 正项级数收敛性的充分判定法4.任意项级数绝对收敛5.广义积分的收敛性6.T- 函数II. 函数项级数7.函数项级数的一般概念8.一致收敛及一致收敛级数的基本性质III 幂级数9.幂级数的收敛半径10.幂级数的运算11.泰勒级数12.初等函数的展开式13.泰勒级数在近似计算上的应用14.复变量的指数函数欧拉公式第十一章傅立叶级数1.三角级数三角函数系的正交性2.欧拉-傅立叶公式3.傅立叶级数4.偶函数及奇函数的傅立叶级数5.函数展开为正弦和余弦级数6.任意区间上的傅立叶级数第十二章多元函数的微分法及其应用1.一般概念2.二元函数的极限及连续性3.偏导数4.全增量及全微分5.方向导数6.复合函数的微分法7.隐函数及其微分法8.空间曲线的切线及法平面9.曲面的切平面及法线10.高阶偏导数11.二元函数的泰勒公式12.多元函数的极值13.条件极值--拉格朗日乘数法则第十三章重积分1.体积问题二重积分2.二重积分的简单性质中值定理3.二重积分计算法4.利用极坐标计算二重积分5.三重积分及其计算法6.柱面坐标和球面坐标7.曲面的面积8.重积分在静力学中的应用第十四章曲线积分及曲面积分1.对坐标的曲线积分2.对弧长的曲线积分3.格林公式4.曲线积分与路线无关的条件5.曲面积分6.奥斯特罗格拉特斯公式第十五章微分方程1.一般概念2.变量可分离的微分方程3.齐次微分方程4.一阶线性方程5.全微分方程6.高阶微分方程的几个特殊类型7.线性微分方程解的结构8.常系数齐次线性方程9.常系数非齐次线性方程10.欧拉方程11.幂级数解法举例12.常系数线性微分方程组。
高等数学讲义(2)

第3讲 导数与微分高等数学基础课程的主要研究对象是函数,函数是变量之间的对应关系,怎样研究函数的变化是这一讲的主要问题。
3.1 导数的概念一、函数的变化率对于函数)(x f y =,我们要研究y 怎样随x 变化,进一步我们还要研究变化的速率,可以先看看下面这个图我们可以看出,对于相同的自变量的改变量x ∆,所对应的函数改变量y ∆是不同的。
xy∆∆可以表示变化的速率,但这是一个平均速率,怎样考虑函数)(x f y =在一点0x 的变化率呢?二、导数的概念根据前面的介绍,我们给出下面的定义。
定义3.1 设函数)(x f y =在点0x 及其某个邻域U 内有定义,对应于自变量x 在0x 处的改变量x ∆,函数相应的改变量为)()(00x f x x f y -∆+=∆,如果当0→∆x 时极限x y x ∆∆→∆0lim存在,则此极限值称为函数)(x f y =在点0x 处的导数,或在点0x 处函数)(x f 关于自变量x 的变化率,记作)(0x y ',或)(0x f '这时,称函数)(x f y =在点0x 处是可导的。
根据导数定义,我们来求一些基本初等函数的导数。
例1 根据导数定义求c y =在点x 处的导数。
解 根据定义求导数通常分三步: (Ⅰ)求)()(00x f x x f y -∆+=∆:0=-=∆c c y(Ⅱ)求xy ∆∆: 00=∆=∆∆xx y (Ⅲ)求xy x ∆∆→∆0lim:00lim lim00==∆∆→∆→∆x x x y因此得出0)(='x y 。
如果函数)(x f 在其定义域内每一点都可导,那么我们就得到了一个新的函数)(x f ',称)(x f '为)(x f 的导函数。
)(x f '在点0x x =的函数值)(0x f '就是)(x f 在点0x x =的导数。
例2 根据导数定义求2)(x x f =在点x 处的导数。
《高等数学(二)线性代数课件》
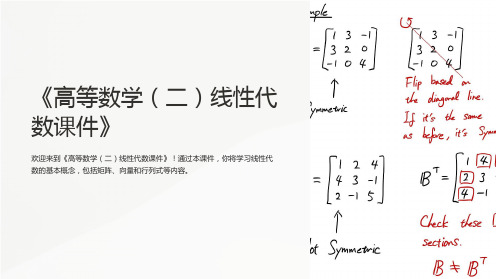
欢迎来到《高等数学(二)线性代数课件》!通过本课件,你将学习线性代 数的基本概念,包括矩阵、向量和行列式等内容。
线性方程组方程组的解法,了解
解的可能情况。
3
二元线性方程组
掌握二元线性方程组的求解方法,理解 解的几何意义。
高阶线性方程组
线性变换的定义
线性变换的性质
探索线性变换的定义和基本性质, 了解线性变换的意义和作用。
学习线性变换的性质和特点,掌 握线性变换的运算规则。
线性变换的标准矩阵
理解线性变换与标准矩阵的关系, 应用标准矩阵进行计算和坐标变 换。
特征值与特征向量
1
特征值
了解特征值的定义和性质,理解特征值在线性代数中的重要作用。
2
特征向量
学习特征向量的定义和特点,掌握特征向量的计算方法和应用。
学习解高阶线性方程组的方法,掌握复 杂方程组求解的技巧。
矩阵运算与特殊矩阵
矩阵的加法与减法
学习矩阵的加法和减法规则, 了解矩阵运算的性质。
矩阵的乘法
掌握矩阵乘法的计算方法, 理解矩阵乘法的几何意义。
对角矩阵和单位矩阵
认识对角矩阵和单位矩阵的 特点和性质,应用到实际问 题中。
线性变换与其标准矩阵表示
高数二课件

421lim )2(4312lim )1(.-+-+∞→∞→∞→n n x x x n x 时的极限(一)=2/3=1/2 1)1tan(lim)3(113lim)2()2(lim 1.22031--++++-→→→x x x x x x x x x x )(极限值等于函数值(二)=2 =1=tan1 )())(lim (,1,1,21,32)()5()()(lim ,0,10,)()4(021=⎪⎩⎪⎨⎧>-=<+==⎩⎨⎧<≥=→→x f f x x x x x x x f x f x x x x f x x 1 6 1ln 1lim )6(1ln lim )5(334lim )4(39lim )3(42lim )2(123lim )1(00.31122323222221-+---+-------+-→→→→→→x x x x x x x x x x x x x x x x x x x x x x x 型极限(三)33lim 3tan lim )2(55lim 5sin lim )1(,~1;~)1ln(;~tan ;~sin 0.0000====-+→→→→→x x x x x x x x x e x x x x x x x x x x x x 如:时,等价无穷小量替代(四)111lim 1)1tan(lim )4(2111lim 1)1sin(lim)3(112121=--=--=--=--→→→→x x x x x x x x x x x x 括号外指数的倒数。
,第二项是)括号内第一项是(型)()幂指函数的极限特点:(的应用重要极限(五)13)01(21)11(lim .∞∞→+=+e xx x x x xx xx x x x )311(lim )3()1(lim )2()31(lim )1(20-+-∞→→∞→3-=e31-=e2e =二 导数(二).利用基本求导公式求导(三).导数乘法、除法运算法则(六).连续 )()(lim )(000x f x f x x x f x x ==→则处连续,在函数)1()0(0,0,12)()2()2(00,20,)()1(22=⎩⎨⎧>≤+===⎩⎨⎧>≤+=f x x x x x f a x x x a x x f ,则设函数处连续,则在设函数h x f h x f x x f x x f x f h x )()(lim )()(lim )(.0000000'-+=∆-∆+=→→∆导数定义(一))3()1()1(lim ,3)1()2.2008.(2)4()1()21(lim ,2)1()2.2007.(10'0'=-+==∆-∆+=→→∆h f h f f x f x f f h x 则已知则已知)(,)14.2009.(7)(,2ln sin )2.2009.(6)(,ln )3.2008.(5)()(,3)()3.2006.(4)(,3)2.2005.(3'''5'3'''3===++====+==+=-y x y y x x y y x y x f e x x f y x y x 2'''''')(v uv v u v u uvv u uv -=⎪⎭⎫ ⎝⎛+=)()1(,ln )()3.2009.(12)(,cos )13.2008.(11)(,ln )13.2007.(10)(,sin )22.2006.(9)(,cos )22.2005.(8'''43==========f x e x f y x x y y xxy dy x x y dy x x y x(五).多元函数一阶偏导数(六).多元函数二阶偏导数(七)多元函数全微分)(,)22.2009.(18)(),1sin()5.2007.(17)(,2sin )14.2006.(16)(,5)2.2006.(15)()0(,)14.2005.(14)()0(,2cos )()3.2005.(13sin 2'''2''2'===-====+=====dy e y dy x y y x y y e y y e y f x x f x x x )(),tan()8.2009.(22)(,3)8.2008.(21)(,)8.2006.(20)(,)8.2005.(193=∂∂==∂∂+==∂∂==∂∂=+x z xy z x z y x z x ze z x z e z xy y x )()(,),()9.2009.(26)(,)9.2008.(25)(),cos()9.2006.(24)(,)19.2005.(232222222222)1,1(223=∂∂+===∂∂==∂∂+==∂∂+=xzu f y x u u f z x z y x z xz y x z x z e x z y 二阶可导,则且dy y z dx x z dz y x f z ∂∂+∂∂==则),,()(),ln()20.2009.(31)()20.2008.(30)(,)19.2007.(29)(,)20.2006.(28)(),ln()20.2005.(2722=+==∂∂∂∂=====+=+dz y x z dz y zx z dz x z dz e z dz y x z y y x ,则、数设存在一阶连续的偏导三、导数应用(二)驻点与拐点(三)单调区间和极值z x z x yx F F z F y F y z F F z F xF x z z y x F F F y F xFdx dy y x F '''''',,0),,(,0),(-=∂∂∂∂-=∂∂-=∂∂∂∂-=∂∂=-=∂∂∂∂-==则则.),()28.2005.(32222dz e z y x y x z z z 确定的隐函数,求是由方程=++=dy e z ydx e z x dz e z y y z e z x x z e z F y F x F e z y x z y x F z zz z z z y x z ----=--=∂∂--=∂∂-====-++=222222,222,2,20),,('''222,于是则解:设.0),()24.2008.(35.),()24.2007.(34.1),()28.2006.(332223x z e y x y x z z dz e z y x y x z z dz e z y x y x z z z z z ∂∂=-+==++==+++=所确定的隐函数,求是由方程所确定的隐函数,求是由方程所确定的隐函数,求是由方程))((),(),()(00'00'00x x x f y y x f k y x x f y -=-==切线方程为:切线斜率为处的在点线斜率及方程(一)曲线上一点的切)1(,121.3._____2x 2__________)0,1(.2).2()1,0(.123=-===-=-==+=a x y x ax y y x x y k x e y x 则处的切线平行于直线在已知切线方程为点处的在处的切线斜率在点()),(810.8),1/31(),(131.70,0.6._0_)1ln(.50,0.40023002322323=+-==+-=+==+==y x x x y y x x x y y x z x x y x y 的拐点坐标曲线的拐点坐标曲线)的驻点是(的驻点为)的拐点坐标是(是极大值、是极小值、则时,当时,处连续,当在设函数、、、、)内为单调增加的是(下列函数在)0()0()(,0)(0;0)(00)(.10sin ),(.9''2f B f A A x f x x f x x x f x y D x y C x y B x y A A >><<===-==+∞-∞(四)导数应用题 1.上半部为等边三角形下半部为矩形的窗户(如图所示),其周长为12米,为使窗户的面积S 达到最大,矩形的宽l 应为多少米?四、积分 (一)原函数、不定积分的概念及性质 (二)求不定积分 (三)定积分的概念及性质 (四)求定积分 (五)定积分的应用(一)原函数、不定积分及其性质.______0__.12._____ln ..112===x e y x x y x 的极值点为函数的单调增区间为函数),(1+∞-e 的极小值。
大专-高等数学--第二章-PPT

定义1 设函数 f (x) 在 x0 的某一空心邻域N (xˆ0 , )
内有定义,如果当自变量 x 在N (xˆ0 , ) 内无限接近于 x0
时,相应的函数值无限接近于常数 A ,则 A 为x x0 时
函数
f
( x) 的极限,记作lim xx0
f
(x)
A或
f
(x)
A( x
x0 ) .
2. x x0 时函数 f (x)的极限
x
定理 2 lim f (x) A的充要条件是 x
lim f (x)= lim f (x) A.
x
x
例 3 由图 5 可知: lim 1 0 ; lim 1 0 .
x x
x x
由图 6 可知 lim ex 0 . x
y y ex
y
y
1 x
O
x
O
x
图5
图6
二、数列的极限
1. 数列的概念
设自变量为正整数的函数un f (n)(n 1,2,),其 函数值按自变量 n 由小到大排列成一列数
6. x 时函数 f (x)的极限
定义 6 设函数 f (x)在(, a)内有定义( a为某个 实数),当自变量无限变小(或 x 无限变大)时,相应的 函数值 f (x)无限接近于常数 A,则称 A为 x 时函 数 f (x)的极限,记 lim f (x) A或 f (x) A(x ).
定理 3 (单调有界原理) 单调有界数列必有极限.
三、极限的性质
性质 性质 1 (惟一性) 则A B.
若 lim f (x) A, lim f (x) B,
xx0
xx0
性质 2
(有界性)
若 lim xx0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第八章:多元函数微分8.1 多元函数的极限与连续性8.1.1 定义设函数f(x,y)在开区域(或闭区域)D内有定义,P0(x,y)是D的内点或边界点。
如果对于任意给定的正数ε,总存在正数δ,使得对于适合不等式的一切点P(x,y)∈D,都有|f(x,y)-A|<ε成立,则称常数A为函数f(x,y)当 x→x0,y→y时的极限,记作或f(x,y) →A (ρ→0),这里ρ=|PP|。
例设(x2+y2≠0),求证。
因为,可见,对任何ε>0,取,则当时,总有成立,所以。
我们必须注意,所谓二重极限存在,是指P(x,y)以任何方式趋于P0(x,y)时,函数都无限接近于A。
定义设函数f(x,y)在开区域(或闭区域)D内有定义,P0(x,y)是D的内点或边界点且P∈D。
如果则称函数f(x,y)在点P0(x,y)连续。
8.1.2 性质性质1(最大值和最小值定理)在有界闭区域D上的多元连续函数,在D上一定有最小值和最大值。
性质2(介值定理)在有界闭区域D上的多元连续函数,如果在D上取得两个不同的函数值,则它在D上取得介于这两个值之间的任何值至少一次。
一切多元初等函数在其定义区域内是连续的。
所谓定义区域,是指包含在定义域内的区域或闭区域。
由多元初等函数的连续性,如果要求它在点P0处的极限,而该点又在此函数的定义区域内,则极限值就是函数在该点的函数值,即。
8.2 偏导数的定义及计算法8.2.1 定义设函数z=f(x,y)在点(x0,y)的某一邻域内有定义,当y固定在y而x在x0处有增量Δx时,相应的函数有增量f(x+Δx,y)-f(x,y),如果存在,则称此极限为函数z=f(x,y) 在点(x0,y)处对x的偏导数,记作或 fx (x,y)。
对于函数z=f(x,y),求时,只要把y暂时看作常量而对y求导。
例求z=x2sin2y的偏导数。
解。
8.2.2 高阶偏导数定理如果函数z=f(x,y)的两个二阶混合偏导数在区域D内连续,那末在该区域内这两个二阶混合偏导数必相等。
8.3 多元复合函数求导法则及实例定理如果函数u=φ(t)及ψ(t)都在点t可导,函数z=f(u,v)在对应点(u,v)具有连续偏导数,则复合函数z=f[φ(t), ψ(t)]在点t可导,且其导数可用下列公式计算:。
例设z=eusinv,而u = xy,v = x+y。
求。
解8.4 隐函数的求导公式8.4.1 一个方程的情形隐函数存在定理1 设函数F(x,y)在点P(x0,y)的某一邻域内具有连续的偏导数,且F(x0,y)=0, Fy(x,y) ≠ 0,则方程F(x,y) = 0在点(x,y)的某一邻域内恒能唯一确定一个单值连续且具有连续导数的函数y = f(x),它满足条件y=f(x),并有。
上面公式就是隐函数的求导公式。
隐函数存在定理2 设函数F(x,y,z)在点P(x0,y,z)的某一邻域内具有连续的偏导数,且F(x0,y,z) = 0, Fz(x,y,z) ≠ 0,则方程F(x,y,z) = 0在点(x,y,z)的某一邻域内恒能唯一确定一个单值连续且具有连续导数的函数z = f(x,y),它满足条件z0 = f(x,y),并有。
例设x2+y2+z2-4z = 0,求,解设F(x,y,z)= x2+y2+z2-4z ,则Fx = 2x,Fz= 2z-4。
应同上面公式,得。
再一次对x求偏导数,得。
二、方程组的情形隐函数存在定理3 设F(x,y,u,v)、G(x,y,u,v)在点P(x0,y,u,v)的某一邻域内具有对各个变量的连续偏导数,又F(x0,y,u,v)= 0,G(x,y,u,v)= 0,且偏导数所组成的函数行列式(或称雅可比(Jacobi)式):在点P(x0,y,u,v)不等于零,则方程组F(x,y,u,v)= 0,G(x,y,u,v)= 0在点(x0,y,u,v)的某一邻域内恒能唯一确定一组单值连续且具有连续导数的函数u = u(x,y),v = v(x,y),它们满足条件u0= u(x,y),v= v(x,y),并有。
8.5 微分法在几何上的应用8.5.1 空间曲线的切线与法平面设空间曲线Г的参数方称为x=φ(t),y=ψ(t),z=ω(t),这里假定上式的三个函数都可导。
[插图1]在曲线Г上取对应于t=t0的一点M(x,y,z)。
根据解析几何,可得曲线在点M处的切线方程为。
切线的方向向量称为曲线的切向量。
向量T={φ'(t 0),ψ'(t 0),ω'(t 0)} 就是曲线Г在点M 处的一个切向量。
通过点而与切线垂直的平面称为曲线Г在点M 处的法平面,它是通过点M (x 0,y 0,z 0)而以T 为法向量的平面,因此这法平面的方程为 φ'(t 0)(x-x 0)+ψ'(t 0)(y-y 0)+ω'(t 0)(z-z 0)= 0。
8.5.2 曲面的切平面与法线 [插图2]设曲面Σ由方程F (x,y,z )= 0给出,M (x 0,y 0,z 0)是曲面Σ上的一点,并设函数F (x,y,z )的偏导数在该点连续且不同时为零。
则根据解析几何,可得曲面上通过点M 的一切曲线在点M 的切线都在同一个平面上。
这个平面称为曲面Σ在点M 的切平面。
这切平面的方程是F x (x 0,y 0,z 0)(x-x 0)+F y (x 0,y 0,z 0)(y-y 0)+F z (x 0,y 0,z 0)(z-z 0)= 0 通过点M (x 0,y 0,z 0)而垂直于切平面的直线称为曲面在该点的法线。
法线方程是x=3垂直于曲面上切平面的向量称为曲面的法向量。
向量 n = {F x (x 0,y 0,z 0),F y (x 0,y 0,z 0),F z (x 0,y 0,z 0)} 就是曲面Σ在点M 处的一个法向量。
8.6 多元函数极值的求法8.6.1 多元函数的极值二元函数的极值问题,一般可以利用偏导数来解决。
定理1(必要条件) 设函数z = f(x,y)在点(x 0,y 0)具有偏导数,且在点(x 0,y 0)处有极值,则它在该点的偏导数必然为零: f x (x 0,y 0) = 0,f y (x 0,y 0) = 0。
定理2(充分条件) 设函数z = f(x,y)在点(x 0,y 0)的某领域内连续且有一阶及二阶连续偏导数,又f x (x 0,y 0) = 0,f y (x 0,y 0) = 0,令 f xx (x 0,y 0) = A ,f xy (x 0,y 0) = B ,f yy (x 0,y 0) = C ,则f(x,y)在(x0,y)处是否取得极值的条件如下:(1)AC-B2>0时具有极值,且当A<0时有极大值,当A>0时有极小值;(2)AC-B2<0时没有极值;(2)AC-B2=0时可能有极值,也可能没有极值,还需另作讨论。
利用定理1、2,我们把具有二阶连续偏导数的函数z = f(x,y)的极值的求法叙述如下:第一步解方程组f x (x,y) = 0,fy(x,y) = 0,求得一切实数解,即可求得一切驻点。
第二步对于每一个驻点(x0,y),求出二阶偏导数的值A、B和C。
第三步定出AC-B2的符号,按定理2的结论判定f(x0,y)是否是极值、是极大值还是极小值。
8.6.2 条件极值拉格朗日乘数法拉格朗日乘数法要找函数z = f(x,y)在附加条件φ(x,y) = 0下的可能极值点,可以先构成辅助函数F(x,y)= f(x,y)+λφ(x,y) ,其中λ为某一常数。
求其对x与y的一阶偏导数,并使之为零,然后与方程φ(x,y) = 0联立起来:有这方程组解出x,y及λ,则其中x,y就是函数f(x,y)在附加条件φ(x,y) = 0下的可能极值点的坐标。
这方法还可以推广到自变量多于两个而条件多于一个的情形。
至于如何确定所求得的点是否极值点,在实际问题中往往可根据问题本身的性质来判定。
9.1 二重积分的概念与性质9.1.1 二重积分的概念为引出二重积分的概念,我们先来讨论两个实际问题。
设有一平面薄片占有xOy面上的闭区域D,它在点(x,y)处的面密度为ρ(x,y),这里ρ(x,y)> 0且在D上连续。
现在要计算该薄片的质量M。
由于面密度ρ(x,y)是变量,薄片的质量不能直接用密度公式(M=ρS)来计算。
但ρ(x,y)是连续的,利用积分的思想,把薄片分成许多小块后,只要小块所占的小闭区域D si的直径很小,这些小块就可以近似地看作均匀薄片。
在D s i(这小闭区域的面积也记作D s i)上任取一点(x i,h i),则ρ(xi ,hi)D si(i = 1,2,…,n)可看作第i个小块的质量的近似值[插图1]。
通过求和,再令n个小区域的直径中的最大值(记作λ)趋于零,取和的极限,便自然地得出薄片的质量M,即。
再设有一立体,它的底是xOy面上的闭区域D,它的侧面是以D的边界曲线为准线而母线平行于z轴的柱面,它的顶是曲面z = f(x,y),这里f(x,y)≥ 0且在D上连续。
这种立体叫做曲顶柱体。
现在要计算上述曲顶柱体的体积V。
由于曲顶柱体的高f(x,y)是变量,它的体积不能直接用体积公式来计算。
但仍可采用上面的思想方法,用一组曲线网把D分成n个小闭区域D s1,D s2,…,D s n,在每个D s i上任取一点(x i,h i),则f(x i,h i)D s i(i = 1,2,…,n)可看作以f(xi ,hi)为高而底为D si的平顶柱体的体积[插图2]。
通过求和,取极限,便得出。
上面两个问题所要求的,都归结为同一形式的和的极限。
在其他学科中,由许多物理量和几何量也可归结为这一形式的和的极限。
因此我们要一般地研究这种和的极限,并抽象出下述二重积分的定义。
定义设f(x,y)是有界闭区域D上的有界函数。
将闭区域D任意分成n个小闭区域D s1,D s2,…,D s n,其中D si表示第i个小闭区域,也表示它的面积。
在每个D s i上任取一点(xi ,hi),作乘积 f(xi,hi)D si(i= 1, 2, …, n,),并作和。
如果当各小闭区域的直径中的最大值l趋于零时,这和的极限总存在,则称此极限为函数f(x,y)在闭区域D上的二重积分,记作,即。
(*)其中f(x,y)叫做被积函数,f(x,y)d s叫做被积表达式,d s叫做面积元素,x与y叫做积分变量,D叫做积分区域,叫做积分和。
在二重积分的定义中对闭区域D的划分是任意的,如果在直角坐标系中用平行于坐标轴的直线网来划分D,那末除了包含边界点的一些小闭区域外,其余的小闭区域都是矩形闭区域。
设矩形闭区域D si 的边长为D xj和D yk,则D s= D xj·Dyk。
