计数型测量系统假设试验分析
计数型测量系统分析报告-KAPPA(适用10-50个样品)

料号量具编号量具名称测量者 A 品名量具类型评价人数测量者 B 特性状态定义重复次数测量者 C 零件数量报告人批准日期产品编号A-1A-2A-3B-1B-2B-3C-1C-2C-3真值(REF)12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849501=合格 0=不合格计数型测量系统分析报告计数型#DIV/0!人员更换定期(校准/年度)修复后新购公差变化DataSummary/A*BA*CB*CA*RefB*RefC*Ref0*00000001*00000000*10000001*1000SelfagreementA B C 00A*B Cross01总计Po:#DIV/0!A0计数000期望值#DIV/0!#DIV/0!#DIV/0!Pe:#DIV/0!1计数000期望值#DIV/0!#DIV/0!#DIV/0!总计计数000期望值#DIV/0!#DIV/0!#DIV/0!B*C01总计Po:#DIV/0!B0计数00期望值#DIV/0!#DIV/0!#DIV/0!Pe:#DIV/0!1计数000期望值#DIV/0!#DIV/0!#DIV/0!总计计数0期望值#DIV/0!#DIV/0!#DIV/0!A*CCrosstabulC 01总计Po:#DIV/0!A0计数0期望值#DIV/0!#DIV/0!#DIV/0!Pe:#DIV/0!1计数0期望值#DIV/0!#DIV/0!#DIV/0!总计计数0期望值#DIV/0!#DIV/0!#DIV/0!Reproduci bilityKappa 判定Kappa=(Po-Pe)/(1-Pe)A*REFCrosstabul1总计Po:#DIV/0!A0计数000期望值#DIV/0!#DIV/0!#DIV/0!Pe:#DIV/0!1计数000期望值#DIV/0!#DIV/0!#DIV/0!总计计数000期望值#DIV/0!#DIV/0!#DIV/0!B*REFCrosstabul1总计Po:#DIV/0!B0计数000期望值#DIV/0!#DIV/0!#DIV/0!Pe:#DIV/0!1计数000期望值#DIV/0!#DIV/0!#DIV/0!总计计数000期望值#DIV/0!#DIV/0!#DIV/0!真值#DIV/0!#DIV/0!#DIV/0!真值B C A*B B*C A*C #DIV/0!#DIV/0!#DIV/0!编制:审核:核准:。
计数型测量系统分析报告2024

引言概述:正文内容:1.系统功能分析1.1.计数型测量系统是如何实现计数功能的?1.2.系统能够处理的计数范围和精度是多少?1.3.系统具备哪些自动化控制特性?1.4.系统是否支持多通道计数?1.5.系统是否拥有远程监控和报警功能?2.应用领域分析2.1.在工业生产中,计数型测量系统的应用案例有哪些?2.2.计数型测量系统在科学研究中的应用有哪些?2.3.系统在质量检测和控制中的作用是如何体现的?2.4.系统在仪器仪表校准中的重要性是什么?2.5.系统在数据分析和统计中的应用有哪些独特之处?3.系统性能分析3.1.系统的测量精度和稳定性如何评估?3.2.系统的信噪比和分辨率是如何确定的?3.3.系统的抗干扰性如何进行测试和验证?3.4.系统的响应时间和采样频率有何关联?3.5.系统的可靠性和可维护性如何保证?4.系统优化建议4.1.如何通过硬件升级提升系统的测量精度?4.2.优化信号处理算法可以提高系统的性能吗?4.3.系统的自动校准和自适应控制如何实现?4.4.整合其他测量技术是否能够进一步完善系统?4.5.如何对系统进行定期维护和保养以确保其性能稳定?5.发展趋势和展望5.1.计数型测量系统在工业4.0时代有何新的应用?5.2.系统在物联网和大数据时代的发展前景如何?5.3.新兴技术对系统的影响和挑战是什么?5.4.基于的计数型测量系统有何突破?5.5.未来的研究和发展方向有哪些?总结:通过对计数型测量系统的分析,我们深入了解了系统的功能、应用领域、性能和优化方案。
我们还对系统的发展趋势和展望进行了探讨。
计数型测量系统作为一种重要的测量技术,在工业和科学领域的应用前景广阔。
我们建议用户在使用系统时,根据实际需求选择适合的硬件配置和算法优化方案,并定期对系统进行维护和升级,以提高系统的性能和可靠性。
MSA计数型测量系统分析-假设试验分析法(KAPPA)

B
0.954 Good
C
0.954 Good
测量系 统有效
评价人
零件总数 正确判断数 有效性% 结* 有论效性 = 正确
A
30 29 97% Good
B
30 29 97% Good
C
30 29 97% Good
评价人 的接受
漏发警报的比例
结论
误发警报的比例
A
0%
接受
1%
B
0%
接受
1%
* 漏C发警
0%
D
16
D
D
D
17
A
A
A
18
D
D
D
19
D
D
D
20
D
D
D
21
D
D
D
22
D
D
D
23
D
D
D
24
D
D
D
25
D
D
D
26
D
D
D
27
D
D
D
28
A
A
A
29
D
D
D
30
D
D
D
评价人之间数据报
A1*C1
A D D D D D D D A D D D D D D D A D D D D D D D D D D A D D
A2*C2
1
3
1
1
1
1
1
1
1
1
1
1
4
1
1
1
1
1
1
1
1
1
FM-QCA-SP039A 计数型测量系统分析报告

计算 期望的计算 计算 期望的计算 计算 期望的计算
Po= 0.92
B
0
1
41
7
14.72
33.28
5
97
31.28
70.72
46
104
46.00
104.00
Po= 0.9067
C
0
1
41
5
15.33
30.67
9
95
34.67
69.33
50
100
50.00
100.00
Po= 0.88
评价人
A B
C
相互一致性
A*B
OK
A*C
NG
B*A
OK
B*C
OK
C*A
NG
C*B
OK
与标准 有效性 漏发率 误发率 OK OK NG OK OK OK NG OK
OK NG NG OK
判定 OK OK OK
说明:只有,当一致性、 有效性、漏发率、误发率均为 “OK”时,表示测量系统可接 受;否则测量系统必须改进! 如果测量系统合格,填写下面 的统计报告。
3
样品数 (n)
50
评价人 A
评价人B
评价人C 数据记 录规
数据记录表
A-3 B-1 B-2 B-3 C-1 C-2
1
1
1
1
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
MSA计数型测量系统分析——假设试验分析法(Kappa)

6.136.13 计数型测量系统分析计数型测量系统分析——————假设试验分析法假设试验分析法假设试验分析法((Kappa Kappa))说明:参照张智勇所著《ISO/TS16949五大工具最新版一本通》(机械工业出版社)编写。
计数型测量系统的分析是为了确定不同班次,不同生产线的检查人员是否能正确地区分合格品和不合格品,分析出测量结果与标准值的符合程度,以及他们自身和相互之间重复检查的一致程度。
假设试验分析—交叉表法是一种常用的计数型测量系统分析方法。
交叉表法可以在基准值(分析用样品称为基准,用计量型测量系统对样品进行测量,测量值称为基准值)已知的情况下进行,也可以在基准值未知的情况下进行。
在基准值未知的情况下进行,可以评价测量人之间的一致性,但不能评价测量系统区分好与不好的能力。
在基准值已知的情况下,即可评价测量人之间的一致性,又能评价测量人员与基准值的一致性,以及测量的有效性、漏判率和误判率,从而判断出测量人区分合格和不合格零件的能力。
6.136.13.1 .1 .1 未知基准值的一致性分析未知基准值的一致性分析1)随机选取g=50(一般选取g=30~50个样本)个能够覆盖过程范围的零件,对这些零件进行编号。
零件的编号不要让测量人知道,但分析人应该知道。
2)由3名评价人以随机盲测的方式测量所有零件各m=3次,每人测量次数为n=g×m=50×3=150次。
“接受”记为“1”,“拒绝”记为“0”,将三人所测150×3=450个数据记录于表6-21中。
测量时应按这样的规则进行:先让A 测量人以随机顺序对50个零件进行第1轮测量,然后让B 测量人、C 测量人以随机顺序进行第1轮测量,再让A 测量人进行第2轮测量,以此类推,完成测量工作。
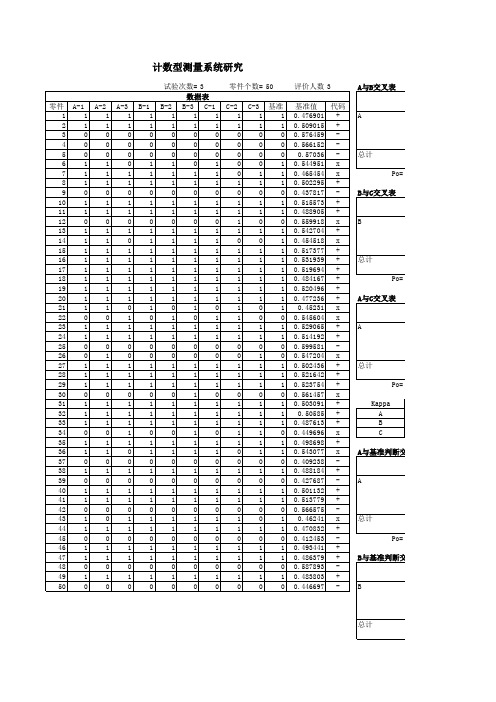
表6-21 计数型测量系统分析数据表零件测量人A 测量人B 测量人C基准基准值代码A-1 A-2 A-3 B-1 B-2 B-3 C-1 C-2 C-31 1 1 1 1 1 1 1 1 1 1 0.476 901 +2 1 1 1 1 1 1 1 1 1 1 0.509015 +3 0 0 0 0 0 0 0 0 0 0 0.576459 -4 0 0 0 0 0 0 0 0 0 0 0.566152 -5 0 0 0 0 0 0 0 0 0 0 0.57036 -6 1 1 0 1 1 0 1 0 0 1 0.544 951 ×7 1 1 1 1 1 1 1 0 1 1 0.465454 ×8 1 1 1 1 1 1 1 1 1 1 0.502295 +9 0 0 0 0 0 0 0 0 0 0 0.437817 -10 1 1 1 1 1 1 1 1 1 1 0.515573 +11 1 1 1 1 1 1 1 1 1 1 0.488905 +12 0 0 0 0 0 0 0 10 0 0.559918 ×13 1 1 1 1 1 1 1 1 1 1 0.542704 +14 1 1 0 1 1 1 1 0 0 1 0.454518 ×15 1 1 1 1 1 1 1 1 1 1 0.517377 +16 1 1 1 1 1 1 1 1 1 1 0.531939 +17 1 1 1 1 1 1 1 1 1 1 0.519694 +18 1 1 1 1 1 1 1 1 1 1 0.484167 +19 1 1 1 1 1 1 1 1 1 1 0.520496 +20 1 1 1 1 1 1 1 1 1 1 0.477236 +21 1 1 0 1 0 1 0 1 0 1 0.452310 ×22 0 0 1 0 1 0 1 10 0 0.545604 ×23 1 1 1 1 1 1 1 1 1 1 0.529065 +24 1 1 1 1 1 1 1 1 1 1 0.514192 +25 0 0 0 0 0 0 0 0 0 0 0.599581 -26 0 1 0 0 0 0 0 0 1 0 0.547204 ×27 1 1 1 1 1 1 1 1 1 1 0.502436 +28 1 1 1 1 1 1 1 1 1 1 0.521642 +29 1 1 1 1 1 1 1 1 1 1 0.523754 +30 0 0 0 0 0 1 0 0 0 0 0.561457 ×31 1 1 1 1 1 1 1 1 1 1 0.503091 +32 1 1 1 1 1 1 1 1 1 1 0.505850 +33 1 1 1 1 1 1 1 1 1 1 0.487613 +34 0 0 1 0 0 1 0 1 1 0 0.449696 ×35 1 1 1 1 1 1 1 1 1 1 0.498698 +36 1 1 0 1 1 1 1 0 1 1 0.543077 ×37 0 0 0 0 0 0 0 0 0 0 0.409238 -38 1 1 1 1 1 1 1 1 1 1 0.488184 +39 0 0 0 0 0 0 0 0 0 0 0.427687 -40 1 1 1 1 1 1 1 1 1 1 0.501132 +41 1 1 1 1 1 1 1 1 1 1 0.513779 +42 0 0 0 0 0 0 0 0 0 0 0.566575 -43 1 0 1 1 1 1 1 1 0 1 0.462410 ×44 1 1 1 1 1 1 1 1 1 1 0.470832 +45 0 0 0 0 0 0 0 0 0 0 0.412453 -46 1 1 1 1 1 1 1 1 1 1 0.493441 +47 1 1 1 1 1 1 1 1 1 1 0.486379 +48 0 0 0 0 0 0 0 0 0 0 0.587893 -49 1 1 1 1 1 1 1 1 1 1 0.483803 +50 0 0 0 0 0 0 0 0 0 0 0.446697 -3)根据表6-21中的0和l 数据的结果将评价人A 和B、B 和C、A 和C 利用交叉表方法进行统计(见表6-22),A*B 栏中“0*0”代表A、B 两人均判拒绝的次数,统计有44个;“0*1”代表A 判拒绝而B 判接受的次数,统计有6个;“1*0”代表A 判接受而B 判拒绝的次数,统计有3个;“1*1”代表AB 两人同时判为接受的次数,统计有97个,将统计结果依次填入表6-22中。
(精品)计数型(通止规)MSA测量系统分析
A-1 1 1 0 0 0 1 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 0 1 1 0 0 1 1 1 0 1 1 1 0 1 1 0 1 0 1 1 0 1 1 0 1 1 0 1 0
A-2 1 1 0 0 0 1 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 0 1 1 0 1 1 1 1 0 1 1 1 0 1 1 0 1 0 1 1 0 0 1 0 1 1 0 1 0
B
总计
Po=
C与基准判断交叉表
C
总计
Po=
Kappa
来源 总受检数 符合的 错误地否定 错误地肯定 混合的 95%置信上限 计算得分 95%置信下限
总受检数 一致数 95%置信上限 计算得分 95%置信下限
注意: 1) 评价人自己在所有试验上都一致 2)评价人在所有试验上都与基准一致 3) 所有评价人自己保持一致,两两间一致 4)所有评价人自己和两两间一致并且于基 5) UCI和LCI分别是上、下置信区间边界线
计数型测量系统研究
零件 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
零件个数= 50
C-2 C-3 基准 111 111 000 000 000 001 011 111 000 111 111 100 111 001 111 111 111 111 111 111 101 100 111 111 000 010 111 111 111 000 111 111 111 110 111 011 000 111 000 111 111 000 101 111 000 111 111 000 111 000
计数型MSA测量系统分析报告
D
D
A
C
D
D
D
D
D
B
C
A
A
A
D
D
D
A
A
A
D
D
D
D
D
D
A
A
A
D
C
B
D
D
D
A
A
A
D
D
D
D
D
D
A
A
A
D
D
D
D
D
D
D
D
D
A
A
A
A
A
A
A
A
A
1
0
3
0
1
分析用表格
A﹡参考
B﹡参考
1
2
3
1
2
3
D
DDDDD NhomakorabeaD
D
D
D
D
D
B
B
B
B
B
B
A
A
A
A
A
A
A
A
A
A
A
A
D
D
B
D
D
B
D
D
D
D
D
D
D
D
D
D
D
D
A
A
A
A
A
A
D
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
计数型测量系统分析报告

1
总计
数量 期望的数量 数量 期望的数量 数量 期望的数量
B*参考 交叉表
B
0
1
总计
C*参考 交叉表
数量 期望的数量 数量 期望的数量 数量 期望的数量
C
0
1
总计
Kappa 判定
数量 期望的数量 数量 期望的数量 数量 期望的数量
A 0.92 一致性好
重复性 检查总数 匹配数 有效性 判定
评价人
A B C
B
C
数
总检查数
50
50
50
50
50
50
型
匹配数
48
48
49
47
47
48
量
95%UCI
99.51% 99.51% 99.95% 98.75% 98.75% 99.51%
计算结果
96.00% 96.00% 98.00% 94.00% 94.00% 96.00%
具
95%LCI
86.29% 86.29% 89.35% 83.45% 83.45% 86.29%
1
1
1
1
1
1
1
0
0
0
0
1
1
1
1
1
1
1
1
0
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
0
0
0
1
1
1
1
0
0
0
计量型和计数性测量系统分析

限
1
• 控制区内表示测量灵敏度
(噪声)。大约一半或更
多的均值应落在控制区外,
那么测量系统能够充分探
测零件之间的变差并能提
供对过程分析和过程控制
有用的信息。
-1
• 同时,可以分析出分析评
价人之间的差异。如有基
准值则可分析出各评价人
-2
的整体偏倚倾向
评价人A 评价人B 评价人C
UCL LCL
极差图
1.0
零件 16 均值
(Xp) .169 -0.851 1.099 0.367 -1.06 -0.186 0.454 17 R==(R-a+R-b+R-c)n =0.3417 18 X-DIFF=MaxX-—MinX- =0.4446 19 UCLR=R=D4 =0.3417*2.58=0.8816
20
8 -0.31 -0.2 -0.17 -0.227 0.14
3)将数据按时间顺序画在X-R控 制图上;
4)结果分析 建立控制限并用标准控制图分 析评价是否稳定
注:如果测量过程是稳定的,数据可 以确定测量系统的偏倚和测量系 统重复性的近似值
5)如不稳定, 需实验设计或其他 分析技术查找原因
稳定性分析示例
工艺小组在工艺中程附 近选择了一个零件,送 测量室测量,确定基准 值为6.01。小组每班测 量这个零件5 次,共测 量4周(20个子组)。 数据收集后作X——R控 制图。
12 2.40 3.80 6.10 7.70 9.40
计算偏倚和均值
使用统计软件计算最佳拟合线:Y=0.7367-0.1317X
X
X
X
X
X
X
X
X
X
计数型量具分析报告(评价人一致性交叉表法)讲稿
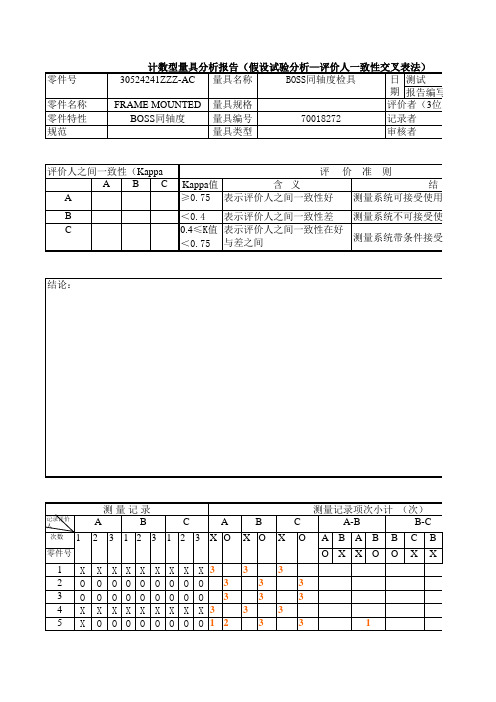
测量记录 B 3 1 2 X O O X O X O O X O X O O X O 3 X O O X O
C 1 2 X O O X O X O O X O
A 3 X O X 3 3 O 3 O X 3 O 1 2
B X O 3 3 3 3 3 3 X 3
C O
测量记录项次小计 (次) A-B B-C A B A B B O C X B X O X X O
1
1 1
1
1
1
2
49 O O O O O O O O O 50 O O X O O O O O O 测量记录项次总计(次) ⑴ ⑵ ⑶ ⑷ 说明:X--- 不合格 O---- -B B O X A O a=⑵-⑺ ⑺ X 总计 C-A C O X 总计 O a=⑹-⑾ 0 ⑿ 0 c=a+⑿ 0 0 ⑻ 0 c=a+⑻ 0 A X ⑾ 0 b=⑸-⑿ 0 d=b+⑾ 0 0 b=⑴-⑻ 0 d=b+⑺ 0
=⑴+⑵=⑶+⑷
=⑶+⑷=⑸+⑹ =⑸+⑹=⑴+⑵
述,说明计算有误
I- Pe
kappa
⑼=⑻-⑹ 150 150 150
⑽=⑺/⑼ 0.00 0.00 0.00
C 0.00
Po- Pe
I
I- Pe
⑺=⑶-⑹ 0 0 0
⑻ 150 150 150
⑼=⑻-⑹ 150 150 150
A A B C
评价人之间一致性 (kappa值) B 0.00
C 0.00
0.00
叉表法) 测试 报告编写 评价者(3位) 记录者 审核者
年 年
月 月
日 日
【MSA】计数型测量系系分析-设试验分析-交叉表法

【MSA】计数型测量系系分析-设试验分析-交叉表法由于小组不知道零件的参考决定,他们展开了交叉表格(cross-tabulations)来比较每个评价者与其它人的结果。
交叉表格的过程为两个或两个以上的分类变量分析了分布数据。
被排列在矩阵表中的结果形成了一个列联表,此表将说明变量之间的依存关系。
第一步是总结观测数据。
通过评审表,该小组审查了每俩观测者的数据。
计算他们对每组评估相同或不相同的结果。
评估结果中,34次A-1=1和B-1=1;32次A-2=1和B-2=1;31次A-3=1和B-3=1,即总共有97次结果致。
下表是用于对观测者A*B俩的数据分布总结。
也准备俩类似的表格对观测者B*C和A*C进行总结。
第二步是估计预期数据分布。
观察者对于纯偶然观测值赞同与否的可能性是什么?在150个观察值中,观察者A拒收这个零件50次,观察者B拒收这个零件47次。
pRA0R = 47/150 = 0.313pRB0R= 50/150= 0.333由于两个观察者是独立的,他们认为这个零件是坏的概率为:p(A0∩ B0) = pRA0R pRB0R= 0.104观察者A和观察者B认为这个零件是坏的预期次数可以通过将他们分别认为零件是坏的次数占总观察数的比例乘以总观察数得到。
150 x (pRA0R pRB0R)=150 x (47/150)x(50/150)= 15.7为了完成下面的表格,小组对每对观察者所作的每组观察都做了相似的评估:这些表格的目的在于确定评价者之间一致性的程度。
为确定这一致性的程度,小组使用了(cohen的)Kappa,这是用来衡量两个评价者对同一物体进行评价时,其评定结论的一致性。
Kappa为1时,表示有完全的一致性,为0时,表示一致性不比可能性来得好。
Kappa仅用于表格,表中两个变数有相同的分类值,且两个变数有相同的分类数量。
Kappa—种对评价者内部一致性的衡量,它测试在诊断区(获得相同评定的零件)中的数量与那些基于可能性期望的数量是否有差别。
MSA计数型测量系统分析指导书

5
10
93% 97% 90% 93% 97% 90%
84% 90% 80% 84% 90% 80%
71% 78% 66% 71% 78% 66%
来源 总受检数 符合的 错误的拒收(由于评价人偏移造成的拒收) 错误的接受(由于评价人偏移造成的接受) 不相配 95%上限 计算得分 95%下限
系统有效结果%
见表1
JT/C-7.6J-004
表1-计数型研究数据表
零 A- A-2 A-3 B-1 B-2 B-3 C-1 C-2 C-3 参 参考值 代
件1
考
码
1 1 1 1 1 1 1 1 1 1 1 0.476 901 2 1 1 1 1 1 1 1 1 1 1 0.509015 3 0 0 0 0 0 0 0 0 0 0 0.576459 - 4 0 0 0 0 0 0 0 0 0 0 0.566152 - 5 0 0 0 0 0 0 0 0 0 0 0.57036 - 6 1 1 0 1 1 0 1 0 0 1 0.544 951 7 1 1 1 1 1 1 1 1 1 1 0.465454 8 1 1 1 1 1 1 1 1 1 1 0.502295 9 0 0 0 0 0 0 0 0 0 0 0.437817 - 10 1 1 1 1 1 1 1 1 1 1 0.515573 11 1 1 1 1 1 1 1 1 1 1 0.488905 12 0 0 0 0 0 0 0 0 0 0 0.559918 13 1 1 1 1 1 1 1 1 1 1 0.542704 14 1 1 0 1 1 1 1 0 0 1 0.454518 15 1 1 1 1 1 1 1 1 1 1 0.517377 16 1 1 1 1 1 1 1 1 1 1 0.531939 17 1 1 1 1 1 1 1 1 1 1 0.519694 18 1 1 1 1 1 1 1 1 1 1 0.484167 19 1 1 1 1 1 1 1 1 1 1 0.520496 20 1 1 1 1 1 1 1 1 1 1 0.477236 21 1 1 0 1 0 1 0 1 0 1 0.452310 22 0 0 1 0 1 0 1 0 1 0 0.545604 23 1 1 1 1 1 1 1 1 1 1 0.529065 24 1 1 1 1 1 1 1 1 1 1 0.514192 25 0 0 0 0 0 0 0 0 0 0 0.599581 - 26 0 1 0 0 0 0 0 0 1 0 0.547204 27 1 1 1 1 1 1 1 1 1 1 0.502436 28 1 1 1 1 1 1 1 1 1 1 0.521642 29 1 1 1 1 1 1 1 1 1 1 0.523754
计数型测量系统分析报告

计数型测量系统分析报告1. 引言计数型测量系统是一种常用于工业生产和科学研究的测量设备。
它通过对待测物体进行计数来获取其数量信息,广泛应用于物流管理、质量控制和统计调查等领域。
本报告将对计数型测量系统进行分析,包括其工作原理、应用场景、优势和局限性。
2. 工作原理计数型测量系统的工作原理基于显微镜技术和图像处理算法。
首先,待测物体被放置在显微镜下,并通过显微镜成像系统进行放大显示。
然后,图像处理算法对显微镜中的图像进行分析,提取物体的特征并对其进行计数。
常用的图像处理算法包括边缘检测、阈值分割和形态学处理等。
3. 应用场景计数型测量系统在许多领域都有广泛的应用。
以下是几个常见的应用场景:3.1. 生物学研究计数型测量系统在生物学研究中被用于细胞计数和微生物计数等。
通过对细胞或微生物图像进行处理和计数,科学家们可以了解样本中的数量信息,帮助研究生物学过程和疾病机理。
3.2. 智能物流计数型测量系统在智能物流中扮演着重要角色。
它可以用于包裹计数和货物分类,提高物流效率和准确性。
通过自动计数和分类,物流企业可以更好地管理库存和跟踪货物位置。
3.3. 工业生产在工业生产中,计数型测量系统可以用于产品质量控制和制程监测。
通过对产品进行计数和缺陷检测,可以及时发现生产异常并采取相应措施,提高产品质量和生产效率。
3.4. 统计调查计数型测量系统在统计调查中也有广泛应用。
例如,人口普查中可以利用计数型测量系统对人口数量进行统计。
此外,市场调查中的样本计数和选择也可以借助计数型测量系统进行。
4. 优势计数型测量系统相比传统方法具有以下优势:4.1. 自动化计数型测量系统可以实现自动化的计数和分析过程,减少了人工操作和人为误差,提高了测量的准确性和效率。
4.2. 高精度通过利用显微镜技术和图像处理算法,计数型测量系统可以实现对微小物体的计数和精确测量,提供高精度的数量信息。
4.3. 大规模计数计数型测量系统能够快速处理大批量物体的计数,适用于大规模的生产和调查应用。
计数型测量系统研究

作出正确决定的次数 有效性= 总决定次数
变差来源 总检查数 相配数
评价人A 50 42
评价人¹ 评价人B 评价人C 50 45 50 40
结果%与归因的比较² 评价人A 评价人B 评价人C 50 42 0 0 8 50 45 0 0 5 97% 90% 78% 50 40 0 0 10 90% 80% 66%
A*B交叉表
B .00 A .00
数量 期望的数量 总计
1.00 6 34.3 97 68.7 103 103.0
44 15.7 3 31.3 47 47.0
50 50.0 100 100.0 150 150.0
1.00 数量
期望的数量 总计 数量 期望的数量
B*C交叉表
C .00 B .00
数量 期望的数量 总计
图29:与测量系统有关的“灰色”区域
p 小组使用了一个%GRR为公差的25%的特定量 具。由于这还没有被小组文件化,于是需要对 这测量系统进行研究。小组已决定从过程中随 机选取50个零件,以获得涵盖了整个过程范围 的零件。 使用3名评价人,每位评价人对每个零件测量 3次。
表 12 计 数 型 研 究 数 据 表
43 17.0 8 34.0 51 51.0
50 50.0 100 100.0 150 150.0
1.00 数量
期望的数量 总计 数量 期望的数量
p 这些表格的目的在于确定评价人之间一致性的 程度。为确定这一致性的程度,小组使用了 (cohen的)Kappa,这是用来衡量两个评价人 对同一物体进行评价时,其评定结论的一致性。 Kappa为1时,表示有完全的一致性,为0时, 表示一致性不比可能性来得好。Kappa仅用于 表格,表中两个变数有相同的分类值,且两个 变数有相同的分类数量。
计数型测量系统分析报告(KAPPA)

1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
1
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
1
1
1
1
1
1
作成:
Prepared by :
Page 1 of 3
Part Number(零件型号)
XXXXXXXXXXXXXXXXXXXXXXX
计数型测量系统分析报告(KAPPA)
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
测量系统分析培训--6 计数型系统分析Kappa

Operator 1
通 / 止规 是 最 常 Operator 2
用的量具,它只有
两种结果;测量的
零件是被接受或是
拒收
NO-GO
GO
-3-
第六章 计数型测量系统分析
ARR分析方法
1.假设性试验分析----Kappa分析法 假设性试验分析方法属于大样法,也叫Kappa分析法。一般使用交 叉表格(cross-tabulations)来比较每个评价者与其它人的结果.
测量系统分析培训教程六
第六章 计数型测量系统分析
Prepared by: fjhuang Apr 05, 2015
第六章 计数型测量系统分析
计数型数据(Attributes Data)
与计量型数据(Variables Data )相对, 可以被分类用 来记录和分析的定性数据.
Go-No Go 数据模式.人为因素主导,情况复杂 统计模型多种多样,统计学上各家争鸣,尚无定论 实践中采用何种形式,取决于实例与统计模型的接近程度 对于以”是”和”不是”为计数基础的定性数据,其GR&R考
• 漏判的几率 Probability of miss(P-miss) - 将“不合格”判为合格的机 会 P(miss)=实际漏判的次数 / 漏判的总机会数.
• 误判的几率 Probability of false alarm(P-FA) - 将“合格”判为不合格 的机会. P(false alarm)=实际误判次数 / 误判的总机会数.
基准 01
合计
计数 45
5 50
预期 16.0 34.0 50.0
计数
3 97 100
预期 32.0 68.0 100.0
计数 48 102 150
测量系统分析(MSA)计数型测量系统研究

测量系统分析(MSA)计数型测量系统研究计数型测量系统研究计数型测量系统属于测量系统中的一类,是一种测量数值为有限的分类数量的测量系统,它与测量结果是连续值的计量型测量系统不同。
最常见的是通过/不通过量具,只可能有两个结果;其它的计数型测量系统,如目视标准,可能产生5~7个分级,如非常好、好、一般、差、非常差等。
MSA前面所介绍的分析方法不能被用来评价这样的系统。
计数型测量系统研究计数型量具的特点是,把每一个零件同一个特定的限定值进行比较。
如果满足限定值就接受这个零件,反之拒绝零件(如通过/不通过量具)。
多数这种类型的量具以一套标准零件为基础进行设定接受与拒绝。
与计量型量具不同的是,这个计数型量具不能指出一个零件有多好或多坏,只能指出零件可接受或拒绝。
计数型测量系统研究-范例计数型测量系统研究-范例表格中的“1”指定为可接受判断,“0”指定为不可接受判断。
表格中的基准判断和计量基准值不预先确定。
表格中的“代码”列还用“-”、“+”、“x”显示了零件是否在第Ⅲ,Ⅱ,Ⅰ,区域。
计数型测量系统研究-范例假设检验分析-交叉表方法由于研究人员不知道零件的基准判断值,他们开发了交叉表比较每个评价人之间的差异。
计数型测量系统研究-范例2016-11-24陈瑞泉8表中(期望的计算)值的计算过程如下:(44+3)(3+97)/150=31.3(6+97)(97+3)/150=68.7(3+44)(44+6)/150=15.7(97+6)(6+44)/150=34.3计数型测量系统研究-范例上述这些表格的目的是确定评价人之间意见一致的程度。
为了确定评价人一致的水平,研究人员用科恩的Kappa来测量两个评价人对同一目标评价值的一致程度。
1值表示完全一致,0值表示一致程度不比偶然的要好。
kappa只用于两个变量具有相同的分级值和相同的分级数的情况。
计数型测量系统研究-范例kappa是一个评价人之间一致性的测量值。
检验是否沿对角线格子中的计数(接收比率一样的零件)与那些仅是偶然的期望不同。
测量系统分析方法

本方法适用于各类测量系统的影响测量结果的变异来源及其分布的分析方法。
主要包括:分辨力、偏差、线性、稳定性、重复性和再现性、假设试验分析等。
分辨力、偏差、线性、稳定性、重复性和再现性的分析方法适用于计量型测量系统的研究,假设试验分析法适用于计数型测量系统的分析,不可重复的测量系统可选用控制图法分析。
2术语2.1测量系统:是对测量单元进行量化或对被测的特性进行评估,其所使用的仪器或量具、标准、操作、方法、夹具、软件、人员、环境及假设的集合;也就是说,用来获得测量结果的整个过程。
2.2测量系统分析:是指检测测量系统以便更好地了解影响测量结果的变异来源及其分布的一种方法。
2.3分辨力指一测量仪器能够检测并忠实地显示相对于参考值的变化量。
2.4偏差是指测量结果的观测平均值与基准值的差值。
2.5稳定性(或称飘移)是指测量系统在某持续时间内测量同一基准或样本的单一特性时获得的测量值总变差。
2.6线性是指在测量设备预期的工作范围内,偏差值的差值。
2.7重复性即设备变差:是指由一个评价人,采用同一测量设备,多次测量同一样本的同一特性时获得的测量值变2.8 再现性即评价人变差:是指由不同的评价人,采用同一测量设备,测量同一样本的同一特性时获得的测量平均值变差。
2.9 计数型测量系统测量数值为一有限的分类数量的测量系统。
2.10计量型测量系统能获得一连串数值结果的测量系统。
3准备工作3.1应该事先决定好测量员数量,测量样本的数量及重复测量的次数。
3.2测量员应该从那些平时经常操作测量设备的人中选出。
3.3测试的样本必须从流程测量中选出,并代表该流程的控制范围,每个样本应被看作代表产品偏差的整个范围来进行分析的,每个样本将会进行多次测量,为了便于认别每个样本,必须对它们进行编号。
3.4按照指定的测量程序,确保测量方式正确。
3.5所有的分析方法都应确保每次读数的统计独立性,为了减少可能得出的错误的结果,应该采取下列步骤:a)测量必须是随机进行,以确保在分析研究中任何测岀的偏差或改变随机分布。
计数型测量系统分析报告MSA范本(带公式未加密)

5 5.15 5.02 5.05 4.98 5.07 5.05 5.16 5.15 5.13 5.12 5.17 5.08 5.08 5.06 5.07 5.01 4.99
5
代码
+ + + + + × + + + × + × + × + × + + + + × + + + × × + + × + + + × + + + × + × + + + + × +
核准:
基准
1 1 0 1 1 1 1 1 1 1 0 1 1 0 1 1 1 0 1 1 1 1 1 0 1 1 1 0 1 1 1 1 1 1 1 0 1 1 0 1 1 1 0 1 1 1 1 1 0 1
基准值
5.12 5.08 4.94 5.12 5.12 5.14
5 5.15 5.02 5.05 4.98 5.07 5.05 5.16 5.15 5.13 5.12 5.17 5.08 5.08 5.06 5.07 5.01 4.99
NO:
XXXXX
量具名称: 外形检
量具编号: MS13H
被测产品: CL-
被测参数下限:
5
零件
操作者A:
1
2
1
1
1
2
1
1
3
0
0
4
1
1
5
1
1
6
1
计数型MSA计算分析(假设试验法入门实例讲解)

计数型MSA研究方法——假设试验分析(交叉表法):实例详解计数型MSA研究对象:定性分析测量系统,外观、通止规等常用方法:假设试验分析操作方式:选择50个产品,其中2/3左右合格品和1/3左右不合格品,3个检验人员分别对其进行3次测量,相当于每人150次测量。
得出的结果,判定合格记录为1,判定不合格记录为0得出以下表格所示的结果:(为便于观察和理解,这里将测量人员判定结果与标准不一致的标成黄色)计数型MSA的指标要求和计算:1、Kappa:判定人员一致性好坏的指标,接收准则:Kappa>0.75 1.1人员之间的一致性:期望发生的次数:根据判定结果的概率,会发生的次数A判定为0的概率=A判定为0的次数/A判定的总次数=(44+6)/150=0.333 A判定为1的概率=A判定为1的次数/A判定的总次数=(3+97)/150=0.667 B判定为0的概率=B判定为0的次数/A判定的总次数=(44+3)/150=0.313 B判定为1的概率=B判定为1的次数/A判定的总次数=(6+97)/150=0.687A判定为0,同时B判定为0的概率=0.333*0.313=0.104A判定为0,同时B判定为1的概率=0.333*0.687=0.229A判定为1,同时B判定为0的概率=0.667*0.313=0.209A判定为1,同时B判定为1的概率=0.667*0.687=0.458A判定为0,同时B判定为0期望的次数=0.104*150=15.6A判定为0,同时B判定为1期望的次数=0.229*150=34.35A判定为1,同时B判定为0期望的次数=0.209*150=31.35A判定为1,同时B判定为1期望的次数=0.458*150=68.7Po:A与B判定结果一致的概率=(44+97)/150=0.94Pe:期望结果一致的概率=(15.6+68.7)/150=0.562Kappa=== 0.863Kappa>0.75,说明A与B一致性较好A与C、B与C按相同方式计算并进行判定1.2人员与标准之间的一致性Po=(45+97)/150=0.947Pe=(16+68)/150=0.56Kappa=(0.947-0.56)/(1-0.56)=0.879Kappa>0.75,说明A与标准一致性较好B、C与标准的一致性按相同方式计算并进行判定2、有效率、漏判率、错判率:判定单个人员好坏的指标有效率:完全判定正确的零件个数/总零件个数漏判率:将不合格判定为合格的次数/标准为不合格的次数(Ⅱ类风险,顾客风险)错判率:将合格判定为不合格的次数/标准为合格的次数(Ⅰ类风险,工厂风险)根据数据计算结果:人员A有效率=42/50=84%人员A漏判率=3/48=6.25%人员A错判率=5/102=4.9%结果表明,人员A有效率位于可接受边缘,漏判率不接受,错判率接受。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A-2 1 1 1 0 1 1 0 0 1 0 1 1 1 0 1 1 0 0 1 0 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 0 1 1
A-3 1 0 1 1 0 0 0 0 1 1 0 0 1 0 0 0 0 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1
C-2 1 1 1 0 1 1 0 0 1 0 1 0 1 0 1 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1
C-3 1 0 1 1 0 0 0 0 1 1 1 0 1 0 0 0 0 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1
P0: Pe:
0.92 0.62
A*C交叉表 B A 0 1 总计 计数 期望计数 计数 期望计数 计数 期望计数 0 35 11.2 5 28.8 40 40.0 1 7 30.8 103 79.2 110 110.0 总计 42.0 42.0 108.0 108.0 150.0 150.0
P0: Pe:
总计 42.0 42.0 108.0 108.0 150.0 150.0
P0: Pe:
0.92 0.61
B*C交叉表 B A 0 1 总计 计数 期望计数 计数 期望计数 计数 期望计数 0 33 10.1 7 29.9 40 40.0 1 5 27.9 105 82.1 110 110.0 总计 38.0 38.0 112.0 112.0 150.0 150.0
B-1 1 1 1 0 1 0 1 0 1 0 1 1 1 1 0 1 0 0 1 0 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 0 1 1
C-1 1 1 1 0 1 0 1 0 1 0 1 0 1 1 0 1 0 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1
C-1 1 1 1 1 1 0 1 1 1 1 0
C-2 1 1 1 1 1 0 1 1 1 1 0
C-3 1 1 1 1 1 1 1 1 1 1 0
基准
B A 0 1 总计 计数 期望计数 计数 期望计数 计数 期望计数 0 34 10.6 4 27.4 38 38.0 1 8 31.4 104 8统分析报告--假设检验交叉表法
零件名称: 量具名称:R规 分度值: 测量日期:7.12 试验次数 3 量具型号:R3.5 测量参数: 分析人员:符进金 零件样品数 50 操作人数 3 数据记录表 B-2 B-3 1 1 1 0 1 1 0 1 1 0 1 0 1 1 0 0 0 1 0 0 1 1 0 1 1 1 0 0 1 0 0 0 0 0 0 1 1 1 0 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 操作员 A B C 1 0 姓名 徐乐云 罗瀚 易宏 Pass/合格 Fail/不合格
基准
零件 40 41 42 43 44 45 46 47 48 49 50
A-1 1 1 1 1 1 0 1 1 1 1 0 A*B交叉表
A-2 1 1 1 1 1 0 0 1 1 1 0
A-3 1 1 1 1 1 1 1 1 1 1 0
B-1 1 1 1 1 1 0 1 1 1 1 0
数据记录表 B-2 B-3 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 0 0
0.92 0.60
kappa=(P0-Pe)/(1-Pe) (>0.75表示有很好的一致性,<0.40则表示一致不好 A*B 0.80 一致好 B*C 0.79 一致好 审核: A*C 0.80 一致好
Kappa 判定 编制:
零件 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39
A-1 1 1 1 0 1 0 1 0 1 0 1 1 1 1 0 0 0 0 1 0 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 0 1 1
