广义最小方差控制

合集下载

第3章自校正算法讲解

（6）应注意的问题
①控制信号可能过大。
u * (k) 1 T (k)
b0 ②对于非最小相位系统，采用自校正调节器还会带来控制系统的不稳定，即上述自校正调节器不适用于非最小相位系统。
3.3 广义最小方差自校正控制器
1.对控制量加以约束的最小方差调节器
（1）设计思想为了克服非最小相位系统对自校正调节器带来的
1) 1)
u(k
-
d)
+
C (zA(z -
1) 1)
w(k
)
（2）假设条件
①被控对象的纯迟延时间d以及多项式A、 B、C的阶次和系数都是已知的； ②被控对象模型是最小相位系统，即多项式B的所有零点位于单位圆内；
③多项式C的所有零点位于单位圆内；
④{w(k)}是均值为零，方差为2。
3.1 最小方差自校正调节器（续）
D( z 1 )u(k )

E ( z 1 ) C ( z 1 )
y(k)
J
D(z1)w(k d ) 2

E ( z 1 ) C ( z 1 )
y(k)

B( z 1 ) D( z 1 ) C ( z 1 )
u(k)
2
第三章自校正控制算法
主要内容
1.最小方差自校正调节器 2.广义最小方差控制器 3.极点配置的自校正调节器
3.1 最小方差自校正调节器
1. 系统结构
u(k )
扰动
y(k)
被控对象
参数估计器
ˆ
自适应律
c
控制器
3.1 最小方差自校正调节器（续）
2. 最小方差控制算法

基于神经网络误差补偿的预测控制研究毕业论文

基于神经网络误差补偿的预测控制研究毕业论文目录摘要............................................... 错误!未定义书签。

1 预测控制 (2)1.1 预测控制的产生 (2)1.2 预测控制的发展 (3)1.3 预测控制算法及应用 (4)1.3.1模型控制算法（Model Algorithmic Control，MAC） (5)1.3.2动态矩阵控制（Dynamic Matrix Control，DMC） (5)1.3.3广义预测控制（Generalized Predictive Control，GPC） (5)1.3.4极点配置广义预测控制 (5)1.3.5内模控制 (5)1.3.6模糊预测控制 (6)1.4 预测控制的基本特征 (6)1.4.1预测模型 (6)1.4.2反馈校正 (6)1.4.3滚动优化 (6)1.5预测控制的现状 (7)2 神经网络 (7)2.1 人工神经网络的生理原理 (8)2.2 神经网络的特征 (10)2.3 神经网络的发展历史 (11)2.4 神经网络的内容 (12)2.5 神经网络的优越性 (14)2.6 神经网络研究方向 (14)2.7 神经网络的应用分析 (14)2.8 神经网络使用注意事项 (17)2.9 神经网络的发展趋势 (18)2.10 BP神经网络 (18)2.10.1 BP神经网络模型 (18)2.10.2 BP网络模型的缺陷分析及优化策略 (19)2.10.3 神经网络仿真 (20)3．动态矩阵控制 (22)3.1 预测模型 (22)3.2 滚动优化 (23)3.3 反馈校正 (24)3.4 有约束多变量动态矩阵控制及其线性化 (27)3.5 动态矩阵控制仿真 (29)4 基于神经网络误差补偿的预测控制 (32)4.1 研究背景 (32)4.2 传统PID控制 (33)4.2.1位置式PID控制 (33)4.2.2 增量式PID控制 (35)4.3 基于神经网络的动态矩阵控制 (37)4.4 基于神经网络输出反馈的动态矩阵控制研究 (40)4.5 基于神经网络误差补偿的动态矩阵控制 (46)4.6 仿真效果验证 (51)总结 (57)参考文献 (58)1 预测控制1.1 预测控制的产生预测控制的产生，并不是理论发展的需要，而首先是工业实践向控制提出的挑战。

广义最小方差自校正控制

将其代入式（4-17）
J
E
P(z1) y(k d
k)
P(z1)E(z 1) (k
d)
R(
z
1
)
yr
(k
)
2
Q(z 1)u(k)2
由于(k d) 与yr (i), u(i), y(i), i „ k 不相关，并且它们的互相关函数为零，所以上式可写为
J E P(z1) y(k d k) R(z1) yr (k)2 Q(z1)u(k)2 P(z1)E(z 1)(k d)2
小很多，对系统输出的影响可忽略不计，根据 z 变换的终值定理和前面导出的表达式，系统输出的稳态值为
zd B(z1)R(z1)
q0 b0
Q(z 1)u(k)
P(z 1)E(z 1) (k
d)
z (k d k) P(z 1)E(z 1) (k d )
式中
(4-21)
z (k d k) P(z 1) y (k d k) R(z 1) yr (k) (q0 / b0 )Q(z 1)u(k) 于是，性能指标函数可表述为
y(k d k) u(k) f0 b0 ,
Q(z1)u(k) u(k)
q0
代入式（4-19），并不考虑符号 “E”，则有
P(
z
1 )
y
(k
d
k) R(z 1) yr (k)
f0
q0Q(z 1)u(k)
0
从而
3
u(k) R(z 1) yr (k) P(z 1) y (k d k) (q0 / b0 )Q(z 1)
(4-20)
除 z(k d) 外，其它符号含义同前。求使性能指标函数 4
J E z2(k d)

预测控制

1.1 引言预测控制是一种基于模型的先进控制技术，它不是某一种统一理论的产物，而是源于工业实践，最大限度地结合了工业实际地要求，并且在实际中取得了许多成功应用的一类新型的计算机控制算法。

由于它采用的是多步测试、滚动优化和反馈校正等控制策略，因而控制效果好，适用于控制不易建立精确数字模型且比较复杂的工业生产过程，所以它一出现就受到国内外工程界的重视，并已在石油、化工、电力、冶金、机械等工业部门的控制系统得到了成功的应用。

工业生产的过程是复杂的，我们建立起来的模型也是不完善的。

就是理论非常复杂的现代控制理论，其控制的效果也往往不尽人意，甚至在某些方面还不及传统的PID控制。

70年代，人们除了加强对生产过程的建模、系统辨识、自适应控制等方面的研究外，开始打破传统的控制思想的观念，试图面向工业开发出一种对各种模型要求低、在线计算方便、控制综合效果好的新型算法。

这样的背景下，预测控制的一种，也就是模型算法控制（MAC -Model Algorithmic Control）首先在法国的工业控制中得到应用。

同时，计算机技术的发展也为算法的实现提供了物质基础。

现在比较流行的算法包括有：模型算法控制（MAC）、动态矩阵控制（DMC ）、广义预测控制（GPC）、广义预测极点（GPP）控制、内模控制（IMC）、推理控制（IC）等等。

随着现代计算机技术的不断发展，人们希望有一个方便使用的软件包来代替复杂的理论分析和数学运算，而Matlab、C、C++等语言很好的满足了我们的要求。

1.2 预测控制的存在问题及发展前景70年代以来，人们从工业过程的特点出发，寻找对模型精度要求不高，而同样能实现高质量控制性能的方法，以克服理论与应用之间的不协调。

预测控制就是在这种背景下发展起来的一种新型控制算法。

它最初由Richalet和Cutler等人提出了建立在脉冲响应基础上的模型预测启发控制（Model Predictive Heuristic Control,简称“MPHC”）,或称模型算法控制(Model Algorithmic Control，简称“MAC”)；Cutler等人提出了建立在阶跃响应基础上的动态矩阵控制(Dynamic Matrix Control，简称“DMC”)，是以被控系统的输出时域响应(单位阶跃响应或单位冲激响应)为模型，控制律基于系统输出预测，控制系统性能有较强的鲁棒性，并且方法原理直观简单、易于计算机实现。

改进广义预测算法的NCS时延补偿

据，从而减少网络延迟和空抽样对 NCS 系统控制性能的影响。 Mu J X 等［6］使用预测控制算法的冗余控制来提高控制性能，并使用改进的史密斯预测器和模型预测器来补偿反馈信道中的延迟。文献［7~ 8］提出了一种约束模型预测控制算法，通过滚动控制时域优化对应终端性能的上限和下限，使用执行器中的缓冲器来保存时延补偿控制量。
112
时维国等：改进广义预测算法的 NCS 时延补偿
第 47 卷
广义预测控制（The generalized predictive control， GPC）算法应用于以太网 NCS 网络延迟的补偿。使用基于最小方差控制的广义预测控制算法来避免 Diophantine 方程，以确保网络控制系统的实时性。将传统的广义预测控制算法和改进的广义预测控制算法在 Matlab 仿真平台上验证算法的优越性。仿真结果表明，改进的广义预测控制算法可以在随机延迟较大的以太网控制环境中使用，可以补偿延迟对系统性能的影响，大大提高系统的控制精度。
SHI Weiguo YAN Xiaoyu WANG Jiasheng （Colllege of Information & Electrical，Dalian Jiaotong University，Dalian 116028）
Abstract Aiming at the shortcomings of traditional generalized predictive control algorithm in Ethernet network control sys⁃ tem，such as large computational complexity，complex system and lack of real time，a generalized predictive control algorithm based on minimum variance control is adopted，which avoids the solution of Diophantine equation，reduces the calculation time， and ensures the real-time network control system. Experimental results show that the improved generalized predictive control algo⁃ rithm can well compensate the influence of delay on system performance and improve the control precision of the system.

基于精校机的广义最小方差的极点配置控制器的仿真与应用

ｔｅｐｏｓｔｏｋｓｏｙｓｅ．Ｉｓａｈｉｉｎｏｆｐｏｅｆｓｔｍｔｉｐｐｌｏｔｌｔｏ－ｉｔｈｅｅｅｒｈｙｄａｉｄｅｃｒｕｌｐｏｓｔｏｇＶｙｓｅｆｔｅｐｒｃｓｃｉｉｎＳＴＯａｔｏｄＡｐｐｉａｉｎｏｌｃｔｏｆＰｏｋａｅｅｎｔｏｌｒｏｈｅｉｅＳｔａｇｅｎｅＰｌｃｍｎｔＣｏｒｌｅｎｔｅＰｒｃｓｒｉｈｔｎｉｇＭａｈｉｃｎｅ’ ｎｅａｉｅｉｉｕｍｒａｃＳＧｅｒｌｄＭｎｍｚＶａｉｎｅ
Ａｂｔａｃ：Ａｅｅａｉｄｍｉｍｕａｉｎｃｅｆｔｉｇｃｎｒｌｒｉｐｉａｅｔｈｅｒｎｄｍｙｓｅｆｏｔｉｓｒｔｇｎｒｌｚｅｎｉｍｖｒａｅｓｌ－ｕｎｏｔｏｌｓａｐｌｂｌｏｔａｏｓｔｍｏｕｓｄｅｎｅｃ
ｃｎｒｌａｈｈａｔｉｔｃｈｃｒｉｐｌｉｈｅｉｄｅｉａｒｎｇｏｔｗｉｅｉｒｃｏｔｏｌｈｔｅｃａｃｅｓｉｓｗｉｈａｅｓｒｅｓｒｒｍｅａｔｍｔｃａａｌｃｒｙｉｕｔａｓｔｍｃｏｏｍｐｕｅ，ｒｎｓｙｈｔｒＳｔａｐｒｃｉａｌ．ＴｈｉｐｅｏｓｓｈｇｎｒｌｅｉｉｕＯｉｓｈａｔｌｖａｕｅｃｓｐａｒｐｒｐｏｅｔｅｅｅａｉｄｍｎｍｍｖｒａｃｅｆｔｎｇｃｎｔｏｌａｄｚａｉｎｅｓｌ－ｕｉｏｒｌｎｎｒｅ

非线性广义最小方差控制律综述

第１１卷第２期２０１３年６月
１６７２－６５５３／２０１３／１１（２）／１０２－７
动力学与控制学报
ＪＯＵＲＮＡＬＯＦＤＹＮＡＭＩＣＳＡＮＤＣＯＮＴＲＯＬ
Ｖｏ１．１１Ｎｏ．２
２０１２－０５－２１收到第１稿，２０１２０－５－３０收到修改稿．．国家自然科学基金资助项目（６１００４０４１），辽宁省自然科学基金资助项目（２０１１０２０３６），新世纪优秀人才计划资助（ＮＣＥＴ・１１－００５４）十通讯作者Ｅ・ｍａｉｌ：ｙｐａｎｇ＠ｄｌｕｔ．ｅｄｕ．Ｃｒｌ
控制系统中的非线性一般有两个来源５Ｊ：一是系统自身的不完善，而这种不完善实际中是不可避免的，例如随动系统的齿轮传动具有的间隙和
干摩擦；二是系统的固有特性，例如高速运动机械
ＭｉｎｉｍｕｍＶａｒｉａｎｃｅ，ＮＧＭＶ）控制是在广义最小方差（ＧｅｎｅｒａｌｉｚｅｄＭｉｎｉｍｕｍＶａｒｉａｎｃｅ，ＧＭＶ）控制基础上的进一步扩展应用，对非线性控制问题提出了一种新的解决方案．ＮＧＭＶ控制的系统模型组成为：输入通道或输出通道中的延时项；非线性输
提高，建立在线性系统基础上的传统设计已经无

极小广义方差法

极小广义方差法1. 引言极小广义方差法（Minimum Generalized Variance, MGV）是一种用于求解优化问题的数值方法。

它可以用于寻找一个函数的最小值点，或者在给定约束条件下找到使目标函数最小化的变量取值。

MGV方法在数学和工程领域都有广泛的应用，特别是在非线性优化、控制理论和机器学习等领域。

本文将介绍极小广义方差法的基本原理、算法步骤以及应用示例，并探讨其优缺点和改进方法。

2. 基本原理极小广义方差法是基于方差的概念进行优化的一种方法。

在确定目标函数最小时，我们希望找到一组变量取值，使得这组取值下目标函数的方差最小。

因此，MGV方法通过调整变量取值来寻找最小方差点。

具体而言，假设我们有一个目标函数f(x)，其中x是一个n维向量。

我们希望找到一个x，使得f(x)最小，并且满足一系列约束条件g(x)<=0。

那么可以定义一个新的函数J(x)，即广义方差函数：J(x) = f(x) + λ * Σ(g(x))²其中λ是一个非负的参数，用于平衡目标函数和约束条件。

当λ趋近于无穷大时，J(x)的最小值点就是满足约束条件的最小值点。

3. 算法步骤极小广义方差法包括以下几个基本步骤：步骤1：确定初始点选择一个合适的初始点x0作为算法的起始点。

步骤2：计算梯度和海森矩阵计算目标函数f(x)在当前点xk处的梯度gk和海森矩阵Hk。

梯度表示了目标函数在当前点的变化率，而海森矩阵则表示了梯度的变化率。

步骤3：求解线性方程组解决下面的线性方程组，找到一个搜索方向pk：Hk * pk = -gk这个方程组可以通过各种数值方法来求解，例如共轭梯度法、牛顿法等。

步骤4：确定步长确定一个合适的步长αk，使得在搜索方向上移动一段距离。

常用的方法有Armijo 准则、Wolfe-Powell准则等。

步骤5：更新变量更新变量xk+1 = xk + αk * pk，并计算新的目标函数值和梯度。

步骤6：判断停止条件根据一定的停止条件判断算法是否终止。

广义预测控制,算法及仿真实例

广义预测控制算法及实例分析一．广义预测控制算法1.广义预测控制的提出广义预测控制是预测控制中三种常见算法之一。

预测控制的提出并不是某一种统一理论的产物，而是源于工业实践，并在工业实践过程中发展和完善起来的一类新型计算机控制算法。

预测控制不会过分依赖被控对象的精确数学模型，能很好的应对工业对象的结构、参数的不确定性，且用工业计算机较容易实现。

2.广义预测控制的基本原理广义预测控制是预测控制中最具代表性的算法，他有三方面的特点：基于传统的参数模型，模型参数少；是在自适应发展过称中发展起来的，保留了自适应发展的优点且更具鲁棒性；采用多步预测、滚动优化、反馈校正更适于工业应用。

广义预测控制基本原理：预测模型、滚动优化、反馈校正预测模型：预测控制的模型称为预测模型。

预测控制对模型的要求只强调其功能而非结构，只要模型可利用过去己知数据信息预测系统未来的输出行为，就可以作为预测模型。

在DMC、MAC等预测控制策略中，采用了阶跃响应、脉冲响应等非参数模型，而GPC预测控制策略则多选择CARIMA参数模型。

滚动优化：预测控制是一种优化控制算法，通过某一性能指标的最优来确定未来的控制作用。

预测控制的优化标准不是采用一成不变的全局最优化目标，而是采用滚动式的有限时域优化策略。

优化不是一次离线进行，而是反复在线进行。

在每一采样时刻，优化性能指标只涉及到未来有限的时域，而到下一采样时刻，这一优化时域同时向前推移。

因此，预测控制在每一时刻有一个相对于该时刻的优化性能指标，即实现滚动优化。

反馈校正：预测控制算法在进行滚动优化时，优化的基点应与系统实际一致。

但作为基础的预测模型，只是对象动态特性的粗略描述，可能与实时状态不慎符合。

这就需要用附加的预测手段补充模型预测的不足，或对基础模型进行在线修正。

预测控制算法在通过优化确定了一系列未来的控制作用后，每次只是实施当前时刻的控制作用。

到下一采样时刻，则首先检测对象的实际输出，并利用这一实时信息对基于模型的预测进行修正，然后再进行新的优化。

广义最小方差自校正控制(直接算法)

%广义最小方差自校正控制(直接算法)考虑如下系统：() 1.7(1)0.7(2)(4)0.5(5)()0.2(1)y k y k y k u k u k k k ξξ--+-=-+-++- 式中ξ(k )为方差为0.1的白噪声。

取111()1,()1,()2P z R z Q z ---===，期望输出y r (k )为幅值为10的方波信号。

clear all;close all;a=[1 -1.7 0.7];b=[1 2];c=[1 0.2];d=4;na=length(a)-1;nb=length(b)-1;nc=length(c)-1;nf=nb+d-1;ng=na-1;Pw=1;R=1;Q=2; %加权多项式np=length(Pw)-1;nr=length(R)-1;nq=length(Q)-1;L=400;uk=zeros(d+nf,1);yk=zeros(d+ng,1);yek=zeros(nc,1);yrk=zeros(nc,1);xik=zeros(nc,1);%xiek=zeros(nc,1);yr=10*[ones(L/4,1);-ones(L/4,1);ones(L/4,1);-ones(L/4+d,1)]; xi=sqrt(0.1)*randn(L,1);%RELS初值设定thetaek=zeros(na+nb+d+nc,d);P=10^6*eye(na+nb+d+nc);for k=1:Ltime(k)=k;y(k)=-a(2:na+1)*yk(1:na)+b*uk(d:d+nb)+c*[xi(k);xik];%递推最小二乘法phie=[yk(d:d+ng);uk(d:d+nf);-yek(1:nc)];K=P*phie/(1+phie'*P*phie);thetae(:,k)=thetaek(:,1)+K*(y(k)-phie'*thetaek(:,1));P=(eye(na+nb+d+nc)-K*phie')*P;ye=phie'*thetaek(:,d); %最优预测输出估计值% xie=y(k)-phie'*thetae(:,k);%白噪声估计值%提取辨识参数ge=thetae(1:ng+1,k)';fe=thetae(ng+2:ng+nf+2,k)';ce=[1 thetae(ng+nf+3:ng+nf+2+nc,k)'];if abs(ce(2))>0.9ce(2)=sign(ce(2))*0.9;endif fe(1)<0.1fe(1)=0.1;end%[e,f,g]=singlediophantine(ae,be,ce,d);CQ=conv(ce,Q);FP=conv(fe,Pw);CR=conv(ce,R);GP=conv(ge,Pw);u1=-Q(1)*CQ(2:nc+nq+1)*uk(1:nc+nq)/fe(1)-FP(2:np+nf+1)*uk(1:np+n f);u2=CR*[yr(k+d:-1:k+d-min(d,nr+nc));yrk(1:nr+nc-d)];u(k)=(u1+u2-GP*[y(k);yk(1:np+ng)])/(Q(1)*Q(1)/fe(1)+fe(1));%更新数据for i=d:-1:2thetaek(:,i)=thetaek(:,i-1);endthetaek(:,1)=thetae(:,k);for i=d+nf:-1:2uk(i)=uk(i-1);enduk(1)=u(k);for i=d+ng:-1:2yk(i)=yk(i-1);endyk(1)=y(k);for i=nc:-1:2yek(i)=yek(i-1);yrk(i)=yrk(i-1);xik(i)=xik(i-1);endif nc>0yek(1)=ye;yrk(1)=yr(k);xik(1)=xi(k);endendfigure(1);subplot(2,1,1);plot(time,yr(1:L),'r:',time,y);xlabel('k');ylabel('y_r(k),y(k)');legend('y_r(k)','y(k)');axis([0 L -20 20]);subplot(2,1,2);plot(time,u);xlabel('k');ylabel('u(k)');axis([0 L -10 10]);figure(2);subplot(211);plot([1:L],thetae(1:ng+1,:),[1:L],thetae(ng+nf+3:ng+2+nf+nc,:)); xlabel('k');ylabel('参数估计g,c');legend('g_0','g_1','c_1');axis([0 L -3 4]);subplot(212);plot([1:L],thetae(ng+2:ng+2+nf,:));xlabel('k');ylabel('参数估计f');legend('f_0','f_1','f_2','f_3','f_4');axis([0 L 0 8]);。

多步预测自校正控制

多步预测自校正控制1 多步预测自校正控制介绍多步预测自校正控制业称为广义预测控制（Generalize Predictive Control ）,它是再最小方差自校正控制和广义最小方差自校正控制得基础上发展起来得。

它保留了最小方差自校正控制的优点，同时增加了一些新亮点。

如最小方差控制中的预测模型，控制优化和反馈控制在多步预测控制中得到了继承，并且增加了多步预测，多步控制，实施一步，循环滚动等措施。

因而控制效果更好，系统的鲁棒性更强，更能适应复杂的过程或对象，使多步预测控制升华为一种性能卓越，适应性强的控制策略。

它不仅适用于稳定的开环系统，而且还适用于非最小相位系统，开环不稳定系统，以及非线性系统。

与最小方差自校正控制不同的是，预测控制可以预测未来多步模型的输出，并且在多步时段内控制也有多步作用，于是，在输出的预测，既有原来施加控制的影响，我们称之为零输入作用下的预测，简称为零输入预测，又有新加入的控制产生的作用，我们称之为零状态下的预测，简称为零状态预测。

按某种性能指标函数优化控制，并且仅实施最近的一步控制量。

从整个系统的控制过程看，每个周期的控制不是最优的，但它却是周期中最好的。

因此，对系统时刻可能遭受到的模型失配，参数变化，干扰等不良影响，系统都能及时的有效抵御。

2 控制算法步骤（1）已知a n ,b n ，根据被控对象和要求确定N ，u N ，R 和Q ，初始化P(0)， θ(0)，等值；（2）读取y(k),r y (k+j),用式 ()(1)()[()()(1)]T k k K k y k k k θθϕθ=-+∆--估计 θ(k)；（3）用 ()k θ中的 1()A z -和 1()B z -代替1()A z -和1()B z -，并求1()A z -；（4）递推法求1()j E z -,1()j G z -,1()j L z -和1()j H z -;（5）构成据政L ，H 和G ；（6）求的第一行T q l ；（7）式()(1)[()()()]T q r u k u k l Y k j H U k j GY k =-++-∆--求u(k)，并执行；（8）k →k+1,转步骤（2）。

一种用于ASM测试的改进RLS广义最小方差自适应控制

》ｒｕｓｈｖｓｏｇｌｔｔａｔｅｅｈｄｃｎａａｔｈｈｎｅｏａｅｕｋ，ｈｈ《ｅｌａｅｔｎｌｉｕｒｅｔｔｈｎｗｍｔｏｄｅｃａｇｆｌｄｖｒｑｉｌｗｉｓｔｒｙｌｓａｄｈｅｏｐｔｏｙｃｙｃ；ｍｋｓｈｓｍｂｉｅａｄａｌＴｕｔｅｉａｓｏｎｏｅｒｔａｉａｐｉｔｎａｅ；ａｅｔｓｔｎｏｒｅｅ．ｓｈｄｓｎｓｈｗａｉｌｎｐｌａｏｕｓｅｙｅｅｇｐｔｅｙｅｇｈｓｈｔｂｐｃｃｃｉｖ．ｌ
李恒宾刘平任庆平 Fra bibliotek熊建国侯彦羽
（青海交通职业技术学院汽车工程系，，西宁８０２）１０８（西南交通大学机械工程学院，成都６０３）１０１
Ａｅｆｔｎｎｏｔｏｌｒｏｅｅａｉｅｎｍｕｖｒｎｅｗｉｒｖｄｓｌｕｉｇｃｎｒｌｆｇｎｒｌｄｍｉｉｍａｉｃｔｉｏｅ－ｅｚａｈｍｐＩａｔｓａｅｇｒｈｕｄｒｅｓ— ｑｕｒｓａｌｏｉｍｎｅｔＡＳＭｅｔｔｓＬｅｇｂｎ，Ｉｉｇ，ＥｉｇｐｎＸＯＧＪｎｇｏ，Ｏａ－ｕＩｎ－ｉＬＵＰｎＲＮＱｎ－ｉｇ，ＩＮａ－ｕＨＵＹｎｙＨｉ（ＤｐｒｎｆｕｏｏｉｎｉｅｒｇＱｎｈｉｏｕｉｔｎｅｈｉａＣｌｇ，ｉｉｇ８２，ｈｎ）ｅａｔｔｔｍｔｅＥｇｅｉ，ｉｇａＣｍｍｎｃｉｓｃｎｃｌｏｅｅＸｎｎ１０８ＣｉａｍｅｏＡｖｎｎａｏＴｌ０（ｃｏｌｆｃａｉａＥｇｎｅｉｇＳｕｈｅｔｉｔｇＵｉｅｓｙＣｅｇｕ６３，ｈｎ）２ｈｏｏｈｎｃｌｎｉｅｒ，ｏｔｗｓＪｏｎｎｖｒｉ，ｈｎｄ０ＣｉａＳＭｅｎａｏｔ１１０

多个解释变量异方差修正命令_解释说明

多个解释变量异方差修正命令解释说明1. 引言1.1 概述在经济学和统计学领域，研究人员常常使用多元回归模型来分析变量之间的关系。

然而，在进行多元回归分析时，我们必须考虑到可能存在的异方差问题，即误差项的方差随着解释变量的变化而发生改变。

异方差问题会导致回归系数估计的不准确性，从而影响对实际关系的解释。

为了解决异方差问题，研究人员提出了许多修正方法。

其中一种常见的方法是利用多个解释变量对异方差进行修正。

本文将详细介绍这种修正方法及其应用。

1.2 文章结构本文将分为五个部分进行阐述。

首先，在引言部分我们将概述本文的主题和目标，并描述文章的结构安排。

接下来，在第二部分中我们将介绍异方差问题的引出以及解释变量对异方差修正的影响。

紧接着，第三部分将重点论述多个解释变量的异方差修正方法，并列举具体要点进行解释说明。

在第四部分中，我们进一步探讨另一个角度下解释说明该方法，并提出一些相关要点。

最后，在结论部分，我们将总结讨论结果，展望未来研究方向，并分析本研究的局限性。

1.3 目的本文的目的是系统介绍多个解释变量异方差修正命令及其解释说明。

通过对该方法的详细阐述，读者可以了解到如何使用多个解释变量对回归模型进行异方差修正以获得更准确和可靠的估计结果。

同时，本文还旨在提供有关该方法的具体步骤和要点以供实践应用。

希望读者在阅读完本文后能够对多个解释变量异方差修正命令有一个清晰全面的了解，并能够在实际研究中灵活运用该方法来解决异方差问题。

2. 多个解释变量异方差修正命令2.1 异方差问题的引出在实证研究和统计分析中，我们常常会使用回归模型来研究一个或多个解释变量对于一个因变量的影响。

然而，在实际应用中，我们会发现回归模型假设了误差项具有同方差性。

但是，在许多情况下，误差项可能表现出异方差性，即其方差随着解释变量的不同取值而发生改变。

这可能会导致一些问题，例如参数估计结果的无效性、显著性检验结果的失真以及预测精度的降低。

第10章-广义预测控制

10.1.1 预测模型
其中
Gj
(z1)
g j,0
g
z1
j,1
g j, j1z j1
H (z ) h z 则由式(10.1.4)和式(10.11.5)可以得到1
j
j,1
hj ,2 z 2
hj,nb znb
式出y信((1k0息.1及.4未)j、|来式k的)(1输0.入1G.5值j)(、, z就式可1()1以0.u预1.(7测k)和对式象j(未10来.11的.|8)k输都)出可。作H为jG(PzC1的)预u测(模k)型。F这j样(z, 根1)据y(已k知) 的(输10入.1输.7)
(k
)
FN
(
z
1
)
y
(k
)
均可由 k 时刻已知的信息 y , ≤k 以及 u , k 计算。
(10.1.15)
如果记
y(k | k) y(k 1| k), , y(k N | k)T
u(k | k) u(k | k), ,u(k Nu 1| k)T
f (k) f1(k), , fN (k)T
给出了一个
E j、(z1) Fj (的z递1)推算法。
首先, 根据式(10.1.3)可写出
1 Ej (z1)A(z1) z j Fj (z1)
1 Ej1(z1)A(z1) z( j1) Fj1(z1)
两式相减可得
A(z1
)[E
j
1 ( z 1
)
E
j
(z
1
)]
z
j
[
z
F 1 j 1
(z1
)
Fj
10.1.1 预测模型
式中，z 1 是后移算子，表示后退一个采样周期的相应的量，即 z1y(k) y(k 1) ，z1u(k) u(k 1)；

广义最小方差自校正重置PID控制器及其在压力系统中的应用研究

广义最小方差自校正重置PID控制器及其在压力系统中的应用研究作者：贺建军吴高亮喻寿益来源：《计算技术与自动化》2013年第01期摘要：针对压力系统的纯延迟、大惯性、非线性、时变等特点，本文将重置控制和以广义最小方差为性能指标的自校正PID控制相结合，提出一种广义最小方差自校正重置PID控制方法。

该方法首先根据被控对象的数学模型，以广义最小方差为目标设计广义最小方差控制器，通过选择该控制器的分母多项式，求解Diophantine方程，得到具有PID结构形式的广义最小方差控制器，再在该控制器的积分项中引入重置控制，构成广义最小方差重置PID控制；对于模型未知或参数慢时变的被控对象，通过采用带遗忘因子的递推最小二乘法构建系统的自适应机制，增强控制系统的自适应能力和鲁棒性。

最后，将该控制方法应用于压力容器的恒值控制中，获得了比较满意的控制效果。

关键词：最小方差；自校正控制；重置控制；压力系统中图分类号：TP13文献标识码：A1引言压力系统是过程控制的主要控制对象之一，在工业生产中有着极其重要的地位。

在有色金属冶炼和化工化学生产中，该系统常被用作反应容器，为相应的化学反应提供所需的压力条件；另一方面，压力系统也可作为气动设备如气泵执行部件、气动传感器等的气源。

因此压力系统的运行情况对整个生产过程的安全生产和产品质量有直接影响，合理、有效地对压力值进行控制至关重要。

然而，压力系统具有纯延迟、大惯性、非线性等特点，其过程参数甚至模型结构都会随着时间和工作环境的变化而改变，使得基于可编程逻辑控制器的传统PID算法对压力系统的控制不能获得满意的控制效果。

因此许多学者针对这一类复杂系统不断地提出新算法。

杨云飞[1]提出了一种基于可编程逻辑控制器的自适应模糊PID控制算法，通过查表的方式对压力系统进行控制。

由于其大量的模糊规则和隶属度函数的设定都是依据经验来进行选择，因此模糊规则的制定和隶属度函数的设置需要耗费大量的时间；Ryouta Hoshino[2] 提出了一种广义最小方差自校正控制方法。

GPC文档

qˆ
(
k
)
=
qˆ
(
k
-1)
+
1
+
f
P(k T (k)
-1)f (k ) P (k -1)f
(k
)
éëDy
(
k
)
-
qˆT
(k
-1)f
(
k
)ùû
（21）
P
(
k
)
=
P
(k
-1)
-
P
(k -1)f (k )fT 1+fT (k)P(k
(k)P - 1)f
(k (k
-
)
1)
（22）
4
姓名：牛攀峰
学号：2120100307
方程
EjB = Gj + z-jH j
G j = g0 + g1z-1 + L + g j-1z-( j-1)
Hj
=
hj0
+ hj1z-1
+L +
h z -(nb-1) jnb-1
将（6）式代入（5）式，得
（6）
( ) yˆ (k + j | k ) = Gj + z- j H j Du (k + j -1) + Fj y (k )
由图（3）发现系统在刚开始时跟踪效果比较差，这是因为系统模型参数最初时未知，模型参数需要进过一段时间的辨识之后才能获得，之后就会很快进入到稳定状态了。
之后我们再设 na=4， nb=2，得到的仿真结果为：
图（4）
结果中,辨识的模型系数 A 为[1,-0.88496,-0.31555，0.1684,0.076418], 模型系数 B 为[1.079,1.2983,0.59091]，得到的辨识模型为：

【国家自然科学基金】_广义最小方差控制_基金支持热词逐年推荐_【万方软件创新助手】_20140802

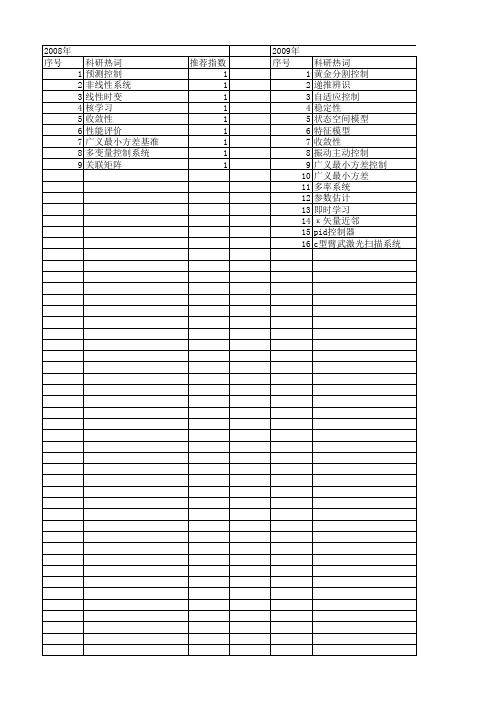
科研热词黄金分割控制递推辨识自适应控制稳定性状态空间模型特征模型收敛性振动主动控制广义最小方差控制广义最小方差多率系统参数估计即时学习 κ 矢量近邻 pid控制器 c型臂武激光扫描系统
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年序号 1 2 3 4 5 6 7 8 9 10 11 12 13
2012年序号 1 2 3 4
科研热词方差约束指标相容性广义系统 h∞指标
推荐指数 1 1 1 1
2013年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
科研热词性能评价广义最小方差非线性重置控制输出方差限制自校正控制线性时变扰动矩阵加权融合准则状态空间描述系统最小方差最优控制参数时滞控制器设计广义系统广义最小方差(gmv) 广义多变量系统对角关联矩阵多项式系统多变量系统复杂有色噪声压力系统卡尔曼仿真分析 pi控制
2008年序号 1 2 3 4 5 6 7 8 9
科研热词预测控制非线性系统线性时变核学习收敛性性能评价广义最小方差基准多变量控制系统关联矩阵
推荐指数 1 1 1 1 1 1 1 1 1
2009年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
推荐指数 3 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2014年序号 1 2 3 4 5 6 7 8 9
2014年科研热词飞行试验非线性线性混杂自动机等价模型状态依赖空间模型滤波涵道无人直升机广义最小方差参数辨识推荐指数 1 1 1 1 1 1 1 1 1

最小方差控制

2 2
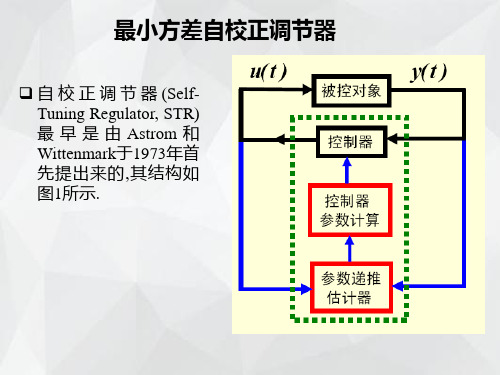
2 最小方差控制
最小方差控制的目的是要确定u(k)，使得输出的方差为最小，由于u(k)最早只能影响到y(k+d)，因此选择性能指标为
J E{ y(k d ) }
2
(14)
上式可改写为：
ˆ (k d k ) ~ J E{ y (k d ) 2 } E{[ y y (k d k )]2 } ˆ (k d k ) 2 } E{~ E{ y y (k d k ) 2 }
在最小方差调节器的研究中,所讨论的被控系统的模型为 A(q-1)y(k)=B(q-1)u(k-d)+C(q-1)e(k) (1)
1 1 n A ( q ) 1 a q a q 其中： 1 n
B (q 1 ) b0 b1q 1 bn q n C (q 1 ) 1 c1q 1 cn q n
刻及以前的输入输出的函数。若对预测的要求是使预测的误差平方即系统误差的方差为最小，则损失函数可表示为：
ˆ (k d k ) y (k d )]2 } J E{[ y
1 1 1 B ( q ) F ( q ) G ( q ) 1 2 ˆ ( k d k ) F ( q )e( k d ) E{[ y u ( k ) y ( k )] } 1 1 C (q ) C (q ) (10) 上式中F(q-1)e(k+d)与其它项均不相关，且由于{e(k)}为零均值白噪声序列，式(10)可写为
1 最小方差预测
设在k时刻已观测到输出值y(k),y(k-1),…等，希望由此得到预测值 y ˆ (k d k ) 。
1 1 B ( q ) C ( q ) 由式(1)有： y (k d ) u (k ) e(k d ) 1 1 A(q ) A(q )

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

[e,f,g]=singlediophantine(a,b,c,d); CQ=conv(c,Q);FP=conv(f,P);CR=conv(c,R);GP=conv(g,P);
for k=1:L time(k)=k; y(k)=-a(2:na+1)*yk+b*uk(d:d+nb)+c*[xi(k);xik];
%广义最小方差控制显示控制广义最小方差控制(显示控制广义最小方差控制显示控制)
考虑如下系统：
y (k ) − 1.7 y (k − 1) + 0.7 y (k − 2) = u (k − 4) + 0.5u (k − 5) + ξ (k ) + 0.2ξ (k − 1)
式中ξ(k)为方差为 0.1 的白噪声。取 P( z −1 ) = 1, R( z −1 ) = 1, Q( z −1 ) = 2 ，期望输出 yr(k)为幅值为 10 的方波信号。
subplot(2,1,1); plot(time,yr(1:L),'r:',time,y); xlabel('k');ylabel('y_r(k),y(k)'); legend('y_r(k)','y(k)'); subplot(2,1,2); plot(time,u); xlabel('k');ylabel('u(k)');
u1=-Q(1)*CQ(2:nc+nq+1)*uk(1:nc+nq)/b(1)-FP(2:np+nf+1)*uk(1:np+nf ); u2=CR*[yr(k+d:-1:k+d-min(d,nr+nc));yrk(1:nr+nc-d)]; u(k)=(u1+u2-GP*[y(k);yk(1:np+ng)])/(Q(1)*CQ(1)/b(1)+FP(1));
%更新数据 for i=d+nb:-1:2 uk(i)=uk(i-1); end uk(1)=u(k);
for i=na:-1:2 yk(i)=yk(i-1);
end yk(1)=y(k);
for i=nc:-1:2 yrk(i)=yrk(i-1); xik(i)=xik(i-1); end if nc>0 yrk(1)=yr(k); xik(1)=xi(k); end end
clear all;close all; a=[1 -1.7 0.7];b=[1 2];c=[1 0.2];d=4; na=length(a)-1;nb=length(b)-1;nc=length(c)-1; nf=nb+d-1;ng=na-1;
P=1;R=1;Q=2; %加权多项式 np=length(P)-1;nr=length(R)-1;nq=length(Q)-1;
Hale Waihona Puke L=400; uk=zeros(d+nb,1); yk=zeros(na,1); yrk=zeros(nc,1); xik=zeros(nc,1); yr=10*[ones(L/4,1);-ones(L/4,1);ones(L/4,1);-ones(L/4+d,1)];
xi=sqrt(0.1)*randn(L,1);