多边形的面积等积变形
小学五年级上学期数学《多边形的面积》教案精选全文完整版

可编辑修改精选全文完整版小学五年级上学期数学《多边形的面积》教案•相关推荐小学五年级上学期数学《多边形的面积》教案(通用8篇)在教学工作者实际的教学活动中,很有必要精心设计一份教案,教案是备课向课堂教学转化的关节点。
那么应当如何写教案呢?下面是小编精心整理的小学五年级上学期数学《多边形的面积》教案,仅供参考,欢迎大家阅读。
小学五年级上学期数学《多边形的面积》教案篇1学习目标:1.复习面积的意义、常用的面积单位、长方形和正方形的面积计算公式,初步建立图形的等积变形思想。
2.体会转化、估计等解决问题的策略,为教学平行四边形等图形的面积计算作比较充分的知识准备和思想准备。
3.学习重难点:对图形进行分解与组合、分割与移拼的转化方法学具准备:学具盒学习过程:一、分一分、数一数1、下面两个图形的面积相等吗?2、怎样数的?在小组里交流一下。
二、移一移、数一数1、怎样移动右边图形中的一部分,能很快数出它的面积?2、利用分割与平移,保持面积不变,把多边形转化为长方形,计算它的面积。
这个图形的面积是多少?三、数一数、算一算1、下面是牧场中一个池塘的平面图。
先把池塘上面整格的和不满整格的分别涂上不同的颜色,数一数各有多少个,再算出池塘面积大约是多少平方米?(不满整格的,都按半格计算)。
2、你算出的面积大约是多少?这样的算法合理吗?在小组里说说自己的想法。
3、你能算出右边树叶的面积大约是多少平方厘米吗?四、估一估、算一算1、采集几片树叶,先估计他们的面积个是多少平方厘米,再把树叶描在第122页的方格纸上,用数方格的方法算促他们的面积。
2、你能用这样的方法算出自己手掌的面积吗?五、小结:今天我们进行面积是多少实践活动,怎样计算不规则图形的面积呢?小学五年级上学期数学《多边形的面积》教案篇2【教学内容】:课本79页到81页的内容【教学目标】:1、知识与能力目标:使学生在理解的基础上掌握平行四边形面积的计算公式,并会运用公式正确地计算平行四边形的面积.2、过程与方法:通过操作、观察、比较,发展学生的空间观念,培养学生运用转化的思考方法解决问题的能力和逻辑思维能力.3、情感态度价值观:通过解决问题,使学生体会所学知识在生活中的应用,增强学生学好数学的兴趣和意识。
多边形的面积(教案)

第五单元多边形的面积本单元教材包括四部分内容:平行四边形的面积,三角形的面积,梯形的面积,组合图形的面积。
教学目标:1、利用方格纸和割补、拼摆等方法,探索并掌握平行四边形、三角形和梯形的面积计算公式。
会计算平行四边形、三角形和梯形的面积。
2、使学生通过列表、画图等策略,整理平面图形的面积公式,加深对各种图形特征及其面积计算公式之间内在联系的认识。
3、使学生经历操作、观察、填表、讨论、分析、归纳等数学活动过程,体会等积变形、转化等数学思想,发展空间观念,发展初步的推理能力。
4、使学生在操作、思考的过程中,提高对“空间与图形”内容的学习兴趣,逐步形成积极的数学情感。
教学重点:平行四边形、三角形、梯形的面积计算公式教学难点:理解三种图形面积公式的推导过程,运用公式解决面积的计算问题。
课时安排:9课时教学建议:1、加强知识之间的联系,促进知识的迁移和学习能力的提高。
在认识这些图形时是按照四边形和三角形分类编排,学习这些图形的面积计算则以长方形面积计算为基础,以图形内在联系为线索,以未知向已知转化为基本方法开展学习。
2、体现动手操作、合作学习的学习方式,让学生经历自主探索的过程。
各类图形面积公式的推导均采用让学生动手实验,先将图形转化为已经学过的图形,再通过合作学习的方式,探索转化后的图形与原来图形的联系,发现新图形的面积计算公式这样一个过程。
同时按照学习的先后顺序,探索的要求逐步提高。
平行四边形面积的计算,是先借助数方格的方法,得到平行四边形的面积;再引导学生将平行四边形转化为一个长方形,推导出平行四边形的面积计算公式。
三角形的面积计算就直接要求学生将三角形转化为已学过的图形推导出面积计算公式。
到梯形面积的计算,要求学生综合运用学过的方法自己推导出面积计算公式。
每一种图形教材均没有给出推导的过程和计算公式,以便于学生从多种途径探索,自己得出结论,从而给教师和学生都留以较大的创造空间。
3、注意练习的探索性,形式多样化,以促进学生对知识的理解和灵活运用。
五年级奥数寒假讲义
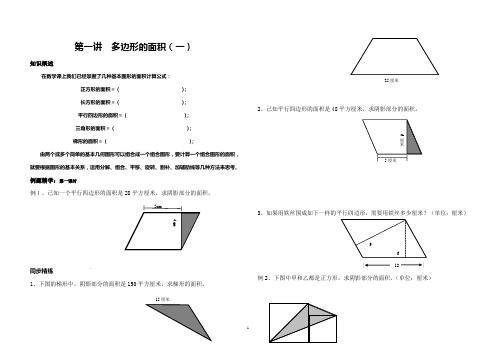
第一讲多边形的面积(一)知识概述在数学课上我们已经掌握了几种基本图形的面积计算公式:正方形的面积=();长方形的面积=();平行四边形的面积=();三角形的面积=();梯形的面积=();由两个或多个简单的基本几何图形可以组合成一个组合图形,要计算一个组合图形的面积,就要根据图形的基本关系,运用分解、组合、平移、旋转、割补、加辅助线等几种方法来思考。
例题精学:第一课时例1、已知一个平行四边形的面积是28平方厘米,求阴影部分的面积。
同步精练1、下图的梯形中,阴影部分的面积是150平方厘米,求梯形的面积。
2、已知平行四边形的面积是48平方厘米,求阴影部分的面积。
3、如果用铁丝围成如下一样的平行四边形,需要用铁丝多少厘米?(单位:厘米)| 12|例2、下图中甲和乙都是正方形,求阴影部分的面积。
(单位:厘米)5cm4cm 15厘米25厘米5厘米6厘米96 6 4甲乙同步精练1、求右图中阴影部分的面积。
(单位:厘米)2、求右图中的阴影部分的面积。
(单位:厘米)3、如图所示,四边形ABCD 是一个长方形草坪,长20米,宽14米,中间有一条宽2米的曲折小路,求小路的面积。
例题精学 第二课时:例3、如图所示,甲三角形的面积比乙三角形的面积大6平方厘米,求CE 的长度。
同步精练1、四边形ABCD 是一个长为10厘米,宽为6厘米的长方形,三角形ADE 的面积比三角形CEF 的面积大10平方厘米。
求CF 的长是多少厘米?4厘米3厘米DCAB8厘米5厘米甲A 乙 CB EDF4 厘米 4厘米FEADC B2、平行四边形ABCD 的边长BC=10厘米,直角三角形BCE 的直角边EC 长为8厘米,已知阴影部分三角形ABG 和三角形CDF 的面积和比三角形EFG 的面积大10平方厘米。
求CF 的长。
3、正方形ABCD 的边长是12厘米,已知DE 是EC 长度的2倍,求: (1)三角形DEF 的面积; (2)CF 的长。
例4、两条对角线把梯形ABCD 分割成四个三角形。
五年级数学上册《多边形的面积》知识点总结

《多边形的面积》知识点总结一、图形的面积计算公式以及变式①长方形的面积=长×宽S=ab长方形的长=面积÷宽长方形的宽=面积÷长②正方形的面积=边长×边长S=a2正方形的边长=面积÷边长③平行四边形的面积=底×高S=a h平行四边形的底=面积÷高平行四边形的高=面积÷底④三角形的面积=底×高÷2S=a h÷2三角形的底=三角形的面积×2÷高三角形的高=三角形的面积×2÷底⑤梯形的面积=(上底+下底)×高÷2S=(a+b)× h ÷2梯形的高=梯形的面积×2÷(上底+下底)二、难点解析①两个完全一样的三角形可以拼成一个平行四边形。
原来三角形的底和拼成的平行四边形的底相等,原来三角形的底和拼成的平行四边形的高相等,三角形的面积是拼成的平行四边形面积的一半。
②两个完全一样的梯形可以拼成一个平行四边形,原来梯形的上底与下底之和等于拼成的平行四边形的底,原来梯形的高等于拼成的平行四边形的高,原来梯形的面积等于拼成的平行四边形面积的一半。
③同底等高的平行四边形面积相等。
三角形的面积是与它等底等高的平行四边形面积的一半。
三、三角形与平行四边形之间的一些联系。
①面积相等,底相等,三角形的高是平行四边形高的2倍。
②面积相等,高相等,三角形的底是平行四边形底的2倍。
③高相等,底相等,三角形的面积是平行四边形面积的一半。
多边形面积(三)组合图形面积求解

白色的长方形的面积: (10+5)×10=150(cm2)
黄色三角形面积: 10×10÷2=50(cm2) 绿色三角形面积: 5×5÷2=12.5(cm2) 红色三角形面积: (10+5)×5÷2=37.5(cm2)
蓝色三角形面积=白色的长方形的面积-三个直角三角形的面积 150-50-12.5-37.5=50(cm2)
一块梯形布料(如下图),如果在这块布料中 减下一个最大的三角形,那么剩余布料的面积 是多少?
要想在这个梯形中剪去一个最大的三角形,必须把梯形的下底 作为三角形的底,把梯形的高作为三角形的高,则剩下的图形 的面积就是以梯形的上底为底,梯形的高为高的三角形的面积, 据此利用三角形的面积公式计算即可解。
剩余布料就是蓝色三角形的。 5.5×8÷2=22(m2) 剩余的布料是22m2。
长方形的面积是am2,在长方形内画一个最大 的三角形,这个三角形是多少m2?
在一个长方形内画一个最大的三角形,如果三角 形面积最大,那么它的底和高都要取最大,则最 大的三角形的底=长方形的长,最大的三角形的高 =长方形的宽。
大长方形的面积: (10+8)×10=180(cm2)
黄色三角形的面积: 10×10÷2=50(cm2)
蓝色阴影部分的面积: 180-50-72-16=42(cm2) 阴影部分的面积42cm2
红色三角形的面积: (10+8)×8÷2=72(cm2)
黄色小长方形的面积: 8×(10-8)=16(cm2)
正方形ABCD的边长是10厘米, 正方形BEFG的边长是6厘米。
梯形CDFE的上底EF:6厘米 下底CD:10厘米 高EC:10-6=4(厘米)
梯形CDFE的面积:(6+10)×4÷2=32(平方厘米)
五年级数学上册《多边形的面积》知识点汇总

五年级数学上册《多边形的面积》知识点汇总五年级数学上册《多边形的面积》知识点汇总(精选2篇)五年级数学上册《多边形的面积》知识点汇总篇11、公式:长方形:周长=(长+宽)×2 字母公式:c=(a+b)×2面积=长×宽字母公式:s=ab正方形:周长=边长×4 字母公式:c=4a面积=边长×边长字母公式:s=a平行四边形的面积=底×高字母公式: s=ah底=面积÷高高=面积÷底三角形的面积=底×高÷2 字母公式:s=ah÷2(底=面积×2÷高;高=面积×2÷底)梯形的面积=(上底+下底)×高÷2 字母公式: s=(a+b)h÷2 上底=面积×2÷高-下底下底=面积×2÷高-上底高=面积×2÷(上底+下底)2、单位换算的方法:大化小,乘进率;小化大,除以进率。
3、常用的单位间的进率长度单位:1千米=1000米 1米=10分米 1分米=10厘米 1厘米=10毫米面积单位:1平方千米=100公顷 1公顷=10000平方米1平方米=100平方分米 1平方分米=100平方厘米4、图形之间的关系:两个完全相同的三角形可以拼成一个平行四边形。
两个完全相同的梯形可以拼成一个平行四边形。
等底等高的平行四边形面积相等;等底等高的三角形面积相等。
等底等高的平行四边形面积是三角形面积的2倍。
如果一个三角形和一个平行四边形等面积,等底,则三角形的高是平行四边形的2倍。
如果一个三角形和一个平行四边形等面积,等高,则三角形的底是平行四边形的2倍。
5、把长方形框架拉成平行四边形,周长不变,面积变小了。
6、求组合图形面积的方法:(1)仔细观察,确定组合图形可以分割或添补成哪些可以计算面积的基本图形。
1五年级上册第二单元《多边形的面积》教案+实录+反思
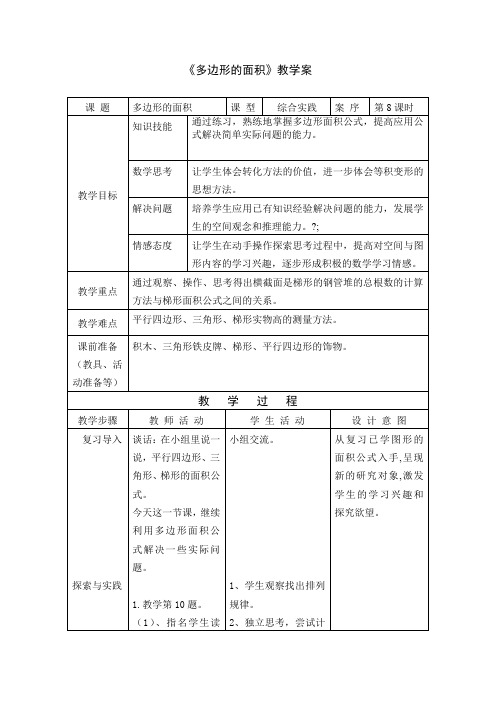
《多边形的面积》教学案《多边形的面积》课堂实录——探索与实践课题:苏教版小学数学五年级上册第二单元《多边形的面积》教学过程:一、复习导入师:在小组里说一说,平行四边形、三角形、梯形的面积公式。
师:今天这一节课,继续利用多边形面积公式解决一些实际问题。
二、探索与实践1、教学第10题(1)、指名学生读题。
(2)、出示完整的截面示意图。
(3)、师:这些钢管的排列有什么规律?生:下面一层都比上一层多一根。
师:请大家独立思考,尝试计算出这堆钢管的根数。
师:小组讨论,交流算法。
(4)、全班交流算法。
生1:因为下面一层都比上面一层多一根,所以用9+10+11+12+13+14+15+16=(9+16)×8÷2=100(根)生2:用两个完全一样的梯形拼成一个平行四边形,每层有:9+16=25(根),8层共有:25×8=200(根),这堆钢管一共有:200÷2=100(根)。
生3:列成综合算式是:(9+16)×8÷2=100(根)师:这堆钢管总根数的计算方法和梯形的计算方法有联系吗?生1:有。
梯形钢管堆的上层根数相当于梯形的上底,下层根数相当于梯形的下底,层数相当于梯形的高。
生2:因为梯形的面积是(上底+下底)×高÷2,所以横截面是梯形的钢管堆总根数等于(上层根数+下层根数)×层数÷2。
2、教学第11题。
(1)师:各小组测量出平行四边形、三角形、梯形实物的底和高的长度,小组长认真做好分工和记录。
教师指导学生正确掌握测量高度的方法。
(2)各小组汇报测量的数据。
(3)根据测量数据计算它们的面积。
3、教学思考题(1)、学生独立操作。
师:在第131页的方格纸上画出一个三角形和一个梯形,通过剪、拼分别把它们转化成平行四边形。
你能根据转化成的平行四边形与原来图形的关系,推想出三角形和梯形的面积公式吗?(2)、分组讨论,探索出把三角形和梯形转化成平行四边形的不同方法。
苏教版小学数学五年级上册:《多边形的面积》单元教学分析

《多边形的面积》单元教学分析(一)教学目标1.使学生通过剪拼、平移、旋转等方法,探索并掌握平行四边形、三角形和梯形的面积公式,能正确计算它们的面积;会通过割、补、拼以及数方格等操作活动,计算简单组合图形的面积,估计不规则图形的面积;能解决一些与图形面积计算相关的实际问题。
2.使学生认识常用土地面积单位公顷和平方千米;通过观察、计算、推理和想象等活动,初步建立1公顷实际大小的观念;发现平方米、公顷和平方千米之间的进率,能进行相应的单位换算;会解决一些与土地面积计算有关的实际问题。
3.使学生经历探索各种多边形面积公式的过程,体会等积变形、转化等数学思想方法,培养初步的推理能力,发展解决问题的策略,增强空间观念。
4.使学生在探索学习活动中,获得一些成功的体验,进一步培养与他人合作的能力,体会面积计算和测量与实际生活的联系,感受图形与几何的学习价值,提高数学学习的兴趣和学好数学的信心。
(二)教材说明和教学建议本单元教学内容及其前后联系如下图:本单元内容大体分三段安排:第一段主要引导学生探索平行四边形、三角形的面积公式,并应用面积公式解决实际问题;第二段引导学生探索梯形面积公式并进行应用,教学常用的土地面积单位公顷和平方千米;第三段教学计算简单组合图形面积、估计不规则图形面积的方法。
在这三段内容的教学之后,还安排了整个单元的“整理与练习”。
本单元教学内容的基本结构如下页图:本单元的教学重点是探索并掌握平行四边形、三角形和梯形的面积公式。
这是因为,探索并掌握平行四边形、三角形和梯形的面积公式,不仅是探索简单组合图形面积、解决与多边形面积计算有关的实际问题等学习活动所应具备的前提条件,也是今后进一步学习图形与几何领域其他内容的重要基础。
本单元的教学难点是不规则图形面积的估计。
这不仅是因为不规则图形面积的估计方法与多边形面积的计算方法存在明显差异,学生习惯了间接计量方法之后,反而对直接计量方法不太适应;而且是因为用数方格的方法估计不规则图形的面积时,需要特别细致的态度,稍有不慎就会出现重复或遗漏的情况。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三讲多边形的面积(等积变形)知识概述
三角形面积的公式是底×高÷2,两个三角形只要是底和高分别相等,它们的面积就相等,而这两个三角形的形状不一定完全相同,例如,下面的两个三角形面积就是相等的。
在解答一些平面图形的面积时,我们可以2等底等高两个三角形面积相等的方法来解答。
例题精学
例1 四边形ABCD中,M为AB的中点,N为CD的中点,如果四边形ABCD的面积时80平方厘米,求阴影部分的面积时多少平方厘米。
思路点拨图中阴影部分BNDM是一个不规则的四边形,不能直接求出它的面积。
如果用一条对角线BD将四边形ABCD分成两个三角形。
(如右图所示)。
在△ABD和△BDC中,由于M,N分别是AB,CD的中
点,根据等底等高三角形面积相等的道理,可知S
△AMD =S
△MBD
,S
△DNB
=S
△CNB。
所以阴
影部分的面积与空白部分的两个三角形的面积之和相等。
同步精练
1. 如图,六边形ABCDEF的面积时16平方厘米,M,N,P,Q分别是AB,CD,DE,AF,的中点,求图中阴影部分的面积。
2. 如图,平行四边形的面积为50平方厘米,P是期中任意一点,求阴影面积
3. 如图,正方形的边长是6厘米,E,H是所在边的二等分点,F,G,L,M是所在边的三等分点,求阴影部分的面积和。
例2 如下图,三角形ABC为等边三角形,D为AB边上的中点。
已知三角形BDF的面积为5平方厘米。
求等边三角形ABC
的面积。
思路点拨我们在三角形ABC的AC边上取中点F,BC边上取中点
G,然后连接DF,FG,GD(如右图)。
我们看到,三角形ADF,BDG,FGC,GFD为四个完全一样的
等边三角形。
因为DE为△DBG底BG上的高,所以S
△DBE =S
△DGE。
由此,
我们可以想到三角形ABC的面积是三角形DBE面积的8倍同步精练
1. 如图,平行四边形ABCD中,AE=EF=FB,AG=2CG,三角形GEF的面积是6平方厘米,平行
四边形的面积时多少平方厘米?
2. 如图,已知长方形ABCD,三角形ABG的面积为20平方厘米,三角形CDQ的面积为35平方厘米,求
阴影部分的面积时多少平方厘米?
3. 如图,在一个等边三角形中任意取一点P,连接PA,PB,PC,过P点作三角形三边的垂线,E,F,G分别为垂足。
三角形ABC被分成6个三角形。
已知三角形ABC的面积为40平方厘米,求图中阴影部分的面积。
例3下图中正方形ABCD的边长是4厘米,长方形DEFG
的长DG=5厘米,问长方形的宽DE为多少厘米?
思路点拨因为长方形面积=长×宽,现在已知长方形DEFG
的长DG是5厘米,要求宽DE的长度,就要求出长方形DE
FG的面积。
而正方形的面积可以求出,长方形的面积与正方形
的面积有什么关系呢?
观察长方形和正方形的重叠部分可以发现,如果连接AG,则三角形AGD的面积既是正方形面积的一半,也是长方形面积的一半,这样就可以说明正方形的面积和长方形的面积相等。
同步精练
1. 如图,两个相同的直角三角形叠放在一起,求阴影部
分的面积。
(单位:分米)
2. 如图,ABCD为长方形,AB=10厘米,BC=
6厘米,E,F分别为AB,AD的中点,且FG=2
GE。
求阴影部分的面积。
3. 如图,ABCD是直角梯形,其中AD=12厘米,
AB=8厘米,BC=15厘米,且三角形ADE、四
边形DEBF及三角形CDF的面积相等,三角形EBF(阴
影部分)的面积是多少平方厘米?
例3 下图是两个正方形拼成的图形,其中小正方形的边长是4厘米,求阴影部分的面积。
思路点拨在上一讲我们曾经做过已知大、小两个正方形的边长再求图中阴影部分面积的题目。
而现在只知道小正方形的边长,又该如何求阴影部分的面积呢?
如上图,我们可以连接AC,S
△AGC =GC×AB÷2,S
△
ACE
=CE×AD÷2,GC和CE都是小正方形的边长,AB和AD都是
大正方形的边长,所以S
△AGC =S
△ACE。
而这两个三角形分别去掉
它们的共同部分(△ACH),则它们剩下的部分也应相等,即S
△AGH =S
△CEH。
这样原图中阴影部分就可以转化为△GCE的面积,而S
△GCE
等于小正方形面积的一半。
同步精练
1. 如果下图中大正方形的边长是6分米,求阴影部分的面积。
2. 如图,AD=2AB,CF=3AC,BE=4BC,已知△ABC的面积为5平方厘米,求△DEF的面积。
FC,已知△ABC的面积为90平方厘3. 如图,AE=ED,AF=1
2
米,求阴影部分的面积。
练习卷
1.如图,在平行四边形ABCD中,EF与AC平行,如果三
角形BFC的面积是35平方厘米,那么三角形AEB的面积
能不能确定?如果能,它的面积是多少?
2.在三角形ABC中,AD垂直于BC,CE垂直于AB,AD=8
厘米,CE=7厘米,AB+BC=21厘米,求三角形ABC的面积。
3.如图,AB=6厘米,BC=4厘米,AC=2CD,BE=BD,求三
角形ADE的面积。
4.如图,三角形ABC的面积是30平方厘米,D是BC的
中点,AE的长是ED的2倍,求三角形CDE的面积。
5.三角形ABC的面积是180平方厘米,D是BC的中点,AD的长是AE长的3倍,EF的长是BF的3倍,求三角形AEF的面积。
6.下图中,正方形ABCD的边长是12厘米,P是AB边上任意一点,M,N,I,H分别是BC,AD的三等分点,E,F,G是CD的四等分点,求图中阴影部分的面积。
7.正三角形ABC的边长为12厘米,BD,DE,EF,FG四条线段把它的面积5等分,求AF,FD,DC,AG,GE,EB的长。
8.下图中,BD=2DC,AE=BE,已知三角形ABC的面积
是18平方厘米,求四边形AEDC的面积等于多少平方
厘米。
