一维连续型随机变量和其概率密度
合集下载
概率论第三章部分习题解答
ydxdy.
定理1 cov(X ,Y ) E( XY ) E( X )E(Y )
定理2 若X与Y 独立，则：covX ,Y 0. 逆命题不成立。
注 设X与Y是任两个随机变量，
10
D( X Y ) D( X ) D(Y ) 2cov(X ,Y )
2、X与Y 的相关系数
定义 R( X ,Y ) cov( X ,Y )
EX
xf
xdx
1
二、二维随机变量的数学期望
（1）设二维离散随机变量(X,Y)的联合概率函数为p(xi , yj)，则
随机变量X及Y 的数学期望分别定义如下：
EX xi p xi , y j , EY y j p xi , y j .
i j
ji
即： EX xi pX xi , EY y j pY y j .
第三章 随机变量的数字特征
（一）基本内容 一、一维随机变量的数学期望
定义1：设X是一离散型随机变量，其分布列为：
X x1 x2 xi
P p( x1 ) p( x2 )p( xi )
则随机变量X 的数学期望为: EX xi pxi
i
定义2：设X是一连续型随机变量，其分布密度为 f x,
则随机变量X的数学期望为
i
j
假定级数是绝对收敛的.
（2）设二维连续随机变量(X,Y)的联合概率密度为f(x, y)，则
随机变量X及Y 的数学期望分别定义如下：
EX
xf
x,
ydxdy,
EY
yf x, ydxdy.
即：EX
xf X x dx,
EY
yfY y dy.
2
假定积分是绝对收敛的.
一维连续型随机变量
第六讲 一维连续型随机变量教学任务：1．随机变量的分布函数的定义； 2．常见的连续型随机变量。
教学重点：常见的连续型随机变量教学目的：1． 让学生理解随机变量的分布函数的定义； 2． 理解连续型随机变量的定义；3． 学会求一些简单的连续随机变量的密度； 4． 掌握常见的连续型随机变量。
教学方法：课堂教学。
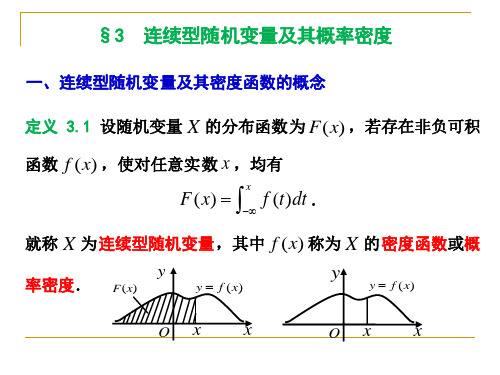
三、随机变量的分布函数对于非离散随机变量, 由于其所有可能取值不能一个一个列举出来, 因此不能用分布律来表示. 而是关心这种随机变量落在一个区间的概率, 并不关心它取各个值的概率. 如测量误差, 考虑落在某一区间内的概率, 产品寿命大于某个数的概率等. 为此, 我们首先引进随机变量分布函数的概念.分布函数的定义 设X 是一个随机变量, 对任意实数x, 则称)()(x X P x F ≤= (2.8)为随机变量X 的分布函数.通过分布函数能用数学分析的方法研究随机变量.分布函数的性质: （1）单调不减函数, 若, 则21x x <)()(21x F x F ≤ 事实上, 当时, 21x x <},{}{21x X x X ≤⊂≤有),()(21x X P x X P ≤≤≤则 )()(21x F x F ≤（2）右连续性 即)0()(+=x F x F（3）, 0)()(lim =−∞=−∞→F x F x 0)()(lim =−∞=∞→F x F x不论随机变量是离散型随机变量或非离散型随机变量, 分布函数)(x F 全面地描述了随机变量的统计规律性.另外，显然有：)()()()()(121221x F x F x X P x X P x X x P −=≤−≤=≤<例题2.7 一袋中装有2个白球和3个黑球, 每次从中任取1个球, 不放回抽样, 直至取到白球为止, 求 (1) 取球次数X 的分布函数; (2) )1(≤X P ; (3) )32/3(≤<X P ; (4))42(≤≤X P .解 X 的概率分布为X 1 2 3 4 )(k X P = 0.4 0.3 0.2 0.1(1) X 的分布函数为⎪⎪⎩⎪⎪⎨⎧≤<≤<≤<≤<=xx x x x x F 41439.0327.0214.010)( )(x F 的图形是一条阶梯形的曲线, 在x=1,2,3,4处有跳跃点, 跳跃值分别为0.4, 0.3, 0.2, 0.1.(3) 5.04.09.0)2/3()3()32/3(=−=−=≤<F F X P(4) 6.03.07.01)2()2()4()42(=+−==+−=≤≤X P F F X P一般地, 设离散型随机变量X 的分布律为 k k p x X P ==)(, L .2.1=k 则X 的分布函数为∑∑≤≤===≤=xx k xx k k k p x X P x X P x F )()()( (2.9)和式是对所有满足的k 求和. x x k ≤)(x F 在k x x =处有跳跃, 其跳跃值. )(k k x X P p ==四、 连续型随机变量及其概率密度连续型随机变量的定义 设)(x F 为随机变量X 的分布函数, 如果存在非负函数)(x f , 使对于任意实数x , 有(2.10)∫∞−=xdt t f x F )()(则称X 为连续型随机变量, 称)(x f 为的概率密度函数.由式(2.10)知, 几何上解释, )(x F 表示曲线)(x f 下，x 轴上方的面积, 所以)(x F 是连续函数. 本书主要讨论两类随机变量: 离散型随机变量和连续型随机变量. 概率密度具有如下性质: (1)非负性 0)(≥x f (2) 归一性∫∞∞−=1)(dx x f (3)∫=≤<21)()(21x x dx x f x X x P (1) 若)(x f 在点x 处连续, 则)()('x f x F =随机变量X 落在小区间],(x x x Δ+上的概率为x x f x x X x P Δ≈Δ+≤<)()( (2,11)x x f Δ)(称为概率微分.连续型随机变量取任一指定的实数值a 的概率为0, 即0)(==a XP .事实上, }{}{a X x a a X≤<Δ−⊂=得)()()(){0x a F a F a X x a a X P Δ−−=≤<Δ−≤=≤0)]()([lim ){lim 00=Δ−−≤=≤→Δ→Δx a F a F a X P x x所以0)(==a XP . 根据这一结果, 则有)()()(b X a P b X a P b X a P <<=≤≤=≤<另有, 若φ=A , 则0)(=A P ; 反之, 若0)(=A P , 并不一定意味着A 是不可能事件.常用的连续型随机变量及其概率密度(1) 均匀分布如果连续型随机变量X 的概率密度为⎪⎩⎪⎨⎧<<−=其他1)(b x a ab x f (2.12) 则称X 在区间(a , b )上服从均匀分布， 简记为),(~b a U X ，∞<<<∞−b a 为参数。
概率论与数理统计连续型随机变量函数的密度函数
答案：
f
S
(
y)
2
1
y
,
y 4 ,
0,
otherwise,
10
此类问题的基本做法:先确定Y的取值范围,其密度 函数在此范围外的取值为零,对此范围内用公式法 或者分布函数求导法,最后写出函数. 以下练习:
例题1,…
11
练习题:
12
2.分段严格单调可导函数
定理3.2 若随机变量X和随机变量Y=g(X)的密度 函数分别为f X (x), fY (y), 当g(x)在不相重叠的区间
x ,
2
则 Y X 2 概率密度函数为：
fY
y
1
2
1 y
y 2e 2 ,
0,
y0 y0
此时称Y 服从自由度为1的-2分布,记作 Y ~ 2 1
结论：若 X ~ N,则0,1 X 2 ~ 2 1. 14
解 1).公式法 (自己看)
首先注意到 y x2 , 则 y 0 因此对于 y 0, 有 fY ( y) 0.
17
例3.15(3). 设X的密度函数
f
(x)
8
9
2
(x
2
),
2
x
,
0,
otherwise,
求 Y sin X 的密度函数.
解. 因为 1 Y 1, 所以只要考虑 1 y 1.
当 1 y 0 时,
FY ( y) P{Y y} P{sin X y}
P{
2
X
arcsin
基本方法(分布函数求导法),分2个步骤:
(1) 求Y的分布函数 FY ( y)
FY ( y)
根据分布函数 的定义
连续型随机变量的概率密度
x
F ( x) f ( x)dx
则称X为连续型随机变量，称 f (x)为X的概率密度函数，简称 概率密度或密度.
概率论与数理统计
2
❖ 一.连续型随机变量的概率密度 1.概念
x
F ( x) f ( x)dx
➢ 从几何上看, 连续型随机变量X的分
布函数是由概率密度曲线 f (x), x轴,
概率论与数理统计
3
❖ 一.连续型随机变量的概率密度 1.概念
x
F ( x) f ( x)dx
➢ 根据高等数学的知识，容易得到，连续型随机变量的分布函
数一定是连续函数，且在F(x)的导数存在的点上有
F( x) f (x).
➢ 由上述定义，显然，对于任意的实数 x1 x2 ，均有
P
x1 X x2
试求(1)
常数A,
1 Aex1 , x 1.
B的值；(2) 概率密度f
(x)；
(3)
P(X
1 ).
2
➢ 解 (1) 由分布函数的连续性知 lim F( x) F(0), lim F( x) F(1),
x0
x1
可得
A
B,1
A
B,
则
A
B
1 2
.
1 2
e
x
,
故分布函数为：F
(
x
)
1
,
2
x 0, 0 x 1,
概率论与数理统计
❖ 一.连续型随机变量的概率密度 1.概念
➢ 由于连续型随机变量是在实数集上连续取值的随机变量，其 概率分布与离散型完全不同，由于其取值有无穷多个，不能 一一列举，需要用新的方法来研究其分布律. 对于这类随机变 量，用概率密度来描绘连续型随机变量的概率分布.
F ( x) f ( x)dx
则称X为连续型随机变量，称 f (x)为X的概率密度函数，简称 概率密度或密度.
概率论与数理统计
2
❖ 一.连续型随机变量的概率密度 1.概念
x
F ( x) f ( x)dx
➢ 从几何上看, 连续型随机变量X的分
布函数是由概率密度曲线 f (x), x轴,
概率论与数理统计
3
❖ 一.连续型随机变量的概率密度 1.概念
x
F ( x) f ( x)dx
➢ 根据高等数学的知识，容易得到，连续型随机变量的分布函
数一定是连续函数，且在F(x)的导数存在的点上有
F( x) f (x).
➢ 由上述定义，显然，对于任意的实数 x1 x2 ，均有
P
x1 X x2
试求(1)
常数A,
1 Aex1 , x 1.
B的值；(2) 概率密度f
(x)；
(3)
P(X
1 ).
2
➢ 解 (1) 由分布函数的连续性知 lim F( x) F(0), lim F( x) F(1),
x0
x1
可得
A
B,1
A
B,
则
A
B
1 2
.
1 2
e
x
,
故分布函数为：F
(
x
)
1
,
2
x 0, 0 x 1,
概率论与数理统计
❖ 一.连续型随机变量的概率密度 1.概念
➢ 由于连续型随机变量是在实数集上连续取值的随机变量，其 概率分布与离散型完全不同，由于其取值有无穷多个，不能 一一列举，需要用新的方法来研究其分布律. 对于这类随机变 量，用概率密度来描绘连续型随机变量的概率分布.
2.3一维连续型随机变量及其概率密度
2 解： (1) f ( x ) dx 0 (ax b)dx 2a 2b 1
P{1 X 3}
3 1 f
( x )dx
2 1 (ax b)dx
1.5a b 0.25
a 0.5, b 1
0.5 x 1 0 x 2 f ( x) 其他 0
0t 2 其他
t f (t ) 2 0
F ( x)
x
f ( t )dt
定义2.3.1 设随机变量X 的分布函数为F (x), 若存 在非负函数 f (x), 使得对 x R 有
x F ( x) f ( t )dt
则称X 为连续型随机变量, f (x)为X 的概率密度函数,
u
x
t
1 e 2
( t )2 2 2
dt
x dt du
( x )
1 2
u2 e 2
du
* X ~ N ( , 2 ),
x X x F ( x ) P{ X x } P b a P {a X b} a P{ X a } 2 1
b a
f ( x )dx
(4) 在 f ( x ) 的连续点x 上，F ( x ) f ( x )；
(5) c R,
P{ X c} 0.
性质（4）： 在 f (x)的连续点 x 处
F ( x x ) F ( x ) f ( x ) lim x 0 x P { x X x x } lim x 0 x
P{1 X 3}
3 1 f
( x )dx
2 1 (ax b)dx
1.5a b 0.25
a 0.5, b 1
0.5 x 1 0 x 2 f ( x) 其他 0
0t 2 其他
t f (t ) 2 0
F ( x)
x
f ( t )dt
定义2.3.1 设随机变量X 的分布函数为F (x), 若存 在非负函数 f (x), 使得对 x R 有
x F ( x) f ( t )dt
则称X 为连续型随机变量, f (x)为X 的概率密度函数,
u
x
t
1 e 2
( t )2 2 2
dt
x dt du
( x )
1 2
u2 e 2
du
* X ~ N ( , 2 ),
x X x F ( x ) P{ X x } P b a P {a X b} a P{ X a } 2 1
b a
f ( x )dx
(4) 在 f ( x ) 的连续点x 上，F ( x ) f ( x )；
(5) c R,
P{ X c} 0.
性质（4）： 在 f (x)的连续点 x 处
F ( x x ) F ( x ) f ( x ) lim x 0 x P { x X x x } lim x 0 x
连续型随机变量的概率密度
解：⑴．P1 X 5 F (5) F (1)
(5 2) (1 2)
3
3
1
1 3
1 1 1
3
0.84134 0.62930 1
0.47064
⑵．PX 2 6 1 PX 2 6
1 P 6 X 2 6
x
令 u t
1
t2 x
e 2 dt
2
1
(2) (0) P( X 0) 1 2
() 1 ;() 0
引理：
设X ~ N ， 2 ，则 Y X ~ N ( 0, 1 )
FY
y
PY
y
P{ X
P{X y} 1
y}
y
e
t 2
2 2
dt
2
作变换
u
t
，du
dt
FY y
使用了s 小时，它总共能使用至少 s t
指数分布
若 X 表示某一元件的寿命，则 (*)式表明：已知元件 使用了s 小时，它总共能使用至少 s t 小时的条件 概率与从开始使用时算起它至少能使用 t小时的概 率相等，即元件对它使用过 s 小时没有记忆,具有这
一性质是指数分布具有广泛应用的重要原因.
设X ~ N ， 2 ，则 Y X ~ N ( 0, 1 )
(2)若X~N(,2),
P{X x} P{ X x }
( x )
(3) 若X~N(,2),对于任意区间(x1,x2]有
P( x1
X
x2 )
P
x1
X
x2
x2
x1
【例5】 设 随 机 变 量 X ~ N 2， 9 求 ： ⑴ P1 X 5；⑵ PX 2 6；⑶ PX 0．
一维连续型随机变量函数的分布
解
1 1 fY ( y ) fX ( y 2) 3 3
1 2 y 3 2 y 2 2e 0 3 3 0 其它
2 2( y3 2） e 3 0
y2 其它
x , 0 x4 例： X ~ f ( x) 8 时，定理为真
例1.已知 X 的 d.f.为 f X ( x), Y aX b, a, b为常数，且 a 0, 求 fY ( y ) 解 y b
y g ( x) ax b, x h( y ) 1 h( y) . a
a
,
fY ( y ) f X (h( y )) h( y )
一维连续型随机变量 函数的分布
一般地,对 y= g(x)是严格单调函数,有下面的结论.
定理 设X是一个连续型随机变量，其密度函数
为 f(x), 又函数 y= g(x) 严格单调，其反函数 h ( y ) 有连续导数，则 Y = g (X) 也是一个连续型随机 变量，且其密度函数为
f X [ h( y )] h( y ) fY ( y ) 0
1 3
Y X 3， fY ( y )。 求
y g ( x) x3， x y h ( y ) 解：
g '( x) 3x 0， fY ( y) 1 y f X ( y ) 3
2
2 3 1 3
1 1 y 3 , 0 y 64 fY ( y ) 24 0, 其他
Y ~ N (a b, a )
2 2
一般若X ~ N ( , 2 )， aX b Y ~ N (a b, a 2 2 ) Y
特别地 ，若
概率论与数理统计第3章
试求常数a和b。
π F xlim F x a b 2 0 解： F lim F x a b π 1 x 2
1 1 a , b 2 π
P ( 2 4) P ( 2) P ( 2 4) 0.3 0.6 0.5 0.4
P ( 3) 1 P ( 3) 1 0.5 0.5
6
例3：设r.v. 的分布函数
F x a b arctan x
b a
因此求概率可从分布函数与密度函数两条途径入手。
5、密度的图像称分布曲线，相应有两个特征： ⑴ 曲线在x轴上方；
概率面积
y
f(x)分布曲线
⑵ 曲线于x轴之间的 面积是1。
x c o d
10
例4：设 的密度在[a,b]以外为0，在[a,b]内为
一常数 ，
， a x b f ( x) 0， 其它
x2 2
16
⑶ f(x)符合密度函数的两性质： ① f(x) > 0；②
f x d x 1。
x2 2
以标准正态分布为例， e
e d t e
t2 2 2 x2 2
d x 称为高斯积分。
dy
r2 2 0
从F(x)求f(x)： f x F x 从f(x)求F(x)： F x f t d t
x
9
4、对于连续型随机变量 ，
⑴ P a 0 ，即某指定点的概率为0； ⑵ Pa b Pa b
Pa b Pa b f x d x
连续型随机变量及其概率密度
问：怎样求一般正态分布的概率？
对一般的正态分布 ：X ~ N ( , 2)
其分布函数 F( x)
1
e d t x
(t )2 2 2
2
作变量代换s
t
F(x)
1 2
x
s2
e 2ds
x
即 X ~ N ( , 2) 则 X ~ N ( 0 ,1)
P{a
X
b}
F (b)
222 0.3830
3) 0.6826 4) 0.4981
0.02
-10
-5
a
5
b
x
例1 有一批晶体管，已知每只的使用寿命 X 为 连续型随机变量，其概率密度函数为
f
(
x)
c x2
,
0,
x 1000 其它
( c 为常数)
(1) 求常数 c
(2) 已知一只收音机上装有3只这样的晶体管，
每只晶体管能否正常工作相互独立，求在
使用的最初1500小时只有一个损坏的概率.
(3) P(X>1.76)= 1 – P(X≤1.76)= 1 – Φ(1.76)
=1 – 0.9608 =0.0392 (4) P(X< – 0.78)= Φ(- 0.78) =1-Φ(0.78)
=1 – 0.7823 =0.2177 (5) P(|X|<1.55)= 2Φ(1.55) – 1 (6) P(|X|>1.55)= 1 – P(|X|<1.55)
即： P( X a) 0, a为任一指定值
事实上 { X a} {a x X a}
x 0
0 P{ X a} P{a x X a} aax f ( x)d x
连续型随机变量及其概率密度
1. 均匀分布
设连续型随机变量
X
具有概率密度f
(
x)
b
1
a
,
a x b,
0,
其它,
则称 X 在区间 (a, b) 区间上服从均匀分布,记为 X ~ U (a, b).
说明：
对c, l R, 如果(c, c l ) (a, b), 则
cl
l
P(c X c l ) c
f ( x)dx ba
1
( x )2
e , 2 2
2
x
, ( 0)为常数, 则称X服从正态分布,记作:X : N(, 2).
0, 1时, X : N (0,1)
概率密度: ( x)
1
x2
e2
2
说明：
f(x)满足概率条件: f(x) 0,
+ f(x)dx 1 -
证明(2): 令 x- t, 则x t, dx dt
解 : (1) 由概率密度的定义 :
f ( x)dx 1
-
f ( x)dx
3 C(9 x2 )dx 1
-
-3
C 1 36
(2)
P{ X 0}
0 -3
1 36
(9
x2 )dx
1 36
(9x
x3 3
)
|03
1 2
P{1 X 1} 1 1 (9 x2 )dx 13
-1 36
k 0
n大，p小，np=3，用=np=3的泊松近似
上式 1 N 3k e3 0.01
k0 k !
N 3k e3 0.99
k0 k !
查泊松分布表，最小N=8。至少配8名维修工。
2.4连续型随机变量及其概率密度函数
x2 2a
[ e
x 2a
]
x 0
1 e
x 2a
0 综合上述得: F ( x ) x2 2a 1 e
x0 x0
1 2a
(2). P (0 X 1) F (1) F (0) 1 e
2014-2-23 北邮概率统计课件
f ( x )dx 1
f (x)
这两条性质是判定 一个函数 f(x)是否为某 随机变量X 的概率密度 函数的充要条件.
面积为1
o
2014-2-23
x
概率统计
北邮概率统计课件
性质3
P ( x1 X x2 ) F ( x2 ) F ( x1 )
x2 x1
f ( x )dx
P ( x1 X x2 ) f ( x )dx F ( x2 ) F ( x1 )
x1
x2
▲ P () 0 (不可能的事件的概率为0),但概率 为零的事不一定是不可能事件.
2014-2-23
概率统计
北邮概率统计课件
2. 概率密度函数的性质 性质1 性质2
f ( x) 0
是一个连续型随机变量的概率密度函数.
f ( x ) 0 ( x )
f ( x )dx
一般只需验 证f(x)性质中 的这两条即 可.
2014-2-23
1 0 x 1 x e dx e dx 2 2 0 1 1 1 2 2
2014-2-23
概率统计
北邮概率统计课件
注： P ( x X x x ) F ( x x ) F ( x )
概率2-3连续型随机变量及其概率密度-2
x
e
dt , x
概率论
( x)
( x )
概率论
7. 标准正态分布与一般正态分布的关系 定理1
X 若 X ~ N , , 则 Z ~ N 0 , 1 .
2
标准正态分布的重要性在于，任何一个一 般的正态分布都可以通过线性变换转化为标准 正态分布.
概率论
例2 在一公共汽车站有甲、乙、丙 3人，分别等1、2、3路公交车，设 每人等车时间（分钟）都服从[0，5] 上的均匀分布，求3人中至少有2人 等车时间不超过2分钟的概率。
概率论
（II）指数分布 1. 含义：随机变量X描述对某一事件发生的 等待时间，各种不会变老的物品寿命。 2. 密度函数：若 r .v. X具有概率密度
x 2
2
Φ(x)
概率论
作业
58页，24，25，26，27，29，30
概率论
3σ准则
由标准正态分布的查表计算可以求得，
当X～N(0,1)时， P{|X| ≤ 1}=2 Φ(1)-1=0.6826 P{|X| ≤ 2}=2 Φ(2)-1=0.9544 P{|X| ≤ 3}=2 Φ(3)-1=0.9974 这说明，X的取值几乎全部集中在[-3,3]区间
内，超出这个范围的可能性仅占不到0.3%.
概率论
(2) X ~ N ( , 2 ), 求区间概率
X 若 X ~ N ( , ), 则 Y ~N(0,1)
2
P{ a X
a b Y } b} P{
b a ( ) ( )
概率论
例3 若 r. v. X～N(10,4),求 P{10<X<13}, P{│X-10│<2}. 例4 若 r. v. X～N(μ,σ2), P{X ≤ -1.6}=0.036， P{X ≤ 5.9}=0.758，求 P{X> 0}
一维连续型随机变量和密度函数的概念
证明：
f (x0 ) F(x0 )
F(x0 x) F(x0 )
x0 x f (x)dx
x0
x
x
f ( )x f ( )
x
在x0与x0 x之间
两边取极限，有
F ( x0 )
lim
x0
F ( x0
x) x
F ( x0 )
lim
x0
f
( )
f
( x0 )
(5) 设x为 f(x)的连续点，当x >0且较小时,则有
一般地，设D是数轴上一些不相交的区 间之和，若X的概率密度为
f
(x)
1 D的长度
,xD
0
,xD
则称X在D上服从均匀分布。
2 指数分布 若随机变量 X 的概率密度为
ex , x 0
f (x) 0, x 0
其中常数>0 ，则称X 服从参数为的指数
分布，相应的分布函数为
1 ex x 0 F(x)
概率密度函数的性质
（1） f (x) 0
（2） f (x)dx 1 f (x)
这两条性质是判定一个 函数 f(x)是否为某r.v. X的 概率密度函数的充要条件.
面积为1
o
x
b
(3) P {a < X b}=F(b)F(a) f ( x)dx a
(4) 在 f (x) 的连续点 x0 处，有
( x)
(x) 1
x t2
e 2 dt
2
注意：Φ(0)=0.5
Φ(x)=1 Φ(x)
若 X～N(0, 1)
x x
P(a X b) (b) (a)
7. 正态分布的计算
x
F(x)
一维连续型随机变量及其概率密度
P { X > 2000, X > 1000} = P { X > 1000} P { X > 2000} = P { X > 1000}
1 − P{ X ≤ 2000} = 1 − P { X ≤ 1000}
1 − F ( 2000) = 1 − F (1000) =e
− 1 2
≈ 0.607.
第2.3节 一维连续型随机变量 2.3节 及其概率密度
一、连续型随机变量及其概率密度 二、常见连续型随机变量的分布 三、小结
一、概率密度的概念与性质 1.定义 定义
设 X为随机变量 ， F ( x )为 X 的分布函数 , 若存在 F ( x) =
非负可积函数 p( x ), 使对于任意实数 x 有
7 7 ( 3) P {1 < X ≤ } = F ( ) − F (1) = 41 . 2 2 48
二、常见连续型随机变量的分布 1. 均匀分布
定义 设连续型随机变量 X 具有概率密度 1 , a < x < b, p( x ) = b − a 0, 其它, 则称 X 在区间 (a , b ) 区间上服从均匀分布 , 记为 X ~ U (a , b ).
正态分布下的概率计算 原函数不是 初等函数
x 1 P { X ≤ x }= F ( x ) = ∫−∞e 2πσ ( t − µ )2 − 2σ 2
dt
=?
方法一:利用 软件包计算(演示 方法一 利用MATLAB软件包计算 演示 利用 软件包计算 演示) 方法二:转化为标准正态分布查表计算 方法二 转化为标准正态分布查表计算
因而有
2 Y ~ B 3, . 3
2 2 3
2.4一维连续型随机变量
信息系刘康泽
例 4、设随机变量 的密度函数为：
ax b 0 x 1 p( x) ， 其它 0 5 1 1 a 且 P ( ) ，求（1） , b ； （2）P( „ ) 。 8 4 2
解： （1）由 ：
a 1 p( x)dx (ax b)dx b 0 2 1 5 3 b P ( ) 1 ( ax b )dx a 8 8 2 2 1 解得： a 1, b 2
a a
b
a
b
信息系刘康泽 (4) a R , 有：P{ a} 0 。
即：连续型随机变量取某个特定点的概率为0。
证明：
P( a) lim P(a „ a x)
lim
x 0
x 0
a x
a
p( x)dx 0
【注】此性质可以说明:概率为0的事件不一定是不可 能事件。同理： 概率为1的事件也不一定是必然事件. 由此，对于连续型随机变量有：
信息系刘康泽
第2-4节 一维连续型随机变量
有些随机变量所有可能的取值充满了一个区 间, 对这种类型的随机变量, 不能象离散型随机变 量那样, 以指定它取每个值概率的方式, 去给出 其概率分布, 而是通过给出所谓“概率密度函数” 的方式，这就是连续性随机变量。
信息系刘康泽
1、引例：武汉年降雨量的分布
1 2
（1） （2）
信息系刘康泽 ) P( ) （2） P(sin 2 6 2
1 3 6 2 106 P ( ) p ( x)dx 1 ( x )dx 。 5 135 3 5 5 3 1 3
p 例 6、 （选择题）设随机变量 的密度函数为( x) ， 且 p ( x) p ( x), F ( x)是 的分布函数， 则对任意的实
一维连续型随机变量及其概率密度
设 A 表示“一次观测中X的值大于 3 ”,
即 A={ X >3 }.
由于 P( A) P{ X 3}
51
2
dx ,
33
3
设Y 表示3次独立观测中观测值大于3的次数,
则 Y ~ B 3, 2 . 3
因而有
P{Y
2}
C2032.
2 3
2
1
2 3
C33
2 3
3
1
2 3
0
27
2. 指数分布
(4)曲线在 x μ σ 处有拐点;
(5) 曲线以 x 轴为渐近线;
p(x)
(6) 当 固 定σ, 改 变 μ 的大小时, p(x) 图形的形状不变,只 是 沿 着 x 轴作平移变换;
p(x)
(7) 当固定μ, 改变 σ 的大小时, p(x) 图形的对称轴 不变,而形状在改变, σ 越小,图形越高越瘦, σ越大, 图 形 越 矮 越 胖.
P{1
X
7} 2
F(7) 2
F (1)
41 . 48
二、常见连续型随机变量的分布
1. 均匀分布
定义 设连续型随机变量X 具有概率密度
p(
x)
b
1
a
,
a x b,
0,
其 它,
则称 X 在区间(a, b)区间上服从均匀分布,
记为 X ~ U(a,b).
概率密度
p( x)
函数图形
ao
b
分布函数
证明F(x) x .
解 F(x) P{X x} x
令 t μ u, σ
xμ
σ
1
e d t
(tμ)2 2σ 2
2-3连续型随机变量及其概率密度
f
(x)
b
1
a
,
a x b,
0,
其它,
就称 X 服从[a,b] 上的均匀分布，记为 X ~ U[a,b]．
【注】 X 的分布函数为
0, x a,
F ( x)
x
b
a a
,
a
x
b,
1, b x.
均匀分布与第一章中介绍的几何概型原理相通，适用于一维
的几何概型试验．此时， X 落入某区间 I 内（上）的概率为 P{X I} P{X I I [a,b]} I I [a,b]的长度 ． ba
(b ) (a ) ．
特别地， P{X b} (b ), P{X a} 1 ( a ) 。
其中 (a ) 和 (b ) 可查表得．
•22
例 3.5 设随机变量 X ~ N(1, 4) ，分别计算
P{X 3}， P{1 X 5} ．
解 由题意知， 1, 2 ．
y (x)
y
y (x) 1
1 2
O
x
O
x
•20
由于(x) 为偶函数，利用本节例 3.2 的结论，有
F(x()x)
F((x)x)
1；1；F(0()0)
1
1；；P{PX{ X
x}x}
2F(Fx)(x)1．1．
22
当 x 0 时， (x) 可以通过直接查标准正态分布表求得．
当 x 0 时， (x) 1 (x) ，再查标准正态分布表可得．
【注 7】如果 X ~ N(0,1) ，则对于任意的实数 a,b (a b) ， P{a X b} (b) (a) ，
其中 (a), (b) 可查标准正态分布表计算．
•21
正态分布的计算、一维连续型函数的分布
2
因为
P2
X
4
4
2
2
2
2
0
2
0.5
0.3
2
0.8
所以
PX
0
0
2
1
2
0.2
8
例3 设 ~ N 1.5, 4, 1 求 P0.5 1.5
1
x2
e 2 dx 0.8413
2
解：P0.5 1.5 F 1.5 F 0.5
1 2
0.5 1.5 2
1 2
1
解：（2）FV v PV v P eX v
当 v 0 时，FV v 0 fV v 0
当
v
0
时，FV
v
PX
ln v
1
FX
ln v
ln v, 1 v e
fV
v
fX
ln v 1
v
v
2 ln v 1 ,
v
e v e2
综上所述，. . . . . .
0,
其它
20
例9 若 X ~ N , 2 , Y aX b, a 0
1 P3 X 3 1 F 3 F 3
1
3
1.5 2
3
1.5 2
10.75 2.25
10.75 12.25
2 0.7734 0.9878 0.2388
21 F 3
7
例2 若 X ~ N 2, 2 , 且 P2 X 4 0.3, 求 PX 0
解： PX
0
0
2
1
x
3 Pa X b F b F a
b
a
4
P
X
c
2
§3.1 一维连续型随机变量及其分布
求分布函数 F ( x ).
设随机变量X的分布函数为 例 设随机变量 的分布函数为
A / 2e x , x≤0 F ( x ) = 0.5, 0 < x ≤ 1 B + Ce −( x −1) , x > 1 求A，B，C的值 .
A 设随机变量X有密度 例 设随机变量 有密度 f ( x ) = x , x ∈ R, −x e +e
面积为 F ( x )
f ( x)
O
x
x
连续型随机变量的分布函数的性质： 连续型随机变量的分布函数的性质： 1) 0 ≤ F ( x ) ≤ 1；
F 2)F(x)单调不减，即当 x1 ≤ x2 时， ( x1 ) ≤ F ( x2 ); 单调不减， 单调不减
3) F ( −∞ ) = xlim F ( x ) = 0, F ( +∞ ) = xlim F ( x ) = 1; → −∞ → +∞ 4)F(x)右连续，即对任意实数 x , F ( x + 0) = F ( x ). 右连续， 右连续
密度函数一定连续吗？ 问题 (1) 密度函数一定连续吗？ (2) 对于一个给定的连续型随机变量， 对于一个给定的连续型随机变量， 其密度函数唯一吗？ 其密度函数唯一吗？ (3) 连续型随机变量与离散型随机变量 的本质区别是什么? 的本质区别是什么
连续型随机变量与离散型随机变量的本质 区别在于： 区别在于：连续型随机变量取单个值的概率 为零，也离散型不一定， 为零，也离散型不一定，这主要是由于积分 的性质.由此，便有下列的等价形式： 的性质 由此，便有下列的等价形式： 由此
d F ( x ) = f ( x ). dx
设连续型随机变量X有分布函数 例 设连续型随机变量 有分布函数
连续型随机变量及概率密度
(4) 可由分布函数求分布密度，对于 F(x)不存在 的点可人为的补充定义.
2021/8/17
7
0 x 0
ex1.设X的分布函数为 F(x) x 0 x 1,
求X的分布密度 f (x).
1 x 1
解 f(x ) F (x ),
而端点处情况可人为规定.
f(x)10
0x1 其它
orf(x) 10
1(1e2)5.
2021/8/17
16
三、正态分布
1. 正态分布的定义
如果连续型随机变量X的概率密度为
f(x)
1
(x)2
e 22
2
( x)
其 , 中 (0 )为,常 则 X 服 数 称从 , 参 的数 正
分布或 .记 高 X 为 ~N 斯 (,2)分 . 布
特,令 别 0 ,地 1 得 (x) 1 2ex22 ( x)
且 1 (z) ( z) 2
2
2
从 2021/8而 /17 (z2)12
z
2
( x)
O z x
( x)
2
O z x
2
26
e5 .x 设 X ~ N (1,9 0 ) N 8 (1,3 0 2 )8 , (1 )求 P { 1.1 0 X 1 1.6 1 }7 ;
( 2 ) 求 a 使 P { X a } 0 .9 ;
f (x)
面积为1
o
x
( 3 )P { x 1 X x 2 } F ( x 2 ) F ( x 1 ) x x 1 2 f ( x ) d ;x
(4)在 f(x)的连,F 续 (x)点 f(x);处
2021/8/17
5
在 f(x)的不连 ,F续 (x)不 点 存 ;处 在 (用 F (x 0 ) lx i0 F m (x 0 x x ) F (x 0 )证 ) 明 (5 )对任 a ,P { X 意 a } F ( 实 a ) F (a 数 0 ) 0 ;
2021/8/17
7
0 x 0
ex1.设X的分布函数为 F(x) x 0 x 1,
求X的分布密度 f (x).
1 x 1
解 f(x ) F (x ),
而端点处情况可人为规定.
f(x)10
0x1 其它
orf(x) 10
1(1e2)5.
2021/8/17
16
三、正态分布
1. 正态分布的定义
如果连续型随机变量X的概率密度为
f(x)
1
(x)2
e 22
2
( x)
其 , 中 (0 )为,常 则 X 服 数 称从 , 参 的数 正
分布或 .记 高 X 为 ~N 斯 (,2)分 . 布
特,令 别 0 ,地 1 得 (x) 1 2ex22 ( x)
且 1 (z) ( z) 2
2
2
从 2021/8而 /17 (z2)12
z
2
( x)
O z x
( x)
2
O z x
2
26
e5 .x 设 X ~ N (1,9 0 ) N 8 (1,3 0 2 )8 , (1 )求 P { 1.1 0 X 1 1.6 1 }7 ;
( 2 ) 求 a 使 P { X a } 0 .9 ;
f (x)
面积为1
o
x
( 3 )P { x 1 X x 2 } F ( x 2 ) F ( x 1 ) x x 1 2 f ( x ) d ;x
(4)在 f(x)的连,F 续 (x)点 f(x);处
2021/8/17
5
在 f(x)的不连 ,F续 (x)不 点 存 ;处 在 (用 F (x 0 ) lx i0 F m (x 0 x x ) F (x 0 )证 ) 明 (5 )对任 a ,P { X 意 a } F ( 实 a ) F (a 数 0 ) 0 ;
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
若X是连续性随机变量,则
P{X a} 0,
显然 {X a} 是可能发生的
事实上:
x R, p(x) 0; p(x)dx 1
是 p(x) 是某连续性随机变量X的密度函数的充要条件.
例1 设随机变量X 具有概率密度
kx, 0 x 3,
p( x)
2
x 2
,
3 x 4,
0,
其 它.
S p(x) d x 1
1
0
x
(3)
P{ x1
X
x2 }
F(x2)
F ( x1)
x2 x1
p( x)dx
证明 P{x1 X x2} PX x2 X x1 PX x2 PX x1 F(x2) F(x1)
x2 p( x) d x
x1 p( x) d x
x2 p( x)d x.p(x)来自b1 a
,
a x b,
0,
其 它,
则称 X 在区间(a, b)区间上服从均匀分布,
记为 X ~ U(a,b).
概率密度
p( x)
函数图形
ao
b
分布函数
0,
x a,
F(x)
F
(
x)
x b
a a
,
a x b,
1•
1,
x b.
•
•
ao
b
x
均匀分布分布函数图形演示
例3 设随机变量 X 在 [ 2, 5 ]上服从均匀分布, 现 对 X 进行三次独立观测 ,试求至少有两次观测值 大于3 的概率.
上的概率.
(2) 有一只这种灯管已经正常使用了1000 小时以
上,求还能使用1000小时以上的概率.
解 X 的分布函数为
F
(
x)
1
e
1 2000
x
,
x 0,
0,
x 0.
(1) P{X 1000} 1 P{X 1000} 1 F (1000)
1
e 2 0.607.
(2) P{ X 2000 X 1000} P{ X 2000, X 1000} P{ X 1000} P{ X 2000} P{ X 1000}
其中 μ, σ(σ 0) 为常数,则称 X 服从参数为μ, σ
由 F (x) x p(t) d t 得
当x 0时 ,
x
F (x) 0dt 0
x
当 0 x 3时 , F (x) p(t)dt
0
0dt
xt
dt x2
06
12
当3
x
4时
,F ( x)
0
0dt
3
0
t 6
dt
x
3 (2
t )dt 2
3 2x x2
4
当x 4时 ,
F(x)
0
0dt
3 t dt
4 2 t dt
x
0dt
06
3 2
4
1
0,
x 0,
x
2
,
0 x 3,
即
F(x)
12
3
2x
x2 4
,
3 x 4,
1,
x 4.
(3)
P{1
X
7} 2
F(7) 2
F (1)
41 . 48
二、常见连续型随机变量的分布
1. 均匀分布
定义 设连续型随机变量X 具有概率密度
1 P{ X 2000} 1 P{ X 1000}
1 F (2000) 1 F (1000)
1
e 2 0.607.
指数分布的重要性质 :“无记忆性”.
3. 正态分布(或高斯分布)
高斯资料
定义 设连续型随机变量X 的概率密度为
图形演示 p(x)
1
e
(
xμ) 2σ 2
2
,
x
,
2 πσ
2 3
2
1
2 3
C33
2 3
3
1
2 3
0
27
2. 指数分布
定义 设连续型随机变量X 的概率密度为
ex , x 0,
p(x)
0,
x 0.
其中 0 为常数,则称 X 服从参数为的指数
分 布.
p(x)
3
1
1 2
指数分布密度 函数图形演示
分布函数
1 ex , x 0,
x1
同时得以下计算公式
P{X a} F(a)
a
p( x)d
x,
P{X a} 1 P{X a} 1 F(a)
a
p(x) d x p(x) d x
a p(x) d x.
(4) 若 p( x) 在点 x 处连续,则有 F( x) p( x).
(5)P{X=a}=0. 证: 由于P{X=a}=F(a)-F(a-0),
而F(x)在R上连续, 所以P{X=a}=0.
由此可得
P{a X b} P{a X b} P{a X b}
b
P{a X b} a p(x)dx s1
连续型随机变量的概率与区间的开闭无关 p( x)
S1
0
a•
•
b
x
注意
不可能事件的概率一定为0,而概率为0 的事件不一定是不可能事件.
第2.3节 一维连续型随机变量 及其概率密度
一、连续型随机变量及其概率密度 二、常见连续型随机变量的分布 三、小结
一、概率密度的概念与性质
1.定义
设X为 随 机 变 量，F ( x)为X 的 分 布 函 数,若 存 在
非 负 可 积 函 数p( x),使 对 于 任 意 实 数x 有
x
F ( x) p(t)d t,
F(x) 0,
x 0.
3 1
1 2
指数分布分布函数图形演示
应用与背景
某些元件或设备的寿命服从指数分布.例如 无线电元件的寿命 , 电力设备的寿命, 动物的寿 命等都服从指数分布.
例4 设某类日光灯管的使用寿命 X 服从参数为
=1/2000的指数分布(单位:小时)
(1)任取一只这种灯管, 求能正常使用1000小时以
(1) 确 定 常 数k; (2) 求 X 的 分 布 函 数;
(3) 求 P{1 X 7}. 2
解
(1) 由
p(x) d x 1,
得
3
kx d x
4
(2
x)d
x
1,
0
3
2
(2)由 k 1 知 X 的概率密度为 6
解之得
k 1. 6
x 6
,
p( x)
2
x 2
,
0,
0 x 3, 3 x 4, 其 它.
解 X 的分布密度函数为
p(
x)
1 3
,
0,
2 x 5, 其 它.
设 A 表示“一次观测中X的值大于 3 ”,
即 A={ X >3 }.
由于 P( A) P{ X 3}
51
2
dx ,
33
3
设Y 表示3次独立观测中观测值大于3的次数,
则 Y ~ B 3, 2 . 3
因而有
P{Y
2}
C2032.
则 称 X 为 连 续 型 随 机 变 量, 其 中 p( x) 称 为 X的 概
率 密 度 函 数,简 称 概 率 密 度.
性质 (1) 对任意的x, p( x) 0. (2)
p(x) d x 1.
证明 (2) 1 F () lim
x
p(t) d t p(x) d x.
x
p( x)
P{X a} 0,
显然 {X a} 是可能发生的
事实上:
x R, p(x) 0; p(x)dx 1
是 p(x) 是某连续性随机变量X的密度函数的充要条件.
例1 设随机变量X 具有概率密度
kx, 0 x 3,
p( x)
2
x 2
,
3 x 4,
0,
其 它.
S p(x) d x 1
1
0
x
(3)
P{ x1
X
x2 }
F(x2)
F ( x1)
x2 x1
p( x)dx
证明 P{x1 X x2} PX x2 X x1 PX x2 PX x1 F(x2) F(x1)
x2 p( x) d x
x1 p( x) d x
x2 p( x)d x.p(x)来自b1 a
,
a x b,
0,
其 它,
则称 X 在区间(a, b)区间上服从均匀分布,
记为 X ~ U(a,b).
概率密度
p( x)
函数图形
ao
b
分布函数
0,
x a,
F(x)
F
(
x)
x b
a a
,
a x b,
1•
1,
x b.
•
•
ao
b
x
均匀分布分布函数图形演示
例3 设随机变量 X 在 [ 2, 5 ]上服从均匀分布, 现 对 X 进行三次独立观测 ,试求至少有两次观测值 大于3 的概率.
上的概率.
(2) 有一只这种灯管已经正常使用了1000 小时以
上,求还能使用1000小时以上的概率.
解 X 的分布函数为
F
(
x)
1
e
1 2000
x
,
x 0,
0,
x 0.
(1) P{X 1000} 1 P{X 1000} 1 F (1000)
1
e 2 0.607.
(2) P{ X 2000 X 1000} P{ X 2000, X 1000} P{ X 1000} P{ X 2000} P{ X 1000}
其中 μ, σ(σ 0) 为常数,则称 X 服从参数为μ, σ
由 F (x) x p(t) d t 得
当x 0时 ,
x
F (x) 0dt 0
x
当 0 x 3时 , F (x) p(t)dt
0
0dt
xt
dt x2
06
12
当3
x
4时
,F ( x)
0
0dt
3
0
t 6
dt
x
3 (2
t )dt 2
3 2x x2
4
当x 4时 ,
F(x)
0
0dt
3 t dt
4 2 t dt
x
0dt
06
3 2
4
1
0,
x 0,
x
2
,
0 x 3,
即
F(x)
12
3
2x
x2 4
,
3 x 4,
1,
x 4.
(3)
P{1
X
7} 2
F(7) 2
F (1)
41 . 48
二、常见连续型随机变量的分布
1. 均匀分布
定义 设连续型随机变量X 具有概率密度
1 P{ X 2000} 1 P{ X 1000}
1 F (2000) 1 F (1000)
1
e 2 0.607.
指数分布的重要性质 :“无记忆性”.
3. 正态分布(或高斯分布)
高斯资料
定义 设连续型随机变量X 的概率密度为
图形演示 p(x)
1
e
(
xμ) 2σ 2
2
,
x
,
2 πσ
2 3
2
1
2 3
C33
2 3
3
1
2 3
0
27
2. 指数分布
定义 设连续型随机变量X 的概率密度为
ex , x 0,
p(x)
0,
x 0.
其中 0 为常数,则称 X 服从参数为的指数
分 布.
p(x)
3
1
1 2
指数分布密度 函数图形演示
分布函数
1 ex , x 0,
x1
同时得以下计算公式
P{X a} F(a)
a
p( x)d
x,
P{X a} 1 P{X a} 1 F(a)
a
p(x) d x p(x) d x
a p(x) d x.
(4) 若 p( x) 在点 x 处连续,则有 F( x) p( x).
(5)P{X=a}=0. 证: 由于P{X=a}=F(a)-F(a-0),
而F(x)在R上连续, 所以P{X=a}=0.
由此可得
P{a X b} P{a X b} P{a X b}
b
P{a X b} a p(x)dx s1
连续型随机变量的概率与区间的开闭无关 p( x)
S1
0
a•
•
b
x
注意
不可能事件的概率一定为0,而概率为0 的事件不一定是不可能事件.
第2.3节 一维连续型随机变量 及其概率密度
一、连续型随机变量及其概率密度 二、常见连续型随机变量的分布 三、小结
一、概率密度的概念与性质
1.定义
设X为 随 机 变 量，F ( x)为X 的 分 布 函 数,若 存 在
非 负 可 积 函 数p( x),使 对 于 任 意 实 数x 有
x
F ( x) p(t)d t,
F(x) 0,
x 0.
3 1
1 2
指数分布分布函数图形演示
应用与背景
某些元件或设备的寿命服从指数分布.例如 无线电元件的寿命 , 电力设备的寿命, 动物的寿 命等都服从指数分布.
例4 设某类日光灯管的使用寿命 X 服从参数为
=1/2000的指数分布(单位:小时)
(1)任取一只这种灯管, 求能正常使用1000小时以
(1) 确 定 常 数k; (2) 求 X 的 分 布 函 数;
(3) 求 P{1 X 7}. 2
解
(1) 由
p(x) d x 1,
得
3
kx d x
4
(2
x)d
x
1,
0
3
2
(2)由 k 1 知 X 的概率密度为 6
解之得
k 1. 6
x 6
,
p( x)
2
x 2
,
0,
0 x 3, 3 x 4, 其 它.
解 X 的分布密度函数为
p(
x)
1 3
,
0,
2 x 5, 其 它.
设 A 表示“一次观测中X的值大于 3 ”,
即 A={ X >3 }.
由于 P( A) P{ X 3}
51
2
dx ,
33
3
设Y 表示3次独立观测中观测值大于3的次数,
则 Y ~ B 3, 2 . 3
因而有
P{Y
2}
C2032.
则 称 X 为 连 续 型 随 机 变 量, 其 中 p( x) 称 为 X的 概
率 密 度 函 数,简 称 概 率 密 度.
性质 (1) 对任意的x, p( x) 0. (2)
p(x) d x 1.
证明 (2) 1 F () lim
x
p(t) d t p(x) d x.
x
p( x)