胶体化学
物理化学第七章

粗分散物系
>10-7m
混浊泥水,牛 奶,豆浆
3、胶体四大特征:(同溶液相比较)
①聚结不稳定性(热不稳自发聚沉)②多相不均匀性 聚结不稳定性 ②多相不均匀性(一相分散 于另一相,有相界面)③高分散性 ③高分散性(颗粒大小及胶团量不相同) 结构组成不确定性(受添加剂或添加物影响) ④结构组成不确定性 (真溶液:热稳,均相物系,组成,结构,分子量恒定) 4、胶体化学研究内容:表面现象,分散物系及高分子溶液 5、表面:物体处于真空或与本身饱和蒸气达平衡的面。 6、界面:物体与空气或其他物体相接触的面(存在于两相之间 几个nm厚度薄层) 7、表面现象(Surface phenomenon):凡物质处于凝聚状态时, 其界面上发生的一切物理化学现象。(包括s-g,s-l,l-g,ss,l-l等统称表面)严格讲为界面现象,如:毛细现象,润湿 作用,液体过热,蒸气过饱和,吸附作用等统称界面现象 AS Sο (Interface phenomenon)。
(1)按分散相和分散介质的聚集状态分类
分散相 分散介质 名称 气 泡沫 液 液 乳状液 固 悬浮体,溶液胶 气 液 固 固溶胶 固 气 液 气 气溶胶 固
实例 肥皂泡沫 牛奶 泥浆,金溶胶 浮石,泡沫玻璃 珍珠,某些矿石 某些合金 雾 烟
(2)按分散相的分散度分类
类型 低分子 分散物系 分散相粒子半 径 <10-9m 分散相 原子 离子,小分子 性质 均相,热力学稳定物 系,扩散快,能透过 半透膜,形成真溶液 均相,热力学稳定物 系,扩散慢,不能透 过半透膜,形成真溶 液 举例 NaCI、蔗糖的 水溶液,混合 气体等 聚乙烯醇水溶 液
之一):当毛细管插入润湿性液体水中时,管内液面呈凹面, △P背向 液面,使液体受到向上提升力而沿管内壁上升,当液柱产生的静压 力ρgh=△P时达平衡停止移动;反之,当毛细管插入非润湿性液体 汞中时产生管内凸液面,因△P向下,使管内液面下降至ρgh=△P 达平衡时停止,此为毛细现象。
物理化学第十四章胶体化学

过程是自发过程。
固体的溶解度与颗粒的大小有关,颗粒半径与其相 应的溶解度之间服从Kelvin公式:
lns2 s1
M RT
2
1 R2'
1 R1'
若有大小不同的颗粒同时在一个溶胶中,较小颗粒 附近的饱和浓度大于较大颗粒的饱和浓度,结果是小者 愈小,大者愈大,直到小颗粒全部溶解为止。
而大颗粒大到一定程度即发生沉淀,这就是产生老 化过程的原因。
14.2 溶胶的制备与纯化
一、溶胶制备
粗分 散 分 体 散 胶 系 法 体 凝 体 聚 系 分 法 子分
1.分散法 (1)研磨法 (2)超声分散法 (3)电孤法 2.凝聚法
(1)物理凝聚法
(2)化学凝聚法
化学凝聚法
通过各种化学反应使初生成的难溶物微粒 结合成胶粒,在少量稳定剂存在下形成溶胶。 稳定剂:某一过量的反应物。
四、均分散胶体的制备和应用 1. 制备
在严格控制的条件下,有可能制备出形状 相同、尺寸相差不大的沉淀颗粒,组成均分散 系统。颗粒的尺寸在胶体颗粒范围之内的均分 散系统则称为均分散胶体系统。
Perrin用大小均匀的藤黄粒子作悬浮体,证 明了Einstein理论的正确性:
D RT 1
L 6 r
制备均分散系统的方法有:(1) 沉淀法; (2) 相转移法;(3) 多组分阳离子法;(4) 粒子 “包封法”;(5) 气溶胶反应法;(6) 微乳液 法等。
3.粗分散体系
分散相粒子半径大于1000 nm,多相体系,热力 学不稳定。
按分散相和介质聚集状态分类 1.液溶胶
将液体作为分散介质所形成的溶胶。当分散 相为不同状态时,则形成不同的液溶胶:
A.液-固溶胶 如油漆,AgI溶胶 B.液-液溶胶 如牛奶,石油原油等乳状液 C.液-气溶胶 如泡沫
关于胶体化学的几个基本概念

一、概述1.关于胶体化学的几个基本概念(1)相和相界面相是指那些物质的物理性质和化学性质都完全相同的均匀部分。
体系中有两个或两个以上的相,称为多相体。
相与相之间的接触面称为相接面。
(2) 分散相与分散介质在多相分散体系中,被分散的物质叫做分散相。
包围分散相的另一相,称为分散介质。
例如,水基钻井液中,粘土颗粒分散在水中,粘土为分散相,水为分散介质。
(3)分散度和比表面分散度是某一分散程度的量度,通常用分散相颗粒平均直径或长度的倒数来表示。
如果用D表示分散度,用a表示颗粒的平均直径或长度,则分散度可表示为D=1/a。
比表面是物质分散度的另一种量度,其数值等于全部分散相颗粒的总面积与总质量(或总体积)之比。
如果用S代表总表面积,用V表示总体积,用m表示总质量,则比表面可表示为:=S/V (m-1) (2-2)S比或 S=S/m (m-1/kg) (2-3)比物质的颗粒愈小,分散度愈高,比表面愈大,界面能与界面性质就会发生惊人的变化。
所有颗粒分散体系的共性是具有极大的比表(界)面。
按分散度不同,可将分散体系分为细分散体系与粗分散体系。
胶体实际上是细分散体系,其分散相的比表面≥104 m2/kg,其颗粒长度在1 nm~1 μm 之间。
悬浮体则属于粗分散体系,其比表面大致不超过104m2/kg分散相的颗粒直径在1~40/μm之间。
钻井液是复杂的胶体分散体系。
水基钻井液基本上是溶胶和悬浮体的混合物,本书中统称为胶体分散体系。
(4)吸附作用物质在两相界面上自动浓集(界面浓度大于内部浓度)的现象,称为吸附。
被吸附的物质称为吸附质,吸附吸附质的物质称为吸附剂。
按吸附的作用力性质不同,可将吸附分为物理吸附和化学吸附两类。
仅由范德华引力引起的吸附,是物理吸附。
这类吸附一般无选择性,吸附热较小,容易脱附。
若吸附质与吸附剂之间的作用力为化学键力,这类吸附叫化学吸附。
化学吸附具有选择性,吸附热较大,不易脱附。
2.沉降与沉降平衡钻井液中的粘土粒子,在重力场的作用下会沉降。
10胶体化学

NaAuO2是上述方法制得金溶胶的稳定剂,写出该金溶胶
胶团结构的表示式。
解:该金溶胶胶团结构为: {[Au]m nAuO2- (n-x)Na+}x- xNa+
12.11.在Ba(NO3)2溶液中滴加Na2SO4溶液可制备BaSO4溶 胶。分别写出(1) Ba(NO3)2溶液过量,(2) Na2SO4溶液过量 时的胶团结构表示式。 解:(1) Ba(NO3)2溶液过量时,胶团结构为: {[BaSO4]m nBa2+(2n-x)NO3-}x+ xNO3(2) Na2SO4溶液过量时,胶团结构为: {[BaSO4]m nSO42-(2n-x)Na+}x- xNa+
胶核:胶体粒子内由分子、原子或离子
形成的固态微粒
胶团:整个扩散层及其所包围的胶体粒子
构成的电中性的整体
例: AgNO3 + KI AgI + KNO3 KI过量 :
AgI溶胶吸附I-带负电,K+为反离子 AgNO3过量: AgI溶胶吸附Ag+带正电,NO3-为反离子
特点:
(1) 胶 核 : 首 先 吸附过量的成 核离子,然后 吸附反离子; (2) 胶 团 整 体 为 电中性。
分散系统分类(按分散相与分散介质的聚集状态): (1) 均相系统(真溶液) 分散相以分子形式溶于分散介质 (2) 多相系统 分散相不溶于分散介质
分散 分散相 介质 气
名称 气溶胶 泡沫 乳状液 液溶胶或悬浮液
实例
液 固
气 液 固 气 液 固
云、雾 烟、尘
肥皂泡沫 牛奶 泥浆、油漆 泡沫塑料 珍珠 有色玻璃
物理化学第十四章胶体化学

一、分散体系的分类
•真溶液 按分散相粒子的大小分类: •胶体分散体系
•粗分散体系 •液溶胶
按胶体溶液的稳定性分类
1.憎液溶胶 胶体化学的主要研究体系 半径在1 nm~100 nm之间的难溶物固体粒子
分散在液体介质中。溶剂与粒子间亲合力弱。
溶剂蒸发后,再加入溶剂无法再形成溶胶。 不可逆体系。
2.亲液溶胶 大分子溶液
溶剂与粒子(大分子 )间亲合力强。溶剂蒸 发后,产生凝聚,再加入溶剂,又可形成溶胶。 热力学上稳定、可逆的体系。
按分散相和介质的聚集状态分类: •固溶胶 •气溶胶
按胶体溶液的稳定性分类: •憎液溶胶 •亲液溶胶
按分散相粒子的大小分类
1.真溶液(分子分散体系)
分散相与分散介质以分子或离子形式均匀的单 相,热力学稳定。分散相粒子半径小于1 nm。
2.胶体分散体系 分散相粒子半径1 nm~100 nm。高分散的多相 体系,粒子有自动聚集的趋势,热力学不稳定。
A.复分解反应制硫化砷溶胶 2H3AsO3(稀)+ 3H2S →As2S3(溶胶)+6H2O
B.水解反应制氢氧化铁溶胶 FeCl3 +3H2O (热)→ Fe(OH)3 (溶胶)+3HCl
C.氧化还原反应制备硫溶胶 2H2S(稀)+ SO2(g) → 2H2O +3S (溶胶) Na2S2O3 +2HCl → 2NaCl +H2O +SO2 +S (溶胶)
高等水化学胶体化学

按胶体分散系统的性质分类
• (2)亲液溶胶 • 半径落在胶体粒子范围内的大分子物质,
溶解在合适的溶剂中形成的溶胶。 • 分散相分子本身的大小已达到胶粒范围,
它的扩散速率小、不能透过半透膜等性质 与胶体系统相似。 • 亲液溶胶是热力学上稳定,可逆的系统。
§12-1 胶体系统的制备与净化
粗分散系统 分散法 胶体系统 凝聚法 分子分散系统
第二章 胶体化学
Chapter 2 Colloidal Chemistry
“胶体”这个名词是英国化学家 Graham于1861年提出的
胶体(colloid)
任一质点,其某个线度 在10-7和10-9m之间即认为 是胶体分散系统
(一)胶体分散系统及其基本性质
胶体是一种分散系统
分散系统:一种或几种物质分散在另一种物质之中 分散相:被分散的物质 (dispersed phase) 分散介质:另一种连续分布的物质
1nm 散慢,不能透过半透膜,有一定 高浓度肥皂水
~100nm 的光散射
溶液
热力学不稳定,但动力学稳 金溶胶、硫溶
1nm 定的多相系统,扩散慢,不能透 胶、牛奶、豆
~100nm
过半透膜,光散射强,在超显微 镜下可以看见
浆、雾、烟、 各种泡沫
>100nm
热力学不稳定,动力学不稳 定的多相系统,扩散慢,不能透 过半透膜,光散射强,在普通显 微镜下可以看见
2
1 cos 2
I0
I :散射光强度 ;
I0 : 入射光强度;
V :一个粒子的体积; C :单位体积中的粒子数;
n : 分散相的折射率; n0:分散介质的折射率;
:散射角(观测方向与入射光方向间夹角);
表面化学-胶体化学

表面化学-胶体化学表面化学-胶体化学表面化学是研究物质表面的性质和现象的一门学科,而胶体化学则是表面化学的一个重要分支,研究胶体溶液中物质的性质和行为。
胶体化学的研究内容涉及到胶体的形成、稳定性、表面性质、胶体颗粒的相互作用以及胶体溶液的性质等。
本文将介绍表面化学和胶体化学的基本概念、研究方法以及应用领域。
表面化学最早起源于对溶液表面现象的研究,如水的表面张力、液滴的形成和液体的湿润性等。
表面化学研究的对象是固体和液体的界面以及液体和气体的界面,主要涉及到界面上的吸附现象、界面能和界面活性物质等。
固体-液体界面上的吸附现象包括离子吸附、分子吸附和表面电荷等,而液体-气体界面上的吸附现象则涉及到液滴形成和表面张力等。
胶体化学研究的是胶体溶液中胶体颗粒的性质和行为。
胶体是一种介于溶液和悬浮液之间的物质,其特点是颗粒很小,约为1纳米到1微米大小,并且能够在溶液中均匀分散。
胶体的稳定性是胶体化学研究的重要内容,稳定性的源于胶体颗粒表面的电荷,正负电荷的平衡使得颗粒之间相互排斥,从而保持胶体溶液的稳定性。
此外,胶体溶液中还包含着胶体的吸附、吸附剂的选择、界面张力、胶体性质的测定以及胶体与其他物质的相互作用等方面的研究内容。
表面化学和胶体化学的研究方法主要包括物理化学方法和化学方法两种。
物理化学方法包括表面张力测定、界面能测定、电化学方法、X射线衍射、电子显微镜等。
而化学方法包括有机合成、溶胶-凝胶法、聚合法、共沉淀法等多种方法。
表面化学和胶体化学在许多领域中都有重要的应用。
在光学领域中,胶体颗粒可以通过改变其尺寸和组成来调控其光学性质,从而应用于光学传感器、太阳能电池、红外吸收材料等。
在材料科学领域中,胶体颗粒可以通过自组装形成多孔材料和有序结构,具有较大的比表面积和孔径,被广泛用于催化剂、分离膜和储能材料等。
此外,表面化学和胶体化学还在生物医学、环境污染治理、油水分离、食品加工等领域发挥着重要的作用。
综上所述,表面化学和胶体化学是研究物质表面性质和胶体溶液行为的学科,涉及到物质界面的吸附现象、界面能、表面张力等。
9胶体化学详解

(emulsion),泡沫
(二)胶体的基本特征 (1)多相(multiphase)性 在胶体系 统中,分散相粒子由众多分子或离子 组成,粒子内部与外部分散介质的许 多物理和化学性质都不相同,所以性 质是不均匀的,因而是多相系统。包 围胶体粒子的界面是相界面。
(一)分散(dispersion)法
直接将大块物质粉碎为小颗粒,并
使之分散于介质中。
机械分散法; 超声波(ultrasonic)
分散法; 电分散法; 胶溶法。
(二)凝聚(agglomeration)法
将分子或离子凝聚成胶体颗粒。
化学凝聚法
通过化学反应(如复分解反应、水解反应、氧化或还原反 应等)使生成物呈过饱和状态,然后粒子再结合成溶胶。
(二)沉降(sedimentation)平衡
当溶胶中颗粒的密度大 于介质时,颗粒在重力场作 用下有向下沉降的趋势;沉 降的结果使底部粒子浓度大 于上部,即造成上下的浓差, 而粒子的扩散将促使浓度趋 于均一。当沉降与扩散达平 衡时,称为沉降平衡;此时, 颗粒浓度自下而上降低,有 一个分布。
沉降平衡中粒子的分布
热力学电势ф0 :固体表面与溶液本体间的电势差 斯特恩电势фδ :斯特恩面同溶液本体之间的电势差 ξ电势:滑动面与溶液本体之间的电势差
ξ 电势的特点:
ξ 电势的绝对值小于热力学电势 的绝对值ф 0 •ξ 电势是衡量胶粒所带净电荷多 少的物理量; •ξ 电势的符号由胶粒所吸附离子
的电荷决定
•胶粒表面吸附正离子,ξ 电势为 正;胶粒表面吸附负离子,ξ 电 势为负 •少量外加电解质会对ξ 电势产生 很大的影响 •处于等电态的胶体质点不带电
(3)斯特恩双电层模型
11-胶体化学

布朗运动
返回
二、扩散
在有浓度梯度时,胶体粒子因热运动而发生宏观上定向 迁移运动。
三、沉降与沉降平衡
多相分散系统中物质的粒子因受重力作用而下沉的过程 叫沉降。
沉降过程产生浓度梯度,而扩散过程是消除浓度梯度, 当两者达平衡时叫做沉降平衡。 即:沉降速度=扩散速度
a
4
1、电泳
在外电场作用下,胶粒在分散介质中的定向移动。 (胶粒带电、带正电的胶粒移向负极)
+
-
NaOH
Fe(OH)3
电泳速度
∝
粒子带电量、外加电位 梯度 介质的黏度、粒子的大 小
电泳演示
2.电渗:
在多孔膜(或毛细管)两端加电压,液体分散 介质作定向移动。
3.流动电势:
电渗演示
在外力作用下,迫使分散介质通过多孔膜作定向移 动,在多孔膜两端产生的电势差。
4.沉降电势:
分散相粒子在重力场(或离心力场)作用下迅 速移动,产生的电势差。
电泳现象
返回
电渗现象
返回
二、扩散双电层理论 胶粒带电
1、胶粒从溶液中选择性吸附某种离子而带电(Fanjes规则); 2、胶粒分子本身电离作用使离子进入溶液而带电。
双电层电位:
5
扩散双电层理论
问题提出: 1、液体在远离胶粒的液层是流动的,在胶粒附近不流动? 2、电位与电极电位有何区别, │ζ│<│ϕ│? 3、电解质为何能影响ζ电位的大小? 4、 ζ电位的符号不但与固相有关,也与溶液中某种离子过
{[
AgI
]m
nAg
+
⋅ (n
−
x
)
NO
− 3
高一化学必修一知识点化学胶体

高一化学必修一知识点化学胶体1、胶体的定义:分散质粒子直径大小在10-9~10-7m之间的分散系。
2、胶体的分类:①.根据分散界定质微粒组成的状况分类:如:胶体胶粒是由许多汇聚等小分子聚集一起形成的微粒,其直径在1nm~100nm之间,这样的胶体叫粒子胶体。
又如:淀粉属高分子化合物,其单个分子的直径约在1nm~100nm范围之内,这样的胶体叫分子胶体。
②.根据分散剂的状态划分:如:烟、云、雾等的分散剂为气体,这样的胶体叫做气溶胶;AgI溶胶、溶胶、溶胶,其分散剂为水,分散剂胶体为液体的胶体叫做液显色;有色玻璃、烟水晶均以固体为分散剂,这样的胶体叫做固溶胶。
3、胶体的制备A.物理方法①机械法:利用机械磨碎法将固体固体直接磨成胶粒的大小②溶解法:高分子化合物分散在合适的溶剂中形成胶体,如蛋白质溶于水,淀粉溶于水、聚乙烯熔于某氯气等。
B.化学方法①水解促进法:FeCl3+3H2O(沸)=(胶体)+3HCl②复分解反应法:KI+AgNO3=AgI(胶体)+KNO3Na2SiO3+2HCl=H2SiO3(胶体)+2NaCl思考:若上述两种反应物的量两类中均为大量,则可观察到什么现象?如何表达对应的两个反应方程式?提示:KI+AgNO3=AgI↓+KNO3(黄色↓)Na2SiO3+2HCl=H2SiO3↓+2NaCl(白色↓)4、胶体的性质:①丁达尔效应——丁达尔效应是粒子对光散射作用的结果,是一种物理现象。
丁达尔现象产生的其原因,是因为胶体微粒直径大小恰当,当光照射胶粒上时,胶粒将光从各个方面全部反射,胶粒即成前段光源(这一现象叫光的热辐射),故可明显地看到由小光源形成的光亮“通路”。
当光照在比较大或小的颗粒或微粒上则无此现象,只发生反射或将光全部吸收的现象,而以溶液和浊液无丁达尔现象,所以丁达尔效应常用于鉴别胶体和其他分散系。
②布朗运动——在胶体中,由于胶粒在各个方向所受的力不能相互平衡而产生运动无规则的的,称为布朗运动。
胶体化学

二、 高分子溶液的性质
表11-8
高分子溶液的渗透压:溶质分子的柔性及溶剂化,渗透压 较相同浓度的小分子溶液大。
高分子溶液的黏度:黏度大
原因:
1)高分子的柔性使得高分子在溶液中占的体积很大,对介 质流动形成阻力
2)高分子溶剂化,溶剂分子被高分子束缚,流动性差 3)高分子链段间相互作用形成一定结构,流动阻力增大,
乳状液的制备
自然乳化分散法 瞬间成皂法 界面复合物生成法 交替添加法
三 乳状液的转型与破坏
(1)乳状液转型 转型:由W/O变成O/W或者由O/W变成W/O 外加物质使乳化剂的性质发生改变而引起
加入量少------不能转型 加入量适中---转型 加入量多------破坏乳液 温度改变(非离子型表面活性剂) 转型温度
溶胶的净化
在制备溶胶的过程中,常生成一些多余的电解质,
在制备溶胶的过程中,常生成一些多余的 如制电备解F质e(O,H如)3溶制胶备时生Fe成(O的HH)C3l溶。胶时生成的HCl。
少量电解质可以作为溶胶的稳定剂,但是过多的电解质存在会 使溶胶不稳定,容易聚沉,所以必须除去。 净化的方法主要有渗析法和超过滤法。
第二节 溶胶的制备和净化
制备: 1)由小分子溶液聚集 物理聚集法、化学反应法、更换溶剂法 2)由粗分散系统分散
研磨法、电弧法、超声分散法
由小分子溶液聚集
水解反应制氢氧化铁溶胶 FeCl3 (稀)+3H2O (热)→ Fe(OH)3 (溶胶)+3HCl
由粗分散系统分散
电弧法主要用于制备金、银、铂等金属溶胶。制备过程包括先分 散后凝聚两个过程。将金属做成两个电极,浸在水中,盛水的盘子放 在冷浴中。在水中加入少量NaOH 作为稳定剂。 制备时在两电极上施加 100V 左右的直流电,调节电极之间的距离,使 之发生电火花,这时表面金属蒸发,是分散过程,接着金属蒸气立即 被水冷却而凝聚为胶粒。
胶体化学

的形状对胶体性质有重要影响。
胶粒的形状
例如:(1)聚苯乙烯胶乳是球形质点
(2) V2O5 溶胶是带状的质点 (3) Fe(OH)3 溶胶是丝状的质点
§14.5 溶胶的稳定和聚沉
溶胶是热力学不稳定系统,但有些溶胶却能在相 当长时间内稳定存在。 1、溶胶的经典稳定理论—DLVO理论 胶体带电是其稳定存在的主要原因 (1)胶团之间既存在引力势能,也存在斥力势能。
例1:AgNO3 + KI→KNO3 + AgI↓ 过量的 KI 作稳定剂 胶团的结构表达式 : [(AgI)m n I – (n-x)K+]x– xK+ 胶核 胶粒(带负电) 胶团的图示式: 胶核 胶粒
胶团
胶团(电中性)
例2:AgNO3 + KI → KNO3 + AgI↓
过量的 AgNO3 作稳定剂
溶胶的电动现象体现在以下四个方面: 电泳:在外电场作用下,胶体粒子在分散介质中定 向移动的现象。
1、溶胶的电动现象 电渗:在多孔膜(或毛细管)两端施加一定电压,
液体将通过多孔膜而定向移动。在外电场作用下,胶
体粒子相对静止,分散介质定向移动的现象。 流动电势:在外力的作用下,迫使液体通过多孔膜 (或毛细管)定向流动,多孔膜两端所产生的电势差 沉降电势:分散相粒子在重力场或离心力场的作用
的最简便的方法。
光散射现象 当光束通过分散系统时,一部分自由地通过,一 部分被吸收、反射或散射。 入射光频率与分子的固有频率相同时,吸收 入射光波长小于分散粒子尺寸时,反射
入射光波长大于分散粒子尺寸时,散射
散射光的强度可利用瑞利公式进行计算
2、瑞利公式 I=
9π2V 2C
2λ4l 2
2 n2 - n 0 2 ( 2 ) (1 + cos2α)I0 2 n + 2n 0
胶体化学在生活中的应用

胶体化学在生活中的应用胶体化学是一门研究物质在粘度和流变方面的物理性质的学科,是胶体物理学和表面活性剂学的总称,它研究了胶体的性质和结构、悬浮的性质和稳定性等问题,以及胶体的传输现象和物理加工技术。
胶体化学是物理化学和材料科学的一个重要分支,涉及其他学科,如物理学、化学、生物学和核科学等。
二、胶体化学在生活中的应用1、食品、医药、农药和化妆品中的应用大多数食品、医药、农药和化妆品中都含有胶体,胶体具有乳化、增稠、悬浮、调节水分、降解解质等功能,可以改变物质的性质,达到提高食品、医药、农药和化妆品的质量的目的。
此外,特殊的胶体还可以用于增加生产效率和减少产品成本,对生产高品质食品、医药、农药和化妆品具有重要意义。
2、新材料中的应用随着科学技术的进步,新材料的应用日益广泛,胶体技术是其中的重要组成部分。
胶体制备的新型材料具有新型复合材料、功能材料和高分子材料等特性,其均匀性好、分散性佳和可控加工性,可以极大地促进新材料的发展。
3、环境保护与能源利用中的应用当今社会,保护环境和高效利用能源已经成为生活的基本需求。
胶体化学技术可以帮助在环境保护方面取得长足进展。
比如,微胶体可以起到活性剂的作用,有助于环境污染物的降解和净化;另外,离子型胶体也可以有效地把废水中有害物质汇集起来,从而减少污染物的流失;在能源利用方面,比如,胶体表面技术可以有效地减少燃料消耗,以及提高燃料的利用率。
三、结论从上面可以看出,胶体化学在食品、医药、农药、化妆品、新材料、环境保护和节能利用等方面都发挥了重要作用,为我们生活带来很大的便利。
未来,随着胶体化学技术的不断发展和完善,我们将能够更好地发挥胶体化学在生活中的作用,促进人类文明的进程。
胶体化学教案中的胶体的定义与分类

胶体化学教案中的胶体的定义与分类胶体是一种介于溶液和悬浊液之间的物质状态,其特点是细小的颗粒悬浮于连续相中。
在胶体化学中,胶体的定义与分类是非常重要的基础概念。
本教案将详细介绍胶体的定义以及常见的胶体分类,帮助学生全面了解胶体的本质和不同种类。
一、胶体的定义胶体的定义可以从微观和宏观两个方面来分析。
从微观角度来看,胶体由一种或多种微粒组成,这些微粒的直径通常在1纳米到1微米之间。
这些微粒在连续相中保持着悬浮状态,不沉降、不析出和不沉淀,形成一个均匀的、稳定的体系。
从宏观角度来看,胶体呈现出浑浊、半透明的性质,具有独特的光学和流变学特性。
二、胶体的分类胶体可以根据其组成、性质和来源等方面进行分类。
下面将介绍一些常见的胶体分类。
1. 溶胶溶胶是由固体微粒(溶质)悬浮在液体(溶剂)中所形成的胶体体系。
在溶胶中,固体微粒的尺寸较小,且呈现出分散均匀的状态。
常见的溶胶包括金溶胶、银溶胶和硅溶胶等。
2. 凝胶凝胶是由连续相(溶剂)中的大量溶质形成的胶体体系。
溶质能够形成三维网状结构,从而使得连续相变得不流动,呈现出凝固状态。
常见的凝胶包括凝胶体和凝胶体系。
3. 乳胶乳胶是由液体微粒(分散相)悬浮在液体介质(连续相)中所形成的胶体体系。
乳胶通常呈现出白色、乳白色或淡黄色的外观,常见的乳胶有牛奶、乳胶漆等。
4. 气溶胶气溶胶是由固体或液体微粒(溶质)悬浮在气体介质(溶剂)中所形成的胶体体系。
气溶胶可分为烟雾、霾和雾等。
其中,烟雾由细小的固体或液体微粒悬浮在空气中形成,霾由大气中微粒、颗粒物质和汽车尾气等污染物组成,雾由水蒸气凝结为微小的水滴悬浮在空气中形成。
5. 胶体溶液胶体溶液是由胶体颗粒悬浮在液体介质中所形成的胶体体系。
它不具备自己的形状和表面,可以用胶体颗粒的分散性质来描述,例如胶体溶液的浑浊度、粒径分布等。
在实际应用中,胶体的分类还可以根据其化学成分、电荷性质、表面活性剂的存在与否以及溶质和溶剂的性质等来细分。
高一化学胶体课件

胶体制备与提纯的注意事项
注意安全
在制备和提纯过程中,应避免使用有 毒有害的试剂,并确保操作安全。
控制条件
制备和提纯过程中,应控制好温度、 压力、浓度等条件,以保证实验结果 的准确性和可靠性。
实验操作规范
在实验过程中,应遵循实验操作规范 ,避免污染和交叉污染。
实验后处理
实验结束后,应对废液进行妥善处理 ,避免对环境和人体造成危害。
胶体在医学中的应用
胶体在医学中也有着重要的应 用,如医用胶、血液透析等。
医用胶是一种常用的外科手术 材料,具有快速止血、促进伤 口愈合等作用,广泛应用于手 术和创伤治疗中。
血液透析则是利用胶体的渗透 作用,将血液中的毒素和多余 水分滤出,以治疗肾功能衰竭 等疾病。
胶体在其他领域的应用
除了化学工业和医学领域,胶体 在其他领域也有着广泛的应用。
如胶体在环保领域中可以用于污 水处理、土壤修复等;在农业领 域中可以用于农药和肥料的缓释
剂等。
此外,胶体还在化妆品、食品、 墨水等领域中有着广泛的应用, 如隐形眼镜护理液、墨水等产品
中都含有胶体成分。
05
胶体的实验研究
胶体实验的目的与原理
目的
通过实验了解胶体的性质和特点,加深对胶体概念的理解。
原理
胶体是一种分散质粒子直径在1nm-100nm之间的分散系,具有介稳性、丁达 尔效应等特点。实验通过观察胶体的电泳、聚沉等性质,探究胶体的本质。
实验步骤与操作方法
步骤一
制备胶体。将一定量的Fe(OH)3固体溶解在沸水中,得到Fe(OH)3胶体。
步骤二
进行电泳实验。将胶体置于电场中,观察胶体粒子在电场中的移动情况。
氧化铝等。
胶体化学
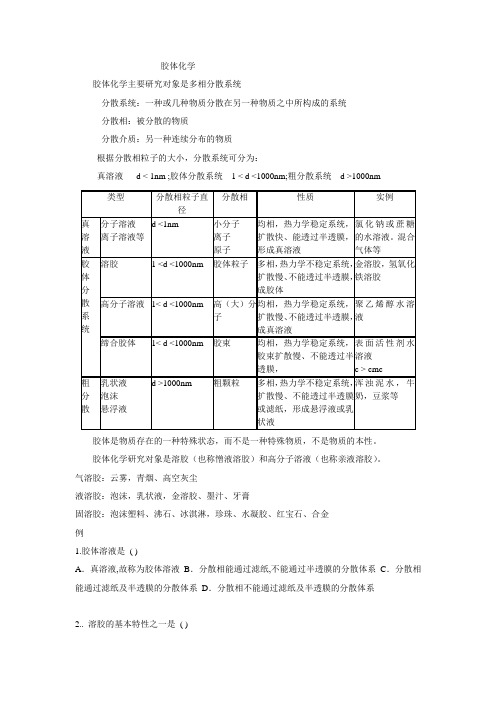
胶体化学胶体化学主要研究对象是多相分散系统分散系统:一种或几种物质分散在另一种物质之中所构成的系统分散相:被分散的物质分散介质:另一种连续分布的物质根据分散相粒子的大小,分散系统可分为:真溶液 d < 1nm ;胶体分散系统 1 < d <1000nm;粗分散系统 d >1000nm胶体是物质存在的一种特殊状态,而不是一种特殊物质,不是物质的本性。
胶体化学研究对象是溶胶(也称憎液溶胶)和高分子溶液(也称亲液溶胶)。
气溶胶:云雾,青烟、高空灰尘液溶胶:泡沫,乳状液,金溶胶、墨汁、牙膏固溶胶:泡沫塑料、沸石、冰淇淋,珍珠、水凝胶、红宝石、合金例1.胶体溶液是( )A.真溶液,故称为胶体溶液B.分散相能通过滤纸,不能通过半透膜的分散体系C.分散相能通过滤纸及半透膜的分散体系D.分散相不能通过滤纸及半透膜的分散体系2.. 溶胶的基本特性之一是( )A.热力学上和动力学上皆属于稳定体系B.热力学上和动力学上皆属不稳定体系C.热力学上不稳定而动力学上稳定体系D.热力学上稳定而动力学上不稳定体系3.. 雾属于分散体系,其分散介质是( )A.液体B.气体C.固体D.气体或固体4. 将高分子溶液作为胶体体系来研究,因为它( )A.是多相体系B.热力学不稳定体系C.对电解质很敏感D.粒子大小在胶体范围内5. 溶胶与大分子溶液的区别主要在于( )A.粒子大小不同B.渗透压不同C.丁达尔效应的强弱不同D.相状态和热力学稳定性不同6. 下列物系中,不属于胶体的是( )A.云雾B.烟C.珍珠D.空气7. 对于胶体与大分子溶液( )A.都属于同类的分散体系B.两者的分散相质点均能通过滤纸,因此都属于均相混和物C.胶体属于介稳体系,大分子溶液属于稳定体系D.粘度都大1.溶胶的制备与净化1).溶胶制备的一般条件:(1)分散相在介质中的溶解度必须极小(2)必须有稳定剂存在2).胶体的制备方法:(1)凝聚法: ①蒸气凝聚法,②过饱和法(2)分散法: ①胶体磨, ②气流粉碎机(又称喷射磨)③电弧法—用于制备贵金属的水溶胶2.溶胶的光学性质1).光散射(1)丁达尔效应:以一束强光射入溶胶后,在入射光的垂直方向可以看到一道明亮的光带,被称为丁达尔效应光本质是电磁波,当光波作用到介质中小于光波波长的粒子上时,粒子中的电子被迫振动(其振动频率与入射光波的频率相同),成为二次波源,向各个方向发射电磁波,这就是散射光波也就是我们看到的散射光。
胶体化学

系统 真溶液 胶体系统 粗分散系统
分散系统的分类及特征(总结)
分散相粒子 直径 d
系统相态
热力学稳定性
实例
d < 1 nm
均相
各种分子、原子、离子溶液
稳定
多相不稳定, 如乙醇水溶液、NaCl 水溶液、
空气等
多相 1<d<1000nm
不稳定
为什么? 各种溶胶
二 胶体系统的动力学性质
解释胶粒能扩散、渗透以及因重力作用而不聚沉下来的原因。
以后发现,线度小于4000nm的粒子,在分散介质中都 有这种运动。(胶体尺度 1 ~ 1000nm)
这种现象产生的原因是,分 散介质分子处于不断的热运动中, 从四面八方不断的撞击分散相粒 子。对于大小在胶体尺度下的分 散相粒子,粒子受到撞击次数较 小,从各个方向受到的撞击力不能 完全互相抵消,在某一时刻,粒子 从某一方向得到的冲量即可发生 位移。此即布朗运动。
h1 h2
4.沉降速度与粒子半径的关系
阻力F为: F=4/3лr3dg-4/3 лr3dog
= 4/3лr3(d-do)g
根据斯托克斯公式: 4/3лr3(d-do)g=6 лŋru 因此: r=[9 ŋu/2(d-do)g]1/2
r-粒子半径; d-粒子密度; d0-分散介质密度;u-粒子沉降速度; ŋ-介质粘度
溶胶是一个高度分散的非均相系统。分散相粒子 与分散介质间有明显的相界面。实验发现,在外电场 下,固、液两相可发生相对运动;反之,若迫使固、 液两相作相对运动时,又可产生电势差。溶胶的这种 与电势差有关的相对运动称为电动现象,电泳和电渗 都属于电动现象
电动现象说明,溶胶粒子表面带有电荷。而溶胶粒 子带有电荷也正是它能长期稳定存在的原因。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
胶体化学
一、主要概念
均相分散系统(溶液),胶体系统(亲液溶胶,憎液溶胶),粗分散系统,胶体的光学、动力和电性质,胶团结构,双电层DLVO理论,乳状液,纳米材料
二、主要性质与公式
1.胶体的性质:高度分散性、多相性和热力学不稳定性。
体现如下:
(1)光学性质-丁达尔效应:胶体对光的散射现象。
散射光强度-雷利公式: (定性记忆)
式中:I0及l分别为入射光强度和波长,V为每个分散相粒子的体积,c为单位体积中的粒子数,n及n0分别为分散相及介质的折射率,a为散射角,l
为观察者与散射中心的距离。
此公式适用于粒子的尺寸远小于入射光的波长,把粒子看成点光源;不考虑粒子散射光之间的相互干涉;粒子不导电。
应用解释:浊度计原理;超显微镜原理;早上、下午太阳红色,中午天空蓝色。
(2)动力性质
i. 布郎运动:在超显微镜下,观察到胶粒不断地作不规则的运动,称为布郎运动。
ii. 扩散:在有浓度梯度存在时,物质粒子因热运动而发生宏观上的定向迁移的现象。
iii. 沉降与沉降平衡:当扩散速率等于沉降速率时,粒子浓度c随高度h的分布。
(3) 电学性质
i. 电泳:在外电场的作用下,胶体粒子在分散介质中定向移动的现象。
ii. 电渗:在多孔膜(或毛细管)的两端施加一定电压,液体通过多孔膜而定向流动的现象
iii. 流动电势:在外力的作用下,液体通过多孔膜(或毛细管)定向流动时在多孔膜两端产生的电势差。
iv. 沉降电势:分散相粒子在重力场或离心力的作用下迅速移动时,在移动方向的两端所产生的电势差。
v.从电泳速率或电渗速率计算z 电势 (准确记忆)
式中e为分散介质的介电常数,e=e r e
0,e r为相对介电常数,e
为真空介
电常数。
E为电势梯度,h为介质粘度。
2.憎液溶胶的胶团结构
根据扩散双电层理论,胶团结构由胶核、胶粒和滑动部分三个层次组成。
双电层由紧密层和扩散层组成,它们之间存在一个滑动面。
具体如下:
(1)胶核由固体微粒和选择性吸附的离子组成,该离子通常为构成固体微粒的离子,并且决定着胶粒所带的电荷,一般为溶液中过量物质(起着稳定剂的作用)的成核离子。
(2)紧密层和扩散层的离子其电荷与胶粒吸附的离子电荷相反,称为反离子,通常为稳定剂中的非成核的离子。
(3)写胶团结构的关键是确定稳定剂,稳定剂一旦确定,吸附的离子便确定。
注意:
(1) 在胶团结构中, m, n, x均为不定数。
(2) 胶粒虽带电,但整个胶团结构是电中性。
(3) 对于固体分散成的溶胶,胶团结构要具体分析。
3.扩散双电层理论
双电层由紧密层和扩散层组成。
双电层结构可用下图模型表示。
ψ热力学电势:固体表面与溶液本体之间的电势差。
yδ斯特恩电势:斯特恩层与溶液本体之间的电势差。
z电势(或电动电势):滑动面与溶液本体之间的电势差,只有在固液两相发生相对移动时,才能呈现出来。
z电势在数值上小于热力学电势。
图1 斯特恩双电层模型
例如:10ml 0.1 mol×dm-3 KI + 9 ml 0.1 mol×dm-3 AgNO3制备AgI溶胶,由于KI稍过量,起着稳定剂作用,固体微粒优先吸附与其自身有相同元素的离子,即I-,反离子为稳定剂的另一个离子K+,故AgI溶胶的胶团结构可表示为图12-1,胶粒带负电,电泳时朝正极移动。
若AgNO3稍过量则为稳定剂,胶团结构变为图12-2,胶粒带正电,电泳时朝负极移动。
图2 KI稍过量时的胶团结构
稍过量时的胶团
图3 AgNO
3
4.电解质对溶胶的聚沉作用
使溶胶发生明显的聚沉所需电解质的最小浓度,称为该电解质的聚沉值,聚沉值的倒数定义为聚沉能力。
(1)起聚沉作用的是与胶粒带相反电荷的离子(即反离子);
(2)反离子价数越高,聚沉能力愈大,聚沉值愈小。
(3)与溶胶具有同样电荷的离子能削弱反离子的聚沉能力,且价数愈高,削弱作用愈强。
(4)有机化合物的离子都具有很强的聚沉能力。
5.DLVO理论:能较好解释带电溶胶稳定的原因。
除胶粒带电是溶胶稳定的主要因素外,溶剂化作用和布郎运动也是溶胶稳定的原因。
6. 乳状液:稳定,加入稳定剂;去乳化手段。
三、典型题型
计算胶体的性质(主要是z电势),写出胶团结构,比较电解质对胶体稳定性的大小,及DLVO理论的理解是本章的主要内容。
粗分散系统的性质仅需了解。
例题1:混合等体积的0.1 mo1·dm-3 KI和0.09 mo1·dm-3 AgNO3溶液所得的溶胶。
(1) 试写出胶团结构式;
(2) 指明电泳方向;
(3) 比较MgSO4,Na2SO4,CaCl2电解质对溶胶的聚沉能力并简述原因。
(6分)
解:(1) [ (AgI)m n I- · (n-x)K+]x-·x K+
(2)胶粒带负电,往正极移动
(3)聚沉能力为: Na2SO4 < MgSO4< CaCl2
因为胶粒带负电,反离子起聚沉作用,其价数越高,聚沉能力越大,故Ca2+、Mg2+ > Na+。
又因与胶粒带同种电荷的离子能削弱反离子作用,高价强于低价,即聚沉能力有SO42-< Cl-,因此可得到上面的聚沉能力次序。
简述热力学三个定律及其应用。
例题2:在浓度为10 mol·m-3的20cm3 AgNO3溶液中,缓慢滴加浓度为15 mol·m-3的KBr溶液10cm3 ,以制备AgBr溶胶。
(1) 写出AgBr溶胶的胶团结构表达式,指出电泳方向。
(2) 在三个分别盛10cm3 AgBr溶胶的烧杯中,各加入KNO3、K2SO4、
K3PO4溶液使其聚沉,最少需加电解质的数量为:1.0 mol·m-3的KNO3 5.8 cm3 ;
0.01 mol·m-3的K2SO4;8.8 cm3 ;1.5×10-3 mol·m-3的K3PO48.0 cm3 ;计算各电解质的聚沉值以及它们的聚沉能力之比。
(3) 293K时,在两极距离为35cm的电泳池中施加的电压为188V,通电40min 15s,测得AgBr溶胶粒子移动了3.8cm。
问该溶胶的ξ电势为多大?已知293K时分散介质的相对介电常数εr=80,粘度η=1.03×10-3 Pa·s ,真空介电常数ε0=8.854×10-12F·m-1。
(10分)
解:(1) AgNO3过量,为稳定剂,胶团结构为
[(AgBr)m n Ag+·(n-x)NO3-]x+ ·x NO3-
胶粒带正电,电泳时向负极移动。
(2) KNO3的聚沉值: 1.0mol·dm-3×5.8cm3 / (10+5.8) cm3 = 0.367 mol·dm-3
K2SO4的聚沉值: 0.01 mol·dm-3×8.8cm3 / (10+8.8) cm3 =
4.68×10-3 mol·dm-3
K3PO4的聚沉值;0.0015 mol·dm-3×8.0cm3 / (10+8.0) cm3 =
6.67×10-4 mol·dm-3
聚沉能力之比KNO3:K2SO4:K3PO4
= (1/0.357):(1/4.48×10-3):(1/6.67×10-4) =1:79.7:535
(3) 由公式u =εEζ/η=ε(V/l) ζ/ η得
ζ = u lη /εV = u lη /εrε0 V
= (0.038m/2415s) ×0.35m ×1.03×10-3Pa·s/ (80×8.854×10-12F·m-1×188V)
= 0.0426V。
