GERRETSEN不等式的对偶律(1)
jensen不等式的理解

jensen不等式的理解Jensen不等式是数学中的一个重要不等式,它在函数凸性的研究中具有重要的应用价值。
本文将从凸函数、Jensen不等式的定义和推导以及其在实际问题中的应用等方面进行阐述。
一、凸函数的定义和性质在了解Jensen不等式之前,我们首先需要了解凸函数的概念。
在实数域上,给定函数f(x),如果对于任意的x1和x2以及0≤λ≤1,都有f(λx1+(1-λ)x2)≤λf(x1)+(1-λ)f(x2),那么我们称函数f(x)是凸函数。
凸函数的图像呈现凸状,也就是说,函数曲线上任意两点之间的连线位于曲线的上方或者与曲线相切。
凸函数具有以下性质:1. 凸函数的上确界和下确界都是函数的值域的端点;2. 凸函数的导函数是递增的;3. 凸函数的和、积、复合仍然是凸函数。
二、 Jensen不等式的定义和推导Jensen不等式是由丹麦数学家Johan Jensen于1906年提出的,它描述了凸函数在随机变量上的平均值与函数值之间的关系。
设X 是一个随机变量,f(x)是定义在X的取值范围上的凸函数,那么对于任意的X的取值x1,x2,...,xn以及对应的概率p1,p2,...,pn,Jensen不等式可以表述为:f(p1x1+p2x2+...+pnxn) ≤ p1f(x1) + p2f(x2) + ... + pnf(xn)其中,p1+p2+...+pn=1且pi≥0。
Jensen不等式的推导可以通过数学归纳法进行证明。
当n=2时,根据凸函数的定义,我们有:f(p1x1+(1-p1)x2) ≤ p1f(x1) + (1-p1)f(x2)将上式中的p1替换为λ,(1-p1)替换为(1-λ),则有:f(λx1+(1-λ)x2) ≤ λf(x1) + (1-λ)f(x2)这与Jensen不等式的定义完全一致。
因此,Jensen不等式成立。
三、 Jensen不等式的应用Jensen不等式在数学和实际问题中有着广泛的应用。
对偶律公式证明

对偶律公式证明对偶律公式是数学中常见的概念,它是指在布尔代数或逻辑学中,一个表述的逆命题可以由原表述的对偶形式得到,即使得原表述中的与运算变为或运算,或运算变为与运算,真值不变。
对偶律公式是数学中的重要性质之一,下面介绍如何证明它。
首先,我们需要了解两个定义,分别是“补”和“对偶”。
补是指对于一个布尔变量x,取反符号写为~x,则~x被定义为x的补。
对偶是指将一个布尔表达式中的符号~(非)、&(与)、|(或)分别替换成|(或)、&(与)、~(非),得到的布尔表达式称作其对偶。
根据上述定义,我们可以得到以下两条定理:1. ~(~x) = x2. ~(|x&y) = (~x)|(~y)下面根据这两条定理,证明对偶律公式。
对偶律公式的表述如下:对偶律1: ~(x&y) = (~x)|(~y)对偶律2: ~(x|y) = (~x)&(~y)证明对偶律1:1. 将x&y的对偶,即(~x)|(~y)表示为(~x&~y)。
(根据对偶定义,~(x&y)的对偶为~x|~y,然后再根据德摩根定律将其转化为~x&~y)2. 我们对比原式和上式,发现它们恰好只是x和~x互换了,y和~y互换了,因此它们的真值等价,即可得出对偶律1。
证明对偶律2:1. 将x|y的对偶,即(~x)&(~y)表示为(~x|~y)。
(根据对偶定义,~(x|y)的对偶为~x&~y,然后再根据德摩根定律将其转化为~x|~y)2. 我们对比原式和上式,发现它们恰好只是x和~x互换了,y和~y互换了,并且原式和上式都加了一个取反符号,因此它们的真值等价,即可得出对偶律2。
综上所述,我们完成了对偶律公式的证明,它可以用于简化布尔代数中的表达式,具有广泛的应用价值。
jensen不等式
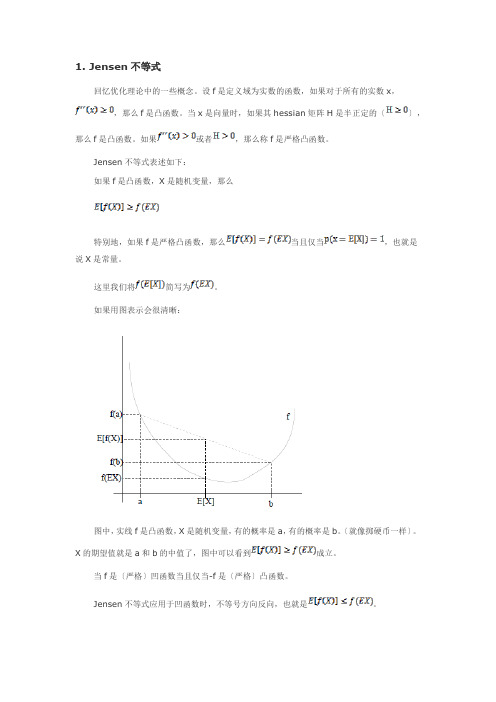
1. Jensen不等式回忆优化理论中的一些概念。
设f是定义域为实数的函数,如果对于所有的实数x,,那么f是凸函数。
当x是向量时,如果其hessian矩阵H是半正定的〔〕,那么f是凸函数。
如果或者,那么称f是严格凸函数。
Jensen不等式表述如下:如果f是凸函数,X是随机变量,那么特别地,如果f是严格凸函数,那么当且仅当,也就是说X是常量。
这里我们将简写为。
如果用图表示会很清晰:图中,实线f是凸函数,X是随机变量,有的概率是a,有的概率是b。
〔就像掷硬币一样〕。
X的期望值就是a和b的中值了,图中可以看到成立。
当f是〔严格〕凹函数当且仅当-f是〔严格〕凸函数。
Jensen不等式应用于凹函数时,不等号方向反向,也就是。
先验概率与后验概率事情还没有发生,要求这件事情发生的可能性的大小,是先验概率. 事情已经发生,要求这件事情发生的原因是由某个因素引起的可能性的大小,是后验概率.一、先验概率是指根据以往经历和分析得到的概率,如全概率公式,它往往作为“由因求果〞问题中的“因〞出现。
后验概率是指在得到“结果〞的信息后重新修正的概率,如贝叶斯公式中的,是“执果寻因〞问题中的“因〞。
先验概率与后验概率有不可分割的联系,后验概率的计算要以先验概率为根底。
二、A prior probability is a marginal probability, interpreted as a description of what is known about a variable in the absence of some evidence. The posterior probability is then the conditional probability of the variable taking the evidence into account. The posterior probability is computed from the prior and the likelihood function via Bayes' theorem.三、先验概率与后验概率通俗释义事情有N种发生的可能,我们不能控制结果的发生,或者影响结果的机理是我们不知道或是太复杂超过我们的运算能力。
如何理解克劳修斯不等式

如何理解克劳修斯不等式如何理解克劳修斯不等式克劳修斯不等式是概率论中很重要的一条不等式,它描述了两个随机变量之间的关系。
克劳修斯不等式在信息论中也有广泛的应用。
这篇文章将介绍克劳修斯不等式的定义、推导和应用。
1. 克劳修斯不等式的定义首先,我们需要了解一下随机变量的概念。
随机变量是指在某个随机实验中可能出现的各种结果。
比如在掷一枚硬币的实验中,正面向上和反面向上就是两种可能的结果。
我们可以用随机变量X代表正面向上时的结果,用随机变量Y代表反面向上时的结果。
克劳修斯不等式描述的是两个随机变量之间的关系。
如果X和Y是两个随机变量,它们的概率分布分别为P(x)和Q(y),则克劳修斯不等式可以表示为:H(P,Q)≥0其中,H(P,Q)是X和Y之间的交叉熵。
交叉熵在信息论中也有重要的应用,它衡量了用一个概率分布Q来表示实际分布P的效率。
对于两个概率分布P和Q,它们的交叉熵表示为:H(P,Q)=-∑P(x)logQ(x)2. 克劳修斯不等式的推导克劳修斯不等式看起来很简单,但是它的证明并不容易理解。
下面我们将简要介绍一下克劳修斯不等式的推导过程。
假设有一个函数f(x),它是单调递减的。
我们定义一个概率分布P'(x)=f(x)P(x)和Q'(x)=f(x)Q(x)。
可以证明P'(x)和Q'(x)也是概率分布,且它们的交叉熵H(P',Q')等于H(P,Q)-D(f||1/f),其中D(f||1/f)是KL散度。
KL散度是另一个在信息论中常用的指标,它可以用来衡量两个概率分布的差距。
KL散度的具体定义为:D(P||Q)=∑P(x)log(P(x)/Q(x))由于KL散度始终大于等于0,所以可以得出H(P,Q)≥D(f||1/f)。
当f(x)=1/x时,D(f||1/f)达到最小值,也就是0,此时H(P,Q)达到最小值。
3. 克劳修斯不等式的应用克劳修斯不等式在信息论中有广泛的应用。
柯西不等式的对偶式及应用

柯西不等式的对偶式及应用柯西不等式是一个重要的数学定理,它提供了一种有效的方法来证明函数的最大值和最小值。
它的对偶式也是一个重要的数学定理,它可以用来求解优化问题,并在经济学、运筹学、控制论等领域有广泛的应用。
柯西不等式的原式是:设f(x)是定义在区间[a,b]上的连续函数,则有:$$\int_{a}^{b}f(x)dx\geqslant\frac{1}{b-a}[f(a)+f(b)]$$柯西不等式的对偶式是:设f(x)是定义在区间[a,b]上的连续函数,则有:$$\frac{1}{b-a}[f(a)+f(b)]\geqslant\frac{1}{2}[f(\frac{a+b}{2})]$$柯西不等式的对偶式可以用来求解优化问题,即求解函数f(x)在区间[a,b]上的最大值和最小值。
具体的做法是:首先,将区间[a,b]分成n 个子区间,每个子区间的宽度为$\frac{b-a}{n}$,然后,在每个子区间上取一个点,使得函数f(x)在该点取得最大值或最小值,最后,将这些点代入柯西不等式的对偶式,即可求出函数f(x)在区间[a,b]上的最大值和最小值。
柯西不等式的对偶式在经济学、运筹学、控制论等领域有广泛的应用。
在经济学中,柯西不等式的对偶式可以用来求解最优化问题,如求解最优生产组合、最优投资组合等。
在运筹学中,柯西不等式的对偶式可以用来求解最短路径问题、最小生成树问题等。
在控制论中,柯西不等式的对偶式可以用来求解最优控制问题,如最优控制策略、最优控制结构等。
总之,柯西不等式的对偶式是一个重要的数学定理,它可以用来求解优化问题,并在经济学、运筹学、控制论等领域有广泛的应用。
高中赫尔德不等式

高中赫尔德不等式高中赫尔德不等式=================一、引言在数学中,不等式是研究和应用最广泛的数学概念之一。
不等式不仅在基础数学中具有重要的地位,而且在各个领域中都具有广泛的应用,包括数论、代数、几何和概率论等。
在这篇文章中,我们将着重讨论高中阶段学习中重要的不等式之一——赫尔德不等式。
二、赫尔德不等式的定义赫尔德不等式是由德国数学家奥图·赫尔德(Otto Ludwig Hölder)在1889年提出的。
它是一种针对实数集合间的不等式,特别适用于处理函数的平均值和积分的估计等问题。
赫尔德不等式可以用以下形式表示:其中,ui 和 vi 是实数,p 是一个大于 1 的实数。
三、赫尔德不等式的证明我们可以通过一种简单的方式来证明赫尔德不等式,基本思想是利用柯西-施瓦茨不等式。
根据柯西-施瓦茨不等式,我们有:应用柯西-施瓦茨不等式的思想,我们可以得到:根据不等式的性质,我们可以看出赫尔德不等式成立。
四、应用示例赫尔德不等式可以应用于许多领域,如概率论、数论和几何学等。
下面我们举一个简单的实例来说明其应用。
假设有两个实数序列 {ai} 和 {bi},我们想要估计它们的内积。
根据赫尔德不等式,我们可以得到:通过这个估计,我们可以得到内积的一个上界值。
这在概率论中经常应用于估计协方差等问题。
五、总结与回顾通过对赫尔德不等式的深入讨论,我们可以得出以下要点:- 赫尔德不等式是一种适用于实数集合的不等式,特别适合用于处理函数的平均值和积分问题。
- 赫尔德不等式可以通过柯西-施瓦茨不等式进行证明。
- 赫尔德不等式在概率论、数论和几何学中具有广泛的应用。
六、观点与理解赫尔德不等式作为数学中的一种基本不等式,在高中数学中也是重要的学习内容之一。
通过了解和掌握赫尔德不等式,我们可以提升我们处理函数积分和平均值等问题的能力。
赫尔德不等式还可以为我们打开更深入的数学领域,为我们进一步学习和研究提供基础。
代数函数的jensen不等式的加细与推广

代数函数的jensen不等式的加细与推广Jensen不等式是数学和统计学中发挥重要作用的数学定理,它以一个有限个变量构成的累积函数形式,对这些变量的累积函数的期望进行有限的界定及求解。
下面就Jensen不等式的加细与推广作一进一步的讨论:一、 Jensen不等式的加细1、基本的Jensen不等式:即假设函数f(x)是连续可微函数,而X是一个有限个变量构成的随机变量,那么对任意可行赋值θ,有:E(f(X))≥f(E(X)),这就是基本的Jensen不等式。
2、海森堡不等式:假设fx(x1, x2, ..., xn)在[αi, βi]下是一个凸函数,Then, for any arbitrary set of values θ1, θ2, ..., θn, there is:E[f(X)]≥f[E(X1), E(X2), ..., E(Xn)],这就是海森堡不等式。
3、勒贝格不等式:前提条件是函数f(x)是可微的,对任意可行赋值θ,有:E[f(X)]≥E(g(X)),其中g(X)=E{f(X′) |X=θ} ,这就是提出了勒贝格不等式。
4、贝叶斯不等式:前提条件是f(x)是可微的,对任意可行赋值θ,有:E[f(X)]≥E{g(X)|X=θ},其中g(x)是贝叶斯可合并的,这就是贝叶斯不等式。
二、Jensen不等式的推广1、统计不等式:假设f(x)是连续可微函数,而X是一个有限个变量构成的随机变量,那么对任意可行赋值θ,有:E[f(X)]≤f[E(X1), E(X2), ..., E(Xn)],这称为统计不等式。
2、博弈论不等式:博弈论中,假设f(x)是一个单局博弈积分函数,X是一个等概率随机策略,则Frame‐Stewart不等式规定:E[f(X)]≤f[E(X1), E(X2), ..., E(Xn)],这称为博弈论不等式。
3、期望函数不等式:期望函数不等式指的是在一个期望函数的类中,存在某种非负函数f,有:E[f(X)]≤f(E(X)),这就是期望函数不等式。
Gronwall不等式

格朗沃尔不等式在数学中,格朗沃尔引理或格朗沃尔不等式说明了对于满足一定的微分方程或积分方程的函数,有相应的关于此微分方程或积分方程的不等式。
格朗沃尔不等式有两种形式,分别是积分形式和微分形式。
积分形式下的不等式可以有几种不同的写法。
格朗沃尔不等式常常被用来估计常微分方程的解的取值范围。
比如,它可以用来证明初值问题的解的唯一性(见柯西-利普希茨定理)。
格朗沃尔不等式的名称来自多玛·哈肯·格朗沃尔。
格朗沃尔是一位瑞典的数学家,后来移居美国。
格朗沃尔不等式的微分形式首先由格朗沃尔在1919年证明[1]。
而积分形式则是由理查德·贝尔曼(Richard Bellman)在1943年证明[2]。
微分形式设I是一个实数区间,记为:[a, ∞) 或[a, b] 或[a, b),其中a < b。
又设β和u为定义在I上的实数值的连续函数。
假设u 是一个在I的内部(也就是不包括端点)可微的函数,并且满足如下的微分不等式:那么对于所有的,函数u都小于等于以下微分方程的解:注意:不等式对函数β和u的符号没有任何要求。
证明如果设是以下微分方程其中v(a) = 1 的解,那么对所有的t都有v(t) > 0,因此根据复合函数求导法则中的除法定则:对所有的t > a成立,因此于是格朗沃尔不等式得证。
积分形式设I是一个实数区间,记为:[a, ∞) 或[a, b] 或[a, b),其中a < b。
又设α、β和u为定义在I上的实数值的函数。
假设β和u是连续的,则有:∙(a) 如果β是非负函数并且u满足如下的积分不等式:,那么(b) 如果在之前的条件下,α还是一个常数,那么注意:∙不等式的成立条件里并没有限制α和u的符号;∙相比于微分形式,积分形式中对函数u的可微性没有做要求;证明(a) 定义则运用复合函数求导法则中的乘法法则、链式法则、指数函数的求导法则以及微积分基本定理,可以得到:由于注意到括号中的部分小于α,可以得到相应的不等式,并进行积分。
克劳修斯不等式

克劳修斯不等式
卡诺定理指出,任何一个热机的效率都不能大于工作在相同的两个高温热源和低温热源之间的可逆卡诺热机的效率,即
或
式中的等号只适用于可逆卡诺循环,不等号则适用于不可逆循环。
由上式可得下面的关系式
或
上式中的Q
1和Q
2
都是正的,若把吸收的热量记为Q,把放出的热量记为一Q,则
上式便可写成如下形式:
式中Q
1是工作物质从温度为T
1
的高温热源处所吸收的热量;Q
2
是从温度为T
2
的
低温热源处所吸收的热量。
对可逆卡诺循环,上式应取等号;对不可逆循环,则上式应取不等号。
如果工作物质(即系统)的状态是连续改变的,则可以认为它与一系列连续改变温度的高温热源和低温热源进行热量交换,且每次交换微量的热量dQ,就可用下列积分形式:
这个公式称克劳修斯等式,不等式,其中取“=”时,即克劳修斯等式,取“<”号时即克劳修斯不等式。
它是热力学第二定律最普遍的数学表达式。
这里,热量不写成dQ,而写成dQ是因为传递热量与具体经历的过程有关。
从数学上讲,dQ不是一个全微分,故写成dQ,以此表示和全微分
说,这个积分等于零,对不可逆循环,这个积分小于零。
涉及jensen函数的不等式

涉及jensen函数的不等式涉及Jensen函数的不等式是一种统计学和数学中应用十分广泛的不等式,其源于由著名的数学家J.L. Jensen 在1906年提出的定理,也被称为Jensen不等式。
这个不等式最早由Jensen(1906)提出,它是以实立方体上一点(x,y,z)为例来推导出来的,Jensen函数的不等式可以用来阐明概率变量之间的关系,它表明如果某一变量是另一变量的函数,那么它们之间必然存在不等式关系。
Jensen不等式得出的结论是:如果一个变量X是另一个变量Y的函数,则X和Y之间存在不等式关系。
它的条件是,对于X的任意取值,Y的取值都要大于等于X的取值,或者说,Y的函数值要大于等于X的函数值。
Jensen不等式的一般形式是:E[f(X)]≤f(E[X]),其中E[X]表示X的期望值,而f(X)表示X的函数值。
Jensen不等式是求解多变量函数最大值和最小值的重要工具,并在信息论、统计学、经济学、运筹学、控制论、图论和机器学习等领域有着广泛的应用。
Jensen函数的不等式可以用来分析多变量函数的性质,它有助于推导出一些重要的不等式,如Cauchy-Schwarz不等式和Hölder不等式,以及Markov不等式等。
此外,Jensen不等式也常常用于证明优化问题的最优解。
它可以用来证明某种约束优化问题的最优解是一个唯一最优解,同时也可以用来证明某种无约束优化问题的最优解是一个唯一最优解。
Jensen函数的不等式还可以用来证明某些重要的概率不等式,比如Chebyshev不等式和Markov不等式。
它还可以用来研究多变量函数的极值特性,这有助于证明某些函数的最大值和最小值的存在性。
Jensen函数的不等式也可以用来证明某些重要的最优化问题,比如最小二乘法拟合问题也可以使用Jensen函数的不等式来求解。
总之,Jensen函数的不等式是一种非常重要的不等式,它在概率论、统计学、经济学、运筹学、机器学习等领域有着广泛的应用,它可以用来证明某些重要的不等式,以及求解优化问题的最优解等。
赫尔德不等式知乎

赫尔德不等式知乎赫尔德不等式是数学中的一种重要不等式,它在数学分析、概率论、统计学等领域都有广泛的应用。
在知乎上,也有很多关于赫尔德不等式的讨论和解答。
本文将从数学、应用和解答三个方面来介绍赫尔德不等式在知乎上的应用和讨论。
数学赫尔德不等式是数学中的一种重要不等式,它是由德国数学家赫尔德于1889年提出的。
赫尔德不等式的形式为:对于任意的实数a1,a2,...,an和b1,b2,...,bn,以及任意的p,q>0,满足1/p+1/q=1,则有:(a1b1+a2b2+...+anbn)≤(a1^p+a2^p+...+an^p)^(1/p)×(b1^q+b2^q+...+bn^q)^ (1/q)这个不等式的证明比较复杂,需要运用到一些高等数学知识,但是它的应用却非常广泛。
应用赫尔德不等式在数学分析、概率论、统计学等领域都有广泛的应用。
在数学分析中,赫尔德不等式可以用来证明一些重要的定理,如柯西-施瓦茨不等式、霍尔德不等式等。
在概率论中,赫尔德不等式可以用来证明一些重要的概率不等式,如马尔可夫不等式、切比雪夫不等式等。
在统计学中,赫尔德不等式可以用来证明一些重要的统计不等式,如柯西-施瓦茨不等式、切比雪夫不等式等。
解答在知乎上,也有很多关于赫尔德不等式的讨论和解答。
有些人会问,赫尔德不等式有什么应用?有些人会问,赫尔德不等式的证明过程是什么?还有些人会问,赫尔德不等式和其他不等式有什么区别?对于这些问题,知乎上的数学专家们都给出了详细的解答。
他们用通俗易懂的语言,解释了赫尔德不等式的应用和证明过程,还比较了赫尔德不等式和其他不等式的区别。
这些解答不仅帮助了提问者,也让更多的人了解了赫尔德不等式的重要性和应用价值。
总结赫尔德不等式是数学中的一种重要不等式,它在数学分析、概率论、统计学等领域都有广泛的应用。
在知乎上,也有很多关于赫尔德不等式的讨论和解答。
通过这些讨论和解答,我们可以更好地了解赫尔德不等式的应用和证明过程,也可以更好地掌握数学知识。
jensen不等式的理解

jensen不等式的理解Jensen不等式的理解Jensen不等式是数学中的一种重要不等式,被广泛应用于概率论、统计学和优化理论等领域。
它是由丹麦数学家约翰·约瑟夫·昂森(Johann Jensen)在1906年提出的,因此被称为Jensen不等式。
Jensen不等式的核心思想是描述凸函数与其自变量的关系。
在数学中,凸函数是一种具有特殊性质的函数,它的弧线上的任意两点连线都位于弧线上方或者弧线上,简单来说就是函数图像上的任意两点之间的线段都位于或者在函数图像上方。
Jensen不等式的表述形式如下:设函数f(x)在区间[a,b]上连续,且f(x)是凸函数,那么对于[a,b]上的任意n个实数x1,x2, (x)以及非负系数λ1,λ2,...,λn且满足λ1+λ2+...+λn=1,有以下不等式成立:f(λ1x1+λ2x2+...+λnxn) ≤ λ1f(x1)+λ2f(x2)+...+λnf(xn)这个不等式的意义在于描述了凸函数的线性性质。
它表明,对于凸函数而言,函数值的线性组合在函数值上是保持凸性的。
也就是说,凸函数的函数值的线性组合不会超过对应自变量的函数值的线性组合。
为了更好地理解Jensen不等式,我们可以通过一个具体的例子来说明。
假设有一家公司要根据员工的绩效进行奖金发放,奖金的总额为100万元。
根据Jensen不等式,假设有三个员工,他们的绩效分别为x1、x2和x3,且绩效的权重分别为λ1、λ2和λ3。
那么根据Jensen不等式,奖金的分配方式应该满足以下条件:λ1x1+λ2x2+λ3x3 ≤ λ1f(x1)+λ2f(x2)+λ3f(x3)其中,f(x)是奖金与绩效之间的函数关系,可以是线性函数、指数函数或者其他函数。
这个不等式告诉我们,根据员工的绩效以及绩效的权重,我们可以通过函数f(x)来确定每个员工所获得的奖金。
而Jensen不等式则保证了这种奖金分配方式是公平且符合凸函数的性质。
Jensen不等式

凸函數、Jensen 不等式與Legendre 變換一、前言凸函數的出現絕非偶然,在古典力學中的動能,就是最自然直接的凸函數,其他如熵(entropy)……等皆是,當然從幾何的角度而言就是拋物線。
近代分析由於受凸分析研究所得之進展的影響,使得在非線性分析,非線性微分方程皆有長足之進展與突破,其中較重要的就是逐漸將非線性 (nonlinearity)視為一個體,而非只是線性化 (linearization) 而已。
凸函數是如此地美麗且重要,而一般教科書只是提個定義然後定理之後便是習題。
對於這樣的數學,我們實在不滿足地無法忍受,畢竟數學要教導我們聰明並學習如何去思考。
因此本文秉持此原則,將著重於幾何與物理直觀,並與一些相關聯的領域作一些對應,以思索在我們前面的那些數學巨人是如何思考問題。
二、凸函數我們從凸函數之定義開始定義:f為一定義在區間上之一實值函數 (real-valuedfunction)若對任意的, ,f滿足下式則稱f為一凸函數 (convex function)。
圖一其幾何意義為連接(a,f(a)),(b,f(b))兩點的弦,永遠在弧y=f(x)之上(圖一)。
利用分點公式我們可將(1)式表為下列之形式:由(2)式可得即圖二其幾何意義從圖形上之斜率可知。
我們的主要目的在於如何將(1)式推廣至一般情形。
首先同時也是自然而然地(在數學上 2 與n是沒有差別的)將(1)式推廣至n個點x1,…,x n。
(可用歸納法)其中, , ,。
有時候我們(有目的地)令則(4)式可改寫為這就是 Jensen 不等式之一形式。
若取特殊的p i,例如:則(6)式可表為典型的凸函數有底下的類型:在尚未做進一步推廣前,Jensen 不等式最直接的應用就是幾何平均與算數平均之關係;讀者可自行練習例題 1:(幾何-算數平均)試證(a)(b)三、Jensen 不等式的意義我們感興趣的問題是關於 Jensen 不等式(6)式或(7)式之幾何意義與物理意義,首先介紹質量中心:假設平面上有n個點且它們皆有相同之質量,其位置向量為,,則質量中心之位置向量為或這意思是從點到各點之向量彼此互相抵消。
赫尔德不等式

赫尔德不等式在赫尔德共轭的定义中,1/∞意味着零。
如果1 ≤ p,q < ∞,那么||f ||p和||g||q表示(可能无穷的)表达式:以及如果p = ∞,那么||f ||∞表示|f |的本性上确界,||g||∞也类似。
在赫尔德不等式的右端,0乘以∞以及∞乘以0意味着 0。
把a > 0乘以∞,则得出∞。
赫尔德不等式有许多证明,主要的想法是杨氏不等式。
如果||f ||p = 0,那么fμ-几乎处处为零,且乘积fgμ-几乎处处为零,因此赫尔德不等式的左端为零。
如果||g||q = 0也是这样。
因此,我们可以假设||f ||p > 0且||g||q > 0。
如果||f||p = ∞或||g||q = ∞,那么不等式的右端为无穷大。
因此,我们可以假设||f ||p和||g||q位于(0,∞)内。
如果p= ∞且q = 1,那么几乎处处有|fg| ≤ ||f||∞ |g|,不等式就可以从勒贝格积分的单调性推出。
对于p = 1和q= ∞,情况也类似。
因此,我们还可以假设p, q∈ (1,∞)。
分别用f和g除||f ||p||g||q,我们可以假设:我们现在使用杨氏不等式:对于所有非负的a和b,当且仅当a = b时等式成立。
因此:两边积分,得:这便证明了赫尔德不等式。
在p∈ (1,∞)和||f ||p = ||g||q = 1的假设下,等式成立当且仅当几乎处处有|f |p = |g|q。
更一般地,如果||f ||p和||g||q位于(0,∞)内,那么赫尔德不等式变为等式,当且仅当存在α, β > 0(即α = ||g||q 且β = ||f ||p),使得:μ-几乎处处 (*) ||f ||p = 0的情况对应于(*)中的β = 0。
||g||q = 的情况对应于(*)中的α = 0。
如何理解克劳修斯不等式

如何理解克劳修斯不等式引言克劳修斯不等式是数学中的一个重要不等式,它在概率论、统计学和信息论等领域有着广泛的应用。
本文将详细介绍克劳修斯不等式的定义、推导过程以及其应用场景,帮助读者深入理解该不等式。
1. 克劳修斯不等式的定义克劳修斯不等式是概率论中用来估计随机变量之间关系的重要工具。
对于两个实数随机变量X和Y,克劳修斯不等式给出了它们联合概率分布和边缘概率分布之间的关系,即:H(X,Y) ≤ H(X) + H(Y)其中,H(X,Y)表示X和Y的联合熵,H(X)表示X的熵,H(Y)表示Y的熵。
2. 克劳修斯不等式的推导为了推导克劳修斯不等式,需要引入香农熵的概念。
2.1 香农熵香农熵是信息论中衡量随机变量不确定性的度量。
对于一个离散随机变量X,其熵定义为:H(X) = -∑P(x)logP(x)其中,P(x)表示随机变量X取值为x的概率。
2.2 联合熵与条件熵对于两个随机变量X和Y,它们的联合熵H(X,Y)定义为:H(X,Y) = -∑∑P(x,y)logP(x,y)其中,P(x,y)表示随机变量X取值为x且随机变量Y取值为y的概率。
条件熵H(Y|X)表示在已知随机变量X的取值的条件下,随机变量Y的不确定性。
它定义为:H(Y|X) = -∑∑P(x,y)logP(y|x)其中,P(y|x)表示在随机变量X的取值为x的条件下,随机变量Y的取值为y的概率。
克劳修斯不等式的推导基于以下定理:H(X,Y) = H(X) + H(Y|X)将联合熵H(X,Y)的定义代入上式,可以得到:H(X) + H(Y|X) = -∑∑P(x,y)logP(x,y) = -∑∑P(x,y)(logP(x) + logP(y|x))将右侧的式子进行展开并重新排序,得到:-∑∑P(x,y)logP(x) - ∑∑P(x,y)logP(y|x)第一项是关于X的熵,第二项是关于Y的条件熵。
根据熵的定义可以得知,它们都是非负的。
因此,我们有:H(X,Y) ≤ H(X) + H(Y|X)即克劳修斯不等式成立。
反赫尔德不等式

反赫尔德不等式反赫尔德不等式是一种数学定理,它给出了一种关于线性空间中两个向量的关系。
具体来说,对于任意两个向量x和y,它给出了以下不等式:||x+y||^2 + ||x-y||^2 >= 2(||x||^2 + ||y||^2)这个不等式通常用来证明其他定理或者优化算法。
反赫尔德不等式也经常被用在几何学和波动力学中,在这些领域中,它可以用来证明一些重要的定理,例如点积不等式和欧几里得不等式。
反赫尔德不等式是由德国数学家阿尔伯特·赫尔德(Albert Heine)于1909年首先提出的。
在线性代数中,反赫尔德不等式是一个基本的工具,可以用来证明向量空间中的一些性质,例如范数的三角不等式。
举个例子,假设有两个向量x = (1,2,3) 和y = (4,5,6)。
我们可以用反赫尔德不等式来证明以下不等式:||x+y||^2 + ||x-y||^2 >= 2(||x||^2 + ||y||^2)首先, 我们计算出x+y = (1+4, 2+5, 3+6) = (5,7,9), x-y = (1-4, 2-5, 3-6) = (-3,-3,-3)||x+y|| = sqrt(5^2 + 7^2 + 9^2) = sqrt(169) = 13, ||x-y|| = sqrt(-3^2 + -3^2 + -3^2) = sqrt(27) = 3.同时,||x||=sqrt(1^2+2^2+3^2)=sqrt(14),||y||=sqrt(4^2+5^2+6^2)=sqrt(77)所以, 我们可以得到:13^2 + 3^2 >= 2(14+77)169 + 9 >= 196178 >= 196此时不等式左边与右边不等, 所以我们发现这个不等式是不成立的这只是一个简单的例子, 在实际应用中, 反赫尔德不等式可能会更加复杂, 但原理是相同的.。
对偶律德摩根公式

对偶律德摩根公式对偶律和德摩根公式是数学逻辑中的重要概念,对于我们理解和处理逻辑关系有着关键的作用。
先来说说对偶律。
对偶律简单来说,就像是逻辑世界里的一对“双胞胎”,它们有着相似但又略有不同的特点。
比如说,在集合运算中,“并”和“交”这对兄弟就遵循着对偶律。
我记得有一次给学生们讲这个知识点的时候,有个小同学一脸迷茫地问我:“老师,这对偶律到底有啥用啊?”我笑了笑,给他举了个例子。
假设我们有两个班级,一班喜欢数学的同学组成了集合 A,二班喜欢数学的同学组成了集合B。
那么两个班中喜欢数学的同学的总和,就是 A 并 B。
而两个班中都喜欢数学的同学,就是 A 交 B。
通过这个小小的例子,他似乎有点明白了。
再说说德摩根公式。
这德摩根公式啊,就像是逻辑世界里的一把神奇钥匙,可以帮助我们打开复杂逻辑关系的大门。
它把“或”与“且”的否定巧妙地联系了起来。
还记得有一回,在课堂上我出了一道题:假设全集 U 是所有整数,集合 A 是所有偶数,集合 B 是所有奇数。
让同学们求(A 并 B)的补集和(A 的补集)交(B 的补集)。
一开始,大家都有点摸不着头脑,经过我一步步的引导,利用德摩根公式,终于算出了答案,同学们脸上露出了恍然大悟的表情。
在实际应用中,对偶律和德摩根公式经常会一起出现,帮助我们解决各种各样的逻辑问题。
比如说在计算机编程中,判断条件的设置就经常会用到这两个公式。
又比如在电路设计中,通过这两个公式可以优化电路的逻辑结构,提高效率。
其实,学习对偶律和德摩根公式就像是在搭建一座逻辑的大厦。
每一个概念、每一道例题都是一块坚实的砖头,只有把它们都砌好了,这座大厦才能稳固。
而我们在这个过程中,也能锻炼自己的思维能力,让我们的大脑变得更加聪明、灵活。
对于初学者来说,可能一开始会觉得这些公式有点抽象、难以理解。
但别担心,只要多做一些练习题,多结合实际的例子去思考,慢慢地就能掌握其中的精髓啦。
总之,对偶律和德摩根公式虽然看起来有点复杂,但只要我们用心去学,就一定能攻克它们,让我们的逻辑思维更上一层楼!。
德摩根律——精选推荐

德摩根律徳摩根律(对偶律)德·摩根律是属于逻辑学的定律。
德·摩根定律(或称德·摩根定理)是形式逻辑中有关否定所描述的系统方式中的逻辑运算符对偶对的一系列法则。
由此引出的关系也就被称为“德·摩根二重性”。
德·摩根首先发现了在命题逻辑中存在的这些关系而他的发现也影响了乔治·布尔从事的逻辑问题代数解法的研究,这巩固了德·摩根作为该定律的发现者的地位,尽管亚里士多德也曾注意到类似现象、且这也为古希腊与中世纪的逻辑学家熟知。
徳摩根律(对偶律)德摩根律(德·摩根)的公式表述DeMorgan's Theorem 1.Cs (A∩B)=CsA U CsB2.Cs (A∪B)=CsA ∩CsB文字表述1.集合A与集合B的交集的补集等于集合A的补集与集合B的补集的并集;2.集合A与集合B的并集的补集等于集合A的补集与集合B的补集的交集。
发展历程与表达形式奥古斯都•德•摩根首先发现了在命题逻辑中存在着下面这些关系:非(p 且 q)=(非p)或(非q)非(p 或 q)=(非p)且(非q)德•摩根的发现影响了乔治•布尔从事的逻辑问题代数解法的研究,这巩固了德•摩根作为该规律的发现者的地位,尽管亚里士多德也曾注意到类似现象、且这也为古希腊与中世纪的逻辑学家熟知(引自bocheński《形式逻辑历史》)。
形式逻辑中此定律表达形式:\neg(p\wedge q)=(\neg p)\vee(\neg q)\neg(p\vee q)=(\neg p)\wedge(\neg q)在集合论中:(a\cap b)^c=a^c\cup b^c(a\cup b)^c=a^c\cap b^c.在经典命题逻辑的外延中,此二元性依然有效(即对于任意的逻辑运算符,我们都能找他它的对偶),由于存在于调节否定关系的恒等式中,人们总会引入作为一个算符的德•摩根对偶的另一个算符。
克劳修斯不等式PPT资料优选版

= 可逆循环
克劳修斯 不等式
< 不可逆循环
> 循环不可能
克劳修斯不等式总结
正循环(可逆、不可逆)
Q 0 吸热
反循环(可逆、不可逆)
Q 0 放热
Q
T
0
可逆 = 不可逆 <
克劳修斯不等式例题
A 热机是否能实现
Q
T
2000 1000
800 300
可能
0.667kJ/K 0
1000 K 2000 kJ
如果:W=1500 kJ
Q
T
2000 1000
500 300
不可能
0.333kJ/K 0
A 1200 kJ 1500 kJ
800 kJ 500 kJ
300 K
注意:热量的正和负是站在循环的立场上
克劳修斯不等式
研究对象:循环
实际热机的循环都是不可逆的,尽可能地 使实际循环接近可逆循环是提高循环热效率的 基本途径。循环不可逆性的大小如何度量?
用途:判断一个循环 是否可能、 是否可逆
克劳修斯不等式不可逆
循环分割成多个微元循环
根据卡诺定理推论二有
t
1
q2 q1
1
T2 T1
q2 T2 q1 T1
q2 q1 T2 T1
q1 q2 0(q为绝对值)
T1 T2
q2 q1 0(q为代数值)
T2 T1
克劳修斯不等式
q
任何可逆循环 0 正循环(可逆、不可逆)
热二律任∴表何对达不任式可意之逆循一环循环 TqTTq 0 0 用A用AA用正 反反如循正正用 <正用反反AA如<如A用正实<正用不不不一一一循循循果环循循一循一循循果果一循际循一热热热热热热可可可组 组 组 环环 环 : 不 环 环 组环 组 环 环 : : 组 环 热 环 组机机机机机机逆逆逆可可可( ((W可((可 (可((WW可(机(可是是是是是是循循循===逆逆逆可 可可逆可可逆 可逆可可逆可的可逆否否否否否否111环环环绝绝绝逆 逆逆性逆逆绝 逆绝逆逆绝逆循逆绝555能能能能能能000热热热、 、、的、、热 、热、、热、环、热实实实实实实000 线线线不 不不大不不线 不线不不线不都不线kkk现现现现现现JJJ将将将可 可可小可可将 可将可可将可是可将不不不逆 逆逆如逆逆不 逆不逆逆不逆不逆不可可可)))何))可)可))可)可)可逆逆逆度逆 逆逆逆逆循循循量循 循循的循环环环?环 环环,环分分分分 分分尽分割割割割 割割可割成成成成 成成能成多多多多 多多地多个个个个 个个使个微微微微 微微实微元元元元 元元际元循循循循 循循循循环环环环 环环环环接近可逆循环是提高循环热效率的基本途径。
