固体物理学(题库,黄昆著)
黄昆版固体物理学课后答案解析答案

《固体物理学》习题解答黄昆 原着 韩汝琦改编 (陈志远解答,仅供参考)第一章 晶体结构1.1、解:实验表明,很多元素的原子或离子都具有或接近于球形对称结构。
因此,可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。
这样,一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。
它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比,即:晶体原胞的空间利用率, VcnVx = (1)对于简立方结构:(见教材P2图1-1)a=2r , V=3r 34π,Vc=a 3,n=1∴52.06r 8r34a r 34x 3333=π=π=π= (2)对于体心立方:晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯= (3)对于面心立方:晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4,Vc=a 3(4)对于六角密排:a=2r 晶胞面积:S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积:V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个 (5)对于金刚石结构,晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 31.2、试证:六方密排堆积结构中633.1)38(a c 2/1≈= 证明:在六角密堆积结构中,第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形,第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切,于是: NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。
…1.3、证明:面心立方的倒格子是体心立方;体心立方的倒格子是面心立方。
证明:(1)面心立方的正格子基矢(固体物理学原胞基矢):123()2()2()2a a j k a a i k a a i j ⎧=+⎪⎪⎪=+⎨⎪⎪=+⎪⎩由倒格子基矢的定义:1232()b a a π=⨯Ω31230,,22(),0,224,,022a aa a a a a a a a Ω=⋅⨯==,223,,,0,()224,,022i j ka a a a a i j k a a ⨯==-++ 同理可得:232()2()b i j k ab i j k aππ=-+=+-即面心立方的倒格子基矢与体心立方的正格基矢相同。
(黄昆版)固体物理试题2

《固体物理学》模拟试题 2(时间 120 分钟)
题号
一
二
三
四
五
得分
得分
1.晶格常数为 a 的体心立方晶格,原胞体积Ω等于
。
2.金刚石结构中,相邻两共价键之间的夹角为 cosθ =
(or θ = )。
3.含有 N 个初基原胞的铜晶体,晶格振动的声学波支数为
, 晶格振动的光学波支数
为
。
4.由 N 个原胞组成的简单晶体,不考虑能带交叠,则每个 S 能带可容纳的电子数为
2. 什么叫简正振动模式?简正振动数目、格波数目或格波振动模式数目是否是一回事?
《固体物理学》试卷 共 !语法错误,)页 第
3.四角晶系中为什么没有底心四角和面心四角点阵?
4.在布里渊区边界上电子的能带有何特点?
得分 评卷人 复核人 四、计算题(每小题 10 分,共 30 分)
1. 有一由同种原子组成的晶格,其固体物理学原胞的基失为:
。
5.三维晶格振动按德拜模型,模式密度与 成正比。
6.晶体的价带处于近满带时,其导电性质可归结为“空穴”在外电场作用下的运动。空穴有如下
基本性质:
。
得分 评卷人 复核人 二、单项选择题(将正确的选项号如 A…填入括号 内,每小题 2 分,共 12 分)
1. 一个二维简单正交晶格的第一布里渊区形状是( )。 A、长方形 B、正六边形 C、圆 D、 圆球
a 1 =3i,a 2 =3j,a 3 =1.5(i+j+2k)。 (1)此晶格属什么晶系?是哪种布喇菲点阵?求单胞基矢; (2)求其倒格子基矢; (3)(1,1,1)晶列与(1,-1,1)晶列之间的夹角是多少?
!语法错误,)页
固体物理习题第一章(黄昆)资料

对于构成金刚石结构,n= 4 8 1 6 1 8 ,V= ( 8r )3,
则有:x=
8* 4 πr3 3
( 8r )3
3 16
π
8
≈0.34
2
3
3
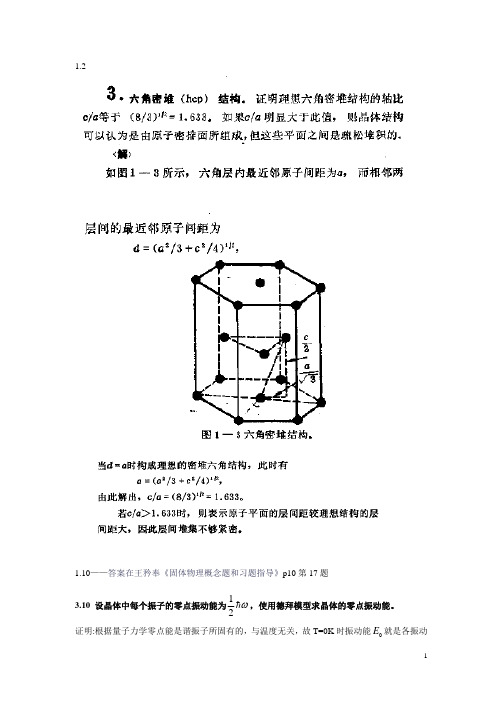
1.2 试证六方密排堆积结构中 c (8 )1/ 2 1.633. a3
证明:如图所示,六方密排中取出一个正四
面体,有c=2h
在正四面体中有:
]
a1VC
(2 )3
VC
即倒格子原胞体积为(2)3 Vc .
1.5指证数明为(:h倒1h格2h子3)矢的量晶面G系 h.1b1 h2b2 h3b3 垂直于密勒
证明:如图所示,ABC是晶面族(h1h
2
h
)
3
中离原点最近的一晶面.
因为
AC
( a3
a1 )
BC
( a 3
a2 )
h3 h1
k
0 a2i
i (a3 a1) 0
j 0
k
a a2 j
00a
a00
i (a1 a2) a
j 0
k
0 a2k
0a0
代入有:b1
2
a
i ,b2
2
a
j , b3
2
k
a
2
2 2
倒格子矢量:G hb1 kb2 lb3 h
i k a
a
j l
k a
则密勒指数为(hkl)的晶面系,面间距d为:
2
a -a a
2
22
代入有:b1
2
a2 ( 2 a3
j
k)
2
a
(
j
k)
黄昆版固体物理学课后答案解析答案

《固体物理学》习题解答黄昆 原着 韩汝琦改编 (陈志远解答,仅供参考)第一章 晶体结构1.1、解:实验表明,很多元素的原子或离子都具有或接近于球形对称结构。
因此,可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。
这样,一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。
它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比,即:晶体原胞的空间利用率, VcnVx = (1)对于简立方结构:(见教材P2图1-1)a=2r , V=3r 34π,Vc=a 3,n=1∴52.06r 8r34a r 34x 3333=π=π=π= (2)对于体心立方:晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯= (3)对于面心立方:晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4,Vc=a 3(4)对于六角密排:a=2r 晶胞面积:S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积:V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个 (5)对于金刚石结构,晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 31.2、试证:六方密排堆积结构中633.1)38(a c 2/1≈= 证明:在六角密堆积结构中,第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形,第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切,于是: NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。
…1.3、证明:面心立方的倒格子是体心立方;体心立方的倒格子是面心立方。
证明:(1)面心立方的正格子基矢(固体物理学原胞基矢):123()2()2()2a a j k a a i k a a i j ⎧=+⎪⎪⎪=+⎨⎪⎪=+⎪⎩由倒格子基矢的定义:1232()b a a π=⨯Ω31230,,22(),0,224,,022a aa a a a a a a a Ω=⋅⨯==,223,,,0,()224,,022i j ka a a a a i j k a a ⨯==-++ 同理可得:232()2()b i j k ab i j k aππ=-+=+-即面心立方的倒格子基矢与体心立方的正格基矢相同。
黄昆固体物理习题-第一章 晶体结构

第一章习题参考解答解答:设立方晶格的边长为a,一个晶胞中的原子数为n,原子球半径为R,晶胞体积为V,则致密度(或叫填充率)K为:V Rn K3 34π•= ch1.1 题略3343===0.52(2)6R K R ππ(1) 简单立方,晶胞内含有一个原子n=1,原子球半径为R ,立方晶格的顶点原子球相切,立方边长a=2R ,体积为(2R)3,所以VR n K 334π•=(2)体心立方晶胞内有2个原子,n=2,原子球半径为R ,晶胞边长为a ,立方晶格的体对角线原子球相切,体对角线长为4个原子半径,所以ππ83)34(342,3433=⨯=R R K R =0.68ππ83)34(342,3433=⨯==R R K R a(3)面心立方晶胞内有4个原子,晶胞的面对角线原子球相切,面对角线长度为4个原子半径,立方体边长为a ,ππ62)24(34433=⨯=R RK =0.74,24R a =(4)六角密排原胞内中含2个原子,正四面体四个顶点处的原子球相切,边长为a ,六角柱高h =0.74ππ62322]321)2[(34223=•⨯⨯⨯=a R R K hs 斜边2R=a[(2R)2-[(2Rsin60)х2/3]2=(h/2)2底边竖直边ππ16383433=⨯=a R K =0.34(5)金刚石在单位晶格中含有8个原子,碳原子最近邻长度2R 为体对角线1/4长,体对角线为,38a R =证明1:设六角层内最近邻原子间距为a ,相邻两层间的最近邻为d ,则633.13/8,])2()3[(,])2()3[(21222122≈=+==+=a c c a a a d c a d 由此解出此时有构,时构成理想的密堆积结当ch1.2 题略a d证明2:设六角层内最近邻原子间距为a,相邻两层间的最近邻为d,则a dch1.3 题略解:对于体心立方,原胞基矢为:对于体心立方原胞体积为:1.3)(21k j a a +=)(22i k a a +=)(23j i a a +=对于面心立方,原胞基矢为:根据倒格子基矢定义,并将体心原胞基矢代入计算之,可得:将计算所得到的倒格子基矢与面心立方原胞基矢相同,可知体心立方的倒格子是面心立方。
固体物理学_答案

《固体物理学》习题解答黄昆 原著 韩汝琦改编第一章 晶体结构1.1、解:实验表明,很多元素的原子或离子都具有或接近于球形对称结构。
因此,可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。
这样,一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。
它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比,即:晶体原胞的空间利用率, VcnVx = (1)对于简立方结构:(见教材P2图1-1)a=2r , V=3r 34π,Vc=a 3,n=1 ∴52.06r 8r34a r 34x 3333=π=π=π= (2)对于体心立方:晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯=(3)对于面心立方:晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4,Vc=a 374.062)r 22(r 344a r 344x 3333≈π=π⨯=π⨯= (4)对于六角密排:a=2r 晶胞面积:S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积:V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个 74.062r224r346x 33≈π=π⨯= (5)对于金刚石结构,晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 334.063r 338r 348a r 348x 33333≈π=π⨯=π⨯=1.2、试证:六方密排堆积结构中633.1)38(a c 2/1≈= 证明:在六角密堆积结构中,第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形,第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切,于是: NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。
黄昆版固体物理学课后答案解析答案

《固体物理学》习题解答黄昆 原著 韩汝琦改编 (陈志远解答,仅供参考)第一章 晶体结构1.1、解:实验表明,很多元素的原子或离子都具有或接近于球形对称结构。
因此,可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。
这样,一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。
它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比,即:晶体原胞的空间利用率, VcnVx = (1)对于简立方结构:(见教材P2图1-1)a=2r , V=3r 34π,Vc=a 3,n=1 ∴52.06r 8r34a r 34x 3333=π=π=π= (2)对于体心立方:晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯= (3)对于面心立方:晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4,Vc=a 374.062)r 22(r 344a r 344x 3333≈π=π⨯=π⨯= (4)对于六角密排:a=2r 晶胞面积:S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积:V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个 74.062r224r 346x 33≈π=π⨯= (5)对于金刚石结构,晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 334.063r 338r 348a r 348x 33333≈π=π⨯=π⨯=1.2、试证:六方密排堆积结构中633.1)38(a c 2/1≈= 证明:在六角密堆积结构中,第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形,第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切,于是: NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。
习题5固体物理习题黄昆版共25页

谢谢你的阅读
❖ 知识就是财富 ❖ 丰富你的人生
71、既然我已经踏上这条道路,那么,任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远,吾将上下而求索。——屈原 75、内外相应,言行相称。—一条件。——黑格 尔 7、纪律是集体的面貌,集体的声音, 集体的 动作, 集体的 表情, 集体的 信念。 ——马 卡连柯
8、我们现在必须完全保持党的纪律, 否则一 切都会 陷入污 泥中。 ——马 克思 9、学校没有纪律便如磨坊没有水。— —夸美 纽斯
10、一个人应该:活泼而守纪律,天 真而不 幼稚, 勇敢而 鲁莽, 倔强而 有原则 ,热情 而不冲 动,乐 观而不 盲目。 ——马 克思
习题6固体物理习题黄昆版

2m q k / 2m
*
3 2m q E
* 2
295K
1 1.61 10
3
8
6.21 10 S
7
20 K
1 0.038 10
2
8
2.63 10 S
9
Ag 10.5 10 kg / m
3
Z 107.87
3
3
近自由电子近似情况下
电阻率=1.61×10-6 · cm(295 K)
0.038×10-6 · cm(20 K)
解:(1)Ag的费米能为
EF
2 2 2
( 3 n ) 3
34
2
(3
M 原子
2
)3
2
2m ( 1.055 10 )
2m
2
(1)
2 9.11 10
19
31
( 3
3
10
6 2
2 3 3.14 )
/( 6.022 10
23
)
5.95 10J Βιβλιοθήκη 3.72e V费米温度TF为
TF EF kB 4.31 10 K
4
6.2 在低温下金属K的摩尔电子热容的实验结果为 Ce=2.08 mJ/mol· K。在自由电子气模型下估算K 的费米温度TF和费米面上的能态密度N(EF) 解:摩尔电子热容,考虑材料含一摩尔K原子, 电子数N=NA,电子热容为
10.5 10 107.87 10
3
3
10
6 2 23
2 3 3.14 )
/( 6.022 10
(黄昆版)固体物理试题4答案

0 度 TK 答:
时有何差别?简要说明原因。 时,绝缘体的热容量遵从 T
3
0 温度 TK 定律,即
CT V :
0 而金属的热容量在温度 TK
时,
3
;
。 (3分) 造成差别的原因在于金属中有大量的近自由电 子,它们对热容量的贡献为
CTbT V
3
CT V :
图1.1
2.(5分)温度一定,一个光学波的声子数目多 呢, 还是声学波的声子数目多?而对同一个振动 模式, 温度高时的声子数目多呢, 还是温度低 时的声子数目多? 答: 频率为 的格波的(平均) 声子数为
n
hoB / kT h AB / kT
1 e
h / kT B
1
因为光学波的频率 O 比声学波的频率 A 高,
(3分)
2.(7分)NaCl型离子晶体排斥势的幂指数为:
n 1,
72 00 R 4 e2 (M为马德龙常数,K为体弹模量)
证明:
Q 晶体平衡时的体积弹性模量为
V
2 dU dV 2
V0
e2 B A VNr 4 0 r n ), 其中, e 2 n 1 dU r0 0 418 00 R 4 平衡条件 dr ,结合诸式可得 44 41872 RR 0000 n 11 22 ee
A UrN 3 2 ,U=N( r
3.(7分)在经典近似下,晶格的自由能可以表示为:
(3分)
(4分)
FUkT 0
证明: 晶格的自由能为
B
ln kT
q
h
B
经典极限相当于(温度较高) 所以
《固体物理学(黄昆)》课后习题答案(2)
1.10——答案在王矜奉《固体物理概念题和习题指导》p10 第 17 题
3.10 设晶体中每个振子的零点振动能为
1 ,使用德拜模型求晶体的零点振动能。 2
证明:根据量子力学零点能是谐振子所固有的,与温度无关,故 T=0K 时振动能 E0 就是各振动
1
模零点能之和。 E0
m
0
E0 g d 将E0
将
M
us ueisKa e it , Vs VeisKa e it . 代入上式有
M 2u C 10 e ika V 11Cu , M 2V C eika 10 u 11CV ,
4
是 U,v 的线性齐次方程组,存在非零解的条件为
2 2 2 2 Kx , 2m 2m a 2m a
2 2 2 2 2 2 2 2 B点能量 B K x K y 2 m 2 , 所以 B / A 2 2m a a 2m a
所以 B / A 3
(c)如果二价金属具有简单立方品格结构,布里渊区如图 7—2 所示.根据自由电子理
2 2 论,自由电子的能量为 K x2 K y K z2 ,FerM 面应为球面.由(b)可知,内切于 2m
4 点的内切球的体积
3
4 3
,于是在 K 空间中,内切球内能容纳的电子数为 a
当 K= / a 时
2 20C / M , 2 2C / M ,
当 K=0 时,
2 22C / M , 2 0,
2 与 K 的关系如下图所示.这是一个双原子(例如 H 2 )晶体
黄昆固体物理试题及答案

山东大学试题专用纸物理系-----年级----班 课程名称: 固体物理 共1页 学号: 姓名:一. 填空(20分, 每题2分)1.对晶格常数为a 的SC 晶体,与正格矢R =a i +2a j +2a k 正交的倒格子晶面族的面指数为( ), 其面间距为( ).2.典型离子晶体的体积为V , 最近邻两离子的距离为R , 晶体的格波数目为( ), 长光学波的( )波会引起离子晶体宏观上的极化.3. 金刚石晶体的结合类型是典型的( )晶体, 它有( )支格波.4. 当电子遭受到某一晶面族的强烈反射时, 电子平行于晶面族的平均速度( )零, 电子波矢的末端处在( )边界上.5. 两种不同金属接触后, 费米能级高的带( )电. 对导电有贡献的是 ( )的电子. 二. (25分)1. 证明立方晶系的晶列[hkl ]与晶面族(hkl )正交.2. 设晶格常数为a , 求立方晶系密勒指数为(hkl )的晶面族的面间距. 三. (25分)设质量为m 的同种原子组成的一维双原子分子链, 分子内部的力系数为β1, 分子间相邻原子的力系数为β2, 分子的两原子的间距为d , 晶格常数为a , 1. 列出原子运动方程. 2. 求出格波的振动谱ω(q ). 四. (30分)对于晶格常数为a 的SC 晶体1. 以紧束缚近似求非简并s 态电子的能带.2. 画出第一布里渊区[110]方向的能带曲线, 求出带宽.3.当电子的波矢k =a πi +a πj 时,求导致电子产生布拉格反射的晶面族的面指数. (试题随答卷上交)答案:一. 填空(20分, 每题2分)1.对晶格常数为a 的SC 晶体,与正格矢R =a i +2a j +2a k 正交的倒格子晶面族的面指数为( 122 ), 其面间距为( a 32π).2.典型离子晶体的体积为V , 最近邻两离子的距离为R , 晶体的格波数目为( 33R V ), 长光学波的( 纵 )波会引起离子晶体宏观上的极化.3. 金刚石晶体的结合类型是典型的(共价结合)晶体, 它有( 6 )支格波.4. 当电子遭受到某一晶面族的强烈反射时, 电子平行于晶面族的平均速度(不为 )零, 电子波矢的末端处在(布里渊区)边界上.5. 两种不同金属接触后, 费米能级高的带(正)电.对导电有贡献的是 (费米面附近)的电子.二. (25分)1.设d 为晶面族()hkl 的面间距为, n 为单位法矢量, 根据晶面族的定义,晶面族()hkl 将c b a 、、分别截为l k h 、、等份, 即 a =⋅n a cos (a ,n )==a cos (a ,n )=hd , b =⋅n b cos (b ,n )= a cos (b ,n ) =kd , c =⋅n c cos (c ,n )= a cos (c ,n ) =ld .于是有n =a dh i +a d kj +a d l k =a d(h i +k j +l k ). (1)其中, i 、j 、k 分别为平行于c b a 、、三个坐标轴的单位矢量. 而晶列[]hkl 的方向矢量为=R ha i +ka j +la k=a (h i +k j +l k ).(2)由(1)、(2)两式得n =2a dR ,即n 与R 平行. 因此晶列[]hkl 与晶面()hkl 正交.2. 立方晶系密勒指数为(hkl )的晶面族的面间距22222222l k h aa l a k a h d hkl hkl ++=++==kj i K πππππ三. (25分) 1.原子运动方程) (2t qna i n Ae u ω-= ) (12t qna i n Be u ω-+= 1. 1.格波的振动谱ω(q )=()2/12/1222121222212sin 16422⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+-±+qa m m m m ββββββ四. (30分) 1. 紧束缚近似非简并s 态电子的能带()a k a k a k J C E E z y x s s at s s cos cos cos 2)(++--=k2.[110]方向的能带曲线带宽为8J s 。
《固体物理学》基础知识训练题及其参考标准答案

《固体物理学》基础知识训练题及其参考标准答案《固体物理》基础知识训练题及其参考答案说明:本内容是以黄昆原著、韩汝琦改编的《固体物理学》为蓝本,重点训练读者在固体物理方面的基础知识,具体以19次作业的形式展开训练。
第一章作业1:1.固体物理的研究对象有那些?答:(1)固体的结构;(2)组成固体的粒子之间的相互作用与运动规律;(3)固体的性能与用途。
2.晶体和非晶体原子排列各有什么特点?答:晶体中原子排列是周期性的,即晶体中的原子排列具有长程有序性。
非晶体中原子排列没有严格的周期性,即非晶体中的原子排列具有短程有序而长程无序的特性。
3.试说明体心立方晶格,面心立方晶格,六角密排晶格的原子排列各有何特点?试画图说明。
有那些单质晶体分别属于以上三类。
答:体心立方晶格:除了在立方体的每个棱角位置上有1个原子以外,在该立方体的体心位置还有一个原子。
常见的体心立方晶体有:Li,Na,K,Rb,Cs,Fe等。
面心立方晶格:除了在立方体的每个棱角位置上有1个原子以外,在该立方体每个表面的中心还都有1个原子。
常见的面心立方晶体有:Cu, Ag, Au, Al等。
六角密排晶格:以ABAB形式排列,第一层原子单元是在正六边形的每个角上分布1个原子,且在该正六边形的中心还有1个原子;第二层原子单元是由3个原子组成正三边形的角原子,且其中心在第一层原子平面上的投影位置在对应原子集合的最低凹陷处。
常见的六角密排晶体有:Be,Mg,Zn,Cd等。
4.试说明, NaCl,金刚石,CsCl, ZnS晶格的粒子排列规律。
答:NaCl:先将两套相同的面心立方晶格,并让它们重合,然后,将一套晶格沿另一套晶格的棱边滑行1/2个棱长,就组成Nacl晶格;金刚石:先将碳原子组成两套相同的面心立方体,并让它们重合,然后将一套晶格沿另一套晶格的空角对角线滑行1/4个对角线的长度,就组成金刚石晶格;Cscl::先将组成两套相同的简单立方,并让它们重合,然后将一套晶格沿另一套晶格的体对角线滑行1/2个体对角线的长度,就组成Cscl晶格。
固体物理学-黄昆-题库-精品资料

PART ONE 填空问题 Q01_01_001 原胞中有p 个原子。
那么在晶体中有3支声学波和33p -支光学波?Q01_01_002 按结构划分,晶体可分为7大晶系, 共14布喇菲格子?Q01_01_004 面心立方原胞的体积为314a =;其第一布里渊区的体积为334(2)*aπ?=Q01_01_005 体心立方原胞的体积为32a=;第一布里渊区的体积为332(2)*aπ=Q01_01_006 对于立方晶系,有简单立方、体心立方和面心立方三种布喇菲格子。
Q01_01_007 金刚石晶体是复式格子,由两个面心立方结构的子晶格沿空间对角线位移1/4 的长度套构而成,晶胞中有8个碳原子。
Q01_01_008 原胞是最小的晶格重复单元。
对于布喇菲格子,原胞只包含1个原子;Q01_01_009 晶面有规则、对称配置的固体,具有长程有序特点的固体称为晶体;在凝结过程中不经过结晶(即有序化)的阶段,原子的排列为长程无序的固体称为非晶体。
由晶粒组成的固体,称为多晶。
Q01_01_010 由完全相同的一种原子构成的格子,格子中只有一个原子,称为布喇菲格子。
满足ij j i b a πδ2=?G G ?≠===)(0)(2j i j i π关系的1b G ,2b G ,3b G 为基矢,由322211b h b h b h G h K K K K ++=构成的格子,称作倒格子。
由若干个布喇菲格子相套而成的格子,叫做复式格子。
其原胞中有两个以上的原子。
Q01_03_001 由N 个原胞构成的晶体,原胞中有l 个原子,晶体共有3lN 个独立振动的正则频率。
Q01_03_002 声子的角频率为ω,声子的能量和动量表示为ω=和q K=。
Q01_03_003 光学波声子又可以分为纵光学波声子和横光学波声子,它们分别被称为极化声子和电磁声子Q01_03_004 一维复式原子链振动中,在布里渊区中心和边界,声学波的频率为→±==0,02,)2(211q a q Mπβω;光学波的频率???±=→=aq mq 2)2(0)2(21212πβμβωQ01_04_001 金属的线度为L ,一维运动的自由电子波函数ikxe Lx 1)(=ψ;能量m k E 222==;波矢的取值Lnk π2=Q01_04_002 电子在三维周期性晶格中波函数方程的解具有()()ik r kr e u r k ψ?=K KK K K K 形式?式中()k u r KK 在晶格平移下保持不变。
黄昆固体物理习题解答-完整版

0⎞ ⎟ 0⎟ ε3 ⎟ ⎠
1.12 比较面心立方晶格、金刚石晶格、闪锌矿晶格、Nacl 晶格的晶系、布拉伐格子、平 移群、点群、空间群。 晶格 面心立方晶格 金刚石晶格 闪锌矿晶格 Nacl 晶格的晶系 晶系 立方 立方 立方 立方 布拉伐格子 面心立方 面心立方 面心立方 面心立方 点群 Oh Oh Td Oh 空间群 Fm3m Fd3m
F43m
Fm3m
感谢大家对木虫和物理版的支持!
5
《固体物理》习题解答
第二章
习 题
2.1.证明两种一价离子组成的一维晶格的马德隆常数为 α = 2 ln 2 . 证 设想一个由正负两种离子相间排列的无限长的离子键,取任一负离子作参考离子 (这样马德隆常数中的正负号可以这样取,即遇正离子取正号,遇负离子取负号) ,用 r 表 示相邻离子间的距离,于是有
3π / 8 ≈ 0.68
2π / 6 ≈ 0.74 2π / 6 ≈ 0.74 3π /16 ≈ 0.34
解 设n为一个晶胞中的刚性原子数,r表示刚性原子球半径,V表示晶胞体积,则致
密度为: ρ = 结构 简单立方 体心立方 面心立方 六方密排 金刚石
4π nr 3 (设立方晶格的边长为a) r取原子球相切是的半径于是 3V
6 a
3a / 2
6 a
2a
1.7
画体心立方和面心立方晶格结构的金属在 (100) , (110) , (111) 面上 解:
原子排列.
感谢大家对木虫和物理版的支持!
3
《固体物理》习题解答
体心立方
面心立方
1.9 指出立方晶格(111)面与(100)面,(111)面与(110)面的交线的晶向 解 (111)面与(100)面的交线的 AB-AB 平移, A 与 O 重合。B 点位矢 RB = −aj + ak (111) 与 (100) 面的交线的晶向 AB = − aj + ak —— 晶 向指数 ⎡011⎤
黄昆固体物理习题

β N −m Nα m r0 (α − )= (1 − )r0− m nβ n 2 2 mα m Nα m nβ − n − = (1 − )( ) m 2 n mα
则平均单个原子的结合能为
m 1 m nβ − n − α (1 − )( ) m 2 n mα
(3)体变模量为
K = (V
以及 其中 Z 为一个与结构有关的常数。 有
= aj , a3 = ak ,可以马上求出:
b1 = 2π 2π 2π i , b2 = j , b3 = k a a a
因为倒格子基矢互相正交,因此其大小为
h k l 2π Ghkl = (hb1 ) 2 + (kb2 ) 2 + (lb3 ) 2 = 2π ( ) 2 + ( ) 2 + ( ) 2 = a a a a
U = N [−
但是现在
A′ B + ] r rn
A′ =
同样在平衡位置满足
α q ′2 ,而 q′ = 2q 。 4πε 0
∂U =0 ∂r
则求得晶格常数为
B 1 n −1 = r0′ A′ n
所以
B n1 r0′ = ( n) −1 A′
与原来的晶体相比,为
B n −1 1 r0′ ( A′ n) A n1 1− n −1 ( ) 4 = = = 1 r0 A′ B ( n) n −1 A
第一章、 晶体结构 1.1 如果将等体积球分别排列成下列结构,设 x 表示钢球所占体积与总体积之比,证明 x 结构 简单立方 体心立方 面心立方 六方密排 金刚石
π / 6 ≈ 0.52
3π / 8 ≈ 0.68
2π / 6 ≈ 0.74 2π / 6 ≈ 0.74
固体物理学(黄昆_高教版)_答案

《固体物理学》习题解答黄昆 原著 韩汝琦改编第一章 晶体结构1.1、解:实验表明,很多元素的原子或离子都具有或接近于球形对称结构。
因此,可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。
这样,一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。
它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比,即:晶体原胞的空间利用率, VcnV x =(1)对于简立方结构:(见教材P2图1-1) a=2r , V=3r 34π,Vc=a 3,n=1 ∴52.06r8r34ar 34x 3333=π=π=π=(2)对于体心立方:晶胞的体对角线BG=x 334a r 4a 3=⇒=n=2, Vc=a 3∴68.083)r 334(r 342ar342x 3333≈π=π⨯=π⨯=(3)对于面心立方:晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4,Vc=a 374.062)r 22(r344ar344x 3333≈π=π⨯=π⨯=(4)对于六角密排:a=2r 晶胞面积:S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233晶胞的体积:V=332r 224a 23a 38a 233C S ==⨯=⨯n=32126112+⨯+⨯=6个74.062r224r 346x 33≈π=π⨯=(5)对于金刚石结构,晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 334.063r338r 348ar348x 33333≈π=π⨯=π⨯=1.2、试证:六方密排堆积结构中633.1)38(a c2/1≈= 证明:在六角密堆积结构中,第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形,第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切,于是: NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。
(黄昆版)固体物理试题2答案

EEJe k s
(1)
g 0JR s ikR RS 0
邻 近 最
s
简立方中一个原子最临近的有六个原子R n : a(1,00),a(-1,0,0),a(0,1,0),a(0,-1,0),a(0,0,1),a(0,0,-1)
e
RS
ikR g
S
∴
=2(cosk x a+cosk y a+cosk z a)
22m
41 sin m 2 2N
1/2
五、证明题(每小题题10分,共 30
1、金属Na的晶体结构为体心立方点阵,则 衍射的几何结构因子满足如下关系
分)
其X射线
F(h,k,l)= 证: 每个单胞有两个同种原子,位矢为
2f Na 0
h+k+l= 数 偶 当 h+k+l= 数 奇 当
2f Na 0
h+k+l= 数 偶 当 h+k+l= 数 奇 当
Ne 2 1 W 1 4 00 rn
证:
e2 A B r n ),A= 4 0 内聚能为U=N( r dU B 1 n 1 r0 r0 0 An 由平衡条件 dr
k Euu k
kk
=
k E k
1 k En k =h
简正振动数目、格波数目或格波振动模式数目是一回事, 这个数目等于晶体中所有原子 的自由度数之和, 即等于3N.(或3Nn,N为原胞数,n为原胞中不同原子数)。 3、四角晶系中为什么没有底心四角和面心四角点阵? 解答: 底心四角实际即 简单四角(如图), 面心四角实际即 体心四角(如图)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3Nk B
( =Z0 kBT
)2
=Z0
e kBT
āāᠸ⍘Ꮥ⮳ᠶᒑᐾ䭼ѽ喌̽Ⴭ侻㐂 CV
AT 3 ̼さȡ
❠ఏಕὐᔬ⪔εळᵫ∑⮳䷀⢶ጝݚȡ
Q02_04_001 ᵨᢝ㘬ፕ⤵䃩ク䔟䜀ᆍȠࡹᄫ҂㐌㑇҂⮳ᄫ⩤ᕖ喛
第 3 页,共 32 页
ᄨν䜀ᆍ喚⩤ၿ㘬ፕ͜⮳කٴञДᒑ̼␐ፕ喌ࢢᄫፕ喌ఏₓႲЛ̯㝛᭞ᄫ҂ȡᄨνࡹᄫ҂喚 Ͻ㘬ፕ㐂ᲳᲔⰺ̽㐌㑇҂⮳Ⱗѫ喌ѵࡹᄫ҂⺰ፕწᏕ䒲㐌㑇҂⮳音喌ӌ䲏☜⓯ऀࢢञДᄵ␐ፕ͜⮳ ⩤ၿ⓯ऀݟᄫፕ͜喌ఏ㔻ڦᄫ⩤㘬ߊȡ
G ai
G bj
2SG ij
®
¯
2S 0
(i j)
GG G
K
(i z j) ڢ㈪⮳ b1 , b2 , b3 ͩഩⴑ喌⩠ Gh
KK K h1b1 h2b2 h2b3 Ჳ⮳ᵫၿ喌
土ҋՁᵫၿȡ ⩠㠔Ꭱ͙ጲશ㤡ᵫၿⰧຆ㔻⮳ᵫၿ喌च։ᐾᵫၿȡ࣎ڥ㘍͓͙͜Д̹⮳࣎ၿȡ
Q01_03_001 ⩠ N ͙࣎㘍Ჳ⮳ᮥ҂喌࣎㘍͜ l ͙࣎ၿ喌ᮥ҂ڠ 3lN ͙⠛⿺ᡞߗ⮳ₒ݈䷀⢶ȡ
Q01_06_002
㜙⩠⩤ၿ⅃㈪㐎⮳䉨ㆢ㘬㏖ͩ
E
0 F
,
k 阜䬣䉨ㆢࡹᒳ kF
2mE
0 F
喛
=
⩤ၿ⮳Ꭲ㘬䛾 EKin
3 5
E F0
Q01_06_003 ⍘Ꮥͩ 0 K ᬥ喌 N ͙㜙⩠⩤ၿᲳ⮳̸㐣㜙⩠⩤ၿ⅃喌҂㈪⮳㘬䛾 E0
3 5
NEF0
Q01_07_001 N ࡹᄫ҂ͪ㺰ग़̯ͪ喌ັͪ⮳㘬㏖᭞ ED 喌ͪ⊂Ꮥͩ N D 喌䋢๎ѽ⮳
Q01_04_002
⩤ၿ̸㐣গᱎᕖᮥᵫ͜∑ܬ彡⮳㼒ڦ\
K k
(rK
)
eikKrK
uK k
(rK
)
ᒑᐾ喟ᐾ͜
uK k
(
rK
)
ᮥᵫᎢ尢̺Ԍᠰ̼इȡ
Q01_04_003 ັ̯ϊ㘬䛾ࡩഎ͜喌∑ߗ彡̼ႇڦጲ≊䊚ܬᒑᐾ⮳㼒喌䔈ϊ㘬䛾ࡩഎ土ͩ ⺰ፕ喌ࢢፕ䯈喛㘬ፕ⮳㶗មᆄ㘬ࡩభᐾ∄ Ƞク㏕ጲ䛻⌹ࡩభᐾ∄Ƞগᱎᕖ㘬ࡩభᐾ∄̸భᐾȡ
Q02_06_001 Ͻ⩤ၿ☜შ䛾ၿ⤵䃩ク䔟䜀ᆍ͜⮳⩤ၿᄨ҂☜შ⮳䉐⡝ȡ
䛾ၿ⤵䃩͜喌๖้⩤ၿ⮳㘬䛾䔋䔋ѽν䉨ჵ㘬䛾 EF0 喌⩠νआ⮳⤵࣎ݘ∐ݟ䭿̼ݥ㘬ࣱ̽☜
⓯ऀ喌ङ
E
0 F
䭳䔀㏕
~
kBT
㠲ణ⩤ڴၿࣱ̽☜⓯ऀ喌ᄨ䜀ᆍ⮳☜შ䛾䉐⡝ȡ䃐テ㐂㶗ᬽ⩤ၿ
⮳☜შ䛾̽⍘Ꮥ̯⁐ₒ℃ȡ
䃧้䜀ᆍ⮳ഩᱛᕖ䉗अۢν㘬䛾 EF 䭳䔀⮳⩤ၿ喌⩤ၿ⮳☜შ䛾 CV
N
(
E
0 F
)
ₒ℃喌⩠⩤ၿ⮳☜შ䛾ञД㣦ᓆ䉨ㆢ䲑䭳䔀㘬ᔰჵᏕ⮳Ԑᖞȡ
[S 2 3
N
(
E
0 F
)(kBT )]kB
̽
䓶⍐ ㉏ٲMnȠFeȠCo Ni ڦ䒲倇⮳⩤ၿ☜შ䛾喌ࣼεႲЛ䉨ㆢ䲑䭳䔀ڦ䒲๖⮳㘬ᔰჵᏕȡ
E
)
1 2
,
®M
°¯0,
q
r
S 2a
喛ٸ႕∑⮳䷀⢶ Z 2
qo0
°°(
2E P
)
1 2
® °°¯(
2E m
)
1 2
qo0 q rS
2a
Q01_04_001 䜀ᆍ⮳㏮Ꮥͩ L喌̯㐣䓿ߗ⮳㜙⩠⩤ၿ∑ܬ\ ( x)
1 eikx 喛㘬䛾 E
=2k 2
喛
L
2m
第 1 页,共 32 页
∑ⴑ⮳अի k 2Sn L
3$5721( ငଥႜ
Q01_01_001 ࣎㘍͜ p ͙࣎ၿȡ䗒ͷᮥ҂͜ 3 ᩞฟ႕∑ 3 p 3 ᩞٸ႕∑喟
Q01_01_002 ᠸ㐂Ჳ݁ܵ喌ᮥ҂ञܵͩ 7 ๖ᮥ㈪, ڠ14 ጲશ㤡ᵫၿ?
Q01_01_004 䲑ᓲ⿺࣎㘍⮳҂囗ͩ :
1 a3 喛ڥせ̯ጲ䛻⌹ࡩ⮳҂囗ͩ :* 4
1
Q01_04_004 㘬䛾ᴶᏕ̺喌䉨ㆢ㜙⩠⩤ၿ⅃㈪㐎⮳ᔰჵᏕ N (E) CE 2 ȡ
K Q01_04_005 ߗ䛾ᴶᏕ̺喌䉨ㆢ㜙⩠⩤ၿ⅃㈪㐎⮳ᔰჵᏕ N (k )
Vc 4S 3
ȡ
Q01_04_006 ⩤ၿᢝε̯͙㘬ፕ͜ᝯ⮳⟥ᔰ喌土䄔㘬ፕͩ␐ፕ喛⇐Ъ҄⩤ၿᢝ喈කٴ喉⮳ 㘬ፕ喌土ͩ阜ፕ喛ᄫፕД̺⮳せ̯͙␐ፕ喌ᝅ㔴ᰯ̹䲑⮳̯͙␐ፕ土ͩЦፕ喛ᰯ̺䲑⮳̯͙阜ፕ土 ͩᄫፕ喛͓͙㘬ፕͺ䬣喌ٰ̼䃧ႇ⮳㘬㏖წᏕ喌土ͩፕ䯈ȡ
Q02_03_002 ϯͷ᭞҂℃☜⮳ᓦ᠋ὐ喟Ꭵク䔟䃐テ㐂⮳ᘾȡ
ᓦ᠋ܩД䔍㐜Ϻ䉗⮳ᑨᕖ∑ᲔВ㶗ᵫ∑喌ᄵጲશ㤡ᮥᵫⰺҋ᭞ळीऻᕖ⮳䔍㐜Ϻ䉗喌 1 ͙㏤ ∑ 2 ͙⠛⿺⮳Ὑ∑ȡ
䃐テ㐂㶗ᬽѽ⍘Ჰ䭿̺喚 CV (T / 4D )
12S 4 R( T )3 ā̽⍘Ꮥ⮳ 3 ⁐ₒ℃ȡ 15 4D
⍘Ꮥᘷѽ喌ᓦ᠋䔀ѫᘷຬ喌䄣ᬽ⍘Ꮥᒷѽᬥ喌ङ䪮∑ᵫ∑⮳⓯ऀ᭞ͪ㺰⮳ȡ
Q02_03_003 ϯͷ᭞҂℃☜⮳❠ఏಕὐ喟Ꭵク䔟䃐テ㐂⮳ᘾȡ
ᄨνN͙࣎ၿᲳ⮳ᮥ҂喌ᮥ҂͜ᝯ⮳࣎ၿДⰧऻ⮳䷀⢶Z0ᡞߗȡ
䃐テ㐂㶗ᬽ⍘Ꮥ䒲倇ᬥ喚 CV # 3NkB āā ̽䮵喍⣯ᰮᒺ̯㜣ȡ
⍘Ꮥ䲍፧ѽᬥ喚CV
䓿ߗᒑ
⮳⩤≰
̯͙ፕₒ
(k1) 䓿ߗ⮳㇁ၿᝯϖ⩎⮳⩤≰Ⱗऻȡ䔈͙阜⟥ᔰ土ͩ阜酉ȡ
⩤㢦
e
喌Д
k1
⟥ᔰ
⩤ၿ䕎Ꮥ
Q02_05_002 ᄵ㇁ၿⰺҋ᭞㏾ڧ㇁ၿᬥ喌Ⴒ⮳䕎Ꮥ䓿ߗ彡᭞ϯͷ喟
K ⩤ၿ⟥ᔰइࡅഩᱛڛᐾ喚 d (=k )
dt
K F
;
⩤ၿ⮳䕎Ꮥ喚 vKk
1 =
k
E
Q02_05_003 ク䔟ᄫፕ͜⮳⩤ၿๅ౩ҋ⩗̺ϖ⩎⩤≰⮳࣎ఏȡ
㉖㑉䔀ѫ∄⮳ᕌᘢ喚⩤ၿ̯͙࣎ၿ喈ᵫ◨喉䭳䔀ᬥ喌ͪ㺰आݟ䄔࣎ၿ߮౩⮳ҋ⩗喌㔻ᄵڥ Ⴒ࣎ၿ喈ᵫ◨喉߮౩⮳ҋ⩗ⰺҋ᭞ᓝស喌ᄵᮥ҂͜⩤ၿ⮳∑ܬ䔀ѫⰺ࣎ၿ䒗䖂∑ܬ⮳㏮ᕖ㏳ ष喌䔈ᵦञДᓆ࣎ݟၿ㘬㏖ᮥ҂͜㘬ፕͺ䬣⮳ڢ㈪ȡ
̯͙࣎ၿ㘬㏖HiᄨᏃ̯͙㘬ፕ喌̼ऻ⮳࣎ၿ㘬㏖ᄨᏃ̼ऻ⮳㘬ፕȡᒂ࣎ၿᒑ҂ऽ喌ᒑε̯㈪݆ ⮳㘬ፕȡ
Q02_06_003 ͩϯͷ⍘Ꮥ䒲ѽᬥञДᓴ䶪㔲㮀⩤ၿᄨ҂☜შ䛾⮳䉐⡝喟
ѽ⍘㠲ణ̺喌ᮥᵫᡞߗ⮳☜შ䛾ᠸ⍘Ꮥ⮳ 3 ⁐䊺ν䰥喌㔻⩤ၿ⮳☜შ䛾̽⍘Ꮥ 1 ⁐ₒ℃喌 䮾⍘Ꮥ̺䭼इࡅ℃䒲㑂ᚑ喌ₓᬥ⩤ၿ⮳☜შ䛾ञДᮥᵫᡞߗ⮳☜შ䛾Ⱗ℃䒲喌̼㘬ᔬ⪔ȡ
Q02_06_004 ͩϯͷ㐌ᄨ䰥Ꮥᬥ喌䜀ᆍ͜⮳⩤ၿϼ♥ڦ䒲倇⮳㘬䛾喟
Q01_01_008 ࣎㘍᭞ᰯᄾ⮳ᮥᵫ䛼ࢄٲȡᄨνጲશ㤡ᵫၿ喌࣎㘍ङ࠴ग़ 1 ͙࣎ၿ喛
Q01_01_009 ᮥ䲑㻳݈Ƞᄨ土䙼㒝⮳҂喌ڦ䪮彡Ꮎ➨◨⮳҂土ͩᮥ҂喛܌㐂䓶彡̼͜ ㏾䓶㐂ᮥ喈ࢢᎾࡅ喉⮳䭥⃤喌࣎ၿ⮳ᣁ݆ͩ䪮彡ᬏᎾ⮳҂土ͩ䲍ᮥ҂ȡ⩠ᮥ㇁㏳⮳҂喌土 ้ͩᮥȡ
Q01_01_010 ⩠Ⴛ̯࣎⮳ऻⰧڗၿᲳ⮳ᵫၿ喌ᵫၿ͜ङ̯͙࣎ၿ喌土ͩጲશ㤡ᵫၿȡ␐䋢
4(2S )3 a3
Q01_01_005 ҂ᓲ⿺࣎㘍⮳҂囗ͩ :
a3 喛せ̯ጲ䛻⌹ࡩ⮳҂囗ͩ :* 2
2(2S )3 a3
Q01_01_006 ᄨν⿺ᮥ㈪喌クࢄ⿺Ƞ҂ᓲ⿺䲑ᓲ⿺̸ጲશ㤡ᵫၿȡ
Q01_01_007 䜀݉ⴢᮥ҂᭞ᐾᵫၿ喌⩠͓͙䲑ᓲ⿺㐂Ჳ⮳ၿᮥᵫ⇮阜䬣ᄨ㼁㏮Ѽ尢 1喏4 ⮳䪮 ᏕຆᲳ㔻喌ᮥ㘍͜ 8 ͙ⷢ࣎ၿȡ
㘬䛾䒲ѽ⮳㘬㏖ᄨᏃڴᅱ⩤ၿ喌ڥ䒗䖂䒲ᄾ喌࣎ၿͺ䬣ڴᅱ⩤ၿ⮳∑ܬⰧρ䛼ए䒲ᅀ喌ᝯДᄨᏃ ⮳㘬ፕ䒲音ȡ
㘬䛾䒲倇⮳㘬㏖ᄨᏃๅᅱ⩤ၿ喌ڥ䒗䖂䒲๖喌࣎ၿͺ䬣ๅᅱ⩤ၿ⮳∑ܬⰧρ䛼ए䒲้喌ᝯДᄨᏃ ⮳㘬ፕ䒲წȡ
Q02_05_001 ϯͷ᭞阜酉喟
K
K
vKe
̯
K
͙阜⮳
k1
⟥ᔰ⮳
䔀␐ፕ͜
ᝯ⩤ၿ
ำ⤵ȡᒂ͓͙⩠Ⱗρ㜙⩠⮳ⴘ䭤⟥ٲᔰ k k ' k Gn ⮳䰥㏖㘬䛾Ⱗへᬥ喌̯㏖ԝₒ∑ܬλ㏖
㘬䛾ԝₒ䊺νᬏ金๖ȡ
K2 ࢢ喚 k
⮳㘬ፕȡ
K k
K Gn
2
K 喌ᝅ㔴 Gn
K (k
1 2
K Gn )
0 喌ጲ䛻⌹ࡩ⮳䓨⩻ำ喌㘬䛾ऀ革ܩइ喌ᒑ̯㈪݆
Q02_04_003 ク䔟㉖㑉䔀ѫὐ⮳ᕌᘢͪ㺰㐂䃩ȡ
⻪ၿᕖ㐂ष喚ₒȠ䉎⻪ၿͺ䬣䲏ᏂЀ१ᑄߊҋ⩗㔻Ⱗρ䲏䔀喌ᒂ䲏䔀̯ݟ彡Ꮥᬥ喌⩠ν∐̼ݘ Ⱗშ࣎⤵喌͓͙⻪ၿ⮳䬜षยᅱ⮳⩤ၿπ⮳ϓ䔜щϖ⩎ᑩ๖⮳ᣁߊȡᒂᣁߊ१ᑄߊⰧρᎢ㶐 ᬥ喌ᒑ甘⮳⻪ၿᮥ҂喛
ڠЦᕖ㐂ष喚䲏͓͙࣎ၿळ䉐⡝ၿ⮳ᰯๅᅱ⩤ၿͩᝯ࣎ၿᝯڠ喌ఏₓ㐂ष䜀ᆍᮥ҂ᬥ喌 ࣪εᰯๅᅱ喈Ц喉⩤ၿ⮳࣎ၿჍĆ↸⊧ć⩠Ц⩤ၿ㏳⮳Ć⩤ၿπć͜ȡ䔈ᗴ̺ۤ喌⩤ၿ π࣎ၿჍͺ䬣ႇᏂЀҋ⩗喌҂囗䊹ᄾ⩤ၿπჵᏕ䊹倇喌ᏂЀⰧρҋ⩗⮳ᏂЀ㘬ᘷѽ喌㶗⣟ͩ࣎ ၿ㖉ष䊦Ე⮳ҋ⩗ȡ
⍘Ꮥ̺喌䒬≰ၿͪ㺰᭞Ͻͪ㘬㏖⓯ऀݟᄫፕ⮳⩤ၿȡᒂ⍘Ꮥᒷѽᬥ喌ङᒷᅀ⮳ͪ㷚⩤⻪ȡᒂ ⍘Ꮥ䋢๎倇ᬥ喌ͪͽڗ䘗㷚⩤⻪喌ᄫፕ͜⮳⩤ၿᣔ䔀νͪȡ
第 2 页,共 32 页
3$577:2 ਨཐႜ
Q02_02_001 ࣎ၿ㐂षᮥ҂ᬥ喌࣎ၿ⮳Ц⩤ၿϖ⩎䛼ܵጲ喌Ͻ㔻ϖ⩎̼ऻ⮳㐂षߊ喌ܵᲿ⻪ၿ ᕖȠڠЦᕖȠ䜀ᆍᕖ㠲ᓦ⨕㕢ᕖ㐂षߊ⮳➨◨ȡ
ᄫፕ͜ङ䘗ܵ⟥ᔰ㷚⩤ၿකٴ喌ๅ౩⮳ҋ⩗щҮጲ䛻⌹ࡩ⮳⟥ᔰܵጲऀ⩎इࡅȡᝯ⮳⩤ၿ⟥ ᔰДⰧऻ⮳䕎Ꮥ⇮Ɐ⩤౩⮳ࣼी䓿ߗ喌ѵ⩠ν㘬ፕ᭞̼␐ፕ喌䔵⩤౩ी̹䓿ߗ⮳⩤ၿ䒲้喌ఏ ₓϖ⩎⩤≰ȡ
