高一数学期末复习天天练17
高中数学期末综合复习练习试卷(必修 )

期末综合复习练习试卷(必修3、4)(第一卷)本试卷分第一卷(选择题)和第二卷(填空题、解答题)两部分。
第一卷1至2页,第二卷3至6页,共21题,合计100分。
第一卷的选择题和第二卷的填空题、解答题都要答在第二卷上。
考试时间120分钟。
一、选择题:本大题共12小题,每小题3分,共36分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、 下面的结论不正确的是( )(A )一个程序的算法、步骤是不可逆的 (B )完成一件事情的算法是惟一的(C )设计算法要本着简单方便、明确有效的原则 (D )一个算法,执行的步骤总是有限次的 2、 把389化成四进制数的末位为( ) (A )1 (B )2 (C ) 3 (D )03、 人们常用来反映数据n x x x ,,,21 的变异特征的量是( ) (A )中位数 (B )众数 (C )标准差 (D )平均值4、 观察新生婴儿的体重,其频率分布直方图如图所示,则新生婴儿的体重在[2700,3000]的频率为( ) (A )0.001 (B )0.01 (C )0.003 (D )0.35、 在500mL 的水中有一个草履虫,现从中随机取出2mL 水样放到显微镜镜下观察,则发现草履虫的概率为( )(A )0 (B )0.002 (C )0.004 (D )1 6、 函数R x x y ∈+=),2cos(π( )(A )是奇函数 (B )是偶函数 (C )既不是奇函数,又不是偶函数 (D )有无奇偶性不能确定7、 将函数x y 2tan =的图象向左平移6π个单位,得到图象的函数解析式是( ) (A ))62tan(π+=x y (B ))32tan(π+=x y(C ))62tan(π-=x y (D ))32tan(π-=x y8、在ABC ∆中,b CA a CB ==,,则=AB ( )(A )b a + (B ))(b a +- (C )b a - (D )a b -9、已知平行四边形ABCD 的顶点A (-1,-2),B (3,-1),C (5,6),则顶点D 的坐标是( )(A )(9,7) (B )(1,5) (C )(-3,-9) (D )(2,6) 10、化简)4(sin )4(cos 22απαπ---得到( )(A )α2sin (B )α2sin - (C )α2cos (D )α2cos -11、函数)20(cos 2π≤≤=x x y 的图象和直线2=y 围成一个封闭的平面图形,则这个封闭图形的面积是( )(A ) π (B )π2 (C )π3 (D )π412、已知ABC ∆的三个顶点A 、B 、C 及平面内一点P ,若,AB PC PB PA =++则点P 与ABC ∆的位置关系是( )(A ) P 在AC 上 (B )P 在AB 边上或其延长线上 (C )P 在ABC ∆外部 (D )P 在ABC ∆内部(第二卷)一.选择题:本大题共12小题,每小题3分,共36分。
高一数学 数学天天练

2.在检查产品尺寸过程中,将其尺寸分成若干组,[,)a b 是其中一组,抽查出的个体在该组上频率 为m ,该组上的直方图的高为h ,则||a b -=( ).A.hmB. mh C. hm D.h m +3.“22a b>”是 “22log log a b >”的( ).A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.已知函数21(01)()2(20)xx x f x a x ⎧+≤≤⎪=⎨+-≤<⎪⎩,且112()1f -=-,则函数()f x 的值域为__________.5.已知ABC ∆三内角A 、B 、C 成等差数列,(1cos 2,2sin )m A C =+-,(tan ,cos )n A C =. (Ⅰ)若m n ⊥,判断ABC ∆形状;(Ⅱ)求m n ⋅取得最大值时ABC ∆三内角的大小.数学天天练之二1.等比数列中,483a a +=-,则62610(2)a a a a ++的值为( ).A.9B.9-C.6D.6-2.已知22(,)ππθ∈-,且sin cos a θθ+=,其中(0,1)a ∈,则关于tan θ的值,以下四个答案中,可能正确的是( ).A.3-B.3或13 C.13-D.3-或13-3.若3132()nxx -的展开式中含有常数项,则这样的正整数n 的最小值是( ).A.a c+数学天天练之十1、已知53sin ),,2(=∈a a ππ,则=a tan A .34- B .43-C .43D .342、下列函数中,在其定义域内既是奇函数又是增函数的是A .3x y =,x ∈R B .x y sin =,x ∈RC .x y -=,x ∈RD .xy )21(=,x ∈R 3.已知a>b ,则下列不等式中正确的是A .a 1<b 1B .2a >2b C .b a +>ab 2 D .22b a +>ab 24.抛物线22x y =的焦点坐标是 .5.如右图在棱长为1的正方体ABCD —A ′B ′C ′D ′中,E 、F 分别是OD ′,BD 中点,G 在棱CD 上,且CD CG 41=。
高一数学期末练习题
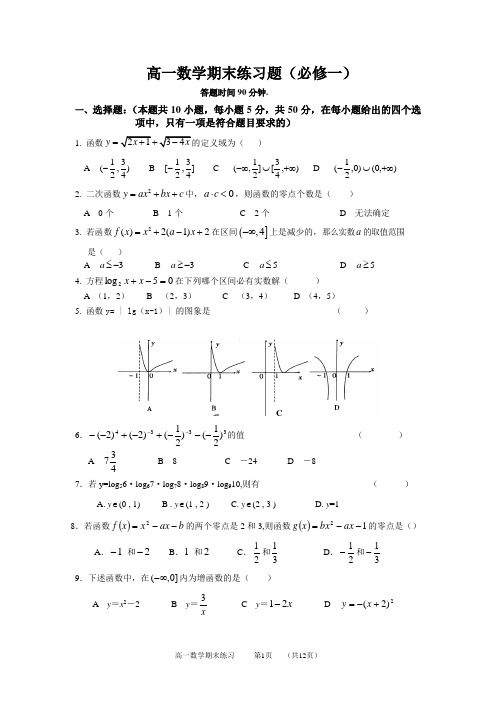
高一数学期末练习题(必修一)答题时间90分钟.一、选择题:(本题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.函数y = )A )43,21(- B ]43,21[- C ),43[]21,(+∞⋃-∞ D ),0()0,21(+∞⋃- 2. 二次函数2y ax bx c =++中,0a c ⋅<,则函数的零点个数是( ) A 0个 B 1个 C 2个 D 无法确定 3. 若函数2()2(1)2f x x a x =+-+在区间(],4-∞上是减少的,那么实数a 的取值范围 是( )A 3-≤aB 3-≥aC 5≤aD 5≥a 4. 方程05log 2=-+x x 在下列哪个区间必有实数解( ) A (1,2) B (2,3) C (3,4) D (4,5) 5. 函数y= | lg (x-1)| 的图象是 ( )6.3334)21()21()2()2(---+-+----的值 ( )A 437B 8C -24D -8 7.若y=log 56·log 67·log 78·log 89·log 910,则有 ( )A. y ∈(0 , 1) B . y ∈(1 , 2 ) C. y ∈(2 , 3 ) D. y =18.若函数()b ax x x f --=2的两个零点是2和3,则函数()12--=ax bx x g 的零点是()A .1- 和2-B .1 和2C .21和31 D .21-和31- 9.下述函数中,在]0,(-∞内为增函数的是( )A y =x 2-2B y =x3 C y =12x - D 2)2(+-=x y C10.下面四个结论:①偶函数的图象一定与y 轴相交;②奇函数的图象一定通过原点;③偶函数的图象关于y 轴对称;④既是奇函数又是偶函数的函数一定是()f x =0(x ∈R ),其中正确命题的个数是( )A 4B 3C 2D 1二、填空题(本大题共5小题,每小题5分,共25分)11.已知函数f(x)的定义域为[0,1],则f(2x )的定义域为 。
2020版试吧高中全程训练打算数学文天天练17

天天练17 平面向量的大体定理及坐标表示小题狂练⑰一、选择题1.[2019·昆明调研]已知向量a =(-1,2),b =(1,3),那么|2a -b |=( ) A. 2 B .2 C.10 D .10答案:C解析:由已知,易患2a -b =2(-1,2)-(1,3)=(-3,1),因此|2a -b |=-32+12=10.应选C.2.[2019·桂林模拟]以下各组向量中,能够作为基底的是( ) A .e 1=(0,0),e 2=(1,-2) B .e 1=(-1,2),e 2=(5,7) C .e 1=(3,5),e 2=(6,10)D .e 1=(2,-3),e 2=⎝ ⎛⎭⎪⎫12,-34答案:B解析:两个不共线的非零向量组成一组基底,A 中向量e 1为零向量,C ,D 中两向量共线,B 中e 1≠0,e 2≠0,且e 1与e 2不共线,应选B.3.若是e 1、e 2是平面α内两个不共线的向量,那么以下说法中不正确的选项是( )①a =λe 1+μe 2(λ、μ∈R )能够表示平面α内的所有向量;②关于平面α内任一贯量a ,使a =λe 1+μe 2的实数对(λ,μ)有无穷多个;③假设向量λ1e 1+μ1e 2与λ2e 1+μ2e 2共线,那么λ1λ2=μ1μ2.④假设实数λ、μ使得λe 1+μe 2=0,那么λ=μ=0.A .①②B .②③C .③④D .② 答案:B解析:由平面向量大体定理可知,①④是正确的.关于②,由平面向量大体定理可知,一旦一个平面的基底确信,那么任意一个向量在此基底下的实数对是唯一的.关于③,当λ1λ2=0或μ1μ2=0时不必然成立,应为λ1μ2-λ2μ1=0.应选B.4.[2019·天津红桥区模拟]假设向量a =(2,3),b =(-1,2),那么a +b 的坐标为( )A .(1,5)B .(1,1)C .(3,1)D .(3,5) 答案:A解析:∵向量a =(2,3),b =(-1,2),∴a +b =(1,5).应选A.5.[2018·全国卷Ⅰ]在△ABC 中,AD 为BC 边上的中线,E 为AD 的中点,那么EB→=( ) A.34AB →-14AC → B.14AB →-34AC → C.34AB →+14AC → D.14AB →+34AC → 答案:A解析:作出示用意如下图.EB→=ED →+DB →=12AD →+12CB → =12×12(AB →+AC →)+12(AB →-AC →) =34AB →-14AC →. 应选A.6.[2019·吉林一中等五校模拟]已知向量a =⎝ ⎛⎭⎪⎫13,tan α,b =(cos α,1),α∈⎝ ⎛⎭⎪⎫π2,π,且a ∥b ,那么sin ⎝ ⎛⎭⎪⎫α-π2=( )A .-13 B.13C.223 D .-223答案:C解析:因为向量a =⎝ ⎛⎭⎪⎫13,tan α,b =(cos α,1),且a ∥b ,因此13=tan αcos α=sin α.因为α∈⎝ ⎛⎭⎪⎫π2,π,因此sin ⎝ ⎛⎭⎪⎫α-π2=-cos α=1-sin 2α=223.应选C.7.[2019·宜昌模拟]已知点A (1,3),B (4,-1),那么与AB→同方向的单位向量是( )A.⎝ ⎛⎭⎪⎫35,-45B.⎝ ⎛⎭⎪⎫45,-35C.⎝ ⎛⎭⎪⎫-35,45D.⎝ ⎛⎭⎪⎫-45,35 答案:A解析:因为AB →=(3,-4),因此与AB →同方向的单位向量为AB →|AB →|=⎝⎛⎭⎪⎫35,-45.8.假设A ,B ,C ,D 四点共线,且知足AB →=(3a,2a )(a ≠0),CD →=(2,t ),那么t 等于( )A.34B.43C .3D .-3 答案:B解析:因为A ,B ,C ,D 四点共线,因此AB →∥CD →,故3a ·t =2a ·2,t =43.应选B.二、非选择题9.在平面直角坐标系xOy 中,已知a =(3,1),假设将向量-2a 绕坐标原点O 逆时针旋转120°取得向量b ,那么b 的坐标为________.答案:(23,-2)解析:因为a =(3,1),因此-2a =(-23,-2),如下图,易知向量-2a 与x 轴正半轴的夹角α=150°.向量-2a 绕坐标原点O 逆时针旋转120°取得向量b ,由图可知,b 在第四象限,且与x 轴正半轴的夹角β=30°,因此b =(23,-2).10.已知向量a =(m,4),b =(3,-2),且a ∥b ,那么m =________________. 答案:-6解析:由题意知-2m -12=0,m =-6.11.设向量a ,b 知足|a |=25,b =(2,1),且a 与b 的方向相反,那么a 的坐标为________.答案:(-4,-2)解析:因为b =(2,1),且a 与b 的方向相反,因此设a =(2λ,λ)(λ<0),因为|a |=2 5.因此4λ2+λ2=20,λ2=4,λ=-2.因此a =(-4,-2).12.已知A (2,1),B (3,5),C (3,2),AP →=AB →+tAC →(t ∈R ),假设点P 在第二象限,那么实数t 的取值范围是________.答案:(-5,-3)解析:设点P (x ,y ),那么由AP→=AB →+tAC →(t ∈R ),得(x -2,y -1)=(1,4)+t (1,1)=(1+t,4+t ),因此⎩⎨⎧ x -2=1+t ,y -1=4+t ,解得⎩⎨⎧x =3+t ,y =5+t ,由点P 在第二象限,得⎩⎨⎧x =3+t <0,y =5+t >0,解得-5<t <-3,因此实数t 的取值范围为(-5,-3).课时测评⑰一、选择题1.已知向量a =(-3,-4),那么以下能使a =λe 1+μe 2(λ,μ∈R )成立的一组向量e 1,e 2是( )A .e 1=(0,0),e 2=(-1,2)B .e 1=(-1,3),e 2=(2,-6)C .e 1=(-1,2),e 2=(3,-1)D .e 1=⎝ ⎛⎭⎪⎫-12,1,e 2=(1,-2)答案:C解析:作为基底,其应该知足的条件为不共线向量.A 中,零向量与任意向量共线;B 中,e 1=(-1,3),e 2=(2,-6)共线;C 中,e 1=(-1,2),e 2=(3,-1)不共线;D 中,e 1=⎝ ⎛⎭⎪⎫-12,1,e 2=(1,-2)共线.2.已知向量AB →与向量a =(1,-2)反向共线,|AB →|=25,点A 的坐标为(3,-4),那么点B 的坐标为( )A .(1,0)B .(0,1)C .(5,-8)D .(-8,5) 答案:A解析:依题意,设AB→=λa ,其中λ<0,那么有|AB →|=|λa |=-λ|a |,即25=-5λ,∴λ=-2,AB→=-2a =(-2,4),因此点B 的坐标是(-2,4)+(3,-4)=(1,0),应选A.3.如图,向量e 1,e 2,a 的起点与终点均在正方形网格的格点上,那么向量a 可用基底e 1,e 2表示为( )A .e 1+e 2B .-2e 1+e 2C .2e 1-e 2D .2e 1+e 2 答案:B解析:由题意可取e 1=(1,0),e 2=(-1,1),a =(-3,1),设a =x e 1+y e 2=x (1,0)+y (-1,1)=(x -y ,y ),那么⎩⎨⎧ x -y =-3,y =1,解得⎩⎨⎧x =-2,y =1,故a =-2e 1+e 2.4.[2019·重庆第八中学适应性考试(一)]已知向量a =(1,m ),b =(3,-2),且(a +b )∥b ,那么m =( )A .-23 B.23C .-8D .8 答案:A解析:由题意得a +b =(4,m -2).因为(a +b )∥b ,因此43=m -2-2,解得m =-23.应选A.5.[2019·湖南省五校联考]已知圆心为O ,半径为1的圆上有不同的三个点A ,B ,C ,其中OA →·OB →=0,存在实数λ,μ知足OC →+λOA →+μOB →=0,那么实数λ,μ的关系为( ) A .λ2+μ2=1 B.1λ+1μ=1 C .λμ=1 D .λ+μ=1 答案:A解析:解法一 取特殊点,取C 点为优弧AB 的中点,现在易患λ=μ=22,只有A 符合.应选A.解法二 依题意得|OA →|=|OB →|=|OC →|=1,-OC →=λOA →+μOB →,两边平方得1=λ2+μ2.应选A.6.如图,OC →=2OP →,AB →=2AC →,OM →=mOB →,ON →=nOA →,假设m =38,那么n 等于( )A.12B.2334 D.4 5C.答案:C解析:因为AB →=2AC →,因此C 为AB 中点,故OC →=12OA →+12OB →=2OP →,因此OP →=14OA →+14OB .由OM →=mOB →,ON →=nOA →,因此OB →=1m OM →,OA →=1n ON →,因此OP →=14m OM →+14n ON →,因为M ,P ,N 三点共线,故14m +14n =1,当m =38时,n =34.应选C.7.[2019·安徽淮南模拟]已知G 是△ABC 的重心,过点G 作直线MN 与AB ,AC 别离交于点M ,N ,且AM→=xAB →,AN →=yAC →(x ,y >0),那么3x +y 的最小值是( )A.83B.72C.52D.43+233 答案:D 解析:如图.AC →=1y AN →,AB →=1x AM →,又∵AG →=13AB →+13AC →, ∴AG→=13x AM →+13yAN →, 又∵M ,G ,N 三点共线,∴13x +13y =1.∵x >0,y >0,∴3x +y =(3x +y )⎝ ⎛⎭⎪⎫13x +13y =1+13+y 3x +x y ≥43+233.当且仅当y =3x 时取等号.应选D.8.[2019·福建质量检测]正五角星是一个超级优美的几何图形,且与黄金分割有着紧密的关系.在如下图的正五角星中,以A ,B ,C ,D ,E为极点的多边形为正五边形,且PTAT =5-12.以下关系中正确的选项是( )A.BP →-TS →=5+12RS →B.CQ →+TP →=5+12TS →C.ES →-AP →=5-12BQ →D.AT →+BQ →=5-12CR → 答案:A解析:由题意,知BP →-TS →=TE →-TS →=SE →,RS SE =PT AT =5-12,因此SE →=5+12RS →,故A 正确;CQ →+TP →=PA →-PT →=TA →=5+12ST →,故B 错误;ES →-AP →=RC→-QC →=RQ →=5-12QB →,故C 错误;因为AT →+BQ →=SD →+RD →,5-12CR →=RS→=RD →-SD →,假设AT →+BQ →=5-12CR →成立,那么SD →=0,不合题意,故D 错误.应选A.二、非选择题 9.如图,在四边形ABCD 中,AC 和BD 相交于点O ,设AD→=a ,AB →=b ,假设AB→=2DC →,那么AO →=________(用向量a 和b 表示). 答案:23a +13b解析:由AB→=2DC →知,AB ∥DC 且|AB →|=2|DC →|,从而|BO →|=2|OD →|.因此BO →=23BD →=23(AD →-AB →)=23(a -b ),因此AO →=AB →+BO →=b +23(a -b )=23a +13b .10.[2018·全国卷Ⅲ]已知向量a =(1,2),b =(2,-2),c =(1,λ).假设c ∥(2a +b ),那么λ=________.答案:12解析:2a +b =(4,2),因为c ∥(2a +b ),因此4λ=2,得λ=12.11.已知e 1,e 2是平面内两个不共线的非零向量,AB →=2e 1+e 2,BE →=-e 1+λe 2,EC→=-2e 1+e 2,且A ,E ,C 三点共线. (1)求实数λ的值;假设e 1=(2,1),e 2=(2,-2),求BC→的坐标; (2)已知点D (3,5),在(1)的条件下,假设ABCD 四点组成平行四边形,求点A 的坐标.解析:(1)AE→=AB →+BE →=(2e 1+e 2)+(-e 1+λe 2) =e 1+(1+λ)e 2.∵A ,E ,C 三点共线,∴存在实数k ,使得AE →=kEC →, 即e 1+(1+λ)e 2=k (-2e 1+e 2), 得(1+2k )e 1=(k -1-λ)e 2.∵e 1,e 2是平面内两个不共线的非零向量,∴⎩⎨⎧1+2k =0,λ=k -1,解得k =-12,λ=-32.BC →=BE →+EC →=-3e 1-12e 2 =(-6,-3)+(-1,1)=(-7,-2).(2)∵ABCD 四点组成平行四边形,∴AD →=BC →. 设A (x ,y ),那么AD→=(3-x,5-y ), 又BC →=(-7,-2),∴⎩⎨⎧3-x =-7,5-y =-2,解得⎩⎨⎧x =10,y =7,点A (10,7).。
【优质文档】2018–2019学年度高一数学第一学期期末复习试卷(十七)含详解

A. y x
By
log
x 1
2
C. y
2sin
4.设角 a 的终边过点 P(1,-2), 则
的值是
cos
(x 1)2
A.-4
B.-2
C.2
Dy x 2
D.4
5.方程 ex x 2 0 的解的个数是
A.0
6.已知 cos( 2
4
A.
3
B. 1
C.2
3
)
,且 ( , ) ,则 tan(
5
2
3
B.
4
4
C
3
已知函数 f ( x) Asin( x )( A 0, 0,
为 ,且图象上有一个最低点为
4
(I) 求函数 f(x)的解析式
7 M ( , 3)
12
的一个对称中心到相邻对称轴的距离
2
(Ⅱ )求函数 f( x)在 [0, ] 上的单调递增区间
18.(本小题满分 12 分
第 3 页 共 11 页
16. 设 函 数 f ( x)( x R) 满 足 f ( x ) f ( x) c o, xs当 13
f ( ) ______________________。 6
x 0 时 ,f( x)=0, 则
三、解答题 :(本大题共 6 小题 ,共 70 分 .解答应写出文字说明 ,证明过程或演算步骤
17.(本小题满分 10 分
D. a<b<c
9.已知定义在
R 上的奇函数
f (x)在 (-∞ ,0]上递减 ,且 f(-1)=1, 则足
f
(log
x 2
)
范围是
1 的 x 的取值
高一数学复习精练17 试题

数学根底知识复习数学精练 〔17〕{|32}M m m =∈-<<Z {|13}N n n M N =∈-=Z 则,≤≤〔 〕A .{}01,B .{}101-,,C .{}012,,D .{}1012-,,,2.以下四个函数中,在〔0,∞〕上为增函数的是〔 〕A.f 〔x 〕=3-xB.f 〔x 〕=x 2-3xC.f 〔x 〕=-|x |D.f 〔x 〕=-23+x 2211()31x x f x x x x ⎧-⎪=⎨-->⎪⎩,,,, ≤那么1(3)f f ⎛⎫⎪⎝⎭的值是〔 〕A .1516 B .2716- C .89 D .184.83=-x ,那么x 等于〔 〕A .2B .2-C .2±D .212()2(1)2f x x a x =+-+在区间(],4-∞上是减少的,那么实数a 的取值范围是〔〕A 、3a -≤B 、3a -≥C 、a ≤5D 、a ≥5y=x x ++192是( )A .奇函数B .偶函数C .既是奇函数又是偶函数D .非奇非偶函数7.{1,2}⊆M {1,2,3,4},那么这样的集合M 有〔 〕个A .2B .3C .4D .58. 函数()2f x x =,那么()1f a +的值是 〔 〕A 、22a a ++B 、21a +C 、222a a ++D 、221a a ++9.化简3a a 的结果是〔 〕A .aB .21aC .2aD .31a10.假设函数)(x f 为奇函数,且当,10)(,0x x f x =>时那么)2(-f 的值是〔〕 A .100- B .1001 C .100 D .1001- 11. 函数y=f(x)在R 上为减函数,且f(0)=1,f(1)=0,那么f(x)〉0的解集是〔 〕A.〔0,+∞〕B.(0,1)C.(1,+ ∞)D.(- ∞,1)12.0<c ,那么以下不等式中成立的一个是〔 〕A .c c 2>B .cc )21(>C .c c )21(2>D .c c )21(2<答案BDCDA BBDBA DD励志赠言经典语录精选句;挥动**,放飞梦想。
高一数学下学期期末冲刺卷17答案

高一数学下学期期末冲刺卷(17)答案一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知角的终边经过点,则()A. B. C. D.【答案】A【解析】分析:先求出角的终边上的点P(﹣1,3)到原点的距离为 r,再利用任意角的三角函数的定义求出结果.详解::角的终边上的点P(﹣1,3)到原点的距离为:r==,由任意角的三角函数的定义得cos==﹣.故选:A.点睛:本题考查任意角的三角函数的定义,两点间的距离公式的应用,考查计算能力,属于基础题.2.在利用最小二乘法求回归方程时,用到了下面表中的组数据,则表格中的值为()A. B. C. D.【答案】D【解析】分析:由题意设要求的数据为,求得代入回归方程,由于回归直线过样本点的中心(,),得到,即可得的值.详解:由题意可得(10+20+30+40+50)=30,(62++75+81+89因为回归直线=0.67x+54.9,过样本点的中心(,),所以(+307)=0.67×30+54.9,解得=68故选:B.点睛:本题考查线性回归方程,利用回归直线过样本中心点(,)是解决问题的关键,属于基础题.3.已知集合,,则下列结论正确的是()A. B. C. D.【答案】D【解析】分析:求出A中函数的定义域确定出A,确定出A与B的交集,并集以及包含关系.详解:由集合A中的函数y=ln(x+3),得到x+3>0,即x>﹣3,∴A=(﹣3,+∞),∵B={x|x≥2}=[2,+∞),∴A≠B,A∩B=[2,+∞),A⊇B,故选:D.点睛:此题考查了交集及其运算,考查了集合相等及子集概念,熟练掌握交集的定义是解本题的关键.4.若直线与圆相切,则的值是()A. 或B. 或C. 或D. 或【答案】C【解析】分析:由圆的标准方程求出圆心坐标和半径,由圆心到直线的距离等于圆的半径列式求得b值.详解:∵圆的标准方程为(x﹣1)2+(y﹣1)2=1,∴圆心坐标为(1,1),半径为1,∵直线与圆相切,∴圆心(1,1)到直线3x+4y﹣b=0的距离等于圆的半径,即,解得:b=2或b=12.故选:C.点睛:本题考查圆的切线方程,考查了点到直线的距离公式的应用,属于基础题.5.一程序框图如图所示,如果输出的函数值在区间上,那么输入的实数的取值范围是()A. B.C. D.【答案】D【解析】分析:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是计算分段函数的函数值.根据函数的解析式,结合输出的函数值在区间,即可得到答案.详解::根据题意,得当x∈[﹣2,2]时,f(x)=2x,∴1≤2x≤2,∴0≤x≤1;当x∉[﹣2,2]时,f(x)=3,不符合,∴x的取值范围是[0,1].故选:D.点睛:本题考查了程序框图的应用问题,也考查了分段函数的应用问题,解题时应模拟程序框图的运行过程,以便正确解答问题,属于基础题.6.一个几何体的三视图如图1所示,已知这个几何体的体积为,则( )A. B. C. D.【答案】B【解析】试题分析:由三视图可知,该几何体是四棱锥,底面积,体积,解得,故答案为B.考点:由三视图求几何体的体积.7.若向量,不共线,,,,则下列关系式中正确的是()A. B. C. D.【答案】B【解析】分析:根据条件计算向量,可得,从而可得出正确选项.详解:由条件可得=++=﹣8﹣2=2,则关系式中正确的是,故选:B.点睛:本题考查向量的共线问题,考查向量的运算法则及向量的线性运算,属于基础题.8.若,则()A. B. C. D.【答案】A【解析】试题分析:,故选A.考点:两角和与差的正切公式.【此处有视频,请去附件查看】9.已知,则函数有零点的概率为()A. B. C. D.【答案】A【解析】分析:求出函数有零点的等价条件,利用几何概型的概率公式即可得到结论.详解:若函数f(x)=x2+2ax+1有零点,则判别式△=4a2﹣4≥0,解得a≥1或a≤﹣1,∵a∈[﹣2,2],∴﹣2≤a≤﹣1或1≤a≤2,则根据几何概型的概率公式可得函数f(x)=x2+2ax+1有零点的概率为,故选:A.点睛:几何概型概率公式的应用:(1)一般地,一个连续变量可建立与长度有关的几何概型,只需把这个变量放在坐标轴上即可;(2)若一个随机事件需要用两个变量来描述,则可用这两个变量的有序实数对来表示它的基本事件,然后利用平面直角坐标系就能顺利地建立与面积有关的几何概型;(3)若一个随机事件需要用三个连续变量来描述,则可用这三个变量组成的有序数组来表示基本事件,利用空间直角坐标系建立与体积有关的几何概型.10.已知是定义在上的偶函数,且在区间上单调递增.若实数满足,则的取值范围是()A. B. C. D.【答案】B【解析】分析:根据函数的对称性可知f(x)在(0,+∞)递减,故只需令<即可.详解:∵f(x)是定义在R上的偶函数,且在区间(﹣∞,0)上单调递增,∴f(x)在(0,+∞)上单调递减.∵>0,f(﹣)=f(),即∴0<a<.故选:B.点睛:本题主要考查抽象函数的定义域、抽象函数的单调性及抽象函数解不等式.根据抽象函数的单调性解不等式应注意以下三点:(1)一定注意抽象函数的定义域(这一点是同学们容易疏忽的地方,不能掉以轻心);(2)注意应用函数的奇偶性(往往需要先证明是奇函数还是偶函数);(3)化成后再利用单调性和定义域列不等式组.11.若将函数的图形向右平移个单位,所得图象关于轴对称,则的最小正值是()A. B. C. D.【答案】C【解析】试题分析:函数的图象向右移的单位,可得,其图关轴对称,可得,即,结合,得的最小值为.故选:C.考点:(1)函数的图象变换;(2)三角函数中的恒等变换.12.已知圆及三个函数:①;②;③其中图像能等分圆面积的函数个数为()A. B. C. D.【答案】C【解析】分析:要使图象能等分圆C面积,则函数必须关于原点对称.详解:圆O关于原点O对称.函数f(x)=x3与函数f(x)=tanx是定义域上的奇函数,其图象关于原点对称,能等分圆O面积;而f(x)=xsinx是R上的偶函数,其图象关于y轴对称,且当0<x≤1时,f(x)=xsinx>0不能等分圆O面积.故满足条件的函数只有①②.故选:B.点睛:本题主要考查函数的奇偶性的性质的应用,正确理解题意是解决本题的关键.二、填空题(每题5分,满分20分,将答案填在答题纸上)13.若函数如下表所示:则__________.【答案】1【解析】【详解】分析:由表直接得出f(1)=2,再由表得出结果.详解:由表可知,f(1)=2,而f(2)=1所以f[f(1)]=f(2)=1故答案为:1点睛:本题考查根据图表求函数值.14.已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为_______.【答案】【解析】分析:根据正方体和球的关系,得到正方体的体对角线等于球的直径,结合球的体积公式进行计算即可.详解:设正方体的棱长为,因为这个正方体的表面积为,所以,解得,因为一个正方体所有的顶点在一个球面上,所以正方体的体对角线等于球的直径,即,即解得,则球的体积为.点睛:本题主要考查了空间正方体和球的关系,及球的体积的计算,利用正方体的体对角线等于球的直径,结合球的体积公式是解答的关键,着重考查了空间想象能力,以及推理与运算能力.15.设点是圆上的动点,点是直线上的动点,则的最小值为__________.【答案】4【解析】分析:过圆心A作AQ⊥直线x=﹣3,与圆交于点P,此时|PQ|最小,由此能求出|PQ|的最小值.详解:过圆心A作AQ⊥直线x=﹣3,与圆交于点P,此时|PQ|最小,由圆的方程得到A(3,﹣1),半径r=2,则|PQ|=|AQ|﹣r=6﹣2=4.故答案为:4.点睛:这个题目考查的是直线和圆的位置关系,一般直线和圆的题很多情况下是利用数形结合来解决的,联立的时候较少;还有就是在求圆上的点到直线或者定点的距离时,一般是转化为圆心到直线或者圆心到定点的距离,再加减半径,分别得到最大值和最小值.16.在中,,,是斜边上的两个动点,且,则的取值范围为__________.【答案】【解析】试题分析:根据题意可以C为原点建立平面直角坐标系,则,直线AB方程为:,可设点,由,即,化简得:,由,又,结合二次函数的图象可得:.考点:1.向量的数量积;2.二次函数的最值.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知向量=(cosα,sinα),=(cosβ,sinβ),0<β<α<π.(1)若|﹣|=,求证:⊥;(2)设c=(0,1),若+=c,求α,β的值.【分析】(1)由向量的平方即为模的平方,化简整理,结合向量垂直的条件,即可得证;(2)先求出+的坐标,根据条件即可得到,两边分别平方并相加便可得到sinβ=,进而得到sinα=,根据条件0<β<α<π即可得出α,β.【解答】解:(1)证明:由|﹣|=,即(﹣)2=2﹣2•+2=2,又因为2=2=||2=||2=1.所以2﹣2•=2,即•=0,故⊥;(2)因为+=(cosα+cosβ,sinα+sinβ)=(0,1),所以,即,两边分别平方再相加得1=2﹣2sinβ,∴sinβ=,sinα=,又∵0<β<α<π,∴α=,β=.18.在每年的3月份,濮阳市政府都会发动市民参与到植树绿化活动中去林业管理部门为了保证树苗的质量都会在植树前对树苗进行检测,现从甲、乙两种树苗中各抽测了株树苗,量出它们的高度如下(单位:厘米),甲:37,21,31,20,29,19,32,23,25,33;乙:10,30,47,27,46,14,26,10,44,46.(1)画出两组数据的茎叶图并根据茎叶图对甲、乙两种树苗的高度作比较,写出两个统计结论;(2)设抽测的株甲种树苗高度平均值为,将这株树苗的高度依次输人,按程序框(如图)进行运算,问输出的大小为多少?并说明的统计学意义,【答案】(1)见解析;(2)见解析【解析】分析:(1)画出茎叶图,通过图能判断甲,乙两种树苗的平均高度、分散情况、中位数的值.(2)直接利用均值与方差公式求解,说明几何意义即可.详解:(1)茎叶图:统计结论:(答案不唯一,任意两个即可)①甲种树苗的平均高度小于乙种树苗的平均高度;②甲种树苗比乙种树苗长得整齐;③甲种树苗的中位数为,乙种树苗的中位数为;④甲种树苗的高度基本上是对称的,而且大多数集中在平均数附近,乙种树苗的高度分布比较分散.(2)根据十个数据求得:,由框图可求得,表示株甲种树苗高度的方差.越小,表示长得越整齐,值越大,表示长得越参差不齐.点睛:平均数与方差都是重要的数字特征,是对总体的一种简明的描述,它们所反映的情况有着重要的实际意义,平均数、中位数、众数描述其集中趋势,方差和标准差描述其波动大小,方差或标准差越小,则数据分布波动较小,相对比较稳定;茎叶图的优点是保留了原始数据,便于记录及表示,能反映数据在各段上的分布情况.茎叶图不能直接反映总体的分布情况,这就需要通过茎叶图给出的数据求出数据的数字特征,进一步估计总体情况.19.如图,在底面是正方形的四棱锥中,面,交于点,是中点,为上一点.()求证:.()确定点在线段上的位置,使平面,并说明理由.【答案】(1)见解析;(2)见解析.【解析】试题分析:(Ⅰ)要证,只需证明平面即可;(Ⅱ)当点位于的中点时,要证明平面,即可.试题解析:()证明:∵面,平面,∴,∵底面是正方形,∴,又,平面,平面,∴平面,又∵平面,∴.()当点位于的中点时,平面,理由如下:连结,∵在中,是的中点,是的中点,∴,又平面,平面,∴平面.20.已知函数的最大值为.(1)求的值及的最小正周期;(2)在坐标系上作出在上的图像,要求标出关键点的坐标.【答案】(1),;(2)见解析【解析】分析:(1)先根据两角和公式对函数进行化简整理得f(x)═,再根据最大值确定a值,结合正弦函数的性质求得函数的最小正周期;(2)依据图表,分别求得0,,,,,时,f(x)的值,进而描点画出图象.详解:(1),,∵的最大值为,∴,最小正周期(2)关键点的坐标,,,,,要求正确标出四个以上,图像略.点睛:作函数图象的方法(1)作三角函数图象的基本方法就是把看作一个整体,利用五点法画图,此法注意在作出一个周期上的简图后,应向两端伸展一下,以示整个定义域上的图像;(2)变换法作图象的关键是看x轴上是先平移后伸缩还是先伸缩后平移,对于后者可利用来确定平移单位.21.四边形中,,,,.(1)求与的关系式;(2)若,求、的值以及四边形的面积.【答案】(1);(2)16【解析】本试题主要是考查了向量的共线与向量的加减法表示和向量的数量积的运用。
高一数学第一学期期末测试题和答案

高一数学第一学期期末测试题本试卷共4页,20题,满分为150分钟,考试用时120分钟。
一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.集合{13,4,5,7,9}=A ,B {3,5,7,8,10}=,那么=AB ( )A 、{13,4,5,7,8,9},B 、{1,4,8,9}C 、{3,5,7}D 、{3,5,7,8} 2.cos()6π-的值是( )A B . C .12 D .12- 3.函数)1ln()(-=x x f 的定义域是( )A . ),1(+∞B .),1[+∞C . ),0(+∞D .),0[+∞ 4.函数cos y x =的一个单调递增区间为 ( ) A .,22ππ⎛⎫-⎪⎝⎭ B .()0,π C .3,22ππ⎛⎫⎪⎝⎭D .(),2ππ 5.函数tan(2)4y x π=+的最小正周期为( )A .4π B .2πC .πD .2π 6.函数2()ln f x x x=-的零点所在的大致区间是 ( ) A .(1,2) B .(,3)e C .(2,)e D .(,)e +∞7.已知0.30.2a=,0.2log 3b =,0.2log 4c =,则( )A. a>b>cB. a>c>bC. b>c>aD. c>b>a 8.若函数23()(23)m f x m x-=+是幂函数,则m 的值为( )A 、1-B 、0C 、1D 、2 9.若1tan()47πα+=,则tan α=( )A 、34 B 、43C 、34-D 、43-10.函数22cos 14y x π⎛⎫=-- ⎪⎝⎭是( ) A.最小正周期为π的奇函数 B.最小正周期为2π的奇函数 C.最小正周期为π的偶函数 D.最小正周期为2π的偶函数二、填空题:本大题共4小题,每小题5分,满分20分.11.已知函数()()()2log 030x x x f x x >⎧⎪=⎨⎪⎩,则()0f f =⎡⎤⎣⎦ . 12.已知3tan =α,则ααααsin 3cos 5cos 2sin 4+-= ;13.若cos α=﹣,且α∈(π,),则tan α= .14.设{1,2,3,4,5,6},B {1,2,7,8},A ==定义A 与B 的差集为{|},A B x x A x B A A B -=∈∉--,且则()三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.15.(满分12分)(1)4253sin cos tan()364πππ-(2)22lg 4lg 25ln 2e -+-+16.(满分12分)已知函数()2sin 23f x x π⎛⎫=+⎪⎝⎭)(R x ∈ (1)求()f x 的振幅和初相;(2)该函数图象可由)(sin R x x y ∈=的图象经过怎样的平移和伸缩变换得到?17.(本题满分14分) 已知函数()sin 2cos 21f x x x =+-(1)把函数化为()sin(),(0,0)f x A x B A ωϕω=++>>的形式,并求()f x 的最小正周期;(2)求函数()f x 的最大值及()f x 取得最大值时x 的集合; 18.(满分14分)()2sin(),(0,0,),()62.1(0)228730(),(),sin 35617f x x A x R f x f ABC A B C f A f B C πωωπωππ=->>∈+=+=-已知函数且的最小正周期是()求和的值;()已知锐角的三个内角分别为,,,若求的值。
高三数学天天练17 解三角形及其应用

天天练17 解三角形及其应用一、选择题1.在△ABC 中,如果sin A :sin B :sin C =2:3:4,那么cos C 等于( )A .23B .-23C .-13D .-142.(·河西五市二联)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且满足(b -a)sin A =(b -c)(sin B +sin C),则角C 等于( )A .π3B .π6C .π4D .2π33.在△ABC 中,若c =2a cos B ,则△ABC 是 ( )A .直角三角形B .等腰三角形C .等腰或直角三角形D .等腰直角三角形4.(·大连双基)△ABC 中,AB =2,AC =3,B =60°,则cos C =( )A .33B .±63C .-63D .635.(·新课标全国卷Ⅲ)在△ABC 中,B =π4,BC 边上的高等于13BC ,则cos A =( )A .31010B .1010C .-1010D .-310106.(·天津,3)在△ABC 中,若AB =13,BC =3,∠C =120°,则AC =( )A .1B .2C .3D .47.(·太原五中检测)在锐角△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c.若sin A =223,a =2,S △ABC =2,则b 的值为( )A . 3B .322C .2 2D .238.在△ABC 中,a ,b ,c 分别为角A ,B ,C 的对边,且cos 2B+cos B +cos (A -C)=1,则( )A .a ,b ,c 成等差数列B .a ,b ,c 成等比数列C .a ,c ,b 成等差数列D .a ,c ,b 成等比数列二、填空题9.在△ABC 中,a =4,b =5,c =6,则sin 2A sin C =__________.10.(·长沙一模)△ABC 的周长等于2(sin A +sin B +sin C),则其外接圆半径等于__________.11.某观察站C 与两灯塔A 、B 的距离分别为300米和500米,测得灯塔A 在观察站C 北偏东30°方向,灯塔B 在观察站C 正西方向,则两灯塔A 、B 间的距离为__________米.三、解答题12.(·山东,16)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c.已知2(tan A +tan B)=tan A cos B +tan B cos A .(1)证明:a +b =2c ;(2)求cos C 的最小值.天天练17 解三角形及其应用1.D 由正弦定理a sin A =b sin B =c sin C 可知a :b :c =sin A :sin B :sin C =2:3:4,设a =2k ,b =3k ,c =4k ,cos C =a 2+b 2-c 22ab=4k 2+9k 2-16k 22×2k ×3k=-14,答案选D. 2.A 由题意得,(b -a )a =(b -c )(b +c ),∴ab =a 2+b 2-c 2,∴cos C =a 2+b 2-c 22ab =12,∴C =π3,故选A.3.B 根据题意,结合着正弦定理,可知sin C =2sin A cos B ,即。
高一下学期数学期末考试易错题总结及详解

a
的取值范围是
( ,
8] .
【解答】解:由
1
A
可得,
a(1 2) 1 3
2
第3页共7页
a 8 故答案为: ( , 8]
11.设 a , b 0 , a b 5 ,则 a 1 b 3 的最大值为 3 2 . 【解答】解:由题意, ( a 1 b 3)2(1 1)(a 1 b 3) 18 ,
C.当 k 2 时, ABC 是钝角三角形
D.当 k 1 时, ABC 是钝角三角形
【解答】解: sin A sin B sin C (k 为非零实数),可得: sin A : sin B : sin C k : 3 : 4 ,
k
3
4
由正弦定理 a b c 2R ,可得: a : b : c k : 3 : 4 , sin A sin B sin C
m n1 【解答】解:正实数 m , n 满足 m n 3 , 所以: m (n 1) 4 ,
则: m(n 1)4 ,
则 m2 1 n2 , m n1
m 1 (n 1 1)2 , m n1
m n12 1 1 , m n1
2 1 1 , m n1
2 2 1 , m(n 1)
在 B 中,由正弦定理得: a b , a sin B b sin A ,故 B 正确; sin A sin B
在 C 中, a b cos C c cos B ,
由余弦定理得: a b a2 b2 c2 c a2 c2 b2 ,
2ab
2ac
整理,得 2a2 2a2 ,故 C 正确;
2A 2B 或 2 A 2 2B , AB或AB ,
2 ABC 是等腰三角形或直角三角形,因此是假命题, C 错误.
〖人教版〗高一数学下册期末复习试卷17

〖人教版〗高一数学下册期末复习试卷第二学期期末教学质量检查一、选择题(本大题共10小题,每小题5分,共50分. 每小题各有四个选择支,仅有一个选择支正确.请用2B 铅笔把答题卡中所选答案的标号涂黑.) 1.22cos 22.5sin 22.5︒-︒的值为A .1B .12C D 2.已知点)1,1,1(A ,)3,3,3(---B ,则线段AB 的长为A. 34B. 32C. 24D. 23 3.角α的终边过)4,3(-P ,则下列结论正确的是A .54sin =αB .53cos =αC .43tan -=α D.34tan =α 4.已知1sin()23πα+=,则)cos(απ+的值为A.31 B.31- C. 31± D.322-5.北京奥运会上,七位裁判为某运动员打出的分数如茎叶图所示,则去掉一个最高分和一个最低分 后,所剩数据的平均数和方差分别为 A .84,8 B .84,1.6C .85,1147D .85,876.已知单位向量)21,(m =,则实数m 的值为A.23 B .23- C . 21 D. 23± 7.已知函数()sin (0)f x x ωωπ⎛⎫=+> ⎪3⎝⎭的最小正周期为π,则该函数的图象A .关于直线x π=4对称 B .关于点0π⎛⎫ ⎪4⎝⎭,对称C .关于点0π⎛⎫ ⎪3⎝⎭,对称D .关于直线x π=3对称 8.边长为1的等边ABC ∆中,⋅的值为A.21B.21- C.23 D.23-9.某流程图如右图所示,现输入如下四个函数,则可以输出的 函数为A.1)(+=x x fB.xx f 1)(=C.6)(+=xe xf D.)2cos()(x x f +=π10.在平行四边形ABCD 中,E 和F 分别是边CD 和BC 的中点,AC AE AF λμ=+,其中,R λμ∈,则λμ+= A.12 B.23 C.43 D.12- 二、填空题(本大题共4小题,每小题5分,共20分.请把答案填在答题卡中相应的位置上.)11.某单位为了了解用电量y 度与气温C x之间的关系,随机统计了某4天的用电量与当天气温,并由此得到线性回归方程602ˆ+-=x y.当气温为C 05时,可以预测这一天该单位的用电量约为度.12.已知扇形的圆心角为2,半径为3,则扇形的面积是. 13.如图,阴影部分为圆O 的内接等腰直角三角形(斜边为圆O 的直径),假设你在图形上随机撒一粒黄豆,则它落到阴影部分的概率为14.以点)1,2(-为圆心且与直线3450x y -+=相切的圆的方程 为.三、解答题(本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.) 15.(本小题满分13分)同时掷两枚骰子,计算: (1)两枚骰子向上的点数相等的概率;(2)两枚骰子点数之和(第9题图)(第13题图)是7的倍数的概率. 16.(本小题满分13分)某市统计局就某地居民的月收入调查了10000人,他们的月收入均在)4000,1000[内.现根据所得数据画出了该样本的频率分布直方图如下.(每个分组包括左端点,不包括右端点,如第一组表示月收入在)1500,1000[内) (1)求某居民月收入在)4000,3000[内的频率;(2)根据该频率分布直方图估计居民的月收入的中位数;(3)为了分析居民的月收入与年龄、职业等方面的关系,需再从这10000人中利用分层抽样的方法抽取100人作进一步分析,则应从月收入在)3500,3000[内的居民中抽取多少人?17.(本小题满分13已知α(1)ααsin sin 2⋅-(2)()sin 4cos 24πααπ⎛⎫+ ⎪⎝⎭+18.(本小题满分13分)已知函数23cos sin cos 3)(2-+=x x x x f . (1)求)(x f 的单调递增区间;(2)函数)(x f 的图象经过怎样的平移可使其对应的函数成为偶函数?请写出一种正确的平移方法,并说明理由. 19.(本小题满分14分)如图,已知︒=∠︒=∠60,90AOC AOB ,1||,2||,2||===OB OC OA . (1)试用向量,OA OB 来表示向量OC ;(2)若向量,OA OB ,k OC 的终点在一条直线上,频率/组距(第16题图)O A BC求实数k 的值; (3)设()13OD OA tOB t R =+∈,当⊥时,求t 的值. 20. (本小题满分14分)在平面直角坐标系xoy 中,已知圆4)1()3(:221=-++y x C 和圆16)5()4(:222=-+-y x C .(1)若直线l 过点)0,6(A ,且被圆2C 截得的弦长为34,求直线l 的方程; (2)在平面内是否存在一点P ,使得过点P 有无穷多对互相垂直的直线1l 和2l ,它们分别与圆1C 和圆2C 相交,且直线1l 被圆1C 截得的弦长的2倍与直线2l 被圆2C 截得的弦长相等?若存在,求出所有满足条件的P 点的坐标;若不存在,请说明理由.一、选择题(本大题共10小题,每小题5CAABB DCBDC二、填空题(本大题共4小题,每小题511.50 12.9 13.π1三、解答题(本大题共6小题,共80分.15.(本小题满分13分) 解:(1)若用),(b a (1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),………(6,1),(6,2),(6,3),(6,4),(6,5),(6,6),共36种.……………3分两枚骰子向上的点数相等的结果有:(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),共6种.……………5分 所以两个骰子向上的点数相等的概率是:61366==P .……………7分 (2)点数之和是7的倍数的结果有:(1,6),(2,5),(3,4),(4,3),(5,2),(6,1),共6种; …………10分所以两枚骰子点数之和是7的倍数的概率是:61366==P .…………13分 16.(本小题满分13分)解: (1)由频率分布直方图可知,居民月收入在)4000,3000[内的频率为(0.0002+0.0003)×500=0.25.…………2分 (2)由频率分布直方图可知(第19题图)0.0001×500=0.05, 0.0004×500=0.20, 0.0005×500=0.25,从而有0.0001×500+0.0004×500+0.0005×500=0.5,…………6分 所以可以估计居民的月收入的中位数为2500(元).…………7分(3)由频率分布直方图可知,居民月收入在)3500,3000[内的频率为0.0003×500=0.15,…………9分所以这10000人中月收入在)3500,3000[内的人数为0.15×10000=1500(人),…………11分再从这10000人中利用分层抽样的方法抽取100人,则应从月收入在)3500,3000[内的居民中抽取15100001500100=⨯(人).…………13分17.(本小题满分13分) 解:由于3cos 5α=,且α是第一象限的角,所以有 54cos 1sin 2=-=αα,…………2分34cos sin tan ==ααα.…………4分从而有(1)752123425354)54(tan 2cos sin sin 22=⨯+⋅-=+⋅-αααα.…………7分 (2))42cos()4sin(παπα++=ααα2cos )sin (cos 22+…………9分ααααααsin cos 122sin cos )sin (cos 2222-⋅=-+=…………11分 =2255453122-=-⨯.…………13分 18.(本小题满分13分) 解: (1)23cos sin cos 3)(2-+=x x x x f x x 2sin 212cos 23+=…………4分).32sin(π+=x …………5分由,223222πππππk x k +≤+≤+-得,12125ππππk x k +≤≤+-…………7分 所以)(x f 的单调递增区间为)](12,125[Z k k k ∈++-ππππ.…………8分(2)将函数)(x f 的图象向左平移12π个单位,其对应的函数为 x x x y 2cos )22sin(]3)12(2sin[=+=++=πππ,…………12分由于x y 2cos =是偶函数,所以将)(x f 的图象向左平移12π个单位,其对应的函数可成为偶函数.…………13分(说出正确的一种平移即可,但如果没有说明理由,则扣3分) 19.(本小题满分14分)解:(1)以直线OA 为x 轴,OB 为y 轴,如图建立直角坐标系则)3,1(),1,0(),0,2(===.…………2分 令n m +=,则有即⎪⎩⎪⎨⎧==,3,21n m …………4分 所以21+=. …………5分 (2)令)3,(k k k ==,则有)1,2(-=-=,)3,2(k k -=-=.…………6分又由题意知:AB ∥AE ,…………7分 所以0)2(132=-⨯-⨯-k k ,…………9分解得112343212-=+=k .…………10分 (3)),32(31t t =+=.…………11分 OAB Cxy由于AB OD ⊥,所以0=⋅AB OD ,从而有0)1,2(),32(=-⋅t , 即034=+-t .…………12分解得34=t .…………13分所以当⊥时,34=t . …………14分20. (本小题满分14分)解:(1)若直线l 的斜率不存在,则过点)0,6(A 的直线为6=x ,此时圆心2C )5,4(到直线6=x 的距离为2,l 被圆2C 截得的弦长为344162=-,符合题意,所以直线6=x 为所求.…………2分若直线l 的斜率存在,可设直线l 的方程为(6)y k x =-,即60kx y k --=,所以圆心2C 到直线l 的距离1|52|1|654|22++=+--=k k k k k d . …………3分又直线l 被圆2C 截得的弦长为34,圆2C 的半径为4,所以圆心2C 到直线l 的距离应为2)32(422=-,即有21|52|2=++k k ,解得:2021-=k . …………4分 因此,所求直线l 的方程为6=x 或)6(2021--=x y , 即6=x 或01262021=-+y x . …………5分 (2) 设P 点坐标为(,)m n ,直线1l 的斜率为k (不妨设)0≠k ,则21,l l 的方程分别为:)(:1m x k n y l -=-即0:1=-+-km n y kx l ,)(12m x kn y l --=-即0:2=--+m kn ky x l . …………6分因为直线1l 被圆1C 截得的弦长的2倍与直线2l 被圆2C 截得的弦长相等,又已知圆2C 的半径是圆1C 的半径的2倍.由垂径定理得:圆心1C 到直线1l 的距离的2倍与2C 直线2l 的距离相等.…………7分故有1|54|1|13|222+--+=+-+--k m kn k k km n k ,…………10分化简得:|54||13|2m nk k km n k --+=+-+,即有(21)(22)0m n k m n +++--=或(211)(62)0m n k n m -++--=.…………11分由于关于k 的方程有无穷多解,所以有210220m n m n ++=⎧⎨--=⎩或2110260m n m n -+=⎧⎨--+=⎩, …………12分 解之得:⎩⎨⎧-==10n m 或⎪⎩⎪⎨⎧=-=523516n m , …………13分 所以所有满足条件的P 点坐标为)1,0(-或)523,516(-.…………14分。
天天练17

数 学 天 天 练17
姓名: 班级: 分数:
一、填空题(每空5分)
1、将原点O 向右平移3个单位长度所得的点A 表示的数为_ ___,点O 与点A 之间的距离为 __。
2、如果在数轴上点A 表示-4,将A 向右移动7个单位长度,那么终点B 表示的数为 ____,AB 间的距离为___ __。
与点A 相距7个单位长度的点所表示的数为_____ _____。
3、如果点A 表示-4,将A 向右移动7个单位长度,再向左移动4个单位长度,那么终点B 表示的数为______,AB 间的距离是______.
4、已知数a,b,c 的关系是a<0,b>0,c<0,且|c|>|b|>|a|, 化简a+b|-|c-b|+|c-a|=
5、(1)已知 ,则 (2)已知 ,则
6、(20分)①若│x-3│+│y │=0, 求x 、y 的值。
②若│2x-1│+│2+3y │ =0,求│x │+│y │的值。
③若│x │=7,│y │=12,且x>y,则求x+y 的值。
7、计算(30分)
(1) (2) 2-=+b b a a __________=ab ab 22222)1.0(]2716)412(42)21(5.0[÷⨯+----+-)411(323)2132(215-÷÷-⨯-1-=++c c b b a a ________=abc abc。
人教版高一数学期末复习(公式总结与综合练习和答案)

1 sin x
8.已 x
的值是
2
sin x 1
9.将函数 y f ( x) 的图象上的每一点的纵坐标变为原来的
象限角 . .
.
1 得到图象 C1 ,再将 C1 上每一点的横坐标变为原来的 3
1 得到 2
图象 C2 ,再将 C2 上的每一点向右平移
为
.
个长度单位得到图象 C3 ,若 C3 的表达式为 y sin x ,则 y 3
f (x) 的解析式
1
12.已知 f
2
log 1
2
x
x 1. x1
( 1)求 f (x) 的解析式;
( 2)判断 f (x) 的奇偶性;
( 3)判断 f (x) 的单调性并证明.
13.已知函数 y= 1 cos2x+
3
sinxcosx+1,x ∈ R .
2
2
(1)求它的振幅、周期和初相;
(2)用五点法作出它的简图;
f ( x1) f (x2 ) 0即 f (x1 ) f ( x2 ) 则认为该函数在其定义域内单调递减。 (具体情况具体定)
函数的周期: 若 f ( x T ) f (x) ,则 T 为函数周期。
必修四:
4、关于扇形的计算公式: l
2π R 2 R; S
π R2 1 R2 1 Rl
2π
2π
2
2
l ——弧长α——圆心角(弧度制 R ——扇形半径 S——面积
(3)该函数的图象是由 y=sinx(x ∈ R)的图象经过怎样的平移和伸缩变换得到的?
人教版高中数学必修一至必修四公式(必会)
人教版高中数学必修一至必修四公式(必会)
1. 3 个 2.0.5 3
天一高一数学试卷期末

一、选择题(每题5分,共50分)1. 若 \(a > b\),则下列不等式中正确的是:A. \(a^2 > b^2\)B. \(a + 1 > b + 1\)C. \(\frac{a}{b} > \frac{b}{a}\)D. \(a - b < 0\)2. 下列函数中,定义域为全体实数的是:A. \(y = \sqrt{x - 1}\)B. \(y = \frac{1}{x}\)C. \(y = |x|\)D. \(y = \sqrt[3]{x}\)3. 若 \(m, n\) 是方程 \(x^2 - (m + 1)x + n = 0\) 的两个实数根,则 \(m + n\) 的值是:A. 2B. 3C. 4D. 54. 下列数列中,是等比数列的是:A. 1, 3, 9, 27, ...B. 1, 2, 4, 8, ...C. 1, 3, 6, 10, ...D. 1, 2, 4, 7, ...5. 若 \(A\) 和 \(B\) 是两个不等事件,且 \(P(A) = 0.4\),\(P(B) = 0.6\),\(P(A \cap B) = 0.2\),则 \(P(A \cup B)\) 的值是:A. 0.5B. 0.6C. 0.8D. 16. 已知 \(f(x) = 2x + 3\),则 \(f(-1)\) 的值是:A. -1B. 1C. 2D. 57. 在直角坐标系中,点 \(A(2, 3)\) 关于直线 \(y = x\) 的对称点是:A. (2, 3)B. (3, 2)C. (-2, -3)D. (-3, -2)8. 若 \(x^2 - 5x + 6 = 0\),则 \(x^3 - 15x^2 + 54x\) 的值是:A. 0B. 1C. 2D. 39. 下列函数中,是奇函数的是:A. \(y = x^2\)B. \(y = \frac{1}{x}\)C. \(y = |x|\)D. \(y = x + 1\)10. 在等腰三角形 \(ABC\) 中,\(AB = AC\),\(BC = 6\),\(AD\) 是底边\(BC\) 的中线,则 \(AD\) 的长度是:A. 3B. 4C. 5D. 6二、填空题(每题5分,共50分)1. 若 \(a + b = 5\),\(ab = 6\),则 \(a^2 + b^2\) 的值是 _______。
