第3章_时域瞬态响应分析_3.5高阶系统的瞬态响应
《控制工程基础》课程作业习题(含解答)
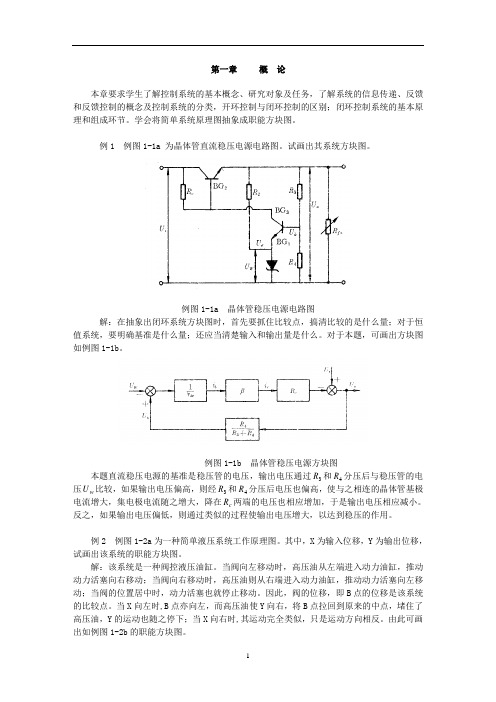
第一章概论本章要求学生了解控制系统的基本概念、研究对象及任务,了解系统的信息传递、反馈和反馈控制的概念及控制系统的分类,开环控制与闭环控制的区别;闭环控制系统的基本原理和组成环节。
学会将简单系统原理图抽象成职能方块图。
例1 例图1-1a 为晶体管直流稳压电源电路图。
试画出其系统方块图。
例图1-1a 晶体管稳压电源电路图解:在抽象出闭环系统方块图时,首先要抓住比较点,搞清比较的是什么量;对于恒值系统,要明确基准是什么量;还应当清楚输入和输出量是什么。
对于本题,可画出方块图如例图1-1b。
例图1-1b 晶体管稳压电源方块图本题直流稳压电源的基准是稳压管的电压,输出电压通过R和4R分压后与稳压管的电3压U比较,如果输出电压偏高,则经3R和4R分压后电压也偏高,使与之相连的晶体管基极w电流增大,集电极电流随之增大,降在R两端的电压也相应增加,于是输出电压相应减小。
c反之,如果输出电压偏低,则通过类似的过程使输出电压增大,以达到稳压的作用。
例2 例图1-2a为一种简单液压系统工作原理图。
其中,X为输入位移,Y为输出位移,试画出该系统的职能方块图。
解:该系统是一种阀控液压油缸。
当阀向左移动时,高压油从左端进入动力油缸,推动动力活塞向右移动;当阀向右移动时,高压油则从右端进入动力油缸,推动动力活塞向左移动;当阀的位置居中时,动力活塞也就停止移动。
因此,阀的位移,即B点的位移是该系统的比较点。
当X向左时,B点亦向左,而高压油使Y向右,将B点拉回到原来的中点,堵住了高压油,Y的运动也随之停下;当X向右时,其运动完全类似,只是运动方向相反。
由此可画出如例图1-2b的职能方块图。
例图1-2a 简单液压系统例图1-2b 职能方块图1.在给出的几种答案里,选择出正确的答案。
(1)以同等精度元件组成的开环系统和闭环系统,其精度比较为_______ (A )开环高; (B )闭环高; (C )相差不多; (D )一样高。
(2)系统的输出信号对控制作用的影响 (A )开环有; (B )闭环有; (C )都没有; (D )都有。
瞬态响应及误差分析(时域分析法)

10K O 10K O K OG ( S ) 10K O 1 10K H ( s) 0.2s 1 0.2 1 K H G ( s) 1 10K H 0.2s 1 10K H s 1 0.2s 1 1 10K H 10K O 1 10K K * 10 K O 10 0.2 H T * 0.02 K H 0.9 1 10K H
12
3. 选取试验输入信号的原则:
选取的输入信号应反映系统工作的大部分实际情况; 形式简单,便于用数学式表达及分析处理,实际中可 以实现或近似实现; 应选取那些能够使系统工作在最不利的情形下的输入 信号作为典型试验信号;
•如控制系统的输入量是突变的,采用阶跃信号。如室温 调节系统 。 •如控制系统的输入量是随时间等速变化,采用斜坡信号 作为实验信号 •如控制系统的输入量是随时间等加速变化,采用抛物线 信号; 宇宙飞船控制系统 •如控制系统为冲击输入量,则采用脉冲信号
特征点: 1 A点 : xo (T ) 0.368 xo (0) ) 2)零时刻点: xo (t )
1 T
2e
t T t 0
1 2 ; x o ( 0) T T
24
1
一阶系统单位脉冲响应的特点: 1. 瞬态响应:(1/T )e –t/T;稳态响应0; 2. 瞬态响应的特性反映系统本身的特性,时间常数大的 系统,其响应速度慢于时间常数小的系统。 3. 输入试验信号仅是为了识别系统特性,系统特性只取 决于组成系统的参数,不取决于外作用的形式。 4. xo(0)=1/T,随时间的推移,xo(t)指数衰减。 5.
量从初始状态到稳定状态的响应过程。
稳态响应:当某一输入信号的作用下,系统的响应
第3章_时域瞬态响应分析_3.2一阶系统的瞬态响应

(t ≥ 0)
1 斜率 − 2 T
1 0.368 T
1 − t /T xo (t ) = e T
T
一阶系统三种典型输入信号及响应关系: 一阶系统三种典型输入信号及响应关系:
xi (t ) = t
输 入
xt (t ) = t − T + Te x1 (t ) = 1 − e 1 1 −T t xδ (t ) = e T
x0(t) 1
1/T
xo(t)=1-e-t/T
86.5%
0
63.2%
95.0%
98.2%
T
2T
3T
4T
t
特点 一阶惯性系统总是稳定的,无振荡。 (1)一阶惯性系统总是稳定的,无振荡。 曲线上升到0.632的高度 。 反过来 , 的高度。 ( 2 ) 经过时间 T , 曲线上升到 的高度 反过来, 如果用实验的方法测出响应曲线达到0.632的时间 , 的时间, 如果用实验的方法测出响应曲线达到 的时间 即是惯性环节的时间常数。 即是惯性环节的时间常数。 经过时间3 响应曲线达稳定值的95 95% (3)经过时间 3T~ 4T,响应曲线达稳定值的95%~ 98% 可以认为其调整过程已经完成, 98 % , 可以认为其调整过程已经完成 , 故一般取调 整时间( 整时间(3~4)T。 响应曲线的切线斜率为1/T。 (4)在t=0处,响应曲线的切线斜率为 。
注意: 该性质只适用于线性定常系统, 注意 : 该性质只适用于线性定常系统 , 不适用于 线性时变系统和非线性系统。 线性时变系统和非线性系统。
1 T T = 2− + s s s+ 1 T
单位斜坡响应为 x0 (t ) = t − T + Te
第三章 时域瞬态响应

时域瞬态响应
汇报人:XX
目录
CONTENTS
01 添加目录标题
02 时域瞬态响应的基 本概念
03 时域瞬态响应的分 析方法
04 时域瞬态响应在工 程中的应用
05 时域瞬态响应的未 来发展
添加章节标题
时域瞬态响应的基本概 念
定义与特性
时域瞬态响应:描 述系统在时域中的 瞬态响应特性
定义:系统在输入 信号作用下的输出 信号随时间的域信号进行分析
现代分析方法
快速傅里叶变换(FFT):快速计 算傅里叶变换,适用于长信号分析
添加标题
添加标题
添加标题
添加标题
拉普拉斯变换:将时域信号转换为 复频域信号进行分析
小波变换:将时域信号分解为不同 尺度的小波,适用于非平稳信号分 析
优缺点比较
优点:能够直观地反映系统的动态特性,易于理解和分析 缺点:需要大量的数据,计算量较大 优点:可以分析系统的稳定性和稳定性裕度 缺点:不能直接反映系统的频率特性,需要进一步处理才能得到频率响应
瞬态激励:通常 采用阶跃函数、 脉冲函数等作为 瞬态激励
响应测量:通过 测量系统在瞬态 激励下的输出信 号来获取系统的 瞬态响应
数据处理:对测 量数据进行处理 和分析,以获取 系统的瞬态特性 参数
时域瞬态响应的分析方 法
经典分析方法
傅里叶变换:将时域信号转换为频域信号,便于分析 拉普拉斯变换:将时域信号转换为复频域信号,便于分析 卷积定理:用于分析两个信号的卷积,得到新的信号 傅里叶级数:将时域信号分解为傅里叶级数的形式,便于分析 拉普拉斯变换的逆变换:将复频域信号转换为时域信号,便于分析 傅里叶变换的逆变换:将频域信号转换为时域信号,便于分析
控制工程基础大作业

控制工程基础大作业第一篇:控制工程基础大作业控制工程基础(B)大作业一、查阅相关资料,撰写读书报告通过广泛的资料查阅,以论文形式就控制领域发展状况提交相关读书报告,以培养学生文献检索和阅读能力。
要求:至少阅读5篇2008年以后的文献资料,并在上交时附上相应的参考文献或网址,阅读报告的字数不得少于3000汉字。
二、应用Matlab软件绘制Nyquist图及Bode图1、自己从教材上的例题或者课后作业中选择一个系统,绘制其Bode图。
2、已知系统的开环传递函数为G(s)=100k,用Matlab分s(s+5)(s+10)别绘制k=1,8,20时系统Nyquist 图,并判断系统的稳定性。
试分析k对系统稳定性的影响。
三、控制系统典型环节性能分析熟悉Matlab软件Simulink的基本使用方法,利用Simulink建立各典型环节的仿真模型,并通过仿真得到各典型环节的单位阶跃响应曲线,给出各典型环节相关参数变化对典型环节动态性能的影响。
要求:每个学生的文件名包括姓名、班级和学号(1~2位数字)。
该部分主要是考察大家的自学能力,网上有很多资料可下载、查阅。
大作业以报告形式撰写,由各班长(或者学习委员)负责收齐电子文档,并于6月12日上交,其中电子文档以班为单位打包后发送至邮箱:*****************附:本课程成绩评定方法考勤、课堂表现、平时作业、实验报告、大作业及期末考试相结合,其中:考勤、课堂表现、平时作业与实验报告占20%,大作业占20%,期末考试成绩占60%。
任课教师:江老师2013年5月第二篇:控制工程基础试卷序号一、试写出图示机械装置(物体与地面无摩擦)在外力F作用下的运动(微分)方程,并求该系统的传递函数Y0(s)/F(s)。
(10分)二、试求图示框图的传递函数C(s)/R(s)(方法不限,10分)。
序号三、某单位负反馈控制系统如图。
已知K=4,设输入信号为单位阶跃函数,求:(15分)(1)闭环传递函数C(s)/R(s);(2)单位阶跃响应c(t)(3)调整时间ts;(4)最大超调量。
第三章系统时域响应分析

s1 s2
[s平面]
系统可视为两个一阶系统的串或并联
图1)
2) 1,有两个相等负实根,
s ,
1,2
n
系统称为临界阻尼系统。
s1,2
2020/8/17
jω
图2)
3)0 1,有两共轭复根,
s 2
j 1
,
1,2
n
n
系统称为欠阻尼系统。
4) 0,有两个共轭虚根,
s j ,
1,2
)
p
(
2
1
)sin(
n
d tp )
t
n
p
e
cos(
2
d tp )
1
0
d
2020/8/17
t t sin ) (co s ) 0 ( .
n dp
d
dp
t 当cos( )0 (1) dp
2
2
1
1
t 有tg(
) d n
dp
tg
n
n
t k, dp
t t 由定义取 。
,
n
(s)1 s2 n
Xo s s s
s s 1
2
1
1
s 2 21
21 21
ss1
ss2
xo
e e (t)1
xo
s s 2
st 1
st 2
n ( )1
2
1 1
2
2020/8/17
0
t
s 2)1,系统为临界阻 尼系 统 。,
1,2
n
n
X(s)1s2
o
s s
2020/8/17
2、描述欠阻尼二阶系统单位阶跃响应的特性, 常用的性能指标:
自动控制原理第3章
自动控制原理
17
调量越小, 响应的振荡 越弱,系统 的平稳性越 好,灵敏性?
越大,超
自动控制原理
18
3-3-2 二阶系统的单位阶跃响应
一定时 ,瞬态分 量衰减速 度取 n e 决于 n 故 衰减系数
自动控制原理
19
3-3-2 二阶系统的单位阶跃响应
(2)等幅振荡型
h(t ) 0 1 e nt 1
c (s)
自动控制原理
12
3-3-1 二阶系统的数学模型
开环传递函数
K G(s) s(Tm s 1)
c ( s) K ( s) r ( s ) Tm s 2 s K
R(S) C(S)
闭环传递函数
二阶系统微分方程 系统的闭环传递函数的标准形式:
2 n ( s) 2 2 s 2 n s n
自动控制原理
4
3-1 系统的时域性能指标
动态性能指标
在阶跃函数作用下测定或计算系统的动态性能指标 因为阶跃输入可以表征系统受到的最严峻的工作状态 (1)延迟时间
td
h ()
(2)上升时间
(3)峰值时间 (4)调节时间
tr
tp
0.9h() 0.5h() 0.1h()
td
ts
tr
ts
tp
5
误差带:±5%, ±2%
3-3-3 欠阻尼二阶系统的动态过程分析
(3)峰值时间 t p 的计算
dh(t ) n t e n p sin( d t p ) 0 dt t t p 1 2
则 sin( d t p ) 0
d t p 0, ,2 , d t p
第三章 时域瞬态响应分析

特征方程的根为:
2 s1,2 ξωn jωn 1 -ξ
上式中,令: σ=ξωn , 衰减系数
2 ωd ωn 1 ξ , 阻尼振荡频率
三、二阶系统的时域分析
31
1、定义(续)
二阶振荡环节为:
2 n 2 ωn G s 2 2 s ξωn jωd s ξωn jωd s 2 n s n
注意:
–系统的时域性能指标往往选择阶跃函数作为输入来定义。 –分析系统的频率特性一般用正弦函数作为典型输入信号。
一、时域响应及性能指标
6
(二)、典型输入信号
• 单位阶跃函数 1(t)
• 单位脉冲函数 δ(t)
• 单位加速度函数 (½)t2
• 单位斜坡函数 t
• 正弦函数 A sin(wt+ø)
一、时域响应及性能指标
二、一阶系统的时域分析 20
3、一阶系统的单位脉冲响应
单位脉冲输入x i t δt的象函数为X i s 1,则
1 X o s Gs Xi s 1 Gs 1 Ts 1 s T 1 1 Tt 进行拉氏反变换:x o t e 1t T 1 T
特征方程的特征根为:
2 s1,2 jωd ξωn jωn 1 -ξ
分类讨论: 1) ξ 0,负阻尼,两个正实 部的特征根,系统发散 。 2) ξ=0 ,零阻尼,一对纯虚根 ,瞬态响应为等幅振荡 。 3) 0 ξ 1,欠阻尼,一对共轭 复根,位于左半s平面 。 4) ξ=1 ,临界阻尼,两个相等 的负实根。 5) ξ 1,过阻尼,两个不等 的负实根。
三、二阶系统的时域分析 32
2、二阶系统单位阶跃响应
1 单位阶跃输入x i t 1t的象函数为X i s ,则 s 2 ωn 1 X o s Gs Xi s 2 2 s 2ξωns ωn s ωn 1 = s ξωn jωd s ξωn jωd s
第三章 时域瞬态响应分析

第三章时域瞬态响应分析3.1 典型输入信号和性能指标3.2 一阶系统的瞬态响应3.3 二阶系统的瞬态响应3.4 高阶系统的瞬态响应时域分析法:根据系统在一定的输入信号作用下其输出随时间变化的关系,分析系统稳定性、瞬态性能和稳态性能的方法。
一、瞬态响应和稳态响应1.瞬态响应:系统在输入信号作用下,输出量从初始状态过渡到稳定状态的响应过程。
决定于:①系统结构参数;②输入信号的形式;③初始状态。
2. 稳态响应:信号输入后,时间趋向于无穷大时系统的输出状态。
x o(ωn t)x i(ωn t)=1(t)ωn t3. 时域响应分析中,往往选择典型输入信号①数学处理简单,给定典型信号下的性能指标,便于分析和综合系统。
②典型输入下的响应往往作为分析复杂输入时系统性能的基础;③便于进行系统辨识,确定未知环节的传递函数。
任一时间函数信号输入时系统的响应①任一时间函数信号x i (t )可分解为一系列脉冲信号【x i (τk )Δτ】的叠加。
②线性系统对x i (t )输入的响应x o (t )等于这一系列脉冲信号各个单独作用下系统响应【x i (τk )Δτ g (t -τk )】的叠加。
()()()()()()()1o i i i 0lim d *n tk k n k x t x g t x g t x t g t ττττττ-→∞==∆⋅-=-=∑⎰结论:任一时间函数信号输入下,系统的输出响应x o (t )为输入信号x i (t )与脉冲响应函数g (t )的卷积,即:x o (t ) =x i (t ) *g (t )。
()i x t ()o x t ()()i k k x g t τττ∆⋅-()()()1o i 0n k k k x t x g t τττ-==∆⋅-∑()i k x τx i (t )x o (t )=x i (t ) *g (t )5. 正弦信号()i sin 000a t t x t t ω>⎧=⎨<⎩ 系统分析时,典型输入信号的选择:视系统具体工作状况而定。
三章时域瞬态响应

则
Xo s
Xo Xi
s s
Xi
s
1 1 Ts 1
1
T
s
1 T
进行拉氏反变换
xo
(t)
1 T
1t
eT
1t
xo(t)
1 T
1t
eT
1t
3.2节小结
一阶系统的瞬态响应:
1. 单位斜坡响应 xot(t)tTTeT 1t 1t 2. 单位阶跃响应 xo1(t)1eT1t 1t
1
1
1 2( 2
2 11) 2( 2
2 11)
s s n n 2 1 s n n 2 1
进行拉氏反变换,得
x o (t) 1 2212 1 1e 2 1 n t 2212 1 1e 2 1 n t 1t
n
1 2
3. 求取最大超调量
Mp
将上式代入到单位阶跃响应表达式中,得
Mp xo (tp ) 1
=
1-
-n
e
n
1- 2
sin
arctan
1- 2
=e =e
-n
n
1- 2
xo
(t)
1t 1e T
1t
常数
故 T1lgetlg1xo(t)
据此鉴别系统是否为一阶惯性环节。
Lg[1-xo(t)] t
实验三 高阶系统的瞬态响应和稳定性分析

实验三 高阶系统的瞬态响应和稳定性分析一、实验目的1. 通过实验,进一步理解线性系统的稳定性仅取决于系统本身的结构和参数,它与外作用及初始条件均无关的特性;2. 研究系统的开环增益K 或其它参数的变化对闭环系统稳定性的影响。
二、实验设备同实验一。
三、实验内容观测三阶系统的开环增益K 为不同数值时的阶跃响应曲线;四、实验原理三阶系统及三阶以上的系统统称为高阶系统。
一个高阶系统的瞬态响应是由一阶和二阶系统的瞬态响应组成。
控制系统能投入实际应用必须首先满足稳定的要求。
线性系统稳定的充要条件是其特征方程式的根全部位于S 平面的左方。
应用劳斯判断就可以判别闭环特征方程式的根在S 平面上的具体分布,从而确定系统是否稳定。
本实验是研究一个三阶系统的稳定性与其参数K对系统性能的关系。
三阶系统的方框图和模拟电路图如图3-1、图3-2所示。
图3-1 三阶系统的方框图图3-2 三阶系统的模拟电路图(电路参考单元为:U 3、U 8、U 5、U 6、反相器单元)图3-1的开环传递函数为 系统开环传递函数为:)15.0)(11.0()1)(1()(2121++=++=S S S K K S T S T S K s G τ 式中τ=1s ,S T 1.01=,S T 5.02=,τ21K K K =,11=K ,5102XK R =(其中待定电阻R x 的单位为K Ω),改变R x 的阻值,可改变系统的放大系数K 。
由开环传递函数得到系统的特征方程为020201223=+++K S S S由劳斯判据得0<K<12 系统稳定K =12 系统临界稳定K>12 系统不稳定 其三种状态的不同响应曲线如图3-3的a)、b)、c)所示。
a) 不稳定 b) 临界 c)稳定图3-3三阶系统在不同放大系数的单位阶跃响应曲线五、实验步骤根据图3-2所示的三阶系统的模拟电路图,设计并组建该系统的模拟电路。
当系统输入一单位阶跃信号时,在下列几种情况下,用上位软件观测并记录不同K 值时的实验曲线。
时域瞬态响应分析 三章时域分析法

1 t T
]
t
)
当t时,e()=T 当输入为单位斜坡函数时, 一阶系 统存在稳态误差T 。
3. 一阶系统的单位脉冲响应
单位脉冲输入为 输出为
xi (t ) (t )
xo(t)
X i ( s) 1
X 0 ( s) G( s) X i ( s)
单位脉冲响应为
如控制系统的输入随时间往复变化时,采用正弦信号
3.2 一阶系统的瞬态响应
能够用一阶微分方程描述的系统称为一阶系统。
它的典型形式为一阶惯性环节
X 0 ( s) 1 G( s) X i ( s) Ts 1
1.一阶系统的单位阶跃响应
单位阶跃输入为 输出为
1 1 1 T 1 X 0 ( s) G( s) X i ( s) Ts 1 s s Ts 1 s 1 s 1 T
第3章 时域瞬态响应分析
3.1 时域分析中的典型信号 3.2 一阶系统的瞬态响应 3.3 二阶系统的瞬态响应 3.4 二阶系统的瞬态响应性能指标 *3.8 高阶系统的瞬态响应
3.1 时域分析中的典型信号
时域分析是指在时间域内研究系统在一定输入信号
的作用下,其输出信号随时间的变化情况。
控制系统的输出响应是由瞬态响应和稳态响应两部分 组成。
能用二阶微分方程描述的系统称为二阶系统。二阶系统 总包含两个贮能元件,能量在两个元件之间相互转换,引起 系统具有往复振荡的趋势 。RLC就是一个典型的二阶系统。 一. 二阶系统的典型传递函数
Xi (s) 2 n s(s +2n ) Xo (s)
闭环传递函数
2 X o ( s) n (s) 2 2 X i (s) s 2 n s n
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
×
1
偶极子 -1
0
s2×
相距很近的一对零点和极点叫作偶极子。 相距很近的一对零点和极点叫作偶极子。 一对靠得很近的零点和极点,在输出中, 一对靠得很近的零点和极点,在输出中,与该极 点相对应的分量可以忽略, 点相对应的分量可以忽略,也即这一对靠得很近的零 点和极点可以一起消掉,这种情况称为偶极子相消。 点和极点可以一起消掉,这种情况称为偶极子相消。 经验指出, 经验指出,如果闭环零点和极点之间的距离比它 们本身的模值小一个数量级时, 们本身的模值小一个数量级时,则这一对零点和极点 就构成了偶极子。 就构成了偶极子。 偶极子的概念对控制系统的综合设计是很有用的, 偶极子的概念对控制系统的综合设计是很有用的, 有时可以有目的地在系统中加入适当的零点, 有时可以有目的地在系统中加入适当的零点,以抵消 对动态性能影响较大的不利的极点, 对动态性能影响较大的不利的极点,使系统的性能得 到改善。 到改善。
m m −1 m m −1 X o ( s ) K ( s + b1s + L + bm −1s + bm ) K ( s + b1s + L + bm−1s + bm ) = q = n n −1 r Xi (s) s + a1s + L + an −1s + an ( s + pi ) ∏ ( s 2 + 2ξ jω j s + ω 2j ) ∏ i =1 j =1
《控制工程基础》 控制工程基础》
第3章 时域瞬态响应分析 章 3.5 高阶系统的瞬态响应
3.5.1 高阶系统的单位阶跃响应
一般的高阶机电系统可以分解成若干一阶惯 性环节和二阶振荡环节的叠加。 性环节和二阶振荡环节的叠加。其瞬态响应即是由 这些一阶惯性环节和二阶振荡环节的响应函数叠加 组成。对于一般单输入、单输出的线性定常系统, 组成。对于一般单输入、单输出的线性定常系统, 其传递函数可表示为
低阶系统G1的单位阶跃响应(用红色表示): 低阶系统 的单位阶跃响应(用红色表示): 的单位阶跃响应
将高阶系统G 用蓝色表示)和低阶系统G1 (用红色表示)的 用红色表示) 将高阶系统 (用蓝色表示)和低阶系统 单位阶跃响应画在同一张图上进行对比,发现二者非常近似: 单位阶跃响应画在同一张图上进行对比,发现二者非常近似:
注意:近似时应保证 系统增益G(0)不变。
近似前后的单位阶跃响应曲线
近似 xo(t)
xo(t)
10 1 例:G ( s ) = 2 ≈ 2 2 ( s + s + 1)( s + 5s + 10) s + s + 1
在一般情况下, 在一般情况下 , 当 某些极点与虚轴的距离 是其它极点与虚轴距离 的 4-5 倍及 以 上时 , 这 些极点可以略去。 些极点可以略去。
s3
×
1.94 s平面 平面
s1 ×
-0.5
0.87 0
-2.5
s2 × s4
×
近似 xo(t) xo(t)
结论: 结论: ①高阶系统的各个闭环极点对系统时间响应的影响程度是不相 同的。 平面左半平面内,距离虚轴越远的极点, 同的。在s平面左半平面内,距离虚轴越远的极点,其负实部 的绝对值就越大, 的绝对值就越大,与这些极点相对应的指数项分量与阻尼指数 项分量衰减越快。因此, 项分量衰减越快。因此,对高阶系统的时间响应进行近似分析 可以忽略这些分量的影响。 时,可以忽略这些分量的影响。 相反地, ②相反地,距离虚轴很近的极点则对系统的时间响应起主导作 因而这种极点就被称为主导极点。 用,因而这种极点就被称为主导极点。 在工程上,一般将高阶系统中距离虚轴最近、 ③在工程上,一般将高阶系统中距离虚轴最近、其实部的绝对 值为其它极点绝对值的1/5或更小的闭环极点作为主导极点。 1/5或更小的闭环极点作为主导极点 值为其它极点绝对值的1/5或更小的闭环极点作为主导极点。 主导极点对高阶系统的瞬态响应起主导作用。 主导极点对高阶系统的瞬态响应起主导作用。 对于高阶系统,如果能够找到主导极点, ④对于高阶系统,如果能够找到主导极点,就可以忽略其它远 离虚轴的极点的影响,近似为一阶或二阶系统进行处理。 离虚轴的极点的影响,近似为一阶或二阶系统进行处理。
例1:已知某高阶系统 :已知某高阶系统G(s)的传递函数为 的传递函数为
G (s ) = s 2 + 20s + 100 s 6 + 15s 5 + 84s 4 + 223s 3 + 309s 2 + 240s + 100
试求该系统的单位阶跃响应。 试求该系统的单位阶跃响应。 解:采用MATLAB软件计算 采用 软件计算 numerator=[1 20 100]; denominator=[1 15 84 223 309 240 100]; t=(0:0.1:20); step(numerator,denominator,t);
(s + a + δ) 2a ⋅ 例:G(s) = a + δ (s + a)(s 2 + 2 s + 2 ) δ << a
情况(1): 情况(1): (1)
1.8182(s + 2.2 ) (1) G(s) = -2.2 (s + 2 )(s 2 + 2 s + 2 ) •× 2 -2 ≈ 2 ? s + 2s + 2 偶极子
s平面 平面
×
j
×
主导 极点
s平面 平面 s1 × β s2×
j 主导 极点 0
s1
×
0
×
×
×
5 1 例:G ( s ) = ≈ ( s + 1)( s + 5) s + 1
1 1 或G ( s ) = ≈ ( s + 1)(0.2 s + 1) s + 1
时间常数<<1(主导极点 ( 时间常数 对应的时间常数) 对应的时间常数)
s1
(s + a + δ) 2a 例:G(s) = ⋅ 2 a + δ (s + a)(s + 2 s + 2 ) δ << a
×
1
偶极子 -1
• ×
0
s2× 讨论不同位置偶极子对系统响应的影响: 讨论不同位置偶极子对系统响应的影响: (1)远离原点的偶极子,其影响可略。 )远离原点的偶极子,其影响可略。 (2)接近原点的偶极子,其影响必须考虑。 )接近原点的偶极子,其影响必须考虑。
xo (t ) = α 0 + ∑ α i e
i =1 q − pi t
+ ∑ β je
j =1
r
−ζ j ω j t
cos(ω j 1 − ζ l 2 )t
+ ∑ γ je
j
r
−ζ j ω j t
sin ω j 1 − ζ l 2 )t
可见, 可见,一般高阶系统瞬态响应是由若干一阶惯性环节和二阶振荡环节 的响应函数叠加组成的。当所有极点均具有负实部时,系统稳定。 的响应函数叠加组成的。 当所有极点均具有负实部时 , 系统稳定 。 极点的性 质决定瞬态分量的类型: 质决定瞬态分量的类型: ●实数极点 非周期瞬态分量 阻尼振荡瞬态分量。 ●共轭复数极点 阻尼振荡瞬态分量。 类似于低阶系统,高阶系统的极点的位置决定系统响应的基本形态: 类似于低阶系统,高阶系统的极点的位置决定系统响应的基本形态: ●极点位于除原点外的虚轴上 ⇒ 等幅振荡 ●极点位于右半复平面 ⇒ 发散 ●极点位于左半复平面 ⇒ 收敛 在收敛的情况下,收敛速度取决于极点与虚轴的距离: ●在收敛的情况下,收敛速度取决于极点与虚轴的距离:极点与虚轴 的距离越大,收敛速度越快。 的距离越大,收敛速度越快。 在收敛的情况下,收敛的平稳性(波动性) ●在收敛的情况下,收敛的平稳性(波动性)基本取决于极点与负实 轴的夹角(阻尼) 零点也有影响。 轴的夹角(阻尼),零点也有影响。
z1 s3×2 Nhomakorabeas1× 0.87
-5 -0.5
-10
z2
s2×
0 -2
xo(t) 近似 xo(t)
3.5.3 偶极子相消
系统零点分布对时域响应的影响
c(t ) = a + ∑ a j e
j =1 q − p jt
+ ∑ bk2 + ck2 e −ζ k ωk t sin(ω k 1 − ζ k2 t + ϕ k )
k =1
r
高阶系统的各个闭环极点 对系统时间响应的影响程度还 取决于在各个闭环极点上的留 数的相对大小。 数的相对大小。如果有一对靠 得很近的零点和极点, 得很近的零点和极点,那么就 会使此极点上的留数很小, 会使此极点上的留数很小,这 可以从计算留数的公式中看出。 可以从计算留数的公式中看出。
s1 • ×
G1 (s ) = 1 s 2 + 1 s + s + 1 2
2
(
)
=
(s + 2)2 (s 2 + s + 1)
s s 100 + 1 + 1 s 2 + s + 1 5 2 4
(
)
采用MATLAB软件计算低阶系统 的单位阶跃响应: 软件计算低阶系统G1的单位阶跃响应 采用 软件计算低阶系统 的单位阶跃响应: numerator1=[4]; denominator1=conv([1 4 4],[1 1 1]); system1=tf(numerator1,denominator1); t=(0:0.1:20); step(system1,'r',t);
