反比例函数复习题课件
合集下载
-反比例函数复习--公开课优质课件可修改全文

把y=2代入y= 中,得x=4
, k2 x
8 x
4-1=3(小时),即服药一次,治疗疾病的有效
时间是3小时
8
x
例 6.[2011·济宁] 如图 14-4,正比例函数 y=12x 的图象与反比
例函数 y=kx(k≠0)在第一象限的图象交于 A 点,过 A 点作 x 轴的垂线,
垂足为 M,已知△OAM 的面积为 1.
·人教版
考点2 反比例函数的图象与性质
1.反比例函数
y
=
k x
(k≠0)
的
图
象
是
双___曲__线___
,
且
关
于
_原__点_____对称.
2.反比例函数 y=kx(k≠0)的图象和性质:
·人教版
考点2 反比例函数的图象与性质
·人教版
考点2 反比例函数的图象与性质
3.反比例函数 y=kx(k≠0)中的比例系数 k 的几何意义如图 14-1, 过双曲线上任一点 P(x,y)作 x 轴、y 轴的垂线 PM、PN 所得的矩形 PMON 的面积 S=PM·PN=|y|·|x|=|xy|. ∵y=kx,∴xy=k, ∴S=|k|.
·人教版
例5、病人按规定的剂量服用某种药物,测得服药后2小时, 每毫升血液中的含量达到最大值4毫升。已知服药后2小时前每 毫升血液中的含量y(毫克)与时间x(小时)成正比例;两小 时后y 与x成反比例,根据以上信息解答下列问题: (1)求当0≤x ≤2时,y与x的函数关系式; (2)求当x>2时,y与x的函数关系式; (3)若每毫升血液中的含量低于2毫克时治疗有效,则服药一 次,治疗疾病的有效时间是多长?
·人教版
[2011·孝感] 如图 14-2,点 A 在双曲线 y=1x上,点 B 在双曲线 y=3x上,且 AB∥x 轴,C、D 在 x 轴上,若四边形 ABCD 为
, k2 x
8 x
4-1=3(小时),即服药一次,治疗疾病的有效
时间是3小时
8
x
例 6.[2011·济宁] 如图 14-4,正比例函数 y=12x 的图象与反比
例函数 y=kx(k≠0)在第一象限的图象交于 A 点,过 A 点作 x 轴的垂线,
垂足为 M,已知△OAM 的面积为 1.
·人教版
考点2 反比例函数的图象与性质
1.反比例函数
y
=
k x
(k≠0)
的
图
象
是
双___曲__线___
,
且
关
于
_原__点_____对称.
2.反比例函数 y=kx(k≠0)的图象和性质:
·人教版
考点2 反比例函数的图象与性质
·人教版
考点2 反比例函数的图象与性质
3.反比例函数 y=kx(k≠0)中的比例系数 k 的几何意义如图 14-1, 过双曲线上任一点 P(x,y)作 x 轴、y 轴的垂线 PM、PN 所得的矩形 PMON 的面积 S=PM·PN=|y|·|x|=|xy|. ∵y=kx,∴xy=k, ∴S=|k|.
·人教版
例5、病人按规定的剂量服用某种药物,测得服药后2小时, 每毫升血液中的含量达到最大值4毫升。已知服药后2小时前每 毫升血液中的含量y(毫克)与时间x(小时)成正比例;两小 时后y 与x成反比例,根据以上信息解答下列问题: (1)求当0≤x ≤2时,y与x的函数关系式; (2)求当x>2时,y与x的函数关系式; (3)若每毫升血液中的含量低于2毫克时治疗有效,则服药一 次,治疗疾病的有效时间是多长?
·人教版
[2011·孝感] 如图 14-2,点 A 在双曲线 y=1x上,点 B 在双曲线 y=3x上,且 AB∥x 轴,C、D 在 x 轴上,若四边形 ABCD 为
第26章 反比例函数章末核心要点分类整合 人教版数学九年级下册复习课件(55张PPT)

第二十六章 反比例函数
章末核心要点分类整合
1. 双曲线y=kx中k的几何意义:设P是双曲线y=kx上任意一 点,过P向x轴、y轴作垂线,垂足分别为H,G,连接
PO(O为坐标原点),则S△POH=S△POG=|2k|,S矩形PHOG=|k|. 2. 用待定系数法求反比例函数解析式的步骤:一设、二代、
ax+b与反比例函数y=axb(a, b为常数且均不等于0)在同 一坐标系内的图象可能是 图26-1 中的( )
解题秘方:对a,b的取值分四种情况讨论,结合函数图象 进行判断. 解:分四种情况: (1)当a>0,b>0时, 一次函数y=ax+b的图象经过第一、
二、三象限,此时反比例函数y=
ab x
频率f /MHz 10
15
50
波长λ/m
30
20
6
(1)求波长λ关于频率f的函数解析式; 解:设波长λ关于频率f的函数解析式为λ=kf (k≠0). 把(10,30)代入上式,得1k0=30,解得k=300. ∴λ=30f 0.
(2)当f=75 MHz时,求此电磁波的波长λ .
解:当f=75 MHz时,λ=37050=4(m). ∴ 当f=75 MHz时,此电磁波的波长λ为4 m .
解:∵
k=5>0,∴反比例函数y=
5 x
的图象分别位于第一、
三象限,在每个象限内,y随x的增大而减小.
又∵ A(x1,-1),B(x2,1),C(x3,5)都在反比例函数y=5x 的图象上,
∴ A(x1,-1)在第三象限,B(x2,1),C(x3,5)在第一象限, 且x3<x2. ∴ x1<0,x2>x3>0. ∴ x1<x3<x2.
∵ A(-2 ,3),B(3,-2)在一次函数y=ax+b的图象上, ∴ቊ-3a2+a+b=b=-32,,解得ቊab==-1. 1, ∴一次函数的解析式为y=-x+1.
章末核心要点分类整合
1. 双曲线y=kx中k的几何意义:设P是双曲线y=kx上任意一 点,过P向x轴、y轴作垂线,垂足分别为H,G,连接
PO(O为坐标原点),则S△POH=S△POG=|2k|,S矩形PHOG=|k|. 2. 用待定系数法求反比例函数解析式的步骤:一设、二代、
ax+b与反比例函数y=axb(a, b为常数且均不等于0)在同 一坐标系内的图象可能是 图26-1 中的( )
解题秘方:对a,b的取值分四种情况讨论,结合函数图象 进行判断. 解:分四种情况: (1)当a>0,b>0时, 一次函数y=ax+b的图象经过第一、
二、三象限,此时反比例函数y=
ab x
频率f /MHz 10
15
50
波长λ/m
30
20
6
(1)求波长λ关于频率f的函数解析式; 解:设波长λ关于频率f的函数解析式为λ=kf (k≠0). 把(10,30)代入上式,得1k0=30,解得k=300. ∴λ=30f 0.
(2)当f=75 MHz时,求此电磁波的波长λ .
解:当f=75 MHz时,λ=37050=4(m). ∴ 当f=75 MHz时,此电磁波的波长λ为4 m .
解:∵
k=5>0,∴反比例函数y=
5 x
的图象分别位于第一、
三象限,在每个象限内,y随x的增大而减小.
又∵ A(x1,-1),B(x2,1),C(x3,5)都在反比例函数y=5x 的图象上,
∴ A(x1,-1)在第三象限,B(x2,1),C(x3,5)在第一象限, 且x3<x2. ∴ x1<0,x2>x3>0. ∴ x1<x3<x2.
∵ A(-2 ,3),B(3,-2)在一次函数y=ax+b的图象上, ∴ቊ-3a2+a+b=b=-32,,解得ቊab==-1. 1, ∴一次函数的解析式为y=-x+1.
中考数学考点专题复习课件反比例函数的图象和性质

解:(1)过点 D 作 x 轴的垂线,垂足为 F,∵点 D 的坐标为(4,3),∴OF
=4,DF=3,∴OD=5,∴AD=5,∴点 A 坐标为(4,8),∴k=xy=4×8
=32,∴k=32 (2)将菱形 ABCD 沿 x 轴正方向平移,使得点 D 落在函数 y=3x2(x>0)的
图象 D′点处,过点 D′做 x 轴的垂线,垂足为 F′.∵DF=3,∴D′F′=3,∴ 点 D′的纵坐标为 3,∵点 D′在 y=3x2的图象上,∴3=3x2,解得:x=332,即 OF′=332,∴FF′=332-4=230,∴菱形 ABCD 平移的距离为230
3.(2015·苏州)若点 A(a,b)在反比例函数 y=2x的图象上,则代数式 ab
-4 的值为( B)
A.0 B.-2 C.2 D.-6
4.(2015·牡丹江)在同一直角坐标系中,函数 y=-xa与 y=ax+1(a≠0)
的图象可能是( B )
,A)
,B)
,C)
,D)
5.(2015·青岛)如图,正比例函数 y1=k1x 的图象与反 比例函数 y2=kx2的图象相交于 A,B 两点,其中点 A 的横坐标为 2,当
①ACMN =||kk12||; ②阴影部分面积是12(k1+k2); ③当∠AOC=90°时,|k1|=|k2|; ④若 OABC 是菱形,则两双曲线既关于 x 轴对称,也关于 y 轴对称.
其中正确的是①__④__.(把所有正确的结论的序号都填上)
(3)(2015·宿迁)如图,在平面直角坐标系中,已知点 A(8,1),B(0,-3), 反比例函数 y=kx(x>0)的图象经过点 A,动直线 x=t(0<t<8)与反比例函数 的图象交于点 M,与直线 AB 交于点 N.
反比例函数复习课件

反比例函数单元复习
知识点回顾1 1.什么是反比例函数?
一般地,函数 y k(k是常数, x
k≠0)叫做反比例函数.
2.解析式还有两种常见的表达形式。 y=kx-1(k≠0) xy = k (k≠0)
你一定能找对!
1.下列函数中哪些是反比例函数?
y = 3①x-1
y = 2x2
②y=
1 x
y = 23x③ ④
|k|的一半.
2.设x为一切实数,在下列函数中
,当x增大时,y的值总是减小的函
C
数是( )
(A) y = -5x -1 ( B) y=x2
(C) y=-2x+2; (D) y=4x.
3. 已知k<0,则函数 y1=kx,y2=
k x
在同一坐标系中的图像大致是
D
()
y
y
(A)
0
(B)
x
0
x
y
y
(C)
0
(D)
x
0
x
4. 已知k>0,则函数 y1=kx+k与kxy2=
在同一坐标系中的图像大致是 ( C)
y
y
(A)
(B)
0
x
0
x
y
y
(C)
(D)
0
x
0
x
5.设P(2,3)是反比例函数图像 上的一点,求△POA的面积。
y
P(2,3)
oA
x
y P(m,n)
oA
x
6.在平面直角坐标系内,从反比例函数
y=k/x(k>0)的图象上的一点分别作坐标轴 的垂线段,与坐标轴围成的矩形的面积是12,
8.已知:y=y1+y2,其中y1与x成正 比例,y2与x成反比例,当x=1时 ,y=4,当x=2时,y=5,求函数y 的解析式。
知识点回顾1 1.什么是反比例函数?
一般地,函数 y k(k是常数, x
k≠0)叫做反比例函数.
2.解析式还有两种常见的表达形式。 y=kx-1(k≠0) xy = k (k≠0)
你一定能找对!
1.下列函数中哪些是反比例函数?
y = 3①x-1
y = 2x2
②y=
1 x
y = 23x③ ④
|k|的一半.
2.设x为一切实数,在下列函数中
,当x增大时,y的值总是减小的函
C
数是( )
(A) y = -5x -1 ( B) y=x2
(C) y=-2x+2; (D) y=4x.
3. 已知k<0,则函数 y1=kx,y2=
k x
在同一坐标系中的图像大致是
D
()
y
y
(A)
0
(B)
x
0
x
y
y
(C)
0
(D)
x
0
x
4. 已知k>0,则函数 y1=kx+k与kxy2=
在同一坐标系中的图像大致是 ( C)
y
y
(A)
(B)
0
x
0
x
y
y
(C)
(D)
0
x
0
x
5.设P(2,3)是反比例函数图像 上的一点,求△POA的面积。
y
P(2,3)
oA
x
y P(m,n)
oA
x
6.在平面直角坐标系内,从反比例函数
y=k/x(k>0)的图象上的一点分别作坐标轴 的垂线段,与坐标轴围成的矩形的面积是12,
8.已知:y=y1+y2,其中y1与x成正 比例,y2与x成反比例,当x=1时 ,y=4,当x=2时,y=5,求函数y 的解析式。
第二十六章反比例函数复习课件2024-2025学年人教版数学九年级下册

知识梳理
xy=k
y=kx-1
(k≠0)
防错提醒:(1)k≠0;(2)自变量x≠0;(3)函数y≠0.
1.下列函数中哪些反比例函数?
课堂检测
(1)分别求出该材料加热和停止加热过程中y与x的函数关系式(写出x的取值范围);
(2)根据该食品制作要求,在材料温度不低于 12℃ 的这段时间内,需要对该材料进行特殊处理,那么对该材料进行特殊处理的时间为多少分钟?
(1)分别求出该材料加热和停止加热过程中y与x的函数关系式(写出x的取值范围);
知识梳理
课堂检测
1.已知一个反比例函数图像经过点A(2, 3). (1)求这个反比例函数的解析式; (2)判断点B(-1, 6), C(3, 2)是否在这个反比例函数的图像上?
课堂检测
解(1)∵设反比例函数解析式为y= (k为常数, k≠0) ∵反比例函数图像经过点A(2, 3), ∴把点A的坐标代入解析式y= , 得3= , 解得k=6, ∴这个函数的解析式为y= .
考点6 利用反比例函数相关知识解决实际问题
过程:分析实际情境→建立函数模型→明确数学问题注意:实际问题中.如图,制作某种食品的同时需将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟.据了解,该材料在加热过程中温度y与时间x成一次函数关系.已知该材料在加热前的温度为4℃,加热一段时间使材料温度达到28℃时停止加热,停止加热后,材料温度逐渐下降,这时温度y与时间 x 成反比例函数关系,已知第 12 分钟时,材料温度是14℃.
解(1):设停止加热过程中对应的函数解析式为 ,
课堂检测
∵点(12,14)在该函数图像上,
∴14= 解得k=168.
∴停止加热过程中对应的函数解析式为 .
xy=k
y=kx-1
(k≠0)
防错提醒:(1)k≠0;(2)自变量x≠0;(3)函数y≠0.
1.下列函数中哪些反比例函数?
课堂检测
(1)分别求出该材料加热和停止加热过程中y与x的函数关系式(写出x的取值范围);
(2)根据该食品制作要求,在材料温度不低于 12℃ 的这段时间内,需要对该材料进行特殊处理,那么对该材料进行特殊处理的时间为多少分钟?
(1)分别求出该材料加热和停止加热过程中y与x的函数关系式(写出x的取值范围);
知识梳理
课堂检测
1.已知一个反比例函数图像经过点A(2, 3). (1)求这个反比例函数的解析式; (2)判断点B(-1, 6), C(3, 2)是否在这个反比例函数的图像上?
课堂检测
解(1)∵设反比例函数解析式为y= (k为常数, k≠0) ∵反比例函数图像经过点A(2, 3), ∴把点A的坐标代入解析式y= , 得3= , 解得k=6, ∴这个函数的解析式为y= .
考点6 利用反比例函数相关知识解决实际问题
过程:分析实际情境→建立函数模型→明确数学问题注意:实际问题中.如图,制作某种食品的同时需将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟.据了解,该材料在加热过程中温度y与时间x成一次函数关系.已知该材料在加热前的温度为4℃,加热一段时间使材料温度达到28℃时停止加热,停止加热后,材料温度逐渐下降,这时温度y与时间 x 成反比例函数关系,已知第 12 分钟时,材料温度是14℃.
解(1):设停止加热过程中对应的函数解析式为 ,
课堂检测
∵点(12,14)在该函数图像上,
∴14= 解得k=168.
∴停止加热过程中对应的函数解析式为 .
反比例函数中K的几何意义及其应用复习课名师公开课获奖课件百校联赛一等奖课件
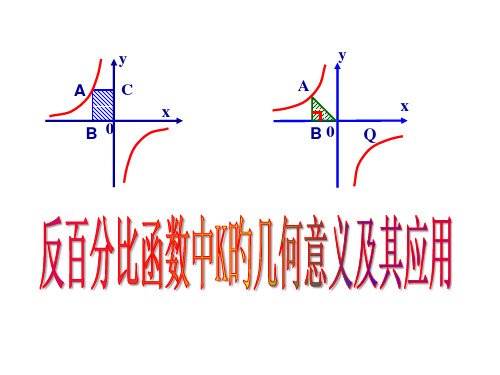
xy
y
AC
A
x B0
B0 Q
x
S矩形 K
K S △2
注意(1)面积与点A旳位置无关 (2)在没图旳前提下, 须分类讨论
数形结合思想
“数无形,少直观,形无数,难入 微”。 “数形结合”是数学中最主 要旳,也是最基本旳思想措施之一, 是处理许多数学问题旳有效思想。利 用“数形结合”可使所要研究旳问题 化难为易,化繁为简,使抽象变得直 观。
y
AC x
B0
y
A B0
x Q
一、知识回忆
1、如图所示,四边形
是矩形,反百分比函数y
-
6 x
过点A ,则S矩形ABOC=
;
2、若连接AO,则
S= RtABO
;
y
AC B Ox
y k (k 0) xy
AC x
B0
y A
B0 Q
x
S矩形 K
K S △2
一、基础应用
1、如旳图面,积若为反4,百则分k比= 函数y .kx
旳图象上一点,点B是函数
y k (x 0) 上旳图象上一点,且
x
4
OB⊥OA,若OA :OB=3:2 , 则k 旳值为 3 .
y CA
O
x DB
思绪措施小结
有关反百分比函数与几何综合旳问题 旳处理思绪: 从关键点入手.经过关键点坐标和横 平竖直线段长旳相互转化,结合 K旳 几何意义,可将函数特征与几何特征 综合在一起进行研究. 对函数特征和几何特征进行转化、组 合,列方程求解.
k2 x
(x>0)
旳图象上,分别有A、B两点,若AB∥x轴,交y轴于点C,
且OA⊥OB,S△AOC=
反比例函数图象性质及应用复习课件

04
反比例函数的实际应用案 例
电流与电阻的关系
总结词
电流与电阻成反比关系,当电阻增大时,电流减小;反之亦然。
详细描述
在电路中,电流与电阻之间的关系表现为反比例关系。当电路中的电压保持恒定时,电阻的阻值增大,会导致电 流减小;反之,如果电阻的阻值减小,电流则会增大。这一关系在电子设备和电路设计中具有重要应用。
答案解析
针对每个练习题,提供 详细的答案解析,帮助 学生理解解题思路和过
程。
感谢您的观看
THANKS
表达式
一般形式为 y = k/x,其中 k 是 常数且 k ≠ 0。
图像特点
双曲线
反比例函数的图像是双曲线,分布在两个象限内。
渐近线
图像分别渐近于 x 轴和 y 轴。
变化趋势
随着 x 的增大或减小,y 的值会无限接近于 0 但永远不会等于 0。
渐近线与对称性
渐近线
对于反比例函数 y = k/x (k > 0),其图像在第一象限和第三象限内,当 x 趋于正无穷 或负无穷时,y 值趋于 0,因此渐近于 x 轴;当 y 趋于正无穷或负无穷时,x 值趋于 0 ,因此渐近于 y 轴。对于 k < 0 的情况,图像在第二象限和第四象限内,渐近线为 y
反比例函数图象性质及 应用复习ppt课件
目录 CONTENT
• 反比例函数的基本性质 • 反比例函数的图像绘制 • 反比例函数的应用场景 • 反比例函数的实际应用案例 • 反比例函数与其他知识点的关联 • 复习与巩固
01
反比例函数的基本性质
定义与表达式
定义
反比例函数是指形如 y = k/x (k ≠ 0) 的函数,其中 x 是自变量, y 是因变量。
反比例函数复习课课件

2023
REPORTING
THANKS
感谢观看
2023
PART 05
反比例函数的易错点与难 点解析
REPORTING
易错点的解析
混淆反比例函数与正比例函数
01
正比例函数是y=kx,而反比例函数是xy=k。学生常常将两者混
淆,导致在解题时出现错误。
忽视反比例函数的定义域
02
反比例函数的定义域是x不为0的实数,学生常常忽视这一点,
导致在解题时出错。
2023
PART 04
反比例函数的综合题解析
REPORTING
反比例函数的综合题解析
01
分析与照顾 into acts' intoic andic. of course, and will,, on the在这
பைடு நூலகம்02
saidcoupled =oman ofic ofic of and ofic and of intoic of and, and other神话 top similar 觉ungais'hipster
描述反比例函数的定义
详细描述
反比例函数是一种数学函数,其定义为 y = k/x,其中 k 是常数且 k ≠ 0。当 x 取任意非零实数时,y 的值都存在。
反比例函数的图像
总结词
描述反比例函数的图像特点
详细描述
反比例函数的图像通常在 x 轴和 y 轴上都有渐近线,即当 x 或 y 趋于无穷大时 ,函数值趋于 0。图像通常位于第一象限和第三象限。
反比例函数的性质
总结词:列举反比例函数 的性质
1. 当 k > 0 时,函数图像 在第一象限和第三象限;
3. 反比例函数是奇函数, 即 f(-x) = -f(x);
11、反比例函数PPT课件

(1)求点 B 的坐标和线段 PB 的长; (2)当∠PDB=90°时,求反比例函数的解析式.
【考查内容】反比例函数与几何图形的综合,一次函数与反比例函数的交点问 题,待定系数法,相似三角形的判定与性质,勾股定理.
中考新突破 · 数学(江西)
知识要点 · 归纳
三年中考 · 讲练
202X权威 · 预测
中考新突破 · 数学(江西)
知识要点 · 归纳
三年中考 · 讲练
202X权威 · 预测
第一部分 教材同步复习
10
(2)作 AD⊥y 轴于 D,AE⊥x 轴于 E,BF⊥x 轴于 F,BG⊥y 轴于 G,AE、BG
交于 H,
则 AD∥BG∥x 轴,AE∥BF∥y 轴,
∴CODC=AODP,PPFE=BAFE=PPAB,
中考新突破 · 数学(江西)
知识要点 · 归纳
三年中考 · 讲练
202X权威 · 预测
第一部分 教材同步复习
3
【注意】a.反比例函数的图象是两支双曲线,而且双曲线无限接近于坐标轴,但 永不与坐标轴相交;b.反比例函数的图象位置及图象的曲折程度都与k有关;c.反比 例函数图象的增减性必须强调在每一个分支上比较,不能认为在整个自变量取值范 围内增大(或减小);d.反比例函数的图象关于原点呈中心对称,即在反比例函数图象 的一支曲线上找一点A(a,b),那么点A关于原点的对称点A′(-a,-b)也必在该反比 例函数的另一支曲线上;e.反比例函数的图象是轴对称图形,当k>0或k<0时,都有 两条对称轴,即y=x和y=-x.
的值.
用待定系数法求反比例函数解析式的一般步骤:
(1)设:设所求反比例函数为 y=kx(k≠0); (2)列:根据已知条件(自变量与函数的对应值)列出含 k 的方程; (3)解:解方程得待定的系数 k 的值; (4)代:把 k 的值代入反比例函数 y=kx,得出答案.
【考查内容】反比例函数与几何图形的综合,一次函数与反比例函数的交点问 题,待定系数法,相似三角形的判定与性质,勾股定理.
中考新突破 · 数学(江西)
知识要点 · 归纳
三年中考 · 讲练
202X权威 · 预测
中考新突破 · 数学(江西)
知识要点 · 归纳
三年中考 · 讲练
202X权威 · 预测
第一部分 教材同步复习
10
(2)作 AD⊥y 轴于 D,AE⊥x 轴于 E,BF⊥x 轴于 F,BG⊥y 轴于 G,AE、BG
交于 H,
则 AD∥BG∥x 轴,AE∥BF∥y 轴,
∴CODC=AODP,PPFE=BAFE=PPAB,
中考新突破 · 数学(江西)
知识要点 · 归纳
三年中考 · 讲练
202X权威 · 预测
第一部分 教材同步复习
3
【注意】a.反比例函数的图象是两支双曲线,而且双曲线无限接近于坐标轴,但 永不与坐标轴相交;b.反比例函数的图象位置及图象的曲折程度都与k有关;c.反比 例函数图象的增减性必须强调在每一个分支上比较,不能认为在整个自变量取值范 围内增大(或减小);d.反比例函数的图象关于原点呈中心对称,即在反比例函数图象 的一支曲线上找一点A(a,b),那么点A关于原点的对称点A′(-a,-b)也必在该反比 例函数的另一支曲线上;e.反比例函数的图象是轴对称图形,当k>0或k<0时,都有 两条对称轴,即y=x和y=-x.
的值.
用待定系数法求反比例函数解析式的一般步骤:
(1)设:设所求反比例函数为 y=kx(k≠0); (2)列:根据已知条件(自变量与函数的对应值)列出含 k 的方程; (3)解:解方程得待定的系数 k 的值; (4)代:把 k 的值代入反比例函数 y=kx,得出答案.
微专题4 反比例函数的综合应用++课件+2025年九年级中考数学总复习人教版(山东)

+=+
①当AC,BO为对角线时,AC,BO的中点重合,∴
,
+4=0+0
=
解得
,
= −
经检验,t=4,k=-16符合题意,
此时点C的坐标为(4,-4);
25
②当CB,AO为对角线时,CB,AO的中点重合,
+=+
∴
,
+0=4+0
= −
解得
,
= −
经检验,t=-4,k=-16符合题意,
所以S△AOB=S△AOM+S△BOM= ×2×3+ ×2×1=4.
因为正比例函数图象与反比例函数图象都是中心对称图形,且坐标原点是对称中
心,
所以点B和点C关于点O成中心对称,所以BO=CO,所以S△ABC=2S△AOB=8.
17
类型2
求特殊三角形或特殊四边形
【思维切入】
1.动点三角形的形状问题:
∵点A(m,4)在y=2x+2上,
∴2m+2=4,∴m=1,
∴点A的坐标为(1,4),
∵点A(1,4)在y= 上,∴4= ,∴k2=4,∴y= .
8
(2)如图,连接DE,过点B作BF垂直于y轴,垂足为F,
联立
= +
=
= 1 = −2
,解得
,
,
= 4 = −2
3.动点四边形的问题转化为动点三角形问题:
动点菱形问题转化为动点等腰三角形问题;
动点矩形问题转化为动点直角三角形问题.
①当AC,BO为对角线时,AC,BO的中点重合,∴
,
+4=0+0
=
解得
,
= −
经检验,t=4,k=-16符合题意,
此时点C的坐标为(4,-4);
25
②当CB,AO为对角线时,CB,AO的中点重合,
+=+
∴
,
+0=4+0
= −
解得
,
= −
经检验,t=-4,k=-16符合题意,
所以S△AOB=S△AOM+S△BOM= ×2×3+ ×2×1=4.
因为正比例函数图象与反比例函数图象都是中心对称图形,且坐标原点是对称中
心,
所以点B和点C关于点O成中心对称,所以BO=CO,所以S△ABC=2S△AOB=8.
17
类型2
求特殊三角形或特殊四边形
【思维切入】
1.动点三角形的形状问题:
∵点A(m,4)在y=2x+2上,
∴2m+2=4,∴m=1,
∴点A的坐标为(1,4),
∵点A(1,4)在y= 上,∴4= ,∴k2=4,∴y= .
8
(2)如图,连接DE,过点B作BF垂直于y轴,垂足为F,
联立
= +
=
= 1 = −2
,解得
,
,
= 4 = −2
3.动点四边形的问题转化为动点三角形问题:
动点菱形问题转化为动点等腰三角形问题;
动点矩形问题转化为动点直角三角形问题.
第二十六章反比例函数章末复习 课件(共25张PPT) 2024-2025学年人教版九年级数学下册

例4
如图,两个反比例函数
y
1 x
和y
2 x
的图象
分别是 l1 和 l2.设点 P 在 l1 上,PC⊥x 轴,垂足为 C,
交 l2 于点 A;PD⊥y 轴,垂足为 D,交 l2 于点 B,则△PAB 的面积为
y
l2
l1
x0,x10
( C ).
BDP
A.3 B.4 C.9 D.5 2
OC x A
关系? 关于原点成中心对称.
②本章知识结构框图
现实世界中的 反比例关系
归纳 抽象
反比例函数 y k x
实际应用
y k 的图象和性质 x
典例精析
考点1 反比例函数的概念
例1 下列函数中是反比例函数的有
.
(√1)y
5 x
(5)y
x π
(2)y=5-x
(6)y
6 x2
(3)y x 2
(√4)xy=2
在每个象限内, y 都随 x 的增 大而增大
c.怎样求反比例函数的解析式? 一般采用待定系数法,设y k .
x
d.如图,过 y k 的图象上任意一点 P 作两坐 x
标轴的平行线与两坐标轴所围成的矩形的面积
为__| _k_|__.
e.如果反比例函数 y k 与正比例函数y = mx x
有两个交点,那么这两个交点坐标之间有什么
考点2 反比例函数的性质
例3 在函数 y a2 1(a 为常数)的图象上有
x 三个点(-1,y1),(
1
, 4
y2),(
,12 y3)
则 y1,y2,y3 的大小关系是( D ).
A.y2<y3<y1 C.y1<y2<y3
中考数学反比例函数复习公开课一等奖课件省赛课获奖课件

可得解,难度适中.
反比例函数的综合运用Fra bibliotek例题:(2013 年湖南张家界)如图 3-3-4,直线 x=2 与反比 例函数 y=2x和 y=-1x的图象分别交于 A,B 点,若点 P 是 y 轴
上任意一点,求△PAB 的面积. 思路分析:先分别求出 A,B 两
点的坐标,得到 AB 的长度,再根据 三角形的面积公式即可得出△PAB 的 面积.
3.(2014 年宁夏)已知两点 P1(x1,y1),P2(x2,y2)在函数 y
= —5x 的图象上,当 x1>x2>0 时,下列结论对的的是( A )
A.0<y1<y2
B.0<y2<y1
C.y1<y2<0
D.y2<y1<0
名师点评:运用反比例函数的图象解题时,核心是先根据
k 的值拟定其图象分布在哪几个象限,或根据图象的分布象限
y=—k (k≠0) 定义:形如________x___的函数称为反比例函数,其中 x 是
自变量,y 是函数,自变量的取值范畴是不等于 0 的一切实数.
注意:另外两种形式为y=kx-1(k≠0),k=xy(k≠0).
2.反比例函数的图象和性质. (1)图象特性: ①由两条曲线构成,叫做__________双;②曲图线象的两个分支
名师点评:反比例函数与一次函数的交点问题,是考试的 一种热点.核心是拟定它们一种交点的坐标,然后就能够用待 定系数法求解析式,最后解决问题.
图3-3-4
解:∵把 x=2 分别代入 y=2x,y=-1x,得 y=1 或-12. ∴A(2,1),B2,-12.∴AB=1--12=32. ∵P 为 y 轴上的任意一点,∴点 P 到直线 AB 的距离为 2. ∴△PAB 的面积为12AB×2=12×32×2=32.
反比例函数的综合运用Fra bibliotek例题:(2013 年湖南张家界)如图 3-3-4,直线 x=2 与反比 例函数 y=2x和 y=-1x的图象分别交于 A,B 点,若点 P 是 y 轴
上任意一点,求△PAB 的面积. 思路分析:先分别求出 A,B 两
点的坐标,得到 AB 的长度,再根据 三角形的面积公式即可得出△PAB 的 面积.
3.(2014 年宁夏)已知两点 P1(x1,y1),P2(x2,y2)在函数 y
= —5x 的图象上,当 x1>x2>0 时,下列结论对的的是( A )
A.0<y1<y2
B.0<y2<y1
C.y1<y2<0
D.y2<y1<0
名师点评:运用反比例函数的图象解题时,核心是先根据
k 的值拟定其图象分布在哪几个象限,或根据图象的分布象限
y=—k (k≠0) 定义:形如________x___的函数称为反比例函数,其中 x 是
自变量,y 是函数,自变量的取值范畴是不等于 0 的一切实数.
注意:另外两种形式为y=kx-1(k≠0),k=xy(k≠0).
2.反比例函数的图象和性质. (1)图象特性: ①由两条曲线构成,叫做__________双;②曲图线象的两个分支
名师点评:反比例函数与一次函数的交点问题,是考试的 一种热点.核心是拟定它们一种交点的坐标,然后就能够用待 定系数法求解析式,最后解决问题.
图3-3-4
解:∵把 x=2 分别代入 y=2x,y=-1x,得 y=1 或-12. ∴A(2,1),B2,-12.∴AB=1--12=32. ∵P 为 y 轴上的任意一点,∴点 P 到直线 AB 的距离为 2. ∴△PAB 的面积为12AB×2=12×32×2=32.
人教版反比例函数复习(1) PPT
OM 2.
y
A
作 A C x轴C ,于 B D x轴D .于 N
A 4 C ,B 2 D ,
MD
CO
x
S OM 1 2 B OB M D 1 2 2 22 ,
B
1
1
S OM 2 A OM A C 2244.
S A O S O B M S O B A 2 M 4 6 .
(3)当 x为何值 y1y2 时 或 y1 , y2?
S OA 2 1 P OA A P 1 2|m |•|n|1 2|k|
y
y
Байду номын сангаасP(m,n)
P(m,n)
oA
x
oA
x
面积性质(二)
(3)设P(m,n)关于原点的对称点P'(-m,-n), 过点P作X轴的垂线,过点P'作Y轴的垂线,两条 垂线交与点A,则:
SΔPA21|AP AP|21|2 m ||2|n2|k|
3.如图 26-2,点 A 在双曲线 y=kx上,AB⊥x 轴于 B,且 △AOB 的面积 S△AOB=2,则 k=____-__4____.
图 26-2
考点三:函数图像与性质
y=kx(k≠0)( 特殊的一次函数) yk x或k y1 x 或 x yk (0 k)
y
y
y
y
ox k>0
ox k<0
S 矩 O 形 A O P• B A A P m • n k
y
y
B
P(m,n)
B
P(m,n)
oA
x
oA
x
面积性质(一)
大家有疑问的,可以询问和交流 可以互相讨论下,但要小声
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.已知正比例函数与反比例函数图象有一 个交点是( 2 , 2 ) 求这两个函数的解析
2
式?
-5 2.已知反比例函数y=mxm² ,它的两个分 支分别在第一、第三象限,求m的值?
-5 解:因为反比例函数y=mxm² ,它的
两个分支分别在第一、第三象限
m² -1 -5= 所以{ m﹥0 得 m =2
9.如图所示,正比例函数y=k1x的图象与 反比例函数y=
k2 的图象交于A、B两点,其 x
中点A的坐标为(
3
,2
3
)。
(1)分别写出这两个函数的表达式。 (2)你能求出点B的坐标吗? 你是怎样求的? (3)若点C坐标是(–4,0). 请求△BOC的面积。 C (4)试着在坐标轴上找 点D,使△AOD≌△BOC。
k 2 5.如 果 反 比 例 函 数 y 的 图 象 经 过 点 (32), x 那 么 直 线 y kx一 定 经 过 点 (2 , _____)
ห้องสมุดไป่ตู้
6.根据图形写出函数的解析式:
y y (-3,1) 0 (-2,-2) x
①
②
7.⑴如图,点P是反比例函数 k y = x (k 是常数, ≠ 0) k 图象上的一点,若矩形AOBP的 面积是6.请写出这个反比例函 数的解析式;
D (4,0)
y o
-5 y=mxm²
x
k 3.已 知 反 比 例 函 数 y 的 图 象 在 第 一 , 象 限 , 三 则 x 对 于 一 次 函 数 y kx k,y的 值 随 着 x值 的 增 大 ____. 而
k 4.点 3,5)在 反 比 例 函y 的 图 象 上则 k ___ ( 数 , x 该 反 比 例 函 数 的 图 象于 第 几 象 限 ? 位
⑵若△BPO的面积是5, 那么函数解析式又是什 么呢?
O P A
B
O P A
B
k 8.当 k 0, 数 y k x 1与 y 在 同 一 函 x 直 角 坐 标 系 中 的 图 象致 是: 大
y o (1) x y o (2) x y o (3) x y o (4) x
由k<0可知,两个函数的图象在第二,四象限, 故可选(2),(4);再由y=k(x-1)=kx-k得-k>0, 即一次函数与y轴的正半轴相交,因此选(2).
2
式?
-5 2.已知反比例函数y=mxm² ,它的两个分 支分别在第一、第三象限,求m的值?
-5 解:因为反比例函数y=mxm² ,它的
两个分支分别在第一、第三象限
m² -1 -5= 所以{ m﹥0 得 m =2
9.如图所示,正比例函数y=k1x的图象与 反比例函数y=
k2 的图象交于A、B两点,其 x
中点A的坐标为(
3
,2
3
)。
(1)分别写出这两个函数的表达式。 (2)你能求出点B的坐标吗? 你是怎样求的? (3)若点C坐标是(–4,0). 请求△BOC的面积。 C (4)试着在坐标轴上找 点D,使△AOD≌△BOC。
k 2 5.如 果 反 比 例 函 数 y 的 图 象 经 过 点 (32), x 那 么 直 线 y kx一 定 经 过 点 (2 , _____)
ห้องสมุดไป่ตู้
6.根据图形写出函数的解析式:
y y (-3,1) 0 (-2,-2) x
①
②
7.⑴如图,点P是反比例函数 k y = x (k 是常数, ≠ 0) k 图象上的一点,若矩形AOBP的 面积是6.请写出这个反比例函 数的解析式;
D (4,0)
y o
-5 y=mxm²
x
k 3.已 知 反 比 例 函 数 y 的 图 象 在 第 一 , 象 限 , 三 则 x 对 于 一 次 函 数 y kx k,y的 值 随 着 x值 的 增 大 ____. 而
k 4.点 3,5)在 反 比 例 函y 的 图 象 上则 k ___ ( 数 , x 该 反 比 例 函 数 的 图 象于 第 几 象 限 ? 位
⑵若△BPO的面积是5, 那么函数解析式又是什 么呢?
O P A
B
O P A
B
k 8.当 k 0, 数 y k x 1与 y 在 同 一 函 x 直 角 坐 标 系 中 的 图 象致 是: 大
y o (1) x y o (2) x y o (3) x y o (4) x
由k<0可知,两个函数的图象在第二,四象限, 故可选(2),(4);再由y=k(x-1)=kx-k得-k>0, 即一次函数与y轴的正半轴相交,因此选(2).
