【2014东营二模】山东省东营市2014届高三第二次模拟 数学理 Word版含答案
山东省东营市2014届高三第二次模拟数学(理)试题(有答案)

保密★启用前 试卷类型:A教学质量检测 理科数学注意事项:1.本试卷分为第Ⅰ卷和第Ⅱ卷两部分.第Ⅰ卷为选择题,第Ⅱ卷为非选择题,考试时间为120分钟, 满分150分.2.把选择题选出的答案标号涂在答题卡上.3.第Ⅱ卷用黑色签字笔在答题纸规定的位置作答,否则不予评分.第Ⅰ卷 选择题(共50分)一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.将正确答案填写在答题卷相应位置. 1.已知集合{}{}R x y y N x x x M x∈==≥=,2,2,则MN = ( )A .)(1,0B .]1,0[C .)1,0[D .]1,0(2.“实数1a =”是“复数(1)ai i +(,a R i ∈的 ( ) A .充分非必要条件 B .必要非充分条件 C .充要条件 D .既非充分条件又不必要条件 3.数列{}n a 的前n 项和为n S ,若1(1)n a n n =+,则6S 等于 ( )A .142B .45C .56D .674.已知某几何体的三视图(单位:cm )如图所示,则该几何体的体积是 ( ) A .48cm 3 B .98cm 3 C .88cm 3 D .78cm 35.执行如图所示的程序框图,输出的S 值为( )A .2B .2-C .4D .4-6.已知0ω>,函数()sin()4f x x πω=+在(,)2ππ上单调递减.则ω的取值范围是 ( )A .15[,]24B . 13[,]24C . 1(0,]2D .(0,2]7.函数()f x 的部分图像如图所示,则()f x 的解析式可以是 ( )x D .3()()()22f x x x x ππ=--8小的两个编号分别为007,032,则样本中最大的编号应该为 ( ) A . 480 B . 481 C . 482 D . 4839. 偶函数)(x f 满足)1()1(+=-x f x f ,且在]1,0[∈x 时,2)(x x f =,则关于x 的方程xx f ⎪⎭⎫⎝⎛=101)(在]3,2[-上的根的个数是 ( ) A .3 B .4 C .5 D .610.已知1F ,2F 是双曲线22221(0,0)x y a b a b-=>>的左,右焦点,若双曲线左支上存在一点P 与点2F 关于直线bxy a=对称,则该双曲线的离心率为 ( ) A B C D .2第Ⅱ卷 非选择题(共100分)二.填空题:本大题共5小题,每小题5分,共25分.11.某公司一年购买某种货物400吨,每次都购买x 吨,运费为4万元/次,一年的总存储费用为x 4万元,要使一年的总运费与总存储费用之和最小,则=x ___ ____ 吨.12.设8280128()x a a a x a x a x -=++++,若685-=+a a ,则实数a 的值为 .13.已知x ,y 满足约束条件⎪⎩⎪⎨⎧≥++≤≥+-0306k y x x y x ,且y x z 42+=的最小值为6,则常数k = .14.已知直角梯形ABCD ,AB AD ⊥,CD AD ⊥,222AB AD CD ===,沿AC 折叠成三棱锥,当三棱锥体积最大时,三棱锥外接球的体积为 .15.如图,在正方形ABCD 中,E 为AB 的中点,P 为以A 为圆心,AB 为半径的圆弧上的任意一点,设向量的最小值为则μλμλ++=,AP DE AC .三.解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤. 16.(本小题满分12分)在ABC ∆中,角C B A 、、所对的边为c b a 、、,且满足cos 2cos 22cos cos 66A B A A ππ⎛⎫⎛⎫-=-+⎪ ⎪⎝⎭⎝⎭(Ⅰ)求角B 的值; (Ⅱ)若3=b 且a b ≤,求c a 21-的取值范围. 17.(本小题满分12分)在对某渔业产品的质量调研中,从甲,乙两地出产的该产品中各随机抽取10件,测量该产品中某种元素的含量(单位:毫克). 下表是测量数据的茎叶图:规定:当产品中的此种元素含量15≥毫克时为优质品.(Ⅰ)试用上述样本数据估计甲,乙两地该产品的优质品率(优质品件数/总件数);(Ⅱ)从乙地抽出的上述10件产品中,随机抽取3件,求抽到的3件产品中优质品数ξ的分布列及数学期望()E ξ.21006542098874286438210乙地甲地18.(本小题满分12分)如图,在底面是正方形的四棱锥P —ABCD 中,PA ⊥面ABCD ,BD 交AC 于点E ,F 是PC 中点,G 为AC 上一点. (Ⅰ)求证:BD ⊥FG ;(Ⅱ)确定点G 在线段AC 上的位置,使FG//平面PBD ,并说明理由. (Ⅲ)当二面角B —PC —D 的大小为32π时,求PC 与底面ABCD 所成角的正切值.19.(本小题满分12分)设数列{}n a 为等差数列,且145=a ,720a =,数列{}n b 的前n 项和为n S ,123b =且132(2,)n n S S n n N -=+≥∈.(Ⅰ)求数列{}n a ,{}n b 的通项公式; (Ⅱ)若,1,2,3,n n n c a b n =⋅=,n T 为数列{}n c 的前n 项和,n T m <对*n N ∈恒成立,求m 的最小值.20.(本小题满分13分)如图,已知椭圆134:22=+y x C ,直线l 的方程为4=x ,过右焦点F 的直线'l 与椭圆交于异于左顶点A 的Q P ,两点,直线AP ,AQ 交直线l 分别于点M ,N . (Ⅰ)当29=⋅AQ AP 时,求此时直线'l 的方程; (Ⅱ)试问M ,N 两点的纵坐标之积是否为定值?若是,求出该定值;若不是,请说明理由.21.(本小题满分14分)设函数ax xxx f -=ln )(. (Ⅰ)若函数)(x f 在),1(+∞上为减函数,求实数a 的最小值;(Ⅱ)若存在212,,x x e e ⎡⎤∈⎣⎦,使a x f x f +'≤)()(21成立,求实数a 的取值范围.教学质量检测 理科数学参考答案一.选择题:DADBD ACCCB 二.填空题:11.20; 12.21; 13.-3; 14.43π; 15.21三.解答题:16.(本小题满分12分)解:(Ⅰ)由已知⎪⎭⎫⎝⎛+⎪⎭⎫⎝⎛-=-A A B A 6cos 6cos 22cos 2cos ππ 得2222312sin 2sin 2cos sin 44B A A A ⎛⎫-=-⎪⎝⎭……………………………………………………………3分 化简得23sin =B ………………………………………………………………………………………………5分 故323ππ或=B .………………………………………………………………………………………………6分 (Ⅱ)因为b a ≤,所以3B π=,……………………………………………………………………………7分由正弦定理2sin sin sin 2a c bA C B====,得C c A a sin 2,sin 2==, 故A A A A C A c a cos 23sin 2332sin sin 2sin sin 221-=⎪⎭⎫ ⎝⎛--=-=-π6A π⎛⎫=- ⎪⎝⎭ ……9分因为b a ≤,所以323ππ<≤A ,266πππ<-≤A ,……………………………………………………10分 所以⎪⎪⎭⎫⎢⎣⎡∈⎪⎭⎫ ⎝⎛-=-3,236sin 321πA c a . ……………………………………………………12分17.(本小题满分12分)解:(Ⅰ)甲厂抽取的样品中优等品有7件,优等品率为710,……………………………………2分 乙厂抽取的样品中优等品有8件,优等品率为84105=.…………………………………………………4分 (Ⅱ)ξ的取值为1,2,3.………………………………………………………………………………6分12823101(1)15C C P C ξ⋅===,21823107(2)15C C P C ξ⋅===,157)3(3100238=⋅==C C C P ξ……………………9分所以ξ的分布列为…………………………………………………………………………………………………………………10分 故的数学期望为17712123.1515155E ξ=⨯+⨯+⨯=() …………………………………………………12分 18.(本小题满分12分)解:方法一:(Ⅰ)∵PA ⊥面ABCD ,四边形ABCD 是正方形,其对角线BD ,AC 交于点E∴PA ⊥BD ,AC ⊥BD , ∴BD ⊥平面APC ………………………………………………………2分 ∵FG ⊂平面PAC ,∴BD ⊥FG ……………………………………………………………………3分 (Ⅱ)当G 为EC 中点,即AG=34AC 时,FG ∥平面PBD ,……………………………………………4分 连接PE ,由F 为PC 中点,G 为EC 中点,知FG ∥PE ,………………………………………………5分 而FG ⊄平面PBD ,PB ⊂平面PBD ,故FG ∥平面PBD .……………………………………………6分 (Ⅲ)作BH ⊥PC 于H ,连接DH ,∵PA ⊥面ABCD ,四边形ABCD 是正方形,∴PB=PD ,又∵BC=DC ,PC=PC ,∴△PCB ≌△PCD ,∴DH ⊥PC ,且DH=BH ,∴∠BHD 是二面角B -PC -D 的平面角.即,32π=∠BHD ………………………………………………………………………………………7分 ∵PA ⊥面ABCD ,∴∠PCA 就是PC 与底面ABCD 所成的角 …………………………………8分连结EH ,则PC EH BHE BD EH ⊥=∠⊥,3,π,tan BEBHE EH∴∠==而BE EC =,,33sin ,3==∠∴=∴EC EH PCA EH EC …………………………………………10分,22tan =∠∴PCA ……………………………………………………………………………………11分 ∴PC 与底面ABCD 所成角的正切值是22………………………………………………………12分 方法二:(Ⅰ)以A 为原点,AB ,AD ,PA 所在的直线分别为x ,y ,z 轴建立空间直角坐标系,设正方形ABCD 的边长为1,则A (0,0,0),B (1,0,0),C (1,1,0)D (0,1,0),P (0,0,a )(a>0),)20)(0,,(),2,21,21(),0,21,21(<<m m m G a F E …………1分∵11(1,1,0),(,,)222a BD FG m m =-=---,110022BD FG m m ⎛⎫⎛⎫⋅=--+-+= ⎪ ⎪⎝⎭⎝⎭…………2分∴BD ⊥FG ………………………………………………………………………………3分(Ⅱ)要使FG//平面PBD ,只需FG//EP ,而11,,22EP a ⎛⎫=-- ⎪⎝⎭,由FG EP λ=,可得:11222m a a λλ⎧-=-⎪⎪⎨⎪-=⎪⎩,解得12λ=-,34m =,…………………………………………………………………………………5分 33,,044G ⎛⎫∴ ⎪⎝⎭,34AG AC =,故当34AG AC =时,FG//平面PBD ………………………6分(Ⅲ)设平面PBC 的一个法向量为(),,u x y z =则⎪⎩⎪⎨⎧=⋅=⋅0BC u PC u ,而)0,1,0(),,1,1(=-=BC a PC ⎩⎨⎧==-+∴0y az y x ,取1z =,得)1,0,(a u =,……………………8分 同理可得平面PDC 的一个法向量)1,,0(a v =,设v u ,所成的角为θ,则,21|32cos||cos |==πθ 即,21111,21||||22=+⋅+∴=a a v u v u 1=∴a …………………………………………10分∵PA ⊥面ABCD ,∴∠PCA 就是PC 与底面ABCD 所成的角,2221tan ===∠∴AC PA PCA ∴PC 与底面ABCD 所成角的正切值是22…………………………………………………………12分 19.(本小题满分12分)解:(Ⅰ) 数列{}n a 为等差数列,公差751() 3 2d a a ==-,易得21=a , 所以 13-=n a n ……………………………………………………………………………………1分 由132n n S S -=+,得32n n n S S b =-+,即22n n b S =-, 所以21222()b b b =-+,又123b =,所以229b =,2113b b = ………………………………………2分由132n n S S -=+, 当3n ≥时,得1232n n S S --=+,两式相减得:1123()n n n n S S S S ----=-,即13n n b b -=,所以)3≥…………………4分 ,所以{}n b 是以……………5分6分 8分9分11分∵n T m <对n N +∈恒成立,∴2≥m ∴m 的最小值是2………………………………12分20. (本小题满分13分)解:(Ⅰ)①当直线PQ 的斜率不存在时,由)0,1(F 可知PQ 方程为1=x代入椭圆134:22=+y x C 得)23,1(),23,1(-Q P 又)0,2(-A ),23,3(),23,3(-==∴274AP AQ ⋅=不满足……………………………………2分 ②当直线PQ 的斜率存在时,设PQ 方程为)0)(1(≠-=k x k y代入椭圆134:22=+y x C 得01248)43(2222=-+-+k x k x k …………………………3分 设),(),,(2211y x Q y x P 得2221222143124,438k k x x k k x x +-=+=+…………………………4分 222121221221439)1()1)(1(k k x x x x k x x k y y +-=++--=--=2943274)(2)2)(2(222121212121=+=++++=+++=⋅k k y y x x x x y y x x AQ AP26±=∴k 故直线'l 的方程; ()126-±=x y ………………………………………………6分 (Ⅱ)AP 的方程为11(2)2y y x x =++与l 的方程:4x =联立 得:116(4,)2y M x + 同理得226(4,)2y N x +…………………………………………………8分 12121212126636222()4M N y y y y y y x x x x x x ∴⋅=⋅=+++++ ①k 不存在时,3336()22912(11)4M N y y ⋅⋅-⋅==-+++………………………………………………9分 ②k 存在时,2222223243494121643434M N k k y y k kk k-+⋅==--++++………………………………………12分 M ,N 两点的纵坐标之积为定值9- …………………………………………13分21.(本小题满分14分) 解:(Ⅰ)由已知得x >0,x ≠1.因f (x )在(1)+∞,上为减函数,故2ln 1()0(ln )x f x a x -'=-≤在(1)+∞,上恒成立. ………………1分所以当(1)x ∈+∞,时,max ()0f x '≤. 又()22ln 111()ln ln (ln )x f x a a x xx -'=-=-+-()2111ln 24a x =--+-,………………………………2分 故当11ln 2x =,即2x e =时,max 1()4f x a '=-. 所以10,4a -≤于是14a ≥,故a 的最小值为14. ……………………………………………4分(Ⅱ)命题“若存在212,[,],x x e e ∈使()12()f x f x a '+≤成立”等价于“当2[,]x e e ∈时,有()min max ()f x f x a '+≤”. …………………………………………………5分 由(Ⅰ),当2[,]x e e ∈时,max 1()4f x a '=-,∴()max 14f x a '+=.问题等价于:“当2[,]x e e ∈时,有min 1()4f x ≤”. ………………………………………………6分①当14a ≥时,由(1),()f x 在2[,]e e 上为减函数,则min ()f x =2221()24e f e ae =-≤,故21124a e -≥. ……………………………………………8分②当a <14时,由于'2111()()ln 24f x a x =--+-在2,e e ⎡⎤⎣⎦上的值域为1,4a a ⎡⎤--⎢⎥⎣⎦(ⅰ)0a -≥,即0a ≤,'()0f x ≥在2,e e ⎡⎤⎣⎦恒成立,故()f x 在2,e e ⎡⎤⎣⎦上为增函数,于是,min 1()()4f x f e e ae e ==-≥>,矛盾.……………………………………………10分 (ⅱ)0a -<,即104a <<,由'()f x 的单调性和值域知, 存在唯一20(,)x e e ∈,使'()0f x =,且满足:当0(,)x e x ∈时,'()0f x <,()f x 为减函数;当20(,)x x e ∈时,'()0f x >,()f x 为增函数;所以,0min 0001()()ln 4x f x f x ax x ==-≤,20(,)x e e ∈…………………………………………12分 所以,2001111111ln 4ln 4244a x x e e ≥->->-=,与104a <<矛盾.………………………13分 综上,得21124a e≥-………………………………………………………………………………14分。
山东东营2014届中考数学二模试题有解析

山东东营2014届中考数学二模试题(有解析)(时间:120分钟;满分:120分)一、选择题(每小题只有一个正确答案,每小题3分,计30分) 1.2sin 30o的倒数是 ( )A. 0.5B.14 C.4 D.-42.下面是一位同学做的四道题: ①633a a a =+;②632x x x =⋅;③a a a 22)(2=÷-;④63326-)2-(y x xy =.其中做对了几道题 ( )A.0B.1C.2D.33.如图①,有6张写有实数的卡片,它们的背面都相同,现将它们背面朝上洗匀后如图②摆放,从中任意翻开两张都是无理数的概率是( )A.12B.16C.13D.154.两圆的半径分别为,a b ,圆心距为4.若25440a b a a +-+-+=,则两圆( )A .内含B .相交C .外切D .外离5.已知整数x 满足是不等式组⎪⎩⎪⎨⎧+-<--<613424)1(32x x x x ,则x 的算术平方根为( ) A .2B .±2C . 2D . 46.如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1、S2,则1212s s s s k -+=的值为 ( )A .16B .17C .18D .197.如图,在△ABC 中,∠C=90°,∠B=30°,以A 为圆心,任意长为半径画弧分别交AB 、AC 于点M 和N ,再分别以M 、N 为圆心,大于MN 的长为半径画弧,两弧交于点P ,连结AP 并延长交BC 于点D ,则下列说法中正确的个数是( )①AD 是∠BAC 的平分线;②∠ADC=60°;③点D 在AB 的中垂线上;④S △DAC :S △ABC=1:3 A.1 B.2 C.3 D.48. 如图,正六边形边长为a 的六角螺帽在桌面上滚动(没有滑动)一周,则它的中心O 点所经过的路径长为( )A .6aB .5aC .2a π Dπ 9.给出以下命题:①已知8215-可以被在60~70之间的两个整数整除,则这两个数是63、65; ②若,2=xa ,3=ya 则yx a -2=34;③已知关于x 的方程322=-+x mx 的解是正数,则m 的取值范围为6-≠->m m 或;其中正确的是( )A .①②B .②③C .①③ D.①②③10.如图①,在梯形ABCD 中,AD ∥BC ,∠A=60°,动点P 从A 点出发,以1cm/s 的速度沿着A →B →C →D 的方向不停移动,直到点P 到达点D 后才停止.已知△PAD 的面积s(单位:cm2)与点P 移动的时间t (单位:s )的函数如图②所示,则下列结论:①AB =BC =2cm ;②cos ∠CDA =12;③梯形A BCD的面积为;④点P 从开始移动到停止移动一共用了(4+秒;其中正确的结论是( )A .①②B .①③C .①③④D .①②③④二、填空题(每小题3分,计24分)11. 2014年3月8日马航失踪后,据央视报道,我国已划定长90海里,宽25海里,总面积约2250平方海里(约合7717平方公里)的长方形区域为12日前的海上搜救范围,1平方公里=1×106平方米,对7717平方公里用科学计数法表示为__________ 平方米.(保留两个有效数字) 12.分解因式: 22a ax ax -+ .14.如图,菱形ABCD 中,60DAB ∠=︒,DF AB ⊥于点E ,且DF DC =,连接FC ,则ACF ∠的度数为 度。
最新2014年全国高考理科数学二模试题及答案-山东卷

最新2014年全国高考理科数学二模试题及答案-山东卷解析:C对于f(x)=ax,当a1时,f(x)在R上是增函数。
对于g(x)=(2-a)x,当2-a>0时,g(x)在R上是增函数;当2-a<0时,g(x)在R上是减函数。
所以当a>2时,f(x)是减函数,g(x)是增函数,两者同时成立,为充分必要条件。
答案选C。
4在平面直角坐标系内,点A(0,0),点B(3,4),点C(4,3),则△ABC的面积为A5B6C7D8解析:BABC的面积可以用向量叉积求解,设向量BA=(3,-4),向量CA=(4,-3),则ABC的面积为1/2|BA×CA|=1/2|3×(-3)-4×4|=6.答案选B。
5已知集合A={x|x2-2x-3<0},则A的取值范围是A(-∞,1)∪(3,∞)B(-∞,1)∪(3,∞)C(-∞,-1)∪(3,∞)D(-∞,-1)∪(1,3)∪(3,∞)解析:Dx2-2x-3=(x-3)(x+1)<0,解得x∈(-∞,-1)∪(3,∞)。
答案选D。
6已知函数f(x)=x3-3x2+5x-1,则f(x)的单调递减区间为A(-∞,1)B(1,2)C(2,+∞)D(1,+∞)解析:Af'(x)=3x2-6x+5,判别式△=6-4×3×5=-560的解不存在,f(x)在R上单调递减。
答案选A。
7已知集合A={x|x2+px+q>0},其中p,q∈R,若A中至少有一个元素,则下列说法正确的是A p2-4q≤0B p2-4q>0C p2+4q≤0D p2+4q>0解析:B当A中至少有一个元素时,x2+px+q>0,即判别式△=p2-4q0.答案选B。
8已知函数f(x)=x2-2ax+a2+3a-1,若对于任意实数x,都有f(x)≥0,则a的取值范围是A(-∞,-2]∪[1,2]B(-∞,-2]∪[2,+∞)C[-1,2]D(-∞,-1]∪[2,+∞)解析:Bf(x)=x2-2ax+a2+3a-1=(x-a)2+(3a-1),当a≥2或a≤-2时,(3a-1)≤0,所以f(x)≤0,不符合条件。
数学_2014年山东省某校高考数学二模试卷(理科)_(含答案)

2014年山东省某校高考数学二模试卷(理科)一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的(本大题共10小题,每小题5分,共50分).1. 已知集合A ={x ∈R||x|≤2},B ={x ∈R|x ≤1},则A ∩B =( ) A (−∞, 2] B [1, 2] C [−2, 2] D [−2, 1]2. 函数f(x)是R 上的增函数且f(a)+f(b)>f(−a)+f(−b)则( ) A a >b >0 B a −b >0 C a +b >0 D a >0,b >03. 过点(1, 0)且与直线x −2y −2=0平行的直线方程是( )A x −2y −1=0B x −2y +1=0C 2x +y −2=0D x +2y −1=04. 阅读如图所示的程序框图,如果输出i =4,那么空白的判断框中应填入的条件是( )A S <8B S <9C S <10D S <115. 样本中共有五个个体,其值分别为a ,0,1,2,3.若该样本的平均值为1,则样本方差为( )A √65 B 65C √2D 26. 设定义在R 上的函数f(x)满足f(x)⋅f(x +2)=13,若f(1)=2,则f(99)=( ) A 13 B 2 C 132D 2137. 由0,1,2,3,4这5个数字组成没有重复数字且个位上的数字不能为1的3位数共有( )A 28个B 36个C 39个D 42个8. 实数x ,y 满足{y ≥1y ≤2x −1x +y ≤b ,如果目标函数z =x −y 的最小值为−2,则实数b 的值为( )A 0B 6C 7D 89. 在ABC 中,a ,b ,c 分别为角A ,B ,C 的对边,且角A =60∘,若S △ABC =15√34,且5sinB =3sinC ,则ABC 的周长等于( )A 8+√19B 14C 10+3√5D 1810. 设互不相等的平面向量组a i (i =1, 2, 3,…),满足①|a i |=1;②a i ⋅a i+1=0.若T m =a 1+a 2+...+a m (m ≥2),则|T m |的取值集合为( )A {0, √2}B {1, √3}C {1, √2, √3}D {0, 1, √2}二、填空题:把答案填在答题卷中的横线上(本大题共4小题,每小题5分,共25分). 11. 双曲线x 24−y 2m =1的焦距为4√2,则m =________. 12. 二项式(ax 2√x)5的展开式中常数项为160,则a 的值为________.13. 已知√2+23=2√23,√3+38=3√38,√4+415=4√415…,照此规律,第五个等式为________.14. 某制冷设备厂设计生产一种长方形薄板,如图所示,长方形ABCD(AB>AD)的周长为4米,沿AC折叠使B到B′位置,AB′交DC于P.研究发现当ADP的面积最大时最节能,则最节能时长方形ABCD的面积为________.二、请在下列三题中任选一题作答,如果多做,则按所做的第一题评分。
【2014济南二模】山东省济南市2014届高三5月针对性训练 理科数学 Word版含答案

2014年高考针对性训练(山东卷)理 科 数 学本试卷分为第I 卷和第Ⅱ卷两部分,共5页.训练时间120分钟,满分150分,考试结束后,将本试卷和答题卡一并交回.注意事项:1.答题前,考生务必用0.5毫米黑色签字笔将自己的姓名、座号、考生号、县区和科类写在答题卡和试卷规定的位置上.2.第I 卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号,答案不能答在试卷上.3.第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效.4.填空题请直接填写答案,解答题应写出文字说明、证明过程或演算步骤. 参考公式:如果事件A ,B 互斥,那么()()()P A B P A P B ⋃=+;如果事件A ,B 独立,那么()()()P A B P A P B ⋂=⋅.第I 卷(共50分)一、选择题:本大题共10个小题,每小题5分,共50分.每小题给出的四个选项中只有一项是符合题目要求的.1.设集合{}2320A x x x =-+=,则满足{}0,1,2A B ⋃=的集合B 的个数是 A.1 B.3 C.4 D.62.如图,在复平面内,复数12,z z 对应的向量分别是,OA OB ,则12z z +=A.1B.C.2D.3 3. 22log sinlog cos 212ππ+的值为 A.2-B. 2-C.12D.14.设等差数列{}n a 的前n 项和为357899,30n S S S a a a ==++=,若,则A.27B.36C.42D.635.一个空间几何体的三视图如图所示,该几何体的表面积为A.96B.136C.152D.1926.如图,在1,3ABC AB AC ∆==中,,D 是BC 的中点,则AD BC ⋅=A.3B.4C.5D.不能确定7.函数()()2cos x f x xπ=的图象大致是8.执行右面的程序框图,输出的S 的值为A.0B. 2C.1D.9.设曲线y x =轴所围成的区域为D ,向区域D 内随机设一点,则该点落入区域(){}22,2x y D xy ∈+<的概率是 A. 1ππ- B. 1ππ+ C.23 D. 3410.已知定义域为R 的函数()()33sin cos 2cos bx x bx x f x a a b R x++=+∈+、有最大值和最小值,且最大值与最小值和为6,则32a b -= A.7B.8C.9D.10 第II 卷(共100分)二、填空题:本大题共5个小题,每小题5分,共25分.11.已知关于x 的不等式21x a x -+->的解集为全体实数R ,则实数a 的取值范围是________.12.已知()()611ax x ++的展开式中2x 的系数为3,则a =__________. 13.设0x 是方程10lg x x -=的解,且()()0,1=x k k k Z k ∈+∈,则___________.14.设变量,x y 满足约束条件32210,28y x y x y x x y ≤-⎧⎪⎪-+≤⎨⎪+≤⎪⎩则的最大值是____________. 15.过双曲线()222210,0x y a b a b-=>>的左焦点()(),00F c c ->,作倾斜角为6π的直线EF 交该双曲线右支于点P ,O 为坐标原点,若()102OE OF OP OE EF =+⋅=且,则双曲线的离心率为__________.三、解答题:本大题共6小题,共75分.16.(本小题满分12分)在ABC ∆中,角A ,B ,C对应的边分别是,,.2a b c a b A B ==∠=∠且. (I )求cos B 的值;(II )求c 的值.甲地区有10名人大代表,其中有4名女代表;乙地区有5名人大代表,其中有3名女代表,现采用分层抽样方法从甲、乙两地区共抽取3名代表进行座谈.(I )求从甲、乙两地区各抽取的代表数;(II )求从甲组抽取的代表中至少有1名女代表的概率;(III )记ξ表示抽取的3名代表中女代表数,求ξ的分布列及数学期望.18.(本小题满分12分)在四面体A B C D A -⊥中,平面BCD ,302,BC CD DBC AD BD ⊥∠===,,M 是AD 的中点,P 是BM 的中点,点Q 在线段AC 上,且AQ=3QC.(I )证明:PQ//平面BCD ;(II )求二面角C BM D --的大小.19.(本小题满分12分)已知数列{}n b 满足{}11117242n n n n b b b T b +=+=,且,为的前n 项和. (I )求证:数列12n b ⎧⎫-⎨⎬⎩⎭是等比数列,并求{}n b 的通项公式; (II )如果对任意的2*22321045n n T n N n n k -+-∈≤++,不等式恒成立,求实数k 的取值范围.20.(本小题满分13分)已知曲线C 上任意一点P 到点F (0,1)的距离比它到直线:2l y =-的距离小1,一个圆的圆心为A (0,4),过点A 的直线与曲线C 交于D ,E 两点.(I )求曲线C 的方程;(II )当线段DE 长度最短时,曲线C 过D 点的切线与圆A ,求此时圆A 的方程.已知函数()()21,x ax f x e x g x x e =--=.(I )求()f x 的最小值;(II )求()g x 的单调区间;(III )当1a =时,对于在(0,1)中的任一个常数m ,是否存在正数0x 使得()()002m f x g x >成立?如果存在,求出符合条件的一个0x ;否则说明理由.。
2014山东省实验中学高三二模考试数学理试题及答案
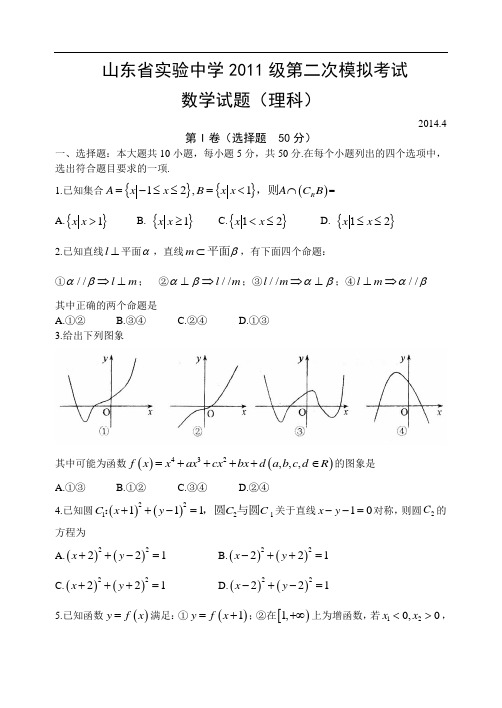
山东省实验中学2011级第二次模拟考试数学试题(理科)2014.4第I 卷(选择题 50分)一、选择题:本大题共10小题,每小题5分,共50分.在每个小题列出的四个选项中,选出符合题目要求的一项.1.已知集合{}{}()12,1R A x x B x x A C B =-≤≤=<⋂,则= A.{}1x x > B. {}1x x ≥ C.{}2x x 1<≤ D. {}2x x 1≤≤ 2.已知直线l ⊥平面α,直线m β⊂平面,有下面四个命题:①//l m αβ⇒⊥; ②//l m αβ⊥⇒;③//l m αβ⇒⊥;④//l m αβ⊥⇒ 其中正确的两个命题是A.①②B.③④C.②④D.①③3.给出下列图象其中可能为函数()()432,,,f x x ax cx bx d a b c d R =++++∈的图象是 A.①③ B.①②C.③④D.②④ 4.已知圆()()22121111C x y C C ++-=:,圆与圆关于直线10x y --=对称,则圆2C 的方程为A.()()22221x y ++-=B.()()22221x y -++= C.()()22221x y +++= D.()()22221x y -+-= 5.已知函数()y f x =满足:①()1y f x =+;②在[)1,+∞上为增函数,若120,0x x <>,且()()12122x x f x f x +<---,则与的大小关系是A.()()12f x f x -=-B. ()()12f x f x -<-C.()()12f x f x ->-D.无法确定6.已知G 是ABC ∆的重心,点P 是GBC ∆内一点,若AP AB AC λμλμ=++,则的取值范围是 A.112⎛⎫⎪⎝⎭, B.213⎛⎫⎪⎝⎭, C.312⎛⎫⎪⎝⎭, D.()12,7.已知点(),M a b 在由不等式组002x y x y ≥⎧⎪≥⎨⎪+≤⎩确定的平面区域内,则点(),N a b a b +-所在平面区域的面积是A.4B.2C.1D.88.已知离心率为e的双曲线和离心率为2的椭圆有相同的焦点12F F P 、,是两曲线的一个公共点,若123F PF e π∠=,则等于A.2B. 2C.52D.3 9.设αβ,为锐角,那么“()22sinsin sin αβαβ+=+”是“2παβ+=”的A.充分非必要条件B.必要非充分条件C.充要条件D.既不充分也不必要条件 10.已知函数()31,0,9,0x x f x xx x ⎧+>⎪=⎨⎪+≤⎩若关于x 的方程()()22f x x a a R +=∈有六个不同的实根,则a 的取值范围是A.(]2,8B.(]2,9C.()8,9D. (]8,9二、填空题:本大题共5小题,每小题5分,共25分.11.阅读下面程序框图,则输出的数据S 为______.12.几何体的三视图如图所示(单位:m ),则该几何体的体积为________m 3.13.已知对于任意的x R ∈,不等式35x x a -+->恒成立,则实数a 的取值范围是________.14.如图,用四种不同颜色给三棱柱111ABC A B C -的六个顶点涂色,要求四种颜色全都用上,每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色.则不同的涂色方法的种数为_________(用数字做答).15.设S 为非空数集,若,x yS ∀∈,都有,,x y x y xy S +-∈,则称S 为封闭集.下列命题①实数集是封闭集; ②全体虚数组成的集合是封闭集;③封闭集一定是无限集; ④若S 为封闭集,则一定有0S ∈;⑤若S ,T 为封闭集,且满足S U T ⊆⊆,则集合U 也是封闭集.其中真命题是_________________.三、解答题:本大题共6小题,共75分.解答应写出文字说明,演算步骤或证明过程.16.(本小题满分12分)已知ABC ∆的面积为1,且满足02AB AC AB AC <⋅≤,设和的夹角为θ. (I )求θ的取值范围;(II )求函数()22sin cos 246f ππθθθ⎛⎫⎛⎫=+-+ ⎪ ⎪⎝⎭⎝⎭的最大值及取得最大值时的θ值. 17.(本小题满分12分)如图,正三棱柱111ABC A B C -的所有棱长都为2,D 为1CC 中点.(I )求证:1AB ⊥平面1A BD ;(II )求二面角1A A D B --的大小.18.(本小题满分12分)盒中装有5个乒乓球用作比赛,其中2个是旧球,另外3个是新球,新球使用后...即成为了旧球.(I )每次比赛从盒中随机抽取1个球使用,使用后...放回盒中,求第2次比赛结束后盒内剩余的新球数为2个的概率P ;(II )每次比赛从盒中随机抽取2个球使用,使用后放回盒中,设第2次比赛结束后盒内剩余的新球数为X ,求X 的分布列和数学期望.19.(本小题满分12分)已知数列{}()*n a n N ∈的前n 项和为n S ,数列n S n ⎧⎫⎨⎬⎩⎭是首项为0,公差为12的等差数列. (I )求数列{}n a 的通项公式;(II )设()()*4215n a n b n N =⋅-∈,对任意的正整数k ,将集合{}21221,,k k k b b b -+中的三个元素排成一个递增的等差数列,其公差为x d ,求数列{}k d 的通项公式.(III )对(II )中的x d ,求集合{}1,k k x d x d x Z +<<∈的元素个数.20.(本小题满分13分)已知椭圆()2222:1x y C a b a b +=>>0的两个左、右焦点分别是())12,F F ,且经过点33A ⎛ ⎝⎭.(I )求椭圆C 的方程;(II )若椭圆C 上两点M ,N 使(),0,2OM ON OA OMN λλ+=∈∆求面积的最大值.21.(本小题满分14分)已知函数()2ln ,f x x ax x a R =+-∈.(I )若函数()[]12f x 在,上是减函数,求实数a 的取值范围;(II )令()()2g x f x x =-,是否存在实数(]0,a x e ∈,当(e 是自然常数)时,函数()g x 的最小值是3,若存在,求出a 的值;若不存,说明理由;(III )当(]0,x e ∈时,证明:()2251ln 2e x x x x ->+.。
山东省东营市数学高三理数第二次联考试卷

山东省东营市数学高三理数第二次联考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)设,,,则= ()A .B .C .D .2. (2分)(2019·江南模拟) 复数满足,则()A .B . 3C .D . 53. (2分)若a,b为非零实数,且a<b,则下列命题成立的是()A .B . a2<b2C . a2b<ab2D . a3<b34. (2分)(2020·淮北模拟) 已知圆直线,则“ ”是“ 上恰有两个不同的点到的离为1”的()A . 充要条件B . 充分不必要条件C . 必要不充分条件D . 既不充分也不必要条件5. (2分)等差数列{an}的前n项和为Sn ,且S3=6,a1=4,则公差d等于()A . 1B .C . -2D . 36. (2分) (2019高二上·张家口期中) 如图是一个正方体的平面展开图,则在正方体中直线AB与CD的位置关系为A . 相交B . 平行C . 异面而且垂直D . 异面但不垂直7. (2分) (2015高二上·海林期末) 已知P是抛物线y2=4x上的一个动点,则点P到直线l1:3x﹣4y+12=0和l2:x+2=0的距离之和的最小值是()A . 1B . 2C . 3D . 48. (2分) (2019高二上·阜阳月考) 已知点是抛物线上的一动点,为抛物线的焦点,是圆:上一动点,则的最小值为()A . 3B . 4C . 5D . 69. (2分)已知正整数a,b满足4a+b=30,使得取最小值时,则实数对(a,b)是()A . (5,10)B . (6,6)C . (10,5)D . (7,2)10. (2分)集合A={﹣1,0,1},A的子集中,含有元素0的子集共有()A . 2个B . 4个C . 6个D . 8个11. (2分)(2017·襄阳模拟) 已知,在矩形ABCD中,AB=2,AD=1,点P为矩形ABCD内一点,则使得的概率为()A .B .C .D .12. (2分)先将函数的图像向左平移个长度单位,再保持所有点的纵坐标不变横坐标压缩为原的,得到函数g(x)的图像.则使g(x)为增函数的一个区间是()A .B .C .D .二、填空题 (共4题;共4分)13. (1分)非负实数x、y满足,则x+3y的最大值为________.14. (1分)《广告法》对插播广告的时间有一定的规定,某人对某台的电视节目做了长期的统计后得出结论,他任意时间打开电视机看该台节目,看不到广告的概率为,那么该台每小时约有________ 分钟的广告.15. (1分)(2020·江西模拟) 已知函数的图象关于对称,记函数的所有极值点之和与积分别为,,则 ________.16. (1分)如图,在正方体ABCD﹣A1B1C1D1 ,若E是AD的中点,则异面直线A1B与C1E所成角等于________三、解答题 (共7题;共70分)17. (10分)(2017·石家庄模拟) 棉花的纤维长度是评价棉花质量的重要指标,某农科所的专家在土壤环境不同的甲、乙两块实验地分别种植某品种的棉花,为了评价该品种的棉花质量,在棉花成熟后,分别从甲、乙两地的棉花中各随机抽取20根棉花纤维进行统计,结果如下表:(记纤维长度不低于300mm的为“长纤维”,其余为“短纤维”)纤维长度(0,100)[100,200)[200,300)[300,400)[400,500]甲地(根数)34454乙地(根数)112106(1)由以上统计数据,填写下面2×2列联表,并判断能否在犯错误概率不超过0.025的前提下认为“纤维长度与土壤环境有关系”.甲地乙地总计长纤维________________________短纤维________________________总计________________________附:(1);(2)临界值表;P(K2≥k0)0.100.050.0250.0100.0050.001k0 2.706 3.841 5.024 6.6357.87910.828(2)现从上述40根纤维中,按纤维长度是否为“长纤维”还是“短纤维”采用分层抽样的方法抽取8根进行检测,在这8根纤维中,记乙地“短纤维”的根数为X,求X的分布列及数学期望.18. (10分) (2017高二上·河南月考) 如图,在四棱锥中,平面,底面是菱形.(1)求证:平面;(2)若,求与平面所成角的正弦值.19. (10分) (2016高三上·成都期中) 已知公差不为0的等差数列{an}中,a1=2,且a2+1,a4+1,a8+1成等比数列.(1)求数列{an}通项公式;(2)设数列{bn}满足bn= ,求适合方程b1b2+b2b3+…+bnbn+1= 的正整数n的值.20. (10分)(2018·天津模拟) 已知椭圆左顶点为M ,上顶点为N ,直线MN的斜率为.(Ⅰ)求椭圆的离心率;(Ⅱ)直线l:与椭圆交于A , C两点,与y轴交于点P ,以线段AC为对角线作正方形ABCD ,若.()求椭圆方程;()若点E在直线MN上,且满足,求使得最长时,直线AC的方程.21. (10分) (2017高一上·厦门期末) 已知函数f(x)=x2+ax(a>0)在[﹣1,2]上的最大值为8,函数g (x)是h(x)=ex的反函数.(1)求函数g(f(x))的单调区间;(2)求证:函数y=f(x)h(x)﹣(x>0)恰有一个零点x0,且g(x0)<x02h(x0)﹣1(参考数据:e=2.71828…,ln2≈0.693).22. (10分)(2018·河北模拟) 以平面直角坐标系的原点为极点,轴的正半轴为极轴,取相同的长度单位建立极坐标系,已知直线的极坐标方程是,圆的参数方程为(为参数,).(1)若直线与圆有公共点,求实数的取值范围;(2)当时,过点且与直线平行的直线交圆于两点,求的值.23. (10分)已知函数f(x)=x+ .(1)用定义证明f(x)在[1,+∞)上是增函数;(2)求f(x)在[1,4]上的最大值及最小值.参考答案一、单选题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共7题;共70分)17-1、17-2、18-1、18-2、19-1、19-2、21-1、21-2、22-1、22-2、23-1、23-2、。
数学_2014年山东省聊城市高考数学二模试卷(理科)_(含答案)

2014年山东省聊城市高考数学二模试卷(理科)一、选择题(本大题共10小题,每小题5分,共50分)1. 若集合A ={x||x|≤1, x ∈R},B ={x|y =√x},则A ∩B =( ) A {x|−1≤x ≤1} B {x|x ≥0} C {x|0≤x ≤1} D ⌀2. 设i 是虚数单位,复数1+ai 2−i为纯虚数,则实数a 为( )A 2B −2C −12 D 123. 已知某几何体的三视图如图所示,则该几何体的体积为( )A 8π3 B 3π C 10π3 D 6π4. 设函数f(x)={(12)x−1,x ≤11+log 2x ,x >1,则满足f(x)≤2的x 的取值范围是( )A [−1, 2]B [0, 2]C [1, +∞)D [0, +∞)5. 设x ,y ∈R ,向量a →=(x, 1),b →=(1, y),c →=(2, −4)且a →⊥c →,b → // c →,则|a →+b →|= ( )A √5B √10C 2√5D 106. 执行如图所示的程序框图,输出的结果是( )A 2B 3C 6D 97. (x 2+2)(1x 3−1)3的展开式中的常数项是( ) A 2 B 3 C −3 D −28. 若M(x, y)为由不等式组{0≤x ≤√2y ≤2x −√2y ≤0确定的平面区域D 上的动点,点A 的坐标为(√2, 1),则z =OM →⋅OA →的最大值为( )A 3B 4C 3√2D 4√29. 函数f(x)=(1−cosx)sinx在[−π, π]的图象大致为()A B C D10. 设f(x)与g(x)是定义在R上的两个函数,若对任意x∈[a, b],都有|f(x)−g(x)|≤1成立,则称f(x)和g(x)在[a, b]上是“密切函数”.若f(x)=x2−3x+4与g(x)=2x+t在[2, 3]上时“密切函数”,则实数t的取值范围是()A [−3, −1]B [−234, −54] C [−54, −1] D [−3, −54]二、填空题(本大题共5个小题,每小题5分,共25分)11. 某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40, 50),[50, 60),[60, 70),[70, 80),[80, 90),[90, 100]加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为________.12. 等轴双曲线C的中心在原点,焦点在x轴上,若双曲线C与抛物线y2=16x的准线交于A,B两点,|AB|=4√3,则双曲线C的实轴长为________.13. 在△ABC中,角A、B、C所对边的长分别为a、b、c,若a2+b2=2c2,则cosC的最小值等于________.14. 已知f(x, y)=2x−y+2,某公司的QQ在线等级计算方法如下:设等级为n级需要的天数为a n(n∈N∗),a1=5,a2=12,a3=f(a2, a1)=21,a4=f(a3, a2)=32,a5=f(a4, a3)=45,…,根据以上事实,由归纳推理可得,当n≥3时,a n=f(a n−1, a n−2)=________.(用n表示)15. 若式子σ(a, b, c)对任意a,b,c∈R,都有σ(a, b, c)=σ(c, a, b),则称σ(a, b, c)为轮换对称式,给出如下三个式子:①σ(a, b, c)=abc;②σ(a, b, c)=a2−b2+c2;③σ(A, B, C)=cosC⋅cos(A−B)−cos2C(A,B,C是△ABC的内角).则其中所有轮换对称式的序号是________.三、解答题(本大题共6小题,共75分)16. 已知向量a →=(cosωx −sinωx, sinωx),b →=(−cosωx −sinωx, 2√3cosωx)(ω>0),函数f(x)=a →⋅b →的最小正周期为2π. (1)求ω的值;(2)将函数y =f(x)的图象上各点的横坐标缩短到原来的12倍,纵坐标不变,得到函数y =g(x)的图象,求函数y =g(x)在区间[0, π2]上的取值范围.17. 等比数列{a n }的各项均为正数,且2a 1+3a 2=1,a 32=9a 2a 6,设b n =log 13a n ,n ∈N ∗.(1)求数列{a n },{b n }的通项公式;(2)设{b n }的前n 项和为S n ,求数列{1S n }(n ∈N ∗)的前n 项和T n .18. 在如图所示的几何体中,PO ⊥平面ABCD ,点O 在AB 上,EA // PO ,四边形ABCD 为直角梯形,BC ⊥AB ,PO =OB =BC =CD ,EA =AO =12CD .(1)求证:PE ⊥平面PBC ;(2)求二面角E −BD −A 的余弦值.19. “辽宁舰”是中国第一艘航母,为保证航母的动力安全性,拟增加运用某项新技术,该项新技术要进入试用阶段前必须对其中的三项不同指标甲、乙、丙进行量化检测,已知各项指标检测结果互不影响,且指标甲、乙、丙检测合格的概率分别为34、23、12.记指标甲、乙、丙合格分别得4分、2分、4分,某项指标不合格,则该项指标得0分. (1)求该项新技术量化得分不低于8分的概率;(2)记该项新技术的三项指标甲、乙、丙量化检测得分之和为随机变量X ,求X 的分布列与数学期望E(X).20. 已知椭圆C:x 2a2+y 2b 2=1(a >b >0)的左、右焦点分别为F 1(−1, 0),F 2(1, 0),点(1, e)在椭圆上,其中e 为椭圆的离心率. (1)求椭圆C 的方程;(2)设A 、B 是椭圆上位于x 轴上方的两点,且直线AF 1与直线BF 2平行,AF 2与BF 1交于点P .试用|AF 1|,|BF 2|表示|PF 1|+|PF 2|,并证明|PF 1|+|PF 2|是定值. 21. 已知函数f(x)=e x (e =2.71828…是自然对数的底数),x ∈R . (1)求函数y =f(x)的图象过原点的切线方程;(2)设x >0,讨论曲线y =f(x)与曲线y =mx 2(m >0)公共点的个数; (3)设a <b ,证明f(a)+f(b)2>f(b)−f(a)b−a.2014年山东省聊城市高考数学二模试卷(理科)答案1. C2. A3. A4. B5. B6. D7. D8. B9. C 10. D 11. 480 12. 4 13. 1214. n(n +4) 15. ①③16. 解:(1)函数f(x)=a →⋅b →=(cosωx −sinωx)⋅(−cosωx −sinωx)+sinωx ⋅2√3cosωx =sin 2ωx −cos 2ωx +√3sin2ωx =−cos2ωx +√3sin2ωx =2sin(2ωx −π6),再根据f(x)的周期为2π,可得2π2ω=2π,∴ ω=12,故f(x)=2sin(x −π6).(2)将f(x)=2sin(x −π6)图象上各点的横坐标缩短到原来的12倍,纵坐标不变,得到函数y =g(x)=2sin(2x −π6)的图象, ∵ 0≤x ≤π2,∴ −π6≤2x −π6≤5π6,∴ sin(2x −π6)∈[−12, 1],∴ g(x)∈[−1, 2].17. 解:(1)设数列{a n }的公比为q ,由a 32=9a 2a 6得a 32=9a 42,所以q 2=19,由条件可知各项均为正数,所以q =13, 由2a 1+3a 2=1得2a 1+3a 1q =1,所以a 1=13 所以数列{a n }的通项式为a n =13⋅13n−1=13n ,则b n =log 13a n =n ;(2)由(1)得,S n =1+2+3+...+n =n(1+n)2,所以1S n=2n(n+1)=2(1n −1n+1),所以T n =2[(1−12)+(12−13)+(13−14)+...+(1n−1n+1)]=2(1−1n+1)=2nn+1.18. (1)证明:EA // OP ,AO ⊂平面ABP , ∴ 点A ,B ,P ,E 共面,∵ PO ⊥平面ABCD ,PO ⊂平面PEAB ,∴ 平面PEAB ∩平面ABCD =AB , ∴ BC ⊥平面PEAB ,∴ PE ⊥BC , 取OP 中点F ,连接EF ,∵ EA =AO =12CD ,OP =CD ,∴ EA =OF ,∴ EFOA 是平行四边形, ∵ PO ⊥平面ABCD , ∴ OP ⊥AB ,∴ EFOA 是正方形, ∴ EF ⊥PF , ∵ EF =PF , ∴ ∠EPF =45∘,∵ PO =OB ,OP ⊥AB , ∴ ∠OPB =45∘, ∴ ∠EPB =90∘, ∴ PE ⊥PB∴ PE ⊥平面PBC .(2)解:由已知知四边形BCDO 是正方形,OD 、OB 、OP 两两垂直, 如图建立空间直角坐标系,设DC =1, 则B(0, 1, 0),D(1, 0, 0),E(0, −0.5, 0.5), 设平面BDE 的一个法向量为n 1→=(x, y, z),BD →=(1, −1, 0),BE →=(0, −1.5, 0.5),∴ {x −y =0−1.5y +0.5z =0,取y =1,则x =1,z =3,从而n 1→=(1, 1, 3). 取平面ABD 的一个法向量为n 2→=(0, 0, 1). cos <n 1→,n 2→>=3√1111, 故二面角E −BD −A 的余弦值为3√1111. 19. 解:(1)记该项新技术的三项指标甲、乙、丙检测合格分别为A ,B ,C , 则事件“得分不低于8分”表示为ABC +AB ¯C , ∵ ABC 与AB ¯C 为互斥事件,且A ,B ,C 彼此独立, ∴ 该项新技术量化得分不低于8分的概率为: P(ABC +AB ¯C)=34×23×12+34×13×12=38.(2)该项新技术的三项指标甲、乙、丙量化检测得分之和为随机变量X ,由题意知X =0,2,4,6,8,10, P(X =0)=P(A ¯B ¯C ¯)=14×13×12=124, P(X =2)=P(A ¯BC ¯)=14×23×12=112,P(X =4)=P(AB ¯C ¯)+P(A ¯B ¯C)=34×13×12+14×13×12=16,P(X =6)=P(ABC ¯)=+P(A ¯BC)=34×23×12+14×23×12=13,P(X =8)=38,P(X =10)=14EX =0×124+2×112+4×16+6×13+8×18+10×14=193.20. 解:(1)由题设知c =1,由点(1, e)在椭圆上,得1a 2+e 2b 2=1,∴ b =1,a =√2.∴ 椭圆的方程为x 22+y 2=1.(2)∵ 直线AF 1与直线BF 2平行,∴ 设AF 1与BF 2的方程分别为x +1=my ,x −1=my . 设A(x 1, y 1),B(x 2, y 2),y 1>0,y 2>0,∴ 由{x 122+y 12=1x 1+1=my 1,可得(m 2+2)y 12−2my 1−1=0. ∴ y 1=m+√2m 2+2m 2+2,∴ |AF 1|=√m 2+1×|0−y 1|=√2(m 2+1)+m√m 2+1m 2+2① 同理|BF 2|=√2(m 2+1)−m√m 2+1m 2+2②∵ 直线AF 1与直线BF 2平行,∴ PB PF 1=BF 2AF 1,即PF 1=AF1AF 1+BF 2×BF 1.由点B 在椭圆上知,BF 1+BF 2=2√2,∴ PF 1=AF 1AF 1+BF 2×(2√2−BF 2).同理PF 2=BF 2AF 1+BF 2×(2√2−AF 1).∴ |PF 1|+|PF 2|=AF 1AF 1+BF 2×(2√2−BF 2)+BF 2AF 1+BF 2×(2√2−AF 1)=2√2−2AF 1×BF 2AF 1+BF 2.由①②得,|AF 1|+|BF 2|=2√2(m 2+1)m 2+2,|AF 1||BF 2|=m 2+1m 2+2,∴ |PF 1|+|PF 2|=3√22. ∴ PF 1+PF 2是定值.21. (1)解:设切线方程为y =kx ,切点为(x 0, y 0),则{kx 0=e x 0k =e x 0∴ x 0=1,k =e ,∴ 函数y =f(x)的图象过原点的切线方程为y =ex ; (2)解:当x >0,m >0时,令f(x)=mx 2,化为m =e x x 2,令ℎ(x)=e x x 2(x >0),则ℎ′(x)=e x (x−2)x 3,则x ∈(0, 2)时,ℎ′(x)<0,ℎ(x)单调递减;x ∈(2, +∞)时,ℎ′(x)>0,ℎ(x)单调递增. ∴ 当x =2时,ℎ(x)取得极小值即最小值,ℎ(2)=e 24.∴ 当m ∈(0, e 24)时,曲线y =f (x) 与曲线y =mx 2(m >0)公共点的个数为0; 当m =e 24时,曲线y =f (x) 与曲线y =mx 2(m >0)公共点的个数为1; 当m >e 24时,曲线y =f (x) 与曲线y =mx 2(m >0)公共点个数为2.(3)证明:f(a)+f(b)2>f(b)−f(a)b−a=(b−a+2)+(b−a−2)e b−a2(b−a)e a ,令g(x)=x +2+(x −2)e x (x >0),则g′(x)=1+(x −1)e x . g ′′(x)=xe x >0,∴ g′(x)在(0, +∞)上单调递增,且g′(0)=0, ∴ g′(x)>0,∴ g(x)在(0, +∞)上单调递增,而g(0)=0,∴ 在(0, +∞)上,有g(x)>g(0)=0.∵ 当x>0时,g(x)=x+2+(x−2)⋅e x>0,且a<b,∴ (b−a+2)+(b−a−2)e b−a2(b−a)e a>0,即当a<b时,f(a)+f(b)2>f(b)−f(a)b−a.。
【2014东营市二模】山东省东营市2014届高三第二次模拟化学Word版含答案

化学试题7.化学与人类生产、生活、社会可持续发展密切相关。
下列有关说法错误..的是A.煤经气化、液化和干馏三个物理变化过程,可变为清洁能源B.在汽车排气管上加装“催化转化器”是为了减少有害气体的排放C.硬铝属于合金材料,瓷器属于硅酸盐制品D.食醋可去除水垢,NH4Cl溶液可去除铁锈8.右图是部分短周期元素化合价与原子序数的关系图,下列说法正确的是A.原子半径:Z>Y>XB.气态氢化物的还原性:W>RC.WX3和水反应形成的化合物是离子化合物D.含Z的盐溶液一定显示酸性9.下列说法正确的是A.CH3CH2CH2CH3的二氯取代产物只有5种结构B.油脂的种类很多,但它们水解后都有一相同产物C.乙烯、苯、纤维素均属于烃类化合物D.苯和乙烯都能使溴水层褪色,均与溴水发生加成反应10.下列说法正确的是A.SO2通入品红溶液,溶液褪色的原理与SO2通入溴水后褪色的原理相同B.浓硫酸具有强氧化性,稀硫酸不具有氧化性C.用浓FeCl3溶液和NaOH溶液混合制备Fe(OH)3胶体D.明矾和漂白粉常用于自来水的净化和杀菌消毒,但二者的作用原理不同11.设N A为阿伏加德罗常数的数值,下列说法中正确的是A.标准状况下,11.2L Cl2和H2混合气体原子数为2N AB.常温下,pH=l的H2SO4溶液中含有的H+的数目为0.2N AC.在含Al3+总数为N A的AlCl3溶液中,Cl-总数大于3N AD.标准状况下,2.24LCl2溶于水,转移的电子数目为0.1N A12.下列实验设计能够成功的是13.碘单质难溶于小却易溶于KI溶液。
碘水中加入KI溶液发生反应:I2(aq)+I-(aq) I3-(aq),该反应的平衡常数与温度的关系如右图,下列说法不正确的是A.上述正反应为放热反应B.上述体系中加入苯,平衡不移动C.可运用该反应原理除去硫粉中少量的碘单质D.实验室配制碘水时,为增大碘单质的溶解度可加入适量KI溶液28.(20分)I.(1)一定条件下Fe(OH)3与KClO在KOH溶液中反应可制得K2FeO4,该反应的化学方程式为;生成0.1molK2FeO4转移的电子的物质的量mol。
山东省2014届高三高考仿真模拟冲刺考试(二)数学理 Word版含答案.pdf

高考仿真模拟冲刺考试(二)数学(理)试题 满分150分 考试用时120分钟 参考公式: 如果事件A,B互斥,那么P(A+B)=P(A)+P(B); 如果事件A,B独立,那么P(AB)=P(A)·P(B). 如果事件A在一次试验中发生的概率是p,那么n次独立重复试验中事件A恰好发生k次的概 率: 第Ⅰ卷(选择题 共50分) 一、选择题:本大题共10小题.每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设全集,集合和,则 A.或 B. C. D. 2.下面是关于复数的四个命题:其中的真命题为( ) 的共轭复数为 的虚部为 A. . . . 3.“”是“直线与圆相交”的 A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分又不必要条件4.已知数列,若利用如图所示的程序框图计算该数列的第10项,则判断框内的条件是( ) A. B. C. D. 5.,,,且,和的夹角是 ( ) A. B.C. D. 6. A.20 B.24 C.16 D.12 7.函数f(x)的定义域为R,f(-1)=2,对任意,,则的解集为( ) A.(-1,1) B.(-1,+∞)C.(-∞,-l)D.(-∞,+∞) 8.若函数与函数在上的单调性相同,则的一个值为 A. B. C. D. 9.内的正弦曲线y=sinx与x轴围成的区域记为D,随机往圆O内投一个点A,则点A落在区域D内的概率是( ) A.B. C.D. 10.已知函数是定义在上的奇函数,且满足,当时,,则满足的的值是 A.B. C.D.第Ⅱ卷(非选择题 共100分) 二、填空题:本大题共5小题,每小题5分,共25分. 11.方程的实数解为_________________; 12.数列{an}的前n项和为Sn,若a1=1,,则=________. 13.已知抛物线的焦点与双曲线的一个焦点重合,则该双曲线的离心率为______________; 14.设二项式的展开式中常数项为,则________. 15.具有性质:的函数,我们称为满足“倒负”交换的函数,下列函数: ①②③中满足“倒负”变换的函数是 . 三、解答题:本大题共6小题,共75分,解答时应写出必要的文字说明、证明过程或演算步骤. 16.(本小题满分12分)在中,角的对边分别为,且. (Ⅰ)求的值; (Ⅱ)若,,求向量在方向上的投影.17.(本小题满分12分) 下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天. (Ⅰ)求此人到达当日空气重度污染的概率; (Ⅱ)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望; (Ⅲ)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)18.(本小题满分12分) 在如图1所示的等腰梯形中,,且,为中点.若沿将三角形折起,使平面平面,连结,得到如图2所示的几何体,在图2中解答以下问题: (Ⅰ)设为中点,求证:; (Ⅱ)求二面角的正弦值.19.(本小题满分12分) 设是数列()的前项和,已知,,设. (Ⅰ)证明:数列是等比数列,并求数列的通项公式; (Ⅱ)令,求数列的前项和.20.(本小题满分13分) 已知函数 (Ⅰ)求函数的单调区间; (Ⅱ)若不等式在区间上恒成立,求实数k的取值范围.21.(本小题满分14分) 已知椭圆:的左焦点为,其左、右顶点为、,椭圆与轴正半轴的交点为,的外接圆的圆心在直线上. (Ⅰ)求椭圆的方程; (Ⅱ)已知直线,是椭圆上的动点,,垂足为,是否存在点,使得为等腰三角形?若存在,求出点的坐标,若不存在,请说明理由.理科数学(二) 二、填空题:1. .3× 1. 1. 1.①③ 三、解答题: 17.解:设表示事件“此人于3月日到达该市”(=1,2,,13). 根据题意, ,且. (I)设B为事件“此人到达当日空气重度污染”,则, 所以. (II)由题意可知,X的所有可能取值为0,1,2,且 P(X=1)=P(A3∪A6∪A7∪A11)=P(A3)+P(A6)+P(A7)+P(A11)=, P(X=2)=P(A1∪A2∪A12∪A13)=P(A1)+P(A2)+P(A12)+P(A13)=, P(X=0)=1-P(X=1)-P(X=2)=, 所以X的分布列为: 故X的期望. (III)从3月5日开始连续三天的空气质量指数方差最大. 1.证明: (Ⅰ)取中点,连结,连结, 面平面, 所以平面,平面, 所以,因为为平行四边形,, 所以,为菱形,, ;因为平面,平面,且, 所以平面,又平面,所以。
数学_2014年山东省某校高考数学二模试卷(文科)(1)_(含答案)

2014年山东省某校高考数学二模试卷(文科)(1)一、选择题:(本大题共10小题,每小题5分,共50分.) 1. 在复平面内,复数−1+i i对应的点位于( )A 第一象限B 第二象限C 第三象限D 第四象限2. 定义集合A ∗B ={x|x ∈A, 且x ∉B},若A ={1, 3, 5, 7},B ={2, 3, 5},则A ∗B 的子集个数为( )A 1B 2C 3D 43. 等比数列{a n ]中,“a 1<a 3”是“a 4<a 6”的( )A 充分而不必要条件B 必要而不充分条件C 充要条件D 既不充分又不必要条件 4. 已知函数y =f(x)是奇函数,当x >0时,f(x)=lgx ,则f(f(1100))的值等于( )A 1lg2 B −1lg2C lg2D −lg25. 给出的图象中可能为函数f(x)=x 4+ax 3+cx 2+bx +d(a, b, c, d ∈R)的图象是( )A ①③B ①②C ③④D ②④6. 如图是一个组合几何体的三视图,则该几何体的体积是( )A27√32+64π B27√32+128π C 12+64π D 36+128π7. 如图,共顶点的椭圆①、②与双曲线③、④的离心率分别为e 1、e 2、e 3、e 4,其大小关系为( )A e 1<e 2<e 4<e 3B e 1<e 2<e 3<e 4C e 2<e 1<e 3<e 4D e 2<e 1<e 4<e 38. 已知函数f(x)的部分图象如图所示,则f(x)的解析式可能为( )A f(x)=2cos(x 2−π3) B f(x)=√2cos(4x +π4) C f(x)=2sin(x 2−π6) D f(x)=2sin(4x +π4)9. 已知z =2x +y ,x ,y 满足{y ≥xx +y ≤2x ≥m ,且z 的最大值是最小值的4倍,则m 的值是( )A 14B 15C 16D 1710. 若函数f(x)在给定区间M 上,存在正数t ,使得对于任意x ∈M ,有x +t ∈M ,且f(x +t)≥f(x),则称f(x)为M 上的t 级类增函数,则以下命题正确的是( )A 函数f(x)=4x +x 是(1,+∞)上的1级类增函数 B 函数f(x)=|log 2(x −1)|是(1, +∞)上的1级类增函数 C 若函数f(x)=sinx +ax 为[π2,+∞)上的π3级类增函数,则实数a 的最小值为2 D 若函数f(x)=x 2−3x 为[1, +∞)上的t 级类增函数,则实数t 的取值范围为[1, +∞)二、填空题:本大题共5小题,每小题5分,共25分. 11. 阅读程序框图,则输出的数据S 为________.12. 200辆汽车经过某一雷达地区,时速频率分布直方图如图所示,则时速不低于60km/ℎ的汽车数量为________辆.13. 已知抛物线y 2=2px(p >0)的准线与圆x 2+y 2−6x −7=0相切,则p 的值为________. 14. 设0<m <12,若1m+21−2m≥k 恒成立,则k 的最大值为________.15. 在四边形ABCD 中,AB →=DC →=(1, 1),1|BA →|BA →+1|BC →|BC →=√3|BD →|BD →,则四边形ABCD 的面积是________.三、解答题:本大题共6小题,共75分.解答应写出文字说明,演算步骤或证明过程.16. 已知f(x)=cos(2x+π3)+1−2cos2x.(1)求函数f(x)的单调递减区间;(2)在△ABC中,a,b,c分别是角A,B,C的对边,且a=1,b+c=2,f(A)=−12,求△ABC的面积.17. 袋子中放有大小和形状相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个,已知从袋子随机抽取1个小球,取到标号为2的小球的概率是12.(I)求n的值;(II)从袋子中不放回地随机抽取2个球,记第一次取出的小球标号为a,第二次取出的小球标号为b.①记“a+b=2”为事件A,求事件A的概率;②在区间[0, 2]内任取2个实数x,y,求事件“x2+y2>(a−b)2恒成立”的概率.18. 已知矩形ABCD所在的平面和梯形ABEF所在的平面互相垂直,AB // FE,G, H分别为AB, CF的中点,AB=2,AD=EF=1,∠AFB=π2.(1)求证:GH // 平面DAF;(2)AF⊥平面BFC;(3)求平面CBF将几何体EFABCD分成两个锥体F−ABCD与F−BCE的体积之比.19. 已知数列{a n}(n∈N⋅)的前n项和为S n,数列{S nn }是首项为0,公差为12的等差数列.(1)求数列{a n}的通项公式;(2)设b n=415⋅(−2)a n(n∈N⋅),对任意的正整数k,将集合{b2k−1, b2k, b2k+1}中的三个元素排成一个递增的等差数列,其公差为d x,求数列{d k}的通项公式.(3)对(2)中的{d k}的前n项和T n.20. 设椭圆C:x2a2+y2b2=1(a>b>0)的离心率e=12,短轴的一个端点与两焦点构成的三角形的面积为√3,O为坐标原点.(1)求椭圆C的方程;(2)过点O作两条互相垂直的射线,与椭圆C分别交于A,B两点,证明:点O到直线AB的距离为定值,并求弦AB长度的最小值.21. 已知函数f(x)=xlnx,g(x)=−x2+ax−3.(1)求函数f(x)的最小值;(2)对一切x∈(0, +∞),2f(x)≥g(x)恒成立,求实数a的取值范围;(3)证明:对一切x∈(0, +∞),都有lnx>1e x −2ex成立.2014年山东省某校高考数学二模试卷(文科)(1)答案1. A2. D3. D4. D5. A6. D7. A8. A9. A10. D11. 412. 7613. 214. 815. √316. 解:(1)f(x)=cos(2x+π3)+1−2cos2x=12cos2x−√32sin2x−cos2x=−12cos2x−√3 2sin2x=−sin(2x+π6).由要求函数f(x)的单调递减区间,即求y=sin(2x+π6)的递增区间,由−π2+2kπ≤2x+π6≤π2+2kπ,即kπ−π3≤x≤π6+kπ.即函数的单调递减区间为[kπ−π3, π6+kπ],k∈Z.(2)∵ f(A)=−12,∴ sin(2A+π6)=12,∵ 0<A<π,则π6<2A+π6<13π6,即2A+π6=5π6,解得A=π3,在△ABC中,a=1,b+c=2,A=π3,则由余弦定理得1=b2+c2−2bccosA,即1=(b+c)2−3bc=4−3bc,故bc=1,则△ABC的面积S=12bcsinA=12×1×√32=√34.17. 解:(1)由题意,根据从袋子随机抽取1个小球,取到标号为2的小球的概率是12,可得n1+1+n =12∴ n=2(2)①从袋子中不放回地随机抽取2个球,共有基本事件12个,其中“a+b=2”为事件A的基本事件有4个∴ P(A)=412=13②记“x2+y2>(a−b)2恒成立”为事件B,则事件B等价于“x2+y2>4恒成立,(x, y)可以看成平面中的点,则全部结果所构成的区域为Ω={(x, y)|0≤x≤2, 0≤y≤2, x, y∈R},而事件B构成的区域B={(x, y)|x2+y2>4, (x, y)∈Ω}∴ P(B)=1−π418. (1)证明:设DF的中点为M,连接AM,MH则MH // CD,MH=12CD,又矩形ABCD中,G是中点,∴ MH // AG,MH=AG,∴ 四边形MHGA为平行四边形,∴ AM // GH,又AM⊂平面DAF,GH⊄平面DAF,∴ GH // 平面DAF;(2)证明:∵ 平面ABCD⊥平面ABEF,CB⊥AB,平面ABCD∩平面ABEF=AB,∴ CB⊥平面ABEF,而AF⊂平面ABEF,∴ AF⊥CB.∵ AB为圆O的直径,∴ AF⊥BF.又BF∩CB=B,∴ AF⊥平面CBF;(3)解:过点F作FO⊥AB于O,∵ 平面ABCD⊥平面ABEF,∴ FO⊥平面ABCD,∴ V F−ABCD=2V F−ACD=2V D−AFB=23FO.∵ CB⊥平面ABEF,∴ V F−CBE=V C−FBE=13⋅12⋅EF⋅FO⋅CB=16FO,∴ V F−ABCD :V F−CBE=4:1.19. 解:(1)由已知得S nn =0+(n−1)⋅12=n2(n−1),∴ a n=n−1(2)由(1)可知,b n=415⋅(−2)n−1,∴ b2k−1=415(−2)2k−2=415⋅22k−2,b2k=415(−2)2k−1b2k=−415⋅22k−1,b2k+1=415(−2)2k=415⋅22k由2b2k−1=b k+b k+1及b2k<b2k−1<b2k+1得b2k,b2k−1,b2k+1依次成递增的等差数列,∴ d k=b2k+1−b2k−1=4k5,(3)由(2)得d k+1d k =4k+154k5=4,∴ 数列{d k}为等比数列,∴ T n=45−4n5 1−4=415(4n−1)20. (1)解:∵ 椭圆C:x2a2+y2b2=1(a>b>0)的离心率e=12,短轴的一个端点与两焦点构成的三角形的面积为√3,∴ {ca=121 2⋅2c⋅b=√3,解得a=2,b=√3,∴ 椭圆C的方程为x24+y23=1,(2)证明:设A(x1, y1),B(x2, y2),当直线AB的斜率不存在时,AB的方程为x=±2√217,∴ 原点O到直线AB的距离为2√217,当直线AB斜率存在时,设直线的方程为y=kx+m,联立{x24+y23=1y=kx+m,得(4k2+3)x2+8kmx+(4m2−12)=0,∴ x1+x2=−8km4k2+3,x1x2=4m2−124k2+3,∵ OA ⊥OB ,∴ x 1x 2+y 1y 2=0, ∴ x 1x 2+(kx 1+m)(kx 2+m)=0, ∴ (k 2+1)4m 2−123+4k 2−8k 2m 23+4k 2+m 2=0,整理,得7m 2=12(k 2+1), ∴ 原点O 到直线AB 的距离d =√1+k 2=2√217为定值, 综上所述O 到直线AB 的距离d =2√217为定值, ∵ OA ⊥OB ,d ⋅AB =OA ⋅OB ≤OA 2+OB 22=AB 22,∴ AB ≥2d =4√217, ∴ 当OA =OB 时,弦AB 长的最小值为4√217. 21. 解:(1)f(x)的定义域为(0, +∞),f(x)的导数f ′(x)=1+lnx . 令f ′(x)>0,解得x >1e ; 令f ′(x)<0,解得0<x <1e .从而f(x)在(0, 1e )单调递减,在(1e , +∞)单调递增. 所以,当x =1e 时,f(x)取得最小值−1e . (2)若2f(x)≥g(x),则a ≤2lnx +x +3x ,设ℎ(x)=2lnx +x +3x,则ℎ′(x)=2x +1−3x 2=x 2+2x−3x 2=(x+3)(x−1)x 2∵ x ∈(0, 1)时,ℎ′(x)<0,ℎ(x)单调递减, x ∈(1, +∞)时,ℎ′(x)>0,ℎ(x)单调递增, ∴ ℎ(x)min =ℎ(1)=4 故a ≤4即实数a 的取值范围为(−∞, 4] 证明: (3)若lnx >1e x−2ex则lnx ⋅x >xe x −2e ,由(1)得:lnx ⋅x ≥−1e ,当且仅当x =1e 时,取最小值; 设m(x)=xe x −2e ,则m′(x)=1−x e x,∵ x∈(0, 1)时,m′(x)>0,m(x)单调递增,x∈(1, +∞)时,m′(x)<0,m(x)单调递减,故当x=1时,m(x)取最大值−1e故对一切x∈(0, +∞),都有lnx>1e x −2ex成立.。
山东省东营市高三数学下学期第二次模拟试卷 理(含解析

2015年山东省东营市高考数学二模试卷(理科)一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.将正确答案填写在答题卷相应位置.1.已知i是虚数单位,则=()A. 1﹣2i B. 2﹣i C. 2+i D. 1+2i2.若集合A={x|},B={x|x2<2x},则A∩B=()A. {x|0<x<1} B. {x|0≤x<1} C. {x|0<x≤1} D. {x|0≤x≤1}3.已知α,β角的终边均在第一象限,则“α>β”是“sinα>sinβ”的()A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分也不必要条件4.已知函数f(x+1)是偶函数,当x∈(1,+∞)时,函数f(x)=sinx﹣x,设a=f(﹣),b=f(3),c=f(0),则a、b、c的大小关系为()A. b<a<c B. c<a<b C. b<c<a D. a<b<c5.一个几何体的三视图如图所示,该几何体外接球的表面积为()A. 9π B. C. 8π D. 7π6.已知{a n}是首项为1的等比数列,S n是{a n}的前n项和,且9S3=S6,则数列的前5项和为()A.或5 B.或5 C. D.7.执行如图所示的程序框图,若输入的x,t均为2,则输出的S=()A. 4 B. 5 C. 6 D. 78.从左至右依次站着甲、乙、丙3个人,从中随机抽取2个人进行位置调换,则经过两次这样的调换后,甲在乙左边的概率是()A. B. C. D.9.已知焦点在x轴上的椭圆方程为+=1,随着a的增大该椭圆的形状()A.越接近于圆 B.越扁C.先接近于圆后越扁 D.先越扁后接近于圆10.如图是某果园的平面图,实线部分DE、DF、EF游客观赏道路,其中曲线部分EF是以AB为直径的半圆上的一段弧,点O为圆心,△ABD是以AB为斜边的等腰直角三角形,其中AB=2千米,∠EOA=∠FOB=2x(0<x<),若游客在路线DE、DF上观赏所获得的“满意度”是路线长度的2倍,在路线EF上观赏所获得的“满意度”是路线的长度,假定该果园的“社会满意度”y是游客在所有路线上观赏所获得的“满意度”之和,则下面图象中能较准确的反映y与x的函数关系的是()A. B.C. D.二.填空题:本大题共5小题,每小题5分,共25分.11.已知9a=3,lgx=a 则x= .12.的展开式中的常数项为a,则直线y=ax与曲线y=x2围成图形的面积为.13.已知若f[f(x0)]=3,则x0= .14.设x,t满足约束条件,若目标函数z=4ax+by(a>0,b>0)的最大值为8,则a= 时,+取得最小值.15.在平面直角坐标系中,O为原点A(﹣1,0),B(0,),C(3,0),动点D满足||=1,则||的最大值是.三.解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤.16.在△ABC中,三个内角A,B,C的对边分别为a,b,c,其中c=2,且==.(Ⅰ)求a,b,C.(Ⅱ)如右图,设圆O过A,B,C三点,点P位于劣弧上,记∠PAB=θ,求△PAC面积最大值.17.现有两种投资方案,一年后投资盈亏的情况如下:(1)投资股市:投资结果获利40% 不赔不赚亏损20%概率(2)购买基金:投资结果获利20% 不赔不赚亏损10%概率 p q(Ⅰ)当时,求q的值;(Ⅱ)已知甲、乙两人分别选择了“投资股市”和“购买基金”进行投资,如果一年后他们中至少有一人获利的概率大于,求p的取值范围;(Ⅲ)丙要将家中闲置的10万元钱进行投资,决定在“投资股市”和“购买基金”这两种方案中选择一种,已知,,那么丙选择哪种投资方案,才能使得一年后投资收益的数学期望较大?给出结果并说明理由.18.已知正项数列{a n},其前n项和S n满足,且a2是a1和a7的等比中项.(Ⅰ)求数列的通项公式;(Ⅱ)符号[x]表示不超过实数x的最大整数,记,求.19.在三棱柱ABC﹣A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1=,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1.(Ⅰ)证明:BC⊥AB1;(Ⅱ)若OC=OA,求直线C1D与平面ABC所成角的正弦值.20.设A,B是椭圆W:+=1上不关于坐标轴对称的两个点,直线AB交x轴于点M(与点A,B不重合),O为坐标原点.(Ⅰ)如果点M是椭圆W的右焦点,线段MB的中点在y轴上,求直线AB的方程;(Ⅱ)设N为x轴上一点,且•=4,直线AN与椭圆W的另外一个交点为C,证明:点B与点C关x轴对称.21.已知函数.(Ⅰ)函数f(x)在区间(0,+∞)上是增函数还是减函数?证明你的结论;(Ⅱ)当x>0时,恒成立,求整数k的最大值;(Ⅲ)试证明:(1+1•2)•(1+2•3)•(1+3•4)•…•(1+n(n+1))>e2n﹣3.2015年山东省东营市高考数学二模试卷(理科)参考答案与试题解析一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.将正确答案填写在答题卷相应位置.1.已知i是虚数单位,则=()A. 1﹣2i B. 2﹣i C. 2+i D. 1+2i考点:复数代数形式的乘除运算.专题:数系的扩充和复数.分析:由题意,可对复数代数式分子与分母都乘以1+i,再由进行计算即可得到答案.解答:解:故选D点评:本题考查复数代数形式的乘除运算,解题的关键是分子分母都乘以分母的共轭,复数的四则运算是复数考查的重要内容,要熟练掌握.2.若集合A={x|},B={x|x2<2x},则A∩B=()A. {x|0<x<1} B. {x|0≤x<1} C. {x|0<x≤1} D. {x|0≤x≤1}考点:交集及其运算.专题:计算题.分析:分别求解分式不等式和一元二次不等式化简集合A与集合B,然后直接利用交集运算求解.解答:解:由,得,解得0≤x<1.所以{x|}={x|0≤x<1},又B={x|x2<2x}={x|0<x<2},所以A∩B={x|0≤x<1}∩{x|0<x<2}={x|0<x<1}.故选A.点评:本题考查了交集及其运算,考查了分式不等式及二次不等式的解法,是基础的运算题.3.已知α,β角的终边均在第一象限,则“α>β”是“sinα>sinβ”的()A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分也不必要条件考点:必要条件、充分条件与充要条件的判断;正弦函数的单调性.专题:计算题.分析:取特值验证可得α>β不是sinα>sinβ的充分条件;α>β不是sinα>sinβ的必要条件,所以α>β是sinα>sinβ的即不充分也不必要条件.解答:解:由题意得当α=390°,β=60°时有sinα<sinβ所以α>β不是sinα>sinβ的充分条件.当sinα=,sinβ=时因为α,β角的终边均在第一象限所以不妨取α=60°,β=390°所以α>β不是sinα>sinβ的必要条件.因此α>β是sinα>sinβ的即不充分也不必要条件.故选D.点评:本题以判断是否是充要条件作为考查工具考查三角函数的知识点,由于本题是选择题因此可以利用特值的方法判断.特值法是做选择题时一种快速灵活简便的方法.4.已知函数f(x+1)是偶函数,当x∈(1,+∞)时,函数f(x)=sinx﹣x,设a=f(﹣),b=f(3),c=f(0),则a、b、c的大小关系为()A. b<a<c B. c<a<b C. b<c<a D. a<b<c考点:函数单调性的性质;函数奇偶性的性质;不等式比较大小.专题:函数的性质及应用.分析:易得函数f(x)的图象关于直线x=1对称,且当x∈(1,+∞)时,函数f(x)=sinx ﹣x单调递减,由对称性可得a=f(),c=f(2),由单调性可得答案.解答:解:∵函数f(x+1)是偶函数,∴函数f(x)的图象关于直线x=1对称,又∵当x∈(1,+∞)时,函数f(x)=sinx﹣x,∴b=f(3),a=f(﹣)=f(),c=f(0)=f(2),又x∈(1,+∞)时,f′(x)=cosx﹣1≤0,∴当x∈(1,+∞)时,函数f(x)=sinx﹣x单调递减,∴b<a<c故选:A点评:本题考查函数的单调性和对称性,涉及导数法判函数的单调性,属基础题.5.一个几何体的三视图如图所示,该几何体外接球的表面积为()A. 9π B. C. 8π D. 7π考点:由三视图求面积、体积.专题:空间位置关系与距离.分析:由已知中的三视图可得,该几何体是一个以正视图为底面的四棱锥,其外接球,与以俯视图为底面,以2为高的正三棱柱的外接球相同,进而可得该几何体外接球的表面积.解答:解:由已知中的三视图可得,该几何体是一个以正视图为底面的四棱锥,其外接球,与以俯视图为底面,以2为高的正三棱柱的外接球相同,如图所示:由底面边长为2,可得底面外接圆的半径为:,由棱柱高为2,可得球心距为1,故外接球半径为:=,故外接球的表面积S=4πr2=,故选:B点评:本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.6.已知{a n}是首项为1的等比数列,S n是{a n}的前n项和,且9S3=S6,则数列的前5项和为()A.或5 B.或5 C. D.考点:等比数列的前n项和;等比数列的性质.专题:等差数列与等比数列.分析:利用等比数列求和公式代入9s3=s6求得q,进而根据等比数列求和公式求得数列的前5项和.解答:解:显然q≠1,所以,所以是首项为1,公比为的等比数列,前5项和.故选:C点评:本题主要考查等比数列前n项和公式及等比数列的性质,属于中等题.在进行等比数列运算时要注意约分,降低幂的次数,同时也要注意基本量法的应用.7.执行如图所示的程序框图,若输入的x,t均为2,则输出的S=()A. 4 B. 5 C. 6 D. 7考点:程序框图.专题:算法和程序框图.分析:根据条件,依次运行程序,即可得到结论.解答:解:若x=t=2,则第一次循环,1≤2成立,则M=,S=2+3=5,k=2,第二次循环,2≤2成立,则M=,S=2+5=7,k=3,此时3≤2不成立,输出S=7,故选:D.点评:本题主要考查程序框图的识别和判断,比较基础.8.从左至右依次站着甲、乙、丙3个人,从中随机抽取2个人进行位置调换,则经过两次这样的调换后,甲在乙左边的概率是()A. B. C. D.考点:古典概型及其概率计算公式.专题:概率与统计.分析:从左至右依次站着甲、乙、丙3个人,从中随机抽取2个人进行位置调换,则经过两次这样的调换,基本事件总数为n=9,经过两次这样的调换后,甲在乙左边包含的基本事件个数m=6,由此能求出经过两次这样的调换后,甲在乙左边的概率.解答:解:从左至右依次站着甲、乙、丙3个人,从中随机抽取2个人进行位置调换,则经过两次这样的调换,基本事件总数为n==9,左至右依次站着甲、乙、丙3个人,从中随机抽取2个人进行位置调换,第一次调换后,对后的位置关系有三种:甲丙乙、乙甲丙、丙乙甲,第二次调换后甲在乙左边对应的关系有:,,,丙乙甲,∴经过两次这样的调换后,甲在乙左边包含的基本事件个数m=6,∴经过两次这样的调换后,甲在乙左边的概率:P==,故选:C.点评:本题考查概率的求法,是中档题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.9.已知焦点在x轴上的椭圆方程为+=1,随着a的增大该椭圆的形状()A.越接近于圆 B.越扁C.先接近于圆后越扁 D.先越扁后接近于圆考点:椭圆的简单性质.专题:圆锥曲线的定义、性质与方程.分析:首先根据椭圆成立的条件求出a的取值范围,进一步利用函数的单调性求出椭圆中的短轴的变化规律,最后确定结果.解答:解:椭圆方程为焦点在x轴上的椭圆方程,所以:解得:由于a在不断的增大,所以对函数y=a2﹣1()为单调递增函数.即短轴中的b2在不断增大.即离心率不断减小.所以椭圆的形状越来越接近于圆.故选:A点评:本题考查的知识要点:椭圆成立的条件,椭圆中a、b、c的关系及函数的性质的应用.属于基础题型.10.如图是某果园的平面图,实线部分DE、DF、EF游客观赏道路,其中曲线部分EF是以AB为直径的半圆上的一段弧,点O为圆心,△ABD是以AB为斜边的等腰直角三角形,其中AB=2千米,∠EOA=∠FOB=2x(0<x<),若游客在路线DE、DF上观赏所获得的“满意度”是路线长度的2倍,在路线EF上观赏所获得的“满意度”是路线的长度,假定该果园的“社会满意度”y是游客在所有路线上观赏所获得的“满意度”之和,则下面图象中能较准确的反映y与x的函数关系的是()A. B.C. D.考点:函数的图象.专题:函数的性质及应用.分析:根据三角函数关系,求出DE,DF,和EF的长度,利用满意度的定义,建立函数关系,即可得到结论.解答:解:(Ⅰ)因为OA=AB=1,∠EOA=∠FOB=2x,连结OD,由OD=OE=OF=1,得∠FOD=∠EOD=,∴DE=DF==(sinx+cosx),∠EOF=π﹣4x,∠C0E=,则EF=2CE=2OEsin()=2cos2x,∵游客在路线DE、DF上观赏所获得的“满意度”是路线长度的2倍,在路线EF上观赏所获得的“满意度”是路线的长度,∴y=4(sinx+cosx)+2cos2x,∴对应的图象为A.故选:A.点评:本题主要考查函数图象的识别和判断,利用条件求出DE,EF,DF的长度是解决本题的关键,综合性较强,难度较大.二.填空题:本大题共5小题,每小题5分,共25分.11.已知9a=3,lgx=a 则x= .考点:对数的运算性质.专题:函数的性质及应用.分析:根据幂的运算性质求出a的值,再根据对数的运算性质求出x的值.解答:解:∵9a=3,∴32a=3,∴a=,∵lgx=a==lg,∴x=,故答案为:.点评:本题考查了幂和对数的运算性质,属于基础题.12.的展开式中的常数项为a,则直线y=ax与曲线y=x2围成图形的面积为.考点:定积分在求面积中的应用;二项式系数的性质.专题:导数的综合应用.分析:先根据二项式定理求出常数a,然后利用积分的几何意义求区域面积.解答:解:=,则(1+x3)3的展开式的通项公式为,当k=1时,展开式的常数项a=,即a=3,此时直线y=ax=3x,由得x2=3x,解得x=0或x=3,则由积分公式得=()|=,故答案为:;点评:本题主要考查利用积分求区域面积,利用二项式定理的知识求出常数项a是解决本题的关键.13.已知若f[f(x0)]=3,则x0= 或.考点:运用诱导公式化简求值.专题:计算题.分析:当 x0≤0时,由题意知 f(x0)=x02≥0,f[f(x0)]=﹣2sinx02,不可能等于 3.当π>x0>0时,由题意知 f(x0)=﹣2sinx0<0,f[f(x0)]=4sin2x0=3,解得sinx0=,可得 x0的值.解答:解:当x0≤0时,由题意知 f(x0)=x02≥0,f[f(x0)]=﹣2sinx02,不可能等于3.当π>x0>0时,由题意知 f(x0)=﹣2sinx0<0,f[f(x0)]=4sin2x0=3,∴sinx0=,∴x0=或,故答案为或.点评:本题考查应用诱导公式化简三角函数式,要特别注意符号的选取,这是解题的易错点.14.设x,t满足约束条件,若目标函数z=4ax+by(a>0,b>0)的最大值为8,则a= 时,+取得最小值.考点:简单线性规划.专题:不等式的解法及应用.分析:作出不等式组对应的平面区域,利用线性规划求出最优解,结合基本不等式求解即可.解答:解:作出不等式组对应的平面区域如图:由z=4ax+by得y=﹣x+,∵a>0,b>0,∴目标函数的斜率k=﹣<0,平移直线y=﹣x+,由图象知当直线y=﹣x+,经过点B时,直线的截距最大,此时z最大为8,由,解得,即B(1,4),此时4a+4b=8,即+=1,则+=+=++≥+2=+1=,当且仅当=,即b=2a时取得号,∵4a+4b=8,∴4a+8a=8,解得a==,故答案为:.点评:本题考查了简单的线性规划,考查了数形结合的解题思想方法,训练了基本不等式的应用,是中档题.15.在平面直角坐标系中,O为原点A(﹣1,0),B(0,),C(3,0),动点D满足||=1,则||的最大值是 4 .考点:平面向量数量积的运算.专题:平面向量及应用.分析:设D(x,y),由题意和两点之间的距离公式求出动点D的轨迹方程和轨迹,由向量的坐标运算求出的坐标,再判断出的几何意义,并求出最大值.解答:解:设D(x,y),因为C(3,0),动点D满足||=1,所以(x﹣3)2+y2=1,则动点D的轨迹是以(3,0)为圆心、以1为半径的圆,由A(﹣1,0),B(0,)得,=(x﹣1,y+),则的几何意义是点(1,﹣)到圆(x﹣3)2+y2=1上的点的距离,因为点(1,﹣)在圆外,所以的最大值是:+1=4,故答案为:4.点评:本题考查了向量的坐标运算,两点之间的距离公式,动点的轨迹方程,以及代数式子的几何意义,属于中档题.三.解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤.16.在△ABC中,三个内角A,B,C的对边分别为a,b,c,其中c=2,且==.(Ⅰ)求a,b,C.(Ⅱ)如右图,设圆O过A,B,C三点,点P位于劣弧上,记∠PAB=θ,求△PAC面积最大值.考点:正弦定理;余弦定理.专题:解三角形.分析:(Ⅰ)由正弦定理结合已知得sinAcosA=sinBcosB,即sin2A=sin2B,然后根据角的范围求得,即C=,△ABC是直角三角形,再由=,c=2,结合勾股定理求得a,b的值;(Ⅱ)设∠PAB=θ(),则,在Rt△PAB中,可得PA=AB•cosθ=2cosθ,代入三角形面积公式并整理得S△PAC=,再由θ的范围求得△PAC面积最大值.解答:解:(Ⅰ)由正弦定理得,整理为sinAcosA=sinBcosB,即sin2A=sin2B,又0<2A,2B<2π,∴2A=2B或2A+2B=π,即A=B或A+B=.∵,∴A=B舍去,故.由可知C=,∴△ABC是直角三角形;∵b=,c=2,又a2+b2=c2,可得a=1,b=;(Ⅱ)设∠PAB=θ(),则,在Rt△PAB中,PA=AB•cosθ=2cosθ,∴===.∵,∴,当,即时,S△PAC最大值等于.点评:本题考查正弦定理和余弦定理的应用,考查了两角和与差的正弦和余弦,关键是辅助角公式的应用,是中档题.17.现有两种投资方案,一年后投资盈亏的情况如下:(1)投资股市:投资结果获利40% 不赔不赚亏损20%概率(2)购买基金:投资结果获利20% 不赔不赚亏损10%概率 p q(Ⅰ)当时,求q的值;(Ⅱ)已知甲、乙两人分别选择了“投资股市”和“购买基金”进行投资,如果一年后他们中至少有一人获利的概率大于,求p的取值范围;(Ⅲ)丙要将家中闲置的10万元钱进行投资,决定在“投资股市”和“购买基金”这两种方案中选择一种,已知,,那么丙选择哪种投资方案,才能使得一年后投资收益的数学期望较大?给出结果并说明理由.考点:互斥事件的概率加法公式;相互独立事件的概率乘法公式.专题:概率与统计.分析:(Ⅰ)根据p++q=1解出即可;(Ⅱ)设出各个事件后得,根据,,从而求出P的范围;(Ⅲ)分别求出EX,EY在值,通过比较得到结论.解答:(Ⅰ)解:因为“购买基金”后,投资结果只有“获利”、“不赔不赚”、“亏损”三种,且三种投资结果相互独立,所以p++q=1.…(2分)又因为,所以q=.…(3分)(Ⅱ)解:记事件A为“甲投资股市且盈利”,事件B为“乙购买基金且盈利”,事件C为“一年后甲、乙两人中至少有一人投资获利”,…(4分)则,且A,B独立.由上表可知,,P(B)=p.所以…(5分)==.…(6分)因为,所以.…(7分)又因为,q≥0,所以.所以.…(8分)(Ⅲ)解:假设丙选择“投资股票”方案进行投资,且记X为丙投资股票的获利金额(单位:万元),所以随机变量X的分布列为:X 4 0 ﹣2P…(9分)则.…10 分假设丙选择“购买基金”方案进行投资,且记Y为丙购买基金的获利金额(单位:万元),所以随机变量Y的分布列为:Y 2 0 ﹣1P…(11分)则.…(12分)因为EX>EY,所以丙选择“投资股市”,才能使得一年后的投资收益的数学期望较大.…(13分)点评:本题考查了互斥事件的概率问题,考查了期望问题,是一道基础题.18.已知正项数列{a n},其前n项和S n满足,且a2是a1和a7的等比中项.(Ⅰ)求数列的通项公式;(Ⅱ)符号[x]表示不超过实数x的最大整数,记,求.考点:数列的求和;数列递推式.专题:点列、递归数列与数学归纳法.分析:(Ⅰ)在给出的数列递推式中,取n=n﹣1得另一递推式,两式作差后整理,得到(a n ﹣a n﹣1﹣4)(a n+a n﹣1)=0,结合已知进一步得到a n﹣a n﹣1=4,再由已知递推式求出首项,取符合a2是a1和a7的等比中项的值,然后代入等差数列的通项公式求得数列的通项公式;(Ⅱ)把数列的通项公式代入,依据[x]表示不超过实数x的最大整数得到b 1,b2,…,的值,总结规律后利用错位相减法求.解答:解:(Ⅰ)由①得②①﹣②得:8a n=(a n﹣a n﹣1)(a n+a n﹣1)+4a n﹣4a n﹣1,整理得:(a n﹣a n﹣1﹣4)(a n+a n﹣1)=0(n≥2,n∈N),∵{a n}为正项数列,∴a n+a n﹣1>0,则a n﹣a n﹣1=4(n≥2,n∈N),∴{a n}为公差为4的等差数列,由,得a1=3或a1=1,当a1=3时,a2=7,a7=27,不满足a2是a1和a7的等比中项.当a1=1时,a2=5,a7=25,满足a2是a1和a7的等比中项.∴a n=1+(n﹣1)×4=4n﹣3;(Ⅱ)由a n=4n﹣3,得,由符号[x]表示不超过实数x的最大整数知,当2m≤n<2m+1时,[log2n]=m,令=0+1+1+2+…+3+…+4+…+n﹣1+…+n∴S=1×21+2×22+3×23+4×24+(n﹣1)×2n﹣1+n ①2S=1×22+2×23+3×24+4×25+(n﹣1)×2n+2n ②①﹣②得:=,∴S=(n﹣2)2n+n+2,即=(n﹣2)2n+n+2.点评:本题考查数列递推式,考查了数列的和的求法,解答的关键是对b n的值的规律总结,是中档题.19.在三棱柱ABC﹣A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1=,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1.(Ⅰ)证明:BC⊥AB1;(Ⅱ)若OC=OA,求直线C1D与平面ABC所成角的正弦值.考点:用空间向量求直线与平面的夹角;直线与平面所成的角.专题:证明题;空间位置关系与距离.分析:(Ⅰ)要证明BC⊥AB1,可证明AB1垂直于BC所在的平面BCD,已知CO垂直于侧面ABB1A1,所以CO垂直于AB1,只要在矩形ABB1A1内证明BD垂直于AB1即可,可利用角的关系加以证明;(Ⅱ)分别以OD,OB1,OC所在的直线为x,y,z轴,以O为原点,建立空间直角坐标系,求出,平面ABC的一个法向量,利用向量的夹角公式,即可得出结论.解答:(I)证明:由题意,因为ABB1A1是矩形,D为AA1中点,AB=1,AA1=,AD=,所以在直角三角形ABB1中,tan∠AB1B=,在直角三角形ABD中,tan∠ABD=,所以∠AB1B=∠ABD,又∠BAB1+∠AB1B=90°,∠BAB1+∠ABD=90°,所以在直角三角形ABO中,故∠BOA=90°,即BD⊥AB1,又因为CO⊥侧面ABB1A1,AB1⊂侧面ABB1A1,所以CO⊥AB1所以,AB1⊥面BCD,因为BC⊂面BCD,所以BC⊥AB1.(Ⅱ)解:如图,分别以OD,OB1,OC所在的直线为x,y,z轴,以O为原点,建立空间直角坐标系,则A(0,﹣,0),B(﹣,0,0),C(0,0,),B1(0,,0),D (,0,0),又因为=2,所以所以=(﹣,,0),=(0,,),=(),设平面ABC的法向量为=(x,y,z),则根据可得=(1,,﹣)是平面ABC的一个法向量,设直线C1D与平面ABC所成角为α,则sinα=.点评:本题考查了直线与平面垂直的性质,考查线面角,考查向量方法的运用,属于中档题.20.设A,B是椭圆W:+=1上不关于坐标轴对称的两个点,直线AB交x轴于点M(与点A,B不重合),O为坐标原点.(Ⅰ)如果点M是椭圆W的右焦点,线段MB的中点在y轴上,求直线AB的方程;(Ⅱ)设N为x轴上一点,且•=4,直线AN与椭圆W的另外一个交点为C,证明:点B与点C关x轴对称.考点:直线与圆锥曲线的综合问题.专题:圆锥曲线中的最值与范围问题.分析:(Ⅰ)由已知条件推导出点B的坐标为(﹣1,±),由此能求出直线AB(即MB)的方程.(Ⅱ)设点B关于x轴的对称点为B1(在椭圆W上),要证点B与点C关于x轴对称,只要证点B1与点C重合,又因为直线AN与椭圆W的交点为C(与点A不重合),所以只要证明点A,N,B1三点共线.解答:(Ⅰ)解:椭圆W:+=1的右焦点为M(1,0),因为线段MB的中点在y轴上,所以点B的横坐标为﹣1,因为点B在椭圆W上,将x=﹣1代入椭圆W的方程,得点B的坐标为(﹣1,±).所以直线AB(即MB)的方程为3x﹣4y﹣3=0或3x+4y﹣3=0.(Ⅱ)证明:设点B关于x轴的对称点为B1(在椭圆W上),要证点B与点C关于x轴对称,只要证点B1与点C重合,.又因为直线AN与椭圆W的交点为C(与点A不重合),所以只要证明点A,N,B1三点共线.以下给出证明:由题意,设直线AB的方程为y=kx+m,(k≠0),A(x1,y1),B(x2,y2),则B1(x2,﹣y2).由,得(3+4k2)x2+8kmx+4m2﹣12=0,所以△=(8km)2﹣4(3+4k2)(4m2﹣12)>0,,.在y=kx+m中,令y=0,得点M的坐标为(﹣,0),由,得点N的坐标为N(﹣,0),设直线NA,NB1的斜率分别为k NA,,则==,因为===2k×()+(m+)(﹣)+8k==0.所以,所以点A,N,B1三点共线,即点B与点C关于x轴对称.点评:本题考查直线方程的求法,考查两点关于x轴对称的证明,解题时要认真审题,注意等价转化思想的合理运用.21.已知函数.(Ⅰ)函数f(x)在区间(0,+∞)上是增函数还是减函数?证明你的结论;(Ⅱ)当x>0时,恒成立,求整数k的最大值;(Ⅲ)试证明:(1+1•2)•(1+2•3)•(1+3•4)•…•(1+n(n+1))>e2n﹣3.考点:利用导数研究函数的单调性;导数在最大值、最小值问题中的应用;不等式的证明.专题:综合题;压轴题;导数的综合应用.分析:(Ⅰ)求导函数,确定导数的符号,即可得到结论;(Ⅱ)当x>0时,恒成立,即在(0,+∞)上恒成立,构造函数,求出函数的最小值,即可求整数k的最大值;(Ⅲ)由(Ⅱ)知:,从而令,即可证得结论.解答:(Ⅰ)解:由题,…(2分)故f(x)在区间(0,+∞)上是减函数;…(3分)(Ⅱ)解:当x>0时,恒成立,即在(0,+∞)上恒成立,取,则,…(5分)再取g(x)=x﹣1﹣ln(x+1),则,故g(x)在(0,+∞)上单调递增,而g(1)=﹣ln2<0,g(2)=1﹣ln3<0,g(3)=2﹣2ln2>0,…(7分)故g(x)=0在(0,+∞)上存在唯一实数根a∈(2,3),a﹣1﹣ln(a+1)=0,故x∈(0,a)时,g(x)<0;x∈(a,+∞)时,g(x)>0,故,故k max=3…(8分)(Ⅲ)证明:由(Ⅱ)知:,∴令,…(10分)又ln[(1+1•2)•(1+2•3)•(1+3•4)•…•(1+n(n+1))]=ln(1+1×2)+ln(1+2×3)+…+ln (1+n×(n+1))=即:(1+1•2)•(1+2•3)•(1+3•4)•…•[1+n(n+1)]>e2n﹣3…(14分)点评:本题考查导数知识的运用,考查函数的单调性,考查恒成立问题,考查不等式的证明,属于中档题.。
【2014东营市二模】山东省东营市2014届高三第二次模拟 地理

2014年东营市高三二模检测题本试卷分第I卷和第II卷两部分,共13页。
满分300分。
考试用时150分钟。
答题前务必用0.5毫米黑色签字笔将自己的姓名、座号、考生号、区县和科类填写在试卷和答题卡规定的位置。
考试结束后,将本试卷和答题卡一并交回。
第I卷选择题(必做,共140分)注意事项:1.第I卷共35小题,每小题4分,共140分。
在每小题给出的四个选项中,只有一项是最符合题目要求的。
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
不涂在答题卡上,只答在试卷上不得分。
目前,京津冀协同发展上升为国家重大战略。
读图完成1~2题。
1.保定在参与京津冀协同发展中,具有的突出优势条件是()A.科技力量雄厚B.距离北京、天津和石家庄较近,交通便捷C.矿产资源和水资源丰富D.市场广阔2.保定为承接京津产业转移需要做好哪些方面的工作()①建设产业转移基地②为大力发展重化工业腾出足够的空间③全面加强基础设施和生态环境建设④快速推动城市化,为产业转入储备足够的劳动力A.①②B.③④C.①③D.②④随着经济的快速发展,我国能源消费总量由2003年的1204.2百万吨油当量上升到2012年的2735.2百万吨油当量;能源消费构成也发生了变化,如下图中外圆为2012年、内圆表示2003年能源消费结构,读下结构图回答3~4题。
3.关于能源消费变化说法正确的是()A.煤炭消费量变化较小B.原油消费量明显增加C.水电消费比重下降D.核电和再生能源发展速度最慢4.下列关于能源消费变化影响表述合理的是()①减少灰霾天气②减少紫外线辐射③加剧全球温室效应 ④加剧能源供应紧缺程度A.①②B.②③C.③④D.①④读某经济开发区规划图,完成5~6题。
5.图中①②③功能用地预开发成商业用地、住宅用地、工业用地、,下列合理的是( )A. 工业用地、住宅用地、商业用地B. 商业用地、住宅用地、工业用地C. 商业用地、工业用地、住宅用地D. 住宅用地、商业金融业用地、工业用地6.该经济开发区可能位于( )A.西欧B.中国东南地区C.中国北方地区D.印度下图为10°S 附近某区域的遥感影像,其中深色部分为植被覆盖区,浅色部分为荒漠区;图中终年冰雪覆盖的山脉主峰海拔6768米,距海约120千米。
山东省东营市2024年数学(高考)部编版第二次模拟(评估卷)模拟试卷

山东省东营市2024年数学(高考)部编版第二次模拟(评估卷)模拟试卷一、单项选择题(本题包含8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题已知函数,,命题:,命题:,则是的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件第(2)题下列结论不正确的是()A.若事件与互斥,则B.若事件与相互独立,则C.如果分别是两个独立的随机变量,那么D.若随机变量的方差,则第(3)题已知,,,则()A.,B.,C.,D.,第(4)题设全集,集合,则()A.B.C.D.第(5)题下列说法不正确的是()A.若,则B.命题,,则:,C.回归直线方程为,则样本点的中心可以为D.在中,角的对边分别为则“”是“”的充要条件第(6)题已知函数,函数有4个零点,则实数的取值范围是()A.B.C.D.第(7)题若复数是实数,则()A.1B.3C.5D.7第(8)题不等式的解集为()A.或B.或C.D.或二、多项选择题(本题包含3小题,每小题6分,共18分。
在每小题给出的四个选项中,至少有两个选项正确。
全部选对的得6分,选对但不全的得3分,有选错或不答的得0分) (共3题)第(1)题已知正方体中,E,F,G,H,I分别是线段,,,AB,的中点,则()A.B.C.D.第(2)题函数,则下列说法正确的是()A.若,则B.函数在上为增函数C .函数的图象关于点对称D .函数的图象可以由的图象向左平移个单位长度得到第(3)题如图,在正四棱柱中,,,点在棱上,且,点在上底面运动,则下列结论正确的是()A.存在点使B.不存在点使平面平面C.若,,,四点共面,则的最小值为D.若,,,,五点共球面,则的最小值为三、填空(本题包含3个小题,每小题5分,共15分。
请按题目要求作答,并将答案填写在答题纸上对应位置) (共3题)第(1)题围棋在中国古时称"弈",是一种策略性二人棋类游戏.围棋棋盘由纵横各19条等距离、垂直交叉的平行线构成.则围棋棋盘上的矩形数量为_____________.(用数字作答)第(2)题已知,,则______.第(3)题已知椭圆的左、右焦点分别为,,点P在椭圆上,且,的延长线交椭圆于点Q,若椭圆的离心率,___________.四、解答题(本题包含5小题,共77分。
【2014潍坊市二模】山东省潍坊市2014届高三4月模拟考试理科数学Word版含答案

高三数学(理)本试卷共4页,分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟.第I 卷(选择题共50分)注意事项:1.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、准考证号、考试科目填写在规定的位置上。
2.第I 卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
3.第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置;如需改动,先划掉原来的答案,然后再写上新的答案,不得使用涂改液,胶带纸、修正带和其他笔。
4.不按以上要求作答以及将答案写在试题卷上的,答案无效。
一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.若复数z 满足 (1)i z i +⋅=,则z 的虚部为A . 2i -B . 12-C .2iD .122.设集合 {}{}|213,|lg(1)A x x B x y x =-≤==-,则 A B =A.(1,2)B.[1,2]C.(1,2]D.[1,2)3.下列结论正确的是A.若向量a ∥b ,则存在唯一的实数 λ使 a b λ=B.已知向量a ,b 为非零向量,则“a ,b 的夹角为钝角”的充要条件是“a ⋅b<0’’ c .“若 3πθ=,则 1cos 2θ=”的否命题为“若 3πθ≠,则 1cos 2θ≠” D .若命题 2:,10p x R x x ∃∈-+<,则 2:,10p x R x x ⌝∀∈-+>4.已知 21()sin(),'()42f x x x f x π=++为 ()f x 的导函数,则 '()y f x =的图象大致是5.已知 ,αβ表示平面,m ,n 表示直线, ,m βαβ⊥⊥,给出下列四个结论:① ,n n αβ∀⊂⊥;② ,n m n β∀⊂⊥;③,//n m n α∀⊂;④ ,n m n α∃⊂⊥, 则上述结论中正确的个数为A .1B .2C .3D .46.已知函数 2()f x x x =+,执行右边的程序框图,若输出的结果是3132,则 判断框中的条件应是A. 30n ≤ B . 31n ≤C . 32n ≤D . 33n ≤ 7.已知双曲线 2222:1(0,0)x y C a b a b-=>>的左、右焦点分别是1F 、2F 过 2F 垂直x 轴的直线与双曲线C 的两渐近线的交点分别是M 、N ,若1MF N ∆为正三角形,则该双曲线的离心率为A .B .C .D .2+8.某几何体的三视图如图所示,则该几何体外接球的表面积为A .43π B . 323π C . 4π D . 16π 9.在区间[-3,3]上任取两数x ,y ,使 210x y --<成立的概率为A . 827B . 727C . 16D . 42710.已知定义在R 上的函数 ()y f x =对任意的x 满足 (1)()f x f x +=-,当-l ≤x<l时, 3()f x x =.函数 log ,0,()1,0a x x g x x x⎧>⎪=⎨-<⎪⎩若函数在 [)6,-+∞上有6个零点,则实数a 的取值范围是A . 1(0,)(7,)7+∞ B. (]11,7,997⎡⎤⎢⎥⎣⎦C. (]1,1,1,99⎡⎫⎪⎢⎣⎭ D . [)11,7,997⎛⎤ ⎥⎝⎦第Ⅱ卷 (非选择题共1 00分)注意事项:将第Ⅱ卷答案用0. 5mm 的黑色签字笔答在答题卡的相应位置上,二、填空题:本大题共5小题,每小题5分,共25分.1 1.已知 12,e e 是夹角为 60的两个单位向量,若向量 1232a e e =+,则 a =________.12.现将如图所示的5个小正方形涂上红、黄两种颜色,其中3个涂红色,2个涂黄色,若恰有两个相邻的小正方形涂红色,则不同的涂法种数共有_________.(用数字作答)13.已知抛物线 2:2(0)C y px p =>上一点 (2,)(0)P m m >,若P 到焦点F 的距离为4,则以P 为圆心且与抛物线C 的准线相切的圆的标准方程为_________.14.曲线 sin y x =在点 (,),(,)2222A B ππππ-处的切线分别为 12,l l ,设 12,l l 及直线 x-2y+2=0围成的区域为D(包括边界).设点P(x ,y)是区域D 内任意一点,则x+2y 的最大值为________.15.如右图所示,位于东海某岛的雷达观测站A ,发现其北偏东 45,与观测站A 距离 B 处有一货船正匀速直线行驶,半小时后,又测得该货船位于观测站A 东偏北 (045)θθ<<的C 处,且 4cos 5θ=,已知A 、C 两处的距离为10海里,则该货船的船速为 海里/小时___________.三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.16.(本小题满分12分)已知函数 ()sin()(0,0)4f x A x A πωω=+>>的振幅为2,其图象的相邻两个对称中心之间的距离为 3π.(I)若 26(),03125f a a ππ+=<<,求sina ; (Ⅱ)将函数 ()y f x =的图象向右平移 6π个单位得到 ()y g x =的图象,若函数()y g x k =-是在 110,36π⎡⎤⎢⎥⎣⎦上有零点,求实数 k 的取值范围. 17.(本小题满分1 2分)直三棱柱 111ABC A B C -中,,AB BC BC ⊥=,112,BB AC =与1AC 交于一点P ,延长 1B B 到D ,使得BD=AB ,连接DC ,DA ,得到如图所示几何体.(I)若AB=1,求证:BP ∥平面ACD,(Ⅱ)若直线 1CA 与平面 11BCC B 所成的角为 30,求二面角 1D AC C --的余弦值.18.(本小题满分12分)某超市制定“五一”期间促销方案,当天一次性购物消费额满1000元的顾客可参加“摸球抽奖赢代金券”活动,规则如下:①每位参与抽奖的顾客从一个装有2个红球和4个白球的箱子中逐次随机摸球,一次只摸出一个球;②若摸出白球,将其放回箱中,并再次摸球;若摸出红球则不放回,工作人员往箱中补放一白球后,再次摸球;③如果连续两次摸出白球或两个红球全被摸出,则停止摸球.停止摸球后根据摸出的红球个数领取代金券,代金券数额Y 与摸出的红球个数x 满足如下关系:Y=144+72x(单位:元).(I)求一位参与抽奖顾客恰好摸球三次即停止摸球的概率;(Ⅱ)求随机变量Y 的分布列与期望.19.(本小题满分12分)已知等差数列 {}135468,42,69n a a a a a a a ++=++=;等比数列 {}1,2n b b =, 2123log ()6b b b =.(I)求数列 {}n a 和数列 {}n b 的通项公式;(Ⅱ)设 n n n c a b =-,求数列{}nc 的前n 项和 nT . 20.(本小题满分13分)如图,椭圆 2222:1(0)x y C a b a b+=>>的短轴长为2,点P 为上顶点,圆 222:O x y b +=将椭圆C 的长轴三等分,直线 4:(0)5l y mx m =-≠与椭圆C 交于A 、B 两点,PA 、PB 与圆O 交于M 、N 两点.(I)求椭圆C 的方程;(Ⅱ)求证△APB 为直角三角形;(Ⅲ)设直线MN 的斜率为n ,求证: m n为定值.21.(本小题满分14分)已知函数 2()ln (01)x f x a x x a a a =+->≠且. ( I)求函数 ()f x 的单调区间;(Ⅱ)a>l ,证明:当 (0,)x ∈+∞时, ()()f x f x >-; (Ⅲ)若对任意 1212,,x x x x ≠,且当 12()()f x f x =时,有 120x x +<,求a 的取值范围,。
数学_2014年山东省高考数学模拟试卷(二)(理科)_(含答案)

2014年山东省高考数学模拟试卷(二)(理科)一、选择题:本大题共10小题.每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设全集U =R ,集合A ={x|(12)x ≥2},B ={y|y =lg(x 2+1)},则(∁U A)∩B =( ) A {x|x ≤−1或x ≥0} B {(x, y)|x ≤−1, y ≥0} C {x|x ≥0} D {x|x >−1} 2. 下面是关于复数z =2−1+i 的四个命题:其中的真命题为( )p 1:|z|=2, p 2:z 2=2i ,p 3:z 的共轭复数为1+i , p 4:z 的虚部为−1.A p 2,p 3B p 1,p 2C p 2,p 4D p 3,p 43. “k =1”是“直线x −y +k =0与圆x 2+y 2=1相交”的( )A 充分不必要条件B 必要不充分条件C 充分必要条件D 即不充分也不必要条件4.已知数列{a n }中,a 1=1,a n+1=a n +n ,若利用如图所示的种序框图计算该数列的第10项,则判断框内的条件是( ) A n ≤8? B n ≤9? C n ≤10? D n ≤11?5. 已知向量a →、b →,其中|a →|=√2,|b →|=2,且(a →−b →)⊥a →,则向量a →和b →的夹角是( ) A π4B π6C 3π4D 5π66. 已知实数x 、y 满足约束条件{x ≥2y ≥2x +y ≤6,则z =2x +4y 的最大值为( )A 24B 20C 16D 127. 函数f(x)的定义域为R ,f(−1)=2,对任意x ∈R ,f′(x)>2,则f(x)>2x +4的解集为( )A (−1, 1)B (−1, +∞)C (−∞, −l)D (−∞, +∞)8. 若函数y =cos2x 与函数y =sin(x +φ)在区间[0,π2]上的单调性相同,则φ的一个值是( )A π6 B π4 C π3 D π29. 如图,圆O:x 2+y 2=π2内的正弦曲线y =sinx 与x 轴围成的区域记为M (图中阴影部分),随机往圆O 内投一个点A ,则点A 落在区域M 内的概率是( ) A 4π2 B 4π3 C 2π2 D 2π310. 已知函数f(x)是定义在R 上的奇函数,且满足f(x +2)=−f(x),当0≤x ≤1时,f(x)=12x ,则使f(x)=−12的x 的值是( )A 2n(n ∈Z)B 2n −1(n ∈Z)C 4n +1(n ∈Z)D 4n −1(n ∈Z)二、填空题:本大题共5小题,每小题5分,共25分. 11. 方程33x −1+13=3x−1的实数解为________.12. 数列{a n }的前n 项和为S n ,若a 1=1,a n+1=3S n (n ≥1),则a 6=________. 13. 已知抛物线 y 2=8x 的焦点与双曲线x 2a 2−y 2=1的一个焦点重合,则该双曲线的离心率为________.14. 设二项式(√x −√x 3)5的展开式中常数项为A ,则A =________.15. 具有性质:f(1x)=−f(x)的函数,我们称为满足“倒负”变换的函数,下列函数:①y =x −1x ;②y =x +1x ;③y =lnx(x >0)④y ={x,(0<x <1)0,(x =1)−1x (x >1)其中满足“倒负”变换的函数是________.三、解答题:本大题共6小题,共75分,解答时应写出必要的文字说明、证明过程或演算步骤.16. 在△ABC 中,2cos 2A−B 2cosB −sin(A −B)sinB +cos(A +C)=−35.(1)求cosA 的值;(2)若a =4√2,b =5,求BA →在BC →方向上的投影.17. 如图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染.某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.(1)求此人到达当日空气重度污染的概率;(2)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望;(3)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)18. 在如图1所示的等腰梯形ABCD中,AB // CD,CD=a,E为CD中点.若沿AE将三角形DAE折起,使平面DAE⊥平且AB=AD=BC=12面ABCE,连接DB,DC,得到如图2所示的几何体D−ABCE,在图2中解答以下问题:(1)设F为AB中点,求证:DF⊥AC;(2)求二面角A−BD−C的正弦值.19. 设S n是数列{a n}(n∈N∗)的前n项和,已知a1=4,a n+1=S n+3n,设b n=S n−3n.(1)证明:数列{b n}是等比数列,并求数列{b n}的通项公式;+2,求数列{c n}的前n项和T n.(2)令c n=2log2b n−nb n20. 已知函数f(x)=kx,g(x)=lnx.x(1)求函数g(x)=lnx的单调区间;x(2)若不等式f(x)≥g(x)在区间(0, +∞)上恒成立,求实数k的取值范围.21. 已知椭圆D:x2+y2=1(0<b<1)的左焦点为F,其左右顶点为A、C,椭圆与y轴正半b2轴的交点为B,△FBC的外接圆的圆心P(m, n)在直线x+y=0上.(1)求椭圆D的方程;(2)已知直线l:x=−√2,N是椭圆D上的动点,NM⊥l,垂足为M,是否存在点N,使得△FMN为等腰三角形?若存在,求出点N的坐标,若不存在,请说明理由.2014年山东省高考数学模拟试卷(二)(理科)答案1. C2. C3. A4. B5. A6. B7. B8. D9. B 10. D 11. log 34 12. 768 13.2√3314. −10 15. ①③④ 16. 由2cos 2A−B 2cosB −sin(A −B)sinB +cos(A +C)=−35可得cos(A −B)cosB −sin(A −B)sinB =−35, 即cos(A −B +B)=−35,即cosA =−35,由正弦定理,a sinA =b sinB ,所以sinB =bsinA a =√22, 由题意可知a >b ,即A >B ,所以B =π4,由余弦定理可知(4√2)2=52+c 2−2×5c ×(−35).解得c =1,c =−7(舍去).向量BA →在BC →方向上的投影:|BA →|cosB =ccosB =√22. 17. 解:(1)设“此人到达当日空气重度污染”为事件A . 因为此人随机选择某一天到达该城市且停留2天,因此他必须在3月1日至13日的某一天到达该城市,由图可以看出期间有2天属于重度污染, 故P(A)=213.(2)由题意可知X 所有可能取值为0,1,2.由图可以看出在3月1日至14日属于优良天气的共有7天.①当此人在3月4号,5号,8号,9号,10号这5天的某一天到达该城市时,停留的2天都不是优良天气, 故P(X =0)=513;②当此人在3月3号,6号,7号,11号,这4天的某一天到达该城市时,停留的2天中的1天不是优良天气1天是优良天气, 故P(X =1)=413;③当此人在3月1号,2号,12号,13号,这4天的某一天到达该城市时,停留的2天都是优良天气, 故P(X =2)=413.故X 的分布列为∴ E(X)=0×513+1×413+2×413=1213.(3)由图判断从3月5日开始连续三天的空气质量指数波动最大,因此方差最大.18. (1)证明:取AE 中点H ,连接HF ,连接EB因为△DAE 为等边三角形,所以DH ⊥AE因为平面DAE ⊥平面ABCE ,平面DAE ∩平面ABCE =AE 所以DH ⊥平面ABCE , 因为AC ⊂平面ABCE 所以AC ⊥DH…因为ABCE 为平行四边形,CE =BC =a 所以ABCE 为菱形,所以AC ⊥BE因为H 、F 分别为AE 、AB 中点,所以HF // BE 所以AC ⊥HF…因为HF ⊂平面DHF ,DH ⊂平面DHF ,且HF ∩DH =H 所以AC ⊥平面DHF ,又DF ⊂平面DHF 所以DF ⊥AC…(2)解:连接BH ,EB由题意得三角形ABE 为等边三角形,所以BH ⊥AE由(1)知DH ⊥底面ABCE 以H 为原点,分别以HA ,HB ,HD 所在直线为x ,y ,z 轴 建立空间直角坐标系,如图所示 则A(a2,0,0),B(0,√32a,0),D(0,0,√32a),C(−a,√32a,0) 所以BD →=(0,−√32a,√32a),BC→=(−a,0,0)设面DCB 的法向量为m →=(x,y,z),则{−ax =0−√32ay +√32az =0不妨设m →=(0,1,1)…设面DAB 的法向量n →=(x′,y′,z′),又DA →=(a2,0,−√32a) 则{x′−√3z′=0y′−z′=0,取n →=(1,√33,√33)…所以cos <m →,n →>=|m →|⋅|n →|˙=√105 所以二面角A −BD −C 的正弦值为√155… 19. (1)证明:∵ a n+1=S n +3n ,∴ S n+1−S n =S n +3n , 即S n+1=2S n +3n ,∴ S n+1−3n+1=2S n +3n −3n+1=2(S n −3n ), ∴ b n+1=2b n .又b 1=S 1−3=a 1−3=1,∴ {b n }是首项为1,公比为2的等比数列, 故数列{b n }的通项公式为b n =2n−1. (2)解:由(1)得:c n =2log 2b n −n b n+2=2n −n 2n−1,设M =1+22+322+423+...+n−12n−2+n2n−1,①则12M =12+222+323+424+...+n−12n−1+n2n ,② ①−②得:12M =1+12+122+123+124+...+12n−1−n 2n =2−12n−1−n2n ,∴ M =4−12n−2−n2n−1=4−2+n2n−1, ∴ T n =n(n +1)+2+n 2n−1−4.20. (本题满分12分) 解:(1)∵ g(x)=lnx x,x >0,故其定义域为(0, +∞),∴ g ′(x)=1−lnx x 2,令g′(x)>0,得0<x <e , 令g′(x)<0,得x >e , 故函数g(x)=lnx x的单调递增区间为(0, e),单调递减区间为(e, +∞).(2)∵ x >0,kx ≥lnx x,∴ k ≥lnx x 2,令ℎ(x)=lnx x 2,又ℎ′(x)=1−2lnxx3,令ℎ′(x)=0,解得x=√e,当x在(0, +∞)内变化时,ℎ′(x),ℎ(x)变化如下表由表知,当时函数ℎ(x)有最大值,且最大值为12e,所以k≥12e.21. 解:(1)由题意知,圆心P既在FC的垂直平分线上,也在BC的垂直平分线上,设F的坐标为(−c, 0)(c>0),则FC的垂直平分线方程为x=1−c2…①因为BC的中点坐标为(12,b2),BC的斜率为−b所以BC的垂直平分线的方程为y−b2=1b(x−12)…②联立①②解得:x=1−c2,y=b2−c2b即m=1−c2,n=b2−c2b因为P(m, n)在直线x+y=0上,所以1−c2+b2−c2b=0…即(1+b)(b−c)=0因为1+b>0,所以b=c再由b2=1−c2求得b2=c2=12所以椭圆D的方程为x2+2y2=1…(2)由(1)知:F(−√22,0),椭圆上的点横坐标满足−1≤x≤1设N(x, y),由题意得M(−√2,y),则|MN|=x+√2,|FN|=√22),|MF|=√12+y2①若|MN|=|FN|,即√(x+√2)2=√22)与x2+2y2=1联立,解得x=−√2<−1,显然不符合条件…②|MN|=|MF|,即√(x+√2)2=√12+y2与x2+2y2=1联立,解得:x=−√23,x=−√2<−1(显然不符合条件,舍去)所以满足条件的点N 的坐标为(−√23,±√146)… ③若|FN|=|MF|,即√22)=√12+y 2解得x =0,x =−√2<−1(显然不符合条件,舍去) 此时所以满足条件的点N 的坐标为(0,±√22)… 综上,存在点N(−√23,±√146)或(0,±√22),使得△FMN 为等腰三角形…。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
保密★启用前 试卷类型:A教学质量检测 理科数学注意事项:1.本试卷分为第Ⅰ卷和第Ⅱ卷两部分.第Ⅰ卷为选择题,第Ⅱ卷为非选择题,考试时间为120分钟, 满分150分.2.把选择题选出的答案标号涂在答题卡上.3.第Ⅱ卷用黑色签字笔在答题纸规定的位置作答,否则不予评分.第Ⅰ卷 选择题(共50分)一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.将正确答案填写在答题卷相应位置. 1.已知集合{}{}R x y y N x x x M x∈==≥=,2,2,则MN = ( )A .)(1,0 B .]1,0[ C .)1,0[ D .]1,0( 2.“实数1a =”是“复数(1)ai i +(,a R i ∈的 ( ) A .充分非必要条件 B .必要非充分条件 C .充要条件 D .既非充分条件又不必要条件 3.数列{}n a 的前n 项和为n S ,若1(1)n a n n =+,则6S 等于 ( )A .142B .45C .56D .674.已知某几何体的三视图(单位:cm )如图所示,则该几何体的体积是 ( ) A .48cm 3 B .98cm 3 C .88cm 3 D .78cm 35.执行如图所示的程序框图,输出的S 值为( )A .2B .2-C .4D .4-6.已知0ω>,函数()sin()4f x x πω=+在(,)2ππ上单调递减.则ω的取值范围是 ( )A .15[,]24B . 13[,]24C . 1(0,]2 D .(0,2]7.函数()f x 的部分图像如图所示,则()f x 的解析式可以是 ( )x D .3()()()22f x x x x ππ=--8小的两个编号分别为007,032,则样本中最大的编号应该为 ( ) A . 480 B . 481 C . 482 D . 4839. 偶函数)(x f 满足)1()1(+=-x f x f ,且在]1,0[∈x 时,2)(x x f =,则关于x 的方程xx f ⎪⎭⎫⎝⎛=101)(在]3,2[-上的根的个数是 ( ) A .3 B .4 C .5 D .610.已知1F ,2F 是双曲线22221(0,0)x y a b a b-=>>的左,右焦点,若双曲线左支上存在一点P 与点2F 关于直线bxy a=对称,则该双曲线的离心率为 ( ) A B C D .2第Ⅱ卷 非选择题(共100分)二.填空题:本大题共5小题,每小题5分,共25分.11.某公司一年购买某种货物400吨,每次都购买x 吨,运费为4万元/次,一年的总存储费用为x 4万元,要使一年的总运费与总存储费用之和最小,则=x ___ ____ 吨. 12.设8280128()x a a a x a x a x -=++++,若685-=+a a ,则实数a 的值为 .13.已知x ,y 满足约束条件⎪⎩⎪⎨⎧≥++≤≥+-0306k y x x y x ,且y x z 42+=的最小值为6,则常数k = .14.已知直角梯形ABCD ,AB AD ⊥,CD AD ⊥,222AB AD CD ===,沿AC 折叠成三棱锥,当三棱锥体积最大时,三棱锥外接球的体积为 .15.如图,在正方形ABCD 中,E 为AB 的中点,P 为以A 为圆心,AB 为半径的圆弧上的任意一点,设向量的最小值为则μλμλ++=, .三.解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤. 16.(本小题满分12分)在ABC ∆中,角C B A 、、所对的边为c b a 、、,且满足cos 2cos 22cos cos 66A B A A ππ⎛⎫⎛⎫-=-+⎪ ⎪⎝⎭⎝⎭(Ⅰ)求角B 的值; (Ⅱ)若3=b 且a b ≤,求c a 21-的取值范围.17.(本小题满分12分)在对某渔业产品的质量调研中,从甲,乙两地出产的该产品中各随机抽取10件,测量该产品中某种元素的含量(单位:毫克). 下表是测量数据的茎叶图:规定:当产品中的此种元素含量15≥毫克时为优质品.(Ⅰ)试用上述样本数据估计甲,乙两地该产品的优质品率(优质品件数/总件数);(Ⅱ)从乙地抽出的上述10件产品中,随机抽取3件,求抽到的3件产品中优质品数ξ的分布列及数学期望()E ξ.21006542098874286438210乙地甲地18.(本小题满分12分)如图,在底面是正方形的四棱锥P —ABCD 中,PA ⊥面ABCD ,BD 交AC 于点E ,F 是PC 中点,G 为AC 上一点. (Ⅰ)求证:BD ⊥FG ;(Ⅱ)确定点G 在线段AC 上的位置,使FG//平面PBD ,并说明理由. (Ⅲ)当二面角B —PC —D 的大小为32π时,求PC 与底面ABCD 所成角的正切值.19.(本小题满分12分)设数列{}n a 为等差数列,且145=a ,720a =,数列{}n b 的前n 项和为n S ,132(2,)n n S S n n N -=+≥∈.(Ⅰ)求数列{}n a ,{}n b 的通项公式; (Ⅱ)若,1,2,3,n n n c a b n =⋅=,n T 为数列{}n c 的前n 项和,n T m <对*n N ∈恒成立,求m 的最小值.20.(本小题满分13分)如图,已知椭圆134:22=+y x C ,直线l 的方程为4=x ,过右焦点F 的直线'l 与椭圆交于异于左顶点A 的Q P ,两点,直线AP ,AQ 交直线l 分别于点M ,N . (Ⅰ)当29=⋅AQ AP 时,求此时直线'l 的方程; (Ⅱ)试问M ,N 两点的纵坐标之积是否为定值?若是,求出该定值;若不是,请说明理由.21.(本小题满分14分)设函数ax xxx f -=ln )(. (Ⅰ)若函数)(x f 在),1(+∞上为减函数,求实数a 的最小值;(Ⅱ)若存在212,,x x e e ⎡⎤∈⎣⎦,使a x f x f +'≤)()(21成立,求实数a 的取值范围.教学质量检测 理科数学参考答案一.选择题:DADBD ACCCB 二.填空题:11.20; 12.21; 13.-3; 14.43π; 15.21三.解答题:16.(本小题满分12分)解:(Ⅰ)由已知⎪⎭⎫⎝⎛+⎪⎭⎫⎝⎛-=-A A B A 6cos 6cos 22cos 2cos ππ 得2222312sin 2sin 2cos sin 44B A A A ⎛⎫-=-⎪⎝⎭……………………………………………………………3分 化简得23sin =B ………………………………………………………………………………………………5分 故323ππ或=B .………………………………………………………………………………………………6分 (Ⅱ)因为b a ≤,所以3B π=,……………………………………………………………………………7分由正弦定理2sin sin sin a c bA C B====,得C c A a sin 2,sin 2==, 故A A A A C A c a cos 23sin 2332sin sin 2sin sin 221-=⎪⎭⎫ ⎝⎛--=-=-π6A π⎛⎫=- ⎪⎝⎭ ……9分因为b a ≤,所以323ππ<≤A ,266πππ<-≤A ,……………………………………………………10分 所以⎪⎪⎭⎫⎢⎣⎡∈⎪⎭⎫ ⎝⎛-=-3,236sin 321πA c a . ……………………………………………………12分17.(本小题满分12分)解:(Ⅰ)甲厂抽取的样品中优等品有7件,优等品率为710,……………………………………2分 乙厂抽取的样品中优等品有8件,优等品率为84105=.…………………………………………………4分 (Ⅱ)ξ的取值为1,2,3.………………………………………………………………………………6分12823101(1)15C C P C ξ⋅===,21823107(2)15C C P C ξ⋅===,157)3(3100238=⋅==C C C P ξ……………………9分所以ξ的分布列为…………………………………………………………………………………………………………………10分故的数学期望为17712123.1515155Eξ=⨯+⨯+⨯=() …………………………………………………12分 18.(本小题满分12分)解:方法一:(Ⅰ)∵PA ⊥面ABCD ,四边形ABCD 是正方形,其对角线BD ,AC 交于点E∴PA ⊥BD ,AC ⊥BD , ∴BD ⊥平面APC ………………………………………………………2分 ∵FG ⊂平面PAC ,∴BD ⊥FG ……………………………………………………………………3分 (Ⅱ)当G 为EC 中点,即AG=34AC 时,FG ∥平面PBD ,……………………………………………4分 连接PE ,由F 为PC 中点,G 为EC 中点,知FG ∥PE ,………………………………………………5分 而FG ⊄平面PBD ,PB ⊂平面PBD ,故FG ∥平面PBD .……………………………………………6分 (Ⅲ)作BH ⊥PC 于H ,连接DH ,∵PA ⊥面ABCD ,四边形ABCD 是正方形,∴PB=PD ,又∵BC=DC ,PC=PC ,∴△PCB ≌△PCD ,∴DH ⊥PC ,且DH=BH ,∴∠BHD 是二面角B -PC -D 的平面角.即,32π=∠BHD ………………………………………………………………………………………7分 ∵PA ⊥面ABCD ,∴∠PCA 就是PC 与底面ABCD 所成的角 …………………………………8分连结EH ,则PC EH BHE BD EH ⊥=∠⊥,3,π,tan BEBHE EH∴∠==而BE EC =,,33sin ,3==∠∴=∴EC EH PCA EH EC …………………………………………10分,22tan =∠∴PCA ……………………………………………………………………………………11分 ∴PC 与底面ABCD 所成角的正切值是22………………………………………………………12分 方法二:(Ⅰ)以A 为原点,AB ,AD ,PA 所在的直线分别为x ,y ,z 轴建立空间直角坐标系,设正方形ABCD 的边长为1,则A (0,0,0),B (1,0,0),C (1,1,0)D (0,1,0),P (0,0,a )(a>0),)20)(0,,(),2,21,21(),0,21,21(<<m m m G aF E …………1分 ∵11(1,1,0),(,,)222a BD FG m m =-=---,110022BD FG m m ⎛⎫⎛⎫⋅=--+-+= ⎪ ⎪⎝⎭⎝⎭…………2分 ∴BD ⊥FG ………………………………………………………………………………3分(Ⅱ)要使FG//平面PBD ,只需FG//EP ,而11,,22EP a ⎛⎫=-- ⎪⎝⎭,由F G E P λ=,可得:11222m a a λλ⎧-=-⎪⎪⎨⎪-=⎪⎩,解得12λ=-,34m =,…………………………………………………………………………………5分 33,,044G ⎛⎫∴ ⎪⎝⎭,34AG AC =,故当34AG AC =时,FG//平面PBD ………………………6分(Ⅲ)设平面PBC 的一个法向量为(),,u x y z =则⎪⎩⎪⎨⎧=⋅=⋅0,而)0,1,0(),,1,1(=-=BC a PC ⎩⎨⎧==-+∴0y az y x ,取1z =,得)1,0,(a =,……………………8分 同理可得平面PDC 的一个法向量)1,,0(a =,设,所成的角为θ,则,21|32cos||cos |==πθ ,21111,21||||22=+⋅+∴=a a v u 1=∴a …………………………………………10分∵PA ⊥面ABCD ,∴∠PCA 就是PC 与底面ABCD 所成的角,2221tan ===∠∴AC PA PCA ∴PC 与底面ABCD 所成角的正切值是22…………………………………………………………12分 19.(本小题满分12分)解:(Ⅰ) 数列{}n a 为等差数列,公差,易得21=a , 所以 13-=n a n ……………………………………………………………………………………1分 由132n n S S -=+,得32n n n S S b =-+,即22n n b S =-, 所以21222()b b b =-+,又123b =2分 由132n n S S -=+, 当3n ≥时,得1232n n S S --=+, 两式相减得:1123()n n n n S S S S ----=-,即13n n b b -=,所以)3≥…………………4分,所以{}n b 是以……………5分6分8分9分11分∵nT m<对n N+∈恒成立,∴2≥m∴m的最小值是2………………………………12分20.(本小题满分13分)解:(Ⅰ)①当直线PQ的斜率不存在时,由)0,1(F可知PQ方程为1=x代入椭圆134:22=+yxC得)23,1(),23,1(-QP又)0,2(-A),23,3(),23,3(-==∴274AP AQ⋅=不满足……………………………………2分②当直线PQ的斜率存在时,设PQ方程为)0)(1(≠-=kxky代入椭圆134:22=+yxC得01248)43(2222=-+-+kxkxk…………………………3分设),(),,(2211yxQyxP得2221222143124,438kkxxkkxx+-=+=+…………………………4分222121221221439)1()1)(1(kkxxxxkxxkyy+-=++--=--=2943274)(2)2)(2(222121212121=+=++++=+++=⋅kkyyxxxxyyxx26±=∴k故直线'l的方程;()126-±=xy………………………………………………6分(Ⅱ)AP 的方程为11(2)2y y x x =++与l 的方程:4x =联立 得:116(4,)2y M x + 同理得226(4,)2y N x +…………………………………………………8分12121212126636222()4M N y y y y y y x x x x x x ∴⋅=⋅=+++++ ①k 不存在时,3336()22912(11)4M N y y ⋅⋅-⋅==-+++………………………………………………9分 ②k 存在时,2222223243494121643434M N k k y y k k k k -+⋅==--++++………………………………………12分M ,N 两点的纵坐标之积为定值9- …………………………………………13分21.(本小题满分14分) 解:(Ⅰ)由已知得x >0,x ≠1.因f (x )在(1)+∞,上为减函数,故2ln 1()0(ln )x f x a x -'=-≤在(1)+∞,上恒成立. ………………1分所以当(1)x ∈+∞,时,max ()0f x '≤. 又()22ln 111()ln ln (ln )x f x a a x xx -'=-=-+-()2111ln 24a x =--+-,………………………………2分 故当11ln 2x =,即2x e =时,max 1()4f x a '=-. 所以10,4a -≤于是14a ≥,故a 的最小值为14. ……………………………………………4分(Ⅱ)命题“若存在212,[,],x x e e ∈使()12()f x f x a '+≤成立”等价于“当2[,]x e e ∈时,有()min max ()f x f x a '+≤”. …………………………………………………5分 由(Ⅰ),当2[,]x e e ∈时,max 1()4f x a '=-,∴()max 14f x a '+=.问题等价于:“当2[,]x e e ∈时,有min 1()4f x ≤”. ………………………………………………6分①当14a ≥时,由(1),()f x 在2[,]e e 上为减函数,则min ()f x =2221()24e f e ae =-≤,故21124a e -≥. ……………………………………………8分②当a <14时,由于'2111()()ln 24f x a x =--+-在2,e e ⎡⎤⎣⎦上的值域为1,4a a ⎡⎤--⎢⎥⎣⎦(ⅰ)0a -≥,即0a ≤,'()0f x ≥在2,e e ⎡⎤⎣⎦恒成立,故()f x 在2,e e ⎡⎤⎣⎦上为增函数,于是,min 1()()4f x f e e ae e ==-≥>,矛盾.……………………………………………10分 (ⅱ)0a -<,即104a <<,由'()f x 的单调性和值域知, 存在唯一20(,)x e e ∈,使'()0f x =,且满足:当0(,)x e x ∈时,'()0f x <,()f x 为减函数;当20(,)x x e ∈时,'()0f x >,()f x 为增函数; 所以,0min 0001()()ln 4x f x f x ax x ==-≤,20(,)x e e ∈…………………………………………12分 所以,2001111111ln 4ln 4244a x x e e ≥->->-=,与104a <<矛盾.………………………13分 综上,得21124a e≥-………………………………………………………………………………14分。
