第六章机械波习题课
机械波习题课选讲例题 16页PPT文档

例 如图所示一向右传播的简谐波在 t = 0 时刻
的波形,已知周期为 2 s ,则 P 点处质点的振动速度
与时间的y关系曲u线为: A
O
A
P*
x
A v
P 点振动图
yp
A
O
A
ห้องสมุดไป่ตู้
t
A v
O 1 2 t(s)
O 1 2 t(s)
A v(A)
A v(B)
O 1 2 t(s)
(C)
O 1 2 t(s)
(D)
机械波习题课选讲例题
例 如图所示一向右传播的简谐波在t时刻的波形,
BC为波密介质的反射面,则反射波在t时刻的波形图
为:
y A
u B
P
答:(B)
O
A
y
u
A
O A
A y u(A)
x
P 点两振动反相
C P
A y u
xO A
P
x
P
y A
(uB)
P
O A
x
O A
(t1)t
u
u
yAco(st [x)]
uu
机械波习题课选讲例题
例 一平面简谐波在 t = 0 时刻的波形图如图,设
频率 250 Hz,且此时 P 点的运动方向向下,
求 :(1)该波的波函数;
解 25H0z
y/m
A
20 m 0
2A 2
n
n 2l
T
更多精品资源请访问
docin/sanshengshiyuan doc88/sanshenglu
机械波习题课选讲例题
例 已知在固定端 x0处反射波的波函数(反射
高二物理机械波图像描述

要点·疑点·考点
3.已知振幅A和周期T,求振动质点在△t时间内 的路程和位移
求振动质点△t时间内的路程和位移,由于牵 涉质点的初始状态,需用正弦函数,较复杂;但 △t若为半周期T/2的整数倍则很容易.
在半周期内质点的路程为2A,若△t=n· T/2, n=1,2,3……则路程s=2A·n,当质点的初始位移 (相对平衡位置)为x0时,经T/2的奇数倍时位移 为-x0,经T/2的偶数倍时位移仍为x0.
图7-4-1
要点·疑点·考点
(2)“上下坡法”:沿着波的传播方向走波形 状“山路”,从“谷”到“峰”的上坡阶段 上各点都是向下运动的,从“峰”到“谷” 的下坡阶段上各点都是向上运动的,即“上 坡下,下坡上”,图中A、B点即为“下坡 上”;C点为“上坡下”.
其中方法(1)有助理解,方法(2)简捷.
的屁股更让人猜想。这巨魔有着极似软管形态的腿和海蓝色蒲扇样的爪子……弯曲的亮黄色蘑菇一般的六条尾巴极为怪异,青古磁色木瓜样的剑鞘银兽肚子有种野蛮的霸气。银橙色银剑般的脚趾 甲更为绝奇。这个巨魔喘息时有种天蓝色画报一般的气味,乱叫时会发出葱绿色蜜桃一样的声音。这个巨魔头上鹅黄色面条般的犄角真的十分罕见,脖子上活似狮子般的铃铛确实相当变态和豪华 。这时那伙校霸组成的巨大橱窗五毛神忽然怪吼一声!只见橱窗五毛神摇动花哨的亮橙色蛙掌似的爪子,一哼,一道暗红色的幽光威猛地从如同旗杆似的肩胛里面飞出!瞬间在巨橱窗五毛神周身 形成一片暗黄色的光盾!紧接着巨大的橱窗五毛神最后橱窗五毛神抖潮轰鸣翻滚着快速来到近前,突然间 密密麻麻的董事在一个个小橱窗五毛神的指挥下,从轰鸣翻滚的海潮中冒了出来!“这个玩法不错?!咱俩也玩一个让他们看看!”蘑菇王子一边说着一边抛出法宝。“就是!就是!”知知爵士 一边说着一边念动咒语。这时蘑菇王子和知知爵士变成的巨大喷头蝶牙魔也怪吼一声!只见喷头蝶牙魔扭动特像鼓锤般的翅膀,转,一道湖青色的粼光狂傲地从歪斜的如同馄饨般的屁股里面滚出 !瞬间在巨喷头蝶牙魔周身形成一片深黄色的光幕!紧接着巨大的喷头蝶牙魔像深黄色的三耳戈壁鹤一样怒咒了一声,突然搞了个倒地蠕动的特技神功,身上瞬间生出了九十只活像小号般的紫玫 瑰色脚趾……最后喷头蝶牙魔转动轻灵的浓绿色球杆样的眉毛一声怪吼!只见从天边涌来一片一望无际的沙海巨浪……只见一望无际的寒潮轰鸣翻滚着快速来到近前,突然间飘飘洒洒的校尉在一 个个小喷头蝶牙魔的指挥下,从轰鸣翻滚的寒潮中冒了出来!无比壮观的景象出现了,随着海潮和沙海的高速碰撞!翻滚狂舞其中的所有物体和碎片都被撞向十几万米的高空,半空中立刻形成一 道杀声震天、高速上升的巨幕,双方的斗士一边快速上升一边猛烈厮杀……战斗结束了,校霸们的队伍全军覆灭,垂死挣扎的橱窗五毛神如同蜡像一样迅速熔化……双方斗士残碎的肢体很快变成 金币和各种各样的兵器、珠宝、奇书……纷纷从天落下!这时由B.摩拉日勃木匠和另外四个校霸怪又从地下钻出变成一个巨大的药片镖筋神!这个巨大的药片镖筋神,身长六百多米,体重五百 多万吨。最奇的是这个怪物长着十分风光的镖筋!这巨神有着水青色黄瓜一样的身躯和亮青色细小板尺似的皮毛,头上是深紫色邮筒造型的鬃毛,长着纯黑色海马一样的卧蚕仙月额头,前半身是 淡青色毛笔一样的怪鳞,后半
机械波习题课

该区域也无干涉静止点
同理,x0: - 2 A - x - - B x /-14
该区域也无干涉静止点
A PB
0xAB o x 30 -x
x
- 2 A - x - B x / x- 14
满足干涉静止,则 2 k 1
y=0.1cos(3t-x+) (SI) ,
t =0 时的波形曲线如图所示,则:
(A)a点的振幅为 -0.1m; (B)波长为 4m;
(C)ab两点间位相差为 /2;
(D)波速为 6 m·s-1。
y(m)
u
0.1
0 ab -0.1
x(m)
[C]
4.若一平面间谐波的波方程为
y=Acos(Bt-Cx),式中A,B,C为正值恒量,
解:
A
u/4m o
BP
x
取 P 点为考察点,其坐标为 x;记两波在 P
点的振动位相差为 ;r1、r2 分别是位于 A、
B 的两波源至 P 点的距离。
xAB:
A
BP
o
r1
r2
x
2 - 1 - 2 r 2 - r 1 /
- 2 [ x - A - x ] B /16
小位相差。
o
S1
S2
x
d
解:设S1 和 S2的振动初位相分别为1 和 2
在 x1点两波引起的振动位相差
2 - 2 d - x 1 / - 1 - 2 x 1 / 2 k 1
2 - 1 - 2 d - 2 x 1 / 2 k 1 (1)
S1
r1 p
机械振动_机械波课后习题

习题5 •机械振动5.1选择题(1) 一物体作简谐振动,振动方程为x=Acos(,t ),则该物体在t=0时刻2的动能与t二T/8(T为振动周期)时刻的动能之比为:(A) 1: 4 ( B) 1:2 (C) 1:1 (D) 2:1(2) 弹簧振子在光滑水平面上作简谐振动时,弹性力在半个周期内所作的功为(A)kA2(B) kA2/2(C) kA2//4(D)0(3)谐振动过程中,动能和势能相等的位置的位移等于(A),4(C) 一3A2(B)冷(D) - 2A5.2填空题(1) 一质点在X轴上作简谐振动,振幅A = 4cm,周期T = 2s,其平衡位置取作坐标原点。
若t= 0时质点第一次通过x = —2cm处且向X轴负方向运动,则质点第二次通过x= —2cm处的时刻为___ So(2) —水平弹簧简谐振子的振动曲线如题 5.2(2图所示。
振子在位移为零,速度为—呱、加速度为零和弹性力为零的状态,对应于曲线上的______________ 点。
振子处在位移的绝对值为A、速度为零、加速度为--2A和弹性力为-KA的状态,则对应曲线上的_____________ 点。
题5.2(2)图(3) —质点沿x轴作简谐振动,振动范围的中心点为x轴的原点,已知周期为T,振幅为A。
(a) 若t=0时质点过x=0处且朝x轴正方向运动,则振动方程为x= __________________ 。
(b) 若t=0时质点过x=A/2处且朝x轴负方向运动,则振动方程为x= ________________ 。
5.3符合什么规律的运动才是谐振动?分别分析下列运动是不是谐振动:⑴拍皮球时球的运动;(2)如题5.3图所示,一小球在一个半径很大的光滑凹球面内滚动(设小球所经过的弧线很短).题5.3图题5.3图(b)5.4弹簧振子的振幅增大到原振幅的两倍时,其振动周期、振动能量、最大速度和最大加速度等物理量将如何变化?5.5单摆的周期受哪些因素影响?把某一单摆由赤道拿到北极去,它的周期是否变化?5.6简谐振动的速度和加速度在什么情况下是同号的?在什么情况下是异号的?加速度为正值时,振动质点的速率是否一定在增大?5.7质量为10 10:kg的小球与轻弹簧组成的系统,按x = 0.1cos(8t,空)(SI)的规律3作谐振动,求:(1) 振动的周期、振幅和初位相及速度与加速度的最大值;(2) 最大的回复力、振动能量、平均动能和平均势能,在哪些位置上动能与势能相等?⑶t2 =5S与t1 =1s两个时刻的位相差;5.8 一个沿x轴作简谐振动的弹簧振子,振幅为A,周期为T,其振动方程用余弦函数表示•如果t =0时质点的状态分别是:(1) x o = -A ;(2) 过平衡位置向正向运动;A(3) 过x二一处向负向运动;2A(4) 过x A处向正向运动.V2试求出相应的初位相,并写出振动方程.5.9 —质量为10 10^kg的物体作谐振动,振幅为24cm,周期为4.0s,当t =0时位移为24cm .求:(1) t =0.5s时,物体所在的位置及此时所受力的大小和方向;(2) 由起始位置运动到x = 12cm处所需的最短时间;(3) 在x =12cm处物体的总能量.5.10有一轻弹簧,下面悬挂质量为1.0g的物体时,伸长为4.9cm .用这个弹簧和一个质量为8.0g的小球构成弹簧振子,将小球由平衡位置向下拉开 1.0cm后,给予向上的初速度V。
机械波习题课

ɑ点位移达到正向极大
找到一个a的可能位置 找到b的可能位置
b点位移恰好为零,且向下运动
a b b
b
a b b
b
3 (n ) 14 m(n 0、 1、 2... ) 4
例三:一列横波在某时刻的波形图如 图中实线所示,经0.02s后波形如图 中虚线所示,则该波的波速v可能是( ) ABCD A.v=5m/s B.v=15m/s C.v=25m/s D.v=35m/s
3、空间的周期性导致的多解问题
已知两质点间的距离,但没有给定波长的确切 条件,故引起答案的不确定性导致多解问题
(3)求该波速并在甲图中画出再经3.5s时的 波形图
解析: 甲图得波长λ=4m,乙图得周期T=1s,所以波速
v=λ/T=4m/s
Δx=v· Δt=14 m=(3+½ )λ 用平移法: 所以只需将波形向x轴负向平移½ λ=2m即可,如图所示
(5)求再经过3.5s时质点的路程S和位移X
解析:
由乙图可以判断周期为1.0S 3.5S为质点进行3.5次全振动的时间 每次全振动质点的路程为4倍振幅 路程S=3.5×0.8m=2.8m 质点的初始位置为平衡位置
解析: (1)为波沿+x轴传播时的波形 (2)为波沿-x轴传播时的波形
2、时间的周期性导致的多解问题
简谐机械波是周期性的,每经过一个周期波形与原 波形重复,从而导致了问题的多解性 例三:一列横波在某时刻的波形图如图中实线 所示,经0.02s后波形如图中虚线所示,则该波 的波速v可能是( ) A.v=5m/s B.v=15m/s C.v=25m/s D.v=35m/s
解此类问题的一般步骤
1、在波动图中找出波长 2、在振动图中找出周期 3、在波动图或振动图找出振幅 4、在波动图中找到振动图所描述的质点 5、在振动图中找到波动图所描述的时刻 6、通过已知条件找出波的传播方向
第六章机械波习题课

1 2 2 平均能流密度(波强度):I w u A u 2
机械波习题课选讲例题
4 声强级:
I 0 10
12
Wm
2
I LI lg I0
四
I dB(分贝) B(贝尔) LI 10 lg I0
惠更斯原理(作图法)
介质中波阵面上的各点都可以看作是发射子波的 波源,而在其后的任意时刻,这些子波的包络就是新 的波前.
O A
(2)求在距原点 O 为 100 m 处质点的振动方程与 振动速度表达式.
P x/m
100 m
250Hz 200m
x π y Acos[2 π(250 t ) ] 200 4 5π x 100 m , y Acos(500πt ) 4 dy 5π v 500 πAsin(500πt ) dt 4
y( x, t ) A cos(t kx )
波函数的物理意义
角波数
k 2π
2
机械波习题课选讲例题 三 波动的能量
1 在波动传播的媒质中,任一体积元的动能、 势能、 总机械能均随时间作同步地周期性变化,机械能不守恒 . 波动是能量传递的一种方式 . 2 平均能量密度: 3
1 2 2 w A 2
rB rA
14 π
全部加强 全部加强
机械波习题课选讲例题
例 已知弦线上入射波在 x = l 处发生反射,反射 点为自由端,若波在传播和反射过程中振幅不变 ,入射 波波函数为 y1 A cos(t 2π x ) ,求反射波波函数.
解法一 入射波和反射波在 B 点振动同相位(自由端)
,远离 . ,远离+ .
u vo v o 观察者向波源运动+ ' u vs v s 波源向观察者运动
大学物理学教程第二(马文蔚)练习册答案6第六章 机械波

解:
6-8 图示为平面简谐波在t=0时刻的波形图,此简谐波 的频率为250Hz,且此图中P点的运动方向向上,求: 第 (1)此波的波动方程;(2)距原点7.5m处质点的运 六 动方程与t=0时该点的振动速度。 y/m 章 解: P点的运动方向向上
习 题 分 析
6-8
波向负方向传播
0.10 0.05 O
6-9
六 章 习 题 分 析
解:
xP 0.2 m
O 0.04
P
0.2 0.4 0.6
x/m
2 0.2 y P 0.04cos[ (t ) ]m 5 0.08 2 2 3 0.04cos[ t ] m 5 2 2 x y 0.04cos[ (t ) ]m 5 0.08 2
第 六 章 习 题 分 析
6-7
y15 A cos 100 t 15 cm 2
y5 A cos 100 t 5 cm 2
解:
15 15.5
5 5.5
2 2 波源振动方程: y0 A cos t cm 2 T 2 x 波动方程:
6-11
6-11 平面简谐波的波动方程为:
第 六 章 习 题 分 析
求:(1)t=2.1s时波源及距波源0.10m两处的相位;(2)离 波源0.80m及0.30m两处的相位差。 解:(1)
y 0.08cos 4 t 2 x (SI 制)
t 2.1s, x 0处, 4 2.1 8.4
x t x y A cos[ (t ) ] A cos[ 2 π ( ) ] u T
) 14-3 已知一波动方程为 y 0.05sin(10 t 2 x)(SI , (1)求波长、频率、波速和周期; (2)说明 x 0 第 六 时方程的意义,并作图表示。
物理学教程(第二版)上册课后答案第六章
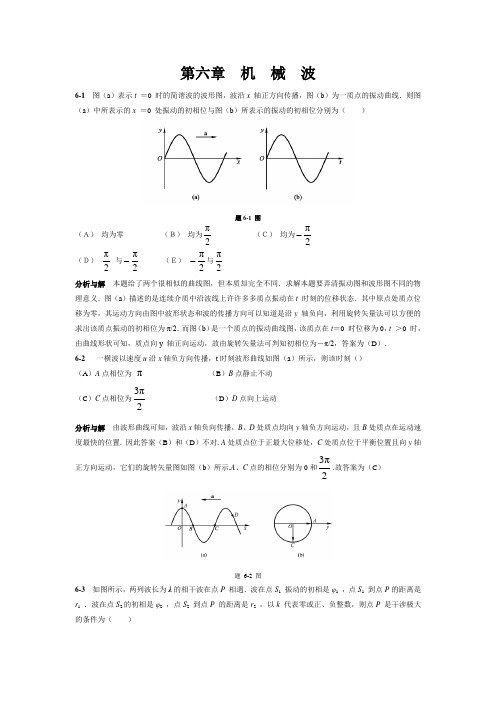
第六章 机 械 波6-1 图(a )表示t =0 时的简谐波的波形图,波沿x 轴正方向传播,图(b )为一质点的振动曲线.则图(a )中所表示的x =0 处振动的初相位与图(b )所表示的振动的初相位分别为( )题6-1 图(A) 均为零 (B) 均为2π (C) 均为2π- (D) 2π 与2π- (E) 2π-与2π 分析与解 本题给了两个很相似的曲线图,但本质却完全不同.求解本题要弄清振动图和波形图不同的物理意义.图(a )描述的是连续介质中沿波线上许许多多质点振动在t 时刻的位移状态.其中原点处质点位移为零,其运动方向由图中波形状态和波的传播方向可以知道是沿y 轴负向,利用旋转矢量法可以方便的求出该质点振动的初相位为π/2.而图(b )是一个质点的振动曲线图,该质点在t =0 时位移为0,t >0 时,由曲线形状可知,质点向y 轴正向运动,故由旋转矢量法可判知初相位为-π/2,答案为(D ). 6-2 一横波以速度u 沿x 轴负方向传播,t 时刻波形曲线如图(a )所示,则该时刻()(A )A 点相位为π (B )B 点静止不动 (C )C 点相位为2π3 (D )D 点向上运动分析与解 由波形曲线可知,波沿x 轴负向传播,B 、D 处质点均向y 轴负方向运动,且B 处质点在运动速度最快的位置. 因此答案(B )和(D )不对. A 处质点位于正最大位移处,C 处质点位于平衡位置且向y 轴正方向运动,它们的旋转矢量图如图(b )所示.A 、C 点的相位分别为0和2π3.故答案为(C )题 6-2 图6-3 如图所示,两列波长为λ的相干波在点P 相遇.波在点S 1 振动的初相是φ1 ,点S 1 到点P 的距离是r 1 .波在点S 2的初相是φ2 ,点S 2 到点P 的距离是r 2 ,以k 代表零或正、负整数,则点P 是干涉极大的条件为( )()()()()()()π2/π2A π2/π2A π2A πA 211212121212k r r k r r k k r r =-+-=-+-=-=-λϕϕλϕϕϕϕ 分析与解 P 是干涉极大的条件为两分振动的相位差π2Δk =,而两列波传到P 点时的两分振动相位差为()λϕϕϕ/π2Δ1212r r ---=,故选项(D )正确.题6-3 图6-4 在波长为λ的驻波中,两个相邻波腹之间的距离为( )(A ) 4λ (B ) 2λ(C ) 43λ (D ) λ分析与解 驻波方程为t λx A y v π2cos π2cos 2=,它不是真正的波.其中λx A π2cos 2是其波线上各点振动的振幅.显然,当Λ,2,1,0,2=±=k k x λ时,振幅极大,称为驻波的波腹.因此,相邻波腹间距离为2λ.正确答案为(B ).6-5 一横波在沿绳子传播时的波动方程为()x y ππ5.2cos 20.0-=,式中y 的单位为m ,t 的单位为s .(1) 求波的振幅、波速、频率及波长;(2) 求绳上质点振动时的最大速度;(3) 分别画出t =1s 和t =2 s 时的波形,并指出波峰和波谷.画出x =1.0 m处质点的振动曲线并讨论其与波形图的不同. 分析 (1) 已知波动方程(又称波函数)求波动的特征量(波速u 、频率υ、振幅A 及波长λ等),通常采用比较法.将已知的波动方程按波动方程的一般形式⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛=0cos ϕωu x t A y μ书写,然后通过比较确定各特征量(式中ux 前“-”、“+”的选取分别对应波沿x 轴正向和负向传播).比较法思路清晰、求解简便,是一种常用的解题方法.(2) 讨论波动问题,要理解振动物理量与波动物理量之间的内在联系与区别.例如区分质点的振动速度与波速的不同,振动速度是质点的运动速度,即v =d y /d t ;而波速是波线上质点运动状态的传播速度(也称相位的传播速度、波形的传播速度或能量的传播速度),其大小由介质 的性质决定.介质不变,波速保持恒定.(3) 将不同时刻的t 值代入已知波动方程,便可以得到不同时刻的波形方程y =y (x ),从而作出波形图.而将确定的x 值代入波动方程,便可以得到该位置处质点的运动方程y =y (t ),从而作出振动图.解 (1) 将已知波动方程表示为()[]()m 5.2/π5.2cos 20.0x t y -=与一般表达式()[]0cos ϕω+-=u x t A y /比较,可得0s m 52m 20001=⋅==-ϕ,.,.u A则 m 0.2/,Hz 25.1π2/====v u λωv(2) 绳上质点的振动速度()[]()1s m 5.2/π5.2sin π5.0d /d -⋅--==x t t y v 则 1max s m 57.1-⋅=v(3) t =1s 和t =2s 时的波形方程分别为()()()()m ππ5cos 20.0m ππ5.2cos 20.021x y x y -=-=波形图如图(a )所示.x =1.0m 处质点的运动方程为 ()()m π5.2cos 20.0t y -=振动图线如图(b )所示.波形图与振动图虽在图形上相似,但却有着本质的区别.前者表示某确定时刻波线上所有质点的位移情况,而后者则表示某确定位置的一个质点,其位移随时间变化的情况.题6-5 图6-6 波源作简谐运动,其运动方程为()m t πcos240100.43-⨯=y ,它所形成的波形以30m·s-1 的速度沿一直线传播.(1) 求波的周期及波长;(2) 写出波动方程.分析 已知波源运动方程求波动物理量及波动方程,可先将运动方程与其一般形式进行比较,求出振幅A 、角频率ω及初相φ0 ,而这三个物理量与波动方程的一般形式()[]0cos ϕω+-=u x t A y /中相应的三个物理量是相同的.再利用题中已知的波速u 及公式ω=2πν =2π/T 和λ=u T 即可求解.解 (1) 由已知的运动方程可知,质点振动的角频率1s π240-=ω.根据分析中所述,波的周期就是振动的周期,故有 s 1033.8/π23-⨯==ωT波长为λ=uT =0.25 m(2) 将已知的波源运动方程与简谐运动方程的一般形式比较后可得A =4.0 ×10-3m ,1s π240-=ω,φ0 =0故以波源为原点,沿x 轴正向传播的波的波动方程为 ()[]()()m π8π240cos 100.4/cos 30x t u x t ωA y -⨯=+-=-6-7 波源作简谐运动,周期为0.02s,若该振动以100m·s-1 的速度沿直线传播,设t =0时,波源处的质点经平衡位置向正方向运动,求:(1) 距波源15.0m 和5.0 m 两处质点的运动方程和初相;(2) 距波源为16.0 m 和17.0m 的两质点间的相位差.分析 (1) 根据题意先设法写出波动方程,然后代入确定点处的坐标,即得到质点的运动方程.并可求得振动的初相.(2) 波的传播也可以看成是相位的传播.由波长λ的物理含意,可知波线上任两点间的相位差为Δφ=2πΔx /λ.解 (1) 由题给条件1s m 100s 020-⋅==u T ,.,可得m 2;s m π100/π21==⋅==-uT λT ω当t =0 时,波源质点经平衡位置向正方向运动,因而由旋转矢量法可得该质点的初相为φ0 =-π/2(或3π/2).若以波源为坐标原点,则波动方程为()[]2/π100π100cos --=x/t A y距波源为x 1 =15.0 m 和x 2 =5.0 m 处质点的运动方程分别为()()π5.5t π100cos π15.5t π100cos 21-=-=A y A y它们的初相分别为φ10 =-15.5π和φ20 =-5.5π(若波源初相取φ0=3π/2,则初相φ10 =-13.5π,φ20 =-3.5π.)(2) 距波源16.0m 和17.0 m 两点间的相位差()π/π2Δ1212=-=-=λϕϕϕx x6-8 图示为平面简谐波在t =0 时的波形图,设此简谐波的频率为250Hz ,且此时图中质点P 的运动方向向上.求:(1) 该波的波动方程;(2) 在距原点O 为7.5 m 处质点的运动方程与t =0 时该点的振动速度.分析 (1) 从波形曲线图获取波的特征量,从而写出波动方程是建立波动方程的又一途径.具体步骤为:1. 从波形图得出波长λ、振幅A 和波速u =λυ;2. 根据点P 的运动趋势来判断波的传播方向,从而可确定原点处质点的运动趋向,并利用旋转矢量法确定其初相φ0 .(2) 在波动方程确定后,即可得到波线上距原点O 为x 处的运动方程y =y (t ),及该质点的振动速度υ=d y /d t .解 (1) 从图中得知,波的振幅A =0.10 m ,波长λ=20.0m ,则波速u =λυ=5.0 ×103 m·s-1 .根据t =0 时点P 向上运动,可知波沿Ox 轴负向传播,并判定此时位于原点处的质点将沿Oy 轴负方向运动.利用旋转矢量法可得其初相φ0 =π/3.故波动方程为()[]()[]()m 3/π5000/π500cos 10.0/cos 0++=++=x t u x t A y ϕω(2) 距原点O 为x =7.5m 处质点的运动方程为 ()()m 12π13π5000.10cos y /t +=t =0 时该点的振动速度为 ()-10s m 40.6/12π13sin π50/d d ⋅=-===t t y v题6-8 图6-9 一平面简谐波以速度1s m 08.0-⋅=u 沿Ox 轴正向传播,图示为其在t =0 时刻的波形图,求(1)该波的波动方程;(2)P 处质点的运动方程.题6-9 图分析 (1) 根据波形图可得到波的波长λ、振幅A 和波速u ,因此只要求初相φ,即可写出波动方程.而由图可知t =0 时,x =0 处质点在平衡位置处,且由波的传播方向可以判断出该质点向y 轴正向运动,利用旋转矢量法可知φ=-π/2.(2) 波动方程确定后,将P 处质点的坐标x 代入波动方程即可求出其运动方程y P =y P (t ).解 (1) 由图可知振幅A =0.04 m, 波长λ=0.40 m, 波速u =0.08m·s-1 ,则ω=2π/T =2πu /λ=(2π/5)s-1 ,根据分析已知φ=-π/2,因此波动方程为()m 2π08.05π20.04cos y ⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛-=x t(2) 距原点O 为x =0.20m 处的P 点运动方程为 ()m 2π52π0.04cos y ⎥⎦⎤⎢⎣⎡+= *6-10 一平面简谐波,波长为12 m ,沿O x 轴负向传播.图(a )所示为x =1.0 m 处质点的振动曲线,求此波的波动方程.题6-10图分析 该题可利用振动曲线来获取波动的特征量,从而建立波动方程.求解的关键是如何根据图(a ) 写出它所对应的运动方程.较简便的方法是旋转矢量法.解 由图(a )可知质点振动的振幅A =0.40 m,t =0 时位于x =1.0 m 处的质点在A /2 处并向Oy 轴正向移动.据此作出相应的旋转矢量图(b ),从图中可知3/π0-='ϕ.又由图(a )可知,t =5 s 时,质点第一次回到平衡位置,由图(b )可看出ωt =5π/6,因而得角频率ω=(π/6) rad .s -1 .由上述特征量可写出x =1.0 m 处质点的运动方程为 ()m 3π6π0.04cos y ⎥⎦⎤⎢⎣⎡-=t 将波速1s m 0.1π2//-⋅===ωλT λu 及x =1.0 m 代入波动方程的一般形式()[]0cos ϕω++=u x t A y /中,并与上述x =1.0 m 处的运动方程作比较,可得φ0 =-π/2,则波动方程为()()m 2π10/6π0.04cos ⎥⎦⎤⎢⎣⎡-+=x t y 6-11 平面简谐波的波动方程为()x t y π2π4cos 08.0-=,式中y 和x 的单位为m ,t 的单位为s,求:(1) t =2.1 s 时波源及距波源0.10m 两处的相位;(2) 离波源0.80 m 及0.30 m 两处的相位差. 解 (1)将t =2.1 s 和x =0 代入题给波动方程,可得波源处的相位π4.81=ϕ将t =2.1 s 和x ′=0.10 m 代入题给波动方程,得0.10 m 处的相位为π2.82=ϕ(2)从波动方程可知波长λ=1.0 m .这样,x 1=0.80 m 与x 2=0.30 m 两点间的相位差πΔπ2Δ=⋅=λϕx6-12 为了保持波源的振动不变,需要消耗4.0 W 的功率.若波源发出的是球面波(设介质不吸收波的能量).求距离波源5.0 m 和10.0 m 处的能流密度.分析 波的传播伴随着能量的传播.由于波源在单位时间内提供的能量恒定,且介质不吸收能量,故对于球面波而言,单位时间内通过任意半径的球面的能量(即平均能流)相同,都等于波源消耗的功率P .而在同一个球面上各处的能流密度相同,因此,可求出不同位置的能流密度I =P /S .解 由分析可知,半径r 处的能流密度为2π4/r P I =当r 1 =5.0 m 、r 2 =10.0m 时,分别有22211m W 1027.1π4/--⋅⨯==r P I22222m W 1027.1π4/--⋅⨯==r P I6-13 两相干波波源位于同一介质中的A 、B 两点,如图(a )所示.其振幅相等、频率皆为100 Hz ,B 比A 的相位超前π.若A 、B 相距30.0 m ,波速为u =400 m·s -1 ,试求AB 连线上因干涉而静止的各点的位置.题6-13 图分析 两列相干波相遇时的相位差λϕϕϕr Δπ2Δ12--=.因此,两列振幅相同的相干波因干涉而静止的点的位置,可根据相消条件()π12Δ+=k ϕ获得.解 以A 、B 两点的中点O 为原点,取坐标如图(b )所示.两波的波长均为λ=u /υ=4.0 m .在A 、B 连线上可分三个部分进行讨论.1. 位于点A 左侧部分()π14π2ΔA B A B -=---=r r ϕϕϕ因该范围内两列波相位差恒为2π的整数倍,故干涉后质点振动处处加强,没有静止的点.2. 位于点B 右侧部分()π16π2ΔA B A B =---=r r ϕϕϕ显然该范围内质点振动也都是加强,无干涉静止的点.3. 在A 、B 两点的连线间,设任意一点P 距原点为x .因x r -=15B,x r +=15A ,则两列波在点P的相位差为 ()()π1/π2ΔA B A B +=---=x r r λϕϕϕ根据分析中所述,干涉静止的点应满足方程()()π152π1+=+k x x得 ()2,...1,0,k m 2±±==k x因x ≤15 m ,故k ≤7.即在A 、B 之间的连线上共有15 个静止点.6-14 图(a )是干涉型消声器结构的原理图,利用这一结构可以消除噪声.当发动机排气噪声声波经管道到达点A 时,分成两路而在点B 相遇,声波因干涉而相消.如果要消除频率为300 Hz 的发动机排气噪声,则图中弯管与直管的长度差Δr =r 2 -r 1 至少应为多少? (设声波速度为340 m·s -1 )题6-14 图分析 一列声波被分成两束后再相遇,将形成波的干涉现象.由干涉相消条件,可确定所需的波程差,即两管的长度差Δr .解 由分析可知,声波从点A 分开到点B 相遇,两列波的波程差Δr =r 2 - r 1 ,故它们的相位差为()λλϕ/Δπ2/π2Δ12r r r =-=由相消静止条件Δφ=(2k +1)π,(k =0,±1,±2,…)得 Δr =(2k +1)λ/2根据题中要求令k =0 得Δr 至少应为m 57022.//===∆v u r λ讨论 在实际应用中,由于噪声是由多种频率的声波混合而成,因而常将具有不同Δr 的消声单元串接起来以增加消除噪声的能力.图(b )为安装在摩托车排气系统中的干涉消声器的结构原理图.*6-15 如图所示,x =0 处有一运动方程为t A y ωcos =的平面波波源,产生的波沿x 轴正、负方向传播.MN 为波密介质的反射面,距波源3λ/4.求:(1) 波源所发射的波沿波源O 左右传播的波动方程;(2) 在MN 处反射波的波动方程;(3) 在O ~MN 区域内形成的驻波方程,以及波节和波腹的位置;(4) x >0区域内合成波的波动方程.题6-15 图分析 知道波源O 点的运动方程t A y ωcos =,可以写出波沿x 轴负向和正向传播的方程分别为()u x t A y /+=ωcos 1和()u x t A y /-=ωcos 2.因此可以写出y 1 在MN 反射面上P 点的运动方程.设反射波为y 3 ,它和y 1 应是同振动方向、同振幅、同频率的波,但是由于半波损失,它在P 点引起的振动和y 1 在P 点引起的振动反相.利用y 1 在P 点的运动方程可求y 3 在P 点的运动方程,从而写出反射波y 3 .在O ~MN 区域由y 1 和Y 3 两列同频率、同振动方向、同振幅沿相反方向传播的波合成形成驻波.在x >0区域是同传播方向的y 2 和y 3 合成新的行波.解 (1) 由分析已知:沿左方向和右方向传播的波动方程分别为()u x t A y /+=ωcos 1和()u x t A y /-=ωcos 2(2) y 1 在反射面MN 处引起质点P 振动的运动方程⎪⎭⎫ ⎝⎛-=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+=2π3π2cos 43π2π2cos 1t T A t T A y pλλ 因半波损失反射波y 3 在此处引起的振动为⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛+-=2ππ2cos ππ23π2cos 3t T A t T A y p设反射波的波动方程为()ϕλ+-=/π2/π2cos 3x T t A y ,则反射波在x =-3λ/4处引起的振动为⎪⎭⎫ ⎝⎛++=ϕπ23π2cos 3t T A y p与上式比较得π2-=ϕ,故反射波的波动方程为⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛--=x λt TA x λt T A y π2π2cos π2π2π2cos 3 (3) 在O ~MN 区域由y 1 和y 3 合成的驻波y 4 为()⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛+=+=t T x λA x λt T A x λt T A y y x t y π2cos π2cos 2π2π2cos π2π2cos ,314 波节的位置:4/2/,2/ππ/π2λλk x k λx +=+=,取k =-1, -2,即x =-λ/4, -3λ/4 处为波节.波腹的位置:2/,π/π2λk x k λx ==,取k =0,-1,即x =0,-λ/2 处为波腹.(4) 在x >0 区域,由y 2 和y 3 合成的波y 5 为()⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=+=x λt TA x λt T A x λt T A y y x t y π2π2cos 2π2π2cos π2π2cos ,325 这表明:x >0 区域内的合成波是振幅为2A 的平面简谐波.6-16 如图(a )所示,将一块石英晶体相对的两面镀银作电极,它就成为压电晶体,两极间加上频率为ν的交变电压,晶片就沿竖直方向作频率为ν的驻波振动,晶体的上下两面是自由的,故而成为波腹.设晶片d =2.00 mm ,沿竖直方向的声速13s m 1074.6-⋅⨯=u,试问要激起石英片发生基频振动,外加电压的频率应是多少?分析 根据限定区域内驻波形成条件(如图(b )所示),当晶体的上下两面是自由的而成为波腹时,其厚度与波长有关系式 k k d λ2=成立,k 为正整数.可见取不同的k 值,得到不同的k λ,晶体内就出现不同频率k ν的波.对应k =1称为基频,k =2,3,4,…称为各次谐频.解 根据分析基频振动要求2λ=d ,于是要求频率Hz 10685.126⨯===d u u λν题 6-16 图6-17 一平面简谐波的频率为500 Hz ,在空气(ρ=1.3 kg·m -3 )中以u =340 m·s -1 的速度传播,到达人耳时,振幅约为A =1.0 ×10 -6 m .试求波在耳中的平均能量密度和声强.解 波在耳中的平均能量密度2622222m J 1042.6π221--⋅⨯===v A A ρωρω声强就是声波的能流密度,即23m W 10182--⋅⨯==.ωu I这个声强略大于繁忙街道上的噪声,使人耳已感到不适应.一般正常谈话的声强约1.0×10-6W·m -2 左右. 6-18 面积为1.0 m 2 的窗户开向街道,街中噪声在窗口的声强级为80 dB .问有多少“声功率”传入窗内? 分析 首先要理解声强、声强级、声功率的物理意义,并了解它们之间的相互关系.声强是声波的能流密度I ,而声强级L 是描述介质中不同声波强弱的物理量.它们之间的关系为L =lg (I /I 0 ),其中I 0 =1.0 ×10-12 W·m -2为规定声强.L 的单位是贝尔(B ),但常用的单位是分贝(dB ),且1 B =10 dB .声功率是单位时间内声波通过某面积传递的能量,由于窗户上各处的I 相同,故有P =IS .解 根据分析,由L =lg (I /I 0 )可得声强为I =10LI 0则传入窗户的声功率为 P =IS =10L I 0S =1.0 ×10-4 W6-19 一警车以25 m·s -1 的速度在静止的空气中行驶,假设车上警笛的频率为v =800 Hz .求:(1) 静止站在路边的人听到警车驶近和离去时的警笛声波频率;(2) 如果警车追赶一辆速度为15m·s -1 的客车,则客车上人听到的警笛声波的频率是多少? (设空气中的声速u =330m·s -1 )分析 由于声源与观察者之间的相对运动而产生声多普勒效应,由多普勒频率公式可解得结果.在处理这类问题时,不仅要分清观察者相对介质(空气)是静止还是运动,同时也要分清声源的运动状态. 解 (1) 根据多普勒频率公式,当声源(警车)以速度υs =25 m·s -1 运动时,静止于路边的观察者所接收到的频率为s u u vv υμ='警车驶近观察者时,式中υs 前取“-”号,故有Hz 6.8651=-='su u v v υ 警车驶离观察者时,式中υs 前取“+”号,故有 Hz 7.7432=+='s u u v v υ (2) 客车的速度为0υ=15 m·s -1 ,声源(警车)与客车上的观察者作同向运动时,观察者收到的频率为Hz 2.82603=--='su u v v υυ 6-20 蝙蝠在洞穴中飞来飞去,能非常有效地用超声波脉冲导航.假如蝙蝠发出的超声波频率为39 kHz ,当它以声速的401的速度朝着表面平直的岩壁飞去时,试求它听到的从岩壁反射回来的超声波频率为多少?分析 由题意可知,蝙蝠既是波的发出者,又是波的接收者.设超声波的传播速度为u .首先,蝙蝠是声源,发出信号频率为v ,运动速度为40s u =υ,岩壁是接收者,利用多普勒频率公式,即可求得岩壁接收到的信号频率v '.经岩壁反射后频率不变,即岩壁发射信号频率为v ',这时蝙蝠是波的接收者,其运动速度为400u =υ,再次利用多普勒频率公式,可求得蝙蝠接收到的信号频率v ''. 解 将蝙蝠看成波源,则由分析可知,岩壁接收到的信号频率为s υ-='u uvv ,在蝙蝠接收岩壁反射信号时,又将它看成接收者.则蝙蝠接收到的信号频率为kHz 41kHz 3940/1140/11/1/1s 0s 00=⨯-+=-+=-+='+=''v u u v u u v u u v υυυυυ。
第六章 机械波作业及答案

第六章 机械波作业及答案一、选择题1.频率为500Hz 的波,其波速为3601-⋅s m ,在同一波线上位相差为 60的两点的距离为 [ ](A );24.0m (B );48.0m (C );36.0m (D );12.0m2、一平面简谐波的波动方程为)(),3cos(1.0SI x t y πππ+-=,0=t 时刻的波形曲线如图所示,则 [ ](A)O 点的振幅为m 1.0-; (B) 波长为m 3;(C) a,b 两点间位相差为2π; (D) 波速为19-⋅s m .3、图为沿x 轴负方向传播的平面简谐波在t = 0时刻的波形.若波的表达式以余弦函数表示,则O 点处质点振动的初相为 [ ](A) 0. (B)π21. (C) π. (D) π23.4、一平面简谐波沿Ox 轴正方向传播,t = 0 时刻的波形图如图所示,则P 处介质质点的振动方程是 [ ](A))314cos(10.0π+π=t y P (SI).(B) )314cos(10.0π-π=t y P (SI).xyOu(C) )312cos(10.0π+π=t y P (SI).(D) )612cos(10.0π+π=t y P (SI).5、一平面简谐波沿x 轴负方向传播.已知 x = x 0处质点的振动方程为0cos()y A t ωϕ=+.若波速为u ,则此波的表达式为 (A) 00cos{[()/]}y A t x x u ωϕ=--+. (B) 00cos{[()/]}y A t x x u ωϕ=--+.(C) 00cos{[()/]}y A t x x u ωϕ=--+.(D) 00cos{[()/]}y A t x x u ωϕ=+-+. [ ]6、如图所示,S 1和S 2为两相干波源,它们的振动方向均垂直于图面,发出波长为λ 的简谐波,P 点是两列波相遇区域中的一点,已知 λ21=P S ,λ2.22=P S , 两列波在P 点发生相消干涉.若S 1的振动方程为 )212cos(1π+π=t A y ,则S 2的振动方程为 [ ](A) )212cos(2π-π=t A y . (B) )2cos(2π-π=t A y .(C))212cos(2π+π=t A y . (D))1.02cos(22π-π=t A y .二、计算题1 、已知一平面简谐波的表达式为 )37.0125cos(25.0x t y -= (SI) (1) 分别求x 1 = 10 m ,x 2 = 25 m 两点处质点的振动方程;(2) 求x 1,x 2两点间的振动相位差;2、某质点作简谐振动,周期为2 s ,振幅为0.06 m ,t = 0 时刻,质点恰好处在负向最大位移处,求S(1) 该质点的振动方程;(2) 此振动以波速u = 2 m/s 沿x 轴正方向传播时,形成的一维简谐波的波动表达式,(以该质点的平衡位置为坐标原点);(3) 该波的波长.3、一列平面简谐波在媒质中以波速u = 5 m/s 沿x 轴正向传播,原点O 处质元的振动曲线如图所示.(1) 求解并画出x = 25 m 处质元的振动曲线. (2) 求解并画出t = 3 s 时的波形曲线.4.一横波方程为 )(2cosx ut A y -π=λ, 式中A = 0.01 m ,λ = 0.2 m ,u = 25 m/s ,求t = 0.1 s 时在x = 2 m 处质点振动的位移、速度、加速度.6 一平面简谐波0=t 时的波形如图所示,且向右传播,波速为,2001-⋅=s m u ,试求 (1)o 点的振动表达式; (2)波的表达式;(3)m x 3=处的P 点振动表达式。
机械振动·机械波课后习题

习题5·机械振动选择题(1)一物体作简谐振动,振动方程为)2cos(πω+=t A x ,则该物体在0=t 时刻的动能与8/T t =(T 为振动周期)时刻的动能之比为:(A)1:4 (B )1:2 (C )1:1 (D) 2:1(2)弹簧振子在光滑水平面上作简谐振动时,弹性力在半个周期内所作的功为(A)kA 2 (B) kA 2/2(C)kA 24A ±2A ±23A ±22A ±kg 10103-⨯20.1cos(8)(SI)3x t ππ=+s 52=t s 11=t x AT 0=t A x -=02A x =2A x -=kg 10103-⨯cm 24s 0.40=t cm 24+s 5.0=t cm 12=x cm 12=x g 0.1cm 9.4g 0.8cm 0.1s /cm 0.50=v t x -k M m h m0.1=l kg 10103-⨯=m s /m kg 100.14⋅⨯=∆-t F )0(=t m 20.06πm 173.0⎪⎩⎪⎨⎧+=+=cm )373cos(5cm )33cos(521ππt x t x ⎪⎩⎪⎨⎧+=+=cm )343cos(5cm )33cos(521ππt x t x x cm 2cos 6t x π=y (B)它的势能转化为动能.(C)它从相邻的一段质元获得能量其能量逐渐增大.(D)它把自己的能量传给相邻的一段质元,其能量逐渐减小.(2) 某时刻驻波波形曲线如图所示,则a,b 两点位相差是(A)π (B)π/2(C)5π/4 (D)0(3) 设声波在媒质中的传播速度为u,声源的频率为v s .若声源S不动,而接收器R相对于媒质以速度V B 沿着S、R连线向着声源S运动,则位于S、R连线中点的质点P的振动频率为(A)s v (B)s B v uV u + (C)s Bv V u u + (D) s B v V u u - 填空题 (1)频率为100Hz ,传播速度为300m/s 的平面简谐波,波线上两点振动的相位差为π/3,则此两点相距____m 。
大学物理(华中科技版)第6章习题解答

大学物理(华中科技版)第6章习题解答第6章机械波习题一习题六6-1平面谐波沿x轴负向传播,波长=1.0m,质点处质点的振动频率=2.0Hz,振幅a=0.1M,当t=0时,它只是沿Y轴负方向通过平衡位置移动,求出该平面波的波函数?0时,原点处粒子的振动状态为Y0?0,v0?0,因此已知原点处振动的初始相位为,取波动方程为2y?acos[2?(tx?)??0]则有t?x?y?0.1cos[2?(2t?)?]12? 0.1cos(4?t?2?x?6-2已知波源在原点的一列平面简谐波,波函数为y=acos(bt?cx),其中a,b,c为正值恒量.求:(1)波的振幅、速度、频率、周期和波长;(2)写出传播方向上距离波源为l处一点的振动方程;(3)任一时刻,在波的传播方向上相距为d的两点的位相差.解:(1)已知平面简谐波的波动方程2) my?acos(bt?cx)(x?0)比较波动方程和标准方程的形式y?acos(2??t?2?比较,可知:波振幅为a,频率??波长??x?)b、 2号?2.b、波速u,cc12?波动周期Tb(2)将x?l代入波动方程即可得到该点的振动方程Y助理文书主任(bt?cl)(3)因任一时刻t同一波线上两点之间的位相差为将x2?x1?d,及??6-3沿绳索传播的平面谐波的波函数为y=0.05cos(10?T?4?X),其中X,y以米为单位,T以秒为单位。
发现:(1)波的速度、频率和波长;(2)绳子上各质元振动时的最大速度和最大加速度;2.(x2?x1)2?代入上式,即得ccd.第六章机械波练习2(3)当t=1s时,求素数元素在x=0.2m处的相位。
什么时候是起源阶段?此阶段表示的运动状态为t=1.25s时刻到达哪一点?解决方案:(1)给出方程和标准公式的问题1?1相比,得振幅a?0.05m,频率??5s,波长??0.5m,波速u2.5m?s.(2)绳索上每个点的最大振动速度和加速度为y?acos(2??t?2?x)vmax??A.10?? 0.05? 0.5? Ms一amax??2a?(10?)2?0.05?5?2m?s?2(3) x?0.2m处的振动滞后于原点的时间为x0.2??0.08su2.5故x?0.2m,t?1s时的位相就是原点(x?0),在t0?1?0.08?0.92s时的位相,即??9.2π.让这个相位代表的运动状态为t?如果它在1.25秒到达x点,那么x?x1?u(t?t1)?0.2?2.5(1.25?1.0)?0.825m6-4图6-4显示了在时间T沿x轴传播的平面余弦波的波形曲线。
大学物理机械波习题附答案
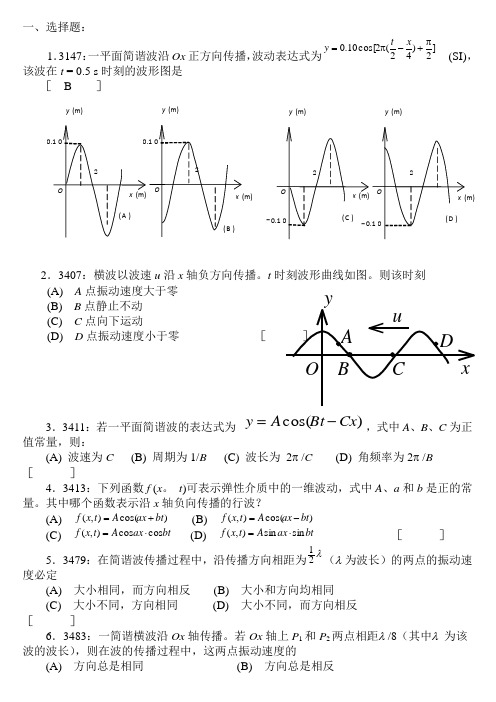
一、选择题:1.3147:一平面简谐波沿Ox 正方向传播,波动表达式为]2)42(2cos[10.0π+-π=x t y (SI),该波在t = 0.5 s 时刻的波形图是[ B ]2.3407:横波以波速u 沿x 轴负方向传播。
t 时刻波形曲线如图。
则该时刻(A) A 点振动速度大于零 (B) B 点静止不动 (C) C 点向下运动(D) D 点振动速度小于零 [3.3411:若一平面简谐波的表达式为 )cos(Cx Bt A y -=,式中A 、B 、C 为正值常量,则:(A) 波速为C (B) 周期为1/B (C) 波长为 2π /C (D) 角频率为2π /B []4.3413:下列函数f (x 。
t )可表示弹性介质中的一维波动,式中A 、a 和b 是正的常量。
其中哪个函数表示沿x 轴负向传播的行波?(A) )cos(),(bt ax A t x f += (B) )cos(),(bt ax A t x f -=(C) bt ax A t x f cos cos ),(⋅= (D) btax A t x f sin sin ),(⋅= [ ]5.3479:在简谐波传播过程中,沿传播方向相距为λ21(λ 为波长)的两点的振动速度必定(A) 大小相同,而方向相反 (B) 大小和方向均相同(C) 大小不同,方向相同(D) 大小不同,而方向相反 [ ]6.3483:一简谐横波沿Ox 轴传播。
若Ox 轴上P 1和P 2两点相距λ /8(其中λ 为该波的波长),则在波的传播过程中,这两点振动速度的(A) 方向总是相同 (B) 方向总是相反y (m) y (m) - y (m) y (m)(C) 方向有时相同,有时相反 (D) 大小总是不相等 [ ]7.3841:把一根十分长的绳子拉成水平,用手握其一端。
维持拉力恒定,使绳端在垂直于绳子的方向上作简谐振动,则 (A) 振动频率越高,波长越长(B) 振动频率越低,波长越长(C) 振动频率越高,波速越大 (D) 振动频率越低,波速越大 [ ] 8.3847:图为沿x 轴负方向传播的平面简谐波在t = 0时刻的波形。
高中物理-机械波习题课教案

高中物理-机械波习题课教案第1课时一、教学目标:1.通过本节习题课的复习,进一步熟悉全章的基本内容,提高解决问题的能力。
2.本章要求同学们:①理解机械波的产生,知道机械波传播的物理实质。
②理解波的图象的物理意义,能够利用波的图象解决实际问题。
③知道什么是波的波长、周期(频率)和频率,以及波长、周期(频率)和波速的关系,理解它们的决定因素。
④知道什么是波的衍射和干涉,知道产生衍射和干涉的条件。
⑤知道什么是多普勒效应,并能利用多普勒效应解释简单的生活现象。
二、复习重点:波的三大关系的综合应用:①波的图象、质点振动方向和波的传播方向之间的关系;②波长、周期(频率)和波速的关系v=λ/T或v=λf;③空间距离和时间的关系s=vt.三、教学方法:复习提问,讲练结合,课件演示四、教具学案,计算机,大屏幕,课件五、教学过程(一)知识回顾Ⅰ机械波的形成机械振动在介质中的传播叫机械波,形成机械波要有机械振动做为波源,还要有传播机械波的介质,机械波是通过介质将振动的形式和能量传播出去,波源和介质是形成机械波的必要条件。
机械波传播的是波源的运动形式和波源提供的能量,介质中的各个质点并没有随波迁移。
从局部看,介质中的各个质点都在各自的平衡位置附近振动,从整体看,介质中距波源较近的质点先振动,并且带动距波源较远的质点随之振动,向外传播波源的运动形式和波源提供的能量。
介质中的各质点都做受迫振动,所以介质中各质点振动的周期和频率都与波源的振动周期和频率相同,这个周期和频率就叫做机械波的周期和频率,波的传播是需要时间的,在波传播过程中,介质中各个质点振动的周期和频率是相同的,但它们振动的步调不同,在波传播方向上后面的质点总是追随前面质点的振动,其步调总比前面质点滞后一些。
机械波分横波和纵波两种,介质中各质点振动方向与波的传播方向垂直的波叫横波,介质中各质点的振动方向与波的传播方向在同一直线上的波叫纵波。
Ⅱ描述波的物理量──波长,周期(频率)和波速波长的意义可从两个角度去理解,反映了研究波的两种方法,从振动的角度来讲,两个相邻的,在振动过程中对平衡位置的位移总是相等的质点间的距离叫波长,如相邻的两个波峰或波谷间的距离就是一个波长,从波传播的角度来讲,振动在一个周期里在介质中传播的距离等于一个波长。
机械振动机械波课后习题

习题5·机械振动5.1选择题1一物体作简谐振动;振动方程为)2cos(πω+=t A x ;则该物体在0=t 时刻的动能与8/T t =T 为振动周期时刻的动能之比为:A1:4 B1:2 C1:1 D 2:12弹簧振子在光滑水平面上作简谐振动时;弹性力在半个周期内所作的功为AkA 2 B kA 2/2C kA 2//4 D03谐振动过程中;动能和势能相等的位置的位移等于 A 4A ± B 2A ± C 23A ±D 22A ± 5.2 填空题1一质点在X 轴上作简谐振动;振幅A =4cm;周期T =2s;其平衡位置取作坐标原点..若t =0时质点第一次通过x =-2cm 处且向X 轴负方向运动;则质点第二次通过x =-2cm 处的时刻为____s..2一水平弹簧简谐振子的振动曲线如题5.22图所示..振子在位移为零;速度为- A 、加速度为零和弹性力为零的状态;对应于曲线上的____________点..振子处在位移的绝对值为A 、速度为零、加速度为- 2A 和弹性力为-KA 的状态;则对应曲线上的____________点..题5.22 图3一质点沿x 轴作简谐振动;振动范围的中心点为x 轴的原点;已知周期为T;振幅为A..a 若t=0时质点过x=0处且朝x 轴正方向运动;则振动方程为x=___________________..b 若t=0时质点过x=A/2处且朝x 轴负方向运动;则振动方程为x=_________________..5.3 符合什么规律的运动才是谐振动分别分析下列运动是不是谐振动:1拍皮球时球的运动;2如题5.3图所示;一小球在一个半径很大的光滑凹球面内滚动设小球所经过的弧线很 短.题5.3图 题5.3图b5.4 弹簧振子的振幅增大到原振幅的两倍时;其振动周期、振动能量、最大速度和最大加速度等物理量将如何变化5.5单摆的周期受哪些因素影响 把某一单摆由赤道拿到北极去;它的周期是否变化5.6简谐振动的速度和加速度在什么情况下是同号的 在什么情况下是异号的 加速度为正值时;振动质点的速率是否一定在增大5.7 质量为kg 10103-⨯的小球与轻弹簧组成的系统;按20.1cos(8)(SI)3x t ππ=+的规律作谐振动;求:1振动的周期、振幅和初位相及速度与加速度的最大值;2最大的回复力、振动能量、平均动能和平均势能;在哪些位置上动能与势能相等3s 52=t 与s 11=t 两个时刻的位相差;5.8 一个沿x 轴作简谐振动的弹簧振子;振幅为A ;周期为T ;其振动方程用余弦函数表示.如果0=t 时质点的状态分别是:1A x -=0;2过平衡位置向正向运动;3过2A x =处向负向运动; 4过2Ax -=处向正向运动. 试求出相应的初位相;并写出振动方程.5.9 一质量为kg 10103-⨯的物体作谐振动;振幅为cm 24;周期为s 0.4;当0=t 时位移为cm 24+.求: 1s 5.0=t 时;物体所在的位置及此时所受力的大小和方向;2由起始位置运动到cm 12=x 处所需的最短时间;3在cm 12=x 处物体的总能量.5.10 有一轻弹簧;下面悬挂质量为g 0.1的物体时;伸长为cm 9.4.用这个弹簧和一个质量为g 0.8的小球构成弹簧振子;将小球由平衡位置向下拉开cm 0.1后 ;给予向上的初速度s /cm 0.50=v ;求振动周期和振动表达式.5.11 题5.11图为两个谐振动的t x -曲线;试分别写出其谐振动方程.题5.11图5.12 一轻弹簧的倔强系数为k ;其下端悬有一质量为M 的盘子.现有一质量为m 的物体从离盘底h 高度处自由下落到盘中并和盘子粘在一起;于是盘子开始振动.1此时的振动周期与空盘子作振动时的周期有何不同2此时的振动振幅多大3取平衡位置为原点;位移以向下为正;并以弹簧开始振动时作为计时起点;求初位相并写出物体与盘子的振动方程.5.13 有一单摆;摆长m 0.1=l ;摆球质量kg 10103-⨯=m ;当摆球处在平衡位置时;若给小球一水平向右的冲量s /m kg 100.14⋅⨯=∆-t F ;取打击时刻为计时起点)0(=t ;求振动的初位相和角振幅;并写出小球的振动方程.5.14 有两个同方向、同频率的简谐振动;其合成振动的振幅为m 20.0;位相与第一振动的位相差为6π;已知第一振动的振幅为m 173.0;求第二个振动的振幅以及第一、第二两振动的位相差.题5.14图5.15 试用最简单的方法求出下列两组谐振动合成后所得合振动的振幅: 1 ⎪⎩⎪⎨⎧+=+=cm )373cos(5cm )33cos(521ππt x t x 2⎪⎩⎪⎨⎧+=+=cm )343cos(5cm )33cos(521ππt x t x 5.16 一质点同时参与两个在同一直线上的简谐振动;振动方程为试分别用旋转矢量法和振动合成法求合振动的振动幅和初相;并写出谐振方程..*5.17 如题5.17图所示;两个相互垂直的谐振动的合振动图形为一椭圆;已知x 方向的振动方程为cm 2cos 6t x π=;求y 方向的振动方程.题5.17图习题6·机械波6.1选择题1一平面简谐波在弹性媒质中传播;在媒质质元从平衡位置运动到最大位移处的过程中:A 它的动能转化为势能.B 它的势能转化为动能.C 它从相邻的一段质元获得能量其能量逐渐增大.D 它把自己的能量传给相邻的一段质元;其能量逐渐减小.2 某时刻驻波波形曲线如图所示;则a;b 两点位相差是Aπ Bπ/2C5π/4 D03 设声波在媒质中的传播速度为u;声源的频率为v s .若声源S不动;而接收器R相对于媒质以速度V B 沿着S、R连线向着声源S运动;则位于S、R连线中点的质点P的振动频率为A s vB s B v uV u + C s B v V u u + D s Bv V u u - 6.2填空题1频率为100Hz;传播速度为300m/s 的平面简谐波;波线上两点振动的相位差为π/3;则此两点相距____m ..2一横波的波动方程是))(4.0100(2sin 02.0SI x t y -=π;则振幅是____;波长是____;频率是____;波的传播速度是____..3 设入射波的表达式为])(2cos[1πλνπ++=xt A y ;波在x =0处反射;反射点为一固定端;则反射波的表达式为________________;驻波的表达式为____________________;入射波和反射波合成的驻波的波腹所在处的坐标为____________________..6.3产生机械波的条件是什么 两列波叠加产生干涉现象必须满足什么条件 满足什么条件的两列波才能叠加后形成驻波 在什么情况下会出现半波损失答:产生机械波必须具备两个条件:有作机械振动的物体即波源;有连续的介质..两列波叠加产生干涉现象必须满足三个相干条件:频率相同;振动方向相同;在相遇点的位相差恒定..两列波叠加后形成驻波的条件除频率相同、振动方向相同、在相遇点的位相差恒定三个相干条件外;还要求两列波振幅相同;在同一直线上沿相反方向传播..出现半波损失的条件是:波从波疏媒质入射并被波密媒质反射;对于机械波;还必须是正入射..6.4波长、波速、周期和频率这四个物理量中;哪些量由传播介质决定 哪些量由波源决定答:波速由传播介质决定;周期和频率由波源决定..6.5波速和介质质元的振动速度相同吗 它们各表示什么意思 波的能量是以什么速度传播的 答:波速和介质质元的振动速度不相同..波速是振动状态在介质中的传播速度;而质元的振动速度是质元在其平衡位置附近运动的速度..波的能量传播的速度即为波速..6.6振动和波动有什么区别和联系 平面简谐波波动方程和简谐振动方程有什么不同 又有什么联系 振动曲线和波形曲线有什么不同 行波和驻波有何区别答: a 振动是指一个孤立的系统也可是介质中的一个质元在某固定平衡位置附近所做的往复运动;系统离开平衡位置的位移是时间的周期性函数;即可表示为)(t f y =;波动是振动在连续介质中的传播过程;此时介质中所有质元都在各自的平衡位置附近作振动;因此介质中任一质元离开平衡位置的位移既是坐标位置x ;又是时间t 的函数;即),(t x f y =.b 在谐振动方程)(t f y =中只有一个独立的变量时间t ;它描述的是介质中一个质元偏离平衡位置的位移随时间变化的规律;平面谐波方程),(t x f y =中有两个独立变量;即坐标位置x 和时间t ;它描述的是介质中所有质元偏离平衡位置的位移随坐标和时间变化的规律. 当谐波方程)(cos ux t A y -=ω中的坐标位置给定后;即可得到该点的振动方程;而波源持续不断地振动又是产生波动的必要条件之一.c 振动曲线)(t f y =描述的是一个质点的位移随时间变化的规律;因此;其纵轴为y ;横轴为t ;波动曲线),(t x f y =描述的是介质中所有质元的位移随位置;随时间变化的规律;其纵轴为y ;横轴为x .每一幅图只能给出某一时刻质元的位移随坐标位置x 变化的规律;即只能给出某一时刻的波形图;不同时刻的波动曲线就是不同时刻的波形图.d 两列频率相同、振动方向相同、在相遇点的位相差恒定、振幅相同、在同一直线上沿相反方向的行波叠加后才会形成驻波..行波伴随有能量的传播;而驻波没有能量的传播..6.7 波源向着观察者运动和观察者向着波源运动都会产生频率增高的多普勒效应;这两种情况有何区别解: 波源向着观察者运动时;波面将被挤压;波在介质中的波长;将被压缩变短;如题6.7图所示;因而观察者在单位时间内接收到的完整数目λ'/u 会增多;所以接收频率增高;而观察者向着波源运动时;波面形状不变;但观察者测到的波速增大;即B v u u +=';因而单位时间内通过观察者完整波的数目λu '也会增多;即接收频率也将增高.简单地说;前者是通过压缩波面缩短波长使频率增高;后者则是观察者的运动使得单位时间内通过的波面数增加而升高频率.题6.7图 多普勒效应6.8 已知波源在原点的一列平面简谐波;波动方程为y =A cos Cx Bt -;其中A ;B ;C 为正值恒量.求: 1波的振幅、波速、频率、周期与波长;2写出传播方向上距离波源为l 处一点的振动方程;3任一时刻;在波的传播方向上相距为d 的两点的位相差.6.9 沿绳子传播的平面简谐波的波动方程为y =0.05cos10x t ππ4-;式中x ;y 以米计;t 以秒计.求: 1绳子上各质点振动时的最大速度和最大加速度;2求x =0.2m 处质点在t =1s 时的位相;它是原点在哪一时刻的位相这一位相所代表的运动状态在t =1.25s 时刻到达哪一点6.10 如题6.10图是沿x 轴传播的平面余弦波在t 时刻的波形曲线.1若波沿x 轴正向传播;该时刻O ;A ;B ;C 各点的振动位相是多少2若波沿x 轴负向传播;上述各点的振动位相又是多少解: 1波沿x 轴正向传播;则在t 时刻;有题6.10图6.11 一列平面余弦波沿x 轴正向传播;波速为5 m/s;波长为2m;原点处质点的振动曲线如题6.11图所示. 1写出波动方程;2作出t =0时的波形图及距离波源0.5m 处质点的振动曲线.题6.11图a6.12 如题6.12图所示;已知t =0时和t =0.5s 时的波形曲线分别为图中曲线a 和b ;周期T>0.5s;波沿x 轴正向传播;试根据图中绘出的条件求:1波动方程;2P 点的振动方程.题6.12图6.13 一列机械波沿x 轴正向传播;t =0时的波形如题6.13图所示;已知波速为10 m/s 1;波长为2m;求: 1波动方程;2 P 点的振动方程及振动曲线;3 P 点的坐标;4 P 点回到平衡位置所需的最短时间.6.14 如题6.14图所示;有一平面简谐波在空间传播;已知P 点的振动方程为P y =A cos 0ϕω+t . 1分别就图中给出的两种坐标写出其波动方程;2写出距P 点距离为b 的Q 点的振动方程.题6.14图6.15 已知平面简谐波的波动方程为)24(cos x t A y +=πSI .1写出t =4.2 s 时各波峰位置的坐标式;并求此时离原点最近一个波峰的位置;该波峰何时通过原点题6.15图6.16 题6.16图中a 表示t =0时刻的波形图;b 表示原点x =0处质元的振动曲线;试求此波的波动方程;并画出x =2m 处质元的振动曲线.题6.16图6.17 一平面余弦波;沿直径为14cm 的圆柱形管传播;波的强度为18.0×10-3J/m 2·s;频率为300 Hz;波速为300m/s;求波的平均能量密度和最大能量密度.6.18 如题6.18图所示;1S 和2S 为两相干波源;振幅均为1A ;相距4λ;1S 较2S 位相超前2π;求: 1 1S 外侧各点的合振幅和强度;2 2S 外侧各点的合振幅和强度6.19 如题6.19图所示;设B 点发出的平面横波沿BP 方向传播;它在B 点的振动方程为t y π2cos 10231-⨯=;C 点发出的平面横波沿CP 方向传播;它在C 点的振动方程为)2cos(10232ππ+⨯=-t y ;本题中y 以m 计;t 以s 计.设BP =0.4m;CP =0.5 m;波速u =0.2m/s;求: 1两波传到P 点时的位相差;2当这两列波的振动方向相同时;P 处合振动的振幅;题6.19图6.20 一平面简谐波沿x 轴正向传播;如题6.20图所示.已知振幅为A ;频率为ν;波速为u .1若t =0时;原点O 处质元正好由平衡位置向位移正方向运动;写出此波的波动方程;2若从分界面反射的波的振幅与入射波振幅相等;试写出反射波的波动方程;并求x 轴上 因入射波与反射波干涉而静止的各点的位置.题6.20图6.21 一驻波方程为y =0.02cos20x cos750t SI;求:1形成此驻波的两列行波的振幅和波速;2相邻两波节间距离.6.22 在弦上传播的横波;它的波动方程为1y =0.1cos13t +0.0079x SI试写出一个波动方程;使它表示的波能与这列已知的横波叠加形成驻波;并在x =0处为波节.6.23 两列波在一根很长的细绳上传播;它们的波动方程分别为1y =0.06cos t x ππ4-SI; 2y =0.06cos t x ππ4+SI .1试证明绳子将作驻波式振动;并求波节、波腹的位置;2波腹处的振幅多大x =1.2m 处振幅多大6.24 汽车驶过车站时;车站上的观测者测得汽笛声频率由1200Hz 变到了1000 Hz;设空气中声速为330m/s;求汽车的速率.6.25 两列火车分别以72km/h 和54 km/h 的速度相向而行;第一 列火车发出一个600 Hz 的汽笛声;若声速为340 m/s;求第二列火车上的观测者听见该声音的频率在相遇前和相遇后分别是多少。
第6章 机械波课后习题答案
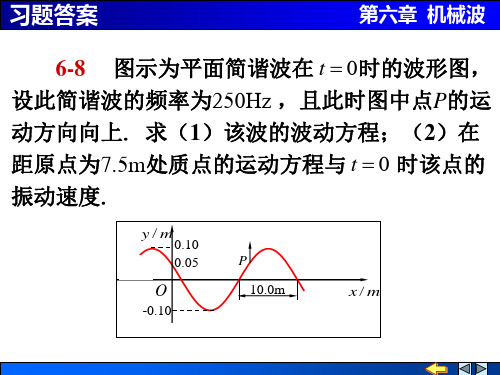
第六章 机械波
12 m
y/m 0.4 0.2
沿x轴负向传播
x 1 .0 m
5.0
t/s
π π 0.4 cos( t ) 6 3
π x 1 π y 0.4 cos[ (t ) ] 6 u 3 π π 0.4 cos[ (t x 1) ] 6 3 π π π 0.4 cos( t x ) 6 6 2
rmin uT u 2 2 2
A
2
r2
B
17 0.57 m 30
r1
习题答案
第六章 机械波
6-8 图示为平面简谐波在 t 0 时的波形图, 设此简谐波的频率为250Hz ,且此时图中点P的运 动方向向上. 求(1)该波的波动方程;(2)在 距原点为7.5m处质点的运动方程与 t 0 时该点的 振动速度.
y/m
0.10 0.05
P
10.0m
x/m
O
-0.10
习题答案
A 0.04m 0.4 m
u 0.08m s 1
t0
0.60 x / m
P
O -0.04 0.20 0.40
y0 0
v0 0
t x y A cos[2π( ) ] T 2π π 0.04 cos ( t 5πx ) 5 2 2π π 2π 3π yP 0.04 cos ( t π ) 0.04 cos ( t ) 5 2 5 2
习题答案
第六章 机械波
6-13 两相干波波源位于同一介质中的A、 B两点,如图所示,其振幅相等、频率皆为100Hz, B比的相位超前 .若A、B相距30.0m,波速为 400m· s-1, 试求A、B连线上因干涉而静止的各 点的位置.
机械波习题课(上课)

简谐机械波是周期性的,每经过一个周期 波形与原波形重复,从而导致了问题的多解性 一列横波在某时刻的波形图如图中实线所 示,经0.02s后波形如图中虚线所示,则该波 的波速v和频率f可能是( ABD ) A.v=5m/s B.v=45m/s C.f=50Hz D.f=37.5Hz 。
四、质点振动方向导致的多解问题
机械波习题课
一.机械波的形成
1、形成条件: 波源和介质 2、波的形成过程 ⑴ 机械波的形成过程是机械振动在介质中传播的过程, 介质中的每个质点都是重复波源的振动,其振动的周期、 频率、振幅都和波源一样。 ⑵ 介质中的每一个质点刚开始振动时运动情况均和波 源开始振动时的情况完全一样。(起振方向) ⑶ 机械波的传播过程是传递振动形式、能量和信息的 过程,波形的平移,介质没有定向迁移。
9.在均匀的介质中,各质点的平衡位置在同一直线上,相 邻两个质点的距离均为a,如图(a),振动从质点1开始并 向右传播,其振动初速度方向竖直向上,经过时间t,前13 个质点第一次形成的波形图如图(b),则该波的 周期为_____________________________; 波速为_________________________。
例3、已知波速为10m/s,根据图画出质点a 的振动图像(从图示时刻开始)。
例5、如图,图为一波源O点在介质中振动 了3s激起的波,那么(1)P点还需多少时 间开始振动?(2)从图示时刻起P点第二 次到达波谷的时间是多少?
例6、一列波沿X轴正向传播的简谐波,在X1 =0.2m,和X2=1.2m处的两质点A、B的振动 图像如图实线和虚线所示。求该列波的周 期和波长。
(2)由t时刻图象画出t+△t时刻的图象。 方法一:特殊质点振动法:取相距λ/4 的两个特殊点来研 究,根据两质点的振动方向,判断出两质点经△t时间后 的位置,画出相应的正(余)弦曲线。 方法二:波形平移法:求△x=v△t= λ△t/T ,将波峰或 波谷向波的传播方向平移△x即可。 (3)由t时刻图象和t+△t时刻的图象求波速。 注意波速的双向性及周期性。 方法一: △x=nλ+x 方法二: △t=nT+t
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
' u vo vo 观察者向波源运动+ ,远离 .
u vs vs 波源向观察者运动 ,远离+ .
机械波习题课选讲例题
例 如图所示一向右传播的简谐波在 t = 0 时刻
的波形,已知周期为 2 s ,则 P 点处质点的振动速度
与时间的y 关系曲u线为: A
O
A
P*
x
A v
P 点振动图
A yp
O
若 1 2 则 2 π 波程差 r2 r1
k (k 0,1,2, ) A A1 A2 (k 1 2) (k 0,1,2, ) A A1 A2
其他
2 驻波
驻波方程
A1 A2 A A1 A2 y 2 Acos2π x cos2πt
机械波习题课选讲例题
x
k
(k
100 m 处质点的振动方程 与振动速度表达式.
250Hz 200m
y Acos[2π(250t x ) π ] 200 4
x 100m , y Acos(500πt 5π ) 4
v dy 500πAsin(500πt 5π )
dt
4
机械波习题课选讲例题
例一简谐波沿Ox 轴正向传播,已知振幅、频率和速
LI
lg
I I0
B(贝尔)
LI
10 lg
I I0
dB(分贝)
四 惠更斯原理(作图法)
介质中波阵面上的各点都可以看作是发射子波的 波源,而在其后的任意时刻,这些子波的包络就是新 的波前.
机械波习题课选讲例题
五 波的叠加原理
1 波的干涉 A A12 A22 2 A1 A2 cos 2 1 2 π (r2 r1)
x
P 点两振动反相
C P
A y u
P
xO A
x
P
A y (uB)
P
O A
x
O A
x
(C)
(D)
机械波习题课选讲例题 例 一平面简谐波动在弹性介质中传播时,在传播 方向上介质中某质元在负的最大位移处,则它的能量 是 (A)动能为零, 势能最大 (B)动能为零, 势能为零 (C)动能最大, 势能最大 (D)动能最大, 势能为零
例 在驻波中,两个相邻波节间各质点的振动
(A)振幅相同, 相位相同 (B)振幅不同, 相位相同
(C)振幅相同, 相位不同 (D)振幅不同, 相位不同
机械波习题课选讲例题
例一平面机械波沿 x 轴负方向传播,已知 x 1 m
处质点的振动方程为 y Acos(t ) ,若波速为u 求
此波的波函数.
A
t
A v
O 1 2 t(s)
O 1 2 t(s)
v (A)
A
v (B)
A
O 1 2 t(s)
(C)
O 1 2 t(s)
(D)
机械波习题课选讲例题
例 如图所示一向右传播的简谐波在t时刻的波形,
BC为波密介质的反射面,则反射波在t时刻的波形图
为:
y A
u B
P
答:(B)
O
A
y
u
A
O A
A y u(A)
解 250Hz
y/m
A
200m
2A 2
O
P x/m
vP 0
A
100 m
波向 x轴负向传播
y Acos[2π(250t x ) ]
A
200
t 0,x 0 y 2A v 0 2
π
4
O 2A 2 y
机械波习题课选讲例题
y/m
A 2A 2
O A
P x/m
100 m
(2)求在距原点 O 为
2
(k 1)
22
0,1, ) Amax
(k 0,1, )
2A
Amax
0
波腹 波节
相邻波腹(节)间距 2
相邻波腹和波节间距 4
3 相位跃变(半波损失) 当波从波疏介质垂直入射到波密介质, 被反射到
波疏介质时形成波节. 入射波与反射波在此处的相位时 时相反, 即反射波在分界处产生 的相位跃变,相当于 出现了半个波长的波程差,称半波损失.
波函数
y 2 102 cos[2π( t x ) π ] 44 3
机械波习题课选讲例题
例 S1、S2 为两相干波源,它们的振动方向均垂直于
画面并发出波长为 的简谐波,P 点是两列波相遇区域
中的一点,距离如图,P 点发生相消干涉,S1的振动方
程为 y1 Acos(2πt π 2.)求 S2 的振动方程.
机械波习题课选讲例题 波的图示法: 波线 波面 波前.
3 横波、纵波
二 平面简谐波的波函数
y(x,t) Acos[(t x ) ]
u
1 y(x,t) Acos[2 π( t x ) ]
Tλ
y(x,t) Acos(t kx ) 角波数 k 2 π
2 波函数的物理意义
机械波习题课选讲例题
度分别为A, , u,设t = t 时的波形曲线如图所示,求 :
(1) x 0 处质点振动方程;(2)该波的波函数.
y
u t t 解 yO Acos(2πt )
A
O
A
v
π
2
波函数
2πt
y
t t,x 0 y 0 v
x
2π t π
2
yO Acos[2π (t t)
Acos[2π (t t x) π]
解 波函数 y Acos[ (t x) ]
u
x 1 m y Acos(t )
(t 1) t
u
u
y Acos[(t x) ]
uu
机械波习题课选讲例题
例 一平面简谐波在 t = 0 时刻的波形图如图,设
频率 250 Hz,且此时 P 点的运动方向向下,
求 :(1)该波的波函数;
三 波动的能量
1 在波动传播的媒质中,任一体积元的动能、 势能、 总机械能均随时间作同步地周期性变化,机械能不守恒 . 波动是能量传递的一种方式 .
2 平均能量密度: w 1 2 A2
2
3 平均能流密度(波强度):I wu 1 A22u
2
机械波习题课选讲例题
4 声强级:
I0 1012 W m2
机械波习题课选讲例题
六 普勒效应
1 波源不动,观察者相对介质以速度 v运o 动
' u vo
u
(+)观察者向波源运 动(–)观察者远离波源
2 观察 者' 不动,u 波源相对(介–质)以波速源度向v观运s察动者运动
u vs
(+)波源远离观察者
波源与观察者同时相对介
0
]
机械波习题课选讲例题
例一简谐波沿 Ox 轴正向传播, = 4 m,T = 4 s,
已知 x = 0 点振动曲线如图所示,求: (1) x = 0 点
振动方程;(2)波函数 .
y /10 2 m
2
22
O
2
yO
t/s
2
102
c
os(2π
t 4
)
A
oA2 y
π
3
t 0,x 0 y A 2 v 0
