广东省佛山市顺德区罗定邦中学高中数学《不等式》测试题 新人教A版必修5
高中数学 第三章 不等式同步测试卷(含解析)新人教A版必修5(1)(2021年最新整理)

高中数学第三章不等式同步测试卷(含解析)新人教A版必修5(1) 编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(高中数学第三章不等式同步测试卷(含解析)新人教A版必修5(1))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为高中数学第三章不等式同步测试卷(含解析)新人教A版必修5(1)的全部内容。
不等式(时间:120分钟,满分:150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(2015·高考山东卷)已知集合A={x|x2-4x+3<0},B={x|2<x<4},则A∩B=()A.(1,3) B.(1,4) C.(2,3) D.(2,4)2.(2015·高考北京卷)若集合A={x|-5<x<2},B={x|-3<x<3},则A∩B=()A.{x|-3<x<2} B.{x|-5<x<2} C.{x|-3<x<3} D.{x|-5<x<3}3.(2014·高考课标全国卷Ⅱ)设x,y满足约束条件错误!则z=2x-y的最大值为() A.10 B.8 C.3 D.24.(2015·高考天津卷)设变量x,y满足约束条件错误!则目标函数z=x+6y的最大值为( )A.3 B.4 C.18 D.405.(2015·高考湖南卷)若实数a,b满足错误!+错误!=错误!,则ab的最小值为( )A.错误! B.2 C.2错误! D.46。
在如图所示的锐角三角形空地中,欲建一个面积不小于300 m2的内接矩形花园(阴影部分),则其边长x(单位:m)的取值范围是()A.[15,20]B.[12,25]C.[10,30] D.[20,30]7.(2014·高考重庆卷)若log4(3a+4b)=log2ab,则a+b的最小值是()A.6+2错误! B.7+2错误! C.6+4错误! D.7+4错误!8.(2015·高考重庆卷)若不等式组错误!表示的平面区域为三角形,且其面积等于错误!,则m的值为( )A.-3 B.1 C。
人教A版高中数学必修五高一数学必修五第三单元:不等式.docx

高中数学学习材料马鸣风萧萧*整理制作高一数学必修五第三单元:不等式单元过关试卷一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.不等式(x+3)2<1的解集是()A.{x|x>-2}B.{x|x<-4}C.{x|-4<x<-2}D.{x|-4≤x≤-2}2.已知t=a+2b,s=a+b2+1,则t和s的大小关系正确的是()A.t>sB.t≥sC.t<sD.t≤s3.不等式组0,34,34xx yx y≥⎧⎪+≥⎨⎪+≤⎩所表示的平面区域的面积等于()A. 32B.23C.43D.344.已知函数f(x)=log2(x+1)且a>b>c>0,则()f aa、()f bb、()f cc的大小关系是()A.()f aa>()f bb>()f ccB.()f cc>()f bb>()f aaC.()f bb>()f aa>()f ccD.()f aa>()f cc>()f bb5.已知不等式(x+y)(1ax y+)≥9对任意正实数x,y恒成立,则正实数a的最小值为()A.2B.4C.6D.86.满足不等式y2-x2≥0的点(x,y)的集合(用阴影表示)是()7.已知函数f(x)=1,1,0,x xx x-+<0,⎧⎨-≥⎩则不等式x+(x+1)· f(x+1)≤1的解集是()A.{x|-1≤x≤2-1}B.{x|x≤1}C.{x|x≤2-1}D.{x|-2-1≤x≤2-1}8.设M=(1a-1)(1b-1)(1c-1),且a+b+c=1(a、b、c∈R+),则M的取值范围是()A.[0,18] B.[18,1)C.[1,8)D.[8,+∞)9.对于满足等式x2+(y-1)2=1的一切实数x、y,不等式x+y+c≥0恒成立,则实数c的取值范围是()A.(-∞,0]B.[2,+∞)C.[2-1,+∞)D.[1-2,+∞)10.如果正数a ,b ,c ,d 满足a+b=cd=4,那么( )A.ab ≤c+d 且等号成立时,a ,b ,c ,d 的取值唯一B.ab ≥c+d 且等号成立时,a ,b ,c ,d 的取值唯一C.ab ≤c+d 且等号成立时,a ,b ,c ,d 的取值不唯一D.ab ≥c+d ,且等号成立时,a ,b ,c ,d 的取值不唯一二、填空题(本大题共2小题,每小题5分,共10分.把答案填在题中横线上)11.不等式2242x x +-≤12的解集为 . 12.函数y=1x a -(a >0,a ≠1)的图象恒过定点A ,若点A 在直线mx+ny-1=0(mn >0)上,则1m +1n 的最小值为 .13.不等式组⎩⎪⎨⎪⎧ x +y -1≤0x -y +1≥0,y ≥0表示的平面区域内到直线y =2x -4的距离最远的点的坐标为________.14.(2012·江苏卷)已知函数f (x )=x 2+ax +b (a ,b ∈R)的值域为[0,+∞),若关于x 的不等式f (x )<c 的解集为(m ,m +6),则实数c 的值为________.15.设集合A ={x |x 2<4},B =⎩⎨⎧⎭⎬⎫x ⎪⎪ 1<4x +3. (1)求集合A ∩B ;(2)若不等式2x 2+ax +b <0的解集为B ,求a ,b 的值.三、解答题16.(12分)如图,要设计一张矩形广告,该广告含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏目的面积之和为18 000 cm 2,四周空白的宽度为10 cm ,两栏之间的中缝空白的宽度为5 cm.怎样确定广告的高与宽的尺寸(单位:cm )能使矩形广告的面积最小?17.(12分)不等式(m 2-2m-3)x 2-(m-3)x-1<0对一切x ∈R 恒成立,求实数m 的取值范围.18.(12分)制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目,根据预测,甲、乙两个项目可能的最大盈利率分别为100%和50%,可能的最大亏损率分别为30%和10%,投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元,则投资人对甲、乙两个项目各投资多少万元才能使可能的盈利最大? 19.(12分)已知二次函数f (x )满足f (-2)=0,且2x ≤f (x )≤242x +对一切实数x 都成立. (1)求f (2)的值;(2)求f (x )的解析式(3)设b n =1()f n ,数列{b n }的前n 项和为S n , 求证:S n >43(3)n n +. 20.(13分)某村计划建造一个室内面积为72 m 2的矩形蔬菜温室.在温室内,沿左、右两侧与后侧内墙各保留1 m 宽的通道,沿前侧内墙保留3 m 宽的空地.当矩形温室的边长各为多少时蔬菜的种植面积最大?最大种植面积是多少?21.已知函数f (x )=|x -a |.(1)若不等式f (x )≤3的解集为{x |-1≤x ≤5},求实数a 的值;(2)在(1)的条件下,若f (x )+f (x +5)≥m 对一切实数x 恒成立,求实数m 的取值范围.(备选题):22.(本题14分)已知函数()g x =sin x x λ+是区间[,]22ππ-上的增函数. (1)求λ的取值集合D ;(2)是否存在实数t ,使得()g x 21t t λ>++对∀[1,1]x ∈-且D λ∈恒成立; (3)讨论关于x 的方程2ln sin ()(2)x x g x x e x k xλ+=+-++的根的个数. 第三章 不等式(数学人教实验A 版必修5)答案一、选择题1.C 解析:原不等式可化为x 2+6x+8<0,解得-4<x<-2.2.D 解析:∵ t-s=a+2b-a-b 2-1=-(b-1)2≤0,∴ t ≤s.3.C 解析:不等式组表示的平面区域如图所示, 由34,34x y x y +=⎧⎨+=⎩得交点A 的坐标为(1,1), 又B ,C 两点的坐标分别为(0,4),(0,43), 故S △ABC =12 (4-43)×1=43. 4.B 解析:特殊值法.令a=7,b=3,c=1,满足a >b >c >0,∴ 2log (11)1+>2log (31)3+>2log (71)7+. 5.B 解析:不等式(x+y )(1a x y +)≥9对任意正实数x ,y 恒成立,则1+a+y ax x y +≥a+2a +1≥9, ∴ a ≥2或a ≤-4(舍去),∴ 正实数a 的最小值为4.6.B 解析:取测试点(0,1)可知C ,D 错;再取测试点(0,-1)可知A 错,故选B.7.C 解析:依题意得10,10,(1)()1(1)1x x x x x x x x +<+≥⎧⎧⎨⎨++-≤++≤⎩⎩或, 所以1,1,2121x x x x ≥-⎧<-⎧⎪⇒⎨⎨∈--≤≤-⎪⎩⎩R 或x <-1或-1≤x ≤2-1x ≤2-1,选C. 8. D 解析:M=b c a +·a c b +·a b c+≥8ab bc ac abc ∙∙=8. 9.C 解析:令x= cos θ,y=1+ sin θ,则-(x+y )=- sin θ-cos θ-1=-2sin (θ+π4)-1. ∴ -(x+y )max =2-1.∵ x+y+c ≥0恒成立,故c ≥-(x+y )max =2-1,故选C.10.A 解析:因为a+b=cd=4,由基本不等式得a+b ≥2ab ,故ab ≤4.又cd ≤2()4c d +,故c+d ≥4,所以ab ≤c+d ,当且仅当a=b=c=d=2时,等号成立.故应选A. 11.{x|-3≤x ≤1} 解析:依题意x 2+2x-4≤-1(x+3)(x-1)≤0x ∈[-3,1].12.4 解析:由题意知A (1,1),∴ m+n-1=0,即 m+n=1,∴1m +1n =(1m +1n )(m+n )=2+n m +m n ≥2+2n m m n∙=4. 13.解析: 在坐标平面内画出不等式组表示的平面区域及直线y =2x -4,结合图形可知,在该平面区域内所有的点中,点(-1,0)到直线y =2x -4的距离最远.答案: (-1,0)14.解析: ∵f (x )=x 2+ax +b 的值域为[0,+∞),∴Δ=0,∴b -a 24=0,∴f (x )=x 2+ax +14a 2=⎝⎛⎭⎫x +12a 2.又∵f (x )<c 的解集为(m ,m +6),∴m ,m +6是方程x 2+ax +a24-c =0的两根.由一元二次方程根与系数的关系得⎩⎪⎨⎪⎧2m +6=-a ,m (m +6)=a 24-c ,解得c =9.答案: 915解析: A ={x |x 2<4}={x |-2<x <2},B =⎩⎨⎧⎭⎬⎫x ⎪⎪ 1<4x +3=⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪ x -1x +3<0={x |-3<x <1}, (1)A ∩B ={x |-2<x <1};(2)因为2x 2+ax +b <0的解集为B ={x |-3<x <1},所以-3和1为2x 2+ax +b =0的两根.故⎩⎨⎧ -a 2=-3+1,b 2=-3×1,所以a =4,b =-6.三.解答题:16.解:设矩形栏目的高为a cm ,宽为b cm ,则ab=9 000.①广告的高为a+20,宽为2b+25,其中a >0,b >0.广告的面积S=(a+20)(2b+25)=2ab+40b+25a+500=18 500+25a+40b≥18 500+22540a b ∙=18 500+21000ab =24 500.当且仅当25a=40b 时等号成立,此时b=58a ,代入①式得a=120,从而b=75, 即当a=120,b=75时,S 取得最小值24 500.故广告的高为140 cm ,宽为175 cm 时,可使广告的面积最小.17.解:若m 2-2m-3=0,则m=-1或m=3.当m=-1时,不合题意;当m=3时,符合题意.若m 2-2m-3≠0,设f (x )=(m 2-2m-3)x 2-(m-3)x-1, 则由题意,得22230,230,m m m m m ∆2⎧--<⎨=[-(-3)]+4(--)<⎩解得-15<m<3. 综上所述,-15<m ≤3. 18.解:设投资人分别用x ,y 万元投资甲,乙两个项目,由题意,得10,0.30.1 1.8,0,0,x y x y x y +≤⎧⎪+≤⎪⎨≥⎪⎪≥⎩目标函数为z =x+0.5y. 上述不等式组表示的平面区域如图所示,阴影部分(含边界)即为可行域.作直线l 0:x+0.5y=0,并作平行于直线l 0的一组直线x+0.5y=z ,z ∈R ,与可行域相交,其中有一条直线经过可行域上的点M ,此时z 最大,这里点M 是直线x+y=10与直线0.3x+0.1y=1.8的交点.解方程组10,0.30.1 1.8,x y x y +=⎧⎨+=⎩得4,6,x y =⎧⎨=⎩此时,z=4+0.5×6=7(万元). ∴ 当x=4,y=6时,z 取得最大值.答:投资人用4万元投资甲项目,6万元投资乙项目,才能使可能的盈利最大.19.(1)解:∵ 2x ≤f (x )≤242x +对一切实数都成立, ∴ 4≤f (2)≤4,∴ f (2)=4.(2)解:设f (x )=ax 2+bx+c (a ≠0).∵ f (-2)=0,f (2)=4,∴424,1,42024.a b c b a b c c a ++==⎧⎧⇒⎨⎨-+==-⎩⎩∵ ax 2+bx+c ≥2x ,即ax 2-x+2-4a ≥0,∴ Δ=1-4a (2-4a )≤0⇒(4a-1)2≤0, ∴ a=14,c=2-4a=1,故f (x )=24x +x+1. (3)证明:∵ b n =1()f n =24(2)n +>4(2)(3)n n ++=4(12n +-13n +), ∴ S n =b 1+b 2+…+b n >4[(13-14)+(14-15)+…+(12n +-13n +)]=4×1133n ⎛⎫- ⎪+⎝⎭=43(3)n n +. 20.解:设矩形温室的左侧边长为a m ,后侧边长为b m ,则ab=72,蔬菜的种植面积S=(a-4)(b-2)=ab-4b-2a+8=80-2(a+2b )≤80-42ab =32(m 2). 当且仅当a=2b ,即a=12,b=6时,S max =32.答:当矩形温室的边长为6 m ,12 m 时,蔬菜的种植面积最大,最大种植面积是32 m 2.21.解析: (1)由f (x )≤3,得|x -a |≤3,解得a -3≤x ≤a +3.又已知不等式f (x )≤3的解集为{x |-1≤x ≤5},所以⎩⎪⎨⎪⎧a -3=-1,a +3=5,解得a =2. (2)方法一:当a =2时,f (x )=|x -2|,设g (x )=f (x )+f (x +5)=|x -2|+|x +3|.由|x -2|+|x +3|≥|(x -2)-(x +3)|=5,当且仅当-3≤x ≤2时等号成立,得g (x )的最小值为5.从而,若f (x )+f (x +5)≥m 对一切实数x 恒成立,实数m 的取值范围为(-∞,5]. 方法二:当a =2时,f (x )=|x -2|,设g (x )=f (x )+f (x +5)=|x -2|+|x +3|.于是g (x )=|x -2|+|x +3|=⎩⎪⎨⎪⎧ -2x -1,x <-3,5,-3≤x ≤2,2x +1,x >2.所以当x <-3时,g (x )>5;当-3≤x ≤2时,g (x )=5;当x >2时,g (x )>5.综上可得,g (x )的最小值为5.从而,若f (x )+f (x +5)≥m 对一切实数x 恒成立,实数m 的取值范围为(-∞,5].22.解:(1)因为()g x 在[,]22ππ-上单调递增,所以'()cos 0g x x λ=+≥, 即cos x λ≥-在[,]22ππ-恒成立 …………………2分 所以0λ≥,所以D=[0,)+∞ ………………4分(2)由题意min ()(1)sin1g x g λ=-=-- ………………5分 所以只需sin1λ-->21t t λ++ ………………6分所以2(1)sin11t t λ++++<0(0λ≥)恒成立, 令=)(λh 2(1)sin11t t λ++++,则需10(0)0t h +<⎧⎨<⎩………………7分 而(0)h 2sin11t =++恒正,故上式无解所以不存在实数,使得()g x 21t t λ>++对∀[1,1]x ∈-且D λ∈恒成立.………8分 (3)方程2ln sin ()(2)x x g x x e x k x λ+=+-++即2ln (2)x x ex k x--= 令()f x =2ln (2)x x ex x --,因为'()f x 21ln 2()x e x x -=+- 当(0,)x e ∈时,'()f x 0>;当(,)x e ∈+∞时,'()f x 0<所以()f x 在(0,)e 递增,(,)e +∞上递减所以max ()f x ()f e =21e e =+ …………… ………………11分 所以当k >21e e +时方程无解; 当k =21e e+时方程有一个根; 当k <21e e+时方程有两个根 …………………………………………14分。
2021年高中数学 不等式复习试题 新人教A版必修5

2021年高中数学不等式复习试题新人教A版必修5考点一:二元一次不等式(组)与平面区域画二元一次不等式表示的平面区域常采用“直线定界,特殊点定域”的方法.由于对在直线同一侧的所有点(),把它的坐标()代入,所得到实数的符号都相同,所以只需在此直线的某一侧取一特殊点,从的正负即可判断表示直线哪一侧的平面区域.例1画出下列不等式(组)表示的平面区域(1)(2)变式1:知识点二:简单的线性规划问题(一)与线性规划问题有关的概念(二)解题步骤(1)在平面直角坐标系内作出;(2)考虑目标函数的几何意义,将目标函数进行变形,线性问题一般变形为;(3)确定最优解:在可行域内平行移动目标函数变形后的直线,从而确定最优解;(4)求最值:将最优解代入目标函数即可求出最大值或最小值例2、若变量满足约束条件,则的最小值为()A.17B.14C.5D.3变式2:若变量满足约束条件,则目标函数的最大值和最小值分别为()A.3,-11B.-3,-11C.11,3D.11,3知识点三:简单的线性规划问题的实际应用步骤:(1)设元,并列出相应的约束条件和目标函数(2)作图,准确作图,平移找点(3)求解,代入求解,准确计算(4)检验,根据结果,检验反馈例3、某运输公司有7辆可载6t的A型卡车与4辆可载10t的B型卡车,有9名驾驶员,建筑某段高速公路站,此公司承包了每天至少搬运360t沥青的任务,已知每辆卡车每天往返的次数为A型车8次,B型车6次,每辆卡车每天往返成本费为A型车160元,B型车252元,每天派出A型车和B型车各多少辆,公司所花的成本费最低?变式3:某服装制造商现有10的棉布料,10的羊毛料,和6的丝绸料。
做一条裤子需要1的棉布料,2的羊毛料,1的丝绸料。
一条裙子需要1的棉布料,1的羊毛料,1的丝绸料。
一条裤子的纯收益是20元,一条裙子的纯收益是40元,为了使收益达到最大,需要安排生产这两种服装的计划请你列出生产这两种服装件数所要满足的数学关系式,并画出图形知识点四:基本不等式(1)重要不等式:若,则(当且仅当时,等号成立)(2)基本不等式:若,则(当且仅当时,等号成立)其中可变性为,(3)在利用基本不等式求最值时,应具备三个条件:一正二定三相等例4、(1)若,求的最小值,并求此时x的值。
2021年高中数学 不等式练习题 新人教A版必修5

2021年高中数学不等式练习题新人教A版必修5一、选择题1.若xy>0,则对xy+yx说法正确的是( )A.有最大值-2 B.有最小值2C.无最大值和最小值D.无法确定2.已知,则在不等式2x-3y+1≤0表示的平面区域内的点是()(A)P1、P2(B)P2(C)P2、P3(D)P33.函数y=3x2+6x2+1的最小值是( )A.32-3 B.-3 C.6 2 D.62-34变量x、y满足条件:212,2936,2324,0,0.x yx yx yx y+≥⎧⎪+≥⎪⎨+=⎪⎪≥≥⎩则使z=3x+2y的值最小的(x,y)是()(A)(4.5,3) (B)(3,6) (C)(9,2) (D)(6,4)5设动点坐标(x,y)满足,则x2+y2的最小值为(A) (B) (C) (D)10 6.给出下面四个推导过程:①∵a,b∈(0,+∞),∴ba +ab≥2ba·ab=2;②∵x,y∈(0,+∞),∴lg x+lg y≥2lg x·lg y;③∵a∈R,a≠0,∴4a+a≥24a·a=4;④∵x,y∈R,,xy<0,∴xy +yx=-[(-xy)+(-yx)]≤-2-xy-yx=-2.其中正确的推导过程为( )A.①②B.②③C.③④D.①④7.已知x、y均为正数,xy=8x+2y,则xy有( )A.最大值64 B.最大值1 64C.最小值64 D.最小值1 648.已知x,y满足则z=2x+4y的最值为(A)zmax =16,zmin=-2 (B)zmax=14,zmin=-2 (C)zmax=2,zmin=-2 (D)zmax=2,z min =-149.已知a >0,b >0,则1a +1b+2ab 的最小值是( )A .2B .22C .4D .510图中阴影部分表示的平面区域可用二元一次不等式组表示成 (A) (B) (C) (D)二.填空题1. 若实数满足,则的最小值是 .。
广东省佛山市顺德区罗定邦中学高中数学周测题 新人教A

广东省佛山市顺德区罗定邦中学高中数学周测题 新人教A 版必修52012.5.20班级________组号______姓名_________学号________一、单项选择题(每题5分,把答案填入后面的表格中)1. 已知a,b 均为正数,a+b=1,则1abA.有最大值4B. 有最小值4C.既无最大值也无最小值D.4既不是最大值也不是最小值 2. 将29(10)化为二进制数的结果是A. 11101(2)B.10111(2)C.1101(2)D. 1011(2)3. 用秦九韶算法求当0x x =时()5432126294f x x x x x x =-+-+-+的值,做的乘法次数为A.21B.20C.5D.4 4. 图4框图输出的结果是A. 41B. 40C. 121D.非以上结果图4图7图8开始结束 输出a1=a31a a =+40?a >是 否5. 要使图5的程序输出结果小于2,则输入的x 的范围是_____A.(-13,2)B.(-∞,-13)∪(2,+∞)C.(-2, 13)D.(-∞,-2)∪(13,+∞)INPUT “x=”;x PRINT 3*x*x+5*x END 图5 INPUT “a,b=”;a,b c=b b=a a=c PRINT a,b,c END 图6 a=-1 m=2 n=1 WHILE n<=5 a=a+m^2 n=n+1 WEND PRINT a END图126. 程序输入1,2,则输出 ______A. 2 2 2B. 1 1 2C. 1 2 2D. 2 1 27. 图7框图要计算12+14+16+...+1100,则判断框应填入______A. i<50?B. i>50?C. i≥50?D. i=50? 8. 图8程序循环体被运行的次数是_______A.13B.14C. 15D.16 请把选择题答案填入下面表格 1 2 3 4 5 6 7 8 BACCCDBC二、填空题(每空5分)9. f(x)= sin(x+π3)+cos(x -π6)的最小值为______ 10. 3721与2257的最大公约数结果是_____11. 已知x+2y=6,x,y 都是正数,则xy 的最大值为 ______12. 图12程序输出的结果是______ 19三、解答题13. 为求一块四边形土地面积,测量可知∠ABC=∠BCD=120°,AB=4 m ,BC=CD=2 m ,(1)求BD长。
新课标人教版必修5高中第3章不等式单元检测试卷及答案解析(原始打印版)

新课标人教版必修5高中数学 第3章 不等式单元检测试卷1.设a b <,c d <,则下列不等式中一定成立的是 ( )A .d b c a ->-B .bd ac >C .d b c a +>+D .c b d a +>+2. “0>>b a ”是“222b a ab +<”的 ( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件3.不等式b ax >的解集不可能是 ( )A .φB .RC .),(+∞a bD .),(ab --∞ 4.不等式022>++bx ax 的解集是)31,21(-,则b a -的值等于 ( ) A .-14 B .14 C .-10 D .105.不等式||x x x <的解集是 ( ) A .{|01}x x <<B .{|11}x x -<<C .{|01x x <<或1}x <-D .{|10,1}x x x -<<> 6.若011<<ba ,则下列结论不正确的是 ( ) A .22b a < B .2b ab < C .2>+ba ab D .||||||b a b a +>+7.若13)(2+-=x x x f ,12)(2-+=x x x g ,则)(x f 与)(x g 的大小关系为 ( )A .)()(x g x f >B .)()(x g x f =C .)()(x g x f <D .随x 值变化而变化 8.下列各式中最小值是2的是 ( )A .y x +x yB .4522++x x C .tan x +cot x D . x x -+229.下列各组不等式中,同解的一组是 ( )A .02>x 与0>xB .01)2)(1(<-+-x x x 与02<+xC .0)23(log 21>+x 与123<+x D .112≤--x x 与112≤--x x 10.如果a x x >+++|9||1|对任意实数x 总成立,则a 的取值范围是 ( )A. }8|{<a aB. }8|{>a aC. }8|{≥a aD. }8|{≤a a 11.若+∈R b a ,,则b a 11+与ba +1的大小关系是 .12.函数121lg+-=x xy 的定义域是 . 13.某公司一年购买某种货物400吨,每次都购买x 吨,运费为4万元/次,一年的总存储费用为4x 万元,要使一年的总运费与总存储费用之和最小,则x = 吨.14. 已知0()1,0x x f x x ≥⎧=⎨-<⎩,, 则不等式3)2(≤+x f 的解集___ _ ____.15.已知()f x 是奇函数,且在(-∞,0)上是增函数,(2)0f =,则不等式()0xf x <的解集是___ _ ____. 16.解不等式:21582≥+-x x x17.已知1<a ,解关于x 的不等式12>-x ax.18.已知0=++c b a ,求证:0≤++ca bc ab 。
2020年高中数学 人教A版 必修5 章末优化试卷 《不等式》(含答案解析)

2020年高中数学 人教A 版 必修5 章末优化试卷《不等式》一、选择题1.不等式(x +3)2<1的解集是( )A .{x|x>-2}B .{x|x<-4}C .{x|-4<x<-2}D .{x|-4≤x≤-2}2.若a ,b ,c ∈R ,且a>b ,则下列不等式一定成立的是( )A .a +c≥b+cB .ac>bc C.c 2a -b >0 D.c2a -b≥03.设M=2a(a-2),N=(a +1)(a-3),则有( )A .M>NB .M ≥NC .M<ND .M≤N4.已知关于x 的不等式mx 2+8mx +28<0的解集为{x|-7<x<-1},则实数m 的值为( )A .1B .2C .3D .45.设x ,y 为正数,则(x +y)⎝ ⎛⎭⎪⎫1x +4y 的最小值为( ) A .6 B .9 C .12 D .15 6.若x ,y 满足约束条件⎩⎪⎨⎪⎧x≥0,x +2y≥3,2x +y≤3,则z=x-y 的最小值是( )A .-3B .0 C.32D .37.不等式组⎩⎪⎨⎪⎧-2x -3>10,x 2+7x +12≤0的解集为( )A .[-4,-3]B .[-4,-2]C .[-3,-2]D .∅8.已知实数x ,y 满足x 2+y 2=1,则(1-xy)(1+xy)有( )A .最小值12和最大值1B .最小值34和最大值1C .最小值12和最大值34D .最小值19.若关于x 的不等式2x 2-8x-4-a≥0在1≤x≤4内有解,则实数a 的取值范围是( )A .a≤-4B .a≥-4C .a≥-12D .a≤-1210.设a 、b 是实数,且a+b=3,则2a +2b的最小值是( )A .6B .4 2C .2 6D .811.某农户计划种植黄瓜和韭菜,种植面积不超过50亩,投入资金不超过54万元,假设种植黄瓜和韭菜的产量、成本和售价如下表:为使一年的种植总利润(总利润=总销售收入-总种植成本)最大,那么黄瓜和韭菜的种植面积(单位:亩)分别为( )A .50,0B .30,20C .20,30D .0,5012.设变量x ,y 满足约束条件⎩⎪⎨⎪⎧2x -y -6≤0,x -y +2≥0,x>0,y>0,若目标函数z=ax +by(a>0,b>0)的最大值为40,则5a +1b的最小值为( )A.256B.94 C .1 D .4二、填空题13.函数y=2-x-4x(x>0)的值域为________.14.不等式x +1x≤3的解集为________.15.已知不等式x 2-ax-b<0的解集为(2,3),则不等式bx 2-ax-1>0的解集为________.16.设D 是不等式组⎩⎪⎨⎪⎧x +2y≤10,2x +y≥3,0≤x≤4,y≥1表示的平面区域,则D 中的点P(x ,y)到直线x +y=10的距离的最大值是________.三、解答题17.已知f(x)=x 2+2x +2a-a 2,若对任意x ∈[1,+∞),f(x)>0恒成立,求实数a 的取值范围.18.已知f(x)=x 2-(a +1a)x +1,(1)当a=12时,解不等式f(x)≤0;(2)若a >0,解关于x 的不等式f(x)≤0.19.一个农民有田2亩,根据他的经验,若种水稻,则每亩每期产量为400千克;若种花生,则每亩每期产量为100千克,但水稻成本较高,每亩每期需240元,而花生只要80元,且花生每千克可卖5元,稻米每千克只卖3元,现在他只能凑足400元,问这位农民对两种作物各种多少亩,才能得到最大利润?20.已知关于x的不等式kx2-2x+6k<0(k≠0).(1)若不等式的解集是{x|x<-3或x>-2},求k的值;(2)若不等式的解集是R,求k的取值范围.21.某外商到一开发区投资72万美元建起一座蔬菜加工厂,第一年各种经费12万美元,以后每年增加4万美元,每年销售蔬菜收入50万美元.设f(n)表示前n年的纯利润总和.(注:f(n)=前n年的总收入-前n年的总支出-投资额)(1)从第几年开始获利?(2)若干年后,外商为开发新项目,有两种处理方案:①年平均利润最大时,以48万美元出售该厂;②纯利润总和最大时,以16万美元出售该厂.问哪种方案最合算?为什么?22.设函数f(x)=x+ax+1,x∈[0,+∞).(1)当a=2时,求函数f(x)的最小值;(2)当0<a<1时,求函数f(x)的最小值.答案解析1.答案为:C ;解析:原不等式可化为x 2+6x +8<0,解得-4<x<-2.2.答案为:D ;解析:∵a>b ,∴a-b>0,c 2≥0∴c 2a -b≥0.3.答案为:A ;解析:因为M-N=2a 2-4a-(a 2-2a-3)=a 2-2a +3=(a-1)2+2>0,所以M>N ,故选A.4.答案为:D ;解析:因为不等式mx 2+8mx +28<0的解集为{x|-7<x<-1},所以-7,-1是方程mx 2+8mx +28=0的两个根,且m>0,所以⎩⎪⎨⎪⎧-7-1=-8mm ,-7×-1=28m ,∴m=4.5.答案为:B ;解析:x ,y 为正数,(x +y)⎝ ⎛⎭⎪⎫1x +4y =1+4+y x +4x y ≥9,当且仅当y=2x 等号成立,选B.6.答案为:A ;解析:可行域为如图所示的阴影部分,可知z=x-y 在点A(0,3)处取得最小值,∴z 最小值=-3.7.答案为:A ;解析:⎩⎪⎨⎪⎧-2x -3>10x 2+7x +12≤0⇒⎩⎪⎨⎪⎧x -3<-5x +3x +4≤0⇒⎩⎪⎨⎪⎧x<-2-4≤x≤-3⇒-4≤x≤-3.8.答案为:B ;解析:∵x 2y 2≤⎝ ⎛⎭⎪⎫x 2+y 222=14,当且仅当x 2=y 2=12时,等号成立,∴(1-xy)(1+xy)=1-x 2y 2≥34.∴x 2y 2≥0,∴34≤1-x 2y 2≤1.9.答案为:A ;解析:令y=2x 2-8x-4(1≤x≤4),则y=2x 2-8x-4在x=4时取得最大值-4,∴当a≤-4时,2x 2-8x-4≥a 在1≤x≤4内有解.10.答案为:B ;解析:∵a ,b 是实数,∴2a >0,2b>0,于是2a +2b ≥22a ·2b =22a +b =223=42,当且仅当a=b=32时取得最小值4 2.11.答案为:B ;解析:设黄瓜和韭菜的种植面积分别为x ,y 亩,总利润为z 万元, 则目标函数为z=(0.55×4x -1.2x)+(0.3×6y -0.9y)=x +0.9y.线性约束条件为⎩⎪⎨⎪⎧x +y≤50,1.2x +0.9y≤54,x≥0,y≥0,即⎩⎪⎨⎪⎧x +y≤50,4x +3y≤180,x≥0,y≥0作出不等式组⎩⎪⎨⎪⎧x +y≤50,4x +3y≤180,x≥0,y≥0.表示的可行域如图,易求得点A(0,50),B(30,20),C(45,0).平移直线x +0.9y=0,可知当直线经过点B(30,20),即x=30,y=20时,z 取得最大值,且z max =48.故选B.12.答案为:B ;解析:作出可行域如图阴影部分所示(不包括坐标轴边界上的点).由z=ax +by 得y=-a b x +1b z.因为a>0,b>0,所以-a b <0,作直线l 0:y=-abx 并向上平移,数形结合知,当l 0平移至过点A 时z 取得最大值. 由⎩⎪⎨⎪⎧2x -y -6=0,x -y +2=0得点A 的坐标为(8,10),即z max =8a +10b=40,得a 5+b 4=1,于是⎝ ⎛⎭⎪⎫5a +1b ⎝ ⎛⎭⎪⎫a 5+b 4=54+⎝ ⎛⎭⎪⎫5b 4a +a 5b ≥54+214=94⎝ ⎛⎭⎪⎫当且仅当5b 4a =a 5b 时取“=”.∴⎝ ⎛⎭⎪⎫5a +1b min =94.13.答案为:(-∞,-2];解析:当x>0时,y=2-⎝ ⎛⎭⎪⎫x +4x ≤2-2x ×4x =-2.当且仅当x=4x ,x=2时取等号.14.答案为:(-∞,0)∪[12,+∞);解析:x +1x ≤3⇔x +1-3x x ≤0,即2x -1x ≥0,∴x <0或x≥12.15.答案为:⎝ ⎛⎭⎪⎫-12,-13;解析:方程x 2-ax-b=0的根为2,3.根据韦达定理得:a=5,b=-6,所以不等式为6x 2+5x +1<0,解得解集为⎝ ⎛⎭⎪⎫-12,-13.16.答案为:42;解析:画出可行域,由图知最优解为A(1,1),故A 到x +y=10的距离为d=4 2.17.解:设g(x)=x 2+2x.因为f(x)>0,所以x 2+2x>a 2-2a.只要使g(x)在[1,+∞)上的最小值大于a 2-2a 即可.因为g(x)=x 2+2x 在[1,+∞)上单调递增, 所以g(x)min =g(1)=3.所以a 2-2a<3,解此一元二次不等式,得-1<a<3. 所以实数a 的取值范围是(-1,3). 18.解:(1)当a=12时,有不等式f(x)=x 2-52x +1≤0,∴(x-12)(x-2)≤0,∴不等式的解集为{x|12≤x≤2}.(2)∵不等式f(x)=(x-1a )(x-a)≤0,当0<a <1时,有1a>a ,不等式的解集为{x|a≤x≤1a};当a >1时,有1a <a ,不等式的解集为{x|1a≤x≤a};当a=1时,不等式的解集为{x|x=1}.19.解:设水稻种x 亩,花生种y 亩,则由题意得⎩⎪⎨⎪⎧x +y≤2,240x +80y≤400,x≥0,y≥0.即⎩⎪⎨⎪⎧x +y≤2,3x +y≤5,x≥0,y≥0,画出可行域如图阴影部分所示.而利润P=(3×400-240)x +(5×100-80)y=960x +420y(目标函数),可联立⎩⎪⎨⎪⎧x +y =2,3x +y =5,得交点B(1.5,0.5).故当x=1.5,y=0.5时,P 最大值=960×1.5+420×0.5=1 650, 即水稻种1.5亩,花生种0.5亩时所得到的利润最大.20.解:(1)因为不等式的解集为{x|x<-3或x>-2},所以-3,-2是方程kx 2-2x +6k=0的两根且k<0.由根与系数的关系得⎩⎪⎨⎪⎧-3×-2=6,-3+-2=2k ,解得k=-25.所以⎩⎪⎨⎪⎧ k<0,Δ=4-4k·6k<0,即⎩⎪⎨⎪⎧ k<0,k>66或k<-66.所以k<-66. 即k 的取值范围是⎝⎛⎭⎪⎫-∞,-66.21.解:由题意知,每年的经费是以12为首项,4为公差的等差数列,则f(n)=50n-⎣⎢⎡⎦⎥⎤12n +n n -12×4-72=-2n 2+40n-72. (1)获利就是要求f(n)>0,所以-2n 2+40n-72>0,解得2<n<18.由n ∈N 知从第三年开始获利.(2)①年平均利润=f n n =40-2⎝⎛⎭⎪⎫n +36n ≤16. 当且仅当n=6时取等号,故此方案共获利6×16+48=144(万美元),此时n=6.②f(n)=-2(n-10)2+128.当n=10时,f(n)max =128.故第②种方案共获利128+16=144(万美元).故比较两种方案,获利都是144万美元.但第①种方案只需6年,而第②种方案需10年,故选择第①种方案.22.解:(1)把a=2代入f(x)=x +a x +1,得f(x)=x +2x +1=(x +1)+2x +1-1, ∵x ∈[0,+∞),∴x +1>0,2x +1>0, ∴x +1+2x +1≥2 2. 当且仅当x +1=2x +1,即x=2-1时,f(x)取最小值. 此时,f(x)min =22-1.(2)当0<a<1时,f(x)=x +1+a x +1-1. 若x +1+a x +1≥2a , 则当且仅当x +1=a x +1时取等号,此时x=a-1<0(不合题意),因此,上式等号取不到. 设x 1>x 2≥0,则f(x 1)-f(x 2)=x 1+a x 1+1-x 2-a x 2+1=(x 1-x 2)⎣⎢⎡⎦⎥⎤1-a x 1+1x 2+1, ∵x 1>x 2≥0,∴x 1-x 2>0,x 1+1>1,x 2+1≥1.∴(x 1+1)(x 2+1)>1,而0<a<1.∴a x 1+1x 2+1<1, ∴f(x 1)-f(x 2)>0,∴f(x)在[0,+∞)上单调递增,∴f(x)min=f(0)=a.。
广东省佛山市顺德区罗定邦中学高中数学模拟题 新人教A版必修5

广东省佛山市顺德区罗定邦中学高中数学模拟题 新人教A 版必修51. 已知函数22()3cos 23sin cos sin f x x x x x =++ (1)求f(x)的最小正周期(1) 求函数的单调增区间(3)当[,]44x ππ∈-时,求函数的最大值、最小值及何时取到2. 已知226sin sin cos 2cos 0,(,),sin(2)23ππαααααπα+-=∈+求的值.3. 在△ABC 中,A 、B 、C 所对的边为a 、b 、c ,且2sin (2)sin (2)sin a A b c B c b C =+++(1)求A 的大小;(2)若sinB+sinC=1试判断△ABC 的形状.4. 今年入夏以来,松花江哈尔滨段水位不断下降,达到历史最低水位,一条船在松花江某水段自西向东沿直线航行,在A 处测得航标C 在北偏东60°的方向上,前进100米到达B 处,又测得航标C 在北偏东45°方向上,如图.在以航标C 为圆心,120米长为半径的圆形区域内有浅滩,如果这条船继续前进,是否有被浅滩阻碍的危险?(错误!未找到引用源。
)5. 正数数列{}n a 的前n 项的和为n S ,满足21(2).8n n S a =+(1)求证:数列{}n a 是等差数列;(2)设1302n n b a =-,求数列{}n b 的前n 项和'n S 的最小值.6. 已知数列{}n a 的前n 项和为*1(1),(),3n n S a n N =-∈求证:数列{}n a 是等比数列,并求出通项公式.7. 已知正项等差数列错误!未找到引用源。
的前n 项和为错误!未找到引用源。
,若错误!未找到引用源。
=12,且2错误!未找到引用源。
,错误!未找到引用源。
,错误!未找到引用源。
+1成等比数列.(1) 求错误!未找到引用源。
的通项公式; (2)记3nn n a b =的前n 项和为n T ,求n T .一、 原式=31+cos2x 2+3sin2x+1-cos2x 2 降幂公式 =2+cos2x+3sin2x = 2+2sin(2x+π6) 辅助角公式 周期π (1)由-π2+2kπ≤2x+π6≤π2+2kπ得-π3+kπ≤x≤π6+kπ即增区间[-π3+kπ,π6+kπ],k ∈Z(3)设t=2x+π6,当-π4≤x≤π4时,求出t 的范围[-π3,2π3]画出正弦曲线sint ,截取[-π3,2π3]的一段,观察最值。
新人教A版必修5不等式练习题及答案1

不等式练习题(一)一、若a>b ,下列不等式中必然成立的是( )A 、b a 11<B 、1<ab C 、22a b > D 、0lg()a b -> 二、若-1<a<b<1,则下列不等式中成立的是( )A 、-2<a-b<0B 、-2<a-b<-1C 、-1<a-b<0D 、-1<a-b<13、与不等式1232≥--x x 同解的不等式是( ) A 、01≥-x B 、0232≥+-x x C 、lg (232+-x x )>0 D 、02123≥--+-x x x x 4.已知二次不等式210ax bx ++>的解集为{}21x x -<<,则,a b 的值为( ) 11221 D.122.,.,.,A a b B a b C a b a b =-=-=-=-==-== 5.方程2210()mx m x m -++=有两个不相等的实数解,则m 的取值范围是( )1110000444....A m B m C m m D m m >->-<<><>或或 6.若223121(),()f x x x g x x x =-+=+-,则(),()f x g x 的大小关系是( ).()().()().()().A f x g x B f x g x C f x g x D >=<随x 的值转变而转变 7、不等式x x 283)31(2-->的解集是8.若 0112,,x y ≤≤-≤≤则4z x y =+的最小值为_______,最大值为_______.9.已知不等式240x ax ++<的解集为空集,则a 的取值范围是_______________.10、已知14x y -<+<且23x y <-<,则 23z x y =-的取值范围是__________.11.(1)已知函数231()log ()f x ax ax =-+的概念域为R ,求实数a 的取值范围;(2)已知函数231()log ()f x ax ax =-+的值域为R ,求实数a 的取值范围;1二、已知不等式250ax x b -+>解集是{}32x x -<<-,求不等式250bx x a -+<的解集13.已知函数22222()()y a x a x =-+--的图象在x 轴下方,求实数a 的取值范围.14.解关于x 的不等式222ax x ax -≥-不等式练习题一 参考答案 1-6 C A D C C A 7.{}24x x -<< ,99. {}44a a -≤≤ 10.(3,8) 1110424.()()a a ≤<≥{}111223.x x x <->-或 13.(学案62页11题){}02a a <≤14.0a =时,{}1x x ≤- 0a >时,{}21x x x a ≤-≥或 20a -<<时, {}21x x a≤≤- 2a =-时,{}1x x =-2a <-时,{}21x x a-≤≤。
(完整版)高中数学不等式测试题(基础卷)新人教A版必修5

不等式测试题(基础卷)1.如果01,0<<-<b a ,那么下列不等式成立的是( )A .2ab ab a >>B .a ab ab >>2C .2ab a ab >>D .a ab ab >>22.若b a >,则下列不等式中恒成立的是( )A .1>ba B .b a lg lg > C .b a 22> D .22b a > 3.下列函数中,最小值为4的是( )A .x x x f 4)(+=B .x x x f cos 4cos )(+=C .x x x f -⨯+=343)(D 10log lg )(x x x f +=. 4.若10,10<<<<b a ,则22,2,2,b a ab ab b a ++中最大的一个是 。
5.已知1,0,0=+>>b a b a ,则ba 11+的取值范围是 。
解:422211=⨯+≥++=+++=+b a a b b a a b b b a a b a b a ,当且仅当21==b a 时取“=”。
6.若不等式022>++bx ax 解集为⎭⎬⎫⎩⎨⎧<<-3121|x x ,则b a +的值为 。
解:31,21-分别是方程022=++bx ax 的两个根,即:31212,3121⨯-=+-=-a a b ,解得:2,12-=-=b a ,所以14-=+b a 。
7.当0>a 时,解关于x 的不等式01)1(2<++-x a ax 。
8.如果不等式)0(02≠<++a c bx ax 解集为∅,那么( )A .0,0>∆<aB .0,0≤∆<aC .0,0≤∆>aD .0,0≥∆>a9. 设123)(+-=a ax x f ,若存在)1,1(0-∈x ,使0)(0=x f ,则实数a 的取值范围是( )10.不等式02>++k x x 恒成立,则k 的取值范围是 。
人教版高中数学必修5不等式练习题及答案

第三章 不等式一、选择题1.假设a =2,b =log π3,c =log πsin 52π,则( ). A .a >b >cB .b >a >cC .c >a >bD .b >c >a2.设a ,b 是非零实数,且a <b ,则以下不等式成立的是( ). A .a 2<b 2B .ab 2<a 2bC .21ab<b a 21 D .a b <ba3.假设对任意实数x ∈R ,不等式|x |≥ax 恒成立,则实数a 的取值范围是( ). A .a <-1B .|a |≤1C .|a |<1D .a ≥14.不等式x 3-x ≥0的解集为( ). A .(1,+∞)B .[1,+∞)C .[0,1)∪(1,+∞)D .[-1,0]∪[1,+∞)5.已知f (x )在R 上是减函数,则满足f (11-x )>f (1)的实数取值范围是( ). A .(-∞,1)B .(2,+∞)C .(-∞,1)∪(2,+∞)D .(1,2)6.已知不等式f (x )=ax 2-x -c >0的解集为{x |-2<x <1},则函数y =f (-x )的图象为图中( ).A B C D7.设变量x ,y 满足约束条件⎪⎩⎪⎨⎧yx y x y x 2++- 则目标函数z =5x +y 的最大值是( ). A .2 B .3 C .4 D .58.设变量x ,y 满足⎪⎩⎪⎨⎧5--31+-3-+y x y x y x 设y =kx ,则k 的取值范围是( ).A .[21,34] B .[34,2] C .[21,2] D .[21,+∞) ≥0 ≤1≥1 ≥0≥1 ≤1 (第6题)9.已知a ,b ∈R ,则使|a |+|b |≥1成立的一个充分不必要条件是( ). A .|a +b |<1 B .a ≤1,且b ≤1 C .a <1,且b <1D .a 2+b 2≥110.假设lg x +lg y =2,则x1+y 1的最小值为( ). A .201B .51 C .21 D .2二、填空题11.以下四个不等式:①a <0<b ,②b <a <0,③b <0<a ,④0<b <a ,其中使a 1<b1成立的充分条件是 .12.设函数f (x )=⎩⎨⎧-11 则不等式xf (x )+x ≤4的解集是____________.13.假设不等式(-1)na <2+nn 1)1(+-对任意正整数n 恒成立, 则a 的取值范围是 .14.关于x 的不等式x 2-(a +a 1+1)x +a +a1<0(a >0)的解集为__________________. 15.假设不等式x 2-2x +3≤a 2-2a -1在R 上的解集是空集,则a 的取值范围是 .三、解答题16.已知函数f (x )=x 2-2x +2194)(x -,x ∈(-∞,1)∪(1,+∞),求f (x )的最小值.(x >0),(x <0).17.甲乙两人同时同地沿同一路线走向同一地点,甲有一半时间以速度m行走,另一半时间以速度n行走;乙有一半路程以速度m行走,另一半路程以速度n行走,假设m≠n,问甲乙两人谁先到达指定地点?18*.已知关于x的不等式(ax-5)(x2-a)<0的解集为M.(1)当a=4时,求集合M;(2)当3∈M,且5∈M时,求实数a的取值范围.第三章不等式参考答案一、选择题 1.A解析:三个以上的实数比较大小,可以先估算,进行分类(与0比较或与1比较),再应用不等式性质或作差法.因为π>1,0<sin52π<1,所以c =log π sin 52π<0. 又因为3>1,所以b =log π3>0,而a =2>0,故c 最小,只需再比较a 与b 的大小. 由指数函数的性质知,2>1而且0<log π 3<log π π=1,所以a >b ,即a >b >c . 2.C解析:比较两个实数的大小,可采用作差法,也可用特殊值排除法,以下用作差法. ∵a 2-b 2=(a +b )(a -b ),当a <b ,且a ,b 均为负数时,(a +b )( a -b )>0,a 2 >b 2,排除A . ∵ab 2-a 2b =ab (b -a ),由于b -a >0,当a ,b 同号时(比方a =1,b =2),ab (b -a )>0,ab 2>a 2b ,排除B .∵21ab -b a 21=22-b a b a <0,即21ab <b a 21. 同样可以用作差法判断a b <ba是错误的. 3.B解析:由于不等号两边的函数比较熟悉,可以尝试数形结合法. 令f (x )=|x |,g (x )=ax ,画出图象如右图, 由图可以看出|a |≤1. 4.D解析:用数轴标根法求解. x 3-x ≥0可化为 x (x -1)(x +1)≥0,如图,原不等式的解集为{x |-1≤x ≤0,或x ≥1}. 5.C解析:关键是利用单调性去掉“f ”,转化为不含“f ”的不等式求解.(第3题)(第4题)∵f (x )在R 上是减函数, ∴f (11-x )>f (1)⇔11-x <1⇔12--x x >0⇔x <1或x >2. 6.B解析:首先根据方程ax 2-x -c =0的根确定a ,c ,再求出f (-x ). 由已知,方程ax 2-x -c =0的两个实根为-2和1,则(-2)+1=a 1,(-2)×1=ac -,解得a =-1,c =-2,则f (x )=-x 2-x +2,f (-x )=-x 2+x +2=-(x -21)2+49,由开口方向和对称轴位置判断为B .7.D解:先画可行域如图.作直线l 0:5x +y =0,平行移动直线l 0至直线l ,从图形中可以发现,当直线l 经过平面区域内的点A 时,直线在y 轴的截距最大,此时z 最大.由⎩⎨⎧1=+1=2+y x y x ,解得⎩⎨⎧0=1=y x ,即A (1,0), ∴z =5×1+0=5.(第7题)8.C解析:k 的几何意义是可行域内的点与原点连线的斜率.解: 先画出题中不等式组所表示的区域(如图),可以看出k OA 最小,k OB 最大.由⎩⎨⎧⇔⎩⎨⎧1=2=0=3-+0=5--3y x y x y x 得A (2,1), k OA =-20-1=21; 由⎩⎨⎧⇔⎩⎨⎧2=1=0=3-+0=1+-y x y x y x 得B (1,2), k OB =0-10-2=2.∴21≤k ≤2,即k ∈[21,2].9.D分析:如果①:某选项能推出|a |+|b |≥1,则充分性成立;还需要②:|a |+|b |≥1不能推出该选项,①和②满足,该选项就是充分不必要条件.解:假设a 2+b 2≥1,则(|a |+|b |)2=a 2+2|ab |+b 2≥a 2+b 2≥1,|a |+|b |≥1,充分性成立.但|a |+|b |≥1时,未必有a 2+b 2≥1,例如21+21=1,然而221⎪⎭⎫ ⎝⎛+221⎪⎭⎫⎝⎛<1.10.B解:∵lg x +lg y =2,∴xy =100,且x >0,y >0, ∴x 1+y 1≥2y x 11⋅=xy2,即x 1+y 1≥51, 当且仅当⎩⎨⎧100==xy yx x =10,y =10时取等号.二、填空题 11.①②④. 解:a <0<b ⇒a 1<0<b1,充分性成立; b <a <0⇒ab >0,b -a <0⇒aba b -<0,即a 1<b 1,充分性成立;b <0<a ⇒b 1<0,a1>0⇒a 1>b 1,充分性不成立; (第8题)0<b <a ⇒ab >0,b -a <0⇒a 1<b1,充分性成立. 12.{x |0<x ≤2,或x <0}.解析:由于f (x )是分段函数,所以要分别对每一段(分别在x >0,x <0条件下)解不等式.由⎩⎨⎧ ⇔⎩⎨⎧ ⇔0<x ≤2, 由⎩⎨⎧ ⇔⎩⎨⎧ ⇔x <0, ∴0<x ≤2或x <0. 13.[-2,23). 解析:首先处理(-1)n ,需要对n 的奇偶性进行讨论. 假设n 为奇数,原不等式⇔-a <2+n 1⇔ a >-(2+n 1),即a >-(2+n1)对任意正奇数n 恒成立,因为-(2+n 1)=-2-n1<-2,所以只需a ≥-2. 假设n 为偶数,原不等式⇔a <2-n 1,即a <2-n1对任意正偶数n 恒成立, 只需a <(2-n 1)最小值=2-21=23,即a <23. 所以假设对任意正整数n 不等式恒成立,以上应同时满足, 故-2≤a <23. 14.{x |1<x <a +a1}. 解析:首先判断方程x 2-(a +a 1+1)x +a +a1=0(a >0)是否有实数根,实数根大小是否确定.x 2-(a +a 1+1)x +a +a 1<0可化为(x -1)[x -(a +a1)]<0, ∵a >0,a +a 1≥2>1,∴1<x <a +a1. 15.{x |-1<a <3}.解析:把问题等价转化为“恒成立”问题. x 2-2x +3≤a 2-2a -1在R 上的解集是空集, ⇔ x 2-2x +3>a 2-2a -1在R 上恒成立,x >0 xf (x )+x ≤4 x >0x ·1+x ≤4 x <0 xf (x )+x ≤4 x <0x ·(-1)+x ≤4⇔ x 2-2x -a 2+2a +4>0在R 上恒成立.因为抛物线y =x 2-2x -a 2+2a +4开口向上,故只需△=4-4(-a 2+2a +4)<0, 即x 2-2x +3<0⇔-1<a <3. 三、解答题16.解析:f (x )=(x -1)2+2194)(x --1≥294-1=31. 当x -1=2194)(x -时,即x =1±36时,f (x )取到最小值31. 17.分析:行走时间短者先到达指定地点,问题的实质是比较两个实数(式子)的大小,用作差法.解:设从出发地到指定地点的路程是s ,甲乙两人走完这段路程所用的时间分别为t 1,t 2,则s n t m t =2+211,2=2+2t n s m s ,所以t 1=n m s +2,t 2=mnsn m 2+)(. t 1-t 2=mns n m n m s 2+-+2)(=)(])([n m mn s n m mn +2+-42)()(n m mn s n m +2-=-2, 因为s ,m ,n 均为正数且m ≠n ,所以t 1-t 2<0,即t 1<t 2, 所以甲比乙先到达指定地点.18*.解:(1)当a =4时,(ax -5)(x 2-a )<0⇔(x -45)(x -2)(x +2)<0,由数轴标根法得x <-2,或45<x <2. 故M ={x |x <-2,或45<x <2}. (2)3∈M ,且5∈M⎪⎩⎪⎨⎧⇔ ⎪⎩⎪⎨⎧⇔))(())((25-1-9-35-a a a a ⎪⎩⎪⎨⎧⇔ ⇔1≤a <35,或9<a ≤25.故实数a 的取值范围是{x |1≤a <35,或9<a ≤25}. (3a -5)(9-a )<0(5a -5)(25-a )≥0 ≤0 a <35,或a >9 1≤a ≤25>0 (第18题)。
新人教版必修5第三章不等式练习题及答案ABC卷

数学5(必修)第三章:不等式[基础训练A 组]一、选择题1.若02522>-+-x x ,则221442-++-x x x 等于( )A .54-xB .3-C .3D .x 45-2.下列各对不等式中同解的是( )A .72<x 与 x x x +<+72B .0)1(2>+x 与 01≠+xC .13>-x 与13>-xD .33)1(x x >+与x x 111<+ 3.若122+x ≤()142x -,则函数2x y =的值域是( ) A .1[,2)8 B .1[,2]8 C .1(,]8-∞ D .[2,)+∞ 4.设11a b >>>-,则下列不等式中恒成立的是 ( )A .b a 11<B .b a 11>C .2a b >D .22a b > 5.如果实数,x y 满足221x y +=,则(1)(1)xy xy +-有 ( )A .最小值21和最大值1 B .最大值1和最小值43 C .最小值43而无最大值 D .最大值1而无最小值 6.二次方程22(1)20x a x a +++-=,有一个根比1大,另一个根比1-小, 则a 的取值范围是 ( )A .31a -<<B .20a -<<C .10a -<<D .02a <<二、填空题1.若方程2222(1)34420x m x m mn n ++++++=有实根,则实数m =_______;且实数n =_______。
2.一个两位数的个位数字比十位数字大2,若这个两位数小于30, 则这个两位数为________________。
3.设函数23()lg()4f x x x =--,则()f x 的单调递减区间是 。
4.当=x ______时,函数)2(22x x y -=有最_______值,且最值是_________。
人教A版高中数学必修五单元测评 不等式.docx
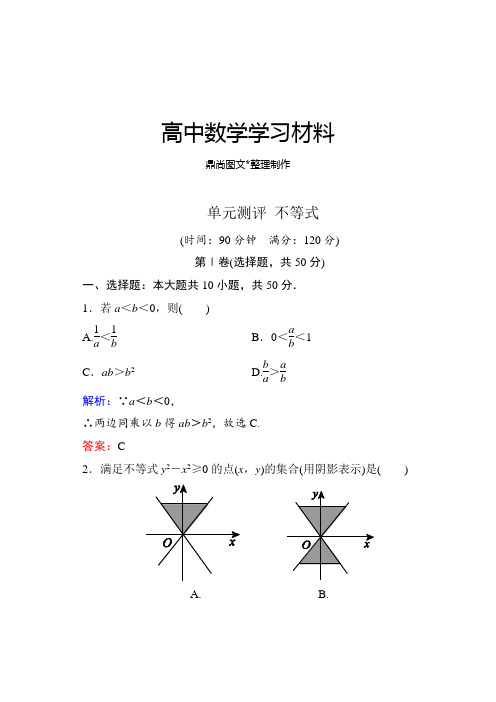
高中数学学习材料鼎尚图文*整理制作单元测评 不等式(时间:90分钟 满分:120分) 第Ⅰ卷(选择题,共50分)一、选择题:本大题共10小题,共50分. 1.若a <b <0,则( ) A.1a <1b B .0<ab <1 C .ab >b 2D.b a >a b解析:∵a <b <0,∴两边同乘以b 得ab >b 2,故选C. 答案:C2.满足不等式y 2-x 2≥0的点(x ,y )的集合(用阴影表示)是( )A. B.C. D.解析:取测试点(0,1)可知C ,D 错;再取测试点(0,-1)可知A 错,故选B.答案:B3.若a ,b ∈R ,则下列恒成立的不等式是( ) A.|a +b |2≥|ab | B.b a +ab ≥2C.a 2+b 22≥⎝ ⎛⎭⎪⎫a +b 22D .(a +b )⎝⎛⎭⎪⎫1a +1b ≥4解析:⎝ ⎛⎭⎪⎫a +b 22=a 2+b 2+2ab 4≤a 2+b 2+a 2+b 24=a 2+b 22,当且仅当a =b 时取等号,∴a 2+b 22≥⎝⎛⎭⎪⎫a +b 22. 答案:C4.在R 上定义运算☆,a ☆b =ab +2a +b ,则满足x ☆(x -2)<0的实数x 的取值范围为( )A .(0,2)B .(-2,1)C .(-∞,-2)∪(1,+∞)D .(-1,2)解析:根据定义得:x ☆(x -2)=x (x -2)+2x +(x -2)=x 2+x -2<0,解得-2<x <1,所以实数x 的取值范围为(-2,1),故选B.答案:B5.已知a ,b ,c ∈R +,且ab +bc +ca =1,那么下列不等式中正确的是( )A .a 2+b 2+c 2≥2B .(a +b +c )2≥3 C.1a +1b +1c ≥2 3D .abc (a +b +c )≤13解析:∵a 2+b 2≥2ab ,b 2+c 2≥2bc ,c 2+a 2≥2ac ,三式相加可知2(a 2+b 2+c 2)≥2(bc +ab +ac ),∴a 2+b 2+c 2≥1.∴a 2+b 2+c 2+2ab +2bc +2ca ≥1+2.∴(a +b +c )2≥3.答案:B6.若不等式⎝ ⎛⎭⎪⎫13x 2-2ax <33x +a2恒成立,则a 的取值范围为( )A .0<a <1B .a >34 C .0<a <34D .a <34解析:由题意得-x 2+2ax <3x +a 2恒成立,即x 2+(3-2a )x +a 2>0恒成立.所以Δ=(3-2a )2-4a 2<0,解得a >34,故选B.答案:B7.已知变量x ,y 满足⎩⎪⎨⎪⎧x ≥1,y ≥1,x +y -3≤0,目标函数是z =2x +y ,则有( )A .z max =5,z min =3B .z max =5,z 无最小值C .z min =3,z 无最大值D .z 既无最大值,也无最小值 解析:可行域为:如图所示:z 在A 点取得最小值,z min =3, z 在B 点取得最大值,z max =5. 答案:A8.若关于x 的方程9x +(4+a )·3x +4=0有解,则实数a 的取值范围是( )A .(-∞,-8]∪[0,+∞)B .(-∞,-4]C .(-∞,4]D .(-∞,-8]解析:分离变量:-(4+a )=3x+43x ≥4,得a ≤-8.故选D. 答案:D9.设奇函数f (x )在(0,+∞)上为增函数,且f (1)=0,则不等式f (x )-f (-x )x <0的解集为( )A .(-1,0)∪(1,+∞)B .(-∞,-1)∪(0,1)C .(-∞,-1)∪(1,+∞)D .(-1,0)∪(0,1)解析:f (x )-f (-x )x =2f (x )x <0. (1)当x >0时,f (x )<0,又∵f (x )在(0,+∞)上为增函数,f (1)=0,∴0<x <1.(2)当x <0时,f (x )>0,∵f (x )在(-∞,0)上也为增函数,f (-1)=0, ∴-1<x <0. 答案:D10.已知a ,b ,c ∈R ,a +b +c =0,abc >0,T =1a +1b +1c ,则( ) A .T >0 B .T <0 C .T =0D .T ≥0解析:方法一:取特殊值,a =2,b =c =-1, 则T =-32<0,排除A ,C ,D ,可知选B.方法二:由a +b +c =0,abc >0,知三数中一正两负,不妨设a >0,b <0,c <0,则T =1a +1b +1c =ab +bc +ca abc =ab +c (b +a )abc=ab -c 2abc . ∵ab <0,-c 2<0,abc >0,故T <0,应选B. 答案:B第Ⅱ卷(非选择题,共70分)二、填空题:本大题共4小题,每小题5分,共20分. 11.函数y =16-x -x2的定义域是__________. 解析:要使函数有意义,只需6-x -x 2>0,即x 2+x -6<0. ∵Δ=1+24=25>0,∴方程x 2+x -6=0有两个不相等的实数根分别为-3,2.∴不等式x 2+x -6<0的解为-3<x <2, ∴函数的定义域为{x |-3<x <2}.答案:{x |-3<x <2}12.若x >y >z >1,则xyz ,xy ,yz ,zx 从大到小依次排列为__________.解析:取特殊值法,由x >y >z >1, 可取x =4,y =3,z =2,分别代入得xyz =26,xy =23,yz =6,zx =2 2. 故xyz >xy >xz >yz . 答案:xyz >xy >xz >yz13.已知不等式(x +y )⎝ ⎛⎭⎪⎫1x +a y ≥9对任意正实数x ,y 恒成立,则正实数a 的最小值为__________.解析:∵(x +y )⎝ ⎛⎭⎪⎫1x +a y =1+ax y +yx +a ≥1+a +2a =(a +1)2,∴(a +1)2≥9,∴a ≥4.答案:414.若正数x ,y 满足2x +y -3=0,则x +2yxy 的最小值为__________. 解析:由题意:2x +y -3=0⇒2x 3+y3=1,∴x +2y xy =2x +1y =⎝⎛⎭⎪⎫2x +1y ·⎝⎛⎭⎪⎫2x 3+y 3=23⎝⎛⎭⎪⎫y x +x y +53≥23·2+53=3,当且仅当x =y =1时取得最小值. 答案:3三、解答题:本大题共4小题,满分50分.15.(12分)已知a ,b 是不相等的两个正数,求证:(a +b )(a 3+b 3)>(a 2+b 2)2.证明:∵(a +b )(a 3+b 3)-(a 2+b 2)2=(a 4+ab 3+ba 3+b 4)-(a 4+2a 2b 2+b 4) =ab (a -b )2,(6分) ∵a ,b ∈R +且a ≠b , ∴ab >0,(a -b )2>0, ∴ab (a -b )2>0.∴(a +b )(a 3+b 3)>(a 2+b 2)2.(12分)16.(12分)已知函数f (x )=-3x 2+a (6-a )x +c . (1)当c =19时,解关于a 的不等式f (1)>0.(2)若关于x 的不等式f (x )>0的解集是(-1,3),求实数a ,c 的值. 解:(1)由已知有:f (1)=-3+a (6-a )+19>0, 即a 2-6a -16<0,解得:-2<a <8. 所以不等式的解集为:(-2,8).(6分)(2)由关于x 的不等式f (x )>0的解集是(-1,3)可知:-1,3是关于x 的方程3x 2-a (6-a )x -c =0的两个根,则有⎩⎪⎨⎪⎧Δ>0,-1+3=a (6-a )3,-1×3=-c 3解得:a =3±3,c =9.(12分)17.(12分)已知α,β是方程x 2+ax +2b =0的两根,且α∈[0,1],β∈[1,2],a ,b ∈R ,求b -3a -1的最大值和最小值.解:∵⎩⎪⎨⎪⎧α+β=-a ,αβ=2b ,∴⎩⎨⎧a =-(α+β),b =αβ2.∵0≤α≤1,1≤β≤2,∴1≤α+β≤3,0≤αβ≤2.∴⎩⎪⎨⎪⎧-3≤a ≤-1,0≤b ≤1.(4分) 建立平面直角坐标系aOb ,则上述不等式组表示的平面区域如图所示.令k =b -3a -1,可以看成动点P (a ,b )与定点A (1,3)的连线的斜率.取B (-1,0),C (-3,1),则k AB =32,k AC =12. ∴12≤b -3a -1≤32.故b -3a -1的最大值是32,最小值是12.(12分) 18.(14分)某投资公司计划投资A ,B 两种金融产品,根据市场调查与预测,A 产品的利润y 1与投资金额x 的函数关系为y 1=18-180x +10,B 产品的利润y 2与投资金额x 的函数关系为y 2=x5,(注:利润与投资金额单位:万元)(1)该公司已有100万元资金,并全部投入A ,B 两种产品中,其中x 万元资金投入A 产品,试把A ,B 两种产品利润总和表示为x 的函数,并写出定义域;(2)试问:怎样分配这100万元资金,才能使公司获得最大利润?其最大利润为多少万元?解:(1)其中x 万元资金投入A 产品,则剩余的100-x (万元)资金投入B产品,利润总和f (x )=18-180x +10+100-x5=38-x 5-180x +10(x ∈[0,100])(6分)(2)∵f (x )=40-⎝ ⎛⎭⎪⎫x +105+180x +10,x ∈[0,100], ∴由基本不等式得:f (x )≤40-236=28,取等号当且仅当x +105=180x +10时,即x =20.(12分)答:分别用20万元和80万元资金投资A 、B 两种金融产品,可以使公司获得最大利润,最大利润为28万元.(14分)。
广东省佛山市顺德区罗定邦中学高中数学《不等式》测试题 新人教A版必修5

广东省佛山市顺德区罗定邦中学高中数学《不等式》测试题 新人教A版必修5班别_______组号______姓名_______学号______一、 选择题1.下列推导不正确的是( B )A .c a c b a b -<-⇒> B.,0c cc a b a b<>⇒> C.0,0a b a b c d d c>>>>⇒> D.*()n n a b n N a b <∈⇒< 2.不等式2610x x -++≥的解集为( )A .11[,]23- B.11[,]32 C.11,32⎡⎤-⎢⎥⎣⎦D.11[,]23--3. 设a >1>b >-1,则下列不等式中恒成立的是 ( ) A .ba 11< B .b a 11> C .a >b 2 D .a 2>2b4. 不等式3x -2y -6>0表示的区域在直线3x -2y -6=0 的( )A .右上方B .右下方C .左上方D .左下方 5. 一元二次不等式ax 2+bx +2>0的解集是(-21,31),则a +b 的值是 A. 10 B. -10 C. 14 D. -146. 不等式组1121032x y y x y ⎧-≥⎪⎪+>⎨⎪+≤⎪⎩的可行域是( )A. B.C. D.7. 当x>0时,下列各函数中最小值为2的是 ( ) A 、422+-=x x y B 、xx y 16+= C .21222+++=x x yD .xx y 1+= 8. 函数y =log21(x +41x ++1) (x > -1)的最大值是 ( )A .-2B .2C .-3D .3 请把..选择题答案填入下面表格........... 1 2 3 4 5 6 7 811.已知0,0,x y >>且42,x y +=则xy 的最大值为 ____________ 12.已知0<x<8,则(162)x x -的最大值为____________13. 已知不等式x 2-ax-b<0的解集为(2,3),则不等式bx 2-ax-1>0的解集为______________14. 对于任意实数x ,不等式()()222240a x a x ----<恒成立,则实数a 的取值范围是_______________三、解答题16.如下图所示,动物园要围成四间相同面积的长方形虎笼,一面可利用原有的墙,其他各面可用钢筋网围成.(1)现有可围36m长的材料,每间虎笼的长、宽设计为多少时,可使每间虎笼面积最大?(2)若使每间虎笼面积为24㎡,则每间虎笼的长、宽设计为多少时,可使围成四间虎笼的钢筋网总长最小?15.某厂拟生产甲、乙两种销售产品,每件销售收入分别为3000元、2000元.甲、乙产品都需要在A、B两种设备上加工,在每台A、B设备上加工1件甲设备所需工时分别为1h、2h,加工1件乙设备所需工时分别为2h、1h,A、B两种设备每月有效使用台时数分别为400h和500h。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广东省佛山市顺德区罗定邦中学高中数学《不等式》测试题 新人教A
版必修5
班别_______组号______姓名_______学号______
一、 选择题
1.下列推导不正确的是( B )
A .c a c b a b -<-⇒> B.
,0c c
c a b a b
<>⇒>
C.0,0a b c d >>>>⇒
>*
)n N a b <∈⇒< 2.不等式2
610x x -++≥的解集为( ) A .11[,]23-
B.11[,]32
C.11,32⎡⎤
-⎢⎥⎣⎦
D.11[,]23-- 3. 设a >1>b >-1,则下列不等式中恒成立的是 ( ) A .
b
a 11< B .
b a 1
1> C .a >b 2 D .a 2>2b
4. 不等式3x -2y -6>0表示的区域在直线3x -2y -6=0 的( )
A .右上方
B .右下方
C .左上方
D .左下方 5. 一元二次不等式ax 2
+bx +2>0的解集是(-
21,3
1
),则a +b 的值是 A. 10 B. -10 C. 14 D. -14
6. 不等式组1
121032x y y x y ⎧-≥⎪⎪
+>⎨⎪+≤⎪⎩
的可行域是( )
A. B.
C. D.
7. 当x>0时,下列各函数中最小值为2的是 ( ) A 、422
+-=x x y B 、x
x y 16+
= C .2
1222++
+=
x x y
D .x
x y 1+
= 8. 函数y =log
2
1(x +4
1x ++1) (x > -1)的最大值是 ( )
A .-2
B .2
C .-3
D .3 请把..选择题答案填入下面表格........... 6 11.已知0,0,x y >>且42,x y +=则xy 的最大值为 ____________ 12.已知0<x<8,则(162)x x -的最大值为
____________
13. 已知不等式x 2-ax-b<0的解集为(2,3),则不等式bx 2
-ax-1>0的解集为
______________
14. 对于任意实数x ,不等式()()2
22240a x a x ----<恒成立,则实数a 的取值范围是
_______________
三、解答题
16.如下图所示,动物园要围成四间相同面积的长方形虎笼,一面可利用原有的墙,其他各面可用钢筋网围成.
(1)现有可围36m长的材料,每间虎笼的长、
宽设计为多少时,可使每间虎笼面积最大?
(2)若使每间虎笼面积为24㎡,则每间虎
15.某厂拟生产甲、乙两种销售产品,每件销售收入分别为3000元、2000元.甲、乙产品都需要在A、B两种设备上加工,在每台A、B设备上加工1件甲设备所需工时分别为1h、2h,加工1件乙设备所需工时分别为2h、1h,A、B两种设备每月有效使用台时数分别为400h和500h。
如何安排生产可使收入最大?最大收入为多少?
17. 已知f(x)=x2-2kx-3k2
(1)解方程f(x)=0. (3分)。
