线性代数-矩阵的概念
矩阵的基本概念

矩阵的基本概念矩阵是线性代数中的重要概念,广泛应用于各个领域,如物理学、计算机科学、经济学等。
本文将介绍矩阵的基本概念,包括定义、表示、运算以及特殊类型的矩阵。
一、定义矩阵是一个二维数组,由m行n列的元素构成,示例如下: [a₁₁, a₁₂, ..., a₁ₙ][a₂₁, a₂₂, ..., a₂ₙ][ ... , ... , ..., ... ][aₙ₁, aₙ₂, ..., aₙₙ]其中aₙₙ表示矩阵中第k行第l列的元素。
二、表示矩阵可以用多种方式进行表示,常见的有行向量、列向量、分块矩阵和矩阵方程。
1. 行向量:将矩阵的一行元素写成一个行向量,示例如下:[a₁₁, a₁₂, ..., a₁ₙ]2. 列向量:将矩阵的一列元素写成一个列向量,示例如下:[a₁₁][a₂₁][ ... ][aₙ₁]3. 分块矩阵:将一个大矩阵划分为多个小矩阵组成的矩阵,示例如下:[A₁₁, A₁₂; A₂₁, A₂₂]4. 矩阵方程:将矩阵和向量之间的关系表示为矩阵方程,示例如下:AX = B三、运算矩阵有多种运算,包括加法、数乘、乘法和转置等。
1. 加法:两个矩阵的对应元素相加得到新的矩阵,示例如下:[A₁₁, A₁₂] [B₁₁, B₁₂] [A₁₁ + B₁₁, A₁₂ + B₁₂][A₂₁, A₂₂] + [B₂₁, B₂₂] = [A₂₁ + B₂₁, A₂₂ + B₂₂]2. 数乘:将矩阵中的每个元素乘以一个常数,示例如下:c * [A₁₁, A₁₂] = [cA₁₁, cA₁₂][A₂₁, A₂₂] [cA₂₁, cA₂₂]3. 乘法:两个矩阵的对应元素相乘然后相加得到新的矩阵,示例如下:[A₁₁, A₁₂] [B₁₁, B₁₂] [A₁₁B₁₁ + A₁₂B₂₁,A₁₁B₁₂ + A₁₂B₂₂][A₂₁, A₂₂] * [B₂₁, B₂₂] = [A₂₁B₁₁ + A₂₂B₂₁,A₂₁B₁₂ + A₂₂B₂₂]4. 转置:将矩阵的行和列互换得到新的矩阵,示例如下:[A₁₁, A₁₂, A₁₃] [A₁₁, A₂₁][A₂₁, A₂₂, A₂₃] -> [A₁₂, A₂₂][A₃₁, A₃₂, A₃₃] [A₁₃, A₂₃]四、特殊类型的矩阵矩阵还有一些特殊类型,包括零矩阵、单位矩阵、对角矩阵和方阵等。
矩阵的基本概念和运算

矩阵的基本概念和运算矩阵是线性代数中的基本概念之一,广泛应用于数学、工程学、计算机科学和物理学等领域。
它是一个由数字排列成的矩形阵列,其中的数字称为矩阵的元素。
本文将详细介绍矩阵的基本概念和运算。
一、矩阵的基本概念矩阵由m行n列的数字排列组成,可以表示为一个m×n的矩阵。
其中,m为矩阵的行数,n为矩阵的列数。
每个元素可以用下标表示,例如矩阵A的第i行第j列的元素可以用A(i,j)表示。
二、矩阵的表示和分类矩阵可以用方括号表示,例如A = [aij],其中aij表示矩阵A的第i 行第j列的元素。
矩阵还可以分为不同的类型,如行矩阵、列矩阵、方阵等。
行矩阵是只有一行的矩阵,可以表示为A = [a1, a2, ..., an],其中ai 为矩阵A的第i个元素。
列矩阵是只有一列的矩阵,可以表示为A = [a1; a2; ...; an],其中ai 为矩阵A的第i个元素。
方阵是行数和列数相等的矩阵,可以表示为A = [aij],其中i和j都从1到n。
三、矩阵的运算1. 矩阵的加法对于两个相同大小的矩阵A和B,它们的加法可以定义为A + B = [aij+ bij],其中aij和bij分别为矩阵A和B的对应元素。
2. 矩阵的减法对于两个相同大小的矩阵A和B,它们的减法可以定义为A - B = [aij- bij],其中aij和bij分别为矩阵A和B的对应元素。
3. 矩阵的数乘对于一个矩阵A和一个实数k,它们的数乘可以定义为kA = [kaij],其中aij为矩阵A的元素。
4. 矩阵的乘法对于两个矩阵A和B,它们的乘法可以定义为C = AB,其中C的第i行第j列的元素可以表示为C(i,j) = ∑(ai,k * bk,j),其中k从1到n,n为矩阵A和B的列数。
四、矩阵的转置矩阵的转置是将矩阵的行和列互换得到的新矩阵。
例如,若A = [aij]为一个m×n的矩阵,它的转置矩阵记作AT,即AT = [aji],其中a ji为矩阵A的第j行第i列的元素。
线性代数—矩阵的基本概念

n
注 对角阵是主对角元素不全为零, 其余元素都为零的方阵.
注 对角元素足以确定对角方阵本身.
(6) 标量阵和单位阵
当一对角阵的对角元全为同一非零常量时称为标量
阵(scalar matrix) ,如
5 0 0 0
K
0 0 0
5 0 0
0 5 0
0 50
1 0 0
形如
E
En
0
1
0
的方阵,称为单位阵或称
(1)零行(即其元素全为零的行)位于全部非零行的下方(如 果矩阵有零行的话);
(2)非零行的首非零元 (即位于最左边的非零元) 的列标随 其行标严格递增.
定义 若梯矩阵具有如下特征就称之为简化梯矩阵 (1) 非零行的首非零元为1; (2) 非零行的首非零元所在列的其余元素皆为零.
例
2 1 1 3
A
3
2
1
0
1
5 4 3 2 1
7 6 5 4 3
2、一些特殊的矩阵
元素是实数的矩阵称为实矩阵,
至少有一个元素是复数的矩阵称为复矩阵.
例
1
9
0 6
3 4
5
3
是一个2×4实矩阵;
13 6 2i
2
2i
2
是一个3×3 复矩阵;
2 2 2
1
2 3 5 9 是一个1×4实矩阵;
2
是一个3×1实矩阵;
yA x′
α
O
x
写成矩阵形式,记为
过渡矩阵
x y
cos
sin
sin x '
cos
y
'
例 (线性代数方程组)一般形式的线性方程组,即
线性代数中的矩阵:概念与基本性质

线性代数中的矩阵:概念与基本性质矩阵是线性代数中最基本、也是最常用的概念之一。
它是由若干个按照规定大小和次序排列的数构成的矩形阵列,常用大写字母表示。
下面将介绍矩阵的概念与基本性质。
一、矩阵的定义设有m行n列的数a_ij排成一个m×n的矩形阵列,则称这个m×n的阵列为一个矩阵,记作A=(a_ij),其中1≤i≤m,1≤j≤n。
在矩阵A中,a_ij称为矩阵A的第i行第j列的元素,第i行的元素排列在一起,构成了矩阵A的第i行,第j列的元素排列在一起,构成了矩阵A的第j列。
二、矩阵的基本性质1、矩阵的加法设矩阵A=(a_ij)与B=(b_ij)的大小及相对应的元素都相同,则A 与B的和C=A+B的元素c_ij=a_ij+b_ij,1≤i≤m,1≤j≤n。
矩阵加法具有结合律、交换律和分配律。
2、矩阵的数乘设k是一个数,矩阵A=(a_ij),则kA的元素为(k·a_ij),1≤i≤m,1≤j≤n。
矩阵数乘同样具有分配律和结合律。
3、矩阵的乘法设矩阵A=(a_ij)的大小为m×p,矩阵B=(b_ij)的大小为p×n,矩阵C=(c_ij)的大小为m×n,则称C=AB,如果c_ij=a_i1b_1j+a_i2b_2j+…+a_ipb_pj,1≤i≤m,1≤j≤n。
在矩阵C中,第i行第j列的元素c_ij是矩阵A的第i行的元素和矩阵B的第j列的元素的乘积和。
矩阵乘法不具有交换律。
4、矩阵的转置设矩阵A=(a_ij)的大小为m×n,则称A的转置矩阵为A^T=(b_ij),大小为n×m,其中b_ij=a_ji。
矩阵的转置具有分配律和结合律。
5、矩阵的逆设方阵A的大小为n×n,如果存在一个n×n的方阵B,使得AB=BA=E,其中E是n阶单位矩阵,那么称矩阵A是可逆的。
矩阵B称为矩阵A的逆矩阵,记作A^(-1)。
如果矩阵A是可逆的,则其逆矩阵唯一。
线性代数课件第2章矩阵

于乘法中的数1. 课件
20
定义5 方阵 A 的 n 次幂定义为 n 个方阵 A 连
乘,即
6 47n个48
An A AL A
其中 n 为正整数,规定 A0 E ,其运算规律:
(1)AkAl Akl ;
(2)(Ak)l Akl (k,l为正整数) .
因为矩阵乘法不满足交换律,所以两个 n 阶方
数,记 A ( a ij ) , A 称为 A的共轭矩阵.
其运算规律(设 A,B为复矩阵,为复数,且
运算都是可行的):
(1) ABAB; (2) AA ;
(3) ABAB.
课件
27
2.3 逆矩阵
课件
28
2.3.1 逆矩阵的定义及性质
定义9 设 A 为 n 阶方阵,若存在 n 阶方阵 B ,
课件
23
所以
0 17
( A B )T
1
4
1
3
3 1 0
解法2 (AB)TBTAT
1 4 2 2 1 0 17 7 2 0 0 314 13
1 3 11 2 3 10
课件
24
定义7 设 A为 n阶方阵,若满足 AT A ,则
称 A为对称矩阵,即 ai jaji(i,j1 ,2,,n)
a21
b21
M
a12 b12 L a22 b22 L
M
am1
bm1
am2 bm2
L
a1n b1n
a2n
b2n
M
amn
bmn
= (aij + bij ) 课件
10
例1 设
A
3 1
0 4
75,
则
线性代数1矩阵概念

矩阵是数学中的一个重要的基本概念,是代数学的一个主要研究对象,也是数 学研究和应用的一个重要工具。“矩阵”这个词是由西尔维斯特首先使用的,他是 为了将数字的矩形阵列区别于行列式而发明了这个述语。而实际上,矩阵这个课题 在诞生之前就已经发展的很好了。从行列式的大量工作中明显的表现出来,为了很 多目的,不管行列式的值是否与问题有关,方阵本身都可以研究和使用,矩阵的许 多基本性质也是在行列式的发展中建立起来的。在逻辑上,矩阵的概念应先于行列
amn
这个矩形表就称为矩阵
例1 设有线性方程组
x1 5x2 x3 x4 1
3xxx111
2x2 8x2 9x2
x3 x3 3x3
3x4 x4 7x4
3 1
7
这个方程组未知量系数及常数项按方程组中的顺序组成一个
4行5列的矩形阵列如下来自1 1315 2
8 9
1 1 1 3
1 3 1 7
0,就得到一个数表:
A
B
A B
C D
改成1,空白地方填上
C
D
0 1 1 0
1 0 1 0
1 0
0 1
0 0
1 0
这个数表反映了四城市间交通联接情况.
定义(矩阵)
由mn个数aij(i1 2 m j1 2 n)排成的一个m行n 列的矩形表称为一个mn矩阵(matrix) 记作
a11 a21
一、矩阵的加法
定义(矩阵加法)
两个mn矩阵A(aij)mn B(bij)mn将它们的对应位置元素 相加,得到的mn矩阵称为矩阵A与矩阵B的和 记为AB 即
AB(aij)mn(bij)mn(aijbij )mn
a11 b11
A
B
线性代数 第一章、矩阵

张一 98 90 87 72 李二 89 90 86 98 王三 97 84 75 87 刘六 85 88 85 88
解: 用矩阵表示为
98
89
90 90
87 86
72
98
97 84 75 87
85 88 85 88
11
几种比较特殊的矩阵:
行矩阵:只有一行的矩阵
列矩阵:只有一列的矩阵
L
L L L
称为线性变换的系数矩阵。
am1
am 2
0 0 3
14
数量矩阵:对角矩阵中当 1 2 n时
例如:
5 0 0 0
0
5
0
0
就是一个数量矩阵
0 0 5 0
0
0
0
5
也就是说,数量矩阵是对角矩阵的一种特例
15
单位矩阵:当数量矩阵中对角线上的常数为1,
称为单位矩阵,用字母 E 或 En 表示
1 0 L 0
即
M M O M
ym am1 x1 am2 x2 amn xn .
称为由变量x1 ,x2 , ... ,xn到变量y1 ,y2 , ... ,ym的
变换为线性变换。线性变换由 m 个 n元函数
组成,每个函数都是变量的一次幂,故而称
之为线性变换。
17
a11 a12 L
其中,由系数构成的矩阵
A
a21
a22
0
0
L
1
特点:从左上角到右下角的直线(主对角线)上
的元素都是1,其他元素都是0。
16
定义1.4
线性变换:
如果变量y1 ,y2 ,... ,ym可由变量x1 ,x2 ,... ,xn线性表示,
线性代数第一章 矩阵

16 150 160 140
丁 25
16 180 150 150
甲乙丙丁 单价 20 50 30 25 重量 16 20 16 16
200 180 190 100 120 100 150 160 140 180 150 150
第一章 矩阵
§1.1 矩阵概念
例2. 四个城市间的单向航线如图所示.
1
4
甲 220 185 200
乙 105 120 110
第二次
两次累计:
产品
发到各商场的数量
ABC
甲 420
乙
第一章 矩阵
§1.2 矩阵的基本运算
§1.2 矩阵的基本运算
一. 矩阵的线性运算
1. 加法
例3.
产品
发到各商场的数量
ABC
甲 200 180 190
乙 100 120 100
第一次
产品
发到各商场的数量
例如A =
1 0
1 0
,B=
1 1
0 0
,
AB =
2 0
0 0
,
A2 =
1 0
1 0
= A, B2 =1 10ຫໍສະໝຸດ 0=B,(AB)2 =
4 0
0 0
,
A2B2 = AB =
2 0
0 0
,
第一章 矩阵
§1.2 矩阵的基本运算
例:
1 设A = BC, 其中B = 2 , C = [1 2 3],
2
3
若用aij表示从i市到j市航线的条数, 则上图信息可表示为
a11 a12 a13 a14
01 1 1
a21 a22 a23 a24 a31 a32 a33 a34
矩阵的基本概念与运算

矩阵的基本概念与运算矩阵是线性代数中的重要概念,广泛应用于数学、物理、计算机科学等领域。
本文将介绍矩阵的基本概念、运算规则以及常见的应用。
一、矩阵的基本概念矩阵是由数个数排列成的矩形阵列。
矩阵可以用方括号表示,例如:A = [a11, a12, a13;a21, a22, a23;a31, a32, a33]其中a11、a12等为矩阵元素,按行排列。
矩阵的行数为m,列数为n,则该矩阵称为m×n矩阵。
矩阵可以是实数矩阵,也可以是复数矩阵。
实数矩阵的元素全为实数,复数矩阵的元素可以是复数。
例如:B = [3+2i, -4-7i, 5+6i;-2+3i, 1-5i, -2i]二、矩阵的运算1. 矩阵的加法和减法若A、B为同型矩阵(行数和列数相同),则有:A +B = [a11+b11, a12+b12, a13+b13;a21+b21, a22+b22, a23+b23;a31+b31, a32+b32, a33+b33]A -B = [a11-b11, a12-b12, a13-b13;a21-b21, a22-b22, a23-b23;a31-b31, a32-b32, a33-b33]2. 矩阵的数乘若A为m×n矩阵,k为标量,则有:kA = [ka11, ka12, ka13;ka21, ka22, ka23;ka31, ka32, ka33]3. 矩阵的乘法若A为m×n矩阵,B为n×p矩阵,则它们的乘积AB为m×p矩阵,满足:AB = [c11, c12, c13;c21, c22, c23;c31, c32, c33]其中:c11 = a11b11 + a12b21 + a13b31c12 = a11b12 + a12b22 + a13b32c13 = a11b13 + a12b23 + a13b33...c33 = a31b13 + a32b23 + a33b334. 矩阵的转置若A为m×n矩阵,则其转置记作A^T,为n×m矩阵,满足:A^T = [a11, a21, a31;a12, a22, a32;a13, a23, a33]三、矩阵的应用1. 网络图论矩阵可以用于表示和分析网络图论中的关系和连接。
第一章线性代数
2. 初等矩阵的性质 定理1.1. 定理1.1. 对m×n矩阵A施行一次初等行变换 矩阵A施行一次初等行 相当于在A 相当于在A的左边乘以相应的初等 矩阵; 施行一次初等列 矩阵; 对A施行一次初等列变换相 当于在A 当于在A的右边乘以相应的初等矩 阵.
第一章 矩阵
§1.5 方阵的逆矩阵
§1.5 方阵的逆矩阵 一. 逆矩阵的概念 1. 定义: 设A为方阵, 若存在方阵B, 使得 定义: 为方阵, 若存在方阵B AB = BA = E, 则称A可逆, 并称B 则称A可逆, 并称B为A的逆矩阵. 逆矩阵. 2. 逆矩阵是唯一的, A−1. 逆矩阵是唯一的, 记为A 记为 3. 性质:设A, B为同阶可逆方阵, 数k ≠ 0. 则 性质: 为同阶可逆方阵, (1) (A−1)−1 = A. (2) (AT)−1 = (A−1)T. (A (3) (kA)−1 = k−1A−1. (4) (AB)−1 = B−1A−1.
则λA =
λA11 λA12 … λA1r λA21 λA22 … λA2r
… … … … . λAs1 λAs2 … λAsr
第一章 矩阵
§1.3 分块矩阵
3. 分块乘法
设A为m×l矩阵, B为l ×n矩阵, 将它们分块如下 矩阵, 矩阵, A11 A12 … A1t B11 B12 … B1r A21 A22 … A2t B21 B22 … B2r A= … … … … , B= … … … … , As1 As2 … Ast Bt1 Bt2 … Btr 其中A 的列数分别与B 其中Ai1, Ai2, …, Ait的列数分别与B1j, B2j, …, Btj的 行数相等. 行数相等. C11 C12 … C1r t C21 C22 … C2r 其中C 则AB = … … … … , 其中Cij = Σ AikBkj , k=1 Cs1 Cs2 … Csr (i = 1, 2, …, s; j = 1, 2, …, r.)
矩阵的概念与性质

矩阵的概念与性质矩阵是线性代数中的重要概念,广泛应用于数学、计算机科学、物理学等领域。
它是一种由数值排列成的矩形阵列。
在本文中,我们将介绍矩阵的基本概念以及其一些重要的性质。
一、矩阵的定义矩阵是由m行n列数值组成的矩形阵列,通常用大写字母表示。
其中m表示矩阵的行数,n表示矩阵的列数。
矩阵中的每个数值称为元素,表示为aij,其中i表示元素所在的行号,j表示元素所在的列号。
例如,一个3行2列的矩阵可以表示为:[ a11 a12 ][ a21 a22 ][ a31 a32 ]二、矩阵的类型根据矩阵的性质,可以将矩阵分为以下几种类型:1. 零矩阵:所有元素都为零的矩阵,通常用0表示。
2. 方阵:行数等于列数的矩阵称为方阵。
例如,一个3行3列的方阵可以表示为:[ a11 a12 a13 ][ a21 a22 a23 ][ a31 a32 a33 ]3. 对角矩阵:除了对角线上的元素外,其余元素都为零的矩阵称为对角矩阵。
例如,一个3行3列的对角矩阵可以表示为:[ a11 0 0 ][ 0 a22 0 ][ 0 0 a33 ]4. 单位矩阵:对角线上的元素都为1,其余元素都为零的矩阵称为单位矩阵。
单位矩阵通常表示为I。
5. 转置矩阵:将矩阵的行列互换得到的矩阵称为转置矩阵。
例如,对于矩阵A的转置矩阵表示为AT。
三、矩阵的性质矩阵具有许多重要的性质,下面我们将介绍几个常见的性质:1. 加法性质:对于两个同型矩阵A和B,它们的和矩阵C等于对应元素相加得到的矩阵。
即C = A + B。
2. 数乘性质:矩阵A的每个元素都乘以一个标量k得到的矩阵称为矩阵的数乘。
即kA。
3. 乘法性质:对于两个矩阵A和B,当A的列数等于B的行数时,它们可以相乘得到一个新的矩阵C。
即C = AB。
4. 逆矩阵:如果一个方阵A存在一个矩阵B,满足AB = BA = I,那么矩阵B称为矩阵A的逆矩阵。
只有可逆矩阵才能求逆矩阵。
5. 矩阵的转置性质:对于矩阵A,它的转置矩阵AT的转置矩阵等于A。
矩阵的概念和计算

矩阵的概念和计算矩阵是线性代数中一种重要的数学工具,广泛应用于各个领域,包括物理、工程、计算机科学等。
本文将详细介绍矩阵的概念,以及矩阵的基本运算和计算方法。
一、矩阵的概念矩阵是由数个数按一定的规律排列成的长方形阵列。
矩阵由m行n列元素组成,可以表示成一个m×n的形式。
其中,m表示矩阵的行数,n表示矩阵的列数。
每个元素在矩阵中由其所在的行号和列号来确定。
例如,一个3×2的矩阵可以表示为:A = [a11, a12;a21, a22;a31, a32]其中,a11, a12, a21, a22, a31, a32分别表示矩阵A中的元素。
二、矩阵的基本运算1. 矩阵的加法矩阵的加法是指对应元素相加,要求两个矩阵具有相同的行数和列数。
例如,对于两个3×2的矩阵A和B,其加法可以表示为:C = A + B = [a11 + b11, a12 + b12;a21 + b21, a22 + b22;a31 + b31, a32 + b32]2. 矩阵的减法矩阵的减法是指对应元素相减,同样需要两个矩阵具有相同的行数和列数。
例如,对于两个3×2的矩阵A和B,其减法可以表示为:C = A - B = [a11 - b11, a12 - b12;a21 - b21, a22 - b22;a31 - b31, a32 - b32]3. 矩阵的数乘矩阵的数乘是指矩阵中的每个元素都乘以一个常数。
例如,对于一个3×2的矩阵A和一个常数k,其数乘可以表示为:B = kA = [ka11, ka12;ka21, ka22;ka31, ka32]4. 矩阵的乘法矩阵的乘法是指满足前一个矩阵的列数等于后一个矩阵的行数的情况下,将相应的元素相乘再相加得到新的矩阵。
例如,对于一个m×n 的矩阵A和一个n×p的矩阵B,其乘法可以表示为:C = AB = [c11, c12, ..., c1p;c21, c22, ..., c2p;...cm1, cm2, ..., cmp]其中,cij表示矩阵C中第i行第j列的元素,其计算方法为:cij = a[i1]b[1j] + a[i2]b[2j] + ... + a[in]b[nj]三、矩阵的计算方法1. 矩阵的转置矩阵的转置指的是将矩阵的行和列互换得到的新矩阵。
线性代数的矩阵理论

线性代数的矩阵理论线性代数是数学中的一个重要分支,涉及向量空间以及在这些空间中的线性变换。
矩阵是线性代数核心的工具之一,其不仅在理论上具有深远的意义,还在计算和应用中起着不可或缺的作用。
本文将探讨矩阵的基本概念、性质、运算以及在实际中的应用。
一、矩阵的基本概念定义矩阵是按照矩形排列的复数或实数集合,用方括号或圆括号表示。
一个 m 行 n 列的矩阵称为 m x n 矩阵。
矩阵元素通常用 a_ij 表示,其中 i 表示行索引,j 表示列索引。
特例矩阵零矩阵:所有元素均为零的矩阵称为零矩阵,记作 O。
单位矩阵:对角线元素为1,其余元素为0的方阵称为单位矩阵,记作 I。
对称矩阵:若 A = A^T(A 的转置),则称 A 为对称矩阵。
逆矩阵:若存在一个 B 使得 AB = I,则 B 称为 A 的逆矩阵,记作 A^(-1)。
二、矩阵的性质加法性质两个同型矩阵相加结果也是同型矩阵,即对于任意的 m x n 矩阵 A 和 B,有 C = A + B 也是 m x n 矩阵。
乘法性质矩阵乘法并不满足交换律,但满足结合律和分配律。
在计算时,如果 A 是 m x n 矩阵,B 是 n x p 矩阵,则 C = AB 是 m x p 矩阵。
转置性质矩阵的转置乘积法则为 (AB)^T = B^T A^T,可以利用这个性质简化计算。
行列式与迹方阵的行列式是标量,拥有判别矩阵可逆性的意义。
迹是方阵对角线元素之和,在多种计算中具有重要作用。
三、矩阵运算加法与减法对于同型矩阵,可以逐元素进行加法或减法。
例如:数乘对任意实数或复数 k,与矩阵 A 的乘积 kA 是新的一组修改后的元素,该运算对每个元素进行扩展。
乘法假设 A 为 m x n 矩阵,B 为 n x p 矩阵,对应元素乘积规则如下:转置与逆转置是一种符号操作,将行列互换。
逆是求解 Ax = b 的重要方法,只有当行列式不为零时才存在。
四、特征值与特征向量定义及求解给定一个方阵 A,若存在标量λ 和非零向量 v,使得 Av = λv,则称λ 为 A 的特征值,而 v 为对应的特征向量。
线性代数教学课件:矩阵的概念

代
当i>j时, aij 0
数
2 3 0 1
如
0
1
1
1
=
0 0 0 2 0 0 0 1
=
▪下三角矩阵
a11 0
0
a21
a22
0
线
an1 , aij 0
1 0 0 0
数
如
2
4
0
0
=
3 0 1 0
1 2 1 1
=
可以建立线性方程组与矩阵的一一对应:
=
0 0 1
可以建立线性方程组与矩阵的一一对应:
如,称 A 2 1 1
线
1 0 1
为线性代数方程组
2 x1 x1
x2
x3 x3
1 的系数矩阵; 2
性 代
系数及常数项组成的矩阵
—
A
2
1
1
1
数
1 0 1 2
称为方程组的增广矩阵.
=
=
1.1 矩阵及其运算
同型矩阵: Amn , Bmn
例1.2 某企业生产4种产品,各种产品的季度产值
(单位:万元)如下表:
线
产值
季节 产品1 产品2 产品3 产品4
性
1 80 58 75 78
代
2 98 70 85 84
3 90 75 90 90
数
4 88 70 82 80
80
这个数表 98
90
58 70 75
75 85 90
78 84
具体描述了这家企业各种产品 各季度的产值,同时也揭示了
代
▪行矩阵或行向量
a1 a2 an 如(1 0 1 2) 数
线性代数第一章

a1n aM2n , amn
称为m行n 列矩阵, 简称m n 矩阵. 其中aij称为矩阵
的第i行第 j 列元素, 也称为矩阵的(i, j)元.
矩阵常用大写英文字母表示,如 A, B,C,L . 有时记作 [aij ], Amn,或[aij ]mn .
a11 a12 L
A
a21 M
a22 M
65 3 2
6 0
r2 2r1
r3 r1 r3 4r1
0 0
1 1
2 2
0 0
3 3
2 2
4 7 6 14 5 12
0 1 2 2 1 4
1 2 1 3 1 2
1 2 1 0 5 7
r3 r2
r3 r2
0
1
2 0 3 2 12r3 0 1
20
3
2
r3 r4 0 0 0 2 4 6 r13r3 0 0 0 1 2 3
L
am1 am2 L
a1n aM2n aij amn
当P = R时 , 矩阵A称为实矩阵; 当P = C时 , 矩阵A称为复矩阵.
特殊矩阵
(1)零矩阵:元素全为零的矩阵,记作 Osn , 或O .
(2)行向量(矩阵):只有一行的矩阵. (3)列向量(矩阵):只有一列的矩阵.
同型矩阵:行数、列数均相等的两个矩 阵.
转置矩阵
定义1.2.3 将一个m n矩阵
a11 a12 L
A
a21
a22
L
M M
am1 am2 L
a1n
a2
n
M
amn
的行依次变列(或列依次变行)所得到的n m 矩阵
a11 a21 L
a12
线性代数 矩阵的概念

矩阵矩阵的概念⏹矩阵的概念⏹方阵的行列式矩阵的概念111212122212n n m m mn a a a a a a A a a a 简记为.ij n m ij n m a a A A 元的矩阵n m A ,定义由m ×n 个数排列成m 行n 列的数表叫做m n 矩阵.这记作个数,称为A 的元素, 简称为元.m ×n 矩阵的概念矩阵的概念注意:矩阵和行列式是两个完全不同的概念, 行列式表示一个数, 而矩阵一个数表.●元素是实数的矩阵称为实矩阵. ●元素是复数的矩阵称为复矩阵.矩阵的概念例如654254012是一个实矩阵,42242549944427321i 是一个复矩阵,334221 是一个矩阵,41 4是一个矩阵.11矩阵的概念●如果A, B 都是m ×n 矩阵, 就说A 与B 是同型的.●如果A m ×n 矩阵的所有的元都是零的矩阵称为零矩阵,记为0mxn .例如00000000是一个零矩阵.42矩阵的概念在m n 矩阵A =(a ij )中, 当m =n 时,称为n 阶方阵, 简记为(a ij )n .111212122212,n n n n nn a a a a a a A a a a在n 阶方阵A=(a ij )n 中, 连接元素a 11,a 22,…,a nn 的直线称为方阵A 的主对角线, 这里a 11,a 22,…,a nn 称为主对角元素.矩阵的概念132609422是一个3阶方阵.例如矩阵的概念●只有一行的矩阵 ,,,,21n a a a A 称为行矩阵(或行向量).,21n a a a B 称为列矩阵(或列向量).●只有一列的矩阵●介绍几种特殊形状的矩阵矩阵的概念(3)形如O O 不全为0若全为1若全为k ●称这样的矩阵为对角矩阵.●称这样的矩阵为n 阶单位矩阵,记为: .nE ●称这样的矩阵为数量矩阵,k 为数字.12000000n 的方阵,21001E 3100010001E 100010001n E矩阵的概念 nn n n a a a a a a ...00...0 (22211211)nn n n a a a a a a 21222111000为上三角形矩阵.为下三角形矩阵.形如形如O O 上、下三角形矩阵矩阵的概念定义设n 阶方阵:则称与此n 阶方阵A 相对应的n 阶行列式:为方阵A 的行列式,记为A (或det A ). nn n n a a a A :222211111212......::...n n a a a a a a 方阵的行列式111212122212......:::...n n n n nn a a a a a a a a a。
矩阵知识点归纳

矩阵知识点归纳矩阵是线性代数中一种重要的数学工具,它广泛应用于科学、工程、计算机科学等领域。
本文将对矩阵的基本概念、运算法则以及常见的矩阵类型进行归纳总结。
一、矩阵的基本概念1. 矩阵的定义:矩阵是由m行n列的元素排列而成的矩形阵列,用大写字母表示,如A。
其中,m表示矩阵的行数,n表示矩阵的列数。
2. 元素:矩阵中的数值称为元素,用小写字母表示,如a。
矩阵A的第i行第j列的元素表示为a_ij。
3. 零矩阵:所有元素都为0的矩阵,用0表示。
4. 单位矩阵:主对角线上的元素为1,其他元素为0的矩阵,用I表示。
5. 行向量和列向量:只有一行的矩阵称为行向量,只有一列的矩阵称为列向量。
二、矩阵的运算法则1. 矩阵的加法:两个相同维数的矩阵相加,即对应位置的元素相加。
2. 矩阵的减法:两个相同维数的矩阵相减,即对应位置的元素相减。
3. 矩阵的数乘:用一个数乘以矩阵的每个元素。
4. 矩阵的乘法:矩阵乘法需要满足左矩阵的列数等于右矩阵的行数。
若A是m×n的矩阵,B是n×p的矩阵,那么A与B的乘积AB是m×p的矩阵,且AB的第i行第j列元素为A的第i行与B的第j列对应元素的乘积之和。
5. 转置:将矩阵的行和列对调得到的矩阵称为原矩阵的转置。
若A为m×n的矩阵,其转置记作A^T,即A的第i行第j列元素等于A^T的第j行第i列元素。
三、常见的矩阵类型1. 方阵:行数和列数相等的矩阵称为方阵。
2. 对角矩阵:主对角线以外的元素都为0的方阵称为对角矩阵。
3. 上三角矩阵:主对角线以下的元素都为0的方阵称为上三角矩阵。
4. 下三角矩阵:主对角线以上的元素都为0的方阵称为下三角矩阵。
5. 对称矩阵:元素满足a_ij=a_ji的方阵称为对称矩阵。
6. 反对称矩阵:元素满足a_ij=-a_ji的方阵称为反对称矩阵。
7. 单位矩阵:主对角线上的元素为1,其他元素为0的方阵称为单位矩阵。
四、矩阵的性质1. 矩阵的零点乘法:任何矩阵与零矩阵相乘,结果都是零矩阵。
矩阵的总结知识点

矩阵的总结知识点一、矩阵的基本概念1. 矩阵的定义矩阵是一个按照矩形排列的数学对象。
矩阵的概念最早出现在线性代数理论中,它是由m行n列的数字排成的矩形阵列。
通常表示为一个大写字母,比如A,而矩阵中的元素通常用小写字母表示,比如a_ij,表示在第i行第j列的元素。
2. 矩阵的类型根据矩阵的形状和性质不同,可以将矩阵分为多种类型,比如方阵、对称矩阵、对角矩阵、三角矩阵等。
方阵是指行数和列数相等的矩阵,对称矩阵是指矩阵关于主对角线对称,对角矩阵是指除了主对角线上的元素外,其他元素都为零,而三角矩阵是指上三角或下三角矩阵。
3. 矩阵的运算矩阵的运算包括矩阵的加法、减法、数乘、矩阵的乘法等。
其中,矩阵的加法和减法要求相加的矩阵具有相同的形状,即行数和列数相同;而矩阵的数乘是指矩阵中的每个元素都乘以一个标量;矩阵的乘法是指矩阵A的列数等于矩阵B的行数时,可以进行矩阵乘法运算。
4. 矩阵的转置和逆矩阵矩阵的转置是指将矩阵的行和列对调得到一个新的矩阵,记作A^T。
而逆矩阵是指如果一个矩阵A存在逆矩阵A^(-1),使得A*A^(-1)=I,其中I是单位矩阵,则称矩阵A可逆,否则称矩阵A为奇异矩阵。
二、矩阵的应用1. 线性方程组的求解矩阵可以用来表示和求解线性方程组,线性方程组可以表示成AX=B的形式,其中A是系数矩阵,X是未知数矩阵,B是常数矩阵。
通过矩阵的基本变换和行列式的计算,可以求解线性方程组的解。
2. 数据处理和分析在数据处理和分析领域,矩阵可以用来表示和处理大规模的数据集。
比如,在机器学习算法中,可以通过矩阵的运算和矩阵分解来进行数据的降维和特征的提取。
3. 控制理论在控制理论中,矩阵可以用来描述线性系统的状态方程和控制方程,通过对状态矩阵和控制矩阵的计算和分析,可以得到系统的稳定性和控制性能。
4. 计算机图形学在计算机图形学中,矩阵可以用来描述和处理图形的旋转、平移、缩放等变换,通过矩阵的运算和矩阵乘法,可以实现图形的变换和动画效果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
的解取决于
系数 aiji, j 1,2,,n,
常数项 bi i 1,2,,n
一、矩阵概念的引入
线性方程组的系数与常数项按原位置可排为
a11 a21
a12 a22
a1n a2n
b1 b2
an1 an2 ann bn
2. 某航空公司在A,B,C,D四
对线性方程组的 研究可转化为对 这张表的研究.
是一个 11 矩阵.
三、几类特殊矩阵
几种特殊矩阵
(1)行数与列数都等于 n 的矩阵 A ,称为 n 阶
方阵.也可记作 An .
例如
13 2
6 2
2i 2
是一个3 阶方阵.
2 2 2
(2)只有一行的矩阵
A a1,a2 ,,an ,
称为行矩阵(或行向量).
三、几类特殊矩阵
只有一列的矩阵
a1
例1 n个变量x1, x2,, xn与m个变量y1, y2,, ym之 间的关系式
y1 a11x1 a12 x2 a1n xn ,
y2 a21x1 a22 x2 a2n xn ,
ym am1 x1 am2 x2 amn xn .
表示一个从变量x1, x2,, xn 到变量 y1, y2,, ym的 线性变换. 其中 aij为常数.
例如
0 0 0 0
0 0
0 0
0 0
0 0
0
0
0
0.
0 0 0 0
三、几类特殊矩阵
(5)方阵
1 0 0
E
En
0
1
O
0
O 0 0
1
称为单位矩阵(或单位阵).
(6)方阵
a 0
aE
aEn
0
O
a
0 0
O
0 0
a
称为数量矩阵(或数量阵).
全为1 全为a
三、几类特殊矩阵
同型矩阵与矩阵相等的概念
B
a2
,
an
称为列矩阵(或列向量). 不全为0
1 0
(3)形如
0
2
0 O 0
0
O0
的方阵,称为对角
n
矩阵(或对角阵).
三、几类特殊矩阵
记作 A diag1,2,,n .
(4)元素全为零的矩阵称为零矩阵,m n 零
矩阵记作 omn 或 o .
注意 不同阶数的零矩阵是不相等的.
记作
A Amn
aij
mn
aij
.
矩阵是线性代数的一个最基本的概念; 它最早是由英国数学家薛尔维斯特 (J.J.sylvester)于1850年提出的,用来 指行列式所联系的那个数字阵列,矩阵的 性质研究是在行列式理论研究中逐渐发展 起来的。
1858年,英国数学家凯莱(A.Cayley) 系统阐述了关于矩阵的理论,他被公认为 矩阵论的创始人。
A
B
C
D
A
B
C
D
0
1
1
0
1
0
1
0
1
0
0
1
0
1
0
0
这个数表反映了四城市间交通联接情况.
二、矩阵的概念
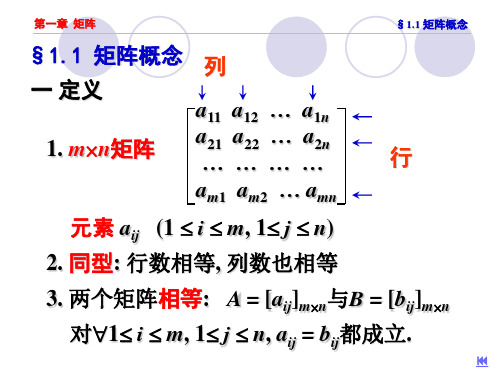
由 m n 个数 aij i 1,2,,m; j 1,2,,n
排成的 m行 n列的数表
a11 a12 a1n
a21 a22 a2n
am1 am2 amn
称为 m n矩阵.简称 m n 矩阵.
§2.1
矩 阵 的 概 念
• 一、引例 • 二、矩阵的概念 • 三、特殊矩阵 • 复习小结
一、矩阵概念的引入
a11 x1 a12 x2 a1n xn b1
1.
线性方程组
a21 x1 a22 x2 a2n xn b2
an1 x1 an2 x2 ann xn bn
这m n个数称为A的元素,简称为元. 元素是实数的矩阵称为实矩阵, 元素是复数的矩阵称为复矩阵.
二、矩阵的概念
例如
1 9
0 6
3 4
5 3
是一个 2 4 实矩阵,
13 2
6 2
2i 2
是一个
33
复矩阵,
1 2
2 2 2
4
2 3 5 9
是一个 3 1 矩阵,
4
是一个 1 4 矩阵,
三、几类特殊矩阵
y1 a11x1 a12 x2 a1n xn ,
y2 a21x1 a22 x2 a2n xn ,
ym am1 x1 am2 x2 amn xn .
a11
A
a21
a12 a22
a1n a2n 系数矩阵
am1 am1 amn
小结
(1)矩阵的概念 m行n列的一个数表
a11
A
a21
a12
a22
a1n a2n
am1 am1 amn
(2) 特殊矩阵
方阵
m n;
a1
行矩阵与列矩阵; A
单位矩阵;
数量矩阵与对角矩阵;
1001aB110,a022, aan2,,a00n ,00.
零矩阵.
00 0 0 1 n
矩阵与行列式的有何区别?
矩阵与行列式有本质的区别,行列式是一个 算式,一个数字行列式经过计算可求得其值,而 矩阵仅仅是一个数表,它的行数和列数可以不同.
siny, cosy.
对应
cos sin sin cos
这是一个以原点为中心
旋转 角的旋转变换.
Y P1 x1, y1
Px, y
Oቤተ መጻሕፍቲ ባይዱ
X
三、几类特殊矩阵
例2 设 A 1 2 3, 3 1 2
B 1 x 3, y 1 z
已知 A B,求 x, y, z. 解 A B,
x 2, y 3, z 2.
B
城市之间开辟了若干航线 ,
如图所示表示了四城市间的 A
C
航班图,如果从A到B有航班,
则用带箭头的线连接 A 与B.
D
一、矩阵概念的引入
四城市间的航班图情况常用表格来表示: 到站
A
B
C
D
A
发站 B C
D
其中 表示有航班.
为了便于计算,把表中的 0,就得到一个数表:
改成1,空白地方填上
一、矩阵概念的引入
1.两个矩阵的行数相等,列数相等时,称为同型矩阵.
例如
1 5
62 与 184
3 4
为同型矩阵.
3 7 3 9
对应元2.素两相个等矩,阵即A aij 与B bij 为同型矩阵,并且
aij bij i 1,2,,m; j 1,2,,n,
则称矩阵 A与B相等,记作 A B.
三、几类特殊矩阵
矩阵是把一组数用一张表的形式联系 在一起,视为一个整体,当作一个“量” 来运算,用它来论述问题,可以使问题变 得简捷明了,更容易把握问题的整体和本 质。
二、矩阵的概念
a11
A
a21
a12
a22
a1n a2n
am1 am1 amn
矩阵A的
m, n元
注意:矩阵的写法(与行列式的区别)
三、几类特殊矩阵
线性变换与矩阵之间存在着一一对应关系.
若线性变换为
y1 x1,
y2 x2 ,
yn xn
y1 x1,
y2 x2 ,
yn xn
称之为恒等变换.
对应
1 0
0 1
0
0
单位阵.
0 0 1
三、几类特殊矩阵
线性变换
x1 y1
cosx sinx
