(完整版)信号与线性系统分析_(吴大正_第四版)第一章习题答案
(NEW)吴大正《信号与线性系统分析》(第4版)配套题库【名校考研真题+课后习题+章节题库+模拟试题】上册

二、判断题
任何系统的全响应必为零状态响应与零输入响应之和。( )[北京 邮电大学2012研]
【答案】×
【解析】零输入响应为仅由起始状态所产生的响应。零状态响应是系统 的初始状态为零时,仅由输入信号引起的响应。由此可知仅当系统满足 线性时,其全响应必为零状态响应与零输入响应之和。
三、分析计算题
1.已知某系统的转移函数 ,求系统的零状态响应
【答案】
【解析】设f1(t)=ε(t)由LTI系统的线性和时不变性得(由于该题 没有给出系统的初始状态,所以这里不考虑)
f(t)=ε(t-1)-ε(t-2)=f1(t-1)-f1(t-2)
3.已知某LTI系统,当t>0时有: 当输入f(t)=(e-t+2e-2t)ε(t)时,输出响应为(e-t+5e-2t) ε(t); 当输入f(t)=(2e-t+e-2t)ε(t)时,输出响应为(5e-t+e-2t) ε(t); 当输入f(t)=(e-t+e-2t)ε(t)时,输出响应为(e-t+e-2t) ε(t); 则当输入为f(t)=(e-t-e-2t)ε(t)时,系统的输出响应为 ______。[长沙理工大学2006研]
整理得:
则
关) 取其逆变换得:
(仅与输入有关) (仅与系统的初始状态有
第3章 离散系统的时域分析 一、选择题
1.有限长序列 的长度为4,欲使 与 的圆卷积和线卷积相同, 则长度L的最小值为( )。[中国科学院研究生院2012研] A.5 B.6 C.7 D.8 【答案】C
【解析】 的长度为4,则其线卷积的长度为4+4-1=7。当 与 的圆卷积 时, 与 的圆卷积和线卷积相同,可知L的最小
【答案】
;
;稳定
【解析】由
可知,该系统任意两个相邻的输出值之差就是该
信号与线性系统分析_(吴大正_第四版)习题答案12264精编版
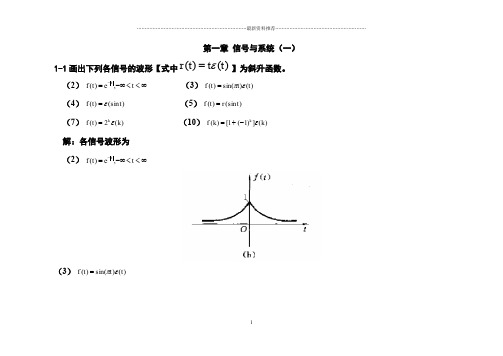
第一章 信号与系统(一)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 解:各信号波形为 (2)∞<<-∞=-t e t f t ,)((3))()sin()(t t t f επ=(4))fεt=(sin)(t(5))trf=(sin)(t(7))t(kf kε=)(2(10))f kεk-=(k+(])1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k---=εε 解:各信号波形为 (1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
吴大正《信号与线性系统分析》(第4版)笔记和课后习题(含考研

6.2课后习题详解
6.1复习笔记
6.3名校考研真题 详解
7.2课后习题详解
7.1复习笔记
7.3名校考研真题 详解
8.2课后习题详解
8.1复习笔记
8.3名校考研真题 详解
作者介绍
这是《吴大正《信号与线性系统分析》(第4版)笔记和课后习题(含考研真题)详解》的读书笔记模板,暂 无该书作者的介绍。
读书笔记
这是《吴大正《信号与线性系统分析》(第4版)笔记和课后习题(含考研真题)详解》的读书笔记模板,可 以替换为自己的心得。
精彩摘录
这是《吴大正《信号与线性系统分析》(第4版)笔记和课后习题(含考研真题)详解》的读书笔记模板,可 以替换为自己的精彩内容摘录。
感谢观看
暂无内容
目录分析
1.2课后习题详解
1.1复习笔记
1.3名校考研真题 详解
2.2课后习题详解
2.1复习笔记
2.3名校考研真题 详解
3.2课后习题详解
3.1复习笔记
3.3名校考研真题 详解
4.2课后习题详解
4.1复习笔记
4.3名校考研真题 详解
5.2课后习题详解
5.1复习笔记
5.3名校考研真题 详解
吴大正《信号与线性系统分析》 (第4版)笔记和课后习题 (含考研
读书笔记模板
01 思维导图
03 目录分析 05 读书笔记
目录
02 内容摘要 04 作者介绍 06 精彩摘录
思维导图
本书关键字分析思维导图
复习
域
笔记
习题
ห้องสมุดไป่ตู้时域
真题
频域
分析
内容
笔记 名校
状态变量
第版
信号与线性系统分析吴大正习题答案1_2

1-1画出下列各信号的波形【式中r(t) t (t)】为斜升函数。
(2) f(t) e N, t (4) f(t) (si nt) (7) f(t) 2k (k) 解:各信号波形为(2) f(t) e N, t (3) f(t) sin( t) (t) (5) f (t) r(sint) (10) f(k) [1 ( 1)k] (k)(hl(3) f(t) sin( t) (t)(4) f(t) (si nt)(d)(5) f(t) r(si nt)(7) f(t) 2k (k)(10) f(k) [1 ( 1)k] (k)2卜〔■■ 4* *0::2 3 4 5( 5 21-2画出下列各信号的波形[式中r(t)t (t)为斜升函数]。
(1) f(t) 2 (t 1) 3 (t1) (t 2)(2) f (t) r(t)2r(t1) r(t 2)(5) f(t)r(2t) (2 t)(8) f(k)k[ (k)(k 5)](11) f(k)k(k 7)](12) f(k)2k[ (3k) ( k)] sin( )[ (k)6解:各信号波形为⑴ f(t) 2 (t 1) 3 (t 1) (t 2)(5)f(t) r(2t) (2 t)r(t) 2r(t 1)r(t 2)j/O)Z\1 a7(b)⑵ f(t)4P -OF ■"■(8)f(k) k[ (k) (k 5)]O3)2 13,2<k(11)f(k) sin(~6)[ (k) (k 7)]fa)■MB -»r1.4 1 L_ K _o! 2 3 4 5 6(k)(12)f(k) 2k[ (3k) ( k)]g 8.I~o| 1 2 3 k(I)1-3写出图仁3所示各波形的表达式解图示各波形的表示式分别为:(a) /(f) — 2e(z — 1)—€(『一1) — F (t — 2.) (b)/ (t ) — (t —1)e (r — 1)—2(/—1)c ( f —1) — (t — 3)c ( / 一3)(= 10sint7rZ )_£(?) 一 M — 1 丿_= 1 — 2(r + 2) £(? + 2) — £(r + l)] + (r — 1) c(t H-l) —— 1)12.Ar>1.LIo i tb/(r)正菠函數—1 O l 23(b) I AO(d)1-4写出图1-4所示各序列的闭合形式表达式解图示各序列的闭台形式表示式分别为:(a)/(A)=讥+ 2) (b)/(A) = —3)——7)(c)/«) =e(-^+2) (d)f(k)= (一1)¥⑷1-5判别下列各序列是否为周期性的。
信与线性系统分析习题答案吴大正第四版高等教育出版社

第一章信号与系统(二)1-1画出下列各信号的波形【式中r(t)t(t)】为斜升函数。
(2)f(t) et t(3)f(t)sin( t) (t)(4)f (t) (sint)(5)f(t)r(sin t)(7)f(t) 2k (k)(10f(k) [1 ( 1)k] (k))解:各信号波形为(2)f(t) e N, t(3)f(t)sin( t)(t)(4)f(t)(s int)(5)f(t)r(si n t)(7)f(t)2k (k)(10)f(k)[1 (1)k] (k)1-2画出下列各信号的波形[式中r(t) t (t)为斜升函数]。
(1)f(t) 2 (t 1) 3 (t 1) (t 2) (2)f (t) r(t) 2r(t 1) r(t 2)(5)f (t) r(2t) (2 t) (8)f(k) k[ (k) (k 5)](11) f(k) ksin( )[ (k) (k 7)]6(12)f(k) 2k[ (3 k) ( k)]解:: 各信号波「形为(1) f(t) 2 (t 1) 3 (t 1) (t 2)(2) f(t) r(t) 2r(t 1) r(t2)(5) f(t)r(2t) (2 t)(8)f(k)k[ (k) (k 5)](11)f(k)ksin( § )[ (k) (k7)](12) f(k) 2k [ (3 k) ( k)]1-3写出图1-3所示各波形的表达式。
1-4写出图1-4所示各序列的闭合形式表达式。
1-5判别下列各序列是否为周期性的。
如果是,确定其周期。
Q■(2) f 2(k) cos(- k ) cos(—k )(5) f 5(t)3cost 2sin( t)4 4 3 6解:1-6已知信号f(t)的波形如图1-5所示,画出下列各函数的波形。
(6)f(0.5t 2)(1) f(t 1) (t) (2) f(t 1) (t 1) (5) f (1 2t)df (t) t(7) K ( 8) f(X)dx解:各信号波形为(1)f(t 1) (t)(2)f(t 1) (t 1)(5)f(1 2t)(6) f (0.5t 2)df(t)(7)dtt(8) f (x)dx1-7已知序列f(k)的图形如图1-7所示,画出下列各序列的图形。
(NEW)吴大正《信号与线性系统分析》(第4版)笔记和课后习题(含考研真题)详解

目 录第1章 信号与系统1.1 复习笔记1.2 课后习题详解1.3 名校考研真题详解第2章 连续系统的时域分析2.1 复习笔记2.2 课后习题详解2.3 名校考研真题详解第3章 离散系统的时域分析3.1 复习笔记3.2 课后习题详解3.3 名校考研真题详解第4章 傅里叶变换和系统的频域分析4.1 复习笔记4.2 课后习题详解4.3 名校考研真题详解第5章 连续系统的s域分析5.1 复习笔记5.2 课后习题详解5.3 名校考研真题详解第6章 离散系统的z域分析6.1 复习笔记6.2 课后习题详解6.3 名校考研真题详解第7章 系统函数7.1 复习笔记7.2 课后习题详解7.3 名校考研真题详解第8章 系统的状态变量分析8.1 复习笔记8.2 课后习题详解8.3 名校考研真题详解第1章 信号与系统1.1 复习笔记一、信号的基本概念与分类信号是载有信息的随时间变化的物理量或物理现象,其图像为信号的波形。
根据信号的不同特性,可对信号进行不同的分类:确定信号与随机信号;周期信号与非周期信号;连续时间信号与离散时间信号;实信号与复信号;能量信号与功率信号等。
二、信号的基本运算1加法和乘法f1(t)±f2(t)或f1(t)×f2(t)两信号f1(·)和f2(·)的相加、减、乘指同一时刻两信号之值对应相加、减、乘。
2.反转和平移(1)反转f(-t)f(-t)波形为f(t)波形以t=0为轴反转。
图1-1(2)平移f(t+t0)t0>0,f(t+t0)为f(t)波形在t轴上左移t0;t0<0,f(t+t0)为f(t)波形在t轴上右移t0。
图1-2平移的应用:在雷达系统中,雷达接收到的目标回波信号比发射信号延迟了时间t0,利用该延迟时间t0可以计算出目标与雷达之间的距离。
这里雷达接收到的目标回波信号就是延时信号。
3.尺度变换f(at)若a>1,则f(at)波形为f(t)的波形在时间轴上压缩为原来的;若0<a<1,则f(at)波形为f(t)的波形在时间轴上扩展为原来的;若a<0,则f(at)波形为f(t)的波形反转并压缩或展宽至。
信号与线性系统分析_(第四版)习题答案

专业课习题解析课程xxxxxx大学844信号与系统专业课习题解析课程第1讲第一章信号与系统(一)专业课习题解析课程第2讲第一章 信号与系统(二)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f =(7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为(2)∞<<-∞=-t e t f t ,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))tf=r)(sin(t(7))f kε=t)(2(k(10))(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=kkkkfεεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的辯达式。
1-4 写出图1-4所示各序列的闭合形式辯达式。
信号与线性系统分析课后答案_吴大正
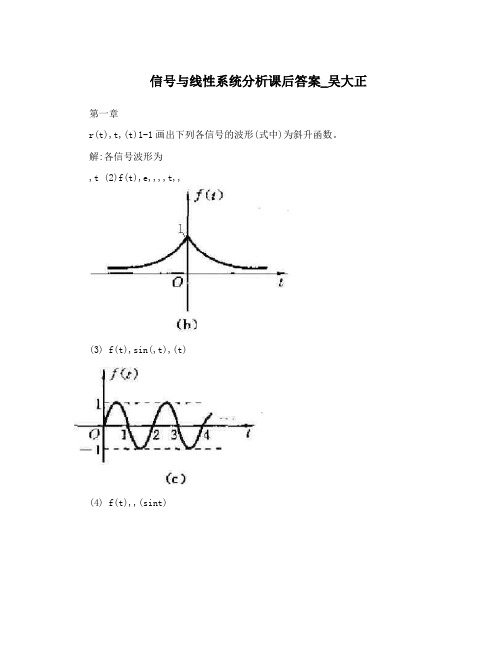
信号与线性系统分析课后答案_吴大正第一章r(t),t,(t)1-1画出下列各信号的波形(式中)为斜升函数。
解:各信号波形为,t (2)f(t),e,,,,t,,(3) f(t),sin(,t),(t)(4) f(t),,(sint)(5) f(t),r(sint)k(7) f(t),2,(k)k(10) f(k),[1,(,1)],(k)r(t),t,(t)1-2 画出下列各信号的波形[为斜升函数]。
f(t),r(t),2r(t,1),r(t,2)f(t),2,(t,1),3,(t,1),,(t,2) (1) (2) f(k),k[,(k),,(k,5)]f(t),r(2t),(2,t) (5) (8),kkf(k),sin()[,(k),,(k,7)]f(k),2[,(3,k),,(,k)](11) (12) 6解:各信号波形为f(t),2,(t,1),3,(t,1),,(t,2) (1)f(t),r(t),2r(t,1),r(t,2) (2)f(t),r(2t),(2,t) (5)f(k),k[,(k),,(k,5)] (8),kf(k),sin()[,(k),,(k,7)](11) 6kf(k),2[,(3,k),,(,k)](12)1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
3,,,,f(t),3cost,2sin(,t)f(k),cos(k,),cos(k,) (2) (5) 524436 解:f(t)1-6 已知信号的波形如图1-5所示,画出下列各函数的波形。
f(0.5t,2)f(1,2t)f(t,1),(t)f(t,1),(t,1) (1) (2) (5) (6) tdf(t)f(x)dx (7) (8) ,,,dt解:各信号波形为f(t,1),(t) (1)f(t,1),(t,1) (2)f(1,2t) (5) f(0.5t,2) (6)df(t)(7) dttf(x)dx (8) ,,,f(k)1-7 已知序列的图形如图1-7所示,画出下列各序列的图形。
信号与系统(吴大正)--完整版答案--纠错修改后版本之欧阳家百创编

欧阳索引创编 2021.02.02第一章 信号与系统欧阳家百(2021.03.07)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+=解:各信号波形为 (2)∞<<-∞=-t e t f t,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(ttt rε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=ttttfεεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε(8))]5()([)(--=kkkkfεε(11))]7()()[6sin()(--=kkkkfεεπ(12))]()3([2)(kkkf k---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=ttttfεεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε(8))]5()([)(--=kkkkfεε(11))]7()()[6sin()(--=kkkkfεεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
欧阳索引创编 2021.02.02欧阳索引创编 2021.02.021-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
信号与线性系统分析吴大正习题答案1_2

1-1画出下列各信号的波形【式中r(t) t (t)】为斜升函数。
(2) f(t) e N, t (4) f(t) (si nt) (7) f(t) 2k (k) 解:各信号波形为(2) f(t) e N, t (3) f(t) sin( t) (t) (5) f (t) r(sint) (10) f(k) [1 ( 1)k] (k)(hl(3) f(t) sin( t) (t)(4) f(t) (si nt)(d)(5) f(t) r(si nt)(7) f(t) 2k (k)(10) f(k) [1 ( 1)k] (k)2卜〔■■ 4* *0::2 3 4 5( 5 21-2画出下列各信号的波形[式中r(t)t (t)为斜升函数]。
(1) f(t) 2 (t 1) 3 (t1) (t 2)(2) f (t) r(t)2r(t1) r(t 2)(5) f(t)r(2t) (2 t)(8) f(k)k[ (k)(k 5)](11) f(k)k(k 7)](12) f(k)2k[ (3k) ( k)] sin( )[ (k)6解:各信号波形为⑴ f(t) 2 (t 1) 3 (t 1) (t 2)(5)f(t) r(2t) (2 t)r(t) 2r(t 1)r(t 2)j/O)Z\1 a7(b)⑵ f(t)4P -OF ■"■(8)f(k) k[ (k) (k 5)]O3)2 13,2<k(11)f(k) sin(~6)[ (k) (k 7)]fa)■MB -»r1.4 1 L_ K _o! 2 3 4 5 6(k)(12)f(k) 2k[ (3k) ( k)]g 8.I~o| 1 2 3 k(I)1-3写出图仁3所示各波形的表达式解图示各波形的表示式分别为:(a) /(f) — 2e(z — 1)—€(『一1) — F (t — 2.) (b)/ (t ) — (t —1)e (r — 1)—2(/—1)c ( f —1) — (t — 3)c ( / 一3)(= 10sint7rZ )_£(?) 一 M — 1 丿_= 1 — 2(r + 2) £(? + 2) — £(r + l)] + (r — 1) c(t H-l) —— 1)12.Ar>1.LIo i tb/(r)正菠函數—1 O l 23(b) I AO(d)1-4写出图1-4所示各序列的闭合形式表达式解图示各序列的闭台形式表示式分别为:(a)/(A)=讥+ 2) (b)/(A) = —3)——7)(c)/«) =e(-^+2) (d)f(k)= (一1)¥⑷1-5判别下列各序列是否为周期性的。
(NEW)吴大正《信号与线性系统分析》(第4版)配套题库【名校考研真题+课后习题+章节题库+模拟试题】上册

【答案】
【解析】设f1(t)=ε(t)由LTI系统的线性和时不变性得(由于该题 没有给出系统的初始状态,所以这里不考虑)
f(t)=ε(t-1)-ε(t-2)=f1(t-1)-f1(t-2)
3.已知某LTI系统,当t>0时有: 当输入f(t)=(e-t+2e-2t)ε(t)时,输出响应为(e-t+5e-2t) ε(t); 当输入f(t)=(2e-t+e-2t)ε(t)时,输出响应为(5e-t+e-2t) ε(t); 当输入f(t)=(e-t+e-2t)ε(t)时,输出响应为(e-t+e-2t) ε(t); 则当输入为f(t)=(e-t-e-2t)ε(t)时,系统的输出响应为 ______。[长沙理工大学2006研]
【答案】
;
;稳定
【解析】由
可知,该系统任意两个相邻的输出值之差就是该
系统的输入值,即
,因此其逆系统的方程是
。
又因为
可知该逆系统的单位冲激响应为
为有限长序列,则其收敛域包含整个坐标平面。可见包含单位圆,则稳 定。
二、选择题 1.用下列差分方程描述的系统为线性系统的是( )。[西安电子科 技大学研] A.y(k)+y(k-1)=2f(k)+3 B.y(k)+y(k-1)y(k-2)=2f(k) C.y(k)+ky(k-2)=f(1-k)+2f(k-1) D.y(k)+2y(k-2)=2|f(k)| 【答案】C
图2-3 解:由框图可知,系统函数
令 因输入
,由于两共轭零点实部为1,可以求得 ,故 。
,即
时,系统全响应
,即
① 由此可知 的三个一阶极点分别为 , , ,分别代入传 递函数特征方程式
,从而可得
根据
可写出系统微分方程为
对方程两边取单边拉氏变换,将 由式①=②,可求得
信号与系统(吴大正)--完整版答案--纠错修改后版本之欧阳历创编

欧阳历创编 2021..02.09第一章 信号与系统1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+=解:各信号波形为 (2)∞<<-∞=-t e t f t,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε=欧阳历创编 2021..02.09(10))(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f (5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε 解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ欧阳历创编 2021..02.09(12))]()3([2)(k k k f k---=εε1-3 写出图1-3所示各波形的表达式。
信号与线性系统分析_(吴大正_第四版)习题答案
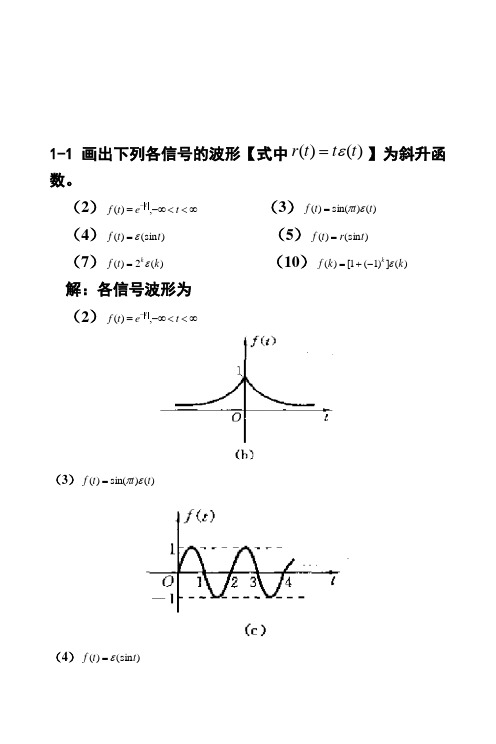
1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))f=rt)(sin(t(7))t=(kf kε(2)(10))f kεk=(k+-((])1)1[1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
信号与线性系统分析吴大正习题答案

专业课习题解析课程西安电子科技大学844信号与系统专业课习题解析课程第2讲第一章信号与系统(二)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))fεt=(sin)(t (5))f=t(sin)(tr(7))(2)(k t f k ε=(10))(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f (5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε (11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
吴大正《信号与线性系统分析》(第4版)配套题库【名校考研真题+模拟试题】(上册)【圣才出品】

x
t
0.5
t
1 2
2. sin nt dt ______。[天津工业大学 2006 研]
t
1 / 62
圣才电子书 十万种考研考证电子书、题库视频学习平台
【答案】
【解析】
sin nt dt t
sin nt nt
dnt
令t1 nt
Sa
t1 dt1 。
圣才电子书
第一部分 名校考研真题
十万种考研考证电子书、题库视频学习平台
第 1 章 信号与系统
一、填空题
1.设 x(t) et 0.5 (2t 1) ,则 x(t) =______。[华中科技大学 2008 研] 【答案】 x(t) 0.5 (t 0.5)
【解析】根据冲激函数的尺度变换,有
y(2t)
f ( )h(2t )d 21
f
(21)h(2t
21)d 21
2
f
(21)h[2(t
1)]d1
2
f
(2t) h(2t)。
另解:此题也可以使用傅里叶变换性质得到:
设 f t F ,ht H , yt Y
则Y F H ,由尺度变换特性得
y
2t
1 2
Y
1 2
函数。
四、画图题
信号
x(t)如图
1-1
所示,画出信号
y(t
)
2
x
1 3
t
2 3
的图形。[北京邮电大学
2012
研]
图 1-1
解:
yt
2x
1 3
t
2
如图
1-2(d)所示:
(a)
(b)
吴大正《信号与线性系统分析》(第4版)笔记和课后习题考研真题详解

第 7 章 系统函数 7.1 复习笔记 7.2 课后习题详解 7.3 名校考研真题详解
第 8 章 系统的状态变量分析 8.1 复习笔记 8.2 课后习题详解 8.3 名校考研真题详解
吴大正《信号与线性系统分பைடு நூலகம்》(第 4 版)笔记和课后习题(含考研真题)详
解完整版>精研学习 wang>无偿试用 20%资料
全国 547 所院校视频及题库资料
考研全套>视频资料>课后答案>往年真题>职称考试
第 1 章 信号与系统 1.1 复习笔记 1.2 课后习题详解 1.3 名校考研真题详解
第 2 章 连续系统的时域分析 2.1 复习笔记 2.2 课后习题详解 2.3 名校考研真题详解
第 3 章 离散系统的时域分析 3.1 复习笔记 3.2 课后习题详解 3.3 名校考研真题详解
第 4 章 傅里叶变换和系统的频域分析 4.1 复习笔记 4.2 课后习题详解 4.3 名校考研真题详解
第 5 章 连续系统的 s 域分析 5.1 复习笔记 5.2 课后习题详解 5.3 名校考研真题详解
(完整版)信号与线性系统分析_(吴大正_第四版)第一章习题答案

专业课习题解析课程第1讲第一章信号与系统(一)专业课习题解析课程第2讲第一章 信号与系统(二)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))tf=r)(sin(t(7))f kε=t)(2(k(10))(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε (11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k---=εε 解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=kkkkfεεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
信号与系统吴大正--完整版答案详解--纠错修改后版本
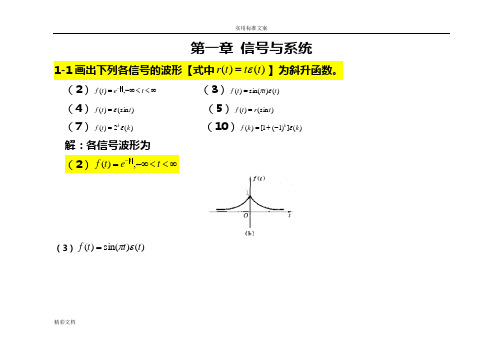
精彩文档第一章 信号与系统1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为(2)∞<<-∞=-t e t f t,)((3))()sin()(t t t f επ=精彩文档(4))(sin )(t t f ε=(5))(sin )(t r t f =(7))(2)(k t f k ε=精彩文档(10))(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f (5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε (11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k---=εε 解:各信号波形为精彩文档(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε精彩文档(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε1-3 写出图1-3所示各波形的表达式。
精彩文档1-4 写出图1-4所示各序列的闭合形式表达式。
信号与线性系统分析吴大正习题答案

专业课习题解析课程西安电子科技大学844信号与系统精选专业课习题解析课程第2讲第一章信号与系统(二)精选精选1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))fε=t)(sin(t(5))tf=r(t)(sin精选(7))t(kf kε=)(2(10))f kεk-=(k+(])1()1[精选精选1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f (5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε (11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k---=εε 解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε精选精选(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε精选1-3 写出图1-3所示各波形的表达式。
精选1-4 写出图1-4所示各序列的闭合形式表达式。
信号与线性系统分析_(第四版)习题答案

专业课习题解析课程xxxxxx大学844信号与系统专业课习题解析课程第1讲第一章信号与系统(一)专业课习题解析课程第2讲第一章 信号与系统(二)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f =(7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为(2)∞<<-∞=-t e t f t ,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))tf=r)(sin(t(7))f kε=t)(2(k(10))(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=kkkkfεεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的辯达式。
1-4 写出图1-4所示各序列的闭合形式辯达式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专业课习题解析课程
第1讲
第一章信号与系统(一)
专业课习题解析课程
第2讲
第一章 信号与系统(二)
1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e
t f t
,)( (3))()sin()(t t t f επ=
(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k
ε= (10))(])1(1[)(k k f k
ε-+=
解:各信号波形为 (2)∞<<-∞=-t e
t f t
,)(
(3))()sin()(t t t f επ=
(4))(sin )(t t f ε=
(5))
t
f=
r
)
(sin
(t
(7))
f kε
=
t
)
(
2
(k
(10))(])1(1[)(k k f k ε-+=
1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f
(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε (11)
)]7()()[6
sin(
)(--=k k k k f εεπ
(12)
)]()3([2)(k k k f k
---=εε 解:各信号波形为
(1))2()1(3)1(2)(-+--+=t t t t f εεε
(2)
)2()1(2)()(-+--=t r t r t r t f
(5)
)2()2()(t t r t f -=ε
(8)
)]5()([)(--=k k k k f εε
(11)
)]
7
(
)
(
)[
6
sin(
)
(-
-
=k
k
k
k
fε
ε
π
(12)
)]
(
)
3(
[
2
)
(k
k
k
f k-
-
-
=ε
ε
1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))6
3cos()443cos()(2π
πππ+++=k k k f
(5))sin(2cos 3)(5t t t f π+=
解:
1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
(1))()1(t t f ε- (2))1()1(--t t f ε (5)
)21(t f - (6))25.0(-t f
(7)dt
t df )
( (8)dx x f t ⎰∞-)(
解:各信号波形为 (1))()1(t t f ε-
(2)
)1()1(--t t f ε
(5)
)21(t f -
(6)
)25.0( t f
(7)dt t df )(
(8)
dx
x
f
t
⎰∞-)(
1-7 已知序列)(k f 的图形如图1-7所示,画出下列各序列的图形。
(1))()2(k k f ε- (2))2()2(--k k f ε
(3))]4()()[2(---k k k f εε (4))2(--k f (5)
)1()2(+-+-k k f ε (6))3()(--k f k f
解:
1-9 已知信号的波形如图1-11所示,分别画出)(t f
和dt t df )
(的波形。
解:由图1-11知,)3(t f -的波形如图1-12(a)所示()3(t f -波形是由对)23(t f -的波形展宽为原来的两倍而得)。
将)3(t f -的波形反转而得到)3(+t f 的波形,如图1-12(b)所示。
再将)3(+t f 的波形右移3个单位,就得到了)(t f ,如图1-12(c)所示。
dt
t df )
(的波形如图1-12(d)所示。
1-10 计算下列各题。
(1)[]{})()2sin(cos 22
t t t dt
d ε+ (2))]([)1(t
e dt d t t δ--
(5)
dt t t
t )2()]4
sin([2
++⎰
∞
∞-δπ (8)
dx x x t
)(')1(δ⎰
∞
--
1-12 如图1-13所示的电路,写出
(1)以)(t u C 为响应的微分方程。
(2)以)(t i L 为响应的微分方程。
1-20 写出图1-18各系统的微分或差分方程。
1-23 设系统的初始状态为)0(x ,激励为)(⋅f ,各系统的全响应)(⋅y 与激励和初始状态的关系如下,试分析各系统是否是线性的。
(1)⎰+=-t t dx x xf x e t y 0)(sin )0()( (2)⎰+=t
dx x f x t f t y 0)()0()()( (3)⎰+=t
dx x f t x t y 0)(])0(sin[)(
(
4))2()()0()5.0()(-+=k f k f x k y k (5)∑=+=k
j j f kx k y 0)
()0()(
1-25 设激励为)(⋅f ,下列是各系统的零状态响应)(⋅zs y 。
判断各系统是否是线性的、时不变的、因果的、稳定的?
(1)dt t df
t y zs )()(= (2))()(t f t y zs = (3))2cos()()(t t f t y zs π= (4))()(t f t y zs -= (5))1()()(-=k f k f k y zs
(
6))()2()(k f k k y zs -= (7)∑==k
j zs j f k y 0)()( (8))1()(k f k y zs -=
1-28 某一阶LTI离散系统,其初始状态为)0(x。
已知当激励为)(
)
(
1k
k
yε
=时,其全响应为
若初始状态不变,当激励为)(k f-时,其全响应为)(]1
)5.0(2[
)
(
2k
k
y kε
-
=
若初始状态为)0(2x,当激励为)(
4k
f时,求其全响应。
